problem
stringlengths 14
7.96k
| solution
stringlengths 3
10k
| answer
stringlengths 1
91
| problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | question_type
stringclasses 1
value | problem_type
stringclasses 8
values | problem_raw
stringlengths 14
7.96k
| solution_raw
stringlengths 3
10k
| metadata
dict | uuid
stringlengths 36
36
| id
int64 22.6k
612k
|
|---|---|---|---|---|---|---|---|---|---|---|---|
A regular 12-sided polygon is inscribed in a circle of radius 1. How many chords of the circle that join two of the vertices of the 12-gon have lengths whose squares are rational? (No proof is necessary.)
|
The chords joining vertices subtend minor arcs of $30^{\circ}, 60^{\circ}, 90^{\circ}, 120^{\circ}, 150^{\circ}$, or $180^{\circ}$. There are 12 chords of each of the first five kinds and 6 diameters. For a chord with central angle $\theta$, we can draw radii from the two endpoints of the chord to the center of the circle. By the law of cosines, the square of the length of the chord is $1+1-2 \cos \theta$, which is rational when $\theta$ is $60^{\circ}, 90^{\circ}, 120^{\circ}$, or $180^{\circ}$. The answer is thus $12+12+12+6=42$.
|
42
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
A regular 12-sided polygon is inscribed in a circle of radius 1. How many chords of the circle that join two of the vertices of the 12-gon have lengths whose squares are rational? (No proof is necessary.)
|
The chords joining vertices subtend minor arcs of $30^{\circ}, 60^{\circ}, 90^{\circ}, 120^{\circ}, 150^{\circ}$, or $180^{\circ}$. There are 12 chords of each of the first five kinds and 6 diameters. For a chord with central angle $\theta$, we can draw radii from the two endpoints of the chord to the center of the circle. By the law of cosines, the square of the length of the chord is $1+1-2 \cos \theta$, which is rational when $\theta$ is $60^{\circ}, 90^{\circ}, 120^{\circ}$, or $180^{\circ}$. The answer is thus $12+12+12+6=42$.
|
{
"resource_path": "HarvardMIT/segmented/en-92-2006-feb-team2-solutions.jsonl",
"problem_match": "\n8. [25]",
"solution_match": "\nSolution: "
}
|
75c38285-e875-5238-b8be-6d16ff322e51
| 611,543
|
Find the largest positive integer $n$ such that $1!+2!+3!+\cdots+n$ ! is a perfect square. Prove that your answer is correct.
|
Clearly $1!+2!+3!=9$ works. For $n \geq 4$, we have
$$
1!+2!+3!+\cdots+n!\equiv 1!+2!+3!+4!\equiv 3 \quad(\bmod 5)
$$
but there are no squares congruent to 3 modulo 5 .
|
3
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Find the largest positive integer $n$ such that $1!+2!+3!+\cdots+n$ ! is a perfect square. Prove that your answer is correct.
|
Clearly $1!+2!+3!=9$ works. For $n \geq 4$, we have
$$
1!+2!+3!+\cdots+n!\equiv 1!+2!+3!+4!\equiv 3 \quad(\bmod 5)
$$
but there are no squares congruent to 3 modulo 5 .
|
{
"resource_path": "HarvardMIT/segmented/en-92-2006-feb-team2-solutions.jsonl",
"problem_match": "\n11. [15]",
"solution_match": "\nSolution: "
}
|
154c6346-7e13-5011-a284-1a849b0bb4fd
| 611,546
|
Four circles with radii $1,2,3$, and $r$ are externally tangent to one another. Compute $r$. (No proof is necessary.)
|
Let $A, B, C, P$ be the centers of the circles with radii $1,2,3$, and $r$, respectively. Then, $A B C$ is a 3-4-5 right triangle. Using the law of cosines in $\triangle P A B$ yields
$$
\cos \angle P A B=\frac{3^{2}+(1+r)^{2}-(2+r)^{2}}{2 \cdot 3 \cdot(1+r)}=\frac{3-r}{3(1+r)}
$$
Similarly,
$$
\cos \angle P A C=\frac{4^{2}+(1+r)^{2}-(3+r)^{2}}{2 \cdot 4 \cdot(1+r)}=\frac{2-r}{2(1+r)}
$$
We can now use the equation $(\cos \angle P A B)^{2}+(\cos \angle P A C)^{2}=1$, which yields $0=$ $23 r^{2}+132 r-36=(23 r-6)(r+6)$, or $r=6 / 23$.
|
\frac{6}{23}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Four circles with radii $1,2,3$, and $r$ are externally tangent to one another. Compute $r$. (No proof is necessary.)
|
Let $A, B, C, P$ be the centers of the circles with radii $1,2,3$, and $r$, respectively. Then, $A B C$ is a 3-4-5 right triangle. Using the law of cosines in $\triangle P A B$ yields
$$
\cos \angle P A B=\frac{3^{2}+(1+r)^{2}-(2+r)^{2}}{2 \cdot 3 \cdot(1+r)}=\frac{3-r}{3(1+r)}
$$
Similarly,
$$
\cos \angle P A C=\frac{4^{2}+(1+r)^{2}-(3+r)^{2}}{2 \cdot 4 \cdot(1+r)}=\frac{2-r}{2(1+r)}
$$
We can now use the equation $(\cos \angle P A B)^{2}+(\cos \angle P A C)^{2}=1$, which yields $0=$ $23 r^{2}+132 r-36=(23 r-6)(r+6)$, or $r=6 / 23$.
|
{
"resource_path": "HarvardMIT/segmented/en-92-2006-feb-team2-solutions.jsonl",
"problem_match": "\n13. [25]",
"solution_match": "\nSolution: "
}
|
576f643c-9e65-5481-aeeb-813251ca6922
| 611,548
|
Find the prime factorization of
$$
2006^{2} \cdot 2262-669^{2} \cdot 3599+1593^{2} \cdot 1337
$$
(No proof is necessary.)
|
Upon observing that $2262=669+1593,3599=1593+2006$, and $1337=$ $2006-669$, we are inspired to write $a=2006, b=669, c=-1593$. The expression in question then rewrites as $a^{2}(b-c)+b^{2}(c-a)+c^{2}(a-b)$. But, by experimenting in the general case (e.g. setting $a=b$ ), we find that this polynomial is zero when two of $a, b, c$ are equal. Immediately we see that it factors as $(b-a)(c-b)(a-c)$, so the original expression is a way of writing $(-1337) \cdot(-2262) \cdot(3599)$. Now, $1337=7 \cdot 191$, $2262=2 \cdot 3 \cdot 13 \cdot 29$, and $3599=60^{2}-1^{2}=59 \cdot 61$.
|
(-1337) \cdot(-2262) \cdot(3599)
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Find the prime factorization of
$$
2006^{2} \cdot 2262-669^{2} \cdot 3599+1593^{2} \cdot 1337
$$
(No proof is necessary.)
|
Upon observing that $2262=669+1593,3599=1593+2006$, and $1337=$ $2006-669$, we are inspired to write $a=2006, b=669, c=-1593$. The expression in question then rewrites as $a^{2}(b-c)+b^{2}(c-a)+c^{2}(a-b)$. But, by experimenting in the general case (e.g. setting $a=b$ ), we find that this polynomial is zero when two of $a, b, c$ are equal. Immediately we see that it factors as $(b-a)(c-b)(a-c)$, so the original expression is a way of writing $(-1337) \cdot(-2262) \cdot(3599)$. Now, $1337=7 \cdot 191$, $2262=2 \cdot 3 \cdot 13 \cdot 29$, and $3599=60^{2}-1^{2}=59 \cdot 61$.
|
{
"resource_path": "HarvardMIT/segmented/en-92-2006-feb-team2-solutions.jsonl",
"problem_match": "\n14. [40]",
"solution_match": "\nSolution: "
}
|
79f98328-6313-53b0-ac32-9c3a3e320303
| 611,549
|
Determine the smallest number $M$ such that the inequality $$ \left|a b\left(a^{2}-b^{2}\right)+b c\left(b^{2}-c^{2}\right)+c a\left(c^{2}-a^{2}\right)\right| \leq M\left(a^{2}+b^{2}+c^{2}\right)^{2} $$ holds for all real numbers $a, b, c$. (Ireland)
|
We first consider the cubic polynomial $$ P(t)=t b\left(t^{2}-b^{2}\right)+b c\left(b^{2}-c^{2}\right)+c t\left(c^{2}-t^{2}\right) . $$ It is easy to check that $P(b)=P(c)=P(-b-c)=0$, and therefore $$ P(t)=(b-c)(t-b)(t-c)(t+b+c), $$ since the cubic coefficient is $b-c$. The left-hand side of the proposed inequality can therefore be written in the form $$ \left|a b\left(a^{2}-b^{2}\right)+b c\left(b^{2}-c^{2}\right)+c a\left(c^{2}-a^{2}\right)\right|=|P(a)|=|(b-c)(a-b)(a-c)(a+b+c)| . $$ The problem comes down to finding the smallest number $M$ that satisfies the inequality $$ |(b-c)(a-b)(a-c)(a+b+c)| \leq M \cdot\left(a^{2}+b^{2}+c^{2}\right)^{2} \text {. } $$ Note that this expression is symmetric, and we can therefore assume $a \leq b \leq c$ without loss of generality. With this assumption, $$ |(a-b)(b-c)|=(b-a)(c-b) \leq\left(\frac{(b-a)+(c-b)}{2}\right)^{2}=\frac{(c-a)^{2}}{4} $$ with equality if and only if $b-a=c-b$, i.e. $2 b=a+c$. Also $$ \left(\frac{(c-b)+(b-a)}{2}\right)^{2} \leq \frac{(c-b)^{2}+(b-a)^{2}}{2} $$ or equivalently, $$ 3(c-a)^{2} \leq 2 \cdot\left[(b-a)^{2}+(c-b)^{2}+(c-a)^{2}\right], $$ again with equality only for $2 b=a+c$. From (2) and (3) we get $$ \begin{aligned} & |(b-c)(a-b)(a-c)(a+b+c)| \\ \leq & \frac{1}{4} \cdot\left|(c-a)^{3}(a+b+c)\right| \\ = & \frac{1}{4} \cdot \sqrt{(c-a)^{6}(a+b+c)^{2}} \\ \leq & \frac{1}{4} \cdot \sqrt{\left(\frac{2 \cdot\left[(b-a)^{2}+(c-b)^{2}+(c-a)^{2}\right]}{3}\right)^{3} \cdot(a+b+c)^{2}} \\ = & \frac{\sqrt{2}}{2} \cdot\left(\sqrt[4]{\left(\frac{(b-a)^{2}+(c-b)^{2}+(c-a)^{2}}{3}\right)^{3} \cdot(a+b+c)^{2}}\right)^{2} . \end{aligned} $$ By the weighted AM-GM inequality this estimate continues as follows: $$ \begin{aligned} & |(b-c)(a-b)(a-c)(a+b+c)| \\ \leq & \frac{\sqrt{2}}{2} \cdot\left(\frac{(b-a)^{2}+(c-b)^{2}+(c-a)^{2}+(a+b+c)^{2}}{4}\right)^{2} \\ = & \frac{9 \sqrt{2}}{32} \cdot\left(a^{2}+b^{2}+c^{2}\right)^{2} . \end{aligned} $$ We see that the inequality (1) is satisfied for $M=\frac{9}{32} \sqrt{2}$, with equality if and only if $2 b=a+c$ and $$ \frac{(b-a)^{2}+(c-b)^{2}+(c-a)^{2}}{3}=(a+b+c)^{2} $$ Plugging $b=(a+c) / 2$ into the last equation, we bring it to the equivalent form $$ 2(c-a)^{2}=9(a+c)^{2} . $$ The conditions for equality can now be restated as $$ 2 b=a+c \quad \text { and } \quad(c-a)^{2}=18 b^{2} \text {. } $$ Setting $b=1$ yields $a=1-\frac{3}{2} \sqrt{2}$ and $c=1+\frac{3}{2} \sqrt{2}$. We see that $M=\frac{9}{32} \sqrt{2}$ is indeed the smallest constant satisfying the inequality, with equality for any triple $(a, b, c)$ proportional to $\left(1-\frac{3}{2} \sqrt{2}, 1,1+\frac{3}{2} \sqrt{2}\right)$, up to permutation. Comment. With the notation $x=b-a, y=c-b, z=a-c, s=a+b+c$ and $r^{2}=a^{2}+b^{2}+c^{2}$, the inequality (1) becomes just $|s x y z| \leq M r^{4}$ (with suitable constraints on $s$ and $r$ ). The original asymmetric inequality turns into a standard symmetric one; from this point on the solution can be completed in many ways. One can e.g. use the fact that, for fixed values of $\sum x$ and $\sum x^{2}$, the product $x y z$ is a maximum/minimum only if some of $x, y, z$ are equal, thus reducing one degree of freedom, etc. As observed by the proposer, a specific attraction of the problem is that the maximum is attained at a point $(a, b, c)$ with all coordinates distinct.
|
\frac{9}{32} \sqrt{2}
|
Yes
|
Yes
|
math-word-problem
|
Inequalities
|
Determine the smallest number $M$ such that the inequality $$ \left|a b\left(a^{2}-b^{2}\right)+b c\left(b^{2}-c^{2}\right)+c a\left(c^{2}-a^{2}\right)\right| \leq M\left(a^{2}+b^{2}+c^{2}\right)^{2} $$ holds for all real numbers $a, b, c$. (Ireland)
|
We first consider the cubic polynomial $$ P(t)=t b\left(t^{2}-b^{2}\right)+b c\left(b^{2}-c^{2}\right)+c t\left(c^{2}-t^{2}\right) . $$ It is easy to check that $P(b)=P(c)=P(-b-c)=0$, and therefore $$ P(t)=(b-c)(t-b)(t-c)(t+b+c), $$ since the cubic coefficient is $b-c$. The left-hand side of the proposed inequality can therefore be written in the form $$ \left|a b\left(a^{2}-b^{2}\right)+b c\left(b^{2}-c^{2}\right)+c a\left(c^{2}-a^{2}\right)\right|=|P(a)|=|(b-c)(a-b)(a-c)(a+b+c)| . $$ The problem comes down to finding the smallest number $M$ that satisfies the inequality $$ |(b-c)(a-b)(a-c)(a+b+c)| \leq M \cdot\left(a^{2}+b^{2}+c^{2}\right)^{2} \text {. } $$ Note that this expression is symmetric, and we can therefore assume $a \leq b \leq c$ without loss of generality. With this assumption, $$ |(a-b)(b-c)|=(b-a)(c-b) \leq\left(\frac{(b-a)+(c-b)}{2}\right)^{2}=\frac{(c-a)^{2}}{4} $$ with equality if and only if $b-a=c-b$, i.e. $2 b=a+c$. Also $$ \left(\frac{(c-b)+(b-a)}{2}\right)^{2} \leq \frac{(c-b)^{2}+(b-a)^{2}}{2} $$ or equivalently, $$ 3(c-a)^{2} \leq 2 \cdot\left[(b-a)^{2}+(c-b)^{2}+(c-a)^{2}\right], $$ again with equality only for $2 b=a+c$. From (2) and (3) we get $$ \begin{aligned} & |(b-c)(a-b)(a-c)(a+b+c)| \\ \leq & \frac{1}{4} \cdot\left|(c-a)^{3}(a+b+c)\right| \\ = & \frac{1}{4} \cdot \sqrt{(c-a)^{6}(a+b+c)^{2}} \\ \leq & \frac{1}{4} \cdot \sqrt{\left(\frac{2 \cdot\left[(b-a)^{2}+(c-b)^{2}+(c-a)^{2}\right]}{3}\right)^{3} \cdot(a+b+c)^{2}} \\ = & \frac{\sqrt{2}}{2} \cdot\left(\sqrt[4]{\left(\frac{(b-a)^{2}+(c-b)^{2}+(c-a)^{2}}{3}\right)^{3} \cdot(a+b+c)^{2}}\right)^{2} . \end{aligned} $$ By the weighted AM-GM inequality this estimate continues as follows: $$ \begin{aligned} & |(b-c)(a-b)(a-c)(a+b+c)| \\ \leq & \frac{\sqrt{2}}{2} \cdot\left(\frac{(b-a)^{2}+(c-b)^{2}+(c-a)^{2}+(a+b+c)^{2}}{4}\right)^{2} \\ = & \frac{9 \sqrt{2}}{32} \cdot\left(a^{2}+b^{2}+c^{2}\right)^{2} . \end{aligned} $$ We see that the inequality (1) is satisfied for $M=\frac{9}{32} \sqrt{2}$, with equality if and only if $2 b=a+c$ and $$ \frac{(b-a)^{2}+(c-b)^{2}+(c-a)^{2}}{3}=(a+b+c)^{2} $$ Plugging $b=(a+c) / 2$ into the last equation, we bring it to the equivalent form $$ 2(c-a)^{2}=9(a+c)^{2} . $$ The conditions for equality can now be restated as $$ 2 b=a+c \quad \text { and } \quad(c-a)^{2}=18 b^{2} \text {. } $$ Setting $b=1$ yields $a=1-\frac{3}{2} \sqrt{2}$ and $c=1+\frac{3}{2} \sqrt{2}$. We see that $M=\frac{9}{32} \sqrt{2}$ is indeed the smallest constant satisfying the inequality, with equality for any triple $(a, b, c)$ proportional to $\left(1-\frac{3}{2} \sqrt{2}, 1,1+\frac{3}{2} \sqrt{2}\right)$, up to permutation. Comment. With the notation $x=b-a, y=c-b, z=a-c, s=a+b+c$ and $r^{2}=a^{2}+b^{2}+c^{2}$, the inequality (1) becomes just $|s x y z| \leq M r^{4}$ (with suitable constraints on $s$ and $r$ ). The original asymmetric inequality turns into a standard symmetric one; from this point on the solution can be completed in many ways. One can e.g. use the fact that, for fixed values of $\sum x$ and $\sum x^{2}$, the product $x y z$ is a maximum/minimum only if some of $x, y, z$ are equal, thus reducing one degree of freedom, etc. As observed by the proposer, a specific attraction of the problem is that the maximum is attained at a point $(a, b, c)$ with all coordinates distinct.
|
{
"resource_path": "IMO/segmented/en-IMO2006SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
ada6190f-c3c7-5d2c-b5e3-6a67a926cb07
| 23,542
|
A diagonal of a regular 2006-gon is called odd if its endpoints divide the boundary into two parts, each composed of an odd number of sides. Sides are also regarded as odd diagonals. Suppose the 2006-gon has been dissected into triangles by 2003 nonintersecting diagonals. Find the maximum possible number of isosceles triangles with two odd sides. (Serbia)
|
Call an isosceles triangle odd if it has two odd sides. Suppose we are given a dissection as in the problem statement. A triangle in the dissection which is odd and isosceles will be called iso-odd for brevity. Lemma. Let $A B$ be one of dissecting diagonals and let $\mathcal{L}$ be the shorter part of the boundary of the 2006-gon with endpoints $A, B$. Suppose that $\mathcal{L}$ consists of $n$ segments. Then the number of iso-odd triangles with vertices on $\mathcal{L}$ does not exceed $n / 2$. Proof. This is obvious for $n=2$. Take $n$ with $2<n \leq 1003$ and assume the claim to be true for every $\mathcal{L}$ of length less than $n$. Let now $\mathcal{L}$ (endpoints $A, B$ ) consist of $n$ segments. Let $P Q$ be the longest diagonal which is a side of an iso-odd triangle $P Q S$ with all vertices on $\mathcal{L}$ (if there is no such triangle, there is nothing to prove). Every triangle whose vertices lie on $\mathcal{L}$ is obtuse or right-angled; thus $S$ is the summit of $P Q S$. We may assume that the five points $A, P, S, Q, B$ lie on $\mathcal{L}$ in this order and partition $\mathcal{L}$ into four pieces $\mathcal{L}_{A P}, \mathcal{L}_{P S}, \mathcal{L}_{S Q}, \mathcal{L}_{Q B}$ (the outer ones possibly reducing to a point). By the definition of $P Q$, an iso-odd triangle cannot have vertices on both $\mathcal{L}_{A P}$ and $\mathcal{L}_{Q B}$. Therefore every iso-odd triangle within $\mathcal{L}$ has all its vertices on just one of the four pieces. Applying to each of these pieces the induction hypothesis and adding the four inequalities we get that the number of iso-odd triangles within $\mathcal{L}$ other than $P Q S$ does not exceed $n / 2$. And since each of $\mathcal{L}_{P S}, \mathcal{L}_{S Q}$ consists of an odd number of sides, the inequalities for these two pieces are actually strict, leaving a $1 / 2+1 / 2$ in excess. Hence the triangle $P S Q$ is also covered by the estimate $n / 2$. This concludes the induction step and proves the lemma. The remaining part of the solution in fact repeats the argument from the above proof. Consider the longest dissecting diagonal $X Y$. Let $\mathcal{L}_{X Y}$ be the shorter of the two parts of the boundary with endpoints $X, Y$ and let $X Y Z$ be the triangle in the dissection with vertex $Z$ not on $\mathcal{L}_{X Y}$. Notice that $X Y Z$ is acute or right-angled, otherwise one of the segments $X Z, Y Z$ would be longer than $X Y$. Denoting by $\mathcal{L}_{X Z}, \mathcal{L}_{Y Z}$ the two pieces defined by $Z$ and applying the lemma to each of $\mathcal{L}_{X Y}, \mathcal{L}_{X Z}, \mathcal{L}_{Y Z}$ we infer that there are no more than 2006/2 iso-odd triangles in all, unless $X Y Z$ is one of them. But in that case $X Z$ and $Y Z$ are odd diagonals and the corresponding inequalities are strict. This shows that also in this case the total number of iso-odd triangles in the dissection, including $X Y Z$, is not greater than 1003 . This bound can be achieved. For this to happen, it just suffices to select a vertex of the 2006-gon and draw a broken line joining every second vertex, starting from the selected one. Since 2006 is even, the line closes. This already gives us the required 1003 iso-odd triangles. Then we can complete the triangulation in an arbitrary fashion.
|
1003
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
A diagonal of a regular 2006-gon is called odd if its endpoints divide the boundary into two parts, each composed of an odd number of sides. Sides are also regarded as odd diagonals. Suppose the 2006-gon has been dissected into triangles by 2003 nonintersecting diagonals. Find the maximum possible number of isosceles triangles with two odd sides. (Serbia)
|
Call an isosceles triangle odd if it has two odd sides. Suppose we are given a dissection as in the problem statement. A triangle in the dissection which is odd and isosceles will be called iso-odd for brevity. Lemma. Let $A B$ be one of dissecting diagonals and let $\mathcal{L}$ be the shorter part of the boundary of the 2006-gon with endpoints $A, B$. Suppose that $\mathcal{L}$ consists of $n$ segments. Then the number of iso-odd triangles with vertices on $\mathcal{L}$ does not exceed $n / 2$. Proof. This is obvious for $n=2$. Take $n$ with $2<n \leq 1003$ and assume the claim to be true for every $\mathcal{L}$ of length less than $n$. Let now $\mathcal{L}$ (endpoints $A, B$ ) consist of $n$ segments. Let $P Q$ be the longest diagonal which is a side of an iso-odd triangle $P Q S$ with all vertices on $\mathcal{L}$ (if there is no such triangle, there is nothing to prove). Every triangle whose vertices lie on $\mathcal{L}$ is obtuse or right-angled; thus $S$ is the summit of $P Q S$. We may assume that the five points $A, P, S, Q, B$ lie on $\mathcal{L}$ in this order and partition $\mathcal{L}$ into four pieces $\mathcal{L}_{A P}, \mathcal{L}_{P S}, \mathcal{L}_{S Q}, \mathcal{L}_{Q B}$ (the outer ones possibly reducing to a point). By the definition of $P Q$, an iso-odd triangle cannot have vertices on both $\mathcal{L}_{A P}$ and $\mathcal{L}_{Q B}$. Therefore every iso-odd triangle within $\mathcal{L}$ has all its vertices on just one of the four pieces. Applying to each of these pieces the induction hypothesis and adding the four inequalities we get that the number of iso-odd triangles within $\mathcal{L}$ other than $P Q S$ does not exceed $n / 2$. And since each of $\mathcal{L}_{P S}, \mathcal{L}_{S Q}$ consists of an odd number of sides, the inequalities for these two pieces are actually strict, leaving a $1 / 2+1 / 2$ in excess. Hence the triangle $P S Q$ is also covered by the estimate $n / 2$. This concludes the induction step and proves the lemma. The remaining part of the solution in fact repeats the argument from the above proof. Consider the longest dissecting diagonal $X Y$. Let $\mathcal{L}_{X Y}$ be the shorter of the two parts of the boundary with endpoints $X, Y$ and let $X Y Z$ be the triangle in the dissection with vertex $Z$ not on $\mathcal{L}_{X Y}$. Notice that $X Y Z$ is acute or right-angled, otherwise one of the segments $X Z, Y Z$ would be longer than $X Y$. Denoting by $\mathcal{L}_{X Z}, \mathcal{L}_{Y Z}$ the two pieces defined by $Z$ and applying the lemma to each of $\mathcal{L}_{X Y}, \mathcal{L}_{X Z}, \mathcal{L}_{Y Z}$ we infer that there are no more than 2006/2 iso-odd triangles in all, unless $X Y Z$ is one of them. But in that case $X Z$ and $Y Z$ are odd diagonals and the corresponding inequalities are strict. This shows that also in this case the total number of iso-odd triangles in the dissection, including $X Y Z$, is not greater than 1003 . This bound can be achieved. For this to happen, it just suffices to select a vertex of the 2006-gon and draw a broken line joining every second vertex, starting from the selected one. Since 2006 is even, the line closes. This already gives us the required 1003 iso-odd triangles. Then we can complete the triangulation in an arbitrary fashion.
|
{
"resource_path": "IMO/segmented/en-IMO2006SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
5816615c-7dd4-5732-80bf-344ac953b604
| 23,548
|
Let $n>1$ be an integer. In the space, consider the set $$ S=\{(x, y, z) \mid x, y, z \in\{0,1, \ldots, n\}, x+y+z>0\} $$ Find the smallest number of planes that jointly contain all $(n+1)^{3}-1$ points of $S$ but none of them passes through the origin. (Netherlands) Answer. $3 n$ planes.
|
It is easy to find $3 n$ such planes. For example, planes $x=i, y=i$ or $z=i$ $(i=1,2, \ldots, n)$ cover the set $S$ but none of them contains the origin. Another such collection consists of all planes $x+y+z=k$ for $k=1,2, \ldots, 3 n$. We show that $3 n$ is the smallest possible number. Lemma 1. Consider a nonzero polynomial $P\left(x_{1}, \ldots, x_{k}\right)$ in $k$ variables. Suppose that $P$ vanishes at all points $\left(x_{1}, \ldots, x_{k}\right)$ such that $x_{1}, \ldots, x_{k} \in\{0,1, \ldots, n\}$ and $x_{1}+\cdots+x_{k}>0$, while $P(0,0, \ldots, 0) \neq 0$. Then $\operatorname{deg} P \geq k n$. Proof. We use induction on $k$. The base case $k=0$ is clear since $P \neq 0$. Denote for clarity $y=x_{k}$. Let $R\left(x_{1}, \ldots, x_{k-1}, y\right)$ be the residue of $P$ modulo $Q(y)=y(y-1) \ldots(y-n)$. Polynomial $Q(y)$ vanishes at each $y=0,1, \ldots, n$, hence $P\left(x_{1}, \ldots, x_{k-1}, y\right)=R\left(x_{1}, \ldots, x_{k-1}, y\right)$ for all $x_{1}, \ldots, x_{k-1}, y \in\{0,1, \ldots, n\}$. Therefore, $R$ also satisfies the condition of the Lemma; moreover, $\operatorname{deg}_{y} R \leq n$. Clearly, $\operatorname{deg} R \leq \operatorname{deg} P$, so it suffices to prove that $\operatorname{deg} R \geq n k$. Now, expand polynomial $R$ in the powers of $y$ : $$ R\left(x_{1}, \ldots, x_{k-1}, y\right)=R_{n}\left(x_{1}, \ldots, x_{k-1}\right) y^{n}+R_{n-1}\left(x_{1}, \ldots, x_{k-1}\right) y^{n-1}+\cdots+R_{0}\left(x_{1}, \ldots, x_{k-1}\right) $$ We show that polynomial $R_{n}\left(x_{1}, \ldots, x_{k-1}\right)$ satisfies the condition of the induction hypothesis. Consider the polynomial $T(y)=R(0, \ldots, 0, y)$ of degree $\leq n$. This polynomial has $n$ roots $y=1, \ldots, n$; on the other hand, $T(y) \not \equiv 0$ since $T(0) \neq 0$. Hence $\operatorname{deg} T=n$, and its leading coefficient is $R_{n}(0,0, \ldots, 0) \neq 0$. In particular, in the case $k=1$ we obtain that coefficient $R_{n}$ is nonzero. Similarly, take any numbers $a_{1}, \ldots, a_{k-1} \in\{0,1, \ldots, n\}$ with $a_{1}+\cdots+a_{k-1}>0$. Substituting $x_{i}=a_{i}$ into $R\left(x_{1}, \ldots, x_{k-1}, y\right)$, we get a polynomial in $y$ which vanishes at all points $y=0, \ldots, n$ and has degree $\leq n$. Therefore, this polynomial is null, hence $R_{i}\left(a_{1}, \ldots, a_{k-1}\right)=0$ for all $i=0,1, \ldots, n$. In particular, $R_{n}\left(a_{1}, \ldots, a_{k-1}\right)=0$. Thus, the polynomial $R_{n}\left(x_{1}, \ldots, x_{k-1}\right)$ satisfies the condition of the induction hypothesis. So, we have $\operatorname{deg} R_{n} \geq(k-1) n$ and $\operatorname{deg} P \geq \operatorname{deg} R \geq \operatorname{deg} R_{n}+n \geq k n$. Now we can finish the solution. Suppose that there are $N$ planes covering all the points of $S$ but not containing the origin. Let their equations be $a_{i} x+b_{i} y+c_{i} z+d_{i}=0$. Consider the polynomial $$ P(x, y, z)=\prod_{i=1}^{N}\left(a_{i} x+b_{i} y+c_{i} z+d_{i}\right) $$ It has total degree $N$. This polynomial has the property that $P\left(x_{0}, y_{0}, z_{0}\right)=0$ for any $\left(x_{0}, y_{0}, z_{0}\right) \in S$, while $P(0,0,0) \neq 0$. Hence by Lemma 1 we get $N=\operatorname{deg} P \geq 3 n$, as desired. Comment 1. There are many other collections of $3 n$ planes covering the set $S$ but not covering the origin.
|
3 n
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Let $n>1$ be an integer. In the space, consider the set $$ S=\{(x, y, z) \mid x, y, z \in\{0,1, \ldots, n\}, x+y+z>0\} $$ Find the smallest number of planes that jointly contain all $(n+1)^{3}-1$ points of $S$ but none of them passes through the origin. (Netherlands) Answer. $3 n$ planes.
|
It is easy to find $3 n$ such planes. For example, planes $x=i, y=i$ or $z=i$ $(i=1,2, \ldots, n)$ cover the set $S$ but none of them contains the origin. Another such collection consists of all planes $x+y+z=k$ for $k=1,2, \ldots, 3 n$. We show that $3 n$ is the smallest possible number. Lemma 1. Consider a nonzero polynomial $P\left(x_{1}, \ldots, x_{k}\right)$ in $k$ variables. Suppose that $P$ vanishes at all points $\left(x_{1}, \ldots, x_{k}\right)$ such that $x_{1}, \ldots, x_{k} \in\{0,1, \ldots, n\}$ and $x_{1}+\cdots+x_{k}>0$, while $P(0,0, \ldots, 0) \neq 0$. Then $\operatorname{deg} P \geq k n$. Proof. We use induction on $k$. The base case $k=0$ is clear since $P \neq 0$. Denote for clarity $y=x_{k}$. Let $R\left(x_{1}, \ldots, x_{k-1}, y\right)$ be the residue of $P$ modulo $Q(y)=y(y-1) \ldots(y-n)$. Polynomial $Q(y)$ vanishes at each $y=0,1, \ldots, n$, hence $P\left(x_{1}, \ldots, x_{k-1}, y\right)=R\left(x_{1}, \ldots, x_{k-1}, y\right)$ for all $x_{1}, \ldots, x_{k-1}, y \in\{0,1, \ldots, n\}$. Therefore, $R$ also satisfies the condition of the Lemma; moreover, $\operatorname{deg}_{y} R \leq n$. Clearly, $\operatorname{deg} R \leq \operatorname{deg} P$, so it suffices to prove that $\operatorname{deg} R \geq n k$. Now, expand polynomial $R$ in the powers of $y$ : $$ R\left(x_{1}, \ldots, x_{k-1}, y\right)=R_{n}\left(x_{1}, \ldots, x_{k-1}\right) y^{n}+R_{n-1}\left(x_{1}, \ldots, x_{k-1}\right) y^{n-1}+\cdots+R_{0}\left(x_{1}, \ldots, x_{k-1}\right) $$ We show that polynomial $R_{n}\left(x_{1}, \ldots, x_{k-1}\right)$ satisfies the condition of the induction hypothesis. Consider the polynomial $T(y)=R(0, \ldots, 0, y)$ of degree $\leq n$. This polynomial has $n$ roots $y=1, \ldots, n$; on the other hand, $T(y) \not \equiv 0$ since $T(0) \neq 0$. Hence $\operatorname{deg} T=n$, and its leading coefficient is $R_{n}(0,0, \ldots, 0) \neq 0$. In particular, in the case $k=1$ we obtain that coefficient $R_{n}$ is nonzero. Similarly, take any numbers $a_{1}, \ldots, a_{k-1} \in\{0,1, \ldots, n\}$ with $a_{1}+\cdots+a_{k-1}>0$. Substituting $x_{i}=a_{i}$ into $R\left(x_{1}, \ldots, x_{k-1}, y\right)$, we get a polynomial in $y$ which vanishes at all points $y=0, \ldots, n$ and has degree $\leq n$. Therefore, this polynomial is null, hence $R_{i}\left(a_{1}, \ldots, a_{k-1}\right)=0$ for all $i=0,1, \ldots, n$. In particular, $R_{n}\left(a_{1}, \ldots, a_{k-1}\right)=0$. Thus, the polynomial $R_{n}\left(x_{1}, \ldots, x_{k-1}\right)$ satisfies the condition of the induction hypothesis. So, we have $\operatorname{deg} R_{n} \geq(k-1) n$ and $\operatorname{deg} P \geq \operatorname{deg} R \geq \operatorname{deg} R_{n}+n \geq k n$. Now we can finish the solution. Suppose that there are $N$ planes covering all the points of $S$ but not containing the origin. Let their equations be $a_{i} x+b_{i} y+c_{i} z+d_{i}=0$. Consider the polynomial $$ P(x, y, z)=\prod_{i=1}^{N}\left(a_{i} x+b_{i} y+c_{i} z+d_{i}\right) $$ It has total degree $N$. This polynomial has the property that $P\left(x_{0}, y_{0}, z_{0}\right)=0$ for any $\left(x_{0}, y_{0}, z_{0}\right) \in S$, while $P(0,0,0) \neq 0$. Hence by Lemma 1 we get $N=\operatorname{deg} P \geq 3 n$, as desired. Comment 1. There are many other collections of $3 n$ planes covering the set $S$ but not covering the origin.
|
{
"resource_path": "IMO/segmented/en-IMO2007SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
13039424-17f8-5aea-a6ab-71ae796ea0c1
| 23,642
|
In the coordinate plane consider the set $S$ of all points with integer coordinates. For a positive integer $k$, two distinct points $A, B \in S$ will be called $k$-friends if there is a point $C \in S$ such that the area of the triangle $A B C$ is equal to $k$. A set $T \subset S$ will be called a $k$-clique if every two points in $T$ are $k$-friends. Find the least positive integer $k$ for which there exists a $k$-clique with more than 200 elements.
|
To begin, let us describe those points $B \in S$ which are $k$-friends of the point $(0,0)$. By definition, $B=(u, v)$ satisfies this condition if and only if there is a point $C=(x, y) \in S$ such that $\frac{1}{2}|u y-v x|=k$. (This is a well-known formula expressing the area of triangle $A B C$ when $A$ is the origin.) To say that there exist integers $x, y$ for which $|u y-v x|=2 k$, is equivalent to saying that the greatest common divisor of $u$ and $v$ is also a divisor of $2 k$. Summing up, a point $B=(u, v) \in S$ is a $k$-friend of $(0,0)$ if and only if $\operatorname{gcd}(u, v)$ divides $2 k$. Translation by a vector with integer coordinates does not affect $k$-friendship; if two points are $k$-friends, so are their translates. It follows that two points $A, B \in S, A=(s, t), B=(u, v)$, are $k$-friends if and only if the point $(u-s, v-t)$ is a $k$-friend of $(0,0)$; i.e., if $\operatorname{gcd}(u-s, v-t) \mid 2 k$. Let $n$ be a positive integer which does not divide $2 k$. We claim that a $k$-clique cannot have more than $n^{2}$ elements. Indeed, all points $(x, y) \in S$ can be divided into $n^{2}$ classes determined by the remainders that $x$ and $y$ leave in division by $n$. If a set $T$ has more than $n^{2}$ elements, some two points $A, B \in T, A=(s, t), B=(u, v)$, necessarily fall into the same class. This means that $n \mid u-s$ and $n \mid v-t$. Hence $n \mid d$ where $d=\operatorname{gcd}(u-s, v-t)$. And since $n$ does not divide $2 k$, also $d$ does not divide $2 k$. Thus $A$ and $B$ are not $k$-friends and the set $T$ is not a $k$-clique. Now let $M(k)$ be the least positive integer which does not divide $2 k$. Write $M(k)=m$ for the moment and consider the set $T$ of all points $(x, y)$ with $0 \leq x, y<m$. There are $m^{2}$ of them. If $A=(s, t), B=(u, v)$ are two distinct points in $T$ then both differences $|u-s|,|v-t|$ are integers less than $m$ and at least one of them is positive. By the definition of $m$, every positive integer less than $m$ divides $2 k$. Therefore $u-s$ (if nonzero) divides $2 k$, and the same is true of $v-t$. So $2 k$ is divisible by $\operatorname{gcd}(u-s, v-t)$, meaning that $A, B$ are $k$-friends. Thus $T$ is a $k$-clique. It follows that the maximum size of a $k$-clique is $M(k)^{2}$, with $M(k)$ defined as above. We are looking for the minimum $k$ such that $M(k)^{2}>200$. By the definition of $M(k), 2 k$ is divisible by the numbers $1,2, \ldots, M(k)-1$, but not by $M(k)$ itself. If $M(k)^{2}>200$ then $M(k) \geq 15$. Trying to hit $M(k)=15$ we get a contradiction immediately ( $2 k$ would have to be divisible by 3 and 5 , but not by 15 ). So let us try $M(k)=16$. Then $2 k$ is divisible by the numbers $1,2, \ldots, 15$, hence also by their least common multiple $L$, but not by 16 . And since $L$ is not a multiple of 16 , we infer that $k=L / 2$ is the least $k$ with $M(k)=16$. Finally, observe that if $M(k) \geq 17$ then $2 k$ must be divisible by the least common multiple of $1,2, \ldots, 16$, which is equal to $2 L$. Then $2 k \geq 2 L$, yielding $k>L / 2$. In conclusion, the least $k$ with the required property is equal to $L / 2=180180$.
|
180180
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
In the coordinate plane consider the set $S$ of all points with integer coordinates. For a positive integer $k$, two distinct points $A, B \in S$ will be called $k$-friends if there is a point $C \in S$ such that the area of the triangle $A B C$ is equal to $k$. A set $T \subset S$ will be called a $k$-clique if every two points in $T$ are $k$-friends. Find the least positive integer $k$ for which there exists a $k$-clique with more than 200 elements.
|
To begin, let us describe those points $B \in S$ which are $k$-friends of the point $(0,0)$. By definition, $B=(u, v)$ satisfies this condition if and only if there is a point $C=(x, y) \in S$ such that $\frac{1}{2}|u y-v x|=k$. (This is a well-known formula expressing the area of triangle $A B C$ when $A$ is the origin.) To say that there exist integers $x, y$ for which $|u y-v x|=2 k$, is equivalent to saying that the greatest common divisor of $u$ and $v$ is also a divisor of $2 k$. Summing up, a point $B=(u, v) \in S$ is a $k$-friend of $(0,0)$ if and only if $\operatorname{gcd}(u, v)$ divides $2 k$. Translation by a vector with integer coordinates does not affect $k$-friendship; if two points are $k$-friends, so are their translates. It follows that two points $A, B \in S, A=(s, t), B=(u, v)$, are $k$-friends if and only if the point $(u-s, v-t)$ is a $k$-friend of $(0,0)$; i.e., if $\operatorname{gcd}(u-s, v-t) \mid 2 k$. Let $n$ be a positive integer which does not divide $2 k$. We claim that a $k$-clique cannot have more than $n^{2}$ elements. Indeed, all points $(x, y) \in S$ can be divided into $n^{2}$ classes determined by the remainders that $x$ and $y$ leave in division by $n$. If a set $T$ has more than $n^{2}$ elements, some two points $A, B \in T, A=(s, t), B=(u, v)$, necessarily fall into the same class. This means that $n \mid u-s$ and $n \mid v-t$. Hence $n \mid d$ where $d=\operatorname{gcd}(u-s, v-t)$. And since $n$ does not divide $2 k$, also $d$ does not divide $2 k$. Thus $A$ and $B$ are not $k$-friends and the set $T$ is not a $k$-clique. Now let $M(k)$ be the least positive integer which does not divide $2 k$. Write $M(k)=m$ for the moment and consider the set $T$ of all points $(x, y)$ with $0 \leq x, y<m$. There are $m^{2}$ of them. If $A=(s, t), B=(u, v)$ are two distinct points in $T$ then both differences $|u-s|,|v-t|$ are integers less than $m$ and at least one of them is positive. By the definition of $m$, every positive integer less than $m$ divides $2 k$. Therefore $u-s$ (if nonzero) divides $2 k$, and the same is true of $v-t$. So $2 k$ is divisible by $\operatorname{gcd}(u-s, v-t)$, meaning that $A, B$ are $k$-friends. Thus $T$ is a $k$-clique. It follows that the maximum size of a $k$-clique is $M(k)^{2}$, with $M(k)$ defined as above. We are looking for the minimum $k$ such that $M(k)^{2}>200$. By the definition of $M(k), 2 k$ is divisible by the numbers $1,2, \ldots, M(k)-1$, but not by $M(k)$ itself. If $M(k)^{2}>200$ then $M(k) \geq 15$. Trying to hit $M(k)=15$ we get a contradiction immediately ( $2 k$ would have to be divisible by 3 and 5 , but not by 15 ). So let us try $M(k)=16$. Then $2 k$ is divisible by the numbers $1,2, \ldots, 15$, hence also by their least common multiple $L$, but not by 16 . And since $L$ is not a multiple of 16 , we infer that $k=L / 2$ is the least $k$ with $M(k)=16$. Finally, observe that if $M(k) \geq 17$ then $2 k$ must be divisible by the least common multiple of $1,2, \ldots, 16$, which is equal to $2 L$. Then $2 k \geq 2 L$, yielding $k>L / 2$. In conclusion, the least $k$ with the required property is equal to $L / 2=180180$.
|
{
"resource_path": "IMO/segmented/en-IMO2008SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
1fc0e9b7-0711-5be2-aff5-b6aae982cf62
| 23,740
|
Let $n$ and $k$ be fixed positive integers of the same parity, $k \geq n$. We are given $2 n$ lamps numbered 1 through $2 n$; each of them can be on or off. At the beginning all lamps are off. We consider sequences of $k$ steps. At each step one of the lamps is switched (from off to on or from on to off). Let $N$ be the number of $k$-step sequences ending in the state: lamps $1, \ldots, n$ on, lamps $n+1, \ldots, 2 n$ off. Let $M$ be the number of $k$-step sequences leading to the same state and not touching lamps $n+1, \ldots, 2 n$ at all. Find the ratio $N / M$.
|
A sequence of $k$ switches ending in the state as described in the problem statement (lamps $1, \ldots, n$ on, lamps $n+1, \ldots, 2 n$ off) will be called an admissible process. If, moreover, the process does not touch the lamps $n+1, \ldots, 2 n$, it will be called restricted. So there are $N$ admissible processes, among which $M$ are restricted. In every admissible process, restricted or not, each one of the lamps $1, \ldots, n$ goes from off to on, so it is switched an odd number of times; and each one of the lamps $n+1, \ldots, 2 n$ goes from off to off, so it is switched an even number of times. Notice that $M>0$; i.e., restricted admissible processes do exist (it suffices to switch each one of the lamps $1, \ldots, n$ just once and then choose one of them and switch it $k-n$ times, which by hypothesis is an even number). Consider any restricted admissible process $\mathbf{p}$. Take any lamp $\ell, 1 \leq \ell \leq n$, and suppose that it was switched $k_{\ell}$ times. As noticed, $k_{\ell}$ must be odd. Select arbitrarily an even number of these $k_{\ell}$ switches and replace each of them by the switch of lamp $n+\ell$. This can be done in $2^{k_{\ell}-1}$ ways (because a $k_{\ell}$-element set has $2^{k_{\ell}-1}$ subsets of even cardinality). Notice that $k_{1}+\cdots+k_{n}=k$. These actions are independent, in the sense that the action involving lamp $\ell$ does not affect the action involving any other lamp. So there are $2^{k_{1}-1} \cdot 2^{k_{2}-1} \cdots 2^{k_{n}-1}=2^{k-n}$ ways of combining these actions. In any of these combinations, each one of the lamps $n+1, \ldots, 2 n$ gets switched an even number of times and each one of the lamps $1, \ldots, n$ remains switched an odd number of times, so the final state is the same as that resulting from the original process $\mathbf{p}$. This shows that every restricted admissible process $\mathbf{p}$ can be modified in $2^{k-n}$ ways, giving rise to $2^{k-n}$ distinct admissible processes (with all lamps allowed). Now we show that every admissible process $\mathbf{q}$ can be achieved in that way. Indeed, it is enough to replace every switch of a lamp with a label $\ell>n$ that occurs in $\mathbf{q}$ by the switch of the corresponding lamp $\ell-n$; in the resulting process $\mathbf{p}$ the lamps $n+1, \ldots, 2 n$ are not involved. Switches of each lamp with a label $\ell>n$ had occurred in $\mathbf{q}$ an even number of times. So the performed replacements have affected each lamp with a label $\ell \leq n$ also an even number of times; hence in the overall effect the final state of each lamp has remained the same. This means that the resulting process $\mathbf{p}$ is admissible - and clearly restricted, as the lamps $n+1, \ldots, 2 n$ are not involved in it any more. If we now take process $\mathbf{p}$ and reverse all these replacements, then we obtain process $\mathbf{q}$. These reversed replacements are nothing else than the modifications described in the foregoing paragraphs. Thus there is a one-to $-\left(2^{k-n}\right)$ correspondence between the $M$ restricted admissible processes and the total of $N$ admissible processes. Therefore $N / M=2^{k-n}$.
|
2^{k-n}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Let $n$ and $k$ be fixed positive integers of the same parity, $k \geq n$. We are given $2 n$ lamps numbered 1 through $2 n$; each of them can be on or off. At the beginning all lamps are off. We consider sequences of $k$ steps. At each step one of the lamps is switched (from off to on or from on to off). Let $N$ be the number of $k$-step sequences ending in the state: lamps $1, \ldots, n$ on, lamps $n+1, \ldots, 2 n$ off. Let $M$ be the number of $k$-step sequences leading to the same state and not touching lamps $n+1, \ldots, 2 n$ at all. Find the ratio $N / M$.
|
A sequence of $k$ switches ending in the state as described in the problem statement (lamps $1, \ldots, n$ on, lamps $n+1, \ldots, 2 n$ off) will be called an admissible process. If, moreover, the process does not touch the lamps $n+1, \ldots, 2 n$, it will be called restricted. So there are $N$ admissible processes, among which $M$ are restricted. In every admissible process, restricted or not, each one of the lamps $1, \ldots, n$ goes from off to on, so it is switched an odd number of times; and each one of the lamps $n+1, \ldots, 2 n$ goes from off to off, so it is switched an even number of times. Notice that $M>0$; i.e., restricted admissible processes do exist (it suffices to switch each one of the lamps $1, \ldots, n$ just once and then choose one of them and switch it $k-n$ times, which by hypothesis is an even number). Consider any restricted admissible process $\mathbf{p}$. Take any lamp $\ell, 1 \leq \ell \leq n$, and suppose that it was switched $k_{\ell}$ times. As noticed, $k_{\ell}$ must be odd. Select arbitrarily an even number of these $k_{\ell}$ switches and replace each of them by the switch of lamp $n+\ell$. This can be done in $2^{k_{\ell}-1}$ ways (because a $k_{\ell}$-element set has $2^{k_{\ell}-1}$ subsets of even cardinality). Notice that $k_{1}+\cdots+k_{n}=k$. These actions are independent, in the sense that the action involving lamp $\ell$ does not affect the action involving any other lamp. So there are $2^{k_{1}-1} \cdot 2^{k_{2}-1} \cdots 2^{k_{n}-1}=2^{k-n}$ ways of combining these actions. In any of these combinations, each one of the lamps $n+1, \ldots, 2 n$ gets switched an even number of times and each one of the lamps $1, \ldots, n$ remains switched an odd number of times, so the final state is the same as that resulting from the original process $\mathbf{p}$. This shows that every restricted admissible process $\mathbf{p}$ can be modified in $2^{k-n}$ ways, giving rise to $2^{k-n}$ distinct admissible processes (with all lamps allowed). Now we show that every admissible process $\mathbf{q}$ can be achieved in that way. Indeed, it is enough to replace every switch of a lamp with a label $\ell>n$ that occurs in $\mathbf{q}$ by the switch of the corresponding lamp $\ell-n$; in the resulting process $\mathbf{p}$ the lamps $n+1, \ldots, 2 n$ are not involved. Switches of each lamp with a label $\ell>n$ had occurred in $\mathbf{q}$ an even number of times. So the performed replacements have affected each lamp with a label $\ell \leq n$ also an even number of times; hence in the overall effect the final state of each lamp has remained the same. This means that the resulting process $\mathbf{p}$ is admissible - and clearly restricted, as the lamps $n+1, \ldots, 2 n$ are not involved in it any more. If we now take process $\mathbf{p}$ and reverse all these replacements, then we obtain process $\mathbf{q}$. These reversed replacements are nothing else than the modifications described in the foregoing paragraphs. Thus there is a one-to $-\left(2^{k-n}\right)$ correspondence between the $M$ restricted admissible processes and the total of $N$ admissible processes. Therefore $N / M=2^{k-n}$.
|
{
"resource_path": "IMO/segmented/en-IMO2008SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
15a757e1-f1f1-500e-a2da-abe81a5109df
| 23,742
|
CZE Find the largest possible integer $k$, such that the following statement is true: Let 2009 arbitrary non-degenerated triangles be given. In every triangle the three sides are colored, such that one is blue, one is red and one is white. Now, for every color separately, let us sort the lengths of the sides. We obtain $$ \begin{aligned} & b_{1} \leq b_{2} \\ & \leq \ldots \leq b_{2009} \quad \text { the lengths of the blue sides, } \\ r_{1} & \leq r_{2} \leq \ldots \leq r_{2009} \quad \text { the lengths of the red sides, } \\ \text { and } \quad w_{1} & \leq w_{2} \leq \ldots \leq w_{2009} \quad \text { the lengths of the white sides. } \end{aligned} $$ Then there exist $k$ indices $j$ such that we can form a non-degenerated triangle with side lengths $b_{j}, r_{j}, w_{j}$ 。
|
We will prove that the largest possible number $k$ of indices satisfying the given condition is one. Firstly we prove that $b_{2009}, r_{2009}, w_{2009}$ are always lengths of the sides of a triangle. Without loss of generality we may assume that $w_{2009} \geq r_{2009} \geq b_{2009}$. We show that the inequality $b_{2009}+r_{2009}>w_{2009}$ holds. Evidently, there exists a triangle with side lengths $w, b, r$ for the white, blue and red side, respectively, such that $w_{2009}=w$. By the conditions of the problem we have $b+r>w, b_{2009} \geq b$ and $r_{2009} \geq r$. From these inequalities it follows $$ b_{2009}+r_{2009} \geq b+r>w=w_{2009} $$ Secondly we will describe a sequence of triangles for which $w_{j}, b_{j}, r_{j}$ with $j<2009$ are not the lengths of the sides of a triangle. Let us define the sequence $\Delta_{j}, j=1,2, \ldots, 2009$, of triangles, where $\Delta_{j}$ has a blue side of length $2 j$, a red side of length $j$ for all $j \leq 2008$ and 4018 for $j=2009$, and a white side of length $j+1$ for all $j \leq 2007$, 4018 for $j=2008$ and 1 for $j=2009$. Since $$ \begin{array}{rrrl} (j+1)+j>2 j & \geq j+1>j, & \text { if } & j \leq 2007 \\ 2 j+j>4018>2 j \quad>j, & \text { if } & j=2008 \\ 4018+1>2 j & =4018>1, & \text { if } & j=2009 \end{array} $$ such a sequence of triangles exists. Moreover, $w_{j}=j, r_{j}=j$ and $b_{j}=2 j$ for $1 \leq j \leq 2008$. Then $$ w_{j}+r_{j}=j+j=2 j=b_{j} $$ i.e., $b_{j}, r_{j}$ and $w_{j}$ are not the lengths of the sides of a triangle for $1 \leq j \leq 2008$.
|
1
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
CZE Find the largest possible integer $k$, such that the following statement is true: Let 2009 arbitrary non-degenerated triangles be given. In every triangle the three sides are colored, such that one is blue, one is red and one is white. Now, for every color separately, let us sort the lengths of the sides. We obtain $$ \begin{aligned} & b_{1} \leq b_{2} \\ & \leq \ldots \leq b_{2009} \quad \text { the lengths of the blue sides, } \\ r_{1} & \leq r_{2} \leq \ldots \leq r_{2009} \quad \text { the lengths of the red sides, } \\ \text { and } \quad w_{1} & \leq w_{2} \leq \ldots \leq w_{2009} \quad \text { the lengths of the white sides. } \end{aligned} $$ Then there exist $k$ indices $j$ such that we can form a non-degenerated triangle with side lengths $b_{j}, r_{j}, w_{j}$ 。
|
We will prove that the largest possible number $k$ of indices satisfying the given condition is one. Firstly we prove that $b_{2009}, r_{2009}, w_{2009}$ are always lengths of the sides of a triangle. Without loss of generality we may assume that $w_{2009} \geq r_{2009} \geq b_{2009}$. We show that the inequality $b_{2009}+r_{2009}>w_{2009}$ holds. Evidently, there exists a triangle with side lengths $w, b, r$ for the white, blue and red side, respectively, such that $w_{2009}=w$. By the conditions of the problem we have $b+r>w, b_{2009} \geq b$ and $r_{2009} \geq r$. From these inequalities it follows $$ b_{2009}+r_{2009} \geq b+r>w=w_{2009} $$ Secondly we will describe a sequence of triangles for which $w_{j}, b_{j}, r_{j}$ with $j<2009$ are not the lengths of the sides of a triangle. Let us define the sequence $\Delta_{j}, j=1,2, \ldots, 2009$, of triangles, where $\Delta_{j}$ has a blue side of length $2 j$, a red side of length $j$ for all $j \leq 2008$ and 4018 for $j=2009$, and a white side of length $j+1$ for all $j \leq 2007$, 4018 for $j=2008$ and 1 for $j=2009$. Since $$ \begin{array}{rrrl} (j+1)+j>2 j & \geq j+1>j, & \text { if } & j \leq 2007 \\ 2 j+j>4018>2 j \quad>j, & \text { if } & j=2008 \\ 4018+1>2 j & =4018>1, & \text { if } & j=2009 \end{array} $$ such a sequence of triangles exists. Moreover, $w_{j}=j, r_{j}=j$ and $b_{j}=2 j$ for $1 \leq j \leq 2008$. Then $$ w_{j}+r_{j}=j+j=2 j=b_{j} $$ i.e., $b_{j}, r_{j}$ and $w_{j}$ are not the lengths of the sides of a triangle for $1 \leq j \leq 2008$.
|
{
"resource_path": "IMO/segmented/en-IMO2009SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
67a9b319-ee7d-5944-9b7a-abb8e49053cc
| 23,794
|
CZE Find the largest possible integer $k$, such that the following statement is true: Let 2009 arbitrary non-degenerated triangles be given. In every triangle the three sides are colored, such that one is blue, one is red and one is white. Now, for every color separately, let us sort the lengths of the sides. We obtain $$ \begin{array}{rlrl} b_{1} & \leq b_{2} & \leq \ldots \leq b_{2009} \quad & \\ & & \text { the lengths of the blue sides, } \\ r_{1} & \leq r_{2} & \leq \ldots \leq r_{2009} \quad \text { the lengths of the red sides, } \\ w_{1} & \leq w_{2} & \leq \ldots \leq w_{2009} \quad \text { the lengths of the white sides. } \end{array} $$ Then there exist $k$ indices $j$ such that we can form a non-degenerated triangle with side lengths $b_{j}, r_{j}, w_{j}$ 。
|
We will prove that the largest possible number $k$ of indices satisfying the given condition is one. Firstly we prove that $b_{2009}, r_{2009}, w_{2009}$ are always lengths of the sides of a triangle. Without loss of generality we may assume that $w_{2009} \geq r_{2009} \geq b_{2009}$. We show that the inequality $b_{2009}+r_{2009}>w_{2009}$ holds. Evidently, there exists a triangle with side lengths $w, b, r$ for the white, blue and red side, respectively, such that $w_{2009}=w$. By the conditions of the problem we have $b+r>w, b_{2009} \geq b$ and $r_{2009} \geq r$. From these inequalities it follows $$ b_{2009}+r_{2009} \geq b+r>w=w_{2009} $$ Secondly we will describe a sequence of triangles for which $w_{j}, b_{j}, r_{j}$ with $j<2009$ are not the lengths of the sides of a triangle. Let us define the sequence $\Delta_{j}, j=1,2, \ldots, 2009$, of triangles, where $\Delta_{j}$ has a blue side of length $2 j$, a red side of length $j$ for all $j \leq 2008$ and 4018 for $j=2009$, and a white side of length $j+1$ for all $j \leq 2007$, 4018 for $j=2008$ and 1 for $j=2009$. Since $$ \begin{array}{rrrl} (j+1)+j>2 j & \geq j+1>j, & \text { if } & j \leq 2007 \\ 2 j+j>4018>2 j \quad>j, & \text { if } & j=2008 \\ 4018+1>2 j & =4018>1, & \text { if } & j=2009 \end{array} $$ such a sequence of triangles exists. Moreover, $w_{j}=j, r_{j}=j$ and $b_{j}=2 j$ for $1 \leq j \leq 2008$. Then $$ w_{j}+r_{j}=j+j=2 j=b_{j} $$ i.e., $b_{j}, r_{j}$ and $w_{j}$ are not the lengths of the sides of a triangle for $1 \leq j \leq 2008$.
|
1
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
CZE Find the largest possible integer $k$, such that the following statement is true: Let 2009 arbitrary non-degenerated triangles be given. In every triangle the three sides are colored, such that one is blue, one is red and one is white. Now, for every color separately, let us sort the lengths of the sides. We obtain $$ \begin{array}{rlrl} b_{1} & \leq b_{2} & \leq \ldots \leq b_{2009} \quad & \\ & & \text { the lengths of the blue sides, } \\ r_{1} & \leq r_{2} & \leq \ldots \leq r_{2009} \quad \text { the lengths of the red sides, } \\ w_{1} & \leq w_{2} & \leq \ldots \leq w_{2009} \quad \text { the lengths of the white sides. } \end{array} $$ Then there exist $k$ indices $j$ such that we can form a non-degenerated triangle with side lengths $b_{j}, r_{j}, w_{j}$ 。
|
We will prove that the largest possible number $k$ of indices satisfying the given condition is one. Firstly we prove that $b_{2009}, r_{2009}, w_{2009}$ are always lengths of the sides of a triangle. Without loss of generality we may assume that $w_{2009} \geq r_{2009} \geq b_{2009}$. We show that the inequality $b_{2009}+r_{2009}>w_{2009}$ holds. Evidently, there exists a triangle with side lengths $w, b, r$ for the white, blue and red side, respectively, such that $w_{2009}=w$. By the conditions of the problem we have $b+r>w, b_{2009} \geq b$ and $r_{2009} \geq r$. From these inequalities it follows $$ b_{2009}+r_{2009} \geq b+r>w=w_{2009} $$ Secondly we will describe a sequence of triangles for which $w_{j}, b_{j}, r_{j}$ with $j<2009$ are not the lengths of the sides of a triangle. Let us define the sequence $\Delta_{j}, j=1,2, \ldots, 2009$, of triangles, where $\Delta_{j}$ has a blue side of length $2 j$, a red side of length $j$ for all $j \leq 2008$ and 4018 for $j=2009$, and a white side of length $j+1$ for all $j \leq 2007$, 4018 for $j=2008$ and 1 for $j=2009$. Since $$ \begin{array}{rrrl} (j+1)+j>2 j & \geq j+1>j, & \text { if } & j \leq 2007 \\ 2 j+j>4018>2 j \quad>j, & \text { if } & j=2008 \\ 4018+1>2 j & =4018>1, & \text { if } & j=2009 \end{array} $$ such a sequence of triangles exists. Moreover, $w_{j}=j, r_{j}=j$ and $b_{j}=2 j$ for $1 \leq j \leq 2008$. Then $$ w_{j}+r_{j}=j+j=2 j=b_{j} $$ i.e., $b_{j}, r_{j}$ and $w_{j}$ are not the lengths of the sides of a triangle for $1 \leq j \leq 2008$.
|
{
"resource_path": "IMO/segmented/en-IMO2009SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
3d17de47-6887-57fa-be6d-e92e699106e4
| 23,897
|
Let $x_{1}, \ldots, x_{100}$ be nonnegative real numbers such that $x_{i}+x_{i+1}+x_{i+2} \leq 1$ for all $i=1, \ldots, 100$ (we put $x_{101}=x_{1}, x_{102}=x_{2}$ ). Find the maximal possible value of the sum $$ S=\sum_{i=1}^{100} x_{i} x_{i+2} $$ (Russia) Answer. $\frac{25}{2}$.
|
Let $x_{2 i}=0, x_{2 i-1}=\frac{1}{2}$ for all $i=1, \ldots, 50$. Then we have $S=50 \cdot\left(\frac{1}{2}\right)^{2}=\frac{25}{2}$. So, we are left to show that $S \leq \frac{25}{2}$ for all values of $x_{i}$ 's satisfying the problem conditions. Consider any $1 \leq i \leq 50$. By the problem condition, we get $x_{2 i-1} \leq 1-x_{2 i}-x_{2 i+1}$ and $x_{2 i+2} \leq 1-x_{2 i}-x_{2 i+1}$. Hence by the AM-GM inequality we get $$ \begin{aligned} x_{2 i-1} x_{2 i+1} & +x_{2 i} x_{2 i+2} \leq\left(1-x_{2 i}-x_{2 i+1}\right) x_{2 i+1}+x_{2 i}\left(1-x_{2 i}-x_{2 i+1}\right) \\ & =\left(x_{2 i}+x_{2 i+1}\right)\left(1-x_{2 i}-x_{2 i+1}\right) \leq\left(\frac{\left(x_{2 i}+x_{2 i+1}\right)+\left(1-x_{2 i}-x_{2 i+1}\right)}{2}\right)^{2}=\frac{1}{4} \end{aligned} $$ Summing up these inequalities for $i=1,2, \ldots, 50$, we get the desired inequality $$ \sum_{i=1}^{50}\left(x_{2 i-1} x_{2 i+1}+x_{2 i} x_{2 i+2}\right) \leq 50 \cdot \frac{1}{4}=\frac{25}{2} $$ Comment. This solution shows that a bit more general fact holds. Namely, consider $2 n$ nonnegative numbers $x_{1}, \ldots, x_{2 n}$ in a row (with no cyclic notation) and suppose that $x_{i}+x_{i+1}+x_{i+2} \leq 1$ for all $i=1,2, \ldots, 2 n-2$. Then $\sum_{i=1}^{2 n-2} x_{i} x_{i+2} \leq \frac{n-1}{4}$. The proof is the same as above, though if might be easier to find it (for instance, applying induction). The original estimate can be obtained from this version by considering the sequence $x_{1}, x_{2}, \ldots, x_{100}, x_{1}, x_{2}$.
|
\frac{25}{2}
|
Yes
|
Yes
|
math-word-problem
|
Inequalities
|
Let $x_{1}, \ldots, x_{100}$ be nonnegative real numbers such that $x_{i}+x_{i+1}+x_{i+2} \leq 1$ for all $i=1, \ldots, 100$ (we put $x_{101}=x_{1}, x_{102}=x_{2}$ ). Find the maximal possible value of the sum $$ S=\sum_{i=1}^{100} x_{i} x_{i+2} $$ (Russia) Answer. $\frac{25}{2}$.
|
Let $x_{2 i}=0, x_{2 i-1}=\frac{1}{2}$ for all $i=1, \ldots, 50$. Then we have $S=50 \cdot\left(\frac{1}{2}\right)^{2}=\frac{25}{2}$. So, we are left to show that $S \leq \frac{25}{2}$ for all values of $x_{i}$ 's satisfying the problem conditions. Consider any $1 \leq i \leq 50$. By the problem condition, we get $x_{2 i-1} \leq 1-x_{2 i}-x_{2 i+1}$ and $x_{2 i+2} \leq 1-x_{2 i}-x_{2 i+1}$. Hence by the AM-GM inequality we get $$ \begin{aligned} x_{2 i-1} x_{2 i+1} & +x_{2 i} x_{2 i+2} \leq\left(1-x_{2 i}-x_{2 i+1}\right) x_{2 i+1}+x_{2 i}\left(1-x_{2 i}-x_{2 i+1}\right) \\ & =\left(x_{2 i}+x_{2 i+1}\right)\left(1-x_{2 i}-x_{2 i+1}\right) \leq\left(\frac{\left(x_{2 i}+x_{2 i+1}\right)+\left(1-x_{2 i}-x_{2 i+1}\right)}{2}\right)^{2}=\frac{1}{4} \end{aligned} $$ Summing up these inequalities for $i=1,2, \ldots, 50$, we get the desired inequality $$ \sum_{i=1}^{50}\left(x_{2 i-1} x_{2 i+1}+x_{2 i} x_{2 i+2}\right) \leq 50 \cdot \frac{1}{4}=\frac{25}{2} $$ Comment. This solution shows that a bit more general fact holds. Namely, consider $2 n$ nonnegative numbers $x_{1}, \ldots, x_{2 n}$ in a row (with no cyclic notation) and suppose that $x_{i}+x_{i+1}+x_{i+2} \leq 1$ for all $i=1,2, \ldots, 2 n-2$. Then $\sum_{i=1}^{2 n-2} x_{i} x_{i+2} \leq \frac{n-1}{4}$. The proof is the same as above, though if might be easier to find it (for instance, applying induction). The original estimate can be obtained from this version by considering the sequence $x_{1}, x_{2}, \ldots, x_{100}, x_{1}, x_{2}$.
|
{
"resource_path": "IMO/segmented/en-IMO2010SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
a52d081b-c67d-5acf-80bd-9a0c6f9f6fdc
| 23,913
|
In a concert, 20 singers will perform. For each singer, there is a (possibly empty) set of other singers such that he wishes to perform later than all the singers from that set. Can it happen that there are exactly 2010 orders of the singers such that all their wishes are satisfied? (Austria) Answer. Yes, such an example exists.
|
We say that an order of singers is good if it satisfied all their wishes. Next, we say that a number $N$ is realizable by $k$ singers (or $k$-realizable) if for some set of wishes of these singers there are exactly $N$ good orders. Thus, we have to prove that a number 2010 is 20-realizable. We start with the following simple Lemma. Suppose that numbers $n_{1}, n_{2}$ are realizable by respectively $k_{1}$ and $k_{2}$ singers. Then the number $n_{1} n_{2}$ is $\left(k_{1}+k_{2}\right)$-realizable. Proof. Let the singers $A_{1}, \ldots, A_{k_{1}}$ (with some wishes among them) realize $n_{1}$, and the singers $B_{1}$, $\ldots, B_{k_{2}}$ (with some wishes among them) realize $n_{2}$. Add to each singer $B_{i}$ the wish to perform later than all the singers $A_{j}$. Then, each good order of the obtained set of singers has the form $\left(A_{i_{1}}, \ldots, A_{i_{k_{1}}}, B_{j_{1}}, \ldots, B_{j_{k_{2}}}\right)$, where $\left(A_{i_{1}}, \ldots, A_{i_{k_{1}}}\right)$ is a good order for $A_{i}$ 's and $\left(B_{j_{1}}, \ldots, B_{j_{k_{2}}}\right)$ is a good order for $B_{j}$ 's. Conversely, each order of this form is obviously good. Hence, the number of good orders is $n_{1} n_{2}$. In view of Lemma, we show how to construct sets of singers containing 4, 3 and 13 singers and realizing the numbers 5, 6 and 67 , respectively. Thus the number $2010=6 \cdot 5 \cdot 67$ will be realizable by $4+3+13=20$ singers. These companies of singers are shown in Figs. 1-3; the wishes are denoted by arrows, and the number of good orders for each Figure stands below in the brackets.  (5) Fig. 1  (67) Fig. 3 For Fig. 1, there are exactly 5 good orders $(a, b, c, d),(a, b, d, c),(b, a, c, d),(b, a, d, c)$, $(b, d, a, c)$. For Fig. 2, each of 6 orders is good since there are no wishes. Finally, for Fig. 3, the order of $a_{1}, \ldots, a_{11}$ is fixed; in this line, singer $x$ can stand before each of $a_{i}(i \leq 9)$, and singer $y$ can stand after each of $a_{j}(j \geq 5)$, thus resulting in $9 \cdot 7=63$ cases. Further, the positions of $x$ and $y$ in this line determine the whole order uniquely unless both of them come between the same pair $\left(a_{i}, a_{i+1}\right)$ (thus $5 \leq i \leq 8$ ); in the latter cases, there are two orders instead of 1 due to the order of $x$ and $y$. Hence, the total number of good orders is $63+4=67$, as desired. Comment. The number 20 in the problem statement is not sharp and is put there to respect the original formulation. So, if necessary, the difficulty level of this problem may be adjusted by replacing 20 by a smaller number. Here we present some improvements of the example leading to a smaller number of singers. Surely, each example with $<20$ singers can be filled with some "super-stars" who should perform at the very end in a fixed order. Hence each of these improvements provides a different solution for the problem. Moreover, the large variety of ideas standing behind these examples allows to suggest that there are many other examples. 1. Instead of building the examples realizing 5 and 6 , it is more economic to make an example realizing 30; it may seem even simpler. Two possible examples consisting of 5 and 6 singers are shown in Fig. 4; hence the number 20 can be decreased to 19 or 18 . For Fig. 4a, the order of $a_{1}, \ldots, a_{4}$ is fixed, there are 5 ways to add $x$ into this order, and there are 6 ways to add $y$ into the resulting order of $a_{1}, \ldots, a_{4}, x$. Hence there are $5 \cdot 6=30$ good orders. On Fig. 4b, for 5 singers $a, b_{1}, b_{2}, c_{1}, c_{2}$ there are $5!=120$ orders at all. Obviously, exactly one half of them satisfies the wish $b_{1} \leftarrow b_{2}$, and exactly one half of these orders satisfies another wish $c_{1} \leftarrow c_{2}$; hence, there are exactly $5!/ 4=30$ good orders.  2. One can merge the examples for 30 and 67 shown in Figs. 4 b and 3 in a smarter way, obtaining a set of 13 singers representing 2010. This example is shown in Fig. 5; an arrow from/to group $\left\{b_{1}, \ldots, b_{5}\right\}$ means that there exists such arrow from each member of this group. Here, as in Fig. 4b, one can see that there are exactly 30 orders of $b_{1}, \ldots, b_{5}, a_{6}, \ldots, a_{11}$ satisfying all their wishes among themselves. Moreover, one can prove in the same way as for Fig. 3 that each of these orders can be complemented by $x$ and $y$ in exactly 67 ways, hence obtaining $30 \cdot 67=2010$ good orders at all. Analogously, one can merge the examples in Figs. 1-3 to represent 2010 by 13 singers as is shown in Fig. 6.  3. Finally, we will present two other improvements; the proofs are left to the reader. The graph in Fig. 7 shows how 10 singers can represent 67 . Moreover, even a company of 10 singers representing 2010 can be found; this company is shown in Fig. 8.
|
2010
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
In a concert, 20 singers will perform. For each singer, there is a (possibly empty) set of other singers such that he wishes to perform later than all the singers from that set. Can it happen that there are exactly 2010 orders of the singers such that all their wishes are satisfied? (Austria) Answer. Yes, such an example exists.
|
We say that an order of singers is good if it satisfied all their wishes. Next, we say that a number $N$ is realizable by $k$ singers (or $k$-realizable) if for some set of wishes of these singers there are exactly $N$ good orders. Thus, we have to prove that a number 2010 is 20-realizable. We start with the following simple Lemma. Suppose that numbers $n_{1}, n_{2}$ are realizable by respectively $k_{1}$ and $k_{2}$ singers. Then the number $n_{1} n_{2}$ is $\left(k_{1}+k_{2}\right)$-realizable. Proof. Let the singers $A_{1}, \ldots, A_{k_{1}}$ (with some wishes among them) realize $n_{1}$, and the singers $B_{1}$, $\ldots, B_{k_{2}}$ (with some wishes among them) realize $n_{2}$. Add to each singer $B_{i}$ the wish to perform later than all the singers $A_{j}$. Then, each good order of the obtained set of singers has the form $\left(A_{i_{1}}, \ldots, A_{i_{k_{1}}}, B_{j_{1}}, \ldots, B_{j_{k_{2}}}\right)$, where $\left(A_{i_{1}}, \ldots, A_{i_{k_{1}}}\right)$ is a good order for $A_{i}$ 's and $\left(B_{j_{1}}, \ldots, B_{j_{k_{2}}}\right)$ is a good order for $B_{j}$ 's. Conversely, each order of this form is obviously good. Hence, the number of good orders is $n_{1} n_{2}$. In view of Lemma, we show how to construct sets of singers containing 4, 3 and 13 singers and realizing the numbers 5, 6 and 67 , respectively. Thus the number $2010=6 \cdot 5 \cdot 67$ will be realizable by $4+3+13=20$ singers. These companies of singers are shown in Figs. 1-3; the wishes are denoted by arrows, and the number of good orders for each Figure stands below in the brackets.  (5) Fig. 1  (67) Fig. 3 For Fig. 1, there are exactly 5 good orders $(a, b, c, d),(a, b, d, c),(b, a, c, d),(b, a, d, c)$, $(b, d, a, c)$. For Fig. 2, each of 6 orders is good since there are no wishes. Finally, for Fig. 3, the order of $a_{1}, \ldots, a_{11}$ is fixed; in this line, singer $x$ can stand before each of $a_{i}(i \leq 9)$, and singer $y$ can stand after each of $a_{j}(j \geq 5)$, thus resulting in $9 \cdot 7=63$ cases. Further, the positions of $x$ and $y$ in this line determine the whole order uniquely unless both of them come between the same pair $\left(a_{i}, a_{i+1}\right)$ (thus $5 \leq i \leq 8$ ); in the latter cases, there are two orders instead of 1 due to the order of $x$ and $y$. Hence, the total number of good orders is $63+4=67$, as desired. Comment. The number 20 in the problem statement is not sharp and is put there to respect the original formulation. So, if necessary, the difficulty level of this problem may be adjusted by replacing 20 by a smaller number. Here we present some improvements of the example leading to a smaller number of singers. Surely, each example with $<20$ singers can be filled with some "super-stars" who should perform at the very end in a fixed order. Hence each of these improvements provides a different solution for the problem. Moreover, the large variety of ideas standing behind these examples allows to suggest that there are many other examples. 1. Instead of building the examples realizing 5 and 6 , it is more economic to make an example realizing 30; it may seem even simpler. Two possible examples consisting of 5 and 6 singers are shown in Fig. 4; hence the number 20 can be decreased to 19 or 18 . For Fig. 4a, the order of $a_{1}, \ldots, a_{4}$ is fixed, there are 5 ways to add $x$ into this order, and there are 6 ways to add $y$ into the resulting order of $a_{1}, \ldots, a_{4}, x$. Hence there are $5 \cdot 6=30$ good orders. On Fig. 4b, for 5 singers $a, b_{1}, b_{2}, c_{1}, c_{2}$ there are $5!=120$ orders at all. Obviously, exactly one half of them satisfies the wish $b_{1} \leftarrow b_{2}$, and exactly one half of these orders satisfies another wish $c_{1} \leftarrow c_{2}$; hence, there are exactly $5!/ 4=30$ good orders.  2. One can merge the examples for 30 and 67 shown in Figs. 4 b and 3 in a smarter way, obtaining a set of 13 singers representing 2010. This example is shown in Fig. 5; an arrow from/to group $\left\{b_{1}, \ldots, b_{5}\right\}$ means that there exists such arrow from each member of this group. Here, as in Fig. 4b, one can see that there are exactly 30 orders of $b_{1}, \ldots, b_{5}, a_{6}, \ldots, a_{11}$ satisfying all their wishes among themselves. Moreover, one can prove in the same way as for Fig. 3 that each of these orders can be complemented by $x$ and $y$ in exactly 67 ways, hence obtaining $30 \cdot 67=2010$ good orders at all. Analogously, one can merge the examples in Figs. 1-3 to represent 2010 by 13 singers as is shown in Fig. 6.  3. Finally, we will present two other improvements; the proofs are left to the reader. The graph in Fig. 7 shows how 10 singers can represent 67 . Moreover, even a company of 10 singers representing 2010 can be found; this company is shown in Fig. 8.
|
{
"resource_path": "IMO/segmented/en-IMO2010SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
8448cec8-e96e-564c-b232-7b7d3b121cfa
| 23,936
|
On some planet, there are $2^{N}$ countries $(N \geq 4)$. Each country has a flag $N$ units wide and one unit high composed of $N$ fields of size $1 \times 1$, each field being either yellow or blue. No two countries have the same flag. We say that a set of $N$ flags is diverse if these flags can be arranged into an $N \times N$ square so that all $N$ fields on its main diagonal will have the same color. Determine the smallest positive integer $M$ such that among any $M$ distinct flags, there exist $N$ flags forming a diverse set. (Croatia) Answer. $M=2^{N-2}+1$.
|
When speaking about the diagonal of a square, we will always mean the main diagonal. Let $M_{N}$ be the smallest positive integer satisfying the problem condition. First, we show that $M_{N}>2^{N-2}$. Consider the collection of all $2^{N-2}$ flags having yellow first squares and blue second ones. Obviously, both colors appear on the diagonal of each $N \times N$ square formed by these flags. We are left to show that $M_{N} \leq 2^{N-2}+1$, thus obtaining the desired answer. We start with establishing this statement for $N=4$. Suppose that we have 5 flags of length 4 . We decompose each flag into two parts of 2 squares each; thereby, we denote each flag as $L R$, where the $2 \times 1$ flags $L, R \in \mathcal{S}=\{\mathrm{BB}, \mathrm{BY}, \mathrm{YB}, \mathrm{YY}\}$ are its left and right parts, respectively. First, we make two easy observations on the flags $2 \times 1$ which can be checked manually. (i) For each $A \in \mathcal{S}$, there exists only one $2 \times 1$ flag $C \in \mathcal{S}$ (possibly $C=A$ ) such that $A$ and $C$ cannot form a $2 \times 2$ square with monochrome diagonal (for part BB, that is YY, and for BY that is YB). (ii) Let $A_{1}, A_{2}, A_{3} \in \mathcal{S}$ be three distinct elements; then two of them can form a $2 \times 2$ square with yellow diagonal, and two of them can form a $2 \times 2$ square with blue diagonal (for all parts but BB , a pair $(\mathrm{BY}, \mathrm{YB})$ fits for both statements, while for all parts but BY, these pairs are $(\mathrm{YB}, \mathrm{YY})$ and (BB, YB)). Now, let $\ell$ and $r$ be the numbers of distinct left and right parts of our 5 flags, respectively. The total number of flags is $5 \leq r \ell$, hence one of the factors (say, $r$ ) should be at least 3 . On the other hand, $\ell, r \leq 4$, so there are two flags with coinciding right part; let them be $L_{1} R_{1}$ and $L_{2} R_{1}\left(L_{1} \neq L_{2}\right)$. Next, since $r \geq 3$, there exist some flags $L_{3} R_{3}$ and $L_{4} R_{4}$ such that $R_{1}, R_{3}, R_{4}$ are distinct. Let $L^{\prime} R^{\prime}$ be the remaining flag. By (i), one of the pairs $\left(L^{\prime}, L_{1}\right)$ and $\left(L^{\prime}, L_{2}\right)$ can form a $2 \times 2$ square with monochrome diagonal; we can assume that $L^{\prime}, L_{2}$ form a square with a blue diagonal. Finally, the right parts of two of the flags $L_{1} R_{1}, L_{3} R_{3}, L_{4} R_{4}$ can also form a $2 \times 2$ square with a blue diagonal by (ii). Putting these $2 \times 2$ squares on the diagonal of a $4 \times 4$ square, we find a desired arrangement of four flags. We are ready to prove the problem statement by induction on $N$; actually, above we have proved the base case $N=4$. For the induction step, assume that $N>4$, consider any $2^{N-2}+1$ flags of length $N$, and arrange them into a large flag of size $\left(2^{N-2}+1\right) \times N$. This flag contains a non-monochrome column since the flags are distinct; we may assume that this column is the first one. By the pigeonhole principle, this column contains at least $\left\lceil\frac{2^{N-2}+1}{2}\right\rceil=2^{N-3}+1$ squares of one color (say, blue). We call the flags with a blue first square good. Consider all the good flags and remove the first square from each of them. We obtain at least $2^{N-3}+1 \geq M_{N-1}$ flags of length $N-1$; by the induction hypothesis, $N-1$ of them can form a square $Q$ with the monochrome diagonal. Now, returning the removed squares, we obtain a rectangle $(N-1) \times N$, and our aim is to supplement it on the top by one more flag. If $Q$ has a yellow diagonal, then we can take each flag with a yellow first square (it exists by a choice of the first column; moreover, it is not used in $Q$ ). Conversely, if the diagonal of $Q$ is blue then we can take any of the $\geq 2^{N-3}+1-(N-1)>0$ remaining good flags. So, in both cases we get a desired $N \times N$ square.
|
2^{N-2}+1
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
On some planet, there are $2^{N}$ countries $(N \geq 4)$. Each country has a flag $N$ units wide and one unit high composed of $N$ fields of size $1 \times 1$, each field being either yellow or blue. No two countries have the same flag. We say that a set of $N$ flags is diverse if these flags can be arranged into an $N \times N$ square so that all $N$ fields on its main diagonal will have the same color. Determine the smallest positive integer $M$ such that among any $M$ distinct flags, there exist $N$ flags forming a diverse set. (Croatia) Answer. $M=2^{N-2}+1$.
|
When speaking about the diagonal of a square, we will always mean the main diagonal. Let $M_{N}$ be the smallest positive integer satisfying the problem condition. First, we show that $M_{N}>2^{N-2}$. Consider the collection of all $2^{N-2}$ flags having yellow first squares and blue second ones. Obviously, both colors appear on the diagonal of each $N \times N$ square formed by these flags. We are left to show that $M_{N} \leq 2^{N-2}+1$, thus obtaining the desired answer. We start with establishing this statement for $N=4$. Suppose that we have 5 flags of length 4 . We decompose each flag into two parts of 2 squares each; thereby, we denote each flag as $L R$, where the $2 \times 1$ flags $L, R \in \mathcal{S}=\{\mathrm{BB}, \mathrm{BY}, \mathrm{YB}, \mathrm{YY}\}$ are its left and right parts, respectively. First, we make two easy observations on the flags $2 \times 1$ which can be checked manually. (i) For each $A \in \mathcal{S}$, there exists only one $2 \times 1$ flag $C \in \mathcal{S}$ (possibly $C=A$ ) such that $A$ and $C$ cannot form a $2 \times 2$ square with monochrome diagonal (for part BB, that is YY, and for BY that is YB). (ii) Let $A_{1}, A_{2}, A_{3} \in \mathcal{S}$ be three distinct elements; then two of them can form a $2 \times 2$ square with yellow diagonal, and two of them can form a $2 \times 2$ square with blue diagonal (for all parts but BB , a pair $(\mathrm{BY}, \mathrm{YB})$ fits for both statements, while for all parts but BY, these pairs are $(\mathrm{YB}, \mathrm{YY})$ and (BB, YB)). Now, let $\ell$ and $r$ be the numbers of distinct left and right parts of our 5 flags, respectively. The total number of flags is $5 \leq r \ell$, hence one of the factors (say, $r$ ) should be at least 3 . On the other hand, $\ell, r \leq 4$, so there are two flags with coinciding right part; let them be $L_{1} R_{1}$ and $L_{2} R_{1}\left(L_{1} \neq L_{2}\right)$. Next, since $r \geq 3$, there exist some flags $L_{3} R_{3}$ and $L_{4} R_{4}$ such that $R_{1}, R_{3}, R_{4}$ are distinct. Let $L^{\prime} R^{\prime}$ be the remaining flag. By (i), one of the pairs $\left(L^{\prime}, L_{1}\right)$ and $\left(L^{\prime}, L_{2}\right)$ can form a $2 \times 2$ square with monochrome diagonal; we can assume that $L^{\prime}, L_{2}$ form a square with a blue diagonal. Finally, the right parts of two of the flags $L_{1} R_{1}, L_{3} R_{3}, L_{4} R_{4}$ can also form a $2 \times 2$ square with a blue diagonal by (ii). Putting these $2 \times 2$ squares on the diagonal of a $4 \times 4$ square, we find a desired arrangement of four flags. We are ready to prove the problem statement by induction on $N$; actually, above we have proved the base case $N=4$. For the induction step, assume that $N>4$, consider any $2^{N-2}+1$ flags of length $N$, and arrange them into a large flag of size $\left(2^{N-2}+1\right) \times N$. This flag contains a non-monochrome column since the flags are distinct; we may assume that this column is the first one. By the pigeonhole principle, this column contains at least $\left\lceil\frac{2^{N-2}+1}{2}\right\rceil=2^{N-3}+1$ squares of one color (say, blue). We call the flags with a blue first square good. Consider all the good flags and remove the first square from each of them. We obtain at least $2^{N-3}+1 \geq M_{N-1}$ flags of length $N-1$; by the induction hypothesis, $N-1$ of them can form a square $Q$ with the monochrome diagonal. Now, returning the removed squares, we obtain a rectangle $(N-1) \times N$, and our aim is to supplement it on the top by one more flag. If $Q$ has a yellow diagonal, then we can take each flag with a yellow first square (it exists by a choice of the first column; moreover, it is not used in $Q$ ). Conversely, if the diagonal of $Q$ is blue then we can take any of the $\geq 2^{N-3}+1-(N-1)>0$ remaining good flags. So, in both cases we get a desired $N \times N$ square.
|
{
"resource_path": "IMO/segmented/en-IMO2010SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
9520af31-fa45-50de-b7a3-43a6338f847e
| 23,939
|
2500 chess kings have to be placed on a $100 \times 100$ chessboard so that (i) no king can capture any other one (i.e. no two kings are placed in two squares sharing a common vertex); (ii) each row and each column contains exactly 25 kings. Find the number of such arrangements. (Two arrangements differing by rotation or symmetry are supposed to be different.) (Russia) Answer. There are two such arrangements.
|
Suppose that we have an arrangement satisfying the problem conditions. Divide the board into $2 \times 2$ pieces; we call these pieces blocks. Each block can contain not more than one king (otherwise these two kings would attack each other); hence, by the pigeonhole principle each block must contain exactly one king. Now assign to each block a letter T or B if a king is placed in its top or bottom half, respectively. Similarly, assign to each block a letter L or R if a king stands in its left or right half. So we define $T$-blocks, $B$-blocks, $L$-blocks, and $R$-blocks. We also combine the letters; we call a block a TL-block if it is simultaneously T-block and L-block. Similarly we define TR-blocks, $B L$-blocks, and BR-blocks. The arrangement of blocks determines uniquely the arrangement of kings; so in the rest of the solution we consider the $50 \times 50$ system of blocks (see Fig. 1). We identify the blocks by their coordinate pairs; the pair $(i, j)$, where $1 \leq i, j \leq 50$, refers to the $j$ th block in the $i$ th row (or the $i$ th block in the $j$ th column). The upper-left block is $(1,1)$. The system of blocks has the following properties.. ( $\left.\mathrm{i}^{\prime}\right)$ If $(i, j)$ is a B-block then $(i+1, j)$ is a B-block: otherwise the kings in these two blocks can take each other. Similarly: if $(i, j)$ is a T-block then $(i-1, j)$ is a T-block; if $(i, j)$ is an L-block then $(i, j-1)$ is an L-block; if $(i, j)$ is an R-block then $(i, j+1)$ is an R-block. (ii') Each column contains exactly 25 L-blocks and 25 R-blocks, and each row contains exactly 25 T -blocks and 25 B-blocks. In particular, the total number of L-blocks (or R-blocks, or T-blocks, or B-blocks) is equal to $25 \cdot 50=1250$. Consider any B-block of the form $(1, j)$. By ( $\mathrm{i}^{\prime}$ ), all blocks in the $j$ th column are B-blocks; so we call such a column $B$-column. By (ii'), we have 25 B-blocks in the first row, so we obtain 25 B-columns. These 25 B-columns contain 1250 B-blocks, hence all blocks in the remaining columns are T-blocks, and we obtain 25 T-columns. Similarly, there are exactly $25 L$-rows and exactly $25 R$-rows. Now consider an arbitrary pair of a T-column and a neighboring B-column (columns with numbers $j$ and $j+1$ ). 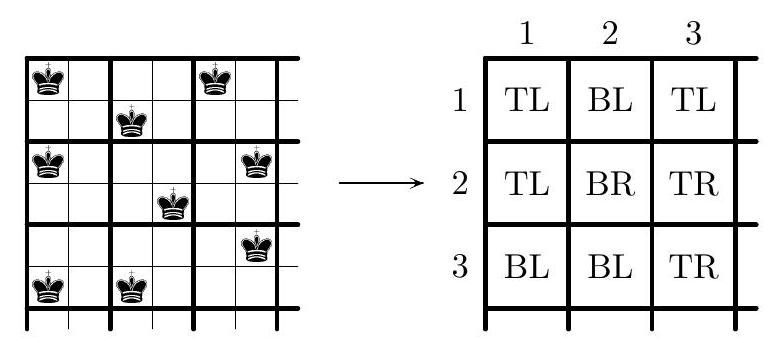 Fig. 1 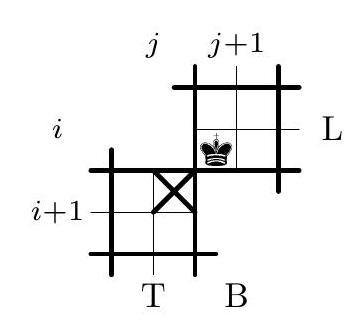 Fig. 2 Case 1. Suppose that the $j$ th column is a T-column, and the $(j+1)$ th column is a Bcolumn. Consider some index $i$ such that the $i$ th row is an L-row; then $(i, j+1)$ is a BL-block. Therefore, $(i+1, j)$ cannot be a TR-block (see Fig. 2), hence $(i+1, j)$ is a TL-block, thus the $(i+1)$ th row is an L-row. Now, choosing the $i$ th row to be the topmost L-row, we successively obtain that all rows from the $i$ th to the 50 th are L-rows. Since we have exactly 25 L-rows, it follows that the rows from the 1st to the 25 th are R-rows, and the rows from the 26 th to the 50th are L-rows. Now consider the neighboring R-row and L-row (that are the rows with numbers 25 and 26). Replacing in the previous reasoning rows by columns and vice versa, the columns from the 1 st to the 25 th are T-columns, and the columns from the 26 th to the 50 th are B-columns. So we have a unique arrangement of blocks that leads to the arrangement of kings satisfying the condition of the problem (see Fig. 3). 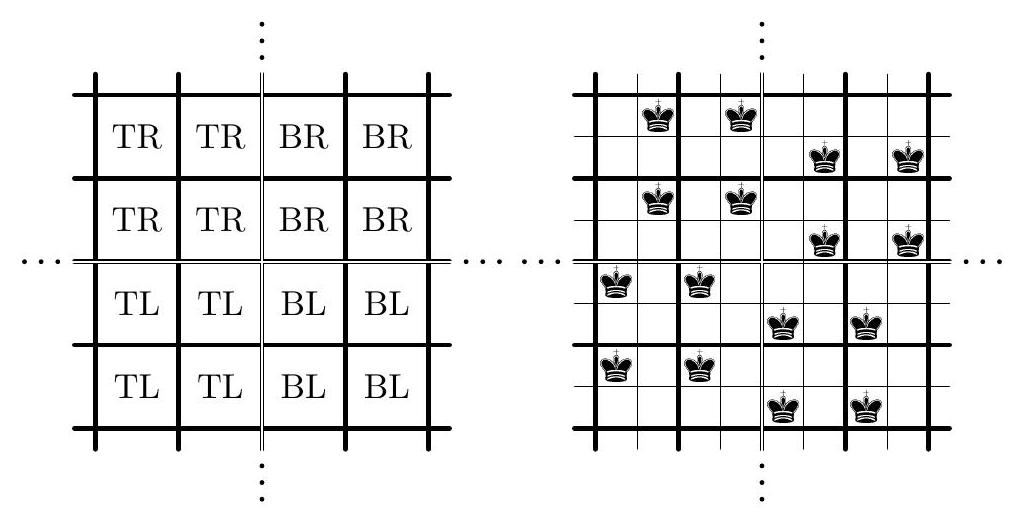 Fig. 3 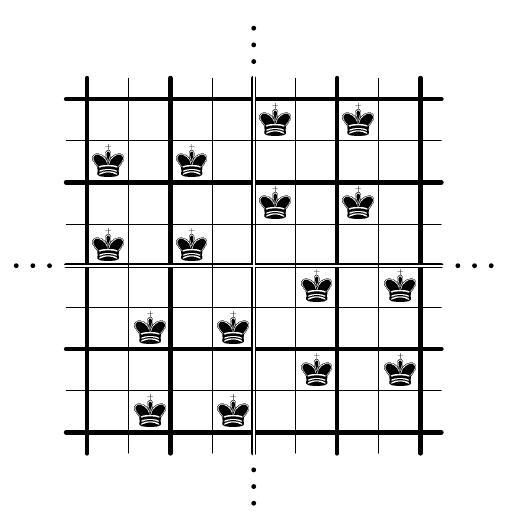 Fig. 4 Case 2. Suppose that the $j$ th column is a B-column, and the $(j+1)$ th column is a T-column. Repeating the arguments from Case 1, we obtain that the rows from the 1st to the 25th are L-rows (and all other rows are R-rows), the columns from the 1st to the 25 th are B-columns (and all other columns are T-columns), so we find exactly one more arrangement of kings (see Fig. 4).
|
2
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
2500 chess kings have to be placed on a $100 \times 100$ chessboard so that (i) no king can capture any other one (i.e. no two kings are placed in two squares sharing a common vertex); (ii) each row and each column contains exactly 25 kings. Find the number of such arrangements. (Two arrangements differing by rotation or symmetry are supposed to be different.) (Russia) Answer. There are two such arrangements.
|
Suppose that we have an arrangement satisfying the problem conditions. Divide the board into $2 \times 2$ pieces; we call these pieces blocks. Each block can contain not more than one king (otherwise these two kings would attack each other); hence, by the pigeonhole principle each block must contain exactly one king. Now assign to each block a letter T or B if a king is placed in its top or bottom half, respectively. Similarly, assign to each block a letter L or R if a king stands in its left or right half. So we define $T$-blocks, $B$-blocks, $L$-blocks, and $R$-blocks. We also combine the letters; we call a block a TL-block if it is simultaneously T-block and L-block. Similarly we define TR-blocks, $B L$-blocks, and BR-blocks. The arrangement of blocks determines uniquely the arrangement of kings; so in the rest of the solution we consider the $50 \times 50$ system of blocks (see Fig. 1). We identify the blocks by their coordinate pairs; the pair $(i, j)$, where $1 \leq i, j \leq 50$, refers to the $j$ th block in the $i$ th row (or the $i$ th block in the $j$ th column). The upper-left block is $(1,1)$. The system of blocks has the following properties.. ( $\left.\mathrm{i}^{\prime}\right)$ If $(i, j)$ is a B-block then $(i+1, j)$ is a B-block: otherwise the kings in these two blocks can take each other. Similarly: if $(i, j)$ is a T-block then $(i-1, j)$ is a T-block; if $(i, j)$ is an L-block then $(i, j-1)$ is an L-block; if $(i, j)$ is an R-block then $(i, j+1)$ is an R-block. (ii') Each column contains exactly 25 L-blocks and 25 R-blocks, and each row contains exactly 25 T -blocks and 25 B-blocks. In particular, the total number of L-blocks (or R-blocks, or T-blocks, or B-blocks) is equal to $25 \cdot 50=1250$. Consider any B-block of the form $(1, j)$. By ( $\mathrm{i}^{\prime}$ ), all blocks in the $j$ th column are B-blocks; so we call such a column $B$-column. By (ii'), we have 25 B-blocks in the first row, so we obtain 25 B-columns. These 25 B-columns contain 1250 B-blocks, hence all blocks in the remaining columns are T-blocks, and we obtain 25 T-columns. Similarly, there are exactly $25 L$-rows and exactly $25 R$-rows. Now consider an arbitrary pair of a T-column and a neighboring B-column (columns with numbers $j$ and $j+1$ ).  Fig. 1  Fig. 2 Case 1. Suppose that the $j$ th column is a T-column, and the $(j+1)$ th column is a Bcolumn. Consider some index $i$ such that the $i$ th row is an L-row; then $(i, j+1)$ is a BL-block. Therefore, $(i+1, j)$ cannot be a TR-block (see Fig. 2), hence $(i+1, j)$ is a TL-block, thus the $(i+1)$ th row is an L-row. Now, choosing the $i$ th row to be the topmost L-row, we successively obtain that all rows from the $i$ th to the 50 th are L-rows. Since we have exactly 25 L-rows, it follows that the rows from the 1st to the 25 th are R-rows, and the rows from the 26 th to the 50th are L-rows. Now consider the neighboring R-row and L-row (that are the rows with numbers 25 and 26). Replacing in the previous reasoning rows by columns and vice versa, the columns from the 1 st to the 25 th are T-columns, and the columns from the 26 th to the 50 th are B-columns. So we have a unique arrangement of blocks that leads to the arrangement of kings satisfying the condition of the problem (see Fig. 3).  Fig. 3  Fig. 4 Case 2. Suppose that the $j$ th column is a B-column, and the $(j+1)$ th column is a T-column. Repeating the arguments from Case 1, we obtain that the rows from the 1st to the 25th are L-rows (and all other rows are R-rows), the columns from the 1st to the 25 th are B-columns (and all other columns are T-columns), so we find exactly one more arrangement of kings (see Fig. 4).
|
{
"resource_path": "IMO/segmented/en-IMO2010SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
aa661286-a907-5a78-b6f0-3ae59f7d10e5
| 23,943
|
Find the least positive integer $n$ for which there exists a set $\left\{s_{1}, s_{2}, \ldots, s_{n}\right\}$ consisting of $n$ distinct positive integers such that $$ \left(1-\frac{1}{s_{1}}\right)\left(1-\frac{1}{s_{2}}\right) \ldots\left(1-\frac{1}{s_{n}}\right)=\frac{51}{2010} $$ $\mathbf{N} 1^{\prime}$. Same as Problem N1, but the constant $\frac{51}{2010}$ is replaced by $\frac{42}{2010}$. (Canada) Answer for Problem N1. $n=39$. Solution for Problem N1. Suppose that for some $n$ there exist the desired numbers; we may assume that $s_{1}<s_{2}<\cdots<s_{n}$. Surely $s_{1}>1$ since otherwise $1-\frac{1}{s_{1}}=0$. So we have $2 \leq s_{1} \leq s_{2}-1 \leq \cdots \leq s_{n}-(n-1)$, hence $s_{i} \geq i+1$ for each $i=1, \ldots, n$. Therefore $$ \begin{aligned} \frac{51}{2010} & =\left(1-\frac{1}{s_{1}}\right)\left(1-\frac{1}{s_{2}}\right) \ldots\left(1-\frac{1}{s_{n}}\right) \\ & \geq\left(1-\frac{1}{2}\right)\left(1-\frac{1}{3}\right) \ldots\left(1-\frac{1}{n+1}\right)=\frac{1}{2} \cdot \frac{2}{3} \cdots \frac{n}{n+1}=\frac{1}{n+1} \end{aligned} $$ which implies $$ n+1 \geq \frac{2010}{51}=\frac{670}{17}>39 $$ so $n \geq 39$. Now we are left to show that $n=39$ fits. Consider the set $\{2,3, \ldots, 33,35,36, \ldots, 40,67\}$ which contains exactly 39 numbers. We have $$ \frac{1}{2} \cdot \frac{2}{3} \cdots \frac{32}{33} \cdot \frac{34}{35} \cdots \frac{39}{40} \cdot \frac{66}{67}=\frac{1}{33} \cdot \frac{34}{40} \cdot \frac{66}{67}=\frac{17}{670}=\frac{51}{2010} $$ hence for $n=39$ there exists a desired example. Comment. One can show that the example (1) is unique. Answer for Problem N1' ${ }^{\prime} n=48$. Solution for Problem N1'. Suppose that for some $n$ there exist the desired numbers. In the same way we obtain that $s_{i} \geq i+1$. Moreover, since the denominator of the fraction $\frac{42}{2010}=\frac{7}{335}$ is divisible by 67 , some of $s_{i}$ 's should be divisible by 67 , so $s_{n} \geq s_{i} \geq 67$. This means that $$ \frac{42}{2010} \geq \frac{1}{2} \cdot \frac{2}{3} \cdots \frac{n-1}{n} \cdot\left(1-\frac{1}{67}\right)=\frac{66}{67 n} $$ which implies $$ n \geq \frac{2010 \cdot 66}{42 \cdot 67}=\frac{330}{7}>47 $$ so $n \geq 48$. Now we are left to show that $n=48$ fits. Consider the set $\{2,3, \ldots, 33,36,37, \ldots, 50,67\}$ which contains exactly 48 numbers. We have $$ \frac{1}{2} \cdot \frac{2}{3} \cdots \frac{32}{33} \cdot \frac{35}{36} \cdots \frac{49}{50} \cdot \frac{66}{67}=\frac{1}{33} \cdot \frac{35}{50} \cdot \frac{66}{67}=\frac{7}{335}=\frac{42}{2010} $$ hence for $n=48$ there exists a desired example. Comment 1. In this version of the problem, the estimate needs one more step, hence it is a bit harder. On the other hand, the example in this version is not unique. Another example is $$ \frac{1}{2} \cdot \frac{2}{3} \cdots \frac{46}{47} \cdot \frac{66}{67} \cdot \frac{329}{330}=\frac{1}{67} \cdot \frac{66}{330} \cdot \frac{329}{47}=\frac{7}{67 \cdot 5}=\frac{42}{2010} . $$ Comment 2. N1' was the Proposer's formulation of the problem. We propose N1 according to the number of current IMO.
|
None
|
48
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Find the least positive integer $n$ for which there exists a set $\left\{s_{1}, s_{2}, \ldots, s_{n}\right\}$ consisting of $n$ distinct positive integers such that $$ \left(1-\frac{1}{s_{1}}\right)\left(1-\frac{1}{s_{2}}\right) \ldots\left(1-\frac{1}{s_{n}}\right)=\frac{51}{2010} $$ $\mathbf{N} 1^{\prime}$. Same as Problem N1, but the constant $\frac{51}{2010}$ is replaced by $\frac{42}{2010}$. (Canada) Answer for Problem N1. $n=39$. Solution for Problem N1. Suppose that for some $n$ there exist the desired numbers; we may assume that $s_{1}<s_{2}<\cdots<s_{n}$. Surely $s_{1}>1$ since otherwise $1-\frac{1}{s_{1}}=0$. So we have $2 \leq s_{1} \leq s_{2}-1 \leq \cdots \leq s_{n}-(n-1)$, hence $s_{i} \geq i+1$ for each $i=1, \ldots, n$. Therefore $$ \begin{aligned} \frac{51}{2010} & =\left(1-\frac{1}{s_{1}}\right)\left(1-\frac{1}{s_{2}}\right) \ldots\left(1-\frac{1}{s_{n}}\right) \\ & \geq\left(1-\frac{1}{2}\right)\left(1-\frac{1}{3}\right) \ldots\left(1-\frac{1}{n+1}\right)=\frac{1}{2} \cdot \frac{2}{3} \cdots \frac{n}{n+1}=\frac{1}{n+1} \end{aligned} $$ which implies $$ n+1 \geq \frac{2010}{51}=\frac{670}{17}>39 $$ so $n \geq 39$. Now we are left to show that $n=39$ fits. Consider the set $\{2,3, \ldots, 33,35,36, \ldots, 40,67\}$ which contains exactly 39 numbers. We have $$ \frac{1}{2} \cdot \frac{2}{3} \cdots \frac{32}{33} \cdot \frac{34}{35} \cdots \frac{39}{40} \cdot \frac{66}{67}=\frac{1}{33} \cdot \frac{34}{40} \cdot \frac{66}{67}=\frac{17}{670}=\frac{51}{2010} $$ hence for $n=39$ there exists a desired example. Comment. One can show that the example (1) is unique. Answer for Problem N1' ${ }^{\prime} n=48$. Solution for Problem N1'. Suppose that for some $n$ there exist the desired numbers. In the same way we obtain that $s_{i} \geq i+1$. Moreover, since the denominator of the fraction $\frac{42}{2010}=\frac{7}{335}$ is divisible by 67 , some of $s_{i}$ 's should be divisible by 67 , so $s_{n} \geq s_{i} \geq 67$. This means that $$ \frac{42}{2010} \geq \frac{1}{2} \cdot \frac{2}{3} \cdots \frac{n-1}{n} \cdot\left(1-\frac{1}{67}\right)=\frac{66}{67 n} $$ which implies $$ n \geq \frac{2010 \cdot 66}{42 \cdot 67}=\frac{330}{7}>47 $$ so $n \geq 48$. Now we are left to show that $n=48$ fits. Consider the set $\{2,3, \ldots, 33,36,37, \ldots, 50,67\}$ which contains exactly 48 numbers. We have $$ \frac{1}{2} \cdot \frac{2}{3} \cdots \frac{32}{33} \cdot \frac{35}{36} \cdots \frac{49}{50} \cdot \frac{66}{67}=\frac{1}{33} \cdot \frac{35}{50} \cdot \frac{66}{67}=\frac{7}{335}=\frac{42}{2010} $$ hence for $n=48$ there exists a desired example. Comment 1. In this version of the problem, the estimate needs one more step, hence it is a bit harder. On the other hand, the example in this version is not unique. Another example is $$ \frac{1}{2} \cdot \frac{2}{3} \cdots \frac{46}{47} \cdot \frac{66}{67} \cdot \frac{329}{330}=\frac{1}{67} \cdot \frac{66}{330} \cdot \frac{329}{47}=\frac{7}{67 \cdot 5}=\frac{42}{2010} . $$ Comment 2. N1' was the Proposer's formulation of the problem. We propose N1 according to the number of current IMO.
|
None
|
{
"resource_path": "IMO/segmented/en-IMO2010SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
e030207e-d161-56dd-aed9-099d6d9e7330
| 23,989
|
Find the smallest number $n$ such that there exist polynomials $f_{1}, f_{2}, \ldots, f_{n}$ with rational coefficients satisfying $$ x^{2}+7=f_{1}(x)^{2}+f_{2}(x)^{2}+\cdots+f_{n}(x)^{2} . $$ (Poland) Answer. The smallest $n$ is 5 .
|
The equality $x^{2}+7=x^{2}+2^{2}+1^{2}+1^{2}+1^{2}$ shows that $n \leq 5$. It remains to show that $x^{2}+7$ is not a sum of four (or less) squares of polynomials with rational coefficients. Suppose by way of contradiction that $x^{2}+7=f_{1}(x)^{2}+f_{2}(x)^{2}+f_{3}(x)^{2}+f_{4}(x)^{2}$, where the coefficients of polynomials $f_{1}, f_{2}, f_{3}$ and $f_{4}$ are rational (some of these polynomials may be zero). Clearly, the degrees of $f_{1}, f_{2}, f_{3}$ and $f_{4}$ are at most 1 . Thus $f_{i}(x)=a_{i} x+b_{i}$ for $i=1,2,3,4$ and some rationals $a_{1}, b_{1}, a_{2}, b_{2}, a_{3}, b_{3}, a_{4}, b_{4}$. It follows that $x^{2}+7=\sum_{i=1}^{4}\left(a_{i} x+b_{i}\right)^{2}$ and hence $$ \sum_{i=1}^{4} a_{i}^{2}=1, \quad \sum_{i=1}^{4} a_{i} b_{i}=0, \quad \sum_{i=1}^{4} b_{i}^{2}=7 $$ Let $p_{i}=a_{i}+b_{i}$ and $q_{i}=a_{i}-b_{i}$ for $i=1,2,3,4$. Then $$ \begin{aligned} \sum_{i=1}^{4} p_{i}^{2} & =\sum_{i=1}^{4} a_{i}^{2}+2 \sum_{i=1}^{4} a_{i} b_{i}+\sum_{i=1}^{4} b_{i}^{2}=8 \\ \sum_{i=1}^{4} q_{i}^{2} & =\sum_{i=1}^{4} a_{i}^{2}-2 \sum_{i=1}^{4} a_{i} b_{i}+\sum_{i=1}^{4} b_{i}^{2}=8 \\ \text { and } \quad \sum_{i=1}^{4} p_{i} q_{i} & =\sum_{i=1}^{4} a_{i}^{2}-\sum_{i=1}^{4} b_{i}^{2}=-6 \end{aligned} $$ which means that there exist a solution in integers $x_{1}, y_{1}, x_{2}, y_{2}, x_{3}, y_{3}, x_{4}, y_{4}$ and $m>0$ of the system of equations (i) $\sum_{i=1}^{4} x_{i}^{2}=8 m^{2}$, (ii) $\sum_{i=1}^{4} y_{i}^{2}=8 m^{2}$, (iii) $\sum_{i=1}^{4} x_{i} y_{i}=-6 m^{2}$. We will show that such a solution does not exist. Assume the contrary and consider a solution with minimal $m$. Note that if an integer $x$ is odd then $x^{2} \equiv 1(\bmod 8)$. Otherwise (i.e., if $x$ is even) we have $x^{2} \equiv 0(\bmod 8)$ or $x^{2} \equiv 4$ $(\bmod 8)$. Hence, by (i), we get that $x_{1}, x_{2}, x_{3}$ and $x_{4}$ are even. Similarly, by (ii), we get that $y_{1}, y_{2}, y_{3}$ and $y_{4}$ are even. Thus the LHS of (iii) is divisible by 4 and $m$ is also even. It follows that $\left(\frac{x_{1}}{2}, \frac{y_{1}}{2}, \frac{x_{2}}{2}, \frac{y_{2}}{2}, \frac{x_{3}}{2}, \frac{y_{3}}{2}, \frac{x_{4}}{2}, \frac{y_{4}}{2}, \frac{m}{2}\right)$ is a solution of the system of equations (i), (ii) and (iii), which contradicts the minimality of $m$.
|
5
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Find the smallest number $n$ such that there exist polynomials $f_{1}, f_{2}, \ldots, f_{n}$ with rational coefficients satisfying $$ x^{2}+7=f_{1}(x)^{2}+f_{2}(x)^{2}+\cdots+f_{n}(x)^{2} . $$ (Poland) Answer. The smallest $n$ is 5 .
|
The equality $x^{2}+7=x^{2}+2^{2}+1^{2}+1^{2}+1^{2}$ shows that $n \leq 5$. It remains to show that $x^{2}+7$ is not a sum of four (or less) squares of polynomials with rational coefficients. Suppose by way of contradiction that $x^{2}+7=f_{1}(x)^{2}+f_{2}(x)^{2}+f_{3}(x)^{2}+f_{4}(x)^{2}$, where the coefficients of polynomials $f_{1}, f_{2}, f_{3}$ and $f_{4}$ are rational (some of these polynomials may be zero). Clearly, the degrees of $f_{1}, f_{2}, f_{3}$ and $f_{4}$ are at most 1 . Thus $f_{i}(x)=a_{i} x+b_{i}$ for $i=1,2,3,4$ and some rationals $a_{1}, b_{1}, a_{2}, b_{2}, a_{3}, b_{3}, a_{4}, b_{4}$. It follows that $x^{2}+7=\sum_{i=1}^{4}\left(a_{i} x+b_{i}\right)^{2}$ and hence $$ \sum_{i=1}^{4} a_{i}^{2}=1, \quad \sum_{i=1}^{4} a_{i} b_{i}=0, \quad \sum_{i=1}^{4} b_{i}^{2}=7 $$ Let $p_{i}=a_{i}+b_{i}$ and $q_{i}=a_{i}-b_{i}$ for $i=1,2,3,4$. Then $$ \begin{aligned} \sum_{i=1}^{4} p_{i}^{2} & =\sum_{i=1}^{4} a_{i}^{2}+2 \sum_{i=1}^{4} a_{i} b_{i}+\sum_{i=1}^{4} b_{i}^{2}=8 \\ \sum_{i=1}^{4} q_{i}^{2} & =\sum_{i=1}^{4} a_{i}^{2}-2 \sum_{i=1}^{4} a_{i} b_{i}+\sum_{i=1}^{4} b_{i}^{2}=8 \\ \text { and } \quad \sum_{i=1}^{4} p_{i} q_{i} & =\sum_{i=1}^{4} a_{i}^{2}-\sum_{i=1}^{4} b_{i}^{2}=-6 \end{aligned} $$ which means that there exist a solution in integers $x_{1}, y_{1}, x_{2}, y_{2}, x_{3}, y_{3}, x_{4}, y_{4}$ and $m>0$ of the system of equations (i) $\sum_{i=1}^{4} x_{i}^{2}=8 m^{2}$, (ii) $\sum_{i=1}^{4} y_{i}^{2}=8 m^{2}$, (iii) $\sum_{i=1}^{4} x_{i} y_{i}=-6 m^{2}$. We will show that such a solution does not exist. Assume the contrary and consider a solution with minimal $m$. Note that if an integer $x$ is odd then $x^{2} \equiv 1(\bmod 8)$. Otherwise (i.e., if $x$ is even) we have $x^{2} \equiv 0(\bmod 8)$ or $x^{2} \equiv 4$ $(\bmod 8)$. Hence, by (i), we get that $x_{1}, x_{2}, x_{3}$ and $x_{4}$ are even. Similarly, by (ii), we get that $y_{1}, y_{2}, y_{3}$ and $y_{4}$ are even. Thus the LHS of (iii) is divisible by 4 and $m$ is also even. It follows that $\left(\frac{x_{1}}{2}, \frac{y_{1}}{2}, \frac{x_{2}}{2}, \frac{y_{2}}{2}, \frac{x_{3}}{2}, \frac{y_{3}}{2}, \frac{x_{4}}{2}, \frac{y_{4}}{2}, \frac{m}{2}\right)$ is a solution of the system of equations (i), (ii) and (iii), which contradicts the minimality of $m$.
|
{
"resource_path": "IMO/segmented/en-IMO2010SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
f93d2d77-70fc-5fcd-adc9-964e38ba78b1
| 23,993
|
Let $m$ be a positive integer and consider a checkerboard consisting of $m$ by $m$ unit squares. At the midpoints of some of these unit squares there is an ant. At time 0 , each ant starts moving with speed 1 parallel to some edge of the checkerboard. When two ants moving in opposite directions meet, they both turn $90^{\circ}$ clockwise and continue moving with speed 1 . When more than two ants meet, or when two ants moving in perpendicular directions meet, the ants continue moving in the same direction as before they met. When an ant reaches one of the edges of the checkerboard, it falls off and will not re-appear. Considering all possible starting positions, determine the latest possible moment at which the last ant falls off the checkerboard or prove that such a moment does not necessarily exist.
|
For $m=1$ the answer is clearly correct, so assume $m>1$. In the sequel, the word collision will be used to denote meeting of exactly two ants, moving in opposite directions. If at the beginning we place an ant on the southwest corner square facing east and an ant on the southeast corner square facing west, then they will meet in the middle of the bottom row at time $\frac{m-1}{2}$. After the collision, the ant that moves to the north will stay on the board for another $m-\frac{1}{2}$ time units and thus we have established an example in which the last ant falls off at time $\frac{m-1}{2}+m-\frac{1}{2}=\frac{3 m}{2}-1$. So, we are left to prove that this is the latest possible moment. Consider any collision of two ants $a$ and $a^{\prime}$. Let us change the rule for this collision, and enforce these two ants to turn anticlockwise. Then the succeeding behavior of all the ants does not change; the only difference is that $a$ and $a^{\prime}$ swap their positions. These arguments may be applied to any collision separately, so we may assume that at any collision, either both ants rotate clockwise or both of them rotate anticlockwise by our own choice. For instance, we may assume that there are only two types of ants, depending on their initial direction: $N E$-ants, which move only north or east, and $S W$-ants, moving only south and west. Then we immediately obtain that all ants will have fallen off the board after $2 m-1$ time units. However, we can get a better bound by considering the last moment at which a given ant collides with another ant. Choose a coordinate system such that the corners of the checkerboard are $(0,0),(m, 0),(m, m)$ and $(0, m)$. At time $t$, there will be no NE-ants in the region $\{(x, y): x+y<t+1\}$ and no $\mathrm{SW}$-ants in the region $\{(x, y): x+y>2 m-t-1\}$. So if two ants collide at $(x, y)$ at time $t$, we have $$ t+1 \leq x+y \leq 2 m-t-1 $$ Analogously, we may change the rules so that each ant would move either alternatingly north and west, or alternatingly south and east. By doing so, we find that apart from (1) we also have $|x-y| \leq m-t-1$ for each collision at point $(x, y)$ and time $t$. To visualize this, put $$ B(t)=\left\{(x, y) \in[0, m]^{2}: t+1 \leq x+y \leq 2 m-t-1 \text { and }|x-y| \leq m-t-1\right\} . $$ An ant can thus only collide with another ant at time $t$ if it happens to be in the region $B(t)$. The following figure displays $B(t)$ for $t=\frac{1}{2}$ and $t=\frac{7}{2}$ in the case $m=6$ :  Now suppose that an NE-ant has its last collision at time $t$ and that it does so at the point $(x, y)$ (if the ant does not collide at all, it will fall off the board within $m-\frac{1}{2}<\frac{3 m}{2}-1$ time units, so this case can be ignored). Then we have $(x, y) \in B(t)$ and thus $x+y \geq t+1$ and $x-y \geq-(m-t-1)$. So we get $$ x \geq \frac{(t+1)-(m-t-1)}{2}=t+1-\frac{m}{2} $$ By symmetry we also have $y \geq t+1-\frac{m}{2}$, and hence $\min \{x, y\} \geq t+1-\frac{m}{2}$. After this collision, the ant will move directly to an edge, which will take at $\operatorname{most} m-\min \{x, y\}$ units of time. In sum, the total amount of time the ant stays on the board is at most $$ t+(m-\min \{x, y\}) \leq t+m-\left(t+1-\frac{m}{2}\right)=\frac{3 m}{2}-1 $$ By symmetry, the same bound holds for $\mathrm{SW}$-ants as well.
|
\frac{3 m}{2}-1
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Let $m$ be a positive integer and consider a checkerboard consisting of $m$ by $m$ unit squares. At the midpoints of some of these unit squares there is an ant. At time 0 , each ant starts moving with speed 1 parallel to some edge of the checkerboard. When two ants moving in opposite directions meet, they both turn $90^{\circ}$ clockwise and continue moving with speed 1 . When more than two ants meet, or when two ants moving in perpendicular directions meet, the ants continue moving in the same direction as before they met. When an ant reaches one of the edges of the checkerboard, it falls off and will not re-appear. Considering all possible starting positions, determine the latest possible moment at which the last ant falls off the checkerboard or prove that such a moment does not necessarily exist.
|
For $m=1$ the answer is clearly correct, so assume $m>1$. In the sequel, the word collision will be used to denote meeting of exactly two ants, moving in opposite directions. If at the beginning we place an ant on the southwest corner square facing east and an ant on the southeast corner square facing west, then they will meet in the middle of the bottom row at time $\frac{m-1}{2}$. After the collision, the ant that moves to the north will stay on the board for another $m-\frac{1}{2}$ time units and thus we have established an example in which the last ant falls off at time $\frac{m-1}{2}+m-\frac{1}{2}=\frac{3 m}{2}-1$. So, we are left to prove that this is the latest possible moment. Consider any collision of two ants $a$ and $a^{\prime}$. Let us change the rule for this collision, and enforce these two ants to turn anticlockwise. Then the succeeding behavior of all the ants does not change; the only difference is that $a$ and $a^{\prime}$ swap their positions. These arguments may be applied to any collision separately, so we may assume that at any collision, either both ants rotate clockwise or both of them rotate anticlockwise by our own choice. For instance, we may assume that there are only two types of ants, depending on their initial direction: $N E$-ants, which move only north or east, and $S W$-ants, moving only south and west. Then we immediately obtain that all ants will have fallen off the board after $2 m-1$ time units. However, we can get a better bound by considering the last moment at which a given ant collides with another ant. Choose a coordinate system such that the corners of the checkerboard are $(0,0),(m, 0),(m, m)$ and $(0, m)$. At time $t$, there will be no NE-ants in the region $\{(x, y): x+y<t+1\}$ and no $\mathrm{SW}$-ants in the region $\{(x, y): x+y>2 m-t-1\}$. So if two ants collide at $(x, y)$ at time $t$, we have $$ t+1 \leq x+y \leq 2 m-t-1 $$ Analogously, we may change the rules so that each ant would move either alternatingly north and west, or alternatingly south and east. By doing so, we find that apart from (1) we also have $|x-y| \leq m-t-1$ for each collision at point $(x, y)$ and time $t$. To visualize this, put $$ B(t)=\left\{(x, y) \in[0, m]^{2}: t+1 \leq x+y \leq 2 m-t-1 \text { and }|x-y| \leq m-t-1\right\} . $$ An ant can thus only collide with another ant at time $t$ if it happens to be in the region $B(t)$. The following figure displays $B(t)$ for $t=\frac{1}{2}$ and $t=\frac{7}{2}$ in the case $m=6$ :  Now suppose that an NE-ant has its last collision at time $t$ and that it does so at the point $(x, y)$ (if the ant does not collide at all, it will fall off the board within $m-\frac{1}{2}<\frac{3 m}{2}-1$ time units, so this case can be ignored). Then we have $(x, y) \in B(t)$ and thus $x+y \geq t+1$ and $x-y \geq-(m-t-1)$. So we get $$ x \geq \frac{(t+1)-(m-t-1)}{2}=t+1-\frac{m}{2} $$ By symmetry we also have $y \geq t+1-\frac{m}{2}$, and hence $\min \{x, y\} \geq t+1-\frac{m}{2}$. After this collision, the ant will move directly to an edge, which will take at $\operatorname{most} m-\min \{x, y\}$ units of time. In sum, the total amount of time the ant stays on the board is at most $$ t+(m-\min \{x, y\}) \leq t+m-\left(t+1-\frac{m}{2}\right)=\frac{3 m}{2}-1 $$ By symmetry, the same bound holds for $\mathrm{SW}$-ants as well.
|
{
"resource_path": "IMO/segmented/en-IMO2011SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
01beb1da-3294-58ee-96f1-187b23d086fc
| 24,034
|
Let $m$ be a positive integer and consider a checkerboard consisting of $m$ by $m$ unit squares. At the midpoints of some of these unit squares there is an ant. At time 0 , each ant starts moving with speed 1 parallel to some edge of the checkerboard. When two ants moving in opposite directions meet, they both turn $90^{\circ}$ clockwise and continue moving with speed 1 . When more than two ants meet, or when two ants moving in perpendicular directions meet, the ants continue moving in the same direction as before they met. When an ant reaches one of the edges of the checkerboard, it falls off and will not re-appear. Considering all possible starting positions, determine the latest possible moment at which the last ant falls off the checkerboard or prove that such a moment does not necessarily exist. Antswer. The latest possible moment for the last ant to fall off is $\frac{3 m}{2}-1$.
|
For $m=1$ the answer is clearly correct, so assume $m>1$. In the sequel, the word collision will be used to denote meeting of exactly two ants, moving in opposite directions. If at the beginning we place an ant on the southwest corner square facing east and an ant on the southeast corner square facing west, then they will meet in the middle of the bottom row at time $\frac{m-1}{2}$. After the collision, the ant that moves to the north will stay on the board for another $m-\frac{1}{2}$ time units and thus we have established an example in which the last ant falls off at time $\frac{m-1}{2}+m-\frac{1}{2}=\frac{3 m}{2}-1$. So, we are left to prove that this is the latest possible moment. Consider any collision of two ants $a$ and $a^{\prime}$. Let us change the rule for this collision, and enforce these two ants to turn anticlockwise. Then the succeeding behavior of all the ants does not change; the only difference is that $a$ and $a^{\prime}$ swap their positions. These arguments may be applied to any collision separately, so we may assume that at any collision, either both ants rotate clockwise or both of them rotate anticlockwise by our own choice. For instance, we may assume that there are only two types of ants, depending on their initial direction: $N E$-ants, which move only north or east, and $S W$-ants, moving only south and west. Then we immediately obtain that all ants will have fallen off the board after $2 m-1$ time units. However, we can get a better bound by considering the last moment at which a given ant collides with another ant. Choose a coordinate system such that the corners of the checkerboard are $(0,0),(m, 0),(m, m)$ and $(0, m)$. At time $t$, there will be no NE-ants in the region $\{(x, y): x+y<t+1\}$ and no $\mathrm{SW}$-ants in the region $\{(x, y): x+y>2 m-t-1\}$. So if two ants collide at $(x, y)$ at time $t$, we have $$ t+1 \leq x+y \leq 2 m-t-1 $$ Analogously, we may change the rules so that each ant would move either alternatingly north and west, or alternatingly south and east. By doing so, we find that apart from (1) we also have $|x-y| \leq m-t-1$ for each collision at point $(x, y)$ and time $t$. To visualize this, put $$ B(t)=\left\{(x, y) \in[0, m]^{2}: t+1 \leq x+y \leq 2 m-t-1 \text { and }|x-y| \leq m-t-1\right\} . $$ An ant can thus only collide with another ant at time $t$ if it happens to be in the region $B(t)$. The following figure displays $B(t)$ for $t=\frac{1}{2}$ and $t=\frac{7}{2}$ in the case $m=6$ :  Now suppose that an NE-ant has its last collision at time $t$ and that it does so at the point $(x, y)$ (if the ant does not collide at all, it will fall off the board within $m-\frac{1}{2}<\frac{3 m}{2}-1$ time units, so this case can be ignored). Then we have $(x, y) \in B(t)$ and thus $x+y \geq t+1$ and $x-y \geq-(m-t-1)$. So we get $$ x \geq \frac{(t+1)-(m-t-1)}{2}=t+1-\frac{m}{2} $$ By symmetry we also have $y \geq t+1-\frac{m}{2}$, and hence $\min \{x, y\} \geq t+1-\frac{m}{2}$. After this collision, the ant will move directly to an edge, which will take at $\operatorname{most} m-\min \{x, y\}$ units of time. In sum, the total amount of time the ant stays on the board is at most $$ t+(m-\min \{x, y\}) \leq t+m-\left(t+1-\frac{m}{2}\right)=\frac{3 m}{2}-1 $$ By symmetry, the same bound holds for $\mathrm{SW}$-ants as well.
|
\frac{3 m}{2}-1
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Let $m$ be a positive integer and consider a checkerboard consisting of $m$ by $m$ unit squares. At the midpoints of some of these unit squares there is an ant. At time 0 , each ant starts moving with speed 1 parallel to some edge of the checkerboard. When two ants moving in opposite directions meet, they both turn $90^{\circ}$ clockwise and continue moving with speed 1 . When more than two ants meet, or when two ants moving in perpendicular directions meet, the ants continue moving in the same direction as before they met. When an ant reaches one of the edges of the checkerboard, it falls off and will not re-appear. Considering all possible starting positions, determine the latest possible moment at which the last ant falls off the checkerboard or prove that such a moment does not necessarily exist. Antswer. The latest possible moment for the last ant to fall off is $\frac{3 m}{2}-1$.
|
For $m=1$ the answer is clearly correct, so assume $m>1$. In the sequel, the word collision will be used to denote meeting of exactly two ants, moving in opposite directions. If at the beginning we place an ant on the southwest corner square facing east and an ant on the southeast corner square facing west, then they will meet in the middle of the bottom row at time $\frac{m-1}{2}$. After the collision, the ant that moves to the north will stay on the board for another $m-\frac{1}{2}$ time units and thus we have established an example in which the last ant falls off at time $\frac{m-1}{2}+m-\frac{1}{2}=\frac{3 m}{2}-1$. So, we are left to prove that this is the latest possible moment. Consider any collision of two ants $a$ and $a^{\prime}$. Let us change the rule for this collision, and enforce these two ants to turn anticlockwise. Then the succeeding behavior of all the ants does not change; the only difference is that $a$ and $a^{\prime}$ swap their positions. These arguments may be applied to any collision separately, so we may assume that at any collision, either both ants rotate clockwise or both of them rotate anticlockwise by our own choice. For instance, we may assume that there are only two types of ants, depending on their initial direction: $N E$-ants, which move only north or east, and $S W$-ants, moving only south and west. Then we immediately obtain that all ants will have fallen off the board after $2 m-1$ time units. However, we can get a better bound by considering the last moment at which a given ant collides with another ant. Choose a coordinate system such that the corners of the checkerboard are $(0,0),(m, 0),(m, m)$ and $(0, m)$. At time $t$, there will be no NE-ants in the region $\{(x, y): x+y<t+1\}$ and no $\mathrm{SW}$-ants in the region $\{(x, y): x+y>2 m-t-1\}$. So if two ants collide at $(x, y)$ at time $t$, we have $$ t+1 \leq x+y \leq 2 m-t-1 $$ Analogously, we may change the rules so that each ant would move either alternatingly north and west, or alternatingly south and east. By doing so, we find that apart from (1) we also have $|x-y| \leq m-t-1$ for each collision at point $(x, y)$ and time $t$. To visualize this, put $$ B(t)=\left\{(x, y) \in[0, m]^{2}: t+1 \leq x+y \leq 2 m-t-1 \text { and }|x-y| \leq m-t-1\right\} . $$ An ant can thus only collide with another ant at time $t$ if it happens to be in the region $B(t)$. The following figure displays $B(t)$ for $t=\frac{1}{2}$ and $t=\frac{7}{2}$ in the case $m=6$ :  Now suppose that an NE-ant has its last collision at time $t$ and that it does so at the point $(x, y)$ (if the ant does not collide at all, it will fall off the board within $m-\frac{1}{2}<\frac{3 m}{2}-1$ time units, so this case can be ignored). Then we have $(x, y) \in B(t)$ and thus $x+y \geq t+1$ and $x-y \geq-(m-t-1)$. So we get $$ x \geq \frac{(t+1)-(m-t-1)}{2}=t+1-\frac{m}{2} $$ By symmetry we also have $y \geq t+1-\frac{m}{2}$, and hence $\min \{x, y\} \geq t+1-\frac{m}{2}$. After this collision, the ant will move directly to an edge, which will take at $\operatorname{most} m-\min \{x, y\}$ units of time. In sum, the total amount of time the ant stays on the board is at most $$ t+(m-\min \{x, y\}) \leq t+m-\left(t+1-\frac{m}{2}\right)=\frac{3 m}{2}-1 $$ By symmetry, the same bound holds for $\mathrm{SW}$-ants as well.
|
{
"resource_path": "IMO/segmented/en-IMO2011SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
c2628f72-93a8-59ed-9619-f9c18a030a7d
| 24,123
|
On a square table of 2011 by 2011 cells we place a finite number of napkins that each cover a square of 52 by 52 cells. In each cell we write the number of napkins covering it, and we record the maximal number $k$ of cells that all contain the same nonzero number. Considering all possible napkin configurations, what is the largest value of $k$ ? Answer. $2011^{2}-\left(\left(52^{2}-35^{2}\right) \cdot 39-17^{2}\right)=4044121-57392=3986729$.
|
Let $m=39$, then $2011=52 m-17$. We begin with an example showing that there can exist 3986729 cells carrying the same positive number.  To describe it, we number the columns from the left to the right and the rows from the bottom to the top by $1,2, \ldots, 2011$. We will denote each napkin by the coordinates of its lowerleft cell. There are four kinds of napkins: first, we take all napkins $(52 i+36,52 j+1)$ with $0 \leq j \leq i \leq m-2$; second, we use all napkins $(52 i+1,52 j+36)$ with $0 \leq i \leq j \leq m-2$; third, we use all napkins $(52 i+36,52 i+36)$ with $0 \leq i \leq m-2$; and finally the napkin $(1,1)$. Different groups of napkins are shown by different types of hatchings in the picture. Now except for those squares that carry two or more different hatchings, all squares have the number 1 written into them. The number of these exceptional cells is easily computed to be $\left(52^{2}-35^{2}\right) m-17^{2}=57392$. We are left to prove that 3986729 is an upper bound for the number of cells containing the same number. Consider any configuration of napkins and any positive integer $M$. Suppose there are $g$ cells with a number different from $M$. Then it suffices to show $g \geq 57392$. Throughout the solution, a line will mean either a row or a column. Consider any line $\ell$. Let $a_{1}, \ldots, a_{52 m-17}$ be the numbers written into its consecutive cells. For $i=1,2, \ldots, 52$, let $s_{i}=\sum_{t \equiv i(\bmod 52)} a_{t}$. Note that $s_{1}, \ldots, s_{35}$ have $m$ terms each, while $s_{36}, \ldots, s_{52}$ have $m-1$ terms each. Every napkin intersecting $\ell$ contributes exactly 1 to each $s_{i}$; hence the number $s$ of all those napkins satisfies $s_{1}=\cdots=s_{52}=s$. Call the line $\ell$ rich if $s>(m-1) M$ and poor otherwise. Suppose now that $\ell$ is rich. Then in each of the sums $s_{36}, \ldots, s_{52}$ there exists a term greater than $M$; consider all these terms and call the corresponding cells the rich bad cells for this line. So, each rich line contains at least 17 cells that are bad for this line. If, on the other hand, $\ell$ is poor, then certainly $s<m M$ so in each of the sums $s_{1}, \ldots, s_{35}$ there exists a term less than $M$; consider all these terms and call the corresponding cells the poor bad cells for this line. So, each poor line contains at least 35 cells that are bad for this line. Let us call all indices congruent to $1,2, \ldots$, or 35 modulo 52 small, and all other indices, i.e. those congruent to $36,37, \ldots$, or 52 modulo 52 , big. Recall that we have numbered the columns from the left to the right and the rows from the bottom to the top using the numbers $1,2, \ldots, 52 m-17$; we say that a line is big or small depending on whether its index is big or small. By definition, all rich bad cells for the rows belong to the big columns, while the poor ones belong to the small columns, and vice versa. In each line, we put a strawberry on each cell that is bad for this line. In addition, for each small rich line we put an extra strawberry on each of its (rich) bad cells. A cell gets the strawberries from its row and its column independently. Notice now that a cell with a strawberry on it contains a number different from $M$. If this cell gets a strawberry by the extra rule, then it contains a number greater than $M$. Moreover, it is either in a small row and in a big column, or vice versa. Suppose that it is in a small row, then it is not bad for its column. So it has not more than two strawberries in this case. On the other hand, if the extra rule is not applied to some cell, then it also has not more than two strawberries. So, the total number $N$ of strawberries is at most $2 g$. We shall now estimate $N$ in a different way. For each of the $2 \cdot 35 m$ small lines, we have introduced at least 34 strawberries if it is rich and at least 35 strawberries if it is poor, so at least 34 strawberries in any case. Similarly, for each of the $2 \cdot 17(m-1)$ big lines, we put at least $\min (17,35)=17$ strawberries. Summing over all lines we obtain $$ 2 g \geq N \geq 2(35 m \cdot 34+17(m-1) \cdot 17)=2(1479 m-289)=2 \cdot 57392 $$ as desired. Comment. The same reasoning applies also if we replace 52 by $R$ and 2011 by $R m-H$, where $m, R$, and $H$ are integers with $m, R \geq 1$ and $0 \leq H \leq \frac{1}{3} R$. More detailed information is provided after the next solution.
|
3986729
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
On a square table of 2011 by 2011 cells we place a finite number of napkins that each cover a square of 52 by 52 cells. In each cell we write the number of napkins covering it, and we record the maximal number $k$ of cells that all contain the same nonzero number. Considering all possible napkin configurations, what is the largest value of $k$ ? Answer. $2011^{2}-\left(\left(52^{2}-35^{2}\right) \cdot 39-17^{2}\right)=4044121-57392=3986729$.
|
Let $m=39$, then $2011=52 m-17$. We begin with an example showing that there can exist 3986729 cells carrying the same positive number.  To describe it, we number the columns from the left to the right and the rows from the bottom to the top by $1,2, \ldots, 2011$. We will denote each napkin by the coordinates of its lowerleft cell. There are four kinds of napkins: first, we take all napkins $(52 i+36,52 j+1)$ with $0 \leq j \leq i \leq m-2$; second, we use all napkins $(52 i+1,52 j+36)$ with $0 \leq i \leq j \leq m-2$; third, we use all napkins $(52 i+36,52 i+36)$ with $0 \leq i \leq m-2$; and finally the napkin $(1,1)$. Different groups of napkins are shown by different types of hatchings in the picture. Now except for those squares that carry two or more different hatchings, all squares have the number 1 written into them. The number of these exceptional cells is easily computed to be $\left(52^{2}-35^{2}\right) m-17^{2}=57392$. We are left to prove that 3986729 is an upper bound for the number of cells containing the same number. Consider any configuration of napkins and any positive integer $M$. Suppose there are $g$ cells with a number different from $M$. Then it suffices to show $g \geq 57392$. Throughout the solution, a line will mean either a row or a column. Consider any line $\ell$. Let $a_{1}, \ldots, a_{52 m-17}$ be the numbers written into its consecutive cells. For $i=1,2, \ldots, 52$, let $s_{i}=\sum_{t \equiv i(\bmod 52)} a_{t}$. Note that $s_{1}, \ldots, s_{35}$ have $m$ terms each, while $s_{36}, \ldots, s_{52}$ have $m-1$ terms each. Every napkin intersecting $\ell$ contributes exactly 1 to each $s_{i}$; hence the number $s$ of all those napkins satisfies $s_{1}=\cdots=s_{52}=s$. Call the line $\ell$ rich if $s>(m-1) M$ and poor otherwise. Suppose now that $\ell$ is rich. Then in each of the sums $s_{36}, \ldots, s_{52}$ there exists a term greater than $M$; consider all these terms and call the corresponding cells the rich bad cells for this line. So, each rich line contains at least 17 cells that are bad for this line. If, on the other hand, $\ell$ is poor, then certainly $s<m M$ so in each of the sums $s_{1}, \ldots, s_{35}$ there exists a term less than $M$; consider all these terms and call the corresponding cells the poor bad cells for this line. So, each poor line contains at least 35 cells that are bad for this line. Let us call all indices congruent to $1,2, \ldots$, or 35 modulo 52 small, and all other indices, i.e. those congruent to $36,37, \ldots$, or 52 modulo 52 , big. Recall that we have numbered the columns from the left to the right and the rows from the bottom to the top using the numbers $1,2, \ldots, 52 m-17$; we say that a line is big or small depending on whether its index is big or small. By definition, all rich bad cells for the rows belong to the big columns, while the poor ones belong to the small columns, and vice versa. In each line, we put a strawberry on each cell that is bad for this line. In addition, for each small rich line we put an extra strawberry on each of its (rich) bad cells. A cell gets the strawberries from its row and its column independently. Notice now that a cell with a strawberry on it contains a number different from $M$. If this cell gets a strawberry by the extra rule, then it contains a number greater than $M$. Moreover, it is either in a small row and in a big column, or vice versa. Suppose that it is in a small row, then it is not bad for its column. So it has not more than two strawberries in this case. On the other hand, if the extra rule is not applied to some cell, then it also has not more than two strawberries. So, the total number $N$ of strawberries is at most $2 g$. We shall now estimate $N$ in a different way. For each of the $2 \cdot 35 m$ small lines, we have introduced at least 34 strawberries if it is rich and at least 35 strawberries if it is poor, so at least 34 strawberries in any case. Similarly, for each of the $2 \cdot 17(m-1)$ big lines, we put at least $\min (17,35)=17$ strawberries. Summing over all lines we obtain $$ 2 g \geq N \geq 2(35 m \cdot 34+17(m-1) \cdot 17)=2(1479 m-289)=2 \cdot 57392 $$ as desired. Comment. The same reasoning applies also if we replace 52 by $R$ and 2011 by $R m-H$, where $m, R$, and $H$ are integers with $m, R \geq 1$ and $0 \leq H \leq \frac{1}{3} R$. More detailed information is provided after the next solution.
|
{
"resource_path": "IMO/segmented/en-IMO2011SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
3ab902c8-e456-58f8-a185-6defe4e560e3
| 24,126
|
Let $n \geq 1$ be an integer. What is the maximum number of disjoint pairs of elements of the set $\{1,2, \ldots, n\}$ such that the sums of the different pairs are different integers not exceeding $n$ ?
|
Consider $x$ such pairs in $\{1,2, \ldots, n\}$. The sum $S$ of the $2 x$ numbers in them is at least $1+2+\cdots+2 x$ since the pairs are disjoint. On the other hand $S \leq n+(n-1)+\cdots+(n-x+1)$ because the sums of the pairs are different and do not exceed $n$. This gives the inequality $$ \frac{2 x(2 x+1)}{2} \leq n x-\frac{x(x-1)}{2}, $$ which leads to $x \leq \frac{2 n-1}{5}$. Hence there are at most $\left\lfloor\frac{2 n-1}{5}\right\rfloor$ pairs with the given properties. We show a construction with exactly $\left\lfloor\frac{2 n-1}{5}\right\rfloor$ pairs. First consider the case $n=5 k+3$ with $k \geq 0$, where $\left\lfloor\frac{2 n-1}{5}\right\rfloor=2 k+1$. The pairs are displayed in the following table. | Pairs | $3 k+1$ | $3 k$ | $\cdots$ | $2 k+2$ | $4 k+2$ | $4 k+1$ | $\cdots$ | $3 k+3$ | $3 k+2$ | | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | | | 2 | 4 | $\cdots$ | $2 k$ | 1 | 3 | $\cdots$ | $2 k-1$ | $2 k+1$ | | Sums | $3 k+3$ | $3 k+4$ | $\cdots$ | $4 k+2$ | $4 k+3$ | $4 k+4$ | $\cdots$ | $5 k+2$ | $5 k+3$ | The $2 k+1$ pairs involve all numbers from 1 to $4 k+2$; their sums are all numbers from $3 k+3$ to $5 k+3$. The same construction works for $n=5 k+4$ and $n=5 k+5$ with $k \geq 0$. In these cases the required number $\left\lfloor\frac{2 n-1}{5}\right\rfloor$ of pairs equals $2 k+1$ again, and the numbers in the table do not exceed $5 k+3$. In the case $n=5 k+2$ with $k \geq 0$ one needs only $2 k$ pairs. They can be obtained by ignoring the last column of the table (thus removing $5 k+3$ ). Finally, $2 k$ pairs are also needed for the case $n=5 k+1$ with $k \geq 0$. Now it suffices to ignore the last column of the table and then subtract 1 from each number in the first row. Comment. The construction above is not unique. For instance, the following table shows another set of $2 k+1$ pairs for the cases $n=5 k+3, n=5 k+4$, and $n=5 k+5$. | Pairs | 1 | 2 | $\cdots$ | $k$ | $k+1$ | $k+2$ | $\cdots$ | $2 k+1$ | | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | | | $4 k+1$ | $4 k-1$ | $\cdots$ | $2 k+3$ | $4 k+2$ | $4 k$ | $\cdots$ | $2 k+2$ | | Sums | $4 k+2$ | $4 k+1$ | $\cdots$ | $3 k+3$ | $5 k+3$ | $5 k+2$ | $\cdots$ | $4 k+3$ | The table for the case $n=5 k+2$ would be the same, with the pair $(k+1,4 k+2)$ removed. For the case $n=5 k+1$ remove the last column and subtract 2 from each number in the second row.
|
\left\lfloor\frac{2 n-1}{5}\right\rfloor
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Let $n \geq 1$ be an integer. What is the maximum number of disjoint pairs of elements of the set $\{1,2, \ldots, n\}$ such that the sums of the different pairs are different integers not exceeding $n$ ?
|
Consider $x$ such pairs in $\{1,2, \ldots, n\}$. The sum $S$ of the $2 x$ numbers in them is at least $1+2+\cdots+2 x$ since the pairs are disjoint. On the other hand $S \leq n+(n-1)+\cdots+(n-x+1)$ because the sums of the pairs are different and do not exceed $n$. This gives the inequality $$ \frac{2 x(2 x+1)}{2} \leq n x-\frac{x(x-1)}{2}, $$ which leads to $x \leq \frac{2 n-1}{5}$. Hence there are at most $\left\lfloor\frac{2 n-1}{5}\right\rfloor$ pairs with the given properties. We show a construction with exactly $\left\lfloor\frac{2 n-1}{5}\right\rfloor$ pairs. First consider the case $n=5 k+3$ with $k \geq 0$, where $\left\lfloor\frac{2 n-1}{5}\right\rfloor=2 k+1$. The pairs are displayed in the following table. | Pairs | $3 k+1$ | $3 k$ | $\cdots$ | $2 k+2$ | $4 k+2$ | $4 k+1$ | $\cdots$ | $3 k+3$ | $3 k+2$ | | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | | | 2 | 4 | $\cdots$ | $2 k$ | 1 | 3 | $\cdots$ | $2 k-1$ | $2 k+1$ | | Sums | $3 k+3$ | $3 k+4$ | $\cdots$ | $4 k+2$ | $4 k+3$ | $4 k+4$ | $\cdots$ | $5 k+2$ | $5 k+3$ | The $2 k+1$ pairs involve all numbers from 1 to $4 k+2$; their sums are all numbers from $3 k+3$ to $5 k+3$. The same construction works for $n=5 k+4$ and $n=5 k+5$ with $k \geq 0$. In these cases the required number $\left\lfloor\frac{2 n-1}{5}\right\rfloor$ of pairs equals $2 k+1$ again, and the numbers in the table do not exceed $5 k+3$. In the case $n=5 k+2$ with $k \geq 0$ one needs only $2 k$ pairs. They can be obtained by ignoring the last column of the table (thus removing $5 k+3$ ). Finally, $2 k$ pairs are also needed for the case $n=5 k+1$ with $k \geq 0$. Now it suffices to ignore the last column of the table and then subtract 1 from each number in the first row. Comment. The construction above is not unique. For instance, the following table shows another set of $2 k+1$ pairs for the cases $n=5 k+3, n=5 k+4$, and $n=5 k+5$. | Pairs | 1 | 2 | $\cdots$ | $k$ | $k+1$ | $k+2$ | $\cdots$ | $2 k+1$ | | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | | | $4 k+1$ | $4 k-1$ | $\cdots$ | $2 k+3$ | $4 k+2$ | $4 k$ | $\cdots$ | $2 k+2$ | | Sums | $4 k+2$ | $4 k+1$ | $\cdots$ | $3 k+3$ | $5 k+3$ | $5 k+2$ | $\cdots$ | $4 k+3$ | The table for the case $n=5 k+2$ would be the same, with the pair $(k+1,4 k+2)$ removed. For the case $n=5 k+1$ remove the last column and subtract 2 from each number in the second row.
|
{
"resource_path": "IMO/segmented/en-IMO2012SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
a86a2168-227a-5d95-a2a9-265664ee43a3
| 24,167
|
In a $999 \times 999$ square table some cells are white and the remaining ones are red. Let $T$ be the number of triples $\left(C_{1}, C_{2}, C_{3}\right)$ of cells, the first two in the same row and the last two in the same column, with $C_{1}$ and $C_{3}$ white and $C_{2}$ red. Find the maximum value $T$ can attain.
|
We prove that in an $n \times n$ square table there are at most $\frac{4 n^{4}}{27}$ such triples. Let row $i$ and column $j$ contain $a_{i}$ and $b_{j}$ white cells respectively, and let $R$ be the set of red cells. For every red cell $(i, j)$ there are $a_{i} b_{j}$ admissible triples $\left(C_{1}, C_{2}, C_{3}\right)$ with $C_{2}=(i, j)$, therefore $$ T=\sum_{(i, j) \in R} a_{i} b_{j} $$ We use the inequality $2 a b \leq a^{2}+b^{2}$ to obtain $$ T \leq \frac{1}{2} \sum_{(i, j) \in R}\left(a_{i}^{2}+b_{j}^{2}\right)=\frac{1}{2} \sum_{i=1}^{n}\left(n-a_{i}\right) a_{i}^{2}+\frac{1}{2} \sum_{j=1}^{n}\left(n-b_{j}\right) b_{j}^{2} $$ This is because there are $n-a_{i}$ red cells in row $i$ and $n-b_{j}$ red cells in column $j$. Now we maximize the right-hand side. By the AM-GM inequality we have $$ (n-x) x^{2}=\frac{1}{2}(2 n-2 x) \cdot x \cdot x \leq \frac{1}{2}\left(\frac{2 n}{3}\right)^{3}=\frac{4 n^{3}}{27} $$ with equality if and only if $x=\frac{2 n}{3}$. By putting everything together, we get $$ T \leq \frac{n}{2} \frac{4 n^{3}}{27}+\frac{n}{2} \frac{4 n^{3}}{27}=\frac{4 n^{4}}{27} $$ If $n=999$ then any coloring of the square table with $x=\frac{2 n}{3}=666$ white cells in each row and column attains the maximum as all inequalities in the previous argument become equalities. For example color a cell $(i, j)$ white if $i-j \equiv 1,2, \ldots, 666(\bmod 999)$, and red otherwise. Therefore the maximum value $T$ can attain is $T=\frac{4 \cdot 999^{4}}{27}$. Comment. One can obtain a better preliminary estimate with the CAUCHY-SCHWARZ inequality: $$ T=\sum_{(i, j) \in R} a_{i} b_{j} \leq\left(\sum_{(i, j) \in R} a_{i}^{2}\right)^{\frac{1}{2}} \cdot\left(\sum_{(i, j) \in R} b_{j}^{2}\right)^{\frac{1}{2}}=\left(\sum_{i=1}^{n}\left(n-a_{i}\right) a_{i}^{2}\right)^{\frac{1}{2}} \cdot\left(\sum_{j=1}^{n}\left(n-b_{j}\right) b_{j}^{2}\right)^{\frac{1}{2}} $$ It can be used to reach the same conclusion.
|
\frac{4 \cdot 999^{4}}{27}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
In a $999 \times 999$ square table some cells are white and the remaining ones are red. Let $T$ be the number of triples $\left(C_{1}, C_{2}, C_{3}\right)$ of cells, the first two in the same row and the last two in the same column, with $C_{1}$ and $C_{3}$ white and $C_{2}$ red. Find the maximum value $T$ can attain.
|
We prove that in an $n \times n$ square table there are at most $\frac{4 n^{4}}{27}$ such triples. Let row $i$ and column $j$ contain $a_{i}$ and $b_{j}$ white cells respectively, and let $R$ be the set of red cells. For every red cell $(i, j)$ there are $a_{i} b_{j}$ admissible triples $\left(C_{1}, C_{2}, C_{3}\right)$ with $C_{2}=(i, j)$, therefore $$ T=\sum_{(i, j) \in R} a_{i} b_{j} $$ We use the inequality $2 a b \leq a^{2}+b^{2}$ to obtain $$ T \leq \frac{1}{2} \sum_{(i, j) \in R}\left(a_{i}^{2}+b_{j}^{2}\right)=\frac{1}{2} \sum_{i=1}^{n}\left(n-a_{i}\right) a_{i}^{2}+\frac{1}{2} \sum_{j=1}^{n}\left(n-b_{j}\right) b_{j}^{2} $$ This is because there are $n-a_{i}$ red cells in row $i$ and $n-b_{j}$ red cells in column $j$. Now we maximize the right-hand side. By the AM-GM inequality we have $$ (n-x) x^{2}=\frac{1}{2}(2 n-2 x) \cdot x \cdot x \leq \frac{1}{2}\left(\frac{2 n}{3}\right)^{3}=\frac{4 n^{3}}{27} $$ with equality if and only if $x=\frac{2 n}{3}$. By putting everything together, we get $$ T \leq \frac{n}{2} \frac{4 n^{3}}{27}+\frac{n}{2} \frac{4 n^{3}}{27}=\frac{4 n^{4}}{27} $$ If $n=999$ then any coloring of the square table with $x=\frac{2 n}{3}=666$ white cells in each row and column attains the maximum as all inequalities in the previous argument become equalities. For example color a cell $(i, j)$ white if $i-j \equiv 1,2, \ldots, 666(\bmod 999)$, and red otherwise. Therefore the maximum value $T$ can attain is $T=\frac{4 \cdot 999^{4}}{27}$. Comment. One can obtain a better preliminary estimate with the CAUCHY-SCHWARZ inequality: $$ T=\sum_{(i, j) \in R} a_{i} b_{j} \leq\left(\sum_{(i, j) \in R} a_{i}^{2}\right)^{\frac{1}{2}} \cdot\left(\sum_{(i, j) \in R} b_{j}^{2}\right)^{\frac{1}{2}}=\left(\sum_{i=1}^{n}\left(n-a_{i}\right) a_{i}^{2}\right)^{\frac{1}{2}} \cdot\left(\sum_{j=1}^{n}\left(n-b_{j}\right) b_{j}^{2}\right)^{\frac{1}{2}} $$ It can be used to reach the same conclusion.
|
{
"resource_path": "IMO/segmented/en-IMO2012SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
1adfa912-e8de-5691-9ff6-7c74afee91c0
| 24,171
|
Players $A$ and $B$ play a game with $N \geq 2012$ coins and 2012 boxes arranged around a circle. Initially $A$ distributes the coins among the boxes so that there is at least 1 coin in each box. Then the two of them make moves in the order $B, A, B, A, \ldots$ by the following rules: - On every move of his $B$ passes 1 coin from every box to an adjacent box. - On every move of hers $A$ chooses several coins that were not involved in $B$ 's previous move and are in different boxes. She passes every chosen coin to an adjacent box. Player $A$ 's goal is to ensure at least 1 coin in each box after every move of hers, regardless of how $B$ plays and how many moves are made. Find the least $N$ that enables her to succeed.
|
We argue for a general $n \geq 7$ instead of 2012 and prove that the required minimum $N$ is $2 n-2$. For $n=2012$ this gives $N_{\min }=4022$. a) If $N=2 n-2$ player $A$ can achieve her goal. Let her start the game with a regular distribution: $n-2$ boxes with 2 coins and 2 boxes with 1 coin. Call the boxes of the two kinds red and white respectively. We claim that on her first move $A$ can achieve a regular distribution again, regardless of $B$ 's first move $M$. She acts according as the following situation $S$ occurs after $M$ or not: The initial distribution contains a red box $R$ with 2 white neighbors, and $R$ receives no coins from them on move $M$. Suppose that $S$ does not occur. Exactly one of the coins $c_{1}$ and $c_{2}$ in a given red box $X$ is involved in $M$, say $c_{1}$. If $M$ passes $c_{1}$ to the right neighbor of $X$, let $A$ pass $c_{2}$ to its left neighbor, and vice versa. By doing so with all red boxes $A$ performs a legal move $M^{\prime}$. Thus $M$ and $M^{\prime}$ combined move the 2 coins of every red box in opposite directions. Hence after $M$ and $M^{\prime}$ are complete each neighbor of a red box $X$ contains exactly 1 coin that was initially in $X$. So each box with a red neighbor is non-empty after $M^{\prime}$. If initially there is a box $X$ with 2 white neighbors ( $X$ is red and unique) then $X$ receives a coin from at least one of them on move $M$ since $S$ does not occur. Such a coin is not involved in $M^{\prime}$, so $X$ is also non-empty after $M^{\prime}$. Furthermore each box $Y$ has given away its initial content after $M$ and $M^{\prime}$. A red neighbor of $Y$ adds 1 coin to it; a white neighbor adds at most 1 coin because it is not involved in $M^{\prime}$. Hence each box contains 1 or 2 coins after $M^{\prime}$. Because $N=2 n-2$, such a distribution is regular. Now let $S$ occur after move $M$. Then $A$ leaves untouched the exceptional red box $R$. With all remaining red boxes she proceeds like in the previous case, thus making a legal move $M^{\prime \prime}$. Box $R$ receives no coins from its neighbors on either move, so there is 1 coin in it after $M^{\prime \prime}$. Like above $M$ and $M^{\prime \prime}$ combined pass exactly 1 coin from every red box different from $R$ to each of its neighbors. Every box except $R$ has a red neighbor different from $R$, hence all boxes are non-empty after $M^{\prime \prime}$. Next, each box $Y$ except $R$ loses its initial content after $M$ and $M^{\prime \prime}$. A red neighbor of $Y$ adds at most 1 coin to it; a white neighbor also adds at most 1 coin as it does not participate in $M^{\prime \prime}$. Thus each box has 1 or 2 coins after $M^{\prime \prime}$, and the obtained distribution is regular. Player $A$ can apply the described strategy indefinitely, so $N=2 n-2$ enables her to succeed. b) For $N \leq 2 n-3$ player $B$ can achieve an empty box after some move of $A$. Let $\alpha$ be a set of $\ell$ consecutive boxes containing a total of $N(\alpha)$ coins. We call $\alpha$ an arc if $\ell \leq n-2$ and $N(\alpha) \leq 2 \ell-3$. Note that $\ell \geq 2$ by the last condition. Moreover if both extremes of $\alpha$ are non-empty boxes then $N(\alpha) \geq 2$, so that $N(\alpha) \leq 2 \ell-3$ implies $\ell \geq 3$. Observe also that if an extreme $X$ of $\alpha$ has more than 1 coin then ignoring $X$ yields a shorter arc. It follows that every arc contains an arc whose extremes have at most 1 coin each. Given a clockwise labeling $1,2, \ldots, n$ of the boxes, suppose that boxes $1,2, \ldots, \ell$ form an arc $\alpha$, with $\ell \leq n-2$ and $N(\alpha) \leq 2 \ell-3$. Suppose also that all $n \geq 7$ boxes are non-empty. Then $B$ can move so that an arc $\alpha^{\prime}$ with $N\left(\alpha^{\prime}\right)<N(\alpha)$ will appear after any response of $A$. One may assume exactly 1 coin in boxes 1 and $\ell$ by a previous remark. Let $B$ pass 1 coin in counterclockwise direction from box 1 and box $n$, and in clockwise direction from each remaining box. This leaves $N(\alpha)-2$ coins in the boxes of $\alpha$. In addition, due to $3 \leq \ell \leq n-2$, box $\ell$ has exactly 1 coin $c$, the one received from box $\ell-1$. Let player $A$ 's next move $M$ pass $k \leq 2$ coins to boxes $1,2, \ldots, \ell$ from the remaining ones. Only boxes 1 and $\ell$ can receive such coins, at most 1 each. If $k<2$ then after move $M$ boxes $1,2, \ldots, \ell$ form an arc $\alpha^{\prime}$ with $N\left(\alpha^{\prime}\right)<N(\alpha)$. If $k=2$ then $M$ adds a coin to box $\ell$. Also $M$ does not move coin $c$ from $\ell$ because $c$ is involved in the previous move of $B$. In summary boxes $1,2, \ldots, \ell$ contain $N(\alpha)$ coins like before, so they form an arc. However there are 2 coins now in the extreme $\ell$ of the arc. Ignore $\ell$ to obtain a shorter arc $\alpha^{\prime}$ with $N\left(\alpha^{\prime}\right)<N(\alpha)$. Consider any initial distribution without empty boxes. Since $N \leq 2 n-3$, there are at least 3 boxes in it with exactly 1 coin. It follows from $n \geq 7$ that some 2 of them are the extremes of an $\operatorname{arc} \alpha$. Hence $B$ can make the move described above, which leads to an arc $\alpha^{\prime}$ with $N\left(\alpha^{\prime}\right)<N(\alpha)$ after $A^{\prime}$ 's response. If all boxes in the new distribution are non-empty he can repeat the same, and so on. Because $N(\alpha)$ cannot decrease indefinitely, an empty box will occur after some move of $A$.
|
4022
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Players $A$ and $B$ play a game with $N \geq 2012$ coins and 2012 boxes arranged around a circle. Initially $A$ distributes the coins among the boxes so that there is at least 1 coin in each box. Then the two of them make moves in the order $B, A, B, A, \ldots$ by the following rules: - On every move of his $B$ passes 1 coin from every box to an adjacent box. - On every move of hers $A$ chooses several coins that were not involved in $B$ 's previous move and are in different boxes. She passes every chosen coin to an adjacent box. Player $A$ 's goal is to ensure at least 1 coin in each box after every move of hers, regardless of how $B$ plays and how many moves are made. Find the least $N$ that enables her to succeed.
|
We argue for a general $n \geq 7$ instead of 2012 and prove that the required minimum $N$ is $2 n-2$. For $n=2012$ this gives $N_{\min }=4022$. a) If $N=2 n-2$ player $A$ can achieve her goal. Let her start the game with a regular distribution: $n-2$ boxes with 2 coins and 2 boxes with 1 coin. Call the boxes of the two kinds red and white respectively. We claim that on her first move $A$ can achieve a regular distribution again, regardless of $B$ 's first move $M$. She acts according as the following situation $S$ occurs after $M$ or not: The initial distribution contains a red box $R$ with 2 white neighbors, and $R$ receives no coins from them on move $M$. Suppose that $S$ does not occur. Exactly one of the coins $c_{1}$ and $c_{2}$ in a given red box $X$ is involved in $M$, say $c_{1}$. If $M$ passes $c_{1}$ to the right neighbor of $X$, let $A$ pass $c_{2}$ to its left neighbor, and vice versa. By doing so with all red boxes $A$ performs a legal move $M^{\prime}$. Thus $M$ and $M^{\prime}$ combined move the 2 coins of every red box in opposite directions. Hence after $M$ and $M^{\prime}$ are complete each neighbor of a red box $X$ contains exactly 1 coin that was initially in $X$. So each box with a red neighbor is non-empty after $M^{\prime}$. If initially there is a box $X$ with 2 white neighbors ( $X$ is red and unique) then $X$ receives a coin from at least one of them on move $M$ since $S$ does not occur. Such a coin is not involved in $M^{\prime}$, so $X$ is also non-empty after $M^{\prime}$. Furthermore each box $Y$ has given away its initial content after $M$ and $M^{\prime}$. A red neighbor of $Y$ adds 1 coin to it; a white neighbor adds at most 1 coin because it is not involved in $M^{\prime}$. Hence each box contains 1 or 2 coins after $M^{\prime}$. Because $N=2 n-2$, such a distribution is regular. Now let $S$ occur after move $M$. Then $A$ leaves untouched the exceptional red box $R$. With all remaining red boxes she proceeds like in the previous case, thus making a legal move $M^{\prime \prime}$. Box $R$ receives no coins from its neighbors on either move, so there is 1 coin in it after $M^{\prime \prime}$. Like above $M$ and $M^{\prime \prime}$ combined pass exactly 1 coin from every red box different from $R$ to each of its neighbors. Every box except $R$ has a red neighbor different from $R$, hence all boxes are non-empty after $M^{\prime \prime}$. Next, each box $Y$ except $R$ loses its initial content after $M$ and $M^{\prime \prime}$. A red neighbor of $Y$ adds at most 1 coin to it; a white neighbor also adds at most 1 coin as it does not participate in $M^{\prime \prime}$. Thus each box has 1 or 2 coins after $M^{\prime \prime}$, and the obtained distribution is regular. Player $A$ can apply the described strategy indefinitely, so $N=2 n-2$ enables her to succeed. b) For $N \leq 2 n-3$ player $B$ can achieve an empty box after some move of $A$. Let $\alpha$ be a set of $\ell$ consecutive boxes containing a total of $N(\alpha)$ coins. We call $\alpha$ an arc if $\ell \leq n-2$ and $N(\alpha) \leq 2 \ell-3$. Note that $\ell \geq 2$ by the last condition. Moreover if both extremes of $\alpha$ are non-empty boxes then $N(\alpha) \geq 2$, so that $N(\alpha) \leq 2 \ell-3$ implies $\ell \geq 3$. Observe also that if an extreme $X$ of $\alpha$ has more than 1 coin then ignoring $X$ yields a shorter arc. It follows that every arc contains an arc whose extremes have at most 1 coin each. Given a clockwise labeling $1,2, \ldots, n$ of the boxes, suppose that boxes $1,2, \ldots, \ell$ form an arc $\alpha$, with $\ell \leq n-2$ and $N(\alpha) \leq 2 \ell-3$. Suppose also that all $n \geq 7$ boxes are non-empty. Then $B$ can move so that an arc $\alpha^{\prime}$ with $N\left(\alpha^{\prime}\right)<N(\alpha)$ will appear after any response of $A$. One may assume exactly 1 coin in boxes 1 and $\ell$ by a previous remark. Let $B$ pass 1 coin in counterclockwise direction from box 1 and box $n$, and in clockwise direction from each remaining box. This leaves $N(\alpha)-2$ coins in the boxes of $\alpha$. In addition, due to $3 \leq \ell \leq n-2$, box $\ell$ has exactly 1 coin $c$, the one received from box $\ell-1$. Let player $A$ 's next move $M$ pass $k \leq 2$ coins to boxes $1,2, \ldots, \ell$ from the remaining ones. Only boxes 1 and $\ell$ can receive such coins, at most 1 each. If $k<2$ then after move $M$ boxes $1,2, \ldots, \ell$ form an arc $\alpha^{\prime}$ with $N\left(\alpha^{\prime}\right)<N(\alpha)$. If $k=2$ then $M$ adds a coin to box $\ell$. Also $M$ does not move coin $c$ from $\ell$ because $c$ is involved in the previous move of $B$. In summary boxes $1,2, \ldots, \ell$ contain $N(\alpha)$ coins like before, so they form an arc. However there are 2 coins now in the extreme $\ell$ of the arc. Ignore $\ell$ to obtain a shorter arc $\alpha^{\prime}$ with $N\left(\alpha^{\prime}\right)<N(\alpha)$. Consider any initial distribution without empty boxes. Since $N \leq 2 n-3$, there are at least 3 boxes in it with exactly 1 coin. It follows from $n \geq 7$ that some 2 of them are the extremes of an $\operatorname{arc} \alpha$. Hence $B$ can make the move described above, which leads to an arc $\alpha^{\prime}$ with $N\left(\alpha^{\prime}\right)<N(\alpha)$ after $A^{\prime}$ 's response. If all boxes in the new distribution are non-empty he can repeat the same, and so on. Because $N(\alpha)$ cannot decrease indefinitely, an empty box will occur after some move of $A$.
|
{
"resource_path": "IMO/segmented/en-IMO2012SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
b9b4f603-6d62-50dc-883d-066ef80f8788
| 24,173
|
Let $n$ be a positive integer. Find the smallest integer $k$ with the following property: Given any real numbers $a_{1}, \ldots, a_{d}$ such that $a_{1}+a_{2}+\cdots+a_{d}=n$ and $0 \leqslant a_{i} \leqslant 1$ for $i=1,2, \ldots, d$, it is possible to partition these numbers into $k$ groups (some of which may be empty) such that the sum of the numbers in each group is at most 1 . (Poland)
|
If $d=2 n-1$ and $a_{1}=\cdots=a_{2 n-1}=n /(2 n-1)$, then each group in such a partition can contain at most one number, since $2 n /(2 n-1)>1$. Therefore $k \geqslant 2 n-1$. It remains to show that a suitable partition into $2 n-1$ groups always exists. We proceed by induction on $d$. For $d \leqslant 2 n-1$ the result is trivial. If $d \geqslant 2 n$, then since $$ \left(a_{1}+a_{2}\right)+\ldots+\left(a_{2 n-1}+a_{2 n}\right) \leqslant n $$ we may find two numbers $a_{i}, a_{i+1}$ such that $a_{i}+a_{i+1} \leqslant 1$. We "merge" these two numbers into one new number $a_{i}+a_{i+1}$. By the induction hypothesis, a suitable partition exists for the $d-1$ numbers $a_{1}, \ldots, a_{i-1}, a_{i}+a_{i+1}, a_{i+2}, \ldots, a_{d}$. This induces a suitable partition for $a_{1}, \ldots, a_{d}$.
|
2n-1
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Let $n$ be a positive integer. Find the smallest integer $k$ with the following property: Given any real numbers $a_{1}, \ldots, a_{d}$ such that $a_{1}+a_{2}+\cdots+a_{d}=n$ and $0 \leqslant a_{i} \leqslant 1$ for $i=1,2, \ldots, d$, it is possible to partition these numbers into $k$ groups (some of which may be empty) such that the sum of the numbers in each group is at most 1 . (Poland)
|
If $d=2 n-1$ and $a_{1}=\cdots=a_{2 n-1}=n /(2 n-1)$, then each group in such a partition can contain at most one number, since $2 n /(2 n-1)>1$. Therefore $k \geqslant 2 n-1$. It remains to show that a suitable partition into $2 n-1$ groups always exists. We proceed by induction on $d$. For $d \leqslant 2 n-1$ the result is trivial. If $d \geqslant 2 n$, then since $$ \left(a_{1}+a_{2}\right)+\ldots+\left(a_{2 n-1}+a_{2 n}\right) \leqslant n $$ we may find two numbers $a_{i}, a_{i+1}$ such that $a_{i}+a_{i+1} \leqslant 1$. We "merge" these two numbers into one new number $a_{i}+a_{i+1}$. By the induction hypothesis, a suitable partition exists for the $d-1$ numbers $a_{1}, \ldots, a_{i-1}, a_{i}+a_{i+1}, a_{i+2}, \ldots, a_{d}$. This induces a suitable partition for $a_{1}, \ldots, a_{d}$.
|
{
"resource_path": "IMO/segmented/en-IMO2013SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
18b2c3fa-2dd0-5464-b295-f782af11a287
| 24,264
|
In the plane, 2013 red points and 2014 blue points are marked so that no three of the marked points are collinear. One needs to draw $k$ lines not passing through the marked points and dividing the plane into several regions. The goal is to do it in such a way that no region contains points of both colors. Find the minimal value of $k$ such that the goal is attainable for every possible configuration of 4027 points. (Australia)
|
Firstly, let us present an example showing that $k \geqslant 2013$. Mark 2013 red and 2013 blue points on some circle alternately, and mark one more blue point somewhere in the plane. The circle is thus split into 4026 arcs, each arc having endpoints of different colors. Thus, if the goal is reached, then each arc should intersect some of the drawn lines. Since any line contains at most two points of the circle, one needs at least 4026/2 $=2013$ lines. It remains to prove that one can reach the goal using 2013 lines. First of all, let us mention that for every two points $A$ and $B$ having the same color, one can draw two lines separating these points from all other ones. Namely, it suffices to take two lines parallel to $A B$ and lying on different sides of $A B$ sufficiently close to it: the only two points between these lines will be $A$ and $B$. Now, let $P$ be the convex hull of all marked points. Two cases are possible. Case 1. Assume that $P$ has a red vertex $A$. Then one may draw a line separating $A$ from all the other points, pair up the other 2012 red points into 1006 pairs, and separate each pair from the other points by two lines. Thus, 2013 lines will be used. Case 2. Assume now that all the vertices of $P$ are blue. Consider any two consecutive vertices of $P$, say $A$ and $B$. One may separate these two points from the others by a line parallel to $A B$. Then, as in the previous case, one pairs up all the other 2012 blue points into 1006 pairs, and separates each pair from the other points by two lines. Again, 2013 lines will be used. Comment 1. Instead of considering the convex hull, one may simply take a line containing two marked points $A$ and $B$ such that all the other marked points are on one side of this line. If one of $A$ and $B$ is red, then one may act as in Case 1; otherwise both are blue, and one may act as in Case 2.
|
2013
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
In the plane, 2013 red points and 2014 blue points are marked so that no three of the marked points are collinear. One needs to draw $k$ lines not passing through the marked points and dividing the plane into several regions. The goal is to do it in such a way that no region contains points of both colors. Find the minimal value of $k$ such that the goal is attainable for every possible configuration of 4027 points. (Australia)
|
Firstly, let us present an example showing that $k \geqslant 2013$. Mark 2013 red and 2013 blue points on some circle alternately, and mark one more blue point somewhere in the plane. The circle is thus split into 4026 arcs, each arc having endpoints of different colors. Thus, if the goal is reached, then each arc should intersect some of the drawn lines. Since any line contains at most two points of the circle, one needs at least 4026/2 $=2013$ lines. It remains to prove that one can reach the goal using 2013 lines. First of all, let us mention that for every two points $A$ and $B$ having the same color, one can draw two lines separating these points from all other ones. Namely, it suffices to take two lines parallel to $A B$ and lying on different sides of $A B$ sufficiently close to it: the only two points between these lines will be $A$ and $B$. Now, let $P$ be the convex hull of all marked points. Two cases are possible. Case 1. Assume that $P$ has a red vertex $A$. Then one may draw a line separating $A$ from all the other points, pair up the other 2012 red points into 1006 pairs, and separate each pair from the other points by two lines. Thus, 2013 lines will be used. Case 2. Assume now that all the vertices of $P$ are blue. Consider any two consecutive vertices of $P$, say $A$ and $B$. One may separate these two points from the others by a line parallel to $A B$. Then, as in the previous case, one pairs up all the other 2012 blue points into 1006 pairs, and separates each pair from the other points by two lines. Again, 2013 lines will be used. Comment 1. Instead of considering the convex hull, one may simply take a line containing two marked points $A$ and $B$ such that all the other marked points are on one side of this line. If one of $A$ and $B$ is red, then one may act as in Case 1; otherwise both are blue, and one may act as in Case 2.
|
{
"resource_path": "IMO/segmented/en-IMO2013SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
55bc9343-8861-5def-80d7-80895b6a4c3c
| 24,268
|
In the plane, 2013 red points and 2014 blue points are marked so that no three of the marked points are collinear. One needs to draw $k$ lines not passing through the marked points and dividing the plane into several regions. The goal is to do it in such a way that no region contains points of both colors. Find the minimal value of $k$ such that the goal is attainable for every possible configuration of 4027 points. (Australia) Answer. $k=2013$.
|
Firstly, let us present an example showing that $k \geqslant 2013$. Mark 2013 red and 2013 blue points on some circle alternately, and mark one more blue point somewhere in the plane. The circle is thus split into 4026 arcs, each arc having endpoints of different colors. Thus, if the goal is reached, then each arc should intersect some of the drawn lines. Since any line contains at most two points of the circle, one needs at least 4026/2 $=2013$ lines. It remains to prove that one can reach the goal using 2013 lines. First of all, let us mention that for every two points $A$ and $B$ having the same color, one can draw two lines separating these points from all other ones. Namely, it suffices to take two lines parallel to $A B$ and lying on different sides of $A B$ sufficiently close to it: the only two points between these lines will be $A$ and $B$. Now, let $P$ be the convex hull of all marked points. Two cases are possible. Case 1. Assume that $P$ has a red vertex $A$. Then one may draw a line separating $A$ from all the other points, pair up the other 2012 red points into 1006 pairs, and separate each pair from the other points by two lines. Thus, 2013 lines will be used. Case 2. Assume now that all the vertices of $P$ are blue. Consider any two consecutive vertices of $P$, say $A$ and $B$. One may separate these two points from the others by a line parallel to $A B$. Then, as in the previous case, one pairs up all the other 2012 blue points into 1006 pairs, and separates each pair from the other points by two lines. Again, 2013 lines will be used. Comment 1. Instead of considering the convex hull, one may simply take a line containing two marked points $A$ and $B$ such that all the other marked points are on one side of this line. If one of $A$ and $B$ is red, then one may act as in Case 1; otherwise both are blue, and one may act as in Case 2.
|
2013
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
In the plane, 2013 red points and 2014 blue points are marked so that no three of the marked points are collinear. One needs to draw $k$ lines not passing through the marked points and dividing the plane into several regions. The goal is to do it in such a way that no region contains points of both colors. Find the minimal value of $k$ such that the goal is attainable for every possible configuration of 4027 points. (Australia) Answer. $k=2013$.
|
Firstly, let us present an example showing that $k \geqslant 2013$. Mark 2013 red and 2013 blue points on some circle alternately, and mark one more blue point somewhere in the plane. The circle is thus split into 4026 arcs, each arc having endpoints of different colors. Thus, if the goal is reached, then each arc should intersect some of the drawn lines. Since any line contains at most two points of the circle, one needs at least 4026/2 $=2013$ lines. It remains to prove that one can reach the goal using 2013 lines. First of all, let us mention that for every two points $A$ and $B$ having the same color, one can draw two lines separating these points from all other ones. Namely, it suffices to take two lines parallel to $A B$ and lying on different sides of $A B$ sufficiently close to it: the only two points between these lines will be $A$ and $B$. Now, let $P$ be the convex hull of all marked points. Two cases are possible. Case 1. Assume that $P$ has a red vertex $A$. Then one may draw a line separating $A$ from all the other points, pair up the other 2012 red points into 1006 pairs, and separate each pair from the other points by two lines. Thus, 2013 lines will be used. Case 2. Assume now that all the vertices of $P$ are blue. Consider any two consecutive vertices of $P$, say $A$ and $B$. One may separate these two points from the others by a line parallel to $A B$. Then, as in the previous case, one pairs up all the other 2012 blue points into 1006 pairs, and separates each pair from the other points by two lines. Again, 2013 lines will be used. Comment 1. Instead of considering the convex hull, one may simply take a line containing two marked points $A$ and $B$ such that all the other marked points are on one side of this line. If one of $A$ and $B$ is red, then one may act as in Case 1; otherwise both are blue, and one may act as in Case 2.
|
{
"resource_path": "IMO/segmented/en-IMO2013SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
b100bf85-cad8-503f-976a-e20988486adb
| 24,356
|
For a sequence $x_{1}, x_{2}, \ldots, x_{n}$ of real numbers, we define its price as $$ \max _{1 \leqslant i \leqslant n}\left|x_{1}+\cdots+x_{i}\right| $$ Given $n$ real numbers, Dave and George want to arrange them into a sequence with a low price. Diligent Dave checks all possible ways and finds the minimum possible price $D$. Greedy George, on the other hand, chooses $x_{1}$ such that $\left|x_{1}\right|$ is as small as possible; among the remaining numbers, he chooses $x_{2}$ such that $\left|x_{1}+x_{2}\right|$ is as small as possible, and so on. Thus, in the $i^{\text {th }}$ step he chooses $x_{i}$ among the remaining numbers so as to minimise the value of $\left|x_{1}+x_{2}+\cdots+x_{i}\right|$. In each step, if several numbers provide the same value, George chooses one at random. Finally he gets a sequence with price $G$. Find the least possible constant $c$ such that for every positive integer $n$, for every collection of $n$ real numbers, and for every possible sequence that George might obtain, the resulting values satisfy the inequality $G \leqslant c D$. (Georgia)
|
If the initial numbers are $1,-1,2$, and -2 , then Dave may arrange them as $1,-2,2,-1$, while George may get the sequence $1,-1,2,-2$, resulting in $D=1$ and $G=2$. So we obtain $c \geqslant 2$. Therefore, it remains to prove that $G \leqslant 2 D$. Let $x_{1}, x_{2}, \ldots, x_{n}$ be the numbers Dave and George have at their disposal. Assume that Dave and George arrange them into sequences $d_{1}, d_{2}, \ldots, d_{n}$ and $g_{1}, g_{2}, \ldots, g_{n}$, respectively. Put $$ M=\max _{1 \leqslant i \leqslant n}\left|x_{i}\right|, \quad S=\left|x_{1}+\cdots+x_{n}\right|, \quad \text { and } \quad N=\max \{M, S\} $$ We claim that $$ \begin{aligned} & D \geqslant S, \\ & D \geqslant \frac{M}{2}, \quad \text { and } \\ & G \leqslant N=\max \{M, S\} \end{aligned} $$ These inequalities yield the desired estimate, as $G \leqslant \max \{M, S\} \leqslant \max \{M, 2 S\} \leqslant 2 D$. The inequality (1) is a direct consequence of the definition of the price. To prove (2), consider an index $i$ with $\left|d_{i}\right|=M$. Then we have $$ M=\left|d_{i}\right|=\left|\left(d_{1}+\cdots+d_{i}\right)-\left(d_{1}+\cdots+d_{i-1}\right)\right| \leqslant\left|d_{1}+\cdots+d_{i}\right|+\left|d_{1}+\cdots+d_{i-1}\right| \leqslant 2 D $$ as required. It remains to establish (3). Put $h_{i}=g_{1}+g_{2}+\cdots+g_{i}$. We will prove by induction on $i$ that $\left|h_{i}\right| \leqslant N$. The base case $i=1$ holds, since $\left|h_{1}\right|=\left|g_{1}\right| \leqslant M \leqslant N$. Notice also that $\left|h_{n}\right|=S \leqslant N$. For the induction step, assume that $\left|h_{i-1}\right| \leqslant N$. We distinguish two cases. Case 1. Assume that no two of the numbers $g_{i}, g_{i+1}, \ldots, g_{n}$ have opposite signs. Without loss of generality, we may assume that they are all nonnegative. Then one has $h_{i-1} \leqslant h_{i} \leqslant \cdots \leqslant h_{n}$, thus $$ \left|h_{i}\right| \leqslant \max \left\{\left|h_{i-1}\right|,\left|h_{n}\right|\right\} \leqslant N $$ Case 2. Among the numbers $g_{i}, g_{i+1}, \ldots, g_{n}$ there are positive and negative ones. Then there exists some index $j \geqslant i$ such that $h_{i-1} g_{j} \leqslant 0$. By the definition of George's sequence we have $$ \left|h_{i}\right|=\left|h_{i-1}+g_{i}\right| \leqslant\left|h_{i-1}+g_{j}\right| \leqslant \max \left\{\left|h_{i-1}\right|,\left|g_{j}\right|\right\} \leqslant N $$ Thus, the induction step is established. Comment 1. One can establish the weaker inequalities $D \geqslant \frac{M}{2}$ and $G \leqslant D+\frac{M}{2}$ from which the result also follows. Comment 2. One may ask a more specific question to find the maximal suitable $c$ if the number $n$ is fixed. For $n=1$ or 2 , the answer is $c=1$. For $n=3$, the answer is $c=\frac{3}{2}$, and it is reached e.g., for the collection $1,2,-4$. Finally, for $n \geqslant 4$ the answer is $c=2$. In this case the arguments from the solution above apply, and the answer is reached e.g., for the same collection $1,-1,2,-2$, augmented by several zeroes.
|
2
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
For a sequence $x_{1}, x_{2}, \ldots, x_{n}$ of real numbers, we define its price as $$ \max _{1 \leqslant i \leqslant n}\left|x_{1}+\cdots+x_{i}\right| $$ Given $n$ real numbers, Dave and George want to arrange them into a sequence with a low price. Diligent Dave checks all possible ways and finds the minimum possible price $D$. Greedy George, on the other hand, chooses $x_{1}$ such that $\left|x_{1}\right|$ is as small as possible; among the remaining numbers, he chooses $x_{2}$ such that $\left|x_{1}+x_{2}\right|$ is as small as possible, and so on. Thus, in the $i^{\text {th }}$ step he chooses $x_{i}$ among the remaining numbers so as to minimise the value of $\left|x_{1}+x_{2}+\cdots+x_{i}\right|$. In each step, if several numbers provide the same value, George chooses one at random. Finally he gets a sequence with price $G$. Find the least possible constant $c$ such that for every positive integer $n$, for every collection of $n$ real numbers, and for every possible sequence that George might obtain, the resulting values satisfy the inequality $G \leqslant c D$. (Georgia)
|
If the initial numbers are $1,-1,2$, and -2 , then Dave may arrange them as $1,-2,2,-1$, while George may get the sequence $1,-1,2,-2$, resulting in $D=1$ and $G=2$. So we obtain $c \geqslant 2$. Therefore, it remains to prove that $G \leqslant 2 D$. Let $x_{1}, x_{2}, \ldots, x_{n}$ be the numbers Dave and George have at their disposal. Assume that Dave and George arrange them into sequences $d_{1}, d_{2}, \ldots, d_{n}$ and $g_{1}, g_{2}, \ldots, g_{n}$, respectively. Put $$ M=\max _{1 \leqslant i \leqslant n}\left|x_{i}\right|, \quad S=\left|x_{1}+\cdots+x_{n}\right|, \quad \text { and } \quad N=\max \{M, S\} $$ We claim that $$ \begin{aligned} & D \geqslant S, \\ & D \geqslant \frac{M}{2}, \quad \text { and } \\ & G \leqslant N=\max \{M, S\} \end{aligned} $$ These inequalities yield the desired estimate, as $G \leqslant \max \{M, S\} \leqslant \max \{M, 2 S\} \leqslant 2 D$. The inequality (1) is a direct consequence of the definition of the price. To prove (2), consider an index $i$ with $\left|d_{i}\right|=M$. Then we have $$ M=\left|d_{i}\right|=\left|\left(d_{1}+\cdots+d_{i}\right)-\left(d_{1}+\cdots+d_{i-1}\right)\right| \leqslant\left|d_{1}+\cdots+d_{i}\right|+\left|d_{1}+\cdots+d_{i-1}\right| \leqslant 2 D $$ as required. It remains to establish (3). Put $h_{i}=g_{1}+g_{2}+\cdots+g_{i}$. We will prove by induction on $i$ that $\left|h_{i}\right| \leqslant N$. The base case $i=1$ holds, since $\left|h_{1}\right|=\left|g_{1}\right| \leqslant M \leqslant N$. Notice also that $\left|h_{n}\right|=S \leqslant N$. For the induction step, assume that $\left|h_{i-1}\right| \leqslant N$. We distinguish two cases. Case 1. Assume that no two of the numbers $g_{i}, g_{i+1}, \ldots, g_{n}$ have opposite signs. Without loss of generality, we may assume that they are all nonnegative. Then one has $h_{i-1} \leqslant h_{i} \leqslant \cdots \leqslant h_{n}$, thus $$ \left|h_{i}\right| \leqslant \max \left\{\left|h_{i-1}\right|,\left|h_{n}\right|\right\} \leqslant N $$ Case 2. Among the numbers $g_{i}, g_{i+1}, \ldots, g_{n}$ there are positive and negative ones. Then there exists some index $j \geqslant i$ such that $h_{i-1} g_{j} \leqslant 0$. By the definition of George's sequence we have $$ \left|h_{i}\right|=\left|h_{i-1}+g_{i}\right| \leqslant\left|h_{i-1}+g_{j}\right| \leqslant \max \left\{\left|h_{i-1}\right|,\left|g_{j}\right|\right\} \leqslant N $$ Thus, the induction step is established. Comment 1. One can establish the weaker inequalities $D \geqslant \frac{M}{2}$ and $G \leqslant D+\frac{M}{2}$ from which the result also follows. Comment 2. One may ask a more specific question to find the maximal suitable $c$ if the number $n$ is fixed. For $n=1$ or 2 , the answer is $c=1$. For $n=3$, the answer is $c=\frac{3}{2}$, and it is reached e.g., for the collection $1,2,-4$. Finally, for $n \geqslant 4$ the answer is $c=2$. In this case the arguments from the solution above apply, and the answer is reached e.g., for the same collection $1,-1,2,-2$, augmented by several zeroes.
|
{
"resource_path": "IMO/segmented/en-IMO2014SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
37c8fe66-355e-5ec0-9a49-0195f287d322
| 24,392
|
We are given an infinite deck of cards, each with a real number on it. For every real number $x$, there is exactly one card in the deck that has $x$ written on it. Now two players draw disjoint sets $A$ and $B$ of 100 cards each from this deck. We would like to define a rule that declares one of them a winner. This rule should satisfy the following conditions: 1. The winner only depends on the relative order of the 200 cards: if the cards are laid down in increasing order face down and we are told which card belongs to which player, but not what numbers are written on them, we can still decide the winner. 2. If we write the elements of both sets in increasing order as $A=\left\{a_{1}, a_{2}, \ldots, a_{100}\right\}$ and $B=\left\{b_{1}, b_{2}, \ldots, b_{100}\right\}$, and $a_{i}>b_{i}$ for all $i$, then $A$ beats $B$. 3. If three players draw three disjoint sets $A, B, C$ from the deck, $A$ beats $B$ and $B$ beats $C$, then $A$ also beats $C$. How many ways are there to define such a rule? Here, we consider two rules as different if there exist two sets $A$ and $B$ such that $A$ beats $B$ according to one rule, but $B$ beats $A$ according to the other. (Russia)
|
We prove a more general statement for sets of cardinality $n$ (the problem being the special case $n=100$, then the answer is $n$ ). In the following, we write $A>B$ or $B<A$ for " $A$ beats $B$ ". Part I. Let us first define $n$ different rules that satisfy the conditions. To this end, fix an index $k \in\{1,2, \ldots, n\}$. We write both $A$ and $B$ in increasing order as $A=\left\{a_{1}, a_{2}, \ldots, a_{n}\right\}$ and $B=\left\{b_{1}, b_{2}, \ldots, b_{n}\right\}$ and say that $A$ beats $B$ if and only if $a_{k}>b_{k}$. This rule clearly satisfies all three conditions, and the rules corresponding to different $k$ are all different. Thus there are at least $n$ different rules. Part II. Now we have to prove that there is no other way to define such a rule. Suppose that our rule satisfies the conditions, and let $k \in\{1,2, \ldots, n\}$ be minimal with the property that $$ A_{k}=\{1,2, \ldots, k, n+k+1, n+k+2, \ldots, 2 n\} \prec B_{k}=\{k+1, k+2, \ldots, n+k\} $$ Clearly, such a $k$ exists, since this holds for $k=n$ by assumption. Now consider two disjoint sets $X=\left\{x_{1}, x_{2}, \ldots, x_{n}\right\}$ and $Y=\left\{y_{1}, y_{2}, \ldots, y_{n}\right\}$, both in increasing order (i.e., $x_{1}<x_{2}<\cdots<x_{n}$ and $y_{1}<y_{2}<\cdots<y_{n}$ ). We claim that $X<Y$ if (and only if - this follows automatically) $x_{k}<y_{k}$. To prove this statement, pick arbitrary real numbers $u_{i}, v_{i}, w_{i} \notin X \cup Y$ such that $$ u_{1}<u_{2}<\cdots<u_{k-1}<\min \left(x_{1}, y_{1}\right), \quad \max \left(x_{n}, y_{n}\right)<v_{k+1}<v_{k+2}<\cdots<v_{n} $$ and $$ x_{k}<v_{1}<v_{2}<\cdots<v_{k}<w_{1}<w_{2}<\cdots<w_{n}<u_{k}<u_{k+1}<\cdots<u_{n}<y_{k}, $$ and set $$ U=\left\{u_{1}, u_{2}, \ldots, u_{n}\right\}, V=\left\{v_{1}, v_{2}, \ldots, v_{n}\right\}, W=\left\{w_{1}, w_{2}, \ldots, w_{n}\right\} $$ Then - $u_{i}<y_{i}$ and $x_{i}<v_{i}$ for all $i$, so $U<Y$ and $X<V$ by the second condition. - The elements of $U \cup W$ are ordered in the same way as those of $A_{k-1} \cup B_{k-1}$, and since $A_{k-1}>B_{k-1}$ by our choice of $k$, we also have $U>W$ (if $k=1$, this is trivial). - The elements of $V \cup W$ are ordered in the same way as those of $A_{k} \cup B_{k}$, and since $A_{k} \prec B_{k}$ by our choice of $k$, we also have $V \prec W$. It follows that $$ X \prec V \prec W \prec U \prec Y $$ so $X<Y$ by the third condition, which is what we wanted to prove.
|
100
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
We are given an infinite deck of cards, each with a real number on it. For every real number $x$, there is exactly one card in the deck that has $x$ written on it. Now two players draw disjoint sets $A$ and $B$ of 100 cards each from this deck. We would like to define a rule that declares one of them a winner. This rule should satisfy the following conditions: 1. The winner only depends on the relative order of the 200 cards: if the cards are laid down in increasing order face down and we are told which card belongs to which player, but not what numbers are written on them, we can still decide the winner. 2. If we write the elements of both sets in increasing order as $A=\left\{a_{1}, a_{2}, \ldots, a_{100}\right\}$ and $B=\left\{b_{1}, b_{2}, \ldots, b_{100}\right\}$, and $a_{i}>b_{i}$ for all $i$, then $A$ beats $B$. 3. If three players draw three disjoint sets $A, B, C$ from the deck, $A$ beats $B$ and $B$ beats $C$, then $A$ also beats $C$. How many ways are there to define such a rule? Here, we consider two rules as different if there exist two sets $A$ and $B$ such that $A$ beats $B$ according to one rule, but $B$ beats $A$ according to the other. (Russia)
|
We prove a more general statement for sets of cardinality $n$ (the problem being the special case $n=100$, then the answer is $n$ ). In the following, we write $A>B$ or $B<A$ for " $A$ beats $B$ ". Part I. Let us first define $n$ different rules that satisfy the conditions. To this end, fix an index $k \in\{1,2, \ldots, n\}$. We write both $A$ and $B$ in increasing order as $A=\left\{a_{1}, a_{2}, \ldots, a_{n}\right\}$ and $B=\left\{b_{1}, b_{2}, \ldots, b_{n}\right\}$ and say that $A$ beats $B$ if and only if $a_{k}>b_{k}$. This rule clearly satisfies all three conditions, and the rules corresponding to different $k$ are all different. Thus there are at least $n$ different rules. Part II. Now we have to prove that there is no other way to define such a rule. Suppose that our rule satisfies the conditions, and let $k \in\{1,2, \ldots, n\}$ be minimal with the property that $$ A_{k}=\{1,2, \ldots, k, n+k+1, n+k+2, \ldots, 2 n\} \prec B_{k}=\{k+1, k+2, \ldots, n+k\} $$ Clearly, such a $k$ exists, since this holds for $k=n$ by assumption. Now consider two disjoint sets $X=\left\{x_{1}, x_{2}, \ldots, x_{n}\right\}$ and $Y=\left\{y_{1}, y_{2}, \ldots, y_{n}\right\}$, both in increasing order (i.e., $x_{1}<x_{2}<\cdots<x_{n}$ and $y_{1}<y_{2}<\cdots<y_{n}$ ). We claim that $X<Y$ if (and only if - this follows automatically) $x_{k}<y_{k}$. To prove this statement, pick arbitrary real numbers $u_{i}, v_{i}, w_{i} \notin X \cup Y$ such that $$ u_{1}<u_{2}<\cdots<u_{k-1}<\min \left(x_{1}, y_{1}\right), \quad \max \left(x_{n}, y_{n}\right)<v_{k+1}<v_{k+2}<\cdots<v_{n} $$ and $$ x_{k}<v_{1}<v_{2}<\cdots<v_{k}<w_{1}<w_{2}<\cdots<w_{n}<u_{k}<u_{k+1}<\cdots<u_{n}<y_{k}, $$ and set $$ U=\left\{u_{1}, u_{2}, \ldots, u_{n}\right\}, V=\left\{v_{1}, v_{2}, \ldots, v_{n}\right\}, W=\left\{w_{1}, w_{2}, \ldots, w_{n}\right\} $$ Then - $u_{i}<y_{i}$ and $x_{i}<v_{i}$ for all $i$, so $U<Y$ and $X<V$ by the second condition. - The elements of $U \cup W$ are ordered in the same way as those of $A_{k-1} \cup B_{k-1}$, and since $A_{k-1}>B_{k-1}$ by our choice of $k$, we also have $U>W$ (if $k=1$, this is trivial). - The elements of $V \cup W$ are ordered in the same way as those of $A_{k} \cup B_{k}$, and since $A_{k} \prec B_{k}$ by our choice of $k$, we also have $V \prec W$. It follows that $$ X \prec V \prec W \prec U \prec Y $$ so $X<Y$ by the third condition, which is what we wanted to prove.
|
{
"resource_path": "IMO/segmented/en-IMO2014SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
b9d6d44a-363e-53a5-b3ea-4e33b476dd67
| 24,421
|
We are given an infinite deck of cards, each with a real number on it. For every real number $x$, there is exactly one card in the deck that has $x$ written on it. Now two players draw disjoint sets $A$ and $B$ of 100 cards each from this deck. We would like to define a rule that declares one of them a winner. This rule should satisfy the following conditions: 1. The winner only depends on the relative order of the 200 cards: if the cards are laid down in increasing order face down and we are told which card belongs to which player, but not what numbers are written on them, we can still decide the winner. 2. If we write the elements of both sets in increasing order as $A=\left\{a_{1}, a_{2}, \ldots, a_{100}\right\}$ and $B=\left\{b_{1}, b_{2}, \ldots, b_{100}\right\}$, and $a_{i}>b_{i}$ for all $i$, then $A$ beats $B$. 3. If three players draw three disjoint sets $A, B, C$ from the deck, $A$ beats $B$ and $B$ beats $C$, then $A$ also beats $C$. How many ways are there to define such a rule? Here, we consider two rules as different if there exist two sets $A$ and $B$ such that $A$ beats $B$ according to one rule, but $B$ beats $A$ according to the other. (Russia) Answer. 100.
|
We prove a more general statement for sets of cardinality $n$ (the problem being the special case $n=100$, then the answer is $n$ ). In the following, we write $A>B$ or $B<A$ for " $A$ beats $B$ ". Part I. Let us first define $n$ different rules that satisfy the conditions. To this end, fix an index $k \in\{1,2, \ldots, n\}$. We write both $A$ and $B$ in increasing order as $A=\left\{a_{1}, a_{2}, \ldots, a_{n}\right\}$ and $B=\left\{b_{1}, b_{2}, \ldots, b_{n}\right\}$ and say that $A$ beats $B$ if and only if $a_{k}>b_{k}$. This rule clearly satisfies all three conditions, and the rules corresponding to different $k$ are all different. Thus there are at least $n$ different rules. Part II. Now we have to prove that there is no other way to define such a rule. Suppose that our rule satisfies the conditions, and let $k \in\{1,2, \ldots, n\}$ be minimal with the property that $$ A_{k}=\{1,2, \ldots, k, n+k+1, n+k+2, \ldots, 2 n\} \prec B_{k}=\{k+1, k+2, \ldots, n+k\} $$ Clearly, such a $k$ exists, since this holds for $k=n$ by assumption. Now consider two disjoint sets $X=\left\{x_{1}, x_{2}, \ldots, x_{n}\right\}$ and $Y=\left\{y_{1}, y_{2}, \ldots, y_{n}\right\}$, both in increasing order (i.e., $x_{1}<x_{2}<\cdots<x_{n}$ and $y_{1}<y_{2}<\cdots<y_{n}$ ). We claim that $X<Y$ if (and only if - this follows automatically) $x_{k}<y_{k}$. To prove this statement, pick arbitrary real numbers $u_{i}, v_{i}, w_{i} \notin X \cup Y$ such that $$ u_{1}<u_{2}<\cdots<u_{k-1}<\min \left(x_{1}, y_{1}\right), \quad \max \left(x_{n}, y_{n}\right)<v_{k+1}<v_{k+2}<\cdots<v_{n} $$ and $$ x_{k}<v_{1}<v_{2}<\cdots<v_{k}<w_{1}<w_{2}<\cdots<w_{n}<u_{k}<u_{k+1}<\cdots<u_{n}<y_{k}, $$ and set $$ U=\left\{u_{1}, u_{2}, \ldots, u_{n}\right\}, V=\left\{v_{1}, v_{2}, \ldots, v_{n}\right\}, W=\left\{w_{1}, w_{2}, \ldots, w_{n}\right\} $$ Then - $u_{i}<y_{i}$ and $x_{i}<v_{i}$ for all $i$, so $U<Y$ and $X<V$ by the second condition. - The elements of $U \cup W$ are ordered in the same way as those of $A_{k-1} \cup B_{k-1}$, and since $A_{k-1}>B_{k-1}$ by our choice of $k$, we also have $U>W$ (if $k=1$, this is trivial). - The elements of $V \cup W$ are ordered in the same way as those of $A_{k} \cup B_{k}$, and since $A_{k} \prec B_{k}$ by our choice of $k$, we also have $V \prec W$. It follows that $$ X \prec V \prec W \prec U \prec Y $$ so $X<Y$ by the third condition, which is what we wanted to prove.
|
100
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
We are given an infinite deck of cards, each with a real number on it. For every real number $x$, there is exactly one card in the deck that has $x$ written on it. Now two players draw disjoint sets $A$ and $B$ of 100 cards each from this deck. We would like to define a rule that declares one of them a winner. This rule should satisfy the following conditions: 1. The winner only depends on the relative order of the 200 cards: if the cards are laid down in increasing order face down and we are told which card belongs to which player, but not what numbers are written on them, we can still decide the winner. 2. If we write the elements of both sets in increasing order as $A=\left\{a_{1}, a_{2}, \ldots, a_{100}\right\}$ and $B=\left\{b_{1}, b_{2}, \ldots, b_{100}\right\}$, and $a_{i}>b_{i}$ for all $i$, then $A$ beats $B$. 3. If three players draw three disjoint sets $A, B, C$ from the deck, $A$ beats $B$ and $B$ beats $C$, then $A$ also beats $C$. How many ways are there to define such a rule? Here, we consider two rules as different if there exist two sets $A$ and $B$ such that $A$ beats $B$ according to one rule, but $B$ beats $A$ according to the other. (Russia) Answer. 100.
|
We prove a more general statement for sets of cardinality $n$ (the problem being the special case $n=100$, then the answer is $n$ ). In the following, we write $A>B$ or $B<A$ for " $A$ beats $B$ ". Part I. Let us first define $n$ different rules that satisfy the conditions. To this end, fix an index $k \in\{1,2, \ldots, n\}$. We write both $A$ and $B$ in increasing order as $A=\left\{a_{1}, a_{2}, \ldots, a_{n}\right\}$ and $B=\left\{b_{1}, b_{2}, \ldots, b_{n}\right\}$ and say that $A$ beats $B$ if and only if $a_{k}>b_{k}$. This rule clearly satisfies all three conditions, and the rules corresponding to different $k$ are all different. Thus there are at least $n$ different rules. Part II. Now we have to prove that there is no other way to define such a rule. Suppose that our rule satisfies the conditions, and let $k \in\{1,2, \ldots, n\}$ be minimal with the property that $$ A_{k}=\{1,2, \ldots, k, n+k+1, n+k+2, \ldots, 2 n\} \prec B_{k}=\{k+1, k+2, \ldots, n+k\} $$ Clearly, such a $k$ exists, since this holds for $k=n$ by assumption. Now consider two disjoint sets $X=\left\{x_{1}, x_{2}, \ldots, x_{n}\right\}$ and $Y=\left\{y_{1}, y_{2}, \ldots, y_{n}\right\}$, both in increasing order (i.e., $x_{1}<x_{2}<\cdots<x_{n}$ and $y_{1}<y_{2}<\cdots<y_{n}$ ). We claim that $X<Y$ if (and only if - this follows automatically) $x_{k}<y_{k}$. To prove this statement, pick arbitrary real numbers $u_{i}, v_{i}, w_{i} \notin X \cup Y$ such that $$ u_{1}<u_{2}<\cdots<u_{k-1}<\min \left(x_{1}, y_{1}\right), \quad \max \left(x_{n}, y_{n}\right)<v_{k+1}<v_{k+2}<\cdots<v_{n} $$ and $$ x_{k}<v_{1}<v_{2}<\cdots<v_{k}<w_{1}<w_{2}<\cdots<w_{n}<u_{k}<u_{k+1}<\cdots<u_{n}<y_{k}, $$ and set $$ U=\left\{u_{1}, u_{2}, \ldots, u_{n}\right\}, V=\left\{v_{1}, v_{2}, \ldots, v_{n}\right\}, W=\left\{w_{1}, w_{2}, \ldots, w_{n}\right\} $$ Then - $u_{i}<y_{i}$ and $x_{i}<v_{i}$ for all $i$, so $U<Y$ and $X<V$ by the second condition. - The elements of $U \cup W$ are ordered in the same way as those of $A_{k-1} \cup B_{k-1}$, and since $A_{k-1}>B_{k-1}$ by our choice of $k$, we also have $U>W$ (if $k=1$, this is trivial). - The elements of $V \cup W$ are ordered in the same way as those of $A_{k} \cup B_{k}$, and since $A_{k} \prec B_{k}$ by our choice of $k$, we also have $V \prec W$. It follows that $$ X \prec V \prec W \prec U \prec Y $$ so $X<Y$ by the third condition, which is what we wanted to prove.
|
{
"resource_path": "IMO/segmented/en-IMO2014SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
71bfb157-39cc-51f7-a9fc-9a80bbbc7413
| 24,515
|
Let $n \geqslant 2$ be an integer, and let $A_{n}$ be the set $$ A_{n}=\left\{2^{n}-2^{k} \mid k \in \mathbb{Z}, 0 \leqslant k<n\right\} . $$ Determine the largest positive integer that cannot be written as the sum of one or more (not necessarily distinct) elements of $A_{n}$. (Serbia) Answer. $(n-2) 2^{n}+1$.
|
Part I. First we show that every integer greater than $(n-2) 2^{n}+1$ can be represented as such a sum. This is achieved by induction on $n$. For $n=2$, the set $A_{n}$ consists of the two elements 2 and 3 . Every positive integer $m$ except for 1 can be represented as the sum of elements of $A_{n}$ in this case: as $m=2+2+\cdots+2$ if $m$ is even, and as $m=3+2+2+\cdots+2$ if $m$ is odd. Now consider some $n>2$, and take an integer $m>(n-2) 2^{n}+1$. If $m$ is even, then consider $$ \frac{m}{2} \geqslant \frac{(n-2) 2^{n}+2}{2}=(n-2) 2^{n-1}+1>(n-3) 2^{n-1}+1 $$ By the induction hypothesis, there is a representation of the form $$ \frac{m}{2}=\left(2^{n-1}-2^{k_{1}}\right)+\left(2^{n-1}-2^{k_{2}}\right)+\cdots+\left(2^{n-1}-2^{k_{r}}\right) $$ for some $k_{i}$ with $0 \leqslant k_{i}<n-1$. It follows that $$ m=\left(2^{n}-2^{k_{1}+1}\right)+\left(2^{n}-2^{k_{2}+1}\right)+\cdots+\left(2^{n}-2^{k_{r}+1}\right) $$ giving us the desired representation as a sum of elements of $A_{n}$. If $m$ is odd, we consider $$ \frac{m-\left(2^{n}-1\right)}{2}>\frac{(n-2) 2^{n}+1-\left(2^{n}-1\right)}{2}=(n-3) 2^{n-1}+1 $$ By the induction hypothesis, there is a representation of the form $$ \frac{m-\left(2^{n}-1\right)}{2}=\left(2^{n-1}-2^{k_{1}}\right)+\left(2^{n-1}-2^{k_{2}}\right)+\cdots+\left(2^{n-1}-2^{k_{r}}\right) $$ for some $k_{i}$ with $0 \leqslant k_{i}<n-1$. It follows that $$ m=\left(2^{n}-2^{k_{1}+1}\right)+\left(2^{n}-2^{k_{2}+1}\right)+\cdots+\left(2^{n}-2^{k_{r}+1}\right)+\left(2^{n}-1\right) $$ giving us the desired representation of $m$ once again. Part II. It remains to show that there is no representation for $(n-2) 2^{n}+1$. Let $N$ be the smallest positive integer that satisfies $N \equiv 1\left(\bmod 2^{n}\right)$, and which can be represented as a sum of elements of $A_{n}$. Consider a representation of $N$, i.e., $$ N=\left(2^{n}-2^{k_{1}}\right)+\left(2^{n}-2^{k_{2}}\right)+\cdots+\left(2^{n}-2^{k_{r}}\right) $$ where $0 \leqslant k_{1}, k_{2}, \ldots, k_{r}<n$. Suppose first that two of the terms in the sum are the same, i.e., $k_{i}=k_{j}$ for some $i \neq j$. If $k_{i}=k_{j}=n-1$, then we can simply remove these two terms to get a representation for $$ N-2\left(2^{n}-2^{n-1}\right)=N-2^{n} $$ as a sum of elements of $A_{n}$, which contradicts our choice of $N$. If $k_{i}=k_{j}=k<n-1$, replace the two terms by $2^{n}-2^{k+1}$, which is also an element of $A_{n}$, to get a representation for $$ N-2\left(2^{n}-2^{k}\right)+2^{n}-2^{k+1}=N-2^{n} . $$ This is a contradiction once again. Therefore, all $k_{i}$ have to be distinct, which means that $$ 2^{k_{1}}+2^{k_{2}}+\cdots+2^{k_{r}} \leqslant 2^{0}+2^{1}+2^{2}+\cdots+2^{n-1}=2^{n}-1 $$ On the other hand, taking (1) modulo $2^{n}$, we find $$ 2^{k_{1}}+2^{k_{2}}+\cdots+2^{k_{r}} \equiv-N \equiv-1 \quad\left(\bmod 2^{n}\right) $$ Thus we must have $2^{k_{1}}+2^{k_{2}}+\cdots+2^{k_{r}}=2^{n}-1$, which is only possible if each element of $\{0,1, \ldots, n-1\}$ occurs as one of the $k_{i}$. This gives us $$ N=n 2^{n}-\left(2^{0}+2^{1}+\cdots+2^{n-1}\right)=(n-1) 2^{n}+1 . $$ In particular, this means that $(n-2) 2^{n}+1$ cannot be represented as a sum of elements of $A_{n}$.
|
(n-2) 2^{n}+1
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Let $n \geqslant 2$ be an integer, and let $A_{n}$ be the set $$ A_{n}=\left\{2^{n}-2^{k} \mid k \in \mathbb{Z}, 0 \leqslant k<n\right\} . $$ Determine the largest positive integer that cannot be written as the sum of one or more (not necessarily distinct) elements of $A_{n}$. (Serbia) Answer. $(n-2) 2^{n}+1$.
|
Part I. First we show that every integer greater than $(n-2) 2^{n}+1$ can be represented as such a sum. This is achieved by induction on $n$. For $n=2$, the set $A_{n}$ consists of the two elements 2 and 3 . Every positive integer $m$ except for 1 can be represented as the sum of elements of $A_{n}$ in this case: as $m=2+2+\cdots+2$ if $m$ is even, and as $m=3+2+2+\cdots+2$ if $m$ is odd. Now consider some $n>2$, and take an integer $m>(n-2) 2^{n}+1$. If $m$ is even, then consider $$ \frac{m}{2} \geqslant \frac{(n-2) 2^{n}+2}{2}=(n-2) 2^{n-1}+1>(n-3) 2^{n-1}+1 $$ By the induction hypothesis, there is a representation of the form $$ \frac{m}{2}=\left(2^{n-1}-2^{k_{1}}\right)+\left(2^{n-1}-2^{k_{2}}\right)+\cdots+\left(2^{n-1}-2^{k_{r}}\right) $$ for some $k_{i}$ with $0 \leqslant k_{i}<n-1$. It follows that $$ m=\left(2^{n}-2^{k_{1}+1}\right)+\left(2^{n}-2^{k_{2}+1}\right)+\cdots+\left(2^{n}-2^{k_{r}+1}\right) $$ giving us the desired representation as a sum of elements of $A_{n}$. If $m$ is odd, we consider $$ \frac{m-\left(2^{n}-1\right)}{2}>\frac{(n-2) 2^{n}+1-\left(2^{n}-1\right)}{2}=(n-3) 2^{n-1}+1 $$ By the induction hypothesis, there is a representation of the form $$ \frac{m-\left(2^{n}-1\right)}{2}=\left(2^{n-1}-2^{k_{1}}\right)+\left(2^{n-1}-2^{k_{2}}\right)+\cdots+\left(2^{n-1}-2^{k_{r}}\right) $$ for some $k_{i}$ with $0 \leqslant k_{i}<n-1$. It follows that $$ m=\left(2^{n}-2^{k_{1}+1}\right)+\left(2^{n}-2^{k_{2}+1}\right)+\cdots+\left(2^{n}-2^{k_{r}+1}\right)+\left(2^{n}-1\right) $$ giving us the desired representation of $m$ once again. Part II. It remains to show that there is no representation for $(n-2) 2^{n}+1$. Let $N$ be the smallest positive integer that satisfies $N \equiv 1\left(\bmod 2^{n}\right)$, and which can be represented as a sum of elements of $A_{n}$. Consider a representation of $N$, i.e., $$ N=\left(2^{n}-2^{k_{1}}\right)+\left(2^{n}-2^{k_{2}}\right)+\cdots+\left(2^{n}-2^{k_{r}}\right) $$ where $0 \leqslant k_{1}, k_{2}, \ldots, k_{r}<n$. Suppose first that two of the terms in the sum are the same, i.e., $k_{i}=k_{j}$ for some $i \neq j$. If $k_{i}=k_{j}=n-1$, then we can simply remove these two terms to get a representation for $$ N-2\left(2^{n}-2^{n-1}\right)=N-2^{n} $$ as a sum of elements of $A_{n}$, which contradicts our choice of $N$. If $k_{i}=k_{j}=k<n-1$, replace the two terms by $2^{n}-2^{k+1}$, which is also an element of $A_{n}$, to get a representation for $$ N-2\left(2^{n}-2^{k}\right)+2^{n}-2^{k+1}=N-2^{n} . $$ This is a contradiction once again. Therefore, all $k_{i}$ have to be distinct, which means that $$ 2^{k_{1}}+2^{k_{2}}+\cdots+2^{k_{r}} \leqslant 2^{0}+2^{1}+2^{2}+\cdots+2^{n-1}=2^{n}-1 $$ On the other hand, taking (1) modulo $2^{n}$, we find $$ 2^{k_{1}}+2^{k_{2}}+\cdots+2^{k_{r}} \equiv-N \equiv-1 \quad\left(\bmod 2^{n}\right) $$ Thus we must have $2^{k_{1}}+2^{k_{2}}+\cdots+2^{k_{r}}=2^{n}-1$, which is only possible if each element of $\{0,1, \ldots, n-1\}$ occurs as one of the $k_{i}$. This gives us $$ N=n 2^{n}-\left(2^{0}+2^{1}+\cdots+2^{n-1}\right)=(n-1) 2^{n}+1 . $$ In particular, this means that $(n-2) 2^{n}+1$ cannot be represented as a sum of elements of $A_{n}$.
|
{
"resource_path": "IMO/segmented/en-IMO2014SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
f7fc25e5-4a45-5496-8a52-cd864048c67f
| 24,536
|
Let $n$ be a fixed positive integer. Find the maximum possible value of $$ \sum_{1 \leqslant r<s \leqslant 2 n}(s-r-n) x_{r} x_{s} $$ where $-1 \leqslant x_{i} \leqslant 1$ for all $i=1,2, \ldots, 2 n$.
|
Let $Z$ be the expression to be maximized. Since this expression is linear in every variable $x_{i}$ and $-1 \leqslant x_{i} \leqslant 1$, the maximum of $Z$ will be achieved when $x_{i}=-1$ or 1 . Therefore, it suffices to consider only the case when $x_{i} \in\{-1,1\}$ for all $i=1,2, \ldots, 2 n$. For $i=1,2, \ldots, 2 n$, we introduce auxiliary variables $$ y_{i}=\sum_{r=1}^{i} x_{r}-\sum_{r=i+1}^{2 n} x_{r} $$ Taking squares of both sides, we have $$ \begin{aligned} y_{i}^{2} & =\sum_{r=1}^{2 n} x_{r}^{2}+\sum_{r<s \leqslant i} 2 x_{r} x_{s}+\sum_{i<r<s} 2 x_{r} x_{s}-\sum_{r \leqslant i<s} 2 x_{r} x_{s} \\ & =2 n+\sum_{r<s \leqslant i} 2 x_{r} x_{s}+\sum_{i<r<s} 2 x_{r} x_{s}-\sum_{r \leqslant i<s} 2 x_{r} x_{s}, \end{aligned} $$ where the last equality follows from the fact that $x_{r} \in\{-1,1\}$. Notice that for every $r<s$, the coefficient of $x_{r} x_{s}$ in (1) is 2 for each $i=1, \ldots, r-1, s, \ldots, 2 n$, and this coefficient is -2 for each $i=r, \ldots, s-1$. This implies that the coefficient of $x_{r} x_{s}$ in $\sum_{i=1}^{2 n} y_{i}^{2}$ is $2(2 n-s+r)-2(s-r)=$ $4(n-s+r)$. Therefore, summing (1) for $i=1,2, \ldots, 2 n$ yields $$ \sum_{i=1}^{2 n} y_{i}^{2}=4 n^{2}+\sum_{1 \leqslant r<s \leqslant 2 n} 4(n-s+r) x_{r} x_{s}=4 n^{2}-4 Z $$ Hence, it suffices to find the minimum of the left-hand side. Since $x_{r} \in\{-1,1\}$, we see that $y_{i}$ is an even integer. In addition, $y_{i}-y_{i-1}=2 x_{i}= \pm 2$, and so $y_{i-1}$ and $y_{i}$ are consecutive even integers for every $i=2,3, \ldots, 2 n$. It follows that $y_{i-1}^{2}+y_{i}^{2} \geqslant 4$, which implies $$ \sum_{i=1}^{2 n} y_{i}^{2}=\sum_{j=1}^{n}\left(y_{2 j-1}^{2}+y_{2 j}^{2}\right) \geqslant 4 n $$ Combining (2) and (3), we get $$ 4 n \leqslant \sum_{i=1}^{2 n} y_{i}^{2}=4 n^{2}-4 Z $$ Hence, $Z \leqslant n(n-1)$. If we set $x_{i}=1$ for odd indices $i$ and $x_{i}=-1$ for even indices $i$, then we obtain equality in (3) (and thus in (4)). Therefore, the maximum possible value of $Z$ is $n(n-1)$, as desired. Comment 1. $Z=n(n-1)$ can be achieved by several other examples. In particular, $x_{i}$ needs not be $\pm 1$. For instance, setting $x_{i}=(-1)^{i}$ for all $2 \leqslant i \leqslant 2 n$, we find that the coefficient of $x_{1}$ in $Z$ is 0 . Therefore, $x_{1}$ can be chosen arbitrarily in the interval $[-1,1]$. Nevertheless, if $x_{i} \in\{-1,1\}$ for all $i=1,2, \ldots, 2 n$, then the equality $Z=n(n-1)$ holds only when $\left(y_{1}, y_{2}, \ldots, y_{2 n}\right)=(0, \pm 2,0, \pm 2, \ldots, 0, \pm 2)$ or $( \pm 2,0, \pm 2,0, \ldots, \pm 2,0)$. In each case, we can reconstruct $x_{i}$ accordingly. The sum $\sum_{i=1}^{2 n} x_{i}$ in the optimal cases needs not be 0 , but it must equal 0 or $\pm 2$. Comment 2. Several variations in setting up the auxiliary variables are possible. For instance, one may let $x_{2 n+i}=-x_{i}$ and $y_{i}^{\prime}=x_{i}+x_{i+1}+\cdots+x_{i+n-1}$ for any $1 \leqslant i \leqslant 2 n$. Similarly to Solution 1 , we obtain $Y:=y_{1}^{\prime 2}+y_{2}^{\prime 2}+\cdots+y_{2 n}^{\prime 2}=2 n^{2}-2 Z$. Then, it suffices to show that $Y \geqslant 2 n$. If $n$ is odd, then each $y_{i}^{\prime}$ is odd, and so $y_{i}^{\prime 2} \geqslant 1$. If $n$ is even, then each $y_{i}^{\prime}$ is even. We can check that at least one of $y_{i}^{\prime}, y_{i+1}^{\prime}, y_{n+i}^{\prime}$, and $y_{n+i+1}^{\prime}$ is nonzero, so that $y_{i}^{\prime 2}+y_{i+1}^{\prime 2}+y_{n+i}^{\prime 2}+y_{n+i+1}^{\prime 2} \geqslant 4$; summing these up for $i=1,3, \ldots, n-1$ yields $Y \geqslant 2 n$.
|
n(n-1)
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Let $n$ be a fixed positive integer. Find the maximum possible value of $$ \sum_{1 \leqslant r<s \leqslant 2 n}(s-r-n) x_{r} x_{s} $$ where $-1 \leqslant x_{i} \leqslant 1$ for all $i=1,2, \ldots, 2 n$.
|
Let $Z$ be the expression to be maximized. Since this expression is linear in every variable $x_{i}$ and $-1 \leqslant x_{i} \leqslant 1$, the maximum of $Z$ will be achieved when $x_{i}=-1$ or 1 . Therefore, it suffices to consider only the case when $x_{i} \in\{-1,1\}$ for all $i=1,2, \ldots, 2 n$. For $i=1,2, \ldots, 2 n$, we introduce auxiliary variables $$ y_{i}=\sum_{r=1}^{i} x_{r}-\sum_{r=i+1}^{2 n} x_{r} $$ Taking squares of both sides, we have $$ \begin{aligned} y_{i}^{2} & =\sum_{r=1}^{2 n} x_{r}^{2}+\sum_{r<s \leqslant i} 2 x_{r} x_{s}+\sum_{i<r<s} 2 x_{r} x_{s}-\sum_{r \leqslant i<s} 2 x_{r} x_{s} \\ & =2 n+\sum_{r<s \leqslant i} 2 x_{r} x_{s}+\sum_{i<r<s} 2 x_{r} x_{s}-\sum_{r \leqslant i<s} 2 x_{r} x_{s}, \end{aligned} $$ where the last equality follows from the fact that $x_{r} \in\{-1,1\}$. Notice that for every $r<s$, the coefficient of $x_{r} x_{s}$ in (1) is 2 for each $i=1, \ldots, r-1, s, \ldots, 2 n$, and this coefficient is -2 for each $i=r, \ldots, s-1$. This implies that the coefficient of $x_{r} x_{s}$ in $\sum_{i=1}^{2 n} y_{i}^{2}$ is $2(2 n-s+r)-2(s-r)=$ $4(n-s+r)$. Therefore, summing (1) for $i=1,2, \ldots, 2 n$ yields $$ \sum_{i=1}^{2 n} y_{i}^{2}=4 n^{2}+\sum_{1 \leqslant r<s \leqslant 2 n} 4(n-s+r) x_{r} x_{s}=4 n^{2}-4 Z $$ Hence, it suffices to find the minimum of the left-hand side. Since $x_{r} \in\{-1,1\}$, we see that $y_{i}$ is an even integer. In addition, $y_{i}-y_{i-1}=2 x_{i}= \pm 2$, and so $y_{i-1}$ and $y_{i}$ are consecutive even integers for every $i=2,3, \ldots, 2 n$. It follows that $y_{i-1}^{2}+y_{i}^{2} \geqslant 4$, which implies $$ \sum_{i=1}^{2 n} y_{i}^{2}=\sum_{j=1}^{n}\left(y_{2 j-1}^{2}+y_{2 j}^{2}\right) \geqslant 4 n $$ Combining (2) and (3), we get $$ 4 n \leqslant \sum_{i=1}^{2 n} y_{i}^{2}=4 n^{2}-4 Z $$ Hence, $Z \leqslant n(n-1)$. If we set $x_{i}=1$ for odd indices $i$ and $x_{i}=-1$ for even indices $i$, then we obtain equality in (3) (and thus in (4)). Therefore, the maximum possible value of $Z$ is $n(n-1)$, as desired. Comment 1. $Z=n(n-1)$ can be achieved by several other examples. In particular, $x_{i}$ needs not be $\pm 1$. For instance, setting $x_{i}=(-1)^{i}$ for all $2 \leqslant i \leqslant 2 n$, we find that the coefficient of $x_{1}$ in $Z$ is 0 . Therefore, $x_{1}$ can be chosen arbitrarily in the interval $[-1,1]$. Nevertheless, if $x_{i} \in\{-1,1\}$ for all $i=1,2, \ldots, 2 n$, then the equality $Z=n(n-1)$ holds only when $\left(y_{1}, y_{2}, \ldots, y_{2 n}\right)=(0, \pm 2,0, \pm 2, \ldots, 0, \pm 2)$ or $( \pm 2,0, \pm 2,0, \ldots, \pm 2,0)$. In each case, we can reconstruct $x_{i}$ accordingly. The sum $\sum_{i=1}^{2 n} x_{i}$ in the optimal cases needs not be 0 , but it must equal 0 or $\pm 2$. Comment 2. Several variations in setting up the auxiliary variables are possible. For instance, one may let $x_{2 n+i}=-x_{i}$ and $y_{i}^{\prime}=x_{i}+x_{i+1}+\cdots+x_{i+n-1}$ for any $1 \leqslant i \leqslant 2 n$. Similarly to Solution 1 , we obtain $Y:=y_{1}^{\prime 2}+y_{2}^{\prime 2}+\cdots+y_{2 n}^{\prime 2}=2 n^{2}-2 Z$. Then, it suffices to show that $Y \geqslant 2 n$. If $n$ is odd, then each $y_{i}^{\prime}$ is odd, and so $y_{i}^{\prime 2} \geqslant 1$. If $n$ is even, then each $y_{i}^{\prime}$ is even. We can check that at least one of $y_{i}^{\prime}, y_{i+1}^{\prime}, y_{n+i}^{\prime}$, and $y_{n+i+1}^{\prime}$ is nonzero, so that $y_{i}^{\prime 2}+y_{i+1}^{\prime 2}+y_{n+i}^{\prime 2}+y_{n+i+1}^{\prime 2} \geqslant 4$; summing these up for $i=1,3, \ldots, n-1$ yields $Y \geqslant 2 n$.
|
{
"resource_path": "IMO/segmented/en-IMO2015SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
ebc5d58a-f8a8-5113-8092-1614701597f1
| 24,558
|
Let $n$ be a fixed positive integer. Find the maximum possible value of $$ \sum_{1 \leqslant r<s \leqslant 2 n}(s-r-n) x_{r} x_{s}, $$ where $-1 \leqslant x_{i} \leqslant 1$ for all $i=1,2, \ldots, 2 n$. (Austria) Answer. $n(n-1)$.
|
Let $Z$ be the expression to be maximized. Since this expression is linear in every variable $x_{i}$ and $-1 \leqslant x_{i} \leqslant 1$, the maximum of $Z$ will be achieved when $x_{i}=-1$ or 1 . Therefore, it suffices to consider only the case when $x_{i} \in\{-1,1\}$ for all $i=1,2, \ldots, 2 n$. For $i=1,2, \ldots, 2 n$, we introduce auxiliary variables $$ y_{i}=\sum_{r=1}^{i} x_{r}-\sum_{r=i+1}^{2 n} x_{r} $$ Taking squares of both sides, we have $$ \begin{aligned} y_{i}^{2} & =\sum_{r=1}^{2 n} x_{r}^{2}+\sum_{r<s \leqslant i} 2 x_{r} x_{s}+\sum_{i<r<s} 2 x_{r} x_{s}-\sum_{r \leqslant i<s} 2 x_{r} x_{s} \\ & =2 n+\sum_{r<s \leqslant i} 2 x_{r} x_{s}+\sum_{i<r<s} 2 x_{r} x_{s}-\sum_{r \leqslant i<s} 2 x_{r} x_{s}, \end{aligned} $$ where the last equality follows from the fact that $x_{r} \in\{-1,1\}$. Notice that for every $r<s$, the coefficient of $x_{r} x_{s}$ in (1) is 2 for each $i=1, \ldots, r-1, s, \ldots, 2 n$, and this coefficient is -2 for each $i=r, \ldots, s-1$. This implies that the coefficient of $x_{r} x_{s}$ in $\sum_{i=1}^{2 n} y_{i}^{2}$ is $2(2 n-s+r)-2(s-r)=$ $4(n-s+r)$. Therefore, summing (1) for $i=1,2, \ldots, 2 n$ yields $$ \sum_{i=1}^{2 n} y_{i}^{2}=4 n^{2}+\sum_{1 \leqslant r<s \leqslant 2 n} 4(n-s+r) x_{r} x_{s}=4 n^{2}-4 Z $$ Hence, it suffices to find the minimum of the left-hand side. Since $x_{r} \in\{-1,1\}$, we see that $y_{i}$ is an even integer. In addition, $y_{i}-y_{i-1}=2 x_{i}= \pm 2$, and so $y_{i-1}$ and $y_{i}$ are consecutive even integers for every $i=2,3, \ldots, 2 n$. It follows that $y_{i-1}^{2}+y_{i}^{2} \geqslant 4$, which implies $$ \sum_{i=1}^{2 n} y_{i}^{2}=\sum_{j=1}^{n}\left(y_{2 j-1}^{2}+y_{2 j}^{2}\right) \geqslant 4 n $$ Combining (2) and (3), we get $$ 4 n \leqslant \sum_{i=1}^{2 n} y_{i}^{2}=4 n^{2}-4 Z $$ Hence, $Z \leqslant n(n-1)$. If we set $x_{i}=1$ for odd indices $i$ and $x_{i}=-1$ for even indices $i$, then we obtain equality in (3) (and thus in (4)). Therefore, the maximum possible value of $Z$ is $n(n-1)$, as desired. Comment 1. $Z=n(n-1)$ can be achieved by several other examples. In particular, $x_{i}$ needs not be $\pm 1$. For instance, setting $x_{i}=(-1)^{i}$ for all $2 \leqslant i \leqslant 2 n$, we find that the coefficient of $x_{1}$ in $Z$ is 0 . Therefore, $x_{1}$ can be chosen arbitrarily in the interval $[-1,1]$. Nevertheless, if $x_{i} \in\{-1,1\}$ for all $i=1,2, \ldots, 2 n$, then the equality $Z=n(n-1)$ holds only when $\left(y_{1}, y_{2}, \ldots, y_{2 n}\right)=(0, \pm 2,0, \pm 2, \ldots, 0, \pm 2)$ or $( \pm 2,0, \pm 2,0, \ldots, \pm 2,0)$. In each case, we can reconstruct $x_{i}$ accordingly. The sum $\sum_{i=1}^{2 n} x_{i}$ in the optimal cases needs not be 0 , but it must equal 0 or $\pm 2$. Comment 2. Several variations in setting up the auxiliary variables are possible. For instance, one may let $x_{2 n+i}=-x_{i}$ and $y_{i}^{\prime}=x_{i}+x_{i+1}+\cdots+x_{i+n-1}$ for any $1 \leqslant i \leqslant 2 n$. Similarly to Solution 1 , we obtain $Y:=y_{1}^{\prime 2}+y_{2}^{\prime 2}+\cdots+y_{2 n}^{\prime 2}=2 n^{2}-2 Z$. Then, it suffices to show that $Y \geqslant 2 n$. If $n$ is odd, then each $y_{i}^{\prime}$ is odd, and so $y_{i}^{\prime 2} \geqslant 1$. If $n$ is even, then each $y_{i}^{\prime}$ is even. We can check that at least one of $y_{i}^{\prime}, y_{i+1}^{\prime}, y_{n+i}^{\prime}$, and $y_{n+i+1}^{\prime}$ is nonzero, so that $y_{i}^{\prime 2}+y_{i+1}^{\prime 2}+y_{n+i}^{\prime 2}+y_{n+i+1}^{\prime 2} \geqslant 4$; summing these up for $i=1,3, \ldots, n-1$ yields $Y \geqslant 2 n$.
|
n(n-1)
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Let $n$ be a fixed positive integer. Find the maximum possible value of $$ \sum_{1 \leqslant r<s \leqslant 2 n}(s-r-n) x_{r} x_{s}, $$ where $-1 \leqslant x_{i} \leqslant 1$ for all $i=1,2, \ldots, 2 n$. (Austria) Answer. $n(n-1)$.
|
Let $Z$ be the expression to be maximized. Since this expression is linear in every variable $x_{i}$ and $-1 \leqslant x_{i} \leqslant 1$, the maximum of $Z$ will be achieved when $x_{i}=-1$ or 1 . Therefore, it suffices to consider only the case when $x_{i} \in\{-1,1\}$ for all $i=1,2, \ldots, 2 n$. For $i=1,2, \ldots, 2 n$, we introduce auxiliary variables $$ y_{i}=\sum_{r=1}^{i} x_{r}-\sum_{r=i+1}^{2 n} x_{r} $$ Taking squares of both sides, we have $$ \begin{aligned} y_{i}^{2} & =\sum_{r=1}^{2 n} x_{r}^{2}+\sum_{r<s \leqslant i} 2 x_{r} x_{s}+\sum_{i<r<s} 2 x_{r} x_{s}-\sum_{r \leqslant i<s} 2 x_{r} x_{s} \\ & =2 n+\sum_{r<s \leqslant i} 2 x_{r} x_{s}+\sum_{i<r<s} 2 x_{r} x_{s}-\sum_{r \leqslant i<s} 2 x_{r} x_{s}, \end{aligned} $$ where the last equality follows from the fact that $x_{r} \in\{-1,1\}$. Notice that for every $r<s$, the coefficient of $x_{r} x_{s}$ in (1) is 2 for each $i=1, \ldots, r-1, s, \ldots, 2 n$, and this coefficient is -2 for each $i=r, \ldots, s-1$. This implies that the coefficient of $x_{r} x_{s}$ in $\sum_{i=1}^{2 n} y_{i}^{2}$ is $2(2 n-s+r)-2(s-r)=$ $4(n-s+r)$. Therefore, summing (1) for $i=1,2, \ldots, 2 n$ yields $$ \sum_{i=1}^{2 n} y_{i}^{2}=4 n^{2}+\sum_{1 \leqslant r<s \leqslant 2 n} 4(n-s+r) x_{r} x_{s}=4 n^{2}-4 Z $$ Hence, it suffices to find the minimum of the left-hand side. Since $x_{r} \in\{-1,1\}$, we see that $y_{i}$ is an even integer. In addition, $y_{i}-y_{i-1}=2 x_{i}= \pm 2$, and so $y_{i-1}$ and $y_{i}$ are consecutive even integers for every $i=2,3, \ldots, 2 n$. It follows that $y_{i-1}^{2}+y_{i}^{2} \geqslant 4$, which implies $$ \sum_{i=1}^{2 n} y_{i}^{2}=\sum_{j=1}^{n}\left(y_{2 j-1}^{2}+y_{2 j}^{2}\right) \geqslant 4 n $$ Combining (2) and (3), we get $$ 4 n \leqslant \sum_{i=1}^{2 n} y_{i}^{2}=4 n^{2}-4 Z $$ Hence, $Z \leqslant n(n-1)$. If we set $x_{i}=1$ for odd indices $i$ and $x_{i}=-1$ for even indices $i$, then we obtain equality in (3) (and thus in (4)). Therefore, the maximum possible value of $Z$ is $n(n-1)$, as desired. Comment 1. $Z=n(n-1)$ can be achieved by several other examples. In particular, $x_{i}$ needs not be $\pm 1$. For instance, setting $x_{i}=(-1)^{i}$ for all $2 \leqslant i \leqslant 2 n$, we find that the coefficient of $x_{1}$ in $Z$ is 0 . Therefore, $x_{1}$ can be chosen arbitrarily in the interval $[-1,1]$. Nevertheless, if $x_{i} \in\{-1,1\}$ for all $i=1,2, \ldots, 2 n$, then the equality $Z=n(n-1)$ holds only when $\left(y_{1}, y_{2}, \ldots, y_{2 n}\right)=(0, \pm 2,0, \pm 2, \ldots, 0, \pm 2)$ or $( \pm 2,0, \pm 2,0, \ldots, \pm 2,0)$. In each case, we can reconstruct $x_{i}$ accordingly. The sum $\sum_{i=1}^{2 n} x_{i}$ in the optimal cases needs not be 0 , but it must equal 0 or $\pm 2$. Comment 2. Several variations in setting up the auxiliary variables are possible. For instance, one may let $x_{2 n+i}=-x_{i}$ and $y_{i}^{\prime}=x_{i}+x_{i+1}+\cdots+x_{i+n-1}$ for any $1 \leqslant i \leqslant 2 n$. Similarly to Solution 1 , we obtain $Y:=y_{1}^{\prime 2}+y_{2}^{\prime 2}+\cdots+y_{2 n}^{\prime 2}=2 n^{2}-2 Z$. Then, it suffices to show that $Y \geqslant 2 n$. If $n$ is odd, then each $y_{i}^{\prime}$ is odd, and so $y_{i}^{\prime 2} \geqslant 1$. If $n$ is even, then each $y_{i}^{\prime}$ is even. We can check that at least one of $y_{i}^{\prime}, y_{i+1}^{\prime}, y_{n+i}^{\prime}$, and $y_{n+i+1}^{\prime}$ is nonzero, so that $y_{i}^{\prime 2}+y_{i+1}^{\prime 2}+y_{n+i}^{\prime 2}+y_{n+i+1}^{\prime 2} \geqslant 4$; summing these up for $i=1,3, \ldots, n-1$ yields $Y \geqslant 2 n$.
|
{
"resource_path": "IMO/segmented/en-IMO2015SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
31ebab3e-859f-59ac-8276-ceb3c8d3a936
| 24,673
|
For a finite set $A$ of positive integers, we call a partition of $A$ into two disjoint nonempty subsets $A_{1}$ and $A_{2}$ good if the least common multiple of the elements in $A_{1}$ is equal to the greatest common divisor of the elements in $A_{2}$. Determine the minimum value of $n$ such that there exists a set of $n$ positive integers with exactly 2015 good partitions. (Ukraine) Answer. 3024.
|
Let $A=\left\{a_{1}, a_{2}, \ldots, a_{n}\right\}$, where $a_{1}<a_{2}<\cdots<a_{n}$. For a finite nonempty set $B$ of positive integers, denote by $\operatorname{lcm} B$ and $\operatorname{gcd} B$ the least common multiple and the greatest common divisor of the elements in $B$, respectively. Consider any good partition $\left(A_{1}, A_{2}\right)$ of $A$. By definition, $\operatorname{lcm} A_{1}=d=\operatorname{gcd} A_{2}$ for some positive integer $d$. For any $a_{i} \in A_{1}$ and $a_{j} \in A_{2}$, we have $a_{i} \leqslant d \leqslant a_{j}$. Therefore, we have $A_{1}=\left\{a_{1}, a_{2}, \ldots, a_{k}\right\}$ and $A_{2}=\left\{a_{k+1}, a_{k+2}, \ldots, a_{n}\right\}$ for some $k$ with $1 \leqslant k<n$. Hence, each good partition is determined by an element $a_{k}$, where $1 \leqslant k<n$. We call such $a_{k}$ partitioning. It is convenient now to define $\ell_{k}=\operatorname{lcm}\left(a_{1}, a_{2}, \ldots, a_{k}\right)$ and $g_{k}=\operatorname{gcd}\left(a_{k+1}, a_{k+2}, \ldots, a_{n}\right)$ for $1 \leqslant k \leqslant n-1$. So $a_{k}$ is partitioning exactly when $\ell_{k}=g_{k}$. We proceed by proving some properties of partitioning elements, using the following claim. Claim. If $a_{k-1}$ and $a_{k}$ are partitioning where $2 \leqslant k \leqslant n-1$, then $g_{k-1}=g_{k}=a_{k}$. Proof. Assume that $a_{k-1}$ and $a_{k}$ are partitioning. Since $\ell_{k-1}=g_{k-1}$, we have $\ell_{k-1} \mid a_{k}$. Therefore, $g_{k}=\ell_{k}=\operatorname{lcm}\left(\ell_{k-1}, a_{k}\right)=a_{k}$, and $g_{k-1}=\operatorname{gcd}\left(a_{k}, g_{k}\right)=a_{k}$, as desired.  Proof. Suppose, to the contrary, that all three numbers $a_{k-1}, a_{k}$, and $a_{k+1}$ are partitioning. The claim yields that $a_{k+1}=g_{k}=a_{k}$, a contradiction. Property 2. The elements $a_{1}$ and $a_{2}$ cannot be simultaneously partitioning. Also, $a_{n-2}$ and $\overline{a_{n-1} \text { cannot be simultaneously partitioning }}$ Proof. Assume that $a_{1}$ and $a_{2}$ are partitioning. By the claim, it follows that $a_{2}=g_{1}=\ell_{1}=$ $\operatorname{lcm}\left(a_{1}\right)=a_{1}$, a contradiction. Similarly, assume that $a_{n-2}$ and $a_{n-1}$ are partitioning. The claim yields that $a_{n-1}=g_{n-1}=$ $\operatorname{gcd}\left(a_{n}\right)=a_{n}$, a contradiction. Now let $A$ be an $n$-element set with exactly 2015 good partitions. Clearly, we have $n \geqslant 5$. Using Property 2, we find that there is at most one partitioning element in each of $\left\{a_{1}, a_{2}\right\}$ and $\left\{a_{n-2}, a_{n-1}\right\}$. By Property 1 , there are at least $\left\lfloor\frac{n-5}{3}\right\rfloor$ non-partitioning elements in $\left\{a_{3}, a_{4}, \ldots, a_{n-3}\right\}$. Therefore, there are at most $(n-1)-2-\left\lfloor\frac{n-5}{3}\right\rfloor=\left\lceil\frac{2(n-2)}{3}\right\rceil$ partitioning elements in $A$. Thus, $\left\lceil\frac{2(n-2)}{3}\right\rceil \geqslant 2015$, which implies that $n \geqslant 3024$. Finally, we show that there exists a set of 3024 positive integers with exactly 2015 partitioning elements. Indeed, in the set $A=\left\{2 \cdot 6^{i}, 3 \cdot 6^{i}, 6^{i+1} \mid 0 \leqslant i \leqslant 1007\right\}$, each element of the form $3 \cdot 6^{i}$ or $6^{i}$, except $6^{1008}$, is partitioning. Therefore, the minimum possible value of $n$ is 3024 . Comment. Here we will work out the general case when 2015 is replaced by an arbitrary positive integer $m$. Note that the bound $\left\lceil\frac{2(n-2)}{3}\right\rceil \geqslant m$ obtained in the solution is, in fact, true for any positive integers $m$ and $n$. Using this bound, one can find that $n \geqslant\left\lceil\frac{3 m}{2}\right\rceil+1$. To show that the bound is sharp, one constructs a set of $\left\lceil\frac{3 m}{2}\right\rceil+1$ elements with exactly $m$ good partitions. Indeed, the minimum is attained on the set $\left\{6^{i}, 2 \cdot 6^{i}, 3 \cdot 6^{i} \mid 0 \leqslant i \leqslant t-1\right\} \cup\left\{6^{t}\right\}$ for every even $m=2 t$, and $\left\{2 \cdot 6^{i}, 3 \cdot 6^{i}, 6^{i+1} \mid 0 \leqslant i \leqslant t-1\right\}$ for every odd $m=2 t-1$.
|
3024
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
For a finite set $A$ of positive integers, we call a partition of $A$ into two disjoint nonempty subsets $A_{1}$ and $A_{2}$ good if the least common multiple of the elements in $A_{1}$ is equal to the greatest common divisor of the elements in $A_{2}$. Determine the minimum value of $n$ such that there exists a set of $n$ positive integers with exactly 2015 good partitions. (Ukraine) Answer. 3024.
|
Let $A=\left\{a_{1}, a_{2}, \ldots, a_{n}\right\}$, where $a_{1}<a_{2}<\cdots<a_{n}$. For a finite nonempty set $B$ of positive integers, denote by $\operatorname{lcm} B$ and $\operatorname{gcd} B$ the least common multiple and the greatest common divisor of the elements in $B$, respectively. Consider any good partition $\left(A_{1}, A_{2}\right)$ of $A$. By definition, $\operatorname{lcm} A_{1}=d=\operatorname{gcd} A_{2}$ for some positive integer $d$. For any $a_{i} \in A_{1}$ and $a_{j} \in A_{2}$, we have $a_{i} \leqslant d \leqslant a_{j}$. Therefore, we have $A_{1}=\left\{a_{1}, a_{2}, \ldots, a_{k}\right\}$ and $A_{2}=\left\{a_{k+1}, a_{k+2}, \ldots, a_{n}\right\}$ for some $k$ with $1 \leqslant k<n$. Hence, each good partition is determined by an element $a_{k}$, where $1 \leqslant k<n$. We call such $a_{k}$ partitioning. It is convenient now to define $\ell_{k}=\operatorname{lcm}\left(a_{1}, a_{2}, \ldots, a_{k}\right)$ and $g_{k}=\operatorname{gcd}\left(a_{k+1}, a_{k+2}, \ldots, a_{n}\right)$ for $1 \leqslant k \leqslant n-1$. So $a_{k}$ is partitioning exactly when $\ell_{k}=g_{k}$. We proceed by proving some properties of partitioning elements, using the following claim. Claim. If $a_{k-1}$ and $a_{k}$ are partitioning where $2 \leqslant k \leqslant n-1$, then $g_{k-1}=g_{k}=a_{k}$. Proof. Assume that $a_{k-1}$ and $a_{k}$ are partitioning. Since $\ell_{k-1}=g_{k-1}$, we have $\ell_{k-1} \mid a_{k}$. Therefore, $g_{k}=\ell_{k}=\operatorname{lcm}\left(\ell_{k-1}, a_{k}\right)=a_{k}$, and $g_{k-1}=\operatorname{gcd}\left(a_{k}, g_{k}\right)=a_{k}$, as desired.  Proof. Suppose, to the contrary, that all three numbers $a_{k-1}, a_{k}$, and $a_{k+1}$ are partitioning. The claim yields that $a_{k+1}=g_{k}=a_{k}$, a contradiction. Property 2. The elements $a_{1}$ and $a_{2}$ cannot be simultaneously partitioning. Also, $a_{n-2}$ and $\overline{a_{n-1} \text { cannot be simultaneously partitioning }}$ Proof. Assume that $a_{1}$ and $a_{2}$ are partitioning. By the claim, it follows that $a_{2}=g_{1}=\ell_{1}=$ $\operatorname{lcm}\left(a_{1}\right)=a_{1}$, a contradiction. Similarly, assume that $a_{n-2}$ and $a_{n-1}$ are partitioning. The claim yields that $a_{n-1}=g_{n-1}=$ $\operatorname{gcd}\left(a_{n}\right)=a_{n}$, a contradiction. Now let $A$ be an $n$-element set with exactly 2015 good partitions. Clearly, we have $n \geqslant 5$. Using Property 2, we find that there is at most one partitioning element in each of $\left\{a_{1}, a_{2}\right\}$ and $\left\{a_{n-2}, a_{n-1}\right\}$. By Property 1 , there are at least $\left\lfloor\frac{n-5}{3}\right\rfloor$ non-partitioning elements in $\left\{a_{3}, a_{4}, \ldots, a_{n-3}\right\}$. Therefore, there are at most $(n-1)-2-\left\lfloor\frac{n-5}{3}\right\rfloor=\left\lceil\frac{2(n-2)}{3}\right\rceil$ partitioning elements in $A$. Thus, $\left\lceil\frac{2(n-2)}{3}\right\rceil \geqslant 2015$, which implies that $n \geqslant 3024$. Finally, we show that there exists a set of 3024 positive integers with exactly 2015 partitioning elements. Indeed, in the set $A=\left\{2 \cdot 6^{i}, 3 \cdot 6^{i}, 6^{i+1} \mid 0 \leqslant i \leqslant 1007\right\}$, each element of the form $3 \cdot 6^{i}$ or $6^{i}$, except $6^{1008}$, is partitioning. Therefore, the minimum possible value of $n$ is 3024 . Comment. Here we will work out the general case when 2015 is replaced by an arbitrary positive integer $m$. Note that the bound $\left\lceil\frac{2(n-2)}{3}\right\rceil \geqslant m$ obtained in the solution is, in fact, true for any positive integers $m$ and $n$. Using this bound, one can find that $n \geqslant\left\lceil\frac{3 m}{2}\right\rceil+1$. To show that the bound is sharp, one constructs a set of $\left\lceil\frac{3 m}{2}\right\rceil+1$ elements with exactly $m$ good partitions. Indeed, the minimum is attained on the set $\left\{6^{i}, 2 \cdot 6^{i}, 3 \cdot 6^{i} \mid 0 \leqslant i \leqslant t-1\right\} \cup\left\{6^{t}\right\}$ for every even $m=2 t$, and $\left\{2 \cdot 6^{i}, 3 \cdot 6^{i}, 6^{i+1} \mid 0 \leqslant i \leqslant t-1\right\}$ for every odd $m=2 t-1$.
|
{
"resource_path": "IMO/segmented/en-IMO2015SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
decafbe8-3c52-5965-a630-4efd59b0f583
| 24,691
|
Let $A B C$ be an acute triangle, and let $M$ be the midpoint of $A C$. A circle $\omega$ passing through $B$ and $M$ meets the sides $A B$ and $B C$ again at $P$ and $Q$, respectively. Let $T$ be the point such that the quadrilateral $B P T Q$ is a parallelogram. Suppose that $T$ lies on the circumcircle of the triangle $A B C$. Determine all possible values of $B T / B M$. (Russia) Answer. $\sqrt{2}$.
|
Let $S$ be the center of the parallelogram $B P T Q$, and let $B^{\prime} \neq B$ be the point on the ray $B M$ such that $B M=M B^{\prime}$ (see Figure 1). It follows that $A B C B^{\prime}$ is a parallelogram. Then, $\angle A B B^{\prime}=\angle P Q M$ and $\angle B B^{\prime} A=\angle B^{\prime} B C=\angle M P Q$, and so the triangles $A B B^{\prime}$ and $M Q P$ are similar. It follows that $A M$ and $M S$ are corresponding medians in these triangles. Hence, $$ \angle S M P=\angle B^{\prime} A M=\angle B C A=\angle B T A . $$ Since $\angle A C T=\angle P B T$ and $\angle T A C=\angle T B C=\angle B T P$, the triangles $T C A$ and $P B T$ are similar. Again, as $T M$ and $P S$ are corresponding medians in these triangles, we have $$ \angle M T A=\angle T P S=\angle B Q P=\angle B M P . $$ Now we deal separately with two cases. Case 1. $\quad S$ does not lie on $B M$. Since the configuration is symmetric between $A$ and $C$, we may assume that $S$ and $A$ lie on the same side with respect to the line $B M$. Applying (1) and (2), we get $$ \angle B M S=\angle B M P-\angle S M P=\angle M T A-\angle B T A=\angle M T B, $$ and so the triangles $B S M$ and $B M T$ are similar. We now have $B M^{2}=B S \cdot B T=B T^{2} / 2$, so $B T=\sqrt{2} B M$. Case 2. $\quad S$ lies on $B M$. It follows from (2) that $\angle B C A=\angle M T A=\angle B Q P=\angle B M P$ (see Figure 2). Thus, $P Q \| A C$ and $P M \| A T$. Hence, $B S / B M=B P / B A=B M / B T$, so $B T^{2}=2 B M^{2}$ and $B T=\sqrt{2} B M$.  Figure 1  Figure 2 Comment 1. Here is another way to show that the triangles $B S M$ and $B M T$ are similar. Denote by $\Omega$ the circumcircle of the triangle $A B C$. Let $R$ be the second point of intersection of $\omega$ and $\Omega$, and let $\tau$ be the spiral similarity centered at $R$ mapping $\omega$ to $\Omega$. Then, one may show that $\tau$ maps each point $X$ on $\omega$ to a point $Y$ on $\Omega$ such that $B, X$, and $Y$ are collinear (see Figure 3). If we let $K$ and $L$ be the second points of intersection of $B M$ with $\Omega$ and of $B T$ with $\omega$, respectively, then it follows that the triangle $M K T$ is the image of $S M L$ under $\tau$. We now obtain $\angle B S M=\angle T M B$, which implies the desired result.  Figure 3  Figure 4
|
\sqrt{2}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $A B C$ be an acute triangle, and let $M$ be the midpoint of $A C$. A circle $\omega$ passing through $B$ and $M$ meets the sides $A B$ and $B C$ again at $P$ and $Q$, respectively. Let $T$ be the point such that the quadrilateral $B P T Q$ is a parallelogram. Suppose that $T$ lies on the circumcircle of the triangle $A B C$. Determine all possible values of $B T / B M$. (Russia) Answer. $\sqrt{2}$.
|
Let $S$ be the center of the parallelogram $B P T Q$, and let $B^{\prime} \neq B$ be the point on the ray $B M$ such that $B M=M B^{\prime}$ (see Figure 1). It follows that $A B C B^{\prime}$ is a parallelogram. Then, $\angle A B B^{\prime}=\angle P Q M$ and $\angle B B^{\prime} A=\angle B^{\prime} B C=\angle M P Q$, and so the triangles $A B B^{\prime}$ and $M Q P$ are similar. It follows that $A M$ and $M S$ are corresponding medians in these triangles. Hence, $$ \angle S M P=\angle B^{\prime} A M=\angle B C A=\angle B T A . $$ Since $\angle A C T=\angle P B T$ and $\angle T A C=\angle T B C=\angle B T P$, the triangles $T C A$ and $P B T$ are similar. Again, as $T M$ and $P S$ are corresponding medians in these triangles, we have $$ \angle M T A=\angle T P S=\angle B Q P=\angle B M P . $$ Now we deal separately with two cases. Case 1. $\quad S$ does not lie on $B M$. Since the configuration is symmetric between $A$ and $C$, we may assume that $S$ and $A$ lie on the same side with respect to the line $B M$. Applying (1) and (2), we get $$ \angle B M S=\angle B M P-\angle S M P=\angle M T A-\angle B T A=\angle M T B, $$ and so the triangles $B S M$ and $B M T$ are similar. We now have $B M^{2}=B S \cdot B T=B T^{2} / 2$, so $B T=\sqrt{2} B M$. Case 2. $\quad S$ lies on $B M$. It follows from (2) that $\angle B C A=\angle M T A=\angle B Q P=\angle B M P$ (see Figure 2). Thus, $P Q \| A C$ and $P M \| A T$. Hence, $B S / B M=B P / B A=B M / B T$, so $B T^{2}=2 B M^{2}$ and $B T=\sqrt{2} B M$.  Figure 1  Figure 2 Comment 1. Here is another way to show that the triangles $B S M$ and $B M T$ are similar. Denote by $\Omega$ the circumcircle of the triangle $A B C$. Let $R$ be the second point of intersection of $\omega$ and $\Omega$, and let $\tau$ be the spiral similarity centered at $R$ mapping $\omega$ to $\Omega$. Then, one may show that $\tau$ maps each point $X$ on $\omega$ to a point $Y$ on $\Omega$ such that $B, X$, and $Y$ are collinear (see Figure 3). If we let $K$ and $L$ be the second points of intersection of $B M$ with $\Omega$ and of $B T$ with $\omega$, respectively, then it follows that the triangle $M K T$ is the image of $S M L$ under $\tau$. We now obtain $\angle B S M=\angle T M B$, which implies the desired result.  Figure 3  Figure 4
|
{
"resource_path": "IMO/segmented/en-IMO2015SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
779f8772-73e8-5cb0-998a-42041fcafdbc
| 24,706
|
Find the smallest real constant $C$ such that for any positive real numbers $a_{1}, a_{2}, a_{3}, a_{4}$ and $a_{5}$ (not necessarily distinct), one can always choose distinct subscripts $i, j, k$ and $l$ such that $$ \left|\frac{a_{i}}{a_{j}}-\frac{a_{k}}{a_{l}}\right| \leqslant C $$
|
We first show that $C \leqslant \frac{1}{2}$. For any positive real numbers $a_{1} \leqslant a_{2} \leqslant a_{3} \leqslant a_{4} \leqslant a_{5}$, consider the five fractions $$ \frac{a_{1}}{a_{2}}, \frac{a_{3}}{a_{4}}, \frac{a_{1}}{a_{5}}, \frac{a_{2}}{a_{3}}, \frac{a_{4}}{a_{5}} . $$ Each of them lies in the interval $(0,1]$. Therefore, by the Pigeonhole Principle, at least three of them must lie in $\left(0, \frac{1}{2}\right]$ or lie in $\left(\frac{1}{2}, 1\right]$ simultaneously. In particular, there must be two consecutive terms in (2) which belong to an interval of length $\frac{1}{2}$ (here, we regard $\frac{a_{1}}{a_{2}}$ and $\frac{a_{4}}{a_{5}}$ as consecutive). In other words, the difference of these two fractions is less than $\frac{1}{2}$. As the indices involved in these two fractions are distinct, we can choose them to be $i, j, k, l$ and conclude that $C \leqslant \frac{1}{2}$. Next, we show that $C=\frac{1}{2}$ is best possible. Consider the numbers $1,2,2,2, n$ where $n$ is a large real number. The fractions formed by two of these numbers in ascending order are $\frac{1}{n}, \frac{2}{n}, \frac{1}{2}, \frac{2}{2}, \frac{2}{1}, \frac{n}{2}, \frac{n}{1}$. Since the indices $i, j, k, l$ are distinct, $\frac{1}{n}$ and $\frac{2}{n}$ cannot be chosen simultaneously. Therefore the minimum value of the left-hand side of (1) is $\frac{1}{2}-\frac{2}{n}$. When $n$ tends to infinity, this value approaches $\frac{1}{2}$, and so $C$ cannot be less than $\frac{1}{2}$. These conclude that $C=\frac{1}{2}$ is the smallest possible choice. Comment. The conclusion still holds if $a_{1}, a_{2}, \ldots, a_{5}$ are pairwise distinct, since in the construction, we may replace the 2's by real numbers sufficiently close to 2 . There are two possible simplifications for this problem: (i) the answer $C=\frac{1}{2}$ is given to the contestants; or (ii) simply ask the contestants to prove the inequality (1) for $C=\frac{1}{2}$.
|
\frac{1}{2}
|
Yes
|
Yes
|
math-word-problem
|
Inequalities
|
Find the smallest real constant $C$ such that for any positive real numbers $a_{1}, a_{2}, a_{3}, a_{4}$ and $a_{5}$ (not necessarily distinct), one can always choose distinct subscripts $i, j, k$ and $l$ such that $$ \left|\frac{a_{i}}{a_{j}}-\frac{a_{k}}{a_{l}}\right| \leqslant C $$
|
We first show that $C \leqslant \frac{1}{2}$. For any positive real numbers $a_{1} \leqslant a_{2} \leqslant a_{3} \leqslant a_{4} \leqslant a_{5}$, consider the five fractions $$ \frac{a_{1}}{a_{2}}, \frac{a_{3}}{a_{4}}, \frac{a_{1}}{a_{5}}, \frac{a_{2}}{a_{3}}, \frac{a_{4}}{a_{5}} . $$ Each of them lies in the interval $(0,1]$. Therefore, by the Pigeonhole Principle, at least three of them must lie in $\left(0, \frac{1}{2}\right]$ or lie in $\left(\frac{1}{2}, 1\right]$ simultaneously. In particular, there must be two consecutive terms in (2) which belong to an interval of length $\frac{1}{2}$ (here, we regard $\frac{a_{1}}{a_{2}}$ and $\frac{a_{4}}{a_{5}}$ as consecutive). In other words, the difference of these two fractions is less than $\frac{1}{2}$. As the indices involved in these two fractions are distinct, we can choose them to be $i, j, k, l$ and conclude that $C \leqslant \frac{1}{2}$. Next, we show that $C=\frac{1}{2}$ is best possible. Consider the numbers $1,2,2,2, n$ where $n$ is a large real number. The fractions formed by two of these numbers in ascending order are $\frac{1}{n}, \frac{2}{n}, \frac{1}{2}, \frac{2}{2}, \frac{2}{1}, \frac{n}{2}, \frac{n}{1}$. Since the indices $i, j, k, l$ are distinct, $\frac{1}{n}$ and $\frac{2}{n}$ cannot be chosen simultaneously. Therefore the minimum value of the left-hand side of (1) is $\frac{1}{2}-\frac{2}{n}$. When $n$ tends to infinity, this value approaches $\frac{1}{2}$, and so $C$ cannot be less than $\frac{1}{2}$. These conclude that $C=\frac{1}{2}$ is the smallest possible choice. Comment. The conclusion still holds if $a_{1}, a_{2}, \ldots, a_{5}$ are pairwise distinct, since in the construction, we may replace the 2's by real numbers sufficiently close to 2 . There are two possible simplifications for this problem: (i) the answer $C=\frac{1}{2}$ is given to the contestants; or (ii) simply ask the contestants to prove the inequality (1) for $C=\frac{1}{2}$.
|
{
"resource_path": "IMO/segmented/en-IMO2016SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
f159e380-3446-5a7a-9e8c-f59f6eab18df
| 24,732
|
The equation $$ (x-1)(x-2) \cdots(x-2016)=(x-1)(x-2) \cdots(x-2016) $$ is written on the board. One tries to erase some linear factors from both sides so that each side still has at least one factor, and the resulting equation has no real roots. Find the least number of linear factors one needs to erase to achieve this.
|
Since there are 2016 common linear factors on both sides, we need to erase at least 2016 factors. We claim that the equation has no real roots if we erase all factors $(x-k)$ on the left-hand side with $k \equiv 2,3(\bmod 4)$, and all factors $(x-m)$ on the right-hand side with $m \equiv 0,1(\bmod 4)$. Therefore, it suffices to show that no real number $x$ satisfies $$ \prod_{j=0}^{503}(x-4 j-1)(x-4 j-4)=\prod_{j=0}^{503}(x-4 j-2)(x-4 j-3) $$ - Case 1. $x=1,2, \ldots, 2016$. In this case, one side of (1) is zero while the other side is not. This shows $x$ cannot satisfy (1). - Case 2. $4 k+1<x<4 k+2$ or $4 k+3<x<4 k+4$ for some $k=0,1, \ldots, 503$. For $j=0,1, \ldots, 503$ with $j \neq k$, the product $(x-4 j-1)(x-4 j-4)$ is positive. For $j=k$, the product $(x-4 k-1)(x-4 k-4)$ is negative. This shows the left-hand side of (1) is negative. On the other hand, each product $(x-4 j-2)(x-4 j-3)$ on the right-hand side of (1) is positive. This yields a contradiction. - Case 3. $x<1$ or $x>2016$ or $4 k<x<4 k+1$ for some $k=1,2, \ldots, 503$. The equation (1) can be rewritten as $$ 1=\prod_{j=0}^{503} \frac{(x-4 j-1)(x-4 j-4)}{(x-4 j-2)(x-4 j-3)}=\prod_{j=0}^{503}\left(1-\frac{2}{(x-4 j-2)(x-4 j-3)}\right) $$ Note that $(x-4 j-2)(x-4 j-3)>2$ for $0 \leqslant j \leqslant 503$ in this case. So each term in the product lies strictly between 0 and 1 , and the whole product must be less than 1 , which is impossible. - Case 4. $4 k+2<x<4 k+3$ for some $k=0,1, \ldots, 503$. This time we rewrite (1) as $$ \begin{aligned} 1 & =\frac{x-1}{x-2} \cdot \frac{x-2016}{x-2015} \prod_{j=1}^{503} \frac{(x-4 j)(x-4 j-1)}{(x-4 j+1)(x-4 j-2)} \\ & =\frac{x-1}{x-2} \cdot \frac{x-2016}{x-2015} \prod_{j=1}^{503}\left(1+\frac{2}{(x-4 j+1)(x-4 j-2)}\right) \end{aligned} $$ Clearly, $\frac{x-1}{x-2}$ and $\frac{x-2016}{x-2015}$ are both greater than 1 . For the range of $x$ in this case, each term in the product is also greater than 1 . Then the right-hand side must be greater than 1 and hence a contradiction arises. From the four cases, we conclude that (1) has no real roots. Hence, the minimum number of linear factors to be erased is 2016. Comment. We discuss the general case when 2016 is replaced by a positive integer $n$. The above solution works equally well when $n$ is divisible by 4 . If $n \equiv 2(\bmod 4)$, one may leave $l(x)=(x-1)(x-2) \cdots\left(x-\frac{n}{2}\right)$ on the left-hand side and $r(x)=\left(x-\frac{n}{2}-1\right)\left(x-\frac{n}{2}-2\right) \cdots(x-n)$ on the right-hand side. One checks that for $x<\frac{n+1}{2}$, we have $|l(x)|<|r(x)|$, while for $x>\frac{n+1}{2}$, we have $|l(x)|>|r(x)|$. If $n \equiv 3(\bmod 4)$, one may leave $l(x)=(x-1)(x-2) \cdots\left(x-\frac{n+1}{2}\right)$ on the left-hand side and $r(x)=\left(x-\frac{n+3}{2}\right)\left(x-\frac{x+5}{2}\right) \cdots(x-n)$ on the right-hand side. For $x<1$ or $\frac{n+1}{2}<x<\frac{n+3}{2}$, we have $l(x)>0>r(x)$. For $1<x<\frac{n+1}{2}$, we have $|l(x)|<|r(x)|$. For $x>\frac{n+3}{2}$, we have $|l(x)|>|r(x)|$. If $n \equiv 1(\bmod 4)$, as the proposer mentioned, the situation is a bit more out of control. Since the construction for $n-1 \equiv 0(\bmod 4)$ works, the answer can be either $n$ or $n-1$. For $n=5$, we can leave the products $(x-1)(x-2)(x-3)(x-4)$ and $(x-5)$. For $n=9$, the only example that works is $l(x)=(x-1)(x-2)(x-9)$ and $r(x)=(x-3)(x-4) \cdots(x-8)$, while there seems to be no such partition for $n=13$.
|
2016
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
The equation $$ (x-1)(x-2) \cdots(x-2016)=(x-1)(x-2) \cdots(x-2016) $$ is written on the board. One tries to erase some linear factors from both sides so that each side still has at least one factor, and the resulting equation has no real roots. Find the least number of linear factors one needs to erase to achieve this.
|
Since there are 2016 common linear factors on both sides, we need to erase at least 2016 factors. We claim that the equation has no real roots if we erase all factors $(x-k)$ on the left-hand side with $k \equiv 2,3(\bmod 4)$, and all factors $(x-m)$ on the right-hand side with $m \equiv 0,1(\bmod 4)$. Therefore, it suffices to show that no real number $x$ satisfies $$ \prod_{j=0}^{503}(x-4 j-1)(x-4 j-4)=\prod_{j=0}^{503}(x-4 j-2)(x-4 j-3) $$ - Case 1. $x=1,2, \ldots, 2016$. In this case, one side of (1) is zero while the other side is not. This shows $x$ cannot satisfy (1). - Case 2. $4 k+1<x<4 k+2$ or $4 k+3<x<4 k+4$ for some $k=0,1, \ldots, 503$. For $j=0,1, \ldots, 503$ with $j \neq k$, the product $(x-4 j-1)(x-4 j-4)$ is positive. For $j=k$, the product $(x-4 k-1)(x-4 k-4)$ is negative. This shows the left-hand side of (1) is negative. On the other hand, each product $(x-4 j-2)(x-4 j-3)$ on the right-hand side of (1) is positive. This yields a contradiction. - Case 3. $x<1$ or $x>2016$ or $4 k<x<4 k+1$ for some $k=1,2, \ldots, 503$. The equation (1) can be rewritten as $$ 1=\prod_{j=0}^{503} \frac{(x-4 j-1)(x-4 j-4)}{(x-4 j-2)(x-4 j-3)}=\prod_{j=0}^{503}\left(1-\frac{2}{(x-4 j-2)(x-4 j-3)}\right) $$ Note that $(x-4 j-2)(x-4 j-3)>2$ for $0 \leqslant j \leqslant 503$ in this case. So each term in the product lies strictly between 0 and 1 , and the whole product must be less than 1 , which is impossible. - Case 4. $4 k+2<x<4 k+3$ for some $k=0,1, \ldots, 503$. This time we rewrite (1) as $$ \begin{aligned} 1 & =\frac{x-1}{x-2} \cdot \frac{x-2016}{x-2015} \prod_{j=1}^{503} \frac{(x-4 j)(x-4 j-1)}{(x-4 j+1)(x-4 j-2)} \\ & =\frac{x-1}{x-2} \cdot \frac{x-2016}{x-2015} \prod_{j=1}^{503}\left(1+\frac{2}{(x-4 j+1)(x-4 j-2)}\right) \end{aligned} $$ Clearly, $\frac{x-1}{x-2}$ and $\frac{x-2016}{x-2015}$ are both greater than 1 . For the range of $x$ in this case, each term in the product is also greater than 1 . Then the right-hand side must be greater than 1 and hence a contradiction arises. From the four cases, we conclude that (1) has no real roots. Hence, the minimum number of linear factors to be erased is 2016. Comment. We discuss the general case when 2016 is replaced by a positive integer $n$. The above solution works equally well when $n$ is divisible by 4 . If $n \equiv 2(\bmod 4)$, one may leave $l(x)=(x-1)(x-2) \cdots\left(x-\frac{n}{2}\right)$ on the left-hand side and $r(x)=\left(x-\frac{n}{2}-1\right)\left(x-\frac{n}{2}-2\right) \cdots(x-n)$ on the right-hand side. One checks that for $x<\frac{n+1}{2}$, we have $|l(x)|<|r(x)|$, while for $x>\frac{n+1}{2}$, we have $|l(x)|>|r(x)|$. If $n \equiv 3(\bmod 4)$, one may leave $l(x)=(x-1)(x-2) \cdots\left(x-\frac{n+1}{2}\right)$ on the left-hand side and $r(x)=\left(x-\frac{n+3}{2}\right)\left(x-\frac{x+5}{2}\right) \cdots(x-n)$ on the right-hand side. For $x<1$ or $\frac{n+1}{2}<x<\frac{n+3}{2}$, we have $l(x)>0>r(x)$. For $1<x<\frac{n+1}{2}$, we have $|l(x)|<|r(x)|$. For $x>\frac{n+3}{2}$, we have $|l(x)|>|r(x)|$. If $n \equiv 1(\bmod 4)$, as the proposer mentioned, the situation is a bit more out of control. Since the construction for $n-1 \equiv 0(\bmod 4)$ works, the answer can be either $n$ or $n-1$. For $n=5$, we can leave the products $(x-1)(x-2)(x-3)(x-4)$ and $(x-5)$. For $n=9$, the only example that works is $l(x)=(x-1)(x-2)(x-9)$ and $r(x)=(x-3)(x-4) \cdots(x-8)$, while there seems to be no such partition for $n=13$.
|
{
"resource_path": "IMO/segmented/en-IMO2016SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
ad72a2c6-a10e-5596-b233-7e5e38161411
| 24,745
|
Determine the largest real number $a$ such that for all $n \geqslant 1$ and for all real numbers $x_{0}, x_{1}, \ldots, x_{n}$ satisfying $0=x_{0}<x_{1}<x_{2}<\cdots<x_{n}$, we have $$ \frac{1}{x_{1}-x_{0}}+\frac{1}{x_{2}-x_{1}}+\cdots+\frac{1}{x_{n}-x_{n-1}} \geqslant a\left(\frac{2}{x_{1}}+\frac{3}{x_{2}}+\cdots+\frac{n+1}{x_{n}}\right) . $$
|
We first show that $a=\frac{4}{9}$ is admissible. For each $2 \leqslant k \leqslant n$, by the CauchySchwarz Inequality, we have $$ \left(x_{k-1}+\left(x_{k}-x_{k-1}\right)\right)\left(\frac{(k-1)^{2}}{x_{k-1}}+\frac{3^{2}}{x_{k}-x_{k-1}}\right) \geqslant(k-1+3)^{2}, $$ which can be rewritten as $$ \frac{9}{x_{k}-x_{k-1}} \geqslant \frac{(k+2)^{2}}{x_{k}}-\frac{(k-1)^{2}}{x_{k-1}} $$ Summing (2) over $k=2,3, \ldots, n$ and adding $\frac{9}{x_{1}}$ to both sides, we have $$ 9 \sum_{k=1}^{n} \frac{1}{x_{k}-x_{k-1}} \geqslant 4 \sum_{k=1}^{n} \frac{k+1}{x_{k}}+\frac{n^{2}}{x_{n}}>4 \sum_{k=1}^{n} \frac{k+1}{x_{k}} . $$ This shows (1) holds for $a=\frac{4}{9}$. Next, we show that $a=\frac{4}{9}$ is the optimal choice. Consider the sequence defined by $x_{0}=0$ and $x_{k}=x_{k-1}+k(k+1)$ for $k \geqslant 1$, that is, $x_{k}=\frac{1}{3} k(k+1)(k+2)$. Then the left-hand side of (1) equals $$ \sum_{k=1}^{n} \frac{1}{k(k+1)}=\sum_{k=1}^{n}\left(\frac{1}{k}-\frac{1}{k+1}\right)=1-\frac{1}{n+1} $$ while the right-hand side equals $$ a \sum_{k=1}^{n} \frac{k+1}{x_{k}}=3 a \sum_{k=1}^{n} \frac{1}{k(k+2)}=\frac{3}{2} a \sum_{k=1}^{n}\left(\frac{1}{k}-\frac{1}{k+2}\right)=\frac{3}{2}\left(1+\frac{1}{2}-\frac{1}{n+1}-\frac{1}{n+2}\right) a . $$ When $n$ tends to infinity, the left-hand side tends to 1 while the right-hand side tends to $\frac{9}{4} a$. Therefore $a$ has to be at most $\frac{4}{9}$. Hence the largest value of $a$ is $\frac{4}{9}$.
|
\frac{4}{9}
|
Yes
|
Yes
|
math-word-problem
|
Inequalities
|
Determine the largest real number $a$ such that for all $n \geqslant 1$ and for all real numbers $x_{0}, x_{1}, \ldots, x_{n}$ satisfying $0=x_{0}<x_{1}<x_{2}<\cdots<x_{n}$, we have $$ \frac{1}{x_{1}-x_{0}}+\frac{1}{x_{2}-x_{1}}+\cdots+\frac{1}{x_{n}-x_{n-1}} \geqslant a\left(\frac{2}{x_{1}}+\frac{3}{x_{2}}+\cdots+\frac{n+1}{x_{n}}\right) . $$
|
We first show that $a=\frac{4}{9}$ is admissible. For each $2 \leqslant k \leqslant n$, by the CauchySchwarz Inequality, we have $$ \left(x_{k-1}+\left(x_{k}-x_{k-1}\right)\right)\left(\frac{(k-1)^{2}}{x_{k-1}}+\frac{3^{2}}{x_{k}-x_{k-1}}\right) \geqslant(k-1+3)^{2}, $$ which can be rewritten as $$ \frac{9}{x_{k}-x_{k-1}} \geqslant \frac{(k+2)^{2}}{x_{k}}-\frac{(k-1)^{2}}{x_{k-1}} $$ Summing (2) over $k=2,3, \ldots, n$ and adding $\frac{9}{x_{1}}$ to both sides, we have $$ 9 \sum_{k=1}^{n} \frac{1}{x_{k}-x_{k-1}} \geqslant 4 \sum_{k=1}^{n} \frac{k+1}{x_{k}}+\frac{n^{2}}{x_{n}}>4 \sum_{k=1}^{n} \frac{k+1}{x_{k}} . $$ This shows (1) holds for $a=\frac{4}{9}$. Next, we show that $a=\frac{4}{9}$ is the optimal choice. Consider the sequence defined by $x_{0}=0$ and $x_{k}=x_{k-1}+k(k+1)$ for $k \geqslant 1$, that is, $x_{k}=\frac{1}{3} k(k+1)(k+2)$. Then the left-hand side of (1) equals $$ \sum_{k=1}^{n} \frac{1}{k(k+1)}=\sum_{k=1}^{n}\left(\frac{1}{k}-\frac{1}{k+1}\right)=1-\frac{1}{n+1} $$ while the right-hand side equals $$ a \sum_{k=1}^{n} \frac{k+1}{x_{k}}=3 a \sum_{k=1}^{n} \frac{1}{k(k+2)}=\frac{3}{2} a \sum_{k=1}^{n}\left(\frac{1}{k}-\frac{1}{k+2}\right)=\frac{3}{2}\left(1+\frac{1}{2}-\frac{1}{n+1}-\frac{1}{n+2}\right) a . $$ When $n$ tends to infinity, the left-hand side tends to 1 while the right-hand side tends to $\frac{9}{4} a$. Therefore $a$ has to be at most $\frac{4}{9}$. Hence the largest value of $a$ is $\frac{4}{9}$.
|
{
"resource_path": "IMO/segmented/en-IMO2016SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
51293bac-61fe-52a1-92bc-b3e6de848b7f
| 24,754
|
Let $n \geqslant 3$ be a positive integer. Find the maximum number of diagonals of a regular $n$-gon one can select, so that any two of them do not intersect in the interior or they are perpendicular to each other.
|
We consider two cases according to the parity of $n$. - Case 1. $n$ is odd. We first claim that no pair of diagonals is perpendicular. Suppose $A, B, C, D$ are vertices where $A B$ and $C D$ are perpendicular, and let $E$ be the vertex lying on the perpendicular bisector of $A B$. Let $E^{\prime}$ be the opposite point of $E$ on the circumcircle of the regular polygon. Since $E C=E^{\prime} D$ and $C, D, E$ are vertices of the regular polygon, $E^{\prime}$ should also belong to the polygon. This contradicts the fact that a regular polygon with an odd number of vertices does not contain opposite points on the circumcircle.  Therefore in the odd case we can only select diagonals which do not intersect. In the maximal case these diagonals should divide the regular $n$-gon into $n-2$ triangles, so we can select at most $n-3$ diagonals. This can be done, for example, by selecting all diagonals emanated from a particular vertex. - Case 2. $n$ is even. If there is no intersection, then the proof in the odd case works. Suppose there are two perpendicular diagonals selected. We consider the set $S$ of all selected diagonals parallel to one of them which intersect with some selected diagonals. Suppose $S$ contains $k$ diagonals and the number of distinct endpoints of the $k$ diagonals is $l$. Firstly, consider the longest diagonal in one of the two directions in $S$. No other diagonal in $S$ can start from either endpoint of that diagonal, since otherwise it has to meet another longer diagonal in $S$. The same holds true for the other direction. Ignoring these two longest diagonals and their four endpoints, the remaining $k-2$ diagonals share $l-4$ endpoints where each endpoint can belong to at most two diagonals. This gives $2(l-4) \geqslant 2(k-2)$, so that $k \leqslant l-2$.  Consider a group of consecutive vertices of the regular $n$-gon so that each of the two outermost vertices is an endpoint of a diagonal in $S$, while the interior points are not. There are $l$ such groups. We label these groups $P_{1}, P_{2}, \ldots, P_{l}$ in this order. We claim that each selected diagonal outside $S$ must connect vertices of the same group $P_{i}$. Consider any diagonal $d$ joining vertices from distinct groups $P_{i}$ and $P_{j}$. Let $d_{1}$ and $d_{2}$ be two diagonals in $S$ each having one of the outermost points of $P_{i}$ as endpoint. Then $d$ must meet either $d_{1}, d_{2}$ or a diagonal in $S$ which is perpendicular to both $d_{1}$ and $d_{2}$. In any case $d$ should belong to $S$ by definition, which is a contradiction. Within the same group $P_{i}$, there are no perpendicular diagonals since the vertices belong to the same side of a diameter of the circumcircle. Hence there can be at most $\left|P_{i}\right|-2$ selected diagonals within $P_{i}$, including the one joining the two outermost points of $P_{i}$ when $\left|P_{i}\right|>2$. Therefore, the maximum number of diagonals selected is $$ \sum_{i=1}^{l}\left(\left|P_{i}\right|-2\right)+k=\sum_{i=1}^{l}\left|P_{i}\right|-2 l+k=(n+l)-2 l+k=n-l+k \leqslant n-2 $$ This upper bound can be attained as follows. We take any vertex $A$ and let $A^{\prime}$ be the vertex for which $A A^{\prime}$ is a diameter of the circumcircle. If we select all diagonals emanated from $A$ together with the diagonal $d^{\prime}$ joining the two neighbouring vertices of $A^{\prime}$, then the only pair of diagonals that meet each other is $A A^{\prime}$ and $d^{\prime}$, which are perpendicular to each other. In total we can take $n-2$ diagonals. 
|
n-2
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Let $n \geqslant 3$ be a positive integer. Find the maximum number of diagonals of a regular $n$-gon one can select, so that any two of them do not intersect in the interior or they are perpendicular to each other.
|
We consider two cases according to the parity of $n$. - Case 1. $n$ is odd. We first claim that no pair of diagonals is perpendicular. Suppose $A, B, C, D$ are vertices where $A B$ and $C D$ are perpendicular, and let $E$ be the vertex lying on the perpendicular bisector of $A B$. Let $E^{\prime}$ be the opposite point of $E$ on the circumcircle of the regular polygon. Since $E C=E^{\prime} D$ and $C, D, E$ are vertices of the regular polygon, $E^{\prime}$ should also belong to the polygon. This contradicts the fact that a regular polygon with an odd number of vertices does not contain opposite points on the circumcircle.  Therefore in the odd case we can only select diagonals which do not intersect. In the maximal case these diagonals should divide the regular $n$-gon into $n-2$ triangles, so we can select at most $n-3$ diagonals. This can be done, for example, by selecting all diagonals emanated from a particular vertex. - Case 2. $n$ is even. If there is no intersection, then the proof in the odd case works. Suppose there are two perpendicular diagonals selected. We consider the set $S$ of all selected diagonals parallel to one of them which intersect with some selected diagonals. Suppose $S$ contains $k$ diagonals and the number of distinct endpoints of the $k$ diagonals is $l$. Firstly, consider the longest diagonal in one of the two directions in $S$. No other diagonal in $S$ can start from either endpoint of that diagonal, since otherwise it has to meet another longer diagonal in $S$. The same holds true for the other direction. Ignoring these two longest diagonals and their four endpoints, the remaining $k-2$ diagonals share $l-4$ endpoints where each endpoint can belong to at most two diagonals. This gives $2(l-4) \geqslant 2(k-2)$, so that $k \leqslant l-2$.  Consider a group of consecutive vertices of the regular $n$-gon so that each of the two outermost vertices is an endpoint of a diagonal in $S$, while the interior points are not. There are $l$ such groups. We label these groups $P_{1}, P_{2}, \ldots, P_{l}$ in this order. We claim that each selected diagonal outside $S$ must connect vertices of the same group $P_{i}$. Consider any diagonal $d$ joining vertices from distinct groups $P_{i}$ and $P_{j}$. Let $d_{1}$ and $d_{2}$ be two diagonals in $S$ each having one of the outermost points of $P_{i}$ as endpoint. Then $d$ must meet either $d_{1}, d_{2}$ or a diagonal in $S$ which is perpendicular to both $d_{1}$ and $d_{2}$. In any case $d$ should belong to $S$ by definition, which is a contradiction. Within the same group $P_{i}$, there are no perpendicular diagonals since the vertices belong to the same side of a diameter of the circumcircle. Hence there can be at most $\left|P_{i}\right|-2$ selected diagonals within $P_{i}$, including the one joining the two outermost points of $P_{i}$ when $\left|P_{i}\right|>2$. Therefore, the maximum number of diagonals selected is $$ \sum_{i=1}^{l}\left(\left|P_{i}\right|-2\right)+k=\sum_{i=1}^{l}\left|P_{i}\right|-2 l+k=(n+l)-2 l+k=n-l+k \leqslant n-2 $$ This upper bound can be attained as follows. We take any vertex $A$ and let $A^{\prime}$ be the vertex for which $A A^{\prime}$ is a diameter of the circumcircle. If we select all diagonals emanated from $A$ together with the diagonal $d^{\prime}$ joining the two neighbouring vertices of $A^{\prime}$, then the only pair of diagonals that meet each other is $A A^{\prime}$ and $d^{\prime}$, which are perpendicular to each other. In total we can take $n-2$ diagonals. 
|
{
"resource_path": "IMO/segmented/en-IMO2016SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
0ec240f0-4397-5a2e-8cd3-b04da17ab997
| 24,769
|
Let $n$ be a positive integer. Determine the smallest positive integer $k$ with the following property: it is possible to mark $k$ cells on a $2 n \times 2 n$ board so that there exists a unique partition of the board into $1 \times 2$ and $2 \times 1$ dominoes, none of which contains two marked cells.
|
We first construct an example of marking $2 n$ cells satisfying the requirement. Label the rows and columns $1,2, \ldots, 2 n$ and label the cell in the $i$-th row and the $j$-th column $(i, j)$. For $i=1,2, \ldots, n$, we mark the cells $(i, i)$ and $(i, i+1)$. We claim that the required partition exists and is unique. The two diagonals of the board divide the board into four regions. Note that the domino covering cell $(1,1)$ must be vertical. This in turn shows that each domino covering $(2,2),(3,3), \ldots,(n, n)$ is vertical. By induction, the dominoes in the left region are all vertical. By rotational symmetry, the dominoes in the bottom region are horizontal, and so on. This shows that the partition exists and is unique.  It remains to show that this value of $k$ is the smallest possible. Assume that only $k<2 n$ cells are marked, and there exists a partition $P$ satisfying the requirement. It suffices to show there exists another desirable partition distinct from $P$. Let $d$ be the main diagonal of the board. Construct the following graph with edges of two colours. Its vertices are the cells of the board. Connect two vertices with a red edge if they belong to the same domino of $P$. Connect two vertices with a blue edge if their reflections in $d$ are connected by a red edge. It is possible that two vertices are connected by edges of both colours. Clearly, each vertex has both red and blue degrees equal to 1 . Thus the graph splits into cycles where the colours of edges in each cycle alternate (a cycle may have length 2). Consider any cell $c$ lying on the diagonal $d$. Its two edges are symmetrical with respect to $d$. Thus they connect $c$ to different cells. This shows $c$ belongs to a cycle $C(c)$ of length at least 4. Consider a part of this cycle $c_{0}, c_{1}, \ldots, c_{m}$ where $c_{0}=c$ and $m$ is the least positive integer such that $c_{m}$ lies on $d$. Clearly, $c_{m}$ is distinct from $c$. From the construction, the path symmetrical to this with respect to $d$ also lies in the graph, and so these paths together form $C(c)$. Hence, $C(c)$ contains exactly two cells from $d$. Then all $2 n$ cells in $d$ belong to $n$ cycles $C_{1}, C_{2}, \ldots, C_{n}$, each has length at least 4. By the Pigeonhole Principle, there exists a cycle $C_{i}$ containing at most one of the $k$ marked cells. We modify $P$ as follows. We remove all dominoes containing the vertices of $C_{i}$, which correspond to the red edges of $C_{i}$. Then we put the dominoes corresponding to the blue edges of $C_{i}$. Since $C_{i}$ has at least 4 vertices, the resultant partition $P^{\prime}$ is different from $P$. Clearly, no domino in $P^{\prime}$ contains two marked cells as $C_{i}$ contains at most one marked cell. This shows the partition is not unique and hence $k$ cannot be less than $2 n$.
|
2n
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Let $n$ be a positive integer. Determine the smallest positive integer $k$ with the following property: it is possible to mark $k$ cells on a $2 n \times 2 n$ board so that there exists a unique partition of the board into $1 \times 2$ and $2 \times 1$ dominoes, none of which contains two marked cells.
|
We first construct an example of marking $2 n$ cells satisfying the requirement. Label the rows and columns $1,2, \ldots, 2 n$ and label the cell in the $i$-th row and the $j$-th column $(i, j)$. For $i=1,2, \ldots, n$, we mark the cells $(i, i)$ and $(i, i+1)$. We claim that the required partition exists and is unique. The two diagonals of the board divide the board into four regions. Note that the domino covering cell $(1,1)$ must be vertical. This in turn shows that each domino covering $(2,2),(3,3), \ldots,(n, n)$ is vertical. By induction, the dominoes in the left region are all vertical. By rotational symmetry, the dominoes in the bottom region are horizontal, and so on. This shows that the partition exists and is unique.  It remains to show that this value of $k$ is the smallest possible. Assume that only $k<2 n$ cells are marked, and there exists a partition $P$ satisfying the requirement. It suffices to show there exists another desirable partition distinct from $P$. Let $d$ be the main diagonal of the board. Construct the following graph with edges of two colours. Its vertices are the cells of the board. Connect two vertices with a red edge if they belong to the same domino of $P$. Connect two vertices with a blue edge if their reflections in $d$ are connected by a red edge. It is possible that two vertices are connected by edges of both colours. Clearly, each vertex has both red and blue degrees equal to 1 . Thus the graph splits into cycles where the colours of edges in each cycle alternate (a cycle may have length 2). Consider any cell $c$ lying on the diagonal $d$. Its two edges are symmetrical with respect to $d$. Thus they connect $c$ to different cells. This shows $c$ belongs to a cycle $C(c)$ of length at least 4. Consider a part of this cycle $c_{0}, c_{1}, \ldots, c_{m}$ where $c_{0}=c$ and $m$ is the least positive integer such that $c_{m}$ lies on $d$. Clearly, $c_{m}$ is distinct from $c$. From the construction, the path symmetrical to this with respect to $d$ also lies in the graph, and so these paths together form $C(c)$. Hence, $C(c)$ contains exactly two cells from $d$. Then all $2 n$ cells in $d$ belong to $n$ cycles $C_{1}, C_{2}, \ldots, C_{n}$, each has length at least 4. By the Pigeonhole Principle, there exists a cycle $C_{i}$ containing at most one of the $k$ marked cells. We modify $P$ as follows. We remove all dominoes containing the vertices of $C_{i}$, which correspond to the red edges of $C_{i}$. Then we put the dominoes corresponding to the blue edges of $C_{i}$. Since $C_{i}$ has at least 4 vertices, the resultant partition $P^{\prime}$ is different from $P$. Clearly, no domino in $P^{\prime}$ contains two marked cells as $C_{i}$ contains at most one marked cell. This shows the partition is not unique and hence $k$ cannot be less than $2 n$.
|
{
"resource_path": "IMO/segmented/en-IMO2016SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
25a478b5-e168-5a76-ae05-4772cc03001c
| 24,779
|
Define $P(n)=n^{2}+n+1$. For any positive integers $a$ and $b$, the set $$ \{P(a), P(a+1), P(a+2), \ldots, P(a+b)\} $$ is said to be fragrant if none of its elements is relatively prime to the product of the other elements. Determine the smallest size of a fragrant set.
|
We have the following observations. (i) $(P(n), P(n+1))=1$ for any $n$. We have $(P(n), P(n+1))=\left(n^{2}+n+1, n^{2}+3 n+3\right)=\left(n^{2}+n+1,2 n+2\right)$. Noting that $n^{2}+n+1$ is odd and $\left(n^{2}+n+1, n+1\right)=(1, n+1)=1$, the claim follows. (ii) $(P(n), P(n+2))=1$ for $n \not \equiv 2(\bmod 7)$ and $(P(n), P(n+2))=7$ for $n \equiv 2(\bmod 7)$. From $(2 n+7) P(n)-(2 n-1) P(n+2)=14$ and the fact that $P(n)$ is odd, $(P(n), P(n+2))$ must be a divisor of 7 . The claim follows by checking $n \equiv 0,1, \ldots, 6(\bmod 7)$ directly. (iii) $(P(n), P(n+3))=1$ for $n \not \equiv 1(\bmod 3)$ and $3 \mid(P(n), P(n+3))$ for $n \equiv 1(\bmod 3)$. From $(n+5) P(n)-(n-1) P(n+3)=18$ and the fact that $P(n)$ is odd, $(P(n), P(n+3))$ must be a divisor of 9 . The claim follows by checking $n \equiv 0,1,2(\bmod 3)$ directly. Suppose there exists a fragrant set with at most 5 elements. We may assume it contains exactly 5 elements $P(a), P(a+1), \ldots, P(a+4)$ since the following argument also works with fewer elements. Consider $P(a+2)$. From (i), it is relatively prime to $P(a+1)$ and $P(a+3)$. Without loss of generality, assume $(P(a), P(a+2))>1$. From (ii), we have $a \equiv 2(\bmod 7)$. The same observation implies $(P(a+1), P(a+3))=1$. In order that the set is fragrant, $(P(a), P(a+3))$ and $(P(a+1), P(a+4))$ must both be greater than 1. From (iii), this holds only when both $a$ and $a+1$ are congruent to $1 \bmod 3$, which is a contradiction. It now suffices to construct a fragrant set of size 6. By the Chinese Remainder Theorem, we can take a positive integer $a$ such that $$ a \equiv 7 \quad(\bmod 19), \quad a+1 \equiv 2 \quad(\bmod 7), \quad a+2 \equiv 1 \quad(\bmod 3) $$ For example, we may take $a=197$. From (ii), both $P(a+1)$ and $P(a+3)$ are divisible by 7. From (iii), both $P(a+2)$ and $P(a+5)$ are divisible by 3 . One also checks from $19 \mid P(7)=57$ and $19 \mid P(11)=133$ that $P(a)$ and $P(a+4)$ are divisible by 19. Therefore, the set $\{P(a), P(a+1), \ldots, P(a+5)\}$ is fragrant. Therefore, the smallest size of a fragrant set is 6 . Comment. "Fragrant Harbour" is the English translation of "Hong Kong". A stronger version of this problem is to show that there exists a fragrant set of size $k$ for any $k \geqslant 6$. We present a proof here. For each even positive integer $m$ which is not divisible by 3 , since $m^{2}+3 \equiv 3(\bmod 4)$, we can find a prime $p_{m} \equiv 3(\bmod 4)$ such that $p_{m} \mid m^{2}+3$. Clearly, $p_{m}>3$. If $b=2 t \geqslant 6$, we choose $a$ such that $3 \mid 2(a+t)+1$ and $p_{m} \mid 2(a+t)+1$ for each $1 \leqslant m \leqslant b$ with $m \equiv 2,4(\bmod 6)$. For $0 \leqslant r \leqslant t$ and $3 \mid r$, we have $a+t \pm r \equiv 1(\bmod 3)$ so that $3 \mid P(a+t \pm r)$. For $0 \leqslant r \leqslant t$ and $(r, 3)=1$, we have $$ 4 P(a+t \pm r) \equiv(-1 \pm 2 r)^{2}+2(-1 \pm 2 r)+4=4 r^{2}+3 \equiv 0 \quad\left(\bmod p_{2 r}\right) . $$ Hence, $\{P(a), P(a+1), \ldots, P(a+b)\}$ is fragrant. If $b=2 t+1 \geqslant 7$ (the case $b=5$ has been done in the original problem), we choose $a$ such that $3 \mid 2(a+t)+1$ and $p_{m} \mid 2(a+t)+1$ for $1 \leqslant m \leqslant b$ with $m \equiv 2,4(\bmod 6)$, and that $a+b \equiv 9(\bmod 13)$. Note that $a$ exists by the Chinese Remainder Theorem since $p_{m} \neq 13$ for all $m$. The even case shows that $\{P(a), P(a+1), \ldots, P(a+b-1)\}$ is fragrant. Also, one checks from $13 \mid P(9)=91$ and $13 \mid P(3)=13$ that $P(a+b)$ and $P(a+b-6)$ are divisible by 13. The proof is thus complete.
|
6
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Define $P(n)=n^{2}+n+1$. For any positive integers $a$ and $b$, the set $$ \{P(a), P(a+1), P(a+2), \ldots, P(a+b)\} $$ is said to be fragrant if none of its elements is relatively prime to the product of the other elements. Determine the smallest size of a fragrant set.
|
We have the following observations. (i) $(P(n), P(n+1))=1$ for any $n$. We have $(P(n), P(n+1))=\left(n^{2}+n+1, n^{2}+3 n+3\right)=\left(n^{2}+n+1,2 n+2\right)$. Noting that $n^{2}+n+1$ is odd and $\left(n^{2}+n+1, n+1\right)=(1, n+1)=1$, the claim follows. (ii) $(P(n), P(n+2))=1$ for $n \not \equiv 2(\bmod 7)$ and $(P(n), P(n+2))=7$ for $n \equiv 2(\bmod 7)$. From $(2 n+7) P(n)-(2 n-1) P(n+2)=14$ and the fact that $P(n)$ is odd, $(P(n), P(n+2))$ must be a divisor of 7 . The claim follows by checking $n \equiv 0,1, \ldots, 6(\bmod 7)$ directly. (iii) $(P(n), P(n+3))=1$ for $n \not \equiv 1(\bmod 3)$ and $3 \mid(P(n), P(n+3))$ for $n \equiv 1(\bmod 3)$. From $(n+5) P(n)-(n-1) P(n+3)=18$ and the fact that $P(n)$ is odd, $(P(n), P(n+3))$ must be a divisor of 9 . The claim follows by checking $n \equiv 0,1,2(\bmod 3)$ directly. Suppose there exists a fragrant set with at most 5 elements. We may assume it contains exactly 5 elements $P(a), P(a+1), \ldots, P(a+4)$ since the following argument also works with fewer elements. Consider $P(a+2)$. From (i), it is relatively prime to $P(a+1)$ and $P(a+3)$. Without loss of generality, assume $(P(a), P(a+2))>1$. From (ii), we have $a \equiv 2(\bmod 7)$. The same observation implies $(P(a+1), P(a+3))=1$. In order that the set is fragrant, $(P(a), P(a+3))$ and $(P(a+1), P(a+4))$ must both be greater than 1. From (iii), this holds only when both $a$ and $a+1$ are congruent to $1 \bmod 3$, which is a contradiction. It now suffices to construct a fragrant set of size 6. By the Chinese Remainder Theorem, we can take a positive integer $a$ such that $$ a \equiv 7 \quad(\bmod 19), \quad a+1 \equiv 2 \quad(\bmod 7), \quad a+2 \equiv 1 \quad(\bmod 3) $$ For example, we may take $a=197$. From (ii), both $P(a+1)$ and $P(a+3)$ are divisible by 7. From (iii), both $P(a+2)$ and $P(a+5)$ are divisible by 3 . One also checks from $19 \mid P(7)=57$ and $19 \mid P(11)=133$ that $P(a)$ and $P(a+4)$ are divisible by 19. Therefore, the set $\{P(a), P(a+1), \ldots, P(a+5)\}$ is fragrant. Therefore, the smallest size of a fragrant set is 6 . Comment. "Fragrant Harbour" is the English translation of "Hong Kong". A stronger version of this problem is to show that there exists a fragrant set of size $k$ for any $k \geqslant 6$. We present a proof here. For each even positive integer $m$ which is not divisible by 3 , since $m^{2}+3 \equiv 3(\bmod 4)$, we can find a prime $p_{m} \equiv 3(\bmod 4)$ such that $p_{m} \mid m^{2}+3$. Clearly, $p_{m}>3$. If $b=2 t \geqslant 6$, we choose $a$ such that $3 \mid 2(a+t)+1$ and $p_{m} \mid 2(a+t)+1$ for each $1 \leqslant m \leqslant b$ with $m \equiv 2,4(\bmod 6)$. For $0 \leqslant r \leqslant t$ and $3 \mid r$, we have $a+t \pm r \equiv 1(\bmod 3)$ so that $3 \mid P(a+t \pm r)$. For $0 \leqslant r \leqslant t$ and $(r, 3)=1$, we have $$ 4 P(a+t \pm r) \equiv(-1 \pm 2 r)^{2}+2(-1 \pm 2 r)+4=4 r^{2}+3 \equiv 0 \quad\left(\bmod p_{2 r}\right) . $$ Hence, $\{P(a), P(a+1), \ldots, P(a+b)\}$ is fragrant. If $b=2 t+1 \geqslant 7$ (the case $b=5$ has been done in the original problem), we choose $a$ such that $3 \mid 2(a+t)+1$ and $p_{m} \mid 2(a+t)+1$ for $1 \leqslant m \leqslant b$ with $m \equiv 2,4(\bmod 6)$, and that $a+b \equiv 9(\bmod 13)$. Note that $a$ exists by the Chinese Remainder Theorem since $p_{m} \neq 13$ for all $m$. The even case shows that $\{P(a), P(a+1), \ldots, P(a+b-1)\}$ is fragrant. Also, one checks from $13 \mid P(9)=91$ and $13 \mid P(3)=13$ that $P(a+b)$ and $P(a+b-6)$ are divisible by 13. The proof is thus complete.
|
{
"resource_path": "IMO/segmented/en-IMO2016SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
fd57bbb8-51a8-5fc9-8cdb-d365de164d54
| 24,828
|
Find the smallest real constant $C$ such that for any positive real numbers $a_{1}, a_{2}, a_{3}, a_{4}$ and $a_{5}$ (not necessarily distinct), one can always choose distinct subscripts $i, j, k$ and $l$ such that $$ \left|\frac{a_{i}}{a_{j}}-\frac{a_{k}}{a_{l}}\right| \leqslant C . $$ Answer. The smallest $C$ is $\frac{1}{2}$.
|
We first show that $C \leqslant \frac{1}{2}$. For any positive real numbers $a_{1} \leqslant a_{2} \leqslant a_{3} \leqslant a_{4} \leqslant a_{5}$, consider the five fractions $$ \frac{a_{1}}{a_{2}}, \frac{a_{3}}{a_{4}}, \frac{a_{1}}{a_{5}}, \frac{a_{2}}{a_{3}}, \frac{a_{4}}{a_{5}} . $$ Each of them lies in the interval $(0,1]$. Therefore, by the Pigeonhole Principle, at least three of them must lie in $\left(0, \frac{1}{2}\right]$ or lie in $\left(\frac{1}{2}, 1\right]$ simultaneously. In particular, there must be two consecutive terms in (2) which belong to an interval of length $\frac{1}{2}$ (here, we regard $\frac{a_{1}}{a_{2}}$ and $\frac{a_{4}}{a_{5}}$ as consecutive). In other words, the difference of these two fractions is less than $\frac{1}{2}$. As the indices involved in these two fractions are distinct, we can choose them to be $i, j, k, l$ and conclude that $C \leqslant \frac{1}{2}$. Next, we show that $C=\frac{1}{2}$ is best possible. Consider the numbers $1,2,2,2, n$ where $n$ is a large real number. The fractions formed by two of these numbers in ascending order are $\frac{1}{n}, \frac{2}{n}, \frac{1}{2}, \frac{2}{2}, \frac{2}{1}, \frac{n}{2}, \frac{n}{1}$. Since the indices $i, j, k, l$ are distinct, $\frac{1}{n}$ and $\frac{2}{n}$ cannot be chosen simultaneously. Therefore the minimum value of the left-hand side of (1) is $\frac{1}{2}-\frac{2}{n}$. When $n$ tends to infinity, this value approaches $\frac{1}{2}$, and so $C$ cannot be less than $\frac{1}{2}$. These conclude that $C=\frac{1}{2}$ is the smallest possible choice. Comment. The conclusion still holds if $a_{1}, a_{2}, \ldots, a_{5}$ are pairwise distinct, since in the construction, we may replace the 2's by real numbers sufficiently close to 2 . There are two possible simplifications for this problem: (i) the answer $C=\frac{1}{2}$ is given to the contestants; or (ii) simply ask the contestants to prove the inequality (1) for $C=\frac{1}{2}$.
|
\frac{1}{2}
|
Yes
|
Yes
|
math-word-problem
|
Inequalities
|
Find the smallest real constant $C$ such that for any positive real numbers $a_{1}, a_{2}, a_{3}, a_{4}$ and $a_{5}$ (not necessarily distinct), one can always choose distinct subscripts $i, j, k$ and $l$ such that $$ \left|\frac{a_{i}}{a_{j}}-\frac{a_{k}}{a_{l}}\right| \leqslant C . $$ Answer. The smallest $C$ is $\frac{1}{2}$.
|
We first show that $C \leqslant \frac{1}{2}$. For any positive real numbers $a_{1} \leqslant a_{2} \leqslant a_{3} \leqslant a_{4} \leqslant a_{5}$, consider the five fractions $$ \frac{a_{1}}{a_{2}}, \frac{a_{3}}{a_{4}}, \frac{a_{1}}{a_{5}}, \frac{a_{2}}{a_{3}}, \frac{a_{4}}{a_{5}} . $$ Each of them lies in the interval $(0,1]$. Therefore, by the Pigeonhole Principle, at least three of them must lie in $\left(0, \frac{1}{2}\right]$ or lie in $\left(\frac{1}{2}, 1\right]$ simultaneously. In particular, there must be two consecutive terms in (2) which belong to an interval of length $\frac{1}{2}$ (here, we regard $\frac{a_{1}}{a_{2}}$ and $\frac{a_{4}}{a_{5}}$ as consecutive). In other words, the difference of these two fractions is less than $\frac{1}{2}$. As the indices involved in these two fractions are distinct, we can choose them to be $i, j, k, l$ and conclude that $C \leqslant \frac{1}{2}$. Next, we show that $C=\frac{1}{2}$ is best possible. Consider the numbers $1,2,2,2, n$ where $n$ is a large real number. The fractions formed by two of these numbers in ascending order are $\frac{1}{n}, \frac{2}{n}, \frac{1}{2}, \frac{2}{2}, \frac{2}{1}, \frac{n}{2}, \frac{n}{1}$. Since the indices $i, j, k, l$ are distinct, $\frac{1}{n}$ and $\frac{2}{n}$ cannot be chosen simultaneously. Therefore the minimum value of the left-hand side of (1) is $\frac{1}{2}-\frac{2}{n}$. When $n$ tends to infinity, this value approaches $\frac{1}{2}$, and so $C$ cannot be less than $\frac{1}{2}$. These conclude that $C=\frac{1}{2}$ is the smallest possible choice. Comment. The conclusion still holds if $a_{1}, a_{2}, \ldots, a_{5}$ are pairwise distinct, since in the construction, we may replace the 2's by real numbers sufficiently close to 2 . There are two possible simplifications for this problem: (i) the answer $C=\frac{1}{2}$ is given to the contestants; or (ii) simply ask the contestants to prove the inequality (1) for $C=\frac{1}{2}$.
|
{
"resource_path": "IMO/segmented/en-IMO2016SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
a8f7b450-e8b5-5d04-a90c-a9b3c637a25a
| 24,850
|
The equation $$ (x-1)(x-2) \cdots(x-2016)=(x-1)(x-2) \cdots(x-2016) $$ is written on the board. One tries to erase some linear factors from both sides so that each side still has at least one factor, and the resulting equation has no real roots. Find the least number of linear factors one needs to erase to achieve this. Answer. 2016.
|
Since there are 2016 common linear factors on both sides, we need to erase at least 2016 factors. We claim that the equation has no real roots if we erase all factors $(x-k)$ on the left-hand side with $k \equiv 2,3(\bmod 4)$, and all factors $(x-m)$ on the right-hand side with $m \equiv 0,1(\bmod 4)$. Therefore, it suffices to show that no real number $x$ satisfies $$ \prod_{j=0}^{503}(x-4 j-1)(x-4 j-4)=\prod_{j=0}^{503}(x-4 j-2)(x-4 j-3) $$ - Case 1. $x=1,2, \ldots, 2016$. In this case, one side of (1) is zero while the other side is not. This shows $x$ cannot satisfy (1). - Case 2. $4 k+1<x<4 k+2$ or $4 k+3<x<4 k+4$ for some $k=0,1, \ldots, 503$. For $j=0,1, \ldots, 503$ with $j \neq k$, the product $(x-4 j-1)(x-4 j-4)$ is positive. For $j=k$, the product $(x-4 k-1)(x-4 k-4)$ is negative. This shows the left-hand side of (1) is negative. On the other hand, each product $(x-4 j-2)(x-4 j-3)$ on the right-hand side of (1) is positive. This yields a contradiction. - Case 3. $x<1$ or $x>2016$ or $4 k<x<4 k+1$ for some $k=1,2, \ldots, 503$. The equation (1) can be rewritten as $$ 1=\prod_{j=0}^{503} \frac{(x-4 j-1)(x-4 j-4)}{(x-4 j-2)(x-4 j-3)}=\prod_{j=0}^{503}\left(1-\frac{2}{(x-4 j-2)(x-4 j-3)}\right) $$ Note that $(x-4 j-2)(x-4 j-3)>2$ for $0 \leqslant j \leqslant 503$ in this case. So each term in the product lies strictly between 0 and 1 , and the whole product must be less than 1 , which is impossible. - Case 4. $4 k+2<x<4 k+3$ for some $k=0,1, \ldots, 503$. This time we rewrite (1) as $$ \begin{aligned} 1 & =\frac{x-1}{x-2} \cdot \frac{x-2016}{x-2015} \prod_{j=1}^{503} \frac{(x-4 j)(x-4 j-1)}{(x-4 j+1)(x-4 j-2)} \\ & =\frac{x-1}{x-2} \cdot \frac{x-2016}{x-2015} \prod_{j=1}^{503}\left(1+\frac{2}{(x-4 j+1)(x-4 j-2)}\right) \end{aligned} $$ Clearly, $\frac{x-1}{x-2}$ and $\frac{x-2016}{x-2015}$ are both greater than 1 . For the range of $x$ in this case, each term in the product is also greater than 1 . Then the right-hand side must be greater than 1 and hence a contradiction arises. From the four cases, we conclude that (1) has no real roots. Hence, the minimum number of linear factors to be erased is 2016. Comment. We discuss the general case when 2016 is replaced by a positive integer $n$. The above solution works equally well when $n$ is divisible by 4 . If $n \equiv 2(\bmod 4)$, one may leave $l(x)=(x-1)(x-2) \cdots\left(x-\frac{n}{2}\right)$ on the left-hand side and $r(x)=\left(x-\frac{n}{2}-1\right)\left(x-\frac{n}{2}-2\right) \cdots(x-n)$ on the right-hand side. One checks that for $x<\frac{n+1}{2}$, we have $|l(x)|<|r(x)|$, while for $x>\frac{n+1}{2}$, we have $|l(x)|>|r(x)|$. If $n \equiv 3(\bmod 4)$, one may leave $l(x)=(x-1)(x-2) \cdots\left(x-\frac{n+1}{2}\right)$ on the left-hand side and $r(x)=\left(x-\frac{n+3}{2}\right)\left(x-\frac{x+5}{2}\right) \cdots(x-n)$ on the right-hand side. For $x<1$ or $\frac{n+1}{2}<x<\frac{n+3}{2}$, we have $l(x)>0>r(x)$. For $1<x<\frac{n+1}{2}$, we have $|l(x)|<|r(x)|$. For $x>\frac{n+3}{2}$, we have $|l(x)|>|r(x)|$. If $n \equiv 1(\bmod 4)$, as the proposer mentioned, the situation is a bit more out of control. Since the construction for $n-1 \equiv 0(\bmod 4)$ works, the answer can be either $n$ or $n-1$. For $n=5$, we can leave the products $(x-1)(x-2)(x-3)(x-4)$ and $(x-5)$. For $n=9$, the only example that works is $l(x)=(x-1)(x-2)(x-9)$ and $r(x)=(x-3)(x-4) \cdots(x-8)$, while there seems to be no such partition for $n=13$.
|
2016
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
The equation $$ (x-1)(x-2) \cdots(x-2016)=(x-1)(x-2) \cdots(x-2016) $$ is written on the board. One tries to erase some linear factors from both sides so that each side still has at least one factor, and the resulting equation has no real roots. Find the least number of linear factors one needs to erase to achieve this. Answer. 2016.
|
Since there are 2016 common linear factors on both sides, we need to erase at least 2016 factors. We claim that the equation has no real roots if we erase all factors $(x-k)$ on the left-hand side with $k \equiv 2,3(\bmod 4)$, and all factors $(x-m)$ on the right-hand side with $m \equiv 0,1(\bmod 4)$. Therefore, it suffices to show that no real number $x$ satisfies $$ \prod_{j=0}^{503}(x-4 j-1)(x-4 j-4)=\prod_{j=0}^{503}(x-4 j-2)(x-4 j-3) $$ - Case 1. $x=1,2, \ldots, 2016$. In this case, one side of (1) is zero while the other side is not. This shows $x$ cannot satisfy (1). - Case 2. $4 k+1<x<4 k+2$ or $4 k+3<x<4 k+4$ for some $k=0,1, \ldots, 503$. For $j=0,1, \ldots, 503$ with $j \neq k$, the product $(x-4 j-1)(x-4 j-4)$ is positive. For $j=k$, the product $(x-4 k-1)(x-4 k-4)$ is negative. This shows the left-hand side of (1) is negative. On the other hand, each product $(x-4 j-2)(x-4 j-3)$ on the right-hand side of (1) is positive. This yields a contradiction. - Case 3. $x<1$ or $x>2016$ or $4 k<x<4 k+1$ for some $k=1,2, \ldots, 503$. The equation (1) can be rewritten as $$ 1=\prod_{j=0}^{503} \frac{(x-4 j-1)(x-4 j-4)}{(x-4 j-2)(x-4 j-3)}=\prod_{j=0}^{503}\left(1-\frac{2}{(x-4 j-2)(x-4 j-3)}\right) $$ Note that $(x-4 j-2)(x-4 j-3)>2$ for $0 \leqslant j \leqslant 503$ in this case. So each term in the product lies strictly between 0 and 1 , and the whole product must be less than 1 , which is impossible. - Case 4. $4 k+2<x<4 k+3$ for some $k=0,1, \ldots, 503$. This time we rewrite (1) as $$ \begin{aligned} 1 & =\frac{x-1}{x-2} \cdot \frac{x-2016}{x-2015} \prod_{j=1}^{503} \frac{(x-4 j)(x-4 j-1)}{(x-4 j+1)(x-4 j-2)} \\ & =\frac{x-1}{x-2} \cdot \frac{x-2016}{x-2015} \prod_{j=1}^{503}\left(1+\frac{2}{(x-4 j+1)(x-4 j-2)}\right) \end{aligned} $$ Clearly, $\frac{x-1}{x-2}$ and $\frac{x-2016}{x-2015}$ are both greater than 1 . For the range of $x$ in this case, each term in the product is also greater than 1 . Then the right-hand side must be greater than 1 and hence a contradiction arises. From the four cases, we conclude that (1) has no real roots. Hence, the minimum number of linear factors to be erased is 2016. Comment. We discuss the general case when 2016 is replaced by a positive integer $n$. The above solution works equally well when $n$ is divisible by 4 . If $n \equiv 2(\bmod 4)$, one may leave $l(x)=(x-1)(x-2) \cdots\left(x-\frac{n}{2}\right)$ on the left-hand side and $r(x)=\left(x-\frac{n}{2}-1\right)\left(x-\frac{n}{2}-2\right) \cdots(x-n)$ on the right-hand side. One checks that for $x<\frac{n+1}{2}$, we have $|l(x)|<|r(x)|$, while for $x>\frac{n+1}{2}$, we have $|l(x)|>|r(x)|$. If $n \equiv 3(\bmod 4)$, one may leave $l(x)=(x-1)(x-2) \cdots\left(x-\frac{n+1}{2}\right)$ on the left-hand side and $r(x)=\left(x-\frac{n+3}{2}\right)\left(x-\frac{x+5}{2}\right) \cdots(x-n)$ on the right-hand side. For $x<1$ or $\frac{n+1}{2}<x<\frac{n+3}{2}$, we have $l(x)>0>r(x)$. For $1<x<\frac{n+1}{2}$, we have $|l(x)|<|r(x)|$. For $x>\frac{n+3}{2}$, we have $|l(x)|>|r(x)|$. If $n \equiv 1(\bmod 4)$, as the proposer mentioned, the situation is a bit more out of control. Since the construction for $n-1 \equiv 0(\bmod 4)$ works, the answer can be either $n$ or $n-1$. For $n=5$, we can leave the products $(x-1)(x-2)(x-3)(x-4)$ and $(x-5)$. For $n=9$, the only example that works is $l(x)=(x-1)(x-2)(x-9)$ and $r(x)=(x-3)(x-4) \cdots(x-8)$, while there seems to be no such partition for $n=13$.
|
{
"resource_path": "IMO/segmented/en-IMO2016SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
d0483a95-5898-5610-9caf-22a7d65b088f
| 24,860
|
Determine the largest real number $a$ such that for all $n \geqslant 1$ and for all real numbers $x_{0}, x_{1}, \ldots, x_{n}$ satisfying $0=x_{0}<x_{1}<x_{2}<\cdots<x_{n}$, we have $$ \frac{1}{x_{1}-x_{0}}+\frac{1}{x_{2}-x_{1}}+\cdots+\frac{1}{x_{n}-x_{n-1}} \geqslant a\left(\frac{2}{x_{1}}+\frac{3}{x_{2}}+\cdots+\frac{n+1}{x_{n}}\right) . $$ Answer. The largest $a$ is $\frac{4}{9}$.
|
We first show that $a=\frac{4}{9}$ is admissible. For each $2 \leqslant k \leqslant n$, by the CauchySchwarz Inequality, we have $$ \left(x_{k-1}+\left(x_{k}-x_{k-1}\right)\right)\left(\frac{(k-1)^{2}}{x_{k-1}}+\frac{3^{2}}{x_{k}-x_{k-1}}\right) \geqslant(k-1+3)^{2}, $$ which can be rewritten as $$ \frac{9}{x_{k}-x_{k-1}} \geqslant \frac{(k+2)^{2}}{x_{k}}-\frac{(k-1)^{2}}{x_{k-1}} $$ Summing (2) over $k=2,3, \ldots, n$ and adding $\frac{9}{x_{1}}$ to both sides, we have $$ 9 \sum_{k=1}^{n} \frac{1}{x_{k}-x_{k-1}} \geqslant 4 \sum_{k=1}^{n} \frac{k+1}{x_{k}}+\frac{n^{2}}{x_{n}}>4 \sum_{k=1}^{n} \frac{k+1}{x_{k}} . $$ This shows (1) holds for $a=\frac{4}{9}$. Next, we show that $a=\frac{4}{9}$ is the optimal choice. Consider the sequence defined by $x_{0}=0$ and $x_{k}=x_{k-1}+k(k+1)$ for $k \geqslant 1$, that is, $x_{k}=\frac{1}{3} k(k+1)(k+2)$. Then the left-hand side of (1) equals $$ \sum_{k=1}^{n} \frac{1}{k(k+1)}=\sum_{k=1}^{n}\left(\frac{1}{k}-\frac{1}{k+1}\right)=1-\frac{1}{n+1} $$ while the right-hand side equals $$ a \sum_{k=1}^{n} \frac{k+1}{x_{k}}=3 a \sum_{k=1}^{n} \frac{1}{k(k+2)}=\frac{3}{2} a \sum_{k=1}^{n}\left(\frac{1}{k}-\frac{1}{k+2}\right)=\frac{3}{2}\left(1+\frac{1}{2}-\frac{1}{n+1}-\frac{1}{n+2}\right) a . $$ When $n$ tends to infinity, the left-hand side tends to 1 while the right-hand side tends to $\frac{9}{4} a$. Therefore $a$ has to be at most $\frac{4}{9}$. Hence the largest value of $a$ is $\frac{4}{9}$.
|
\frac{4}{9}
|
Yes
|
Yes
|
math-word-problem
|
Inequalities
|
Determine the largest real number $a$ such that for all $n \geqslant 1$ and for all real numbers $x_{0}, x_{1}, \ldots, x_{n}$ satisfying $0=x_{0}<x_{1}<x_{2}<\cdots<x_{n}$, we have $$ \frac{1}{x_{1}-x_{0}}+\frac{1}{x_{2}-x_{1}}+\cdots+\frac{1}{x_{n}-x_{n-1}} \geqslant a\left(\frac{2}{x_{1}}+\frac{3}{x_{2}}+\cdots+\frac{n+1}{x_{n}}\right) . $$ Answer. The largest $a$ is $\frac{4}{9}$.
|
We first show that $a=\frac{4}{9}$ is admissible. For each $2 \leqslant k \leqslant n$, by the CauchySchwarz Inequality, we have $$ \left(x_{k-1}+\left(x_{k}-x_{k-1}\right)\right)\left(\frac{(k-1)^{2}}{x_{k-1}}+\frac{3^{2}}{x_{k}-x_{k-1}}\right) \geqslant(k-1+3)^{2}, $$ which can be rewritten as $$ \frac{9}{x_{k}-x_{k-1}} \geqslant \frac{(k+2)^{2}}{x_{k}}-\frac{(k-1)^{2}}{x_{k-1}} $$ Summing (2) over $k=2,3, \ldots, n$ and adding $\frac{9}{x_{1}}$ to both sides, we have $$ 9 \sum_{k=1}^{n} \frac{1}{x_{k}-x_{k-1}} \geqslant 4 \sum_{k=1}^{n} \frac{k+1}{x_{k}}+\frac{n^{2}}{x_{n}}>4 \sum_{k=1}^{n} \frac{k+1}{x_{k}} . $$ This shows (1) holds for $a=\frac{4}{9}$. Next, we show that $a=\frac{4}{9}$ is the optimal choice. Consider the sequence defined by $x_{0}=0$ and $x_{k}=x_{k-1}+k(k+1)$ for $k \geqslant 1$, that is, $x_{k}=\frac{1}{3} k(k+1)(k+2)$. Then the left-hand side of (1) equals $$ \sum_{k=1}^{n} \frac{1}{k(k+1)}=\sum_{k=1}^{n}\left(\frac{1}{k}-\frac{1}{k+1}\right)=1-\frac{1}{n+1} $$ while the right-hand side equals $$ a \sum_{k=1}^{n} \frac{k+1}{x_{k}}=3 a \sum_{k=1}^{n} \frac{1}{k(k+2)}=\frac{3}{2} a \sum_{k=1}^{n}\left(\frac{1}{k}-\frac{1}{k+2}\right)=\frac{3}{2}\left(1+\frac{1}{2}-\frac{1}{n+1}-\frac{1}{n+2}\right) a . $$ When $n$ tends to infinity, the left-hand side tends to 1 while the right-hand side tends to $\frac{9}{4} a$. Therefore $a$ has to be at most $\frac{4}{9}$. Hence the largest value of $a$ is $\frac{4}{9}$.
|
{
"resource_path": "IMO/segmented/en-IMO2016SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
7115cdfd-a432-5324-af85-27fc73c2633a
| 24,863
|
Find all positive integers $n$ for which all positive divisors of $n$ can be put into the cells of a rectangular table under the following constraints: - each cell contains a distinct divisor; - the sums of all rows are equal; and - the sums of all columns are equal. Answer. 1.
|
Suppose all positive divisors of $n$ can be arranged into a rectangular table of size $k \times l$ where the number of rows $k$ does not exceed the number of columns $l$. Let the sum of numbers in each column be $s$. Since $n$ belongs to one of the columns, we have $s \geqslant n$, where equality holds only when $n=1$. For $j=1,2, \ldots, l$, let $d_{j}$ be the largest number in the $j$-th column. Without loss of generality, assume $d_{1}>d_{2}>\cdots>d_{l}$. Since these are divisors of $n$, we have $$ d_{l} \leqslant \frac{n}{l} $$ As $d_{l}$ is the maximum entry of the $l$-th column, we must have $$ d_{l} \geqslant \frac{s}{k} \geqslant \frac{n}{k} . $$ The relations (1) and (2) combine to give $\frac{n}{l} \geqslant \frac{n}{k}$, that is, $k \geqslant l$. Together with $k \leqslant l$, we conclude that $k=l$. Then all inequalities in (1) and (2) are equalities. In particular, $s=n$ and so $n=1$, in which case the conditions are clearly satisfied.
|
1
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Find all positive integers $n$ for which all positive divisors of $n$ can be put into the cells of a rectangular table under the following constraints: - each cell contains a distinct divisor; - the sums of all rows are equal; and - the sums of all columns are equal. Answer. 1.
|
Suppose all positive divisors of $n$ can be arranged into a rectangular table of size $k \times l$ where the number of rows $k$ does not exceed the number of columns $l$. Let the sum of numbers in each column be $s$. Since $n$ belongs to one of the columns, we have $s \geqslant n$, where equality holds only when $n=1$. For $j=1,2, \ldots, l$, let $d_{j}$ be the largest number in the $j$-th column. Without loss of generality, assume $d_{1}>d_{2}>\cdots>d_{l}$. Since these are divisors of $n$, we have $$ d_{l} \leqslant \frac{n}{l} $$ As $d_{l}$ is the maximum entry of the $l$-th column, we must have $$ d_{l} \geqslant \frac{s}{k} \geqslant \frac{n}{k} . $$ The relations (1) and (2) combine to give $\frac{n}{l} \geqslant \frac{n}{k}$, that is, $k \geqslant l$. Together with $k \leqslant l$, we conclude that $k=l$. Then all inequalities in (1) and (2) are equalities. In particular, $s=n$ and so $n=1$, in which case the conditions are clearly satisfied.
|
{
"resource_path": "IMO/segmented/en-IMO2016SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
86dddf9f-6590-57c4-b871-c6e1c6112da1
| 24,872
|
Let $n$ be a positive integer. Determine the smallest positive integer $k$ with the following property: it is possible to mark $k$ cells on a $2 n \times 2 n$ board so that there exists a unique partition of the board into $1 \times 2$ and $2 \times 1$ dominoes, none of which contains two marked cells. Answer. $2 n$.
|
We first construct an example of marking $2 n$ cells satisfying the requirement. Label the rows and columns $1,2, \ldots, 2 n$ and label the cell in the $i$-th row and the $j$-th column $(i, j)$. For $i=1,2, \ldots, n$, we mark the cells $(i, i)$ and $(i, i+1)$. We claim that the required partition exists and is unique. The two diagonals of the board divide the board into four regions. Note that the domino covering cell $(1,1)$ must be vertical. This in turn shows that each domino covering $(2,2),(3,3), \ldots,(n, n)$ is vertical. By induction, the dominoes in the left region are all vertical. By rotational symmetry, the dominoes in the bottom region are horizontal, and so on. This shows that the partition exists and is unique.  It remains to show that this value of $k$ is the smallest possible. Assume that only $k<2 n$ cells are marked, and there exists a partition $P$ satisfying the requirement. It suffices to show there exists another desirable partition distinct from $P$. Let $d$ be the main diagonal of the board. Construct the following graph with edges of two colours. Its vertices are the cells of the board. Connect two vertices with a red edge if they belong to the same domino of $P$. Connect two vertices with a blue edge if their reflections in $d$ are connected by a red edge. It is possible that two vertices are connected by edges of both colours. Clearly, each vertex has both red and blue degrees equal to 1 . Thus the graph splits into cycles where the colours of edges in each cycle alternate (a cycle may have length 2). Consider any cell $c$ lying on the diagonal $d$. Its two edges are symmetrical with respect to $d$. Thus they connect $c$ to different cells. This shows $c$ belongs to a cycle $C(c)$ of length at least 4. Consider a part of this cycle $c_{0}, c_{1}, \ldots, c_{m}$ where $c_{0}=c$ and $m$ is the least positive integer such that $c_{m}$ lies on $d$. Clearly, $c_{m}$ is distinct from $c$. From the construction, the path symmetrical to this with respect to $d$ also lies in the graph, and so these paths together form $C(c)$. Hence, $C(c)$ contains exactly two cells from $d$. Then all $2 n$ cells in $d$ belong to $n$ cycles $C_{1}, C_{2}, \ldots, C_{n}$, each has length at least 4. By the Pigeonhole Principle, there exists a cycle $C_{i}$ containing at most one of the $k$ marked cells. We modify $P$ as follows. We remove all dominoes containing the vertices of $C_{i}$, which correspond to the red edges of $C_{i}$. Then we put the dominoes corresponding to the blue edges of $C_{i}$. Since $C_{i}$ has at least 4 vertices, the resultant partition $P^{\prime}$ is different from $P$. Clearly, no domino in $P^{\prime}$ contains two marked cells as $C_{i}$ contains at most one marked cell. This shows the partition is not unique and hence $k$ cannot be less than $2 n$.
|
2n
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Let $n$ be a positive integer. Determine the smallest positive integer $k$ with the following property: it is possible to mark $k$ cells on a $2 n \times 2 n$ board so that there exists a unique partition of the board into $1 \times 2$ and $2 \times 1$ dominoes, none of which contains two marked cells. Answer. $2 n$.
|
We first construct an example of marking $2 n$ cells satisfying the requirement. Label the rows and columns $1,2, \ldots, 2 n$ and label the cell in the $i$-th row and the $j$-th column $(i, j)$. For $i=1,2, \ldots, n$, we mark the cells $(i, i)$ and $(i, i+1)$. We claim that the required partition exists and is unique. The two diagonals of the board divide the board into four regions. Note that the domino covering cell $(1,1)$ must be vertical. This in turn shows that each domino covering $(2,2),(3,3), \ldots,(n, n)$ is vertical. By induction, the dominoes in the left region are all vertical. By rotational symmetry, the dominoes in the bottom region are horizontal, and so on. This shows that the partition exists and is unique.  It remains to show that this value of $k$ is the smallest possible. Assume that only $k<2 n$ cells are marked, and there exists a partition $P$ satisfying the requirement. It suffices to show there exists another desirable partition distinct from $P$. Let $d$ be the main diagonal of the board. Construct the following graph with edges of two colours. Its vertices are the cells of the board. Connect two vertices with a red edge if they belong to the same domino of $P$. Connect two vertices with a blue edge if their reflections in $d$ are connected by a red edge. It is possible that two vertices are connected by edges of both colours. Clearly, each vertex has both red and blue degrees equal to 1 . Thus the graph splits into cycles where the colours of edges in each cycle alternate (a cycle may have length 2). Consider any cell $c$ lying on the diagonal $d$. Its two edges are symmetrical with respect to $d$. Thus they connect $c$ to different cells. This shows $c$ belongs to a cycle $C(c)$ of length at least 4. Consider a part of this cycle $c_{0}, c_{1}, \ldots, c_{m}$ where $c_{0}=c$ and $m$ is the least positive integer such that $c_{m}$ lies on $d$. Clearly, $c_{m}$ is distinct from $c$. From the construction, the path symmetrical to this with respect to $d$ also lies in the graph, and so these paths together form $C(c)$. Hence, $C(c)$ contains exactly two cells from $d$. Then all $2 n$ cells in $d$ belong to $n$ cycles $C_{1}, C_{2}, \ldots, C_{n}$, each has length at least 4. By the Pigeonhole Principle, there exists a cycle $C_{i}$ containing at most one of the $k$ marked cells. We modify $P$ as follows. We remove all dominoes containing the vertices of $C_{i}$, which correspond to the red edges of $C_{i}$. Then we put the dominoes corresponding to the blue edges of $C_{i}$. Since $C_{i}$ has at least 4 vertices, the resultant partition $P^{\prime}$ is different from $P$. Clearly, no domino in $P^{\prime}$ contains two marked cells as $C_{i}$ contains at most one marked cell. This shows the partition is not unique and hence $k$ cannot be less than $2 n$.
|
{
"resource_path": "IMO/segmented/en-IMO2016SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
4f13f78b-e8a4-588c-854b-20de1b2e75f6
| 24,887
|
Define $P(n)=n^{2}+n+1$. For any positive integers $a$ and $b$, the set $$ \{P(a), P(a+1), P(a+2), \ldots, P(a+b)\} $$ is said to be fragrant if none of its elements is relatively prime to the product of the other elements. Determine the smallest size of a fragrant set. Answer. 6.
|
We have the following observations. (i) $(P(n), P(n+1))=1$ for any $n$. We have $(P(n), P(n+1))=\left(n^{2}+n+1, n^{2}+3 n+3\right)=\left(n^{2}+n+1,2 n+2\right)$. Noting that $n^{2}+n+1$ is odd and $\left(n^{2}+n+1, n+1\right)=(1, n+1)=1$, the claim follows. (ii) $(P(n), P(n+2))=1$ for $n \not \equiv 2(\bmod 7)$ and $(P(n), P(n+2))=7$ for $n \equiv 2(\bmod 7)$. From $(2 n+7) P(n)-(2 n-1) P(n+2)=14$ and the fact that $P(n)$ is odd, $(P(n), P(n+2))$ must be a divisor of 7 . The claim follows by checking $n \equiv 0,1, \ldots, 6(\bmod 7)$ directly. (iii) $(P(n), P(n+3))=1$ for $n \not \equiv 1(\bmod 3)$ and $3 \mid(P(n), P(n+3))$ for $n \equiv 1(\bmod 3)$. From $(n+5) P(n)-(n-1) P(n+3)=18$ and the fact that $P(n)$ is odd, $(P(n), P(n+3))$ must be a divisor of 9 . The claim follows by checking $n \equiv 0,1,2(\bmod 3)$ directly. Suppose there exists a fragrant set with at most 5 elements. We may assume it contains exactly 5 elements $P(a), P(a+1), \ldots, P(a+4)$ since the following argument also works with fewer elements. Consider $P(a+2)$. From (i), it is relatively prime to $P(a+1)$ and $P(a+3)$. Without loss of generality, assume $(P(a), P(a+2))>1$. From (ii), we have $a \equiv 2(\bmod 7)$. The same observation implies $(P(a+1), P(a+3))=1$. In order that the set is fragrant, $(P(a), P(a+3))$ and $(P(a+1), P(a+4))$ must both be greater than 1. From (iii), this holds only when both $a$ and $a+1$ are congruent to $1 \bmod 3$, which is a contradiction. It now suffices to construct a fragrant set of size 6. By the Chinese Remainder Theorem, we can take a positive integer $a$ such that $$ a \equiv 7 \quad(\bmod 19), \quad a+1 \equiv 2 \quad(\bmod 7), \quad a+2 \equiv 1 \quad(\bmod 3) $$ For example, we may take $a=197$. From (ii), both $P(a+1)$ and $P(a+3)$ are divisible by 7. From (iii), both $P(a+2)$ and $P(a+5)$ are divisible by 3 . One also checks from $19 \mid P(7)=57$ and $19 \mid P(11)=133$ that $P(a)$ and $P(a+4)$ are divisible by 19. Therefore, the set $\{P(a), P(a+1), \ldots, P(a+5)\}$ is fragrant. Therefore, the smallest size of a fragrant set is 6 . Comment. "Fragrant Harbour" is the English translation of "Hong Kong". A stronger version of this problem is to show that there exists a fragrant set of size $k$ for any $k \geqslant 6$. We present a proof here. For each even positive integer $m$ which is not divisible by 3 , since $m^{2}+3 \equiv 3(\bmod 4)$, we can find a prime $p_{m} \equiv 3(\bmod 4)$ such that $p_{m} \mid m^{2}+3$. Clearly, $p_{m}>3$. If $b=2 t \geqslant 6$, we choose $a$ such that $3 \mid 2(a+t)+1$ and $p_{m} \mid 2(a+t)+1$ for each $1 \leqslant m \leqslant b$ with $m \equiv 2,4(\bmod 6)$. For $0 \leqslant r \leqslant t$ and $3 \mid r$, we have $a+t \pm r \equiv 1(\bmod 3)$ so that $3 \mid P(a+t \pm r)$. For $0 \leqslant r \leqslant t$ and $(r, 3)=1$, we have $$ 4 P(a+t \pm r) \equiv(-1 \pm 2 r)^{2}+2(-1 \pm 2 r)+4=4 r^{2}+3 \equiv 0 \quad\left(\bmod p_{2 r}\right) . $$ Hence, $\{P(a), P(a+1), \ldots, P(a+b)\}$ is fragrant. If $b=2 t+1 \geqslant 7$ (the case $b=5$ has been done in the original problem), we choose $a$ such that $3 \mid 2(a+t)+1$ and $p_{m} \mid 2(a+t)+1$ for $1 \leqslant m \leqslant b$ with $m \equiv 2,4(\bmod 6)$, and that $a+b \equiv 9(\bmod 13)$. Note that $a$ exists by the Chinese Remainder Theorem since $p_{m} \neq 13$ for all $m$. The even case shows that $\{P(a), P(a+1), \ldots, P(a+b-1)\}$ is fragrant. Also, one checks from $13 \mid P(9)=91$ and $13 \mid P(3)=13$ that $P(a+b)$ and $P(a+b-6)$ are divisible by 13. The proof is thus complete.
|
6
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Define $P(n)=n^{2}+n+1$. For any positive integers $a$ and $b$, the set $$ \{P(a), P(a+1), P(a+2), \ldots, P(a+b)\} $$ is said to be fragrant if none of its elements is relatively prime to the product of the other elements. Determine the smallest size of a fragrant set. Answer. 6.
|
We have the following observations. (i) $(P(n), P(n+1))=1$ for any $n$. We have $(P(n), P(n+1))=\left(n^{2}+n+1, n^{2}+3 n+3\right)=\left(n^{2}+n+1,2 n+2\right)$. Noting that $n^{2}+n+1$ is odd and $\left(n^{2}+n+1, n+1\right)=(1, n+1)=1$, the claim follows. (ii) $(P(n), P(n+2))=1$ for $n \not \equiv 2(\bmod 7)$ and $(P(n), P(n+2))=7$ for $n \equiv 2(\bmod 7)$. From $(2 n+7) P(n)-(2 n-1) P(n+2)=14$ and the fact that $P(n)$ is odd, $(P(n), P(n+2))$ must be a divisor of 7 . The claim follows by checking $n \equiv 0,1, \ldots, 6(\bmod 7)$ directly. (iii) $(P(n), P(n+3))=1$ for $n \not \equiv 1(\bmod 3)$ and $3 \mid(P(n), P(n+3))$ for $n \equiv 1(\bmod 3)$. From $(n+5) P(n)-(n-1) P(n+3)=18$ and the fact that $P(n)$ is odd, $(P(n), P(n+3))$ must be a divisor of 9 . The claim follows by checking $n \equiv 0,1,2(\bmod 3)$ directly. Suppose there exists a fragrant set with at most 5 elements. We may assume it contains exactly 5 elements $P(a), P(a+1), \ldots, P(a+4)$ since the following argument also works with fewer elements. Consider $P(a+2)$. From (i), it is relatively prime to $P(a+1)$ and $P(a+3)$. Without loss of generality, assume $(P(a), P(a+2))>1$. From (ii), we have $a \equiv 2(\bmod 7)$. The same observation implies $(P(a+1), P(a+3))=1$. In order that the set is fragrant, $(P(a), P(a+3))$ and $(P(a+1), P(a+4))$ must both be greater than 1. From (iii), this holds only when both $a$ and $a+1$ are congruent to $1 \bmod 3$, which is a contradiction. It now suffices to construct a fragrant set of size 6. By the Chinese Remainder Theorem, we can take a positive integer $a$ such that $$ a \equiv 7 \quad(\bmod 19), \quad a+1 \equiv 2 \quad(\bmod 7), \quad a+2 \equiv 1 \quad(\bmod 3) $$ For example, we may take $a=197$. From (ii), both $P(a+1)$ and $P(a+3)$ are divisible by 7. From (iii), both $P(a+2)$ and $P(a+5)$ are divisible by 3 . One also checks from $19 \mid P(7)=57$ and $19 \mid P(11)=133$ that $P(a)$ and $P(a+4)$ are divisible by 19. Therefore, the set $\{P(a), P(a+1), \ldots, P(a+5)\}$ is fragrant. Therefore, the smallest size of a fragrant set is 6 . Comment. "Fragrant Harbour" is the English translation of "Hong Kong". A stronger version of this problem is to show that there exists a fragrant set of size $k$ for any $k \geqslant 6$. We present a proof here. For each even positive integer $m$ which is not divisible by 3 , since $m^{2}+3 \equiv 3(\bmod 4)$, we can find a prime $p_{m} \equiv 3(\bmod 4)$ such that $p_{m} \mid m^{2}+3$. Clearly, $p_{m}>3$. If $b=2 t \geqslant 6$, we choose $a$ such that $3 \mid 2(a+t)+1$ and $p_{m} \mid 2(a+t)+1$ for each $1 \leqslant m \leqslant b$ with $m \equiv 2,4(\bmod 6)$. For $0 \leqslant r \leqslant t$ and $3 \mid r$, we have $a+t \pm r \equiv 1(\bmod 3)$ so that $3 \mid P(a+t \pm r)$. For $0 \leqslant r \leqslant t$ and $(r, 3)=1$, we have $$ 4 P(a+t \pm r) \equiv(-1 \pm 2 r)^{2}+2(-1 \pm 2 r)+4=4 r^{2}+3 \equiv 0 \quad\left(\bmod p_{2 r}\right) . $$ Hence, $\{P(a), P(a+1), \ldots, P(a+b)\}$ is fragrant. If $b=2 t+1 \geqslant 7$ (the case $b=5$ has been done in the original problem), we choose $a$ such that $3 \mid 2(a+t)+1$ and $p_{m} \mid 2(a+t)+1$ for $1 \leqslant m \leqslant b$ with $m \equiv 2,4(\bmod 6)$, and that $a+b \equiv 9(\bmod 13)$. Note that $a$ exists by the Chinese Remainder Theorem since $p_{m} \neq 13$ for all $m$. The even case shows that $\{P(a), P(a+1), \ldots, P(a+b-1)\}$ is fragrant. Also, one checks from $13 \mid P(9)=91$ and $13 \mid P(3)=13$ that $P(a+b)$ and $P(a+b-6)$ are divisible by 13. The proof is thus complete.
|
{
"resource_path": "IMO/segmented/en-IMO2016SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
4d2086c1-927d-5b0c-88eb-6ef847714b4f
| 24,897
|
An integer $n \geqslant 3$ is given. We call an $n$-tuple of real numbers $\left(x_{1}, x_{2}, \ldots, x_{n}\right)$ Shiny if for each permutation $y_{1}, y_{2}, \ldots, y_{n}$ of these numbers we have $$ \sum_{i=1}^{n-1} y_{i} y_{i+1}=y_{1} y_{2}+y_{2} y_{3}+y_{3} y_{4}+\cdots+y_{n-1} y_{n} \geqslant-1 $$ Find the largest constant $K=K(n)$ such that $$ \sum_{1 \leqslant i<j \leqslant n} x_{i} x_{j} \geqslant K $$ holds for every Shiny $n$-tuple $\left(x_{1}, x_{2}, \ldots, x_{n}\right)$.
|
We present another proof that $\sum_{i<j} x_{i} x_{j} \geqslant-(n-1) / 2$ for any Shiny $n$-tuple $\left(x_{1}, \ldots, x_{n}\right)$. Assume an ordering of the $x_{i}$ as in (2), and let $\ell=n-k$. Assume without loss of generality that $k \geqslant \ell$. Also assume $k \neq n$, (as otherwise, all of the $x_{i}$ are nonpositive, and so the inequality is trivial). Define the sets of indices $S=\{1,2, \ldots, k\}$ and $T=\{k+1, \ldots, n\}$. Define the following sums: $$ K=\sum_{\substack{i<j \\ i, j \in S}} x_{i} x_{j}, \quad M=\sum_{\substack{i \in S \\ j \in T}} x_{i} x_{j}, \quad \text { and } \quad L=\sum_{\substack{i<j \\ i, j \in T}} x_{i} x_{j} $$ By definition, $K, L \geqslant 0$ and $M \leqslant 0$. We aim to show that $K+L+M \geqslant-(n-1) / 2$. We split into cases based on whether $k=\ell$ or $k>\ell$. Case 1: $k>\ell$. Consider all permutations $\phi:\{1,2, \ldots, n\} \rightarrow\{1,2, \ldots, n\}$ such that $\phi^{-1}(T)=\{2,4, \ldots, 2 \ell\}$. Note that there are $k!!$ ! such permutations $\phi$. Define $$ f(\phi)=\sum_{i=1}^{n-1} x_{\phi(i)} x_{\phi(i+1)} $$ We know that $f(\phi) \geqslant-1$ for every permutation $\phi$ with the above property. Averaging $f(\phi)$ over all $\phi$ gives $$ -1 \leqslant \frac{1}{k!\ell!} \sum_{\phi} f(\phi)=\frac{2 \ell}{k \ell} M+\frac{2(k-\ell-1)}{k(k-1)} K $$ where the equality holds because there are $k \ell$ products in $M$, of which $2 \ell$ are selected for each $\phi$, and there are $k(k-1) / 2$ products in $K$, of which $k-\ell-1$ are selected for each $\phi$. We now have $$ K+L+M \geqslant K+L+\left(-\frac{k}{2}-\frac{k-\ell-1}{k-1} K\right)=-\frac{k}{2}+\frac{\ell}{k-1} K+L $$ Since $k \leqslant n-1$ and $K, L \geqslant 0$, we get the desired inequality. Case 2: $k=\ell=n / 2$. We do a similar approach, considering all $\phi:\{1,2, \ldots, n\} \rightarrow\{1,2, \ldots, n\}$ such that $\phi^{-1}(T)=$ $\{2,4, \ldots, 2 \ell\}$, and defining $f$ the same way. Analogously to Case 1 , we have $$ -1 \leqslant \frac{1}{k!\ell!} \sum_{\phi} f(\phi)=\frac{2 \ell-1}{k \ell} M $$ because there are $k \ell$ products in $M$, of which $2 \ell-1$ are selected for each $\phi$. Now, we have that $$ K+L+M \geqslant M \geqslant-\frac{n^{2}}{4(n-1)} \geqslant-\frac{n-1}{2} $$ where the last inequality holds because $n \geqslant 4$.
|
-(n-1)/2
|
Yes
|
Yes
|
math-word-problem
|
Inequalities
|
An integer $n \geqslant 3$ is given. We call an $n$-tuple of real numbers $\left(x_{1}, x_{2}, \ldots, x_{n}\right)$ Shiny if for each permutation $y_{1}, y_{2}, \ldots, y_{n}$ of these numbers we have $$ \sum_{i=1}^{n-1} y_{i} y_{i+1}=y_{1} y_{2}+y_{2} y_{3}+y_{3} y_{4}+\cdots+y_{n-1} y_{n} \geqslant-1 $$ Find the largest constant $K=K(n)$ such that $$ \sum_{1 \leqslant i<j \leqslant n} x_{i} x_{j} \geqslant K $$ holds for every Shiny $n$-tuple $\left(x_{1}, x_{2}, \ldots, x_{n}\right)$.
|
We present another proof that $\sum_{i<j} x_{i} x_{j} \geqslant-(n-1) / 2$ for any Shiny $n$-tuple $\left(x_{1}, \ldots, x_{n}\right)$. Assume an ordering of the $x_{i}$ as in (2), and let $\ell=n-k$. Assume without loss of generality that $k \geqslant \ell$. Also assume $k \neq n$, (as otherwise, all of the $x_{i}$ are nonpositive, and so the inequality is trivial). Define the sets of indices $S=\{1,2, \ldots, k\}$ and $T=\{k+1, \ldots, n\}$. Define the following sums: $$ K=\sum_{\substack{i<j \\ i, j \in S}} x_{i} x_{j}, \quad M=\sum_{\substack{i \in S \\ j \in T}} x_{i} x_{j}, \quad \text { and } \quad L=\sum_{\substack{i<j \\ i, j \in T}} x_{i} x_{j} $$ By definition, $K, L \geqslant 0$ and $M \leqslant 0$. We aim to show that $K+L+M \geqslant-(n-1) / 2$. We split into cases based on whether $k=\ell$ or $k>\ell$. Case 1: $k>\ell$. Consider all permutations $\phi:\{1,2, \ldots, n\} \rightarrow\{1,2, \ldots, n\}$ such that $\phi^{-1}(T)=\{2,4, \ldots, 2 \ell\}$. Note that there are $k!!$ ! such permutations $\phi$. Define $$ f(\phi)=\sum_{i=1}^{n-1} x_{\phi(i)} x_{\phi(i+1)} $$ We know that $f(\phi) \geqslant-1$ for every permutation $\phi$ with the above property. Averaging $f(\phi)$ over all $\phi$ gives $$ -1 \leqslant \frac{1}{k!\ell!} \sum_{\phi} f(\phi)=\frac{2 \ell}{k \ell} M+\frac{2(k-\ell-1)}{k(k-1)} K $$ where the equality holds because there are $k \ell$ products in $M$, of which $2 \ell$ are selected for each $\phi$, and there are $k(k-1) / 2$ products in $K$, of which $k-\ell-1$ are selected for each $\phi$. We now have $$ K+L+M \geqslant K+L+\left(-\frac{k}{2}-\frac{k-\ell-1}{k-1} K\right)=-\frac{k}{2}+\frac{\ell}{k-1} K+L $$ Since $k \leqslant n-1$ and $K, L \geqslant 0$, we get the desired inequality. Case 2: $k=\ell=n / 2$. We do a similar approach, considering all $\phi:\{1,2, \ldots, n\} \rightarrow\{1,2, \ldots, n\}$ such that $\phi^{-1}(T)=$ $\{2,4, \ldots, 2 \ell\}$, and defining $f$ the same way. Analogously to Case 1 , we have $$ -1 \leqslant \frac{1}{k!\ell!} \sum_{\phi} f(\phi)=\frac{2 \ell-1}{k \ell} M $$ because there are $k \ell$ products in $M$, of which $2 \ell-1$ are selected for each $\phi$. Now, we have that $$ K+L+M \geqslant M \geqslant-\frac{n^{2}}{4(n-1)} \geqslant-\frac{n-1}{2} $$ where the last inequality holds because $n \geqslant 4$.
|
{
"resource_path": "IMO/segmented/en-IMO2017SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
a0d182e9-d4db-5773-b6ac-d6bba77cb680
| 24,924
|
Call a rational number short if it has finitely many digits in its decimal expansion. For a positive integer $m$, we say that a positive integer $t$ is $m$-tastic if there exists a number $c \in\{1,2,3, \ldots, 2017\}$ such that $\frac{10^{t}-1}{c \cdot m}$ is short, and such that $\frac{10^{k}-1}{c \cdot m}$ is not short for any $1 \leqslant k<t$. Let $S(m)$ be the set of $m$-tastic numbers. Consider $S(m)$ for $m=1,2, \ldots$. What is the maximum number of elements in $S(m)$ ? (Turkey)
|
First notice that $x \in \mathbb{Q}$ is short if and only if there are exponents $a, b \geqslant 0$ such that $2^{a} \cdot 5^{b} \cdot x \in \mathbb{Z}$. In fact, if $x$ is short, then $x=\frac{n}{10^{k}}$ for some $k$ and we can take $a=b=k$; on the other hand, if $2^{a} \cdot 5^{b} \cdot x=q \in \mathbb{Z}$ then $x=\frac{2^{b} \cdot 5^{a} q}{10^{a+b}}$, so $x$ is short. If $m=2^{a} \cdot 5^{b} \cdot s$, with $\operatorname{gcd}(s, 10)=1$, then $\frac{10^{t}-1}{m}$ is short if and only if $s$ divides $10^{t}-1$. So we may (and will) suppose without loss of generality that $\operatorname{gcd}(m, 10)=1$. Define $$ C=\{1 \leqslant c \leqslant 2017: \operatorname{gcd}(c, 10)=1\} . $$ The $m$-tastic numbers are then precisely the smallest exponents $t>0$ such that $10^{t} \equiv 1$ $(\bmod \mathrm{cm})$ for some integer $c \in C$, that is, the set of orders of 10 modulo cm . In other words, $$ S(m)=\left\{\operatorname{ord}_{c m}(10): c \in C\right\} $$ Since there are $4 \cdot 201+3=807$ numbers $c$ with $1 \leqslant c \leqslant 2017$ and $\operatorname{gcd}(c, 10)=1$, namely those such that $c \equiv 1,3,7,9(\bmod 10)$, $$ |S(m)| \leqslant|C|=807 $$ Now we find $m$ such that $|S(m)|=807$. Let $$ P=\{1<p \leqslant 2017: p \text { is prime, } p \neq 2,5\} $$ and choose a positive integer $\alpha$ such that every $p \in P$ divides $10^{\alpha}-1$ (e.g. $\alpha=\varphi(T), T$ being the product of all primes in $P$ ), and let $m=10^{\alpha}-1$. Claim. For every $c \in C$, we have $$ \operatorname{ord}_{c m}(10)=c \alpha $$ As an immediate consequence, this implies $|S(m)|=|C|=807$, finishing the problem. Proof. Obviously $\operatorname{ord}_{m}(10)=\alpha$. Let $t=\operatorname{ord}_{c m}(10)$. Then $$ c m\left|10^{t}-1 \quad \Longrightarrow \quad m\right| 10^{t}-1 \quad \Longrightarrow \quad \alpha \mid t $$ Hence $t=k \alpha$ for some $k \in \mathbb{Z}_{>0}$. We will show that $k=c$. Denote by $\nu_{p}(n)$ the number of prime factors $p$ in $n$, that is, the maximum exponent $\beta$ for which $p^{\beta} \mid n$. For every $\ell \geqslant 1$ and $p \in P$, the Lifting the Exponent Lemma provides $$ \nu_{p}\left(10^{\ell \alpha}-1\right)=\nu_{p}\left(\left(10^{\alpha}\right)^{\ell}-1\right)=\nu_{p}\left(10^{\alpha}-1\right)+\nu_{p}(\ell)=\nu_{p}(m)+\nu_{p}(\ell) $$ so $$ \begin{aligned} c m \mid 10^{k \alpha}-1 & \Longleftrightarrow \forall p \in P ; \nu_{p}(c m) \leqslant \nu_{p}\left(10^{k \alpha}-1\right) \\ & \Longleftrightarrow \forall p \in P ; \nu_{p}(m)+\nu_{p}(c) \leqslant \nu_{p}(m)+\nu_{p}(k) \\ & \Longleftrightarrow \forall p \in P ; \nu_{p}(c) \leqslant \nu_{p}(k) \\ & \Longleftrightarrow c \mid k . \end{aligned} $$ The first such $k$ is $k=c$, so $\operatorname{ord}_{c m}(10)=c \alpha$. Comment. The Lifting the Exponent Lemma states that, for any odd prime $p$, any integers $a, b$ coprime with $p$ such that $p \mid a-b$, and any positive integer exponent $n$, $$ \nu_{p}\left(a^{n}-b^{n}\right)=\nu_{p}(a-b)+\nu_{p}(n), $$ and, for $p=2$, $$ \nu_{2}\left(a^{n}-b^{n}\right)=\nu_{2}\left(a^{2}-b^{2}\right)+\nu_{p}(n)-1 . $$ Both claims can be proved by induction on $n$.
|
807
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Call a rational number short if it has finitely many digits in its decimal expansion. For a positive integer $m$, we say that a positive integer $t$ is $m$-tastic if there exists a number $c \in\{1,2,3, \ldots, 2017\}$ such that $\frac{10^{t}-1}{c \cdot m}$ is short, and such that $\frac{10^{k}-1}{c \cdot m}$ is not short for any $1 \leqslant k<t$. Let $S(m)$ be the set of $m$-tastic numbers. Consider $S(m)$ for $m=1,2, \ldots$. What is the maximum number of elements in $S(m)$ ? (Turkey)
|
First notice that $x \in \mathbb{Q}$ is short if and only if there are exponents $a, b \geqslant 0$ such that $2^{a} \cdot 5^{b} \cdot x \in \mathbb{Z}$. In fact, if $x$ is short, then $x=\frac{n}{10^{k}}$ for some $k$ and we can take $a=b=k$; on the other hand, if $2^{a} \cdot 5^{b} \cdot x=q \in \mathbb{Z}$ then $x=\frac{2^{b} \cdot 5^{a} q}{10^{a+b}}$, so $x$ is short. If $m=2^{a} \cdot 5^{b} \cdot s$, with $\operatorname{gcd}(s, 10)=1$, then $\frac{10^{t}-1}{m}$ is short if and only if $s$ divides $10^{t}-1$. So we may (and will) suppose without loss of generality that $\operatorname{gcd}(m, 10)=1$. Define $$ C=\{1 \leqslant c \leqslant 2017: \operatorname{gcd}(c, 10)=1\} . $$ The $m$-tastic numbers are then precisely the smallest exponents $t>0$ such that $10^{t} \equiv 1$ $(\bmod \mathrm{cm})$ for some integer $c \in C$, that is, the set of orders of 10 modulo cm . In other words, $$ S(m)=\left\{\operatorname{ord}_{c m}(10): c \in C\right\} $$ Since there are $4 \cdot 201+3=807$ numbers $c$ with $1 \leqslant c \leqslant 2017$ and $\operatorname{gcd}(c, 10)=1$, namely those such that $c \equiv 1,3,7,9(\bmod 10)$, $$ |S(m)| \leqslant|C|=807 $$ Now we find $m$ such that $|S(m)|=807$. Let $$ P=\{1<p \leqslant 2017: p \text { is prime, } p \neq 2,5\} $$ and choose a positive integer $\alpha$ such that every $p \in P$ divides $10^{\alpha}-1$ (e.g. $\alpha=\varphi(T), T$ being the product of all primes in $P$ ), and let $m=10^{\alpha}-1$. Claim. For every $c \in C$, we have $$ \operatorname{ord}_{c m}(10)=c \alpha $$ As an immediate consequence, this implies $|S(m)|=|C|=807$, finishing the problem. Proof. Obviously $\operatorname{ord}_{m}(10)=\alpha$. Let $t=\operatorname{ord}_{c m}(10)$. Then $$ c m\left|10^{t}-1 \quad \Longrightarrow \quad m\right| 10^{t}-1 \quad \Longrightarrow \quad \alpha \mid t $$ Hence $t=k \alpha$ for some $k \in \mathbb{Z}_{>0}$. We will show that $k=c$. Denote by $\nu_{p}(n)$ the number of prime factors $p$ in $n$, that is, the maximum exponent $\beta$ for which $p^{\beta} \mid n$. For every $\ell \geqslant 1$ and $p \in P$, the Lifting the Exponent Lemma provides $$ \nu_{p}\left(10^{\ell \alpha}-1\right)=\nu_{p}\left(\left(10^{\alpha}\right)^{\ell}-1\right)=\nu_{p}\left(10^{\alpha}-1\right)+\nu_{p}(\ell)=\nu_{p}(m)+\nu_{p}(\ell) $$ so $$ \begin{aligned} c m \mid 10^{k \alpha}-1 & \Longleftrightarrow \forall p \in P ; \nu_{p}(c m) \leqslant \nu_{p}\left(10^{k \alpha}-1\right) \\ & \Longleftrightarrow \forall p \in P ; \nu_{p}(m)+\nu_{p}(c) \leqslant \nu_{p}(m)+\nu_{p}(k) \\ & \Longleftrightarrow \forall p \in P ; \nu_{p}(c) \leqslant \nu_{p}(k) \\ & \Longleftrightarrow c \mid k . \end{aligned} $$ The first such $k$ is $k=c$, so $\operatorname{ord}_{c m}(10)=c \alpha$. Comment. The Lifting the Exponent Lemma states that, for any odd prime $p$, any integers $a, b$ coprime with $p$ such that $p \mid a-b$, and any positive integer exponent $n$, $$ \nu_{p}\left(a^{n}-b^{n}\right)=\nu_{p}(a-b)+\nu_{p}(n), $$ and, for $p=2$, $$ \nu_{2}\left(a^{n}-b^{n}\right)=\nu_{2}\left(a^{2}-b^{2}\right)+\nu_{p}(n)-1 . $$ Both claims can be proved by induction on $n$.
|
{
"resource_path": "IMO/segmented/en-IMO2017SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
dea78875-6919-501b-8e61-37922ea24b91
| 25,014
|
Find the smallest positive integer $n$, or show that no such $n$ exists, with the following property: there are infinitely many distinct $n$-tuples of positive rational numbers ( $a_{1}, a_{2}, \ldots, a_{n}$ ) such that both $$ a_{1}+a_{2}+\cdots+a_{n} \quad \text { and } \quad \frac{1}{a_{1}}+\frac{1}{a_{2}}+\cdots+\frac{1}{a_{n}} $$ are integers. (Singapore)
|
For $n=1, a_{1} \in \mathbb{Z}_{>0}$ and $\frac{1}{a_{1}} \in \mathbb{Z}_{>0}$ if and only if $a_{1}=1$. Next we show that (i) There are finitely many $(x, y) \in \mathbb{Q}_{>0}^{2}$ satisfying $x+y \in \mathbb{Z}$ and $\frac{1}{x}+\frac{1}{y} \in \mathbb{Z}$ Write $x=\frac{a}{b}$ and $y=\frac{c}{d}$ with $a, b, c, d \in \mathbb{Z}_{>0}$ and $\operatorname{gcd}(a, b)=\operatorname{gcd}(c, d)=1$. Then $x+y \in \mathbb{Z}$ and $\frac{1}{x}+\frac{1}{y} \in \mathbb{Z}$ is equivalent to the two divisibility conditions $$ b d \mid a d+b c \quad(1) \quad \text { and } \quad a c \mid a d+b c $$ Condition (1) implies that $d|a d+b c \Longleftrightarrow d| b c \Longleftrightarrow d \mid b$ since $\operatorname{gcd}(c, d)=1$. Still from (1) we get $b|a d+b c \Longleftrightarrow b| a d \Longleftrightarrow b \mid d$ since $\operatorname{gcd}(a, b)=1$. From $b \mid d$ and $d \mid b$ we have $b=d$. An analogous reasoning with condition (2) shows that $a=c$. Hence $x=\frac{a}{b}=\frac{c}{d}=y$, i.e., the problem amounts to finding all $x \in \mathbb{Q}_{>0}$ such that $2 x \in \mathbb{Z}_{>0}$ and $\frac{2}{x} \in \mathbb{Z}_{>0}$. Letting $n=2 x \in \mathbb{Z}_{>0}$, we have that $\frac{2}{x} \in \mathbb{Z}_{>0} \Longleftrightarrow \frac{4}{n} \in \mathbb{Z}_{>0} \Longleftrightarrow n=1,2$ or 4 , and there are finitely many solutions, namely $(x, y)=\left(\frac{1}{2}, \frac{1}{2}\right),(1,1)$ or $(2,2)$. (ii) There are infinitely many triples $(x, y, z) \in \mathbb{Q}_{>0}^{2}$ such that $x+y+z \in \mathbb{Z}$ and $\frac{1}{x}+\frac{1}{y}+\frac{1}{z} \in \mathbb{Z}$. We will look for triples such that $x+y+z=1$, so we may write them in the form $$ (x, y, z)=\left(\frac{a}{a+b+c}, \frac{b}{a+b+c}, \frac{c}{a+b+c}\right) \quad \text { with } a, b, c \in \mathbb{Z}_{>0} $$ We want these to satisfy $$ \frac{1}{x}+\frac{1}{y}+\frac{1}{z}=\frac{a+b+c}{a}+\frac{a+b+c}{b}+\frac{a+b+c}{c} \in \mathbb{Z} \Longleftrightarrow \frac{b+c}{a}+\frac{a+c}{b}+\frac{a+b}{c} \in \mathbb{Z} $$ Fixing $a=1$, it suffices to find infinitely many pairs $(b, c) \in \mathbb{Z}_{>0}^{2}$ such that $$ \frac{1}{b}+\frac{1}{c}+\frac{c}{b}+\frac{b}{c}=3 \Longleftrightarrow b^{2}+c^{2}-3 b c+b+c=0 $$ To show that equation (*) has infinitely many solutions, we use Vieta jumping (also known as root flipping): starting with $b=2, c=3$, the following algorithm generates infinitely many solutions. Let $c \geqslant b$, and view (*) as a quadratic equation in $b$ for $c$ fixed: $$ b^{2}-(3 c-1) \cdot b+\left(c^{2}+c\right)=0 $$ Then there exists another root $b_{0} \in \mathbb{Z}$ of ( $\left.* *\right)$ which satisfies $b+b_{0}=3 c-1$ and $b \cdot b_{0}=c^{2}+c$. Since $c \geqslant b$ by assumption, $$ b_{0}=\frac{c^{2}+c}{b} \geqslant \frac{c^{2}+c}{c}>c $$ Hence from the solution $(b, c)$ we obtain another one $\left(c, b_{0}\right)$ with $b_{0}>c$, and we can then "jump" again, this time with $c$ as the "variable" in the quadratic (*). This algorithm will generate an infinite sequence of distinct solutions, whose first terms are $(2,3),(3,6),(6,14),(14,35),(35,90),(90,234),(234,611),(611,1598),(1598,4182), \ldots$ Comment. Although not needed for solving this problem, we may also explicitly solve the recursion given by the Vieta jumping. Define the sequence $\left(x_{n}\right)$ as follows: $$ x_{0}=2, \quad x_{1}=3 \quad \text { and } \quad x_{n+2}=3 x_{n+1}-x_{n}-1 \text { for } n \geqslant 0 $$ Then the triple $$ (x, y, z)=\left(\frac{1}{1+x_{n}+x_{n+1}}, \frac{x_{n}}{1+x_{n}+x_{n+1}}, \frac{x_{n+1}}{1+x_{n}+x_{n+1}}\right) $$ satisfies the problem conditions for all $n \in \mathbb{N}$. It is easy to show that $x_{n}=F_{2 n+1}+1$, where $F_{n}$ denotes the $n$-th term of the Fibonacci sequence ( $F_{0}=0, F_{1}=1$, and $F_{n+2}=F_{n+1}+F_{n}$ for $n \geqslant 0$ ).
|
3
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Find the smallest positive integer $n$, or show that no such $n$ exists, with the following property: there are infinitely many distinct $n$-tuples of positive rational numbers ( $a_{1}, a_{2}, \ldots, a_{n}$ ) such that both $$ a_{1}+a_{2}+\cdots+a_{n} \quad \text { and } \quad \frac{1}{a_{1}}+\frac{1}{a_{2}}+\cdots+\frac{1}{a_{n}} $$ are integers. (Singapore)
|
For $n=1, a_{1} \in \mathbb{Z}_{>0}$ and $\frac{1}{a_{1}} \in \mathbb{Z}_{>0}$ if and only if $a_{1}=1$. Next we show that (i) There are finitely many $(x, y) \in \mathbb{Q}_{>0}^{2}$ satisfying $x+y \in \mathbb{Z}$ and $\frac{1}{x}+\frac{1}{y} \in \mathbb{Z}$ Write $x=\frac{a}{b}$ and $y=\frac{c}{d}$ with $a, b, c, d \in \mathbb{Z}_{>0}$ and $\operatorname{gcd}(a, b)=\operatorname{gcd}(c, d)=1$. Then $x+y \in \mathbb{Z}$ and $\frac{1}{x}+\frac{1}{y} \in \mathbb{Z}$ is equivalent to the two divisibility conditions $$ b d \mid a d+b c \quad(1) \quad \text { and } \quad a c \mid a d+b c $$ Condition (1) implies that $d|a d+b c \Longleftrightarrow d| b c \Longleftrightarrow d \mid b$ since $\operatorname{gcd}(c, d)=1$. Still from (1) we get $b|a d+b c \Longleftrightarrow b| a d \Longleftrightarrow b \mid d$ since $\operatorname{gcd}(a, b)=1$. From $b \mid d$ and $d \mid b$ we have $b=d$. An analogous reasoning with condition (2) shows that $a=c$. Hence $x=\frac{a}{b}=\frac{c}{d}=y$, i.e., the problem amounts to finding all $x \in \mathbb{Q}_{>0}$ such that $2 x \in \mathbb{Z}_{>0}$ and $\frac{2}{x} \in \mathbb{Z}_{>0}$. Letting $n=2 x \in \mathbb{Z}_{>0}$, we have that $\frac{2}{x} \in \mathbb{Z}_{>0} \Longleftrightarrow \frac{4}{n} \in \mathbb{Z}_{>0} \Longleftrightarrow n=1,2$ or 4 , and there are finitely many solutions, namely $(x, y)=\left(\frac{1}{2}, \frac{1}{2}\right),(1,1)$ or $(2,2)$. (ii) There are infinitely many triples $(x, y, z) \in \mathbb{Q}_{>0}^{2}$ such that $x+y+z \in \mathbb{Z}$ and $\frac{1}{x}+\frac{1}{y}+\frac{1}{z} \in \mathbb{Z}$. We will look for triples such that $x+y+z=1$, so we may write them in the form $$ (x, y, z)=\left(\frac{a}{a+b+c}, \frac{b}{a+b+c}, \frac{c}{a+b+c}\right) \quad \text { with } a, b, c \in \mathbb{Z}_{>0} $$ We want these to satisfy $$ \frac{1}{x}+\frac{1}{y}+\frac{1}{z}=\frac{a+b+c}{a}+\frac{a+b+c}{b}+\frac{a+b+c}{c} \in \mathbb{Z} \Longleftrightarrow \frac{b+c}{a}+\frac{a+c}{b}+\frac{a+b}{c} \in \mathbb{Z} $$ Fixing $a=1$, it suffices to find infinitely many pairs $(b, c) \in \mathbb{Z}_{>0}^{2}$ such that $$ \frac{1}{b}+\frac{1}{c}+\frac{c}{b}+\frac{b}{c}=3 \Longleftrightarrow b^{2}+c^{2}-3 b c+b+c=0 $$ To show that equation (*) has infinitely many solutions, we use Vieta jumping (also known as root flipping): starting with $b=2, c=3$, the following algorithm generates infinitely many solutions. Let $c \geqslant b$, and view (*) as a quadratic equation in $b$ for $c$ fixed: $$ b^{2}-(3 c-1) \cdot b+\left(c^{2}+c\right)=0 $$ Then there exists another root $b_{0} \in \mathbb{Z}$ of ( $\left.* *\right)$ which satisfies $b+b_{0}=3 c-1$ and $b \cdot b_{0}=c^{2}+c$. Since $c \geqslant b$ by assumption, $$ b_{0}=\frac{c^{2}+c}{b} \geqslant \frac{c^{2}+c}{c}>c $$ Hence from the solution $(b, c)$ we obtain another one $\left(c, b_{0}\right)$ with $b_{0}>c$, and we can then "jump" again, this time with $c$ as the "variable" in the quadratic (*). This algorithm will generate an infinite sequence of distinct solutions, whose first terms are $(2,3),(3,6),(6,14),(14,35),(35,90),(90,234),(234,611),(611,1598),(1598,4182), \ldots$ Comment. Although not needed for solving this problem, we may also explicitly solve the recursion given by the Vieta jumping. Define the sequence $\left(x_{n}\right)$ as follows: $$ x_{0}=2, \quad x_{1}=3 \quad \text { and } \quad x_{n+2}=3 x_{n+1}-x_{n}-1 \text { for } n \geqslant 0 $$ Then the triple $$ (x, y, z)=\left(\frac{1}{1+x_{n}+x_{n+1}}, \frac{x_{n}}{1+x_{n}+x_{n+1}}, \frac{x_{n+1}}{1+x_{n}+x_{n+1}}\right) $$ satisfies the problem conditions for all $n \in \mathbb{N}$. It is easy to show that $x_{n}=F_{2 n+1}+1$, where $F_{n}$ denotes the $n$-th term of the Fibonacci sequence ( $F_{0}=0, F_{1}=1$, and $F_{n+2}=F_{n+1}+F_{n}$ for $n \geqslant 0$ ).
|
{
"resource_path": "IMO/segmented/en-IMO2017SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
b322fe47-9f40-5de6-bc10-29c40db264df
| 25,020
|
An integer $n \geqslant 3$ is given. We call an $n$-tuple of real numbers $\left(x_{1}, x_{2}, \ldots, x_{n}\right)$ Shiny if for each permutation $y_{1}, y_{2}, \ldots, y_{n}$ of these numbers we have $$ \sum_{i=1}^{n-1} y_{i} y_{i+1}=y_{1} y_{2}+y_{2} y_{3}+y_{3} y_{4}+\cdots+y_{n-1} y_{n} \geqslant-1 $$ Find the largest constant $K=K(n)$ such that $$ \sum_{1 \leqslant i<j \leqslant n} x_{i} x_{j} \geqslant K $$ holds for every Shiny $n$-tuple $\left(x_{1}, x_{2}, \ldots, x_{n}\right)$. (Serbia)
|
We present another proof that $\sum_{i<j} x_{i} x_{j} \geqslant-(n-1) / 2$ for any Shiny $n$-tuple $\left(x_{1}, \ldots, x_{n}\right)$. Assume an ordering of the $x_{i}$ as in (2), and let $\ell=n-k$. Assume without loss of generality that $k \geqslant \ell$. Also assume $k \neq n$, (as otherwise, all of the $x_{i}$ are nonpositive, and so the inequality is trivial). Define the sets of indices $S=\{1,2, \ldots, k\}$ and $T=\{k+1, \ldots, n\}$. Define the following sums: $$ K=\sum_{\substack{i<j \\ i, j \in S}} x_{i} x_{j}, \quad M=\sum_{\substack{i \in S \\ j \in T}} x_{i} x_{j}, \quad \text { and } \quad L=\sum_{\substack{i<j \\ i, j \in T}} x_{i} x_{j} $$ By definition, $K, L \geqslant 0$ and $M \leqslant 0$. We aim to show that $K+L+M \geqslant-(n-1) / 2$. We split into cases based on whether $k=\ell$ or $k>\ell$. Case 1: $k>\ell$. Consider all permutations $\phi:\{1,2, \ldots, n\} \rightarrow\{1,2, \ldots, n\}$ such that $\phi^{-1}(T)=\{2,4, \ldots, 2 \ell\}$. Note that there are $k!!$ ! such permutations $\phi$. Define $$ f(\phi)=\sum_{i=1}^{n-1} x_{\phi(i)} x_{\phi(i+1)} $$ We know that $f(\phi) \geqslant-1$ for every permutation $\phi$ with the above property. Averaging $f(\phi)$ over all $\phi$ gives $$ -1 \leqslant \frac{1}{k!\ell!} \sum_{\phi} f(\phi)=\frac{2 \ell}{k \ell} M+\frac{2(k-\ell-1)}{k(k-1)} K $$ where the equality holds because there are $k \ell$ products in $M$, of which $2 \ell$ are selected for each $\phi$, and there are $k(k-1) / 2$ products in $K$, of which $k-\ell-1$ are selected for each $\phi$. We now have $$ K+L+M \geqslant K+L+\left(-\frac{k}{2}-\frac{k-\ell-1}{k-1} K\right)=-\frac{k}{2}+\frac{\ell}{k-1} K+L $$ Since $k \leqslant n-1$ and $K, L \geqslant 0$, we get the desired inequality. Case 2: $k=\ell=n / 2$. We do a similar approach, considering all $\phi:\{1,2, \ldots, n\} \rightarrow\{1,2, \ldots, n\}$ such that $\phi^{-1}(T)=$ $\{2,4, \ldots, 2 \ell\}$, and defining $f$ the same way. Analogously to Case 1 , we have $$ -1 \leqslant \frac{1}{k!\ell!} \sum_{\phi} f(\phi)=\frac{2 \ell-1}{k \ell} M $$ because there are $k \ell$ products in $M$, of which $2 \ell-1$ are selected for each $\phi$. Now, we have that $$ K+L+M \geqslant M \geqslant-\frac{n^{2}}{4(n-1)} \geqslant-\frac{n-1}{2} $$ where the last inequality holds because $n \geqslant 4$.
|
-(n-1) / 2
|
Yes
|
Yes
|
math-word-problem
|
Inequalities
|
An integer $n \geqslant 3$ is given. We call an $n$-tuple of real numbers $\left(x_{1}, x_{2}, \ldots, x_{n}\right)$ Shiny if for each permutation $y_{1}, y_{2}, \ldots, y_{n}$ of these numbers we have $$ \sum_{i=1}^{n-1} y_{i} y_{i+1}=y_{1} y_{2}+y_{2} y_{3}+y_{3} y_{4}+\cdots+y_{n-1} y_{n} \geqslant-1 $$ Find the largest constant $K=K(n)$ such that $$ \sum_{1 \leqslant i<j \leqslant n} x_{i} x_{j} \geqslant K $$ holds for every Shiny $n$-tuple $\left(x_{1}, x_{2}, \ldots, x_{n}\right)$. (Serbia) Answer: $K=-(n-1) / 2$.
|
We present another proof that $\sum_{i<j} x_{i} x_{j} \geqslant-(n-1) / 2$ for any Shiny $n$-tuple $\left(x_{1}, \ldots, x_{n}\right)$. Assume an ordering of the $x_{i}$ as in (2), and let $\ell=n-k$. Assume without loss of generality that $k \geqslant \ell$. Also assume $k \neq n$, (as otherwise, all of the $x_{i}$ are nonpositive, and so the inequality is trivial). Define the sets of indices $S=\{1,2, \ldots, k\}$ and $T=\{k+1, \ldots, n\}$. Define the following sums: $$ K=\sum_{\substack{i<j \\ i, j \in S}} x_{i} x_{j}, \quad M=\sum_{\substack{i \in S \\ j \in T}} x_{i} x_{j}, \quad \text { and } \quad L=\sum_{\substack{i<j \\ i, j \in T}} x_{i} x_{j} $$ By definition, $K, L \geqslant 0$ and $M \leqslant 0$. We aim to show that $K+L+M \geqslant-(n-1) / 2$. We split into cases based on whether $k=\ell$ or $k>\ell$. Case 1: $k>\ell$. Consider all permutations $\phi:\{1,2, \ldots, n\} \rightarrow\{1,2, \ldots, n\}$ such that $\phi^{-1}(T)=\{2,4, \ldots, 2 \ell\}$. Note that there are $k!!$ ! such permutations $\phi$. Define $$ f(\phi)=\sum_{i=1}^{n-1} x_{\phi(i)} x_{\phi(i+1)} $$ We know that $f(\phi) \geqslant-1$ for every permutation $\phi$ with the above property. Averaging $f(\phi)$ over all $\phi$ gives $$ -1 \leqslant \frac{1}{k!\ell!} \sum_{\phi} f(\phi)=\frac{2 \ell}{k \ell} M+\frac{2(k-\ell-1)}{k(k-1)} K $$ where the equality holds because there are $k \ell$ products in $M$, of which $2 \ell$ are selected for each $\phi$, and there are $k(k-1) / 2$ products in $K$, of which $k-\ell-1$ are selected for each $\phi$. We now have $$ K+L+M \geqslant K+L+\left(-\frac{k}{2}-\frac{k-\ell-1}{k-1} K\right)=-\frac{k}{2}+\frac{\ell}{k-1} K+L $$ Since $k \leqslant n-1$ and $K, L \geqslant 0$, we get the desired inequality. Case 2: $k=\ell=n / 2$. We do a similar approach, considering all $\phi:\{1,2, \ldots, n\} \rightarrow\{1,2, \ldots, n\}$ such that $\phi^{-1}(T)=$ $\{2,4, \ldots, 2 \ell\}$, and defining $f$ the same way. Analogously to Case 1 , we have $$ -1 \leqslant \frac{1}{k!\ell!} \sum_{\phi} f(\phi)=\frac{2 \ell-1}{k \ell} M $$ because there are $k \ell$ products in $M$, of which $2 \ell-1$ are selected for each $\phi$. Now, we have that $$ K+L+M \geqslant M \geqslant-\frac{n^{2}}{4(n-1)} \geqslant-\frac{n-1}{2} $$ where the last inequality holds because $n \geqslant 4$.
|
{
"resource_path": "IMO/segmented/en-IMO2017SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
02d0f90f-b6ac-5b8e-9bc6-70b213545ccb
| 25,040
|
Queenie and Horst play a game on a $20 \times 20$ chessboard. In the beginning the board is empty. In every turn, Horst places a black knight on an empty square in such a way that his new knight does not attack any previous knights. Then Queenie places a white queen on an empty square. The game gets finished when somebody cannot move. Find the maximal positive $K$ such that, regardless of the strategy of Queenie, Horst can put at least $K$ knights on the board. (Armenia)
|
We show two strategies, one for Horst to place at least 100 knights, and another strategy for Queenie that prevents Horst from putting more than 100 knights on the board. A strategy for Horst: Put knights only on black squares, until all black squares get occupied. Colour the squares of the board black and white in the usual way, such that the white and black squares alternate, and let Horst put his knights on black squares as long as it is possible. Two knights on squares of the same colour never attack each other. The number of black squares is $20^{2} / 2=200$. The two players occupy the squares in turn, so Horst will surely find empty black squares in his first 100 steps. A strategy for Queenie: Group the squares into cycles of length 4, and after each step of Horst, occupy the opposite square in the same cycle. Consider the squares of the board as vertices of a graph; let two squares be connected if two knights on those squares would attack each other. Notice that in a $4 \times 4$ board the squares can be grouped into 4 cycles of length 4 , as shown in Figure 1. Divide the board into parts of size $4 \times 4$, and perform the same grouping in every part; this way we arrange the 400 squares of the board into 100 cycles (Figure 2).  Figure 1  Figure 2  Figure 3 The strategy of Queenie can be as follows: Whenever Horst puts a new knight to a certain square $A$, which is part of some cycle $A-B-C-D-A$, let Queenie put her queen on the opposite square $C$ in that cycle (Figure 3). From this point, Horst cannot put any knight on $A$ or $C$ because those squares are already occupied, neither on $B$ or $D$ because those squares are attacked by the knight standing on $A$. Hence, Horst can put at most one knight on each cycle, that is at most 100 knights in total. Comment 1. Queenie's strategy can be prescribed by a simple rule: divide the board into $4 \times 4$ parts; whenever Horst puts a knight in a part $P$, Queenie reflects that square about the centre of $P$ and puts her queen on the reflected square. Comment 2. The result remains the same if Queenie moves first. In the first turn, she may put her first queen arbitrarily. Later, if she has to put her next queen on a square that already contains a queen, she may move arbitrarily again.
|
100
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Queenie and Horst play a game on a $20 \times 20$ chessboard. In the beginning the board is empty. In every turn, Horst places a black knight on an empty square in such a way that his new knight does not attack any previous knights. Then Queenie places a white queen on an empty square. The game gets finished when somebody cannot move. Find the maximal positive $K$ such that, regardless of the strategy of Queenie, Horst can put at least $K$ knights on the board. (Armenia)
|
We show two strategies, one for Horst to place at least 100 knights, and another strategy for Queenie that prevents Horst from putting more than 100 knights on the board. A strategy for Horst: Put knights only on black squares, until all black squares get occupied. Colour the squares of the board black and white in the usual way, such that the white and black squares alternate, and let Horst put his knights on black squares as long as it is possible. Two knights on squares of the same colour never attack each other. The number of black squares is $20^{2} / 2=200$. The two players occupy the squares in turn, so Horst will surely find empty black squares in his first 100 steps. A strategy for Queenie: Group the squares into cycles of length 4, and after each step of Horst, occupy the opposite square in the same cycle. Consider the squares of the board as vertices of a graph; let two squares be connected if two knights on those squares would attack each other. Notice that in a $4 \times 4$ board the squares can be grouped into 4 cycles of length 4 , as shown in Figure 1. Divide the board into parts of size $4 \times 4$, and perform the same grouping in every part; this way we arrange the 400 squares of the board into 100 cycles (Figure 2).  Figure 1  Figure 2  Figure 3 The strategy of Queenie can be as follows: Whenever Horst puts a new knight to a certain square $A$, which is part of some cycle $A-B-C-D-A$, let Queenie put her queen on the opposite square $C$ in that cycle (Figure 3). From this point, Horst cannot put any knight on $A$ or $C$ because those squares are already occupied, neither on $B$ or $D$ because those squares are attacked by the knight standing on $A$. Hence, Horst can put at most one knight on each cycle, that is at most 100 knights in total. Comment 1. Queenie's strategy can be prescribed by a simple rule: divide the board into $4 \times 4$ parts; whenever Horst puts a knight in a part $P$, Queenie reflects that square about the centre of $P$ and puts her queen on the reflected square. Comment 2. The result remains the same if Queenie moves first. In the first turn, she may put her first queen arbitrarily. Later, if she has to put her next queen on a square that already contains a queen, she may move arbitrarily again.
|
{
"resource_path": "IMO/segmented/en-IMO2018SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
7880bd3a-c6f9-525f-85dd-87b017685f07
| 23,566
|
Let $a_{0}, a_{1}, a_{2}, \ldots$ be a sequence of real numbers such that $a_{0}=0, a_{1}=1$, and for every $n \geqslant 2$ there exists $1 \leqslant k \leqslant n$ satisfying $$ a_{n}=\frac{a_{n-1}+\cdots+a_{n-k}}{k} $$ Find the maximal possible value of $a_{2018}-a_{2017}$. (Belgium)
|
We present a different proof of the estimate $a_{2018}-a_{2017} \leqslant \frac{2016}{2017^{2}}$. We keep the same notations of $S(n, k), m_{n}$ and $M_{n}$ from the previous solution. Notice that $S(n, n)=S(n, n-1)$, as $a_{0}=0$. Also notice that for $0 \leqslant k \leqslant \ell \leqslant n$ we have $S(n, \ell)=S(n, k)+S(n-k, \ell-k)$. Claim 2. For every positive integer $n$, we have $m_{n} \leqslant m_{n+1}$ and $M_{n+1} \leqslant M_{n}$, so the segment $\left[m_{n+1}, M_{n+1}\right]$ is contained in $\left[m_{n}, M_{n}\right]$. Proof. Choose a positive integer $k \leqslant n+1$ such that $m_{n+1}=S(n+1, k) / k$. Then we have $$ k m_{n+1}=S(n+1, k)=a_{n}+S(n, k-1) \geqslant m_{n}+(k-1) m_{n}=k m_{n}, $$ which establishes the first inequality in the Claim. The proof of the second inequality is similar. Claim 3. For every positive integers $k \geqslant n$, we have $m_{n} \leqslant a_{k} \leqslant M_{n}$. Proof. By Claim 2, we have $\left[m_{k}, M_{k}\right] \subseteq\left[m_{k-1}, M_{k-1}\right] \subseteq \cdots \subseteq\left[m_{n}, M_{n}\right]$. Since $a_{k} \in\left[m_{k}, M_{k}\right]$, the claim follows. Claim 4. For every integer $n \geqslant 2$, we have $M_{n}=S(n, n-1) /(n-1)$ and $m_{n}=S(n, n) / n$. Proof. We use induction on $n$. The base case $n=2$ is routine. To perform the induction step, we need to prove the inequalities $$ \frac{S(n, n)}{n} \leqslant \frac{S(n, k)}{k} \quad \text { and } \quad \frac{S(n, k)}{k} \leqslant \frac{S(n, n-1)}{n-1} $$ for every positive integer $k \leqslant n$. Clearly, these inequalities hold for $k=n$ and $k=n-1$, as $S(n, n)=S(n, n-1)>0$. In the sequel, we assume that $k<n-1$. Now the first inequality in (1) rewrites as $n S(n, k) \geqslant k S(n, n)=k(S(n, k)+S(n-k, n-k))$, or, cancelling the terms occurring on both parts, as $$ (n-k) S(n, k) \geqslant k S(n-k, n-k) \Longleftrightarrow S(n, k) \geqslant k \cdot \frac{S(n-k, n-k)}{n-k} $$ By the induction hypothesis, we have $S(n-k, n-k) /(n-k)=m_{n-k}$. By Claim 3, we get $a_{n-i} \geqslant m_{n-k}$ for all $i=1,2, \ldots, k$. Summing these $k$ inequalities we obtain $$ S(n, k) \geqslant k m_{n-k}=k \cdot \frac{S(n-k, n-k)}{n-k} $$ as required. The second inequality in (1) is proved similarly. Indeed, this inequality is equivalent to $$ \begin{aligned} (n-1) S(n, k) \leqslant k S(n, n-1) & \Longleftrightarrow(n-k-1) S(n, k) \leqslant k S(n-k, n-k-1) \\ & \Longleftrightarrow S(n, k) \leqslant k \cdot \frac{S(n-k, n-k-1)}{n-k-1}=k M_{n-k} ; \end{aligned} $$ the last inequality follows again from Claim 3, as each term in $S(n, k)$ is at most $M_{n-k}$. Now we can prove the required estimate for $a_{2018}-a_{2017}$. Set $N=2017$. By Claim 4 , $$ \begin{aligned} a_{N+1}-a_{N} \leqslant M_{N+1}-a_{N}=\frac{S(N+1, N)}{N}-a_{N} & =\frac{a_{N}+S(N, N-1)}{N}-a_{N} \\ & =\frac{S(N, N-1)}{N}-\frac{N-1}{N} \cdot a_{N} . \end{aligned} $$ On the other hand, the same Claim yields $$ a_{N} \geqslant m_{N}=\frac{S(N, N)}{N}=\frac{S(N, N-1)}{N} . $$ Noticing that each term in $S(N, N-1)$ is at most 1 , so $S(N, N-1) \leqslant N-1$, we finally obtain $$ a_{N+1}-a_{N} \leqslant \frac{S(N, N-1)}{N}-\frac{N-1}{N} \cdot \frac{S(N, N-1)}{N}=\frac{S(N, N-1)}{N^{2}} \leqslant \frac{N-1}{N^{2}} . $$ Comment 1. Claim 1 in Solution 1 can be deduced from Claims 2 and 4 in Solution 2. By Claim 4 we have $M_{n}=\frac{S(n, n-1)}{n-1}$ and $m_{n}=\frac{S(n, n)}{n}=\frac{S(n, n-1)}{n}$. It follows that $\Delta_{n}=M_{n}-m_{n}=$ $\frac{S(n, n-1)}{(n-1) n}$ and so $M_{n}=n \Delta_{n}$ and $m_{n}=(n-1) \Delta_{n}$ Similarly, $M_{n-1}=(n-1) \Delta_{n-1}$ and $m_{n-1}=(n-2) \Delta_{n-1}$. Then the inequalities $m_{n-1} \leqslant m_{n}$ and $M_{n} \leqslant M_{n-1}$ from Claim 2 write as $(n-2) \Delta_{n-1} \leqslant(n-1) \Delta_{n}$ and $n \Delta_{n} \leqslant(n-1) \Delta_{n-1}$. Hence we have the double inequality $$ \frac{n-2}{n-1} \Delta_{n-1} \leqslant \Delta_{n} \leqslant \frac{n-1}{n} \Delta_{n-1} $$ Comment 2. Both solutions above discuss the properties of an arbitrary sequence satisfying the problem conditions. Instead, one may investigate only an optimal sequence which maximises the value of $a_{2018}-a_{2017}$. Here we present an observation which allows to simplify such investigation - for instance, the proofs of Claim 1 in Solution 1 and Claim 4 in Solution 2. The sequence $\left(a_{n}\right)$ is uniquely determined by choosing, for every $n \geqslant 2$, a positive integer $k(n) \leqslant n$ such that $a_{n}=S(n, k(n)) / k(n)$. Take an arbitrary $2 \leqslant n_{0} \leqslant 2018$, and assume that all such integers $k(n)$, for $n \neq n_{0}$, are fixed. Then, for every $n$, the value of $a_{n}$ is a linear function in $a_{n_{0}}$ (whose possible values constitute some discrete subset of $\left[m_{n_{0}}, M_{n_{0}}\right]$ containing both endpoints). Hence, $a_{2018}-a_{2017}$ is also a linear function in $a_{n_{0}}$, so it attains its maximal value at one of the endpoints of the segment $\left[m_{n_{0}}, M_{n_{0}}\right]$. This shows that, while dealing with an optimal sequence, we may assume $a_{n} \in\left\{m_{n}, M_{n}\right\}$ for all $2 \leqslant n \leqslant 2018$. Now one can easily see that, if $a_{n}=m_{n}$, then $m_{n+1}=m_{n}$ and $M_{n+1} \leqslant \frac{m_{n}+n M_{n}}{n+1} ;$ similar estimates hold in the case $a_{n}=M_{n}$. This already establishes Claim 1, and simplifies the inductive proof of Claim 4, both applied to an optimal sequence.
|
\frac{2016}{2017^{2}}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Let $a_{0}, a_{1}, a_{2}, \ldots$ be a sequence of real numbers such that $a_{0}=0, a_{1}=1$, and for every $n \geqslant 2$ there exists $1 \leqslant k \leqslant n$ satisfying $$ a_{n}=\frac{a_{n-1}+\cdots+a_{n-k}}{k} $$ Find the maximal possible value of $a_{2018}-a_{2017}$. (Belgium) Answer: The maximal value is $\frac{2016}{2017^{2}}$.
|
We present a different proof of the estimate $a_{2018}-a_{2017} \leqslant \frac{2016}{2017^{2}}$. We keep the same notations of $S(n, k), m_{n}$ and $M_{n}$ from the previous solution. Notice that $S(n, n)=S(n, n-1)$, as $a_{0}=0$. Also notice that for $0 \leqslant k \leqslant \ell \leqslant n$ we have $S(n, \ell)=S(n, k)+S(n-k, \ell-k)$. Claim 2. For every positive integer $n$, we have $m_{n} \leqslant m_{n+1}$ and $M_{n+1} \leqslant M_{n}$, so the segment $\left[m_{n+1}, M_{n+1}\right]$ is contained in $\left[m_{n}, M_{n}\right]$. Proof. Choose a positive integer $k \leqslant n+1$ such that $m_{n+1}=S(n+1, k) / k$. Then we have $$ k m_{n+1}=S(n+1, k)=a_{n}+S(n, k-1) \geqslant m_{n}+(k-1) m_{n}=k m_{n}, $$ which establishes the first inequality in the Claim. The proof of the second inequality is similar. Claim 3. For every positive integers $k \geqslant n$, we have $m_{n} \leqslant a_{k} \leqslant M_{n}$. Proof. By Claim 2, we have $\left[m_{k}, M_{k}\right] \subseteq\left[m_{k-1}, M_{k-1}\right] \subseteq \cdots \subseteq\left[m_{n}, M_{n}\right]$. Since $a_{k} \in\left[m_{k}, M_{k}\right]$, the claim follows. Claim 4. For every integer $n \geqslant 2$, we have $M_{n}=S(n, n-1) /(n-1)$ and $m_{n}=S(n, n) / n$. Proof. We use induction on $n$. The base case $n=2$ is routine. To perform the induction step, we need to prove the inequalities $$ \frac{S(n, n)}{n} \leqslant \frac{S(n, k)}{k} \quad \text { and } \quad \frac{S(n, k)}{k} \leqslant \frac{S(n, n-1)}{n-1} $$ for every positive integer $k \leqslant n$. Clearly, these inequalities hold for $k=n$ and $k=n-1$, as $S(n, n)=S(n, n-1)>0$. In the sequel, we assume that $k<n-1$. Now the first inequality in (1) rewrites as $n S(n, k) \geqslant k S(n, n)=k(S(n, k)+S(n-k, n-k))$, or, cancelling the terms occurring on both parts, as $$ (n-k) S(n, k) \geqslant k S(n-k, n-k) \Longleftrightarrow S(n, k) \geqslant k \cdot \frac{S(n-k, n-k)}{n-k} $$ By the induction hypothesis, we have $S(n-k, n-k) /(n-k)=m_{n-k}$. By Claim 3, we get $a_{n-i} \geqslant m_{n-k}$ for all $i=1,2, \ldots, k$. Summing these $k$ inequalities we obtain $$ S(n, k) \geqslant k m_{n-k}=k \cdot \frac{S(n-k, n-k)}{n-k} $$ as required. The second inequality in (1) is proved similarly. Indeed, this inequality is equivalent to $$ \begin{aligned} (n-1) S(n, k) \leqslant k S(n, n-1) & \Longleftrightarrow(n-k-1) S(n, k) \leqslant k S(n-k, n-k-1) \\ & \Longleftrightarrow S(n, k) \leqslant k \cdot \frac{S(n-k, n-k-1)}{n-k-1}=k M_{n-k} ; \end{aligned} $$ the last inequality follows again from Claim 3, as each term in $S(n, k)$ is at most $M_{n-k}$. Now we can prove the required estimate for $a_{2018}-a_{2017}$. Set $N=2017$. By Claim 4 , $$ \begin{aligned} a_{N+1}-a_{N} \leqslant M_{N+1}-a_{N}=\frac{S(N+1, N)}{N}-a_{N} & =\frac{a_{N}+S(N, N-1)}{N}-a_{N} \\ & =\frac{S(N, N-1)}{N}-\frac{N-1}{N} \cdot a_{N} . \end{aligned} $$ On the other hand, the same Claim yields $$ a_{N} \geqslant m_{N}=\frac{S(N, N)}{N}=\frac{S(N, N-1)}{N} . $$ Noticing that each term in $S(N, N-1)$ is at most 1 , so $S(N, N-1) \leqslant N-1$, we finally obtain $$ a_{N+1}-a_{N} \leqslant \frac{S(N, N-1)}{N}-\frac{N-1}{N} \cdot \frac{S(N, N-1)}{N}=\frac{S(N, N-1)}{N^{2}} \leqslant \frac{N-1}{N^{2}} . $$ Comment 1. Claim 1 in Solution 1 can be deduced from Claims 2 and 4 in Solution 2. By Claim 4 we have $M_{n}=\frac{S(n, n-1)}{n-1}$ and $m_{n}=\frac{S(n, n)}{n}=\frac{S(n, n-1)}{n}$. It follows that $\Delta_{n}=M_{n}-m_{n}=$ $\frac{S(n, n-1)}{(n-1) n}$ and so $M_{n}=n \Delta_{n}$ and $m_{n}=(n-1) \Delta_{n}$ Similarly, $M_{n-1}=(n-1) \Delta_{n-1}$ and $m_{n-1}=(n-2) \Delta_{n-1}$. Then the inequalities $m_{n-1} \leqslant m_{n}$ and $M_{n} \leqslant M_{n-1}$ from Claim 2 write as $(n-2) \Delta_{n-1} \leqslant(n-1) \Delta_{n}$ and $n \Delta_{n} \leqslant(n-1) \Delta_{n-1}$. Hence we have the double inequality $$ \frac{n-2}{n-1} \Delta_{n-1} \leqslant \Delta_{n} \leqslant \frac{n-1}{n} \Delta_{n-1} $$ Comment 2. Both solutions above discuss the properties of an arbitrary sequence satisfying the problem conditions. Instead, one may investigate only an optimal sequence which maximises the value of $a_{2018}-a_{2017}$. Here we present an observation which allows to simplify such investigation - for instance, the proofs of Claim 1 in Solution 1 and Claim 4 in Solution 2. The sequence $\left(a_{n}\right)$ is uniquely determined by choosing, for every $n \geqslant 2$, a positive integer $k(n) \leqslant n$ such that $a_{n}=S(n, k(n)) / k(n)$. Take an arbitrary $2 \leqslant n_{0} \leqslant 2018$, and assume that all such integers $k(n)$, for $n \neq n_{0}$, are fixed. Then, for every $n$, the value of $a_{n}$ is a linear function in $a_{n_{0}}$ (whose possible values constitute some discrete subset of $\left[m_{n_{0}}, M_{n_{0}}\right]$ containing both endpoints). Hence, $a_{2018}-a_{2017}$ is also a linear function in $a_{n_{0}}$, so it attains its maximal value at one of the endpoints of the segment $\left[m_{n_{0}}, M_{n_{0}}\right]$. This shows that, while dealing with an optimal sequence, we may assume $a_{n} \in\left\{m_{n}, M_{n}\right\}$ for all $2 \leqslant n \leqslant 2018$. Now one can easily see that, if $a_{n}=m_{n}$, then $m_{n+1}=m_{n}$ and $M_{n+1} \leqslant \frac{m_{n}+n M_{n}}{n+1} ;$ similar estimates hold in the case $a_{n}=M_{n}$. This already establishes Claim 1, and simplifies the inductive proof of Claim 4, both applied to an optimal sequence.
|
{
"resource_path": "IMO/segmented/en-IMO2018SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
24df5dc3-bc2d-51c8-a991-103820d89fc6
| 23,647
|
Find the maximal value of $$ S=\sqrt[3]{\frac{a}{b+7}}+\sqrt[3]{\frac{b}{c+7}}+\sqrt[3]{\frac{c}{d+7}}+\sqrt[3]{\frac{d}{a+7}} $$ where $a, b, c, d$ are nonnegative real numbers which satisfy $a+b+c+d=100$. (Taiwan)
|
Since the value $8 / \sqrt[3]{7}$ is reached, it suffices to prove that $S \leqslant 8 / \sqrt[3]{7}$. Assume that $x, y, z, t$ is a permutation of the variables, with $x \leqslant y \leqslant z \leqslant t$. Then, by the rearrangement inequality, $$ S \leqslant\left(\sqrt[3]{\frac{x}{t+7}}+\sqrt[3]{\frac{t}{x+7}}\right)+\left(\sqrt[3]{\frac{y}{z+7}}+\sqrt[3]{\frac{z}{y+7}}\right) $$ Claim. The first bracket above does not exceed $\sqrt[3]{\frac{x+t+14}{7}}$. Proof. Since $$ X^{3}+Y^{3}+3 X Y Z-Z^{3}=\frac{1}{2}(X+Y-Z)\left((X-Y)^{2}+(X+Z)^{2}+(Y+Z)^{2}\right) $$ the inequality $X+Y \leqslant Z$ is equivalent (when $X, Y, Z \geqslant 0$ ) to $X^{3}+Y^{3}+3 X Y Z \leqslant Z^{3}$. Therefore, the claim is equivalent to $$ \frac{x}{t+7}+\frac{t}{x+7}+3 \sqrt[3]{\frac{x t(x+t+14)}{7(x+7)(t+7)}} \leqslant \frac{x+t+14}{7} $$ Notice that $$ \begin{array}{r} 3 \sqrt[3]{\frac{x t(x+t+14)}{7(x+7)(t+7)}}=3 \sqrt[3]{\frac{t(x+7)}{7(t+7)} \cdot \frac{x(t+7)}{7(x+7)} \cdot \frac{7(x+t+14)}{(t+7)(x+7)}} \\ \leqslant \frac{t(x+7)}{7(t+7)}+\frac{x(t+7)}{7(x+7)}+\frac{7(x+t+14)}{(t+7)(x+7)} \end{array} $$ by the AM-GM inequality, so it suffices to prove $$ \frac{x}{t+7}+\frac{t}{x+7}+\frac{t(x+7)}{7(t+7)}+\frac{x(t+7)}{7(x+7)}+\frac{7(x+t+14)}{(t+7)(x+7)} \leqslant \frac{x+t+14}{7} . $$ A straightforward check verifies that the last inequality is in fact an equality. The claim leads now to $$ S \leqslant \sqrt[3]{\frac{x+t+14}{7}}+\sqrt[3]{\frac{y+z+14}{7}} \leqslant 2 \sqrt[3]{\frac{x+y+z+t+28}{14}}=\frac{8}{\sqrt[3]{7}} $$ the last inequality being due to the AM-CM inequality (or to the fact that $\sqrt[3]{ }$ is concave on $[0, \infty))$.
|
\frac{8}{\sqrt[3]{7}}
|
Yes
|
Yes
|
math-word-problem
|
Inequalities
|
Find the maximal value of $$ S=\sqrt[3]{\frac{a}{b+7}}+\sqrt[3]{\frac{b}{c+7}}+\sqrt[3]{\frac{c}{d+7}}+\sqrt[3]{\frac{d}{a+7}} $$ where $a, b, c, d$ are nonnegative real numbers which satisfy $a+b+c+d=100$. (Taiwan) Answer: $\frac{8}{\sqrt[3]{7}}$, reached when $(a, b, c, d)$ is a cyclic permutation of $(1,49,1,49)$.
|
Since the value $8 / \sqrt[3]{7}$ is reached, it suffices to prove that $S \leqslant 8 / \sqrt[3]{7}$. Assume that $x, y, z, t$ is a permutation of the variables, with $x \leqslant y \leqslant z \leqslant t$. Then, by the rearrangement inequality, $$ S \leqslant\left(\sqrt[3]{\frac{x}{t+7}}+\sqrt[3]{\frac{t}{x+7}}\right)+\left(\sqrt[3]{\frac{y}{z+7}}+\sqrt[3]{\frac{z}{y+7}}\right) $$ Claim. The first bracket above does not exceed $\sqrt[3]{\frac{x+t+14}{7}}$. Proof. Since $$ X^{3}+Y^{3}+3 X Y Z-Z^{3}=\frac{1}{2}(X+Y-Z)\left((X-Y)^{2}+(X+Z)^{2}+(Y+Z)^{2}\right) $$ the inequality $X+Y \leqslant Z$ is equivalent (when $X, Y, Z \geqslant 0$ ) to $X^{3}+Y^{3}+3 X Y Z \leqslant Z^{3}$. Therefore, the claim is equivalent to $$ \frac{x}{t+7}+\frac{t}{x+7}+3 \sqrt[3]{\frac{x t(x+t+14)}{7(x+7)(t+7)}} \leqslant \frac{x+t+14}{7} $$ Notice that $$ \begin{array}{r} 3 \sqrt[3]{\frac{x t(x+t+14)}{7(x+7)(t+7)}}=3 \sqrt[3]{\frac{t(x+7)}{7(t+7)} \cdot \frac{x(t+7)}{7(x+7)} \cdot \frac{7(x+t+14)}{(t+7)(x+7)}} \\ \leqslant \frac{t(x+7)}{7(t+7)}+\frac{x(t+7)}{7(x+7)}+\frac{7(x+t+14)}{(t+7)(x+7)} \end{array} $$ by the AM-GM inequality, so it suffices to prove $$ \frac{x}{t+7}+\frac{t}{x+7}+\frac{t(x+7)}{7(t+7)}+\frac{x(t+7)}{7(x+7)}+\frac{7(x+t+14)}{(t+7)(x+7)} \leqslant \frac{x+t+14}{7} . $$ A straightforward check verifies that the last inequality is in fact an equality. The claim leads now to $$ S \leqslant \sqrt[3]{\frac{x+t+14}{7}}+\sqrt[3]{\frac{y+z+14}{7}} \leqslant 2 \sqrt[3]{\frac{x+y+z+t+28}{14}}=\frac{8}{\sqrt[3]{7}} $$ the last inequality being due to the AM-CM inequality (or to the fact that $\sqrt[3]{ }$ is concave on $[0, \infty))$.
|
{
"resource_path": "IMO/segmented/en-IMO2018SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
9f856afe-eab8-5d72-9acf-c2db760b49e9
| 23,655
|
On a flat plane in Camelot, King Arthur builds a labyrinth $\mathfrak{L}$ consisting of $n$ walls, each of which is an infinite straight line. No two walls are parallel, and no three walls have a common point. Merlin then paints one side of each wall entirely red and the other side entirely blue. At the intersection of two walls there are four corners: two diagonally opposite corners where a red side and a blue side meet, one corner where two red sides meet, and one corner where two blue sides meet. At each such intersection, there is a two-way door connecting the two diagonally opposite corners at which sides of different colours meet. After Merlin paints the walls, Morgana then places some knights in the labyrinth. The knights can walk through doors, but cannot walk through walls. Let $k(\mathfrak{L})$ be the largest number $k$ such that, no matter how Merlin paints the labyrinth $\mathfrak{L}$, Morgana can always place at least $k$ knights such that no two of them can ever meet. For each $n$, what are all possible values for $k(\mathfrak{L})$, where $\mathfrak{L}$ is a labyrinth with $n$ walls? (Canada)
|
First we show by induction that the $n$ walls divide the plane into $\binom{n+1}{2}+1$ regions. The claim is true for $n=0$ as, when there are no walls, the plane forms a single region. When placing the $n^{\text {th }}$ wall, it intersects each of the $n-1$ other walls exactly once and hence splits each of $n$ of the regions formed by those other walls into two regions. By the induction hypothesis, this yields $\left(\binom{n}{2}+1\right)+n=\binom{n+1}{2}+1$ regions, proving the claim. Now let $G$ be the graph with vertices given by the $\binom{n+1}{2}+1$ regions, and with two regions connected by an edge if there is a door between them. We now show that no matter how Merlin paints the $n$ walls, Morgana can place at least $n+1$ knights. No matter how the walls are painted, there are exactly $\binom{n}{2}$ intersection points, each of which corresponds to a single edge in $G$. Consider adding the edges of $G$ sequentially and note that each edge reduces the number of connected components by at most one. Therefore the number of connected components of G is at least $\binom{n+1}{2}+1-\binom{n}{2}=n+1$. If Morgana places a knight in regions corresponding to different connected components of $G$, then no two knights can ever meet. Now we give a construction showing that, no matter what shape the labyrinth is, Merlin can colour it such that there are exactly $n+1$ connected components, allowing Morgana to place at most $n+1$ knights. First, we choose a coordinate system on the labyrinth so that none of the walls run due north-south, or due east-west. We then have Merlin paint the west face of each wall red, and the east face of each wall blue. We label the regions according to how many walls the region is on the east side of: the labels are integers between 0 and $n$. We claim that, for each $i$, the regions labelled $i$ are connected by doors. First, we note that for each $i$ with $0 \leqslant i \leqslant n$ there is a unique region labelled $i$ which is unbounded to the north. Now, consider a knight placed in some region with label $i$, and ask them to walk north (moving east or west by following the walls on the northern sides of regions, as needed). This knight will never get stuck: each region is convex, and so, if it is bounded to the north, it has a single northernmost vertex with a door northwards to another region with label $i$. Eventually it will reach a region which is unbounded to the north, which will be the unique such region with label $i$. Hence every region with label $i$ is connected to this particular region, and so all regions with label $i$ are connected to each other. As a result, there are exactly $n+1$ connected components, and Morgana can place at most $n+1$ knights. Comment. Variations on this argument exist: some of them capture more information, and some of them capture less information, about the connected components according to this system of numbering. For example, it can be shown that the unbounded regions are numbered $0,1, \ldots, n-1, n, n-1, \ldots, 1$ as one cycles around them, that the regions labelled 0 and $n$ are the only regions in their connected components, and that each other connected component forms a single chain running between the two unbounded ones. It is also possible to argue that the regions are acyclic without revealing much about their structure.
|
n+1
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
On a flat plane in Camelot, King Arthur builds a labyrinth $\mathfrak{L}$ consisting of $n$ walls, each of which is an infinite straight line. No two walls are parallel, and no three walls have a common point. Merlin then paints one side of each wall entirely red and the other side entirely blue. At the intersection of two walls there are four corners: two diagonally opposite corners where a red side and a blue side meet, one corner where two red sides meet, and one corner where two blue sides meet. At each such intersection, there is a two-way door connecting the two diagonally opposite corners at which sides of different colours meet. After Merlin paints the walls, Morgana then places some knights in the labyrinth. The knights can walk through doors, but cannot walk through walls. Let $k(\mathfrak{L})$ be the largest number $k$ such that, no matter how Merlin paints the labyrinth $\mathfrak{L}$, Morgana can always place at least $k$ knights such that no two of them can ever meet. For each $n$, what are all possible values for $k(\mathfrak{L})$, where $\mathfrak{L}$ is a labyrinth with $n$ walls? (Canada)
|
First we show by induction that the $n$ walls divide the plane into $\binom{n+1}{2}+1$ regions. The claim is true for $n=0$ as, when there are no walls, the plane forms a single region. When placing the $n^{\text {th }}$ wall, it intersects each of the $n-1$ other walls exactly once and hence splits each of $n$ of the regions formed by those other walls into two regions. By the induction hypothesis, this yields $\left(\binom{n}{2}+1\right)+n=\binom{n+1}{2}+1$ regions, proving the claim. Now let $G$ be the graph with vertices given by the $\binom{n+1}{2}+1$ regions, and with two regions connected by an edge if there is a door between them. We now show that no matter how Merlin paints the $n$ walls, Morgana can place at least $n+1$ knights. No matter how the walls are painted, there are exactly $\binom{n}{2}$ intersection points, each of which corresponds to a single edge in $G$. Consider adding the edges of $G$ sequentially and note that each edge reduces the number of connected components by at most one. Therefore the number of connected components of G is at least $\binom{n+1}{2}+1-\binom{n}{2}=n+1$. If Morgana places a knight in regions corresponding to different connected components of $G$, then no two knights can ever meet. Now we give a construction showing that, no matter what shape the labyrinth is, Merlin can colour it such that there are exactly $n+1$ connected components, allowing Morgana to place at most $n+1$ knights. First, we choose a coordinate system on the labyrinth so that none of the walls run due north-south, or due east-west. We then have Merlin paint the west face of each wall red, and the east face of each wall blue. We label the regions according to how many walls the region is on the east side of: the labels are integers between 0 and $n$. We claim that, for each $i$, the regions labelled $i$ are connected by doors. First, we note that for each $i$ with $0 \leqslant i \leqslant n$ there is a unique region labelled $i$ which is unbounded to the north. Now, consider a knight placed in some region with label $i$, and ask them to walk north (moving east or west by following the walls on the northern sides of regions, as needed). This knight will never get stuck: each region is convex, and so, if it is bounded to the north, it has a single northernmost vertex with a door northwards to another region with label $i$. Eventually it will reach a region which is unbounded to the north, which will be the unique such region with label $i$. Hence every region with label $i$ is connected to this particular region, and so all regions with label $i$ are connected to each other. As a result, there are exactly $n+1$ connected components, and Morgana can place at most $n+1$ knights. Comment. Variations on this argument exist: some of them capture more information, and some of them capture less information, about the connected components according to this system of numbering. For example, it can be shown that the unbounded regions are numbered $0,1, \ldots, n-1, n, n-1, \ldots, 1$ as one cycles around them, that the regions labelled 0 and $n$ are the only regions in their connected components, and that each other connected component forms a single chain running between the two unbounded ones. It is also possible to argue that the regions are acyclic without revealing much about their structure.
|
{
"resource_path": "IMO/segmented/en-IMO2019SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
000bdf7c-70b1-5ae2-8c1a-b697750182f2
| 23,731
|
Let $\mathcal{A}$ denote the set of all polynomials in three variables $x, y, z$ with integer coefficients. Let $\mathcal{B}$ denote the subset of $\mathcal{A}$ formed by all polynomials which can be expressed as $$ (x+y+z) P(x, y, z)+(x y+y z+z x) Q(x, y, z)+x y z R(x, y, z) $$ with $P, Q, R \in \mathcal{A}$. Find the smallest non-negative integer $n$ such that $x^{i} y^{j} z^{k} \in \mathcal{B}$ for all nonnegative integers $i, j, k$ satisfying $i+j+k \geqslant n$. (Venezuela)
|
We start by showing that $n \leqslant 4$, i.e., any monomial $f=x^{i} y^{j} z^{k}$ with $i+j+k \geqslant 4$ belongs to $\mathcal{B}$. Assume that $i \geqslant j \geqslant k$, the other cases are analogous. Let $x+y+z=p, x y+y z+z x=q$ and $x y z=r$. Then $$ 0=(x-x)(x-y)(x-z)=x^{3}-p x^{2}+q x-r $$ therefore $x^{3} \in \mathcal{B}$. Next, $x^{2} y^{2}=x y q-(x+y) r \in \mathcal{B}$. If $k \geqslant 1$, then $r$ divides $f$, thus $f \in \mathcal{B}$. If $k=0$ and $j \geqslant 2$, then $x^{2} y^{2}$ divides $f$, thus we have $f \in \mathcal{B}$ again. Finally, if $k=0, j \leqslant 1$, then $x^{3}$ divides $f$ and $f \in \mathcal{B}$ in this case also. In order to prove that $n \geqslant 4$, we show that the monomial $x^{2} y$ does not belong to $\mathcal{B}$. Assume the contrary: $$ x^{2} y=p P+q Q+r R $$ for some polynomials $P, Q, R$. If polynomial $P$ contains the monomial $x^{2}$ (with nonzero coefficient), then $p P+q Q+r R$ contains the monomial $x^{3}$ with the same nonzero coefficient. So $P$ does not contain $x^{2}, y^{2}, z^{2}$ and we may write $$ x^{2} y=(x+y+z)(a x y+b y z+c z x)+(x y+y z+z x)(d x+e y+f z)+g x y z $$ where $a, b, c ; d, e, f ; g$ are the coefficients of $x y, y z, z x ; x, y, z ; x y z$ in the polynomials $P$; $Q ; R$, respectively (the remaining coefficients do not affect the monomials of degree 3 in $p P+q Q+r R)$. By considering the coefficients of $x y^{2}$ we get $e=-a$, analogously $e=-b$, $f=-b, f=-c, d=-c$, thus $a=b=c$ and $f=e=d=-a$, but then the coefficient of $x^{2} y$ in the right hand side equals $a+d=0 \neq 1$. Comment 1. The general question is the following. Call a polynomial $f\left(x_{1}, \ldots, x_{n}\right)$ with integer coefficients nice, if $f(0,0, \ldots, 0)=0$ and $f\left(x_{\pi_{1}}, \ldots, x_{\pi_{n}}\right)=f\left(x_{1}, \ldots, x_{n}\right)$ for any permutation $\pi$ of $1, \ldots, n$ (in other words, $f$ is symmetric and its constant term is zero.) Denote by $\mathcal{I}$ the set of polynomials of the form $$ p_{1} q_{1}+p_{2} q_{2}+\ldots+p_{m} q_{m} $$ where $m$ is an integer, $q_{1}, \ldots, q_{m}$ are polynomials with integer coefficients, and $p_{1}, \ldots, p_{m}$ are nice polynomials. Find the least $N$ for which any monomial of degree at least $N$ belongs to $\mathcal{I}$. The answer is $n(n-1) / 2+1$. The lower bound follows from the following claim: the polynomial $$ F\left(x_{1}, \ldots, x_{n}\right)=x_{2} x_{3}^{2} x_{4}^{3} \cdot \ldots \cdot x_{n}^{n-1} $$ does not belong to $\mathcal{I}$. Assume that $F=\sum p_{i} q_{i}$, according to (2). By taking only the monomials of degree $n(n-1) / 2$, we can additionally assume that every $p_{i}$ and every $q_{i}$ is homogeneous, $\operatorname{deg} p_{i}>0$, and $\operatorname{deg} p_{i}+\operatorname{deg} q_{i}=$ $\operatorname{deg} F=n(n-1) / 2$ for all $i$. Consider the alternating sum $$ \sum_{\pi} \operatorname{sign}(\pi) F\left(x_{\pi_{1}}, \ldots, x_{\pi_{n}}\right)=\sum_{i=1}^{m} p_{i} \sum_{\pi} \operatorname{sign}(\pi) q_{i}\left(x_{\pi_{1}}, \ldots, x_{\pi_{n}}\right):=S $$ where the summation is done over all permutations $\pi$ of $1, \ldots n$, and $\operatorname{sign}(\pi)$ denotes the sign of the permutation $\pi$. Since $\operatorname{deg} q_{i}=n(n-1) / 2-\operatorname{deg} p_{i}<n(n-1) / 2$, in any monomial $Q$ of $q_{i}$, there are at least two variables, say $x_{\alpha}$ and $x_{\beta}$, with equal exponents. Therefore $\sum_{\pi} \operatorname{sign}(\pi) Q\left(x_{\pi_{1}}, \ldots, x_{\pi_{n}}\right)=0$, because each pair of terms that corresponds to permutations which differ by the transposition of $\alpha$ and $\beta$, cancels out. This holds for any $i=1, \ldots, m$ and any monomial of $q_{i}$, so $S=0$. But the left hand side of (3) is a non-zero polynomial. This is a contradiction. Let us now prove, using induction on $n$, that any monomial $h=x_{1}^{c_{1}} \ldots x_{n}^{c_{n}}$ of degree $n(n-1) / 2+1$ belongs to $\mathcal{I}$, and additionally all $p_{i}, q_{i}$ in the representation (2) can be chosen homogeneous with sum of degrees equal to $n(n-1) / 2+1$. (Obviously, any monomial of degree at least $n(n-1) / 2+1$ is divisible by a monomial of degree exactly $n(n-1) / 2+1$, thus this suffices.) The proposition is true for $n=1$, so assume that $n>1$ and that the proposition is proved for smaller values of $n$. We proceed by an internal induction on $S:=\left|\left\{i: c_{i}=0\right\}\right|$. In the base case $S=0$ the monomial $h$ is divisible by the nice polynomial $x_{1} \cdot \ldots x_{n}$, therefore $h \in \mathcal{I}$. Now assume that $S>0$ and that the claim holds for smaller values of $S$. Let $T=n-S$. We may assume that $c_{T+1}=\ldots=c_{n}=0$ and $h=x_{1} \cdot \ldots \cdot x_{T} g\left(x_{1}, \ldots, x_{n-1}\right)$, where $\operatorname{deg} g=n(n-1) / 2-T+1 \geqslant(n-1)(n-2) / 2+1$. Using the outer induction hypothesis we represent $g$ as $p_{1} q_{1}+\ldots+p_{m} q_{m}$, where $p_{i}\left(x_{1}, \ldots, x_{n-1}\right)$ are nice polynomials in $n-1$ variables. There exist nice homogeneous polynomials $P_{i}\left(x_{1}, \ldots, x_{n}\right)$ such that $P_{i}\left(x_{1}, \ldots, x_{n-1}, 0\right)=p_{i}\left(x_{1}, \ldots, x_{n-1}\right)$. In other words, $\Delta_{i}:=p_{i}\left(x_{1}, \ldots, x_{n-1}\right)-P_{i}\left(x_{1}, \ldots, x_{n-1}, x_{n}\right)$ is divisible by $x_{n}$, let $\Delta_{i}=x_{n} g_{i}$. We get $$ h=x_{1} \cdot \ldots \cdot x_{T} \sum p_{i} q_{i}=x_{1} \cdot \ldots \cdot x_{T} \sum\left(P_{i}+x_{n} g_{i}\right) q_{i}=\left(x_{1} \cdot \ldots \cdot x_{T} x_{n}\right) \sum g_{i} q_{i}+\sum P_{i} q_{i} \in \mathcal{I} $$ The first term belongs to $\mathcal{I}$ by the inner induction hypothesis. This completes both inductions. Comment 2. The solutions above work smoothly for the versions of the original problem and its extensions to the case of $n$ variables, where all polynomials are assumed to have real coefficients. In the version with integer coefficients, the argument showing that $x^{2} y \notin \mathcal{B}$ can be simplified: it is not hard to show that in every polynomial $f \in \mathcal{B}$, the sum of the coefficients of $x^{2} y, x^{2} z, y^{2} x, y^{2} z, z^{2} x$ and $z^{2} y$ is even. A similar fact holds for any number of variables and also implies that $N \geqslant n(n-1) / 2+1$ in terms of the previous comment.
|
4
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Let $\mathcal{A}$ denote the set of all polynomials in three variables $x, y, z$ with integer coefficients. Let $\mathcal{B}$ denote the subset of $\mathcal{A}$ formed by all polynomials which can be expressed as $$ (x+y+z) P(x, y, z)+(x y+y z+z x) Q(x, y, z)+x y z R(x, y, z) $$ with $P, Q, R \in \mathcal{A}$. Find the smallest non-negative integer $n$ such that $x^{i} y^{j} z^{k} \in \mathcal{B}$ for all nonnegative integers $i, j, k$ satisfying $i+j+k \geqslant n$. (Venezuela)
|
We start by showing that $n \leqslant 4$, i.e., any monomial $f=x^{i} y^{j} z^{k}$ with $i+j+k \geqslant 4$ belongs to $\mathcal{B}$. Assume that $i \geqslant j \geqslant k$, the other cases are analogous. Let $x+y+z=p, x y+y z+z x=q$ and $x y z=r$. Then $$ 0=(x-x)(x-y)(x-z)=x^{3}-p x^{2}+q x-r $$ therefore $x^{3} \in \mathcal{B}$. Next, $x^{2} y^{2}=x y q-(x+y) r \in \mathcal{B}$. If $k \geqslant 1$, then $r$ divides $f$, thus $f \in \mathcal{B}$. If $k=0$ and $j \geqslant 2$, then $x^{2} y^{2}$ divides $f$, thus we have $f \in \mathcal{B}$ again. Finally, if $k=0, j \leqslant 1$, then $x^{3}$ divides $f$ and $f \in \mathcal{B}$ in this case also. In order to prove that $n \geqslant 4$, we show that the monomial $x^{2} y$ does not belong to $\mathcal{B}$. Assume the contrary: $$ x^{2} y=p P+q Q+r R $$ for some polynomials $P, Q, R$. If polynomial $P$ contains the monomial $x^{2}$ (with nonzero coefficient), then $p P+q Q+r R$ contains the monomial $x^{3}$ with the same nonzero coefficient. So $P$ does not contain $x^{2}, y^{2}, z^{2}$ and we may write $$ x^{2} y=(x+y+z)(a x y+b y z+c z x)+(x y+y z+z x)(d x+e y+f z)+g x y z $$ where $a, b, c ; d, e, f ; g$ are the coefficients of $x y, y z, z x ; x, y, z ; x y z$ in the polynomials $P$; $Q ; R$, respectively (the remaining coefficients do not affect the monomials of degree 3 in $p P+q Q+r R)$. By considering the coefficients of $x y^{2}$ we get $e=-a$, analogously $e=-b$, $f=-b, f=-c, d=-c$, thus $a=b=c$ and $f=e=d=-a$, but then the coefficient of $x^{2} y$ in the right hand side equals $a+d=0 \neq 1$. Comment 1. The general question is the following. Call a polynomial $f\left(x_{1}, \ldots, x_{n}\right)$ with integer coefficients nice, if $f(0,0, \ldots, 0)=0$ and $f\left(x_{\pi_{1}}, \ldots, x_{\pi_{n}}\right)=f\left(x_{1}, \ldots, x_{n}\right)$ for any permutation $\pi$ of $1, \ldots, n$ (in other words, $f$ is symmetric and its constant term is zero.) Denote by $\mathcal{I}$ the set of polynomials of the form $$ p_{1} q_{1}+p_{2} q_{2}+\ldots+p_{m} q_{m} $$ where $m$ is an integer, $q_{1}, \ldots, q_{m}$ are polynomials with integer coefficients, and $p_{1}, \ldots, p_{m}$ are nice polynomials. Find the least $N$ for which any monomial of degree at least $N$ belongs to $\mathcal{I}$. The answer is $n(n-1) / 2+1$. The lower bound follows from the following claim: the polynomial $$ F\left(x_{1}, \ldots, x_{n}\right)=x_{2} x_{3}^{2} x_{4}^{3} \cdot \ldots \cdot x_{n}^{n-1} $$ does not belong to $\mathcal{I}$. Assume that $F=\sum p_{i} q_{i}$, according to (2). By taking only the monomials of degree $n(n-1) / 2$, we can additionally assume that every $p_{i}$ and every $q_{i}$ is homogeneous, $\operatorname{deg} p_{i}>0$, and $\operatorname{deg} p_{i}+\operatorname{deg} q_{i}=$ $\operatorname{deg} F=n(n-1) / 2$ for all $i$. Consider the alternating sum $$ \sum_{\pi} \operatorname{sign}(\pi) F\left(x_{\pi_{1}}, \ldots, x_{\pi_{n}}\right)=\sum_{i=1}^{m} p_{i} \sum_{\pi} \operatorname{sign}(\pi) q_{i}\left(x_{\pi_{1}}, \ldots, x_{\pi_{n}}\right):=S $$ where the summation is done over all permutations $\pi$ of $1, \ldots n$, and $\operatorname{sign}(\pi)$ denotes the sign of the permutation $\pi$. Since $\operatorname{deg} q_{i}=n(n-1) / 2-\operatorname{deg} p_{i}<n(n-1) / 2$, in any monomial $Q$ of $q_{i}$, there are at least two variables, say $x_{\alpha}$ and $x_{\beta}$, with equal exponents. Therefore $\sum_{\pi} \operatorname{sign}(\pi) Q\left(x_{\pi_{1}}, \ldots, x_{\pi_{n}}\right)=0$, because each pair of terms that corresponds to permutations which differ by the transposition of $\alpha$ and $\beta$, cancels out. This holds for any $i=1, \ldots, m$ and any monomial of $q_{i}$, so $S=0$. But the left hand side of (3) is a non-zero polynomial. This is a contradiction. Let us now prove, using induction on $n$, that any monomial $h=x_{1}^{c_{1}} \ldots x_{n}^{c_{n}}$ of degree $n(n-1) / 2+1$ belongs to $\mathcal{I}$, and additionally all $p_{i}, q_{i}$ in the representation (2) can be chosen homogeneous with sum of degrees equal to $n(n-1) / 2+1$. (Obviously, any monomial of degree at least $n(n-1) / 2+1$ is divisible by a monomial of degree exactly $n(n-1) / 2+1$, thus this suffices.) The proposition is true for $n=1$, so assume that $n>1$ and that the proposition is proved for smaller values of $n$. We proceed by an internal induction on $S:=\left|\left\{i: c_{i}=0\right\}\right|$. In the base case $S=0$ the monomial $h$ is divisible by the nice polynomial $x_{1} \cdot \ldots x_{n}$, therefore $h \in \mathcal{I}$. Now assume that $S>0$ and that the claim holds for smaller values of $S$. Let $T=n-S$. We may assume that $c_{T+1}=\ldots=c_{n}=0$ and $h=x_{1} \cdot \ldots \cdot x_{T} g\left(x_{1}, \ldots, x_{n-1}\right)$, where $\operatorname{deg} g=n(n-1) / 2-T+1 \geqslant(n-1)(n-2) / 2+1$. Using the outer induction hypothesis we represent $g$ as $p_{1} q_{1}+\ldots+p_{m} q_{m}$, where $p_{i}\left(x_{1}, \ldots, x_{n-1}\right)$ are nice polynomials in $n-1$ variables. There exist nice homogeneous polynomials $P_{i}\left(x_{1}, \ldots, x_{n}\right)$ such that $P_{i}\left(x_{1}, \ldots, x_{n-1}, 0\right)=p_{i}\left(x_{1}, \ldots, x_{n-1}\right)$. In other words, $\Delta_{i}:=p_{i}\left(x_{1}, \ldots, x_{n-1}\right)-P_{i}\left(x_{1}, \ldots, x_{n-1}, x_{n}\right)$ is divisible by $x_{n}$, let $\Delta_{i}=x_{n} g_{i}$. We get $$ h=x_{1} \cdot \ldots \cdot x_{T} \sum p_{i} q_{i}=x_{1} \cdot \ldots \cdot x_{T} \sum\left(P_{i}+x_{n} g_{i}\right) q_{i}=\left(x_{1} \cdot \ldots \cdot x_{T} x_{n}\right) \sum g_{i} q_{i}+\sum P_{i} q_{i} \in \mathcal{I} $$ The first term belongs to $\mathcal{I}$ by the inner induction hypothesis. This completes both inductions. Comment 2. The solutions above work smoothly for the versions of the original problem and its extensions to the case of $n$ variables, where all polynomials are assumed to have real coefficients. In the version with integer coefficients, the argument showing that $x^{2} y \notin \mathcal{B}$ can be simplified: it is not hard to show that in every polynomial $f \in \mathcal{B}$, the sum of the coefficients of $x^{2} y, x^{2} z, y^{2} x, y^{2} z, z^{2} x$ and $z^{2} y$ is even. A similar fact holds for any number of variables and also implies that $N \geqslant n(n-1) / 2+1$ in terms of the previous comment.
|
{
"resource_path": "IMO/segmented/en-IMO2020SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
79f99487-8aa4-5bd1-b540-4f70f7346359
| 23,931
|
Suppose that $a, b, c, d$ are positive real numbers satisfying $(a+c)(b+d)=a c+b d$. Find the smallest possible value of $$ \frac{a}{b}+\frac{b}{c}+\frac{c}{d}+\frac{d}{a} $$
|
To show that $S \geqslant 8$, apply the AM-GM inequality twice as follows: $$ \left(\frac{a}{b}+\frac{c}{d}\right)+\left(\frac{b}{c}+\frac{d}{a}\right) \geqslant 2 \sqrt{\frac{a c}{b d}}+2 \sqrt{\frac{b d}{a c}}=\frac{2(a c+b d)}{\sqrt{a b c d}}=\frac{2(a+c)(b+d)}{\sqrt{a b c d}} \geqslant 2 \cdot \frac{2 \sqrt{a c} \cdot 2 \sqrt{b d}}{\sqrt{a b c d}}=8 . $$ The above inequalities turn into equalities when $a=c$ and $b=d$. Then the condition $(a+c)(b+d)=a c+b d$ can be rewritten as $4 a b=a^{2}+b^{2}$. So it is satisfied when $a / b=2 \pm \sqrt{3}$. Hence, $S$ attains value 8 , e.g., when $a=c=1$ and $b=d=2+\sqrt{3}$.
|
8
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Suppose that $a, b, c, d$ are positive real numbers satisfying $(a+c)(b+d)=a c+b d$. Find the smallest possible value of $$ \frac{a}{b}+\frac{b}{c}+\frac{c}{d}+\frac{d}{a} $$
|
To show that $S \geqslant 8$, apply the AM-GM inequality twice as follows: $$ \left(\frac{a}{b}+\frac{c}{d}\right)+\left(\frac{b}{c}+\frac{d}{a}\right) \geqslant 2 \sqrt{\frac{a c}{b d}}+2 \sqrt{\frac{b d}{a c}}=\frac{2(a c+b d)}{\sqrt{a b c d}}=\frac{2(a+c)(b+d)}{\sqrt{a b c d}} \geqslant 2 \cdot \frac{2 \sqrt{a c} \cdot 2 \sqrt{b d}}{\sqrt{a b c d}}=8 . $$ The above inequalities turn into equalities when $a=c$ and $b=d$. Then the condition $(a+c)(b+d)=a c+b d$ can be rewritten as $4 a b=a^{2}+b^{2}$. So it is satisfied when $a / b=2 \pm \sqrt{3}$. Hence, $S$ attains value 8 , e.g., when $a=c=1$ and $b=d=2+\sqrt{3}$.
|
{
"resource_path": "IMO/segmented/en-IMO2020SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
711c9bce-4143-5b1d-a2f1-94906dcc6914
| 23,933
|
Players $A$ and $B$ play a game on a blackboard that initially contains 2020 copies of the number 1. In every round, player $A$ erases two numbers $x$ and $y$ from the blackboard, and then player $B$ writes one of the numbers $x+y$ and $|x-y|$ on the blackboard. The game terminates as soon as, at the end of some round, one of the following holds: (1) one of the numbers on the blackboard is larger than the sum of all other numbers; (2) there are only zeros on the blackboard. Player $B$ must then give as many cookies to player $A$ as there are numbers on the blackboard. Player $A$ wants to get as many cookies as possible, whereas player $B$ wants to give as few as possible. Determine the number of cookies that $A$ receives if both players play optimally.
|
For a positive integer $n$, we denote by $S_{2}(n)$ the sum of digits in its binary representation. We prove that, in fact, if a board initially contains an even number $n>1$ of ones, then A can guarantee to obtain $S_{2}(n)$, but not more, cookies. The binary representation of 2020 is $2020=\overline{11111100100}_{2}$, so $S_{2}(2020)=7$, and the answer follows. A strategy for $A$. At any round, while possible, A chooses two equal nonzero numbers on the board. Clearly, while $A$ can make such choice, the game does not terminate. On the other hand, $A$ can follow this strategy unless the game has already terminated. Indeed, if $A$ always chooses two equal numbers, then each number appearing on the board is either 0 or a power of 2 with non-negative integer exponent, this can be easily proved using induction on the number of rounds. At the moment when $A$ is unable to follow the strategy all nonzero numbers on the board are distinct powers of 2 . If the board contains at least one such power, then the largest of those powers is greater than the sum of the others. Otherwise there are only zeros on the blackboard, in both cases the game terminates. For every number on the board, define its range to be the number of ones it is obtained from. We can prove by induction on the number of rounds that for any nonzero number $k$ written by $B$ its range is $k$, and for any zero written by $B$ its range is a power of 2 . Thus at the end of each round all the ranges are powers of two, and their sum is $n$. Since $S_{2}(a+b) \leqslant S_{2}(a)+S_{2}(b)$ for any positive integers $a$ and $b$, the number $n$ cannot be represented as a sum of less than $S_{2}(n)$ powers of 2 . Thus at the end of each round the board contains at least $S_{2}(n)$ numbers, while $A$ follows the above strategy. So $A$ can guarantee at least $S_{2}(n)$ cookies for himself. Comment. There are different proofs of the fact that the presented strategy guarantees at least $S_{2}(n)$ cookies for $A$. For instance, one may denote by $\Sigma$ the sum of numbers on the board, and by $z$ the number of zeros. Then the board contains at least $S_{2}(\Sigma)+z$ numbers; on the other hand, during the game, the number $S_{2}(\Sigma)+z$ does not decrease, and its initial value is $S_{2}(n)$. The claim follows. A strategy for $B$. Denote $s=S_{2}(n)$. Let $x_{1}, \ldots, x_{k}$ be the numbers on the board at some moment of the game after $B$ 's turn or at the beginning of the game. Say that a collection of $k$ signs $\varepsilon_{1}, \ldots, \varepsilon_{k} \in\{+1,-1\}$ is balanced if $$ \sum_{i=1}^{k} \varepsilon_{i} x_{i}=0 $$ We say that a situation on the board is good if $2^{s+1}$ does not divide the number of balanced collections. An appropriate strategy for $B$ can be explained as follows: Perform a move so that the situation remains good, while it is possible. We intend to show that in this case $B$ will not lose more than $S_{2}(n)$ cookies. For this purpose, we prove several lemmas. For a positive integer $k$, denote by $\nu_{2}(k)$ the exponent of the largest power of 2 that divides $k$. Recall that, by Legendre's formula, $\nu_{2}(n!)=n-S_{2}(n)$ for every positive integer $n$. Lemma 1. The initial situation is good. Proof. In the initial configuration, the number of balanced collections is equal to $\binom{n}{n / 2}$. We have $$ \nu_{2}\left(\binom{n}{n / 2}\right)=\nu_{2}(n!)-2 \nu_{2}((n / 2)!)=\left(n-S_{2}(n)\right)-2\left(\frac{n}{2}-S_{2}(n / 2)\right)=S_{2}(n)=s $$ Hence $2^{\text {s+1 }}$ does not divide the number of balanced collections, as desired. Lemma 2. B may play so that after each round the situation remains good. Proof. Assume that the situation $\left(x_{1}, \ldots, x_{k}\right)$ before a round is good, and that $A$ erases two numbers, $x_{p}$ and $x_{q}$. Let $N$ be the number of all balanced collections, $N_{+}$be the number of those having $\varepsilon_{p}=\varepsilon_{q}$, and $N_{-}$be the number of other balanced collections. Then $N=N_{+}+N_{-}$. Now, if $B$ replaces $x_{p}$ and $x_{q}$ by $x_{p}+x_{q}$, then the number of balanced collections will become $N_{+}$. If $B$ replaces $x_{p}$ and $x_{q}$ by $\left|x_{p}-x_{q}\right|$, then this number will become $N_{-}$. Since $2^{s+1}$ does not divide $N$, it does not divide one of the summands $N_{+}$and $N_{-}$, hence $B$ can reach a good situation after the round. Lemma 3. Assume that the game terminates at a good situation. Then the board contains at most $s$ numbers. Proof. Suppose, one of the numbers is greater than the sum of the other numbers. Then the number of balanced collections is 0 and hence divisible by $2^{s+1}$. Therefore, the situation is not good. Then we have only zeros on the blackboard at the moment when the game terminates. If there are $k$ of them, then the number of balanced collections is $2^{k}$. Since the situation is good, we have $k \leqslant s$. By Lemmas 1 and 2, $B$ may act in such way that they keep the situation good. By Lemma 3, when the game terminates, the board contains at most $s$ numbers. This is what we aimed to prove. Comment 1. If the initial situation had some odd number $n>1$ of ones on the blackboard, player $A$ would still get $S_{2}(n)$ cookies, provided that both players act optimally. The proof of this fact is similar to the solution above, after one makes some changes in the definitions. Such changes are listed below. Say that a collection of $k$ signs $\varepsilon_{1}, \ldots, \varepsilon_{k} \in\{+1,-1\}$ is positive if $$ \sum_{i=1}^{k} \varepsilon_{i} x_{i}>0 $$ For every index $i=1,2, \ldots, k$, we denote by $N_{i}$ the number of positive collections such that $\varepsilon_{i}=1$. Finally, say that a situation on the board is good if $2^{s-1}$ does not divide at least one of the numbers $N_{i}$. Now, a strategy for $B$ again consists in preserving the situation good, after each round. Comment 2. There is an easier strategy for $B$, allowing, in the game starting with an even number $n$ of ones, to lose no more than $d=\left\lfloor\log _{2}(n+2)\right\rfloor-1$ cookies. If the binary representation of $n$ contains at most two zeros, then $d=S_{2}(n)$, and hence the strategy is optimal in that case. We outline this approach below. First of all, we can assume that $A$ never erases zeros from the blackboard. Indeed, $A$ may skip such moves harmlessly, ignoring the zeros in the further process; this way, $A$ 's win will just increase. We say that a situation on the blackboard is pretty if the numbers on the board can be partitioned into two groups with equal sums. Clearly, if the situation before some round is pretty, then $B$ may play so as to preserve this property after the round. The strategy for $B$ is as follows: - $B$ always chooses a move that leads to a pretty situation. - If both possible moves of $B$ lead to pretty situations, then $B$ writes the sum of the two numbers erased by $A$. Since the situation always remains pretty, the game terminates when all numbers on the board are zeros. Suppose that, at the end of the game, there are $m \geqslant d+1=\left\lfloor\log _{2}(n+2)\right\rfloor$ zeros on the board; then $2^{m}-1>n / 2$. Now we analyze the whole process of the play. Let us number the zeros on the board in order of appearance. During the play, each zero had appeared after subtracting two equal numbers. Let $n_{1}, \ldots, n_{m}$ be positive integers such that the first zero appeared after subtracting $n_{1}$ from $n_{1}$, the second zero appeared after subtracting $n_{2}$ from $n_{2}$, and so on. Since the sum of the numbers on the blackboard never increases, we have $2 n_{1}+\ldots+2 n_{m} \leqslant n$, hence $$ n_{1}+\ldots+n_{m} \leqslant n / 2<2^{m}-1 $$ There are $2^{m}$ subsets of the set $\{1,2, \ldots, m\}$. For $I \subseteq\{1,2, \ldots, m\}$, denote by $f(I)$ the sum $\sum_{i \in I} n_{i}$. There are less than $2^{m}$ possible values for $f(I)$, so there are two distinct subsets $I$ and $J$ with $f(I)=f(J)$. Replacing $I$ and $J$ with $I \backslash J$ and $J \backslash I$, we assume that $I$ and $J$ are disjoint. Let $i_{0}$ be the smallest number in $I \cup J$; without loss of generality, $i_{0} \in I$. Consider the round when $A$ had erased two numbers equal to $n_{i_{0}}$, and $B$ had put the $i_{0}{ }^{\text {th }}$ zero instead, and the situation before that round. For each nonzero number $z$ which is on the blackboard at this moment, we can keep track of it during the further play until it enters one of the numbers $n_{i}, i \geqslant i_{0}$, which then turn into zeros. For every $i=i_{0}, i_{0}+1, \ldots, m$, we denote by $X_{i}$ the collection of all numbers on the blackboard that finally enter the first copy of $n_{i}$, and by $Y_{i}$ the collection of those finally entering the second copy of $n_{i}$. Thus, each of $X_{i_{0}}$ and $Y_{i_{0}}$ consists of a single number. Since $A$ never erases zeros, the 2(m-iol $i_{0}$ ) defined sets are pairwise disjoint. Clearly, for either of the collections $X_{i}$ and $Y_{i}$, a signed sum of its elements equals $n_{i}$, for a proper choice of the signs. Therefore, for every $i=i_{0}, i_{0}+1, \ldots, m$ one can endow numbers in $X_{i} \cup Y_{i}$ with signs so that their sum becomes any of the numbers $-2 n_{i}, 0$, or $2 n_{i}$. Perform such endowment so as to get $2 n_{i}$ from each collection $X_{i} \cup Y_{i}$ with $i \in I,-2 n_{j}$ from each collection $X_{j} \cup Y_{j}$ with $j \in J$, and 0 from each remaining collection. The obtained signed sum of all numbers on the blackboard equals $$ \sum_{i \in I} 2 n_{i}-\sum_{i \in J} 2 n_{i}=0 $$ and the numbers in $X_{i_{0}}$ and $Y_{i_{0}}$ have the same (positive) sign. This means that, at this round, $B$ could add up the two numbers $n_{i_{0}}$ to get a pretty situation. According to the strategy, $B$ should have performed that, instead of subtracting the numbers. This contradiction shows that $m \leqslant d$, as desired. This page is intentionally left blank
|
7
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Players $A$ and $B$ play a game on a blackboard that initially contains 2020 copies of the number 1. In every round, player $A$ erases two numbers $x$ and $y$ from the blackboard, and then player $B$ writes one of the numbers $x+y$ and $|x-y|$ on the blackboard. The game terminates as soon as, at the end of some round, one of the following holds: (1) one of the numbers on the blackboard is larger than the sum of all other numbers; (2) there are only zeros on the blackboard. Player $B$ must then give as many cookies to player $A$ as there are numbers on the blackboard. Player $A$ wants to get as many cookies as possible, whereas player $B$ wants to give as few as possible. Determine the number of cookies that $A$ receives if both players play optimally.
|
For a positive integer $n$, we denote by $S_{2}(n)$ the sum of digits in its binary representation. We prove that, in fact, if a board initially contains an even number $n>1$ of ones, then A can guarantee to obtain $S_{2}(n)$, but not more, cookies. The binary representation of 2020 is $2020=\overline{11111100100}_{2}$, so $S_{2}(2020)=7$, and the answer follows. A strategy for $A$. At any round, while possible, A chooses two equal nonzero numbers on the board. Clearly, while $A$ can make such choice, the game does not terminate. On the other hand, $A$ can follow this strategy unless the game has already terminated. Indeed, if $A$ always chooses two equal numbers, then each number appearing on the board is either 0 or a power of 2 with non-negative integer exponent, this can be easily proved using induction on the number of rounds. At the moment when $A$ is unable to follow the strategy all nonzero numbers on the board are distinct powers of 2 . If the board contains at least one such power, then the largest of those powers is greater than the sum of the others. Otherwise there are only zeros on the blackboard, in both cases the game terminates. For every number on the board, define its range to be the number of ones it is obtained from. We can prove by induction on the number of rounds that for any nonzero number $k$ written by $B$ its range is $k$, and for any zero written by $B$ its range is a power of 2 . Thus at the end of each round all the ranges are powers of two, and their sum is $n$. Since $S_{2}(a+b) \leqslant S_{2}(a)+S_{2}(b)$ for any positive integers $a$ and $b$, the number $n$ cannot be represented as a sum of less than $S_{2}(n)$ powers of 2 . Thus at the end of each round the board contains at least $S_{2}(n)$ numbers, while $A$ follows the above strategy. So $A$ can guarantee at least $S_{2}(n)$ cookies for himself. Comment. There are different proofs of the fact that the presented strategy guarantees at least $S_{2}(n)$ cookies for $A$. For instance, one may denote by $\Sigma$ the sum of numbers on the board, and by $z$ the number of zeros. Then the board contains at least $S_{2}(\Sigma)+z$ numbers; on the other hand, during the game, the number $S_{2}(\Sigma)+z$ does not decrease, and its initial value is $S_{2}(n)$. The claim follows. A strategy for $B$. Denote $s=S_{2}(n)$. Let $x_{1}, \ldots, x_{k}$ be the numbers on the board at some moment of the game after $B$ 's turn or at the beginning of the game. Say that a collection of $k$ signs $\varepsilon_{1}, \ldots, \varepsilon_{k} \in\{+1,-1\}$ is balanced if $$ \sum_{i=1}^{k} \varepsilon_{i} x_{i}=0 $$ We say that a situation on the board is good if $2^{s+1}$ does not divide the number of balanced collections. An appropriate strategy for $B$ can be explained as follows: Perform a move so that the situation remains good, while it is possible. We intend to show that in this case $B$ will not lose more than $S_{2}(n)$ cookies. For this purpose, we prove several lemmas. For a positive integer $k$, denote by $\nu_{2}(k)$ the exponent of the largest power of 2 that divides $k$. Recall that, by Legendre's formula, $\nu_{2}(n!)=n-S_{2}(n)$ for every positive integer $n$. Lemma 1. The initial situation is good. Proof. In the initial configuration, the number of balanced collections is equal to $\binom{n}{n / 2}$. We have $$ \nu_{2}\left(\binom{n}{n / 2}\right)=\nu_{2}(n!)-2 \nu_{2}((n / 2)!)=\left(n-S_{2}(n)\right)-2\left(\frac{n}{2}-S_{2}(n / 2)\right)=S_{2}(n)=s $$ Hence $2^{\text {s+1 }}$ does not divide the number of balanced collections, as desired. Lemma 2. B may play so that after each round the situation remains good. Proof. Assume that the situation $\left(x_{1}, \ldots, x_{k}\right)$ before a round is good, and that $A$ erases two numbers, $x_{p}$ and $x_{q}$. Let $N$ be the number of all balanced collections, $N_{+}$be the number of those having $\varepsilon_{p}=\varepsilon_{q}$, and $N_{-}$be the number of other balanced collections. Then $N=N_{+}+N_{-}$. Now, if $B$ replaces $x_{p}$ and $x_{q}$ by $x_{p}+x_{q}$, then the number of balanced collections will become $N_{+}$. If $B$ replaces $x_{p}$ and $x_{q}$ by $\left|x_{p}-x_{q}\right|$, then this number will become $N_{-}$. Since $2^{s+1}$ does not divide $N$, it does not divide one of the summands $N_{+}$and $N_{-}$, hence $B$ can reach a good situation after the round. Lemma 3. Assume that the game terminates at a good situation. Then the board contains at most $s$ numbers. Proof. Suppose, one of the numbers is greater than the sum of the other numbers. Then the number of balanced collections is 0 and hence divisible by $2^{s+1}$. Therefore, the situation is not good. Then we have only zeros on the blackboard at the moment when the game terminates. If there are $k$ of them, then the number of balanced collections is $2^{k}$. Since the situation is good, we have $k \leqslant s$. By Lemmas 1 and 2, $B$ may act in such way that they keep the situation good. By Lemma 3, when the game terminates, the board contains at most $s$ numbers. This is what we aimed to prove. Comment 1. If the initial situation had some odd number $n>1$ of ones on the blackboard, player $A$ would still get $S_{2}(n)$ cookies, provided that both players act optimally. The proof of this fact is similar to the solution above, after one makes some changes in the definitions. Such changes are listed below. Say that a collection of $k$ signs $\varepsilon_{1}, \ldots, \varepsilon_{k} \in\{+1,-1\}$ is positive if $$ \sum_{i=1}^{k} \varepsilon_{i} x_{i}>0 $$ For every index $i=1,2, \ldots, k$, we denote by $N_{i}$ the number of positive collections such that $\varepsilon_{i}=1$. Finally, say that a situation on the board is good if $2^{s-1}$ does not divide at least one of the numbers $N_{i}$. Now, a strategy for $B$ again consists in preserving the situation good, after each round. Comment 2. There is an easier strategy for $B$, allowing, in the game starting with an even number $n$ of ones, to lose no more than $d=\left\lfloor\log _{2}(n+2)\right\rfloor-1$ cookies. If the binary representation of $n$ contains at most two zeros, then $d=S_{2}(n)$, and hence the strategy is optimal in that case. We outline this approach below. First of all, we can assume that $A$ never erases zeros from the blackboard. Indeed, $A$ may skip such moves harmlessly, ignoring the zeros in the further process; this way, $A$ 's win will just increase. We say that a situation on the blackboard is pretty if the numbers on the board can be partitioned into two groups with equal sums. Clearly, if the situation before some round is pretty, then $B$ may play so as to preserve this property after the round. The strategy for $B$ is as follows: - $B$ always chooses a move that leads to a pretty situation. - If both possible moves of $B$ lead to pretty situations, then $B$ writes the sum of the two numbers erased by $A$. Since the situation always remains pretty, the game terminates when all numbers on the board are zeros. Suppose that, at the end of the game, there are $m \geqslant d+1=\left\lfloor\log _{2}(n+2)\right\rfloor$ zeros on the board; then $2^{m}-1>n / 2$. Now we analyze the whole process of the play. Let us number the zeros on the board in order of appearance. During the play, each zero had appeared after subtracting two equal numbers. Let $n_{1}, \ldots, n_{m}$ be positive integers such that the first zero appeared after subtracting $n_{1}$ from $n_{1}$, the second zero appeared after subtracting $n_{2}$ from $n_{2}$, and so on. Since the sum of the numbers on the blackboard never increases, we have $2 n_{1}+\ldots+2 n_{m} \leqslant n$, hence $$ n_{1}+\ldots+n_{m} \leqslant n / 2<2^{m}-1 $$ There are $2^{m}$ subsets of the set $\{1,2, \ldots, m\}$. For $I \subseteq\{1,2, \ldots, m\}$, denote by $f(I)$ the sum $\sum_{i \in I} n_{i}$. There are less than $2^{m}$ possible values for $f(I)$, so there are two distinct subsets $I$ and $J$ with $f(I)=f(J)$. Replacing $I$ and $J$ with $I \backslash J$ and $J \backslash I$, we assume that $I$ and $J$ are disjoint. Let $i_{0}$ be the smallest number in $I \cup J$; without loss of generality, $i_{0} \in I$. Consider the round when $A$ had erased two numbers equal to $n_{i_{0}}$, and $B$ had put the $i_{0}{ }^{\text {th }}$ zero instead, and the situation before that round. For each nonzero number $z$ which is on the blackboard at this moment, we can keep track of it during the further play until it enters one of the numbers $n_{i}, i \geqslant i_{0}$, which then turn into zeros. For every $i=i_{0}, i_{0}+1, \ldots, m$, we denote by $X_{i}$ the collection of all numbers on the blackboard that finally enter the first copy of $n_{i}$, and by $Y_{i}$ the collection of those finally entering the second copy of $n_{i}$. Thus, each of $X_{i_{0}}$ and $Y_{i_{0}}$ consists of a single number. Since $A$ never erases zeros, the 2(m-iol $i_{0}$ ) defined sets are pairwise disjoint. Clearly, for either of the collections $X_{i}$ and $Y_{i}$, a signed sum of its elements equals $n_{i}$, for a proper choice of the signs. Therefore, for every $i=i_{0}, i_{0}+1, \ldots, m$ one can endow numbers in $X_{i} \cup Y_{i}$ with signs so that their sum becomes any of the numbers $-2 n_{i}, 0$, or $2 n_{i}$. Perform such endowment so as to get $2 n_{i}$ from each collection $X_{i} \cup Y_{i}$ with $i \in I,-2 n_{j}$ from each collection $X_{j} \cup Y_{j}$ with $j \in J$, and 0 from each remaining collection. The obtained signed sum of all numbers on the blackboard equals $$ \sum_{i \in I} 2 n_{i}-\sum_{i \in J} 2 n_{i}=0 $$ and the numbers in $X_{i_{0}}$ and $Y_{i_{0}}$ have the same (positive) sign. This means that, at this round, $B$ could add up the two numbers $n_{i_{0}}$ to get a pretty situation. According to the strategy, $B$ should have performed that, instead of subtracting the numbers. This contradiction shows that $m \leqslant d$, as desired. This page is intentionally left blank
|
{
"resource_path": "IMO/segmented/en-IMO2020SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
b8ff11b9-bc7b-546c-a711-565c5eea14e1
| 23,975
|
Suppose that $a, b, c, d$ are positive real numbers satisfying $(a+c)(b+d)=a c+b d$. Find the smallest possible value of $$ S=\frac{a}{b}+\frac{b}{c}+\frac{c}{d}+\frac{d}{a} $$ (Israel)
|
To show that $S \geqslant 8$, apply the AM-GM inequality twice as follows: $$ \left(\frac{a}{b}+\frac{c}{d}\right)+\left(\frac{b}{c}+\frac{d}{a}\right) \geqslant 2 \sqrt{\frac{a c}{b d}}+2 \sqrt{\frac{b d}{a c}}=\frac{2(a c+b d)}{\sqrt{a b c d}}=\frac{2(a+c)(b+d)}{\sqrt{a b c d}} \geqslant 2 \cdot \frac{2 \sqrt{a c} \cdot 2 \sqrt{b d}}{\sqrt{a b c d}}=8 . $$ The above inequalities turn into equalities when $a=c$ and $b=d$. Then the condition $(a+c)(b+d)=a c+b d$ can be rewritten as $4 a b=a^{2}+b^{2}$. So it is satisfied when $a / b=2 \pm \sqrt{3}$. Hence, $S$ attains value 8 , e.g., when $a=c=1$ and $b=d=2+\sqrt{3}$.
|
8
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Suppose that $a, b, c, d$ are positive real numbers satisfying $(a+c)(b+d)=a c+b d$. Find the smallest possible value of $$ S=\frac{a}{b}+\frac{b}{c}+\frac{c}{d}+\frac{d}{a} $$ (Israel) Answer: The smallest possible value is 8.
|
To show that $S \geqslant 8$, apply the AM-GM inequality twice as follows: $$ \left(\frac{a}{b}+\frac{c}{d}\right)+\left(\frac{b}{c}+\frac{d}{a}\right) \geqslant 2 \sqrt{\frac{a c}{b d}}+2 \sqrt{\frac{b d}{a c}}=\frac{2(a c+b d)}{\sqrt{a b c d}}=\frac{2(a+c)(b+d)}{\sqrt{a b c d}} \geqslant 2 \cdot \frac{2 \sqrt{a c} \cdot 2 \sqrt{b d}}{\sqrt{a b c d}}=8 . $$ The above inequalities turn into equalities when $a=c$ and $b=d$. Then the condition $(a+c)(b+d)=a c+b d$ can be rewritten as $4 a b=a^{2}+b^{2}$. So it is satisfied when $a / b=2 \pm \sqrt{3}$. Hence, $S$ attains value 8 , e.g., when $a=c=1$ and $b=d=2+\sqrt{3}$.
|
{
"resource_path": "IMO/segmented/en-IMO2020SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
e37987ec-64a6-5344-a72a-c86216d0d52a
| 24,048
|
Players $A$ and $B$ play a game on a blackboard that initially contains 2020 copies of the number 1. In every round, player $A$ erases two numbers $x$ and $y$ from the blackboard, and then player $B$ writes one of the numbers $x+y$ and $|x-y|$ on the blackboard. The game terminates as soon as, at the end of some round, one of the following holds: (1) one of the numbers on the blackboard is larger than the sum of all other numbers; (2) there are only zeros on the blackboard. Player $B$ must then give as many cookies to player $A$ as there are numbers on the blackboard. Player $A$ wants to get as many cookies as possible, whereas player $B$ wants to give as few as possible. Determine the number of cookies that $A$ receives if both players play optimally. (Austria)
|
For a positive integer $n$, we denote by $S_{2}(n)$ the sum of digits in its binary representation. We prove that, in fact, if a board initially contains an even number $n>1$ of ones, then A can guarantee to obtain $S_{2}(n)$, but not more, cookies. The binary representation of 2020 is $2020=\overline{11111100100}_{2}$, so $S_{2}(2020)=7$, and the answer follows. A strategy for $A$. At any round, while possible, A chooses two equal nonzero numbers on the board. Clearly, while $A$ can make such choice, the game does not terminate. On the other hand, $A$ can follow this strategy unless the game has already terminated. Indeed, if $A$ always chooses two equal numbers, then each number appearing on the board is either 0 or a power of 2 with non-negative integer exponent, this can be easily proved using induction on the number of rounds. At the moment when $A$ is unable to follow the strategy all nonzero numbers on the board are distinct powers of 2 . If the board contains at least one such power, then the largest of those powers is greater than the sum of the others. Otherwise there are only zeros on the blackboard, in both cases the game terminates. For every number on the board, define its range to be the number of ones it is obtained from. We can prove by induction on the number of rounds that for any nonzero number $k$ written by $B$ its range is $k$, and for any zero written by $B$ its range is a power of 2 . Thus at the end of each round all the ranges are powers of two, and their sum is $n$. Since $S_{2}(a+b) \leqslant S_{2}(a)+S_{2}(b)$ for any positive integers $a$ and $b$, the number $n$ cannot be represented as a sum of less than $S_{2}(n)$ powers of 2 . Thus at the end of each round the board contains at least $S_{2}(n)$ numbers, while $A$ follows the above strategy. So $A$ can guarantee at least $S_{2}(n)$ cookies for himself. Comment. There are different proofs of the fact that the presented strategy guarantees at least $S_{2}(n)$ cookies for $A$. For instance, one may denote by $\Sigma$ the sum of numbers on the board, and by $z$ the number of zeros. Then the board contains at least $S_{2}(\Sigma)+z$ numbers; on the other hand, during the game, the number $S_{2}(\Sigma)+z$ does not decrease, and its initial value is $S_{2}(n)$. The claim follows. A strategy for $B$. Denote $s=S_{2}(n)$. Let $x_{1}, \ldots, x_{k}$ be the numbers on the board at some moment of the game after $B$ 's turn or at the beginning of the game. Say that a collection of $k$ signs $\varepsilon_{1}, \ldots, \varepsilon_{k} \in\{+1,-1\}$ is balanced if $$ \sum_{i=1}^{k} \varepsilon_{i} x_{i}=0 $$ We say that a situation on the board is good if $2^{s+1}$ does not divide the number of balanced collections. An appropriate strategy for $B$ can be explained as follows: Perform a move so that the situation remains good, while it is possible. We intend to show that in this case $B$ will not lose more than $S_{2}(n)$ cookies. For this purpose, we prove several lemmas. For a positive integer $k$, denote by $\nu_{2}(k)$ the exponent of the largest power of 2 that divides $k$. Recall that, by Legendre's formula, $\nu_{2}(n!)=n-S_{2}(n)$ for every positive integer $n$. Lemma 1. The initial situation is good. Proof. In the initial configuration, the number of balanced collections is equal to $\binom{n}{n / 2}$. We have $$ \nu_{2}\left(\binom{n}{n / 2}\right)=\nu_{2}(n!)-2 \nu_{2}((n / 2)!)=\left(n-S_{2}(n)\right)-2\left(\frac{n}{2}-S_{2}(n / 2)\right)=S_{2}(n)=s $$ Hence $2^{\text {s+1 }}$ does not divide the number of balanced collections, as desired. Lemma 2. B may play so that after each round the situation remains good. Proof. Assume that the situation $\left(x_{1}, \ldots, x_{k}\right)$ before a round is good, and that $A$ erases two numbers, $x_{p}$ and $x_{q}$. Let $N$ be the number of all balanced collections, $N_{+}$be the number of those having $\varepsilon_{p}=\varepsilon_{q}$, and $N_{-}$be the number of other balanced collections. Then $N=N_{+}+N_{-}$. Now, if $B$ replaces $x_{p}$ and $x_{q}$ by $x_{p}+x_{q}$, then the number of balanced collections will become $N_{+}$. If $B$ replaces $x_{p}$ and $x_{q}$ by $\left|x_{p}-x_{q}\right|$, then this number will become $N_{-}$. Since $2^{s+1}$ does not divide $N$, it does not divide one of the summands $N_{+}$and $N_{-}$, hence $B$ can reach a good situation after the round. Lemma 3. Assume that the game terminates at a good situation. Then the board contains at most $s$ numbers. Proof. Suppose, one of the numbers is greater than the sum of the other numbers. Then the number of balanced collections is 0 and hence divisible by $2^{s+1}$. Therefore, the situation is not good. Then we have only zeros on the blackboard at the moment when the game terminates. If there are $k$ of them, then the number of balanced collections is $2^{k}$. Since the situation is good, we have $k \leqslant s$. By Lemmas 1 and 2, $B$ may act in such way that they keep the situation good. By Lemma 3, when the game terminates, the board contains at most $s$ numbers. This is what we aimed to prove. Comment 1. If the initial situation had some odd number $n>1$ of ones on the blackboard, player $A$ would still get $S_{2}(n)$ cookies, provided that both players act optimally. The proof of this fact is similar to the solution above, after one makes some changes in the definitions. Such changes are listed below. Say that a collection of $k$ signs $\varepsilon_{1}, \ldots, \varepsilon_{k} \in\{+1,-1\}$ is positive if $$ \sum_{i=1}^{k} \varepsilon_{i} x_{i}>0 $$ For every index $i=1,2, \ldots, k$, we denote by $N_{i}$ the number of positive collections such that $\varepsilon_{i}=1$. Finally, say that a situation on the board is good if $2^{s-1}$ does not divide at least one of the numbers $N_{i}$. Now, a strategy for $B$ again consists in preserving the situation good, after each round. Comment 2. There is an easier strategy for $B$, allowing, in the game starting with an even number $n$ of ones, to lose no more than $d=\left\lfloor\log _{2}(n+2)\right\rfloor-1$ cookies. If the binary representation of $n$ contains at most two zeros, then $d=S_{2}(n)$, and hence the strategy is optimal in that case. We outline this approach below. First of all, we can assume that $A$ never erases zeros from the blackboard. Indeed, $A$ may skip such moves harmlessly, ignoring the zeros in the further process; this way, $A$ 's win will just increase. We say that a situation on the blackboard is pretty if the numbers on the board can be partitioned into two groups with equal sums. Clearly, if the situation before some round is pretty, then $B$ may play so as to preserve this property after the round. The strategy for $B$ is as follows: - $B$ always chooses a move that leads to a pretty situation. - If both possible moves of $B$ lead to pretty situations, then $B$ writes the sum of the two numbers erased by $A$. Since the situation always remains pretty, the game terminates when all numbers on the board are zeros. Suppose that, at the end of the game, there are $m \geqslant d+1=\left\lfloor\log _{2}(n+2)\right\rfloor$ zeros on the board; then $2^{m}-1>n / 2$. Now we analyze the whole process of the play. Let us number the zeros on the board in order of appearance. During the play, each zero had appeared after subtracting two equal numbers. Let $n_{1}, \ldots, n_{m}$ be positive integers such that the first zero appeared after subtracting $n_{1}$ from $n_{1}$, the second zero appeared after subtracting $n_{2}$ from $n_{2}$, and so on. Since the sum of the numbers on the blackboard never increases, we have $2 n_{1}+\ldots+2 n_{m} \leqslant n$, hence $$ n_{1}+\ldots+n_{m} \leqslant n / 2<2^{m}-1 $$ There are $2^{m}$ subsets of the set $\{1,2, \ldots, m\}$. For $I \subseteq\{1,2, \ldots, m\}$, denote by $f(I)$ the sum $\sum_{i \in I} n_{i}$. There are less than $2^{m}$ possible values for $f(I)$, so there are two distinct subsets $I$ and $J$ with $f(I)=f(J)$. Replacing $I$ and $J$ with $I \backslash J$ and $J \backslash I$, we assume that $I$ and $J$ are disjoint. Let $i_{0}$ be the smallest number in $I \cup J$; without loss of generality, $i_{0} \in I$. Consider the round when $A$ had erased two numbers equal to $n_{i_{0}}$, and $B$ had put the $i_{0}{ }^{\text {th }}$ zero instead, and the situation before that round. For each nonzero number $z$ which is on the blackboard at this moment, we can keep track of it during the further play until it enters one of the numbers $n_{i}, i \geqslant i_{0}$, which then turn into zeros. For every $i=i_{0}, i_{0}+1, \ldots, m$, we denote by $X_{i}$ the collection of all numbers on the blackboard that finally enter the first copy of $n_{i}$, and by $Y_{i}$ the collection of those finally entering the second copy of $n_{i}$. Thus, each of $X_{i_{0}}$ and $Y_{i_{0}}$ consists of a single number. Since $A$ never erases zeros, the 2(m-iol $i_{0}$ ) defined sets are pairwise disjoint. Clearly, for either of the collections $X_{i}$ and $Y_{i}$, a signed sum of its elements equals $n_{i}$, for a proper choice of the signs. Therefore, for every $i=i_{0}, i_{0}+1, \ldots, m$ one can endow numbers in $X_{i} \cup Y_{i}$ with signs so that their sum becomes any of the numbers $-2 n_{i}, 0$, or $2 n_{i}$. Perform such endowment so as to get $2 n_{i}$ from each collection $X_{i} \cup Y_{i}$ with $i \in I,-2 n_{j}$ from each collection $X_{j} \cup Y_{j}$ with $j \in J$, and 0 from each remaining collection. The obtained signed sum of all numbers on the blackboard equals $$ \sum_{i \in I} 2 n_{i}-\sum_{i \in J} 2 n_{i}=0 $$ and the numbers in $X_{i_{0}}$ and $Y_{i_{0}}$ have the same (positive) sign. This means that, at this round, $B$ could add up the two numbers $n_{i_{0}}$ to get a pretty situation. According to the strategy, $B$ should have performed that, instead of subtracting the numbers. This contradiction shows that $m \leqslant d$, as desired. This page is intentionally left blank
|
7
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Players $A$ and $B$ play a game on a blackboard that initially contains 2020 copies of the number 1. In every round, player $A$ erases two numbers $x$ and $y$ from the blackboard, and then player $B$ writes one of the numbers $x+y$ and $|x-y|$ on the blackboard. The game terminates as soon as, at the end of some round, one of the following holds: (1) one of the numbers on the blackboard is larger than the sum of all other numbers; (2) there are only zeros on the blackboard. Player $B$ must then give as many cookies to player $A$ as there are numbers on the blackboard. Player $A$ wants to get as many cookies as possible, whereas player $B$ wants to give as few as possible. Determine the number of cookies that $A$ receives if both players play optimally. (Austria)
|
For a positive integer $n$, we denote by $S_{2}(n)$ the sum of digits in its binary representation. We prove that, in fact, if a board initially contains an even number $n>1$ of ones, then A can guarantee to obtain $S_{2}(n)$, but not more, cookies. The binary representation of 2020 is $2020=\overline{11111100100}_{2}$, so $S_{2}(2020)=7$, and the answer follows. A strategy for $A$. At any round, while possible, A chooses two equal nonzero numbers on the board. Clearly, while $A$ can make such choice, the game does not terminate. On the other hand, $A$ can follow this strategy unless the game has already terminated. Indeed, if $A$ always chooses two equal numbers, then each number appearing on the board is either 0 or a power of 2 with non-negative integer exponent, this can be easily proved using induction on the number of rounds. At the moment when $A$ is unable to follow the strategy all nonzero numbers on the board are distinct powers of 2 . If the board contains at least one such power, then the largest of those powers is greater than the sum of the others. Otherwise there are only zeros on the blackboard, in both cases the game terminates. For every number on the board, define its range to be the number of ones it is obtained from. We can prove by induction on the number of rounds that for any nonzero number $k$ written by $B$ its range is $k$, and for any zero written by $B$ its range is a power of 2 . Thus at the end of each round all the ranges are powers of two, and their sum is $n$. Since $S_{2}(a+b) \leqslant S_{2}(a)+S_{2}(b)$ for any positive integers $a$ and $b$, the number $n$ cannot be represented as a sum of less than $S_{2}(n)$ powers of 2 . Thus at the end of each round the board contains at least $S_{2}(n)$ numbers, while $A$ follows the above strategy. So $A$ can guarantee at least $S_{2}(n)$ cookies for himself. Comment. There are different proofs of the fact that the presented strategy guarantees at least $S_{2}(n)$ cookies for $A$. For instance, one may denote by $\Sigma$ the sum of numbers on the board, and by $z$ the number of zeros. Then the board contains at least $S_{2}(\Sigma)+z$ numbers; on the other hand, during the game, the number $S_{2}(\Sigma)+z$ does not decrease, and its initial value is $S_{2}(n)$. The claim follows. A strategy for $B$. Denote $s=S_{2}(n)$. Let $x_{1}, \ldots, x_{k}$ be the numbers on the board at some moment of the game after $B$ 's turn or at the beginning of the game. Say that a collection of $k$ signs $\varepsilon_{1}, \ldots, \varepsilon_{k} \in\{+1,-1\}$ is balanced if $$ \sum_{i=1}^{k} \varepsilon_{i} x_{i}=0 $$ We say that a situation on the board is good if $2^{s+1}$ does not divide the number of balanced collections. An appropriate strategy for $B$ can be explained as follows: Perform a move so that the situation remains good, while it is possible. We intend to show that in this case $B$ will not lose more than $S_{2}(n)$ cookies. For this purpose, we prove several lemmas. For a positive integer $k$, denote by $\nu_{2}(k)$ the exponent of the largest power of 2 that divides $k$. Recall that, by Legendre's formula, $\nu_{2}(n!)=n-S_{2}(n)$ for every positive integer $n$. Lemma 1. The initial situation is good. Proof. In the initial configuration, the number of balanced collections is equal to $\binom{n}{n / 2}$. We have $$ \nu_{2}\left(\binom{n}{n / 2}\right)=\nu_{2}(n!)-2 \nu_{2}((n / 2)!)=\left(n-S_{2}(n)\right)-2\left(\frac{n}{2}-S_{2}(n / 2)\right)=S_{2}(n)=s $$ Hence $2^{\text {s+1 }}$ does not divide the number of balanced collections, as desired. Lemma 2. B may play so that after each round the situation remains good. Proof. Assume that the situation $\left(x_{1}, \ldots, x_{k}\right)$ before a round is good, and that $A$ erases two numbers, $x_{p}$ and $x_{q}$. Let $N$ be the number of all balanced collections, $N_{+}$be the number of those having $\varepsilon_{p}=\varepsilon_{q}$, and $N_{-}$be the number of other balanced collections. Then $N=N_{+}+N_{-}$. Now, if $B$ replaces $x_{p}$ and $x_{q}$ by $x_{p}+x_{q}$, then the number of balanced collections will become $N_{+}$. If $B$ replaces $x_{p}$ and $x_{q}$ by $\left|x_{p}-x_{q}\right|$, then this number will become $N_{-}$. Since $2^{s+1}$ does not divide $N$, it does not divide one of the summands $N_{+}$and $N_{-}$, hence $B$ can reach a good situation after the round. Lemma 3. Assume that the game terminates at a good situation. Then the board contains at most $s$ numbers. Proof. Suppose, one of the numbers is greater than the sum of the other numbers. Then the number of balanced collections is 0 and hence divisible by $2^{s+1}$. Therefore, the situation is not good. Then we have only zeros on the blackboard at the moment when the game terminates. If there are $k$ of them, then the number of balanced collections is $2^{k}$. Since the situation is good, we have $k \leqslant s$. By Lemmas 1 and 2, $B$ may act in such way that they keep the situation good. By Lemma 3, when the game terminates, the board contains at most $s$ numbers. This is what we aimed to prove. Comment 1. If the initial situation had some odd number $n>1$ of ones on the blackboard, player $A$ would still get $S_{2}(n)$ cookies, provided that both players act optimally. The proof of this fact is similar to the solution above, after one makes some changes in the definitions. Such changes are listed below. Say that a collection of $k$ signs $\varepsilon_{1}, \ldots, \varepsilon_{k} \in\{+1,-1\}$ is positive if $$ \sum_{i=1}^{k} \varepsilon_{i} x_{i}>0 $$ For every index $i=1,2, \ldots, k$, we denote by $N_{i}$ the number of positive collections such that $\varepsilon_{i}=1$. Finally, say that a situation on the board is good if $2^{s-1}$ does not divide at least one of the numbers $N_{i}$. Now, a strategy for $B$ again consists in preserving the situation good, after each round. Comment 2. There is an easier strategy for $B$, allowing, in the game starting with an even number $n$ of ones, to lose no more than $d=\left\lfloor\log _{2}(n+2)\right\rfloor-1$ cookies. If the binary representation of $n$ contains at most two zeros, then $d=S_{2}(n)$, and hence the strategy is optimal in that case. We outline this approach below. First of all, we can assume that $A$ never erases zeros from the blackboard. Indeed, $A$ may skip such moves harmlessly, ignoring the zeros in the further process; this way, $A$ 's win will just increase. We say that a situation on the blackboard is pretty if the numbers on the board can be partitioned into two groups with equal sums. Clearly, if the situation before some round is pretty, then $B$ may play so as to preserve this property after the round. The strategy for $B$ is as follows: - $B$ always chooses a move that leads to a pretty situation. - If both possible moves of $B$ lead to pretty situations, then $B$ writes the sum of the two numbers erased by $A$. Since the situation always remains pretty, the game terminates when all numbers on the board are zeros. Suppose that, at the end of the game, there are $m \geqslant d+1=\left\lfloor\log _{2}(n+2)\right\rfloor$ zeros on the board; then $2^{m}-1>n / 2$. Now we analyze the whole process of the play. Let us number the zeros on the board in order of appearance. During the play, each zero had appeared after subtracting two equal numbers. Let $n_{1}, \ldots, n_{m}$ be positive integers such that the first zero appeared after subtracting $n_{1}$ from $n_{1}$, the second zero appeared after subtracting $n_{2}$ from $n_{2}$, and so on. Since the sum of the numbers on the blackboard never increases, we have $2 n_{1}+\ldots+2 n_{m} \leqslant n$, hence $$ n_{1}+\ldots+n_{m} \leqslant n / 2<2^{m}-1 $$ There are $2^{m}$ subsets of the set $\{1,2, \ldots, m\}$. For $I \subseteq\{1,2, \ldots, m\}$, denote by $f(I)$ the sum $\sum_{i \in I} n_{i}$. There are less than $2^{m}$ possible values for $f(I)$, so there are two distinct subsets $I$ and $J$ with $f(I)=f(J)$. Replacing $I$ and $J$ with $I \backslash J$ and $J \backslash I$, we assume that $I$ and $J$ are disjoint. Let $i_{0}$ be the smallest number in $I \cup J$; without loss of generality, $i_{0} \in I$. Consider the round when $A$ had erased two numbers equal to $n_{i_{0}}$, and $B$ had put the $i_{0}{ }^{\text {th }}$ zero instead, and the situation before that round. For each nonzero number $z$ which is on the blackboard at this moment, we can keep track of it during the further play until it enters one of the numbers $n_{i}, i \geqslant i_{0}$, which then turn into zeros. For every $i=i_{0}, i_{0}+1, \ldots, m$, we denote by $X_{i}$ the collection of all numbers on the blackboard that finally enter the first copy of $n_{i}$, and by $Y_{i}$ the collection of those finally entering the second copy of $n_{i}$. Thus, each of $X_{i_{0}}$ and $Y_{i_{0}}$ consists of a single number. Since $A$ never erases zeros, the 2(m-iol $i_{0}$ ) defined sets are pairwise disjoint. Clearly, for either of the collections $X_{i}$ and $Y_{i}$, a signed sum of its elements equals $n_{i}$, for a proper choice of the signs. Therefore, for every $i=i_{0}, i_{0}+1, \ldots, m$ one can endow numbers in $X_{i} \cup Y_{i}$ with signs so that their sum becomes any of the numbers $-2 n_{i}, 0$, or $2 n_{i}$. Perform such endowment so as to get $2 n_{i}$ from each collection $X_{i} \cup Y_{i}$ with $i \in I,-2 n_{j}$ from each collection $X_{j} \cup Y_{j}$ with $j \in J$, and 0 from each remaining collection. The obtained signed sum of all numbers on the blackboard equals $$ \sum_{i \in I} 2 n_{i}-\sum_{i \in J} 2 n_{i}=0 $$ and the numbers in $X_{i_{0}}$ and $Y_{i_{0}}$ have the same (positive) sign. This means that, at this round, $B$ could add up the two numbers $n_{i_{0}}$ to get a pretty situation. According to the strategy, $B$ should have performed that, instead of subtracting the numbers. This contradiction shows that $m \leqslant d$, as desired. This page is intentionally left blank
|
{
"resource_path": "IMO/segmented/en-IMO2020SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
daf34ef9-4126-5a45-bf78-dae13fdcf4ca
| 24,074
|
Given a positive integer $n$, find the smallest value of $\left\lfloor\frac{a_{1}}{1}\right\rfloor+\left\lfloor\frac{a_{2}}{2}\right\rfloor+\cdots+\left\lfloor\frac{a_{n}}{n}\right\rfloor$ over all permutations $\left(a_{1}, a_{2}, \ldots, a_{n}\right)$ of $(1,2, \ldots, n)$.
|
Suppose that $2^{k} \leqslant n<2^{k+1}$ with some nonnegative integer $k$. First we show a permutation $\left(a_{1}, a_{2}, \ldots, a_{n}\right)$ such that $\left\lfloor\frac{a_{1}}{1}\right\rfloor+\left\lfloor\frac{a_{2}}{2}\right\rfloor+\cdots+\left\lfloor\frac{a_{n}}{n}\right\rfloor=k+1$; then we will prove that $\left\lfloor\frac{a_{1}}{1}\right\rfloor+\left\lfloor\frac{a_{2}}{2}\right\rfloor+\cdots+\left\lfloor\frac{a_{n}}{n}\right\rfloor \geqslant k+1$ for every permutation. Hence, the minimal possible value will be $k+1$. I. Consider the permutation $$ \begin{gathered} \left(a_{1}\right)=(1), \quad\left(a_{2}, a_{3}\right)=(3,2), \quad\left(a_{4}, a_{5}, a_{6}, a_{7}\right)=(7,4,5,6) \\ \left(a_{2^{k-1}}, \ldots, a_{2^{k}-1}\right)=\left(2^{k}-1,2^{k-1}, 2^{k-1}+1, \ldots, 2^{k}-2\right) \\ \left(a_{2^{k}}, \ldots, a_{n}\right)=\left(n, 2^{k}, 2^{k}+1, \ldots, n-1\right) \end{gathered} $$ This permutation consists of $k+1$ cycles. In every cycle $\left(a_{p}, \ldots, a_{q}\right)=(q, p, p+1, \ldots, q-1)$ we have $q<2 p$, so $$ \sum_{i=p}^{q}\left\lfloor\frac{a_{i}}{i}\right\rfloor=\left\lfloor\frac{q}{p}\right\rfloor+\sum_{i=p+1}^{q}\left\lfloor\frac{i-1}{i}\right\rfloor=1 ; $$ The total sum over all cycles is precisely $k+1$. II. In order to establish the lower bound, we prove a more general statement. Claim. If $b_{1}, \ldots, b_{2^{k}}$ are distinct positive integers then $$ \sum_{i=1}^{2^{k}}\left\lfloor\frac{b_{i}}{i}\right\rfloor \geqslant k+1 $$ From the Claim it follows immediately that $\sum_{i=1}^{n}\left\lfloor\frac{a_{i}}{i}\right\rfloor \geqslant \sum_{i=1}^{2^{k}}\left\lfloor\frac{a_{i}}{i}\right\rfloor \geqslant k+1$. Proof of the Claim. Apply induction on $k$. For $k=1$ the claim is trivial, $\left\lfloor\frac{b_{1}}{1}\right\rfloor \geqslant 1$. Suppose the Claim holds true for some positive integer $k$, and consider $k+1$. If there exists an index $j$ such that $2^{k}<j \leqslant 2^{k+1}$ and $b_{j} \geqslant j$ then $$ \sum_{i=1}^{2^{k+1}}\left\lfloor\frac{b_{i}}{i}\right\rfloor \geqslant \sum_{i=1}^{2^{k}}\left\lfloor\frac{b_{i}}{i}\right\rfloor+\left\lfloor\frac{b_{j}}{j}\right\rfloor \geqslant(k+1)+1 $$ by the induction hypothesis, so the Claim is satisfied. Otherwise we have $b_{j}<j \leqslant 2^{k+1}$ for every $2^{k}<j \leqslant 2^{k+1}$. Among the $2^{k+1}$ distinct numbers $b_{1}, \ldots, b_{2^{k+1}}$ there is some $b_{m}$ which is at least $2^{k+1}$; that number must be among $b_{1} \ldots, b_{2^{k}}$. Hence, $1 \leqslant m \leqslant 2^{k}$ and $b_{m} \geqslant 2^{k+1}$. We will apply the induction hypothesis to the numbers $$ c_{1}=b_{1}, \ldots, c_{m-1}=b_{m-1}, \quad c_{m}=b_{2^{k}+1}, \quad c_{m+1}=b_{m+1}, \ldots, c_{2^{k}}=b_{2^{k}} $$ so take the first $2^{k}$ numbers but replace $b_{m}$ with $b_{2^{k}+1}$. Notice that $$ \left\lfloor\frac{b_{m}}{m}\right\rfloor \geqslant\left\lfloor\frac{2^{k+1}}{m}\right\rfloor=\left\lfloor\frac{2^{k}+2^{k}}{m}\right\rfloor \geqslant\left\lfloor\frac{b_{2^{k}+1}+m}{m}\right\rfloor=\left\lfloor\frac{c_{m}}{m}\right\rfloor+1 $$ For the other indices $i$ with $1 \leqslant i \leqslant 2^{k}, i \neq m$ we have $\left\lfloor\frac{b_{i}}{i}\right\rfloor=\left\lfloor\frac{c_{i}}{i}\right\rfloor$, so $$ \sum_{i=1}^{2^{k+1}}\left\lfloor\frac{b_{i}}{i}\right\rfloor=\sum_{i=1}^{2^{k}}\left\lfloor\frac{b_{i}}{i}\right\rfloor \geqslant \sum_{i=1}^{2^{k}}\left\lfloor\frac{c_{i}}{i}\right\rfloor+1 \geqslant(k+1)+1 $$ That proves the Claim and hence completes the solution.
|
k+1
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Given a positive integer $n$, find the smallest value of $\left\lfloor\frac{a_{1}}{1}\right\rfloor+\left\lfloor\frac{a_{2}}{2}\right\rfloor+\cdots+\left\lfloor\frac{a_{n}}{n}\right\rfloor$ over all permutations $\left(a_{1}, a_{2}, \ldots, a_{n}\right)$ of $(1,2, \ldots, n)$.
|
Suppose that $2^{k} \leqslant n<2^{k+1}$ with some nonnegative integer $k$. First we show a permutation $\left(a_{1}, a_{2}, \ldots, a_{n}\right)$ such that $\left\lfloor\frac{a_{1}}{1}\right\rfloor+\left\lfloor\frac{a_{2}}{2}\right\rfloor+\cdots+\left\lfloor\frac{a_{n}}{n}\right\rfloor=k+1$; then we will prove that $\left\lfloor\frac{a_{1}}{1}\right\rfloor+\left\lfloor\frac{a_{2}}{2}\right\rfloor+\cdots+\left\lfloor\frac{a_{n}}{n}\right\rfloor \geqslant k+1$ for every permutation. Hence, the minimal possible value will be $k+1$. I. Consider the permutation $$ \begin{gathered} \left(a_{1}\right)=(1), \quad\left(a_{2}, a_{3}\right)=(3,2), \quad\left(a_{4}, a_{5}, a_{6}, a_{7}\right)=(7,4,5,6) \\ \left(a_{2^{k-1}}, \ldots, a_{2^{k}-1}\right)=\left(2^{k}-1,2^{k-1}, 2^{k-1}+1, \ldots, 2^{k}-2\right) \\ \left(a_{2^{k}}, \ldots, a_{n}\right)=\left(n, 2^{k}, 2^{k}+1, \ldots, n-1\right) \end{gathered} $$ This permutation consists of $k+1$ cycles. In every cycle $\left(a_{p}, \ldots, a_{q}\right)=(q, p, p+1, \ldots, q-1)$ we have $q<2 p$, so $$ \sum_{i=p}^{q}\left\lfloor\frac{a_{i}}{i}\right\rfloor=\left\lfloor\frac{q}{p}\right\rfloor+\sum_{i=p+1}^{q}\left\lfloor\frac{i-1}{i}\right\rfloor=1 ; $$ The total sum over all cycles is precisely $k+1$. II. In order to establish the lower bound, we prove a more general statement. Claim. If $b_{1}, \ldots, b_{2^{k}}$ are distinct positive integers then $$ \sum_{i=1}^{2^{k}}\left\lfloor\frac{b_{i}}{i}\right\rfloor \geqslant k+1 $$ From the Claim it follows immediately that $\sum_{i=1}^{n}\left\lfloor\frac{a_{i}}{i}\right\rfloor \geqslant \sum_{i=1}^{2^{k}}\left\lfloor\frac{a_{i}}{i}\right\rfloor \geqslant k+1$. Proof of the Claim. Apply induction on $k$. For $k=1$ the claim is trivial, $\left\lfloor\frac{b_{1}}{1}\right\rfloor \geqslant 1$. Suppose the Claim holds true for some positive integer $k$, and consider $k+1$. If there exists an index $j$ such that $2^{k}<j \leqslant 2^{k+1}$ and $b_{j} \geqslant j$ then $$ \sum_{i=1}^{2^{k+1}}\left\lfloor\frac{b_{i}}{i}\right\rfloor \geqslant \sum_{i=1}^{2^{k}}\left\lfloor\frac{b_{i}}{i}\right\rfloor+\left\lfloor\frac{b_{j}}{j}\right\rfloor \geqslant(k+1)+1 $$ by the induction hypothesis, so the Claim is satisfied. Otherwise we have $b_{j}<j \leqslant 2^{k+1}$ for every $2^{k}<j \leqslant 2^{k+1}$. Among the $2^{k+1}$ distinct numbers $b_{1}, \ldots, b_{2^{k+1}}$ there is some $b_{m}$ which is at least $2^{k+1}$; that number must be among $b_{1} \ldots, b_{2^{k}}$. Hence, $1 \leqslant m \leqslant 2^{k}$ and $b_{m} \geqslant 2^{k+1}$. We will apply the induction hypothesis to the numbers $$ c_{1}=b_{1}, \ldots, c_{m-1}=b_{m-1}, \quad c_{m}=b_{2^{k}+1}, \quad c_{m+1}=b_{m+1}, \ldots, c_{2^{k}}=b_{2^{k}} $$ so take the first $2^{k}$ numbers but replace $b_{m}$ with $b_{2^{k}+1}$. Notice that $$ \left\lfloor\frac{b_{m}}{m}\right\rfloor \geqslant\left\lfloor\frac{2^{k+1}}{m}\right\rfloor=\left\lfloor\frac{2^{k}+2^{k}}{m}\right\rfloor \geqslant\left\lfloor\frac{b_{2^{k}+1}+m}{m}\right\rfloor=\left\lfloor\frac{c_{m}}{m}\right\rfloor+1 $$ For the other indices $i$ with $1 \leqslant i \leqslant 2^{k}, i \neq m$ we have $\left\lfloor\frac{b_{i}}{i}\right\rfloor=\left\lfloor\frac{c_{i}}{i}\right\rfloor$, so $$ \sum_{i=1}^{2^{k+1}}\left\lfloor\frac{b_{i}}{i}\right\rfloor=\sum_{i=1}^{2^{k}}\left\lfloor\frac{b_{i}}{i}\right\rfloor \geqslant \sum_{i=1}^{2^{k}}\left\lfloor\frac{c_{i}}{i}\right\rfloor+1 \geqslant(k+1)+1 $$ That proves the Claim and hence completes the solution.
|
{
"resource_path": "IMO/segmented/en-IMO2021SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
856302e8-7bf6-57c1-9269-85686e955c0e
| 24,128
|
Determine all integers $n \geqslant 1$ for which there exists a pair of positive integers $(a, b)$ such that no cube of a prime divides $a^{2}+b+3$ and $$ \frac{a b+3 b+8}{a^{2}+b+3}=n $$
|
As $b \equiv-a^{2}-3\left(\bmod a^{2}+b+3\right)$, the numerator of the given fraction satisfies $$ a b+3 b+8 \equiv a\left(-a^{2}-3\right)+3\left(-a^{2}-3\right)+8 \equiv-(a+1)^{3} \quad\left(\bmod a^{2}+b+3\right) $$ As $a^{2}+b+3$ is not divisible by $p^{3}$ for any prime $p$, if $a^{2}+b+3$ divides $(a+1)^{3}$ then it does also divide $(a+1)^{2}$. Since $$ 0<(a+1)^{2}<2\left(a^{2}+b+3\right) $$ we conclude $(a+1)^{2}=a^{2}+b+3$. This yields $b=2(a-1)$ and $n=2$. The choice $(a, b)=(2,2)$ with $a^{2}+b+3=9$ shows that $n=2$ indeed is a solution.
|
2
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Determine all integers $n \geqslant 1$ for which there exists a pair of positive integers $(a, b)$ such that no cube of a prime divides $a^{2}+b+3$ and $$ \frac{a b+3 b+8}{a^{2}+b+3}=n $$
|
As $b \equiv-a^{2}-3\left(\bmod a^{2}+b+3\right)$, the numerator of the given fraction satisfies $$ a b+3 b+8 \equiv a\left(-a^{2}-3\right)+3\left(-a^{2}-3\right)+8 \equiv-(a+1)^{3} \quad\left(\bmod a^{2}+b+3\right) $$ As $a^{2}+b+3$ is not divisible by $p^{3}$ for any prime $p$, if $a^{2}+b+3$ divides $(a+1)^{3}$ then it does also divide $(a+1)^{2}$. Since $$ 0<(a+1)^{2}<2\left(a^{2}+b+3\right) $$ we conclude $(a+1)^{2}=a^{2}+b+3$. This yields $b=2(a-1)$ and $n=2$. The choice $(a, b)=(2,2)$ with $a^{2}+b+3=9$ shows that $n=2$ indeed is a solution.
|
{
"resource_path": "IMO/segmented/en-IMO2021SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
6f1213bc-ceb2-5dfc-906b-b214eb9849e4
| 24,205
|
Version 1. Let $n$ be a fixed positive integer, and let S be the set of points $(x, y)$ on the Cartesian plane such that both coordinates $x$ and $y$ are nonnegative integers smaller than $2 n$ (thus $|\mathrm{S}|=4 n^{2}$ ). Assume that $\mathcal{F}$ is a set consisting of $n^{2}$ quadrilaterals such that all their vertices lie in $S$, and each point in $S$ is a vertex of exactly one of the quadrilaterals in $\mathcal{F}$. Determine the largest possible sum of areas of all $n^{2}$ quadrilaterals in $\mathcal{F}$. Version 2. Let $n$ be a fixed positive integer, and let $\mathbf{S}$ be the set of points $(x, y)$ on the Cartesian plane such that both coordinates $x$ and $y$ are nonnegative integers smaller than $2 n$ (thus $|\mathrm{S}|=4 n^{2}$ ). Assume that $\mathcal{F}$ is a set of polygons such that all vertices of polygons in $\mathcal{F}$ lie in S , and each point in S is a vertex of exactly one of the polygons in $\mathcal{F}$. Determine the largest possible sum of areas of all polygons in $\mathcal{F}$. Answer for both Versions: The largest possible sum of areas is $\Sigma(n):=\frac{1}{3} n^{2}(2 n+1)(2 n-1)$. Common remarks. Throughout all solutions, the area of a polygon $P$ will be denoted by $[P]$. We say that a polygon is legal if all its vertices belong to S . Let $O=\left(n-\frac{1}{2}, n-\frac{1}{2}\right)$ be the centre of S . We say that a legal square is central if its centre is situated at $O$. Finally, say that a set $\mathcal{F}$ of polygons is acceptable if it satisfies the problem requirements, i.e. if all polygons in $\mathcal{F}$ are legal, and each point in $S$ is a vertex of exactly one polygon in $\mathcal{F}$. For an acceptable set $\mathcal{F}$, we denote by $\Sigma(\mathcal{F})$ the sum of areas of polygons in $\mathcal{F}$. Solution 1, for both Versions. Each point in $S$ is a vertex of a unique central square. Thus the set $\mathcal{G}$ of central squares is acceptable. We will show that $$ \Sigma(\mathcal{F}) \leqslant \Sigma(\mathcal{G})=\Sigma(n) $$ thus establishing the answer. We will use the following key lemma. Lemma 1. Let $P=A_{1} A_{2} \ldots A_{m}$ be a polygon, and let $O$ be an arbitrary point in the plane. Then $$ [P] \leqslant \frac{1}{2} \sum_{i=1}^{m} O A_{i}^{2} $$ moreover, if $P$ is a square centred at $O$, then the inequality (2) turns into an equality. Proof. Put $A_{n+1}=A_{1}$. For each $i=1,2, \ldots, m$, we have $$ \left[O A_{i} A_{i+1}\right] \leqslant \frac{O A_{i} \cdot O A_{i+1}}{2} \leqslant \frac{O A_{i}^{2}+O A_{i+1}^{2}}{4} $$ Therefore, $$ [P] \leqslant \sum_{i=1}^{m}\left[O A_{i} A_{i+1}\right] \leqslant \frac{1}{4} \sum_{i=1}^{m}\left(O A_{i}^{2}+O A_{i+1}^{2}\right)=\frac{1}{2} \sum_{i=1}^{m} O A_{i}^{2} $$ which proves (2). Finally, all the above inequalities turn into equalities when $P$ is a square centred at $O$. Back to the problem, consider an arbitrary acceptable set $\mathcal{F}$. Applying Lemma 1 to each element in $\mathcal{F}$ and to each element in $\mathcal{G}$ (achieving equality in the latter case), we obtain $$ \Sigma(\mathcal{F}) \leqslant \frac{1}{2} \sum_{A \in \mathrm{~S}} O A^{2}=\Sigma(\mathcal{G}) $$ which establishes the left inequality in (1). It remains to compute $\Sigma(\mathcal{G})$. We have $$ \begin{aligned} \Sigma(\mathcal{G})=\frac{1}{2} & \sum_{A \in S} O A^{2}=\frac{1}{2} \sum_{i=0}^{2 n-1} \sum_{j=0}^{2 n-1}\left(\left(n-\frac{1}{2}-i\right)^{2}+\left(n-\frac{1}{2}-j\right)^{2}\right) \\ & =\frac{1}{8} \cdot 4 \cdot 2 n \sum_{i=0}^{n-1}(2 n-2 i-1)^{2}=n \sum_{j=0}^{n-1}(2 j+1)^{2}=n\left(\sum_{j=1}^{2 n} j^{2}-\sum_{j=1}^{n}(2 j)^{2}\right) \\ & =n\left(\frac{2 n(2 n+1)(4 n+1)}{6}-4 \cdot \frac{n(n+1)(2 n+1)}{6}\right)=\frac{n^{2}(2 n+1)(2 n-1)}{3}=\Sigma(n) . \end{aligned} $$ Comment. There are several variations of the above solution, also working for both versions of the problem. E.g., one may implement only the inequality $\left[O A_{i} A_{i+1}\right] \leqslant \frac{1}{2} O A_{i} \cdot O A_{i+1}$ to obtain $$ \Sigma(\mathcal{F}) \leqslant \frac{1}{2} \sum_{i=1}^{4 n^{2}} O K_{i} \cdot O L_{i} $$ where both $\left(K_{i}\right)$ and $\left(L_{i}\right)$ are permutations of all points in S . The right hand side can then be bounded from above by means of the rearrangement inequality; the bound is also achieved on the collection $\mathcal{G}$. However, Version 2 seems to be more difficult than Version 1. First of all, the optimal model for this version is much less easy to guess, until one finds an idea for proving the upper bound. Moreover, Version 1 allows different solutions which do not seem to be generalized easily - such as Solution 2 below. Solution 2, for Version 1. Let $\mathcal{F}$ be an accessible set of quadrilaterals. For every quadrilateral $A B C D$ in $\mathcal{F}$ write $$ [A B C D]=\frac{A C \cdot B D}{2} \sin \phi \leqslant \frac{A C^{2}+B D^{2}}{4} $$ where $\phi$ is the angle between $A C$ and $B D$. Applying this estimate to all members in $\mathcal{F}$ we obtain $$ \Sigma(\mathcal{F}) \leqslant \frac{1}{4} \sum_{i=1}^{2 n^{2}} A_{i} B_{i}^{2} $$ where $A_{1}, A_{2}, \ldots, A_{2 n^{2}}, B_{1}, B_{2}, \ldots, B_{2 n^{2}}$ is some permutation of S . For brevity, denote $$ f\left(\left(A_{i}\right),\left(B_{i}\right)\right):=\sum_{i=1}^{2 n^{2}} A_{i} B_{i}^{2} $$ The rest of the solution is based on the following lemma. Lemma 2. The maximal value of $f\left(\left(A_{i}\right),\left(B_{i}\right)\right)$ over all permutations of $S$ equals $\frac{4}{3} n^{2}\left(4 n^{2}-1\right)$ and is achieved when $A_{i}$ is symmetric to $B_{i}$ with respect to $O$, for every $i=1,2, \ldots, 2 n^{2}$. Proof. Let $A_{i}=\left(p_{i}, q_{i}\right)$ and $B_{i}=\left(r_{i}, s_{i}\right)$, for $i=1,2, \ldots, 2 n^{2}$. We have $$ f\left(\left(A_{i}\right),\left(B_{i}\right)\right)=\sum_{i=1}^{2 n^{2}}\left(p_{i}-r_{i}\right)^{2}+\sum_{i=1}^{2 n^{2}}\left(q_{i}-s_{i}\right)^{2} $$ it suffices to bound the first sum, the second is bounded similarly. This can be done, e.g., by means of the QM-AM inequality as follows: $$ \begin{aligned} \sum_{i=1}^{2 n^{2}}\left(p_{i}-r_{i}\right)^{2}=\sum_{i=1}^{2 n^{2}}\left(2 p_{i}^{2}\right. & \left.+2 r_{i}^{2}-\left(p_{i}+r_{i}\right)^{2}\right)=4 n \sum_{j=0}^{2 n-1} j^{2}-\sum_{i=1}^{2 n^{2}}\left(p_{i}+r_{i}\right)^{2} \\ \leqslant 4 n \sum_{j=0}^{2 n-1} j^{2} & -\frac{1}{2 n^{2}}\left(\sum_{i=1}^{2 n^{2}}\left(p_{i}+r_{i}\right)\right)^{2}=4 n \sum_{j=0}^{2 n-1} j^{2}-\frac{1}{2 n^{2}}\left(2 n \cdot \sum_{j=0}^{2 n-1} j\right)^{2} \\ & =4 n \cdot \frac{2 n(2 n-1)(4 n-1)}{6}-2 n^{2}(2 n-1)^{2}=\frac{2 n^{2}(2 n-1)(2 n+1)}{3} \end{aligned} $$ All the estimates are sharp if $p_{i}+r_{i}=2 n-1$ for all $i$. Thus, $$ f\left(\left(A_{i}\right),\left(B_{i}\right)\right) \leqslant \frac{4 n^{2}\left(4 n^{2}-1\right)}{3} $$ and the estimate is sharp when $p_{i}+r_{i}=q_{i}+s_{i}=2 n-1$ for all $i$, i.e. when $A_{i}$ and $B_{i}$ are symmetric with respect to $O$. Lemma 2 yields $$ \Sigma(\mathcal{F}) \leqslant \frac{1}{4} \cdot \frac{4 n^{2}\left(4 n^{2}-1\right)}{3}=\frac{n^{2}(2 n-1)(2 n+1)}{3} . $$ Finally, all estimates are achieved simultaneously on the set $\mathcal{G}$ of central squares. Comment 2. Lemma 2 also allows different proofs. E.g., one may optimize the sum $\sum_{i} p_{i} r_{i}$ step by step: if $p_{i}<p_{j}$ and $r_{i}<r_{j}$, then a swap $r_{i} \leftrightarrow r_{j}$ increases the sum. By applying a proper chain of such replacements (possibly swapping elements in some pairs ( $\left.p_{i}, r_{i}\right)$ ), one eventually comes to a permutation where $p_{i}+r_{i}=2 n-1$ for all $i$. Comment 3. Version 2 can also be considered for a square grid with odd number $n$ of points on each side. If we allow a polygon consisting of one point, then Solution 1 is applied verbatim, providing an answer $\frac{1}{12} n^{2}\left(n^{2}-1\right)$. If such polygons are not allowed, then one needs to subtract $\frac{1}{2}$ from the answer.
|
None
|
\frac{1}{3} n^{2}(2 n+1)(2 n-1)
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Version 1. Let $n$ be a fixed positive integer, and let S be the set of points $(x, y)$ on the Cartesian plane such that both coordinates $x$ and $y$ are nonnegative integers smaller than $2 n$ (thus $|\mathrm{S}|=4 n^{2}$ ). Assume that $\mathcal{F}$ is a set consisting of $n^{2}$ quadrilaterals such that all their vertices lie in $S$, and each point in $S$ is a vertex of exactly one of the quadrilaterals in $\mathcal{F}$. Determine the largest possible sum of areas of all $n^{2}$ quadrilaterals in $\mathcal{F}$. Version 2. Let $n$ be a fixed positive integer, and let $\mathbf{S}$ be the set of points $(x, y)$ on the Cartesian plane such that both coordinates $x$ and $y$ are nonnegative integers smaller than $2 n$ (thus $|\mathrm{S}|=4 n^{2}$ ). Assume that $\mathcal{F}$ is a set of polygons such that all vertices of polygons in $\mathcal{F}$ lie in S , and each point in S is a vertex of exactly one of the polygons in $\mathcal{F}$. Determine the largest possible sum of areas of all polygons in $\mathcal{F}$. Answer for both Versions: The largest possible sum of areas is $\Sigma(n):=\frac{1}{3} n^{2}(2 n+1)(2 n-1)$. Common remarks. Throughout all solutions, the area of a polygon $P$ will be denoted by $[P]$. We say that a polygon is legal if all its vertices belong to S . Let $O=\left(n-\frac{1}{2}, n-\frac{1}{2}\right)$ be the centre of S . We say that a legal square is central if its centre is situated at $O$. Finally, say that a set $\mathcal{F}$ of polygons is acceptable if it satisfies the problem requirements, i.e. if all polygons in $\mathcal{F}$ are legal, and each point in $S$ is a vertex of exactly one polygon in $\mathcal{F}$. For an acceptable set $\mathcal{F}$, we denote by $\Sigma(\mathcal{F})$ the sum of areas of polygons in $\mathcal{F}$. Solution 1, for both Versions. Each point in $S$ is a vertex of a unique central square. Thus the set $\mathcal{G}$ of central squares is acceptable. We will show that $$ \Sigma(\mathcal{F}) \leqslant \Sigma(\mathcal{G})=\Sigma(n) $$ thus establishing the answer. We will use the following key lemma. Lemma 1. Let $P=A_{1} A_{2} \ldots A_{m}$ be a polygon, and let $O$ be an arbitrary point in the plane. Then $$ [P] \leqslant \frac{1}{2} \sum_{i=1}^{m} O A_{i}^{2} $$ moreover, if $P$ is a square centred at $O$, then the inequality (2) turns into an equality. Proof. Put $A_{n+1}=A_{1}$. For each $i=1,2, \ldots, m$, we have $$ \left[O A_{i} A_{i+1}\right] \leqslant \frac{O A_{i} \cdot O A_{i+1}}{2} \leqslant \frac{O A_{i}^{2}+O A_{i+1}^{2}}{4} $$ Therefore, $$ [P] \leqslant \sum_{i=1}^{m}\left[O A_{i} A_{i+1}\right] \leqslant \frac{1}{4} \sum_{i=1}^{m}\left(O A_{i}^{2}+O A_{i+1}^{2}\right)=\frac{1}{2} \sum_{i=1}^{m} O A_{i}^{2} $$ which proves (2). Finally, all the above inequalities turn into equalities when $P$ is a square centred at $O$. Back to the problem, consider an arbitrary acceptable set $\mathcal{F}$. Applying Lemma 1 to each element in $\mathcal{F}$ and to each element in $\mathcal{G}$ (achieving equality in the latter case), we obtain $$ \Sigma(\mathcal{F}) \leqslant \frac{1}{2} \sum_{A \in \mathrm{~S}} O A^{2}=\Sigma(\mathcal{G}) $$ which establishes the left inequality in (1). It remains to compute $\Sigma(\mathcal{G})$. We have $$ \begin{aligned} \Sigma(\mathcal{G})=\frac{1}{2} & \sum_{A \in S} O A^{2}=\frac{1}{2} \sum_{i=0}^{2 n-1} \sum_{j=0}^{2 n-1}\left(\left(n-\frac{1}{2}-i\right)^{2}+\left(n-\frac{1}{2}-j\right)^{2}\right) \\ & =\frac{1}{8} \cdot 4 \cdot 2 n \sum_{i=0}^{n-1}(2 n-2 i-1)^{2}=n \sum_{j=0}^{n-1}(2 j+1)^{2}=n\left(\sum_{j=1}^{2 n} j^{2}-\sum_{j=1}^{n}(2 j)^{2}\right) \\ & =n\left(\frac{2 n(2 n+1)(4 n+1)}{6}-4 \cdot \frac{n(n+1)(2 n+1)}{6}\right)=\frac{n^{2}(2 n+1)(2 n-1)}{3}=\Sigma(n) . \end{aligned} $$ Comment. There are several variations of the above solution, also working for both versions of the problem. E.g., one may implement only the inequality $\left[O A_{i} A_{i+1}\right] \leqslant \frac{1}{2} O A_{i} \cdot O A_{i+1}$ to obtain $$ \Sigma(\mathcal{F}) \leqslant \frac{1}{2} \sum_{i=1}^{4 n^{2}} O K_{i} \cdot O L_{i} $$ where both $\left(K_{i}\right)$ and $\left(L_{i}\right)$ are permutations of all points in S . The right hand side can then be bounded from above by means of the rearrangement inequality; the bound is also achieved on the collection $\mathcal{G}$. However, Version 2 seems to be more difficult than Version 1. First of all, the optimal model for this version is much less easy to guess, until one finds an idea for proving the upper bound. Moreover, Version 1 allows different solutions which do not seem to be generalized easily - such as Solution 2 below. Solution 2, for Version 1. Let $\mathcal{F}$ be an accessible set of quadrilaterals. For every quadrilateral $A B C D$ in $\mathcal{F}$ write $$ [A B C D]=\frac{A C \cdot B D}{2} \sin \phi \leqslant \frac{A C^{2}+B D^{2}}{4} $$ where $\phi$ is the angle between $A C$ and $B D$. Applying this estimate to all members in $\mathcal{F}$ we obtain $$ \Sigma(\mathcal{F}) \leqslant \frac{1}{4} \sum_{i=1}^{2 n^{2}} A_{i} B_{i}^{2} $$ where $A_{1}, A_{2}, \ldots, A_{2 n^{2}}, B_{1}, B_{2}, \ldots, B_{2 n^{2}}$ is some permutation of S . For brevity, denote $$ f\left(\left(A_{i}\right),\left(B_{i}\right)\right):=\sum_{i=1}^{2 n^{2}} A_{i} B_{i}^{2} $$ The rest of the solution is based on the following lemma. Lemma 2. The maximal value of $f\left(\left(A_{i}\right),\left(B_{i}\right)\right)$ over all permutations of $S$ equals $\frac{4}{3} n^{2}\left(4 n^{2}-1\right)$ and is achieved when $A_{i}$ is symmetric to $B_{i}$ with respect to $O$, for every $i=1,2, \ldots, 2 n^{2}$. Proof. Let $A_{i}=\left(p_{i}, q_{i}\right)$ and $B_{i}=\left(r_{i}, s_{i}\right)$, for $i=1,2, \ldots, 2 n^{2}$. We have $$ f\left(\left(A_{i}\right),\left(B_{i}\right)\right)=\sum_{i=1}^{2 n^{2}}\left(p_{i}-r_{i}\right)^{2}+\sum_{i=1}^{2 n^{2}}\left(q_{i}-s_{i}\right)^{2} $$ it suffices to bound the first sum, the second is bounded similarly. This can be done, e.g., by means of the QM-AM inequality as follows: $$ \begin{aligned} \sum_{i=1}^{2 n^{2}}\left(p_{i}-r_{i}\right)^{2}=\sum_{i=1}^{2 n^{2}}\left(2 p_{i}^{2}\right. & \left.+2 r_{i}^{2}-\left(p_{i}+r_{i}\right)^{2}\right)=4 n \sum_{j=0}^{2 n-1} j^{2}-\sum_{i=1}^{2 n^{2}}\left(p_{i}+r_{i}\right)^{2} \\ \leqslant 4 n \sum_{j=0}^{2 n-1} j^{2} & -\frac{1}{2 n^{2}}\left(\sum_{i=1}^{2 n^{2}}\left(p_{i}+r_{i}\right)\right)^{2}=4 n \sum_{j=0}^{2 n-1} j^{2}-\frac{1}{2 n^{2}}\left(2 n \cdot \sum_{j=0}^{2 n-1} j\right)^{2} \\ & =4 n \cdot \frac{2 n(2 n-1)(4 n-1)}{6}-2 n^{2}(2 n-1)^{2}=\frac{2 n^{2}(2 n-1)(2 n+1)}{3} \end{aligned} $$ All the estimates are sharp if $p_{i}+r_{i}=2 n-1$ for all $i$. Thus, $$ f\left(\left(A_{i}\right),\left(B_{i}\right)\right) \leqslant \frac{4 n^{2}\left(4 n^{2}-1\right)}{3} $$ and the estimate is sharp when $p_{i}+r_{i}=q_{i}+s_{i}=2 n-1$ for all $i$, i.e. when $A_{i}$ and $B_{i}$ are symmetric with respect to $O$. Lemma 2 yields $$ \Sigma(\mathcal{F}) \leqslant \frac{1}{4} \cdot \frac{4 n^{2}\left(4 n^{2}-1\right)}{3}=\frac{n^{2}(2 n-1)(2 n+1)}{3} . $$ Finally, all estimates are achieved simultaneously on the set $\mathcal{G}$ of central squares. Comment 2. Lemma 2 also allows different proofs. E.g., one may optimize the sum $\sum_{i} p_{i} r_{i}$ step by step: if $p_{i}<p_{j}$ and $r_{i}<r_{j}$, then a swap $r_{i} \leftrightarrow r_{j}$ increases the sum. By applying a proper chain of such replacements (possibly swapping elements in some pairs ( $\left.p_{i}, r_{i}\right)$ ), one eventually comes to a permutation where $p_{i}+r_{i}=2 n-1$ for all $i$. Comment 3. Version 2 can also be considered for a square grid with odd number $n$ of points on each side. If we allow a polygon consisting of one point, then Solution 1 is applied verbatim, providing an answer $\frac{1}{12} n^{2}\left(n^{2}-1\right)$. If such polygons are not allowed, then one needs to subtract $\frac{1}{2}$ from the answer.
|
None
|
{
"resource_path": "IMO/segmented/en-IMO2021SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
b8575e39-9b6a-5eda-9c1d-c20b5172de41
| 24,258
|
Let $\mathbb{R}$ be the set of real numbers. We denote by $\mathcal{F}$ the set of all functions $f: \mathbb{R} \rightarrow \mathbb{R}$ such that $$ f(x+f(y))=f(x)+f(y) $$ for every $x, y \in \mathbb{R}$. Find all rational numbers $q$ such that for every function $f \in \mathcal{F}$, there exists some $z \in \mathbb{R}$ satisfying $f(z)=q z$. (Indonesia)
|
Let $Z$ be the set of all rational numbers $q$ such that for every function $f \in \mathcal{F}$, there exists some $z \in \mathbb{R}$ satisfying $f(z)=q z$. Let further $$ S=\left\{\frac{n+1}{n}: n \in \mathbb{Z}, n \neq 0\right\} $$ We prove that $Z=S$ by showing the two inclusions: $S \subseteq Z$ and $Z \subseteq S$. We first prove that $S \subseteq Z$. Let $f \in \mathcal{F}$ and let $P(x, y)$ be the relation $f(x+f(y))=f(x)+$ $f(y)$. First note that $P(0,0)$ gives $f(f(0))=2 f(0)$. Then, $P(0, f(0))$ gives $f(2 f(0))=3 f(0)$. We claim that $$ f(k f(0))=(k+1) f(0) $$ for every integer $k \geqslant 1$. The claim can be proved by induction. The cases $k=1$ and $k=2$ have already been established. Assume that $f(k f(0))=(k+1) f(0)$ and consider $P(0, k f(0))$ which gives $$ f((k+1) f(0))=f(0)+f(k f(0))=(k+2) f(0) $$ This proves the claim. We conclude that $\frac{k+1}{k} \in Z$ for every integer $k \geqslant 1$. Note that $P(-f(0), 0)$ gives $f(-f(0))=0$. We now claim that $$ f(-k f(0))=(-k+1) f(0) $$ for every integer $k \geqslant 1$. The proof by induction is similar to the one above. We conclude that $\frac{-k+1}{-k} \in Z$ for every integer $k \geqslant 1$. This shows that $S \subseteq Z$. We now prove that $Z \subseteq S$. Let $p$ be a rational number outside the set $S$. We want to prove that $p$ does not belong to $Z$. To that end, we construct a function $f \in \mathcal{F}$ such that $f(z) \neq p z$ for every $z \in \mathbb{R}$. The strategy is to first construct a function $$ g:[0,1) \rightarrow \mathbb{Z} $$ and then define $f$ as $f(x)=g(\{x\})+\lfloor x\rfloor$. This function $f$ belongs to $\mathcal{F}$. Indeed, $$ \begin{aligned} f(x+f(y)) & =g(\{x+f(y)\})+\lfloor x+f(y)\rfloor \\ & =g(\{x+g(\{y\})+\lfloor y\rfloor\})+\lfloor x+g(\{y\})+\lfloor y\rfloor\rfloor \\ & =g(\{x\})+\lfloor x\rfloor+g(\{y\})+\lfloor y\rfloor \\ & =f(x)+f(y) \end{aligned} $$ where we used that $g$ only takes integer values. Lemma 1. For every $\alpha \in[0,1)$, there exists $m \in \mathbb{Z}$ such that $$ m+n \neq p(\alpha+n) $$ for every $n \in \mathbb{Z}$. Proof. Note that if $p=1$ the claim is trivial. If $p \neq 1$, then the claim is equivalent to the existence of an integer $m$ such that $$ \frac{m-p \alpha}{p-1} $$ is never an integer. Assume the contrary. That would mean that both $$ \frac{m-p \alpha}{p-1} \quad \text { and } \quad \frac{(m+1)-p \alpha}{p-1} $$ are integers, and so is their difference. The latter is equal to $$ \frac{1}{p-1} $$ Since we assumed $p \notin S, 1 /(p-1)$ is never an integer. This is a contradiction. Define $g:[0,1) \rightarrow \mathbb{Z}$ by $g(\alpha)=m$ for any integer $m$ that satisfies the conclusion of Lemma 1. Note that $f(z) \neq p z$ if and and only if $$ g(\{z\})+\lfloor z\rfloor \neq p(\{z\}+\lfloor z\rfloor) $$ The latter is guaranteed by the construction of the function $g$. We conclude that $p \notin Z$ as desired. This shows that $Z \subset S$.
|
S
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Let $\mathbb{R}$ be the set of real numbers. We denote by $\mathcal{F}$ the set of all functions $f: \mathbb{R} \rightarrow \mathbb{R}$ such that $$ f(x+f(y))=f(x)+f(y) $$ for every $x, y \in \mathbb{R}$. Find all rational numbers $q$ such that for every function $f \in \mathcal{F}$, there exists some $z \in \mathbb{R}$ satisfying $f(z)=q z$. (Indonesia)
|
Let $Z$ be the set of all rational numbers $q$ such that for every function $f \in \mathcal{F}$, there exists some $z \in \mathbb{R}$ satisfying $f(z)=q z$. Let further $$ S=\left\{\frac{n+1}{n}: n \in \mathbb{Z}, n \neq 0\right\} $$ We prove that $Z=S$ by showing the two inclusions: $S \subseteq Z$ and $Z \subseteq S$. We first prove that $S \subseteq Z$. Let $f \in \mathcal{F}$ and let $P(x, y)$ be the relation $f(x+f(y))=f(x)+$ $f(y)$. First note that $P(0,0)$ gives $f(f(0))=2 f(0)$. Then, $P(0, f(0))$ gives $f(2 f(0))=3 f(0)$. We claim that $$ f(k f(0))=(k+1) f(0) $$ for every integer $k \geqslant 1$. The claim can be proved by induction. The cases $k=1$ and $k=2$ have already been established. Assume that $f(k f(0))=(k+1) f(0)$ and consider $P(0, k f(0))$ which gives $$ f((k+1) f(0))=f(0)+f(k f(0))=(k+2) f(0) $$ This proves the claim. We conclude that $\frac{k+1}{k} \in Z$ for every integer $k \geqslant 1$. Note that $P(-f(0), 0)$ gives $f(-f(0))=0$. We now claim that $$ f(-k f(0))=(-k+1) f(0) $$ for every integer $k \geqslant 1$. The proof by induction is similar to the one above. We conclude that $\frac{-k+1}{-k} \in Z$ for every integer $k \geqslant 1$. This shows that $S \subseteq Z$. We now prove that $Z \subseteq S$. Let $p$ be a rational number outside the set $S$. We want to prove that $p$ does not belong to $Z$. To that end, we construct a function $f \in \mathcal{F}$ such that $f(z) \neq p z$ for every $z \in \mathbb{R}$. The strategy is to first construct a function $$ g:[0,1) \rightarrow \mathbb{Z} $$ and then define $f$ as $f(x)=g(\{x\})+\lfloor x\rfloor$. This function $f$ belongs to $\mathcal{F}$. Indeed, $$ \begin{aligned} f(x+f(y)) & =g(\{x+f(y)\})+\lfloor x+f(y)\rfloor \\ & =g(\{x+g(\{y\})+\lfloor y\rfloor\})+\lfloor x+g(\{y\})+\lfloor y\rfloor\rfloor \\ & =g(\{x\})+\lfloor x\rfloor+g(\{y\})+\lfloor y\rfloor \\ & =f(x)+f(y) \end{aligned} $$ where we used that $g$ only takes integer values. Lemma 1. For every $\alpha \in[0,1)$, there exists $m \in \mathbb{Z}$ such that $$ m+n \neq p(\alpha+n) $$ for every $n \in \mathbb{Z}$. Proof. Note that if $p=1$ the claim is trivial. If $p \neq 1$, then the claim is equivalent to the existence of an integer $m$ such that $$ \frac{m-p \alpha}{p-1} $$ is never an integer. Assume the contrary. That would mean that both $$ \frac{m-p \alpha}{p-1} \quad \text { and } \quad \frac{(m+1)-p \alpha}{p-1} $$ are integers, and so is their difference. The latter is equal to $$ \frac{1}{p-1} $$ Since we assumed $p \notin S, 1 /(p-1)$ is never an integer. This is a contradiction. Define $g:[0,1) \rightarrow \mathbb{Z}$ by $g(\alpha)=m$ for any integer $m$ that satisfies the conclusion of Lemma 1. Note that $f(z) \neq p z$ if and and only if $$ g(\{z\})+\lfloor z\rfloor \neq p(\{z\}+\lfloor z\rfloor) $$ The latter is guaranteed by the construction of the function $g$. We conclude that $p \notin Z$ as desired. This shows that $Z \subset S$.
|
{
"resource_path": "IMO/segmented/en-IMO2022SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
f6c133ae-e55c-57f6-9093-47f3f63c17ad
| 24,304
|
A $\pm 1$-sequence is a sequence of 2022 numbers $a_{1}, \ldots, a_{2022}$, each equal to either +1 or -1 . Determine the largest $C$ so that, for any $\pm 1$-sequence, there exists an integer $k$ and indices $1 \leqslant t_{1}<\ldots<t_{k} \leqslant 2022$ so that $t_{i+1}-t_{i} \leqslant 2$ for all $i$, and $$ \left|\sum_{i=1}^{k} a_{t_{i}}\right| \geqslant C $$ (Czech Republic)
|
First, we prove that this can always be achieved. Without loss of generality, suppose at least $\frac{2022}{2}=1011$ terms of the $\pm 1$-sequence are +1 . Define a subsequence as follows: starting at $t=0$, if $a_{t}=+1$ we always include $a_{t}$ in the subsequence. Otherwise, we skip $a_{t}$ if we can (i.e. if we included $a_{t-1}$ in the subsequence), otherwise we include it out of necessity, and go to the next $t$. Clearly, this subsequence will include all +1 s . Also, for each -1 included in the sequence, a -1 must have been skipped, so at most $\left\lfloor\frac{1011}{2}\right\rfloor=505$ can be included. Hence the sum is at least $1011-505=506$, as desired. Next, we prove that, for the $\pm 1$-sequence $$ (\{-1\},\{+1,+1\},\{-1,-1\},\{+1,+1\}, \ldots,\{+1,+1\},\{-1,-1\},\{+1\}) $$ each admissible subsequence $a_{t_{i}}$ has $-506 \leqslant \sum_{i} a_{t_{i}} \leqslant 506$. We say that the terms inside each curly bracket is a block. In total, there are 1012 blocks - 506 of them hold +1-s, and 506 of them hold -1 s . (The two blocks at each end hold 1 number each, each other block holds 2.) Suppose an admissible subsequence includes terms from $k$ blocks holding +1 -s. Then, in each -1 -pair in between the +1 -pairs, the subsequence must also include at least one -1 . There can be at most two +1 s included from each +1 -block, and at least one -1 must be included from each -1 -block, so the sum is at most $2 k-(k-1)=k+1$. For $k<506$, this is at most 506. If $k=506$, one of the +1 -blocks must be the one at the end, meaning it can only include one +1 , so that the maximum in this case is only $k$, not $k+1$, so in this case the sum is also at most 506. Hence we have shown that for any admissible subsequence, $\sum_{i} a_{t_{i}} \leqslant 506$. Analogously we can show that $-506 \leqslant \sum_{i} a_{t_{i}}$, meaning that $C \leqslant 506$ as desired. Comment. A possible reformulation of the problem is the following. 2022 buckets of water are arranged in a row, each coloured either red or blue. Sally the salmon plays a game in the following way: first, she chooses any bucket she likes to start in. Then, any number of times she may jump either to the next bucket in the row, or across it to land in the bucket after that. (She may not jump across more than one bucket.) At any point, she may finish the game. At that time, her score is the absolute value of the difference between the number of red and blue buckets she visited during the game. Determine the largest $C$ so that no matter how the buckets are coloured, Sally can achieve a score of at least $C$.
|
506
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
A $\pm 1$-sequence is a sequence of 2022 numbers $a_{1}, \ldots, a_{2022}$, each equal to either +1 or -1 . Determine the largest $C$ so that, for any $\pm 1$-sequence, there exists an integer $k$ and indices $1 \leqslant t_{1}<\ldots<t_{k} \leqslant 2022$ so that $t_{i+1}-t_{i} \leqslant 2$ for all $i$, and $$ \left|\sum_{i=1}^{k} a_{t_{i}}\right| \geqslant C $$ (Czech Republic)
|
First, we prove that this can always be achieved. Without loss of generality, suppose at least $\frac{2022}{2}=1011$ terms of the $\pm 1$-sequence are +1 . Define a subsequence as follows: starting at $t=0$, if $a_{t}=+1$ we always include $a_{t}$ in the subsequence. Otherwise, we skip $a_{t}$ if we can (i.e. if we included $a_{t-1}$ in the subsequence), otherwise we include it out of necessity, and go to the next $t$. Clearly, this subsequence will include all +1 s . Also, for each -1 included in the sequence, a -1 must have been skipped, so at most $\left\lfloor\frac{1011}{2}\right\rfloor=505$ can be included. Hence the sum is at least $1011-505=506$, as desired. Next, we prove that, for the $\pm 1$-sequence $$ (\{-1\},\{+1,+1\},\{-1,-1\},\{+1,+1\}, \ldots,\{+1,+1\},\{-1,-1\},\{+1\}) $$ each admissible subsequence $a_{t_{i}}$ has $-506 \leqslant \sum_{i} a_{t_{i}} \leqslant 506$. We say that the terms inside each curly bracket is a block. In total, there are 1012 blocks - 506 of them hold +1-s, and 506 of them hold -1 s . (The two blocks at each end hold 1 number each, each other block holds 2.) Suppose an admissible subsequence includes terms from $k$ blocks holding +1 -s. Then, in each -1 -pair in between the +1 -pairs, the subsequence must also include at least one -1 . There can be at most two +1 s included from each +1 -block, and at least one -1 must be included from each -1 -block, so the sum is at most $2 k-(k-1)=k+1$. For $k<506$, this is at most 506. If $k=506$, one of the +1 -blocks must be the one at the end, meaning it can only include one +1 , so that the maximum in this case is only $k$, not $k+1$, so in this case the sum is also at most 506. Hence we have shown that for any admissible subsequence, $\sum_{i} a_{t_{i}} \leqslant 506$. Analogously we can show that $-506 \leqslant \sum_{i} a_{t_{i}}$, meaning that $C \leqslant 506$ as desired. Comment. A possible reformulation of the problem is the following. 2022 buckets of water are arranged in a row, each coloured either red or blue. Sally the salmon plays a game in the following way: first, she chooses any bucket she likes to start in. Then, any number of times she may jump either to the next bucket in the row, or across it to land in the bucket after that. (She may not jump across more than one bucket.) At any point, she may finish the game. At that time, her score is the absolute value of the difference between the number of red and blue buckets she visited during the game. Determine the largest $C$ so that no matter how the buckets are coloured, Sally can achieve a score of at least $C$.
|
{
"resource_path": "IMO/segmented/en-IMO2022SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
60e447c9-f0d2-5a65-8d91-a43080cd8d9a
| 24,312
|
Alice fills the fields of an $n \times n$ board with numbers from 1 to $n^{2}$, each number being used exactly once. She then counts the total number of good paths on the board. A good path is a sequence of fields of arbitrary length (including 1) such that: (i) The first field in the sequence is one that is only adjacent to fields with larger numbers, (ii) Each subsequent field in the sequence is adjacent to the previous field, (iii) The numbers written on the fields in the sequence are in increasing order. Two fields are considered adjacent if they share a common side. Find the smallest possible number of good paths Alice can obtain, as a function of $n$. (Serbia)
|
We will call any field that is only adjacent to fields with larger numbers a well. Other fields will be called non-wells. Let us make a second $n \times n$ board $B$ where in each field we will write the number of good sequences which end on the corresponding field in the original board $A$. We will thus look for the minimal possible value of the sum of all entries in $B$. We note that any well has just one good path ending in it, consisting of just the well, and that any other field has the number of good paths ending in it equal to the sum of this quantity for all the adjacent fields with smaller values, since a good path can only come into the field from a field of lower value. Therefore, if we fill in the fields in $B$ in increasing order with respect to their values in $A$, it follows that each field not adjacent to any already filled field will receive a 1, while each field adjacent to already filled fields will receive the sum of the numbers already written on these adjacent fields. We note that there is at least one well in $A$, that corresponding with the field with the entry 1 in $A$. Hence, the sum of values of fields in $B$ corresponding to wells in $A$ is at least 1 . We will now try to minimize the sum of the non-well entries, i.e. of the entries in $B$ corresponding to the non-wells in $A$. We note that we can ascribe to each pair of adjacent fields the value of the lower assigned number and that the sum of non-well entries will then equal to the sum of the ascribed numbers. Since the lower number is still at least 1, the sum of non-well entries will at least equal the number of pairs of adjacent fields, which is $2 n(n-1)$. Hence, the total minimum sum of entries in $B$ is at least $2 n(n-1)+1=2 n^{2}-2 n+1$. The necessary conditions for the minimum to be achieved is for there to be only one well and for no two entries in $B$ larger than 1 to be adjacent to each other. We will now prove that the lower limit of $2 n^{2}-2 n+1$ entries can be achieved. This amounts to finding a way of marking a certain set of squares, those that have a value of 1 in $B$, such that no two unmarked squares are adjacent and that the marked squares form a connected tree with respect to adjacency. For $n=1$ and $n=2$ the markings are respectively the lone field and the L-trimino. Now, for $n>2$, let $s=2$ for $n \equiv 0,2 \bmod 3$ and $s=1$ for $n \equiv 1 \bmod 3$. We will take indices $k$ and $l$ to be arbitrary non-negative integers. For $n \geqslant 3$ we will construct a path of marked squares in the first two columns consisting of all squares of the form $(1, i)$ where $i$ is not of the form $6 k+s$ and $(2, j)$ where $j$ is of the form $6 k+s-1,6 k+s$ or $6+s+1$. Obviously, this path is connected. Now, let us consider the fields $(2,6 k+s)$ and $(1,6 k+s+3)$. For each considered field $(i, j)$ we will mark all squares of the form $(l, j)$ for $l>i$ and $(i+2 k, j \pm 1)$. One can easily see that no set of marked fields will produce a cycle, that the only fields of the unmarked form $(1,6 k+s),(2+2 l+1,6 k+s \pm 1)$ and $(2+2 l, 6 k+s+3 \pm 1)$ and that no two are adjacent, since the consecutive considered fields are in columns of opposite parity. Examples of markings are given for $n=3,4,5,6,7$, and the corresponding constructions for $A$ and $B$ are given for $n=5$. 
|
2 n^{2}-2 n+1
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Alice fills the fields of an $n \times n$ board with numbers from 1 to $n^{2}$, each number being used exactly once. She then counts the total number of good paths on the board. A good path is a sequence of fields of arbitrary length (including 1) such that: (i) The first field in the sequence is one that is only adjacent to fields with larger numbers, (ii) Each subsequent field in the sequence is adjacent to the previous field, (iii) The numbers written on the fields in the sequence are in increasing order. Two fields are considered adjacent if they share a common side. Find the smallest possible number of good paths Alice can obtain, as a function of $n$. (Serbia)
|
We will call any field that is only adjacent to fields with larger numbers a well. Other fields will be called non-wells. Let us make a second $n \times n$ board $B$ where in each field we will write the number of good sequences which end on the corresponding field in the original board $A$. We will thus look for the minimal possible value of the sum of all entries in $B$. We note that any well has just one good path ending in it, consisting of just the well, and that any other field has the number of good paths ending in it equal to the sum of this quantity for all the adjacent fields with smaller values, since a good path can only come into the field from a field of lower value. Therefore, if we fill in the fields in $B$ in increasing order with respect to their values in $A$, it follows that each field not adjacent to any already filled field will receive a 1, while each field adjacent to already filled fields will receive the sum of the numbers already written on these adjacent fields. We note that there is at least one well in $A$, that corresponding with the field with the entry 1 in $A$. Hence, the sum of values of fields in $B$ corresponding to wells in $A$ is at least 1 . We will now try to minimize the sum of the non-well entries, i.e. of the entries in $B$ corresponding to the non-wells in $A$. We note that we can ascribe to each pair of adjacent fields the value of the lower assigned number and that the sum of non-well entries will then equal to the sum of the ascribed numbers. Since the lower number is still at least 1, the sum of non-well entries will at least equal the number of pairs of adjacent fields, which is $2 n(n-1)$. Hence, the total minimum sum of entries in $B$ is at least $2 n(n-1)+1=2 n^{2}-2 n+1$. The necessary conditions for the minimum to be achieved is for there to be only one well and for no two entries in $B$ larger than 1 to be adjacent to each other. We will now prove that the lower limit of $2 n^{2}-2 n+1$ entries can be achieved. This amounts to finding a way of marking a certain set of squares, those that have a value of 1 in $B$, such that no two unmarked squares are adjacent and that the marked squares form a connected tree with respect to adjacency. For $n=1$ and $n=2$ the markings are respectively the lone field and the L-trimino. Now, for $n>2$, let $s=2$ for $n \equiv 0,2 \bmod 3$ and $s=1$ for $n \equiv 1 \bmod 3$. We will take indices $k$ and $l$ to be arbitrary non-negative integers. For $n \geqslant 3$ we will construct a path of marked squares in the first two columns consisting of all squares of the form $(1, i)$ where $i$ is not of the form $6 k+s$ and $(2, j)$ where $j$ is of the form $6 k+s-1,6 k+s$ or $6+s+1$. Obviously, this path is connected. Now, let us consider the fields $(2,6 k+s)$ and $(1,6 k+s+3)$. For each considered field $(i, j)$ we will mark all squares of the form $(l, j)$ for $l>i$ and $(i+2 k, j \pm 1)$. One can easily see that no set of marked fields will produce a cycle, that the only fields of the unmarked form $(1,6 k+s),(2+2 l+1,6 k+s \pm 1)$ and $(2+2 l, 6 k+s+3 \pm 1)$ and that no two are adjacent, since the consecutive considered fields are in columns of opposite parity. Examples of markings are given for $n=3,4,5,6,7$, and the corresponding constructions for $A$ and $B$ are given for $n=5$. 
|
{
"resource_path": "IMO/segmented/en-IMO2022SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
c5c5e2cd-a9bb-53e9-8e0e-63c55f0ccbbc
| 24,333
|
A number is called Norwegian if it has three distinct positive divisors whose sum is equal to 2022. Determine the smallest Norwegian number. (Note: The total number of positive divisors of a Norwegian number is allowed to be larger than 3.) (Cyprus)
|
Observe that 1344 is a Norwegian number as 6, 672 and 1344 are three distinct divisors of 1344 and $6+672+1344=2022$. It remains to show that this is the smallest such number. Assume for contradiction that $N<1344$ is Norwegian and let $N / a, N / b$ and $N / c$ be the three distinct divisors of $N$, with $a<b<c$. Then $$ 2022=N\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)<1344\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right) $$ and so $$ \left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)>\frac{2022}{1344}=\frac{337}{224}=\frac{3}{2}+\frac{1}{224} $$ If $a>1$ then $$ \frac{1}{a}+\frac{1}{b}+\frac{1}{c} \leqslant \frac{1}{2}+\frac{1}{3}+\frac{1}{4}=\frac{13}{12}<\frac{3}{2} $$ so it must be the case that $a=1$. Similarly, it must hold that $b<4$ since otherwise $$ 1+\frac{1}{b}+\frac{1}{c} \leqslant 1+\frac{1}{4}+\frac{1}{5}<\frac{3}{2} . $$ This leaves two cases to check, $b=2$ and $b=3$. Case $b=3$. Then $$ \frac{1}{c}>\frac{3}{2}+\frac{1}{224}-1-\frac{1}{3}>\frac{1}{6}, $$ so $c=4$ or $c=5$. If $c=4$ then $$ 2022=N\left(1+\frac{1}{3}+\frac{1}{4}\right)=\frac{19}{12} N $$ but this is impossible as $19 \nmid 2022$. If $c=5$ then $$ 2022=N\left(1+\frac{1}{3}+\frac{1}{5}\right)=\frac{23}{15} N $$ which again is impossible, as $23 \nmid 2022$. Case $b=2$. Note that $c<224$ since $$ \frac{1}{c}>\frac{3}{2}+\frac{1}{224}-1-\frac{1}{2}=\frac{1}{224} $$ It holds that $$ 2022=N\left(1+\frac{1}{2}+\frac{1}{c}\right)=\frac{3 c+2}{2 c} N \Rightarrow(3 c+2) N=4044 c $$ Since $(c, 3 c-2)=(c, 2) \in\{1,2\}$, then $3 c+2 \mid 8088=2^{3} \cdot 3 \cdot 337$ which implies that $3 c+2 \mid 2^{3} \cdot 337$. But since $3 c+2 \geqslant 3 \cdot 3+2>8=2^{3}$ and $3 c+2 \neq 337$, then it must hold that $3 c+2 \geqslant 2 \cdot 337$, contradicting $c<224$.
|
1344
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
A number is called Norwegian if it has three distinct positive divisors whose sum is equal to 2022. Determine the smallest Norwegian number. (Note: The total number of positive divisors of a Norwegian number is allowed to be larger than 3.) (Cyprus)
|
Observe that 1344 is a Norwegian number as 6, 672 and 1344 are three distinct divisors of 1344 and $6+672+1344=2022$. It remains to show that this is the smallest such number. Assume for contradiction that $N<1344$ is Norwegian and let $N / a, N / b$ and $N / c$ be the three distinct divisors of $N$, with $a<b<c$. Then $$ 2022=N\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)<1344\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right) $$ and so $$ \left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)>\frac{2022}{1344}=\frac{337}{224}=\frac{3}{2}+\frac{1}{224} $$ If $a>1$ then $$ \frac{1}{a}+\frac{1}{b}+\frac{1}{c} \leqslant \frac{1}{2}+\frac{1}{3}+\frac{1}{4}=\frac{13}{12}<\frac{3}{2} $$ so it must be the case that $a=1$. Similarly, it must hold that $b<4$ since otherwise $$ 1+\frac{1}{b}+\frac{1}{c} \leqslant 1+\frac{1}{4}+\frac{1}{5}<\frac{3}{2} . $$ This leaves two cases to check, $b=2$ and $b=3$. Case $b=3$. Then $$ \frac{1}{c}>\frac{3}{2}+\frac{1}{224}-1-\frac{1}{3}>\frac{1}{6}, $$ so $c=4$ or $c=5$. If $c=4$ then $$ 2022=N\left(1+\frac{1}{3}+\frac{1}{4}\right)=\frac{19}{12} N $$ but this is impossible as $19 \nmid 2022$. If $c=5$ then $$ 2022=N\left(1+\frac{1}{3}+\frac{1}{5}\right)=\frac{23}{15} N $$ which again is impossible, as $23 \nmid 2022$. Case $b=2$. Note that $c<224$ since $$ \frac{1}{c}>\frac{3}{2}+\frac{1}{224}-1-\frac{1}{2}=\frac{1}{224} $$ It holds that $$ 2022=N\left(1+\frac{1}{2}+\frac{1}{c}\right)=\frac{3 c+2}{2 c} N \Rightarrow(3 c+2) N=4044 c $$ Since $(c, 3 c-2)=(c, 2) \in\{1,2\}$, then $3 c+2 \mid 8088=2^{3} \cdot 3 \cdot 337$ which implies that $3 c+2 \mid 2^{3} \cdot 337$. But since $3 c+2 \geqslant 3 \cdot 3+2>8=2^{3}$ and $3 c+2 \neq 337$, then it must hold that $3 c+2 \geqslant 2 \cdot 337$, contradicting $c<224$.
|
{
"resource_path": "IMO/segmented/en-IMO2022SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
079530cc-2973-5d53-a2ce-3b57bf2e2ba7
| 24,367
|
Find all positive integers $n>2$ such that $$ n!\mid \prod_{\substack{p<q \leq n, p, q \text { primes }}}(p+q) $$ (Nigeria)
|
Assume that $n$ satisfies $n!\mid \prod_{p<q \leqslant n}(p+q)$ and let $2=p_{1}<p_{2}<\cdots<p_{m} \leqslant n$ be the primes in $\{1,2, \ldots, n\}$. Each such prime divides $n$ !. In particular, $p_{m} \mid p_{i}+p_{j}$ for some $p_{i}<p_{j} \leqslant n$. But $$ 0<\frac{p_{i}+p_{j}}{p_{m}}<\frac{p_{m}+p_{m}}{p_{m}}=2 $$ so $p_{m}=p_{i}+p_{j}$ which implies $m \geqslant 3, p_{i}=2$ and $p_{m}=2+p_{j}=2+p_{m-1}$. Similarly, $p_{m-1} \mid p_{k}+p_{l}$ for some $p_{k}<p_{l} \leqslant n$. But $$ 0<\frac{p_{l}+p_{k}}{p_{m-1}} \leqslant \frac{p_{m}+p_{m-1}}{p_{m-1}}=\frac{2 p_{m-1}+2}{p_{m-1}}<3 $$ so either $p_{m-1}=p_{l}+p_{k}$ or $2 p_{m-1}=p_{l}+p_{k}$. As above, the former case gives $p_{m-1}=2+p_{m-2}$. If $2 p_{m-1}=p_{l}+p_{k}$, then $p_{m-1}<p_{k}$, so $k=m$ and $$ 2 p_{m-1}=p_{l}+p_{m-1}+2 \Rightarrow p_{m-1}=p_{l}+2=p_{m-2}+2 $$ Either way, $p_{m-2}>2$ and 3 divides one of $p_{m-2}, p_{m-1}=p_{m-2}+2$ and $p_{m}=p_{m-2}+4$. This implies $p_{m-2}=3$ and thus $p_{m}=7$, giving $7 \leqslant n<11$. Finally, a quick computation shows that $7!\mid \prod_{p<q \leqslant 7}(p+q)$ but $8!\nmid \prod_{p<q \leqslant 7}(p+q)$, so neither does 9 ! and 10 !.
|
7
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Find all positive integers $n>2$ such that $$ n!\mid \prod_{\substack{p<q \leq n, p, q \text { primes }}}(p+q) $$ (Nigeria)
|
Assume that $n$ satisfies $n!\mid \prod_{p<q \leqslant n}(p+q)$ and let $2=p_{1}<p_{2}<\cdots<p_{m} \leqslant n$ be the primes in $\{1,2, \ldots, n\}$. Each such prime divides $n$ !. In particular, $p_{m} \mid p_{i}+p_{j}$ for some $p_{i}<p_{j} \leqslant n$. But $$ 0<\frac{p_{i}+p_{j}}{p_{m}}<\frac{p_{m}+p_{m}}{p_{m}}=2 $$ so $p_{m}=p_{i}+p_{j}$ which implies $m \geqslant 3, p_{i}=2$ and $p_{m}=2+p_{j}=2+p_{m-1}$. Similarly, $p_{m-1} \mid p_{k}+p_{l}$ for some $p_{k}<p_{l} \leqslant n$. But $$ 0<\frac{p_{l}+p_{k}}{p_{m-1}} \leqslant \frac{p_{m}+p_{m-1}}{p_{m-1}}=\frac{2 p_{m-1}+2}{p_{m-1}}<3 $$ so either $p_{m-1}=p_{l}+p_{k}$ or $2 p_{m-1}=p_{l}+p_{k}$. As above, the former case gives $p_{m-1}=2+p_{m-2}$. If $2 p_{m-1}=p_{l}+p_{k}$, then $p_{m-1}<p_{k}$, so $k=m$ and $$ 2 p_{m-1}=p_{l}+p_{m-1}+2 \Rightarrow p_{m-1}=p_{l}+2=p_{m-2}+2 $$ Either way, $p_{m-2}>2$ and 3 divides one of $p_{m-2}, p_{m-1}=p_{m-2}+2$ and $p_{m}=p_{m-2}+4$. This implies $p_{m-2}=3$ and thus $p_{m}=7$, giving $7 \leqslant n<11$. Finally, a quick computation shows that $7!\mid \prod_{p<q \leqslant 7}(p+q)$ but $8!\nmid \prod_{p<q \leqslant 7}(p+q)$, so neither does 9 ! and 10 !.
|
{
"resource_path": "IMO/segmented/en-IMO2022SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
572e871d-6a00-50d1-aff8-f53c11d88e31
| 24,369
|
Find all positive integers $n>2$ such that $$ n!\mid \prod_{\substack{p<q \leqslant n, p, q \text { primes }}}(p+q) . $$ (Nigeria)
|
Assume that $n$ satisfies $n!\mid \prod_{p<q \leqslant n}(p+q)$ and let $2=p_{1}<p_{2}<\cdots<p_{m} \leqslant n$ be the primes in $\{1,2, \ldots, n\}$. Each such prime divides $n$ !. In particular, $p_{m} \mid p_{i}+p_{j}$ for some $p_{i}<p_{j} \leqslant n$. But $$ 0<\frac{p_{i}+p_{j}}{p_{m}}<\frac{p_{m}+p_{m}}{p_{m}}=2 $$ so $p_{m}=p_{i}+p_{j}$ which implies $m \geqslant 3, p_{i}=2$ and $p_{m}=2+p_{j}=2+p_{m-1}$. Similarly, $p_{m-1} \mid p_{k}+p_{l}$ for some $p_{k}<p_{l} \leqslant n$. But $$ 0<\frac{p_{l}+p_{k}}{p_{m-1}} \leqslant \frac{p_{m}+p_{m-1}}{p_{m-1}}=\frac{2 p_{m-1}+2}{p_{m-1}}<3 $$ so either $p_{m-1}=p_{l}+p_{k}$ or $2 p_{m-1}=p_{l}+p_{k}$. As above, the former case gives $p_{m-1}=2+p_{m-2}$. If $2 p_{m-1}=p_{l}+p_{k}$, then $p_{m-1}<p_{k}$, so $k=m$ and $$ 2 p_{m-1}=p_{l}+p_{m-1}+2 \Rightarrow p_{m-1}=p_{l}+2=p_{m-2}+2 $$ Either way, $p_{m-2}>2$ and 3 divides one of $p_{m-2}, p_{m-1}=p_{m-2}+2$ and $p_{m}=p_{m-2}+4$. This implies $p_{m-2}=3$ and thus $p_{m}=7$, giving $7 \leqslant n<11$. Finally, a quick computation shows that $7!\mid \prod_{p<q \leqslant 7}(p+q)$ but $8!\nmid \prod_{p<q \leqslant 7}(p+q)$, so neither does 9 ! and 10 !.
|
7
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Find all positive integers $n>2$ such that $$ n!\mid \prod_{\substack{p<q \leqslant n, p, q \text { primes }}}(p+q) . $$ (Nigeria) Answer: This only holds for $n=7$.
|
Assume that $n$ satisfies $n!\mid \prod_{p<q \leqslant n}(p+q)$ and let $2=p_{1}<p_{2}<\cdots<p_{m} \leqslant n$ be the primes in $\{1,2, \ldots, n\}$. Each such prime divides $n$ !. In particular, $p_{m} \mid p_{i}+p_{j}$ for some $p_{i}<p_{j} \leqslant n$. But $$ 0<\frac{p_{i}+p_{j}}{p_{m}}<\frac{p_{m}+p_{m}}{p_{m}}=2 $$ so $p_{m}=p_{i}+p_{j}$ which implies $m \geqslant 3, p_{i}=2$ and $p_{m}=2+p_{j}=2+p_{m-1}$. Similarly, $p_{m-1} \mid p_{k}+p_{l}$ for some $p_{k}<p_{l} \leqslant n$. But $$ 0<\frac{p_{l}+p_{k}}{p_{m-1}} \leqslant \frac{p_{m}+p_{m-1}}{p_{m-1}}=\frac{2 p_{m-1}+2}{p_{m-1}}<3 $$ so either $p_{m-1}=p_{l}+p_{k}$ or $2 p_{m-1}=p_{l}+p_{k}$. As above, the former case gives $p_{m-1}=2+p_{m-2}$. If $2 p_{m-1}=p_{l}+p_{k}$, then $p_{m-1}<p_{k}$, so $k=m$ and $$ 2 p_{m-1}=p_{l}+p_{m-1}+2 \Rightarrow p_{m-1}=p_{l}+2=p_{m-2}+2 $$ Either way, $p_{m-2}>2$ and 3 divides one of $p_{m-2}, p_{m-1}=p_{m-2}+2$ and $p_{m}=p_{m-2}+4$. This implies $p_{m-2}=3$ and thus $p_{m}=7$, giving $7 \leqslant n<11$. Finally, a quick computation shows that $7!\mid \prod_{p<q \leqslant 7}(p+q)$ but $8!\nmid \prod_{p<q \leqslant 7}(p+q)$, so neither does 9 ! and 10 !.
|
{
"resource_path": "IMO/segmented/en-IMO2022SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
b02fbc11-d02b-58be-bae4-0b5be5397742
| 24,447
|
Professor Oak is feeding his 100 Pokémon. Each Pokémon has a bowl whose capacity is a positive real number of kilograms. These capacities are known to Professor Oak. The total capacity of all the bowls is 100 kilograms. Professor Oak distributes 100 kilograms of food in such a way that each Pokémon receives a non-negative integer number of kilograms of food (which may be larger than the capacity of their bowl). The dissatisfaction level of a Pokémon who received $N$ kilograms of food and whose bowl has a capacity of $C$ kilograms is equal to $|N-C|$. Find the smallest real number $D$ such that, regardless of the capacities of the bowls, Professor Oak can distribute the food in a way that the sum of the dissatisfaction levels over all the 100 Pokémon is at most $D$. (Ukraine)
|
First, consider the situation where 99 bowls have a capacity of 0.5 kilograms and the last bowl has a capacity of 50.5 kilograms. No matter how Professor Oak distributes the food, the dissatisfaction level of every Pokémon will be at least 0.5 . This amounts to a total dissatisfaction level of at least 50 , proving that $D \geqslant 50$. Now we prove that no matter what the capacities of the bowls are, Professor Oak can always distribute food in a way that the total dissatisfaction level is at most 50 . We start by fixing some notation. We number the Pokémon from 1 to 100 . Let $C_{i}>0$ be the capacity of the bowl of the $i^{\text {th }}$ Pokémon. By assumption, we have $C_{1}+C_{2}+\cdots+C_{100}=100$. We write $F_{i}:=C_{i}-\left\lfloor C_{i}\right\rfloor$ for the fractional part of $C_{i}$. Without loss of generality, we may assume that $F_{1} \leqslant F_{2} \leqslant \cdots \leqslant F_{100}$. Here is a strategy: Professor Oak starts by giving $\left\lfloor C_{i}\right\rfloor$ kilograms of food to the $i^{\text {th }}$ Pokémon. Let $$ R:=100-\left\lfloor C_{1}\right\rfloor-\left\lfloor C_{2}\right\rfloor-\cdots-\left\lfloor C_{100}\right\rfloor=F_{1}+F_{2}+\cdots+F_{100} \geqslant 0 $$ be the amount of food left. He continues by giving an extra kilogram of food to the $R$ Pokémon numbered $100-R+1,100-R+2, \ldots, 100$, i.e. the Pokémon with the $R$ largest values of $F_{i}$. By doing so, Professor Oak distributed 100 kilograms of food. The total dissatisfaction level with this strategy is $$ d:=F_{1}+\cdots+F_{100-R}+\left(1-F_{100-R+1}\right)+\cdots+\left(1-F_{100}\right) . $$ We can rewrite $$ \begin{aligned} d & =2\left(F_{1}+\cdots+F_{100-R}\right)+R-\left(F_{1}+\cdots+F_{100}\right) \\ & =2\left(F_{1}+\cdots+F_{100-R}\right) . \end{aligned} $$ Now, observe that the arithmetic mean of $F_{1}, F_{2}, \ldots, F_{100-R}$ is not greater than the arithmetic mean of $F_{1}, F_{2}, \ldots, F_{100}$, because we assumed $F_{1} \leqslant F_{2} \leqslant \cdots \leqslant F_{100}$. Therefore $$ d \leqslant 2(100-R) \cdot \frac{F_{1}+\cdots+F_{100}}{100}=2 \cdot \frac{R(100-R)}{100} $$ Finally, we use the AM-GM inequality to see that $R(100-R) \leqslant \frac{100^{2}}{2^{2}}$ which implies $d \leqslant 50$. We conclude that there is always a distribution for which the total dissatisfaction level is at most 50 , proving that $D \leqslant 50$.
|
50
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Professor Oak is feeding his 100 Pokémon. Each Pokémon has a bowl whose capacity is a positive real number of kilograms. These capacities are known to Professor Oak. The total capacity of all the bowls is 100 kilograms. Professor Oak distributes 100 kilograms of food in such a way that each Pokémon receives a non-negative integer number of kilograms of food (which may be larger than the capacity of their bowl). The dissatisfaction level of a Pokémon who received $N$ kilograms of food and whose bowl has a capacity of $C$ kilograms is equal to $|N-C|$. Find the smallest real number $D$ such that, regardless of the capacities of the bowls, Professor Oak can distribute the food in a way that the sum of the dissatisfaction levels over all the 100 Pokémon is at most $D$. (Ukraine)
|
First, consider the situation where 99 bowls have a capacity of 0.5 kilograms and the last bowl has a capacity of 50.5 kilograms. No matter how Professor Oak distributes the food, the dissatisfaction level of every Pokémon will be at least 0.5 . This amounts to a total dissatisfaction level of at least 50 , proving that $D \geqslant 50$. Now we prove that no matter what the capacities of the bowls are, Professor Oak can always distribute food in a way that the total dissatisfaction level is at most 50 . We start by fixing some notation. We number the Pokémon from 1 to 100 . Let $C_{i}>0$ be the capacity of the bowl of the $i^{\text {th }}$ Pokémon. By assumption, we have $C_{1}+C_{2}+\cdots+C_{100}=100$. We write $F_{i}:=C_{i}-\left\lfloor C_{i}\right\rfloor$ for the fractional part of $C_{i}$. Without loss of generality, we may assume that $F_{1} \leqslant F_{2} \leqslant \cdots \leqslant F_{100}$. Here is a strategy: Professor Oak starts by giving $\left\lfloor C_{i}\right\rfloor$ kilograms of food to the $i^{\text {th }}$ Pokémon. Let $$ R:=100-\left\lfloor C_{1}\right\rfloor-\left\lfloor C_{2}\right\rfloor-\cdots-\left\lfloor C_{100}\right\rfloor=F_{1}+F_{2}+\cdots+F_{100} \geqslant 0 $$ be the amount of food left. He continues by giving an extra kilogram of food to the $R$ Pokémon numbered $100-R+1,100-R+2, \ldots, 100$, i.e. the Pokémon with the $R$ largest values of $F_{i}$. By doing so, Professor Oak distributed 100 kilograms of food. The total dissatisfaction level with this strategy is $$ d:=F_{1}+\cdots+F_{100-R}+\left(1-F_{100-R+1}\right)+\cdots+\left(1-F_{100}\right) . $$ We can rewrite $$ \begin{aligned} d & =2\left(F_{1}+\cdots+F_{100-R}\right)+R-\left(F_{1}+\cdots+F_{100}\right) \\ & =2\left(F_{1}+\cdots+F_{100-R}\right) . \end{aligned} $$ Now, observe that the arithmetic mean of $F_{1}, F_{2}, \ldots, F_{100-R}$ is not greater than the arithmetic mean of $F_{1}, F_{2}, \ldots, F_{100}$, because we assumed $F_{1} \leqslant F_{2} \leqslant \cdots \leqslant F_{100}$. Therefore $$ d \leqslant 2(100-R) \cdot \frac{F_{1}+\cdots+F_{100}}{100}=2 \cdot \frac{R(100-R)}{100} $$ Finally, we use the AM-GM inequality to see that $R(100-R) \leqslant \frac{100^{2}}{2^{2}}$ which implies $d \leqslant 50$. We conclude that there is always a distribution for which the total dissatisfaction level is at most 50 , proving that $D \leqslant 50$.
|
{
"resource_path": "IMO/segmented/en-IMO2023SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
9f6b0cf7-cfeb-569f-a509-60f142704ff9
| 607,734
|
Let $n$ be a positive integer. We arrange $1+2+\cdots+n$ circles in a triangle with $n$ rows, such that the $i^{\text {th }}$ row contains exactly $i$ circles. The following figure shows the case $n=6$.  In this triangle, a ninja-path is a sequence of circles obtained by repeatedly going from a circle to one of the two circles directly below it. In terms of $n$, find the largest value of $k$ such that if one circle from every row is coloured red, we can always find a ninja-path in which at least $k$ of the circles are red. (Netherlands)
|
Write $N=\left\lfloor\log _{2} n\right\rfloor$ so that we have $2^{N} \leqslant n \leqslant 2^{N+1}-1$. We first provide a construction where every ninja-path passes through at most $N+1$ red circles. For the row $i=2^{a}+b$ for $0 \leqslant a \leqslant N$ and $0 \leqslant b<2^{a}$, we colour the $(2 b+1)^{\text {th }}$ circle.  Then every ninja-path passes through at most one red circle in each of the rows $2^{a}, 2^{a}+$ $1, \ldots, 2^{a+1}-1$ for each $0 \leqslant a \leqslant N$. It follows that every ninja-path passes through at most $N+1$ red circles. We now prove that for every colouring, there exists a ninja-path going through at least $N+1$ red circles. For each circle $C$, we assign the maximum number of red circles in a ninja-path that starts at the top of the triangle and ends at $C$. 
|
N+1
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Let $n$ be a positive integer. We arrange $1+2+\cdots+n$ circles in a triangle with $n$ rows, such that the $i^{\text {th }}$ row contains exactly $i$ circles. The following figure shows the case $n=6$.  In this triangle, a ninja-path is a sequence of circles obtained by repeatedly going from a circle to one of the two circles directly below it. In terms of $n$, find the largest value of $k$ such that if one circle from every row is coloured red, we can always find a ninja-path in which at least $k$ of the circles are red. (Netherlands)
|
Write $N=\left\lfloor\log _{2} n\right\rfloor$ so that we have $2^{N} \leqslant n \leqslant 2^{N+1}-1$. We first provide a construction where every ninja-path passes through at most $N+1$ red circles. For the row $i=2^{a}+b$ for $0 \leqslant a \leqslant N$ and $0 \leqslant b<2^{a}$, we colour the $(2 b+1)^{\text {th }}$ circle.  Then every ninja-path passes through at most one red circle in each of the rows $2^{a}, 2^{a}+$ $1, \ldots, 2^{a+1}-1$ for each $0 \leqslant a \leqslant N$. It follows that every ninja-path passes through at most $N+1$ red circles. We now prove that for every colouring, there exists a ninja-path going through at least $N+1$ red circles. For each circle $C$, we assign the maximum number of red circles in a ninja-path that starts at the top of the triangle and ends at $C$. 
|
{
"resource_path": "IMO/segmented/en-IMO2023SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
2c8e7147-265c-59a4-a46a-a5e8af97500b
| 607,743
|
Let $a_{1}, a_{2}, \ldots, a_{n}, b_{1}, b_{2}, \ldots, b_{n}$ be $2 n$ positive integers such that the $n+1$ products $$ \begin{gathered} a_{1} a_{2} a_{3} \cdots a_{n} \\ b_{1} a_{2} a_{3} \cdots a_{n} \\ b_{1} b_{2} a_{3} \cdots a_{n} \\ \vdots \\ b_{1} b_{2} b_{3} \cdots b_{n} \end{gathered} $$ form a strictly increasing arithmetic progression in that order. Determine the smallest positive integer that could be the common difference of such an arithmetic progression. (Canada)
|
The condition in the problem is equivalent to $$ D=\left(b_{1}-a_{1}\right) a_{2} a_{3} \cdots a_{n}=b_{1}\left(b_{2}-a_{2}\right) a_{3} a_{4} \cdots a_{n}=\cdots=b_{1} b_{2} \cdots b_{n-1}\left(b_{n}-a_{n}\right), $$ where $D$ is the common difference. Since the progression is strictly increasing, $D>0$, hence $b_{i}>a_{i}$ for every $1 \leqslant i \leqslant n$. Individually, these equalities simplify to $$ \left(b_{i}-a_{i}\right) a_{i+1}=b_{i}\left(b_{i+1}-a_{i+1}\right) \text { for every } 1 \leqslant i \leqslant n-1 $$ If $g_{i}:=\operatorname{gcd}\left(a_{i}, b_{i}\right)>1$ for some $1 \leqslant i \leqslant n$, then we can replace $a_{i}$ with $\frac{a_{i}}{g_{i}}$ and $b_{i}$ with $\frac{b_{i}}{g_{i}}$ to get a smaller common difference. Hence we may assume $\operatorname{gcd}\left(a_{i}, b_{i}\right)=1$ for every $1 \leqslant i \leqslant n$. Then, we have $\operatorname{gcd}\left(b_{i}-a_{i}, b_{i}\right)=\operatorname{gcd}\left(a_{i}, b_{i}\right)=1$ and $\operatorname{gcd}\left(a_{i+1}, b_{i+1}-a_{i+1}\right)=\operatorname{gcd}\left(a_{i+1}, b_{i+1}\right)=1$ for every $1 \leqslant i \leqslant n-1$. The equality (1) implies $a_{i+1}=b_{i}$ and $b_{i}-a_{i}=b_{i+1}-a_{i+1}$. Thus, $$ a_{1}, \quad b_{1}=a_{2}, \quad b_{2}=a_{3}, \quad \ldots, \quad b_{n-1}=a_{n}, \quad b_{n} $$ is an arithmetic progression with positive common difference. Since $a_{1} \geqslant 1$, we have $a_{i} \geqslant i$ for every $1 \leqslant i \leqslant n$, so $$ D=\left(b_{1}-a_{1}\right) a_{2} a_{3} \cdots a_{n} \geqslant 1 \cdot 2 \cdot 3 \cdots n=n! $$ Equality is achieved when $b_{i}-a_{i}=1$ for $1 \leqslant i \leqslant n$ and $a_{1}=1$, i.e. $a_{i}=i$ and $b_{i}=i+1$ for every $1 \leqslant i \leqslant n$. Indeed, it is straightforward to check that these integers produce an arithmetic progression with common difference $n!$. Solution 2 (Variant of Solution 1). Similarly to Solution 1, we may assume $\operatorname{gcd}\left(a_{i}, b_{i}\right)=1$ for every $1 \leqslant i \leqslant n$. Denote by $p_{1}, p_{2}, \ldots, p_{n+1}$ the sequence obtained as the product in the problem statement. Then we have $\frac{p_{i+1}}{p_{i}}=\frac{b_{i}}{a_{i}}>1$, so $b_{i}>a_{i}$. Since $p_{1}, p_{2}, \ldots, p_{n+1}$ is an arithmetic progression, we have $p_{i+2}=2 p_{i+1}-p_{i}$ hence $$ 2-\frac{a_{i}}{b_{i}}=\frac{2 b_{i}-a_{i}}{b_{i}}=\frac{2 p_{i+1}-p_{i}}{p_{i+1}}=\frac{p_{i+2}}{p_{i+1}}=\frac{b_{i+1}}{a_{i+1}} . $$ But since the fractions on the left-hand side and the right-hand side are both irreducible, we conclude that $b_{i}=a_{i+1}$, so $2-\frac{a_{i}}{a_{i+1}}=\frac{a_{i+2}}{a_{i+1}}$. Then we have $a_{i}+a_{i+2}=2 a_{i+1}$, which means that $a_{1}, a_{2}, \ldots, a_{n}$ is an arithmetic progression with positive common difference. We conclude as in Solution 1.
|
n!
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Let $a_{1}, a_{2}, \ldots, a_{n}, b_{1}, b_{2}, \ldots, b_{n}$ be $2 n$ positive integers such that the $n+1$ products $$ \begin{gathered} a_{1} a_{2} a_{3} \cdots a_{n} \\ b_{1} a_{2} a_{3} \cdots a_{n} \\ b_{1} b_{2} a_{3} \cdots a_{n} \\ \vdots \\ b_{1} b_{2} b_{3} \cdots b_{n} \end{gathered} $$ form a strictly increasing arithmetic progression in that order. Determine the smallest positive integer that could be the common difference of such an arithmetic progression. (Canada) Answer: The smallest common difference is $n!$.
|
The condition in the problem is equivalent to $$ D=\left(b_{1}-a_{1}\right) a_{2} a_{3} \cdots a_{n}=b_{1}\left(b_{2}-a_{2}\right) a_{3} a_{4} \cdots a_{n}=\cdots=b_{1} b_{2} \cdots b_{n-1}\left(b_{n}-a_{n}\right), $$ where $D$ is the common difference. Since the progression is strictly increasing, $D>0$, hence $b_{i}>a_{i}$ for every $1 \leqslant i \leqslant n$. Individually, these equalities simplify to $$ \left(b_{i}-a_{i}\right) a_{i+1}=b_{i}\left(b_{i+1}-a_{i+1}\right) \text { for every } 1 \leqslant i \leqslant n-1 $$ If $g_{i}:=\operatorname{gcd}\left(a_{i}, b_{i}\right)>1$ for some $1 \leqslant i \leqslant n$, then we can replace $a_{i}$ with $\frac{a_{i}}{g_{i}}$ and $b_{i}$ with $\frac{b_{i}}{g_{i}}$ to get a smaller common difference. Hence we may assume $\operatorname{gcd}\left(a_{i}, b_{i}\right)=1$ for every $1 \leqslant i \leqslant n$. Then, we have $\operatorname{gcd}\left(b_{i}-a_{i}, b_{i}\right)=\operatorname{gcd}\left(a_{i}, b_{i}\right)=1$ and $\operatorname{gcd}\left(a_{i+1}, b_{i+1}-a_{i+1}\right)=\operatorname{gcd}\left(a_{i+1}, b_{i+1}\right)=1$ for every $1 \leqslant i \leqslant n-1$. The equality (1) implies $a_{i+1}=b_{i}$ and $b_{i}-a_{i}=b_{i+1}-a_{i+1}$. Thus, $$ a_{1}, \quad b_{1}=a_{2}, \quad b_{2}=a_{3}, \quad \ldots, \quad b_{n-1}=a_{n}, \quad b_{n} $$ is an arithmetic progression with positive common difference. Since $a_{1} \geqslant 1$, we have $a_{i} \geqslant i$ for every $1 \leqslant i \leqslant n$, so $$ D=\left(b_{1}-a_{1}\right) a_{2} a_{3} \cdots a_{n} \geqslant 1 \cdot 2 \cdot 3 \cdots n=n! $$ Equality is achieved when $b_{i}-a_{i}=1$ for $1 \leqslant i \leqslant n$ and $a_{1}=1$, i.e. $a_{i}=i$ and $b_{i}=i+1$ for every $1 \leqslant i \leqslant n$. Indeed, it is straightforward to check that these integers produce an arithmetic progression with common difference $n!$. Solution 2 (Variant of Solution 1). Similarly to Solution 1, we may assume $\operatorname{gcd}\left(a_{i}, b_{i}\right)=1$ for every $1 \leqslant i \leqslant n$. Denote by $p_{1}, p_{2}, \ldots, p_{n+1}$ the sequence obtained as the product in the problem statement. Then we have $\frac{p_{i+1}}{p_{i}}=\frac{b_{i}}{a_{i}}>1$, so $b_{i}>a_{i}$. Since $p_{1}, p_{2}, \ldots, p_{n+1}$ is an arithmetic progression, we have $p_{i+2}=2 p_{i+1}-p_{i}$ hence $$ 2-\frac{a_{i}}{b_{i}}=\frac{2 b_{i}-a_{i}}{b_{i}}=\frac{2 p_{i+1}-p_{i}}{p_{i+1}}=\frac{p_{i+2}}{p_{i+1}}=\frac{b_{i+1}}{a_{i+1}} . $$ But since the fractions on the left-hand side and the right-hand side are both irreducible, we conclude that $b_{i}=a_{i+1}$, so $2-\frac{a_{i}}{a_{i+1}}=\frac{a_{i+2}}{a_{i+1}}$. Then we have $a_{i}+a_{i+2}=2 a_{i+1}$, which means that $a_{1}, a_{2}, \ldots, a_{n}$ is an arithmetic progression with positive common difference. We conclude as in Solution 1.
|
{
"resource_path": "IMO/segmented/en-IMO2023SL.jsonl",
"problem_match": null,
"solution_match": null
}
|
6f5524c5-48dc-5f1a-ada8-8afc7126841c
| 607,782
|
1. (POL) Find the smallest natural number $n$ with the following properties: (a) In decimal representation it ends with 6. (b) If we move this digit to the front of the number, we get a number 4 times larger.
|
1. From the conditions of the problem we have $n=10 x+6$ and $4 n=$ $6 \cdot 10^{m}+x$ for some integer $x$. Eliminating $x$ from these two equations, we get $40 n=6 \cdot 10^{m+1}+n-6 \Rightarrow n=2\left(10^{m+1}-1\right) / 13$. Hence we must find the smallest $m$ such that this fraction is an integer. By inspection, this happens for $m=6$, and for this $m$ we obtain $n=153846$, which indeed satisfies the conditions of the problem.
|
153846
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
1. (POL) Find the smallest natural number $n$ with the following properties: (a) In decimal representation it ends with 6. (b) If we move this digit to the front of the number, we get a number 4 times larger.
|
1. From the conditions of the problem we have $n=10 x+6$ and $4 n=$ $6 \cdot 10^{m}+x$ for some integer $x$. Eliminating $x$ from these two equations, we get $40 n=6 \cdot 10^{m+1}+n-6 \Rightarrow n=2\left(10^{m+1}-1\right) / 13$. Hence we must find the smallest $m$ such that this fraction is an integer. By inspection, this happens for $m=6$, and for this $m$ we obtain $n=153846$, which indeed satisfies the conditions of the problem.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
a27684ac-7a7a-5e74-b270-3241fd682c5b
| 24,523
|
3. (CZS) A cube $A B C D A^{\prime} B^{\prime} C^{\prime} D^{\prime}$ is given. The point $X$ is moving at a constant speed along the square $A B C D$ in the direction from $A$ to $B$. The point $Y$ is moving with the same constant speed along the square $B C C^{\prime} B^{\prime}$ in the direction from $B^{\prime}$ to $C^{\prime}$. Initially, $X$ and $Y$ start out from $A$ and $B^{\prime}$ respectively. Find the locus of all the midpoints of $X Y$. Second Day
|
3. By inspecting the four different stages of this periodic motion we easily obtain that the locus of the midpoints of $X Y$ is the edges of $M N C Q$, where $M, N$, and $Q$ are the centers of $A B B^{\prime} A^{\prime}, B C C^{\prime} B^{\prime}$, and $A B C D$, respectively.
|
M N C Q
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
3. (CZS) A cube $A B C D A^{\prime} B^{\prime} C^{\prime} D^{\prime}$ is given. The point $X$ is moving at a constant speed along the square $A B C D$ in the direction from $A$ to $B$. The point $Y$ is moving with the same constant speed along the square $B C C^{\prime} B^{\prime}$ in the direction from $B^{\prime}$ to $C^{\prime}$. Initially, $X$ and $Y$ start out from $A$ and $B^{\prime}$ respectively. Find the locus of all the midpoints of $X Y$. Second Day
|
3. By inspecting the four different stages of this periodic motion we easily obtain that the locus of the midpoints of $X Y$ is the edges of $M N C Q$, where $M, N$, and $Q$ are the centers of $A B B^{\prime} A^{\prime}, B C C^{\prime} B^{\prime}$, and $A B C D$, respectively.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
e368d7a0-96bf-57d0-b506-0f1013c56075
| 24,527
|
1. (CZS) Determine all real solutions of the equation $\sqrt{x^{2}-p}+2 \sqrt{x^{2}-1}=$ $x$, where $p$ is a real number.
|
1. Obviously, $x \geq 0$; hence squaring the given equation yields an equivalent equation $5 x^{2}-p-4+4 \sqrt{\left(x^{2}-1\right)\left(x^{2}-p\right)}=x^{2}$, i.e., $4 \sqrt{\left(x^{2}-1\right)\left(x^{2}-p\right)}=$ $(p+4)-4 x^{2}$. If $4 x^{2} \leq(p+4)$, we may square the equation once again to get $-16(p+1) x^{2}+16 p=-8(p+4) x^{2}+(p+4)^{2}$, which is equivalent to $x^{2}=(4-p)^{2} /[4(4-2 p)]$, i.e., $x=(4-p) /(2 \sqrt{4-2 p})$. For this to be a solution we must have $p \leq 2$ and $(4-p)^{2} /(4-2 p)=4 x^{2} \leq(p+4)$. Hence $4 / 3 \leq p \leq 2$. Otherwise there is no solution.
|
\frac{4-p}{2\sqrt{4-2p}}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
1. (CZS) Determine all real solutions of the equation $\sqrt{x^{2}-p}+2 \sqrt{x^{2}-1}=$ $x$, where $p$ is a real number.
|
1. Obviously, $x \geq 0$; hence squaring the given equation yields an equivalent equation $5 x^{2}-p-4+4 \sqrt{\left(x^{2}-1\right)\left(x^{2}-p\right)}=x^{2}$, i.e., $4 \sqrt{\left(x^{2}-1\right)\left(x^{2}-p\right)}=$ $(p+4)-4 x^{2}$. If $4 x^{2} \leq(p+4)$, we may square the equation once again to get $-16(p+1) x^{2}+16 p=-8(p+4) x^{2}+(p+4)^{2}$, which is equivalent to $x^{2}=(4-p)^{2} /[4(4-2 p)]$, i.e., $x=(4-p) /(2 \sqrt{4-2 p})$. For this to be a solution we must have $p \leq 2$ and $(4-p)^{2} /(4-2 p)=4 x^{2} \leq(p+4)$. Hence $4 / 3 \leq p \leq 2$. Otherwise there is no solution.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
2cda1ca6-ba7e-5e26-bd93-b122918d6c2b
| 24,540
|
3. (YUG) The incircle is inscribed in a triangle $A B C$ with sides $a, b, c$. Three tangents to the incircle are drawn, each of which is parallel to one side of the triangle $A B C$. These tangents form three smaller triangles (internal to $\triangle A B C$ ) with the sides of $\triangle A B C$. In each of these triangles an incircle is inscribed. Determine the sum of areas of all four incircles. Second Day
|
3. Let $r$ be the radius of the incircle of $\triangle A B C, r_{a}, r_{b}, r_{c}$ the radii of the smaller circles corresponding to $A, B, C$, and $h_{a}, h_{b}, h_{c}$ the altitudes from $A, B, C$ respectively. The coefficient of similarity between the smaller triangle at $A$ and the triangle $A B C$ is $1-2 r / h_{a}$, from which we easily obtain $r_{a}=\left(h_{a}-2 r\right) r / h_{a}=(s-a) r / s$. Similarly, $r_{b}=(s-b) r / s$ and $r_{c}=(s-c) r / s$. Now a straightforward computation gives that the sum of areas of the four circles is given by $$ \Sigma=\frac{(b+c-a)(c+a-b)(a+b-c)\left(a^{2}+b^{2}+c^{2}\right) \pi}{(a+b+c)^{3}} $$
|
\frac{(b+c-a)(c+a-b)(a+b-c)\left(a^{2}+b^{2}+c^{2}\right) \pi}{(a+b+c)^{3}}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
3. (YUG) The incircle is inscribed in a triangle $A B C$ with sides $a, b, c$. Three tangents to the incircle are drawn, each of which is parallel to one side of the triangle $A B C$. These tangents form three smaller triangles (internal to $\triangle A B C$ ) with the sides of $\triangle A B C$. In each of these triangles an incircle is inscribed. Determine the sum of areas of all four incircles. Second Day
|
3. Let $r$ be the radius of the incircle of $\triangle A B C, r_{a}, r_{b}, r_{c}$ the radii of the smaller circles corresponding to $A, B, C$, and $h_{a}, h_{b}, h_{c}$ the altitudes from $A, B, C$ respectively. The coefficient of similarity between the smaller triangle at $A$ and the triangle $A B C$ is $1-2 r / h_{a}$, from which we easily obtain $r_{a}=\left(h_{a}-2 r\right) r / h_{a}=(s-a) r / s$. Similarly, $r_{b}=(s-b) r / s$ and $r_{c}=(s-c) r / s$. Now a straightforward computation gives that the sum of areas of the four circles is given by $$ \Sigma=\frac{(b+c-a)(c+a-b)(a+b-c)\left(a^{2}+b^{2}+c^{2}\right) \pi}{(a+b+c)^{3}} $$
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
7aabc6d2-5971-5c82-bda6-0297f0eda9cb
| 24,561
|
5. (ROM) Five points are given in the plane. Among the lines that connect these five points, no two coincide and no two are parallel or perpendicular. Through each point we construct an altitude to each of the other lines. What is the maximal number of intersection points of these altitudes (excluding the initial five points)?
|
5. Let us first compute the number of intersection points of the perpendiculars passing through two distinct points $B$ and $C$. The perpendiculars from $B$ to the lines through $C$ other than $B C$ meet all perpendiculars from $C$, which counts to $3 \cdot 6=18$ intersection points. Each perpendicular from $B$ to the 3 lines not containing $C$ can intersect at most 5 of the perpendiculars passing through $C$, which counts to another $3 \cdot 5=15$ intersection points. Thus there are $18+15=33$ intersection points corresponding to $B, C$. It follows that the required total number is at most $10 \cdot 33=330$. But some of these points, namely the orthocenters of the triangles with vertices at the given points, are counted thrice. There are 10 such points. Hence the maximal number of intersection points is $330-2 \cdot 10=310$. Remark. The jury considered only the combinatorial part of the problem and didn't require an example in which 310 points appear. However, it is "easily" verified that, for instance, the set of points $A(1,1), B(e, \pi)$, $C\left(e^{2}, \pi^{2}\right), D\left(e^{3}, \pi^{3}\right), E\left(e^{4}, \pi^{4}\right)$ works.
|
310
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
5. (ROM) Five points are given in the plane. Among the lines that connect these five points, no two coincide and no two are parallel or perpendicular. Through each point we construct an altitude to each of the other lines. What is the maximal number of intersection points of these altitudes (excluding the initial five points)?
|
5. Let us first compute the number of intersection points of the perpendiculars passing through two distinct points $B$ and $C$. The perpendiculars from $B$ to the lines through $C$ other than $B C$ meet all perpendiculars from $C$, which counts to $3 \cdot 6=18$ intersection points. Each perpendicular from $B$ to the 3 lines not containing $C$ can intersect at most 5 of the perpendiculars passing through $C$, which counts to another $3 \cdot 5=15$ intersection points. Thus there are $18+15=33$ intersection points corresponding to $B, C$. It follows that the required total number is at most $10 \cdot 33=330$. But some of these points, namely the orthocenters of the triangles with vertices at the given points, are counted thrice. There are 10 such points. Hence the maximal number of intersection points is $330-2 \cdot 10=310$. Remark. The jury considered only the combinatorial part of the problem and didn't require an example in which 310 points appear. However, it is "easily" verified that, for instance, the set of points $A(1,1), B(e, \pi)$, $C\left(e^{2}, \pi^{2}\right), D\left(e^{3}, \pi^{3}\right), E\left(e^{4}, \pi^{4}\right)$ works.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
123a0a7c-f7f0-507c-b84b-37252906fe79
| 24,567
|
3. (CZS) A tetrahedron $A B C D$ is given. The lengths of the edges $A B$ and $C D$ are $a$ and $b$, respectively, the distance between the lines $A B$ and $C D$ is $d$, and the angle between them is equal to $\omega$. The tetrahedron is divided into two parts by the plane $\pi$ parallel to the lines $A B$ and $C D$. Calculate the ratio of the volumes of the parts if the ratio between the distances of the plane $\pi$ from $A B$ and $C D$ is equal to $k$. Second Day
|
3. Let $d$ denote the distance between the lines $A B$ and $C D$. Being parallel to $A B$ and $C D$, the plane $\pi$ intersects the faces of the tetrahedron in a parallelogram $E F G H$. Let $X \in A B$ be a points such that $H X \| D B$. Clearly $V_{A E H B F G}=V_{A X E H}+$ $V_{X E H B F G}$. Let $M N$ be the common perpendicular to lines $A B$ and $C D(M \in A B, N \in C D)$ and let $M N, B N$ meet the plane $\pi$ at $Q$ and $R$ respectively. Then it holds that $B R / R N=M Q / Q N=k$ and consequently $A X / X B=A E / E C=$ $A H / H D=B F / F C=B G / G D=$ $k$. Now we have $V_{A X E H} / V_{A B C D}=$  $k^{3} /(k+1)^{3}$ 。 Furthermore, if $h=3 V_{A B C D} / S_{A B C}$ is the height of $A B C D$ from $D$, then $$ \begin{aligned} V_{X E H B F G} & =\frac{1}{2} S_{X B F E} \frac{k}{k+1} h \text { and } \\ S_{X B F E} & =S_{A B C}-S_{A X E}-S_{E F C}=\frac{(k+1)^{2}-1-k^{2}}{(k+1)^{2}}=\frac{2 k}{(1+k)^{2}} \end{aligned} $$ These relations give us $V_{X E H B F G} / V_{A B C D}=3 k^{2} /(1+k)^{3}$. Finally, $$ \frac{V_{A E H B F G}}{V_{A B C D}}=\frac{k^{3}+3 k^{2}}{(k+1)^{3}} $$ Similarly, $V_{C E F D H G} / V_{A B C D}=(3 k+1) /(k+1)^{3}$, and hence the required ratio is $\left(k^{3}+3 k^{2}\right) /(3 k+1)$.
|
\frac{k^{3}+3 k^{2}}{3 k+1}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
3. (CZS) A tetrahedron $A B C D$ is given. The lengths of the edges $A B$ and $C D$ are $a$ and $b$, respectively, the distance between the lines $A B$ and $C D$ is $d$, and the angle between them is equal to $\omega$. The tetrahedron is divided into two parts by the plane $\pi$ parallel to the lines $A B$ and $C D$. Calculate the ratio of the volumes of the parts if the ratio between the distances of the plane $\pi$ from $A B$ and $C D$ is equal to $k$. Second Day
|
3. Let $d$ denote the distance between the lines $A B$ and $C D$. Being parallel to $A B$ and $C D$, the plane $\pi$ intersects the faces of the tetrahedron in a parallelogram $E F G H$. Let $X \in A B$ be a points such that $H X \| D B$. Clearly $V_{A E H B F G}=V_{A X E H}+$ $V_{X E H B F G}$. Let $M N$ be the common perpendicular to lines $A B$ and $C D(M \in A B, N \in C D)$ and let $M N, B N$ meet the plane $\pi$ at $Q$ and $R$ respectively. Then it holds that $B R / R N=M Q / Q N=k$ and consequently $A X / X B=A E / E C=$ $A H / H D=B F / F C=B G / G D=$ $k$. Now we have $V_{A X E H} / V_{A B C D}=$  $k^{3} /(k+1)^{3}$ 。 Furthermore, if $h=3 V_{A B C D} / S_{A B C}$ is the height of $A B C D$ from $D$, then $$ \begin{aligned} V_{X E H B F G} & =\frac{1}{2} S_{X B F E} \frac{k}{k+1} h \text { and } \\ S_{X B F E} & =S_{A B C}-S_{A X E}-S_{E F C}=\frac{(k+1)^{2}-1-k^{2}}{(k+1)^{2}}=\frac{2 k}{(1+k)^{2}} \end{aligned} $$ These relations give us $V_{X E H B F G} / V_{A B C D}=3 k^{2} /(1+k)^{3}$. Finally, $$ \frac{V_{A E H B F G}}{V_{A B C D}}=\frac{k^{3}+3 k^{2}}{(k+1)^{3}} $$ Similarly, $V_{C E F D H G} / V_{A B C D}=(3 k+1) /(k+1)^{3}$, and hence the required ratio is $\left(k^{3}+3 k^{2}\right) /(3 k+1)$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
013e4a89-7527-5ce3-8448-ebd1eac7cf39
| 24,577
|
1. (USS) Three problems $A, B$, and $C$ were given on a mathematics olympiad. All 25 students solved at least one of these problems. The number of students who solved $B$ and not $A$ is twice the number of students who solved $C$ and not $A$. The number of students who solved only $A$ is greater by 1 than the number of students who along with $A$ solved at least one other problem. Among the students who solved only one problem, half solved $A$. How many students solved only $B$ ?
|
1. Let $N_{a}, N_{b}, N_{c}, N_{a b}, N_{a c}, N_{b c}, N_{a b c}$ denote the number of students who solved exactly the problems whose letters are stated in the index of the variable. From the conditions of the problem we have $$ \begin{gathered} N_{a}+N_{b}+N_{c}+N_{a b}+N_{b c}+N_{a c}+N_{a b c}=25 \\ N_{b}+N_{b c}=2\left(N_{c}+N_{b c}\right), \quad N_{a}-1=N_{a c}+N_{a b c}+N_{a b}, \quad N_{a}=N_{b}+N_{c} . \end{gathered} $$ From the first and third equations we get $2 N_{a}+N_{b}+N_{c}+N_{b c}=26$, and from the second and fourth we get $4 N_{b}+N_{c}=26$ and thus $N_{b} \leq 6$. On the other hand, we have from the second equation $N_{b}=2 N_{c}+N_{b c} \Rightarrow$ $N_{c} \leq N_{b} / 2 \Rightarrow 26 \leq 9 N_{b} / 2 \Rightarrow N_{b} \geq 6$; hence $N_{b}=6$.
|
6
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
1. (USS) Three problems $A, B$, and $C$ were given on a mathematics olympiad. All 25 students solved at least one of these problems. The number of students who solved $B$ and not $A$ is twice the number of students who solved $C$ and not $A$. The number of students who solved only $A$ is greater by 1 than the number of students who along with $A$ solved at least one other problem. Among the students who solved only one problem, half solved $A$. How many students solved only $B$ ?
|
1. Let $N_{a}, N_{b}, N_{c}, N_{a b}, N_{a c}, N_{b c}, N_{a b c}$ denote the number of students who solved exactly the problems whose letters are stated in the index of the variable. From the conditions of the problem we have $$ \begin{gathered} N_{a}+N_{b}+N_{c}+N_{a b}+N_{b c}+N_{a c}+N_{a b c}=25 \\ N_{b}+N_{b c}=2\left(N_{c}+N_{b c}\right), \quad N_{a}-1=N_{a c}+N_{a b c}+N_{a b}, \quad N_{a}=N_{b}+N_{c} . \end{gathered} $$ From the first and third equations we get $2 N_{a}+N_{b}+N_{c}+N_{b c}=26$, and from the second and fourth we get $4 N_{b}+N_{c}=26$ and thus $N_{b} \leq 6$. On the other hand, we have from the second equation $N_{b}=2 N_{c}+N_{b c} \Rightarrow$ $N_{c} \leq N_{b} / 2 \Rightarrow 26 \leq 9 N_{b} / 2 \Rightarrow N_{b} \geq 6$; hence $N_{b}=6$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
627dd740-4c7a-51a5-89a9-ff827854d302
| 24,589
|
10. (CZS 4) The square $A B C D$ is to be decomposed into $n$ triangles (nonoverlapping) all of whose angles are acute. Find the smallest integer $n$ for which there exists a solution to this problem and construct at least one decomposition for this $n$. Answer whether it is possible to ask additionally that (at least) one of these triangles has a perimeter less than an arbitrarily given positive number.
|
10. Let $n$ be the number of triangles and let $b$ and $i$ be the numbers of vertices on the boundary and in the interior of the square, respectively. Since all the triangles are acute, each of the vertices of the square belongs to at least two triangles. Additionally, every vertex on the boundary belongs to at least three, and every vertex in the interior belongs to at least five triangles. Therefore $$ 3 n \geq 8+3 b+5 i $$ Moreover, the sum of angles at any vertex that lies in the interior, on the boundary, or at a vertex of the square is equal to $2 \pi, \pi, \pi / 2$ respectively. The sum of all angles of the triangles equals $n \pi$, which gives us $n \pi=4 \cdot \pi / 2+b \pi+2 i \pi$, i.e., $n=$ $2+b+2 i$. This relation together with (1) easily yields that $i \geq 2$. Since each of the vertices inside the square belongs to at least five triangles, and at most two contain both, it follows that $n \geq 8$.  It is shown in the figure that the square can be decomposed into eight acute triangles. Obviously one of them can have an arbitrarily small perimeter.
|
8
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
10. (CZS 4) The square $A B C D$ is to be decomposed into $n$ triangles (nonoverlapping) all of whose angles are acute. Find the smallest integer $n$ for which there exists a solution to this problem and construct at least one decomposition for this $n$. Answer whether it is possible to ask additionally that (at least) one of these triangles has a perimeter less than an arbitrarily given positive number.
|
10. Let $n$ be the number of triangles and let $b$ and $i$ be the numbers of vertices on the boundary and in the interior of the square, respectively. Since all the triangles are acute, each of the vertices of the square belongs to at least two triangles. Additionally, every vertex on the boundary belongs to at least three, and every vertex in the interior belongs to at least five triangles. Therefore $$ 3 n \geq 8+3 b+5 i $$ Moreover, the sum of angles at any vertex that lies in the interior, on the boundary, or at a vertex of the square is equal to $2 \pi, \pi, \pi / 2$ respectively. The sum of all angles of the triangles equals $n \pi$, which gives us $n \pi=4 \cdot \pi / 2+b \pi+2 i \pi$, i.e., $n=$ $2+b+2 i$. This relation together with (1) easily yields that $i \geq 2$. Since each of the vertices inside the square belongs to at least five triangles, and at most two contain both, it follows that $n \geq 8$.  It is shown in the figure that the square can be decomposed into eight acute triangles. Obviously one of them can have an arbitrarily small perimeter.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
15c87a3c-9d1f-599e-809d-c390c0acc923
| 24,607
|
13. (GDR 1) Find whether among all quadrilaterals whose interiors lie inside a semicircle of radius $r$ there exists one (or more) with maximal area. If so, determine their shape and area.
|
13. The maximum area is $3 \sqrt{3} r^{2} / 4$ (where $r$ is the radius of the semicircle) and is attained in the case of a trapezoid with two vertices at the endpoints of the diameter of the semicircle and the other two vertices dividing the semicircle into three equal arcs.
|
\frac{3 \sqrt{3} r^{2}}{4}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
13. (GDR 1) Find whether among all quadrilaterals whose interiors lie inside a semicircle of radius $r$ there exists one (or more) with maximal area. If so, determine their shape and area.
|
13. The maximum area is $3 \sqrt{3} r^{2} / 4$ (where $r$ is the radius of the semicircle) and is attained in the case of a trapezoid with two vertices at the endpoints of the diameter of the semicircle and the other two vertices dividing the semicircle into three equal arcs.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
c803b8dc-a414-51f8-a845-626e823bd9c1
| 24,615
|
14. (GDR 2) Which fraction $p / q$, where $p, q$ are positive integers less than 100 , is closest to $\sqrt{2}$ ? Find all digits after the decimal point in the decimal representation of this fraction that coincide with digits in the decimal representation of $\sqrt{2}$ (without using any tables).
|
14. We have that $$ \left|\frac{p}{q}-\sqrt{2}\right|=\frac{|p-q \sqrt{2}|}{q}=\frac{\left|p^{2}-2 q^{2}\right|}{q(p+q \sqrt{2})} \geq \frac{1}{q(p+q \sqrt{2})} $$ because $\left|p^{2}-2 q^{2}\right| \geq 1$. The greatest solution to the equation $\left|p^{2}-2 q^{2}\right|=1$ with $p, q \leq 100$ is $(p, q)=(99,70)$. It is easy to verify using (1) that $\frac{99}{70}$ best approximates $\sqrt{2}$ among the fractions $p / q$ with $p, q \leq 100$. Second solution. By using some basic facts about Farey sequences one can find that $\frac{41}{29}<\sqrt{2}<\frac{99}{70}$ and that $\frac{41}{29}<\frac{p}{q}<\frac{99}{70}$ implies $p \geq 41+99>100$ because $99 \cdot 29-41 \cdot 70=1$. Of the two fractions $41 / 29$ and $99 / 70$, the latter is closer to $\sqrt{2}$.
|
\frac{99}{70}
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
14. (GDR 2) Which fraction $p / q$, where $p, q$ are positive integers less than 100 , is closest to $\sqrt{2}$ ? Find all digits after the decimal point in the decimal representation of this fraction that coincide with digits in the decimal representation of $\sqrt{2}$ (without using any tables).
|
14. We have that $$ \left|\frac{p}{q}-\sqrt{2}\right|=\frac{|p-q \sqrt{2}|}{q}=\frac{\left|p^{2}-2 q^{2}\right|}{q(p+q \sqrt{2})} \geq \frac{1}{q(p+q \sqrt{2})} $$ because $\left|p^{2}-2 q^{2}\right| \geq 1$. The greatest solution to the equation $\left|p^{2}-2 q^{2}\right|=1$ with $p, q \leq 100$ is $(p, q)=(99,70)$. It is easy to verify using (1) that $\frac{99}{70}$ best approximates $\sqrt{2}$ among the fractions $p / q$ with $p, q \leq 100$. Second solution. By using some basic facts about Farey sequences one can find that $\frac{41}{29}<\sqrt{2}<\frac{99}{70}$ and that $\frac{41}{29}<\frac{p}{q}<\frac{99}{70}$ implies $p \geq 41+99>100$ because $99 \cdot 29-41 \cdot 70=1$. Of the two fractions $41 / 29$ and $99 / 70$, the latter is closer to $\sqrt{2}$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
d2bfeba8-1fc8-56f5-add9-5b60d4740015
| 24,617
|
21. (HUN 2) Without using any tables, find the exact value of the product $$ P=\cos \frac{\pi}{15} \cos \frac{2 \pi}{15} \cos \frac{3 \pi}{15} \cos \frac{4 \pi}{15} \cos \frac{5 \pi}{15} \cos \frac{6 \pi}{15} \cos \frac{7 \pi}{15} $$
|
21. Using the formula $$ \cos x \cos 2 x \cos 4 x \cdots \cos 2^{n-1} x=\frac{\sin 2^{n} x}{2^{n} \sin x} $$ which is shown by simple induction, we obtain $$ \begin{gathered} \cos \frac{\pi}{15} \cos \frac{2 \pi}{15} \cos \frac{4 \pi}{15} \cos \frac{7 \pi}{15}=-\cos \frac{\pi}{15} \cos \frac{2 \pi}{15} \cos \frac{4 \pi}{15} \cos \frac{8 \pi}{15}=\frac{1}{16} \\ \cos \frac{3 \pi}{15} \cos \frac{6 \pi}{15} \end{gathered}=\frac{1}{4}, \quad \cos \frac{5 \pi}{15}=\frac{1}{2} . $$ Multiplying these equalities, we get that the required product $P$ equals 1/128.
|
\frac{1}{128}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
21. (HUN 2) Without using any tables, find the exact value of the product $$ P=\cos \frac{\pi}{15} \cos \frac{2 \pi}{15} \cos \frac{3 \pi}{15} \cos \frac{4 \pi}{15} \cos \frac{5 \pi}{15} \cos \frac{6 \pi}{15} \cos \frac{7 \pi}{15} $$
|
21. Using the formula $$ \cos x \cos 2 x \cos 4 x \cdots \cos 2^{n-1} x=\frac{\sin 2^{n} x}{2^{n} \sin x} $$ which is shown by simple induction, we obtain $$ \begin{gathered} \cos \frac{\pi}{15} \cos \frac{2 \pi}{15} \cos \frac{4 \pi}{15} \cos \frac{7 \pi}{15}=-\cos \frac{\pi}{15} \cos \frac{2 \pi}{15} \cos \frac{4 \pi}{15} \cos \frac{8 \pi}{15}=\frac{1}{16} \\ \cos \frac{3 \pi}{15} \cos \frac{6 \pi}{15} \end{gathered}=\frac{1}{4}, \quad \cos \frac{5 \pi}{15}=\frac{1}{2} . $$ Multiplying these equalities, we get that the required product $P$ equals 1/128.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
f352ef91-2609-5e91-904f-5800aadf7299
| 24,638
|
30. (MON 1) Given $m+n$ numbers $a_{i}(i=1,2, \ldots, m), b_{j}(j=1,2, \ldots, n)$, determine the number of pairs $\left(a_{i}, b_{j}\right)$ for which $|i-j| \geq k$, where $k$ is a nonnegative integer.
|
30. We assume w.l.o.g. that $m \leq n$. Let $r$ and $s$ be the numbers of pairs for which $i-j \geq k$ and of those for which $j-i \geq k$. The desired number is $r+s$. We easily find that $$ \begin{aligned} & r= \begin{cases}(m-k)(m-k+1) / 2, & k<m \\ 0, & k \geq m\end{cases} \\ & s= \begin{cases}m(2 n-2 k-m+1) / 2, & k<n-m \\ (n-k)(n-k+1) / 2, & n-m \leq k<n \\ 0, & k \geq n\end{cases} \end{aligned} $$
|
r+s
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
30. (MON 1) Given $m+n$ numbers $a_{i}(i=1,2, \ldots, m), b_{j}(j=1,2, \ldots, n)$, determine the number of pairs $\left(a_{i}, b_{j}\right)$ for which $|i-j| \geq k$, where $k$ is a nonnegative integer.
|
30. We assume w.l.o.g. that $m \leq n$. Let $r$ and $s$ be the numbers of pairs for which $i-j \geq k$ and of those for which $j-i \geq k$. The desired number is $r+s$. We easily find that $$ \begin{aligned} & r= \begin{cases}(m-k)(m-k+1) / 2, & k<m \\ 0, & k \geq m\end{cases} \\ & s= \begin{cases}m(2 n-2 k-m+1) / 2, & k<n-m \\ (n-k)(n-k+1) / 2, & n-m \leq k<n \\ 0, & k \geq n\end{cases} \end{aligned} $$
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
5367df9f-9445-54cb-9a26-e35df1aa4cb1
| 24,664
|
42. (ROM 1) Decompose into real factors the expression $1-\sin ^{5} x-\cos ^{5} x$.
|
42. $E=(1-\sin x)(1-\cos x)[3+2(\sin x+\cos x)+2 \sin x \cos x+\sin x \cos x(\sin x+$ $\cos x)]$.
|
(1-\sin x)(1-\cos x)[3+2(\sin x+\cos x)+2 \sin x \cos x+\sin x \cos x(\sin x+\cos x)]
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
42. (ROM 1) Decompose into real factors the expression $1-\sin ^{5} x-\cos ^{5} x$.
|
42. $E=(1-\sin x)(1-\cos x)[3+2(\sin x+\cos x)+2 \sin x \cos x+\sin x \cos x(\sin x+$ $\cos x)]$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
0788ec65-89ca-561a-b2c8-91e018c9a176
| 24,700
|
51. (SWE 4) A subset $S$ of the set of integers $0, \ldots, 99$ is said to have property A if it is impossible to fill a crossword puzzle with 2 rows and 2 columns with numbers in $S$ ( 0 is written as 00,1 as 01 , and so on). Determine the maximal number of elements in sets $S$ with property A.
|
51. If there exist two numbers $\overline{a b}, \overline{b c} \in S$, then one can fill a crossword puzzle as $\left(\begin{array}{ll}a & b \\ b & c\end{array}\right)$. The converse is obvious. Hence the set $S$ has property $A$ if and only if the set of first digits and the set of second digits of numbers in $S$ are disjoint. Thus the maximum size of $S$ is 25 .
|
25
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
51. (SWE 4) A subset $S$ of the set of integers $0, \ldots, 99$ is said to have property A if it is impossible to fill a crossword puzzle with 2 rows and 2 columns with numbers in $S$ ( 0 is written as 00,1 as 01 , and so on). Determine the maximal number of elements in sets $S$ with property A.
|
51. If there exist two numbers $\overline{a b}, \overline{b c} \in S$, then one can fill a crossword puzzle as $\left(\begin{array}{ll}a & b \\ b & c\end{array}\right)$. The converse is obvious. Hence the set $S$ has property $A$ if and only if the set of first digits and the set of second digits of numbers in $S$ are disjoint. Thus the maximum size of $S$ is 25 .
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
232b4490-681c-5a92-8dfc-ccd361b14732
| 24,726
|
59. (USS 6) On the circle with center $O$ and radius 1 the point $A_{0}$ is fixed and points $A_{1}, A_{2}, \ldots, A_{999}, A_{1000}$ are distributed in such a way that $\angle A_{0} O A_{k}=k$ (in radians). Cut the circle at points $A_{0}, A_{1}, \ldots, A_{1000}$. How many arcs with different lengths are obtained? ### 3.10 The Tenth IMO
|
59. By the $\operatorname{arc} A B$ we shall always mean the positive $\operatorname{arc} A B$. We denote by $|A B|$ the length of arc $A B$. Let a basic arc be one of the $n+1$ arcs into which the circle is partitioned by the points $A_{0}, A_{1}, \ldots, A_{n}$, where $n \in \mathbb{N}$. Suppose that $A_{p} A_{0}$ and $A_{0} A_{q}$ are the basic arcs with an endpoint at $A_{0}$, and that $x_{n}, y_{n}$ are their lengths, respectively. We show by induction on $n$ that for each $n$ the length of a basic arc is equal to $x_{n}, y_{n}$ or $x_{n}+y_{n}$. The statement is trivial for $n=1$. Assume that it holds for $n$, and let $A_{i} A_{n+1}, A_{n+1} A_{j}$ be basic arcs. We shall prove that these two arcs have lengths $x_{n}, y_{n}$, or $x_{n}+y_{n}$. If $i, j$ are both strictly positive, then $\left|A_{i} A_{n+1}\right|=$ $\left|A_{i-1} A_{n}\right|$ and $\left|A_{n+1} A_{j}\right|=\left|A_{n} A_{j-1}\right|$ are equal to $x_{n}, y_{n}$, or $x_{n}+y_{n}$ by the inductive hypothesis. Let us assume now that $i=0$, i.e., that $A_{p} A_{n+1}$ and $A_{n+1} A_{0}$ are basic arcs. Then $\left|A_{p} A_{n+1}\right|=\left|A_{0} A_{n+1-p}\right| \geq\left|A_{0} A_{q}\right|=y_{n}$ and similarly $\left|A_{n+1} A_{q}\right| \geq x_{n}$, but $\left|A_{p} A_{q}\right|=x_{n}+y_{n}$, from which it follows that $\left|A_{p} A_{n+1}\right|=\left|A_{0} A_{q}\right|=y_{n}$ and consequently $n+1=p+q$. Also, $x_{n+1}=\left|A_{n+1} A_{0}\right|=y_{n}-x_{n}$ and $y_{n+1}=y_{n}$. Now, all basic arcs have lengths $y_{n}-x_{n}, x_{n}, y_{n}, x_{n}+y_{n}$. A presence of a basic arc of length $x_{n}+y_{n}$ would spoil our inductive step. However, if any basic arc $A_{k} A_{l}$ has length $x_{n}+y_{n}$, then we must have $l-q=k-p$ because $2 \pi$ is irrational, and therefore the arc $A_{k} A_{l}$ contains either the point $A_{k-p}$ (if $k \geq p$ ) or the point $A_{k+q}$ (if $k<p$ ), which is impossible; hence, the proof is complete for $i=0$. The proof for $j=0$ is analogous. This completes the induction. It can be also seen from the above considerations that the basic arcs take only two distinct lengths if and only if $n=p+q-1$. If we denote by $n_{k}$ the sequence of $n$ 's for which this holds, and by $p_{k}, q_{k}$ the sequences of the corresponding $p, q$, we have $p_{1}=q_{1}=1$ and $$ \left(p_{k+1}, q_{k+1}\right)=\left\{\begin{array}{l} \left(p_{k}+q_{k}, q_{k}\right), \text { if }\left\{p_{k} /(2 \pi)\right\}+\left\{q_{k} /(2 \pi)\right\}>1 \\ \left(p_{k}, p_{k}+q_{k}\right), \text { if }\left\{p_{k} /(2 \pi)\right\}+\left\{q_{k} /(2 \pi)\right\}<1 \end{array}\right. $$ It is now "easy" to calculate that $p_{19}=p_{20}=333, q_{19}=377, q_{20}=710$, and thus $n_{19}=709<1000<1042=n_{20}$. It follows that the lengths of the basic arcs for $n=1000$ take exactly three different values.
|
3
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
59. (USS 6) On the circle with center $O$ and radius 1 the point $A_{0}$ is fixed and points $A_{1}, A_{2}, \ldots, A_{999}, A_{1000}$ are distributed in such a way that $\angle A_{0} O A_{k}=k$ (in radians). Cut the circle at points $A_{0}, A_{1}, \ldots, A_{1000}$. How many arcs with different lengths are obtained? ### 3.10 The Tenth IMO
|
59. By the $\operatorname{arc} A B$ we shall always mean the positive $\operatorname{arc} A B$. We denote by $|A B|$ the length of arc $A B$. Let a basic arc be one of the $n+1$ arcs into which the circle is partitioned by the points $A_{0}, A_{1}, \ldots, A_{n}$, where $n \in \mathbb{N}$. Suppose that $A_{p} A_{0}$ and $A_{0} A_{q}$ are the basic arcs with an endpoint at $A_{0}$, and that $x_{n}, y_{n}$ are their lengths, respectively. We show by induction on $n$ that for each $n$ the length of a basic arc is equal to $x_{n}, y_{n}$ or $x_{n}+y_{n}$. The statement is trivial for $n=1$. Assume that it holds for $n$, and let $A_{i} A_{n+1}, A_{n+1} A_{j}$ be basic arcs. We shall prove that these two arcs have lengths $x_{n}, y_{n}$, or $x_{n}+y_{n}$. If $i, j$ are both strictly positive, then $\left|A_{i} A_{n+1}\right|=$ $\left|A_{i-1} A_{n}\right|$ and $\left|A_{n+1} A_{j}\right|=\left|A_{n} A_{j-1}\right|$ are equal to $x_{n}, y_{n}$, or $x_{n}+y_{n}$ by the inductive hypothesis. Let us assume now that $i=0$, i.e., that $A_{p} A_{n+1}$ and $A_{n+1} A_{0}$ are basic arcs. Then $\left|A_{p} A_{n+1}\right|=\left|A_{0} A_{n+1-p}\right| \geq\left|A_{0} A_{q}\right|=y_{n}$ and similarly $\left|A_{n+1} A_{q}\right| \geq x_{n}$, but $\left|A_{p} A_{q}\right|=x_{n}+y_{n}$, from which it follows that $\left|A_{p} A_{n+1}\right|=\left|A_{0} A_{q}\right|=y_{n}$ and consequently $n+1=p+q$. Also, $x_{n+1}=\left|A_{n+1} A_{0}\right|=y_{n}-x_{n}$ and $y_{n+1}=y_{n}$. Now, all basic arcs have lengths $y_{n}-x_{n}, x_{n}, y_{n}, x_{n}+y_{n}$. A presence of a basic arc of length $x_{n}+y_{n}$ would spoil our inductive step. However, if any basic arc $A_{k} A_{l}$ has length $x_{n}+y_{n}$, then we must have $l-q=k-p$ because $2 \pi$ is irrational, and therefore the arc $A_{k} A_{l}$ contains either the point $A_{k-p}$ (if $k \geq p$ ) or the point $A_{k+q}$ (if $k<p$ ), which is impossible; hence, the proof is complete for $i=0$. The proof for $j=0$ is analogous. This completes the induction. It can be also seen from the above considerations that the basic arcs take only two distinct lengths if and only if $n=p+q-1$. If we denote by $n_{k}$ the sequence of $n$ 's for which this holds, and by $p_{k}, q_{k}$ the sequences of the corresponding $p, q$, we have $p_{1}=q_{1}=1$ and $$ \left(p_{k+1}, q_{k+1}\right)=\left\{\begin{array}{l} \left(p_{k}+q_{k}, q_{k}\right), \text { if }\left\{p_{k} /(2 \pi)\right\}+\left\{q_{k} /(2 \pi)\right\}>1 \\ \left(p_{k}, p_{k}+q_{k}\right), \text { if }\left\{p_{k} /(2 \pi)\right\}+\left\{q_{k} /(2 \pi)\right\}<1 \end{array}\right. $$ It is now "easy" to calculate that $p_{19}=p_{20}=333, q_{19}=377, q_{20}=710$, and thus $n_{19}=709<1000<1042=n_{20}$. It follows that the lengths of the basic arcs for $n=1000$ take exactly three different values.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
2e51b4a3-8fed-59a6-8c44-5ded97796ba1
| 24,749
|
1. (SWE 2) Two ships sail on the sea with constant speeds and fixed directions. It is known that at 9:00 the distance between them was 20 miles; at 9:35, 15 miles; and at 9:55, 13 miles. At what moment were the ships the smallest distance from each other, and what was that distance?
|
1. Since the ships are sailing with constant speeds and directions, the second ship is sailing at a constant speed and direction in reference to the first ship. Let $A$ be the constant position of the first ship in this frame. Let $B_{1}$, $B_{2}, B_{3}$, and $B$ on line $b$ defining the trajectory of the ship be positions of the second ship with respect to the first ship at 9:00, 9:35, 9:55, and at the moment the two ships were closest. Then we have the following equations for distances (in miles): $$ \begin{gathered} A B_{1}=20, \quad A B_{2}=15, \quad A B_{3}=13 \\ B_{1} B_{2}: B_{2} B_{3}=7: 4, \quad A B_{i}^{2}=A B^{2}+B B_{i}^{2} \end{gathered} $$ Since $B B_{1}>B B_{2}>B B_{3}$, it follows that $\mathcal{B}\left(B_{3}, B, B_{2}, B_{1}\right)$ or $\mathcal{B}\left(B, B_{3}, B_{2}\right.$, $B_{1}$ ). We get a system of three quadratic equations with three unknowns: $A B, B B_{3}$ and $B_{3} B_{2}$ ( $B B_{3}$ being negative if $\mathcal{B}\left(B_{3}, B, B_{1}, B_{2}\right)$, positive otherwise). This can be solved by eliminating $A B$ and then $B B_{3}$. The unique solution ends up being $$ A B=12, \quad B B_{3}=5, \quad B_{3} B_{2}=4 $$ and consequently, the two ships are closest at 10:20 when they are at a distance of 12 miles.
|
12
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
1. (SWE 2) Two ships sail on the sea with constant speeds and fixed directions. It is known that at 9:00 the distance between them was 20 miles; at 9:35, 15 miles; and at 9:55, 13 miles. At what moment were the ships the smallest distance from each other, and what was that distance?
|
1. Since the ships are sailing with constant speeds and directions, the second ship is sailing at a constant speed and direction in reference to the first ship. Let $A$ be the constant position of the first ship in this frame. Let $B_{1}$, $B_{2}, B_{3}$, and $B$ on line $b$ defining the trajectory of the ship be positions of the second ship with respect to the first ship at 9:00, 9:35, 9:55, and at the moment the two ships were closest. Then we have the following equations for distances (in miles): $$ \begin{gathered} A B_{1}=20, \quad A B_{2}=15, \quad A B_{3}=13 \\ B_{1} B_{2}: B_{2} B_{3}=7: 4, \quad A B_{i}^{2}=A B^{2}+B B_{i}^{2} \end{gathered} $$ Since $B B_{1}>B B_{2}>B B_{3}$, it follows that $\mathcal{B}\left(B_{3}, B, B_{2}, B_{1}\right)$ or $\mathcal{B}\left(B, B_{3}, B_{2}\right.$, $B_{1}$ ). We get a system of three quadratic equations with three unknowns: $A B, B B_{3}$ and $B_{3} B_{2}$ ( $B B_{3}$ being negative if $\mathcal{B}\left(B_{3}, B, B_{1}, B_{2}\right)$, positive otherwise). This can be solved by eliminating $A B$ and then $B B_{3}$. The unique solution ends up being $$ A B=12, \quad B B_{3}=5, \quad B_{3} B_{2}=4 $$ and consequently, the two ships are closest at 10:20 when they are at a distance of 12 miles.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
5b170c84-1c87-5fb1-80ba-4c3c40a689fb
| 24,761
|
14. (BUL 5) A line in the plane of a triangle $A B C$ intersects the sides $A B$ and $A C$ respectively at points $X$ and $Y$ such that $B X=C Y$. Find the locus of the center of the circumcircle of triangle $X A Y$.
|
14. Let $O, D, E$ be the circumcenter of $\triangle A B C$ and the midpoints of $A B$ and $A C$, and given arbitrary $X \in A B$ and $Y \in A C$ such that $B X=C Y$, let $O_{1}, D_{1}, E_{1}$ be the circumcenter of $\triangle A X Y$ and the midpoints of $A X$ and $A Y$, respectively. Since $A D=A B / 2$ and $A D_{1}=A X / 2$, it follows that $D D_{1}=B X / 2$ and similarly $E E_{1}=C Y / 2$. Hence $O_{1}$ is at the same distance $B X / 2=C Y / 2$ from the lines $O D$ and $O E$ and lies on the halfline bisector $l$ of $\angle D O E$. If we let $X, Y$ vary along the segments $A B$ and $A C$, we obtain that the locus of $O_{1}$ is the segment $O P$, where $P \in l$ is a point at distance $\min (A B, A C) / 2$ from $O D$ and $O E$.
|
O P
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
14. (BUL 5) A line in the plane of a triangle $A B C$ intersects the sides $A B$ and $A C$ respectively at points $X$ and $Y$ such that $B X=C Y$. Find the locus of the center of the circumcircle of triangle $X A Y$.
|
14. Let $O, D, E$ be the circumcenter of $\triangle A B C$ and the midpoints of $A B$ and $A C$, and given arbitrary $X \in A B$ and $Y \in A C$ such that $B X=C Y$, let $O_{1}, D_{1}, E_{1}$ be the circumcenter of $\triangle A X Y$ and the midpoints of $A X$ and $A Y$, respectively. Since $A D=A B / 2$ and $A D_{1}=A X / 2$, it follows that $D D_{1}=B X / 2$ and similarly $E E_{1}=C Y / 2$. Hence $O_{1}$ is at the same distance $B X / 2=C Y / 2$ from the lines $O D$ and $O E$ and lies on the halfline bisector $l$ of $\angle D O E$. If we let $X, Y$ vary along the segments $A B$ and $A C$, we obtain that the locus of $O_{1}$ is the segment $O P$, where $P \in l$ is a point at distance $\min (A B, A C) / 2$ from $O D$ and $O E$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
31b13fd6-c067-5fb8-8ca4-eef8408d3774
| 24,775
|
19. (ITA 5) We are given a fixed point on the circle of radius 1, and going from this point along the circumference in the positive direction on curved distances $0,1,2, \ldots$ from it we obtain points with abscisas $n=0,1,2, \ldots$ respectively. How many points among them should we take to ensure that some two of them are less than the distance $1 / 5$ apart?
|
19. We shall denote by $d_{n}$ the shortest curved distance from the initial point to the $n$th point in the positive direction. The sequence $d_{n}$ goes as follows: $0,1,2,3,4,5,6,0.72,1.72, \ldots, 5.72,0.43,1.43, \ldots, 5.43,0.15=d_{19}$. Hence the required number of points is 20 .
|
20
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
19. (ITA 5) We are given a fixed point on the circle of radius 1, and going from this point along the circumference in the positive direction on curved distances $0,1,2, \ldots$ from it we obtain points with abscisas $n=0,1,2, \ldots$ respectively. How many points among them should we take to ensure that some two of them are less than the distance $1 / 5$ apart?
|
19. We shall denote by $d_{n}$ the shortest curved distance from the initial point to the $n$th point in the positive direction. The sequence $d_{n}$ goes as follows: $0,1,2,3,4,5,6,0.72,1.72, \ldots, 5.72,0.43,1.43, \ldots, 5.43,0.15=d_{19}$. Hence the required number of points is 20 .
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
b84e0026-ad28-54ec-ad72-7291729dfa39
| 24,789
|
22. (CZS 3) ${ }^{\mathrm{IMO} 2}$ Find all positive integers $x$ for which $p(x)=x^{2}-10 x-22$, where $p(x)$ denotes the product of the digits of $x$.
|
22. It can be shown by induction on the number of digits of $x$ that $p(x) \leq x$ for all $x \in \mathbb{N}$. It follows that $x^{2}-10 x-22 \leq x$, which implies $x \leq 12$. Since $0<x^{2}-10 x-22=(x-12)(x+2)+2$, one easily obtains $x \geq 12$. Now one can directly check that $x=12$ is indeed a solution, and thus the only one.
|
12
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
22. (CZS 3) ${ }^{\mathrm{IMO} 2}$ Find all positive integers $x$ for which $p(x)=x^{2}-10 x-22$, where $p(x)$ denotes the product of the digits of $x$.
|
22. It can be shown by induction on the number of digits of $x$ that $p(x) \leq x$ for all $x \in \mathbb{N}$. It follows that $x^{2}-10 x-22 \leq x$, which implies $x \leq 12$. Since $0<x^{2}-10 x-22=(x-12)(x+2)+2$, one easily obtains $x \geq 12$. Now one can directly check that $x=12$ is indeed a solution, and thus the only one.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
4248577d-b8b5-51d0-83ff-675d5cc4544d
| 24,799
|
3. (GDR 1) Knowing that the system $$ \begin{aligned} x+y+z & =3, \\ x^{3}+y^{3}+z^{3} & =15, \\ x^{4}+y^{4}+z^{4} & =35, \end{aligned} $$ has a real solution $x, y, z$ for which $x^{2}+y^{2}+z^{2}<10$, find the value of $x^{5}+y^{5}+z^{5}$ for that solution.
|
3. Let $x, y, z$ be a solution of the given system with $x^{2}+y^{2}+z^{2}=\alpha<10$. Then $$ x y+y z+z x=\frac{(x+y+z)^{2}-\left(x^{2}+y^{2}+z^{2}\right)}{2}=\frac{9-\alpha}{2} . $$ Furthermore, $3 x y z=x^{3}+y^{3}+z^{3}-(x+y+z)\left(x^{2}+y^{2}+z^{2}-x y-y z-z x\right)$, which gives us $x y z=3(9-\alpha) / 2-4$. We now have $$ \begin{aligned} 35= & x^{4}+y^{4}+z^{4}=\left(x^{3}+y^{3}+z^{3}\right)(x+y+z) \\ & -\left(x^{2}+y^{2}+z^{2}\right)(x y+y z+z x)+x y z(x+y+z) \\ = & 45-\frac{\alpha(9-\alpha)}{2}+\frac{9(9-\alpha)}{2}-12 . \end{aligned} $$ The solutions in $\alpha$ are $\alpha=7$ and $\alpha=11$. Therefore $\alpha=7$, xyz $=-1$, $x y+x z+y z=1$, and $$ \begin{aligned} x^{5}+y^{5}+z^{5}= & \left(x^{4}+y^{4}+z^{4}\right)(x+y+z) \\ & -\left(x^{3}+y^{3}+z^{3}\right)(x y+x z+y z)+x y z\left(x^{2}+y^{2}+z^{2}\right) \\ = & 35 \cdot 3-15 \cdot 1+7 \cdot(-1)=83 . \end{aligned} $$
|
83
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
3. (GDR 1) Knowing that the system $$ \begin{aligned} x+y+z & =3, \\ x^{3}+y^{3}+z^{3} & =15, \\ x^{4}+y^{4}+z^{4} & =35, \end{aligned} $$ has a real solution $x, y, z$ for which $x^{2}+y^{2}+z^{2}<10$, find the value of $x^{5}+y^{5}+z^{5}$ for that solution.
|
3. Let $x, y, z$ be a solution of the given system with $x^{2}+y^{2}+z^{2}=\alpha<10$. Then $$ x y+y z+z x=\frac{(x+y+z)^{2}-\left(x^{2}+y^{2}+z^{2}\right)}{2}=\frac{9-\alpha}{2} . $$ Furthermore, $3 x y z=x^{3}+y^{3}+z^{3}-(x+y+z)\left(x^{2}+y^{2}+z^{2}-x y-y z-z x\right)$, which gives us $x y z=3(9-\alpha) / 2-4$. We now have $$ \begin{aligned} 35= & x^{4}+y^{4}+z^{4}=\left(x^{3}+y^{3}+z^{3}\right)(x+y+z) \\ & -\left(x^{2}+y^{2}+z^{2}\right)(x y+y z+z x)+x y z(x+y+z) \\ = & 45-\frac{\alpha(9-\alpha)}{2}+\frac{9(9-\alpha)}{2}-12 . \end{aligned} $$ The solutions in $\alpha$ are $\alpha=7$ and $\alpha=11$. Therefore $\alpha=7$, xyz $=-1$, $x y+x z+y z=1$, and $$ \begin{aligned} x^{5}+y^{5}+z^{5}= & \left(x^{4}+y^{4}+z^{4}\right)(x+y+z) \\ & -\left(x^{3}+y^{3}+z^{3}\right)(x y+x z+y z)+x y z\left(x^{2}+y^{2}+z^{2}\right) \\ = & 35 \cdot 3-15 \cdot 1+7 \cdot(-1)=83 . \end{aligned} $$
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
13082925-2cba-51a8-8793-2297b6ecacda
| 24,908
|
11. (SWE 4) ${ }^{\mathrm{IMO} 3}$ Determine the minimum of $a^{2}+b^{2}$ if $a$ and $b$ are real numbers for which the equation $$ x^{4}+a x^{3}+b x^{2}+a x+1=0 $$ has at least one real solution.
|
11. Putting $x+\frac{1}{x}=t$ we also get $x^{2}+\frac{1}{x^{2}}=t^{2}-2$, and the given equation reduces to $t^{2}+a t+b-2=0$. Since $x=\frac{t \pm \sqrt{t^{2}-4}}{2}, x$ will be real if and only if $|t| \geq 2, t \in \mathbb{R}$. Thus we need the minimum value of $a^{2}+b^{2}$ under the condition $a t+b=-\left(t^{2}-2\right),|t| \geq 2$. However, by the Cauchy-Schwarz inequality we have $$ \left(a^{2}+b^{2}\right)\left(t^{2}+1\right) \geq(a t+b)^{2}=\left(t^{2}-2\right)^{2} $$ It follows that $a^{2}+b^{2} \geq h(t)=\frac{\left(t^{2}-2\right)^{2}}{t^{2}+1}$. Since $h(t)=\left(t^{2}+1\right)+\frac{9}{t^{2}+1}-6$ is increasing for $t \geq 2$, we conclude that $a^{2}+b^{2} \geq h(2)=\frac{4}{5}$. The cases of equality are easy to examine: These are $a= \pm \frac{4}{5}$ and $b=-\frac{2}{5}$. Second solution. In fact, there was no need for considering $x=t+1 / t$. By the Cauchy-Schwarz inequality we have $\left(a^{2}+2 b^{2}+a^{2}\right)\left(x^{6}+x^{4} / 2+x^{2}\right) \geq$ $\left(a x^{3}+b x^{2}+a x\right)^{2}=\left(x^{4}+1\right)^{2}$. Hence $$ a^{2}+b^{2} \geq \frac{\left(x^{4}+1\right)^{2}}{2 x^{6}+x^{4}+2 x^{2}} \geq \frac{4}{5} $$ with equality for $x=1$.
|
\frac{4}{5}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
11. (SWE 4) ${ }^{\mathrm{IMO} 3}$ Determine the minimum of $a^{2}+b^{2}$ if $a$ and $b$ are real numbers for which the equation $$ x^{4}+a x^{3}+b x^{2}+a x+1=0 $$ has at least one real solution.
|
11. Putting $x+\frac{1}{x}=t$ we also get $x^{2}+\frac{1}{x^{2}}=t^{2}-2$, and the given equation reduces to $t^{2}+a t+b-2=0$. Since $x=\frac{t \pm \sqrt{t^{2}-4}}{2}, x$ will be real if and only if $|t| \geq 2, t \in \mathbb{R}$. Thus we need the minimum value of $a^{2}+b^{2}$ under the condition $a t+b=-\left(t^{2}-2\right),|t| \geq 2$. However, by the Cauchy-Schwarz inequality we have $$ \left(a^{2}+b^{2}\right)\left(t^{2}+1\right) \geq(a t+b)^{2}=\left(t^{2}-2\right)^{2} $$ It follows that $a^{2}+b^{2} \geq h(t)=\frac{\left(t^{2}-2\right)^{2}}{t^{2}+1}$. Since $h(t)=\left(t^{2}+1\right)+\frac{9}{t^{2}+1}-6$ is increasing for $t \geq 2$, we conclude that $a^{2}+b^{2} \geq h(2)=\frac{4}{5}$. The cases of equality are easy to examine: These are $a= \pm \frac{4}{5}$ and $b=-\frac{2}{5}$. Second solution. In fact, there was no need for considering $x=t+1 / t$. By the Cauchy-Schwarz inequality we have $\left(a^{2}+2 b^{2}+a^{2}\right)\left(x^{6}+x^{4} / 2+x^{2}\right) \geq$ $\left(a x^{3}+b x^{2}+a x\right)^{2}=\left(x^{4}+1\right)^{2}$. Hence $$ a^{2}+b^{2} \geq \frac{\left(x^{4}+1\right)^{2}}{2 x^{6}+x^{4}+2 x^{2}} \geq \frac{4}{5} $$ with equality for $x=1$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
25fbb410-5d28-5528-8dcf-214880643ef4
| 24,964
|
13. (YUG 4) Find the sphere of maximal radius that can be placed inside every tetrahedron that has all altitudes of length greater than or equal to 1.
|
13. Let $S_{1}, S_{2}, S_{3}, S_{4}$ denote the areas of the faces of the tetrahedron, $V$ its volume, $h_{1}, h_{2}, h_{3}, h_{4}$ its altitudes, and $r$ the radius of its inscribed sphere. Since $$ 3 V=S_{1} h_{1}=S_{2} h_{2}=S_{3} h_{3}=S_{4} h_{4}=\left(S_{1}+S_{2}+S_{3}+S_{4}\right) r, $$ it follows that $$ \frac{1}{h_{1}}+\frac{1}{h_{2}}+\frac{1}{h_{3}}+\frac{1}{h_{4}}=\frac{1}{r} . $$ In our case, $h_{1}, h_{2}, h_{3}, h_{4} \geq 1$, hence $r \geq 1 / 4$. On the other hand, it is clear that a sphere of radius greater than $1 / 4$ cannot be inscribed in a tetrahedron all of whose altitudes have length equal to 1 . Thus the answer is $1 / 4$.
|
\frac{1}{4}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
13. (YUG 4) Find the sphere of maximal radius that can be placed inside every tetrahedron that has all altitudes of length greater than or equal to 1.
|
13. Let $S_{1}, S_{2}, S_{3}, S_{4}$ denote the areas of the faces of the tetrahedron, $V$ its volume, $h_{1}, h_{2}, h_{3}, h_{4}$ its altitudes, and $r$ the radius of its inscribed sphere. Since $$ 3 V=S_{1} h_{1}=S_{2} h_{2}=S_{3} h_{3}=S_{4} h_{4}=\left(S_{1}+S_{2}+S_{3}+S_{4}\right) r, $$ it follows that $$ \frac{1}{h_{1}}+\frac{1}{h_{2}}+\frac{1}{h_{3}}+\frac{1}{h_{4}}=\frac{1}{r} . $$ In our case, $h_{1}, h_{2}, h_{3}, h_{4} \geq 1$, hence $r \geq 1 / 4$. On the other hand, it is clear that a sphere of radius greater than $1 / 4$ cannot be inscribed in a tetrahedron all of whose altitudes have length equal to 1 . Thus the answer is $1 / 4$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
3d22a63b-5e4a-51c0-bcd6-95561270790e
| 24,970
|
14. (YUG 5) ${ }^{\mathrm{IMO} 4} \mathrm{~A}$ soldier has to investigate whether there are mines in an area that has the form of an equilateral triangle. The radius of his detector is equal to one-half of an altitude of the triangle. The soldier starts from one vertex of the triangle. Determine the shortest path that the soldier has to traverse in order to check the whole region.
|
14. Suppose that the soldier starts at the vertex $A$ of the equilateral triangle $A B C$ of side length $a$. Let $\varphi, \psi$ be the arcs of circles with centers $B$ and $C$ and radii $a \sqrt{3} / 4$ respectively, that lie inside the triangle. In order to check the vertices $B, C$, he must visit some points $D \in \varphi$ and $E \in \psi$.  Thus his path cannot be shorter than the path $A D E$ (or $A E D$ ) itself. The length of the path $A D E$ is $A D+D E \geq A D+D C-a \sqrt{3} / 4$. Let $F$ be the reflection of $C$ across the line $M N$, where $M, N$ are the midpoints of $A B$ and $B C$. Then $D C \geq D F$ and hence $A D+D C \geq A D+D F \geq A F$. Consequently $A D+D E \geq A F-a \frac{\sqrt{3}}{4}=a\left(\frac{\sqrt{7}}{2}-\frac{\sqrt{3}}{4}\right)$, with equality if and only if $D$ is the midpoint of $\operatorname{arc} \varphi$ and $E=(C D) \cap \psi$. Moreover, it is easy to verify that, in following the path $A D E$, the soldier will check the whole region. Therefore this path (as well as the one symmetric to it) is shortest possible path that the soldier can take in order to check the entire field.
|
a\left(\frac{\sqrt{7}}{2}-\frac{\sqrt{3}}{4}\right)
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
14. (YUG 5) ${ }^{\mathrm{IMO} 4} \mathrm{~A}$ soldier has to investigate whether there are mines in an area that has the form of an equilateral triangle. The radius of his detector is equal to one-half of an altitude of the triangle. The soldier starts from one vertex of the triangle. Determine the shortest path that the soldier has to traverse in order to check the whole region.
|
14. Suppose that the soldier starts at the vertex $A$ of the equilateral triangle $A B C$ of side length $a$. Let $\varphi, \psi$ be the arcs of circles with centers $B$ and $C$ and radii $a \sqrt{3} / 4$ respectively, that lie inside the triangle. In order to check the vertices $B, C$, he must visit some points $D \in \varphi$ and $E \in \psi$.  Thus his path cannot be shorter than the path $A D E$ (or $A E D$ ) itself. The length of the path $A D E$ is $A D+D E \geq A D+D C-a \sqrt{3} / 4$. Let $F$ be the reflection of $C$ across the line $M N$, where $M, N$ are the midpoints of $A B$ and $B C$. Then $D C \geq D F$ and hence $A D+D C \geq A D+D F \geq A F$. Consequently $A D+D E \geq A F-a \frac{\sqrt{3}}{4}=a\left(\frac{\sqrt{7}}{2}-\frac{\sqrt{3}}{4}\right)$, with equality if and only if $D$ is the midpoint of $\operatorname{arc} \varphi$ and $E=(C D) \cap \psi$. Moreover, it is easy to verify that, in following the path $A D E$, the soldier will check the whole region. Therefore this path (as well as the one symmetric to it) is shortest possible path that the soldier can take in order to check the entire field.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
d196ca07-f8e7-54bc-bb21-3ec5be6df52a
| 24,973
|
4. (GBR 1) Let $P$ be a set of 7 different prime numbers and $C$ a set of 28 different composite numbers each of which is a product of two (not necessarily different) numbers from $P$. The set $C$ is divided into 7 disjoint four-element subsets such that each of the numbers in one set has a common prime divisor with at least two other numbers in that set. How many such partitions of $C$ are there?
|
4. Each of the subsets must be of the form $\left\{a^{2}, a b, a c, a d\right\}$ or $\left\{a^{2}, a b, a c, b c\right\}$. It is now easy to count up the partitions. The result is 26460 .
|
26460
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
4. (GBR 1) Let $P$ be a set of 7 different prime numbers and $C$ a set of 28 different composite numbers each of which is a product of two (not necessarily different) numbers from $P$. The set $C$ is divided into 7 disjoint four-element subsets such that each of the numbers in one set has a common prime divisor with at least two other numbers in that set. How many such partitions of $C$ are there?
|
4. Each of the subsets must be of the form $\left\{a^{2}, a b, a c, a d\right\}$ or $\left\{a^{2}, a b, a c, b c\right\}$. It is now easy to count up the partitions. The result is 26460 .
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
ff0234fe-1970-590d-8f40-427500029800
| 24,988
|
5. (FRA 2) A circle of radius 1 is located in a right-angled trihedron and touches all its faces. Find the locus of centers of such circles.
|
5. Let $O$ be the vertex of the trihedron, $Z$ the center of a circle $k$ inscribed in the trihedron, and $A, B, C$ points in which the plane of the circle meets the edges of the trihedron. We claim that the distance $O Z$ is constant. Set $O A=x, O B=y, O C=z, B C=a, C A=b, A B=c$, and let $S$ and $r=1$ be the area and inradius of $\triangle A B C$. Since $Z$ is the incenter of $A B C$, we have $(a+b+c) \overrightarrow{O Z}=a \overrightarrow{O A}+b \overrightarrow{O B}+c \overrightarrow{O C}$. Hence $$ (a+b+c)^{2} O Z^{2}=(a \overrightarrow{O A}+b \overrightarrow{O B}+c \overrightarrow{O C})^{2}=a^{2} x^{2}+b^{2} y^{2}+c^{2} z^{2} $$ But since $y^{2}+z^{2}=a^{2}, z^{2}+x^{2}=b^{2}$ and $x^{2}+y^{2}=c^{2}$, we obtain $x^{2}=\frac{-a^{2}+b^{2}+c^{2}}{2}, y^{2}=\frac{a^{2}-b^{2}+c^{2}}{2}, z^{2}=\frac{a^{2}+b^{2}-c^{2}}{2}$. Substituting these values in (1) yields $$ \begin{aligned} (a+b+c)^{2} O Z^{2} & =\frac{2 a^{2} b^{2}+2 b^{2} c^{2}+2 c^{2} a^{2}-a^{4}-b^{4}-c^{4}}{2} \\ & =8 S^{2}=2(a+b+c)^{2} r^{2} \end{aligned} $$ Hence $O Z=r \sqrt{2}=\sqrt{2}$, and $Z$ belongs to a sphere $\sigma$ with center $O$ and radius $\sqrt{2}$. Moreover, the distances of $Z$ from the faces of the trihedron do not exceed 1 ; hence $Z$ belongs to a part of $\sigma$ that lies inside the unit cube with three faces lying on the faces of the trihedron. It is easy to see that this part of $\sigma$ is exactly the required locus.
|
\sqrt{2}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
5. (FRA 2) A circle of radius 1 is located in a right-angled trihedron and touches all its faces. Find the locus of centers of such circles.
|
5. Let $O$ be the vertex of the trihedron, $Z$ the center of a circle $k$ inscribed in the trihedron, and $A, B, C$ points in which the plane of the circle meets the edges of the trihedron. We claim that the distance $O Z$ is constant. Set $O A=x, O B=y, O C=z, B C=a, C A=b, A B=c$, and let $S$ and $r=1$ be the area and inradius of $\triangle A B C$. Since $Z$ is the incenter of $A B C$, we have $(a+b+c) \overrightarrow{O Z}=a \overrightarrow{O A}+b \overrightarrow{O B}+c \overrightarrow{O C}$. Hence $$ (a+b+c)^{2} O Z^{2}=(a \overrightarrow{O A}+b \overrightarrow{O B}+c \overrightarrow{O C})^{2}=a^{2} x^{2}+b^{2} y^{2}+c^{2} z^{2} $$ But since $y^{2}+z^{2}=a^{2}, z^{2}+x^{2}=b^{2}$ and $x^{2}+y^{2}=c^{2}$, we obtain $x^{2}=\frac{-a^{2}+b^{2}+c^{2}}{2}, y^{2}=\frac{a^{2}-b^{2}+c^{2}}{2}, z^{2}=\frac{a^{2}+b^{2}-c^{2}}{2}$. Substituting these values in (1) yields $$ \begin{aligned} (a+b+c)^{2} O Z^{2} & =\frac{2 a^{2} b^{2}+2 b^{2} c^{2}+2 c^{2} a^{2}-a^{4}-b^{4}-c^{4}}{2} \\ & =8 S^{2}=2(a+b+c)^{2} r^{2} \end{aligned} $$ Hence $O Z=r \sqrt{2}=\sqrt{2}$, and $Z$ belongs to a sphere $\sigma$ with center $O$ and radius $\sqrt{2}$. Moreover, the distances of $Z$ from the faces of the trihedron do not exceed 1 ; hence $Z$ belongs to a part of $\sigma$ that lies inside the unit cube with three faces lying on the faces of the trihedron. It is easy to see that this part of $\sigma$ is exactly the required locus.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
3d99d153-a1f0-5700-86ba-d28b15437741
| 24,991
|
11. II 5 (BUL 1) ${ }^{\mathrm{IMO} 4}$ Consider a partition of an $8 \times 8$ chessboard into $p$ rectangles whose interiors are disjoint such that each of them has an equal number of white and black cells. Assume that $a_{1}<a_{2}<\cdots<a_{p}$, where $a_{i}$ denotes the number of white cells in the $i$ th rectangle. Find the maximal $p$ for which such a partition is possible and for that $p$ determine all possible corresponding sequences $a_{1}, a_{2}, \ldots, a_{p}$.
|
11. First, we notice that $a_{1}+a_{2}+\cdots+a_{p}=32$. The numbers $a_{i}$ are distinct, and consequently $a_{i} \geq i$ and $a_{1}+\cdots+a_{p} \geq p(p+1) / 2$. Therefore $p \leq 7$. The number 32 can be represented as a sum of 7 mutually distinct positive integers in the following ways: (1) $32=1+2+3+4+5+6+11$; (2) $32=1+2+3+4+5+7+10$; (3) $32=1+2+3+4+5+8+9$; (4) $32=1+2+3+4+6+7+9$; (5) $32=1+2+3+5+6+7+8$. The case (1) is eliminated because there is no rectangle with 22 cells on an $8 \times 8$ chessboard. In the other cases the partitions are realized as below.  Case (2)  Case (3)  Case (4)  Case (5)
|
7
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
11. II 5 (BUL 1) ${ }^{\mathrm{IMO} 4}$ Consider a partition of an $8 \times 8$ chessboard into $p$ rectangles whose interiors are disjoint such that each of them has an equal number of white and black cells. Assume that $a_{1}<a_{2}<\cdots<a_{p}$, where $a_{i}$ denotes the number of white cells in the $i$ th rectangle. Find the maximal $p$ for which such a partition is possible and for that $p$ determine all possible corresponding sequences $a_{1}, a_{2}, \ldots, a_{p}$.
|
11. First, we notice that $a_{1}+a_{2}+\cdots+a_{p}=32$. The numbers $a_{i}$ are distinct, and consequently $a_{i} \geq i$ and $a_{1}+\cdots+a_{p} \geq p(p+1) / 2$. Therefore $p \leq 7$. The number 32 can be represented as a sum of 7 mutually distinct positive integers in the following ways: (1) $32=1+2+3+4+5+6+11$; (2) $32=1+2+3+4+5+7+10$; (3) $32=1+2+3+4+5+8+9$; (4) $32=1+2+3+4+6+7+9$; (5) $32=1+2+3+5+6+7+8$. The case (1) is eliminated because there is no rectangle with 22 cells on an $8 \times 8$ chessboard. In the other cases the partitions are realized as below.  Case (2)  Case (3)  Case (4)  Case (5)
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
d4eb6473-1184-5c5a-b859-445a6e61f603
| 25,010
|
3. (USA) Find the integer represented by $\left[\sum_{n=1}^{10^{9}} n^{-2 / 3}\right]$. Here $[x]$ denotes the greatest integer less than or equal to $x$ (e.g. $[\sqrt{2}]=1$ ).
|
3. From $\left((k+1)^{2 / 3}+(k+1)^{1 / 3} k^{1 / 3}+k^{2 / 3}\right)\left((k+1)^{1 / 3}-k^{1 / 3}\right)=1$ and $3 k^{2 / 3}<(k+1)^{2 / 3}+(k+1)^{1 / 3} k^{1 / 3}+k^{2 / 3}<3(k+1)^{2 / 3}$ we obtain $$ 3\left((k+1)^{1 / 3}-k^{1 / 3}\right)<k^{-2 / 3}<3\left(k^{1 / 3}-(k-1)^{1 / 3}\right) . $$ Summing from 1 to $n$ we get $$ 1+3\left((n+1)^{1 / 3}-2^{1 / 3}\right)<\sum_{k=1}^{n} k^{-2 / 3}<1+3\left(n^{1 / 3}-1\right) $$ In particular, for $n=10^{9}$ this inequality gives $$ 2997<1+3\left(\left(10^{9}+1\right)^{1 / 3}-2^{1 / 3}\right)<\sum_{k=1}^{10^{9}} k^{-2 / 3}<2998 $$ Therefore $\left[\sum_{k=1}^{10^{9}} k^{-2 / 3}\right]=2997$.
|
2997
|
Yes
|
Yes
|
math-word-problem
|
Calculus
|
3. (USA) Find the integer represented by $\left[\sum_{n=1}^{10^{9}} n^{-2 / 3}\right]$. Here $[x]$ denotes the greatest integer less than or equal to $x$ (e.g. $[\sqrt{2}]=1$ ).
|
3. From $\left((k+1)^{2 / 3}+(k+1)^{1 / 3} k^{1 / 3}+k^{2 / 3}\right)\left((k+1)^{1 / 3}-k^{1 / 3}\right)=1$ and $3 k^{2 / 3}<(k+1)^{2 / 3}+(k+1)^{1 / 3} k^{1 / 3}+k^{2 / 3}<3(k+1)^{2 / 3}$ we obtain $$ 3\left((k+1)^{1 / 3}-k^{1 / 3}\right)<k^{-2 / 3}<3\left(k^{1 / 3}-(k-1)^{1 / 3}\right) . $$ Summing from 1 to $n$ we get $$ 1+3\left((n+1)^{1 / 3}-2^{1 / 3}\right)<\sum_{k=1}^{n} k^{-2 / 3}<1+3\left(n^{1 / 3}-1\right) $$ In particular, for $n=10^{9}$ this inequality gives $$ 2997<1+3\left(\left(10^{9}+1\right)^{1 / 3}-2^{1 / 3}\right)<\sum_{k=1}^{10^{9}} k^{-2 / 3}<2998 $$ Therefore $\left[\sum_{k=1}^{10^{9}} k^{-2 / 3}\right]=2997$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
18b5dba1-c3ca-5e53-9c87-6212532b9b89
| 25,059
|
6. (USS) ${ }^{\mathrm{IMO} 04}$ Let $A$ be the sum of the digits of the number $16^{16}$ and $B$ the sum of the digits of the number $A$. Find the sum of the digits of the number $B$ without calculating $16^{16}$.
|
6. Let us denote by $C$ the sum of digits of $B$. We know that $16^{16} \equiv A \equiv$ $B \equiv C(\bmod 9)$. Since $16^{16}=2^{64}=2^{6 \cdot 10+4} \equiv 2^{4} \equiv 7$, we get $C \equiv 7(\bmod$ 9). Moreover, $16^{16}<100^{16}=10^{32}$, hence $A$ cannot exceed $9 \cdot 32=288$; consequently, $B$ cannot exceed 19 and $C$ is at most 10 . Therefore $C=7$.
|
7
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
6. (USS) ${ }^{\mathrm{IMO} 04}$ Let $A$ be the sum of the digits of the number $16^{16}$ and $B$ the sum of the digits of the number $A$. Find the sum of the digits of the number $B$ without calculating $16^{16}$.
|
6. Let us denote by $C$ the sum of digits of $B$. We know that $16^{16} \equiv A \equiv$ $B \equiv C(\bmod 9)$. Since $16^{16}=2^{64}=2^{6 \cdot 10+4} \equiv 2^{4} \equiv 7$, we get $C \equiv 7(\bmod$ 9). Moreover, $16^{16}<100^{16}=10^{32}$, hence $A$ cannot exceed $9 \cdot 32=288$; consequently, $B$ cannot exceed 19 and $C$ is at most 10 . Therefore $C=7$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
1e7eedf0-c19b-58d3-b478-45855c1bcbf3
| 25,068
|
10. (USA 6) ${ }^{\mathrm{IMO}}$ Find the largest number obtainable as the product of positive integers whose sum is 1976.
|
10. Let $a_{1}<a_{2}<\cdots<a_{n}$ be positive integers whose sum is 1976 . Let $M$ denote the maximal value of $a_{1} a_{2} \cdots a_{n}$. We make the following observations: (1) $a_{1}=1$ does not yield the maximum, since replacing $1, a_{2}$ by $1+a_{2}$ increases the product. (2) $a_{j}-a_{i} \geq 2$ does not yield the maximal value, since replacing $a_{i}, a_{j}$ by $a_{i}+1, a_{j}-1$ increases the product. (3) $a_{i} \geq 5$ does not yield the maximal value, since $2\left(a_{i}-2\right)=2 a_{i}-4>a_{i}$. Since $4=2^{2}$, we may assume that all $a_{i}$ are either 2 or 3 , and $M=2^{k} 3^{l}$, where $2 k+3 l=1976$. (4) $k \geq 3$ does not yield the maximal value, since $2 \cdot 2 \cdot 2<3 \cdot 3$. Hence $k \leq 2$ and $2 k \equiv 1976(\bmod 3)$ gives us $k=1, l=658$ and $M=2 \cdot 3^{658}$.
|
2 \cdot 3^{658}
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
10. (USA 6) ${ }^{\mathrm{IMO}}$ Find the largest number obtainable as the product of positive integers whose sum is 1976.
|
10. Let $a_{1}<a_{2}<\cdots<a_{n}$ be positive integers whose sum is 1976 . Let $M$ denote the maximal value of $a_{1} a_{2} \cdots a_{n}$. We make the following observations: (1) $a_{1}=1$ does not yield the maximum, since replacing $1, a_{2}$ by $1+a_{2}$ increases the product. (2) $a_{j}-a_{i} \geq 2$ does not yield the maximal value, since replacing $a_{i}, a_{j}$ by $a_{i}+1, a_{j}-1$ increases the product. (3) $a_{i} \geq 5$ does not yield the maximal value, since $2\left(a_{i}-2\right)=2 a_{i}-4>a_{i}$. Since $4=2^{2}$, we may assume that all $a_{i}$ are either 2 or 3 , and $M=2^{k} 3^{l}$, where $2 k+3 l=1976$. (4) $k \geq 3$ does not yield the maximal value, since $2 \cdot 2 \cdot 2<3 \cdot 3$. Hence $k \leq 2$ and $2 k \equiv 1976(\bmod 3)$ gives us $k=1, l=658$ and $M=2 \cdot 3^{658}$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
a423233b-6faa-5d82-a42d-1bf75fcb3a7a
| 25,081
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.