problem
stringlengths 14
7.96k
| solution
stringlengths 3
10k
| answer
stringlengths 1
91
| problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | question_type
stringclasses 1
value | problem_type
stringclasses 8
values | problem_raw
stringlengths 14
7.96k
| solution_raw
stringlengths 3
10k
| metadata
dict | uuid
stringlengths 36
36
| id
int64 22.6k
612k
|
|---|---|---|---|---|---|---|---|---|---|---|---|
All the squares of a $2024 \times 2024$ board are coloured white. In one move, Mohit can select one row or column whose every square is white, choose exactly 1000 squares in this row or column, and colour all of them red. Find the maximum number of squares that Mohit can colour red in a finite number of moves.
|
Let $n=2024$ and $k=1000$. We claim that the maximum number of squares that can be coloured in this way is $k(2 n-k)$, which evaluates to 3048000 .
Indeed, call a row/column bad if it has at least one red square. After the first move, there are exactly $k+1$ bad rows and columns: if a row was picked, then that row and the $k$ columns corresponding to the chosen squares are all bad. Any subsequent move increases the number of bad rows/columns by at least 1 . Since there are only $2 n$ rows and columns, we can make at most $2 n-(k+1)$ moves after the first one, and so at most $2 n-k$ moves can be made in total. Thus we can have at most $k(2 n-k)$ red squares.
To prove this is achievable, let's choose each of the $n$ columns in the first $n$ moves, and colour the top $k$ cells in these columns. Then, the bottom $n-k$ rows are still uncoloured, so we can make $n-k$ more moves, colouring $k(n+n-k)$ cells in total.
|
3048000
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
All the squares of a $2024 \times 2024$ board are coloured white. In one move, Mohit can select one row or column whose every square is white, choose exactly 1000 squares in this row or column, and colour all of them red. Find the maximum number of squares that Mohit can colour red in a finite number of moves.
|
Let $n=2024$ and $k=1000$. We claim that the maximum number of squares that can be coloured in this way is $k(2 n-k)$, which evaluates to 3048000 .
Indeed, call a row/column bad if it has at least one red square. After the first move, there are exactly $k+1$ bad rows and columns: if a row was picked, then that row and the $k$ columns corresponding to the chosen squares are all bad. Any subsequent move increases the number of bad rows/columns by at least 1 . Since there are only $2 n$ rows and columns, we can make at most $2 n-(k+1)$ moves after the first one, and so at most $2 n-k$ moves can be made in total. Thus we can have at most $k(2 n-k)$ red squares.
To prove this is achievable, let's choose each of the $n$ columns in the first $n$ moves, and colour the top $k$ cells in these columns. Then, the bottom $n-k$ rows are still uncoloured, so we can make $n-k$ more moves, colouring $k(n+n-k)$ cells in total.
|
{
"resource_path": "INMO/segmented/en-INMO_2024_final_solutions.jsonl",
"problem_match": "\nProblem 2.",
"solution_match": "\nSolution."
}
|
76b55b7c-d06c-5556-9e24-7c48fbffd38a
| 607,873
|
There are four basket-ball players $A, B, C, D$. Initially, the ball is with $A$. The ball is always passed from one person to a different person. In how many ways can the ball come back to $A$ after seven passes? (For example $A \rightarrow C \rightarrow B \rightarrow D \rightarrow A \rightarrow B \rightarrow C \rightarrow A$ and
$A \rightarrow D \rightarrow A \rightarrow D \rightarrow C \rightarrow A \rightarrow B \rightarrow A$ are two ways in which the ball can come back to $A$ after seven passes.)
|
Let $x_{n}$ be the number of ways in which $A$ can get back the ball after $n$ passes. Let $y_{n}$ be the number of ways in which the ball goes back to a fixed person other than $A$ after $n$ passes. Then
$$
x_{n}=3 y_{n-1} \text {, }
$$
and
$$
y_{n}=x_{n-1}+2 y_{n-1}
$$
We also have $x_{1}=0, x_{2}=3, y_{1}=1$ and $y_{2}=2$.
Eliminating $y_{n}$ and $y_{n-1}$, we get $x_{n+1}=3 x_{n-1}+2 x_{n}$. Thus
$$
\begin{aligned}
& x_{3}=3 x_{1}+2 x_{2}=2 \times 3=6 \\
& x_{4}=3 x_{2}+2 x_{3}=(3 \times 3)+(2 \times 6)=9+12=21 \\
& x_{5}=3 x_{3}+2 x_{4}=(3 \times 6)+(2 \times 21)=18+42=60 \\
& x_{6}=3 x_{4}+2 x_{5}=(3 \times 21)+(2 \times 60)=63+120=183 \\
& x_{7}=3 x_{5}+2 x_{6}=(3 \times 60)+(2 \times 183)=180+366=546
\end{aligned}
$$
Alternate solution: Since the ball goes back to one of the other 3 persons, we have
$$
x_{n}+3 y_{n}=3^{n}
$$
since there are $3^{n}$ ways of passing the ball in $n$ passes. Using $x_{n}=$ $3 y_{n-1}$, we obtain
$$
x_{n-1}+x_{n}=3^{n-1}
$$
with $x_{1}=0$. Thus
$$
\begin{array}{r}
x_{7}=3^{6}-x_{6}=3^{6}-3^{5}+x_{5}=3^{6}-3^{5}+3^{4}-x_{4}=3^{6}-3^{5}+3^{4}-3^{3}+x_{3} \\
=3^{6}-3^{5}+3^{4}-3^{3}+3^{2}-x_{2}=3^{6}-3^{5}+3^{4}-3^{3}+3^{2}-3 \\
=\left(2 \times 3^{5}\right)+\left(2 \times 3^{3}\right)+(2 \times 3)=486+54+6=546
\end{array}
$$
|
546
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
There are four basket-ball players $A, B, C, D$. Initially, the ball is with $A$. The ball is always passed from one person to a different person. In how many ways can the ball come back to $A$ after seven passes? (For example $A \rightarrow C \rightarrow B \rightarrow D \rightarrow A \rightarrow B \rightarrow C \rightarrow A$ and
$A \rightarrow D \rightarrow A \rightarrow D \rightarrow C \rightarrow A \rightarrow B \rightarrow A$ are two ways in which the ball can come back to $A$ after seven passes.)
|
Let $x_{n}$ be the number of ways in which $A$ can get back the ball after $n$ passes. Let $y_{n}$ be the number of ways in which the ball goes back to a fixed person other than $A$ after $n$ passes. Then
$$
x_{n}=3 y_{n-1} \text {, }
$$
and
$$
y_{n}=x_{n-1}+2 y_{n-1}
$$
We also have $x_{1}=0, x_{2}=3, y_{1}=1$ and $y_{2}=2$.
Eliminating $y_{n}$ and $y_{n-1}$, we get $x_{n+1}=3 x_{n-1}+2 x_{n}$. Thus
$$
\begin{aligned}
& x_{3}=3 x_{1}+2 x_{2}=2 \times 3=6 \\
& x_{4}=3 x_{2}+2 x_{3}=(3 \times 3)+(2 \times 6)=9+12=21 \\
& x_{5}=3 x_{3}+2 x_{4}=(3 \times 6)+(2 \times 21)=18+42=60 \\
& x_{6}=3 x_{4}+2 x_{5}=(3 \times 21)+(2 \times 60)=63+120=183 \\
& x_{7}=3 x_{5}+2 x_{6}=(3 \times 60)+(2 \times 183)=180+366=546
\end{aligned}
$$
Alternate solution: Since the ball goes back to one of the other 3 persons, we have
$$
x_{n}+3 y_{n}=3^{n}
$$
since there are $3^{n}$ ways of passing the ball in $n$ passes. Using $x_{n}=$ $3 y_{n-1}$, we obtain
$$
x_{n-1}+x_{n}=3^{n-1}
$$
with $x_{1}=0$. Thus
$$
\begin{array}{r}
x_{7}=3^{6}-x_{6}=3^{6}-3^{5}+x_{5}=3^{6}-3^{5}+3^{4}-x_{4}=3^{6}-3^{5}+3^{4}-3^{3}+x_{3} \\
=3^{6}-3^{5}+3^{4}-3^{3}+3^{2}-x_{2}=3^{6}-3^{5}+3^{4}-3^{3}+3^{2}-3 \\
=\left(2 \times 3^{5}\right)+\left(2 \times 3^{3}\right)+(2 \times 3)=486+54+6=546
\end{array}
$$
|
{
"resource_path": "INMO/segmented/en-inmosol-15.jsonl",
"problem_match": "\n4.",
"solution_match": "\nSolution:"
}
|
e5360540-52f5-5320-bad2-e8c0ac460da2
| 607,899
|
Let $X=\{0,1,2,3,4,5,6,7,8,9\}$. Let $S \subseteq X$ be such that any nonnegative integer $n$ can be written as $p+q$ where the nonnegative integers $p, q$ have all their digits in $S$. Find the smallest possible number of elements in $S$.
|
We show that 5 numbers will suffice. Take $S=\{0,1,3,4,6\}$. Observe the following splitting:
| $n$ | $a$ | $b$ |
| :--- | :--- | :--- |
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 2 | 1 | 1 |
| 3 | 0 | 3 |
| 4 | 1 | 3 |
| 5 | 1 | 4 |
| 6 | 3 | 3 |
| 7 | 3 | 4 |
| 8 | 4 | 4 |
| 9 | 3 | 6 |
Thus each digit in a given nonnegative integer is split according to the above and can be written as a sum of two numbers each having digits in $S$.
We show that $|S|>4$. Suppose $|S| \leq 4$. We may take $|S|=4$ as adding extra numbers to $S$ does not alter our argument. Let $S=\{a, b, c, d\}$. Since the last digit can be any one of the numbers $0,1,2, \ldots, 9$, we must be able to write this as a sum of digits from $S$, modulo 10. Thus the collection
$$
A=\{x+y \quad(\bmod 10) \mid x, y \in S\}
$$
must contain $\{0,1,2, \ldots, 9\}$ as a subset. But $A$ has at most 10 elements $\left(\binom{4}{2}+4\right)$. Thus each element of the form $x+y(\bmod 10)$, as $x, y$ vary over $S$, must give different numbers from $\{0,1,2, \ldots, 9\}$.
Consider $a+a, b+b, c+c, d+d$ modulo 10. They must give 4 even numbers. Hence the remaining even number must be from the remaining 6 elements obtained by adding two distinct members of $S$. We may assume that even number is $a+b(\bmod 10)$. Then $a, b$ must have same parity. If any one of $c, d$ has same parity as that of $a$, then its sum with $a$ gives an even number, which is impossible. Hence $c, d$ must have same parity, in which case $c+d(\bmod 10)$ is even, which leads to a contradiction. We conclude that $|S| \geq 5$.
|
5
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Let $X=\{0,1,2,3,4,5,6,7,8,9\}$. Let $S \subseteq X$ be such that any nonnegative integer $n$ can be written as $p+q$ where the nonnegative integers $p, q$ have all their digits in $S$. Find the smallest possible number of elements in $S$.
|
We show that 5 numbers will suffice. Take $S=\{0,1,3,4,6\}$. Observe the following splitting:
| $n$ | $a$ | $b$ |
| :--- | :--- | :--- |
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 2 | 1 | 1 |
| 3 | 0 | 3 |
| 4 | 1 | 3 |
| 5 | 1 | 4 |
| 6 | 3 | 3 |
| 7 | 3 | 4 |
| 8 | 4 | 4 |
| 9 | 3 | 6 |
Thus each digit in a given nonnegative integer is split according to the above and can be written as a sum of two numbers each having digits in $S$.
We show that $|S|>4$. Suppose $|S| \leq 4$. We may take $|S|=4$ as adding extra numbers to $S$ does not alter our argument. Let $S=\{a, b, c, d\}$. Since the last digit can be any one of the numbers $0,1,2, \ldots, 9$, we must be able to write this as a sum of digits from $S$, modulo 10. Thus the collection
$$
A=\{x+y \quad(\bmod 10) \mid x, y \in S\}
$$
must contain $\{0,1,2, \ldots, 9\}$ as a subset. But $A$ has at most 10 elements $\left(\binom{4}{2}+4\right)$. Thus each element of the form $x+y(\bmod 10)$, as $x, y$ vary over $S$, must give different numbers from $\{0,1,2, \ldots, 9\}$.
Consider $a+a, b+b, c+c, d+d$ modulo 10. They must give 4 even numbers. Hence the remaining even number must be from the remaining 6 elements obtained by adding two distinct members of $S$. We may assume that even number is $a+b(\bmod 10)$. Then $a, b$ must have same parity. If any one of $c, d$ has same parity as that of $a$, then its sum with $a$ gives an even number, which is impossible. Hence $c, d$ must have same parity, in which case $c+d(\bmod 10)$ is even, which leads to a contradiction. We conclude that $|S| \geq 5$.
|
{
"resource_path": "INMO/segmented/en-sol-inmo-20.jsonl",
"problem_match": "\n3.",
"solution_match": "\nSolution:"
}
|
5b35f95a-e104-54a8-a6ed-6dbfbf25a349
| 607,904
|
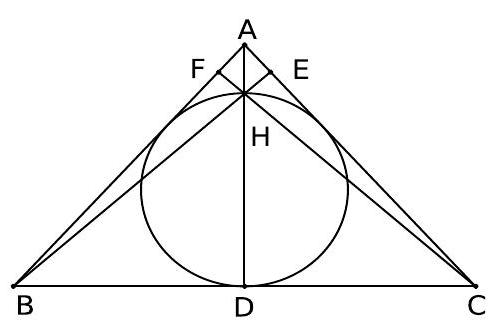
Let $A B C$ be triangle in which $A B=A C$. Suppose the orthocentre of the triangle lies on the in-circle. Find the ratio $A B / B C$.
|
Since the triangle is isosceles, the orthocentre lies on the perpendicular $A D$ from $A$ on to $B C$. Let it cut the in-circle at $H$. Now we are given that $H$ is the orthocentre of the triangle. Let $A B=A C=b$ and $B C=2 a$. Then $B D=a$. Observe that $b>a$ since $b$ is the hypotenuse and $a$ is a leg of a right-angled triangle. Let $B H$ meet $A C$ in $E$ and $C H$ meet $A B$ in $F$. By Pythagoras theorem applied to $\triangle B D H$, we get
$$
B H^{2}=H D^{2}+B D^{2}=4 r^{2}+a^{2}
$$
where $r$ is the in-radius of $A B C$. We want to compute $B H$ in another way. Since $A, F, H, E$ are con-cyclic, we have
$$
B H \cdot B E=B F \cdot B A
$$
But $B F \cdot B A=B D \cdot B C=2 a^{2}$, since $A, F, D, C$ are con-cyclic. Hence $B H^{2}=4 a^{4} / B E^{2}$. But
$$
B E^{2}=4 a^{2}-C E^{2}=4 a^{2}-B F^{2}=4 a^{2}-\left(\frac{2 a^{2}}{b}\right)^{2}=\frac{4 a^{2}\left(b^{2}-a^{2}\right)}{b^{2}}
$$
This leads to
$$
B H^{2}=\frac{a^{2} b^{2}}{b^{2}-a^{2}}
$$
Thus we get
$$
\frac{a^{2} b^{2}}{b^{2}-a^{2}}=a^{2}+4 r^{2}
$$
This simplifies to $\left(a^{4} /\left(b^{2}-a^{2}\right)\right)=4 r^{2}$. Now we relate $a, b, r$ in another way using area. We know that $[A B C]=r s$, where $s$ is the semi-perimeter of $A B C$. We have $s=(b+b+2 a) / 2=b+a$. On the other hand area can be calculated using Heron's formula::
$$
[A B C]^{2}=s(s-2 a)(s-b)(s-b)=(b+a)(b-a) a^{2}=a^{2}\left(b^{2}-a^{2}\right)
$$
Hence
$$
r^{2}=\frac{[A B C]^{2}}{s^{2}}=\frac{a^{2}\left(b^{2}-a^{2}\right)}{(b+a)^{2}}
$$
Using this we get
$$
\frac{a^{4}}{b^{2}-a^{2}}=4\left(\frac{a^{2}\left(b^{2}-a^{2}\right)}{(b+a)^{2}}\right)
$$
Therefore $a^{2}=4(b-a)^{2}$, which gives $a=2(b-a)$ or $2 b=3 a$. Finally,
$$
\frac{A B}{B C}=\frac{b}{2 a}=\frac{3}{4}
$$
## Alternate Solution 1:
We use the known facts $B H=2 R \cos B$ and $r=4 R \sin (A / 2) \sin (B / 2) \sin (C / 2)$, where $R$ is the circumradius of $\triangle A B C$ and $r$ its in-radius. Therefore
$$
H D=B H \sin \angle H B D=2 R \cos B \sin \left(\frac{\pi}{2}-C\right)=2 R \cos ^{2} B
$$
since $\angle C=\angle B$. But $\angle B=(\pi-\angle A) / 2$, since $A B C$ is isosceles. Thus we obtain
$$
H D=2 R \cos ^{2}\left(\frac{\pi}{2}-\frac{A}{2}\right)
$$
However $H D$ is also the diameter of the in circle. Therefore $H D=2 r$. Thus we get
$$
2 R \cos ^{2}\left(\frac{\pi}{2}-\frac{A}{2}\right)=2 r=8 R \sin (A / 2) \sin ^{2}((\pi-A) / 4)
$$
This reduces to
$$
\sin (A / 2)=2(1-\sin (A / 2))
$$
Therefore $\sin (A / 2)=2 / 3$. We also observe that $\sin (A / 2)=B D / A B$. Finally
$$
\frac{A B}{B C}=\frac{A B}{2 B D}=\frac{1}{2 \sin (A / 2)}=\frac{3}{4}
$$
## Alternate Solution 2:
Let $D$ be the mid-point of $B C$. Extend $A D$ to meet the circumcircle in $L$. Then we know that $H D=D L$. But $H D=2 r$. Thus $D L=2 r$. Therefore $I L=I D+D L=r+2 r=3 r$. We also know that $L B=L I$. Therefore $L B=3 r$. This gives
$$
\frac{B L}{L D}=\frac{3 r}{2 r}=\frac{3}{2}
$$
But $\triangle B L D$ is similar to $\triangle A B D$. So
$$
\frac{A B}{B D}=\frac{B L}{L D}=\frac{3}{2}
$$
Finally,
$$
\frac{A B}{B C}=\frac{A B}{2 B D}=\frac{3}{4}
$$
## Alternate Solution 3:
Let $D$ be the mid-point of $B C$ and $E$ be the mid-point of $D C$. Since $D I=I H(=r)$ and $D E=E C$, the mid-point theorem implies that $I E \| C H$. But $C H \perp A B$. Therefore $E I \perp A B$. Let $E I$ meet $A B$ in $F$. Then $F$ is the point of tangency of the incircle of $\triangle A B C$ with $A B$. Since the incircle is also tangent to $B C$ at $D$, we have $B F=B D$. Observe that $\triangle B F E$ is similar to $\triangle B D A$. Hence
$$
\frac{A B}{B D}=\frac{B E}{B F}=\frac{B E}{B D}=\frac{B D+D E}{B D}=1+\frac{D E}{B D}=\frac{3}{2}
$$
This gives
$$
\frac{A B}{B C}=\frac{3}{4}
$$
|
\frac{3}{4}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $A B C$ be triangle in which $A B=A C$. Suppose the orthocentre of the triangle lies on the in-circle. Find the ratio $A B / B C$.
|
Since the triangle is isosceles, the orthocentre lies on the perpendicular $A D$ from $A$ on to $B C$. Let it cut the in-circle at $H$. Now we are given that $H$ is the orthocentre of the triangle. Let $A B=A C=b$ and $B C=2 a$. Then $B D=a$. Observe that $b>a$ since $b$ is the hypotenuse and $a$ is a leg of a right-angled triangle. Let $B H$ meet $A C$ in $E$ and $C H$ meet $A B$ in $F$. By Pythagoras theorem applied to $\triangle B D H$, we get

$$
B H^{2}=H D^{2}+B D^{2}=4 r^{2}+a^{2}
$$
where $r$ is the in-radius of $A B C$. We want to compute $B H$ in another way. Since $A, F, H, E$ are con-cyclic, we have
$$
B H \cdot B E=B F \cdot B A
$$
But $B F \cdot B A=B D \cdot B C=2 a^{2}$, since $A, F, D, C$ are con-cyclic. Hence $B H^{2}=4 a^{4} / B E^{2}$. But
$$
B E^{2}=4 a^{2}-C E^{2}=4 a^{2}-B F^{2}=4 a^{2}-\left(\frac{2 a^{2}}{b}\right)^{2}=\frac{4 a^{2}\left(b^{2}-a^{2}\right)}{b^{2}}
$$
This leads to
$$
B H^{2}=\frac{a^{2} b^{2}}{b^{2}-a^{2}}
$$
Thus we get
$$
\frac{a^{2} b^{2}}{b^{2}-a^{2}}=a^{2}+4 r^{2}
$$
This simplifies to $\left(a^{4} /\left(b^{2}-a^{2}\right)\right)=4 r^{2}$. Now we relate $a, b, r$ in another way using area. We know that $[A B C]=r s$, where $s$ is the semi-perimeter of $A B C$. We have $s=(b+b+2 a) / 2=b+a$. On the other hand area can be calculated using Heron's formula::
$$
[A B C]^{2}=s(s-2 a)(s-b)(s-b)=(b+a)(b-a) a^{2}=a^{2}\left(b^{2}-a^{2}\right)
$$
Hence
$$
r^{2}=\frac{[A B C]^{2}}{s^{2}}=\frac{a^{2}\left(b^{2}-a^{2}\right)}{(b+a)^{2}}
$$
Using this we get
$$
\frac{a^{4}}{b^{2}-a^{2}}=4\left(\frac{a^{2}\left(b^{2}-a^{2}\right)}{(b+a)^{2}}\right)
$$
Therefore $a^{2}=4(b-a)^{2}$, which gives $a=2(b-a)$ or $2 b=3 a$. Finally,
$$
\frac{A B}{B C}=\frac{b}{2 a}=\frac{3}{4}
$$
## Alternate Solution 1:
We use the known facts $B H=2 R \cos B$ and $r=4 R \sin (A / 2) \sin (B / 2) \sin (C / 2)$, where $R$ is the circumradius of $\triangle A B C$ and $r$ its in-radius. Therefore
$$
H D=B H \sin \angle H B D=2 R \cos B \sin \left(\frac{\pi}{2}-C\right)=2 R \cos ^{2} B
$$
since $\angle C=\angle B$. But $\angle B=(\pi-\angle A) / 2$, since $A B C$ is isosceles. Thus we obtain
$$
H D=2 R \cos ^{2}\left(\frac{\pi}{2}-\frac{A}{2}\right)
$$
However $H D$ is also the diameter of the in circle. Therefore $H D=2 r$. Thus we get
$$
2 R \cos ^{2}\left(\frac{\pi}{2}-\frac{A}{2}\right)=2 r=8 R \sin (A / 2) \sin ^{2}((\pi-A) / 4)
$$
This reduces to
$$
\sin (A / 2)=2(1-\sin (A / 2))
$$
Therefore $\sin (A / 2)=2 / 3$. We also observe that $\sin (A / 2)=B D / A B$. Finally
$$
\frac{A B}{B C}=\frac{A B}{2 B D}=\frac{1}{2 \sin (A / 2)}=\frac{3}{4}
$$
## Alternate Solution 2:
Let $D$ be the mid-point of $B C$. Extend $A D$ to meet the circumcircle in $L$. Then we know that $H D=D L$. But $H D=2 r$. Thus $D L=2 r$. Therefore $I L=I D+D L=r+2 r=3 r$. We also know that $L B=L I$. Therefore $L B=3 r$. This gives
$$
\frac{B L}{L D}=\frac{3 r}{2 r}=\frac{3}{2}
$$
But $\triangle B L D$ is similar to $\triangle A B D$. So
$$
\frac{A B}{B D}=\frac{B L}{L D}=\frac{3}{2}
$$
Finally,
$$
\frac{A B}{B C}=\frac{A B}{2 B D}=\frac{3}{4}
$$
## Alternate Solution 3:
Let $D$ be the mid-point of $B C$ and $E$ be the mid-point of $D C$. Since $D I=I H(=r)$ and $D E=E C$, the mid-point theorem implies that $I E \| C H$. But $C H \perp A B$. Therefore $E I \perp A B$. Let $E I$ meet $A B$ in $F$. Then $F$ is the point of tangency of the incircle of $\triangle A B C$ with $A B$. Since the incircle is also tangent to $B C$ at $D$, we have $B F=B D$. Observe that $\triangle B F E$ is similar to $\triangle B D A$. Hence
$$
\frac{A B}{B D}=\frac{B E}{B F}=\frac{B E}{B D}=\frac{B D+D E}{B D}=1+\frac{D E}{B D}=\frac{3}{2}
$$
This gives
$$
\frac{A B}{B C}=\frac{3}{4}
$$
|
{
"resource_path": "INMO/segmented/en-sol-inmo16.jsonl",
"problem_match": "\n1.",
"solution_match": "\nSolution:"
}
|
1dae100a-b4dc-5363-adfa-08d97515f883
| 607,908
|
Find the number of triples $(x, a, b)$ where $x$ is a real number and $a, b$ belong to the set $\{1,2,3,4,5,6,7,8,9\}$ such that
$$
x^{2}-a\{x\}+b=0
$$
where $\{x\}$ denotes the fractional part of the real number $x$. (For example $\{1.1\}=0.1=$ $\{-0.9\}$.
|
Let us write $x=n+f$ where $n=[x]$ and $f=\{x\}$. Then
$$
f^{2}+(2 n-a) f+n^{2}+b=0
$$
Observe that the product of the roots of (1) is $n^{2}+b \geq 1$. If this equation has to have a solution $0 \leq f<1$, the larger root of (1) is greater 1 . We conclude that the equation (1) has a real root less than 1 only if $P(1)<0$ where $P(y)=y^{2}+(2 n-a) y+n^{2}+2 b$. This gives
$$
1+2 n-a+n^{2}+2 b<0
$$
Therefore we have $(n+1)^{2}+b<a$. If $n \geq 2$, then $(n+1)^{2}+b \geq 10>a$. Hence $n \leq 1$. If $n \leq-4$, then again $(n+1)^{2}+b \geq 10>a$. Thus we have the range for $n:-3,-2,-1,0,1$. If $n=-3$ or $n=1$, we have $(n+1)^{2}=4$. Thus we must have $4+b<a$. If $a=9$, we must have $b=4,3,2,1$ giving 4 values. For $a=8$, we must have $b=3,2,1$ giving 3 values. Similarly, for $a=7$ we get 2 values of $b$ and $a=6$ leads to 1 value of $b$. In each case we get a real value of $f<1$ and this leads to a solution for $x$. Thus we get totally $2(4+3+2+1)=20$ values of the triple $(x, a, b)$.
For $n=-2$ and $n=0$, we have $(n+1)^{2}=1$. Hence we require $1+b<a$. We again count pairs $(a, b)$ such that $a-b>1$. For $a=9$, we get 7 values of $b$; for $a=8$ we get 6 values of $b$ and so on. Thus we get $2(7+6+5+4+3+2+1)=56$ values for the triple $(x, a, b)$.
Suppose $n=-1$ so that $(n+1)^{2}=0$. In this case we require $b<a$. We get $8+7+6+5+$ $4+3+2+1=36$ values for the triple $(x, a, b)$.
Thus the total number of triples $(x, a, b)$ is $20+56+36=112$.
|
112
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Find the number of triples $(x, a, b)$ where $x$ is a real number and $a, b$ belong to the set $\{1,2,3,4,5,6,7,8,9\}$ such that
$$
x^{2}-a\{x\}+b=0
$$
where $\{x\}$ denotes the fractional part of the real number $x$. (For example $\{1.1\}=0.1=$ $\{-0.9\}$.
|
Let us write $x=n+f$ where $n=[x]$ and $f=\{x\}$. Then
$$
f^{2}+(2 n-a) f+n^{2}+b=0
$$
Observe that the product of the roots of (1) is $n^{2}+b \geq 1$. If this equation has to have a solution $0 \leq f<1$, the larger root of (1) is greater 1 . We conclude that the equation (1) has a real root less than 1 only if $P(1)<0$ where $P(y)=y^{2}+(2 n-a) y+n^{2}+2 b$. This gives
$$
1+2 n-a+n^{2}+2 b<0
$$
Therefore we have $(n+1)^{2}+b<a$. If $n \geq 2$, then $(n+1)^{2}+b \geq 10>a$. Hence $n \leq 1$. If $n \leq-4$, then again $(n+1)^{2}+b \geq 10>a$. Thus we have the range for $n:-3,-2,-1,0,1$. If $n=-3$ or $n=1$, we have $(n+1)^{2}=4$. Thus we must have $4+b<a$. If $a=9$, we must have $b=4,3,2,1$ giving 4 values. For $a=8$, we must have $b=3,2,1$ giving 3 values. Similarly, for $a=7$ we get 2 values of $b$ and $a=6$ leads to 1 value of $b$. In each case we get a real value of $f<1$ and this leads to a solution for $x$. Thus we get totally $2(4+3+2+1)=20$ values of the triple $(x, a, b)$.
For $n=-2$ and $n=0$, we have $(n+1)^{2}=1$. Hence we require $1+b<a$. We again count pairs $(a, b)$ such that $a-b>1$. For $a=9$, we get 7 values of $b$; for $a=8$ we get 6 values of $b$ and so on. Thus we get $2(7+6+5+4+3+2+1)=56$ values for the triple $(x, a, b)$.
Suppose $n=-1$ so that $(n+1)^{2}=0$. In this case we require $b<a$. We get $8+7+6+5+$ $4+3+2+1=36$ values for the triple $(x, a, b)$.
Thus the total number of triples $(x, a, b)$ is $20+56+36=112$.
|
{
"resource_path": "INMO/segmented/en-sol-inmo_17.jsonl",
"problem_match": "\n3.",
"solution_match": "\nSolution:"
}
|
584c287f-af14-58ab-9d16-9b8690b56364
| 607,916
|
There are given 100 distinct positive integers. We call a pair of integers among them good if the ratio of its elements is either 2 or 3 . What is the maximum number $g$ of good pairs that these 100 numbers can form? (A same number can be used in several pairs.)
|
Like so often in Russian problems, numbers are used instead of generic symbols. Let us therefore denote $10=n>1,2=k>1,3=\ell>1$, with the extra condition both $k$ and $\ell$ aren't powers of a same number. Consider the digraph $G$ whose set of vertices $V(G)$ is made of $v=n^{2}$ distinct positive integers, and whose set of edges $E(G)$ is made by the pairs $(a, b) \in V(G) \times V(G)$ with $a \mid b$. For each positive integer $m$ consider now the (not induced) spanning subdigraph $G_{m}$ of $G$ (with $V\left(G_{m}\right)=V(G)$ and so $v_{m}=v=n^{2}$ vertices), and whose edges are the pairs $(a, b) \in G \times G$ with $b=m a$. Moreover, it is clear that $E\left(G_{m^{\prime}}\right) \cap E\left(G_{m^{\prime \prime}}\right)=\emptyset$ for $m^{\prime} \neq m^{\prime \prime}$ (since if $(a, b) \in E(G)$ then $(a, b) \in E\left(G_{b / a}\right)$ only), and also $\bigcup_{m \geq 1} E\left(G_{m}\right)=E(G)$ (but that is irrelevant). Since the good pairs are precisely the edges of $G_{k}$ and $G_{\ell}$ together, we need to maximize their number $g$.
A digraph $G_{m}$ is clearly a union of some $n_{m}$ disjoint (directed) paths $P_{m, i}$, with lengths $\lambda\left(P_{m, i}\right)=\lambda_{m, i}, 0 \leq \lambda_{m, i} \leq n^{2}-1$, such that $\sum_{i=1}^{n_{m}}\left(\lambda_{m, i}+1\right)=n^{2}$, and containing $e_{m}=\sum_{i=1}^{n_{m}} \lambda_{m, i}$ edges (zero-length paths, i.e. isolated vertices, are possible, allowed, and duly considered). The defect of the graph $G_{m}$ is taken to be $v-e_{m}=n_{m}$. We therefore need to maximize $g=e_{k}+e_{\ell}$, or equivalently, to minimize the defect $\delta=n_{k}+n_{\ell}$.
Using the model $V(G)=V_{x}=\left\{k^{i-1} \ell^{j-1} x \mid 1 \leq i, j \leq n\right\}$, we have $n_{k}=n_{\ell}=n$, therefore $\delta=2 n$, so $g=2 n(n-1)$. To prove value $2 n$ is a minimum for $\delta$ is almost obvious. We have $\lambda_{k, i} \leq n_{\ell}-1$ for all $1 \leq i \leq n_{k}$ (by the condition on $k$ and $\ell$, we have $\left|P_{k, i} \cap P_{\ell, j}\right| \leq 1$ for all $1 \leq i \leq n_{k}$ and $\left.1 \leq j \leq n_{\ell}\right),{ }^{2}$ so $n^{2}-n_{k}=e_{k}=\sum_{i=1}^{n_{k}} \lambda_{k, i} \leq \sum_{i=1}^{n_{k}}\left(n_{\ell}-1\right)=n_{k} n_{\ell}-n_{k}$, therefore $n^{2} \leq n_{k} n_{\ell}$, and so $\delta=n_{k}+n_{\ell} \geq 2 \sqrt{n_{k} n_{\ell}}=2 n$. Moreover, we see equality occurs if and only if $n_{k}=n_{\ell}=n$ and $\lambda_{k, i}=\lambda_{\ell, i}=n-1$ for all $1 \leq i \leq n$, thus only for the sets $V_{x}$ described above. Răspunsul este deci $g=180$.
Comentarii. Odată ce ideea vine, problema este aproape trivială, cu detaliile tehnice fiind aproape "forţate". Valorile particulare folosite aruncă doar un văl de umbră asupra situaţiei de fapt (mai ales ocultul $100=10^{2}$ )! Laticea de divizibilitate a celor $n^{2}$ numere este considerată în mod natural, şi conduce la facila numărătoare de mai sus.[^1]
## Second Day - Solutions
|
180
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
There are given 100 distinct positive integers. We call a pair of integers among them good if the ratio of its elements is either 2 or 3 . What is the maximum number $g$ of good pairs that these 100 numbers can form? (A same number can be used in several pairs.)
|
Like so often in Russian problems, numbers are used instead of generic symbols. Let us therefore denote $10=n>1,2=k>1,3=\ell>1$, with the extra condition both $k$ and $\ell$ aren't powers of a same number. Consider the digraph $G$ whose set of vertices $V(G)$ is made of $v=n^{2}$ distinct positive integers, and whose set of edges $E(G)$ is made by the pairs $(a, b) \in V(G) \times V(G)$ with $a \mid b$. For each positive integer $m$ consider now the (not induced) spanning subdigraph $G_{m}$ of $G$ (with $V\left(G_{m}\right)=V(G)$ and so $v_{m}=v=n^{2}$ vertices), and whose edges are the pairs $(a, b) \in G \times G$ with $b=m a$. Moreover, it is clear that $E\left(G_{m^{\prime}}\right) \cap E\left(G_{m^{\prime \prime}}\right)=\emptyset$ for $m^{\prime} \neq m^{\prime \prime}$ (since if $(a, b) \in E(G)$ then $(a, b) \in E\left(G_{b / a}\right)$ only), and also $\bigcup_{m \geq 1} E\left(G_{m}\right)=E(G)$ (but that is irrelevant). Since the good pairs are precisely the edges of $G_{k}$ and $G_{\ell}$ together, we need to maximize their number $g$.
A digraph $G_{m}$ is clearly a union of some $n_{m}$ disjoint (directed) paths $P_{m, i}$, with lengths $\lambda\left(P_{m, i}\right)=\lambda_{m, i}, 0 \leq \lambda_{m, i} \leq n^{2}-1$, such that $\sum_{i=1}^{n_{m}}\left(\lambda_{m, i}+1\right)=n^{2}$, and containing $e_{m}=\sum_{i=1}^{n_{m}} \lambda_{m, i}$ edges (zero-length paths, i.e. isolated vertices, are possible, allowed, and duly considered). The defect of the graph $G_{m}$ is taken to be $v-e_{m}=n_{m}$. We therefore need to maximize $g=e_{k}+e_{\ell}$, or equivalently, to minimize the defect $\delta=n_{k}+n_{\ell}$.
Using the model $V(G)=V_{x}=\left\{k^{i-1} \ell^{j-1} x \mid 1 \leq i, j \leq n\right\}$, we have $n_{k}=n_{\ell}=n$, therefore $\delta=2 n$, so $g=2 n(n-1)$. To prove value $2 n$ is a minimum for $\delta$ is almost obvious. We have $\lambda_{k, i} \leq n_{\ell}-1$ for all $1 \leq i \leq n_{k}$ (by the condition on $k$ and $\ell$, we have $\left|P_{k, i} \cap P_{\ell, j}\right| \leq 1$ for all $1 \leq i \leq n_{k}$ and $\left.1 \leq j \leq n_{\ell}\right),{ }^{2}$ so $n^{2}-n_{k}=e_{k}=\sum_{i=1}^{n_{k}} \lambda_{k, i} \leq \sum_{i=1}^{n_{k}}\left(n_{\ell}-1\right)=n_{k} n_{\ell}-n_{k}$, therefore $n^{2} \leq n_{k} n_{\ell}$, and so $\delta=n_{k}+n_{\ell} \geq 2 \sqrt{n_{k} n_{\ell}}=2 n$. Moreover, we see equality occurs if and only if $n_{k}=n_{\ell}=n$ and $\lambda_{k, i}=\lambda_{\ell, i}=n-1$ for all $1 \leq i \leq n$, thus only for the sets $V_{x}$ described above. Răspunsul este deci $g=180$.
Comentarii. Odată ce ideea vine, problema este aproape trivială, cu detaliile tehnice fiind aproape "forţate". Valorile particulare folosite aruncă doar un văl de umbră asupra situaţiei de fapt (mai ales ocultul $100=10^{2}$ )! Laticea de divizibilitate a celor $n^{2}$ numere este considerată în mod natural, şi conduce la facila numărătoare de mai sus.[^1]
## Second Day - Solutions
|
{
"resource_path": "IZho/segmented/en-2014_zhautykov_resenja_e.jsonl",
"problem_match": "\nProblem 3.",
"solution_match": "\nSolution."
}
|
cccb2214-f230-5016-bc1e-467d2a7603ec
| 604,188
|
Determine the maximum integer $n$ with the property that for each positive integer $k \leq \frac{n}{2}$ there exist two positive divisors of $n$ with difference $k$.
|
If there exists a positive integer $p \leq\lfloor n / 6\rfloor$ such that $p \nmid n$, then we have $\lfloor n / 2\rfloor>\lfloor n / 6\rfloor$, and taking $k=\lfloor n / 2\rfloor-p \geq 2$ and two positive divisors $d, d+k$ of $n$, we need $d+(\lfloor n / 2\rfloor-p)$ to divide $n$. But $d+(\lfloor n / 2\rfloor-p) \geq d+\lfloor n / 2\rfloor-\lfloor n / 6\rfloor>d+(n / 2-1)-n / 6 \geq n / 3$, so $d+(\lfloor n / 2\rfloor-p) \in\{n / 2, n\}$, the only possible divisors of $n$ larger than $n / 3$. However, $d+(\lfloor n / 2\rfloor-p)=n / 2$ yields $d=p$, absurd (since $d \mid n$ but $p \nmid n$ ), while $d+(\lfloor n / 2\rfloor-p)=n$ yields $d>n / 2$, thus $d=n$ (since $d \mid n$ ), forcing $p=\lfloor n / 2\rfloor>\lfloor n / 6\rfloor$, again absurd. Therefore all positive integers not larger than $\lfloor n / 6\rfloor$ must divide $n$.
Denote $u=\lfloor n / 6\rfloor$. Since $\operatorname{gcd}(u, u-1)=1$, it follows $u(u-1) \mid n$, so $u(u-1) \leq n=6(n / 6)<6(u+1)$, forcing $u \leq 7$. For $u \geq 4$ we need $\operatorname{lcm}[1,2,3,4]=12 \mid n$, and we can see that $n=24$ satisfies, and moreover is an acceptable value. For $n=36$ we get $u=6$, but $\operatorname{lcm}[1,2,3,4,5,6]=60 \nmid n$. And for $n \geq 48$ we have $u \geq 8$, not acceptable. Thus the answer is $n=24$.
We may in fact quite easily exhibit the full set $\{1,2,4,6,8,12,18,24\}$ of such positive integers $n$ (for $n=1$ the condition is vacuously fulfilled). The related question of which are the positive integers satisfying the above property for all $1 \leq k \leq n-1$ can also easily be answered; the full set is $\{1,2,4,6\}$.
Comentarii. O problemă extrem de drăguţă, şi nu tocmai simplă dacă ne străduim să evităm discutarea a prea multe cazuri. Analiza numerelor $n$ mici ne sugerează imediat că $n>1$ nu poate să fie impar (ceea ce este trivial), şi prin faptul că singurul $k$ defect pentru $n=36$ este $k=13$, ideea pentru soluţia dată mai sus. Oricum, o idee proaspătă, şi care se implementează elegant şi cu calcule minime.
|
24
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Determine the maximum integer $n$ with the property that for each positive integer $k \leq \frac{n}{2}$ there exist two positive divisors of $n$ with difference $k$.
|
If there exists a positive integer $p \leq\lfloor n / 6\rfloor$ such that $p \nmid n$, then we have $\lfloor n / 2\rfloor>\lfloor n / 6\rfloor$, and taking $k=\lfloor n / 2\rfloor-p \geq 2$ and two positive divisors $d, d+k$ of $n$, we need $d+(\lfloor n / 2\rfloor-p)$ to divide $n$. But $d+(\lfloor n / 2\rfloor-p) \geq d+\lfloor n / 2\rfloor-\lfloor n / 6\rfloor>d+(n / 2-1)-n / 6 \geq n / 3$, so $d+(\lfloor n / 2\rfloor-p) \in\{n / 2, n\}$, the only possible divisors of $n$ larger than $n / 3$. However, $d+(\lfloor n / 2\rfloor-p)=n / 2$ yields $d=p$, absurd (since $d \mid n$ but $p \nmid n$ ), while $d+(\lfloor n / 2\rfloor-p)=n$ yields $d>n / 2$, thus $d=n$ (since $d \mid n$ ), forcing $p=\lfloor n / 2\rfloor>\lfloor n / 6\rfloor$, again absurd. Therefore all positive integers not larger than $\lfloor n / 6\rfloor$ must divide $n$.
Denote $u=\lfloor n / 6\rfloor$. Since $\operatorname{gcd}(u, u-1)=1$, it follows $u(u-1) \mid n$, so $u(u-1) \leq n=6(n / 6)<6(u+1)$, forcing $u \leq 7$. For $u \geq 4$ we need $\operatorname{lcm}[1,2,3,4]=12 \mid n$, and we can see that $n=24$ satisfies, and moreover is an acceptable value. For $n=36$ we get $u=6$, but $\operatorname{lcm}[1,2,3,4,5,6]=60 \nmid n$. And for $n \geq 48$ we have $u \geq 8$, not acceptable. Thus the answer is $n=24$.
We may in fact quite easily exhibit the full set $\{1,2,4,6,8,12,18,24\}$ of such positive integers $n$ (for $n=1$ the condition is vacuously fulfilled). The related question of which are the positive integers satisfying the above property for all $1 \leq k \leq n-1$ can also easily be answered; the full set is $\{1,2,4,6\}$.
Comentarii. O problemă extrem de drăguţă, şi nu tocmai simplă dacă ne străduim să evităm discutarea a prea multe cazuri. Analiza numerelor $n$ mici ne sugerează imediat că $n>1$ nu poate să fie impar (ceea ce este trivial), şi prin faptul că singurul $k$ defect pentru $n=36$ este $k=13$, ideea pentru soluţia dată mai sus. Oricum, o idee proaspătă, şi care se implementează elegant şi cu calcule minime.
|
{
"resource_path": "IZho/segmented/en-2015_zhautykov_resenja_e.jsonl",
"problem_match": "\nProblem 4.",
"solution_match": "\nSolution."
}
|
30c53e84-0548-56fb-9f55-dfd98e1ec71a
| 604,297
|
The Crocodile thought of four unit squares of a $2018 \times 2018$ forming a rectangle with sides 1 and 4 . The Bear can choose any square formed by 9 unit squares and ask whether it contains at least one of the four Crocodile's squares. What minimum number of questions should he ask to be sure of at least one affirmative answer?
The answer is $\frac{673^{2}-1}{2}=226464$.
|
We call checked any square chosen by the Bear, and all its unit squares. The position of a unit square in the table can be defined by the numbers of its row and column, that is, the square $(x, y)$ is in the $x$-th row and $y$-th column.
First we prove that $\frac{673^{2}-1}{2}$ questions is enough even on a $2019 \times 2019$ table. Let us divide this table into $3 \times 3$ squares and apply chess colouring to these large squares so that the corners are white. Thet it is enough to check all the black $3 \times 3$ squares: no row or column contains four consecutive white squares.
To prove that we need so many questions, we select all the unit squares with coordinates $(3 m+1,3 n+1)$, where $0 \leqslant m, n \leqslant 672$. A $3 \times 3$ square obviously can not contain two selected unit squares. On the other hand, if two selected squares lie at distance 3 (i.e., one of them is $(x, y)$, and another is $(x, y+3)$ or $(x+3, y)$ ), the Bear must check at least one of these two squares (because if neither is checked, then so are the two unit squares between them, and the Crocodile can place his rectangle on the unchecked squares).
Thus it is enough to produce $\frac{673^{2}-1}{2}$ pairs of selected unit squares at distance 3 . One can take pairs $(6 k+1,3 n+1)$, $(6 k+4,3 n+1), 0 \leqslant k \leqslant 335,0 \leqslant n \leqslant 672$, and $(2017,6 n+1),(2017,6 n+4), 0 \leqslant n \leqslant 335$.
|
226464
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
The Crocodile thought of four unit squares of a $2018 \times 2018$ forming a rectangle with sides 1 and 4 . The Bear can choose any square formed by 9 unit squares and ask whether it contains at least one of the four Crocodile's squares. What minimum number of questions should he ask to be sure of at least one affirmative answer?
The answer is $\frac{673^{2}-1}{2}=226464$.
|
We call checked any square chosen by the Bear, and all its unit squares. The position of a unit square in the table can be defined by the numbers of its row and column, that is, the square $(x, y)$ is in the $x$-th row and $y$-th column.
First we prove that $\frac{673^{2}-1}{2}$ questions is enough even on a $2019 \times 2019$ table. Let us divide this table into $3 \times 3$ squares and apply chess colouring to these large squares so that the corners are white. Thet it is enough to check all the black $3 \times 3$ squares: no row or column contains four consecutive white squares.
To prove that we need so many questions, we select all the unit squares with coordinates $(3 m+1,3 n+1)$, where $0 \leqslant m, n \leqslant 672$. A $3 \times 3$ square obviously can not contain two selected unit squares. On the other hand, if two selected squares lie at distance 3 (i.e., one of them is $(x, y)$, and another is $(x, y+3)$ or $(x+3, y)$ ), the Bear must check at least one of these two squares (because if neither is checked, then so are the two unit squares between them, and the Crocodile can place his rectangle on the unchecked squares).
Thus it is enough to produce $\frac{673^{2}-1}{2}$ pairs of selected unit squares at distance 3 . One can take pairs $(6 k+1,3 n+1)$, $(6 k+4,3 n+1), 0 \leqslant k \leqslant 335,0 \leqslant n \leqslant 672$, and $(2017,6 n+1),(2017,6 n+4), 0 \leqslant n \leqslant 335$.
|
{
"resource_path": "IZho/segmented/en-2018_zhautykov_resenja_e.jsonl",
"problem_match": "\n4.",
"solution_match": "\nSolution."
}
|
70dc1bbb-4d68-55cb-a420-31a2790b116b
| 604,358
|
In a set of 20 elements there are $2 k+1$ different subsets of 7 elements such that each of these subsets intersects exactly $k$ other subsets. Find the maximum $k$ for which this is possible.
The answer is $k=2$.
|
Let $M$ be the set of residues mod20. An example is given by the sets $A_{i}=\{4 i+1,4 i+$ $2,4 i+3,4 i+4,4 i+5,4 i+6,4 i+7\} \subset M, i=0,1,2,3,4$.
Let $k \geq 2$. Obviously among any three 7-element subsets there are two intersecting subsets.
Let $A$ be any of the $2 k+1$ subsets. It intersects $k$ other subsets $B_{1}, \ldots, B_{k}$. The remaining subsets $C_{1}$, $\ldots, C_{k}$ do not intersect $A$ and are therefore pairwise intersecting. Since each $C_{i}$ intersects $k$ other subsets, it intersects exactly one $B_{j}$. This $B_{j}$ can not be the same for all $C_{i}$ because $B_{j}$ can not intersect $k+1$ subsets.
Thus there are two different $C_{i}$ intersecting different $B_{j}$; let $C_{1}$ intersect $B_{1}$ and $C_{2}$ intersect $B_{2}$. All the subsets that do not intersect $C_{1}$ must intersect each other; there is $A$ among them, therefore they are $A$ and all $B_{i}, i \neq 1$. Hence every $B_{j}$ and $B_{j}, i \neq 1, j \neq 1$, intersect. Applying the same argument to $C_{2}$ we see that any $B_{i}$ and $B_{j}, i \neq 2, j \neq 2$, intersect. We see that the family $A, B_{1}, \ldots, B_{k}$ contains only one pair, $B_{1}$ and $B_{2}$, of non-untersecting subsets, while $B_{1}$ intersects $C_{1}$ and $B_{2}$ intersects $C_{2}$. For each $i$ this list contains $k$ subsets intersecting $B_{i}$. It follows that no $C_{i}$ with $i>2$ intersects any $B_{j}$, that is, there are no such $C_{i}$, and $k \leq 2$.
|
2
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
In a set of 20 elements there are $2 k+1$ different subsets of 7 elements such that each of these subsets intersects exactly $k$ other subsets. Find the maximum $k$ for which this is possible.
The answer is $k=2$.
|
Let $M$ be the set of residues mod20. An example is given by the sets $A_{i}=\{4 i+1,4 i+$ $2,4 i+3,4 i+4,4 i+5,4 i+6,4 i+7\} \subset M, i=0,1,2,3,4$.
Let $k \geq 2$. Obviously among any three 7-element subsets there are two intersecting subsets.
Let $A$ be any of the $2 k+1$ subsets. It intersects $k$ other subsets $B_{1}, \ldots, B_{k}$. The remaining subsets $C_{1}$, $\ldots, C_{k}$ do not intersect $A$ and are therefore pairwise intersecting. Since each $C_{i}$ intersects $k$ other subsets, it intersects exactly one $B_{j}$. This $B_{j}$ can not be the same for all $C_{i}$ because $B_{j}$ can not intersect $k+1$ subsets.
Thus there are two different $C_{i}$ intersecting different $B_{j}$; let $C_{1}$ intersect $B_{1}$ and $C_{2}$ intersect $B_{2}$. All the subsets that do not intersect $C_{1}$ must intersect each other; there is $A$ among them, therefore they are $A$ and all $B_{i}, i \neq 1$. Hence every $B_{j}$ and $B_{j}, i \neq 1, j \neq 1$, intersect. Applying the same argument to $C_{2}$ we see that any $B_{i}$ and $B_{j}, i \neq 2, j \neq 2$, intersect. We see that the family $A, B_{1}, \ldots, B_{k}$ contains only one pair, $B_{1}$ and $B_{2}$, of non-untersecting subsets, while $B_{1}$ intersects $C_{1}$ and $B_{2}$ intersects $C_{2}$. For each $i$ this list contains $k$ subsets intersecting $B_{i}$. It follows that no $C_{i}$ with $i>2$ intersects any $B_{j}$, that is, there are no such $C_{i}$, and $k \leq 2$.
|
{
"resource_path": "IZho/segmented/en-2020_zhautykov_resenja_e.jsonl",
"problem_match": "\n2.",
"solution_match": "\nSolution."
}
|
38364def-1c4d-5c64-828c-3bb7af51fd1a
| 604,498
|
Some squares of a $n \times n$ table $(n>2)$ are black, the rest are white. In every white square we write the number of all the black squares having at least one common vertex with it. Find the maximum possible sum of all these numbers.
The answer is $3 n^{2}-5 n+2$.
|
The sum attains this value when all squares in even rows are black and the rest are white. It remains to prove that this is the maximum value.
The sum in question is the number of pairs of differently coloured squares sharing at least one vertex. There are two kinds of such pairs: sharing a side and sharing only one vertex. Let us count the number of these pairs in another way.
We start with zeroes in all the vertices. Then for each pair of the second kind we add 1 to the (only) common vertex of this pair, and for each pair of the first kind we add $\frac{1}{2}$ to each of the two common vertices of its squares. For each pair the sum of all the numbers increases by 1 , therefore in the end it is equal to the number of pairs.
Simple casework shows that
(i) 3 is written in an internal vertex if and only if this vertex belongs to two black squares sharing a side and two white squares sharing a side;
(ii) the numbers in all the other internal vertices do not exceed 2 ;
(iii) a border vertex is marked with $\frac{1}{2}$ if it belongs to two squares of different colours, and 0 otherwise; (iv) all the corners are marked with 0 .
Note: we have already proved that the sum in question does not exceed $3 \times(n-1)^{2}+\frac{1}{2}(4 n-4)=$ $=3 n^{2}-4 n+1$. This estimate is valuable in itself.
Now we prove that the numbers in all the vertices can not be maximum possible simultaneously. To be more precise we need some definitions.
Definition. The number in a vertex is maximum if the vertex is internal and the number is 3 , or the vertex is on the border and the number is $\frac{1}{2}$.
Definition. A path - is a sequence of vertices such that every two consecutive vertices are one square side away.
Lemma. In each colouring of the table every path that starts on a horizontal side, ends on a vertical side and does not pass through corners, contains a number which is not maximum.
Proof. Assume the contrary. Then if the colour of any square containing the initial vertex is chosen, the colours of all the other squares containing the vertices of the path is uniquely defined, and the number in the last vertex is 0 .
Now we can prove that the sum of the numbers in any colouring does not exceed the sum of all the maximum numbers minus quarter of the number of all border vertices (not including corners). Consider the squares $1 \times 1,2 \times 2, \ldots,(N-1) \times(N-1)$ with a vertex in the lower left corner of the table. The right side and the upper side of such square form a path satisfying the conditions of the Lemma. Similar set of $N-1$ paths is produced by the squares $1 \times 1,2 \times 2, \ldots,(N-1) \times(N-1)$ with a vertex in the upper right corner of the table. Each border vertex is covered by one of these $2 n-2$ paths, and each internal vertex by two.
In any colouring of the table each of these paths contains a number which is not maximum. If this number is on the border, it is smaller than the maximum by (at least) $\frac{1}{2}$ and does not belong to any other path. If this number is in an internal vertex, it belongs to two paths and is smaller than the maximum at least by 1. Thus the contribution of each path in the sum in question is less than the maximum possible at least by $\frac{1}{2}$, q.e.d.
An interesting question: is it possible to count all the colourings with maximum sum using this argument?
|
3 n^{2}-5 n+2
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Some squares of a $n \times n$ table $(n>2)$ are black, the rest are white. In every white square we write the number of all the black squares having at least one common vertex with it. Find the maximum possible sum of all these numbers.
The answer is $3 n^{2}-5 n+2$.
|
The sum attains this value when all squares in even rows are black and the rest are white. It remains to prove that this is the maximum value.
The sum in question is the number of pairs of differently coloured squares sharing at least one vertex. There are two kinds of such pairs: sharing a side and sharing only one vertex. Let us count the number of these pairs in another way.
We start with zeroes in all the vertices. Then for each pair of the second kind we add 1 to the (only) common vertex of this pair, and for each pair of the first kind we add $\frac{1}{2}$ to each of the two common vertices of its squares. For each pair the sum of all the numbers increases by 1 , therefore in the end it is equal to the number of pairs.
Simple casework shows that
(i) 3 is written in an internal vertex if and only if this vertex belongs to two black squares sharing a side and two white squares sharing a side;
(ii) the numbers in all the other internal vertices do not exceed 2 ;
(iii) a border vertex is marked with $\frac{1}{2}$ if it belongs to two squares of different colours, and 0 otherwise; (iv) all the corners are marked with 0 .
Note: we have already proved that the sum in question does not exceed $3 \times(n-1)^{2}+\frac{1}{2}(4 n-4)=$ $=3 n^{2}-4 n+1$. This estimate is valuable in itself.
Now we prove that the numbers in all the vertices can not be maximum possible simultaneously. To be more precise we need some definitions.
Definition. The number in a vertex is maximum if the vertex is internal and the number is 3 , or the vertex is on the border and the number is $\frac{1}{2}$.
Definition. A path - is a sequence of vertices such that every two consecutive vertices are one square side away.
Lemma. In each colouring of the table every path that starts on a horizontal side, ends on a vertical side and does not pass through corners, contains a number which is not maximum.
Proof. Assume the contrary. Then if the colour of any square containing the initial vertex is chosen, the colours of all the other squares containing the vertices of the path is uniquely defined, and the number in the last vertex is 0 .
Now we can prove that the sum of the numbers in any colouring does not exceed the sum of all the maximum numbers minus quarter of the number of all border vertices (not including corners). Consider the squares $1 \times 1,2 \times 2, \ldots,(N-1) \times(N-1)$ with a vertex in the lower left corner of the table. The right side and the upper side of such square form a path satisfying the conditions of the Lemma. Similar set of $N-1$ paths is produced by the squares $1 \times 1,2 \times 2, \ldots,(N-1) \times(N-1)$ with a vertex in the upper right corner of the table. Each border vertex is covered by one of these $2 n-2$ paths, and each internal vertex by two.
In any colouring of the table each of these paths contains a number which is not maximum. If this number is on the border, it is smaller than the maximum by (at least) $\frac{1}{2}$ and does not belong to any other path. If this number is in an internal vertex, it belongs to two paths and is smaller than the maximum at least by 1. Thus the contribution of each path in the sum in question is less than the maximum possible at least by $\frac{1}{2}$, q.e.d.
An interesting question: is it possible to count all the colourings with maximum sum using this argument?
|
{
"resource_path": "IZho/segmented/en-2020_zhautykov_resenja_e.jsonl",
"problem_match": "\n№6.",
"solution_match": "\nSolution."
}
|
942431d0-f2bf-5b08-a166-6a6897dae34c
| 604,549
|
On a party with 99 guests, hosts Ann and Bob play a game (the hosts are not regarded as guests). There are 99 chairs arranged in a circle; initially, all guests hang around those chairs. The hosts take turns alternately. By a turn, a host orders any standing guest to sit on an unoccupied chair $c$. If some chair adjacent to $c$ is already occupied, the same host orders one guest on such chair to stand up (if both chairs adjacent to $c$ are occupied, the host chooses exactly one of them). All orders are carried out immediately. Ann makes the first move; her goal is to fulfill, after some move of hers, that at least $k$ chairs are occupied. Determine the largest $k$ for which Ann can reach the goal, regardless of Bob's play.
Answer. $k=34$.
|
Preliminary notes. Let $F$ denote the number of occupied chairs at the current position in the game. Notice that, on any turn, $F$ does not decrease. Thus, we need to determine the maximal value of $F$ Ann can guarantee after an arbitrary move (either hers or her opponent's).
Say that the situation in the game is stable if every unoccupied chair is adjacent to an occupied one. In a stable situation, we have $F \geq 33$, since at most $3 F$ chairs are either occupied or adjacent to such. Moreover, the same argument shows that there is a unique (up to rotation) stable situation with $F=33$, in which exactly every third chair is occupied; call such stable situation bad.
If the situation after Bob's move is stable, then Bob can act so as to preserve the current value of $F$ indefinitely. Namely, if $A$ puts some guest on chair $a$, she must free some chair $b$ adjacent to $a$. Then Bob merely puts a guest on $b$ and frees $a$, returning to the same stable position.
On the other hand, if the situation after Bob's move is unstable, then Ann may increase $F$ in her turn by putting a guest on a chair having no adjacent occupied chairs.
Strategy for Ann, if $k \leq 34$. In short, Ann's strategy is to increase $F$ avoiding appearance of a bad situation after Bob's move (conversely, Ann creates a bad situation in her turn, if she can).
So, on each her turn, Ann takes an arbitrary turn increasing $F$ if there is no danger that Bob reaches a bad situation in the next turn (thus, Ann always avoids forcing any guest to stand up). The exceptional cases are listed below.
Case 1. After possible Ann's move (consisting in putting a guest on chair $a$ ), we have $F=32$, and Bob can reach a bad situation by putting a guest on some chair. This means that, after Ann's move, every third chair would be occupied, with one exception. But this means that, by her move, Ann could put a guest on a chair adjacent to $a$, avoiding the danger.
Case 2. After possible Ann's move (by putting a guest on chair $a$ ), we have $F=33$, and Bob can reach a stable situation by putting a guest on some chair $b$ and freeing an adjacent chair $c$. If $a=c$, then Ann could put her guest on $b$ to create a stable situation after her turn; that enforces Bob to break stability in his turn. Otherwise, as in the previous case, Ann could put a guest on some chair adjacent to $a$, still increasing the value of $F$, but with no danger of bad situation arising.
So, acting as described, Ann increases the value of $F$ on each turn of hers whenever $F \leq 33$. Thus, she reaches $F=34$ after some her turn.
Strategy for Bob, if $k \geq 35$. Split all chairs into 33 groups each consisting of three consecutive chairs, and number the groups by $1,2, \ldots, 33$ so that Ann's first turn uses a chair from group 1. In short, Bob's strategy is to ensure, after each his turn, that
$(*)$ In group 1, at most two chairs are occupied; in every other group, only the central chair may be occupied.
If $(*)$ is satisfied after Bob's turn, then $F \leq 34<k$; thus, property $(*)$ ensures that Bob will not lose. It remains to show that Bob can always preserve $(*)$. after any his turn. Clearly, he can do that oat the first turn.
Suppose first that Ann, in her turn, puts a guest on chair $a$ and frees an adjacent chair $b$, then Bob may revert her turn by putting a guest on chair $b$ and freeing chair $a$.
Suppose now that Ann just puts a guest on some chair $a$, and the chairs adjacent to $a$ are unoccupied. In particular, group 1 still contains at most two occupied chairs. If the obtained situation satisfies (*), then Bob just makes a turn by putting a guest into group 1 (preferably, on its central chair), and, possibly, removing another guest from that group. Otherwise, $a$ is a non-central chair in some group $i \geq 2$; in this case Bob puts a guest to the central chair in group $i$ and frees chair $a$.
So Bob indeed can always preserve (*).
|
34
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
On a party with 99 guests, hosts Ann and Bob play a game (the hosts are not regarded as guests). There are 99 chairs arranged in a circle; initially, all guests hang around those chairs. The hosts take turns alternately. By a turn, a host orders any standing guest to sit on an unoccupied chair $c$. If some chair adjacent to $c$ is already occupied, the same host orders one guest on such chair to stand up (if both chairs adjacent to $c$ are occupied, the host chooses exactly one of them). All orders are carried out immediately. Ann makes the first move; her goal is to fulfill, after some move of hers, that at least $k$ chairs are occupied. Determine the largest $k$ for which Ann can reach the goal, regardless of Bob's play.
Answer. $k=34$.
|
Preliminary notes. Let $F$ denote the number of occupied chairs at the current position in the game. Notice that, on any turn, $F$ does not decrease. Thus, we need to determine the maximal value of $F$ Ann can guarantee after an arbitrary move (either hers or her opponent's).
Say that the situation in the game is stable if every unoccupied chair is adjacent to an occupied one. In a stable situation, we have $F \geq 33$, since at most $3 F$ chairs are either occupied or adjacent to such. Moreover, the same argument shows that there is a unique (up to rotation) stable situation with $F=33$, in which exactly every third chair is occupied; call such stable situation bad.
If the situation after Bob's move is stable, then Bob can act so as to preserve the current value of $F$ indefinitely. Namely, if $A$ puts some guest on chair $a$, she must free some chair $b$ adjacent to $a$. Then Bob merely puts a guest on $b$ and frees $a$, returning to the same stable position.
On the other hand, if the situation after Bob's move is unstable, then Ann may increase $F$ in her turn by putting a guest on a chair having no adjacent occupied chairs.
Strategy for Ann, if $k \leq 34$. In short, Ann's strategy is to increase $F$ avoiding appearance of a bad situation after Bob's move (conversely, Ann creates a bad situation in her turn, if she can).
So, on each her turn, Ann takes an arbitrary turn increasing $F$ if there is no danger that Bob reaches a bad situation in the next turn (thus, Ann always avoids forcing any guest to stand up). The exceptional cases are listed below.
Case 1. After possible Ann's move (consisting in putting a guest on chair $a$ ), we have $F=32$, and Bob can reach a bad situation by putting a guest on some chair. This means that, after Ann's move, every third chair would be occupied, with one exception. But this means that, by her move, Ann could put a guest on a chair adjacent to $a$, avoiding the danger.
Case 2. After possible Ann's move (by putting a guest on chair $a$ ), we have $F=33$, and Bob can reach a stable situation by putting a guest on some chair $b$ and freeing an adjacent chair $c$. If $a=c$, then Ann could put her guest on $b$ to create a stable situation after her turn; that enforces Bob to break stability in his turn. Otherwise, as in the previous case, Ann could put a guest on some chair adjacent to $a$, still increasing the value of $F$, but with no danger of bad situation arising.
So, acting as described, Ann increases the value of $F$ on each turn of hers whenever $F \leq 33$. Thus, she reaches $F=34$ after some her turn.
Strategy for Bob, if $k \geq 35$. Split all chairs into 33 groups each consisting of three consecutive chairs, and number the groups by $1,2, \ldots, 33$ so that Ann's first turn uses a chair from group 1. In short, Bob's strategy is to ensure, after each his turn, that
$(*)$ In group 1, at most two chairs are occupied; in every other group, only the central chair may be occupied.
If $(*)$ is satisfied after Bob's turn, then $F \leq 34<k$; thus, property $(*)$ ensures that Bob will not lose. It remains to show that Bob can always preserve $(*)$. after any his turn. Clearly, he can do that oat the first turn.
Suppose first that Ann, in her turn, puts a guest on chair $a$ and frees an adjacent chair $b$, then Bob may revert her turn by putting a guest on chair $b$ and freeing chair $a$.
Suppose now that Ann just puts a guest on some chair $a$, and the chairs adjacent to $a$ are unoccupied. In particular, group 1 still contains at most two occupied chairs. If the obtained situation satisfies (*), then Bob just makes a turn by putting a guest into group 1 (preferably, on its central chair), and, possibly, removing another guest from that group. Otherwise, $a$ is a non-central chair in some group $i \geq 2$; in this case Bob puts a guest to the central chair in group $i$ and frees chair $a$.
So Bob indeed can always preserve (*).
|
{
"resource_path": "IZho/segmented/en-2021_zhautykov_resenja_e.jsonl",
"problem_match": "\n№5.",
"solution_match": "\nSolution."
}
|
e71b10cd-12d6-567c-81ec-37de86b7c2da
| 604,677
|
The function $\mathrm{f}(\mathrm{n})$ is defined on the positive integers and takes non-negative integer values. It satisfies (1) $f(m n)=f(m)+f(n),(2) f(n)=0$ if the last digit of $n$ is 3 , (3) $f(10)=0$. Find $\mathrm{f}(1985)$.
|
If $\mathrm{f}(\mathrm{mn})=0$, then $\mathrm{f}(\mathrm{m})+\mathrm{f}(\mathrm{n})=0($ by $(1))$. But $\mathrm{f}(\mathrm{m})$ and $\mathrm{f}(\mathrm{n})$ are non-negative, so $\mathrm{f}(\mathrm{m})=\mathrm{f}(\mathrm{n})=$ 0 . Thus $f(10)=0$ implies $f(5)=0$. Similarly $f(3573)=0$ by (2), so $f(397)=0$. Hence $f(1985)$ $=\mathrm{f}(5)+\mathrm{f}(397)=0$.
|
0
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
The function $\mathrm{f}(\mathrm{n})$ is defined on the positive integers and takes non-negative integer values. It satisfies (1) $f(m n)=f(m)+f(n),(2) f(n)=0$ if the last digit of $n$ is 3 , (3) $f(10)=0$. Find $\mathrm{f}(1985)$.
|
If $\mathrm{f}(\mathrm{mn})=0$, then $\mathrm{f}(\mathrm{m})+\mathrm{f}(\mathrm{n})=0($ by $(1))$. But $\mathrm{f}(\mathrm{m})$ and $\mathrm{f}(\mathrm{n})$ are non-negative, so $\mathrm{f}(\mathrm{m})=\mathrm{f}(\mathrm{n})=$ 0 . Thus $f(10)=0$ implies $f(5)=0$. Similarly $f(3573)=0$ by (2), so $f(397)=0$. Hence $f(1985)$ $=\mathrm{f}(5)+\mathrm{f}(397)=0$.
|
{
"resource_path": "IberoAmerican_MO/segmented/en-1985-2003-IberoamericanMO.jsonl",
"problem_match": "\n## Problem B2",
"solution_match": "\n## Solution"
}
|
f43a5baa-76cf-512b-8898-06634088185f
| 604,757
|
Find a number $\mathrm{N}$ with five digits, all different and none zero, which equals the sum of all distinct three digit numbers whose digits are all different and are all digits of $\mathrm{N}$.
|
Answer: 35964
There are $4.3=12$ numbers with a given digit of $n$ in the units place. Similarly, there are 12 with it in the tens place and 12 with it in the hundreds place. So the sum of the 3 digit numbers is $12.111(\mathrm{a}+\mathrm{b}+\mathrm{c}+\mathrm{d}+\mathrm{e})$, where $\mathrm{n}=\mathrm{abcde}$. So $8668 \mathrm{a}=332 \mathrm{~b}+1232 \mathrm{c}+1322 \mathrm{~d}+$ 1331e. We can easily see that $\mathrm{a}=1$ is too small and $\mathrm{a}=4$ is too big, so $\mathrm{a}=2$ or 3 . Obviously e must be even. 0 is too small, so $\mathrm{e}=2,4,6$ or 8 . Working mod 11 , we see that $0=2 \mathrm{~b}+2 \mathrm{~d}$, so $\mathrm{b}+\mathrm{d}=11$. Working $\bmod 7$, we see that $2 \mathrm{a}=3 \mathrm{~b}+6 \mathrm{~d}+\mathrm{e}$. Using the $\bmod 11$ result, $\mathrm{b}=2, \mathrm{~d}=$ 9 or $b=3, d=8$ or $b=4, d=7$ or $b=5, d=6$ or $b=6, d=5$ or $b=7, d=4$ or $b=8, d=3$ or $\mathrm{b}=9, \mathrm{~d}=2$. Putting each of these into the $\bmod 7$ result gives $2 \mathrm{a}-\mathrm{e}=4,1,5,2,6,3,0,4$ mod 7. So putting $\mathrm{a}=2$ and remembering that $\mathrm{e}$ must be $2,4,6,8$ and that all digits must be different gives a, b, d, e = 2,4, 7, 6 or 2, 7, 4, 8 or 2, 8, 3, 4 as the only possibilities. It is then straightforward but tiresome to check that none of these give a solution for $\mathrm{c}$. Similarly putting $\mathrm{a}=4$, gives $\mathrm{a}, \mathrm{b}, \mathrm{d}, \mathrm{e}=3,4,7,8$ or $3,5,6,4$ as the only possibilities. Checking, we find the solution above and no others.
|
35964
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Find a number $\mathrm{N}$ with five digits, all different and none zero, which equals the sum of all distinct three digit numbers whose digits are all different and are all digits of $\mathrm{N}$.
|
Answer: 35964
There are $4.3=12$ numbers with a given digit of $n$ in the units place. Similarly, there are 12 with it in the tens place and 12 with it in the hundreds place. So the sum of the 3 digit numbers is $12.111(\mathrm{a}+\mathrm{b}+\mathrm{c}+\mathrm{d}+\mathrm{e})$, where $\mathrm{n}=\mathrm{abcde}$. So $8668 \mathrm{a}=332 \mathrm{~b}+1232 \mathrm{c}+1322 \mathrm{~d}+$ 1331e. We can easily see that $\mathrm{a}=1$ is too small and $\mathrm{a}=4$ is too big, so $\mathrm{a}=2$ or 3 . Obviously e must be even. 0 is too small, so $\mathrm{e}=2,4,6$ or 8 . Working mod 11 , we see that $0=2 \mathrm{~b}+2 \mathrm{~d}$, so $\mathrm{b}+\mathrm{d}=11$. Working $\bmod 7$, we see that $2 \mathrm{a}=3 \mathrm{~b}+6 \mathrm{~d}+\mathrm{e}$. Using the $\bmod 11$ result, $\mathrm{b}=2, \mathrm{~d}=$ 9 or $b=3, d=8$ or $b=4, d=7$ or $b=5, d=6$ or $b=6, d=5$ or $b=7, d=4$ or $b=8, d=3$ or $\mathrm{b}=9, \mathrm{~d}=2$. Putting each of these into the $\bmod 7$ result gives $2 \mathrm{a}-\mathrm{e}=4,1,5,2,6,3,0,4$ mod 7. So putting $\mathrm{a}=2$ and remembering that $\mathrm{e}$ must be $2,4,6,8$ and that all digits must be different gives a, b, d, e = 2,4, 7, 6 or 2, 7, 4, 8 or 2, 8, 3, 4 as the only possibilities. It is then straightforward but tiresome to check that none of these give a solution for $\mathrm{c}$. Similarly putting $\mathrm{a}=4$, gives $\mathrm{a}, \mathrm{b}, \mathrm{d}, \mathrm{e}=3,4,7,8$ or $3,5,6,4$ as the only possibilities. Checking, we find the solution above and no others.
|
{
"resource_path": "IberoAmerican_MO/segmented/en-1985-2003-IberoamericanMO.jsonl",
"problem_match": "\n## Problem B1",
"solution_match": "\n## Solution"
}
|
af2e0667-9918-5e98-a691-1eb266db83ff
| 604,425
|
$a_{n}$ is the last digit of $1+2+\ldots+n$. Find $a_{1}+a_{2}+\ldots+a_{1992}$.
|
It is easy to compile the following table, from which we see that $\mathrm{a}_{\mathrm{n}}$ is periodic with period 20 , and indeed the sum for each decade (from 0 to 9 ) is 35 . Thus the sum for 1992 is $199.35+5+$ $6+8=6984$.
| $\mathrm{n}$ | | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- |
| 17 | 18 | 19 | 20 | | | | | | | | | | | | | | | |
| $a_{\mathrm{n}}$ | | 0 | 1 | 3 | 6 | 0 | 5 | 1 | 8 | 6 | 5 | 5 | 6 | 8 | 1 | 5 | 0 | 6 |
| 3 | 1 | 0 | 0 | | | | | | | | | | 6 | | 1 | 5 | | |
| sum | | 0 | 1 | 4 | 10 | 10 | 15 | 16 | 24 | 30 | 35 | 40 | 46 | 54 | 55 | 60 | 60 | 66 |
| 69 | 70 | 70 | 70 | | | | | | | | | | | | | | | |
|
6984
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
$a_{n}$ is the last digit of $1+2+\ldots+n$. Find $a_{1}+a_{2}+\ldots+a_{1992}$.
|
It is easy to compile the following table, from which we see that $\mathrm{a}_{\mathrm{n}}$ is periodic with period 20 , and indeed the sum for each decade (from 0 to 9 ) is 35 . Thus the sum for 1992 is $199.35+5+$ $6+8=6984$.
| $\mathrm{n}$ | | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- |
| 17 | 18 | 19 | 20 | | | | | | | | | | | | | | | |
| $a_{\mathrm{n}}$ | | 0 | 1 | 3 | 6 | 0 | 5 | 1 | 8 | 6 | 5 | 5 | 6 | 8 | 1 | 5 | 0 | 6 |
| 3 | 1 | 0 | 0 | | | | | | | | | | 6 | | 1 | 5 | | |
| sum | | 0 | 1 | 4 | 10 | 10 | 15 | 16 | 24 | 30 | 35 | 40 | 46 | 54 | 55 | 60 | 60 | 66 |
| 69 | 70 | 70 | 70 | | | | | | | | | | | | | | | |
|
{
"resource_path": "IberoAmerican_MO/segmented/en-1985-2003-IberoamericanMO.jsonl",
"problem_match": "\n## Problem A1",
"solution_match": "\n## Solution"
}
|
e0e71d23-0809-5691-91a4-f95fa638095a
| 604,464
|
Let $f(x)=a_{1} /\left(x+a_{1}\right)+a_{2} /\left(x+a_{2}\right)+\ldots+a_{n} /\left(x+a_{n}\right)$, where $a_{i}$ are unequal positive reals. Find the sum of the lengths of the intervals in which $f(x) \geq 1$.
Answer
$\sum a_{i}$
|
wlog $a_{1}>a_{2}>\ldots>a_{n}$. The graph of each $a_{i} /\left(x+a_{i}\right)$ is a rectangular hyberbola with asymptotes $x=-a_{i}$ and $y=0$. So it is not hard to see that the graph of $f(x)$ is made up of $n+1$ strictly decreasing parts. For $\mathrm{x}<-\mathrm{a}_{1}, \mathrm{f}(\mathrm{x})$ is negative. For $\mathrm{x} \square\left(-\mathrm{a}_{\mathrm{i}},-\mathrm{a}_{\mathrm{i}+1}\right), \mathrm{f}(\mathrm{x})$ decreases from $\infty$ to $-\infty$. Finally, for $\mathrm{x}>-\mathrm{a}_{\mathrm{n}}, \mathrm{f}(\mathrm{x})$ decreases from $\infty$ to 0 . Thus $\mathrm{f}(\mathrm{x})=1$ at $\mathrm{n}$ values $\mathrm{b}_{1}<\mathrm{b}_{2}<\ldots<\mathrm{b}_{\mathrm{n}}$, and $f(x) \geq 1$ on the $n$ intervals $\left(-a_{1}, b_{1}\right),\left(-a_{2}, b_{2}\right), \ldots,\left(-a_{n}, b_{n}\right)$. So the sum of the lengths of these intervals is $\sum\left(a_{i}+b_{i}\right)$. We show that $\sum b_{i}=0$.
Multiplying $f(x)=1$ by $\prod\left(x+a_{j}\right)$ we get a polynomial of degree $n$ :
$$
\Pi\left(x+a_{j}\right)-\sum_{i}\left(a_{i} \prod_{j \neq i}\left(x+a_{j}\right)\right)=0
$$
The coefficient of $x^{n}$ is 1 and the coefficient of $x^{n-1}$ is $\sum a_{j}-\sum a_{i}=0$. Hence the sum of the roots, which is $\sum b_{i}$, is zero.
|
\sum a_{i}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Let $f(x)=a_{1} /\left(x+a_{1}\right)+a_{2} /\left(x+a_{2}\right)+\ldots+a_{n} /\left(x+a_{n}\right)$, where $a_{i}$ are unequal positive reals. Find the sum of the lengths of the intervals in which $f(x) \geq 1$.
Answer
$\sum a_{i}$
|
wlog $a_{1}>a_{2}>\ldots>a_{n}$. The graph of each $a_{i} /\left(x+a_{i}\right)$ is a rectangular hyberbola with asymptotes $x=-a_{i}$ and $y=0$. So it is not hard to see that the graph of $f(x)$ is made up of $n+1$ strictly decreasing parts. For $\mathrm{x}<-\mathrm{a}_{1}, \mathrm{f}(\mathrm{x})$ is negative. For $\mathrm{x} \square\left(-\mathrm{a}_{\mathrm{i}},-\mathrm{a}_{\mathrm{i}+1}\right), \mathrm{f}(\mathrm{x})$ decreases from $\infty$ to $-\infty$. Finally, for $\mathrm{x}>-\mathrm{a}_{\mathrm{n}}, \mathrm{f}(\mathrm{x})$ decreases from $\infty$ to 0 . Thus $\mathrm{f}(\mathrm{x})=1$ at $\mathrm{n}$ values $\mathrm{b}_{1}<\mathrm{b}_{2}<\ldots<\mathrm{b}_{\mathrm{n}}$, and $f(x) \geq 1$ on the $n$ intervals $\left(-a_{1}, b_{1}\right),\left(-a_{2}, b_{2}\right), \ldots,\left(-a_{n}, b_{n}\right)$. So the sum of the lengths of these intervals is $\sum\left(a_{i}+b_{i}\right)$. We show that $\sum b_{i}=0$.
Multiplying $f(x)=1$ by $\prod\left(x+a_{j}\right)$ we get a polynomial of degree $n$ :
$$
\Pi\left(x+a_{j}\right)-\sum_{i}\left(a_{i} \prod_{j \neq i}\left(x+a_{j}\right)\right)=0
$$
The coefficient of $x^{n}$ is 1 and the coefficient of $x^{n-1}$ is $\sum a_{j}-\sum a_{i}=0$. Hence the sum of the roots, which is $\sum b_{i}$, is zero.
|
{
"resource_path": "IberoAmerican_MO/segmented/en-1985-2003-IberoamericanMO.jsonl",
"problem_match": "\n## Problem A2",
"solution_match": "\n## Solution"
}
|
7b623153-948f-527e-9be5-8b2fba21dcc8
| 604,476
|
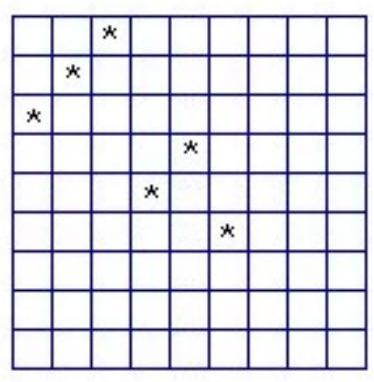
$\mathrm{ABCD}$ is an $\mathrm{n} \mathrm{x}$ board. We call a diagonal row of cells a positive diagonal if it is parallel to AC. How many coins must be placed on an $\mathrm{n} x \mathrm{n}$ board such that every cell either has a coin or is in the same row, column or positive diagonal as a coin?
## Answer
smallest integer $\geq(2 n-1) / 3$
[so $2 \mathrm{~m}-1$ for $\mathrm{n}=3 \mathrm{~m}-1,2 \mathrm{~m}$ for $\mathrm{n}=3 \mathrm{~m}, 2 \mathrm{~m}+1$ for $\mathrm{n}=3 \mathrm{~m}+1$ ]
|
There must be at least $\mathrm{n}-\mathrm{k}$ rows without a coin and at least $\mathrm{n}-\mathrm{k}$ columns without a coin. Let $\mathrm{r}_{1}$, $\mathrm{r}_{2}, \ldots, \mathrm{r}_{\mathrm{n}-\mathrm{k}}$ be cells in the top row without a coin which are also in a column without a coin. Let $\mathrm{r}_{1}, \mathrm{c}_{2}, \mathrm{c}_{3}, \ldots, \mathrm{c}_{\mathrm{n}-\mathrm{k}}$ be cells in the first column without a coin which are also in a row without a coin. Each of the $2 \mathrm{n}-2 \mathrm{k}-1 \mathrm{r}_{\mathrm{i}}$ and $\mathrm{c}_{\mathrm{j}}$ are on a different positive diagonal, so we must have $\mathrm{k} \geq$ $2 n-2 k-1$ and hence $k \geq(2 n-1) / 3$.
Let (i,j) denote the cell in row $\mathrm{i}$, col $\mathrm{j}$. For $\mathrm{n}=3 \mathrm{~m}-1$, put coins in (m,1), $(\mathrm{m}-1,2),(m-2,3), \ldots$, $(1, m)$ and in $(2 m-1, m+1),(2 m-2, m+2), \ldots,(m+1,2 m-1)$. It is easy to check that this works. For $\mathrm{n}=3 \mathrm{~m}$, put an additional coin in ( $2 \mathrm{~m}, 2 \mathrm{~m}$ ), it is easy to check that works. For $\mathrm{n}=3 \mathrm{~m}+1$ we can use the same arrangement as for $3 m+2$.
|
(2 n-1) / 3
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
$\mathrm{ABCD}$ is an $\mathrm{n} \mathrm{x}$ board. We call a diagonal row of cells a positive diagonal if it is parallel to AC. How many coins must be placed on an $\mathrm{n} x \mathrm{n}$ board such that every cell either has a coin or is in the same row, column or positive diagonal as a coin?
## Answer
smallest integer $\geq(2 n-1) / 3$
[so $2 \mathrm{~m}-1$ for $\mathrm{n}=3 \mathrm{~m}-1,2 \mathrm{~m}$ for $\mathrm{n}=3 \mathrm{~m}, 2 \mathrm{~m}+1$ for $\mathrm{n}=3 \mathrm{~m}+1$ ]
|
There must be at least $\mathrm{n}-\mathrm{k}$ rows without a coin and at least $\mathrm{n}-\mathrm{k}$ columns without a coin. Let $\mathrm{r}_{1}$, $\mathrm{r}_{2}, \ldots, \mathrm{r}_{\mathrm{n}-\mathrm{k}}$ be cells in the top row without a coin which are also in a column without a coin. Let $\mathrm{r}_{1}, \mathrm{c}_{2}, \mathrm{c}_{3}, \ldots, \mathrm{c}_{\mathrm{n}-\mathrm{k}}$ be cells in the first column without a coin which are also in a row without a coin. Each of the $2 \mathrm{n}-2 \mathrm{k}-1 \mathrm{r}_{\mathrm{i}}$ and $\mathrm{c}_{\mathrm{j}}$ are on a different positive diagonal, so we must have $\mathrm{k} \geq$ $2 n-2 k-1$ and hence $k \geq(2 n-1) / 3$.
Let (i,j) denote the cell in row $\mathrm{i}$, col $\mathrm{j}$. For $\mathrm{n}=3 \mathrm{~m}-1$, put coins in (m,1), $(\mathrm{m}-1,2),(m-2,3), \ldots$, $(1, m)$ and in $(2 m-1, m+1),(2 m-2, m+2), \ldots,(m+1,2 m-1)$. It is easy to check that this works. For $\mathrm{n}=3 \mathrm{~m}$, put an additional coin in ( $2 \mathrm{~m}, 2 \mathrm{~m}$ ), it is easy to check that works. For $\mathrm{n}=3 \mathrm{~m}+1$ we can use the same arrangement as for $3 m+2$.

|
{
"resource_path": "IberoAmerican_MO/segmented/en-1985-2003-IberoamericanMO.jsonl",
"problem_match": "\n## Problem B1",
"solution_match": "\n## Solution"
}
|
5bd22e5b-473b-5ee7-ad38-c7949e05ed2a
| 604,679
|
Find the smallest positive integer $\mathrm{n}$ so that a cube with side $\mathrm{n}$ can be divided into 1996 cubes each with side a positive integer.
|
Answer: 13.
Divide all the cubes into unit cubes. Then the 1996 cubes must each contain at least one unit cube, so the large cube contains at least 1996 unit cubes. But $12^{3}=1728<1996<2197=13^{3}$, so it is certainly not possible for $\mathrm{n}<13$.
It can be achieved with 13 by $1.5^{3}+11.2^{3}+1984.1^{3}=13^{3}$ (actually packing the cubes together to form a $13 \times 13 \times 13$ cube is trivial since there are so many unit cubes).
## Problem 2
$\mathrm{M}$ is the midpoint of the median $\mathrm{AD}$ of the triangle $\mathrm{ABC}$. The ray $\mathrm{BM}$ meets $\mathrm{AC}$ at $N$. Show that $\mathrm{AB}$ is tangent to the circumcircle of $\mathrm{NBC}$ iff $\mathrm{BM} / \mathrm{BN}=(\mathrm{BC} / \mathrm{BN})^{2}$.
|
13
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Find the smallest positive integer $\mathrm{n}$ so that a cube with side $\mathrm{n}$ can be divided into 1996 cubes each with side a positive integer.
|
Answer: 13.
Divide all the cubes into unit cubes. Then the 1996 cubes must each contain at least one unit cube, so the large cube contains at least 1996 unit cubes. But $12^{3}=1728<1996<2197=13^{3}$, so it is certainly not possible for $\mathrm{n}<13$.
It can be achieved with 13 by $1.5^{3}+11.2^{3}+1984.1^{3}=13^{3}$ (actually packing the cubes together to form a $13 \times 13 \times 13$ cube is trivial since there are so many unit cubes).
## Problem 2
$\mathrm{M}$ is the midpoint of the median $\mathrm{AD}$ of the triangle $\mathrm{ABC}$. The ray $\mathrm{BM}$ meets $\mathrm{AC}$ at $N$. Show that $\mathrm{AB}$ is tangent to the circumcircle of $\mathrm{NBC}$ iff $\mathrm{BM} / \mathrm{BN}=(\mathrm{BC} / \mathrm{BN})^{2}$.
|
{
"resource_path": "IberoAmerican_MO/segmented/en-1985-2003-IberoamericanMO.jsonl",
"problem_match": "\n## Problem A1",
"solution_match": "\n## Solution"
}
|
355a613d-8bb8-5ac8-bfc5-9134703a639a
| 604,704
|
Find the smallest number $\mathrm{n}$ such that given any $\mathrm{n}$ distinct numbers from $\{1,2,3, \ldots, 999\}$, one can choose four different numbers $\mathrm{a}, \mathrm{b}, \mathrm{c}, \mathrm{d}$ such that $\mathrm{a}+2 \mathrm{~b}+3 \mathrm{c}=\mathrm{d}$.
|
Answer: $\mathrm{n}=835$.
Consider the set $S=\{166,167, \ldots, 999\}$. The smallest possible value for $a+2 b+3 c$, for distinct $\mathrm{a}, \mathrm{b}, \mathrm{c}$ in $\mathrm{S}$ is $168+2.167+3.166=1000$. So we cannot find distinct $\mathrm{a}, \mathrm{b}, \mathrm{c}, \mathrm{d}$ in $\mathrm{S}$ with $a+2 b+3 c=d$. So the smallest $n>834$.
Now suppose $\mathrm{S}$ is any subset of 835 elements which satisfies the condition. Take it elements to be $\mathrm{m}=\mathrm{a}_{1}<\mathrm{a}_{2}<\ldots<\mathrm{a}_{835}=\mathrm{M}$. Obviously $\mathrm{M} \geq \mathrm{m}+834 \geq 835$, so $-3 \mathrm{~m} \geq 3.834-3 \mathrm{M}$ and hence $M-3 \mathrm{~m} \geq 2502-2 \mathrm{M} \geq 2502-2.999=504$. Put $\mathrm{k}=\mathrm{M}-3 \mathrm{~m}$.
There are at least 167 disjoint pairs (a,b) of numbers taken from $\{1,2, \ldots, 999\}$ with $a+2 b=$ $\mathrm{k}$, namely
```
(k- - 2, 1)
(k-4, 2)
```
```
```

```
(k-334, 167) - note that in the extreme case k = 504 this is (170, 167)
```
At least one number from each pair must either (1) be $\mathrm{M}$ or $\mathrm{m}$ or (2) not belong to $\mathrm{S}$ - or otherwise we would have $a+2 b+3 m=M$ for distinct elements $a, b, m$ and $M$ in $S$. None of the numbers can be $M$ and at most one of them can be $m$, so we have at least 166 numbers which are not in S. That means S contains at most $999-166=833$ numbers. Contradiction.
So $\mathrm{S}$ cannot have 835 elements. Nor can it have more than 835 elements (or we just take a subset of 835 elements, which must also satisfy the condition, and get a contradiction).
|
835
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Find the smallest number $\mathrm{n}$ such that given any $\mathrm{n}$ distinct numbers from $\{1,2,3, \ldots, 999\}$, one can choose four different numbers $\mathrm{a}, \mathrm{b}, \mathrm{c}, \mathrm{d}$ such that $\mathrm{a}+2 \mathrm{~b}+3 \mathrm{c}=\mathrm{d}$.
|
Answer: $\mathrm{n}=835$.
Consider the set $S=\{166,167, \ldots, 999\}$. The smallest possible value for $a+2 b+3 c$, for distinct $\mathrm{a}, \mathrm{b}, \mathrm{c}$ in $\mathrm{S}$ is $168+2.167+3.166=1000$. So we cannot find distinct $\mathrm{a}, \mathrm{b}, \mathrm{c}, \mathrm{d}$ in $\mathrm{S}$ with $a+2 b+3 c=d$. So the smallest $n>834$.
Now suppose $\mathrm{S}$ is any subset of 835 elements which satisfies the condition. Take it elements to be $\mathrm{m}=\mathrm{a}_{1}<\mathrm{a}_{2}<\ldots<\mathrm{a}_{835}=\mathrm{M}$. Obviously $\mathrm{M} \geq \mathrm{m}+834 \geq 835$, so $-3 \mathrm{~m} \geq 3.834-3 \mathrm{M}$ and hence $M-3 \mathrm{~m} \geq 2502-2 \mathrm{M} \geq 2502-2.999=504$. Put $\mathrm{k}=\mathrm{M}-3 \mathrm{~m}$.
There are at least 167 disjoint pairs (a,b) of numbers taken from $\{1,2, \ldots, 999\}$ with $a+2 b=$ $\mathrm{k}$, namely
```
(k- - 2, 1)
(k-4, 2)
```
```
```

```
(k-334, 167) - note that in the extreme case k = 504 this is (170, 167)
```
At least one number from each pair must either (1) be $\mathrm{M}$ or $\mathrm{m}$ or (2) not belong to $\mathrm{S}$ - or otherwise we would have $a+2 b+3 m=M$ for distinct elements $a, b, m$ and $M$ in $S$. None of the numbers can be $M$ and at most one of them can be $m$, so we have at least 166 numbers which are not in S. That means S contains at most $999-166=833$ numbers. Contradiction.
So $\mathrm{S}$ cannot have 835 elements. Nor can it have more than 835 elements (or we just take a subset of 835 elements, which must also satisfy the condition, and get a contradiction).
|
{
"resource_path": "IberoAmerican_MO/segmented/en-1985-2003-IberoamericanMO.jsonl",
"problem_match": "\n## Problem A3",
"solution_match": "\n## Solution"
}
|
c6e9d613-83ec-5249-b173-158411300f40
| 604,897
|
Representatives from $n>1$ different countries sit around a table. If two people are from the same country then their respective right hand neighbors are from different countries. Find the maximum number of people who can sit at the table for each $\mathrm{n}$.
|
Answer: $n^{2}$.
Obviously there cannot be more than $\mathrm{n}^{2}$ people. For if there were, then at least one country would have more than $n$ representatives. But there are only $n$ different countries to choose their right-hand neighbours from. Contradiction.
Represent someone from country i by i. Then for $\mathrm{n}=2$, the arrangement 1122 works. [It wraps round, so that the second 2 is adjacent to the first 1.] Suppose we have an arrangement for $\mathrm{n}$. Then each of $11,22, \ldots$, nn must occur just once in the arrangement. Replace 11 by $1(n+1) 11,22$ by $2(n+1) 22, \ldots$, and $(n-1)(n-1)$ by $(n-1)(n+1)(n-1)(n-1)$. Finally replace $n n$ by $\mathrm{n}(\mathrm{n}+1)(\mathrm{n}+1) \mathrm{nn}$. It is easy to check that we now have an arrangement for $\mathrm{n}+1$. We have added one additional representative for each of the countries 1 to $\mathrm{n}$ and $\mathrm{n}+1$ representatives for country $\mathrm{n}+1$, so we have indeed got $(\mathrm{n}+1)^{2}$ people in all. We have also given a representative of each country 1 to $n$ a neighbour from country $n+1$ on his right and we have given the ( $n+1$ ) representatives from country $n+1$ neighbours (on their right) from each of the other countries. Otherwise we have left the seating unchanged.
|
n^2
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Representatives from $n>1$ different countries sit around a table. If two people are from the same country then their respective right hand neighbors are from different countries. Find the maximum number of people who can sit at the table for each $\mathrm{n}$.
|
Answer: $n^{2}$.
Obviously there cannot be more than $\mathrm{n}^{2}$ people. For if there were, then at least one country would have more than $n$ representatives. But there are only $n$ different countries to choose their right-hand neighbours from. Contradiction.
Represent someone from country i by i. Then for $\mathrm{n}=2$, the arrangement 1122 works. [It wraps round, so that the second 2 is adjacent to the first 1.] Suppose we have an arrangement for $\mathrm{n}$. Then each of $11,22, \ldots$, nn must occur just once in the arrangement. Replace 11 by $1(n+1) 11,22$ by $2(n+1) 22, \ldots$, and $(n-1)(n-1)$ by $(n-1)(n+1)(n-1)(n-1)$. Finally replace $n n$ by $\mathrm{n}(\mathrm{n}+1)(\mathrm{n}+1) \mathrm{nn}$. It is easy to check that we now have an arrangement for $\mathrm{n}+1$. We have added one additional representative for each of the countries 1 to $\mathrm{n}$ and $\mathrm{n}+1$ representatives for country $\mathrm{n}+1$, so we have indeed got $(\mathrm{n}+1)^{2}$ people in all. We have also given a representative of each country 1 to $n$ a neighbour from country $n+1$ on his right and we have given the ( $n+1$ ) representatives from country $n+1$ neighbours (on their right) from each of the other countries. Otherwise we have left the seating unchanged.
|
{
"resource_path": "IberoAmerican_MO/segmented/en-1985-2003-IberoamericanMO.jsonl",
"problem_match": "\n## Problem B1",
"solution_match": "\n## Solution"
}
|
70583725-3bd6-5724-807a-b54ab8957937
| 604,908
|
$\mathrm{P}_{1}, \mathrm{P}_{2}, \ldots, \mathrm{P}_{\mathrm{n}}$ are points in the plane and $\mathrm{r}_{1}, \mathrm{r}_{2}, \ldots, \mathrm{r}_{\mathrm{n}}$ are real numbers such that the distance between $P_{i}$ and $P_{j}$ is $r_{i}+r_{j}$ (for $i$ not equal to $j$ ). Find the largest $n$ for which this is possible.
|
Answer: $\mathrm{n}=4$.
Draw a circle radius $r_{i}$ at $P_{i}$. Then each pair of circles must touch. But that is possible iff $n \leq 4$.
|
4
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
$\mathrm{P}_{1}, \mathrm{P}_{2}, \ldots, \mathrm{P}_{\mathrm{n}}$ are points in the plane and $\mathrm{r}_{1}, \mathrm{r}_{2}, \ldots, \mathrm{r}_{\mathrm{n}}$ are real numbers such that the distance between $P_{i}$ and $P_{j}$ is $r_{i}+r_{j}$ (for $i$ not equal to $j$ ). Find the largest $n$ for which this is possible.
|
Answer: $\mathrm{n}=4$.
Draw a circle radius $r_{i}$ at $P_{i}$. Then each pair of circles must touch. But that is possible iff $n \leq 4$.

|
{
"resource_path": "IberoAmerican_MO/segmented/en-1985-2003-IberoamericanMO.jsonl",
"problem_match": "\n## Problem B2",
"solution_match": "\n## Solution"
}
|
d4be8beb-ab7a-598b-b1ed-138ddbd2e1e9
| 604,923
|
$\mathrm{k}$ is the positive root of the equation $\mathrm{x}^{2}-1998 \mathrm{x}-1=0$. Define the sequence $\mathrm{x}_{0}, \mathrm{x}_{1}, \mathrm{x}_{2}, \ldots$ by $\mathrm{x}_{0}$ $=1, \mathrm{x}_{\mathrm{n}+1}=\left[\mathrm{k} \mathrm{x}_{\mathrm{n}}\right]$. Find the remainder when $\mathrm{x}_{1998}$ is divided by 1998.
|
Put $\mathrm{p}(\mathrm{x})=\mathrm{x}^{2}-1998 \mathrm{x}-1$. Then $\mathrm{p}(1998)=-1, \mathrm{p}(1999)=1998$, so $1998<\mathrm{k}<1999$. Also $\mathrm{k}$ is irrational (using the formula for the root of a quadratic). We have $x_{n}=\left[k x_{n-1}\right]$, so $x_{n}<k x_{n-1}$ and $>\mathrm{kx}_{\mathrm{n}-1}-1$. Hence $\mathrm{x}_{\mathrm{n}} / \mathrm{k}<\mathrm{x}_{\mathrm{n}-1}<\mathrm{x}_{\mathrm{n}} / \mathrm{k}+1 / \mathrm{k}$, so $\left[\mathrm{x}_{\mathrm{n}} / \mathrm{k}\right]=\mathrm{x}_{\mathrm{n}-1}-1$.
$\mathrm{k}=(1998 \mathrm{k}+1) / \mathrm{k}=1998+1 / \mathrm{k}$. Hence $\mathrm{kx}_{\mathrm{n}}=1998 \mathrm{x}_{\mathrm{n}}+\mathrm{x} / \mathrm{k}$. Hence $\mathrm{x}_{\mathrm{n}+1}=\left[\mathrm{kx}_{\mathrm{n}}\right]=1998 \mathrm{x}_{\mathrm{n}}+$ $\left[\mathrm{x}_{\mathrm{n}} / \mathrm{k}\right]=1998 \mathrm{x}_{\mathrm{n}}+\mathrm{x}_{\mathrm{n}-1}-1$. Hence $\mathrm{x}_{\mathrm{n}+1}=\mathrm{x}_{\mathrm{n}-1}-1 \bmod 1998$. So $\mathrm{x}_{1998}=1-999=1000 \bmod$ 1998.
|
1000
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
$\mathrm{k}$ is the positive root of the equation $\mathrm{x}^{2}-1998 \mathrm{x}-1=0$. Define the sequence $\mathrm{x}_{0}, \mathrm{x}_{1}, \mathrm{x}_{2}, \ldots$ by $\mathrm{x}_{0}$ $=1, \mathrm{x}_{\mathrm{n}+1}=\left[\mathrm{k} \mathrm{x}_{\mathrm{n}}\right]$. Find the remainder when $\mathrm{x}_{1998}$ is divided by 1998.
|
Put $\mathrm{p}(\mathrm{x})=\mathrm{x}^{2}-1998 \mathrm{x}-1$. Then $\mathrm{p}(1998)=-1, \mathrm{p}(1999)=1998$, so $1998<\mathrm{k}<1999$. Also $\mathrm{k}$ is irrational (using the formula for the root of a quadratic). We have $x_{n}=\left[k x_{n-1}\right]$, so $x_{n}<k x_{n-1}$ and $>\mathrm{kx}_{\mathrm{n}-1}-1$. Hence $\mathrm{x}_{\mathrm{n}} / \mathrm{k}<\mathrm{x}_{\mathrm{n}-1}<\mathrm{x}_{\mathrm{n}} / \mathrm{k}+1 / \mathrm{k}$, so $\left[\mathrm{x}_{\mathrm{n}} / \mathrm{k}\right]=\mathrm{x}_{\mathrm{n}-1}-1$.
$\mathrm{k}=(1998 \mathrm{k}+1) / \mathrm{k}=1998+1 / \mathrm{k}$. Hence $\mathrm{kx}_{\mathrm{n}}=1998 \mathrm{x}_{\mathrm{n}}+\mathrm{x} / \mathrm{k}$. Hence $\mathrm{x}_{\mathrm{n}+1}=\left[\mathrm{kx}_{\mathrm{n}}\right]=1998 \mathrm{x}_{\mathrm{n}}+$ $\left[\mathrm{x}_{\mathrm{n}} / \mathrm{k}\right]=1998 \mathrm{x}_{\mathrm{n}}+\mathrm{x}_{\mathrm{n}-1}-1$. Hence $\mathrm{x}_{\mathrm{n}+1}=\mathrm{x}_{\mathrm{n}-1}-1 \bmod 1998$. So $\mathrm{x}_{1998}=1-999=1000 \bmod$ 1998.
|
{
"resource_path": "IberoAmerican_MO/segmented/en-1985-2003-IberoamericanMO.jsonl",
"problem_match": "\n## Problem B3",
"solution_match": "\n## Solution"
}
|
0cea2807-3780-5baf-9c23-44688a23cfae
| 604,934
|
The numbers $1,2, \ldots, 2002$ are written in order on a blackboard. Then the 1 st, 4 th, 7 th, $\ldots$, $3 \mathrm{k}+1$ th, $\ldots$ numbers in the list are erased. Then the 1 st, $4 \mathrm{th}, 7 \mathrm{th}, \ldots 3 \mathrm{k}+1$ th numbers in the remaining list are erased (leaving $3,5,8,9,12, \ldots$ ). This process is carried out repeatedly until there are no numbers left. What is the last number to be erased?
|
Answer: 1598.
Let $\mathrm{a}_{\mathrm{n}}$ be the first number remaining after $\mathrm{n}$ iterations, so $\mathrm{a}_{0}=1, \mathrm{a}_{1}=2, \mathrm{a}_{3}=3, \mathrm{a}_{4}=5$ etc. We claim that:
```
\(a_{n+1}=3 / 2 a_{n} \quad\) if \(a_{n}\) is even, and
\(3 / 2\left(a_{n}+1\right)-1\) if \(a_{n}\) is odd.
```
We use induction on $n$. Suppose $a_{n}=2 N$. Consider the number $3 N$. There are initially $\mathrm{N}$ smaller numbers $=1 \mathrm{mod} 3$. So after the first iteration, it will lie in 2Nth place. Hence, it will lie in first place after $n+1$ iterations. Similarly, suppose $\mathrm{a}_{\mathrm{n}}=2 \mathrm{~N}+1$. Consider $3 N+2$. There are initially $\mathrm{N}+1$ smaller numbers $=1 \bmod 3$. So after the first iteration, it will lie in $2 \mathrm{~N}+1$ st place. Hence, it will lie in first place after $\mathrm{n}+1$ iterations. That completes the induction.
We may now calculate successively the members of the sequence: $1,2,3,5,8,12,18,27,41$, $62,93,140,210,315,473,710,1065,1598,2397$. Hence 1598 is the last surviving number from $1,2, \ldots, 2002$.
|
1598
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
The numbers $1,2, \ldots, 2002$ are written in order on a blackboard. Then the 1 st, 4 th, 7 th, $\ldots$, $3 \mathrm{k}+1$ th, $\ldots$ numbers in the list are erased. Then the 1 st, $4 \mathrm{th}, 7 \mathrm{th}, \ldots 3 \mathrm{k}+1$ th numbers in the remaining list are erased (leaving $3,5,8,9,12, \ldots$ ). This process is carried out repeatedly until there are no numbers left. What is the last number to be erased?
|
Answer: 1598.
Let $\mathrm{a}_{\mathrm{n}}$ be the first number remaining after $\mathrm{n}$ iterations, so $\mathrm{a}_{0}=1, \mathrm{a}_{1}=2, \mathrm{a}_{3}=3, \mathrm{a}_{4}=5$ etc. We claim that:
```
\(a_{n+1}=3 / 2 a_{n} \quad\) if \(a_{n}\) is even, and
\(3 / 2\left(a_{n}+1\right)-1\) if \(a_{n}\) is odd.
```
We use induction on $n$. Suppose $a_{n}=2 N$. Consider the number $3 N$. There are initially $\mathrm{N}$ smaller numbers $=1 \mathrm{mod} 3$. So after the first iteration, it will lie in 2Nth place. Hence, it will lie in first place after $n+1$ iterations. Similarly, suppose $\mathrm{a}_{\mathrm{n}}=2 \mathrm{~N}+1$. Consider $3 N+2$. There are initially $\mathrm{N}+1$ smaller numbers $=1 \bmod 3$. So after the first iteration, it will lie in $2 \mathrm{~N}+1$ st place. Hence, it will lie in first place after $\mathrm{n}+1$ iterations. That completes the induction.
We may now calculate successively the members of the sequence: $1,2,3,5,8,12,18,27,41$, $62,93,140,210,315,473,710,1065,1598,2397$. Hence 1598 is the last surviving number from $1,2, \ldots, 2002$.
|
{
"resource_path": "IberoAmerican_MO/segmented/en-1985-2003-IberoamericanMO.jsonl",
"problem_match": "\n## Problem A1",
"solution_match": "\n## Solution"
}
|
e131c124-62ca-5156-a0f6-d1ab6cd108ca
| 605,114
|
A $\square\{1,2,3, \ldots, 49\}$ does not contain six consecutive integers. Find the largest possible value of |A|. How many such subsets are there (of the maximum size)?
## Answer
$\max =41$; no. ways 495
|
We must exclude at least one element of each of the 8 sets $\{1,2, \ldots, 6\},\{7, \ldots, 12\},\{13, \ldots$, $18\}, \ldots,\{43, \ldots, 48\}$. So $|\mathrm{A}| \leq 41$. But a value of 41 is certainly possible, for example, exclude $2,8,14, \ldots, 44$.
The largest excluded element must be at least 44 (or we have the 6 consecutive elements 44, 45, 46, 47, 48, 49). The smallest excluded element must be at most 6 . If we exclude 2 and 44, then the difference between them is 7.6 and so the other 6 excluded elements are fixed. But if we exclude 3 and 44, for example, then there are several possible choices for the other elements.
There are 5 ways of choosing the smallest and largest excluded element to get a difference of 7. 6 between them ( 2 and 44, 3 and 45, 4 and 46, 5 and 47,6 and 48). There are 4 ways to get a difference of 7. $6-1$ ( 3 and 44, 4 and 45, 5 and 46, 6 and 47). There are 3 ways to get a difference of 7. $6-2$ ( 4 and 44, 5 and 45, 6 and 46), 2 ways to get a difference of 7. $6-3$ (5 and 44, 6 and 45), and 1 way to get a difference of 7. $6-4$ (6 and 44).
If the difference is $7.6-1$, then we can shorten any of the 7 gaps, so there are 7 possibilities. For example, with 3 and 44, we could shorten the first gap, so excluding 3, 8, 14, 20, 26, 32, 38 and 44 , or the second gap, so excluding $3,9,14,20,26,32,38$ and 44 , and so on.
If the difference is $7 \cdot 6-2$, then we can shorten one gap by two ( 7 possibilities) or two gaps by one (21 possibilities), total 28 . If the difference is $7 \cdot 6-3$, then we can shorten on gap by three (7), one by two and one by one (42) or three by one (35), total 84. Finally, if the difference is 7. 6 - 4, we can shorten one by four (7), one by three and one by 1 (42), two by two (21), one by two and two by one (105), or four by one (35), total 210.
So the total number of possibilities is $5 \cdot 1+4 \cdot 7+3 \cdot 28+2 \cdot 84+1 \cdot 210=495$.
|
495
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
A $\square\{1,2,3, \ldots, 49\}$ does not contain six consecutive integers. Find the largest possible value of |A|. How many such subsets are there (of the maximum size)?
## Answer
$\max =41$; no. ways 495
|
We must exclude at least one element of each of the 8 sets $\{1,2, \ldots, 6\},\{7, \ldots, 12\},\{13, \ldots$, $18\}, \ldots,\{43, \ldots, 48\}$. So $|\mathrm{A}| \leq 41$. But a value of 41 is certainly possible, for example, exclude $2,8,14, \ldots, 44$.
The largest excluded element must be at least 44 (or we have the 6 consecutive elements 44, 45, 46, 47, 48, 49). The smallest excluded element must be at most 6 . If we exclude 2 and 44, then the difference between them is 7.6 and so the other 6 excluded elements are fixed. But if we exclude 3 and 44, for example, then there are several possible choices for the other elements.
There are 5 ways of choosing the smallest and largest excluded element to get a difference of 7. 6 between them ( 2 and 44, 3 and 45, 4 and 46, 5 and 47,6 and 48). There are 4 ways to get a difference of 7. $6-1$ ( 3 and 44, 4 and 45, 5 and 46, 6 and 47). There are 3 ways to get a difference of 7. $6-2$ ( 4 and 44, 5 and 45, 6 and 46), 2 ways to get a difference of 7. $6-3$ (5 and 44, 6 and 45), and 1 way to get a difference of 7. $6-4$ (6 and 44).
If the difference is $7.6-1$, then we can shorten any of the 7 gaps, so there are 7 possibilities. For example, with 3 and 44, we could shorten the first gap, so excluding 3, 8, 14, 20, 26, 32, 38 and 44 , or the second gap, so excluding $3,9,14,20,26,32,38$ and 44 , and so on.
If the difference is $7 \cdot 6-2$, then we can shorten one gap by two ( 7 possibilities) or two gaps by one (21 possibilities), total 28 . If the difference is $7 \cdot 6-3$, then we can shorten on gap by three (7), one by two and one by one (42) or three by one (35), total 84. Finally, if the difference is 7. 6 - 4, we can shorten one by four (7), one by three and one by 1 (42), two by two (21), one by two and two by one (105), or four by one (35), total 210.
So the total number of possibilities is $5 \cdot 1+4 \cdot 7+3 \cdot 28+2 \cdot 84+1 \cdot 210=495$.
|
{
"resource_path": "IberoAmerican_MO/segmented/en-1985-2003-IberoamericanMO.jsonl",
"problem_match": "\n## Problem B1",
"solution_match": "\n## Solution"
}
|
6fb75f3e-b80f-5473-bd05-42aa9e0b78ff
| 605,223
|
For any set $A=\left\{x_{1}, x_{2}, x_{3}, x_{4}, x_{5}\right\}$ of five distinct positive integers denote by $S_{A}$ the sum of its elements, and denote by $T_{A}$ the number of triples $(i, j, k)$ with $1 \leqslant i<j<k \leqslant 5$ for which $x_{i}+x_{j}+x_{k}$ divides $S_{A}$.
Find the largest possible value of $T_{A}$.
|
We will prove that the maximum value that $T_{A}$ can attain is 4 . Let $A=$ $\left\{x_{1}, x_{2}, x_{3}, x_{4}, x_{5}\right\}$ be a set of five positive integers such that $x_{1}<x_{2}<x_{3}<x_{4}<x_{5}$. Call a triple $(i, j, k)$ with $1 \leqslant i<j<k \leqslant 5$ good if $x_{i}+x_{j}+x_{k}$ divides $S_{A}$. None of the triples $(3,4,5),(2,4,5),(1,4,5),(2,3,5),(1,3,5)$ is good, since, for example
$$
x_{5}+x_{3}+x_{1}\left|S_{A} \Rightarrow x_{5}+x_{3}+x_{1}\right| x_{2}+x_{4}
$$
which is impossible since $x_{5}>x_{4}$ and $x_{3}>x_{2}$. Analogously we can show that any triple of form $(x, y, 5)$ where $y>2$ isn't good.
By above, the number of good triples can be at most 5 and only triples $(1,2,5),(2,3,4)$, $(1,3,4),(1,2,4),(1,2,3)$ can be good. But if triples $(1,2,5)$ and $(2,3,4)$ are simultaneously good we have that:
$$
x_{1}+x_{2}+x_{5} \mid x_{3}+x_{4} \Rightarrow x_{5}<x_{3}+x_{4}
$$
and
$$
x_{2}+x_{3}+x_{4} \mid x_{1}+x_{5} \Rightarrow x_{2}+x_{3}+x_{4} \leqslant x_{1}+x_{5} \stackrel{(1)}{<} x_{1}+x_{3}+x_{4}<x_{2}+x_{3}+x_{4},
$$
which is impossible. Therefore, $T_{A} \leqslant 4$.
Alternatively, one can prove the statement above by adding up the two inequalities $x_{1}+x_{2}+x_{4}<x_{3}+x_{4}$ and $x_{2}+x_{3}+x_{4}<x_{1}+x_{5}$ that are derived from the divisibilities.
To show that $T_{A}=4$ is possible, consider the numbers $1,2,3,4,494$. This works because $6|498,7| 497,8 \mid 496$, and $9 \mid 495$.
Remark. The motivation for construction is to realize that if we choose $x_{1}, x_{2}, x_{3}, x_{4}$ we can get all the conditions $x_{5}$ must satisfy. Let $S=x_{1}+x_{2}+x_{3}+x_{4}$. Now we have to choose $x_{5}$ such that
$$
S-x_{i} \mid x_{i}+x_{5} \text {, i.e. } x_{5} \equiv-x_{i} \quad \bmod \left(S-x_{i}\right) \forall i \in\{1,2,3,4\}
$$
By the Chinese Remainder Theorem it is obvious that if $S-x_{1}, S-x_{2}, S-x_{3}, S-x_{4}$ are pairwise coprime, such $x_{5}$ must exist. To make all these numbers pairwise coprime it's natural to take $x_{1}, x_{2}, x_{3}, x_{4}$ to be all odd and then solve mod 3 issues. Fortunately it can be seen that $1,5,7,11$ easily works because $13,17,19,23$ are pairwise coprime.
However, even without the knowledge of this theorem it makes sense intuitively that this system must have a solution for some $x_{1}, x_{2}, x_{3}, x_{4}$. By taking $\left(x_{1}, x_{2}, x_{3}, x_{4}\right)=$ $(1,2,3,4)$ we get pretty simple system which can be solved by hand rather easily.
|
4
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
For any set $A=\left\{x_{1}, x_{2}, x_{3}, x_{4}, x_{5}\right\}$ of five distinct positive integers denote by $S_{A}$ the sum of its elements, and denote by $T_{A}$ the number of triples $(i, j, k)$ with $1 \leqslant i<j<k \leqslant 5$ for which $x_{i}+x_{j}+x_{k}$ divides $S_{A}$.
Find the largest possible value of $T_{A}$.
|
We will prove that the maximum value that $T_{A}$ can attain is 4 . Let $A=$ $\left\{x_{1}, x_{2}, x_{3}, x_{4}, x_{5}\right\}$ be a set of five positive integers such that $x_{1}<x_{2}<x_{3}<x_{4}<x_{5}$. Call a triple $(i, j, k)$ with $1 \leqslant i<j<k \leqslant 5$ good if $x_{i}+x_{j}+x_{k}$ divides $S_{A}$. None of the triples $(3,4,5),(2,4,5),(1,4,5),(2,3,5),(1,3,5)$ is good, since, for example
$$
x_{5}+x_{3}+x_{1}\left|S_{A} \Rightarrow x_{5}+x_{3}+x_{1}\right| x_{2}+x_{4}
$$
which is impossible since $x_{5}>x_{4}$ and $x_{3}>x_{2}$. Analogously we can show that any triple of form $(x, y, 5)$ where $y>2$ isn't good.
By above, the number of good triples can be at most 5 and only triples $(1,2,5),(2,3,4)$, $(1,3,4),(1,2,4),(1,2,3)$ can be good. But if triples $(1,2,5)$ and $(2,3,4)$ are simultaneously good we have that:
$$
x_{1}+x_{2}+x_{5} \mid x_{3}+x_{4} \Rightarrow x_{5}<x_{3}+x_{4}
$$
and
$$
x_{2}+x_{3}+x_{4} \mid x_{1}+x_{5} \Rightarrow x_{2}+x_{3}+x_{4} \leqslant x_{1}+x_{5} \stackrel{(1)}{<} x_{1}+x_{3}+x_{4}<x_{2}+x_{3}+x_{4},
$$
which is impossible. Therefore, $T_{A} \leqslant 4$.
Alternatively, one can prove the statement above by adding up the two inequalities $x_{1}+x_{2}+x_{4}<x_{3}+x_{4}$ and $x_{2}+x_{3}+x_{4}<x_{1}+x_{5}$ that are derived from the divisibilities.
To show that $T_{A}=4$ is possible, consider the numbers $1,2,3,4,494$. This works because $6|498,7| 497,8 \mid 496$, and $9 \mid 495$.
Remark. The motivation for construction is to realize that if we choose $x_{1}, x_{2}, x_{3}, x_{4}$ we can get all the conditions $x_{5}$ must satisfy. Let $S=x_{1}+x_{2}+x_{3}+x_{4}$. Now we have to choose $x_{5}$ such that
$$
S-x_{i} \mid x_{i}+x_{5} \text {, i.e. } x_{5} \equiv-x_{i} \quad \bmod \left(S-x_{i}\right) \forall i \in\{1,2,3,4\}
$$
By the Chinese Remainder Theorem it is obvious that if $S-x_{1}, S-x_{2}, S-x_{3}, S-x_{4}$ are pairwise coprime, such $x_{5}$ must exist. To make all these numbers pairwise coprime it's natural to take $x_{1}, x_{2}, x_{3}, x_{4}$ to be all odd and then solve mod 3 issues. Fortunately it can be seen that $1,5,7,11$ easily works because $13,17,19,23$ are pairwise coprime.
However, even without the knowledge of this theorem it makes sense intuitively that this system must have a solution for some $x_{1}, x_{2}, x_{3}, x_{4}$. By taking $\left(x_{1}, x_{2}, x_{3}, x_{4}\right)=$ $(1,2,3,4)$ we get pretty simple system which can be solved by hand rather easily.
|
{
"resource_path": "JBMO/segmented/en-official/en-2021_jbmo_problems_and_sol.jsonl",
"problem_match": "\nProblem 2.",
"solution_match": "\nSolution."
}
|
da9e65ea-8465-51cf-8661-8a40f3c6ef7f
| 605,270
|
Let $M$ be a subset of the set of 2021 integers $\{1,2,3, \ldots, 2021\}$ such that for any three elements (not necessarily distinct) $a, b, c$ of $M$ we have $|a+b-c|>10$. Determine the largest possible number of elements of $M$.
|
The set $M=\{1016,1017, \ldots, 2021\}$ has 1006 elements and satisfies the required property, since $a, b, c \in M$ implies that $a+b-c \geqslant 1016+1016-2021=11$. We will show that this is optimal.
Suppose $M$ satisfies the condition in the problem. Let $k$ be the minimal element of $M$. Then $k=|k+k-k|>10 \Rightarrow k \geqslant 11$. Note also that for every $m$, the integers $m, m+k-10$ cannot both belong to $M$, since $k+m-(m+k-10)=10$.
Claim 1: $M$ contains at most $k-10$ out of any $2 k-20$ consecutive integers.
Proof: We can partition the set $\{m, m+1, \ldots, m+2 k-21\}$ into $k-10$ pairs as follows:
$$
\{m, m+k-10\},\{m+1, m+k-9\}, \ldots,\{m+k-11, m+2 k-21\}
$$
It remains to note that $M$ can contain at most one element of each pair.
Claim 2: $M$ contains at most $[(t+k-10) / 2]$ out of any $t$ consecutive integers.
Proof: Write $t=q(2 k-20)+r$ with $r \in\{0,1,2 \ldots, 2 k-21\}$. From the set of the first $q(2 k-20)$ integers, by Claim 1 at most $q(k-10)$ can belong to $M$. Also by claim 1, it follows that from the last $r$ integers, at $\operatorname{most} \min \{r, k-10\}$ can belong to $M$.
Thus,
- If $r \leqslant k-10$, then at most
$$
q(k-10)+r=\frac{t+r}{2} \leqslant \frac{t+k-10}{2} \text { integers belong to } M
$$
- If $r>k-10$, then at most
$$
q(k-10)+k-10=\frac{t-r+2(k-10)}{2} \leqslant \frac{t+k-10}{2} \text { integers belong to } M
$$
By Claim 2, the number of elements of $M$ amongst $k+1, k+2, \ldots, 2021$ is at most
$$
\left[\frac{(2021-k)+(k-10)}{2}\right]=1005
$$
Since amongst $\{1,2, \ldots, k\}$ only $k$ belongs to $M$, we conclude that $M$ has at most 1006 elements as claimed.
|
1006
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Let $M$ be a subset of the set of 2021 integers $\{1,2,3, \ldots, 2021\}$ such that for any three elements (not necessarily distinct) $a, b, c$ of $M$ we have $|a+b-c|>10$. Determine the largest possible number of elements of $M$.
|
The set $M=\{1016,1017, \ldots, 2021\}$ has 1006 elements and satisfies the required property, since $a, b, c \in M$ implies that $a+b-c \geqslant 1016+1016-2021=11$. We will show that this is optimal.
Suppose $M$ satisfies the condition in the problem. Let $k$ be the minimal element of $M$. Then $k=|k+k-k|>10 \Rightarrow k \geqslant 11$. Note also that for every $m$, the integers $m, m+k-10$ cannot both belong to $M$, since $k+m-(m+k-10)=10$.
Claim 1: $M$ contains at most $k-10$ out of any $2 k-20$ consecutive integers.
Proof: We can partition the set $\{m, m+1, \ldots, m+2 k-21\}$ into $k-10$ pairs as follows:
$$
\{m, m+k-10\},\{m+1, m+k-9\}, \ldots,\{m+k-11, m+2 k-21\}
$$
It remains to note that $M$ can contain at most one element of each pair.
Claim 2: $M$ contains at most $[(t+k-10) / 2]$ out of any $t$ consecutive integers.
Proof: Write $t=q(2 k-20)+r$ with $r \in\{0,1,2 \ldots, 2 k-21\}$. From the set of the first $q(2 k-20)$ integers, by Claim 1 at most $q(k-10)$ can belong to $M$. Also by claim 1, it follows that from the last $r$ integers, at $\operatorname{most} \min \{r, k-10\}$ can belong to $M$.
Thus,
- If $r \leqslant k-10$, then at most
$$
q(k-10)+r=\frac{t+r}{2} \leqslant \frac{t+k-10}{2} \text { integers belong to } M
$$
- If $r>k-10$, then at most
$$
q(k-10)+k-10=\frac{t-r+2(k-10)}{2} \leqslant \frac{t+k-10}{2} \text { integers belong to } M
$$
By Claim 2, the number of elements of $M$ amongst $k+1, k+2, \ldots, 2021$ is at most
$$
\left[\frac{(2021-k)+(k-10)}{2}\right]=1005
$$
Since amongst $\{1,2, \ldots, k\}$ only $k$ belongs to $M$, we conclude that $M$ has at most 1006 elements as claimed.
|
{
"resource_path": "JBMO/segmented/en-official/en-2021_jbmo_problems_and_sol.jsonl",
"problem_match": "\nProblem 4.",
"solution_match": "\nSolution."
}
|
578e1f57-7233-5e5d-bf6e-f031082470af
| 605,294
|
We call an even positive integer $n$ nice if the set $\{1,2, \ldots, n\}$ can be partitioned into $\frac{n}{2}$ two-element subsets, such that the sum of the elements in each subset is a power of 3 . For example, 6 is nice, because the set $\{1,2,3,4,5,6\}$ can be partitioned into subsets $\{1,2\},\{3,6\},\{4,5\}$. Find the number of nice positive integers which are smaller than $3^{2022}$.
|
For a nice number $n$ and a given partition of the set $\{1,2, \ldots, n\}$ into twoelement subsets such that the sum of the elements in each subset is a power of 3 , we say that $a, b \in\{1,2, \ldots, n\}$ are paired if both of them belong to the same subset.
Let $x$ be a nice number and $k$ be a (unique) non-negative integer such that $3^{k} \leq x<3^{k+1}$. Suppose that $x$ is paired with $y<x$. Then, $x+y=3^{s}$, for some positive integer $s$. Since
$$
3^{s}=x+y<2 x<2 \cdot 3^{k+1}<3^{k+2}
$$
we must have $s<k+2$. On the other hand, the inequality
$$
x+y \geq 3^{k}+1>3^{k}
$$
implies that $s>k$. From these we conclude that $s$ must be equal to $k+1$, so $x+y=3^{k+1}$. The last equation, combined with $x>y$, implies that $x>\frac{3^{k+1}}{2}$.
Similarly as above, we can conclude that each number $z$ from the closed interval $\left[3^{k+1}-x, x\right]$ is paired with $3^{k+1}-z$. Namely, for any such $z$, the larger of the numbers $z$ and $3^{k+1}-z$ is greater than $\frac{3^{k+1}}{2}$ which is greater than $3^{k}$, so the numbers $z$ and $3^{k+1}-z$ must necessarily be in the same subset. In other words, each number from the interval $\left[3^{k+1}-x, x\right]$ is paired with another number from this interval. Note that this implies that all numbers smaller than $3^{k+1}-x$ are paired among themselves, so the number $3^{k+1}-x-1$ is either nice or equals zero. Also, the number $3^{k}$ must be paired with $2 \cdot 3^{k}$, so $x \geq 2 \cdot 3^{k}$.
Finally, we prove by induction that $a_{n}=2^{n}-1$, where $a_{n}$ is the number of nice positive integers smaller than $3^{n}$. For $n=1$, the claim is obviously true, because 2 is the only nice positive integer smaller than 3 . Now, assume that $a_{n}=2^{n}-1$ for some positive integer $n$. We will prove that $a_{n+1}=2^{n+1}-1$. To prove this, first observe that the number of nice positive integers between $2 \cdot 3^{n}$ and $3^{n+1}$ is exactly $a_{n+1}-a_{n}$. Next, observe that $3^{n+1}-1$ is nice. For every nice number $2 \cdot 3^{n} \leq x<3^{n+1}-1$, the number $3^{n+1}-x-1$ is also nice and is strictly smaller than $3^{n}$. Also, for every positive integer $y<3^{n}$, obviously there is a unique number $x$ such that $2 \cdot 3^{n} \leq x<3^{n+1}-1$ and $3^{n+1}-x-1=y$. Thus,
$$
a_{n+1}-a_{n}=a_{n}+1 \Leftrightarrow a_{n+1}=2 a_{n}+1=2\left(2^{n}-1\right)+1=2^{n+1}-1
$$
completing the proof.
In summary, there are $2^{2022}-1$ nice positive integers smaller than $3^{2022}$.
|
2^{2022}-1
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
We call an even positive integer $n$ nice if the set $\{1,2, \ldots, n\}$ can be partitioned into $\frac{n}{2}$ two-element subsets, such that the sum of the elements in each subset is a power of 3 . For example, 6 is nice, because the set $\{1,2,3,4,5,6\}$ can be partitioned into subsets $\{1,2\},\{3,6\},\{4,5\}$. Find the number of nice positive integers which are smaller than $3^{2022}$.
|
For a nice number $n$ and a given partition of the set $\{1,2, \ldots, n\}$ into twoelement subsets such that the sum of the elements in each subset is a power of 3 , we say that $a, b \in\{1,2, \ldots, n\}$ are paired if both of them belong to the same subset.
Let $x$ be a nice number and $k$ be a (unique) non-negative integer such that $3^{k} \leq x<3^{k+1}$. Suppose that $x$ is paired with $y<x$. Then, $x+y=3^{s}$, for some positive integer $s$. Since
$$
3^{s}=x+y<2 x<2 \cdot 3^{k+1}<3^{k+2}
$$
we must have $s<k+2$. On the other hand, the inequality
$$
x+y \geq 3^{k}+1>3^{k}
$$
implies that $s>k$. From these we conclude that $s$ must be equal to $k+1$, so $x+y=3^{k+1}$. The last equation, combined with $x>y$, implies that $x>\frac{3^{k+1}}{2}$.
Similarly as above, we can conclude that each number $z$ from the closed interval $\left[3^{k+1}-x, x\right]$ is paired with $3^{k+1}-z$. Namely, for any such $z$, the larger of the numbers $z$ and $3^{k+1}-z$ is greater than $\frac{3^{k+1}}{2}$ which is greater than $3^{k}$, so the numbers $z$ and $3^{k+1}-z$ must necessarily be in the same subset. In other words, each number from the interval $\left[3^{k+1}-x, x\right]$ is paired with another number from this interval. Note that this implies that all numbers smaller than $3^{k+1}-x$ are paired among themselves, so the number $3^{k+1}-x-1$ is either nice or equals zero. Also, the number $3^{k}$ must be paired with $2 \cdot 3^{k}$, so $x \geq 2 \cdot 3^{k}$.
Finally, we prove by induction that $a_{n}=2^{n}-1$, where $a_{n}$ is the number of nice positive integers smaller than $3^{n}$. For $n=1$, the claim is obviously true, because 2 is the only nice positive integer smaller than 3 . Now, assume that $a_{n}=2^{n}-1$ for some positive integer $n$. We will prove that $a_{n+1}=2^{n+1}-1$. To prove this, first observe that the number of nice positive integers between $2 \cdot 3^{n}$ and $3^{n+1}$ is exactly $a_{n+1}-a_{n}$. Next, observe that $3^{n+1}-1$ is nice. For every nice number $2 \cdot 3^{n} \leq x<3^{n+1}-1$, the number $3^{n+1}-x-1$ is also nice and is strictly smaller than $3^{n}$. Also, for every positive integer $y<3^{n}$, obviously there is a unique number $x$ such that $2 \cdot 3^{n} \leq x<3^{n+1}-1$ and $3^{n+1}-x-1=y$. Thus,
$$
a_{n+1}-a_{n}=a_{n}+1 \Leftrightarrow a_{n+1}=2 a_{n}+1=2\left(2^{n}-1\right)+1=2^{n+1}-1
$$
completing the proof.
In summary, there are $2^{2022}-1$ nice positive integers smaller than $3^{2022}$.
|
{
"resource_path": "JBMO/segmented/en-official/en-jbmo-2022-solutions.jsonl",
"problem_match": "\nProblem 4.",
"solution_match": "\nSolution."
}
|
1aeb3bd1-e40e-5387-8a88-feebc98dfccc
| 605,367
|
Consider a regular $2 n$-gon $P, A_{1} A_{2} \ldots A_{2 n}$ in the plane, where $n$ is a positive integer. We say that a point $S$ on one of the sides of $P$ can be seen from a point $E$ that is external to $P$, if the line segment $S E$ contains no other points that lie on the sides of $P$ except $S$. We color the sides of $P$ in 3 different colors (ignore the vertices of $P$, we consider them colorless), such that every side is colored in exactly one color, and each color is used at least once. Moreover, from every point in the plane external to $P$, points of at most 2 different colors on $P$ can be seen. Find the number of distinct such colorings of $P$ (two colorings are considered distinct if at least one of the sides is colored differently).
|
Answer: For $n=2$, the answer is 36 ; for $n=3$, the answer is 30 and for $n \geq 4$, the answer is $6 n$.
Lemma 1. Given a regular $2 n$-gon in the plane and a sequence of $n$ consecutive sides $s_{1}, s_{2}, \ldots, s_{n}$ there is an external point $Q$ in the plane, such that the color of each $s_{i}$ can be seen from $Q$, for $i=1,2, \ldots, n$.
Proof. It is obvious that for a semi-circle $S$, there is a point $R$ in the plane far enough on the bisector of its diameter such that almost the entire semi-circle can be seen from $R$.
Now, it is clear that looking at the circumscribed circle around the $2 n$-gon, there is a semi-circle $S$ such that each $s_{i}$ either has both endpoints on it, or has an endpoint that's on the semi-circle, and is not on the semi-circle's end. So, take $Q$ to be a point in the plane from which almost all of $S$ can be seen, clearly, the color of each $s_{i}$ can be seen from $Q$.
Lemma 2. Given a regular $2 n$-gon in the plane, and a sequence of $n+1$ consecutive sides $s_{1}, s_{2}, \ldots, s_{n+1}$ there is no external point $Q$ in the plane, such that the color of each $s_{i}$ can be seen from $Q$, for $i=1,2, \ldots, n+1$.
Proof. Since $s_{1}$ and $s_{n+1}$ are parallel opposite sides of the $2 n$-gon, they cannot be seen at the same time from an external point.
For $n=2$, we have a square, so all we have to do is make sure each color is used. Two sides will be of the same color, and we have to choose which are these 2 sides, and then assign colors according to this choice, so the answer is $\binom{4}{2} .3 .2=36$.
For $n=3$, we have a hexagon. Denote the sides as $a_{1}, a_{2}, \ldots q_{6}$, in that order. There must be 2 consecutive sides of different colors, say $a_{1}$ is red, $a_{2}$ is blue. We must have a green side, and only $a_{4}$ and $a_{5}$ can be green. We have 3 possibilities:
1) $a_{4}$ is green, $a_{5}$ is not. So, $a_{3}$ must be blue and $a_{5}$ must be blue (by elimination) and $a_{6}$ must be blue, so we get a valid coloring.
2) Both $a_{4}$ and $a_{5}$ are green, thus $a_{6}$ must be red and $a_{5}$ must be blue, and we get the coloring rbbggr.
3) $a_{5}$ is green, $a_{4}$ is not. Then $a_{6}$ must be red. Subsequently, $a_{4}$ must be red (we assume it is not green). It remains that $a_{3}$ must be red, and the coloring is rbrrgr.
Thus, we have 2 kinds of configurations:
i) 2 opposite sides have 2 opposite colors and all other sides are of the third color. This can happen in 3.(3.2.1) $=18$ ways (first choosing the pair of opposite sides, then assigning colors),
ii) 3 pairs of consecutive sides, each pair in one of the 3 colors. This can happen in $2.6=12$ ways (2 partitioning into pairs of consecutive sides, for each partitioning, 6 ways to assign the colors).
Thus, for $n=3$, the answer is $18+12=30$.
Finally, let's address the case $n \geq 4$. The important thing now is that any 4 consecutive sides can be seen from an external point, by Lemma 1 .
Denote the sides as $a_{1}, a_{2}, \ldots, a_{2 n}$. Again, there must be 2 adjacent sides that are of different colors, say $a_{1}$ is blue and $a_{2}$ is red. We must have a green side, and by Lemma 1 , that can only be $a_{n+1}$ or $a_{n+2}$. So, we have 2 cases:
Case 1: $a_{n+1}$ is green, so $a_{n}$ must be red (cannot be green due to Lemma 1 applied to $a_{1}, a_{2}, \ldots, a_{n}$, cannot be blue for the sake of $a_{2}, \ldots, a_{n+1}$. If $a_{n+2}$ is red, so are $a_{n+3}, \ldots, a_{2 n}$, and we get a valid coloring: $a_{1}$ is blue, $a_{n+1}$ is green, and all the others are red.
If $a_{n+2}$ is green:
a) $a_{n+3}$ cannot be green, because of $a_{2}, a_{1}, a_{2 n} \ldots, a_{n+3}$.
b) $a_{n+3}$ cannot be blue, because the 4 adjacent sides $a_{n}, \ldots, a_{n+3}$ can be seen (this is the case that makes the separate treatment of $n \geq 4$ necessary)
c) $a_{n+3}$ cannot be red, because of $a_{1}, a_{2 n}, \ldots, a_{n+2}$.
So, in the case that $a_{n+2}$ is also green, we cannot get a valid coloring.
Case 2: $a_{n+2}$ is green is treated the same way as Case 1.
This means that the only valid configuration for $n \geq 4$ is having 2 opposite sides colored in 2 different colors, and all other sides colored in the third color. This can be done in $n .3 .2=6 n$ ways.
|
6n
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Consider a regular $2 n$-gon $P, A_{1} A_{2} \ldots A_{2 n}$ in the plane, where $n$ is a positive integer. We say that a point $S$ on one of the sides of $P$ can be seen from a point $E$ that is external to $P$, if the line segment $S E$ contains no other points that lie on the sides of $P$ except $S$. We color the sides of $P$ in 3 different colors (ignore the vertices of $P$, we consider them colorless), such that every side is colored in exactly one color, and each color is used at least once. Moreover, from every point in the plane external to $P$, points of at most 2 different colors on $P$ can be seen. Find the number of distinct such colorings of $P$ (two colorings are considered distinct if at least one of the sides is colored differently).
|
Answer: For $n=2$, the answer is 36 ; for $n=3$, the answer is 30 and for $n \geq 4$, the answer is $6 n$.
Lemma 1. Given a regular $2 n$-gon in the plane and a sequence of $n$ consecutive sides $s_{1}, s_{2}, \ldots, s_{n}$ there is an external point $Q$ in the plane, such that the color of each $s_{i}$ can be seen from $Q$, for $i=1,2, \ldots, n$.
Proof. It is obvious that for a semi-circle $S$, there is a point $R$ in the plane far enough on the bisector of its diameter such that almost the entire semi-circle can be seen from $R$.
Now, it is clear that looking at the circumscribed circle around the $2 n$-gon, there is a semi-circle $S$ such that each $s_{i}$ either has both endpoints on it, or has an endpoint that's on the semi-circle, and is not on the semi-circle's end. So, take $Q$ to be a point in the plane from which almost all of $S$ can be seen, clearly, the color of each $s_{i}$ can be seen from $Q$.
Lemma 2. Given a regular $2 n$-gon in the plane, and a sequence of $n+1$ consecutive sides $s_{1}, s_{2}, \ldots, s_{n+1}$ there is no external point $Q$ in the plane, such that the color of each $s_{i}$ can be seen from $Q$, for $i=1,2, \ldots, n+1$.
Proof. Since $s_{1}$ and $s_{n+1}$ are parallel opposite sides of the $2 n$-gon, they cannot be seen at the same time from an external point.
For $n=2$, we have a square, so all we have to do is make sure each color is used. Two sides will be of the same color, and we have to choose which are these 2 sides, and then assign colors according to this choice, so the answer is $\binom{4}{2} .3 .2=36$.
For $n=3$, we have a hexagon. Denote the sides as $a_{1}, a_{2}, \ldots q_{6}$, in that order. There must be 2 consecutive sides of different colors, say $a_{1}$ is red, $a_{2}$ is blue. We must have a green side, and only $a_{4}$ and $a_{5}$ can be green. We have 3 possibilities:
1) $a_{4}$ is green, $a_{5}$ is not. So, $a_{3}$ must be blue and $a_{5}$ must be blue (by elimination) and $a_{6}$ must be blue, so we get a valid coloring.
2) Both $a_{4}$ and $a_{5}$ are green, thus $a_{6}$ must be red and $a_{5}$ must be blue, and we get the coloring rbbggr.
3) $a_{5}$ is green, $a_{4}$ is not. Then $a_{6}$ must be red. Subsequently, $a_{4}$ must be red (we assume it is not green). It remains that $a_{3}$ must be red, and the coloring is rbrrgr.
Thus, we have 2 kinds of configurations:
i) 2 opposite sides have 2 opposite colors and all other sides are of the third color. This can happen in 3.(3.2.1) $=18$ ways (first choosing the pair of opposite sides, then assigning colors),
ii) 3 pairs of consecutive sides, each pair in one of the 3 colors. This can happen in $2.6=12$ ways (2 partitioning into pairs of consecutive sides, for each partitioning, 6 ways to assign the colors).
Thus, for $n=3$, the answer is $18+12=30$.
Finally, let's address the case $n \geq 4$. The important thing now is that any 4 consecutive sides can be seen from an external point, by Lemma 1 .
Denote the sides as $a_{1}, a_{2}, \ldots, a_{2 n}$. Again, there must be 2 adjacent sides that are of different colors, say $a_{1}$ is blue and $a_{2}$ is red. We must have a green side, and by Lemma 1 , that can only be $a_{n+1}$ or $a_{n+2}$. So, we have 2 cases:
Case 1: $a_{n+1}$ is green, so $a_{n}$ must be red (cannot be green due to Lemma 1 applied to $a_{1}, a_{2}, \ldots, a_{n}$, cannot be blue for the sake of $a_{2}, \ldots, a_{n+1}$. If $a_{n+2}$ is red, so are $a_{n+3}, \ldots, a_{2 n}$, and we get a valid coloring: $a_{1}$ is blue, $a_{n+1}$ is green, and all the others are red.
If $a_{n+2}$ is green:
a) $a_{n+3}$ cannot be green, because of $a_{2}, a_{1}, a_{2 n} \ldots, a_{n+3}$.
b) $a_{n+3}$ cannot be blue, because the 4 adjacent sides $a_{n}, \ldots, a_{n+3}$ can be seen (this is the case that makes the separate treatment of $n \geq 4$ necessary)
c) $a_{n+3}$ cannot be red, because of $a_{1}, a_{2 n}, \ldots, a_{n+2}$.
So, in the case that $a_{n+2}$ is also green, we cannot get a valid coloring.
Case 2: $a_{n+2}$ is green is treated the same way as Case 1.
This means that the only valid configuration for $n \geq 4$ is having 2 opposite sides colored in 2 different colors, and all other sides colored in the third color. This can be done in $n .3 .2=6 n$ ways.
|
{
"resource_path": "JBMO/segmented/en-official/en-jbmo_2017_english_solutions.jsonl",
"problem_match": "\nProblem 4.",
"solution_match": "\nSolution "
}
|
2ffad5b6-f37d-55b2-8a30-694e676f4e7e
| 605,485
|
Let $n$ three-digit numbers satisfy the following properties:
(1) No number contains the digit 0 .
(2) The sum of the digits of each number is 9 .
(3) The units digits of any two numbers are different.
(4) The tens digits of any two numbers are different.
(5) The hundreds digits of any two numbers are different.
Find the largest possible value of $n$.
|
Let $S$ denote the set of three-digit numbers that have digit sum equal to 9 and no digit equal to 0 . We will first find the cardinality of $S$. We start from the number 111 and each element of $S$ can be obtained from 111 by a string of 6 A's (which means that we add 1 to the current digit) and $2 G$ 's (which means go to the next digit). Then for example 324 can be obtained from 111 by the string AAGAGAAA. There are in total
$$
\frac{8!}{6!\cdot 2!}=28
$$
such words, so $S$ contains 28 numbers. Now, from the conditions (3), (4), (5), if $\overline{a b c}$ is in $T$ then each of the other numbers of the form $\overline{* c}$ cannot be in $T$, neither $\overline{* *}$ can be, nor $\overline{a * *}$. Since there are $a+b-2$ numbers of the first category, $a+c-2$ from the second and $b+c-2$ from the third one. In these three categories there are
$$
(a+b-2)+(b+c-2)+(c+a-2)=2(a+b+c)-6=2 \cdot 9-6=12
$$
distinct numbers that cannot be in $T$ if $\overline{a b c}$ is in $T$. So, if $T$ has $n$ numbers, then $12 n$ are the forbidden ones that are in $S$, but each number from $S$ can be a forbidden number no more than three times, once for each of its digits, so
$$
n+\frac{12 n}{3} \leq 28 \Longleftrightarrow n \leq \frac{28}{5}
$$
and since $n$ is an integer, we get $n \leq 5$. A possible example for $n=5$ is
$$
T=\{144,252,315,423,531\}
$$
Comment by PSC. It is classical to compute the cardinality of $S$ and this can be done in many ways. In general, the number of solutions of the equation
$$
x_{1}+x_{2}+\cdots+x_{k}=n
$$
in positive integers, where the order of $x_{i}$ matters, is well known that equals to $\binom{n-1}{k-1}$. In our case, we want to count the number of positive solutions to $a+b+c=9$. By the above, this equals to $\binom{9-1}{3-1}=28$. Using the general result above, we can also find that there are $a+b-2$ numbers of the form $\overline{* c}$.
|
5
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Let $n$ three-digit numbers satisfy the following properties:
(1) No number contains the digit 0 .
(2) The sum of the digits of each number is 9 .
(3) The units digits of any two numbers are different.
(4) The tens digits of any two numbers are different.
(5) The hundreds digits of any two numbers are different.
Find the largest possible value of $n$.
|
Let $S$ denote the set of three-digit numbers that have digit sum equal to 9 and no digit equal to 0 . We will first find the cardinality of $S$. We start from the number 111 and each element of $S$ can be obtained from 111 by a string of 6 A's (which means that we add 1 to the current digit) and $2 G$ 's (which means go to the next digit). Then for example 324 can be obtained from 111 by the string AAGAGAAA. There are in total
$$
\frac{8!}{6!\cdot 2!}=28
$$
such words, so $S$ contains 28 numbers. Now, from the conditions (3), (4), (5), if $\overline{a b c}$ is in $T$ then each of the other numbers of the form $\overline{* c}$ cannot be in $T$, neither $\overline{* *}$ can be, nor $\overline{a * *}$. Since there are $a+b-2$ numbers of the first category, $a+c-2$ from the second and $b+c-2$ from the third one. In these three categories there are
$$
(a+b-2)+(b+c-2)+(c+a-2)=2(a+b+c)-6=2 \cdot 9-6=12
$$
distinct numbers that cannot be in $T$ if $\overline{a b c}$ is in $T$. So, if $T$ has $n$ numbers, then $12 n$ are the forbidden ones that are in $S$, but each number from $S$ can be a forbidden number no more than three times, once for each of its digits, so
$$
n+\frac{12 n}{3} \leq 28 \Longleftrightarrow n \leq \frac{28}{5}
$$
and since $n$ is an integer, we get $n \leq 5$. A possible example for $n=5$ is
$$
T=\{144,252,315,423,531\}
$$
Comment by PSC. It is classical to compute the cardinality of $S$ and this can be done in many ways. In general, the number of solutions of the equation
$$
x_{1}+x_{2}+\cdots+x_{k}=n
$$
in positive integers, where the order of $x_{i}$ matters, is well known that equals to $\binom{n-1}{k-1}$. In our case, we want to count the number of positive solutions to $a+b+c=9$. By the above, this equals to $\binom{9-1}{3-1}=28$. Using the general result above, we can also find that there are $a+b-2$ numbers of the form $\overline{* c}$.
|
{
"resource_path": "JBMO/segmented/en-official/en-jbmo_2018_solutions.jsonl",
"problem_match": "\nProblem 2.",
"solution_match": "\nSolution."
}
|
424dc650-a890-5da4-83d0-129ce12362d3
| 605,510
|
A $5 \times 100$ table is divided into 500 unit square cells, where $n$ of them are coloured black and the rest are coloured white. Two unit square cells are called adjacent if they share a common side. Each of the unit square cells has at most two adjacent black unit square cells. Find the largest possible value of $n$.
|
Alternative Solution. Consider the cells adjacent to all cells of the second and fourth row. Counting multiplicity, each cell in the first and fifth row is counted once, each cell in the third row twice, while each cell in the second and fourth row is also counted twice apart from their first and last cells which are counted only once.
So there are 204 cells counted once and 296 cells counted twice. Those cells contain, counting multiplicity, at most 400 black cells. Suppose $a$ of the cells have multiplicity one and $b$ of them have multiplicity 2 . Then $a+2 b \leqslant 400$ and $a \leqslant 204$. Thus
$$
2 a+2 b \leqslant 400+a \leqslant 604
$$
and so $a+b \leqslant 302$ as required.
Remark. The alternative solution shows that if we have equality, then all cells in the perimeter of the table except perhaps the two cells of the third row must be coloured black. No other cell in the second or fourth row can be coloured black as this will give a cell in the first or fifth row with at least three neighbouring black cells. For similar reasons we cannot colour black the second and last-but-one cell of the third row. So we must colour black all other cells of the third row and therefore the colouring is unique.
|
302
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
A $5 \times 100$ table is divided into 500 unit square cells, where $n$ of them are coloured black and the rest are coloured white. Two unit square cells are called adjacent if they share a common side. Each of the unit square cells has at most two adjacent black unit square cells. Find the largest possible value of $n$.
|
Alternative Solution. Consider the cells adjacent to all cells of the second and fourth row. Counting multiplicity, each cell in the first and fifth row is counted once, each cell in the third row twice, while each cell in the second and fourth row is also counted twice apart from their first and last cells which are counted only once.
So there are 204 cells counted once and 296 cells counted twice. Those cells contain, counting multiplicity, at most 400 black cells. Suppose $a$ of the cells have multiplicity one and $b$ of them have multiplicity 2 . Then $a+2 b \leqslant 400$ and $a \leqslant 204$. Thus
$$
2 a+2 b \leqslant 400+a \leqslant 604
$$
and so $a+b \leqslant 302$ as required.
Remark. The alternative solution shows that if we have equality, then all cells in the perimeter of the table except perhaps the two cells of the third row must be coloured black. No other cell in the second or fourth row can be coloured black as this will give a cell in the first or fifth row with at least three neighbouring black cells. For similar reasons we cannot colour black the second and last-but-one cell of the third row. So we must colour black all other cells of the third row and therefore the colouring is unique.
|
{
"resource_path": "JBMO/segmented/en-official/en-optimizedjbmo_2019_problems_and_solutions_english.jsonl",
"problem_match": "\nProblem 4.",
"solution_match": "\nSolution."
}
|
6eab0a66-f817-5540-b84f-4b01141aacdf
| 605,638
|
Let $a, b, c$ be positive real numbers such that $a+b+c=3$. Find the minimum value of the expression
$$
A=\frac{2-a^{3}}{a}+\frac{2-b^{3}}{b}+\frac{2-c^{3}}{c}
$$

$19^{\text {th }}$ Junior Balkan Mathematical Olympiad June 24-29, 2015, Belgrade, Serbia
|
We can rewrite $A$ as follows:
$$
\begin{aligned}
& A=\frac{2-a^{3}}{a}+\frac{2-b^{3}}{b}+\frac{2-c^{3}}{c}=2\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)-a^{2}-b^{2}-c^{2}= \\
& 2\left(\frac{a b+b c+c a}{a b c}\right)-\left(a^{2}+b^{2}+c^{2}\right)=2\left(\frac{a b+b c+c a}{a b c}\right)-\left((a+b+c)^{2}-2(a b+b c+c a)\right)= \\
& 2\left(\frac{a b+b c+c a}{a b c}\right)-(9-2(a b+b c+c a))=2\left(\frac{a b+b c+c a}{a b c}\right)+2(a b+b c+c a)-9= \\
& 2(a b+b c+c a)\left(\frac{1}{a b c}+1\right)-9
\end{aligned}
$$
Recall now the well-known inequality $(x+y+z)^{2} \geq 3(x y+y z+z x)$ and set $x=a b, y=b c, z=c a$, to obtain $(a b+b c+c a)^{2} \geq 3 a b c(a+b+c)=9 a b c$, where we have used $a+b+c=3$. By taking the square roots on both sides of the last one we obtain:
$$
a b+b c+c a \geq 3 \sqrt{a b c}
$$
Also by using AM-GM inequality we get that
$$
\frac{1}{a b c}+1 \geq 2 \sqrt{\frac{1}{a b c}}
$$
Multiplication of (1) and (2) gives:
$$
(a b+b c+c a)\left(\frac{1}{a b c}+1\right) \geq 3 \sqrt{a b c} \cdot 2 \sqrt{\frac{1}{a b c}}=6
$$
So $A \geq 2 \cdot 6-9=3$ and the equality holds if and only if $a=b=c=1$, so the minimum value is 3.
|
3
|
Yes
|
Yes
|
math-word-problem
|
Inequalities
|
Let $a, b, c$ be positive real numbers such that $a+b+c=3$. Find the minimum value of the expression
$$
A=\frac{2-a^{3}}{a}+\frac{2-b^{3}}{b}+\frac{2-c^{3}}{c}
$$

$19^{\text {th }}$ Junior Balkan Mathematical Olympiad June 24-29, 2015, Belgrade, Serbia
|
We can rewrite $A$ as follows:
$$
\begin{aligned}
& A=\frac{2-a^{3}}{a}+\frac{2-b^{3}}{b}+\frac{2-c^{3}}{c}=2\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)-a^{2}-b^{2}-c^{2}= \\
& 2\left(\frac{a b+b c+c a}{a b c}\right)-\left(a^{2}+b^{2}+c^{2}\right)=2\left(\frac{a b+b c+c a}{a b c}\right)-\left((a+b+c)^{2}-2(a b+b c+c a)\right)= \\
& 2\left(\frac{a b+b c+c a}{a b c}\right)-(9-2(a b+b c+c a))=2\left(\frac{a b+b c+c a}{a b c}\right)+2(a b+b c+c a)-9= \\
& 2(a b+b c+c a)\left(\frac{1}{a b c}+1\right)-9
\end{aligned}
$$
Recall now the well-known inequality $(x+y+z)^{2} \geq 3(x y+y z+z x)$ and set $x=a b, y=b c, z=c a$, to obtain $(a b+b c+c a)^{2} \geq 3 a b c(a+b+c)=9 a b c$, where we have used $a+b+c=3$. By taking the square roots on both sides of the last one we obtain:
$$
a b+b c+c a \geq 3 \sqrt{a b c}
$$
Also by using AM-GM inequality we get that
$$
\frac{1}{a b c}+1 \geq 2 \sqrt{\frac{1}{a b c}}
$$
Multiplication of (1) and (2) gives:
$$
(a b+b c+c a)\left(\frac{1}{a b c}+1\right) \geq 3 \sqrt{a b c} \cdot 2 \sqrt{\frac{1}{a b c}}=6
$$
So $A \geq 2 \cdot 6-9=3$ and the equality holds if and only if $a=b=c=1$, so the minimum value is 3.
|
{
"resource_path": "JBMO/segmented/en-official/en-solutions-english-jbmo2015.jsonl",
"problem_match": "\nProblem 2.",
"solution_match": "## Solution:"
}
|
2ead2ebf-68d2-529a-ab00-91d04415fda0
| 605,667
|
Consider an acute triangle $A B C$ with area S. Let $C D \perp A B \quad(D \in A B)$, $D M \perp A C \quad(M \in A C)$ and $\quad D N \perp B C \quad(N \in B C)$. Denote by $H_{1}$ and $H_{2}$ the orthocentres of the triangles $M N C$ and $M N D$ respectively. Find the area of the quadrilateral $\mathrm{AH}_{1} \mathrm{BH}_{2}$ in terms of $S$.
|
1. Let $O, P, K, R$ and $T$ be the mid-points of the segments $C D, M N$, $C N, C H_{1}$ and $M H_{1}$, respectively. From $\triangle M N C$ we have that $\overline{P K}=\frac{1}{2} \overline{M C}$ and $P K \| M C$. Analogously, from $\Delta M H_{1} C$ we have that $\overline{T R}=\frac{1}{2} \overline{M C}$ and $T R \| M C$. Consequently, $\overline{P K}=\overline{T R}$ and $P K \| T R$. Also $O K \| D N \quad$ (from
$\triangle C D N$ ) and since $D N \perp B C$ and $M H_{1} \perp B C$, it follows that $T H_{1} \| O K$. Since $O$ is the circumcenter of $\triangle C M N, O P \perp M N$. Thus, $C H_{1} \perp M N$ implies $O P \| C H_{1}$. We conclude $\triangle T R H_{1} \cong \triangle K P O \quad$ (they have parallel sides and $\overline{T R}=\overline{P K}$ ), hence $\overline{R H_{1}}=\overline{P O}$, i.e. $\overline{C H_{1}}=2 \overline{P O}$ and $C H_{1} \| P O$.
Analogously, $\overline{D H_{2}}=2 \overline{P O} \quad$ and $\quad D H_{2} \| P O$. From $\quad \overline{C H_{1}}=2 \overline{P O}=\overline{D H_{2}} \quad$ and $C H_{1}\|P O\| D H_{2}$ the quadrilateral $C H_{1} H_{2} D$ is a parallelogram, thus $\overline{H_{1} H_{2}}=\overline{C D}$ and $H_{1} H_{2} \| C D$. Therefore the area of the quadrilateral $A H_{1} B H_{2}$ is $\frac{\overline{A B} \cdot \overline{H_{1} H_{2}}}{2}=\frac{\overline{A B} \cdot \overline{C D}}{2}=S$.
Solution 2. Since $M H_{1} \| D N$ and $N H_{1} \| D M, M D N H_{1}$ is a parallelogram. Similarly, $N H_{2} \| C M$ and $M H_{2} \| C N$ imply $M C N H_{2}$ is a parallelogram . Let $P$ be the midpoint of the segment $\overline{M N}$. Then $\sigma_{P}(D)=H_{1}$ and $\sigma_{P}(C)=H_{2}$, thus $C D \| H_{1} H_{2}$ and $\overline{C D}=\overline{H_{1} H_{2}}$. From $C D \perp A B$ we deduce $A_{A H_{1} B H_{2}}=\frac{1}{2} \overline{A B} \cdot \overline{C D}=S$.
|
S
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Consider an acute triangle $A B C$ with area S. Let $C D \perp A B \quad(D \in A B)$, $D M \perp A C \quad(M \in A C)$ and $\quad D N \perp B C \quad(N \in B C)$. Denote by $H_{1}$ and $H_{2}$ the orthocentres of the triangles $M N C$ and $M N D$ respectively. Find the area of the quadrilateral $\mathrm{AH}_{1} \mathrm{BH}_{2}$ in terms of $S$.
|
1. Let $O, P, K, R$ and $T$ be the mid-points of the segments $C D, M N$, $C N, C H_{1}$ and $M H_{1}$, respectively. From $\triangle M N C$ we have that $\overline{P K}=\frac{1}{2} \overline{M C}$ and $P K \| M C$. Analogously, from $\Delta M H_{1} C$ we have that $\overline{T R}=\frac{1}{2} \overline{M C}$ and $T R \| M C$. Consequently, $\overline{P K}=\overline{T R}$ and $P K \| T R$. Also $O K \| D N \quad$ (from

$\triangle C D N$ ) and since $D N \perp B C$ and $M H_{1} \perp B C$, it follows that $T H_{1} \| O K$. Since $O$ is the circumcenter of $\triangle C M N, O P \perp M N$. Thus, $C H_{1} \perp M N$ implies $O P \| C H_{1}$. We conclude $\triangle T R H_{1} \cong \triangle K P O \quad$ (they have parallel sides and $\overline{T R}=\overline{P K}$ ), hence $\overline{R H_{1}}=\overline{P O}$, i.e. $\overline{C H_{1}}=2 \overline{P O}$ and $C H_{1} \| P O$.
Analogously, $\overline{D H_{2}}=2 \overline{P O} \quad$ and $\quad D H_{2} \| P O$. From $\quad \overline{C H_{1}}=2 \overline{P O}=\overline{D H_{2}} \quad$ and $C H_{1}\|P O\| D H_{2}$ the quadrilateral $C H_{1} H_{2} D$ is a parallelogram, thus $\overline{H_{1} H_{2}}=\overline{C D}$ and $H_{1} H_{2} \| C D$. Therefore the area of the quadrilateral $A H_{1} B H_{2}$ is $\frac{\overline{A B} \cdot \overline{H_{1} H_{2}}}{2}=\frac{\overline{A B} \cdot \overline{C D}}{2}=S$.
Solution 2. Since $M H_{1} \| D N$ and $N H_{1} \| D M, M D N H_{1}$ is a parallelogram. Similarly, $N H_{2} \| C M$ and $M H_{2} \| C N$ imply $M C N H_{2}$ is a parallelogram . Let $P$ be the midpoint of the segment $\overline{M N}$. Then $\sigma_{P}(D)=H_{1}$ and $\sigma_{P}(C)=H_{2}$, thus $C D \| H_{1} H_{2}$ and $\overline{C D}=\overline{H_{1} H_{2}}$. From $C D \perp A B$ we deduce $A_{A H_{1} B H_{2}}=\frac{1}{2} \overline{A B} \cdot \overline{C D}=S$.
|
{
"resource_path": "JBMO/segmented/en-official/en-solutions_en-jbmo2014.jsonl",
"problem_match": "\nProblem 2.",
"solution_match": "\nSolution "
}
|
29411fd8-582d-51e0-b4f9-b5b763f561ad
| 605,710
|
For a positive integer $n$, two players A and B play the following game: Given a pile of $s$ stones, the players take turn alternatively with A going first. On each turn the player is allowed to take either one stone, or a prime number of stones, or a multiple of $n$ stones. The winner is the one who takes the last stone. Assuming both $\mathrm{A}$ and $\mathrm{B}$ play perfectly, for how many values of $s$ the player A cannot win?
|
Denote by $k$ the sought number and let $\left\{s_{1}, \mathrm{~s}_{2}, \ldots, \mathrm{s}_{k}\right\}$ be the corresponding values for $s$. We call each $s_{i}$ a losing number and every other nonnegative integer a winning numbers.
## Clearly every multiple of $n$ is a winning number.
Suppose there are two different losing numbers $s_{i}>s_{j}$, which are congruent modulo $n$. Then, on his first turn of play, player $A$ may remove $s_{i}-s_{j}$ stones (since $n \mid s_{i}-s_{j}$ ), leaving a pile with $s_{j}$ stones for B. This is in contradiction with both $s_{i}$ and $s_{j}$ being losing numbers.
Hence, there are at most $n-1$ losing numbers, i.e. $k \leq n-1$.
Suppose there exists an integer $r \in\{1,2, \ldots, n-1\}$, such that $m n+r$ is a winning number for every $m \in \mathbb{N}_{0}$. Let us denote by $u$ the greatest losing number (if $k>0$ ) or 0 (if $k=0)$, and let $s=\operatorname{LCM}(2,3, \ldots, u+n+1)$. Note that all the numbers $s+2, s+3, \ldots$, $s+u+n+1 \quad$ are composite. Let $m^{\prime} \in \mathbb{N}_{0}$, be such that $s+u+2 \leq m^{\prime} n+r \leq s+u+n+1$. In order for $m^{\prime} n+r$ to be a winning number, there must exist an integer $p$, which is either one, or prime, or a positive multiple of $n$, such that $m^{\prime} n+r-p$ is a losing number or 0 , and hence lesser than or equal to $u$. Since $s+2 \leq m^{\prime} n+r-u \leq p \leq m^{\prime} n+r \leq s+u+n+1, p$ must be a composite, hence $p$ is a multiple of $n$ (say $p=q n$ ). But then $m^{\prime} n+r-p=\left(m^{\prime}-q\right) n+r$ must be a winning number, according to our assumption. This contradicts our assumption that all numbers $m n+r, m \in \mathbb{N}_{0}$ are winning.
Hence, each nonzero residue class modulo $n$ contains a loosing number.
There are exactly $n-1$ losing numbers .
Lemma: No pair $(u, n)$ of positive integers satisfies the following property:
$(*) \quad$ In $\mathbb{N}$ exists an arithmetic progression $\left(a_{t}\right)_{t=1}^{\infty}$ with difference $n$ such that each segment
$\left[a_{i}-u, a_{i}+u\right]$ contains a prime.
Proof of the lemma: Suppose such a pair $(u, n)$ and a corresponding arithmetic progression $\left(\mathrm{a}_{t}\right)_{t=1}^{\infty}$ exist. In $\mathbb{N}$ exist arbitrarily long patches of consecutive composites. Take such a patch $P$ of length $3 u n$. Then, at least one segment $\left[a_{i}-u, a_{i}+u\right]$ is fully contained in $P$, a contradiction.
Suppose such a nonzero residue class modulo $n$ exists (hence $n>1$ ). Let $u \in \mathbb{N}$ be greater than every loosing number. Consider the members of the supposed residue class which are greater than $u$. They form an arithmetic progression with the property $\left({ }^{*}\right)$, a contradiction (by the lemma).
|
n-1
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
For a positive integer $n$, two players A and B play the following game: Given a pile of $s$ stones, the players take turn alternatively with A going first. On each turn the player is allowed to take either one stone, or a prime number of stones, or a multiple of $n$ stones. The winner is the one who takes the last stone. Assuming both $\mathrm{A}$ and $\mathrm{B}$ play perfectly, for how many values of $s$ the player A cannot win?
|
Denote by $k$ the sought number and let $\left\{s_{1}, \mathrm{~s}_{2}, \ldots, \mathrm{s}_{k}\right\}$ be the corresponding values for $s$. We call each $s_{i}$ a losing number and every other nonnegative integer a winning numbers.
## Clearly every multiple of $n$ is a winning number.
Suppose there are two different losing numbers $s_{i}>s_{j}$, which are congruent modulo $n$. Then, on his first turn of play, player $A$ may remove $s_{i}-s_{j}$ stones (since $n \mid s_{i}-s_{j}$ ), leaving a pile with $s_{j}$ stones for B. This is in contradiction with both $s_{i}$ and $s_{j}$ being losing numbers.
Hence, there are at most $n-1$ losing numbers, i.e. $k \leq n-1$.
Suppose there exists an integer $r \in\{1,2, \ldots, n-1\}$, such that $m n+r$ is a winning number for every $m \in \mathbb{N}_{0}$. Let us denote by $u$ the greatest losing number (if $k>0$ ) or 0 (if $k=0)$, and let $s=\operatorname{LCM}(2,3, \ldots, u+n+1)$. Note that all the numbers $s+2, s+3, \ldots$, $s+u+n+1 \quad$ are composite. Let $m^{\prime} \in \mathbb{N}_{0}$, be such that $s+u+2 \leq m^{\prime} n+r \leq s+u+n+1$. In order for $m^{\prime} n+r$ to be a winning number, there must exist an integer $p$, which is either one, or prime, or a positive multiple of $n$, such that $m^{\prime} n+r-p$ is a losing number or 0 , and hence lesser than or equal to $u$. Since $s+2 \leq m^{\prime} n+r-u \leq p \leq m^{\prime} n+r \leq s+u+n+1, p$ must be a composite, hence $p$ is a multiple of $n$ (say $p=q n$ ). But then $m^{\prime} n+r-p=\left(m^{\prime}-q\right) n+r$ must be a winning number, according to our assumption. This contradicts our assumption that all numbers $m n+r, m \in \mathbb{N}_{0}$ are winning.
Hence, each nonzero residue class modulo $n$ contains a loosing number.
There are exactly $n-1$ losing numbers .
Lemma: No pair $(u, n)$ of positive integers satisfies the following property:
$(*) \quad$ In $\mathbb{N}$ exists an arithmetic progression $\left(a_{t}\right)_{t=1}^{\infty}$ with difference $n$ such that each segment
$\left[a_{i}-u, a_{i}+u\right]$ contains a prime.
Proof of the lemma: Suppose such a pair $(u, n)$ and a corresponding arithmetic progression $\left(\mathrm{a}_{t}\right)_{t=1}^{\infty}$ exist. In $\mathbb{N}$ exist arbitrarily long patches of consecutive composites. Take such a patch $P$ of length $3 u n$. Then, at least one segment $\left[a_{i}-u, a_{i}+u\right]$ is fully contained in $P$, a contradiction.
Suppose such a nonzero residue class modulo $n$ exists (hence $n>1$ ). Let $u \in \mathbb{N}$ be greater than every loosing number. Consider the members of the supposed residue class which are greater than $u$. They form an arithmetic progression with the property $\left({ }^{*}\right)$, a contradiction (by the lemma).
|
{
"resource_path": "JBMO/segmented/en-official/en-solutions_en-jbmo2014.jsonl",
"problem_match": "\nProblem 4.",
"solution_match": "\nSolution."
}
|
94e3fc1b-1f61-596d-a41c-fb975863eb54
| 605,755
|
Let $x, y$ be positive real numbers such that $x^{3}+y^{3} \leq x^{2}+y^{2}$. Find the greatest possible value of the product $x y$.
|
We have $(x+y)\left(x^{2}+y^{2}\right) \geq(x+y)\left(x^{3}+y^{3}\right) \geq\left(x^{2}+y^{2}\right)^{2}$, hence $x+y \geq x^{2}+y^{2}$. Now $2(x+y) \geq(1+1)\left(x^{2}+y^{2}\right) \geq(x+y)^{2}$, thus $2 \geq x+y$. Because $x+y \geq 2 \sqrt{x y}$, we will obtain $1 \geq x y$. Equality holds when $x=y=1$.
So the greatest possible value of the product $x y$ is 1 .
## Solution 2
By $A M-G M$ we have $x^{3}+y^{3} \geq \sqrt{x y} \cdot\left(x^{2}+y^{2}\right)$, hence $1 \geq \sqrt{x y}$ since $x^{2}+y^{2} \geq x^{3}+y^{3}$. Equality holds when $x=y=1$. So the greatest possible value of the product $x y$ is 1 .
|
1
|
Yes
|
Yes
|
math-word-problem
|
Inequalities
|
Let $x, y$ be positive real numbers such that $x^{3}+y^{3} \leq x^{2}+y^{2}$. Find the greatest possible value of the product $x y$.
|
We have $(x+y)\left(x^{2}+y^{2}\right) \geq(x+y)\left(x^{3}+y^{3}\right) \geq\left(x^{2}+y^{2}\right)^{2}$, hence $x+y \geq x^{2}+y^{2}$. Now $2(x+y) \geq(1+1)\left(x^{2}+y^{2}\right) \geq(x+y)^{2}$, thus $2 \geq x+y$. Because $x+y \geq 2 \sqrt{x y}$, we will obtain $1 \geq x y$. Equality holds when $x=y=1$.
So the greatest possible value of the product $x y$ is 1 .
## Solution 2
By $A M-G M$ we have $x^{3}+y^{3} \geq \sqrt{x y} \cdot\left(x^{2}+y^{2}\right)$, hence $1 \geq \sqrt{x y}$ since $x^{2}+y^{2} \geq x^{3}+y^{3}$. Equality holds when $x=y=1$. So the greatest possible value of the product $x y$ is 1 .
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-alg-20111.jsonl",
"problem_match": "\nA4 ",
"solution_match": "## Solution 1"
}
|
eccc7305-140c-5fb2-b49d-cda2f577f272
| 605,796
|
Can we divide an equilateral triangle $\triangle A B C$ into 2011 small triangles using 122 straight lines? (there should be 2011 triangles that are not themselves divided into smaller parts and there should be no polygons which are not triangles)
|
Firstly, for each side of the triangle, we draw 37 equidistant, parallel lines to it. In this way we get $38^{2}=1444$ triangles. Then we erase 11 lines which are closest to the vertex $A$ and parallel to the side $B C$ and we draw 21 lines perpendicular to $B C$, the first starting from the vertex $A$ and 10 on each of the two sides, the lines which are closest to the vertex $A$, distributed symmetrically. In this way we get $26 \cdot 21+10=$ 556 new triangles. Therefore we obtain a total of 2000 triangles and we have used $37 \cdot 3-11+21=121$ lines. Let $D$ be the $12^{\text {th }}$ point on side $A B$, starting from $B$ (including it). The perpendicular to $B C$ passing through $D$ will be the last line we draw. In this way we obtain the required configuration.
|
2011
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Can we divide an equilateral triangle $\triangle A B C$ into 2011 small triangles using 122 straight lines? (there should be 2011 triangles that are not themselves divided into smaller parts and there should be no polygons which are not triangles)
|
Firstly, for each side of the triangle, we draw 37 equidistant, parallel lines to it. In this way we get $38^{2}=1444$ triangles. Then we erase 11 lines which are closest to the vertex $A$ and parallel to the side $B C$ and we draw 21 lines perpendicular to $B C$, the first starting from the vertex $A$ and 10 on each of the two sides, the lines which are closest to the vertex $A$, distributed symmetrically. In this way we get $26 \cdot 21+10=$ 556 new triangles. Therefore we obtain a total of 2000 triangles and we have used $37 \cdot 3-11+21=121$ lines. Let $D$ be the $12^{\text {th }}$ point on side $A B$, starting from $B$ (including it). The perpendicular to $B C$ passing through $D$ will be the last line we draw. In this way we obtain the required configuration.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-combi-2011.jsonl",
"problem_match": "\nC2 ",
"solution_match": "## Solution"
}
|
934d42e4-4f40-5da8-ae50-ced409decfc3
| 605,869
|
We can change a natural number $n$ in three ways:
a) If the number $n$ has at least two digits, we erase the last digit and we subtract that digit from the remaining number (for example, from 123 we get $12-3=9$ );
b) If the last digit is different from 0 , we can change the order of the digits in the opposite one (for example, from 123 we get 321 );
c) We can multiply the number $n$ by a number from the set $\{1,2,3, \ldots, 2010\}$.
Can we get the number 21062011 from the number 1012011?
|
The answer is NO. We will prove that if the first number is divisible by 11, then all the numbers which we can get from $n$, are divisible by 11 . When we use $a$ ), from the number $10 a+b$, we will get the number $m=a-b=11 a-n$, so $11 \mid m$ since $11 \mid n$. It's well-known that a number is divisible by 11 if and only if the difference between sum of digits on even places and sum of digits on odd places is divisible by 11 . Hence, when we use $b$ ), from a number which is divisible by 11, we will get a number which is also divisible by 11 . When we use $c$ ), the obtained number remains divisible by 11 . So, the answer is NO since 1012011 is divisible by 11 and 21062011 is not.
|
NO
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
We can change a natural number $n$ in three ways:
a) If the number $n$ has at least two digits, we erase the last digit and we subtract that digit from the remaining number (for example, from 123 we get $12-3=9$ );
b) If the last digit is different from 0 , we can change the order of the digits in the opposite one (for example, from 123 we get 321 );
c) We can multiply the number $n$ by a number from the set $\{1,2,3, \ldots, 2010\}$.
Can we get the number 21062011 from the number 1012011?
|
The answer is NO. We will prove that if the first number is divisible by 11, then all the numbers which we can get from $n$, are divisible by 11 . When we use $a$ ), from the number $10 a+b$, we will get the number $m=a-b=11 a-n$, so $11 \mid m$ since $11 \mid n$. It's well-known that a number is divisible by 11 if and only if the difference between sum of digits on even places and sum of digits on odd places is divisible by 11 . Hence, when we use $b$ ), from a number which is divisible by 11, we will get a number which is also divisible by 11 . When we use $c$ ), the obtained number remains divisible by 11 . So, the answer is NO since 1012011 is divisible by 11 and 21062011 is not.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-combi-2011.jsonl",
"problem_match": "\nC3 ",
"solution_match": "\nSolution"
}
|
e1d7b93f-ae5b-57d1-a62c-fe0835456806
| 605,877
|
In a group of $n$ people, each one had a different ball. They performed a sequence of swaps; in each swap, two people swapped the ball they had at that moment. Each pair of people performed at least one swap. In the end each person had the ball he/she had at the start. Find the least possible number of swaps, if: $a$ ) $n=5$; b) $n=6$.
|
We will denote the people by $A, B, C, \ldots$ and their initial balls by the corresponding small letters. Thus the initial state is $A a, B b, C c, D d, E e(, F f)$. A swap is denoted by the (capital) letters of the people involved.
a) Five people form 10 pairs, so at least 10 swaps are necessary.
In fact, 10 swaps are sufficient:
Swap $A B$, then $B C$, then $C A$; the state is now $A a, B c, C b, D d, E e$.
Swap $A D$, then $D E$, then $E A$; the state is now $A a, B c, C b, D e, E d$.
Swap $B E$, then $C D$; the state is now $A a, B d, C e, D b, E c$.
Swap $B D$, then $C E$; the state is now $A a, B b, C c, D d, E e$.
All requirements are fulfilled now, so the answer is 10 .
b) Six people form 15 pairs, so at least 15 swaps are necessary. We will prove that the final number of swaps must be even. Call a pair formed by a ball and a person inverted if letter of the ball lies after letter of the person in the alphabet. Let $T$ be the number of inverted pairs; at the start we have $T=0$. Each swap changes $T$ by 1 , so it changes the parity of $T$. Since in the end $T=0$, the total number of swaps must be even. Hence, at least 16 swaps are necessary. In fact 16 swaps are sufficient:
Swap $A B$, then $B C$, then $C A$; the state is now $A a, B c, C b, D d, E e, F f$. Swap $A D$, then $D E$, then $E A$; the state is now $A a, B c, C b, D e, E d, F f$. Swap $F B$, then $B E$, then $E F$; the state is now $A a, B d, C b, D e, E c, F f$. Swap $F C$, then $C D$, then $D F$; the state is now $A a, B d, C e, D b, E c, F f$. Swap $B D$, then $C E$, then twice $A F$, the state is now $A a, B b, C c, D d, E e, F f$. All requirements are fulfilled now, so the answer is 16 .
|
10
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
In a group of $n$ people, each one had a different ball. They performed a sequence of swaps; in each swap, two people swapped the ball they had at that moment. Each pair of people performed at least one swap. In the end each person had the ball he/she had at the start. Find the least possible number of swaps, if: $a$ ) $n=5$; b) $n=6$.
|
We will denote the people by $A, B, C, \ldots$ and their initial balls by the corresponding small letters. Thus the initial state is $A a, B b, C c, D d, E e(, F f)$. A swap is denoted by the (capital) letters of the people involved.
a) Five people form 10 pairs, so at least 10 swaps are necessary.
In fact, 10 swaps are sufficient:
Swap $A B$, then $B C$, then $C A$; the state is now $A a, B c, C b, D d, E e$.
Swap $A D$, then $D E$, then $E A$; the state is now $A a, B c, C b, D e, E d$.
Swap $B E$, then $C D$; the state is now $A a, B d, C e, D b, E c$.
Swap $B D$, then $C E$; the state is now $A a, B b, C c, D d, E e$.
All requirements are fulfilled now, so the answer is 10 .
b) Six people form 15 pairs, so at least 15 swaps are necessary. We will prove that the final number of swaps must be even. Call a pair formed by a ball and a person inverted if letter of the ball lies after letter of the person in the alphabet. Let $T$ be the number of inverted pairs; at the start we have $T=0$. Each swap changes $T$ by 1 , so it changes the parity of $T$. Since in the end $T=0$, the total number of swaps must be even. Hence, at least 16 swaps are necessary. In fact 16 swaps are sufficient:
Swap $A B$, then $B C$, then $C A$; the state is now $A a, B c, C b, D d, E e, F f$. Swap $A D$, then $D E$, then $E A$; the state is now $A a, B c, C b, D e, E d, F f$. Swap $F B$, then $B E$, then $E F$; the state is now $A a, B d, C b, D e, E c, F f$. Swap $F C$, then $C D$, then $D F$; the state is now $A a, B d, C e, D b, E c, F f$. Swap $B D$, then $C E$, then twice $A F$, the state is now $A a, B b, C c, D d, E e, F f$. All requirements are fulfilled now, so the answer is 16 .
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-combi-2011.jsonl",
"problem_match": "\nC4 ",
"solution_match": "## Solution"
}
|
c36e183f-3765-529d-aac7-a63d824b6ffb
| 605,886
|
A set $S$ of natural numbers is called good, if for each element $x \in S, x$ does not divide the sum of the remaining numbers in $S$. Find the maximal possible number of elements of a good set which is a subset of the set $A=\{1,2,3, \ldots, 63\}$.
|
Let set $B$ be the good subset of $A$ which have the maximum number of elements. We can easily see that the number 1 does not belong to $B$ since 1 divides all natural numbers. Based on the property of divisibility, we know that $x$ divides the sum of the remaining numbers if and only if $x$ divides the sum of all numbers in the set $B$. If $B$ has exactly 62 elements, than $B=\{2,3,4, \ldots, 62\}$, but this set can't be good since the sum of its elements is 2015 which is divisible by 5 . Therefore $B$ has at most 61 elements. Now we are looking for the set, whose elements does not divide their sum, so the best way to do that is making a sum of elements be a prime number. $2+3+4+\ldots+63=2015$ and if we remove the number 4, we will obtain the prime number 2011. Hence the set $B=\{2,3,5,6,7, \ldots, 63\}$ is a good one. We conclude that our number is 61 .
|
61
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
A set $S$ of natural numbers is called good, if for each element $x \in S, x$ does not divide the sum of the remaining numbers in $S$. Find the maximal possible number of elements of a good set which is a subset of the set $A=\{1,2,3, \ldots, 63\}$.
|
Let set $B$ be the good subset of $A$ which have the maximum number of elements. We can easily see that the number 1 does not belong to $B$ since 1 divides all natural numbers. Based on the property of divisibility, we know that $x$ divides the sum of the remaining numbers if and only if $x$ divides the sum of all numbers in the set $B$. If $B$ has exactly 62 elements, than $B=\{2,3,4, \ldots, 62\}$, but this set can't be good since the sum of its elements is 2015 which is divisible by 5 . Therefore $B$ has at most 61 elements. Now we are looking for the set, whose elements does not divide their sum, so the best way to do that is making a sum of elements be a prime number. $2+3+4+\ldots+63=2015$ and if we remove the number 4, we will obtain the prime number 2011. Hence the set $B=\{2,3,5,6,7, \ldots, 63\}$ is a good one. We conclude that our number is 61 .
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-combi-2011.jsonl",
"problem_match": "\nC5 ",
"solution_match": "\nSolution"
}
|
deb0a48e-df4b-5712-b4d0-ec90783b6064
| 605,898
|
Let $n>3$ be a positive integer. An equilateral triangle $\triangle A B C$ is divided into $n^{2}$ smaller congruent equilateral triangles (with sides parallel to its sides).
Let $m$ be the number of rhombuses that contain two small equilateral triangles and $d$ the number of rhombuses that contain eight small equilateral triangles. Find the difference $m-d$ in terms of $n$.
|
We will count the rhombuses having their large diagonal perpendicular to one side of the large triangle, then we will multiply by 3 . So consider the horizontal side, and then the other $n-1$ horizontal dividing lines, plus a horizontal line through the apex. Index them by $1,2, \ldots, n$, from top down (the basis remains unindexed). Then each indexed $k$ line contains exactly $k$ nodes of this triangular lattice.
The top vertex of a rhombus containing two small triangles, and with its large diagonal vertical, may (and has to) a node of this triangular lattice found on the top $n-1$ lines, so there are $m=3[1+2+\ldots+(n-1)]=\frac{3 n(n-1)}{2}$ such rhombuses.
The top vertex of a rhombus containing eight small triangles, and with its large diagonal vertical, may (and has to) be a node of this triangular lattice found on the top $n-3$ lines, so there are $d=3[1+2+\cdots+(n-3)]=\frac{3(n-3)(n-2)}{2}$ such rhombuses. Finally we have $m-d=\frac{3}{2} \cdot\left(n^{2}-n-n^{2}+5 n-6\right)=6 n-9$.
|
6n-9
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Let $n>3$ be a positive integer. An equilateral triangle $\triangle A B C$ is divided into $n^{2}$ smaller congruent equilateral triangles (with sides parallel to its sides).
Let $m$ be the number of rhombuses that contain two small equilateral triangles and $d$ the number of rhombuses that contain eight small equilateral triangles. Find the difference $m-d$ in terms of $n$.
|
We will count the rhombuses having their large diagonal perpendicular to one side of the large triangle, then we will multiply by 3 . So consider the horizontal side, and then the other $n-1$ horizontal dividing lines, plus a horizontal line through the apex. Index them by $1,2, \ldots, n$, from top down (the basis remains unindexed). Then each indexed $k$ line contains exactly $k$ nodes of this triangular lattice.
The top vertex of a rhombus containing two small triangles, and with its large diagonal vertical, may (and has to) a node of this triangular lattice found on the top $n-1$ lines, so there are $m=3[1+2+\ldots+(n-1)]=\frac{3 n(n-1)}{2}$ such rhombuses.
The top vertex of a rhombus containing eight small triangles, and with its large diagonal vertical, may (and has to) be a node of this triangular lattice found on the top $n-3$ lines, so there are $d=3[1+2+\cdots+(n-3)]=\frac{3(n-3)(n-2)}{2}$ such rhombuses. Finally we have $m-d=\frac{3}{2} \cdot\left(n^{2}-n-n^{2}+5 n-6\right)=6 n-9$.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-combi-2011.jsonl",
"problem_match": "\nC6 ",
"solution_match": "## Solution"
}
|
0289f189-15fc-5af8-8091-1eaeb66fbe12
| 605,906
|
Inside the square $A B C D$, the equilateral triangle $\triangle A B E$ is constructed. Let $M$ be an interior point of the triangle $\triangle A B E$ such that $M B=\sqrt{2}, M C=\sqrt{6}, M D=\sqrt{5}$ and $M E=\sqrt{3}$. Find the area of the square $A B C D$.
|
Let $K, F, H, Z$ be the projections of point $M$ on the sides of the square.
Then by Pythagorean Theorem we can prove that $M A^{2}+M C^{2}=M B^{2}+M D^{2}$.
From the given condition we obtain $M A=1$.
With center $A$ and angle $60^{\circ}$, we rotate $\triangle A M E$, so we construct the triangle $A N B$.
Since $A M=A N$ and $\widehat{M A N}=60^{\circ}$, it follows that $\triangle A M N$ is equilateral and $M N=1$. Hence $\triangle B M N$ is right-angled because $B M^{2}+M N^{2}=B N^{2}$.
So $m(\widehat{B M A})=m(\widehat{B M N})+m(\widehat{A M N})=150^{\circ}$.
Applying Pythagorean Generalized Theorem in $\triangle A M B$, we get:
$A B^{2}=A M^{2}+B M^{2}-2 A M \cdot B M \cdot \cos 150^{\circ}=1+2+2 \sqrt{2} \cdot \sqrt{3}: 2=3+\sqrt{6}$.
We conclude that the area of the square $A B C D$ is $3+\sqrt{6}$.
|
3+\sqrt{6}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Inside the square $A B C D$, the equilateral triangle $\triangle A B E$ is constructed. Let $M$ be an interior point of the triangle $\triangle A B E$ such that $M B=\sqrt{2}, M C=\sqrt{6}, M D=\sqrt{5}$ and $M E=\sqrt{3}$. Find the area of the square $A B C D$.
|
Let $K, F, H, Z$ be the projections of point $M$ on the sides of the square.
Then by Pythagorean Theorem we can prove that $M A^{2}+M C^{2}=M B^{2}+M D^{2}$.
From the given condition we obtain $M A=1$.
With center $A$ and angle $60^{\circ}$, we rotate $\triangle A M E$, so we construct the triangle $A N B$.

Since $A M=A N$ and $\widehat{M A N}=60^{\circ}$, it follows that $\triangle A M N$ is equilateral and $M N=1$. Hence $\triangle B M N$ is right-angled because $B M^{2}+M N^{2}=B N^{2}$.
So $m(\widehat{B M A})=m(\widehat{B M N})+m(\widehat{A M N})=150^{\circ}$.
Applying Pythagorean Generalized Theorem in $\triangle A M B$, we get:
$A B^{2}=A M^{2}+B M^{2}-2 A M \cdot B M \cdot \cos 150^{\circ}=1+2+2 \sqrt{2} \cdot \sqrt{3}: 2=3+\sqrt{6}$.
We conclude that the area of the square $A B C D$ is $3+\sqrt{6}$.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-geome-2011.jsonl",
"problem_match": "\nG5 ",
"solution_match": "## Solution"
}
|
541ac522-7a97-578c-8c3f-80a80c0cac69
| 605,994
|
Natural numbers 1,2,3, .., 2003 are written in an arbitrary sequence $a_{1}, a_{2}, a_{3}, \ldots a_{2003}$. Let $b_{1}=1 a_{1}, b_{2}=2 a_{2}, b_{3}=3 a_{3}, \ldots, b_{2003}=2003 a_{2003}$, and $B$ be the maximum of the numbers $b_{1}, b_{2}, b_{3}, \ldots, b_{2003}$.
a) If $a_{1}=2003, a_{2}=2002, a_{3}=2001, \ldots, a_{2002}=2, a_{2003}=1$, find the value of $B$.
b) Prove that $B \geq 1002^{2}$.
|
a) Using the inequality between the arithmetical and geometrical mean, we obtain that $b_{n}=n(2004-n) \leq\left(\frac{n+(2004-n)}{2}\right)^{2}=1002^{2}$ for $n=1,2,3, \ldots, 2003$. The equality holds if and only if $n=2004-n$, i.e. $n=1002$. Therefore, $B=b_{1002}=1002 \times(2004-1002)=1002^{2}$. b) Let $a_{1}, a_{2}, a_{3}, \ldots a_{2003}$ be an arbitrary order of the numbers $1,2,3, \ldots, 2003$. First, we will show that numbers $1002,1003,1004, \ldots, 2003$ cannot occulpy the places numbered $1,2,3$, $\ldots, 1001$ only. Indeed, we have $(2003-1002)+1=1002$ numbers and 1002 places. This means that at least one of the numbers $1002,1003,1004, \ldots, 2003$, say $a_{m}$, lies on a place which number $m$ is greater than 1001 . Therefore, $B \geq m a \geq 1002 \times 1002=1002^{2}$.
|
1002^2
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Natural numbers 1,2,3, .., 2003 are written in an arbitrary sequence $a_{1}, a_{2}, a_{3}, \ldots a_{2003}$. Let $b_{1}=1 a_{1}, b_{2}=2 a_{2}, b_{3}=3 a_{3}, \ldots, b_{2003}=2003 a_{2003}$, and $B$ be the maximum of the numbers $b_{1}, b_{2}, b_{3}, \ldots, b_{2003}$.
a) If $a_{1}=2003, a_{2}=2002, a_{3}=2001, \ldots, a_{2002}=2, a_{2003}=1$, find the value of $B$.
b) Prove that $B \geq 1002^{2}$.
|
a) Using the inequality between the arithmetical and geometrical mean, we obtain that $b_{n}=n(2004-n) \leq\left(\frac{n+(2004-n)}{2}\right)^{2}=1002^{2}$ for $n=1,2,3, \ldots, 2003$. The equality holds if and only if $n=2004-n$, i.e. $n=1002$. Therefore, $B=b_{1002}=1002 \times(2004-1002)=1002^{2}$. b) Let $a_{1}, a_{2}, a_{3}, \ldots a_{2003}$ be an arbitrary order of the numbers $1,2,3, \ldots, 2003$. First, we will show that numbers $1002,1003,1004, \ldots, 2003$ cannot occulpy the places numbered $1,2,3$, $\ldots, 1001$ only. Indeed, we have $(2003-1002)+1=1002$ numbers and 1002 places. This means that at least one of the numbers $1002,1003,1004, \ldots, 2003$, say $a_{m}$, lies on a place which number $m$ is greater than 1001 . Therefore, $B \geq m a \geq 1002 \times 1002=1002^{2}$.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo-2003_shl.jsonl",
"problem_match": "\nCOM 2 ",
"solution_match": "\nSolution:"
}
|
c84be181-3b04-5916-a00b-bbe5ce245e5b
| 606,095
|
Is there a triangle whose area is $12 \mathrm{~cm}^{2}$ and whose perimeter is $12 \mathrm{~cm}$.
|
No. Let $\mathrm{r}$ be the radius of the inscribed circle. Then $12=6 \mathrm{r}$, i.e. $\mathrm{r}=2 \mathrm{~cm}$. But the area of the inscribed circle is $4 \pi>12$, and it is known that the area of any triangle is bigger than the area of its inscribed circle.
|
No
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Is there a triangle whose area is $12 \mathrm{~cm}^{2}$ and whose perimeter is $12 \mathrm{~cm}$.
|
No. Let $\mathrm{r}$ be the radius of the inscribed circle. Then $12=6 \mathrm{r}$, i.e. $\mathrm{r}=2 \mathrm{~cm}$. But the area of the inscribed circle is $4 \pi>12$, and it is known that the area of any triangle is bigger than the area of its inscribed circle.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo-2003_shl.jsonl",
"problem_match": "\nGEO 2.",
"solution_match": "\nSolution."
}
|
4ef1f283-1d1b-5ab0-9945-1fc7d44cc4f1
| 606,134
|
Find all four digit numbers A such that
$$
\frac{1}{3} A+2000=\frac{2}{3} \bar{A}
$$
where $\bar{A}$ is the number with the same digits as $A$, but written in opposite order. (For example, $\overline{1234}=4321$.)
|
Let $A=1000 a+100 b+10 c+d$. Then we obtain the equality
$$
\frac{1}{3}(1000 n+100 b+10 c+d)+2000=\frac{2}{3}(1000 d+100 c+10 b+a)
$$
ol
$$
1999 d+190 c=80 b+998 a+6000
$$
It is clear that $d$ is even digit and $d>2$. So we have to investigate three cases: (i) $d=4$ : (ii) $d=6$; (iii) $d=8$.
(i) If $d=4$. comparing the last digits in the upper equality we see that $a=2$ or $a=\overline{1}$.
If $a=2$ then $19 c=80$, which is possible only when $40=c=0$. Hence the number $4=2004$ satisfies the condition.
If $a=\overline{7}$ then $19 c-8 b=490$, which is impossible.
(ii) If $d=6$ then $190 c+5994=80 b+998$ r. Comparing the last digits we obtain tilat. $a=3$ or $a=8$.
If $a=3$ then $80 b+998 a<80 \cdot 9+1000 \cdot 3<5994$.
If $a=8$ then $306+998 a \geq 998 \cdot \delta=7984=5994+1990>599+190 c$.
(iii) If $d=8$ then $190 c+9992=80 b+998 a$. Now $80 b+998 a \leq 80 \cdot 9+998 \cdot 9=9702<$ $9992+190 c$
Hence we have the only solution $4=2004$.
|
2004
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Find all four digit numbers A such that
$$
\frac{1}{3} A+2000=\frac{2}{3} \bar{A}
$$
where $\bar{A}$ is the number with the same digits as $A$, but written in opposite order. (For example, $\overline{1234}=4321$.)
|
Let $A=1000 a+100 b+10 c+d$. Then we obtain the equality
$$
\frac{1}{3}(1000 n+100 b+10 c+d)+2000=\frac{2}{3}(1000 d+100 c+10 b+a)
$$
ol
$$
1999 d+190 c=80 b+998 a+6000
$$
It is clear that $d$ is even digit and $d>2$. So we have to investigate three cases: (i) $d=4$ : (ii) $d=6$; (iii) $d=8$.
(i) If $d=4$. comparing the last digits in the upper equality we see that $a=2$ or $a=\overline{1}$.
If $a=2$ then $19 c=80$, which is possible only when $40=c=0$. Hence the number $4=2004$ satisfies the condition.
If $a=\overline{7}$ then $19 c-8 b=490$, which is impossible.
(ii) If $d=6$ then $190 c+5994=80 b+998$ r. Comparing the last digits we obtain tilat. $a=3$ or $a=8$.
If $a=3$ then $80 b+998 a<80 \cdot 9+1000 \cdot 3<5994$.
If $a=8$ then $306+998 a \geq 998 \cdot \delta=7984=5994+1990>599+190 c$.
(iii) If $d=8$ then $190 c+9992=80 b+998 a$. Now $80 b+998 a \leq 80 \cdot 9+998 \cdot 9=9702<$ $9992+190 c$
Hence we have the only solution $4=2004$.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo-2004_shl.jsonl",
"problem_match": "\nNT2.",
"solution_match": "\nSolution."
}
|
1aad75df-fc45-5065-b142-290c6f4d347a
| 606,202
|
Let $p_{1}, p_{2}, \ldots, p_{2005}$ be different prime numbers. Let $\mathrm{S}$ be a set of natural numbers which elements have the property that their simple divisors are some of the numbers $p_{1}, p_{2}, \ldots, p_{2005}$ and product of any two elements from $\mathrm{S}$ is not perfect square.
What is the maximum number of elements in $\mathrm{S}$ ?
|
Let $a, b$ be two arbitrary numbers from $\mathrm{S}$. They can be written as
$$
a=p_{1}^{a_{1}} p_{2}^{a_{2}} \cdots p_{2005}^{a_{2005}} \text { and } b=p_{1}^{\beta_{1}} p_{2}^{\beta_{2}} \cdots p_{2005}^{\beta_{2005}}
$$
In order for the product of the elements $a$ and $b$ to be a square all the sums of the corresponding exponents need to be even from where we can conclude that for every $i, a_{i}$ and $\beta_{i}$ have the same parity. If we replace all exponents of $\mathrm{a}$ and $b$ by their remainders modulo 2 , then we get two numbers $a^{\prime}, b^{\prime}$ whose product is a perfect square if and only if ab is a perfect square.
In order for the product $a^{\prime} b^{\prime}$ not to be a perfect square, at least one pair of the corresponding exponents modulo 2, need to be of opposite parity.
Since we form 2005 such pairs modulo 2, and each number in these pairs is 1 or 2 , we conclude that we can obtain $2^{2005}$ distinct products none of which is a perfect square.
Now if we are given $2^{2005}+1$ numbers, thanks to Dirichlet's principle, there are at least two with the same sequence of modulo 2 exponents, thus giving a product equal to a square.
So, the maximal number of the elements of $S$ is $2^{2005}$.
|
2^{2005}
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Let $p_{1}, p_{2}, \ldots, p_{2005}$ be different prime numbers. Let $\mathrm{S}$ be a set of natural numbers which elements have the property that their simple divisors are some of the numbers $p_{1}, p_{2}, \ldots, p_{2005}$ and product of any two elements from $\mathrm{S}$ is not perfect square.
What is the maximum number of elements in $\mathrm{S}$ ?
|
Let $a, b$ be two arbitrary numbers from $\mathrm{S}$. They can be written as
$$
a=p_{1}^{a_{1}} p_{2}^{a_{2}} \cdots p_{2005}^{a_{2005}} \text { and } b=p_{1}^{\beta_{1}} p_{2}^{\beta_{2}} \cdots p_{2005}^{\beta_{2005}}
$$
In order for the product of the elements $a$ and $b$ to be a square all the sums of the corresponding exponents need to be even from where we can conclude that for every $i, a_{i}$ and $\beta_{i}$ have the same parity. If we replace all exponents of $\mathrm{a}$ and $b$ by their remainders modulo 2 , then we get two numbers $a^{\prime}, b^{\prime}$ whose product is a perfect square if and only if ab is a perfect square.
In order for the product $a^{\prime} b^{\prime}$ not to be a perfect square, at least one pair of the corresponding exponents modulo 2, need to be of opposite parity.
Since we form 2005 such pairs modulo 2, and each number in these pairs is 1 or 2 , we conclude that we can obtain $2^{2005}$ distinct products none of which is a perfect square.
Now if we are given $2^{2005}+1$ numbers, thanks to Dirichlet's principle, there are at least two with the same sequence of modulo 2 exponents, thus giving a product equal to a square.
So, the maximal number of the elements of $S$ is $2^{2005}$.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo-2005_shl.jsonl",
"problem_match": "\nC4.",
"solution_match": "## Solution"
}
|
a6fd72fd-23ad-5410-b74c-18da4dcccafd
| 604,419
|
The nonnegative integer $n$ and $(2 n+1) \times(2 n+1)$ chessboard with squares colored alternatively black and white are given. For every natural number $m$ with $1<m<2 n+1$, an $m \times m$ square of the given chessboard that has more than half of its area colored in black, is called a $B$-square. If the given chessboard is a $B$-square, find in terms of $n$ the total number of $B$-squares of this chessboard.
|
Every square with even side length will have an equal number of black and white $1 \times 1$ squares, so it isn't a $B$-square. In a square with odd side length, there is one more $1 \times 1$ black square than white squares, if it has black corner squares. So, a square with odd side length is a $B$-square either if it is a $1 \times 1$ black square or it has black corners.
Let the given $(2 n+1) \times(2 n+1)$ chessboard be a $B$-square and denote by $b_{i}(i=$ $1,2, \ldots, n+1)$ the lines of the chessboard, which have $n+1$ black $1 \times 1$ squares, by $w_{i}(i=1,2, \ldots, n)$ the lines of the chessboard, which have $n$ black $1 \times 1$ squares and by $T_{m}(m=1,3,5, \ldots, 2 n-1,2 n+1)$ the total number of $B$-squares of dimension $m \times m$ of the given chessboard.
For $T_{1}$ we obtain $T_{1}=(n+1)(n+1)+n \cdot n=(n+1)^{2}+n^{2}$.
For computing $T_{3}$ we observe that there are $n 3 \times 3 B$-squares, which have the black corners on each pair of lines $\left(b_{i}, b_{i+1}\right)$ for $i=1,2, \ldots, n$ and there are $n-13 \times 3 B$-squares, which have the black corners on each pair of lines $\left(w_{i}, w_{i+1}\right)$ for $i=1,2, \ldots, n-1$. So, we have
$$
T_{3}=n \cdot n+(n-1)(n-1)=n^{2}+(n-1)^{2} \text {. }
$$
By using similar arguments for each pair of lines $\left(b_{i}, b_{i+2}\right)$ for $i=1,2, \ldots, n-1$ and for each pair of lines $\left(w_{i}, w_{i+2}\right)$ for $i=1,2, \ldots, n-2$ we compute
$$
T_{5}=(n-1)(n-1)+(n-2)(n-2)=(n-1)^{2}+(n-2)^{2}
$$
Step by step, we obtain
$$
\begin{gathered}
T_{7}=(n-2)(n-2)+(n-3)(n-3)=(n-2)^{2}+(n-3)^{2} \\
\ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \\
T_{2 n-1}=2 \cdot 2+1 \cdot 1=2^{2}+1^{2} \\
T_{2 n+1}=1 \cdot 1=1^{2}
\end{gathered}
$$
The total number of $B$-squares of the given chessboard equals to
$$
\begin{gathered}
T_{1}+T_{3}+T_{5}+\ldots+T_{2 n+1}=2\left(1^{2}+2^{2}+\ldots+n^{2}\right)+(n+1)^{2}= \\
\frac{n(n+1)(2 n+1)}{3}+(n+1)^{2}=\frac{(n+1)\left(2 n^{2}+4 n+3\right)}{3}
\end{gathered}
$$
The problem is solved.
### 2.3 Geometry
|
\frac{(n+1)\left(2 n^{2}+4 n+3\right)}{3}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
The nonnegative integer $n$ and $(2 n+1) \times(2 n+1)$ chessboard with squares colored alternatively black and white are given. For every natural number $m$ with $1<m<2 n+1$, an $m \times m$ square of the given chessboard that has more than half of its area colored in black, is called a $B$-square. If the given chessboard is a $B$-square, find in terms of $n$ the total number of $B$-squares of this chessboard.
|
Every square with even side length will have an equal number of black and white $1 \times 1$ squares, so it isn't a $B$-square. In a square with odd side length, there is one more $1 \times 1$ black square than white squares, if it has black corner squares. So, a square with odd side length is a $B$-square either if it is a $1 \times 1$ black square or it has black corners.
Let the given $(2 n+1) \times(2 n+1)$ chessboard be a $B$-square and denote by $b_{i}(i=$ $1,2, \ldots, n+1)$ the lines of the chessboard, which have $n+1$ black $1 \times 1$ squares, by $w_{i}(i=1,2, \ldots, n)$ the lines of the chessboard, which have $n$ black $1 \times 1$ squares and by $T_{m}(m=1,3,5, \ldots, 2 n-1,2 n+1)$ the total number of $B$-squares of dimension $m \times m$ of the given chessboard.
For $T_{1}$ we obtain $T_{1}=(n+1)(n+1)+n \cdot n=(n+1)^{2}+n^{2}$.
For computing $T_{3}$ we observe that there are $n 3 \times 3 B$-squares, which have the black corners on each pair of lines $\left(b_{i}, b_{i+1}\right)$ for $i=1,2, \ldots, n$ and there are $n-13 \times 3 B$-squares, which have the black corners on each pair of lines $\left(w_{i}, w_{i+1}\right)$ for $i=1,2, \ldots, n-1$. So, we have
$$
T_{3}=n \cdot n+(n-1)(n-1)=n^{2}+(n-1)^{2} \text {. }
$$
By using similar arguments for each pair of lines $\left(b_{i}, b_{i+2}\right)$ for $i=1,2, \ldots, n-1$ and for each pair of lines $\left(w_{i}, w_{i+2}\right)$ for $i=1,2, \ldots, n-2$ we compute
$$
T_{5}=(n-1)(n-1)+(n-2)(n-2)=(n-1)^{2}+(n-2)^{2}
$$
Step by step, we obtain
$$
\begin{gathered}
T_{7}=(n-2)(n-2)+(n-3)(n-3)=(n-2)^{2}+(n-3)^{2} \\
\ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \\
T_{2 n-1}=2 \cdot 2+1 \cdot 1=2^{2}+1^{2} \\
T_{2 n+1}=1 \cdot 1=1^{2}
\end{gathered}
$$
The total number of $B$-squares of the given chessboard equals to
$$
\begin{gathered}
T_{1}+T_{3}+T_{5}+\ldots+T_{2 n+1}=2\left(1^{2}+2^{2}+\ldots+n^{2}\right)+(n+1)^{2}= \\
\frac{n(n+1)(2 n+1)}{3}+(n+1)^{2}=\frac{(n+1)\left(2 n^{2}+4 n+3\right)}{3}
\end{gathered}
$$
The problem is solved.
### 2.3 Geometry
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo-2007_shl.jsonl",
"problem_match": "\nC3 ",
"solution_match": "## Solution"
}
|
5ceccb38-1871-5182-89a0-e454b98c47a3
| 604,519
|
Consider an integer $n \geq 4$ and a sequence of real numbers $x_{1}, x_{2}, x_{3}, \ldots, x_{n}$. An operation consists in eliminating all numbers not having the rank of the form $4 k+3$, thus leaving only the numbers $x_{3}, x_{7}, x_{11}, \ldots$ (for example, the sequence $4,5,9,3,6,6,1,8$ produces the sequence 9,1 . Upon the sequence $1,2,3, \ldots, 1024$ the operation is performed successively for 5 times. Show that at the end only 1 number remains and find this number.
|
After the first operation 256 number remain; after the second one, 64 are left, then 16, next 4 and ultimately only one number.
Notice that the 256 numbers left after the first operation are $3,7, \ldots, 1023$, hence they are in arithmetical progression of common difference 4. Successively, the 64 numbers left after the second operation are in arithmetical progression of ratio 16 and so on.
Let $a_{1}, a_{2}, a_{3}, a_{4}, a_{5}$ be the first term in the 5 sequences obtained after each of the 5 operations. Thus $a_{1}=3$ and $a_{5}$ is the requested number. The sequence before the fifth operation has 4 numbers, namely
$$
a_{4}, a_{4}+256, a_{4}+512, a_{4}+768
$$
and $a_{5}=a_{4}+512$. Similarly, $a_{4}=a_{3}+128, a_{3}=a_{2}+32, a_{2}=a_{1}+8$.
Summing up yields $a_{5}=a_{1}+8+32+128+512=3+680=683$.
### 2.2 Combinatorics
|
683
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Consider an integer $n \geq 4$ and a sequence of real numbers $x_{1}, x_{2}, x_{3}, \ldots, x_{n}$. An operation consists in eliminating all numbers not having the rank of the form $4 k+3$, thus leaving only the numbers $x_{3}, x_{7}, x_{11}, \ldots$ (for example, the sequence $4,5,9,3,6,6,1,8$ produces the sequence 9,1 . Upon the sequence $1,2,3, \ldots, 1024$ the operation is performed successively for 5 times. Show that at the end only 1 number remains and find this number.
|
After the first operation 256 number remain; after the second one, 64 are left, then 16, next 4 and ultimately only one number.
Notice that the 256 numbers left after the first operation are $3,7, \ldots, 1023$, hence they are in arithmetical progression of common difference 4. Successively, the 64 numbers left after the second operation are in arithmetical progression of ratio 16 and so on.
Let $a_{1}, a_{2}, a_{3}, a_{4}, a_{5}$ be the first term in the 5 sequences obtained after each of the 5 operations. Thus $a_{1}=3$ and $a_{5}$ is the requested number. The sequence before the fifth operation has 4 numbers, namely
$$
a_{4}, a_{4}+256, a_{4}+512, a_{4}+768
$$
and $a_{5}=a_{4}+512$. Similarly, $a_{4}=a_{3}+128, a_{3}=a_{2}+32, a_{2}=a_{1}+8$.
Summing up yields $a_{5}=a_{1}+8+32+128+512=3+680=683$.
### 2.2 Combinatorics
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo-2008_shl.jsonl",
"problem_match": "\nA9 ",
"solution_match": "## Solution"
}
|
3955bef6-893d-5268-9961-2a59c13b74f4
| 604,731
|
The vertices $A$ and $B$ of an equilateral $\triangle A B C$ lie on a circle $k$ of radius 1 , and the vertex $C$ is inside $k$. The point $D \neq B$ lies on $k, A D=A B$ and the line $D C$ intersects $k$ for the second time in point $E$. Find the length of the segment $C E$.
|
As $A D=A C, \triangle C D A$ is isosceles. If $\varangle A D C=\varangle A C D=\alpha$ and $\varangle B C E=\beta$, then $\beta=120^{\circ}-\alpha$. The quadrilateral $A B E D$ is cyclic, so $\varangle A B E=180^{\circ}-\alpha$. Then $\varangle C B E=$ $120^{\circ}-\alpha$ so $\varangle C B E=\beta$. Thus $\triangle C B E$ is isosceles, so $A E$ is the perpendicular bisector of $B C$, so it bisects $\varangle B A C$. Now the arc $B E$ is intercepted by a $30^{\circ}$ inscribed angle, so it measures $60^{\circ}$. Then $B E$ equals the radius of $k$, namely 1 . Hence $C E=B E=1$.
|
1
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
The vertices $A$ and $B$ of an equilateral $\triangle A B C$ lie on a circle $k$ of radius 1 , and the vertex $C$ is inside $k$. The point $D \neq B$ lies on $k, A D=A B$ and the line $D C$ intersects $k$ for the second time in point $E$. Find the length of the segment $C E$.
|
As $A D=A C, \triangle C D A$ is isosceles. If $\varangle A D C=\varangle A C D=\alpha$ and $\varangle B C E=\beta$, then $\beta=120^{\circ}-\alpha$. The quadrilateral $A B E D$ is cyclic, so $\varangle A B E=180^{\circ}-\alpha$. Then $\varangle C B E=$ $120^{\circ}-\alpha$ so $\varangle C B E=\beta$. Thus $\triangle C B E$ is isosceles, so $A E$ is the perpendicular bisector of $B C$, so it bisects $\varangle B A C$. Now the arc $B E$ is intercepted by a $30^{\circ}$ inscribed angle, so it measures $60^{\circ}$. Then $B E$ equals the radius of $k$, namely 1 . Hence $C E=B E=1$.

|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo-2008_shl.jsonl",
"problem_match": "\nG3 ",
"solution_match": "## Solution"
}
|
cec3c9c7-be58-558e-838b-8d1904f6a0c0
| 604,830
|
Let $A B C$ be an isosceles triangle with $A C=B C$. The point $D$ lies on the side $A B$ such that the semicircle with diameter $[B D]$ and center $O$ is tangent to the side $A C$ in the point $P$ and intersects the side $B C$ at the point $Q$. The radius $O P$ intersects the chord $D Q$ at the point $E$ such that $5 \cdot P E=3 \cdot D E$. Find the ratio $\frac{A B}{B C}$.
|
We denote $O P=O D=O B=R, A C=B C=b$ and $A B=2 a$. Because $O P \perp A C$ and $D Q \perp B C$, then the right triangles $A P O$ and $B Q D$ are similar and $\varangle B D Q=\varangle A O P$. So, the triangle $D E O$ is isosceles with $D E=O E$. It follows that
$$
\frac{P E}{D E}=\frac{P E}{O E}=\frac{3}{5}
$$
Let $F$ and $G$ are the orthogonal projections of the points $E$ and $P$ respectively on the side $A B$ and $M$ is the midpoint of the side $[A B]$. The triangles $O F E, O G P, O P A$ and $C M A$ are similar. We obtain the following relations
$$
\frac{O F}{O E}=\frac{O G}{O P}=\frac{C M}{A C}=\frac{O P}{O A}
$$
But $C M=\sqrt{b^{2}-a^{2}}$ and we have $O G=\frac{R}{b} \cdot \sqrt{b^{2}-a^{2}}$. In isosceles triangle $D E O$ the point $F$ is the midpoint of the radius $D O$. So, $O F=R / 2$. By using Thales' theorem we obtain
$$
\frac{3}{5}=\frac{P E}{O E}=\frac{G F}{O F}=\frac{O G-O F}{O F}=\frac{O G}{O F}-1=2 \cdot \sqrt{1-\left(\frac{a}{b}\right)^{2}}-1
$$
From the last relations it is easy to obtain that $\frac{a}{b}=\frac{3}{5}$ and $\frac{A B}{B C}=\frac{6}{5}$.
The problem is solved.
|
\frac{6}{5}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $A B C$ be an isosceles triangle with $A C=B C$. The point $D$ lies on the side $A B$ such that the semicircle with diameter $[B D]$ and center $O$ is tangent to the side $A C$ in the point $P$ and intersects the side $B C$ at the point $Q$. The radius $O P$ intersects the chord $D Q$ at the point $E$ such that $5 \cdot P E=3 \cdot D E$. Find the ratio $\frac{A B}{B C}$.
|
We denote $O P=O D=O B=R, A C=B C=b$ and $A B=2 a$. Because $O P \perp A C$ and $D Q \perp B C$, then the right triangles $A P O$ and $B Q D$ are similar and $\varangle B D Q=\varangle A O P$. So, the triangle $D E O$ is isosceles with $D E=O E$. It follows that
$$
\frac{P E}{D E}=\frac{P E}{O E}=\frac{3}{5}
$$
Let $F$ and $G$ are the orthogonal projections of the points $E$ and $P$ respectively on the side $A B$ and $M$ is the midpoint of the side $[A B]$. The triangles $O F E, O G P, O P A$ and $C M A$ are similar. We obtain the following relations
$$
\frac{O F}{O E}=\frac{O G}{O P}=\frac{C M}{A C}=\frac{O P}{O A}
$$
But $C M=\sqrt{b^{2}-a^{2}}$ and we have $O G=\frac{R}{b} \cdot \sqrt{b^{2}-a^{2}}$. In isosceles triangle $D E O$ the point $F$ is the midpoint of the radius $D O$. So, $O F=R / 2$. By using Thales' theorem we obtain
$$
\frac{3}{5}=\frac{P E}{O E}=\frac{G F}{O F}=\frac{O G-O F}{O F}=\frac{O G}{O F}-1=2 \cdot \sqrt{1-\left(\frac{a}{b}\right)^{2}}-1
$$
From the last relations it is easy to obtain that $\frac{a}{b}=\frac{3}{5}$ and $\frac{A B}{B C}=\frac{6}{5}$.
The problem is solved.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo-2008_shl.jsonl",
"problem_match": "\nG7 ",
"solution_match": "## Solution"
}
|
ff38383a-c8d3-59a7-b4fe-8382082291c5
| 604,882
|
Let $s(a)$ denote the sum of digits of a given positive integer $a$. The sequence $a_{1}, a_{2}, \ldots a_{n}, \ldots$ of positive integers is such that $a_{n+1}=a_{n}+s\left(a_{n}\right)$ for each positive integer $n$. Find the greatest possible $n$ for which it is possible to have $a_{n}=2008$.
|
Since $a_{n-1} \equiv s\left(a_{n-1}\right)$ (all congruences are modulo 9 ), we have $2 a_{n-1} \equiv a_{n} \equiv 2008 \equiv 10$, so $a_{n-1} \equiv 5$. But $a_{n-1}<2008$, so $s\left(a_{n-1}\right) \leq 28$ and thus $s\left(a_{n-1}\right)$ can equal 5,14 or 23 . We check $s(2008-5)=s(2003)=5, s(2008-14)=s(1994)=23, s(2008-23)=s(1985)=$ 23. Thus $a_{n-1}$ can equal 1985 or 2003 . As above $2 a_{n-2} \equiv a_{n-1} \equiv 5 \equiv 14$, so $a_{n-2} \equiv 7$. But $a_{n-2}<2003$, so $s\left(a_{n-2}\right) \leq 28$ and thus $s\left(a_{n-2}\right)$ can equal 16 or 25 . Checking as above we see that the only possibility is $s(2003-25)=s(1978)=25$. Thus $a_{n-2}$ can be only 1978. Now $2 a_{n-3} \equiv a_{n-2} \equiv 7 \equiv 16$ and $a_{n-3} \equiv 8$. But $s\left(a_{n-3}\right) \leq 27$ and thus $s\left(a_{n-3}\right)$ can equal 17 or 26 . The check works only for $s(1978-17)=s(1961)=17$. Thus $a_{n-3}=1961$ and similarly $a_{n-4}=1939 \equiv 4, a_{n-5}=1919 \equiv 2$ (if they exist). The search for $a_{n-6}$ requires a residue of 1 . But $a_{n-6}<1919$, so $s\left(a_{n-6}\right) \leq 27$ and thus $s\left(a_{n-6}\right)$ can be equal only to 10 or 19 . The check fails for both $s(1919-10)=s(1909)=19$ and $s(1919-19)=s(1900)=10$. Thus $n \leq 6$ and the case $n=6$ is constructed above (1919, 1939, 1961, 1978, 2003, 2008).
|
6
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Let $s(a)$ denote the sum of digits of a given positive integer $a$. The sequence $a_{1}, a_{2}, \ldots a_{n}, \ldots$ of positive integers is such that $a_{n+1}=a_{n}+s\left(a_{n}\right)$ for each positive integer $n$. Find the greatest possible $n$ for which it is possible to have $a_{n}=2008$.
|
Since $a_{n-1} \equiv s\left(a_{n-1}\right)$ (all congruences are modulo 9 ), we have $2 a_{n-1} \equiv a_{n} \equiv 2008 \equiv 10$, so $a_{n-1} \equiv 5$. But $a_{n-1}<2008$, so $s\left(a_{n-1}\right) \leq 28$ and thus $s\left(a_{n-1}\right)$ can equal 5,14 or 23 . We check $s(2008-5)=s(2003)=5, s(2008-14)=s(1994)=23, s(2008-23)=s(1985)=$ 23. Thus $a_{n-1}$ can equal 1985 or 2003 . As above $2 a_{n-2} \equiv a_{n-1} \equiv 5 \equiv 14$, so $a_{n-2} \equiv 7$. But $a_{n-2}<2003$, so $s\left(a_{n-2}\right) \leq 28$ and thus $s\left(a_{n-2}\right)$ can equal 16 or 25 . Checking as above we see that the only possibility is $s(2003-25)=s(1978)=25$. Thus $a_{n-2}$ can be only 1978. Now $2 a_{n-3} \equiv a_{n-2} \equiv 7 \equiv 16$ and $a_{n-3} \equiv 8$. But $s\left(a_{n-3}\right) \leq 27$ and thus $s\left(a_{n-3}\right)$ can equal 17 or 26 . The check works only for $s(1978-17)=s(1961)=17$. Thus $a_{n-3}=1961$ and similarly $a_{n-4}=1939 \equiv 4, a_{n-5}=1919 \equiv 2$ (if they exist). The search for $a_{n-6}$ requires a residue of 1 . But $a_{n-6}<1919$, so $s\left(a_{n-6}\right) \leq 27$ and thus $s\left(a_{n-6}\right)$ can be equal only to 10 or 19 . The check fails for both $s(1919-10)=s(1909)=19$ and $s(1919-19)=s(1900)=10$. Thus $n \leq 6$ and the case $n=6$ is constructed above (1919, 1939, 1961, 1978, 2003, 2008).
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo-2008_shl.jsonl",
"problem_match": "\nNT3 ",
"solution_match": "## Solution"
}
|
ab7da857-3ed8-5d1c-8a78-d27658a1a81b
| 604,976
|
Let $f: \mathbb{N} \rightarrow \mathbb{R}$ be a function, satisfying the following condition:
for every integer $n>1$, there exists a prime divisor $p$ of $n$ such that $f(n)=f\left(\frac{n}{p}\right)-f(p)$. If
$$
f\left(2^{2007}\right)+f\left(3^{2008}\right)+f\left(5^{2009}\right)=2006
$$
determine the value of
$$
f\left(2007^{2}\right)+f\left(2008^{3}\right)+f\left(2009^{5}\right)
$$
|
If $n=p$ is prime number, we have
$$
f(p)=f\left(\frac{p}{p}\right)-f(p)=f(1)-f(p)
$$
i.e.
$$
f(p)=\frac{f(1)}{2}
$$
If $n=p q$, where $p$ and $q$ are prime numbers, then
$$
f(n)=f\left(\frac{n}{p}\right)-f(p)=f(q)-f(p)=\frac{f(1)}{2}-\frac{f(1)}{2}=0
$$
If $n$ is a product of three prime numbers, we have
$$
f(n)=f\left(\frac{n}{p}\right)-f(p)=0-f(p)=-f(p)=-\frac{f(1)}{2}
$$
With mathematical induction by a number of prime multipliers we shell prove that: if $n$ is a product of $k$ prime numbers then
$$
f(n)=(2-k) \frac{f(1)}{2}
$$
For $k=1$, clearly the statement (2), holds.
Let statement (2) holds for all integers $n$, where $n$ is a product of $k$ prime numbers.
Now let $n$ be a product of $k+1$ prime numbers. Then we have $n=n_{1} p$, where $n_{1}$ is a product of $k$ prime numbers.
So
$$
f(n)=f\left(\frac{n}{p}\right)-f(p)=f\left(n_{1}\right)-f(p)=(2-k) \frac{f(1)}{2}-\frac{f(1)}{2}=(2-(k+1)) \frac{f(1)}{2}
$$
So (2) holds for every integer $n>1$.
Now from $f\left(2^{2007}\right)+f\left(3^{2008}\right)+f\left(5^{2009}\right)=2006$ and because of (2) we have
$$
\begin{aligned}
2006 & =f\left(2^{2007}\right)+f\left(3^{2008}\right)+f\left(5^{2009}\right) \\
& =\frac{2-2007}{2} f(1)+\frac{2-2008}{2} f(1)+\frac{2-2009}{2} f(1)=-\frac{3 \cdot 2006}{2} f(1)
\end{aligned}
$$
i.e.
$$
f(1)=-\frac{2}{3}
$$
Since
$$
2007=3^{2} \cdot 223,2008=2^{3} \cdot 251,2009=7^{2} \cdot 41
$$
and because of (2) and (3), we get
$$
\begin{aligned}
f\left(2007^{2}\right)+f\left(2008^{3}\right)+f\left(2009^{5}\right) & =\frac{2-6}{2} f(1)+\frac{2-12}{2} f(1)+\frac{2-15}{2} f(1) \\
& =-\frac{27}{2} f(1)=-\frac{27}{2} \cdot\left(-\frac{2}{3}\right)=9
\end{aligned}
$$
|
9
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Let $f: \mathbb{N} \rightarrow \mathbb{R}$ be a function, satisfying the following condition:
for every integer $n>1$, there exists a prime divisor $p$ of $n$ such that $f(n)=f\left(\frac{n}{p}\right)-f(p)$. If
$$
f\left(2^{2007}\right)+f\left(3^{2008}\right)+f\left(5^{2009}\right)=2006
$$
determine the value of
$$
f\left(2007^{2}\right)+f\left(2008^{3}\right)+f\left(2009^{5}\right)
$$
|
If $n=p$ is prime number, we have
$$
f(p)=f\left(\frac{p}{p}\right)-f(p)=f(1)-f(p)
$$
i.e.
$$
f(p)=\frac{f(1)}{2}
$$
If $n=p q$, where $p$ and $q$ are prime numbers, then
$$
f(n)=f\left(\frac{n}{p}\right)-f(p)=f(q)-f(p)=\frac{f(1)}{2}-\frac{f(1)}{2}=0
$$
If $n$ is a product of three prime numbers, we have
$$
f(n)=f\left(\frac{n}{p}\right)-f(p)=0-f(p)=-f(p)=-\frac{f(1)}{2}
$$
With mathematical induction by a number of prime multipliers we shell prove that: if $n$ is a product of $k$ prime numbers then
$$
f(n)=(2-k) \frac{f(1)}{2}
$$
For $k=1$, clearly the statement (2), holds.
Let statement (2) holds for all integers $n$, where $n$ is a product of $k$ prime numbers.
Now let $n$ be a product of $k+1$ prime numbers. Then we have $n=n_{1} p$, where $n_{1}$ is a product of $k$ prime numbers.
So
$$
f(n)=f\left(\frac{n}{p}\right)-f(p)=f\left(n_{1}\right)-f(p)=(2-k) \frac{f(1)}{2}-\frac{f(1)}{2}=(2-(k+1)) \frac{f(1)}{2}
$$
So (2) holds for every integer $n>1$.
Now from $f\left(2^{2007}\right)+f\left(3^{2008}\right)+f\left(5^{2009}\right)=2006$ and because of (2) we have
$$
\begin{aligned}
2006 & =f\left(2^{2007}\right)+f\left(3^{2008}\right)+f\left(5^{2009}\right) \\
& =\frac{2-2007}{2} f(1)+\frac{2-2008}{2} f(1)+\frac{2-2009}{2} f(1)=-\frac{3 \cdot 2006}{2} f(1)
\end{aligned}
$$
i.e.
$$
f(1)=-\frac{2}{3}
$$
Since
$$
2007=3^{2} \cdot 223,2008=2^{3} \cdot 251,2009=7^{2} \cdot 41
$$
and because of (2) and (3), we get
$$
\begin{aligned}
f\left(2007^{2}\right)+f\left(2008^{3}\right)+f\left(2009^{5}\right) & =\frac{2-6}{2} f(1)+\frac{2-12}{2} f(1)+\frac{2-15}{2} f(1) \\
& =-\frac{27}{2} f(1)=-\frac{27}{2} \cdot\left(-\frac{2}{3}\right)=9
\end{aligned}
$$
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo-2008_shl.jsonl",
"problem_match": "\nNT6 ",
"solution_match": "## Solution"
}
|
f3298ef6-0418-5db1-a520-7d05bc22cd81
| 605,010
|
Determine the minimal prime number $p>3$ for which no natural number $n$ satisfies
$$
2^{n}+3^{n} \equiv 0(\bmod p)
$$
|
We put $A(n)=2^{n}+3^{n}$. From Fermat's little theorem, we have $2^{p-1} \equiv 1(\bmod p)$ and $3^{p-1} \equiv 1(\bmod p)$ from which we conclude $A(n) \equiv 2(\bmod p)$. Therefore, after $p-1$ steps
at most, we will have repetition of the power. It means that in order to determine the minimal prime number $p$ we seek, it is enough to determine a complete set of remainders $S(p)=\{0,1, \ldots, p-1\}$ such that $2^{n}+3^{n} \not \equiv 0(\bmod p)$, for every $n \in S(p)$.
For $p=5$ and $n=1$ we have $A(1) \equiv 0(\bmod 5)$.
For $p=7$ and $n=3$ we have $A(3) \equiv 0(\bmod 7)$.
For $p=11$ and $n=5$ we have $A(5) \equiv 0(\bmod 11)$.
For $p=13$ and $n=2$ we have $A(2) \equiv 0(\bmod 13)$.
For $p=17$ and $n=8$ we have $A(8) \equiv 0(\bmod 17)$.
For $p=19$ we have $A(n) \not \equiv 0(\bmod 19)$, for all $n \in S(19)$.
Hence the minimal value of $p$ is 19 .
|
19
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Determine the minimal prime number $p>3$ for which no natural number $n$ satisfies
$$
2^{n}+3^{n} \equiv 0(\bmod p)
$$
|
We put $A(n)=2^{n}+3^{n}$. From Fermat's little theorem, we have $2^{p-1} \equiv 1(\bmod p)$ and $3^{p-1} \equiv 1(\bmod p)$ from which we conclude $A(n) \equiv 2(\bmod p)$. Therefore, after $p-1$ steps
at most, we will have repetition of the power. It means that in order to determine the minimal prime number $p$ we seek, it is enough to determine a complete set of remainders $S(p)=\{0,1, \ldots, p-1\}$ such that $2^{n}+3^{n} \not \equiv 0(\bmod p)$, for every $n \in S(p)$.
For $p=5$ and $n=1$ we have $A(1) \equiv 0(\bmod 5)$.
For $p=7$ and $n=3$ we have $A(3) \equiv 0(\bmod 7)$.
For $p=11$ and $n=5$ we have $A(5) \equiv 0(\bmod 11)$.
For $p=13$ and $n=2$ we have $A(2) \equiv 0(\bmod 13)$.
For $p=17$ and $n=8$ we have $A(8) \equiv 0(\bmod 17)$.
For $p=19$ we have $A(n) \not \equiv 0(\bmod 19)$, for all $n \in S(19)$.
Hence the minimal value of $p$ is 19 .
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo-2008_shl.jsonl",
"problem_match": "\nNT7 ",
"solution_match": "## Solution"
}
|
ee90bb4a-22c5-5605-84e8-a07c848b4926
| 605,021
|
Find the maximum value of $z+x$, if $(x, y, z, t)$ satisfies the conditions:
$$
\left\{\begin{array}{l}
x^{2}+y^{2}=4 \\
z^{2}+t^{2}=9 \\
x t+y z \geq 6
\end{array}\right.
$$
|
I: From the conditions we have
$$
36=\left(x^{2}+y^{2}\right)\left(z^{2}+t^{2}\right)=(x t+y z)^{2}+(x z-y t)^{2} \geq 36+(x z-y t)^{2}
$$
and this implies $x z-y t=0$.
Now it is clear that
$$
x^{2}+z^{2}+y^{2}+t^{2}=(x+z)^{2}+(y-t)^{2}=13
$$
and the maximum value of $z+x$ is $\sqrt{13}$. It is achieved for $x=\frac{4}{\sqrt{13}}, y=t=\frac{6}{\sqrt{13}}$ and $z=\frac{9}{\sqrt{13}}$.
Solution II: From inequality $x t+y z \geq 6$ and problem conditions we have:
$$
\begin{gathered}
(x t+y z)^{2}-36 \geq 0 \Leftrightarrow \\
(x t+y z)^{2}-\left(x^{2}+y^{2}\right)\left(z^{2}+t^{2}\right) \geq 0 \Leftrightarrow \\
2 x y z t-x^{2} y^{2}-y^{2} t^{2} \geq 0 \Leftrightarrow \\
-(x z-y t)^{2} \geq 0
\end{gathered}
$$
From here we have $x z=y t$.
Furthermore,
$$
x^{2}+y^{2}+z^{2}+t^{2}=(x+z)^{2}+(y-t)^{2}=13
$$
and it follows that
$$
(x+z)^{2} \leq 13
$$
Thus,
$$
x+z \leq \sqrt{13}
$$
Equality $x+z=\sqrt{13}$ holds if we have $y=t$ and $z^{2}-x^{2}=5$, which leads to $z-x=\frac{5}{\sqrt{13}}$. Therefore, $x=\frac{4}{\sqrt{13}}, y=t=\frac{6}{\sqrt{13}}, z=\frac{9}{\sqrt{13}}$.
|
\sqrt{13}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Find the maximum value of $z+x$, if $(x, y, z, t)$ satisfies the conditions:
$$
\left\{\begin{array}{l}
x^{2}+y^{2}=4 \\
z^{2}+t^{2}=9 \\
x t+y z \geq 6
\end{array}\right.
$$
|
I: From the conditions we have
$$
36=\left(x^{2}+y^{2}\right)\left(z^{2}+t^{2}\right)=(x t+y z)^{2}+(x z-y t)^{2} \geq 36+(x z-y t)^{2}
$$
and this implies $x z-y t=0$.
Now it is clear that
$$
x^{2}+z^{2}+y^{2}+t^{2}=(x+z)^{2}+(y-t)^{2}=13
$$
and the maximum value of $z+x$ is $\sqrt{13}$. It is achieved for $x=\frac{4}{\sqrt{13}}, y=t=\frac{6}{\sqrt{13}}$ and $z=\frac{9}{\sqrt{13}}$.
Solution II: From inequality $x t+y z \geq 6$ and problem conditions we have:
$$
\begin{gathered}
(x t+y z)^{2}-36 \geq 0 \Leftrightarrow \\
(x t+y z)^{2}-\left(x^{2}+y^{2}\right)\left(z^{2}+t^{2}\right) \geq 0 \Leftrightarrow \\
2 x y z t-x^{2} y^{2}-y^{2} t^{2} \geq 0 \Leftrightarrow \\
-(x z-y t)^{2} \geq 0
\end{gathered}
$$
From here we have $x z=y t$.
Furthermore,
$$
x^{2}+y^{2}+z^{2}+t^{2}=(x+z)^{2}+(y-t)^{2}=13
$$
and it follows that
$$
(x+z)^{2} \leq 13
$$
Thus,
$$
x+z \leq \sqrt{13}
$$
Equality $x+z=\sqrt{13}$ holds if we have $y=t$ and $z^{2}-x^{2}=5$, which leads to $z-x=\frac{5}{\sqrt{13}}$. Therefore, $x=\frac{4}{\sqrt{13}}, y=t=\frac{6}{\sqrt{13}}, z=\frac{9}{\sqrt{13}}$.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo-2009_shl.jsonl",
"problem_match": "\nA2 ",
"solution_match": "\nSolution "
}
|
46d684aa-f7ec-52fa-9333-fe9f762e7867
| 605,095
|
Each one of 2009 distinct points in the plane is coloured in blue or red, so that on every blue-centered unit circle there are exactly two red points. Find the gratest possible number of blue points.
|
Each pair of red points can belong to at most two blue-centered unit circles. As $n$ red points form $\frac{n(n-1)}{2}$ pairs, we can have not more than twice that number of blue points, i.e. $n(n-1)$ blue points. Thus, the total number of points can not exceed
$$
n+n(n-1)=n^{2}
$$
As $44^{2}<2009, n$ must be at least 45 . We can arrange 45 distinct red points on a segment of length 1 , and color blue all but $16\left(=45^{2}-2009\right)$ points on intersections of the redcentered unit circles (all points of intersection are distinct, as no blue-centered unit circle can intersect the segment more than twice). Thus, the greatest possible number of blue points is $2009-45=1964$.
|
1964
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Each one of 2009 distinct points in the plane is coloured in blue or red, so that on every blue-centered unit circle there are exactly two red points. Find the gratest possible number of blue points.
|
Each pair of red points can belong to at most two blue-centered unit circles. As $n$ red points form $\frac{n(n-1)}{2}$ pairs, we can have not more than twice that number of blue points, i.e. $n(n-1)$ blue points. Thus, the total number of points can not exceed
$$
n+n(n-1)=n^{2}
$$
As $44^{2}<2009, n$ must be at least 45 . We can arrange 45 distinct red points on a segment of length 1 , and color blue all but $16\left(=45^{2}-2009\right)$ points on intersections of the redcentered unit circles (all points of intersection are distinct, as no blue-centered unit circle can intersect the segment more than twice). Thus, the greatest possible number of blue points is $2009-45=1964$.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo-2009_shl.jsonl",
"problem_match": "\nC1 ",
"solution_match": "\nSolution:"
}
|
ae883c11-b84d-559f-afd5-26219675de5a
| 605,139
|
Five players $(A, B, C, D, E)$ take part in a bridge tournament. Every two players must play (as partners) against every other two players. Any two given players can be partners not more than once per day. What is the least number of days needed for this tournament?
|
A given pair must play with three other pairs and these plays must be in different days, so at three days are needed. Suppose that three days suffice. Let the pair $A B$ play against $C D$ on day $x$. Then $A B-D E$ and $C D-B E$ cannot play on day $x$. Then one of the other two plays of $D E$ (with $A C$ and $B C$ ) must be on day $x$. Similarly, one of the plays of $B E$ with $A C$ or $A D$ must be on day $x$. Thus, two of the plays in the chain $B C-D E-A C-B E-A D$ are on day $x$ (more than two among these cannot be on one day).
Consider the chain $A B-C D-E A-B D-C E-A B$. At least three days are needed for playing all the matches within it. For each of these days we conclude (as above) that there are exactly two of the plays in the chain $B C-D E-A C-B E-A D-B C$ on that day. This is impossible, as this chain consists of five plays.
It remains to show that four days will suffice:
Day 1: $A B-C D, A C-D E, A D-C E, A E-B C$
Day 2: $A B-D E, A C-B D, A D-B C, B E-C D$
Day 3: $A B-C E, A D-B E, A E-B D, B C-D E$
Day 4: $A C-B E, A E-C D, B D-C E$.
Remark: It is possible to have 5 games in one day (but not on each day).
## Alternative solution:
There are 10 pairs. Each of them plays 3 games, so the tournament needs to last at least 3 days. Assume the tournament could finish in 3 days. Then every pair must play one game on each day. There are 15 games to be played, so you must have 5 games on each day. Call "Day 1" the day AB plays against CD, "Day 2" the day AB plays against DE
and "Day 3" the day AB plays against CE. Let us examine the other possible games on Day 1. CE can't play $\mathrm{AB}$, so it must play either $\mathrm{AD}$ or $\mathrm{BD}$. $\mathrm{DE}$ can't play $\mathrm{AB}$, so it must play AC or BC. Similarly, AE can't play CD, so it must play BC or BD, and BE must play either $\mathrm{AC}$ or $\mathrm{AD}$. We obtain the following circular diagram in which exact every other game has to take place on Day 1, either the red ones or the blue ones:
Similar reasoning leads un to the following diagram for Day 2. Here again, either all the red matches have to take place, or all the blue matches have to take place on Day 2.
One can't have the blue matches on both Day 1 and Day 2 because AD-BE would repeat itself.
We can't have the red mathes on both days as this would repeat the match BD-CE.
We can not have the blue matches on Day 1 and the red matches on Day 2 because this would repeat the game AC-BE. Finally, choosing the red matches on Day 1 and the blue ones on Day 2 won't work either as the game AE-BC would repeat itself.
In conclusion, the tournament has to last at least four days. An example of how it could
be organized in four days is given in the previous solution.
|
4
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Five players $(A, B, C, D, E)$ take part in a bridge tournament. Every two players must play (as partners) against every other two players. Any two given players can be partners not more than once per day. What is the least number of days needed for this tournament?
|
A given pair must play with three other pairs and these plays must be in different days, so at three days are needed. Suppose that three days suffice. Let the pair $A B$ play against $C D$ on day $x$. Then $A B-D E$ and $C D-B E$ cannot play on day $x$. Then one of the other two plays of $D E$ (with $A C$ and $B C$ ) must be on day $x$. Similarly, one of the plays of $B E$ with $A C$ or $A D$ must be on day $x$. Thus, two of the plays in the chain $B C-D E-A C-B E-A D$ are on day $x$ (more than two among these cannot be on one day).
Consider the chain $A B-C D-E A-B D-C E-A B$. At least three days are needed for playing all the matches within it. For each of these days we conclude (as above) that there are exactly two of the plays in the chain $B C-D E-A C-B E-A D-B C$ on that day. This is impossible, as this chain consists of five plays.
It remains to show that four days will suffice:
Day 1: $A B-C D, A C-D E, A D-C E, A E-B C$
Day 2: $A B-D E, A C-B D, A D-B C, B E-C D$
Day 3: $A B-C E, A D-B E, A E-B D, B C-D E$
Day 4: $A C-B E, A E-C D, B D-C E$.
Remark: It is possible to have 5 games in one day (but not on each day).
## Alternative solution:
There are 10 pairs. Each of them plays 3 games, so the tournament needs to last at least 3 days. Assume the tournament could finish in 3 days. Then every pair must play one game on each day. There are 15 games to be played, so you must have 5 games on each day. Call "Day 1" the day AB plays against CD, "Day 2" the day AB plays against DE
and "Day 3" the day AB plays against CE. Let us examine the other possible games on Day 1. CE can't play $\mathrm{AB}$, so it must play either $\mathrm{AD}$ or $\mathrm{BD}$. $\mathrm{DE}$ can't play $\mathrm{AB}$, so it must play AC or BC. Similarly, AE can't play CD, so it must play BC or BD, and BE must play either $\mathrm{AC}$ or $\mathrm{AD}$. We obtain the following circular diagram in which exact every other game has to take place on Day 1, either the red ones or the blue ones:

Similar reasoning leads un to the following diagram for Day 2. Here again, either all the red matches have to take place, or all the blue matches have to take place on Day 2.

One can't have the blue matches on both Day 1 and Day 2 because AD-BE would repeat itself.
We can't have the red mathes on both days as this would repeat the match BD-CE.
We can not have the blue matches on Day 1 and the red matches on Day 2 because this would repeat the game AC-BE. Finally, choosing the red matches on Day 1 and the blue ones on Day 2 won't work either as the game AE-BC would repeat itself.
In conclusion, the tournament has to last at least four days. An example of how it could
be organized in four days is given in the previous solution.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo-2009_shl.jsonl",
"problem_match": "\nC2 ",
"solution_match": "\nSolution:"
}
|
6a425a57-3229-5aa6-ac9b-6a8cb73c515a
| 605,148
|
In a right trapezoid $A B C D(A B \| C D)$ the angle at vertex $B$ measures $75^{\circ}$. Point $H$ is the foot of the perpendicular from point $A$ to the line $B C$. If $B H=D C$ and $A D+A H=8$, find the area of $A B C D$.
|
Produce the legs of the trapezoid until they intersect at point $E$. The triangles $A B H$ and $E C D$ are congruent (ASA). The area of $A B C D$ is equal to area of triangle $E A H$ of hypotenuse
$$
A E=A D+D E=A D+A H=8
$$
Let $M$ be the midpoint of $A E$. Then
$$
M E=M A=M H=4
$$
and $\angle A M H=30^{\circ}$. Now, the altitude from $H$ to AM equals one half of $M H$, namely 2. Finally, the area is 8 .
|
8
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
In a right trapezoid $A B C D(A B \| C D)$ the angle at vertex $B$ measures $75^{\circ}$. Point $H$ is the foot of the perpendicular from point $A$ to the line $B C$. If $B H=D C$ and $A D+A H=8$, find the area of $A B C D$.
|
Produce the legs of the trapezoid until they intersect at point $E$. The triangles $A B H$ and $E C D$ are congruent (ASA). The area of $A B C D$ is equal to area of triangle $E A H$ of hypotenuse
$$
A E=A D+D E=A D+A H=8
$$
Let $M$ be the midpoint of $A E$. Then
$$
M E=M A=M H=4
$$
and $\angle A M H=30^{\circ}$. Now, the altitude from $H$ to AM equals one half of $M H$, namely 2. Finally, the area is 8 .

|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo-2009_shl.jsonl",
"problem_match": "\nG2 ",
"solution_match": "\nSolution:"
}
|
389a026f-d77f-5dfd-803c-2548234b5e1a
| 605,193
|
A group of $n>1$ pirates of different age owned total of 2009 coins. Initially each pirate (except for the youngest one) had one coin more than the next younger.
a) Find all possible values of $n$.
b) Every day a pirate was chosen. The chosen pirate gave a coin to each of the other pirates. If $n=7$, find the largest possible number of coins a pirate can have after several days.
|
a) If $n$ is odd, then it is a divisor of $2009=7 \times 7 \times 41$. If $n>49$, then $n$ is at least $7 \times 41$, while the average pirate has 7 coins, so the initial division is impossible. So, we can have $n=7, n=41$ or $n=49$. Each of these cases is possible (e.g. if $n=49$, the average pirate has 41 coins, so the initial amounts are from $41-24=17$ to $41+24=65$ ).
If $n$ is even, then 2009 is multiple of the sum $S$ of the oldest and the youngest pirate. If $S<7 \times 41$, then $S$ is at most 39 and the pairs of pirates of sum $S$ is at least 41 , so we must have at least 82 pirates, a contradiction. So we can have just $S=7 \times 41=287$ and $S=49 \times 41=2009$; respectively, $n=2 \times 7=14$ or $n=2 \times 1=2$. Each of these cases is possible (e.g. if $n=14$, the initial amounts are from $144-7=137$ to $143+7=150$ ). In total, $n$ is one of the numbers $2,7,13,41$ and 49 .
b) If $n=7$, the average pirate has $7 \times 41=287$ coins, so the initial amounts are from 284 to 290; they have different residues modulo 7. The operation decreases one of the amounts by 6 and increases the other ones by 1 , so the residues will be different at all times. The largest possible amount in one pirate's possession will be achieved if all the others have as little as possible, namely $0,1,2,3,4$ and 5 coins (the residues modulo 7 have to be different). If this happens, the wealthiest pirate will have $2009-14=1994$ coins. Indeed, this can be achieved e.g. if every day (until that moment) the coins are given by the second wealthiest: while he has more than 5 coins, he can provide the 6 coins needed, and when he has no more than five, the coins at the poorest six pirates have to be $0,1,2,3,4,5$. Thus, $n=1994$ can be achieved.
|
1994
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
A group of $n>1$ pirates of different age owned total of 2009 coins. Initially each pirate (except for the youngest one) had one coin more than the next younger.
a) Find all possible values of $n$.
b) Every day a pirate was chosen. The chosen pirate gave a coin to each of the other pirates. If $n=7$, find the largest possible number of coins a pirate can have after several days.
|
a) If $n$ is odd, then it is a divisor of $2009=7 \times 7 \times 41$. If $n>49$, then $n$ is at least $7 \times 41$, while the average pirate has 7 coins, so the initial division is impossible. So, we can have $n=7, n=41$ or $n=49$. Each of these cases is possible (e.g. if $n=49$, the average pirate has 41 coins, so the initial amounts are from $41-24=17$ to $41+24=65$ ).
If $n$ is even, then 2009 is multiple of the sum $S$ of the oldest and the youngest pirate. If $S<7 \times 41$, then $S$ is at most 39 and the pairs of pirates of sum $S$ is at least 41 , so we must have at least 82 pirates, a contradiction. So we can have just $S=7 \times 41=287$ and $S=49 \times 41=2009$; respectively, $n=2 \times 7=14$ or $n=2 \times 1=2$. Each of these cases is possible (e.g. if $n=14$, the initial amounts are from $144-7=137$ to $143+7=150$ ). In total, $n$ is one of the numbers $2,7,13,41$ and 49 .
b) If $n=7$, the average pirate has $7 \times 41=287$ coins, so the initial amounts are from 284 to 290; they have different residues modulo 7. The operation decreases one of the amounts by 6 and increases the other ones by 1 , so the residues will be different at all times. The largest possible amount in one pirate's possession will be achieved if all the others have as little as possible, namely $0,1,2,3,4$ and 5 coins (the residues modulo 7 have to be different). If this happens, the wealthiest pirate will have $2009-14=1994$ coins. Indeed, this can be achieved e.g. if every day (until that moment) the coins are given by the second wealthiest: while he has more than 5 coins, he can provide the 6 coins needed, and when he has no more than five, the coins at the poorest six pirates have to be $0,1,2,3,4,5$. Thus, $n=1994$ can be achieved.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo-2009_shl.jsonl",
"problem_match": "\nNT2 ",
"solution_match": "## Solution:"
}
|
10d0ad47-3255-59b9-9397-2186676a929d
| 605,252
|
Determine all four digit numbers $\overline{a b c d}$ such that
$$
a(a+b+c+d)\left(a^{2}+b^{2}+c^{2}+d^{2}\right)\left(a^{6}+2 b^{6}+3 c^{6}+4 d^{6}\right)=\overline{a b c d}
$$
|
From $\overline{a b c d}<10000$ and
$$
a^{10} \leq a(a+b+c+d)\left(a^{2}+b^{2}+c^{2}+d^{2}\right)\left(a^{6}+2 b^{6}+3 c^{6}+4 d^{6}\right)=\overline{a b c d}
$$
follows that $a \leq 2$. We thus have two cases:
Case I: $a=1$.
Obviously $2000>\overline{1 b c d}=(1+b+c+d)\left(1+b^{2}+c^{2}+d^{2}\right)\left(1+2 b^{6}+3 c^{6}+4 d^{6}\right) \geq$ $(b+1)\left(b^{2}+1\right)\left(2 b^{6}+1\right)$, so $b \leq 2$. Similarly one gets $c<2$ and $d<2$. By direct check there is no solution in this case.
Case II: $a=2$.
We have $3000>\overline{2 b c d}=2(2+b+c+d)\left(4+b^{2}+c^{2}+d^{2}\right)\left(64+2 b^{6}+3 c^{6}+4 d^{6}\right) \geq$ $2(b+2)\left(b^{2}+4\right)\left(2 b^{6}+64\right)$, imposing $b \leq 1$. In the same way one proves $c<2$ and $d<2$. By direct check, we find out that 2010 is the only solution.
|
2010
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Determine all four digit numbers $\overline{a b c d}$ such that
$$
a(a+b+c+d)\left(a^{2}+b^{2}+c^{2}+d^{2}\right)\left(a^{6}+2 b^{6}+3 c^{6}+4 d^{6}\right)=\overline{a b c d}
$$
|
From $\overline{a b c d}<10000$ and
$$
a^{10} \leq a(a+b+c+d)\left(a^{2}+b^{2}+c^{2}+d^{2}\right)\left(a^{6}+2 b^{6}+3 c^{6}+4 d^{6}\right)=\overline{a b c d}
$$
follows that $a \leq 2$. We thus have two cases:
Case I: $a=1$.
Obviously $2000>\overline{1 b c d}=(1+b+c+d)\left(1+b^{2}+c^{2}+d^{2}\right)\left(1+2 b^{6}+3 c^{6}+4 d^{6}\right) \geq$ $(b+1)\left(b^{2}+1\right)\left(2 b^{6}+1\right)$, so $b \leq 2$. Similarly one gets $c<2$ and $d<2$. By direct check there is no solution in this case.
Case II: $a=2$.
We have $3000>\overline{2 b c d}=2(2+b+c+d)\left(4+b^{2}+c^{2}+d^{2}\right)\left(64+2 b^{6}+3 c^{6}+4 d^{6}\right) \geq$ $2(b+2)\left(b^{2}+4\right)\left(2 b^{6}+64\right)$, imposing $b \leq 1$. In the same way one proves $c<2$ and $d<2$. By direct check, we find out that 2010 is the only solution.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo-2010_shl.jsonl",
"problem_match": "\nProblem A2.",
"solution_match": "\nSolution."
}
|
408f6b56-a3e7-5484-97e0-7c54b608232f
| 605,299
|
There are two piles of coins, each containing 2010 pieces. Two players A and B play a game taking turns (A plays first). At each turn, the player on play has to take one or more coins from one pile or exactly one coin from each pile. Whoever takes the last coin is the winner. Which player will win if they both play in the best possible way?
|
B wins.
In fact, we will show that A will lose if the total number of coins is a multiple of 3 and the two piles differ by not more than one coin (call this a balanced position). To this end, firstly notice that it is not possible to move from one balanced position to another. The winning strategy for B consists in returning A to a balanced position (notice that the initial position is a balanced position).
There are two types of balanced positions; for each of them consider the moves of $\mathrm{A}$ and the replies of B.
If the number in each pile is a multiple of 3 and there is at least one coin:
- if A takes $3 n$ coins from one pile, then $\mathrm{B}$ takes $3 n$ coins from the other one.
- if A takes $3 n+1$ coins from one pile, then $\mathrm{B}$ takes $3 n+2$ coins from the other one.
- if A takes $3 n+2$ coins from one pile, then $\mathrm{B}$ takes $3 n+1$ coins from the other one.
- if A takes a coin from each pile, then $\mathrm{B}$ takes one coin from one pile.
If the numbers are not multiples of 3 , then we have $3 m+1$ coins in one pile and $3 m+2$ in the other one. Hence:
- if A takes $3 n$ coins from one pile, then $\mathrm{B}$ takes $3 n$ coins from the other one.
- if A takes $3 n+1$ coins from the first pile $(n \leq m)$, then $\mathrm{B}$ takes $3 n+2$ coins from the second one.
- if A takes $3 n+2$ coins from the second pile $(n \leq m)$, then $\mathrm{B}$ takes $3 n+1$ coins from the first one.
- if A takes $3 n+2$ coins from the first pile $(n \leq m-1)$, then $\mathrm{B}$ takes $3 n+4$ coins from the second one.
- if A takes $3 n+1$ coins from the second pile $(n \leq m)$, then $\mathrm{B}$ takes $3 n-1$ coins from the first one. This is impossible if A has taken only one coin from the second pile; in this case $\mathrm{B}$ takes one coin from each pile.
- if A takes a coin from each pile, then B takes one coin from the second pile.
In all these cases, the position after B's move is again a balanced position. Since the number of coins decreases and $(0 ; 0)$ is a balanced position, after a finite number of moves, there will be no coins left after B's move. Thus, B wins.
|
B wins
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
There are two piles of coins, each containing 2010 pieces. Two players A and B play a game taking turns (A plays first). At each turn, the player on play has to take one or more coins from one pile or exactly one coin from each pile. Whoever takes the last coin is the winner. Which player will win if they both play in the best possible way?
|
B wins.
In fact, we will show that A will lose if the total number of coins is a multiple of 3 and the two piles differ by not more than one coin (call this a balanced position). To this end, firstly notice that it is not possible to move from one balanced position to another. The winning strategy for B consists in returning A to a balanced position (notice that the initial position is a balanced position).
There are two types of balanced positions; for each of them consider the moves of $\mathrm{A}$ and the replies of B.
If the number in each pile is a multiple of 3 and there is at least one coin:
- if A takes $3 n$ coins from one pile, then $\mathrm{B}$ takes $3 n$ coins from the other one.
- if A takes $3 n+1$ coins from one pile, then $\mathrm{B}$ takes $3 n+2$ coins from the other one.
- if A takes $3 n+2$ coins from one pile, then $\mathrm{B}$ takes $3 n+1$ coins from the other one.
- if A takes a coin from each pile, then $\mathrm{B}$ takes one coin from one pile.
If the numbers are not multiples of 3 , then we have $3 m+1$ coins in one pile and $3 m+2$ in the other one. Hence:
- if A takes $3 n$ coins from one pile, then $\mathrm{B}$ takes $3 n$ coins from the other one.
- if A takes $3 n+1$ coins from the first pile $(n \leq m)$, then $\mathrm{B}$ takes $3 n+2$ coins from the second one.
- if A takes $3 n+2$ coins from the second pile $(n \leq m)$, then $\mathrm{B}$ takes $3 n+1$ coins from the first one.
- if A takes $3 n+2$ coins from the first pile $(n \leq m-1)$, then $\mathrm{B}$ takes $3 n+4$ coins from the second one.
- if A takes $3 n+1$ coins from the second pile $(n \leq m)$, then $\mathrm{B}$ takes $3 n-1$ coins from the first one. This is impossible if A has taken only one coin from the second pile; in this case $\mathrm{B}$ takes one coin from each pile.
- if A takes a coin from each pile, then B takes one coin from the second pile.
In all these cases, the position after B's move is again a balanced position. Since the number of coins decreases and $(0 ; 0)$ is a balanced position, after a finite number of moves, there will be no coins left after B's move. Thus, B wins.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo-2010_shl.jsonl",
"problem_match": "\nProblem C1.",
"solution_match": "\nSolution."
}
|
7c628d15-c8b9-5a23-ac25-5b3daf32fcc6
| 605,381
|
Find the largest possible value of the expression $\left|\sqrt{x^{2}+4 x+8}-\sqrt{x^{2}+8 x+17}\right|$ where $x$ is a real number.
|
We observe that
$$
\left|\sqrt{x^{2}+4 x+8}-\sqrt{x^{2}+8 x+17}\right|=\left|\sqrt{(x-(-2))^{2}+(0-2)^{2}}-\sqrt{\left.(x-(-4))^{2}+(0-1)^{2}\right)}\right|
$$
is the absolute difference of the distances from the point $P(x, 0)$ in the $x y$-plane to the points $A(-2,2)$ and $B(-4,1)$.
By the Triangle Inequality, $|P A-P B| \leq|A B|$ and the equality occurs exactly when $P$ lies on the line passing through $A$ and $B$, but not between them.
If $P, A, B$ are collinear, then $(x-(-2)) /(0-2)=((-4)-(-2)) /(1-2)$. This gives $x=-6$, and as $-6<-4<-2$,
$$
\left|\sqrt{(-6)^{2}+4(-6)+8}-\sqrt{(-6)^{2}+8(-6)+17}\right|=|\sqrt{20}-\sqrt{5}|=\sqrt{5}
$$
is the largest possible value of the expression.
|
\sqrt{5}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Find the largest possible value of the expression $\left|\sqrt{x^{2}+4 x+8}-\sqrt{x^{2}+8 x+17}\right|$ where $x$ is a real number.
|
We observe that
$$
\left|\sqrt{x^{2}+4 x+8}-\sqrt{x^{2}+8 x+17}\right|=\left|\sqrt{(x-(-2))^{2}+(0-2)^{2}}-\sqrt{\left.(x-(-4))^{2}+(0-1)^{2}\right)}\right|
$$
is the absolute difference of the distances from the point $P(x, 0)$ in the $x y$-plane to the points $A(-2,2)$ and $B(-4,1)$.
By the Triangle Inequality, $|P A-P B| \leq|A B|$ and the equality occurs exactly when $P$ lies on the line passing through $A$ and $B$, but not between them.
If $P, A, B$ are collinear, then $(x-(-2)) /(0-2)=((-4)-(-2)) /(1-2)$. This gives $x=-6$, and as $-6<-4<-2$,
$$
\left|\sqrt{(-6)^{2}+4(-6)+8}-\sqrt{(-6)^{2}+8(-6)+17}\right|=|\sqrt{20}-\sqrt{5}|=\sqrt{5}
$$
is the largest possible value of the expression.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo_2013.jsonl",
"problem_match": "\nA2.",
"solution_match": "\nSolution."
}
|
25ca4af7-a6ba-5881-b7e0-c2ed6876a4c5
| 605,429
|
For any real number a, let $\lfloor a\rfloor$ denote the greatest integer not exceeding a. In positive real numbers solve the following equation
$$
n+\lfloor\sqrt{n}\rfloor+\lfloor\sqrt[3]{n}\rfloor=2014
$$
|
Obviously $n$ must be positive integer. Now note that $44^{2}=1936<2014<2025=45^{2}$ and $12^{3}<1900<2014<13^{3}$.
If $n<1950$ than $2014=n+\lfloor\sqrt{n}\rfloor+\lfloor\sqrt[3]{n}\rfloor<1950+44+12=2006$, a contradiction!
So $n \geq 1950$. Also if $n>2000$ than $2014=n+\lfloor\sqrt{n}\rfloor+\lfloor\sqrt[3]{n}\rfloor>2000+44+12=2056$, a contradiction!
So $1950 \leq n \leq 2000$, therefore $\lfloor\sqrt{n}\rfloor=44$ and $\lfloor\sqrt[3]{n}\rfloor=12$. Plugging that into the original equation we get:
$$
n+\lfloor\sqrt{n}\rfloor+\lfloor\sqrt[3]{n}\rfloor=n+44+12=2014
$$
From which we get $n=1956$, which is the only solution.
Solution2. Obviously $n$ must be positive integer. Since $n \leq 2014, \sqrt{n}<45$ and $\sqrt[3]{n}<13$.
Form $n=2014-\lfloor\sqrt{n}\rfloor-\lfloor\sqrt[3]{n}\rfloor>2014-45-13=1956, \sqrt{n}>44$ and $\sqrt[3]{n}>12$, thus $\lfloor\sqrt{n}\rfloor=44$ and $\lfloor\sqrt[3]{n}\rfloor=12$ and $n=2014-\lfloor\sqrt{n}\rfloor-\lfloor\sqrt[3]{n}\rfloor=2014-44-12=1958$.
|
1956
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
For any real number a, let $\lfloor a\rfloor$ denote the greatest integer not exceeding a. In positive real numbers solve the following equation
$$
n+\lfloor\sqrt{n}\rfloor+\lfloor\sqrt[3]{n}\rfloor=2014
$$
|
Obviously $n$ must be positive integer. Now note that $44^{2}=1936<2014<2025=45^{2}$ and $12^{3}<1900<2014<13^{3}$.
If $n<1950$ than $2014=n+\lfloor\sqrt{n}\rfloor+\lfloor\sqrt[3]{n}\rfloor<1950+44+12=2006$, a contradiction!
So $n \geq 1950$. Also if $n>2000$ than $2014=n+\lfloor\sqrt{n}\rfloor+\lfloor\sqrt[3]{n}\rfloor>2000+44+12=2056$, a contradiction!
So $1950 \leq n \leq 2000$, therefore $\lfloor\sqrt{n}\rfloor=44$ and $\lfloor\sqrt[3]{n}\rfloor=12$. Plugging that into the original equation we get:
$$
n+\lfloor\sqrt{n}\rfloor+\lfloor\sqrt[3]{n}\rfloor=n+44+12=2014
$$
From which we get $n=1956$, which is the only solution.
Solution2. Obviously $n$ must be positive integer. Since $n \leq 2014, \sqrt{n}<45$ and $\sqrt[3]{n}<13$.
Form $n=2014-\lfloor\sqrt{n}\rfloor-\lfloor\sqrt[3]{n}\rfloor>2014-45-13=1956, \sqrt{n}>44$ and $\sqrt[3]{n}>12$, thus $\lfloor\sqrt{n}\rfloor=44$ and $\lfloor\sqrt[3]{n}\rfloor=12$ and $n=2014-\lfloor\sqrt{n}\rfloor-\lfloor\sqrt[3]{n}\rfloor=2014-44-12=1958$.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo_2014.jsonl",
"problem_match": "## A1",
"solution_match": "\nSolution1."
}
|
947b6851-3721-5e1f-9d3c-b4cd941e55f1
| 605,585
|
In a country with $n$ cities, all direct airlines are two-way. There are $r>2014$ routes between pairs of different cities that include no more than one intermediate stop (the direction of each route matters). Find the least possible $n$ and the least possible $r$ for that value of $n$.
|
Denote by $X_{1}, X_{2}, \ldots X_{n}$ the cities in the country and let $X_{i}$ be connected to exactly $m_{i}$ other cities by direct two-way airline. Then $X_{i}$ is a final destination of $m_{i}$ direct routes and an intermediate stop of $m_{i}\left(m_{i}-1\right)$ non-direct routes. Thus $r=m_{1}^{2}+\ldots+m_{n}^{2}$. As each $m_{i}$ is at most $n-1$ and $13 \cdot 12^{2}<2014$, we deduce $n \geq 14$.
Consider $n=14$. As each route appears in two opposite directions, $r$ is even, so $r \geq 2016$. We can achieve $r=2016$ by arranging the 14 cities uniformly on a circle connect (by direct two-way airlines) all of them, except the diametrically opposite pairs. This way, there are exactly $14 \cdot 12^{2}=2016$ routes.
|
2016
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
In a country with $n$ cities, all direct airlines are two-way. There are $r>2014$ routes between pairs of different cities that include no more than one intermediate stop (the direction of each route matters). Find the least possible $n$ and the least possible $r$ for that value of $n$.
|
Denote by $X_{1}, X_{2}, \ldots X_{n}$ the cities in the country and let $X_{i}$ be connected to exactly $m_{i}$ other cities by direct two-way airline. Then $X_{i}$ is a final destination of $m_{i}$ direct routes and an intermediate stop of $m_{i}\left(m_{i}-1\right)$ non-direct routes. Thus $r=m_{1}^{2}+\ldots+m_{n}^{2}$. As each $m_{i}$ is at most $n-1$ and $13 \cdot 12^{2}<2014$, we deduce $n \geq 14$.
Consider $n=14$. As each route appears in two opposite directions, $r$ is even, so $r \geq 2016$. We can achieve $r=2016$ by arranging the 14 cities uniformly on a circle connect (by direct two-way airlines) all of them, except the diametrically opposite pairs. This way, there are exactly $14 \cdot 12^{2}=2016$ routes.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo_2014.jsonl",
"problem_match": "## C2",
"solution_match": "\nSolution."
}
|
9fcc110f-5e84-57e7-a06a-839b09d28235
| 605,669
|
For a given positive integer n, two players $A$ and B play the following game: Given is pile of $\boldsymbol{\Omega}$ stones. The players take turn alternatively with A going first. On each turn the player is allowed to take one stone, a prime number of stones, or a multiple of $n$ stones. The winner is the one who takes the last stone. Assuming perfect play, find the number of values for $S_{\infty}$, for which A cannot win.
|
Denote by $k$ the sought number and let $\left\{a_{1}, a_{2}, \ldots, a_{k}\right\}$ be the corresponding values for $a$. We will call each $a_{i}$ a losing number and every other positive integer a winning numbers. Clearly every multiple of $n$ is a winning number.
Suppose there are two different losing numbers $a_{i}>a_{j}$, which are congruent modulo $n$. Then, on his first turn of play, the player $A$ may remove $a_{i}-a_{j}$ stones (since $n \mid a_{i}-a_{j}$ ), leaving a pile with $a_{j}$ stones for B. This is in contradiction with both $a_{i}$ and $a_{j}$ being losing numbers. Therefore there are at most $n-1$ losing numbers, i.e. $k \leq n-1$.
Suppose there exists an integer $r \in\{1,2, \ldots, n-1\}$, such that $m n+r$ is a winning number for every $m \in \mathbb{N}_{0}$. Let us denote by $u$ the greatest losing number (if $k>0$ ) or 0 (if $k=0$ ), and let $s=\operatorname{LCM}(2,3, \ldots, u+n+1)$. Note that all the numbers $s+2, s+3, \ldots, s+u+n+1$ are composite. Let $m^{\prime} \in \mathbb{N}_{0}$, be such that $s+u+2 \leq m^{\prime} n+r \leq s+u+n+1$. In order for $m^{\prime} n+r$ to be a winning number, there must exist an integer $p$, which is either one, or prime, or a positive multiple of $n$, such that $m^{\prime} n+r-p$ is a losing number or 0 , and hence lesser than or equal to $u$. Since $s+2 \leq m^{\prime} n+r-u \leq p \leq m^{\prime} n+r \leq s+u+n+1, p$ must be a composite, hence $p$ is a multiple of $n$ (say $p=q n$ ). But then $m^{\prime} n+r-p=\left(m^{\prime}-q\right) n+r$ must be a winning number, according to our assumption. This contradicts our assumption that all numbers $m n+r, m \in \mathbb{N}_{0}$ are winning.
Hence there are exactly $n-1$ losing numbers (one for each residue $r \in\{1,2, \ldots, n-1\}$ ).
|
n-1
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
For a given positive integer n, two players $A$ and B play the following game: Given is pile of $\boldsymbol{\Omega}$ stones. The players take turn alternatively with A going first. On each turn the player is allowed to take one stone, a prime number of stones, or a multiple of $n$ stones. The winner is the one who takes the last stone. Assuming perfect play, find the number of values for $S_{\infty}$, for which A cannot win.
|
Denote by $k$ the sought number and let $\left\{a_{1}, a_{2}, \ldots, a_{k}\right\}$ be the corresponding values for $a$. We will call each $a_{i}$ a losing number and every other positive integer a winning numbers. Clearly every multiple of $n$ is a winning number.
Suppose there are two different losing numbers $a_{i}>a_{j}$, which are congruent modulo $n$. Then, on his first turn of play, the player $A$ may remove $a_{i}-a_{j}$ stones (since $n \mid a_{i}-a_{j}$ ), leaving a pile with $a_{j}$ stones for B. This is in contradiction with both $a_{i}$ and $a_{j}$ being losing numbers. Therefore there are at most $n-1$ losing numbers, i.e. $k \leq n-1$.
Suppose there exists an integer $r \in\{1,2, \ldots, n-1\}$, such that $m n+r$ is a winning number for every $m \in \mathbb{N}_{0}$. Let us denote by $u$ the greatest losing number (if $k>0$ ) or 0 (if $k=0$ ), and let $s=\operatorname{LCM}(2,3, \ldots, u+n+1)$. Note that all the numbers $s+2, s+3, \ldots, s+u+n+1$ are composite. Let $m^{\prime} \in \mathbb{N}_{0}$, be such that $s+u+2 \leq m^{\prime} n+r \leq s+u+n+1$. In order for $m^{\prime} n+r$ to be a winning number, there must exist an integer $p$, which is either one, or prime, or a positive multiple of $n$, such that $m^{\prime} n+r-p$ is a losing number or 0 , and hence lesser than or equal to $u$. Since $s+2 \leq m^{\prime} n+r-u \leq p \leq m^{\prime} n+r \leq s+u+n+1, p$ must be a composite, hence $p$ is a multiple of $n$ (say $p=q n$ ). But then $m^{\prime} n+r-p=\left(m^{\prime}-q\right) n+r$ must be a winning number, according to our assumption. This contradicts our assumption that all numbers $m n+r, m \in \mathbb{N}_{0}$ are winning.
Hence there are exactly $n-1$ losing numbers (one for each residue $r \in\{1,2, \ldots, n-1\}$ ).
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo_2014.jsonl",
"problem_match": "## C3",
"solution_match": "\nSolution."
}
|
41777f12-b54a-5033-b37c-782c3bbb13c6
| 605,682
|
Let $A=1 \cdot 4 \cdot 7 \cdot \ldots \cdot 2014$ be the product of the numbers less or equal to 2014 that give remainder 1 when divided by 3 . Find the last non-zero digit of $A$.
|
Grouping the elements of the product by ten we get:
$$
\begin{aligned}
& (30 k+1)(30 k+4)(30 k+7)(30 k+10)(30 k+13)(30 k+16) \\
& (30 k+19)(30 k+22)(30 k+25)(30 k+28)= \\
& =(30 k+1)(15 k+2)(30 k+7)(120 k+40)(30 k+13)(15 k+8) \\
& (30 k+19)(15 k+11)(120 k+100)(15 k+14)
\end{aligned}
$$
(We divide all even numbers not divisible by five, by two and multiply all numbers divisible by five with four.)
We denote $P_{k}=(30 k+1)(15 k+2)(30 k+7)(30 k+13)(15 k+8)(30 k+19)(15 k+11)(15 k+14)$. For all the numbers not divisible by five, only the last digit affects the solution, since the power of two in the numbers divisible by five is greater than the power of five. Considering this, for even $k, P_{k}$ ends with the same digit as $1 \cdot 2 \cdot 7 \cdot 3 \cdot 8 \cdot 9 \cdot 1 \cdot 4$, i.e. six and for odd $k, P_{k}$ ends with the same digit as $1 \cdot 7 \cdot 7 \cdot 3 \cdot 3 \cdot 9 \cdot 6 \cdot 9$, i.e. six. Thus $P_{0} P_{1} \ldots P_{66}$ ends with six. If we remove one zero from the end of all numbers divisible with five, we get that the last nonzero digit of the given product is the same as the one from $6 \cdot 2011 \cdot 2014 \cdot 4 \cdot 10 \cdot 16 \cdot \ldots .796 \cdot 802$. Considering that $4 \cdot 6 \cdot 2 \cdot 8$ ends with four and removing one zero from every fifth number we get that the last nonzero digit is the same as in $4 \cdot 4^{26} \cdot 784 \cdot 796 \cdot 802 \cdot 1 \cdot 4 \cdot \ldots \cdot 76 \cdot 79$. Repeating the process we did for the starting sequence we conclude that the last nonzero number will be the same as in $2 \cdot 6 \cdot 6 \cdot 40 \cdot 100 \cdot 160 \cdot 220 \cdot 280 \cdot 61 \cdot 32 \cdot 67 \cdot 73 \cdot 38 \cdot 79$, which is two.
Let $A B C$ be a triangle with $\measuredangle B=\measuredangle C=40^{\circ}$. The bisector of the $\measuredangle B$ meets $A C$ at the point $D$ . Prove that $\overline{B D}+\overline{D A}=\overline{B C}$.
Solution. Since $\measuredangle B A C=100^{\circ}$ and $\measuredangle B D C=120^{\circ}$ we have $\overline{B D}<\overline{B C}$. Let $E$ be the point on $\overline{B C}$ such that $\overline{B D}=\overline{B E}$. Then $\measuredangle D E C=100^{\circ}$ and $\measuredangle E D C=40^{\circ}$, hence $\overline{D E}=\overline{E C}$, and $\measuredangle B A C+\measuredangle D E B=180^{\circ}$. So $A, B, E$ and $D$ are concyclic, implying $\overline{A D}=\overline{D E}$ (since $\measuredangle A B D=\measuredangle D B C=20^{\circ}$ ), which completes the proof.
|
2
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Let $A=1 \cdot 4 \cdot 7 \cdot \ldots \cdot 2014$ be the product of the numbers less or equal to 2014 that give remainder 1 when divided by 3 . Find the last non-zero digit of $A$.
|
Grouping the elements of the product by ten we get:
$$
\begin{aligned}
& (30 k+1)(30 k+4)(30 k+7)(30 k+10)(30 k+13)(30 k+16) \\
& (30 k+19)(30 k+22)(30 k+25)(30 k+28)= \\
& =(30 k+1)(15 k+2)(30 k+7)(120 k+40)(30 k+13)(15 k+8) \\
& (30 k+19)(15 k+11)(120 k+100)(15 k+14)
\end{aligned}
$$
(We divide all even numbers not divisible by five, by two and multiply all numbers divisible by five with four.)
We denote $P_{k}=(30 k+1)(15 k+2)(30 k+7)(30 k+13)(15 k+8)(30 k+19)(15 k+11)(15 k+14)$. For all the numbers not divisible by five, only the last digit affects the solution, since the power of two in the numbers divisible by five is greater than the power of five. Considering this, for even $k, P_{k}$ ends with the same digit as $1 \cdot 2 \cdot 7 \cdot 3 \cdot 8 \cdot 9 \cdot 1 \cdot 4$, i.e. six and for odd $k, P_{k}$ ends with the same digit as $1 \cdot 7 \cdot 7 \cdot 3 \cdot 3 \cdot 9 \cdot 6 \cdot 9$, i.e. six. Thus $P_{0} P_{1} \ldots P_{66}$ ends with six. If we remove one zero from the end of all numbers divisible with five, we get that the last nonzero digit of the given product is the same as the one from $6 \cdot 2011 \cdot 2014 \cdot 4 \cdot 10 \cdot 16 \cdot \ldots .796 \cdot 802$. Considering that $4 \cdot 6 \cdot 2 \cdot 8$ ends with four and removing one zero from every fifth number we get that the last nonzero digit is the same as in $4 \cdot 4^{26} \cdot 784 \cdot 796 \cdot 802 \cdot 1 \cdot 4 \cdot \ldots \cdot 76 \cdot 79$. Repeating the process we did for the starting sequence we conclude that the last nonzero number will be the same as in $2 \cdot 6 \cdot 6 \cdot 40 \cdot 100 \cdot 160 \cdot 220 \cdot 280 \cdot 61 \cdot 32 \cdot 67 \cdot 73 \cdot 38 \cdot 79$, which is two.
Let $A B C$ be a triangle with $\measuredangle B=\measuredangle C=40^{\circ}$. The bisector of the $\measuredangle B$ meets $A C$ at the point $D$ . Prove that $\overline{B D}+\overline{D A}=\overline{B C}$.
Solution. Since $\measuredangle B A C=100^{\circ}$ and $\measuredangle B D C=120^{\circ}$ we have $\overline{B D}<\overline{B C}$. Let $E$ be the point on $\overline{B C}$ such that $\overline{B D}=\overline{B E}$. Then $\measuredangle D E C=100^{\circ}$ and $\measuredangle E D C=40^{\circ}$, hence $\overline{D E}=\overline{E C}$, and $\measuredangle B A C+\measuredangle D E B=180^{\circ}$. So $A, B, E$ and $D$ are concyclic, implying $\overline{A D}=\overline{D E}$ (since $\measuredangle A B D=\measuredangle D B C=20^{\circ}$ ), which completes the proof.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo_2014.jsonl",
"problem_match": "## C4",
"solution_match": "\nSolution."
}
|
a0924b6e-a0c7-5111-ad49-337ad1a98810
| 605,694
|
Let $C D \perp A B(D \in A B), D M \perp A C(M \in A C)$ and $D N \perp B C(N \in B C)$ for an acute triangle ABC with area $S$. If $H_{1}$ and $H_{2}$ are the orthocentres of the triangles $M N C$ and MND respectively. Evaluate the area of the quadrilateral $\mathrm{AH}_{1} \mathrm{BH}_{2}$.
|
Let $O, P, K, R$ and $T$ be the midpoints of the segments $C D, M N, C N, C H_{1}$ and $M H_{1}$, respectively. From $\triangle M N C$ we have that $\overline{P K}=\frac{1}{2} \overline{M C}$ and $P K \| M C$. Analogously, from $\Delta M H_{1} C$ we have that $\overline{T R}=\frac{1}{2} \overline{M C}$ and $T R \| M C$. Consequently, $\overline{P K}=\overline{T R}$ and $P K \| T R$. Also $O K \| D N$
(from $\triangle C D N$ ) and since $D N \perp B C$ and $M H_{1} \perp B C$, it follows that $T H_{1} \| O K$. Since $O$ is the circumcenter of $\triangle C M N, O P \perp M N$. Thus, $C H_{1} \perp M N$ implies $O P \| C H_{1}$. We conclude $\Delta T R H_{1} \cong \triangle K P O$ (they have parallel sides and $\overline{T R}=\overline{P K}$ ), hence $\overline{R H_{1}}=\overline{P O}$, i.e. $\overline{C H_{1}}=2 \overline{P O}$ and $\mathrm{CH}_{1} \| \mathrm{PO}$.
Analogously, $\overline{D H_{2}}=2 \overline{P O}$ and $D H_{2} \| P O$. From $\overline{C H_{1}}=2 \overline{P O}=\overline{D H_{2}}$ and
$H_{1} H_{2} \| C D$. Therefore the area of the quadrilateral $A H_{1} B H_{2}$ is $\frac{\overline{A B} \cdot \overline{H_{1} H_{2}}}{2}=\frac{\overline{A B} \cdot \overline{C D}}{2}=S$.
Solution2. Since $M H_{1} \| D N$ and $N H_{1} \| D M, M D N H_{1}$ is a parallelogram. Similarly, $\mathrm{NH}_{2} \| C M$ and $\mathrm{MH}_{2} \| \mathrm{CN}$ imply $\mathrm{MCNH}_{2}$ is a parallelogram. Let $P$ be the midpoint of the segment $\overline{M N}$. Then $\sigma_{P}(D)=H_{1}$ and $\sigma_{P}(C)=H_{2}$, thus $C D \| H_{1} H_{2}$ and $\overline{C D}=\overline{H_{1} H_{2}}$. From $C D \perp A B$ we deduce $A_{A H_{1} B H_{2}}=\frac{1}{2} \overline{A B} \cdot \overline{C D}=S$.
|
S
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $C D \perp A B(D \in A B), D M \perp A C(M \in A C)$ and $D N \perp B C(N \in B C)$ for an acute triangle ABC with area $S$. If $H_{1}$ and $H_{2}$ are the orthocentres of the triangles $M N C$ and MND respectively. Evaluate the area of the quadrilateral $\mathrm{AH}_{1} \mathrm{BH}_{2}$.
|
Let $O, P, K, R$ and $T$ be the midpoints of the segments $C D, M N, C N, C H_{1}$ and $M H_{1}$, respectively. From $\triangle M N C$ we have that $\overline{P K}=\frac{1}{2} \overline{M C}$ and $P K \| M C$. Analogously, from $\Delta M H_{1} C$ we have that $\overline{T R}=\frac{1}{2} \overline{M C}$ and $T R \| M C$. Consequently, $\overline{P K}=\overline{T R}$ and $P K \| T R$. Also $O K \| D N$

(from $\triangle C D N$ ) and since $D N \perp B C$ and $M H_{1} \perp B C$, it follows that $T H_{1} \| O K$. Since $O$ is the circumcenter of $\triangle C M N, O P \perp M N$. Thus, $C H_{1} \perp M N$ implies $O P \| C H_{1}$. We conclude $\Delta T R H_{1} \cong \triangle K P O$ (they have parallel sides and $\overline{T R}=\overline{P K}$ ), hence $\overline{R H_{1}}=\overline{P O}$, i.e. $\overline{C H_{1}}=2 \overline{P O}$ and $\mathrm{CH}_{1} \| \mathrm{PO}$.
Analogously, $\overline{D H_{2}}=2 \overline{P O}$ and $D H_{2} \| P O$. From $\overline{C H_{1}}=2 \overline{P O}=\overline{D H_{2}}$ and
$H_{1} H_{2} \| C D$. Therefore the area of the quadrilateral $A H_{1} B H_{2}$ is $\frac{\overline{A B} \cdot \overline{H_{1} H_{2}}}{2}=\frac{\overline{A B} \cdot \overline{C D}}{2}=S$.
Solution2. Since $M H_{1} \| D N$ and $N H_{1} \| D M, M D N H_{1}$ is a parallelogram. Similarly, $\mathrm{NH}_{2} \| C M$ and $\mathrm{MH}_{2} \| \mathrm{CN}$ imply $\mathrm{MCNH}_{2}$ is a parallelogram. Let $P$ be the midpoint of the segment $\overline{M N}$. Then $\sigma_{P}(D)=H_{1}$ and $\sigma_{P}(C)=H_{2}$, thus $C D \| H_{1} H_{2}$ and $\overline{C D}=\overline{H_{1} H_{2}}$. From $C D \perp A B$ we deduce $A_{A H_{1} B H_{2}}=\frac{1}{2} \overline{A B} \cdot \overline{C D}=S$.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo_2014.jsonl",
"problem_match": "## G3",
"solution_match": "\nSolution1."
}
|
62d5dcf3-abb9-55ce-86ec-c8a7793753ae
| 605,711
|
Let $a$ and $b$ be positive real numbers such that $3 a^{2}+2 b^{2}=3 a+2 b$. Find the minimum value of
$$
A=\sqrt{\frac{a}{b(3 a+2)}}+\sqrt{\frac{b}{a(2 b+3)}}
$$
|
By the Cauchy-Schwarz inequality we have that
$$
5\left(3 a^{2}+2 b^{2}\right)=5\left(a^{2}+a^{2}+a^{2}+b^{2}+b^{2}\right) \geq(3 a+2 b)^{2}
$$
(or use that the last inequality is equivalent to $(a-b)^{2} \geq 0$ ).
So, with the help of the given condition we get that $3 a+2 b \leq 5$. Now, by the AM-GM inequality we have that
$$
A \geq 2 \sqrt{\sqrt{\frac{a}{b(3 a+2)}} \cdot \sqrt{\frac{b}{a(2 b+3)}}}=\frac{2}{\sqrt[4]{(3 a+2)(2 b+3)}}
$$
Finally, using again the AM-GM inequality, we get that
$$
(3 a+2)(2 b+3) \leq\left(\frac{3 a+2 b+5}{2}\right)^{2} \leq 25
$$
so $A \geq 2 / \sqrt{5}$ and the equality holds if and only if $a=b=1$.
|
\frac{2}{\sqrt{5}}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Let $a$ and $b$ be positive real numbers such that $3 a^{2}+2 b^{2}=3 a+2 b$. Find the minimum value of
$$
A=\sqrt{\frac{a}{b(3 a+2)}}+\sqrt{\frac{b}{a(2 b+3)}}
$$
|
By the Cauchy-Schwarz inequality we have that
$$
5\left(3 a^{2}+2 b^{2}\right)=5\left(a^{2}+a^{2}+a^{2}+b^{2}+b^{2}\right) \geq(3 a+2 b)^{2}
$$
(or use that the last inequality is equivalent to $(a-b)^{2} \geq 0$ ).
So, with the help of the given condition we get that $3 a+2 b \leq 5$. Now, by the AM-GM inequality we have that
$$
A \geq 2 \sqrt{\sqrt{\frac{a}{b(3 a+2)}} \cdot \sqrt{\frac{b}{a(2 b+3)}}}=\frac{2}{\sqrt[4]{(3 a+2)(2 b+3)}}
$$
Finally, using again the AM-GM inequality, we get that
$$
(3 a+2)(2 b+3) \leq\left(\frac{3 a+2 b+5}{2}\right)^{2} \leq 25
$$
so $A \geq 2 / \sqrt{5}$ and the equality holds if and only if $a=b=1$.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo_2017_short_list.jsonl",
"problem_match": "\nA2.",
"solution_match": "\nSolution."
}
|
59d9e080-4578-5f68-8228-8614f3e05c38
| 605,790
|
Consider a regular $2 n$-gon $P$ in the plane, where $n$ is a positive integer. We say that a point $S$ on one of the sides of $P$ can be seen from a point $E$ that is external to $P$, if the line segment $S E$ contains no other points that lie on the sides of $P$ except $S$. We want to color the sides of $P$ in 3 colors, such that every side is colored in exactly one color, and each color must be used at least once. Moreover, from every point in the plane external to $P$, at most 2 different colors on $P$ can be seen (ignore the vertices of $P$, we consider them colorless). Find the number of distinct such colorings of $P$ (two colorings are considered distinct if at least one side is colored differently).
|
Answer: For $n=2$, the answer is 36 ; for $n=3$, the answer is 30 and for $n \geq 4$, the answer is $6 n$.
Lemma 1. Given a regular $2 n$-gon in the plane and a sequence of $n$ consecutive sides $s_{1}, s_{2}, \ldots, s_{n}$ there is an external point $Q$ in the plane, such that the color of each $s_{i}$ can be seen from $Q$, for $i=1,2, \ldots, n$.
Proof. It is obvious that for a semi-circle $S$, there is a point $R$ in the plane far enough on the bisector of its diameter such that almost the entire semi-circle can be seen from $R$.
Now, it is clear that looking at the circumscribed circle around the $2 n$-gon, there is a semi-circle $S$ such that each $s_{i}$ either has both endpoints on it, or has an endpoint that's on the semi-circle, and is not on the semi-circle's end. So, take $Q$ to be a point in the plane from which almost all of $S$ can be seen, clearly, the color of each $s_{i}$ can be seen from $Q$.
Lemma 2. Given a regular $2 n$-gon in the plane, and a sequence of $n+1$ consecutive sides $s_{1}, s_{2}, \ldots, s_{n+1}$ there is no external point $Q$ in the plane, such that the color of each $s_{i}$ can be seen from $Q$, for $i=1,2, \ldots, n+1$.
Proof. Since $s_{1}$ and $s_{n+1}$ are parallel opposite sides of the $2 n$-gon, they cannot be seen at the same time from an external point.
For $n=2$, we have a square, so all we have to do is make sure each color is used. Two sides will be of the same color, and we have to choose which are these 2 sides, and then assign colors
according to this choice, so the answer is $\binom{4}{2} \cdot 3 \cdot 2=36$.
For $n=3$, we have a hexagon. Denote the sides as $a_{1}, a_{2}, \ldots q_{6}$, in that order. There must be 2 consecutive sides of different colors, say $a_{1}$ is red, $a_{2}$ is blue. We must have a green side, and only $a_{4}$ and $a_{5}$ can be green. We have 3 possibilities:
1) $a_{4}$ is green, $a_{5}$ is not. So, $a_{3}$ must be blue and $a_{5}$ must be blue (by elimination) and $a_{6}$ must be blue, so we get a valid coloring.
2) Both $a_{4}$ and $a_{5}$ are green, thus $a_{6}$ must be red and $a_{5}$ must be blue, and we get the coloring rbbggr.
3) $a_{5}$ is green, $a_{4}$ is not. Then $a_{6}$ must be red. Subsequently, $a_{4}$ must be red (we assume it is not green). It remains that $a_{3}$ must be red, and the coloring is rbrrgr.
Thus, we have 2 kinds of configurations:
i) 2 opposite sides have 2 opposite colors and all other sides are of the third color. This can happen in 3.(3.2.1) $=18$ ways (first choosing the pair of opposite sides, then assigning colors), ii) 3 pairs of consecutive sides, each pair in one of the 3 colors. This can happen in $2.6=12$ ways (2 partitioning into pairs of consecutive sides, for each partitioning, 6 ways to assign the colors).
Thus, for $n=3$, the answer is $18+12=30$.
Finally, let's address the case $n \geq 4$. The important thing now is that any 4 consecutive sides can be seen from an external point, by Lemma 1.
Denote the sides as $a_{1}, a_{2}, \ldots, a_{2 n}$. Again, there must be 2 adjacent sides that are of different colors, say $a_{1}$ is blue and $a_{2}$ is red. We must have a green side, and by Lemma 1, that can only be $a_{n+1}$ or $a_{n+2}$. So, we have 2 cases:
Case 1: $a_{n+1}$ is green, so $a_{n}$ must be red (cannot be green due to Lemma 1 applied to $a_{1}, a_{2}, \ldots, a_{n}$, cannot be blue for the sake of $a_{2}, \ldots, a_{n+1}$. If $a_{n+2}$ is red, so are $a_{n+3}, \ldots, a_{2 n}$, and we get a valid coloring: $a_{1}$ is blue, $a_{n+1}$ is green, and all the others are red.
If $a_{n+2}$ is green:
a) $a_{n+3}$ cannot be green, because of $a_{2}, a_{1}, a_{2 n} \ldots, a_{n+3}$.
b) $a_{n+3}$ cannot be blue, because the 4 adjacent sides $a_{n}, \ldots, a_{n+3}$ can be seen (this is the case that makes the separate treatment of $n \geq 4$ necessary)
c) $a_{n+3}$ cannot be red, because of $a_{1}, a_{2 n}, \ldots, a_{n+2}$.
So, in the case that $a_{n+2}$ is also green, we cannot get a valid coloring.
Case 2: $a_{n+2}$ is green is treated the same way as Case 1.
This means that the only valid configuration for $n \geq 4$ is having 2 opposite sides colored in 2 different colors, and all other sides colored in the third color. This can be done in $n \cdot 3 \cdot 2=6 n$ ways.
|
6n
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Consider a regular $2 n$-gon $P$ in the plane, where $n$ is a positive integer. We say that a point $S$ on one of the sides of $P$ can be seen from a point $E$ that is external to $P$, if the line segment $S E$ contains no other points that lie on the sides of $P$ except $S$. We want to color the sides of $P$ in 3 colors, such that every side is colored in exactly one color, and each color must be used at least once. Moreover, from every point in the plane external to $P$, at most 2 different colors on $P$ can be seen (ignore the vertices of $P$, we consider them colorless). Find the number of distinct such colorings of $P$ (two colorings are considered distinct if at least one side is colored differently).
|
Answer: For $n=2$, the answer is 36 ; for $n=3$, the answer is 30 and for $n \geq 4$, the answer is $6 n$.
Lemma 1. Given a regular $2 n$-gon in the plane and a sequence of $n$ consecutive sides $s_{1}, s_{2}, \ldots, s_{n}$ there is an external point $Q$ in the plane, such that the color of each $s_{i}$ can be seen from $Q$, for $i=1,2, \ldots, n$.
Proof. It is obvious that for a semi-circle $S$, there is a point $R$ in the plane far enough on the bisector of its diameter such that almost the entire semi-circle can be seen from $R$.
Now, it is clear that looking at the circumscribed circle around the $2 n$-gon, there is a semi-circle $S$ such that each $s_{i}$ either has both endpoints on it, or has an endpoint that's on the semi-circle, and is not on the semi-circle's end. So, take $Q$ to be a point in the plane from which almost all of $S$ can be seen, clearly, the color of each $s_{i}$ can be seen from $Q$.
Lemma 2. Given a regular $2 n$-gon in the plane, and a sequence of $n+1$ consecutive sides $s_{1}, s_{2}, \ldots, s_{n+1}$ there is no external point $Q$ in the plane, such that the color of each $s_{i}$ can be seen from $Q$, for $i=1,2, \ldots, n+1$.
Proof. Since $s_{1}$ and $s_{n+1}$ are parallel opposite sides of the $2 n$-gon, they cannot be seen at the same time from an external point.
For $n=2$, we have a square, so all we have to do is make sure each color is used. Two sides will be of the same color, and we have to choose which are these 2 sides, and then assign colors
according to this choice, so the answer is $\binom{4}{2} \cdot 3 \cdot 2=36$.
For $n=3$, we have a hexagon. Denote the sides as $a_{1}, a_{2}, \ldots q_{6}$, in that order. There must be 2 consecutive sides of different colors, say $a_{1}$ is red, $a_{2}$ is blue. We must have a green side, and only $a_{4}$ and $a_{5}$ can be green. We have 3 possibilities:
1) $a_{4}$ is green, $a_{5}$ is not. So, $a_{3}$ must be blue and $a_{5}$ must be blue (by elimination) and $a_{6}$ must be blue, so we get a valid coloring.
2) Both $a_{4}$ and $a_{5}$ are green, thus $a_{6}$ must be red and $a_{5}$ must be blue, and we get the coloring rbbggr.
3) $a_{5}$ is green, $a_{4}$ is not. Then $a_{6}$ must be red. Subsequently, $a_{4}$ must be red (we assume it is not green). It remains that $a_{3}$ must be red, and the coloring is rbrrgr.
Thus, we have 2 kinds of configurations:
i) 2 opposite sides have 2 opposite colors and all other sides are of the third color. This can happen in 3.(3.2.1) $=18$ ways (first choosing the pair of opposite sides, then assigning colors), ii) 3 pairs of consecutive sides, each pair in one of the 3 colors. This can happen in $2.6=12$ ways (2 partitioning into pairs of consecutive sides, for each partitioning, 6 ways to assign the colors).
Thus, for $n=3$, the answer is $18+12=30$.
Finally, let's address the case $n \geq 4$. The important thing now is that any 4 consecutive sides can be seen from an external point, by Lemma 1.
Denote the sides as $a_{1}, a_{2}, \ldots, a_{2 n}$. Again, there must be 2 adjacent sides that are of different colors, say $a_{1}$ is blue and $a_{2}$ is red. We must have a green side, and by Lemma 1, that can only be $a_{n+1}$ or $a_{n+2}$. So, we have 2 cases:
Case 1: $a_{n+1}$ is green, so $a_{n}$ must be red (cannot be green due to Lemma 1 applied to $a_{1}, a_{2}, \ldots, a_{n}$, cannot be blue for the sake of $a_{2}, \ldots, a_{n+1}$. If $a_{n+2}$ is red, so are $a_{n+3}, \ldots, a_{2 n}$, and we get a valid coloring: $a_{1}$ is blue, $a_{n+1}$ is green, and all the others are red.
If $a_{n+2}$ is green:
a) $a_{n+3}$ cannot be green, because of $a_{2}, a_{1}, a_{2 n} \ldots, a_{n+3}$.
b) $a_{n+3}$ cannot be blue, because the 4 adjacent sides $a_{n}, \ldots, a_{n+3}$ can be seen (this is the case that makes the separate treatment of $n \geq 4$ necessary)
c) $a_{n+3}$ cannot be red, because of $a_{1}, a_{2 n}, \ldots, a_{n+2}$.
So, in the case that $a_{n+2}$ is also green, we cannot get a valid coloring.
Case 2: $a_{n+2}$ is green is treated the same way as Case 1.
This means that the only valid configuration for $n \geq 4$ is having 2 opposite sides colored in 2 different colors, and all other sides colored in the third color. This can be done in $n \cdot 3 \cdot 2=6 n$ ways.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo_2017_short_list.jsonl",
"problem_match": "\nC2.",
"solution_match": "\nSolution."
}
|
583a05b1-57e1-582a-a4a3-fc1f71af6ebb
| 605,827
|
We have two piles with 2000 and 2017 coins respectively. Ann and Bob take alternate turns making the following moves: The player whose turn is to move picks a pile with at least two coins, removes from that pile $t$ coins for some $2 \leqslant t \leqslant 4$, and adds to the other pile 1 coin. The players can choose a different $t$ at each turn, and the player who cannot make a move loses. If Ann plays first determine which player has a winning strategy.
|
Denote the number of coins in the two piles by $X$ and $Y$. We say that the pair $(X, Y)$ is losing if the player who begins the game loses and that the pair $(X, Y)$ is winning otherwise. We shall prove that $(X, Y)$ is loosing if $X-Y \equiv 0,1,7 \bmod 8$, and winning if $X-Y \equiv 2,3,4,5,6 \bmod 8$.
Lemma 1. If we have a winning pair $(X, Y)$ then we can always play in such a way that the other player is then faced with a losing pair.
Proof of Lemma 1. Assume $X \geq Y$ and write $X=Y+8 k+\ell$ for some non-negative integer $k$ and some $\ell \in\{2,3,4,5,6\}$. If $\ell=2,3,4$ then we remove two coins from the first pile and add one coin to the second pile. If $\ell=5,6$ then we remove four coins from the first pile and add one coin to the second pile. In each case we then obtain loosing pair
Lemma 2. If we are faced with a losing distribution then either we cannot play, or, however we play, the other player is faced with a winning distribution.
Proof of Lemma 2. Without loss of generality we may assume that we remove $k$ coins from the first pile. The following table show the new difference for all possible values of $k$ and all possible differences $X-Y$. So however we move, the other player will be faced with a winning distribution.
| $k \backslash X-Y$ | 0 | 1 | 7 |
| :---: | :---: | :---: | :---: |
| 2 | 5 | 6 | 4 |
| 3 | 4 | 5 | 3 |
| 4 | 3 | 4 | 2 |
Since initially the coin difference is 1 mod 8 , by Lemmas 1 and 2 Bob has a winning strategy: He can play so that he is always faced with a winning distribution while Ann is always faced with a losing distribution. So Bob cannot lose. On the other hand the game finishes after at most 4017 moves, so Ann has to lose.
## Geometry
|
Bob
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
We have two piles with 2000 and 2017 coins respectively. Ann and Bob take alternate turns making the following moves: The player whose turn is to move picks a pile with at least two coins, removes from that pile $t$ coins for some $2 \leqslant t \leqslant 4$, and adds to the other pile 1 coin. The players can choose a different $t$ at each turn, and the player who cannot make a move loses. If Ann plays first determine which player has a winning strategy.
|
Denote the number of coins in the two piles by $X$ and $Y$. We say that the pair $(X, Y)$ is losing if the player who begins the game loses and that the pair $(X, Y)$ is winning otherwise. We shall prove that $(X, Y)$ is loosing if $X-Y \equiv 0,1,7 \bmod 8$, and winning if $X-Y \equiv 2,3,4,5,6 \bmod 8$.
Lemma 1. If we have a winning pair $(X, Y)$ then we can always play in such a way that the other player is then faced with a losing pair.
Proof of Lemma 1. Assume $X \geq Y$ and write $X=Y+8 k+\ell$ for some non-negative integer $k$ and some $\ell \in\{2,3,4,5,6\}$. If $\ell=2,3,4$ then we remove two coins from the first pile and add one coin to the second pile. If $\ell=5,6$ then we remove four coins from the first pile and add one coin to the second pile. In each case we then obtain loosing pair
Lemma 2. If we are faced with a losing distribution then either we cannot play, or, however we play, the other player is faced with a winning distribution.
Proof of Lemma 2. Without loss of generality we may assume that we remove $k$ coins from the first pile. The following table show the new difference for all possible values of $k$ and all possible differences $X-Y$. So however we move, the other player will be faced with a winning distribution.
| $k \backslash X-Y$ | 0 | 1 | 7 |
| :---: | :---: | :---: | :---: |
| 2 | 5 | 6 | 4 |
| 3 | 4 | 5 | 3 |
| 4 | 3 | 4 | 2 |
Since initially the coin difference is 1 mod 8 , by Lemmas 1 and 2 Bob has a winning strategy: He can play so that he is always faced with a winning distribution while Ann is always faced with a losing distribution. So Bob cannot lose. On the other hand the game finishes after at most 4017 moves, so Ann has to lose.
## Geometry
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo_2017_short_list.jsonl",
"problem_match": "\nC3.",
"solution_match": "\nSolution."
}
|
a6963100-1d42-5071-a704-2ba750a81ca0
| 605,837
|
Let $A$ and $B$ be two non-empty subsets of $X=\{1,2, \ldots, 11\}$ with $A \cup B=X$. Let $P_{A}$ be the product of all elements of $A$ and let $P_{B}$ be the product of all elements of $B$. Find the minimum and maximum possible value of $P_{A}+P_{B}$ and find all possible equality cases.
|
For the maximum, we use the fact that $\left(P_{A}-1\right)\left(P_{B}-1\right) \geqslant 0$, to get that $P_{A}+P_{B} \leqslant P_{A} P_{B}+1=11!+1$. Equality holds if and only if $A=\{1\}$ or $B=\{1\}$.
For the minimum observe, first that $P_{A} \cdot P_{B}=11!=c$. Without loss of generality let $P_{A} \leqslant P_{B}$. In this case $P_{A} \leqslant \sqrt{c}$. We write $P_{A}+P_{B}=P_{A}+\frac{c}{P_{A}}$ and consider the function $f(x)=x+\frac{c}{x}$ for $x \leqslant \sqrt{c}$. Since
$$
f(x)-f(y)=x-y+\frac{c(y-x)}{y x}=\frac{(x-y)(x y-c)}{x y}
$$
then $f$ is decreasing for $x \in(0, c]$.
Since $x$ is an integer and cannot be equal with $\sqrt{c}$, the minimum is attained to the closest integer to $\sqrt{c}$. We have $\lfloor\sqrt{11!}\rfloor=\left\lfloor\sqrt{2^{8} \cdot 3^{4} \cdot 5^{2} \cdot 7 \cdot 11}\right\rfloor=\lfloor 720 \sqrt{77}\rfloor=6317$ and the closest integer which can be a product of elements of $X$ is $6300=2 \cdot 5 \cdot 7 \cdot 9 \cdot 10$.
Therefore the minimum is $f(6300)=6300+6336=12636$ and it is achieved for example for $A=\{2,5,7,9,10\}, B=\{1,3,4,6,8,11\}$.
Suppose now that there are different sets $A$ and $B$ such that $P_{A}+P_{B}=402$. Then the pairs of numbers $(6300,6336)$ and $\left(P_{A}, P_{B}\right)$ have the same sum and the same product, thus the equality case is unique for the numbers 6300 and 6336. It remains to find all possible subsets $A$ with product $6300=2^{2} \cdot 3^{2} \cdot 5^{2} \cdot 7$. It is immediate that $5,7,10 \in A$ and from here it is easy to see that all posibilities are $A=\{2,5,7,9,10\},\{1,2,5,7,9,10\},\{3,5,6,7,10\}$ and $\{1,3,5,6,7,10\}$.
Alternative Solution by PSC. We have $P_{A}+P_{B} \geqslant 2 \sqrt{P_{A} P_{B}}=2 \sqrt{11!}=1440 \sqrt{77}$. Since $P_{A}+P_{B}$ is an integer, we have $P_{A}+P_{B} \geqslant\lceil 1440 \sqrt{77}\rceil=12636$. One can then follow the approach of the first solution to find all equality cases.
Remark by PSC. We can increase the difficulty of the alternative solution by taking $X=\{1,2, \ldots, 9\}$. Following the first solution we have $\lfloor\sqrt{9!}\rfloor=\lfloor 72 \sqrt{70}\rfloor=602$ and the closest integer which can be a product of elements of $X$ is $2 \cdot 4 \cdot 8 \cdot 9=576$. The minimum is $f(576)=576+630=1206$ achieved by $A=\{1,2,4,8,9\}$ and $B=\{3,5,6,7\}$. For equality, the set with product 630 must contain 5 and 7 , either 2 and 9 or 3 and 6 , and finally it is allowed to either contain 1 or not.
Our alternative solution would give $P_{A}+P_{B} \geqslant\lceil 144 \sqrt{70}\rceil=1205$. One would then need to find a way to show that $P_{A}+P_{B} \neq 1205$. To do this we can assume without loss of generality that $5 \in A$. Then the last digit of $P_{A}$ is either 5 or 0 . In the first case the last digit of $P_{B}$ would be 0 and so $P_{B}$ would also be a multiple of 5 which is impossible. The second case is analogous.
The computation of the expresions here might be a bit simpler. For example $9!=362880$ so one expects $\sqrt{9!}$ to be slightly larger than 600 .
|
12636
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Let $A$ and $B$ be two non-empty subsets of $X=\{1,2, \ldots, 11\}$ with $A \cup B=X$. Let $P_{A}$ be the product of all elements of $A$ and let $P_{B}$ be the product of all elements of $B$. Find the minimum and maximum possible value of $P_{A}+P_{B}$ and find all possible equality cases.
|
For the maximum, we use the fact that $\left(P_{A}-1\right)\left(P_{B}-1\right) \geqslant 0$, to get that $P_{A}+P_{B} \leqslant P_{A} P_{B}+1=11!+1$. Equality holds if and only if $A=\{1\}$ or $B=\{1\}$.
For the minimum observe, first that $P_{A} \cdot P_{B}=11!=c$. Without loss of generality let $P_{A} \leqslant P_{B}$. In this case $P_{A} \leqslant \sqrt{c}$. We write $P_{A}+P_{B}=P_{A}+\frac{c}{P_{A}}$ and consider the function $f(x)=x+\frac{c}{x}$ for $x \leqslant \sqrt{c}$. Since
$$
f(x)-f(y)=x-y+\frac{c(y-x)}{y x}=\frac{(x-y)(x y-c)}{x y}
$$
then $f$ is decreasing for $x \in(0, c]$.
Since $x$ is an integer and cannot be equal with $\sqrt{c}$, the minimum is attained to the closest integer to $\sqrt{c}$. We have $\lfloor\sqrt{11!}\rfloor=\left\lfloor\sqrt{2^{8} \cdot 3^{4} \cdot 5^{2} \cdot 7 \cdot 11}\right\rfloor=\lfloor 720 \sqrt{77}\rfloor=6317$ and the closest integer which can be a product of elements of $X$ is $6300=2 \cdot 5 \cdot 7 \cdot 9 \cdot 10$.
Therefore the minimum is $f(6300)=6300+6336=12636$ and it is achieved for example for $A=\{2,5,7,9,10\}, B=\{1,3,4,6,8,11\}$.
Suppose now that there are different sets $A$ and $B$ such that $P_{A}+P_{B}=402$. Then the pairs of numbers $(6300,6336)$ and $\left(P_{A}, P_{B}\right)$ have the same sum and the same product, thus the equality case is unique for the numbers 6300 and 6336. It remains to find all possible subsets $A$ with product $6300=2^{2} \cdot 3^{2} \cdot 5^{2} \cdot 7$. It is immediate that $5,7,10 \in A$ and from here it is easy to see that all posibilities are $A=\{2,5,7,9,10\},\{1,2,5,7,9,10\},\{3,5,6,7,10\}$ and $\{1,3,5,6,7,10\}$.
Alternative Solution by PSC. We have $P_{A}+P_{B} \geqslant 2 \sqrt{P_{A} P_{B}}=2 \sqrt{11!}=1440 \sqrt{77}$. Since $P_{A}+P_{B}$ is an integer, we have $P_{A}+P_{B} \geqslant\lceil 1440 \sqrt{77}\rceil=12636$. One can then follow the approach of the first solution to find all equality cases.
Remark by PSC. We can increase the difficulty of the alternative solution by taking $X=\{1,2, \ldots, 9\}$. Following the first solution we have $\lfloor\sqrt{9!}\rfloor=\lfloor 72 \sqrt{70}\rfloor=602$ and the closest integer which can be a product of elements of $X$ is $2 \cdot 4 \cdot 8 \cdot 9=576$. The minimum is $f(576)=576+630=1206$ achieved by $A=\{1,2,4,8,9\}$ and $B=\{3,5,6,7\}$. For equality, the set with product 630 must contain 5 and 7 , either 2 and 9 or 3 and 6 , and finally it is allowed to either contain 1 or not.
Our alternative solution would give $P_{A}+P_{B} \geqslant\lceil 144 \sqrt{70}\rceil=1205$. One would then need to find a way to show that $P_{A}+P_{B} \neq 1205$. To do this we can assume without loss of generality that $5 \in A$. Then the last digit of $P_{A}$ is either 5 or 0 . In the first case the last digit of $P_{B}$ would be 0 and so $P_{B}$ would also be a multiple of 5 which is impossible. The second case is analogous.
The computation of the expresions here might be a bit simpler. For example $9!=362880$ so one expects $\sqrt{9!}$ to be slightly larger than 600 .
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo_shortlist_2019-1.jsonl",
"problem_match": "\nA3.",
"solution_match": "\nSolution."
}
|
6053c462-7051-50d6-81f5-80e2f227188e
| 605,962
|
In a $5 \times 100$ table we have coloured black $n$ of its cells. Each of the 500 cells has at most two adjacent (by side) cells coloured black. Find the largest possible value of $n$.
|
If we colour all the cells along all edges of the board together with the entire middle row except the second and the last-but-one cell, the condition is satisfied and there are 302 black cells. The figure below exhibits this colouring for the $5 \times 8$ case.

We can cover the table by one fragment like the first one on the figure below, 24 fragments like the middle one, and one fragment like the third one.
In each fragment, among the cells with the same letter, there are at most two coloured black, so the total number of coloured cells is at most $(5+24 \cdot 6+1) \cdot 2+2=302$.
Alternative Solution by PSC. Consider the cells adjacent to all cells of the second and fourth row. Counting multiplicity, each cell in the first and fifth row is counted once, each cell in the third row twice, while each cell in the second and fourth row is also counted twice apart from their first and last cells which are counted only once.
So there are 204 cells counted once and 296 cells counted twice. Those cells contain, counting multiplicity, at most 400 black cells. Suppose $a$ of the cells have multiplicity one and $b$ of them have multiplicity 2 . Then $a+2 b \leqslant 400$ and $a \leqslant 204$. Thus
$$
2 a+2 b \leqslant 400+a \leqslant 604
$$
and so $a+b \leqslant 302$ as required.
Remark by PSC. The alternative solution shows that if we have equality, then all cells in the perimeter of the table except perhaps the two cells of the third row must be coloured black. No other cell in the second or fourth row can be coloured black as this will give a cell in the first or fifth row with at least three neighbouring black cells. For similar reasons we cannot colour black the second and last-but-one cell of the third row. So we must colour black all other cells of the third row and therefore the colouring is unique.
|
302
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
In a $5 \times 100$ table we have coloured black $n$ of its cells. Each of the 500 cells has at most two adjacent (by side) cells coloured black. Find the largest possible value of $n$.
|
If we colour all the cells along all edges of the board together with the entire middle row except the second and the last-but-one cell, the condition is satisfied and there are 302 black cells. The figure below exhibits this colouring for the $5 \times 8$ case.

We can cover the table by one fragment like the first one on the figure below, 24 fragments like the middle one, and one fragment like the third one.

In each fragment, among the cells with the same letter, there are at most two coloured black, so the total number of coloured cells is at most $(5+24 \cdot 6+1) \cdot 2+2=302$.
Alternative Solution by PSC. Consider the cells adjacent to all cells of the second and fourth row. Counting multiplicity, each cell in the first and fifth row is counted once, each cell in the third row twice, while each cell in the second and fourth row is also counted twice apart from their first and last cells which are counted only once.
So there are 204 cells counted once and 296 cells counted twice. Those cells contain, counting multiplicity, at most 400 black cells. Suppose $a$ of the cells have multiplicity one and $b$ of them have multiplicity 2 . Then $a+2 b \leqslant 400$ and $a \leqslant 204$. Thus
$$
2 a+2 b \leqslant 400+a \leqslant 604
$$
and so $a+b \leqslant 302$ as required.
Remark by PSC. The alternative solution shows that if we have equality, then all cells in the perimeter of the table except perhaps the two cells of the third row must be coloured black. No other cell in the second or fourth row can be coloured black as this will give a cell in the first or fifth row with at least three neighbouring black cells. For similar reasons we cannot colour black the second and last-but-one cell of the third row. So we must colour black all other cells of the third row and therefore the colouring is unique.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo_shortlist_2019-1.jsonl",
"problem_match": "\nC3.",
"solution_match": "\nSolution."
}
|
ab64b5f2-0322-57b1-9edf-aee954757872
| 606,028
|
We have a group of $n$ kids. For each pair of kids, at least one has sent a message to the other one. For each kid $A$, among the kids to whom $A$ has sent a message, exactly $25 \%$ have sent a message to $A$. How many possible two-digit values of $n$ are there?
|
If the number of pairs of kids with two-way communication is $k$, then by the given condition the total number of messages is $4 k+4 k=8 k$. Thus the number of pairs of kids is $\frac{n(n-1)}{2}=7 k$. This is possible only if $n \equiv 0,1 \bmod 7$.
- In order to obtain $n=7 m+1$, arrange the kids in a circle and let each kid send a message to the first $4 m$ kids to its right and hence receive a message from the first $4 m$ kids to its left. Thus there are exactly $m$ kids to which it has both sent and received messages.
- In order to obtain $n=7 m$, let kid $X$ send no messages (and receive from every other kid). Arrange the remaining $7 m-1$ kids in a circle and let each kid on the circle send a message to the first $4 m-1$ kids to its right and hence receive a message from the first $4 m-1$ kids to its left. Thus there are exactly $m$ kids to which it has both sent and received messages.
There are 26 two-digit numbers with remainder 0 or 1 modulo 7 . (All numbers of the form $7 m$ and $7 m+1$ with $2 \leqslant m \leqslant 14$.)
Alternative Solution by PSC. Suppose kid $x_{i}$ sent $4 d_{i}$ messages. (Guaranteed by the conditions to be a multiple of 4.) Then it received $d_{i}$ messages from the kids that it has sent a message to, and another $n-1-4 d_{i}$ messages from the rest of the kids. So it received a total of $n-1-3 d_{i}$ messages. Since the total number of messages sent is equal to the total number of mesages received, we must have:
$$
d_{1}+\cdots+d_{n}=\left(n-1-3 d_{1}\right)+\cdots+\left(n-1-3 d_{n}\right)
$$
This gives $7\left(d_{1}+\cdots+d_{n}\right)=n(n-1)$ from which we get $n \equiv 0,1 \bmod 7$ as in the first solution.
We also present an alternative inductive construction (which turns out to be different from the construction in the first solution).
For the case $n \equiv 0 \bmod 7$, we start with a construction for $7 k$ kids, say $x_{1}, \ldots, x_{7 k}$, and another construction with 7 kids, say $y_{1}, \ldots, y_{7}$. We merge them by demanding that in addition, each kid $x_{i}$ sends and receives gifts according to the following table:
| $i \bmod 7$ | Sends | Receives |
| :---: | :---: | :---: |
| 0 | $y_{1}, y_{2}, y_{3}, y_{4}$ | $y_{4}, y_{5}, y_{6}, y_{7}$ |
| 1 | $y_{2}, y_{3}, y_{4}, y_{5}$ | $y_{5}, y_{6}, y_{7}, y_{1}$ |
| 2 | $y_{3}, y_{4}, y_{5}, y_{6}$ | $y_{6}, y_{7}, y_{1}, y_{2}$ |
| 3 | $y_{4}, y_{5}, y_{6}, y_{7}$ | $y_{7}, y_{1}, y_{2}, y_{3}$ |
| 4 | $y_{5}, y_{6}, y_{7}, y_{1}$ | $y_{1}, y_{2}, y_{3}, y_{4}$ |
| 5 | $y_{6}, y_{7}, y_{1}, y_{2}$ | $y_{2}, y_{3}, y_{4}, y_{5}$ |
| 6 | $y_{7}, y_{1}, y_{2}, y_{3}$ | $y_{3}, y_{4}, y_{5}, y_{6}$ |
So each kid $x_{i}$ sends an additional four messages and receives a message from only one of those four additional kids. Also, each kid $y_{j}$ sends an additional $4 k$ messages and receives from exactly $k$ of those additional kids. So this is a valid construction for $7(k+1)$ kids.
For the case $n \equiv 1 \bmod 7$, we start with a construction for $7 k+1$ kids, say $x_{1}, \ldots, x_{7 k+1}$, and we take another 7 kids, say $y_{1}, \ldots, y_{7}$ for which we do not yet mention how they exchange gifts. The kids $x_{1}, \ldots, x_{7 k+1}$ exchange gifts with the kids $y_{1}, \ldots, y_{7}$ according to the previous table. As before, each kid $x_{i}$ satisfies the conditions. We now put $y_{1}, \ldots, y_{7}$ on a circle and demand that each of $y_{1}, \ldots, y_{3}$ sends gifts to the next four kids on the circle and each of $y_{4}, \ldots, y_{7}$ sends gifts to the next three kids on the circle. It is each to check that the condition is satisfied by each $y_{i}$ as well.
|
26
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
We have a group of $n$ kids. For each pair of kids, at least one has sent a message to the other one. For each kid $A$, among the kids to whom $A$ has sent a message, exactly $25 \%$ have sent a message to $A$. How many possible two-digit values of $n$ are there?
|
If the number of pairs of kids with two-way communication is $k$, then by the given condition the total number of messages is $4 k+4 k=8 k$. Thus the number of pairs of kids is $\frac{n(n-1)}{2}=7 k$. This is possible only if $n \equiv 0,1 \bmod 7$.
- In order to obtain $n=7 m+1$, arrange the kids in a circle and let each kid send a message to the first $4 m$ kids to its right and hence receive a message from the first $4 m$ kids to its left. Thus there are exactly $m$ kids to which it has both sent and received messages.
- In order to obtain $n=7 m$, let kid $X$ send no messages (and receive from every other kid). Arrange the remaining $7 m-1$ kids in a circle and let each kid on the circle send a message to the first $4 m-1$ kids to its right and hence receive a message from the first $4 m-1$ kids to its left. Thus there are exactly $m$ kids to which it has both sent and received messages.
There are 26 two-digit numbers with remainder 0 or 1 modulo 7 . (All numbers of the form $7 m$ and $7 m+1$ with $2 \leqslant m \leqslant 14$.)
Alternative Solution by PSC. Suppose kid $x_{i}$ sent $4 d_{i}$ messages. (Guaranteed by the conditions to be a multiple of 4.) Then it received $d_{i}$ messages from the kids that it has sent a message to, and another $n-1-4 d_{i}$ messages from the rest of the kids. So it received a total of $n-1-3 d_{i}$ messages. Since the total number of messages sent is equal to the total number of mesages received, we must have:
$$
d_{1}+\cdots+d_{n}=\left(n-1-3 d_{1}\right)+\cdots+\left(n-1-3 d_{n}\right)
$$
This gives $7\left(d_{1}+\cdots+d_{n}\right)=n(n-1)$ from which we get $n \equiv 0,1 \bmod 7$ as in the first solution.
We also present an alternative inductive construction (which turns out to be different from the construction in the first solution).
For the case $n \equiv 0 \bmod 7$, we start with a construction for $7 k$ kids, say $x_{1}, \ldots, x_{7 k}$, and another construction with 7 kids, say $y_{1}, \ldots, y_{7}$. We merge them by demanding that in addition, each kid $x_{i}$ sends and receives gifts according to the following table:
| $i \bmod 7$ | Sends | Receives |
| :---: | :---: | :---: |
| 0 | $y_{1}, y_{2}, y_{3}, y_{4}$ | $y_{4}, y_{5}, y_{6}, y_{7}$ |
| 1 | $y_{2}, y_{3}, y_{4}, y_{5}$ | $y_{5}, y_{6}, y_{7}, y_{1}$ |
| 2 | $y_{3}, y_{4}, y_{5}, y_{6}$ | $y_{6}, y_{7}, y_{1}, y_{2}$ |
| 3 | $y_{4}, y_{5}, y_{6}, y_{7}$ | $y_{7}, y_{1}, y_{2}, y_{3}$ |
| 4 | $y_{5}, y_{6}, y_{7}, y_{1}$ | $y_{1}, y_{2}, y_{3}, y_{4}$ |
| 5 | $y_{6}, y_{7}, y_{1}, y_{2}$ | $y_{2}, y_{3}, y_{4}, y_{5}$ |
| 6 | $y_{7}, y_{1}, y_{2}, y_{3}$ | $y_{3}, y_{4}, y_{5}, y_{6}$ |
So each kid $x_{i}$ sends an additional four messages and receives a message from only one of those four additional kids. Also, each kid $y_{j}$ sends an additional $4 k$ messages and receives from exactly $k$ of those additional kids. So this is a valid construction for $7(k+1)$ kids.
For the case $n \equiv 1 \bmod 7$, we start with a construction for $7 k+1$ kids, say $x_{1}, \ldots, x_{7 k+1}$, and we take another 7 kids, say $y_{1}, \ldots, y_{7}$ for which we do not yet mention how they exchange gifts. The kids $x_{1}, \ldots, x_{7 k+1}$ exchange gifts with the kids $y_{1}, \ldots, y_{7}$ according to the previous table. As before, each kid $x_{i}$ satisfies the conditions. We now put $y_{1}, \ldots, y_{7}$ on a circle and demand that each of $y_{1}, \ldots, y_{3}$ sends gifts to the next four kids on the circle and each of $y_{4}, \ldots, y_{7}$ sends gifts to the next three kids on the circle. It is each to check that the condition is satisfied by each $y_{i}$ as well.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo_shortlist_2019-1.jsonl",
"problem_match": "\nC4.",
"solution_match": "\nSolution."
}
|
00447e07-a330-58d2-b2fd-d44ca2096c27
| 606,038
|
Find all triples of positive real numbers $(a, b, c)$ so that the expression
$$
M=\frac{(a+b)(b+c)(a+b+c)}{a b c}
$$
gets its least value.
|
The expression $M$ is homogeneous, therefore we can assume that $a b c=1$. We set $s=a+c$ and $p=a c$ and using $b=\frac{1}{a c}$, we get
$$
M=\left(a+\frac{1}{a c}\right)\left(\frac{1}{a c}+c\right)\left(a+\frac{1}{a c}+c\right)=\left(a+p^{-1}\right)\left(c+p^{-1}\right)\left(s+p^{-1}\right)
$$
Expanding the right-hand side we get
$$
M=p s+\frac{s^{2}}{p}+1+\frac{2 s}{p^{2}}+\frac{1}{p^{3}}
$$
Now by $s \geq 2 \sqrt{p}$ and setting $x=p \sqrt{p}>0$ we get
$$
M \geq 2 x+5+\frac{4}{x}+\frac{1}{x^{2}}
$$
We will now prove that
$$
2 x+5+\frac{4}{x}+\frac{1}{x^{2}} \geq \frac{11+5 \sqrt{5}}{2} \text {. }
$$
Indeed, the latter is equivalent to $4 x^{3}-(5 \sqrt{5}+1) x^{2}+8 x+2 \geq 0$, which can be rewritten as
$$
\left(x-\frac{1+\sqrt{5}}{2}\right)^{2}(4 x+3-\sqrt{5}) \geq 0
$$
which is true.
Remark: Notice that the equality holds for $a=c=\sqrt{p}=\sqrt[3]{\frac{1+\sqrt{5}}{2}}$ and $b=\frac{1}{a c}$.
|
\frac{11+5\sqrt{5}}{2}
|
Yes
|
Yes
|
math-word-problem
|
Inequalities
|
Find all triples of positive real numbers $(a, b, c)$ so that the expression
$$
M=\frac{(a+b)(b+c)(a+b+c)}{a b c}
$$
gets its least value.
|
The expression $M$ is homogeneous, therefore we can assume that $a b c=1$. We set $s=a+c$ and $p=a c$ and using $b=\frac{1}{a c}$, we get
$$
M=\left(a+\frac{1}{a c}\right)\left(\frac{1}{a c}+c\right)\left(a+\frac{1}{a c}+c\right)=\left(a+p^{-1}\right)\left(c+p^{-1}\right)\left(s+p^{-1}\right)
$$
Expanding the right-hand side we get
$$
M=p s+\frac{s^{2}}{p}+1+\frac{2 s}{p^{2}}+\frac{1}{p^{3}}
$$
Now by $s \geq 2 \sqrt{p}$ and setting $x=p \sqrt{p}>0$ we get
$$
M \geq 2 x+5+\frac{4}{x}+\frac{1}{x^{2}}
$$
We will now prove that
$$
2 x+5+\frac{4}{x}+\frac{1}{x^{2}} \geq \frac{11+5 \sqrt{5}}{2} \text {. }
$$
Indeed, the latter is equivalent to $4 x^{3}-(5 \sqrt{5}+1) x^{2}+8 x+2 \geq 0$, which can be rewritten as
$$
\left(x-\frac{1+\sqrt{5}}{2}\right)^{2}(4 x+3-\sqrt{5}) \geq 0
$$
which is true.
Remark: Notice that the equality holds for $a=c=\sqrt{p}=\sqrt[3]{\frac{1+\sqrt{5}}{2}}$ and $b=\frac{1}{a c}$.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo_shortlist_2020.jsonl",
"problem_match": "\nA 3.",
"solution_match": "\nSolution."
}
|
90be8f3a-c660-599a-b87f-788af19b745e
| 606,230
|
Alice and Bob play the following game: Alice begins by picking a natural number $n \geqslant 2$. Then, with Bob starting first, they alternately choose one number from the set $A=\{1,2, \ldots, n\}$ according to the following condition: The number chosen at each step should be distinct from all the already chosen numbers, and should differ by 1 from an already chosen number. (At the very first step Bob can choose any number he wants.) The game ends when all numbers from the set $A$ are chosen.
For example, if Alice picks $n=4$, then a valid game would be for Bob to choose 2, then Alice to choose 3, then Bob to choose 1, and then Alice to choose 4 .
Alice wins if the sum $S$ of all of the numbers that she has chosen is composite. Otherwise Bob wins. (In the above example $S=7$, so Bob wins.)
Decide which player has a winning strategy.
|
Alice has a winning strategy. She initially picks $n=8$. We will give a strategy so that she can end up with $S$ even, or $S=15$, or $S=21$, so she wins.
Case 1: If Bob chooses 1, then the game ends with Alice choosing 2,4,6,8 so $S$ is even (larger than 2) and Alice wins.
Case 2: If Bob chooses 2, then Alice chooses 3. Bob can now choose either 1 or 3 .
Case 2A: If Bob chooses 1, then Alice's numbers are $3,4,6,8$. So $S=21$ and Alice wins.
Case 2B: If Bob chooses 4, then Alice chooses 1 and ends with the numbers 1,3,6,8. So $S$ is even and alice wins.
Case 3: If Bob chooses 3, then Alice chooses 2. Bob can now choose either 1 or 4 .
Case 3A: If Bob chooses 1, then Alice's numbers are 2,4,6,8. So $S$ is even and Alice wins.
Case 3B: If Bob chooses 4, then Alice chooses 5. Bob can now choose either 1 or 6 .
Case 3Bi: If Bob chooses 1, then Alice's numbers are 2,5,6,8. So $S=21$ and Alice wins.
Case 3Bii: If Bob chooses 6 , then Alice chooses 1. Then Alice's numbers are 2,5,1,8. So $S$ is even and Alice wins.
Case 4: If Bob chooses 4, then Alice chooses 5. Bob can now choose either 3 or 6 .
Case 4A: If Bob chooses 3, then Alice chooses 6. Bob can now choose either 2 or 7 .
Case 4Ai: If Bob chooses 2, then Alice chooses 1 and ends up with 5,6,1,8. So $S$ is even and Alice wins.
Case 4Aii: If Bob chooses 7, then Alice chooses 8 and ends up with $5,6,8,1$. So $S$ is even and Alice wins.
Case 4B: If Bob chooses 6, then Alice chooses 7. Bob can now choose either 3 or 8 .
Case 4Bi: If Bob chooses 3, then Alice chooses 2 and ends up with 5,7,2 and either 1 or 8 . So $S=15$ or $S=22$ and Alice wins.
Case 4Bii: If Bob chooses 8, then Alice's numbers are $5,7,3,1$. So $S$ is even and Alice wins.
Cases 5-8: If Bob chooses $k \in\{5,6,7,8\}$ then Alice follows the strategy in case $9-k$ but whenever she had to choose $\ell$, she instead chooses $9-\ell$. If at the end of that strategy she ended up with $S$, she will now end up with $S^{\prime}=4 \cdot 9-S=36-S$. Then $S^{\prime}$ is even or $S^{\prime}=15$ or $S^{\prime}=21$ so again she wins.
## GEOMETRY
|
1
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Alice and Bob play the following game: Alice begins by picking a natural number $n \geqslant 2$. Then, with Bob starting first, they alternately choose one number from the set $A=\{1,2, \ldots, n\}$ according to the following condition: The number chosen at each step should be distinct from all the already chosen numbers, and should differ by 1 from an already chosen number. (At the very first step Bob can choose any number he wants.) The game ends when all numbers from the set $A$ are chosen.
For example, if Alice picks $n=4$, then a valid game would be for Bob to choose 2, then Alice to choose 3, then Bob to choose 1, and then Alice to choose 4 .
Alice wins if the sum $S$ of all of the numbers that she has chosen is composite. Otherwise Bob wins. (In the above example $S=7$, so Bob wins.)
Decide which player has a winning strategy.
|
Alice has a winning strategy. She initially picks $n=8$. We will give a strategy so that she can end up with $S$ even, or $S=15$, or $S=21$, so she wins.
Case 1: If Bob chooses 1, then the game ends with Alice choosing 2,4,6,8 so $S$ is even (larger than 2) and Alice wins.
Case 2: If Bob chooses 2, then Alice chooses 3. Bob can now choose either 1 or 3 .
Case 2A: If Bob chooses 1, then Alice's numbers are $3,4,6,8$. So $S=21$ and Alice wins.
Case 2B: If Bob chooses 4, then Alice chooses 1 and ends with the numbers 1,3,6,8. So $S$ is even and alice wins.
Case 3: If Bob chooses 3, then Alice chooses 2. Bob can now choose either 1 or 4 .
Case 3A: If Bob chooses 1, then Alice's numbers are 2,4,6,8. So $S$ is even and Alice wins.
Case 3B: If Bob chooses 4, then Alice chooses 5. Bob can now choose either 1 or 6 .
Case 3Bi: If Bob chooses 1, then Alice's numbers are 2,5,6,8. So $S=21$ and Alice wins.
Case 3Bii: If Bob chooses 6 , then Alice chooses 1. Then Alice's numbers are 2,5,1,8. So $S$ is even and Alice wins.
Case 4: If Bob chooses 4, then Alice chooses 5. Bob can now choose either 3 or 6 .
Case 4A: If Bob chooses 3, then Alice chooses 6. Bob can now choose either 2 or 7 .
Case 4Ai: If Bob chooses 2, then Alice chooses 1 and ends up with 5,6,1,8. So $S$ is even and Alice wins.
Case 4Aii: If Bob chooses 7, then Alice chooses 8 and ends up with $5,6,8,1$. So $S$ is even and Alice wins.
Case 4B: If Bob chooses 6, then Alice chooses 7. Bob can now choose either 3 or 8 .
Case 4Bi: If Bob chooses 3, then Alice chooses 2 and ends up with 5,7,2 and either 1 or 8 . So $S=15$ or $S=22$ and Alice wins.
Case 4Bii: If Bob chooses 8, then Alice's numbers are $5,7,3,1$. So $S$ is even and Alice wins.
Cases 5-8: If Bob chooses $k \in\{5,6,7,8\}$ then Alice follows the strategy in case $9-k$ but whenever she had to choose $\ell$, she instead chooses $9-\ell$. If at the end of that strategy she ended up with $S$, she will now end up with $S^{\prime}=4 \cdot 9-S=36-S$. Then $S^{\prime}$ is even or $S^{\prime}=15$ or $S^{\prime}=21$ so again she wins.
## GEOMETRY
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo_shortlist_2020.jsonl",
"problem_match": "\nC 3.",
"solution_match": "\nSolution."
}
|
2ad2f8c5-acb4-50de-8a74-76793efcb0ca
| 604,200
|
Find the largest integer $k(k \geq 2)$, for which there exists an integer $n(n \geq k)$ such that from any collection of $n$ consecutive positive integers one can always choose $k$ numbers, which verify the following conditions:
1. each chosen number is not divisible by 6 , by 7 and by 8 ;
2. the positive difference of any two different chosen numbers is not divisible by at least one of the numbers 6,7 or 8 .
|
An integer is divisible by 6,7 and 8 if and only if it is divisible by their Least Common Multiple, which equals $6 \times 7 \times 4=168$.
Let $n$ be a positive integer and let $A$ be an arbitrary set of $n$ consecutive positive integers. Replace each number $a_{i}$ from $A$ with its remainder $r_{i}$ ( mod 168). The number $a_{i}$ is divisible by 6 ( 7 or 8 ) if and only if its remainder $r_{i}$ is divisible by 6 (respectively 7 or 8 ). The difference $\left|a_{i}-a_{j}\right|$ is divisible by 168 if and only if their remainders $r_{i}=r_{j}$.
Choosing $k$ numbers from the initial set $A$, which verify the required conditions, is the same as choosing $k$ their remainders ( mod 168) such that:
1. each chosen remainder is not divisible by 6,7 and 8 ;
2. all chosen remainders are different.
Suppose we have chosen $k$ numbers from $A$, which verify the conditions. Therefore, all remainders are different and $k \leq 168$ (otherwise, there would be two equal remainders).
Denote by $B=\{0,1,2,3, \ldots, 167\}$ the set of all possible remainders ( $\bmod 168)$ and by $B_{m}$ the subset of all elements of $B$, which are divisible by $m$. Compute the number of elements of the following subsets:
$$
\begin{gathered}
\left|B_{6}\right|=168: 6=28, \quad\left|B_{7}\right|=168: 7=24, \quad\left|B_{8}\right|=168: 8=21 \\
\left|B_{6} \cap B_{7}\right|=\left|B_{42}\right|=168: 42=4, \quad\left|B_{6} \cap B_{8}\right|=\left|B_{24}\right|=168: 24=7 \\
\left|B_{7} \cap B_{8}\right|=\left|B_{56}\right|=168: 56=3, \quad\left|B_{6} \cap B_{7} \cap B_{8}\right|=\left|B_{168}\right|=1
\end{gathered}
$$
Denote by $D=B_{6} \cup B_{7} \cup B_{8}$, the subset of all elements of $B$, which are divisible by at least one of the numbers 6,7 or 8 . By the Inclusion-Exclusion principle we got
$$
\begin{gathered}
|D|=\left|B_{6}\right|+\left|B_{7}\right|+\left|B_{8}\right|-\left(\left|B_{6} \cap B_{7}\right|+\left|B_{6} \cap B_{8}\right|+\left|B_{7} \cap B_{8}\right|\right)+\left|B_{6} \cap B_{7} \cap B_{8}\right|= \\
28+24+21-(4+7+3)+1=60 .
\end{gathered}
$$
Each chosen remainder belongs to the subset $B \backslash D$, since it is not divisible by 6,7 and 8 . Hence, $k \leq|B \backslash D|=168-60=108$.
Let us show that the greatest possible value is $k=108$. Consider $n=168$. Given any collection $A$ of 168 consecutive positive integers, replace each number with its remainder ( $\bmod 168$ ). Choose from these remainders 108 numbers, which constitute the set $B \backslash D$. Finally, take 108 numbers from the initial set $A$, having exactly these remainders. These $k=108$ numbers verify the required conditions.
|
108
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Find the largest integer $k(k \geq 2)$, for which there exists an integer $n(n \geq k)$ such that from any collection of $n$ consecutive positive integers one can always choose $k$ numbers, which verify the following conditions:
1. each chosen number is not divisible by 6 , by 7 and by 8 ;
2. the positive difference of any two different chosen numbers is not divisible by at least one of the numbers 6,7 or 8 .
|
An integer is divisible by 6,7 and 8 if and only if it is divisible by their Least Common Multiple, which equals $6 \times 7 \times 4=168$.
Let $n$ be a positive integer and let $A$ be an arbitrary set of $n$ consecutive positive integers. Replace each number $a_{i}$ from $A$ with its remainder $r_{i}$ ( mod 168). The number $a_{i}$ is divisible by 6 ( 7 or 8 ) if and only if its remainder $r_{i}$ is divisible by 6 (respectively 7 or 8 ). The difference $\left|a_{i}-a_{j}\right|$ is divisible by 168 if and only if their remainders $r_{i}=r_{j}$.
Choosing $k$ numbers from the initial set $A$, which verify the required conditions, is the same as choosing $k$ their remainders ( mod 168) such that:
1. each chosen remainder is not divisible by 6,7 and 8 ;
2. all chosen remainders are different.
Suppose we have chosen $k$ numbers from $A$, which verify the conditions. Therefore, all remainders are different and $k \leq 168$ (otherwise, there would be two equal remainders).
Denote by $B=\{0,1,2,3, \ldots, 167\}$ the set of all possible remainders ( $\bmod 168)$ and by $B_{m}$ the subset of all elements of $B$, which are divisible by $m$. Compute the number of elements of the following subsets:
$$
\begin{gathered}
\left|B_{6}\right|=168: 6=28, \quad\left|B_{7}\right|=168: 7=24, \quad\left|B_{8}\right|=168: 8=21 \\
\left|B_{6} \cap B_{7}\right|=\left|B_{42}\right|=168: 42=4, \quad\left|B_{6} \cap B_{8}\right|=\left|B_{24}\right|=168: 24=7 \\
\left|B_{7} \cap B_{8}\right|=\left|B_{56}\right|=168: 56=3, \quad\left|B_{6} \cap B_{7} \cap B_{8}\right|=\left|B_{168}\right|=1
\end{gathered}
$$
Denote by $D=B_{6} \cup B_{7} \cup B_{8}$, the subset of all elements of $B$, which are divisible by at least one of the numbers 6,7 or 8 . By the Inclusion-Exclusion principle we got
$$
\begin{gathered}
|D|=\left|B_{6}\right|+\left|B_{7}\right|+\left|B_{8}\right|-\left(\left|B_{6} \cap B_{7}\right|+\left|B_{6} \cap B_{8}\right|+\left|B_{7} \cap B_{8}\right|\right)+\left|B_{6} \cap B_{7} \cap B_{8}\right|= \\
28+24+21-(4+7+3)+1=60 .
\end{gathered}
$$
Each chosen remainder belongs to the subset $B \backslash D$, since it is not divisible by 6,7 and 8 . Hence, $k \leq|B \backslash D|=168-60=108$.
Let us show that the greatest possible value is $k=108$. Consider $n=168$. Given any collection $A$ of 168 consecutive positive integers, replace each number with its remainder ( $\bmod 168$ ). Choose from these remainders 108 numbers, which constitute the set $B \backslash D$. Finally, take 108 numbers from the initial set $A$, having exactly these remainders. These $k=108$ numbers verify the required conditions.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-jbmo_shortlist_2020.jsonl",
"problem_match": "\nNT 3.",
"solution_match": "\nSolution."
}
|
ef850bc4-fe93-5769-a8eb-8ae95d12a556
| 604,301
|
Find the least positive integer such that the sum of its digits is 2011 and the product of its digits is a power of 6 .
|
Denote this number by $N$. Then $N$ can not contain the digits $0,5,7$ and its digits must be written in increasing order. Suppose that $N$ has $x_{1}$ ones, $x_{2}$ twos, $x_{3}$ threes, $x_{4}$ fours, $x_{6}$ sixes, $x_{8}$ eights and $x_{9}$ nines, then $x_{1}+2 x_{2}+3 x_{3}+4 x_{4}+6 x_{6}+8 x_{8}+9 x_{9}=2011$. (1) The product of digits of the number $N$ is a power of 6 when we have the relation $x_{2}+2 x_{4}+x_{6}+3 x_{8}=x_{3}+x_{6}+2 x_{9}$, hence $x_{2}-x_{3}+2 x_{4}+3 x_{8}-2 x_{9}=0$.
Denote by $S$ the number of digits of $N\left(S=x_{1}+x_{2}+\ldots+x_{9}\right)$. In order to make the coefficients of $x_{8}$ and $x_{9}$ equal, we multiply relation (1) by 5 , then we add relation (2). We get $43 x_{9}+43 x_{8}+30 x_{6}+22 x_{4}+14 x_{3}+11 x_{2}+5 x_{1}=10055 \Leftrightarrow 43 S=10055+13 x_{6}+$ $21 x_{4}+29 x_{3}+32 x_{2}+38 x_{1}$. Then $10055+13 x_{6}+21 x_{4}+29 x_{3}+32 x_{2}+38 x_{1}$ is a multiple of 43 not less than 10055. The least such number is 10062 , but the relation $10062=$ $10055+13 x_{6}+21 x_{4}+29 x_{3}+32 x_{2}+38 x_{1}$ means that among $x_{1}, x_{2}, \ldots, x_{6}$ there is at least one positive, so $10062=10055+13 x_{6}+21 x_{4}+29 x_{3}+32 x_{2}+38 x_{1} \geq 10055+13=10068$ which is obviously false. The next multiple of 43 is 10105 and from relation $10105=$ $10055+13 x_{6}+21 x_{4}+29 x_{3}+32 x_{2}+38 x_{1}$ we get $50=13 x_{6}+21 x_{4}+29 x_{3}+32 x_{2}+38 x_{1}$. By writing as $13 x_{6}+21\left(x_{4}-1\right)+29\left(x_{3}-1\right)+32 x_{2}+38 x_{1}=0$, we can easily see that the only possibility is $x_{1}=x_{2}=x_{6}=0$ and $x_{3}=x_{4}=1$. Then $S=235, x_{8}=93, x_{9}=140$. Since $S$ is strictly minimal, we conclude that $N=34 \underbrace{88 \ldots 8}_{93} \underbrace{99 \ldots 9}_{140}$.
|
34\underbrace{88\ldots8}_{93}\underbrace{99\ldots9}_{140}
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Find the least positive integer such that the sum of its digits is 2011 and the product of its digits is a power of 6 .
|
Denote this number by $N$. Then $N$ can not contain the digits $0,5,7$ and its digits must be written in increasing order. Suppose that $N$ has $x_{1}$ ones, $x_{2}$ twos, $x_{3}$ threes, $x_{4}$ fours, $x_{6}$ sixes, $x_{8}$ eights and $x_{9}$ nines, then $x_{1}+2 x_{2}+3 x_{3}+4 x_{4}+6 x_{6}+8 x_{8}+9 x_{9}=2011$. (1) The product of digits of the number $N$ is a power of 6 when we have the relation $x_{2}+2 x_{4}+x_{6}+3 x_{8}=x_{3}+x_{6}+2 x_{9}$, hence $x_{2}-x_{3}+2 x_{4}+3 x_{8}-2 x_{9}=0$.
Denote by $S$ the number of digits of $N\left(S=x_{1}+x_{2}+\ldots+x_{9}\right)$. In order to make the coefficients of $x_{8}$ and $x_{9}$ equal, we multiply relation (1) by 5 , then we add relation (2). We get $43 x_{9}+43 x_{8}+30 x_{6}+22 x_{4}+14 x_{3}+11 x_{2}+5 x_{1}=10055 \Leftrightarrow 43 S=10055+13 x_{6}+$ $21 x_{4}+29 x_{3}+32 x_{2}+38 x_{1}$. Then $10055+13 x_{6}+21 x_{4}+29 x_{3}+32 x_{2}+38 x_{1}$ is a multiple of 43 not less than 10055. The least such number is 10062 , but the relation $10062=$ $10055+13 x_{6}+21 x_{4}+29 x_{3}+32 x_{2}+38 x_{1}$ means that among $x_{1}, x_{2}, \ldots, x_{6}$ there is at least one positive, so $10062=10055+13 x_{6}+21 x_{4}+29 x_{3}+32 x_{2}+38 x_{1} \geq 10055+13=10068$ which is obviously false. The next multiple of 43 is 10105 and from relation $10105=$ $10055+13 x_{6}+21 x_{4}+29 x_{3}+32 x_{2}+38 x_{1}$ we get $50=13 x_{6}+21 x_{4}+29 x_{3}+32 x_{2}+38 x_{1}$. By writing as $13 x_{6}+21\left(x_{4}-1\right)+29\left(x_{3}-1\right)+32 x_{2}+38 x_{1}=0$, we can easily see that the only possibility is $x_{1}=x_{2}=x_{6}=0$ and $x_{3}=x_{4}=1$. Then $S=235, x_{8}=93, x_{9}=140$. Since $S$ is strictly minimal, we conclude that $N=34 \underbrace{88 \ldots 8}_{93} \underbrace{99 \ldots 9}_{140}$.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-nt20111.jsonl",
"problem_match": "\nNT5 ",
"solution_match": "## Solution"
}
|
f9d7d6fa-4c30-502e-94c9-4480ef6bc48d
| 604,426
|
Find the largest positive integer $n$ for which the inequality
$$
\frac{a+b+c}{a b c+1}+\sqrt[n]{a b c} \leq \frac{5}{2}
$$
holds for all $a, b, c \in[0,1]$. Here $\sqrt[1]{a b c}=a b c$.
|
Let $n_{\max }$ be the sought largest value of $n$, and let $E_{a, b, c}(n)=\frac{a+b+c}{a b c+1}+\sqrt[n]{a b c}$. Then $E_{a, b, c}(m)-E_{a, b, c}(n)=\sqrt[m]{a b c}-\sqrt[n]{a b c}$ and since $a . b c \leq 1$ we clearly have $E_{a, b, c}(m) \geq$ $E_{a, b, c}(n)$ for $m \geq n$. So if $E_{a, b, c}(n) \geq \frac{5}{2}$ for some choice of $a, b, c \in[0,1]$, it must be $n_{\max } \leq n$. We use this remark to determine the upper bound $n_{\max } \leq 3$ by plugging some particular values of $a, b, c$ into the given inequality as follow's:
$$
\text { For }(a, b, c)=(1,1, c), c \in[0,1] \text {, inequality (1) implies } \frac{c+2}{c+1}+\sqrt[n]{c} \leq \frac{5}{2} \Leftrightarrow \frac{1}{c+1}+\sqrt[n]{c} \leq
$$
$\frac{3}{2}$. Obviously, every $x \in[0 ; 1]$ is written as $\sqrt[n]{c}$ for some $c \in[0 ; 1]$. So the last inequality is equivalent to:
$$
\begin{aligned}
& \frac{1}{x^{n}+1}+x \leq \frac{3}{2} \Leftrightarrow 2+2 x^{n+1}+2 x \leq 3 x^{n}+3 \Leftrightarrow 3 x^{n}+1 \geq 2 x^{n+1}+2 x \\
\Leftrightarrow & 2 x^{n}(1-x)+(1-x)+(x-1)\left(x^{n-1}+\cdots+x\right) \geq 0 \\
\Leftrightarrow & (1-x)\left[2 x^{n}+1-\left(x^{n-1}+x^{n-2}+\ldots+x\right)\right] \geq 0, \forall x \in[0,1]
\end{aligned}
$$
For $n=4$, the left hand side of the above becomes $(1-x)\left(2 x^{4}+1-x^{3}-x^{2}-x\right)=$ $(1-x)(x-1)\left(2 x^{3}+x^{2}-1\right)=-(1-x)^{2}\left(2 x^{3}+x^{2}-1\right)$ which for $x=0.9$ is negative. Thus. $n_{\max } \leq 3$ as claimed.
Now, we shall prove that for $n=3$ inequality (1) holds for all $a, b, c \in[0,1]$, and this would mean $n_{\max }=3$. We shall use the following Lemma:
Lemma. For all $a, b, c \in[0 ; 1]: a+b+c \leq a b c+2$.
Proof of the Lemma: The required result comes by adding the following two inequalities side by side
$$
\begin{aligned}
& 0 \leq(a-1)(b-1) \Leftrightarrow a+b \leq a b+1 \Leftrightarrow a+b-a b \leq 1 \\
& 0 \leq(a b-1)(c-1) \Leftrightarrow a b+c \leq a b c+1
\end{aligned}
$$
Because of the Lemma, our inequality (1) for $n=3$ wrill be proved if the following weaker inequality is proved for all $a, b, c \in[0,1]$ :
$$
\frac{a b c+2}{a b c+1}+\sqrt[3]{a b c} \leq \frac{5}{2} \Leftrightarrow \frac{1}{a b c+1}+\sqrt[3]{a b c} \leq \frac{3}{2}
$$
Denoting $\sqrt[3]{a b c}=y \in[0 ; 1]$, this inequality becomes:
$$
\begin{aligned}
& \frac{1}{y^{3}+1}+y \leq \frac{3}{2} \Leftrightarrow 2+2 y^{4}+2 y \leq 3 y^{3}+3 \Leftrightarrow-2 y^{4}+3 y^{3}-2 y+1 \geq 0 \\
\Leftrightarrow & 2 y^{3}(1-y)+(y-1) y(y+1)+(1-y) \geq 0 \Leftrightarrow(1-y)\left(2 y^{3}+1-y^{2}-y\right) \geq 0
\end{aligned}
$$
The last inequality is obvious because $1-y \geq 0$ and $2 y^{3}+1-y^{2}-y=y^{3}+(y-1)^{2}(y+1) \geq 0$.
## Geometry
2
|
3
|
Yes
|
Yes
|
math-word-problem
|
Inequalities
|
Find the largest positive integer $n$ for which the inequality
$$
\frac{a+b+c}{a b c+1}+\sqrt[n]{a b c} \leq \frac{5}{2}
$$
holds for all $a, b, c \in[0,1]$. Here $\sqrt[1]{a b c}=a b c$.
|
Let $n_{\max }$ be the sought largest value of $n$, and let $E_{a, b, c}(n)=\frac{a+b+c}{a b c+1}+\sqrt[n]{a b c}$. Then $E_{a, b, c}(m)-E_{a, b, c}(n)=\sqrt[m]{a b c}-\sqrt[n]{a b c}$ and since $a . b c \leq 1$ we clearly have $E_{a, b, c}(m) \geq$ $E_{a, b, c}(n)$ for $m \geq n$. So if $E_{a, b, c}(n) \geq \frac{5}{2}$ for some choice of $a, b, c \in[0,1]$, it must be $n_{\max } \leq n$. We use this remark to determine the upper bound $n_{\max } \leq 3$ by plugging some particular values of $a, b, c$ into the given inequality as follow's:
$$
\text { For }(a, b, c)=(1,1, c), c \in[0,1] \text {, inequality (1) implies } \frac{c+2}{c+1}+\sqrt[n]{c} \leq \frac{5}{2} \Leftrightarrow \frac{1}{c+1}+\sqrt[n]{c} \leq
$$
$\frac{3}{2}$. Obviously, every $x \in[0 ; 1]$ is written as $\sqrt[n]{c}$ for some $c \in[0 ; 1]$. So the last inequality is equivalent to:
$$
\begin{aligned}
& \frac{1}{x^{n}+1}+x \leq \frac{3}{2} \Leftrightarrow 2+2 x^{n+1}+2 x \leq 3 x^{n}+3 \Leftrightarrow 3 x^{n}+1 \geq 2 x^{n+1}+2 x \\
\Leftrightarrow & 2 x^{n}(1-x)+(1-x)+(x-1)\left(x^{n-1}+\cdots+x\right) \geq 0 \\
\Leftrightarrow & (1-x)\left[2 x^{n}+1-\left(x^{n-1}+x^{n-2}+\ldots+x\right)\right] \geq 0, \forall x \in[0,1]
\end{aligned}
$$
For $n=4$, the left hand side of the above becomes $(1-x)\left(2 x^{4}+1-x^{3}-x^{2}-x\right)=$ $(1-x)(x-1)\left(2 x^{3}+x^{2}-1\right)=-(1-x)^{2}\left(2 x^{3}+x^{2}-1\right)$ which for $x=0.9$ is negative. Thus. $n_{\max } \leq 3$ as claimed.
Now, we shall prove that for $n=3$ inequality (1) holds for all $a, b, c \in[0,1]$, and this would mean $n_{\max }=3$. We shall use the following Lemma:
Lemma. For all $a, b, c \in[0 ; 1]: a+b+c \leq a b c+2$.
Proof of the Lemma: The required result comes by adding the following two inequalities side by side
$$
\begin{aligned}
& 0 \leq(a-1)(b-1) \Leftrightarrow a+b \leq a b+1 \Leftrightarrow a+b-a b \leq 1 \\
& 0 \leq(a b-1)(c-1) \Leftrightarrow a b+c \leq a b c+1
\end{aligned}
$$
Because of the Lemma, our inequality (1) for $n=3$ wrill be proved if the following weaker inequality is proved for all $a, b, c \in[0,1]$ :
$$
\frac{a b c+2}{a b c+1}+\sqrt[3]{a b c} \leq \frac{5}{2} \Leftrightarrow \frac{1}{a b c+1}+\sqrt[3]{a b c} \leq \frac{3}{2}
$$
Denoting $\sqrt[3]{a b c}=y \in[0 ; 1]$, this inequality becomes:
$$
\begin{aligned}
& \frac{1}{y^{3}+1}+y \leq \frac{3}{2} \Leftrightarrow 2+2 y^{4}+2 y \leq 3 y^{3}+3 \Leftrightarrow-2 y^{4}+3 y^{3}-2 y+1 \geq 0 \\
\Leftrightarrow & 2 y^{3}(1-y)+(y-1) y(y+1)+(1-y) \geq 0 \Leftrightarrow(1-y)\left(2 y^{3}+1-y^{2}-y\right) \geq 0
\end{aligned}
$$
The last inequality is obvious because $1-y \geq 0$ and $2 y^{3}+1-y^{2}-y=y^{3}+(y-1)^{2}(y+1) \geq 0$.
## Geometry
2
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-shl-2012.jsonl",
"problem_match": "\nA5.",
"solution_match": "\nSolution."
}
|
5d796f65-4b90-5976-99ec-7d20814ca580
| 604,480
|
MLD
Let $x, y, z$ be real numbers, satisfying the relations
$$
\left\{\begin{array}{l}
x \geq 20 \\
y \geq 40 \\
z \geq 1675 \\
x+y+z=2015
\end{array}\right.
$$
Find the greatest value of the product $P=x \cdot y \cdot z$.
|
By virtue of $z \geq 1675$ we have
$$
y+z<2015 \Leftrightarrow y<2015-z \leq 2015-1675<1675
$$
It follows that $(1675-y) \cdot(1675-z) \leq 0 \Leftrightarrow y \cdot z \leq 1675 \cdot(y+z-1675)$.
By using the inequality $u \cdot v \leq\left(\frac{u+v}{2}\right)^{2}$ for all real numbers $u, v$ we obtain
$$
\begin{gathered}
P=x \cdot y \cdot z \leq 1675 \cdot x \cdot(y+z-1675) \leq 1675 \cdot\left(\frac{x+y+z-1675}{2}\right)^{2}= \\
1675 \cdot\left(\frac{2015-1675}{2}\right)^{2}=1675 \cdot 170^{2}=48407500
\end{gathered}
$$
$$
\text { We have } P=x \cdot y \cdot z=48407500 \Leftrightarrow\left\{\begin{array} { l }
{ x + y + z = 2 0 1 5 , } \\
{ z = 1 6 7 5 , } \\
{ x = y + z - 1 6 7 5 }
\end{array} \Leftrightarrow \left\{\begin{array}{l}
x=170 \\
y=170 \\
z=1675
\end{array}\right.\right.
$$
So, the greatest value of the product is $P=x \cdot y \cdot z=48407500$.
## Solution 2:
Let $S=\{(x, y, z) \mid x \geq 20, y \geq 40, z \geq 1675, x+y+z=2015\}$ and $\Pi=\{|x \cdot y \cdot z|(x, y, z) \in S\}$ We have to find the biggest element of $\Pi$. By using the given inequalities we obtain:
$$
\left\{\begin{array}{l}
20 \leq x \leq 300 \\
40 \leq y \leq 320 \\
1675 \leq z \leq 1955 \\
y<1000<z
\end{array}\right.
$$
Let $z=1675+d$. Since $x \leq 300$ so $(1675+d) \cdot x=1675 x+d x \leq 1675 x+1675 d=1675 \cdot(x+d)$ That means that if $(x, y, 1675+d) \in S$ then $(x+d, y, 1675) \in S$, and $x \cdot y \cdot(1675+d) \leq(x+d) \cdot y \cdot 1675$. Therefore $z=1675$ must be for the greatest product.
Furthermore, $x \cdot y \leq\left(\frac{x+y}{2}\right)^{2}=\left(\frac{2015-1675}{2}\right)^{2}=\left(\frac{340}{2}\right)^{2}=170^{2}$. Since $(170,170,1675) \in S$ that means that the biggest element of $\Pi$ is $170 \cdot 170 \cdot 1675=48407500$
|
48407500
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
MLD
Let $x, y, z$ be real numbers, satisfying the relations
$$
\left\{\begin{array}{l}
x \geq 20 \\
y \geq 40 \\
z \geq 1675 \\
x+y+z=2015
\end{array}\right.
$$
Find the greatest value of the product $P=x \cdot y \cdot z$.
|
By virtue of $z \geq 1675$ we have
$$
y+z<2015 \Leftrightarrow y<2015-z \leq 2015-1675<1675
$$
It follows that $(1675-y) \cdot(1675-z) \leq 0 \Leftrightarrow y \cdot z \leq 1675 \cdot(y+z-1675)$.
By using the inequality $u \cdot v \leq\left(\frac{u+v}{2}\right)^{2}$ for all real numbers $u, v$ we obtain
$$
\begin{gathered}
P=x \cdot y \cdot z \leq 1675 \cdot x \cdot(y+z-1675) \leq 1675 \cdot\left(\frac{x+y+z-1675}{2}\right)^{2}= \\
1675 \cdot\left(\frac{2015-1675}{2}\right)^{2}=1675 \cdot 170^{2}=48407500
\end{gathered}
$$
$$
\text { We have } P=x \cdot y \cdot z=48407500 \Leftrightarrow\left\{\begin{array} { l }
{ x + y + z = 2 0 1 5 , } \\
{ z = 1 6 7 5 , } \\
{ x = y + z - 1 6 7 5 }
\end{array} \Leftrightarrow \left\{\begin{array}{l}
x=170 \\
y=170 \\
z=1675
\end{array}\right.\right.
$$
So, the greatest value of the product is $P=x \cdot y \cdot z=48407500$.
## Solution 2:
Let $S=\{(x, y, z) \mid x \geq 20, y \geq 40, z \geq 1675, x+y+z=2015\}$ and $\Pi=\{|x \cdot y \cdot z|(x, y, z) \in S\}$ We have to find the biggest element of $\Pi$. By using the given inequalities we obtain:
$$
\left\{\begin{array}{l}
20 \leq x \leq 300 \\
40 \leq y \leq 320 \\
1675 \leq z \leq 1955 \\
y<1000<z
\end{array}\right.
$$
Let $z=1675+d$. Since $x \leq 300$ so $(1675+d) \cdot x=1675 x+d x \leq 1675 x+1675 d=1675 \cdot(x+d)$ That means that if $(x, y, 1675+d) \in S$ then $(x+d, y, 1675) \in S$, and $x \cdot y \cdot(1675+d) \leq(x+d) \cdot y \cdot 1675$. Therefore $z=1675$ must be for the greatest product.
Furthermore, $x \cdot y \leq\left(\frac{x+y}{2}\right)^{2}=\left(\frac{2015-1675}{2}\right)^{2}=\left(\frac{340}{2}\right)^{2}=170^{2}$. Since $(170,170,1675) \in S$ that means that the biggest element of $\Pi$ is $170 \cdot 170 \cdot 1675=48407500$
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-shl-2015.jsonl",
"problem_match": "## A1 ",
"solution_match": "## Solution 1:"
}
|
edd8ec6c-b163-5ebb-b3cf-825e975a8cc4
| 604,690
|
ALB
3) If $x^{3}-3 \sqrt{3} x^{2}+9 x-3 \sqrt{3}-64=0$, find the value of $x^{6}-8 x^{5}+13 x^{4}-5 x^{3}+49 x^{2}-137 x+2015$.
|
$x^{3}-3 \sqrt{3} x^{2}+9 x-3 \sqrt{3}-64=0 \Leftrightarrow(x-\sqrt{3})^{3}=64 \Leftrightarrow(x-\sqrt{3})=4 \Leftrightarrow x-4=\sqrt{3} \Leftrightarrow x^{2}-8 x+16=3 \Leftrightarrow$ $x^{2}-8 x+13=0$
$x^{6}-8 x^{5}+13 x^{4}-5 x^{3}+49 x^{2}-137 x+2015=\left(x^{2}-8 x+13\right)\left(x^{4}-5 x+9\right)+1898=0+1898=1898$
|
1898
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
ALB
3) If $x^{3}-3 \sqrt{3} x^{2}+9 x-3 \sqrt{3}-64=0$, find the value of $x^{6}-8 x^{5}+13 x^{4}-5 x^{3}+49 x^{2}-137 x+2015$.
|
$x^{3}-3 \sqrt{3} x^{2}+9 x-3 \sqrt{3}-64=0 \Leftrightarrow(x-\sqrt{3})^{3}=64 \Leftrightarrow(x-\sqrt{3})=4 \Leftrightarrow x-4=\sqrt{3} \Leftrightarrow x^{2}-8 x+16=3 \Leftrightarrow$ $x^{2}-8 x+13=0$
$x^{6}-8 x^{5}+13 x^{4}-5 x^{3}+49 x^{2}-137 x+2015=\left(x^{2}-8 x+13\right)\left(x^{4}-5 x+9\right)+1898=0+1898=1898$
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-shl-2015.jsonl",
"problem_match": "## A2 ",
"solution_match": "\nSolution"
}
|
d8cf27bb-2d97-53d5-a385-93fba96ccaff
| 604,699
|
SAU
What is the greatest number of integers that can be selected from a set of 2015 consecutive numbers so that no sum of any two selected numbers is divisible by their difference?
|
We take any two chosen numbers. If their difference is 1 , it is clear that their sum is divisible by their difference. If their difference is 2 , they will be of the same parity, and their sum is divisible by their difference. Therefore, the difference between any chosen numbers will be at least 3 . In other words, we can choose at most one number of any three consecutive numbers. This implies that we can choose at most 672 numbers.
Now, we will show that we can choose 672 such numbers from any 2015 consecutive numbers. Suppose that these numbers are $a, a+1, \ldots, a+2014$. If $a$ is divisible by 3 , we can choose $a+1, a+4, \ldots, a+2014$. If $a$ is not divisible by 3 , we can choose $a, a+3, \ldots, a+$ 2013.
|
672
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
SAU
What is the greatest number of integers that can be selected from a set of 2015 consecutive numbers so that no sum of any two selected numbers is divisible by their difference?
|
We take any two chosen numbers. If their difference is 1 , it is clear that their sum is divisible by their difference. If their difference is 2 , they will be of the same parity, and their sum is divisible by their difference. Therefore, the difference between any chosen numbers will be at least 3 . In other words, we can choose at most one number of any three consecutive numbers. This implies that we can choose at most 672 numbers.
Now, we will show that we can choose 672 such numbers from any 2015 consecutive numbers. Suppose that these numbers are $a, a+1, \ldots, a+2014$. If $a$ is divisible by 3 , we can choose $a+1, a+4, \ldots, a+2014$. If $a$ is not divisible by 3 , we can choose $a, a+3, \ldots, a+$ 2013.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-shl-2015.jsonl",
"problem_match": "\nNT1 ",
"solution_match": "## Solution:"
}
|
1bb3571e-258d-5291-ad46-26cd0b42a3ec
| 604,812
|
GRE
Let $n \geq 1$ be a positive integer. A square of side length $n$ is divided by lines parallel to each side into $n^{2}$ squares of side length 1 . Find the number of parallelograms which have vertices among the vertices of the $n^{2}$ squares of side length 1 , with both sides smaller or equal to 2 , and which have the area equal to 2 .
|
We can divide all these parallelograms into 7 classes (types I-VII), according to Figure.
Type 1: There are $n$ ways to choose the strip for the horizontal (shorter) side of the parallelogram, and $(n-1)$ ways to choose the strip (of the width 2 ) for the vertical (longer) side. So there are $n(n-1)$ parallelograms of the type I.
Type II: There are $(n-1)$ ways to choose the strip (of the width 2 ) for the horizontal (longer) side, and $n$ ways to choose the strip for the vertical (shorter) side. So the number of the parallelogram of this type is also $n(n-1)$.
Type III: Each parallelogram of this type is a square inscribed in a unique square $2 \times 2$ of our grid. The number of such squares is $(n-1)^{2}$. So there are $(n-1)^{2}$ parallelograms of type III. For each of the types IV, V, VI, VII, the strip of the width 1 in which the parallelogram is located can be chosen in $n$ ways and for each such choice there are $n-2$ parallelograms located in the chosen strip.
Summing we obtain that the total number of parallelograms is:
$$
2 n(n-1)+(n-1)^{2}+4 n(n-2)=7 n^{2}-12 n+1
$$
(C5) CYP
We have a $5 \times 5$ chessboard and a supply of $\mathrm{L}$-shaped triominoes, i.e. $2 \times 2$ squares with one comer missing. Two players $A$ and $B$ play the following game: A positive integer $k \leq 25$ is chosen. Starting with $A$, the players take alternating turns marking squares of the chessboard until they mark a total of $k$ squares. (In each turn a player has to mark exactly one new square.)
At the end of the process, player $A$ wins if he can cover without overlapping all but at most 2 unmarked squares with $\mathrm{L}$-shaped triominoes, otherwise player $\boldsymbol{B}$ wins. It is not permitted any
marked squares to be covered.
Find the smallest $\boldsymbol{k}$, if it exists, such that player $\boldsymbol{B}$ has a winning strategy.
## Solution:
We will show that player $A$ wins if $k=1,2$ or 3 , but player $B$ wins if $k=4$. Thus the smallest $k$ for which $B$ has a winning strategy exists and is equal to 4 .
If $k=1$, player $A$ marks the upper left corner of the square and then fills it as follows.

If $k=2$, player $A$ marks the upper left comer of the square. Whatever square player $B$ marks, then player $\boldsymbol{A}$ can fill in the square in exactly the same pattern as above except that he doesn't put the triomino which covers the marked square of $B$. Player $A$ wins because he has left only two unmarked squares uncovered.
For $k=3$, player $\boldsymbol{A}$ wins by following the same strategy. When he has to mark a square for the second time, he marks any yet unmarked square of the triomino that covers the marked square of $B$.
Let us now show that for $k=4$ player $B$ has a wimning strategy. Since there will be 21 unmarked squares, player $\boldsymbol{A}$ will need to cover all of them with seven L-shaped triominoes. We can assume that in his first move, player $\boldsymbol{A}$ does not mark any square in the bottom two rows of the chessboard (otherwise just rotate the chessboard). In his first move player $\boldsymbol{B}$ marks the square labeled 1 in the following figure.

If player $\boldsymbol{A}$ in his next move does not mark any of the squares labeled 2,3 and 4 then player $\boldsymbol{B}$ marks the square labeled 3. Player $\boldsymbol{B}$ wins as the square labeled 2 is left unmarked but cannot be covered with an L-shaped triomino.
If player $\boldsymbol{A}$ in his next move marks the square labeled 2, then player $\boldsymbol{B}$ marks the square labeled 5 . Player $B$ wins as the square labeled 3 is left unmarked but cannot be covered with an L-shaped triomino.
Finally, if player $\boldsymbol{A}$ in his next move marks one of the squares labeled 3 or 4 , player $\boldsymbol{B}$ marks the other of these two squares. Player $\boldsymbol{B}$ wins as the square labeled 2 is left unmarked but cannot be covered with an L-shaped triomino.
Since we have covered all possible cases, player $B$ wins when $k=4$.
|
4
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
GRE
Let $n \geq 1$ be a positive integer. A square of side length $n$ is divided by lines parallel to each side into $n^{2}$ squares of side length 1 . Find the number of parallelograms which have vertices among the vertices of the $n^{2}$ squares of side length 1 , with both sides smaller or equal to 2 , and which have the area equal to 2 .
|
We can divide all these parallelograms into 7 classes (types I-VII), according to Figure.

Type 1: There are $n$ ways to choose the strip for the horizontal (shorter) side of the parallelogram, and $(n-1)$ ways to choose the strip (of the width 2 ) for the vertical (longer) side. So there are $n(n-1)$ parallelograms of the type I.
Type II: There are $(n-1)$ ways to choose the strip (of the width 2 ) for the horizontal (longer) side, and $n$ ways to choose the strip for the vertical (shorter) side. So the number of the parallelogram of this type is also $n(n-1)$.
Type III: Each parallelogram of this type is a square inscribed in a unique square $2 \times 2$ of our grid. The number of such squares is $(n-1)^{2}$. So there are $(n-1)^{2}$ parallelograms of type III. For each of the types IV, V, VI, VII, the strip of the width 1 in which the parallelogram is located can be chosen in $n$ ways and for each such choice there are $n-2$ parallelograms located in the chosen strip.
Summing we obtain that the total number of parallelograms is:
$$
2 n(n-1)+(n-1)^{2}+4 n(n-2)=7 n^{2}-12 n+1
$$
(C5) CYP
We have a $5 \times 5$ chessboard and a supply of $\mathrm{L}$-shaped triominoes, i.e. $2 \times 2$ squares with one comer missing. Two players $A$ and $B$ play the following game: A positive integer $k \leq 25$ is chosen. Starting with $A$, the players take alternating turns marking squares of the chessboard until they mark a total of $k$ squares. (In each turn a player has to mark exactly one new square.)
At the end of the process, player $A$ wins if he can cover without overlapping all but at most 2 unmarked squares with $\mathrm{L}$-shaped triominoes, otherwise player $\boldsymbol{B}$ wins. It is not permitted any
marked squares to be covered.
Find the smallest $\boldsymbol{k}$, if it exists, such that player $\boldsymbol{B}$ has a winning strategy.
## Solution:
We will show that player $A$ wins if $k=1,2$ or 3 , but player $B$ wins if $k=4$. Thus the smallest $k$ for which $B$ has a winning strategy exists and is equal to 4 .
If $k=1$, player $A$ marks the upper left corner of the square and then fills it as follows.

If $k=2$, player $A$ marks the upper left comer of the square. Whatever square player $B$ marks, then player $\boldsymbol{A}$ can fill in the square in exactly the same pattern as above except that he doesn't put the triomino which covers the marked square of $B$. Player $A$ wins because he has left only two unmarked squares uncovered.
For $k=3$, player $\boldsymbol{A}$ wins by following the same strategy. When he has to mark a square for the second time, he marks any yet unmarked square of the triomino that covers the marked square of $B$.
Let us now show that for $k=4$ player $B$ has a wimning strategy. Since there will be 21 unmarked squares, player $\boldsymbol{A}$ will need to cover all of them with seven L-shaped triominoes. We can assume that in his first move, player $\boldsymbol{A}$ does not mark any square in the bottom two rows of the chessboard (otherwise just rotate the chessboard). In his first move player $\boldsymbol{B}$ marks the square labeled 1 in the following figure.

If player $\boldsymbol{A}$ in his next move does not mark any of the squares labeled 2,3 and 4 then player $\boldsymbol{B}$ marks the square labeled 3. Player $\boldsymbol{B}$ wins as the square labeled 2 is left unmarked but cannot be covered with an L-shaped triomino.
If player $\boldsymbol{A}$ in his next move marks the square labeled 2, then player $\boldsymbol{B}$ marks the square labeled 5 . Player $B$ wins as the square labeled 3 is left unmarked but cannot be covered with an L-shaped triomino.
Finally, if player $\boldsymbol{A}$ in his next move marks one of the squares labeled 3 or 4 , player $\boldsymbol{B}$ marks the other of these two squares. Player $\boldsymbol{B}$ wins as the square labeled 2 is left unmarked but cannot be covered with an L-shaped triomino.
Since we have covered all possible cases, player $B$ wins when $k=4$.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-shl-2015.jsonl",
"problem_match": "\nC4",
"solution_match": "\nSolution:"
}
|
5e223dd1-5a36-5b08-8b8c-f575e35f25fc
| 604,903
|
Find the maximum positive integer $k$ such that for any positive integers $m, n$ such that $m^{3}+n^{3}>$ $(m+n)^{2}$, we have
$$
m^{3}+n^{3} \geq(m+n)^{2}+k
$$
|
We see that for $m=3$ and $n=2$ we have $m^{3}+n^{3}>(m+n)^{2}$, thus
$$
3^{3}+2^{3} \geq(3+2)^{2}+k \Rightarrow k \leq 10
$$
We will show that $k=10$ is the desired maximum. In other words, we have to prove that
$$
m^{3}+n^{3} \geq(m+n)^{2}+10
$$
The last inequality is equivalent to
$$
(m+n)\left(m^{2}+n^{2}-m n-m-n\right) \geq 10
$$
If $m+n=2$ or $m+n=3$, then $(m, n)=(1,1),(1,2),(2,1)$ and we can check that none of them satisfies the condition $m^{3}+n^{3}>(m+n)^{2}$.
If $m+n=4$, then $(m, n)=(1,3),(2,2),(3,1)$. The pair $(m, n)=(2,2)$ doesn't satisfy the condition. The pairs $(m, n)=(1,3),(3,1)$ satisfy the condition and we can readily check that $m^{3}+n^{3} \geq(m+$ $n)^{2}+10$.
If $m+n \geq 5$ then we will show that
$$
m^{2}+n^{2}-m n-m-n \geq 2
$$
which is equivalent to
$$
(m-n)^{2}+(m-1)^{2}+(n-1)^{2} \geq 6
$$
If at least one of the numbers $m, n$ is greater or equal to 4 then $(m-1)^{2} \geq 9$ or $(n-1)^{2} \geq 9$ hence the desired result holds. As a result, it remains to check what happens if $m \leq 3$ and $n \leq 3$. Using the condition $m+n \geq 5$ we have that all such pairs are $(m, n)=(2,3),(3,2),(3,3)$.
All of them satisfy the condition and also the inequality $m^{2}+n^{2}-m n-m-n \geq 2$, thus we have the desired result.
Alternative solution by PSC. The problem equivalently asks for to find the minimum value of
$$
A=(m+n)\left(m^{2}+n^{2}-m n-m-n\right)
$$
given that $(m+n)\left(m^{2}+n^{2}-m n-m-n\right)>0$. If $m=n$, we get that $m>2$ and
$$
A=2 m\left(m^{2}-2 m\right) \geq 6\left(3^{2}-6\right)=18
$$
Suppose without loss of generality that $m>n$. If $n=1$, then $m(m+1)(m-2)>0$, therefore $m>2$ and
$$
A \geq 3 \cdot(3+1) \cdot(3-2)=12
$$
If $n \geq 2$, then since $m \geq n+1$ we have
$$
A=(m+n)\left(m(m-n-1)+n^{2}-n\right) \geq(2 n+1)\left(n^{2}-n\right) \geq 5\left(2^{2}-2\right)=10
$$
In all cases $A \geq 10$ and the equality holds if $m=n+1$ and $n=2$, therefore if $m=3$ and $n=2$. It follows that the maximum $k$ is $k=10$.
|
10
|
Yes
|
Yes
|
math-word-problem
|
Inequalities
|
Find the maximum positive integer $k$ such that for any positive integers $m, n$ such that $m^{3}+n^{3}>$ $(m+n)^{2}$, we have
$$
m^{3}+n^{3} \geq(m+n)^{2}+k
$$
|
We see that for $m=3$ and $n=2$ we have $m^{3}+n^{3}>(m+n)^{2}$, thus
$$
3^{3}+2^{3} \geq(3+2)^{2}+k \Rightarrow k \leq 10
$$
We will show that $k=10$ is the desired maximum. In other words, we have to prove that
$$
m^{3}+n^{3} \geq(m+n)^{2}+10
$$
The last inequality is equivalent to
$$
(m+n)\left(m^{2}+n^{2}-m n-m-n\right) \geq 10
$$
If $m+n=2$ or $m+n=3$, then $(m, n)=(1,1),(1,2),(2,1)$ and we can check that none of them satisfies the condition $m^{3}+n^{3}>(m+n)^{2}$.
If $m+n=4$, then $(m, n)=(1,3),(2,2),(3,1)$. The pair $(m, n)=(2,2)$ doesn't satisfy the condition. The pairs $(m, n)=(1,3),(3,1)$ satisfy the condition and we can readily check that $m^{3}+n^{3} \geq(m+$ $n)^{2}+10$.
If $m+n \geq 5$ then we will show that
$$
m^{2}+n^{2}-m n-m-n \geq 2
$$
which is equivalent to
$$
(m-n)^{2}+(m-1)^{2}+(n-1)^{2} \geq 6
$$
If at least one of the numbers $m, n$ is greater or equal to 4 then $(m-1)^{2} \geq 9$ or $(n-1)^{2} \geq 9$ hence the desired result holds. As a result, it remains to check what happens if $m \leq 3$ and $n \leq 3$. Using the condition $m+n \geq 5$ we have that all such pairs are $(m, n)=(2,3),(3,2),(3,3)$.
All of them satisfy the condition and also the inequality $m^{2}+n^{2}-m n-m-n \geq 2$, thus we have the desired result.
Alternative solution by PSC. The problem equivalently asks for to find the minimum value of
$$
A=(m+n)\left(m^{2}+n^{2}-m n-m-n\right)
$$
given that $(m+n)\left(m^{2}+n^{2}-m n-m-n\right)>0$. If $m=n$, we get that $m>2$ and
$$
A=2 m\left(m^{2}-2 m\right) \geq 6\left(3^{2}-6\right)=18
$$
Suppose without loss of generality that $m>n$. If $n=1$, then $m(m+1)(m-2)>0$, therefore $m>2$ and
$$
A \geq 3 \cdot(3+1) \cdot(3-2)=12
$$
If $n \geq 2$, then since $m \geq n+1$ we have
$$
A=(m+n)\left(m(m-n-1)+n^{2}-n\right) \geq(2 n+1)\left(n^{2}-n\right) \geq 5\left(2^{2}-2\right)=10
$$
In all cases $A \geq 10$ and the equality holds if $m=n+1$ and $n=2$, therefore if $m=3$ and $n=2$. It follows that the maximum $k$ is $k=10$.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-shl-jbmo2018.jsonl",
"problem_match": "\nA 2.",
"solution_match": "\nSolution."
}
|
e6e0a67e-a3b8-597e-897a-8a1c75ff1adb
| 604,925
|
Let $A$ be a set of positive integers with the following properties:
(a) If $n$ is an element of $A$ then $n \leqslant 2018$.
(b) If $S$ is a subset of $A$ with $|S|=3$ then there are two elements $n, m$ of $S$ with $|n-m| \geqslant \sqrt{n}+\sqrt{m}$.
What is the maximum number of elements that $A$ can have?
|
Assuming $n>m$ we have
$$
\begin{aligned}
|n-m| \geqslant \sqrt{n}+\sqrt{m} & \Leftrightarrow(\sqrt{n}-\sqrt{m})(\sqrt{n}+\sqrt{m}) \geqslant \sqrt{n}+\sqrt{m} \\
& \Leftrightarrow \sqrt{n} \geqslant \sqrt{m}+1 .
\end{aligned}
$$
Let $A_{k}=\left\{k^{2}, k^{2}+1, \ldots,(k+1)^{2}-1\right\}$. Note that each $A_{k}$ can contain at most two elements of since if $n, m \in$ with $n>m$ then
$$
\sqrt{n}-\sqrt{m} \leqslant \sqrt{(k+1)^{2}-1}-\sqrt{k^{2}}<(k+1)-k=1
$$
In particular, since $\subseteq A_{1} \cup \cdots \cup A_{44}$, we have $|S| \leqslant 2 \cdot 44=88$.
On the other hand we claim that $A=\left\{m^{2}: 1 \leqslant m \leqslant 44\right\} \cup\left\{m^{2}+m: 1 \leqslant m \leqslant 44\right\}$ satisfies the properties and has $|A|=88$. We check property (b) as everything else is trivial.
So let $r, s, t$ be three elements of $A$ and assume $r<s<t$. There are two cases for $r$.
(i) If we have that $r=m^{2}$, then $t \geqslant(m+1)^{2}$ and so $\sqrt{t}-\sqrt{r} \geq 1$ verifying (b).
(ii) If we have that $r=m^{2}+m$, then $t \geqslant(m+1)^{2}+(m+1)$ and
$$
\begin{aligned}
\sqrt{t} \geqslant \sqrt{r}+1 & \Leftrightarrow \sqrt{(m+1)^{2}+(m+1)} \geqslant \sqrt{m^{2}+m}+1 \\
& \Leftrightarrow m^{2}+3 m+2 \geqslant m^{2}+m+1+2 \sqrt{m^{2}+m} \\
& \Leftrightarrow 2 m+1 \geqslant 2 \sqrt{m^{2}+m} \\
& \Leftrightarrow 4 m^{2}+4 m+1 \geqslant 4 m^{2}+4 m .
\end{aligned}
$$
So property (b) holds in this case as well.
## COMBINATORICS
|
88
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Let $A$ be a set of positive integers with the following properties:
(a) If $n$ is an element of $A$ then $n \leqslant 2018$.
(b) If $S$ is a subset of $A$ with $|S|=3$ then there are two elements $n, m$ of $S$ with $|n-m| \geqslant \sqrt{n}+\sqrt{m}$.
What is the maximum number of elements that $A$ can have?
|
Assuming $n>m$ we have
$$
\begin{aligned}
|n-m| \geqslant \sqrt{n}+\sqrt{m} & \Leftrightarrow(\sqrt{n}-\sqrt{m})(\sqrt{n}+\sqrt{m}) \geqslant \sqrt{n}+\sqrt{m} \\
& \Leftrightarrow \sqrt{n} \geqslant \sqrt{m}+1 .
\end{aligned}
$$
Let $A_{k}=\left\{k^{2}, k^{2}+1, \ldots,(k+1)^{2}-1\right\}$. Note that each $A_{k}$ can contain at most two elements of since if $n, m \in$ with $n>m$ then
$$
\sqrt{n}-\sqrt{m} \leqslant \sqrt{(k+1)^{2}-1}-\sqrt{k^{2}}<(k+1)-k=1
$$
In particular, since $\subseteq A_{1} \cup \cdots \cup A_{44}$, we have $|S| \leqslant 2 \cdot 44=88$.
On the other hand we claim that $A=\left\{m^{2}: 1 \leqslant m \leqslant 44\right\} \cup\left\{m^{2}+m: 1 \leqslant m \leqslant 44\right\}$ satisfies the properties and has $|A|=88$. We check property (b) as everything else is trivial.
So let $r, s, t$ be three elements of $A$ and assume $r<s<t$. There are two cases for $r$.
(i) If we have that $r=m^{2}$, then $t \geqslant(m+1)^{2}$ and so $\sqrt{t}-\sqrt{r} \geq 1$ verifying (b).
(ii) If we have that $r=m^{2}+m$, then $t \geqslant(m+1)^{2}+(m+1)$ and
$$
\begin{aligned}
\sqrt{t} \geqslant \sqrt{r}+1 & \Leftrightarrow \sqrt{(m+1)^{2}+(m+1)} \geqslant \sqrt{m^{2}+m}+1 \\
& \Leftrightarrow m^{2}+3 m+2 \geqslant m^{2}+m+1+2 \sqrt{m^{2}+m} \\
& \Leftrightarrow 2 m+1 \geqslant 2 \sqrt{m^{2}+m} \\
& \Leftrightarrow 4 m^{2}+4 m+1 \geqslant 4 m^{2}+4 m .
\end{aligned}
$$
So property (b) holds in this case as well.
## COMBINATORICS
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-shl-jbmo2018.jsonl",
"problem_match": "\nA 7.",
"solution_match": "\nSolution."
}
|
3551a01b-5250-509a-a43f-2d514a8e2766
| 604,982
|
A set $S$ is called neighbouring if it has the following two properties:
a) $S$ has exactly four elements
b) for every element $x$ of $S$, at least one of the numbers $x-1$ or $x+1$ belongs to $S$.
Find the number of all neighbouring subsets of the set $\{1,2, \ldots, n\}$.
|
Let us denote with $a$ and $b$ the smallest and the largest element of a neighbouring set $S$, respectively. Since $a-1 \notin S$, we have that $a+1 \in S$. Similarly, we conclude that $b-1 \in S$. So, every neighbouring set has the following form $\{a, a+1, b-1, b\}$ for $b-a \geq 3$. The number of the neighbouring subsets for which $b-a=3$ is $n-3$. The number of the neighbouring subsets for which $b-a=4$ is $n-4$ and so on. It follows that the number of the neighbouring subsets of the set $\{1,2, \ldots, n\}$ is:
$$
(n-3)+(n-4)+\cdots+3+2+1=\frac{(n-3)(n-2)}{2}
$$
|
\frac{(n-3)(n-2)}{2}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
A set $S$ is called neighbouring if it has the following two properties:
a) $S$ has exactly four elements
b) for every element $x$ of $S$, at least one of the numbers $x-1$ or $x+1$ belongs to $S$.
Find the number of all neighbouring subsets of the set $\{1,2, \ldots, n\}$.
|
Let us denote with $a$ and $b$ the smallest and the largest element of a neighbouring set $S$, respectively. Since $a-1 \notin S$, we have that $a+1 \in S$. Similarly, we conclude that $b-1 \in S$. So, every neighbouring set has the following form $\{a, a+1, b-1, b\}$ for $b-a \geq 3$. The number of the neighbouring subsets for which $b-a=3$ is $n-3$. The number of the neighbouring subsets for which $b-a=4$ is $n-4$ and so on. It follows that the number of the neighbouring subsets of the set $\{1,2, \ldots, n\}$ is:
$$
(n-3)+(n-4)+\cdots+3+2+1=\frac{(n-3)(n-2)}{2}
$$
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-shl-jbmo2018.jsonl",
"problem_match": "\nC 1.",
"solution_match": "\nSolution."
}
|
c976402e-ee9f-5a8a-bc22-77938d3c19cb
| 604,992
|
A set $T$ of $n$ three-digit numbers has the following five properties:
(1) No number contains the digit 0 .
(2) The sum of the digits of each number is 9 .
(3) The units digits of any two numbers are different.
(4) The tens digits of any two numbers are different.
(5) The hundreds digits of any two numbers are different.
Find the largest possible value of $n$.
|
Let $S$ denote the set of three-digit numbers that have digit sum equal to 9 and no digit equal to 0 . We will first find the cardinality of $S$. We start from the number 111 and each element of $S$ can be obtained from 111 by a string of $6 A$ 's (which means that we add 1 to the current digit) and 2 G's (which means go to the next digit). Then for example 324 can be obtained from 111 by the
string AAGAGAAA. There are in total
$$
\frac{8!}{6!\cdot 2!}=28
$$
such words, so $S$ contains 28 numbers. Now, from the conditions (3), (4), (5), if $\overline{a b c}$ is in $T$ then each of the other numbers of the form $\overline{* c}$ cannot be in $T$, neither $\overline{* * *}$ can be, nor $\overline{a * *}$. Since there are $a+b-2$ numbers of the first category, $a+c-2$ from the second and $b+c-2$ from the third one. In
these three categories there are
$$
(a+b-2)+(b+c-2)+(c+a-2)=2(a+b+c)-6=2 \cdot 9-6=12
$$
distinct numbers that cannot be in $T$ if $\overline{a b c}$ is in $T$. So, if $T$ has $n$ numbers, then $12 n$ are the forbidden ones that are in $S$, but each number from $S$ can be a forbidden number no more than three times, once for each of its digits, so
$$
n+\frac{12 n}{3} \leq 28 \Longleftrightarrow n \leq \frac{28}{5}
$$
and since $n$ is an integer, we get $n \leq 5$. A possible example for $n=5$ is
$$
T=\{144,252,315,423,531\}
$$
Comment by PSC. It is classical to compute the cardinality of $S$ and this can be done in many ways. In general, the number of solutions of the equation
$$
x_{1}+x_{2}+\cdots+x_{k}=n
$$
in positive integers, where the order of $x_{i}$ matters, is well known that equals to $\binom{n-1}{k-1}$. In our case,
we want to count the number of positive solutions to we want to count the number of positive solutions to $a+b+c=9$. By the above, this equals to $\binom{9-1}{3-1}=28$. Using the general result above, we can also find that there are $a+b-2$ numbers of the
form $\overline{* * c}$.
|
5
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
A set $T$ of $n$ three-digit numbers has the following five properties:
(1) No number contains the digit 0 .
(2) The sum of the digits of each number is 9 .
(3) The units digits of any two numbers are different.
(4) The tens digits of any two numbers are different.
(5) The hundreds digits of any two numbers are different.
Find the largest possible value of $n$.
|
Let $S$ denote the set of three-digit numbers that have digit sum equal to 9 and no digit equal to 0 . We will first find the cardinality of $S$. We start from the number 111 and each element of $S$ can be obtained from 111 by a string of $6 A$ 's (which means that we add 1 to the current digit) and 2 G's (which means go to the next digit). Then for example 324 can be obtained from 111 by the
string AAGAGAAA. There are in total
$$
\frac{8!}{6!\cdot 2!}=28
$$
such words, so $S$ contains 28 numbers. Now, from the conditions (3), (4), (5), if $\overline{a b c}$ is in $T$ then each of the other numbers of the form $\overline{* c}$ cannot be in $T$, neither $\overline{* * *}$ can be, nor $\overline{a * *}$. Since there are $a+b-2$ numbers of the first category, $a+c-2$ from the second and $b+c-2$ from the third one. In
these three categories there are
$$
(a+b-2)+(b+c-2)+(c+a-2)=2(a+b+c)-6=2 \cdot 9-6=12
$$
distinct numbers that cannot be in $T$ if $\overline{a b c}$ is in $T$. So, if $T$ has $n$ numbers, then $12 n$ are the forbidden ones that are in $S$, but each number from $S$ can be a forbidden number no more than three times, once for each of its digits, so
$$
n+\frac{12 n}{3} \leq 28 \Longleftrightarrow n \leq \frac{28}{5}
$$
and since $n$ is an integer, we get $n \leq 5$. A possible example for $n=5$ is
$$
T=\{144,252,315,423,531\}
$$
Comment by PSC. It is classical to compute the cardinality of $S$ and this can be done in many ways. In general, the number of solutions of the equation
$$
x_{1}+x_{2}+\cdots+x_{k}=n
$$
in positive integers, where the order of $x_{i}$ matters, is well known that equals to $\binom{n-1}{k-1}$. In our case,
we want to count the number of positive solutions to we want to count the number of positive solutions to $a+b+c=9$. By the above, this equals to $\binom{9-1}{3-1}=28$. Using the general result above, we can also find that there are $a+b-2$ numbers of the
form $\overline{* * c}$.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-shl-jbmo2018.jsonl",
"problem_match": "\nC 2.",
"solution_match": "\nSolution."
}
|
9228c1f2-540e-5bfe-9d62-07283b6b0196
| 605,006
|
The cells of a $8 \times 8$ table are initially white. Alice and Bob play a game. First Alice paints $n$ of the fields in red. Then Bob chooses 4 rows and 4 columns from the table and paints all fields in them in black. Alice wins if there is at least one red field left. Find the least value of $n$ such that Alice can win the game no matter how Bob plays.
|
We will show that the least value of $n$ is $n=13$.
If $n \leq 12$, Bob wins by painting black the 4 rows containing the highest numbers of red cells. Indeed, if at least 5 red cells remain, then one of the rows not blackened contains at least 2 red cells. Thus, each one of the rows blackened contained at least 2 red cells, and then all blackened cells were at least 8. However, in this case, at most 4 would be not blackened, a contradiction. It follows that at most 4 red cells remain which can be easily blackened by Bob choosing the 4 columns that they are in.
Now let $n=13$. Enumerate the rows and the columns from 1 to 8 and each field will be referred to by the pair (row,column) it is in. Let Alice paint in red the fields
$$
(1,1),(1,2),(2,1),(2,3),(3,2),(3,4),(4,3),(4,5),(5,4),(5,5),(6,6),(7,7),(8,8)
$$
as in the following figure.

Suppose that Bob has managed to paint all red fields in black. The cells $(6,6),(7,7),(8,8)$ are painted black by three different lines (rows or columns) containing no other red felds, so the remaining 10 red fields have to be painted black by the remaining 5 lines. As no line contains more than 2 red fields, each red field has to be contained in exactly one of these lines. Assume that $(1,1)$ is painted black by a row, that is, row 1 is painted black. Let $k$ be the least positive integer such that row $k$ has not been painted black, where $2 \leq k \leq 5$. Then field $(k, k-1)$ should be painted black by column $k-1$. However, in this column there is another red field $(j, k-1)$ contained in the painted row with number $j<k$, which is a contradiction. Similar reasoning works if $(1,1)$ is painted black by a column.
Comment by PSC. Here is another reasoning to conclude that if Alice paints the table as above, then she wins.
Let $A$ be the $5 \times 5$ square defined by the corners $(1,1)$ and $(5,5)$.
Case 1: If Bob chooses 3 rows to paint black the cells $(6,6),(7,7)$ and $(8,8)$ then he has to use 1 row and 4 columns to paint in black the remaining 10 red squares in $A$. Then no matter which 4 columns
Bob select, the remaining 1 column in A contains two red squares which cannot be painted in black using only 1 row. Similar reasoning stands if Bob chooses 3 columns.
Case 2: If Bob chooses 2 rows and 1 column to paint black the cells $(6,6),(7,7)$ and $(8,8)$, then he has to use 3 columns and 2 rows to paint in black the remaining 10 red squares in $A$. Then, no matter which 3 columns Bob select, the remaining 2 columns in $A$ contain 4 red squares in 3 different rows which cannot be painted in black using only 2 rows. Similar reasoning stands if
Bob chooses 1 row and 2 columns.
## GEOMETRY
|
13
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
The cells of a $8 \times 8$ table are initially white. Alice and Bob play a game. First Alice paints $n$ of the fields in red. Then Bob chooses 4 rows and 4 columns from the table and paints all fields in them in black. Alice wins if there is at least one red field left. Find the least value of $n$ such that Alice can win the game no matter how Bob plays.
|
We will show that the least value of $n$ is $n=13$.
If $n \leq 12$, Bob wins by painting black the 4 rows containing the highest numbers of red cells. Indeed, if at least 5 red cells remain, then one of the rows not blackened contains at least 2 red cells. Thus, each one of the rows blackened contained at least 2 red cells, and then all blackened cells were at least 8. However, in this case, at most 4 would be not blackened, a contradiction. It follows that at most 4 red cells remain which can be easily blackened by Bob choosing the 4 columns that they are in.
Now let $n=13$. Enumerate the rows and the columns from 1 to 8 and each field will be referred to by the pair (row,column) it is in. Let Alice paint in red the fields
$$
(1,1),(1,2),(2,1),(2,3),(3,2),(3,4),(4,3),(4,5),(5,4),(5,5),(6,6),(7,7),(8,8)
$$
as in the following figure.

Suppose that Bob has managed to paint all red fields in black. The cells $(6,6),(7,7),(8,8)$ are painted black by three different lines (rows or columns) containing no other red felds, so the remaining 10 red fields have to be painted black by the remaining 5 lines. As no line contains more than 2 red fields, each red field has to be contained in exactly one of these lines. Assume that $(1,1)$ is painted black by a row, that is, row 1 is painted black. Let $k$ be the least positive integer such that row $k$ has not been painted black, where $2 \leq k \leq 5$. Then field $(k, k-1)$ should be painted black by column $k-1$. However, in this column there is another red field $(j, k-1)$ contained in the painted row with number $j<k$, which is a contradiction. Similar reasoning works if $(1,1)$ is painted black by a column.
Comment by PSC. Here is another reasoning to conclude that if Alice paints the table as above, then she wins.
Let $A$ be the $5 \times 5$ square defined by the corners $(1,1)$ and $(5,5)$.
Case 1: If Bob chooses 3 rows to paint black the cells $(6,6),(7,7)$ and $(8,8)$ then he has to use 1 row and 4 columns to paint in black the remaining 10 red squares in $A$. Then no matter which 4 columns
Bob select, the remaining 1 column in A contains two red squares which cannot be painted in black using only 1 row. Similar reasoning stands if Bob chooses 3 columns.
Case 2: If Bob chooses 2 rows and 1 column to paint black the cells $(6,6),(7,7)$ and $(8,8)$, then he has to use 3 columns and 2 rows to paint in black the remaining 10 red squares in $A$. Then, no matter which 3 columns Bob select, the remaining 2 columns in $A$ contain 4 red squares in 3 different rows which cannot be painted in black using only 2 rows. Similar reasoning stands if
Bob chooses 1 row and 2 columns.
## GEOMETRY
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-shl-jbmo2018.jsonl",
"problem_match": "\nC 3.",
"solution_match": "\nSolution."
}
|
d7113dc5-b92c-510e-a7d3-4f7391f2b66f
| 605,017
|
Find all four-digit positive integers $\overline{a b c d}=10^{3} a+10^{2} b+10 c+d$, with $a \neq 0$, such that
$$
\overline{a b c d}=a^{a+b+c+d}-a^{-a+b-c+d}+a
$$
|
It is obvious that $a \neq 1$ and $-a+b-c+d \geq 0$. It follows that $b+d \geq c+a \geq a$. Then,
$$
\begin{aligned}
10000>\overline{a b c d} & =a^{a+b+c+d}-a^{-a+b-c+d}+a \\
& >a^{a+b+c+d}-a^{a+b+c+d-2} \\
& =a^{a+b+c+d-2}\left(a^{2}-1\right) \\
& \geq a^{2 a-2}\left(a^{2}-1\right)
\end{aligned}
$$
For $a \geq 4$, we have
$$
a^{2 a-2}\left(a^{2}-1\right)=4^{6} \cdot 15>4^{5} \cdot 10=10240>10000
$$
a contradiction. This means that $a=2$ or $a=3$.
Case 1: If $\mathrm{a}=3$, then since $3^{7}=2187<3000$, we conclude that $a+b+c+d \geq 8$ and like in the previous paragraph we get
$$
3^{a+b+c+d}-3^{-a+b-c+d}+3>3^{a+b+c+d-2} \cdot 8 \geq 729 \cdot 8>4000
$$
which is again a contradiction.
Case 2: If $a=2$ then $2^{10}=1024<2000$, thus $a+b+c+d \geq 11$. If $a+b+c+d \geq 12$, we have again as above that
$$
\overline{a b c d}>2^{a+b+c+d-2} \cdot 3=1024 \cdot 3>3000
$$
which is absurd and we conclude that $a+b+c+d=11$. Then $\overline{a b c d}<2^{11}+2=2050$, so $b=0$. Moreover, from
$$
2050-2^{d-c-2} \geq 2000 \Longleftrightarrow 2^{d-c-2} \leq 50
$$
we get $d-c-2 \leq 5$. However, from $d+c=9$ we have that $d-c-2$ is odd, so $d-c-2 \in\{1,3,5\}$. This means that
$$
\overline{a b c d}=2050-2^{d-c-2} \in\{2048,2042,2018\}
$$
The only number that satisfies $a+b+c+d=11$ is 2018 , so it is the only solution.
Comment by PSC. After proving $b+d \geq a+c \geq 2$, we can alternatively conclude that $a \leq 3$, as follows. If $a \geq 4$, then
$$
\begin{aligned}
\overline{a b c d} & =a^{a+b+c+d}-a^{-a+b-c+d}+a \\
& >a^{b+d-a-c}\left(a^{2 a+2 c}-1\right) \\
& >a^{2 a+2 c}-1 \\
& \geq 4^{8}-1=65535
\end{aligned}
$$
a contradiction.
|
2018
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Find all four-digit positive integers $\overline{a b c d}=10^{3} a+10^{2} b+10 c+d$, with $a \neq 0$, such that
$$
\overline{a b c d}=a^{a+b+c+d}-a^{-a+b-c+d}+a
$$
|
It is obvious that $a \neq 1$ and $-a+b-c+d \geq 0$. It follows that $b+d \geq c+a \geq a$. Then,
$$
\begin{aligned}
10000>\overline{a b c d} & =a^{a+b+c+d}-a^{-a+b-c+d}+a \\
& >a^{a+b+c+d}-a^{a+b+c+d-2} \\
& =a^{a+b+c+d-2}\left(a^{2}-1\right) \\
& \geq a^{2 a-2}\left(a^{2}-1\right)
\end{aligned}
$$
For $a \geq 4$, we have
$$
a^{2 a-2}\left(a^{2}-1\right)=4^{6} \cdot 15>4^{5} \cdot 10=10240>10000
$$
a contradiction. This means that $a=2$ or $a=3$.
Case 1: If $\mathrm{a}=3$, then since $3^{7}=2187<3000$, we conclude that $a+b+c+d \geq 8$ and like in the previous paragraph we get
$$
3^{a+b+c+d}-3^{-a+b-c+d}+3>3^{a+b+c+d-2} \cdot 8 \geq 729 \cdot 8>4000
$$
which is again a contradiction.
Case 2: If $a=2$ then $2^{10}=1024<2000$, thus $a+b+c+d \geq 11$. If $a+b+c+d \geq 12$, we have again as above that
$$
\overline{a b c d}>2^{a+b+c+d-2} \cdot 3=1024 \cdot 3>3000
$$
which is absurd and we conclude that $a+b+c+d=11$. Then $\overline{a b c d}<2^{11}+2=2050$, so $b=0$. Moreover, from
$$
2050-2^{d-c-2} \geq 2000 \Longleftrightarrow 2^{d-c-2} \leq 50
$$
we get $d-c-2 \leq 5$. However, from $d+c=9$ we have that $d-c-2$ is odd, so $d-c-2 \in\{1,3,5\}$. This means that
$$
\overline{a b c d}=2050-2^{d-c-2} \in\{2048,2042,2018\}
$$
The only number that satisfies $a+b+c+d=11$ is 2018 , so it is the only solution.
Comment by PSC. After proving $b+d \geq a+c \geq 2$, we can alternatively conclude that $a \leq 3$, as follows. If $a \geq 4$, then
$$
\begin{aligned}
\overline{a b c d} & =a^{a+b+c+d}-a^{-a+b-c+d}+a \\
& >a^{b+d-a-c}\left(a^{2 a+2 c}-1\right) \\
& >a^{2 a+2 c}-1 \\
& \geq 4^{8}-1=65535
\end{aligned}
$$
a contradiction.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-shl-jbmo2018.jsonl",
"problem_match": "\nNT 3.",
"solution_match": "\nSolution."
}
|
860e4b14-fc39-58f6-a4bf-83d6452466e7
| 605,125
|
Determine the number of pairs of integers $(m, n)$ such that
$$
\sqrt{n+\sqrt{2016}}+\sqrt{m-\sqrt{2016}} \in \mathbb{Q}
$$
|
Let $r=\sqrt{n+\sqrt{2016}}+\sqrt{m-\sqrt{2016}}$. Then
$$
n+m+2 \sqrt{n+\sqrt{2016}} \cdot \sqrt{m-\sqrt{2016}}=r^{2}
$$
and
$$
(m-n) \sqrt{2106}=\frac{1}{4}\left(r^{2}-m-n\right)^{2}-m n+2016 \in \mathbb{Q}
$$
Since $\sqrt{2016} \notin \mathbb{Q}$, it follows that $m=n$. Then
$$
\sqrt{n^{2}-2016}=\frac{1}{2}\left(r^{2}-2 n\right) \in \mathbb{Q}
$$
Hence, there is some nonnegative integer $p$ such that $n^{2}-2016=p^{2}$ and (1) becomes $2 n+2 p=r^{2}$.
It follows that $2(n+p)=r^{2}$ is the square of a rational and also an integer, hence a perfect square. On the other hand, $2016=(n-p)(n+p)$ and $n+p$ is a divisor of 2016, larger than $\sqrt{2016}$. Since $n+p$ is even, so is also $n-p$, and $r^{2}=2(n+p)$ is a divisor of $2016=2^{5} \cdot 3^{2} \cdot 7$, larger than $2 \sqrt{2016}>88$. The only possibility is $r^{2}=2^{4} \cdot 3^{2}=12^{2}$. Hence, $n+p=72$ and $n-p=28$, and we conclude that $n=m=50$. Thus, there is only one such pair.
|
1
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Determine the number of pairs of integers $(m, n)$ such that
$$
\sqrt{n+\sqrt{2016}}+\sqrt{m-\sqrt{2016}} \in \mathbb{Q}
$$
|
Let $r=\sqrt{n+\sqrt{2016}}+\sqrt{m-\sqrt{2016}}$. Then
$$
n+m+2 \sqrt{n+\sqrt{2016}} \cdot \sqrt{m-\sqrt{2016}}=r^{2}
$$
and
$$
(m-n) \sqrt{2106}=\frac{1}{4}\left(r^{2}-m-n\right)^{2}-m n+2016 \in \mathbb{Q}
$$
Since $\sqrt{2016} \notin \mathbb{Q}$, it follows that $m=n$. Then
$$
\sqrt{n^{2}-2016}=\frac{1}{2}\left(r^{2}-2 n\right) \in \mathbb{Q}
$$
Hence, there is some nonnegative integer $p$ such that $n^{2}-2016=p^{2}$ and (1) becomes $2 n+2 p=r^{2}$.
It follows that $2(n+p)=r^{2}$ is the square of a rational and also an integer, hence a perfect square. On the other hand, $2016=(n-p)(n+p)$ and $n+p$ is a divisor of 2016, larger than $\sqrt{2016}$. Since $n+p$ is even, so is also $n-p$, and $r^{2}=2(n+p)$ is a divisor of $2016=2^{5} \cdot 3^{2} \cdot 7$, larger than $2 \sqrt{2016}>88$. The only possibility is $r^{2}=2^{4} \cdot 3^{2}=12^{2}$. Hence, $n+p=72$ and $n-p=28$, and we conclude that $n=m=50$. Thus, there is only one such pair.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-shortlist_jbmo_2016_v7-1.jsonl",
"problem_match": "\nA3.",
"solution_match": "\nSolution."
}
|
efbbbbe1-76e2-5ba2-be56-383bb4829dbf
| 605,169
|
Let $S_{n}$ be the sum of reciprocal values of non-zero digits of all positive integers up to (and including) $n$. For instance, $S_{13}=\frac{1}{1}+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}+\frac{1}{6}+\frac{1}{7}+\frac{1}{8}+\frac{1}{9}+\frac{1}{1}+\frac{1}{1}+\frac{1}{1}+\frac{1}{1}+\frac{1}{2}+\frac{1}{1}+\frac{1}{3}$. Find the least positive integer $k$ making the number $k!\cdot S_{2016}$ an integer.
|
We will first calculate $S_{999}$, then $S_{1999}-S_{999}$, and then $S_{2016}-S_{1999}$.
Writing the integers from 1 to 999 as 001 to 999, adding eventually also 000 (since 0 digits actually do not matter), each digit appears exactly 100 times in each position(as unit, ten, or hundred). Hence
$$
S_{999}=300 \cdot\left(\frac{1}{1}+\frac{1}{2}+\cdots+\frac{1}{9}\right)
$$
For the numbers in the interval $1000 \rightarrow 1999$, compared to $0 \rightarrow 999$, there are precisely 1000 more digits 1 . We get
$$
S_{1999}-S_{999}=1000+S_{999} \Longrightarrow S_{1999}=1000+600 \cdot\left(\frac{1}{1}+\frac{1}{2}+\cdots+\frac{1}{9}\right)
$$
Finally, in the interval $2000 \rightarrow 2016$, the digit 1 appears twice as unit and seven times as a ten, the digit 2 twice as a unit and 17 times as a thousand, the digits $3,4,5$, and 6 each appear exactly twice as units, and the digits 7,8 , and 9 each appear exactly once as a unit. Hence
$$
S_{2016}-S_{1999}=9 \cdot 1+19 \cdot \frac{1}{2}+2 \cdot\left(\frac{1}{3}+\frac{1}{4}+\frac{1}{5}+\frac{1}{6}\right)+1 \cdot\left(\frac{1}{7}+\frac{1}{8}+\frac{1}{9}\right)
$$
In the end, we get
$$
\begin{aligned}
S_{2016} & =1609 \cdot 1+619 \cdot \frac{1}{2}+602 \cdot\left(\frac{1}{3}+\frac{1}{4}+\frac{1}{5}+\frac{1}{6}\right)+601 \cdot\left(\frac{1}{7}+\frac{1}{8}+\frac{1}{9}\right) \\
& =m+\frac{1}{2}+\frac{2}{3}+\frac{2}{4}+\frac{2}{5}+\frac{2}{6}+\frac{6}{7}+\frac{1}{8}+\frac{7}{9}=n+\frac{p}{2^{3} \cdot 3^{2} \cdot 5 \cdot 7}
\end{aligned}
$$
where $m, n$, and $p$ are positive integers, $p$ coprime to $2^{3} \cdot 3^{2} \cdot 5 \cdot 7$. Then $k!\cdot S_{2016}$ is an integer precisely when $k$ ! is a multiple of $2^{3} \cdot 3^{2} \cdot 5 \cdot 7$. Since $7 \mid k!$, it follows that $k \geq 7$. Also, $7!=2^{4} \cdot 3^{2} \cdot 5 \cdot 7$, implying that the least $k$ satisfying $k!\cdot S_{2016} \in \mathbb{Z}$ is $k=7$.
|
7
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Let $S_{n}$ be the sum of reciprocal values of non-zero digits of all positive integers up to (and including) $n$. For instance, $S_{13}=\frac{1}{1}+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}+\frac{1}{6}+\frac{1}{7}+\frac{1}{8}+\frac{1}{9}+\frac{1}{1}+\frac{1}{1}+\frac{1}{1}+\frac{1}{1}+\frac{1}{2}+\frac{1}{1}+\frac{1}{3}$. Find the least positive integer $k$ making the number $k!\cdot S_{2016}$ an integer.
|
We will first calculate $S_{999}$, then $S_{1999}-S_{999}$, and then $S_{2016}-S_{1999}$.
Writing the integers from 1 to 999 as 001 to 999, adding eventually also 000 (since 0 digits actually do not matter), each digit appears exactly 100 times in each position(as unit, ten, or hundred). Hence
$$
S_{999}=300 \cdot\left(\frac{1}{1}+\frac{1}{2}+\cdots+\frac{1}{9}\right)
$$
For the numbers in the interval $1000 \rightarrow 1999$, compared to $0 \rightarrow 999$, there are precisely 1000 more digits 1 . We get
$$
S_{1999}-S_{999}=1000+S_{999} \Longrightarrow S_{1999}=1000+600 \cdot\left(\frac{1}{1}+\frac{1}{2}+\cdots+\frac{1}{9}\right)
$$
Finally, in the interval $2000 \rightarrow 2016$, the digit 1 appears twice as unit and seven times as a ten, the digit 2 twice as a unit and 17 times as a thousand, the digits $3,4,5$, and 6 each appear exactly twice as units, and the digits 7,8 , and 9 each appear exactly once as a unit. Hence
$$
S_{2016}-S_{1999}=9 \cdot 1+19 \cdot \frac{1}{2}+2 \cdot\left(\frac{1}{3}+\frac{1}{4}+\frac{1}{5}+\frac{1}{6}\right)+1 \cdot\left(\frac{1}{7}+\frac{1}{8}+\frac{1}{9}\right)
$$
In the end, we get
$$
\begin{aligned}
S_{2016} & =1609 \cdot 1+619 \cdot \frac{1}{2}+602 \cdot\left(\frac{1}{3}+\frac{1}{4}+\frac{1}{5}+\frac{1}{6}\right)+601 \cdot\left(\frac{1}{7}+\frac{1}{8}+\frac{1}{9}\right) \\
& =m+\frac{1}{2}+\frac{2}{3}+\frac{2}{4}+\frac{2}{5}+\frac{2}{6}+\frac{6}{7}+\frac{1}{8}+\frac{7}{9}=n+\frac{p}{2^{3} \cdot 3^{2} \cdot 5 \cdot 7}
\end{aligned}
$$
where $m, n$, and $p$ are positive integers, $p$ coprime to $2^{3} \cdot 3^{2} \cdot 5 \cdot 7$. Then $k!\cdot S_{2016}$ is an integer precisely when $k$ ! is a multiple of $2^{3} \cdot 3^{2} \cdot 5 \cdot 7$. Since $7 \mid k!$, it follows that $k \geq 7$. Also, $7!=2^{4} \cdot 3^{2} \cdot 5 \cdot 7$, implying that the least $k$ satisfying $k!\cdot S_{2016} \in \mathbb{Z}$ is $k=7$.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-shortlist_jbmo_2016_v7-1.jsonl",
"problem_match": "\nC1.",
"solution_match": "## Solution."
}
|
759f8bbe-0b83-5f7e-b3ad-227573562c5b
| 605,208
|
The natural numbers from 1 to 50 are written down on the blackboard. At least how many of them should be deleted, in order that the sum of any two of the remaining numbers is not a prime?
|
Notice that if the odd, respectively even, numbers are all deleted, then the sum of any two remaining numbers is even and exceeds 2 , so it is certainly not a prime. We prove that 25 is the minimal number of deleted numbers. To this end, we group the positive integers from 1 to 50 in 25 pairs, such that the sum of the numbers within each pair is a prime:
$$
\begin{aligned}
& (1,2),(3,4),(5,6),(7,10),(8,9),(11,12),(13,16),(14,15),(17,20) \\
& (18,19),(21,22),(23,24),(25,28),(26,27),(29,30),(31,36),(32,35) \\
& (33,34),(37,42),(38,41),(39,40),(43,46),(44,45),(47,50),(48,49)
\end{aligned}
$$
Since at least one number from each pair has to be deleted, the minimal number is 25 .
|
25
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
The natural numbers from 1 to 50 are written down on the blackboard. At least how many of them should be deleted, in order that the sum of any two of the remaining numbers is not a prime?
|
Notice that if the odd, respectively even, numbers are all deleted, then the sum of any two remaining numbers is even and exceeds 2 , so it is certainly not a prime. We prove that 25 is the minimal number of deleted numbers. To this end, we group the positive integers from 1 to 50 in 25 pairs, such that the sum of the numbers within each pair is a prime:
$$
\begin{aligned}
& (1,2),(3,4),(5,6),(7,10),(8,9),(11,12),(13,16),(14,15),(17,20) \\
& (18,19),(21,22),(23,24),(25,28),(26,27),(29,30),(31,36),(32,35) \\
& (33,34),(37,42),(38,41),(39,40),(43,46),(44,45),(47,50),(48,49)
\end{aligned}
$$
Since at least one number from each pair has to be deleted, the minimal number is 25 .
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-shortlist_jbmo_2016_v7-1.jsonl",
"problem_match": "\nC2.",
"solution_match": "\nSolution."
}
|
908c8b1e-f734-5e9d-98b2-d4fa596407bf
| 605,221
|
Consider any four pairwise distinct real numbers and write one of these numbers in each cell of a $5 \times 5$ array so that each number occurs exactly once in every $2 \times 2$ subarray. The sum over all entries of the array is called the total sum of that array. Determine the maximum number of distinct total sums that may be obtained in this way.
|
We will prove that the maximum number of total sums is 60 .
The proof is based on the following claim.
Claim. Either each row contains exactly two of the numbers, or each column contains exactly two of the numbers.
Proof of the Claim. Indeed, let $R$ be a row containing at least three of the numbers. Then, in row $R$ we can find three of the numbers in consecutive positions, let $x, y, z$ be the numbers in consecutive positions(where $\{x, y, s, z\}=\{a, b, c, d\}$ ). Due to our hypothesis that in every $2 \times 2$ subarray each number is used exactly once, in the row above $\mathrm{R}$ (if there is such a row), precisely above the numbers $x, y, z$ will be the numbers $z, t, x$ in this order. And above them will be the numbers $x, y, z$ in this order. The same happens in the rows below $R$ (see at the following figure).
$$
\left(\begin{array}{lllll}
\bullet & x & y & z & \bullet \\
\bullet & z & t & x & \bullet \\
\bullet & x & y & z & \bullet \\
\bullet & z & t & x & \bullet \\
\bullet & x & y & z & \bullet
\end{array}\right)
$$
Completing all the array, it easily follows that each column contains exactly two of the numbers and our claim has been proven.
Rotating the matrix (if it is necessary), we may assume that each row contains exactly two of the numbers. If we forget the first row and column from the array, we obtain a $4 \times 4$ array, that can be divided into four $2 \times 2$ subarrays, containing thus each number exactly four times, with a total sum of $4(a+b+c+d)$. It suffices to find how many different ways are there to put the numbers in the first row $R_{1}$ and the first column $C_{1}$.
Denoting by $a_{1}, b_{1}, c_{1}, d_{1}$ the number of appearances of $a, b, c$, and respectively $d$ in $R_{1}$ and $C_{1}$, the total sum of the numbers in the entire $5 \times 5$ array will be
$$
S=4(a+b+c+d)+a_{1} \cdot a+b_{1} \cdot b+c_{1} \cdot c+d_{1} \cdot d
$$
If the first, the third and the fifth row contain the numbers $x, y$, with $x$ denoting the number at the entry $(1,1)$, then the second and the fourth row will contain only the numbers $z, t$, with $z$ denoting the number at the entry $(2,1)$. Then $x_{1}+y_{1}=7$ and $x_{1} \geqslant 3$, $y_{1} \geqslant 2, z_{1}+t_{1}=2$, and $z_{1} \geqslant t_{1}$. Then $\left\{x_{1}, y_{1}\right\}=\{5,2\}$ or $\left\{x_{1}, y_{1}\right\}=\{4,3\}$, respectively $\left\{z_{1}, t_{1}\right\}=\{2,0\}$ or $\left\{z_{1}, t_{1}\right\}=\{1,1\}$. Then $\left(a_{1}, b_{1}, c_{1}, d_{1}\right)$ is obtained by permuting one of the following quadruples:
$$
(5,2,2,0),(5,2,1,1),(4,3,2,0),(4,3,1,1)
$$
There are a total of $\frac{4!}{2!}=12$ permutations of $(5,2,2,0)$, also 12 permutations of $(5,2,1,1)$, 24 permutations of $(4,3,2,0)$ and finally, there are 12 permutations of $(4,3,1,1)$. Hence, there are at most 60 different possible total sums.
We can obtain indeed each of these 60 combinations: take three rows ababa alternating
with two rows $c d c d c$ to get $(5,2,2,0)$; take three rows ababa alternating with one row $c d c d c$ and a row $(d c d c d)$ to get $(5,2,1,1)$; take three rows $a b a b c$ alternating with two rows $c d c d a$ to get $(4,3,2,0)$; take three rows abcda alternating with two rows $c d a b c$ to get $(4,3,1,1)$. By choosing for example $a=10^{3}, b=10^{2}, c=10, d=1$, we can make all these sums different. Hence, 60 is indeed the maximum possible number of different sums.
|
60
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Consider any four pairwise distinct real numbers and write one of these numbers in each cell of a $5 \times 5$ array so that each number occurs exactly once in every $2 \times 2$ subarray. The sum over all entries of the array is called the total sum of that array. Determine the maximum number of distinct total sums that may be obtained in this way.
|
We will prove that the maximum number of total sums is 60 .
The proof is based on the following claim.
Claim. Either each row contains exactly two of the numbers, or each column contains exactly two of the numbers.
Proof of the Claim. Indeed, let $R$ be a row containing at least three of the numbers. Then, in row $R$ we can find three of the numbers in consecutive positions, let $x, y, z$ be the numbers in consecutive positions(where $\{x, y, s, z\}=\{a, b, c, d\}$ ). Due to our hypothesis that in every $2 \times 2$ subarray each number is used exactly once, in the row above $\mathrm{R}$ (if there is such a row), precisely above the numbers $x, y, z$ will be the numbers $z, t, x$ in this order. And above them will be the numbers $x, y, z$ in this order. The same happens in the rows below $R$ (see at the following figure).
$$
\left(\begin{array}{lllll}
\bullet & x & y & z & \bullet \\
\bullet & z & t & x & \bullet \\
\bullet & x & y & z & \bullet \\
\bullet & z & t & x & \bullet \\
\bullet & x & y & z & \bullet
\end{array}\right)
$$
Completing all the array, it easily follows that each column contains exactly two of the numbers and our claim has been proven.
Rotating the matrix (if it is necessary), we may assume that each row contains exactly two of the numbers. If we forget the first row and column from the array, we obtain a $4 \times 4$ array, that can be divided into four $2 \times 2$ subarrays, containing thus each number exactly four times, with a total sum of $4(a+b+c+d)$. It suffices to find how many different ways are there to put the numbers in the first row $R_{1}$ and the first column $C_{1}$.
Denoting by $a_{1}, b_{1}, c_{1}, d_{1}$ the number of appearances of $a, b, c$, and respectively $d$ in $R_{1}$ and $C_{1}$, the total sum of the numbers in the entire $5 \times 5$ array will be
$$
S=4(a+b+c+d)+a_{1} \cdot a+b_{1} \cdot b+c_{1} \cdot c+d_{1} \cdot d
$$
If the first, the third and the fifth row contain the numbers $x, y$, with $x$ denoting the number at the entry $(1,1)$, then the second and the fourth row will contain only the numbers $z, t$, with $z$ denoting the number at the entry $(2,1)$. Then $x_{1}+y_{1}=7$ and $x_{1} \geqslant 3$, $y_{1} \geqslant 2, z_{1}+t_{1}=2$, and $z_{1} \geqslant t_{1}$. Then $\left\{x_{1}, y_{1}\right\}=\{5,2\}$ or $\left\{x_{1}, y_{1}\right\}=\{4,3\}$, respectively $\left\{z_{1}, t_{1}\right\}=\{2,0\}$ or $\left\{z_{1}, t_{1}\right\}=\{1,1\}$. Then $\left(a_{1}, b_{1}, c_{1}, d_{1}\right)$ is obtained by permuting one of the following quadruples:
$$
(5,2,2,0),(5,2,1,1),(4,3,2,0),(4,3,1,1)
$$
There are a total of $\frac{4!}{2!}=12$ permutations of $(5,2,2,0)$, also 12 permutations of $(5,2,1,1)$, 24 permutations of $(4,3,2,0)$ and finally, there are 12 permutations of $(4,3,1,1)$. Hence, there are at most 60 different possible total sums.
We can obtain indeed each of these 60 combinations: take three rows ababa alternating
with two rows $c d c d c$ to get $(5,2,2,0)$; take three rows ababa alternating with one row $c d c d c$ and a row $(d c d c d)$ to get $(5,2,1,1)$; take three rows $a b a b c$ alternating with two rows $c d c d a$ to get $(4,3,2,0)$; take three rows abcda alternating with two rows $c d a b c$ to get $(4,3,1,1)$. By choosing for example $a=10^{3}, b=10^{2}, c=10, d=1$, we can make all these sums different. Hence, 60 is indeed the maximum possible number of different sums.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-shortlist_jbmo_2016_v7-1.jsonl",
"problem_match": "\nC3.",
"solution_match": "\nSolution."
}
|
846f6b4a-9eb0-5cfc-bc41-080e9f7dcd60
| 605,234
|
A splitting of a planar polygon is a finite set of triangles whose interiors are pairwise disjoint, and whose union is the polygon in question. Given an integer $n \geq 3$, determine the largest integer $m$ such that no planar $n$-gon splits into less than $m$ triangles.
|
The required maximum is $\lceil n / 3\rceil$, the least integer greater than or equal to $n / 3$. To describe a planar $n$-gon splitting into this many triangles, write $n=3 m-r$, where $m$ is a positive integer and $r=0,1,2$, and consider $m$ coplanar equilateral triangles $A_{3 i} A_{3 i+1} A_{3 i+2}$, $i=0, \ldots, m-1$, where the $A_{i}$ are pairwise distinct, the $A$ 's of rank congruent to 0 or 2 modulo 3 are all collinear, $A_{2}, A_{3}, A_{5}, \ldots, A_{3 m-3}, A_{3 m-1}, A_{0}$, in order, and the line $A_{0} A_{2}$ separates $A_{1}$ from the remaining $A$ 's of rank congruent to 1 modulo 3 . The polygon $A_{0} A_{1} A_{2} A_{3} A_{4} A_{5} \ldots A_{3 m-3} A_{3 m-2} A_{3 m-1}$ settles the case $r=0$; removal of $A_{3}$ from the list settles the case $r=1$; and removal of $A_{3}$ and $A_{3 m-1}$ settles the case $r=2$.
Next, we prove that no planar $n$-gon splits into less than $n / 3$ triangles. Alternatively, but equivalently, if a planar polygon splits into $t$ triangles, then its boundary has (combinatorial) length at most $3 t$. Proceed by induction on $t$. The base case $t=1$ is clear, so let $t>1$.
The vertices of the triangles in the splitting may subdivide the boundary of the polygon, making it into a possibly combinatorially longer simple loop $\Omega$. Clearly, it is sufficient to prove that the length of $\Omega$ does not exceed $3 t$.
To this end, consider a triangle in the splitting whose boundary $\omega$ meets $\Omega$ along at least one of its edges. Trace $\Omega$ counterclockwise and let $\alpha_{1}, \ldots, \alpha_{k}$, in order, be the connected components of $\Omega-\omega$. Each $\alpha_{i}$ is a path along $\Omega$ with distinct end points, whose terminal point is joined to the starting point of $\alpha_{i+1}$ by a (possibly constant) path $\beta_{i}$ along $\omega$. Trace $\omega$ clockwise from the terminal point of $\alpha_{i}$ to its starting point to obtain a path $\alpha_{i}^{\prime}$ of positive length, and notice that $\alpha_{i}+\alpha_{i}^{\prime}$ is the boundary of a polygon split into $t_{i}<t$ triangles. By the induction hypothesis, the length of $\alpha_{i}+\alpha_{i}^{\prime}$ does not exceed $3 t_{i}$, and since $\alpha_{i}^{\prime}$ has positive length, the length of $\alpha_{i}$ is at most $3 t_{i}-1$. Consequently, the length of $\Omega-\omega$ does not exceed $\sum_{i=1}^{k}\left(3 t_{i}-1\right)=3 t-3-k$.
Finally, we prove that the total length of the $\beta_{i}$ does not exceed $k+3$. Begin by noticing that no $\beta_{i}$ has length greater than 4 , at most one has length greater than 2 , and at most three have length 2 . If some $\beta_{i}$ has length 4 , then the remaining $k-1$ are all of length at most 1 , so the total length of the $\beta$ 's does not exceed $4+(k-1)=k+3$. Otherwise, either some $\beta_{i}$ has length 3 , in which case at most one other has length 2 and the remaining $k-2$ all have length at most 1 , or the $\beta_{i}$ all have length less than 3 , in which case there are at most three of length 2 and the remaining $k-3$ all have length at most 1 ; in the former case, the total length of the $\beta$ 's does not exceed $3+2+(k-2)=k+3$, and in the latter, the total length of the $\beta$ 's does not exceed $3 \cdot 2+(k-3)=k+3$. The conclusion follows.
## Chapter 3
## Geometry
|
\lceil n / 3\rceil
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
A splitting of a planar polygon is a finite set of triangles whose interiors are pairwise disjoint, and whose union is the polygon in question. Given an integer $n \geq 3$, determine the largest integer $m$ such that no planar $n$-gon splits into less than $m$ triangles.
|
The required maximum is $\lceil n / 3\rceil$, the least integer greater than or equal to $n / 3$. To describe a planar $n$-gon splitting into this many triangles, write $n=3 m-r$, where $m$ is a positive integer and $r=0,1,2$, and consider $m$ coplanar equilateral triangles $A_{3 i} A_{3 i+1} A_{3 i+2}$, $i=0, \ldots, m-1$, where the $A_{i}$ are pairwise distinct, the $A$ 's of rank congruent to 0 or 2 modulo 3 are all collinear, $A_{2}, A_{3}, A_{5}, \ldots, A_{3 m-3}, A_{3 m-1}, A_{0}$, in order, and the line $A_{0} A_{2}$ separates $A_{1}$ from the remaining $A$ 's of rank congruent to 1 modulo 3 . The polygon $A_{0} A_{1} A_{2} A_{3} A_{4} A_{5} \ldots A_{3 m-3} A_{3 m-2} A_{3 m-1}$ settles the case $r=0$; removal of $A_{3}$ from the list settles the case $r=1$; and removal of $A_{3}$ and $A_{3 m-1}$ settles the case $r=2$.
Next, we prove that no planar $n$-gon splits into less than $n / 3$ triangles. Alternatively, but equivalently, if a planar polygon splits into $t$ triangles, then its boundary has (combinatorial) length at most $3 t$. Proceed by induction on $t$. The base case $t=1$ is clear, so let $t>1$.
The vertices of the triangles in the splitting may subdivide the boundary of the polygon, making it into a possibly combinatorially longer simple loop $\Omega$. Clearly, it is sufficient to prove that the length of $\Omega$ does not exceed $3 t$.
To this end, consider a triangle in the splitting whose boundary $\omega$ meets $\Omega$ along at least one of its edges. Trace $\Omega$ counterclockwise and let $\alpha_{1}, \ldots, \alpha_{k}$, in order, be the connected components of $\Omega-\omega$. Each $\alpha_{i}$ is a path along $\Omega$ with distinct end points, whose terminal point is joined to the starting point of $\alpha_{i+1}$ by a (possibly constant) path $\beta_{i}$ along $\omega$. Trace $\omega$ clockwise from the terminal point of $\alpha_{i}$ to its starting point to obtain a path $\alpha_{i}^{\prime}$ of positive length, and notice that $\alpha_{i}+\alpha_{i}^{\prime}$ is the boundary of a polygon split into $t_{i}<t$ triangles. By the induction hypothesis, the length of $\alpha_{i}+\alpha_{i}^{\prime}$ does not exceed $3 t_{i}$, and since $\alpha_{i}^{\prime}$ has positive length, the length of $\alpha_{i}$ is at most $3 t_{i}-1$. Consequently, the length of $\Omega-\omega$ does not exceed $\sum_{i=1}^{k}\left(3 t_{i}-1\right)=3 t-3-k$.
Finally, we prove that the total length of the $\beta_{i}$ does not exceed $k+3$. Begin by noticing that no $\beta_{i}$ has length greater than 4 , at most one has length greater than 2 , and at most three have length 2 . If some $\beta_{i}$ has length 4 , then the remaining $k-1$ are all of length at most 1 , so the total length of the $\beta$ 's does not exceed $4+(k-1)=k+3$. Otherwise, either some $\beta_{i}$ has length 3 , in which case at most one other has length 2 and the remaining $k-2$ all have length at most 1 , or the $\beta_{i}$ all have length less than 3 , in which case there are at most three of length 2 and the remaining $k-3$ all have length at most 1 ; in the former case, the total length of the $\beta$ 's does not exceed $3+2+(k-2)=k+3$, and in the latter, the total length of the $\beta$ 's does not exceed $3 \cdot 2+(k-3)=k+3$. The conclusion follows.
## Chapter 3
## Geometry
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-shortlist_jbmo_2016_v7-1.jsonl",
"problem_match": "\nC4.",
"solution_match": "\nSolution."
}
|
3d795476-6099-570d-8b89-4eb6841e5da0
| 605,245
|
Determine the largest positive integer $n$ that divides $p^{6}-1$ for all primes $p>7$.
|
Note that
$$
p^{6}-1=(p-1)(p+1)\left(p^{2}-p+1\right)\left(p^{2}+p+1\right)
$$
For $p=11$ we have
$$
p^{6}-1=1771560=2^{3} \cdot 3^{2} \cdot 5 \cdot 7 \cdot 19 \cdot 37
$$
For $p=13$ we have
$$
p^{6}-1=2^{3} \cdot 3^{2} \cdot 7 \cdot 61 \cdot 157
$$
From the last two calculations we find evidence to try showing that $p^{6}-1$ is divisible by $2^{3} \cdot 3^{2} \cdot 7=504$ and this would be the largest positive integer that divides $p^{6}-1$ for all primes greater than 7 .
By Fermat's theorem, $7 \mid p^{6}-1$.
Next, since $p$ is odd, $8 \mid p^{2}-1=(p-1)(p+1)$, hence $8 \mid p^{6}-1$.
It remains to show that $9 \mid p^{6}-1$.
Any prime number $p, p>3$ is 1 or -1 modulo 3 .
In the first case both $p-1$ and $p^{2}+p+1$ are divisible by 3 , and in the second case, both $p+1$ and $p^{2}-p+1$ are divisible by 3 .
Consequently, the required number is indeed 504
## Alternative solution
Let $q$ be a (positive) prime factor of $n$. Then $q \leq 7$, as $q \nmid q^{6}-1$. Also, $q$ is not 5 , as the last digit of $13^{6}-1$ is 8 .
Hence, the prime factors of $n$ are among 2,3 , and 7 .
Next, from $11^{6}-1=2^{3} \cdot 3^{2} \cdot 5 \cdot 7 \cdot 19 \cdot 37$ it follows that the largest integer $n$ such that $n \mid p^{6}-1$ for all primes $p$ greater than 7 is at most $2^{3} \cdot 3^{2} \cdot 7$, and it remains to prove that 504 divides $p^{6}-1$ for all primes grater than 7 .
|
504
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Determine the largest positive integer $n$ that divides $p^{6}-1$ for all primes $p>7$.
|
Note that
$$
p^{6}-1=(p-1)(p+1)\left(p^{2}-p+1\right)\left(p^{2}+p+1\right)
$$
For $p=11$ we have
$$
p^{6}-1=1771560=2^{3} \cdot 3^{2} \cdot 5 \cdot 7 \cdot 19 \cdot 37
$$
For $p=13$ we have
$$
p^{6}-1=2^{3} \cdot 3^{2} \cdot 7 \cdot 61 \cdot 157
$$
From the last two calculations we find evidence to try showing that $p^{6}-1$ is divisible by $2^{3} \cdot 3^{2} \cdot 7=504$ and this would be the largest positive integer that divides $p^{6}-1$ for all primes greater than 7 .
By Fermat's theorem, $7 \mid p^{6}-1$.
Next, since $p$ is odd, $8 \mid p^{2}-1=(p-1)(p+1)$, hence $8 \mid p^{6}-1$.
It remains to show that $9 \mid p^{6}-1$.
Any prime number $p, p>3$ is 1 or -1 modulo 3 .
In the first case both $p-1$ and $p^{2}+p+1$ are divisible by 3 , and in the second case, both $p+1$ and $p^{2}-p+1$ are divisible by 3 .
Consequently, the required number is indeed 504
## Alternative solution
Let $q$ be a (positive) prime factor of $n$. Then $q \leq 7$, as $q \nmid q^{6}-1$. Also, $q$ is not 5 , as the last digit of $13^{6}-1$ is 8 .
Hence, the prime factors of $n$ are among 2,3 , and 7 .
Next, from $11^{6}-1=2^{3} \cdot 3^{2} \cdot 5 \cdot 7 \cdot 19 \cdot 37$ it follows that the largest integer $n$ such that $n \mid p^{6}-1$ for all primes $p$ greater than 7 is at most $2^{3} \cdot 3^{2} \cdot 7$, and it remains to prove that 504 divides $p^{6}-1$ for all primes grater than 7 .
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-shortlist_jbmo_2016_v7-1.jsonl",
"problem_match": "\nN1.",
"solution_match": "\nSolution."
}
|
36ca2008-2d50-5ade-b225-138520e9648a
| 605,331
|
Find the maximum number of natural numbers $x_{1}, x_{2}, \ldots, x_{m}$ satisfying the conditions:
a) No $x_{i}-x_{j}, 1 \leq i<j \leq m$ is divisible by 11 ; and
b) The sum $x_{2} x_{3} \ldots x_{m}+x_{1} x_{3} \ldots x_{m}+\cdots+x_{1} x_{2} \ldots x_{m-1}$ is divisible by 11 .
|
The required maximum is 10 .
According to a), the numbers $x_{i}, 1 \leq i \leq m$, are all different $(\bmod 11)$ (1)
Hence, the number of natural numbers satisfying the conditions is at most 11.
If $x_{j} \equiv 0(\bmod 11)$ for some $j$, then
$$
x_{2} x_{3} \ldots x_{m}+x_{1} x_{3} \ldots x_{m}+\cdots+x_{1} x_{2} \ldots x_{m-1} \equiv x_{1} \ldots x_{j-1} x_{j+1} \ldots x_{m} \quad(\bmod 11)
$$
which would lead to $x_{i} \equiv 0(\bmod 11)$ for some $i \neq j$, contradicting (1).
We now prove that 10 is indeed the required maximum.
Consider $x_{i}=i$, for all $i \in\{1,2, \ldots, 10\}$. The products $2 \cdot 3 \cdots \cdot 10,1 \cdot 3 \cdots \cdots 10, \ldots$, $1 \cdot 2 \cdots \cdot 9$ are all different $(\bmod 11)$, and so
$$
2 \cdot 3 \cdots \cdots 10+1 \cdot 3 \cdots \cdots 10+\cdots+1 \cdot 2 \cdots \cdot 9 \equiv 1+2+\cdots+10 \quad(\bmod 11)
$$
and condition b) is satisfied, since $1+2+\cdots+10=55=5 \cdot 11$.
|
10
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Find the maximum number of natural numbers $x_{1}, x_{2}, \ldots, x_{m}$ satisfying the conditions:
a) No $x_{i}-x_{j}, 1 \leq i<j \leq m$ is divisible by 11 ; and
b) The sum $x_{2} x_{3} \ldots x_{m}+x_{1} x_{3} \ldots x_{m}+\cdots+x_{1} x_{2} \ldots x_{m-1}$ is divisible by 11 .
|
The required maximum is 10 .
According to a), the numbers $x_{i}, 1 \leq i \leq m$, are all different $(\bmod 11)$ (1)
Hence, the number of natural numbers satisfying the conditions is at most 11.
If $x_{j} \equiv 0(\bmod 11)$ for some $j$, then
$$
x_{2} x_{3} \ldots x_{m}+x_{1} x_{3} \ldots x_{m}+\cdots+x_{1} x_{2} \ldots x_{m-1} \equiv x_{1} \ldots x_{j-1} x_{j+1} \ldots x_{m} \quad(\bmod 11)
$$
which would lead to $x_{i} \equiv 0(\bmod 11)$ for some $i \neq j$, contradicting (1).
We now prove that 10 is indeed the required maximum.
Consider $x_{i}=i$, for all $i \in\{1,2, \ldots, 10\}$. The products $2 \cdot 3 \cdots \cdot 10,1 \cdot 3 \cdots \cdots 10, \ldots$, $1 \cdot 2 \cdots \cdot 9$ are all different $(\bmod 11)$, and so
$$
2 \cdot 3 \cdots \cdots 10+1 \cdot 3 \cdots \cdots 10+\cdots+1 \cdot 2 \cdots \cdot 9 \equiv 1+2+\cdots+10 \quad(\bmod 11)
$$
and condition b) is satisfied, since $1+2+\cdots+10=55=5 \cdot 11$.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-shortlist_jbmo_2016_v7-1.jsonl",
"problem_match": "\nN2.",
"solution_match": "\nSolution."
}
|
5e108f20-65e2-5b26-9d9c-606c32f33b5b
| 605,338
|
Determine all four-digit numbers $\overline{a b c d}$ such that
$$
(a+b)(a+c)(a+d)(b+c)(b+d)(c+d)=\overline{a b c d}
$$
|
Depending on the parity of $a, b, c, d$, at least two of the factors $(a+b),(a+c)$, $(a+d),(b+c),(b+d),(c+d)$ are even, so that $4 \mid \overline{a b c d}$.
We claim that $3 \mid \overline{a b c d}$.
Assume $a+b+c+d \equiv 2(\bmod 3)$. Then $x+y \equiv 1(\bmod 3)$, for all distinct $x, y \in\{a, b, c, d\}$. But then the left hand side in the above equality is congruent to $1(\bmod 3)$ and the right hand side congruent to $2(\bmod 3)$, contradiction.
Assume $a+b+c+d \equiv 1(\bmod 3)$. Then $x+y \equiv 2(\bmod 3)$, for all distinct $x, y \in\{a, b, c, d\}$, and $x \equiv 1(\bmod 3)$, for all $x, y \in\{a, b, c, d\}$. Hence, $a, b, c, d \in\{1,4,7\}$, and since $4 \mid \overline{a b c d}$, we have $c=d=4$. Therefore, $8 \mid \overline{a b 44}$, and since at least one more factor is even, it follows that $16 \overline{a b 44}$. Then $b \neq 4$, and the only possibilities are $b=1$, implying $a=4$, which is impossible because 4144 is not divisible by $5=1+4$, or $b=7$, implying $11 \mid \overline{a 744}$, hence $a=7$, which is also impossible because 7744 is not divisible by $14=7+7$.
We conclude that $3 \mid \overline{a b c d}$, hence also $3 \mid a+b+c+d$. Then at least one factor $x+y$ of $(a+b),(a+c),(a+d),(b+c),(b+d),(c+d)$ is a multiple of 3 , implying that also $3 \mid a+b+c+d-x-y$, so $9 \mid \overline{a b c d}$. Then $9 \mid a+b+c+d$, and $a+b+c+d \in\{9,18,27,36\}$. Using the inequality $x y \geq x+y-1$, valid for all $x, y \in \mathbb{N}^{*}$, if $a+b+c+d \in\{27,36\}$, then
$$
\overline{a b c d}=(a+b)(a+c)(a+d)(b+c)(b+d)(c+d) \geq 26^{3}>10^{4}
$$
which is impossible.
Using the inequality $x y \geq 2(x+y)-4$ for all $x, y \geq 2$, if $a+b+c+d=18$ and all two-digit sums are greater than 1 , then $\overline{a b c d} \geq 32^{3}>10^{4}$. Hence, if $a+b+c+d=18$, some two-digit sum must be 1 , hence the complementary sum will be 17 , and the digits are $\{a, b, c, d\}=\{0,1,8,9\}$. But then $\overline{a b c d}=1 \cdot 17 \cdot 8 \cdot 9^{2} \cdot 10>10^{4}$.
We conclude that $a+b+c+d=9$. Then among $a, b, c, d$ there are either three odd or three even numbers, and $8 \mid \overline{a b c d}$.
If three of the digits are odd, then $d$ is even and since $c$ is odd, divisibility by 8 implies that $d \in\{2,6\}$. If $d=6$, then $a=b=c=1$. But 1116 is not divisible by 7 , so this is not a solution. If $d=2$, then $a, b, c$ are either $1,1,5$ or $1,3,3$ in some order. In the first case $2 \cdot 6^{2} \cdot 3^{2} \cdot 7=4536 \neq \overline{a b c d}$. The second case cannot hold because the resulting number is not a multiple of 5 .
Hence, there has to be one odd and three even digits. At least one of the two-digits sums of even digits is a multiple of 4 , and since there cannot be two zero digits, we have either $x+y=4$ and $z+t=5$, or $x+y=8$ and $z+t=1$ for some ordering $x, y, z, t$ of $a, b, c, d$. In the first case we have $d=0$ and the digits are $0,1,4,4$, or $0,2,3,4$, or $0,2,2,5$. None of these is a solution because $1 \cdot 4^{2} \cdot 5^{2} \cdot 8=3200,2 \cdot 3 \cdot 4 \cdot 5 \cdot 6 \cdot 7=5040$ and $2^{2} \cdot 5 \cdot 4 \cdot 7^{2}=3920$. In the second case two of the digits are 0 and 1 , and the other two have to be either 4 and 4 , or 2 and 6 . We already know that the first possibility fails. For the second, we get
$$
(0+1) \cdot(0+2) \cdot(0+6) \cdot(1+2) \cdot(1+6) \cdot(2+6)=2016
$$
and $\overline{a b c d}=2016$ is the only solution.
|
2016
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Determine all four-digit numbers $\overline{a b c d}$ such that
$$
(a+b)(a+c)(a+d)(b+c)(b+d)(c+d)=\overline{a b c d}
$$
|
Depending on the parity of $a, b, c, d$, at least two of the factors $(a+b),(a+c)$, $(a+d),(b+c),(b+d),(c+d)$ are even, so that $4 \mid \overline{a b c d}$.
We claim that $3 \mid \overline{a b c d}$.
Assume $a+b+c+d \equiv 2(\bmod 3)$. Then $x+y \equiv 1(\bmod 3)$, for all distinct $x, y \in\{a, b, c, d\}$. But then the left hand side in the above equality is congruent to $1(\bmod 3)$ and the right hand side congruent to $2(\bmod 3)$, contradiction.
Assume $a+b+c+d \equiv 1(\bmod 3)$. Then $x+y \equiv 2(\bmod 3)$, for all distinct $x, y \in\{a, b, c, d\}$, and $x \equiv 1(\bmod 3)$, for all $x, y \in\{a, b, c, d\}$. Hence, $a, b, c, d \in\{1,4,7\}$, and since $4 \mid \overline{a b c d}$, we have $c=d=4$. Therefore, $8 \mid \overline{a b 44}$, and since at least one more factor is even, it follows that $16 \overline{a b 44}$. Then $b \neq 4$, and the only possibilities are $b=1$, implying $a=4$, which is impossible because 4144 is not divisible by $5=1+4$, or $b=7$, implying $11 \mid \overline{a 744}$, hence $a=7$, which is also impossible because 7744 is not divisible by $14=7+7$.
We conclude that $3 \mid \overline{a b c d}$, hence also $3 \mid a+b+c+d$. Then at least one factor $x+y$ of $(a+b),(a+c),(a+d),(b+c),(b+d),(c+d)$ is a multiple of 3 , implying that also $3 \mid a+b+c+d-x-y$, so $9 \mid \overline{a b c d}$. Then $9 \mid a+b+c+d$, and $a+b+c+d \in\{9,18,27,36\}$. Using the inequality $x y \geq x+y-1$, valid for all $x, y \in \mathbb{N}^{*}$, if $a+b+c+d \in\{27,36\}$, then
$$
\overline{a b c d}=(a+b)(a+c)(a+d)(b+c)(b+d)(c+d) \geq 26^{3}>10^{4}
$$
which is impossible.
Using the inequality $x y \geq 2(x+y)-4$ for all $x, y \geq 2$, if $a+b+c+d=18$ and all two-digit sums are greater than 1 , then $\overline{a b c d} \geq 32^{3}>10^{4}$. Hence, if $a+b+c+d=18$, some two-digit sum must be 1 , hence the complementary sum will be 17 , and the digits are $\{a, b, c, d\}=\{0,1,8,9\}$. But then $\overline{a b c d}=1 \cdot 17 \cdot 8 \cdot 9^{2} \cdot 10>10^{4}$.
We conclude that $a+b+c+d=9$. Then among $a, b, c, d$ there are either three odd or three even numbers, and $8 \mid \overline{a b c d}$.
If three of the digits are odd, then $d$ is even and since $c$ is odd, divisibility by 8 implies that $d \in\{2,6\}$. If $d=6$, then $a=b=c=1$. But 1116 is not divisible by 7 , so this is not a solution. If $d=2$, then $a, b, c$ are either $1,1,5$ or $1,3,3$ in some order. In the first case $2 \cdot 6^{2} \cdot 3^{2} \cdot 7=4536 \neq \overline{a b c d}$. The second case cannot hold because the resulting number is not a multiple of 5 .
Hence, there has to be one odd and three even digits. At least one of the two-digits sums of even digits is a multiple of 4 , and since there cannot be two zero digits, we have either $x+y=4$ and $z+t=5$, or $x+y=8$ and $z+t=1$ for some ordering $x, y, z, t$ of $a, b, c, d$. In the first case we have $d=0$ and the digits are $0,1,4,4$, or $0,2,3,4$, or $0,2,2,5$. None of these is a solution because $1 \cdot 4^{2} \cdot 5^{2} \cdot 8=3200,2 \cdot 3 \cdot 4 \cdot 5 \cdot 6 \cdot 7=5040$ and $2^{2} \cdot 5 \cdot 4 \cdot 7^{2}=3920$. In the second case two of the digits are 0 and 1 , and the other two have to be either 4 and 4 , or 2 and 6 . We already know that the first possibility fails. For the second, we get
$$
(0+1) \cdot(0+2) \cdot(0+6) \cdot(1+2) \cdot(1+6) \cdot(2+6)=2016
$$
and $\overline{a b c d}=2016$ is the only solution.
|
{
"resource_path": "JBMO/segmented/en-shortlist/en-shortlist_jbmo_2016_v7-1.jsonl",
"problem_match": "\nN5.",
"solution_match": "\nSolution."
}
|
57ca1898-4b26-5151-ade2-f08b8db5e037
| 605,369
|
Let $f$ be a strictly increasing function defined in the set of natural numbers satisfying the conditions $f(2)=a>2$ and $f(m n)=f(m) f(n)$ for all natural numbers $m$ and $n$. Determine the smallest possible value of $a$.
|
Since $f(n)=n^{2}$ is a function satisfying the conditions of the problem, the smallest posiible $a$ is at most 4. Assume $a=3$. It is easy to prove by induction that $f\left(n^{k}\right)=f(n)^{k}$ for all $k \geq 1$. So, taking into account that $f$ is strictly increasing, we get
$$
\begin{gathered}
f(3)^{4}=f\left(3^{4}\right)=f(81)>f(64)=f\left(2^{6}\right)=f(2)^{6} \\
=3^{6}=27^{2}>25^{2}=5^{4}
\end{gathered}
$$
as well as
$$
\begin{aligned}
& f(3)^{8}=f\left(3^{8}\right)=f(6561)<f(8192) \\
& \quad=f\left(2^{13}\right)=f(2)^{13}=3^{13}<6^{8}
\end{aligned}
$$
So we arrive at $5<f(3)<6$. But this is not possible, since $f(3)$ is an integer. So $a=4$.
|
4
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Let $f$ be a strictly increasing function defined in the set of natural numbers satisfying the conditions $f(2)=a>2$ and $f(m n)=f(m) f(n)$ for all natural numbers $m$ and $n$. Determine the smallest possible value of $a$.
|
Since $f(n)=n^{2}$ is a function satisfying the conditions of the problem, the smallest posiible $a$ is at most 4. Assume $a=3$. It is easy to prove by induction that $f\left(n^{k}\right)=f(n)^{k}$ for all $k \geq 1$. So, taking into account that $f$ is strictly increasing, we get
$$
\begin{gathered}
f(3)^{4}=f\left(3^{4}\right)=f(81)>f(64)=f\left(2^{6}\right)=f(2)^{6} \\
=3^{6}=27^{2}>25^{2}=5^{4}
\end{gathered}
$$
as well as
$$
\begin{aligned}
& f(3)^{8}=f\left(3^{8}\right)=f(6561)<f(8192) \\
& \quad=f\left(2^{13}\right)=f(2)^{13}=3^{13}<6^{8}
\end{aligned}
$$
So we arrive at $5<f(3)<6$. But this is not possible, since $f(3)$ is an integer. So $a=4$.
|
{
"resource_path": "Nordic_MO/segmented/en-1987-2011-sol.jsonl",
"problem_match": "\n87.3. ",
"solution_match": "\nSolution. "
}
|
2c63a937-3e25-5a6c-acda-fd84a5ceccf8
| 607,922
|
The positive integer $n$ has the following property: if the three last digits of $n$ are removed, the number $\sqrt[3]{n}$ remains. Find $n$.
|
If $x=\sqrt[3]{n}$, and $y, 0 \leq y<1000$, is the number formed by the three last digits of $n$, we have
$$
x^{3}=1000 x+y
$$
So $x^{3} \geq 1000 x, x^{2}>1000$, and $x>31$. On the other hand, $x^{3}<1000 x+1000$, or $x\left(x^{2}-1000\right)<1000$. The left hand side of this inequality is an increasing function of $x$, and $x=33$ does not satisfy the inequality. So $x<33$. Since $x$ is an integer, $x=32$ and $n=32^{3}=32768$.
|
32768
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
The positive integer $n$ has the following property: if the three last digits of $n$ are removed, the number $\sqrt[3]{n}$ remains. Find $n$.
|
If $x=\sqrt[3]{n}$, and $y, 0 \leq y<1000$, is the number formed by the three last digits of $n$, we have
$$
x^{3}=1000 x+y
$$
So $x^{3} \geq 1000 x, x^{2}>1000$, and $x>31$. On the other hand, $x^{3}<1000 x+1000$, or $x\left(x^{2}-1000\right)<1000$. The left hand side of this inequality is an increasing function of $x$, and $x=33$ does not satisfy the inequality. So $x<33$. Since $x$ is an integer, $x=32$ and $n=32^{3}=32768$.
|
{
"resource_path": "Nordic_MO/segmented/en-1987-2011-sol.jsonl",
"problem_match": "\n88.1. ",
"solution_match": "\nSolution. "
}
|
edebe7f1-e636-5d56-962d-78ace5d71ca7
| 607,924
|
Determine the last two digits of the number
$$
2^{5}+2^{5^{2}}+2^{5^{3}}+\cdots+2^{5^{1991}}
$$
written in decimal notation.
|
We first show that all numbers $2^{5^{k}}$ are of the form $100 p+32$. This can be shown by induction. The case $k=1$ is clear $\left(2^{5}=32\right)$. Assume $2^{5^{k}}=100 p+32$. Then, by the binomial formula,
$$
2^{5^{k+1}}=\left(2^{5^{k}}\right)^{5}=(100 p+32)^{5}=100 q+32^{5}
$$
and
$$
\begin{gathered}
(30+2)^{5}=30^{5}+5 \cdot 30^{4} \cdot 2+10 \cdot 30^{3} \cdot 4+10 \cdot 30^{2} \cdot 8+5 \cdot 30 \cdot 16+32 \\
=100 r+32
\end{gathered}
$$
So the last two digits of the sum in the problem are the same as the last digits of the number $1991 \cdot 32$, or 12 .
|
12
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Determine the last two digits of the number
$$
2^{5}+2^{5^{2}}+2^{5^{3}}+\cdots+2^{5^{1991}}
$$
written in decimal notation.
|
We first show that all numbers $2^{5^{k}}$ are of the form $100 p+32$. This can be shown by induction. The case $k=1$ is clear $\left(2^{5}=32\right)$. Assume $2^{5^{k}}=100 p+32$. Then, by the binomial formula,
$$
2^{5^{k+1}}=\left(2^{5^{k}}\right)^{5}=(100 p+32)^{5}=100 q+32^{5}
$$
and
$$
\begin{gathered}
(30+2)^{5}=30^{5}+5 \cdot 30^{4} \cdot 2+10 \cdot 30^{3} \cdot 4+10 \cdot 30^{2} \cdot 8+5 \cdot 30 \cdot 16+32 \\
=100 r+32
\end{gathered}
$$
So the last two digits of the sum in the problem are the same as the last digits of the number $1991 \cdot 32$, or 12 .
|
{
"resource_path": "Nordic_MO/segmented/en-1987-2011-sol.jsonl",
"problem_match": "\n91.1. ",
"solution_match": "\nSolution. "
}
|
4c703fa2-551b-5de5-b25a-856309fa7381
| 607,933
|
Peter has many squares of equal side. Some of the squares are black, some are white. Peter wants to assemble a big square, with side equal to $n$ sides of the small squares, so that the big square has no rectangle formed by the small squares such that all the squares in the vertices of the rectangle are of equal colour. How big a square is Peter able to assemble?
|
We show that Peter only can make a $4 \times 4$ square. The construction is possible, if $n=4$ :

Now consider the case $n=5$. We may assume that at least 13 of the 25 squares are black. If five black squares are on one horizontal row, the remaining eight ones are distributed on the other four rows. At least one row has two black squres. A rectangle with all corners black is created. Next assume that one row has four black squares. Of the remaing 9 squares, at least three are one row. At least two of these three have to be columns having the assumed four black squares. If no row has more than four black squares, there have to be at least three rows with exactly three black squares. Denote these rows by $A, B$, and $C$. Let us call the columns in which the black squares on row $A$ lie black columns, and the other two columns white columns. If either row $B$ or row $C$ has at least two black squares which are on black columns, a rectancle with black corners arises. If both rows $B$ and $C$ have only one black square on the black columns, then both of them have two black squares on the two white columns, and they make the black corners of a rectangle. So Peter cannot make a $5 \times 5$ square in the way he wishes.
|
4
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Peter has many squares of equal side. Some of the squares are black, some are white. Peter wants to assemble a big square, with side equal to $n$ sides of the small squares, so that the big square has no rectangle formed by the small squares such that all the squares in the vertices of the rectangle are of equal colour. How big a square is Peter able to assemble?
|
We show that Peter only can make a $4 \times 4$ square. The construction is possible, if $n=4$ :

Now consider the case $n=5$. We may assume that at least 13 of the 25 squares are black. If five black squares are on one horizontal row, the remaining eight ones are distributed on the other four rows. At least one row has two black squres. A rectangle with all corners black is created. Next assume that one row has four black squares. Of the remaing 9 squares, at least three are one row. At least two of these three have to be columns having the assumed four black squares. If no row has more than four black squares, there have to be at least three rows with exactly three black squares. Denote these rows by $A, B$, and $C$. Let us call the columns in which the black squares on row $A$ lie black columns, and the other two columns white columns. If either row $B$ or row $C$ has at least two black squares which are on black columns, a rectancle with black corners arises. If both rows $B$ and $C$ have only one black square on the black columns, then both of them have two black squares on the two white columns, and they make the black corners of a rectangle. So Peter cannot make a $5 \times 5$ square in the way he wishes.
|
{
"resource_path": "Nordic_MO/segmented/en-1987-2011-sol.jsonl",
"problem_match": "\n92.4. ",
"solution_match": "\nSolution. "
}
|
2c204676-9dce-5b93-b72d-a099c12091a8
| 607,939
|
Messages are coded using sequences consisting of zeroes and ones only. Only sequences with at most two consecutive ones or zeroes are allowed. (For instance the sequence 011001 is allowed, but 011101 is not.) Determine the number of sequences consisting of exactly 12 numbers.
|
Let $S_{n}$ be the set of acceptable sequences consisting of $2 n$ digits. We partition $S_{n}$ in subsets $A_{n}, B_{n}, C_{n}$, and $D_{n}$, on the basis of the two last digits of the sequence. Sequences ending in 00 are in $A_{n}$, those ending in 01 are in $B_{n}$, those ending in 10 are in $C_{n}$, and those ending in 11 are in $D_{n}$. Denote by $x_{n}, a_{n}, b_{n}, c_{n}$, and $d_{n}$ the number of elements in $S_{n}, A_{n}, B_{n}, C_{n}$, and $D_{n}$. We compute $x_{6}$. Because $S_{1}=\{00,01,10,11\}$, $x_{1}=4$ and $a_{1}=b_{1}=c_{1}=d_{1}=1$. Every element of $A_{n+1}$ can be obtained in a unique manner from an element of $B_{n}$ or $D_{n}$ by adjoining 00 to the end. So $a_{n+1}=b_{n}+d_{n}$. The elements of $B_{n+1}$ are similarly obtained from elements of $B_{n}, C_{n}$, and $D_{n}$ by adjoining 01 to the end. So $b_{n+1}=b_{n}+c_{n}+d_{n}$. In a similar manner we obtain the recursion formulas $c_{n+1}=a_{n}+b_{n}+c_{n}$ and $d_{n+1}=a_{n}+c_{n}$. So $a_{n+1}+d_{n+1}=\left(b_{n}+d_{n}\right)+\left(a_{n}+c_{n}\right)=x_{n}$ and $x_{n+1}=2 a_{n}+3 b_{n}+3 c_{n}+2 d_{n}=3 x_{n}-\left(a_{n}+b_{n}\right)=3 x_{n}-x_{n-1}$. Starting from the initial values $a_{1}=b_{1}=c_{1}=d_{1}=1$, we obtain $a_{2}=d_{2}=2, b_{2}=c_{2}=3$, and $x_{2}=10$. So $x_{3}=3 x_{2}-x_{1}=3 \cdot 10-4=26, x_{4}=3 \cdot 26-10=68, x_{5}=3 \cdot 68-26=178$, and $x_{6}=3 \cdot 178-68=466$.
|
466
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Messages are coded using sequences consisting of zeroes and ones only. Only sequences with at most two consecutive ones or zeroes are allowed. (For instance the sequence 011001 is allowed, but 011101 is not.) Determine the number of sequences consisting of exactly 12 numbers.
|
Let $S_{n}$ be the set of acceptable sequences consisting of $2 n$ digits. We partition $S_{n}$ in subsets $A_{n}, B_{n}, C_{n}$, and $D_{n}$, on the basis of the two last digits of the sequence. Sequences ending in 00 are in $A_{n}$, those ending in 01 are in $B_{n}$, those ending in 10 are in $C_{n}$, and those ending in 11 are in $D_{n}$. Denote by $x_{n}, a_{n}, b_{n}, c_{n}$, and $d_{n}$ the number of elements in $S_{n}, A_{n}, B_{n}, C_{n}$, and $D_{n}$. We compute $x_{6}$. Because $S_{1}=\{00,01,10,11\}$, $x_{1}=4$ and $a_{1}=b_{1}=c_{1}=d_{1}=1$. Every element of $A_{n+1}$ can be obtained in a unique manner from an element of $B_{n}$ or $D_{n}$ by adjoining 00 to the end. So $a_{n+1}=b_{n}+d_{n}$. The elements of $B_{n+1}$ are similarly obtained from elements of $B_{n}, C_{n}$, and $D_{n}$ by adjoining 01 to the end. So $b_{n+1}=b_{n}+c_{n}+d_{n}$. In a similar manner we obtain the recursion formulas $c_{n+1}=a_{n}+b_{n}+c_{n}$ and $d_{n+1}=a_{n}+c_{n}$. So $a_{n+1}+d_{n+1}=\left(b_{n}+d_{n}\right)+\left(a_{n}+c_{n}\right)=x_{n}$ and $x_{n+1}=2 a_{n}+3 b_{n}+3 c_{n}+2 d_{n}=3 x_{n}-\left(a_{n}+b_{n}\right)=3 x_{n}-x_{n-1}$. Starting from the initial values $a_{1}=b_{1}=c_{1}=d_{1}=1$, we obtain $a_{2}=d_{2}=2, b_{2}=c_{2}=3$, and $x_{2}=10$. So $x_{3}=3 x_{2}-x_{1}=3 \cdot 10-4=26, x_{4}=3 \cdot 26-10=68, x_{5}=3 \cdot 68-26=178$, and $x_{6}=3 \cdot 178-68=466$.
|
{
"resource_path": "Nordic_MO/segmented/en-1987-2011-sol.jsonl",
"problem_match": "\n95.2. ",
"solution_match": "\nSolution 1. "
}
|
284c774a-8739-506e-97b6-a24e9660afcb
| 607,949
|
Let A be a set of seven positive numbers. Determine the maximal number of triples $(x, y, z)$ of elements of A satisfying $x<y$ and $x+y=z$.
|
Let $0<a_{1}<a_{2}<\ldots<a_{7}$ be the elements of the set $A$. If $\left(a_{i}, a_{j}, a_{k}\right)$ is a triple of the kind required in the problem, then $a_{i}<a_{j}<a_{i}+a_{j}=a_{k}$. There are at most $k-1$ pairs $\left(a_{i}, a_{j}\right)$ such that $a_{i}+a_{j}=a_{k}$. The number of pairs satisfying $a_{i}<a_{j}$ is at most $\left\lfloor\frac{k-1}{2}\right\rfloor$. The total number of pairs is at most
$$
\sum_{k=3}^{7}\left\lfloor\frac{k-1}{2}\right\rfloor=1+1+2+2+3=9
$$
The value 9 can be reached, if $A=\{1,2, \ldots, 7\}$. In this case the triples $(1,2,3),(1,3,4)$, $(1,4,5),(1,5,6),(1,6,7),(2,3,5),(2,4,6),(2,5,7)$, and $(3,4,7)$ satisfy the conditions of the problem.
|
9
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Let A be a set of seven positive numbers. Determine the maximal number of triples $(x, y, z)$ of elements of A satisfying $x<y$ and $x+y=z$.
|
Let $0<a_{1}<a_{2}<\ldots<a_{7}$ be the elements of the set $A$. If $\left(a_{i}, a_{j}, a_{k}\right)$ is a triple of the kind required in the problem, then $a_{i}<a_{j}<a_{i}+a_{j}=a_{k}$. There are at most $k-1$ pairs $\left(a_{i}, a_{j}\right)$ such that $a_{i}+a_{j}=a_{k}$. The number of pairs satisfying $a_{i}<a_{j}$ is at most $\left\lfloor\frac{k-1}{2}\right\rfloor$. The total number of pairs is at most
$$
\sum_{k=3}^{7}\left\lfloor\frac{k-1}{2}\right\rfloor=1+1+2+2+3=9
$$
The value 9 can be reached, if $A=\{1,2, \ldots, 7\}$. In this case the triples $(1,2,3),(1,3,4)$, $(1,4,5),(1,5,6),(1,6,7),(2,3,5),(2,4,6),(2,5,7)$, and $(3,4,7)$ satisfy the conditions of the problem.
|
{
"resource_path": "Nordic_MO/segmented/en-1987-2011-sol.jsonl",
"problem_match": "\n97.1. ",
"solution_match": "\nSolution. "
}
|
62b4052b-08a9-5149-9b70-903b59bd2481
| 607,956
|
Let $A, B, C$, and $D$ be four different points in the plane. Three of the line segments $A B, A C, A D, B C, B D$, and $C D$ have length a. The other three have length $b$, where $b>a$. Determine all possible values of the quotient $\frac{b}{a}$.
|
If the three segments of length $a$ share a common endpoint, say $A$, then the other three points are on a circle of radius $a$, centered at $A$, and they are the vertices of an equilateral triangle of side length $b$. But this means that $A$ is the center of the triangle $B C D$, and
$$
\frac{b}{a}=\frac{b}{\frac{2}{3} \frac{\sqrt{3}}{2} b}=\sqrt{3}
$$
Assume then that of the segments emanating from $A$ at least one has lenght $a$ and at least one has length $b$. We may assume $A B=a$ and $A D=b$. If only one segment of length $a$ would emanate from each of the four poits, then the number of segments of length $a$ would be two, as every segment is counted twice when we count the emanating segments. So we may assume that $A C$ has length $a$, too. If $B C=a$, then $A B C$ would be an equilateral triangle, and the distance of $D$ from each of its vertices would be $b$. This is not possible, since $b>a$. So $B C=b$. Of the segments $C D$ and $B D$ one has length $a$. We may assume $D C=a$. The segments $D C$ and $A B$ are either on one side of thye line $A C$ or on opposite sides of it. In the latter case, $A B C D$ is a parallelogram with a pair of sides of length $a$ and a pair of sides of length $b$, and its diagonals have lengths $a$ and $b$. This is not possible, due to the fact that the sum of the squares of the diagonals of the parallelogram, $a^{2}+b^{2}$, would be equal to the sum of the squares of its sides, i.e. $2 a^{2}+2 b^{2}$. This means that we may assume that $B A C D$ is a convex quadrilateral. Let $\angle A B C=\alpha$ and $\angle A D B=\beta$. From isosceles triangles we obtain for instance $\angle C B D=\beta$, and from the triangle $A B D$ in particular $2 \alpha+2 \beta+\beta=\pi$ as well as $\angle C D A=\alpha, \angle D C B=\frac{1}{2}(\pi-\beta), \angle C A D=\alpha$. The triangle $A D C$ thus yields $\alpha+\alpha+\alpha+\frac{1}{2}(\pi-\beta)=\pi$. From this we solve $\alpha=\frac{1}{5} \pi=36^{\circ}$. The sine theorem applied to $A B C$ gives
$$
\frac{b}{a}=\frac{\sin 108^{\circ}}{\sin 36^{\circ}}=\frac{\sin 72^{\circ}}{\sin 36^{\circ}}=2 \cos 36^{\circ}=\frac{\sqrt{5}+1}{2}
$$
(In fact, $a$ is the side of a regular pentagon, and $b$ is its diagonal.) - Another way of finding the ratio $\frac{b}{a}$ is to consider the trapezium $C D B A$, with $C D \| A B$; if $E$ is the orthogonal projection of $B$ on the segment $C D$, then $C E=b-\frac{1}{2}(b-a)=\frac{1}{2}(b+a)$. The right triangles $B C E$ and $D C E$ yield $C E^{2}=b^{2}-\left(\frac{b+a}{2}\right)^{2}=a^{2}-\left(\frac{b-a}{2}\right)^{2}$, which can be written as $b^{2}-a b-a^{2}=0$. From this we solve $\frac{b}{a}=\frac{\sqrt{5}+1}{2}$.
|
\frac{\sqrt{5}+1}{2}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $A, B, C$, and $D$ be four different points in the plane. Three of the line segments $A B, A C, A D, B C, B D$, and $C D$ have length a. The other three have length $b$, where $b>a$. Determine all possible values of the quotient $\frac{b}{a}$.
|
If the three segments of length $a$ share a common endpoint, say $A$, then the other three points are on a circle of radius $a$, centered at $A$, and they are the vertices of an equilateral triangle of side length $b$. But this means that $A$ is the center of the triangle $B C D$, and
$$
\frac{b}{a}=\frac{b}{\frac{2}{3} \frac{\sqrt{3}}{2} b}=\sqrt{3}
$$
Assume then that of the segments emanating from $A$ at least one has lenght $a$ and at least one has length $b$. We may assume $A B=a$ and $A D=b$. If only one segment of length $a$ would emanate from each of the four poits, then the number of segments of length $a$ would be two, as every segment is counted twice when we count the emanating segments. So we may assume that $A C$ has length $a$, too. If $B C=a$, then $A B C$ would be an equilateral triangle, and the distance of $D$ from each of its vertices would be $b$. This is not possible, since $b>a$. So $B C=b$. Of the segments $C D$ and $B D$ one has length $a$. We may assume $D C=a$. The segments $D C$ and $A B$ are either on one side of thye line $A C$ or on opposite sides of it. In the latter case, $A B C D$ is a parallelogram with a pair of sides of length $a$ and a pair of sides of length $b$, and its diagonals have lengths $a$ and $b$. This is not possible, due to the fact that the sum of the squares of the diagonals of the parallelogram, $a^{2}+b^{2}$, would be equal to the sum of the squares of its sides, i.e. $2 a^{2}+2 b^{2}$. This means that we may assume that $B A C D$ is a convex quadrilateral. Let $\angle A B C=\alpha$ and $\angle A D B=\beta$. From isosceles triangles we obtain for instance $\angle C B D=\beta$, and from the triangle $A B D$ in particular $2 \alpha+2 \beta+\beta=\pi$ as well as $\angle C D A=\alpha, \angle D C B=\frac{1}{2}(\pi-\beta), \angle C A D=\alpha$. The triangle $A D C$ thus yields $\alpha+\alpha+\alpha+\frac{1}{2}(\pi-\beta)=\pi$. From this we solve $\alpha=\frac{1}{5} \pi=36^{\circ}$. The sine theorem applied to $A B C$ gives
$$
\frac{b}{a}=\frac{\sin 108^{\circ}}{\sin 36^{\circ}}=\frac{\sin 72^{\circ}}{\sin 36^{\circ}}=2 \cos 36^{\circ}=\frac{\sqrt{5}+1}{2}
$$
(In fact, $a$ is the side of a regular pentagon, and $b$ is its diagonal.) - Another way of finding the ratio $\frac{b}{a}$ is to consider the trapezium $C D B A$, with $C D \| A B$; if $E$ is the orthogonal projection of $B$ on the segment $C D$, then $C E=b-\frac{1}{2}(b-a)=\frac{1}{2}(b+a)$. The right triangles $B C E$ and $D C E$ yield $C E^{2}=b^{2}-\left(\frac{b+a}{2}\right)^{2}=a^{2}-\left(\frac{b-a}{2}\right)^{2}$, which can be written as $b^{2}-a b-a^{2}=0$. From this we solve $\frac{b}{a}=\frac{\sqrt{5}+1}{2}$.
|
{
"resource_path": "Nordic_MO/segmented/en-1987-2011-sol.jsonl",
"problem_match": "\n97.3. ",
"solution_match": "\nSolution. "
}
|
acc009a9-ba39-5fb1-8848-c51a60bd50d5
| 607,958
|
Consider 7-gons inscribed in a circle such that all sides of the 7-gon are of different length. Determine the maximal number of $120^{\circ}$ angles in this kind of a 7-gon.
|
It is easy to give examples of heptagons $A B C D E F G$ inscribed in a circle with all sides unequal and two angles equal to $120^{\circ}$. These angles cannot lie on adjacent vertices of the heptagon. In fact, if $\angle A B C=\angle B C D=120^{\circ}$, and arc $B C$ equals $b^{\circ}$, then arcs $A B$ and $C D$ both are $120^{\circ}-b^{\circ}$ (compute angles in isosceles triangles with center of the circle as the to vertex), and $A B=C D$, contrary to the assumption. So if the heptagon has three angles of $120^{\circ}$, their vertices are, say $A, C$, and $E$. Then each of the arcs $G A B, B C D$, $D E F$ are $360^{\circ}-240^{\circ}=120^{\circ}$. The arcs are disjoint, so they cover the whole circumference. The $F$ has to coincide with $G$, and the heptagon degenerates to a hexagon. There can be at most two $120^{\circ}$ angles.
|
2
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Consider 7-gons inscribed in a circle such that all sides of the 7-gon are of different length. Determine the maximal number of $120^{\circ}$ angles in this kind of a 7-gon.
|
It is easy to give examples of heptagons $A B C D E F G$ inscribed in a circle with all sides unequal and two angles equal to $120^{\circ}$. These angles cannot lie on adjacent vertices of the heptagon. In fact, if $\angle A B C=\angle B C D=120^{\circ}$, and arc $B C$ equals $b^{\circ}$, then arcs $A B$ and $C D$ both are $120^{\circ}-b^{\circ}$ (compute angles in isosceles triangles with center of the circle as the to vertex), and $A B=C D$, contrary to the assumption. So if the heptagon has three angles of $120^{\circ}$, their vertices are, say $A, C$, and $E$. Then each of the arcs $G A B, B C D$, $D E F$ are $360^{\circ}-240^{\circ}=120^{\circ}$. The arcs are disjoint, so they cover the whole circumference. The $F$ has to coincide with $G$, and the heptagon degenerates to a hexagon. There can be at most two $120^{\circ}$ angles.
|
{
"resource_path": "Nordic_MO/segmented/en-1987-2011-sol.jsonl",
"problem_match": "\n99.2. ",
"solution_match": "\nSolution. "
}
|
57bf2eff-c4a3-56cb-80a7-66c18e1056d8
| 607,965
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.