problem
stringlengths 14
7.96k
| solution
stringlengths 3
10k
| answer
stringlengths 1
91
| problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | question_type
stringclasses 1
value | problem_type
stringclasses 8
values | problem_raw
stringlengths 14
7.96k
| solution_raw
stringlengths 3
10k
| metadata
dict | uuid
stringlengths 36
36
| id
int64 22.6k
612k
|
|---|---|---|---|---|---|---|---|---|---|---|---|
The vertices of a regular hexagon are labeled $\cos (\theta), \cos (2 \theta), \ldots, \cos (6 \theta)$. For every pair of vertices, Bob draws a blue line through the vertices if one of these functions can be expressed as a polynomial function of the other (that holds for all real $\theta$ ), and otherwise Roberta draws a red line through the
vertices. In the resulting graph, how many triangles whose vertices lie on the hexagon have at least one red and at least one blue edge?
|
14 Solution: The existence of the Chebyshev polynomials, which express $\cos (n \theta)$ as a polynomial in $\cos (\theta)$, imply that Bob draws a blue line between $\cos (\theta)$ and each other vertex, and also between $\cos (2 \theta)$ and $\cos (4 \theta)$, between $\cos (2 \theta)$ and $\cos (6 \theta)$, and between $\cos (3 \theta)$ and $\cos (6 \theta)$ (by substituting $\theta^{\prime}=2 \theta$ or $3 \theta$ as necessary). We now show that Roberta draws a red line through each other pair of vertices.
Let $m$ and $n$ be positive integers. Notice that $\cos (n \theta)$ is a periodic function with period $\frac{2 \pi}{n}$, and $\cos (m \theta)$ is periodic with period $\frac{2 \pi}{m}$. Thus, any polynomial in $\cos (m \theta)$ is also periodic of period $\frac{2 \pi}{m}$. This may not be the minimum period of the polynomial, however, so the minimum period is $\frac{2 \pi}{m k}$ for some $k$. Therefore, if $\cos (n \theta)$ can be expressed as a polynomial in $\cos (m \theta)$ then $\frac{2 \pi}{n}=\frac{2 \pi}{m k}$ for some $k$, so $m \mid n$. This shows that there is a blue line between two vertices $\cos (a \theta)$ and $\cos (b \theta)$ if and only if one of $a$ or $b$ divides the other.
Drawing the graph, one can easily count that there are 3 triangles with all blue edges, 3 triangles with all red edges, and $\binom{6}{3}=20$ triangles total. Thus there are $20-3-3=14$ triangles having at least one red and at least one blue edge.
|
14
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
The vertices of a regular hexagon are labeled $\cos (\theta), \cos (2 \theta), \ldots, \cos (6 \theta)$. For every pair of vertices, Bob draws a blue line through the vertices if one of these functions can be expressed as a polynomial function of the other (that holds for all real $\theta$ ), and otherwise Roberta draws a red line through the
vertices. In the resulting graph, how many triangles whose vertices lie on the hexagon have at least one red and at least one blue edge?
|
14 Solution: The existence of the Chebyshev polynomials, which express $\cos (n \theta)$ as a polynomial in $\cos (\theta)$, imply that Bob draws a blue line between $\cos (\theta)$ and each other vertex, and also between $\cos (2 \theta)$ and $\cos (4 \theta)$, between $\cos (2 \theta)$ and $\cos (6 \theta)$, and between $\cos (3 \theta)$ and $\cos (6 \theta)$ (by substituting $\theta^{\prime}=2 \theta$ or $3 \theta$ as necessary). We now show that Roberta draws a red line through each other pair of vertices.
Let $m$ and $n$ be positive integers. Notice that $\cos (n \theta)$ is a periodic function with period $\frac{2 \pi}{n}$, and $\cos (m \theta)$ is periodic with period $\frac{2 \pi}{m}$. Thus, any polynomial in $\cos (m \theta)$ is also periodic of period $\frac{2 \pi}{m}$. This may not be the minimum period of the polynomial, however, so the minimum period is $\frac{2 \pi}{m k}$ for some $k$. Therefore, if $\cos (n \theta)$ can be expressed as a polynomial in $\cos (m \theta)$ then $\frac{2 \pi}{n}=\frac{2 \pi}{m k}$ for some $k$, so $m \mid n$. This shows that there is a blue line between two vertices $\cos (a \theta)$ and $\cos (b \theta)$ if and only if one of $a$ or $b$ divides the other.
Drawing the graph, one can easily count that there are 3 triangles with all blue edges, 3 triangles with all red edges, and $\binom{6}{3}=20$ triangles total. Thus there are $20-3-3=14$ triangles having at least one red and at least one blue edge.
|
{
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-guts-solutions.jsonl",
"problem_match": "\n28. [15]",
"solution_match": "\nAnswer: "
}
|
0092aa2f-4a36-589d-a4a6-e98f88dfb362
| 608,538
|
The average of a set of distinct primes is 27 . What is the largest prime that can be in this set?
|
139 Solution: Denote the set of these primes by $A$ and the number of elements in $A$ by
$n$. There are 9 primes smaller than 27 , namely $2,3,5,7,11,13,17,19$ and 23 . Since 27 is odd and all primes except 2 are odd, $2 \notin A$. Thus the largest prime $p$ is at most $27 \cdot 9-3-5-7-11-13-17-19-23=145$, so $p \leq 141$. When the primes are $3,5,7,11,13,17,19,23,29,31$ and 139 , their average is 27 . Therefore $p=139$.
|
139
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
The average of a set of distinct primes is 27 . What is the largest prime that can be in this set?
|
139 Solution: Denote the set of these primes by $A$ and the number of elements in $A$ by
$n$. There are 9 primes smaller than 27 , namely $2,3,5,7,11,13,17,19$ and 23 . Since 27 is odd and all primes except 2 are odd, $2 \notin A$. Thus the largest prime $p$ is at most $27 \cdot 9-3-5-7-11-13-17-19-23=145$, so $p \leq 141$. When the primes are $3,5,7,11,13,17,19,23,29,31$ and 139 , their average is 27 . Therefore $p=139$.
|
{
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-guts-solutions.jsonl",
"problem_match": "\n29. [15]",
"solution_match": "\nAnswer: "
}
|
5719aba0-0c09-5e25-b612-152c78b35f74
| 608,539
|
Let $f$ be a polynomial with integer coefficients such that the greatest common divisor of all its coefficients is 1 . For any $n \in \mathbb{N}, f(n)$ is a multiple of 85 . Find the smallest possible degree of $f$.
|
17 Solution: Notice that, if $p$ is a prime and $g$ is a polynomial with integer coefficients
such that $g(n) \equiv 0(\bmod p)$ for some $n$, then $g(n+m p)$ is divisible by $p$ as well for any integer multiple $m p$ of $p$. Therefore, it suffices to find the smallest possible degree of a polynomial $f$ for which $f(0), f(1), f(2), \ldots, f(16)$ are divisible by 17 and by 5 .
There is a polynomial of degree 17 with integer coefficients having $f(0)=f(1)=\cdots=f(16)=0$, namely $f(x)=(x)(x-1)(x-2) \cdots(x-16)$. Thus the minimal degree is no larger than 17 .
Now, let $f$ be such a polynomial and consider $f$ modulo 17 . The polynomial has 17 roots, so it must be at least degree 17 when taken modulo 17 . Thus $f$ has degree at least 17 as well.
## $12^{\text {th }}$ HARVARD-MIT MATHEMATICS TOURNAMENT, 21 FEBRUARY 2009 - GUTS ROUND
|
17
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Let $f$ be a polynomial with integer coefficients such that the greatest common divisor of all its coefficients is 1 . For any $n \in \mathbb{N}, f(n)$ is a multiple of 85 . Find the smallest possible degree of $f$.
|
17 Solution: Notice that, if $p$ is a prime and $g$ is a polynomial with integer coefficients
such that $g(n) \equiv 0(\bmod p)$ for some $n$, then $g(n+m p)$ is divisible by $p$ as well for any integer multiple $m p$ of $p$. Therefore, it suffices to find the smallest possible degree of a polynomial $f$ for which $f(0), f(1), f(2), \ldots, f(16)$ are divisible by 17 and by 5 .
There is a polynomial of degree 17 with integer coefficients having $f(0)=f(1)=\cdots=f(16)=0$, namely $f(x)=(x)(x-1)(x-2) \cdots(x-16)$. Thus the minimal degree is no larger than 17 .
Now, let $f$ be such a polynomial and consider $f$ modulo 17 . The polynomial has 17 roots, so it must be at least degree 17 when taken modulo 17 . Thus $f$ has degree at least 17 as well.
## $12^{\text {th }}$ HARVARD-MIT MATHEMATICS TOURNAMENT, 21 FEBRUARY 2009 - GUTS ROUND
|
{
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-guts-solutions.jsonl",
"problem_match": "\n30. [15]",
"solution_match": "\nAnswer: "
}
|
51b81f45-b45c-5bd3-b0e1-b0d807b14ba0
| 608,540
|
How many ways are there to win tic-tac-toe in $\mathbb{R}^{n}$ ? (That is, how many lines pass through three of the lattice points $\left(a_{1}, \ldots, a_{n}\right)$ in $\mathbb{R}^{n}$ with each coordinate $a_{i}$ in $\{1,2,3\} ?$ ) Express your answer in terms of $n$.
|
$\quad\left(5^{n}-3^{n}\right) / 2$ Solution: A line consists of three points. Each coordinate can do one of three things passing from the first point to the last point: increase by 1 each time, stay the same, or decrease by 1 each time. There are three ways to stay the same (three coordinates), one way to increase by 1 , and one way to decrease by 1 , so there are $5^{n}$ possible types of behavior. Determining this behavior uniquely determines the end point and start point except that we have traced every line exactly twice (forwards and backwards) and incorrectly counted the $3^{n}$ "lines" where each coordinate stays the same, so we subtract $3^{n}$ and divide by 2 .
|
\left(5^{n}-3^{n}\right) / 2
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
How many ways are there to win tic-tac-toe in $\mathbb{R}^{n}$ ? (That is, how many lines pass through three of the lattice points $\left(a_{1}, \ldots, a_{n}\right)$ in $\mathbb{R}^{n}$ with each coordinate $a_{i}$ in $\{1,2,3\} ?$ ) Express your answer in terms of $n$.
|
$\quad\left(5^{n}-3^{n}\right) / 2$ Solution: A line consists of three points. Each coordinate can do one of three things passing from the first point to the last point: increase by 1 each time, stay the same, or decrease by 1 each time. There are three ways to stay the same (three coordinates), one way to increase by 1 , and one way to decrease by 1 , so there are $5^{n}$ possible types of behavior. Determining this behavior uniquely determines the end point and start point except that we have traced every line exactly twice (forwards and backwards) and incorrectly counted the $3^{n}$ "lines" where each coordinate stays the same, so we subtract $3^{n}$ and divide by 2 .
|
{
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-guts-solutions.jsonl",
"problem_match": "\n31. [18]",
"solution_match": "\nAnswer: "
}
|
29c201ed-b0ff-51a3-a765-6b91c0b29478
| 608,541
|
Circle $\Omega$ has radius 13. Circle $\omega$ has radius 14 and its center $P$ lies on the boundary of circle $\Omega$. Points $A$ and $B$ lie on $\Omega$ such that chord $A B$ has length 24 and is tangent to $\omega$ at point $T$. Find $A T \cdot B T$.
|
56 Solution: Let $M$ be the midpoint of chord $A B$; then $A M=B M=12$ and Pythagoras on triangle $A M O$ gives $M O=5$. Note that $\angle A O M=\angle A O B / 2=\angle A P B=\angle A P T+\angle T P B$ or $\tan (\angle A O M)=\tan (\angle A P T+\angle T P B)$. Applying the tangent addition formula,
$$
\begin{aligned}
\frac{A M}{M O} & =\frac{\frac{A T}{T P}+\frac{B T}{T P}}{1-\frac{A T}{T P} \cdot \frac{B T}{T P}} \\
& =\frac{A B \cdot T P}{T P^{2}-A T \cdot B T}
\end{aligned}
$$
from which $A T \cdot B T=T P^{2}-A B \cdot T P \cdot M O / A M=14^{2}-24 \cdot 14 \cdot 5 / 12=56$.
|
56
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Circle $\Omega$ has radius 13. Circle $\omega$ has radius 14 and its center $P$ lies on the boundary of circle $\Omega$. Points $A$ and $B$ lie on $\Omega$ such that chord $A B$ has length 24 and is tangent to $\omega$ at point $T$. Find $A T \cdot B T$.
|
56 Solution: Let $M$ be the midpoint of chord $A B$; then $A M=B M=12$ and Pythagoras on triangle $A M O$ gives $M O=5$. Note that $\angle A O M=\angle A O B / 2=\angle A P B=\angle A P T+\angle T P B$ or $\tan (\angle A O M)=\tan (\angle A P T+\angle T P B)$. Applying the tangent addition formula,
$$
\begin{aligned}
\frac{A M}{M O} & =\frac{\frac{A T}{T P}+\frac{B T}{T P}}{1-\frac{A T}{T P} \cdot \frac{B T}{T P}} \\
& =\frac{A B \cdot T P}{T P^{2}-A T \cdot B T}
\end{aligned}
$$
from which $A T \cdot B T=T P^{2}-A B \cdot T P \cdot M O / A M=14^{2}-24 \cdot 14 \cdot 5 / 12=56$.
|
{
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-guts-solutions.jsonl",
"problem_match": "\n32. [18]",
"solution_match": "\nAnswer: "
}
|
8f683171-2529-51ae-a944-ae1a7acf7538
| 608,542
|
Descartes's Blackjack: How many integer lattice points (points of the form $(m, n)$ for integers $m$ and $n$ ) lie inside or on the boundary of the disk of radius 2009 centered at the origin?
If your answer is higher than the correct answer, you will receive 0 points. If your answer is $d$ less than the correct answer, your score on this problem will be the larger of 0 and $25-\lfloor d / 10\rfloor$.
|
12679605
|
12679605
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Descartes's Blackjack: How many integer lattice points (points of the form $(m, n)$ for integers $m$ and $n$ ) lie inside or on the boundary of the disk of radius 2009 centered at the origin?
If your answer is higher than the correct answer, you will receive 0 points. If your answer is $d$ less than the correct answer, your score on this problem will be the larger of 0 and $25-\lfloor d / 10\rfloor$.
|
12679605
|
{
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-guts-solutions.jsonl",
"problem_match": "\n34. $[\\leq \\mathbf{2 5}]$",
"solution_match": "\nAnswer: "
}
|
1099224e-cf01-5156-bab7-2e014c911b36
| 608,544
|
Von Neumann's Poker: The first step in Von Neumann's game is selecting a random number on $[0,1]$. To generate this number, Chebby uses the factorial base: the number $0 . A_{1} A_{2} A_{3} A_{4} \ldots$ stands for $\sum_{n=0}^{\infty} \frac{A_{n}}{(n+1)!}$, where each $A_{n}$ is an integer between 0 and $n$, inclusive.
Chebby has an infinite number of cards labeled $\mathbf{0}, \mathbf{1}, \mathbf{2}, \ldots$. He begins by putting cards $\mathbf{0}$ and $\mathbf{1}$ into a hat and drawing randomly to determine $A_{1}$. The card assigned $A_{1}$ does not get reused. Chebby then adds in card 2 and draws for $A_{2}$, and continues in this manner to determine the random number. At each step, he only draws one card from two in the hat.
Unfortunately, this method does not result in a uniform distribution. What is the expected value of Chebby's final number?
Your score on this problem will be the larger of 0 and $\lfloor 25(1-d)\rfloor$, where $d$ is the positive difference between your answer and the correct answer.
|
.57196
|
0.57196
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Von Neumann's Poker: The first step in Von Neumann's game is selecting a random number on $[0,1]$. To generate this number, Chebby uses the factorial base: the number $0 . A_{1} A_{2} A_{3} A_{4} \ldots$ stands for $\sum_{n=0}^{\infty} \frac{A_{n}}{(n+1)!}$, where each $A_{n}$ is an integer between 0 and $n$, inclusive.
Chebby has an infinite number of cards labeled $\mathbf{0}, \mathbf{1}, \mathbf{2}, \ldots$. He begins by putting cards $\mathbf{0}$ and $\mathbf{1}$ into a hat and drawing randomly to determine $A_{1}$. The card assigned $A_{1}$ does not get reused. Chebby then adds in card 2 and draws for $A_{2}$, and continues in this manner to determine the random number. At each step, he only draws one card from two in the hat.
Unfortunately, this method does not result in a uniform distribution. What is the expected value of Chebby's final number?
Your score on this problem will be the larger of 0 and $\lfloor 25(1-d)\rfloor$, where $d$ is the positive difference between your answer and the correct answer.
|
.57196
|
{
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-guts-solutions.jsonl",
"problem_match": "\n35. $[\\leq \\mathbf{2 5}]$",
"solution_match": "\nAnswer: "
}
|
4dfec1b9-dda0-5dd0-b6d1-98d43d70516c
| 608,545
|
A $k$-clique of a graph is a set of $k$ vertices such that all pairs of vertices in the clique are adjacent. The clique number of a graph is the size of the largest clique in the graph. Does there exist a graph which has a clique number smaller than its chromatic number?
|
Consider a graph with 5 vertices arranged in a circle, with each vertex connected to its two neighbors. If only two colors are used, it is impossible to alternate colors to avoid using the same color on two adjacent vertices, so the chromatic number is 3 . Its clique number is 2 , so we have found such a graph.
|
2
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
A $k$-clique of a graph is a set of $k$ vertices such that all pairs of vertices in the clique are adjacent. The clique number of a graph is the size of the largest clique in the graph. Does there exist a graph which has a clique number smaller than its chromatic number?
|
Consider a graph with 5 vertices arranged in a circle, with each vertex connected to its two neighbors. If only two colors are used, it is impossible to alternate colors to avoid using the same color on two adjacent vertices, so the chromatic number is 3 . Its clique number is 2 , so we have found such a graph.
|
{
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-team2-solutions.jsonl",
"problem_match": "\n5. [10]",
"solution_match": "\nSolution: "
}
|
daf500c4-8eee-5246-948e-1efd0f3a1632
| 608,558
|
Evaluate the sum:
$$
11^{2}-1^{2}+12^{2}-2^{2}+13^{2}-3^{2}+\ldots+20^{2}-10^{2}
$$
|
2100 This sum can be written as $\sum_{a=1}^{10}(a+10)^{2}-a^{2}=\sum_{a=1}^{10} 10(2 a+10)=10 * 10 *$ $11+10 * 10 * 10=2100$.
|
2100
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Evaluate the sum:
$$
11^{2}-1^{2}+12^{2}-2^{2}+13^{2}-3^{2}+\ldots+20^{2}-10^{2}
$$
|
2100 This sum can be written as $\sum_{a=1}^{10}(a+10)^{2}-a^{2}=\sum_{a=1}^{10} 10(2 a+10)=10 * 10 *$ $11+10 * 10 * 10=2100$.
|
{
"resource_path": "HarvardMIT/segmented/en-131-2009-nov-gen1-solutions.jsonl",
"problem_match": "\n1. [2]",
"solution_match": "\nAnswer: "
}
|
afd88728-baa9-5c89-b951-30642354a508
| 608,560
|
Given that $a+b+c=5$ and that $1 \leq a, b, c \leq 2$, what is the minimum possible value of $\frac{1}{a+b}+\frac{1}{b+c}$ ?
|
| $\frac{4}{7}$ | If $a>1$ and $b<2$, we can decrease the sum by decreasing $a$ and increasing $b$. You can |
| :---: | :---: | follow a similar procedure if $c>1$ and $b<2$. Therefore, the sum is minimized when $b=2$. We can then cross-multiply the two fractions and see that we are trying to minimize $\frac{a+c+4}{(a+2)(c+2)}=\frac{7}{(a+2)(c+2)}$. The product of two numbers with a fixed sum is maximized when those two numbers are equal, so $\frac{7}{(a+2)(c+2)}$ is minimized for $a=c=\frac{3}{2}$, which gives us an answer of $\frac{4}{7}$.
|
\frac{4}{7}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Given that $a+b+c=5$ and that $1 \leq a, b, c \leq 2$, what is the minimum possible value of $\frac{1}{a+b}+\frac{1}{b+c}$ ?
|
| $\frac{4}{7}$ | If $a>1$ and $b<2$, we can decrease the sum by decreasing $a$ and increasing $b$. You can |
| :---: | :---: | follow a similar procedure if $c>1$ and $b<2$. Therefore, the sum is minimized when $b=2$. We can then cross-multiply the two fractions and see that we are trying to minimize $\frac{a+c+4}{(a+2)(c+2)}=\frac{7}{(a+2)(c+2)}$. The product of two numbers with a fixed sum is maximized when those two numbers are equal, so $\frac{7}{(a+2)(c+2)}$ is minimized for $a=c=\frac{3}{2}$, which gives us an answer of $\frac{4}{7}$.
|
{
"resource_path": "HarvardMIT/segmented/en-131-2009-nov-gen1-solutions.jsonl",
"problem_match": "\n2. [3]",
"solution_match": "\nAnswer: "
}
|
79ce44df-cc29-5581-a83b-c260120263e0
| 608,561
|
What is the period of the function $f(x)=\cos (\cos (x))$ ?
|
$\pi$ Since $f(x)$ never equals $\cos (1)$ for $x \in(0, \pi)$ but $f(0)=\cos (1)$, the period is at least $\pi$. However, $\cos (x+\pi)=-\cos (x)$, so $\cos (\cos (x+\pi))=\cos (\cos (x))$.
|
\pi
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
What is the period of the function $f(x)=\cos (\cos (x))$ ?
|
$\pi$ Since $f(x)$ never equals $\cos (1)$ for $x \in(0, \pi)$ but $f(0)=\cos (1)$, the period is at least $\pi$. However, $\cos (x+\pi)=-\cos (x)$, so $\cos (\cos (x+\pi))=\cos (\cos (x))$.
|
{
"resource_path": "HarvardMIT/segmented/en-131-2009-nov-gen1-solutions.jsonl",
"problem_match": "\n3. [3]",
"solution_match": "\nAnswer: "
}
|
b788f531-37c2-5b2b-8341-2d40cb52778f
| 608,562
|
How many subsets $A$ of $\{1,2,3,4,5,6,7,8,9,10\}$ have the property that no two elements of $A$ sum to 11 ?
|
243 For each element listed, there is exactly one other element such that the two elements sum to 11. Thus, we can list all the 10 numbers above as 5 pairs of numbers, such that each pair sums to 11. The problem then can be solved as follows: in any given subset with no two elements summing to 11 , at most one element from each pair can be present. Thus, there are 3 ways in which each pair can contribute to a given subset (no element, the first element in the pair, or the second element in the pair). Since there are 5 pairs, the total number of ways to construct a subset with no two elements summing to 11 is $3^{5}=243$.
|
243
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
How many subsets $A$ of $\{1,2,3,4,5,6,7,8,9,10\}$ have the property that no two elements of $A$ sum to 11 ?
|
243 For each element listed, there is exactly one other element such that the two elements sum to 11. Thus, we can list all the 10 numbers above as 5 pairs of numbers, such that each pair sums to 11. The problem then can be solved as follows: in any given subset with no two elements summing to 11 , at most one element from each pair can be present. Thus, there are 3 ways in which each pair can contribute to a given subset (no element, the first element in the pair, or the second element in the pair). Since there are 5 pairs, the total number of ways to construct a subset with no two elements summing to 11 is $3^{5}=243$.
|
{
"resource_path": "HarvardMIT/segmented/en-131-2009-nov-gen1-solutions.jsonl",
"problem_match": "\n4. [4]",
"solution_match": "\nAnswer: "
}
|
f88e7974-1c8b-579a-b54a-0390fef001f3
| 608,563
|
A polyhedron has faces that are all either triangles or squares. No two square faces share an edge, and no two triangular faces share an edge. What is the ratio of the number of triangular faces to the number of square faces?
|
| $\frac{4}{3}$ | Let $s$ be the number of square faces and $t$ be the number of triangular faces. Every |
| :---: | :---: | :---: | edge is adjacent to exactly one square face and one triangular face. Therefore, the number of edges is equal to $4 s$, and it is also equal to $3 t$. Thus $4 s=3 t$ and $\frac{t}{s}=\frac{4}{3}$
|
\frac{4}{3}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
A polyhedron has faces that are all either triangles or squares. No two square faces share an edge, and no two triangular faces share an edge. What is the ratio of the number of triangular faces to the number of square faces?
|
| $\frac{4}{3}$ | Let $s$ be the number of square faces and $t$ be the number of triangular faces. Every |
| :---: | :---: | :---: | edge is adjacent to exactly one square face and one triangular face. Therefore, the number of edges is equal to $4 s$, and it is also equal to $3 t$. Thus $4 s=3 t$ and $\frac{t}{s}=\frac{4}{3}$
|
{
"resource_path": "HarvardMIT/segmented/en-131-2009-nov-gen1-solutions.jsonl",
"problem_match": "\n5. [5]",
"solution_match": "\nAnswer: "
}
|
d78bcfc1-5f36-5b21-a55a-f96f7b5eb1b3
| 608,564
|
Find the maximum value of $x+y$, given that $x^{2}+y^{2}-3 y-1=0$.
|
$\frac{\sqrt{26}+3}{2}$ We can rewrite $x^{2}+y^{2}-3 y-1=0$ as $x^{2}+\left(y-\frac{3}{2}\right)^{2}=\frac{13}{4}$. We then see that the set of solutions to $x^{2}-y^{2}-3 y-1=0$ is the circle of radius $\frac{\sqrt{13}}{2}$ and center $\left(0, \frac{3}{2}\right)$. This can be written as $x=\frac{\sqrt{13}}{2} \cos (\theta)$ and $y=\frac{\sqrt{13}}{2} \sin (\theta)+\frac{3}{2}$. Thus, $x+y=\frac{3}{2}+\frac{\sqrt{13}}{2}(\cos (\theta)+\sin (\theta))=\frac{3}{2}+\frac{\sqrt{13}}{2} \sqrt{2} \sin \left(\theta+45^{\circ}\right)$, which is maximized for $\theta=45^{\circ}$ and gives $\frac{\sqrt{26}+3}{2}$. (We could also solve this geometrically by noting that if $x+y$ attains a maximum value of $s$ then the line $x+y=s$ is tangent to the circle.)
|
\frac{\sqrt{26}+3}{2}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Find the maximum value of $x+y$, given that $x^{2}+y^{2}-3 y-1=0$.
|
$\frac{\sqrt{26}+3}{2}$ We can rewrite $x^{2}+y^{2}-3 y-1=0$ as $x^{2}+\left(y-\frac{3}{2}\right)^{2}=\frac{13}{4}$. We then see that the set of solutions to $x^{2}-y^{2}-3 y-1=0$ is the circle of radius $\frac{\sqrt{13}}{2}$ and center $\left(0, \frac{3}{2}\right)$. This can be written as $x=\frac{\sqrt{13}}{2} \cos (\theta)$ and $y=\frac{\sqrt{13}}{2} \sin (\theta)+\frac{3}{2}$. Thus, $x+y=\frac{3}{2}+\frac{\sqrt{13}}{2}(\cos (\theta)+\sin (\theta))=\frac{3}{2}+\frac{\sqrt{13}}{2} \sqrt{2} \sin \left(\theta+45^{\circ}\right)$, which is maximized for $\theta=45^{\circ}$ and gives $\frac{\sqrt{26}+3}{2}$. (We could also solve this geometrically by noting that if $x+y$ attains a maximum value of $s$ then the line $x+y=s$ is tangent to the circle.)
|
{
"resource_path": "HarvardMIT/segmented/en-131-2009-nov-gen1-solutions.jsonl",
"problem_match": "\n6. [5]",
"solution_match": "\nAnswer: "
}
|
d3c86379-7854-5978-895e-0514a8f4d74b
| 608,565
|
There are 15 stones placed in a line. In how many ways can you mark 5 of these stones so that there are an odd number of stones between any two of the stones you marked?
|
77 Number the stones 1 through 15 in order. We note that the condition is equivalent to stipulating that the stones have either all odd numbers or all even numbers. There are $\binom{8}{5}$ ways to choose 5 odd-numbered stones, and $\binom{7}{5}$ ways to choose all even-numbered stones, so the total number
of ways to pick the stones is $\binom{8}{5}+\binom{7}{5}=77$. $\binom{n}{k}$ is the number of ways to choose $k$ out of $n$ items. It equals $\left.\frac{n!}{k!(n-k)!}\right)$.
|
77
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
There are 15 stones placed in a line. In how many ways can you mark 5 of these stones so that there are an odd number of stones between any two of the stones you marked?
|
77 Number the stones 1 through 15 in order. We note that the condition is equivalent to stipulating that the stones have either all odd numbers or all even numbers. There are $\binom{8}{5}$ ways to choose 5 odd-numbered stones, and $\binom{7}{5}$ ways to choose all even-numbered stones, so the total number
of ways to pick the stones is $\binom{8}{5}+\binom{7}{5}=77$. $\binom{n}{k}$ is the number of ways to choose $k$ out of $n$ items. It equals $\left.\frac{n!}{k!(n-k)!}\right)$.
|
{
"resource_path": "HarvardMIT/segmented/en-131-2009-nov-gen1-solutions.jsonl",
"problem_match": "\n7. [6]",
"solution_match": "\nAnswer: "
}
|
9adce821-ffcb-5c33-941c-f6be2b0437f1
| 608,566
|
Let $\triangle A B C$ be an equilateral triangle with height 13 , and let $O$ be its center. Point $X$ is chosen at random from all points inside $\triangle A B C$. Given that the circle of radius 1 centered at $X$ lies entirely inside $\triangle A B C$, what is the probability that this circle contains $O$ ?
|
$\frac{\sqrt{3} \pi}{100}$ The set of points $X$ such that the circle of radius 1 centered at $X$ lies entirely inside $\triangle A B C$ is itself a triangle, $A^{\prime} B^{\prime} C^{\prime}$, such that $A B$ is parallel to $A^{\prime} B^{\prime}, B C$ is parallel to $B^{\prime} C^{\prime}$, and $C A$ is parallel to $C^{\prime} A^{\prime}$, and furthermore $A B$ and $A^{\prime} B^{\prime}, B C$ and $B^{\prime} C^{\prime}$, and $C A$ and $C^{\prime} A^{\prime}$ are all 1 unit apart. We can use this to calculate that $A^{\prime} B^{\prime} C^{\prime}$ is an equilateral triangle with height 10, and hence has area $\frac{100}{\sqrt{3}}$. On the other hand, the set of points $X$ such that the circle of radius 1 centered at $X$ contains $O$ is a circle of radius 1 , centered at $O$, and hence has area $\pi$. The probability that the circle centered at $X$ contains $O$ given that it also lies in $A B C$ is then the ratio of the two areas, that is, $\frac{\pi}{\frac{100}{\sqrt{3}}}=\frac{\sqrt{3} \pi}{100}$.
|
\frac{\sqrt{3} \pi}{100}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $\triangle A B C$ be an equilateral triangle with height 13 , and let $O$ be its center. Point $X$ is chosen at random from all points inside $\triangle A B C$. Given that the circle of radius 1 centered at $X$ lies entirely inside $\triangle A B C$, what is the probability that this circle contains $O$ ?
|
$\frac{\sqrt{3} \pi}{100}$ The set of points $X$ such that the circle of radius 1 centered at $X$ lies entirely inside $\triangle A B C$ is itself a triangle, $A^{\prime} B^{\prime} C^{\prime}$, such that $A B$ is parallel to $A^{\prime} B^{\prime}, B C$ is parallel to $B^{\prime} C^{\prime}$, and $C A$ is parallel to $C^{\prime} A^{\prime}$, and furthermore $A B$ and $A^{\prime} B^{\prime}, B C$ and $B^{\prime} C^{\prime}$, and $C A$ and $C^{\prime} A^{\prime}$ are all 1 unit apart. We can use this to calculate that $A^{\prime} B^{\prime} C^{\prime}$ is an equilateral triangle with height 10, and hence has area $\frac{100}{\sqrt{3}}$. On the other hand, the set of points $X$ such that the circle of radius 1 centered at $X$ contains $O$ is a circle of radius 1 , centered at $O$, and hence has area $\pi$. The probability that the circle centered at $X$ contains $O$ given that it also lies in $A B C$ is then the ratio of the two areas, that is, $\frac{\pi}{\frac{100}{\sqrt{3}}}=\frac{\sqrt{3} \pi}{100}$.
|
{
"resource_path": "HarvardMIT/segmented/en-131-2009-nov-gen1-solutions.jsonl",
"problem_match": "\n8. [7]",
"solution_match": "\nAnswer: "
}
|
a2950879-ced4-5c07-bd30-4745da1ea308
| 608,567
|
A set of points is convex if the points are the vertices of a convex polygon (that is, a non-selfintersecting polygon with all angles less than or equal to $180^{\circ}$ ). Let $S$ be the set of points $(x, y)$ such that $x$ and $y$ are integers and $1 \leq x, y \leq 26$. Find the number of ways to choose a convex subset of $S$ that contains exactly 98 points.
|
4958 For this problem, let $n=26$. A convex set may be divided into four subsets: a set of points with maximal $y$ coordinate, a set of points with minimal $y$ coordinate, the points to the left of one of these subsets, and the points to the right of one of these subsets (the left, top, right, and bottom of the corresponding convex polygon). Each of these four parts contains at most $n$ points. (All points in the top or bottom have distinct $x$ coordinates while all points in the left or right have distinct $y$ coordinates.) Moreover, there are four corners each of which is contained in two of these regions. This implies that at most $4 n-4$ distinct points are in any convex set. To find a set of size $4 n-6$ we can remove 2 additional points. Either exactly one of the top, bottom, left, or right contains exactly $n-2$ points or some two of them each contain exactly $n-1$ points.
Any of the $\binom{100}{98}=4950$ sets of 98 points with either $x$ or $y$ coordinate either 1 or 26 have this property. Suppose instead that some of the points have $x$ coordinate and $y$ coordinate both different from 1 and from 26. In this case we can check that it is impossible for one side to have $n-2$ points. If two opposite sides (top/bottom or left/right) have $n-1$ points, then we obtain all the points on the boundary of an $n-1$ by $n$ rectangle (of which there are four). If two adjacent sides (any of the other pairs) have $n-1$ points, then we obtain the points on the boundary of an $n$ by $n$ square with the points $(1,1),(1,2)$, $(2,1)$ missing and the point $(2,2)$ added (or one of its rotations). There are an additional 4 such sets, for a total of 4958.
|
4958
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
A set of points is convex if the points are the vertices of a convex polygon (that is, a non-selfintersecting polygon with all angles less than or equal to $180^{\circ}$ ). Let $S$ be the set of points $(x, y)$ such that $x$ and $y$ are integers and $1 \leq x, y \leq 26$. Find the number of ways to choose a convex subset of $S$ that contains exactly 98 points.
|
4958 For this problem, let $n=26$. A convex set may be divided into four subsets: a set of points with maximal $y$ coordinate, a set of points with minimal $y$ coordinate, the points to the left of one of these subsets, and the points to the right of one of these subsets (the left, top, right, and bottom of the corresponding convex polygon). Each of these four parts contains at most $n$ points. (All points in the top or bottom have distinct $x$ coordinates while all points in the left or right have distinct $y$ coordinates.) Moreover, there are four corners each of which is contained in two of these regions. This implies that at most $4 n-4$ distinct points are in any convex set. To find a set of size $4 n-6$ we can remove 2 additional points. Either exactly one of the top, bottom, left, or right contains exactly $n-2$ points or some two of them each contain exactly $n-1$ points.
Any of the $\binom{100}{98}=4950$ sets of 98 points with either $x$ or $y$ coordinate either 1 or 26 have this property. Suppose instead that some of the points have $x$ coordinate and $y$ coordinate both different from 1 and from 26. In this case we can check that it is impossible for one side to have $n-2$ points. If two opposite sides (top/bottom or left/right) have $n-1$ points, then we obtain all the points on the boundary of an $n-1$ by $n$ rectangle (of which there are four). If two adjacent sides (any of the other pairs) have $n-1$ points, then we obtain the points on the boundary of an $n$ by $n$ square with the points $(1,1),(1,2)$, $(2,1)$ missing and the point $(2,2)$ added (or one of its rotations). There are an additional 4 such sets, for a total of 4958.
|
{
"resource_path": "HarvardMIT/segmented/en-131-2009-nov-gen1-solutions.jsonl",
"problem_match": "\n9. [7]",
"solution_match": "\nAnswer: "
}
|
5fcd0954-19e5-56ba-b102-872e2bc9fd8c
| 608,568
|
Compute
$$
\prod_{n=0}^{\infty}\left(1-\left(\frac{1}{2}\right)^{3^{n}}+\left(\frac{1}{4}\right)^{3^{n}}\right)
$$
|
| $\frac{2}{3}$ |
| :---: |
| We can rewrite each term as $\frac{1+\left(\frac{1}{2}\right)^{3^{n+1}}}{1+\left(\frac{1}{2}\right)^{3^{n}}}$. In the infinite product, each term of the form | $1+\left(\frac{1}{2}\right)^{3^{n}}$ with $n>0$ appears once in the numerator and once in the denominator. The only remaining term is $1+\left(\frac{1}{2}\right)^{1}$ in the first denominator.
|
\frac{2}{3}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Compute
$$
\prod_{n=0}^{\infty}\left(1-\left(\frac{1}{2}\right)^{3^{n}}+\left(\frac{1}{4}\right)^{3^{n}}\right)
$$
|
| $\frac{2}{3}$ |
| :---: |
| We can rewrite each term as $\frac{1+\left(\frac{1}{2}\right)^{3^{n+1}}}{1+\left(\frac{1}{2}\right)^{3^{n}}}$. In the infinite product, each term of the form | $1+\left(\frac{1}{2}\right)^{3^{n}}$ with $n>0$ appears once in the numerator and once in the denominator. The only remaining term is $1+\left(\frac{1}{2}\right)^{1}$ in the first denominator.
|
{
"resource_path": "HarvardMIT/segmented/en-131-2009-nov-gen1-solutions.jsonl",
"problem_match": "\n10. [8]",
"solution_match": "\nAnswer: "
}
|
ba9acd92-a60a-5a0f-a09a-bff8a94388c5
| 608,569
|
Paul starts with the number 19. In one step, he can add 1 to his number, divide his number by 2 , or divide his number by 3 . What is the minimum number of steps Paul needs to get to 1 ?
|
6 One possible path is $19 \rightarrow 20 \rightarrow 10 \rightarrow 5 \rightarrow 6 \rightarrow 2 \rightarrow 1$.
|
6
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Paul starts with the number 19. In one step, he can add 1 to his number, divide his number by 2 , or divide his number by 3 . What is the minimum number of steps Paul needs to get to 1 ?
|
6 One possible path is $19 \rightarrow 20 \rightarrow 10 \rightarrow 5 \rightarrow 6 \rightarrow 2 \rightarrow 1$.
|
{
"resource_path": "HarvardMIT/segmented/en-131-2009-nov-gen2-solutions.jsonl",
"problem_match": "\n1. [3]",
"solution_match": "\nAnswer: "
}
|
90d43bb5-cada-532a-ab5c-50db7845d482
| 608,570
|
You start with a number. Every second, you can add or subtract any number of the form $n$ ! to your current number to get a new number. In how many ways can you get from 0 to 100 in 4 seconds? ( $n!$ is defined as $n \times(n-1) \times(n-2) \times \cdots \times 2 \times 1$, so $1!=1,2!=2,3!=6,4!=24$, etc.)
|
36 To get to 100 , you have to use one number which is at least $5!=120$, because $24 \times 4=96$, which is less than 100 . If you use $6!=720$ or anything larger, you need to get back from 720 to 100 (or further) in three seconds. Since $3 \cdot 5!<620$, there is no way to do this in 3 seconds. This means you have to use 5 ! at least once. The remaining numbers must get you from 120 to 100 . If you use three numbers all at most 3 !, you can move by at most $3 \cdot 3!=18<120-100$. This means you have to use 4 !. From $120-24=96$, there are two ways to get to 100: adding 6 then subtracting 2 , or adding 2 twice. So, to get to 100 from 0 in four seconds, you must either add 120 , subtract 24 , add 6 , and subtract 2 , or add 120 , subtract 24 , and add 2 twice. You can do these steps in any order, so the first sequence yields 24 paths and the second sequence yields 12 .
|
36
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
You start with a number. Every second, you can add or subtract any number of the form $n$ ! to your current number to get a new number. In how many ways can you get from 0 to 100 in 4 seconds? ( $n!$ is defined as $n \times(n-1) \times(n-2) \times \cdots \times 2 \times 1$, so $1!=1,2!=2,3!=6,4!=24$, etc.)
|
36 To get to 100 , you have to use one number which is at least $5!=120$, because $24 \times 4=96$, which is less than 100 . If you use $6!=720$ or anything larger, you need to get back from 720 to 100 (or further) in three seconds. Since $3 \cdot 5!<620$, there is no way to do this in 3 seconds. This means you have to use 5 ! at least once. The remaining numbers must get you from 120 to 100 . If you use three numbers all at most 3 !, you can move by at most $3 \cdot 3!=18<120-100$. This means you have to use 4 !. From $120-24=96$, there are two ways to get to 100: adding 6 then subtracting 2 , or adding 2 twice. So, to get to 100 from 0 in four seconds, you must either add 120 , subtract 24 , add 6 , and subtract 2 , or add 120 , subtract 24 , and add 2 twice. You can do these steps in any order, so the first sequence yields 24 paths and the second sequence yields 12 .
|
{
"resource_path": "HarvardMIT/segmented/en-131-2009-nov-gen2-solutions.jsonl",
"problem_match": "\n2. [4]",
"solution_match": "\nAnswer: "
}
|
b09239b3-1b5f-5a9e-a760-f2c1584e3659
| 608,571
|
Let $C$ be the circle of radius 12 centered at $(0,0)$. What is the length of the shortest path in the plane between $(8 \sqrt{3}, 0)$ and $(0,12 \sqrt{2})$ that does not pass through the interior of $C$ ?
|
$12+4 \sqrt{3}+\pi$ The shortest path consists of a tangent to the circle, a circular arc, and then another tangent. The first tangent, from $(8 \sqrt{3}, 0)$ to the circle, has length $4 \sqrt{3}$, because it is a leg of a 30-60-90 right triangle. The $15^{\circ}$ arc has length $\frac{15}{360}(24 \pi)$, or $\pi$, and the final tangent, to $(0,12 \sqrt{2})$, has length 12.
|
12+4 \sqrt{3}+\pi
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $C$ be the circle of radius 12 centered at $(0,0)$. What is the length of the shortest path in the plane between $(8 \sqrt{3}, 0)$ and $(0,12 \sqrt{2})$ that does not pass through the interior of $C$ ?
|
$12+4 \sqrt{3}+\pi$ The shortest path consists of a tangent to the circle, a circular arc, and then another tangent. The first tangent, from $(8 \sqrt{3}, 0)$ to the circle, has length $4 \sqrt{3}$, because it is a leg of a 30-60-90 right triangle. The $15^{\circ}$ arc has length $\frac{15}{360}(24 \pi)$, or $\pi$, and the final tangent, to $(0,12 \sqrt{2})$, has length 12.
|
{
"resource_path": "HarvardMIT/segmented/en-131-2009-nov-gen2-solutions.jsonl",
"problem_match": "\n3. [5]",
"solution_match": "\nAnswer: "
}
|
5fdcb07d-64b8-5b7c-b515-30cf4e365c07
| 608,572
|
You are given a $5 \times 6$ checkerboard with squares alternately shaded black and white. The bottomleft square is white. Each square has side length 1 unit. You can normally travel on this board at a speed of 2 units per second, but while you travel through the interior (not the boundary) of a black square, you are slowed down to 1 unit per second. What is the shortest time it takes to travel from the bottom-left corner to the top-right corner of the board?
|
$\frac{1+5 \sqrt{2}}{2}$ It is always faster to take a path around a black square than through it, since the length of the hypotenuse of any right triangle is greater than half the sum of the length of its legs. Therefore, an optimal path always stays on white squares or on boundaries, and the shortest such path has length $1+5 \sqrt{2}$.
|
\frac{1+5 \sqrt{2}}{2}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
You are given a $5 \times 6$ checkerboard with squares alternately shaded black and white. The bottomleft square is white. Each square has side length 1 unit. You can normally travel on this board at a speed of 2 units per second, but while you travel through the interior (not the boundary) of a black square, you are slowed down to 1 unit per second. What is the shortest time it takes to travel from the bottom-left corner to the top-right corner of the board?
|
$\frac{1+5 \sqrt{2}}{2}$ It is always faster to take a path around a black square than through it, since the length of the hypotenuse of any right triangle is greater than half the sum of the length of its legs. Therefore, an optimal path always stays on white squares or on boundaries, and the shortest such path has length $1+5 \sqrt{2}$.
|
{
"resource_path": "HarvardMIT/segmented/en-131-2009-nov-gen2-solutions.jsonl",
"problem_match": "\n4. [6]",
"solution_match": "\nAnswer: "
}
|
071a2176-f797-5fb0-8c57-e27d6dad7eea
| 608,573
|
The following grid represents a mountain range; the number in each cell represents the height of the mountain located there. Moving from a mountain of height $a$ to a mountain of height $b$ takes $(b-a)^{2}$ time. Suppose that you start on the mountain of height 1 and that you can move up, down, left, or right to get from one mountain to the next. What is the minimum amount of time you need to get to the mountain of height 49 ?
| 1 | 3 | 6 | 10 | 15 | 21 | 28 |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| 2 | 5 | 9 | 14 | 20 | 27 | 34 |
| 4 | 8 | 13 | 19 | 26 | 33 | 39 |
| 7 | 12 | 18 | 25 | 32 | 38 | 43 |
| 11 | 17 | 24 | 31 | 37 | 42 | 46 |
| 16 | 23 | 30 | 36 | 41 | 45 | 48 |
| 22 | 29 | 35 | 40 | 44 | 47 | 49 |
|
212 Consider the diagonals of the board running up and to the right - so the first diagonal is the square 1 , the second diagonal is the squares 2 and 3 , and so on. The $i$ th ascent is the largest step taken from a square in the $i$ th diagonal to a square in the $i+1$ st. Since you must climb from square 1 to square 49 , the sum of the ascents is at least 48 . Since there are 12 ascents, the average ascent is at least 4.
The 1 st and 12 th ascents are at most 2 , and the 2 nd and 11 th ascents are at most 3 . The 6 th and 7 th ascents are at least 6 , and the 5 th and 8 th ascents are at least 5 . Because $f(x)=x^{2}$ is convex, the sum of squares of the ascents is minimized when they are as close together as possible. One possible shortest path is then $1 \rightarrow 3 \rightarrow 6 \rightarrow 10 \rightarrow 14 \rightarrow 19 \rightarrow 25 \rightarrow 31 \rightarrow 36 \rightarrow 40 \rightarrow 44 \rightarrow 47 \rightarrow 49$, which has ascents of size $2,3,4,4,5,6,6,5,4,4,3$, and 2 . Thus, our answer is 212 , the sums of the squares of these ascents. There are other solutions to this problem. One alternative problem involves computing the shortest path to each square of the graph, recursively, starting from squares 2 and 3 .
## Five Guys
|
212
|
Yes
|
Yes
|
math-word-problem
|
Logic and Puzzles
|
The following grid represents a mountain range; the number in each cell represents the height of the mountain located there. Moving from a mountain of height $a$ to a mountain of height $b$ takes $(b-a)^{2}$ time. Suppose that you start on the mountain of height 1 and that you can move up, down, left, or right to get from one mountain to the next. What is the minimum amount of time you need to get to the mountain of height 49 ?
| 1 | 3 | 6 | 10 | 15 | 21 | 28 |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| 2 | 5 | 9 | 14 | 20 | 27 | 34 |
| 4 | 8 | 13 | 19 | 26 | 33 | 39 |
| 7 | 12 | 18 | 25 | 32 | 38 | 43 |
| 11 | 17 | 24 | 31 | 37 | 42 | 46 |
| 16 | 23 | 30 | 36 | 41 | 45 | 48 |
| 22 | 29 | 35 | 40 | 44 | 47 | 49 |
|
212 Consider the diagonals of the board running up and to the right - so the first diagonal is the square 1 , the second diagonal is the squares 2 and 3 , and so on. The $i$ th ascent is the largest step taken from a square in the $i$ th diagonal to a square in the $i+1$ st. Since you must climb from square 1 to square 49 , the sum of the ascents is at least 48 . Since there are 12 ascents, the average ascent is at least 4.
The 1 st and 12 th ascents are at most 2 , and the 2 nd and 11 th ascents are at most 3 . The 6 th and 7 th ascents are at least 6 , and the 5 th and 8 th ascents are at least 5 . Because $f(x)=x^{2}$ is convex, the sum of squares of the ascents is minimized when they are as close together as possible. One possible shortest path is then $1 \rightarrow 3 \rightarrow 6 \rightarrow 10 \rightarrow 14 \rightarrow 19 \rightarrow 25 \rightarrow 31 \rightarrow 36 \rightarrow 40 \rightarrow 44 \rightarrow 47 \rightarrow 49$, which has ascents of size $2,3,4,4,5,6,6,5,4,4,3$, and 2 . Thus, our answer is 212 , the sums of the squares of these ascents. There are other solutions to this problem. One alternative problem involves computing the shortest path to each square of the graph, recursively, starting from squares 2 and 3 .
## Five Guys
|
{
"resource_path": "HarvardMIT/segmented/en-131-2009-nov-gen2-solutions.jsonl",
"problem_match": "\n5. [7]",
"solution_match": "\nAnswer: "
}
|
cb0a5517-9baf-5a07-88ce-0c2a7a564b9c
| 608,574
|
Five guys are eating hamburgers. Each one puts a top half and a bottom half of a hamburger bun on the grill. When the buns are toasted, each guy randomly takes two pieces of bread off of the grill. What is the probability that each guy gets a top half and a bottom half?
|
$\frac{8}{63}$ Say a guy is content if he gets a top half and a bottom half. Suppose, without loss of generality, that the first guy's first piece of bread is a top. Then there is a $\frac{5}{9}$ chance that his second piece of bread is a bottom. By the same reasoning, given that the first guy is content, there is a $\frac{4}{7}$ chance that the second guy is content. Given that the first two guys are content, there is a $\frac{3}{5}$ chance that the third guy is content, and so on. Our final answer is $\frac{5}{9} \cdot \frac{4}{7} \cdot \frac{3}{5} \cdot \frac{2}{3} \cdot \frac{1}{1}=\frac{8}{63}$.
|
\frac{8}{63}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Five guys are eating hamburgers. Each one puts a top half and a bottom half of a hamburger bun on the grill. When the buns are toasted, each guy randomly takes two pieces of bread off of the grill. What is the probability that each guy gets a top half and a bottom half?
|
$\frac{8}{63}$ Say a guy is content if he gets a top half and a bottom half. Suppose, without loss of generality, that the first guy's first piece of bread is a top. Then there is a $\frac{5}{9}$ chance that his second piece of bread is a bottom. By the same reasoning, given that the first guy is content, there is a $\frac{4}{7}$ chance that the second guy is content. Given that the first two guys are content, there is a $\frac{3}{5}$ chance that the third guy is content, and so on. Our final answer is $\frac{5}{9} \cdot \frac{4}{7} \cdot \frac{3}{5} \cdot \frac{2}{3} \cdot \frac{1}{1}=\frac{8}{63}$.
|
{
"resource_path": "HarvardMIT/segmented/en-131-2009-nov-gen2-solutions.jsonl",
"problem_match": "\n7. [4]",
"solution_match": "\nAnswer: "
}
|
6729decd-fa68-56f8-afb3-edd4bf26a439
| 73,857
|
A single burger is not enough to satisfy a guy's hunger. The five guys go to Five Guys' Restaurant, which has 20 different meals on the menu. Each meal costs a different integer dollar amount between $\$ 1$ and $\$ 20$. The five guys have $\$ 20$ to split between them, and they want to use all the money to order five different meals. How many sets of five meals can the guys choose?
|
7 Suppose the meals, sorted in descending order, cost $5+x_{1}, 4+x_{2}, \ldots, 1+x_{5}$. To satisfy the conditions in the problem, the $x_{i}$ must be a non-increasing sequence of non-negative integers which sums to 5 . Therefore, there is exactly one order for each partition of 5 : order the elements of the partition from largest to smallest and use these parts as the $x_{i}$. For example, the partition $3+2$ corresponds to the order $5+3,4+2,3,2,1$. There are thus 7 orders, corresponding to the 7 partitions of 5 below.
$$
1+1+1+1+1,1+1+1+2,1+2+2,1+1+3,2+3,1+4,5
$$
These partitions yield the following seven orders:
$$
(2,3,4,5,6),(1,3,4,5,7),(1,2,4,6,7),(1,2,3,5,7)
$$
$(1,2,3,6,8),(1,2,3,5,9),(1,2,3,4,10)$
|
7
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
A single burger is not enough to satisfy a guy's hunger. The five guys go to Five Guys' Restaurant, which has 20 different meals on the menu. Each meal costs a different integer dollar amount between $\$ 1$ and $\$ 20$. The five guys have $\$ 20$ to split between them, and they want to use all the money to order five different meals. How many sets of five meals can the guys choose?
|
7 Suppose the meals, sorted in descending order, cost $5+x_{1}, 4+x_{2}, \ldots, 1+x_{5}$. To satisfy the conditions in the problem, the $x_{i}$ must be a non-increasing sequence of non-negative integers which sums to 5 . Therefore, there is exactly one order for each partition of 5 : order the elements of the partition from largest to smallest and use these parts as the $x_{i}$. For example, the partition $3+2$ corresponds to the order $5+3,4+2,3,2,1$. There are thus 7 orders, corresponding to the 7 partitions of 5 below.
$$
1+1+1+1+1,1+1+1+2,1+2+2,1+1+3,2+3,1+4,5
$$
These partitions yield the following seven orders:
$$
(2,3,4,5,6),(1,3,4,5,7),(1,2,4,6,7),(1,2,3,5,7)
$$
$(1,2,3,6,8),(1,2,3,5,9),(1,2,3,4,10)$
|
{
"resource_path": "HarvardMIT/segmented/en-131-2009-nov-gen2-solutions.jsonl",
"problem_match": "\n8. [5]",
"solution_match": "\nAnswer: "
}
|
ad5a4e6b-434a-5637-9eae-0412c94116da
| 608,576
|
Five guys each have a positive integer (the integers are not necessarily distinct). The greatest common divisor of any two guys' numbers is always more than 1 , but the greatest common divisor of all the numbers is 1 . What is the minimum possible value of the product of the numbers?
|
32400 Let $\omega(n)$ be the number of distinct prime divisors of a number. Each of the guys' numbers must have $\omega(n) \geq 2$, since no prime divides all the numbers. Therefore, if the answer has prime factorization $p_{1}^{e_{1}} p_{2}^{e_{2}} \ldots p_{k}^{e_{k}}$, then $e_{1}+e_{2}+\ldots+e_{k} \geq 10$. If $p^{2}$ divided any of the guys' numbers, we could divide their number by $p$ to reduce the product. Therefore we may assume $e_{i} \leq 4$ for each $i$, so the smallest possible product is $2^{4} 3^{4} 5^{2}$. This bound is achievable: give the guys the numbers $10,6,6,6$, and 15 .
|
32400
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Five guys each have a positive integer (the integers are not necessarily distinct). The greatest common divisor of any two guys' numbers is always more than 1 , but the greatest common divisor of all the numbers is 1 . What is the minimum possible value of the product of the numbers?
|
32400 Let $\omega(n)$ be the number of distinct prime divisors of a number. Each of the guys' numbers must have $\omega(n) \geq 2$, since no prime divides all the numbers. Therefore, if the answer has prime factorization $p_{1}^{e_{1}} p_{2}^{e_{2}} \ldots p_{k}^{e_{k}}$, then $e_{1}+e_{2}+\ldots+e_{k} \geq 10$. If $p^{2}$ divided any of the guys' numbers, we could divide their number by $p$ to reduce the product. Therefore we may assume $e_{i} \leq 4$ for each $i$, so the smallest possible product is $2^{4} 3^{4} 5^{2}$. This bound is achievable: give the guys the numbers $10,6,6,6$, and 15 .
|
{
"resource_path": "HarvardMIT/segmented/en-131-2009-nov-gen2-solutions.jsonl",
"problem_match": "\n9. [6]",
"solution_match": "\nAnswer: "
}
|
72843d95-b930-57e2-9a72-683bd62d171e
| 608,577
|
Five guys join five girls for a night of bridge. Bridge games are always played by a team of two guys against a team of two girls. The guys and girls want to make sure that every guy and girl play against each other an equal number of times. Given that at least one game is played, what is the least number of games necessary to accomplish this?
|
25 Suppose that each guy plays each girl $t$ times. Since each guy plays against two girls in one game, the total number of games each guy plays is $\frac{5 t}{2}$. Then the total number of games is $\frac{25 t}{4}$, which is a multiple of 25 and therefore at least 25 . To check that 25 games is enough, we arrange the guys and girls in two circles. A good pair of guys is a pair of guys who are adjacent in the circle; a good pair of girls is defined similarly. There are 5 good pairs of guys and girls - making each good pair of guys play each good pair of girls works.
|
25
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Five guys join five girls for a night of bridge. Bridge games are always played by a team of two guys against a team of two girls. The guys and girls want to make sure that every guy and girl play against each other an equal number of times. Given that at least one game is played, what is the least number of games necessary to accomplish this?
|
25 Suppose that each guy plays each girl $t$ times. Since each guy plays against two girls in one game, the total number of games each guy plays is $\frac{5 t}{2}$. Then the total number of games is $\frac{25 t}{4}$, which is a multiple of 25 and therefore at least 25 . To check that 25 games is enough, we arrange the guys and girls in two circles. A good pair of guys is a pair of guys who are adjacent in the circle; a good pair of girls is defined similarly. There are 5 good pairs of guys and girls - making each good pair of guys play each good pair of girls works.
|
{
"resource_path": "HarvardMIT/segmented/en-131-2009-nov-gen2-solutions.jsonl",
"problem_match": "\n10. [7]",
"solution_match": "\nAnswer: "
}
|
55ec6679-3efc-52b2-aec7-5dd59d011408
| 608,578
|
If $f(x)=x /(x+1)$, what is $f(f(f(f(2009))))$ ?
|
$\frac{2009}{8037} f(f(x))=\frac{(x /(x+1))}{(x /(x+1))+1}=x / 2 x+1, f(f(f(f(x))))=x / 4 x+1=\frac{2009}{8037}$
|
\frac{2009}{8037}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
If $f(x)=x /(x+1)$, what is $f(f(f(f(2009))))$ ?
|
$\frac{2009}{8037} f(f(x))=\frac{(x /(x+1))}{(x /(x+1))+1}=x / 2 x+1, f(f(f(f(x))))=x / 4 x+1=\frac{2009}{8037}$
|
{
"resource_path": "HarvardMIT/segmented/en-131-2009-nov-guts-solutions.jsonl",
"problem_match": "\n1. [5]",
"solution_match": "\nAnswer: "
}
|
6230c9ec-4fab-5256-9f57-35af6388b26b
| 608,579
|
A knight begins on the lower-left square of a standard chessboard. How many squares could the knight end up at after exactly 2009 legal knight's moves? (A knight's move is 2 squares either horizontally or vertically, followed by 1 square in a direction perpendicular to the first.)
|
32 The knight goes from a black square to a white square on every move, or vice versa, so after 2009 moves he must be on a square whose color is opposite of what he started on. So he can only land on half the squares after 2009 moves. Note that he can access any of the 32 squares (there are no other parity issues) because any single jump can also be accomplished in 3 jumps, so with 2009 jumps, he can land on any of the squares of the right color.
|
32
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
A knight begins on the lower-left square of a standard chessboard. How many squares could the knight end up at after exactly 2009 legal knight's moves? (A knight's move is 2 squares either horizontally or vertically, followed by 1 square in a direction perpendicular to the first.)
|
32 The knight goes from a black square to a white square on every move, or vice versa, so after 2009 moves he must be on a square whose color is opposite of what he started on. So he can only land on half the squares after 2009 moves. Note that he can access any of the 32 squares (there are no other parity issues) because any single jump can also be accomplished in 3 jumps, so with 2009 jumps, he can land on any of the squares of the right color.
|
{
"resource_path": "HarvardMIT/segmented/en-131-2009-nov-guts-solutions.jsonl",
"problem_match": "\n2. [5]",
"solution_match": "\nAnswer: "
}
|
15774e16-95a3-5311-b9ca-b002cb604fde
| 608,580
|
Consider a square, inside which is inscribed a circle, inside which is inscribed a square, inside which is inscribed a circle, and so on, with the outermost square having side length 1. Find the difference between the sum of the areas of the squares and the sum of the areas of the circles.
|
$2-\frac{\pi}{2}$
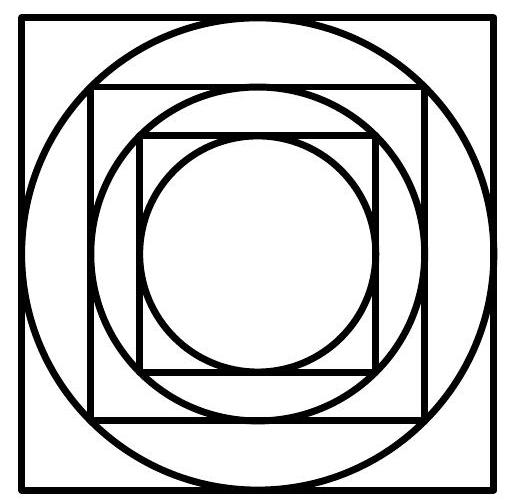
The ratio of the area of each square and the circle immediately inside it is $\frac{4}{\pi}$. The total sum of the areas of the squares is $1+\frac{1}{2}+\frac{1}{4}+\ldots=2$. Difference in area is then $2-2 \cdot \frac{4}{\pi}$.
$2^{\text {nd }}$ ANNUAL HARVARD-MIT NOVEMBER TOURNAMENT, 7 NOVEMBER $2009 —$ GUTS ROUND
|
2-\frac{\pi}{2}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Consider a square, inside which is inscribed a circle, inside which is inscribed a square, inside which is inscribed a circle, and so on, with the outermost square having side length 1. Find the difference between the sum of the areas of the squares and the sum of the areas of the circles.
|
$2-\frac{\pi}{2}$

The ratio of the area of each square and the circle immediately inside it is $\frac{4}{\pi}$. The total sum of the areas of the squares is $1+\frac{1}{2}+\frac{1}{4}+\ldots=2$. Difference in area is then $2-2 \cdot \frac{4}{\pi}$.
$2^{\text {nd }}$ ANNUAL HARVARD-MIT NOVEMBER TOURNAMENT, 7 NOVEMBER $2009 —$ GUTS ROUND
|
{
"resource_path": "HarvardMIT/segmented/en-131-2009-nov-guts-solutions.jsonl",
"problem_match": "\n3. [5]",
"solution_match": "\nAnswer: "
}
|
9e4173e5-e3b8-53a3-9ba1-1d4b0302b982
| 608,581
|
A cube has side length 1. Find the product of the lengths of the diagonals of this cube (a diagonal is a line between two vertices that is not an edge).
|
576 There are 12 diagonals that go along a face and 4 that go through the center of the cube, so the answer is $\sqrt{2}^{12} \cdot \sqrt{3}^{4}=576$.
|
576
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
A cube has side length 1. Find the product of the lengths of the diagonals of this cube (a diagonal is a line between two vertices that is not an edge).
|
576 There are 12 diagonals that go along a face and 4 that go through the center of the cube, so the answer is $\sqrt{2}^{12} \cdot \sqrt{3}^{4}=576$.
|
{
"resource_path": "HarvardMIT/segmented/en-131-2009-nov-guts-solutions.jsonl",
"problem_match": "\n4. [6]",
"solution_match": "\nAnswer: "
}
|
ca5b5ffb-55a5-5b86-aabd-2176380fa405
| 608,582
|
Tanks has a pile of 5 blue cards and 5 red cards. Every morning, he takes a card and throws it down a well. What is the probability that the first card he throws down and the last card he throws down are the same color?
|
| $\frac{4}{9}$ | Once he has thrown the first card down the well, there are 9 remaining cards, and only |
| :---: | :---: | 4 have the same color as the card that was thrown down. Therefore, the probability that the last card he throws down has the same color is $\frac{4}{9}$.
|
\frac{4}{9}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Tanks has a pile of 5 blue cards and 5 red cards. Every morning, he takes a card and throws it down a well. What is the probability that the first card he throws down and the last card he throws down are the same color?
|
| $\frac{4}{9}$ | Once he has thrown the first card down the well, there are 9 remaining cards, and only |
| :---: | :---: | 4 have the same color as the card that was thrown down. Therefore, the probability that the last card he throws down has the same color is $\frac{4}{9}$.
|
{
"resource_path": "HarvardMIT/segmented/en-131-2009-nov-guts-solutions.jsonl",
"problem_match": "\n5. [6]",
"solution_match": "\nAnswer: "
}
|
f505a884-f3f0-52bf-96e7-a6272bf925cf
| 608,583
|
Find the last two digits of $1032^{1032}$. Express your answer as a two-digit number.
|
76 The last two digits of $1032^{1032}$ is the same as the last two digits of $32^{1032}$. The last two digits of $32^{n}$ repeat with a period of four as $32,24,68,76,32,24,68,76, \ldots$.
$2^{\text {nd }}$ ANNUAL HARVARD-MIT NOVEMBER TOURNAMENT, 7 NOVEMBER 2009 - GUTS ROUND
|
76
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Find the last two digits of $1032^{1032}$. Express your answer as a two-digit number.
|
76 The last two digits of $1032^{1032}$ is the same as the last two digits of $32^{1032}$. The last two digits of $32^{n}$ repeat with a period of four as $32,24,68,76,32,24,68,76, \ldots$.
$2^{\text {nd }}$ ANNUAL HARVARD-MIT NOVEMBER TOURNAMENT, 7 NOVEMBER 2009 - GUTS ROUND
|
{
"resource_path": "HarvardMIT/segmented/en-131-2009-nov-guts-solutions.jsonl",
"problem_match": "\n6. [6]",
"solution_match": "\nAnswer: "
}
|
33626920-ea45-51ea-95ae-10e9f5c4a6af
| 608,584
|
A computer program is a function that takes in 4 bits, where each bit is either a 0 or a 1 , and outputs TRUE or FALSE. How many computer programs are there?
|
65536 The function has $2^{4}$ inputs and 2 outputs for each possible input, so the answer is $2^{2^{4}}=2^{16}=65536$.
|
65536
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
A computer program is a function that takes in 4 bits, where each bit is either a 0 or a 1 , and outputs TRUE or FALSE. How many computer programs are there?
|
65536 The function has $2^{4}$ inputs and 2 outputs for each possible input, so the answer is $2^{2^{4}}=2^{16}=65536$.
|
{
"resource_path": "HarvardMIT/segmented/en-131-2009-nov-guts-solutions.jsonl",
"problem_match": "\n7. [7]",
"solution_match": "\nAnswer: "
}
|
fff425cd-9d0a-595e-8666-d6c036562309
| 608,585
|
The angles of a convex $n$-sided polygon form an arithmetic progression whose common difference (in degrees) is a non-zero integer. Find the largest possible value of $n$ for which this is possible. (A polygon is convex if its interior angles are all less than $180^{\circ}$.)
|
27 The exterior angles form an arithmetic sequence too (since they are each $180^{\circ}$ minus the corresponding interior angle). The sum of this sequence must be $360^{\circ}$. Let the smallest exterior angle be $x$ and the common difference be $d$. The sum of the exterior angles is then $x+(x+a)+(x+$ $2 a)+\ldots+(x+(n-1) a)=\frac{n(n-1)}{2} \cdot a+n x$. Setting this to 360 , and using $n x>0$, we get $n(n-1)<720$, so $n \leq 27$.
|
27
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
The angles of a convex $n$-sided polygon form an arithmetic progression whose common difference (in degrees) is a non-zero integer. Find the largest possible value of $n$ for which this is possible. (A polygon is convex if its interior angles are all less than $180^{\circ}$.)
|
27 The exterior angles form an arithmetic sequence too (since they are each $180^{\circ}$ minus the corresponding interior angle). The sum of this sequence must be $360^{\circ}$. Let the smallest exterior angle be $x$ and the common difference be $d$. The sum of the exterior angles is then $x+(x+a)+(x+$ $2 a)+\ldots+(x+(n-1) a)=\frac{n(n-1)}{2} \cdot a+n x$. Setting this to 360 , and using $n x>0$, we get $n(n-1)<720$, so $n \leq 27$.
|
{
"resource_path": "HarvardMIT/segmented/en-131-2009-nov-guts-solutions.jsonl",
"problem_match": "\n8. [7]",
"solution_match": "\nAnswer: "
}
|
c729cc86-f0bc-5cd3-a4d9-eb8c9a829620
| 608,586
|
Daniel wrote all the positive integers from 1 to $n$ inclusive on a piece of paper. After careful observation, he realized that the sum of all the digits that he wrote was exactly 10,000 . Find $n$.
|
799 Let $S(n)$ denote the sum of the digits of $n$, and let $f(x)=\sum_{n=0}^{x} S(n)$. (We may add $n=0$ because $S(0)=0$.) Observe that:
$$
f(99)=\sum_{a=0}^{9}\left(\sum_{b=0}^{9}(a+b)\right)=10 \sum_{b=0}^{9} b+10 \sum_{a=0}^{9} a=900
$$
If $a$ is an integer between 1 and 9 inclusive, then:
$$
\sum_{n=100 a}^{100 a+99} S(n)=\sum_{n=100 a}^{100 a+99}(a+S(n-100 a))=100 a+f(99)=100 a+900
$$
Summing, we get:
$$
f(100 a+99)=\sum_{n=0}^{a}(100 a+900)=900(a+1)+50 a(a+1)
$$
This formula can be used to find benchmarks. However, it turns out that this formula alone will suffice, as things turn out rather nicely:
$$
\begin{aligned}
900(a+1)+50 a(a+1) & =10000 \\
50 a^{2}+950 a+900 & =10000 \\
50 a^{2}+950 a-9100 & =0 \\
50(a+26)(a-7) & =0 \\
a & =7
\end{aligned}
$$
Therefore $f(799)=10000$, and our answer is 799 .
## $2^{\text {nd }}$ ANNUAL HARVARD-MIT NOVEMBER TOURNAMENT, 7 NOVEMBER 2009 - GUTS ROUND
|
799
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Daniel wrote all the positive integers from 1 to $n$ inclusive on a piece of paper. After careful observation, he realized that the sum of all the digits that he wrote was exactly 10,000 . Find $n$.
|
799 Let $S(n)$ denote the sum of the digits of $n$, and let $f(x)=\sum_{n=0}^{x} S(n)$. (We may add $n=0$ because $S(0)=0$.) Observe that:
$$
f(99)=\sum_{a=0}^{9}\left(\sum_{b=0}^{9}(a+b)\right)=10 \sum_{b=0}^{9} b+10 \sum_{a=0}^{9} a=900
$$
If $a$ is an integer between 1 and 9 inclusive, then:
$$
\sum_{n=100 a}^{100 a+99} S(n)=\sum_{n=100 a}^{100 a+99}(a+S(n-100 a))=100 a+f(99)=100 a+900
$$
Summing, we get:
$$
f(100 a+99)=\sum_{n=0}^{a}(100 a+900)=900(a+1)+50 a(a+1)
$$
This formula can be used to find benchmarks. However, it turns out that this formula alone will suffice, as things turn out rather nicely:
$$
\begin{aligned}
900(a+1)+50 a(a+1) & =10000 \\
50 a^{2}+950 a+900 & =10000 \\
50 a^{2}+950 a-9100 & =0 \\
50(a+26)(a-7) & =0 \\
a & =7
\end{aligned}
$$
Therefore $f(799)=10000$, and our answer is 799 .
## $2^{\text {nd }}$ ANNUAL HARVARD-MIT NOVEMBER TOURNAMENT, 7 NOVEMBER 2009 - GUTS ROUND
|
{
"resource_path": "HarvardMIT/segmented/en-131-2009-nov-guts-solutions.jsonl",
"problem_match": "\n9. [7]",
"solution_match": "\nAnswer: "
}
|
289d106c-c45c-562f-8050-81f8afff99cf
| 608,587
|
Admiral Ackbar needs to send a 5-character message through hyperspace to the Rebels. Each character is a lowercase letter, and the same letter may appear more than once in a message. When the message is beamed through hyperspace, the characters come out in a random order. Ackbar chooses his message so that the Rebels have at least a $\frac{1}{2}$ chance of getting the same message he sent. How many distinct messages could he send?
|
26 If there is more than one distinct letter sent in the message, then there will be at most a $1 / 5$ chance of transmitting the right message. So the message must consist of one letter repeated five times, so there are 26 possible messages.
|
26
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Admiral Ackbar needs to send a 5-character message through hyperspace to the Rebels. Each character is a lowercase letter, and the same letter may appear more than once in a message. When the message is beamed through hyperspace, the characters come out in a random order. Ackbar chooses his message so that the Rebels have at least a $\frac{1}{2}$ chance of getting the same message he sent. How many distinct messages could he send?
|
26 If there is more than one distinct letter sent in the message, then there will be at most a $1 / 5$ chance of transmitting the right message. So the message must consist of one letter repeated five times, so there are 26 possible messages.
|
{
"resource_path": "HarvardMIT/segmented/en-131-2009-nov-guts-solutions.jsonl",
"problem_match": "\n10. [8]",
"solution_match": "\nAnswer: "
}
|
3eaafea0-94cb-5456-b4d1-5e6799341296
| 608,588
|
Lily and Sarah are playing a game. They each choose a real number at random between -1 and 1 . They then add the squares of their numbers together. If the result is greater than or equal to 1 , Lily wins, and if the result is less than 1, Sarah wins. What is the probability that Sarah wins?
|
$\frac{\pi}{4}$ If we let $x$ denote Lily's choice of number and $y$ denote Sarah's, then all possible outcomes are represented by the square with vertices $(-1,-1),(-1,1),(1,-1)$, and $(1,1)$. Sarah wins if $x^{2}+y^{2} \leq 1$, which is the area inside the unit circle. Since this has an area of $\pi$ and the entire square has an area of 4 , the probability that Sarah wins is $\frac{\pi}{4}$.
|
\frac{\pi}{4}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Lily and Sarah are playing a game. They each choose a real number at random between -1 and 1 . They then add the squares of their numbers together. If the result is greater than or equal to 1 , Lily wins, and if the result is less than 1, Sarah wins. What is the probability that Sarah wins?
|
$\frac{\pi}{4}$ If we let $x$ denote Lily's choice of number and $y$ denote Sarah's, then all possible outcomes are represented by the square with vertices $(-1,-1),(-1,1),(1,-1)$, and $(1,1)$. Sarah wins if $x^{2}+y^{2} \leq 1$, which is the area inside the unit circle. Since this has an area of $\pi$ and the entire square has an area of 4 , the probability that Sarah wins is $\frac{\pi}{4}$.
|
{
"resource_path": "HarvardMIT/segmented/en-131-2009-nov-guts-solutions.jsonl",
"problem_match": "\n11. [8]",
"solution_match": "\nAnswer: "
}
|
ed06dfcf-a057-5e09-b94e-b3b497aab820
| 608,589
|
Let $\omega$ be a circle of radius 1 centered at $O$. Let $B$ be a point on $\omega$, and let $l$ be the line tangent to $\omega$ at $B$. Let $A$ be on $l$ such that $\angle A O B=60^{\circ}$. Let $C$ be the foot of the perpendicular from $B$ to $O A$. Find the length of line segment $O C$.
|
$\frac{1}{2}$ We have $O C / O B=\cos \left(60^{\circ}\right)$. Since $O B=1, O C=\frac{1}{2}$.
$2^{\text {nd }}$ ANNUAL HARVARD-MIT NOVEMBER TOURNAMENT, 7 NOVEMBER 2009 - GUTS ROUND
|
\frac{1}{2}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $\omega$ be a circle of radius 1 centered at $O$. Let $B$ be a point on $\omega$, and let $l$ be the line tangent to $\omega$ at $B$. Let $A$ be on $l$ such that $\angle A O B=60^{\circ}$. Let $C$ be the foot of the perpendicular from $B$ to $O A$. Find the length of line segment $O C$.
|
$\frac{1}{2}$ We have $O C / O B=\cos \left(60^{\circ}\right)$. Since $O B=1, O C=\frac{1}{2}$.
$2^{\text {nd }}$ ANNUAL HARVARD-MIT NOVEMBER TOURNAMENT, 7 NOVEMBER 2009 - GUTS ROUND
|
{
"resource_path": "HarvardMIT/segmented/en-131-2009-nov-guts-solutions.jsonl",
"problem_match": "\n12. [8]",
"solution_match": "\nAnswer: "
}
|
298a24cb-d741-51e2-88df-6af5a3c4219e
| 608,590
|
8 students are practicing for a math contest, and they divide into pairs to take a practice test. In how many ways can they be split up?
|
105 We create the pairs one at a time. The first person has 7 possible partners. Set this pair aside. Of the remaining six people, pick a person. He or she has 5 possible partners. Set this pair aside. Of the remaining four people, pick a person. He or she has 3 possible partners. Set this pair aside. Then the last two must be partners. So there are $7 \cdot 5 \cdot 3=105$ possible groupings. Alternatively, we can consider the 8 ! permutations of the students in a line, where the first two are a pair, the next two are a pair, etc. Given a grouping, there are 4 ! ways to arrange the four pairs in order, and in each pair, 2 ways to order the students. So our answer is $\frac{8!}{4!2^{4}}=7 \cdot 5 \cdot 3=105$.
|
105
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
8 students are practicing for a math contest, and they divide into pairs to take a practice test. In how many ways can they be split up?
|
105 We create the pairs one at a time. The first person has 7 possible partners. Set this pair aside. Of the remaining six people, pick a person. He or she has 5 possible partners. Set this pair aside. Of the remaining four people, pick a person. He or she has 3 possible partners. Set this pair aside. Then the last two must be partners. So there are $7 \cdot 5 \cdot 3=105$ possible groupings. Alternatively, we can consider the 8 ! permutations of the students in a line, where the first two are a pair, the next two are a pair, etc. Given a grouping, there are 4 ! ways to arrange the four pairs in order, and in each pair, 2 ways to order the students. So our answer is $\frac{8!}{4!2^{4}}=7 \cdot 5 \cdot 3=105$.
|
{
"resource_path": "HarvardMIT/segmented/en-131-2009-nov-guts-solutions.jsonl",
"problem_match": "\n13. [8]",
"solution_match": "\nAnswer: "
}
|
8fc8f3ad-b319-5dc1-8620-dd4cc654c40b
| 608,591
|
Let $f(x)=x^{4}+a x^{3}+b x^{2}+c x+d$ be a polynomial whose roots are all negative integers. If $a+b+c+d=2009$, find $d$.
|
528 Call the roots $-x_{1},-x_{2},-x_{3}$, and $-x_{4}$. Then $f(x)$ must factor as $\left(x+x_{1}\right)\left(x+x_{2}\right)(x+$ $\left.x_{3}\right)\left(x+x_{4}\right)$. If we evaluate $f$ at 1 , we get $\left(1+x_{1}\right)\left(1+x_{2}\right)\left(1+x_{3}\right)\left(1+x_{4}\right)=a+b+c+d+1=$ $2009+1=2010$. $2010=2 \cdot 3 \cdot 5 \cdot 67$. $d$ is the product of the four roots, so $d=(-1) \cdot(-2) \cdot(-4) \cdot(-66)$.
|
528
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Let $f(x)=x^{4}+a x^{3}+b x^{2}+c x+d$ be a polynomial whose roots are all negative integers. If $a+b+c+d=2009$, find $d$.
|
528 Call the roots $-x_{1},-x_{2},-x_{3}$, and $-x_{4}$. Then $f(x)$ must factor as $\left(x+x_{1}\right)\left(x+x_{2}\right)(x+$ $\left.x_{3}\right)\left(x+x_{4}\right)$. If we evaluate $f$ at 1 , we get $\left(1+x_{1}\right)\left(1+x_{2}\right)\left(1+x_{3}\right)\left(1+x_{4}\right)=a+b+c+d+1=$ $2009+1=2010$. $2010=2 \cdot 3 \cdot 5 \cdot 67$. $d$ is the product of the four roots, so $d=(-1) \cdot(-2) \cdot(-4) \cdot(-66)$.
|
{
"resource_path": "HarvardMIT/segmented/en-131-2009-nov-guts-solutions.jsonl",
"problem_match": "\n14. [8]",
"solution_match": "\nAnswer: "
}
|
5b347d1b-fcb0-571a-97ea-9f3af017f099
| 608,592
|
The curves $x^{2}+y^{2}=36$ and $y=x^{2}-7$ intersect at four points. Find the sum of the squares of the $x$-coordinates of these points.
|
26 If we use the system of equations to solve for $y$, we get $y^{2}+y-29=0$ (since $x^{2}=y+7$ ). The sum of the roots of this equation is -1 . Combine this with $x^{2}=y+7$ to see that the sum of the square of the possible values of $x$ is $2 \cdot(-1+7 \cdot 2)=26$.
|
26
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
The curves $x^{2}+y^{2}=36$ and $y=x^{2}-7$ intersect at four points. Find the sum of the squares of the $x$-coordinates of these points.
|
26 If we use the system of equations to solve for $y$, we get $y^{2}+y-29=0$ (since $x^{2}=y+7$ ). The sum of the roots of this equation is -1 . Combine this with $x^{2}=y+7$ to see that the sum of the square of the possible values of $x$ is $2 \cdot(-1+7 \cdot 2)=26$.
|
{
"resource_path": "HarvardMIT/segmented/en-131-2009-nov-guts-solutions.jsonl",
"problem_match": "\n15. [8]",
"solution_match": "\nAnswer: "
}
|
68ced284-bdcb-59f9-b78c-71fbbff911b9
| 608,593
|
A circle passes through the points $(2,0)$ and $(4,0)$ and is tangent to the line $y=x$. Find the sum of all possible values for the $y$-coordinate of the center of the circle.
|
-6 First, we see that the x coordinate must be 3. Let the y coordinate be y. Now, we see that the radius is $r=\sqrt{1+y^{2}}$. The line from the center of the circle to the point of tangency with the line $x=y$ is perpendicular to the line $x=y$. Hence, the distance from the center of the circle to the line $x=y$ is $d=\sqrt{2}(3-y)$. Letting $r=d$ we see that the two possible values for y are 1 and -7 , which sum to -6 .
|
-6
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
A circle passes through the points $(2,0)$ and $(4,0)$ and is tangent to the line $y=x$. Find the sum of all possible values for the $y$-coordinate of the center of the circle.
|
-6 First, we see that the x coordinate must be 3. Let the y coordinate be y. Now, we see that the radius is $r=\sqrt{1+y^{2}}$. The line from the center of the circle to the point of tangency with the line $x=y$ is perpendicular to the line $x=y$. Hence, the distance from the center of the circle to the line $x=y$ is $d=\sqrt{2}(3-y)$. Letting $r=d$ we see that the two possible values for y are 1 and -7 , which sum to -6 .
|
{
"resource_path": "HarvardMIT/segmented/en-131-2009-nov-guts-solutions.jsonl",
"problem_match": "\n17. [9]",
"solution_match": "\nAnswer: "
}
|
70eb8927-72af-5b9c-a97b-6710fd123f2a
| 608,595
|
Let $f$ be a function that takes in a triple of integers and outputs a real number. Suppose that $f$ satisfies the equations
$$
\begin{aligned}
f(a, b, c) & =\frac{f(a+1, b, c)+f(a-1, b, c)}{2} \\
f(a, b, c) & =\frac{f(a, b+1, c)+f(a, b-1, c)}{2} \\
f(a, b, c) & =\frac{f(a, b, c+1)+f(a, b, c-1)}{2}
\end{aligned}
$$
for all integers $a, b, c$. What is the minimum number of triples at which we need to evaluate $f$ in order to know its value everywhere?
|
8 Note that if we have the value of $f$ at the 8 points: $(0,0,0),(1,0,0),(0,1,0),(0,0,1),(0,1,1),(1,0,1),(1,1,0),(1,1,1)$, we can calculate the value for any triple of points because we have that $f(a+1, b, c)-(a, b, c)$ constant for any $a$, if $b$ and $c$ are fixed (and similarly for the other coordinates). To see why we cannot do this with less points, notice that we need to determine what the value of these 8 points anyways, and there is no "more efficient" way to determine them all in fewer evaluations.
$2^{\text {nd }}$ ANNUAL HARVARD-MIT NOVEMBER TOURNAMENT, 7 NOVEMBER 2009 - GUTS ROUND
|
8
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Let $f$ be a function that takes in a triple of integers and outputs a real number. Suppose that $f$ satisfies the equations
$$
\begin{aligned}
f(a, b, c) & =\frac{f(a+1, b, c)+f(a-1, b, c)}{2} \\
f(a, b, c) & =\frac{f(a, b+1, c)+f(a, b-1, c)}{2} \\
f(a, b, c) & =\frac{f(a, b, c+1)+f(a, b, c-1)}{2}
\end{aligned}
$$
for all integers $a, b, c$. What is the minimum number of triples at which we need to evaluate $f$ in order to know its value everywhere?
|
8 Note that if we have the value of $f$ at the 8 points: $(0,0,0),(1,0,0),(0,1,0),(0,0,1),(0,1,1),(1,0,1),(1,1,0),(1,1,1)$, we can calculate the value for any triple of points because we have that $f(a+1, b, c)-(a, b, c)$ constant for any $a$, if $b$ and $c$ are fixed (and similarly for the other coordinates). To see why we cannot do this with less points, notice that we need to determine what the value of these 8 points anyways, and there is no "more efficient" way to determine them all in fewer evaluations.
$2^{\text {nd }}$ ANNUAL HARVARD-MIT NOVEMBER TOURNAMENT, 7 NOVEMBER 2009 - GUTS ROUND
|
{
"resource_path": "HarvardMIT/segmented/en-131-2009-nov-guts-solutions.jsonl",
"problem_match": "\n18. [9]",
"solution_match": "\nAnswer: "
}
|
03876752-19f5-59e3-9c94-519ab49e84bf
| 608,596
|
You are trapped in ancient Japan, and a giant enemy crab is approaching! You must defeat it by cutting off its two claws and six legs and attacking its weak point for massive damage. You cannot cut off any of its claws until you cut off at least three of its legs, and you cannot attack its weak point until you have cut off all of its claws and legs. In how many ways can you defeat the giant enemy crab? (Note that the legs are distinguishable, as are the claws.)
|
14400 The answer is given by $6!2!\binom{5}{2}$, because we can cut off the claws and legs in any order and there are $\binom{5}{2}$ ways to decide when to cut off the two claws (since we can do it at any time among the last 5 cuts).
|
14400
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
You are trapped in ancient Japan, and a giant enemy crab is approaching! You must defeat it by cutting off its two claws and six legs and attacking its weak point for massive damage. You cannot cut off any of its claws until you cut off at least three of its legs, and you cannot attack its weak point until you have cut off all of its claws and legs. In how many ways can you defeat the giant enemy crab? (Note that the legs are distinguishable, as are the claws.)
|
14400 The answer is given by $6!2!\binom{5}{2}$, because we can cut off the claws and legs in any order and there are $\binom{5}{2}$ ways to decide when to cut off the two claws (since we can do it at any time among the last 5 cuts).
|
{
"resource_path": "HarvardMIT/segmented/en-131-2009-nov-guts-solutions.jsonl",
"problem_match": "\n19. [11]",
"solution_match": "\nAnswer: "
}
|
97cb54b0-d68a-5162-9cef-22e2e301e4a6
| 608,597
|
Consider an equilateral triangle and a square both inscribed in a unit circle such that one side of the square is parallel to one side of the triangle. Compute the area of the convex heptagon formed by the vertices of both the triangle and the square.
|
$\frac{3+\sqrt{3}}{2}$
Consider the diagram above. We see that the shape is a square plus 3 triangles. The top and bottom triangles have base $\sqrt{2}$ and height $\frac{1}{2}(\sqrt{3}-\sqrt{2})$, and the triangle on the side has the same base and height $1-\frac{\sqrt{2}}{2}$ Adding their areas, we get the answer.
|
\frac{3+\sqrt{3}}{2}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Consider an equilateral triangle and a square both inscribed in a unit circle such that one side of the square is parallel to one side of the triangle. Compute the area of the convex heptagon formed by the vertices of both the triangle and the square.
|
$\frac{3+\sqrt{3}}{2}$

Consider the diagram above. We see that the shape is a square plus 3 triangles. The top and bottom triangles have base $\sqrt{2}$ and height $\frac{1}{2}(\sqrt{3}-\sqrt{2})$, and the triangle on the side has the same base and height $1-\frac{\sqrt{2}}{2}$ Adding their areas, we get the answer.
|
{
"resource_path": "HarvardMIT/segmented/en-131-2009-nov-guts-solutions.jsonl",
"problem_match": "\n20. [11]",
"solution_match": "\nAnswer: "
}
|
5e196e1f-f4fb-5196-8aa2-72ee3dc3ffa0
| 608,598
|
Let $f(x)=x^{2}+2 x+1$. Let $g(x)=f(f(\cdots f(x)))$, where there are $2009 f \mathrm{~s}$ in the expression for $g(x)$. Then $g(x)$ can be written as
$$
g(x)=x^{2^{2009}}+a_{2^{2009}-1} x^{2^{2009}-1}+\cdots+a_{1} x+a_{0}
$$
where the $a_{i}$ are constants. Compute $a_{2^{2009}-1}$.
|
$2^{2009} f(x)=(x+1)^{2}$, so $f\left(x^{n}+c x^{n-1}+\ldots\right)=\left(x^{n}+c x^{n-1}+\ldots+1\right)^{2}=x^{2 n}+2 c x^{2 n-1}+\ldots$. Applying the preceding formula repeatedly shows us that the coefficient of the term of second highest degree in the polynomial doubles each time, so after 2009 applications of $f$ it is $2^{2009}$.
$2^{\text {nd }}$ ANNUAL HARVARD-MIT NOVEMBER TOURNAMENT, 7 NOVEMBER 2009 - GUTS ROUND
|
2^{2009}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Let $f(x)=x^{2}+2 x+1$. Let $g(x)=f(f(\cdots f(x)))$, where there are $2009 f \mathrm{~s}$ in the expression for $g(x)$. Then $g(x)$ can be written as
$$
g(x)=x^{2^{2009}}+a_{2^{2009}-1} x^{2^{2009}-1}+\cdots+a_{1} x+a_{0}
$$
where the $a_{i}$ are constants. Compute $a_{2^{2009}-1}$.
|
$2^{2009} f(x)=(x+1)^{2}$, so $f\left(x^{n}+c x^{n-1}+\ldots\right)=\left(x^{n}+c x^{n-1}+\ldots+1\right)^{2}=x^{2 n}+2 c x^{2 n-1}+\ldots$. Applying the preceding formula repeatedly shows us that the coefficient of the term of second highest degree in the polynomial doubles each time, so after 2009 applications of $f$ it is $2^{2009}$.
$2^{\text {nd }}$ ANNUAL HARVARD-MIT NOVEMBER TOURNAMENT, 7 NOVEMBER 2009 - GUTS ROUND
|
{
"resource_path": "HarvardMIT/segmented/en-131-2009-nov-guts-solutions.jsonl",
"problem_match": "\n21. [11]",
"solution_match": "\nAnswer: "
}
|
c3745e9d-b65b-5429-ab05-91fcc0aeec5f
| 608,599
|
Five cards labeled A, B, C, D, and E are placed consecutively in a row. How many ways can they be re-arranged so that no card is moved more than one position away from where it started? (Not moving the cards at all counts as a valid re-arrangement.)
|
8 The only things we can do is leave cards where they are or switch them with adjacent cards. There is 1 way to leave them all where they are, 4 ways to switch just one adjacent pair, and 3 ways to switch two different adjacent pairs, for 8 possibilities total.
|
8
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Five cards labeled A, B, C, D, and E are placed consecutively in a row. How many ways can they be re-arranged so that no card is moved more than one position away from where it started? (Not moving the cards at all counts as a valid re-arrangement.)
|
8 The only things we can do is leave cards where they are or switch them with adjacent cards. There is 1 way to leave them all where they are, 4 ways to switch just one adjacent pair, and 3 ways to switch two different adjacent pairs, for 8 possibilities total.
|
{
"resource_path": "HarvardMIT/segmented/en-131-2009-nov-guts-solutions.jsonl",
"problem_match": "\n22. [12]",
"solution_match": "\nAnswer: "
}
|
93dd62b4-f1ca-52eb-892c-f7bd4904c573
| 608,600
|
Let $a_{0}, a_{1}, \ldots$ be a sequence such that $a_{0}=3, a_{1}=2$, and $a_{n+2}=a_{n+1}+a_{n}$ for all $n \geq 0$. Find
$$
\sum_{n=0}^{8} \frac{a_{n}}{a_{n+1} a_{n+2}}
$$
|
$\frac{105}{212}$ We can re-write $\frac{a_{n}}{a_{n+1} a_{n+2}}$ as $\frac{a_{n+2}-a_{n+1}}{a_{n+1} a_{n+2}}=\frac{1}{a_{n+1}}-\frac{1}{a_{n+2}}$. We can thus re-write the sum as
$$
\left(\frac{1}{a_{1}}-\frac{1}{a_{2}}\right)+\left(\frac{1}{a_{2}}-\frac{1}{a_{3}}\right)+\left(\frac{1}{a_{4}}-\frac{1}{a_{3}}\right)+\ldots+\left(\frac{1}{a_{9}}-\frac{1}{a_{10}}\right)=\frac{1}{a_{1}}-\frac{1}{a_{10}}=\frac{1}{2}-\frac{1}{212}=\frac{105}{212} .
$$
|
\frac{105}{212}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Let $a_{0}, a_{1}, \ldots$ be a sequence such that $a_{0}=3, a_{1}=2$, and $a_{n+2}=a_{n+1}+a_{n}$ for all $n \geq 0$. Find
$$
\sum_{n=0}^{8} \frac{a_{n}}{a_{n+1} a_{n+2}}
$$
|
$\frac{105}{212}$ We can re-write $\frac{a_{n}}{a_{n+1} a_{n+2}}$ as $\frac{a_{n+2}-a_{n+1}}{a_{n+1} a_{n+2}}=\frac{1}{a_{n+1}}-\frac{1}{a_{n+2}}$. We can thus re-write the sum as
$$
\left(\frac{1}{a_{1}}-\frac{1}{a_{2}}\right)+\left(\frac{1}{a_{2}}-\frac{1}{a_{3}}\right)+\left(\frac{1}{a_{4}}-\frac{1}{a_{3}}\right)+\ldots+\left(\frac{1}{a_{9}}-\frac{1}{a_{10}}\right)=\frac{1}{a_{1}}-\frac{1}{a_{10}}=\frac{1}{2}-\frac{1}{212}=\frac{105}{212} .
$$
|
{
"resource_path": "HarvardMIT/segmented/en-131-2009-nov-guts-solutions.jsonl",
"problem_match": "\n23. [12]",
"solution_match": "\nAnswer: "
}
|
221c417d-df6f-5af8-9a92-6854d6ee30e5
| 608,601
|
Penta chooses 5 of the vertices of a unit cube. What is the maximum possible volume of the figure whose vertices are the 5 chosen points?
|
$\frac{1}{2}$ Label the vertices of the cube $A, B, C, D, E, F, G, H$, such that $A B C D$ is the top face of the cube, $E$ is directly below $A, F$ is directly below $B, G$ is directly below $C$, and $H$ is directly
below $D$. We can obtain a volume of $\frac{1}{2}$ by taking the vertices $A, B, C, F$, and $H$. To compute the volume of $A C B F H$, we will instead compute the volume of the parts of the cube that are not part of $A B C F H$. This is just the three tetrahedrons $C F G H, A E F H$, and $A C D H$, which each have volume $\frac{1}{6}$ (by using the $\frac{1}{3} b h$ formula for the area of a pyramid). Therefore, the volume not contained in $A C B F H$ is $3 \cdot \frac{1}{6}=\frac{1}{2}$, so the volume contained in $A C B F H$ is $1-\frac{1}{2}=\frac{1}{2}$.
$2^{\text {nd }}$ ANNUAL HARVARD-MIT NOVEMBER TOURNAMENT, 7 NOVEMBER 2009 - GUTS ROUND
|
\frac{1}{2}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Penta chooses 5 of the vertices of a unit cube. What is the maximum possible volume of the figure whose vertices are the 5 chosen points?
|
$\frac{1}{2}$ Label the vertices of the cube $A, B, C, D, E, F, G, H$, such that $A B C D$ is the top face of the cube, $E$ is directly below $A, F$ is directly below $B, G$ is directly below $C$, and $H$ is directly
below $D$. We can obtain a volume of $\frac{1}{2}$ by taking the vertices $A, B, C, F$, and $H$. To compute the volume of $A C B F H$, we will instead compute the volume of the parts of the cube that are not part of $A B C F H$. This is just the three tetrahedrons $C F G H, A E F H$, and $A C D H$, which each have volume $\frac{1}{6}$ (by using the $\frac{1}{3} b h$ formula for the area of a pyramid). Therefore, the volume not contained in $A C B F H$ is $3 \cdot \frac{1}{6}=\frac{1}{2}$, so the volume contained in $A C B F H$ is $1-\frac{1}{2}=\frac{1}{2}$.
$2^{\text {nd }}$ ANNUAL HARVARD-MIT NOVEMBER TOURNAMENT, 7 NOVEMBER 2009 - GUTS ROUND
|
{
"resource_path": "HarvardMIT/segmented/en-131-2009-nov-guts-solutions.jsonl",
"problem_match": "\n24. [12]",
"solution_match": "\nAnswer: "
}
|
919a0476-dccb-5b30-9174-b7b14dd394f2
| 608,602
|
In how many ways can the positive integers from 1 to 100 be arranged in a circle such that the sum of every two integers placed opposite each other is the same? (Arrangements that are rotations of each other count as the same.) Express your answer in the form $a!\cdot b^{c}$.
|
$49!\cdot 2^{49}$ Split the integers up into pairs of the form $(x, 101-x)$. In the top half of the circle, exactly one element from each pair occurs, and there are thus 50 ! ways to arrange them. and also $2^{50}$ ways to decide whether the larger or smaller number in each pair occurs in the top half of the circle. We then need to divide by 100 since rotations are not considered distinct, so we get $\frac{50!2^{50}}{100}=49!\cdot 2^{49}$.
|
49!\cdot 2^{49}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
In how many ways can the positive integers from 1 to 100 be arranged in a circle such that the sum of every two integers placed opposite each other is the same? (Arrangements that are rotations of each other count as the same.) Express your answer in the form $a!\cdot b^{c}$.
|
$49!\cdot 2^{49}$ Split the integers up into pairs of the form $(x, 101-x)$. In the top half of the circle, exactly one element from each pair occurs, and there are thus 50 ! ways to arrange them. and also $2^{50}$ ways to decide whether the larger or smaller number in each pair occurs in the top half of the circle. We then need to divide by 100 since rotations are not considered distinct, so we get $\frac{50!2^{50}}{100}=49!\cdot 2^{49}$.
|
{
"resource_path": "HarvardMIT/segmented/en-131-2009-nov-guts-solutions.jsonl",
"problem_match": "\n26. [14]",
"solution_match": "\nAnswer: "
}
|
16607fdb-a33f-5b4a-9ba7-19f6e8390704
| 608,604
|
$A B C D$ is a regular tetrahedron of volume 1. Maria glues regular tetrahedra $A^{\prime} B C D, A B^{\prime} C D$, $A B C^{\prime} D$, and $A B C D^{\prime}$ to the faces of $A B C D$. What is the volume of the tetrahedron $A^{\prime} B^{\prime} C^{\prime} D^{\prime}$ ?
|
$\frac{125}{27}$ Consider the tetrahedron with vertices at $W=(1,0,0), X=(0,1,0), Y=(0,0,1)$, and $Z=(1,1,1)$. This tetrahedron is similar to $A B C D$. It has center $O=\left(\frac{1}{2}, \frac{1}{2}, \frac{1}{2}\right)$. We can construct a tetrahedron $W^{\prime} X^{\prime} Y^{\prime} Z^{\prime}$ in the same way that $A^{\prime} B^{\prime} C^{\prime} D^{\prime}$ was constructed by letting $W^{\prime}$ be the reflection of $W$ across $X Y Z$ and so forth. Then we see that $Z^{\prime}=\left(-\frac{1}{3},-\frac{1}{3},-\frac{1}{3}\right)$, so $O Z^{\prime}$ has length $\frac{5}{6} \sqrt{3}$, whereas $O Z$ has length $\frac{1}{2} \sqrt{3}$. We thus see that $W^{\prime} X^{\prime} Y^{\prime} Z^{\prime}$ has a side length $\frac{\frac{5}{6}}{\frac{1}{2}}=\frac{5}{3}$ that of $W X Y Z$, so by similarity the same is true of $A^{\prime} B^{\prime} C^{\prime} D^{\prime}$ and $A B C D$. In particular, the volume of $A^{\prime} B^{\prime} C^{\prime} D^{\prime}$ is $\left(\frac{5}{3}\right)^{3}$ that of $A B C D$, so it is $\frac{125}{27}$.
## $2^{\text {nd }}$ ANNUAL HARVARD-MIT NOVEMBER TOURNAMENT, 7 NOVEMBER 2009 - GUTS ROUND
|
\frac{125}{27}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
$A B C D$ is a regular tetrahedron of volume 1. Maria glues regular tetrahedra $A^{\prime} B C D, A B^{\prime} C D$, $A B C^{\prime} D$, and $A B C D^{\prime}$ to the faces of $A B C D$. What is the volume of the tetrahedron $A^{\prime} B^{\prime} C^{\prime} D^{\prime}$ ?
|
$\frac{125}{27}$ Consider the tetrahedron with vertices at $W=(1,0,0), X=(0,1,0), Y=(0,0,1)$, and $Z=(1,1,1)$. This tetrahedron is similar to $A B C D$. It has center $O=\left(\frac{1}{2}, \frac{1}{2}, \frac{1}{2}\right)$. We can construct a tetrahedron $W^{\prime} X^{\prime} Y^{\prime} Z^{\prime}$ in the same way that $A^{\prime} B^{\prime} C^{\prime} D^{\prime}$ was constructed by letting $W^{\prime}$ be the reflection of $W$ across $X Y Z$ and so forth. Then we see that $Z^{\prime}=\left(-\frac{1}{3},-\frac{1}{3},-\frac{1}{3}\right)$, so $O Z^{\prime}$ has length $\frac{5}{6} \sqrt{3}$, whereas $O Z$ has length $\frac{1}{2} \sqrt{3}$. We thus see that $W^{\prime} X^{\prime} Y^{\prime} Z^{\prime}$ has a side length $\frac{\frac{5}{6}}{\frac{1}{2}}=\frac{5}{3}$ that of $W X Y Z$, so by similarity the same is true of $A^{\prime} B^{\prime} C^{\prime} D^{\prime}$ and $A B C D$. In particular, the volume of $A^{\prime} B^{\prime} C^{\prime} D^{\prime}$ is $\left(\frac{5}{3}\right)^{3}$ that of $A B C D$, so it is $\frac{125}{27}$.
## $2^{\text {nd }}$ ANNUAL HARVARD-MIT NOVEMBER TOURNAMENT, 7 NOVEMBER 2009 - GUTS ROUND
|
{
"resource_path": "HarvardMIT/segmented/en-131-2009-nov-guts-solutions.jsonl",
"problem_match": "\n27. [14]",
"solution_match": "\nAnswer: "
}
|
c937dc0f-9600-582a-8873-6f73a3c71172
| 608,605
|
Six men and their wives are sitting at a round table with 12 seats. These men and women are very jealous - no man will allow his wife to sit next to any man except for himself, and no woman will allow her husband to sit next to any woman except for herself. In how many distinct ways can these 12 people be seated such that these conditions are satisfied? (Rotations of a valid seating are considered distinct.)
|
288000 Think of this problem in terms of "blocks" of men and women, that is, groups of men and women sitting together. Each block must contain at least two people; otherwise you have a man sitting next to two women (or vice-versa).
We will define the notation $\left[a_{1}, b_{1}, a_{2}, b_{2}, \ldots\right]$ to mean a seating arrangement consisting of, going in order, $a_{1}$ men, $b_{1}$ women, $a_{2}$ men, $b_{2}$ women, and so on.
Split the problem into three cases, each based on the number of blocks of men and women:
Case 1: One block of each, $[6,6]$.
There are 12 ways to choose the seats where the men sit, and $6!$ ways to arrange those men. The two women on either side of the men are uniquely determined by the men they sit next to. There are 4 ! ways to arrange the other four women. This gives $6!\cdot 288$ ways.
Case 2: Two blocks of each.
The arrangement is $[a, b, c, d]$, where $a+c=b+d=6$. There are five distinct block schematics: $[2,2,4,4],[2,3,4,3],[2,4,4,2],[3,2,3,4]$, and $[3,3,3,3]$. (The others are rotations of one of the above.) For each of these, there are 6 ! ways to arrange the men. In addition, four women are uniquely determined because they sit next to a man. There are 2 ways to arrange the other two women. Each of the first four possible block schematics gives 12 distinct rotations, while the fifth one gives 6 . This gives $6!(2)(12+12+12+12+6)=6!\cdot 108$ ways.
Case 3: Three blocks of each, $[2,2,2,2,2,2]$.
There are 4 ways to choose where the men sit and 6 ! ways to arrange those men. Each placement of men will uniquely determine the placement of each women. This gives $6!\cdot 4$ ways.
Then we have a grand total of $6!\cdot(288+108+4)=6!\cdot 400=288000$ seating arrangements.
|
288000
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Six men and their wives are sitting at a round table with 12 seats. These men and women are very jealous - no man will allow his wife to sit next to any man except for himself, and no woman will allow her husband to sit next to any woman except for herself. In how many distinct ways can these 12 people be seated such that these conditions are satisfied? (Rotations of a valid seating are considered distinct.)
|
288000 Think of this problem in terms of "blocks" of men and women, that is, groups of men and women sitting together. Each block must contain at least two people; otherwise you have a man sitting next to two women (or vice-versa).
We will define the notation $\left[a_{1}, b_{1}, a_{2}, b_{2}, \ldots\right]$ to mean a seating arrangement consisting of, going in order, $a_{1}$ men, $b_{1}$ women, $a_{2}$ men, $b_{2}$ women, and so on.
Split the problem into three cases, each based on the number of blocks of men and women:
Case 1: One block of each, $[6,6]$.
There are 12 ways to choose the seats where the men sit, and $6!$ ways to arrange those men. The two women on either side of the men are uniquely determined by the men they sit next to. There are 4 ! ways to arrange the other four women. This gives $6!\cdot 288$ ways.
Case 2: Two blocks of each.
The arrangement is $[a, b, c, d]$, where $a+c=b+d=6$. There are five distinct block schematics: $[2,2,4,4],[2,3,4,3],[2,4,4,2],[3,2,3,4]$, and $[3,3,3,3]$. (The others are rotations of one of the above.) For each of these, there are 6 ! ways to arrange the men. In addition, four women are uniquely determined because they sit next to a man. There are 2 ways to arrange the other two women. Each of the first four possible block schematics gives 12 distinct rotations, while the fifth one gives 6 . This gives $6!(2)(12+12+12+12+6)=6!\cdot 108$ ways.
Case 3: Three blocks of each, $[2,2,2,2,2,2]$.
There are 4 ways to choose where the men sit and 6 ! ways to arrange those men. Each placement of men will uniquely determine the placement of each women. This gives $6!\cdot 4$ ways.
Then we have a grand total of $6!\cdot(288+108+4)=6!\cdot 400=288000$ seating arrangements.
|
{
"resource_path": "HarvardMIT/segmented/en-131-2009-nov-guts-solutions.jsonl",
"problem_match": "\n28. [17]",
"solution_match": "\nAnswer: "
}
|
0f5967af-4a5c-56e4-b9c4-d68790f21395
| 608,606
|
For how many integer values of $b$ does there exist a polynomial function with integer coefficients such that $f(2)=2010$ and $f(b)=8$ ?
|
32 We can take $f(x)=-\frac{2002}{d}(x-b)+2010$ for all divisors $d$ of -2002 . To see that we can't get any others, note that $b-2$ must divide $f(b)-f(2)$, so $b-2$ divides -2002 (this is because $b-2$ divides $b^{n}-2^{n}$ and hence any sum of numbers of the form $b^{n}-2^{n}$ ).
|
32
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
For how many integer values of $b$ does there exist a polynomial function with integer coefficients such that $f(2)=2010$ and $f(b)=8$ ?
|
32 We can take $f(x)=-\frac{2002}{d}(x-b)+2010$ for all divisors $d$ of -2002 . To see that we can't get any others, note that $b-2$ must divide $f(b)-f(2)$, so $b-2$ divides -2002 (this is because $b-2$ divides $b^{n}-2^{n}$ and hence any sum of numbers of the form $b^{n}-2^{n}$ ).
|
{
"resource_path": "HarvardMIT/segmented/en-131-2009-nov-guts-solutions.jsonl",
"problem_match": "\n29. [17]",
"solution_match": "\nAnswer: "
}
|
45469582-7e4a-570c-af76-81b0b1787e2b
| 608,607
|
Regular hexagon $A B C D E F$ has side length 2. A laser beam is fired inside the hexagon from point $A$ and hits $\overline{B C}$ at point $G$. The laser then reflects off $\overline{B C}$ and hits the midpoint of $\overline{D E}$. Find $B G$.
|
$\frac{2}{5}$ Look at the diagram below, in which points $J, K, M, T$, and $X$ have been defined. $M$ is the midpoint of $\overline{D E}, B C J K$ is a rhombus with $J$ lying on the extension of $\overline{C D}, T$ is the intersection of lines $\overline{C D}$ and $\overline{G M}$ when extended, and $X$ is on $\overline{J T}$ such that $\overline{X M} \| \overline{J K}$.
It can be shown that $m \angle M D X=m \angle M X D=60^{\circ}$, so $\triangle D M X$ is equilateral, which yields $X M=1$. The diagram indicates that $J X=5$. One can show by angle-angle similarity that $\triangle T X M \sim \triangle T J K$, which yields $T X=5$.
One can also show by angle-angle similarity that $\triangle T J K \sim \triangle T C G$, which yields the proportion $\frac{T J}{J K}=\frac{T C}{C G}$. We know everything except $C G$, which we can solve for. This yields $C G=\frac{8}{5}$, so $B G=\frac{2}{5}$.
$2^{\text {nd }}$ ANNUAL HARVARD-MIT NOVEMBER TOURNAMENT, 7 NOVEMBER 2009 - GUTS ROUND
|
\frac{2}{5}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Regular hexagon $A B C D E F$ has side length 2. A laser beam is fired inside the hexagon from point $A$ and hits $\overline{B C}$ at point $G$. The laser then reflects off $\overline{B C}$ and hits the midpoint of $\overline{D E}$. Find $B G$.
|
$\frac{2}{5}$ Look at the diagram below, in which points $J, K, M, T$, and $X$ have been defined. $M$ is the midpoint of $\overline{D E}, B C J K$ is a rhombus with $J$ lying on the extension of $\overline{C D}, T$ is the intersection of lines $\overline{C D}$ and $\overline{G M}$ when extended, and $X$ is on $\overline{J T}$ such that $\overline{X M} \| \overline{J K}$.

It can be shown that $m \angle M D X=m \angle M X D=60^{\circ}$, so $\triangle D M X$ is equilateral, which yields $X M=1$. The diagram indicates that $J X=5$. One can show by angle-angle similarity that $\triangle T X M \sim \triangle T J K$, which yields $T X=5$.
One can also show by angle-angle similarity that $\triangle T J K \sim \triangle T C G$, which yields the proportion $\frac{T J}{J K}=\frac{T C}{C G}$. We know everything except $C G$, which we can solve for. This yields $C G=\frac{8}{5}$, so $B G=\frac{2}{5}$.
$2^{\text {nd }}$ ANNUAL HARVARD-MIT NOVEMBER TOURNAMENT, 7 NOVEMBER 2009 - GUTS ROUND
|
{
"resource_path": "HarvardMIT/segmented/en-131-2009-nov-guts-solutions.jsonl",
"problem_match": "\n30. [17]",
"solution_match": "\nAnswer: "
}
|
44664c6f-5c7e-5199-9494-7dfd47c52641
| 608,608
|
There are two buildings facing each other, each 5 stories high. How many ways can Kevin string ziplines between the buildings so that:
(a) each zipline starts and ends in the middle of a floor.
(b) ziplines can go up, stay flat, or go down, but can't touch each other (this includes touching at their endpoints).
Note that you can't string a zipline between two floors of the same building.
|
252 Associate with each configuration of ziplines a path in the plane as follows: Suppose there are $k$ ziplines. Let $a_{0}, \ldots, a_{k}$ be the distances between consecutive ziplines on the left building
( $a_{0}$ is the floor on which the first zipline starts, and $a_{k}$ is the distance from the last zipline to the top of the building). Define $b_{0}, \ldots, b_{k}$ analogously for the right building. The path in the plane consists of starting at $(0,0)$ and going a distance $a_{0}$ to the right, $b_{0}$ up, $a_{1}$ to the right, $b_{1}$ up, etc. We thus go from $(0,0)$ to $(5,5)$ while traveling only up and to the right between integer coordinates. We can check that there is exactly one configuration of ziplines for each such path, so the answer is the number of paths from $(0,0)$ to $(5,5)$ where you only travel up and to the right. This is equal to $\binom{10}{5}=252$, since there are 10 total steps to make, and we must choose which 5 of them go to the right.
|
252
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
There are two buildings facing each other, each 5 stories high. How many ways can Kevin string ziplines between the buildings so that:
(a) each zipline starts and ends in the middle of a floor.
(b) ziplines can go up, stay flat, or go down, but can't touch each other (this includes touching at their endpoints).
Note that you can't string a zipline between two floors of the same building.
|
252 Associate with each configuration of ziplines a path in the plane as follows: Suppose there are $k$ ziplines. Let $a_{0}, \ldots, a_{k}$ be the distances between consecutive ziplines on the left building
( $a_{0}$ is the floor on which the first zipline starts, and $a_{k}$ is the distance from the last zipline to the top of the building). Define $b_{0}, \ldots, b_{k}$ analogously for the right building. The path in the plane consists of starting at $(0,0)$ and going a distance $a_{0}$ to the right, $b_{0}$ up, $a_{1}$ to the right, $b_{1}$ up, etc. We thus go from $(0,0)$ to $(5,5)$ while traveling only up and to the right between integer coordinates. We can check that there is exactly one configuration of ziplines for each such path, so the answer is the number of paths from $(0,0)$ to $(5,5)$ where you only travel up and to the right. This is equal to $\binom{10}{5}=252$, since there are 10 total steps to make, and we must choose which 5 of them go to the right.
|
{
"resource_path": "HarvardMIT/segmented/en-131-2009-nov-guts-solutions.jsonl",
"problem_match": "\n31. [20]",
"solution_match": "\nAnswer: "
}
|
738f6bbc-cd5a-5475-bfe2-9d95aa657de2
| 608,609
|
A circle $\omega_{1}$ of radius 15 intersects a circle $\omega_{2}$ of radius 13 at points $P$ and $Q$. Point $A$ is on line $P Q$ such that $P$ is between $A$ and $Q . R$ and $S$ are the points of tangency from $A$ to $\omega_{1}$ and $\omega_{2}$, respectively, such that the line $A S$ does not intersect $\omega_{1}$ and the line $A R$ does not intersect $\omega_{2}$. If $P Q=24$ and $\angle R A S$ has a measure of $90^{\circ}$, compute the length of $A R$.
|
$\sqrt[{14+\sqrt{97}}]{ }$ Let $O_{1}$ be the center of $\omega_{1}$ and $O_{2}$ be the center of $\omega_{2}$. Then $O_{1} O_{2}$ and $P Q$ are perpendicular. Let their point of intersection be $X$. Using the Pythagorean theorem, the fact that $P Q=24$, and our knowledge of the radii of the circles, we can compute that $O_{1} X=9$ and $O_{2} X=5$, so $O_{1} O_{2}=14$. Let $S O_{1}$ and $R O_{2}$ meet at $Y$. Then $S A R Y$ is a square, say of side length $s$. Then $O_{1} Y=s-15$ and $O_{2} Y=s-13$. So, $O_{1} O_{2} Y$ is a right triangle with sides $14, s-15$, and $s-13$. By the Pythagorean theorem, $(s-13)^{2}+(s-15)^{2}=14^{2}$. We can write this as $2 s^{2}-4 \cdot 14 s+198=0$, or $s^{2}-28 s+99=0$. The quadratic formula then gives $s=\frac{28 \pm \sqrt{388}}{2}=14 \pm \sqrt{97}$. Since $14-\sqrt{97}<15$ and $Y O_{1}>15$, we can discard the root of $14-\sqrt{97}$, and the answer is therefore $14+\sqrt{97}$.
|
14+\sqrt{97}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
A circle $\omega_{1}$ of radius 15 intersects a circle $\omega_{2}$ of radius 13 at points $P$ and $Q$. Point $A$ is on line $P Q$ such that $P$ is between $A$ and $Q . R$ and $S$ are the points of tangency from $A$ to $\omega_{1}$ and $\omega_{2}$, respectively, such that the line $A S$ does not intersect $\omega_{1}$ and the line $A R$ does not intersect $\omega_{2}$. If $P Q=24$ and $\angle R A S$ has a measure of $90^{\circ}$, compute the length of $A R$.
|
$\sqrt[{14+\sqrt{97}}]{ }$ Let $O_{1}$ be the center of $\omega_{1}$ and $O_{2}$ be the center of $\omega_{2}$. Then $O_{1} O_{2}$ and $P Q$ are perpendicular. Let their point of intersection be $X$. Using the Pythagorean theorem, the fact that $P Q=24$, and our knowledge of the radii of the circles, we can compute that $O_{1} X=9$ and $O_{2} X=5$, so $O_{1} O_{2}=14$. Let $S O_{1}$ and $R O_{2}$ meet at $Y$. Then $S A R Y$ is a square, say of side length $s$. Then $O_{1} Y=s-15$ and $O_{2} Y=s-13$. So, $O_{1} O_{2} Y$ is a right triangle with sides $14, s-15$, and $s-13$. By the Pythagorean theorem, $(s-13)^{2}+(s-15)^{2}=14^{2}$. We can write this as $2 s^{2}-4 \cdot 14 s+198=0$, or $s^{2}-28 s+99=0$. The quadratic formula then gives $s=\frac{28 \pm \sqrt{388}}{2}=14 \pm \sqrt{97}$. Since $14-\sqrt{97}<15$ and $Y O_{1}>15$, we can discard the root of $14-\sqrt{97}$, and the answer is therefore $14+\sqrt{97}$.
|
{
"resource_path": "HarvardMIT/segmented/en-131-2009-nov-guts-solutions.jsonl",
"problem_match": "\n32. [20]",
"solution_match": "\nAnswer: "
}
|
890ea497-3237-5154-9fb4-77afb62323c3
| 608,610
|
Compute
$$
\sum_{n=2009}^{\infty} \frac{1}{\binom{n}{2009}}
$$
Note that $\binom{n}{k}$ is defined as $\frac{n!}{k!(n-k)!}$.
|
$\frac{2009}{2008}$ Observe that
$$
\begin{aligned}
\frac{k+1}{k}\left(\frac{1}{\binom{n-1}{k}}-\frac{1}{\binom{n}{k}}\right) & =\frac{k+1}{k} \frac{\binom{n}{k}-\binom{n-1}{k}}{\binom{n}{k}\binom{n-1}{k}} \\
& =\frac{k+1}{k} \frac{\binom{n-1}{k-1}}{\binom{n}{k}\binom{n-1}{k}} \\
& =\frac{k+1}{k} \frac{(n-1)!k!k!(n-k-1)!(n-k)!}{n!(n-1)!(k-1)!(n-k)!} \\
& =\frac{k+1}{k} \frac{k \cdot k!(n-k-1)!}{n!} \\
& =\frac{(k+1)!(n-k-1)!}{n!} \\
& =\frac{1}{\binom{n}{k+1}}
\end{aligned}
$$
Now apply this with $k=2008$ and sum across all $n$ from 2009 to $\infty$. We get
$$
\sum_{n=2009}^{\infty} \frac{1}{\binom{n}{2009}}=\frac{2009}{2008} \sum_{n=2009}^{\infty} \frac{1}{\binom{n-1}{2008}}-\frac{1}{\binom{n}{2008}}
$$
All terms from the sum on the right-hand-side cancel, except for the initial $\frac{1}{\binom{2008}{2008}}$, which is equal to 1 , so we get $\sum_{n=2009}^{\infty} \frac{1}{\binom{n}{2009}}=\frac{2009}{2008}$.
|
\frac{2009}{2008}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Compute
$$
\sum_{n=2009}^{\infty} \frac{1}{\binom{n}{2009}}
$$
Note that $\binom{n}{k}$ is defined as $\frac{n!}{k!(n-k)!}$.
|
$\frac{2009}{2008}$ Observe that
$$
\begin{aligned}
\frac{k+1}{k}\left(\frac{1}{\binom{n-1}{k}}-\frac{1}{\binom{n}{k}}\right) & =\frac{k+1}{k} \frac{\binom{n}{k}-\binom{n-1}{k}}{\binom{n}{k}\binom{n-1}{k}} \\
& =\frac{k+1}{k} \frac{\binom{n-1}{k-1}}{\binom{n}{k}\binom{n-1}{k}} \\
& =\frac{k+1}{k} \frac{(n-1)!k!k!(n-k-1)!(n-k)!}{n!(n-1)!(k-1)!(n-k)!} \\
& =\frac{k+1}{k} \frac{k \cdot k!(n-k-1)!}{n!} \\
& =\frac{(k+1)!(n-k-1)!}{n!} \\
& =\frac{1}{\binom{n}{k+1}}
\end{aligned}
$$
Now apply this with $k=2008$ and sum across all $n$ from 2009 to $\infty$. We get
$$
\sum_{n=2009}^{\infty} \frac{1}{\binom{n}{2009}}=\frac{2009}{2008} \sum_{n=2009}^{\infty} \frac{1}{\binom{n-1}{2008}}-\frac{1}{\binom{n}{2008}}
$$
All terms from the sum on the right-hand-side cancel, except for the initial $\frac{1}{\binom{2008}{2008}}$, which is equal to 1 , so we get $\sum_{n=2009}^{\infty} \frac{1}{\binom{n}{2009}}=\frac{2009}{2008}$.
|
{
"resource_path": "HarvardMIT/segmented/en-131-2009-nov-guts-solutions.jsonl",
"problem_match": "\n33. [20]",
"solution_match": "\nAnswer: "
}
|
3d683e69-a814-5694-83ce-b68e794c2a12
| 608,611
|
Call an integer $n>1$ radical if $2^{n}-1$ is prime. What is the 20 th smallest radical number? If $A$ is your answer, and $S$ is the correct answer, you will get $\max \left(25\left(1-\frac{|A-S|}{S}\right), 0\right)$ points, rounded to the nearest integer.
|
4423
|
4423
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Call an integer $n>1$ radical if $2^{n}-1$ is prime. What is the 20 th smallest radical number? If $A$ is your answer, and $S$ is the correct answer, you will get $\max \left(25\left(1-\frac{|A-S|}{S}\right), 0\right)$ points, rounded to the nearest integer.
|
4423
|
{
"resource_path": "HarvardMIT/segmented/en-131-2009-nov-guts-solutions.jsonl",
"problem_match": "\n35. [25]",
"solution_match": "\nAnswer: "
}
|
f9acbcf1-2bb9-5ec3-ab43-155431f006ff
| 608,613
|
In how many ways can the ball be launched so that it will return again to a vertex for the first time after 2009 bounces?
|
502 We will use the same idea as in the previous problem. We first note that every vertex of a triangle can be written uniquely in the form $a(5,0)+b\left(\frac{5}{2}, \frac{5 \sqrt{3}}{2}\right)$, where $a$ and $b$ are non-negative integers. Furthermore, if a ball ends at $a(5,0)+b\left(\frac{5}{2}, \frac{5 \sqrt{3}}{2}\right)$, then it bounches off of a wall $2(a+b)-3$ times. Therefore, the possible directions that you can launch the ball in correspond to solutions to $2(a+b)-3=2009$, or $a+b=1006$. However, if $a$ and $b$ have a common factor, say, $k$, then the ball will pass through the vertex corresponding to $\frac{a}{k}$ and $\frac{b}{k}$ before it passes through the vertex corresponding to $a$ and $b$. Therefore, we must discount all such pairs $a, b$. This corresponds to when $a$ is even or $a=503$, so after removing these we are left with 502 remaining possible values of $a$, hence 502 possible directions in which to launch the ball.
## Super Mario 64!
Mario is once again on a quest to save Princess Peach. Mario enters Peach's castle and finds himself in a room with 4 doors. This room is the first in a sequence of 2 indistinugishable rooms. In each room, 1 door leads to the next room in the sequence (or, for the second room, into Bowser's level), while the other 3 doors lead to the first room.
|
502
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
In how many ways can the ball be launched so that it will return again to a vertex for the first time after 2009 bounces?
|
502 We will use the same idea as in the previous problem. We first note that every vertex of a triangle can be written uniquely in the form $a(5,0)+b\left(\frac{5}{2}, \frac{5 \sqrt{3}}{2}\right)$, where $a$ and $b$ are non-negative integers. Furthermore, if a ball ends at $a(5,0)+b\left(\frac{5}{2}, \frac{5 \sqrt{3}}{2}\right)$, then it bounches off of a wall $2(a+b)-3$ times. Therefore, the possible directions that you can launch the ball in correspond to solutions to $2(a+b)-3=2009$, or $a+b=1006$. However, if $a$ and $b$ have a common factor, say, $k$, then the ball will pass through the vertex corresponding to $\frac{a}{k}$ and $\frac{b}{k}$ before it passes through the vertex corresponding to $a$ and $b$. Therefore, we must discount all such pairs $a, b$. This corresponds to when $a$ is even or $a=503$, so after removing these we are left with 502 remaining possible values of $a$, hence 502 possible directions in which to launch the ball.
## Super Mario 64!
Mario is once again on a quest to save Princess Peach. Mario enters Peach's castle and finds himself in a room with 4 doors. This room is the first in a sequence of 2 indistinugishable rooms. In each room, 1 door leads to the next room in the sequence (or, for the second room, into Bowser's level), while the other 3 doors lead to the first room.
|
{
"resource_path": "HarvardMIT/segmented/en-131-2009-nov-team-solutions.jsonl",
"problem_match": "\n8. [6]",
"solution_match": "\nAnswer: "
}
|
176115bb-557d-5d93-a11c-f8142e3ddd4c
| 608,619
|
Suppose that in every room, Mario randomly picks a door to walk through. What is the expected number of doors (not including Mario's initial entrance to the first room) through which Mario will pass before he reaches Bowser's level?
|
20 Let $E_{i}$ be the expected number of doors through which Mario will pass in the future if he is currently in room $i$ for $i=1,2,3$ (we will set $E_{3}=0$ ). We claim that $E_{i}=1+\frac{3}{4} E_{1}+\frac{1}{4} E_{i+1}$. Indeed, the 1 at the beginning comes from the fact that we need to pass through a door to leave the room, the $\frac{3}{4} E_{1}$ comes from the fact that there is a $\frac{3}{4}$ chance of ending up in room 1 , and the $\frac{1}{4} E_{i+1}$ corresponds to the fact that there is a $\frac{1}{4}$ chance of ending up in $E_{i+1}$. Using this, we get $E_{1}=1+\frac{3}{4} E_{1}+\frac{1}{4} E_{2}$, or $E_{1}=4+E_{2}$. We also get $E_{2}=1+\frac{3}{4} E_{1}$. Solving this system of equations yields $E_{1}=20$.
|
20
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Suppose that in every room, Mario randomly picks a door to walk through. What is the expected number of doors (not including Mario's initial entrance to the first room) through which Mario will pass before he reaches Bowser's level?
|
20 Let $E_{i}$ be the expected number of doors through which Mario will pass in the future if he is currently in room $i$ for $i=1,2,3$ (we will set $E_{3}=0$ ). We claim that $E_{i}=1+\frac{3}{4} E_{1}+\frac{1}{4} E_{i+1}$. Indeed, the 1 at the beginning comes from the fact that we need to pass through a door to leave the room, the $\frac{3}{4} E_{1}$ comes from the fact that there is a $\frac{3}{4}$ chance of ending up in room 1 , and the $\frac{1}{4} E_{i+1}$ corresponds to the fact that there is a $\frac{1}{4}$ chance of ending up in $E_{i+1}$. Using this, we get $E_{1}=1+\frac{3}{4} E_{1}+\frac{1}{4} E_{2}$, or $E_{1}=4+E_{2}$. We also get $E_{2}=1+\frac{3}{4} E_{1}$. Solving this system of equations yields $E_{1}=20$.
|
{
"resource_path": "HarvardMIT/segmented/en-131-2009-nov-team-solutions.jsonl",
"problem_match": "\n9. [3]",
"solution_match": "\nAnswer: "
}
|
62857ac9-0587-589c-88a8-e9bb23173ac4
| 608,620
|
In general, if there are $d$ doors in every room (but still only 1 correct door) and $r$ rooms, the last of which leads into Bowser's level, what is the expected number of doors through which Mario will pass before he reaches Bowser's level?
|
$\frac{d\left(d^{r}-1\right)}{d-1}$ Let $E_{i}$ be the expected number of doors through which Mario will pass in the future if he is currently in room $i$ for $i=1,2, \ldots, r+1$ (we will set $E_{r+1}=0$ ). We claim that $E_{i}=1+\frac{d-1}{d} E_{1}+\frac{1}{d} E_{i+1}$. This is because, as before, there is a $\frac{d-1}{d}$ chance of ending up in room 1, and a $\frac{1}{d}$ chance of ending up in room $i+1$. Note that we can re-write this equation as $d E_{i}=d+(d-1) E_{1}+E_{i+1}$.
We can solve this system of equation as follows: let $E_{1}=E_{i}+c_{i}$. Then we can re-write each equation as $d E_{1}-d \cdot c_{i}=d+(d-1) E_{1}+E_{1}-c_{i+1}$, so $c_{i+1}=d \cdot c_{i}+d$, and $c_{1}=0$. We can then see that $c_{i}=d \frac{d^{i-1}-1}{d-1}$ (either by finding the pattern or by using more advanced techniques, such as those given at http://en.wikipedia.org/wiki/Recurrence_relation). Solving for $E_{1}$ using $E_{1}=E_{r}+c_{r}$ and $E_{r}=1+\frac{d-1}{d} E_{1}$, we get $E_{1}=\frac{d\left(d^{r}-1\right)}{d-1}$.
|
\frac{d\left(d^{r}-1\right)}{d-1}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
In general, if there are $d$ doors in every room (but still only 1 correct door) and $r$ rooms, the last of which leads into Bowser's level, what is the expected number of doors through which Mario will pass before he reaches Bowser's level?
|
$\frac{d\left(d^{r}-1\right)}{d-1}$ Let $E_{i}$ be the expected number of doors through which Mario will pass in the future if he is currently in room $i$ for $i=1,2, \ldots, r+1$ (we will set $E_{r+1}=0$ ). We claim that $E_{i}=1+\frac{d-1}{d} E_{1}+\frac{1}{d} E_{i+1}$. This is because, as before, there is a $\frac{d-1}{d}$ chance of ending up in room 1, and a $\frac{1}{d}$ chance of ending up in room $i+1$. Note that we can re-write this equation as $d E_{i}=d+(d-1) E_{1}+E_{i+1}$.
We can solve this system of equation as follows: let $E_{1}=E_{i}+c_{i}$. Then we can re-write each equation as $d E_{1}-d \cdot c_{i}=d+(d-1) E_{1}+E_{1}-c_{i+1}$, so $c_{i+1}=d \cdot c_{i}+d$, and $c_{1}=0$. We can then see that $c_{i}=d \frac{d^{i-1}-1}{d-1}$ (either by finding the pattern or by using more advanced techniques, such as those given at http://en.wikipedia.org/wiki/Recurrence_relation). Solving for $E_{1}$ using $E_{1}=E_{r}+c_{r}$ and $E_{r}=1+\frac{d-1}{d} E_{1}$, we get $E_{1}=\frac{d\left(d^{r}-1\right)}{d-1}$.
|
{
"resource_path": "HarvardMIT/segmented/en-131-2009-nov-team-solutions.jsonl",
"problem_match": "\n11. [5]",
"solution_match": "\nAnswer: "
}
|
673ecda3-efda-5ad2-8c00-dcf685eea4a5
| 608,622
|
Suppose that $x$ and $y$ are positive reals such that
$$
x-y^{2}=3, \quad x^{2}+y^{4}=13
$$
Find $x$.
|
$\frac{3+\sqrt{17}}{2}$ Squaring both sides of $x-y^{2}=3$ gives $x^{2}+y^{4}-2 x y^{2}=9$. Subtract this equation from twice the second given to get $x^{2}+2 x y^{2}+y^{4}=17 \Longrightarrow x+y^{2}= \pm 17$. Combining this equation with the first given, we see that $x=\frac{3 \pm \sqrt{17}}{2}$. Since $x$ is a positive real, $x$ must be $\frac{3+\sqrt{17}}{2}$.
|
\frac{3+\sqrt{17}}{2}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Suppose that $x$ and $y$ are positive reals such that
$$
x-y^{2}=3, \quad x^{2}+y^{4}=13
$$
Find $x$.
|
$\frac{3+\sqrt{17}}{2}$ Squaring both sides of $x-y^{2}=3$ gives $x^{2}+y^{4}-2 x y^{2}=9$. Subtract this equation from twice the second given to get $x^{2}+2 x y^{2}+y^{4}=17 \Longrightarrow x+y^{2}= \pm 17$. Combining this equation with the first given, we see that $x=\frac{3 \pm \sqrt{17}}{2}$. Since $x$ is a positive real, $x$ must be $\frac{3+\sqrt{17}}{2}$.
|
{
"resource_path": "HarvardMIT/segmented/en-132-2010-feb-alg-solutions.jsonl",
"problem_match": "\n1. [3]",
"solution_match": "\nAnswer: "
}
|
10fd318c-80b8-5161-89d9-228d593f3df7
| 608,623
|
Let $S_{0}=0$ and let $S_{k}$ equal $a_{1}+2 a_{2}+\ldots+k a_{k}$ for $k \geq 1$. Define $a_{i}$ to be 1 if $S_{i-1}<i$ and -1 if $S_{i-1} \geq i$. What is the largest $k \leq 2010$ such that $S_{k}=0$ ?
|
1092 Suppose that $S_{N}=0$ for some $N \geq 0$. Then $a_{N+1}=1$ because $N+1 \geq S_{N}$. The following table lists the values of $a_{k}$ and $S_{k}$ for a few $k \geq N$ :
| $k$ | $a_{k}$ | $S_{k}$ |
| :--- | ---: | :--- |
| $N$ | | 0 |
| $N+1$ | 1 | $N+1$ |
| $N+2$ | 1 | $2 N+3$ |
| $N+3$ | -1 | $N$ |
| $N+4$ | 1 | $2 N+4$ |
| $N+5$ | -1 | $N-1$ |
| $N+6$ | 1 | $2 N+5$ |
| $N+7$ | -1 | $N-2$ |
We see inductively that, for every $i \geq 1$,
$$
S_{N+2 i}=2 N+2+i
$$
and
$$
S_{N+1+2 i}=N+1-i
$$
thus $S_{3 N+3}=0$ is the next $k$ for which $S_{k}=0$. The values of $k$ for which $S_{k}=0$ satisfy the recurrence relation $p_{n+1}=3 p_{n}+3$, and we compute that the first terms of the sequence are $0,3,12,39,120,363,1092$; hence 1092 is our answer.
|
1092
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Let $S_{0}=0$ and let $S_{k}$ equal $a_{1}+2 a_{2}+\ldots+k a_{k}$ for $k \geq 1$. Define $a_{i}$ to be 1 if $S_{i-1}<i$ and -1 if $S_{i-1} \geq i$. What is the largest $k \leq 2010$ such that $S_{k}=0$ ?
|
1092 Suppose that $S_{N}=0$ for some $N \geq 0$. Then $a_{N+1}=1$ because $N+1 \geq S_{N}$. The following table lists the values of $a_{k}$ and $S_{k}$ for a few $k \geq N$ :
| $k$ | $a_{k}$ | $S_{k}$ |
| :--- | ---: | :--- |
| $N$ | | 0 |
| $N+1$ | 1 | $N+1$ |
| $N+2$ | 1 | $2 N+3$ |
| $N+3$ | -1 | $N$ |
| $N+4$ | 1 | $2 N+4$ |
| $N+5$ | -1 | $N-1$ |
| $N+6$ | 1 | $2 N+5$ |
| $N+7$ | -1 | $N-2$ |
We see inductively that, for every $i \geq 1$,
$$
S_{N+2 i}=2 N+2+i
$$
and
$$
S_{N+1+2 i}=N+1-i
$$
thus $S_{3 N+3}=0$ is the next $k$ for which $S_{k}=0$. The values of $k$ for which $S_{k}=0$ satisfy the recurrence relation $p_{n+1}=3 p_{n}+3$, and we compute that the first terms of the sequence are $0,3,12,39,120,363,1092$; hence 1092 is our answer.
|
{
"resource_path": "HarvardMIT/segmented/en-132-2010-feb-alg-solutions.jsonl",
"problem_match": "\n3. [4]",
"solution_match": "\nAnswer: "
}
|
52a2df19-7968-5bd1-9941-147ec11e00a5
| 608,625
|
Suppose that $x$ and $y$ are complex numbers such that $x+y=1$ and that $x^{20}+y^{20}=20$. Find the sum of all possible values of $x^{2}+y^{2}$.
|
-90 We have $x^{2}+y^{2}+2 x y=1$. Define $a=2 x y$ and $b=x^{2}+y^{2}$ for convenience. Then $a+b=1$ and $b-a=x^{2}+y^{2}-2 x y=(x-y)^{2}=2 b-1$ so that $x, y=\frac{\sqrt{2 b-1} \pm 1}{2}$. Then
$$
\begin{aligned}
x^{20}+y^{20} & =\left(\frac{\sqrt{2 b-1}+1}{2}\right)^{20}+\left(\frac{\sqrt{2 b-1}-1}{2}\right)^{20} \\
& =\frac{1}{2^{20}}\left[(\sqrt{2 b-1}+1)^{20}+(\sqrt{2 b-1}-1)^{20}\right] \\
& =\frac{2}{2^{20}}\left[(\sqrt{2 b-1})^{20}+\binom{20}{2}(\sqrt{2 b-1})^{18}+\binom{20}{4}(\sqrt{2 b-1})^{16}+\ldots\right] \\
& =\frac{2}{2^{20}}\left[(2 b-1)^{10}+\binom{20}{2}(2 b-1)^{9}+\binom{20}{4}(2 b-1)^{8}+\ldots\right] \\
& =20
\end{aligned}
$$
We want to find the sum of distinct roots of the above polynomial in $b$; we first prove that the original polynomial is square-free. The conditions $x+y=1$ and $x^{20}+y^{20}=20$ imply that $x^{20}+(1-x)^{20}-20=0$; let $p(x)=x^{20}+(1-x)^{20}-20 . p$ is square-free if and only if $G C D\left(p, p^{\prime}\right)=c$ for some constant $c$ :
$$
\begin{aligned}
\operatorname{GCD}\left(p, p^{\prime}\right) & =\operatorname{GCD}\left(x^{20}+(1-x)^{20}-20,20\left(x^{19}-(1-x)^{19}\right)\right) \\
& =\operatorname{GCD}\left(x^{20}-x(1-x)^{19}+(1-x)^{19}-20,20\left(x^{19}-(1-x)^{19}\right)\right) \\
& =G C D\left((1-x)^{19}-20, x^{19}-(1-x)^{19}\right) \\
& =G C D\left((1-x)^{19}-20, x^{19}-20\right)
\end{aligned}
$$
The roots of $x^{19}-20$ are $\sqrt[19]{20^{k}} \exp \left(\frac{2 \pi i k}{19}\right)$ for some $k=0,1, \ldots, 18$; the roots of $(1-x)^{19}-20$ are $1-\sqrt[19]{20^{k}} \exp \left(\frac{2 \pi i k}{19}\right)$ for some $k=0,1, \ldots, 18$. If $x^{19}-20$ and $(1-x)^{19}-20$ share a common root, then there exist integers $m, n$ such that $\sqrt[19]{20^{m}} \exp \left(\frac{2 \pi i m}{19}\right)=1-\sqrt[19]{20^{n}} \exp \left(\frac{2 \pi i n}{19}\right)$; since the imaginary parts of both sides must be the same, we have $m=n$ and $\sqrt[19]{20^{m}} \exp \left(\frac{2 \pi i m}{19}\right)=\frac{1}{2} \Longrightarrow 20^{m}=\frac{1}{2^{19}}$, a contradiction. Thus we have proved that the polynomial in $x$ has no double roots. Since for each $b$ there exists a unique pair ( $x, y$ ) (up to permutations) that satisfies $x^{2}+y^{2}=b$ and $(x+y)^{2}=1$, the polynomial in $b$ has no double roots.
Let the coefficient of $b^{n}$ in the above equation be $\left[b^{n}\right]$. By Vieta's Formulas, the sum of all possible values of $b=x^{2}+y^{2}$ is equal to $-\frac{\left[b^{9}\right]}{\left[b^{0}\right]} .\left[b^{10}\right]=\frac{2}{2^{20}}\left(2^{10}\right)$ and $\left[b^{9}\right]=\frac{2}{2^{20}}\left(-\binom{10}{1} 2^{9}+\binom{20}{2} 2^{9}\right)$; thus $-\frac{\left[b^{9}\right]}{\left[b^{10}\right]}=-\frac{\binom{10}{1} 2^{9}-\binom{20}{2_{2}}^{9}}{2^{10}}=-90$.
|
-90
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Suppose that $x$ and $y$ are complex numbers such that $x+y=1$ and that $x^{20}+y^{20}=20$. Find the sum of all possible values of $x^{2}+y^{2}$.
|
-90 We have $x^{2}+y^{2}+2 x y=1$. Define $a=2 x y$ and $b=x^{2}+y^{2}$ for convenience. Then $a+b=1$ and $b-a=x^{2}+y^{2}-2 x y=(x-y)^{2}=2 b-1$ so that $x, y=\frac{\sqrt{2 b-1} \pm 1}{2}$. Then
$$
\begin{aligned}
x^{20}+y^{20} & =\left(\frac{\sqrt{2 b-1}+1}{2}\right)^{20}+\left(\frac{\sqrt{2 b-1}-1}{2}\right)^{20} \\
& =\frac{1}{2^{20}}\left[(\sqrt{2 b-1}+1)^{20}+(\sqrt{2 b-1}-1)^{20}\right] \\
& =\frac{2}{2^{20}}\left[(\sqrt{2 b-1})^{20}+\binom{20}{2}(\sqrt{2 b-1})^{18}+\binom{20}{4}(\sqrt{2 b-1})^{16}+\ldots\right] \\
& =\frac{2}{2^{20}}\left[(2 b-1)^{10}+\binom{20}{2}(2 b-1)^{9}+\binom{20}{4}(2 b-1)^{8}+\ldots\right] \\
& =20
\end{aligned}
$$
We want to find the sum of distinct roots of the above polynomial in $b$; we first prove that the original polynomial is square-free. The conditions $x+y=1$ and $x^{20}+y^{20}=20$ imply that $x^{20}+(1-x)^{20}-20=0$; let $p(x)=x^{20}+(1-x)^{20}-20 . p$ is square-free if and only if $G C D\left(p, p^{\prime}\right)=c$ for some constant $c$ :
$$
\begin{aligned}
\operatorname{GCD}\left(p, p^{\prime}\right) & =\operatorname{GCD}\left(x^{20}+(1-x)^{20}-20,20\left(x^{19}-(1-x)^{19}\right)\right) \\
& =\operatorname{GCD}\left(x^{20}-x(1-x)^{19}+(1-x)^{19}-20,20\left(x^{19}-(1-x)^{19}\right)\right) \\
& =G C D\left((1-x)^{19}-20, x^{19}-(1-x)^{19}\right) \\
& =G C D\left((1-x)^{19}-20, x^{19}-20\right)
\end{aligned}
$$
The roots of $x^{19}-20$ are $\sqrt[19]{20^{k}} \exp \left(\frac{2 \pi i k}{19}\right)$ for some $k=0,1, \ldots, 18$; the roots of $(1-x)^{19}-20$ are $1-\sqrt[19]{20^{k}} \exp \left(\frac{2 \pi i k}{19}\right)$ for some $k=0,1, \ldots, 18$. If $x^{19}-20$ and $(1-x)^{19}-20$ share a common root, then there exist integers $m, n$ such that $\sqrt[19]{20^{m}} \exp \left(\frac{2 \pi i m}{19}\right)=1-\sqrt[19]{20^{n}} \exp \left(\frac{2 \pi i n}{19}\right)$; since the imaginary parts of both sides must be the same, we have $m=n$ and $\sqrt[19]{20^{m}} \exp \left(\frac{2 \pi i m}{19}\right)=\frac{1}{2} \Longrightarrow 20^{m}=\frac{1}{2^{19}}$, a contradiction. Thus we have proved that the polynomial in $x$ has no double roots. Since for each $b$ there exists a unique pair ( $x, y$ ) (up to permutations) that satisfies $x^{2}+y^{2}=b$ and $(x+y)^{2}=1$, the polynomial in $b$ has no double roots.
Let the coefficient of $b^{n}$ in the above equation be $\left[b^{n}\right]$. By Vieta's Formulas, the sum of all possible values of $b=x^{2}+y^{2}$ is equal to $-\frac{\left[b^{9}\right]}{\left[b^{0}\right]} .\left[b^{10}\right]=\frac{2}{2^{20}}\left(2^{10}\right)$ and $\left[b^{9}\right]=\frac{2}{2^{20}}\left(-\binom{10}{1} 2^{9}+\binom{20}{2} 2^{9}\right)$; thus $-\frac{\left[b^{9}\right]}{\left[b^{10}\right]}=-\frac{\binom{10}{1} 2^{9}-\binom{20}{2_{2}}^{9}}{2^{10}}=-90$.
|
{
"resource_path": "HarvardMIT/segmented/en-132-2010-feb-alg-solutions.jsonl",
"problem_match": "\n5. [5]",
"solution_match": "\nAnswer: "
}
|
16f2293d-d4b4-5fb8-b300-24c4256837f8
| 608,627
|
Suppose that a polynomial of the form $p(x)=x^{2010} \pm x^{2009} \pm \cdots \pm x \pm 1$ has no real roots. What is the maximum possible number of coefficients of -1 in $p$ ?
|
1005 Let $p(x)$ be a polynomial with the maximum number of minus signs. $p(x)$ cannot have more than 1005 minus signs, otherwise $p(1)<0$ and $p(2) \geq 2^{2010}-2^{2009}-\ldots-2-1=$ 1 , which implies, by the Intermediate Value Theorem, that $p$ must have a root greater than 1 .
Let $p(x)=\frac{x^{2011}+1}{x+1}=x^{2010}-x^{2009}+x^{2008}-\ldots-x+1$. -1 is the only real root of $x^{2011}+1=0$ but $p(-1)=2011$; therefore $p$ has no real roots. Since $p$ has 1005 minus signs, it is the desired polynomial.
|
1005
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Suppose that a polynomial of the form $p(x)=x^{2010} \pm x^{2009} \pm \cdots \pm x \pm 1$ has no real roots. What is the maximum possible number of coefficients of -1 in $p$ ?
|
1005 Let $p(x)$ be a polynomial with the maximum number of minus signs. $p(x)$ cannot have more than 1005 minus signs, otherwise $p(1)<0$ and $p(2) \geq 2^{2010}-2^{2009}-\ldots-2-1=$ 1 , which implies, by the Intermediate Value Theorem, that $p$ must have a root greater than 1 .
Let $p(x)=\frac{x^{2011}+1}{x+1}=x^{2010}-x^{2009}+x^{2008}-\ldots-x+1$. -1 is the only real root of $x^{2011}+1=0$ but $p(-1)=2011$; therefore $p$ has no real roots. Since $p$ has 1005 minus signs, it is the desired polynomial.
|
{
"resource_path": "HarvardMIT/segmented/en-132-2010-feb-alg-solutions.jsonl",
"problem_match": "\n6. [5]",
"solution_match": "\nAnswer: "
}
|
9cabab8c-9bcc-5b91-812f-a7d34ba82326
| 608,628
|
Let $a, b, c, x, y$, and $z$ be complex numbers such that
$$
a=\frac{b+c}{x-2}, \quad b=\frac{c+a}{y-2}, \quad c=\frac{a+b}{z-2} .
$$
If $x y+y z+z x=67$ and $x+y+z=2010$, find the value of $x y z$.
|
-5892 Manipulate the equations to get a common denominator: $a=\frac{b+c}{x-2} \Longrightarrow x-2=$ $\frac{b+c}{a} \Longrightarrow x-1=\frac{a+b+c}{a} \Longrightarrow \frac{1}{x-1}=\frac{a}{a+b+c}$; similarly, $\frac{1}{y-1}=\frac{b}{a+b+c}$ and $\frac{1}{z-1}=\frac{c}{a+b+c}$. Thus
$$
\begin{aligned}
\frac{1}{x-1}+\frac{1}{y-1}+\frac{1}{z-1} & =1 \\
(y-1)(z-1)+(x-1)(z-1)+(x-1)(y-1) & =(x-1)(y-1)(z-1) \\
x y+y z+z x-2(x+y+z)+3 & =x y z-(x y+y z+z x)+(x+y+z)-1 \\
x y z-2(x y+y z+z x)+3(x+y+z)-4 & =0 \\
x y z-2(67)+3(2010)-4 & =0 \\
x y z & =-5892
\end{aligned}
$$
|
-5892
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Let $a, b, c, x, y$, and $z$ be complex numbers such that
$$
a=\frac{b+c}{x-2}, \quad b=\frac{c+a}{y-2}, \quad c=\frac{a+b}{z-2} .
$$
If $x y+y z+z x=67$ and $x+y+z=2010$, find the value of $x y z$.
|
-5892 Manipulate the equations to get a common denominator: $a=\frac{b+c}{x-2} \Longrightarrow x-2=$ $\frac{b+c}{a} \Longrightarrow x-1=\frac{a+b+c}{a} \Longrightarrow \frac{1}{x-1}=\frac{a}{a+b+c}$; similarly, $\frac{1}{y-1}=\frac{b}{a+b+c}$ and $\frac{1}{z-1}=\frac{c}{a+b+c}$. Thus
$$
\begin{aligned}
\frac{1}{x-1}+\frac{1}{y-1}+\frac{1}{z-1} & =1 \\
(y-1)(z-1)+(x-1)(z-1)+(x-1)(y-1) & =(x-1)(y-1)(z-1) \\
x y+y z+z x-2(x+y+z)+3 & =x y z-(x y+y z+z x)+(x+y+z)-1 \\
x y z-2(x y+y z+z x)+3(x+y+z)-4 & =0 \\
x y z-2(67)+3(2010)-4 & =0 \\
x y z & =-5892
\end{aligned}
$$
|
{
"resource_path": "HarvardMIT/segmented/en-132-2010-feb-alg-solutions.jsonl",
"problem_match": "\n7. [5]",
"solution_match": "\nAnswer: "
}
|
c289c1d3-9b95-5d61-a765-dc71e2b1efc1
| 608,629
|
How many polynomials of degree exactly 5 with real coefficients send the set $\{1,2,3,4,5,6\}$ to a permutation of itself?
|
714 For every permutation $\sigma$ of $\{1,2,3,4,5,6\}$, Lagrange Interpolation ${ }^{1}$ gives a polynomial of degree at most 5 with $p(x)=\sigma(x)$ for every $x=1,2,3,4,5,6$. Additionally, this polynomial is unique: assume that there exist two polynomials $p, q$ of degree $\leq 5$ such that they map $\{1,2,3,4,5,6\}$ to the same permutation. Then $p-q$ is a nonzero polynomial of degree $\leq 5$ with 6 distinct roots, a contradiction. Thus an upper bound for the answer is $6!=720$ polynomials.
However, not every polynomial obtained by Lagrange interpolation is of degree 5 (for example, $p(x)=$ $x$ ). We can count the number of invalid polynomials using finite differences ${ }^{2}$ A polynomial has degree less than 5 if and only if the sequence of 5 th finite differences is 0 . The 5 th finite difference of $p(1), p(2), p(3), p(4), p(5), p(6)$ is $p(1)-5 p(2)+10 p(3)-10 p(4)+5 p(5)-p(6)$; thus we want to solve $p(1)-5 p(2)+10 p(3)-10 p(4)+5 p(5)-p(6)=0$ with $\{p(1), p(2), p(3), p(4), p(5), p(6)\}=\{1,2,3,4,5,6\}$.
Taking the above equation modulo 5 , we get $p(1)=p(6)(\bmod 5) \Longrightarrow\{p(1), p(6)\}=\{1,6\}$. Note that $1-5 p(2)+10 p(3)-10 p(4)+5 p(5)-6=0$ if and only if $6-5 p(5)+10 p(4)-10 p(3)+5 p(2)-1=0$, so we may assume that $p(1)=1$ and double our result later. Then we have $\{p(2), p(3), p(4), p(5)\}=\{2,3,4,5\}$ and
$$
-p(2)+2 p(3)-2 p(4)+p(5)=1
$$
The above equation taken modulo 2 implies that $p(2), p(5)$ are of opposite parity, so $p(3), p(4)$ are of opposite parity. We do casework on $\{p(2), p(5)\}$ :
(a) $p(2)=2, p(5)=3 ; 2 p(3)-2 p(4)=0$ is a contradiction
(b) $p(2)=2, p(5)=5 ; 2 p(3)-2 p(4)=-2 \Longrightarrow p(3)-p(4)=-1 \Longrightarrow p(3)=3, p(4)=4$
(c) $p(2)=3, p(5)=2 ; 2 p(3)-2 p(4)=-2 \Longrightarrow p(3)-p(4)=-1 \Longrightarrow p(3)=4, p(4)=5$
(d) $p(2)=3, p(5)=4 ; 2 p(3)-2 p(4)=0$ is a contradiction
(e) $p(2)=4, p(5)=3 ; 2 p(3)-2 p(4)=2 \Longrightarrow p(3)-p(4)=1$ but $\{p(3), p(4)\}=\{2,5\}$, contradiction
(f) $p(2)=4, p(5)=5 ; 2 p(3)-2 p(4)=0$ is a contradiction
(g) $p(2)=5, p(5)=2 ; 2 p(3)-2 p(4)=4 \Longrightarrow p(3)-p(4)=2$, contradiction
(h) $p(2)=5, p(5)=4 ; 2 p(3)-2 p(4)=2 \Longrightarrow p(3)-p(4)=1 \Longrightarrow p(3)=3, p(4)=2$
Hence there are a total of $720-2(3)=714$ polynomials.
|
714
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
How many polynomials of degree exactly 5 with real coefficients send the set $\{1,2,3,4,5,6\}$ to a permutation of itself?
|
714 For every permutation $\sigma$ of $\{1,2,3,4,5,6\}$, Lagrange Interpolation ${ }^{1}$ gives a polynomial of degree at most 5 with $p(x)=\sigma(x)$ for every $x=1,2,3,4,5,6$. Additionally, this polynomial is unique: assume that there exist two polynomials $p, q$ of degree $\leq 5$ such that they map $\{1,2,3,4,5,6\}$ to the same permutation. Then $p-q$ is a nonzero polynomial of degree $\leq 5$ with 6 distinct roots, a contradiction. Thus an upper bound for the answer is $6!=720$ polynomials.
However, not every polynomial obtained by Lagrange interpolation is of degree 5 (for example, $p(x)=$ $x$ ). We can count the number of invalid polynomials using finite differences ${ }^{2}$ A polynomial has degree less than 5 if and only if the sequence of 5 th finite differences is 0 . The 5 th finite difference of $p(1), p(2), p(3), p(4), p(5), p(6)$ is $p(1)-5 p(2)+10 p(3)-10 p(4)+5 p(5)-p(6)$; thus we want to solve $p(1)-5 p(2)+10 p(3)-10 p(4)+5 p(5)-p(6)=0$ with $\{p(1), p(2), p(3), p(4), p(5), p(6)\}=\{1,2,3,4,5,6\}$.
Taking the above equation modulo 5 , we get $p(1)=p(6)(\bmod 5) \Longrightarrow\{p(1), p(6)\}=\{1,6\}$. Note that $1-5 p(2)+10 p(3)-10 p(4)+5 p(5)-6=0$ if and only if $6-5 p(5)+10 p(4)-10 p(3)+5 p(2)-1=0$, so we may assume that $p(1)=1$ and double our result later. Then we have $\{p(2), p(3), p(4), p(5)\}=\{2,3,4,5\}$ and
$$
-p(2)+2 p(3)-2 p(4)+p(5)=1
$$
The above equation taken modulo 2 implies that $p(2), p(5)$ are of opposite parity, so $p(3), p(4)$ are of opposite parity. We do casework on $\{p(2), p(5)\}$ :
(a) $p(2)=2, p(5)=3 ; 2 p(3)-2 p(4)=0$ is a contradiction
(b) $p(2)=2, p(5)=5 ; 2 p(3)-2 p(4)=-2 \Longrightarrow p(3)-p(4)=-1 \Longrightarrow p(3)=3, p(4)=4$
(c) $p(2)=3, p(5)=2 ; 2 p(3)-2 p(4)=-2 \Longrightarrow p(3)-p(4)=-1 \Longrightarrow p(3)=4, p(4)=5$
(d) $p(2)=3, p(5)=4 ; 2 p(3)-2 p(4)=0$ is a contradiction
(e) $p(2)=4, p(5)=3 ; 2 p(3)-2 p(4)=2 \Longrightarrow p(3)-p(4)=1$ but $\{p(3), p(4)\}=\{2,5\}$, contradiction
(f) $p(2)=4, p(5)=5 ; 2 p(3)-2 p(4)=0$ is a contradiction
(g) $p(2)=5, p(5)=2 ; 2 p(3)-2 p(4)=4 \Longrightarrow p(3)-p(4)=2$, contradiction
(h) $p(2)=5, p(5)=4 ; 2 p(3)-2 p(4)=2 \Longrightarrow p(3)-p(4)=1 \Longrightarrow p(3)=3, p(4)=2$
Hence there are a total of $720-2(3)=714$ polynomials.
|
{
"resource_path": "HarvardMIT/segmented/en-132-2010-feb-alg-solutions.jsonl",
"problem_match": "\n8. [6]",
"solution_match": "\nAnswer: "
}
|
25379aac-ca39-5e69-9eb6-c9dbac7e13b5
| 608,630
|
Let $f(x)=c x(x-1)$, where $c$ is a positive real number. We use $f^{n}(x)$ to denote the polynomial obtained by composing $f$ with itself $n$ times. For every positive integer $n$, all the roots of $f^{n}(x)$ are real. What is the smallest possible value of $c$ ?
|
2 We first prove that all roots of $f^{n}(x)$ are greater than or equal to $-\frac{c}{4}$ and less than or equal to $1+\frac{c}{4}$. Suppose that $r$ is a root of $f^{n}(x)$. If $r=-\frac{c}{4}, f^{-1}(r)=\left\{\frac{1}{2}\right\}$ and $-\frac{c}{4}<\frac{1}{2}<1+\frac{c}{4}$ since $c$ is positive. Suppose $r \neq-\frac{c}{4}$; by the quadratic formula, there exist two complex numbers $r_{1}, r_{2}$ such that $r_{1}+r_{2}=1$ and $f\left(r_{1}\right)=f\left(r_{2}\right)=r$. Thus all the roots of $f^{n}(x)$ (except $\frac{1}{2}$ ) come in pairs that sum to 1 . No root $r$ of $f^{n}(x)$ can be less than $-\frac{c}{4}$, otherwise $f^{n+1}(x)$ has an imaginary root, $f^{-1}(r)$. Also, no root $r$ of $f^{n}(x)$ can be greater than $1+\frac{c}{4}$, otherwise its "conjugate" root will be less than $-\frac{c}{4}$.
Define $g(x)=\frac{1}{2}\left(1+\sqrt{1+\frac{4 x}{c}}\right)$, the larger inverse of $f(x)$. Note that $g^{n}(x)$ is the largest element of $f^{-n}(x)$ (which is a set). $g^{n}(0)$ should be less than or equal to $1+\frac{c}{4}$ for all $n$. Let $x_{0}$ be the nonzero real number such that $g\left(x_{0}\right)=x_{0}$; then $c x_{0}\left(x_{0}-1\right)=x_{0} \Longrightarrow x_{o}=1+\frac{1}{c}$. $x_{0}<g(x)<x$ if $x>x_{0}$ and $x<g(x)<x_{0}$ if $x<x_{0}$; it can be proved that $g^{n}$ converges to $x_{0}$. Hence we have the requirement that $x_{0}=1+\frac{1}{c} \leq 1+\frac{c}{4} \Longrightarrow c \geq 2$.
We verify that $c=2$ is possible. All the roots of $f^{-} n(x)$ will be real if $g(0) \leq 1+\frac{c}{4}=\frac{3}{2}$. We know that $0<\frac{3}{2} \Longrightarrow g(0)<\frac{3}{2}$, so $g^{2}(0)<\frac{3}{2}$ and $g^{n}(0)<g^{n+1}(0)<\frac{3}{2}$ for all $n$. Therefore all the roots of $f^{n}(x)$ are real.
|
2
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Let $f(x)=c x(x-1)$, where $c$ is a positive real number. We use $f^{n}(x)$ to denote the polynomial obtained by composing $f$ with itself $n$ times. For every positive integer $n$, all the roots of $f^{n}(x)$ are real. What is the smallest possible value of $c$ ?
|
2 We first prove that all roots of $f^{n}(x)$ are greater than or equal to $-\frac{c}{4}$ and less than or equal to $1+\frac{c}{4}$. Suppose that $r$ is a root of $f^{n}(x)$. If $r=-\frac{c}{4}, f^{-1}(r)=\left\{\frac{1}{2}\right\}$ and $-\frac{c}{4}<\frac{1}{2}<1+\frac{c}{4}$ since $c$ is positive. Suppose $r \neq-\frac{c}{4}$; by the quadratic formula, there exist two complex numbers $r_{1}, r_{2}$ such that $r_{1}+r_{2}=1$ and $f\left(r_{1}\right)=f\left(r_{2}\right)=r$. Thus all the roots of $f^{n}(x)$ (except $\frac{1}{2}$ ) come in pairs that sum to 1 . No root $r$ of $f^{n}(x)$ can be less than $-\frac{c}{4}$, otherwise $f^{n+1}(x)$ has an imaginary root, $f^{-1}(r)$. Also, no root $r$ of $f^{n}(x)$ can be greater than $1+\frac{c}{4}$, otherwise its "conjugate" root will be less than $-\frac{c}{4}$.
Define $g(x)=\frac{1}{2}\left(1+\sqrt{1+\frac{4 x}{c}}\right)$, the larger inverse of $f(x)$. Note that $g^{n}(x)$ is the largest element of $f^{-n}(x)$ (which is a set). $g^{n}(0)$ should be less than or equal to $1+\frac{c}{4}$ for all $n$. Let $x_{0}$ be the nonzero real number such that $g\left(x_{0}\right)=x_{0}$; then $c x_{0}\left(x_{0}-1\right)=x_{0} \Longrightarrow x_{o}=1+\frac{1}{c}$. $x_{0}<g(x)<x$ if $x>x_{0}$ and $x<g(x)<x_{0}$ if $x<x_{0}$; it can be proved that $g^{n}$ converges to $x_{0}$. Hence we have the requirement that $x_{0}=1+\frac{1}{c} \leq 1+\frac{c}{4} \Longrightarrow c \geq 2$.
We verify that $c=2$ is possible. All the roots of $f^{-} n(x)$ will be real if $g(0) \leq 1+\frac{c}{4}=\frac{3}{2}$. We know that $0<\frac{3}{2} \Longrightarrow g(0)<\frac{3}{2}$, so $g^{2}(0)<\frac{3}{2}$ and $g^{n}(0)<g^{n+1}(0)<\frac{3}{2}$ for all $n$. Therefore all the roots of $f^{n}(x)$ are real.
|
{
"resource_path": "HarvardMIT/segmented/en-132-2010-feb-alg-solutions.jsonl",
"problem_match": "\n9. [7]",
"solution_match": "\nAnswer: "
}
|
1a90b295-6914-5b15-aaec-f7e9e7ca153f
| 608,631
|
Suppose that $p(x)$ is a polynomial and that $p(x)-p^{\prime}(x)=x^{2}+2 x+1$. Compute $p(5)$.
|
50 Observe that $p(x)$ must be quadratic. Let $p(x)=a x^{2}+b x+c$. Comparing coefficients gives $a=1, b-2 a=2$, and $c-b=1$. So $b=4, c=5, p(x)=x^{2}+4 x+5$ and $p(5)=25+20+5=50$.
|
50
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Suppose that $p(x)$ is a polynomial and that $p(x)-p^{\prime}(x)=x^{2}+2 x+1$. Compute $p(5)$.
|
50 Observe that $p(x)$ must be quadratic. Let $p(x)=a x^{2}+b x+c$. Comparing coefficients gives $a=1, b-2 a=2$, and $c-b=1$. So $b=4, c=5, p(x)=x^{2}+4 x+5$ and $p(5)=25+20+5=50$.
|
{
"resource_path": "HarvardMIT/segmented/en-132-2010-feb-calc-solutions.jsonl",
"problem_match": "\n1. [3]",
"solution_match": "\nAnswer: "
}
|
72846768-87b1-5306-9dcc-ad1cb4935a5c
| 608,633
|
Let $f$ be a function such that $f(0)=1, f^{\prime}(0)=2$, and
$$
f^{\prime \prime}(t)=4 f^{\prime}(t)-3 f(t)+1
$$
for all $t$. Compute the 4th derivative of $f$, evaluated at 0 .
|
54 Putting $t=0$ gives $f^{\prime \prime}(0)=6$. By differentiating both sides, we get $f^{(3)}(t)=4 f^{\prime \prime}(t)-$ $3 f^{\prime}(t)$ and $f^{(3)}(0)=4 \cdot 6-3 \cdot 2=18$. Similarly, $f^{(4)}(t)=4 f^{(3)}(t)-3 f^{\prime \prime}(t)$ and $f^{(4)}(0)=4 \cdot 18-3 \cdot 6=54$.
|
54
|
Yes
|
Yes
|
math-word-problem
|
Calculus
|
Let $f$ be a function such that $f(0)=1, f^{\prime}(0)=2$, and
$$
f^{\prime \prime}(t)=4 f^{\prime}(t)-3 f(t)+1
$$
for all $t$. Compute the 4th derivative of $f$, evaluated at 0 .
|
54 Putting $t=0$ gives $f^{\prime \prime}(0)=6$. By differentiating both sides, we get $f^{(3)}(t)=4 f^{\prime \prime}(t)-$ $3 f^{\prime}(t)$ and $f^{(3)}(0)=4 \cdot 6-3 \cdot 2=18$. Similarly, $f^{(4)}(t)=4 f^{(3)}(t)-3 f^{\prime \prime}(t)$ and $f^{(4)}(0)=4 \cdot 18-3 \cdot 6=54$.
|
{
"resource_path": "HarvardMIT/segmented/en-132-2010-feb-calc-solutions.jsonl",
"problem_match": "\n2. [3]",
"solution_match": "\nAnswer: "
}
|
84235504-cabd-55e4-a150-176180c1b2cd
| 608,634
|
Let $p$ be a monic cubic polynomial such that $p(0)=1$ and such that all the zeros of $p^{\prime}(x)$ are also zeros of $p(x)$. Find $p$. Note: monic means that the leading coefficient is 1 .
|
$(x+1)^{3}$ A root of a polynomial $p$ will be a double root if and only if it is also a root of $p^{\prime}$. Let $a$ and $b$ be the roots of $p^{\prime}$. Since $a$ and $b$ are also roots of $p$, they are double roots of $p$. But $p$ can have only three roots, so $a=b$ and $a$ becomes a double root of $p^{\prime}$. This makes $p^{\prime}(x)=3 c(x-a)^{2}$ for some constant $3 c$, and thus $p(x)=c(x-a)^{3}+d$. Because $a$ is a root of $p$ and $p$ is monic, $d=0$ and $c=1$. From $p(0)=1$ we get $p(x)=(x+1)^{3}$.
|
(x+1)^{3}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Let $p$ be a monic cubic polynomial such that $p(0)=1$ and such that all the zeros of $p^{\prime}(x)$ are also zeros of $p(x)$. Find $p$. Note: monic means that the leading coefficient is 1 .
|
$(x+1)^{3}$ A root of a polynomial $p$ will be a double root if and only if it is also a root of $p^{\prime}$. Let $a$ and $b$ be the roots of $p^{\prime}$. Since $a$ and $b$ are also roots of $p$, they are double roots of $p$. But $p$ can have only three roots, so $a=b$ and $a$ becomes a double root of $p^{\prime}$. This makes $p^{\prime}(x)=3 c(x-a)^{2}$ for some constant $3 c$, and thus $p(x)=c(x-a)^{3}+d$. Because $a$ is a root of $p$ and $p$ is monic, $d=0$ and $c=1$. From $p(0)=1$ we get $p(x)=(x+1)^{3}$.
|
{
"resource_path": "HarvardMIT/segmented/en-132-2010-feb-calc-solutions.jsonl",
"problem_match": "\n3. [4]",
"solution_match": "\nAnswer: "
}
|
a1664b3b-7694-5843-9216-bebf4af0b07b
| 608,635
|
Compute $\lim _{n \rightarrow \infty} \frac{\sum_{k=1}^{n}|\cos (k)|}{n}$.
|
$\frac{2}{\pi}$ The main idea lies on the fact that positive integers are uniformly distributed modulo $\pi$. (In the other words, if each integer $n$ is written as $q \pi+r$ where $q$ is an integer and $0 \leq r<\pi$, the value of $r$ will distribute uniformly in the interval $[0, \pi]$.) Using this fact, the summation is equivalent to the average value (using the Riemann summation) of the function $|\cos (k)|$ over the interval $[0, \pi]$. Therefore, the answer is $\frac{1}{\pi} \int_{0}^{\pi}|\cos (k)|=\frac{2}{\pi}$.
|
\frac{2}{\pi}
|
Yes
|
Yes
|
math-word-problem
|
Calculus
|
Compute $\lim _{n \rightarrow \infty} \frac{\sum_{k=1}^{n}|\cos (k)|}{n}$.
|
$\frac{2}{\pi}$ The main idea lies on the fact that positive integers are uniformly distributed modulo $\pi$. (In the other words, if each integer $n$ is written as $q \pi+r$ where $q$ is an integer and $0 \leq r<\pi$, the value of $r$ will distribute uniformly in the interval $[0, \pi]$.) Using this fact, the summation is equivalent to the average value (using the Riemann summation) of the function $|\cos (k)|$ over the interval $[0, \pi]$. Therefore, the answer is $\frac{1}{\pi} \int_{0}^{\pi}|\cos (k)|=\frac{2}{\pi}$.
|
{
"resource_path": "HarvardMIT/segmented/en-132-2010-feb-calc-solutions.jsonl",
"problem_match": "\n4. [4]",
"solution_match": "\nAnswer: "
}
|
2bd98966-1411-572f-a653-65b67a61fc4b
| 608,636
|
Let the functions $f(\alpha, x)$ and $g(\alpha)$ be defined as
$$
f(\alpha, x)=\frac{\left(\frac{x}{2}\right)^{\alpha}}{x-1} \quad g(\alpha)=\left.\frac{d^{4} f}{d x^{4}}\right|_{x=2}
$$
Then $g(\alpha)$ is a polynomial in $\alpha$. Find the leading coefficient of $g(\alpha)$.
|
$\frac{1}{16}$ Write the first equation as $(x-1) f=\left(\frac{x}{2}\right)^{\alpha}$. For now, treat $\alpha$ as a constant. From this equation, repeatedly applying derivative with respect to $x$ gives
$$
\begin{aligned}
(x-1) f^{\prime}+f & =\left(\frac{\alpha}{2}\right)\left(\frac{x}{2}\right)^{\alpha-1} \\
(x-1) f^{\prime \prime}+2 f^{\prime} & =\left(\frac{\alpha}{2}\right)\left(\frac{\alpha-1}{2}\right)\left(\frac{x}{2}\right)^{\alpha-2} \\
(x-1) f^{(3)}+3 f^{\prime \prime} & =\left(\frac{\alpha}{2}\right)\left(\frac{\alpha-1}{2}\right)\left(\frac{\alpha-2}{2}\right)\left(\frac{x}{2}\right)^{\alpha-3} \\
(x-1) f^{(4)}+4 f^{(3)} & =\left(\frac{\alpha}{2}\right)\left(\frac{\alpha-1}{2}\right)\left(\frac{\alpha-2}{2}\right)\left(\frac{\alpha-3}{2}\right)\left(\frac{x}{2}\right)^{\alpha-4}
\end{aligned}
$$
Substituting $x=2$ to all equations gives $g(\alpha)=f^{(4)}(\alpha, 2)=\left(\frac{\alpha}{2}\right)\left(\frac{\alpha-1}{2}\right)\left(\frac{\alpha-2}{2}\right)\left(\frac{\alpha-3}{2}\right)-4 f^{(3)}(\alpha, 2)$. Because $f^{(3)}(\alpha, 2)$ is a cubic polynomial in $\alpha$, the leading coefficient of $g(\alpha)$ is $\frac{1}{16}$.
|
\frac{1}{16}
|
Yes
|
Yes
|
math-word-problem
|
Calculus
|
Let the functions $f(\alpha, x)$ and $g(\alpha)$ be defined as
$$
f(\alpha, x)=\frac{\left(\frac{x}{2}\right)^{\alpha}}{x-1} \quad g(\alpha)=\left.\frac{d^{4} f}{d x^{4}}\right|_{x=2}
$$
Then $g(\alpha)$ is a polynomial in $\alpha$. Find the leading coefficient of $g(\alpha)$.
|
$\frac{1}{16}$ Write the first equation as $(x-1) f=\left(\frac{x}{2}\right)^{\alpha}$. For now, treat $\alpha$ as a constant. From this equation, repeatedly applying derivative with respect to $x$ gives
$$
\begin{aligned}
(x-1) f^{\prime}+f & =\left(\frac{\alpha}{2}\right)\left(\frac{x}{2}\right)^{\alpha-1} \\
(x-1) f^{\prime \prime}+2 f^{\prime} & =\left(\frac{\alpha}{2}\right)\left(\frac{\alpha-1}{2}\right)\left(\frac{x}{2}\right)^{\alpha-2} \\
(x-1) f^{(3)}+3 f^{\prime \prime} & =\left(\frac{\alpha}{2}\right)\left(\frac{\alpha-1}{2}\right)\left(\frac{\alpha-2}{2}\right)\left(\frac{x}{2}\right)^{\alpha-3} \\
(x-1) f^{(4)}+4 f^{(3)} & =\left(\frac{\alpha}{2}\right)\left(\frac{\alpha-1}{2}\right)\left(\frac{\alpha-2}{2}\right)\left(\frac{\alpha-3}{2}\right)\left(\frac{x}{2}\right)^{\alpha-4}
\end{aligned}
$$
Substituting $x=2$ to all equations gives $g(\alpha)=f^{(4)}(\alpha, 2)=\left(\frac{\alpha}{2}\right)\left(\frac{\alpha-1}{2}\right)\left(\frac{\alpha-2}{2}\right)\left(\frac{\alpha-3}{2}\right)-4 f^{(3)}(\alpha, 2)$. Because $f^{(3)}(\alpha, 2)$ is a cubic polynomial in $\alpha$, the leading coefficient of $g(\alpha)$ is $\frac{1}{16}$.
|
{
"resource_path": "HarvardMIT/segmented/en-132-2010-feb-calc-solutions.jsonl",
"problem_match": "\n5. [4]",
"solution_match": "\nAnswer: "
}
|
0d9061de-7037-58c9-998d-5b8d0fa943f5
| 608,637
|
Let $f(x)=x^{3}-x^{2}$. For a given value of $c$, the graph of $f(x)$, together with the graph of the line $c+x$, split the plane up into regions. Suppose that $c$ is such that exactly two of these regions have finite area. Find the value of $c$ that minimizes the sum of the areas of these two regions.
|
$-\frac{11}{27}$ Observe that $f(x)$ can be written as $\left(x-\frac{1}{3}\right)^{3}-\frac{1}{3}\left(x-\frac{1}{3}\right)-\frac{2}{27}$, which has $180^{\circ}$ symmetry around the point $\left(\frac{1}{3},-\frac{2}{27}\right)$. Suppose the graph of $f$ cuts the line $y=c+x$ into two segments of lengths $a$ and $b$. When we move the line toward point $P$ with a small distance $\Delta x$ (measured along the line perpendicular to $y=x+c)$, the sum of the enclosed areas will increase by $|a-b|(\Delta x)$. As long as the line $x+c$ does not passes through $P$, we can find a new line $x+c^{*}$ that increases the sum of the enclosed areas. Therefore, the sum of the areas reaches its maximum when the line passes through $P$. For that line, we can find that $c=y-x=-\frac{2}{27}-\frac{1}{3}=-\frac{11}{27}$.
|
-\frac{11}{27}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Let $f(x)=x^{3}-x^{2}$. For a given value of $c$, the graph of $f(x)$, together with the graph of the line $c+x$, split the plane up into regions. Suppose that $c$ is such that exactly two of these regions have finite area. Find the value of $c$ that minimizes the sum of the areas of these two regions.
|
$-\frac{11}{27}$ Observe that $f(x)$ can be written as $\left(x-\frac{1}{3}\right)^{3}-\frac{1}{3}\left(x-\frac{1}{3}\right)-\frac{2}{27}$, which has $180^{\circ}$ symmetry around the point $\left(\frac{1}{3},-\frac{2}{27}\right)$. Suppose the graph of $f$ cuts the line $y=c+x$ into two segments of lengths $a$ and $b$. When we move the line toward point $P$ with a small distance $\Delta x$ (measured along the line perpendicular to $y=x+c)$, the sum of the enclosed areas will increase by $|a-b|(\Delta x)$. As long as the line $x+c$ does not passes through $P$, we can find a new line $x+c^{*}$ that increases the sum of the enclosed areas. Therefore, the sum of the areas reaches its maximum when the line passes through $P$. For that line, we can find that $c=y-x=-\frac{2}{27}-\frac{1}{3}=-\frac{11}{27}$.
|
{
"resource_path": "HarvardMIT/segmented/en-132-2010-feb-calc-solutions.jsonl",
"problem_match": "\n6. [5]",
"solution_match": "\nAnswer: "
}
|
6262764d-75ac-5f77-91af-a52a51b386f4
| 608,638
|
Let $a_{1}, a_{2}$, and $a_{3}$ be nonzero complex numbers with non-negative real and imaginary parts. Find the minimum possible value of
$$
\frac{\left|a_{1}+a_{2}+a_{3}\right|}{\sqrt[3]{\left|a_{1} a_{2} a_{3}\right|}}
$$
|
$\sqrt{3} \sqrt[3]{2}$ Write $a_{1}$ in its polar form $r e^{i \theta}$ where $0 \leq \theta \leq \frac{\pi}{2}$. Suppose $a_{2}, a_{3}$ and $r$ are fixed so that the denominator is constant. Write $a_{2}+a_{3}$ as $s e^{i \phi}$. Since $a_{2}$ and $a_{3}$ have non-negative real and imaginary parts, the angle $\phi$ lies between 0 and $\frac{\pi}{2}$. Consider the function
$$
f(\theta)=\left|a_{1}+a_{2}+a_{3}\right|^{2}=\left|r e^{i \theta}+s e^{i \phi}\right|^{2}=r^{2}+2 r s \cos (\theta-\phi)+s^{2}
$$
Its second derivative is $\left.f^{\prime \prime}(\theta)=-2 \operatorname{rs}(\cos (\theta-\phi))\right)$. Since $-\frac{\pi}{2} \leq(\theta-\phi) \leq \frac{\pi}{2}$, we know that $f^{\prime \prime}(\theta)<0$ and $f$ is concave. Therefore, to minimize $f$, the angle $\theta$ must be either 0 or $\frac{\pi}{2}$. Similarly, each of $a_{1}, a_{2}$ and $a_{3}$ must be either purely real or purely imaginary to minimize $f$ and the original fraction.
By the AM-GM inequality, if $a_{1}, a_{2}$ and $a_{3}$ are all real or all imaginary, then the minimum value of the fraction is 3 . Now suppose only two of the $a_{i}$ 's, say, $a_{1}$ and $a_{2}$ are real. Since the fraction is homogenous, we may fix $a_{1}+a_{2}$ - let the sum be 2 . The term $a_{1} a_{2}$ in the denominator acheives its maximum only when $a_{1}$ and $a_{2}$ are equal, i.e. when $a_{1}=a_{2}=1$. Then, if $a_{3}=k i$ for some real number $k$, then the expression equals
$$
\frac{\sqrt{k^{2}+4}}{\sqrt[3]{k}}
$$
Squaring and taking the derivative, we find that the minimum value of the fraction is $\sqrt{3} \sqrt[3]{2}$, attained when $k=\sqrt{2}$. With similar reasoning, the case where only one of the $a_{i}$ 's is real yields the same minimum value.
|
\sqrt{3} \sqrt[3]{2}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Let $a_{1}, a_{2}$, and $a_{3}$ be nonzero complex numbers with non-negative real and imaginary parts. Find the minimum possible value of
$$
\frac{\left|a_{1}+a_{2}+a_{3}\right|}{\sqrt[3]{\left|a_{1} a_{2} a_{3}\right|}}
$$
|
$\sqrt{3} \sqrt[3]{2}$ Write $a_{1}$ in its polar form $r e^{i \theta}$ where $0 \leq \theta \leq \frac{\pi}{2}$. Suppose $a_{2}, a_{3}$ and $r$ are fixed so that the denominator is constant. Write $a_{2}+a_{3}$ as $s e^{i \phi}$. Since $a_{2}$ and $a_{3}$ have non-negative real and imaginary parts, the angle $\phi$ lies between 0 and $\frac{\pi}{2}$. Consider the function
$$
f(\theta)=\left|a_{1}+a_{2}+a_{3}\right|^{2}=\left|r e^{i \theta}+s e^{i \phi}\right|^{2}=r^{2}+2 r s \cos (\theta-\phi)+s^{2}
$$
Its second derivative is $\left.f^{\prime \prime}(\theta)=-2 \operatorname{rs}(\cos (\theta-\phi))\right)$. Since $-\frac{\pi}{2} \leq(\theta-\phi) \leq \frac{\pi}{2}$, we know that $f^{\prime \prime}(\theta)<0$ and $f$ is concave. Therefore, to minimize $f$, the angle $\theta$ must be either 0 or $\frac{\pi}{2}$. Similarly, each of $a_{1}, a_{2}$ and $a_{3}$ must be either purely real or purely imaginary to minimize $f$ and the original fraction.
By the AM-GM inequality, if $a_{1}, a_{2}$ and $a_{3}$ are all real or all imaginary, then the minimum value of the fraction is 3 . Now suppose only two of the $a_{i}$ 's, say, $a_{1}$ and $a_{2}$ are real. Since the fraction is homogenous, we may fix $a_{1}+a_{2}$ - let the sum be 2 . The term $a_{1} a_{2}$ in the denominator acheives its maximum only when $a_{1}$ and $a_{2}$ are equal, i.e. when $a_{1}=a_{2}=1$. Then, if $a_{3}=k i$ for some real number $k$, then the expression equals
$$
\frac{\sqrt{k^{2}+4}}{\sqrt[3]{k}}
$$
Squaring and taking the derivative, we find that the minimum value of the fraction is $\sqrt{3} \sqrt[3]{2}$, attained when $k=\sqrt{2}$. With similar reasoning, the case where only one of the $a_{i}$ 's is real yields the same minimum value.
|
{
"resource_path": "HarvardMIT/segmented/en-132-2010-feb-calc-solutions.jsonl",
"problem_match": "\n7. [6]",
"solution_match": "\nAnswer: "
}
|
98aa53ec-1d8b-532f-8da7-3a0c69256293
| 608,639
|
Let $f(n)=\sum_{k=2}^{\infty} \frac{1}{k^{n} \cdot k!}$. Calculate $\sum_{n=2}^{\infty} f(n)$.
|
$3-e$
$$
\begin{aligned}
\sum_{n=2}^{\infty} f(n) & =\sum_{k=2}^{\infty} \sum_{n=2}^{\infty} \frac{1}{k^{n} \cdot k!} \\
& =\sum_{k=2}^{\infty} \frac{1}{k!} \sum_{n=2}^{\infty} \frac{1}{k^{n}} \\
& =\sum_{k=2}^{\infty} \frac{1}{k!} \cdot \frac{1}{k(k-1)} \\
& =\sum_{k=2}^{\infty} \frac{1}{(k-1)!} \cdot \frac{1}{k^{2}(k-1)}
\end{aligned}
$$
$$
\begin{aligned}
& =\sum_{k=2}^{\infty} \frac{1}{(k-1)!}\left(\frac{1}{k-1}-\frac{1}{k^{2}}-\frac{1}{k}\right) \\
& =\sum_{k=2}^{\infty}\left(\frac{1}{(k-1)(k-1)!}-\frac{1}{k \cdot k!}-\frac{1}{k!}\right) \\
& =\sum_{k=2}^{\infty}\left(\frac{1}{(k-1)(k-1)!}-\frac{1}{k \cdot k!}\right)-\sum_{k=2}^{\infty} \frac{1}{k!} \\
& =\frac{1}{1 \cdot 1!}-\left(e-\frac{1}{0!}-\frac{1}{1!}\right) \\
& =3-e
\end{aligned}
$$
|
3-e
|
Yes
|
Yes
|
math-word-problem
|
Calculus
|
Let $f(n)=\sum_{k=2}^{\infty} \frac{1}{k^{n} \cdot k!}$. Calculate $\sum_{n=2}^{\infty} f(n)$.
|
$3-e$
$$
\begin{aligned}
\sum_{n=2}^{\infty} f(n) & =\sum_{k=2}^{\infty} \sum_{n=2}^{\infty} \frac{1}{k^{n} \cdot k!} \\
& =\sum_{k=2}^{\infty} \frac{1}{k!} \sum_{n=2}^{\infty} \frac{1}{k^{n}} \\
& =\sum_{k=2}^{\infty} \frac{1}{k!} \cdot \frac{1}{k(k-1)} \\
& =\sum_{k=2}^{\infty} \frac{1}{(k-1)!} \cdot \frac{1}{k^{2}(k-1)}
\end{aligned}
$$
$$
\begin{aligned}
& =\sum_{k=2}^{\infty} \frac{1}{(k-1)!}\left(\frac{1}{k-1}-\frac{1}{k^{2}}-\frac{1}{k}\right) \\
& =\sum_{k=2}^{\infty}\left(\frac{1}{(k-1)(k-1)!}-\frac{1}{k \cdot k!}-\frac{1}{k!}\right) \\
& =\sum_{k=2}^{\infty}\left(\frac{1}{(k-1)(k-1)!}-\frac{1}{k \cdot k!}\right)-\sum_{k=2}^{\infty} \frac{1}{k!} \\
& =\frac{1}{1 \cdot 1!}-\left(e-\frac{1}{0!}-\frac{1}{1!}\right) \\
& =3-e
\end{aligned}
$$
|
{
"resource_path": "HarvardMIT/segmented/en-132-2010-feb-calc-solutions.jsonl",
"problem_match": "\n8. [6]",
"solution_match": "\nAnswer: "
}
|
8a8517a9-cd46-5f76-b699-59dba0822109
| 608,640
|
Let $x(t)$ be a solution to the differential equation
$$
\left(x+x^{\prime}\right)^{2}+x \cdot x^{\prime \prime}=\cos t
$$
with $x(0)=x^{\prime}(0)=\sqrt{\frac{2}{5}}$. Compute $x\left(\frac{\pi}{4}\right)$.
|
$\frac{\sqrt[4]{450}}{5}$ Rewrite the equation as $x^{2}+2 x x^{\prime}+\left(x x^{\prime}\right)^{\prime}=\cos t$. Let $y=x^{2}$, so $y^{\prime}=2 x x^{\prime}$ and the equation becomes $y+y^{\prime}+\frac{1}{2} y^{\prime \prime}=\cos t$. The term $\cos t$ suggests that the particular solution should be in the form $A \sin t+B \cos t$. By substitution and coefficient comparison, we get $A=\frac{4}{5}$ and $B=\frac{2}{5}$. Since the function $y(t)=\frac{4}{5} \sin t+\frac{2}{5} \cos t$ already satisfies the initial conditions $y(0)=x(0)^{2}=\frac{2}{5}$ and $y^{\prime}(0)=2 x(0) x^{\prime}(0)=\frac{4}{5}$, the function $y$ also solves the initial value problem. Note that since $x$ is positive at $t=0$ and $y=x^{2}$ never reaches zero before $t$ reaches $\frac{\pi}{4}$, the value of $x\left(\frac{\pi}{4}\right)$ must be positive. Therefore, $x\left(\frac{\pi}{4}\right)=+\sqrt{y\left(\frac{\pi}{4}\right)}=\sqrt{\frac{6}{5} \cdot \frac{\sqrt{2}}{2}}=\frac{\sqrt[4]{450}}{5}$.
|
\frac{\sqrt[4]{450}}{5}
|
Yes
|
Yes
|
math-word-problem
|
Calculus
|
Let $x(t)$ be a solution to the differential equation
$$
\left(x+x^{\prime}\right)^{2}+x \cdot x^{\prime \prime}=\cos t
$$
with $x(0)=x^{\prime}(0)=\sqrt{\frac{2}{5}}$. Compute $x\left(\frac{\pi}{4}\right)$.
|
$\frac{\sqrt[4]{450}}{5}$ Rewrite the equation as $x^{2}+2 x x^{\prime}+\left(x x^{\prime}\right)^{\prime}=\cos t$. Let $y=x^{2}$, so $y^{\prime}=2 x x^{\prime}$ and the equation becomes $y+y^{\prime}+\frac{1}{2} y^{\prime \prime}=\cos t$. The term $\cos t$ suggests that the particular solution should be in the form $A \sin t+B \cos t$. By substitution and coefficient comparison, we get $A=\frac{4}{5}$ and $B=\frac{2}{5}$. Since the function $y(t)=\frac{4}{5} \sin t+\frac{2}{5} \cos t$ already satisfies the initial conditions $y(0)=x(0)^{2}=\frac{2}{5}$ and $y^{\prime}(0)=2 x(0) x^{\prime}(0)=\frac{4}{5}$, the function $y$ also solves the initial value problem. Note that since $x$ is positive at $t=0$ and $y=x^{2}$ never reaches zero before $t$ reaches $\frac{\pi}{4}$, the value of $x\left(\frac{\pi}{4}\right)$ must be positive. Therefore, $x\left(\frac{\pi}{4}\right)=+\sqrt{y\left(\frac{\pi}{4}\right)}=\sqrt{\frac{6}{5} \cdot \frac{\sqrt{2}}{2}}=\frac{\sqrt[4]{450}}{5}$.
|
{
"resource_path": "HarvardMIT/segmented/en-132-2010-feb-calc-solutions.jsonl",
"problem_match": "\n9. [7]",
"solution_match": "\nAnswer: "
}
|
f8c7e705-c1c5-5064-841e-2440c70477af
| 608,641
|
Let $S=\{1,2,3,4,5,6,7,8,9,10\}$. How many (potentially empty) subsets $T$ of $S$ are there such that, for all $x$, if $x$ is in $T$ and $2 x$ is in $S$ then $2 x$ is also in $T$ ?
|
180 We partition the elements of $S$ into the following subsets: $\{1,2,4,8\},\{3,6\},\{5,10\}$, $\{7\},\{9\}$. Consider the first subset, $\{1,2,4,8\}$. Say 2 is an element of $T$. Because $2 \cdot 2=4$ is in $S, 4$ must also be in $T$. Furthermore, since $4 \cdot 2=8$ is in $S, 8$ must also be in $T$. So if $T$ contains 2 , it must also contain 4 and 8 . Similarly, if $T$ contains 1 , it must also contain 2,4 , and 8 . So $T$ can contain the following subsets of the subset $\{1,2,4,8\}$ : the empty set, $\{8\},\{4,8\},\{2,4,8\}$, or $\{1,2,4,8\}$. This gives 5 possibilities for the first subset. In general, we see that if $T$ contains an element $q$ of one of these subsets, it must also contain the elements in that subset that are larger than $q$, because we created the subsets for this to be true. So there are 3 possibilities for $\{3,6\}, 3$ for $\{5,10\}, 2$ for $\{7\}$, and 2 for $\{9\}$. This gives a total of $5 \cdot 3 \cdot 3 \cdot 2 \cdot 2=180$ possible subsets $T$.
|
180
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Let $S=\{1,2,3,4,5,6,7,8,9,10\}$. How many (potentially empty) subsets $T$ of $S$ are there such that, for all $x$, if $x$ is in $T$ and $2 x$ is in $S$ then $2 x$ is also in $T$ ?
|
180 We partition the elements of $S$ into the following subsets: $\{1,2,4,8\},\{3,6\},\{5,10\}$, $\{7\},\{9\}$. Consider the first subset, $\{1,2,4,8\}$. Say 2 is an element of $T$. Because $2 \cdot 2=4$ is in $S, 4$ must also be in $T$. Furthermore, since $4 \cdot 2=8$ is in $S, 8$ must also be in $T$. So if $T$ contains 2 , it must also contain 4 and 8 . Similarly, if $T$ contains 1 , it must also contain 2,4 , and 8 . So $T$ can contain the following subsets of the subset $\{1,2,4,8\}$ : the empty set, $\{8\},\{4,8\},\{2,4,8\}$, or $\{1,2,4,8\}$. This gives 5 possibilities for the first subset. In general, we see that if $T$ contains an element $q$ of one of these subsets, it must also contain the elements in that subset that are larger than $q$, because we created the subsets for this to be true. So there are 3 possibilities for $\{3,6\}, 3$ for $\{5,10\}, 2$ for $\{7\}$, and 2 for $\{9\}$. This gives a total of $5 \cdot 3 \cdot 3 \cdot 2 \cdot 2=180$ possible subsets $T$.
|
{
"resource_path": "HarvardMIT/segmented/en-132-2010-feb-comb-solutions.jsonl",
"problem_match": "\n1. [2]",
"solution_match": "\nAnswer: "
}
|
843a0eaf-d927-5fe6-b224-40b868522ed1
| 608,643
|
How many positive integers less than or equal to 240 can be expressed as a sum of distinct factorials? Consider 0! and 1! to be distinct.
|
39 Note that $1=0!, 2=0!+1!, 3=0!+2$ !, and $4=0!+1!+2$ !. These are the only numbers less than 6 that can be written as the sum of factorials. The only other factorials less than 240 are $3!=6,4!=24$, and $5!=120$. So a positive integer less than or equal to 240 can only contain 3 !, 4 !, 5 !, and/or one of $1,2,3$, or 4 in its sum. If it contains any factorial larger than 5 !, it will be larger than 240 . So a sum less than or equal to 240 will will either include 3 ! or not ( 2 ways), 4 ! or not ( 2 ways), 5 ! or not ( 2 ways), and add an additional $0,1,2,3$ or 4 ( 5 ways). This gives $2 \cdot 2 \cdot 2 \cdot 5=40$ integers less than 240 . However, we want only positive integers, so we must not count 0 . So there are 39 such positive integers.
|
39
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
How many positive integers less than or equal to 240 can be expressed as a sum of distinct factorials? Consider 0! and 1! to be distinct.
|
39 Note that $1=0!, 2=0!+1!, 3=0!+2$ !, and $4=0!+1!+2$ !. These are the only numbers less than 6 that can be written as the sum of factorials. The only other factorials less than 240 are $3!=6,4!=24$, and $5!=120$. So a positive integer less than or equal to 240 can only contain 3 !, 4 !, 5 !, and/or one of $1,2,3$, or 4 in its sum. If it contains any factorial larger than 5 !, it will be larger than 240 . So a sum less than or equal to 240 will will either include 3 ! or not ( 2 ways), 4 ! or not ( 2 ways), 5 ! or not ( 2 ways), and add an additional $0,1,2,3$ or 4 ( 5 ways). This gives $2 \cdot 2 \cdot 2 \cdot 5=40$ integers less than 240 . However, we want only positive integers, so we must not count 0 . So there are 39 such positive integers.
|
{
"resource_path": "HarvardMIT/segmented/en-132-2010-feb-comb-solutions.jsonl",
"problem_match": "\n2. [3]",
"solution_match": "\nAnswer: "
}
|
ab0813b1-50da-51ce-8a48-4c650106403f
| 608,644
|
How many ways are there to choose 2010 functions $f_{1}, \ldots, f_{2010}$ from $\{0,1\}$ to $\{0,1\}$ such that $f_{2010} \circ f_{2009} \circ \cdots \circ f_{1}$ is constant? Note: a function $g$ is constant if $g(a)=g(b)$ for all $a, b$ in the domain of $g$.
|
$4^{2010}-2^{2010}$ If all 2010 functions are bijective ${ }^{1}$, then the composition $f_{2010} \circ f_{2009} \circ \cdots \circ f_{1}$ will be bijective also, and therefore not constant. If, however, one of $f_{1}, \ldots, f_{2010}$ is not bijective, say $f_{k}$, then $f_{k}(0)=f_{k}(1)=q$, so $f_{2010} \circ f_{2009} \circ \cdots \circ f_{k+1} \circ f_{k} \circ \cdots f_{1}(0)=f_{2010} \circ f_{2009} \circ \cdots \circ f_{k+1}(q)=$ $f_{2010} \circ f_{2009} \circ \cdots \circ f_{k+1} \circ f_{k} \circ \cdots f_{1}(1)$. So the composition will be constant unless all $f_{i}$ are bijective. Since there are 4 possible functions ${ }^{2}$ from $\{0,1\}$ to $\{0,1\}$ and 2 of them are bijective, we subtract the cases where all the functions are bijective from the total to get $4^{2010}-2^{2010}$.
|
4^{2010}-2^{2010}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
How many ways are there to choose 2010 functions $f_{1}, \ldots, f_{2010}$ from $\{0,1\}$ to $\{0,1\}$ such that $f_{2010} \circ f_{2009} \circ \cdots \circ f_{1}$ is constant? Note: a function $g$ is constant if $g(a)=g(b)$ for all $a, b$ in the domain of $g$.
|
$4^{2010}-2^{2010}$ If all 2010 functions are bijective ${ }^{1}$, then the composition $f_{2010} \circ f_{2009} \circ \cdots \circ f_{1}$ will be bijective also, and therefore not constant. If, however, one of $f_{1}, \ldots, f_{2010}$ is not bijective, say $f_{k}$, then $f_{k}(0)=f_{k}(1)=q$, so $f_{2010} \circ f_{2009} \circ \cdots \circ f_{k+1} \circ f_{k} \circ \cdots f_{1}(0)=f_{2010} \circ f_{2009} \circ \cdots \circ f_{k+1}(q)=$ $f_{2010} \circ f_{2009} \circ \cdots \circ f_{k+1} \circ f_{k} \circ \cdots f_{1}(1)$. So the composition will be constant unless all $f_{i}$ are bijective. Since there are 4 possible functions ${ }^{2}$ from $\{0,1\}$ to $\{0,1\}$ and 2 of them are bijective, we subtract the cases where all the functions are bijective from the total to get $4^{2010}-2^{2010}$.
|
{
"resource_path": "HarvardMIT/segmented/en-132-2010-feb-comb-solutions.jsonl",
"problem_match": "\n3. [4]",
"solution_match": "\nAnswer: "
}
|
de166431-a53e-50cb-8e3c-f1e9b9217b0a
| 608,645
|
Manya has a stack of $85=1+4+16+64$ blocks comprised of 4 layers (the $k$ th layer from the top has $4^{k-1}$ blocks; see the diagram below). Each block rests on 4 smaller blocks, each with dimensions half those of the larger block. Laura removes blocks one at a time from this stack, removing only blocks that currently have no blocks on top of them. Find the number of ways Laura can remove precisely 5 blocks from Manya's stack (the order in which they are removed matters).
|
3384 Each time Laura removes a block, 4 additional blocks are exposed, increasing the total number of exposed blocks by 3 . She removes 5 blocks, for a total of $1 \cdot 4 \cdot 7 \cdot 10 \cdot 13$ ways. However, the stack originally only has 4 layers, so we must subtract the cases where removing a block on the bottom layer does not expose any new blocks. There are $1 \cdot 4 \cdot 4 \cdot 4 \cdot 4=256$ of these (the last factor of 4 is from the 4 blocks that we counted as being exposed, but were not actually). So our final answer is $1 \cdot 4 \cdot 7 \cdot 10 \cdot 13-1 \cdot 4 \cdot 4 \cdot 4 \cdot 4=3384$.
|
3384
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Manya has a stack of $85=1+4+16+64$ blocks comprised of 4 layers (the $k$ th layer from the top has $4^{k-1}$ blocks; see the diagram below). Each block rests on 4 smaller blocks, each with dimensions half those of the larger block. Laura removes blocks one at a time from this stack, removing only blocks that currently have no blocks on top of them. Find the number of ways Laura can remove precisely 5 blocks from Manya's stack (the order in which they are removed matters).

|
3384 Each time Laura removes a block, 4 additional blocks are exposed, increasing the total number of exposed blocks by 3 . She removes 5 blocks, for a total of $1 \cdot 4 \cdot 7 \cdot 10 \cdot 13$ ways. However, the stack originally only has 4 layers, so we must subtract the cases where removing a block on the bottom layer does not expose any new blocks. There are $1 \cdot 4 \cdot 4 \cdot 4 \cdot 4=256$ of these (the last factor of 4 is from the 4 blocks that we counted as being exposed, but were not actually). So our final answer is $1 \cdot 4 \cdot 7 \cdot 10 \cdot 13-1 \cdot 4 \cdot 4 \cdot 4 \cdot 4=3384$.
|
{
"resource_path": "HarvardMIT/segmented/en-132-2010-feb-comb-solutions.jsonl",
"problem_match": "\n4. [4]",
"solution_match": "\nAnswer: "
}
|
503a5cf7-3246-516a-a117-f0ea461a532a
| 608,646
|
John needs to pay 2010 dollars for his dinner. He has an unlimited supply of 2, 5, and 10 dollar notes. In how many ways can he pay?
|
20503
Let the number of 2,5 , and 10 dollar notes John can use be $x, y$, and $z$ respectively. We wish to find the number of nonnegative integer solutions to $2 x+5 y+10 z=2010$. Consider this equation $\bmod 2$. Because $2 x, 10 z$, and 2010 are even, $5 y$ must also be even, so $y$ must be even. Now consider the equation mod 5 . Because $5 y, 10 z$, and 2010 are divisible by $5,2 x$ must also be divisible by 5 , so $x$ must be divisible by 5 . So both $2 x$ and $5 y$ are divisible by 10 . So the equation is equivalent to $10 x^{\prime}+10 y^{\prime}+10 z=2010$, or $x^{\prime}+y^{\prime}+z=201$, with $x^{\prime}, y^{\prime}$, and $z$ nonnegative integers. There is a well-known bijection between solutions of this equation and picking 2 of 203 balls in a row on the table (explained in further detail below), so there are $\binom{203}{2}=20503$ ways.
The bijection between solutions of $x^{\prime}+y^{\prime}+z=201$ and arrangements of 203 balls in a row is as follows. Given a solution of the equation, we put $x^{\prime}$ white balls in a row, then a black ball, then $y^{\prime}$ white balls, then a black ball, then $z$ white balls. This is like having 203 balls in a row on a table and picking two of them to be black. To go from an arrangement of balls to a solution of the equation, we just read off $x^{\prime}, y^{\prime}$, and $z$ from the number of white balls in a row. There are $\binom{203}{2}$ ways to choose 2 of 203 balls to be black, so there are $\binom{203}{2}$ solutions to $x^{\prime}+y^{\prime}+z=201$.
|
20503
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
John needs to pay 2010 dollars for his dinner. He has an unlimited supply of 2, 5, and 10 dollar notes. In how many ways can he pay?
|
20503
Let the number of 2,5 , and 10 dollar notes John can use be $x, y$, and $z$ respectively. We wish to find the number of nonnegative integer solutions to $2 x+5 y+10 z=2010$. Consider this equation $\bmod 2$. Because $2 x, 10 z$, and 2010 are even, $5 y$ must also be even, so $y$ must be even. Now consider the equation mod 5 . Because $5 y, 10 z$, and 2010 are divisible by $5,2 x$ must also be divisible by 5 , so $x$ must be divisible by 5 . So both $2 x$ and $5 y$ are divisible by 10 . So the equation is equivalent to $10 x^{\prime}+10 y^{\prime}+10 z=2010$, or $x^{\prime}+y^{\prime}+z=201$, with $x^{\prime}, y^{\prime}$, and $z$ nonnegative integers. There is a well-known bijection between solutions of this equation and picking 2 of 203 balls in a row on the table (explained in further detail below), so there are $\binom{203}{2}=20503$ ways.
The bijection between solutions of $x^{\prime}+y^{\prime}+z=201$ and arrangements of 203 balls in a row is as follows. Given a solution of the equation, we put $x^{\prime}$ white balls in a row, then a black ball, then $y^{\prime}$ white balls, then a black ball, then $z$ white balls. This is like having 203 balls in a row on a table and picking two of them to be black. To go from an arrangement of balls to a solution of the equation, we just read off $x^{\prime}, y^{\prime}$, and $z$ from the number of white balls in a row. There are $\binom{203}{2}$ ways to choose 2 of 203 balls to be black, so there are $\binom{203}{2}$ solutions to $x^{\prime}+y^{\prime}+z=201$.
|
{
"resource_path": "HarvardMIT/segmented/en-132-2010-feb-comb-solutions.jsonl",
"problem_match": "\n5. [5]",
"solution_match": "\nAnswer: "
}
|
56ddd9ea-2f32-530c-9360-a850a6c7d7df
| 608,647
|
For each integer $x$ with $1 \leq x \leq 10$, a point is randomly placed at either $(x, 1)$ or $(x,-1)$ with equal probability. What is the expected area of the convex hull of these points? Note: the convex hull of a finite set is the smallest convex polygon containing it.
|
$\frac{1793}{\frac{1728}{128}}$ Let $n=10$. Given a random variable $X$, let $\mathbb{E}(X)$ denote its expected value. If all points are collinear, then the convex hull has area zero. This happens with probability $\frac{2}{2^{n}}$ (either all points are at $y=1$ or all points are at $y=-1$ ). Otherwise, the points form a trapezoid with height 2 (the trapezoid is possibly degenerate, but this won't matter for our calculation). Let $x_{1, l}$ be the $x$-coordinate of the left-most point at $y=1$ and $x_{1, r}$ be the $x$-coordinate of the right-most point at $y=1$. Define $x_{-1, l}$ and $x_{-1, r}$ similarly for $y=-1$. Then the area of the trapezoid is
$$
2 \cdot \frac{\left(x_{1, r}-x_{1, l}\right)+\left(x_{-1, r}-x_{-1, l}\right)}{2}=x_{1, r}+x_{-1, r}-x_{1, l}-x_{-1, l} .
$$
The expected area of the convex hull (assuming the points are not all collinear) is then, by linearity of expectation,
$$
\mathbb{E}\left(x_{1, r}+x_{-1, r}-x_{1, l}-x_{-1, l}\right)=\mathbb{E}\left(x_{1, r}\right)+\mathbb{E}\left(x_{-1, r}\right)-\mathbb{E}\left(x_{1, l}\right)-\mathbb{E}\left(x_{-1, l}\right) .
$$
We need only compute the expected values given in the above equation. Note that $x_{1, r}$ is equal to $k$ with probability $\frac{2^{k-1}}{2^{n}-2}$, except that it is equal to $n$ with probability $\frac{2^{n-1}-1}{2^{n}-2}$ (the denominator is $2^{n}-2$ instead of $2^{n}$ because we need to exclude the case where all points are collinear). Therefore, the expected value of $x_{1, r}$ is equal to
$$
\begin{aligned}
& \frac{1}{2^{n}-2}\left(\left(\sum_{k=1}^{n} k \cdot 2^{k-1}\right)-n \cdot 1\right) \\
& \quad=\frac{1}{2^{n}-2}\left(\left(1+2+\cdots+2^{n-1}\right)+\left(2+4+\cdots+2^{n-1}\right)+\cdots+2^{n-1}-n\right) \\
& =\frac{1}{2^{n}-2}\left(\left(2^{n}-1\right)+\left(2^{n}-2\right)+\cdots+\left(2^{n}-2^{n-1}\right)-n\right) \\
& =\frac{1}{2^{n}-2}\left(n \cdot 2^{n}-\left(2^{n}-1\right)-n\right) \\
& \quad=(n-1) \frac{2^{n}-1}{2^{n}-2}
\end{aligned}
$$
Similarly, the expected value of $x_{-1, r}$ is also $(n-1) \frac{2^{n}-1}{2^{n}-2}$. By symmetry, the expected value of both $x_{1, l}$ and $x_{-1, l}$ is $n+1-(n-1) \frac{\frac{2}{n}^{n}-1}{2^{n}-2}$. This says that if the points are not all collinear then the expected area is $2 \cdot\left((n-1) \frac{2^{n}-1}{2^{n-1}-1}-(n+1)\right)$. So, the expected area is
$$
\begin{aligned}
\frac{2}{2^{n}} \cdot 0+(1- & \left.\frac{2}{2^{n}}\right) \cdot 2 \cdot\left((n-1) \frac{2^{n}-1}{2^{n-1}-1}-(n+1)\right) \\
& =2 \cdot \frac{2^{n-1}-1}{2^{n-1}} \cdot\left((n-1) \frac{2^{n}-1}{2^{n-1}-1}-(n+1)\right) \\
& =2 \cdot \frac{(n-1)\left(2^{n}-1\right)-(n+1)\left(2^{n-1}-1\right)}{2^{n-1}} \\
& =2 \cdot \frac{((2 n-2)-(n+1)) 2^{n-1}+2}{2^{n-1}} \\
& =2 n-6+\frac{1}{2^{n-3}}
\end{aligned}
$$
Plugging in $n=10$, we get $14+\frac{1}{128}=\frac{1793}{128}$.
|
\frac{1793}{128}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
For each integer $x$ with $1 \leq x \leq 10$, a point is randomly placed at either $(x, 1)$ or $(x,-1)$ with equal probability. What is the expected area of the convex hull of these points? Note: the convex hull of a finite set is the smallest convex polygon containing it.
|
$\frac{1793}{\frac{1728}{128}}$ Let $n=10$. Given a random variable $X$, let $\mathbb{E}(X)$ denote its expected value. If all points are collinear, then the convex hull has area zero. This happens with probability $\frac{2}{2^{n}}$ (either all points are at $y=1$ or all points are at $y=-1$ ). Otherwise, the points form a trapezoid with height 2 (the trapezoid is possibly degenerate, but this won't matter for our calculation). Let $x_{1, l}$ be the $x$-coordinate of the left-most point at $y=1$ and $x_{1, r}$ be the $x$-coordinate of the right-most point at $y=1$. Define $x_{-1, l}$ and $x_{-1, r}$ similarly for $y=-1$. Then the area of the trapezoid is
$$
2 \cdot \frac{\left(x_{1, r}-x_{1, l}\right)+\left(x_{-1, r}-x_{-1, l}\right)}{2}=x_{1, r}+x_{-1, r}-x_{1, l}-x_{-1, l} .
$$
The expected area of the convex hull (assuming the points are not all collinear) is then, by linearity of expectation,
$$
\mathbb{E}\left(x_{1, r}+x_{-1, r}-x_{1, l}-x_{-1, l}\right)=\mathbb{E}\left(x_{1, r}\right)+\mathbb{E}\left(x_{-1, r}\right)-\mathbb{E}\left(x_{1, l}\right)-\mathbb{E}\left(x_{-1, l}\right) .
$$
We need only compute the expected values given in the above equation. Note that $x_{1, r}$ is equal to $k$ with probability $\frac{2^{k-1}}{2^{n}-2}$, except that it is equal to $n$ with probability $\frac{2^{n-1}-1}{2^{n}-2}$ (the denominator is $2^{n}-2$ instead of $2^{n}$ because we need to exclude the case where all points are collinear). Therefore, the expected value of $x_{1, r}$ is equal to
$$
\begin{aligned}
& \frac{1}{2^{n}-2}\left(\left(\sum_{k=1}^{n} k \cdot 2^{k-1}\right)-n \cdot 1\right) \\
& \quad=\frac{1}{2^{n}-2}\left(\left(1+2+\cdots+2^{n-1}\right)+\left(2+4+\cdots+2^{n-1}\right)+\cdots+2^{n-1}-n\right) \\
& =\frac{1}{2^{n}-2}\left(\left(2^{n}-1\right)+\left(2^{n}-2\right)+\cdots+\left(2^{n}-2^{n-1}\right)-n\right) \\
& =\frac{1}{2^{n}-2}\left(n \cdot 2^{n}-\left(2^{n}-1\right)-n\right) \\
& \quad=(n-1) \frac{2^{n}-1}{2^{n}-2}
\end{aligned}
$$
Similarly, the expected value of $x_{-1, r}$ is also $(n-1) \frac{2^{n}-1}{2^{n}-2}$. By symmetry, the expected value of both $x_{1, l}$ and $x_{-1, l}$ is $n+1-(n-1) \frac{\frac{2}{n}^{n}-1}{2^{n}-2}$. This says that if the points are not all collinear then the expected area is $2 \cdot\left((n-1) \frac{2^{n}-1}{2^{n-1}-1}-(n+1)\right)$. So, the expected area is
$$
\begin{aligned}
\frac{2}{2^{n}} \cdot 0+(1- & \left.\frac{2}{2^{n}}\right) \cdot 2 \cdot\left((n-1) \frac{2^{n}-1}{2^{n-1}-1}-(n+1)\right) \\
& =2 \cdot \frac{2^{n-1}-1}{2^{n-1}} \cdot\left((n-1) \frac{2^{n}-1}{2^{n-1}-1}-(n+1)\right) \\
& =2 \cdot \frac{(n-1)\left(2^{n}-1\right)-(n+1)\left(2^{n-1}-1\right)}{2^{n-1}} \\
& =2 \cdot \frac{((2 n-2)-(n+1)) 2^{n-1}+2}{2^{n-1}} \\
& =2 n-6+\frac{1}{2^{n-3}}
\end{aligned}
$$
Plugging in $n=10$, we get $14+\frac{1}{128}=\frac{1793}{128}$.
|
{
"resource_path": "HarvardMIT/segmented/en-132-2010-feb-comb-solutions.jsonl",
"problem_match": "\n7. [6]",
"solution_match": "\nAnswer: "
}
|
b6b75202-110d-5719-a98e-b76e78a02743
| 608,649
|
Rosencrantz and Guildenstern are playing a game where they repeatedly flip coins. Rosencrantz wins if 1 heads followed by 2009 tails appears. Guildenstern wins if 2010 heads come in a row. They will flip coins until someone wins. What is the probability that Rosencrantz wins?
|
$\frac{2^{2009}-1}{3 \cdot 2^{2008}-1}$ We can assume the first throw is heads (because neither player can win starting from a string of only tails). Let $x$ be the probability that Rosencrantz wins. Let $y$ be the probability that Rosencrantz wins after HT.
Whenever there is a string of less than 2009 tails followed by a heads, the heads basically means the two are starting from the beginning, where Rosencrantz has probability $x$ of winning.
We also know that $x=y\left(1-\frac{1}{2^{2009}}\right)$. This is because from the initial heads there is a $\left(1-\frac{1}{2^{2009}}\right)$ chance Rosencrantz doesn't lose, and in this case the last two flips are HT, in which case Rosencrantz has probability $y$ of winning.
If the first two throws are HT, there is a $\frac{1}{2^{2008}}$ chance Rosencrantz wins; otherwise, there is eventually a heads, and so we are back in the case of starting from a heads, which corresponds to $x$. Therefore, $y=\frac{1}{2^{2008}}+x\left(1-\frac{1}{2^{2008}}\right)$. Putting this together with the previous equation, we get:
$$
\begin{aligned}
x & =\left(\frac{1}{2^{2008}}+x\left(1-\frac{1}{2^{2008}}\right)\right)\left(1-\frac{1}{2^{2009}}\right) \\
\Longrightarrow \quad x & =\left(\frac{1+2^{2008} x-x}{2^{2008}}\right)\left(\frac{2^{2009}-1}{\left.2^{2009}\right)}\right. \\
\Longrightarrow \quad 2^{4017} x & =x\left(2^{4017}-2^{2009}-2^{2008}+1\right)+2^{2009}-1 \\
\Longrightarrow \quad x & =\frac{2^{2009}-1}{2^{2009}+2^{2008}-1},
\end{aligned}
$$
so the answer is $\frac{2^{2009}-1}{2^{2009}+2^{2008}-1}=\frac{2^{2009}-1}{3 \cdot 2^{2008}-1}$.
|
\frac{2^{2009}-1}{3 \cdot 2^{2008}-1}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Rosencrantz and Guildenstern are playing a game where they repeatedly flip coins. Rosencrantz wins if 1 heads followed by 2009 tails appears. Guildenstern wins if 2010 heads come in a row. They will flip coins until someone wins. What is the probability that Rosencrantz wins?
|
$\frac{2^{2009}-1}{3 \cdot 2^{2008}-1}$ We can assume the first throw is heads (because neither player can win starting from a string of only tails). Let $x$ be the probability that Rosencrantz wins. Let $y$ be the probability that Rosencrantz wins after HT.
Whenever there is a string of less than 2009 tails followed by a heads, the heads basically means the two are starting from the beginning, where Rosencrantz has probability $x$ of winning.
We also know that $x=y\left(1-\frac{1}{2^{2009}}\right)$. This is because from the initial heads there is a $\left(1-\frac{1}{2^{2009}}\right)$ chance Rosencrantz doesn't lose, and in this case the last two flips are HT, in which case Rosencrantz has probability $y$ of winning.
If the first two throws are HT, there is a $\frac{1}{2^{2008}}$ chance Rosencrantz wins; otherwise, there is eventually a heads, and so we are back in the case of starting from a heads, which corresponds to $x$. Therefore, $y=\frac{1}{2^{2008}}+x\left(1-\frac{1}{2^{2008}}\right)$. Putting this together with the previous equation, we get:
$$
\begin{aligned}
x & =\left(\frac{1}{2^{2008}}+x\left(1-\frac{1}{2^{2008}}\right)\right)\left(1-\frac{1}{2^{2009}}\right) \\
\Longrightarrow \quad x & =\left(\frac{1+2^{2008} x-x}{2^{2008}}\right)\left(\frac{2^{2009}-1}{\left.2^{2009}\right)}\right. \\
\Longrightarrow \quad 2^{4017} x & =x\left(2^{4017}-2^{2009}-2^{2008}+1\right)+2^{2009}-1 \\
\Longrightarrow \quad x & =\frac{2^{2009}-1}{2^{2009}+2^{2008}-1},
\end{aligned}
$$
so the answer is $\frac{2^{2009}-1}{2^{2009}+2^{2008}-1}=\frac{2^{2009}-1}{3 \cdot 2^{2008}-1}$.
|
{
"resource_path": "HarvardMIT/segmented/en-132-2010-feb-comb-solutions.jsonl",
"problem_match": "\n9. [7]",
"solution_match": "\nAnswer: "
}
|
99f2a340-9815-5f64-81a1-438a12f8c9d0
| 608,651
|
In a $16 \times 16$ table of integers, each row and column contains at most 4 distinct integers. What is the maximum number of distinct integers that there can be in the whole table?
|
49 First, we show that 50 is too big. Assume for sake of contradiction that a labeling with at least 50 distinct integers exists. By the Pigeonhole Principle, there must be at least one row, say the first row, with at least 4 distinct integers in it; in this case, that is exactly 4 , since that is the maximum number of distinct integers in one row. Then, in the remaining 15 rows there must be at least 46 distinct integers (these 46 will also be distinct from the 4 in the first row). Using Pigeonhole again, there will be another row, say the second row, with 4 distinct integers in it. Call the set of integers in the first and second rows $S$. Because the 4 distinct integers in the second row are distinct from the 4 in the first row, there are 8 distinct values in the first two rows, so $|S|=8$. Now consider the subcolumns containing the cells in rows 3 to 16 . In each subcolumn, there are at most 2 values not in $S$, because there are already two distinct values in that column from the cells in the first two rows. So, the maximum number of distinct values in the table is $16 \cdot 2+8=40$, a contradiction. So a valid labeling must have fewer than 50 distinct integers. Below, we show by example that 49 is attainable.
| 1 | 17 | 33 | - | - | - | - | - | - | - | - | - | - | - | - | - |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| - | 2 | 18 | 34 | - | - | - | - | - | - | - | - | - | - | - | - |
| - | - | 3 | 19 | 35 | - | - | - | - | - | - | - | - | - | - | - |
| - | - | - | 4 | 20 | 36 | - | - | - | - | - | - | - | - | - | - |
| - | - | - | - | 5 | 21 | 37 | - | - | - | - | - | - | - | - | - |
| - | - | - | - | - | 6 | 22 | 38 | - | - | - | - | - | - | - | - |
| - | - | - | - | - | - | 7 | 23 | 39 | - | - | - | - | - | - | - |
| - | - | - | - | - | - | - | 8 | 24 | 40 | - | - | - | - | - | - |
| - | - | - | - | - | - | - | - | 9 | 25 | 41 | - | - | - | - | - |
| - | - | - | - | - | - | - | - | - | 10 | 26 | 42 | - | - | - | - |
| - | - | - | - | - | - | - | - | - | - | 11 | 27 | 43 | - | - | - |
| - | - | - | - | - | - | - | - | - | - | - | 12 | 28 | 44 | - | - |
| - | - | - | - | - | - | - | - | - | - | - | - | 13 | 29 | 45 | - |
| - | - | - | - | - | - | - | - | - | - | - | - | - | 14 | 30 | 46 |
| 47 | - | - | - | - | - | - | - | - | - | - | - | - | - | 15 | 31 |
| 32 | 48 | - | - | - | - | - | - | - | - | - | - | - | - | - | 16 |
Cells that do not contain a number are colored with color 49 .
|
49
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
In a $16 \times 16$ table of integers, each row and column contains at most 4 distinct integers. What is the maximum number of distinct integers that there can be in the whole table?
|
49 First, we show that 50 is too big. Assume for sake of contradiction that a labeling with at least 50 distinct integers exists. By the Pigeonhole Principle, there must be at least one row, say the first row, with at least 4 distinct integers in it; in this case, that is exactly 4 , since that is the maximum number of distinct integers in one row. Then, in the remaining 15 rows there must be at least 46 distinct integers (these 46 will also be distinct from the 4 in the first row). Using Pigeonhole again, there will be another row, say the second row, with 4 distinct integers in it. Call the set of integers in the first and second rows $S$. Because the 4 distinct integers in the second row are distinct from the 4 in the first row, there are 8 distinct values in the first two rows, so $|S|=8$. Now consider the subcolumns containing the cells in rows 3 to 16 . In each subcolumn, there are at most 2 values not in $S$, because there are already two distinct values in that column from the cells in the first two rows. So, the maximum number of distinct values in the table is $16 \cdot 2+8=40$, a contradiction. So a valid labeling must have fewer than 50 distinct integers. Below, we show by example that 49 is attainable.
| 1 | 17 | 33 | - | - | - | - | - | - | - | - | - | - | - | - | - |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| - | 2 | 18 | 34 | - | - | - | - | - | - | - | - | - | - | - | - |
| - | - | 3 | 19 | 35 | - | - | - | - | - | - | - | - | - | - | - |
| - | - | - | 4 | 20 | 36 | - | - | - | - | - | - | - | - | - | - |
| - | - | - | - | 5 | 21 | 37 | - | - | - | - | - | - | - | - | - |
| - | - | - | - | - | 6 | 22 | 38 | - | - | - | - | - | - | - | - |
| - | - | - | - | - | - | 7 | 23 | 39 | - | - | - | - | - | - | - |
| - | - | - | - | - | - | - | 8 | 24 | 40 | - | - | - | - | - | - |
| - | - | - | - | - | - | - | - | 9 | 25 | 41 | - | - | - | - | - |
| - | - | - | - | - | - | - | - | - | 10 | 26 | 42 | - | - | - | - |
| - | - | - | - | - | - | - | - | - | - | 11 | 27 | 43 | - | - | - |
| - | - | - | - | - | - | - | - | - | - | - | 12 | 28 | 44 | - | - |
| - | - | - | - | - | - | - | - | - | - | - | - | 13 | 29 | 45 | - |
| - | - | - | - | - | - | - | - | - | - | - | - | - | 14 | 30 | 46 |
| 47 | - | - | - | - | - | - | - | - | - | - | - | - | - | 15 | 31 |
| 32 | 48 | - | - | - | - | - | - | - | - | - | - | - | - | - | 16 |
Cells that do not contain a number are colored with color 49 .
|
{
"resource_path": "HarvardMIT/segmented/en-132-2010-feb-comb-solutions.jsonl",
"problem_match": "\n10. [8]",
"solution_match": "\nAnswer: "
}
|
1a4f8428-e1c5-56d2-b884-078306612aba
| 608,652
|
A rectangular piece of paper is folded along its diagonal (as depicted below) to form a non-convex pentagon that has an area of $\frac{7}{10}$ of the area of the original rectangle. Find the ratio of the longer side of the rectangle to the shorter side of the rectangle.
|
$\sqrt{5}$
Given a polygon $P_{1} P_{2} \cdots P_{k}$, let $\left[P_{1} P_{2} \cdots P_{k}\right]$ denote its area. Let $A B C D$ be the rectangle. Suppose we fold $B$ across $\overline{A C}$, and let $E$ be the intersection of $\overline{A D}$ and $\overline{B^{\prime} C}$. Then we end up with the pentagon $A C D E B^{\prime}$, depicted above. Let's suppose, without loss of generality, that $A B C D$ has area 1. Then $\triangle A E C$ must have area $\frac{3}{10}$, since
$$
\begin{aligned}
{[A B C D] } & =[A B C]+[A C D] \\
& =\left[A B^{\prime} C\right]+[A C D] \\
& =\left[A B^{\prime} E\right]+2[A E C]+[E D C] \\
& =\left[A C D E B^{\prime}\right]+[A E C] \\
& =\frac{7}{10}[A B C D]+[A E C],
\end{aligned}
$$
That is, $[A E C]=\frac{3}{10}[A B C D]=\frac{3}{10}$.
Since $\triangle E C D$ is congruent to $\triangle E A B^{\prime}$, both triangles have area $\frac{1}{5}$. Note that $\triangle A B^{\prime} C, \triangle A B C$, and $\triangle C D A$ are all congruent, and all have area $\frac{1}{2}$. Since $\triangle A E C$ and $\triangle E D C$ share altitude $\overline{D C}$, $\frac{D E}{E A}=\frac{[D E C]}{[A E C]}=\frac{2}{3}$. Because $\triangle C A E$ is isosceles, $C E=E A$. Let $A E=3 x$. The $C E=3 x, D E=2 x$, and $C D=x \sqrt{9-4}=x \sqrt{5}$. Then $\frac{A D}{D C}=\frac{A E+E D}{D C}=\frac{3+2}{\sqrt{5}}=\sqrt{5}$.
|
\sqrt{5}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
A rectangular piece of paper is folded along its diagonal (as depicted below) to form a non-convex pentagon that has an area of $\frac{7}{10}$ of the area of the original rectangle. Find the ratio of the longer side of the rectangle to the shorter side of the rectangle.

|
$\sqrt{5}$

Given a polygon $P_{1} P_{2} \cdots P_{k}$, let $\left[P_{1} P_{2} \cdots P_{k}\right]$ denote its area. Let $A B C D$ be the rectangle. Suppose we fold $B$ across $\overline{A C}$, and let $E$ be the intersection of $\overline{A D}$ and $\overline{B^{\prime} C}$. Then we end up with the pentagon $A C D E B^{\prime}$, depicted above. Let's suppose, without loss of generality, that $A B C D$ has area 1. Then $\triangle A E C$ must have area $\frac{3}{10}$, since
$$
\begin{aligned}
{[A B C D] } & =[A B C]+[A C D] \\
& =\left[A B^{\prime} C\right]+[A C D] \\
& =\left[A B^{\prime} E\right]+2[A E C]+[E D C] \\
& =\left[A C D E B^{\prime}\right]+[A E C] \\
& =\frac{7}{10}[A B C D]+[A E C],
\end{aligned}
$$
That is, $[A E C]=\frac{3}{10}[A B C D]=\frac{3}{10}$.
Since $\triangle E C D$ is congruent to $\triangle E A B^{\prime}$, both triangles have area $\frac{1}{5}$. Note that $\triangle A B^{\prime} C, \triangle A B C$, and $\triangle C D A$ are all congruent, and all have area $\frac{1}{2}$. Since $\triangle A E C$ and $\triangle E D C$ share altitude $\overline{D C}$, $\frac{D E}{E A}=\frac{[D E C]}{[A E C]}=\frac{2}{3}$. Because $\triangle C A E$ is isosceles, $C E=E A$. Let $A E=3 x$. The $C E=3 x, D E=2 x$, and $C D=x \sqrt{9-4}=x \sqrt{5}$. Then $\frac{A D}{D C}=\frac{A E+E D}{D C}=\frac{3+2}{\sqrt{5}}=\sqrt{5}$.
|
{
"resource_path": "HarvardMIT/segmented/en-132-2010-feb-gen1-solutions.jsonl",
"problem_match": "\n3. [4]",
"solution_match": "\nAnswer: "
}
|
763b10b0-7d6e-549d-91f6-12e39d48ce9a
| 608,653
|
Manya has a stack of $85=1+4+16+64$ blocks comprised of 4 layers (the $k$ th layer from the top has $4^{k-1}$ blocks; see the diagram below). Each block rests on 4 smaller blocks, each with dimensions half those of the larger block. Laura removes blocks one at a time from this stack, removing only blocks that currently have no blocks on top of them. Find the number of ways Laura can remove precisely 5 blocks from Manya's stack (the order in which they are removed matters).

|
3384 Each time Laura removes a block, 4 additional blocks are exposed, increasing the total number of exposed blocks by 3 . She removes 5 blocks, for a total of $1 \cdot 4 \cdot 7 \cdot 10 \cdot 13$ ways. However, the stack originally only has 4 layers, so we must subtract the cases where removing a block on the bottom layer does not expose any new blocks. There are $1 \cdot 4 \cdot 4 \cdot 4 \cdot 4=256$ of these (the last factor of 4 is from the 4 blocks that we counted as being exposed, but were not actually). So our final answer is $1 \cdot 4 \cdot 7 \cdot 10 \cdot 13-1 \cdot 4 \cdot 4 \cdot 4 \cdot 4=3384$.
|
3384
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Manya has a stack of $85=1+4+16+64$ blocks comprised of 4 layers (the $k$ th layer from the top has $4^{k-1}$ blocks; see the diagram below). Each block rests on 4 smaller blocks, each with dimensions half those of the larger block. Laura removes blocks one at a time from this stack, removing only blocks that currently have no blocks on top of them. Find the number of ways Laura can remove precisely 5 blocks from Manya's stack (the order in which they are removed matters).

|
3384 Each time Laura removes a block, 4 additional blocks are exposed, increasing the total number of exposed blocks by 3 . She removes 5 blocks, for a total of $1 \cdot 4 \cdot 7 \cdot 10 \cdot 13$ ways. However, the stack originally only has 4 layers, so we must subtract the cases where removing a block on the bottom layer does not expose any new blocks. There are $1 \cdot 4 \cdot 4 \cdot 4 \cdot 4=256$ of these (the last factor of 4 is from the 4 blocks that we counted as being exposed, but were not actually). So our final answer is $1 \cdot 4 \cdot 7 \cdot 10 \cdot 13-1 \cdot 4 \cdot 4 \cdot 4 \cdot 4=3384$.
|
{
"resource_path": "HarvardMIT/segmented/en-132-2010-feb-gen1-solutions.jsonl",
"problem_match": "\n5. [4]",
"solution_match": "\nAnswer: "
}
|
19a5371b-35f7-54d2-a57c-91aa40fa2dbe
| 608,654
|
A sphere is the set of points at a fixed positive distance $r$ from its center. Let $\mathcal{S}$ be a set of 2010dimensional spheres. Suppose that the number of points lying on every element of $\mathcal{S}$ is a finite number $n$. Find the maximum possible value of $n$.
|
2 The answer is 2 for any number of dimensions. We prove this by induction on the dimension.
Note that 1-dimensional spheres are pairs of points, and 2-dimensional spheres are circles.
Base case, $d=2$ : The intersection of two circles is either a circle (if the original circles are identical, and in the same place), a pair of points, a single point (if the circles are tangent), or the empty set. Thus, in dimension 2 , the largest finite number of intersection points is 2 , because the number of pairwise intersection points is 0,1 , or 2 for distinct circles.
We now prove that the intersection of two $k$-dimensional spheres is either the empty set, a $(k-1)$ dimensional sphere, a $k$-dimensional sphere (which only occurs if the original spheres are identical and coincident). Consider two spheres in $k$-dimensional space, and impose a coordinate system such that the centers of the two spheres lie on one coordinate axis. Then the equations for the two spheres become identical in all but one coordinate:
$$
\begin{aligned}
& \left(x_{1}-a_{1}\right)^{2}+x_{2}^{2}+\ldots+x_{k}^{2}=r_{1}^{2} \\
& \left(x_{1}-a_{2}\right)^{2}+x_{2}^{2}+\ldots+x_{k}^{2}=r_{2}^{2}
\end{aligned}
$$
If $a_{1}=a_{2}$, the spheres are concentric, and so they are either nonintersecting or coincident, intersecting in a $k$-dimensional sphere. If $a_{1} \neq a_{2}$, then subtracting the equations and solving for $x_{1}$ yields $x_{1}=\frac{r_{1}^{2}-a_{1}^{2}-r_{2}^{2}+a_{2}^{2}}{2\left(a_{2}-a_{2}\right)}$. Plugging this in to either equation above yields a single equation equation that describes a $(k-1)$-dimensional sphere.
Assume we are in dimension $d$, and suppose for induction that for all $k$ less than $d$, any two distinct $k$-dimensional spheres intersecting in a finite number of points intersect in at most two points. Suppose we have a collection of $d$-dimensional spheres $s_{1}, s_{2}, \ldots, s_{m}$. Without loss of generality, suppose the $s_{i}$ are distinct. Let $t_{i}$ be the intersection of $s_{i}$ and $s_{i+1}$ for $1 \leq i<m$. If any $t_{i}$ are the empty set, then the intersection of the $t_{i}$ is empty. None of the $t_{i}$ is a $d$-dimensional sphere because the $s_{i}$ are distinct. Thus each of $t_{1}, t_{2}, \ldots, t_{m-1}$ is a $(d-1)$-dimensional sphere, and the intersection of all of them is the same as the intersection of the $d$-dimensional spheres. We can then apply the inductive hypothesis to find that $t_{1}, \ldots, t_{m-1}$ intersect in at most two points. Thus, by induction, a set of spheres in any dimension which intersect at only finitely many points intersect at at most two points.
We now exhibit a set of $2^{2009}$ 2010-dimensional spheres, and prove that their intersection contains exactly two points. Take the spheres with radii $\sqrt{2013}$ and centers $(0, \pm 1, \pm 1, \ldots, \pm 1)$, where the sign of each coordinate is independent from the sign of every other coordinate. Because of our choice of radius, all these spheres pass through the points $( \pm 2,0,0, \ldots 0)$. Then the intersection is the set of points $\left(x_{1}, x_{2}, \ldots, x_{2010}\right)$ which satisfy the equations $x_{1}^{2}+\left(x_{2} \pm 1\right)^{2}+\cdots+\left(x_{2010} \pm 1\right)^{2}=2013$. The only solutions to these equations are the points $( \pm 2,0,0, \ldots, 0)$ (since $\left(x_{i}+1\right)^{2}$ must be the same as $\left(x_{i}-1\right)^{2}$ for all $i>1$, because we may hold all but one of the $\pm$ choices constant, and change the remaining one).
|
2
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
A sphere is the set of points at a fixed positive distance $r$ from its center. Let $\mathcal{S}$ be a set of 2010dimensional spheres. Suppose that the number of points lying on every element of $\mathcal{S}$ is a finite number $n$. Find the maximum possible value of $n$.
|
2 The answer is 2 for any number of dimensions. We prove this by induction on the dimension.
Note that 1-dimensional spheres are pairs of points, and 2-dimensional spheres are circles.
Base case, $d=2$ : The intersection of two circles is either a circle (if the original circles are identical, and in the same place), a pair of points, a single point (if the circles are tangent), or the empty set. Thus, in dimension 2 , the largest finite number of intersection points is 2 , because the number of pairwise intersection points is 0,1 , or 2 for distinct circles.
We now prove that the intersection of two $k$-dimensional spheres is either the empty set, a $(k-1)$ dimensional sphere, a $k$-dimensional sphere (which only occurs if the original spheres are identical and coincident). Consider two spheres in $k$-dimensional space, and impose a coordinate system such that the centers of the two spheres lie on one coordinate axis. Then the equations for the two spheres become identical in all but one coordinate:
$$
\begin{aligned}
& \left(x_{1}-a_{1}\right)^{2}+x_{2}^{2}+\ldots+x_{k}^{2}=r_{1}^{2} \\
& \left(x_{1}-a_{2}\right)^{2}+x_{2}^{2}+\ldots+x_{k}^{2}=r_{2}^{2}
\end{aligned}
$$
If $a_{1}=a_{2}$, the spheres are concentric, and so they are either nonintersecting or coincident, intersecting in a $k$-dimensional sphere. If $a_{1} \neq a_{2}$, then subtracting the equations and solving for $x_{1}$ yields $x_{1}=\frac{r_{1}^{2}-a_{1}^{2}-r_{2}^{2}+a_{2}^{2}}{2\left(a_{2}-a_{2}\right)}$. Plugging this in to either equation above yields a single equation equation that describes a $(k-1)$-dimensional sphere.
Assume we are in dimension $d$, and suppose for induction that for all $k$ less than $d$, any two distinct $k$-dimensional spheres intersecting in a finite number of points intersect in at most two points. Suppose we have a collection of $d$-dimensional spheres $s_{1}, s_{2}, \ldots, s_{m}$. Without loss of generality, suppose the $s_{i}$ are distinct. Let $t_{i}$ be the intersection of $s_{i}$ and $s_{i+1}$ for $1 \leq i<m$. If any $t_{i}$ are the empty set, then the intersection of the $t_{i}$ is empty. None of the $t_{i}$ is a $d$-dimensional sphere because the $s_{i}$ are distinct. Thus each of $t_{1}, t_{2}, \ldots, t_{m-1}$ is a $(d-1)$-dimensional sphere, and the intersection of all of them is the same as the intersection of the $d$-dimensional spheres. We can then apply the inductive hypothesis to find that $t_{1}, \ldots, t_{m-1}$ intersect in at most two points. Thus, by induction, a set of spheres in any dimension which intersect at only finitely many points intersect at at most two points.
We now exhibit a set of $2^{2009}$ 2010-dimensional spheres, and prove that their intersection contains exactly two points. Take the spheres with radii $\sqrt{2013}$ and centers $(0, \pm 1, \pm 1, \ldots, \pm 1)$, where the sign of each coordinate is independent from the sign of every other coordinate. Because of our choice of radius, all these spheres pass through the points $( \pm 2,0,0, \ldots 0)$. Then the intersection is the set of points $\left(x_{1}, x_{2}, \ldots, x_{2010}\right)$ which satisfy the equations $x_{1}^{2}+\left(x_{2} \pm 1\right)^{2}+\cdots+\left(x_{2010} \pm 1\right)^{2}=2013$. The only solutions to these equations are the points $( \pm 2,0,0, \ldots, 0)$ (since $\left(x_{i}+1\right)^{2}$ must be the same as $\left(x_{i}-1\right)^{2}$ for all $i>1$, because we may hold all but one of the $\pm$ choices constant, and change the remaining one).
|
{
"resource_path": "HarvardMIT/segmented/en-132-2010-feb-gen1-solutions.jsonl",
"problem_match": "\n8. [6]",
"solution_match": "\nAnswer: "
}
|
9da70d1a-dbfd-5ad1-90cd-efb1fc885a87
| 608,655
|
Three unit circles $\omega_{1}, \omega_{2}$, and $\omega_{3}$ in the plane have the property that each circle passes through the centers of the other two. A square $S$ surrounds the three circles in such a way that each of its four sides is tangent to at least one of $\omega_{1}, \omega_{2}$ and $\omega_{3}$. Find the side length of the square $S$.
|
$\frac{\sqrt{6}+\sqrt{2}+8}{4}$
By the Pigeonhole Principle, two of the sides must be tangent to the same circle, say $\omega_{1}$. Since $S$ surrounds the circles, these two sides must be adjacent, so we can let $A$ denote the common vertex of the two sides tangent to $\omega_{1}$. Let $B, C$, and $D$ be the other vertices of $S$ in clockwise order, and let $P, Q$, and $R$ be the centers of $\omega_{1}, \omega_{2}$, and $\omega_{3}$ respectively, and suppose WLOG that they are also in clockwise order. Then $A C$ passes through the center of $\omega_{1}$, and by symmetry ( since $A B=A D$ ) it
must also pass through the other intersection point of $\omega_{2}$ and $\omega_{3}$. That is, $A C$ is the radical axis of $\omega_{2}$ and $\omega_{3}$.
Now, let $M$ and $N$ be the feet of the perpendiculars from $P$ and $R$, respectively, to side $A D$. Let $E$ and $F$ be the feet of the perpendiculars from $P$ to $A B$ and from $R$ to $D C$, respectively. Then $P E A M$ and $N R F D$ are rectangles, and $P E$ and $R F$ are radii of $\omega_{1}$ and $\omega_{2}$ respectively. Thus $A M=E P=1$ and $N D=R F=1$. Finally, we have
$$
\begin{aligned}
M N & =P R \cdot \cos \left(180^{\circ}-\angle E P R\right) \\
& =\cos \left(180^{\circ}-E P Q-R P Q\right) \\
& =-\cos \left(\left(270^{\circ}-60^{\circ}\right) / 2+60^{\circ}\right) \\
& =-\cos \left(165^{\circ}\right) \\
& =\cos \left(15^{\circ}\right) \\
& =\frac{\sqrt{6}+\sqrt{2}}{4} .
\end{aligned}
$$
Thus $A D=A M+M N+N D=1+\frac{\sqrt{6}+\sqrt{2}}{4}+1=\frac{\sqrt{6}+\sqrt{2}+8}{4}$ as claimed.
|
\frac{\sqrt{6}+\sqrt{2}+8}{4}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Three unit circles $\omega_{1}, \omega_{2}$, and $\omega_{3}$ in the plane have the property that each circle passes through the centers of the other two. A square $S$ surrounds the three circles in such a way that each of its four sides is tangent to at least one of $\omega_{1}, \omega_{2}$ and $\omega_{3}$. Find the side length of the square $S$.
|
$\frac{\sqrt{6}+\sqrt{2}+8}{4}$

By the Pigeonhole Principle, two of the sides must be tangent to the same circle, say $\omega_{1}$. Since $S$ surrounds the circles, these two sides must be adjacent, so we can let $A$ denote the common vertex of the two sides tangent to $\omega_{1}$. Let $B, C$, and $D$ be the other vertices of $S$ in clockwise order, and let $P, Q$, and $R$ be the centers of $\omega_{1}, \omega_{2}$, and $\omega_{3}$ respectively, and suppose WLOG that they are also in clockwise order. Then $A C$ passes through the center of $\omega_{1}$, and by symmetry ( since $A B=A D$ ) it
must also pass through the other intersection point of $\omega_{2}$ and $\omega_{3}$. That is, $A C$ is the radical axis of $\omega_{2}$ and $\omega_{3}$.
Now, let $M$ and $N$ be the feet of the perpendiculars from $P$ and $R$, respectively, to side $A D$. Let $E$ and $F$ be the feet of the perpendiculars from $P$ to $A B$ and from $R$ to $D C$, respectively. Then $P E A M$ and $N R F D$ are rectangles, and $P E$ and $R F$ are radii of $\omega_{1}$ and $\omega_{2}$ respectively. Thus $A M=E P=1$ and $N D=R F=1$. Finally, we have
$$
\begin{aligned}
M N & =P R \cdot \cos \left(180^{\circ}-\angle E P R\right) \\
& =\cos \left(180^{\circ}-E P Q-R P Q\right) \\
& =-\cos \left(\left(270^{\circ}-60^{\circ}\right) / 2+60^{\circ}\right) \\
& =-\cos \left(165^{\circ}\right) \\
& =\cos \left(15^{\circ}\right) \\
& =\frac{\sqrt{6}+\sqrt{2}}{4} .
\end{aligned}
$$
Thus $A D=A M+M N+N D=1+\frac{\sqrt{6}+\sqrt{2}}{4}+1=\frac{\sqrt{6}+\sqrt{2}+8}{4}$ as claimed.
|
{
"resource_path": "HarvardMIT/segmented/en-132-2010-feb-gen1-solutions.jsonl",
"problem_match": "\n9. [7]",
"solution_match": "\nAnswer: "
}
|
c88b4497-a395-5433-bcb9-cc7f9cc412c8
| 608,656
|
How many positive integers less than or equal to 240 can be expressed as a sum of distinct factorials? Consider 0 ! and 1 ! to be distinct.
|
39 Note that $1=0!, 2=0!+1!, 3=0!+2$ !, and $4=0!+1!+2$ !. These are the only numbers less than 6 that can be written as the sum of factorials. The only other factorials less than 240 are $3!=6,4!=24$, and $5!=120$. So a positive integer less than or equal to 240 can only contain $3!, 4!, 5$ !, and/or one of $1,2,3$, or 4 in its sum. If it contains any factorial larger than 5 !, it will be larger than 240 . So a sum less than or equal to 240 will will either include 3 ! or not ( 2 ways), 4 ! or not ( 2 ways), 5 ! or not ( 2 ways), and add an additional $0,1,2,3$ or 4 ( 5 ways). This gives $2 \cdot 2 \cdot 2 \cdot 5=40$ integers less than 240 . However, we want only positive integers, so we must not count 0 . So there are 39 such positive integers.
|
39
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
How many positive integers less than or equal to 240 can be expressed as a sum of distinct factorials? Consider 0 ! and 1 ! to be distinct.
|
39 Note that $1=0!, 2=0!+1!, 3=0!+2$ !, and $4=0!+1!+2$ !. These are the only numbers less than 6 that can be written as the sum of factorials. The only other factorials less than 240 are $3!=6,4!=24$, and $5!=120$. So a positive integer less than or equal to 240 can only contain $3!, 4!, 5$ !, and/or one of $1,2,3$, or 4 in its sum. If it contains any factorial larger than 5 !, it will be larger than 240 . So a sum less than or equal to 240 will will either include 3 ! or not ( 2 ways), 4 ! or not ( 2 ways), 5 ! or not ( 2 ways), and add an additional $0,1,2,3$ or 4 ( 5 ways). This gives $2 \cdot 2 \cdot 2 \cdot 5=40$ integers less than 240 . However, we want only positive integers, so we must not count 0 . So there are 39 such positive integers.
|
{
"resource_path": "HarvardMIT/segmented/en-132-2010-feb-gen2-solutions.jsonl",
"problem_match": "\n3. [4]",
"solution_match": "\nAnswer: "
}
|
f2bfdb4f-ec42-5b4e-a03f-a30e829006d2
| 608,658
|
For $0 \leq y \leq 2$, let $D_{y}$ be the half-disk of diameter 2 with one vertex at $(0, y)$, the other vertex on the positive $x$-axis, and the curved boundary further from the origin than the straight boundary. Find the area of the union of $D_{y}$ for all $0 \leq y \leq 2$.
|
$\pi$
From the picture above, we see that the union of the half-disks will be a quarter-circle with radius 2 , and therefore area $\pi$. To prove that this is the case, we first prove that the boundary of every half-disk intersects the quarter-circle with radius 2 , and then that the half-disk is internally tangent to the quarter-circle at that point. This is sufficient because it is clear from the diagram that we need not worry about covering the interior of the quarter-circle.
Let $O$ be the origin. For a given half-disk $D_{y}$, label the vertex on the $y$-axis $A$ and the vertex on the $x$-axis $B$. Let $M$ be the midpoint of line segment $\overline{A B}$. Draw segment $O M$, and extend it until it intersects the curved boundary of $D_{y}$. Label the intersection point $C$. This construction is shown in the diagram below.
We first prove that $C$ lies on the quarter-circle, centered at the origin, with radius 2 . Since $M$ is the midpoint of $\overline{A B}$, and $A$ is on the $y$-axis, $M$ is horizontally halfway between $B$ and the $y$-axis. Since
$O$ and $B$ are on the $x$-axis (which is perpendicular to the $y$-axis), segments $\overline{O M}$ and $\overline{M B}$ have the same length. Since $M$ is the midpoint of $\overline{A B}$, and $A B=2, O M=1$. Since $D_{y}$ is a half-disk with radius 1 , all points on its curved boundary are 1 away from its center, $M$. Then $C$ is 2 away from the origin, and the quarter-circle consists of all points which are 2 away from the origin. Thus, $C$ is an intersection of the half-disk $D_{y}$ with the positive quarter-circle of radius 2 .
It remains to show that the half-disk $D_{y}$ is internally tangent to the quarter-circle. Since $\overline{O C}$ is a radius of the quarter-circle, it is perpendicular to the tangent of the quarter-circle at $C$. Since $\overline{M C}$ is a radius of the half-disk, it is perpendicular to the tangent of the half-disk at $C$. Then the tangents lines of the half-disk and the quarter-circle coincide, and the half-disk is tangent to the quarter-circle. It is obvious from the diagram that the half-disk lies at least partially inside of the quarter-circle, the half-disk $D_{y}$ is internally tangent to the quarter-circle.
Then the union of the half-disks is be a quarter-circle with radius 2 , and has area $\pi$.
|
\pi
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
For $0 \leq y \leq 2$, let $D_{y}$ be the half-disk of diameter 2 with one vertex at $(0, y)$, the other vertex on the positive $x$-axis, and the curved boundary further from the origin than the straight boundary. Find the area of the union of $D_{y}$ for all $0 \leq y \leq 2$.
|
$\pi$

From the picture above, we see that the union of the half-disks will be a quarter-circle with radius 2 , and therefore area $\pi$. To prove that this is the case, we first prove that the boundary of every half-disk intersects the quarter-circle with radius 2 , and then that the half-disk is internally tangent to the quarter-circle at that point. This is sufficient because it is clear from the diagram that we need not worry about covering the interior of the quarter-circle.
Let $O$ be the origin. For a given half-disk $D_{y}$, label the vertex on the $y$-axis $A$ and the vertex on the $x$-axis $B$. Let $M$ be the midpoint of line segment $\overline{A B}$. Draw segment $O M$, and extend it until it intersects the curved boundary of $D_{y}$. Label the intersection point $C$. This construction is shown in the diagram below.

We first prove that $C$ lies on the quarter-circle, centered at the origin, with radius 2 . Since $M$ is the midpoint of $\overline{A B}$, and $A$ is on the $y$-axis, $M$ is horizontally halfway between $B$ and the $y$-axis. Since
$O$ and $B$ are on the $x$-axis (which is perpendicular to the $y$-axis), segments $\overline{O M}$ and $\overline{M B}$ have the same length. Since $M$ is the midpoint of $\overline{A B}$, and $A B=2, O M=1$. Since $D_{y}$ is a half-disk with radius 1 , all points on its curved boundary are 1 away from its center, $M$. Then $C$ is 2 away from the origin, and the quarter-circle consists of all points which are 2 away from the origin. Thus, $C$ is an intersection of the half-disk $D_{y}$ with the positive quarter-circle of radius 2 .
It remains to show that the half-disk $D_{y}$ is internally tangent to the quarter-circle. Since $\overline{O C}$ is a radius of the quarter-circle, it is perpendicular to the tangent of the quarter-circle at $C$. Since $\overline{M C}$ is a radius of the half-disk, it is perpendicular to the tangent of the half-disk at $C$. Then the tangents lines of the half-disk and the quarter-circle coincide, and the half-disk is tangent to the quarter-circle. It is obvious from the diagram that the half-disk lies at least partially inside of the quarter-circle, the half-disk $D_{y}$ is internally tangent to the quarter-circle.
Then the union of the half-disks is be a quarter-circle with radius 2 , and has area $\pi$.
|
{
"resource_path": "HarvardMIT/segmented/en-132-2010-feb-gen2-solutions.jsonl",
"problem_match": "\n4. [4]",
"solution_match": "\nAnswer: "
}
|
d0b73004-c0b7-5006-9ee0-022bf7f932fd
| 608,659
|
Let $A B C D$ be an isosceles trapezoid such that $A B=10, B C=15, C D=28$, and $D A=15$. There is a point $E$ such that $\triangle A E D$ and $\triangle A E B$ have the same area and such that $E C$ is minimal. Find $E C$.
|
| $\frac{216}{\sqrt{145}}$ |
| :---: |
The locus of points $E$ such that $[A E D]=[A E B]$ forms a line, since area is a linear function of the coordinates of $E$; setting the areas equal gives a linear equation in the coordinates $E^{2}$. Note that $A$ and $M$, the midpoint of $\overline{D B}$, are on this line; $A$ because both areas are 0 , and $M$ because the triangles share an altitude, and bases $\overline{D M}$ and $\overline{M B}$ are equal in length. Then $\overline{A M}$ is the set of points satisfying the area condition. The point $E$, then, is such that $\triangle A E C$ is a right angle (to make the distance minimal) and $E$ lies on $\overline{A M}$.
Let $X$ be the point of intersection of $\overline{A M}$ and $\overline{C D}$. Then $\triangle A M B \sim \triangle X M D$, and since $M D=B M$, they are in fact congruent. Thus $D X=A B=10$, and $X C=18$. Similarly, $B X=15$, so $A B X D$ is a parallelogram. Let $Y$ be the foot of the perpendicular from $A$ to $\overline{D C}$, so that $D Y=\frac{D C-A B}{2}=9$. Then
[^1]$A Y=\sqrt{A D^{2}-D Y^{2}}=\sqrt{225-81}=12$. Then $Y X=D X-D Y=1$ and $A X=\sqrt{A Y^{2}+Y X^{2}}=$ $\sqrt{144+1}=\sqrt{145}$. Since both $\triangle A X Y$ and $\triangle C X E$ have a right angle, and $\angle E X C$ and $\angle Y X A$ are congruent because they are vertical angles, $\triangle A X Y \sim \triangle C X E$. Then $\frac{C E}{A Y}=\frac{C X}{A X}$, so $C E=12 \cdot \frac{18}{\sqrt{145}}=$ $\frac{216}{\sqrt{145}}$.
|
\frac{216}{\sqrt{145}}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $A B C D$ be an isosceles trapezoid such that $A B=10, B C=15, C D=28$, and $D A=15$. There is a point $E$ such that $\triangle A E D$ and $\triangle A E B$ have the same area and such that $E C$ is minimal. Find $E C$.
|
| $\frac{216}{\sqrt{145}}$ |
| :---: |

The locus of points $E$ such that $[A E D]=[A E B]$ forms a line, since area is a linear function of the coordinates of $E$; setting the areas equal gives a linear equation in the coordinates $E^{2}$. Note that $A$ and $M$, the midpoint of $\overline{D B}$, are on this line; $A$ because both areas are 0 , and $M$ because the triangles share an altitude, and bases $\overline{D M}$ and $\overline{M B}$ are equal in length. Then $\overline{A M}$ is the set of points satisfying the area condition. The point $E$, then, is such that $\triangle A E C$ is a right angle (to make the distance minimal) and $E$ lies on $\overline{A M}$.
Let $X$ be the point of intersection of $\overline{A M}$ and $\overline{C D}$. Then $\triangle A M B \sim \triangle X M D$, and since $M D=B M$, they are in fact congruent. Thus $D X=A B=10$, and $X C=18$. Similarly, $B X=15$, so $A B X D$ is a parallelogram. Let $Y$ be the foot of the perpendicular from $A$ to $\overline{D C}$, so that $D Y=\frac{D C-A B}{2}=9$. Then
[^1]$A Y=\sqrt{A D^{2}-D Y^{2}}=\sqrt{225-81}=12$. Then $Y X=D X-D Y=1$ and $A X=\sqrt{A Y^{2}+Y X^{2}}=$ $\sqrt{144+1}=\sqrt{145}$. Since both $\triangle A X Y$ and $\triangle C X E$ have a right angle, and $\angle E X C$ and $\angle Y X A$ are congruent because they are vertical angles, $\triangle A X Y \sim \triangle C X E$. Then $\frac{C E}{A Y}=\frac{C X}{A X}$, so $C E=12 \cdot \frac{18}{\sqrt{145}}=$ $\frac{216}{\sqrt{145}}$.
|
{
"resource_path": "HarvardMIT/segmented/en-132-2010-feb-gen2-solutions.jsonl",
"problem_match": "\n6. [5]",
"solution_match": "\nAnswer: "
}
|
25b94423-88a3-566e-bee7-6552e1315da7
| 608,660
|
You are standing in an infinitely long hallway with sides given by the lines $x=0$ and $x=6$. You start at $(3,0)$ and want to get to $(3,6)$. Furthermore, at each instant you want your distance to $(3,6)$ to either decrease or stay the same. What is the area of the set of points that you could pass through on your journey from $(3,0)$ to $(3,6)$ ?
|
$9 \sqrt{3}+\frac{21 \pi}{2}$
If you draw concentric circles around the destination point, the condition is equivalent to the restriction that you must always go inwards towards the destination. In the diagram above, the regions through which you might pass are shaded.
We find the areas of regions $\mathrm{A}, \mathrm{B}$, and C separately, and add them up (doubling the area of region A, because there are two of them).
The hypotenuse of triangle A is of length 6 , and the base is of length 3 , so it is a $\frac{\pi}{6}-\frac{\pi}{3}-\frac{\pi}{2}$ triangle (30-60-90 triangle) with area $\frac{9 \sqrt{3}}{2}$. Then the total area of the regions labeled A is $9 \sqrt{3}$.
Since the angle of triangle A nearest the center of the circle (the destination point) is $\frac{\pi}{3}$, sector B has central angle $\frac{\pi}{3}$. Then the area of sector B is $\frac{1}{2} r^{2} \theta=\frac{1}{2} \cdot 36 \cdot \frac{\pi}{3}=6 \pi$.
Region C is a half-disc of radius 3 , so its area is $\frac{9 \pi}{2}$.
Thus, the total area is $9 \sqrt{3}+\frac{21 \pi}{2}$.
|
9 \sqrt{3}+\frac{21 \pi}{2}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
You are standing in an infinitely long hallway with sides given by the lines $x=0$ and $x=6$. You start at $(3,0)$ and want to get to $(3,6)$. Furthermore, at each instant you want your distance to $(3,6)$ to either decrease or stay the same. What is the area of the set of points that you could pass through on your journey from $(3,0)$ to $(3,6)$ ?
|
$9 \sqrt{3}+\frac{21 \pi}{2}$

If you draw concentric circles around the destination point, the condition is equivalent to the restriction that you must always go inwards towards the destination. In the diagram above, the regions through which you might pass are shaded.
We find the areas of regions $\mathrm{A}, \mathrm{B}$, and C separately, and add them up (doubling the area of region A, because there are two of them).
The hypotenuse of triangle A is of length 6 , and the base is of length 3 , so it is a $\frac{\pi}{6}-\frac{\pi}{3}-\frac{\pi}{2}$ triangle (30-60-90 triangle) with area $\frac{9 \sqrt{3}}{2}$. Then the total area of the regions labeled A is $9 \sqrt{3}$.
Since the angle of triangle A nearest the center of the circle (the destination point) is $\frac{\pi}{3}$, sector B has central angle $\frac{\pi}{3}$. Then the area of sector B is $\frac{1}{2} r^{2} \theta=\frac{1}{2} \cdot 36 \cdot \frac{\pi}{3}=6 \pi$.
Region C is a half-disc of radius 3 , so its area is $\frac{9 \pi}{2}$.
Thus, the total area is $9 \sqrt{3}+\frac{21 \pi}{2}$.
|
{
"resource_path": "HarvardMIT/segmented/en-132-2010-feb-gen2-solutions.jsonl",
"problem_match": "\n9. [7]",
"solution_match": "\nAnswer: "
}
|
ace34874-8c16-5fd4-88c7-f1a5ebc2e2b9
| 608,661
|
A rectangular piece of paper is folded along its diagonal (as depicted below) to form a non-convex pentagon that has an area of $\frac{7}{10}$ of the area of the original rectangle. Find the ratio of the longer side of the rectangle to the shorter side of the rectangle.
|
$\sqrt{5}$
[^0]
Given a polygon $P_{1} P_{2} \cdots P_{k}$, let $\left[P_{1} P_{2} \cdots P_{k}\right]$ denote its area. Let $A B C D$ be the rectangle. Suppose we fold $B$ across $\overline{A C}$, and let $E$ be the intersection of $\overline{A D}$ and $\overline{B^{\prime} C}$. Then we end up with the pentagon $A C D E B^{\prime}$, depicted above. Let's suppose, without loss of generality, that $A B C D$ has area 1. Then $\triangle A E C$ must have area $\frac{3}{10}$, since
$$
\begin{aligned}
{[A B C D] } & =[A B C]+[A C D] \\
& =\left[A B^{\prime} C\right]+[A C D] \\
& =\left[A B^{\prime} E\right]+2[A E C]+[E D C] \\
& =\left[A C D E B^{\prime}\right]+[A E C] \\
& =\frac{7}{10}[A B C D]+[A E C]
\end{aligned}
$$
That is, $[A E C]=\frac{3}{10}[A B C D]=\frac{3}{10}$.
Since $\triangle E C D$ is congruent to $\triangle E A B^{\prime}$, both triangles have area $\frac{1}{5}$. Note that $\triangle A B^{\prime} C, \triangle A B C$, and $\triangle C D A$ are all congruent, and all have area $\frac{1}{2}$. Since $\triangle A E C$ and $\triangle E D C$ share altitude $\overline{D C}$, $\frac{D E}{E A}=\frac{[D E C]}{[A E C]}=\frac{2}{3}$. Because $\triangle C A E$ is isosceles, $C E=E A$. Let $A E=3 x$. The $C E=3 x, D E=2 x$, and $C D=x \sqrt{9-4}=x \sqrt{5}$. Then $\frac{A D}{D C}=\frac{A E+E D}{D C}=\frac{3+2}{\sqrt{5}}=\sqrt{5}$.
|
\sqrt{5}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
A rectangular piece of paper is folded along its diagonal (as depicted below) to form a non-convex pentagon that has an area of $\frac{7}{10}$ of the area of the original rectangle. Find the ratio of the longer side of the rectangle to the shorter side of the rectangle.

|
$\sqrt{5}$
[^0]
Given a polygon $P_{1} P_{2} \cdots P_{k}$, let $\left[P_{1} P_{2} \cdots P_{k}\right]$ denote its area. Let $A B C D$ be the rectangle. Suppose we fold $B$ across $\overline{A C}$, and let $E$ be the intersection of $\overline{A D}$ and $\overline{B^{\prime} C}$. Then we end up with the pentagon $A C D E B^{\prime}$, depicted above. Let's suppose, without loss of generality, that $A B C D$ has area 1. Then $\triangle A E C$ must have area $\frac{3}{10}$, since
$$
\begin{aligned}
{[A B C D] } & =[A B C]+[A C D] \\
& =\left[A B^{\prime} C\right]+[A C D] \\
& =\left[A B^{\prime} E\right]+2[A E C]+[E D C] \\
& =\left[A C D E B^{\prime}\right]+[A E C] \\
& =\frac{7}{10}[A B C D]+[A E C]
\end{aligned}
$$
That is, $[A E C]=\frac{3}{10}[A B C D]=\frac{3}{10}$.
Since $\triangle E C D$ is congruent to $\triangle E A B^{\prime}$, both triangles have area $\frac{1}{5}$. Note that $\triangle A B^{\prime} C, \triangle A B C$, and $\triangle C D A$ are all congruent, and all have area $\frac{1}{2}$. Since $\triangle A E C$ and $\triangle E D C$ share altitude $\overline{D C}$, $\frac{D E}{E A}=\frac{[D E C]}{[A E C]}=\frac{2}{3}$. Because $\triangle C A E$ is isosceles, $C E=E A$. Let $A E=3 x$. The $C E=3 x, D E=2 x$, and $C D=x \sqrt{9-4}=x \sqrt{5}$. Then $\frac{A D}{D C}=\frac{A E+E D}{D C}=\frac{3+2}{\sqrt{5}}=\sqrt{5}$.
|
{
"resource_path": "HarvardMIT/segmented/en-132-2010-feb-geo-solutions.jsonl",
"problem_match": "\n2. [3]",
"solution_match": "\nAnswer: "
}
|
efe05137-bb9f-5162-aeee-88229619f7b7
| 608,663
|
Let $O$ be the point $(0,0)$. Let $A, B, C$ be three points in the plane such that $A O=15, B O=15$, and $C O=7$, and such that the area of triangle $A B C$ is maximal. What is the length of the shortest side of $A B C$ ?
|
20 We claim that $O$ should be the orthocenter of the triangle $A B C$. If $O$ is not on an altitude of $\triangle A B C$, suppose (without loss of generality) that $\overline{A O}$ is not perpendicular to $\overline{B C}$. We can
rotate $A$ around $O$, leaving $B$ and $C$ fixed, to make $\overline{A O}$ perpendicular to $\overline{B C}$, which strictly increases the area. Therefore, if $[A B C]$ is maximal then $\triangle A B C$ is an isosceles triangle with orthocenter $O$ and base $\overline{A B}$.
Let $F$ be the foot of the perpendicular from $C$ to $\overline{A B}$. Since $\angle F O A$ and $\angle C O E$ are vertical, $\angle F A O=$ $\angle O C E$. Then $\triangle F A O$ is similar to $\triangle F C B$, so we have $\frac{A F}{O F}=\frac{C F}{B F}=\frac{O F+7}{A F}$, so $A F^{2}=O F^{2}+7 \cdot O F$. Since $A F^{2}=225-O F^{2}, 2 \cdot O F^{2}+7 \cdot O F-225=0$, so $O F=9$. Then $A F=12$, so $A B=24$ and $B C=20$. Thus, the length of the shortest side of $\triangle A B C$ is 20 .
|
20
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $O$ be the point $(0,0)$. Let $A, B, C$ be three points in the plane such that $A O=15, B O=15$, and $C O=7$, and such that the area of triangle $A B C$ is maximal. What is the length of the shortest side of $A B C$ ?
|
20 We claim that $O$ should be the orthocenter of the triangle $A B C$. If $O$ is not on an altitude of $\triangle A B C$, suppose (without loss of generality) that $\overline{A O}$ is not perpendicular to $\overline{B C}$. We can
rotate $A$ around $O$, leaving $B$ and $C$ fixed, to make $\overline{A O}$ perpendicular to $\overline{B C}$, which strictly increases the area. Therefore, if $[A B C]$ is maximal then $\triangle A B C$ is an isosceles triangle with orthocenter $O$ and base $\overline{A B}$.

Let $F$ be the foot of the perpendicular from $C$ to $\overline{A B}$. Since $\angle F O A$ and $\angle C O E$ are vertical, $\angle F A O=$ $\angle O C E$. Then $\triangle F A O$ is similar to $\triangle F C B$, so we have $\frac{A F}{O F}=\frac{C F}{B F}=\frac{O F+7}{A F}$, so $A F^{2}=O F^{2}+7 \cdot O F$. Since $A F^{2}=225-O F^{2}, 2 \cdot O F^{2}+7 \cdot O F-225=0$, so $O F=9$. Then $A F=12$, so $A B=24$ and $B C=20$. Thus, the length of the shortest side of $\triangle A B C$ is 20 .
|
{
"resource_path": "HarvardMIT/segmented/en-132-2010-feb-geo-solutions.jsonl",
"problem_match": "\n8. [6]",
"solution_match": "\nAnswer: "
}
|
7d3b2b87-5ba3-532b-a0f2-4938fb88b1c2
| 608,664
|
Circles $\omega_{1}$ and $\omega_{2}$ intersect at points $A$ and $B$. Segment $P Q$ is tangent to $\omega_{1}$ at $P$ and to $\omega_{2}$ at $Q$, and $A$ is closer to $P Q$ than $B$. Point $X$ is on $\omega_{1}$ such that $P X \| Q B$, and point $Y$ is on $\omega_{2}$ such that $Q Y \| P B$. Given that $\angle A P Q=30^{\circ}$ and $\angle P Q A=15^{\circ}$, find the ratio $A X / A Y$.
|
$2-\sqrt{3}$
Let $C$ be the fourth vertex of parallelogram $A P C Q$. The midpoint $M$ of $\overline{P Q}$ is the intersection of the diagonals of this parallelogram. Because $M$ has equal power ${ }^{3}$ with respect to the two circles $\omega_{1}$ and $\omega_{2}$, it lies on $\overleftrightarrow{A B}$, the circles' radical axis $4^{4}$. Therefore, $C$ lies on $\overleftrightarrow{A B}$ as well.
Using a series of parallel lines and inscribed arcs, we have:
$$
\angle A P C=\angle A P Q+\angle C P Q=\angle A P Q+\angle P Q A=\angle A B P+\angle Q B A=\angle P B Q=\angle X P B
$$
where the last equality follows from the fact that $P X \| Q B$.
[^2]We also know that $\angle B X P=180^{\circ}-\angle P A B=\angle C A P$, so triangles $B X P$ and $C A P$ are similar. By the spiral similarity theorem triangles $B P C$ and $X P A$ are similar, too.
By analogous reasoning, triangles $B Q C$ and $Y Q A$ are similar. Then we have:
$$
\frac{A X}{A Y}=\frac{A X / B C}{A Y / B C}=\frac{A P / C P}{A Q / C Q}=\frac{A P^{2}}{A Q^{2}}
$$
where the last inequality holds because $A P C Q$ is a parallelogram. Using the Law of Sines, the last expression equals $\frac{\sin ^{2} 15^{\circ}}{\sin ^{2} 30^{\circ}}=2-\sqrt{3}$.
[^3]
[^0]: ${ }^{1}$ http://en.wikipedia.org/wiki/Inscribed_angle_theorem
[^1]: ${ }^{2}$ The notation $\left[A_{1} A_{2} \ldots A_{n}\right]$ means the area of polygon $A_{1} A_{2} \ldots A_{n}$.
[^2]: $\sqrt[3]{ }$ http://en.wikipedia.org/wiki/Power_of_a_point
4 http://en.wikipedia.org/wiki/Radical_axis
[^3]: ${ }^{5}$ This theorem states that if $\triangle P A B$ and $\triangle P X Y$ are similar and oriented the same way, then $\triangle P A X$ and $\triangle P B Y$ are similar too. It is true because the first similarity implies that $A P / B P=X P / Y P$ and $\angle A P B=\angle X P Y$, which proves the second similarity.
|
2-\sqrt{3}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Circles $\omega_{1}$ and $\omega_{2}$ intersect at points $A$ and $B$. Segment $P Q$ is tangent to $\omega_{1}$ at $P$ and to $\omega_{2}$ at $Q$, and $A$ is closer to $P Q$ than $B$. Point $X$ is on $\omega_{1}$ such that $P X \| Q B$, and point $Y$ is on $\omega_{2}$ such that $Q Y \| P B$. Given that $\angle A P Q=30^{\circ}$ and $\angle P Q A=15^{\circ}$, find the ratio $A X / A Y$.
|
$2-\sqrt{3}$

Let $C$ be the fourth vertex of parallelogram $A P C Q$. The midpoint $M$ of $\overline{P Q}$ is the intersection of the diagonals of this parallelogram. Because $M$ has equal power ${ }^{3}$ with respect to the two circles $\omega_{1}$ and $\omega_{2}$, it lies on $\overleftrightarrow{A B}$, the circles' radical axis $4^{4}$. Therefore, $C$ lies on $\overleftrightarrow{A B}$ as well.
Using a series of parallel lines and inscribed arcs, we have:
$$
\angle A P C=\angle A P Q+\angle C P Q=\angle A P Q+\angle P Q A=\angle A B P+\angle Q B A=\angle P B Q=\angle X P B
$$
where the last equality follows from the fact that $P X \| Q B$.
[^2]We also know that $\angle B X P=180^{\circ}-\angle P A B=\angle C A P$, so triangles $B X P$ and $C A P$ are similar. By the spiral similarity theorem triangles $B P C$ and $X P A$ are similar, too.
By analogous reasoning, triangles $B Q C$ and $Y Q A$ are similar. Then we have:
$$
\frac{A X}{A Y}=\frac{A X / B C}{A Y / B C}=\frac{A P / C P}{A Q / C Q}=\frac{A P^{2}}{A Q^{2}}
$$
where the last inequality holds because $A P C Q$ is a parallelogram. Using the Law of Sines, the last expression equals $\frac{\sin ^{2} 15^{\circ}}{\sin ^{2} 30^{\circ}}=2-\sqrt{3}$.
[^3]
[^0]: ${ }^{1}$ http://en.wikipedia.org/wiki/Inscribed_angle_theorem
[^1]: ${ }^{2}$ The notation $\left[A_{1} A_{2} \ldots A_{n}\right]$ means the area of polygon $A_{1} A_{2} \ldots A_{n}$.
[^2]: $\sqrt[3]{ }$ http://en.wikipedia.org/wiki/Power_of_a_point
4 http://en.wikipedia.org/wiki/Radical_axis
[^3]: ${ }^{5}$ This theorem states that if $\triangle P A B$ and $\triangle P X Y$ are similar and oriented the same way, then $\triangle P A X$ and $\triangle P B Y$ are similar too. It is true because the first similarity implies that $A P / B P=X P / Y P$ and $\angle A P B=\angle X P Y$, which proves the second similarity.
|
{
"resource_path": "HarvardMIT/segmented/en-132-2010-feb-geo-solutions.jsonl",
"problem_match": "\n10. [8]",
"solution_match": "\nAnswer: "
}
|
061fa514-b9ca-5e89-b015-9b83b67d6e92
| 608,666
|
If $A=10^{9}-987654321$ and $B=\frac{123456789+1}{10}$, what is the value of $\sqrt{A B}$ ?
|
12345679 Both $A$ and $B$ equal 12345679, so $\sqrt{A B}=12345679$ as well.
|
12345679
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
If $A=10^{9}-987654321$ and $B=\frac{123456789+1}{10}$, what is the value of $\sqrt{A B}$ ?
|
12345679 Both $A$ and $B$ equal 12345679, so $\sqrt{A B}=12345679$ as well.
|
{
"resource_path": "HarvardMIT/segmented/en-132-2010-feb-guts-solutions.jsonl",
"problem_match": "\n1. [4]",
"solution_match": "\nAnswer: "
}
|
0d07772c-6939-5582-8c71-20aaa133f1d1
| 608,667
|
Suppose that $x, y$, and $z$ are non-negative real numbers such that $x+y+z=1$. What is the maximum possible value of $x+y^{2}+z^{3}$ ?
|
1 Since $0 \leq y, z \leq 1$, we have $y^{2} \leq y$ and $z^{3} \leq z$. Therefore $x+y^{2}+z^{3} \leq x+y+z=1$. We can get $x+y^{2}+z^{3}=1$ by setting $(x, y, z)=(1,0,0)$.
|
1
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Suppose that $x, y$, and $z$ are non-negative real numbers such that $x+y+z=1$. What is the maximum possible value of $x+y^{2}+z^{3}$ ?
|
1 Since $0 \leq y, z \leq 1$, we have $y^{2} \leq y$ and $z^{3} \leq z$. Therefore $x+y^{2}+z^{3} \leq x+y+z=1$. We can get $x+y^{2}+z^{3}=1$ by setting $(x, y, z)=(1,0,0)$.
|
{
"resource_path": "HarvardMIT/segmented/en-132-2010-feb-guts-solutions.jsonl",
"problem_match": "\n2. [4]",
"solution_match": "\nAnswer: "
}
|
84f2f9d6-c43b-597a-8b74-982463a41474
| 608,668
|
In a group of people, there are 13 who like apples, 9 who like blueberries, 15 who like cantaloupe, and 6 who like dates. (A person can like more than 1 kind of fruit.) Each person who likes blueberries also likes exactly one of apples and cantaloupe. Each person who likes cantaloupe also likes exactly one of blueberries and dates. Find the minimum possible number of people in the group.
|
22 Everyone who likes cantaloupe likes exactly one of blueberries and dates. However, there are 15 people who like cantaloupe, 9 who like blueberries, and 6 who like dates. Thus, everyone who likes blueberries or dates must also like cantaloupes (because if any of them didn't, we would end up with less than 15 people who like cantaloupe).
Since everyone who likes blueberries likes cantaloupes, none of them can like apples. However, the 6 people who like both cantaloupe and dates can also like apples. So, we could have a group where 7 people like apples alone, 9 like blueberries and cantaloupe, and 6 like apples, cantaloupe, and dates. This gives 22 people in the group, which is optimal.
$13^{\text {th }}$ ANNUAL HARVARD-MIT MATHEMATICS TOURNAMENT, 20 FEBRUARY 2010 - GUTS ROUND
|
22
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
In a group of people, there are 13 who like apples, 9 who like blueberries, 15 who like cantaloupe, and 6 who like dates. (A person can like more than 1 kind of fruit.) Each person who likes blueberries also likes exactly one of apples and cantaloupe. Each person who likes cantaloupe also likes exactly one of blueberries and dates. Find the minimum possible number of people in the group.
|
22 Everyone who likes cantaloupe likes exactly one of blueberries and dates. However, there are 15 people who like cantaloupe, 9 who like blueberries, and 6 who like dates. Thus, everyone who likes blueberries or dates must also like cantaloupes (because if any of them didn't, we would end up with less than 15 people who like cantaloupe).
Since everyone who likes blueberries likes cantaloupes, none of them can like apples. However, the 6 people who like both cantaloupe and dates can also like apples. So, we could have a group where 7 people like apples alone, 9 like blueberries and cantaloupe, and 6 like apples, cantaloupe, and dates. This gives 22 people in the group, which is optimal.
$13^{\text {th }}$ ANNUAL HARVARD-MIT MATHEMATICS TOURNAMENT, 20 FEBRUARY 2010 - GUTS ROUND
|
{
"resource_path": "HarvardMIT/segmented/en-132-2010-feb-guts-solutions.jsonl",
"problem_match": "\n3. [4]",
"solution_match": "\nAnswer: "
}
|
67c69c9d-a261-5b52-b26d-c5c778203344
| 608,669
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.