Dataset Viewer
problem
stringlengths 14
7.96k
| solution
stringlengths 3
10k
| answer
stringlengths 1
91
| problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | question_type
stringclasses 1
value | problem_type
stringclasses 8
values | problem_raw
stringlengths 14
7.96k
| solution_raw
stringlengths 3
10k
| metadata
dict | uuid
stringlengths 36
36
| id
int64 22.6k
612k
|
|---|---|---|---|---|---|---|---|---|---|---|---|
Let $A_{1}, A_{2}, A_{3}$ be three points in the plane, and for convenience,let $A_{4}=A_{1}, A_{5}=A_{2}$. For $n=1,2$, and 3 , suppose that $B_{n}$ is the midpoint of $A_{n} A_{n+1}$, and suppose that $C_{n}$ is the midpoint of $A_{n} B_{n}$. Suppose that $A_{n} C_{n+1}$ and $B_{n} A_{n+2}$ meet at $D_{n}$, and that $A_{n} B_{n+1}$ and $C_{n} A_{n+2}$ meet at $E_{n}$. Calculate the ratio of the area of triangle $D_{1} D_{2} D_{3}$ to the area of triangle $E_{1} E_{2} E_{3}$.
|
Let $G$ be the centroid of triangle $A B C$, and also the intersection point of $A_{1} B_{2}, A_{2} B_{3}$, and $A_{3} B_{1}$ 。
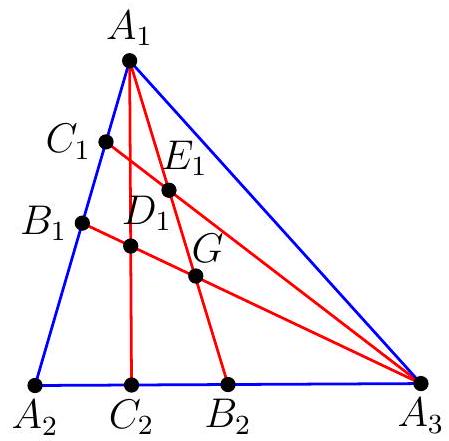
By Menelao's theorem on triangle $B_{1} A_{2} A_{3}$ and line $A_{1} D_{1} C_{2}$,
$$
\frac{A_{1} B_{1}}{A_{1} A_{2}} \cdot \frac{D_{1} A_{3}}{D_{1} B_{1}} \cdot \frac{C_{2} A_{2}}{C_{2} A_{3}}=1 \Longleftrightarrow \frac{D_{1} A_{3}}{D_{1} B_{1}}=2 \cdot 3=6 \Longleftrightarrow \frac{D_{1} B_{1}}{A_{3} B_{1}}=\frac{1}{7}
$$
Since $A_{3} G=\frac{2}{3} A_{3} B_{1}$, if $A_{3} B_{1}=21 t$ then $G A_{3}=14 t, D_{1} B_{1}=\frac{21 t}{7}=3 t, A_{3} D_{1}=18 t$, and $G D_{1}=A_{3} D_{1}-A_{3} G=18 t-14 t=4 t$, and
$$
\frac{G D_{1}}{G A_{3}}=\frac{4}{14}=\frac{2}{7}
$$
Similar results hold for the other medians, therefore $D_{1} D_{2} D_{3}$ and $A_{1} A_{2} A_{3}$ are homothetic with center $G$ and ratio $-\frac{2}{7}$.
By Menelao's theorem on triangle $A_{1} A_{2} B_{2}$ and line $C_{1} E_{1} A_{3}$,
$$
\frac{C_{1} A_{1}}{C_{1} A_{2}} \cdot \frac{E_{1} B_{2}}{E_{1} A_{1}} \cdot \frac{A_{3} A_{2}}{A_{3} B_{2}}=1 \Longleftrightarrow \frac{E_{1} B_{2}}{E_{1} A_{1}}=3 \cdot \frac{1}{2}=\frac{3}{2} \Longleftrightarrow \frac{A_{1} E_{1}}{A_{1} B_{2}}=\frac{2}{5}
$$
If $A_{1} B_{2}=15 u$, then $A_{1} G=\frac{2}{3} \cdot 15 u=10 u$ and $G E_{1}=A_{1} G-A_{1} E_{1}=10 u-\frac{2}{5} \cdot 15 u=4 u$, and
$$
\frac{G E_{1}}{G A_{1}}=\frac{4}{10}=\frac{2}{5}
$$
Similar results hold for the other medians, therefore $E_{1} E_{2} E_{3}$ and $A_{1} A_{2} A_{3}$ are homothetic with center $G$ and ratio $\frac{2}{5}$.
Then $D_{1} D_{2} D_{3}$ and $E_{1} E_{2} E_{3}$ are homothetic with center $G$ and ratio $-\frac{2}{7}: \frac{2}{5}=-\frac{5}{7}$, and the ratio of their area is $\left(\frac{5}{7}\right)^{2}=\frac{25}{49}$.
|
\frac{25}{49}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $A_{1}, A_{2}, A_{3}$ be three points in the plane, and for convenience,let $A_{4}=A_{1}, A_{5}=A_{2}$. For $n=1,2$, and 3 , suppose that $B_{n}$ is the midpoint of $A_{n} A_{n+1}$, and suppose that $C_{n}$ is the midpoint of $A_{n} B_{n}$. Suppose that $A_{n} C_{n+1}$ and $B_{n} A_{n+2}$ meet at $D_{n}$, and that $A_{n} B_{n+1}$ and $C_{n} A_{n+2}$ meet at $E_{n}$. Calculate the ratio of the area of triangle $D_{1} D_{2} D_{3}$ to the area of triangle $E_{1} E_{2} E_{3}$.
Answer: $\frac{25}{49}$.
|
Let $G$ be the centroid of triangle $A B C$, and also the intersection point of $A_{1} B_{2}, A_{2} B_{3}$, and $A_{3} B_{1}$ 。

By Menelao's theorem on triangle $B_{1} A_{2} A_{3}$ and line $A_{1} D_{1} C_{2}$,
$$
\frac{A_{1} B_{1}}{A_{1} A_{2}} \cdot \frac{D_{1} A_{3}}{D_{1} B_{1}} \cdot \frac{C_{2} A_{2}}{C_{2} A_{3}}=1 \Longleftrightarrow \frac{D_{1} A_{3}}{D_{1} B_{1}}=2 \cdot 3=6 \Longleftrightarrow \frac{D_{1} B_{1}}{A_{3} B_{1}}=\frac{1}{7}
$$
Since $A_{3} G=\frac{2}{3} A_{3} B_{1}$, if $A_{3} B_{1}=21 t$ then $G A_{3}=14 t, D_{1} B_{1}=\frac{21 t}{7}=3 t, A_{3} D_{1}=18 t$, and $G D_{1}=A_{3} D_{1}-A_{3} G=18 t-14 t=4 t$, and
$$
\frac{G D_{1}}{G A_{3}}=\frac{4}{14}=\frac{2}{7}
$$
Similar results hold for the other medians, therefore $D_{1} D_{2} D_{3}$ and $A_{1} A_{2} A_{3}$ are homothetic with center $G$ and ratio $-\frac{2}{7}$.
By Menelao's theorem on triangle $A_{1} A_{2} B_{2}$ and line $C_{1} E_{1} A_{3}$,
$$
\frac{C_{1} A_{1}}{C_{1} A_{2}} \cdot \frac{E_{1} B_{2}}{E_{1} A_{1}} \cdot \frac{A_{3} A_{2}}{A_{3} B_{2}}=1 \Longleftrightarrow \frac{E_{1} B_{2}}{E_{1} A_{1}}=3 \cdot \frac{1}{2}=\frac{3}{2} \Longleftrightarrow \frac{A_{1} E_{1}}{A_{1} B_{2}}=\frac{2}{5}
$$
If $A_{1} B_{2}=15 u$, then $A_{1} G=\frac{2}{3} \cdot 15 u=10 u$ and $G E_{1}=A_{1} G-A_{1} E_{1}=10 u-\frac{2}{5} \cdot 15 u=4 u$, and
$$
\frac{G E_{1}}{G A_{1}}=\frac{4}{10}=\frac{2}{5}
$$
Similar results hold for the other medians, therefore $E_{1} E_{2} E_{3}$ and $A_{1} A_{2} A_{3}$ are homothetic with center $G$ and ratio $\frac{2}{5}$.
Then $D_{1} D_{2} D_{3}$ and $E_{1} E_{2} E_{3}$ are homothetic with center $G$ and ratio $-\frac{2}{7}: \frac{2}{5}=-\frac{5}{7}$, and the ratio of their area is $\left(\frac{5}{7}\right)^{2}=\frac{25}{49}$.
|
{
"resource_path": "APMO/segmented/en-apmo1989_sol.jsonl",
"problem_match": "# Problem 3",
"solution_match": "\nSolution\n"
}
|
83c5357e-cc64-51e7-8925-9bd682bff7b7
| 604,178
|
Find the total number of different integer values the function
$$
f(x)=[x]+[2 x]+\left[\frac{5 x}{3}\right]+[3 x]+[4 x]
$$
takes for real numbers $x$ with $0 \leq x \leq 100$.
Note: $[t]$ is the largest integer that does not exceed $t$.
|
Note that, since $[x+n]=[x]+n$ for any integer $n$,
$$
f(x+3)=[x+3]+[2(x+3)]+\left[\frac{5(x+3)}{3}\right]+[3(x+3)]+[4(x+3)]=f(x)+35,
$$
one only needs to investigate the interval $[0,3)$.
The numbers in this interval at which at least one of the real numbers $x, 2 x, \frac{5 x}{3}, 3 x, 4 x$ is an integer are
- $0,1,2$ for $x$;
- $\frac{n}{2}, 0 \leq n \leq 5$ for $2 x$;
- $\frac{3 n}{5}, 0 \leq n \leq 4$ for $\frac{5 x}{3}$;
- $\frac{n}{3}, 0 \leq n \leq 8$ for $3 x$;
- $\frac{n}{4}, 0 \leq n \leq 11$ for $4 x$.
Of these numbers there are
- 3 integers $(0,1,2)$;
- 3 irreducible fractions with 2 as denominator (the numerators are $1,3,5$ );
- 6 irreducible fractions with 3 as denominator (the numerators are $1,2,4,5,7,8$ );
- 6 irreducible fractions with 4 as denominator (the numerators are $1,3,5,7,9,11,13,15$ );
- 4 irreducible fractions with 5 as denominator (the numerators are 3,6,9,12).
Therefore $f(x)$ increases 22 times per interval. Since $100=33 \cdot 3+1$, there are $33 \cdot 22$ changes of value in $[0,99)$. Finally, there are 8 more changes in [99,100]: 99, 100, $99 \frac{1}{2}, 99 \frac{1}{3}, 99 \frac{2}{3}, 99 \frac{1}{4}$, $99 \frac{3}{4}, 99 \frac{3}{5}$.
The total is then $33 \cdot 22+8=734$.
Comment: A more careful inspection shows that the range of $f$ are the numbers congruent modulo 35 to one of
$$
0,1,2,4,5,6,7,11,12,13,14,16,17,18,19,23,24,25,26,28,29,30
$$
in the interval $[0, f(100)]=[0,1166]$. Since $1166 \equiv 11(\bmod 35)$, this comprises 33 cycles plus the 8 numbers in the previous list.
|
734
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Find the total number of different integer values the function
$$
f(x)=[x]+[2 x]+\left[\frac{5 x}{3}\right]+[3 x]+[4 x]
$$
takes for real numbers $x$ with $0 \leq x \leq 100$.
Note: $[t]$ is the largest integer that does not exceed $t$.
Answer: 734.
|
Note that, since $[x+n]=[x]+n$ for any integer $n$,
$$
f(x+3)=[x+3]+[2(x+3)]+\left[\frac{5(x+3)}{3}\right]+[3(x+3)]+[4(x+3)]=f(x)+35,
$$
one only needs to investigate the interval $[0,3)$.
The numbers in this interval at which at least one of the real numbers $x, 2 x, \frac{5 x}{3}, 3 x, 4 x$ is an integer are
- $0,1,2$ for $x$;
- $\frac{n}{2}, 0 \leq n \leq 5$ for $2 x$;
- $\frac{3 n}{5}, 0 \leq n \leq 4$ for $\frac{5 x}{3}$;
- $\frac{n}{3}, 0 \leq n \leq 8$ for $3 x$;
- $\frac{n}{4}, 0 \leq n \leq 11$ for $4 x$.
Of these numbers there are
- 3 integers $(0,1,2)$;
- 3 irreducible fractions with 2 as denominator (the numerators are $1,3,5$ );
- 6 irreducible fractions with 3 as denominator (the numerators are $1,2,4,5,7,8$ );
- 6 irreducible fractions with 4 as denominator (the numerators are $1,3,5,7,9,11,13,15$ );
- 4 irreducible fractions with 5 as denominator (the numerators are 3,6,9,12).
Therefore $f(x)$ increases 22 times per interval. Since $100=33 \cdot 3+1$, there are $33 \cdot 22$ changes of value in $[0,99)$. Finally, there are 8 more changes in [99,100]: 99, 100, $99 \frac{1}{2}, 99 \frac{1}{3}, 99 \frac{2}{3}, 99 \frac{1}{4}$, $99 \frac{3}{4}, 99 \frac{3}{5}$.
The total is then $33 \cdot 22+8=734$.
Comment: A more careful inspection shows that the range of $f$ are the numbers congruent modulo 35 to one of
$$
0,1,2,4,5,6,7,11,12,13,14,16,17,18,19,23,24,25,26,28,29,30
$$
in the interval $[0, f(100)]=[0,1166]$. Since $1166 \equiv 11(\bmod 35)$, this comprises 33 cycles plus the 8 numbers in the previous list.
|
{
"resource_path": "APMO/segmented/en-apmo1993_sol.jsonl",
"problem_match": "# Problem 2",
"solution_match": "# Solution\n\n"
}
|
bd5d8315-f23a-5686-b090-d21bea91e8e5
| 604,509
|
Find the smallest positive integer $n$ with the following property : There does not exist an arithmetic progression of 1993 terms of real numbers containing exactly $n$ integers.
|
and Marking Scheme:
We first note that the integer terms of any arithmetic progression are "equally spaced", because if the $i$ th term $a_{i}$ and the $(i+j)$ th term $a_{i+j}$ of an arithmetic progression are both integers, then so is the $(i+2 j)$ th term $a_{i+2 j}=a_{i+j}+\left(a_{i+j}-a_{i}\right)$.
1 POINT for realizing that the integers must be "equally spaced".
Thus, by scaling and translation, we can assume that the integer terms of the arithmetic progression are $1,2, \cdots, n$ and we need only to consider arithmetic progression of the form
$$
1,1+\frac{1}{k}, 1+\frac{2}{k}, \cdots, 1+\frac{k-1}{k}, 2,2+\frac{1}{k}, \cdots, n-1, \cdots, n-1+\frac{k-1}{k}, n
$$
This has $k n-k+1$ terms of which exactly $n$ are integers. Moreover we can add up to $k-1$ terms on either end and get another arithmetic progression without changing the number of integer terms.
2 POINTS for noticing that the maximal sequence has an equal number of terms on either side of the integers appearing in the sequence (this includes the 1 POINT above). In other words, 2 POINTS for the scaled and translated form of the progression including the $k-1$ terms on either side.
Thus there are arithmetic progressions with $n$ integers whose length is any integer lying in the interval $[k n-k+1, k n+k-1]$, where $k$ is any positive integer. Thus we want to find the smallest $n>0$ so that, if $k$ is the largest integer satisfying $k n+k-1 \leq 1998$, then $(k+1) n-(k+1)+1 \geq 2000$.
4 POINTS for clarifying the nature of the number $n$ in this way, which includes counting the terms of the maximal and minimal sequences containing $n$ integers and bounding them accordingly (this includes the 2 POINTS above).
That is, putting $k=\lfloor 1999 /(n+1)\rfloor$, we want the smallest integer $n$ so that
$$
\left\lfloor\frac{1999}{n+1}\right\rfloor(n-1)+n \geq 2000
$$
This inequality does not hold if
$$
\frac{1999}{n+1} \cdot(n-1)+n<2000
$$
2 POINTS for setting up an inequality for $n$.
This simplifies to $n^{2}<3999$, that is, $n \leq 63$. Now we check integers from $n=64$ on:
$$
\begin{aligned}
& \text { for } n=64,\left\lfloor\frac{1999}{65}\right\rfloor \cdot 63+64=30 \cdot 63+64=1954<2000 ; \\
& \text { for } n=65,\left\lfloor\frac{1999}{66}\right\rfloor \cdot 64+65=30 \cdot 64+65=1985<2000 ; \\
& \text { for } n=66,\left\lfloor\frac{1999}{67}\right\rfloor \cdot 65+66=29 \cdot 65+66=1951<2000 ; \\
& \text { for } n=67,\left\lfloor\left\lfloor\frac{1999}{68}\right\rfloor \cdot 66+67=29 \cdot 66+67=1981<2000 ;\right. \\
& \text { for } n=68,\left\lfloor\frac{1999}{69}\right\rfloor \cdot 67+68=28 \cdot 67+68=1944<2000 ; \\
& \text { for } n=69,\left\lfloor\frac{1999}{70}\right\rfloor \cdot 68+69=28 \cdot 68+69=1973<2000 ; \\
& \text { for } n=70,\left\lfloor\frac{1999}{71}\right\rfloor \cdot 69+70=28 \cdot 69+70=2002 \geq 2000 .
\end{aligned}
$$
Thus the answer is $n=70$.
1.POINT for checking these rumbers and finding that $n=70$.
|
70
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Find the smallest positive integer $n$ with the following property : There does not exist an arithmetic progression of 1993 terms of real numbers containing exactly $n$ integers.
|
and Marking Scheme:
We first note that the integer terms of any arithmetic progression are "equally spaced", because if the $i$ th term $a_{i}$ and the $(i+j)$ th term $a_{i+j}$ of an arithmetic progression are both integers, then so is the $(i+2 j)$ th term $a_{i+2 j}=a_{i+j}+\left(a_{i+j}-a_{i}\right)$.
1 POINT for realizing that the integers must be "equally spaced".
Thus, by scaling and translation, we can assume that the integer terms of the arithmetic progression are $1,2, \cdots, n$ and we need only to consider arithmetic progression of the form
$$
1,1+\frac{1}{k}, 1+\frac{2}{k}, \cdots, 1+\frac{k-1}{k}, 2,2+\frac{1}{k}, \cdots, n-1, \cdots, n-1+\frac{k-1}{k}, n
$$
This has $k n-k+1$ terms of which exactly $n$ are integers. Moreover we can add up to $k-1$ terms on either end and get another arithmetic progression without changing the number of integer terms.
2 POINTS for noticing that the maximal sequence has an equal number of terms on either side of the integers appearing in the sequence (this includes the 1 POINT above). In other words, 2 POINTS for the scaled and translated form of the progression including the $k-1$ terms on either side.
Thus there are arithmetic progressions with $n$ integers whose length is any integer lying in the interval $[k n-k+1, k n+k-1]$, where $k$ is any positive integer. Thus we want to find the smallest $n>0$ so that, if $k$ is the largest integer satisfying $k n+k-1 \leq 1998$, then $(k+1) n-(k+1)+1 \geq 2000$.
4 POINTS for clarifying the nature of the number $n$ in this way, which includes counting the terms of the maximal and minimal sequences containing $n$ integers and bounding them accordingly (this includes the 2 POINTS above).
That is, putting $k=\lfloor 1999 /(n+1)\rfloor$, we want the smallest integer $n$ so that
$$
\left\lfloor\frac{1999}{n+1}\right\rfloor(n-1)+n \geq 2000
$$
This inequality does not hold if
$$
\frac{1999}{n+1} \cdot(n-1)+n<2000
$$
2 POINTS for setting up an inequality for $n$.
This simplifies to $n^{2}<3999$, that is, $n \leq 63$. Now we check integers from $n=64$ on:
$$
\begin{aligned}
& \text { for } n=64,\left\lfloor\frac{1999}{65}\right\rfloor \cdot 63+64=30 \cdot 63+64=1954<2000 ; \\
& \text { for } n=65,\left\lfloor\frac{1999}{66}\right\rfloor \cdot 64+65=30 \cdot 64+65=1985<2000 ; \\
& \text { for } n=66,\left\lfloor\frac{1999}{67}\right\rfloor \cdot 65+66=29 \cdot 65+66=1951<2000 ; \\
& \text { for } n=67,\left\lfloor\left\lfloor\frac{1999}{68}\right\rfloor \cdot 66+67=29 \cdot 66+67=1981<2000 ;\right. \\
& \text { for } n=68,\left\lfloor\frac{1999}{69}\right\rfloor \cdot 67+68=28 \cdot 67+68=1944<2000 ; \\
& \text { for } n=69,\left\lfloor\frac{1999}{70}\right\rfloor \cdot 68+69=28 \cdot 68+69=1973<2000 ; \\
& \text { for } n=70,\left\lfloor\frac{1999}{71}\right\rfloor \cdot 69+70=28 \cdot 69+70=2002 \geq 2000 .
\end{aligned}
$$
Thus the answer is $n=70$.
1.POINT for checking these rumbers and finding that $n=70$.
|
{
"resource_path": "APMO/segmented/en-apmo1999_sol.jsonl",
"problem_match": "\nProblem 1.",
"solution_match": "\nSolution "
}
|
2b064b65-5764-50a4-aaaf-18dcc2829667
| 604,646
|
Compute the sum $S=\sum_{i=0}^{101} \frac{x_{i}^{3}}{1-3 x_{i}+3 x_{i}^{2}}$ for $x_{i}=\frac{i}{101}$.
|
Since $x_{101-i}=\frac{101-i}{101}=1-\frac{i}{101}=1-x_{i}$ and
$$
1-3 x_{i}+3 x_{i}^{2}=\left(1-3 x_{i}+3 x_{i}^{2}-x_{i}^{3}\right)+x_{i}^{3}=\left(1-x_{i}\right)^{3}+x_{i}^{3}=x_{101-i}^{3}+x_{i}^{3},
$$
we have, by replacing $i$ by $101-i$ in the second sum,
$$
2 S=S+S=\sum_{i=0}^{101} \frac{x_{i}^{3}}{x_{101-i}^{3}+x_{i}^{3}}+\sum_{i=0}^{101} \frac{x_{101-i}^{3}}{x_{i}^{3}+x_{101-i}^{3}}=\sum_{i=0}^{101} \frac{x_{i}^{3}+x_{101-i}^{3}}{x_{101-i}^{3}+x_{i}^{3}}=102,
$$
so $S=51$.
|
51
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Compute the sum $S=\sum_{i=0}^{101} \frac{x_{i}^{3}}{1-3 x_{i}+3 x_{i}^{2}}$ for $x_{i}=\frac{i}{101}$.
Answer: $S=51$.
|
Since $x_{101-i}=\frac{101-i}{101}=1-\frac{i}{101}=1-x_{i}$ and
$$
1-3 x_{i}+3 x_{i}^{2}=\left(1-3 x_{i}+3 x_{i}^{2}-x_{i}^{3}\right)+x_{i}^{3}=\left(1-x_{i}\right)^{3}+x_{i}^{3}=x_{101-i}^{3}+x_{i}^{3},
$$
we have, by replacing $i$ by $101-i$ in the second sum,
$$
2 S=S+S=\sum_{i=0}^{101} \frac{x_{i}^{3}}{x_{101-i}^{3}+x_{i}^{3}}+\sum_{i=0}^{101} \frac{x_{101-i}^{3}}{x_{i}^{3}+x_{101-i}^{3}}=\sum_{i=0}^{101} \frac{x_{i}^{3}+x_{101-i}^{3}}{x_{101-i}^{3}+x_{i}^{3}}=102,
$$
so $S=51$.
|
{
"resource_path": "APMO/segmented/en-apmo2000_sol.jsonl",
"problem_match": "# Problem 1",
"solution_match": "# Solution\n\n"
}
|
9b4fe559-cb6b-5f2d-b86c-bacaacc657cb
| 604,724
|
Let $a, b, c, d, e, f$ be real numbers such that the polynomial
$$
p(x)=x^{8}-4 x^{7}+7 x^{6}+a x^{5}+b x^{4}+c x^{3}+d x^{2}+e x+f
$$
factorises into eight linear factors $x-x_{i}$, with $x_{i}>0$ for $i=1,2, \ldots, 8$. Determine all possible values of $f$.
|
From
$$
x^{8}-4 x^{7}+7 x^{6}+a x^{5}+b x^{4}+c x^{3}+d x^{2}+e x+f=\left(x-x_{1}\right)\left(x-x_{2}\right) \ldots\left(x-x_{8}\right)
$$
we have
$$
\sum_{i=1}^{8} x_{i}=4 \quad \text { and } \quad \sum x_{i} x_{j}=7
$$
where the second sum is over all pairs $(i, j)$ of integers where $1 \leq i<j \leq 8$. Since this sum can also be written
$$
\frac{1}{2}\left[\left(\sum_{i=1}^{8} x_{i}\right)^{2}-\sum_{i=1}^{8} x_{i}^{2}\right]
$$
we get
$$
14=\left(\sum_{i=1}^{8} x_{i}\right)^{2}-\sum_{i=1}^{8} x_{i}^{2}=16-\sum_{i=1}^{8} x_{i}^{2}
$$
so
$$
\sum_{i=1}^{8} x_{i}^{2}=2 \quad \text { while } \quad \sum_{i=1}^{8} x_{i}=4 . \quad[3 \text { marks }]
$$
Now
$$
\sum_{i=1}^{8}\left(2 x_{i}-1\right)^{2}=4 \sum_{i=1}^{8} x_{i}^{2}-4 \sum_{i=1}^{8} x_{i}+8=4(2)-4(4)+8=0
$$
which forces $x_{i}=1 / 2$ for all $i$. [3 marks] Therefore
$$
f=\prod_{i=1}^{8} x_{i}=\left(\frac{1}{2}\right)^{8}=\frac{1}{256} . \quad[1 m x]
$$
Alternate solution: After obtaining (1) [3 marks], use Cauchy's inequality to get
$$
16=\left(x_{1} \cdot 1+x_{2} \cdot 1+\cdots+x_{8} \cdot 1\right)^{2} \leq\left(x_{1}^{2-}+x_{2}^{2}+\cdots+x_{8}^{2}\right)\left(1^{2}+1^{2}+\cdots+1^{2}\right)=8 \cdot 2=16
$$
or the power mean inequality to get
$$
\frac{1}{2}=\frac{1}{8} \sum_{i=1}^{8} x_{i} \leq\left(\frac{1}{8} \sum_{i=1}^{8} x_{i}^{2}\right)^{1 / 2}=\frac{1}{2} . \quad[2 \text { marks }]
$$
Either way, equality must hold, which can only happen if all the terms $x_{i}$ are equal, that is, if $x_{i}=1 / 2$ for all $i$. [1 mark] Thus $f=1 / 256$ as above. [ 1 mark]
|
\frac{1}{256}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Let $a, b, c, d, e, f$ be real numbers such that the polynomial
$$
p(x)=x^{8}-4 x^{7}+7 x^{6}+a x^{5}+b x^{4}+c x^{3}+d x^{2}+e x+f
$$
factorises into eight linear factors $x-x_{i}$, with $x_{i}>0$ for $i=1,2, \ldots, 8$. Determine all possible values of $f$.
|
From
$$
x^{8}-4 x^{7}+7 x^{6}+a x^{5}+b x^{4}+c x^{3}+d x^{2}+e x+f=\left(x-x_{1}\right)\left(x-x_{2}\right) \ldots\left(x-x_{8}\right)
$$
we have
$$
\sum_{i=1}^{8} x_{i}=4 \quad \text { and } \quad \sum x_{i} x_{j}=7
$$
where the second sum is over all pairs $(i, j)$ of integers where $1 \leq i<j \leq 8$. Since this sum can also be written
$$
\frac{1}{2}\left[\left(\sum_{i=1}^{8} x_{i}\right)^{2}-\sum_{i=1}^{8} x_{i}^{2}\right]
$$
we get
$$
14=\left(\sum_{i=1}^{8} x_{i}\right)^{2}-\sum_{i=1}^{8} x_{i}^{2}=16-\sum_{i=1}^{8} x_{i}^{2}
$$
so
$$
\sum_{i=1}^{8} x_{i}^{2}=2 \quad \text { while } \quad \sum_{i=1}^{8} x_{i}=4 . \quad[3 \text { marks }]
$$
Now
$$
\sum_{i=1}^{8}\left(2 x_{i}-1\right)^{2}=4 \sum_{i=1}^{8} x_{i}^{2}-4 \sum_{i=1}^{8} x_{i}+8=4(2)-4(4)+8=0
$$
which forces $x_{i}=1 / 2$ for all $i$. [3 marks] Therefore
$$
f=\prod_{i=1}^{8} x_{i}=\left(\frac{1}{2}\right)^{8}=\frac{1}{256} . \quad[1 m x]
$$
Alternate solution: After obtaining (1) [3 marks], use Cauchy's inequality to get
$$
16=\left(x_{1} \cdot 1+x_{2} \cdot 1+\cdots+x_{8} \cdot 1\right)^{2} \leq\left(x_{1}^{2-}+x_{2}^{2}+\cdots+x_{8}^{2}\right)\left(1^{2}+1^{2}+\cdots+1^{2}\right)=8 \cdot 2=16
$$
or the power mean inequality to get
$$
\frac{1}{2}=\frac{1}{8} \sum_{i=1}^{8} x_{i} \leq\left(\frac{1}{8} \sum_{i=1}^{8} x_{i}^{2}\right)^{1 / 2}=\frac{1}{2} . \quad[2 \text { marks }]
$$
Either way, equality must hold, which can only happen if all the terms $x_{i}$ are equal, that is, if $x_{i}=1 / 2$ for all $i$. [1 mark] Thus $f=1 / 256$ as above. [ 1 mark]
|
{
"resource_path": "APMO/segmented/en-apmo2003_sol.jsonl",
"problem_match": "\n1. ",
"solution_match": "# Solution."
}
|
c13852dc-b4a2-516c-ba98-28de916b4f95
| 607,119
|
In a small town, there are $n \times n$ houses indexed by $(i, j)$ for $1 \leq i, j \leq n$ with $(1,1)$ being the house at the top left corner, where $i$ and $j$ are the row and column indices, respectively. At time 0 , a fire breaks out at the house indexed by $(1, c)$, where $c \leq \frac{n}{2}$. During each subsequent time interval $[t, t+1]$, the fire fighters defend a house which is not yet on fire while the fire spreads to all undefended neighbors of each house which was on fire at time $t$. Once a house is defended, it remains so all the time. The process ends when the fire can no longer spread. At most how many houses can be saved by the fire fighters? A house indexed by $(i, j)$ is a neighbor of a house indexed by $(k, \ell)$ if $|i-k|+|j-\ell|=1$.
|
At most $n^{2}+c^{2}-n c-c$ houses can be saved. This can be achieved under the following order of defending:
$$
\begin{gathered}
(2, c),(2, c+1) ;(3, c-1),(3, c+2) ;(4, c-2),(4, c+3) ; \ldots \\
(c+1,1),(c+1,2 c) ;(c+1,2 c+1), \ldots,(c+1, n)
\end{gathered}
$$
Under this strategy, there are
2 columns (column numbers $c, c+1$ ) at which $n-1$ houses are saved
2 columns (column numbers $c-1, c+2$ ) at which $n-2$ houses are saved
...
2 columns (column numbers $1,2 c$ ) at which $n-c$ houses are saved
$n-2 c$ columns (column numbers $n-2 c+1, \ldots, n$ ) at which $n-c$ houses are saved
Adding all these we obtain :
$$
2[(n-1)+(n-2)+\cdots+(n-c)]+(n-2 c)(n-c)=n^{2}+c^{2}-c n-c
$$
We say that a house indexed by $(i, j)$ is at level $t$ if $|i-1|+|j-c|=t$. Let $d(t)$ be the number of houses at level $t$ defended by time $t$, and $p(t)$ be the number of houses at levels greater than $t$ defended by time $t$. It is clear that
$$
p(t)+\sum_{i=1}^{t} d(i) \leq t \text { and } p(t+1)+d(t+1) \leq p(t)+1
$$
Let $s(t)$ be the number of houses at level $t$ which are not burning at time $t$. We prove that
$$
s(t) \leq t-p(t) \leq t
$$
for $1 \leq t \leq n-1$ by induction. It is obvious when $t=1$. Assume that it is true for $t=k$. The union of the neighbors of any $k-p(k)+1$ houses at level $k+1$ contains at least $k-p(k)+1$ vertices at level $k$. Since $s(k) \leq k-p(k)$, one of these houses at level $k$ is burning. Therefore, at most $k-p(k)$ houses at level $k+1$ have no neighbor burning. Hence we have
$$
\begin{aligned}
s(k+1) & \leq k-p(k)+d(k+1) \\
& =(k+1)-(p(k)+1-d(k+1)) \\
& \leq(k+1)-p(k+1)
\end{aligned}
$$
We now prove that the strategy given above is optimal. Since
$$
\sum_{t=1}^{n-1} s(t) \leq\binom{ n}{2}
$$
the maximum number of houses at levels less than or equal to $n-1$, that can be saved under any strategy is at most $\binom{n}{2}$, which is realized by the strategy above. Moreover, at levels bigger than $n-1$, every house is saved under the strategy above.
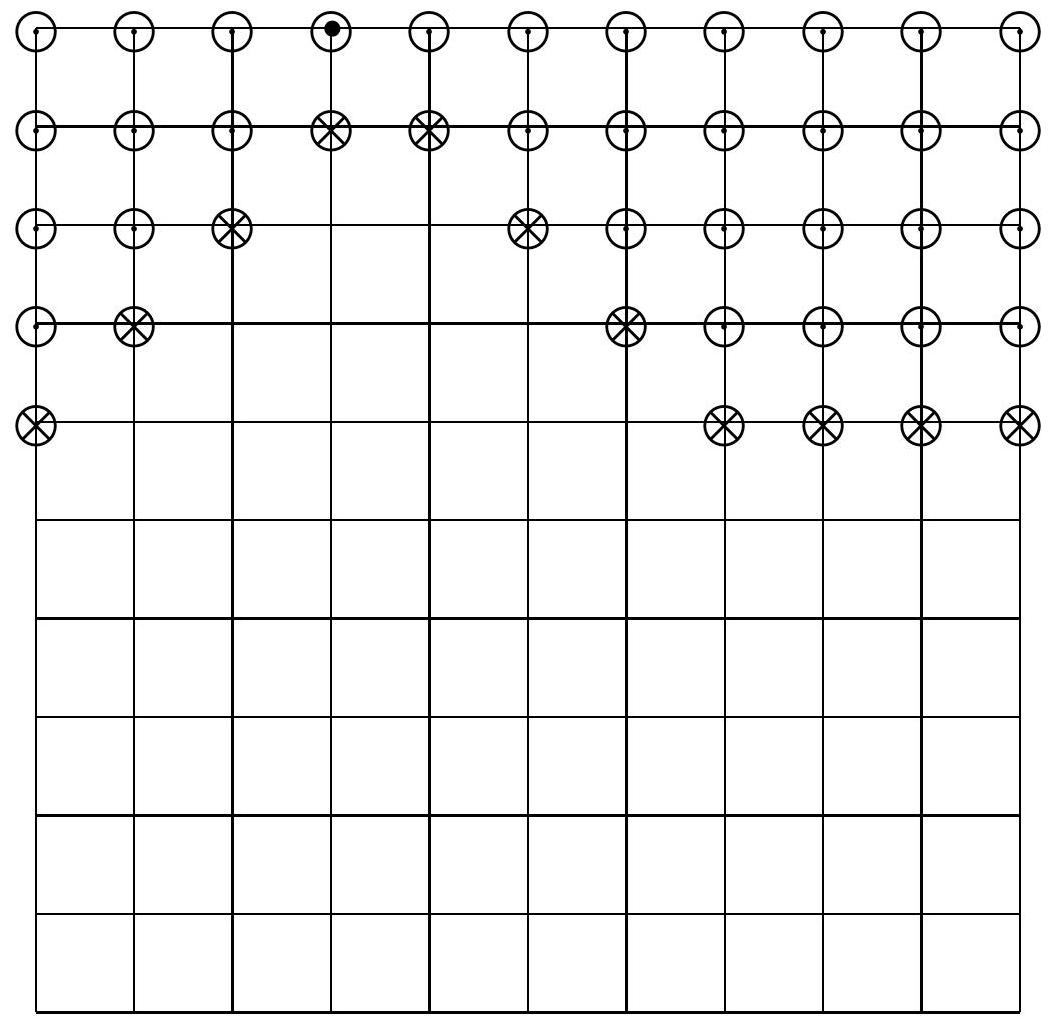
The following is an example when $n=11$ and $c=4$. The houses with $\bigcirc$ mark are burned. The houses with $\otimes$ mark are blocked ones and hence those and the houses below them are saved.
|
n^{2}+c^{2}-n c-c
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
In a small town, there are $n \times n$ houses indexed by $(i, j)$ for $1 \leq i, j \leq n$ with $(1,1)$ being the house at the top left corner, where $i$ and $j$ are the row and column indices, respectively. At time 0 , a fire breaks out at the house indexed by $(1, c)$, where $c \leq \frac{n}{2}$. During each subsequent time interval $[t, t+1]$, the fire fighters defend a house which is not yet on fire while the fire spreads to all undefended neighbors of each house which was on fire at time $t$. Once a house is defended, it remains so all the time. The process ends when the fire can no longer spread. At most how many houses can be saved by the fire fighters? A house indexed by $(i, j)$ is a neighbor of a house indexed by $(k, \ell)$ if $|i-k|+|j-\ell|=1$.
|
At most $n^{2}+c^{2}-n c-c$ houses can be saved. This can be achieved under the following order of defending:
$$
\begin{gathered}
(2, c),(2, c+1) ;(3, c-1),(3, c+2) ;(4, c-2),(4, c+3) ; \ldots \\
(c+1,1),(c+1,2 c) ;(c+1,2 c+1), \ldots,(c+1, n)
\end{gathered}
$$
Under this strategy, there are
2 columns (column numbers $c, c+1$ ) at which $n-1$ houses are saved
2 columns (column numbers $c-1, c+2$ ) at which $n-2$ houses are saved
...
2 columns (column numbers $1,2 c$ ) at which $n-c$ houses are saved
$n-2 c$ columns (column numbers $n-2 c+1, \ldots, n$ ) at which $n-c$ houses are saved
Adding all these we obtain :
$$
2[(n-1)+(n-2)+\cdots+(n-c)]+(n-2 c)(n-c)=n^{2}+c^{2}-c n-c
$$
We say that a house indexed by $(i, j)$ is at level $t$ if $|i-1|+|j-c|=t$. Let $d(t)$ be the number of houses at level $t$ defended by time $t$, and $p(t)$ be the number of houses at levels greater than $t$ defended by time $t$. It is clear that
$$
p(t)+\sum_{i=1}^{t} d(i) \leq t \text { and } p(t+1)+d(t+1) \leq p(t)+1
$$
Let $s(t)$ be the number of houses at level $t$ which are not burning at time $t$. We prove that
$$
s(t) \leq t-p(t) \leq t
$$
for $1 \leq t \leq n-1$ by induction. It is obvious when $t=1$. Assume that it is true for $t=k$. The union of the neighbors of any $k-p(k)+1$ houses at level $k+1$ contains at least $k-p(k)+1$ vertices at level $k$. Since $s(k) \leq k-p(k)$, one of these houses at level $k$ is burning. Therefore, at most $k-p(k)$ houses at level $k+1$ have no neighbor burning. Hence we have
$$
\begin{aligned}
s(k+1) & \leq k-p(k)+d(k+1) \\
& =(k+1)-(p(k)+1-d(k+1)) \\
& \leq(k+1)-p(k+1)
\end{aligned}
$$
We now prove that the strategy given above is optimal. Since
$$
\sum_{t=1}^{n-1} s(t) \leq\binom{ n}{2}
$$
the maximum number of houses at levels less than or equal to $n-1$, that can be saved under any strategy is at most $\binom{n}{2}$, which is realized by the strategy above. Moreover, at levels bigger than $n-1$, every house is saved under the strategy above.
The following is an example when $n=11$ and $c=4$. The houses with $\bigcirc$ mark are burned. The houses with $\otimes$ mark are blocked ones and hence those and the houses below them are saved.

|
{
"resource_path": "APMO/segmented/en-apmo2005_sol.jsonl",
"problem_match": "\nProblem 4.",
"solution_match": "(Solution)"
}
|
ab2e01d6-9893-55dd-a5ef-36ae08e81cdd
| 604,978
|
In a circus, there are $n$ clowns who dress and paint themselves up using a selection of 12 distinct colours. Each clown is required to use at least five different colours. One day, the ringmaster of the circus orders that no two clowns have exactly the same set
of colours and no more than 20 clowns may use any one particular colour. Find the largest number $n$ of clowns so as to make the ringmaster's order possible.
|
Let $C$ be the set of $n$ clowns. Label the colours $1,2,3, \ldots, 12$. For each $i=1,2, \ldots, 12$, let $E_{i}$ denote the set of clowns who use colour $i$. For each subset $S$ of $\{1,2, \ldots, 12\}$, let $E_{S}$ be the set of clowns who use exactly those colours in $S$. Since $S \neq S^{\prime}$ implies $E_{S} \cap E_{S^{\prime}}=\emptyset$, we have
$$
\sum_{S}\left|E_{S}\right|=|C|=n
$$
where $S$ runs over all subsets of $\{1,2, \ldots, 12\}$. Now for each $i$,
$$
E_{S} \subseteq E_{i} \quad \text { if and only if } \quad i \in S
$$
and hence
$$
\left|E_{i}\right|=\sum_{i \in S}\left|E_{S}\right|
$$
By assumption, we know that $\left|E_{i}\right| \leq 20$ and that if $E_{S} \neq \emptyset$, then $|S| \geq 5$. From this we obtain
$$
20 \times 12 \geq \sum_{i=1}^{12}\left|E_{i}\right|=\sum_{i=1}^{12}\left(\sum_{i \in S}\left|E_{S}\right|\right) \geq 5 \sum_{S}\left|E_{S}\right|=5 n
$$
Therefore $n \leq 48$.
Now, define a sequence $\left\{c_{i}\right\}_{i=1}^{52}$ of colours in the following way:
$1234|5678| 9101112 \mid$
$4123|8567| 1291011 \mid$
$3412|7856| 1112910 \mid$
$2341|6785| 1011129 \mid 1234$
The first row lists $c_{1}, \ldots, c_{12}$ in order, the second row lists $c_{13}, \ldots, c_{24}$ in order, the third row lists $c_{25}, \ldots, c_{36}$ in order, and finally the last row lists $c_{37}, \ldots, c_{52}$ in order. For each $j, 1 \leq j \leq 48$, assign colours $c_{j}, c_{j+1}, c_{j+2}, c_{j+3}, c_{j+4}$ to the $j$-th clown. It is easy to check that this assignment satisfies all conditions given above. So, 48 is the largest for $n$.
Remark: The fact that $n \leq 48$ can be obtained in a much simpler observation that
$$
5 n \leq 12 \times 20=240
$$
There are many other ways of constructing 48 distinct sets consisting of 5 colours. For example, consider the sets
$$
\begin{array}{cccc}
\{1,2,3,4,5,6\}, & \{3,4,5,6,7,8\}, & \{5,6,7,8,9,10\}, & \{7,8,9,10,11,12\}, \\
\{9,10,11,12,1,2\}, & \{11,12,1,2,3,4\}, & \{1,2,5,6,9,10\}, & \{3,4,7,8,11,12\} .
\end{array}
$$
Each of the above 8 sets has 6 distinct subsets consisting of exactly 5 colours. It is easy to check that the 48 subsets obtained in this manner are all distinct.
|
48
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
In a circus, there are $n$ clowns who dress and paint themselves up using a selection of 12 distinct colours. Each clown is required to use at least five different colours. One day, the ringmaster of the circus orders that no two clowns have exactly the same set
of colours and no more than 20 clowns may use any one particular colour. Find the largest number $n$ of clowns so as to make the ringmaster's order possible.
|
Let $C$ be the set of $n$ clowns. Label the colours $1,2,3, \ldots, 12$. For each $i=1,2, \ldots, 12$, let $E_{i}$ denote the set of clowns who use colour $i$. For each subset $S$ of $\{1,2, \ldots, 12\}$, let $E_{S}$ be the set of clowns who use exactly those colours in $S$. Since $S \neq S^{\prime}$ implies $E_{S} \cap E_{S^{\prime}}=\emptyset$, we have
$$
\sum_{S}\left|E_{S}\right|=|C|=n
$$
where $S$ runs over all subsets of $\{1,2, \ldots, 12\}$. Now for each $i$,
$$
E_{S} \subseteq E_{i} \quad \text { if and only if } \quad i \in S
$$
and hence
$$
\left|E_{i}\right|=\sum_{i \in S}\left|E_{S}\right|
$$
By assumption, we know that $\left|E_{i}\right| \leq 20$ and that if $E_{S} \neq \emptyset$, then $|S| \geq 5$. From this we obtain
$$
20 \times 12 \geq \sum_{i=1}^{12}\left|E_{i}\right|=\sum_{i=1}^{12}\left(\sum_{i \in S}\left|E_{S}\right|\right) \geq 5 \sum_{S}\left|E_{S}\right|=5 n
$$
Therefore $n \leq 48$.
Now, define a sequence $\left\{c_{i}\right\}_{i=1}^{52}$ of colours in the following way:
$1234|5678| 9101112 \mid$
$4123|8567| 1291011 \mid$
$3412|7856| 1112910 \mid$
$2341|6785| 1011129 \mid 1234$
The first row lists $c_{1}, \ldots, c_{12}$ in order, the second row lists $c_{13}, \ldots, c_{24}$ in order, the third row lists $c_{25}, \ldots, c_{36}$ in order, and finally the last row lists $c_{37}, \ldots, c_{52}$ in order. For each $j, 1 \leq j \leq 48$, assign colours $c_{j}, c_{j+1}, c_{j+2}, c_{j+3}, c_{j+4}$ to the $j$-th clown. It is easy to check that this assignment satisfies all conditions given above. So, 48 is the largest for $n$.
Remark: The fact that $n \leq 48$ can be obtained in a much simpler observation that
$$
5 n \leq 12 \times 20=240
$$
There are many other ways of constructing 48 distinct sets consisting of 5 colours. For example, consider the sets
$$
\begin{array}{cccc}
\{1,2,3,4,5,6\}, & \{3,4,5,6,7,8\}, & \{5,6,7,8,9,10\}, & \{7,8,9,10,11,12\}, \\
\{9,10,11,12,1,2\}, & \{11,12,1,2,3,4\}, & \{1,2,5,6,9,10\}, & \{3,4,7,8,11,12\} .
\end{array}
$$
Each of the above 8 sets has 6 distinct subsets consisting of exactly 5 colours. It is easy to check that the 48 subsets obtained in this manner are all distinct.
|
{
"resource_path": "APMO/segmented/en-apmo2006_sol.jsonl",
"problem_match": "\nProblem 5.",
"solution_match": "(Solution)"
}
|
5b2a8169-c2ad-5a85-9550-581891fe4e37
| 261,512
|
Consider $n$ disks $C_{1}, C_{2}, \ldots, C_{n}$ in a plane such that for each $1 \leq i<n$, the center of $C_{i}$ is on the circumference of $C_{i+1}$, and the center of $C_{n}$ is on the circumference of $C_{1}$. Define the score of such an arrangement of $n$ disks to be the number of pairs $(i, j)$ for which $C_{i}$ properly contains $C_{j}$. Determine the maximum possible score.
|
The answer is $(n-1)(n-2) / 2$.
Let's call a set of $n$ disks satisfying the given conditions an $n$-configuration. For an $n$ configuration $\mathcal{C}=\left\{C_{1}, \ldots, C_{n}\right\}$, let $S_{\mathcal{C}}=\left\{(i, j) \mid C_{i}\right.$ properly contains $\left.C_{j}\right\}$. So, the score of an $n$-configuration $\mathcal{C}$ is $\left|S_{\mathcal{C}}\right|$.
We'll show that (i) there is an $n$-configuration $\mathcal{C}$ for which $\left|S_{\mathcal{C}}\right|=(n-1)(n-2) / 2$, and that (ii) $\left|S_{\mathcal{C}}\right| \leq(n-1)(n-2) / 2$ for any $n$-configuration $\mathcal{C}$.
Let $C_{1}$ be any disk. Then for $i=2, \ldots, n-1$, take $C_{i}$ inside $C_{i-1}$ so that the circumference of $C_{i}$ contains the center of $C_{i-1}$. Finally, let $C_{n}$ be a disk whose center is on the circumference of $C_{1}$ and whose circumference contains the center of $C_{n-1}$. This gives $S_{\mathcal{C}}=\{(i, j) \mid 1 \leq i<j \leq n-1\}$ of size $(n-1)(n-2) / 2$, which proves (i).
For any $n$-configuration $\mathcal{C}, S_{\mathcal{C}}$ must satisfy the following properties:
(1) $(i, i) \notin S_{\mathcal{C}}$,
(2) $(i+1, i) \notin S_{\mathcal{C}},(1, n) \notin S_{\mathcal{C}}$,
(3) if $(i, j),(j, k) \in S_{\mathcal{C}}$, then $(i, k) \in S_{\mathcal{C}}$,
(4) if $(i, j) \in S_{\mathcal{C}}$, then $(j, i) \notin S_{\mathcal{C}}$.
Now we show that a set $G$ of ordered pairs of integers between 1 and $n$, satisfying the conditions $(1) \sim(4)$, can have no more than $(n-1)(n-2) / 2$ elements. Suppose that there exists a set $G$ that satisfies the conditions (1) $\sim(4)$, and has more than $(n-1)(n-2) / 2$ elements. Let $n$ be the least positive integer with which there exists such a set $G$. Note that $G$ must have $(i, i+1)$ for some $1 \leq i \leq n$ or $(n, 1)$, since otherwise $G$ can have at most
$$
\binom{n}{2}-n=\frac{n(n-3)}{2}<\frac{(n-1)(n-2)}{2}
$$
elements. Without loss of generality we may assume that $(n, 1) \in G$. Then $(1, n-1) \notin G$, since otherwise the condition (3) yields $(n, n-1) \in G$ contradicting the condition (2). Now let $G^{\prime}=\{(i, j) \in G \mid 1 \leq i, j \leq n-1\}$, then $G^{\prime}$ satisfies the conditions (1) (4), with $n-1$.
We now claim that $\left|G-G^{\prime}\right| \leq n-2$ :
Suppose that $\left|G-G^{\prime}\right|>n-2$, then $\left|G-G^{\prime}\right|=n-1$ and hence for each $1 \leq i \leq n-1$, either $(i, n)$ or $(n, i)$ must be in $G$. We already know that $(n, 1) \in G$ and $(n-1, n) \in G$ (because $(n, n-1) \notin G$ ) and this implies that $(n, n-2) \notin G$ and $(n-2, n) \in G$. If we keep doing this process, we obtain $(1, n) \in G$, which is a contradiction.
Since $\left|G-G^{\prime}\right| \leq n-2$, we obtain
$$
\left|G^{\prime}\right| \geq \frac{(n-1)(n-2)}{2}-(n-2)=\frac{(n-2)(n-3)}{2}
$$
This, however, contradicts the minimality of $n$, and hence proves (ii).
|
(n-1)(n-2) / 2
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Consider $n$ disks $C_{1}, C_{2}, \ldots, C_{n}$ in a plane such that for each $1 \leq i<n$, the center of $C_{i}$ is on the circumference of $C_{i+1}$, and the center of $C_{n}$ is on the circumference of $C_{1}$. Define the score of such an arrangement of $n$ disks to be the number of pairs $(i, j)$ for which $C_{i}$ properly contains $C_{j}$. Determine the maximum possible score.
|
The answer is $(n-1)(n-2) / 2$.
Let's call a set of $n$ disks satisfying the given conditions an $n$-configuration. For an $n$ configuration $\mathcal{C}=\left\{C_{1}, \ldots, C_{n}\right\}$, let $S_{\mathcal{C}}=\left\{(i, j) \mid C_{i}\right.$ properly contains $\left.C_{j}\right\}$. So, the score of an $n$-configuration $\mathcal{C}$ is $\left|S_{\mathcal{C}}\right|$.
We'll show that (i) there is an $n$-configuration $\mathcal{C}$ for which $\left|S_{\mathcal{C}}\right|=(n-1)(n-2) / 2$, and that (ii) $\left|S_{\mathcal{C}}\right| \leq(n-1)(n-2) / 2$ for any $n$-configuration $\mathcal{C}$.
Let $C_{1}$ be any disk. Then for $i=2, \ldots, n-1$, take $C_{i}$ inside $C_{i-1}$ so that the circumference of $C_{i}$ contains the center of $C_{i-1}$. Finally, let $C_{n}$ be a disk whose center is on the circumference of $C_{1}$ and whose circumference contains the center of $C_{n-1}$. This gives $S_{\mathcal{C}}=\{(i, j) \mid 1 \leq i<j \leq n-1\}$ of size $(n-1)(n-2) / 2$, which proves (i).
For any $n$-configuration $\mathcal{C}, S_{\mathcal{C}}$ must satisfy the following properties:
(1) $(i, i) \notin S_{\mathcal{C}}$,
(2) $(i+1, i) \notin S_{\mathcal{C}},(1, n) \notin S_{\mathcal{C}}$,
(3) if $(i, j),(j, k) \in S_{\mathcal{C}}$, then $(i, k) \in S_{\mathcal{C}}$,
(4) if $(i, j) \in S_{\mathcal{C}}$, then $(j, i) \notin S_{\mathcal{C}}$.
Now we show that a set $G$ of ordered pairs of integers between 1 and $n$, satisfying the conditions $(1) \sim(4)$, can have no more than $(n-1)(n-2) / 2$ elements. Suppose that there exists a set $G$ that satisfies the conditions (1) $\sim(4)$, and has more than $(n-1)(n-2) / 2$ elements. Let $n$ be the least positive integer with which there exists such a set $G$. Note that $G$ must have $(i, i+1)$ for some $1 \leq i \leq n$ or $(n, 1)$, since otherwise $G$ can have at most
$$
\binom{n}{2}-n=\frac{n(n-3)}{2}<\frac{(n-1)(n-2)}{2}
$$
elements. Without loss of generality we may assume that $(n, 1) \in G$. Then $(1, n-1) \notin G$, since otherwise the condition (3) yields $(n, n-1) \in G$ contradicting the condition (2). Now let $G^{\prime}=\{(i, j) \in G \mid 1 \leq i, j \leq n-1\}$, then $G^{\prime}$ satisfies the conditions (1) (4), with $n-1$.
We now claim that $\left|G-G^{\prime}\right| \leq n-2$ :
Suppose that $\left|G-G^{\prime}\right|>n-2$, then $\left|G-G^{\prime}\right|=n-1$ and hence for each $1 \leq i \leq n-1$, either $(i, n)$ or $(n, i)$ must be in $G$. We already know that $(n, 1) \in G$ and $(n-1, n) \in G$ (because $(n, n-1) \notin G$ ) and this implies that $(n, n-2) \notin G$ and $(n-2, n) \in G$. If we keep doing this process, we obtain $(1, n) \in G$, which is a contradiction.
Since $\left|G-G^{\prime}\right| \leq n-2$, we obtain
$$
\left|G^{\prime}\right| \geq \frac{(n-1)(n-2)}{2}-(n-2)=\frac{(n-2)(n-3)}{2}
$$
This, however, contradicts the minimality of $n$, and hence proves (ii).
|
{
"resource_path": "APMO/segmented/en-apmo2007_sol.jsonl",
"problem_match": "\nProblem 3.",
"solution_match": "\nSolution."
}
|
8d33c1d3-c1d3-5bf1-b208-ed86249f3b44
| 261,138
|
Let $a_{1}, a_{2}, a_{3}, a_{4}, a_{5}$ be real numbers satisfying the following equations:
$$
\frac{a_{1}}{k^{2}+1}+\frac{a_{2}}{k^{2}+2}+\frac{a_{3}}{k^{2}+3}+\frac{a_{4}}{k^{2}+4}+\frac{a_{5}}{k^{2}+5}=\frac{1}{k^{2}} \text { for } k=1,2,3,4,5
$$
Find the value of $\frac{a_{1}}{37}+\frac{a_{2}}{38}+\frac{a_{3}}{39}+\frac{a_{4}}{40}+\frac{a_{5}}{41}$. (Express the value in a single fraction.)
|
Let $R(x):=\frac{a_{1}}{x^{2}+1}+\frac{a_{2}}{x^{2}+2}+\frac{a_{3}}{x^{2}+3}+\frac{a_{4}}{x^{2}+4}+\frac{a_{5}}{x^{2}+5}$. Then $R( \pm 1)=1$, $R( \pm 2)=\frac{1}{4}, R( \pm 3)=\frac{1}{9}, R( \pm 4)=\frac{1}{16}, R( \pm 5)=\frac{1}{25}$ and $R(6)$ is the value to be found. Let's put $P(x):=\left(x^{2}+1\right)\left(x^{2}+2\right)\left(x^{2}+3\right)\left(x^{2}+4\right)\left(x^{2}+5\right)$ and $Q(x):=R(x) P(x)$. Then for $k= \pm 1, \pm 2, \pm 3, \pm 4, \pm 5$, we get $Q(k)=R(k) P(k)=\frac{P(k)}{k^{2}}$, that is, $P(k)-k^{2} Q(k)=0$. Since $P(x)-x^{2} Q(x)$ is a polynomial of degree 10 with roots $\pm 1, \pm 2, \pm 3, \pm 4, \pm 5$, we get
$$
P(x)-x^{2} Q(x)=A\left(x^{2}-1\right)\left(x^{2}-4\right)\left(x^{2}-9\right)\left(x^{2}-16\right)\left(x^{2}-25\right)
$$
Putting $x=0$, we get $A=\frac{P(0)}{(-1)(-4)(-9)(-16)(-25)}=-\frac{1}{120}$. Finally, dividing both sides of $(*)$ by $P(x)$ yields
$$
1-x^{2} R(x)=1-x^{2} \frac{Q(x)}{P(x)}=-\frac{1}{120} \cdot \frac{\left(x^{2}-1\right)\left(x^{2}-4\right)\left(x^{2}-9\right)\left(x^{2}-16\right)\left(x^{2}-25\right)}{\left(x^{2}+1\right)\left(x^{2}+2\right)\left(x^{2}+3\right)\left(x^{2}+4\right)\left(x^{2}+5\right)}
$$
and hence that
$$
1-36 R(6)=-\frac{35 \times 32 \times 27 \times 20 \times 11}{120 \times 37 \times 38 \times 39 \times 40 \times 41}=-\frac{3 \times 7 \times 11}{13 \times 19 \times 37 \times 41}=-\frac{231}{374699}
$$
which implies $R(6)=\frac{187465}{6744582}$.
Remark. We can get $a_{1}=\frac{1105}{72}, a_{2}=-\frac{2673}{40}, a_{3}=\frac{1862}{15}, a_{4}=-\frac{1885}{18}, a_{5}=\frac{1323}{40}$ by solving the given system of linear equations, which is extremely messy and takes a lot of time.
|
\frac{187465}{6744582}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Let $a_{1}, a_{2}, a_{3}, a_{4}, a_{5}$ be real numbers satisfying the following equations:
$$
\frac{a_{1}}{k^{2}+1}+\frac{a_{2}}{k^{2}+2}+\frac{a_{3}}{k^{2}+3}+\frac{a_{4}}{k^{2}+4}+\frac{a_{5}}{k^{2}+5}=\frac{1}{k^{2}} \text { for } k=1,2,3,4,5
$$
Find the value of $\frac{a_{1}}{37}+\frac{a_{2}}{38}+\frac{a_{3}}{39}+\frac{a_{4}}{40}+\frac{a_{5}}{41}$. (Express the value in a single fraction.)
|
Let $R(x):=\frac{a_{1}}{x^{2}+1}+\frac{a_{2}}{x^{2}+2}+\frac{a_{3}}{x^{2}+3}+\frac{a_{4}}{x^{2}+4}+\frac{a_{5}}{x^{2}+5}$. Then $R( \pm 1)=1$, $R( \pm 2)=\frac{1}{4}, R( \pm 3)=\frac{1}{9}, R( \pm 4)=\frac{1}{16}, R( \pm 5)=\frac{1}{25}$ and $R(6)$ is the value to be found. Let's put $P(x):=\left(x^{2}+1\right)\left(x^{2}+2\right)\left(x^{2}+3\right)\left(x^{2}+4\right)\left(x^{2}+5\right)$ and $Q(x):=R(x) P(x)$. Then for $k= \pm 1, \pm 2, \pm 3, \pm 4, \pm 5$, we get $Q(k)=R(k) P(k)=\frac{P(k)}{k^{2}}$, that is, $P(k)-k^{2} Q(k)=0$. Since $P(x)-x^{2} Q(x)$ is a polynomial of degree 10 with roots $\pm 1, \pm 2, \pm 3, \pm 4, \pm 5$, we get
$$
P(x)-x^{2} Q(x)=A\left(x^{2}-1\right)\left(x^{2}-4\right)\left(x^{2}-9\right)\left(x^{2}-16\right)\left(x^{2}-25\right)
$$
Putting $x=0$, we get $A=\frac{P(0)}{(-1)(-4)(-9)(-16)(-25)}=-\frac{1}{120}$. Finally, dividing both sides of $(*)$ by $P(x)$ yields
$$
1-x^{2} R(x)=1-x^{2} \frac{Q(x)}{P(x)}=-\frac{1}{120} \cdot \frac{\left(x^{2}-1\right)\left(x^{2}-4\right)\left(x^{2}-9\right)\left(x^{2}-16\right)\left(x^{2}-25\right)}{\left(x^{2}+1\right)\left(x^{2}+2\right)\left(x^{2}+3\right)\left(x^{2}+4\right)\left(x^{2}+5\right)}
$$
and hence that
$$
1-36 R(6)=-\frac{35 \times 32 \times 27 \times 20 \times 11}{120 \times 37 \times 38 \times 39 \times 40 \times 41}=-\frac{3 \times 7 \times 11}{13 \times 19 \times 37 \times 41}=-\frac{231}{374699}
$$
which implies $R(6)=\frac{187465}{6744582}$.
Remark. We can get $a_{1}=\frac{1105}{72}, a_{2}=-\frac{2673}{40}, a_{3}=\frac{1862}{15}, a_{4}=-\frac{1885}{18}, a_{5}=\frac{1323}{40}$ by solving the given system of linear equations, which is extremely messy and takes a lot of time.
|
{
"resource_path": "APMO/segmented/en-apmo2009_sol.jsonl",
"problem_match": "\nProblem 2.",
"solution_match": "(Solution)"
}
|
149fe16f-5e4d-586c-aea5-aafc6a7e9dea
| 605,313
|
Let $n$ be a positive integer. $n$ people take part in a certain party. For any pair of the participants, either the two are acquainted with each other or they are not. What is the maximum possible number of the pairs for which the two are not acquainted but have a common acquaintance among the participants?
|
When 1 participant, say the person $A$, is mutually acquainted with each of the remaining $n-1$ participants, and if there are no other acquaintance relationships among the participants, then for any pair of participants not involving $A$, the two are not mutual acquaintances, but they have a common acquaintance, namely $A$, so any such pair satisfies the requirement. Thus, the number desired in this case is $\frac{(n-1)(n-2)}{2}=\frac{n^{2}-3 n+2}{2}$.
Let us show that $\frac{n^{2}-3 n+2}{2}$ is the maximum possible number of the pairs satisfying the requirement of the problem. First, let us observe that in the process of trying to find the maximum possible number of such pairs, if we split the participants into two non-empty subsets $T$ and $S$ which are disjoint, we may assume that there is a pair consisting of one person chosen from $T$ and the other chosen from $S$ who are mutual acquaintances. This is so, since if there are no such pair for some splitting $T$ and $S$, then among the pairs consisting of one person chosen from $T$ and the other chosen from $S$, there is no pair for which the two have a common acquaintance among participants, and therefore, if we arbitrarily choose a person $A \in T$ and $B \in S$ and declare that $A$ and $B$ are mutual acquaintances, the number of the pairs satisfying the requirement of the problem does not decrease.
Let us now call a set of participants a group if it satisfies the following 2 conditions:
- One can connect any person in the set with any other person in the set by tracing a chain of mutually acquainted pairs. More precisely, for any pair of people $A, B$ in the set there exists a sequence of people $A_{0}, A_{1}, \cdots, A_{n}$ for which $A_{0}=A, A_{n}=B$ and, for each $i: 0 \leq i \leq n-1, A_{i}$ and $A_{i+1}$ are mutual acquaintances.
- No person in this set can be connected with a person not belonging to this set by tracing a chain of mutually acquainted pairs.
In view of the discussions made above, we may assume that the set of all the participants to the party forms a group of $n$ people. Let us next consider the following lemma.
Lemma. In a group of $n$ people, there are at least $n-1$ pairs of mutual acquaintances.
Proof: If you choose a mutually acquainted pair in a group and declare the two in the pair are not mutually acquainted, then either the group stays the same or splits into 2 groups. This means that by changing the status of a mutually acquainted pair in a group to that of a non-acquainted pair, one can increase the number of groups at most by 1 . Now if in a group of $n$ people you change the status of all of the mutually acquainted pairs to that of non-acquainted pairs, then obviously, the number of groups increases from 1 to $n$. Therefore, there must be at least $n-1$ pairs of mutually acquainted pairs in a group consisting of $n$ people.
The lemma implies that there are at most $\frac{n(n-1)}{2}-(n-1)=\frac{n^{2}-3 n+2}{2}$ pairs satisfying the condition of the problem. Thus the desired maximum number of pairs satisfying the requirement of the problem is $\frac{n^{2}-3 n+2}{2}$.
Remark: One can give a somewhat different proof by separating into 2 cases depending on whether there are at least $n-1$ mutually acquainted pairs, or at most $n-2$ such pairs. In the former case, one can argue in the same way as the proof above, while in the latter case, the Lemma above implies that there would be 2 or more groups to start with, but then, in view of the comment made before the definition of a group above, these groups can be combined to form one group, thereby one can reduce the argument to the former case.
Alternate Solution 1: The construction of an example for the case for which the number $\frac{n^{2}-3 n+2}{2}$ appears, and the argument for the case where there is only 1 group would be the same as in the preceding proof.
Suppose, then, $n$ participants are separated into $k(k \geq 2)$ groups, and the number of people in each group is given by $a_{i}, i=1, \cdots, k$. In such a case, the number of pairs for which paired people are not mutually acquainted but have a common acquaintance is at most $\sum_{i=1}^{k} a_{i} C_{2}$, where we set ${ }_{1} C_{2}=0$ for convenience. Since ${ }_{a} C_{2}+{ }_{b} C_{2} \leq{ }_{a+b} C_{2}$ holds for any pair of positive integers $a, b$, we have $\sum_{i=1}^{k} a_{i} C_{2} \leq{ }_{a_{1}} C_{2}+{ }_{n-a_{1}} C_{2}$. From
$$
{ }_{a_{1}} C_{2}+{ }_{n-a_{1}} C_{2}=a_{1}^{2}-n a_{1}+\frac{n^{2}-n}{2}=\left(a_{1}-\frac{n}{2}\right)^{2}+\frac{n^{2}-2 n}{4}
$$
it follows that ${ }_{a} C_{2}+{ }_{n-a_{1}} C_{2}$ takes its maximum value when $a_{1}=1, n-1$. Therefore, we have $\sum_{i=1}^{k}{ }_{a} C_{2} \leq{ }_{n-1} C_{2}$, which shows that in the case where the number of groups are 2 or more, the number of the pairs for which paired people are not mutually acquainted but have a common acquaintance is at most ${ }_{n-1} C_{2}=\frac{n^{2}-3 n+2}{2}$, and hence the desired maximum number of the pairs satisfying the requirement is $\frac{n^{2}-3 n+2}{2}$.
Alternate Solution 2: Construction of an example would be the same as the preceding proof.
For a participant, say $A$, call another participant, say $B$, a familiar face if $A$ and $B$ are not mutually acquainted but they have a common acquaintance among the participants, and in this case call the pair $A, B$ a familiar pair.
Suppose there is a participant $P$ who is mutually acquainted with $d$ participants. Denote by $S$ the set of these $d$ participants, and by $T$ the set of participants different from $P$ and not belonging to the set $S$. Suppose there are $e$ pairs formed by a person in $S$ and a person in $T$ who are mutually acquainted.
Then the number of participants who are familiar faces to $P$ is at most $e$. The number of pairs formed by two people belonging to the set $S$ and are mutually acquainted is at most ${ }_{d} C_{2}$. The number of familiar pairs formed by two people belonging to the set $T$ is at most ${ }_{n-d-1} C_{2}$. Since there are $e$ pairs formed by a person in the set $S$ and a person in the set $T$ who are mutually acquainted (and so the pairs are not familiar pairs), we have at most $d(n-1-d)-e$ familiar pairs formed by a person chosen from $S$ and a person chosen from $T$. Putting these together we conclude that there are at most $e+{ }_{d} C_{2}+{ }_{n-1-d} C_{2}+d(n-1-d)-e$ familiar pairs. Since
$$
e+{ }_{d} C_{2}+{ }_{n-1-d} C_{2}+d(n-1-d)-e=\frac{n^{2}-3 n+2}{2}
$$
the number we seek is at most $\frac{n^{2}-3 n+2}{2}$, and hence this is the desired solution to the problem.
|
\frac{n^{2}-3 n+2}{2}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Let $n$ be a positive integer. $n$ people take part in a certain party. For any pair of the participants, either the two are acquainted with each other or they are not. What is the maximum possible number of the pairs for which the two are not acquainted but have a common acquaintance among the participants?
|
When 1 participant, say the person $A$, is mutually acquainted with each of the remaining $n-1$ participants, and if there are no other acquaintance relationships among the participants, then for any pair of participants not involving $A$, the two are not mutual acquaintances, but they have a common acquaintance, namely $A$, so any such pair satisfies the requirement. Thus, the number desired in this case is $\frac{(n-1)(n-2)}{2}=\frac{n^{2}-3 n+2}{2}$.
Let us show that $\frac{n^{2}-3 n+2}{2}$ is the maximum possible number of the pairs satisfying the requirement of the problem. First, let us observe that in the process of trying to find the maximum possible number of such pairs, if we split the participants into two non-empty subsets $T$ and $S$ which are disjoint, we may assume that there is a pair consisting of one person chosen from $T$ and the other chosen from $S$ who are mutual acquaintances. This is so, since if there are no such pair for some splitting $T$ and $S$, then among the pairs consisting of one person chosen from $T$ and the other chosen from $S$, there is no pair for which the two have a common acquaintance among participants, and therefore, if we arbitrarily choose a person $A \in T$ and $B \in S$ and declare that $A$ and $B$ are mutual acquaintances, the number of the pairs satisfying the requirement of the problem does not decrease.
Let us now call a set of participants a group if it satisfies the following 2 conditions:
- One can connect any person in the set with any other person in the set by tracing a chain of mutually acquainted pairs. More precisely, for any pair of people $A, B$ in the set there exists a sequence of people $A_{0}, A_{1}, \cdots, A_{n}$ for which $A_{0}=A, A_{n}=B$ and, for each $i: 0 \leq i \leq n-1, A_{i}$ and $A_{i+1}$ are mutual acquaintances.
- No person in this set can be connected with a person not belonging to this set by tracing a chain of mutually acquainted pairs.
In view of the discussions made above, we may assume that the set of all the participants to the party forms a group of $n$ people. Let us next consider the following lemma.
Lemma. In a group of $n$ people, there are at least $n-1$ pairs of mutual acquaintances.
Proof: If you choose a mutually acquainted pair in a group and declare the two in the pair are not mutually acquainted, then either the group stays the same or splits into 2 groups. This means that by changing the status of a mutually acquainted pair in a group to that of a non-acquainted pair, one can increase the number of groups at most by 1 . Now if in a group of $n$ people you change the status of all of the mutually acquainted pairs to that of non-acquainted pairs, then obviously, the number of groups increases from 1 to $n$. Therefore, there must be at least $n-1$ pairs of mutually acquainted pairs in a group consisting of $n$ people.
The lemma implies that there are at most $\frac{n(n-1)}{2}-(n-1)=\frac{n^{2}-3 n+2}{2}$ pairs satisfying the condition of the problem. Thus the desired maximum number of pairs satisfying the requirement of the problem is $\frac{n^{2}-3 n+2}{2}$.
Remark: One can give a somewhat different proof by separating into 2 cases depending on whether there are at least $n-1$ mutually acquainted pairs, or at most $n-2$ such pairs. In the former case, one can argue in the same way as the proof above, while in the latter case, the Lemma above implies that there would be 2 or more groups to start with, but then, in view of the comment made before the definition of a group above, these groups can be combined to form one group, thereby one can reduce the argument to the former case.
Alternate Solution 1: The construction of an example for the case for which the number $\frac{n^{2}-3 n+2}{2}$ appears, and the argument for the case where there is only 1 group would be the same as in the preceding proof.
Suppose, then, $n$ participants are separated into $k(k \geq 2)$ groups, and the number of people in each group is given by $a_{i}, i=1, \cdots, k$. In such a case, the number of pairs for which paired people are not mutually acquainted but have a common acquaintance is at most $\sum_{i=1}^{k} a_{i} C_{2}$, where we set ${ }_{1} C_{2}=0$ for convenience. Since ${ }_{a} C_{2}+{ }_{b} C_{2} \leq{ }_{a+b} C_{2}$ holds for any pair of positive integers $a, b$, we have $\sum_{i=1}^{k} a_{i} C_{2} \leq{ }_{a_{1}} C_{2}+{ }_{n-a_{1}} C_{2}$. From
$$
{ }_{a_{1}} C_{2}+{ }_{n-a_{1}} C_{2}=a_{1}^{2}-n a_{1}+\frac{n^{2}-n}{2}=\left(a_{1}-\frac{n}{2}\right)^{2}+\frac{n^{2}-2 n}{4}
$$
it follows that ${ }_{a} C_{2}+{ }_{n-a_{1}} C_{2}$ takes its maximum value when $a_{1}=1, n-1$. Therefore, we have $\sum_{i=1}^{k}{ }_{a} C_{2} \leq{ }_{n-1} C_{2}$, which shows that in the case where the number of groups are 2 or more, the number of the pairs for which paired people are not mutually acquainted but have a common acquaintance is at most ${ }_{n-1} C_{2}=\frac{n^{2}-3 n+2}{2}$, and hence the desired maximum number of the pairs satisfying the requirement is $\frac{n^{2}-3 n+2}{2}$.
Alternate Solution 2: Construction of an example would be the same as the preceding proof.
For a participant, say $A$, call another participant, say $B$, a familiar face if $A$ and $B$ are not mutually acquainted but they have a common acquaintance among the participants, and in this case call the pair $A, B$ a familiar pair.
Suppose there is a participant $P$ who is mutually acquainted with $d$ participants. Denote by $S$ the set of these $d$ participants, and by $T$ the set of participants different from $P$ and not belonging to the set $S$. Suppose there are $e$ pairs formed by a person in $S$ and a person in $T$ who are mutually acquainted.
Then the number of participants who are familiar faces to $P$ is at most $e$. The number of pairs formed by two people belonging to the set $S$ and are mutually acquainted is at most ${ }_{d} C_{2}$. The number of familiar pairs formed by two people belonging to the set $T$ is at most ${ }_{n-d-1} C_{2}$. Since there are $e$ pairs formed by a person in the set $S$ and a person in the set $T$ who are mutually acquainted (and so the pairs are not familiar pairs), we have at most $d(n-1-d)-e$ familiar pairs formed by a person chosen from $S$ and a person chosen from $T$. Putting these together we conclude that there are at most $e+{ }_{d} C_{2}+{ }_{n-1-d} C_{2}+d(n-1-d)-e$ familiar pairs. Since
$$
e+{ }_{d} C_{2}+{ }_{n-1-d} C_{2}+d(n-1-d)-e=\frac{n^{2}-3 n+2}{2}
$$
the number we seek is at most $\frac{n^{2}-3 n+2}{2}$, and hence this is the desired solution to the problem.
|
{
"resource_path": "APMO/segmented/en-apmo2010_sol.jsonl",
"problem_match": "\nProblem 3.",
"solution_match": "\nSolution:"
}
|
8217e940-8b0a-5b7b-b8b8-51d1b25d50a6
| 65,014
|
Let $S=\{1,2, \ldots, 2014\}$. For each non-empty subset $T \subseteq S$, one of its members is chosen as its representative. Find the number of ways to assign representatives to all non-empty subsets of $S$ so that if a subset $D \subseteq S$ is a disjoint union of non-empty subsets $A, B, C \subseteq S$, then the representative of $D$ is also the representative of at least one of $A, B, C$. (Warut Suksompong, Thailand)
|
Answer: 108 - 2014!.
For any subset $X$ let $r(X)$ denotes the representative of $X$. Suppose that $x_{1}=r(S)$. First, we prove the following fact:
$$
\text { If } x_{1} \in X \text { and } X \subseteq S \text {, then } x_{1}=r(X) \text {. }
$$
If $|X| \leq 2012$, then we can write $S$ as a disjoint union of $X$ and two other subsets of $S$, which gives that $x_{1}=r(X)$. If $|X|=2013$, then let $y \in X$ and $y \neq x_{1}$. We can write $X$ as a disjoint union of $\left\{x_{1}, y\right\}$ and two other subsets. We already proved that $r\left(\left\{x_{1}, y\right\}\right)=x_{1}$ (since $\left|\left\{x_{1}, y\right\}\right|=2<2012$ ) and it follows that $y \neq r(X)$ for every $y \in X$ except $x_{1}$. We have proved the fact.
Note that this fact is true and can be proved similarly, if the ground set $S$ would contain at least 5 elements.
There are 2014 ways to choose $x_{1}=r(S)$ and for $x_{1} \in X \subseteq S$ we have $r(X)=x_{1}$. Let $S_{1}=S \backslash\left\{x_{1}\right\}$. Analogously, we can state that there are 2013 ways to choose $x_{2}=r\left(S_{1}\right)$ and for $x_{2} \in X \subseteq S_{1}$ we have $r(X)=x_{2}$. Proceeding similarly (or by induction), there are $2014 \cdot 2013 \cdots 5$ ways to choose $x_{1}, x_{2}, \ldots, x_{2010} \in S$ so that for all $i=1,2 \ldots, 2010$, $x_{i}=r(X)$ for each $X \subseteq S \backslash\left\{x_{1}, \ldots, x_{i-1}\right\}$ and $x_{i} \in X$.
We are now left with four elements $Y=\left\{y_{1}, y_{2}, y_{3}, y_{4}\right\}$. There are 4 ways to choose $r(Y)$. Suppose that $y_{1}=r(Y)$. Then we clearly have $y_{1}=r\left(\left\{y_{1}, y_{2}\right\}\right)=r\left(\left\{y_{1}, y_{3}\right\}\right)=r\left(\left\{y_{1}, y_{4}\right\}\right)$. The only subsets whose representative has not been assigned yet are $\left\{y_{1}, y_{2}, y_{3}\right\},\left\{y_{1}, y_{2}, y_{4}\right\}$, $\left\{y_{1}, y_{3}, y_{4}\right\},\left\{y_{2}, y_{3}, y_{4}\right\},\left\{y_{2}, y_{3}\right\},\left\{y_{2}, y_{4}\right\},\left\{y_{3}, y_{4}\right\}$. These subsets can be assigned in any way, hence giving $3^{4} \cdot 2^{3}$ more choices.
In conclusion, the total number of assignments is $2014 \cdot 2013 \cdots 4 \cdot 3^{4} \cdot 2^{3}=108 \cdot 2014$ !.
|
108 \cdot 2014!
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Let $S=\{1,2, \ldots, 2014\}$. For each non-empty subset $T \subseteq S$, one of its members is chosen as its representative. Find the number of ways to assign representatives to all non-empty subsets of $S$ so that if a subset $D \subseteq S$ is a disjoint union of non-empty subsets $A, B, C \subseteq S$, then the representative of $D$ is also the representative of at least one of $A, B, C$. (Warut Suksompong, Thailand)
|
Answer: 108 - 2014!.
For any subset $X$ let $r(X)$ denotes the representative of $X$. Suppose that $x_{1}=r(S)$. First, we prove the following fact:
$$
\text { If } x_{1} \in X \text { and } X \subseteq S \text {, then } x_{1}=r(X) \text {. }
$$
If $|X| \leq 2012$, then we can write $S$ as a disjoint union of $X$ and two other subsets of $S$, which gives that $x_{1}=r(X)$. If $|X|=2013$, then let $y \in X$ and $y \neq x_{1}$. We can write $X$ as a disjoint union of $\left\{x_{1}, y\right\}$ and two other subsets. We already proved that $r\left(\left\{x_{1}, y\right\}\right)=x_{1}$ (since $\left|\left\{x_{1}, y\right\}\right|=2<2012$ ) and it follows that $y \neq r(X)$ for every $y \in X$ except $x_{1}$. We have proved the fact.
Note that this fact is true and can be proved similarly, if the ground set $S$ would contain at least 5 elements.
There are 2014 ways to choose $x_{1}=r(S)$ and for $x_{1} \in X \subseteq S$ we have $r(X)=x_{1}$. Let $S_{1}=S \backslash\left\{x_{1}\right\}$. Analogously, we can state that there are 2013 ways to choose $x_{2}=r\left(S_{1}\right)$ and for $x_{2} \in X \subseteq S_{1}$ we have $r(X)=x_{2}$. Proceeding similarly (or by induction), there are $2014 \cdot 2013 \cdots 5$ ways to choose $x_{1}, x_{2}, \ldots, x_{2010} \in S$ so that for all $i=1,2 \ldots, 2010$, $x_{i}=r(X)$ for each $X \subseteq S \backslash\left\{x_{1}, \ldots, x_{i-1}\right\}$ and $x_{i} \in X$.
We are now left with four elements $Y=\left\{y_{1}, y_{2}, y_{3}, y_{4}\right\}$. There are 4 ways to choose $r(Y)$. Suppose that $y_{1}=r(Y)$. Then we clearly have $y_{1}=r\left(\left\{y_{1}, y_{2}\right\}\right)=r\left(\left\{y_{1}, y_{3}\right\}\right)=r\left(\left\{y_{1}, y_{4}\right\}\right)$. The only subsets whose representative has not been assigned yet are $\left\{y_{1}, y_{2}, y_{3}\right\},\left\{y_{1}, y_{2}, y_{4}\right\}$, $\left\{y_{1}, y_{3}, y_{4}\right\},\left\{y_{2}, y_{3}, y_{4}\right\},\left\{y_{2}, y_{3}\right\},\left\{y_{2}, y_{4}\right\},\left\{y_{3}, y_{4}\right\}$. These subsets can be assigned in any way, hence giving $3^{4} \cdot 2^{3}$ more choices.
In conclusion, the total number of assignments is $2014 \cdot 2013 \cdots 4 \cdot 3^{4} \cdot 2^{3}=108 \cdot 2014$ !.
|
{
"resource_path": "APMO/segmented/en-apmo2014_sol.jsonl",
"problem_match": "\nProblem 2.",
"solution_match": "\nSolution."
}
|
541b1cb1-d6a3-5fee-aff1-899a319fd3fc
| 261,240
|
A sequence of real numbers $a_{0}, a_{1}, \ldots$ is said to be good if the following three conditions hold.
(i) The value of $a_{0}$ is a positive integer.
(ii) For each non-negative integer $i$ we have $a_{i+1}=2 a_{i}+1$ or $a_{i+1}=\frac{a_{i}}{a_{i}+2}$.
(iii) There exists a positive integer $k$ such that $a_{k}=2014$.
Find the smallest positive integer $n$ such that there exists a good sequence $a_{0}, a_{1}, \ldots$ of real numbers with the property that $a_{n}=2014$.
|
Note that
$$
a_{i+1}+1=2\left(a_{i}+1\right) \text { or } a_{i+1}+1=\frac{a_{i}+a_{i}+2}{a_{i}+2}=\frac{2\left(a_{i}+1\right)}{a_{i}+2} .
$$
Hence
$$
\frac{1}{a_{i+1}+1}=\frac{1}{2} \cdot \frac{1}{a_{i}+1} \text { or } \frac{1}{a_{i+1}+1}=\frac{a_{i}+2}{2\left(a_{i}+1\right)}=\frac{1}{2} \cdot \frac{1}{a_{i}+1}+\frac{1}{2} .
$$
Therefore,
$$
\frac{1}{a_{k}+1}=\frac{1}{2^{k}} \cdot \frac{1}{a_{0}+1}+\sum_{i=1}^{k} \frac{\varepsilon_{i}}{2^{k-i+1}}
$$
where $\varepsilon_{i}=0$ or 1 . Multiplying both sides by $2^{k}\left(a_{k}+1\right)$ and putting $a_{k}=2014$, we get
$$
2^{k}=\frac{2015}{a_{0}+1}+2015 \cdot\left(\sum_{i=1}^{k} \varepsilon_{i} \cdot 2^{i-1}\right)
$$
where $\varepsilon_{i}=0$ or 1 . Since $\operatorname{gcd}(2,2015)=1$, we have $a_{0}+1=2015$ and $a_{0}=2014$. Therefore,
$$
2^{k}-1=2015 \cdot\left(\sum_{i=1}^{k} \varepsilon_{i} \cdot 2^{i-1}\right)
$$
where $\varepsilon_{i}=0$ or 1 . We now need to find the smallest $k$ such that $2015 \mid 2^{k}-1$. Since $2015=$ $5 \cdot 13 \cdot 31$, from the Fermat little theorem we obtain $5\left|2^{4}-1,13\right| 2^{12}-1$ and $31 \mid 2^{30}-1$. We also have $\operatorname{lcm}[4,12,30]=60$, hence $5\left|2^{60}-1,13\right| 2^{60}-1$ and $31 \mid 2^{60}-1$, which gives $2015 \mid 2^{60}-1$.
But $5 \nmid 2^{30}-1$ and so $k=60$ is the smallest positive integer such that $2015 \mid 2^{k}-1$. To conclude, the smallest positive integer $k$ such that $a_{k}=2014$ is when $k=60$.
Alternative solution 1. Clearly all members of the sequence are positive rational numbers. For each positive integer $i$, we have $a_{i}=\frac{a_{i+1}-1}{2}$ or $a_{i}=\frac{2 a_{i+1}}{1-a_{i+1}}$. Since $a_{i}>0$ we deduce that
$$
a_{i}=\left\{\begin{array}{cl}
\frac{a_{i+1}-1}{2} & \text { if } a_{i+1}>1 \\
\frac{2 a_{i+1}}{1-a_{i+1}} & \text { if } a_{i+1}<1
\end{array}\right.
$$
Thus $a_{i}$ is uniquely determined from $a_{i+1}$. Hence starting from $a_{k}=2014$, we simply run the sequence backwards until we reach a positive integer. We compute as follows.
$$
\begin{aligned}
& \frac{2014}{1}, \frac{2013}{2}, \frac{2011}{4}, \frac{2007}{8}, \frac{1999}{16}, \frac{1983}{32}, \frac{1951}{64}, \frac{1887}{128}, \frac{1759}{256}, \frac{1503}{512}, \frac{991}{1024}, \frac{1982}{33}, \frac{1949}{66}, \frac{1883}{132}, \frac{1751}{264}, \frac{1487}{528}, \frac{959}{1056}, \frac{1918}{97}, \frac{1821}{194}, \frac{1627}{388}, \\
& \frac{1239}{776}, \frac{463}{1552}, \frac{926}{1089}, \frac{1852}{163}, \frac{1689}{326}, \frac{1363}{652}, \frac{711}{1304}, \frac{1422}{593}, \frac{829}{1186}, \frac{1658}{357}, \frac{1301}{714}, \frac{587}{1428}, \frac{1174}{841}, \frac{333}{1682}, \frac{666}{1349}, \frac{1332}{683}, \frac{649}{1366}, \frac{1298}{717}, \frac{581}{1434}, \frac{1162}{853}, \\
& \frac{309}{1706}, \frac{618}{1397}, \frac{1236}{779}, \frac{457}{1558}, \frac{914}{1101}, \frac{1828}{187}, \frac{1641}{374}, \frac{1267}{748}, \frac{519}{1496}, \frac{1038}{977}, \frac{61}{1954}, \frac{122}{1893}, \frac{244}{1771}, \frac{488}{1527}, \frac{976}{1039}, \frac{1952}{63}, \frac{1889}{126}, \frac{1763}{252}, \frac{1511}{504}, \frac{1007}{1008}, \frac{2014}{1}
\end{aligned}
$$
There are 61 terms in the above list. Thus $k=60$.
Alternative solution 1 is quite computationally intensive. Calculating the first few terms indicates some patterns that are easy to prove. This is shown in the next solution.
Alternative solution 2. Start with $a_{k}=\frac{m_{0}}{n_{0}}$ where $m_{0}=2014$ and $n_{0}=1$ as in alternative solution 1. By inverting the sequence as in alternative solution 1, we have $a_{k-i}=\frac{m_{i}}{n_{i}}$ for $i \geq 0$ where
$$
\left(m_{i+1}, n_{i+1}\right)= \begin{cases}\left(m_{i}-n_{i}, 2 n_{i}\right) & \text { if } m_{i}>n_{i} \\ \left(2 m_{i}, n_{i}-m_{i}\right) & \text { if } m_{i}<n_{i}\end{cases}
$$
Easy inductions show that $m_{i}+n_{i}=2015,1 \leq m_{i}, n_{i} \leq 2014$ and $\operatorname{gcd}\left(m_{i}, n_{i}\right)=1$ for $i \geq 0$. Since $a_{0} \in \mathbb{N}^{+}$and $\operatorname{gcd}\left(m_{k}, n_{k}\right)=1$, we require $n_{k}=1$. An easy induction shows that $\left(m_{i}, n_{i}\right) \equiv\left(-2^{i}, 2^{i}\right)(\bmod 2015)$ for $i=0,1, \ldots, k$.
Thus $2^{k} \equiv 1(\bmod 2015)$. As in the official solution, the smallest such $k$ is $k=60$. This yields $n_{k} \equiv 1(\bmod 2015)$. But since $1 \leq n_{k}, m_{k} \leq 2014$, it follows that $a_{0}$ is an integer.
|
60
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
A sequence of real numbers $a_{0}, a_{1}, \ldots$ is said to be good if the following three conditions hold.
(i) The value of $a_{0}$ is a positive integer.
(ii) For each non-negative integer $i$ we have $a_{i+1}=2 a_{i}+1$ or $a_{i+1}=\frac{a_{i}}{a_{i}+2}$.
(iii) There exists a positive integer $k$ such that $a_{k}=2014$.
Find the smallest positive integer $n$ such that there exists a good sequence $a_{0}, a_{1}, \ldots$ of real numbers with the property that $a_{n}=2014$.
Answer: 60.
|
Note that
$$
a_{i+1}+1=2\left(a_{i}+1\right) \text { or } a_{i+1}+1=\frac{a_{i}+a_{i}+2}{a_{i}+2}=\frac{2\left(a_{i}+1\right)}{a_{i}+2} .
$$
Hence
$$
\frac{1}{a_{i+1}+1}=\frac{1}{2} \cdot \frac{1}{a_{i}+1} \text { or } \frac{1}{a_{i+1}+1}=\frac{a_{i}+2}{2\left(a_{i}+1\right)}=\frac{1}{2} \cdot \frac{1}{a_{i}+1}+\frac{1}{2} .
$$
Therefore,
$$
\frac{1}{a_{k}+1}=\frac{1}{2^{k}} \cdot \frac{1}{a_{0}+1}+\sum_{i=1}^{k} \frac{\varepsilon_{i}}{2^{k-i+1}}
$$
where $\varepsilon_{i}=0$ or 1 . Multiplying both sides by $2^{k}\left(a_{k}+1\right)$ and putting $a_{k}=2014$, we get
$$
2^{k}=\frac{2015}{a_{0}+1}+2015 \cdot\left(\sum_{i=1}^{k} \varepsilon_{i} \cdot 2^{i-1}\right)
$$
where $\varepsilon_{i}=0$ or 1 . Since $\operatorname{gcd}(2,2015)=1$, we have $a_{0}+1=2015$ and $a_{0}=2014$. Therefore,
$$
2^{k}-1=2015 \cdot\left(\sum_{i=1}^{k} \varepsilon_{i} \cdot 2^{i-1}\right)
$$
where $\varepsilon_{i}=0$ or 1 . We now need to find the smallest $k$ such that $2015 \mid 2^{k}-1$. Since $2015=$ $5 \cdot 13 \cdot 31$, from the Fermat little theorem we obtain $5\left|2^{4}-1,13\right| 2^{12}-1$ and $31 \mid 2^{30}-1$. We also have $\operatorname{lcm}[4,12,30]=60$, hence $5\left|2^{60}-1,13\right| 2^{60}-1$ and $31 \mid 2^{60}-1$, which gives $2015 \mid 2^{60}-1$.
But $5 \nmid 2^{30}-1$ and so $k=60$ is the smallest positive integer such that $2015 \mid 2^{k}-1$. To conclude, the smallest positive integer $k$ such that $a_{k}=2014$ is when $k=60$.
Alternative solution 1. Clearly all members of the sequence are positive rational numbers. For each positive integer $i$, we have $a_{i}=\frac{a_{i+1}-1}{2}$ or $a_{i}=\frac{2 a_{i+1}}{1-a_{i+1}}$. Since $a_{i}>0$ we deduce that
$$
a_{i}=\left\{\begin{array}{cl}
\frac{a_{i+1}-1}{2} & \text { if } a_{i+1}>1 \\
\frac{2 a_{i+1}}{1-a_{i+1}} & \text { if } a_{i+1}<1
\end{array}\right.
$$
Thus $a_{i}$ is uniquely determined from $a_{i+1}$. Hence starting from $a_{k}=2014$, we simply run the sequence backwards until we reach a positive integer. We compute as follows.
$$
\begin{aligned}
& \frac{2014}{1}, \frac{2013}{2}, \frac{2011}{4}, \frac{2007}{8}, \frac{1999}{16}, \frac{1983}{32}, \frac{1951}{64}, \frac{1887}{128}, \frac{1759}{256}, \frac{1503}{512}, \frac{991}{1024}, \frac{1982}{33}, \frac{1949}{66}, \frac{1883}{132}, \frac{1751}{264}, \frac{1487}{528}, \frac{959}{1056}, \frac{1918}{97}, \frac{1821}{194}, \frac{1627}{388}, \\
& \frac{1239}{776}, \frac{463}{1552}, \frac{926}{1089}, \frac{1852}{163}, \frac{1689}{326}, \frac{1363}{652}, \frac{711}{1304}, \frac{1422}{593}, \frac{829}{1186}, \frac{1658}{357}, \frac{1301}{714}, \frac{587}{1428}, \frac{1174}{841}, \frac{333}{1682}, \frac{666}{1349}, \frac{1332}{683}, \frac{649}{1366}, \frac{1298}{717}, \frac{581}{1434}, \frac{1162}{853}, \\
& \frac{309}{1706}, \frac{618}{1397}, \frac{1236}{779}, \frac{457}{1558}, \frac{914}{1101}, \frac{1828}{187}, \frac{1641}{374}, \frac{1267}{748}, \frac{519}{1496}, \frac{1038}{977}, \frac{61}{1954}, \frac{122}{1893}, \frac{244}{1771}, \frac{488}{1527}, \frac{976}{1039}, \frac{1952}{63}, \frac{1889}{126}, \frac{1763}{252}, \frac{1511}{504}, \frac{1007}{1008}, \frac{2014}{1}
\end{aligned}
$$
There are 61 terms in the above list. Thus $k=60$.
Alternative solution 1 is quite computationally intensive. Calculating the first few terms indicates some patterns that are easy to prove. This is shown in the next solution.
Alternative solution 2. Start with $a_{k}=\frac{m_{0}}{n_{0}}$ where $m_{0}=2014$ and $n_{0}=1$ as in alternative solution 1. By inverting the sequence as in alternative solution 1, we have $a_{k-i}=\frac{m_{i}}{n_{i}}$ for $i \geq 0$ where
$$
\left(m_{i+1}, n_{i+1}\right)= \begin{cases}\left(m_{i}-n_{i}, 2 n_{i}\right) & \text { if } m_{i}>n_{i} \\ \left(2 m_{i}, n_{i}-m_{i}\right) & \text { if } m_{i}<n_{i}\end{cases}
$$
Easy inductions show that $m_{i}+n_{i}=2015,1 \leq m_{i}, n_{i} \leq 2014$ and $\operatorname{gcd}\left(m_{i}, n_{i}\right)=1$ for $i \geq 0$. Since $a_{0} \in \mathbb{N}^{+}$and $\operatorname{gcd}\left(m_{k}, n_{k}\right)=1$, we require $n_{k}=1$. An easy induction shows that $\left(m_{i}, n_{i}\right) \equiv\left(-2^{i}, 2^{i}\right)(\bmod 2015)$ for $i=0,1, \ldots, k$.
Thus $2^{k} \equiv 1(\bmod 2015)$. As in the official solution, the smallest such $k$ is $k=60$. This yields $n_{k} \equiv 1(\bmod 2015)$. But since $1 \leq n_{k}, m_{k} \leq 2014$, it follows that $a_{0}$ is an integer.
|
{
"resource_path": "APMO/segmented/en-apmo2015_sol.jsonl",
"problem_match": "\nProblem 3.",
"solution_match": "\nSolution."
}
|
35b4378f-60b8-52b6-81e4-64686cfb86f6
| 605,633
|
A positive integer is called fancy if it can be expressed in the form
$$
2^{a_{1}}+2^{a_{2}}+\cdots+2^{a_{100}}
$$
where $a_{1}, a_{2}, \ldots, a_{100}$ are non-negative integers that are not necessarily distinct.
Find the smallest positive integer $n$ such that no multiple of $n$ is a fancy number.
|
Let $k$ be any positive integer less than $2^{101}-1$. Then $k$ can be expressed in binary notation using at most 100 ones, and therefore there exists a positive integer $r$ and non-negative integers $a_{1}, a_{2}, \ldots, a_{r}$ such that $r \leq 100$ and $k=2^{a_{1}}+\cdots+2^{a_{r}}$. Notice that for a positive integer $s$ we have:
$$
\begin{aligned}
2^{s} k & =2^{a_{1}+s}+2^{a_{2}+s}+\cdots+2^{a_{r-1}+s}+\left(1+1+2+\cdots+2^{s-1}\right) 2^{a_{r}} \\
& =2^{a_{1}+s}+2^{a_{2}+s}+\cdots+2^{a_{r-1}+s}+2^{a_{r}}+2^{a_{r}}+\cdots+2^{a_{r}+s-1} .
\end{aligned}
$$
This shows that $k$ has a multiple that is a sum of $r+s$ powers of two. In particular, we may take $s=100-r \geq 0$, which shows that $k$ has a multiple that is a fancy number.
We will now prove that no multiple of $n=2^{101}-1$ is a fancy number. In fact we will prove a stronger statement, namely, that no multiple of $n$ can be expressed as the sum of at most 100 powers of 2 .
For the sake of contradiction, suppose that there exists a positive integer $c$ such that $c n$ is the sum of at most 100 powers of 2 . We may assume that $c$ is the smallest such integer. By repeatedly merging equal powers of two in the representation of $c n$ we may assume that
$$
c n=2^{a_{1}}+2^{a_{2}}+\cdots+2^{a_{r}}
$$
where $r \leq 100$ and $a_{1}<a_{2}<\ldots<a_{r}$ are distinct non-negative integers. Consider the following two cases:
- If $a_{r} \geq 101$, then $2^{a_{r}}-2^{a_{r}-101}=2^{a_{r}-101} n$. It follows that $2^{a_{1}}+2^{a_{2}}+\cdots+2^{a_{r}-1}+2^{a_{r}-101}$ would be a multiple of $n$ that is smaller than $c n$. This contradicts the minimality of $c$.
- If $a_{r} \leq 100$, then $\left\{a_{1}, \ldots, a_{r}\right\}$ is a proper subset of $\{0,1, \ldots, 100\}$. Then
$$
n \leq c n<2^{0}+2^{1}+\cdots+2^{100}=n
$$
This is also a contradiction.
From these contradictions we conclude that it is impossible for cn to be the sum of at most 100 powers of 2 . In particular, no multiple of $n$ is a fancy number.
|
2^{101}-1
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
A positive integer is called fancy if it can be expressed in the form
$$
2^{a_{1}}+2^{a_{2}}+\cdots+2^{a_{100}}
$$
where $a_{1}, a_{2}, \ldots, a_{100}$ are non-negative integers that are not necessarily distinct.
Find the smallest positive integer $n$ such that no multiple of $n$ is a fancy number.
Answer: The answer is $n=2^{101}-1$.
|
Let $k$ be any positive integer less than $2^{101}-1$. Then $k$ can be expressed in binary notation using at most 100 ones, and therefore there exists a positive integer $r$ and non-negative integers $a_{1}, a_{2}, \ldots, a_{r}$ such that $r \leq 100$ and $k=2^{a_{1}}+\cdots+2^{a_{r}}$. Notice that for a positive integer $s$ we have:
$$
\begin{aligned}
2^{s} k & =2^{a_{1}+s}+2^{a_{2}+s}+\cdots+2^{a_{r-1}+s}+\left(1+1+2+\cdots+2^{s-1}\right) 2^{a_{r}} \\
& =2^{a_{1}+s}+2^{a_{2}+s}+\cdots+2^{a_{r-1}+s}+2^{a_{r}}+2^{a_{r}}+\cdots+2^{a_{r}+s-1} .
\end{aligned}
$$
This shows that $k$ has a multiple that is a sum of $r+s$ powers of two. In particular, we may take $s=100-r \geq 0$, which shows that $k$ has a multiple that is a fancy number.
We will now prove that no multiple of $n=2^{101}-1$ is a fancy number. In fact we will prove a stronger statement, namely, that no multiple of $n$ can be expressed as the sum of at most 100 powers of 2 .
For the sake of contradiction, suppose that there exists a positive integer $c$ such that $c n$ is the sum of at most 100 powers of 2 . We may assume that $c$ is the smallest such integer. By repeatedly merging equal powers of two in the representation of $c n$ we may assume that
$$
c n=2^{a_{1}}+2^{a_{2}}+\cdots+2^{a_{r}}
$$
where $r \leq 100$ and $a_{1}<a_{2}<\ldots<a_{r}$ are distinct non-negative integers. Consider the following two cases:
- If $a_{r} \geq 101$, then $2^{a_{r}}-2^{a_{r}-101}=2^{a_{r}-101} n$. It follows that $2^{a_{1}}+2^{a_{2}}+\cdots+2^{a_{r}-1}+2^{a_{r}-101}$ would be a multiple of $n$ that is smaller than $c n$. This contradicts the minimality of $c$.
- If $a_{r} \leq 100$, then $\left\{a_{1}, \ldots, a_{r}\right\}$ is a proper subset of $\{0,1, \ldots, 100\}$. Then
$$
n \leq c n<2^{0}+2^{1}+\cdots+2^{100}=n
$$
This is also a contradiction.
From these contradictions we conclude that it is impossible for cn to be the sum of at most 100 powers of 2 . In particular, no multiple of $n$ is a fancy number.
|
{
"resource_path": "APMO/segmented/en-apmo2016_sol.jsonl",
"problem_match": "\nProblem 2.",
"solution_match": "\nSolution."
}
|
3b0e7405-eba8-5a35-9ddf-4a27ed786d7b
| 605,693
|
The country Dreamland consists of 2016 cities. The airline Starways wants to establish some one-way flights between pairs of cities in such a way that each city has exactly one flight out of it. Find the smallest positive integer $k$ such that no matter how Starways establishes its flights, the cities can always be partitioned into $k$ groups so that from any city it is not possible to reach another city in the same group by using at most 28 flights.
##
|
The flights established by Starways yield a directed graph $G$ on 2016 vertices in which each vertex has out-degree equal to 1.
We first show that we need at least 57 groups. For this, suppose that $G$ has a directed cycle of length 57. Then, for any two cities in the cycle, one is reachable from the other using at most 28 flights. So no two cities in the cycle can belong to the same group. Hence, we need at least 57 groups.
We will now show that 57 groups are enough. Consider another auxiliary directed graph $H$ in which the vertices are the cities of Dreamland and there is an arrow from city $u$ to city $v$ if $u$ can be reached from $v$ using at most 28 flights. Each city has out-degree at most 28 . We will be done if we can split the cities of $H$ in at most 57 groups such that there are no arrows between vertices of the same group. We prove the following stronger statement.
Lemma: Suppose we have a directed graph on $n \geq 1$ vertices such that each vertex has out-degree at most 28. Then the vertices can be partitioned into 57 groups in such a way that no vertices in the same group are connected by an arrow.
Proof: We apply induction. The result is clear for 1 vertex. Now suppose we have more than one vertex. Since the out-degree of each vertex is at most 28 , there is a vertex, say $v$, with in-degree at most 28. If we remove the vertex $v$ we obtain a graph with fewer vertices which still satifies the conditions, so by inductive hypothesis we may split it into at most 57 groups with no adjacent vertices in the same group. Since $v$ has in-degree and out-degree at most 28 , it has at most 56 neighboors in the original directed graph. Therefore, we may add $v$ back and place it in a group in which it has no neighbors. This completes the inductive step.
|
57
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
The country Dreamland consists of 2016 cities. The airline Starways wants to establish some one-way flights between pairs of cities in such a way that each city has exactly one flight out of it. Find the smallest positive integer $k$ such that no matter how Starways establishes its flights, the cities can always be partitioned into $k$ groups so that from any city it is not possible to reach another city in the same group by using at most 28 flights.
## Answer: 57
|
The flights established by Starways yield a directed graph $G$ on 2016 vertices in which each vertex has out-degree equal to 1.
We first show that we need at least 57 groups. For this, suppose that $G$ has a directed cycle of length 57. Then, for any two cities in the cycle, one is reachable from the other using at most 28 flights. So no two cities in the cycle can belong to the same group. Hence, we need at least 57 groups.
We will now show that 57 groups are enough. Consider another auxiliary directed graph $H$ in which the vertices are the cities of Dreamland and there is an arrow from city $u$ to city $v$ if $u$ can be reached from $v$ using at most 28 flights. Each city has out-degree at most 28 . We will be done if we can split the cities of $H$ in at most 57 groups such that there are no arrows between vertices of the same group. We prove the following stronger statement.
Lemma: Suppose we have a directed graph on $n \geq 1$ vertices such that each vertex has out-degree at most 28. Then the vertices can be partitioned into 57 groups in such a way that no vertices in the same group are connected by an arrow.
Proof: We apply induction. The result is clear for 1 vertex. Now suppose we have more than one vertex. Since the out-degree of each vertex is at most 28 , there is a vertex, say $v$, with in-degree at most 28. If we remove the vertex $v$ we obtain a graph with fewer vertices which still satifies the conditions, so by inductive hypothesis we may split it into at most 57 groups with no adjacent vertices in the same group. Since $v$ has in-degree and out-degree at most 28 , it has at most 56 neighboors in the original directed graph. Therefore, we may add $v$ back and place it in a group in which it has no neighbors. This completes the inductive step.
|
{
"resource_path": "APMO/segmented/en-apmo2016_sol.jsonl",
"problem_match": "\nProblem 4.",
"solution_match": "\nSolution."
}
|
842fab19-0a9e-5f76-b92c-64771e2a0233
| 260,724
|
A collection of $n$ squares on the plane is called tri-connected if the following criteria are satisfied:
(i) All the squares are congruent.
(ii) If two squares have a point $P$ in common, then $P$ is a vertex of each of the squares.
(iii) Each square touches exactly three other squares.
How many positive integers $n$ are there with $2018 \leq n \leq 3018$, such that there exists a collection of $n$ squares that is tri-connected?
|
We will prove that there is no tri-connected collection if $n$ is odd, and that tri-connected collections exist for all even $n \geq 38$. Since there are 501 even numbers in the range from 2018 to 3018, this yields 501 as the answer.
For any two different squares $A$ and $B$, let us write $A \sim B$ to mean that square $A$ touches square $B$. Since each square touches exactly three other squares, and there are $n$ squares in total, the total number of instances of $A \sim B$ is $3 n$. But $A \sim B$ if and only if $B \sim A$. Hence the total number of instances of $A \sim B$ is even. Thus $3 n$ and hence also $n$ is even.
We now construct tri-connected collections for each even $n$ in the range. We show two
Construction 1 The idea is to use the following two configurations. Observe that in each configuration every square is related to three squares except for the leftmost and rightmost squares which are related to two squares. Note that the configuration on the left is of variable length. Also observe that multiple copies of the configuration on the right can be chained together to end around corners.

Putting the above two types of configurations together as in the following figure yields a tri-connected collection for every even $n \geq 38$.
Construction 2 Consider a regular $4 n$-gon $A_{1} A_{2} \cdots A_{4 n}$, and make $4 n$ squares on the outside of the $4 n$-gon with one side being on the $4 n$-gon. Reflect squares sharing sides $A_{4 m+2} A_{4 m+3}, A_{4 m+3} A_{4 m+4}$ across line $A_{4 m+2} A_{4 m+4}$, for $0 \leq m \leq n-1$. This will produce a tri-connected set of $6 n$ squares, as long as the squares inside the $4 n$-gon do not intersect. When $n \geq 4$, this will be true. The picture for $n=24$ is as follows:
To treat the other cases, consider the following gadget

Two squares touch 3 other squares, and the squares containing $X, Y$ touch 2 other squares. Take the $4 n$-gon from above, and break it into two along the line $A_{1} A_{2 n}$, moving the two parts away from that line. Do so until the gaps can be exactly filled by inserting two copies of the above figure, so that the vertices $X, Y$ touch the two vertices which used to be $A_{1}$ in one instance, and the two vertices which used to be $A_{2 n}$ in the other.
This gives us a valid configuration for $6 n+8$ squares, $n \geq 4$. Finally, if we had instead spread the two parts out more and inserted two copies of the above figure into each gap, we would get $6 n+16$ for $n \geq 4$, which finishes the proof for all even numbers at least 36 .
|
501
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
A collection of $n$ squares on the plane is called tri-connected if the following criteria are satisfied:
(i) All the squares are congruent.
(ii) If two squares have a point $P$ in common, then $P$ is a vertex of each of the squares.
(iii) Each square touches exactly three other squares.
How many positive integers $n$ are there with $2018 \leq n \leq 3018$, such that there exists a collection of $n$ squares that is tri-connected?
Answer: 501
|
We will prove that there is no tri-connected collection if $n$ is odd, and that tri-connected collections exist for all even $n \geq 38$. Since there are 501 even numbers in the range from 2018 to 3018, this yields 501 as the answer.
For any two different squares $A$ and $B$, let us write $A \sim B$ to mean that square $A$ touches square $B$. Since each square touches exactly three other squares, and there are $n$ squares in total, the total number of instances of $A \sim B$ is $3 n$. But $A \sim B$ if and only if $B \sim A$. Hence the total number of instances of $A \sim B$ is even. Thus $3 n$ and hence also $n$ is even.
We now construct tri-connected collections for each even $n$ in the range. We show two
Construction 1 The idea is to use the following two configurations. Observe that in each configuration every square is related to three squares except for the leftmost and rightmost squares which are related to two squares. Note that the configuration on the left is of variable length. Also observe that multiple copies of the configuration on the right can be chained together to end around corners.

Putting the above two types of configurations together as in the following figure yields a tri-connected collection for every even $n \geq 38$.

Construction 2 Consider a regular $4 n$-gon $A_{1} A_{2} \cdots A_{4 n}$, and make $4 n$ squares on the outside of the $4 n$-gon with one side being on the $4 n$-gon. Reflect squares sharing sides $A_{4 m+2} A_{4 m+3}, A_{4 m+3} A_{4 m+4}$ across line $A_{4 m+2} A_{4 m+4}$, for $0 \leq m \leq n-1$. This will produce a tri-connected set of $6 n$ squares, as long as the squares inside the $4 n$-gon do not intersect. When $n \geq 4$, this will be true. The picture for $n=24$ is as follows:

To treat the other cases, consider the following gadget

Two squares touch 3 other squares, and the squares containing $X, Y$ touch 2 other squares. Take the $4 n$-gon from above, and break it into two along the line $A_{1} A_{2 n}$, moving the two parts away from that line. Do so until the gaps can be exactly filled by inserting two copies of the above figure, so that the vertices $X, Y$ touch the two vertices which used to be $A_{1}$ in one instance, and the two vertices which used to be $A_{2 n}$ in the other.
This gives us a valid configuration for $6 n+8$ squares, $n \geq 4$. Finally, if we had instead spread the two parts out more and inserted two copies of the above figure into each gap, we would get $6 n+16$ for $n \geq 4$, which finishes the proof for all even numbers at least 36 .
|
{
"resource_path": "APMO/segmented/en-apmo2018_sol.jsonl",
"problem_match": "\nProblem 3.",
"solution_match": "\nSolution."
}
|
99df8265-842c-5db0-8573-bcaa6c1c8dd8
| 605,916
|
Find all integers $n$ satisfying $n \geq 2$ and $\frac{\sigma(n)}{p(n)-1}=n$, in which $\sigma(n)$ denotes the sum of all positive divisors of $n$, and $p(n)$ denotes the largest prime divisor of $n$.
|
Let $n=p_{1}^{\alpha_{1}} \cdot \ldots \cdot p_{k}^{\alpha_{k}}$ be the prime factorization of $n$ with $p_{1}<\ldots<p_{k}$, so that $p(n)=p_{k}$ and $\sigma(n)=\left(1+p_{1}+\cdots+p_{1}^{\alpha_{1}}\right) \ldots\left(1+p_{k}+\cdots+p_{k}^{\alpha_{k}}\right)$. Hence
$p_{k}-1=\frac{\sigma(n)}{n}=\prod_{i=1}^{k}\left(1+\frac{1}{p_{i}}+\cdots+\frac{1}{p_{i}^{\alpha_{i}}}\right)<\prod_{i=1}^{k} \frac{1}{1-\frac{1}{p_{i}}}=\prod_{i=1}^{k}\left(1+\frac{1}{p_{i}-1}\right) \leq \prod_{i=1}^{k}\left(1+\frac{1}{i}\right)=k+1$,
that is, $p_{k}-1<k+1$, which is impossible for $k \geq 3$, because in this case $p_{k}-1 \geq 2 k-2 \geq k+1$. Then $k \leq 2$ and $p_{k}<k+2 \leq 4$, which implies $p_{k} \leq 3$.
If $k=1$ then $n=p^{\alpha}$ and $\sigma(n)=1+p+\cdots+p^{\alpha}$, and in this case $n \nmid \sigma(n)$, which is not possible. Thus $k=2$, and $n=2^{\alpha} 3^{\beta}$ with $\alpha, \beta>0$. If $\alpha>1$ or $\beta>1$,
$$
\frac{\sigma(n)}{n}>\left(1+\frac{1}{2}\right)\left(1+\frac{1}{3}\right)=2 .
$$
Therefore $\alpha=\beta=1$ and the only answer is $n=6$.
Comment: There are other ways to deal with the case $n=2^{\alpha} 3^{\beta}$. For instance, we have $2^{\alpha+2} 3^{\beta}=\left(2^{\alpha+1}-1\right)\left(3^{\beta+1}-1\right)$. Since $2^{\alpha+1}-1$ is not divisible by 2 , and $3^{\beta+1}-1$ is not divisible by 3 , we have
$$
\left\{\begin{array} { l }
{ 2 ^ { \alpha + 1 } - 1 = 3 ^ { \beta } } \\
{ 3 ^ { \beta + 1 } - 1 = 2 ^ { \alpha + 2 } }
\end{array} \Longleftrightarrow \left\{\begin{array} { c }
{ 2 ^ { \alpha + 1 } - 1 = 3 ^ { \beta } } \\
{ 3 \cdot ( 2 ^ { \alpha + 1 } - 1 ) - 1 = 2 \cdot 2 ^ { \alpha + 1 } }
\end{array} \Longleftrightarrow \left\{\begin{array}{r}
2^{\alpha+1}=4 \\
3^{\beta}=3
\end{array}\right.\right.\right.
$$
and $n=2^{\alpha} 3^{\beta}=6$.
|
6
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Find all integers $n$ satisfying $n \geq 2$ and $\frac{\sigma(n)}{p(n)-1}=n$, in which $\sigma(n)$ denotes the sum of all positive divisors of $n$, and $p(n)$ denotes the largest prime divisor of $n$.
Answer: $n=6$.
|
Let $n=p_{1}^{\alpha_{1}} \cdot \ldots \cdot p_{k}^{\alpha_{k}}$ be the prime factorization of $n$ with $p_{1}<\ldots<p_{k}$, so that $p(n)=p_{k}$ and $\sigma(n)=\left(1+p_{1}+\cdots+p_{1}^{\alpha_{1}}\right) \ldots\left(1+p_{k}+\cdots+p_{k}^{\alpha_{k}}\right)$. Hence
$p_{k}-1=\frac{\sigma(n)}{n}=\prod_{i=1}^{k}\left(1+\frac{1}{p_{i}}+\cdots+\frac{1}{p_{i}^{\alpha_{i}}}\right)<\prod_{i=1}^{k} \frac{1}{1-\frac{1}{p_{i}}}=\prod_{i=1}^{k}\left(1+\frac{1}{p_{i}-1}\right) \leq \prod_{i=1}^{k}\left(1+\frac{1}{i}\right)=k+1$,
that is, $p_{k}-1<k+1$, which is impossible for $k \geq 3$, because in this case $p_{k}-1 \geq 2 k-2 \geq k+1$. Then $k \leq 2$ and $p_{k}<k+2 \leq 4$, which implies $p_{k} \leq 3$.
If $k=1$ then $n=p^{\alpha}$ and $\sigma(n)=1+p+\cdots+p^{\alpha}$, and in this case $n \nmid \sigma(n)$, which is not possible. Thus $k=2$, and $n=2^{\alpha} 3^{\beta}$ with $\alpha, \beta>0$. If $\alpha>1$ or $\beta>1$,
$$
\frac{\sigma(n)}{n}>\left(1+\frac{1}{2}\right)\left(1+\frac{1}{3}\right)=2 .
$$
Therefore $\alpha=\beta=1$ and the only answer is $n=6$.
Comment: There are other ways to deal with the case $n=2^{\alpha} 3^{\beta}$. For instance, we have $2^{\alpha+2} 3^{\beta}=\left(2^{\alpha+1}-1\right)\left(3^{\beta+1}-1\right)$. Since $2^{\alpha+1}-1$ is not divisible by 2 , and $3^{\beta+1}-1$ is not divisible by 3 , we have
$$
\left\{\begin{array} { l }
{ 2 ^ { \alpha + 1 } - 1 = 3 ^ { \beta } } \\
{ 3 ^ { \beta + 1 } - 1 = 2 ^ { \alpha + 2 } }
\end{array} \Longleftrightarrow \left\{\begin{array} { c }
{ 2 ^ { \alpha + 1 } - 1 = 3 ^ { \beta } } \\
{ 3 \cdot ( 2 ^ { \alpha + 1 } - 1 ) - 1 = 2 \cdot 2 ^ { \alpha + 1 } }
\end{array} \Longleftrightarrow \left\{\begin{array}{r}
2^{\alpha+1}=4 \\
3^{\beta}=3
\end{array}\right.\right.\right.
$$
and $n=2^{\alpha} 3^{\beta}=6$.
|
{
"resource_path": "APMO/segmented/en-apmo2023_sol.jsonl",
"problem_match": "# Problem 2",
"solution_match": "# Solution\n\n"
}
|
8ef1d7ed-6915-53dc-ba6b-a82e5c8b3aae
| 606,316
|
Let $S$ be the set of positive real numbers. Find all functions $f: S^{3} \rightarrow S$ such that, for all positive real numbers $x, y, z$ and $k$, the following three conditions are satisfied:
(i) $x f(x, y, z)=z f(z, y, x)$;
(ii) $f\left(x, k y, k^{2} z\right)=k f(x, y, z)$;
(iii) $f(1, k, k+1)=k+1$.
(United Kingdom)
|
It follows from the properties of function $f$ that, for all $x, y, z, a, b>0$, $f\left(a^{2} x, a b y, b^{2} z\right)=b f\left(a^{2} x, a y, z\right)=b \cdot \frac{z}{a^{2} x} f\left(z, a y, a^{2} x\right)=\frac{b z}{a x} f(z, y, x)=\frac{b}{a} f(x, y, z)$.
We shall choose $a$ and $b$ in such a way that the triple $\left(a^{2} x, a b y, b^{2} z\right)$ is of the form $(1, k, k+1)$ for some $k$ : namely, we take $a=\frac{1}{\sqrt{x}}$ and $b$ satisfying $b^{2} z-a b y=1$, which upon solving the quadratic equation yields $b=\frac{y+\sqrt{y^{2}+4 x z}}{2 z \sqrt{x}}$ and $k=\frac{y\left(y+\sqrt{y^{2}+4 x z}\right)}{2 x z}$. Now we easily obtain
$$
f(x, y, z)=\frac{a}{b} f\left(a^{2} x, a b y, b^{2} z\right)=\frac{a}{b} f(1, k, k+1)=\frac{a}{b}(k+1)=\frac{y+\sqrt{y^{2}+4 x z}}{2 x} .
$$
It is directly verified that $f$ satisfies the problem conditions.
|
\frac{y+\sqrt{y^{2}+4 x z}}{2 x}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Let $S$ be the set of positive real numbers. Find all functions $f: S^{3} \rightarrow S$ such that, for all positive real numbers $x, y, z$ and $k$, the following three conditions are satisfied:
(i) $x f(x, y, z)=z f(z, y, x)$;
(ii) $f\left(x, k y, k^{2} z\right)=k f(x, y, z)$;
(iii) $f(1, k, k+1)=k+1$.
(United Kingdom)
|
It follows from the properties of function $f$ that, for all $x, y, z, a, b>0$, $f\left(a^{2} x, a b y, b^{2} z\right)=b f\left(a^{2} x, a y, z\right)=b \cdot \frac{z}{a^{2} x} f\left(z, a y, a^{2} x\right)=\frac{b z}{a x} f(z, y, x)=\frac{b}{a} f(x, y, z)$.
We shall choose $a$ and $b$ in such a way that the triple $\left(a^{2} x, a b y, b^{2} z\right)$ is of the form $(1, k, k+1)$ for some $k$ : namely, we take $a=\frac{1}{\sqrt{x}}$ and $b$ satisfying $b^{2} z-a b y=1$, which upon solving the quadratic equation yields $b=\frac{y+\sqrt{y^{2}+4 x z}}{2 z \sqrt{x}}$ and $k=\frac{y\left(y+\sqrt{y^{2}+4 x z}\right)}{2 x z}$. Now we easily obtain
$$
f(x, y, z)=\frac{a}{b} f\left(a^{2} x, a b y, b^{2} z\right)=\frac{a}{b} f(1, k, k+1)=\frac{a}{b}(k+1)=\frac{y+\sqrt{y^{2}+4 x z}}{2 x} .
$$
It is directly verified that $f$ satisfies the problem conditions.
|
{
"resource_path": "Balkan_MO/segmented/en-2013-BMO-type2.jsonl",
"problem_match": "\n3.",
"solution_match": "\n3."
}
|
9a3cfccb-47cd-5f74-833c-faf45dc1786a
| 604,314
|
Let $n$ be a positive integer. A regular hexagon with side length $n$ is divided into equilateral triangles with side length 1 by lines parallel to its sides.
Find the number of regular hexagons all of whose vertices are among the vertices of the equilateral triangles.
|
By a lattice hexagon we will mean a regular hexagon whose sides run along edges of the lattice. Given any regular hexagon $H$, we construct a lattice hexagon whose edges pass through the vertices of $H$, as shown in the figure, which we will call the enveloping lattice hexagon of $H$. Given a lattice hexagon $G$ of side length $m$, the number of regular hexagons whose enveloping lattice hexagon is $G$ is exactly $m$.
Yet also there are precisely $3(n-m)(n-m+1)+1$ lattice hexagons of side length $m$ in our lattice: they are those with centres lying at most $n-m$ steps from the centre of the lattice. In particular, the total number of regular hexagons equals
$N=\sum_{m=1}^{n}(3(n-m)(n-m+1)+1) m=\left(3 n^{2}+3 n\right) \sum_{m=1}^{n} m-3(2 m+1) \sum_{m=1}^{n} m^{2}+3 \sum_{m=1}^{n} m^{3}$.
Since $\sum_{m=1}^{n} m=\frac{n(n+1)}{2}, \sum_{m=1}^{n} m^{2}=\frac{n(n+1)(2 n+1)}{6}$ and $\sum_{m=1}^{n} m^{3}=\left(\frac{n(n+1)}{2}\right)^{2}$ it is easily checked that $N=\left(\frac{n(n+1)}{2}\right)^{2}$.
|
\left(\frac{n(n+1)}{2}\right)^{2}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Let $n$ be a positive integer. A regular hexagon with side length $n$ is divided into equilateral triangles with side length 1 by lines parallel to its sides.
Find the number of regular hexagons all of whose vertices are among the vertices of the equilateral triangles.
|
By a lattice hexagon we will mean a regular hexagon whose sides run along edges of the lattice. Given any regular hexagon $H$, we construct a lattice hexagon whose edges pass through the vertices of $H$, as shown in the figure, which we will call the enveloping lattice hexagon of $H$. Given a lattice hexagon $G$ of side length $m$, the number of regular hexagons whose enveloping lattice hexagon is $G$ is exactly $m$.
Yet also there are precisely $3(n-m)(n-m+1)+1$ lattice hexagons of side length $m$ in our lattice: they are those with centres lying at most $n-m$ steps from the centre of the lattice. In particular, the total number of regular hexagons equals

$N=\sum_{m=1}^{n}(3(n-m)(n-m+1)+1) m=\left(3 n^{2}+3 n\right) \sum_{m=1}^{n} m-3(2 m+1) \sum_{m=1}^{n} m^{2}+3 \sum_{m=1}^{n} m^{3}$.
Since $\sum_{m=1}^{n} m=\frac{n(n+1)}{2}, \sum_{m=1}^{n} m^{2}=\frac{n(n+1)(2 n+1)}{6}$ and $\sum_{m=1}^{n} m^{3}=\left(\frac{n(n+1)}{2}\right)^{2}$ it is easily checked that $N=\left(\frac{n(n+1)}{2}\right)^{2}$.
|
{
"resource_path": "Balkan_MO/segmented/en-2014-BMO-type1.jsonl",
"problem_match": "\nProblem 4.",
"solution_match": "\nSolution."
}
|
c2a0bdb9-1b48-5eb4-b675-fc82852509ab
| 604,375
|
Let $k$ be a positive integer. Determine the least integer $n \geqslant k+1$ for which the game below can be played indefinitely:
Consider $n$ boxes, labelled $b_{1}, b_{2}, \ldots, b_{n}$. For each index $i$, box $b_{i}$ contains initially exactly $i$ coins. At each step, the following three substeps are performed in order:
(1) Choose $k+1$ boxes;
(2) Of these $k+1$ boxes, choose $k$ and remove at least half of the coins from each, and add to the remaining box, if labelled $b_{i}$, a number of $i$ coins.
(3) If one of the boxes is left empty, the game ends; otherwise, go to the next step.
|
The required minimum is $n=2^{k}+k-1$.
In this case the game can be played indefinitely by choosing the last $k+1$ boxes, $b_{2^{k}-1}, b_{2^{k}}, \ldots, b_{2^{k}+k-1}$, at each step: At step $r$, if box $b_{2^{k}+i-1}$ has exactly $m_{i}$ coins, then $\left\lceil m_{i} / 2\right\rceil$ coins are removed from that box, unless $i \equiv r-1(\bmod k+1)$, in which case $2^{k}+i-1$ coins are added. Thus, after step $r$ has been performed, box $b_{2^{k}+i-1}$ contains exactly $\left\lfloor m_{i} / 2\right\rfloor$ coins, unless $i \equiv r-1(\bmod k+1)$, in which case it contains exactly $m_{i}+2^{k}+i-1$ coins. This game goes on indefinitely, since each time a box is supplied, at least $2^{k}-1$ coins are added, so it will then contain at least $2^{k}$ coins, good enough to survive the $k$ steps to its next supply.
We now show that no smaller value of $n$ works. So, let $n \leqslant 2^{k}+k-2$ and suppose, if possible, that a game can be played indefinitely. Notice that a box currently containing exactly $m$ coins survives at most $w=\left\lfloor\log _{2} m\right\rfloor$ withdrawals; this $w$ will be referred to as the weight of that box. The sum of the weigths of all boxes will referred to as the total weight. The argument hinges on the lemma below, proved at the end of the solution.
Lemma. Performing a step does not increase the total weight. Moreover, supplying one of the first $2^{k}-2$ boxes strictly decreases the total weight.
Since the total weight cannot strictly decrease indefinitely, $n>2^{k}-2$, and from some stage on none of the first $2^{k}-2$ boxes is ever supplied. Recall that each step involves a $(k+1)$-box choice. Since $n \leqslant 2^{k}+k-2$, from that stage on, each step involves a withdrawal from at least one of the first $2^{k}-2$ boxes. This cannot go on indefinitely, so the game must eventually come to an end, contradicting the assumption.
Consequently, a game that can be played indefinitely requires $n \geqslant 2^{k}+$ $k-1$.
Proof of the Lemma. Since a withdrawal from a box decreases its weight by at least 1 , it is sufficient to show that supplying a box increases its weight by at most $k$; and if the latter is amongst the first $2^{k}-2$ boxes, then its weight increases by at most $k-1$. Let the box to be supplied be $b_{i}$ and let it currently contain exactly $m_{i}$ coins, to proceed by case analysis:
If $m_{i}=1$, the weight increases by $\left\lfloor\log _{2}(i+1)\right\rfloor \leqslant\left\lfloor\log _{2}\left(2^{k}+k-1\right)\right\rfloor \leqslant$ $\left\lfloor\log _{2}\left(2^{k+1}-2\right)\right\rfloor \leqslant k$; and if, in addition, $i \leqslant 2^{k}-2$, then the weight increases by $\left\lfloor\log _{2}(i+1)\right\rfloor \leqslant\left\lfloor\log _{2}\left(2^{k}-1\right)\right\rfloor=k-1$.
If $m_{i}=2$, then the weight increases by $\left\lfloor\log _{2}(i+2)\right\rfloor-\left\lfloor\log _{2} 2\right\rfloor \leqslant$ $\left\lfloor\log _{2}\left(2^{k}+k\right)\right\rfloor-1 \leqslant k-1$.
If $m_{i} \geqslant 3$, then the weight increases by
$$
\begin{aligned}
\left\lfloor\log _{2}\left(i+m_{i}\right)\right\rfloor-\left\lfloor\log _{2} m_{i}\right\rfloor & \leqslant\left\lfloor\log _{2}\left(i+m_{i}\right)-\log _{2} m_{i}\right\rfloor+1 \\
& \leqslant\left\lfloor\log _{2}\left(1+\frac{2^{k}+k-2}{3}\right)\right\rfloor+1 \leqslant k,
\end{aligned}
$$
since $1+\frac{1}{3}\left(2^{k}+k-2\right)=\frac{1}{3}\left(2^{k}+k+1\right)<\frac{1}{3}\left(2^{k}+2^{k+1}\right)=2^{k}$.
Finally, let $i \leqslant 2^{k}-2$ to consider the subcases $m_{i}=3$ and $m_{i} \geqslant 4$. In the former subcase, the weight increases by
$$
\left\lfloor\log _{2}(i+3)\right\rfloor-\left\lfloor\log _{2} 3\right\rfloor \leqslant\left\lfloor\log _{2}\left(2^{k}+1\right)\right\rfloor-1=k-1,
$$
and in the latter by
$$
\begin{aligned}
\left\lfloor\log _{2}\left(i+m_{i}\right)\right\rfloor-\left\lfloor\log _{2} m_{i}\right\rfloor & \leqslant\left\lfloor\log _{2}\left(i+m_{i}\right)-\log _{2} m_{i}\right\rfloor+1 \\
& \leqslant\left\lfloor\log _{2}\left(1+\frac{2^{k}-2}{4}\right)\right\rfloor+1 \leqslant k-1,
\end{aligned}
$$
since $1+\frac{1}{4}\left(2^{k}-2\right)=\frac{1}{4}\left(2^{k}+2\right)<2^{k-2}+1$. This ends the proof and completes the solution.
|
2^{k}+k-1
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Let $k$ be a positive integer. Determine the least integer $n \geqslant k+1$ for which the game below can be played indefinitely:
Consider $n$ boxes, labelled $b_{1}, b_{2}, \ldots, b_{n}$. For each index $i$, box $b_{i}$ contains initially exactly $i$ coins. At each step, the following three substeps are performed in order:
(1) Choose $k+1$ boxes;
(2) Of these $k+1$ boxes, choose $k$ and remove at least half of the coins from each, and add to the remaining box, if labelled $b_{i}$, a number of $i$ coins.
(3) If one of the boxes is left empty, the game ends; otherwise, go to the next step.
|
The required minimum is $n=2^{k}+k-1$.
In this case the game can be played indefinitely by choosing the last $k+1$ boxes, $b_{2^{k}-1}, b_{2^{k}}, \ldots, b_{2^{k}+k-1}$, at each step: At step $r$, if box $b_{2^{k}+i-1}$ has exactly $m_{i}$ coins, then $\left\lceil m_{i} / 2\right\rceil$ coins are removed from that box, unless $i \equiv r-1(\bmod k+1)$, in which case $2^{k}+i-1$ coins are added. Thus, after step $r$ has been performed, box $b_{2^{k}+i-1}$ contains exactly $\left\lfloor m_{i} / 2\right\rfloor$ coins, unless $i \equiv r-1(\bmod k+1)$, in which case it contains exactly $m_{i}+2^{k}+i-1$ coins. This game goes on indefinitely, since each time a box is supplied, at least $2^{k}-1$ coins are added, so it will then contain at least $2^{k}$ coins, good enough to survive the $k$ steps to its next supply.
We now show that no smaller value of $n$ works. So, let $n \leqslant 2^{k}+k-2$ and suppose, if possible, that a game can be played indefinitely. Notice that a box currently containing exactly $m$ coins survives at most $w=\left\lfloor\log _{2} m\right\rfloor$ withdrawals; this $w$ will be referred to as the weight of that box. The sum of the weigths of all boxes will referred to as the total weight. The argument hinges on the lemma below, proved at the end of the solution.
Lemma. Performing a step does not increase the total weight. Moreover, supplying one of the first $2^{k}-2$ boxes strictly decreases the total weight.
Since the total weight cannot strictly decrease indefinitely, $n>2^{k}-2$, and from some stage on none of the first $2^{k}-2$ boxes is ever supplied. Recall that each step involves a $(k+1)$-box choice. Since $n \leqslant 2^{k}+k-2$, from that stage on, each step involves a withdrawal from at least one of the first $2^{k}-2$ boxes. This cannot go on indefinitely, so the game must eventually come to an end, contradicting the assumption.
Consequently, a game that can be played indefinitely requires $n \geqslant 2^{k}+$ $k-1$.
Proof of the Lemma. Since a withdrawal from a box decreases its weight by at least 1 , it is sufficient to show that supplying a box increases its weight by at most $k$; and if the latter is amongst the first $2^{k}-2$ boxes, then its weight increases by at most $k-1$. Let the box to be supplied be $b_{i}$ and let it currently contain exactly $m_{i}$ coins, to proceed by case analysis:
If $m_{i}=1$, the weight increases by $\left\lfloor\log _{2}(i+1)\right\rfloor \leqslant\left\lfloor\log _{2}\left(2^{k}+k-1\right)\right\rfloor \leqslant$ $\left\lfloor\log _{2}\left(2^{k+1}-2\right)\right\rfloor \leqslant k$; and if, in addition, $i \leqslant 2^{k}-2$, then the weight increases by $\left\lfloor\log _{2}(i+1)\right\rfloor \leqslant\left\lfloor\log _{2}\left(2^{k}-1\right)\right\rfloor=k-1$.
If $m_{i}=2$, then the weight increases by $\left\lfloor\log _{2}(i+2)\right\rfloor-\left\lfloor\log _{2} 2\right\rfloor \leqslant$ $\left\lfloor\log _{2}\left(2^{k}+k\right)\right\rfloor-1 \leqslant k-1$.
If $m_{i} \geqslant 3$, then the weight increases by
$$
\begin{aligned}
\left\lfloor\log _{2}\left(i+m_{i}\right)\right\rfloor-\left\lfloor\log _{2} m_{i}\right\rfloor & \leqslant\left\lfloor\log _{2}\left(i+m_{i}\right)-\log _{2} m_{i}\right\rfloor+1 \\
& \leqslant\left\lfloor\log _{2}\left(1+\frac{2^{k}+k-2}{3}\right)\right\rfloor+1 \leqslant k,
\end{aligned}
$$
since $1+\frac{1}{3}\left(2^{k}+k-2\right)=\frac{1}{3}\left(2^{k}+k+1\right)<\frac{1}{3}\left(2^{k}+2^{k+1}\right)=2^{k}$.
Finally, let $i \leqslant 2^{k}-2$ to consider the subcases $m_{i}=3$ and $m_{i} \geqslant 4$. In the former subcase, the weight increases by
$$
\left\lfloor\log _{2}(i+3)\right\rfloor-\left\lfloor\log _{2} 3\right\rfloor \leqslant\left\lfloor\log _{2}\left(2^{k}+1\right)\right\rfloor-1=k-1,
$$
and in the latter by
$$
\begin{aligned}
\left\lfloor\log _{2}\left(i+m_{i}\right)\right\rfloor-\left\lfloor\log _{2} m_{i}\right\rfloor & \leqslant\left\lfloor\log _{2}\left(i+m_{i}\right)-\log _{2} m_{i}\right\rfloor+1 \\
& \leqslant\left\lfloor\log _{2}\left(1+\frac{2^{k}-2}{4}\right)\right\rfloor+1 \leqslant k-1,
\end{aligned}
$$
since $1+\frac{1}{4}\left(2^{k}-2\right)=\frac{1}{4}\left(2^{k}+2\right)<2^{k-2}+1$. This ends the proof and completes the solution.
|
{
"resource_path": "Balkan_MO/segmented/en-2020-BMO-type1.jsonl",
"problem_match": "## 2020 BMO, Problem 3",
"solution_match": "\nSolution."
}
|
21fcc46f-d1ea-5c74-a214-14209ff3879d
| 604,727
|
Problem. Consider an $n \times n$ grid consisting of $n^{2}$ unit cells, where $n \geqslant 3$ is a given odd positive integer. First, Dionysus colours each cell either red or blue. It is known that a frog can hop from one cell to another if and only if these cells have the same colour and share at least one vertex. Then, Xanthias views the colouring and next places $k$ frogs on the cells so that each of the $n^{2}$ cells can be reached by a frog in a finite number (possibly zero) of hops. Find the least value of $k$ for which this is always possible regardless of the colouring chosen by Dionysus.
Note. Dionysus and Xanthias are characters from the play of Aristophanes 'frogs'. Dionysus is the known god of wine and Xanthias is his witty slave.
|
. Let $G$ be the graph whose vertices are all $(n+1)^{2}$ vertices of the grid and where two vertices are adjacent if and only if they are adjacent in the grid and moreover the two cells in either side of the corresponding edge have different colours.
The connnected components of $G$, excluding the isolated vertices, are precisely the boundaries between pairs of monochromatic regions each of which can be covered by a single frog. Each time we add one of these components in the grid, it creates exactly one new monochromatic region. So the number of frogs required is one more than the number of such components of $G$.
It is easy to check that every corner vertex of the grid has degree 0 , every boundary vertex of the grid has degree 0 or 1 and every 'internal' vertex of the grid has degree 0,2 or 4 . It is also easy to see that every component of $G$ which is not an isolated vertex must contain at least four vertices unless it is the boundary of a single corner of the grid, in which case it contains only three vertices.
Writing $N$ for the number of components which are not isolated vertices, we see that in total they contain at least $4 N-4$ vertices. (As at most four of them contain 3 vertices and all others contain 4 vertices.) Since we also have at least 4 components which are isolated vertices, then $4 N=(4 N-4)+4 \leqslant(n+1)^{2}$. Thus $N \leqslant \frac{(n+1)^{2}}{4}$ and therefore the minimal number of frogs required is $\frac{(n+1)^{2}}{4}+1$.

This bound for $n=2 m+1$ is achieved by putting coordinates $(x, y)$ with $x, y \in\{0,1, \ldots, 2 m\}$ in the cells and colouring red all cells both of whose coordinates are even, and blue all other cells. An example for $n=9$ is shown above.
|
\frac{(n+1)^{2}}{4}+1
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Problem. Consider an $n \times n$ grid consisting of $n^{2}$ unit cells, where $n \geqslant 3$ is a given odd positive integer. First, Dionysus colours each cell either red or blue. It is known that a frog can hop from one cell to another if and only if these cells have the same colour and share at least one vertex. Then, Xanthias views the colouring and next places $k$ frogs on the cells so that each of the $n^{2}$ cells can be reached by a frog in a finite number (possibly zero) of hops. Find the least value of $k$ for which this is always possible regardless of the colouring chosen by Dionysus.
Note. Dionysus and Xanthias are characters from the play of Aristophanes 'frogs'. Dionysus is the known god of wine and Xanthias is his witty slave.
|
. Let $G$ be the graph whose vertices are all $(n+1)^{2}$ vertices of the grid and where two vertices are adjacent if and only if they are adjacent in the grid and moreover the two cells in either side of the corresponding edge have different colours.
The connnected components of $G$, excluding the isolated vertices, are precisely the boundaries between pairs of monochromatic regions each of which can be covered by a single frog. Each time we add one of these components in the grid, it creates exactly one new monochromatic region. So the number of frogs required is one more than the number of such components of $G$.
It is easy to check that every corner vertex of the grid has degree 0 , every boundary vertex of the grid has degree 0 or 1 and every 'internal' vertex of the grid has degree 0,2 or 4 . It is also easy to see that every component of $G$ which is not an isolated vertex must contain at least four vertices unless it is the boundary of a single corner of the grid, in which case it contains only three vertices.
Writing $N$ for the number of components which are not isolated vertices, we see that in total they contain at least $4 N-4$ vertices. (As at most four of them contain 3 vertices and all others contain 4 vertices.) Since we also have at least 4 components which are isolated vertices, then $4 N=(4 N-4)+4 \leqslant(n+1)^{2}$. Thus $N \leqslant \frac{(n+1)^{2}}{4}$ and therefore the minimal number of frogs required is $\frac{(n+1)^{2}}{4}+1$.

This bound for $n=2 m+1$ is achieved by putting coordinates $(x, y)$ with $x, y \in\{0,1, \ldots, 2 m\}$ in the cells and colouring red all cells both of whose coordinates are even, and blue all other cells. An example for $n=9$ is shown above.
|
{
"resource_path": "Balkan_MO/segmented/en-2022-BMO-type1.jsonl",
"problem_match": "# Problem 4",
"solution_match": "\nSolution 1"
}
|
b85b77fe-2996-59e8-8f01-d8b24287296b
| 604,919
|
Find the greatest integer $k \leq 2023$ for which the following holds: whenever Alice colours exactly $k$ numbers of the set $\{1,2, \ldots, 2023\}$ in red, Bob can colour some of the remaining uncoloured numbers in blue, such that the sum of the red numbers is the same as the sum of the blue numbers.
|
Answer: 592.
For $k \geq 593$, Alice can color the greatest 593 numbers $1431,1432, \ldots, 2023$ and any other $(k-593)$ numbers so that their sum $s$ would satisfy
$$
s \geq \frac{2023 \cdot 2024}{2}-\frac{1430 \cdot 1431}{2}>\frac{1}{2} \cdot\left(\frac{2023 \cdot 2024}{2}\right),
$$
thus anyhow Bob chooses his numbers, the sum of his numbers will be less than Alice's numbers' sum.
We now show that $k=592$ satisfies the condition. Let $s$ be the sum of Alice's 592 numbers; note that $s<\frac{1}{2} \cdot\left(\frac{2023 \cdot 2024}{2}\right)$. Below is a strategy for Bob to find some of the remaining 1431 numbers so that their sum is
$$
s_{0}=\min \left\{s, \frac{2023.2024}{2}-2 s\right\} \leqslant \frac{1}{3} \cdot\left(\frac{2023 \cdot 2024}{2}\right)
$$
(Clearly, if Bob finds some numbers whose sum is $\frac{2023.2024}{2}-2 s$, then the sum of remaining numbers will be $s$ ).
Case 1. $s_{0} \geq 2024$. Let $s_{0}=2024 a+b$, where $0 \leqslant b \leqslant 2023$. Bob finds two of the remaining numbers with sum $b$ or $2024+b$, then he finds $a$ (or $a-1$ ) pairs among the remaining numbers with sum 2024 . Note that $a \leq 337$ since $s_{0} \leq \frac{1}{3} \cdot\left(\frac{2023 \cdot 2024}{2}\right)$.
The $\left\lfloor\frac{b-1}{2}\right\rfloor$ pairs
$$
(1, b-1),(2, b-2), \ldots,\left(\left\lfloor\frac{b-1}{2}\right\rfloor, b-\left\lfloor\frac{b-1}{2}\right\rfloor\right),
$$
have sum of their components equal to $b$ and the $\left\lfloor\frac{2023+b}{2}\right\rfloor-b$ pairs
$$
(2023, b+1),(2022, b+2), \ldots,\left(2024+b-\left\lfloor\frac{2023+b}{2}\right\rfloor,\left\lfloor\frac{2023+b}{2}\right\rfloor\right)
$$
have sum of their components equal to $2024+b$. The total number of these pairs is
$$
\left\lfloor\frac{2023+b}{2}\right\rfloor-b+\left\lfloor\frac{b-1}{2}\right\rfloor \geq \frac{2022+b}{2}+\frac{b-2}{2}-b=\frac{2020}{2}=1010>592
$$
hence some of these pairs have no red-colored components, so Bob can choose one of these pairs and color those two numbers in blue. Thus 594 numbers are colored so far.
Further, the 1011 pairs
$$
(1,2023),(2,2022), \ldots,(1011,1013)
$$
have sum of the components equal to 2024. Among these, at least $1011-594=417>$ $337 \geq a$ pairs have no components colored, so Bob can choose $a$ (or $a-1$ ) uncolored pairs and color them all blue to achieve a collection of blue numbers with their sum equal to $s_{0}$.
Case 2. $s_{0} \leq 2023$. Note that $s \geq 1+2+\ldots+592>2023$, thus we have $s_{0}=$ $\frac{2023 \cdot 2024}{2}-2 s$, i.e. $s=\frac{2023 \cdot 2024}{4}-\frac{s_{0}}{2}$.
If $s_{0}>2 \cdot 593$, at least one of the 593 pairs
$$
\left(1, s_{0}-1\right),\left(2, s_{0}-2\right), \ldots,\left(593, s_{0}-593\right)
$$
have no red-colored components, so Bob can choose these two numbers and immediately achieve the sum of $s_{0}$. And if $s_{0} \leq 2 \cdot 593$, then
$s=\frac{2023 \cdot 2024}{4}-\frac{s_{0}}{2} \geq(1432+1433+\ldots+2023)-593=839+(1434+1435+\ldots+2023)$,
hence Alice cannot have colored any of the numbers $1,2, \ldots, 838$. Then Bob can easily choose one or two of these numbers having the sum of $s_{0}$.
|
592
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Find the greatest integer $k \leq 2023$ for which the following holds: whenever Alice colours exactly $k$ numbers of the set $\{1,2, \ldots, 2023\}$ in red, Bob can colour some of the remaining uncoloured numbers in blue, such that the sum of the red numbers is the same as the sum of the blue numbers.
|
Answer: 592.
For $k \geq 593$, Alice can color the greatest 593 numbers $1431,1432, \ldots, 2023$ and any other $(k-593)$ numbers so that their sum $s$ would satisfy
$$
s \geq \frac{2023 \cdot 2024}{2}-\frac{1430 \cdot 1431}{2}>\frac{1}{2} \cdot\left(\frac{2023 \cdot 2024}{2}\right),
$$
thus anyhow Bob chooses his numbers, the sum of his numbers will be less than Alice's numbers' sum.
We now show that $k=592$ satisfies the condition. Let $s$ be the sum of Alice's 592 numbers; note that $s<\frac{1}{2} \cdot\left(\frac{2023 \cdot 2024}{2}\right)$. Below is a strategy for Bob to find some of the remaining 1431 numbers so that their sum is
$$
s_{0}=\min \left\{s, \frac{2023.2024}{2}-2 s\right\} \leqslant \frac{1}{3} \cdot\left(\frac{2023 \cdot 2024}{2}\right)
$$
(Clearly, if Bob finds some numbers whose sum is $\frac{2023.2024}{2}-2 s$, then the sum of remaining numbers will be $s$ ).
Case 1. $s_{0} \geq 2024$. Let $s_{0}=2024 a+b$, where $0 \leqslant b \leqslant 2023$. Bob finds two of the remaining numbers with sum $b$ or $2024+b$, then he finds $a$ (or $a-1$ ) pairs among the remaining numbers with sum 2024 . Note that $a \leq 337$ since $s_{0} \leq \frac{1}{3} \cdot\left(\frac{2023 \cdot 2024}{2}\right)$.
The $\left\lfloor\frac{b-1}{2}\right\rfloor$ pairs
$$
(1, b-1),(2, b-2), \ldots,\left(\left\lfloor\frac{b-1}{2}\right\rfloor, b-\left\lfloor\frac{b-1}{2}\right\rfloor\right),
$$
have sum of their components equal to $b$ and the $\left\lfloor\frac{2023+b}{2}\right\rfloor-b$ pairs
$$
(2023, b+1),(2022, b+2), \ldots,\left(2024+b-\left\lfloor\frac{2023+b}{2}\right\rfloor,\left\lfloor\frac{2023+b}{2}\right\rfloor\right)
$$
have sum of their components equal to $2024+b$. The total number of these pairs is
$$
\left\lfloor\frac{2023+b}{2}\right\rfloor-b+\left\lfloor\frac{b-1}{2}\right\rfloor \geq \frac{2022+b}{2}+\frac{b-2}{2}-b=\frac{2020}{2}=1010>592
$$
hence some of these pairs have no red-colored components, so Bob can choose one of these pairs and color those two numbers in blue. Thus 594 numbers are colored so far.
Further, the 1011 pairs
$$
(1,2023),(2,2022), \ldots,(1011,1013)
$$
have sum of the components equal to 2024. Among these, at least $1011-594=417>$ $337 \geq a$ pairs have no components colored, so Bob can choose $a$ (or $a-1$ ) uncolored pairs and color them all blue to achieve a collection of blue numbers with their sum equal to $s_{0}$.
Case 2. $s_{0} \leq 2023$. Note that $s \geq 1+2+\ldots+592>2023$, thus we have $s_{0}=$ $\frac{2023 \cdot 2024}{2}-2 s$, i.e. $s=\frac{2023 \cdot 2024}{4}-\frac{s_{0}}{2}$.
If $s_{0}>2 \cdot 593$, at least one of the 593 pairs
$$
\left(1, s_{0}-1\right),\left(2, s_{0}-2\right), \ldots,\left(593, s_{0}-593\right)
$$
have no red-colored components, so Bob can choose these two numbers and immediately achieve the sum of $s_{0}$. And if $s_{0} \leq 2 \cdot 593$, then
$s=\frac{2023 \cdot 2024}{4}-\frac{s_{0}}{2} \geq(1432+1433+\ldots+2023)-593=839+(1434+1435+\ldots+2023)$,
hence Alice cannot have colored any of the numbers $1,2, \ldots, 838$. Then Bob can easily choose one or two of these numbers having the sum of $s_{0}$.
|
{
"resource_path": "Balkan_MO/segmented/en-2023-BMO-type1.jsonl",
"problem_match": "\nProblem 4.",
"solution_match": "\nSolution."
}
|
3d6962fe-c852-5854-8352-f3b3c572a632
| 604,984
|
There are 2016 costumers who entered a shop on a particular day. Every customer entered the shop exactly once. (i.e. the customer entered the shop, stayed there for some time and then left the shop without returning back.)
Find the maximal $k$ such that the following holds:
There are $k$ customers such that either all of them were in the shop at a specific time instance or no two of them were both in the shop at any time instance.
|
We show that the maximal $k$ is 45 .
First we show that no larger $k$ can be achieved: We break the day at 45 disjoint time intervals and assume that at each time interval there were exactly 45 costumers who stayed in the shop only during that time interval (except in the last interval in which there were only 36 customers). We observe that there are no 46 people with the required property.
Now we show that $k=45$ can be achieved: Suppose that customers $C_{1}, C_{2}, \ldots, C_{2016}$ visited the shop in this order. (If two or more customers entered the shop at exactly the same time then we break ties arbitrarily.)
We define groups $A_{1}, A_{2}, \ldots$ of customers as follows: Starting with $C_{1}$ and proceeding in order, we place customer $C_{j}$ into the group $A_{i}$ where $i$ is the smallest index such that $A_{i}$ contains no customer $C_{j^{\prime}}$ with $j^{\prime}<j$ and such that $C_{j^{\prime}}$ was inside the shop once $C_{j}$ entered it.
Clearly no two customers who are in the same group were inside the shop at the exact same time. So we may assume that every $A_{i}$ has at most 45 customers. Since $44 \cdot 45<2016$, by the pigeonhole principle there must be at least 45 (non-empty) groups.
Let $C_{j}$ be a person in group $A_{45}$ and suppose that $C_{j}$ entered the shop at time $t_{j}$. Since we placed $C_{j}$ in group $A_{45}$ this means that for each $i<45$, there is a $j_{i}<j$ such that $C_{j_{i}} \in A_{i}$ and $C_{j_{i}}$ is still inside the shop at time $t_{j}$.
Thus we have found a specific time instance, namely $t_{j}$, during which at least 45 customers were all inside the shop.
Note: Instead of asking for the maximal $k$, an easier version is the following:
Show that there are 45 customers such that either all of them were in the shop at a specific time instance or no two of them were both in the shop at any time instance.
|
45
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
There are 2016 costumers who entered a shop on a particular day. Every customer entered the shop exactly once. (i.e. the customer entered the shop, stayed there for some time and then left the shop without returning back.)
Find the maximal $k$ such that the following holds:
There are $k$ customers such that either all of them were in the shop at a specific time instance or no two of them were both in the shop at any time instance.
|
We show that the maximal $k$ is 45 .
First we show that no larger $k$ can be achieved: We break the day at 45 disjoint time intervals and assume that at each time interval there were exactly 45 costumers who stayed in the shop only during that time interval (except in the last interval in which there were only 36 customers). We observe that there are no 46 people with the required property.
Now we show that $k=45$ can be achieved: Suppose that customers $C_{1}, C_{2}, \ldots, C_{2016}$ visited the shop in this order. (If two or more customers entered the shop at exactly the same time then we break ties arbitrarily.)
We define groups $A_{1}, A_{2}, \ldots$ of customers as follows: Starting with $C_{1}$ and proceeding in order, we place customer $C_{j}$ into the group $A_{i}$ where $i$ is the smallest index such that $A_{i}$ contains no customer $C_{j^{\prime}}$ with $j^{\prime}<j$ and such that $C_{j^{\prime}}$ was inside the shop once $C_{j}$ entered it.
Clearly no two customers who are in the same group were inside the shop at the exact same time. So we may assume that every $A_{i}$ has at most 45 customers. Since $44 \cdot 45<2016$, by the pigeonhole principle there must be at least 45 (non-empty) groups.
Let $C_{j}$ be a person in group $A_{45}$ and suppose that $C_{j}$ entered the shop at time $t_{j}$. Since we placed $C_{j}$ in group $A_{45}$ this means that for each $i<45$, there is a $j_{i}<j$ such that $C_{j_{i}} \in A_{i}$ and $C_{j_{i}}$ is still inside the shop at time $t_{j}$.
Thus we have found a specific time instance, namely $t_{j}$, during which at least 45 customers were all inside the shop.
Note: Instead of asking for the maximal $k$, an easier version is the following:
Show that there are 45 customers such that either all of them were in the shop at a specific time instance or no two of them were both in the shop at any time instance.
|
{
"resource_path": "Balkan_Shortlist/segmented/en-2016_bmo_shortlist.jsonl",
"problem_match": "\n## C2.",
"solution_match": "\nSolution."
}
|
ebcb4d04-2cb8-5da6-a385-f39daf4d2621
| 605,167
|
What is the least positive integer $k$ such that, in every convex 101 -gon, the sum of any $k$ diagonals is greater than or equal to the sum of the remaining diagonals?
|
Let $P Q=1$. Consider a convex 101 -gon such that one of its vertices is at $P$ and the remaining 100 vertices are within $\varepsilon$ of $Q$ where $\varepsilon$ is an arbitrarily small positive real. Let $k+l$ equal the total number $\frac{101.98}{2}=4949$ of diagonals. When $k \leq 4851$. the sum of the $k$ shortest diagonals is arbitrarily small. When $k \geq 4851$, the sum of the $k$ shortest diagonals is arbitrarily close to $k-4851=98-l$ and the sum of the remaining diagonals is arbitrarily close to $l$. Therefore, we need to have $l \leq 49$ and $k \geq 4900$.
We proceed to show that $k=4900$ works. To this end, colour all $l=49$ remaining diagonals green. To each green diagonal $A B$, apart from, possibly, the last one, we will assign two red diagonals $A C$ and $C B$ so that no green diagonal is ever coloured red and no diagonal is coloured red twice.
Suppose that we have already done this for $0 \leq i \leq 48$ green diagonals (thus forming $i$ red-red-green triangles) and let $A B$ be up next. Let $D$ be the set of all diagonals emanating from $A$ or $B$ and distinct from $A B$ : we have $|D|=2 \cdot 97=194$. Every red-red-green triangle formed thus far has at most two sides in $D$. Therefore, the subset $E$ of all as-of-yetuncoloured diagonals in $D$ contains at least 194-2i elements.
When $i \leq 47,194-2 i \geq 100$. The total number of endpoints distinct from $A$ and $B$ of diagonals in $D$. however, is 99 . Therefore, two diagonals in $E$ have a common endpoint $C$ and we can assign $A C$ and $C B$ to $A B$. as needed.
The case $i=48$ is slightly more tricky: this time, it is possible that no two diagonals in $E$ have a common endpoint other than $A$ and $B$. but, if so, then there are two diagonals in $E$ that intersect in a point interior to both. Otherwise, at least one (say, $a$ ) of the two vertices adjacent to $A$ is cut off from $B$ by the diagonals emanating from $A$ and at least one (say, $b$ ) of the two vertices adjacent to $B$ is cut off from $A$ by the diagonals emanating from $B$ (and $a \neq b$ ). This leaves us with at most 97 suitable endpoints and at least 98 diagonals in $E$. a contradiction.
By the triangle inequality, this completes the solution.
## $\mathbb{O}_{1}^{2}$ $R_{1}$
## Union of Mathematicians of Macedonia
Sponsored by

Homisinan
|
4900
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
What is the least positive integer $k$ such that, in every convex 101 -gon, the sum of any $k$ diagonals is greater than or equal to the sum of the remaining diagonals?
|
Let $P Q=1$. Consider a convex 101 -gon such that one of its vertices is at $P$ and the remaining 100 vertices are within $\varepsilon$ of $Q$ where $\varepsilon$ is an arbitrarily small positive real. Let $k+l$ equal the total number $\frac{101.98}{2}=4949$ of diagonals. When $k \leq 4851$. the sum of the $k$ shortest diagonals is arbitrarily small. When $k \geq 4851$, the sum of the $k$ shortest diagonals is arbitrarily close to $k-4851=98-l$ and the sum of the remaining diagonals is arbitrarily close to $l$. Therefore, we need to have $l \leq 49$ and $k \geq 4900$.
We proceed to show that $k=4900$ works. To this end, colour all $l=49$ remaining diagonals green. To each green diagonal $A B$, apart from, possibly, the last one, we will assign two red diagonals $A C$ and $C B$ so that no green diagonal is ever coloured red and no diagonal is coloured red twice.
Suppose that we have already done this for $0 \leq i \leq 48$ green diagonals (thus forming $i$ red-red-green triangles) and let $A B$ be up next. Let $D$ be the set of all diagonals emanating from $A$ or $B$ and distinct from $A B$ : we have $|D|=2 \cdot 97=194$. Every red-red-green triangle formed thus far has at most two sides in $D$. Therefore, the subset $E$ of all as-of-yetuncoloured diagonals in $D$ contains at least 194-2i elements.
When $i \leq 47,194-2 i \geq 100$. The total number of endpoints distinct from $A$ and $B$ of diagonals in $D$. however, is 99 . Therefore, two diagonals in $E$ have a common endpoint $C$ and we can assign $A C$ and $C B$ to $A B$. as needed.
The case $i=48$ is slightly more tricky: this time, it is possible that no two diagonals in $E$ have a common endpoint other than $A$ and $B$. but, if so, then there are two diagonals in $E$ that intersect in a point interior to both. Otherwise, at least one (say, $a$ ) of the two vertices adjacent to $A$ is cut off from $B$ by the diagonals emanating from $A$ and at least one (say, $b$ ) of the two vertices adjacent to $B$ is cut off from $A$ by the diagonals emanating from $B$ (and $a \neq b$ ). This leaves us with at most 97 suitable endpoints and at least 98 diagonals in $E$. a contradiction.
By the triangle inequality, this completes the solution.
## $\mathbb{O}_{1}^{2}$ $R_{1}$
## Union of Mathematicians of Macedonia
Sponsored by

Homisinan
|
{
"resource_path": "Balkan_Shortlist/segmented/en-2017_bmo_shortlist.jsonl",
"problem_match": "\nC6",
"solution_match": "\n## Solution"
}
|
96677517-ae54-57e1-a5b2-abb6ff75e71f
| 605,552
|
Let $P$ be a point inside a triangle $A B C$ and let $a, b, c$ be the side lengths and $p$ the semi-perimeter of the triangle. Find the maximum value of
$$
\min \left(\frac{P A}{p-a}, \frac{P B}{p-b}, \frac{P C}{p-c}\right)
$$
over all possible choices of triangle $A B C$ and point $P$.
|
If $A B C$ is an equilateral triangle and $P$ its center, then $\frac{P A}{p-a}=\frac{P B}{p-b}=\frac{P C}{p-c}=\frac{2}{\sqrt{3}}$.
We shall prove that $\frac{2}{\sqrt{3}}$ is the required value. Suppose without loss of generality that $\varangle A P B \geqslant 120^{\circ}$. Then
$$
A B^{2} \geqslant P A^{2}+P B^{2}+P A \cdot P B \geqslant \frac{3}{4}(P A+P B)^{2}
$$
i.e. $P A+P B \leqslant \frac{2}{\sqrt{3}} A B=\frac{2}{\sqrt{3}}((p-a)+(p-b))$, so at least one of the ratios $\frac{P A}{p-a}$ and $\frac{P B}{p-b}$ does not exceed $\frac{2}{\sqrt{3}}$.
|
\frac{2}{\sqrt{3}}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $P$ be a point inside a triangle $A B C$ and let $a, b, c$ be the side lengths and $p$ the semi-perimeter of the triangle. Find the maximum value of
$$
\min \left(\frac{P A}{p-a}, \frac{P B}{p-b}, \frac{P C}{p-c}\right)
$$
over all possible choices of triangle $A B C$ and point $P$.
|
If $A B C$ is an equilateral triangle and $P$ its center, then $\frac{P A}{p-a}=\frac{P B}{p-b}=\frac{P C}{p-c}=\frac{2}{\sqrt{3}}$.
We shall prove that $\frac{2}{\sqrt{3}}$ is the required value. Suppose without loss of generality that $\varangle A P B \geqslant 120^{\circ}$. Then
$$
A B^{2} \geqslant P A^{2}+P B^{2}+P A \cdot P B \geqslant \frac{3}{4}(P A+P B)^{2}
$$
i.e. $P A+P B \leqslant \frac{2}{\sqrt{3}} A B=\frac{2}{\sqrt{3}}((p-a)+(p-b))$, so at least one of the ratios $\frac{P A}{p-a}$ and $\frac{P B}{p-b}$ does not exceed $\frac{2}{\sqrt{3}}$.
|
{
"resource_path": "Balkan_Shortlist/segmented/en-2018_bmo_shortlist.jsonl",
"problem_match": "\nG3.",
"solution_match": "\n## Solution."
}
|
53c882ed-44a8-572a-bc80-fe722def841c
| 605,739
|
Let $n(n \geq 1)$ be a positive integer and $U=\{1, \ldots, n\}$. Let $S$ be a nonempty subset of $U$ and let $d(d \neq 1)$ be the smallest common divisor of all elements of the set $S$. Find the smallest positive integer $k$ such that for any subset $T$ of $U$, consisting of $k$ elements, with $S \subset T$, the greatest common divisor of all elements of $T$ is equal to 1 .
|
We will show that $k_{\min }=1+\left[\frac{n}{d}\right]$ (here [.] denotes the integer part).
Obviously, the number of elements of $S$ is not grater than $\left[\frac{n}{d}\right]$, i.e. $|S| \leq\left[\frac{n}{d}\right]$, and $S \neq U$.
If $S \subset T$ and the greatest common divisor of elements of $T$ is equal to 1 , then $|T| \geq|S|+1$.
1) Assume that $|S|<\left[\frac{n}{d}\right]$. Let $T$ be the subset of $U$, consisting of all multiples of $d$ in $U$. Thus, $|T|=\left[\frac{n}{d}\right]$ and $S \subset T$. Therefore, the greatest common divisor of all elements of $T$ is $d>1$. Thus, $k \geq 1+\left[\frac{n}{d}\right]$.
2) Assume $|S|=\left[\frac{n}{d}\right]$. Let $T$ be any subset of $U$ with $S \subset T, S \neq T$. Therefore, $|T| \geq 1+\left[\frac{n}{d}\right]$. Let $q$ be the greatest common divisor of all elements of $T$. Assume that $q>1$. Therefore, $q$ is a common divisor of all elements of $S$ as well. Hence, $q \geq d$. It follows that $|T| \leq\left[\frac{n}{q}\right] \leq\left[\frac{n}{d}\right]$, contradiction. Hence, $q=1$.
Therefore, the minimal possible value of $k$ is $1+\left[\frac{n}{d}\right]$.
[^5]
## COMBINATORICS
|
1+\left[\frac{n}{d}\right]
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Let $n(n \geq 1)$ be a positive integer and $U=\{1, \ldots, n\}$. Let $S$ be a nonempty subset of $U$ and let $d(d \neq 1)$ be the smallest common divisor of all elements of the set $S$. Find the smallest positive integer $k$ such that for any subset $T$ of $U$, consisting of $k$ elements, with $S \subset T$, the greatest common divisor of all elements of $T$ is equal to 1 .
|
We will show that $k_{\min }=1+\left[\frac{n}{d}\right]$ (here [.] denotes the integer part).
Obviously, the number of elements of $S$ is not grater than $\left[\frac{n}{d}\right]$, i.e. $|S| \leq\left[\frac{n}{d}\right]$, and $S \neq U$.
If $S \subset T$ and the greatest common divisor of elements of $T$ is equal to 1 , then $|T| \geq|S|+1$.
1) Assume that $|S|<\left[\frac{n}{d}\right]$. Let $T$ be the subset of $U$, consisting of all multiples of $d$ in $U$. Thus, $|T|=\left[\frac{n}{d}\right]$ and $S \subset T$. Therefore, the greatest common divisor of all elements of $T$ is $d>1$. Thus, $k \geq 1+\left[\frac{n}{d}\right]$.
2) Assume $|S|=\left[\frac{n}{d}\right]$. Let $T$ be any subset of $U$ with $S \subset T, S \neq T$. Therefore, $|T| \geq 1+\left[\frac{n}{d}\right]$. Let $q$ be the greatest common divisor of all elements of $T$. Assume that $q>1$. Therefore, $q$ is a common divisor of all elements of $S$ as well. Hence, $q \geq d$. It follows that $|T| \leq\left[\frac{n}{q}\right] \leq\left[\frac{n}{d}\right]$, contradiction. Hence, $q=1$.
Therefore, the minimal possible value of $k$ is $1+\left[\frac{n}{d}\right]$.
[^5]
## COMBINATORICS
|
{
"resource_path": "Balkan_Shortlist/segmented/en-2019_bmo_shortlist.jsonl",
"problem_match": "\nTN2b. ${ }^{7}$",
"solution_match": "\nSolution."
}
|
9c634123-ce97-511d-833f-16a7312272c2
| 605,977
|
100 couples are invited to a traditional Moldovan dance. The 200 people stand in a line, and then in a step, two of them (not necessarily adjacent) may swap positions. Find the least $C$ such that whatever the initial order, they can arrive at an ordering where everyone is dancing next to their partner in at most $C$ steps.
|
With 100 replaced by $N$, the answer is $C=C(N)=N-1$. Throughout, we will say that the members of a couple have the same.
$N=2$ : We use this as a base case for induction for both bounds. Up to labelling, there is one trivial initial order, and two non-trivial ones, namely
$$
1,1,2,2 ; \quad 1, \sqrt{2,2,1} ; \quad 1, \sqrt{2,1}, 2
$$
The brackets indicate how to arrive at a suitable final ordering with one step. Obviously one step is necessary in the second and third cases.
Upper bound: First we show $C(N) \leq N-1$, by induction. The base case $N=2$ has already been seen. Now suppose the claim is true for $N-1$, and consider an initial arrangement of $N$ couples. Suppose the types of the left-most couples in line are $a$ and $b$. If $a \neq b$, then in the first step, swap the $b$ in place two with the other person with type $a$. If $a=b$, skip this. In both cases, we now have $N-1$ couples distributed among the final $2 N-2$ places, and we know that $N-2$ steps suffices to order them appropriately, by induction. So $N-1$ steps suffices for $N$ couples.
Lower bound: We need to exhibit an example of an initial order for which $N-1$ steps are necessary. Consider
$$
\mathcal{A}_{N}:=1,2,2,3,3, \ldots, N-1, N-1, N, N, 1
$$
Proceed by induction, with the base case $N=2$ trivial. Suppose there is a sequence of at most $N-2$ steps which works. In any suitable final arrangement, a given type must be in positions (odd, even), whereas they start in positions (even, odd). So each type must be involved in at least one step. However, each step involves at most two types, so by the pigeonhole principle, at least four types are involved in at most one step. Pick one such type $a \neq 1$. The one step involving $a$ must be one of
$$
\ldots, ?, a, a, ?, \ldots .
$$
Neither of these steps affects the relative order of the $2 N-2$ other people. So by ignoring this step involving the $a$, we have a sequence of at most $N-3$ steps acting on the other $2 N-2$ people which appropriately sorts them. By induction, this is a contradiction.
Alternative lower bound I: Consider the graph with vertices given by pairs of positions $\{(1,2),(3,4), \ldots,(2 N-1,2 N)\}$. We add an edge between pairs of (different)
vertices if we ever swap two people in places corresponding to those vertices. In particular, at the end, the two people with type $k$ end up in places corresponding to a single vertex.
Suppose we start from the ordering (1) and have some number of steps leading to an ordering where everyone is next to their partner. Then, in the induced graph, there is a path between the vertices corresponding to the places $(2 k-3,2 k-2)$ and $(2 k-1,2 k)$ for each $2 \leq k \leq N$, and also between $(1,2)$ and $(2 N-1,2 N)$. In other words, the graph is connected, and so must have at least $N-1$ edges.
Alternative lower bound II: Consider a bipartite multigraph with vertex classes $\left(v_{1}, \ldots, v_{n}\right)$ and $\left(w_{1}, \ldots, w_{n}\right)$. Connect $v_{i}$ to $w_{j}$ if a person of type $j$ is in positions ( $2 i-1,2 i$ ) (if both positions are taken by the type $j$ couple, then add two edges).
Each step in the dance consists of replacing edges $\left.E=\left\{v_{a} \leftrightarrow w_{c}, v_{b} \leftrightarrow w_{d}\right)\right\}$ with $E^{\prime}=\left\{v_{a} \leftrightarrow w_{d}, v_{b} \leftrightarrow w_{c}\right\}$. However, both before and after the step, the number of components in the graph which include $\left\{v_{a}, v_{b}, w_{c}, w_{d}\right\}$ is either one or two. The structure of other components which do not include these vertices is unaffected by the move.
Therefore, the number of connected components increases by at most 1 in each step.
Starting from configuration (1), the graph initially consists of a single (cyclic) component, so one requires at least $n-1$ steps to get to the final configuration for which there are $n$ connected components.
|
N-1
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
100 couples are invited to a traditional Moldovan dance. The 200 people stand in a line, and then in a step, two of them (not necessarily adjacent) may swap positions. Find the least $C$ such that whatever the initial order, they can arrive at an ordering where everyone is dancing next to their partner in at most $C$ steps.
|
With 100 replaced by $N$, the answer is $C=C(N)=N-1$. Throughout, we will say that the members of a couple have the same.
$N=2$ : We use this as a base case for induction for both bounds. Up to labelling, there is one trivial initial order, and two non-trivial ones, namely
$$
1,1,2,2 ; \quad 1, \sqrt{2,2,1} ; \quad 1, \sqrt{2,1}, 2
$$
The brackets indicate how to arrive at a suitable final ordering with one step. Obviously one step is necessary in the second and third cases.
Upper bound: First we show $C(N) \leq N-1$, by induction. The base case $N=2$ has already been seen. Now suppose the claim is true for $N-1$, and consider an initial arrangement of $N$ couples. Suppose the types of the left-most couples in line are $a$ and $b$. If $a \neq b$, then in the first step, swap the $b$ in place two with the other person with type $a$. If $a=b$, skip this. In both cases, we now have $N-1$ couples distributed among the final $2 N-2$ places, and we know that $N-2$ steps suffices to order them appropriately, by induction. So $N-1$ steps suffices for $N$ couples.
Lower bound: We need to exhibit an example of an initial order for which $N-1$ steps are necessary. Consider
$$
\mathcal{A}_{N}:=1,2,2,3,3, \ldots, N-1, N-1, N, N, 1
$$
Proceed by induction, with the base case $N=2$ trivial. Suppose there is a sequence of at most $N-2$ steps which works. In any suitable final arrangement, a given type must be in positions (odd, even), whereas they start in positions (even, odd). So each type must be involved in at least one step. However, each step involves at most two types, so by the pigeonhole principle, at least four types are involved in at most one step. Pick one such type $a \neq 1$. The one step involving $a$ must be one of
$$
\ldots, ?, a, a, ?, \ldots .
$$
Neither of these steps affects the relative order of the $2 N-2$ other people. So by ignoring this step involving the $a$, we have a sequence of at most $N-3$ steps acting on the other $2 N-2$ people which appropriately sorts them. By induction, this is a contradiction.
Alternative lower bound I: Consider the graph with vertices given by pairs of positions $\{(1,2),(3,4), \ldots,(2 N-1,2 N)\}$. We add an edge between pairs of (different)
vertices if we ever swap two people in places corresponding to those vertices. In particular, at the end, the two people with type $k$ end up in places corresponding to a single vertex.
Suppose we start from the ordering (1) and have some number of steps leading to an ordering where everyone is next to their partner. Then, in the induced graph, there is a path between the vertices corresponding to the places $(2 k-3,2 k-2)$ and $(2 k-1,2 k)$ for each $2 \leq k \leq N$, and also between $(1,2)$ and $(2 N-1,2 N)$. In other words, the graph is connected, and so must have at least $N-1$ edges.
Alternative lower bound II: Consider a bipartite multigraph with vertex classes $\left(v_{1}, \ldots, v_{n}\right)$ and $\left(w_{1}, \ldots, w_{n}\right)$. Connect $v_{i}$ to $w_{j}$ if a person of type $j$ is in positions ( $2 i-1,2 i$ ) (if both positions are taken by the type $j$ couple, then add two edges).
Each step in the dance consists of replacing edges $\left.E=\left\{v_{a} \leftrightarrow w_{c}, v_{b} \leftrightarrow w_{d}\right)\right\}$ with $E^{\prime}=\left\{v_{a} \leftrightarrow w_{d}, v_{b} \leftrightarrow w_{c}\right\}$. However, both before and after the step, the number of components in the graph which include $\left\{v_{a}, v_{b}, w_{c}, w_{d}\right\}$ is either one or two. The structure of other components which do not include these vertices is unaffected by the move.
Therefore, the number of connected components increases by at most 1 in each step.
Starting from configuration (1), the graph initially consists of a single (cyclic) component, so one requires at least $n-1$ steps to get to the final configuration for which there are $n$ connected components.
|
{
"resource_path": "Balkan_Shortlist/segmented/en-2019_bmo_shortlist.jsonl",
"problem_match": "\nC1.",
"solution_match": "\nSolution."
}
|
379abfeb-7d99-5ab7-af81-c8663566089b
| 605,985
|
An $5 \times 5$ array must be completed with all numbers $\{1,2, \ldots, 25\}$, one number in each cell. Find the maximal positive integer $k$, such that for any completion of the array there is a $2 \times 2$ square (subarray), whose numbers have a sum not less than $k$.
|
We will prove that $k_{\max }=45$.
We number the columns and the rows and we select all possible $3^{2}=9$ choices of an odd column with an odd row.
Collecting all such pairs of an odd column with an odd row, we double count some squares. Indeed, we take some $3^{2}$ squares 5 times, some 12 squares 3 times and there are some 4 squares (namely all the intersections of an even column with an even row) that we don't take in such pairs.
It follows that the maximal total sum over all $3^{2}$ choices of an odd column with an odd row is
$$
5 \times(17+18+\cdots+25)+3 \times(5+6+\cdots+16)=1323
$$
So, by an averaging argument, there exists a pair of an odd column with an odd row with sum at most $\frac{1323}{9}=147$.
Then all the other squares of the array will have sum at least
$$
(1+2+\cdots+25)-147=178
$$
But for these squares there is a tiling with $2 \times 2$ arrays, which are 4 in total. So there is an $2 \times 2$ array, whose numbers have a sum at least $\frac{178}{4}>44$. So, there is a $2 \times 2$ array whose numbers have a sum at least 45 . This argument gives that
$$
k_{\max } \geq 45 .
$$
We are going now to give an example of an array, in which 45 is the best possible. We fill the rows of the array as follows:
| 25 | 5 | 24 | 6 | 23 |
| :---: | :---: | :---: | :---: | :---: |
| 11 | 4 | 12 | 3 | 13 |
| 22 | 7 | 21 | 8 | 20 |
| 14 | 2 | 15 | 1 | 16 |
| 19 | 9 | 18 | 10 | 17 |
We are going now to even rows:
In the above array, every $2 \times 2$ subarray has a sum, which is less or equal to 45 . This gives that
$$
k_{\max } \leq 45 .
$$
A combination of (1) and (2) gives that $k_{\max }=45$.
[^6]C3. Anna and Bob play a game on the set of all points of the form $(m, n)$ where $m, n$ are integers with $|m|,|n| \leqslant 2019$. Let us call the lines $x= \pm 2019$ and $y= \pm 2019$ the boundary lines of the game. The points of these lines are called the boundary points. The neighbours of point $(m, n)$ are the points $(m+1, n),(m-1, n),(m, n+1),(m, n-1)$.
Anna starts with a token at the origin ( 0,0 ). With Bob playing first, they alternately perform the following steps: At his turn, Bob deletes two points on each boundary line. On her turn Anna makes a sequences of three moves of the token, where a move of the token consists of picking up the token from its current position and placing it in one of its neighbours.
To win the game Anna must place her token on a boundary point before it is deleted by Bob. Does Anna have a winning strategy?
[Note: At every turn except perhaps her last, Anna must make exactly three moves.]
|
45
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
An $5 \times 5$ array must be completed with all numbers $\{1,2, \ldots, 25\}$, one number in each cell. Find the maximal positive integer $k$, such that for any completion of the array there is a $2 \times 2$ square (subarray), whose numbers have a sum not less than $k$.
|
We will prove that $k_{\max }=45$.
We number the columns and the rows and we select all possible $3^{2}=9$ choices of an odd column with an odd row.
Collecting all such pairs of an odd column with an odd row, we double count some squares. Indeed, we take some $3^{2}$ squares 5 times, some 12 squares 3 times and there are some 4 squares (namely all the intersections of an even column with an even row) that we don't take in such pairs.
It follows that the maximal total sum over all $3^{2}$ choices of an odd column with an odd row is
$$
5 \times(17+18+\cdots+25)+3 \times(5+6+\cdots+16)=1323
$$
So, by an averaging argument, there exists a pair of an odd column with an odd row with sum at most $\frac{1323}{9}=147$.
Then all the other squares of the array will have sum at least
$$
(1+2+\cdots+25)-147=178
$$
But for these squares there is a tiling with $2 \times 2$ arrays, which are 4 in total. So there is an $2 \times 2$ array, whose numbers have a sum at least $\frac{178}{4}>44$. So, there is a $2 \times 2$ array whose numbers have a sum at least 45 . This argument gives that
$$
k_{\max } \geq 45 .
$$
We are going now to give an example of an array, in which 45 is the best possible. We fill the rows of the array as follows:
| 25 | 5 | 24 | 6 | 23 |
| :---: | :---: | :---: | :---: | :---: |
| 11 | 4 | 12 | 3 | 13 |
| 22 | 7 | 21 | 8 | 20 |
| 14 | 2 | 15 | 1 | 16 |
| 19 | 9 | 18 | 10 | 17 |
We are going now to even rows:
In the above array, every $2 \times 2$ subarray has a sum, which is less or equal to 45 . This gives that
$$
k_{\max } \leq 45 .
$$
A combination of (1) and (2) gives that $k_{\max }=45$.
[^6]C3. Anna and Bob play a game on the set of all points of the form $(m, n)$ where $m, n$ are integers with $|m|,|n| \leqslant 2019$. Let us call the lines $x= \pm 2019$ and $y= \pm 2019$ the boundary lines of the game. The points of these lines are called the boundary points. The neighbours of point $(m, n)$ are the points $(m+1, n),(m-1, n),(m, n+1),(m, n-1)$.
Anna starts with a token at the origin ( 0,0 ). With Bob playing first, they alternately perform the following steps: At his turn, Bob deletes two points on each boundary line. On her turn Anna makes a sequences of three moves of the token, where a move of the token consists of picking up the token from its current position and placing it in one of its neighbours.
To win the game Anna must place her token on a boundary point before it is deleted by Bob. Does Anna have a winning strategy?
[Note: At every turn except perhaps her last, Anna must make exactly three moves.]
|
{
"resource_path": "Balkan_Shortlist/segmented/en-2019_bmo_shortlist.jsonl",
"problem_match": "\nC2b. ${ }^{8}$",
"solution_match": "\nSolution."
}
|
9dd429f2-67e5-51d1-b358-a81a695571c6
| 605,995
|
Let $n \geqslant 3$ be an integer and let
$$
M=\left\{\frac{a_{1}+a_{2}+\cdots+a_{k}}{k}: 1 \leqslant k \leqslant n \text { and } 1 \leqslant a_{1}<\cdots<a_{k} \leqslant n\right\}
$$
be the set of the arithmetic means of the elements of all non-empty subsets of $\{1,2, \ldots, n\}$. Find $\min \{|a-b|: a, b \in M$ with $a \neq b\}$.
## Proposed by Romania
|
We observe that $M$ is composed by rational numbers of the form $a=\frac{x}{k}$, where $1 \leqslant k \leqslant n$. As the arithmetic mean of $1, \ldots, n$ is $\frac{n+1}{2}$, if we look at these rational numbers in their irreducible form, we can say that $1 \leqslant k \leqslant n-1$.
A non-zero difference $|a-b|$ with $a, b \in M$ is then of form
$$
\left|\frac{x}{k}-\frac{y}{p}\right|=\frac{\left|p_{0} x-k_{0} y\right|}{[k, p]}
$$
where $[k, p]$ is the l.c.m. of $k, p$, and $k_{0}=\frac{[k, p]}{k}, p_{0}=\frac{[k, p]}{p}$. Then $|a-b| \geqslant \frac{1}{[k, p]}$, as $\left|p_{0} x-k_{0} y\right|$ is a non-zero integer. As
$$
\max \{[k, p] \mid 1 \leqslant k<p \leqslant n-1\}=(n-1)(n-2),
$$
we can say that $m=\min _{\substack{a, b \in M \\ a \neq b}}|a-b| \geqslant \frac{1}{(n-1)(n-2)}$.
To reach this minimum, we seek $x \in\{3,4, \ldots, 2 n-1\}$ and $y \in\{1,2, \ldots, n\}$ for which
$$
\left|\frac{\frac{n(n+1)}{2}-x}{n-2}-\frac{\frac{n(n+1)}{2}-y}{n-1}\right|=\frac{1}{(n-1)(n-2)},
$$
meaning
$$
\left|\frac{n(n+1)}{2}-(n-1) x+(n-2) y\right|=1 .
$$
If $n=2 k$, we can choose $x=k+3$ and $y=2$ and if $n=2 k+1$ we can choose $x=n=2 k+1$ and $y=k$. Therefore, the required minimum is $\frac{1}{(n-1)(n-2)}$.
Comment. For $n \geqslant 5$, the only other possibilities are to take $x=3 k-1, y=2 k-1$ if $n=2 k$ and to take $x=2 k+3, y=k+2$ if $n=2 k+1$. (For $n=3,4$ there are also examples where one of the sets is of size $n$.)
|
\frac{1}{(n-1)(n-2)}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Let $n \geqslant 3$ be an integer and let
$$
M=\left\{\frac{a_{1}+a_{2}+\cdots+a_{k}}{k}: 1 \leqslant k \leqslant n \text { and } 1 \leqslant a_{1}<\cdots<a_{k} \leqslant n\right\}
$$
be the set of the arithmetic means of the elements of all non-empty subsets of $\{1,2, \ldots, n\}$. Find $\min \{|a-b|: a, b \in M$ with $a \neq b\}$.
## Proposed by Romania
|
We observe that $M$ is composed by rational numbers of the form $a=\frac{x}{k}$, where $1 \leqslant k \leqslant n$. As the arithmetic mean of $1, \ldots, n$ is $\frac{n+1}{2}$, if we look at these rational numbers in their irreducible form, we can say that $1 \leqslant k \leqslant n-1$.
A non-zero difference $|a-b|$ with $a, b \in M$ is then of form
$$
\left|\frac{x}{k}-\frac{y}{p}\right|=\frac{\left|p_{0} x-k_{0} y\right|}{[k, p]}
$$
where $[k, p]$ is the l.c.m. of $k, p$, and $k_{0}=\frac{[k, p]}{k}, p_{0}=\frac{[k, p]}{p}$. Then $|a-b| \geqslant \frac{1}{[k, p]}$, as $\left|p_{0} x-k_{0} y\right|$ is a non-zero integer. As
$$
\max \{[k, p] \mid 1 \leqslant k<p \leqslant n-1\}=(n-1)(n-2),
$$
we can say that $m=\min _{\substack{a, b \in M \\ a \neq b}}|a-b| \geqslant \frac{1}{(n-1)(n-2)}$.
To reach this minimum, we seek $x \in\{3,4, \ldots, 2 n-1\}$ and $y \in\{1,2, \ldots, n\}$ for which
$$
\left|\frac{\frac{n(n+1)}{2}-x}{n-2}-\frac{\frac{n(n+1)}{2}-y}{n-1}\right|=\frac{1}{(n-1)(n-2)},
$$
meaning
$$
\left|\frac{n(n+1)}{2}-(n-1) x+(n-2) y\right|=1 .
$$
If $n=2 k$, we can choose $x=k+3$ and $y=2$ and if $n=2 k+1$ we can choose $x=n=2 k+1$ and $y=k$. Therefore, the required minimum is $\frac{1}{(n-1)(n-2)}$.
Comment. For $n \geqslant 5$, the only other possibilities are to take $x=3 k-1, y=2 k-1$ if $n=2 k$ and to take $x=2 k+3, y=k+2$ if $n=2 k+1$. (For $n=3,4$ there are also examples where one of the sets is of size $n$.)
|
{
"resource_path": "Balkan_Shortlist/segmented/en-2021_bmo_shortlist.jsonl",
"problem_match": "\nN1.",
"solution_match": "\nSolution."
}
|
439e6d91-4fd5-535e-b6da-14b56118fa7d
| 604,254
|
Let $A B C$ be a triangle such that $\frac{|B C|}{|A B|-|B C|}=\frac{|A B|+|B C|}{|A C|}$. Determine the ratio $\angle A: \angle C$.
|
Answer: $1: 2$.
Denote $|B C|=a,|A C|=b,|A B|=c$. The condition $\frac{a}{c-a}=\frac{c+a}{b}$ implies $c^{2}=a^{2}+a b$ and
$$
\frac{c}{a+b}=\frac{a}{c} .
$$
Let $D$ be a point on $A B$ such that $|B D|=\frac{a}{a+b} \cdot c$ (see Figure 5). Then
$$
\frac{|B D|}{|B C|}=\frac{c}{a+b}=\frac{a}{c}=\frac{|B C|}{|B A|}
$$
so triangles $B C D$ and $B A C$ are similar, implying $\angle B C D=\angle B A C$. Also, $\frac{|A C|}{|B C|}=\frac{|A D|}{|B D|}$ yields $\frac{|B C|}{|B D|}=\frac{|A C|}{|A D|}$, and hence by the bisector theorem $C D$ is the bisector of $\angle B C A$. So the ratio asked for is $1: 2$.
Figure 5
|
1: 2
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $A B C$ be a triangle such that $\frac{|B C|}{|A B|-|B C|}=\frac{|A B|+|B C|}{|A C|}$. Determine the ratio $\angle A: \angle C$.
|
Answer: $1: 2$.
Denote $|B C|=a,|A C|=b,|A B|=c$. The condition $\frac{a}{c-a}=\frac{c+a}{b}$ implies $c^{2}=a^{2}+a b$ and
$$
\frac{c}{a+b}=\frac{a}{c} .
$$
Let $D$ be a point on $A B$ such that $|B D|=\frac{a}{a+b} \cdot c$ (see Figure 5). Then
$$
\frac{|B D|}{|B C|}=\frac{c}{a+b}=\frac{a}{c}=\frac{|B C|}{|B A|}
$$
so triangles $B C D$ and $B A C$ are similar, implying $\angle B C D=\angle B A C$. Also, $\frac{|A C|}{|B C|}=\frac{|A D|}{|B D|}$ yields $\frac{|B C|}{|B D|}=\frac{|A C|}{|A D|}$, and hence by the bisector theorem $C D$ is the bisector of $\angle B C A$. So the ratio asked for is $1: 2$.

Figure 5
|
{
"resource_path": "BalticWay/segmented/en-bw00sol.jsonl",
"problem_match": "\n5.",
"solution_match": "\n5."
}
|
1cc707c3-6f34-5c4b-ac71-6cc09a4eaead
| 240,339
|
Fourteen friends met at a party. One of them, Fredek, wanted to go to bed early. He said goodbye to 10 of his friends, forgot about the remaining 3 , and went to bed. After a while he returned to the party, said goodbye to 10 of his friends (not necessarily the same as before), and went to bed. Later Fredek came back a number of times, each time saying goodbye to exactly 10 of his friends, and then went back to bed. As soon as he had said goodbye to each of his friends at least once, he did not come back again. In the morning Fredek realised that he had said goodbye a different number of times to each of his thirteen friends! What is the smallest possible number of times that Fredek returned to the party?
|
Answer: Fredek returned at least 32 times.
Assume Fredek returned $k$ times, i.e. he was saying good-bye $k+1$ times to his friends. There exists a friend of Fredek, call him $X_{13}$, about whom Fredek forgot $k$ times in a row, starting from the very first time - otherwise Fredek would have come back less than $k$ times.
Consider the remaining friends of Fredek: $X_{1}, X_{2}, \ldots, X_{12}$. Assume that Fredek forgot $x_{j}$ times about each friend $X_{j}$. Since Fredek forgot a different number of times about each of his friends, so we can assume w.l.o.g. that $x_{j} \geqslant j-1$ for $j=1,2, \ldots, 12$. Since $X_{13}$ was forgotten by Fredek $k$ times, and since Fredek forgot about exactly three of his friends each time, we have
$$
\begin{aligned}
3(k+1) & =x_{1}+x_{2}+x_{3}+\ldots+x_{12}+k \geqslant \\
& \geqslant 0+1+2+3+\ldots+11+k= \\
& =66+k .
\end{aligned}
$$
Therefore $2 k \geqslant 63$, which gives $k \geqslant 32$.
It is possible that Fredek returned 32 times, i.e. he was saying good-bye 33 times to his friends. The following table shows this. The $i$-th column displays the three friends Fredek forgot while saying good-bye for the $i$-th time (i.e. before his $i$-th return). For simplicity we write $j$ in place of $X_{j}$.
$$
\begin{aligned}
& 13 \ldots .131313 \ldots .1313 \ldots .131313131313131311
\end{aligned}
$$
|
32
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Fourteen friends met at a party. One of them, Fredek, wanted to go to bed early. He said goodbye to 10 of his friends, forgot about the remaining 3 , and went to bed. After a while he returned to the party, said goodbye to 10 of his friends (not necessarily the same as before), and went to bed. Later Fredek came back a number of times, each time saying goodbye to exactly 10 of his friends, and then went back to bed. As soon as he had said goodbye to each of his friends at least once, he did not come back again. In the morning Fredek realised that he had said goodbye a different number of times to each of his thirteen friends! What is the smallest possible number of times that Fredek returned to the party?
|
Answer: Fredek returned at least 32 times.
Assume Fredek returned $k$ times, i.e. he was saying good-bye $k+1$ times to his friends. There exists a friend of Fredek, call him $X_{13}$, about whom Fredek forgot $k$ times in a row, starting from the very first time - otherwise Fredek would have come back less than $k$ times.
Consider the remaining friends of Fredek: $X_{1}, X_{2}, \ldots, X_{12}$. Assume that Fredek forgot $x_{j}$ times about each friend $X_{j}$. Since Fredek forgot a different number of times about each of his friends, so we can assume w.l.o.g. that $x_{j} \geqslant j-1$ for $j=1,2, \ldots, 12$. Since $X_{13}$ was forgotten by Fredek $k$ times, and since Fredek forgot about exactly three of his friends each time, we have
$$
\begin{aligned}
3(k+1) & =x_{1}+x_{2}+x_{3}+\ldots+x_{12}+k \geqslant \\
& \geqslant 0+1+2+3+\ldots+11+k= \\
& =66+k .
\end{aligned}
$$
Therefore $2 k \geqslant 63$, which gives $k \geqslant 32$.
It is possible that Fredek returned 32 times, i.e. he was saying good-bye 33 times to his friends. The following table shows this. The $i$-th column displays the three friends Fredek forgot while saying good-bye for the $i$-th time (i.e. before his $i$-th return). For simplicity we write $j$ in place of $X_{j}$.
$$
\begin{aligned}
& 13 \ldots .131313 \ldots .1313 \ldots .131313131313131311
\end{aligned}
$$
|
{
"resource_path": "BalticWay/segmented/en-bw00sol.jsonl",
"problem_match": "\n8.",
"solution_match": "\n8."
}
|
aa416b98-3d44-59d0-8520-368cd65ee518
| 604,506
|
A sequence of positive integers $a_{1}, a_{2}, \ldots$ is such that for each $m$ and $n$ the following holds: if $m$ is a divisor of $n$ and $m<n$, then $a_{m}$ is a divisor of $a_{n}$ and $a_{m}<a_{n}$. Find the least possible value of $a_{2000}$.
|
Answer: 128.
Let $d$ denote the least possible value of $a_{2000}$. We shall prove that $d=128$.
Clearly the sequence defined by $a_{1}=1$ and $a_{n}=2^{\alpha_{1}+\alpha_{2}+\cdots+\alpha_{k}}$ for $n=p_{1}^{\alpha_{1}} p_{2}^{\alpha_{2}} \cdots \cdots p_{k}^{\alpha_{k}}$ has the required property. Since $2000=2^{4} \cdot 5^{3}$, we have $a_{2000}=2^{4+3}=128$ and therefore $d \leqslant 128$.
Note that in the sequence $1<5<25<125<250<500<1000<2000$ each term is divisible by the previous one. As $a_{1} \geqslant 1$ it follows that
$$
a_{2000} \geqslant 2 \cdot a_{1000} \geqslant 2^{2} \cdot a_{500} \geqslant 2^{3} \cdot a_{250} \geqslant \ldots \geqslant 2^{7} \cdot a_{1} \geqslant 2^{7}=128 .
$$
|
128
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
A sequence of positive integers $a_{1}, a_{2}, \ldots$ is such that for each $m$ and $n$ the following holds: if $m$ is a divisor of $n$ and $m<n$, then $a_{m}$ is a divisor of $a_{n}$ and $a_{m}<a_{n}$. Find the least possible value of $a_{2000}$.
|
Answer: 128.
Let $d$ denote the least possible value of $a_{2000}$. We shall prove that $d=128$.
Clearly the sequence defined by $a_{1}=1$ and $a_{n}=2^{\alpha_{1}+\alpha_{2}+\cdots+\alpha_{k}}$ for $n=p_{1}^{\alpha_{1}} p_{2}^{\alpha_{2}} \cdots \cdots p_{k}^{\alpha_{k}}$ has the required property. Since $2000=2^{4} \cdot 5^{3}$, we have $a_{2000}=2^{4+3}=128$ and therefore $d \leqslant 128$.
Note that in the sequence $1<5<25<125<250<500<1000<2000$ each term is divisible by the previous one. As $a_{1} \geqslant 1$ it follows that
$$
a_{2000} \geqslant 2 \cdot a_{1000} \geqslant 2^{2} \cdot a_{500} \geqslant 2^{3} \cdot a_{250} \geqslant \ldots \geqslant 2^{7} \cdot a_{1} \geqslant 2^{7}=128 .
$$
|
{
"resource_path": "BalticWay/segmented/en-bw00sol.jsonl",
"problem_match": "\n11.",
"solution_match": "\n11."
}
|
9c42bd35-eb49-50cd-93ab-ec11d9558097
| 240,391
|
Find all positive integers $n$ such that $n$ is equal to 100 times the number of positive divisors of $n$.
|
Answer: 2000 is the only such integer.
Let $d(n)$ denote the number of positive divisors of $n$ and $p \triangleright n$ denote the exponent of the prime $p$ in the canonical representation of $n$. Let $\delta(n)=\frac{n}{d(n)}$. Using this notation, the problem reformulates as follows: Find all positive integers $n$ such that $\delta(n)=100$.
Lemma: Let $n$ be an integer and $m$ its proper divisor. Then $\delta(m) \leqslant \delta(n)$ and the equality holds if and only if $m$ is odd and $n=2 m$.
Proof. Let $n=m p$ for a prime $p$. By the well-known formula
$$
d(n)=\prod_{p}(1+p \triangleright n)
$$
we have
$$
\frac{\delta(n)}{\delta(m)}=\frac{n}{m} \cdot \frac{d(m)}{d(n)}=p \cdot \frac{1+p \triangleright m}{1+p \triangleright n}=p \cdot \frac{p \triangleright n}{1+p \triangleright n} \geqslant 2 \cdot \frac{1}{2}=1,
$$
hence $\delta(m) \leqslant \delta(n)$. It is also clear that equality holds if and only if $p=2$ and $p \triangleright n=1$, i.e. $m$ is odd and $n=2 m$.
For the general case $n=m s$ where $s>1$ is an arbitrary positive integer, represent $s$ as a product of primes. By elementary induction on the number of factors in the representation we prove $\delta(m) \leqslant \delta(n)$. The equality can hold only if all factors are equal to 2 and the number $m$ as well as any intermediate result of multiplying it by these factors is odd, i.e. the representation of $s$ consists of a single prime 2, which gives $n=2 m$. This proves the lemma.
Now assume that $\delta(n)=100$ for some $n$, i.e. $n=100 \cdot d(n)=2^{2} \cdot 5^{2} \cdot d(n)$. In the following, we estimate the exponents of primes in the canonical representation of $n$, using the fact that 100 is a divisor of $n$.
(1) Observe that $\delta\left(2^{7} \cdot 5^{2}\right)=\frac{2^{5} \cdot 100}{8 \cdot 3}=\frac{3200}{24}>100$. Hence $2 \triangleright n \leqslant 6$, since otherwise $2^{7} \cdot 5^{2}$ divides $n$ and, by the lemma, $\delta(n)>100$.
(2) Observe that $\delta\left(2^{2} \cdot 5^{4}\right)=\frac{5^{2} \cdot 100}{3 \cdot 5}=\frac{2500}{15}>100$. Hence $5 \triangleright n \leqslant 3$, since otherwise $2^{2} \cdot 5^{4}$ divides $n$ and, by the lemma, $\delta(n)>100$.
(3) Observe that $\delta\left(2^{2} \cdot 5^{2} \cdot 3^{4}\right)=\frac{3^{4} \cdot 100}{3 \cdot 3 \cdot 5}=\frac{8100}{45}>100$. Hence $3 \triangleright n \leqslant 3$, since otherwise $2^{2} \cdot 5^{2} \cdot 3^{4}$ divides $n$ and, by the lemma, $\delta(n)>100$.
(4) Take a prime $q>5$ and an integer $k \geqslant 4$. Then
$$
\begin{aligned}
\delta\left(2^{2} \cdot 5^{2} \cdot q^{k}\right) & =\frac{2^{2} \cdot 5^{2} \cdot q^{k}}{d\left(2^{2} \cdot 5^{2} \cdot q^{k}\right)}=\frac{2^{2} \cdot 5^{2} \cdot q^{k}}{d\left(2^{2} \cdot 5^{2} \cdot 3^{k}\right)}>\frac{2^{2} \cdot 5^{2} \cdot 3^{k}}{d\left(2^{2} \cdot 5^{2} \cdot 3^{k}\right)}= \\
& =\delta\left(2^{2} \cdot 5^{2} \cdot 3^{k}\right)>100 .
\end{aligned}
$$
Hence, similarly to the previous cases, we get $q \triangleright n \leqslant 3$.
(5) If a prime $q>7$ divides $n$, then $q$ divides $d(n)$. Thus $q$ divides $1+p \triangleright n$ for some prime $p$. But this is impossible because, as the previous cases showed, $p \triangleright n \leqslant 6$ for all $p$. So $n$ is not divisible by primes greater than 7 .
(6) If 7 divides $n$, then 7 divides $d(n)$ and hence divides $1+p \triangleright n$ for some prime $p$. By (1)-(4), this implies $p=2$ and $2 \triangleright n=6$. At the same time, if $2 \triangleright n=6$, then 7 divides $d(n)$ and $n$. So 7 divides $n$ if and only if $2 \triangleright n=6$. Since $\delta\left(2^{6} \cdot 5^{2} \cdot 7\right)=\frac{2^{4} \cdot 7 \cdot 100}{7 \cdot 3 \cdot 2}=\frac{11200}{42}>100$, both of these conditions cannot hold simultaneously. So $n$ is not divisible by 7 and $2 \triangleright n \leqslant 5$.
(7) If $5 \triangleright n=3$, then 5 divides $d(n)$ and hence divides $1+p \triangleright n$ for some prime $p$. By (1)-(4), this implies $p=2$ and $2 \triangleright n=4$. At the same time, if $2 \triangleright n=4$, then 5 divides $d(n), 5^{3}$ divides $n$ and, by (2), $5 \triangleright n=3$. So $5 \triangleright n=3$ if and only if $2 \triangleright n=4$. Since $\delta\left(2^{4} \cdot 5^{3}\right)=\frac{2^{2} \cdot 5 \cdot 100}{5 \cdot 4}=100$, we find that $n=2^{4} \cdot 5^{3}=2000$ satisfies the required condition. On the other hand, if $2 \triangleright n=4$ and $5 \triangleright n=3$ for some $n \neq 2000$, then $n=2000 s$ for some $s>1$ and, by the lemma, $\delta(n)>100$.
(8) The case $5 \triangleright n=2$ has remained. By (7), we have $2 \triangleright n \neq 4$, so $2 \triangleright n \in\{2,3,5\}$. The condition $5 \triangleright n=2$ implies that 3 divides $d(n)$ and $n$, thus $3 \triangleright n \in\{1,2,3\}$. If $2 \triangleright n=3$, then $d(n)$ is divisible by 2 but not by 4 . At the same time $2 \triangleright n=3$ implies $3+1=4$ divides $d(n)$, a contradiction. Thus $2 \triangleright n \in\{2,5\}$, and $3^{2}$ divides $d(n)$ and $n$, i.e.
$3 \triangleright n \in\{2,3\}$. Now $3 \triangleright n=2$ would imply that $3^{3}$ divides $d(n)$ and $n$, a contradiction; on the other hand $3 \triangleright n=3$ would imply $3 \triangleright d(n)=2$ and hence $3 \triangleright n=2$, a contradiction.
|
2000
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Find all positive integers $n$ such that $n$ is equal to 100 times the number of positive divisors of $n$.
|
Answer: 2000 is the only such integer.
Let $d(n)$ denote the number of positive divisors of $n$ and $p \triangleright n$ denote the exponent of the prime $p$ in the canonical representation of $n$. Let $\delta(n)=\frac{n}{d(n)}$. Using this notation, the problem reformulates as follows: Find all positive integers $n$ such that $\delta(n)=100$.
Lemma: Let $n$ be an integer and $m$ its proper divisor. Then $\delta(m) \leqslant \delta(n)$ and the equality holds if and only if $m$ is odd and $n=2 m$.
Proof. Let $n=m p$ for a prime $p$. By the well-known formula
$$
d(n)=\prod_{p}(1+p \triangleright n)
$$
we have
$$
\frac{\delta(n)}{\delta(m)}=\frac{n}{m} \cdot \frac{d(m)}{d(n)}=p \cdot \frac{1+p \triangleright m}{1+p \triangleright n}=p \cdot \frac{p \triangleright n}{1+p \triangleright n} \geqslant 2 \cdot \frac{1}{2}=1,
$$
hence $\delta(m) \leqslant \delta(n)$. It is also clear that equality holds if and only if $p=2$ and $p \triangleright n=1$, i.e. $m$ is odd and $n=2 m$.
For the general case $n=m s$ where $s>1$ is an arbitrary positive integer, represent $s$ as a product of primes. By elementary induction on the number of factors in the representation we prove $\delta(m) \leqslant \delta(n)$. The equality can hold only if all factors are equal to 2 and the number $m$ as well as any intermediate result of multiplying it by these factors is odd, i.e. the representation of $s$ consists of a single prime 2, which gives $n=2 m$. This proves the lemma.
Now assume that $\delta(n)=100$ for some $n$, i.e. $n=100 \cdot d(n)=2^{2} \cdot 5^{2} \cdot d(n)$. In the following, we estimate the exponents of primes in the canonical representation of $n$, using the fact that 100 is a divisor of $n$.
(1) Observe that $\delta\left(2^{7} \cdot 5^{2}\right)=\frac{2^{5} \cdot 100}{8 \cdot 3}=\frac{3200}{24}>100$. Hence $2 \triangleright n \leqslant 6$, since otherwise $2^{7} \cdot 5^{2}$ divides $n$ and, by the lemma, $\delta(n)>100$.
(2) Observe that $\delta\left(2^{2} \cdot 5^{4}\right)=\frac{5^{2} \cdot 100}{3 \cdot 5}=\frac{2500}{15}>100$. Hence $5 \triangleright n \leqslant 3$, since otherwise $2^{2} \cdot 5^{4}$ divides $n$ and, by the lemma, $\delta(n)>100$.
(3) Observe that $\delta\left(2^{2} \cdot 5^{2} \cdot 3^{4}\right)=\frac{3^{4} \cdot 100}{3 \cdot 3 \cdot 5}=\frac{8100}{45}>100$. Hence $3 \triangleright n \leqslant 3$, since otherwise $2^{2} \cdot 5^{2} \cdot 3^{4}$ divides $n$ and, by the lemma, $\delta(n)>100$.
(4) Take a prime $q>5$ and an integer $k \geqslant 4$. Then
$$
\begin{aligned}
\delta\left(2^{2} \cdot 5^{2} \cdot q^{k}\right) & =\frac{2^{2} \cdot 5^{2} \cdot q^{k}}{d\left(2^{2} \cdot 5^{2} \cdot q^{k}\right)}=\frac{2^{2} \cdot 5^{2} \cdot q^{k}}{d\left(2^{2} \cdot 5^{2} \cdot 3^{k}\right)}>\frac{2^{2} \cdot 5^{2} \cdot 3^{k}}{d\left(2^{2} \cdot 5^{2} \cdot 3^{k}\right)}= \\
& =\delta\left(2^{2} \cdot 5^{2} \cdot 3^{k}\right)>100 .
\end{aligned}
$$
Hence, similarly to the previous cases, we get $q \triangleright n \leqslant 3$.
(5) If a prime $q>7$ divides $n$, then $q$ divides $d(n)$. Thus $q$ divides $1+p \triangleright n$ for some prime $p$. But this is impossible because, as the previous cases showed, $p \triangleright n \leqslant 6$ for all $p$. So $n$ is not divisible by primes greater than 7 .
(6) If 7 divides $n$, then 7 divides $d(n)$ and hence divides $1+p \triangleright n$ for some prime $p$. By (1)-(4), this implies $p=2$ and $2 \triangleright n=6$. At the same time, if $2 \triangleright n=6$, then 7 divides $d(n)$ and $n$. So 7 divides $n$ if and only if $2 \triangleright n=6$. Since $\delta\left(2^{6} \cdot 5^{2} \cdot 7\right)=\frac{2^{4} \cdot 7 \cdot 100}{7 \cdot 3 \cdot 2}=\frac{11200}{42}>100$, both of these conditions cannot hold simultaneously. So $n$ is not divisible by 7 and $2 \triangleright n \leqslant 5$.
(7) If $5 \triangleright n=3$, then 5 divides $d(n)$ and hence divides $1+p \triangleright n$ for some prime $p$. By (1)-(4), this implies $p=2$ and $2 \triangleright n=4$. At the same time, if $2 \triangleright n=4$, then 5 divides $d(n), 5^{3}$ divides $n$ and, by (2), $5 \triangleright n=3$. So $5 \triangleright n=3$ if and only if $2 \triangleright n=4$. Since $\delta\left(2^{4} \cdot 5^{3}\right)=\frac{2^{2} \cdot 5 \cdot 100}{5 \cdot 4}=100$, we find that $n=2^{4} \cdot 5^{3}=2000$ satisfies the required condition. On the other hand, if $2 \triangleright n=4$ and $5 \triangleright n=3$ for some $n \neq 2000$, then $n=2000 s$ for some $s>1$ and, by the lemma, $\delta(n)>100$.
(8) The case $5 \triangleright n=2$ has remained. By (7), we have $2 \triangleright n \neq 4$, so $2 \triangleright n \in\{2,3,5\}$. The condition $5 \triangleright n=2$ implies that 3 divides $d(n)$ and $n$, thus $3 \triangleright n \in\{1,2,3\}$. If $2 \triangleright n=3$, then $d(n)$ is divisible by 2 but not by 4 . At the same time $2 \triangleright n=3$ implies $3+1=4$ divides $d(n)$, a contradiction. Thus $2 \triangleright n \in\{2,5\}$, and $3^{2}$ divides $d(n)$ and $n$, i.e.
$3 \triangleright n \in\{2,3\}$. Now $3 \triangleright n=2$ would imply that $3^{3}$ divides $d(n)$ and $n$, a contradiction; on the other hand $3 \triangleright n=3$ would imply $3 \triangleright d(n)=2$ and hence $3 \triangleright n=2$, a contradiction.
|
{
"resource_path": "BalticWay/segmented/en-bw00sol.jsonl",
"problem_match": "\n14.",
"solution_match": "\n14."
}
|
82bb9477-1cd7-5a98-a5aa-5f31c355e0f0
| 240,419
|
A set of 8 problems was prepared for an examination. Each student was given 3 of them. No two students received more than one common problem. What is the largest possible number of students?
|
Answer: 8 .
Denote the problems by $A, B, C, D, E, F, G, H$, then 8 possible problem sets are $A B C, A D E, A F G, B D G, B F H, C D H, C E F, E G H$. Hence, there could be 8 students.
Suppose that some problem (e.g., $A$ ) was given to 4 students. Then each of these 4 students should receive 2 different "supplementary" problems, and there should be at least 9 problems - a contradiction. Therefore each problem was given to at most 3 students, and there were at most $8 \cdot 3=24$ "awardings" of problems. As each student was "awarded" 3 problems, there were at most 8 students.
|
8
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
A set of 8 problems was prepared for an examination. Each student was given 3 of them. No two students received more than one common problem. What is the largest possible number of students?
|
Answer: 8 .
Denote the problems by $A, B, C, D, E, F, G, H$, then 8 possible problem sets are $A B C, A D E, A F G, B D G, B F H, C D H, C E F, E G H$. Hence, there could be 8 students.
Suppose that some problem (e.g., $A$ ) was given to 4 students. Then each of these 4 students should receive 2 different "supplementary" problems, and there should be at least 9 problems - a contradiction. Therefore each problem was given to at most 3 students, and there were at most $8 \cdot 3=24$ "awardings" of problems. As each student was "awarded" 3 problems, there were at most 8 students.
|
{
"resource_path": "BalticWay/segmented/en-bw01sol.jsonl",
"problem_match": "\n1.",
"solution_match": "\n1."
}
|
451ee0af-4e82-564a-808b-85ae07a108ad
| 240,119
|
The real-valued function $f$ is defined for all positive integers. For any integers $a>1, b>1$ with $d=\operatorname{gcd}(a, b)$, we have
$$
f(a b)=f(d) \cdot\left(f\left(\frac{a}{d}\right)+f\left(\frac{b}{d}\right)\right),
$$
Determine all possible values of $f(2001)$.
|
Answer: 0 and $\frac{1}{2}$.
Obviously the constant functions $f(n)=0$ and $f(n)=\frac{1}{2}$ provide solutions.
We show that there are no other solutions. Assume $f(2001) \neq 0$. Since $2001=3 \cdot 667$ and $\operatorname{gcd}(3,667)=1$, then
$$
f(2001)=f(1) \cdot(f(3)+f(667)),
$$
and $f(1) \neq 0$. Since $\operatorname{gcd}(2001,2001)=2001$ then
$$
f\left(2001^{2}\right)=f(2001)(2 \cdot f(1)) \neq 0 .
$$
Also $\operatorname{gcd}\left(2001,2001^{3}\right)=2001$, so
$$
f\left(2001^{4}\right)=f(2001) \cdot\left(f(1)+f\left(2001^{2}\right)\right)=f(1) f(2001)(1+2 f(2001))
$$
On the other hand, $\operatorname{gcd}\left(2001^{2}, 2001^{2}\right)=2001^{2}$ and
$$
f\left(2001^{4}\right)=f\left(2001^{2}\right) \cdot(f(1)+f(1))=2 f(1) f\left(2001^{2}\right)=4 f(1)^{2} f(2001) .
$$
So $4 f(1)=1+2 f(2001)$ and $f(2001)=2 f(1)-\frac{1}{2}$. Exactly the same
argument starting from $f\left(2001^{2}\right) \neq 0$ instead of $f(2001)$ shows that $f\left(2001^{2}\right)=2 f(1)-\frac{1}{2}$. So
$$
2 f(1)-\frac{1}{2}=2 f(1)\left(2 f(1)-\frac{1}{2}\right) \text {. }
$$
Since $2 f(1)-\frac{1}{2}=f(2001) \neq 0$, we have $f(1)=\frac{1}{2}$, which implies $f(2001)=2 f(1)-\frac{1}{2}=\frac{1}{2}$.
|
\frac{1}{2}
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
The real-valued function $f$ is defined for all positive integers. For any integers $a>1, b>1$ with $d=\operatorname{gcd}(a, b)$, we have
$$
f(a b)=f(d) \cdot\left(f\left(\frac{a}{d}\right)+f\left(\frac{b}{d}\right)\right),
$$
Determine all possible values of $f(2001)$.
|
Answer: 0 and $\frac{1}{2}$.
Obviously the constant functions $f(n)=0$ and $f(n)=\frac{1}{2}$ provide solutions.
We show that there are no other solutions. Assume $f(2001) \neq 0$. Since $2001=3 \cdot 667$ and $\operatorname{gcd}(3,667)=1$, then
$$
f(2001)=f(1) \cdot(f(3)+f(667)),
$$
and $f(1) \neq 0$. Since $\operatorname{gcd}(2001,2001)=2001$ then
$$
f\left(2001^{2}\right)=f(2001)(2 \cdot f(1)) \neq 0 .
$$
Also $\operatorname{gcd}\left(2001,2001^{3}\right)=2001$, so
$$
f\left(2001^{4}\right)=f(2001) \cdot\left(f(1)+f\left(2001^{2}\right)\right)=f(1) f(2001)(1+2 f(2001))
$$
On the other hand, $\operatorname{gcd}\left(2001^{2}, 2001^{2}\right)=2001^{2}$ and
$$
f\left(2001^{4}\right)=f\left(2001^{2}\right) \cdot(f(1)+f(1))=2 f(1) f\left(2001^{2}\right)=4 f(1)^{2} f(2001) .
$$
So $4 f(1)=1+2 f(2001)$ and $f(2001)=2 f(1)-\frac{1}{2}$. Exactly the same
argument starting from $f\left(2001^{2}\right) \neq 0$ instead of $f(2001)$ shows that $f\left(2001^{2}\right)=2 f(1)-\frac{1}{2}$. So
$$
2 f(1)-\frac{1}{2}=2 f(1)\left(2 f(1)-\frac{1}{2}\right) \text {. }
$$
Since $2 f(1)-\frac{1}{2}=f(2001) \neq 0$, we have $f(1)=\frac{1}{2}$, which implies $f(2001)=2 f(1)-\frac{1}{2}=\frac{1}{2}$.
|
{
"resource_path": "BalticWay/segmented/en-bw01sol.jsonl",
"problem_match": "\n11.",
"solution_match": "\n11."
}
|
316d3633-64b3-5913-a882-033261197b3b
| 240,211
|
Let $f$ be a real-valued function defined on the positive integers satisfying the following condition: For all $n>1$ there exists a prime divisor $p$ of $n$ such that
$$
f(n)=f\left(\frac{n}{p}\right)-f(p)
$$
Given that $f(2001)=1$, what is the value of $f(2002)$ ?
|
Answer: 2.
For any prime $p$ we have $f(p)=f(1)-f(p)$ and thus $f(p)=\frac{f(1)}{2}$. If $n$ is a product of two primes $p$ and $q$, then $f(n)=f(p)-f(q)$ or $f(n)=f(q)-f(p)$, so $f(n)=0$. By the same reasoning we find that if $n$ is a product of three primes, then there is a prime $p$ such that
$$
f(n)=f\left(\frac{n}{p}\right)-f(p)=-f(p)=-\frac{f(1)}{2} .
$$
By simple induction we can show that if $n$ is the product of $k$ primes, then $f(n)=(2-k) \cdot \frac{f(1)}{2}$. In particular, $f(2001)=f(3 \cdot 23 \cdot 29)=1$ so $f(1)=-2$. Therefore, $f(2002)=f(2 \cdot 7 \cdot 11 \cdot 13)=-f(1)=2$.
|
2
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Let $f$ be a real-valued function defined on the positive integers satisfying the following condition: For all $n>1$ there exists a prime divisor $p$ of $n$ such that
$$
f(n)=f\left(\frac{n}{p}\right)-f(p)
$$
Given that $f(2001)=1$, what is the value of $f(2002)$ ?
|
Answer: 2.
For any prime $p$ we have $f(p)=f(1)-f(p)$ and thus $f(p)=\frac{f(1)}{2}$. If $n$ is a product of two primes $p$ and $q$, then $f(n)=f(p)-f(q)$ or $f(n)=f(q)-f(p)$, so $f(n)=0$. By the same reasoning we find that if $n$ is a product of three primes, then there is a prime $p$ such that
$$
f(n)=f\left(\frac{n}{p}\right)-f(p)=-f(p)=-\frac{f(1)}{2} .
$$
By simple induction we can show that if $n$ is the product of $k$ primes, then $f(n)=(2-k) \cdot \frac{f(1)}{2}$. In particular, $f(2001)=f(3 \cdot 23 \cdot 29)=1$ so $f(1)=-2$. Therefore, $f(2002)=f(2 \cdot 7 \cdot 11 \cdot 13)=-f(1)=2$.
|
{
"resource_path": "BalticWay/segmented/en-bw01sol.jsonl",
"problem_match": "\n16.",
"solution_match": "\n16."
}
|
63249da3-fd82-594e-b5b4-726b15645a5c
| 605,042
|
What is the smallest positive odd integer having the same number of positive divisors as 360 ?
|
Answer: 31185 .
An integer with the prime factorization $p_{1}^{r_{1}} \cdot p_{2}^{r_{2}} \cdot \ldots \cdot p_{k}^{r_{k}}$ (where $p_{1}, p_{2}, \ldots$, $p_{k}$ are distinct primes) has precisely $\left(r_{1}+1\right) \cdot\left(r_{2}+1\right) \cdot \ldots \cdot\left(r_{k}+1\right)$ distinct positive divisors. Since $360=2^{3} \cdot 3^{2} \cdot 5$, it follows that 360 has $4 \cdot 3 \cdot 2=24$ positive divisors. Since $24=3 \cdot 2 \cdot 2 \cdot 2$, it is easy to check that the smallest odd number with 24 positive divisors is $3^{2} \cdot 5 \cdot 7 \cdot 11=31185$.
|
31185
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
What is the smallest positive odd integer having the same number of positive divisors as 360 ?
|
Answer: 31185 .
An integer with the prime factorization $p_{1}^{r_{1}} \cdot p_{2}^{r_{2}} \cdot \ldots \cdot p_{k}^{r_{k}}$ (where $p_{1}, p_{2}, \ldots$, $p_{k}$ are distinct primes) has precisely $\left(r_{1}+1\right) \cdot\left(r_{2}+1\right) \cdot \ldots \cdot\left(r_{k}+1\right)$ distinct positive divisors. Since $360=2^{3} \cdot 3^{2} \cdot 5$, it follows that 360 has $4 \cdot 3 \cdot 2=24$ positive divisors. Since $24=3 \cdot 2 \cdot 2 \cdot 2$, it is easy to check that the smallest odd number with 24 positive divisors is $3^{2} \cdot 5 \cdot 7 \cdot 11=31185$.
|
{
"resource_path": "BalticWay/segmented/en-bw01sol.jsonl",
"problem_match": "\n19.",
"solution_match": "\n19."
}
|
cc624072-0d9c-5339-981c-b2708ba14fe4
| 605,096
|
End of preview. Expand
in Data Studio
README.md exists but content is empty.
- Downloads last month
- 6