problem
stringlengths 14
7.96k
| solution
stringlengths 3
10k
| answer
stringlengths 1
91
| problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | question_type
stringclasses 1
value | problem_type
stringclasses 8
values | problem_raw
stringlengths 14
7.96k
| solution_raw
stringlengths 3
10k
| metadata
dict | uuid
stringlengths 36
36
| id
int64 22.6k
612k
|
|---|---|---|---|---|---|---|---|---|---|---|---|
Find the largest value of the expression
$$
x y+x \sqrt{1-y^{2}}+y \sqrt{1-x^{2}}-\sqrt{\left(1-x^{2}\right)\left(1-y^{2}\right)}
$$
|
The expression is well-defined only for $|x|,|y| \leq 1$ and we can assume that $x, y \geq 0$. Let $x=\cos \alpha$ and $y=\cos \beta$ for some $0 \leq \alpha, \beta \leq \frac{\pi}{2}$. This reduces the expression to
$$
\cos \alpha \cos \beta+\cos \alpha \sin \beta+\cos \beta \sin \alpha-\sin \alpha \sin \beta=\cos (\alpha+\beta)+\sin (\alpha+\beta)=\sqrt{2} \cdot \sin \left(\alpha+\beta+\frac{\pi}{4}\right)
$$
which does not exceed $\sqrt{2}$. The equality holds when $\alpha+\beta+\frac{\pi}{4}=\frac{\pi}{2}$, for example when $\alpha=\frac{\pi}{4}$ and $\beta=0$, i.e., $x=\frac{\sqrt{2}}{2}$ and $y=1$.
|
\sqrt{2}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Find the largest value of the expression
$$
x y+x \sqrt{1-y^{2}}+y \sqrt{1-x^{2}}-\sqrt{\left(1-x^{2}\right)\left(1-y^{2}\right)}
$$
|
The expression is well-defined only for $|x|,|y| \leq 1$ and we can assume that $x, y \geq 0$. Let $x=\cos \alpha$ and $y=\cos \beta$ for some $0 \leq \alpha, \beta \leq \frac{\pi}{2}$. This reduces the expression to
$$
\cos \alpha \cos \beta+\cos \alpha \sin \beta+\cos \beta \sin \alpha-\sin \alpha \sin \beta=\cos (\alpha+\beta)+\sin (\alpha+\beta)=\sqrt{2} \cdot \sin \left(\alpha+\beta+\frac{\pi}{4}\right)
$$
which does not exceed $\sqrt{2}$. The equality holds when $\alpha+\beta+\frac{\pi}{4}=\frac{\pi}{2}$, for example when $\alpha=\frac{\pi}{4}$ and $\beta=0$, i.e., $x=\frac{\sqrt{2}}{2}$ and $y=1$.
|
{
"resource_path": "BalticWay/segmented/en-bw94sol.jsonl",
"problem_match": "\n3.",
"solution_match": "\nSolution."
}
|
44e17754-419b-5c32-9df1-2e9e34ced892
| 606,375
|
How many positive integers satisfy the following three conditions:
(i) All digits of the number are from the set $\{1,2,3,4,5\}$;
(ii) The absolute value of the difference between any two consecutive digits is 1 ;
(iii) The integer has 1994 digits?
|
Consider all positive integers with $2 n$ digits satisfying conditions $(i)$ and (ii) of the problem. Let the number of such integers beginning with $1,2,3,4$ and 5 be $a_{n}, b_{n}, c_{n}, d_{n}$ and $e_{n}$, respectively. Then, for $n=1$ we have $a_{1}=1$ (integer 12), $b_{1}=2$ (integers 21 and 23), $c_{1}=2$ (integers 32 and 34$), d_{1}=2$ (integers 43 and 45) and $e_{1}=1$ (integer 54). Observe that $c_{1}=a_{1}+e_{1}$.
Suppose now that $n>1$, i.e., the integers have at least four digits. If an integer begins with the digit 1 then the second digit is 2 while the third can be 1 or 3 . This gives the relation
$$
a_{n}=a_{n-1}+c_{n-1} \text {. }
$$
Similarly, if the first digit is 5 , then the second is 4 while the third can be 3 or 5 . This implies
$$
e_{n}=c_{n-1}+e_{n-1}
$$
If the integer begins with 23 then the third digit is 2 or 4 . If the integer begins with 21 then the third digit is 2 . From this we can conclude that
$$
b_{n}=2 b_{n-1}+d_{n-1} \text {. }
$$
In the same manner we can show that
$$
d_{n}=b_{n-1}+2 d_{n-1} .
$$
If the integer begins with 32 then the third digit must be 1 or 3 , and if it begins with 34 the third digit is 3 or 5 . Hence
$$
c_{n}=a_{n-1}+2 c_{n-1}+e_{n-1} \text {. }
$$
From (1), (2) and (5) it follows that $c_{n}=a_{n}+e_{n}$, which is true for all $n \geq 1$. On the other hand, adding the relations (1)-(5) results in
$$
a_{n}+b_{n}+c_{n}+d_{n}+e_{n}=2 a_{n-1}+3 b_{n-1}+4 c_{n-1}+3 d_{n-1}+2 e_{n-1}
$$
and, since $c_{n-1}=a_{n-1}+e_{n-1}$,
$$
a_{n}+b_{n}+c_{n}+d_{n}+e_{n}=3\left(a_{n-1}+b_{n-1}+c_{n-1}+d_{n-1}+e_{n-1}\right)
$$
Thus the number of integers satisfying conditions $(i)$ and $(i i)$ increases three times when we increase the number of digits by 2 . Since the number of such integers with two digits is 8 , and $1994=2+2 \cdot 996$, the number of integers satisfying all three conditions is $8 \cdot 3^{996}$.
|
8 \cdot 3^{996}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
How many positive integers satisfy the following three conditions:
(i) All digits of the number are from the set $\{1,2,3,4,5\}$;
(ii) The absolute value of the difference between any two consecutive digits is 1 ;
(iii) The integer has 1994 digits?
|
Consider all positive integers with $2 n$ digits satisfying conditions $(i)$ and (ii) of the problem. Let the number of such integers beginning with $1,2,3,4$ and 5 be $a_{n}, b_{n}, c_{n}, d_{n}$ and $e_{n}$, respectively. Then, for $n=1$ we have $a_{1}=1$ (integer 12), $b_{1}=2$ (integers 21 and 23), $c_{1}=2$ (integers 32 and 34$), d_{1}=2$ (integers 43 and 45) and $e_{1}=1$ (integer 54). Observe that $c_{1}=a_{1}+e_{1}$.
Suppose now that $n>1$, i.e., the integers have at least four digits. If an integer begins with the digit 1 then the second digit is 2 while the third can be 1 or 3 . This gives the relation
$$
a_{n}=a_{n-1}+c_{n-1} \text {. }
$$
Similarly, if the first digit is 5 , then the second is 4 while the third can be 3 or 5 . This implies
$$
e_{n}=c_{n-1}+e_{n-1}
$$
If the integer begins with 23 then the third digit is 2 or 4 . If the integer begins with 21 then the third digit is 2 . From this we can conclude that
$$
b_{n}=2 b_{n-1}+d_{n-1} \text {. }
$$
In the same manner we can show that
$$
d_{n}=b_{n-1}+2 d_{n-1} .
$$
If the integer begins with 32 then the third digit must be 1 or 3 , and if it begins with 34 the third digit is 3 or 5 . Hence
$$
c_{n}=a_{n-1}+2 c_{n-1}+e_{n-1} \text {. }
$$
From (1), (2) and (5) it follows that $c_{n}=a_{n}+e_{n}$, which is true for all $n \geq 1$. On the other hand, adding the relations (1)-(5) results in
$$
a_{n}+b_{n}+c_{n}+d_{n}+e_{n}=2 a_{n-1}+3 b_{n-1}+4 c_{n-1}+3 d_{n-1}+2 e_{n-1}
$$
and, since $c_{n-1}=a_{n-1}+e_{n-1}$,
$$
a_{n}+b_{n}+c_{n}+d_{n}+e_{n}=3\left(a_{n-1}+b_{n-1}+c_{n-1}+d_{n-1}+e_{n-1}\right)
$$
Thus the number of integers satisfying conditions $(i)$ and $(i i)$ increases three times when we increase the number of digits by 2 . Since the number of such integers with two digits is 8 , and $1994=2+2 \cdot 996$, the number of integers satisfying all three conditions is $8 \cdot 3^{996}$.
|
{
"resource_path": "BalticWay/segmented/en-bw94sol.jsonl",
"problem_match": "\n10.",
"solution_match": "\nSolution."
}
|
09980f99-33ca-5862-b4ae-250d34376d6b
| 241,370
|
Find the smallest number $a$ such that a square of side $a$ can contain five disks of radius 1 so that no two of the disks have a common interior point.
|
Let $P Q R S$ be a square which has the property described in the problem. Clearly, $a>2$. Let $P^{\prime} Q^{\prime} R^{\prime} S^{\prime}$ be the square inside $P Q R S$ whose sides are at distance 1 from the sides of $P Q R S$, and, consequently, are of length $a-2$. Since all the five disks are inside $P Q R S$, their centres are inside $P^{\prime} Q^{\prime} R^{\prime} S^{\prime}$. Divide $P^{\prime} Q^{\prime} R^{\prime} S^{\prime}$ into four congruent squares of side length $\frac{a}{2}-1$. By the pigeonhole principle, at least two of the five centres are in the same small square. Their distance, then, is at most $\sqrt{2}\left(\frac{a}{2}-1\right)$. Since the distance has to be at least 2 , we have $a \geq 2+2 \sqrt{2}$. On the other hand, if $a=2+2 \sqrt{2}$, we can place the five disks in such a way that one is centred at the centre of $P Q R S$ and the other four have centres at $P^{\prime}, Q^{\prime}$, $R^{\prime}$ and $S^{\prime}$.
|
2+2\sqrt{2}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Find the smallest number $a$ such that a square of side $a$ can contain five disks of radius 1 so that no two of the disks have a common interior point.
|
Let $P Q R S$ be a square which has the property described in the problem. Clearly, $a>2$. Let $P^{\prime} Q^{\prime} R^{\prime} S^{\prime}$ be the square inside $P Q R S$ whose sides are at distance 1 from the sides of $P Q R S$, and, consequently, are of length $a-2$. Since all the five disks are inside $P Q R S$, their centres are inside $P^{\prime} Q^{\prime} R^{\prime} S^{\prime}$. Divide $P^{\prime} Q^{\prime} R^{\prime} S^{\prime}$ into four congruent squares of side length $\frac{a}{2}-1$. By the pigeonhole principle, at least two of the five centres are in the same small square. Their distance, then, is at most $\sqrt{2}\left(\frac{a}{2}-1\right)$. Since the distance has to be at least 2 , we have $a \geq 2+2 \sqrt{2}$. On the other hand, if $a=2+2 \sqrt{2}$, we can place the five disks in such a way that one is centred at the centre of $P Q R S$ and the other four have centres at $P^{\prime}, Q^{\prime}$, $R^{\prime}$ and $S^{\prime}$.
|
{
"resource_path": "BalticWay/segmented/en-bw94sol.jsonl",
"problem_match": "\n13.",
"solution_match": "\nSolution."
}
|
ca9fda1c-1549-5350-9ddd-c54cf8fe03a9
| 241,398
|
In a certain kingdom, the king has decided to build 25 new towns on 13 uninhabited islands so that on each island there will be at least one town. Direct ferry connections will be established between any pair of new towns which are on different islands. Determine the least possible number of these connections.
|
Let $a_{1}, \ldots, a_{13}$ be the numbers of towns on each island. Suppose there exist numbers $i$ and $j$ such that $a_{i} \geq a_{j}>1$ and consider an arbitrary town $A$ on the $j$-th island. The number of ferry connections from town $A$ is equal to $25-a_{j}$. On the other hand, if we "move" town $A$ to the $i$-th island then there will be $25-\left(a_{i}+1\right)$ connections from town $A$ while no other connections will be affected by this move. Hence, the smallest number of connections will be achieved if there are 13 towns on one island and one town on each of the other 12 islands. In this case there will be $13 \cdot 12+\frac{12 \cdot 11}{2}=222$ connections.
|
222
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
In a certain kingdom, the king has decided to build 25 new towns on 13 uninhabited islands so that on each island there will be at least one town. Direct ferry connections will be established between any pair of new towns which are on different islands. Determine the least possible number of these connections.
|
Let $a_{1}, \ldots, a_{13}$ be the numbers of towns on each island. Suppose there exist numbers $i$ and $j$ such that $a_{i} \geq a_{j}>1$ and consider an arbitrary town $A$ on the $j$-th island. The number of ferry connections from town $A$ is equal to $25-a_{j}$. On the other hand, if we "move" town $A$ to the $i$-th island then there will be $25-\left(a_{i}+1\right)$ connections from town $A$ while no other connections will be affected by this move. Hence, the smallest number of connections will be achieved if there are 13 towns on one island and one town on each of the other 12 islands. In this case there will be $13 \cdot 12+\frac{12 \cdot 11}{2}=222$ connections.
|
{
"resource_path": "BalticWay/segmented/en-bw94sol.jsonl",
"problem_match": "\n17.",
"solution_match": "\nSolution."
}
|
bcb3d819-d743-54ce-996b-c1755b1d5003
| 241,438
|
In how many ways can the set of integers $\{1,2, \ldots, 1995\}$ be partitioned into three nonempty sets so that none of these sets contains two consecutive integers?
|
We construct the three subsets by adding the numbers successively, and disregard at first the condition that the sets must be non-empty. The numbers 1 and 2 must belong to two different subsets, say $A$ and $B$. We then have two choices for each of the numbers $3,4, \ldots, 1995$, and different choices lead to different partitions. Hence there are $2^{1993}$ such partitions, one of which has an empty part. The number of partitions satisfying the requirements of the problem is therefore $2^{1993}-1$.
|
2^{1993}-1
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
In how many ways can the set of integers $\{1,2, \ldots, 1995\}$ be partitioned into three nonempty sets so that none of these sets contains two consecutive integers?
|
We construct the three subsets by adding the numbers successively, and disregard at first the condition that the sets must be non-empty. The numbers 1 and 2 must belong to two different subsets, say $A$ and $B$. We then have two choices for each of the numbers $3,4, \ldots, 1995$, and different choices lead to different partitions. Hence there are $2^{1993}$ such partitions, one of which has an empty part. The number of partitions satisfying the requirements of the problem is therefore $2^{1993}-1$.
|
{
"resource_path": "BalticWay/segmented/en-bw95sol.jsonl",
"problem_match": "\n11.",
"solution_match": "\nSolution."
}
|
76a6373e-7eb7-5d9f-b4cc-e5d71a00087e
| 241,575
|
In the triangle $A B C$, let $l$ be the bisector of the external angle at $C$. The line through the midpoint $O$ of the segment $A B$ parallel to $l$ meets the line $A C$ at $E$. Determine $|C E|$, if $|A C|=7$ and $|C B|=4$.
|
Let $F$ be the intersection point of $l$ and the line $A B$. Since $|A C|>|B C|$, the point $E$ lies on the segment $A C$, and $F$ lies on the ray $A B$. Let the line through $B$ parallel to $A C$ meet $C F$ at $G$. Then the triangles $A F C$ and $B F G$ are similar. Moreover, we have $\angle B G C=\angle B C G$, and hence the triangle $C B G$ is isosceles with $|B C|=|B G|$. Hence $\frac{|F A|}{|F B|}=\frac{|A C|}{|B G|}=\frac{|A C|}{|B C|}=\frac{7}{4}$. Therefore $\frac{|A O|}{|A F|}=\frac{3}{2} / 7=\frac{3}{14}$. Since the triangles $A C F$ and $A E O$ are similar, $\frac{|A E|}{|A C|}=\frac{|A O|}{|A F|}=\frac{3}{14}$, whence $|A E|=\frac{3}{2}$ and $|E C|=\frac{11}{2}$.
|
\frac{11}{2}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
In the triangle $A B C$, let $l$ be the bisector of the external angle at $C$. The line through the midpoint $O$ of the segment $A B$ parallel to $l$ meets the line $A C$ at $E$. Determine $|C E|$, if $|A C|=7$ and $|C B|=4$.
|
Let $F$ be the intersection point of $l$ and the line $A B$. Since $|A C|>|B C|$, the point $E$ lies on the segment $A C$, and $F$ lies on the ray $A B$. Let the line through $B$ parallel to $A C$ meet $C F$ at $G$. Then the triangles $A F C$ and $B F G$ are similar. Moreover, we have $\angle B G C=\angle B C G$, and hence the triangle $C B G$ is isosceles with $|B C|=|B G|$. Hence $\frac{|F A|}{|F B|}=\frac{|A C|}{|B G|}=\frac{|A C|}{|B C|}=\frac{7}{4}$. Therefore $\frac{|A O|}{|A F|}=\frac{3}{2} / 7=\frac{3}{14}$. Since the triangles $A C F$ and $A E O$ are similar, $\frac{|A E|}{|A C|}=\frac{|A O|}{|A F|}=\frac{3}{14}$, whence $|A E|=\frac{3}{2}$ and $|E C|=\frac{11}{2}$.
|
{
"resource_path": "BalticWay/segmented/en-bw95sol.jsonl",
"problem_match": "\n16.",
"solution_match": "\nSolution."
}
|
f846fbab-0645-55e9-8997-90d8006a7be0
| 241,632
|
The following construction is used for training astronauts: A circle $C_{2}$ of radius $2 R$ rolls along the inside of another, fixed circle $C_{1}$ of radius $n R$, where $n$ is an integer greater than 2 . The astronaut is fastened to a third circle $C_{3}$ of radius $R$ which rolls along the inside of circle $C_{2}$ in such a way that the touching point of the circles $C_{2}$ and $C_{3}$ remains at maximum distance from the touching point of the circles $C_{1}$ and $C_{2}$ at all times (see Figure 3).
How many revolutions (relative to the ground) does the astronaut perform together with the circle $C_{3}$ while the circle $C_{2}$ completes one full lap around the inside of circle $C_{1}$ ?
|
Consider a circle $C_{4}$ with radius $R$ that rolls inside $C_{2}$ in such a way that the two circles always touch in the point opposite to the touching point of $C_{2}$ and $C_{3}$. Then the circles $C_{3}$ and $C_{4}$ follow each other and make the same number of revolutions, and so we will assume that the astronaut is inside the circle $C_{4}$ instead. But the touching point of $C_{2}$ and $C_{4}$ coincides with the touching point of $C_{1}$ and $C_{2}$. Hence the circles $C_{4}$ and $C_{1}$ always touch each other, and we can disregard the circle $C_{2}$ completely.
Suppose the circle $C_{4}$ rolls inside $C_{1}$ in counterclockwise direction. Then the astronaut revolves in clockwise direction. If the circle $C_{4}$ had rolled along a straight line of length $2 \pi n R$ (instead of the inside of $C_{1}$ ), the circle $C_{4}$ would have made $n$ revolutions during its movement. As the path of the circle $C_{4}$ makes a $360^{\circ}$ counterclockwise turn itself, the total number of revolutions of the astronaut relative to the ground is $n-1$.
Remark: The radius of the intermediate circle $C_{2}$ is irrelevant. Moreover, for any number of intermediate circles the answer remains the same, depending only on the radii of the outermost and innermost circles.
|
n-1
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
The following construction is used for training astronauts: A circle $C_{2}$ of radius $2 R$ rolls along the inside of another, fixed circle $C_{1}$ of radius $n R$, where $n$ is an integer greater than 2 . The astronaut is fastened to a third circle $C_{3}$ of radius $R$ which rolls along the inside of circle $C_{2}$ in such a way that the touching point of the circles $C_{2}$ and $C_{3}$ remains at maximum distance from the touching point of the circles $C_{1}$ and $C_{2}$ at all times (see Figure 3).
How many revolutions (relative to the ground) does the astronaut perform together with the circle $C_{3}$ while the circle $C_{2}$ completes one full lap around the inside of circle $C_{1}$ ?
|
Consider a circle $C_{4}$ with radius $R$ that rolls inside $C_{2}$ in such a way that the two circles always touch in the point opposite to the touching point of $C_{2}$ and $C_{3}$. Then the circles $C_{3}$ and $C_{4}$ follow each other and make the same number of revolutions, and so we will assume that the astronaut is inside the circle $C_{4}$ instead. But the touching point of $C_{2}$ and $C_{4}$ coincides with the touching point of $C_{1}$ and $C_{2}$. Hence the circles $C_{4}$ and $C_{1}$ always touch each other, and we can disregard the circle $C_{2}$ completely.
Suppose the circle $C_{4}$ rolls inside $C_{1}$ in counterclockwise direction. Then the astronaut revolves in clockwise direction. If the circle $C_{4}$ had rolled along a straight line of length $2 \pi n R$ (instead of the inside of $C_{1}$ ), the circle $C_{4}$ would have made $n$ revolutions during its movement. As the path of the circle $C_{4}$ makes a $360^{\circ}$ counterclockwise turn itself, the total number of revolutions of the astronaut relative to the ground is $n-1$.
Remark: The radius of the intermediate circle $C_{2}$ is irrelevant. Moreover, for any number of intermediate circles the answer remains the same, depending only on the radii of the outermost and innermost circles.
|
{
"resource_path": "BalticWay/segmented/en-bw95sol.jsonl",
"problem_match": "\n19.",
"solution_match": "\nSolution."
}
|
3fdb652a-896b-55a5-aead-6d34dcebcbfb
| 604,556
|
In the figure below, you see three half-circles. The circle $C$ is tangent to two of the half-circles and to the line $P Q$ perpendicular to the diameter $A B$. The area of the shaded region is $39 \pi$, and the area of the circle $C$ is $9 \pi$. Find the length of the diameter $A B$.

Figure 1
|
Let $r$ and $s$ be the radii of the half-circles with diameters $A P$ and $B P$. Then we have
$$
39 \pi=\frac{\pi}{2}\left((r+s)^{2}-r^{2}-s^{2}\right)-9 \pi
$$
hence $r s=48$. Let $M$ be the midpoint of the diameter $A B, N$ be the midpoint of $P B, O$ be the centre of the circle $C$, and let $F$ be the orthogonal projection of $O$ on $A B$. Since the radius of $C$ is 3 , we have $|M O|=r+s-3,|M F|=r-s+3,|O N|=s+3$, and $|F N|=s-3$.
Applying the Pythagorean theorem to the triangles $M F O$ and $N F O$ yields
$$
(r+s-3)^{2}-(r-s+3)^{2}=|O F|^{2}=(s+3)^{2}-(s-3)^{2},
$$
which implies $r(s-3)=3 s$, so that $3(r+s)=r s=48$. Hence $|A B|=2(r+s)=32$.
|
32
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
In the figure below, you see three half-circles. The circle $C$ is tangent to two of the half-circles and to the line $P Q$ perpendicular to the diameter $A B$. The area of the shaded region is $39 \pi$, and the area of the circle $C$ is $9 \pi$. Find the length of the diameter $A B$.

Figure 1
|
Let $r$ and $s$ be the radii of the half-circles with diameters $A P$ and $B P$. Then we have
$$
39 \pi=\frac{\pi}{2}\left((r+s)^{2}-r^{2}-s^{2}\right)-9 \pi
$$
hence $r s=48$. Let $M$ be the midpoint of the diameter $A B, N$ be the midpoint of $P B, O$ be the centre of the circle $C$, and let $F$ be the orthogonal projection of $O$ on $A B$. Since the radius of $C$ is 3 , we have $|M O|=r+s-3,|M F|=r-s+3,|O N|=s+3$, and $|F N|=s-3$.
Applying the Pythagorean theorem to the triangles $M F O$ and $N F O$ yields
$$
(r+s-3)^{2}-(r-s+3)^{2}=|O F|^{2}=(s+3)^{2}-(s-3)^{2},
$$
which implies $r(s-3)=3 s$, so that $3(r+s)=r s=48$. Hence $|A B|=2(r+s)=32$.
|
{
"resource_path": "BalticWay/segmented/en-bw96sol.jsonl",
"problem_match": "\n2.",
"solution_match": "\nSolution."
}
|
1eecb2b3-3d72-530e-9c46-2fc16f5e37a7
| 604,613
|
Consider the sequence
$$
\begin{aligned}
x_{1} & =19, \\
x_{2} & =95, \\
x_{n+2} & =\operatorname{lcm}\left(x_{n+1}, x_{n}\right)+x_{n},
\end{aligned}
$$
for $n>1$, where $\operatorname{lcm}(a, b)$ means the least common multiple of $a$ and $b$. Find the greatest common divisor of $x_{1995}$ and $x_{1996}$.
|
Let $d=\operatorname{gcd}\left(x_{k}, x_{k+1}\right)$. Then $\operatorname{lcm}\left(x_{k}, x_{k+1}\right)=x_{k} x_{k+1} / d$, and
$$
\operatorname{gcd}\left(x_{k+1}, x_{k+2}\right)=\operatorname{gcd}\left(x_{k+1}, \frac{x_{k} x_{k+1}}{d}+x_{k}\right)=\operatorname{gcd}\left(x_{k+1}, \frac{x_{k}}{d}\left(x_{k+1}+d\right)\right) .
$$
Since $x_{k+1}$ and $x_{k} / d$ are relatively prime, this equals $\operatorname{gcd}\left(x_{k+1}, x_{k+1}+d\right)=d$. It follows by induction that $\operatorname{gcd}\left(x_{n}, x_{n+1}\right)=\operatorname{gcd}\left(x_{1}, x_{2}\right)=19$ for all $n \geq 1$. Hence $\operatorname{gcd}\left(x_{1995}, x_{1996}\right)=19$.
|
19
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Consider the sequence
$$
\begin{aligned}
x_{1} & =19, \\
x_{2} & =95, \\
x_{n+2} & =\operatorname{lcm}\left(x_{n+1}, x_{n}\right)+x_{n},
\end{aligned}
$$
for $n>1$, where $\operatorname{lcm}(a, b)$ means the least common multiple of $a$ and $b$. Find the greatest common divisor of $x_{1995}$ and $x_{1996}$.
|
Let $d=\operatorname{gcd}\left(x_{k}, x_{k+1}\right)$. Then $\operatorname{lcm}\left(x_{k}, x_{k+1}\right)=x_{k} x_{k+1} / d$, and
$$
\operatorname{gcd}\left(x_{k+1}, x_{k+2}\right)=\operatorname{gcd}\left(x_{k+1}, \frac{x_{k} x_{k+1}}{d}+x_{k}\right)=\operatorname{gcd}\left(x_{k+1}, \frac{x_{k}}{d}\left(x_{k+1}+d\right)\right) .
$$
Since $x_{k+1}$ and $x_{k} / d$ are relatively prime, this equals $\operatorname{gcd}\left(x_{k+1}, x_{k+1}+d\right)=d$. It follows by induction that $\operatorname{gcd}\left(x_{n}, x_{n+1}\right)=\operatorname{gcd}\left(x_{1}, x_{2}\right)=19$ for all $n \geq 1$. Hence $\operatorname{gcd}\left(x_{1995}, x_{1996}\right)=19$.
|
{
"resource_path": "BalticWay/segmented/en-bw96sol.jsonl",
"problem_match": "\n8.",
"solution_match": "\nSolution."
}
|
96e18354-b1bf-56b8-b241-9d4fbdd1b52e
| 239,043
|
The graph of the function $f(x)=x^{n}+a_{n-1} x^{n-1}+\cdots+a_{1} x+a_{0}$ (where $n>1$ ), intersects the line $y=b$ at the points $B_{1}, B_{2}, \ldots, B_{n}$ (from left to right), and the line $y=c(c \neq b)$ at the points $C_{1}, C_{2}, \ldots, C_{n}$ (from left to right). Let $P$ be a point on the line $y=c$, to the right to the point $C_{n}$. Find the sum $\cot \angle B_{1} C_{1} P+\cdots+\cot \angle B_{n} C_{n} P$.
|
Let the points $B_{i}$ and $C_{i}$ have the coordinates $\left(b_{i}, b\right)$ and $\left(c_{i}, c\right)$, respectively, for $i=1,2, \ldots, n$. Then we have
$$
\cot \angle B_{1} C_{1} P+\cdots+\cot \angle B_{n} C_{n} P=\frac{1}{b-c} \sum_{i=1}^{n}\left(b_{i}-c_{i}\right)
$$
The numbers $b_{i}$ and $c_{i}$ are the solutions of $f(x)-b=0$ and $f(x)-c=0$, respectively. As $n \geq 2$, it follows from the relationships between the roots and coefficients of a polynomial (Viète's relations) that $\sum_{i=1}^{n} b_{i}=$ $\sum_{i=1}^{n} c_{i}=-a_{n-1}$ regardless of the values of $b$ and $c$, and hence $\cot \angle B_{1} C_{1} P+\cdots+\cot \angle B_{n} C_{n} P=0$.
|
0
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
The graph of the function $f(x)=x^{n}+a_{n-1} x^{n-1}+\cdots+a_{1} x+a_{0}$ (where $n>1$ ), intersects the line $y=b$ at the points $B_{1}, B_{2}, \ldots, B_{n}$ (from left to right), and the line $y=c(c \neq b)$ at the points $C_{1}, C_{2}, \ldots, C_{n}$ (from left to right). Let $P$ be a point on the line $y=c$, to the right to the point $C_{n}$. Find the sum $\cot \angle B_{1} C_{1} P+\cdots+\cot \angle B_{n} C_{n} P$.
|
Let the points $B_{i}$ and $C_{i}$ have the coordinates $\left(b_{i}, b\right)$ and $\left(c_{i}, c\right)$, respectively, for $i=1,2, \ldots, n$. Then we have
$$
\cot \angle B_{1} C_{1} P+\cdots+\cot \angle B_{n} C_{n} P=\frac{1}{b-c} \sum_{i=1}^{n}\left(b_{i}-c_{i}\right)
$$
The numbers $b_{i}$ and $c_{i}$ are the solutions of $f(x)-b=0$ and $f(x)-c=0$, respectively. As $n \geq 2$, it follows from the relationships between the roots and coefficients of a polynomial (Viète's relations) that $\sum_{i=1}^{n} b_{i}=$ $\sum_{i=1}^{n} c_{i}=-a_{n-1}$ regardless of the values of $b$ and $c$, and hence $\cot \angle B_{1} C_{1} P+\cdots+\cot \angle B_{n} C_{n} P=0$.
|
{
"resource_path": "BalticWay/segmented/en-bw96sol.jsonl",
"problem_match": "\n14.",
"solution_match": "\nSolution."
}
|
b2961022-3213-538b-b8e0-9cb3c8c57088
| 604,877
|
Using each of the eight digits $1,3,4,5,6,7,8$ and 9 exactly once, a three-digit number $A$, two twodigit numbers $B$ and $C, B<C$, and a one-digit number $D$ are formed. The numbers are such that $A+D=B+C=143$. In how many ways can this be done?
|
From $A=143-D$ and $1 \leq D \leq 9$, it follows that $134 \leq A \leq 142$. The hundreds digit of $A$ is therefore 1 , and the tens digit is either 3 or 4 . If the tens digit of $A$ is 4 , then the sum of the units digits of
$A$ and $D$ must be 3 , which is impossible, as the digits 0 and 2 are not among the eight digits given. Hence the first two digits of $A$ are uniquely determined as 1 and 3 . The sum of the units digits of $A$ and $D$ must be 13. This can be achieved in six different ways as $13=4+9=5+8=6+7=7+6=8+5=9+4$.
The sum of the units digits of $B$ and $C$ must again be 13, and as $B+C=143$, this must also be true for the tens digits. For each choice of the numbers $A$ and $D$, the remaining four digits form two pairs, both with the sum 13. The units digits of $B$ and $C$ may then be chosen in four ways. The tens digits are then uniquely determined by the remaining pair and the relation $B<C$. The total number of possibilities is therefore $6 \cdot 4=24$.
|
24
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Using each of the eight digits $1,3,4,5,6,7,8$ and 9 exactly once, a three-digit number $A$, two twodigit numbers $B$ and $C, B<C$, and a one-digit number $D$ are formed. The numbers are such that $A+D=B+C=143$. In how many ways can this be done?
|
From $A=143-D$ and $1 \leq D \leq 9$, it follows that $134 \leq A \leq 142$. The hundreds digit of $A$ is therefore 1 , and the tens digit is either 3 or 4 . If the tens digit of $A$ is 4 , then the sum of the units digits of
$A$ and $D$ must be 3 , which is impossible, as the digits 0 and 2 are not among the eight digits given. Hence the first two digits of $A$ are uniquely determined as 1 and 3 . The sum of the units digits of $A$ and $D$ must be 13. This can be achieved in six different ways as $13=4+9=5+8=6+7=7+6=8+5=9+4$.
The sum of the units digits of $B$ and $C$ must again be 13, and as $B+C=143$, this must also be true for the tens digits. For each choice of the numbers $A$ and $D$, the remaining four digits form two pairs, both with the sum 13. The units digits of $B$ and $C$ may then be chosen in four ways. The tens digits are then uniquely determined by the remaining pair and the relation $B<C$. The total number of possibilities is therefore $6 \cdot 4=24$.
|
{
"resource_path": "BalticWay/segmented/en-bw96sol.jsonl",
"problem_match": "\n17.",
"solution_match": "\nSolution."
}
|
6b39b3e1-1c65-5abe-9971-a2b47344aae8
| 604,917
|
Let $x_{1}=1$ and $x_{n+1}=x_{n}+\left\lfloor\frac{x_{n}}{n}\right\rfloor+2$ for $n=1,2,3, \ldots$, where $\lfloor x\rfloor$ denotes the largest integer not greater than $x$. Determine $x_{1997}$.
|
Answer: $x_{1997}=23913$.
Note that if $x_{n}=a n+b$ with $0 \leqslant b<n$, then
$$
x_{n+1}=x_{n}+a+2=a(n+1)+b+2 \text {. }
$$
Hence if $x_{N}=A N$ for some positive integers $A$ and $N$, then for $i=0,1, \ldots, N$ we have $x_{N+i}=A(N+i)+2 i$, and $x_{2 N}=(A+1) \cdot 2 N$. Since for $N=1$ the condition $x_{N}=A N$ holds with $A=1$, then for $N=2^{k}$ (where $k$ is any non-negative integer) it also holds with $A=k+1$. Now for $N=2^{10}=1024$ we have $A=11$ and $x_{N+i}=A(N+i)+2 i$, which for $i=973$ makes $x_{1997}=11 \cdot 1997+2 \cdot 973=23913$.
|
23913
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Let $x_{1}=1$ and $x_{n+1}=x_{n}+\left\lfloor\frac{x_{n}}{n}\right\rfloor+2$ for $n=1,2,3, \ldots$, where $\lfloor x\rfloor$ denotes the largest integer not greater than $x$. Determine $x_{1997}$.
|
Answer: $x_{1997}=23913$.
Note that if $x_{n}=a n+b$ with $0 \leqslant b<n$, then
$$
x_{n+1}=x_{n}+a+2=a(n+1)+b+2 \text {. }
$$
Hence if $x_{N}=A N$ for some positive integers $A$ and $N$, then for $i=0,1, \ldots, N$ we have $x_{N+i}=A(N+i)+2 i$, and $x_{2 N}=(A+1) \cdot 2 N$. Since for $N=1$ the condition $x_{N}=A N$ holds with $A=1$, then for $N=2^{k}$ (where $k$ is any non-negative integer) it also holds with $A=k+1$. Now for $N=2^{10}=1024$ we have $A=11$ and $x_{N+i}=A(N+i)+2 i$, which for $i=973$ makes $x_{1997}=11 \cdot 1997+2 \cdot 973=23913$.
|
{
"resource_path": "BalticWay/segmented/en-bw97sol.jsonl",
"problem_match": "\n3.",
"solution_match": "\n3."
}
|
eca6f684-fda7-5e2f-8d2e-5d1b89a50981
| 238,792
|
On two parallel lines, the distinct points $A_{1}, A_{2}, A_{3}, \ldots$ respectively $B_{1}$, $B_{2}, B_{3}, \ldots$ are marked in such a way that $\left|A_{i} A_{i+1}\right|=1$ and $\left|B_{i} B_{i+1}\right|=2$ for $i=1,2, \ldots$ (see Figure). Provided that $\angle A_{1} A_{2} B_{1}=\alpha$, find the infinite sum $\angle A_{1} B_{1} A_{2}+\angle A_{2} B_{2} A_{3}+\angle A_{3} B_{3} A_{4}+\ldots$
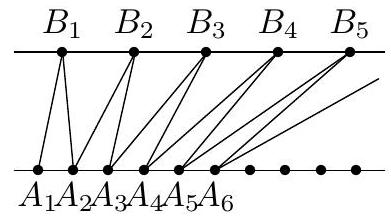
|
Answer: $\pi-\alpha$.
Let $C_{1}, C_{2}, C_{3}, \ldots$ be points on the upper line such that $\left|C_{i} C_{i+1}\right|=1$ and $B_{i}=C_{2 i}$ for each $i=1,2, \ldots$ (see Figure 2 ). Then for any $i=1,2, \ldots$ we have
$$
\angle A_{i} B_{i} A_{i+1}=\angle A_{i} C_{2 i} A_{i+1}=\angle A_{1} C_{i+1} A_{2}=\angle C_{i+1} A_{2} C_{i+2}
$$
Hence
$$
\begin{aligned}
& \angle A_{1} B_{1} A_{2}+\angle A_{2} B_{2} A_{3}+\angle A_{3} B_{3} A_{4}+\ldots= \\
& \quad=\angle C_{2} A_{2} C_{3}+\angle C_{3} A_{2} C_{4}+\angle C_{4} A_{2} C_{5}+\ldots=\pi-\alpha .
\end{aligned}
$$
|
\pi-\alpha
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
On two parallel lines, the distinct points $A_{1}, A_{2}, A_{3}, \ldots$ respectively $B_{1}$, $B_{2}, B_{3}, \ldots$ are marked in such a way that $\left|A_{i} A_{i+1}\right|=1$ and $\left|B_{i} B_{i+1}\right|=2$ for $i=1,2, \ldots$ (see Figure). Provided that $\angle A_{1} A_{2} B_{1}=\alpha$, find the infinite sum $\angle A_{1} B_{1} A_{2}+\angle A_{2} B_{2} A_{3}+\angle A_{3} B_{3} A_{4}+\ldots$

|
Answer: $\pi-\alpha$.
Let $C_{1}, C_{2}, C_{3}, \ldots$ be points on the upper line such that $\left|C_{i} C_{i+1}\right|=1$ and $B_{i}=C_{2 i}$ for each $i=1,2, \ldots$ (see Figure 2 ). Then for any $i=1,2, \ldots$ we have
$$
\angle A_{i} B_{i} A_{i+1}=\angle A_{i} C_{2 i} A_{i+1}=\angle A_{1} C_{i+1} A_{2}=\angle C_{i+1} A_{2} C_{i+2}
$$
Hence
$$
\begin{aligned}
& \angle A_{1} B_{1} A_{2}+\angle A_{2} B_{2} A_{3}+\angle A_{3} B_{3} A_{4}+\ldots= \\
& \quad=\angle C_{2} A_{2} C_{3}+\angle C_{3} A_{2} C_{4}+\angle C_{4} A_{2} C_{5}+\ldots=\pi-\alpha .
\end{aligned}
$$
|
{
"resource_path": "BalticWay/segmented/en-bw97sol.jsonl",
"problem_match": "\n11.",
"solution_match": "\n11."
}
|
9412b696-99e6-5e5c-9a7d-8da523925285
| 238,873
|
A rectangle can be divided into $n$ equal squares. The same rectangle can also be divided into $n+76$ equal squares. Find all possible values of $n$.
|
Answer: $n=324$.
Let $a b=n$ and $c d=n+76$, where $a, b$ and $c, d$ are the numbers of squares in each direction for the partitioning of the rectangle into $n$ and $n+76$ squares, respectively. Then $\frac{a}{c}=\frac{b}{d}$, or $a d=b c$. Denote $u=\operatorname{gcd}(a, c)$ ja $v=\operatorname{gcd}(b, d)$, then there exist positive integers $x$ and $y$ such that $\operatorname{gcd}(x, y)=1, a=u x, c=u y$ and $b=v x, d=v y$. Hence we have
$$
c d-a b=u v\left(y^{2}-x^{2}\right)=u v(y-x)(y+x)=76=2^{2} \cdot 19 .
$$
Since $y-x$ and $y+x$ are positive integers of the same parity and $\operatorname{gcd}(x, y)=1$, we have $y-x=1$ and $y+x=19$ as the only possibility, yielding $y=10, x=9$ and $u v=4$. Finally we have $n=a b=x^{2} u v=324$.
|
324
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
A rectangle can be divided into $n$ equal squares. The same rectangle can also be divided into $n+76$ equal squares. Find all possible values of $n$.
|
Answer: $n=324$.
Let $a b=n$ and $c d=n+76$, where $a, b$ and $c, d$ are the numbers of squares in each direction for the partitioning of the rectangle into $n$ and $n+76$ squares, respectively. Then $\frac{a}{c}=\frac{b}{d}$, or $a d=b c$. Denote $u=\operatorname{gcd}(a, c)$ ja $v=\operatorname{gcd}(b, d)$, then there exist positive integers $x$ and $y$ such that $\operatorname{gcd}(x, y)=1, a=u x, c=u y$ and $b=v x, d=v y$. Hence we have
$$
c d-a b=u v\left(y^{2}-x^{2}\right)=u v(y-x)(y+x)=76=2^{2} \cdot 19 .
$$
Since $y-x$ and $y+x$ are positive integers of the same parity and $\operatorname{gcd}(x, y)=1$, we have $y-x=1$ and $y+x=19$ as the only possibility, yielding $y=10, x=9$ and $u v=4$. Finally we have $n=a b=x^{2} u v=324$.
|
{
"resource_path": "BalticWay/segmented/en-bw97sol.jsonl",
"problem_match": "\n17.",
"solution_match": "\n17."
}
|
8595def0-06cc-5dca-b46a-13976499d6f4
| 605,317
|
We say that an integer $m$ covers the number 1998 if $1,9,9,8$ appear in this order as digits of $m$. (For instance, 1998 is covered by 215993698 but not by 213326798 .) Let $k(n)$ be the number of positive integers that cover 1998 and have exactly $n$ digits $(n \geqslant 5)$, all different from 0 . What is the remainder of $k(n)$ in division by 8 ?
## Solutions
|
Answer: 1.
Let $1 \leqslant g<h<i<j \leqslant n$ be fixed integers. Consider all $n$-digit numbers $a=\overline{a_{1} a_{2} \ldots a_{n}}$ with all digits non-zero, such that $a_{g}=1, a_{h}=9, a_{i}=9$, $a_{j}=8$ and this quadruple 1998 is the leftmost one in $a$; that is,
$$
\begin{cases}a_{l} \neq 1 & \text { if } l<g ; \\ a_{l} \neq 9 & \text { if } g<l<h ; \\ a_{l} \neq 9 & \text { if } h<l<i \\ a_{l} \neq 8 & \text { if } i<l<j\end{cases}
$$
There are $k_{g h i j}(n)=8^{g-1} \cdot 8^{h-g-1} \cdot 8^{i-h-1} \cdot 8^{j-i-1} \cdot 9^{n-j}$ such numbers $a$. Obviously, $k_{g h i j}(n) \equiv 1(\bmod 8)$ for $g=1, h=2, i=3, j=4$, and $k_{g h i j}(n) \equiv 0(\bmod 8)$ in all other cases. Since $k(n)$ is obtained by summing up the values of $k_{g h i j}(n)$ over all possible choicecs of $g, h, i, j$, the remainder we are looking for is 1 .
|
1
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
We say that an integer $m$ covers the number 1998 if $1,9,9,8$ appear in this order as digits of $m$. (For instance, 1998 is covered by 215993698 but not by 213326798 .) Let $k(n)$ be the number of positive integers that cover 1998 and have exactly $n$ digits $(n \geqslant 5)$, all different from 0 . What is the remainder of $k(n)$ in division by 8 ?
## Solutions
|
Answer: 1.
Let $1 \leqslant g<h<i<j \leqslant n$ be fixed integers. Consider all $n$-digit numbers $a=\overline{a_{1} a_{2} \ldots a_{n}}$ with all digits non-zero, such that $a_{g}=1, a_{h}=9, a_{i}=9$, $a_{j}=8$ and this quadruple 1998 is the leftmost one in $a$; that is,
$$
\begin{cases}a_{l} \neq 1 & \text { if } l<g ; \\ a_{l} \neq 9 & \text { if } g<l<h ; \\ a_{l} \neq 9 & \text { if } h<l<i \\ a_{l} \neq 8 & \text { if } i<l<j\end{cases}
$$
There are $k_{g h i j}(n)=8^{g-1} \cdot 8^{h-g-1} \cdot 8^{i-h-1} \cdot 8^{j-i-1} \cdot 9^{n-j}$ such numbers $a$. Obviously, $k_{g h i j}(n) \equiv 1(\bmod 8)$ for $g=1, h=2, i=3, j=4$, and $k_{g h i j}(n) \equiv 0(\bmod 8)$ in all other cases. Since $k(n)$ is obtained by summing up the values of $k_{g h i j}(n)$ over all possible choicecs of $g, h, i, j$, the remainder we are looking for is 1 .
|
{
"resource_path": "BalticWay/segmented/en-bw98sol.jsonl",
"problem_match": "\n20.",
"solution_match": "\n20."
}
|
edbe6e09-0bf6-55b6-b92f-2755b0a2d7ff
| 605,677
|
Determine all positive integers $n$ with the property that the third root of $n$ is obtained by removing the last three decimal digits of $n$.
|
Answer: 32768 is the only such integer.
If $n=m^{3}$ is a solution, then $m$ satisfies $1000 m \leqslant m^{3}<1000(m+1)$. From the first inequality, we get $m^{2} \geqslant 1000$, or $m \geqslant 32$. By the second inequality, we then have
$$
m^{2}<1000 \cdot \frac{m+1}{m} \leqslant 1000 \cdot \frac{33}{32}=1000+\frac{1000}{32} \leqslant 1032,
$$
or $m \leqslant 32$. Hence, $m=32$ and $n=m^{3}=32768$ is the only solution.
|
32768
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Determine all positive integers $n$ with the property that the third root of $n$ is obtained by removing the last three decimal digits of $n$.
|
Answer: 32768 is the only such integer.
If $n=m^{3}$ is a solution, then $m$ satisfies $1000 m \leqslant m^{3}<1000(m+1)$. From the first inequality, we get $m^{2} \geqslant 1000$, or $m \geqslant 32$. By the second inequality, we then have
$$
m^{2}<1000 \cdot \frac{m+1}{m} \leqslant 1000 \cdot \frac{33}{32}=1000+\frac{1000}{32} \leqslant 1032,
$$
or $m \leqslant 32$. Hence, $m=32$ and $n=m^{3}=32768$ is the only solution.
|
{
"resource_path": "BalticWay/segmented/en-bw99sol.jsonl",
"problem_match": "\n2.",
"solution_match": "\n2."
}
|
8016ed30-3a92-51da-87b8-0f753c3dfad1
| 240,895
|
What is the least number of moves it takes a knight to get from one corner of an $n \times n$ chessboard, where $n \geqslant 4$, to the diagonally opposite corner?
|
Answer: $2 \cdot\left\lfloor\frac{n+1}{3}\right\rfloor$.
Label the squares by pairs of integers $(x, y), x, y=1, \ldots, n$, and consider a sequence of moves that takes the knight from square $(1,1)$ to square $(n, n)$.
The total increment of $x+y$ is $2(n-1)$, and the maximal increment in each move is 3 . Furthermore, the parity of $x+y$ shifts in each move, and $1+1$ and $n+n$ are both even. Hence, the number of moves is even and larger than or equal to $\frac{2 \cdot(n-1)}{3}$. If $N=2 m$ is the least integer that satisfies these conditions, then $m$ is the least integer that satisfies $m \geqslant \frac{n-1}{3}$, i.e. $m=\left\lfloor\frac{n+1}{3}\right\rfloor$.
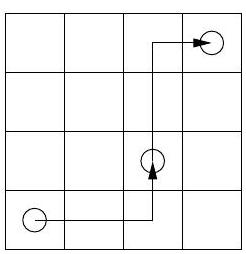
$n=4$
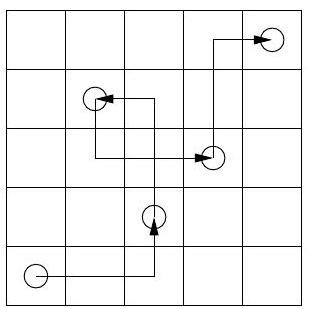
$n=5$
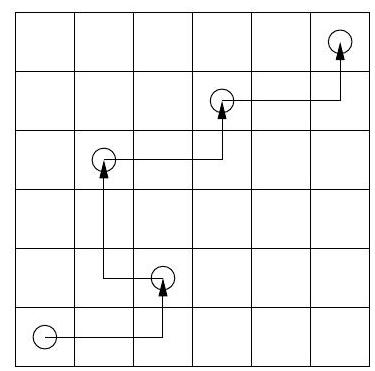
$n=6$
Figure 1
For $n=4, n=5$ and $n=6$ the sequences of moves are easily found that take the knight from square $(1,1)$ to square $(n, n)$ in 2,4 and 4 moves,
respectively (see Figure 1). In particular, the knight may get from square $(k, k)$ to square $(k+3, k+3)$ in 2 moves. Hence, by simple induction, for any $n$ the knight can get from square $(1,1)$ to square $(n, n)$ in a number of moves equal to twice the integer part of $\frac{n+1}{3}$, which is the minimal possible number of moves.
|
2 \cdot\left\lfloor\frac{n+1}{3}\right\rfloor
|
Yes
|
Yes
|
math-word-problem
|
Logic and Puzzles
|
What is the least number of moves it takes a knight to get from one corner of an $n \times n$ chessboard, where $n \geqslant 4$, to the diagonally opposite corner?
|
Answer: $2 \cdot\left\lfloor\frac{n+1}{3}\right\rfloor$.
Label the squares by pairs of integers $(x, y), x, y=1, \ldots, n$, and consider a sequence of moves that takes the knight from square $(1,1)$ to square $(n, n)$.
The total increment of $x+y$ is $2(n-1)$, and the maximal increment in each move is 3 . Furthermore, the parity of $x+y$ shifts in each move, and $1+1$ and $n+n$ are both even. Hence, the number of moves is even and larger than or equal to $\frac{2 \cdot(n-1)}{3}$. If $N=2 m$ is the least integer that satisfies these conditions, then $m$ is the least integer that satisfies $m \geqslant \frac{n-1}{3}$, i.e. $m=\left\lfloor\frac{n+1}{3}\right\rfloor$.

$n=4$

$n=5$

$n=6$
Figure 1
For $n=4, n=5$ and $n=6$ the sequences of moves are easily found that take the knight from square $(1,1)$ to square $(n, n)$ in 2,4 and 4 moves,
respectively (see Figure 1). In particular, the knight may get from square $(k, k)$ to square $(k+3, k+3)$ in 2 moves. Hence, by simple induction, for any $n$ the knight can get from square $(1,1)$ to square $(n, n)$ in a number of moves equal to twice the integer part of $\frac{n+1}{3}$, which is the minimal possible number of moves.
|
{
"resource_path": "BalticWay/segmented/en-bw99sol.jsonl",
"problem_match": "\n6.",
"solution_match": "\n6."
}
|
45c0f129-6a72-5ee8-a9da-36887d7a9e94
| 240,935
|
A cube with edge length 3 is divided into 27 unit cubes. The numbers $1,2, \ldots, 27$ are distributed arbitrarily over the unit cubes, with one number in each cube. We form the 27 possible row sums (there are nine such sums of three integers for each of the three directions parallel to the edges of the cube). At most how many of the 27 row sums can be odd?
|
Answer: 24.
Since each unit cube contributes to exactly three of the row sums, then the total of all the 27 row sums is $3 \cdot(1+2+\ldots+27)=3 \cdot 14 \cdot 27$, which is even. Hence there must be an even number of odd row sums.
(a)
(b)
I
II
III
Figure 2
Figure 3
We shall prove that if one of the three levels of the cube (in any given direction) contains an even row sum, then there is another even row sum within that same level - hence there cannot be 26 odd row sums. Indeed, if this even row sum is formed by three even numbers (case (a) on Figure 2, where + denotes an even number and - denotes an odd number), then in order not to have even column sums (i.e. row sums in the perpendicular direction), we must have another even number in each of the three columns. But then the two remaining rows contain three even and three odd numbers, and hence their row sums cannot both be odd. Consider now the other case when the even row sum is formed by one even number and two odd numbers (case (b) on Figure 2). In order not to have even column sums, the column
containing the even number must contain another even number and an odd number, and each of the other two columns must have two numbers of the same parity. Hence the two other row sums have different parity, and one of them must be even.
It remains to notice that we can achieve 24 odd row sums (see Figure 3, where the three levels of the cube are shown).
|
24
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
A cube with edge length 3 is divided into 27 unit cubes. The numbers $1,2, \ldots, 27$ are distributed arbitrarily over the unit cubes, with one number in each cube. We form the 27 possible row sums (there are nine such sums of three integers for each of the three directions parallel to the edges of the cube). At most how many of the 27 row sums can be odd?
|
Answer: 24.
Since each unit cube contributes to exactly three of the row sums, then the total of all the 27 row sums is $3 \cdot(1+2+\ldots+27)=3 \cdot 14 \cdot 27$, which is even. Hence there must be an even number of odd row sums.

(a)

(b)

I

II

III
Figure 2
Figure 3
We shall prove that if one of the three levels of the cube (in any given direction) contains an even row sum, then there is another even row sum within that same level - hence there cannot be 26 odd row sums. Indeed, if this even row sum is formed by three even numbers (case (a) on Figure 2, where + denotes an even number and - denotes an odd number), then in order not to have even column sums (i.e. row sums in the perpendicular direction), we must have another even number in each of the three columns. But then the two remaining rows contain three even and three odd numbers, and hence their row sums cannot both be odd. Consider now the other case when the even row sum is formed by one even number and two odd numbers (case (b) on Figure 2). In order not to have even column sums, the column
containing the even number must contain another even number and an odd number, and each of the other two columns must have two numbers of the same parity. Hence the two other row sums have different parity, and one of them must be even.
It remains to notice that we can achieve 24 odd row sums (see Figure 3, where the three levels of the cube are shown).
|
{
"resource_path": "BalticWay/segmented/en-bw99sol.jsonl",
"problem_match": "\n9.",
"solution_match": "\n9."
}
|
0c08a1b1-8bfb-540b-940a-8c2e78a269d4
| 240,968
|
Find the smallest positive integer $k$ which is representable in the form $k=19^{n}-5^{m}$ for some positive integers $m$ and $n$.
|
Answer: 14.
Assume that there are integers $n, m$ such that $k=19^{n}-5^{m}$ is a positive integer smaller than $19^{1}-5^{1}=14$. For obvious reasons, $n$ and $m$ must be positive.
Case 1: Assume that $n$ is even. Then the last digit of $k$ is 6 . Consequently, we have $19^{n}-5^{m}=6$. Considering this equation modulo 3 implies that $m$
must be even as well. With $n=2 n^{\prime}$ and $m=2 m^{\prime}$ the above equation can be restated as $\left(19^{n^{\prime}}+5^{m^{\prime}}\right)\left(19^{n^{\prime}}-5^{m^{\prime}}\right)=6$ which evidently has no solution in positive integers.
Case 2: Assume that $n$ is odd. Then the last digit of $k$ is 4 . Consequently, we have $19^{n}-5^{m}=4$. On the other hand, the remainder of $19^{n}-5^{m}$ modulo 3 is never 1 , a contradiction.
|
14
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Find the smallest positive integer $k$ which is representable in the form $k=19^{n}-5^{m}$ for some positive integers $m$ and $n$.
|
Answer: 14.
Assume that there are integers $n, m$ such that $k=19^{n}-5^{m}$ is a positive integer smaller than $19^{1}-5^{1}=14$. For obvious reasons, $n$ and $m$ must be positive.
Case 1: Assume that $n$ is even. Then the last digit of $k$ is 6 . Consequently, we have $19^{n}-5^{m}=6$. Considering this equation modulo 3 implies that $m$
must be even as well. With $n=2 n^{\prime}$ and $m=2 m^{\prime}$ the above equation can be restated as $\left(19^{n^{\prime}}+5^{m^{\prime}}\right)\left(19^{n^{\prime}}-5^{m^{\prime}}\right)=6$ which evidently has no solution in positive integers.
Case 2: Assume that $n$ is odd. Then the last digit of $k$ is 4 . Consequently, we have $19^{n}-5^{m}=4$. On the other hand, the remainder of $19^{n}-5^{m}$ modulo 3 is never 1 , a contradiction.
|
{
"resource_path": "BalticWay/segmented/en-bw99sol.jsonl",
"problem_match": "\n16.",
"solution_match": "\n16."
}
|
a44b8f64-73d9-5bff-8105-57febfae7bf7
| 241,034
|
Let $a, b, c$ and $d$ be prime numbers such that $a>3 b>6 c>12 d$ and $a^{2}-b^{2}+c^{2}-d^{2}=1749$. Determine all possible values of $a^{2}+b^{2}+c^{2}+d^{2}$.
## Solutions
|
Answer: the only possible value is 1999 .
Since $a^{2}-b^{2}+c^{2}-d^{2}$ is odd, one of the primes $a, b, c$ and $d$ must be 2 , and in view of $a>3 b>6 c>12 d$ we must have $d=2$. Now
$$
1749=a^{2}-b^{2}+c^{2}-d^{2}>9 b^{2}-b^{2}+4 d^{2}-d^{2}=8 b^{2}-12,
$$
implying $b \leqslant 13$. From $4<c<\frac{b}{2}$ we now have $c=5$ and $b$ must be either 11 or 13 . It remains to check that $1749+2^{2}-5^{2}+13^{2}=1897$ is not a square of an integer, and $1749+2^{2}-5^{2}+11^{2}=1849=43^{2}$. Hence $b=11$, $a=43$ and
$$
a^{2}+b^{2}+c^{2}+d^{2}=43^{2}+11^{2}+5^{2}+2^{2}=1999
$$
|
1999
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Let $a, b, c$ and $d$ be prime numbers such that $a>3 b>6 c>12 d$ and $a^{2}-b^{2}+c^{2}-d^{2}=1749$. Determine all possible values of $a^{2}+b^{2}+c^{2}+d^{2}$.
## Solutions
|
Answer: the only possible value is 1999 .
Since $a^{2}-b^{2}+c^{2}-d^{2}$ is odd, one of the primes $a, b, c$ and $d$ must be 2 , and in view of $a>3 b>6 c>12 d$ we must have $d=2$. Now
$$
1749=a^{2}-b^{2}+c^{2}-d^{2}>9 b^{2}-b^{2}+4 d^{2}-d^{2}=8 b^{2}-12,
$$
implying $b \leqslant 13$. From $4<c<\frac{b}{2}$ we now have $c=5$ and $b$ must be either 11 or 13 . It remains to check that $1749+2^{2}-5^{2}+13^{2}=1897$ is not a square of an integer, and $1749+2^{2}-5^{2}+11^{2}=1849=43^{2}$. Hence $b=11$, $a=43$ and
$$
a^{2}+b^{2}+c^{2}+d^{2}=43^{2}+11^{2}+5^{2}+2^{2}=1999
$$
|
{
"resource_path": "BalticWay/segmented/en-bw99sol.jsonl",
"problem_match": "\n20.",
"solution_match": "\n20."
}
|
d79dafbc-3bc9-5c67-be8d-005fe2efbce0
| 241,072
|
. A finite set of integers is called bad if its elements add up to 2010. A finite set of integers is a Benelux-set if none of its subsets is bad. Determine the smallest integer $n$ such that the set $\{502,503,504, \ldots, 2009\}$ can be partitioned into $n$ Benelux-sets.
(A partition of a set $S$ into $n$ subsets is a collection of $n$ pairwise disjoint subsets of $S$, the union of which equals $S$.)
|
As $502+1508=2010$, the set $S=\{502,503, \ldots, 2009\}$ is not a Benelux-set, so $n=1$ does not work. We will prove that $n=2$ does work, i.e. that $S$ can be partitioned into 2 Benelux-sets.
Define the following subsets of $S$ :
$$
\begin{aligned}
A & =\{502,503, \ldots, 670\}, \\
B & =\{671,672, \ldots, 1005\}, \\
C & =\{1006,1007, \ldots, 1339\}, \\
D & =\{1340,1341, \ldots, 1508\}, \\
E & =\{1509,1510, \ldots, 2009\} .
\end{aligned}
$$
We will show that $A \cup C \cup E$ and $B \cup D$ are both Benelux-sets.
Note that there does not exist a bad subset of $S$ of one element, since that element would have to be 2010. Also, there does not exist a bad subset of $S$ of more than three elements, since the sum of four or more elements would be at least $502+503+504+505=2014>2010$. So any possible bad subset of $S$ contains two or three elements.
Consider a bad subset of two elements $a$ and $b$. As $a, b \geq 502$ and $a+b=2010$, we have $a, b \leq 2010-502=1508$. Furthermore, exactly one of $a$ and $b$ is smaller than 1005 and one is larger than 1005. So one of them, say $a$, is an element of $A \cup B$, and the other is an element of $C \cup D$. Suppose $a \in A$, then $b \geq 2010-670=1340$, so $b \in D$. On the other hand, suppose $a \in B$, then $b \leq 2010-671=1339$, so $b \in C$. Hence $\{a, b\}$ cannot be a subset of $A \cup C \cup E$, nor of $B \cup D$.
Now consider a bad subset of three elements $a, b$ and $c$. As $a, b, c \geq 502, a+b+c=2010$, and the three elements are pairwise distinct, we have $a, b, c \leq 2010-502-503=1005$. So $a, b, c \in A \cup B$. At least one of the elements, say $a$, is smaller than $\frac{2010}{3}=670$, and at least one of the elements, say $b$, is larger than 670 . So $a \in A$ and $b \in B$. We conclude that $\{a, b, c\}$ cannot be a subset of $A \cup C \cup E$, nor of $B \cup D$.
This proves that $A \cup C \cup E$ and $B \cup D$ are Benelux-sets, and therefore the smallest $n$ for which $S$ can be partitioned into $n$ Benelux-sets is $n=2$.
Remark. Observe that $A \cup C \cup E_{1}$ and $B \cup D \cup E_{2}$ are also Benelux-sets, where $\left\{E_{1}, E_{2}\right\}$ is any partition of $E$.
|
2
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
. A finite set of integers is called bad if its elements add up to 2010. A finite set of integers is a Benelux-set if none of its subsets is bad. Determine the smallest integer $n$ such that the set $\{502,503,504, \ldots, 2009\}$ can be partitioned into $n$ Benelux-sets.
(A partition of a set $S$ into $n$ subsets is a collection of $n$ pairwise disjoint subsets of $S$, the union of which equals $S$.)
|
As $502+1508=2010$, the set $S=\{502,503, \ldots, 2009\}$ is not a Benelux-set, so $n=1$ does not work. We will prove that $n=2$ does work, i.e. that $S$ can be partitioned into 2 Benelux-sets.
Define the following subsets of $S$ :
$$
\begin{aligned}
A & =\{502,503, \ldots, 670\}, \\
B & =\{671,672, \ldots, 1005\}, \\
C & =\{1006,1007, \ldots, 1339\}, \\
D & =\{1340,1341, \ldots, 1508\}, \\
E & =\{1509,1510, \ldots, 2009\} .
\end{aligned}
$$
We will show that $A \cup C \cup E$ and $B \cup D$ are both Benelux-sets.
Note that there does not exist a bad subset of $S$ of one element, since that element would have to be 2010. Also, there does not exist a bad subset of $S$ of more than three elements, since the sum of four or more elements would be at least $502+503+504+505=2014>2010$. So any possible bad subset of $S$ contains two or three elements.
Consider a bad subset of two elements $a$ and $b$. As $a, b \geq 502$ and $a+b=2010$, we have $a, b \leq 2010-502=1508$. Furthermore, exactly one of $a$ and $b$ is smaller than 1005 and one is larger than 1005. So one of them, say $a$, is an element of $A \cup B$, and the other is an element of $C \cup D$. Suppose $a \in A$, then $b \geq 2010-670=1340$, so $b \in D$. On the other hand, suppose $a \in B$, then $b \leq 2010-671=1339$, so $b \in C$. Hence $\{a, b\}$ cannot be a subset of $A \cup C \cup E$, nor of $B \cup D$.
Now consider a bad subset of three elements $a, b$ and $c$. As $a, b, c \geq 502, a+b+c=2010$, and the three elements are pairwise distinct, we have $a, b, c \leq 2010-502-503=1005$. So $a, b, c \in A \cup B$. At least one of the elements, say $a$, is smaller than $\frac{2010}{3}=670$, and at least one of the elements, say $b$, is larger than 670 . So $a \in A$ and $b \in B$. We conclude that $\{a, b, c\}$ cannot be a subset of $A \cup C \cup E$, nor of $B \cup D$.
This proves that $A \cup C \cup E$ and $B \cup D$ are Benelux-sets, and therefore the smallest $n$ for which $S$ can be partitioned into $n$ Benelux-sets is $n=2$.
Remark. Observe that $A \cup C \cup E_{1}$ and $B \cup D \cup E_{2}$ are also Benelux-sets, where $\left\{E_{1}, E_{2}\right\}$ is any partition of $E$.
|
{
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2010-zz.jsonl",
"problem_match": null,
"solution_match": null
}
|
a3fe8e70-6c03-5b06-b40f-cbfe80baa41f
| 605,996
|
Abby and Brian play the following game: They first choose a positive integer $N$. Then they write numbers on a blackboard in turn. Abby starts by writing a 1. Thereafter, when one of them has written the number $n$, the other writes down either $n+1$ or $2 n$, provided that the number is not greater than $N$. The player who writes $N$ on the blackboard wins.
(a) Determine which player has a winning strategy if $N=2011$.
(b) Find the number of positive integers $N \leqslant 2011$ for which Brian has a winning strategy.
#
|
(a) Abby has a winning strategy for odd $N$ : Observe that, whenever any player writes down an odd number, the other player has to write down an even number. By adding 1 to that number, the first player can write down another odd number. Since Abby starts the game by writing down an odd number, she can force Brian to write down even numbers only. Since $N$ is odd, Abby will win the game. In particular, Abby has a winning strategy if $N=2011$.
(b) - Let $N=4 k$. If any player is forced to write down a number $m \in\{k+1, k+2, \ldots, 2 k\}$, the other player wins the game by writing down $2 m \in\{2 k+2,2 k+4, \ldots, 4 k\}$, for the players will have to write down the remaining numbers one after the other. Since there is an even number of numbers remaining, the latter player wins. This implies that the player who can write down $k$, i.e. has a winning strategy for $N=k$, wins the game for $N=4 k$.
- Similarly, let $N=4 k+2$. If any player is forced to write down a number $m \in\{k+1, k+2, \ldots, 2 k+1\}$, the other player wins the game by writing down $2 m \in\{2 k+2,2 k+4, \ldots, 4 k+2\}$, as in the previous case. Analogously, this implies that the player who has a winning strategy for $N=k$ wins the game for $N=4 k+2$.
Since Abby wins the game for $N=1,3$, while Brian wins the game for $N=2$, Brian wins the game for $N=8,10$, as well, and thus for $N=32,34,40,42$, too. Then Brian wins the game for a further 8 values of $N$ between 128 and 170, and thence for a further 16 values between 512 and 682, and for no other values with $N \leqslant 2011$. Hence Brian has a winning strategy for precisely 31 values of $N$ with $N \leqslant 2011$.
|
31
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Abby and Brian play the following game: They first choose a positive integer $N$. Then they write numbers on a blackboard in turn. Abby starts by writing a 1. Thereafter, when one of them has written the number $n$, the other writes down either $n+1$ or $2 n$, provided that the number is not greater than $N$. The player who writes $N$ on the blackboard wins.
(a) Determine which player has a winning strategy if $N=2011$.
(b) Find the number of positive integers $N \leqslant 2011$ for which Brian has a winning strategy.
#
|
(a) Abby has a winning strategy for odd $N$ : Observe that, whenever any player writes down an odd number, the other player has to write down an even number. By adding 1 to that number, the first player can write down another odd number. Since Abby starts the game by writing down an odd number, she can force Brian to write down even numbers only. Since $N$ is odd, Abby will win the game. In particular, Abby has a winning strategy if $N=2011$.
(b) - Let $N=4 k$. If any player is forced to write down a number $m \in\{k+1, k+2, \ldots, 2 k\}$, the other player wins the game by writing down $2 m \in\{2 k+2,2 k+4, \ldots, 4 k\}$, for the players will have to write down the remaining numbers one after the other. Since there is an even number of numbers remaining, the latter player wins. This implies that the player who can write down $k$, i.e. has a winning strategy for $N=k$, wins the game for $N=4 k$.
- Similarly, let $N=4 k+2$. If any player is forced to write down a number $m \in\{k+1, k+2, \ldots, 2 k+1\}$, the other player wins the game by writing down $2 m \in\{2 k+2,2 k+4, \ldots, 4 k+2\}$, as in the previous case. Analogously, this implies that the player who has a winning strategy for $N=k$ wins the game for $N=4 k+2$.
Since Abby wins the game for $N=1,3$, while Brian wins the game for $N=2$, Brian wins the game for $N=8,10$, as well, and thus for $N=32,34,40,42$, too. Then Brian wins the game for a further 8 values of $N$ between 128 and 170, and thence for a further 16 values between 512 and 682, and for no other values with $N \leqslant 2011$. Hence Brian has a winning strategy for precisely 31 values of $N$ with $N \leqslant 2011$.
|
{
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2011-zz.jsonl",
"problem_match": null,
"solution_match": null
}
|
2d30dbf6-a000-5bc7-a68f-dd03958402be
| 606,129
|
. Let $n \geqslant 3$ be an integer. A frog is to jump along the real axis, starting at the point 0 and making $n$ jumps: one of length 1 , one of length $2, \ldots$, one of length $n$. It may perform these $n$ jumps in any order. If at some point the frog is sitting on a number $a \leqslant 0$, its next jump must be to the right (towards the positive numbers). If at some point the frog is sitting on a number $a>0$, its next jump must be to the left (towards the negative numbers). Find the largest positive integer $k$ for which the frog can perform its jumps in such an order that it never lands on any of the numbers $1,2, \ldots, k$.
|
We claim that the largest positive integer $k$ with the given property is $\left\lfloor\frac{n-1}{2}\right\rfloor$, where $\lfloor x\rfloor$ is by definition the largest integer not exceeding $x$.
Consider a sequence of $n$ jumps of length $1,2, \ldots n$ such that the frog never lands on any of the numbers $1,2, \ldots, k$, where $k \geqslant 1$. Note that we must have $k<n$ in order for the frog to be able to make its first jump. As the frog jumps to the right only if it is in a number $a \leqslant 0$, and the largest jump has length $n$, it is impossible to reach numbers greater than $n$. On the other hand, suppose the frog is in a number $a>0$, then it must even be in a number $a \geqslant k+1$, since it is not allowed to hit the numbers $1,2, \ldots, k$. So the frog jumps to the left only if it is in a number $a \geqslant k+1$, and therefore it is impossible to reach numbers less than $(k+1)-n=k-n+1$. This means the frog only possibly lands on the numbers $i$ satisfying
$$
k-n+1 \leqslant i \leqslant 0 \quad \text { or } \quad k+1 \leqslant i \leqslant n \text {. }
$$
When performing a jump of length $k$, the frog has to remain at either side of the numbers $1,2, \ldots, k$. Indeed, jumping over $1,2, \ldots, k$ requires a jump of at least length $k+1$. In case it starts at a number $a>0$ (in fact $k+1 \leqslant a \leqslant n$ ), it lands in $a-k$ and we must also have $a-k \geqslant k+1$. So $2 k+1 \leqslant a \leqslant n$, therefore $2 k+1 \leqslant n$. In case it starts at a number $a \leqslant 0$ (in fact $k-n+1 \leqslant a \leqslant 0$ ), it lands in $a+k$ and we must also have $a+k \leqslant 0$. Adding $k$ to both sides of $k-n+1 \leqslant a$, we obtain $2 k-n+1 \leqslant a+k \leqslant 0$, so in this case we have $2 k+1 \leqslant n$ as well. We conclude that $k \leqslant \frac{n-1}{2}$. Since $k$ is integer, we even have $k \leqslant\left\lfloor\frac{n-1}{2}\right\rfloor$.
Next we prove that this upperbound is sharp: for $k=\left\lfloor\frac{n-1}{2}\right\rfloor$ the frog really can perform its jumps in such an order that it never lands on any of the numbers $1,2, \ldots, k$.
Suppose $n$ is odd, then $\frac{n-1}{2}$ is an integer and we have $k=\frac{n-1}{2}$, so $n=2 k+1$. We claim that when the frog performs the jumps of length $1, \ldots, 2 k+1$ in the following order, it does never land on $1,2, \ldots, k$ : it starts with a jump of length $k+1$, then it performs two jumps, one of length $k+2$ followed by one of length 1 , next two jumps of length $k+3$ and $2, \ldots$, next two jumps of length $k+(i+1)$ and $i, \ldots$, and finally two jumps of length $k+(k+1)$ and $k$. In this order of the jumps every length between 1 and $n=2 k+1$ does occur: it performs a pair of jumps for $1 \leqslant i \leqslant k$, which are the jumps of length $1,2, \ldots$, $k$ and the jumps of length $k+2, k+3, \ldots, 2 k+1$, and it starts with the jump of length $k+1$.
We now prove the correctness of this jumping scheme. After the first jump the frog lands in $k+1>k$. Now suppose the frog is in 0 or $k+1$ and is about to perform the pair of jumps of length $k+(i+1)$ and $i$. Starting from 0 , it lands in $k+(i+1)>k$, after which it lands in $(k+i+1)-i=k+1>k$. If on the contrary it starts in $k+1$, it lands in $(k+1)-(k+(i+1))=-i<1$, after which it lands in $(-i)+i=0$. We see that, starting in 0 , the frog lands in $k+1$ after the pair of jumps, while starting in $k+1$ the frog lands in 0 , while in both cases the jumps do not touch $1,2, \ldots k$. This proves the correctness of its series of jumps. As the frog (after its first jump) alters between $k+1$ and 0 exactly $k$ times, for odd $k$ it will end up in 0 , while for even $k$ it will end up in $k+1$.
Suppose $n$ is even, then $\frac{n-1}{2}$ is not an integer and we have $k=\frac{n-1}{2}-\frac{1}{2}=\frac{n-2}{2}$, so $n=2 k+2$. Let the frog firstly perform the same series of jumps as in the previous case; they still do not touch $1,2, \ldots, k$. Now let the frog make a final extra jump of length $2 k+2$. It will land in $0+(2 k+2)=2 k+2>k$ if $k$ is odd, or in $(k+1)-(2 k+2)=-k-1<1$ if $k$ is even, and its series of jumps is correct again.
We conclude that the largest positive integer $k$ with the given property is $\left\lfloor\frac{n-1}{2}\right\rfloor$.
|
\left\lfloor\frac{n-1}{2}\right\rfloor
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
. Let $n \geqslant 3$ be an integer. A frog is to jump along the real axis, starting at the point 0 and making $n$ jumps: one of length 1 , one of length $2, \ldots$, one of length $n$. It may perform these $n$ jumps in any order. If at some point the frog is sitting on a number $a \leqslant 0$, its next jump must be to the right (towards the positive numbers). If at some point the frog is sitting on a number $a>0$, its next jump must be to the left (towards the negative numbers). Find the largest positive integer $k$ for which the frog can perform its jumps in such an order that it never lands on any of the numbers $1,2, \ldots, k$.
|
We claim that the largest positive integer $k$ with the given property is $\left\lfloor\frac{n-1}{2}\right\rfloor$, where $\lfloor x\rfloor$ is by definition the largest integer not exceeding $x$.
Consider a sequence of $n$ jumps of length $1,2, \ldots n$ such that the frog never lands on any of the numbers $1,2, \ldots, k$, where $k \geqslant 1$. Note that we must have $k<n$ in order for the frog to be able to make its first jump. As the frog jumps to the right only if it is in a number $a \leqslant 0$, and the largest jump has length $n$, it is impossible to reach numbers greater than $n$. On the other hand, suppose the frog is in a number $a>0$, then it must even be in a number $a \geqslant k+1$, since it is not allowed to hit the numbers $1,2, \ldots, k$. So the frog jumps to the left only if it is in a number $a \geqslant k+1$, and therefore it is impossible to reach numbers less than $(k+1)-n=k-n+1$. This means the frog only possibly lands on the numbers $i$ satisfying
$$
k-n+1 \leqslant i \leqslant 0 \quad \text { or } \quad k+1 \leqslant i \leqslant n \text {. }
$$
When performing a jump of length $k$, the frog has to remain at either side of the numbers $1,2, \ldots, k$. Indeed, jumping over $1,2, \ldots, k$ requires a jump of at least length $k+1$. In case it starts at a number $a>0$ (in fact $k+1 \leqslant a \leqslant n$ ), it lands in $a-k$ and we must also have $a-k \geqslant k+1$. So $2 k+1 \leqslant a \leqslant n$, therefore $2 k+1 \leqslant n$. In case it starts at a number $a \leqslant 0$ (in fact $k-n+1 \leqslant a \leqslant 0$ ), it lands in $a+k$ and we must also have $a+k \leqslant 0$. Adding $k$ to both sides of $k-n+1 \leqslant a$, we obtain $2 k-n+1 \leqslant a+k \leqslant 0$, so in this case we have $2 k+1 \leqslant n$ as well. We conclude that $k \leqslant \frac{n-1}{2}$. Since $k$ is integer, we even have $k \leqslant\left\lfloor\frac{n-1}{2}\right\rfloor$.
Next we prove that this upperbound is sharp: for $k=\left\lfloor\frac{n-1}{2}\right\rfloor$ the frog really can perform its jumps in such an order that it never lands on any of the numbers $1,2, \ldots, k$.
Suppose $n$ is odd, then $\frac{n-1}{2}$ is an integer and we have $k=\frac{n-1}{2}$, so $n=2 k+1$. We claim that when the frog performs the jumps of length $1, \ldots, 2 k+1$ in the following order, it does never land on $1,2, \ldots, k$ : it starts with a jump of length $k+1$, then it performs two jumps, one of length $k+2$ followed by one of length 1 , next two jumps of length $k+3$ and $2, \ldots$, next two jumps of length $k+(i+1)$ and $i, \ldots$, and finally two jumps of length $k+(k+1)$ and $k$. In this order of the jumps every length between 1 and $n=2 k+1$ does occur: it performs a pair of jumps for $1 \leqslant i \leqslant k$, which are the jumps of length $1,2, \ldots$, $k$ and the jumps of length $k+2, k+3, \ldots, 2 k+1$, and it starts with the jump of length $k+1$.
We now prove the correctness of this jumping scheme. After the first jump the frog lands in $k+1>k$. Now suppose the frog is in 0 or $k+1$ and is about to perform the pair of jumps of length $k+(i+1)$ and $i$. Starting from 0 , it lands in $k+(i+1)>k$, after which it lands in $(k+i+1)-i=k+1>k$. If on the contrary it starts in $k+1$, it lands in $(k+1)-(k+(i+1))=-i<1$, after which it lands in $(-i)+i=0$. We see that, starting in 0 , the frog lands in $k+1$ after the pair of jumps, while starting in $k+1$ the frog lands in 0 , while in both cases the jumps do not touch $1,2, \ldots k$. This proves the correctness of its series of jumps. As the frog (after its first jump) alters between $k+1$ and 0 exactly $k$ times, for odd $k$ it will end up in 0 , while for even $k$ it will end up in $k+1$.
Suppose $n$ is even, then $\frac{n-1}{2}$ is not an integer and we have $k=\frac{n-1}{2}-\frac{1}{2}=\frac{n-2}{2}$, so $n=2 k+2$. Let the frog firstly perform the same series of jumps as in the previous case; they still do not touch $1,2, \ldots, k$. Now let the frog make a final extra jump of length $2 k+2$. It will land in $0+(2 k+2)=2 k+2>k$ if $k$ is odd, or in $(k+1)-(2 k+2)=-k-1<1$ if $k$ is even, and its series of jumps is correct again.
We conclude that the largest positive integer $k$ with the given property is $\left\lfloor\frac{n-1}{2}\right\rfloor$.
|
{
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2013-zz.jsonl",
"problem_match": null,
"solution_match": null
}
|
767fb025-24f6-54bf-bd57-5922b73036b7
| 606,192
|
Find the smallest possible value of the expression
$$
\left\lfloor\frac{a+b+c}{d}\right\rfloor+\left\lfloor\frac{b+c+d}{a}\right\rfloor+\left\lfloor\frac{c+d+a}{b}\right\rfloor+\left\lfloor\frac{d+a+b}{c}\right\rfloor,
$$
in which $a, b, c$ and $d$ vary over the set of positive integers.
(Here $\lfloor x\rfloor$ denotes the biggest integer which is smaller than or equal to $x$.)
#
|
The answer is 9 .
Notice that $\lfloor x\rfloor>x-1$ for all $x \in \mathbb{R}$. Therefore the given expression is strictly greater than
$$
\frac{a+b+c}{d}+\frac{b+c+d}{a}+\frac{c+d+a}{b}+\frac{d+a+b}{c}-4,
$$
which can be rewritten as
$$
\left(\frac{a}{b}+\frac{b}{a}\right)+\left(\frac{a}{c}+\frac{c}{a}\right)+\left(\frac{a}{d}+\frac{d}{a}\right)+\left(\frac{b}{c}+\frac{c}{b}\right)+\left(\frac{b}{d}+\frac{d}{b}\right)+\left(\frac{c}{d}+\frac{d}{c}\right)-4 .
$$
Since $t+\frac{1}{t} \geq 2$ for $t>0$, we get that $6 \cdot 2-4=8$ is a strict lower bound for the given expression; since it takes integral values only, we actually get that 9 is a lower bound.
It remains to check that 9 can be attained; this happens for $a=b=c=5$ and $d=4$.
#
|
9
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Find the smallest possible value of the expression
$$
\left\lfloor\frac{a+b+c}{d}\right\rfloor+\left\lfloor\frac{b+c+d}{a}\right\rfloor+\left\lfloor\frac{c+d+a}{b}\right\rfloor+\left\lfloor\frac{d+a+b}{c}\right\rfloor,
$$
in which $a, b, c$ and $d$ vary over the set of positive integers.
(Here $\lfloor x\rfloor$ denotes the biggest integer which is smaller than or equal to $x$.)
#
|
The answer is 9 .
Notice that $\lfloor x\rfloor>x-1$ for all $x \in \mathbb{R}$. Therefore the given expression is strictly greater than
$$
\frac{a+b+c}{d}+\frac{b+c+d}{a}+\frac{c+d+a}{b}+\frac{d+a+b}{c}-4,
$$
which can be rewritten as
$$
\left(\frac{a}{b}+\frac{b}{a}\right)+\left(\frac{a}{c}+\frac{c}{a}\right)+\left(\frac{a}{d}+\frac{d}{a}\right)+\left(\frac{b}{c}+\frac{c}{b}\right)+\left(\frac{b}{d}+\frac{d}{b}\right)+\left(\frac{c}{d}+\frac{d}{c}\right)-4 .
$$
Since $t+\frac{1}{t} \geq 2$ for $t>0$, we get that $6 \cdot 2-4=8$ is a strict lower bound for the given expression; since it takes integral values only, we actually get that 9 is a lower bound.
It remains to check that 9 can be attained; this happens for $a=b=c=5$ and $d=4$.
#
|
{
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2014-zz.jsonl",
"problem_match": null,
"solution_match": null
}
|
eed00985-bdbf-58b9-975c-37a7612ee5d1
| 606,243
|
Let $k \geq 1$ be an integer.
We consider $4 k$ chips, $2 k$ of which are red and $2 k$ of which are blue. A sequence of those $4 k$ chips can be transformed into another sequence by a so-called move, consisting of interchanging a number (possibly one) of consecutive red chips with an equal number of consecutive blue chips. For example, we can move from $r \underline{b b b r} \underline{r} b$ to $r \underline{r r} b r \underline{b b b}$ where $r$ denotes a red chip and $b$ denotes a blue chip.
Determine the smallest number $n$ (as a function of $k$ ) such that starting from any initial sequence of the $4 k$ chips, we need at most $n$ moves to reach the state in which the first $2 k$ chips are red.
#
|
The answer is $n=k$.
We will first show that $n \geq k$. Let us count the number $C$ of times a red chip is directly to the right of a blue chip. In the final position this number equals 0 . In the position brbrbr $\cdots b r$ this number equals $2 k$. We claim that any move reduces this number by at most 2 . Denote by $R$ the group of red chips and by $B$ the group of blue chips that are interchanged. Any reduction in $C$ must involve a red chip getting rid of its blue left neighbour or a blue chip getting rid of its red right neighbour. This can only happen with the leftmost chip of $R$ (if its left neighbour is blue) and the rightmost chip of $B$ (if its right neighbour is red), but not with the rightmost chip of $R$ (and its right neighbour) or the leftmost chip of $B$ (and its left neighbour). Hence $C$ is reduced by at most 2 in any move. Therefore the number of moves necessary to change $b r b r b r \cdots b r$ into the final position is at least $\frac{2 k}{2}=k$.
We will now show that $n \leq k$, i.e. that it is always possible to perform at most $k$ moves in order to reach the state in which the first $2 k$ chips are red. Consider the first $2 k$ chips. If at most $k$ of these chips are blue, we can perform one move for each chip, switching it with one of the red chips of the last $2 k$ chips. So then we are done in at most $k$ moves. Now suppose that of the first $2 k$ chips, at least $k+1$ are blue. Then at most $k-1$ chips are red. Hence it is possible to perform at most $k-1$ moves to reach the situation in which the last $2 k$ chips are red. We then perform one final move, switching the first $2 k$ chips and the last $2 k$ chips, ending in the situation in which the first $2 k$ chips are red. Thus, it is always possible to reach the situation in which the first $2 k$ chips are red in at most $k$ steps, hence $n \leq k$.
We have now shown that $n \geq k$ and $n \leq k$, hence $n=k$ as claimed.
#
|
k
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Let $k \geq 1$ be an integer.
We consider $4 k$ chips, $2 k$ of which are red and $2 k$ of which are blue. A sequence of those $4 k$ chips can be transformed into another sequence by a so-called move, consisting of interchanging a number (possibly one) of consecutive red chips with an equal number of consecutive blue chips. For example, we can move from $r \underline{b b b r} \underline{r} b$ to $r \underline{r r} b r \underline{b b b}$ where $r$ denotes a red chip and $b$ denotes a blue chip.
Determine the smallest number $n$ (as a function of $k$ ) such that starting from any initial sequence of the $4 k$ chips, we need at most $n$ moves to reach the state in which the first $2 k$ chips are red.
#
|
The answer is $n=k$.
We will first show that $n \geq k$. Let us count the number $C$ of times a red chip is directly to the right of a blue chip. In the final position this number equals 0 . In the position brbrbr $\cdots b r$ this number equals $2 k$. We claim that any move reduces this number by at most 2 . Denote by $R$ the group of red chips and by $B$ the group of blue chips that are interchanged. Any reduction in $C$ must involve a red chip getting rid of its blue left neighbour or a blue chip getting rid of its red right neighbour. This can only happen with the leftmost chip of $R$ (if its left neighbour is blue) and the rightmost chip of $B$ (if its right neighbour is red), but not with the rightmost chip of $R$ (and its right neighbour) or the leftmost chip of $B$ (and its left neighbour). Hence $C$ is reduced by at most 2 in any move. Therefore the number of moves necessary to change $b r b r b r \cdots b r$ into the final position is at least $\frac{2 k}{2}=k$.
We will now show that $n \leq k$, i.e. that it is always possible to perform at most $k$ moves in order to reach the state in which the first $2 k$ chips are red. Consider the first $2 k$ chips. If at most $k$ of these chips are blue, we can perform one move for each chip, switching it with one of the red chips of the last $2 k$ chips. So then we are done in at most $k$ moves. Now suppose that of the first $2 k$ chips, at least $k+1$ are blue. Then at most $k-1$ chips are red. Hence it is possible to perform at most $k-1$ moves to reach the situation in which the last $2 k$ chips are red. We then perform one final move, switching the first $2 k$ chips and the last $2 k$ chips, ending in the situation in which the first $2 k$ chips are red. Thus, it is always possible to reach the situation in which the first $2 k$ chips are red in at most $k$ steps, hence $n \leq k$.
We have now shown that $n \geq k$ and $n \leq k$, hence $n=k$ as claimed.
#
|
{
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2014-zz.jsonl",
"problem_match": null,
"solution_match": null
}
|
fdbda3a9-86ec-549e-8e29-21df92e6fc0b
| 606,250
|
.
## Determine the smallest positive integer $q$ with the following property:
## for every integer $m$ with $1 \leqslant m \leqslant 1006$, there exists an integer $n$ such that
$$
\frac{m}{1007} q<n<\frac{m+1}{1008} q .
$$
|
. For $m=1006$, we have
$$
q-q / 1007<n<q-q / 1008
$$
for some integer $n$. If $q \leqslant 1007$, then $q-q / 1007$ and $q-q / 1008$ are both numbers that are at least $q-1$ and smaller than $q$, so there can be no integer $n$ in between. Hence $q>1007$ and $q-q / 1008 \leqslant q-1$, implying that $n<q-1$, and that $q-q / 1007<q-2$. By rearranging terms, we find $q>2014$, and hence $q \geqslant 2015$.
Let us prove that $q=2015$ works. Indeed, $m q / 1007=2 m+m / 1007<2 m+1$ and $(m+1) q / 1008=2(m+1)-(m+1) / 1008>2 m+1$ for $1 \leqslant m \leqslant 1006$. Hence each pair of inequalities can be satisfied by taking $n=2 m+1$. This completes the proof, and shows that the smallest possible of $q$ is indeed 2015.
|
2015
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
.
## Determine the smallest positive integer $q$ with the following property:
## for every integer $m$ with $1 \leqslant m \leqslant 1006$, there exists an integer $n$ such that
$$
\frac{m}{1007} q<n<\frac{m+1}{1008} q .
$$
|
. For $m=1006$, we have
$$
q-q / 1007<n<q-q / 1008
$$
for some integer $n$. If $q \leqslant 1007$, then $q-q / 1007$ and $q-q / 1008$ are both numbers that are at least $q-1$ and smaller than $q$, so there can be no integer $n$ in between. Hence $q>1007$ and $q-q / 1008 \leqslant q-1$, implying that $n<q-1$, and that $q-q / 1007<q-2$. By rearranging terms, we find $q>2014$, and hence $q \geqslant 2015$.
Let us prove that $q=2015$ works. Indeed, $m q / 1007=2 m+m / 1007<2 m+1$ and $(m+1) q / 1008=2(m+1)-(m+1) / 1008>2 m+1$ for $1 \leqslant m \leqslant 1006$. Hence each pair of inequalities can be satisfied by taking $n=2 m+1$. This completes the proof, and shows that the smallest possible of $q$ is indeed 2015.
|
{
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2015-zz.jsonl",
"problem_match": null,
"solution_match": null
}
|
8a75e328-6958-5fe4-9592-af9af5a3adee
| 606,271
|
.
An arithmetic progression is a set of the form $\{a, a+d, \ldots, a+k d\}$, where $a, d, k$ are positive integers and $k \geqslant 2$. Thus an arithmetic progression has at least three elements and the successive elements have difference $d$, called the common difference of the arithmetic progression.
Let $n$ be a positive integer. For each partition of the set $\{1,2, \ldots, 3 n\}$ into arithmetic progressions, we consider the sum $S$ of the respective common differences of these arithmetic progressions. What is the maximal value $S$ that can attain?
(A partition of a set $A$ is a collection of disjoint subsets of $A$ whose union is $A$.)
|
The maximum value is $n^{2}$, which is attained for the partition into $n$ arithmetic progressions $\{1, n+1,2 n+1\}, \ldots,\{n, 2 n, 3 n\}$, each of difference $n$.
Suppose indeed that the set has been partioned into $N$ progressions, of respective lengths $\ell_{i}$, and differences $d_{i}$, for $1 \leqslant i \leqslant N$. Since $\ell_{i} \geqslant 3$,
$$
2 \sum_{i=1}^{N} d_{i} \leqslant \sum_{i=1}^{N}\left(\ell_{i}-1\right) d_{i}=\sum_{i=1}^{N} a_{i}-\sum_{i=1}^{N} b_{i}
$$
where $a_{i}$ and $b_{i}$ denote, respectively, the largest and smallest elements of progression $i$. Now
$$
\begin{aligned}
& \sum_{i=1}^{N} b_{i} \geqslant 1+2+\cdots+N=N(N+1) / 2 \\
& \sum_{i=1}^{N} a_{i} \leqslant(3 n-N+1)+\cdots+3 n=N(6 n-N+1) / 2
\end{aligned}
$$
and thus
$$
2 \sum_{i=1}^{N} d_{i} \leqslant N(3 n-N) \leqslant 2 n^{2}
$$
as $N(3 n-N)$ is an increasing of $N$ on the interval $[0,3 n / 2]$ and since $N \leqslant n$. This completes the proof.
Remark. The maximising partition is in fact unique: from the above, it is immediate that all maximal partitions must have $n_{i}=3$ and hence $n=N$. It follows that the minimal and maximal elements of the arithmetic progressions of a maximal partition are precisely $1,2, \ldots, n$ and $2 n+1,2 n+2, \ldots, 3 n$, respectively. Consider the progression $\{n+1-d, n+1, n+1+d\}$ of difference $d$. Then $n+1-d \geqslant 1$ and $n+1+d \geqslant 2 n+1$,
which implies $d=n$, and hence $\{1, n+1,2 n+1\}$ is an element of any maximal partition. By induction, it follows similarly that $\{k, n+k, 2 n+k\}$ is an element of any maximal partition for $1 \leqslant k \leqslant n$, since integers allowing for smaller or larger differences have already been used up. This proves the partition $\{1, n+1,2 n+1\}, \ldots,\{n, 2 n, 3 n\}$ is the unique maximising partition, as claimed.
|
n^2
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
.
An arithmetic progression is a set of the form $\{a, a+d, \ldots, a+k d\}$, where $a, d, k$ are positive integers and $k \geqslant 2$. Thus an arithmetic progression has at least three elements and the successive elements have difference $d$, called the common difference of the arithmetic progression.
Let $n$ be a positive integer. For each partition of the set $\{1,2, \ldots, 3 n\}$ into arithmetic progressions, we consider the sum $S$ of the respective common differences of these arithmetic progressions. What is the maximal value $S$ that can attain?
(A partition of a set $A$ is a collection of disjoint subsets of $A$ whose union is $A$.)
|
The maximum value is $n^{2}$, which is attained for the partition into $n$ arithmetic progressions $\{1, n+1,2 n+1\}, \ldots,\{n, 2 n, 3 n\}$, each of difference $n$.
Suppose indeed that the set has been partioned into $N$ progressions, of respective lengths $\ell_{i}$, and differences $d_{i}$, for $1 \leqslant i \leqslant N$. Since $\ell_{i} \geqslant 3$,
$$
2 \sum_{i=1}^{N} d_{i} \leqslant \sum_{i=1}^{N}\left(\ell_{i}-1\right) d_{i}=\sum_{i=1}^{N} a_{i}-\sum_{i=1}^{N} b_{i}
$$
where $a_{i}$ and $b_{i}$ denote, respectively, the largest and smallest elements of progression $i$. Now
$$
\begin{aligned}
& \sum_{i=1}^{N} b_{i} \geqslant 1+2+\cdots+N=N(N+1) / 2 \\
& \sum_{i=1}^{N} a_{i} \leqslant(3 n-N+1)+\cdots+3 n=N(6 n-N+1) / 2
\end{aligned}
$$
and thus
$$
2 \sum_{i=1}^{N} d_{i} \leqslant N(3 n-N) \leqslant 2 n^{2}
$$
as $N(3 n-N)$ is an increasing of $N$ on the interval $[0,3 n / 2]$ and since $N \leqslant n$. This completes the proof.
Remark. The maximising partition is in fact unique: from the above, it is immediate that all maximal partitions must have $n_{i}=3$ and hence $n=N$. It follows that the minimal and maximal elements of the arithmetic progressions of a maximal partition are precisely $1,2, \ldots, n$ and $2 n+1,2 n+2, \ldots, 3 n$, respectively. Consider the progression $\{n+1-d, n+1, n+1+d\}$ of difference $d$. Then $n+1-d \geqslant 1$ and $n+1+d \geqslant 2 n+1$,
which implies $d=n$, and hence $\{1, n+1,2 n+1\}$ is an element of any maximal partition. By induction, it follows similarly that $\{k, n+k, 2 n+k\}$ is an element of any maximal partition for $1 \leqslant k \leqslant n$, since integers allowing for smaller or larger differences have already been used up. This proves the partition $\{1, n+1,2 n+1\}, \ldots,\{n, 2 n, 3 n\}$ is the unique maximising partition, as claimed.
|
{
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2015-zz.jsonl",
"problem_match": null,
"solution_match": null
}
|
ea986f13-1fcf-5e0c-9543-9401e9f87607
| 606,312
|
. Find the greatest positive integer $N$ with the following property: there exist integers $x_{1}, \ldots, x_{N}$ such that $x_{i}^{2}-x_{i} x_{j}$ is not divisible by 1111 for any $i \neq j$.
|
We prove that the greatest $N$ with the required property is $N=1000$. First note that $x_{i}^{2}-x_{i} x_{j}=x_{i}\left(x_{i}-x_{j}\right)$, and that the prime factorisation of 1111 is $11 \cdot 101$.
We first show that we can find 1000 integers $x_{1}, x_{2}, \ldots, x_{1000}$ such that $x_{i}^{2}-x_{i} x_{j}$ is not divisible by 1111 for any $i \neq j$. Consider the set $\{1,2, \ldots, 1110\}$. This set contains 10 integers divisible by 101, and it contains 100 integers divisible by 11 . None of the integers in the set are divisible by both 11 and 101. If we delete all of these $10+100$ integers from the set, we are left with 1000 integers. Call these $x_{1}, x_{2}, \ldots, x_{1000}$. Now we have $11 \nmid x_{i}$ and $101 \nmid x_{i}$ for all $i$. Suppose there are $i \neq j$ with $1111 \mid x_{i}\left(x_{i}-x_{j}\right)$, then we must have $1111 \mid x_{i}-x_{j}$, which is a contradiction, since $x_{i}, x_{j} \in\{1,2, \ldots, 1110\}$. So this set satisfies the requirement.
We now prove that given 1001 (or more) integers $x_{1}, x_{2}, \ldots, x_{1001}$ there are $i \neq j$ with $1111 \mid x_{i}\left(x_{i}-x_{j}\right)$. Suppose for a contradiction that for all indices $i \neq j$, we have that $x_{i}\left(x_{i}-x_{j}\right)$ is not divisible by 1111, and write $X=\left\{x_{1}, \ldots, x_{1001}\right\}$. We may (after reducing modulo 1111 if necessary) assume that $x_{i} \in\{0,1, \ldots, 1110\}$ for all $i$. Then we know that $x_{i} \neq 0$ for all $i$, and $x_{i} \neq x_{j}$ for all $i \neq j$. Suppose for some $i$ we have $11 \mid x_{i}$. (Since $x_{i} \neq 0$, we know that $101 \nmid x_{i}$.) Then any integer $a \neq x_{i}$ with $a \equiv x_{i} \bmod 101$ cannot be an element of $X$, since $1111 \mid x_{i}\left(x_{i}-a\right)$. In $\{1,2, \ldots, 1110\}$ there are 10 such integers, all of them coprime with $11 \cdot 101$. If there are exactly $k$ different values of $i$ such that $11 \mid x_{i}$, there are $10 k$ different integers from $\{1,2, \ldots, 1110\}$ that cannot be elements of $X$, all of them coprime with $11 \cdot 101$. Similarly, if there are exactly $m$ different values of $i$ such that $101 \mid x_{i}$, then there are $100 \mathrm{~m}$ different integers from $\{1,2, \ldots, 1110\}$ that cannot be elements of $X$, all of them coprime with $11 \cdot 101$. (Note that those $10 k$ and $100 \mathrm{~m}$ integers can overlap.)
In $\{1,2, \ldots, 1110\}$ there are 100 multiples of 11 , there are 10 multiples of 101 and there is no multiple of $11 \cdot 101$, so there are 1000 integers that are coprime with $11 \cdot 101$. In $X$ we have $1001-k-m$ integers that are coprime with $11 \cdot 101$, so exactly $k+m-1$ of the coprime integers in $\{1,2, \ldots, 1110\}$ are not in $X$. This implies that $10 k \leqslant k+m-1$ and $100 m \leqslant k+m-1$. Adding these two inequalities we find $8 k+98 m \leqslant-2$, a clear contradiction. So $N<1001$.
|
1000
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
. Find the greatest positive integer $N$ with the following property: there exist integers $x_{1}, \ldots, x_{N}$ such that $x_{i}^{2}-x_{i} x_{j}$ is not divisible by 1111 for any $i \neq j$.
|
We prove that the greatest $N$ with the required property is $N=1000$. First note that $x_{i}^{2}-x_{i} x_{j}=x_{i}\left(x_{i}-x_{j}\right)$, and that the prime factorisation of 1111 is $11 \cdot 101$.
We first show that we can find 1000 integers $x_{1}, x_{2}, \ldots, x_{1000}$ such that $x_{i}^{2}-x_{i} x_{j}$ is not divisible by 1111 for any $i \neq j$. Consider the set $\{1,2, \ldots, 1110\}$. This set contains 10 integers divisible by 101, and it contains 100 integers divisible by 11 . None of the integers in the set are divisible by both 11 and 101. If we delete all of these $10+100$ integers from the set, we are left with 1000 integers. Call these $x_{1}, x_{2}, \ldots, x_{1000}$. Now we have $11 \nmid x_{i}$ and $101 \nmid x_{i}$ for all $i$. Suppose there are $i \neq j$ with $1111 \mid x_{i}\left(x_{i}-x_{j}\right)$, then we must have $1111 \mid x_{i}-x_{j}$, which is a contradiction, since $x_{i}, x_{j} \in\{1,2, \ldots, 1110\}$. So this set satisfies the requirement.
We now prove that given 1001 (or more) integers $x_{1}, x_{2}, \ldots, x_{1001}$ there are $i \neq j$ with $1111 \mid x_{i}\left(x_{i}-x_{j}\right)$. Suppose for a contradiction that for all indices $i \neq j$, we have that $x_{i}\left(x_{i}-x_{j}\right)$ is not divisible by 1111, and write $X=\left\{x_{1}, \ldots, x_{1001}\right\}$. We may (after reducing modulo 1111 if necessary) assume that $x_{i} \in\{0,1, \ldots, 1110\}$ for all $i$. Then we know that $x_{i} \neq 0$ for all $i$, and $x_{i} \neq x_{j}$ for all $i \neq j$. Suppose for some $i$ we have $11 \mid x_{i}$. (Since $x_{i} \neq 0$, we know that $101 \nmid x_{i}$.) Then any integer $a \neq x_{i}$ with $a \equiv x_{i} \bmod 101$ cannot be an element of $X$, since $1111 \mid x_{i}\left(x_{i}-a\right)$. In $\{1,2, \ldots, 1110\}$ there are 10 such integers, all of them coprime with $11 \cdot 101$. If there are exactly $k$ different values of $i$ such that $11 \mid x_{i}$, there are $10 k$ different integers from $\{1,2, \ldots, 1110\}$ that cannot be elements of $X$, all of them coprime with $11 \cdot 101$. Similarly, if there are exactly $m$ different values of $i$ such that $101 \mid x_{i}$, then there are $100 \mathrm{~m}$ different integers from $\{1,2, \ldots, 1110\}$ that cannot be elements of $X$, all of them coprime with $11 \cdot 101$. (Note that those $10 k$ and $100 \mathrm{~m}$ integers can overlap.)
In $\{1,2, \ldots, 1110\}$ there are 100 multiples of 11 , there are 10 multiples of 101 and there is no multiple of $11 \cdot 101$, so there are 1000 integers that are coprime with $11 \cdot 101$. In $X$ we have $1001-k-m$ integers that are coprime with $11 \cdot 101$, so exactly $k+m-1$ of the coprime integers in $\{1,2, \ldots, 1110\}$ are not in $X$. This implies that $10 k \leqslant k+m-1$ and $100 m \leqslant k+m-1$. Adding these two inequalities we find $8 k+98 m \leqslant-2$, a clear contradiction. So $N<1001$.
|
{
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2016-zz.jsonl",
"problem_match": null,
"solution_match": null
}
|
49d29549-4ba0-5146-8599-f5efc1dab450
| 290,474
|
. Pawns and rooks are placed on a $2019 \times 2019$ chessboard, with at most one piece on each of the $2019^{2}$ squares. A rook can see another rook if they are in the same row or column and all squares between them are empty. What is the maximal number $p$ for which $p$ pawns and $p+2019$ rooks can be placed on the chessboard in such a way that no two rooks can see each other?
|
Answer: the maximal $p$ equals $1009^{2}$.
Write $n=2019$ and $k=1009$; then $n=2 k+1$. We first show that we can place $k^{2}$ pawns and $n+k^{2}$ rooks. Each cell of the chess board has coordinates $(x, y)$ with $1 \leqslant x, y \leqslant n$. We colour each cell black or white depending on whether $x+y$ is even or odd.
Let $A$ be cell $(1, k+1), B$ be cell $(k+1,1), C$ be cell $(2 k+1, k+1)$ and $D$ be cell $(k+1,2 k+1)$, and consider the skew square $A B C D$. We place rooks on the cells of this square which have the same colour as $A$, and we place pawns on the other cells of this square. In this way, no rook can see another rook. Now we have placed $p=k^{2}$ pawns and $(k+1)^{2}=k^{2}+(2 k+1)=p+n$ rooks.
Now we show that we can not place more pawns. Observe that in every row the number of rooks exceeds the number of pawns by at most 1 , since there has to be a pawn between every two neighbouring rooks. So the total number of rooks exceeds the number of pawns by at most $n$. On the other hand we are to place $p$ pawns and $p+n$ rooks, so the number of rooks in every row exceeds the number of pawns by exactly 1 . This means that the rooks and pawns alternate, with rooks at the two ends. For the columns the same holds.
Consider the $\ell$-th row. Let $a$ be the number of pawns in this row and let $b$ be the number of pawns above the $\ell$-th row. For all these pawns, a rook must be somewhere above it. Counting the rooks directly above these $a+b$ pawns, we conclude that there must be at least $a+b$ rooks in the first $\ell-1$ rows. In every row the number of rooks exceeds the number of pawns by 1 , so in these first $\ell-1$ rows we have at least $a+b-(\ell-1)$ pawns. So $b \geqslant a+b-(\ell-1)$, yielding $a \leqslant \ell-1$. We conclude that the $\ell$-th row contains at most $\ell-1$ pawns. The same holds for the $\ell$-th row counted from below (row $(n+1)-\ell$ ): also in this row, there are at most $\ell-1$ pawns. As $n=2 k+1$, the maximal number $p$ is
$$
\sum_{\ell=1}^{k}(\ell-1)+\sum_{\ell=1}^{k+1}(\ell-1)=k+2 \cdot \frac{1}{2} k(k-1)=k+k(k-1)=k^{2}
$$
|
1009^{2}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
. Pawns and rooks are placed on a $2019 \times 2019$ chessboard, with at most one piece on each of the $2019^{2}$ squares. A rook can see another rook if they are in the same row or column and all squares between them are empty. What is the maximal number $p$ for which $p$ pawns and $p+2019$ rooks can be placed on the chessboard in such a way that no two rooks can see each other?
|
Answer: the maximal $p$ equals $1009^{2}$.
Write $n=2019$ and $k=1009$; then $n=2 k+1$. We first show that we can place $k^{2}$ pawns and $n+k^{2}$ rooks. Each cell of the chess board has coordinates $(x, y)$ with $1 \leqslant x, y \leqslant n$. We colour each cell black or white depending on whether $x+y$ is even or odd.
Let $A$ be cell $(1, k+1), B$ be cell $(k+1,1), C$ be cell $(2 k+1, k+1)$ and $D$ be cell $(k+1,2 k+1)$, and consider the skew square $A B C D$. We place rooks on the cells of this square which have the same colour as $A$, and we place pawns on the other cells of this square. In this way, no rook can see another rook. Now we have placed $p=k^{2}$ pawns and $(k+1)^{2}=k^{2}+(2 k+1)=p+n$ rooks.
Now we show that we can not place more pawns. Observe that in every row the number of rooks exceeds the number of pawns by at most 1 , since there has to be a pawn between every two neighbouring rooks. So the total number of rooks exceeds the number of pawns by at most $n$. On the other hand we are to place $p$ pawns and $p+n$ rooks, so the number of rooks in every row exceeds the number of pawns by exactly 1 . This means that the rooks and pawns alternate, with rooks at the two ends. For the columns the same holds.
Consider the $\ell$-th row. Let $a$ be the number of pawns in this row and let $b$ be the number of pawns above the $\ell$-th row. For all these pawns, a rook must be somewhere above it. Counting the rooks directly above these $a+b$ pawns, we conclude that there must be at least $a+b$ rooks in the first $\ell-1$ rows. In every row the number of rooks exceeds the number of pawns by 1 , so in these first $\ell-1$ rows we have at least $a+b-(\ell-1)$ pawns. So $b \geqslant a+b-(\ell-1)$, yielding $a \leqslant \ell-1$. We conclude that the $\ell$-th row contains at most $\ell-1$ pawns. The same holds for the $\ell$-th row counted from below (row $(n+1)-\ell$ ): also in this row, there are at most $\ell-1$ pawns. As $n=2 k+1$, the maximal number $p$ is
$$
\sum_{\ell=1}^{k}(\ell-1)+\sum_{\ell=1}^{k+1}(\ell-1)=k+2 \cdot \frac{1}{2} k(k-1)=k+k(k-1)=k^{2}
$$
|
{
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2019-zz.jsonl",
"problem_match": null,
"solution_match": null
}
|
174c3dbf-28b7-5794-91a0-368ada505415
| 606,401
|
Pebbles are placed on a $2021 \times 2021$ board in such a way that each square contains at most one pebble. The pebble set of a square of the board is the collection of all pebbles which are in the same row or column as this square. Determine the least number of pebbles that can be placed on the board in such a way that no two squares have the same pebble set.
#
|
Let $N \geqslant 1$ be a positive integer. We claim that the least number of pebbles that can be placed on a $(2 N+1) \times(2 N+1)$ chessboard in such a way that no two squares of the board have the same pebble set is $3 N+1$. The problem has $N=1010$, so at least 3031 pebbles are needed.
We begin by placing $(2 N+1)+N=3 N+1$ pebbles on the board as shown. The construction extends to all values of $N$, and one checks that no two squares on the board have the same pebble set.
We are left to show that the number of pebbles, $P$, that must be placed on the board is at least $3 N+1$. Suppose that there exists an empty row. Any other row must then contain at least two pebbles. Indeed, if another row is empty, Figure [1], or contains exactly one pebble, Figure [2], then there are two squares (shaded in the figures below) with the same pebble set. So in this case there are at least $P \geqslant 2(2 N+1-1)=4 N \geqslant 3 N+1$ pebbles on the board. The same argument applies, mutatis mutandis, to the columns of the board.
$[1]$
$[2]$
$[3]$
$[4$

On the other hand, suppose that each each row and each column contains at least one pebble. Let $k$ the number of rows containing precisely one pebble. Counting the number of pebbles per row shows that $P \geqslant k+2(2 N+1-k)$. To count the number of pebbles per column, note that the $k$ pebbles that are the only ones in their row must be in $k$ distinct columns, Figure [3]. Furthermore, at most one of these $k$ columns only has one pebble in it, Figure [4]. So these $k$ columns contain a total of at least $2 k-1$ pebbles, while the remaining columns contain at least one each. Hence $P \geqslant(2 k-1)+(2 N+1-k)$. Adding these two inequalities we get $2 P \geqslant 6 N+2$.
Remark. For a $2 N \times 2 N$ board, at least $3 N$ pebbles are needed. The proof is similar: if there is an empty line, then $P \geqslant 2(2 N-1) \geqslant 3 N$ for $N \geqslant 2$. If there is no empty line, then $2 P \geqslant 6 N-1$. A construction similar to that of the odd boards works. While the construction is unique in the odd case, up to permutation of rows and columns, that is not true for even boards.
#
|
3031
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Pebbles are placed on a $2021 \times 2021$ board in such a way that each square contains at most one pebble. The pebble set of a square of the board is the collection of all pebbles which are in the same row or column as this square. Determine the least number of pebbles that can be placed on the board in such a way that no two squares have the same pebble set.
#
|
Let $N \geqslant 1$ be a positive integer. We claim that the least number of pebbles that can be placed on a $(2 N+1) \times(2 N+1)$ chessboard in such a way that no two squares of the board have the same pebble set is $3 N+1$. The problem has $N=1010$, so at least 3031 pebbles are needed.
We begin by placing $(2 N+1)+N=3 N+1$ pebbles on the board as shown. The construction extends to all values of $N$, and one checks that no two squares on the board have the same pebble set.

We are left to show that the number of pebbles, $P$, that must be placed on the board is at least $3 N+1$. Suppose that there exists an empty row. Any other row must then contain at least two pebbles. Indeed, if another row is empty, Figure [1], or contains exactly one pebble, Figure [2], then there are two squares (shaded in the figures below) with the same pebble set. So in this case there are at least $P \geqslant 2(2 N+1-1)=4 N \geqslant 3 N+1$ pebbles on the board. The same argument applies, mutatis mutandis, to the columns of the board.
$[1]$

$[2]$

$[3]$

$[4$

On the other hand, suppose that each each row and each column contains at least one pebble. Let $k$ the number of rows containing precisely one pebble. Counting the number of pebbles per row shows that $P \geqslant k+2(2 N+1-k)$. To count the number of pebbles per column, note that the $k$ pebbles that are the only ones in their row must be in $k$ distinct columns, Figure [3]. Furthermore, at most one of these $k$ columns only has one pebble in it, Figure [4]. So these $k$ columns contain a total of at least $2 k-1$ pebbles, while the remaining columns contain at least one each. Hence $P \geqslant(2 k-1)+(2 N+1-k)$. Adding these two inequalities we get $2 P \geqslant 6 N+2$.
Remark. For a $2 N \times 2 N$ board, at least $3 N$ pebbles are needed. The proof is similar: if there is an empty line, then $P \geqslant 2(2 N-1) \geqslant 3 N$ for $N \geqslant 2$. If there is no empty line, then $2 P \geqslant 6 N-1$. A construction similar to that of the odd boards works. While the construction is unique in the odd case, up to permutation of rows and columns, that is not true for even boards.
#
|
{
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2021-zz.jsonl",
"problem_match": null,
"solution_match": null
}
|
18d300f9-5061-56a6-bd88-24a432712623
| 606,422
|
A sequence $a_{1}, a_{2}, a_{3}, \ldots$ of positive integers satisfies $a_{1}>5$ and $a_{n+1}=5+6+\cdots+a_{n}$ for all positive integers $n$. Determine all prime numbers $p$ such that, regardless of the value of $a_{1}$, this sequence must contain a multiple of $p$.
#
|
We claim that the only prime number of which the sequence must contain a multiple is $p=2$. To prove this, we begin by noting that
$$
a_{n+1}=\frac{a_{n}\left(a_{n}+1\right)}{2}-10=\frac{\left(a_{n}-4\right)\left(a_{n}+5\right)}{2} .
$$
Let $p>2$ be an odd prime, and choose $a_{1} \equiv-4(\bmod p)$, so $2 a_{2} \equiv(-4-4)(-4+5) \equiv-8(\bmod p)$, whence $a_{2} \equiv-4(\bmod p)$, since $p$ is odd. By induction, $a_{n} \equiv-4(\bmod p) \not \equiv 0(\bmod p)$ for all $n$, and so the sequence need not contain a multiple of $p$.
We are left to show that the sequence must contain an even number. Suppose to the contrary that $a_{n}$ is odd for $n=1,2, \ldots$ We observe that
$$
a_{n+1}-a_{n}=\frac{a_{n}\left(a_{n}+1\right)}{2}-\frac{a_{n-1}\left(a_{n-1}+1\right)}{2}=\frac{a_{n}-a_{n-1}}{2}\left(a_{n}+a_{n-1}+1\right) .
$$
By assumption, $a_{n}+a_{n-1}+1$ is odd for $n=1,2, \ldots$, so this shows that $v_{2}\left(a_{n+1}-a_{n}\right)=v_{2}\left(a_{n}-a_{n-1}\right)-1$, and so there exists $N$ such that $v_{2}\left(a_{N+1}-a_{N}\right)=0$. This is a contradiction, because $a_{n+1}-a_{n}$ is even for $n=1,2, \ldots$ by assumption, and thus completes the proof.
#
|
2
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
A sequence $a_{1}, a_{2}, a_{3}, \ldots$ of positive integers satisfies $a_{1}>5$ and $a_{n+1}=5+6+\cdots+a_{n}$ for all positive integers $n$. Determine all prime numbers $p$ such that, regardless of the value of $a_{1}$, this sequence must contain a multiple of $p$.
#
|
We claim that the only prime number of which the sequence must contain a multiple is $p=2$. To prove this, we begin by noting that
$$
a_{n+1}=\frac{a_{n}\left(a_{n}+1\right)}{2}-10=\frac{\left(a_{n}-4\right)\left(a_{n}+5\right)}{2} .
$$
Let $p>2$ be an odd prime, and choose $a_{1} \equiv-4(\bmod p)$, so $2 a_{2} \equiv(-4-4)(-4+5) \equiv-8(\bmod p)$, whence $a_{2} \equiv-4(\bmod p)$, since $p$ is odd. By induction, $a_{n} \equiv-4(\bmod p) \not \equiv 0(\bmod p)$ for all $n$, and so the sequence need not contain a multiple of $p$.
We are left to show that the sequence must contain an even number. Suppose to the contrary that $a_{n}$ is odd for $n=1,2, \ldots$ We observe that
$$
a_{n+1}-a_{n}=\frac{a_{n}\left(a_{n}+1\right)}{2}-\frac{a_{n-1}\left(a_{n-1}+1\right)}{2}=\frac{a_{n}-a_{n-1}}{2}\left(a_{n}+a_{n-1}+1\right) .
$$
By assumption, $a_{n}+a_{n-1}+1$ is odd for $n=1,2, \ldots$, so this shows that $v_{2}\left(a_{n+1}-a_{n}\right)=v_{2}\left(a_{n}-a_{n-1}\right)-1$, and so there exists $N$ such that $v_{2}\left(a_{N+1}-a_{N}\right)=0$. This is a contradiction, because $a_{n+1}-a_{n}$ is even for $n=1,2, \ldots$ by assumption, and thus completes the proof.
#
|
{
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2021-zz.jsonl",
"problem_match": null,
"solution_match": null
}
|
f4045e30-6f86-5244-82fb-41df27c6cae7
| 290,187
|
Let $n$ be a positive integer. There are $n$ ants walking along a line at constant nonzero speeds. Different ants need not walk at the same speed or walk in the same direction. Whenever two or more ants collide, all the ants involved in this collision instantly change directions. (Different ants need not be moving in opposite directions when they collide, since a faster ant may catch up with a slower one that is moving in the same direction.) The ants keep walking indefinitely.
Assuming that the total number of collisions is finite, determine the largest possible number of collisions in terms of $n$.
#
|
The order of the ants along the line does not change; denote by $v_{1}, v_{2}, \ldots, v_{n}$ the respective speeds of ants $1,2, \ldots, n$ in this order. If $v_{i-1}<v_{i}>v_{i+1}$ for some $i \in\{2, \ldots, n-1\}$, then, at each stage, ant $i$ can catch up with ants $i-1$ or $i+1$ irrespective of the latters' directions of motion, so the number of collisions is infinite. Hence, if the number of collisions is finite, then, up to switching the direction definining the order of the ants, (i) $v_{1} \geqslant \cdots \geqslant v_{n}$ or (ii) $v_{1} \geqslant \cdots \geqslant v_{k-1}>v_{k} \leqslant \cdots \leqslant v_{n}$ for some $k \in\{2, \ldots, n-1\}$. We need the following observation:
Claim. If $v_{1} \geqslant \cdots \geqslant v_{m}$, then ants $m-1$ and $m$ collide at most $m-1$ times.
Proof. The proof goes by induction on $m$, the case $m=1$ being trivial. Since $v_{m-1} \geqslant v_{m}$, ants $m-1$ and $m$ can only collide if the former is moving towards the latter. Hence, between successive collisions with ant $m$, ant $m-1$ must reverse direction by colliding with ant $m-2$. Since ants $m-1$ and $m-2$ collide at most $(m-1)-1=m-2$ times by the inductive hypothesis, ants $m$ and $m-1$ collide at most $(m-2)+1=m-1$ times.
Hence, in case (i), there are at most $0+1+\cdots+(n-1)=n(n-1) / 2$ collisions. In case (ii), applying the claim to ants $1,2, \ldots, k$ and also to ants $n, n-1, \ldots, k$ by switching their order, the number of collisions is at most $k(k-1) / 2+(n-k+1)(n-k) / 2=n(n-1) / 2-(k-1)(n-k)<n(n-1) / 2$.
Now take a coordinate $x$ along the line, and put ants at $x=1,2, \ldots, n$ with positive initial velocities and speeds $v_{1}=\cdots=v_{n-1}=1, v_{n}=\varepsilon$, for some $\varepsilon$. For $\varepsilon=0$, collisions occur according to the pattern shown below for $n=5$, which clearly extends to all values of $n$ in such a way that ants $m$ and $m+1$ collide exactly $m$ times for $m=1,2, \ldots, n-1$. This yield $1+2+\cdots+(n-1)=n(n-1) / 2$ collisions in total. For all sufficiently small $\varepsilon>0$, the number of collisions remains equal to $n(n-1) / 2$.
This shows that the upper bound obtained above can be attained. If the number of collisions is finite, the largest possible number of collisions is therefore indeed $n(n-1) / 2$.
## BxMO 2022: Problems and Solutions
#
|
n(n-1) / 2
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Let $n$ be a positive integer. There are $n$ ants walking along a line at constant nonzero speeds. Different ants need not walk at the same speed or walk in the same direction. Whenever two or more ants collide, all the ants involved in this collision instantly change directions. (Different ants need not be moving in opposite directions when they collide, since a faster ant may catch up with a slower one that is moving in the same direction.) The ants keep walking indefinitely.
Assuming that the total number of collisions is finite, determine the largest possible number of collisions in terms of $n$.
#
|
The order of the ants along the line does not change; denote by $v_{1}, v_{2}, \ldots, v_{n}$ the respective speeds of ants $1,2, \ldots, n$ in this order. If $v_{i-1}<v_{i}>v_{i+1}$ for some $i \in\{2, \ldots, n-1\}$, then, at each stage, ant $i$ can catch up with ants $i-1$ or $i+1$ irrespective of the latters' directions of motion, so the number of collisions is infinite. Hence, if the number of collisions is finite, then, up to switching the direction definining the order of the ants, (i) $v_{1} \geqslant \cdots \geqslant v_{n}$ or (ii) $v_{1} \geqslant \cdots \geqslant v_{k-1}>v_{k} \leqslant \cdots \leqslant v_{n}$ for some $k \in\{2, \ldots, n-1\}$. We need the following observation:
Claim. If $v_{1} \geqslant \cdots \geqslant v_{m}$, then ants $m-1$ and $m$ collide at most $m-1$ times.
Proof. The proof goes by induction on $m$, the case $m=1$ being trivial. Since $v_{m-1} \geqslant v_{m}$, ants $m-1$ and $m$ can only collide if the former is moving towards the latter. Hence, between successive collisions with ant $m$, ant $m-1$ must reverse direction by colliding with ant $m-2$. Since ants $m-1$ and $m-2$ collide at most $(m-1)-1=m-2$ times by the inductive hypothesis, ants $m$ and $m-1$ collide at most $(m-2)+1=m-1$ times.
Hence, in case (i), there are at most $0+1+\cdots+(n-1)=n(n-1) / 2$ collisions. In case (ii), applying the claim to ants $1,2, \ldots, k$ and also to ants $n, n-1, \ldots, k$ by switching their order, the number of collisions is at most $k(k-1) / 2+(n-k+1)(n-k) / 2=n(n-1) / 2-(k-1)(n-k)<n(n-1) / 2$.
Now take a coordinate $x$ along the line, and put ants at $x=1,2, \ldots, n$ with positive initial velocities and speeds $v_{1}=\cdots=v_{n-1}=1, v_{n}=\varepsilon$, for some $\varepsilon$. For $\varepsilon=0$, collisions occur according to the pattern shown below for $n=5$, which clearly extends to all values of $n$ in such a way that ants $m$ and $m+1$ collide exactly $m$ times for $m=1,2, \ldots, n-1$. This yield $1+2+\cdots+(n-1)=n(n-1) / 2$ collisions in total. For all sufficiently small $\varepsilon>0$, the number of collisions remains equal to $n(n-1) / 2$.

This shows that the upper bound obtained above can be attained. If the number of collisions is finite, the largest possible number of collisions is therefore indeed $n(n-1) / 2$.
## BxMO 2022: Problems and Solutions
#
|
{
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2022-zz.jsonl",
"problem_match": null,
"solution_match": null
}
|
fefc693f-676b-56d5-aa09-e19de484004a
| 606,435
|
(a) Let $a_{0}, a_{1}, \ldots, a_{2024}$ be real numbers such that $\left|a_{i+1}-a_{i}\right| \leqslant 1$ for $i=0,1, \ldots, 2023$. Find the minimum possible value of $$ a_{0} a_{1}+a_{1} a_{2}+\cdots+a_{2023} a_{2024} $$ (b) Does there exist a real number $C$ such that $$ a_{0} a_{1}-a_{1} a_{2}+a_{2} a_{3}-a_{3} a_{4}+\cdots+a_{2022} a_{2023}-a_{2023} a_{2024} \geqslant C $$ for all real numbers $a_{0}, a_{1}, \ldots, a_{2024}$ such that $\left|a_{i+1}-a_{i}\right| \leqslant 1$ for $i=0,1, \ldots, 2023$ ?
|
(a) The minimum value is -506 . Note that from $\left|a_{i}-a_{i-1}\right| \leq 1$ it follows that
$$
a_{i} a_{i-1}=\frac{\left(a_{i}+a_{i-1}\right)^{2}-\left(a_{i}-a_{i-1}\right)^{2}}{4} \geq-\frac{\left(a_{i}-a_{i-1}\right)^{2}}{4} \geq-\frac{1}{4}
$$
Adding this for $i=1,2, \ldots, 2024$, we obtain that
$$
a_{0} a_{1}+a_{1} a_{2}+a_{2} a_{3}+\ldots+a_{2023} a_{2024} \geq 2024 \cdot-\frac{1}{4}=-506
$$
We now show that this value can be attained. Indeed, for the sequence $\left(a_{0}, a_{1}, \ldots, a_{2024}\right)=$ $\left(\frac{1}{2},-\frac{1}{2}, \frac{1}{2},-\frac{1}{2}, \frac{1}{2}, \ldots, \frac{1}{2}\right)$ with alternating $\frac{1}{2}$ 's and $-\frac{1}{2}$ 's, each term $a_{i} a_{i-1}$ is equal to $-\frac{1}{4}$, leading to $a_{0} a_{1}+a_{1} a_{2}+a_{2} a_{3}+\ldots+a_{2023} a_{2024}=2024 \cdot-\frac{1}{4}=-506$.
(b) No, such a $C$ does not exist. We argue by contradiction. Suppose $C$ has this property, and consider the sequence defined by $a_{0}=C$ and $a_{i}=C-1$ for $i=1,2, \ldots, 2024$ satisfies the condition in the problem. For this sequence, we have $a_{i} a_{i+1}-a_{i+1} a_{i+2}=0$ for $i=2,4, \ldots$, 2022, so the sum
$$
a_{0} a_{1}-a_{1} a_{2}+a_{2} a_{3}-a_{3} a_{4}+a_{4} a_{5}-a_{5} a_{6}+\ldots+a_{2022} a_{2023}-a_{2023} a_{2024}
$$
is equal to
$$
a_{0} a_{1}-a_{1} a_{2}=C(C-1)-(C-1)^{2}=C-1<C,
$$
contradiction.
|
-506
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
(a) Let $a_{0}, a_{1}, \ldots, a_{2024}$ be real numbers such that $\left|a_{i+1}-a_{i}\right| \leqslant 1$ for $i=0,1, \ldots, 2023$. Find the minimum possible value of $$ a_{0} a_{1}+a_{1} a_{2}+\cdots+a_{2023} a_{2024} $$ (b) Does there exist a real number $C$ such that $$ a_{0} a_{1}-a_{1} a_{2}+a_{2} a_{3}-a_{3} a_{4}+\cdots+a_{2022} a_{2023}-a_{2023} a_{2024} \geqslant C $$ for all real numbers $a_{0}, a_{1}, \ldots, a_{2024}$ such that $\left|a_{i+1}-a_{i}\right| \leqslant 1$ for $i=0,1, \ldots, 2023$ ?
|
(a) The minimum value is -506 . Note that from $\left|a_{i}-a_{i-1}\right| \leq 1$ it follows that
$$
a_{i} a_{i-1}=\frac{\left(a_{i}+a_{i-1}\right)^{2}-\left(a_{i}-a_{i-1}\right)^{2}}{4} \geq-\frac{\left(a_{i}-a_{i-1}\right)^{2}}{4} \geq-\frac{1}{4}
$$
Adding this for $i=1,2, \ldots, 2024$, we obtain that
$$
a_{0} a_{1}+a_{1} a_{2}+a_{2} a_{3}+\ldots+a_{2023} a_{2024} \geq 2024 \cdot-\frac{1}{4}=-506
$$
We now show that this value can be attained. Indeed, for the sequence $\left(a_{0}, a_{1}, \ldots, a_{2024}\right)=$ $\left(\frac{1}{2},-\frac{1}{2}, \frac{1}{2},-\frac{1}{2}, \frac{1}{2}, \ldots, \frac{1}{2}\right)$ with alternating $\frac{1}{2}$ 's and $-\frac{1}{2}$ 's, each term $a_{i} a_{i-1}$ is equal to $-\frac{1}{4}$, leading to $a_{0} a_{1}+a_{1} a_{2}+a_{2} a_{3}+\ldots+a_{2023} a_{2024}=2024 \cdot-\frac{1}{4}=-506$.
(b) No, such a $C$ does not exist. We argue by contradiction. Suppose $C$ has this property, and consider the sequence defined by $a_{0}=C$ and $a_{i}=C-1$ for $i=1,2, \ldots, 2024$ satisfies the condition in the problem. For this sequence, we have $a_{i} a_{i+1}-a_{i+1} a_{i+2}=0$ for $i=2,4, \ldots$, 2022, so the sum
$$
a_{0} a_{1}-a_{1} a_{2}+a_{2} a_{3}-a_{3} a_{4}+a_{4} a_{5}-a_{5} a_{6}+\ldots+a_{2022} a_{2023}-a_{2023} a_{2024}
$$
is equal to
$$
a_{0} a_{1}-a_{1} a_{2}=C(C-1)-(C-1)^{2}=C-1<C,
$$
contradiction.
|
{
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2024-zz.jsonl",
"problem_match": null,
"solution_match": null
}
|
5a7573af-27b6-5d84-ae4c-27b9831d5f2e
| 604,292
|
Let $n \geq 2$ be some fixed positive integer and suppose that $a_{1}, a_{2}, \ldots, a_{n}$ are positive real numbers satisfying $a_{1}+a_{2}+\cdots+a_{n}=2^{n}-1$.
Find the minimum possible value of
$$
\frac{a_{1}}{1}+\frac{a_{2}}{1+a_{1}}+\frac{a_{3}}{1+a_{1}+a_{2}}+\cdots+\frac{a_{n}}{1+a_{1}+a_{2}+\cdots+a_{n-1}} .
$$
|
We claim the the minimum possible value of this expression is $n$. Observe that by AM-GM, we have that
$$
\begin{aligned}
\frac{a_{1}}{1}+ & \frac{a_{2}}{1+a_{1}}+\cdots+\frac{a_{n}}{1+a_{1}+a_{2}+\cdots+a_{n-1}} \\
& =\frac{1+a_{1}}{1}+\frac{1+a_{1}+a_{2}}{1+a_{1}}+\cdots+\frac{1+a_{1}+a_{2}+\cdots+a_{n}}{1+a_{1}+a_{2}+\cdots+a_{n-1}}-n \\
& \geq n \cdot \sqrt[n]{\frac{1+a_{1}}{1} \cdot \frac{1+a_{1}+a_{2}}{1+a_{1}} \cdots \frac{1+a_{1}+a_{2}+\cdots+a_{n}}{1+a_{1}+a_{2}+\cdots+a_{n-1}}}-n \\
& =n \cdot \sqrt[n]{1+a_{1}+a_{2}+\cdots+a_{n}}-n \\
& =2 n-n=n .
\end{aligned}
$$
Furthermore, equality is achieved when $a_{k}=2^{k-1}$ for each $1 \leq k \leq n$.
|
n
|
Yes
|
Yes
|
math-word-problem
|
Inequalities
|
Let $n \geq 2$ be some fixed positive integer and suppose that $a_{1}, a_{2}, \ldots, a_{n}$ are positive real numbers satisfying $a_{1}+a_{2}+\cdots+a_{n}=2^{n}-1$.
Find the minimum possible value of
$$
\frac{a_{1}}{1}+\frac{a_{2}}{1+a_{1}}+\frac{a_{3}}{1+a_{1}+a_{2}}+\cdots+\frac{a_{n}}{1+a_{1}+a_{2}+\cdots+a_{n-1}} .
$$
|
We claim the the minimum possible value of this expression is $n$. Observe that by AM-GM, we have that
$$
\begin{aligned}
\frac{a_{1}}{1}+ & \frac{a_{2}}{1+a_{1}}+\cdots+\frac{a_{n}}{1+a_{1}+a_{2}+\cdots+a_{n-1}} \\
& =\frac{1+a_{1}}{1}+\frac{1+a_{1}+a_{2}}{1+a_{1}}+\cdots+\frac{1+a_{1}+a_{2}+\cdots+a_{n}}{1+a_{1}+a_{2}+\cdots+a_{n-1}}-n \\
& \geq n \cdot \sqrt[n]{\frac{1+a_{1}}{1} \cdot \frac{1+a_{1}+a_{2}}{1+a_{1}} \cdots \frac{1+a_{1}+a_{2}+\cdots+a_{n}}{1+a_{1}+a_{2}+\cdots+a_{n-1}}}-n \\
& =n \cdot \sqrt[n]{1+a_{1}+a_{2}+\cdots+a_{n}}-n \\
& =2 n-n=n .
\end{aligned}
$$
Furthermore, equality is achieved when $a_{k}=2^{k-1}$ for each $1 \leq k \leq n$.
|
{
"resource_path": "Canada_MO/segmented/en-2021CMO_solutions_en-1.jsonl",
"problem_match": "\n## Problem No. 2.",
"solution_match": "\nSolution."
}
|
27cd4d4b-4260-568f-9eac-1755c938c709
| 604,423
|
Assume that real numbers $a$ and $b$ satisfy
$$
a b+\sqrt{a b+1}+\sqrt{a^{2}+b} \cdot \sqrt{b^{2}+a}=0
$$
Find, with proof, the value of
$$
a \sqrt{b^{2}+a}+b \sqrt{a^{2}+b}
$$
|
Let us rewrite the given equation as follows:
$$
a b+\sqrt{a^{2}+b} \sqrt{b^{2}+a}=-\sqrt{a b+1} .
$$
Squaring this gives us
$$
\begin{aligned}
a^{2} b^{2}+2 a b \sqrt{a^{2}+b} \sqrt{b^{2}+a}+\left(a^{2}+b\right)\left(b^{2}+a\right) & =a b+1 \\
\left(a^{2} b^{2}+a^{3}\right)+2 a b \sqrt{a^{2}+b} \sqrt{b^{2}+a}+\left(a^{2} b^{2}+b^{3}\right) & =1 \\
\left(a \sqrt{b^{2}+a}+b \sqrt{a^{2}+b}\right)^{2} & =1 \\
a \sqrt{b^{2}+a}+b \sqrt{a^{2}+b} & = \pm 1 .
\end{aligned}
$$
Next, we show that $a \sqrt{b^{2}+a}+b \sqrt{a^{2}+b}>0$. Note that
$$
a b=-\sqrt{a b+1}-\sqrt{a^{2}+b} \cdot \sqrt{b^{2}+a}<0
$$
so $a$ and $b$ have opposite signs. Without loss of generality, we may assume $a>0>b$. Then rewrite
$$
a \sqrt{b^{2}+a}+b \sqrt{a^{2}+b}=a\left(\sqrt{b^{2}+a}+b\right)-b\left(a-\sqrt{a^{2}+b}\right)
$$
and, since $\sqrt{b^{2}+a}+b$ and $a-\sqrt{a^{2}+b}$ are both positive, the expression above is positive. Therefore,
$$
a \sqrt{b^{2}+a}+b \sqrt{a^{2}+b}=1,
$$
and the proof is finished.
|
1
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Assume that real numbers $a$ and $b$ satisfy
$$
a b+\sqrt{a b+1}+\sqrt{a^{2}+b} \cdot \sqrt{b^{2}+a}=0
$$
Find, with proof, the value of
$$
a \sqrt{b^{2}+a}+b \sqrt{a^{2}+b}
$$
|
Let us rewrite the given equation as follows:
$$
a b+\sqrt{a^{2}+b} \sqrt{b^{2}+a}=-\sqrt{a b+1} .
$$
Squaring this gives us
$$
\begin{aligned}
a^{2} b^{2}+2 a b \sqrt{a^{2}+b} \sqrt{b^{2}+a}+\left(a^{2}+b\right)\left(b^{2}+a\right) & =a b+1 \\
\left(a^{2} b^{2}+a^{3}\right)+2 a b \sqrt{a^{2}+b} \sqrt{b^{2}+a}+\left(a^{2} b^{2}+b^{3}\right) & =1 \\
\left(a \sqrt{b^{2}+a}+b \sqrt{a^{2}+b}\right)^{2} & =1 \\
a \sqrt{b^{2}+a}+b \sqrt{a^{2}+b} & = \pm 1 .
\end{aligned}
$$
Next, we show that $a \sqrt{b^{2}+a}+b \sqrt{a^{2}+b}>0$. Note that
$$
a b=-\sqrt{a b+1}-\sqrt{a^{2}+b} \cdot \sqrt{b^{2}+a}<0
$$
so $a$ and $b$ have opposite signs. Without loss of generality, we may assume $a>0>b$. Then rewrite
$$
a \sqrt{b^{2}+a}+b \sqrt{a^{2}+b}=a\left(\sqrt{b^{2}+a}+b\right)-b\left(a-\sqrt{a^{2}+b}\right)
$$
and, since $\sqrt{b^{2}+a}+b$ and $a-\sqrt{a^{2}+b}$ are both positive, the expression above is positive. Therefore,
$$
a \sqrt{b^{2}+a}+b \sqrt{a^{2}+b}=1,
$$
and the proof is finished.
|
{
"resource_path": "Canada_MO/segmented/en-cmo2022-solutions-en.jsonl",
"problem_match": "\nP1.",
"solution_match": "\nSolution."
}
|
ba735b17-6803-53c2-a34f-31239c79ec21
| 604,475
|
William is thinking of an integer between 1 and 50, inclusive. Victor can choose a positive integer $m$ and ask William: "does $m$ divide your number?", to which William must answer truthfully. Victor continues asking these questions until he determines William's number. What is the minimum number of questions that Victor needs to guarantee this?
|
The minimum number is 15 questions.
First, we show that 14 or fewer questions is not enough to guarantee success. Suppose Victor asks at most 14 questions, and William responds with "no" to each question unless $m=$ 1. Note that these responses are consistent with the secret number being 1. But since there are 15 primes less than 50 , some prime $p$ was never chosen as $m$. That means the responses are also consistent with the secret number being $p$. Therefore, Victor cannot determine the number for sure because 1 and $p$ are both possible options.
Now we show that Victor can always determine the number with 15 questions. Let $N$ be William's secret number. First, Victor asks 4 questions, with $m=2,3,5,7$. We then case on William's responses.
Case 1. William answers " $n o$ " to all four questions.
$N$ can only be divisible by primes that are 11 or larger. This means $N$ cannot have multiple prime factors (otherwise $N \geq 11^{2}>50$ ), so either $N=1$ or $N$ is one of the 11 remaining primes less than 50 . Victor can then ask 11 questions with $m=11,13,17, \ldots, 47$, one for each of the remaining primes, to determine the value of $N$.
Case 2. William answers "yes" to $m=2$, and " $n o$ " to $m=3,5,7$.
There are only 11 possible values of $N$ that match these answers $(2,4,8,16,22,26,32$, 34, 38, 44, and 46). Victor can use his remaining 11 questions on each of these possibilities.
Case 3. William answers "yes" to $m=3$, and " $n o$ " to $m=2,5,7$.
There are 5 possible values of $N(3,9,27,33$, and 39). Similar to Case 2, Victor can ask about these 5 numbers to determine the value of $N$.
Case 4. William answers "yes" to multiple questions, or one "yes" to $m=5$ or $m=7$.
Let $k$ be the product of all $m$ 's that received a "yes" response. Since $N$ is divisible by each of these $m$ 's, $N$ must be divisible by $k$. Since $k \geq 5$, there are at most 10 multiples of $k$ between 1 and 50 . Victor can ask about each of these multiples of $k$ with his remaining questions.
|
15
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
William is thinking of an integer between 1 and 50, inclusive. Victor can choose a positive integer $m$ and ask William: "does $m$ divide your number?", to which William must answer truthfully. Victor continues asking these questions until he determines William's number. What is the minimum number of questions that Victor needs to guarantee this?
|
The minimum number is 15 questions.
First, we show that 14 or fewer questions is not enough to guarantee success. Suppose Victor asks at most 14 questions, and William responds with "no" to each question unless $m=$ 1. Note that these responses are consistent with the secret number being 1. But since there are 15 primes less than 50 , some prime $p$ was never chosen as $m$. That means the responses are also consistent with the secret number being $p$. Therefore, Victor cannot determine the number for sure because 1 and $p$ are both possible options.
Now we show that Victor can always determine the number with 15 questions. Let $N$ be William's secret number. First, Victor asks 4 questions, with $m=2,3,5,7$. We then case on William's responses.
Case 1. William answers " $n o$ " to all four questions.
$N$ can only be divisible by primes that are 11 or larger. This means $N$ cannot have multiple prime factors (otherwise $N \geq 11^{2}>50$ ), so either $N=1$ or $N$ is one of the 11 remaining primes less than 50 . Victor can then ask 11 questions with $m=11,13,17, \ldots, 47$, one for each of the remaining primes, to determine the value of $N$.
Case 2. William answers "yes" to $m=2$, and " $n o$ " to $m=3,5,7$.
There are only 11 possible values of $N$ that match these answers $(2,4,8,16,22,26,32$, 34, 38, 44, and 46). Victor can use his remaining 11 questions on each of these possibilities.
Case 3. William answers "yes" to $m=3$, and " $n o$ " to $m=2,5,7$.
There are 5 possible values of $N(3,9,27,33$, and 39). Similar to Case 2, Victor can ask about these 5 numbers to determine the value of $N$.
Case 4. William answers "yes" to multiple questions, or one "yes" to $m=5$ or $m=7$.
Let $k$ be the product of all $m$ 's that received a "yes" response. Since $N$ is divisible by each of these $m$ 's, $N$ must be divisible by $k$. Since $k \geq 5$, there are at most 10 multiples of $k$ between 1 and 50 . Victor can ask about each of these multiples of $k$ with his remaining questions.
|
{
"resource_path": "Canada_MO/segmented/en-cmo2023-solutions-en.jsonl",
"problem_match": "\nP1.",
"solution_match": "\nSolution."
}
|
d3d30247-3cc7-5f3d-b352-11b51a0b50c4
| 604,544
|
A country with $n$ cities has some two-way roads connecting certain pairs of cities. Someone notices that if the country is split into two parts in any way, then there would be at most $k n$ roads between the two parts (where $k$ is a fixed positive integer). What is the largest integer $m$ (in terms of $n$ and $k$ ) such that there is guaranteed to be a set of $m$ cities, no two of which are directly connected by a road?
|
The answer is $m=\left\lceil\frac{n}{4 k}\right\rceil$
Call a collection of cities independent if no two cities in the collection are joined by a road. Let $r$ and $k$ be integers such that $n=4 k q+r$ where $1 \leq r \leq 4 k$.
First we show that $m \leq\left\lceil\frac{n}{4 k}\right\rceil=q+1$. Let $K_{i}$ denote a set of $i$ cities such that every pair of cities in $K_{i}$ is linked by a road. Consider a country containing $q$ copies of $K_{4 k}$ and one copy of $K_{r}$. An independent set of cities in this country contains at most one city from each $K_{4 k}$ or $K_{r}$ and therefore contains at most $q+1$ cities. Now note that any partition of the cities of the country into two new countries partitions each $K_{4 k}$ and $K_{r}$ into two sets. If $K_{i}$ where $i \leq 4 k$ is partitioned into two sets of cities of sizes $a$ and $b$, then the number of roads between the two sets is $a b \leq \frac{(a+b)^{2}}{4} \leq k i$. Summing this inequality over all copies of $K_{4 k}$ and $K_{r}$ yields that there are at most $k n$ roads between the two new countries. This implies that this particular country satisfies the given condition and it follows that $m \leq\left\lceil\frac{n}{4 k}\right\rceil$.
Now we show that any country satisfying the given condition has an independent set containing at least $\left\lceil\frac{n}{4 k}\right\rceil$ cities. Call a set of cities $i$-separable if it can be partitioned into $i$ disjoint independent sets of cities. Given a country satisfying the conditions, let $S$ be a largest set of cities in the country that is $2 k$-separable. We prove that $|S| \geq n / 2$. By definition of $S$, there exists a partition $A_{1}, A_{2}, \ldots, A_{2 k}$ of the cities in $S$ such that each $A_{i}$ is independent. Let $|S|=t$. Assume for contradiction that $t<\frac{n}{2}$. There are at most $k n$ roads between $S$ and the rest of the country, which by the pigeonhole principle implies that there is a city $u$ not in $S$ that is connected to at most $\frac{k n}{n-t}<2 k$ cities by road. Therefore $u$ is joined by a road to at most $2 k-1$ cities in $S$, and there must be an independent subset $A_{i}$ such that $u$ is not linked by a road to any city in $A_{i}$. Adding $u$ to $S$ maintains the fact that $S$ is $2 k$-separable but contradicts its maximality. Therefore it must follow that $t \geq \frac{n}{2}$. By the pigeonhole principle, one of the sets $A_{1}, A_{2}, \ldots, A_{2 k}$ must contain at least $\frac{t}{2 k} \geq \frac{n}{4 k}$ cities. This proves the claim and therefore $m=\left\lceil\frac{n}{4 k}\right\rceil$.
|
\left\lceil\frac{n}{4 k}\right\rceil
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
A country with $n$ cities has some two-way roads connecting certain pairs of cities. Someone notices that if the country is split into two parts in any way, then there would be at most $k n$ roads between the two parts (where $k$ is a fixed positive integer). What is the largest integer $m$ (in terms of $n$ and $k$ ) such that there is guaranteed to be a set of $m$ cities, no two of which are directly connected by a road?
|
The answer is $m=\left\lceil\frac{n}{4 k}\right\rceil$
Call a collection of cities independent if no two cities in the collection are joined by a road. Let $r$ and $k$ be integers such that $n=4 k q+r$ where $1 \leq r \leq 4 k$.
First we show that $m \leq\left\lceil\frac{n}{4 k}\right\rceil=q+1$. Let $K_{i}$ denote a set of $i$ cities such that every pair of cities in $K_{i}$ is linked by a road. Consider a country containing $q$ copies of $K_{4 k}$ and one copy of $K_{r}$. An independent set of cities in this country contains at most one city from each $K_{4 k}$ or $K_{r}$ and therefore contains at most $q+1$ cities. Now note that any partition of the cities of the country into two new countries partitions each $K_{4 k}$ and $K_{r}$ into two sets. If $K_{i}$ where $i \leq 4 k$ is partitioned into two sets of cities of sizes $a$ and $b$, then the number of roads between the two sets is $a b \leq \frac{(a+b)^{2}}{4} \leq k i$. Summing this inequality over all copies of $K_{4 k}$ and $K_{r}$ yields that there are at most $k n$ roads between the two new countries. This implies that this particular country satisfies the given condition and it follows that $m \leq\left\lceil\frac{n}{4 k}\right\rceil$.
Now we show that any country satisfying the given condition has an independent set containing at least $\left\lceil\frac{n}{4 k}\right\rceil$ cities. Call a set of cities $i$-separable if it can be partitioned into $i$ disjoint independent sets of cities. Given a country satisfying the conditions, let $S$ be a largest set of cities in the country that is $2 k$-separable. We prove that $|S| \geq n / 2$. By definition of $S$, there exists a partition $A_{1}, A_{2}, \ldots, A_{2 k}$ of the cities in $S$ such that each $A_{i}$ is independent. Let $|S|=t$. Assume for contradiction that $t<\frac{n}{2}$. There are at most $k n$ roads between $S$ and the rest of the country, which by the pigeonhole principle implies that there is a city $u$ not in $S$ that is connected to at most $\frac{k n}{n-t}<2 k$ cities by road. Therefore $u$ is joined by a road to at most $2 k-1$ cities in $S$, and there must be an independent subset $A_{i}$ such that $u$ is not linked by a road to any city in $A_{i}$. Adding $u$ to $S$ maintains the fact that $S$ is $2 k$-separable but contradicts its maximality. Therefore it must follow that $t \geq \frac{n}{2}$. By the pigeonhole principle, one of the sets $A_{1}, A_{2}, \ldots, A_{2 k}$ must contain at least $\frac{t}{2 k} \geq \frac{n}{4 k}$ cities. This proves the claim and therefore $m=\left\lceil\frac{n}{4 k}\right\rceil$.
|
{
"resource_path": "Canada_MO/segmented/en-cmo2023-solutions-en.jsonl",
"problem_match": "\nP5.",
"solution_match": "\nSolution."
}
|
56077ab7-8082-5718-a816-b034137b1bb6
| 604,607
|
Let $S$ be a subset of $\{1,2, \ldots, 9\}$, such that the sums formed by adding each unordered pair of distinct numbers from $S$ are all different. For example, the subset $\{1,2,3,5\}$ has this property, but $\{1,2,3,4,5\}$ does not, since the pairs $\{1,4\}$ and $\{2,3\}$ have the same sum, namely 5 .
What is the maximum number of elements that $S$ can contain?
|
It can be checked that all the sums of pairs for the set $\{1,2,3,5,8\}$ are different.
Suppose, for a contradiction, that $S$ is a subset of $\{1, \ldots, 9\}$ containing 6 elements such that all the sums of pairs are different. Now the smallest possible sum for two numbers from $S$ is $1+2=3$ and the largest possible sum is $8+9=17$. That gives 15 possible sums: $3, \ldots, 17$.
Also there are $\left(\begin{array}{l}6 \\ 2\end{array}\right)=15$ pairs from $S$. Thus, each of $3, \ldots, 17$ is the sum of exactly one pair. The only pair from $\{1, \ldots, 9\}$ that adds to 3 is $\{1,2\}$ and to 17 is $\{8,9\}$. Thus $1,2,8,9$ are in $S$. But then $1+9=2+8$, giving a contradiction. It follows that the maximum number of elements that $S$ can contain is 5 .
|
5
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Let $S$ be a subset of $\{1,2, \ldots, 9\}$, such that the sums formed by adding each unordered pair of distinct numbers from $S$ are all different. For example, the subset $\{1,2,3,5\}$ has this property, but $\{1,2,3,4,5\}$ does not, since the pairs $\{1,4\}$ and $\{2,3\}$ have the same sum, namely 5 .
What is the maximum number of elements that $S$ can contain?
|
It can be checked that all the sums of pairs for the set $\{1,2,3,5,8\}$ are different.
Suppose, for a contradiction, that $S$ is a subset of $\{1, \ldots, 9\}$ containing 6 elements such that all the sums of pairs are different. Now the smallest possible sum for two numbers from $S$ is $1+2=3$ and the largest possible sum is $8+9=17$. That gives 15 possible sums: $3, \ldots, 17$.
Also there are $\left(\begin{array}{l}6 \\ 2\end{array}\right)=15$ pairs from $S$. Thus, each of $3, \ldots, 17$ is the sum of exactly one pair. The only pair from $\{1, \ldots, 9\}$ that adds to 3 is $\{1,2\}$ and to 17 is $\{8,9\}$. Thus $1,2,8,9$ are in $S$. But then $1+9=2+8$, giving a contradiction. It follows that the maximum number of elements that $S$ can contain is 5 .
|
{
"resource_path": "Canada_MO/segmented/en-sol2002.jsonl",
"problem_match": "\n1.",
"solution_match": "\n## Solution 1"
}
|
e32bebd5-8f91-524c-8e12-e0ad87a275bd
| 604,743
|
Find the last three digits of the number $2003^{2002^{2001}}$.
|
We must find the remainder when $2003^{2002^{2001}}$ is divided by 1000 , which will be the same as the remainder when $3^{2002^{2001}}$ is divided by 1000 , since $2003 \equiv 3(\bmod 1000)$. To do this we will first find a positive integer $n$ such that $3^{n} \equiv 1(\bmod 1000)$ and then try to express $2002^{2001}$ in the form $n k+r$, so that
$$
2003^{2002^{2001}} \equiv 3^{n k+r} \equiv\left(3^{n}\right)^{k} \cdot 3^{r} \equiv 1^{k} \cdot 3^{r} \equiv 3^{r}(\bmod 1000)
$$
Since $3^{2}=10-1$, we can evaluate $3^{2 m}$ using the binomial theorem:
$$
3^{2 m}=(10-1)^{m}=(-1)^{m}+10 m(-1)^{m-1}+100 \frac{m(m-1)}{2}(-1)^{m-2}+\cdots+10^{m} .
$$
After the first 3 terms of this expansion, all remaining terms are divisible by 1000, so letting $m=2 q$, we have that
$$
3^{4 q} \equiv 1-20 q+100 q(2 q-1)(\bmod 1000)
$$
Using this, we can check that $3^{100} \equiv 1(\bmod 1000)$ and now we wish to find the remainder when $2002^{2001}$ is divided by 100 .
Now $2002^{2001} \equiv 2^{2001}(\bmod 100) \equiv 4 \cdot 2^{1999}(\bmod 4 \cdot 25)$, so we'll investigate powers of 2 modulo 25 . Noting that $2^{10}=1024 \equiv-1(\bmod 25)$, we have
$$
2^{1999}=\left(2^{10}\right)^{199} \cdot 2^{9} \equiv(-1)^{199} \cdot 512 \equiv-12 \equiv 13(\bmod 25) .
$$
Thus $2^{2001} \equiv 4 \cdot 13=52(\bmod 100)$. Therefore $2002^{2001}$ can be written in the form $100 k+52$ for some integer $k$, so
$$
2003^{2002^{2001}} \equiv 3^{52}(\bmod 1000) \equiv 1-20 \cdot 13+1300 \cdot 25 \equiv 241(\bmod 1000)
$$
using equation (1). So the last 3 digits of $2003^{2002^{2001}}$ are 241 .
|
241
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Find the last three digits of the number $2003^{2002^{2001}}$.
|
We must find the remainder when $2003^{2002^{2001}}$ is divided by 1000 , which will be the same as the remainder when $3^{2002^{2001}}$ is divided by 1000 , since $2003 \equiv 3(\bmod 1000)$. To do this we will first find a positive integer $n$ such that $3^{n} \equiv 1(\bmod 1000)$ and then try to express $2002^{2001}$ in the form $n k+r$, so that
$$
2003^{2002^{2001}} \equiv 3^{n k+r} \equiv\left(3^{n}\right)^{k} \cdot 3^{r} \equiv 1^{k} \cdot 3^{r} \equiv 3^{r}(\bmod 1000)
$$
Since $3^{2}=10-1$, we can evaluate $3^{2 m}$ using the binomial theorem:
$$
3^{2 m}=(10-1)^{m}=(-1)^{m}+10 m(-1)^{m-1}+100 \frac{m(m-1)}{2}(-1)^{m-2}+\cdots+10^{m} .
$$
After the first 3 terms of this expansion, all remaining terms are divisible by 1000, so letting $m=2 q$, we have that
$$
3^{4 q} \equiv 1-20 q+100 q(2 q-1)(\bmod 1000)
$$
Using this, we can check that $3^{100} \equiv 1(\bmod 1000)$ and now we wish to find the remainder when $2002^{2001}$ is divided by 100 .
Now $2002^{2001} \equiv 2^{2001}(\bmod 100) \equiv 4 \cdot 2^{1999}(\bmod 4 \cdot 25)$, so we'll investigate powers of 2 modulo 25 . Noting that $2^{10}=1024 \equiv-1(\bmod 25)$, we have
$$
2^{1999}=\left(2^{10}\right)^{199} \cdot 2^{9} \equiv(-1)^{199} \cdot 512 \equiv-12 \equiv 13(\bmod 25) .
$$
Thus $2^{2001} \equiv 4 \cdot 13=52(\bmod 100)$. Therefore $2002^{2001}$ can be written in the form $100 k+52$ for some integer $k$, so
$$
2003^{2002^{2001}} \equiv 3^{52}(\bmod 1000) \equiv 1-20 \cdot 13+1300 \cdot 25 \equiv 241(\bmod 1000)
$$
using equation (1). So the last 3 digits of $2003^{2002^{2001}}$ are 241 .
|
{
"resource_path": "Canada_MO/segmented/en-sol2003.jsonl",
"problem_match": "\n2.",
"solution_match": "\n## Solution\n\n"
}
|
741af07f-2a37-5007-9f70-0174934e9a1b
| 604,894
|
Let $T$ be the set of all positive integer divisors of $2004^{100}$. What is the largest possible number of elements that a subset $S$ of $T$ can have if no element of $S$ is an integer multiple of any other element of $S$ ?
|
Assume throughout that $a, b, c$ are nonnegative integers. Since the prime factorization of 2004 is $2004=2^{2} \cdot 3 \cdot 167$,
$$
T=\left\{2^{a} 3^{b} 167^{c} \mid 0 \leq a \leq 200,0 \leq b, c \leq 100\right\}
$$
Let
$$
S=\left\{2^{200-b-c} 3^{b} 167^{c} \mid 0 \leq b, c \leq 100\right\}
$$
For any $0 \leq b, c \leq 100$, we have $0 \leq 200-b-c \leq 200$, so $S$ is a subset of $T$. Since there are 101 possible values for $b$ and 101 possible values for $c, S$ contains $101^{2}$ elements. We will show that no element of $S$ is a multiple of another and that no larger subset of $T$ satisfies this condition.
Suppose $2^{200-b-c} 3^{b} 167^{c}$ is an integer multiple of $2^{200-j-k} 3^{j} 167^{k}$. Then
$$
200-b-c \geq 200-j-k, \quad b \geq j, \quad c \geq k
$$
But this first inequality implies $b+c \leq j+k$, which together with $b \geq j, c \geq k$ gives $b=j$ and $c=k$. Hence no element of $S$ is an integer multiple of another element of $S$.
Let $U$ be a subset of $T$ with more than $101^{2}$ elements. Since there are only $101^{2}$ distinct pairs $(b, c)$ with $0 \leq b, c \leq 100$, then (by the pigeonhole principle) $U$ must contain two elements $u_{1}=2^{a_{1}} 3^{b_{1}} 167^{c_{1}}$ and $u_{2}=2^{a_{2}} 3^{b_{2}} 167^{c_{2}}$, with $b_{1}=b_{2}$ and $c_{1}=c_{2}$, but $a_{1} \neq a_{2}$. If $a_{1}>a_{2}$, then $u_{1}$ is a multiple of $u_{2}$ and if $a_{1}<a_{2}$, then $u_{2}$ is a multiple of $u_{1}$. Hence $U$ does not satisfy the desired condition.
Therefore the largest possible number of elements that such a subset of $T$ can have is $101^{2}=10201$.
|
10201
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Let $T$ be the set of all positive integer divisors of $2004^{100}$. What is the largest possible number of elements that a subset $S$ of $T$ can have if no element of $S$ is an integer multiple of any other element of $S$ ?
|
Assume throughout that $a, b, c$ are nonnegative integers. Since the prime factorization of 2004 is $2004=2^{2} \cdot 3 \cdot 167$,
$$
T=\left\{2^{a} 3^{b} 167^{c} \mid 0 \leq a \leq 200,0 \leq b, c \leq 100\right\}
$$
Let
$$
S=\left\{2^{200-b-c} 3^{b} 167^{c} \mid 0 \leq b, c \leq 100\right\}
$$
For any $0 \leq b, c \leq 100$, we have $0 \leq 200-b-c \leq 200$, so $S$ is a subset of $T$. Since there are 101 possible values for $b$ and 101 possible values for $c, S$ contains $101^{2}$ elements. We will show that no element of $S$ is a multiple of another and that no larger subset of $T$ satisfies this condition.
Suppose $2^{200-b-c} 3^{b} 167^{c}$ is an integer multiple of $2^{200-j-k} 3^{j} 167^{k}$. Then
$$
200-b-c \geq 200-j-k, \quad b \geq j, \quad c \geq k
$$
But this first inequality implies $b+c \leq j+k$, which together with $b \geq j, c \geq k$ gives $b=j$ and $c=k$. Hence no element of $S$ is an integer multiple of another element of $S$.
Let $U$ be a subset of $T$ with more than $101^{2}$ elements. Since there are only $101^{2}$ distinct pairs $(b, c)$ with $0 \leq b, c \leq 100$, then (by the pigeonhole principle) $U$ must contain two elements $u_{1}=2^{a_{1}} 3^{b_{1}} 167^{c_{1}}$ and $u_{2}=2^{a_{2}} 3^{b_{2}} 167^{c_{2}}$, with $b_{1}=b_{2}$ and $c_{1}=c_{2}$, but $a_{1} \neq a_{2}$. If $a_{1}>a_{2}$, then $u_{1}$ is a multiple of $u_{2}$ and if $a_{1}<a_{2}$, then $u_{2}$ is a multiple of $u_{1}$. Hence $U$ does not satisfy the desired condition.
Therefore the largest possible number of elements that such a subset of $T$ can have is $101^{2}=10201$.
|
{
"resource_path": "Canada_MO/segmented/en-sol2004.jsonl",
"problem_match": "\n5.",
"solution_match": "\n## Solution\n\n"
}
|
f9c92823-c6ff-54b8-bb78-8f38845edce1
| 605,052
|
Consider an equilateral triangle of side length $n$, which is divided into unit triangles, as shown. Let $f(n)$ be the number of paths from the triangle in the top row to the middle triangle in the bottom row, such that adjacent triangles in our path share a common edge and the path never travels up (from a lower row to a higher row) or revisits a triangle. An example of one such path is illustrated below for $n=5$. Determine the value of $f(2005)$.
|
We shall show that $f(n)=(n-1)$ !.
Label the horizontal line segments in the triangle $l_{1}, l_{2}, \ldots$ as in the diagram below. Since the path goes from the top triangle to a triangle in the bottom row and never travels up, the path must cross each of $l_{1}, l_{2}, \ldots, l_{n-1}$ exactly once. The diagonal lines in the triangle divide $l_{k}$ into $k$ unit line segments and the path must cross exactly one of these $k$ segments for each $k$. (In the diagram below, these line segments have been highlighted.) The path is completely determined by the set of $n-1$ line segments which are crossed. So as the path moves from the $k$ th row to the $(k+1)$ st row, there are $k$ possible line segments where the path could cross $l_{k}$. Since there are $1 \cdot 2 \cdot 3 \cdots(n-1)=(n-1)$ ! ways that the path could cross the $n-1$ horizontal lines, and each one corresponds to a unique path, we get $f(n)=(n-1)$ !.
Therefore $f(2005)=(2004)$ !.
|
2004!
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Consider an equilateral triangle of side length $n$, which is divided into unit triangles, as shown. Let $f(n)$ be the number of paths from the triangle in the top row to the middle triangle in the bottom row, such that adjacent triangles in our path share a common edge and the path never travels up (from a lower row to a higher row) or revisits a triangle. An example of one such path is illustrated below for $n=5$. Determine the value of $f(2005)$.

|
We shall show that $f(n)=(n-1)$ !.
Label the horizontal line segments in the triangle $l_{1}, l_{2}, \ldots$ as in the diagram below. Since the path goes from the top triangle to a triangle in the bottom row and never travels up, the path must cross each of $l_{1}, l_{2}, \ldots, l_{n-1}$ exactly once. The diagonal lines in the triangle divide $l_{k}$ into $k$ unit line segments and the path must cross exactly one of these $k$ segments for each $k$. (In the diagram below, these line segments have been highlighted.) The path is completely determined by the set of $n-1$ line segments which are crossed. So as the path moves from the $k$ th row to the $(k+1)$ st row, there are $k$ possible line segments where the path could cross $l_{k}$. Since there are $1 \cdot 2 \cdot 3 \cdots(n-1)=(n-1)$ ! ways that the path could cross the $n-1$ horizontal lines, and each one corresponds to a unique path, we get $f(n)=(n-1)$ !.
Therefore $f(2005)=(2004)$ !.

|
{
"resource_path": "Canada_MO/segmented/en-sol2005.jsonl",
"problem_match": "\n1.",
"solution_match": "\n## Solution\n\n"
}
|
aeba795c-c9fe-511d-b95a-dd54967d4799
| 605,064
|
Let $A B C$ be a triangle with circumradius $R$, perimeter $P$ and area $K$. Determine the maximum value of $K P / R^{3}$.
|
Since similar triangles give the same value of $K P / R^{3}$, we can fix $R=1$ and maximize $K P$ over all triangles inscribed in the unit circle. Fix points $A$ and $B$ on the unit circle. The locus of points $C$ with a given perimeter $P$ is an ellipse that meets the circle in at most four points. The area $K$ is maximized (for a fixed $P$ ) when $C$ is chosen on the perpendicular bisector of $A B$, so we get a maximum value for $K P$ if $C$ is where the perpendicular bisector of $A B$ meets the circle. Thus the maximum value of $K P$ for a given $A B$ occurs when $A B C$ is an isosceles triangle. Repeating this argument with $B C$ fixed, we have that the maximum occurs when $A B C$ is an equilateral triangle.
Consider an equilateral triangle with side length $a$. It has $P=3 a$. It has height equal to $a \sqrt{3} / 2$ giving $K=a^{2} \sqrt{3} / 4$. ¿From the extended law of sines, $2 R=a / \sin (60)$ giving $R=a / \sqrt{3}$. Therefore the maximum value we seek is
$$
K P / R^{3}=\left(\frac{a^{2} \sqrt{3}}{4}\right)(3 a)\left(\frac{\sqrt{3}}{a}\right)^{3}=\frac{27}{4} .
$$
|
\frac{27}{4}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $A B C$ be a triangle with circumradius $R$, perimeter $P$ and area $K$. Determine the maximum value of $K P / R^{3}$.
|
Since similar triangles give the same value of $K P / R^{3}$, we can fix $R=1$ and maximize $K P$ over all triangles inscribed in the unit circle. Fix points $A$ and $B$ on the unit circle. The locus of points $C$ with a given perimeter $P$ is an ellipse that meets the circle in at most four points. The area $K$ is maximized (for a fixed $P$ ) when $C$ is chosen on the perpendicular bisector of $A B$, so we get a maximum value for $K P$ if $C$ is where the perpendicular bisector of $A B$ meets the circle. Thus the maximum value of $K P$ for a given $A B$ occurs when $A B C$ is an isosceles triangle. Repeating this argument with $B C$ fixed, we have that the maximum occurs when $A B C$ is an equilateral triangle.
Consider an equilateral triangle with side length $a$. It has $P=3 a$. It has height equal to $a \sqrt{3} / 2$ giving $K=a^{2} \sqrt{3} / 4$. ¿From the extended law of sines, $2 R=a / \sin (60)$ giving $R=a / \sqrt{3}$. Therefore the maximum value we seek is
$$
K P / R^{3}=\left(\frac{a^{2} \sqrt{3}}{4}\right)(3 a)\left(\frac{\sqrt{3}}{a}\right)^{3}=\frac{27}{4} .
$$
|
{
"resource_path": "Canada_MO/segmented/en-sol2005.jsonl",
"problem_match": "\n4.",
"solution_match": "\n## Solution 1"
}
|
2dc823d9-182a-5647-9bb3-a58a2525ce4f
| 605,143
|
Amy has divided a square up into finitely many white and red rectangles, each with sides parallel to the sides of the square. Within each white rectangle, she writes down its width divided by its height. Within each red rectangle, she writes down its height divided by its width. Finally, she calculates $x$, the sum of these numbers. If the total area of the white rectangles equals the total area of the red rectangles, what is the smallest possible value of $x$ ?
|
Let $a_{i}$ and $b_{i}$ denote the width and height of each white rectangle, and let $c_{i}$ and $d_{i}$ denote the width and height of each red rectangle. Also, let $L$ denote the side length of the original square.
Lemma: Either $\sum a_{i} \geq L$ or $\sum d_{i} \geq L$.
Proof of lemma: Suppose there exists a horizontal line across the square that is covered entirely with white rectangles. Then, the total width of these rectangles is at least $L$, and the claim is proven. Otherwise, there is a red rectangle intersecting every horizontal line, and hence the total height of these rectangles is at least $L$.
Now, let us assume without loss of generality that $\sum a_{i} \geq L$. By the Cauchy-Schwarz inequality,
$$
\begin{aligned}
\left(\sum \frac{a_{i}}{b_{i}}\right) \cdot\left(\sum a_{i} b_{i}\right) & \geq\left(\sum a_{i}\right)^{2} \\
& \geq L^{2}
\end{aligned}
$$
But we know $\sum a_{i} b_{i}=\frac{L^{2}}{2}$, so it follows that $\sum \frac{a_{i}}{b_{i}} \geq 2$. Furthermore, each $c_{i} \leq L$, so
$$
\sum \frac{d_{i}}{c_{i}} \geq \frac{1}{L^{2}} \cdot \sum c_{i} d_{i}=\frac{1}{2}
$$
Therefore, $x$ is at least 2.5. Conversely, $x=2.5$ can be achieved by making the top half of the square one colour, and the bottom half the other colour.
|
2.5
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Amy has divided a square up into finitely many white and red rectangles, each with sides parallel to the sides of the square. Within each white rectangle, she writes down its width divided by its height. Within each red rectangle, she writes down its height divided by its width. Finally, she calculates $x$, the sum of these numbers. If the total area of the white rectangles equals the total area of the red rectangles, what is the smallest possible value of $x$ ?
|
Let $a_{i}$ and $b_{i}$ denote the width and height of each white rectangle, and let $c_{i}$ and $d_{i}$ denote the width and height of each red rectangle. Also, let $L$ denote the side length of the original square.
Lemma: Either $\sum a_{i} \geq L$ or $\sum d_{i} \geq L$.
Proof of lemma: Suppose there exists a horizontal line across the square that is covered entirely with white rectangles. Then, the total width of these rectangles is at least $L$, and the claim is proven. Otherwise, there is a red rectangle intersecting every horizontal line, and hence the total height of these rectangles is at least $L$.
Now, let us assume without loss of generality that $\sum a_{i} \geq L$. By the Cauchy-Schwarz inequality,
$$
\begin{aligned}
\left(\sum \frac{a_{i}}{b_{i}}\right) \cdot\left(\sum a_{i} b_{i}\right) & \geq\left(\sum a_{i}\right)^{2} \\
& \geq L^{2}
\end{aligned}
$$
But we know $\sum a_{i} b_{i}=\frac{L^{2}}{2}$, so it follows that $\sum \frac{a_{i}}{b_{i}} \geq 2$. Furthermore, each $c_{i} \leq L$, so
$$
\sum \frac{d_{i}}{c_{i}} \geq \frac{1}{L^{2}} \cdot \sum c_{i} d_{i}=\frac{1}{2}
$$
Therefore, $x$ is at least 2.5. Conversely, $x=2.5$ can be achieved by making the top half of the square one colour, and the bottom half the other colour.
|
{
"resource_path": "CANADA_MO/segmented/en-sol2011.jsonl",
"problem_match": "\n(3) ",
"solution_match": "\nSolution."
}
|
1c67c89e-9ef8-58e7-8c26-235a10d8c74c
| 605,536
|
Let $m$ and $n$ be odd positive integers. Each square of an $m$ by $n$ board is coloured red or blue. A row is said to be red-dominated if there are more red squares than blue squares in the row. A column is said to be blue-dominated if there are more blue squares than red squares in the column. Determine the maximum possible value of the number of red-dominated rows plus the number of blue-dominated columns. Express your answer in terms of $m$ and $n$.
|
The answer is $m+n-2$ if $m, n \geq 3$ and $\max \{m, n\}$ if one of $m, n$ is equal to 1 .
Note that it is not possible that all rows are red-dominated and all columns are blue-dominated. This is true, since the number of rows and columns are both odd, the number of squares is odd. Hence, there are more squares of one color than the other. Without loss of generality, suppose there are more red squares than blue squares. Then it is not possible that for every column, there are more blue squares than red squares. Hence, every column cannot be blue-dominated.
If one of $m, n$ is equal to 1 , say $m$ without loss of generality, then by the claim, the answer is less than $n+1$. The example where there are $n$ blue-dominated columns is by painting every square blue. There are 0 red-dominated rows. The sum of the two is $n=\max \{m, n\}$.
Now we handle the case $m, n \geq 3$.
There are $m$ rows and $n$ columns on the board. Hence, the answer is at most $m+n$. We have already shown that the answer cannot be $m+n$.
Since $m, n$ are odd, let $m=2 a-1$ and $n=2 b-1$ for some positive integers $a, b$. Since $m, n \geq 3, a, b \geq 2$. We first show that the answer is not $m+n-1$. By symmetry, it suffices to show that we cannot have all rows red-dominated and all-butone column blue-dominated. If all rows are red dominated, then each row has at least $b$ red squares. Hence, there are at least $b m=(2 a-1) b$ red squares. Since all-but-one column is blue-dominated, there are at least $2 b-2$ blue-dominated columns. Each such column then has at least $a$ blue squares. Therefore, there are at least $a(2 b-2)$ blue squares. Therefore, the board has at least $(2 a-1) b+a(2 b-2)=4 a b-b-2 a$ squares. But the total number of squares on the board is
$$
(2 a-1)(2 b-1)=4 a b-2 a-2 b+1=4 a b-2 a-b-b+1<4 a b-2 a-b,
$$
which is true since $b \geq 2$. This is a contradiction. Therefore, the answer is less than $m+n-1$.
## Sun
## Life Financial
We now claim that there is a colouring of the board such that the number of bluedominated columns plus the number of red-dominated rows is $m+n-2$; Colour the first column entirely red, and the first row, minus the top-left corner, entirely blue. The remaining uncoloured square is an even-by-even board. Colour the remaining board in an alternating pattern (i.e. checkerboard pattern). Hence, on this evenby-even board, each row has the same number of red squares as blue squares and each column has the same number of red squares as blue squares. Then on the whole board, since the top row, minus the top-left square is blue, all columns, but the leftmost column, are blue-dominated. Hence, there are $n-1$ blue-dominated columns. Since the left column is red, all rows but the top row are red dominated. Hence, there are $m-1$ red-dominated rows. The sum of these two quantities is $m+n-2$, as desired.
|
m+n-2
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Let $m$ and $n$ be odd positive integers. Each square of an $m$ by $n$ board is coloured red or blue. A row is said to be red-dominated if there are more red squares than blue squares in the row. A column is said to be blue-dominated if there are more blue squares than red squares in the column. Determine the maximum possible value of the number of red-dominated rows plus the number of blue-dominated columns. Express your answer in terms of $m$ and $n$.
|
The answer is $m+n-2$ if $m, n \geq 3$ and $\max \{m, n\}$ if one of $m, n$ is equal to 1 .
Note that it is not possible that all rows are red-dominated and all columns are blue-dominated. This is true, since the number of rows and columns are both odd, the number of squares is odd. Hence, there are more squares of one color than the other. Without loss of generality, suppose there are more red squares than blue squares. Then it is not possible that for every column, there are more blue squares than red squares. Hence, every column cannot be blue-dominated.
If one of $m, n$ is equal to 1 , say $m$ without loss of generality, then by the claim, the answer is less than $n+1$. The example where there are $n$ blue-dominated columns is by painting every square blue. There are 0 red-dominated rows. The sum of the two is $n=\max \{m, n\}$.
Now we handle the case $m, n \geq 3$.
There are $m$ rows and $n$ columns on the board. Hence, the answer is at most $m+n$. We have already shown that the answer cannot be $m+n$.
Since $m, n$ are odd, let $m=2 a-1$ and $n=2 b-1$ for some positive integers $a, b$. Since $m, n \geq 3, a, b \geq 2$. We first show that the answer is not $m+n-1$. By symmetry, it suffices to show that we cannot have all rows red-dominated and all-butone column blue-dominated. If all rows are red dominated, then each row has at least $b$ red squares. Hence, there are at least $b m=(2 a-1) b$ red squares. Since all-but-one column is blue-dominated, there are at least $2 b-2$ blue-dominated columns. Each such column then has at least $a$ blue squares. Therefore, there are at least $a(2 b-2)$ blue squares. Therefore, the board has at least $(2 a-1) b+a(2 b-2)=4 a b-b-2 a$ squares. But the total number of squares on the board is
$$
(2 a-1)(2 b-1)=4 a b-2 a-2 b+1=4 a b-2 a-b-b+1<4 a b-2 a-b,
$$
which is true since $b \geq 2$. This is a contradiction. Therefore, the answer is less than $m+n-1$.
## Sun
## Life Financial
We now claim that there is a colouring of the board such that the number of bluedominated columns plus the number of red-dominated rows is $m+n-2$; Colour the first column entirely red, and the first row, minus the top-left corner, entirely blue. The remaining uncoloured square is an even-by-even board. Colour the remaining board in an alternating pattern (i.e. checkerboard pattern). Hence, on this evenby-even board, each row has the same number of red squares as blue squares and each column has the same number of red squares as blue squares. Then on the whole board, since the top row, minus the top-left square is blue, all columns, but the leftmost column, are blue-dominated. Hence, there are $n-1$ blue-dominated columns. Since the left column is red, all rows but the top row are red dominated. Hence, there are $m-1$ red-dominated rows. The sum of these two quantities is $m+n-2$, as desired.
|
{
"resource_path": "Canada_MO/segmented/en-sol2014.jsonl",
"problem_match": "\n2.",
"solution_match": "\nSolution."
}
|
4a808d25-d6a6-573c-8121-0a677e64655b
| 70,526
|
Let $p$ be a fixed odd prime. A $p$-tuple $\left(a_{1}, a_{2}, a_{3}, \ldots, a_{p}\right)$ of integers is said to be good if
(i) $0 \leq a_{i} \leq p-1$ for all $i$, and
(ii) $a_{1}+a_{2}+a_{3}+\cdots+a_{p}$ is not divisible by $p$, and
(iii) $a_{1} a_{2}+a_{2} a_{3}+a_{3} a_{4}+\cdots+a_{p} a_{1}$ is divisible by $p$.
Determine the number of good $p$-tuples.
|
Let $S$ be the set of all sequences $\left(b_{1}, b_{2}, \ldots, b_{p}\right)$ of numbers from the set $\{0,1,2, \ldots, p-1\}$ such that $b_{1}+b_{2}+\cdots+b_{p}$ is not divisible by $p$. We show that $|S|=p^{p}-p^{p-1}$. For let $b_{1}, b_{2}, \ldots, b_{p-1}$ be an arbitrary sequence of numbers chosen from $\{0,1,2, \ldots, p-1\}$. There are exactly $p-1$ choices for $b_{p}$ such that $b_{1}+b_{2}+\cdots+b_{p-1}+b_{p} \not \equiv 0(\bmod p)$, and therefore $|S|=p^{p-1}(p-1)=p^{p}-p^{p-1}$.
Now it will be shown that the number of good sequences in $S$ is $\frac{1}{p}|S|$. For a sequence $B=\left(b_{1}, b_{2}, \ldots, b_{p}\right)$ in $S$, define the sequence $B_{k}=\left(a_{1}, a_{2}, \ldots, a_{p}\right)$ by
$$
a_{i}=b_{i}-b_{1}+k \bmod p
$$
for $1 \leq i \leq p$. Now note that $B$ in $S$ implies that
$a_{1}+a_{2}+\cdots+a_{p} \equiv\left(b_{1}+b_{2}+\cdots+b_{p}\right)-p b_{1}+p k \equiv\left(b_{1}+b_{2}+\cdots+b_{p}\right) \not \equiv 0 \quad(\bmod p)$
and therefore $B_{k}$ is in $S$ for all non-negative $k$. Now note that $B_{k}$ has first element $k$ for all $0 \leq k \leq p-1$ and therefore the sequences $B_{0}, B_{1}, \ldots, B_{p-1}$ are distinct.
Now define the cycle of $B$ as the set $\left\{B_{0}, B_{1}, \ldots, B_{p-1}\right\}$. Note that $B$ is in its own cycle since $B=B_{k}$ where $k=b_{1}$. Now note that since every sequence in $S$ is in exactly one cycle, $S$ is the disjoint union of cycles.
Now it will be shown that exactly one sequence per cycle is good. Consider an arbitrary cycle $B_{0}, B_{1}, \ldots, B_{p-1}$, and let $B_{0}=\left(b_{1}, b_{2}, \ldots, b_{p}\right)$ where $b_{0}=0$, and note that $B_{k}=\left(b_{1}+k, b_{2}+k, \ldots, b_{p}+k\right) \bmod p$. Let $u=b_{1}+b_{2}+\cdots+b_{p}$, and $v=b_{1} b_{2}+b_{2} b_{3}+\cdots+b_{p} b_{1}$ and note that $\left.\left(b_{1}+k\right)\left(b_{2}+k\right)+\left(b_{2}+k\right)\left(b_{3}+k\right)\right)+\cdots+$ $\left(b_{p}+k\right)\left(b_{1}+k\right)=u+2 k v \bmod p$ for all $0 \leq k \leq p-1$. Since $2 v$ is not divisible by $p$, there is exactly one value of $k$ with $0 \leq k \leq p-1$ such that $p$ divides $u+2 k v$ and it is exactly for this value of $k$ that $B_{k}$ is good. This shows that exactly one sequence per cycle is good and therefore that the number of good sequences in $S$ is $\frac{1}{p}|S|$, which is $p^{p-1}-p^{p-2}$.
|
p^{p-1}-p^{p-2}
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Let $p$ be a fixed odd prime. A $p$-tuple $\left(a_{1}, a_{2}, a_{3}, \ldots, a_{p}\right)$ of integers is said to be good if
(i) $0 \leq a_{i} \leq p-1$ for all $i$, and
(ii) $a_{1}+a_{2}+a_{3}+\cdots+a_{p}$ is not divisible by $p$, and
(iii) $a_{1} a_{2}+a_{2} a_{3}+a_{3} a_{4}+\cdots+a_{p} a_{1}$ is divisible by $p$.
Determine the number of good $p$-tuples.
|
Let $S$ be the set of all sequences $\left(b_{1}, b_{2}, \ldots, b_{p}\right)$ of numbers from the set $\{0,1,2, \ldots, p-1\}$ such that $b_{1}+b_{2}+\cdots+b_{p}$ is not divisible by $p$. We show that $|S|=p^{p}-p^{p-1}$. For let $b_{1}, b_{2}, \ldots, b_{p-1}$ be an arbitrary sequence of numbers chosen from $\{0,1,2, \ldots, p-1\}$. There are exactly $p-1$ choices for $b_{p}$ such that $b_{1}+b_{2}+\cdots+b_{p-1}+b_{p} \not \equiv 0(\bmod p)$, and therefore $|S|=p^{p-1}(p-1)=p^{p}-p^{p-1}$.
Now it will be shown that the number of good sequences in $S$ is $\frac{1}{p}|S|$. For a sequence $B=\left(b_{1}, b_{2}, \ldots, b_{p}\right)$ in $S$, define the sequence $B_{k}=\left(a_{1}, a_{2}, \ldots, a_{p}\right)$ by
$$
a_{i}=b_{i}-b_{1}+k \bmod p
$$
for $1 \leq i \leq p$. Now note that $B$ in $S$ implies that
$a_{1}+a_{2}+\cdots+a_{p} \equiv\left(b_{1}+b_{2}+\cdots+b_{p}\right)-p b_{1}+p k \equiv\left(b_{1}+b_{2}+\cdots+b_{p}\right) \not \equiv 0 \quad(\bmod p)$
and therefore $B_{k}$ is in $S$ for all non-negative $k$. Now note that $B_{k}$ has first element $k$ for all $0 \leq k \leq p-1$ and therefore the sequences $B_{0}, B_{1}, \ldots, B_{p-1}$ are distinct.
Now define the cycle of $B$ as the set $\left\{B_{0}, B_{1}, \ldots, B_{p-1}\right\}$. Note that $B$ is in its own cycle since $B=B_{k}$ where $k=b_{1}$. Now note that since every sequence in $S$ is in exactly one cycle, $S$ is the disjoint union of cycles.
Now it will be shown that exactly one sequence per cycle is good. Consider an arbitrary cycle $B_{0}, B_{1}, \ldots, B_{p-1}$, and let $B_{0}=\left(b_{1}, b_{2}, \ldots, b_{p}\right)$ where $b_{0}=0$, and note that $B_{k}=\left(b_{1}+k, b_{2}+k, \ldots, b_{p}+k\right) \bmod p$. Let $u=b_{1}+b_{2}+\cdots+b_{p}$, and $v=b_{1} b_{2}+b_{2} b_{3}+\cdots+b_{p} b_{1}$ and note that $\left.\left(b_{1}+k\right)\left(b_{2}+k\right)+\left(b_{2}+k\right)\left(b_{3}+k\right)\right)+\cdots+$ $\left(b_{p}+k\right)\left(b_{1}+k\right)=u+2 k v \bmod p$ for all $0 \leq k \leq p-1$. Since $2 v$ is not divisible by $p$, there is exactly one value of $k$ with $0 \leq k \leq p-1$ such that $p$ divides $u+2 k v$ and it is exactly for this value of $k$ that $B_{k}$ is good. This shows that exactly one sequence per cycle is good and therefore that the number of good sequences in $S$ is $\frac{1}{p}|S|$, which is $p^{p-1}-p^{p-2}$.
|
{
"resource_path": "Canada_MO/segmented/en-sol2014.jsonl",
"problem_match": "\n3.",
"solution_match": "\nSolution."
}
|
7d4a0c1c-09f4-5c1d-a80f-8c9f521ca546
| 605,731
|
On a $(4 n+2) \times(4 n+2)$ square grid, a turtle can move between squares sharing a side. The turtle begins in a corner square of the grid and enters each square exactly once, ending in the square where she started. In terms of $n$, what is the largest positive integer $k$ such that there must be a row or column that the turtle has entered at least $k$ distinct times?
|
We shall prove that the answer is $2 n+2$. Number the rows in increasing order, from top to bottom, and number the columns from left to right. By symmetry, we may (and shall) assume that the turtle starts in the top right corner square.
First we shall prove that some row or column must be entered at least $2 n+2$ times. Let $m=4 n+2$. First note that each time the turtle moves, she enters either a row or a column. Let $r_{i}$ denote the number of times the turtle enters row $i$, and let $c_{i}$ be similarly defined for column $i$. Since the turtle moves $m^{2}$ times,
$$
r_{1}+r_{2}+\cdots+r_{m}+c_{1}+c_{2}+\cdots+c_{m}=m^{2}
$$
Now note that each time the turtle enters column 1, the next column she enters must be column 2. Therefore $c_{1}$ is equal to the number of times the turtle enters column 2 from column 1. Furthermore, the turtle must enter column 2 from column 3 at least once, which implies that $c_{2}>c_{1}$. Therefore since the $2 m$ terms $r_{i}$ and $c_{i}$ are not all equal, one must be strictly greater than $m^{2} /(2 m)=2 n+1$ and therefore at least $2 n+2$.
Now we construct an example to show that it is possible that no row or column is entered more than $2 n+2$ times. Partition the square grid into four $(2 n+1) \times(2 n+1)$ quadrants $A, B, C$, and $D$, containing the upper left, upper right, lower left, and lower right corners, respectively. The turtle begins at the top right corner square of $B$, moves one square down, and then moves left through the whole second row of $B$. She then moves one square down and moves right through the whole third row of $B$. She continues in this pattern, moving through each remaining row of $B$ in succession and moving one square down when each row is completed. Since $2 n+1$ is odd, the turtle ends at the bottom right corner of $B$. She then moves one square down into $D$ and through each column of $D$ in turn, moving one square to the left when each column is completed. She ends at the lower left corner of $D$ and moves left into $C$ and through the rows of $C$, moving one square up when each row is completed, ending in the upper left corner of $C$. She then enters $A$ and moves through the columns of $A$, moving one square right when each column is completed. This takes her to the upper right corner of $A$, whereupon she enters $B$ and moves right through the top row of $B$, which returns her to her starting point. Each row passing through $A$ and $B$ is entered at most $2 n+1$ times in $A$ and once in $B$, and thus at most $2 n+2$ times in total. Similarly, each row and column in the grid is entered at most $2 n+2$ times by this path. (See figure below.)
|
2n+2
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
On a $(4 n+2) \times(4 n+2)$ square grid, a turtle can move between squares sharing a side. The turtle begins in a corner square of the grid and enters each square exactly once, ending in the square where she started. In terms of $n$, what is the largest positive integer $k$ such that there must be a row or column that the turtle has entered at least $k$ distinct times?
|
We shall prove that the answer is $2 n+2$. Number the rows in increasing order, from top to bottom, and number the columns from left to right. By symmetry, we may (and shall) assume that the turtle starts in the top right corner square.
First we shall prove that some row or column must be entered at least $2 n+2$ times. Let $m=4 n+2$. First note that each time the turtle moves, she enters either a row or a column. Let $r_{i}$ denote the number of times the turtle enters row $i$, and let $c_{i}$ be similarly defined for column $i$. Since the turtle moves $m^{2}$ times,
$$
r_{1}+r_{2}+\cdots+r_{m}+c_{1}+c_{2}+\cdots+c_{m}=m^{2}
$$
Now note that each time the turtle enters column 1, the next column she enters must be column 2. Therefore $c_{1}$ is equal to the number of times the turtle enters column 2 from column 1. Furthermore, the turtle must enter column 2 from column 3 at least once, which implies that $c_{2}>c_{1}$. Therefore since the $2 m$ terms $r_{i}$ and $c_{i}$ are not all equal, one must be strictly greater than $m^{2} /(2 m)=2 n+1$ and therefore at least $2 n+2$.
Now we construct an example to show that it is possible that no row or column is entered more than $2 n+2$ times. Partition the square grid into four $(2 n+1) \times(2 n+1)$ quadrants $A, B, C$, and $D$, containing the upper left, upper right, lower left, and lower right corners, respectively. The turtle begins at the top right corner square of $B$, moves one square down, and then moves left through the whole second row of $B$. She then moves one square down and moves right through the whole third row of $B$. She continues in this pattern, moving through each remaining row of $B$ in succession and moving one square down when each row is completed. Since $2 n+1$ is odd, the turtle ends at the bottom right corner of $B$. She then moves one square down into $D$ and through each column of $D$ in turn, moving one square to the left when each column is completed. She ends at the lower left corner of $D$ and moves left into $C$ and through the rows of $C$, moving one square up when each row is completed, ending in the upper left corner of $C$. She then enters $A$ and moves through the columns of $A$, moving one square right when each column is completed. This takes her to the upper right corner of $A$, whereupon she enters $B$ and moves right through the top row of $B$, which returns her to her starting point. Each row passing through $A$ and $B$ is entered at most $2 n+1$ times in $A$ and once in $B$, and thus at most $2 n+2$ times in total. Similarly, each row and column in the grid is entered at most $2 n+2$ times by this path. (See figure below.)

|
{
"resource_path": "Canada_MO/segmented/en-sol2015.jsonl",
"problem_match": "\nProblem 3.",
"solution_match": "\nSolution."
}
|
0ceaa974-3e10-513f-b55b-7b6705ff1ea9
| 605,778
|
Let $m$ and $n$ be positive integers. A $2 m \times 2 n$ grid of squares is coloured in the usual chessboard fashion. Find the number of ways of placing $m n$ counters on the white squares, at most one counter per square, so that no two counters are on white squares that are diagonally adjacent. An example of a way to place the counters when $m=2$ and $n=3$ is shown below.
|
Divide the chessboard into $m n 2 \times 2$ squares.

Each $2 \times 2$ square can contain at most one counter. Since we want to place $m n$ counters, each $2 \times 2$ square must contain exactly one counter.
Assume that the lower-right corner of the $2 m \times 2 n$ chessboard is white, so in each $2 \times 2$ square, the upper-left and lower-right squares are white. Call a $2 \times 2$ square UL if the counter it contains is on the upper-left white square, and call it LR if the counter it contains is on the lower-right white square.
Suppose some $2 \times 2$ square is UL. Then the $2 \times 2$ square above it (if it exists) must also be UL, and the $2 \times 2$ square to the left of it (if it exists) must also be UL.
Similarly, if some $2 \times 2$ square is LR, then the $2 \times 2$ square below it (if it exists) must also be LR, and the $2 \times 2$ square to the right of it (if it exists) must also be LR.
Then the collection of UL $2 \times 2$ squares form a region that is top-justified and left-justified, and the collection of LR $2 \times 2$ squares form a region that is bottom-justified and right-justified. This means that the boundary between the two regions forms a path between the lower-left corner and upper-right corner of the $2 m \times 2 n$ chessboard.
Conversely, any path from the lower-left corner to the upper-right corner, where each step consists of two units, can serve as the boundary of the UL squares and LR squares. Thus, the number of ways of placing the counters is equal to the number of paths, which is $\left(\begin{array}{c}m+n \\ m\end{array}\right)$.
|
\left(\begin{array}{c}m+n \\ m\end{array}\right)
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Let $m$ and $n$ be positive integers. A $2 m \times 2 n$ grid of squares is coloured in the usual chessboard fashion. Find the number of ways of placing $m n$ counters on the white squares, at most one counter per square, so that no two counters are on white squares that are diagonally adjacent. An example of a way to place the counters when $m=2$ and $n=3$ is shown below.

|
Divide the chessboard into $m n 2 \times 2$ squares.

Each $2 \times 2$ square can contain at most one counter. Since we want to place $m n$ counters, each $2 \times 2$ square must contain exactly one counter.
Assume that the lower-right corner of the $2 m \times 2 n$ chessboard is white, so in each $2 \times 2$ square, the upper-left and lower-right squares are white. Call a $2 \times 2$ square UL if the counter it contains is on the upper-left white square, and call it LR if the counter it contains is on the lower-right white square.
Suppose some $2 \times 2$ square is UL. Then the $2 \times 2$ square above it (if it exists) must also be UL, and the $2 \times 2$ square to the left of it (if it exists) must also be UL.

Similarly, if some $2 \times 2$ square is LR, then the $2 \times 2$ square below it (if it exists) must also be LR, and the $2 \times 2$ square to the right of it (if it exists) must also be LR.

Then the collection of UL $2 \times 2$ squares form a region that is top-justified and left-justified, and the collection of LR $2 \times 2$ squares form a region that is bottom-justified and right-justified. This means that the boundary between the two regions forms a path between the lower-left corner and upper-right corner of the $2 m \times 2 n$ chessboard.

Conversely, any path from the lower-left corner to the upper-right corner, where each step consists of two units, can serve as the boundary of the UL squares and LR squares. Thus, the number of ways of placing the counters is equal to the number of paths, which is $\left(\begin{array}{c}m+n \\ m\end{array}\right)$.
|
{
"resource_path": "Canada_MO/segmented/en-sol2019.jsonl",
"problem_match": "\n3.",
"solution_match": "\n## Solution."
}
|
139fa062-bc41-5621-a409-836b2437e6e2
| 605,999
|
A purse contains a finite number of coins, each with distinct positive integer values. Is it possible that there are exactly 2020 ways to use coins from the purse to make the value 2020 ?
|
It is possible.
Consider a coin purse with coins of values 2,4,8,2014,2016,2018, 2020 and every odd number between 503 and 1517. Call such a coin big if its value is between 503 and 1517. Call a coin small if its value is 2,4 or 8 and huge if its value is 2014,2016,2018 or 2020. Suppose some subset of these coins contains no huge coins and sums to 2020. If it contains at least four big coins, then its value must be at least $503+505+507+509>2020$. Furthermore since all of the small coins are even in value, if the subset contains exactly one or three big coins, then its value must be odd. Thus the subset must contain exactly two big coins. The eight possible subsets of the small coins have values $0,2,4,6,8,10,12,14$. Therefore the ways to make the value 2020 using no huge coins correspond to the pairs of big coins with sums 2006,2008,2010,2012,2014,2016,2018 and 2020. The numbers of such pairs are $250,251,251,252,252,253,253,254$, respectively. Thus there are exactly 2016 subsets of this coin purse with value 2020 using no huge coins. There are exactly four ways to make a value of 2020 using huge coins; these are $\{2020\},\{2,2018\},\{4,2016\}$ and $\{2,4,2014\}$. Thus there are exactly 2020 ways to make the value 2020 .
Alternate construction: Take the coins $1,2, \ldots, 11,1954,1955, \ldots, 2019$. The only way to get 2020 is a non-empty subset of $1, \ldots, 11$ and a single large coin. There are 2047 non-empty such subsets of sums between 1 and 66 . Thus they each correspond to a unique large coin making 2020, so we have 2047 ways. Thus we only need to remove some large coins, so that we remove exactly 27 small sums. This can be done, for example, by removing coins $2020-n$ for $n=1,5,6,7,8,9$, as these correspond to $1+3+4+5+6+8=27$ partitions into distinct numbers that are at most 11 .
|
2020
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
A purse contains a finite number of coins, each with distinct positive integer values. Is it possible that there are exactly 2020 ways to use coins from the purse to make the value 2020 ?
|
It is possible.
Consider a coin purse with coins of values 2,4,8,2014,2016,2018, 2020 and every odd number between 503 and 1517. Call such a coin big if its value is between 503 and 1517. Call a coin small if its value is 2,4 or 8 and huge if its value is 2014,2016,2018 or 2020. Suppose some subset of these coins contains no huge coins and sums to 2020. If it contains at least four big coins, then its value must be at least $503+505+507+509>2020$. Furthermore since all of the small coins are even in value, if the subset contains exactly one or three big coins, then its value must be odd. Thus the subset must contain exactly two big coins. The eight possible subsets of the small coins have values $0,2,4,6,8,10,12,14$. Therefore the ways to make the value 2020 using no huge coins correspond to the pairs of big coins with sums 2006,2008,2010,2012,2014,2016,2018 and 2020. The numbers of such pairs are $250,251,251,252,252,253,253,254$, respectively. Thus there are exactly 2016 subsets of this coin purse with value 2020 using no huge coins. There are exactly four ways to make a value of 2020 using huge coins; these are $\{2020\},\{2,2018\},\{4,2016\}$ and $\{2,4,2014\}$. Thus there are exactly 2020 ways to make the value 2020 .
Alternate construction: Take the coins $1,2, \ldots, 11,1954,1955, \ldots, 2019$. The only way to get 2020 is a non-empty subset of $1, \ldots, 11$ and a single large coin. There are 2047 non-empty such subsets of sums between 1 and 66 . Thus they each correspond to a unique large coin making 2020, so we have 2047 ways. Thus we only need to remove some large coins, so that we remove exactly 27 small sums. This can be done, for example, by removing coins $2020-n$ for $n=1,5,6,7,8,9$, as these correspond to $1+3+4+5+6+8=27$ partitions into distinct numbers that are at most 11 .
|
{
"resource_path": "Canada_MO/segmented/en-sol2020.jsonl",
"problem_match": "\n3.",
"solution_match": "\nSolution:"
}
|
f34c732b-bf80-5f5f-a76e-2837a7a914a2
| 606,056
|
There are 19,998 people on a social media platform, where any pair of them may or may not be friends. For any group of 9,999 people, there are at least 9,999 pairs of them that are friends. What is the least number of friendships, that is, the least number of pairs of people that are friends, that must be among the 19,998 people?
|
It is $5 \cdot 9999=49995$. One possible construction is as follows: have the 19,998 people form 3,333 groups of 6 people, and within each group every pair of people are friends. Now, for any group of 9,999 people, say that there are $x_{1}, x_{2}, \ldots, x_{3333}$ people in each of the 6 groups, respectively. Then there are
$$
\frac{1}{2} \sum_{i=1}^{3333} x_{i}\left(x_{i}-1\right)
$$
pairs of friendships total. But we have that
$$
x_{i}\left(x_{i}-1\right) \geq 5 x_{i}-9,
$$
so
$$
\frac{1}{2} \sum_{i=1}^{3333} x_{i}\left(x_{i}-1\right) \geq \frac{1}{2} \sum_{i=1}^{3333}\left(5 x_{i}-9\right)=\frac{1}{2}(9999 \cdot 5-9 \cdot 3333)=9999
$$
as desired.
It remains to show that 49995 pairs of friends is optimal. For what follows, let $9999=N$, so that $19,998=2 N$, and assume that the condition is satisfied. Let the number of pairs of friends be $e$. Designate half of the people as red and the other half as blue, so that the number of pairs of friends who are both red is minimized.
Note that this means that for every pair of people, one red and one blue, we have that the number of red friends of the blue person is at least as many as the number of red friends of the red person, and the inequality is strict if the two people are friends. This is because we can otherwise swap the two people. Now, if every blue person is friends with at least 3 red people, then the total number of friendships, $e$, is at least $N+3 N+N=5 N$ ( $N$ each from the red people and blue people and $3 N$ from the pairs), as desired. If some blue person is friends with at most 2 red people, then every red person is friends with at most 2 red people, so the number of pairs of red friends is at most $N$, with equality only if every red person is friends with exactly 2 red people. But then consider a blue person with 2 red friends; then, they must have a red friend with exactly 2 red friends too, a contradiction.
|
49995
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
There are 19,998 people on a social media platform, where any pair of them may or may not be friends. For any group of 9,999 people, there are at least 9,999 pairs of them that are friends. What is the least number of friendships, that is, the least number of pairs of people that are friends, that must be among the 19,998 people?
|
It is $5 \cdot 9999=49995$. One possible construction is as follows: have the 19,998 people form 3,333 groups of 6 people, and within each group every pair of people are friends. Now, for any group of 9,999 people, say that there are $x_{1}, x_{2}, \ldots, x_{3333}$ people in each of the 6 groups, respectively. Then there are
$$
\frac{1}{2} \sum_{i=1}^{3333} x_{i}\left(x_{i}-1\right)
$$
pairs of friendships total. But we have that
$$
x_{i}\left(x_{i}-1\right) \geq 5 x_{i}-9,
$$
so
$$
\frac{1}{2} \sum_{i=1}^{3333} x_{i}\left(x_{i}-1\right) \geq \frac{1}{2} \sum_{i=1}^{3333}\left(5 x_{i}-9\right)=\frac{1}{2}(9999 \cdot 5-9 \cdot 3333)=9999
$$
as desired.
It remains to show that 49995 pairs of friends is optimal. For what follows, let $9999=N$, so that $19,998=2 N$, and assume that the condition is satisfied. Let the number of pairs of friends be $e$. Designate half of the people as red and the other half as blue, so that the number of pairs of friends who are both red is minimized.
Note that this means that for every pair of people, one red and one blue, we have that the number of red friends of the blue person is at least as many as the number of red friends of the red person, and the inequality is strict if the two people are friends. This is because we can otherwise swap the two people. Now, if every blue person is friends with at least 3 red people, then the total number of friendships, $e$, is at least $N+3 N+N=5 N$ ( $N$ each from the red people and blue people and $3 N$ from the pairs), as desired. If some blue person is friends with at most 2 red people, then every red person is friends with at most 2 red people, so the number of pairs of red friends is at most $N$, with equality only if every red person is friends with exactly 2 red people. But then consider a blue person with 2 red friends; then, they must have a red friend with exactly 2 red friends too, a contradiction.
|
{
"resource_path": "Canada_MO/segmented/en-sol2020.jsonl",
"problem_match": "\n5.",
"solution_match": "\nSolution:"
}
|
1ac3ad9d-9478-50cc-a59a-de014c486c4f
| 606,071
|
Consider sequences $a_{1}, a_{2}, a_{3}, \ldots$ of positive integers. Determine the smallest possible value of $a_{2010}$ given:
(i) $a_{n}<a_{n+1}$ for all $n \geq 1$,
(ii) $a_{i}+a_{l}>a_{j}+a_{k}$ for all quadruples $(i, j, k, l)$ with $1 \leq i<j \leq k<l$.
|
We prove by induction that $a_{n}-a_{1} \geq 2^{n-1}-1$ for all $n \geq 2$. For $n=2$, this reads $a_{2}-a_{1} \geq 1$ and that follows from condition (i). Let now $m \geq 2$ and assume that $a_{m}-a_{1} \geq 2^{m-1}-1$. We apply condition (ii) with $i=1, j=k=m$ and $l=m+1$. We find that $a_{1}+a_{m+1}>2 a_{m}$. Thus,
$$
a_{m+1}-a_{1}>2 a_{m}-2 a_{1} \stackrel{\mathrm{IH}}{\geq} 2\left(2^{m-1}-1\right)=2^{m}-2,
$$
and since $a_{m+1}$ is positive and an integer, it follows that $a_{m+1}-a_{1} \geq 2^{m}-1$. This completes the induction.
Now we see that for $n \geq 1$ we have:
$$
a_{n} \geq 2^{n-1}-1+a_{1} \geq 2^{n-1}
$$
and in particular $a_{2010} \geq 2^{2009}$.
On the other hand, we prove that $a_{2010}=2^{2009}$ is possible by showing that the sequence given by $a_{n}=2^{n-1}$ satisfies the conditions. This sequence consists of positive integers and is strictly increasing (condition (i)). Let now $(i, j, k, l)$ be a quadruple satisfying $1 \leq i < j \leq k < l$. We have
$$
a_{j}+a_{k}=2^{j-1}+2^{k-1} \leq 2^{k-1}+2^{k-1}=2^{k} \leq 2^{l-1}<2^{i-1}+2^{l-1},
$$
so condition (ii) is also satisfied.
We conclude that the smallest possible value of $a_{2010}$ is $2^{2009}$.
|
2^{2009}
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Bekijk rijen $a_{1}, a_{2}, a_{3}, \ldots$ van positieve gehele getallen. Bepaal de kleinst mogelijke waarde van $a_{2010}$ als gegeven is:
(i) $a_{n}<a_{n+1}$ voor alle $n \geq 1$,
(ii) $a_{i}+a_{l}>a_{j}+a_{k}$ voor alle viertallen $(i, j, k, l)$ met $1 \leq i<j \leq k<l$.
|
We bewijzen met inductie dat $a_{n}-a_{1} \geq 2^{n-1}-1$ voor alle $n \geq 2$. Voor $n=2$ staat hier $a_{2}-a_{1} \geq 1$ en dat volgt uit voorwaarde (i). $\mathrm{Zij} \mathrm{nu} m \geq 2$ en stel dat $a_{m}-a_{1} \geq 2^{m-1}-1$. We passen voorwaarde (ii) toe met $i=1, j=k=m$ en $l=m+1$. We vinden dat $a_{1}+a_{m+1}>2 a_{m}$. Dus
$$
a_{m+1}-a_{1}>2 a_{m}-2 a_{1} \stackrel{\mathrm{IH}}{\geq} 2\left(2^{m-1}-1\right)=2^{m}-2,
$$
en aangezien $a_{m+1}$ positief en geheel is, volgt hieruit $a_{m+1}-a_{1} \geq 2^{m}-1$. Dit voltooit de inductie.
Nu zien we dat voor $n \geq 1$ geldt:
$$
a_{n} \geq 2^{n-1}-1+a_{1} \geq 2^{n-1}
$$
en in het bijzonder $a_{2010} \geq 2^{2009}$.
Anderzijds bewijzen we dat $a_{2010}=2^{2009}$ mogelijk is door te laten zien dat de rij gegeven door $a_{n}=2^{n-1}$ aan de voorwaarden voldoet. Deze rij bestaat uit positieve gehele getallen en is strikt stijgend (voorwaarde (i)). Zij nu ( $i, j, k, l)$ een viertal dat voldoet aan $1 \leq i<$ $j \leq k<l$. Er geldt
$$
a_{j}+a_{k}=2^{j-1}+2^{k-1} \leq 2^{k-1}+2^{k-1}=2^{k} \leq 2^{l-1}<2^{i-1}+2^{l-1},
$$
dus ook aan voorwaarde (ii) is voldaan.
We concluderen dat de kleinst mogelijke waarde van $a_{2010}$ gelijk is aan $2^{2009}$.
|
{
"resource_path": "Dutch_TST/segmented/nl-2010-D_uitwerkingen.jsonl",
"problem_match": "\nOpgave 1.",
"solution_match": "\nOplossing."
}
|
99b3e824-03d7-5c40-a2e1-8cd998fee100
| 604,324
|
Find all integers $n$ for which $\frac{4 n-2}{n+5}$ is the square of a rational number. (A rational number is a number in $\mathbb{Q}$.)
|
Suppose $\frac{4 n-2}{n+5}$ is the square of a rational number. Then we can write it as $\frac{p^{2}}{q^{2}}$ with $p, q$ non-negative integers, $q \neq 0$ and $\operatorname{gcd}(p, q)=1$. Due to the condition $\operatorname{gcd}(p, q)=1$, $\frac{p^{2}}{q^{2}}$ is the most simplified version of this fraction, so there is an integer $c \neq 0$ such that $4 n-2=c p^{2}$ and $n+5=c q^{2}$. Now,
$$
22=4(n+5)-(4 n-2)=4 c q^{2}-c p^{2}=c\left((2 q)^{2}-p^{2}\right)=c(2 q-p)(2 q+p)
$$
So $c$ is a divisor of 22. Furthermore, 22 is divisible by 2, so the right-hand side is also divisible by 2. If there is a factor of 2 in $2 q-p$, there is also a factor of 2 in $2 q+p$, because these two factors differ by $2 p$ and that is even. Conversely, if $2 q+p$ is divisible by 2, then $2 q-p$ is also divisible by 2. But 22 contains only one factor of 2, so it cannot be that both $2 q-p$ and $2 q+p$ are divisible by 2. We conclude that $2 q-p$ and $2 q+p$ are precisely odd, and $c$ is therefore even. Finally, $p \geq 0$ and $q \geq 1$, so $2 q+p \geq 2$, so the factor 11 from 22 must be in $2 q+p$. We conclude that there are only two possibilities:
- $c=2,2 q+p=11,2 q-p=1$;
- $c=-2,2 q+p=11,2 q-p=-1$.
In the first case, we find $2 p=11-1=10$, so $p=5$ and $q=3$. This gives $4 n-2=50$, so $n=13$. Checking: $\frac{4 n-2}{n+5}=\frac{50}{18}=\frac{25}{9}=\frac{5^{2}}{3^{2}}$, so $n=13$ indeed satisfies. In the second case, we find $2 p=11--1=12$, so $p=6$, but then $q$ cannot be an integer anymore, so this case is invalid. We conclude that there is exactly one solution, and that is $n=13$.
|
13
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Vind alle gehele getallen $n$ waarvoor $\frac{4 n-2}{n+5}$ het kwadraat van een rationaal getal is. (Een rationaal getal is een getal in $\mathbb{Q}$.)
|
Stel dat $\frac{4 n-2}{n+5}$ het kwadraat van een rationaal getal is. Dan kunnen we het dus schrijven als $\frac{p^{2}}{q^{2}}$ met $p, q$ niet-negatieve gehele getallen, $q \neq 0$ en $\operatorname{ggd}(p, q)=1$. Vanwege de voorwaarde $\operatorname{ggd}(p, q)=1$, is $\frac{p^{2}}{q^{2}}$ de meest vereenvoudigde versie van deze breuk, dus er is een gehele $c \neq 0$ zodat $4 n-2=c p^{2}$ en $n+5=c q^{2}$. Nu is
$$
22=4(n+5)-(4 n-2)=4 c q^{2}-c p^{2}=c\left((2 q)^{2}-p^{2}\right)=c(2 q-p)(2 q+p)
$$
Dus $c$ is een deler van 22. Verder is 22 deelbaar door 2, dus de rechterkant is ook deelbaar door 2 . Als er een factor 2 in $2 q-p$ zit, zit er ook een factor 2 in $2 q+p$, want die twee factoren schelen $2 p$ en dat is even. En andersom, als $2 q+p$ deelbaar is door 2 , dan is $2 q-p$ dat ook. Maar 22 bevat maar één factor 2 , dus het kan niet dat $2 q-p$ en $2 q+p$ beide deelbaar zijn door 2 . We concluderen dat $2 q-p$ en $2 q+p$ juist oneven zijn en $c$ dus even is. Ten slotte geldt dat $p \geq 0$ en $q \geq 1$, dus $2 q+p \geq 2$, dus de factor 11 uit 22 moet juist in $2 q+p$ zitten. We concluderen dat er slechts twee mogelijkheden zijn:
- $c=2,2 q+p=11,2 q-p=1$;
- $c=-2,2 q+p=11,2 q-p=-1$.
In het eerste geval vinden we $2 p=11-1=10$, dus $p=5$ en $q=3$. Dit geeft $4 n-2=50$, dus $n=13$. Controleren: $\frac{4 n-2}{n+5}=\frac{50}{18}=\frac{25}{9}=\frac{5^{2}}{3^{2}}$, dus $n=13$ voldoet inderdaad. In het tweede geval vinden we $2 p=11--1=12$, dus $p=6$, maar dan kan $q$ niet meer geheel zijn, dus dit geval valt af. We concluderen dat er precies één oplossing is en dat is $n=13$.
|
{
"resource_path": "Dutch_TST/segmented/nl-2013-C_uitwerkingen.jsonl",
"problem_match": "\nOpgave 2.",
"solution_match": "\nOplossing."
}
|
11f86ed2-7bd9-5108-bb2d-15f04b7dd713
| 605,063
|
Let $n \geq 3$ be an integer and consider an $n \times n$ board, divided into $n^{2}$ unit squares. We have for each $m \geq 1$ arbitrarily many $1 \times m$ rectangles (type I) and arbitrarily many $m \times 1$ rectangles (type II) available. We cover the board with $N$ of these rectangles, which do not overlap and do not extend beyond the board. The total number of type I rectangles on the board must be equal to the total number of type II rectangles on the board. (Note that a $1 \times 1$ rectangle is both of type I and of type II.) What is the smallest value of $N$ for which this is possible?
|
We prove that the minimal value $N=2n-1$. First, we construct an example by induction.
Base case. For $n=3$, $N=5$ is possible, by placing a $1 \times 1$ rectangle in the middle field and covering the remaining fields with four $2 \times 1$ and $1 \times 2$ rectangles. There are then three rectangles with height 1 (type I) and three rectangles with width 1 (type II), where the $1 \times 1$ rectangle is counted twice.
Inductive step. Let $k \geq 3$ and assume that we can cover a $k \times k$ board with $2k-1$ rectangles such that all conditions are met. Consider a $(k+1) \times (k+1)$ board and cover the $k \times k$ sub-square at the bottom right according to the inductive hypothesis. Then cover the left column with a rectangle of width 1 and height $k+1$, and cover the remaining space with a rectangle of height 1 and width $k$. We have now used one more rectangle with width 1 and one more rectangle with height 1, so the condition is satisfied and we have used $2k-1+2=2(k+1)-1$ rectangles. This constructs an example for $n=k+1$.
This proves that it is possible to cover the board with $N=2n-1$ rectangles. We now want to prove that it cannot be done with fewer rectangles. Let $k$ be the number of rectangles with width 1 and height greater than 1. Then the number of rectangles with height 1 and width greater than 1 is also $k$. Let $l$ be the number of $1 \times 1$ rectangles. Thus, $N=2k+l$. If $k \geq n$, then $N \geq 2n$, so there is nothing to prove in this case. We therefore assume that $k < n$ and we will prove that then $l \geq 2n-2k-1$, so that $N \geq 2n-1$.
Each rectangle with width 1 can only cover fields in one column. Therefore, there are $n-k$ columns in which no field is covered by a rectangle with width 1 and height greater than 1. Similarly, there are $n-k$ rows in which no field is covered by a rectangle with height 1 and width greater than 1. Consider the $(n-k)^2$ fields that lie in both such a row and such a column. These fields must be covered by $1 \times 1$ rectangles. Thus, $l \geq (n-k)^2$.
We have $(k-n+1)^2 \geq 0$, so $k^2 + n^2 + 1 - 2kn + 2k - 2n \geq 0$, and thus $n^2 - 2kn + k^2 \geq 2n - 2k - 1$. We conclude that $l \geq (n-k)^2 \geq 2n - 2k - 1$, which is exactly what we wanted to prove. Therefore, in all cases, $N \geq 2n-1$, and this proves that the minimal value of $N$ is $2n-1$.
|
2n-1
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Zij $n \geq 3$ een geheel getal en bekijk een $n \times n$-bord, opgedeeld in $n^{2}$ eenheidsvierkantjes. We hebben voor elke $m \geq 1$ willekeurig veel $1 \times m$-rechthoeken (type I) en willekeurig veel $m \times 1$-rechthoeken (type II) beschikbaar. We bedekken het bord met $N$ van deze rechthoeken, die elkaar niet overlappen en niet uitsteken buiten het bord. Het totaal aantal rechthoeken van type I op het bord moet hierbij gelijk zijn aan het totaal aantal rechthoeken van type II op het bord. (Merk op dat een $1 \times 1$-rechthoek zowel van type I als van type II is.) Wat is de kleinste waarde van $N$ waarvoor dit mogelijk is?
|
We bewijzen dat de minimale waarde $N=2 n-1$ is. We construeren eerst een voorbeeld door middel van inductie.
Inductiebasis. Voor $n=3$ is $N=5$ mogelijk, door in het middelste veld een $1 \times 1$-rechthoek te leggen en de overige velden te bedekken met vier $2 \times 1$ - en $1 \times 2$-rechthoeken. Er zijn dan drie rechthoeken met hoogte 1 (type I) en drie rechthoeken met breedte 1 (type II), waarbij de $1 \times 1$-rechthoek twee keer geteld wordt.
Inductiestap. Zij $k \geq 3$ en neem aan dat we een $k \times k$-bord kunnen bedekken met $2 k-1$ rechthoeken zodat aan alle voorwaarden is voldaan. Bekijk een $(k+1) \times(k+1)$-bord en bedek het $k \times k$-deelvierkant rechtsonder volgens de inductiehypothese. Bedek vervolgens de linkerkolom met een rechthoek met breedte 1 en hoogte $k+1$ en vervolgens de overgebleven ruimte met een rechthoek met hoogte 1 en breedte $k$. We hebben nu één rechthoek met breedte 1 en één rechthoek met hoogte 1 meer gebruikt, dus aan de voorwaarde is voldaan en we hebben $2 k-1+2=2(k+1)-1$ rechthoeken gebruikt. Hiermee hebben we een voorbeeld voor $n=k+1$ geconstrueerd.
Hiermee is bewezen dat het mogelijk is om het bord te bedekken met $N=2 n-1$ rechthoeken. We willen nu nog bewijzen dat het niet met minder rechthoeken kan. Zij $k$ het aantal rechthoeken met breedte 1 en hoogte groter dan 1 . Dan is ook het aantal rechthoeken met hoogte 1 en breedte groter dan 1 , gelijk aan $k$. Zij verder $l$ het aantal rechthoeken van $1 \times 1$. Er geldt dus $N=2 k+l$. Als $k \geq n$, geldt $N \geq 2 n$, dus in dit geval is er niets te bewijzen. We nemen dus aan dat $k<n$ en we gaan bewijzen dat dan $l \geq 2 n-2 k-1$, zodat $N \geq 2 n-1$.
Elke rechthoek met breedte 1 kan alleen velden in één kolom bedekken. Er zijn dus $n-k$ kolommen waarin geen enkel veld wordt bedekt door een rechthoek met breedte 1 en hoogte groter dan 1. Zo ook zijn er $n-k$ rijen waarin geen enkel veld wordt bedekt door een rechthoek met hoogte 1 en breedte groter dan 1. Bekijk de $(n-k)^{2}$ velden die in zowel zo'n rij als zo'n kolom liggen. Deze velden moeten bedekt worden door $1 \times 1$-rechthoeken. Dus $l \geq(n-k)^{2}$.
Er geldt $(k-n+1)^{2} \geq 0$, dus $k^{2}+n^{2}+1-2 k n+2 k-2 n \geq 0$, dus $n^{2}-2 k n+k^{2} \geq 2 n-2 k-1$. We concluderen dat $l \geq(n-k)^{2} \geq 2 n-2 k-1$ en dat is precies wat we wilden bewijzen. Dus in alle gevallen is $N \geq 2 n-1$ en dat bewijst dat de minimale waarde van $N$ gelijk is aan $2 n-1$.
|
{
"resource_path": "Dutch_TST/segmented/nl-2013-C_uitwerkingen.jsonl",
"problem_match": "\nOpgave 4.",
"solution_match": "\nOplossing."
}
|
8e4c942e-96ef-5564-ad1c-4eb85e6a60d9
| 605,111
|
Gegeven is een onbekende rij $a_{1}, a_{2}, a_{3}, \ldots$ van gehele getallen die voldoet aan de volgende eigenschap: voor elk priemgetal $p$ en elk positief geheel getal $k$ geldt
$$
a_{p k+1}=p a_{k}-3 a_{p}+13
$$
Bepaal alle mogelijke waarden van $a_{2013}$.
|
Laat $q$ en $t$ priemgetallen zijn. Vul in $k=q, p=t$ :
$$
a_{q t+1}=t a_{q}-3 a_{t}+13
$$
Vul ook in $k=t, p=q$ :
$$
a_{q t+1}=q a_{t}-3 a_{q}+13
$$
Beide uitdrukkingen rechts zijn dus gelijk aan elkaar, waaruit volgt
$$
t a_{q}-3 a_{t}=q a_{t}-3 a_{q}
$$
oftewel
$$
(t+3) a_{q}=(q+3) a_{t}
$$
In het bijzonder geldt $5 a_{3}=6 a_{2}$ en $5 a_{7}=10 a_{2}$. Vul nu $k=3, p=2$ in:
$$
a_{7}=2 a_{3}-3 a_{2}+13=2 \cdot \frac{6}{5} a_{2}-3 a_{2}+13
$$
Omdat $a_{7}=\frac{10}{5} a_{2}$, vinden we nu
$$
\frac{13}{5} a_{2}=13
$$
dus $a_{2}=5$. Nu geldt voor elk priemgetal $p$ dat $a_{p}=\frac{(p+3) a_{2}}{5}=p+3$.
Vul in $k=4, p=3$ :
$$
a_{13}=3 a_{4}-3 a_{3}+13
$$
We weten dat $a_{13}=16$ en $a_{3}=6$, dus dit geeft $3 a_{4}=21$, oftewel $a_{4}=7$.
Vul ten slotte $k=4$ en $p=503$ in:
$a_{2013}=a_{4 \cdot 503+1}=503 \cdot a_{4}-3 a_{503}+13=503 \cdot 7-3 \cdot(503+3)+13=503 \cdot 4-9+13=2016$.
Dus $a_{2013}=2016$ en dit is de enige mogelijke waarde.
|
2016
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Gegeven is een onbekende rij $a_{1}, a_{2}, a_{3}, \ldots$ van gehele getallen die voldoet aan de volgende eigenschap: voor elk priemgetal $p$ en elk positief geheel getal $k$ geldt
$$
a_{p k+1}=p a_{k}-3 a_{p}+13
$$
Bepaal alle mogelijke waarden van $a_{2013}$.
|
Laat $q$ en $t$ priemgetallen zijn. Vul in $k=q, p=t$ :
$$
a_{q t+1}=t a_{q}-3 a_{t}+13
$$
Vul ook in $k=t, p=q$ :
$$
a_{q t+1}=q a_{t}-3 a_{q}+13
$$
Beide uitdrukkingen rechts zijn dus gelijk aan elkaar, waaruit volgt
$$
t a_{q}-3 a_{t}=q a_{t}-3 a_{q}
$$
oftewel
$$
(t+3) a_{q}=(q+3) a_{t}
$$
In het bijzonder geldt $5 a_{3}=6 a_{2}$ en $5 a_{7}=10 a_{2}$. Vul nu $k=3, p=2$ in:
$$
a_{7}=2 a_{3}-3 a_{2}+13=2 \cdot \frac{6}{5} a_{2}-3 a_{2}+13
$$
Omdat $a_{7}=\frac{10}{5} a_{2}$, vinden we nu
$$
\frac{13}{5} a_{2}=13
$$
dus $a_{2}=5$. Nu geldt voor elk priemgetal $p$ dat $a_{p}=\frac{(p+3) a_{2}}{5}=p+3$.
Vul in $k=4, p=3$ :
$$
a_{13}=3 a_{4}-3 a_{3}+13
$$
We weten dat $a_{13}=16$ en $a_{3}=6$, dus dit geeft $3 a_{4}=21$, oftewel $a_{4}=7$.
Vul ten slotte $k=4$ en $p=503$ in:
$a_{2013}=a_{4 \cdot 503+1}=503 \cdot a_{4}-3 a_{503}+13=503 \cdot 7-3 \cdot(503+3)+13=503 \cdot 4-9+13=2016$.
Dus $a_{2013}=2016$ en dit is de enige mogelijke waarde.
|
{
"resource_path": "Dutch_TST/segmented/nl-2013-D_uitwerkingen.jsonl",
"problem_match": "\nOpgave 3.",
"solution_match": "\nOplossing I."
}
|
48a53520-5393-5861-a3c6-efb2965358dc
| 605,170
|
Given is an unknown sequence $a_{1}, a_{2}, a_{3}, \ldots$ of integers that satisfies the following property: for every prime number $p$ and every positive integer $k$ it holds that
$$
a_{p k+1}=p a_{k}-3 a_{p}+13
$$
Determine all possible values of $a_{2013}$.
|
Leid net als in oplossing I af dat $a_{2}=5$ en $a_{p}=p+3$ voor alle priemgetallen $p$. Dan geldt dus $a_{3}=6$. Invullen van $k=1$ en $p=2$ geeft
$$
a_{3}=2 a_{1}-3 a_{2}+13=2 a_{1}-2,
$$
dus $2 a_{1}=a_{3}+2=8$, dus $a_{1}=4$. Nu hebben we $a_{1}$ en $a_{2}$ berekend. Voor $n \geq 3$ geldt dat er altijd een priemgetal $p$ is met $p \mid n-1$, dus dat we altijd $p$ en $k$ kunnen vinden zodat
$n=k p+1$. Dus ligt de waarde van $a_{n}$ vast als we alle waarden $a_{m}$ met $1 \leq m<n$ al kennen. Er kan dus maar één rij zijn die voldoet. We proberen nu of $a_{n}=n+3$ voldoet. Dan geldt
$$
p a_{k}-3 a_{p}+13=p(k+3)-3(p+3)+13=p k+3 p-3 p-9+13=p k+4=a_{p k+1}
$$
Dus dit voldoet inderdaad. De enige rij die voldoet is dus degene met $a_{n}=n+3$ voor alle $n \geq 1$, waaruit volgt dat de enige mogelijke waarde voor $a_{2013}$ gelijk is aan 2016.
Translate the above text into English, keeping the original text's line breaks and formatting:
From the solution I, we can deduce that $a_{2}=5$ and $a_{p}=p+3$ for all prime numbers $p$. Therefore, $a_{3}=6$. Substituting $k=1$ and $p=2$ gives
$$
a_{3}=2 a_{1}-3 a_{2}+13=2 a_{1}-2,
$$
so $2 a_{1}=a_{3}+2=8$, hence $a_{1}=4$. Now we have calculated $a_{1}$ and $a_{2}$. For $n \geq 3$, there is always a prime number $p$ such that $p \mid n-1$, so we can always find $p$ and $k$ such that
$n=k p+1$. Therefore, the value of $a_{n}$ is fixed if we already know all values $a_{m}$ with $1 \leq m<n$. Thus, there can only be one sequence that satisfies the condition. We now try to see if $a_{n}=n+3$ satisfies the condition. Then we have
$$
p a_{k}-3 a_{p}+13=p(k+3)-3(p+3)+13=p k+3 p-3 p-9+13=p k+4=a_{p k+1}
$$
So this indeed satisfies the condition. The only sequence that satisfies the condition is the one with $a_{n}=n+3$ for all $n \geq 1$, which implies that the only possible value for $a_{2013}$ is 2016.
|
2016
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Gegeven is een onbekende rij $a_{1}, a_{2}, a_{3}, \ldots$ van gehele getallen die voldoet aan de volgende eigenschap: voor elk priemgetal $p$ en elk positief geheel getal $k$ geldt
$$
a_{p k+1}=p a_{k}-3 a_{p}+13
$$
Bepaal alle mogelijke waarden van $a_{2013}$.
|
Leid net als in oplossing I af dat $a_{2}=5$ en $a_{p}=p+3$ voor alle priemgetallen $p$. Dan geldt dus $a_{3}=6$. Invullen van $k=1$ en $p=2$ geeft
$$
a_{3}=2 a_{1}-3 a_{2}+13=2 a_{1}-2,
$$
dus $2 a_{1}=a_{3}+2=8$, dus $a_{1}=4$. Nu hebben we $a_{1}$ en $a_{2}$ berekend. Voor $n \geq 3$ geldt dat er altijd een priemgetal $p$ is met $p \mid n-1$, dus dat we altijd $p$ en $k$ kunnen vinden zodat
$n=k p+1$. Dus ligt de waarde van $a_{n}$ vast als we alle waarden $a_{m}$ met $1 \leq m<n$ al kennen. Er kan dus maar één rij zijn die voldoet. We proberen nu of $a_{n}=n+3$ voldoet. Dan geldt
$$
p a_{k}-3 a_{p}+13=p(k+3)-3(p+3)+13=p k+3 p-3 p-9+13=p k+4=a_{p k+1}
$$
Dus dit voldoet inderdaad. De enige rij die voldoet is dus degene met $a_{n}=n+3$ voor alle $n \geq 1$, waaruit volgt dat de enige mogelijke waarde voor $a_{2013}$ gelijk is aan 2016.
|
{
"resource_path": "Dutch_TST/segmented/nl-2013-D_uitwerkingen.jsonl",
"problem_match": "\nOpgave 3.",
"solution_match": "\nOplossing II."
}
|
48a53520-5393-5861-a3c6-efb2965358dc
| 605,170
|
Let $m \geq 3$ and $n$ be positive integers with $n > m(m-2)$. Find the largest positive integer $d$ such that $d \mid n!$ and $k \nmid d$ for all $k \in \{m, m+1, \ldots, n\}$.
|
We will prove that $d=m-1$ is the largest that satisfies. First, note that $m-1 \mid n$ ! and for $k \geq m$ we have $k \nmid m-1$, so $d=m-1$ indeed satisfies.
Suppose now that for some $d$ we have: $d \mid n$ ! and $k \nmid d$ for all $k \in\{m, m+1, \ldots, n\}$. We will prove that $d \leq m-1$. Write $d=p_{1} p_{2} \cdots p_{t}$ with $p_{i}$ prime for all $i$ (not necessarily all distinct). If $t=0$, then $d=1 \leq m-1$, so we may assume $t \geq 1$. From the first condition on $d$ it follows that $p_{i} \leq n$ for all $i$. From the second condition on $d$ it follows that $p_{i} \notin\{m, m+1, \ldots, n\}$ for all $i$. Thus $p_{i} \leq m-1$ for all $i$. Now consider the numbers $p_{1}, p_{1} p_{2}, \ldots, p_{1} p_{2} \cdots p_{t}$. These are all divisors of $d$ and therefore all different from numbers in $\{m, m+1, \ldots, n\}$. Furthermore, we know that $p_{1} \leq m-1$. Now consider the largest $j \leq t$ for which $p_{1} p_{2} \cdots p_{j} \leq m-1$. If $j<t$ then
$$
p_{1} p_{2} \cdots p_{j} p_{j+1} \leq(m-1) p_{j+1} \leq(m-1)(m-1)=m(m-2)+1 \leq n
$$
But that means that $p_{1} p_{2} \cdots p_{j} p_{j+1} \leq m-1$ as well. Contradiction with the maximality of $j$. So it must be that $j=t$, i.e., $d=p_{1} p_{2} \cdots p_{t} \leq m-1$.
We conclude that $d=m-1$ is indeed the largest $d$ that satisfies the conditions.
|
m-1
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Laat $m \geq 3$ en $n$ positieve gehele getallen zijn met $n>m(m-2)$. Vind het grootste positieve gehele getal $d$ zodat $d \mid n$ ! en $k \nmid d$ voor alle $k \in\{m, m+1, \ldots, n\}$.
|
We gaan bewijzen dat $d=m-1$ de grootste is die voldoet. Merk eerst op dat $m-1 \mid n$ ! en dat voor $k \geq m$ geldt $k \nmid m-1$, dus $d=m-1$ voldoet inderdaad.
Stel nu dat voor zekere $d$ geldt: $d \mid n$ ! en $k \nmid d$ voor alle $k \in\{m, m+1, \ldots, n\}$. We gaan bewijzen dat $d \leq m-1$. Schrijf $d=p_{1} p_{2} \cdots p_{t}$ met $p_{i}$ priem voor alle $i$ (niet noodzakelijk allemaal verschillend). Als $t=0$, is $d=1 \leq m-1$, dus we mogen aannemen $t \geq 1$. Uit de eerste voorwaarde op $d$ volgt $p_{i} \leq n$ voor alle $i$. Uit de tweede voorwaarde op $d$ volgt dat $p_{i} \notin\{m, m+1, \ldots, n\}$ voor alle $i$. Dus $p_{i} \leq m-1$ voor alle $i$. Bekijk nu de getallen $p_{1}, p_{1} p_{2}, \ldots, p_{1} p_{2} \cdots p_{t}$. Dit zijn allemaal delers van $d$ en daarom allemaal ongelijk aan getallen uit $\{m, m+1, \ldots, n\}$. Verder weten we dat $p_{1} \leq m-1$. Bekijk nu de grootste $j \leq t$ waarvoor geldt dat $p_{1} p_{2} \cdots p_{j} \leq m-1$. Als $j<t$ geldt
$$
p_{1} p_{2} \cdots p_{j} p_{j+1} \leq(m-1) p_{j+1} \leq(m-1)(m-1)=m(m-2)+1 \leq n
$$
Maar dat betekent dat ook $p_{1} p_{2} \cdots p_{j} p_{j+1} \leq m-1$. Tegenspraak met de maximaliteit van $j$. Dus moet gelden $j=t$, oftewel $d=p_{1} p_{2} \cdots p_{t} \leq m-1$.
We concluderen dat $d=m-1$ inderdaad de grootste $d$ is die aan de eisen voldoet.
|
{
"resource_path": "Dutch_TST/segmented/nl-2014-B_uitwerkingen.jsonl",
"problem_match": "\nOpgave 4.",
"solution_match": "\nOplossing."
}
|
f3f5d741-e92a-5a4d-a876-55ce09f171af
| 605,271
|
On a $2014 \times 2014$ board, each of the $2014^{2}$ squares contains a lamp. Lamps can be on or off. In the initial situation, some of the lamps are on. In a move, you choose a row or column in which at least 1007 lamps are on and change the status of all 2014 lamps in that row or column (from on to off and from off to on). Find the smallest non-negative integer $k$ such that the following holds: from any initial situation, you can reach a situation in a finite number of steps where at most $k$ lamps are on.
|
Number the rows from 1 to 2014 and the columns as well. Consider the following initial situation: in row $i$, the lamps in columns $i, i+1, \ldots, i+1005$ are on and the rest are off, where we calculate the column numbers modulo 2014. Now, in each row and each column, exactly 1006 lamps are on. Therefore, no move is possible. It is thus not always possible to reach a situation with fewer than 2014 • 1006 lamps on.
Now we show that we can always reach a situation with at most 2014 • 1006 lamps on. Suppose, for the sake of contradiction, that in a certain situation there are at least 2014•1006+1 lamps on and it is not possible to reduce the number of lamps on. If there is a row or column with 1008 or more lamps on, we can change the status of the lamps in this row or column, and there will be fewer lamps on afterward, a contradiction. Therefore, in every row and column, there are at most 1007 lamps on.
Let $I$ be the set of rows with exactly 1007 lamps on, and let $J_{1}$ be the set of columns with exactly 1007 lamps on. We plan to change the status of the lamps in all rows in $I$. This is called the big plan. If after executing the big plan, a column has 1008 or more lamps on, we get a contradiction again, so we assume that this does not happen. Let $J_{2}$ be the set of columns that will have exactly 1007 lamps on after executing the big plan. If there is a cell $(i, j)$ with $i \in I$ and $j \in J_{1}$ where the lamp is off, I can change row $i$ and get more than 1007 lamps on in column $j$, a contradiction. Therefore, every lamp at $(i, j)$ with $i \in I$ and $j \in J_{1}$ is on. If there is a cell $(i, j)$ with $i \in I$ and $j \in J_{2}$ where the lamp is off after executing the big plan, I get a contradiction in the same way. Therefore, every lamp at $(i, j)$ with $i \in I$ and $j \in J_{2}$ is on after executing the big plan. Since the columns in $J_{2}$ each have exactly 1007 lamps on after executing the big plan, they had $1007-|I|$ lamps on before the big plan. (The notation $|X|$ denotes the number of elements in the set $X$.) The columns in $J_{1}$ each have exactly 1007 lamps on, and this also means that $J_{1}$ and $J_{2}$ are disjoint (no overlapping columns). The remaining columns have at most 1006 lamps on. The total number of lamps on before the big plan is thus at most
$(1007-|I|)|J_{2}| + 1007|J_{1}| + 1006(2014 - |J_{1}| - |J_{2}|) = 1006 \cdot 2014 + |J_{1}| + |J_{2}| - |I| \cdot |J_{2}|$.
This must be at least $1006 \cdot 2014 + 1$, so $|J_{1}| + |J_{2}| - |I| \cdot |J_{2}| \geq 1$. This implies $|J_{1}| > (|I| - 1)|J_{2}|$. If $|I| \geq 2$, then $|J_{1}| > |J_{2}|$. By executing the big plan, the number of columns with 1007 lamps on is thus reduced. But then we have a situation again with $|I|$ rows with 1007 lamps on, where $J_{1}$ and $J_{2}$ are exactly swapped. So we can execute a new big plan, which again reduces the number of columns with 1007 lamps on. Contradiction, because we are back in the initial situation. We conclude that $|I| = 1$ must hold.
We thus have the situation that there is exactly one row with exactly 1007 lamps on. Similarly, we can show that there must also be exactly one column with exactly 1007 lamps on. Since there are $1006 \cdot 2014 + 1$ lamps on, there must be exactly 1006 lamps on in every other row and column. Now change the status of the lamps in the row with 1007 lamps on. In 1007 columns, there will then be $1006 + 1 = 1007$ lamps on. We have already seen that in this situation, the number of lamps that are on can be reduced.
We see that if there are more than 1006 • 2014 lamps on, it is always possible to reduce this number. Therefore, the smallest $k$ is $1006 \cdot 2014$.
|
1006 \cdot 2014
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Op een $2014 \times 2014$-bord staat op elk van de $2014^{2}$ vakjes een lamp. Lampen kunnen aan of uit staan. In de beginsituatie is een aantal van de lampen aan. In een zet kies je een rij of kolom waarin minstens 1007 lampen aan staan en verander je van alle 2014 lampen in die rij of kolom de status (van aan naar uit en van uit naar aan). Vind de kleinste niet-negatieve gehele $k$ zodat geldt: vanuit elke beginsituatie kun je in een eindig aantal stappen naar een situatie waarin hoogstens $k$ lampen aan staan.
|
Nummer de rijen van 1 tot en met 2014 en de kolommen ook. Bekijk de volgende beginsituatie: in rij $i$ zijn de lampen in de kolommen $i, i+1, \ldots, i+1005$ aan en de rest uit, waarbij we de kolomnummers modulo 2014 rekenen. Nu zijn in elke rij en in elke kolom precies 1006 lampen aan. Er is dus geen zet mogelijk. Het is dus niet altijd mogelijk om naar een situatie met minder dan 2014 • 1006 lampen aan toe te gaan.
Nu laten we zien dat we wel altijd naar een situatie met hoogstens 2014 • 1006 lampen aan toe kunnen. Stel uit het ongerijmde dat er in een bepaalde situatie minstens 2014•1006+1 lampen aan staan en het toch niet mogelijk is om naar minder lampen aan toe te gaan. Als er een rij of kolom is met 1008 of meer lampen aan, dan kunnen we de status van de lampen in deze rij of kolom veranderen en zijn er daarna minder lampen aan, tegenspraak. Dus in elke rij en kolom staan hoogstens 1007 lampen aan.
Zij $I$ de verzameling rijen met precies 1007 lampen aan en zij $J_{1}$ de verzameling kolommen met precies 1007 lampen aan. We zijn van plan om de status van de lampen in alle rijen in $I$ om te zetten. Dit noemen we het grote plan. Als na het uitvoeren van het grote plan een kolom ontstaat met 1008 of meer lampen aan, krijgen we weer een tegenspraak, dus we nemen aan dat dat niet zo is. $\mathrm{Zij} J_{2}$ de verzameling kolommen die na het uitvoeren van het grote plan precies 1007 lampen aan zullen hebben. Als er een vakje $(i, j)$ bestaat met $i \in I$ en $j \in J_{1}$ waarvan de lamp uit staat, kan ik rij $i$ omzetten en krijg ik in kolom $j$ meer dan 1007 lampen aan, tegenspraak. Dus elke lamp op $(i, j)$ met $i \in I$ en $j \in J_{1}$ is aan. Als er een vakje $(i, j)$ bestaat met $i \in I$ en $j \in J_{2}$ waarvan de lamp na het uitvoeren van het grote plan uit staat, krijg ik op dezelfde manier een tegenspraak. Dus elke lamp op $(i, j)$ met $i \in I$ en $j \in J_{2}$ staat na het uitvoeren van het grote plan aan. Omdat de kolommen in $J_{2}$ na het uitvoeren van het grote plan elk precies 1007 lampen aan hebben, hebben ze vóór het uitvoeren van het grote plan dus $1007-|I|$ lampen aan. (De notatie $|X|$ geeft het aantal elementen in de verzameling $X$ aan.) De kolommen in $J_{1}$ hebben precies 1007 lampen aan en dit betekent ook dat $J_{1}$ en $J_{2}$ disjunct zijn (geen overlappende kolommen hebben). De overige kolommen hebben hoogstens 1006 lampen aan. Het totaal aantal lampen aan vóór het grote plan is dus hoogstens
$(1007-|I|)\left|J_{2}\right|+1007\left|J_{1}\right|+1006\left(2014-\left|J_{1}\right|-\left|J_{2}\right|\right)=1006 \cdot 2014+\left|J_{1}\right|+\left|J_{2}\right|-|I| \cdot\left|J_{2}\right|$.
Dit moet minstens $1006 \cdot 2014+1$ zijn, dus $\left|J_{1}\right|+\left|J_{2}\right|-|I| \cdot\left|J_{2}\right| \geq 1$. Hieruit volgt $\left|J_{1}\right|>(|I|-1)\left|J_{2}\right|$. Als $|I| \geq 2$, dan $\left|J_{1}\right|>\left|J_{2}\right|$. Door het uitvoeren van het grote plan wordt dan dus het aantal kolommen met 1007 lampen aan verkleind. Maar daarna hebben we weer een situatie met $|I|$ rijen met 1007 lampen aan, waarbij $J_{1}$ en $J_{2}$ precies verwisseld zijn. Dus kunnen we hier een nieuw groot plan uitvoeren waardoor het aantal kolommen
met 1007 lampen aan weer kleiner wordt. Tegenspraak, want we zijn nu weer terug in de uitgangssituatie. We concluderen dat moet gelden $|I|=1$.
We hebben dus de situatie dat er precies één rij is met precies 1007 lampen aan. Analoog kunnen we laten zien dat er ook één kolom moet zijn met precies 1007 lampen aan. Omdat er $1006 \cdot 2014+1$ lampen aan staan, moeten er in elke andere rij en kolom precies 1006 lampen aan staan. Verander nu de status van lampen in de rij met 1007 lampen aan. In 1007 kolommen staan vervolgens $1006+1=1007$ lampen aan. We hebben al gezien dat we in deze situatie het aantal lampen dat aan staat, kunnen verminderen.
We zien dat als er meer dan 1006 • 2014 lampen aan staan, het altijd mogelijk is om dit aantal te verminderen. Dus de kleinste $k$ is $1006 \cdot 2014$.
|
{
"resource_path": "Dutch_TST/segmented/nl-2014-C_uitwerkingen.jsonl",
"problem_match": "\nOpgave 5.",
"solution_match": "\nOplossing."
}
|
2bf08a8a-f38a-5e5d-9c24-b26be109fba6
| 605,404
|
Let $f: \mathbb{Z}_{>0} \rightarrow \mathbb{R}$ be a function for which it holds that for all $n>1$ there is a prime divisor $p$ of $n$ such that
$$
f(n)=f\left(\frac{n}{p}\right)-f(p)
$$
Moreover, it is given that $f\left(2^{2014}\right)+f\left(3^{2015}\right)+f\left(5^{2016}\right)=2013$.
Calculate $f\left(2014^{2}\right)+f\left(2015^{3}\right)+f\left(2016^{5}\right)$.
|
When $n=q$ with $q$ prime, there is only one prime divisor of $n$, namely $q$, so it must hold that $f(q)=f(1)-f(q)$, thus $f(q)=\frac{1}{2} f(1)$. If $n=q^{2}$ with $q$ prime, then $n$ also has only one prime divisor, so $f\left(q^{2}\right)=f(q)-f(q)=0$. We now prove by induction on $k$ that $f\left(q^{k}\right)=\frac{2-k}{2} f(1)$ if $q$ is a prime number and $k$ is a positive integer. For $k=1$ and $k=2$, we have already shown this. Suppose now that $f\left(q^{k}\right)=\frac{2-k}{2} f(1)$ for some $k \geq 2$ and substitute $n=q^{k+1}$. It holds that
$$
f\left(q^{k+1}\right)=f\left(q^{k}\right)-f(q)=\frac{2-k}{2} f(1)-\frac{1}{2} f(1)=\frac{2-(k+1)}{2} f(1)
$$
This completes the induction.
Now we use our second given. It holds that
$$
\begin{aligned}
2013 & =f\left(2^{2014}\right)+f\left(3^{2015}\right)+f\left(5^{2016}\right) \\
& =\frac{2-2014}{2} f(1)+\frac{2-2015}{2} f(1)+\frac{2-2016}{2} f(1) \\
& =-\frac{6039}{2} f(1)
\end{aligned}
$$
so $f(1)=\frac{2013 \cdot 2}{-6039}=-\frac{2}{3}$. And then for any prime number $q$, $f(q)=\frac{1}{2} f(1)=-\frac{1}{3}$.
We then prove that if $n=p_{1} p_{2} \cdots p_{m}$ with $p_{1}, p_{2}, \ldots, p_{m}$ not necessarily distinct primes and $m \geq 0$, then $f(n)=\frac{m-2}{3}$. We do this by induction on $m$. For $m=0$, $n=1$ and $f(1)=-\frac{2}{3}=\frac{0-2}{3}$, so it holds for this case. Suppose now that we have proven it for some $m \geq 0$. Consider any $n$ of the form $n=p_{1} p_{2} \cdots p_{m+1}$. Then $n>1$, so there is a prime factor $p \mid n$ for which $f(n)=f\left(\frac{n}{p}\right)-f(p)$; without loss of generality, this is $p=p_{m+1}$. It follows that
$$
f(n)=f\left(p_{1} p_{2} \cdots p_{m}\right)-f\left(p_{m+1}\right)=\frac{m-2}{3}--\frac{1}{3}=\frac{(m+1)-2}{3} .
$$
This completes the induction.
We can now calculate the desired result. The prime factorizations of 2014, 2015, and 2016 are $2014=2 \cdot 19 \cdot 53, 2015=5 \cdot 13 \cdot 31$, and $2016=2^{5} \cdot 3^{2} \cdot 7$, so
$$
f\left(2014^{2}\right)+f\left(2015^{3}\right)+f\left(2016^{5}\right)=\frac{6-2}{3}+\frac{9-2}{3}+\frac{40-2}{3}=\frac{49}{3} .
$$
|
\frac{49}{3}
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Zij $f: \mathbb{Z}_{>0} \rightarrow \mathbb{R}$ een functie waarvoor geldt: voor alle $n>1$ is er een priemdeler $p$ van $n$ zodat
$$
f(n)=f\left(\frac{n}{p}\right)-f(p)
$$
Bovendien is gegeven dat $f\left(2^{2014}\right)+f\left(3^{2015}\right)+f\left(5^{2016}\right)=2013$.
Bereken $f\left(2014^{2}\right)+f\left(2015^{3}\right)+f\left(2016^{5}\right)$.
|
Als $n=q$ met $q$ priem, dan is er maar één priemdeler van $n$, namelijk $q$, dus moet gelden dat $f(q)=f(1)-f(q)$, dus $f(q)=\frac{1}{2} f(1)$. Als $n=q^{2}$ met $q$ priem, dan heeft $n$ ook maar één priemdeler, dus geldt $f\left(q^{2}\right)=f(q)-f(q)=0$. We bewijzen nu met inductie naar $k$ dat $f\left(q^{k}\right)=\frac{2-k}{2} f(1)$ als $q$ een priemgetal is en $k$ een positief geheel getal. Voor $k=1$ en $k=2$ hebben we dit al laten zien. Stel nu dat $f\left(q^{k}\right)=\frac{2-k}{2} f(1)$ voor zekere $k \geq 2$ en vul in $n=q^{k+1}$. Er geldt
$$
f\left(q^{k+1}\right)=f\left(q^{k}\right)-f(q)=\frac{2-k}{2} f(1)-\frac{1}{2} f(1)=\frac{2-(k+1)}{2} f(1)
$$
Dit voltooit de inductie.
Nu gebruiken we ons tweede gegeven. Er geldt
$$
\begin{aligned}
2013 & =f\left(2^{2014}\right)+f\left(3^{2015}\right)+f\left(5^{2016}\right) \\
& =\frac{2-2014}{2} f(1)+\frac{2-2015}{2} f(1)+\frac{2-2016}{2} f(1) \\
& =-\frac{6039}{2} f(1)
\end{aligned}
$$
dus $f(1)=\frac{2013 \cdot 2}{-6039}=-\frac{2}{3}$. En dan geldt voor elk priemgetal $q$ dat $f(q)=\frac{1}{2} f(1)=-\frac{1}{3}$.
We bewijzen vervolgens dat als $n=p_{1} p_{2} \cdots p_{m}$ met $p_{1}, p_{2}, \ldots, p_{m}$ niet noodzakelijk verschillende priemgetallen en $m \geq 0$, dat dan geldt $f(n)=\frac{m-2}{3}$. Dit doen we met inductie naar $m$. Voor $m=0$ is $n=1$ en $f(1)=-\frac{2}{3}=\frac{0-2}{3}$, dus hiervoor klopt het. Stel nu dat we het bewezen hebben voor zekere $m \geq 0$. Bekijk een willekeurige $n$ van de vorm $n=p_{1} p_{2} \cdots p_{m+1}$. Dan is $n>1$, dus is er een priemfactor $p \mid n$ waarvoor geldt $f(n)=f\left(\frac{n}{p}\right)-f(p)$; zonder verlies van algemeenheid is dit $p=p_{m+1}$. Nu volgt
$$
f(n)=f\left(p_{1} p_{2} \cdots p_{m}\right)-f\left(p_{m+1}\right)=\frac{m-2}{3}--\frac{1}{3}=\frac{(m+1)-2}{3} .
$$
Dit voltooit de inductie.
We kunnen nu het gevraagde berekenen. De priemfactorisaties van 2014, 2015 en 2016 zijn $2014=2 \cdot 19 \cdot 53,2015=5 \cdot 13 \cdot 31$ en $2016=2^{5} \cdot 3^{2} \cdot 7$, dus
$$
f\left(2014^{2}\right)+f\left(2015^{3}\right)+f\left(2016^{5}\right)=\frac{6-2}{3}+\frac{9-2}{3}+\frac{40-2}{3}=\frac{49}{3} .
$$
|
{
"resource_path": "Dutch_TST/segmented/nl-2014-D_uitwerkingen.jsonl",
"problem_match": "\nOpgave 1.",
"solution_match": "\nOplossing."
}
|
e84eac5f-58bc-565f-81a0-df6f0cba8fff
| 605,413
|
The sets $A$ and $B$ are subsets of the positive integers. The sum of any two different elements from $A$ is an element of $B$. The quotient of any two different elements from $B$ (where we divide the largest by the smallest) is an element of $A$. Determine the maximum number of elements in $A \cup B$.
|
Suppose $A$ contains at least three elements, say $a<b<c$. Then $B$ contains the three distinct elements $a+b<a+c<b+c$. So $A$ contains the element $\frac{b+c}{a+c}$. This fraction is clearly an integer, so $a+c \mid b+c$. But then it follows that $a+c \mid (b+c)-(a+c)=b-a$. We know $b>a$, so $b-a$ is positive, and thus $a+c \leq b-a$. This gives $c \leq b-2a < b$, a contradiction with $c>b$. Therefore, $A$ contains at most two elements.
Suppose $B$ contains at least four elements, say $a<b<c<d$. Then $A$ contains the three distinct elements $\frac{d}{a}, \frac{d}{b}$, and $\frac{d}{c}$. But $A$ cannot contain three distinct elements, a contradiction. Therefore, $B$ contains at most three elements.
In total, $A \cup B$ contains at most 5 elements. This is possible, for example, with $A=\{2,4\}$ and $B=\{3,6,12\}$. Now, $2+4=6 \in B$ and $\frac{12}{6}=\frac{6}{3}=2 \in A$ and $\frac{12}{3}=4 \in A$, so this pair of sets satisfies the conditions. We conclude that $A \cup B$ contains at most 5 elements.
Finding a pair of sets that satisfies the conditions can be done as follows. Suppose $B$ contains the elements $a<b<c$. Then $A$ contains the elements $\frac{c}{b}, \frac{b}{a}$, and $\frac{c}{a}$, with $\frac{c}{a}$ being the largest. Since $A$ contains only two elements, it must be that $\frac{c}{b}=\frac{b}{a}$. Furthermore, the sum of the two elements in $A$ must be in $B$, so $\frac{b}{a}+\frac{c}{a} \in B$. Write $b=ta$, then $c=tb=t^2a$ and $\frac{b}{a}+\frac{c}{a}=t+t^2$. Now you see that $b$ can equal $t+t^2$ by choosing $a=t+1$. With $t=1$, you get $b=a$, so that does not work; with $t=2$, you get the solution mentioned above.
|
5
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
De verzamelingen $A$ en $B$ zijn deelverzamelingen van de positieve gehele getallen. De som van elke twee verschillende elementen uit $A$ is een element van $B$. Het quotiënt van elke twee verschillende elementen van $B$ (waarbij we de grootste door de kleinste delen) is een element van $A$. Bepaal het maximale aantal elementen in $A \cup B$.
|
Stel dat $A$ minstens drie elementen bevat, zeg $a<b<c$. Dan bevat $B$ de drie verschillende elementen $a+b<a+c<b+c$. Dus $A$ bevat in elk geval het element $\frac{b+c}{a+c}$. Deze breuk is kennelijk geheel, dus $a+c \mid b+c$. Maar dan volgt $a+c \mid(b+c)-(a+c)=b-a$. We weten $b>a$, dus $b-a$ is positief, dus moet gelden $a+c \leq b-a$. Dit geeft $c \leq b-2 a<b$, een tegenspraak met $c>b$. Dus $A$ bevat hoogstens twee elementen.
Stel dat $B$ minstens vier elementen bevat, zeg $a<b<c<d$. Dan bevat $A$ de drie verschillende elementen $\frac{d}{a}, \frac{d}{b}$ en $\frac{d}{c}$. Maar $A$ kan geen drie verschillende elementen bevatten, tegenspraak. Dus $B$ bevat hoogstens drie elementen.
In totaal bevat $A \cup B$ dus hoogstens 5 elementen. Dit is mogelijk, bijvoorbeeld met $A=\{2,4\}$ en $B=\{3,6,12\}$. Nu is $2+4=6 \in B$ en $\frac{12}{6}=\frac{6}{3}=2 \in A$ en $\frac{12}{3}=4 \in A$, dus dit paar verzamelingen voldoet. We concluderen dat $A \cup B$ maximaal 5 elementen bevat.
Het vinden van een paar verzamelingen dat voldoet, kan bijvoorbeeld als volgt. Stel B bevat de elementen $a<b<c$. Dan bevat $A$ de elementen $\frac{c}{b}, \frac{b}{a}$ en $\frac{c}{a}$, waarvan $\frac{c}{a}$ in elk geval de grootste is. Omdat A maar twee elementen bevat, moet wel gelden $\frac{c}{b}=\frac{b}{a}$. Verder moet de som van de twee elementen in $A$ weer in $B$ zitten, dus $\frac{b}{a}+\frac{c}{a} \in B$. Schrijf $b=t a$, dan $c=t b=t^{2} a$ en $\frac{b}{a}+\frac{c}{a}=t+t^{2}$. Nu zie je dat $b$ gelijk kan zijn aan $t+t^{2}$ door $a=t+1$ te kiezen. Met $t=1$ krijg je $b=a$, dus die voldoet niet; met $t=2$ krijg je bovenstaande oplossing.
|
{
"resource_path": "Dutch_TST/segmented/nl-2014-D_uitwerkingen.jsonl",
"problem_match": "\nOpgave 2.",
"solution_match": "\nOplossing."
}
|
83b50a42-e8fe-5d69-a701-6a087ff255a4
| 605,426
|
Let $n \geq 2$ be a positive integer. Each cell of an $n \times n$ board is colored red or blue. We place dominoes on the board, each covering two cells. We call a domino plain if it lies on two red or two blue cells, and colorful if it lies on one red and one blue cell. Find the largest positive integer $k$ with the following property: no matter how the red/blue coloring of the board is done, it is always possible to place $k$ non-overlapping dominoes on the board that are either all plain or all colorful.
|
We prove that $k=\left\lfloor\frac{n^{2}}{4}\right\rfloor$ is the largest possible value.
Suppose $n$ is even. Then it is possible to cover the board with $\frac{n^{2}}{2}$ dominoes (ignoring colors). Since there are $\frac{n^{2}}{2}$ dominoes, all of which are either colorful or plain, there are at least $\left\lfloor\frac{n^{2}}{4}\right\rfloor=\frac{n^{2}}{4}$ colorful or at least $\left\lfloor\frac{n^{2}}{4}\right\rfloor=\frac{n^{2}}{4}$ plain dominoes. If $n$ is odd, we can cover the board with $\frac{n^{2}-1}{2}$ dominoes. (Note that this number is an even integer.) Of these dominoes, there are at least $\frac{n^{2}-1}{4}=\left\lfloor\frac{n^{2}}{4}\right\rfloor$ colorful or at least $\frac{n^{2}-1}{4}=\left\lfloor\frac{n^{2}}{4}\right\rfloor$ plain. This proves that it is always possible to place at least $\left\lfloor\frac{n^{2}}{4}\right\rfloor$ colorful dominoes or at least $\left\lfloor\frac{n^{2}}{4}\right\rfloor$ plain dominoes on the board. We now prove that it is possible to choose the coloring of the squares in red and blue such that there are no more than $\left\lfloor\frac{n^{2}}{4}\right\rfloor$ plain and also no more than $\left\lfloor\frac{n^{2}}{4}\right\rfloor$ colorful dominoes that can be placed.
Color the squares of the board in black and white like a chessboard, so that the bottom-left square is white. If $n$ is even, there are as many white as black squares, namely $\frac{n^{2}}{2}$. If $n$ is odd, there is one fewer black square, and the number of black squares is $\frac{n^{2}-1}{2}=\left\lfloor\frac{n^{2}}{2}\right\rfloor$. In both cases, this is an even number of squares, since for odd $n$ we have $n^{2} \equiv 1$ mod 4. Color half of the black squares red and all other squares blue. Then there are $\left\lfloor\frac{n^{2}}{4}\right\rfloor$ red squares, so we can place at most $\left\lfloor\frac{n^{2}}{4}\right\rfloor$ non-overlapping colorful dominoes on the board: each of these dominoes covers a red square. A plain domino cannot cover two red squares, as no two adjacent squares are red. It must therefore cover two blue squares. At least one of these is a black-blue square, so the number of plain dominoes is at most the number of black-blue squares, which is $\left\lfloor\frac{n^{2}}{4}\right\rfloor$. Therefore, both the colorful and the plain dominoes can have at most $\left\lfloor\frac{n^{2}}{4}\right\rfloor$ placed on the board simultaneously.
We conclude that the maximum $k$ is indeed $k=\left\lfloor\frac{n^{2}}{4}\right\rfloor$.
|
\left\lfloor\frac{n^{2}}{4}\right\rfloor
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Zij $n \geq 2$ een positief geheel getal. Ieder vakje van een $n \times n$-bord wordt rood of blauw gekleurd. We leggen dominostenen op het bord, die elk twee vakjes bedekken. We noemen een dominosteen effen als hij op twee rode of twee blauwe vakjes ligt en kleurrijk als hij op een rood en een blauw vakje ligt. Vind het grootste positieve gehele getal $k$ met de volgende eigenschap: hoe de rood/blauw-kleuring van het bord ook gebeurt, het is altijd mogelijk om $k$ niet-overlappende dominostenen op het bord te leggen die ofwel allemaal effen zijn ofwel allemaal kleurrijk.
|
We bewijzen dat $k=\left\lfloor\frac{n^{2}}{4}\right\rfloor$ de grootst mogelijke waarde is.
Stel dat $n$ even is. Dan is het mogelijk om het bord te bedekken met $\frac{n^{2}}{2}$ dominostenen (zonder op kleuren te letten). Omdat er $\frac{n^{2}}{2}$ dominostenen zijn die allemaal kleurrijk of effen zijn, zijn er of minstens $\left\lfloor\frac{n^{2}}{4}\right\rfloor=\frac{n^{2}}{4}$ kleurrijke of minstens $\left\lfloor\frac{n^{2}}{4}\right\rfloor=\frac{n^{2}}{4}$ effen dominostenen. Als $n$ oneven is, kunnen we het bord bedekken met $\frac{n^{2}-1}{2}$ dominostenen. (Merk op dat dit getal geheel en even is.) Van deze dominostenen zijn er of minstens $\frac{n^{2}-1}{4}=\left\lfloor\frac{n^{2}}{4}\right\rfloor$ kleurrijk, of minstens $\frac{n^{2}-1}{4}=\left\lfloor\frac{n^{2}}{4}\right\rfloor$ effen. Dit bewijst dat het altijd mogelijk is om op het bord minstens $\left\lfloor\frac{n^{2}}{4}\right\rfloor$ kleurrijke dominostenen of minstens $\left\lfloor\frac{n^{2}}{4}\right\rfloor$ effen dominostenen neer te leggen. We bewijzen nu dat het mogelijk is om de kleuring in rode en blauwe vakjes zo te kiezen, dat er niet meer dan $\left\lfloor\frac{n^{2}}{4}\right\rfloor$ effen en ook niet meer dan $\left\lfloor\frac{n^{2}}{4}\right\rfloor$ kleurrijke dominostenen neer te leggen zijn.
Kleur de vakjes van het bord zwart-wit als op een schaakbord, zodat het vakje linksonder wit is. Als $n$ even is, zijn er evenveel witte als zwarte vakjes, namelijk $\frac{n^{2}}{2}$. Als $n$ oneven is, is er een zwart vakje minder en is het aantal zwarte vakjes gelijk aan $\frac{n^{2}-1}{2}=\left\lfloor\frac{n^{2}}{2}\right\rfloor$. In beide gevallen is dit een even aantal vakjes, aangezien voor oneven $n$ geldt dat $n^{2} \equiv 1$ mod 4. Kleur de helft van de zwarte vakjes rood en alle andere vakjes blauw. Dan zijn er $\left\lfloor\frac{n^{2}}{4}\right\rfloor$ rode vakjes, dus we kunnen maximaal $\left\lfloor\frac{n^{2}}{4}\right\rfloor$ niet-overlappende kleurrijke dominostenen op het bord leggen: elk van deze dominostenen bedekt immers een rood vakje. Een effen dominosteen kan geen twee rode vakjes bedekken, want er zijn geen twee vakjes naast elkaar rood gekleurd. Hij moet dus wel twee blauwe vakjes bedekken. Daar zit in elk geval een zwart vakje bij, dus het aantal effen dominostenen is hoogstens het aantal zwart-blauwe vakjes en dat is $\left\lfloor\frac{n^{2}}{4}\right\rfloor$. Dus zowel van de kleurrijke als van de effen dominostenen kunnen er hooguit $\left\lfloor\frac{n^{2}}{4}\right\rfloor$ tegelijk op het bord worden gelegd.
We concluderen dat de maximale $k$ inderdaad $k=\left\lfloor\frac{n^{2}}{4}\right\rfloor$ is.
|
{
"resource_path": "Dutch_TST/segmented/nl-2015-B_uitwerkingen.jsonl",
"problem_match": "\nOpgave 3.",
"solution_match": "\nOplossing."
}
|
ad63fc4e-ef56-5eea-8021-5c55492b0387
| 605,498
|
Determine all positive integers $n$ for which there exist positive integers $a_{1}, a_{2}, \ldots, a_{n}$ such that
$$
a_{1}+2 a_{2}+3 a_{3}+\ldots+n a_{n}=6 n
$$
and
$$
\frac{1}{a_{1}}+\frac{2}{a_{2}}+\frac{3}{a_{3}}+\ldots+\frac{n}{a_{n}}=2+\frac{1}{n}
$$
|
When we apply the inequality of the arithmetic and harmonic mean to $a_{1}$, twice $a_{2}$, three times $a_{3}, \ldots, n$ times $a_{n}$, we find
$$
\frac{6 n}{\frac{1}{2} n(n+1)}=\frac{a_{1}+2 a_{2}+3 a_{3}+\ldots+n a_{n}}{\frac{1}{2} n(n+1)} \geq \frac{\frac{1}{2} n(n+1)}{\frac{1}{a_{1}}+\frac{2}{a_{2}}+\frac{3}{a_{3}}+\ldots+\frac{n}{a_{n}}}=\frac{\frac{1}{2} n(n+1)}{2+\frac{1}{n}}
$$
We have
$$
\frac{6 n}{\frac{1}{2} n(n+1)}=\frac{12}{n+1}<\frac{12}{n}
$$
and
$$
\frac{\frac{1}{2} n(n+1)}{2+\frac{1}{n}}=\frac{\frac{1}{2} n^{2}(n+1)}{2 n+1}>\frac{\frac{1}{2} n^{2}(n+1)}{2 n+2}=\frac{1}{4} n^{2}
$$
Putting everything together, we find $\frac{12}{n}>\frac{1}{4} n^{2}$, or $48>n^{3}$, from which it follows that $n \leq 3$.
With $n=1$, we get $a_{1}=6$ and $\frac{1}{a_{1}}=3$, which contradicts each other. So $n=1$ is not possible.
With $n=2$, we get $a_{1}+2 a_{2}=12$ and $\frac{1}{a_{1}}+\frac{2}{a_{2}}=2+\frac{1}{2}$. If $a_{2} \geq 2$, then $\frac{1}{a_{1}}+\frac{2}{a_{2}} \leq 1+1$ and that is too small. So $a_{2}$ must be $1$, but then we find $a_{1}=12-2=10$ and thus $\frac{1}{a_{1}}+\frac{2}{a_{2}}=\frac{1}{10}+2$, a contradiction. So $n=2$ is not possible.
For $n=3$, there is a solution, namely $a_{1}=6, a_{2}=3$ and $a_{3}=2$ (substitution shows that this satisfies the conditions). So $n=3$ is possible and we conclude that $n=3$ is the only solution.
|
3
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Bepaal alle positieve gehele getallen $n$ waarvoor er positieve gehele getallen $a_{1}, a_{2}, \ldots, a_{n}$ bestaan met
$$
a_{1}+2 a_{2}+3 a_{3}+\ldots+n a_{n}=6 n
$$
en
$$
\frac{1}{a_{1}}+\frac{2}{a_{2}}+\frac{3}{a_{3}}+\ldots+\frac{n}{a_{n}}=2+\frac{1}{n}
$$
|
Als we de ongelijkheid van het rekenkundig en harmonisch gemiddelde toepassen op $a_{1}$, twee keer $a_{2}$, drie keer $a_{3}, \ldots, n$ keer $a_{n}$, dan vinden we
$$
\frac{6 n}{\frac{1}{2} n(n+1)}=\frac{a_{1}+2 a_{2}+3 a_{3}+\ldots+n a_{n}}{\frac{1}{2} n(n+1)} \geq \frac{\frac{1}{2} n(n+1)}{\frac{1}{a_{1}}+\frac{2}{a_{2}}+\frac{3}{a_{3}}+\ldots+\frac{n}{a_{n}}}=\frac{\frac{1}{2} n(n+1)}{2+\frac{1}{n}}
$$
Er geldt
$$
\frac{6 n}{\frac{1}{2} n(n+1)}=\frac{12}{n+1}<\frac{12}{n}
$$
en
$$
\frac{\frac{1}{2} n(n+1)}{2+\frac{1}{n}}=\frac{\frac{1}{2} n^{2}(n+1)}{2 n+1}>\frac{\frac{1}{2} n^{2}(n+1)}{2 n+2}=\frac{1}{4} n^{2}
$$
Alles bij elkaar vinden we $\frac{12}{n}>\frac{1}{4} n^{2}$, oftewel $48>n^{3}$, waaruit volgt $n \leq 3$.
Met $n=1$ krijgen we $a_{1}=6$ en $\frac{1}{a_{1}}=3$, wat in tegenspraak met elkaar is. Dus $n=1$ kan niet.
Met $n=2$ krijgen we $a_{1}+2 a_{2}=12$ en $\frac{1}{a_{1}}+\frac{2}{a_{2}}=2+\frac{1}{2}$. Als $a_{2} \geq 2$ geldt $\frac{1}{a_{1}}+\frac{2}{a_{2}} \leq 1+1$ en dat is te klein. Dus moet $a_{2}=1$, maar dan vinden we $a_{1}=12-2=10$ en dus $\frac{1}{a_{1}}+\frac{2}{a_{2}}=\frac{1}{10}+2$, tegenspraak. Dus $n=2$ kan niet.
Bij $n=3$ is er een oplossing, namelijk $a_{1}=6, a_{2}=3$ en $a_{3}=2$ (invullen laat zien dat deze voldoet). Dus $n=3$ kan wel en we concluderen dat $n=3$ de enige oplossing is.
|
{
"resource_path": "Dutch_TST/segmented/nl-2015-D_uitwerkingen.jsonl",
"problem_match": "\nOpgave 2.",
"solution_match": "\nOplossing."
}
|
d98995cc-6dfc-5985-9ee1-8bc2a21cb0a9
| 605,659
|
You may assign a color to each of the numbers from 1 to 2014, with exactly half being red and the other half blue. Then you examine the number $k$ of positive integers that can be written as the sum of a red and a blue number. Determine the maximum value of $k$ that you can achieve.
|
Let $n=2014$. We will prove that the maximum $k$ is equal to $2n-5$. The smallest number that can be written as the sum of a red and a blue number is $1+2=3$ and the largest number is $(n-1)+n=2n-1$. Therefore, there are at most $2n-3$ numbers that can be written as the sum of a red and a blue number.
Assume that the numbers can be colored in such a way that there are $2n-3$ or $2n-4$ numbers that can be written as the sum of a red and a blue number. There is now at most one number from 3 to $2n-1$ that cannot be written as such. We will first show that we can assume without loss of generality that this number is at least $n+1$. We can create a second coloring where a number $i$ is blue if and only if $n+1-i$ was blue in the first coloring. Then a number $m$ can be written as the sum of red and blue in the second coloring if and only if $2n+2-m$ could be written as the sum of red and blue in the first coloring. Therefore, if a number less than $n+1$ could not be written as the sum of red and blue in the first coloring, then in the second coloring, precisely a number greater than $2n+2-(n+1)=n+1$ cannot be written as the sum of red and blue.
Thus, we can assume that the numbers from 3 to $n$ can all be written as the sum of red and blue. Since red and blue are interchangeable, we can also assume without loss of generality that 1 is colored blue. Since 3 can be written as the sum of red and blue and this can only be $3=1+2$, 2 must be red. Now suppose we know that 2 to $l$ are red, for some $l$ with $2 \leq l \leq n-2$. Then in all possible sums $a+b=l+2$ with $a, b \geq 2$, both numbers are colored red, but we know that we can write $l+2$ as the sum of red and blue (since $l+2 \leq n$), so it must be $1+(l+1)$. Therefore, $l+1$ is also red. By induction, we see that the numbers from 2 to $n-1$ are all red. That is $n-2=2012$ numbers. But there are only $\frac{1}{2}n=1007$ red numbers, contradiction.
We conclude that there are at least two numbers from 3 to $2n-1$ that cannot be written as the sum of a red and a blue number. We will now show that we can color the numbers in such a way that all numbers from 4 to $2n-2$ can be written as the sum of a red and a blue number, so that the maximum $k$ is equal to $2n-5$.
For this, color all even numbers except $n$ blue and also the number 1. All odd numbers except 1 are colored red, and also the number $n$. By adding 1 to an odd number (not equal to 1), we can write all even numbers from 4 to $n$ as the sum of a red and a blue number. By adding 2 to an odd number (not equal to 1), we can write all odd numbers from 5 to $n+1$ as the sum of a red and a blue number. By adding $n-1$ to an even number (not equal to $n$), we can write all odd numbers from $n+1$ to $2n-3$ as the sum of a red and a blue number. By adding $n$ to an even number (not equal to $n$), we can write all even numbers from $n+2$ to $2n-2$ as the sum of a red and a blue number. In total, we can thus write all numbers from 4 to $2n-2$ as the sum of a red and a blue number.
We conclude that the maximum $k$ is equal to $2n-5=4023$.
|
4023
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Je mag elk van de getallen 1 tot en met 2014 een kleur geven, waarbij precies de helft rood moet worden en de andere helft blauw. Vervolgens bekijk je het aantal $k$ van positieve gehele getallen die te schrijven zijn als de som van een rood en een blauw getal. Bepaal de maximale waarde van $k$ die je kunt bereiken.
|
Noem $n=2014$. We gaan bewijzen dat de maximale $k$ gelijk is aan $2 n-5$. Het kleinste getal dat je zou kunnen schrijven als de som van een rood en een blauw getal is $1+2=3$ en het grootste getal is $(n-1)+n=2 n-1$. Er zijn dus hoogstens $2 n-3$ getallen te schrijven als de som van een rood en een blauw getal.
Stel dat de getallen zo gekleurd kunnen worden dat er $2 n-3$ of $2 n-4$ getallen te schrijven zijn als som van een rood en een blauw getal. Er is nu hooguit één getal van 3 tot en met $2 n-1$ dat niet zo te schrijven is. We laten nu eerst zien dat we zonder verlies van algemeenheid mogen aannemen dat dit getal minstens $n+1$ is. We kunnen namelijk een tweede kleuring maken waarbij een getal $i$ blauw is dan en slechts dan als in de eerste kleuring $n+1-i$ blauw was. Dan is een getal $m$ bij de tweede kleuring te schrijven als som van rood en blauw dan en slechts dan als $2 n+2-m$ in de eerste kleuring te schrijven was als som van rood en blauw. Dus als in de eerste kleuring een getal kleiner dan $n+1$ niet te schrijven was als som van rood en blauw, dan is in de tweede kleuring juist een getal groter dan $2 n+2-(n+1)=n+1$ niet te schrijven als som van rood en blauw.
We mogen dus aannemen dat de getallen 3 tot en met $n$ allemaal te schrijven zijn als som van rood en blauw. Omdat rood en blauw verwisselbaar zijn, mogen we ook nog zonder verlies van algemeenheid aannemen dat 1 blauw gekleurd is. Omdat 3 te schrijven is als som van rood en blauw en dat alleen $3=1+2$ kan zijn, moet 2 rood zijn. Stel nu dat we weten dat 2 tot en met $l$ rood zijn, voor zekere $l$ met $2 \leq l \leq n-2$. Dan zijn in alle mogelijke sommen $a+b=l+2$ met $a, b \geq 2$ beide getallen rood gekleurd, maar we weten dat we $l+2$ kunnen schrijven als som van rood en blauw (want $l+2 \leq n$ ), dus moet dat wel $1+(l+1)$ zijn. Dus $l+1$ is ook rood gekleurd. Met inductie zien we nu dus dat de getallen 2 tot en met $n-1$ allemaal rood zijn. Dat zijn $n-2=2012$ getallen. Maar er zijn slechts $\frac{1}{2} n=1007$ getallen rood, tegenspraak.
We concluderen dat er minstens twee getallen van 3 tot en met $2 n-1$ niet te schrijven zijn als som van een rood en een blauw getal. We laten nu zien dat we de getallen zo kunnen kleuren dat alle getallen van 4 tot en met $2 n-2$ te schrijven zijn als som van een rood en een blauw getal, zodat de maximale $k$ gelijk is aan $2 n-5$.
Kleur hiervoor alle even getallen behalve $n$ blauw en verder ook nog het getal 1. Alle oneven getallen behalve 1 kleuren we rood en verder ook nog het getal $n$. Door 1 op te tellen bij een oneven getal (ongelijk aan 1) kunnen we alle even getallen van 4 tot en met $n$ schrijven als som van een rood en een blauw getal. Door 2 op te tellen bij een oneven getal (ongelijk aan 1) kunnen we alle oneven getallen van 5 tot en met $n+1$ schrijven als som van een rood en een blauw getal. Door $n-1$ op te tellen bij een even getal (ongelijk aan $n$ ) kunnen we alle oneven getallen van $n+1$ tot en met $2 n-3$ schrijven als som van een rood en een blauw getal. Door $n$ op te tellen bij een even getal (ongelijk aan $n$ ) kunnen we alle even getallen van $n+2$ tot en met $2 n-2$ schrijven als som van een rood en een
blauw getal. Al met al kunnen we dus alle getallen van 4 tot en met $2 n-2$ schrijven als som van een rood en een blauw getal.
We concluderen dat de maximale $k$ gelijk is aan $2 n-5=4023$.
|
{
"resource_path": "Dutch_TST/segmented/nl-2015-D_uitwerkingen.jsonl",
"problem_match": "\nOpgave 4.",
"solution_match": "\nOplossing."
}
|
a324b23d-e619-5346-9c15-9957de7a034a
| 605,705
|
Find all positive integers $k$ for which the equation
$$
\operatorname{lcm}(m, n)-\operatorname{gcd}(m, n)=k(m-n)
$$
has no positive integer solutions $(m, n)$ with $m \neq n$.
|
Let $d=\operatorname{ggd}(m, n)$ and write $m=d a$ and $n=d b$. It holds that $\operatorname{kgv}(m, n) \cdot \operatorname{ggd}(m, n)=m n$, so we can write the given equation as
$$
\frac{d a \cdot d b}{d}-d=k(d a-d b)
$$
or equivalently
$$
a b-1=k(a-b) .
$$
From now on, we will look at the equivalent problem: find all positive integer $k$ for which this new equation has no positive integer solutions $(a, b)$ with $a \neq b$ and $\operatorname{ggd}(a, b)=1$. Note that if a pair $(a, b)$ satisfies this equation, it automatically follows that $\operatorname{ggd}(a, b)=1$. Suppose that $t \mid a$ and $t \mid b$, then $t \mid a b$ and $t \mid a-b$, so $t \mid 1$, so $a$ and $b$ have no common divisor greater than 1.
Suppose first that $k \geq 3$. We claim that $(a, b)=\left(k^{2}-k-1, k-1\right)$ is a solution. Then we have
$$
a b-1=a(k-1)-1=k a-a-1=k a-k^{2}+k+1-1=k a-k^{2}+k=k(a-k+1)=k(a-b).
$$
We have already seen that this immediately implies that $\operatorname{ggd}(a, b)=1$. We still need to check that $a$ and $b$ are positive and that they are not equal. Since $k \geq 3$, we have $b=k-1 \geq 2$ and $a=k^{2}-k-1 \geq 2 k-k-1=k-1 \geq 2$, so they are both positive. Suppose that $a=b$, then $k^{2}-k-1=k-1$, or $k^{2}=2 k$, or $k=2$, a contradiction. So our pair $(a, b)$ satisfies all the conditions. For every $k \geq 3$, the equation thus has at least one solution $(a, b)$ with $a \neq b$ and $\operatorname{ggd}(a, b)=1$.
Now suppose that $k=1$. We claim that $(a, b)=(2,1)$ is a solution. Clearly, $a$ and $b$ are positive and not equal. Furthermore, we have
$$
a b-1=2-1=1=1 \cdot(2-1)=k(a-b)
$$
So for $k=1$, the equation also has at least one solution $(a, b)$ with $a \neq b$ and $\operatorname{ggd}(a, b)=1$.
Finally, suppose that $k=2$. The equation becomes
$$
a b-1=2(a-b) .
$$
The right-hand side is at most $2 a-2$ because $b$ is positive and integer, so $a b-1 \leq 2 a-2$, so $a b<2 a$, so $b<2$. Therefore, we must have $b=1$. The equation then becomes $a-1=2(a-1)$, which implies $a-1=0$. We then have $a=1$ and $b=1$, so $a=b$. We conclude that there are no solutions $(a, b)$ with $a \neq b$.
Thus, the only $k$ for which the original equation has no positive integer solutions $(m, n)$ with $m \neq n$ is $k=2$.
|
2
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Vind alle positieve gehele $k$ waarvoor de vergelijking
$$
\operatorname{kgv}(m, n)-\operatorname{ggd}(m, n)=k(m-n)
$$
geen positieve gehele oplossingen $(m, n)$ met $m \neq n$ heeft.
|
Noem $d=\operatorname{ggd}(m, n)$ en schrijf $m=d a$ en $n=d b$. Er geldt $\operatorname{kgv}(m, n)$. $\operatorname{ggd}(m, n)=m n$, dus we kunnen de gegeven vergelijking schrijven als
$$
\frac{d a \cdot d b}{d}-d=k(d a-d b)
$$
oftewel
$$
a b-1=k(a-b) .
$$
We kijken vanaf nu naar het equivalente vraagstuk: vind alle positieve gehele $k$ waarvoor deze nieuwe vergelijking geen positieve gehele oplossingen $(a, b)$ met $a \neq b$ en $\operatorname{ggd}(a, b)=1$ heeft. Merk op dat als een paar $(a, b)$ aan deze vergelijking voldoet, automatisch geldt dat $\operatorname{ggd}(a, b)=1$. Stel namelijk dat $t \mid a$ en $t \mid b$, dan geldt $t \mid a b$ en $t \mid a-b$, dus $t \mid 1$, dus $a$ en $b$ hebben geen gemeenschappelijke deler groter dan 1.
Stel eerst dat $k \geq 3$. We beweren dat $(a, b)=\left(k^{2}-k-1, k-1\right)$ een oplossing is. Er geldt dan namelijk
$a b-1=a(k-1)-1=k a-a-1=k a-k^{2}+k+1-1=k a-k^{2}+k=k(a-k+1)=k(a-b)$.
We hebben al gezien dat nu direct volgt dat $\operatorname{ggd}(a, b)=1$. We moeten nog checken dat $a$ en $b$ positief zijn en dat ze ongelijk aan elkaar zijn. Omdat $k \geq 3$, is $b=k-1 \geq 2$ en is $a=k^{2}-k-1 \geq 2 k-k-1=k-1 \geq 2$, dus ze zijn allebei positief. Stel dat $a=b$, dan geldt $k^{2}-k-1=k-1$, oftewel $k^{2}=2 k$, oftewel $k=2$, tegenspraak. Dus ons paar $(a, b)$ voldoet aan alle eisen. Voor elke $k \geq 3$ heeft de vergelijking dus minstens één oplossing $(a, b)$ met $a \neq b$ en $\operatorname{ggd}(a, b)=1$.
Stel nu dat $k=1$. We beweren dat $(a, b)=(2,1)$ een oplossing is. Overduidelijk zijn $a$ en $b$ positief en ongelijk aan elkaar. Verder geldt
$$
a b-1=2-1=1=1 \cdot(2-1)=k(a-b)
$$
Dus voor $k=1$ heeft de vergelijking ook minstens één oplossing $(a, b)$ met $a \neq b$ en $\operatorname{ggd}(a, b)=1$.
Stel ten slotte dat $k=2$. De vergelijking wordt dan
$$
a b-1=2(a-b) .
$$
De rechterkant is hooguit $2 a-2$ omdat $b$ positief en geheel is, dus $a b-1 \leq 2 a-2$, dus $a b<2 a$, dus $b<2$. Er moet dus gelden $b=1$. De vergelijking wordt dan $a-1=2(a-1)$, waaruit volgt $a-1=0$. We hebben dan $a=1$ en $b=1$, dus $a=b$. We concluderen dat er geen oplossingen $(a, b)$ met $a \neq b$ zijn.
Dus de enige $k$ waarvoor de oorspronkelijke vergelijking geen positieve gehele oplossingen $(m, n)$ met $m \neq n$ heeft, is $k=2$.
|
{
"resource_path": "Dutch_TST/segmented/nl-2016-C_uitwerkingen.jsonl",
"problem_match": "\nOpgave 3.",
"solution_match": "\nOplossing."
}
|
0d172a5b-ae5c-5316-9925-e364642fbfff
| 605,825
|
Determine the number of sets $A=\left\{a_{1}, a_{2}, \ldots, a_{1000}\right\}$ of positive integers with $a_{1}<a_{2}<\ldots<a_{1000} \leq 2014$, for which the set
$$
S=\left\{a_{i}+a_{j} \mid 1 \leq i, j \leq 1000 \text { and } i+j \in A\right\}
$$
is a subset of $A$.
|
We prove that there are $2^{14}$ such sets. In particular, we prove that the sets $A$ that satisfy the conditions are of the form $B \cup C$, with $C$ a subset of $\{2001, \ldots, 2014\}$ and $B=\{1,2, \ldots, 1000-|C|\}$. Call sets of this form "nice". Since there are $2^{14}$ subsets of $\{2001, \ldots, 2014\}$, there are $2^{14}$ nice sets. We first show that every nice set $A$ satisfies the conditions. Suppose that $i, j \leq 1000$ with $i+j \in A$. Then $i+j \leq 2000$, so $i+j \in B$. There thus exists a $k$ with $k \leq 1000-|C|$ such that $i+j=a_{k}(=k)$. Since $a_{k} \leq 1000-|C|$, it also holds that $i, j \leq 1000-|C|$, so $a_{i}=i$ and $a_{j}=j$. This means $a_{i}+a_{j}=i+j=a_{k}$ and that is an element of $A$. Therefore, every element of $S$ is an element of $A$, which implies that $A$ satisfies the conditions.
We now show that every set $A$ that satisfies the conditions is nice. Suppose first that there exists a $k$ with $1 \leq k \leq 1000$ such that $a_{k} \in\{1001, \ldots, 2000\}$. Then $a_{k}=1000+i$ for some $i$ with $i \leq 1000$, so $a_{1000}+a_{i}$ is an element of $S$ and must therefore also be an element of $A$. However, $a_{1000}+a_{i}>a_{1000}$, a contradiction. Therefore, such an $a_{k}$ cannot occur. This means that $A$ can be written as the disjoint union $B \cup C$, with $C \subseteq\{2001, \ldots, 2014\}$ and $B \subseteq\{1,2, \ldots, 1000\}$. Let $b$ be the number of elements of $B$. Then $b \geq 986$, because $C$ has at most 14 elements. To prove that $A$ is nice, we need to prove that $B=\{1,2, \ldots, b\}$. It is sufficient to prove that $a_{b}$, the largest element of $B$, is equal to $b$. Therefore, assume for the sake of contradiction that $a_{b}>b$. For $i$ with $i=a_{b}-b$ it then holds that $b+i=a_{b} \leq 1000$, so $i \leq 1000-b \leq 14<b$. Therefore, $a_{i} \leq 1000$ and thus $a_{b}+a_{i} \leq$ 2000. Since $i+b=a_{b} \in A$, it follows that $a_{b}+a_{i} \in S \subset A$, but then $a_{b}+a_{i}$ is a larger element of $B$ than $a_{b}$, the maximal element. Contradiction. Therefore, $a_{b}=b$, which implies that $B=\{1,2, \ldots, b\}$. Thus, $A$ is nice.
|
2^{14}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Bepaal het aantal verzamelingen $A=\left\{a_{1}, a_{2}, \ldots, a_{1000}\right\}$ van positieve gehele getallen met $a_{1}<a_{2}<\ldots<a_{1000} \leq 2014$, waarvoor geldt dat de verzameling
$$
S=\left\{a_{i}+a_{j} \mid 1 \leq i, j \leq 1000 \text { en } i+j \in A\right\}
$$
een deelverzameling is van $A$.
|
We bewijzen dat er $2^{14}$ zulke verzamelingen zijn. We bewijzen in het bijzonder dat de verzamelingen $A$ die voldoen van de vorm $B \cup C$ zijn, met $C$ een deelverzameling van $\{2001, \ldots, 2014\}$ en $B=\{1,2, \ldots, 1000-|C|\}$. Noem verzamelingen van die vorm "leuk". Omdat er $2^{14}$ deelverzamelingen van $\{2001, \ldots, 2014\}$ zijn, zijn er $2^{14}$ leuke verzamelingen. We laten eerst zien dat iedere leuke verzameling $A$ voldoet. Stel dat $i, j \leq 1000$ met $i+j \in A$. Dan is $i+j \leq 2000$, dus $i+j \in B$. Er bestaat dan dus een $k$ met $k \leq 1000-|C|$ zodat $i+j=a_{k}(=k)$. Omdat $a_{k} \leq 1000-|C|$ geldt ook $i, j \leq 1000-|C|$, dus $a_{i}=i$ en $a_{j}=j$. Dat betekent $a_{i}+a_{j}=i+j=a_{k}$ en dat is een element van $A$. Dus elk element van $S$ is een element van $A$, waaruit volgt dat $A$ voldoet.
We laten nu zien dat iedere verzameling $A$ die voldoet, leuk is. Stel allereerst dat er een $k$ met $1 \leq k \leq 1000$ bestaat zodat $a_{k} \in\{1001, \ldots, 2000\}$. Dan is $a_{k}=1000+i$ voor zekere $i$ met $i \leq 1000$, dus $a_{1000}+a_{i}$ is een element van $S$ en moet daarom ook een element van $A$ zijn. Er geldt echter $a_{1000}+a_{i}>a_{1000}$, tegenspraak. Dus zo'n $a_{k}$ kan niet voorkomen. Dit betekent dat $A$ te schrijven is als de disjuncte vereniging $B \cup C$, met $C \subseteq\{2001, \ldots, 2014\}$ en $B \subseteq\{1,2, \ldots, 1000\}$. Zij $b$ het aantal elementen van $B$. Dan is $b \geq 986$, want $C$ heeft hoogstens 14 elementen. Om te bewijzen dat $A$ leuk is, moeten we bewijzen dat $B=\{1,2, \ldots, b\}$. Hiertoe is het voldoende om te bewijzen dat $a_{b}$, het grootste element van $B$, gelijk is aan $b$. Stel daarom uit het ongerijmde dat $a_{b}>b$. Voor $i$ met $i=a_{b}-b$ geldt dan $b+i=a_{b} \leq 1000$, dus $i \leq 1000-b \leq 14<b$. Daarom is $a_{i} \leq 1000$ en dus $a_{b}+a_{i} \leq$ 2000. Omdat $i+b=a_{b} \in A$, geldt $a_{b}+a_{i} \in S \subset A$, maar dan is $a_{b}+a_{i}$ een groter element van $B$ dan $a_{b}$, het maximale element. Tegenspraak. Dus $a_{b}=b$, waaruit volgt dat $B=\{1,2, \ldots, b\}$. Dus $A$ is leuk.
|
{
"resource_path": "Dutch_TST/segmented/nl-2016-D_uitwerkingen.jsonl",
"problem_match": "\nOpgave 4.",
"solution_match": "\nOplossing."
}
|
94cee7ef-4ef8-5f50-98c3-ee7099725974
| 605,888
|
Let $n$ be an even positive integer. A sequence of $n$ real numbers is called complete if for every integer $m$ with $1 \leq m \leq n$, the sum of the first $m$ terms or the sum of the last $m$ terms of the sequence is an integer. Determine the minimum number of integers in a complete sequence of $n$ numbers.
|
We prove that the minimum number of integers in a complete sequence is equal to 2. First, consider the case $n=2$. Let $a_{1}$ and $a_{2}$ be the numbers in the sequence. Then $a_{1}$ or $a_{2}$ is an integer, say without loss of generality $a_{1}$. Furthermore, $a_{1}+a_{2}$ is an integer, but then $a_{2}$ is also an integer. Therefore, the sequence contains at least two integers.
Now consider the case $n>2$. Write $n=2k$ (since $n$ is even) with $k \geq 2$. Then $a_{1}+a_{2}+\ldots+a_{k}$ or $a_{k+1}+a_{k+2}+\ldots+a_{2k}$ is an integer. Since the sum of both expressions is also an integer, they are both integers. Furthermore, $a_{1}+a_{2}+\ldots+a_{k-1}$ or $a_{k+2}+a_{k+3}+\ldots+a_{2k}$ is an integer. This implies that $a_{k}$ or $a_{k+1}$ is an integer. Additionally, we know that $a_{1}$ or $a_{2k}$ is an integer, and these do not coincide with $a_{k}$ or $a_{k+1}$ because $k \geq 2$. Therefore, at least two different numbers are integers.
Finally, we show that for every even $n$ it is possible to construct a complete sequence with exactly two integers. Write $n=2k$ again. If $k$ is odd, we take $a_{1}=a_{k+1}=1$ and all other terms equal to $\frac{1}{2}$. The sum of all numbers in the sequence is an integer, so it suffices to show that the sum of the first or last $m$ terms is an integer with $1 \leq m \leq k$; the cases with $m>k$ follow directly. For odd $m \leq k$, the sum of the first $m$ terms is an integer, and for even $m<k$, the sum of the last $m$ terms is an integer. If $k$ is even, we take $a_{1}=a_{k}=1$ and all other terms equal to $\frac{1}{2}$. Now, for odd $m<k$, the sum of the first $m$ terms is an integer, and for even $m \leq k$, the sum of the last $m$ terms is an integer. Furthermore, the sum of all terms together is an integer, so the required result also follows for $m>k$.
We conclude that the minimum number of integers in a complete sequence of $n$ numbers is 2.
|
2
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Zij $n$ een even positief geheel getal. Een rijtje van $n$ reële getallen noemen we volledig als voor elke gehele $m$ met $1 \leq m \leq n$ geldt dat de som van de eerste $m$ termen of de som van de laatste $m$ termen van het rijtje geheel is. Bepaal het minimale aantal gehele getallen in een volledig rijtje van $n$ getallen.
|
We bewijzen dat het minimale aantal gehele getallen in een volledig rijtje gelijk aan 2 is. Bekijk eerst het geval $n=2$. Noem $a_{1}$ en $a_{2}$ de getallen in het rijtje. Dan is $a_{1}$ of $a_{2}$ geheel, zeg zonder verlies van algemeenheid $a_{1}$. Verder is $a_{1}+a_{2}$ geheel, maar dan is ook $a_{2}$ geheel. Dus het rijtje bevat minstens twee gehele getallen.
Bekijk nu het geval $n>2$. Schrijf $n=2 k$ (want $n$ is even) met $k \geq 2$. Dan is $a_{1}+a_{2}+\ldots+a_{k}$ of $a_{k+1}+a_{k+2}+\ldots+a_{2 k}$ geheel. Maar omdat de som van beide uitdrukkingen ook geheel is, zijn ze allebei geheel. Verder is $a_{1}+a_{2}+\ldots+a_{k-1}$ of $a_{k+2}+a_{k+3}+\ldots+a_{2 k}$ geheel. Hieruit volgt dat $a_{k}$ of $a_{k+1}$ geheel is. Daarnaast weten we dat $a_{1}$ of $a_{2 k}$ geheel is en die vallen niet samen met $a_{k}$ of $a_{k+1}$ omdat $k \geq 2$. Dus minstens twee verschillende getallen zijn geheel.
Ten slotte laten we zien dat het voor elke even $n$ mogelijk is om een volledig rijtje met precies twee gehele getallen te maken. Schrijf weer $n=2 k$. Als $k$ oneven is, nemen we $a_{1}=a_{k+1}=1$ en alle overige termen gelijk aan $\frac{1}{2}$. De som van alle getallen in het rijtje is geheel, dus het is voldoende om nog te laten zien dat de som van de eerste of laatste $m$ termen geheel is met $1 \leq m \leq k$; de gevallen met $m>k$ volgen dan direct. Voor oneven $m \leq k$ zijn de eerste $m$ termen samen geheel, voor even $m<k$ juist de laatste $m$ termen. Als $k$ even is, nemen we juist $a_{1}=a_{k}=1$ en alle overige termen gelijk aan $\frac{1}{2}$. Nu is voor oneven $m<k$ de som van de eerste $m$ termen geheel en voor even $m \leq k$ de som van de laatste $m$ termen. Verder is de som van alle termen bij elkaar geheel, dus het gevraagde volgt ook voor $m>k$.
We concluderen dat het minimale aantal gehele getallen in een volledig rijtje van $n$ getallen 2 is.
|
{
"resource_path": "Dutch_TST/segmented/nl-2017-B_uitwerkingen.jsonl",
"problem_match": "\nOpgave 1.",
"solution_match": "\nOplossing."
}
|
b06049ee-71e8-57cd-97cd-05a029a8b650
| 605,954
|
Given is the function $f: \mathbb{Z}_{>0} \rightarrow \mathbb{Z}$ that satisfies the properties:
(i) $f(p)=1$ for all prime numbers $p$,
(ii) $f(x y)=y f(x)+x f(y)$ for all $x, y \in \mathbb{Z}_{>0}$.
Determine the smallest $n \geq 2016$ with $f(n)=n$.
|
We first prove that for prime numbers $p$ and positive integers $k$, it holds that $f\left(p^{k}\right)=k p^{k-1}$. We do this by induction on $k$. For $k=1$, we have $f(p)=1$ and this is given. Now let $l \geq 1$ and assume we have proven it for $k=l$. Consider $k=l+1$. Then we apply the second property with $x=p$ and $y=p^{l}$:
$$
f\left(p^{l+1}\right)=f\left(p \cdot p^{l}\right)=p^{l} \cdot f(p)+p \cdot f\left(p^{l}\right)=p^{l}+p \cdot l p^{l-1}=(l+1) p^{l} .
$$
This completes the induction. Now we prove that for different prime numbers $p_{1}, p_{2}, \ldots$, $p_{t}$ and positive integers $a_{1}, a_{2}, \ldots, a_{t}$, it holds that
$$
f\left(p_{1}^{a_{1}} p_{2}^{a_{2}} \cdots p_{t}^{a_{t}}\right)=p_{1}^{a_{1}} p_{2}^{a_{2}} \cdots p_{t}^{a_{t}} \cdot\left(\frac{a_{1}}{p_{1}}+\frac{a_{2}}{p_{2}}+\cdots+\frac{a_{t}}{p_{t}}\right) .
$$
We prove this by induction on $t$. For $t=1$, it is exactly the formula we proved earlier. Now let $r \geq 1$ and assume we have proven it for $t=r$. Then we apply the second property again:
$$
\begin{aligned}
f\left(p_{1}^{a_{1}} p_{2}^{a_{2}} \cdots p_{r}^{a_{r}} \cdot p_{r+1}^{a_{r+1}}\right) & =p_{1}^{a_{1}} p_{2}^{a_{2}} \cdots p_{r}^{a_{r}} \cdot f\left(p_{r+1}^{a_{r+1}}\right)+p_{r+1}^{a_{r+1}} \cdot f\left(p_{1}^{a_{1}} p_{2}^{a_{2}} \cdots p_{r}^{a_{r}}\right) \\
& =p_{1}^{a_{1}} p_{2}^{a_{2}} \cdots p_{r}^{a_{r}} \cdot a_{r+1} p_{r+1}^{a_{r+1}-1}+p_{r+1}^{a_{r+1}} \cdot p_{1}^{a_{1}} p_{2}^{a_{2}} \cdots p_{r}^{a_{r}} \cdot\left(\frac{a_{1}}{p_{1}}+\frac{a_{2}}{p_{2}}+\cdots+\frac{a_{r}}{p_{r}}\right) \\
& =p_{1}^{a_{1}} p_{2}^{a_{2}} \cdots p_{r}^{a_{r}} p_{r+1}^{a_{r+1}} \cdot \frac{a_{r+1}}{p_{r+1}}+p_{1}^{a_{1}} p_{2}^{a_{2}} \cdots p_{r}^{a_{r}} p_{r+1}^{a_{r+1}} \cdot\left(\frac{a_{1}}{p_{1}}+\frac{a_{2}}{p_{2}}+\cdots+\frac{a_{r}}{p_{r}}\right) \\
& =p_{1}^{a_{1}} p_{2}^{a_{2}} \cdots p_{r}^{a_{r}} p_{r+1}^{a_{r+1}} \cdot\left(\frac{a_{1}}{p_{1}}+\frac{a_{2}}{p_{2}}+\cdots+\frac{a_{r}}{p_{r}}+\frac{a_{r+1}}{p_{r+1}}\right) .
\end{aligned}
$$
This completes the induction.
For an integer $n>1$ of the form $n=p_{1}^{a_{1}} p_{2}^{a_{2}} \cdots p_{t}^{a_{t}}$ with the $p_{i}$ different prime numbers, the property $f(n)=n$ is thus equivalent to
$$
p_{1}^{a_{1}} p_{2}^{a_{2}} \cdots p_{t}^{a_{t}} \cdot\left(\frac{a_{1}}{p_{1}}+\frac{a_{2}}{p_{2}}+\cdots+\frac{a_{t}}{p_{t}}\right)=p_{1}^{a_{1}} p_{2}^{a_{2}} \cdots p_{t}^{a_{t}}
$$
or equivalently
$$
\frac{a_{1}}{p_{1}}+\frac{a_{2}}{p_{2}}+\cdots+\frac{a_{t}}{p_{t}}=1 .
$$
Multiplying by $p_{1} p_{2} \cdots p_{t}$ gives
$$
a_{1} p_{2} p_{3} \cdots p_{t}+a_{2} p_{1} p_{3} \cdots p_{t}+\ldots+a_{t} p_{1} p_{2} \cdots p_{t-1}=p_{1} p_{2} \cdots p_{t}
$$
Assume without loss of generality that $p_{1}$ is the smallest prime number that occurs in the prime factorization of $n$. In the expression above, $p_{1}$ is a divisor of the right-hand side and of every term on the left-hand side except possibly the first. But then $p_{1}$ must also be a divisor of the first term. Since $p_{2}, \ldots, p_{t}$ are all prime numbers different from $p_{1}$, this can only be if $p_{1} \mid a_{1}$. In particular, then $a_{1} \geq p_{1}$, so $\frac{a_{1}}{p_{1}} \geq 1$. We now see that equality must hold and that $t=1$, because the sum of all $\frac{a_{i}}{p_{i}}$ would otherwise be greater than 1. Thus $n=p^{p}$ for some prime number $p$.
We are looking for the smallest $n \geq 2016$ of the form $n=p^{p}$. We have $3^{3}=27$ and $5^{5}=3125$, so the desired $n$ is equal to 3125.
|
3125
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Gegeven is de functie $f: \mathbb{Z}_{>0} \rightarrow \mathbb{Z}$ die voldoet aan de eigenschappen:
(i) $f(p)=1$ voor alle priemgetallen $p$,
(ii) $f(x y)=y f(x)+x f(y)$ voor alle $x, y \in \mathbb{Z}_{>0}$.
Bepaal de kleinste $n \geq 2016$ met $f(n)=n$.
|
We bewijzen allereerst dat voor priemgetallen $p$ en positieve gehele getallen $k$ geldt dat $f\left(p^{k}\right)=k p^{k-1}$. Dit doen we met inductie naar $k$. Voor $k=1$ staat er $f(p)=1$ en dat is gegeven. Zij nu $l \geq 1$ en stel dat we het bewezen hebben voor $k=l$. Bekijk $k=l+1$. Dan passen we de tweede eigenschap toe met $x=p$ en $y=p^{l}$ :
$$
f\left(p^{l+1}\right)=f\left(p \cdot p^{l}\right)=p^{l} \cdot f(p)+p \cdot f\left(p^{l}\right)=p^{l}+p \cdot l p^{l-1}=(l+1) p^{l} .
$$
Dit voltooit de inductie. Nu bewijzen we dat voor verschillende priemgetallen $p_{1}, p_{2}, \ldots$, $p_{t}$ en positieve gehele getallen $a_{1}, a_{2}, \ldots, a_{t}$ geldt dat
$$
f\left(p_{1}^{a_{1}} p_{2}^{a_{2}} \cdots p_{t}^{a_{t}}\right)=p_{1}^{a_{1}} p_{2}^{a_{2}} \cdots p_{t}^{a_{t}} \cdot\left(\frac{a_{1}}{p_{1}}+\frac{a_{2}}{p_{2}}+\cdots+\frac{a_{t}}{p_{t}}\right) .
$$
We bewijzen dit met inductie naar $t$. Voor $t=1$ is het precies de formule die we hiervoor bewezen hebben. Zij nu $r \geq 1$ en stel dat we het bewezen hebben voor $t=r$. Dan passen we weer de tweede eigenschap toe:
$$
\begin{aligned}
f\left(p_{1}^{a_{1}} p_{2}^{a_{2}} \cdots p_{r}^{a_{r}} \cdot p_{r+1}^{a_{r+1}}\right) & =p_{1}^{a_{1}} p_{2}^{a_{2}} \cdots p_{r}^{a_{r}} \cdot f\left(p_{r+1}^{a_{r+1}}\right)+p_{r+1}^{a_{r+1}} \cdot f\left(p_{1}^{a_{1}} p_{2}^{a_{2}} \cdots p_{r}^{a_{r}}\right) \\
& =p_{1}^{a_{1}} p_{2}^{a_{2}} \cdots p_{r}^{a_{r}} \cdot a_{r+1} p_{r+1}^{a_{r+1}-1}+p_{r+1}^{a_{r+1}} \cdot p_{1}^{a_{1}} p_{2}^{a_{2}} \cdots p_{r}^{a_{r}} \cdot\left(\frac{a_{1}}{p_{1}}+\frac{a_{2}}{p_{2}}+\cdots+\frac{a_{r}}{p_{r}}\right) \\
& =p_{1}^{a_{1}} p_{2}^{a_{2}} \cdots p_{r}^{a_{r}} p_{r+1}^{a_{r+1}} \cdot \frac{a_{r+1}}{p_{r+1}}+p_{1}^{a_{1}} p_{2}^{a_{2}} \cdots p_{r}^{a_{r}} p_{r+1}^{a_{r+1}} \cdot\left(\frac{a_{1}}{p_{1}}+\frac{a_{2}}{p_{2}}+\cdots+\frac{a_{r}}{p_{r}}\right) \\
& =p_{1}^{a_{1}} p_{2}^{a_{2}} \cdots p_{r}^{a_{r}} p_{r+1}^{a_{r+1}} \cdot\left(\frac{a_{1}}{p_{1}}+\frac{a_{2}}{p_{2}}+\cdots+\frac{a_{r}}{p_{r}}+\frac{a_{r+1}}{p_{r+1}}\right) .
\end{aligned}
$$
Dit voltooit de inductie.
Voor een geheel getal $n>1$ van de vorm $n=p_{1}^{a_{1}} p_{2}^{a_{2}} \cdots p_{t}^{a_{t}}$ met de $p_{i}$ verschillende priemgetallen, is de eigenschap $f(n)=n$ dus equivalent met
$$
p_{1}^{a_{1}} p_{2}^{a_{2}} \cdots p_{t}^{a_{t}} \cdot\left(\frac{a_{1}}{p_{1}}+\frac{a_{2}}{p_{2}}+\cdots+\frac{a_{t}}{p_{t}}\right)=p_{1}^{a_{1}} p_{2}^{a_{2}} \cdots p_{t}^{a_{t}}
$$
oftewel
$$
\frac{a_{1}}{p_{1}}+\frac{a_{2}}{p_{2}}+\cdots+\frac{a_{t}}{p_{t}}=1 .
$$
Vermenigvuldigen met $p_{1} p_{2} \cdots p_{t}$ geeft
$$
a_{1} p_{2} p_{3} \cdots p_{t}+a_{2} p_{1} p_{3} \cdots p_{t}+\ldots+a_{t} p_{1} p_{2} \cdots p_{t-1}=p_{1} p_{2} \cdots p_{t}
$$
Neem zonder verlies van algemeenheid aan dat $p_{1}$ het kleinste priemgetal is dat voorkomt in de priemfactorisatie van $n$. In de uitdrukking hierboven is $p_{1}$ een deler van de rechterkant en van elke term aan de linkerkant behalve eventueel de eerste. Maar dan moet $p_{1}$ ook een deler van de eerste term zijn. Aangezien $p_{2}, \ldots, p_{t}$ allemaal priemgetallen ongelijk aan $p_{1}$ zijn, kan dat alleen als $p_{1} \mid a_{1}$. In het bijzonder geldt dan $a_{1} \geq p_{1}$, zodat $\frac{a_{1}}{p_{1}} \geq 1$. We zien nu dat hier gelijkheid moet gelden en dat $t=1$, omdat de som van alle $\frac{a_{i}}{p_{i}}$ anders groter dan 1 wordt. Dus $n=p^{p}$ voor een zeker priemgetal $p$.
We zoeken dus de kleinste $n \geq 2016$ van de vorm $n=p^{p}$. Er geldt $3^{3}=27$ en $5^{5}=3125$, dus de gevraagde $n$ is gelijk aan 3125 .
|
{
"resource_path": "Dutch_TST/segmented/nl-2017-B_uitwerkingen.jsonl",
"problem_match": "\nOpgave 2.",
"solution_match": "\nOplossing."
}
|
7ca4b79b-682d-5860-823b-9bf1f790450c
| 605,965
|
Let $n$ be a positive integer. Given are circular discs with radii $1, 2, \ldots, n$. For each size, we have two discs: a transparent one and an opaque one. Each disc has a hole in the middle, allowing us to stack the discs on a vertical rod. We want to create stacks that meet the following conditions:
- Exactly one disc of each size is on the stack.
- When viewed from directly above, the outer edges of all $n$ discs on the stack can be seen. (This means that if there is an opaque disc on the stack, then no smaller discs may lie below it.)
Determine the number of different stacks that can be made under these conditions. (Two stacks are different if they do not use exactly the same set of discs, but also if they do use exactly the same set of discs but not in the same order.)
|
A stack is considered valid if it meets the conditions. Let $a_{n}$ be the number of valid stacks with $n$ disks (with radii $1, 2, \ldots, n$). We prove by induction that $a_{n}=(n+1)!$. For $n=1$, we can make two stacks: one with the transparent disk of radius 1 and one with the opaque disk of radius 1, so $a_{1}=2=2!$. Suppose now that for some $n \geq 1$ we have proven that $a_{n}=(n+1)!$. Consider a valid stack with $n+1$ disks. If we remove the disk with radius $n+1$, all remaining disks are still visible from above, so we are left with a valid stack of $n$ disks. Every valid stack with $n+1$ disks can thus be created by inserting the disk with radius $n+1$ into a valid stack of $n$ disks at a suitable position. In principle, there are $n+1$ positions where we can insert the disk with radius $n+1$: above the top disk, above the second disk, ..., above the bottom disk, and also below the bottom disk. The disk with radius $n+1$ is always visible, regardless of where we insert it. If we insert the disk with radius $n+1$ below the bottom disk, it can be either transparent or opaque; in both cases, the view of the other disks is not blocked. Thus, there are $2 a_{n}$ valid stacks where the disk with radius $n+1$ is at the bottom. However, if we insert an opaque disk with radius $n+1$ at any other position, it blocks the view of the disks below it. Therefore, we can only insert the transparent disk with radius $n+1$ at the other $n$ positions. Thus, there are $n a_{n}$ valid stacks where the disk with radius $n+1$ is not at the bottom. We find
$$
a_{n+1}=2 a_{n}+n a_{n}=(n+2) a_{n}=(n+2)(n+1)!=(n+2)!
$$
This completes the induction.
|
(n+1)!
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Zij $n$ een positief geheel getal. Gegeven zijn cirkelvormige schijven met stralen $1,2, \ldots, n$. Van elke grootte hebben we twee schijven: een doorzichtige en een ondoorzichtige. In elke schijf zit een gaatje, precies in het midden, waarmee we de schijven op een rechtopstaand staafje kunnen stapelen. We willen nu stapels maken die aan de volgende voorwaarden voldoen:
- Van elke grootte ligt er precies één schijf op de stapel.
- Als we recht van boven kijken, kunnen we de buitenranden van alle $n$ schijven op de stapel zien. (Dat wil zeggen, als er een ondoorzichtige schijf op de stapel ligt, dan mogen daaronder geen kleinere schijven liggen.)
Bepaal het aantal verschillende stapels dat we kunnen maken onder deze voorwaarden. (Twee stapels zijn verschillend als ze niet precies dezelfde verzameling schijven gebruiken, maar ook als ze wel precies dezelfde verzameling schijven gebruiken maar niet in dezelfde volgorde.)
|
Noem een stapel geldig als hij aan de voorwaarden voldoet. Zij $a_{n}$ het aantal geldige stapels met $n$ schijven (met straal $1,2, \ldots, n$ ). We bewijzen met inductie dat $a_{n}=(n+1)!$. Voor $n=1$ kunnen we twee stapels maken: met de doorzichtige schijf met straal 1 en met de ondoorzichtige schijf met straal 1 , dus $a_{1}=2=2$. Stel nu dat we voor zekere $n \geq 1$ bewezen hebben dat $a_{n}=(n+1)$ !. Bekijk een geldige stapel met $n+1$ schijven. Als we de schijf met straal $n+1$ weghalen, zijn nog steeds alle schijven van bovenaf zichtbaar, dus we houden een geldige stapel met $n$ schijven over. Elke geldige stapel met $n+1$ schijven is dus te maken door in een geldige stapel met $n$ schijven de schijf met straal $n+1$ op een geschikte plek in te voegen. In principe zijn er $n+1$ posities waarop we de schijf met straal $n+1$ kunnen invoegen: boven de bovenste schijf, boven de tweede schijf, ..., boven de onderste schijf en ook nog onder de onderste schijf. De schijf met straal $n+1$ zelf is altijd zichtbaar, waar we hem ook invoegen. Als we de schijf met straal $n+1$ invoegen onder de onderste schijf, dan mag hij zowel doorzichtig als ondoorzichtig zijn; in beide gevallen wordt het zicht op de andere schijven niet geblokkeerd. Er zijn dus $2 a_{n}$ geldige stapels waarbij de schijf met straal $n+1$ onderop liggen. Als we echter op een andere positie een ondoorzichtige schijf met straal $n+1$ invoegen, dan blokkeert hij het zicht op de schijven eronder. We kunnen dus op de andere $n$ posities alleen de doorzichtige schijf met straal $n+1$ invoegen. Er zijn dus $n a_{n}$ geldige stapels waarbij de schijf met straal
$n+1$ niet onderop ligt. Zo vinden we
$$
a_{n+1}=2 a_{n}+n a_{n}=(n+2) a_{n}=(n+2)(n+1)!=(n+2)!
$$
Dit voltooit de inductie.
|
{
"resource_path": "Dutch_TST/segmented/nl-2017-C_uitwerkingen.jsonl",
"problem_match": "\nOpgave 1.",
"solution_match": "\nOplossing."
}
|
206e739a-7250-51d3-92b8-565e1d1418af
| 606,000
|
Determine the product of all positive integers $n$ for which $3(n!+1)$ is divisible by $2 n-5$.
将上面的文本翻译成英文,请保留源文本的换行和格式,直接输出翻译结果。
However, it seems there is a note or an additional request in Chinese at the end of your message. If you need the Chinese text translated as well, please let me know! For now, I'll assume you only need the provided Dutch text translated to English. If that's correct, the translation is as above.
|
The numbers $n=1$ to $n=4$ satisfy the condition, because $2n-5$ is then equal to $-3, -1, 1$, and $3$, respectively, and is always a divisor of $3(n!+1)$. From now on, we only consider $n>4$ and then $2n-5>3$.
We first prove that if $n$ satisfies the condition, then $2n-5$ must be prime. We distinguish two cases. Suppose first that $2n-5$ is not prime and has a prime divisor $p>3$. Since $p \neq 2n-5$ and since $2n-5$ is odd, it follows that $p \leq \frac{2n-5}{3} < n$. Therefore, $p \mid n!$, but then $p \nmid n!+1$ and thus also $p \nmid 3(n!+1)$ since $p \neq 3$. Therefore, $2n-5 \nmid 3(n!+1)$, which means that $n$ does not satisfy the condition. Now suppose that $2n-5$ is not prime but has only prime divisors 3; then it is a power of 3 greater than 3. However, for $n>4$, $3 \nmid n!+1$, so $3(n!+1)$ is divisible by exactly one factor of 3 and no more. We see that $n$ cannot satisfy the condition in this case either.
For an $n>4$ that satisfies the condition, we now know that $2n-5$ is a prime number greater than 3. Let $q=2n-5$. Then $q \mid n!+1$, or $n! \equiv -1 \pmod{q}$. Furthermore, Wilson's theorem states that $(q-1)! \equiv -1 \pmod{q}$. Therefore,
$$
\begin{aligned}
-1 & \equiv (2n-6)! \\
& \equiv (2n-6)(2n-7) \cdots (n+1) \cdot n! \\
& \equiv (-1) \cdot (-2) \cdots (-n+6) \cdot n! \\
& \equiv (-1)^{n-6} \cdot (n-6)! \cdot n! \\
& \equiv (-1)^{n} \cdot (n-6)! \cdot -1 \quad \pmod{q}.
\end{aligned}
$$
Thus, $(n-6)! \equiv (-1)^{n} \pmod{q}$. Since $n! \equiv -1 \pmod{q}$, it follows that $n \cdot (n-1) \cdots (n-5) \equiv (-1)^{n-1} \pmod{q}$. We multiply this by $2^6$:
$$
2n \cdot (2n-2) \cdot (2n-4) \cdot (2n-6) \cdot (2n-8) \cdot (2n-10) \equiv (-1)^{n-1} \cdot 64 \pmod{q}.
$$
Modulo $q=2n-5$, the left side is $5 \cdot 3 \cdot 1 \cdot -1 \cdot -3 \cdot -5 = -225$.
Suppose $n$ is odd. Then we have $-225 \equiv 64 \pmod{q}$, so $q \mid -225-64 = -289 = -17^2$. Therefore, $q=17$ and then $n=\frac{17+5}{2}=11$. Now suppose $n$ is even. Then we have $-225 \equiv -64 \pmod{q}$, so $q \mid -225+64 = -161 = -7 \cdot 23$. Therefore, $q=7$ or $q=23$, which gives $n=6$ and $n=14$, respectively.
We check these three possibilities. For $n=11$ and $2n-5=17$:
$$
\begin{aligned}
11! & = 1 \cdot (2 \cdot 9) \cdot (3 \cdot 6) \cdot (5 \cdot 7) \cdot 4 \cdot 8 \cdot 10 \cdot 11 \\
& \equiv 4 \cdot 8 \cdot 10 \cdot 11 = 88 \cdot 40 \equiv 3 \cdot 6 \equiv 1 \quad \pmod{17}
\end{aligned}
$$
so $n=11$ does not satisfy the condition. For $n=14$ and $2n-5=23$:
$$
\begin{aligned}
14! & = 1 \cdot (2 \cdot 12) \cdot (3 \cdot 8) \cdot (4 \cdot 6) \cdot (5 \cdot 14) \cdot (7 \cdot 10) \cdot 9 \cdot 11 \cdot 13 \\
& \equiv 9 \cdot 11 \cdot 13 = 117 \cdot 11 \equiv 2 \cdot 11 \equiv -1 \quad \pmod{23}
\end{aligned}
$$
so $n=14$ satisfies the condition. For $n=6$ and $2n-5=7$, it follows from Wilson's theorem that $6! \equiv -1 \pmod{7}$, so $n=6$ also satisfies the condition.
We conclude that the numbers $n$ that satisfy the condition are: $1, 2, 3, 4, 6$, and 14. The product of these is 2016.
|
2016
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Bepaal het product van alle positieve gehele getallen $n$ waarvoor $3(n!+1)$ deelbaar is door $2 n-5$.
|
De getallen $n=1$ tot en met $n=4$ voldoen, want $2 n-5$ is dan gelijk aan respectievelijk $-3,-1,1$ en 3 , dus altijd een deler dan $3(n!+1)$. Vanaf nu bekijken we alleen $n>4$ en dan is $2 n-5>3$.
We bewijzen eerst dat als $n$ voldoet, dan $2 n-5$ priem moet zijn. We onderscheiden twee gevallen. Stel eerst dat $2 n-5$ niet priem is en een priemdeler $p>3$ heeft. Omdat $p \neq 2 n-5$ en omdat $2 n-5$ oneven is, geldt $p \leq \frac{2 n-5}{3}<n$. Dus $p \mid n!$, maar dan $p \nmid n!+1$ en dus ook $p \nmid 3(n!+1)$ aangezien $p \neq 3$. Dus $2 n-5 \nmid 3(n!+1)$, wat betekent dat $n$ niet voldoet. Stel nu dat $2 n-5$ niet priem is, maar alleen priemdelers 3 heeft; dan is het dus een driemacht groter dan 3. Echter, voor $n>4$ is $3 \nmid n!+1$, dus $3(n!+1)$ is deelbaar door precies één factor 3 en niet meer. We zien dat $n$ ook in dit geval niet kan voldoen.
Voor een $n>4$ die voldoet, weten we nu dat $2 n-5$ een priemgetal groter dan 3 is. Schrijf $q=2 n-5$. Dan $q \mid n!+1$, oftewel $n!\equiv-1 \bmod q$. Verder zegt de stelling van Wilson dat $(q-1)!\equiv-1 \bmod q$. Dus
$$
\begin{aligned}
-1 & \equiv(2 n-6)! \\
& \equiv(2 n-6)(2 n-7) \cdots(n+1) \cdot n! \\
& \equiv(-1) \cdot(-2) \cdots \cdots(-n+6) \cdot n! \\
& \equiv(-1)^{n-6} \cdot(n-6)!\cdot n! \\
& \equiv(-1)^{n} \cdot(n-6)!\cdot-1 \quad \bmod q .
\end{aligned}
$$
Dus $(n-6)!\equiv(-1)^{n} \bmod q$. Omdat $n!\equiv-1 \bmod q$, volgt daaruit $n \cdot(n-1) \cdots \cdot \cdot(n-5) \equiv$ $(-1)^{n-1} \bmod q$. We vermenigvuldigen dit met $2^{6}$ :
$$
2 n \cdot(2 n-2) \cdot(2 n-4) \cdot(2 n-6) \cdot(2 n-8) \cdot(2 n-10) \equiv(-1)^{n-1} \cdot 64 \bmod q .
$$
Modulo $q=2 n-5$ staat links $5 \cdot 3 \cdot 1 \cdot-1 \cdot-3 \cdot-5=-225$.
Stel $n$ is oneven. Dan hebben we dus $-225 \equiv 64 \bmod q$, dus $q \mid-225-64=-289=-17^{2}$. Dus $q=17$ en dan $n=\frac{17+5}{2}=11$. Stel nu $n$ is even. Dan hebben we $-225 \equiv-64 \bmod q$, dus $q \mid-225+64=-161=-7 \cdot 23$. Dus $q=7$ of $q=23$ en dat geeft respectievelijk $n=6$ en $n=14$.
We controleren deze drie mogelijkheden. Voor $n=11$ en $2 n-5=17$ :
$$
\begin{aligned}
11! & =1 \cdot(2 \cdot 9) \cdot(3 \cdot 6) \cdot(5 \cdot 7) \cdot 4 \cdot 8 \cdot 10 \cdot 11 \\
& \equiv 4 \cdot 8 \cdot 10 \cdot 11=88 \cdot 40 \equiv 3 \cdot 6 \equiv 1 \quad \bmod 17
\end{aligned}
$$
dus $n=11$ voldoet niet. Voor $n=14$ en $2 n-5=23$ :
$$
\begin{aligned}
14! & =1 \cdot(2 \cdot 12) \cdot(3 \cdot 8) \cdot(4 \cdot 6) \cdot(5 \cdot 14) \cdot(7 \cdot 10) \cdot 9 \cdot 11 \cdot 13 \\
& \equiv 9 \cdot 11 \cdot 13=117 \cdot 11 \equiv 2 \cdot 11 \equiv-1 \quad \bmod 23
\end{aligned}
$$
dus $n=14$ voldoet. Voor $n=6$ en $2 n-5=7$ ten slotte volgt $6!\equiv-1 \bmod 7$ uit de stelling van Wilson, dus $n=6$ voldoet ook.
We concluderen dat de getallen $n$ die voldoen, zijn: $1,2,3,4,6$ en 14. Het product daarvan is 2016.
|
{
"resource_path": "Dutch_TST/segmented/nl-2017-E_uitwerkingen.jsonl",
"problem_match": "\nOpgave 3.",
"solution_match": "\nOplossing."
}
|
4f36b06d-7c54-57d0-8b6f-5100d0474c05
| 606,126
|
We have 1000 balls in 40 different colors, with exactly 25 balls of each color. Determine the smallest value of $n$ with the following property: if you randomly arrange the 1000 balls in a circle, there will always be $n$ consecutive balls where at least 20 different colors appear.
|
Consider the circle of balls where 25 balls of one color are always next to each other. To have 20 different colors, you need to take at least 18 of these groups plus one ball on one side and one ball on the other side. In total, you need at least \(18 \cdot 25 + 2 = 452\) balls next to each other. Therefore, \(n \geq 452\). Now we prove that in any circle of balls, you need at most 452 balls next to each other to get 20 different colors. For this, consider any random circle of balls and all possible series of balls next to each other that together have exactly 20 colors. (There is at least one such series: take a random ball and add the balls next to it one by one until you have exactly 20 colors.) Take a series with the minimum number of balls. Say the first ball in this series is white. If there is another white ball in the series, we could have omitted the first ball to get a series with the same number of colors but fewer balls. This contradicts the minimality of the series. Therefore, there is no other white ball. In particular, the last ball in the series is not white; say it is black. We see in the same way that no other ball in the series is black. So there is one white ball, one black ball, and balls in 18 other colors, with at most 25 of each color. Together, this is at most \(18 \cdot 25 + 2 = 452\) balls. Therefore, you can always find a series of 452 balls next to each other that contains at least 20 different colors. We conclude that the required minimum \(n\) is 452.
|
452
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
We hebben 1000 ballen in 40 verschillende kleuren, waarbij er van elke kleur precies 25 ballen zijn. Bepaal de kleinste waarde van $n$ met de volgende eigenschap: als je de 1000 ballen willekeurig in een cirkel legt, zijn er altijd $n$ ballen naast elkaar te vinden waarbij minstens 20 verschillende kleuren voorkomen.
|
Bekijk de cirkel van ballen waarbij de 25 ballen van één kleur steeds allemaal naast elkaar liggen. Om nu 20 verschillende kleuren te hebben, moet je minstens 18 van deze groepen nemen plus nog een bal aan de ene kant daarvan en een bal aan de andere kant. Totaal heb je dus minimaal $18 \cdot 25+2=452$ ballen naast elkaar nodig. Dus $n \geq 452$. Nu bewijzen we dat je in elke cirkel van ballen genoeg hebt aan 452 ballen naast elkaar om 20 verschillende kleuren te krijgen. Bekijk daarvoor een willekeurige cirkel van ballen en alle mogelijke series van ballen naast elkaar die samen precies 20 kleuren hebben. (Er bestaat minstens één zo'n serie: pak een willekeurige bal en voeg de ballen ernaast één voor één toe, totdat je precies 20 kleuren hebt.) Neem een serie daarvan met zo min mogelijk ballen erin. Zeg dat de eerste bal daarvan wit is. Als er nog een bal in de serie wit is, dan hadden we de eerste bal kunnen weglaten om een serie te krijgen met evenveel kleuren, maar minder ballen. Dat is een tegenspraak met de minimaliteit van de serie. Dus er is geen enkele andere bal wit. In het bijzonder is ook de laatste bal van de serie niet wit; zeg dat deze zwart is. We zien op dezelfde manier dat geen enkele andere bal in de serie zwart is. Dus er is één witte bal, één zwarte bal en daarnaast nog ballen in 18 andere kleuren, hooguit 25 per kleur. Samen zijn dat hooguit $18 \cdot 25+2=452$ ballen. Dus inderdaad kun je altijd een serie van 452 ballen naast elkaar vinden met daarin minstens 20 verschillende kleuren. We concluderen dat de gevraagde minimale $n$ gelijk is aan 452 .
|
{
"resource_path": "Dutch_TST/segmented/nl-2018-B_uitwerkingen.jsonl",
"problem_match": "\nOpgave 1.",
"solution_match": "\nOplossing I."
}
|
7b911f22-3219-586b-978c-76269d545fab
| 606,145
|
A collection of lines in the plane is called beautiful if each line in the collection intersects an odd number of the other lines in the collection.
Determine the smallest integer $k \geq 0$ with the following property: for any 2018 distinct lines $\ell_{1}, \ell_{2}, \ldots, \ell_{2018}$ in the plane, there exist lines $\ell_{2018+1}, \ell_{2018+2}, \ldots$, $\ell_{2018+k}$ such that the lines $\ell_{1}, \ell_{2}, \ldots, \ell_{2018+k}$ are all distinct and form a beautiful collection.
|
We first prove that in a beautiful collection, the number of lines must be even. Suppose the number of lines is odd. Then on each of the odd number of lines, there is an odd number of intersection points, so the total number of intersection points is also odd. However, each intersection point is counted twice (once for each line it lies on), so the total should be even. Contradiction. Therefore, the number of lines in a beautiful collection must be even. In particular, $2018+k$ must also be even, so $k$ must be even.
Now assume there are 1009 directions such that in each direction, two of the original lines lie. Then each line is parallel to exactly one other line. If $k<1010$, then $k \leq 1008$, so there must be a direction in which we do not add a line. Consider an original line $\ell$ in this direction. It intersects all lines except itself and the line it is parallel to. This is an even number. Therefore, the resulting collection is not beautiful. Thus, there is an example where at least 1010 lines are needed.
We now show that it is possible to add exactly 1010 lines so that the total collection is ultimately beautiful. We consider all directions in which an even number (greater than 0) of the original lines lie. There are at most 1009 such directions. For each of these directions, we add a line. Each line is then parallel to an even number (possibly 0) of other lines. Suppose first that the total number of lines is now even. Then each line intersects an odd number of lines (the total minus itself and an even number of other lines). Suppose now that the total number of lines is now odd. Then each line intersects an even number of lines. We add a line in a new direction that thus intersects all lines (an odd number), so that afterwards each line intersects an odd number of other lines.
Now the collection is beautiful and we have added at most $1009+1=1010$ lines. It is possible that there are really fewer than 1010. In that case, the number of added lines is even, because the total number of lines in a beautiful collection is always even. We choose a direction in which at least one line already runs. We now add pairs of lines in the same direction. These lines intersect all lines in other directions; that is a total of an odd number. The other lines each gain two intersection points,
so they still have an odd number of intersection points. This is also true for the lines that were already in the chosen direction, as they gain zero new intersection points. The collection thus remains beautiful. We keep adding such pairs until we have added a total of 1010 lines.
We conclude that the minimal $k$ that satisfies is $k=1010$.
|
1010
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Een verzameling lijnen in het vlak noemen we mooi indien elke lijn in de verzameling een oneven aantal van de andere lijnen in de verzameling snijdt.
Bepaal het kleinste gehele getal $k \geq 0$ met de volgende eigenschap: voor iedere 2018 verschillende lijnen $\ell_{1}, \ell_{2}, \ldots, \ell_{2018}$ in het vlak bestaan er lijnen $\ell_{2018+1}, \ell_{2018+2}, \ldots$, $\ell_{2018+k}$ zodat de lijnen $\ell_{1}, \ell_{2}, \ldots, \ell_{2018+k}$ allemaal verschillend zijn en een mooie verzameling vormen.
|
We bewijzen eerst dat in een mooie verzameling het aantal lijnen even moet zijn. Stel namelijk dat het aantal lijnen oneven zou zijn. Dan ligt op elk van het oneven aantal lijnen een oneven aantal snijpunten, dus het totale aantal snijpunten is dan ook oneven. Elk snijpunt wordt hier echter twee keer geteld (één keer voor elke lijn waar hij op ligt), dus het totaal zou even moeten zijn. Tegenspraak. Dus het aantal lijnen in een mooie verzameling moet even zijn. In het bijzonder moet $2018+k$ ook even zijn, dus $k$ moet even zijn.
Stel nu dat er 1009 richtingen zijn zodat er in elke richting twee van de oorspronkelijke lijnen liggen. Dan is elke lijn evenwijdig met precies één andere lijn. Als $k<1010$ is $k \leq 1008$, dus moet er een richting zijn waarin we geen lijn toevoegen. Bekijk een oorspronkelijke lijn $\ell$ in deze richting. Die snijdt in de uiteindelijke verzameling alle lijnen behalve zichzelf en de lijn waar hij evenwijdig mee was. Dit is een even aantal. Dus dan is de resulterende verzameling niet mooi. Er is dus een voorbeeld waarbij minstens 1010 lijnen nodig zijn.
We laten nu zien dat het mogelijk is om precies 1010 lijnen toe te voegen zodat de totale verzameling uiteindelijk mooi is. We bekijken alle richtingen waarin een even aantal (groter dan 0) van de oorspronkelijke lijnen liggen. Er zijn hoogstens 1009 van zulke richtingen. Voor elk van deze richtingen voegen we een lijn toe. Elke lijn loopt dan evenwijdig aan een even aantal (mogelijk 0) andere lijnen. Stel eerst dat het totaal aantal lijnen nu even is. Dan snijdt elke lijn een oneven aantal lijnen (het totaal minus zichzelf en een even aantal andere lijnen). Stel nu dat het totaal aantal lijnen nu oneven is. Dan snijdt elke lijn een even aantal lijnen. We voegen een lijn toe in een nieuwe richting die dus alle lijnen snijdt (een oneven aantal), zodat daarna elke lijn een oneven aantal andere lijnen snijdt.
Nu is de verzameling mooi en we hebben hooguit $1009+1=1010$ lijnen toegevoegd. Mogelijk zijn het er echt nog minder dan 1010. In dat geval is het aantal toegevoegde lijnen wel even, want het totaal aantal lijnen van een mooie verzameling is altijd even. We kiezen een richting waarin al minstens één lijn loopt. We voegen nu steeds een tweetal lijnen in diezelfde richting toe. Deze lijnen snijden alle lijnen in andere richtingen; dat is totaal een oneven aantal. Die andere lijnen hebben er elk twee snijpunten bijgekregen,
dus zij houden een oneven aantal snijpunten. Dat laatste geldt ook voor de lijnen die er al waren in de gekozen richting, want zij krijgen nul nieuwe snijpunten. De verzameling blijft dus mooi. We voegen net zo lang zulke tweetallen toe totdat we in totaal 1010 lijnen hebben toegevoegd.
We concluderen dat de minimale $k$ die voldoet $k=1010$ is.
|
{
"resource_path": "Dutch_TST/segmented/nl-2018-E_uitwerkingen.jsonl",
"problem_match": "\nOpgave 1.",
"solution_match": "\nOplossing."
}
|
5a006207-0dc0-58e8-a39d-91f15a7e02bc
| 604,183
|
In a country, there are 2018 cities, some of which are connected by roads. Each city is connected to at least three other cities. It is possible to travel from any arbitrary city to any other arbitrary city via one or more roads. Consider for each pair of cities the shortest route between these two cities. What is the maximum number of roads that could appear in such a shortest route?
|
The largest number of roads that can appear in a shortest route is 1511. We first give a country for which this number is assumed. Divide the cities into 504 groups: two groups of five cities $\left(A_{0}, B_{0}, C_{0}, D_{0}, E_{0}\right)$ and $\left(A_{503}, B_{503}, C_{503}, D_{503}, E_{503}\right)$ and further groups of four cities $\left(A_{i}, B_{i}, C_{i}, D_{i}\right)$ for $1 \leq i \leq 502$. For all $i$ with $0 \leq i \leq 503$: connect $A_{i}$ to $B_{i}$, connect $A_{i}$ to $C_{i}$, connect $B_{i}$ to $D_{i}$, and connect $C_{i}$ to $D_{i}$. Further, connect $E_{0}$ to $A_{0}, B_{0}$, and $C_{0}$. Connect $E_{503}$ to $B_{503}, C_{503}$, and $D_{503}$. For $1 \leq i \leq 502$: connect $B_{i}$ to $C_{i}$. Finally, for $0 \leq i \leq 502$: connect $D_{i}$ to $A_{i+1}$. Now every city is connected to exactly three other cities.
If we now want to go from $A_{0}$ to $D_{503}$, then this must be via all $A_{i}$ and $D_{i}$, because these are the only connections between the different groups and each group is only connected to the previous and next group. Furthermore, for $0 \leq i \leq 503$ the city $A_{i}$ is not connected to $D_{i}$, so the route within group $i$ must go via $B_{i}$ or $C_{i}$. At least three of the four or five cities in such a group are thus visited on the route. In total, the route thus contains at least $3 \cdot 504=1512$ cities and therefore at least 1511 roads.
We then show that a shortest route between two cities never goes through more than 1511 roads. Consider such a shortest route where the cities $A_{0}, A_{1}$, $\ldots, A_{k}$ are visited in sequence. Each of the cities $A_{i}$ is connected to at least one other city besides its neighbors $A_{i-1}$ and $A_{i+1}$, say to $B_{i}$ (here $B_{0}, B_{1}, \ldots, B_{k}$ do not have to be all different cities). Furthermore, $A_{0}$ and $A_{k}$ are also connected to a third city, say $C_{0} \neq B_{0}$ and $C_{k} \neq B_{k}$. If one of the cities $B_{i}$ or $C_{i}$ is equal to one of the cities $A_{j}$, then we could have found a shorter route by going directly from $A_{i}$ to $A_{j}$ (or vice versa), contradiction. Therefore, the cities $B_{i}$ and $C_{i}$ are all different from all cities $A_{j}$.
If one of the cities $B_{i}$ is connected to four cities $A_{j}$, say $B_{i}$ is connected to $A_{i}, A_{m}, A_{n}$, and $A_{p}$ with $i<m<n<p$, then we could shorten the route by going from $A_{i}$ to $B_{i}$ and then to $A_{p}$. We would then skip at least two cities from the original route (namely $A_{m}$ and $A_{n}$) and visit only $B_{i}$ in addition, so this new route would be shorter. Contradiction. The cities $B_{i}$ with $3 \leq i \leq k-3$ are thus at least $\frac{k-5}{3}$ different cities. For $B_{0}$ and $C_{0}$, we can shorten the route if one of these cities is equal to $B_{i}$ with $i \geq 3$. That would be a contradiction, so $B_{0}$ and $C_{0}$ are two different cities different from $B_{i}$ with $i \geq 3$. Similarly, $B_{k}$ and $C_{k}$ are two different cities different from $B_{i}$ with $i \leq k-3$. In total, we have $k+1$ cities on the route itself and at least $\frac{k-5}{3}+2+2$ other cities. So $\frac{k-5}{3}+k+5 \leq 2018$, so $4 k-5+15 \leq 3 \cdot 2018=6054$, so $4 k \leq 6044$, so $k \leq 1511$.
We conclude that the largest possible number of roads in a shortest route is 1511.
|
1511
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
In een land zijn 2018 steden, waarvan sommige met elkaar verbonden zijn door wegen. Elke stad is verbonden met ten minste drie andere steden. Het is mogelijk om van elke willekeurige stad naar elke andere willekeurige stad te reizen via één of meer wegen. Bekijk voor elk tweetal steden de kortste route tussen deze twee steden. Wat is het grootste aantal wegen dat in zo'n kortste route zou kunnen voorkomen?
|
Het grootste aantal wegen dat in een kortste route kan voorkomen, is 1511. We geven eerst een land waarvoor dit aantal aangenomen wordt. Deel de steden op in 504 groepen: twee groepen van vijf steden $\left(A_{0}, B_{0}, C_{0}, D_{0}, E_{0}\right)$ en $\left(A_{503}, B_{503}, C_{503}, D_{503}, E_{503}\right)$ en verder groepen van vier steden $\left(A_{i}, B_{i}, C_{i}, D_{i}\right)$ voor $1 \leq i \leq 502$. Voor alle $i$ met $0 \leq i \leq 503$ : verbind $A_{i}$ met $B_{i}$, verbind $A_{i}$ met $C_{i}$, verbind $B_{i}$ met $D_{i}$ en verbind $C_{i}$ met $D_{i}$. Verbind verder $E_{0}$ met $A_{0}, B_{0}$ en $C_{0}$. Verbind $E_{503}$ met $B_{503}, C_{503}$ en $D_{503}$. Voor $1 \leq i \leq 502$ : verbind $B_{i}$ met $C_{i}$. Ten slotte voor $0 \leq i \leq 502$ : verbind $D_{i}$ met $A_{i+1}$. Nu is elke stad met precies drie andere steden verbonden.
Als we nu van $A_{0}$ naar $D_{503}$ willen, dan moet dat via alle $A_{i}$ en $D_{i}$, omdat daar de enige verbindingen tussen de verschillende groepen lopen en elke groep alleen verbonden is met de vorige en volgende groep. Verder is voor $0 \leq i \leq 503$ de stad $A_{i}$ niet verbonden met $D_{i}$, dus de route binnen groep $i$ moet via $B_{i}$ of $C_{i}$ lopen. Minstens drie van de vier of vijf steden in zo'n groep worden dus aangedaan op de route. In totaal bevat de route dus minstens $3 \cdot 504=1512$ steden en daarmee minstens 1511 wegen.
We laten vervolgens zien dat een kortste route tussen twee steden nooit meer dan 1511 wegen kan doorlopen. Bekijk zo'n korste route waarbij achtereenvolgens de steden $A_{0}, A_{1}$, $\ldots, A_{k}$ worden aangedaan. Elk van de steden $A_{i}$ is behalve met zijn buren $A_{i-1}$ en $A_{i+1}$ nog met minstens één andere stad verbonden, zeg met $B_{i}$ (hierbij hoeven $B_{0}, B_{1}, \ldots, B_{k}$ niet allemaal verschillende steden te zijn). Verder zijn $A_{0}$ en $A_{k}$ nog met een derde stad verbonden, zeg $C_{0} \neq B_{0}$ en $C_{k} \neq B_{k}$. Als één van de steden $B_{i}$ of $C_{i}$ gelijk is aan één van de steden $A_{j}$, dan hadden we een kortere route kunnen vinden door direct van $A_{i}$ naar $A_{j}$ te lopen (of andersom), tegenspraak. Dus de steden $B_{i}$ en $C_{i}$ zijn allemaal ongelijk aan alle steden $A_{j}$.
Als één van de steden $B_{i}$ in totaal met vier steden $A_{j}$ verbonden is, zeg $B_{i}$ is verbonden met $A_{i}, A_{m}, A_{n}$ en $A_{p}$ met $i<m<n<p$, dan zouden we de route kunnen inkorten door van $A_{i}$ naar $B_{i}$ en dan naar $A_{p}$ te lopen. We slaan dan minimaal twee steden uit de oorspronkelijke route over (namelijk $A_{m}$ en $A_{n}$ ) en bezoeken in plaats daarvan alleen $B_{i}$ extra, dus deze nieuwe route is korter. Tegenspraak. De steden $B_{i}$ met $3 \leq i \leq k-3$ zijn dus minstens $\frac{k-5}{3}$ verschillende steden. Voor $B_{0}$ en $C_{0}$ geldt dat we de route kunnen inkorten als één van deze steden gelijk is aan $B_{i}$ met $i \geq 3$. Dat zou een tegenspraak zijn, dus $B_{0}$ en $C_{0}$ zijn twee verschillende steden ongelijk aan $B_{i}$ met $i \geq 3$. Zo ook zijn $B_{k}$ en $C_{k}$ twee verschillende steden ongelijk aan $B_{i}$ met $i \leq k-3$. Al met al hebben we op de route zelf $k+1$ steden en daarnaast nog minstens $\frac{k-5}{3}+2+2$ andere steden. Dus $\frac{k-5}{3}+k+5 \leq 2018$, dus $4 k-5+15 \leq 3 \cdot 2018=6054$, dus $4 k \leq 6044$, dus $k \leq 1511$.
We concluderen dat het grootst mogelijke aantal wegen in een kortste route gelijk aan 1511.
|
{
"resource_path": "Dutch_TST/segmented/nl-2019-B_uitwerkingen.jsonl",
"problem_match": "\nOpgave 5.",
"solution_match": "\nOplossing."
}
|
4730425f-5c92-56a4-9e23-31b01f22056a
| 604,333
|
In a mathematics competition, 300 participants take part. After the competition, some participants play chess. Each pair of participants plays at most one game against each other. There are no three participants at this competition who all play against each other. Determine the maximum $n$ for which it is possible to satisfy the following conditions simultaneously: each participant plays at most $n$ chess games, and for every $m$ with $1 \leq m \leq n$ there is a participant who plays exactly $m$ chess games.
|
We show that $n$ is at most 200. First, we give an example where $n=200$. Consider players $A_{1}, A_{2}, \ldots, A_{200}$ and $B_{1}, B_{2}, \ldots, B_{100}$. This makes a total of 300 players. Let $B_{i}$ play chess against the players $A_{j}$ with $1 \leq j \leq i+100$, while no other participants play against each other. Then $B_{i}$ plays exactly $100+i$ other participants, so for $101 \leq m \leq 200$ there is a participant who plays exactly $m$ games. Furthermore, $A_{j}$ for $j>100$ plays against the participants $B_{i}$ with $i \geq j-100$; there are $100-(j-101)=201-j$ of them. Since $j$ can vary from 101 to 200, this number varies from 100 to 1. Thus, for $1 \leq m \leq 100$ there is also a participant who plays exactly $m$ games. Finally, $A_{j}$ for $j \leq 100$ plays against all $B_{i}$; there are 100 of them. Therefore, there are no participants who play more than 200 games. We see that this example meets the requirements for $n=200$.
Now we prove that $n>200$ is not possible. We do this by contradiction, so assume that $n>200$. Then there is at least one participant $A$ who plays exactly 201 games, against players $B_{1}, B_{2}, \ldots, B_{201}$. There are a total of 300 participants, so apart from them and $A$, there are still $300-1-201=98$ other participants, which we call $C_{1}, \ldots, C_{98}$. If a participant $B_{i}$ plays against another participant $B_{j}$, they form a trio with $A$ who play three games among themselves; this is not allowed. Therefore, $B_{i}$ does not play against another participant $B_{j}$. So he plays at most $1+98=99$ games. This means that the participants who play exactly $m$ other participants with $100 \leq m \leq 200$ must all be among the participants $C_{i}$. However, there are only 98 different people, a contradiction. We conclude that $n>200$ is not possible and that $n=200$ is the maximum.
|
200
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Aan een wiskundewedstrijd doen 300 deelnemers mee. Na de wedstrijd spelen sommige deelnemers wat potjes schaak. Elke twee deelnemers spelen hooguit één keer tegen elkaar. Er zijn geen drie deelnemers bij deze wedstrijd die onderling allemaal tegen elkaar schaken. Bepaal de maximale $n$ waarvoor het mogelijk is dat aan de volgende voorwaarden tegelijk voldaan wordt: elke deelnemer speelt hooguit $n$ potjes schaak, en voor elke $m$ met $1 \leq m \leq n$ is er een deelnemer die precies $m$ potjes schaak speelt.
|
We laten zien dat $n$ maximaal 200 is. We geven eerst een voorbeeld waarin $n=200$ geldt. Bekijk spelers $A_{1}, A_{2}, \ldots, A_{200}$ en $B_{1}, B_{2}, \ldots, B_{100}$. Dit zijn 300 spelers in totaal. Laat $B_{i}$ schaak spelen tegen de spelers $A_{j}$ met $1 \leq j \leq i+100$, terwijl verder geen andere deelnemers tegen elkaar schaken. Dan schaakt $B_{i}$ tegen precies $100+i$ andere deelnemers, dus voor $101 \leq m \leq 200$ is er een deelnemer die precies $m$ potjes schaak speelt. Verder schaakt $A_{j}$ voor $j>100$ tegen de deelnemers $B_{i}$ met $i \geq j-100$; dat zijn er $100-(j-101)=201-j$. Omdat $j$ hier kan variëren van 101 tot en met 200, varieert dit getal van 100 tot en met 1 . Voor $1 \leq m \leq 100$ is er dus ook een deelnemer die precies $m$ potjes schaak speelt. Ten slotte schaakt $A_{j}$ voor $j \leq 100$ tegen alle $B_{i}$; dat zijn er 100. Er zijn dus geen deelnemers die meer dan 200 potjes schaak spelen. We zien dat dit voorbeeld aan de eisen voldoet voor $n=200$.
Nu bewijzen we dat $n>200$ niet kan. Dit doen we uit het ongerijmde, dus stel dat $n>200$. Dan is er in elk geval een deelnemer $A$ die precies 201 potjes schaak speelt, tegen spelers $B_{1}, B_{2}, \ldots, B_{201}$. Er zijn in totaal 300 deelnemers, dus naast hen en $A$ zijn er nog $300-1-201=98$ andere deelnemers, die we $C_{1}, \ldots, C_{98}$ noemen. Als een deelnemer $B_{i}$ schaakt tegen een andere deelnemer $B_{j}$, vormen zij samen met $A$ een drietal dat onderling drie potjes schaakt; dat mag niet. Dus $B_{i}$ schaakt niet tegen een andere deelnemer $B_{j}$. Hij speelt dus hooguit $1+98=99$ potjes schaak. Dat betekent dat de deelnemers die tegen precies $m$ andere deelnemers schaken met $100 \leq m \leq 200$ allemaal onder de deelnemers $C_{i}$ te vinden moeten zijn. Echter, dat zijn maar 98 verschillende mensen, tegenspraak. We concluderen dat $n>200$ niet kan en dat dus $n=200$ maximaal is.
|
{
"resource_path": "Dutch_TST/segmented/nl-2019-E_uitwerkingen.jsonl",
"problem_match": "\nOpgave 4.",
"solution_match": "\nOplossing."
}
|
7e9a4a6d-d807-5a6c-ae2f-f68dbe10a24d
| 604,576
|
For an integer $n \geq 3$ we consider a circle with $n$ points on it. We place a positive integer at each point, where the numbers do not necessarily have to be distinct. Such a placement of numbers is called stable if three consecutive numbers always have the product $n$. For how many values of $n$ with $3 \leq n \leq 2020$ is it possible to place numbers in a stable manner?
|
Suppose $n$ is not a multiple of 3 and we have a stable placement of the numbers $a_{1}, a_{2}, \ldots, a_{n}$, which lie in that order on the circle. Then it holds that $a_{i} a_{i+1} a_{i+2}=3$ for all $i$, where we compute the indices modulo $n$. Thus,
$$
a_{i+1} a_{i+2} a_{i+3}=n=a_{i} a_{i+1} a_{i+2}
$$
from which it follows that $a_{i+3}=a_{i}$ (since all numbers are positive). By induction, we find that for all $k \geq 0$ integers, $a_{3 k+1}=a_{1}$. Since $n$ is not a multiple of 3, the numbers $3 k+1$ for $k \geq 0$ take on all values modulo $n$: indeed, 3 has a multiplicative inverse modulo $n$, so $k \equiv 3^{-1} \cdot(b-1)$ gives $3 k+1 \equiv b \bmod n$ for all $b$. We conclude that all numbers on the circle are equal to $a_{1}$. Therefore, it must hold that $a_{1}^{3}=n$, where $a_{1}$ is a positive integer. Thus, if $n$ is not a multiple of 3, then $n$ must be a cube.
If $n$ is a multiple of 3, then we place the numbers $1,1, n, 1,1, n, \ldots$ consecutively on the circle. The product of three consecutive numbers is now always $1 \cdot 1 \cdot n=n$. If $n$ is a cube, say $n=m^{3}$, then we place the numbers $m, m, m, \ldots$ on the circle. The product of three consecutive numbers is now always $m^{3}=n$.
We conclude that a stable placement is possible if and only if $n$ is a multiple of 3 or a cube. We now need to count this number. The multiples of 3 $n$ with $3 \leq n \leq 2020$ are $3,6,9, \ldots, 2019$ and there are $\frac{2019}{3}=673$ of them. The cubes $n$ with $3 \leq n \leq 2020$ are $2^{3}, 3^{3}, \ldots, 12^{3}$, since $12^{3}=1728 \leq 2020$ and $13^{3}=2197>2020$. This is 11 cubes, of which 4 are divisible by 3, so there are 7 cubes that are not multiples of 3. In total, there are $673+7=680$ values of $n$ that satisfy the condition.
|
680
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Voor een geheel getal $n \geq 3$ bekijken we een cirkel met $n$ punten erop. We plaatsen een positief geheel getal bij elk punt, waarbij de getallen niet noodzakelijk verschillend hoeven te zijn. Zo'n plaatsing van getallen heet stabiel als drie getallen naast elkaar altijd product $n$ hebben. Voor hoeveel waarden van $n$ met $3 \leq n \leq 2020$ is het mogelijk om getallen op een stabiele manier te plaatsen?
|
Stel dat $n$ geen veelvoud van 3 is en dat we een stabiele plaatsing hebben van de getallen $a_{1}, a_{2}, \ldots, a_{n}$, die in die volgorde op de cirkel liggen. Er geldt dan $a_{i} a_{i+1} a_{i+2}=3$ voor alle $i$, waarbij we de indices modulo $n$ rekenen. Dus
$$
a_{i+1} a_{i+2} a_{i+3}=n=a_{i} a_{i+1} a_{i+2}
$$
waaruit volgt dat $a_{i+3}=a_{i}$ (aangezien alle getallen positief zijn). Met inductie vinden we dat voor alle $k \geq 0$ geheel geldt $a_{3 k+1}=a_{1}$. Omdat $n$ geen drievoud is, nemen de getallen $3 k+1$ voor $k \geq 0$ alle waarden modulo $n$ aan: immers, 3 heeft een multiplicatieve inverse modulo $n$, dus $k \equiv 3^{-1} \cdot(b-1)$ geeft $3 k+1 \equiv b \bmod n$ voor alle $b$. We concluderen dat alle getallen op de cirkel gelijk zijn aan $a_{1}$. Er moet dus gelden dat $a_{1}^{3}=n$, waarbij $a_{1}$ positief geheel is. Dus als $n$ geen drievoud is, dan moet $n$ een derdemacht zijn.
Als $n$ een drievoud is, dan zetten we achteraanvolgens de getallen $1,1, n, 1,1, n, \ldots$ neer op de cirkel. Het product van drie getallen naast elkaar is nu altijd $1 \cdot 1 \cdot n=n$. Als $n$ een derdemacht is, zeg $n=m^{3}$, dan zetten we de getallen $m, m, m, \ldots$ neer op de cirkel. Het product van drie getallen naast elkaar is nu altijd $m^{3}=n$.
We conluderen dat er een stabiele plaatsing mogelijk is dan en slechts dan als $n$ een drievoud of een derdemacht is. We moeten nu nog dit aantal tellen. De drievouden $n$ met $3 \leq n \leq 2020$ zijn $3,6,9, \ldots, 2019$ en dat zijn er $\frac{2019}{3}=673$. De derdemachten $n$ met $3 \leq n \leq 2020$ zijn $2^{3}, 3^{3}, \ldots, 12^{3}$, want $12^{3}=1728 \leq 2020$ en $13^{3}=2197>2020$. Dit zijn 11 derdemachten, waarvan er 4 deelbaar zijn door 3 , dus er zijn 7 derdemachten die geen drievoud zijn. Alles bij elkaar zijn er $673+7=680$ waarden van $n$ die voldoen.
|
{
"resource_path": "Dutch_TST/segmented/nl-2020-B2020_uitwerkingen.jsonl",
"problem_match": "\nOpgave 1.",
"solution_match": "\nOplossing."
}
|
b91dec55-46ef-5b15-9edf-4b60e4c1c70a
| 604,587
|
A set $S$ consisting of 2019 (distinct) positive integers has the following property: the product of any 100 elements of $S$ is a divisor of the product of the remaining 1919 elements. What is the maximum number of prime numbers that $S$ can contain?
|
The maximum number of prime numbers is 1819.
We start with the construction. Choose different prime numbers \( p_{1}, p_{2}, \ldots, p_{1819} \) and let \( P = p_{1} p_{2} \cdots p_{1819} \). Take
\[
S = \left\{ p_{1}, p_{2}, \ldots, p_{1819}, P, P \cdot p_{1}, \ldots, P \cdot p_{199} \right\}
\]
For each \( p_{i} \), there are 201 numbers in \( S \) that are divisible by \( p_{i} \) (namely \( p_{i} \) and all numbers divisible by \( P \)). Of these, at most one number has two factors \( p_{i} \); the rest have one factor \( p_{i} \). If we take 100 numbers from \( S \), then their product contains at most 101 factors \( p_{i} \). Among the remaining numbers, there are still at least 101 numbers divisible by \( p_{i} \), so their product has at least 101 factors \( p_{i} \). Since this holds for every \( p_{i} \) and the numbers in \( S \) have no other prime factors, this means that \( S \) has the desired property.
We now prove that \( S \) cannot contain more than 1819 prime numbers. Consider a prime divisor \( q \) of a number in \( S \). Suppose that at most 199 numbers in \( S \) are divisible by \( q \). Then we take the 100 elements of \( S \) with the most factors \( q \); their product always has more factors \( q \) than the remaining elements, contradicting the condition in the problem. Therefore, there must be at least 200 numbers in \( S \) that are divisible by \( q \). If there are exactly 200, it follows that the number of prime factors \( q \) in all these numbers must be the same, otherwise we get a contradiction if we choose the 100 elements with the most factors \( p \).
We now see that \( S \) must contain at least 199 non-prime numbers, because a prime number \( p \) in \( S \) divides at least 199 other elements of \( S \). Suppose now that \( S \) contains exactly 199 non-prime numbers. Then the prime factor \( p \) appears in each of these 199 non-prime numbers exactly once (the same number of times as in the prime number \( p \)). Furthermore, numbers in \( S \) cannot be divisible by a prime number \( r \) that is not in \( S \), because then there must be at least 200 multiples of \( r \) in \( S \), which would be 200 non-prime numbers, a contradiction. This implies that each of the 199 non-prime numbers in \( S \) must be the product of the prime numbers in \( S \) and in particular, these 199 numbers are not distinct from each other. This is a contradiction, so \( S \) must contain at least 200 non-prime numbers and thus at most 1819 prime numbers.
|
1819
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Een verzameling $S$ die bestaat uit 2019 (verschillende) positieve gehele getallen heeft de volgende eigenschap: het product van elke 100 elementen van $S$ is een deler van het product van de overige 1919 elementen. Wat is het maximale aantal priemgetallen dat $S$ kan bevatten?
|
Het maximale aantal priemgetallen is 1819.
We beginnen met de constructie. Kies verschillende priemgetallen $p_{1}, p_{2}, \ldots, p_{1819}$ en zij $P=p_{1} p_{2} \cdots p_{1819}$. Neem
$$
S=\left\{p_{1}, p_{2}, \ldots, p_{1819}, P, P \cdot p_{1}, \ldots, P \cdot p_{199}\right\}
$$
Voor elke $p_{i}$ geldt dat er 201 getallen in $S$ zijn die deelbaar zijn door $p_{i}$ (namelijk $p_{i}$ en alle getallen deelbaar door $P$ ). Hiervan is er hoogstens één getal met twee factoren $p_{i}$; de rest heeft één factor $p_{i}$. Nemen we nu 100 getallen uit $S$, dan zitten in hun product hoogstens 101 factoren $p_{i}$. Bij de overige getallen zitten nog minstens 101 getallen deelbaar door $p_{i}$, dus hun product heeft minstens 101 factoren $p_{i}$. Omdat dit voor elke $p_{i}$ geldt en de getallen uit $S$ geen andere priemfactoren hebben, betekent dit dat $S$ de gewenste eigenschap heeft.
We bewijzen nu dat $S$ niet meer dan 1819 priemgetallen kan bevatten. Bekijk een priemdeler $q$ van een getal in $S$. Stel dat hooguit 199 getallen in $S$ deelbaar zijn door $q$. Dan nemen we de 100 elementen van $S$ met de meeste factoren $q$ erin; die hebben samen altijd meer factoren $q$ dan de overige elemenenten, tegenspraak met de voorwaarde in de opgave. Dus er zijn minstens 200 getallen in $S$ deelbaar door $q$. Als het er precies 200 zijn, volgt bovendien dat het aantal priemfactoren $q$ in al deze getallen gelijk moet zijn, anders krijgen we weer een tegenspraak als we de 100 elementen met de meeste factoren $p$ kiezen.
We zien nu dat $S$ minstens 199 niet-priemgetallen moet bevatten, want een priemgetal $p$ in $S$ deelt nog minstens 199 andere elementen van $S$. Stel nu dat $S$ precies 199 nietpriemgetallen bevat. Dan komt de priemfactor $p$ in elk van deze 199 niet-priemgetallen precies één keer voor (namelijk net zo vaak als in het priemgetal $p$ ). Verder kunnen getallen in $S$ nu niet deelbaar zijn door een priemgetal $r$ dat zelf niet in $S$ zit, want dan moeten er wel in totaal minstens 200 veelvouden van $r$ in $S$ zitten en dat zijn dan 200 niet-priemgetallen, tegenspraak. Hieruit volgt dat elk van de 199 niet-priemgetallen in $S$ het product moet zijn van de priemgetallen in $S$ en in het bijzonder zijn deze 199 getallen dus niet verschillend van elkaar. Dit is een tegenspraak, dus $S$ moet minstens 200 niet-priemgetallen bevatten en daarmee hoogstens 1819 priemgetallen.
|
{
"resource_path": "Dutch_TST/segmented/nl-2020-B2020_uitwerkingen.jsonl",
"problem_match": "\nOpgave 5.",
"solution_match": "\nOplossing."
}
|
ef7f0b38-73b5-5080-b81e-dcc79cbbb9b7
| 604,653
|
For a positive integer $n$, we consider an $n \times n$ board and tiles with dimensions $1 \times 1, 1 \times 2, \ldots, 1 \times n$. In how many ways can exactly $\frac{1}{2} n(n+1)$ squares of the board be colored red, such that the red squares can all be covered by the $n$ tiles placed horizontally, and also by the $n$ tiles placed vertically? Two colorings that are not identical but can be transformed into each other by rotating or reflecting the board are counted as different.
|
The number of red squares is exactly equal to the total number of squares that can be covered by the $n$ tiles, so the tiles are placed only on red squares. Consider a coloring of the board and the corresponding horizontal covering of the tiles (where all tiles lie horizontally) and the vertical covering. We derive several properties of the coloring and then count the number of possibilities. Let the tile with dimensions $1 \times k$ be the $k$-tile.
Since the horizontal covering contains an $n$-tile, each column must contain at least one red square. Therefore, in the vertical covering, there must be at least one tile in each column; since there are exactly $n$ tiles, this means that there must be exactly one tile in each column. Similarly, there must be exactly one tile in each row in the horizontal covering. Number the rows and columns based on the number of the tile that lies in them: so row $i$ is the row in which the $i$-tile lies in the horizontal covering, and analogously for the columns.
We now prove that the square in row $i$ and column $j$ (call this square $(i, j)$) is red if and only if $i+j \geq n+1$. We prove this by induction on $i$. In row 1, there is only one red square, and it must be in the column where the $n$-tile lies in the vertical covering, so in column $n$. Thus, the square $(1, j)$ is red if and only if $j=n$, or equivalently, if and only if $1+j \geq n+1$. Now let $k \geq 1$ and assume we have proven this for all $i \leq k$. We want to prove it for $i=k+1$, that is, that a square $(k+1, j)$ is red if and only if $k+1+j \geq n+1$, or equivalently, if $j \geq n-k$. Consider a column $j \geq n-k$. By the induction hypothesis, we know exactly how many red squares this column has in rows $1,2, \ldots, k$: the square $(i, j)$ is red if and only if $i+j \geq n+1$, or $i \geq n+1-j$, so there are $k-(n-j)=j+k-n$ such squares. In the remaining $n-k$ rows, this column needs $j-(j+k-n)=n-k$ more red squares. Therefore, this column has a red square in each of those rows and in particular also in row $i=k+1$. In row $i=k+1$, the squares $(i, j)$ with $j \geq n-k$ are all red, and there are $k+1$ such squares. Thus, these are exactly all the red squares in row $i=k+1$, so the square $(i, j)$ is red if and only if $j \geq n-k$, or equivalently, if and only if $i+j \geq n-k+k+1=n+1$. This completes the induction.
Now consider two rows directly above each other with row numbers $a$ and $b$, with $a>b$. In column $n-b$, there is a red square in row $a$ (since $a+n-b>n$) but not in row $b$. In the row directly on the other side of row $b$ (if it exists), there should therefore be no red square in column $n-b$, otherwise the red squares in column $n-b$ would not be contiguous and the tile with number $n-b$ could not lie here. The row number of this row must therefore be less than $b$. We conclude that the row numbers cannot first decrease and then increase again. Above and below row $n$, there must be a row with a smaller number (or no more rows at all), so the row numbers must decrease on both sides from there. We see that the row numbers must first be increasing up to row $n$ and then decreasing. The same can be proven for the column numbers.
Conversely, we need to prove that if the row and column numbers are first increasing and then decreasing, we can place both the horizontal and vertical tiles. For this, we color the square $(i, j)$ red if and only if $i+j \geq n+1$. For a fixed $i$, the red squares are thus the squares $(i, j)$ with $j \geq n+1-i$; due to the shape of the column numbers, these columns are contiguous. Therefore, the red squares in each row are contiguous. We can thus place the horizontal tiles exactly on the red squares. The same works for the vertical tiles. We could not have chosen a different coloring with the same row and column numbers that would allow the tiling, because we already know that in every valid tiling, $(i, j)$ is red if and only if $i+j \geq n+1$.
In total, we are looking for the number of ways to choose both the row and column numbers in an order that is first increasing and then decreasing; for each of these choices, there is exactly one way to color the red squares that satisfies the condition. The number of ways to arrange the numbers 1 to $n$ in an order that is first increasing and then decreasing is equal to the number of subsets of $\{1,2, \ldots, n-1\}$, namely the subset of numbers that come before the number $n$; these can be sorted in only one way (increasing) and the rest of the numbers must be sorted in decreasing order and placed after $n$. The number of subsets is $2^{n-1}$. Therefore, the total number of colorings that satisfy the problem is $\left(2^{n-1}\right)^{2}=2^{2 n-2}$.
|
2^{2n-2}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Voor een positief geheel getal $n$ bekijken we een $n \times n$-bord en tegels met afmetingen $1 \times 1,1 \times 2, \ldots, 1 \times n$. Op hoeveel manieren kunnen er precies $\frac{1}{2} n(n+1)$ vakjes van het bord rood worden gekleurd, zodat de rode vakjes allemaal bedekt kunnen worden door de $n$ tegels allemaal horizontaal te plaatsen, maar ook door de $n$ tegels allemaal verticaal te plaatsen? Twee kleuringen die niet identiek zijn, maar door draaiing of spiegeling van het bord in elkaar overgaan, tellen als verschillend.
|
Het aantal rode vakjes is het precies gelijk aan het totaal aantal vakjes dat door de $n$ tegels bedekt kan worden, dus de tegels worden alleen op rode vakjes gelegd. Bekijk een kleuring van het bord en de bijbehorende horizontale bedekking van de tegels (waarin alle tegels horizontaal liggen) en verticale bedekking. We leiden een aantal eigenschappen van de kleuring af en tellen daarna hoeveel mogelijkheden er zijn. Noem de tegel met afmetingen $1 \times k$ de $k$-tegel.
Omdat de horizontale bedekking een $n$-tegel bevat, bevat elke kolom minstens één rood vakje. In de verticale bedekking moet daarom in elke kolom minstens één tegel liggen; omdat er precies $n$ tegels zijn, betekent dat dat er in elke kolom precies één tegel moet liggen. Net zo moet er in de horizontale bedekking in elke rij precies één tegel liggen. Nummer nu de rijen en kolommen afhankelijk van het nummer van de tegel die daarin ligt: dus rij $i$ is de rij waarin de $i$-tegel ligt in de horizontale bedekking, en analoog voor de kolommen.
We bewijzen nu eerst dat het vakje in rij $i$ en kolom $j$ (noem dit vakje $(i, j)$ ) rood is dan en slechts dan als $i+j \geq n+1$. We bewijzen dit met inductie naar $i$. In rij 1 is er slechts één rood vakje en dat moet wel in de kolom zijn waar de $n$-tegel ligt in de verticale bedekking, dus in kolom $n$. Dus het vakje $(1, j)$ is rood dan en slechts als $j=n$, oftewel dan en slechts dan als $1+j \geq n+1$. Zij nu $k \geq 1$ en neem aan dat we dit bewezen hebben voor alle $i \leq k$. We willen het nu bewijzen voor $i=k+1$, dus dat een vakje $(k+1, j)$ rood is dan en slechts dan als $k+1+j \geq n+1$, oftewel als $j \geq n-k$. Bekijk dus een kolom $j \geq n-k$. We weten wegens de inductiehypothese precies hoeveel rode vakjes deze kolom heeft in de rijen $1,2, \ldots, k$ : het vakje $(i, j)$ is namelijk rood dan en slechts dan als $i+j \geq n+1$, oftewel $i \geq n+1-j$, dus dat zijn er $k-(n-j)=j+k-n$. In de overige $n-k$ rijen heeft deze kolom dus nog $j-(j+k-n)=n-k$ rode vakjes nodig. Dus deze kolom heeft een rood vakje in elk van die rijen en in het bijzonder ook in rij $i=k+1$. In rij $i=k+1$ zijn dus de vakjes $(i, j)$ met $j \geq n-k$ allemaal rood en dat zijn er $k+1$. Dus dit zijn precies alle rode vakjes in rij $i=k+1$, dus het vakje $(i, j)$ is rood dan en slechts dan als $j \geq n-k$, oftewel dan en slechts dan als $i+j \geq n-k+k+1=n+1$. Dit voltooit de inductie.
Bekijk nu twee rijen direct boven elkaar met rijnummers $a$ en $b$, met $a>b$. In kolom $n-b$ zit een rood vakje in rij $a$ (want $a+n-b>n$ ) maar niet in rij $b$. In de rij direct aan de andere kant van rij $b$ (als deze bestaat) mag daarom geen rood vakje in kolom $n-b$ zitten, want anders zouden de rode vakjes in kolom $n-b$ niet aaneengesloten zijn en kan de
tegel met nummer $n-b$ hier niet liggen. Het rijnummer van deze rij moet daarom kleiner dan $b$ zijn. We concluderen dat de rijnummers niet eerst kunnen dalen en daarna weer stijgen. Boven en onder rij $n$ moet wel een rij met een kleiner nummer zitten (of helemaal geen rij meer) dus dalen vanaf daar de rijnummers allebei de kanten op. We zien dat de rijnummers van boven naar beneden eerst oplopend moeten zijn tot aan rij $n$ en daarna aflopend. Hetzelfde kunnen we bewijzen voor de kolomnummers.
Andersom moeten we bewijzen dat als de rijnummers en kolomnummers eerst oplopend en dan aflopend zijn, dat we dan de horizontale en verticale tegels allebei neer kunnen leggen. Hiervoor kleuren we de vakje $(i, j)$ rood dan en slechts dan als $i+j \geq n+1$. Voor vaste $i$ zijn de rode vakjes dus de vakjes $(i, j)$ met $j \geq n+1-i$; vanwege de vorm van de kolomnummers zijn die kolommen aaneengesloten. Dus in elke rij zijn de rode vakjes aaneengesloten. We kunnen dus de horizontale tegels precies op de rode vakjes leggen. Net zo goed lukt dit met de verticale tegels. We hadden bij dezelfde rij- en kolomnummers niet een andere kleuring kunnen kiezen waarvoor de betegeling werkt, want we weten al dat bij elke goede betegeling geldt dat $(i, j)$ rood is dan en slechts dan als $i+j \geq n+1$.
Al met al zijn we dus op zoek naar het aantal manieren om zowel de rij- als de kolomnummers te kiezen in een volgorde die eerst oplopend en daarna aflopend is; bij elk van die keuzes hoort precies één manier om de rode vakjes te kleuren die aan de voorwaarde voldoet. Het aantal manieren om de getallen 1 tot en met $n$ in een volgorde te zetten die eerst oplopend en dan aflopend is, is gelijk aan het aantal deelverzamelingen van $\{1,2, \ldots, n-1\}$, namelijk de deelverzameling van getallen die vóór het getal $n$ komen; deze kunnen maar op één manier gesorteerd worden (oplopend) en de rest van de getallen moet juist aflopend gesorteerd worden en na $n$ neergezet worden. Het aantal deelverzamelingen is $2^{n-1}$. Dus het totaal aantal kleuringen dat aan de opgave voldoet is $\left(2^{n-1}\right)^{2}=2^{2 n-2}$.
|
{
"resource_path": "Dutch_TST/segmented/nl-2020-C2020_uitwerkingen.jsonl",
"problem_match": "\nOpgave 3.",
"solution_match": "\nOplossing I."
}
|
aca91a57-735e-5af1-a2ae-6fe9f4695e3b
| 604,712
|
Let $p$ be a prime number greater than 2. Patricia wants to assign 7 not necessarily distinct numbers from $\{1,2, \ldots, p\}$ to the black dots in the figure below, in such a way that the product of the three numbers on a line or circle always has the same remainder when divided by $p$.
(a) Suppose Patricia uses the number $p$ at least once. How many times does she minimally need the number $p$ in total?
(b) Suppose Patricia does not use the number $p$. In how many ways can she then assign the numbers? (Two ways are different if different numbers are assigned to at least one black dot. The figure is not rotated or reflected.)
|
(a) By 'lines' we mean in the following part of this section the six lines and the circle. Whenever the number $p$ is used somewhere, there is a 'line' with a product divisible by $p$, so with a remainder of 0 after division by $p$. Then all 'lines' must give a remainder of 0, so all 'lines' must contain $p$ at least once. This can be achieved by assigning the number $p$ to the bottom three dots. Suppose it can also be done with at most two $p$s. Each dot lies on exactly three 'lines', so then there are at most six 'lines' on which a number $p$ lies. However, there are seven 'lines', so this is not possible. We conclude that it needs $p$ at least three times in total.
(b) Let the bottom three numbers from left to right be $a, b$, and $c$. Let the number in the middle of the left side of the triangle be $d$. We can now calculate all numbers modulo $p$; note that all numbers are invertible modulo $p$ because $p$ itself does not participate and $p$ is prime. The bottom line has the product $a b c$. The left side of the triangle also does, so the number at the very top is congruent modulo $p$ to $a b c(a d)^{-1}=b c d^{-1}$. If we look at the line from the bottom right to the middle of the left side, we see that the middle number must be congruent to $a b c(c d)^{-1}=a b d^{-1}$. By looking at the circle, we find that the number on the right in the middle is $a b c(b d)^{-1} = a c d^{-1}$.
On the right side, we now get the equation $b c d^{-1} \cdot a c d^{-1} \cdot c \equiv a b c \bmod p$, so $c^{2} \equiv d^{2} \bmod p$. Similarly, we find on the vertical line $b^{2} \equiv d^{2}$ and on the line from the bottom left to the middle right $a^{2} \equiv d^{2} \bmod p$. We conclude that the numbers $a, b, c$, and $d$ must all have the same square. From $x^{2} \equiv y^{2}$ follows $(x-y)(x+y) \equiv 0 \bmod p$, so $p \mid x-y$ or $p \mid x+y$, because $p$ is prime. Thus, $x \equiv y$ or $x \equiv -y$. There are two options, because if $y \equiv -y$, then $2 y \equiv 0$, so $p \mid 2 y$, so $p \mid y$ due to $p>2$; contradiction. Therefore, the numbers $b, c$, and $d$ must all be congruent to $a$ or $-a$. If this condition is met, then $a^{2} \equiv b^{2} \equiv c^{2} \equiv d^{2}$ and then it follows from the above that on all six lines and on the circle the product is congruent to $a b c$.
There are $p-1$ possibilities for the number $a$ and then 2 possibilities for each of the numbers $b, c$, and $d$. So in total, there are $8(p-1)$ ways to assign the numbers.
|
8(p-1)
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Zij $p$ een priemgetal groter dan 2. Patricia wil 7 niet-noodzakelijk verschillende getallen uit $\{1,2, \ldots, p\}$ aan de zwarte stippen in onderstaande figuur toekennen, op zo'n manier dat het product van drie getallen op een lijn of cirkel altijd dezelfde rest bij deling door $p$ heeft.

(a) Stel dat Patricia het getal $p$ minstens één keer gebruikt. Hoe vaak heeft ze het getal $p$ dan in totaal minimaal nodig?
(b) Stel dat Patricia het getal $p$ niet gebruikt. Op hoeveel manieren kan zij dan de getallen toekennen? (Twee manieren zijn verschillend als er aan minstens één zwarte stip verschillende getallen zijn toegekend. De figuur wordt niet gedraaid of gespiegeld.)
|
(a) Met 'lijnen' bedoelen we in het vervolg van dit onderdeel de zes lijnen en de cirkel. Zodra het getal $p$ ergens gebruikt wordt, is er een 'lijn' met product deelbaar door $p$, dus met rest 0 na deling door $p$. Alle 'lijnen' moeten dan rest 0 geven, dus alle 'lijnen' bevatten minstens één keer $p$. Dit kunnen we bereiken door het getal $p$ aan de onderste drie stippen toe te kennen. Stel dat het ook al kan met hooguit twee keer $p$. Elke stip ligt op precies drie 'lijnen', dus dan zijn er hooguit zes 'lijnen' waar een getal $p$ op ligt. Er zijn echter zeven 'lijnen', dus dit kan niet. We concluderen dat ze $p$ in totaal minimaal drie keer nodig heeft.
(b) Noem de onderste drie getallen van links naar rechts $a, b$ en $c$. Noem het getal midden op de linkerzijkant van de driehoek $d$. We kunnen nu alle getallen modulo $p$ uitrekenen; merk op dat alle getallen inverteerbaar zijn modulo $p$ omdat $p$ zelf niet meedoet en $p$ priem is. De onderste lijn heeft product $a b c$. De linkerzijde van de driehoek dus ook, dus het getal helemaal bovenin is modulo $p$ congruent aan $a b c(a d)^{-1}=b c d^{-1}$. Als we de lijn van rechtsonder naar het midden van de linkerzijde bekijken, zien we dat het middelste getal congruent moet zijn aan $a b c(c d)^{-1}=a b d^{-1}$. Door de cirkel te bekijken, vinden we dat het getal rechts in het midden $a b c(b d)^{-1}=$ $a c d^{-1}$ is.
Op de rechterzijde krijgen we nu de vergelijking $b c d^{-1} \cdot a c d^{-1} \cdot c \equiv a b c \bmod p$, dus $c^{2} \equiv d^{2} \bmod p$. Analoog vinden we op de verticale lijn $b^{2} \equiv d^{2}$ en op de lijn van linksonder naar rechts midden $a^{2} \equiv d^{2} \bmod p$. We concluderen dat de getallen $a, b, c$ en $d$ allemaal hetzelfde kwadraat moeten hebben. Uit $x^{2} \equiv y^{2} \operatorname{volgt}(x-y)(x+y) \equiv 0$ $\bmod p$, dus $p \mid x-y$ of $p \mid x+y$, want $p$ is priem. Dus geldt $x \equiv y$ of $x \equiv-y$. Dat zijn twee opties, want zou $y \equiv-y$, dan $2 y \equiv 0$, dus $p \mid 2 y$, dus $p \mid y$ wegens $p>2$; tegenspraak. Er geldt dus dat de getallen $b, c$ en $d$ allemaal congruent aan $a$ of $-a$ moeten zijn. Als aan deze voorwaarde voldaan is, dan geldt $a^{2} \equiv b^{2} \equiv c^{2} \equiv d^{2}$ en dan volgt uit het voorgaande dat op alle zes de lijnen en op de cirkel het product congruent aan $a b c$ is.
Er zijn $p-1$ mogelijkheden voor het getal $a$ en daarna 2 mogelijkheden voor elk van de getallen $b, c$ en $d$. Dus totaal zijn er $8(p-1)$ manieren om de getallen toe te kennen.
|
{
"resource_path": "Dutch_TST/segmented/nl-2021-B2021_uitwerkingen.jsonl",
"problem_match": "\nOpgave 3.",
"solution_match": "# Oplossing I."
}
|
98193d56-ac42-5fa9-96c0-078e604ecb37
| 604,936
|
Given is a triangle $ABC$ with the property that $|AB|+|AC|=3|BC|$. Let $T$ be the point on line segment $AC$ such that $|AC|=4|AT|$. Let $K$ and $L$ be points on the interior of line segments $AB$ and $AC$ respectively, such that first, $KL \parallel BC$ and second, $KL$ is tangent to the incircle of $\triangle ABC$. Let $S$ be the intersection of $BT$ and $KL$. Determine the ratio $\frac{|SL|}{|KL|}$.
|
The quadrilateral $K B C L$ touches all its sides to the inscribed circle of $\triangle A B C$. At each vertex, there are two equal tangent segments. Two opposite sides of the quadrilateral consist precisely of the four different tangent segments, so $|K B|+|L C|=|K L|+|B C|$.
Given $K L \| B C$, we have $\triangle A K L \sim \triangle A B C$. Let $t$ be the scaling factor of this similarity, so $|A K|=t|A B|,|A L|=t|A C|$, and $|K L|=t|B C|$. Then $|B K|=$ $|A B|-|A K|=|A B|-t|A B|=(1-t)|A B|$. Similarly, $|C L|=(1-t)|A C|$. Now we have
$t|B C|+|B C|=|K L|+|B C|=|K B|+|L C|=(1-t)|A B|+(1-t)|A C|=3(1-t)|B C|$,
where the last equality holds due to the given condition in the problem. Dividing by $|B C|$ gives $1+t=3-3 t$, or $4 t=2$ thus $t=\frac{1}{2}$. We conclude that $K$ is the midpoint of $A B$ and $L$ is the midpoint of $A C$.
We already knew $\triangle A K L \sim \triangle A B C$, which implies $\frac{|K L|}{|B C|}=\frac{|A L|}{|A C|}$. Given $K L \| B C$, we also have $\triangle T S L \sim \triangle T B C$, so $\frac{|S L|}{|B C|}=\frac{|T L|}{|T C|}$. Combining these ratios, we get
$$
\frac{|S L|}{|K L|}=\frac{|S L|}{|B C|} \cdot \frac{|B C|}{|K L|}=\frac{|T L|}{|T C|} \cdot \frac{|A C|}{|A L|} .
$$
We know that $\frac{|A C|}{|A L|}=2$, since $L$ is the midpoint of $A C$. This also means that $T$ is the midpoint of $A L$, as $4|A T|=|A C|=2|A L|$. Thus $\frac{|T L|}{|T C|}=\frac{\frac{1}{4}|A C|}{\frac{3}{4}|A C|}=\frac{1}{3}$. We conclude that $\frac{|S L|}{|K L|}=\frac{1}{3} \cdot 2=\frac{2}{3}$.
|
\frac{2}{3}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Gegeven is een driehoek $A B C$ met de eigenschap dat $|A B|+|A C|=3|B C|$. Zij $T$ het punt op lijnstuk $A C$ zodat $|A C|=4|A T|$. Laat $K$ en $L$ punten zijn op het inwendige van respectievelijk lijnstukken $A B$ en $A C$ zodat ten eerste $K L \| B C$ en ten tweede $K L$ raakt aan de ingeschreven cirkel van $\triangle A B C$. $\mathrm{Zij} S$ het snijpunt van $B T$ en $K L$. Bepaal de verhouding $\frac{|S L|}{|K L|}$.

|
De vierhoek $K B C L$ raakt met alle zijden aan de ingeschreven cirkel van $\triangle A B C$. Bij elk hoekpunt zitten twee gelijke raaklijnstukjes. Twee overstaande zijden van de vierhoek bestaan samen precies uit de vier verschillende raaklijnstukjes, dus geldt $|K B|+|L C|=|K L|+|B C|$.
Vanwege $K L \| B C$ geldt $\triangle A K L \sim \triangle A B C$. Noem $t$ de vermenigvuldigingsfactor van deze gelijkvormigheid, dus $|A K|=t|A B|,|A L|=t|A C|$ en $|K L|=t|B C|$. Dan is $|B K|=$ $|A B|-|A K|=|A B|-t|A B|=(1-t)|A B|$. Analoog geldt $|C L|=(1-t)|A C|$. Er geldt nu
$t|B C|+|B C|=|K L|+|B C|=|K B|+|L C|=(1-t)|A B|+(1-t)|A C|=3(1-t)|B C|$,
waarbij de laatste gelijkheid geldt vanwege het gegeven in de opgave. Delen door $|B C|$ geeft nu $1+t=3-3 t$, oftewel $4 t=2$ dus $t=\frac{1}{2}$. We concluderen dat $K$ het midden van $A B$ is en $L$ het midden van $A C$.
We wisten al $\triangle A K L \sim \triangle A B C$, waaruit volgt $\frac{|K L|}{|B C|}=\frac{|A L|}{|A C|}$. Er geldt wegens $K L \| B C$ ook $\triangle T S L \sim \triangle T B C$, dus $\frac{|S L|}{|B C|}=\frac{|T L|}{|T C|}$. Combineren we deze verhoudingen, dan krijgen we
$$
\frac{|S L|}{|K L|}=\frac{|S L|}{|B C|} \cdot \frac{|B C|}{|K L|}=\frac{|T L|}{|T C|} \cdot \frac{|A C|}{|A L|} .
$$
We weten dat $\frac{|A C|}{|A L|}=2$, omdat $L$ het midden van $A C$ is. Dit betekent ook dat $T$ het midden van $A L$ is, aangezien $4|A T|=|A C|=2|A L|$. Dus $\frac{|T L|}{|T C|}=\frac{\frac{1}{4}|A C|}{\frac{3}{4}|A C|}=\frac{1}{3}$. We concluderen dat $\frac{|S L|}{|K L|}=\frac{1}{3} \cdot 2=\frac{2}{3}$.
|
{
"resource_path": "Dutch_TST/segmented/nl-2021-B2021_uitwerkingen.jsonl",
"problem_match": "\nOpgave 5.",
"solution_match": "\nOplossing I."
}
|
e75063bd-6f2d-5b1b-9e09-bd42e3908ad8
| 604,981
|
At a fish market, there are 10 stalls, all selling the same 10 types of fish. All the fish are caught in either the North Sea or the Mediterranean Sea, and each stall has only one sea of origin for each type of fish. A number, $k$, of customers buy one fish from each stall such that they have one fish of each type. Furthermore, we know that each pair of customers has at least one fish of a different origin. We consider all possible ways to stock the stalls according to the above rules.
What is the maximum possible value of $k$?
|
The answer is $2^{10}-10$. First, we note that there are $2^{10}$ possible combinations for the origins of each fish species. We will show that there are always at least 10 exceptions (possibilities that are ruled out) and that there is a market setup where there are exactly 10 exceptions.
We order both the stalls and the fish from 1 to 10. For a stall $i$, we define the sequence $a_{i} \in\{M, N\}^{10}$ as the origins of the 10 fish species in this stall (for example, $a_{1}=(M, M, M, N, M, N, N, M, M, M)$). Let $c_{i}$ be the complement of this sequence: we replace all $M$ with $N$ and vice versa. Since every customer has bought a fish from stall $i$, no customer can have the sequence $c_{i}$. If the sequences $c_{i}$ with $1 \leq i \leq 10$ are all different, then we have 10 exceptions.
On the other hand, suppose that stalls $i$ and $j$ sell fish from exactly the same seas, i.e., $a_{i}=a_{j}$. Then also $c_{i}=c_{j}$. We define the sequences $d_{k}$ with $1 \leq k \leq 10$ by swapping the origin of fish $k$ in the sequence $c_{i}$. These are precisely the sequences that match the sequence $a_{i}=a_{j}$ in exactly one sea. If a customer has bought a sequence $d_{k}$, then there can be at most one fish from stall $i$ or $j$ in that sequence. This contradicts the fact that the customer has bought a fish from both stalls. We conclude that in this case, we also have at least 10 exceptions $d_{k}$ (and in fact also $c_{i}$).
We construct a market as follows where you can buy $2^{10}-10$ different combinations of fish origins as described in the problem: stall $i$ sells only fish from the North Sea, with the exception of fish $i$ from the Mediterranean Sea. Let $b \in\{M, N\}^{10}$ be a sequence of origins such that it does not contain exactly one $N$. We will show that we can buy 10 different fish from 10 different stalls so that $b$ is the sequence of origins. We split the fish in $b$ into a set $A$ from the Mediterranean Sea and a set $B$ from the North Sea, that is, $A$ is the set of indices where $b$ has an $M$ and $B$ is the set of indices where $b$ has an $N$. For $i \in A$, we buy fish species $i$ from stall $i$, so we indeed get a fish from the Mediterranean Sea. If $B$ is empty, then we are done. Otherwise, $B$ has at least two elements, and we write $B=\left\{i_{1}, \ldots, i_{n}\right\} \subset\{1, \ldots, 10\}$. For $i_{k} \in B$, we buy fish species $i_{k}$ from stall $i_{k+1}$, where we compute the indices modulo $n$. Since $n \neq 1$, it holds that $i_{k+1} \neq i_{k}$, so this fish indeed comes from the North Sea.
|
2^{10}-10
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Op een vismarkt staan 10 kraampjes die allemaal dezelfde 10 vissoorten verkopen. Alle vissen zijn gevangen in de Noordzee of de Middellandse Zee, en elk kraampje heeft per vissoort maar één zee van afkomst. Een aantal, $k$, klanten koopt van elk kraampje één vis zo dat ze één vis van elke soort hebben. Verder weten we dat elk tweetal klanten een vissoort hebben met verschillende afkomst. We beschouwen alle mogelijke manieren om de kraampjes te vullen volgens de bovenstaande spelregels.
Wat is de maximaal mogelijke waarde van $k$ ?
|
Het antwoord is $2^{10}-10$. Ten eerste merken we op dat er $2^{10}$ mogelijke combinaties zijn voor de afkomsten per vissoort. We gaan laten zien dat er altijd minstens 10 uitzonderingen zijn (mogelijkheden die afvallen) en dat er een marktopzet is waarbij er precies 10 uitzonderingen zijn.
We ordenen zowel de kraampjes als de vissen van 1 tot 10. Voor een kraampje $i$ definiëren we het rijtje $a_{i} \in\{M, N\}^{10}$ als de afkomsten van de 10 vissoorten in dit kraampje (bijvoorbeeld $a_{1}=(M, M, M, N, M, N, N, M, M, M)$ ). Zij $c_{i}$ het complement van dit rijtje: we vervangen alle $M$ door $N$ en vice versa. Aangezien elke klant een vis heeft gekocht van kraampje $i$ kan geen enkele klant het rijtje $c_{i}$ hebben. Als de rijtjes $c_{i}$ met $1 \leq i \leq 10$ allemaal verschillend zijn, dan hebben we dus 10 uitzonderingen.
Stel aan de andere kant dat kraampjes $i$ en $j$ vissen van precies dezelfde zeeën verkopen, oftewel $a_{i}=a_{j}$. Dan ook $c_{i}=c_{j}$. Dan definiëren we de rijtjes $d_{k}$ met $1 \leq k \leq 10$ door in het rijtje $c_{i}$ de afkomst van vis $k$ te wisselen. Dit zijn precies de rijtjes die één zee overeenkomstig hebben met het rijtje $a_{i}=a_{j}$. Als een klant een rijtje $d_{k}$ heeft ingekocht, dan kan daar dus maximaal één vis tussen zitten van kraampje $i$ of $j$. Dit is in tegenspraak met het feit dat de klant bij beide kraampjes een vis heeft gekocht. We concluderen dat we in dat geval ook minstens 10 uitzonderingen $d_{k}$ hebben (en in feite ook nog $c_{i}$ ).
We construeren als volgt een markt waar je $2^{10}-10$ verschillende combinaties van afkomsten van vissen kan kopen zoals in de opgave: kraampje $i$ verkoopt alleen vis uit de Noordzee met uitzondering van vis $i$ uit de Middellandse Zee. Zij $b \in\{M, N\}^{10}$ een rijtje afkomsten zo dat er niet precies één $N$ in voorkomt. We gaan laten zien dat we 10 verschillende vissen van 10 verschillende kraampjes kunnen kopen zo dat $b$ het rijtje afkomsten is. We splitsen de vissen in $b$ op in een verzameling $A$ uit de Middellandse Zee en een verzameling $B$ uit de Noordzee, dat wil zeggen $A$ is de verzameling indices waar in $b$ een $M$ staat en $B$ is de verzameling indices waar een $N$ staat. Voor $i \in A$ kopen we vissoort $i$ bij kraampje $i$, zodat we inderdaad een vis uit de Middellandse Zee krijgen. Als $B$ leeg is, dan zijn we klaar. Anders heeft $B$ minstens twee elementen en schrijven we $B=\left\{i_{1}, \ldots, i_{n}\right\} \subset\{1, \ldots, 10\}$. Voor $i_{k} \in B$ kopen we vissoort $i_{k}$ bij kraampje $i_{k+1}$, waarbij we de indices modulo $n$ rekenen. Omdat $n \neq 1$ geldt dat $i_{k+1} \neq i_{k}$, dus deze vis komt inderdaad uit de Noordzee.
|
{
"resource_path": "Dutch_TST/segmented/nl-2022-B2022_uitwerkingen.jsonl",
"problem_match": "\nOpgave 5.",
"solution_match": "\nOplossing."
}
|
2321a80c-d112-5c44-9205-ee9c9fcc25a9
| 605,277
|
For real numbers $x$ and $y$, we define $M(x, y)$ as the maximum of the three numbers $x y, (x-1)(y-1)$, and $x+y-2 x y$. Determine the smallest possible value of $M(x, y)$ over all real numbers $x$ and $y$ with $0 \leq x, y \leq 1$.
|
We show that the minimum value is $\frac{4}{9}$. This value can be achieved by taking $x=y=\frac{2}{3}$. Then we have $x y=\frac{4}{9}, (x-1)(y-1)=\frac{1}{9}$, and $x+y-2 x y=\frac{4}{9}$, so the maximum is indeed $\frac{4}{9}$.
Now we will prove that $M(x, y) \geq \frac{4}{9}$ for all $x$ and $y$. Let $a=x y, b=(x-1)(y-1)$, and $c=x+y-2 x y$. If we replace $x$ and $y$ with $1-x$ and $1-y$, then $a$ and $b$ are swapped and $c$ remains the same, because $(1-x)+(1-y)-2(1-x)(1-y)=2-x-y-2+2 x+2 y-2 x y=x+y-2 x y$. Thus, $M(1-x, 1-y)=M(x, y)$. We have $x+y=2-(1-x)-(1-y)$, so at least one of $x+y$ and $(1-x)+(1-y)$ is greater than or equal to 1, which means we can assume without loss of generality that $x+y \geq 1$.
Now write $x+y=1+t$ with $t \geq 0$. We also have $t \leq 1$, because $x, y \leq 1$ so $x+y \leq 2$. From the inequality of the arithmetic and geometric means, we get
$$
x y \leq\left(\frac{x+y}{2}\right)^{2}=\frac{(1+t)^{2}}{4}=\frac{t^{2}+2 t+1}{4}
$$
We have $b=x y-x-y+1=x y-(1+t)+1=x y-t=a-t$, so $b \leq a$. Furthermore,
$$
c=x+y-2 x y \geq(1+t)-2 \cdot \frac{t^{2}+2 t+1}{4}=\frac{2+2 t}{2}-\frac{t^{2}+2 t+1}{2}=\frac{1-t^{2}}{2}.
$$
If $t \leq \frac{1}{3}$, then $c \geq \frac{1-t^{2}}{2} \geq \frac{1-\frac{1}{9}}{2}=\frac{4}{9}$, and thus $M(x, y) \geq \frac{4}{9}$.
The remaining case is $t>\frac{1}{3}$. We have $c=x+y-2 x y=1+t-2 a>\frac{4}{3}-2 a$. We have $M(x, y) \geq \max \left(a, \frac{4}{3}-2 a\right)$, so
$$
3 M(x, y) \geq a+a+\left(\frac{4}{3}-2 a\right)=\frac{4}{3},
$$
which implies that $M(x, y) \geq \frac{4}{9}$.
We conclude that the minimum value of $M(x, y)$ is $\frac{4}{9}$.
|
\frac{4}{9}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Voor reële getallen $x$ en $y$ definiëren we $M(x, y)$ als het maximum van de drie getallen $x y,(x-1)(y-1)$ en $x+y-2 x y$. Bepaal de kleinst mogelijke waarde van $M(x, y)$ over alle reële getallen $x$ en $y$ met $0 \leq x, y \leq 1$.
|
We laten zien dat de minimale waarde $\frac{4}{9}$ is. Deze waarde kan bereikt worden door $x=y=\frac{2}{3}$ te nemen. Dan geldt $x y=\frac{4}{9},(x-1)(y-1)=\frac{1}{9}$ en $x+y-2 x y=\frac{4}{9}$, dus dan is het maximum inderdaad $\frac{4}{9}$.
Nu gaan we bewijzen dat $M(x, y) \geq \frac{4}{9}$ voor alle $x$ en $y$. Schrijf $a=x y, b=(x-1)(y-1)$ en $c=x+y-2 x y$. Als we $x$ en $y$ vervangen door $1-x$ en $1-y$, dan worden $a$ en $b$ verwisseld en blijft $c$ gelijk, omdat $(1-x)+(1-y)-2(1-x)(1-y)=2-x-y-2+2 x+2 y-2 x y=x+y-2 x y$. Dus $M(1-x, 1-y)=M(x, y)$. Er geldt $x+y=2-(1-x)-(1-y)$, dus minstens één $\operatorname{van} x+y$ en $(1-x)+(1-y)$ is groter of gelijk aan 1 , wat betekent dat we zonder verlies van algemeemheid mogen aannemen dat $x+y \geq 1$.
Schrijf nu $x+y=1+t$ met $t \geq 0$. Er geldt ook $t \leq 1$, want $x, y \leq 1$ dus $x+y \leq 2$. Uit de ongelijkheid van het rekenkundig en meetkundig gemiddelde volgt
$$
x y \leq\left(\frac{x+y}{2}\right)^{2}=\frac{(1+t)^{2}}{4}=\frac{t^{2}+2 t+1}{4}
$$
Er geldt $b=x y-x-y+1=x y-(1+t)+1=x y-t=a-t$, dus $b \leq a$. Verder is
$$
c=x+y-2 x y \geq(1+t)-2 \cdot \frac{t^{2}+2 t+1}{4}=\frac{2+2 t}{2}-\frac{t^{2}+2 t+1}{2}=\frac{1-t^{2}}{2} .
$$
Als nu $t \leq \frac{1}{3}$, dan geldt $c \geq \frac{1-t^{2}}{2} \geq \frac{1-\frac{1}{9}}{2}=\frac{4}{9}$ en dus ook $M(x, y) \geq \frac{4}{9}$.
Blijft over het geval $t>\frac{1}{3}$. Er geldt $c=x+y-2 x y=1+t-2 a>\frac{4}{3}-2 a$. Er geldt $M(x, y) \geq \max \left(a, \frac{4}{3}-2 a\right)$, dus
$$
3 M(x, y) \geq a+a+\left(\frac{4}{3}-2 a\right)=\frac{4}{3},
$$
waaruit volgt dat $M(x, y) \geq \frac{4}{9}$.
We concluderen dat de minimale waarde van $M(x, y)$ gelijk is aan $\frac{4}{9}$.
|
{
"resource_path": "Dutch_TST/segmented/nl-2022-C2022_uitwerkingen.jsonl",
"problem_match": "\nOpgave 3.",
"solution_match": "\nOplossing I."
}
|
03549d85-dd56-5fb4-a5c1-1994880cc169
| 605,307
|
In a sequence of numbers $a_{1}, a_{2}, \ldots, a_{1000}$ consisting of 1000 different numbers, a pair $\left(a_{i}, a_{j}\right)$ with $i<j$ is called increasing if $a_{i}<a_{j}$ and decreasing if $a_{i}>a_{j}$. Determine the largest positive integer $k$ with the property that in any sequence of 1000 different numbers, there are at least $k$ non-overlapping increasing pairs or at least $k$ non-overlapping decreasing pairs.
|
We will prove that the largest $k$ is equal to 333. First, consider the sequence $1000, 999, 998, \ldots, 669, 668, 1, 2, 3, \ldots, 666, 667$. The first 333 numbers in the sequence are not usable in an increasing pair, because for each of these numbers, only larger numbers are to the left and only smaller numbers are to the right. Therefore, only the last 667 numbers are available for increasing pairs, and this yields at most 333 non-overlapping increasing pairs. For a decreasing pair $\left(a_{i}, a_{j}\right)$ with $i<j$, $a_{i}$ cannot be one of the numbers from 1 to 667, because for each of these numbers, only larger numbers are to the right. Thus, $a_{i}$ must be one of the first 333 numbers, which means there are at most 333 non-overlapping decreasing pairs. We conclude that $k>333$ cannot be satisfied.
Now we prove that for all $t \geq 1$, in a sequence of $3t-1$ different numbers, there are always at least $t$ non-overlapping increasing pairs or $t$ non-overlapping decreasing pairs. We prove this by induction on $t$. For $t=1$, the sequence has length 2, and this pair of numbers is either increasing or decreasing, so it holds. Now let $r \geq 1$ and assume the statement is true for $t=r$. We now consider $t=r+1$ and take an arbitrary sequence $a_{1}, a_{2}, \ldots, a_{3r+2}$ with $3r+2$ different numbers. If the sequence is completely increasing, we can divide the sequence into adjacent pairs, all of which are increasing. There are $\left\lfloor\frac{3r+2}{2}\right\rfloor \geq \frac{2r+2}{2}=r+1$ such pairs. If the sequence is completely decreasing, there are analogously at least $r+1$ decreasing pairs. If the sequence is neither completely increasing nor completely decreasing, there is a point in the sequence where it first increases and then decreases, or vice versa, i.e., there are numbers $a_{i}, a_{i+1}, a_{i+2}$ in the sequence with $a_{i}<a_{i+1}>a_{i+2}$ or $a_{i}>a_{i+1}<a_{i+2}$. In both cases, among these three numbers, there is both an increasing pair and a decreasing pair. Now apply the induction hypothesis to the sequence $a_{1}, a_{2}, \ldots, a_{i-1}, a_{i+3}, a_{i+4}, \ldots, a_{3r+2}$. This is a sequence with $3r+2-3=3r-1$ different numbers, so there are $r$ non-overlapping increasing pairs or $r$ non-overlapping decreasing pairs. In the first case, we add the increasing pair from $a_{i}, a_{i+1}, a_{i+2}$ to these, and in the second case, we add the decreasing pair. This gives us $r+1$ non-overlapping increasing pairs or $r+1$ non-overlapping decreasing pairs. This completes the induction.
Now substitute $t=333$ into this result: in a sequence of 998 different numbers, there are always at least 333 non-overlapping increasing pairs or at least 333 non-overlapping decreasing pairs. This also holds for a sequence of 1000 numbers (ignore the last two numbers in the sequence). Therefore, $k=333$ satisfies the condition and is thus the largest $k$ that satisfies it.
|
333
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
In een getallenrij $a_{1}, a_{2}, \ldots, a_{1000}$ van 1000 verschillende getallen heet een paar $\left(a_{i}, a_{j}\right)$ met $i<j$ stijgend als $a_{i}<a_{j}$ en dalend als $a_{i}>a_{j}$. Bepaal de grootste positieve gehele $k$ met de eigenschap dat in elke rij van 1000 verschillende getallen ten minste $k$ niet-overlappende stijgende paren te vinden zijn of ten minste $k$ niet-overlappende dalende paren.
|
We gaan bewijzen dat de grootste $k$ gelijk aan 333 is. Bekijk ten eerste de rij $1000,999,998, \ldots, 669,668,1,2,3, \ldots, 666,667$. De eerste 333 getallen in de rij zijn niet bruikbaar in een stijgend paar, omdat voor elk van deze getallen geldt dat links van dit getal alleen maar grotere getallen staan en rechts van dit getal alleen maar kleinere getallen. Voor de stijgende paren zijn dus alleen de laatste 667 getallen beschikbaar en dat levert hooguit 333 niet-overlappende stijgende paren op. Voor een dalend paar $\left(a_{i}, a_{j}\right)$ met $i<j$ geldt dat $a_{i}$ niet één van de getallen 1 tot en met 667 kan zijn, want voor elk van deze getallen geldt dat er rechts van dit getal alleen maar grotere getallen staan. Dus $a_{i}$ moet één van de eerste 333 getallen zijn, waaruit volgt dat er hooguit 333 niet-overlappende dalende paren zijn. We concluderen dat $k>333$ niet kan voldoen.
Nu bewijzen we voor alle $t \geq 1$ dat er in een getallenrij van $3 t-1$ verschillende getallen altijd minstens $t$ niet-overlappende stijgende paren of $t$ niet-overlappende dalende paren te vinden zijn. We bewijzen dit met inductie naar $t$. Voor $t=1$ geldt dat de getallenrij lengte 2 heeft en dit paar getallen is ofwel stijgend ofwel dalend, dus het klopt. Zij nu $r \geq 1$ en veronderstel dat de bewering waar is voor $t=r$. We bekijken nu $t=r+1$ en nemen een willekeurige getallenrij $a_{1}, a_{2}, \ldots, a_{3 r+2}$ met $3 r+2$ verschillende getallen. Als de rij volledig stijgend is, dan kunnen we de rij opdelen in buurparen en die zijn allemaal stijgend. Dit zijn er $\left\lfloor\frac{3 r+2}{2}\right\rfloor \geq \frac{2 r+2}{2}=r+1$. Als de rij volledig dalend is, zijn er analoog minstens $r+1$ dalende paren. Als de rij niet volledig stijgend, maar ook niet volledig dalend is, dan is er een plek in de rij waar de rij eerst stijgt en dan daalt of andersom, oftewel: er zijn getallen $a_{i}, a_{i+1}, a_{i+2}$ in de rij met $a_{i}<a_{i+1}>a_{i+2}$ of $a_{i}>a_{i+1}<a_{i+2}$. In beide gevallen zit er in deze drie getallen zowel een stijgend paar als een dalend paar. Pas nu de inductiehypothese toe op de rij $a_{1}, a_{2}, \ldots, a_{i-1}, a_{i+3}, a_{i+4}, \ldots, a_{3 r+2}$. Dit is een rij met $3 r+2-3=3 r-1$ verschillende getallen, dus zijn er $r$ niet-overlappende stijgende paren te vinden of $r$ niet-overlappende dalende paren. In het eerste geval voegen we hier het stijgende paar uit $a_{i}, a_{i+1}, a_{i+2}$ aan toe en in het tweede geval juist het dalende paar. Daarmee hebben we dan $r+1$ niet-overlappende stijgende paren of $r+1$ niet-overlappende dalende paren gevonden. Dat voltooit de inductie.
Vul nu $t=333$ in dit resultaat in: in een rij van 998 verschillende getallen zijn altijd minstens 333 niet-overlappende stijgende paren of minstens 333 niet-overlappende dalende paren te vinden. In een rij van 1000 getallen geldt dit dus ook (negeer de laatste twee getallen in de rij). Dus $k=333$ voldoet en is daarmee de grootste $k$ die voldoet.
|
{
"resource_path": "Dutch_TST/segmented/nl-2022-C2022_uitwerkingen.jsonl",
"problem_match": "\nOpgave 4.",
"solution_match": "\nOplossing."
}
|
d605284a-3119-5e9b-bae0-170c3065481f
| 605,328
|
On the ceiling of a room hang 15 lamps, numbered from 1 to 15. Initially, all the lamps are off. In another room are 15 switches: one switch for lamp 1 and 2, one switch for lamp 2 and 3, one switch for lamp 3 and 4, and so on, up to a switch for lamp 15 and 1. When the switch for such a pair of lamps is flipped, the status of each of those two lamps changes (from on to off or vice versa). The switches are hung in a random order and all look identical. Raymond wants to find out which switch corresponds to which pair of lamps. From the room with the switches, he cannot see the lamps. He can, however, flip a number of switches and then go to the other room to see which lamps are on. He can do this multiple times. How many times must he minimally go to the other room to be certain of which switch corresponds to which pair of lamps?
|
With three rounds of walking, Raymond can never be certain. After all, if you note for each switch whether it is in the initial position or the flipped position in the three rounds, you can get $2^{3}=8$ different patterns. However, there are 15 switches, so there are multiple switches with the same pattern, and Raymond can never distinguish these switches from each other. Therefore, he must walk at least four times. We will prove that this is indeed sufficient.
Assume that Raymond, starting from the situation where all lights are off, flips a number of switches. If he flips all the switches or none at all, then all the lights will remain off afterward. Otherwise, there will always be a light that has been changed by only one flipped switch, so it will be on. Consider such a light $i$ that is on. Then the switch with $i-1$ and $i$ or the switch with $i$ and $i+1$ has been flipped. (Consider the light numbers modulo 15.) First, assume that the latter is the case. Now consider light $i+1$. If it is off, then the switch with $i+1$ and $i+2$ has also been flipped; if the light is on, then that switch has not been used. Next, we can deduce from the status of light $i+2$ whether the switch with $i+2$ and $i+3$ has been flipped or not. By continuing this process, we see that the status of all switches is determined. In the second case, if the switch with $i-1$ and $i$ has been flipped, then the status of all switches is also determined. Therefore, there are exactly two combinations of switches that result in the same status of the lights. If we choose one of these combinations and then flip all 15 switches again, the same lights will be on, so this must result in the second combination of switches. If the first combination of switches contains an even number of switches, then the second combination contains 15 minus that number, so an odd number of switches.
However, Raymond knows himself how many switches he has flipped. He can deduce from the status of the lights which two combinations of switches are possible, and only one of these can match the number of switches he has flipped. Therefore, he can precisely determine which lights the switches he has flipped correspond to; he only does not know which is which within that group of switches.
Write the numbers 1 to 15 in binary notation. For this, a maximum of 4 digits are needed; pad with zeros if necessary so that each number is written with exactly 4 digits. Raymond numbers the switches with these binary numbers. In the first round, he flips the switches whose numbers in binary notation start with a 1 and notes the 8 corresponding light pairs. In the second round, he first resets all switches and then selects the numbers that have a 1 in the second position in binary notation. Similarly, in the third round, he selects the third position in the binary notation, and in the fourth round, the fourth position. In each round, he can determine which light pairs the switches he used correspond to (only not which is which). Since each switch corresponds to a unique combination of rounds, he can then deduce from each switch which light pair it controls. For example, if a certain light pair is turned on in the first round, not in the second round, in the third round, and also in the fourth round, then it corresponds to the switch with binary code 1011, which is switch 11. Therefore, he can succeed in four rounds of walking.
|
4
|
Yes
|
Yes
|
math-word-problem
|
Logic and Puzzles
|
Aan het plafond van een kamer hangen 15 lampen, genummerd van 1 tot en met 15. In het begin zijn de lampen allemaal uit. In een andere kamer zijn 15 schakelaars: een schakelaar voor lamp 1 en 2 , een schakelaar voor lamp 2 en 3 , een schakelaar voor lamp 3 en 4, enzovoorts, tot en met een schakelaar voor lamp 15 en 1. Als de schakelaar voor zo'n tweetal lampen wordt omgezet, verandert elk van die twee lampen van status (van aan naar uit of andersom). De schakelaars hangen in een willekeurige volgorde en zien er allemaal identiek uit. Raymond wil uitzoeken welke schakelaar bij welk tweetal lampen hoort. Vanuit de kamer met de schakelaars kan hij de lampen niet zien. Hij kan wel een aantal schakelaars omzetten en vervolgens naar de andere kamer lopen om te kijken welke lampen er aan staan. Dit kan hij meerdere keren doen. Hoe vaak moet hij minimaal naar de andere kamer lopen om van elke schakelaar zeker te weten bij welk tweetal lampen die hoort?
|
Met drie keer lopen kan Raymond het nooit met zekerheid weten. Immers, als je voor elke schakelaar noteert of hij in de drie rondes in de beginstand of juist de omgezette stand staat, dan kun je $2^{3}=8$ verschillende patronen krijgen. Er zijn echter 15 schakelaars, dus er zijn meerdere schakelaars met hetzelfde patroon en Raymond kan dan nooit deze schakelaars van elkaar onderscheiden. Hij moet dus minimaal vier keer lopen. We bewijzen dat dit inderdaad voldoende is.
Stel dat Raymond vanuit de situatie waarin alle lampen uit staan, een aantal schakelaars om zet. Als hij alle schakelaars om zet of helemaal geen, dan staan daarna alle lampen uit. Anders is er altijd een lamp die maar door één omgezette schakelaar van status is veranderd, dus die aan staat. Bekijk zo'n lamp $i$ die aan staat. Dan is de schakelaar met $i-1$ en $i$ of de schakelaar met $i$ en $i+1$ omgezet. (Reken de lampnummers modulo 15.) Neem eerst aan dat het het tweede is. Bekijk nu lamp $i+1$. Als die uit staat, dan is de schakelaar met $i+1$ en $i+2$ ook omgezet; staat de lamp aan, dan is die schakelaar juist niet gebruikt. Vervolgens kunnen we uit de status van lamp $i+2$ afleiden of de schakelaar met $i+2$ en $i+3$ wel of niet omgezet is. Door zo door te gaan, zien we dat van alle schakelaars vast ligt of ze wel of niet omgezet zijn. In het tweede geval, als juist de schakelaar met $i-1$ en $i$ omgezet is, dan ligt ook van alle schakelaars vast of ze wel of niet omgezet zijn. Er zijn dus precies twee combinaties van schakelaars die samen dezelfde status van de lampen opleveren. Als we één van die combinaties kiezen en vervolgens alle 15 schakelaars nogmaals omzetten, dan staan weer precies dezelfde lampen aan, dus dit moet precies de tweede combinatie van schakelaars opleveren. Als nu de eerste combinatie van schakelaars een even aantal schakelaars bevat, dan bevat de tweede combinatie 15 min dat aantal, dus een oneven aantal schakelaars.
Raymond weet echter zelf hoeveel schakelaars hij heeft omgezet. Hij kan aan de hand van de situatie van de lampen afleiden welke twee combinaties van schakelaars er mogelijk zijn en daarvan kan er maar één kloppen met het aantal schakelaars dat hij heeft omgezet. Hij kan dus precies achterhalen voor welke lampen de schakelaars zijn die hij heeft omgezet;
hij weet alleen binnen die groep schakelaars niet welke welke is.
Schrijf nu de getallen 1 tot en met 15 in binaire notatie. Daarvoor zijn maximaal 4 cijfers nodig; vul eventueel aan met nullen zodat elk getal met precies 4 cijfers geschreven wordt. Raymond nummert de schakelaars met deze binaire getallen. Vervolgens zet hij in de eerste ronde de schakelaars om waarvan het nummer in binaire notatie met een 1 begint en noteert hij de 8 bijbehorende lampentweetallen. In de tweede ronde zet hij eerst alle schakelaars weer terug en kiest hij vervolgens de nummers die in binaire notatie op de tweede positie een 1 hebben. Op dezelfde manier kiest hij in de derde ronde de derde positie in de binaire schrijfwijze en in de vierde ronde de vierde positie. In elke ronde kan hij achterhalen voor welke lampentweetallen de schakelaars zijn die hij heeft gebruikt (alleen niet welke welke is). Omdat elke schakelaar correspondeert met een unieke combinatie van rondes, kan hij vervolgens van elke schakelaar uitpuzzelen welk tweetal lampen die schakelaar bedient. Als bijvoorbeeld een bepaald lampentweetal wel in de eerste ronde, niet in de tweede ronde, wel in de derde en ook in de veride ronde wordt aangezet, dan hoort hier de schakelaar bij met binaire code 1011, dus schakelaar 11. Het lukt hem dus in vier keer lopen.
|
{
"resource_path": "Dutch_TST/segmented/nl-2022-D2022_uitwerkingen.jsonl",
"problem_match": "\nOpgave 3.",
"solution_match": "\nOplossing."
}
|
5a1b8e50-61b7-57ca-829d-e0c28ff4a2d9
| 605,365
|
Let $n>1$ be an integer. In a row, there are $n$ boxes, and we have $n+1$ identical stones. A distribution is a way to distribute the stones over the boxes, with each stone being in exactly one box. We say that two such distributions are a stone's throw away from each other if we can obtain one distribution from the other by moving exactly one stone to a different box. The sociability of a distribution $a$ is defined as the number of distributions that are a stone's throw away from $a$. Determine the average sociability over all possible distributions.
(Two distributions are the same if there are the same number of stones in the $i$-th box of both rows, for all $i \in\{1,2, \ldots, n\}$.)
Answer. $\frac{n^{2}-1}{2}$
In the solutions below, we call two distributions neighbors if they are a stone's throw away from each other.
|
We count the number, $N_{k}$, of distributions that contain exactly $k$ empty boxes with $0 \leq k \leq n-1$ (since not all boxes can be empty). There are $\binom{n}{k}$ ways to choose the empty boxes and by the stars and bars principle $\binom{(k+1)+(n-k)-1}{k+1}=\binom{n}{k+1}$ ways to fill the remaining $n-k$ boxes with $n+1=(n-k)+(k+1)$ stones such that each of these boxes contains at least one stone. This gives a total of $N_{k}=\binom{n}{k} \cdot\binom{n}{k+1}$ distributions with exactly $k$ empty boxes.
Given such a distribution, we can move a stone from one of the $n-k$ non-empty boxes to one of the other $n-1$ boxes. This means that there are $(n-k)(n-1)$ different distributions within one stone move. Thus, the sociability of each of these $N_{k}$ distributions is $(n-k)(n-1)$.
For $k^{\prime}=(n-1)-k$, the number of distributions with exactly $k^{\prime}$ empty boxes is $N_{k^{\prime}}=\binom{n}{k^{\prime}} \cdot\binom{n}{k^{\prime}+1}=\binom{n}{n-1-k} \cdot\binom{n}{n-k}=\binom{n}{k+1} \cdot\binom{n}{k}$, so $N_{k^{\prime}}=N_{k}$. The sociability of these $N_{k}$ distributions is $\left(n-k^{\prime}\right)(n-1)=(k+1)(n-1)$. Therefore, the average sociability of these two (possibly the same) sets of distributions is $\frac{(n-k)+(k+1)}{2}(n-1)=\frac{n+1}{2}(n-1)$. Since this is constant in $k$, it is also the overall average.
|
\frac{n^{2}-1}{2}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Zij $n>1$ een geheel getal. Op een rij staan $n$ dozen, en we hebben $n+1$ identieke stenen. Een verdeling is een manier om de stenen over de dozen te verdelen, waarbij elke steen in precies één doos zit. We zeggen dat twee van zulke verdelingen zich op een steenworp afstand van elkaar bevinden als we de ene verdeling uit de andere kunnen verkrijgen door precies één steen te verplaatsen naar een andere doos. De gezelligheid van een verdeling $a$ is gedefinieerd als het aantal verdelingen dat zich op een steenworp afstand van $a$ bevindt. Bepaal de gemiddelde gezelligheid over alle mogelijke verdelingen.
(Twee verdelingen zijn hetzelfde als er in de $i$-de doos van beide rijen evenveel stenen zitten, voor alle $i \in\{1,2, \ldots, n\}$.)
Antwoord. $\frac{n^{2}-1}{2}$
In de oplossingen hieronder noemen we twee verdelingen buren als ze op een steenworp afstand van elkaar liggen.
|
We tellen het aantal, $N_{k}$, verdelingen dat precies $k$ lege dozen bevat met $0 \leq k \leq n-1$ (aangezien niet alle dozen leeg kunnen zijn). Er zijn $\binom{n}{k}$ manieren om de lege dozen te kiezen en wegens het paaseierenprincipe $\binom{(k+1)+(n-k)-1}{k+1}=\binom{n}{k+1}$ manieren om de overige $n-k$ dozen te vullen met $n+1=(n-k)+(k+1)$ stenen zo dat elke van deze dozen minstens een steen bevat. Dit geeft een totaal van $N_{k}=\binom{n}{k} \cdot\binom{n}{k+1}$ verdelingen met precies $k$ lege dozen.
Gegeven zo'n verdeling kunnen we een steen van een van de de $n-k$ niet-lege dozen verplaatsen naar een van de andere $n-1$ dozen. Dit betekent dat er $(n-k)(n-1)$ verschillende verdelingen op steenworp afstand liggen. Dus de gezelligheid van elk van deze $N_{k}$ verdelingen is $(n-k)(n-1)$.
Voor $k^{\prime}=(n-1)-k$ is het aantal verdelingen met precies $k^{\prime}$ lege dozen gelijk aan $N_{k^{\prime}}=\binom{n}{k^{\prime}} \cdot\binom{n}{k^{\prime}+1}=\binom{n}{n-1-k} \cdot\binom{n}{n-k}=\binom{n}{k+1} \cdot\binom{n}{k}$, dus $N_{k^{\prime}}=N_{k}$. De gezelligheid van deze $N_{k}$ verdelingen is $\left(n-k^{\prime}\right)(n-1)=(k+1)(n-1)$. Dus de gemiddelde gezelligheid van deze twee (mogelijk dezelfde) verzamelingen verdelingen is $\frac{(n-k)+(k+1)}{2}(n-1)=\frac{n+1}{2}(n-1)$. Aangezien dit constant is in $k$, is dit ook het totale gemiddelde.
|
{
"resource_path": "Dutch_TST/segmented/nl-2022-E2022_uitwerkingen.jsonl",
"problem_match": "\nOpgave 2.",
"solution_match": "\nOplossing I."
}
|
e103e672-17d5-53cc-b28d-811e774e1077
| 605,421
|
Determine the largest real number $M$ such that for every infinite sequence $x_{0}, x_{1}, x_{2}, \ldots$ of real numbers that satisfies
a) $x_{0}=1$ and $x_{1}=3$,
b) $x_{0}+x_{1}+\cdots+x_{n-1} \geq 3 x_{n}-x_{n+1}$,
it holds that
$$
\frac{x_{n+1}}{x_{n}}>M
$$
for all $n \geq 0$.
|
Answer: the largest possible constant for which this holds is $M=2$.
This problem is a typical example where it pays to take a stronger induction hypothesis than you strictly need: we show by induction that $x_{n+1}>2 x_{n}>x_{n}+x_{n-1}+\ldots+x_{0}$. For $n=0$, this translates to $x_{1}>2 x_{0}>x_{0}$, which, with the given initial values, translates to $3>2>1$. Now assume as the induction hypothesis that $x_{n+1}>2 x_{n}>x_{n}+x_{n-1}+\ldots+x_{0}$. Then for $x_{n+2}$, using the condition that
$$
\begin{aligned}
x_{n+2} & \geq 3 x_{n+1}-\left(x_{n}+\ldots+x_{0}\right) \\
& >2 x_{n+1} \\
& >x_{n+1}+x_{n}+\ldots+x_{0} .
\end{aligned}
$$
This completes the induction step. From this, it follows that for all possible sequences and all possible $n$, $\frac{x_{n+1}}{x_{n}}>2$.
To show that we cannot find a higher value for $M$, we look at the sequence for which equality holds in b), i.e., $x_{0}+x_{1}+\cdots+x_{n-1}=3 x_{n}-x_{n+1}$. Then we have
$$
\begin{aligned}
x_{n+1} & =3 x_{n}-\left(x_{n-1}+\ldots+x_{0}\right) \\
& =3 x_{n}-x_{n-1}-\left(x_{n-2}+\ldots+x_{0}\right) \\
& =3 x_{n}-x_{n-1}-\left(3 x_{n-1}-x_{n}\right) \\
& =4 x_{n}-4 x_{n-1} .
\end{aligned}
$$
The characteristic equation of this homogeneous recurrence relation is $\lambda^{2}-4 \lambda+4=(\lambda-2)^{2}=0$. Since this has a double root at $\lambda=2$, the two characteristic solutions are $2^{n}$ and $n 2^{n}$. Solving $x_{n}=B 2^{n}+C n 2^{n}$ for the given initial values, we get $B+0=x_{0}=1$ and $2 B+2 C=x_{1}=3$, so $B=1$ and $C=\frac{1}{2}$. The solution for these initial values is thus $x_{n}=1 \cdot 2^{n}+\frac{1}{2} n 2^{n}=(n+2) 2^{n-1}$.
Now that we have solved the recurrence relation, we simply calculate that
$$
\frac{x_{n+1}}{x_{n}}=\frac{(n+3) 2^{n}}{(n+2) 2^{n-1}}=2 \frac{n+3}{n+2}=2\left(1+\frac{1}{n+2}\right)
$$
For large $n$, this fraction approaches 2 arbitrarily closely. To make this precise: suppose $M=2+\epsilon$ with $\epsilon>0$. Then for this sequence and $n>\frac{2}{\epsilon}-2$, we have $\frac{x_{n+1}}{x_{n}}=2+\frac{2}{n+2}<2+\epsilon=M$. Therefore, such an $M$ does not satisfy the condition. The largest value of $M$ that can satisfy is thus 2, and we have seen above that this value does indeed satisfy.
|
2
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Bepaal het grootste reële getal $M$ zodanig dat voor elke oneindige rij $x_{0}, x_{1}, x_{2}, \ldots$ van reële getallen die voldoet aan
a) $x_{0}=1$ en $x_{1}=3$,
b) $x_{0}+x_{1}+\cdots+x_{n-1} \geq 3 x_{n}-x_{n+1}$,
geldt dat
$$
\frac{x_{n+1}}{x_{n}}>M
$$
voor alle $n \geq 0$.
|
Antwoord: de grootst mogelijke constante waarvoor dit geldt is $M=2$.
Deze opgave is een typisch voorbeeld waarbij het baat om een sterkere inductiehypothese te nemen dan je strikt nodig hebt: we laten met inductie zien dat $x_{n+1}>2 x_{n}>x_{n}+x_{n-1}+$ $\ldots+x_{0}$. Voor $n=0$ staat hier dat $x_{1}>2 x_{0}>x_{0}$ wat zich met de gegeven beginwaarden vertaalt naar $3>2>1$. Stel nu als inductiehypothese dat $x_{n+1}>2 x_{n}>x_{n}+x_{n-1}+\ldots+x_{0}$. Dan vinden we voor $x_{n+2}$ met de voorwaarde dat
$$
\begin{aligned}
x_{n+2} & \geq 3 x_{n+1}-\left(x_{n}+\ldots+x_{0}\right) \\
& >2 x_{n+1} \\
& >x_{n+1}+x_{n}+\ldots+x_{0} .
\end{aligned}
$$
Dit voltooit de inductiestap. Hieruit volgt dat voor alle mogelijke rijtjes en alle mogelijk $n$ geldt dat $\frac{x_{n+1}}{x_{n}}>2$.
Om te laten zien dat we geen hogere waarde voor $M$ kunnen vinden, kijken we naar het rijtje waarvoor er gelijkheid geldt in b), oftewel $x_{0}+x_{1}+\cdots+x_{n-1}=3 x_{n}-x_{n+1}$. Dan geldt er dat
$$
\begin{aligned}
x_{n+1} & =3 x_{n}-\left(x_{n-1}+\ldots+x_{0}\right) \\
& =3 x_{n}-x_{n-1}-\left(x_{n-2}+\ldots+x_{0}\right) \\
& =3 x_{n}-x_{n-1}-\left(3 x_{n-1}-x_{n}\right) \\
& =4 x_{n}-4 x_{n-1} .
\end{aligned}
$$
De karakteristieke vergelijking van deze homogene recurrente betrekking is $\lambda^{2}-4 \lambda+4=$ $(\lambda-2)^{2}=0$. Aangezien dit een dubbel nulpunt heeft bij $\lambda=2$, zijn de twee karakteristieke oplossingen $2^{n}$ en $n 2^{n}$. Als we nu $x_{n}=B 2^{n}+C n 2^{n}$ oplossen voor de gegeven startwaarden vinden we $B+0=x_{0}=1$ en $2 B+2 C=x_{1}=3$, dus $B=1$ en $C=\frac{1}{2}$. De oplossing voor deze startwaarden is dus $x_{n}=1 \cdot 2^{n}+\frac{1}{2} n 2^{n}=(n+2) 2^{n-1}$.
Nu we de recurrente betrekking hebben opgelost rekenen we eenvoudig uit dat
$$
\frac{x_{n+1}}{x_{n}}=\frac{(n+3) 2^{n}}{(n+2) 2^{n-1}}=2 \frac{n+3}{n+2}=2\left(1+\frac{1}{n+2}\right)
$$
Voor grote $n$ gaat deze breuk dus willekeurig dicht naar 2. Om dat precies te maken: stel dat $M=2+\epsilon$ met $\epsilon>0$. Dan geldt er voor dit rijtje en $n>\frac{2}{\epsilon}-2$ dat $\frac{x_{n+1}}{x_{n}}=2+\frac{2}{n+2}<$ $2+\epsilon=M$. Dus zo'n $M$ voldoet niet. De grootste waarde van $M$ die kan voldoen is dus 2, en hierboven hebben we gezien dat die ook daadwerkelijk voldoet.
|
{
"resource_path": "Dutch_TST/segmented/nl-2023-C2023_uitwerkingen.jsonl",
"problem_match": "\nOpgave 2.",
"solution_match": "\nOplossing."
}
|
2fccd612-2839-58eb-aade-31bc9ae294e7
| 605,582
|
Find the smallest possible value of
$$
x y+y z+z x+\frac{1}{x}+\frac{2}{y}+\frac{5}{z},
$$
for positive real numbers $x, y$ and $z$.
|
Answer: the smallest possible value is $3 \sqrt[3]{36}$.
Using the arithmetic-geometric mean inequality, we find
$$
\begin{aligned}
x y+\frac{1}{3 x}+\frac{1}{2 y} & \geq 3 \sqrt[3]{x y \frac{1}{3 x} \frac{1}{2 y}}=3 \sqrt[3]{\frac{1}{6}} \\
y z+\frac{3}{2 y}+\frac{3}{z} & \geq 3 \sqrt[3]{y z \frac{3}{2 y} \frac{3}{z}}=3 \sqrt[3]{\frac{9}{2}} \\
x z+\frac{2}{3 x}+\frac{2}{z} & \geq 3 \sqrt[3]{x z \frac{2}{3 x} \frac{2}{z}}=3 \sqrt[3]{\frac{4}{3}}
\end{aligned}
$$
When we add these three inequalities, we get
$$
x y+y z+z x+\frac{1}{x}+\frac{2}{y}+\frac{5}{z} \geq 3\left(\sqrt[3]{\frac{1}{6}}+\sqrt[3]{\frac{9}{2}}+\sqrt[3]{\frac{4}{3}}\right)=3\left(\frac{1}{6}+\frac{1}{2}+\frac{1}{3}\right) \sqrt[3]{36}=3 \sqrt[3]{36}
$$
For each of the three inequalities, equality holds when the three terms are equal. We arrive at an equality case for all three when $(x, y, z)=\left(\frac{1}{3} \sqrt[3]{6}, \frac{1}{2} \sqrt[3]{6}, \sqrt[3]{6}\right)$, which is also easy to verify. Then $x y+y z+z x+\frac{1}{x}+\frac{2}{y}+\frac{5}{z}$ is indeed equal to
$$
\frac{1}{6} \sqrt[3]{36}+\frac{1}{2} \sqrt[3]{36}+\frac{1}{3} \sqrt[3]{36}+3 \frac{1}{\sqrt[3]{6}}+4 \frac{1}{\sqrt[3]{6}}+5 \frac{1}{\sqrt[3]{6}}=\sqrt[3]{36}+12 \frac{1}{\sqrt[3]{6}}=\sqrt[3]{36}+2 \sqrt[3]{36}=3 \sqrt[3]{36}
$$
Remark. After deciding to split the inequality into three inequalities using the arithmetic-geometric mean (one for $x y$, one for $y z$, and one for $x z$), there are different ways to find the coefficients for $\frac{1}{x}, \frac{1}{y}$, and $\frac{1}{z}$. First, you can be guided by examples you have found in your search for the equality case. For example, the expression equals 10 for $(x, y, z)=\left(\frac{2}{3}, 1,2\right)$, and with $(x, y, z)=\left(\frac{3}{5}, \frac{9}{10}, \frac{9}{5}\right)$, you get $\frac{324}{100}+\frac{12}{18} \cdot 10=3.24+6.6666 \ldots=9.9066 \ldots$.
A more structured approach is to introduce variables $a, b, c, d, e, f$ for the inequalities on $x y+a \frac{1}{x}+b \frac{1}{y}, y z+c \frac{1}{y}+d \frac{1}{z}$, and $z x+e \frac{1}{z}+f \frac{1}{x}$. Since these three terms must add up to the desired expressions, we get the conditions
$$
\begin{aligned}
f+a & =1, \\
b+c & =2, \\
d+e & =5 .
\end{aligned}
$$
Furthermore, we want equality to hold for certain $x, y$, and $z$. So the system
$$
\begin{aligned}
& x y=a \frac{1}{x}=b \frac{1}{y} \\
& y z=c \frac{1}{y}=d \frac{1}{z} \\
& z x=e \frac{1}{z}=f \frac{1}{x}
\end{aligned}
$$
must have a solution for some $x, y$, and $z$. From the first equation, it follows that $\frac{x}{y}=\frac{a}{b}$. But using the last two equations, we can also write this as
$$
\frac{x}{y}=\frac{z x}{y z}=\frac{f / x}{c / y}=\frac{f y}{c x} .
$$
This means that $\frac{f}{c}=\frac{x^{2}}{y^{2}}=\frac{a^{2}}{b^{2}}$, or $a^{2} / f=b^{2} / c$. Similarly, it holds that $c^{2} / b=d^{2} / e$ and $e^{2} / d=f^{2} / a$. Together with $f+a=1, b+c=2$, and $d+e=5$, we now have six equations in six variables. Although it is not easy to solve this system, it greatly simplifies the search because it is now easy to check whether $a, b, c, d, e, f$ satisfy the conditions. Other equations that can be derived from this system are, for example, $ace = bdf$ and $ad = be = cf$.
|
3 \sqrt[3]{36}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Vind de kleinst mogelijke waarde van
$$
x y+y z+z x+\frac{1}{x}+\frac{2}{y}+\frac{5}{z},
$$
voor positieve reële getallen $x, y$ en $z$.
|
Antwoord: de kleinst mogelijke waarde is $3 \sqrt[3]{36}$.
Met de ongelijkheid van het rekenkundig-meetkundig gemiddelde vinden we
$$
\begin{aligned}
x y+\frac{1}{3 x}+\frac{1}{2 y} & \geq 3 \sqrt[3]{x y \frac{1}{3 x} \frac{1}{2 y}}=3 \sqrt[3]{\frac{1}{6}} \\
y z+\frac{3}{2 y}+\frac{3}{z} & \geq 3 \sqrt[3]{y z \frac{3}{2 y} \frac{3}{z}}=3 \sqrt[3]{\frac{9}{2}} \\
x z+\frac{2}{3 x}+\frac{2}{z} & \geq 3 \sqrt[3]{x z \frac{2}{3 x} \frac{2}{z}}=3 \sqrt[3]{\frac{4}{3}}
\end{aligned}
$$
Wanneer we deze drie ongelijkheden optellen krijgen we
$$
x y+y z+z x+\frac{1}{x}+\frac{2}{y}+\frac{5}{z} \geq 3\left(\sqrt[3]{\frac{1}{6}}+\sqrt[3]{\frac{9}{2}}+\sqrt[3]{\frac{4}{3}}\right)=3\left(\frac{1}{6}+\frac{1}{2}+\frac{1}{3}\right) \sqrt[3]{36}=3 \sqrt[3]{36}
$$
Voor elke van de drie ongelijkheden geldt gelijkheid wanneer de drie termen gelijk zijn. We komen uit op een gelijkheidsgeval voor alledrie wanneer $(x, y, z)=\left(\frac{1}{3} \sqrt[3]{6}, \frac{1}{2} \sqrt[3]{6}, \sqrt[3]{6}\right)$, wat ook gemakkelijk te controleren is. Dan is $x y+y z+z x+\frac{1}{x}+\frac{2}{y}+\frac{5}{z}$ namelijk gelijk aan
$$
\frac{1}{6} \sqrt[3]{36}+\frac{1}{2} \sqrt[3]{36}+\frac{1}{3} \sqrt[3]{36}+3 \frac{1}{\sqrt[3]{6}}+4 \frac{1}{\sqrt[3]{6}}+5 \frac{1}{\sqrt[3]{6}}=\sqrt[3]{36}+12 \frac{1}{\sqrt[3]{6}}=\sqrt[3]{36}+2 \sqrt[3]{36}=3 \sqrt[3]{36}
$$
Opmerking. Nadat je hebt besloten om de ongelijkheid op te splitsen in drie ongelijkheden met het rekenkundig-meetkundig gemiddelde (één voor $x y$, één voor $y z$ en één voor $x z$ ), zijn er verschillende manieren om de coëfficiënten te vinden voor $\frac{1}{x}, \frac{1}{y}$ en $\frac{1}{z}$. Allereerst kun je je laten leiden door voorbeelden die je hebt gevonden in je zoektocht naar het gelijkheidsgeval. Zo wordt de uitdrukking gelijk aan 10 voor $(x, y, z)=\left(\frac{2}{3}, 1,2\right)$ en met $(x, y, z)=\left(\frac{3}{5}, \frac{9}{10}, \frac{9}{5}\right)$ krijg je $\frac{324}{100}+\frac{12}{18} \cdot 10=3,24+6,6666 \ldots=9,9066 \ldots$.
Een structurelere aanpak is het invoeren van variabelen $a, b, c, d, e, f$ voor de ongelijkheden op $x y+a \frac{1}{x}+b \frac{1}{y}, y z+c \frac{1}{y}+d \frac{1}{z}$ en $z x+e \frac{1}{z}+f \frac{1}{x}$. Omdat deze drie termen op moeten tellen
tot de gevraagde uitdrukkingen, krijgen we de voorwaarden
$$
\begin{aligned}
f+a & =1, \\
b+c & =2, \\
d+e & =5 .
\end{aligned}
$$
Verder willen we dat er gelijkheid geldt voor bepaalde $x, y$ en $z$. Dus het stelsel
$$
\begin{aligned}
& x y=a \frac{1}{x}=b \frac{1}{y} \\
& y z=c \frac{1}{y}=d \frac{1}{z} \\
& z x=e \frac{1}{z}=f \frac{1}{x}
\end{aligned}
$$
moet een oplossing hebben voor een zekere $x, y$ en $z$. Uit de eerste vergelijking volgt dan dat $\frac{x}{y}=\frac{a}{b}$. Maar met behulp van de laatste twee vergelijkingen kunnen we dat ook schrijven als
$$
\frac{x}{y}=\frac{z x}{y z}=\frac{f / x}{c / y}=\frac{f y}{c x} .
$$
Dat betekent dat $\frac{f}{c}=\frac{x^{2}}{y^{2}}=\frac{a^{2}}{b^{2}}$, oftewel $a^{2} / f=b^{2} / c$. Evenzo geldt er dat $c^{2} / b=d^{2} / e$ en $e^{2} / d=f^{2} / a$. Samen met $f+a=1, b+c=2$ en $d+e=5$ hebben we nu zes vergelijkingen in zes variabelen. Hoewel het nog niet eenvoudig is om dit stelsel op te lossen, versimpelt dat de zoektocht enorm doordat het nu makkelijk te controleren is of $a, b, c, d, e, f$ voldoet. Andere vergelijkingen die je uit dit stelsel kan afleiden zijn bijvoorbeeld ace $=b d f$ en $a d=b e=c f$.
|
{
"resource_path": "Dutch_TST/segmented/nl-2023-D2023_uitwerkingen.jsonl",
"problem_match": "\nOpgave 3.",
"solution_match": "\nOplossing."
}
|
96a17d4d-afb1-563b-b7cb-12fbc632013b
| 605,668
|
Every student in the Netherlands receives a finite number of tickets. Each ticket has a real number in the interval $[0,1]$ written on it. (The numbers on different tickets do not have to be distinct.) Find the smallest real number $c>0$ for which the following holds, regardless of the numbers on the tickets that everyone has received.
Every student for whom the sum of the numbers on the tickets is at most 1000, can distribute the tickets over 100 boxes so that the sum of the numbers in each box is at most $c$.
|
Suppose one of the students has received 1001 tickets, each with the number $\frac{1000}{1001}$. Since the sum of the tickets is 1000, this student must be able to distribute the tickets over 100 boxes. By the pigeonhole principle, there is at least one box with 11 tickets. The sum of these 11 tickets is $11 \cdot \frac{1000}{1001}=11\left(1-\frac{1}{1001}\right)=11-\frac{11}{1001}=11-\frac{1}{91}$. We will now show that this is the smallest possible value, $c=11-\frac{1}{91}$.
For any given student, we first choose those distributions in which the maximum of the sums of the tickets per box is as low as possible, and from these distributions, we then choose a distribution in which the fewest number of boxes achieve this maximum. Let $d_{1} \leq d_{2} \leq \ldots \leq d_{100}$ be the total value of the 100 boxes in this distribution, ordered from low to high (where the last $k$ are equal to the maximum). Since the sum of all tickets is at most 1000, we note that
$$
99 d_{1}+d_{100} \leq d_{1}+d_{2}+\ldots+d_{100} \leq 1000
$$
On the other hand, moving a positive ticket from box (with sum) $d_{100}$ to box (with sum) $d_{1}$ should not result in a better distribution by assumption: thus, no distribution with a lower maximum or with fewer than $k$ boxes of this maximum value. This means that the new value of $d_{1}$ must be at least $d_{100}$. If $d_{100} \leq 10$, we are done, since $10<11-\frac{1}{91}$. We can therefore assume that $d_{100}>10$. Since each ticket is at most 1, this means that box $d_{100}$ contains at least 11 positive tickets. This, in turn, implies that there is a ticket in this box with a positive value of at most $\frac{d_{100}}{11}$. If we move this ticket to box $d_{1}$, then it must be true that
$$
d_{1}+\frac{d_{100}}{11} \geq \text { "new value of box } d_{1} " \geq d_{100}
$$
This can be rewritten as $11 d_{1} \geq 10 d_{100}$. If we combine this with the first equation, we find
$$
91 d_{100}=90 d_{100}+d_{100} \leq 99 d_{1}+d_{100} \leq 1000
$$
For every student, the lowest maximum of the sums of the tickets per box is thus $d_{100} \leq \frac{1000}{91}=\frac{1001}{91}-\frac{1}{91}=11-\frac{1}{91}$.
|
11-\frac{1}{91}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Elke scholier in Nederland krijgt een eindig aantal kaartjes. Op elk kaartje staat een reël getal in het interval $[0,1]$. (De getallen op verschillende kaartjes hoeven niet verschillend te zijn.) Vind het kleinste reële getal $c>0$ waarvoor het volgende geldt, onafhankelijk van de getallen op de kaartjes die iedereen heeft gekregen.
Elke scholier waarvan de som van de getallen op de kaartjes hoogstens 1000 is, kan de kaartjes over 100 dozen verdelen zo dat de som van de kaartjes in elke doos hoogstens $c$ is.
|
Stel dat een van de scholieren 1001 kaartjes heeft gekregen met elk het getal $\frac{1000}{1001}$. Aangezien de som van de kaartjes 1000 is, moet deze scholier de kaartjes over de 100 dozen kunnen verdelen. Wegens het ladenprincipe is er minstens een doos met 11 kaartjes. De som van deze 11 kaartjes is $11 \cdot \frac{1000}{1001}=11\left(1-\frac{1}{1001}\right)=11-\frac{11}{1001}=11-\frac{1}{91}$. We gaan nu laten zien dat dit de kleinst mogelijke waarde is, $c=11-\frac{1}{91}$.
Voor een willekeurige scholier kiezen we eerst die verdelingen waarbij het maximum van de sommen van de kaartjes per doos zo laag mogelijk is, en uit deze verdelingen kiezen we vervolgens een verdeling waarbij het minst aantal dozen dit maximum aanneemt. Laat $d_{1} \leq d_{2} \leq \ldots \leq d_{100}$ de totale waarde van de 100 dozen in deze verdeling zijn, geordend van laag naar hoog (waarbij de laatste $k$ gelijk zijn aan het maximum). Omdat de som van alle kaartjes hoogstens 1000 is, merken we op dat
$$
99 d_{1}+d_{100} \leq d_{1}+d_{2}+\ldots+d_{100} \leq 1000
$$
Aan de andere kant mag het verplaatsen van een positief kaartje van doos (met som) $d_{100}$ naar doos (met som) $d_{1}$ geen betere verdeling opleveren per aanname: dus geen verdeling met een lager maximum of met minder dan $k$ dozen van deze maximale waarde. Dit betekent dat de nieuwe waarde van $d_{1}$ minstens gelijk is aan $d_{100}$. Als $d_{100} \leq 10$ zijn we direct klaar, want $10<11-\frac{1}{91}$. We mogen dus aannemen dat $d_{100}>10$. Aangezien elk kaartje hoogstens 1 is, betekent dit dat doos $d_{100}$ minstens 11 positieve kaartjes bevat. Dit impliceert dan weer dat er een kaartje in deze doos zit met positieve waarde hoogstens $\frac{d_{100}}{11}$. Als we dit kaartje naar doos $d_{1}$ verplaatsen, dan moet er dus gelden dat
$$
d_{1}+\frac{d_{100}}{11} \geq \text { "nieuwe waarde van doos } d_{1} " \geq d_{100}
$$
Dit kunnen we herschrijven als $11 d_{1} \geq 10 d_{100}$. Als we dit combineren met de eerste vergelijking vinden we
$$
91 d_{100}=90 d_{100}+d_{100} \leq 99 d_{1}+d_{100} \leq 1000
$$
Voor elke scholier is het laagste maximum van de sommen van de kaartjes per doos dus $d_{100} \leq \frac{1000}{91}=\frac{1001}{91}-\frac{1}{91}=11-\frac{1}{91}$.
|
{
"resource_path": "Dutch_TST/segmented/nl-2023-E2023_uitwerkingen.jsonl",
"problem_match": "\nOpgave 2.",
"solution_match": "\nOplossing."
}
|
ca133b01-8c7f-5fc5-bc24-d741f1447b96
| 605,701
|
Given a natural number $n$. There are $n$ islands with $n-1$ bridges between them such that you can get from any island to any other island. One afternoon, a fire breaks out on one of the islands. Every morning, the fire spreads to all neighboring islands (those islands connected by a bridge). To control the fire, every night a bridge is blown up, as long as the fire still has room to spread. Let $X$ be the minimum number of bridges that must be blown up for a given group of islands and fire origin. Find the maximum of $X$ over all possible island groups and fire origins.
|
The answer is $\lfloor\sqrt{n-1}\rfloor$.
For $n=k^{2}+1$, consider an archipelago with $k^{2}$ islands arranged in a $k \times k$ grid, where the islands are connected row by row, and all islands in the leftmost column are also connected to the last island, where the fire starts. After $\ell<k$ nights, there are still at least $k-\ell>0$ rows where no bridge has been blown up. In such a row, the fire consumes the $\ell^{\text{th}}$ island the next morning. This means that after that morning, there is still an unburned bridge (towards the $k^{\text{th}}$ island) to blow up. Therefore, in this archipelago, you need to blow up at least $k$ bridges. By randomly adding islands to this group, we find that $X \geq\lfloor\sqrt{n-1}\rfloor$.
Now we describe a strategy that shows that for any archipelago, the minimum is also at most $\lfloor\sqrt{n-1}\rfloor$. In this strategy, we blow up the bridge each night to cut off the most islands from the fire. We then consider the situation by collapsing all the islands that are on fire into a single point and forgetting about the isolated islands. This way, we have a situation with one fire source but fewer islands. We then finish it off with induction towards $k=\lfloor\sqrt{n-1}\rfloor$.
The base case $k=0$ gives the only possibility $n=1$, for which there is only one configuration and no bridges need to be blown up (since there are none). Suppose as the induction hypothesis that in all groups with at most $k^{2}$ islands, at most $k-1$ bridges need to be blown up, and consider an archipelago with $n \leq(k+1)^{2}$ islands.
Suppose the fire source had a degree of $d$: the island is connected to $d$ other islands via a bridge. Then, by the pigeonhole principle, there is a branch from the fire source with at least $\frac{n-1}{d}$ islands. In the morning, with this strategy, at least $\frac{n-1}{d}$ islands are removed by blowing up a bridge, and the fire then takes over $d-1$ islands. By collapsing these islands, we thus get a graph with a number of islands that is less than or equal to
$$
n-\frac{n-1}{d}-(d-1)=n+1-\frac{n-1}{d}-d \leq n+1-2 \sqrt{n-1}=(\sqrt{n-1}-1)^{2}+1<k^{2}+1
$$
where the first inequality follows from the arithmetic-geometric mean inequality: $\frac{n-1}{d}+d \geq 2 \sqrt{n-1}$. Since the number of islands is an integer, it follows that there are at most $k^{2}$ islands. Therefore, the archipelago with $n$ islands needs to blow up $1+(k-1)=k$ bridges. This proves the induction step and thus concludes the proof. $\square$
|
\lfloor\sqrt{n-1}\rfloor
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Gegeven is een natuurlijk getal $n$. Er zijn $n$ eilanden met $n-1$ bruggen ertussen zo dat je van elk eiland bij elk ander eiland kan komen. Op een middag breekt er brand uit op een van de eilanden. Elke morgen verspreidt het vuur zich naar alle naburige eilanden (die eilanden die met een brug zijn verbonden). Om het vuur te controleren wordt elke nacht een brug opgeblazen, zolang het vuur nog ruimte heeft om zich te verspreiden. Zij $X$ het minimale aantal bruggen dat men moet opblazen voor een gegeven eilandengroep en brandhaard. Vind het maximum van $X$ over alle mogelijke eilandengroepen en brandhaarden.
|
Het antwoord is $\lfloor\sqrt{n-1}\rfloor$.
Voor $n=k^{2}+1$ beschouwen we de eilandengroep met $k^{2}$ eilanden in een $k \times k$-grid, waarin de eilanden per rij verbonden worden en alle eilanden in de meest linker kolom nog met het laatste eiland worden verbonden, waar ook de brand start. Dan zijn er na $\ell<k$ nachten nog minstens $k-\ell>0$ rijen over waarin nog geen brug is opgeblazen. In zo'n rij verslindt het vuur die morgen het $\ell^{\text {de }}$ eiland. Dat betekent dat er na die morgen nog een onverwoeste brug is (richting het $k^{\text {de }}$ eiland) om op te blazen. Je moet in deze eilandengroep dus minstens $k$ bruggen opblazen. Door random eilanden aan deze groep toe te voegen vinden we dat $X \geq\lfloor\sqrt{n-1}\rfloor$.
Nu beschrijven we een strategie waaruit blijkt dat voor elke eilandengroep het minimum ook hoogstens $\lfloor\sqrt{n-1}\rfloor$ is. In deze strategie blazen we elke nacht de brug op zo dat je de meeste eilanden afsnijdt van het vuur. We beschouwen daarna de situatie door alle eilanden die in brand staan, samen te trekken tot één punt en alle afgesneden eilanden te vergeten. Nu hebben we dus weer een situatie met één brandhaard, maar minder eilanden. Nu maken we het af met inductie naar $k=\lfloor\sqrt{n-1}\rfloor$.
De inductiebasis $k=0$, geeft als enige mogelijkheid $n=1$ waarvoor er maar één configuratie is en er inderdaad geen bruggen hoeven worden opgeblazen (want die zijn er niet). Stel nu als inductiehypothese dat in alle groepen met hoogstens $k^{2}$ eilanden hoogstens $k-1$ bruggen hoeven te worden opgeblazen en bekijk een eilandgroep met $n \leq(k+1)^{2}$ eilanden.
Stel dat de brandhaard een graad had gelijk aan $d$ : het eiland grenst aan $d$ eilanden middels een brug. Dan geldt wegens het ladenprincipe dat er een tak is van de brandhaard met minstens $\frac{n-1}{d}$ eilanden. In de ochtend zijn er met deze strategie dus minstens $\frac{n-1}{d}$ eilanden verwijderd door een brug op te blazen, en daarna heeft het vuur $d-1$ eilanden overgenomen. Met het samentrekken van deze eilanden krijgen we dus een graaf waarvan het aantal eilanden kleiner of gelijk is aan
$$
n-\frac{n-1}{d}-(d-1)=n+1-\frac{n-1}{d}-d \leq n+1-2 \sqrt{n-1}=(\sqrt{n-1}-1)^{2}+1<k^{2}+1
$$
waarbij de eerste ongelijkheid volgt uit de ongelijkheid van rekenkundig-meetkundig gemiddelde: $\frac{n-1}{d}+d \geq 2 \sqrt{n-1}$. Aangezien het aantal eilanden geheel is, volgt hieruit dat het er
hoogstens $k^{2}$ zijn. Dus de eilandgroep met $n$ eilanden heeft er genoeg aan om $1+(k-1)=k$ bruggen op te blazen. Dit bewijst de inductiestap en is daarmee het einde van het bewijs. $\square$
|
{
"resource_path": "Dutch_TST/segmented/nl-2024-D2024_uitwerkingen.jsonl",
"problem_match": "\nOpgave 4.",
"solution_match": "\nOplossing."
}
|
9a4ea8ae-08e5-5ac0-96fa-bd05869138c0
| 605,947
|
On a $2023 \times 2023$ board, some squares contain a beetle, with at most one beetle per square. After one minute, each beetle moves one square to the left, right, up, or down. After each subsequent minute, each beetle moves one square further, but always makes a 90-degree turn. If a beetle moved left or right in one minute, it will move up or down in the next minute, and vice versa. What is the minimum number of beetles that must be on the board to ensure that at some point, two beetles will end up in the same square at the same time, regardless of where the beetles start and how they move (following the rules)?
|
The answer is $2022^{2}+1$.
First, let's show that $2022^{2}$ is indeed insufficient. For this, we divide a $2022 \times 2022$ sub-board into $2 \times 2$ boards. In each such board, we can place four beetles such that they walk in a small circle (square) clockwise.
Now, suppose we have more than $2022^{2}$ beetles. We want to prove that at some point, two will end up in the same square. To this end, we number the squares from $(1,1)$ to $(2023,2023)$ and color the board as follows: the squares in an odd row and odd column are colored $A$, an odd row and even column are colored $B$, an even row and even column are colored $C$, and an even row and odd column are colored $D$. Thus, half of the diagonals are colored with $A$ and $C$, and the other half with $B$ and $D$. Therefore, there are $1012^{2}$ squares $A$, there are $1011^{2}$ squares $C$, and there are $1011 \cdot 1012$ squares of both $B$ and $D$.
Then each beetle follows a cyclic path $A \rightarrow B \rightarrow C \rightarrow D \rightarrow A$ or $A \rightarrow D \rightarrow C \rightarrow B \rightarrow A$. We note that no more than $1011^{2}$ beetles can start in squares $C$, as there are only $1011^{2}$ of them. Since the number of beetles is greater than $2022^{2}$, there must be more than $1011^{2}$ beetles on squares $A$ or more than $2 \cdot 1011^{2}$ beetles on squares $B$ and $D$ together.
In the first case, after two minutes, there are more than $1011^{2}$ beetles in squares $C$, and we conclude that two beetles meet.
In the second case, after the first minute, there are more than $2 \cdot 1011^{2}$ beetles in the squares $A$ and $C$ together. Thus, two beetles meet in $C$ or we find more than $1011^{2}$ beetles on squares $A$. In that case, after the third minute, there are more than $1011^{2}$ beetles in squares $C$, and we conclude that two beetles meet anyway.
|
2022^{2}+1
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Op een $2023 \times 2023$ bord staan er op sommige vakjes een kever, met hoogstens één kever per vakje. Na een minuut gaat elke kever een vakje naar links of rechts, of een vakje naar boven of beneden. Na elke volgende minuut gaat elke kever weer een vakje verder, maar ze maken altijd een bocht van 90 graden. Als een kever de ene minuut naar links of rechts ging dan gaat die dus de volgende minuut naar boven of beneden, en vice versa. Wat is het minimale aantal kevers dat er op het bord moet staan zodat je zeker weet dat er in de loop der tijd een keer twee kevers tegelijk in hetzelfde vakje terecht komen, ongeacht waar de kevers beginnen en hoe ze bewegen (de regels in acht nemende).
|
Het antwoord is $2022^{2}+1$.
Eerst laten we zien dat $2022^{2}$ inderdaad onvoldoende is. Hiervoor delen we een $2022 \times 2022$ deelbord op in $2 \times 2$ bordjes. In elk zo'n bordje kunnen we vier kevers plaatsen zodanig dat ze in een met de klok mee een cirkeltje (vierkantje) lopen.
Stel nu dat we meer dan $2022^{2}$ kevers hebben. We willen bewijzen dat er ooit twee op eenzelfde vakje terecht komen. Hiertoe nummeren we de vakjes van $(1,1) \mathrm{t} / \mathrm{m}(2023,2023)$ en kleuren we het bord als volgt: de vakjes in een oneven rij en oneven kolom kleuren we $A$, een oneven rij en een even kolom kleuren we $B$, een even rij en even kolom kleuren we $C$ en een even rij en oneven kolom kleuren we $D$. De helft van de diagonalen is dus gekleurd met $A$ en $C$ en de andere met $B$ en $D$. Dus er zijn $1012^{2}$ vakjes $A$, er zijn $1011^{2}$ vakjes $C$, en er zijn $1011 \cdot 1012$ vakjes van zowel $B$ als $D$.
Dan volgt elke kever een cyclisch pad $A \rightarrow B \rightarrow C \rightarrow D \rightarrow A$ of $A \rightarrow D \rightarrow C \rightarrow B \rightarrow A$. We merken op dat er niet meer dan $1011^{2}$ kevers in vakjes $C$ kunnen beginnen, want daar zijn er maar $1011^{2}$ van. Omdat het aantal kevers groter is dan $2022^{2}$, moeten er dus meer dan $1011^{2}$ kevers op vakjes $A$ zijn of meer dan $2 \cdot 1011^{2}$ kever op vakjes $B$ en $D$ samen.
In het eerste geval hebben we na twee minuten meer dan $1011^{2}$ kevers in vakjes $C$ en concluderen we dat er twee kevers samenkomen.
In het tweede geval zijn er na de eerste minuut meer dan $2 \cdot 1011^{2}$ kevers in de vakjes $A$ en
$C$ samen. Dan komen er dus twee kevers samen in $C$ of vinden we meer dan $1011^{2}$ kevers op vakjes $A$. In dat geval krijgen we na de derde minuut meer dan $1011^{2}$ kevers in vakjes $C$ en concluderen we alsnog dat er twee kevers samenkomen.
|
{
"resource_path": "Dutch_TST/segmented/nl-2024-E2024_uitwerkingen.jsonl",
"problem_match": "\nOpgave 1.",
"solution_match": "\nOplossing."
}
|
2e2219a1-8b67-5fdb-aedd-403a772663f8
| 605,955
|
Let $n$ be a positive integer. Find the greatest possible integer $m$, in terms of $n$, with the following property: a table with $m$ rows and $n$ columns can be filled with real numbers in such a manner that for any two different rows $\left[a_{1}, a_{2}, \ldots, a_{n}\right]$ and $\left[b_{1}, b_{2}, \ldots, b_{n}\right]$ the following holds:
$$
\max \left(\left|a_{1}-b_{1}\right|,\left|a_{2}-b_{2}\right|, \ldots,\left|a_{n}-b_{n}\right|\right)=1
$$
Origin. Poland (Tomasz Kobos).
|
The largest possible $m$ is equal to $2^{n}$.
In order to see that the value $2^{n}$ can be indeed achieved, consider all binary vectors of length $n$ as rows of the table. We now proceed with proving that this is the maximum value.
Let $\left[a_{k}^{i}\right]$ be a feasible table, where $i=1, \ldots, m$ and $k=1, \ldots, n$. Let us define undirected graphs $G_{1}, G_{2}$, $\ldots, G_{n}$, each with vertex set $\{1,2, \ldots, m\}$, where $i j \in E\left(G_{k}\right)$ if and only if $\left|a_{k}^{i}-a_{k}^{j}\right|=1$ (by $E\left(G_{k}\right)$ we denote the edge set of the graph $G_{k}$ ). Observe the following two properties.
(1) Each graph $G_{k}$ is bipartite. Indeed, if it contained a cycle of odd length, then the sum of $\pm 1$ along this cycle would need to be equal to 0 , which contradicts the length of the cycle being odd.
(2) For every $i \neq j, i j \in E\left(G_{k}\right)$ for some $k$. This follows directly from the problem statement.
For every graph $G_{k}$ fix some bipartition $\left(A_{k}, B_{k}\right)$ of $\{1,2, \ldots, m\}$, i.e., a partition of $\{1,2, \ldots, m\}$ into two disjoint sets $A_{k}, B_{k}$ such that the edges of $G_{k}$ traverse only between $A_{k}$ and $B_{k}$. If $m>2^{n}$, then there are two distinct indices $i, j$ such that they belong to exactly the same parts $A_{k}, B_{k}$, that is, $i \in A_{k}$ if and only if $j \in A_{k}$ for all $k=1,2, \ldots, n$. However, this means that the edge $i j$ cannot be present in any of the graphs $G_{1}, G_{2}$, $\ldots, G_{n}$, which contradicts (2). Therefore, $m \leq 2^{n}$.
|
2^n
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Let $n$ be a positive integer. Find the greatest possible integer $m$, in terms of $n$, with the following property: a table with $m$ rows and $n$ columns can be filled with real numbers in such a manner that for any two different rows $\left[a_{1}, a_{2}, \ldots, a_{n}\right]$ and $\left[b_{1}, b_{2}, \ldots, b_{n}\right]$ the following holds:
$$
\max \left(\left|a_{1}-b_{1}\right|,\left|a_{2}-b_{2}\right|, \ldots,\left|a_{n}-b_{n}\right|\right)=1
$$
Origin. Poland (Tomasz Kobos).
|
The largest possible $m$ is equal to $2^{n}$.
In order to see that the value $2^{n}$ can be indeed achieved, consider all binary vectors of length $n$ as rows of the table. We now proceed with proving that this is the maximum value.
Let $\left[a_{k}^{i}\right]$ be a feasible table, where $i=1, \ldots, m$ and $k=1, \ldots, n$. Let us define undirected graphs $G_{1}, G_{2}$, $\ldots, G_{n}$, each with vertex set $\{1,2, \ldots, m\}$, where $i j \in E\left(G_{k}\right)$ if and only if $\left|a_{k}^{i}-a_{k}^{j}\right|=1$ (by $E\left(G_{k}\right)$ we denote the edge set of the graph $G_{k}$ ). Observe the following two properties.
(1) Each graph $G_{k}$ is bipartite. Indeed, if it contained a cycle of odd length, then the sum of $\pm 1$ along this cycle would need to be equal to 0 , which contradicts the length of the cycle being odd.
(2) For every $i \neq j, i j \in E\left(G_{k}\right)$ for some $k$. This follows directly from the problem statement.
For every graph $G_{k}$ fix some bipartition $\left(A_{k}, B_{k}\right)$ of $\{1,2, \ldots, m\}$, i.e., a partition of $\{1,2, \ldots, m\}$ into two disjoint sets $A_{k}, B_{k}$ such that the edges of $G_{k}$ traverse only between $A_{k}$ and $B_{k}$. If $m>2^{n}$, then there are two distinct indices $i, j$ such that they belong to exactly the same parts $A_{k}, B_{k}$, that is, $i \in A_{k}$ if and only if $j \in A_{k}$ for all $k=1,2, \ldots, n$. However, this means that the edge $i j$ cannot be present in any of the graphs $G_{1}, G_{2}$, $\ldots, G_{n}$, which contradicts (2). Therefore, $m \leq 2^{n}$.
|
{
"resource_path": "EGMO/segmented/en-2012-solutions-day1.jsonl",
"problem_match": "\nProblem 2.",
"solution_match": "\nSolution 1 (submitter)."
}
|
fa5429d6-2ad5-56b7-9659-df3c33f59ae1
| 606,047
|
Let $m$ be a positive integer. Consider a $4 m \times 4 m$ array of square unit cells. Two different cells are related to each other if they are in either the same row or in the same column. No cell is related to itself. Some cells are coloured blue, such that every cell is related to at least two blue cells. Determine the minimum number of blue cells.
|
The required minimum is 6 m and is achieved by a diagonal string of $m 4 \times 4$ blocks of the form below (bullets mark centres of blue cells):
In particular, this configuration shows that the required minimum does not exceed 6 m .
We now show that any configuration of blue cells satisfying the condition in the statement has cardinality at least 6 m .
Fix such a configuration and let $m_{1}^{r}$ be the number of blue cells in rows containing exactly one such, let $m_{2}^{r}$ be the number of blue cells in rows containing exactly two such, and let $m_{3}^{r}$ be the number of blue cells in rows containing at least three such; the numbers $m_{1}^{c}, m_{2}^{c}$ and $m_{3}^{c}$ are defined similarly.
Begin by noticing that $m_{3}^{c} \geq m_{1}^{r}$ and, similarly, $m_{3}^{r} \geq m_{1}^{c}$. Indeed, if a blue cell is alone in its row, respectively column, then there are at least two other blue cells in its column, respectively row, and the claim follows.
Suppose now, if possible, the total number of blue cells is less than 6 m . We will show that $m_{1}^{r}>m_{3}^{r}$ and $m_{1}^{c}>m_{3}^{c}$, and reach a contradiction by the preceding: $m_{1}^{r}>m_{3}^{r} \geq m_{1}^{c}>m_{3}^{c} \geq m_{1}^{r}$.
We prove the first inequality; the other one is dealt with similarly. To this end, notice that there are no empty rows - otherwise, each column would contain at least two blue cells, whence a total of at least $8 m>6 m$ blue cells, which is a contradiction. Next, count rows to get $m_{1}^{r}+m_{2}^{r} / 2+m_{3}^{r} / 3 \geq 4 m$,
and count blue cells to get $m_{1}^{r}+m_{2}^{r}+m_{3}^{r}<6 m$. Subtraction of the latter from the former multiplied by $3 / 2$ yields $m_{1}^{r}-m_{3}^{r}>m_{2}^{r} / 2 \geq 0$, and the conclusion follows.
|
6m
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Let $m$ be a positive integer. Consider a $4 m \times 4 m$ array of square unit cells. Two different cells are related to each other if they are in either the same row or in the same column. No cell is related to itself. Some cells are coloured blue, such that every cell is related to at least two blue cells. Determine the minimum number of blue cells.
|
The required minimum is 6 m and is achieved by a diagonal string of $m 4 \times 4$ blocks of the form below (bullets mark centres of blue cells):
In particular, this configuration shows that the required minimum does not exceed 6 m .
We now show that any configuration of blue cells satisfying the condition in the statement has cardinality at least 6 m .
Fix such a configuration and let $m_{1}^{r}$ be the number of blue cells in rows containing exactly one such, let $m_{2}^{r}$ be the number of blue cells in rows containing exactly two such, and let $m_{3}^{r}$ be the number of blue cells in rows containing at least three such; the numbers $m_{1}^{c}, m_{2}^{c}$ and $m_{3}^{c}$ are defined similarly.
Begin by noticing that $m_{3}^{c} \geq m_{1}^{r}$ and, similarly, $m_{3}^{r} \geq m_{1}^{c}$. Indeed, if a blue cell is alone in its row, respectively column, then there are at least two other blue cells in its column, respectively row, and the claim follows.
Suppose now, if possible, the total number of blue cells is less than 6 m . We will show that $m_{1}^{r}>m_{3}^{r}$ and $m_{1}^{c}>m_{3}^{c}$, and reach a contradiction by the preceding: $m_{1}^{r}>m_{3}^{r} \geq m_{1}^{c}>m_{3}^{c} \geq m_{1}^{r}$.
We prove the first inequality; the other one is dealt with similarly. To this end, notice that there are no empty rows - otherwise, each column would contain at least two blue cells, whence a total of at least $8 m>6 m$ blue cells, which is a contradiction. Next, count rows to get $m_{1}^{r}+m_{2}^{r} / 2+m_{3}^{r} / 3 \geq 4 m$,
and count blue cells to get $m_{1}^{r}+m_{2}^{r}+m_{3}^{r}<6 m$. Subtraction of the latter from the former multiplied by $3 / 2$ yields $m_{1}^{r}-m_{3}^{r}>m_{2}^{r} / 2 \geq 0$, and the conclusion follows.
|
{
"resource_path": "EGMO/segmented/en-2016-solutions.jsonl",
"problem_match": "\nProblem 3.",
"solution_match": "\nSolution 1 (Israel)."
}
|
23cfe301-afa7-58aa-be03-ae3d674c2b83
| 604,833
|
Find the smallest positive integer $k$ for which there exist a colouring of the positive integers $\mathbb{Z}_{>0}$ with $k$ colours and a function $f: \mathbb{Z}_{>0} \rightarrow \mathbb{Z}_{>0}$ with the following two properties:
(i) For all positive integers $m, n$ of the same colour, $f(m+n)=f(m)+f(n)$.
(ii) There are positive integers $m, n$ such that $f(m+n) \neq f(m)+f(n)$.
In a colouring of $\mathbb{Z}_{>0}$ with $k$ colours, every integer is coloured in exactly one of the $k$ colours. In both (i) and (ii) the positive integers $m, n$ are not necessarily different.
Merlijn Staps, the Netherlands
|
The answer is $k=3$.
First we show that there is such a function and coloring for $k=3$. Consider $f: \mathbb{Z}_{>0} \rightarrow \mathbb{Z}_{>0}$ given by $f(n)=n$ for all $n \equiv 1$ or 2 modulo 3 , and $f(n)=2 n$ for $n \equiv 0$ modulo 3 . Moreover, give a positive integer $n$ the $i$-th color if $n \equiv i$ (3).
By construction we have $f(1+2)=6 \neq 3=f(1)+f(2)$ and hence $f$ has property (ii).
Now let $n, m$ be positive integers with the same color $i$. If $i=0$, then $n+m$ has color 0 , so $f(n+m)=$ $2(n+m)=2 n+2 m=f(n)+f(m)$. If $i=1$, then $n+m$ has color 2 , so $f(n+m)=n+m=f(n)+f(m)$. Finally, if $i=2$, then $n+m$ has color 1 , so $f(n+m)=n+m=f(n)+f(m)$. Therefore $f$ also satisfies condition (i).
Next we show that there is no such function and coloring for $k=2$.
Consider any coloring of $\mathbb{Z}_{>0}$ with 2 colors and any function $f: \mathbb{Z}_{>0} \rightarrow \mathbb{Z}_{>0}$ satisfying conditions (i) and (ii). Then there exist positive integers $m$ and $n$ such that $f(m+n) \neq f(m)+f(n)$. Choose $m$ and $n$ such that their sum is minimal among all such $m, n$ and define $a=m+n$. Then in particular for every $b<a$ we have $f(b)=b f(1)$ and $f(a) \neq a f(1)$.
If $a$ is even, then condition (i) for $m=n=\frac{a}{2}$ implies $f(a)=f\left(\frac{a}{2}\right)+f\left(\frac{a}{2}\right)=f(1) a$, a contradiction. Hence $a$ is odd. We will prove two lemmas.
Lemma 1. Any odd integer $b<a$ has a different color than $a$.
Proof. Suppose that $b<a$ is an odd integer, and that $a$ and $b$ have the same color. Then on the one hand, $f(a+b)=f(a)+b f(1)$. On the other hand, we also have $f(a+b)=f\left(\frac{a+b}{2}\right)+f\left(\frac{a+b}{2}\right)=(a+b) f(1)$, as $\frac{a+b}{2}$ is a positive integer smaller than $a$. Hence $f(a)=f(a+b)-b f(1)=(a+b) f(1)-b f(1)=a f(1)$, which is again a contradiction. Therefore all odd integers smaller than $a$ have a color different from that of $a$.
Lemma 2. Any even integer $b<a$ has the same color as $a$
Proof. Suppose $b<a$ is an even integer, and that $a$ and $b$ have different colors. Then $a-b$ is an odd integer smaller than $a$, so it has the same color as $b$. Thus $f(a)=f(a-b)+f(b)=(a-b) f(1)+b f(1)=a f(1)$, a contradiction. Hence all even integers smaller than $a$ have the same color as $a$.
Suppose now $a+1$ has the same color as $a$. As $a>1$, we have $\frac{a+1}{2}<a$ and therefore $f(a+1)=2 f\left(\frac{a+1}{2}\right)=$ $(a+1) f(1)$. As $a-1$ is an even integer smaller than $a$, we have by Lemma 2 that $a-1$ also has the same color as $a$. Hence $2 f(a)=f(2 a)=f(a+1)+f(a-1)=(a+1) f(1)+(a-1) f(1)=2 a f(1)$, which implies that $f(a)=a f(1)$, a contradiction. So $a$ and $a+1$ have different colors.
Since $a-2$ is an odd integer smaller than $a$, by Lemma 1 it has a color different from that of $a$, so $a-2$ and $a+1$ have the same color. Also, we have seen by Lemma 2 that $a-1$ and $a$ have the same color. So $f(a)+f(a-1)=f(2 a-1)=f(a+1)+f(a-2)=(a+1) f(1)+(a-2) f(1)=(2 a-1) f(1)$, from which it follows that $f(a)=(2 a-1) f(1)-f(a-1)=(2 a-1) f(1)-(a-1) f(1)=a f(1)$, which contradicts our choice of $a$ and finishes the proof.
|
3
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Find the smallest positive integer $k$ for which there exist a colouring of the positive integers $\mathbb{Z}_{>0}$ with $k$ colours and a function $f: \mathbb{Z}_{>0} \rightarrow \mathbb{Z}_{>0}$ with the following two properties:
(i) For all positive integers $m, n$ of the same colour, $f(m+n)=f(m)+f(n)$.
(ii) There are positive integers $m, n$ such that $f(m+n) \neq f(m)+f(n)$.
In a colouring of $\mathbb{Z}_{>0}$ with $k$ colours, every integer is coloured in exactly one of the $k$ colours. In both (i) and (ii) the positive integers $m, n$ are not necessarily different.
Merlijn Staps, the Netherlands
|
The answer is $k=3$.
First we show that there is such a function and coloring for $k=3$. Consider $f: \mathbb{Z}_{>0} \rightarrow \mathbb{Z}_{>0}$ given by $f(n)=n$ for all $n \equiv 1$ or 2 modulo 3 , and $f(n)=2 n$ for $n \equiv 0$ modulo 3 . Moreover, give a positive integer $n$ the $i$-th color if $n \equiv i$ (3).
By construction we have $f(1+2)=6 \neq 3=f(1)+f(2)$ and hence $f$ has property (ii).
Now let $n, m$ be positive integers with the same color $i$. If $i=0$, then $n+m$ has color 0 , so $f(n+m)=$ $2(n+m)=2 n+2 m=f(n)+f(m)$. If $i=1$, then $n+m$ has color 2 , so $f(n+m)=n+m=f(n)+f(m)$. Finally, if $i=2$, then $n+m$ has color 1 , so $f(n+m)=n+m=f(n)+f(m)$. Therefore $f$ also satisfies condition (i).
Next we show that there is no such function and coloring for $k=2$.
Consider any coloring of $\mathbb{Z}_{>0}$ with 2 colors and any function $f: \mathbb{Z}_{>0} \rightarrow \mathbb{Z}_{>0}$ satisfying conditions (i) and (ii). Then there exist positive integers $m$ and $n$ such that $f(m+n) \neq f(m)+f(n)$. Choose $m$ and $n$ such that their sum is minimal among all such $m, n$ and define $a=m+n$. Then in particular for every $b<a$ we have $f(b)=b f(1)$ and $f(a) \neq a f(1)$.
If $a$ is even, then condition (i) for $m=n=\frac{a}{2}$ implies $f(a)=f\left(\frac{a}{2}\right)+f\left(\frac{a}{2}\right)=f(1) a$, a contradiction. Hence $a$ is odd. We will prove two lemmas.
Lemma 1. Any odd integer $b<a$ has a different color than $a$.
Proof. Suppose that $b<a$ is an odd integer, and that $a$ and $b$ have the same color. Then on the one hand, $f(a+b)=f(a)+b f(1)$. On the other hand, we also have $f(a+b)=f\left(\frac{a+b}{2}\right)+f\left(\frac{a+b}{2}\right)=(a+b) f(1)$, as $\frac{a+b}{2}$ is a positive integer smaller than $a$. Hence $f(a)=f(a+b)-b f(1)=(a+b) f(1)-b f(1)=a f(1)$, which is again a contradiction. Therefore all odd integers smaller than $a$ have a color different from that of $a$.
Lemma 2. Any even integer $b<a$ has the same color as $a$
Proof. Suppose $b<a$ is an even integer, and that $a$ and $b$ have different colors. Then $a-b$ is an odd integer smaller than $a$, so it has the same color as $b$. Thus $f(a)=f(a-b)+f(b)=(a-b) f(1)+b f(1)=a f(1)$, a contradiction. Hence all even integers smaller than $a$ have the same color as $a$.
Suppose now $a+1$ has the same color as $a$. As $a>1$, we have $\frac{a+1}{2}<a$ and therefore $f(a+1)=2 f\left(\frac{a+1}{2}\right)=$ $(a+1) f(1)$. As $a-1$ is an even integer smaller than $a$, we have by Lemma 2 that $a-1$ also has the same color as $a$. Hence $2 f(a)=f(2 a)=f(a+1)+f(a-1)=(a+1) f(1)+(a-1) f(1)=2 a f(1)$, which implies that $f(a)=a f(1)$, a contradiction. So $a$ and $a+1$ have different colors.
Since $a-2$ is an odd integer smaller than $a$, by Lemma 1 it has a color different from that of $a$, so $a-2$ and $a+1$ have the same color. Also, we have seen by Lemma 2 that $a-1$ and $a$ have the same color. So $f(a)+f(a-1)=f(2 a-1)=f(a+1)+f(a-2)=(a+1) f(1)+(a-2) f(1)=(2 a-1) f(1)$, from which it follows that $f(a)=(2 a-1) f(1)-f(a-1)=(2 a-1) f(1)-(a-1) f(1)=a f(1)$, which contradicts our choice of $a$ and finishes the proof.
|
{
"resource_path": "EGMO/segmented/en-2017-solutions.jsonl",
"problem_match": "# Problem 2",
"solution_match": "# Solution 1:"
}
|
6b79f60e-49ce-5282-bd82-e813e4201184
| 604,961
|
A plane has a special point $O$ called the origin. Let $P$ be a set of 2021 points in the plane, such that
(i) no three points in $P$ lie on a line and
(ii) no two points in $P$ lie on a line through the origin.
A triangle with vertices in $P$ is fat, if $O$ is strictly inside the triangle. Find the maximum number of fat triangles.
(Austria, Veronika Schreitter)
|
We will count minimal number of triangles that are not fat. Let $F$ set of fat triangles, and S set of triangles that are not fat. If triangle $X Y Z \in S$, we call $X$ and $Z$ good vertices if $O Y$ is located between $O X$ and $O Z$. For $A \in P$ let $S_{A} \subseteq S$ be set of triangles in $S$ for which $A$ is one of the good vertex.
It is easy to see that
$$
2|S|=\sum_{A \in P}\left|S_{A}\right|
$$
For $A \in P$, let $R_{A} \subset P$ and $L_{A} \subset P$ be parts of $P \backslash\{A\}$ divided by $A O$. Suppose for $A X Y \in S$ vertex $A$ is good, then clearly $X, Y \in R_{A}$ or $X, Y \in L_{A}$. On the other hand, if $X, Y \in R_{A}$ or $X, Y \in L_{A}$ then clearly $A X Y \in S$ and $A$ is its good vertex. Therefore,
$$
\left|S_{A}\right|=\binom{\left|R_{A}\right|}{2}+\binom{\left|L_{A}\right|}{2}
$$
It is easy to show following identity:
$$
\frac{x(x-1)}{2}+\frac{y(y-1)}{2}-2 \cdot \frac{\frac{x+y}{2}\left(\frac{x+y}{2}-1\right)}{2}=\frac{(x-y)^{2}}{4}
$$
By using (2) and (3) we get
$$
\left|S_{A}\right| \geq 2 \cdot\binom{\frac{\left|R_{A}\right|+\left|L_{A}\right|}{2}}{2}=2 \cdot\binom{1010}{2}=1010 \cdot 1009
$$
and the equality holds when $\left|R_{A}\right|=\left|L_{A}\right|=1010$. Hence
$$
|S|=\frac{\sum_{A \in P}\left|S_{A}\right|}{2} \geq \frac{2021 \cdot 1010 \cdot 1009}{2}=2021 \cdot 505 \cdot 1009
$$
Therefore,
$$
|F|=\binom{2021}{3}-|S| \leq 2021 \cdot 1010 \cdot 673-2021 \cdot 505 \cdot 1009=2021 \cdot 505 \cdot 337
$$
For configuration of points on regular 2021-gon which is centered at $O$, in equalities in (4), (5), (6) become equalities. Hence $2021 \cdot 505 \cdot 337$ is indeed the answer.
|
2021 \cdot 505 \cdot 337
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
A plane has a special point $O$ called the origin. Let $P$ be a set of 2021 points in the plane, such that
(i) no three points in $P$ lie on a line and
(ii) no two points in $P$ lie on a line through the origin.
A triangle with vertices in $P$ is fat, if $O$ is strictly inside the triangle. Find the maximum number of fat triangles.
(Austria, Veronika Schreitter)
Answer: $2021 \cdot 505 \cdot 337$
|
We will count minimal number of triangles that are not fat. Let $F$ set of fat triangles, and S set of triangles that are not fat. If triangle $X Y Z \in S$, we call $X$ and $Z$ good vertices if $O Y$ is located between $O X$ and $O Z$. For $A \in P$ let $S_{A} \subseteq S$ be set of triangles in $S$ for which $A$ is one of the good vertex.
It is easy to see that
$$
2|S|=\sum_{A \in P}\left|S_{A}\right|
$$
For $A \in P$, let $R_{A} \subset P$ and $L_{A} \subset P$ be parts of $P \backslash\{A\}$ divided by $A O$. Suppose for $A X Y \in S$ vertex $A$ is good, then clearly $X, Y \in R_{A}$ or $X, Y \in L_{A}$. On the other hand, if $X, Y \in R_{A}$ or $X, Y \in L_{A}$ then clearly $A X Y \in S$ and $A$ is its good vertex. Therefore,
$$
\left|S_{A}\right|=\binom{\left|R_{A}\right|}{2}+\binom{\left|L_{A}\right|}{2}
$$
It is easy to show following identity:
$$
\frac{x(x-1)}{2}+\frac{y(y-1)}{2}-2 \cdot \frac{\frac{x+y}{2}\left(\frac{x+y}{2}-1\right)}{2}=\frac{(x-y)^{2}}{4}
$$
By using (2) and (3) we get
$$
\left|S_{A}\right| \geq 2 \cdot\binom{\frac{\left|R_{A}\right|+\left|L_{A}\right|}{2}}{2}=2 \cdot\binom{1010}{2}=1010 \cdot 1009
$$
and the equality holds when $\left|R_{A}\right|=\left|L_{A}\right|=1010$. Hence
$$
|S|=\frac{\sum_{A \in P}\left|S_{A}\right|}{2} \geq \frac{2021 \cdot 1010 \cdot 1009}{2}=2021 \cdot 505 \cdot 1009
$$
Therefore,
$$
|F|=\binom{2021}{3}-|S| \leq 2021 \cdot 1010 \cdot 673-2021 \cdot 505 \cdot 1009=2021 \cdot 505 \cdot 337
$$
For configuration of points on regular 2021-gon which is centered at $O$, in equalities in (4), (5), (6) become equalities. Hence $2021 \cdot 505 \cdot 337$ is indeed the answer.
|
{
"resource_path": "EGMO/segmented/en-2021-solutions.jsonl",
"problem_match": "\nProblems 5.",
"solution_match": "# Solution"
}
|
2436e3c8-2b2f-5013-8592-f44fa76efa48
| 605,674
|
Let $k$ be a positive integer. Lexi has a dictionary $\mathcal{D}$ consisting of some $k$-letter strings containing only the letters $A$ and $B$. Lexi would like to write either the letter $A$ or the letter $B$ in each cell of a $k \times k$ grid so that each column contains a string from $\mathcal{D}$ when read from top-to-bottom and each row contains a string from $\mathcal{D}$ when read from left-to-right.
What is the smallest integer $m$ such that if $\mathcal{D}$ contains at least $m$ different strings, then Lexi can fill her grid in this manner, no matter what strings are in $\mathcal{D}$ ?
|
We claim the minimum value of $m$ is $2^{k-1}$.
Firstly, we provide a set $\mathcal{S}$ of size $2^{k-1}-1$ for which Lexi cannot fill her grid. Consider the set of all length- $k$ strings containing only $A$ s and $B$ shich end with a $B$, and remove the string consisting of $k B$ s. Clearly there are 2 independent choices for each of the first $k-1$ letters and 1 for the last letter, and since exactly one string is excluded, there must be exactly $2^{k-1}-1$ strings in this set.
Suppose Lexi tries to fill her grid. For each row to have a valid string, it must end in a $B$. But then the right column would necessarily contain $k B \mathrm{~s}$, and not be in our set. Thus, Lexi cannot fill her grid with our set, and we must have $m \geqslant 2^{k-1}$.
Now, consider any set $\mathcal{S}$ with at least $2^{k-1}$ strings. Clearly, if $\mathcal{S}$ contained either the uniform string with $k A$ s or the string with $k B \mathrm{~s}$, then Lexi could fill her grid with all of the relevant letters and each row and column would contain that string.
Consider the case where $\mathcal{S}$ contains neither of those strings. Among all $2^{k}$ possible length$k$ strings with $A \mathrm{~s}$ and $B \mathrm{~s}$, each has a complement which corresponds to the string with $B$ s in every position where first string had $A$ s and vice-versa. Clearly, the string with all $A$ s is paired with the string with all $B$ s. We may assume that we do not take the two uniform strings and thus applying the pigeonhole principle to the remaining set of strings, we must have two strings which are complementary.
Let this pair of strings be $\ell, \ell^{\prime} \in \mathcal{S}$ in some order. Define the set of indices $\mathcal{J}$ corresponding to the $A$ s in $\ell$ and thus the $B \mathrm{~s}$ in $\ell^{\prime}$, and all other indices (not in $\mathcal{J}$ ) correspond to $B \mathrm{~s}$ in $\ell$ (and thus $A$ s in $\ell^{\prime}$ ). Then, we claim that Lexi puts an $A$ in the cell in row $r$, column $c$ if $r, c \in \mathcal{J}$ or $r, c \notin \mathcal{J}$, and a $B$ otherwise, each row and column contains a string in $\mathcal{S}$.
We illustrate this with a simple example: If $k=6$ and we have that $A A A B A B$ and $B B B A B A$ are both in the dictionary, then Lexi could fill the table as follows:
| A | A | A | B | A | B |
| :---: | :---: | :---: | :---: | :---: | :---: |
| A | A | A | B | A | B |
| A | A | A | B | A | B |
| B | B | B | A | B | A |
| A | A | A | B | A | B |
| B | B | B | A | B | A |
Suppose we are looking at row $i$ or column $i$ for $i \in \mathcal{J}$. Then by construction the string in this row/column contains $A$ s at indices $k$ with $k \in \mathcal{J}$ and $B$ s elsewhere, and thus is precisely $\ell$. Suppose instead we are looking at row $i$ or column $i$ for $i \notin \mathcal{J}$. Then again
by construction the string in this row/column contains $A$ s at indices $k$ with $k \notin \mathcal{J}$ and $B$ s elsewhere, and thus is precisely $\ell^{\prime}$. So each row and column indeed contains a string in $\mathcal{S}$.
Thus, for any $\mathcal{S}$ with $|\mathcal{S}| \geqslant 2^{k-1}$, Lexi can definitely fill the grid appropriately. Since we know $m \geqslant 2^{k-1}$, $2^{k-1}$ is the minimum possible value of $m$ as claimed.
|
2^{k-1}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Let $k$ be a positive integer. Lexi has a dictionary $\mathcal{D}$ consisting of some $k$-letter strings containing only the letters $A$ and $B$. Lexi would like to write either the letter $A$ or the letter $B$ in each cell of a $k \times k$ grid so that each column contains a string from $\mathcal{D}$ when read from top-to-bottom and each row contains a string from $\mathcal{D}$ when read from left-to-right.
What is the smallest integer $m$ such that if $\mathcal{D}$ contains at least $m$ different strings, then Lexi can fill her grid in this manner, no matter what strings are in $\mathcal{D}$ ?
|
We claim the minimum value of $m$ is $2^{k-1}$.
Firstly, we provide a set $\mathcal{S}$ of size $2^{k-1}-1$ for which Lexi cannot fill her grid. Consider the set of all length- $k$ strings containing only $A$ s and $B$ shich end with a $B$, and remove the string consisting of $k B$ s. Clearly there are 2 independent choices for each of the first $k-1$ letters and 1 for the last letter, and since exactly one string is excluded, there must be exactly $2^{k-1}-1$ strings in this set.
Suppose Lexi tries to fill her grid. For each row to have a valid string, it must end in a $B$. But then the right column would necessarily contain $k B \mathrm{~s}$, and not be in our set. Thus, Lexi cannot fill her grid with our set, and we must have $m \geqslant 2^{k-1}$.
Now, consider any set $\mathcal{S}$ with at least $2^{k-1}$ strings. Clearly, if $\mathcal{S}$ contained either the uniform string with $k A$ s or the string with $k B \mathrm{~s}$, then Lexi could fill her grid with all of the relevant letters and each row and column would contain that string.
Consider the case where $\mathcal{S}$ contains neither of those strings. Among all $2^{k}$ possible length$k$ strings with $A \mathrm{~s}$ and $B \mathrm{~s}$, each has a complement which corresponds to the string with $B$ s in every position where first string had $A$ s and vice-versa. Clearly, the string with all $A$ s is paired with the string with all $B$ s. We may assume that we do not take the two uniform strings and thus applying the pigeonhole principle to the remaining set of strings, we must have two strings which are complementary.
Let this pair of strings be $\ell, \ell^{\prime} \in \mathcal{S}$ in some order. Define the set of indices $\mathcal{J}$ corresponding to the $A$ s in $\ell$ and thus the $B \mathrm{~s}$ in $\ell^{\prime}$, and all other indices (not in $\mathcal{J}$ ) correspond to $B \mathrm{~s}$ in $\ell$ (and thus $A$ s in $\ell^{\prime}$ ). Then, we claim that Lexi puts an $A$ in the cell in row $r$, column $c$ if $r, c \in \mathcal{J}$ or $r, c \notin \mathcal{J}$, and a $B$ otherwise, each row and column contains a string in $\mathcal{S}$.
We illustrate this with a simple example: If $k=6$ and we have that $A A A B A B$ and $B B B A B A$ are both in the dictionary, then Lexi could fill the table as follows:
| A | A | A | B | A | B |
| :---: | :---: | :---: | :---: | :---: | :---: |
| A | A | A | B | A | B |
| A | A | A | B | A | B |
| B | B | B | A | B | A |
| A | A | A | B | A | B |
| B | B | B | A | B | A |
Suppose we are looking at row $i$ or column $i$ for $i \in \mathcal{J}$. Then by construction the string in this row/column contains $A$ s at indices $k$ with $k \in \mathcal{J}$ and $B$ s elsewhere, and thus is precisely $\ell$. Suppose instead we are looking at row $i$ or column $i$ for $i \notin \mathcal{J}$. Then again
by construction the string in this row/column contains $A$ s at indices $k$ with $k \notin \mathcal{J}$ and $B$ s elsewhere, and thus is precisely $\ell^{\prime}$. So each row and column indeed contains a string in $\mathcal{S}$.
Thus, for any $\mathcal{S}$ with $|\mathcal{S}| \geqslant 2^{k-1}$, Lexi can definitely fill the grid appropriately. Since we know $m \geqslant 2^{k-1}$, $2^{k-1}$ is the minimum possible value of $m$ as claimed.
|
{
"resource_path": "EGMO/segmented/en-2023-solutions.jsonl",
"problem_match": "\nProblem 3.",
"solution_match": "\nSolution."
}
|
74e0a1fc-b265-52c3-9c70-645581cdb51e
| 606,055
|
Problem. For a sequence $a_{1}<a_{2}<\cdots<a_{n}$ of integers, a pair $\left(a_{i}, a_{j}\right)$ with $1 \leq i<j \leq n$ is called interesting if there exists a pair $\left(a_{k}, a_{l}\right)$ of integers with $1 \leq k<l \leq n$ such that
$$
\frac{a_{l}-a_{k}}{a_{j}-a_{i}}=2
$$
For each $n \geq 3$, find the largest possible number of interesting pairs in a sequence of length $n$.
Answer. $\frac{1}{2}(n-1)(n-2)+1$.
|
Consider the numbers $a_{i}=2^{i}$ for $2 \leq i \leq n$ and $a_{1}=0$, and choose any pair $(i, j)$ with $1 \leq i<j \leq n$.
If $i=1$, the pair $(1, j)$ is interesting for all $2 \leq j \leq n-1$, as $\frac{a_{j+1}-a_{1}}{a_{j}-a_{1}}=\frac{2^{j+1}}{2^{j}}=2$.
If $i \geq 2$, the pair $(i, j)$ is also interesting for all $j$ such that $i+1 \leq j \leq n-1$, since $\frac{a_{j+1}-a_{i+1}}{a_{j}-a_{i}}=\frac{2^{j+1}-2^{i+1}}{2^{j}-2^{i}}=2$.
In addition, the pair $(n-1, n)$ is interesting, as $\frac{a_{n}-a_{0}}{a_{n}-a_{n-1}}=2$.
Hence, all pairs in which $j \leq n-1$, and additionally the pair $(n-1, n)$, are interesting, giving $\frac{1}{2}(n-1)(n-2)+1$ pairs in total.
Now, let's show that there can't be more interesting pairs. To this end we show that at least $\frac{1}{2} n(n-1)-\left(\frac{1}{2}(n-1)(n-2)+1\right)=n-2$ pairs are not interesting. Clearly, the pair $(1, n)$ is not interesting.
Let's make the following observation: if a pair $(i, j)$ is interesting and it's not $(1, n)$, then $a_{j}-a_{i}$ can't exceed $\frac{1}{2}\left(a_{n}-a_{1}\right)$. (Since, if $(i, j)$ is interesting then $a_{l}-a_{k}=2\left(a_{j}-a_{i}\right)$ for some pair $(k, l)$. If then $2\left(a_{j}-a_{i}\right)>a_{n}-a_{1}$ we would have $a_{l}-a_{k}>a_{n}-a_{1}$, which is not possible.)
Finally, for any $2 \leq i \leq n-1$ consider pairs $(1, i)$ and $(i, n)$. If both of them are interesting, then, following the observation above, the only possibility is $a_{i}-a_{1}=a_{n}-a_{i}=\frac{a_{n}-a_{1}}{2}$. Clearly, this is possible for at most one $i$, so for all other $n-3$ values of $i$, at least one of pairs $(1, i)$ and $(i, n)$ is not interesting. Combining with the pair $(1, n)$, we get at least $n-2$ not interesting pairs in total, as desired.
Comment: The originally proposed formulation considered a sequence $a_{1}<a_{2}<\cdots<$ $a_{n}$ of $n$ real numbers, rather than integers. The conclusion is however the same and the solution is identical.
|
\frac{1}{2}(n-1)(n-2)+1
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Problem. For a sequence $a_{1}<a_{2}<\cdots<a_{n}$ of integers, a pair $\left(a_{i}, a_{j}\right)$ with $1 \leq i<j \leq n$ is called interesting if there exists a pair $\left(a_{k}, a_{l}\right)$ of integers with $1 \leq k<l \leq n$ such that
$$
\frac{a_{l}-a_{k}}{a_{j}-a_{i}}=2
$$
For each $n \geq 3$, find the largest possible number of interesting pairs in a sequence of length $n$.
Answer. $\frac{1}{2}(n-1)(n-2)+1$.
|
Consider the numbers $a_{i}=2^{i}$ for $2 \leq i \leq n$ and $a_{1}=0$, and choose any pair $(i, j)$ with $1 \leq i<j \leq n$.
If $i=1$, the pair $(1, j)$ is interesting for all $2 \leq j \leq n-1$, as $\frac{a_{j+1}-a_{1}}{a_{j}-a_{1}}=\frac{2^{j+1}}{2^{j}}=2$.
If $i \geq 2$, the pair $(i, j)$ is also interesting for all $j$ such that $i+1 \leq j \leq n-1$, since $\frac{a_{j+1}-a_{i+1}}{a_{j}-a_{i}}=\frac{2^{j+1}-2^{i+1}}{2^{j}-2^{i}}=2$.
In addition, the pair $(n-1, n)$ is interesting, as $\frac{a_{n}-a_{0}}{a_{n}-a_{n-1}}=2$.
Hence, all pairs in which $j \leq n-1$, and additionally the pair $(n-1, n)$, are interesting, giving $\frac{1}{2}(n-1)(n-2)+1$ pairs in total.
Now, let's show that there can't be more interesting pairs. To this end we show that at least $\frac{1}{2} n(n-1)-\left(\frac{1}{2}(n-1)(n-2)+1\right)=n-2$ pairs are not interesting. Clearly, the pair $(1, n)$ is not interesting.
Let's make the following observation: if a pair $(i, j)$ is interesting and it's not $(1, n)$, then $a_{j}-a_{i}$ can't exceed $\frac{1}{2}\left(a_{n}-a_{1}\right)$. (Since, if $(i, j)$ is interesting then $a_{l}-a_{k}=2\left(a_{j}-a_{i}\right)$ for some pair $(k, l)$. If then $2\left(a_{j}-a_{i}\right)>a_{n}-a_{1}$ we would have $a_{l}-a_{k}>a_{n}-a_{1}$, which is not possible.)
Finally, for any $2 \leq i \leq n-1$ consider pairs $(1, i)$ and $(i, n)$. If both of them are interesting, then, following the observation above, the only possibility is $a_{i}-a_{1}=a_{n}-a_{i}=\frac{a_{n}-a_{1}}{2}$. Clearly, this is possible for at most one $i$, so for all other $n-3$ values of $i$, at least one of pairs $(1, i)$ and $(i, n)$ is not interesting. Combining with the pair $(1, n)$, we get at least $n-2$ not interesting pairs in total, as desired.
Comment: The originally proposed formulation considered a sequence $a_{1}<a_{2}<\cdots<$ $a_{n}$ of $n$ real numbers, rather than integers. The conclusion is however the same and the solution is identical.
|
{
"resource_path": "EGMO/segmented/en-2024-solutions.jsonl",
"problem_match": "# Problem 4 (UKR)\n",
"solution_match": "\nSolution."
}
|
647ac0ef-e3ca-5a10-a98e-b3dda38c6d19
| 606,260
|
Determine all integers $x$ such that $2^{x}+x^{2}+25$ is the cube of a prime number.
|
The exercise will use two ideas:
- Modulos to obtain information about $x$.
- Enclosures comparing $2^{x}$ and $x^{2}$ to show that the left-hand side is often strictly between two consecutive cubes (and therefore cannot be a cube of an integer).
Let $x$ be an integer such that $2^{x}+x^{2}+25$ is the cube of a prime number $p$. Since $2^{x}=p^{3}-x^{2}-25$ is an integer, $x$ is positive. Moreover, $p^{3} \geqslant 25$ so $p>2$ and $p$ is odd.
If $x=0$, then $2^{x}+x^{2}+25=26$ which is not a cube. Thus, $x \geqslant 1$. We deduce that $x^{2}+25$ has the same parity as $p^{3}$, which is odd. This forces $x$ to be even. In particular, $x \geqslant 2$ so $p^{3}>27$ and $p>3$. Let $y$ be the integer such that $x=2 y$. By looking at the equation modulo 3, we find
$$
2^{2 y}+4 y^{2}+25 \equiv 1+y^{2}+25 \equiv 2+y^{2} \quad \bmod 3
$$
If $y$ is not divisible by 3, its square is 1 modulo 3, which implies that 3 divides $p$, which is excluded. Thus, 3 divides $y$. Let $z$ be the integer such that $y=3 z$. The equation becomes
$$
2^{6 z}+36 z^{2}+25=p^{3}
$$
If $z=1$, then the left-hand side is $125=5^{3}$. Thus, $x=6 \times 1$ is a solution.
Let's show that if $z \geqslant 2$, we have $\left(2^{2 z}\right)^{3}<2^{6 z}+36 z^{2}+25<\left(2^{2 z}+1\right)^{3}$, which will show that the left-hand side cannot be the cube of an integer. The left inequality is always true since $36 z^{2}+25>0$. To show the right inequality, we need to show that $3 \times 2^{4 z}+3 \times 2^{2 z}+1>36 z^{2}+25$.
On the one hand, if $z \geqslant 2$, we have $3 \times 2^{2 z} \geqslant 3 \times 16>25$. On the other hand, we show by induction on $z$ that $2^{4 z}>12 z^{2}$.
Initialization: If $z=2$, we have $2^{4 z}=256>48=12 z^{2}$.
Induction: Suppose that $2^{4 z}>12 z^{2}$ for $z \geqslant 2$. Then
$$
2^{4(z+1)}=16 \times 2^{4 z}>16 \times 12 z^{2} \geqslant 12 \times 4 z^{2} \geqslant 12\left(z^{2}+2 z+1\right)=12(z+1)^{2}
$$
where we have used that $z^{2} \geqslant z$ and $z^{2} \geqslant 1$ for $z \geqslant 2$. Thus, the property is true for $z+1$, which completes the induction.
We therefore have $3 \times 2^{4 z}+3 \times 2^{2 z}+1>36 z^{2}+25$, which implies that the left-hand side is not the cube of an integer for $z \geqslant 2$.
The only solution is therefore $x=6$.
|
6
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Déterminer tous les entiers $x$ tels que $2^{x}+x^{2}+25$ est le cube d'un nombre premier.
|
L'exercice va utiliser deux idées:
- Les modulos pour obtenir des informations sur $x$.
- Des encadrements comparant $2^{x}$ et $x^{2}$ afin de montrer que le membre de gauche est souvent strictement compris entre deux cubes consécutifs (et ne peut donc être un cube d'entier).
Soit $x$ un entier tel que $2^{x}+x^{2}+25$ est le cube d'un nombre premier $p$. Puisque $2^{x}=p^{3}-x^{2}-25$ est un entier, $x$ est positif. De plus $p^{3} \geqslant 25$ donc $p>2$ et $p$ est impair.
Si $x=0$, alors $2^{x}+x^{2}+25=26$ qui n'est pas un cube. Ainsi, $x \geqslant 1$. On déduit que $x^{2}+25$ est de la parité de $p^{3}$, c'est-à-dire impair. Ceci force $x$ à être pair. En particulier, $x \geqslant 2$ donc $p^{3}>27$ et $p>3$. Soit y l'entier tel que $x=2 y$. En regardant l'équation modulo 3 , on trouve
$$
2^{2 y}+4 y^{2}+25 \equiv 1+y^{2}+25 \equiv 2+y^{2} \quad \bmod 3
$$
Si y n'est pas divisible par 3 , son carré vaut 1 modulo 3 , ce qui implique que 3 divise $p$, ce qui est exclus. Ainsi, 3 divise $y$. Soit $z$ l'entier tel que $y=3 z$. L'équation devient
$$
2^{6 z}+36 z^{2}+25=p^{3}
$$
Si $z=1$, alors le membre de gauche vaut $125=5^{3}$. Ainsi, $x=6 \times 1$ est solution.
Montrons que si $z \geqslant 2$, on a $\left(2^{2 z}\right)^{3}<2^{6 z}+36 z^{2}+25<\left(2^{2 z}+1\right)^{3}$, ce qui montrera que le côté gauche ne peut être le cube d'un entier. L'inégalité de gauche est toujours vraie car $36 z^{2}+25>0$. Pour montrer l'inégalité de droite, il faut montrer que $3 \times 2^{4 z}+3 \times 2^{2 z}+1>36 z^{2}+25$.
D'une part, si $z \geqslant 2$, on a $3 \times 2^{2 z} \geqslant 3 \times 16>25$. D'autre part, on montre par récurrence sur $z$ que $2^{4 z}>12 z^{2}$.
Initialisation: $\operatorname{Si} z=2$, on a bien $2^{4 z}=256>48=12 z^{2}$.
Hérédité : On suppose que $2^{4 z}>12 z^{2}$ pour $z \geqslant 2$. Alors
$$
2^{4(z+1)}=16 \times 2^{4 z}>16 \times 12 z^{2} \geqslant 12 \times 4 z^{2} \geqslant 12\left(z^{2}+2 z+1\right)=12(z+1)^{2}
$$
où on a utilisé que $z^{2} \geqslant z$ et $z^{2} \geqslant 1$ pour $z \geqslant 2$. Ainsi, la propriété est vraie pour $z+1$, ce qui achève la récurrence.
On a donc bien $3 \times 2^{4 z}+3 \times 2^{2 z}+1>36 z^{2}+25$, ce qui implique que le membre de gauche $n$ 'est pas le cube d'un entier pour $z \geqslant 2$.
L'unique solution est donc $x=6$.
|
{
"resource_path": "French/segmented/envois/fr-Corrige-envoi-5-2023-2024.jsonl",
"problem_match": "\nExercice 7.",
"solution_match": "## Solution de l'exercice 7"
}
|
9ac804d7-9979-5618-8b3e-454cd05388a8
| 607,146
|
We define the sequence $\left(a_{n}\right)$ by $a_{0}=a_{1}=a_{2}=1$ and if $n \geqslant 3$:
$$
a_{n}=\left\lfloor\frac{n}{a_{n-1} a_{n-2} a_{n-3}}\right\rfloor
$$
Determine $\mathrm{a}_{2022}$.
|
By calculating the first terms of the sequence, we make the following conjecture, which we prove by induction on $k$:
$$
\text { If } k \geqslant 1 \text {, then } a_{4 k}=1, a_{4 k+1}=1, a_{4 k+2}=\left\lfloor\frac{4 k+2}{3}\right\rfloor \text { and } a_{4 k+3}=3 .
$$
Initialization: We have $a_{3}=3, a_{4}=1, a_{5}=1, a_{6}=2$ and $a_{7}=3$, so the property is satisfied for $\mathrm{k}=1$.
Hereditary: Suppose the property is satisfied for $k \geqslant 1$ fixed. Then we have successively:
$$
a_{4(k+1)}=\left\lfloor\frac{4(k+1)}{a_{4 k+1} a_{4 k+2} a_{4 k+3}}\right\rfloor=\left\lfloor\frac{4(k+1)}{3\lfloor(4 k+2) / 3\rfloor}\right\rfloor,
$$
and $\frac{4(\mathrm{k}+1)}{3}<2\left(\frac{4 \mathrm{k}+2}{3}-1\right)<2\left\lfloor\frac{4 \mathrm{k}+2}{3}\right\rfloor$ for $k \geqslant 2$ and $\frac{8}{3}<2\left\lfloor\frac{4 \times 1+2}{3}\right\rfloor$, so that $\mathrm{a}_{4(\mathrm{k}+1)}=1$.
$$
\mathbf{a}_{4(k+1)+1}=\left\lfloor\frac{4(k+1)+1}{a_{4 k+2} a_{4 k+3} a_{4(k+1)}}\right\rfloor=\left\lfloor\frac{4(k+1)+1}{3\lfloor(4 k+2) / 3\rfloor}\right\rfloor
$$
and here too, we have $\frac{4(k+1)}{3}<2\left\lfloor\frac{4 k+2}{3}\right\rfloor$, so $a_{4(k+1)+1}=1$.
$$
a_{4(k+1)+2}=\left\lfloor\frac{4(k+1)+2}{a_{4 k+3} a_{4(k+1)} a_{4(k+1)+1}}\right\rfloor=\left\lfloor\frac{4(k+1)+2}{3}\right\rfloor
$$
so $a_{4(k+1)+2}=\left\lfloor\frac{4(k+1)+2}{3}\right\rfloor$.
Finally,
$$
a_{4(k+1)+3}=\left\lfloor\frac{4(k+1)+3}{a_{4(k+1)} a_{4(k+1)+1} a_{4(k+1)+2}}\right\rfloor=\left\lfloor\frac{4(k+1)+3}{\lfloor(4(k+1)+2) / 3\rfloor}\right\rfloor .
$$
We have
$$
4(k+1)+3 \geqslant 3\left(\frac{4(k+1)+2}{3}\right) \geqslant 3\lfloor(4(k+1)+2) / 3\rfloor
$$
and
$$
4(k+1)+3 \leqslant 4\left(\frac{4(k+1)+2}{3}-1\right)<4\lfloor(4(k+1)+2) / 3\rfloor
$$
for $k \geqslant 1$, so $a_{4(k+1)+3}=3$. This completes the induction.
Thus $\mathrm{a}_{2022}=\mathrm{a}_{4 \times 505+2}=\left\lfloor\frac{4 \times 505+2}{3}\right\rfloor=674$.
|
674
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
On définit la suite $\left(a_{n}\right)$ par $a_{0}=a_{1}=a_{2}=1$ et si $n \geqslant 3$ :
$$
a_{n}=\left\lfloor\frac{n}{a_{n-1} a_{n-2} a_{n-3}}\right\rfloor
$$
Déterminer $\mathrm{a}_{2022}$.
|
En calculant les premiers termes de la suite, on effectue la conjecture suivante, que l'on montre par récurrence sur $k$ :
$$
\text { Si } k \geqslant 1 \text {, alors } a_{4 k}=1, a_{4 k+1}=1, a_{4 k+2}=\left\lfloor\frac{4 k+2}{3}\right\rfloor \text { et } a_{4 k+3}=3 .
$$
Initialisation : On a $a_{3}=3, a_{4}=1, a_{5}=1, a_{6}=2$ et $a_{7}=3$, de sorte que la propriété est vérifiée pour $\mathrm{k}=1$.
Hérédité : Supposons la propriété vérifiée pour $k \geqslant 1$ fixée. Alors on a successivement :
$$
a_{4(k+1)}=\left\lfloor\frac{4(k+1)}{a_{4 k+1} a_{4 k+2} a_{4 k+3}}\right\rfloor=\left\lfloor\frac{4(k+1)}{3\lfloor(4 k+2) / 3\rfloor}\right\rfloor,
$$
or $\frac{4(\mathrm{k}+1)}{3}<2\left(\frac{4 \mathrm{k}+2}{3}-1\right)<2\left\lfloor\frac{4 \mathrm{k}+2}{3}\right\rfloor$ pour $k \geqslant 2$ et $\frac{8}{3}<2\left\lfloor\frac{4 \times 1+2}{3}\right\rfloor$, de sorte que $\mathrm{a}_{4(\mathrm{k}+1)}=1$.
$$
\mathbf{a}_{4(k+1)+1}=\left\lfloor\frac{4(k+1)+1}{a_{4 k+2} a_{4 k+3} a_{4(k+1)}}\right\rfloor=\left\lfloor\frac{4(k+1)+1}{3\lfloor(4 k+2) / 3\rfloor}\right\rfloor
$$
et là aussi, on a $\frac{4(k+1)}{3}<2\left\lfloor\frac{4 k+2}{3}\right\rfloor$, de sorte que $a_{4(k+1)+1}=1$.
$$
a_{4(k+1)+2}=\left\lfloor\frac{4(k+1)+2}{a_{4 k+3} a_{4(k+1)} a_{4(k+1)+1}}\right\rfloor=\left\lfloor\frac{4(k+1)+2}{3}\right\rfloor
$$
donc $a_{4(k+1)+2}=\left\lfloor\frac{4(k+1)+2}{3}\right\rfloor$.
Enfin,
$$
a_{4(k+1)+3}=\left\lfloor\frac{4(k+1)+3}{a_{4(k+1)} a_{4(k+1)+1} a_{4(k+1)+2}}\right\rfloor=\left\lfloor\frac{4(k+1)+3}{\lfloor(4(k+1)+2) / 3\rfloor}\right\rfloor .
$$
Or on a bien
$$
4(k+1)+3 \geqslant 3\left(\frac{4(k+1)+2}{3}\right) \geqslant 3\lfloor(4(k+1)+2) / 3\rfloor
$$
et
$$
4(k+1)+3 \leqslant 4\left(\frac{4(k+1)+2}{3}-1\right)<4\lfloor(4(k+1)+2) / 3\rfloor
$$
pour $k \geqslant 1$, de sorte que $a_{4(k+1)+3}=3$. Ceci achève la récurrence.
Ainsi $\mathrm{a}_{2022}=\mathrm{a}_{4 \times 505+2}=\left\lfloor\frac{4 \times 505+2}{3}\right\rfloor=674$.
|
{
"resource_path": "French/segmented/envois/fr-Corrige-envoi-5-2023-2024.jsonl",
"problem_match": "## Exercice 12.",
"solution_match": "\nSolution de l'exercice 12"
}
|
655ffbd8-fbb5-52b2-96e5-608c8c48bcc6
| 607,151
|
Let $n \geqslant 2$ and $a_{1}, \ldots, a_{n} \in[0,1]$ be real numbers. Determine the maximum value that the smallest of the numbers
$$
a_{1}-a_{1} a_{2}, a_{2}-a_{2} a_{3}, \ldots, a_{n}-a_{n} a_{1}
$$
can take.
|
Let $i$ be such that $a_{i}$ is minimal. Then we have $a_{i+1} \geqslant a_{i}$ (where $a_{n+1}=a_{1}$) and thus by the arithmetic-geometric inequality on $a_{i}$ and $1-a_{i}$, we obtain
$$
a_{i}-a_{i} a_{i+1} \leqslant a_{i}-a_{i}^{2}=a_{i}\left(1-a_{i}\right) \leqslant \frac{1}{4}\left(a_{i}+1-a_{i}\right)^{2}=\frac{1}{4}
$$
so the minimum of the numbers is at most $\frac{1}{4}$. It remains to verify that we can find $a_{i}$ such that the minimum is equal to $\frac{1}{4}$. If all the $a_{i}$ are equal to $\frac{1}{2}$, then all the $a_{i}-a_{i} a_{i+1}$ are equal to $\frac{1}{4}$ and the minimum is indeed $\frac{1}{4}$.
Comment from the graders: The problem was generally well done. It contained two steps: proving that the expression is always less than 0.25 and providing an example where this bound is achieved. Some students forget one or the other of these two steps and thus lose valuable points.
|
\frac{1}{4}
|
Yes
|
Yes
|
math-word-problem
|
Inequalities
|
Soit $n \geqslant 2$ et $a_{1}, \ldots, a_{n} \in[0,1]$ des réels. Déterminer la valeur maximale que peut prendre le plus petit des nombres
$$
a_{1}-a_{1} a_{2}, a_{2}-a_{2} a_{3}, \ldots, a_{n}-a_{n} a_{1}
$$
|
Soit $i$ tel que $a_{i}$ soit minimal. Alors on a $a_{i+1} \geqslant a_{i}$ (où $a_{n+1}=a_{1}$ ) et donc par inégalité arithmético-géométrique sur $a_{i}$ et $1-a_{i}$, on obtient
$$
a_{i}-a_{i} a_{i+1} \leqslant a_{i}-a_{i}^{2}=a_{i}\left(1-a_{i}\right) \leqslant \frac{1}{4}\left(a_{i}+1-a_{i}\right)^{2}=\frac{1}{4}
$$
donc le minimum des nombres vaut au plus $\frac{1}{4}$. Il reste à vérifier que l'on peut trouver des $a_{i}$ tel que le minimum soit égal à $\frac{1}{4}$. Si tous les $a_{i}$ valent $\frac{1}{2}$, alors tous les $a_{i}-a_{i} a_{i+1}$ valent $\frac{1}{4}$ et le minimum vaut bien $\frac{1}{4}$.
Commentaire des correcteurs : Le problème est bien réussi dans l'ensemble. Il contenait deux étapes: prouver que l'expresison est toujours plus petite que 0.25 et donner un exemple en lequel cette borne est atteinte. Quelques élèves oublient l'une ou l'autre de ces deux étapes et perdent alors de précieux points.
|
{
"resource_path": "French/segmented/envois/fr-Corrige-envoi-algebre-2023-2024.jsonl",
"problem_match": "\nExercice 5.",
"solution_match": "\nSolution de l'exercice 5"
}
|
8ab9bb28-849b-5dc1-b9f7-011129316478
| 607,162
|
Emile has created an exercise for Benoît. He announces that he has secretly chosen a unitary polynomial $P$ of degree 2023 with integer coefficients, that is, of the form
$$
P(X)=X^{2023}+a_{2022} X^{2022}+a_{2021} X^{2021}+\ldots+a_{1} X+a_{0}
$$
where $a_{0}, a_{1}, \ldots, a_{2022}$ are integers. He gives Benoît $k$ integers $n_{1}, n_{2}, \ldots, n_{k}$, where $k$ is a positive integer, as well as the value of the product $P\left(n_{1}\right) P\left(n_{2}\right) \ldots P\left(n_{k}\right)$. From this information, Benoît must try to determine the polynomial $P$.
Find the smallest integer $k$ such that Emile can find $P$ and $n_{1}, \ldots, n_{k}$ to ensure that the only polynomial matching the information given to Benoît is $P$.
|
Let's show that the minimal $k$ is $k=2023$. Indeed, suppose first that $k<2023$ and that Émile chooses $P$ and $n_{1}, \ldots, n_{k}$. Let
$$
Q = P + (X - n_{1})(X - n_{2}) \ldots (X - n_{k})
$$
which is a polynomial with integer coefficients, always monic of degree 2023, and different from $P$. Then $P$ and $Q$ are equal at each $n_{i}$, and therefore the products $P(n_{1}) \ldots P(n_{k})$ and $Q(n_{1}) \ldots Q(n_{k})$ are equal, so Benoît cannot determine the value of the polynomial $P$.
Now suppose that $k=2023$. Émile can then choose $n_{1}=3, n_{2}=6, \ldots, n_{2023}=3 \cdot 2023$ and set
$$
P = (X-3)(X-6) \ldots (X-3 \cdot 2023) + 1
$$
Then the product $P(n_{1}) P(n_{2}) \ldots P(n_{k})$ is 1. Let $Q$ be a polynomial with integer coefficients, monic of degree 2023, such that the product $Q(n_{1}) \ldots Q(n_{k})$ is equal to 1; we need to show that necessarily $Q=P$. Since all the $Q(n_{i})$ are integers, they are all either 1 or -1. However, we can note that since the $n_{i}$ are divisible by 3, for all $i$, $Q(n_{i})$ is congruent to the constant term of $Q$. Since 1 and -1 are not congruent modulo 3, all the $Q(n_{i})$ are equal. Since 2023 is odd, they cannot all be equal to -1, so they are all 1. Then $P - Q$ is a polynomial of degree at most 2022 (since the terms of order 2023 cancel out) and is zero at each of the 2023 values of the $n_{i}$, so $Q = P$, which concludes.
Comment from the graders: The exercise was generally well understood, and many students thought to create a polynomial $P$ such that the product $P(n_{1}) P(n_{2}) \ldots P(n_{k}) = 1$, which was the right way to solve the exercise. However, be careful to better justify the arguments of polynomial division with integer coefficients; some students were a bit too quick on this step.
|
2023
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Emile a créé un exercice pour Benoît. Il lui annonce qu'il a choisi secrètement un polynôme P unitaire de degré 2023 à coefficients entiers, c'est-à-dire de la forme
$$
P(X)=X^{2023}+a_{2022} X^{2022}+a_{2021} X^{2021}+\ldots+a_{1} X+a_{0}
$$
où $a_{0}, a_{1}, \ldots, a_{2022}$ sont des entiers relatifs. Il donne à Benoît $k$ entiers $n_{1}, n_{2}, \ldots, n_{k}$, où $k$ est un entier positif, ainsi que la valeur du produit $P\left(n_{1}\right) P\left(n_{2}\right) \ldots P\left(n_{k}\right)$. A partir de ces connaissances, Benoît doit essayer de retrouver le polynôme P .
Trouver l'entier $k$ minimal tel que Emile puisse trouver $P$ et $n_{1}, \ldots, n_{k}$ afin de s'assurer que le seul polynôme coincidant avec les informations données à Benoît soit P .
|
Montrons que le $k$ minimal est $k=2023$. En effet, supposons d'abord que $k<2023$ et qu'Emile choisisse $P$ et $n_{1}, \ldots, n_{k}$. Posons
$$
\mathrm{Q}=\mathrm{P}+\left(\mathrm{X}-\mathrm{n}_{1}\right)\left(\mathrm{X}-\mathrm{n}_{2}\right) \ldots\left(\mathrm{X}-\mathrm{n}_{\mathrm{k}}\right)
$$
qui est un polynôme à coefficients entiers, toujours unitaire de degré 2023, et différent de P . Alors P et $Q$ sont égaux en chaque $n_{i}$, et donc les produits $P\left(n_{1}\right) \ldots P\left(n_{k}\right)$ et $Q\left(n_{1}\right) \ldots Q\left(n_{k}\right)$ sont égaux, donc Benoît ne peut pas retrouver la valeur du polynôme $P$.
Supposons maintenant que $k=2023$. Emile peut alors choisir $n_{1}=3, n_{2}=6, \ldots, n_{2023}=3 \cdot 2023$ et poser
$$
P=(X-3)(X-6) \ldots(X-3 \cdot 2023)+1
$$
Alors le produit $\mathrm{P}\left(\mathrm{n}_{1}\right) \mathrm{P}\left(\mathrm{n}_{2}\right) \ldots \mathrm{P}\left(\mathrm{n}_{\mathrm{k}}\right)$ vaut 1 . Soit Q un polynôme à coefficients entiers, unitaire de degré 2023 tel que le produit $Q\left(n_{1}\right) \ldots Q\left(n_{k}\right)$ soit égal à 1 , il faut montrer que nécessairement $Q=P$. Comme tous les $Q\left(n_{i}\right)$ sont entiers, ils valent tous soit 1 , soit -1 . On peut cependant remarquer que comme les $n_{i}$ sont divisibles par 3 alors pour tout $i, Q\left(n_{i}\right)$ est congru au coefficient constant de $Q$. Comme 1 et -1 ne sont pas congrus modulos 3 , tous les $Q\left(n_{i}\right)$ sont égaux. Comme 2023 est impair, ils ne peuvent pas tous être égaux à -1 , donc ils valent tous 1 . Alors $P-Q$ est un polynôme de degré au plus 2022 (car les termes d'ordre 2023 s'annulent) et est nul en chacun des 2023 valeurs des $n_{i}$, donc $\mathrm{Q}=\mathrm{P}$, ce qui conclut.
Commentaire des correcteurs : L'exercice a été plutôt bien compris et beaucoup d'élèves ont penser à créer un polynome P dont le produit $\mathrm{P}\left(\mathrm{n}_{1}\right) \mathrm{P}\left(\mathrm{n}_{2}\right) \ldots \mathrm{P}\left(\mathrm{n}_{\mathrm{k}}\right)=1$ ce qui était la bonne façon de résoudre l'exercice. Attention cepandant à mieux justifier les arguments de division euclidienne sur les polynômes à coefficients entiers, certains sont allés un peu vite sur cette étape.
|
{
"resource_path": "French/segmented/envois/fr-Corrige-envoi-algebre-2023-2024.jsonl",
"problem_match": "\nExercice 14.",
"solution_match": "\nSolution de l'exercice 14"
}
|
d549f54d-55f4-57ea-b264-b077c8485f59
| 607,170
|
Find the number of solutions of $n^{2} m^{6}=180 t+2$ for $n, m$ and $t$ positive integers.
|
We consider the expression modulo 4. The left side is a square and is therefore congruent to 0 or 1. 180 is congruent to 0 modulo 4, so $180 t+2$ is congruent to $0 * t+2=2$. The equation has no solutions modulo 4, so it has no solutions in $\mathbb{N}$
|
0
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Trouver le nombre de solutions de $n^{2} m^{6}=180 t+2$ pour $n, m$ et $t$ des entiers positifs.
|
On considère l'expression modulo 4. La gauche est un carré et est donc congru à 0 ou 1.180 est congru à 0 modulo 4 donc $180 t+2$ est congru à $0 * t+2=2$. L'équation n'a pas de solutions modulo 4 , elle n'en a donc pas non plus dans $\mathbb{N}$
|
{
"resource_path": "French/segmented/envois/fr-corrige-envoi-2.jsonl",
"problem_match": "\nExercice 1.",
"solution_match": "\nSolution de l'exercice 1"
}
|
84be4a5f-4038-50fe-90b3-4ed3656ea876
| 607,208
|
Find the sum of all $n$ such that $n^{2}+8 n+44$ is a perfect square.
|
Let $f$ be the function under study. An idea in this type of exercise is to trap $f(n)$ between two consecutive integer squares $k^{2}<f(n)<(k+1)^{2}$ and to say by contradiction that if $f(n)=\mathfrak{i}^{2}$ then $k<i<k+1$ which is impossible since we are dealing with integers.
Here, the calculations can be shortened by noting that $f$ has the same parity as $n+4$, so if $(n+4)^{2}=n^{2}+8 n+16<f(n)<n^{2}+12 n+36=(n+6)^{2}$ which is true as soon as $n>2, f(n)$ is not a square. For the small cases, 2 is a solution and 1 is not.
|
2
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Trouver la somme des $n$ tels que $n^{2}+8 n+44$ soit un carré parfait.
|
Soit f la fonction étudiée, une idée dans ce genre d'exercice est de coincer $f(n)$ entre 2 carrés d'entiers consécutifs $k^{2}<f(n)<(k+1)^{2}$ et de dire par l'absurde que si $f(n)=\mathfrak{i}^{2}$ alors $k<i<k+1$ ce qui est impossible car on a des entiers.
Ici les calculs peuvent s'abréger en remarquant que f a même parité que $n+4$, ainsi si $(n+4)^{2}=n^{2}+8 n+16<f(n)<n^{2}+12 n+36=(n+6)^{2}$ ce qui est vrai dès que $n>2, f(n)$ n'est pas un carré. Pour les petits cas 2 est solution et 1 non.
|
{
"resource_path": "French/segmented/envois/fr-corrige-envoi-2.jsonl",
"problem_match": "\nExercice 2.",
"solution_match": "\nSolution de l'exercice 2"
}
|
1835e260-8acf-57c9-b2b5-1fe2786e41b7
| 607,209
|
We have five colors and a $99 \times 99$ grid. We color some squares of the grid with one of the five colors such that
- Each color appears the same number of times in the grid.
- No row and no column contains squares of different colors.
What is the maximum number of squares that can be colored while following these rules?
|
Answer: $\mathrm{N}=5 \times 19 \times 20=1900$.
Since each row or column can only contain one color, let's think about it starting from the rows. We say that a row or column is of a certain color (say red) when the only color that the cells in this row or column can have is red. If a row or column has no color, we arbitrarily assign it a color. Thus, a red cell must be at the intersection of a red row and a red column. Consequently, the number of red cells can be bounded by the product of the number of red rows and the number of red columns. Now, let's introduce some notation. We number the available colors from 1 to 5 and denote $x_{i}$ as the number of rows colored with the i-th color, and $y_{i}$ as the number of columns colored with this color. Let's also denote $N$ as the number of cells colored by each color. We want to maximize the total number of colored cells, $5N$. The arguments mentioned above show that $\forall i: N \leqslant x_{i} y_{i}$. We obviously also have $x_{1}+x_{2}+\ldots+x_{5}=y_{1}+y_{2}+\ldots y_{5}=99$. Studying small cases shows that to maximize $N$, the $x_{i}$ and $y_{i}$ should all be roughly equal, each being $\frac{99}{5}$ rounded either up or down. A more in-depth study of small cases where 99 is replaced by a small number congruent to $4 \bmod 5$, like 99, allows us to conjecture that the following construction is optimal:
Here, we have $N=19 \cdot 20$.
Let's now prove the optimality. Suppose, for the sake of contradiction, that we have a valid configuration where $\mathrm{N}>19 \times 20$, so $\forall i: x_{i} y_{i}>19 \times 20$. We then note that $x_{i}+y_{i}>39$. Indeed,
$$
x_{i} y_{i}=\frac{1}{4}\left(\left(x_{i}+y_{i}\right)^{2}-\left(x_{i}-y_{i}\right)^{2}\right)
$$
Thus,
$$
38^{2}<4 \cdot 19 \cdot 20=39^{2}-1<\left(x_{i}+y_{i}\right)^{2}-\left(x_{i}-y_{i}\right)^{2}<\left(x_{i}+y_{i}\right)^{2}
$$
So $38<x_{i}+y_{i}$. Moreover, if $x_{i}+y_{i}=39$, then $\left(x_{i}-y_{i}\right)^{2}<1$ So $x_{i}=y_{i}$, which is impossible because 39 is odd. Therefore, $x_{i}+y_{i} \geqslant 40$.
The final count $2 \cdot 99=\left(x_{1}+y_{1}\right)+\left(x_{2}+y_{2}\right)+\ldots+\left(x_{5}+y_{5}\right) \geqslant 5 \times 40=200$ is a contradiction and completes the proof.
Graders' Comments: The problem was not solved by many students who attempted it. Overall, a good number of students found a configuration that worked for $\mathrm{N}=1900$, which was indeed the maximum answer. However, few of them showed that it was not possible to do better, with many content to say that from the configuration they provided, no more cells could be colored: but this does not mean that another configuration, completely different (and not starting from the configuration at $\mathrm{N}=1900$), could not have more colored cells. Furthermore, a number of students assumed that there must be the same number of rows and columns for each color, leading to 1805: but the constraint was to have the same number of cells for each color in total, with no condition on the number of rows and columns per color, and indeed the optimal configurations do not have the same number of rows and columns per color. Finally, some students had the right reasoning but forgot to answer the question in the statement, which was "what is the maximum number of cells that can be colored in the grid": it is emphasized the importance of reading over and being sure that the question has been answered before submitting a copy.
|
1900
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
On dispose de cinq couleurs et d'une grille $99 \times 99$. On colorie certains carrés de la grille avec l'une des cinq couleurs de sorte que
- Chaque couleur apparaît le même nombre de fois dans la grille.
- Aucune ligne et aucune colonne ne contient des cases de couleur différente.
Quelle est le plus grand nombre possible de cases que l'on peut colorier en suivant ces règles?
|
Réponse : $\mathrm{N}=5 \times 19 \times 20=1900$.
Comme chaque ligne ou colonne ne peut contenir qu'une couleur, on va réfléchir en partant des lignes. On dit qu'une ligne ou colonne est d'une couleur (disons rouge) quand la seule couleur que peuvent avoir des cases de cette ligne ou colonne est le rouge. Si une ligne ou colonne n'a pas de couleur, on lui assigne arbitrairement une couleur. Ainsi, une case rouge se trouve forcément à l'intersection d'une ligne rouge et d'une colonne rouge. Par conséquent, on peut majorer le nombre de case rouge par le produit du nombre de ligne rouges par le nombre de colonnes rouges. Introduisons maintenant des notations. On numérotes les couleurs disponibles de 1 à 5 et on note $x_{i}$ le nombre de lignes colorées de la i-ième couleur, et $y_{i}$ le nombre de colonnes colorées de cette couleur. Notons enfin N le nombre de cases coloriées par couleur. On veut maximiser le nombre total de cases coloriées, 5 N . Les arguments précédemment cités montrent que $\forall i: N \leqslant x_{i} y_{i}$. ON a évidemment aussi, $x_{1}+x_{2}+\ldots+x_{5}=y_{1}+y_{2}+\ldots y_{5}=99$. L'étude des petits cas nous montre que pour maximiser $N$ il faut que les $x_{i}$ et les $y_{i}$ soient tous environs égaux, valant tous $\frac{99}{5}$ arrondi soit par excès ou par défaut. Une étude plus approfondie des petits cas où on remplace 99 par un petit nombre congru à $4 \bmod 5$, comme 99 , nous permet de conjecturer que la construction suivante est optimale :

Ici, on a $N=19 \cdot 20$.
Prouvons maintenant l'optimalité. Supposons par l'absurde disposer d'une configuration valide où $\mathrm{N}>$ $19 \times 20$, donc $\forall i: x_{i} y_{i}>19 \times 20$. On remarque ensuite que $x_{i}+y_{i}>39$. En effet,
$$
x_{i} y_{i}=\frac{1}{4}\left(\left(x_{i}+y_{i}\right)^{2}-\left(x_{i}-y_{i}\right)^{2}\right)
$$
Donc
$$
38^{2}<4 \cdot 19 \cdot 20=39^{2}-1<\left(x_{i}+y_{i}\right)^{2}-\left(x_{i}-y_{i}\right)^{2}<\left(x_{i}+y_{i}\right)^{2}
$$
Donc $38<x_{i}+y_{i}$. De plus, si $x_{i}+y_{i}=39$, alors $\left(x_{i}-y_{i}\right)^{2}<1$ Donc $x_{i}=y_{i}$, ce qui est impossible car 39 est impair. Donc $x_{i}+y_{i} \geqslant 40$.
Le compte final $2 \cdot 99=\left(x_{1}+y_{1}\right)+\left(x_{2}+y_{2}\right)+\ldots+\left(x_{5}+y_{5}\right) \geqslant 5 \times 40=200$ est une contradiction et termine la preuve.
Commentaire des correcteurs : Le problème n'a pas été beaucoup résolu par les élèves qui l'ont abordé. Dans l'ensemble, une bonne partie des élèves ont trouvé une configuration qui marchait pour $\mathrm{N}=1900$, qui était bien la réponse maximale. Mais peu d'entre eux ont montré qu'on ne pouvait pas faire mieux, beaucoup se sont contentés de dire qu'en partant de la configuration qu'ils avaient donnés, on ne pouvait pas colorier plus de cases : mais ceci ne veut pas dire qu'on ne peut pas trouver une autre configuration, complètement différente (et qui ne part pas de la configuration à $\mathrm{N}=1900$ ), avec plus de cases coloriées. Enfin, un certain nombre d'élèves sont partis du principe qu'il devait forcément y avoir le même nombre de ligne et de colonne par couleur, et ont abouti à 1805 : mais la contrainte était d'avoir le même nombre de cases par couleur au total, aucune condition ne portait sur le nombre de lignes et de colonnes par couleur, et d'ailleurs les configurations optimales n'ont pas le même nombre de lignes et de colonnes par couleur. Enfin, certains élèves avaient le bon raisonnement, mais ont oublié de répondre à la question de l'énoncé, qui était "quel est le plus grand nombre de cases possibles à colorier dans la grille" : on souligne l'importance de bien se relire et d'être sûr qu'on a bien répondu à la question posée avant de rendre une copie.
|
{
"resource_path": "French/segmented/envois/fr-corrige-envoi-4-2023-2024.jsonl",
"problem_match": "\nExercice 3.",
"solution_match": "\nSolution de l'exercice 3"
}
|
e2f859bd-71c8-50ac-abe4-8e2dcd9cf5cb
| 607,219
|
Determine the largest even integer $n$ with the following property: no matter how an $n \times n$ grid is tiled with dominoes, there exists a row that cuts the grid into two non-empty parts and does not intersect any domino.
|
Answer: $\mathrm{n}=6$
Let's start by mentioning that the answer can be guessed by trying the exercise for small values of n.
The problem asks to find the largest integer n satisfying a certain property, so it necessarily has two parts. We will first show that 6 satisfies the property, then we will show that if $n \geqslant 8$, there exists a domino configuration that does not respect the property.
Case $\mathrm{n}=\mathbf{6}$: Suppose, to the contrary, that there exists a domino configuration such that every line cutting the board into two non-empty parts cuts at least one domino. We will only consider horizontal lines separating two rows and vertical lines separating two columns of the board, and we call these lines separators, and the two non-empty parts of the board obtained with a separator sections.
On the one hand, a domino can only be intersected by at most one separator (and this separator cuts the domino into two equal squares). On the other hand, a separator intersects an even number of dominos. Indeed, each section obtained contains an even number of cells (the sections are rectangles with one side of length 6). Since each domino sectioned covers exactly one cell of the section and the other cells are covered by dominos contained in the section and are therefore in even numbers, we can deduce that a separator intersects an even number of dominos.
By hypothesis, each separator intersects at least one domino, so it intersects at least 2. There are 10 separators, so at least 20 dominos of the tiling are intersected by a separator. However, the tiling of a $6 \times 6$ square contains exactly 18 dominos. We have reached a contradiction.
Case $n \geqslant 8$: We will provide for every integer $n \geqslant 8$ a tiling of the $n \times n$ grid such that every line cutting the board into two non-empty parts intersects at least one domino.
Consider the following pattern:
We then tile the inside of the gray square with the following pattern:
In this way, we obtain a tiling that satisfies the property stated in the problem.
Comment from the graders: The problem was very little addressed and, in sum, very little solved. Students who submitted an attempt provided good arguments to show that $\mathrm{n} \leqslant 6$ by proposing constructions by induction.
|
6
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Déterminer le plus grand entier $n$ pair ayant la propriété suivante : quelle que soit la façon de paver une grille $\mathrm{n} \times \mathrm{n}$ avec des dominos, il existe une ligne coupant le tableau en deux parties non vides et n'intersectant aucun domino.
|
Réponse: $\mathrm{n}=6$
Mentionnons pour commencer que la réponse peut se deviner en essayant l'exercice pour des petites valeurs de n.
Le problème demande de trouver le plus grand entier n vérifiant une certaine propriété, il comporte donc nécessairement deux parties. Nous allons montrer d'abord que 6 vérifie la propriété, puis nous allons montrer que si $n \geqslant 8$, il existe une configuration de dominos ne respectant pas la propriété.
Cas $\mathrm{n}=\mathbf{6}$ : Supposons au contraire qu'il existe une configuration de dominos telle que chaque ligne coupant le tableau en deux parties non vides coupe au moins un domino. On ne va considérer que les lignes horizontales séparant deux rangées et les lignes verticales séparant deux colonnes du tableau, on appelle ces lignes des séparatrices, et les deux parties non vides du tableau obtenues avec une séparatrice des sections.
D'une part, un domino ne peut être intersecté que par au plus une séparatrice (et cette séparatrice coupe le domino en deux carrés égaux). D'autre part, une séparatrice intersecte un nombre pair de dominos, En effet, chaque section obtenue contient un nombre pair de cases (les sections sont des rectangles dont l'un des côtés est de longueur 6). Comme chaque domino sectionné recouvre exactement une case de la section et que les autres cases sont recouvertes par des dominos inclus dans la section et sont donc en nombre pair, on déduit bien qu'une séparatrice intersecte un nombre pari de dominos.

Par hypothèse, chaque séparatrice intersecte au moins un domino, donc elle en intersecte au moins 2 . Il y a 10 séparatrices, donc au moins 20 dominos du pavage sont intersectés par une séparatrice. Or, le pavage d'un carré $6 \times 6$ contient exactement 18 dominos. On a abouti à une contradiction.
Cas $n \geqslant 8$ : Nous allons donner pour tout entier $n \geqslant 8$ un pavage de la grille $n \times n$ tel que toute ligne coupant le tableau en deux parties non vides intersecte au moins un domino.
On considère le motif suivant:

On pave ensuite l'intérieur du carré grisé avec le motif suivant :

On obtient bien de cette façon un pavage qui vérifie la propriété de l'énoncé.
Commentaire des correcteurs : Le problème a été très peu abordé et en somme très peu résolu. Les élèves ayant rendu une tentative ont donné de bons arguments pour montrer que $\mathrm{n} \leqslant 6$ en proposant des constructions par récurrence.
|
{
"resource_path": "French/segmented/envois/fr-corrige-envoi-4-2023-2024.jsonl",
"problem_match": "\nExercice 7.",
"solution_match": "## Solution de l'exercice 7"
}
|
89ce203b-0004-553d-bc59-0bd49b687233
| 607,223
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.