problem
stringlengths 14
7.96k
| solution
stringlengths 3
10k
| answer
stringlengths 1
91
| problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | question_type
stringclasses 1
value | problem_type
stringclasses 8
values | problem_raw
stringlengths 14
7.96k
| solution_raw
stringlengths 3
10k
| metadata
dict | uuid
stringlengths 36
36
| id
int64 22.6k
612k
|
|---|---|---|---|---|---|---|---|---|---|---|---|
Sam spends his days walking around the following $2 \times 2$ grid of squares.
| 1 | 2 |
| :--- | :--- |
| 4 | 3 |
Say that two squares are adjacent if they share a side. He starts at the square labeled 1 and every second walks to an adjacent square. How many paths can Sam take so that the sum of the numbers on every square he visits in his path is equal to 20 (not counting the square he started on)?
|
Answer: 167
Note that on the first step, Sam can either step on 2 or 4 . On the second step, Sam can either step on 1 or 3 , regardless of whether he is on 2 or 4 . Now, for example, say that Sam takes 8 steps. His total sum will be $2+1+2+1+2+1+2+1+2 a$, where $a$ is the number of times that he decides to step on the larger number of his two choices. Solving gives $a=4$. As he took 8 steps, this gives him $\binom{8}{4}=70$ ways in this case.
We can follow a similar approach by doing casework on the number of steps he takes. I will simply list them out here for brevity. For 8 steps, we get $\binom{8}{4}=70$. For 9 steps, we get $\binom{9}{3}=84$. For 12 steps, we get a contribution on $\binom{12}{1}=12$. For 13 steps, we get a contribution of $\binom{13}{0}=1$. Therefore, the final answer is $70+84+12+1=167$.
|
167
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Sam spends his days walking around the following $2 \times 2$ grid of squares.
| 1 | 2 |
| :--- | :--- |
| 4 | 3 |
Say that two squares are adjacent if they share a side. He starts at the square labeled 1 and every second walks to an adjacent square. How many paths can Sam take so that the sum of the numbers on every square he visits in his path is equal to 20 (not counting the square he started on)?
|
Answer: 167
Note that on the first step, Sam can either step on 2 or 4 . On the second step, Sam can either step on 1 or 3 , regardless of whether he is on 2 or 4 . Now, for example, say that Sam takes 8 steps. His total sum will be $2+1+2+1+2+1+2+1+2 a$, where $a$ is the number of times that he decides to step on the larger number of his two choices. Solving gives $a=4$. As he took 8 steps, this gives him $\binom{8}{4}=70$ ways in this case.
We can follow a similar approach by doing casework on the number of steps he takes. I will simply list them out here for brevity. For 8 steps, we get $\binom{8}{4}=70$. For 9 steps, we get $\binom{9}{3}=84$. For 12 steps, we get a contribution on $\binom{12}{1}=12$. For 13 steps, we get a contribution of $\binom{13}{0}=1$. Therefore, the final answer is $70+84+12+1=167$.
|
{
"resource_path": "HarvardMIT/segmented/en-202-2017-feb-comb-solutions.jsonl",
"problem_match": "\n4. ",
"solution_match": "\nProposed by: Sam Korsky\n"
}
|
13361032-5170-57a1-b9ae-1cb0d135066e
| 609,651
|
Kelvin the Frog likes numbers whose digits strictly decrease, but numbers that violate this condition in at most one place are good enough. In other words, if $d_{i}$ denotes the $i$ th digit, then $d_{i} \leq d_{i+1}$ for at most one value of $i$. For example, Kelvin likes the numbers 43210, 132, and 3, but not the numbers 1337 and 123. How many 5-digit numbers does Kelvin like?
|
## Answer: 14034
Suppose first that no digit violates the constraint; i.e. the digits are in strictly decreasing order. There are $\binom{10}{5}$ ways to choose the digits of the number, and each set of digits can be arranged in exactly one way, so there are $\binom{10}{5}$ such numbers.
We now perform casework on which digit violates the constraint. If it is the final digit, the first four digits must be arranged in decreasing order, which there are $\binom{10}{4}$ ways to do. The final digit can then be any digit, but we have overcounted the ones in which the number is in fully decreasing order (this can happen, for example, if the first 4 digits we chose were $5,4,3$, and 2 - a last digit of 1 was already counted in the first case). Therefore, there are $\binom{10}{4}\binom{10}{1}-252$ new numbers in this case.
If the offending digit is second from the right, the first 3 digits must be decreasing, as must the last 2 digits. There are $\binom{10}{3}\binom{10}{2}$ ways to do this. As before, we overcount the case where the second digit from the right is not actually an offender, so we again overcount the case where all 5 digits decrease. Hence there are $\binom{10}{3}\binom{10}{2}-252$ new numbers in this case.
The case where the third digit is the offender is identical to the previous case, so there are another $\binom{10}{3}\binom{10}{2}-252$ numbers to account for. The final case is when the second digit is the offending digit, in which case there are $\binom{10}{4}$ ways to choose the final 4 digits, but only 9 ways to choose the opening digit (as 0 cannot be a leading digit). Accounting for the usual overcounting, our final answer is
$$
252+\left[\binom{10}{4}\binom{10}{1}-252\right]+2\left[\binom{10}{3}\binom{10}{2}-252\right]+\left[\binom{10}{4} \cdot 9-252\right]
$$
which is easily calculated as 14034 .
|
14034
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Kelvin the Frog likes numbers whose digits strictly decrease, but numbers that violate this condition in at most one place are good enough. In other words, if $d_{i}$ denotes the $i$ th digit, then $d_{i} \leq d_{i+1}$ for at most one value of $i$. For example, Kelvin likes the numbers 43210, 132, and 3, but not the numbers 1337 and 123. How many 5-digit numbers does Kelvin like?
|
## Answer: 14034
Suppose first that no digit violates the constraint; i.e. the digits are in strictly decreasing order. There are $\binom{10}{5}$ ways to choose the digits of the number, and each set of digits can be arranged in exactly one way, so there are $\binom{10}{5}$ such numbers.
We now perform casework on which digit violates the constraint. If it is the final digit, the first four digits must be arranged in decreasing order, which there are $\binom{10}{4}$ ways to do. The final digit can then be any digit, but we have overcounted the ones in which the number is in fully decreasing order (this can happen, for example, if the first 4 digits we chose were $5,4,3$, and 2 - a last digit of 1 was already counted in the first case). Therefore, there are $\binom{10}{4}\binom{10}{1}-252$ new numbers in this case.
If the offending digit is second from the right, the first 3 digits must be decreasing, as must the last 2 digits. There are $\binom{10}{3}\binom{10}{2}$ ways to do this. As before, we overcount the case where the second digit from the right is not actually an offender, so we again overcount the case where all 5 digits decrease. Hence there are $\binom{10}{3}\binom{10}{2}-252$ new numbers in this case.
The case where the third digit is the offender is identical to the previous case, so there are another $\binom{10}{3}\binom{10}{2}-252$ numbers to account for. The final case is when the second digit is the offending digit, in which case there are $\binom{10}{4}$ ways to choose the final 4 digits, but only 9 ways to choose the opening digit (as 0 cannot be a leading digit). Accounting for the usual overcounting, our final answer is
$$
252+\left[\binom{10}{4}\binom{10}{1}-252\right]+2\left[\binom{10}{3}\binom{10}{2}-252\right]+\left[\binom{10}{4} \cdot 9-252\right]
$$
which is easily calculated as 14034 .
|
{
"resource_path": "HarvardMIT/segmented/en-202-2017-feb-comb-solutions.jsonl",
"problem_match": "\n5. ",
"solution_match": "\n## Proposed by: Alexander Katz\n\n"
}
|
9d012250-41ea-58af-a700-18d3ac56f58f
| 609,652
|
Kelvin and 15 other frogs are in a meeting, for a total of 16 frogs. During the meeting, each pair of distinct frogs becomes friends with probability $\frac{1}{2}$. Kelvin thinks the situation after the meeting is cool if for each of the 16 frogs, the number of friends they made during the meeting is a multiple of 4 . Say that the probability of the situation being cool can be expressed in the form $\frac{a}{b}$, where $a$ and $b$ are relatively prime. Find $a$.
|
Consider the multivariate polynomial
$$
\prod_{1 \leq i<j \leq 16}\left(1+x_{i} x_{j}\right)
$$
We're going to filter this by summing over all $4^{16} 16$-tuples $\left(x_{1}, x_{2}, \ldots, x_{16}\right)$ such that $x_{j}= \pm 1, \pm i$. Most of these evaluate to 0 because $i^{2}=(-i)^{2}=-1$, and $1 \cdot-1=-1$. If you do this filtering, you get the following 4 cases:
Case 1: Neither of $i$ or $-i$ appears. Then the only cases we get are when all the $x_{j}$ are 1 , or they're all -1 . Total is $2^{121}$. $\left(120=\binom{16}{2}.\right)$
Case 2: $i$ appears, but $-i$ does not. Then all the remaining $x_{j}$ must be all 1 or all -1 . This contributes a sum of $(1+i)^{15} \cdot 2^{105}+(1-i)^{15} \cdot 2^{105}=2^{113}$. $i$ can be at any position, so we get $16 \cdot 2^{113}$.
Case 3: $-i$ appears, but $i$ does not. Same contribution as above. $16 \cdot 2^{113}$.
Case 4: Both $i$ and $-i$ appear. Then all the rest of the $x_{j}$ must be all 1 or all -1 . This contributes a sum of $2 \cdot(1+i(-i)) \cdot(1+i)^{14} \cdot(1-i)^{14} \cdot 2^{91}=2^{107} \cdot i$ and $-i$ can appear in $16 \cdot 15$ places, so we get $240 \cdot 2^{107}$.
So the final answer is this divided a factor for our filter. $\left(4^{16}=2^{32}\right.$.) So our final answer is $\frac{2^{89}+16 \cdot 2^{82}+240 \cdot 2^{75}}{2^{120}}=$ $\frac{1167}{2^{41}}$.
Therefore, the answer is 1167 .
|
1167
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Kelvin and 15 other frogs are in a meeting, for a total of 16 frogs. During the meeting, each pair of distinct frogs becomes friends with probability $\frac{1}{2}$. Kelvin thinks the situation after the meeting is cool if for each of the 16 frogs, the number of friends they made during the meeting is a multiple of 4 . Say that the probability of the situation being cool can be expressed in the form $\frac{a}{b}$, where $a$ and $b$ are relatively prime. Find $a$.
|
Consider the multivariate polynomial
$$
\prod_{1 \leq i<j \leq 16}\left(1+x_{i} x_{j}\right)
$$
We're going to filter this by summing over all $4^{16} 16$-tuples $\left(x_{1}, x_{2}, \ldots, x_{16}\right)$ such that $x_{j}= \pm 1, \pm i$. Most of these evaluate to 0 because $i^{2}=(-i)^{2}=-1$, and $1 \cdot-1=-1$. If you do this filtering, you get the following 4 cases:
Case 1: Neither of $i$ or $-i$ appears. Then the only cases we get are when all the $x_{j}$ are 1 , or they're all -1 . Total is $2^{121}$. $\left(120=\binom{16}{2}.\right)$
Case 2: $i$ appears, but $-i$ does not. Then all the remaining $x_{j}$ must be all 1 or all -1 . This contributes a sum of $(1+i)^{15} \cdot 2^{105}+(1-i)^{15} \cdot 2^{105}=2^{113}$. $i$ can be at any position, so we get $16 \cdot 2^{113}$.
Case 3: $-i$ appears, but $i$ does not. Same contribution as above. $16 \cdot 2^{113}$.
Case 4: Both $i$ and $-i$ appear. Then all the rest of the $x_{j}$ must be all 1 or all -1 . This contributes a sum of $2 \cdot(1+i(-i)) \cdot(1+i)^{14} \cdot(1-i)^{14} \cdot 2^{91}=2^{107} \cdot i$ and $-i$ can appear in $16 \cdot 15$ places, so we get $240 \cdot 2^{107}$.
So the final answer is this divided a factor for our filter. $\left(4^{16}=2^{32}\right.$.) So our final answer is $\frac{2^{89}+16 \cdot 2^{82}+240 \cdot 2^{75}}{2^{120}}=$ $\frac{1167}{2^{41}}$.
Therefore, the answer is 1167 .
|
{
"resource_path": "HarvardMIT/segmented/en-202-2017-feb-comb-solutions.jsonl",
"problem_match": "\n8. ",
"solution_match": "\nProposed by: Yang Liu\n"
}
|
2261f891-ce1b-5689-a352-b3189bcb63f6
| 609,655
|
Let $m$ be a positive integer, and let $T$ denote the set of all subsets of $\{1,2, \ldots, m\}$. Call a subset $S$ of $T \delta$-good if for all $s_{1}, s_{2} \in S, s_{1} \neq s_{2},\left|\Delta\left(s_{1}, s_{2}\right)\right| \geq \delta m$, where $\Delta$ denotes symmetric difference (the symmetric difference of two sets is the set of elements that is in exactly one of the two sets). Find the largest possible integer $s$ such that there exists an integer $m$ and a $\frac{1024}{2047}$-good set of size $s$.
|
Answer: 2048
Let $n=|S|$. Let the sets in $S$ be $s_{1}, s_{2}, \ldots, s_{n}$. We bound the sum $\sum_{1 \leq i<j \leq n}\left|\Delta\left(s_{i}, s_{j}\right)\right|$ in two ways. On one hand, by the condition we have the obvious bound
$$
\sum_{1 \leq i<j \leq n}\left|\Delta\left(s_{i}, s_{j}\right)\right| \geq\binom{ n}{2} \delta m
$$
On the other hand, for $1 \leq i \leq m$, let $t_{i}=\left|\left\{1 \leq j \leq n: i \in s_{j}\right\}\right|$. Then it is clear that
$$
\sum_{1 \leq i<j \leq n}\left|\Delta\left(s_{i}, s_{j}\right)\right|=\sum_{k=1}^{m} t_{k}\left(n-t_{k}\right) \leq \frac{n^{2}}{4} m
$$
by AM-GM. Therefore, we get the bound
$$
\binom{n}{2} \delta m \leq \frac{n^{2}}{4} m \Rightarrow n \leq \frac{2 \delta}{2 \delta-1}=2048
$$
To give a construction with $n=2048$, take $m=2047$. For the rest of this construction, we will be interpreting the integers $1,2, \ldots, m$ as 11 -digit integers in binary. Given this interpretation, define a dot product $x \odot y$ of two positive integers $0 \leq x, y \leq m$ the following way. If $x=\left(x_{1} x_{2} \ldots x_{11}\right)_{2}, y=$ $\left(y_{1} y_{2} \ldots y_{11}\right)_{2}$ in binary, then
$$
x \odot y=\sum x_{i} y_{i} \quad(\bmod 2)
$$
Now we can define the sets $s_{1}, s_{2}, \ldots, s_{2048}$. Define
$$
s_{i}=\{1 \leq j \leq m:(i-1) \odot j=1 .\}
$$
A computation shows that this construction works.
Some notes: here is the motivation behind the construction. We are treating the integers $0,1, \ldots, m$ as the vector space $V=\mathbb{F}_{2}^{11}$, and the sets $s_{i}$ correspond to linear functionals $f_{i}: V \rightarrow \mathbb{F}_{2}$. In particular, the function $f_{i}: V \rightarrow \mathbb{F}_{2}$ is simply defined as $f_{i}(x)=(i-1) \odot x$, which one can easily check to be linear. This construction corresponds to Hadamard matrices of size $2^{11}$.
|
2048
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Let $m$ be a positive integer, and let $T$ denote the set of all subsets of $\{1,2, \ldots, m\}$. Call a subset $S$ of $T \delta$-good if for all $s_{1}, s_{2} \in S, s_{1} \neq s_{2},\left|\Delta\left(s_{1}, s_{2}\right)\right| \geq \delta m$, where $\Delta$ denotes symmetric difference (the symmetric difference of two sets is the set of elements that is in exactly one of the two sets). Find the largest possible integer $s$ such that there exists an integer $m$ and a $\frac{1024}{2047}$-good set of size $s$.
|
Answer: 2048
Let $n=|S|$. Let the sets in $S$ be $s_{1}, s_{2}, \ldots, s_{n}$. We bound the sum $\sum_{1 \leq i<j \leq n}\left|\Delta\left(s_{i}, s_{j}\right)\right|$ in two ways. On one hand, by the condition we have the obvious bound
$$
\sum_{1 \leq i<j \leq n}\left|\Delta\left(s_{i}, s_{j}\right)\right| \geq\binom{ n}{2} \delta m
$$
On the other hand, for $1 \leq i \leq m$, let $t_{i}=\left|\left\{1 \leq j \leq n: i \in s_{j}\right\}\right|$. Then it is clear that
$$
\sum_{1 \leq i<j \leq n}\left|\Delta\left(s_{i}, s_{j}\right)\right|=\sum_{k=1}^{m} t_{k}\left(n-t_{k}\right) \leq \frac{n^{2}}{4} m
$$
by AM-GM. Therefore, we get the bound
$$
\binom{n}{2} \delta m \leq \frac{n^{2}}{4} m \Rightarrow n \leq \frac{2 \delta}{2 \delta-1}=2048
$$
To give a construction with $n=2048$, take $m=2047$. For the rest of this construction, we will be interpreting the integers $1,2, \ldots, m$ as 11 -digit integers in binary. Given this interpretation, define a dot product $x \odot y$ of two positive integers $0 \leq x, y \leq m$ the following way. If $x=\left(x_{1} x_{2} \ldots x_{11}\right)_{2}, y=$ $\left(y_{1} y_{2} \ldots y_{11}\right)_{2}$ in binary, then
$$
x \odot y=\sum x_{i} y_{i} \quad(\bmod 2)
$$
Now we can define the sets $s_{1}, s_{2}, \ldots, s_{2048}$. Define
$$
s_{i}=\{1 \leq j \leq m:(i-1) \odot j=1 .\}
$$
A computation shows that this construction works.
Some notes: here is the motivation behind the construction. We are treating the integers $0,1, \ldots, m$ as the vector space $V=\mathbb{F}_{2}^{11}$, and the sets $s_{i}$ correspond to linear functionals $f_{i}: V \rightarrow \mathbb{F}_{2}$. In particular, the function $f_{i}: V \rightarrow \mathbb{F}_{2}$ is simply defined as $f_{i}(x)=(i-1) \odot x$, which one can easily check to be linear. This construction corresponds to Hadamard matrices of size $2^{11}$.
|
{
"resource_path": "HarvardMIT/segmented/en-202-2017-feb-comb-solutions.jsonl",
"problem_match": "\n9. ",
"solution_match": "\nProposed by: Yang Liu\n"
}
|
11e32279-4b9b-5332-91a9-096791d28b9c
| 609,656
|
Let $A, B, C, D$ be four points on a circle in that order. Also, $A B=3, B C=5, C D=6$, and $D A=4$. Let diagonals $A C$ and $B D$ intersect at $P$. Compute $\frac{A P}{C P}$.
|
Answer: | $\frac{2}{5}$ |
| :---: |
Note that $\triangle A P B \sim \triangle D P C$ so $\frac{A P}{A B}=\frac{D P}{C D}$. Similarly, $\triangle B P C \sim \triangle A P D$ so $\frac{C P}{B C}=\frac{D P}{D A}$. Dividing these two equations yields
$$
\frac{A P}{C P}=\frac{A B \cdot D A}{B C \cdot C D}=\frac{2}{5}
$$
|
\frac{2}{5}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $A, B, C, D$ be four points on a circle in that order. Also, $A B=3, B C=5, C D=6$, and $D A=4$. Let diagonals $A C$ and $B D$ intersect at $P$. Compute $\frac{A P}{C P}$.
|
Answer: | $\frac{2}{5}$ |
| :---: |
Note that $\triangle A P B \sim \triangle D P C$ so $\frac{A P}{A B}=\frac{D P}{C D}$. Similarly, $\triangle B P C \sim \triangle A P D$ so $\frac{C P}{B C}=\frac{D P}{D A}$. Dividing these two equations yields
$$
\frac{A P}{C P}=\frac{A B \cdot D A}{B C \cdot C D}=\frac{2}{5}
$$
|
{
"resource_path": "HarvardMIT/segmented/en-202-2017-feb-geo-solutions.jsonl",
"problem_match": "\n1. ",
"solution_match": "\nProposed by: Sam Korsky\n\n"
}
|
9bd66560-ec52-5a57-98a1-937ae03545cb
| 609,658
|
Let $A B C$ be a triangle with $A B=13, B C=14$, and $C A=15$. Let $\ell$ be a line passing through two sides of triangle $A B C$. Line $\ell$ cuts triangle $A B C$ into two figures, a triangle and a quadrilateral, that have equal perimeter. What is the maximum possible area of the triangle?
|
Answer: $\frac{1323}{26}$
There are three cases: $\ell$ intersects $A B, A C, \ell$ intersects $A B, B C$, and $\ell$ intersects $A C, B C$. These cases are essentially identical, so let $\ell$ intersect segment $A B$ at $M$ and segment $A C$ at $N$.
Then the condition is equivalent to
$$
\begin{gathered}
A M+M N+A N=M B+B C+C N+M N \\
A M+A N=M B+C N+15
\end{gathered}
$$
but $A N+C N=14$ and $A M+B M=13$, so that
$$
B M+C N=27-A M-A N=A M-A N-15
$$
implying that $A M+A N=21$.
Now let $\angle B A C=\theta$ for convenience, so that
$$
[A M N]=\frac{1}{2} A M \cdot A N \cdot \sin \theta
$$
which is maximized when $A M=A N=\frac{21}{2}$. Further we can easily calculate $\sin \theta=\frac{12}{13}$ (e.g. by LOC); note that this is why the area is maximized in this case (we want to maximize $\sin \theta$, which is equivalent to maximizing $\theta$, so $\theta$ should be opposite the largest side). Our answer is thus
$$
\frac{1}{2} \cdot \frac{21}{2} \cdot \frac{21}{2} \cdot \frac{12}{13}=\frac{1323}{26}
$$
Alternatively we could also calculate
$$
\begin{aligned}
{[A M N] } & =[A B C] \cdot \frac{A M}{A B} \cdot \frac{A N}{A C} \\
& =84 \cdot \frac{21}{23} \cdot \frac{\frac{21}{2}}{14}
\end{aligned}
$$
which gives the same answer.
|
\frac{1323}{26}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $A B C$ be a triangle with $A B=13, B C=14$, and $C A=15$. Let $\ell$ be a line passing through two sides of triangle $A B C$. Line $\ell$ cuts triangle $A B C$ into two figures, a triangle and a quadrilateral, that have equal perimeter. What is the maximum possible area of the triangle?
|
Answer: $\frac{1323}{26}$
There are three cases: $\ell$ intersects $A B, A C, \ell$ intersects $A B, B C$, and $\ell$ intersects $A C, B C$. These cases are essentially identical, so let $\ell$ intersect segment $A B$ at $M$ and segment $A C$ at $N$.
Then the condition is equivalent to
$$
\begin{gathered}
A M+M N+A N=M B+B C+C N+M N \\
A M+A N=M B+C N+15
\end{gathered}
$$
but $A N+C N=14$ and $A M+B M=13$, so that
$$
B M+C N=27-A M-A N=A M-A N-15
$$
implying that $A M+A N=21$.
Now let $\angle B A C=\theta$ for convenience, so that
$$
[A M N]=\frac{1}{2} A M \cdot A N \cdot \sin \theta
$$
which is maximized when $A M=A N=\frac{21}{2}$. Further we can easily calculate $\sin \theta=\frac{12}{13}$ (e.g. by LOC); note that this is why the area is maximized in this case (we want to maximize $\sin \theta$, which is equivalent to maximizing $\theta$, so $\theta$ should be opposite the largest side). Our answer is thus
$$
\frac{1}{2} \cdot \frac{21}{2} \cdot \frac{21}{2} \cdot \frac{12}{13}=\frac{1323}{26}
$$
Alternatively we could also calculate
$$
\begin{aligned}
{[A M N] } & =[A B C] \cdot \frac{A M}{A B} \cdot \frac{A N}{A C} \\
& =84 \cdot \frac{21}{23} \cdot \frac{\frac{21}{2}}{14}
\end{aligned}
$$
which gives the same answer.
|
{
"resource_path": "HarvardMIT/segmented/en-202-2017-feb-geo-solutions.jsonl",
"problem_match": "\n2. ",
"solution_match": "\nProposed by: Sam Korsky\n"
}
|
e03f2bb4-a83b-556c-a509-2fcf4464b0d7
| 609,659
|
Let $A B C D$ be a convex quadrilateral with $A B=5, B C=6, C D=7$, and $D A=8$. Let $M, P, N, Q$ be the midpoints of sides $A B, B C, C D, D A$ respectively. Compute $M N^{2}-P Q^{2}$.
|
Answer: 13
Draw in the diagonals of the quad and use the median formula three times to get $M N^{2}$ in terms of the diagonals. Do the same for $P Q^{2}$ and subtract, the diagonal length terms disappear and the answer is
$$
\frac{B C^{2}+D A^{2}-A B^{2}-C D^{2}}{2}=13
$$
|
13
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $A B C D$ be a convex quadrilateral with $A B=5, B C=6, C D=7$, and $D A=8$. Let $M, P, N, Q$ be the midpoints of sides $A B, B C, C D, D A$ respectively. Compute $M N^{2}-P Q^{2}$.
|
Answer: 13
Draw in the diagonals of the quad and use the median formula three times to get $M N^{2}$ in terms of the diagonals. Do the same for $P Q^{2}$ and subtract, the diagonal length terms disappear and the answer is
$$
\frac{B C^{2}+D A^{2}-A B^{2}-C D^{2}}{2}=13
$$
|
{
"resource_path": "HarvardMIT/segmented/en-202-2017-feb-geo-solutions.jsonl",
"problem_match": "\n4. ",
"solution_match": "\nProposed by: Sam Korsky\n"
}
|
21c1b7e5-6682-5451-b5dd-f4d3040345ee
| 609,661
|
Let $A B C D$ be a quadrilateral with an inscribed circle $\omega$ and let $P$ be the intersection of its diagonals $A C$ and $B D$. Let $R_{1}, R_{2}, R_{3}, R_{4}$ be the circumradii of triangles $A P B, B P C, C P D, D P A$ respectively. If $R_{1}=31$ and $R_{2}=24$ and $R_{3}=12$, find $R_{4}$.
|
Answer: 19
Note that $\angle A P B=180^{\circ}-\angle B P C=\angle C P D=180^{\circ}-\angle D P A$ so $\sin A P B=\sin B P C=\sin C P D=$ $\sin D P A$. Now let $\omega$ touch sides $A B, B C, C D, D A$ at $E, F, G, H$ respectively. Then $A B+C D=$ $A E+B F+C G+D H=B C+D A$ so
$$
\frac{A B}{\sin A P B}+\frac{C D}{\sin C P D}=\frac{B C}{\sin B P C}+\frac{D A}{\sin D P A}
$$
and by the Extended Law of Sines this implies
$$
2 R_{1}+2 R_{3}=2 R_{2}+2 R_{4}
$$
which immediately yields $R_{4}=R_{1}+R_{3}-R_{2}=19$.
|
19
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $A B C D$ be a quadrilateral with an inscribed circle $\omega$ and let $P$ be the intersection of its diagonals $A C$ and $B D$. Let $R_{1}, R_{2}, R_{3}, R_{4}$ be the circumradii of triangles $A P B, B P C, C P D, D P A$ respectively. If $R_{1}=31$ and $R_{2}=24$ and $R_{3}=12$, find $R_{4}$.
|
Answer: 19
Note that $\angle A P B=180^{\circ}-\angle B P C=\angle C P D=180^{\circ}-\angle D P A$ so $\sin A P B=\sin B P C=\sin C P D=$ $\sin D P A$. Now let $\omega$ touch sides $A B, B C, C D, D A$ at $E, F, G, H$ respectively. Then $A B+C D=$ $A E+B F+C G+D H=B C+D A$ so
$$
\frac{A B}{\sin A P B}+\frac{C D}{\sin C P D}=\frac{B C}{\sin B P C}+\frac{D A}{\sin D P A}
$$
and by the Extended Law of Sines this implies
$$
2 R_{1}+2 R_{3}=2 R_{2}+2 R_{4}
$$
which immediately yields $R_{4}=R_{1}+R_{3}-R_{2}=19$.
|
{
"resource_path": "HarvardMIT/segmented/en-202-2017-feb-geo-solutions.jsonl",
"problem_match": "\n5. ",
"solution_match": "\nProposed by: Sam Korsky\n"
}
|
503189c6-5456-565b-acb7-0a7c5311f458
| 609,662
|
In convex quadrilateral $A B C D$ we have $A B=15, B C=16, C D=12, D A=25$, and $B D=20$. Let $M$ and $\gamma$ denote the circumcenter and circumcircle of $\triangle A B D$. Line $C B$ meets $\gamma$ again at $F$, line $A F$ meets $M C$ at $G$, and line $G D$ meets $\gamma$ again at $E$. Determine the area of pentagon $A B C D E$.
|
Answer: 396
Note that $\angle A D B=\angle D C B=90^{\circ}$ and $B C \| A D$. Now by Pascal theorem on $D D E B F A$ implies that $B, M, E$ are collinear. So $[A D E]=[A B D]=150$ and $[B C D]=96$, so the total area is 396 .
|
396
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
In convex quadrilateral $A B C D$ we have $A B=15, B C=16, C D=12, D A=25$, and $B D=20$. Let $M$ and $\gamma$ denote the circumcenter and circumcircle of $\triangle A B D$. Line $C B$ meets $\gamma$ again at $F$, line $A F$ meets $M C$ at $G$, and line $G D$ meets $\gamma$ again at $E$. Determine the area of pentagon $A B C D E$.
|
Answer: 396
Note that $\angle A D B=\angle D C B=90^{\circ}$ and $B C \| A D$. Now by Pascal theorem on $D D E B F A$ implies that $B, M, E$ are collinear. So $[A D E]=[A B D]=150$ and $[B C D]=96$, so the total area is 396 .
|
{
"resource_path": "HarvardMIT/segmented/en-202-2017-feb-geo-solutions.jsonl",
"problem_match": "\n6. ",
"solution_match": "\nProposed by: Evan Chen\n"
}
|
320e5c06-a78d-5aa5-9458-cd3168cca1fe
| 609,663
|
Let $\omega$ and $\Gamma$ by circles such that $\omega$ is internally tangent to $\Gamma$ at a point $P$. Let $A B$ be a chord of $\Gamma$ tangent to $\omega$ at a point $Q$. Let $R \neq P$ be the second intersection of line $P Q$ with $\Gamma$. If the radius of $\Gamma$ is 17 , the radius of $\omega$ is 7 , and $\frac{A Q}{B Q}=3$, find the circumradius of triangle $A Q R$.
|
Answer: $\sqrt{170}$
Let $r$ denote the circumradius of triangle $A Q R$. By Archimedes Lemma, $R$ is the midpoint of arc $A B$ of $\Gamma$. Therefore $\angle R A Q=\angle R P B=\angle R P A$ so $\triangle R A Q \sim \triangle R P A$. By looking at the similarity ratio between the two triangles we have
$$
\frac{r}{17}=\frac{A Q}{A P}
$$
Now, let $A P$ intersect $\omega$ again at $X \neq P$. By homothety we have $X Q \| A R$ so
$$
\frac{A X}{A P}=1-\frac{P Q}{P R}=1-\frac{7}{17}=\frac{10}{17}
$$
But we also know
$$
A X \cdot A P=A Q^{2}
$$
so
$$
\frac{10}{17} A P^{2}=A Q^{2}
$$
Thus
$$
\frac{r}{17}=\frac{A Q}{A P}=\sqrt{\frac{10}{17}}
$$
so we compute $r=\sqrt{170}$ as desired.
|
\sqrt{170}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $\omega$ and $\Gamma$ by circles such that $\omega$ is internally tangent to $\Gamma$ at a point $P$. Let $A B$ be a chord of $\Gamma$ tangent to $\omega$ at a point $Q$. Let $R \neq P$ be the second intersection of line $P Q$ with $\Gamma$. If the radius of $\Gamma$ is 17 , the radius of $\omega$ is 7 , and $\frac{A Q}{B Q}=3$, find the circumradius of triangle $A Q R$.
|
Answer: $\sqrt{170}$
Let $r$ denote the circumradius of triangle $A Q R$. By Archimedes Lemma, $R$ is the midpoint of arc $A B$ of $\Gamma$. Therefore $\angle R A Q=\angle R P B=\angle R P A$ so $\triangle R A Q \sim \triangle R P A$. By looking at the similarity ratio between the two triangles we have
$$
\frac{r}{17}=\frac{A Q}{A P}
$$
Now, let $A P$ intersect $\omega$ again at $X \neq P$. By homothety we have $X Q \| A R$ so
$$
\frac{A X}{A P}=1-\frac{P Q}{P R}=1-\frac{7}{17}=\frac{10}{17}
$$
But we also know
$$
A X \cdot A P=A Q^{2}
$$
so
$$
\frac{10}{17} A P^{2}=A Q^{2}
$$
Thus
$$
\frac{r}{17}=\frac{A Q}{A P}=\sqrt{\frac{10}{17}}
$$
so we compute $r=\sqrt{170}$ as desired.
|
{
"resource_path": "HarvardMIT/segmented/en-202-2017-feb-geo-solutions.jsonl",
"problem_match": "\n7. ",
"solution_match": "\nProposed by: Sam Korsky\n"
}
|
17398e0b-9b50-5e7e-ade6-953bdfe90324
| 609,664
|
Let $A B C$ be a triangle with circumradius $R=17$ and inradius $r=7$. Find the maximum possible value of $\sin \frac{A}{2}$.
|
Answer: $\frac{17+\sqrt{51}}{34}$
Letting $I$ and $O$ denote the incenter and circumcenter of triangle $A B C$ we have by the triangle inequality that
$$
A O \leq A I+O I \Longrightarrow R \leq \frac{r}{\sin \frac{A}{2}}+\sqrt{R(R-2 r)}
$$
and by plugging in our values for $r$ and $R$ we get
$$
\sin \frac{A}{2} \leq \frac{17+\sqrt{51}}{34}
$$
as desired. Equality holds when $A B C$ is isosceles and $I$ lies between $A$ and $O$.
|
\frac{17+\sqrt{51}}{34}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $A B C$ be a triangle with circumradius $R=17$ and inradius $r=7$. Find the maximum possible value of $\sin \frac{A}{2}$.
|
Answer: $\frac{17+\sqrt{51}}{34}$
Letting $I$ and $O$ denote the incenter and circumcenter of triangle $A B C$ we have by the triangle inequality that
$$
A O \leq A I+O I \Longrightarrow R \leq \frac{r}{\sin \frac{A}{2}}+\sqrt{R(R-2 r)}
$$
and by plugging in our values for $r$ and $R$ we get
$$
\sin \frac{A}{2} \leq \frac{17+\sqrt{51}}{34}
$$
as desired. Equality holds when $A B C$ is isosceles and $I$ lies between $A$ and $O$.
|
{
"resource_path": "HarvardMIT/segmented/en-202-2017-feb-geo-solutions.jsonl",
"problem_match": "\n8. ",
"solution_match": "\nProposed by: Sam Korsky\n"
}
|
3b5f3b57-aa22-57c8-b7b6-ca40a020bd31
| 609,665
|
Let $A B C$ be a triangle, and let $B C D E, C A F G, A B H I$ be squares that do not overlap the triangle with centers $X, Y, Z$ respectively. Given that $A X=6, B Y=7$, and $C Z=8$, find the area of triangle $X Y Z$.
|
Answer: $\frac{21 \sqrt{15}}{4}$
By the degenerate case of Von Aubel's Theorem we have that $Y Z=A X=6$ and $Z X=B Y=7$ and $X Y=C Z=8$ so it suffices to find the area of a $6-7-8$ triangle which is given by $\frac{21 \sqrt{15}}{4}$.
To prove that $A X=Y Z$, note that by LoC we get
$$
Y X^{2}=\frac{b^{2}}{2}+\frac{c^{2}}{2}+b c \sin \angle A
$$
and
$$
\begin{aligned}
A X^{2} & =b^{2}+\frac{a^{2}}{2}-a b(\cos \angle C-\sin \angle C) \\
& =c^{2}+\frac{a^{2}}{2}-a c(\cos \angle B-\sin \angle B) \\
& =\frac{b^{2}+c^{2}+a(b \sin \angle C+c \sin \angle B)}{2} \\
& =\frac{b^{2}}{2}+\frac{c^{2}}{2}+a h
\end{aligned}
$$
where $h$ is the length of the $A$-altitude of triangle $A B C$. In these calculations we used the well-known fact that $b \cos \angle C+c \cos \angle B=a$ which can be easily seen by drawing in the $A$-altitude. Then since $b c \sin \angle A$ and $a h$ both equal twice the area of triangle $A B C$, we are done.
|
\frac{21 \sqrt{15}}{4}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $A B C$ be a triangle, and let $B C D E, C A F G, A B H I$ be squares that do not overlap the triangle with centers $X, Y, Z$ respectively. Given that $A X=6, B Y=7$, and $C Z=8$, find the area of triangle $X Y Z$.
|
Answer: $\frac{21 \sqrt{15}}{4}$
By the degenerate case of Von Aubel's Theorem we have that $Y Z=A X=6$ and $Z X=B Y=7$ and $X Y=C Z=8$ so it suffices to find the area of a $6-7-8$ triangle which is given by $\frac{21 \sqrt{15}}{4}$.
To prove that $A X=Y Z$, note that by LoC we get
$$
Y X^{2}=\frac{b^{2}}{2}+\frac{c^{2}}{2}+b c \sin \angle A
$$
and
$$
\begin{aligned}
A X^{2} & =b^{2}+\frac{a^{2}}{2}-a b(\cos \angle C-\sin \angle C) \\
& =c^{2}+\frac{a^{2}}{2}-a c(\cos \angle B-\sin \angle B) \\
& =\frac{b^{2}+c^{2}+a(b \sin \angle C+c \sin \angle B)}{2} \\
& =\frac{b^{2}}{2}+\frac{c^{2}}{2}+a h
\end{aligned}
$$
where $h$ is the length of the $A$-altitude of triangle $A B C$. In these calculations we used the well-known fact that $b \cos \angle C+c \cos \angle B=a$ which can be easily seen by drawing in the $A$-altitude. Then since $b c \sin \angle A$ and $a h$ both equal twice the area of triangle $A B C$, we are done.
|
{
"resource_path": "HarvardMIT/segmented/en-202-2017-feb-geo-solutions.jsonl",
"problem_match": "\n9. ",
"solution_match": "\nProposed by: Sam Korsky\n"
}
|
0e010019-b645-5c9e-b922-f0cfc7770497
| 609,666
|
Let $A B C D$ be a quadrilateral with an inscribed circle $\omega$. Let $I$ be the center of $\omega$ let $I A=12$, $I B=16, I C=14$, and $I D=11$. Let $M$ be the midpoint of segment $A C$. Compute $\frac{I M}{I N}$, where $N$ is the midpoint of segment $B D$.
|
## Answer: $\frac{21}{22}$
Let points $W, X, Y, Z$ be the tangency points between $\omega$ and lines $A B, B C, C D, D A$ respectively. Now invert about $\omega$. Then $A^{\prime}, B^{\prime}, C^{\prime}, D^{\prime}$ are the midpoints of segments $Z W, W X, X Y, Y Z$ respectively. Thus by Varignon's Theorem $A^{\prime} B^{\prime} C^{\prime} D^{\prime}$ is a parallelogram. Then the midpoints of segments $A^{\prime} C^{\prime}$ and $B^{\prime} D^{\prime}$ coincide at a point $P$. Note that figure $I A^{\prime} P C^{\prime}$ is similar to figure $I C M A$ with similitude ratio $\frac{r^{2}}{I A \cdot I C}$ where $r$ is the radius of $\omega$. Similarly figure $I B^{\prime} P D^{\prime}$ is similar to figure $I D M B$ with similitude ratio $\frac{r^{2}}{I B \cdot I D}$. Therefore
$$
I P=\frac{r^{2}}{I A \cdot I C} \cdot I M=\frac{r^{2}}{I B \cdot I D} \cdot I N
$$
which yields
$$
\frac{I M}{I N}=\frac{I A \cdot I C}{I B \cdot I D}=\frac{12 \cdot 14}{16 \cdot 11}=\frac{21}{22}
$$
|
\frac{21}{22}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $A B C D$ be a quadrilateral with an inscribed circle $\omega$. Let $I$ be the center of $\omega$ let $I A=12$, $I B=16, I C=14$, and $I D=11$. Let $M$ be the midpoint of segment $A C$. Compute $\frac{I M}{I N}$, where $N$ is the midpoint of segment $B D$.
|
## Answer: $\frac{21}{22}$
Let points $W, X, Y, Z$ be the tangency points between $\omega$ and lines $A B, B C, C D, D A$ respectively. Now invert about $\omega$. Then $A^{\prime}, B^{\prime}, C^{\prime}, D^{\prime}$ are the midpoints of segments $Z W, W X, X Y, Y Z$ respectively. Thus by Varignon's Theorem $A^{\prime} B^{\prime} C^{\prime} D^{\prime}$ is a parallelogram. Then the midpoints of segments $A^{\prime} C^{\prime}$ and $B^{\prime} D^{\prime}$ coincide at a point $P$. Note that figure $I A^{\prime} P C^{\prime}$ is similar to figure $I C M A$ with similitude ratio $\frac{r^{2}}{I A \cdot I C}$ where $r$ is the radius of $\omega$. Similarly figure $I B^{\prime} P D^{\prime}$ is similar to figure $I D M B$ with similitude ratio $\frac{r^{2}}{I B \cdot I D}$. Therefore
$$
I P=\frac{r^{2}}{I A \cdot I C} \cdot I M=\frac{r^{2}}{I B \cdot I D} \cdot I N
$$
which yields
$$
\frac{I M}{I N}=\frac{I A \cdot I C}{I B \cdot I D}=\frac{12 \cdot 14}{16 \cdot 11}=\frac{21}{22}
$$
|
{
"resource_path": "HarvardMIT/segmented/en-202-2017-feb-geo-solutions.jsonl",
"problem_match": "\n10. ",
"solution_match": "\nProposed by: Sam Korsky\n\n"
}
|
1f1b955b-baae-5bb1-9c9f-8d3da861bdda
| 609,667
|
A random number generator will always output 7 . Sam uses this random number generator once. What is the expected value of the output?
|
Answer: 7
The only output is 7 , so the expected value is 7 .
|
7
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
A random number generator will always output 7 . Sam uses this random number generator once. What is the expected value of the output?
|
Answer: 7
The only output is 7 , so the expected value is 7 .
|
{
"resource_path": "HarvardMIT/segmented/en-202-2017-feb-guts-solutions.jsonl",
"problem_match": "\n1. [4]",
"solution_match": "\nProposed by: Sam Korsky\n"
}
|
2723e3bf-e096-5ddc-914c-50c16197e8d0
| 609,668
|
Let $A, B, C, D, E, F$ be 6 points on a circle in that order. Let $X$ be the intersection of $A D$ and $B E$, $Y$ is the intersection of $A D$ and $C F$, and $Z$ is the intersection of $C F$ and $B E . X$ lies on segments $B Z$ and $A Y$ and $Y$ lies on segment $C Z$. Given that $A X=3, B X=2, C Y=4, D Y=10, E Z=16$, and $F Z=12$, find the perimeter of triangle $X Y Z$.
|
Answer: $\frac{77}{6}$
Let $X Y=z, Y Z=x$, and $Z X=y$. By Power of a Point, we have that
$$
3(z+10)=2(y+16), 4(x+12)=10(z+3), \text { and } 12(x+4)=16(y+2) .
$$
Solving this system gives $X Y=\frac{11}{3}$ and $Y Z=\frac{14}{3}$ and $Z X=\frac{9}{2}$. Therefore, our answer if $X Y+Y Z+$ $Z X=\frac{77}{6}$.
|
\frac{77}{6}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $A, B, C, D, E, F$ be 6 points on a circle in that order. Let $X$ be the intersection of $A D$ and $B E$, $Y$ is the intersection of $A D$ and $C F$, and $Z$ is the intersection of $C F$ and $B E . X$ lies on segments $B Z$ and $A Y$ and $Y$ lies on segment $C Z$. Given that $A X=3, B X=2, C Y=4, D Y=10, E Z=16$, and $F Z=12$, find the perimeter of triangle $X Y Z$.
|
Answer: $\frac{77}{6}$
Let $X Y=z, Y Z=x$, and $Z X=y$. By Power of a Point, we have that
$$
3(z+10)=2(y+16), 4(x+12)=10(z+3), \text { and } 12(x+4)=16(y+2) .
$$
Solving this system gives $X Y=\frac{11}{3}$ and $Y Z=\frac{14}{3}$ and $Z X=\frac{9}{2}$. Therefore, our answer if $X Y+Y Z+$ $Z X=\frac{77}{6}$.
|
{
"resource_path": "HarvardMIT/segmented/en-202-2017-feb-guts-solutions.jsonl",
"problem_match": "\n2. [4]",
"solution_match": "\nProposed by: Sam Korsky\n"
}
|
d3fc1e11-c619-5cd3-8ca9-292ae6fb566e
| 609,669
|
Find the number of pairs of integers $(x, y)$ such that $x^{2}+2 y^{2}<25$.
|
Answer: 55
We do casework on $y$.
If $y=0$, we have $x^{2}<25$, so we get 9 values of $x$. If $y= \pm 1$, then $x^{2}<23$, so we still have 9 values of $x$. If $y= \pm 2$, we have $x^{2}<17$, so we have 9 values of $x$. If $y= \pm 3$, we have $x^{2}<7$, we get 5 values of $x$.
Therefore, the final answer is $9+2(9+9+5)=55$.
|
55
|
Yes
|
Yes
|
math-word-problem
|
Inequalities
|
Find the number of pairs of integers $(x, y)$ such that $x^{2}+2 y^{2}<25$.
|
Answer: 55
We do casework on $y$.
If $y=0$, we have $x^{2}<25$, so we get 9 values of $x$. If $y= \pm 1$, then $x^{2}<23$, so we still have 9 values of $x$. If $y= \pm 2$, we have $x^{2}<17$, so we have 9 values of $x$. If $y= \pm 3$, we have $x^{2}<7$, we get 5 values of $x$.
Therefore, the final answer is $9+2(9+9+5)=55$.
|
{
"resource_path": "HarvardMIT/segmented/en-202-2017-feb-guts-solutions.jsonl",
"problem_match": "\n3. [4]",
"solution_match": "\nProposed by: Allen Liu\n"
}
|
f8fbc5ea-a728-543d-b30a-e8752b849618
| 609,670
|
Find the number of ordered triples of nonnegative integers $(a, b, c)$ that satisfy
$$
(a b+1)(b c+1)(c a+1)=84 .
$$
|
Answer: 12
The solutions are $(0,1,83)$ and $(1,2,3)$ up to permutation. First, we do the case where at least one of $a, b, c$ is 0 . WLOG, say $a=0$. Then we have $1+b c=84 \Longrightarrow b c=83$. As 83 is prime, the only solution is $(0,1,83)$ up to permutation.
Otherwise, we claim that at least one of $a, b, c$ is equal to 1 . Otherwise, all are at least 2 , so $(1+$ $a b)(1+b c)(1+a c) \geq 5^{3}>84$. So WLOG, set $a=1$. We now need $(b+1)(c+1)(b c+1)=84$. Now, WLOG, say $b \leq c$. If $b=1$, then $(c+1)^{2}=42$, which has no solution. If $b \geq 3$, then $(b+1)(c+1)(b c+1) \geq 4^{2} \cdot 10=160>84$. So we need $b=2$. Then we need $(c+1)(2 c+1)=21$. Solving this gives $c=3$, for the solution $(1,2,3)$.
Therefore, the answer is $6+6=12$.
|
12
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Find the number of ordered triples of nonnegative integers $(a, b, c)$ that satisfy
$$
(a b+1)(b c+1)(c a+1)=84 .
$$
|
Answer: 12
The solutions are $(0,1,83)$ and $(1,2,3)$ up to permutation. First, we do the case where at least one of $a, b, c$ is 0 . WLOG, say $a=0$. Then we have $1+b c=84 \Longrightarrow b c=83$. As 83 is prime, the only solution is $(0,1,83)$ up to permutation.
Otherwise, we claim that at least one of $a, b, c$ is equal to 1 . Otherwise, all are at least 2 , so $(1+$ $a b)(1+b c)(1+a c) \geq 5^{3}>84$. So WLOG, set $a=1$. We now need $(b+1)(c+1)(b c+1)=84$. Now, WLOG, say $b \leq c$. If $b=1$, then $(c+1)^{2}=42$, which has no solution. If $b \geq 3$, then $(b+1)(c+1)(b c+1) \geq 4^{2} \cdot 10=160>84$. So we need $b=2$. Then we need $(c+1)(2 c+1)=21$. Solving this gives $c=3$, for the solution $(1,2,3)$.
Therefore, the answer is $6+6=12$.
|
{
"resource_path": "HarvardMIT/segmented/en-202-2017-feb-guts-solutions.jsonl",
"problem_match": "\n4. [4]",
"solution_match": "\n## Proposed by: Evan Chen\n\n"
}
|
9b712657-abe9-50c2-8cd6-2e55dd3655f3
| 609,671
|
Find the number of ordered triples of positive integers $(a, b, c)$ such that
$$
6 a+10 b+15 c=3000
$$
|
Answer: 4851
Note that $6 a$ must be a multiple of 5 , so $a$ must be a multiple of 5 . Similarly, $b$ must be a multiple of 3 , and $c$ must be a multiple of 2 .
Set $a=5 A, b=3 B, c=2 C$. Then the equation reduces to $A+B+C=100$. This has $\binom{99}{2}=4851$ solutions.
|
4851
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Find the number of ordered triples of positive integers $(a, b, c)$ such that
$$
6 a+10 b+15 c=3000
$$
|
Answer: 4851
Note that $6 a$ must be a multiple of 5 , so $a$ must be a multiple of 5 . Similarly, $b$ must be a multiple of 3 , and $c$ must be a multiple of 2 .
Set $a=5 A, b=3 B, c=2 C$. Then the equation reduces to $A+B+C=100$. This has $\binom{99}{2}=4851$ solutions.
|
{
"resource_path": "HarvardMIT/segmented/en-202-2017-feb-guts-solutions.jsonl",
"problem_match": "\n5. [6]",
"solution_match": "\nProposed by: Yang Liu\n"
}
|
f338fde2-6bce-597a-a1b7-1dd453a8e492
| 609,672
|
Let $A B C D$ be a convex quadrilateral with $A C=7$ and $B D=17$. Let $M, P, N, Q$ be the midpoints of sides $A B, B C, C D, D A$ respectively. Compute $M N^{2}+P Q^{2}$
|
Answer: 169
$M P N Q$ is a parallelogram whose side lengths are 3.5 and 8.5 so the sum of squares of its diagonals is $\frac{7^{2}+17^{2}}{2}=169$
|
169
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $A B C D$ be a convex quadrilateral with $A C=7$ and $B D=17$. Let $M, P, N, Q$ be the midpoints of sides $A B, B C, C D, D A$ respectively. Compute $M N^{2}+P Q^{2}$
|
Answer: 169
$M P N Q$ is a parallelogram whose side lengths are 3.5 and 8.5 so the sum of squares of its diagonals is $\frac{7^{2}+17^{2}}{2}=169$
|
{
"resource_path": "HarvardMIT/segmented/en-202-2017-feb-guts-solutions.jsonl",
"problem_match": "\n6. [6]",
"solution_match": "\nProposed by: Sam Korsky\n"
}
|
ee1d09b4-910c-5ba9-af7f-188a10e8cdae
| 609,673
|
An ordered pair of sets $(A, B)$ is good if $A$ is not a subset of $B$ and $B$ is not a subset of $A$. How many ordered pairs of subsets of $\{1,2, \ldots, 2017\}$ are good?
|
Answer: $4^{2017}-2 \cdot 3^{2017}+2^{2017}$
Firstly, there are $4^{2017}$ possible pairs of subsets, as each of the 2017 elements can be in neither subset, in $A$ only, in $B$ only, or in both.
Now let us count the number of pairs of subsets for which $A$ is a subset of $B$. Under these conditions, each of the 2017 elements could be in neither subset, in $B$ only, or in both $A$ and $B$. So there are $3^{2017}$ such pairs.
By symmetry, there are also $3^{2017}$ pairs of subsets where $B$ is a subset of $A$. But this overcounts the pairs in which $A$ is a subset of $B$ and $B$ is a subset of $A$, i.e. $A=B$. There are $2^{2017}$ such subsets.
Thus, in total, there are $4^{2017}-2 \cdot 3^{2017}+2^{2017}$ good pairs of subsets.
|
4^{2017}-2 \cdot 3^{2017}+2^{2017}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
An ordered pair of sets $(A, B)$ is good if $A$ is not a subset of $B$ and $B$ is not a subset of $A$. How many ordered pairs of subsets of $\{1,2, \ldots, 2017\}$ are good?
|
Answer: $4^{2017}-2 \cdot 3^{2017}+2^{2017}$
Firstly, there are $4^{2017}$ possible pairs of subsets, as each of the 2017 elements can be in neither subset, in $A$ only, in $B$ only, or in both.
Now let us count the number of pairs of subsets for which $A$ is a subset of $B$. Under these conditions, each of the 2017 elements could be in neither subset, in $B$ only, or in both $A$ and $B$. So there are $3^{2017}$ such pairs.
By symmetry, there are also $3^{2017}$ pairs of subsets where $B$ is a subset of $A$. But this overcounts the pairs in which $A$ is a subset of $B$ and $B$ is a subset of $A$, i.e. $A=B$. There are $2^{2017}$ such subsets.
Thus, in total, there are $4^{2017}-2 \cdot 3^{2017}+2^{2017}$ good pairs of subsets.
|
{
"resource_path": "HarvardMIT/segmented/en-202-2017-feb-guts-solutions.jsonl",
"problem_match": "\n7. [6]",
"solution_match": "\nProposed by: Alexander Katz\n"
}
|
58d9216e-862a-5f6e-95f5-3ebfbbd92843
| 609,674
|
You have 128 teams in a single elimination tournament. The Engineers and the Crimson are two of these teams. Each of the 128 teams in the tournament is equally strong, so during each match, each team has an equal probability of winning.
Now, the 128 teams are randomly put into the bracket.
What is the probability that the Engineers play the Crimson sometime during the tournament?
|
Answer: $\frac{1}{64}$
There are $\binom{128}{2}=127 \cdot 64$ pairs of teams. In each tournament, 127 of these pairs play.
By symmetry, the answer is $\frac{127}{127 \cdot 64}=\frac{1}{64}$.
|
\frac{1}{64}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
You have 128 teams in a single elimination tournament. The Engineers and the Crimson are two of these teams. Each of the 128 teams in the tournament is equally strong, so during each match, each team has an equal probability of winning.
Now, the 128 teams are randomly put into the bracket.
What is the probability that the Engineers play the Crimson sometime during the tournament?
|
Answer: $\frac{1}{64}$
There are $\binom{128}{2}=127 \cdot 64$ pairs of teams. In each tournament, 127 of these pairs play.
By symmetry, the answer is $\frac{127}{127 \cdot 64}=\frac{1}{64}$.
|
{
"resource_path": "HarvardMIT/segmented/en-202-2017-feb-guts-solutions.jsonl",
"problem_match": "\n8. [6]",
"solution_match": "\nProposed by: Yang Liu\n"
}
|
5127ea48-6e6b-5e97-b467-1c0e843e58ae
| 609,675
|
Jeffrey writes the numbers 1 and $100000000=10^{8}$ on the blackboard. Every minute, if $x, y$ are on the board, Jeffrey replaces them with
$$
\frac{x+y}{2} \text { and } 2\left(\frac{1}{x}+\frac{1}{y}\right)^{-1}
$$
After 2017 minutes the two numbers are $a$ and $b$. Find $\min (a, b)$ to the nearest integer.
|
Answer: 10000
Note that the product of the integers on the board is a constant. Indeed, we have that
$$
\frac{x+y}{2} \cdot 2\left(\frac{1}{x}+\frac{1}{y}\right)^{-1}=x y
$$
Therefore, we expect that the answer to the problem is approximately $\sqrt{1 \cdot 10^{8}}=10^{4}$.
To be more rigorous, we have to show that the process indeed converges quickly enough. To show this, we bound the difference between the integers on the board at time $i$. Say that at time $i$, the integers on the board are $a_{i}<b_{i}$. Note that
$$
\begin{aligned}
d_{i+1}=b_{i+1}-a_{i+1}= & \frac{a_{i}+b_{i}}{2}-2\left(\frac{1}{a_{i}}+\frac{1}{b_{i}}\right)^{-1}=\frac{\left(a_{i}-b_{i}\right)^{2}}{2\left(a_{i}+b_{i}\right)} \\
& <\frac{b_{i}-a_{i}}{2}=\frac{d_{i}}{2}
\end{aligned}
$$
The inequality at the end follows from that obvious fact that $b_{i}-a_{i}<b_{i}+a_{i}$. Therefore, $d_{i+1} \leq \frac{d_{i}}{2}$, so $d_{2017}<\frac{10^{8}}{2^{2017}}$, which is extremely small. So the difference is essentially 0 at time 2017 , which completes the argument.
|
10000
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Jeffrey writes the numbers 1 and $100000000=10^{8}$ on the blackboard. Every minute, if $x, y$ are on the board, Jeffrey replaces them with
$$
\frac{x+y}{2} \text { and } 2\left(\frac{1}{x}+\frac{1}{y}\right)^{-1}
$$
After 2017 minutes the two numbers are $a$ and $b$. Find $\min (a, b)$ to the nearest integer.
|
Answer: 10000
Note that the product of the integers on the board is a constant. Indeed, we have that
$$
\frac{x+y}{2} \cdot 2\left(\frac{1}{x}+\frac{1}{y}\right)^{-1}=x y
$$
Therefore, we expect that the answer to the problem is approximately $\sqrt{1 \cdot 10^{8}}=10^{4}$.
To be more rigorous, we have to show that the process indeed converges quickly enough. To show this, we bound the difference between the integers on the board at time $i$. Say that at time $i$, the integers on the board are $a_{i}<b_{i}$. Note that
$$
\begin{aligned}
d_{i+1}=b_{i+1}-a_{i+1}= & \frac{a_{i}+b_{i}}{2}-2\left(\frac{1}{a_{i}}+\frac{1}{b_{i}}\right)^{-1}=\frac{\left(a_{i}-b_{i}\right)^{2}}{2\left(a_{i}+b_{i}\right)} \\
& <\frac{b_{i}-a_{i}}{2}=\frac{d_{i}}{2}
\end{aligned}
$$
The inequality at the end follows from that obvious fact that $b_{i}-a_{i}<b_{i}+a_{i}$. Therefore, $d_{i+1} \leq \frac{d_{i}}{2}$, so $d_{2017}<\frac{10^{8}}{2^{2017}}$, which is extremely small. So the difference is essentially 0 at time 2017 , which completes the argument.
|
{
"resource_path": "HarvardMIT/segmented/en-202-2017-feb-guts-solutions.jsonl",
"problem_match": "\n9. [7]",
"solution_match": "\nProposed by: Yang Liu\n\n"
}
|
3967ed5f-5edd-5881-a62a-38523faba781
| 609,676
|
Let $A B C$ be a triangle in the plane with $A B=13, B C=14, A C=15$. Let $M_{n}$ denote the smallest possible value of $\left(A P^{n}+B P^{n}+C P^{n}\right)^{\frac{1}{n}}$ over all points $P$ in the plane. Find $\lim _{n \rightarrow \infty} M_{n}$.
|
Answer: 65/8
Let $R$ denote the circumradius of triangle $A B C$. As $A B C$ is an acute triangle, it isn't hard to check that for any point $P$, we have either $A P \geq R, B P \geq R$, or $C P \geq R$. Also, note that if we choose $P=O$ (the circumcenter) then $\left(A P^{n}+B P^{n}+C P^{n}\right)=3 \cdot R^{n}$. Therefore, we have the inequality
$$
R \leq \min _{P \in \mathbb{R}^{2}}\left(A P^{n}+B P^{n}+C P^{n}\right)^{\frac{1}{n}} \leq\left(3 R^{n}\right)^{\frac{1}{n}}=R \cdot 3^{\frac{1}{n}}
$$
Taking $n \rightarrow \infty$ yields
$$
R \leq \lim _{n \rightarrow \infty} M_{n} \leq R
$$
(as $\lim _{n \rightarrow \infty} 3^{\frac{1}{n}}=1$ ), so the answer is $R=\frac{65}{8}$.
|
\frac{65}{8}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $A B C$ be a triangle in the plane with $A B=13, B C=14, A C=15$. Let $M_{n}$ denote the smallest possible value of $\left(A P^{n}+B P^{n}+C P^{n}\right)^{\frac{1}{n}}$ over all points $P$ in the plane. Find $\lim _{n \rightarrow \infty} M_{n}$.
|
Answer: 65/8
Let $R$ denote the circumradius of triangle $A B C$. As $A B C$ is an acute triangle, it isn't hard to check that for any point $P$, we have either $A P \geq R, B P \geq R$, or $C P \geq R$. Also, note that if we choose $P=O$ (the circumcenter) then $\left(A P^{n}+B P^{n}+C P^{n}\right)=3 \cdot R^{n}$. Therefore, we have the inequality
$$
R \leq \min _{P \in \mathbb{R}^{2}}\left(A P^{n}+B P^{n}+C P^{n}\right)^{\frac{1}{n}} \leq\left(3 R^{n}\right)^{\frac{1}{n}}=R \cdot 3^{\frac{1}{n}}
$$
Taking $n \rightarrow \infty$ yields
$$
R \leq \lim _{n \rightarrow \infty} M_{n} \leq R
$$
(as $\lim _{n \rightarrow \infty} 3^{\frac{1}{n}}=1$ ), so the answer is $R=\frac{65}{8}$.
|
{
"resource_path": "HarvardMIT/segmented/en-202-2017-feb-guts-solutions.jsonl",
"problem_match": "\n10. [7]",
"solution_match": "\nProposed by: Yang Liu\n"
}
|
753ea69d-3d0a-55d8-be64-ad4b632d3df7
| 609,677
|
Consider the graph in 3 -space of
$$
0=x y z(x+y)(y+z)(z+x)(x-y)(y-z)(z-x)
$$
This graph divides 3 -space into $N$ connected regions. What is $N$ ?
|
Answer: 48
Note that reflecting for each choice of sign for $x, y, z$, we get new regions. Therefore, we can restrict to the case where $x, y, z>0$. In this case, the sign of the expression only depends on $(x-y)(y-z)(z-x)$. It is easy to see that for this expression, every one of the $3!=6$ orderings for $\{x, y, z\}$ contributes a region.
Therefore, our answer is $2^{3} \cdot 3!=48$.
|
48
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Consider the graph in 3 -space of
$$
0=x y z(x+y)(y+z)(z+x)(x-y)(y-z)(z-x)
$$
This graph divides 3 -space into $N$ connected regions. What is $N$ ?
|
Answer: 48
Note that reflecting for each choice of sign for $x, y, z$, we get new regions. Therefore, we can restrict to the case where $x, y, z>0$. In this case, the sign of the expression only depends on $(x-y)(y-z)(z-x)$. It is easy to see that for this expression, every one of the $3!=6$ orderings for $\{x, y, z\}$ contributes a region.
Therefore, our answer is $2^{3} \cdot 3!=48$.
|
{
"resource_path": "HarvardMIT/segmented/en-202-2017-feb-guts-solutions.jsonl",
"problem_match": "\n11. [7]",
"solution_match": "\nProposed by: Evan Chen\n"
}
|
a0c95ddb-93c0-515c-a8ab-334bedcf4579
| 609,678
|
The game of Penta is played with teams of five players each, and there are five roles the players can play. Each of the five players chooses two of five roles they wish to play. If each player chooses their roles randomly, what is the probability that each role will have exactly two players?
|
Consider a graph with five vertices corresponding to the roles, and draw an edge between two vertices if a player picks both roles. Thus there are exactly 5 edges in the graph, and we want to find the probability that each vertex has degree 2 . In particular, we want to find the probability that the graph is composed entirely of cycles.
Thus there are two cases. The first case is when the graph is itself a 5 -cycle. There are 4 ! ways to choose such a directed cycle (pick an arbitrary vertex $A$ and consider a vertex it connects to, etc.), and thus $\frac{4!}{2}=12$ ways for the undirected graph to be a 5 -cycle. Now, there are $5!$ ways to assign the edges in this cycle to people, giving a total contribution of $12 \cdot 5$ !.
The second case is when the graph is composed of a 2 -cycle and a 3 -cycle, which only requires choosing the two vertices to be the 2 -cycle, and so there are $\binom{5}{2}=10$ ways. To assign the players to edges, there are $\binom{5}{2}=10$ ways to assign the players to the 2 -cycle. For the 3 -cycle, any of the $3!=6$ permutations of the remaining 3 players work. The total contribution is $10 \cdot 10 \cdot 6$.
Therefore, out answer is
$$
\frac{12 \cdot 120+10 \cdot 10 \cdot 6}{10^{5}}=\frac{51}{2500}
$$
|
\frac{51}{2500}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
The game of Penta is played with teams of five players each, and there are five roles the players can play. Each of the five players chooses two of five roles they wish to play. If each player chooses their roles randomly, what is the probability that each role will have exactly two players?
|
Consider a graph with five vertices corresponding to the roles, and draw an edge between two vertices if a player picks both roles. Thus there are exactly 5 edges in the graph, and we want to find the probability that each vertex has degree 2 . In particular, we want to find the probability that the graph is composed entirely of cycles.
Thus there are two cases. The first case is when the graph is itself a 5 -cycle. There are 4 ! ways to choose such a directed cycle (pick an arbitrary vertex $A$ and consider a vertex it connects to, etc.), and thus $\frac{4!}{2}=12$ ways for the undirected graph to be a 5 -cycle. Now, there are $5!$ ways to assign the edges in this cycle to people, giving a total contribution of $12 \cdot 5$ !.
The second case is when the graph is composed of a 2 -cycle and a 3 -cycle, which only requires choosing the two vertices to be the 2 -cycle, and so there are $\binom{5}{2}=10$ ways. To assign the players to edges, there are $\binom{5}{2}=10$ ways to assign the players to the 2 -cycle. For the 3 -cycle, any of the $3!=6$ permutations of the remaining 3 players work. The total contribution is $10 \cdot 10 \cdot 6$.
Therefore, out answer is
$$
\frac{12 \cdot 120+10 \cdot 10 \cdot 6}{10^{5}}=\frac{51}{2500}
$$
|
{
"resource_path": "HarvardMIT/segmented/en-202-2017-feb-guts-solutions.jsonl",
"problem_match": "\n13. [9]",
"solution_match": "\n## Proposed by: Alexander Katz\n\n"
}
|
15bb508b-b660-5671-861a-a6f56ff8ee57
| 59,427
|
Mrs. Toad has a class of 2017 students, with unhappiness levels $1,2, \ldots, 2017$ respectively. Today in class, there is a group project and Mrs. Toad wants to split the class in exactly 15 groups. The unhappiness level of a group is the average unhappiness of its members, and the unhappiness of the class is the sum of the unhappiness of all 15 groups. What's the minimum unhappiness of the class Mrs. Toad can achieve by splitting the class into 15 groups?
|
One can show that the optimal configuration is $\{1\},\{2\}, \ldots,\{14\},\{15, \ldots, 2017\}$. This would give us an answer of $1+2+\cdots+14+\frac{15+2017}{2}=105+1016=1121$.
|
1121
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Mrs. Toad has a class of 2017 students, with unhappiness levels $1,2, \ldots, 2017$ respectively. Today in class, there is a group project and Mrs. Toad wants to split the class in exactly 15 groups. The unhappiness level of a group is the average unhappiness of its members, and the unhappiness of the class is the sum of the unhappiness of all 15 groups. What's the minimum unhappiness of the class Mrs. Toad can achieve by splitting the class into 15 groups?
|
One can show that the optimal configuration is $\{1\},\{2\}, \ldots,\{14\},\{15, \ldots, 2017\}$. This would give us an answer of $1+2+\cdots+14+\frac{15+2017}{2}=105+1016=1121$.
|
{
"resource_path": "HarvardMIT/segmented/en-202-2017-feb-guts-solutions.jsonl",
"problem_match": "\n14. [9]",
"solution_match": "\nProposed by: Yang Liu\n"
}
|
a3c8fdd1-dc7c-5bc6-a75b-62cb90df9d6b
| 609,680
|
Start by writing the integers $1,2,4,6$ on the blackboard. At each step, write the smallest positive integer $n$ that satisfies both of the following properties on the board.
- $n$ is larger than any integer on the board currently.
- $n$ cannot be written as the sum of 2 distinct integers on the board.
Find the 100 -th integer that you write on the board. Recall that at the beginning, there are already 4 integers on the board.
|
Answer: 388
The sequence goes
$$
1,2,4,6,9,12,17,20,25, \ldots
$$
Common differences are $5,3,5,3,5,3, \ldots$, starting from 12. Therefore, the answer is $12+47 \times 8=388$.
|
388
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Start by writing the integers $1,2,4,6$ on the blackboard. At each step, write the smallest positive integer $n$ that satisfies both of the following properties on the board.
- $n$ is larger than any integer on the board currently.
- $n$ cannot be written as the sum of 2 distinct integers on the board.
Find the 100 -th integer that you write on the board. Recall that at the beginning, there are already 4 integers on the board.
|
Answer: 388
The sequence goes
$$
1,2,4,6,9,12,17,20,25, \ldots
$$
Common differences are $5,3,5,3,5,3, \ldots$, starting from 12. Therefore, the answer is $12+47 \times 8=388$.
|
{
"resource_path": "HarvardMIT/segmented/en-202-2017-feb-guts-solutions.jsonl",
"problem_match": "\n15. [9]",
"solution_match": "\nProposed by: Yang Liu\n\n"
}
|
866046fd-6e96-5d8b-b325-0a5d1ab81d75
| 609,681
|
Sean is a biologist, and is looking at a string of length 66 composed of the letters $A, T, C, G$. A substring of a string is a contiguous sequence of letters in the string. For example, the string $A G T C$ has 10 substrings: $A, G, T, C, A G, G T, T C, A G T, G T C, A G T C$. What is the maximum number of distinct substrings of the string Sean is looking at?
|
Answer: 2100
Let's consider the number of distinct substrings of length $\ell$. On one hand, there are obviously at most $4^{\ell}$ distinct substrings. On the other hand, there are $67-\ell$ substrings of length $\ell$ in a length 66 string. Therefore, the number of distinct substrings is at most
$$
\sum_{\ell=1}^{66} \min \left(4^{\ell}, 67-\ell\right)=2100
$$
To show that this bound is achievable, one can do a construction using deBrujin sequences that we won't elaborate on here.
|
2100
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Sean is a biologist, and is looking at a string of length 66 composed of the letters $A, T, C, G$. A substring of a string is a contiguous sequence of letters in the string. For example, the string $A G T C$ has 10 substrings: $A, G, T, C, A G, G T, T C, A G T, G T C, A G T C$. What is the maximum number of distinct substrings of the string Sean is looking at?
|
Answer: 2100
Let's consider the number of distinct substrings of length $\ell$. On one hand, there are obviously at most $4^{\ell}$ distinct substrings. On the other hand, there are $67-\ell$ substrings of length $\ell$ in a length 66 string. Therefore, the number of distinct substrings is at most
$$
\sum_{\ell=1}^{66} \min \left(4^{\ell}, 67-\ell\right)=2100
$$
To show that this bound is achievable, one can do a construction using deBrujin sequences that we won't elaborate on here.
|
{
"resource_path": "HarvardMIT/segmented/en-202-2017-feb-guts-solutions.jsonl",
"problem_match": "\n17. [10]",
"solution_match": "\nProposed by: Yang Liu\n"
}
|
ff955f2f-a3ce-5d1e-9c3f-871fa9804b8b
| 609,683
|
Let $A B C D$ be a quadrilateral with side lengths $A B=2, B C=3, C D=5$, and $D A=4$. What is the maximum possible radius of a circle inscribed in quadrilateral $A B C D$ ?
|
Answer: $\frac{2 \sqrt{30}}{7}$
Let the tangent lengths be $a, b, c, d$ so that
$$
\begin{aligned}
& a+b=2 \\
& b+c=3 \\
& c+d=5 \\
& d+a=4
\end{aligned}
$$
Then $b=2-a$ and $c=1+a$ and $d=4-a$. The radius of the inscribed circle of quadrilateral $A B C D$ is given by
$$
\sqrt{\frac{a b c+a b d+a c d+b c d}{a+b+c+d}}=\sqrt{\frac{-7 a^{2}+16 a+8}{7}}
$$
This is clearly maximized when $a=\frac{8}{7}$ which leads to a radius of $\sqrt{\frac{120}{49}}=\frac{2 \sqrt{30}}{7}$.
|
\frac{2 \sqrt{30}}{7}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $A B C D$ be a quadrilateral with side lengths $A B=2, B C=3, C D=5$, and $D A=4$. What is the maximum possible radius of a circle inscribed in quadrilateral $A B C D$ ?
|
Answer: $\frac{2 \sqrt{30}}{7}$
Let the tangent lengths be $a, b, c, d$ so that
$$
\begin{aligned}
& a+b=2 \\
& b+c=3 \\
& c+d=5 \\
& d+a=4
\end{aligned}
$$
Then $b=2-a$ and $c=1+a$ and $d=4-a$. The radius of the inscribed circle of quadrilateral $A B C D$ is given by
$$
\sqrt{\frac{a b c+a b d+a c d+b c d}{a+b+c+d}}=\sqrt{\frac{-7 a^{2}+16 a+8}{7}}
$$
This is clearly maximized when $a=\frac{8}{7}$ which leads to a radius of $\sqrt{\frac{120}{49}}=\frac{2 \sqrt{30}}{7}$.
|
{
"resource_path": "HarvardMIT/segmented/en-202-2017-feb-guts-solutions.jsonl",
"problem_match": "\n18. [10]",
"solution_match": "\nProposed by: Sam Korsky\n"
}
|
4009552b-1b4b-552b-aafb-082500ba4637
| 609,684
|
Find (in terms of $n \geq 1$ ) the number of terms with odd coefficients after expanding the product:
$$
\prod_{1 \leq i<j \leq n}\left(x_{i}+x_{j}\right)
$$
e.g., for $n=3$ the expanded product is given by $x_{1}^{2} x_{2}+x_{1}^{2} x_{3}+x_{2}^{2} x_{3}+x_{2}^{2} x_{1}+x_{3}^{2} x_{1}+x_{3}^{2} x_{2}+2 x_{1} x_{2} x_{3}$ and so the answer would be 6 .
|
Answer: $n!$
Note that if we take $(\bmod 2)$, we get that
$$
\prod_{1 \leq i<j \leq n}\left(x_{i}+x_{j}\right) \equiv \prod_{1 \leq i<j \leq n}\left(x_{j}-x_{i}\right)=\operatorname{det}(M)
$$
where $M$ is the matrix with $M_{i j}=x_{i}^{j-1}$. This is called a Vandermonde determinant. Expanding this determinant using the formula
$$
\operatorname{det}(M)=\sum_{\sigma} \prod_{i=1}^{n} x_{\sigma(i)}^{i-1},
$$
where the sum if over all $n!$ permutations $\sigma$, gives the result.
|
n!
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Find (in terms of $n \geq 1$ ) the number of terms with odd coefficients after expanding the product:
$$
\prod_{1 \leq i<j \leq n}\left(x_{i}+x_{j}\right)
$$
e.g., for $n=3$ the expanded product is given by $x_{1}^{2} x_{2}+x_{1}^{2} x_{3}+x_{2}^{2} x_{3}+x_{2}^{2} x_{1}+x_{3}^{2} x_{1}+x_{3}^{2} x_{2}+2 x_{1} x_{2} x_{3}$ and so the answer would be 6 .
|
Answer: $n!$
Note that if we take $(\bmod 2)$, we get that
$$
\prod_{1 \leq i<j \leq n}\left(x_{i}+x_{j}\right) \equiv \prod_{1 \leq i<j \leq n}\left(x_{j}-x_{i}\right)=\operatorname{det}(M)
$$
where $M$ is the matrix with $M_{i j}=x_{i}^{j-1}$. This is called a Vandermonde determinant. Expanding this determinant using the formula
$$
\operatorname{det}(M)=\sum_{\sigma} \prod_{i=1}^{n} x_{\sigma(i)}^{i-1},
$$
where the sum if over all $n!$ permutations $\sigma$, gives the result.
|
{
"resource_path": "HarvardMIT/segmented/en-202-2017-feb-guts-solutions.jsonl",
"problem_match": "\n19. [10]",
"solution_match": "\nProposed by: Sam Korsky\n"
}
|
4a0f85d7-e828-5bb4-9dbe-aa92c888f2a9
| 609,685
|
For positive integers $a$ and $N$, let $r(a, N) \in\{0,1, \ldots, N-1\}$ denote the remainder of $a$ when divided by $N$. Determine the number of positive integers $n \leq 1000000$ for which
$$
r(n, 1000)>r(n, 1001)
$$
|
Answer: 499500
Note that $0 \leq r(n, 1000) \leq 999$ and $0 \leq r(n, 1001) \leq 1000$. Consider the $\binom{1000}{2}=499500$ ways to choose pairs $(i, j)$ such that $i>j$.By the Chinese Remainder Theorem, there is exactly one $n$ such that $1 \leq n \leq 1000 \cdot 1001$ such that $n \equiv i(\bmod 1000)$ and $n \equiv j(\bmod 1001)$. Finally, it is easy to check that none of the $n$ in the range 1000001 to 1001000 satisfy the condition, so the answer is exactly 499500 .
|
499500
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
For positive integers $a$ and $N$, let $r(a, N) \in\{0,1, \ldots, N-1\}$ denote the remainder of $a$ when divided by $N$. Determine the number of positive integers $n \leq 1000000$ for which
$$
r(n, 1000)>r(n, 1001)
$$
|
Answer: 499500
Note that $0 \leq r(n, 1000) \leq 999$ and $0 \leq r(n, 1001) \leq 1000$. Consider the $\binom{1000}{2}=499500$ ways to choose pairs $(i, j)$ such that $i>j$.By the Chinese Remainder Theorem, there is exactly one $n$ such that $1 \leq n \leq 1000 \cdot 1001$ such that $n \equiv i(\bmod 1000)$ and $n \equiv j(\bmod 1001)$. Finally, it is easy to check that none of the $n$ in the range 1000001 to 1001000 satisfy the condition, so the answer is exactly 499500 .
|
{
"resource_path": "HarvardMIT/segmented/en-202-2017-feb-guts-solutions.jsonl",
"problem_match": "\n20. [10]",
"solution_match": "\nProposed by: Pakawut Jiradilok\n"
}
|
8a1fd1b9-dc68-54e6-bb47-6af0e38fea3a
| 609,686
|
Let $P$ and $A$ denote the perimeter and area respectively of a right triangle with relatively prime integer side-lengths. Find the largest possible integral value of $\frac{P^{2}}{A}$
|
Assume WLOG that the side lengths of the triangle are pairwise coprime. Then they can be written as $m^{2}-n^{2}, 2 m n, m^{2}+n^{2}$ for some coprime integers $m$ and $n$ where $m>n$ and $m n$ is even. Then we obtain
$$
\frac{P^{2}}{A}=\frac{4 m(m+n)}{n(m-n)}
$$
But $n, m-n, m, m+n$ are all pairwise coprime so for this to be an integer we need $n(m-n) \mid 4$ and by checking each case we find that $(m, n)=(5,4)$ yields the maximum ratio of 45 .
|
45
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $P$ and $A$ denote the perimeter and area respectively of a right triangle with relatively prime integer side-lengths. Find the largest possible integral value of $\frac{P^{2}}{A}$
|
Assume WLOG that the side lengths of the triangle are pairwise coprime. Then they can be written as $m^{2}-n^{2}, 2 m n, m^{2}+n^{2}$ for some coprime integers $m$ and $n$ where $m>n$ and $m n$ is even. Then we obtain
$$
\frac{P^{2}}{A}=\frac{4 m(m+n)}{n(m-n)}
$$
But $n, m-n, m, m+n$ are all pairwise coprime so for this to be an integer we need $n(m-n) \mid 4$ and by checking each case we find that $(m, n)=(5,4)$ yields the maximum ratio of 45 .
|
{
"resource_path": "HarvardMIT/segmented/en-202-2017-feb-guts-solutions.jsonl",
"problem_match": "\n21. [12]",
"solution_match": "\nProposed by: Sam Korsky\n"
}
|
3e37fc5f-468a-576b-a83b-a79c7ddf782c
| 609,687
|
Kelvin the Frog and 10 of his relatives are at a party. Every pair of frogs is either friendly or unfriendly. When 3 pairwise friendly frogs meet up, they will gossip about one another and end up in a fight (but stay friendly anyway). When 3 pairwise unfriendly frogs meet up, they will also end up in a fight. In all other cases, common ground is found and there is no fight. If all $\binom{11}{3}$ triples of frogs meet up exactly once, what is the minimum possible number of fights?
|
Answer: 28
Consider a graph $G$ with 11 vertices - one for each of the frogs at the party - where two vertices are connected by an edge if and only if they are friendly. Denote by $d(v)$ the number of edges emanating from $v$; i.e. the number of friends frog $v$ has. Note that $d(1)+d(2)+\ldots+d(11)=2 e$, where $e$ is the number of edges in this graph.
Focus on a single vertex $v$, and choose two other vertices $u, w$ such that $u v$ is an edge but $w v$ is not. There are then $d(v)$ choices for $u$ and $10-d(v)$ choices for $w$, so there are $d(v)(10-d(v))$ sets of three frogs that include $v$ and do not result in a fight. Each set, however, is counted twice - if $u w$ is an edge, then we count this set both when we focus on $v$ and when we focus on $w$, and otherwise we count it when we focus on $v$ and when we focus on $u$. As such, there are a total of
$$
\frac{1}{2} \sum_{v} d(v)(10-d(v))
$$
sets of 3 frogs that do not result in a fight.
Note that $\frac{d(v)+10-d(v)}{2}=5 \geq \sqrt{d(v)(10-d(v))} \Longrightarrow d(v)(10-d(v)) \leq 25$ by AM-GM. Thus there are a maximum of
$$
\frac{1}{2} \sum_{v} d(v)(10-d(v)) \leq \frac{1}{2}(25 \cdot 11)=\frac{275}{2}
$$
sets of three frogs that do not result in a fight; since this number must be an integer, there are a maximum of 137 such sets. As there are a total of $\binom{11}{3}=165$ sets of 3 frogs, this results in a minimum $165-137=28$ number of fights.
It remains to show that such an arrangement can be constructed. Set $d(1)=d(2)=\ldots=d(10)=5$ and $d(11)=4$. Arrange these in a circle, and connect each to the nearest two clockwise neighbors; this gives each vertex 4 edges. To get the final edge for the first ten vertices, connect 1 to 10,2 to 9,3 to 8,4 to 7 , and 5 to 6 . Thus 28 is constructable, and is thus the true minimum.
|
28
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Kelvin the Frog and 10 of his relatives are at a party. Every pair of frogs is either friendly or unfriendly. When 3 pairwise friendly frogs meet up, they will gossip about one another and end up in a fight (but stay friendly anyway). When 3 pairwise unfriendly frogs meet up, they will also end up in a fight. In all other cases, common ground is found and there is no fight. If all $\binom{11}{3}$ triples of frogs meet up exactly once, what is the minimum possible number of fights?
|
Answer: 28
Consider a graph $G$ with 11 vertices - one for each of the frogs at the party - where two vertices are connected by an edge if and only if they are friendly. Denote by $d(v)$ the number of edges emanating from $v$; i.e. the number of friends frog $v$ has. Note that $d(1)+d(2)+\ldots+d(11)=2 e$, where $e$ is the number of edges in this graph.
Focus on a single vertex $v$, and choose two other vertices $u, w$ such that $u v$ is an edge but $w v$ is not. There are then $d(v)$ choices for $u$ and $10-d(v)$ choices for $w$, so there are $d(v)(10-d(v))$ sets of three frogs that include $v$ and do not result in a fight. Each set, however, is counted twice - if $u w$ is an edge, then we count this set both when we focus on $v$ and when we focus on $w$, and otherwise we count it when we focus on $v$ and when we focus on $u$. As such, there are a total of
$$
\frac{1}{2} \sum_{v} d(v)(10-d(v))
$$
sets of 3 frogs that do not result in a fight.
Note that $\frac{d(v)+10-d(v)}{2}=5 \geq \sqrt{d(v)(10-d(v))} \Longrightarrow d(v)(10-d(v)) \leq 25$ by AM-GM. Thus there are a maximum of
$$
\frac{1}{2} \sum_{v} d(v)(10-d(v)) \leq \frac{1}{2}(25 \cdot 11)=\frac{275}{2}
$$
sets of three frogs that do not result in a fight; since this number must be an integer, there are a maximum of 137 such sets. As there are a total of $\binom{11}{3}=165$ sets of 3 frogs, this results in a minimum $165-137=28$ number of fights.
It remains to show that such an arrangement can be constructed. Set $d(1)=d(2)=\ldots=d(10)=5$ and $d(11)=4$. Arrange these in a circle, and connect each to the nearest two clockwise neighbors; this gives each vertex 4 edges. To get the final edge for the first ten vertices, connect 1 to 10,2 to 9,3 to 8,4 to 7 , and 5 to 6 . Thus 28 is constructable, and is thus the true minimum.
|
{
"resource_path": "HarvardMIT/segmented/en-202-2017-feb-guts-solutions.jsonl",
"problem_match": "\n22. [12]",
"solution_match": "\nProposed by: Alexander Katz\n"
}
|
a46b355a-fe59-508a-87f5-9c15005c3568
| 609,688
|
Five points are chosen uniformly at random on a segment of length 1 . What is the expected distance between the closest pair of points?
|
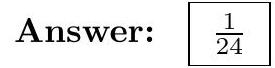
Choose five points arbitrarily at $a_{1}, a_{2}, a_{3}, a_{4}, a_{5}$ in increasing order. Then the intervals $\left(a_{2}-x, a_{2}\right),\left(a_{3}-\right.$ $\left.x, a_{3}\right),\left(a_{4}-x, a_{4}\right),\left(a_{5}-x, a_{5}\right)$ must all be unoccupied. The probability that this happens is the same
as doing the process in reverse: first defining these intervals, then choosing five random points none of which lie in the four intervals. This transformed process clearly has a $(1-4 x)^{5}$ probability of success. It follows that the desired probability is
$$
\int_{0}^{1 / 4}(1-4 x)^{5} d x=\frac{1}{24}
$$
|
\frac{1}{24}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Five points are chosen uniformly at random on a segment of length 1 . What is the expected distance between the closest pair of points?
|
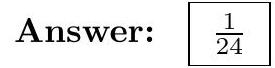
Choose five points arbitrarily at $a_{1}, a_{2}, a_{3}, a_{4}, a_{5}$ in increasing order. Then the intervals $\left(a_{2}-x, a_{2}\right),\left(a_{3}-\right.$ $\left.x, a_{3}\right),\left(a_{4}-x, a_{4}\right),\left(a_{5}-x, a_{5}\right)$ must all be unoccupied. The probability that this happens is the same
as doing the process in reverse: first defining these intervals, then choosing five random points none of which lie in the four intervals. This transformed process clearly has a $(1-4 x)^{5}$ probability of success. It follows that the desired probability is
$$
\int_{0}^{1 / 4}(1-4 x)^{5} d x=\frac{1}{24}
$$
|
{
"resource_path": "HarvardMIT/segmented/en-202-2017-feb-guts-solutions.jsonl",
"problem_match": "\n23. [12]",
"solution_match": "\nProposed by: Meghal Gupta\n"
}
|
c0574e20-78e3-590c-ac87-955a1aa9d4dd
| 609,689
|
At a recent math contest, Evan was asked to find $2^{2016}(\bmod p)$ for a given prime number $p$ with $100<p<500$. Evan has forgotten what the prime $p$ was, but still remembers how he solved it:
- Evan first tried taking 2016 modulo $p-1$, but got a value $e$ larger than 100 .
- However, Evan noted that $e-\frac{1}{2}(p-1)=21$, and then realized the answer was $-2^{21}(\bmod p)$.
What was the prime $p$ ?
|
Answer: 211
Answer is $p=211$. Let $p=2 d+1,50<d<250$. The information in the problem boils down to
$$
2016=d+21 \quad(\bmod 2 d)
$$
From this we can at least read off $d \mid 1995$.
Now factor $1995=3 \cdot 5 \cdot 7 \cdot 19$. The values of $d$ in this interval are $57,95,105,133$. The prime values of $2 d+1$ are then 191 and 211. Of these, we take 211 since $(2 / 191)=+1$ while $(2 / 211)=-1$.
Also, this is (almost) a true story: the contest in question was the PUMaC 2016 Live Round.
|
211
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
At a recent math contest, Evan was asked to find $2^{2016}(\bmod p)$ for a given prime number $p$ with $100<p<500$. Evan has forgotten what the prime $p$ was, but still remembers how he solved it:
- Evan first tried taking 2016 modulo $p-1$, but got a value $e$ larger than 100 .
- However, Evan noted that $e-\frac{1}{2}(p-1)=21$, and then realized the answer was $-2^{21}(\bmod p)$.
What was the prime $p$ ?
|
Answer: 211
Answer is $p=211$. Let $p=2 d+1,50<d<250$. The information in the problem boils down to
$$
2016=d+21 \quad(\bmod 2 d)
$$
From this we can at least read off $d \mid 1995$.
Now factor $1995=3 \cdot 5 \cdot 7 \cdot 19$. The values of $d$ in this interval are $57,95,105,133$. The prime values of $2 d+1$ are then 191 and 211. Of these, we take 211 since $(2 / 191)=+1$ while $(2 / 211)=-1$.
Also, this is (almost) a true story: the contest in question was the PUMaC 2016 Live Round.
|
{
"resource_path": "HarvardMIT/segmented/en-202-2017-feb-guts-solutions.jsonl",
"problem_match": "\n24. [12]",
"solution_match": "\nProposed by: Evan Chen\n"
}
|
0386dd1a-9da4-538b-80ab-5622e7846383
| 609,690
|
Kelvin the Frog is hopping on a number line (extending to infinity in both directions). Kelvin starts at 0 . Every minute, he has a $\frac{1}{3}$ chance of moving 1 unit left, a $\frac{1}{3}$ chance of moving 1 unit right and $\frac{1}{3}$ chance of getting eaten. Find the expected number of times Kelvin returns to 0 (not including the start) before getting eaten.
|
First we compute probability that the mouse returns to 0 before being eaten. Then probability that it is at 0 in $2 n$ minutes without being eaten is given by $\frac{1}{3^{2 n}}\binom{2 n}{n}$. Therefore, the overall expectation is given by
$$
\begin{aligned}
& \sum_{n \geq 1}\binom{2 n}{n} 9^{-n}=-1+\sum_{n \geq 0}\binom{2 n}{n} 9^{-n} \\
= & -1+\frac{1}{\sqrt{1-4 / 9}}=-1+\frac{3}{\sqrt{5}}=\frac{3 \sqrt{5}-5}{5}
\end{aligned}
$$
where we use the well known fact that
$$
\sum_{n \geq 0}\binom{2 n}{n} x^{n}=\frac{1}{\sqrt{1-4 x}}
$$
for $x=\frac{1}{9}$.
|
\frac{3 \sqrt{5}-5}{5}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Kelvin the Frog is hopping on a number line (extending to infinity in both directions). Kelvin starts at 0 . Every minute, he has a $\frac{1}{3}$ chance of moving 1 unit left, a $\frac{1}{3}$ chance of moving 1 unit right and $\frac{1}{3}$ chance of getting eaten. Find the expected number of times Kelvin returns to 0 (not including the start) before getting eaten.
|
First we compute probability that the mouse returns to 0 before being eaten. Then probability that it is at 0 in $2 n$ minutes without being eaten is given by $\frac{1}{3^{2 n}}\binom{2 n}{n}$. Therefore, the overall expectation is given by
$$
\begin{aligned}
& \sum_{n \geq 1}\binom{2 n}{n} 9^{-n}=-1+\sum_{n \geq 0}\binom{2 n}{n} 9^{-n} \\
= & -1+\frac{1}{\sqrt{1-4 / 9}}=-1+\frac{3}{\sqrt{5}}=\frac{3 \sqrt{5}-5}{5}
\end{aligned}
$$
where we use the well known fact that
$$
\sum_{n \geq 0}\binom{2 n}{n} x^{n}=\frac{1}{\sqrt{1-4 x}}
$$
for $x=\frac{1}{9}$.
|
{
"resource_path": "HarvardMIT/segmented/en-202-2017-feb-guts-solutions.jsonl",
"problem_match": "\n26. [15]",
"solution_match": "\nProposed by: Allen Liu\n"
}
|
1d80767e-eb76-5a63-95c5-5077aaab95b6
| 609,692
|
Find the smallest possible value of $x+y$ where $x, y \geq 1$ and $x$ and $y$ are integers that satisfy $x^{2}-29 y^{2}=1$
|
Answer: 11621
Continued fraction convergents to $\sqrt{29}$ are $5, \frac{11}{2}, \frac{16}{3}, \frac{27}{5}, \frac{70}{13}$ and you get $70^{2}-29 \cdot 13^{2}=-1$ so since $(70+13 \sqrt{29})^{2}=9801+1820 \sqrt{29}$ the answer is $9801+1820=11621$
|
11621
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Find the smallest possible value of $x+y$ where $x, y \geq 1$ and $x$ and $y$ are integers that satisfy $x^{2}-29 y^{2}=1$
|
Answer: 11621
Continued fraction convergents to $\sqrt{29}$ are $5, \frac{11}{2}, \frac{16}{3}, \frac{27}{5}, \frac{70}{13}$ and you get $70^{2}-29 \cdot 13^{2}=-1$ so since $(70+13 \sqrt{29})^{2}=9801+1820 \sqrt{29}$ the answer is $9801+1820=11621$
|
{
"resource_path": "HarvardMIT/segmented/en-202-2017-feb-guts-solutions.jsonl",
"problem_match": "\n27. [15]",
"solution_match": "\nProposed by: Sam Korsky\n"
}
|
40ffd1a5-69ab-5767-a457-8b2eb234609d
| 609,693
|
Let $\ldots, a_{-1}, a_{0}, a_{1}, a_{2}, \ldots$ be a sequence of positive integers satisfying the following relations: $a_{n}=0$ for $n<0, a_{0}=1$, and for $n \geq 1$,
$$
a_{n}=a_{n-1}+2(n-1) a_{n-2}+9(n-1)(n-2) a_{n-3}+8(n-1)(n-2)(n-3) a_{n-4} .
$$
Compute
$$
\sum_{n \geq 0} \frac{10^{n} a_{n}}{n!}
$$
|
Answer: $e^{23110}$.
Let $y=\sum_{n \geq 0} \frac{x^{n} a_{n}}{n!}$. Then $y^{\prime}=\left(1+2 x+9 x^{2}+8 x^{3}\right) y$ by definition. So $y=C \exp \left(x+x^{2}+3 x^{3}+2 x^{4}\right)$. Take $x=0$ to get $C=1$. Take $x=10$ to get the answer.
|
e^{23110}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Let $\ldots, a_{-1}, a_{0}, a_{1}, a_{2}, \ldots$ be a sequence of positive integers satisfying the following relations: $a_{n}=0$ for $n<0, a_{0}=1$, and for $n \geq 1$,
$$
a_{n}=a_{n-1}+2(n-1) a_{n-2}+9(n-1)(n-2) a_{n-3}+8(n-1)(n-2)(n-3) a_{n-4} .
$$
Compute
$$
\sum_{n \geq 0} \frac{10^{n} a_{n}}{n!}
$$
|
Answer: $e^{23110}$.
Let $y=\sum_{n \geq 0} \frac{x^{n} a_{n}}{n!}$. Then $y^{\prime}=\left(1+2 x+9 x^{2}+8 x^{3}\right) y$ by definition. So $y=C \exp \left(x+x^{2}+3 x^{3}+2 x^{4}\right)$. Take $x=0$ to get $C=1$. Take $x=10$ to get the answer.
|
{
"resource_path": "HarvardMIT/segmented/en-202-2017-feb-guts-solutions.jsonl",
"problem_match": "\n28. [15]",
"solution_match": "\nProposed by: Yang Liu\n"
}
|
9efbd08c-beb2-594e-a8c2-c3d4628930b9
| 609,694
|
Yang has the sequence of integers $1,2, \ldots, 2017$. He makes 2016 swaps in order, where a swap changes the positions of two integers in the sequence. His goal is to end with $2,3, \ldots, 2017,1$. How many different sequences of swaps can Yang do to achieve his goal?
|
Answer: $2017^{2015}$
Let $n=2017$. The problem is asking to write a cycle permutation of $n$ integers as the product of $n-1$ transpositions. Say that the transpositions Yang uses are ( $a_{i}, b_{i}$ ) (i.e. swapping the $a_{i}$-th integer in the sequence with the $b_{i}$-th integer in the sequence). Draw the graph with edges $\left(a_{i}, b_{i}\right)$. One can show that the result is a cycle if and only if the resulting graph is acyclic, so it must be a tree. There are $n^{n-2}$ trees by Cayley's formula, and for each tree, it can be made in $(n-1)$ ! ways (any ordering of the edges). So the total number of ways to end with a cycle is $n^{n-2} \cdot(n-1)!$. By symmetry, each cycle can be made in the same number of ways, so in particular the cycle $2,3, \ldots, n, 1$ can be made in $\frac{n^{n-2} \cdot(n-1)!}{(n-1)!}=n^{n-2}$ ways.
|
2017^{2015}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Yang has the sequence of integers $1,2, \ldots, 2017$. He makes 2016 swaps in order, where a swap changes the positions of two integers in the sequence. His goal is to end with $2,3, \ldots, 2017,1$. How many different sequences of swaps can Yang do to achieve his goal?
|
Answer: $2017^{2015}$
Let $n=2017$. The problem is asking to write a cycle permutation of $n$ integers as the product of $n-1$ transpositions. Say that the transpositions Yang uses are ( $a_{i}, b_{i}$ ) (i.e. swapping the $a_{i}$-th integer in the sequence with the $b_{i}$-th integer in the sequence). Draw the graph with edges $\left(a_{i}, b_{i}\right)$. One can show that the result is a cycle if and only if the resulting graph is acyclic, so it must be a tree. There are $n^{n-2}$ trees by Cayley's formula, and for each tree, it can be made in $(n-1)$ ! ways (any ordering of the edges). So the total number of ways to end with a cycle is $n^{n-2} \cdot(n-1)!$. By symmetry, each cycle can be made in the same number of ways, so in particular the cycle $2,3, \ldots, n, 1$ can be made in $\frac{n^{n-2} \cdot(n-1)!}{(n-1)!}=n^{n-2}$ ways.
|
{
"resource_path": "HarvardMIT/segmented/en-202-2017-feb-guts-solutions.jsonl",
"problem_match": "\n29. [17]",
"solution_match": "\nProposed by: Yang Liu\n"
}
|
b23fe1ef-e8c4-537a-80d3-888a980ee8ca
| 609,695
|
Consider an equilateral triangular grid $G$ with 20 points on a side, where each row consists of points spaced 1 unit apart. More specifically, there is a single point in the first row, two points in the second row, ..., and 20 points in the last row, for a total of 210 points. Let $S$ be a closed non-selfintersecting polygon which has 210 vertices, using each point in $G$ exactly once. Find the sum of all possible values of the area of $S$.
|
Answer: $52 \sqrt{3}$
Imagine deforming the triangle lattice such that now it looks like a lattice of 45-45-90 right triangles with legs of length 1 . Note that by doing this, the area has multiplied by $\frac{2}{\sqrt{3}}$, so we need to readjust out answer on the isosceles triangle lattice by a factor of $\frac{\sqrt{3}}{2}$ at the end. By Pick's Theorem, the area in the new lattice is given by $I+\frac{P}{2}-1=0+105-1=104$. Therefore, the answer is $104 \cdot \frac{\sqrt{3}}{2}=52 \sqrt{3}$.
|
52 \sqrt{3}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Consider an equilateral triangular grid $G$ with 20 points on a side, where each row consists of points spaced 1 unit apart. More specifically, there is a single point in the first row, two points in the second row, ..., and 20 points in the last row, for a total of 210 points. Let $S$ be a closed non-selfintersecting polygon which has 210 vertices, using each point in $G$ exactly once. Find the sum of all possible values of the area of $S$.
|
Answer: $52 \sqrt{3}$
Imagine deforming the triangle lattice such that now it looks like a lattice of 45-45-90 right triangles with legs of length 1 . Note that by doing this, the area has multiplied by $\frac{2}{\sqrt{3}}$, so we need to readjust out answer on the isosceles triangle lattice by a factor of $\frac{\sqrt{3}}{2}$ at the end. By Pick's Theorem, the area in the new lattice is given by $I+\frac{P}{2}-1=0+105-1=104$. Therefore, the answer is $104 \cdot \frac{\sqrt{3}}{2}=52 \sqrt{3}$.
|
{
"resource_path": "HarvardMIT/segmented/en-202-2017-feb-guts-solutions.jsonl",
"problem_match": "\n30. [17]",
"solution_match": "\nProposed by: Sammy Luo\n"
}
|
82c0a0a0-1a46-5a8c-86a6-293f2f9cc242
| 609,696
|
A baseball league has 6 teams. To decide the schedule for the league, for each pair of teams, a coin is flipped. If it lands head, they will play a game this season, in which one team wins and one team loses. If it lands tails, they don't play a game this season. Define the imbalance of this schedule
to be the minimum number of teams that will end up undefeated, i.e. lose 0 games. Find the expected value of the imbalance in this league.
|
Let $n$ denote the number of teams.
Lemma: Given a connected graph $G$, the imbalance of $G$ is 1 iff $G$ is a tree. Let's just talk in terms of directed graphs and indegree/outdegree.
Proof. If there is a cycle, direct the cycle such that it is a directed cycle. Then from this cycle, point all remaining edges outwards. If $G$ is a tree, induct on the size. Take any leaf. If it wins its game, it is undefeated. Otherwise, it must lose to its neighbor. Then induct on the tree resulting after deleting the leaf.
Now the finish is a simple counting argument using expected values. Using Cayley's formula, for each subset of vertices, we compute the probability that it is a maximal connected component and is a tree. This ends up being
$$
2^{-\binom{n}{2}} \sum_{i=1}^{n}\binom{n}{i} \cdot i^{i-2} \cdot 2^{\binom{n-i}{2}} .
$$
This evaluates to $\frac{5055}{2^{15}}$ for $n=6$.
|
\frac{5055}{2^{15}}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
A baseball league has 6 teams. To decide the schedule for the league, for each pair of teams, a coin is flipped. If it lands head, they will play a game this season, in which one team wins and one team loses. If it lands tails, they don't play a game this season. Define the imbalance of this schedule
to be the minimum number of teams that will end up undefeated, i.e. lose 0 games. Find the expected value of the imbalance in this league.
|
Let $n$ denote the number of teams.
Lemma: Given a connected graph $G$, the imbalance of $G$ is 1 iff $G$ is a tree. Let's just talk in terms of directed graphs and indegree/outdegree.
Proof. If there is a cycle, direct the cycle such that it is a directed cycle. Then from this cycle, point all remaining edges outwards. If $G$ is a tree, induct on the size. Take any leaf. If it wins its game, it is undefeated. Otherwise, it must lose to its neighbor. Then induct on the tree resulting after deleting the leaf.
Now the finish is a simple counting argument using expected values. Using Cayley's formula, for each subset of vertices, we compute the probability that it is a maximal connected component and is a tree. This ends up being
$$
2^{-\binom{n}{2}} \sum_{i=1}^{n}\binom{n}{i} \cdot i^{i-2} \cdot 2^{\binom{n-i}{2}} .
$$
This evaluates to $\frac{5055}{2^{15}}$ for $n=6$.
|
{
"resource_path": "HarvardMIT/segmented/en-202-2017-feb-guts-solutions.jsonl",
"problem_match": "\n31. [17]",
"solution_match": "\nProposed by: Yang Liu\n"
}
|
f953ee6d-cf81-5730-8e6a-728c88353dbe
| 609,697
|
Let $a, b, c$ be non-negative real numbers such that $a b+b c+c a=3$. Suppose that
$$
a^{3} b+b^{3} c+c^{3} a+2 a b c(a+b+c)=\frac{9}{2}
$$
What is the minimum possible value of $a b^{3}+b c^{3}+c a^{3}$ ?
|
Answer: 18
Expanding the inequality $\sum_{\text {cyc }} a b(b+c-2 a)^{2} \geq 0$ gives
$$
\left(\sum_{\text {cyc }} a b^{3}\right)+4\left(\sum_{\text {cyc }} a^{3} b\right)-4\left(\sum_{\text {cyc }} a^{2} b^{2}\right)-a b c(a+b+c) \geq 0
$$
Using $\left(\sum_{\text {cyc }} a^{3} b\right)+2 a b c(a+b+c)=\frac{9}{2}$ in the inequality above yields
$$
\left(\sum_{\text {cyc }} a b^{3}\right)-4(a b+b c+c a)^{2} \geq\left(\sum_{\text {cyc }} a b^{3}\right)-4\left(\sum_{\text {cyc }} a^{2} b^{2}\right)-9 a b c(a+b+c) \geq-18
$$
Since $a b+b c+c a=3$, we have $\sum_{\text {cyc }} a b^{3} \geq 18$ as desired.
The equality occurs when $(a, b, c) \underset{\text { cyc }}{\sim}\left(\sqrt{\frac{3}{2}}, \sqrt{6}, 0\right)$.
|
18
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Let $a, b, c$ be non-negative real numbers such that $a b+b c+c a=3$. Suppose that
$$
a^{3} b+b^{3} c+c^{3} a+2 a b c(a+b+c)=\frac{9}{2}
$$
What is the minimum possible value of $a b^{3}+b c^{3}+c a^{3}$ ?
|
Answer: 18
Expanding the inequality $\sum_{\text {cyc }} a b(b+c-2 a)^{2} \geq 0$ gives
$$
\left(\sum_{\text {cyc }} a b^{3}\right)+4\left(\sum_{\text {cyc }} a^{3} b\right)-4\left(\sum_{\text {cyc }} a^{2} b^{2}\right)-a b c(a+b+c) \geq 0
$$
Using $\left(\sum_{\text {cyc }} a^{3} b\right)+2 a b c(a+b+c)=\frac{9}{2}$ in the inequality above yields
$$
\left(\sum_{\text {cyc }} a b^{3}\right)-4(a b+b c+c a)^{2} \geq\left(\sum_{\text {cyc }} a b^{3}\right)-4\left(\sum_{\text {cyc }} a^{2} b^{2}\right)-9 a b c(a+b+c) \geq-18
$$
Since $a b+b c+c a=3$, we have $\sum_{\text {cyc }} a b^{3} \geq 18$ as desired.
The equality occurs when $(a, b, c) \underset{\text { cyc }}{\sim}\left(\sqrt{\frac{3}{2}}, \sqrt{6}, 0\right)$.
|
{
"resource_path": "HarvardMIT/segmented/en-202-2017-feb-guts-solutions.jsonl",
"problem_match": "\n32. [17]",
"solution_match": "\nProposed by: Pakawut Jiradilok\n"
}
|
3f49bd35-dc4a-526f-9ff6-4cb48c7f28f1
| 609,698
|
Find the sum of all positive integers whose largest proper divisor is 55 . (A proper divisor of $n$ is a divisor that is strictly less than $n$.)
|
Answer: 550
The largest proper divisor of an integer $n$ is $\frac{n}{p}$, where $p$ is the smallest prime divisor of $n$. So $n=55 p$ for some prime $p$. Since $55=5 \cdot 11$, we must have $p \leq 5$, so $p=2,3,5$ gives all solutions. The sum of these solutions is $55(2+3+5)=550$.
|
550
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Find the sum of all positive integers whose largest proper divisor is 55 . (A proper divisor of $n$ is a divisor that is strictly less than $n$.)
|
Answer: 550
The largest proper divisor of an integer $n$ is $\frac{n}{p}$, where $p$ is the smallest prime divisor of $n$. So $n=55 p$ for some prime $p$. Since $55=5 \cdot 11$, we must have $p \leq 5$, so $p=2,3,5$ gives all solutions. The sum of these solutions is $55(2+3+5)=550$.
|
{
"resource_path": "HarvardMIT/segmented/en-211-2017-nov-gen-solutions.jsonl",
"problem_match": "\n1. ",
"solution_match": "\nProposed by: Michael Tang\n"
}
|
3e37a1b4-baec-5240-a838-b226509ea4be
| 609,717
|
Determine the sum of all distinct real values of $x$ such that
$$
|||\cdots|| x|+x|\cdots|+x|+x|=1
$$
where there are $2017 x$ 's in the equation.
|
Answer: $-\frac{2016}{2017}$
Note that $|x+|x||=2 x$ when $x$ is nonnegative, and is equal to 0 otherwise. Thus, when there are 2017 $x$ 's, the expression equals $2017 x$ when $x \geq 0$ and $-x$ otherwise, so the two solutions to the equation are $x=-1$ and $\frac{1}{2017}$, and their sum is $-\frac{2016}{2017}$.
|
-\frac{2016}{2017}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Determine the sum of all distinct real values of $x$ such that
$$
|||\cdots|| x|+x|\cdots|+x|+x|=1
$$
where there are $2017 x$ 's in the equation.
|
Answer: $-\frac{2016}{2017}$
Note that $|x+|x||=2 x$ when $x$ is nonnegative, and is equal to 0 otherwise. Thus, when there are 2017 $x$ 's, the expression equals $2017 x$ when $x \geq 0$ and $-x$ otherwise, so the two solutions to the equation are $x=-1$ and $\frac{1}{2017}$, and their sum is $-\frac{2016}{2017}$.
|
{
"resource_path": "HarvardMIT/segmented/en-211-2017-nov-gen-solutions.jsonl",
"problem_match": "\n2. ",
"solution_match": "\nProposed by: Yuan Yao\n"
}
|
9e02814b-6703-52df-974a-4a28b9195fb0
| 609,718
|
Find the number of integers $n$ with $1 \leq n \leq 2017$ so that $(n-2)(n-0)(n-1)(n-7)$ is an integer multiple of 1001.
|
Answer: 99
Note that $1001=7 \cdot 11 \cdot 13$, so the stated product must be a multiple of 7 , as well as a multiple of 11, as well as a multiple of 13 . There are 4 possible residues of $n$ modulo 11 for which the product is a multiple of 11 ; similarly, there are 4 possible residues of $n$ modulo 13 for which the product is a multiple of 13 . However, there are only 3 possible residues of $n$ modulo 7 for which the product is a multiple of 7 .
Consider each of these $4 \cdot 4 \cdot 3=48$ possible triples of remainders. By the Chinese Remainder Theorem there is exactly one value of $n$ with $1 \leq n \leq 1001$ achieving those remainders, and exactly one value of $n$ with $16 \leq n \leq 1016$ achieving those remainders. Similarly, there is exactly one value of $n$ with $1017 \leq n \leq 2017$ with those same remainders. Hence there are 96 values of $n$ with $16 \leq n \leq 2017$ such that $(n-2)(n-0)(n-1)(n-7)$ is a multiple of 1001 .
It remains to check $n \in\{1,2,3, \ldots, 15\}$. Since the product must be a multiple of 7 , we can narrow the set to $\{1,2,7,8,9,14\}$. The first 3 values work trivially, since the product is 0 . It can be easily checked that none of the remaining values of $n$ yield a product which is a multiple of 11 . Hence, the final answer is $96+3=99$.
|
99
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Find the number of integers $n$ with $1 \leq n \leq 2017$ so that $(n-2)(n-0)(n-1)(n-7)$ is an integer multiple of 1001.
|
Answer: 99
Note that $1001=7 \cdot 11 \cdot 13$, so the stated product must be a multiple of 7 , as well as a multiple of 11, as well as a multiple of 13 . There are 4 possible residues of $n$ modulo 11 for which the product is a multiple of 11 ; similarly, there are 4 possible residues of $n$ modulo 13 for which the product is a multiple of 13 . However, there are only 3 possible residues of $n$ modulo 7 for which the product is a multiple of 7 .
Consider each of these $4 \cdot 4 \cdot 3=48$ possible triples of remainders. By the Chinese Remainder Theorem there is exactly one value of $n$ with $1 \leq n \leq 1001$ achieving those remainders, and exactly one value of $n$ with $16 \leq n \leq 1016$ achieving those remainders. Similarly, there is exactly one value of $n$ with $1017 \leq n \leq 2017$ with those same remainders. Hence there are 96 values of $n$ with $16 \leq n \leq 2017$ such that $(n-2)(n-0)(n-1)(n-7)$ is a multiple of 1001 .
It remains to check $n \in\{1,2,3, \ldots, 15\}$. Since the product must be a multiple of 7 , we can narrow the set to $\{1,2,7,8,9,14\}$. The first 3 values work trivially, since the product is 0 . It can be easily checked that none of the remaining values of $n$ yield a product which is a multiple of 11 . Hence, the final answer is $96+3=99$.
|
{
"resource_path": "HarvardMIT/segmented/en-211-2017-nov-gen-solutions.jsonl",
"problem_match": "\n3. ",
"solution_match": "\nProposed by: Dhruv Rohatgi\n"
}
|
1082bd51-6ae6-5053-8455-9bb3dcbe0669
| 609,719
|
Triangle $A B C$ has $A B=10, B C=17$, and $C A=21$. Point $P$ lies on the circle with diameter $A B$. What is the greatest possible area of $A P C$ ?
|
## Answer: $\frac{189}{2}$
To maximize $[A P C]$, point $P$ should be the farthest point on the circle from $A C$. Let $M$ be the midpoint of $A B$ and $Q$ be the projection of $M$ onto $A C$. Then $P Q=P M+M Q=\frac{1}{2} A B+\frac{1}{2} h_{B}$, where $h_{B}$ is the length of the altitude from $B$ to $A C$. By Heron's formula, one finds that the area of $A B C$ is $\sqrt{24 \cdot 14 \cdot 7 \cdot 3}=84$, so $h_{B}=\frac{2 \cdot 84}{A C}=8$. Then $P Q=\frac{1}{2}(10+8)=9$, so the area of $A P C$ is $\frac{1}{2} \cdot 21 \cdot 9=\frac{189}{2}$.
|
\frac{189}{2}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Triangle $A B C$ has $A B=10, B C=17$, and $C A=21$. Point $P$ lies on the circle with diameter $A B$. What is the greatest possible area of $A P C$ ?
|
## Answer: $\frac{189}{2}$
To maximize $[A P C]$, point $P$ should be the farthest point on the circle from $A C$. Let $M$ be the midpoint of $A B$ and $Q$ be the projection of $M$ onto $A C$. Then $P Q=P M+M Q=\frac{1}{2} A B+\frac{1}{2} h_{B}$, where $h_{B}$ is the length of the altitude from $B$ to $A C$. By Heron's formula, one finds that the area of $A B C$ is $\sqrt{24 \cdot 14 \cdot 7 \cdot 3}=84$, so $h_{B}=\frac{2 \cdot 84}{A C}=8$. Then $P Q=\frac{1}{2}(10+8)=9$, so the area of $A P C$ is $\frac{1}{2} \cdot 21 \cdot 9=\frac{189}{2}$.
|
{
"resource_path": "HarvardMIT/segmented/en-211-2017-nov-gen-solutions.jsonl",
"problem_match": "\n4. ",
"solution_match": "\nProposed by: Michael Tang\n\n"
}
|
4e1943b6-d876-5220-8ebd-6b89888cf34c
| 609,720
|
Given that $a, b, c$ are integers with $a b c=60$, and that complex number $\omega \neq 1$ satisfies $\omega^{3}=1$, find the minimum possible value of $\left|a+b \omega+c \omega^{2}\right|$.
|
Answer: $\sqrt{\sqrt{3}}$
Since $\omega^{3}=1$, and $\omega \neq 1, \omega$ is a third root of unity. For any complex number $z,|z|^{2}=z \cdot \bar{z}$. Letting $z=a+b \omega+c \omega^{2}$, we find that $\bar{z}=a+c \omega+b \omega^{2}$, and
$$
\begin{aligned}
|z|^{2} & =a^{2}+a b \omega+a c \omega^{2}+a b \omega^{2}+b^{2}+b c \omega+a c \omega+b c \omega^{2}+c^{2} \\
& =\left(a^{2}+b^{2}+c^{2}\right)+(a b+b c+c a)(\omega)+(a b+b c+c a)\left(\omega^{2}\right) \\
& =\left(a^{2}+b^{2}+c^{2}\right)-(a b+b c+c a) \\
& =\frac{1}{2}\left((a-b)^{2}+(b-c)^{2}+(c-a)^{2}\right),
\end{aligned}
$$
where we have used the fact that $\omega^{3}=1$ and that $\omega+\omega^{2}=-1$. This quantity is minimized when $a, b$, and $c$ are as close to each other as possible, making $a=3, b=4, c=5$ the optimal choice, giving $|z|^{2}=3$. (A smaller value of $|z|$ requires two of $a, b, c$ to be equal and the third differing from them by at most 2, which is impossible.) So $|z|_{\text {min }}=\sqrt{3}$.
|
\sqrt{3}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Given that $a, b, c$ are integers with $a b c=60$, and that complex number $\omega \neq 1$ satisfies $\omega^{3}=1$, find the minimum possible value of $\left|a+b \omega+c \omega^{2}\right|$.
|
Answer: $\sqrt{\sqrt{3}}$
Since $\omega^{3}=1$, and $\omega \neq 1, \omega$ is a third root of unity. For any complex number $z,|z|^{2}=z \cdot \bar{z}$. Letting $z=a+b \omega+c \omega^{2}$, we find that $\bar{z}=a+c \omega+b \omega^{2}$, and
$$
\begin{aligned}
|z|^{2} & =a^{2}+a b \omega+a c \omega^{2}+a b \omega^{2}+b^{2}+b c \omega+a c \omega+b c \omega^{2}+c^{2} \\
& =\left(a^{2}+b^{2}+c^{2}\right)+(a b+b c+c a)(\omega)+(a b+b c+c a)\left(\omega^{2}\right) \\
& =\left(a^{2}+b^{2}+c^{2}\right)-(a b+b c+c a) \\
& =\frac{1}{2}\left((a-b)^{2}+(b-c)^{2}+(c-a)^{2}\right),
\end{aligned}
$$
where we have used the fact that $\omega^{3}=1$ and that $\omega+\omega^{2}=-1$. This quantity is minimized when $a, b$, and $c$ are as close to each other as possible, making $a=3, b=4, c=5$ the optimal choice, giving $|z|^{2}=3$. (A smaller value of $|z|$ requires two of $a, b, c$ to be equal and the third differing from them by at most 2, which is impossible.) So $|z|_{\text {min }}=\sqrt{3}$.
|
{
"resource_path": "HarvardMIT/segmented/en-211-2017-nov-gen-solutions.jsonl",
"problem_match": "\n5. ",
"solution_match": "\nProposed by: Ashwin Sah\n"
}
|
515d74b1-7167-58c4-a489-126543841a1d
| 609,721
|
A positive integer $n$ is magical if
$$
\lfloor\sqrt{\lceil\sqrt{n}\rceil}\rfloor=\lceil\sqrt{\lfloor\sqrt{n}\rfloor}\rceil,
$$
where $\lfloor\cdot\rfloor$ and $\Gamma \cdot\rceil$ represent the floor and ceiling function respectively. Find the number of magical integers between 1 and 10,000, inclusive.
|
Answer: 1330
First of all, we have $\lfloor\sqrt{n}\rfloor=\lceil\sqrt{n}\rceil$ when $n$ is a perfect square and $\lfloor\sqrt{n}\rfloor=\lceil\sqrt{n}\rceil-1$ otherwise. Therefore, in the first case, the original equation holds if and only if $\sqrt{n}$ is a perfect square itself, i.e., $n$ is a fourth power. In the second case, we need $m=\lfloor\sqrt{n}\rfloor$ to satisfy the equation $\lfloor\sqrt{m+1}\rfloor=\lceil\sqrt{m}\rceil$, which happens if and only if either $m$ or $m+1$ is a perfect square $k^{2}$. Therefore, $n$ is magical if and only if $\left(k^{2}-1\right)^{2}<n<\left(k^{2}+1\right)^{2}$ for some (positive) integer $k$. There are $\left(k^{2}+1\right)^{2}-\left(k^{2}-1\right)^{2}=4 k^{2}-1$ integers in this range. The range in the problem statement includes $k=1,2, \ldots, 9$ and the interval $\left(99^{2}, 100^{2}\right]$, so the total number of magical numbers is
$$
4\left(1^{2}+2^{2}+\cdots+9^{2}\right)-9+\left(100^{2}-99^{2}\right)=4 \cdot \frac{9 \cdot(9+1) \cdot(18+1)}{6}+190=1330 .
$$
|
1330
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
A positive integer $n$ is magical if
$$
\lfloor\sqrt{\lceil\sqrt{n}\rceil}\rfloor=\lceil\sqrt{\lfloor\sqrt{n}\rfloor}\rceil,
$$
where $\lfloor\cdot\rfloor$ and $\Gamma \cdot\rceil$ represent the floor and ceiling function respectively. Find the number of magical integers between 1 and 10,000, inclusive.
|
Answer: 1330
First of all, we have $\lfloor\sqrt{n}\rfloor=\lceil\sqrt{n}\rceil$ when $n$ is a perfect square and $\lfloor\sqrt{n}\rfloor=\lceil\sqrt{n}\rceil-1$ otherwise. Therefore, in the first case, the original equation holds if and only if $\sqrt{n}$ is a perfect square itself, i.e., $n$ is a fourth power. In the second case, we need $m=\lfloor\sqrt{n}\rfloor$ to satisfy the equation $\lfloor\sqrt{m+1}\rfloor=\lceil\sqrt{m}\rceil$, which happens if and only if either $m$ or $m+1$ is a perfect square $k^{2}$. Therefore, $n$ is magical if and only if $\left(k^{2}-1\right)^{2}<n<\left(k^{2}+1\right)^{2}$ for some (positive) integer $k$. There are $\left(k^{2}+1\right)^{2}-\left(k^{2}-1\right)^{2}=4 k^{2}-1$ integers in this range. The range in the problem statement includes $k=1,2, \ldots, 9$ and the interval $\left(99^{2}, 100^{2}\right]$, so the total number of magical numbers is
$$
4\left(1^{2}+2^{2}+\cdots+9^{2}\right)-9+\left(100^{2}-99^{2}\right)=4 \cdot \frac{9 \cdot(9+1) \cdot(18+1)}{6}+190=1330 .
$$
|
{
"resource_path": "HarvardMIT/segmented/en-211-2017-nov-gen-solutions.jsonl",
"problem_match": "\n6. ",
"solution_match": "\nProposed by: Yuan Yao\n"
}
|
ee70d6af-0b02-51d8-8e44-deea45777b02
| 609,722
|
Reimu has a wooden cube. In each step, she creates a new polyhedron from the previous one by cutting off a pyramid from each vertex of the polyhedron along a plane through the trisection point on each adjacent edge that is closer to the vertex. For example, the polyhedron after the first step has six octagonal faces and eight equilateral triangular faces. How many faces are on the polyhedron after the fifth step?
|
Answer: 974
Notice that the number of vertices and edges triple with each step. We always have 3 edges meeting at one vertex, and slicing off a pyramid doesn't change this (we make new vertices from which one edge from the previous step and two of the pyramid edges emanate). So at each step we replace the sliced-off vertex with three new vertices, and to each edge we create four new "half-edges" (two from the pyramid at each endpoint), which is equivalent to tripling the number of vertices and edges. Then, by Euler's Theorem the number of faces is $E-V+2=12 \cdot 3^{5}-8 \cdot 3^{5}+2=974$.
|
974
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Reimu has a wooden cube. In each step, she creates a new polyhedron from the previous one by cutting off a pyramid from each vertex of the polyhedron along a plane through the trisection point on each adjacent edge that is closer to the vertex. For example, the polyhedron after the first step has six octagonal faces and eight equilateral triangular faces. How many faces are on the polyhedron after the fifth step?
|
Answer: 974
Notice that the number of vertices and edges triple with each step. We always have 3 edges meeting at one vertex, and slicing off a pyramid doesn't change this (we make new vertices from which one edge from the previous step and two of the pyramid edges emanate). So at each step we replace the sliced-off vertex with three new vertices, and to each edge we create four new "half-edges" (two from the pyramid at each endpoint), which is equivalent to tripling the number of vertices and edges. Then, by Euler's Theorem the number of faces is $E-V+2=12 \cdot 3^{5}-8 \cdot 3^{5}+2=974$.
|
{
"resource_path": "HarvardMIT/segmented/en-211-2017-nov-gen-solutions.jsonl",
"problem_match": "\n7. ",
"solution_match": "\nProposed by: Qi Qi\n"
}
|
1a4c0e05-5501-5396-9168-d57c67f29fd5
| 59,796
|
Marisa has a collection of $2^{8}-1=255$ distinct nonempty subsets of $\{1,2,3,4,5,6,7,8\}$. For each step she takes two subsets chosen uniformly at random from the collection, and replaces them with either their union or their intersection, chosen randomly with equal probability. (The collection is allowed to contain repeated sets.) She repeats this process $2^{8}-2=254$ times until there is only one set left in the collection. What is the expected size of this set?
|
Answer: $\frac{1024}{255}$
It suffices to compute the probability of each number appearing in the final subset. For any given integer $n \in[1,8]$, there are $2^{7}=128$ subsets with $n$ and $2^{7}-1=127$ without. When we focus on only this element, each operation is equivalent to taking two random sets and discarding one of them randomly. Therefore there is a $\frac{128}{255}$ probability that $n$ is in the final subset, and the expected value of its size is $8 \cdot \frac{128}{255}=\frac{1024}{255}$.
Alternatively, since $|A|+|B|=|A \cup B|+|A \cap B|$, the expected value of the average size of all remaining subsets at a given step is constant, so the answer is simply the average size of all 255 subsets, which is $\frac{8 \cdot 128}{255}=\frac{1024}{255}$.
|
\frac{1024}{255}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Marisa has a collection of $2^{8}-1=255$ distinct nonempty subsets of $\{1,2,3,4,5,6,7,8\}$. For each step she takes two subsets chosen uniformly at random from the collection, and replaces them with either their union or their intersection, chosen randomly with equal probability. (The collection is allowed to contain repeated sets.) She repeats this process $2^{8}-2=254$ times until there is only one set left in the collection. What is the expected size of this set?
|
Answer: $\frac{1024}{255}$
It suffices to compute the probability of each number appearing in the final subset. For any given integer $n \in[1,8]$, there are $2^{7}=128$ subsets with $n$ and $2^{7}-1=127$ without. When we focus on only this element, each operation is equivalent to taking two random sets and discarding one of them randomly. Therefore there is a $\frac{128}{255}$ probability that $n$ is in the final subset, and the expected value of its size is $8 \cdot \frac{128}{255}=\frac{1024}{255}$.
Alternatively, since $|A|+|B|=|A \cup B|+|A \cap B|$, the expected value of the average size of all remaining subsets at a given step is constant, so the answer is simply the average size of all 255 subsets, which is $\frac{8 \cdot 128}{255}=\frac{1024}{255}$.
|
{
"resource_path": "HarvardMIT/segmented/en-211-2017-nov-gen-solutions.jsonl",
"problem_match": "\n8. ",
"solution_match": "\nProposed by: Yuan Yao\n"
}
|
4450a3ff-2a17-5d3f-988a-eaea75c4cd03
| 609,723
|
Find the minimum possible value of
$$
\sqrt{58-42 x}+\sqrt{149-140 \sqrt{1-x^{2}}}
$$
where $-1 \leq x \leq 1$.
|
Answer: $\sqrt{109}$
Substitute $x=\cos \theta$ and $\sqrt{1-x^{2}}=\sin \theta$, and notice that $58=3^{2}+7^{2}, 42=2 \cdot 3 \cdot 7,149=7^{2}+10^{2}$, and $140=2 \cdot 7 \cdot 10$. Therefore the first term is an application of Law of Cosines on a triangle that has two sides 3 and 7 with an angle measuring $\theta$ between them to find the length of the third side; similarly, the second is for a triangle with two sides 7 and 10 that have an angle measuring $90-\theta$ between them. "Gluing" these two triangles together along their sides of length 7 so that the merged triangles form a right angle, we see that the minimum length of the sum of their third sides occurs when the glued triangles form a right triangle. This right triangle has legs of length 3 and 10 , so its hypotenuse has length $\sqrt{109}$.
|
\sqrt{109}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Find the minimum possible value of
$$
\sqrt{58-42 x}+\sqrt{149-140 \sqrt{1-x^{2}}}
$$
where $-1 \leq x \leq 1$.
|
Answer: $\sqrt{109}$
Substitute $x=\cos \theta$ and $\sqrt{1-x^{2}}=\sin \theta$, and notice that $58=3^{2}+7^{2}, 42=2 \cdot 3 \cdot 7,149=7^{2}+10^{2}$, and $140=2 \cdot 7 \cdot 10$. Therefore the first term is an application of Law of Cosines on a triangle that has two sides 3 and 7 with an angle measuring $\theta$ between them to find the length of the third side; similarly, the second is for a triangle with two sides 7 and 10 that have an angle measuring $90-\theta$ between them. "Gluing" these two triangles together along their sides of length 7 so that the merged triangles form a right angle, we see that the minimum length of the sum of their third sides occurs when the glued triangles form a right triangle. This right triangle has legs of length 3 and 10 , so its hypotenuse has length $\sqrt{109}$.
|
{
"resource_path": "HarvardMIT/segmented/en-211-2017-nov-gen-solutions.jsonl",
"problem_match": "\n9. ",
"solution_match": "\nProposed by: Serina $H u$\n"
}
|
46038955-97bc-5a0a-be86-7762a67fb6f7
| 609,724
|
Five equally skilled tennis players named Allen, Bob, Catheryn, David, and Evan play in a round robin tournament, such that each pair of people play exactly once, and there are no ties. In each of the ten games, the two players both have a $50 \%$ chance of winning, and the results of the games are independent. Compute the probability that there exist four distinct players $P_{1}, P_{2}, P_{3}, P_{4}$ such that $P_{i}$ beats $P_{i+1}$ for $i=1,2,3,4$. (We denote $P_{5}=P_{1}$ ).
|
Answer: $\frac{49}{64}$
We make the following claim: if there is a 5 -cycle (a directed cycle involving 5 players) in the tournament, then there is a 4-cycle.
Proof: Assume that $A$ beats $B, B$ beats $C, C$ beats $D, D$ beats $E$ and $E$ beats $A$. If $A$ beats $C$ then $A, C, D, E$ forms a 4-cycle, and similar if $B$ beats $D, C$ beats $E$, and so on. However, if all five reversed matches occur, then $A, D, B, C$ is a 4 -cycle.
Therefore, if there are no 4 -cycles, then there can be only 3 -cycles or no cycles at all.
Case 1: There is a 3 -cycle. Assume that $A$ beats $B, B$ beats $C$, and $C$ beats $A$. (There are $\binom{5}{3}=10$ ways to choose the cycle and 2 ways to orient the cycle.) Then $D$ either beats all three or is beaten by all three, because otherwise there exists two people $X$ and $Y$ in these three people such that $X$ beats $Y$, and $D$ beats $Y$ but is beaten by $X$, and then $X, D, Y, Z$ will form a 4-cycle ( $Z$ is the remaining
person of the three). The same goes for $E$. If $D$ and $E$ both beat all three or are beaten by all three, then there is no restriction on the match between $D$ and $E$. However, if $D$ beats all three and $E$ loses to all three, then $E$ cannot beat $D$ because otherwise $E, D, A, B$ forms a 4 -cycle. This means that $A, B, C$ is the only 3 -cycle in the tournament, and once the cycle is chosen there are $2 \cdot 2+2 \cdot 1=6$ ways to choose the results of remaining matches, for $10 \cdot 2 \cdot 6=120$ ways in total.
Case 2: There are no cycles. This means that the tournament is a complete ordering (the person with a higher rank always beats the person with a lower rank). There are $5!=120$ ways in this case as well. Therefore, the probability of not having a 4 -cycle is $\frac{120+120}{2^{10}}=\frac{15}{64}$, and thus the answer is $1-\frac{15}{64}=\frac{49}{64}$.
|
\frac{49}{64}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Five equally skilled tennis players named Allen, Bob, Catheryn, David, and Evan play in a round robin tournament, such that each pair of people play exactly once, and there are no ties. In each of the ten games, the two players both have a $50 \%$ chance of winning, and the results of the games are independent. Compute the probability that there exist four distinct players $P_{1}, P_{2}, P_{3}, P_{4}$ such that $P_{i}$ beats $P_{i+1}$ for $i=1,2,3,4$. (We denote $P_{5}=P_{1}$ ).
|
Answer: $\frac{49}{64}$
We make the following claim: if there is a 5 -cycle (a directed cycle involving 5 players) in the tournament, then there is a 4-cycle.
Proof: Assume that $A$ beats $B, B$ beats $C, C$ beats $D, D$ beats $E$ and $E$ beats $A$. If $A$ beats $C$ then $A, C, D, E$ forms a 4-cycle, and similar if $B$ beats $D, C$ beats $E$, and so on. However, if all five reversed matches occur, then $A, D, B, C$ is a 4 -cycle.
Therefore, if there are no 4 -cycles, then there can be only 3 -cycles or no cycles at all.
Case 1: There is a 3 -cycle. Assume that $A$ beats $B, B$ beats $C$, and $C$ beats $A$. (There are $\binom{5}{3}=10$ ways to choose the cycle and 2 ways to orient the cycle.) Then $D$ either beats all three or is beaten by all three, because otherwise there exists two people $X$ and $Y$ in these three people such that $X$ beats $Y$, and $D$ beats $Y$ but is beaten by $X$, and then $X, D, Y, Z$ will form a 4-cycle ( $Z$ is the remaining
person of the three). The same goes for $E$. If $D$ and $E$ both beat all three or are beaten by all three, then there is no restriction on the match between $D$ and $E$. However, if $D$ beats all three and $E$ loses to all three, then $E$ cannot beat $D$ because otherwise $E, D, A, B$ forms a 4 -cycle. This means that $A, B, C$ is the only 3 -cycle in the tournament, and once the cycle is chosen there are $2 \cdot 2+2 \cdot 1=6$ ways to choose the results of remaining matches, for $10 \cdot 2 \cdot 6=120$ ways in total.
Case 2: There are no cycles. This means that the tournament is a complete ordering (the person with a higher rank always beats the person with a lower rank). There are $5!=120$ ways in this case as well. Therefore, the probability of not having a 4 -cycle is $\frac{120+120}{2^{10}}=\frac{15}{64}$, and thus the answer is $1-\frac{15}{64}=\frac{49}{64}$.
|
{
"resource_path": "HarvardMIT/segmented/en-211-2017-nov-gen-solutions.jsonl",
"problem_match": "\n10. ",
"solution_match": "\nProposed by: Steven Hao\n"
}
|
68f142cb-ffbe-5f72-9862-9827347d657f
| 609,725
|
Suppose $x$ is a rational number such that $x \sqrt{2}$ is also rational. Find $x$.
|
Answer: 0
Suppose $x \neq 0$. Then $\frac{x \sqrt{2}}{x}=\sqrt{2}$ is the quotient of two nonzero rationals, and so is rational. However, it is well-known that $\sqrt{2}$ is irrational. Therefore any solution $x$ must satisfy $x=0$. We can see that 0 is rational and $0 \sqrt{2}=0$ is rational, so the answer is indeed $x=0$.
|
0
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Suppose $x$ is a rational number such that $x \sqrt{2}$ is also rational. Find $x$.
|
Answer: 0
Suppose $x \neq 0$. Then $\frac{x \sqrt{2}}{x}=\sqrt{2}$ is the quotient of two nonzero rationals, and so is rational. However, it is well-known that $\sqrt{2}$ is irrational. Therefore any solution $x$ must satisfy $x=0$. We can see that 0 is rational and $0 \sqrt{2}=0$ is rational, so the answer is indeed $x=0$.
|
{
"resource_path": "HarvardMIT/segmented/en-211-2017-nov-guts-solutions.jsonl",
"problem_match": "\n1. [2]",
"solution_match": "\nProposed by: Michael Kural\n"
}
|
da706e7c-05c1-5c71-86f2-afa103a1e019
| 609,726
|
The length of a rectangle is three times its width. Given that its perimeter and area are both numerically equal to $k>0$, find $k$.
|
Answer: $\square$
Let $a$ be the width of the rectangle. Then the length of the rectangle is $3 a$, so the perimeter is $2(a+3 a)=8 a$, and the area is $3 a^{2}$. Since the length is numerically equal to the width, we know that
$$
8 a=3 a^{2}=k
$$
Because $k>0$, the rectangle is non-degenerate. It follows that $8=3 a$, so $a=\frac{8}{3}$. Therefore, $k=\frac{64}{3}$.
|
\frac{64}{3}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
The length of a rectangle is three times its width. Given that its perimeter and area are both numerically equal to $k>0$, find $k$.
|
Answer: $\square$
Let $a$ be the width of the rectangle. Then the length of the rectangle is $3 a$, so the perimeter is $2(a+3 a)=8 a$, and the area is $3 a^{2}$. Since the length is numerically equal to the width, we know that
$$
8 a=3 a^{2}=k
$$
Because $k>0$, the rectangle is non-degenerate. It follows that $8=3 a$, so $a=\frac{8}{3}$. Therefore, $k=\frac{64}{3}$.
|
{
"resource_path": "HarvardMIT/segmented/en-211-2017-nov-guts-solutions.jsonl",
"problem_match": "\n3. [2]",
"solution_match": "\nProposed by: Yuan Yao\n"
}
|
14fce066-aae1-5527-8e6e-95453e8297eb
| 609,728
|
Alec wishes to construct a string of 6 letters using the letters A, C, G, and N, such that:
- The first three letters are pairwise distinct, and so are the last three letters;
- The first, second, fourth, and fifth letters are pairwise distinct.
In how many ways can he construct the string?
|
There are $4!=24$ ways to decide the first, second, fourth, and fifth letters because these letters can be selected sequentially without replacement from the four possible letters. Once these four letters are selected, there are 2 ways to select the third letter because two distinct letters have already been selected for the first and second letters, leaving two possibilities. The same analysis applies to the sixth letter. Thus, there are $24 \cdot 2^{2}=96$ total ways to construct the string.
|
96
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Alec wishes to construct a string of 6 letters using the letters A, C, G, and N, such that:
- The first three letters are pairwise distinct, and so are the last three letters;
- The first, second, fourth, and fifth letters are pairwise distinct.
In how many ways can he construct the string?
|
There are $4!=24$ ways to decide the first, second, fourth, and fifth letters because these letters can be selected sequentially without replacement from the four possible letters. Once these four letters are selected, there are 2 ways to select the third letter because two distinct letters have already been selected for the first and second letters, leaving two possibilities. The same analysis applies to the sixth letter. Thus, there are $24 \cdot 2^{2}=96$ total ways to construct the string.
|
{
"resource_path": "HarvardMIT/segmented/en-211-2017-nov-guts-solutions.jsonl",
"problem_match": "\n4. [3]",
"solution_match": "\nProposed by: Yuan Yao\n"
}
|
ecf3f5a2-6aa4-5294-9547-cc360273c823
| 609,729
|
Define a sequence $\left\{a_{n}\right\}$ by $a_{1}=1$ and $a_{n}=\left(a_{n-1}\right)!+1$ for every $n>1$. Find the least $n$ for which $a_{n}>10^{10}$.
|
Answer: 6
We have $a_{2}=2, a_{3}=3, a_{4}=7, a_{5}=7!+1=5041$, and $a_{6}=5041!+1$. But
$$
5041!+1 \gg 5041 \cdot 5040 \cdot 5039>10^{10}
$$
Hence, the answer is 6 .
|
6
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Define a sequence $\left\{a_{n}\right\}$ by $a_{1}=1$ and $a_{n}=\left(a_{n-1}\right)!+1$ for every $n>1$. Find the least $n$ for which $a_{n}>10^{10}$.
|
Answer: 6
We have $a_{2}=2, a_{3}=3, a_{4}=7, a_{5}=7!+1=5041$, and $a_{6}=5041!+1$. But
$$
5041!+1 \gg 5041 \cdot 5040 \cdot 5039>10^{10}
$$
Hence, the answer is 6 .
|
{
"resource_path": "HarvardMIT/segmented/en-211-2017-nov-guts-solutions.jsonl",
"problem_match": "\n5. [3]",
"solution_match": "\nProposed by: Michael Tang\n"
}
|
d2750bfe-d462-5f6f-b49b-302902008309
| 609,730
|
Lunasa, Merlin, and Lyrica each have a distinct hat. Every day, two of these three people, selected randomly, switch their hats. What is the probability that, after 2017 days, every person has their own hat back?
|
Answer: 0
Imagine that the three hats are the vertices of an equilateral triangle. Then each day the exchange is equivalent to reflecting the triangle along one of its three symmetry axes, which changes the orientation of the triangle (from clockwise to counterclockwise or vice versa). Thus, an even number of such exchanges must be performed if the orientation is to be preserved. Since the triangle is reflected 2017 times, it is impossible for the final triangle to have the same orientation as the original triangle, so the desired probability is 0 .
|
0
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Lunasa, Merlin, and Lyrica each have a distinct hat. Every day, two of these three people, selected randomly, switch their hats. What is the probability that, after 2017 days, every person has their own hat back?
|
Answer: 0
Imagine that the three hats are the vertices of an equilateral triangle. Then each day the exchange is equivalent to reflecting the triangle along one of its three symmetry axes, which changes the orientation of the triangle (from clockwise to counterclockwise or vice versa). Thus, an even number of such exchanges must be performed if the orientation is to be preserved. Since the triangle is reflected 2017 times, it is impossible for the final triangle to have the same orientation as the original triangle, so the desired probability is 0 .
|
{
"resource_path": "HarvardMIT/segmented/en-211-2017-nov-guts-solutions.jsonl",
"problem_match": "\n6. [3]",
"solution_match": "\nProposed by: Yuan Yao\n"
}
|
4b4b0278-3a45-5011-bc9a-42ce39bcb980
| 609,731
|
Compute
$$
100^{2}+99^{2}-98^{2}-97^{2}+96^{2}+95^{2}-94^{2}-93^{2}+\ldots+4^{2}+3^{2}-2^{2}-1^{2}
$$
|
Answer: 10100
Note that $(n+3)^{2}-(n+2)^{2}-(n+1)^{2}+n^{2}=4$ for every $n$. Therefore, adding $0^{2}$ to the end of the given sum and applying this identity for every four consecutive terms after $100^{2}$, we see that the given sum is equivalent to $100^{2}+25 \cdot 4=10100$.
Alternatively, we can apply the difference-of-squares factorization to rewrite $100^{2}-98^{2}=(100-$ $98)(100+98)=2(100+98), 99^{2}-97^{2}=(99-97)(99+97)=2(99+97)$, etc. Thus, the given sum is equivalent to $2(100+99+\cdots+2+1)=2 \cdot \frac{100 \cdot 101}{2}=10100$.
|
10100
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Compute
$$
100^{2}+99^{2}-98^{2}-97^{2}+96^{2}+95^{2}-94^{2}-93^{2}+\ldots+4^{2}+3^{2}-2^{2}-1^{2}
$$
|
Answer: 10100
Note that $(n+3)^{2}-(n+2)^{2}-(n+1)^{2}+n^{2}=4$ for every $n$. Therefore, adding $0^{2}$ to the end of the given sum and applying this identity for every four consecutive terms after $100^{2}$, we see that the given sum is equivalent to $100^{2}+25 \cdot 4=10100$.
Alternatively, we can apply the difference-of-squares factorization to rewrite $100^{2}-98^{2}=(100-$ $98)(100+98)=2(100+98), 99^{2}-97^{2}=(99-97)(99+97)=2(99+97)$, etc. Thus, the given sum is equivalent to $2(100+99+\cdots+2+1)=2 \cdot \frac{100 \cdot 101}{2}=10100$.
|
{
"resource_path": "HarvardMIT/segmented/en-211-2017-nov-guts-solutions.jsonl",
"problem_match": "\n7. [3]",
"solution_match": "\nProposed by: Michael Tang\n"
}
|
9608d18a-6d61-5c55-9c4c-7efd5342b545
| 609,732
|
A malfunctioning digital clock shows the time $9: 57 \mathrm{AM}$; however, the correct time is $10: 10 \mathrm{AM}$. There are two buttons on the clock, one of which increases the time displayed by 9 minutes, and another which decreases the time by 20 minutes. What is the minimum number of button presses necessary to correctly set the clock to the correct time?
|
Answer: 24
We need to increase the time by 13 minutes. If we click the 9 minute button $a$ times and the 20 minute button $b$ times, then we must have $9 a-20 b=13$. Note that if this equation is satisfied, then $b$ increases as $a$ increases, so it suffices to minimize $a$. This means that $a$ must end in a 7. However, since $63-20 b=13$ has no integer solution, the next smallest possible value of $a$ is 17 , which gives the solution $(a, b)=(17,7)$, or 24 button presses.
|
24
|
Yes
|
Yes
|
math-word-problem
|
Logic and Puzzles
|
A malfunctioning digital clock shows the time $9: 57 \mathrm{AM}$; however, the correct time is $10: 10 \mathrm{AM}$. There are two buttons on the clock, one of which increases the time displayed by 9 minutes, and another which decreases the time by 20 minutes. What is the minimum number of button presses necessary to correctly set the clock to the correct time?
|
Answer: 24
We need to increase the time by 13 minutes. If we click the 9 minute button $a$ times and the 20 minute button $b$ times, then we must have $9 a-20 b=13$. Note that if this equation is satisfied, then $b$ increases as $a$ increases, so it suffices to minimize $a$. This means that $a$ must end in a 7. However, since $63-20 b=13$ has no integer solution, the next smallest possible value of $a$ is 17 , which gives the solution $(a, b)=(17,7)$, or 24 button presses.
|
{
"resource_path": "HarvardMIT/segmented/en-211-2017-nov-guts-solutions.jsonl",
"problem_match": "\n9. [3]",
"solution_match": "\nProposed by: Kevin Sun\n"
}
|
606c45e0-dc3a-5bea-830c-9724b6141ed5
| 609,734
|
Compute $\frac{x}{w}$ if $w \neq 0$ and $\frac{x+6 y-3 z}{-3 x+4 w}=\frac{-2 y+z}{x-w}=\frac{2}{3}$.
|
Answer:

We have $x+6 y-3 z=\frac{2}{3}(-3 x+4 w)$ and $-2 y+z=\frac{2}{3}(x-w)$, so
$$
\frac{x}{w}=\frac{(x+6 y-3 z)+3(-2 y+z)}{(-3 x+4 w)+3(x-w)}=\frac{\frac{2}{3}(-3 x+4 w)+3 \cdot \frac{2}{3}(x-w)}{(-3 x+4 w)+3(x-w)}=\frac{\frac{2}{3}[(-3 x+4 w)+3(x-w)]}{(-3 x+4 w)+3(x-w)}=\frac{2}{3}
$$
|
\frac{2}{3}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Compute $\frac{x}{w}$ if $w \neq 0$ and $\frac{x+6 y-3 z}{-3 x+4 w}=\frac{-2 y+z}{x-w}=\frac{2}{3}$.
|
Answer:

We have $x+6 y-3 z=\frac{2}{3}(-3 x+4 w)$ and $-2 y+z=\frac{2}{3}(x-w)$, so
$$
\frac{x}{w}=\frac{(x+6 y-3 z)+3(-2 y+z)}{(-3 x+4 w)+3(x-w)}=\frac{\frac{2}{3}(-3 x+4 w)+3 \cdot \frac{2}{3}(x-w)}{(-3 x+4 w)+3(x-w)}=\frac{\frac{2}{3}[(-3 x+4 w)+3(x-w)]}{(-3 x+4 w)+3(x-w)}=\frac{2}{3}
$$
|
{
"resource_path": "HarvardMIT/segmented/en-211-2017-nov-guts-solutions.jsonl",
"problem_match": "\n10. [4]",
"solution_match": "\nProposed by: Angela Deng\n"
}
|
7000aa14-2235-56ed-a082-0a24a6a72c8a
| 609,735
|
Find the sum of all real numbers $x$ for which
$$
\lfloor\lfloor\cdots\lfloor\lfloor\lfloor x\rfloor+x\rfloor+x\rfloor \cdots\rfloor+x\rfloor=2017 \text { and }\{\{\cdots\{\{\{x\}+x\}+x\} \cdots\}+x\}=\frac{1}{2017}
$$
where there are $2017 x$ 's in both equations. ( $\lfloor x\rfloor$ is the integer part of $x$, and $\{x\}$ is the fractional part of $x$.) Express your sum as a mixed number.
|
Answer: $3025 \frac{1}{2017}$ or $\frac{6101426}{2017}$
The two equations are equivalent to $2017\lfloor x\rfloor=2017$ and $\{2017 x\}=\frac{1}{2017}$, respectively. The first equation reduces to $\lfloor x\rfloor=1$, so we must have $x=1+r$ for some real $r$ satisfying $0 \leq r<1$. From the second equation, we deduce that $\{2017 x\}=\{2017+2017 r\}=\{2017 r\}=\frac{1}{2017}$, so $2017 r=n+\frac{1}{2017}$, where $n$ is an integer. Dividing both sides of this equation by 2017 yields $r=\frac{n}{2017}+\frac{1}{2017^{2}}$, where $n=0,1,2, \ldots, 2016$ so that we have $0 \leq r<1$. Thus, we have $x=1+r \underset{1}{=}=1+\frac{n}{2017}+\frac{1}{1017^{2}}$ for $n=0,1,2, \ldots, 2016$. The sum of these solutions is $2017 \cdot 1+\frac{2016 \cdot 2017}{2} \cdot \frac{1}{2017}+2017 \cdot \frac{1}{2017^{2}}=$ $2017+\frac{2016}{2}+\frac{1}{2017}=3025 \frac{1}{2017}$.
|
3025 \frac{1}{2017}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Find the sum of all real numbers $x$ for which
$$
\lfloor\lfloor\cdots\lfloor\lfloor\lfloor x\rfloor+x\rfloor+x\rfloor \cdots\rfloor+x\rfloor=2017 \text { and }\{\{\cdots\{\{\{x\}+x\}+x\} \cdots\}+x\}=\frac{1}{2017}
$$
where there are $2017 x$ 's in both equations. ( $\lfloor x\rfloor$ is the integer part of $x$, and $\{x\}$ is the fractional part of $x$.) Express your sum as a mixed number.
|
Answer: $3025 \frac{1}{2017}$ or $\frac{6101426}{2017}$
The two equations are equivalent to $2017\lfloor x\rfloor=2017$ and $\{2017 x\}=\frac{1}{2017}$, respectively. The first equation reduces to $\lfloor x\rfloor=1$, so we must have $x=1+r$ for some real $r$ satisfying $0 \leq r<1$. From the second equation, we deduce that $\{2017 x\}=\{2017+2017 r\}=\{2017 r\}=\frac{1}{2017}$, so $2017 r=n+\frac{1}{2017}$, where $n$ is an integer. Dividing both sides of this equation by 2017 yields $r=\frac{n}{2017}+\frac{1}{2017^{2}}$, where $n=0,1,2, \ldots, 2016$ so that we have $0 \leq r<1$. Thus, we have $x=1+r \underset{1}{=}=1+\frac{n}{2017}+\frac{1}{1017^{2}}$ for $n=0,1,2, \ldots, 2016$. The sum of these solutions is $2017 \cdot 1+\frac{2016 \cdot 2017}{2} \cdot \frac{1}{2017}+2017 \cdot \frac{1}{2017^{2}}=$ $2017+\frac{2016}{2}+\frac{1}{2017}=3025 \frac{1}{2017}$.
|
{
"resource_path": "HarvardMIT/segmented/en-211-2017-nov-guts-solutions.jsonl",
"problem_match": "\n11. [4]",
"solution_match": "\nProposed by: Yuan Yao\n"
}
|
60d306a7-df86-59b5-b744-119348880b05
| 609,736
|
Trapezoid $A B C D$, with bases $A B$ and $C D$, has side lengths $A B=28, B C=13, C D=14$, and $D A=15$. Let diagonals $A C$ and $B D$ intersect at $P$, and let $E$ and $F$ be the midpoints of $A P$ and $B P$, respectively. Find the area of quadrilateral $C D E F$.
|
Answer: 112
Note that $E F$ is a midline of triangle $A P B$, so $E F$ is parallel to $A B$ and $E F=\frac{1}{2} A B=14=C D$. We also have that $E F$ is parallel to $C D$, and so $C D E F$ is a parallelogram. From this, we have $E P=P C$ as well, so $\frac{C E}{C A}=\frac{2}{3}$. It follows that the height from $C$ to $E F$ is $\frac{2}{3}$ of the height from $C$ to $A B$. We can calculate that the height from $C$ to $A B$ is 12 , so the height from $C$ to $E F$ is 8 . Therefore $C D E F$ is a parallelogram with base 14 and height 8 , and its area is $14 \cdot 8=112$.
|
112
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Trapezoid $A B C D$, with bases $A B$ and $C D$, has side lengths $A B=28, B C=13, C D=14$, and $D A=15$. Let diagonals $A C$ and $B D$ intersect at $P$, and let $E$ and $F$ be the midpoints of $A P$ and $B P$, respectively. Find the area of quadrilateral $C D E F$.
|
Answer: 112
Note that $E F$ is a midline of triangle $A P B$, so $E F$ is parallel to $A B$ and $E F=\frac{1}{2} A B=14=C D$. We also have that $E F$ is parallel to $C D$, and so $C D E F$ is a parallelogram. From this, we have $E P=P C$ as well, so $\frac{C E}{C A}=\frac{2}{3}$. It follows that the height from $C$ to $E F$ is $\frac{2}{3}$ of the height from $C$ to $A B$. We can calculate that the height from $C$ to $A B$ is 12 , so the height from $C$ to $E F$ is 8 . Therefore $C D E F$ is a parallelogram with base 14 and height 8 , and its area is $14 \cdot 8=112$.
|
{
"resource_path": "HarvardMIT/segmented/en-211-2017-nov-guts-solutions.jsonl",
"problem_match": "\n12. [4]",
"solution_match": "\nProposed by: Christopher Shao\n"
}
|
93fbf19c-a550-5e8b-acf3-774a476b9c11
| 609,737
|
Fisica and Ritmo discovered a piece of Notalium shaped like a rectangular box, and wanted to find its volume. To do so, Fisica measured its three dimensions using a ruler with infinite precision, multiplied the results and rounded the product to the nearest cubic centimeter, getting a result of $V$ cubic centimeters. Ritmo, on the other hand, measured each dimension to the nearest centimeter and multiplied the rounded measurements, getting a result of 2017 cubic centimeters. Find the positive difference between the least and greatest possible positive values for $V$.
|
Answer: 4035
The only possible way for Ritmo to get 2017 cubic centimeters is to have his measurements rounded to $1,1,2017$ centimeters respectively. Therefore the largest value of $V$ is achieved when the dimensions are $(1.5-\epsilon)(1.5-\epsilon)(2017.5-\epsilon)=4539.375-\epsilon^{\prime}$ for some very small positive real $\epsilon, \epsilon^{\prime}$, and the smallest value of $V$ is achieved when the dimensions are $(0.5+\epsilon)(0.5+\epsilon)(2016.5+\epsilon)=504.125+\epsilon^{\prime}$ for some very small positive real $\epsilon, \epsilon^{\prime}$. Therefore the positive difference is $4539-504=4035$.
|
4035
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Fisica and Ritmo discovered a piece of Notalium shaped like a rectangular box, and wanted to find its volume. To do so, Fisica measured its three dimensions using a ruler with infinite precision, multiplied the results and rounded the product to the nearest cubic centimeter, getting a result of $V$ cubic centimeters. Ritmo, on the other hand, measured each dimension to the nearest centimeter and multiplied the rounded measurements, getting a result of 2017 cubic centimeters. Find the positive difference between the least and greatest possible positive values for $V$.
|
Answer: 4035
The only possible way for Ritmo to get 2017 cubic centimeters is to have his measurements rounded to $1,1,2017$ centimeters respectively. Therefore the largest value of $V$ is achieved when the dimensions are $(1.5-\epsilon)(1.5-\epsilon)(2017.5-\epsilon)=4539.375-\epsilon^{\prime}$ for some very small positive real $\epsilon, \epsilon^{\prime}$, and the smallest value of $V$ is achieved when the dimensions are $(0.5+\epsilon)(0.5+\epsilon)(2016.5+\epsilon)=504.125+\epsilon^{\prime}$ for some very small positive real $\epsilon, \epsilon^{\prime}$. Therefore the positive difference is $4539-504=4035$.
|
{
"resource_path": "HarvardMIT/segmented/en-211-2017-nov-guts-solutions.jsonl",
"problem_match": "\n13. [5]",
"solution_match": "\nProposed by: Yuan Yao\n"
}
|
fc94701e-fe93-567b-b877-0cc2411f5f81
| 609,738
|
Points $A, B, C$, and $D$ lie on a line in that order such that $\frac{A B}{B C}=\frac{D A}{C D}$. If $A C=3$ and $B D=4$, find $A D$.
|
Answer: 6
Let $B C=x$, then the equation becomes $\frac{3-x}{x}=\frac{7-x}{4-x}$. This simplifies to a quadratic equation with solutions $x=1$ and $x=6$. Since $x<3$, we have $x=1$ and $A D=7-x=6$.
|
6
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Points $A, B, C$, and $D$ lie on a line in that order such that $\frac{A B}{B C}=\frac{D A}{C D}$. If $A C=3$ and $B D=4$, find $A D$.
|
Answer: 6
Let $B C=x$, then the equation becomes $\frac{3-x}{x}=\frac{7-x}{4-x}$. This simplifies to a quadratic equation with solutions $x=1$ and $x=6$. Since $x<3$, we have $x=1$ and $A D=7-x=6$.
|
{
"resource_path": "HarvardMIT/segmented/en-211-2017-nov-guts-solutions.jsonl",
"problem_match": "\n14. [5]",
"solution_match": "\nProposed by: Yuan Yao\n"
}
|
373afca0-a2b1-5efe-bbf8-78877965bf02
| 609,739
|
On a $3 \times 3$ chessboard, each square contains a knight with $\frac{1}{2}$ probability. What is the probability that there are two knights that can attack each other? (In chess, a knight can attack any piece which is two squares away from it in a particular direction and one square away in a perpendicular direction.)
|
Answer: $\square$
Notice that a knight on the center square cannot attack any other square on the chessboard, so whether it contains a knight or not is irrelevant.
For ease of reference, we label the other eight squares as follows:
| 0 | 5 | 2 |
| :---: | :---: | :---: |
| 3 | X | 7 |
| 6 | 1 | 4 |
Notice that a knight in square $i$ attacks both square $i+1$ and $i-1$ (where square numbers are reduced modulo 8). We now consider the number of ways such that no two knights attack each other.
- 0 knights: 1 way.
- 1 knights: 8 ways.
- 2 knights: $\binom{8}{2}-8=20$ ways.
- 3 knights: $8+8=16$ ways, where the two 8 s represent the number of ways such that the "distances" between the knights (index-wise) are $2,2,4$ and $2,3,3$ respectively.
- 4 knights: 2 ways.
Therefore, out of $2^{8}=256$ ways, $1+8+20+16+2=47$ of them doesn't have a pair of attacking knights. Thus the answer is $\frac{256-47}{256}=\frac{209}{256}$.
|
\frac{209}{256}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
On a $3 \times 3$ chessboard, each square contains a knight with $\frac{1}{2}$ probability. What is the probability that there are two knights that can attack each other? (In chess, a knight can attack any piece which is two squares away from it in a particular direction and one square away in a perpendicular direction.)
|
Answer: $\square$
Notice that a knight on the center square cannot attack any other square on the chessboard, so whether it contains a knight or not is irrelevant.
For ease of reference, we label the other eight squares as follows:
| 0 | 5 | 2 |
| :---: | :---: | :---: |
| 3 | X | 7 |
| 6 | 1 | 4 |
Notice that a knight in square $i$ attacks both square $i+1$ and $i-1$ (where square numbers are reduced modulo 8). We now consider the number of ways such that no two knights attack each other.
- 0 knights: 1 way.
- 1 knights: 8 ways.
- 2 knights: $\binom{8}{2}-8=20$ ways.
- 3 knights: $8+8=16$ ways, where the two 8 s represent the number of ways such that the "distances" between the knights (index-wise) are $2,2,4$ and $2,3,3$ respectively.
- 4 knights: 2 ways.
Therefore, out of $2^{8}=256$ ways, $1+8+20+16+2=47$ of them doesn't have a pair of attacking knights. Thus the answer is $\frac{256-47}{256}=\frac{209}{256}$.
|
{
"resource_path": "HarvardMIT/segmented/en-211-2017-nov-guts-solutions.jsonl",
"problem_match": "\n15. [5]",
"solution_match": "\nProposed by: Yuan Yao\n"
}
|
c9e191b5-bb78-5d40-b7b2-c1080521e8f4
| 609,740
|
A repunit is a positive integer, all of whose digits are 1 s. Let $a_{1}<a_{2}<a_{3}<\ldots$ be a list of all the positive integers that can be expressed as the sum of distinct repunits. Compute $a_{111}$.
|
Answer: 1223456
Let $\left\{r_{n}\right\}_{n \geq 0}$ be the repunits (so $r_{0}=1, r_{1}=11$, and so on). We see that for any $n$, there is
$$
r_{n-1}+r_{n-2}+\cdots+r_{0}<\frac{r_{n}}{10}+\frac{r_{n}}{100}+\cdots<\frac{r_{n}}{9}<r_{n}
$$
so $r_{n}$ is only needed when all possible combinations of the first $n$ repunits are exhausted (after $2^{n}$ terms), which shows that there is a bijection between the sequence $\left\{a_{n}\right\}$ and the binary numbers. In particular, if $k=2^{n_{1}}+2^{n_{2}}+\cdots+2^{n_{s}}$ for distinct $n_{i}$ 's, then $a_{k}=r_{n_{1}}+r_{n_{2}}+\cdots+r_{n_{s}}$. Since $111=1101111_{2}=2^{0}+2^{1}+2^{2}+2^{3}+2^{5}+2^{6}$, we have
$$
a_{111}=r_{0}+r_{1}+r_{2}+r_{3}+r_{5}+r_{6}=1223456
$$
|
1223456
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
A repunit is a positive integer, all of whose digits are 1 s. Let $a_{1}<a_{2}<a_{3}<\ldots$ be a list of all the positive integers that can be expressed as the sum of distinct repunits. Compute $a_{111}$.
|
Answer: 1223456
Let $\left\{r_{n}\right\}_{n \geq 0}$ be the repunits (so $r_{0}=1, r_{1}=11$, and so on). We see that for any $n$, there is
$$
r_{n-1}+r_{n-2}+\cdots+r_{0}<\frac{r_{n}}{10}+\frac{r_{n}}{100}+\cdots<\frac{r_{n}}{9}<r_{n}
$$
so $r_{n}$ is only needed when all possible combinations of the first $n$ repunits are exhausted (after $2^{n}$ terms), which shows that there is a bijection between the sequence $\left\{a_{n}\right\}$ and the binary numbers. In particular, if $k=2^{n_{1}}+2^{n_{2}}+\cdots+2^{n_{s}}$ for distinct $n_{i}$ 's, then $a_{k}=r_{n_{1}}+r_{n_{2}}+\cdots+r_{n_{s}}$. Since $111=1101111_{2}=2^{0}+2^{1}+2^{2}+2^{3}+2^{5}+2^{6}$, we have
$$
a_{111}=r_{0}+r_{1}+r_{2}+r_{3}+r_{5}+r_{6}=1223456
$$
|
{
"resource_path": "HarvardMIT/segmented/en-211-2017-nov-guts-solutions.jsonl",
"problem_match": "\n16. [7]",
"solution_match": "\nProposed by: Michael Tang\n"
}
|
80133aa9-b6fc-5cbd-a0ca-78c5ea15b033
| 609,741
|
A standard deck of 54 playing cards (with four cards of each of thirteen ranks, as well as two Jokers) is shuffled randomly. Cards are drawn one at a time until the first queen is reached. What is the probability that the next card is also a queen?
|
## Answer: $\frac{2}{27}$
Since the four queens are equivalent, we can compute the probability that a specific queen, say the queen of hearts, is right after the first queen. Remove the queen of hearts; then for every ordering of the 53 other cards, there are 54 locations for the queen of hearts, and exactly one of those is after the first queen. Therefore the probability that the queen of hearts immediately follows the first queen is $\frac{1}{54}$, and the probability any queen follows the first queen is $\frac{1}{54} \cdot 4=\frac{2}{27}$.
|
\frac{2}{27}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
A standard deck of 54 playing cards (with four cards of each of thirteen ranks, as well as two Jokers) is shuffled randomly. Cards are drawn one at a time until the first queen is reached. What is the probability that the next card is also a queen?
|
## Answer: $\frac{2}{27}$
Since the four queens are equivalent, we can compute the probability that a specific queen, say the queen of hearts, is right after the first queen. Remove the queen of hearts; then for every ordering of the 53 other cards, there are 54 locations for the queen of hearts, and exactly one of those is after the first queen. Therefore the probability that the queen of hearts immediately follows the first queen is $\frac{1}{54}$, and the probability any queen follows the first queen is $\frac{1}{54} \cdot 4=\frac{2}{27}$.
|
{
"resource_path": "HarvardMIT/segmented/en-211-2017-nov-guts-solutions.jsonl",
"problem_match": "\n17. [7]",
"solution_match": "\nProposed by: Serina Hu\n\n"
}
|
9bc4a451-c341-5097-b5be-52917c8cce55
| 609,742
|
Mr. Taf takes his 12 students on a road trip. Since it takes two hours to walk from the school to the destination, he plans to use his car to expedite the journey. His car can take at most 4 students at a time, and travels 15 times as fast as traveling on foot. If they plan their trip optimally, what is the shortest amount of time it takes for them to all reach the destination, in minutes?
|
Answer: 30.4 OR $\frac{152}{5}$
A way to plan the trip is to have Mr. Taf drive 4 students to the $80 \%$ mark, then drive back to the $10 \%$ mark to pick up another 4 students to the $90 \%$ mark, and finally drive back to the $20 \%$ mark to pick up the last 4 students to the destination. All students will reach the destination at the same time, and Mr. Taf would have driven for $(0.8+0.7+0.8+0.7+0.8) \cdot \frac{120}{15}=30.4$ minutes.
Now we show that 30.4 minutes is necessary. First of all, for a trip to be optimal, Mr. Taf must not carry students when he was driving away from the destination, and all student not on the car must keep walking towards the destination. Suppose that among all the students, the student that walked for the longest walked for $15 m$ minutes, where $0 \leq m \leq 8$, then he spent $\frac{120-15 m}{15}=8-m$ minutes on the car, so it took them exactly $14 m+8$ minutes to get to the destination. Moreover, all students must have spent at least $12(8-m)$ minutes on the car total, and Mr. Taf would need to spend at least $3(8-m)=24-3 m$ minutes driving students towards the destination. Since it takes Mr. Taf 8 minutes to drive the entire trip, he would need to drive $3(8-m)-8=16-3 m$ minutes away from the destination, so Mr. Fat drove for at least $40-6 m$ minutes. From this we derive the inequality $40-6 m \geq 14 m+8$, which comes out to $m \geq 1.6$, so the journey is at least $14(1.6)+8=30.4$ minutes.
|
30.4
|
Yes
|
Yes
|
math-word-problem
|
Logic and Puzzles
|
Mr. Taf takes his 12 students on a road trip. Since it takes two hours to walk from the school to the destination, he plans to use his car to expedite the journey. His car can take at most 4 students at a time, and travels 15 times as fast as traveling on foot. If they plan their trip optimally, what is the shortest amount of time it takes for them to all reach the destination, in minutes?
|
Answer: 30.4 OR $\frac{152}{5}$
A way to plan the trip is to have Mr. Taf drive 4 students to the $80 \%$ mark, then drive back to the $10 \%$ mark to pick up another 4 students to the $90 \%$ mark, and finally drive back to the $20 \%$ mark to pick up the last 4 students to the destination. All students will reach the destination at the same time, and Mr. Taf would have driven for $(0.8+0.7+0.8+0.7+0.8) \cdot \frac{120}{15}=30.4$ minutes.
Now we show that 30.4 minutes is necessary. First of all, for a trip to be optimal, Mr. Taf must not carry students when he was driving away from the destination, and all student not on the car must keep walking towards the destination. Suppose that among all the students, the student that walked for the longest walked for $15 m$ minutes, where $0 \leq m \leq 8$, then he spent $\frac{120-15 m}{15}=8-m$ minutes on the car, so it took them exactly $14 m+8$ minutes to get to the destination. Moreover, all students must have spent at least $12(8-m)$ minutes on the car total, and Mr. Taf would need to spend at least $3(8-m)=24-3 m$ minutes driving students towards the destination. Since it takes Mr. Taf 8 minutes to drive the entire trip, he would need to drive $3(8-m)-8=16-3 m$ minutes away from the destination, so Mr. Fat drove for at least $40-6 m$ minutes. From this we derive the inequality $40-6 m \geq 14 m+8$, which comes out to $m \geq 1.6$, so the journey is at least $14(1.6)+8=30.4$ minutes.
|
{
"resource_path": "HarvardMIT/segmented/en-211-2017-nov-guts-solutions.jsonl",
"problem_match": "\n18. [7]",
"solution_match": "\nProposed by: Yuan Yao\n"
}
|
7245a5c2-9d9b-5666-83f9-0cebca81b85d
| 609,743
|
Rebecca has four resistors, each with resistance 1 ohm. Every minute, she chooses any two resistors with resistance of $a$ and $b$ ohms respectively, and combine them into one by one of the following methods:
- Connect them in series, which produces a resistor with resistance of $a+b$ ohms;
- Connect them in parallel, which produces a resistor with resistance of $\frac{a b}{a+b}$ ohms;
- Short-circuit one of the two resistors, which produces a resistor with resistance of either $a$ or $b$ ohms.
Suppose that after three minutes, Rebecca has a single resistor with resistance $R$ ohms. How many possible values are there for $R$ ?
|
Answer: 15
Let $R_{n}$ be the set of all possible resistances using exactly $n$ 1-ohm circuit segments (without shorting any of them), then we get $R_{n}=\bigcup_{i=1}^{n-1}\left(\left\{a+b \mid a \in R_{i}, b \in R_{n-i}\right\} \cup\left\{\left.\frac{a b}{a+b} \right\rvert\, a \in R_{i}, b \in R_{n-i}\right\}\right)$, starting with $R_{1}=\{1\}$, we get:
$$
\begin{aligned}
R_{2} & =\left\{\frac{1}{2}, 2\right\} \\
R_{3} & =\left\{\frac{1}{3}, \frac{2}{3}, \frac{3}{2}, 3\right\} \\
R_{4} & =\left\{\frac{1}{4}, \frac{2}{5}, \frac{3}{5}, \frac{3}{4}, 1, \frac{4}{3}, \frac{5}{3}, \frac{5}{2}, 4\right\}
\end{aligned}
$$
Their union is the set of all possible effective resistances we can get, which contains $2+4+9=15$ values. (Note that $R_{1} \subset R_{4}$ and the sets $R_{2}, R_{3}, R_{4}$ are disjoint.)
|
15
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Rebecca has four resistors, each with resistance 1 ohm. Every minute, she chooses any two resistors with resistance of $a$ and $b$ ohms respectively, and combine them into one by one of the following methods:
- Connect them in series, which produces a resistor with resistance of $a+b$ ohms;
- Connect them in parallel, which produces a resistor with resistance of $\frac{a b}{a+b}$ ohms;
- Short-circuit one of the two resistors, which produces a resistor with resistance of either $a$ or $b$ ohms.
Suppose that after three minutes, Rebecca has a single resistor with resistance $R$ ohms. How many possible values are there for $R$ ?
|
Answer: 15
Let $R_{n}$ be the set of all possible resistances using exactly $n$ 1-ohm circuit segments (without shorting any of them), then we get $R_{n}=\bigcup_{i=1}^{n-1}\left(\left\{a+b \mid a \in R_{i}, b \in R_{n-i}\right\} \cup\left\{\left.\frac{a b}{a+b} \right\rvert\, a \in R_{i}, b \in R_{n-i}\right\}\right)$, starting with $R_{1}=\{1\}$, we get:
$$
\begin{aligned}
R_{2} & =\left\{\frac{1}{2}, 2\right\} \\
R_{3} & =\left\{\frac{1}{3}, \frac{2}{3}, \frac{3}{2}, 3\right\} \\
R_{4} & =\left\{\frac{1}{4}, \frac{2}{5}, \frac{3}{5}, \frac{3}{4}, 1, \frac{4}{3}, \frac{5}{3}, \frac{5}{2}, 4\right\}
\end{aligned}
$$
Their union is the set of all possible effective resistances we can get, which contains $2+4+9=15$ values. (Note that $R_{1} \subset R_{4}$ and the sets $R_{2}, R_{3}, R_{4}$ are disjoint.)
|
{
"resource_path": "HarvardMIT/segmented/en-211-2017-nov-guts-solutions.jsonl",
"problem_match": "\n20. [9]",
"solution_match": "\nProposed by: Yuan Yao\n"
}
|
bd833a1f-5d22-540e-a992-0904782f2d84
| 609,745
|
A box contains three balls, each of a different color. Every minute, Randall randomly draws a ball from the box, notes its color, and then returns it to the box. Consider the following two conditions:
(1) Some ball has been drawn at least three times (not necessarily consecutively).
(2) Every ball has been drawn at least once.
What is the probability that condition (1) is met before condition (2)?
|
Answer: $\square$
At any time, we describe the current state by the number of times each ball is drawn, sorted in nonincreasing order. For example, if the red ball has been drawn twice and green ball once, then the state would be $(2,1,0)$. Given state $S$, let $P_{S}$ be the probability that the state was achieved at some point of time before one of the two conditions are satisfied. Starting with $P_{(0,0,0)}=1$, we compute:
$$
\begin{gathered}
P_{(1,0,0)}=1 ; \\
P_{(1,1,0)}=\frac{2}{3}, P_{(2,0,0)}=\frac{1}{3} ; \\
P_{(1,1,1)}=\frac{1}{3} P_{(1,1,0)}=\frac{2}{9}, P_{(2,1,0)}=\frac{2}{3} P_{(1,1,0)}+\frac{2}{3} P_{(2,0,0)}=\frac{2}{3}, P_{(3,0,0)}=\frac{1}{3} P_{(2,0,0)}=\frac{1}{9} ; \\
P_{(2,1,1)}=P_{(2,2,0)}=P_{(3,1,0)}=\frac{1}{3} P_{(2,1,0)}=\frac{2}{9} ; \\
P_{(2,2,1)}=\frac{1}{3} P_{(2,2,0)}=\frac{2}{27}, P_{(3,2,0)}=\frac{2}{3} P_{(2,2,0)}=\frac{4}{27} .
\end{gathered}
$$
Therefore, the probability that the first condition is satisfied first is $P_{(3,0,0)}+P_{(3,1,0)}+P_{(3,2,0)}=$ $\frac{1}{9}+\frac{2}{9}+\frac{4}{27}=\frac{13}{27}$.
|
\frac{13}{27}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
A box contains three balls, each of a different color. Every minute, Randall randomly draws a ball from the box, notes its color, and then returns it to the box. Consider the following two conditions:
(1) Some ball has been drawn at least three times (not necessarily consecutively).
(2) Every ball has been drawn at least once.
What is the probability that condition (1) is met before condition (2)?
|
Answer: $\square$
At any time, we describe the current state by the number of times each ball is drawn, sorted in nonincreasing order. For example, if the red ball has been drawn twice and green ball once, then the state would be $(2,1,0)$. Given state $S$, let $P_{S}$ be the probability that the state was achieved at some point of time before one of the two conditions are satisfied. Starting with $P_{(0,0,0)}=1$, we compute:
$$
\begin{gathered}
P_{(1,0,0)}=1 ; \\
P_{(1,1,0)}=\frac{2}{3}, P_{(2,0,0)}=\frac{1}{3} ; \\
P_{(1,1,1)}=\frac{1}{3} P_{(1,1,0)}=\frac{2}{9}, P_{(2,1,0)}=\frac{2}{3} P_{(1,1,0)}+\frac{2}{3} P_{(2,0,0)}=\frac{2}{3}, P_{(3,0,0)}=\frac{1}{3} P_{(2,0,0)}=\frac{1}{9} ; \\
P_{(2,1,1)}=P_{(2,2,0)}=P_{(3,1,0)}=\frac{1}{3} P_{(2,1,0)}=\frac{2}{9} ; \\
P_{(2,2,1)}=\frac{1}{3} P_{(2,2,0)}=\frac{2}{27}, P_{(3,2,0)}=\frac{2}{3} P_{(2,2,0)}=\frac{4}{27} .
\end{gathered}
$$
Therefore, the probability that the first condition is satisfied first is $P_{(3,0,0)}+P_{(3,1,0)}+P_{(3,2,0)}=$ $\frac{1}{9}+\frac{2}{9}+\frac{4}{27}=\frac{13}{27}$.
|
{
"resource_path": "HarvardMIT/segmented/en-211-2017-nov-guts-solutions.jsonl",
"problem_match": "\n21. [9]",
"solution_match": "\nProposed by: Yuan Yao\n"
}
|
80dfef5c-c89c-5dcc-a77a-acc4d8921692
| 609,746
|
A sequence of positive integers $a_{1}, a_{2}, \ldots, a_{2017}$ has the property that for all integers $m$ where $1 \leq m \leq 2017,3\left(\sum_{i=1}^{m} a_{i}\right)^{2}=\sum_{i=1}^{m} a_{i}^{3}$. Compute $a_{1337}$.
|
Answer: 4011
I claim that $a_{i}=3 i$ for all $i$. We can conjecture that the sequence should just be the positive multiples of three because the natural numbers satisfy the property that the square of their sum is the sum of their cubes, and prove this by induction. At $i=1$, we have that $3 a_{i}^{2}=a_{i}^{3}$, so $a_{i}=3$. Now assuming this holds for $i=m$, we see that
$$
\begin{aligned}
3\left(\sum_{i=1}^{m+1} a_{i}\right)^{2} & =3\left(a_{m+1}+\sum_{i=1}^{m} a_{i}\right)^{2} \\
& =3 a_{m+1}^{2}+\sum_{i=1}^{m} a_{i}^{3}+6 a_{m+1} \sum_{i=1}^{m} a_{i} \\
& =3 a_{m+1}^{2}+\sum_{i=1}^{m} a_{i}^{3}+6 a_{m+1} \cdot 3\left(\frac{m(m+1)}{2}\right) \\
& =\sum_{i=1}^{m+1} a_{i}^{3}
\end{aligned}
$$
Therefore,
$$
\begin{aligned}
a_{m+1}^{3} & =3 a_{m+1}^{2}+a_{m+1}\left(9 m^{2}+9 m\right) \\
0 & =a_{m+1}^{2}-3 a_{m+1}-\left(9 m^{2}+9 m\right) \\
0 & =\left(a_{m+1}-(3 m+3)\right)\left(a_{m+1}+3 m\right)
\end{aligned}
$$
and because the sequence is positive, $a_{m+1}=3 m+3$, which completes the induction. Then $a_{1337}=$ $1337 \cdot 3=4011$.
|
4011
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
A sequence of positive integers $a_{1}, a_{2}, \ldots, a_{2017}$ has the property that for all integers $m$ where $1 \leq m \leq 2017,3\left(\sum_{i=1}^{m} a_{i}\right)^{2}=\sum_{i=1}^{m} a_{i}^{3}$. Compute $a_{1337}$.
|
Answer: 4011
I claim that $a_{i}=3 i$ for all $i$. We can conjecture that the sequence should just be the positive multiples of three because the natural numbers satisfy the property that the square of their sum is the sum of their cubes, and prove this by induction. At $i=1$, we have that $3 a_{i}^{2}=a_{i}^{3}$, so $a_{i}=3$. Now assuming this holds for $i=m$, we see that
$$
\begin{aligned}
3\left(\sum_{i=1}^{m+1} a_{i}\right)^{2} & =3\left(a_{m+1}+\sum_{i=1}^{m} a_{i}\right)^{2} \\
& =3 a_{m+1}^{2}+\sum_{i=1}^{m} a_{i}^{3}+6 a_{m+1} \sum_{i=1}^{m} a_{i} \\
& =3 a_{m+1}^{2}+\sum_{i=1}^{m} a_{i}^{3}+6 a_{m+1} \cdot 3\left(\frac{m(m+1)}{2}\right) \\
& =\sum_{i=1}^{m+1} a_{i}^{3}
\end{aligned}
$$
Therefore,
$$
\begin{aligned}
a_{m+1}^{3} & =3 a_{m+1}^{2}+a_{m+1}\left(9 m^{2}+9 m\right) \\
0 & =a_{m+1}^{2}-3 a_{m+1}-\left(9 m^{2}+9 m\right) \\
0 & =\left(a_{m+1}-(3 m+3)\right)\left(a_{m+1}+3 m\right)
\end{aligned}
$$
and because the sequence is positive, $a_{m+1}=3 m+3$, which completes the induction. Then $a_{1337}=$ $1337 \cdot 3=4011$.
|
{
"resource_path": "HarvardMIT/segmented/en-211-2017-nov-guts-solutions.jsonl",
"problem_match": "\n22. [12]",
"solution_match": "\nProposed by: Serina Hu\n"
}
|
89068a3a-39a0-5f46-a579-8a6cd21d4af1
| 609,747
|
A string of digits is defined to be similar to another string of digits if it can be obtained by reversing some contiguous substring of the original string. For example, the strings 101 and 110 are similar, but the strings 3443 and 4334 are not. (Note that a string is always similar to itself.) Consider the string of digits
$$
S=01234567890123456789012345678901234567890123456789
$$
consisting of the digits from 0 to 9 repeated five times. How many distinct strings are similar to $S$ ?
|
Answer: 1126
We first count the number of substrings that one could pick to reverse to yield a new substring. If we insert two dividers into the sequence of 50 digits, each arrangement of 2 dividers among the 52 total objects specifies a substring that is contained between the two dividers, for a total of $\binom{52}{2}$ substrings. Next, we account for overcounting. Every substring of length 0 or 1 will give the identity string when reversed, so we are overcounting here by $51+50-1=100$ substrings. Next, for any longer substring $s$ that starts and ends with the same digit, removing the digit from both ends results in a substring $s^{\prime}$, such that reversing $s$ would give the same string as reversing $s^{\prime}$. Therefore, we are overcounting by $10 \cdot\binom{5}{2}$ substrings. Our total number of strings similar to $S$ is therefore $\binom{52}{2}-100-10 \cdot\binom{5}{2}=1126$.
|
1126
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
A string of digits is defined to be similar to another string of digits if it can be obtained by reversing some contiguous substring of the original string. For example, the strings 101 and 110 are similar, but the strings 3443 and 4334 are not. (Note that a string is always similar to itself.) Consider the string of digits
$$
S=01234567890123456789012345678901234567890123456789
$$
consisting of the digits from 0 to 9 repeated five times. How many distinct strings are similar to $S$ ?
|
Answer: 1126
We first count the number of substrings that one could pick to reverse to yield a new substring. If we insert two dividers into the sequence of 50 digits, each arrangement of 2 dividers among the 52 total objects specifies a substring that is contained between the two dividers, for a total of $\binom{52}{2}$ substrings. Next, we account for overcounting. Every substring of length 0 or 1 will give the identity string when reversed, so we are overcounting here by $51+50-1=100$ substrings. Next, for any longer substring $s$ that starts and ends with the same digit, removing the digit from both ends results in a substring $s^{\prime}$, such that reversing $s$ would give the same string as reversing $s^{\prime}$. Therefore, we are overcounting by $10 \cdot\binom{5}{2}$ substrings. Our total number of strings similar to $S$ is therefore $\binom{52}{2}-100-10 \cdot\binom{5}{2}=1126$.
|
{
"resource_path": "HarvardMIT/segmented/en-211-2017-nov-guts-solutions.jsonl",
"problem_match": "\n23. [12]",
"solution_match": "\nProposed by: Kevin Sun\n"
}
|
8d81162c-6f86-5750-b6f8-5d10d383ba38
| 609,748
|
Triangle $A B C$ has side lengths $A B=15, B C=18, C A=20$. Extend $C A$ and $C B$ to points $D$ and $E$ respectively such that $D A=A B=B E$. Line $A B$ intersects the circumcircle of $C D E$ at $P$ and $Q$. Find the length of $P Q$.
|
Answer: 37
WLOG suppose that $P$ is closer to $A$ than to $B$. Let $D A=A B=B E=c=15, B C=a=18, C A=$ $b=20, P A=x$, and $Q B=y$. By Power of a Point on $B$ and $A$, we get $a c=(x+c) y$ and $b c=(y+c) x$, respectively. Subtracting the two equations gives $c y-c x=a c-b c \Rightarrow y-x=a-b$. Substituting $y=x+a-b$ into the first equation gives $a c=(x+c)(x+a-b)=x^{2}+(a-b+c) x+a c-b c$, which is a quadratic with unique positive solution $x=\frac{(b-a-c)+\sqrt{(a-b+c)^{2}+4 b c}}{2}$. Thus,
$P Q=x+y+c=(y-x)+2 x+c=(a-b+c)+(b-a-c)+\sqrt{(a-b+c)^{2}+4 b c}=\sqrt{13^{2}+4 \cdot 20 \cdot 15}=37$.
|
37
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Triangle $A B C$ has side lengths $A B=15, B C=18, C A=20$. Extend $C A$ and $C B$ to points $D$ and $E$ respectively such that $D A=A B=B E$. Line $A B$ intersects the circumcircle of $C D E$ at $P$ and $Q$. Find the length of $P Q$.
|
Answer: 37
WLOG suppose that $P$ is closer to $A$ than to $B$. Let $D A=A B=B E=c=15, B C=a=18, C A=$ $b=20, P A=x$, and $Q B=y$. By Power of a Point on $B$ and $A$, we get $a c=(x+c) y$ and $b c=(y+c) x$, respectively. Subtracting the two equations gives $c y-c x=a c-b c \Rightarrow y-x=a-b$. Substituting $y=x+a-b$ into the first equation gives $a c=(x+c)(x+a-b)=x^{2}+(a-b+c) x+a c-b c$, which is a quadratic with unique positive solution $x=\frac{(b-a-c)+\sqrt{(a-b+c)^{2}+4 b c}}{2}$. Thus,
$P Q=x+y+c=(y-x)+2 x+c=(a-b+c)+(b-a-c)+\sqrt{(a-b+c)^{2}+4 b c}=\sqrt{13^{2}+4 \cdot 20 \cdot 15}=37$.
|
{
"resource_path": "HarvardMIT/segmented/en-211-2017-nov-guts-solutions.jsonl",
"problem_match": "\n24. [12]",
"solution_match": "\nProposed by: Yuan Yao\n"
}
|
e3b502e2-0d78-5d7d-81ea-28e866859462
| 609,749
|
Fisica and Ritmo discovered a piece of Notalium shaped like a rectangular box, and wanted to find its volume. To do so, Fisica measured its three dimensions using a ruler with infinite precision, multiplied the results and rounded the product to the nearest cubic centimeter, getting a result of 2017 cubic centimeters. Ritmo, on the other hand, measured each dimension to the nearest centimeter and multiplied the rounded measurements, getting a result of $V$ cubic centimeters. Find the positive difference between the least and greatest possible positive values for $V$.
|
Answer: 7174
It is not difficult to see that the maximum possible value of $V$ can be achieved when the dimensions are $(0.5+\epsilon) \times(0.5+\epsilon) \times\left(8070-\epsilon^{\prime}\right)=2017.5-\epsilon^{\prime \prime}$ for some very small reals $\epsilon, \epsilon^{\prime}, \epsilon^{\prime \prime}>0$, which when measured by Ritmo, gives $V=1 \cdot 1 \cdot 8070=8070$. Similarly, the minimum possible positive value of $V$ can be achieved when the dimensions are $(1.5-\epsilon) \times(1.5-\epsilon) \times\left(\frac{8066}{9}+\epsilon^{\prime}\right)=2016.5+\epsilon^{\prime \prime}$ for some very small reals $\epsilon, \epsilon^{\prime}, \epsilon^{\prime \prime}>0$, which when measured by Ritmo, gives $V=1 \cdot 1 \cdot 896=896$. Therefore, the difference between the maximum and minimum is $8070-896=7174$.
|
7174
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Fisica and Ritmo discovered a piece of Notalium shaped like a rectangular box, and wanted to find its volume. To do so, Fisica measured its three dimensions using a ruler with infinite precision, multiplied the results and rounded the product to the nearest cubic centimeter, getting a result of 2017 cubic centimeters. Ritmo, on the other hand, measured each dimension to the nearest centimeter and multiplied the rounded measurements, getting a result of $V$ cubic centimeters. Find the positive difference between the least and greatest possible positive values for $V$.
|
Answer: 7174
It is not difficult to see that the maximum possible value of $V$ can be achieved when the dimensions are $(0.5+\epsilon) \times(0.5+\epsilon) \times\left(8070-\epsilon^{\prime}\right)=2017.5-\epsilon^{\prime \prime}$ for some very small reals $\epsilon, \epsilon^{\prime}, \epsilon^{\prime \prime}>0$, which when measured by Ritmo, gives $V=1 \cdot 1 \cdot 8070=8070$. Similarly, the minimum possible positive value of $V$ can be achieved when the dimensions are $(1.5-\epsilon) \times(1.5-\epsilon) \times\left(\frac{8066}{9}+\epsilon^{\prime}\right)=2016.5+\epsilon^{\prime \prime}$ for some very small reals $\epsilon, \epsilon^{\prime}, \epsilon^{\prime \prime}>0$, which when measured by Ritmo, gives $V=1 \cdot 1 \cdot 896=896$. Therefore, the difference between the maximum and minimum is $8070-896=7174$.
|
{
"resource_path": "HarvardMIT/segmented/en-211-2017-nov-guts-solutions.jsonl",
"problem_match": "\n25. [15]",
"solution_match": "\nProposed by: Yuan Yao\n"
}
|
a96038da-a6c6-5484-8708-6b549232816b
| 609,750
|
Points $A, B, C, D$ lie on a circle in that order such that $\frac{A B}{B C}=\frac{D A}{C D}$. If $A C=3$ and $B D=B C=4$, find $A D$.
|
Answer: $\frac{3}{2}$
By Ptolemy's theorem, we have $A B \cdot C D+B C \cdot D A=A C \cdot B D=3 \cdot 4=12$. Since the condition implies $A B \cdot C D=B C \cdot D A$, we have $D A=\frac{6}{B C}=\frac{3}{2}$.
|
\frac{3}{2}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Points $A, B, C, D$ lie on a circle in that order such that $\frac{A B}{B C}=\frac{D A}{C D}$. If $A C=3$ and $B D=B C=4$, find $A D$.
|
Answer: $\frac{3}{2}$
By Ptolemy's theorem, we have $A B \cdot C D+B C \cdot D A=A C \cdot B D=3 \cdot 4=12$. Since the condition implies $A B \cdot C D=B C \cdot D A$, we have $D A=\frac{6}{B C}=\frac{3}{2}$.
|
{
"resource_path": "HarvardMIT/segmented/en-211-2017-nov-guts-solutions.jsonl",
"problem_match": "\n26. [15]",
"solution_match": "\nProposed by: Yuan Yao\n"
}
|
09648599-a82c-5481-aa84-8695bdb460ce
| 609,751
|
On a $3 \times 3$ chessboard, each square contains a Chinese knight with $\frac{1}{2}$ probability. What is the probability that there are two Chinese knights that can attack each other? (In Chinese chess, a Chinese knight can attack any piece which is two squares away from it in a particular direction and one square away in a perpendicular direction, under the condition that there is no other piece immediately adjacent to it in the first direction.)
|
Answer: $\square$
Suppose the $3 \times 3$ square is | A | B | C |
| :---: | :---: | :---: |
| | D | E |
| S | F | We count the number of ways a board could have two knights |
| | G | H | attack each other using PIE. First notice that in any setup with two knights attack each other, the center square must be empty. Also, for any pair of knights that attack each other, one must be in a corner, and the other at the center of a nonadjacent side. There are $8 \cdot 2^{5}$ ways for one pair of knights to attack each other. Next, we count the number of ways two pairs of knights attack each other: up to symmetry, there are four cases: knights at $\mathrm{A}, \mathrm{B}, \mathrm{G}, \mathrm{H}$, and D and E empty; knights at $\mathrm{A}, \mathrm{H}$, F, and B, D, E empty; knights at A, B, H, I, and D, E, F empty; and knights at A, C, H, and D, E, F empty. Four each of these cases, there are four symmetries, so there are a total of $4 \cdot\left(2^{3}+2^{3}+2^{2}+2^{3}\right)$ ways to have two pairs of knights attack each other. Next, there's only one way for three pairs of knights to attack each other, discounting symmetry: A, B, G, H, I have knights, and D, E, F empty. Then there are $4 \cdot 2 \cdot 2$ ways for three knights to attack. Finally, there is only one way for four knights to attack: knights at A, B, C, G, H, I and empty squares at D, E, F, for a total of 2 ways after counting symmetries.
Applying PIE, we get that the total number of boards with at least one pair of knights attacking each other is
$$
8 \cdot 2^{5}-4 \cdot\left(2^{3}+2^{3}+2^{2}+2^{3}\right)+4 \cdot 2 \cdot 2-2=158
$$
Then the probability the $3 \times 3$ board has a pair of knights attacking each other is $\frac{158}{2^{9}}=\frac{79}{256}$.
|
\frac{79}{256}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
On a $3 \times 3$ chessboard, each square contains a Chinese knight with $\frac{1}{2}$ probability. What is the probability that there are two Chinese knights that can attack each other? (In Chinese chess, a Chinese knight can attack any piece which is two squares away from it in a particular direction and one square away in a perpendicular direction, under the condition that there is no other piece immediately adjacent to it in the first direction.)
|
Answer: $\square$
Suppose the $3 \times 3$ square is | A | B | C |
| :---: | :---: | :---: |
| | D | E |
| S | F | We count the number of ways a board could have two knights |
| | G | H | attack each other using PIE. First notice that in any setup with two knights attack each other, the center square must be empty. Also, for any pair of knights that attack each other, one must be in a corner, and the other at the center of a nonadjacent side. There are $8 \cdot 2^{5}$ ways for one pair of knights to attack each other. Next, we count the number of ways two pairs of knights attack each other: up to symmetry, there are four cases: knights at $\mathrm{A}, \mathrm{B}, \mathrm{G}, \mathrm{H}$, and D and E empty; knights at $\mathrm{A}, \mathrm{H}$, F, and B, D, E empty; knights at A, B, H, I, and D, E, F empty; and knights at A, C, H, and D, E, F empty. Four each of these cases, there are four symmetries, so there are a total of $4 \cdot\left(2^{3}+2^{3}+2^{2}+2^{3}\right)$ ways to have two pairs of knights attack each other. Next, there's only one way for three pairs of knights to attack each other, discounting symmetry: A, B, G, H, I have knights, and D, E, F empty. Then there are $4 \cdot 2 \cdot 2$ ways for three knights to attack. Finally, there is only one way for four knights to attack: knights at A, B, C, G, H, I and empty squares at D, E, F, for a total of 2 ways after counting symmetries.
Applying PIE, we get that the total number of boards with at least one pair of knights attacking each other is
$$
8 \cdot 2^{5}-4 \cdot\left(2^{3}+2^{3}+2^{2}+2^{3}\right)+4 \cdot 2 \cdot 2-2=158
$$
Then the probability the $3 \times 3$ board has a pair of knights attacking each other is $\frac{158}{2^{9}}=\frac{79}{256}$.
|
{
"resource_path": "HarvardMIT/segmented/en-211-2017-nov-guts-solutions.jsonl",
"problem_match": "\n27. [15]",
"solution_match": "\nProposed by: Yuan Yao\n"
}
|
5fe5fc22-0813-5954-81ff-0e8932b7636e
| 609,752
|
Compute the number of functions $f:\{1,2, \ldots, 9\} \rightarrow\{1,2, \ldots, 9\}$ which satisfy $f(f(f(f(f(x)))))=$ $x$ for each $x \in\{1,2, \ldots, 9\}$.
|
Answer: 3025
All cycles lengths in the permutation must divide 5 , which is a prime number. Either $f(x)=x$ for all $x$, or there exists exactly one permutation cycle of length 5 . In the latter case, there are $\binom{9}{5}$ ways to choose which numbers are in the cycle and 4 ! ways to create the cycle. The answer is thus $1+\binom{9}{5} \cdot 4!=3025$.
|
3025
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Compute the number of functions $f:\{1,2, \ldots, 9\} \rightarrow\{1,2, \ldots, 9\}$ which satisfy $f(f(f(f(f(x)))))=$ $x$ for each $x \in\{1,2, \ldots, 9\}$.
|
Answer: 3025
All cycles lengths in the permutation must divide 5 , which is a prime number. Either $f(x)=x$ for all $x$, or there exists exactly one permutation cycle of length 5 . In the latter case, there are $\binom{9}{5}$ ways to choose which numbers are in the cycle and 4 ! ways to create the cycle. The answer is thus $1+\binom{9}{5} \cdot 4!=3025$.
|
{
"resource_path": "HarvardMIT/segmented/en-211-2017-nov-guts-solutions.jsonl",
"problem_match": "\n28. [19]",
"solution_match": "\nProposed by: Evan Chen\n"
}
|
0742840a-7dcd-5c02-9256-3b6fb1fafb60
| 609,753
|
Consider a sequence $x_{n}$ such that $x_{1}=x_{2}=1, x_{3}=\frac{2}{3}$. Suppose that $x_{n}=\frac{x_{n-1}^{2} x_{n-2}}{2 x_{n-2}^{2}-x_{n-1} x_{n-3}}$ for all $n \geq 4$. Find the least $n$ such that $x_{n} \leq \frac{1}{10^{6}}$.
|
Answer: 13
The recursion simplifies to $\frac{x_{n-1}}{x_{n}}+\frac{x_{n-3}}{x_{n-2}}=2 \frac{x_{n-2}}{x_{n-1}}$. So if we set $y_{n}=\frac{x_{n-1}}{x_{n}}$ for $n \geq 2$ then we have $y_{n}-y_{n-1}=y_{n-1}-y_{n-2}$ for $n \geq 3$, which means that $\left\{y_{n}\right\}$ is an arithmetic sequence. From the
starting values we have $y_{2}=1, y_{3}=\frac{3}{2}$, so $y_{n}=\frac{n}{2}$ for all $n$. (This means that $x_{n}=\frac{2^{n-1}}{n!}$.) Since $\frac{x_{1}}{x_{n}}=y_{2} y_{3} \cdots y_{n}$, it suffices to find the minimal $n$ such that the RHS is at least $10^{6}$. Note that
$y_{2} y_{3} \cdots y_{12}=1 \cdot(1.5 \cdot 2 \cdot 2.5 \cdot 3 \cdot 3.5) \cdot(4 \cdot 4.5 \cdot 5 \cdot 5.5 \cdot 6)<2.5^{5} \cdot 5^{5}=12.5^{5}<200^{2} \cdot 12.5=500000<10^{6}$,
while
$$
y_{2} y_{3} \cdots y_{13}=1 \cdot(1.5 \cdot 2 \cdot 2.5 \cdot 3) \cdot(3.5 \cdot 4 \cdot 4.5) \cdot(5 \cdot 5.5 \cdot 6 \cdot 6.5)>20 \cdot 60 \cdot 900=1080000>10^{6}
$$
so the answer is 13 .
|
13
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Consider a sequence $x_{n}$ such that $x_{1}=x_{2}=1, x_{3}=\frac{2}{3}$. Suppose that $x_{n}=\frac{x_{n-1}^{2} x_{n-2}}{2 x_{n-2}^{2}-x_{n-1} x_{n-3}}$ for all $n \geq 4$. Find the least $n$ such that $x_{n} \leq \frac{1}{10^{6}}$.
|
Answer: 13
The recursion simplifies to $\frac{x_{n-1}}{x_{n}}+\frac{x_{n-3}}{x_{n-2}}=2 \frac{x_{n-2}}{x_{n-1}}$. So if we set $y_{n}=\frac{x_{n-1}}{x_{n}}$ for $n \geq 2$ then we have $y_{n}-y_{n-1}=y_{n-1}-y_{n-2}$ for $n \geq 3$, which means that $\left\{y_{n}\right\}$ is an arithmetic sequence. From the
starting values we have $y_{2}=1, y_{3}=\frac{3}{2}$, so $y_{n}=\frac{n}{2}$ for all $n$. (This means that $x_{n}=\frac{2^{n-1}}{n!}$.) Since $\frac{x_{1}}{x_{n}}=y_{2} y_{3} \cdots y_{n}$, it suffices to find the minimal $n$ such that the RHS is at least $10^{6}$. Note that
$y_{2} y_{3} \cdots y_{12}=1 \cdot(1.5 \cdot 2 \cdot 2.5 \cdot 3 \cdot 3.5) \cdot(4 \cdot 4.5 \cdot 5 \cdot 5.5 \cdot 6)<2.5^{5} \cdot 5^{5}=12.5^{5}<200^{2} \cdot 12.5=500000<10^{6}$,
while
$$
y_{2} y_{3} \cdots y_{13}=1 \cdot(1.5 \cdot 2 \cdot 2.5 \cdot 3) \cdot(3.5 \cdot 4 \cdot 4.5) \cdot(5 \cdot 5.5 \cdot 6 \cdot 6.5)>20 \cdot 60 \cdot 900=1080000>10^{6}
$$
so the answer is 13 .
|
{
"resource_path": "HarvardMIT/segmented/en-211-2017-nov-guts-solutions.jsonl",
"problem_match": "\n29. [19]",
"solution_match": "\nProposed by: Mehtaab Sawhney\n"
}
|
db20a659-5a3f-535b-bf37-3d515546686e
| 609,754
|
Given complex number $z$, define sequence $z_{0}, z_{1}, z_{2}, \ldots$ as $z_{0}=z$ and $z_{n+1}=2 z_{n}^{2}+2 z_{n}$ for $n \geq 0$. Given that $z_{10}=2017$, find the minimum possible value of $|z|$.
|
Answer: $\frac{\sqrt[1024]{4035-1}}{2}$
Define $w_{n}=z_{n}+\frac{1}{2}$, so $z_{n}=w_{n}-\frac{1}{2}$, and the original equation becomes
$$
w_{n+1}-\frac{1}{2}=2\left(w_{n}-\frac{1}{2}\right)^{2}+2\left(w_{n}-\frac{1}{2}\right)=2 w_{n}^{2}-\frac{1}{2}
$$
which reduces to $w_{n+1}=2 w_{n}^{2}$. it is not difficult to show that
$$
z_{10}+\frac{1}{2}=2017+\frac{1}{2}=\frac{4035}{2}=w_{10}=2^{1023} w_{0}^{1024}
$$
and thus $w_{0}=\frac{\sqrt[1024]{4035}}{2} \omega_{1024}$, where $\omega_{1024}$ is one of the $1024^{\text {th }}$ roots of unity. Since $\left|w_{0}\right|=\frac{\sqrt[1024]{4035}}{2}>\frac{1}{2}$, to minimize the magnitude of $z=w_{0}-\frac{1}{2}$, we need $\omega_{1024}=-1$, which gives $|z|=\frac{\sqrt[1024]{4035}-1}{2}$.
|
\frac{\sqrt[1024]{4035-1}}{2}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Given complex number $z$, define sequence $z_{0}, z_{1}, z_{2}, \ldots$ as $z_{0}=z$ and $z_{n+1}=2 z_{n}^{2}+2 z_{n}$ for $n \geq 0$. Given that $z_{10}=2017$, find the minimum possible value of $|z|$.
|
Answer: $\frac{\sqrt[1024]{4035-1}}{2}$
Define $w_{n}=z_{n}+\frac{1}{2}$, so $z_{n}=w_{n}-\frac{1}{2}$, and the original equation becomes
$$
w_{n+1}-\frac{1}{2}=2\left(w_{n}-\frac{1}{2}\right)^{2}+2\left(w_{n}-\frac{1}{2}\right)=2 w_{n}^{2}-\frac{1}{2}
$$
which reduces to $w_{n+1}=2 w_{n}^{2}$. it is not difficult to show that
$$
z_{10}+\frac{1}{2}=2017+\frac{1}{2}=\frac{4035}{2}=w_{10}=2^{1023} w_{0}^{1024}
$$
and thus $w_{0}=\frac{\sqrt[1024]{4035}}{2} \omega_{1024}$, where $\omega_{1024}$ is one of the $1024^{\text {th }}$ roots of unity. Since $\left|w_{0}\right|=\frac{\sqrt[1024]{4035}}{2}>\frac{1}{2}$, to minimize the magnitude of $z=w_{0}-\frac{1}{2}$, we need $\omega_{1024}=-1$, which gives $|z|=\frac{\sqrt[1024]{4035}-1}{2}$.
|
{
"resource_path": "HarvardMIT/segmented/en-211-2017-nov-guts-solutions.jsonl",
"problem_match": "\n30. [19]",
"solution_match": "\nProposed by: Yuan Yao\n"
}
|
0470fbfe-ec01-5047-b0c6-f55d98ba8648
| 609,755
|
In unit square $A B C D$, points $E, F, G$ are chosen on side $B C, C D, D A$ respectively such that $A E$ is perpendicular to $E F$ and $E F$ is perpendicular to $F G$. Given that $G A=\frac{404}{1331}$, find all possible values of the length of $B E$.
|
Answer: $\frac{9}{11}$
Let $B E=x$, then since triangles $A B E, E C F, F D G$ are all similar, we have $C E=1-x, C F=$ $x(1-x), F D=1-x(1-x), D G=x-x^{2}(1-x), G A=1-x+x^{2}(1-x)=(1-x)\left(x^{2}+1\right)$, therefore it remains to solve the equation
$$
(1-x)\left(x^{2}+1\right)=\frac{404}{1331}
$$
We first seek rational solutions $x=\frac{p}{q}$ for relatively prime positive integers $p, q$. Therefore we have $\frac{(q-p)\left(p^{2}+q^{2}\right)}{q^{3}}=\frac{404}{1331}$. Since both $q-p$ and $p^{2}+q^{2}$ are relatively prime to $q^{3}$, we have $q^{3}=1331 \Rightarrow q=11$, so $(11-p)\left(p^{2}+121\right)=404=2^{2} \cdot 101$, and it is not difficult to see that $p=9$ is the only integral solution. We can therefore rewrite the original equation as
$$
\left(x-\frac{9}{11}\right)\left(x^{2}-\frac{2}{11} x+\frac{103}{121}\right)=0 .
$$
It is not difficult to check that the quadratic factor has no zeroes, therefore $B E=x=\frac{9}{11}$ is the only solution.
|
\frac{9}{11}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
In unit square $A B C D$, points $E, F, G$ are chosen on side $B C, C D, D A$ respectively such that $A E$ is perpendicular to $E F$ and $E F$ is perpendicular to $F G$. Given that $G A=\frac{404}{1331}$, find all possible values of the length of $B E$.
|
Answer: $\frac{9}{11}$
Let $B E=x$, then since triangles $A B E, E C F, F D G$ are all similar, we have $C E=1-x, C F=$ $x(1-x), F D=1-x(1-x), D G=x-x^{2}(1-x), G A=1-x+x^{2}(1-x)=(1-x)\left(x^{2}+1\right)$, therefore it remains to solve the equation
$$
(1-x)\left(x^{2}+1\right)=\frac{404}{1331}
$$
We first seek rational solutions $x=\frac{p}{q}$ for relatively prime positive integers $p, q$. Therefore we have $\frac{(q-p)\left(p^{2}+q^{2}\right)}{q^{3}}=\frac{404}{1331}$. Since both $q-p$ and $p^{2}+q^{2}$ are relatively prime to $q^{3}$, we have $q^{3}=1331 \Rightarrow q=11$, so $(11-p)\left(p^{2}+121\right)=404=2^{2} \cdot 101$, and it is not difficult to see that $p=9$ is the only integral solution. We can therefore rewrite the original equation as
$$
\left(x-\frac{9}{11}\right)\left(x^{2}-\frac{2}{11} x+\frac{103}{121}\right)=0 .
$$
It is not difficult to check that the quadratic factor has no zeroes, therefore $B E=x=\frac{9}{11}$ is the only solution.
|
{
"resource_path": "HarvardMIT/segmented/en-211-2017-nov-guts-solutions.jsonl",
"problem_match": "\n31. [24]",
"solution_match": "\nProposed by: Yuan Yao\n"
}
|
89d10760-aa21-5799-9f74-8f0f506715da
| 609,756
|
Let $P$ be a polynomial with integer coefficients such that $P(0)+P(90)=2018$. Find the least possible value for $|P(20)+P(70)|$.
|
Answer: 782
First, note that $P(x)=x^{2}-3041$ satisfy the condition and gives $|P(70)+P(20)|=|4900+400-6082|=$ 782. To show that 782 is the minimum, we show $2800 \mid P(90)-P(70)-P(20)+P(0)$ for every $P$, since -782 is the only number in the range $[-782,782]$ that is congruent to 2018 modulo 2800.
Proof: It suffices to show that $2800 \mid 90^{n}-70^{n}-20^{n}+0^{n}$ for every $n \geq 0$ (having $0^{0}=1$ ).
Let $Q(n)=90^{n}-70^{n}-20^{n}+0^{n}$, then we note that $Q(0)=Q(1)=0, Q(2)=2800$, and $Q(3)=\left(9^{3}-\right.$ $\left.7^{3}-2^{3}\right) \cdot 10^{3}=378000=135 \cdot 2800$. For $n \geq 4$, we note that 400 divides $10^{4}$, and $90^{n}+0^{n} \equiv 70^{n}+20^{n}$ $(\bmod 7)$. Therefore $2800 \mid Q(n)$ for all $n$.
|
782
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Let $P$ be a polynomial with integer coefficients such that $P(0)+P(90)=2018$. Find the least possible value for $|P(20)+P(70)|$.
|
Answer: 782
First, note that $P(x)=x^{2}-3041$ satisfy the condition and gives $|P(70)+P(20)|=|4900+400-6082|=$ 782. To show that 782 is the minimum, we show $2800 \mid P(90)-P(70)-P(20)+P(0)$ for every $P$, since -782 is the only number in the range $[-782,782]$ that is congruent to 2018 modulo 2800.
Proof: It suffices to show that $2800 \mid 90^{n}-70^{n}-20^{n}+0^{n}$ for every $n \geq 0$ (having $0^{0}=1$ ).
Let $Q(n)=90^{n}-70^{n}-20^{n}+0^{n}$, then we note that $Q(0)=Q(1)=0, Q(2)=2800$, and $Q(3)=\left(9^{3}-\right.$ $\left.7^{3}-2^{3}\right) \cdot 10^{3}=378000=135 \cdot 2800$. For $n \geq 4$, we note that 400 divides $10^{4}$, and $90^{n}+0^{n} \equiv 70^{n}+20^{n}$ $(\bmod 7)$. Therefore $2800 \mid Q(n)$ for all $n$.
|
{
"resource_path": "HarvardMIT/segmented/en-211-2017-nov-guts-solutions.jsonl",
"problem_match": "\n32. [24]",
"solution_match": "\nProposed by: Michael Tang\n"
}
|
682b4b50-dc65-5db5-8c28-9c6a89491ceb
| 609,757
|
Tetrahedron $A B C D$ with volume 1 is inscribed in circumsphere $\omega$ such that $A B=A C=A D=2$ and $B C \cdot C D \cdot D B=16$. Find the radius of $\omega$.
|
## Answer: $\frac{5}{3}$
Let $X$ be the foot of the perpendicular from $A$ to $\Delta B C D$. Since $A B=A C=A D$, it follows that $X$ is the circumcenter of $\triangle B C D$. Denote $X B=X C=X D=r$. By the Pythagorean Theorem on $\triangle A B X$, we have $A X=\sqrt{4-r^{2}}$. Now, from the extended law of sines on $\triangle B C D$, we have the well-known identity
$$
\frac{B C \cdot C D \cdot D B}{4 r}=[B C D]
$$
where $[B C D]$ denotes the area of $\triangle B C D$. However, we have
$$
V=\frac{1}{3} A X \cdot[B C D]
$$
where $V$ is the volume of $A B C D$, which yields the expression
$$
[B C D]=\frac{3}{\sqrt{4-r^{2}}}
$$
Now, given that $B C \cdot C D \cdot D B=16$, we have
$$
\frac{4}{r}=\frac{3}{\sqrt{4-r^{2}}}
$$
Solving, we get $r=\frac{8}{5}$. Now, let $O$ be the center of $\omega$. Since $O B=O C=O D$, it follows that the foot of the perpendicular from $O$ to $\triangle B C D$ must also be the circumcenter of $\triangle B C D$, which is $X$. Thus, $A, X, O$ are collinear. Let $R$ be the radius of $\omega$. Then we have
$$
\begin{aligned}
R & =O A \\
& =O X+X A \\
& =\sqrt{R^{2}-r^{2}}+\sqrt{4-r^{2}} \\
& =\sqrt{R^{2}-\frac{64}{25}}+\frac{6}{5} .
\end{aligned}
$$
Solving, we get $R=\frac{5}{3}$. (Note: solving for $R$ from $O A=O X-X A$ gives a negative value for $R$.)
|
\frac{5}{3}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Tetrahedron $A B C D$ with volume 1 is inscribed in circumsphere $\omega$ such that $A B=A C=A D=2$ and $B C \cdot C D \cdot D B=16$. Find the radius of $\omega$.
|
## Answer: $\frac{5}{3}$
Let $X$ be the foot of the perpendicular from $A$ to $\Delta B C D$. Since $A B=A C=A D$, it follows that $X$ is the circumcenter of $\triangle B C D$. Denote $X B=X C=X D=r$. By the Pythagorean Theorem on $\triangle A B X$, we have $A X=\sqrt{4-r^{2}}$. Now, from the extended law of sines on $\triangle B C D$, we have the well-known identity
$$
\frac{B C \cdot C D \cdot D B}{4 r}=[B C D]
$$
where $[B C D]$ denotes the area of $\triangle B C D$. However, we have
$$
V=\frac{1}{3} A X \cdot[B C D]
$$
where $V$ is the volume of $A B C D$, which yields the expression
$$
[B C D]=\frac{3}{\sqrt{4-r^{2}}}
$$
Now, given that $B C \cdot C D \cdot D B=16$, we have
$$
\frac{4}{r}=\frac{3}{\sqrt{4-r^{2}}}
$$
Solving, we get $r=\frac{8}{5}$. Now, let $O$ be the center of $\omega$. Since $O B=O C=O D$, it follows that the foot of the perpendicular from $O$ to $\triangle B C D$ must also be the circumcenter of $\triangle B C D$, which is $X$. Thus, $A, X, O$ are collinear. Let $R$ be the radius of $\omega$. Then we have
$$
\begin{aligned}
R & =O A \\
& =O X+X A \\
& =\sqrt{R^{2}-r^{2}}+\sqrt{4-r^{2}} \\
& =\sqrt{R^{2}-\frac{64}{25}}+\frac{6}{5} .
\end{aligned}
$$
Solving, we get $R=\frac{5}{3}$. (Note: solving for $R$ from $O A=O X-X A$ gives a negative value for $R$.)
|
{
"resource_path": "HarvardMIT/segmented/en-211-2017-nov-guts-solutions.jsonl",
"problem_match": "\n33. [24]",
"solution_match": "\nProposed by: Caleb He\n\n"
}
|
89592bec-2c95-50be-b127-f5396d819d82
| 609,758
|
A box contains twelve balls, each of a different color. Every minute, Randall randomly draws a ball from the box, notes its color, and then returns it to the box. Consider the following two conditions:
(1) Some ball has been drawn at least twelve times (not necessarily consecutively).
(2) Every ball has been drawn at least once.
What is the probability that condition (1) is met before condition (2)? If the correct answer is $C$ and your answer is $A$, you get $\max \left(\left\lfloor 30\left(1-\frac{1}{2}\left|\log _{2} C-\log _{2} A\right|\right)\right\rfloor, 0\right)$ points.
|
Answer: $0.02236412255 \ldots$
Below is a python implementation to compute the probability, using the same method as the solution to the easier version (with three balls).
```
from fractions import Fraction
N = 12
probs = [{} for i in range((N-1)*(N-1)+2)]
prob1 = Fraction()
prob2 = Fraction()
init = tuple(0 for i in range(N))
probs[0][init] = Fraction(1,1)
for i in range((N-1)*(N-1)+1):
for t in probs[i]:
for j in range(N):
val = probs[i][t] * Fraction(1,N)
l = list(t)
l[j] += 1
l.sort()
l = tuple(l)
if (l[-1] == N):
prob1 = prob1 + val
elif (l[0] == 1):
prob2 = prob2 + val
else:
probs[i+1][l] = probs[i+1].setdefault(l, Fraction()) + val
print(prob1)
```
Intuitively the probability should be quite small, since the distribution tends towards the second condition instead of the first. Indeed, the exact fraction is $p=\frac{M}{N}$, where
$$
\begin{aligned}
M= & 663659309086473387879121984765654681548533307869748367531 \\
& 919050571107782711246694886954585701687513519369602069583 \\
N= & 2967517762021717138065641019865112420616209349876886946382 \\
& 1672067789922444492392280614561539198623553884143178743808 .
\end{aligned}
$$
Note: This is a simplified variant of the Bingo Paradox, which is a phenomenon where horizontal bingos are significantly more frequent than vertical bingos. For more information, see https://www. maa.org/sites/default/files/pdf/Mathhorizons/pdfs/The_Bingo_Paradox_MH_Sept17.pdf.
|
0.02236412255 \ldots
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
A box contains twelve balls, each of a different color. Every minute, Randall randomly draws a ball from the box, notes its color, and then returns it to the box. Consider the following two conditions:
(1) Some ball has been drawn at least twelve times (not necessarily consecutively).
(2) Every ball has been drawn at least once.
What is the probability that condition (1) is met before condition (2)? If the correct answer is $C$ and your answer is $A$, you get $\max \left(\left\lfloor 30\left(1-\frac{1}{2}\left|\log _{2} C-\log _{2} A\right|\right)\right\rfloor, 0\right)$ points.
|
Answer: $0.02236412255 \ldots$
Below is a python implementation to compute the probability, using the same method as the solution to the easier version (with three balls).
```
from fractions import Fraction
N = 12
probs = [{} for i in range((N-1)*(N-1)+2)]
prob1 = Fraction()
prob2 = Fraction()
init = tuple(0 for i in range(N))
probs[0][init] = Fraction(1,1)
for i in range((N-1)*(N-1)+1):
for t in probs[i]:
for j in range(N):
val = probs[i][t] * Fraction(1,N)
l = list(t)
l[j] += 1
l.sort()
l = tuple(l)
if (l[-1] == N):
prob1 = prob1 + val
elif (l[0] == 1):
prob2 = prob2 + val
else:
probs[i+1][l] = probs[i+1].setdefault(l, Fraction()) + val
print(prob1)
```
Intuitively the probability should be quite small, since the distribution tends towards the second condition instead of the first. Indeed, the exact fraction is $p=\frac{M}{N}$, where
$$
\begin{aligned}
M= & 663659309086473387879121984765654681548533307869748367531 \\
& 919050571107782711246694886954585701687513519369602069583 \\
N= & 2967517762021717138065641019865112420616209349876886946382 \\
& 1672067789922444492392280614561539198623553884143178743808 .
\end{aligned}
$$
Note: This is a simplified variant of the Bingo Paradox, which is a phenomenon where horizontal bingos are significantly more frequent than vertical bingos. For more information, see https://www. maa.org/sites/default/files/pdf/Mathhorizons/pdfs/The_Bingo_Paradox_MH_Sept17.pdf.
|
{
"resource_path": "HarvardMIT/segmented/en-211-2017-nov-guts-solutions.jsonl",
"problem_match": "\n36. [30]",
"solution_match": "\nProposed by: Yuan Yao\n"
}
|
a31ec42b-af53-5e6d-8daf-9f6a5429b007
| 609,761
|
A positive integer $k$ is called powerful if there are distinct positive integers $p, q, r, s, t$ such that $p^{2}, q^{3}, r^{5}, s^{7}, t^{11}$ all divide $k$. Find the smallest powerful integer.
|
Answer: 1024
First of all, 1024 is powerful because it can be divided evenly by $16^{2}=256,8^{3}=512,4^{5}=1024,2^{7}=$ 128 , and $1^{11}=1$.
Now we show that 1024 is the smallest powerful number. Since $s \neq t$, at least one of them is at least 2 . If $t \geq 2$ or $s \geq 3$, then we need the number to be divisible by at least $2^{11}=2048$ or $3^{7}=2187$, which both exceed 1024, so we must have $s=2$ and $t=1$. If $r=3$, then the number must be divisible by $3^{5}=243$ and $2^{7}=128$, which means that the number is at least $243 \cdot 128>1024$, so $r \geq 4$, and the number is at least $4^{5}=1024$. Therefore the smallest powerful number is indeed 1024 .
|
1024
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
A positive integer $k$ is called powerful if there are distinct positive integers $p, q, r, s, t$ such that $p^{2}, q^{3}, r^{5}, s^{7}, t^{11}$ all divide $k$. Find the smallest powerful integer.
|
Answer: 1024
First of all, 1024 is powerful because it can be divided evenly by $16^{2}=256,8^{3}=512,4^{5}=1024,2^{7}=$ 128 , and $1^{11}=1$.
Now we show that 1024 is the smallest powerful number. Since $s \neq t$, at least one of them is at least 2 . If $t \geq 2$ or $s \geq 3$, then we need the number to be divisible by at least $2^{11}=2048$ or $3^{7}=2187$, which both exceed 1024, so we must have $s=2$ and $t=1$. If $r=3$, then the number must be divisible by $3^{5}=243$ and $2^{7}=128$, which means that the number is at least $243 \cdot 128>1024$, so $r \geq 4$, and the number is at least $4^{5}=1024$. Therefore the smallest powerful number is indeed 1024 .
|
{
"resource_path": "HarvardMIT/segmented/en-211-2017-nov-team-solutions.jsonl",
"problem_match": "\n1. [15]",
"solution_match": "\nProposed by: Yuan Yao\n"
}
|
55640786-a6b6-5e96-82ff-529816289754
| 609,762
|
How many sequences of integers $\left(a_{1}, \ldots, a_{7}\right)$ are there for which $-1 \leq a_{i} \leq 1$ for every $i$, and
$$
a_{1} a_{2}+a_{2} a_{3}+a_{3} a_{4}+a_{4} a_{5}+a_{5} a_{6}+a_{6} a_{7}=4 ?
$$
|
Answer: 38
For $i=1,2, \ldots, 6$, let $b_{i}=a_{i} a_{i+1}$. From the problem condition each of $b_{1}, b_{2}, \ldots, b_{6}$ can only be $-1,0$, or 1 . Since the sum of these six numbers is 4 , either there are five 1 s and a -1 or there are four 1 s and two 0s.
In the first case, there are 6 ways to choose $i$ such that $b_{i}=-1$. Once that is fixed, determining the value of $a_{1}$ (one of 1 and -1 ) will determine the value of all the remaining $a_{i}$ 's, so there are $6 \cdot 2=12$ possible ways in this case.
In the second case, since if one of $b_{2}, b_{3}, b_{4}, b_{5}$ is zero, then one of the adjacent term to this zero term must also be zero. Therefore the two zeroes must be next to each other or be $b_{1}$ and $b_{6}$.
If $b_{1}=b_{2}=0$, then $a_{2}$ must be zero. $a_{1}$ 's value doesn't matter, and $a_{3}, a_{4}, \ldots, a_{7}$ must have the same sign. The same goes for $b_{5}=b_{6}=0$, giving $3 \cdot 2 \cdot 2=12$ possibilities in these two cases.
If $b_{i}=b_{i+1}=0$ for $i=2,3,4$, then $a_{i+1}$ must be zero. Moreover, $a_{1}, a_{2}, \ldots, a_{i}$ must have the same sign, and so do $a_{i+2}, \ldots, a_{7}$. this gives $2 \cdot 2 \cdot 3=12$ possibilities in these three cases.
If $b_{1}=b_{6}=0$, then $a_{1}=a_{7}=0$. Also, $a_{2}, a_{3}, \ldots, a_{6}$ must have the same sign so there are 2 possibilities. Combining these cases gives $12+12+12+2=38$ possible sequences in total.
|
38
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
How many sequences of integers $\left(a_{1}, \ldots, a_{7}\right)$ are there for which $-1 \leq a_{i} \leq 1$ for every $i$, and
$$
a_{1} a_{2}+a_{2} a_{3}+a_{3} a_{4}+a_{4} a_{5}+a_{5} a_{6}+a_{6} a_{7}=4 ?
$$
|
Answer: 38
For $i=1,2, \ldots, 6$, let $b_{i}=a_{i} a_{i+1}$. From the problem condition each of $b_{1}, b_{2}, \ldots, b_{6}$ can only be $-1,0$, or 1 . Since the sum of these six numbers is 4 , either there are five 1 s and a -1 or there are four 1 s and two 0s.
In the first case, there are 6 ways to choose $i$ such that $b_{i}=-1$. Once that is fixed, determining the value of $a_{1}$ (one of 1 and -1 ) will determine the value of all the remaining $a_{i}$ 's, so there are $6 \cdot 2=12$ possible ways in this case.
In the second case, since if one of $b_{2}, b_{3}, b_{4}, b_{5}$ is zero, then one of the adjacent term to this zero term must also be zero. Therefore the two zeroes must be next to each other or be $b_{1}$ and $b_{6}$.
If $b_{1}=b_{2}=0$, then $a_{2}$ must be zero. $a_{1}$ 's value doesn't matter, and $a_{3}, a_{4}, \ldots, a_{7}$ must have the same sign. The same goes for $b_{5}=b_{6}=0$, giving $3 \cdot 2 \cdot 2=12$ possibilities in these two cases.
If $b_{i}=b_{i+1}=0$ for $i=2,3,4$, then $a_{i+1}$ must be zero. Moreover, $a_{1}, a_{2}, \ldots, a_{i}$ must have the same sign, and so do $a_{i+2}, \ldots, a_{7}$. this gives $2 \cdot 2 \cdot 3=12$ possibilities in these three cases.
If $b_{1}=b_{6}=0$, then $a_{1}=a_{7}=0$. Also, $a_{2}, a_{3}, \ldots, a_{6}$ must have the same sign so there are 2 possibilities. Combining these cases gives $12+12+12+2=38$ possible sequences in total.
|
{
"resource_path": "HarvardMIT/segmented/en-211-2017-nov-team-solutions.jsonl",
"problem_match": "\n2. [20]",
"solution_match": "\nProposed by: mendel keller\n"
}
|
ba61ffb8-133e-520f-a476-605b4548ff53
| 609,763
|
Michael writes down all the integers between 1 and $N$ inclusive on a piece of paper and discovers that exactly $40 \%$ of them have leftmost digit 1 . Given that $N>2017$, find the smallest possible value of $N$.
|
Answer: $1,481,480$
Let $d$ be the number of digits of $N$. Suppose that $N$ does not itself have leftmost digit 1 . Then the number of integers $1,2, \ldots, N$ which have leftmost digit 1 is
$$
1+10+10^{2}+\ldots+10^{d-1}=\frac{10^{d}-1}{9}
$$
so we must have $\frac{10^{d}-1}{9}=\frac{2 N}{5}$, or $5\left(10^{d}-1\right)=18 N$. But the left-hand side is odd, so this is impossible.
Thus $N$ must have leftmost digit 1 . In this case, the number of integers $1,2, \ldots, N$ which have leftmost digit 1 is
$$
\begin{aligned}
& 1+10+10^{2}+\ldots+10^{d-2}+\left(N-10^{d-1}+1\right) \\
= & \frac{10^{d-1}-1}{9}+N-10^{d-1}+1 \\
= & N-8\left(\frac{10^{d-1}-1}{9}\right) .
\end{aligned}
$$
Therefore we need $N-8\left(\frac{10^{d-1}-1}{9}\right)=\frac{2}{5} N$, or $N=\frac{40}{3}\left(\frac{10^{d-1}-1}{9}\right)$. Then, $\frac{10^{d-1}-1}{9}$ must be divisible by 3. The base-ten representation of $\frac{10^{d-1}-1}{9}$ has $d-1$ ones, so $d-1$ must be divisible by 3 . Both $d=1$ and $d=4$ make $N$ less than 2017, but $d=7$ gives the answer $N=\frac{40}{3}(111111)=1481480$.
|
1481480
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Michael writes down all the integers between 1 and $N$ inclusive on a piece of paper and discovers that exactly $40 \%$ of them have leftmost digit 1 . Given that $N>2017$, find the smallest possible value of $N$.
|
Answer: $1,481,480$
Let $d$ be the number of digits of $N$. Suppose that $N$ does not itself have leftmost digit 1 . Then the number of integers $1,2, \ldots, N$ which have leftmost digit 1 is
$$
1+10+10^{2}+\ldots+10^{d-1}=\frac{10^{d}-1}{9}
$$
so we must have $\frac{10^{d}-1}{9}=\frac{2 N}{5}$, or $5\left(10^{d}-1\right)=18 N$. But the left-hand side is odd, so this is impossible.
Thus $N$ must have leftmost digit 1 . In this case, the number of integers $1,2, \ldots, N$ which have leftmost digit 1 is
$$
\begin{aligned}
& 1+10+10^{2}+\ldots+10^{d-2}+\left(N-10^{d-1}+1\right) \\
= & \frac{10^{d-1}-1}{9}+N-10^{d-1}+1 \\
= & N-8\left(\frac{10^{d-1}-1}{9}\right) .
\end{aligned}
$$
Therefore we need $N-8\left(\frac{10^{d-1}-1}{9}\right)=\frac{2}{5} N$, or $N=\frac{40}{3}\left(\frac{10^{d-1}-1}{9}\right)$. Then, $\frac{10^{d-1}-1}{9}$ must be divisible by 3. The base-ten representation of $\frac{10^{d-1}-1}{9}$ has $d-1$ ones, so $d-1$ must be divisible by 3 . Both $d=1$ and $d=4$ make $N$ less than 2017, but $d=7$ gives the answer $N=\frac{40}{3}(111111)=1481480$.
|
{
"resource_path": "HarvardMIT/segmented/en-211-2017-nov-team-solutions.jsonl",
"problem_match": "\n3. [25]",
"solution_match": "\nProposed by: Michael Tang\n"
}
|
89f7f4fa-8db1-5ee2-ac50-f5df8eeca034
| 609,764
|
An equiangular hexagon has side lengths $1,1, a, 1,1, a$ in that order. Given that there exists a circle that intersects the hexagon at 12 distinct points, we have $M<a<N$ for some real numbers $M$ and $N$. Determine the minimum possible value of the ratio $\frac{N}{M}$.
|
Answer: $\frac{3}{\sqrt{3}-1}$ OR $\frac{3 \sqrt{3}+3}{2}$
We claim that the greatest possible value of $M$ is $\sqrt{3}-1$, whereas the least possible value of $N$ is 3 .
To begin, note that the condition requires the circle to intersect each side of the hexagon at two points on its interior. This implies that the center must be inside the hexagon as its projection onto all six sides must be on their interior. Suppose that the hexagon is $A B C D E F$, with $A B=B C=D E=E F=1$, $C D=F A=a$, and the center $O$.
When $a \leq \sqrt{3}-1$, we note that the distance from $O$ to $C D$ (which is $\frac{\sqrt{3}}{2}$ ) is greater than or equal to the distance from $O$ to $B$ or $E$ (which is $\frac{a+1}{2}$ ). However, for the circle to intersect all six sides at two points each, the distance from the center of the circle to $C D$ and to $F A$ must be strictly less than that from the center to $B$ and to $E$, because otherwise any circle that intersects $C D$ and $F A$ at two points each must include $B$ or $E$ on its boundary or interior, which will not satisfy the condition. WLOG assume that the center of the circle is closer to $F A$ than to $C D$, including equality (in other words, the center is on the same side of $B E$ as $F A$, possibly on $B E$ itself), then note that the parabola with foci $B$ and $E$ and common directrix $C D$ intersects on point $O$, which means that there does not exist a point in the hexagon on the same side of $B E$ as $F A$ that lies on the same side of both parabola as $C D$. This means that the center of the circle cannot be chosen.
When $a=\sqrt{3}-1+\epsilon$ for some very small real number $\epsilon>0$, the circle with center $O$ and radius $r=\frac{\sqrt{3}}{2}$ intersects sides $A B, B C, D E, E F$ at two points each and is tangent to $C D$ and $F A$ on their interior. Therefore, there exists a real number $\epsilon^{\prime}>0$ such that the circle with center $O$ and radius $r^{\prime}=r+\epsilon^{\prime}$ satisfy the requirement.
When $a \geq 3$, we note that the projection of $B F$ onto $B C$ has length $\left|\frac{1}{2}-\frac{a}{2}\right| \geq 1$, which means that the projection of $F$ onto side $B C$ is not on its interior, and the same goes for side $E F$ onto $B C$. However, for a circle to intersect both $B C$ and $E F$ at two points, the projection of center of the circle onto the two sides must be on their interior, which cannot happen in this case.
When $a=3-\epsilon$ for some very small real number $\epsilon>0$, a circle with center $O$ and radius $r=\frac{\sqrt{3}}{4}(a+1)$ intersects $A F$ and $C D$ at two points each and is tangent to all four other sides on their interior. Therefore, there exists a real number $\epsilon^{\prime}>0$ such that the circle with center $O$ and radius $r^{\prime}=r+\epsilon^{\prime}$ satisfy the requirement.
With $M \leq \sqrt{3}-1$ and $N \geq 3$, we have $\frac{N}{M} \geq \frac{3}{\sqrt{3}-1}=\frac{3 \sqrt{3}+3}{2}$, which is our answer.
|
\frac{3 \sqrt{3}+3}{2}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
An equiangular hexagon has side lengths $1,1, a, 1,1, a$ in that order. Given that there exists a circle that intersects the hexagon at 12 distinct points, we have $M<a<N$ for some real numbers $M$ and $N$. Determine the minimum possible value of the ratio $\frac{N}{M}$.
|
Answer: $\frac{3}{\sqrt{3}-1}$ OR $\frac{3 \sqrt{3}+3}{2}$
We claim that the greatest possible value of $M$ is $\sqrt{3}-1$, whereas the least possible value of $N$ is 3 .
To begin, note that the condition requires the circle to intersect each side of the hexagon at two points on its interior. This implies that the center must be inside the hexagon as its projection onto all six sides must be on their interior. Suppose that the hexagon is $A B C D E F$, with $A B=B C=D E=E F=1$, $C D=F A=a$, and the center $O$.
When $a \leq \sqrt{3}-1$, we note that the distance from $O$ to $C D$ (which is $\frac{\sqrt{3}}{2}$ ) is greater than or equal to the distance from $O$ to $B$ or $E$ (which is $\frac{a+1}{2}$ ). However, for the circle to intersect all six sides at two points each, the distance from the center of the circle to $C D$ and to $F A$ must be strictly less than that from the center to $B$ and to $E$, because otherwise any circle that intersects $C D$ and $F A$ at two points each must include $B$ or $E$ on its boundary or interior, which will not satisfy the condition. WLOG assume that the center of the circle is closer to $F A$ than to $C D$, including equality (in other words, the center is on the same side of $B E$ as $F A$, possibly on $B E$ itself), then note that the parabola with foci $B$ and $E$ and common directrix $C D$ intersects on point $O$, which means that there does not exist a point in the hexagon on the same side of $B E$ as $F A$ that lies on the same side of both parabola as $C D$. This means that the center of the circle cannot be chosen.
When $a=\sqrt{3}-1+\epsilon$ for some very small real number $\epsilon>0$, the circle with center $O$ and radius $r=\frac{\sqrt{3}}{2}$ intersects sides $A B, B C, D E, E F$ at two points each and is tangent to $C D$ and $F A$ on their interior. Therefore, there exists a real number $\epsilon^{\prime}>0$ such that the circle with center $O$ and radius $r^{\prime}=r+\epsilon^{\prime}$ satisfy the requirement.
When $a \geq 3$, we note that the projection of $B F$ onto $B C$ has length $\left|\frac{1}{2}-\frac{a}{2}\right| \geq 1$, which means that the projection of $F$ onto side $B C$ is not on its interior, and the same goes for side $E F$ onto $B C$. However, for a circle to intersect both $B C$ and $E F$ at two points, the projection of center of the circle onto the two sides must be on their interior, which cannot happen in this case.
When $a=3-\epsilon$ for some very small real number $\epsilon>0$, a circle with center $O$ and radius $r=\frac{\sqrt{3}}{4}(a+1)$ intersects $A F$ and $C D$ at two points each and is tangent to all four other sides on their interior. Therefore, there exists a real number $\epsilon^{\prime}>0$ such that the circle with center $O$ and radius $r^{\prime}=r+\epsilon^{\prime}$ satisfy the requirement.
With $M \leq \sqrt{3}-1$ and $N \geq 3$, we have $\frac{N}{M} \geq \frac{3}{\sqrt{3}-1}=\frac{3 \sqrt{3}+3}{2}$, which is our answer.
|
{
"resource_path": "HarvardMIT/segmented/en-211-2017-nov-team-solutions.jsonl",
"problem_match": "\n4. [30]",
"solution_match": "\nProposed by: Yuan Yao\n"
}
|
b8fd1a77-9906-5f7c-8c8d-f2bfc8089cbc
| 609,765
|
Ashwin the frog is traveling on the $x y$-plane in a series of $2^{2017}-1$ steps, starting at the origin. At the $n^{\text {th }}$ step, if $n$ is odd, then Ashwin jumps one unit to the right. If $n$ is even, then Ashwin jumps $m$ units up, where $m$ is the greatest integer such that $2^{m}$ divides $n$. If Ashwin begins at the origin, what is the area of the polygon bounded by Ashwin's path, the line $x=2^{2016}$, and the $x$-axis?
|
Answer: $2^{2015} \cdot\left(2^{2017}-2018\right)$
Notice that since $v_{2}(x)=v_{2}\left(2^{2017}-x\right)$, the path divides the rectangle bonded by the coordinate axes and the two lines passing through Ashwin's final location parallel to the axes. The answer is therefore half of the product of the coordinates of Ashwin's final coordinates. The $x$-coordinate is the number of odd number steps (which is $2^{2016}$ ). The $y$-coordinate is the number of total powers of 2 in $\left(2^{2017}-1\right)$ !. The final answer is therefore $2^{2015} \cdot\left(2^{2017}-2018\right)$.
|
2^{2015} \cdot\left(2^{2017}-2018\right)
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Ashwin the frog is traveling on the $x y$-plane in a series of $2^{2017}-1$ steps, starting at the origin. At the $n^{\text {th }}$ step, if $n$ is odd, then Ashwin jumps one unit to the right. If $n$ is even, then Ashwin jumps $m$ units up, where $m$ is the greatest integer such that $2^{m}$ divides $n$. If Ashwin begins at the origin, what is the area of the polygon bounded by Ashwin's path, the line $x=2^{2016}$, and the $x$-axis?
|
Answer: $2^{2015} \cdot\left(2^{2017}-2018\right)$
Notice that since $v_{2}(x)=v_{2}\left(2^{2017}-x\right)$, the path divides the rectangle bonded by the coordinate axes and the two lines passing through Ashwin's final location parallel to the axes. The answer is therefore half of the product of the coordinates of Ashwin's final coordinates. The $x$-coordinate is the number of odd number steps (which is $2^{2016}$ ). The $y$-coordinate is the number of total powers of 2 in $\left(2^{2017}-1\right)$ !. The final answer is therefore $2^{2015} \cdot\left(2^{2017}-2018\right)$.
|
{
"resource_path": "HarvardMIT/segmented/en-211-2017-nov-team-solutions.jsonl",
"problem_match": "\n5. [35]",
"solution_match": "\nProposed by: Nikhil Reddy\n"
}
|
02429db4-2517-5c10-963d-ba3152d05597
| 609,766
|
Consider five-dimensional Cartesian space
$$
\mathbb{R}^{5}=\left\{\left(x_{1}, x_{2}, x_{3}, x_{4}, x_{5}\right) \mid x_{i} \in \mathbb{R}\right\}
$$
and consider the hyperplanes with the following equations:
- $x_{i}=x_{j}$ for every $1 \leq i<j \leq 5$;
- $x_{1}+x_{2}+x_{3}+x_{4}+x_{5}=-1 ;$
- $x_{1}+x_{2}+x_{3}+x_{4}+x_{5}=0$;
- $x_{1}+x_{2}+x_{3}+x_{4}+x_{5}=1$.
Into how many regions do these hyperplanes divide $\mathbb{R}^{5}$ ?
|
Answer: 480
(Joint with Junyao Peng)
Note that given a set of plane equations $P_{i}\left(x_{1}, x_{2}, x_{3}, x_{4}, x_{5}\right)=0$, for $i=1,2, \ldots, n$, each region that the planes separate the space into correspond to a $n$-tuple of -1 and 1 , representing the sign of $P_{1}, P_{2}, \ldots P_{n}$ for all points in that region.
Therefore, the first set of planes separate the space into $5!=120$ regions, with each region representing an ordering of the five coordinates by numerical size. Moreover, the next three planes are parallel to each other and perpendicular to all planes in the first set, so these three planes separate each region into 4. Therefore, a total of $4 \cdot 120=480$ regions is created.
|
480
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Consider five-dimensional Cartesian space
$$
\mathbb{R}^{5}=\left\{\left(x_{1}, x_{2}, x_{3}, x_{4}, x_{5}\right) \mid x_{i} \in \mathbb{R}\right\}
$$
and consider the hyperplanes with the following equations:
- $x_{i}=x_{j}$ for every $1 \leq i<j \leq 5$;
- $x_{1}+x_{2}+x_{3}+x_{4}+x_{5}=-1 ;$
- $x_{1}+x_{2}+x_{3}+x_{4}+x_{5}=0$;
- $x_{1}+x_{2}+x_{3}+x_{4}+x_{5}=1$.
Into how many regions do these hyperplanes divide $\mathbb{R}^{5}$ ?
|
Answer: 480
(Joint with Junyao Peng)
Note that given a set of plane equations $P_{i}\left(x_{1}, x_{2}, x_{3}, x_{4}, x_{5}\right)=0$, for $i=1,2, \ldots, n$, each region that the planes separate the space into correspond to a $n$-tuple of -1 and 1 , representing the sign of $P_{1}, P_{2}, \ldots P_{n}$ for all points in that region.
Therefore, the first set of planes separate the space into $5!=120$ regions, with each region representing an ordering of the five coordinates by numerical size. Moreover, the next three planes are parallel to each other and perpendicular to all planes in the first set, so these three planes separate each region into 4. Therefore, a total of $4 \cdot 120=480$ regions is created.
|
{
"resource_path": "HarvardMIT/segmented/en-211-2017-nov-team-solutions.jsonl",
"problem_match": "\n6. [40]",
"solution_match": "\nProposed by: Mehtaab Sawhney\n"
}
|
6b47a539-de84-5a22-b24f-e79b4fdbdd6d
| 609,767
|
Find the number of quadruples $(a, b, c, d)$ of integers with absolute value at most 5 such that
$$
\left(a^{2}+b^{2}+c^{2}+d^{2}\right)^{2}=(a+b+c+d)(a-b+c-d)\left((a-c)^{2}+(b-d)^{2}\right)
$$
|
Answer: 49
Let $x=a+c, y=a-c, w=b+d$, and $z=b-d$. Then
$$
\left(w^{2}+x^{2}+y^{2}+z^{2}\right)^{2}=4\left(x^{2}-w^{2}\right)\left(y^{2}+z^{2}\right)
$$
and since $\left|x^{2}+w^{2}\right| \geq\left|x^{2}-w^{2}\right|$ it follows that $w=0$ or $y=z=0$. Now $y=z=0$ implies $a=b=c=d=0$. Now $w=0$ gives $b=-d$. Then for equality to hold $x^{2}=y^{2}+z^{2}$. This is equivalent to $a c=b^{2}$, which includes the previous case. It suffices to count the number of triples $(a, b, c)$ that satisfy the equation.
When $b=0$, either $a$ or $c$ is zero, which gives $11+11-1=21$ triples.
When $b= \pm 1$, we have $|a|=|c|=1$ and $a, c$ have the same sign, for $2 \cdot 2=4$ triples.
When $b= \pm 2$, we have $(a, c)=(1,4),(2,2),(4,1)$ or their negatives, for $2 \cdot 6=12$ triples.
When $b= \pm 3, \pm 4, \pm 5$, we have $|a|=|b|=|c|$ and $a, c$ have the same sign, for $6 \cdot 2=12$ triples.
So in total there are $21+4+12+12=49$ solutions.
|
49
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Find the number of quadruples $(a, b, c, d)$ of integers with absolute value at most 5 such that
$$
\left(a^{2}+b^{2}+c^{2}+d^{2}\right)^{2}=(a+b+c+d)(a-b+c-d)\left((a-c)^{2}+(b-d)^{2}\right)
$$
|
Answer: 49
Let $x=a+c, y=a-c, w=b+d$, and $z=b-d$. Then
$$
\left(w^{2}+x^{2}+y^{2}+z^{2}\right)^{2}=4\left(x^{2}-w^{2}\right)\left(y^{2}+z^{2}\right)
$$
and since $\left|x^{2}+w^{2}\right| \geq\left|x^{2}-w^{2}\right|$ it follows that $w=0$ or $y=z=0$. Now $y=z=0$ implies $a=b=c=d=0$. Now $w=0$ gives $b=-d$. Then for equality to hold $x^{2}=y^{2}+z^{2}$. This is equivalent to $a c=b^{2}$, which includes the previous case. It suffices to count the number of triples $(a, b, c)$ that satisfy the equation.
When $b=0$, either $a$ or $c$ is zero, which gives $11+11-1=21$ triples.
When $b= \pm 1$, we have $|a|=|c|=1$ and $a, c$ have the same sign, for $2 \cdot 2=4$ triples.
When $b= \pm 2$, we have $(a, c)=(1,4),(2,2),(4,1)$ or their negatives, for $2 \cdot 6=12$ triples.
When $b= \pm 3, \pm 4, \pm 5$, we have $|a|=|b|=|c|$ and $a, c$ have the same sign, for $6 \cdot 2=12$ triples.
So in total there are $21+4+12+12=49$ solutions.
|
{
"resource_path": "HarvardMIT/segmented/en-211-2017-nov-team-solutions.jsonl",
"problem_match": "\n8. [55]",
"solution_match": "\nProposed by: Mehtaab Sawhney\n"
}
|
28958f55-da2e-5e4f-a534-46451bbd04bc
| 609,769
|
Let $A, B, C, D$ be points chosen on a circle, in that order. Line $B D$ is reflected over lines $A B$ and $D A$ to obtain lines $\ell_{1}$ and $\ell_{2}$ respectively. If lines $\ell_{1}, \ell_{2}$, and $A C$ meet at a common point and if $A B=4, B C=3, C D=2$, compute the length $D A$.
|
Answer: $\sqrt{21}$
Let the common point be $E$. Then since lines $B E$ and $B D$ are symmetric about line $B A, B A$ is an exterior bisector of $\angle D B E$, and similarly $D A$ is also an exterior bisector of $\angle B D E$. Therefore $A$ is the $E$-excenter of triangle $B D E$ and thus lie on the interior bisector of $\angle B E D$. Since $C$ lies on line $A E$, and by the fact that $A, B, C, D$ are concyclic, we get that $\angle A B C+\angle A D C=180^{\circ}$, which implies $\angle D B C+\angle B D C=\frac{1}{2}(\angle D B E+\angle B D E)$, so $C$ is the incenter of triangle $B D E$. Thus $\angle A B C=\angle C D A=\frac{\pi}{2}$, and thus $D A^{2}=A C^{2}-C D^{2}=A B^{2}+B C^{2}-C D^{2}=3^{2}+4^{2}-2^{2}=21$. The length of $D A$ is then $\sqrt{21}$.
|
\sqrt{21}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $A, B, C, D$ be points chosen on a circle, in that order. Line $B D$ is reflected over lines $A B$ and $D A$ to obtain lines $\ell_{1}$ and $\ell_{2}$ respectively. If lines $\ell_{1}, \ell_{2}$, and $A C$ meet at a common point and if $A B=4, B C=3, C D=2$, compute the length $D A$.
|
Answer: $\sqrt{21}$
Let the common point be $E$. Then since lines $B E$ and $B D$ are symmetric about line $B A, B A$ is an exterior bisector of $\angle D B E$, and similarly $D A$ is also an exterior bisector of $\angle B D E$. Therefore $A$ is the $E$-excenter of triangle $B D E$ and thus lie on the interior bisector of $\angle B E D$. Since $C$ lies on line $A E$, and by the fact that $A, B, C, D$ are concyclic, we get that $\angle A B C+\angle A D C=180^{\circ}$, which implies $\angle D B C+\angle B D C=\frac{1}{2}(\angle D B E+\angle B D E)$, so $C$ is the incenter of triangle $B D E$. Thus $\angle A B C=\angle C D A=\frac{\pi}{2}$, and thus $D A^{2}=A C^{2}-C D^{2}=A B^{2}+B C^{2}-C D^{2}=3^{2}+4^{2}-2^{2}=21$. The length of $D A$ is then $\sqrt{21}$.
|
{
"resource_path": "HarvardMIT/segmented/en-211-2017-nov-team-solutions.jsonl",
"problem_match": "\n9. [60]",
"solution_match": "\nProposed by: Ashwin Sah\n"
}
|
010f8c19-c23f-5f55-b6b5-479fd5cc4a13
| 609,770
|
Two ordered pairs $(a, b)$ and $(c, d)$, where $a, b, c, d$ are real numbers, form a basis of the coordinate plane if $a d \neq b c$. Determine the number of ordered quadruples $(a, b, c, d)$ of integers between 1 and 3 inclusive for which $(a, b)$ and $(c, d)$ form a basis for the coordinate plane.
|
Answer: 66
Any pair of distinct points will form a basis except when $(a, b)$ and $(c, d)$ are both from $\{(1,1),(2,2),(3,3)\}$, so the answer is $9 \cdot 8-3 \cdot 2=66$.
|
66
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Two ordered pairs $(a, b)$ and $(c, d)$, where $a, b, c, d$ are real numbers, form a basis of the coordinate plane if $a d \neq b c$. Determine the number of ordered quadruples $(a, b, c, d)$ of integers between 1 and 3 inclusive for which $(a, b)$ and $(c, d)$ form a basis for the coordinate plane.
|
Answer: 66
Any pair of distinct points will form a basis except when $(a, b)$ and $(c, d)$ are both from $\{(1,1),(2,2),(3,3)\}$, so the answer is $9 \cdot 8-3 \cdot 2=66$.
|
{
"resource_path": "HarvardMIT/segmented/en-211-2017-nov-thm-solutions.jsonl",
"problem_match": "\n1. ",
"solution_match": "\nProposed by: Ashwin Sah\n"
}
|
90ab39c6-7d15-526b-8263-3e9f3186b4c0
| 609,772
|
Horizontal parallel segments $A B=10$ and $C D=15$ are the bases of trapezoid $A B C D$. Circle $\gamma$ of radius 6 has center within the trapezoid and is tangent to sides $A B, B C$, and $D A$. If side $C D$ cuts out an arc of $\gamma$ measuring $120^{\circ}$, find the area of $A B C D$.
|
Answer: $\frac{225}{2}$
Suppose that the center of the circle is $O$ and the circle intersects $C D$ at $X$ and $Y$. Since $\angle X O Y=120^{\circ}$ and triangle $X O Y$ is isosceles, the distance from $O$ to $X Y$ is $6 \cdot \sin \left(30^{\circ}\right)=3$. On the other hand, the distance from $O$ to $A B$ is 6 as the circle is tangent to $A B$, and $O$ is between $A B$ and $C D$, so the height of the trapezoid is $6+3=9$ and its area is $\frac{9 \cdot(10+15)}{2}=\frac{225}{2}$.
|
\frac{225}{2}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Horizontal parallel segments $A B=10$ and $C D=15$ are the bases of trapezoid $A B C D$. Circle $\gamma$ of radius 6 has center within the trapezoid and is tangent to sides $A B, B C$, and $D A$. If side $C D$ cuts out an arc of $\gamma$ measuring $120^{\circ}$, find the area of $A B C D$.
|
Answer: $\frac{225}{2}$
Suppose that the center of the circle is $O$ and the circle intersects $C D$ at $X$ and $Y$. Since $\angle X O Y=120^{\circ}$ and triangle $X O Y$ is isosceles, the distance from $O$ to $X Y$ is $6 \cdot \sin \left(30^{\circ}\right)=3$. On the other hand, the distance from $O$ to $A B$ is 6 as the circle is tangent to $A B$, and $O$ is between $A B$ and $C D$, so the height of the trapezoid is $6+3=9$ and its area is $\frac{9 \cdot(10+15)}{2}=\frac{225}{2}$.
|
{
"resource_path": "HarvardMIT/segmented/en-211-2017-nov-thm-solutions.jsonl",
"problem_match": "\n2. ",
"solution_match": "\nProposed by: Michael Tang\n"
}
|
babc12a2-8361-5270-ac3e-3c888a00bcce
| 609,773
|
Emilia wishes to create a basic solution with $7 \%$ hydroxide $(\mathrm{OH})$ ions. She has three solutions of different bases available: $10 \%$ rubidium hydroxide $(\mathrm{Rb}(\mathrm{OH})), 8 \%$ cesium hydroxide $(\mathrm{Cs}(\mathrm{OH}))$, and $5 \%$ francium hydroxide $(\mathrm{Fr}(\mathrm{OH})$ ). ( $\mathrm{The} \mathrm{Rb}(\mathrm{OH})$ solution has both $10 \% \mathrm{Rb}$ ions and $10 \% \mathrm{OH}$ ions, and similar for the other solutions.) Since francium is highly radioactive, its concentration in the final solution should not exceed $2 \%$. What is the highest possible concentration of rubidium in her solution?
|
Answer: $1 \%$
Suppose that Emilia uses $R$ liters of $\mathrm{Rb}(\mathrm{OH}), C$ liters of $\mathrm{Cs}(\mathrm{OH})$, and $F$ liters of $\mathrm{Fr}(\mathrm{OH})$, then we have
$$
\frac{10 \% \cdot R+8 \% \cdot C+5 \% \cdot F}{R+C+F}=7 \% \text { and } \frac{5 \% \cdot F}{R+C+F} \leq 2 \%
$$
The equations simplify to $3 R+C=2 F$ and $3 F \leq 2 R+2 C$, which gives
$$
\frac{9 R+3 C}{2} \leq 2 R+2 C \Rightarrow 5 R \leq C
$$
Therefore the concentration of rubidium is maximized when $5 R=C$, so $F=4 R$, and the concentration of rubidium is
$$
\frac{10 \% \cdot R}{R+C+F}=1 \%
$$
|
1 \%
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Emilia wishes to create a basic solution with $7 \%$ hydroxide $(\mathrm{OH})$ ions. She has three solutions of different bases available: $10 \%$ rubidium hydroxide $(\mathrm{Rb}(\mathrm{OH})), 8 \%$ cesium hydroxide $(\mathrm{Cs}(\mathrm{OH}))$, and $5 \%$ francium hydroxide $(\mathrm{Fr}(\mathrm{OH})$ ). ( $\mathrm{The} \mathrm{Rb}(\mathrm{OH})$ solution has both $10 \% \mathrm{Rb}$ ions and $10 \% \mathrm{OH}$ ions, and similar for the other solutions.) Since francium is highly radioactive, its concentration in the final solution should not exceed $2 \%$. What is the highest possible concentration of rubidium in her solution?
|
Answer: $1 \%$
Suppose that Emilia uses $R$ liters of $\mathrm{Rb}(\mathrm{OH}), C$ liters of $\mathrm{Cs}(\mathrm{OH})$, and $F$ liters of $\mathrm{Fr}(\mathrm{OH})$, then we have
$$
\frac{10 \% \cdot R+8 \% \cdot C+5 \% \cdot F}{R+C+F}=7 \% \text { and } \frac{5 \% \cdot F}{R+C+F} \leq 2 \%
$$
The equations simplify to $3 R+C=2 F$ and $3 F \leq 2 R+2 C$, which gives
$$
\frac{9 R+3 C}{2} \leq 2 R+2 C \Rightarrow 5 R \leq C
$$
Therefore the concentration of rubidium is maximized when $5 R=C$, so $F=4 R$, and the concentration of rubidium is
$$
\frac{10 \% \cdot R}{R+C+F}=1 \%
$$
|
{
"resource_path": "HarvardMIT/segmented/en-211-2017-nov-thm-solutions.jsonl",
"problem_match": "\n3. ",
"solution_match": "\nProposed by: Yuan Yao\n"
}
|
be015b50-f45e-5ac6-8a01-8757fb431e2d
| 609,774
|
Mary has a sequence $m_{2}, m_{3}, m_{4}, \ldots$, such that for each $b \geq 2, m_{b}$ is the least positive integer $m$ for which none of the base- $b$ logarithms $\log _{b}(m), \log _{b}(m+1), \ldots, \log _{b}(m+2017)$ are integers. Find the largest number in her sequence.
|
Answer: 2188
It is not difficult to see that for all of the logarithms to be non-integers, they must lie strictly between $n$ and $n+1$ for some integer $n$. Therefore, we require $b^{n+1}-b^{n}>2018$, and so $m_{b}=b^{n}+1$ where $n$ is the smallest integer that satisfies the inequality. In particular, this means that $b^{n}-b^{n-1} \leq 2018$.
Note that $m_{2}=2^{11}+1=2049$ (since $2^{12}-2^{11}=2048>2018$ ) and $m_{3}=3^{7}+1=2188$ (since $3^{8}-3^{7}=4374>2018$ ). we now show that 2188 is the maximum possible value for $m_{b}$.
If $n=0$, then $m_{b}=1+1=2$.
If $n=1$, then $b-1 \leq 2018$ and thus $m_{b}=b+1 \leq 2020$.
If $n=2$, then $b^{2}-b \leq 2018$, which gives $b \leq 45$, and thus $m_{b}=b^{2}+1 \leq 2018+b+1 \leq 2065$.
If $n=3$, then $b^{3}-b^{2} \leq 2018$, which gives $b \leq 12$, and thus $m_{b}=b^{3}+1 \leq 12^{3}+1=1729$.
If $n=4$, then $b^{4}-b^{3} \leq 2018$, which gives $b \leq 6$, and thus $m_{b}=b^{4}+1 \leq 6^{4}+1=1297$.
It then remains to check the value of $m_{4}$ and $m_{5}$. Indeed, $m_{4}=4^{5}+1=1025$ and $m_{5}=5^{4}+1=626$, so no values of $m_{b}$ exceeds 2188 .
|
2188
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Mary has a sequence $m_{2}, m_{3}, m_{4}, \ldots$, such that for each $b \geq 2, m_{b}$ is the least positive integer $m$ for which none of the base- $b$ logarithms $\log _{b}(m), \log _{b}(m+1), \ldots, \log _{b}(m+2017)$ are integers. Find the largest number in her sequence.
|
Answer: 2188
It is not difficult to see that for all of the logarithms to be non-integers, they must lie strictly between $n$ and $n+1$ for some integer $n$. Therefore, we require $b^{n+1}-b^{n}>2018$, and so $m_{b}=b^{n}+1$ where $n$ is the smallest integer that satisfies the inequality. In particular, this means that $b^{n}-b^{n-1} \leq 2018$.
Note that $m_{2}=2^{11}+1=2049$ (since $2^{12}-2^{11}=2048>2018$ ) and $m_{3}=3^{7}+1=2188$ (since $3^{8}-3^{7}=4374>2018$ ). we now show that 2188 is the maximum possible value for $m_{b}$.
If $n=0$, then $m_{b}=1+1=2$.
If $n=1$, then $b-1 \leq 2018$ and thus $m_{b}=b+1 \leq 2020$.
If $n=2$, then $b^{2}-b \leq 2018$, which gives $b \leq 45$, and thus $m_{b}=b^{2}+1 \leq 2018+b+1 \leq 2065$.
If $n=3$, then $b^{3}-b^{2} \leq 2018$, which gives $b \leq 12$, and thus $m_{b}=b^{3}+1 \leq 12^{3}+1=1729$.
If $n=4$, then $b^{4}-b^{3} \leq 2018$, which gives $b \leq 6$, and thus $m_{b}=b^{4}+1 \leq 6^{4}+1=1297$.
It then remains to check the value of $m_{4}$ and $m_{5}$. Indeed, $m_{4}=4^{5}+1=1025$ and $m_{5}=5^{4}+1=626$, so no values of $m_{b}$ exceeds 2188 .
|
{
"resource_path": "HarvardMIT/segmented/en-211-2017-nov-thm-solutions.jsonl",
"problem_match": "\n4. ",
"solution_match": "\nProposed by: Michael Tang\n"
}
|
0139b048-4afb-5fc7-9dc7-77f366c015d3
| 609,775
|
Each of the integers $1,2, \ldots, 729$ is written in its base-3 representation without leading zeroes. The numbers are then joined together in that order to form a continuous string of digits: $12101112202122 \ldots$. . How many times in this string does the substring 012 appear?
|
Answer: 148
Ignore $729=3^{6}=1000000_{3}$ since it will not contribute to a 012 substring. Break into cases on how 012 appears: (i) when an individual integer contains the string 012 ; (ii) when 01 are the last two digits of an integer and 2 is the first digit of the next integer; and (iii) when 0 is the last digit of an integer and 12 are the first two digits of the next integer.
For case (i), we want to find the total number of appearances of the string 012 in $1,2,3, \ldots, N$. Since each number has at most six digits, 012 appears at most once per number. If such a number has $d$ digits, $4 \leq d \leq 6$, then there are $d-3$ possible positions for the substring 012 and $2 \cdot 3^{d-4}$ possible choices for the remaining digits (since the leftmost digit must be nonzero). Thus there are
$$
\sum_{d=4}^{6}(d-3) \cdot\left(2 \cdot 3^{d-4}\right)=1 \cdot 2+2 \cdot 6+3 \cdot 18=68
$$
appearances of 012 in case (i).
For case (ii), we have an integer $n$ for which $n$ ends in 01 and $n+1$ starts with 2 . Then $n$ must also start with 2 . Hence it suffices to count the number of integers $1 \leq n<N$ which start with 2 and end with 01 in base three. If $n$ has $d$ digits, $3 \leq d \leq 6$, then there are $3^{d-3}$ possibilities for the middle digits, so we have
$$
\sum_{d=3}^{6} 3^{d-3}=1+3+9+27=40
$$
appearances of 012 in case (ii).
For case (ii), we have an integer $n$ for which $n$ ends in 0 and $n+1$ starts with 12 . Then $n$ must also start with 12 , so we want to count the number of $1 \leq n<N$ starting with 12 and ending in 0 . Like case (ii), there are also 40 appearances of 012 in case (iii).
In total, the substring 012 appears $68+40+40=148$ times.
|
148
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Each of the integers $1,2, \ldots, 729$ is written in its base-3 representation without leading zeroes. The numbers are then joined together in that order to form a continuous string of digits: $12101112202122 \ldots$. . How many times in this string does the substring 012 appear?
|
Answer: 148
Ignore $729=3^{6}=1000000_{3}$ since it will not contribute to a 012 substring. Break into cases on how 012 appears: (i) when an individual integer contains the string 012 ; (ii) when 01 are the last two digits of an integer and 2 is the first digit of the next integer; and (iii) when 0 is the last digit of an integer and 12 are the first two digits of the next integer.
For case (i), we want to find the total number of appearances of the string 012 in $1,2,3, \ldots, N$. Since each number has at most six digits, 012 appears at most once per number. If such a number has $d$ digits, $4 \leq d \leq 6$, then there are $d-3$ possible positions for the substring 012 and $2 \cdot 3^{d-4}$ possible choices for the remaining digits (since the leftmost digit must be nonzero). Thus there are
$$
\sum_{d=4}^{6}(d-3) \cdot\left(2 \cdot 3^{d-4}\right)=1 \cdot 2+2 \cdot 6+3 \cdot 18=68
$$
appearances of 012 in case (i).
For case (ii), we have an integer $n$ for which $n$ ends in 01 and $n+1$ starts with 2 . Then $n$ must also start with 2 . Hence it suffices to count the number of integers $1 \leq n<N$ which start with 2 and end with 01 in base three. If $n$ has $d$ digits, $3 \leq d \leq 6$, then there are $3^{d-3}$ possibilities for the middle digits, so we have
$$
\sum_{d=3}^{6} 3^{d-3}=1+3+9+27=40
$$
appearances of 012 in case (ii).
For case (ii), we have an integer $n$ for which $n$ ends in 0 and $n+1$ starts with 12 . Then $n$ must also start with 12 , so we want to count the number of $1 \leq n<N$ starting with 12 and ending in 0 . Like case (ii), there are also 40 appearances of 012 in case (iii).
In total, the substring 012 appears $68+40+40=148$ times.
|
{
"resource_path": "HarvardMIT/segmented/en-211-2017-nov-thm-solutions.jsonl",
"problem_match": "\n5. ",
"solution_match": "\nProposed by: Michael Tang\n"
}
|
b11d8e11-ea88-5c0a-a804-10b886cdcce6
| 609,776
|
Rthea, a distant planet, is home to creatures whose DNA consists of two (distinguishable) strands of bases with a fixed orientation. Each base is one of the letters H, M, N, T, and each strand consists of a sequence of five bases, thus forming five pairs. Due to the chemical properties of the bases, each pair must consist of distinct bases. Also, the bases H and M cannot appear next to each other on the same strand; the same is true for N and T . How many possible DNA sequences are there on Rthea?
|
Answer: $12 \cdot 7^{4}$ or 28812
There are $4 \cdot 3=12$ ways to choose the first base pairs, and regardless of which base pair it is, there are 3 possibilities for the next base on one strand and 3 possibilities for the next base on the other
strand. Among these possibilities, exactly 2 of them have identical bases forming a base pair (using one of the base not in the previous base pair if the previous pair is $\mathrm{H}-\mathrm{M}$ or $\mathrm{N}-\mathrm{T}$, or one of the base in the previous pair otherwise), which is not allowed. Therefore there are $3 \cdot 3-2=7$ ways to choose each of the following base pairs. Thus in total there are $12 \cdot 7^{4}=28812$ possible DNA (which is also the maximum number of species).
|
28812
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Rthea, a distant planet, is home to creatures whose DNA consists of two (distinguishable) strands of bases with a fixed orientation. Each base is one of the letters H, M, N, T, and each strand consists of a sequence of five bases, thus forming five pairs. Due to the chemical properties of the bases, each pair must consist of distinct bases. Also, the bases H and M cannot appear next to each other on the same strand; the same is true for N and T . How many possible DNA sequences are there on Rthea?
|
Answer: $12 \cdot 7^{4}$ or 28812
There are $4 \cdot 3=12$ ways to choose the first base pairs, and regardless of which base pair it is, there are 3 possibilities for the next base on one strand and 3 possibilities for the next base on the other
strand. Among these possibilities, exactly 2 of them have identical bases forming a base pair (using one of the base not in the previous base pair if the previous pair is $\mathrm{H}-\mathrm{M}$ or $\mathrm{N}-\mathrm{T}$, or one of the base in the previous pair otherwise), which is not allowed. Therefore there are $3 \cdot 3-2=7$ ways to choose each of the following base pairs. Thus in total there are $12 \cdot 7^{4}=28812$ possible DNA (which is also the maximum number of species).
|
{
"resource_path": "HarvardMIT/segmented/en-211-2017-nov-thm-solutions.jsonl",
"problem_match": "\n6. ",
"solution_match": "\nProposed by: Yuan Yao\n"
}
|
d1b75126-b531-5fde-93f9-e5ebc8bd4e8d
| 609,777
|
New this year at HMNT: the exciting game of $R N G$ baseball! In RNG baseball, a team of infinitely many people play on a square field, with a base at each vertex; in particular, one of the bases is called the home base. Every turn, a new player stands at home base and chooses a number $n$ uniformly at random from $\{0,1,2,3,4\}$. Then, the following occurs:
- If $n>0$, then the player and everyone else currently on the field moves (counterclockwise) around the square by $n$ bases. However, if in doing so a player returns to or moves past the home base, he/she leaves the field immediately and the team scores one point.
- If $n=0$ (a strikeout), then the game ends immediately; the team does not score any more points.
What is the expected number of points that a given team will score in this game?
|
Answer: $\square$
For $i=0,1,2,3$, let $P_{i}$ be the probability that a player on the $i$-th base scores a point before strikeout (with zeroth base being the home base). We have the following equations:
$$
\begin{aligned}
P_{0} & =\frac{1}{5}\left(P_{1}+P_{2}+P_{3}+1\right) \\
P_{1} & =\frac{1}{5}\left(P_{2}+P_{3}+1+1\right) \\
P_{2} & =\frac{1}{5}\left(P_{3}+1+1+1\right) \\
P_{3} & =\frac{1}{5}(1+1+1+1)
\end{aligned}
$$
Solving the system of equations gives $P_{3}=\frac{4}{5}, P_{2}=\frac{19}{25}, P_{1}=\frac{89}{125}, P_{0}=\frac{409}{625}$, so the probability that a batter scores a point himself is $\frac{409}{625}$, given that he is able to enter the game before the game is over. Since the probability that the $n$th player will be able to stand on the home base is $\left(\frac{4}{5}\right)^{n-1}$ (none of the previous $n-1$ players receive a strikeout), the expected value is $\frac{409}{625}\left(1+\frac{4}{5}+\left(\frac{4}{5}\right)^{2}+\cdots\right)=\frac{409}{625} \cdot \frac{1}{1-\frac{4}{5}}=\frac{409}{125}$.
|
\frac{409}{125}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
New this year at HMNT: the exciting game of $R N G$ baseball! In RNG baseball, a team of infinitely many people play on a square field, with a base at each vertex; in particular, one of the bases is called the home base. Every turn, a new player stands at home base and chooses a number $n$ uniformly at random from $\{0,1,2,3,4\}$. Then, the following occurs:
- If $n>0$, then the player and everyone else currently on the field moves (counterclockwise) around the square by $n$ bases. However, if in doing so a player returns to or moves past the home base, he/she leaves the field immediately and the team scores one point.
- If $n=0$ (a strikeout), then the game ends immediately; the team does not score any more points.
What is the expected number of points that a given team will score in this game?
|
Answer: $\square$
For $i=0,1,2,3$, let $P_{i}$ be the probability that a player on the $i$-th base scores a point before strikeout (with zeroth base being the home base). We have the following equations:
$$
\begin{aligned}
P_{0} & =\frac{1}{5}\left(P_{1}+P_{2}+P_{3}+1\right) \\
P_{1} & =\frac{1}{5}\left(P_{2}+P_{3}+1+1\right) \\
P_{2} & =\frac{1}{5}\left(P_{3}+1+1+1\right) \\
P_{3} & =\frac{1}{5}(1+1+1+1)
\end{aligned}
$$
Solving the system of equations gives $P_{3}=\frac{4}{5}, P_{2}=\frac{19}{25}, P_{1}=\frac{89}{125}, P_{0}=\frac{409}{625}$, so the probability that a batter scores a point himself is $\frac{409}{625}$, given that he is able to enter the game before the game is over. Since the probability that the $n$th player will be able to stand on the home base is $\left(\frac{4}{5}\right)^{n-1}$ (none of the previous $n-1$ players receive a strikeout), the expected value is $\frac{409}{625}\left(1+\frac{4}{5}+\left(\frac{4}{5}\right)^{2}+\cdots\right)=\frac{409}{625} \cdot \frac{1}{1-\frac{4}{5}}=\frac{409}{125}$.
|
{
"resource_path": "HarvardMIT/segmented/en-211-2017-nov-thm-solutions.jsonl",
"problem_match": "\n9. ",
"solution_match": "\nProposed by: Yuan Yao\n"
}
|
7994d7f9-9f89-5bee-9b85-3f302e4139cf
| 609,780
|
Denote $\phi=\frac{1+\sqrt{5}}{2}$ and consider the set of all finite binary strings without leading zeroes. Each string $S$ has a "base- $\phi$ " value $p(S)$. For example, $p(1101)=\phi^{3}+\phi^{2}+1$. For any positive integer $n$, let $f(n)$ be the number of such strings $S$ that satisfy $p(S)=\frac{\phi^{48 n}-1}{\phi^{48}-1}$. The sequence of fractions $\frac{f(n+1)}{f(n)}$ approaches a real number $c$ as $n$ goes to infinity. Determine the value of $c$.
|
Answer: $\frac{25+3 \sqrt{69}}{2}$
We write everything in base $\phi$. Notice that
$$
\frac{\phi^{48 n}-1}{\phi^{48}-1}=10 \ldots 010 \ldots 01 \ldots 10 \ldots 01
$$
where there are $n-1$ blocks of 47 zeros each. We can prove that every valid base- $\phi$ representation comes from replacing a consecutive string 100 with a 011 repeatedly. Using this, we can easily classify what base- $\phi$ representations are counted by $f(n)$.
Notice that $10000000=01100000=01011000=01010110$ and similar, so that in each block of zeros we can choose how many times to perform a replacement. It turns out that we can do anywhere from 0 to 24 such replacements, but that if we choose to do 24 then the next block cannot have chosen 0 replacements. (An analogy with lower numbers is $10001000=01101000=01100110=01011110$, with the first block "replaced twice," which was only allowed since the second block had "replaced once," opening up the slot which was filled by the last 1 in the final replacement 011).
Thus we have a bijection from $f(n)$ to sequences in $\{0, \ldots, 24\}^{n-1}$ such that (a) the sequence does not end in 24 and (b) the sequence never has a 24 followed by a 0 .
We let $a_{n}$ denote the number of length- $n$ sequences starting with a $0, b_{n}$ for the number of such sequences starting with any of 1 to 23 , and $c_{n}$ for the number of such sequences starting with 24 . We know $a_{1}=1, b_{1}=23, c_{0}=0$ and that $f(n)=a_{n-1}+b_{n-1}+c_{n-1}$.
Now,
$$
\begin{aligned}
a_{n} & =a_{n-1}+b_{n-1}+c_{n-1} \\
b_{n} & =23\left(a_{n-1}+b_{n-1}+c_{n-1}\right) \\
c_{n} & =b_{n-1}+c_{n-1}
\end{aligned}
$$
so $b_{n}=23 a_{n}$ for all $n$. Substituting gives $a_{n}=24 a_{n-1}+c_{n-1}, c_{n}=23 a_{n-1}+c_{n-1}$. Solving for $c_{n}=a_{n+1}-24 a_{n-1}$ and plugging in gives
$$
a_{n+1}-24 a_{n}=a_{n}-a_{n-1}
$$
which gives a characteristic polynomial of $\lambda^{2}-25 \lambda+1=0$. We easily find that $a_{n}$ grows as $\lambda^{n}$ (where $\lambda$ is the larger solution to the quadratic equation) and thus $b_{n}, c_{n}$ do as well, implying that $f(n)$ grows as $\lambda^{n}$, where
$$
\lambda=\frac{25+\sqrt{25^{2}-4}}{2}=\frac{25+3 \sqrt{69}}{2}
$$
which is our answer.
|
\frac{25+3 \sqrt{69}}{2}
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Denote $\phi=\frac{1+\sqrt{5}}{2}$ and consider the set of all finite binary strings without leading zeroes. Each string $S$ has a "base- $\phi$ " value $p(S)$. For example, $p(1101)=\phi^{3}+\phi^{2}+1$. For any positive integer $n$, let $f(n)$ be the number of such strings $S$ that satisfy $p(S)=\frac{\phi^{48 n}-1}{\phi^{48}-1}$. The sequence of fractions $\frac{f(n+1)}{f(n)}$ approaches a real number $c$ as $n$ goes to infinity. Determine the value of $c$.
|
Answer: $\frac{25+3 \sqrt{69}}{2}$
We write everything in base $\phi$. Notice that
$$
\frac{\phi^{48 n}-1}{\phi^{48}-1}=10 \ldots 010 \ldots 01 \ldots 10 \ldots 01
$$
where there are $n-1$ blocks of 47 zeros each. We can prove that every valid base- $\phi$ representation comes from replacing a consecutive string 100 with a 011 repeatedly. Using this, we can easily classify what base- $\phi$ representations are counted by $f(n)$.
Notice that $10000000=01100000=01011000=01010110$ and similar, so that in each block of zeros we can choose how many times to perform a replacement. It turns out that we can do anywhere from 0 to 24 such replacements, but that if we choose to do 24 then the next block cannot have chosen 0 replacements. (An analogy with lower numbers is $10001000=01101000=01100110=01011110$, with the first block "replaced twice," which was only allowed since the second block had "replaced once," opening up the slot which was filled by the last 1 in the final replacement 011).
Thus we have a bijection from $f(n)$ to sequences in $\{0, \ldots, 24\}^{n-1}$ such that (a) the sequence does not end in 24 and (b) the sequence never has a 24 followed by a 0 .
We let $a_{n}$ denote the number of length- $n$ sequences starting with a $0, b_{n}$ for the number of such sequences starting with any of 1 to 23 , and $c_{n}$ for the number of such sequences starting with 24 . We know $a_{1}=1, b_{1}=23, c_{0}=0$ and that $f(n)=a_{n-1}+b_{n-1}+c_{n-1}$.
Now,
$$
\begin{aligned}
a_{n} & =a_{n-1}+b_{n-1}+c_{n-1} \\
b_{n} & =23\left(a_{n-1}+b_{n-1}+c_{n-1}\right) \\
c_{n} & =b_{n-1}+c_{n-1}
\end{aligned}
$$
so $b_{n}=23 a_{n}$ for all $n$. Substituting gives $a_{n}=24 a_{n-1}+c_{n-1}, c_{n}=23 a_{n-1}+c_{n-1}$. Solving for $c_{n}=a_{n+1}-24 a_{n-1}$ and plugging in gives
$$
a_{n+1}-24 a_{n}=a_{n}-a_{n-1}
$$
which gives a characteristic polynomial of $\lambda^{2}-25 \lambda+1=0$. We easily find that $a_{n}$ grows as $\lambda^{n}$ (where $\lambda$ is the larger solution to the quadratic equation) and thus $b_{n}, c_{n}$ do as well, implying that $f(n)$ grows as $\lambda^{n}$, where
$$
\lambda=\frac{25+\sqrt{25^{2}-4}}{2}=\frac{25+3 \sqrt{69}}{2}
$$
which is our answer.
|
{
"resource_path": "HarvardMIT/segmented/en-211-2017-nov-thm-solutions.jsonl",
"problem_match": "\n10. ",
"solution_match": "\nProposed by: Ashwin Sah\n"
}
|
1a8fb5e8-056b-57bd-8efb-6c79b92ac96b
| 609,781
|
For some real number $c$, the graphs of the equation $y=|x-20|+|x+18|$ and the line $y=x+c$ intersect at exactly one point. What is $c$ ?
|
Answer: 18
We want to know the value of $c$ so that the graph $|x-20|+|x+18|-x=c$ has one solution. The graph of the function $|x-20|+|x+18|-x$ consists of an infinite section of slope -3 for $x \in(-\infty,-18]$, then a finite section of slope -1 for $x \in[-18,20]$, then an infinite section of slope 1 for $x \in[20, \infty)$. Notice that this graph is strictly decreasing on $(-\infty, 20]$ and strictly increasing on $[20, \infty)$. Therefore any horizontal line will intersect this graph 0 or 2 times, except the one that passes through the "vertex" $(20,|20-20|+|20+18|-20)=(20,18)$, giving a value of $c=18$.
|
18
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
For some real number $c$, the graphs of the equation $y=|x-20|+|x+18|$ and the line $y=x+c$ intersect at exactly one point. What is $c$ ?
|
Answer: 18
We want to know the value of $c$ so that the graph $|x-20|+|x+18|-x=c$ has one solution. The graph of the function $|x-20|+|x+18|-x$ consists of an infinite section of slope -3 for $x \in(-\infty,-18]$, then a finite section of slope -1 for $x \in[-18,20]$, then an infinite section of slope 1 for $x \in[20, \infty)$. Notice that this graph is strictly decreasing on $(-\infty, 20]$ and strictly increasing on $[20, \infty)$. Therefore any horizontal line will intersect this graph 0 or 2 times, except the one that passes through the "vertex" $(20,|20-20|+|20+18|-20)=(20,18)$, giving a value of $c=18$.
|
{
"resource_path": "HarvardMIT/segmented/en-212-2018-feb-algnt-solutions.jsonl",
"problem_match": "\n1. ",
"solution_match": "\nProposed by: Henrik Boecken\n"
}
|
b1fbcf8a-be41-5ff4-9f07-7ce6f6af882a
| 609,782
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.