problem
stringlengths 14
7.96k
| solution
stringlengths 3
10k
| answer
stringlengths 1
91
| problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | question_type
stringclasses 1
value | problem_type
stringclasses 8
values | problem_raw
stringlengths 14
7.96k
| solution_raw
stringlengths 3
10k
| metadata
dict | uuid
stringlengths 36
36
| id
int64 22.6k
612k
|
|---|---|---|---|---|---|---|---|---|---|---|---|
For breakfast, Milan is eating a piece of toast shaped like an equilateral triangle. On the piece of toast rests a single sesame seed that is one inch away from one side, two inches away from another side, and four inches away from the third side. He places a circular piece of cheese on top of the toast that is tangent to each side of the triangle. What is the area of this piece of cheese?
|
Answer: $\frac{49 \pi}{9}$
Suppose the toast has side length $s$. If we draw the three line segments from the sesame seed to the three vertices of the triangle, we partition the triangle into three smaller triangles, with areas $\frac{s}{2}$, $s$, and $2 s$, so the entire piece of toast has area $\frac{7 s}{2}$. Suppose the cheese has radius $r$. We similarly see that the toast has area $\frac{3 r s}{2}$. Equating these, we see that $r=\frac{7}{3}$, so the area of the cheese is $\pi\left(\frac{7}{3}\right)^{2}=\frac{49 \pi}{9}$.
|
\frac{49 \pi}{9}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
For breakfast, Milan is eating a piece of toast shaped like an equilateral triangle. On the piece of toast rests a single sesame seed that is one inch away from one side, two inches away from another side, and four inches away from the third side. He places a circular piece of cheese on top of the toast that is tangent to each side of the triangle. What is the area of this piece of cheese?
|
Answer: $\frac{49 \pi}{9}$
Suppose the toast has side length $s$. If we draw the three line segments from the sesame seed to the three vertices of the triangle, we partition the triangle into three smaller triangles, with areas $\frac{s}{2}$, $s$, and $2 s$, so the entire piece of toast has area $\frac{7 s}{2}$. Suppose the cheese has radius $r$. We similarly see that the toast has area $\frac{3 r s}{2}$. Equating these, we see that $r=\frac{7}{3}$, so the area of the cheese is $\pi\left(\frac{7}{3}\right)^{2}=\frac{49 \pi}{9}$.
|
{
"resource_path": "HarvardMIT/segmented/en-231-2019-nov-thm-solutions.jsonl",
"problem_match": "\n3. ",
"solution_match": "\nProposed by: Carl Schildkraut\n"
}
|
e30277a0-81fa-5e65-8160-d6590299e083
| 76,718
|
To celebrate 2019, Faraz gets four sandwiches shaped in the digits 2, 0, 1, and 9 at lunch. However, the four digits get reordered (but not flipped or rotated) on his plate and he notices that they form a 4-digit multiple of 7 . What is the greatest possible number that could have been formed?
|
Answer: 1092
Note that 2 and 9 are equivalent mod 7 . So we will replace the 9 with a 2 for now. Since 7 is a divisor of 21 , a four digit multiple of 7 consisting of $2,0,1$, and 2 cannot have a 2 followed by a 1 (otherwise we could subtract a multiple of 21 to obtain a number of the form $2 \cdot 10^{k}$ ). Thus our number either starts with a 1 or has a 0 followed by a 1 . We can check that 2201 and 2012 are not divisible by 7 . Thus our number starts with a 1. Checking 1220, 1202, and 1022 gives that 1022 is the only possibility. So the answer is 1092.

|
1092
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
To celebrate 2019, Faraz gets four sandwiches shaped in the digits 2, 0, 1, and 9 at lunch. However, the four digits get reordered (but not flipped or rotated) on his plate and he notices that they form a 4-digit multiple of 7 . What is the greatest possible number that could have been formed?

|
Answer: 1092
Note that 2 and 9 are equivalent mod 7 . So we will replace the 9 with a 2 for now. Since 7 is a divisor of 21 , a four digit multiple of 7 consisting of $2,0,1$, and 2 cannot have a 2 followed by a 1 (otherwise we could subtract a multiple of 21 to obtain a number of the form $2 \cdot 10^{k}$ ). Thus our number either starts with a 1 or has a 0 followed by a 1 . We can check that 2201 and 2012 are not divisible by 7 . Thus our number starts with a 1. Checking 1220, 1202, and 1022 gives that 1022 is the only possibility. So the answer is 1092.

|
{
"resource_path": "HarvardMIT/segmented/en-231-2019-nov-thm-solutions.jsonl",
"problem_match": "\n4. ",
"solution_match": "\n## Proposed by: Milan Haiman\n\n"
}
|
b5d880c3-584b-53f7-aff0-d1c3a9fe2673
| 610,105
|
Alison is eating 2401 grains of rice for lunch. She eats the rice in a very peculiar manner: every step, if she has only one grain of rice remaining, she eats it. Otherwise, she finds the smallest positive integer $d>1$ for which she can group the rice into equal groups of size $d$ with none left over. She then groups the rice into groups of size $d$, eats one grain from each group, and puts the rice back into a single pile. How many steps does it take her to finish all her rice?
|
Answer: 17
Note that $2401=7^{4}$. Also, note that the operation is equivalent to replacing $n$ grains of rice with $n \cdot \frac{p-1}{p}$ grains of rice, where $p$ is the smallest prime factor of $n$.
Now, suppose that at some moment Alison has $7^{k}$ grains of rice. After each of the next four steps, she will have $6 \cdot 7^{k-1}, 3 \cdot 7^{k-1}, 2 \cdot 7^{k-1}$, and $7^{k-1}$ grains of rice, respectively. Thus, it takes her 4 steps to decrease the number of grains of rice by a factor of 7 given that she starts at a power of 7 .
Thus, it will take $4 \cdot 4=16$ steps to reduce everything to $7^{0}=1$ grain of rice, after which it will take one step to eat it. Thus, it takes a total of 17 steps for Alison to eat all of the rice.
|
17
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Alison is eating 2401 grains of rice for lunch. She eats the rice in a very peculiar manner: every step, if she has only one grain of rice remaining, she eats it. Otherwise, she finds the smallest positive integer $d>1$ for which she can group the rice into equal groups of size $d$ with none left over. She then groups the rice into groups of size $d$, eats one grain from each group, and puts the rice back into a single pile. How many steps does it take her to finish all her rice?
|
Answer: 17
Note that $2401=7^{4}$. Also, note that the operation is equivalent to replacing $n$ grains of rice with $n \cdot \frac{p-1}{p}$ grains of rice, where $p$ is the smallest prime factor of $n$.
Now, suppose that at some moment Alison has $7^{k}$ grains of rice. After each of the next four steps, she will have $6 \cdot 7^{k-1}, 3 \cdot 7^{k-1}, 2 \cdot 7^{k-1}$, and $7^{k-1}$ grains of rice, respectively. Thus, it takes her 4 steps to decrease the number of grains of rice by a factor of 7 given that she starts at a power of 7 .
Thus, it will take $4 \cdot 4=16$ steps to reduce everything to $7^{0}=1$ grain of rice, after which it will take one step to eat it. Thus, it takes a total of 17 steps for Alison to eat all of the rice.
|
{
"resource_path": "HarvardMIT/segmented/en-231-2019-nov-thm-solutions.jsonl",
"problem_match": "\n5. ",
"solution_match": "\nProposed by: Carl Schilkraut\n"
}
|
b9ce05d0-71c1-5de9-8a5b-d5d1866264ec
| 610,106
|
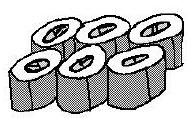
Wendy eats sushi for lunch. She wants to eat six pieces of sushi arranged in a $2 \times 3$ rectangular grid, but sushi is sticky, and Wendy can only eat a piece if it is adjacent to (not counting diagonally) at most two other pieces. In how many orders can Wendy eat the six pieces of sushi, assuming that the pieces of sushi are distinguishable?
|
Answer: 360
Call the sushi pieces $A, B, C$ in the top row and $D, E, F$ in the bottom row of the grid. Note that Wendy must first eat either $A, C, D$, or $F$. Due to the symmetry of the grid, all of these choices are equivalent. Without loss of generality, suppose Wendy eats piece $A$.
Now, note that Wendy cannot eat piece $E$, but can eat all other pieces. If Wendy eats piece $B, D$, or $F$, then in the resulting configuration, all pieces of sushi are adjacent to at most 2 pieces, so she will have 4! ways to eat the sushi. Thus, the total number of possibilities in this case is $4 \cdot 3 \cdot 4!=288$.
If Wendy eats $A$ and then $C$, then Wendy will only have 3 choices for her next piece of sushi, after which she will have 3! ways to eat the remaining 3 pieces of sushi. Thus, the total number of possibilities in this case is $4 \cdot 1 \cdot 3 \cdot 3!=72$.
Thus, the total number of ways for Wendy to eat the sushi is $288+72=360$.
|
360
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Wendy eats sushi for lunch. She wants to eat six pieces of sushi arranged in a $2 \times 3$ rectangular grid, but sushi is sticky, and Wendy can only eat a piece if it is adjacent to (not counting diagonally) at most two other pieces. In how many orders can Wendy eat the six pieces of sushi, assuming that the pieces of sushi are distinguishable?

|
Answer: 360
Call the sushi pieces $A, B, C$ in the top row and $D, E, F$ in the bottom row of the grid. Note that Wendy must first eat either $A, C, D$, or $F$. Due to the symmetry of the grid, all of these choices are equivalent. Without loss of generality, suppose Wendy eats piece $A$.
Now, note that Wendy cannot eat piece $E$, but can eat all other pieces. If Wendy eats piece $B, D$, or $F$, then in the resulting configuration, all pieces of sushi are adjacent to at most 2 pieces, so she will have 4! ways to eat the sushi. Thus, the total number of possibilities in this case is $4 \cdot 3 \cdot 4!=288$.
If Wendy eats $A$ and then $C$, then Wendy will only have 3 choices for her next piece of sushi, after which she will have 3! ways to eat the remaining 3 pieces of sushi. Thus, the total number of possibilities in this case is $4 \cdot 1 \cdot 3 \cdot 3!=72$.
Thus, the total number of ways for Wendy to eat the sushi is $288+72=360$.
|
{
"resource_path": "HarvardMIT/segmented/en-231-2019-nov-thm-solutions.jsonl",
"problem_match": "\n6. ",
"solution_match": "\n## Proposed by: Milan Haiman\n\n"
}
|
5669c47e-510a-5aac-8a69-5a2b20f381d7
| 610,107
|
Carl only eats food in the shape of equilateral pentagons. Unfortunately, for dinner he receives a piece of steak in the shape of an equilateral triangle. So that he can eat it, he cuts off two corners with straight cuts to form an equilateral pentagon. The set of possible perimeters of the pentagon he obtains is exactly the interval $[a, b)$, where $a$ and $b$ are positive real numbers. Compute $\frac{a}{b}$.
|
Answer: $4 \sqrt{3}-6$
Assume that the triangle has side length 1 . We will show the pentagon side length $x$ is in $\left[2 \sqrt{3}-3, \frac{1}{2}\right)$. Call the triangle $A B C$ and let corners $B, C$ be cut. Choose $P$ on $A B, Q, R$ on $B C$, and $S$ on $A C$ such that $A P Q R S$ is equilateral. If $x \geq \frac{1}{2}$ then $Q$ is to the right of $R$, causing self-intersection. Also the distance from $P$ to $B C$ is at most $x$, so
$$
x=P Q \geq P B \sin 60^{\circ}=(1-x) \cdot \frac{\sqrt{3}}{2} .
$$
Solving gives $(2+\sqrt{3}) x \geq \sqrt{3}$, or $x \geq \sqrt{3}(2-\sqrt{3})=2 \sqrt{3}-3$. Finally, these are attainable if we choose $P$ such that $A P=x$, then $Q$ such that $P Q=x$, and so on. Therefore $\frac{a}{b}=4 \sqrt{3}-6$.
|
4 \sqrt{3}-6
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Carl only eats food in the shape of equilateral pentagons. Unfortunately, for dinner he receives a piece of steak in the shape of an equilateral triangle. So that he can eat it, he cuts off two corners with straight cuts to form an equilateral pentagon. The set of possible perimeters of the pentagon he obtains is exactly the interval $[a, b)$, where $a$ and $b$ are positive real numbers. Compute $\frac{a}{b}$.
|
Answer: $4 \sqrt{3}-6$
Assume that the triangle has side length 1 . We will show the pentagon side length $x$ is in $\left[2 \sqrt{3}-3, \frac{1}{2}\right)$. Call the triangle $A B C$ and let corners $B, C$ be cut. Choose $P$ on $A B, Q, R$ on $B C$, and $S$ on $A C$ such that $A P Q R S$ is equilateral. If $x \geq \frac{1}{2}$ then $Q$ is to the right of $R$, causing self-intersection. Also the distance from $P$ to $B C$ is at most $x$, so
$$
x=P Q \geq P B \sin 60^{\circ}=(1-x) \cdot \frac{\sqrt{3}}{2} .
$$
Solving gives $(2+\sqrt{3}) x \geq \sqrt{3}$, or $x \geq \sqrt{3}(2-\sqrt{3})=2 \sqrt{3}-3$. Finally, these are attainable if we choose $P$ such that $A P=x$, then $Q$ such that $P Q=x$, and so on. Therefore $\frac{a}{b}=4 \sqrt{3}-6$.
|
{
"resource_path": "HarvardMIT/segmented/en-231-2019-nov-thm-solutions.jsonl",
"problem_match": "\n7. ",
"solution_match": "\n## Proposed by: Krit Boonsiriseth and Milan Haiman\n\n"
}
|
7a11f968-9d03-5247-bf82-a36551e53e64
| 610,108
|
Omkar, $\mathrm{Krit}_{1}, \mathrm{Krit}_{2}$, and $\mathrm{Krit}_{3}$ are sharing $x>0$ pints of soup for dinner. Omkar always takes 1 pint of soup (unless the amount left is less than one pint, in which case he simply takes all the remaining soup). Krit $_{1}$ always takes $\frac{1}{6}$ of what is left, Krit ${ }_{2}$ always takes $\frac{1}{5}$ of what is left, and Krit ${ }_{3}$ always takes $\frac{1}{4}$ of what is left. They take soup in the order of Omkar, $\mathrm{Krit}_{1}, \mathrm{Krit}_{2}$, $\mathrm{Krit}_{3}$, and then cycle through this order until no soup remains. Find all $x$ for which everyone gets the same amount of soup.
|
Answer: $\frac{49}{3}$
The main observation is that if $x>1$ pints of soup are left, then in one round, Omkar gets 1 and each Krit $_{n}$ gets $\frac{x-1}{6}$, with $\frac{x-1}{2}$ soup left. Thus it is evident that each Krit ${ }_{n}$ gets the same amount of soup, which means it suffices to find $x$ for which Omkar gets $\frac{x}{4}$.
Omkar gets 1 for each cycle and then all the remaining soup when there is less than one pint remaining.
The amount of soup becomes (after each cycle)
$$
x \rightarrow \frac{x-1}{2} \rightarrow \frac{x-3}{4} \rightarrow \cdots \rightarrow \frac{x+1}{2^{n}}-1
$$
so if $n$ is the number of cycles, then Omkar's soup is $n+\frac{x+1}{2^{n}}-1$. Setting this equal to $\frac{x}{4}$, we obtain
$$
x=\frac{n+1 / 2^{n}-1}{1 / 4-1 / 2^{n}}=\frac{(n-1) 2^{n}+1}{2^{n-2}-1}
$$
This immediately implies $n>2$. On the other hand, we necessarily have $0 \leq \frac{x+1}{2^{n}}-1 \leq 1$, so $2^{n} \leq x+1 \leq 2^{n+1}$. But
$$
x+1=\frac{(n-1) 2^{n}+2^{n-2}}{2^{n-2}-1} \leq \frac{(n-1) 2^{n}+2^{n}}{2^{n-3}}=8 n
$$
So $2^{n} \leq 8 n \Longrightarrow n \leq 5$. Testing $n=3,4,5$ :
- For $n=3$ we get $x=17$ which is greater than $2^{4}$.
- For $n=4$ we get $x=\frac{49}{3}$ which works.
- For $n=5$ we get $x=\frac{129}{7}$ which is less than $2^{5}$.
We see that only $n=4$ and $x=\frac{49}{3}$ works.
|
\frac{49}{3}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Omkar, $\mathrm{Krit}_{1}, \mathrm{Krit}_{2}$, and $\mathrm{Krit}_{3}$ are sharing $x>0$ pints of soup for dinner. Omkar always takes 1 pint of soup (unless the amount left is less than one pint, in which case he simply takes all the remaining soup). Krit $_{1}$ always takes $\frac{1}{6}$ of what is left, Krit ${ }_{2}$ always takes $\frac{1}{5}$ of what is left, and Krit ${ }_{3}$ always takes $\frac{1}{4}$ of what is left. They take soup in the order of Omkar, $\mathrm{Krit}_{1}, \mathrm{Krit}_{2}$, $\mathrm{Krit}_{3}$, and then cycle through this order until no soup remains. Find all $x$ for which everyone gets the same amount of soup.

|
Answer: $\frac{49}{3}$
The main observation is that if $x>1$ pints of soup are left, then in one round, Omkar gets 1 and each Krit $_{n}$ gets $\frac{x-1}{6}$, with $\frac{x-1}{2}$ soup left. Thus it is evident that each Krit ${ }_{n}$ gets the same amount of soup, which means it suffices to find $x$ for which Omkar gets $\frac{x}{4}$.
Omkar gets 1 for each cycle and then all the remaining soup when there is less than one pint remaining.
The amount of soup becomes (after each cycle)
$$
x \rightarrow \frac{x-1}{2} \rightarrow \frac{x-3}{4} \rightarrow \cdots \rightarrow \frac{x+1}{2^{n}}-1
$$
so if $n$ is the number of cycles, then Omkar's soup is $n+\frac{x+1}{2^{n}}-1$. Setting this equal to $\frac{x}{4}$, we obtain
$$
x=\frac{n+1 / 2^{n}-1}{1 / 4-1 / 2^{n}}=\frac{(n-1) 2^{n}+1}{2^{n-2}-1}
$$
This immediately implies $n>2$. On the other hand, we necessarily have $0 \leq \frac{x+1}{2^{n}}-1 \leq 1$, so $2^{n} \leq x+1 \leq 2^{n+1}$. But
$$
x+1=\frac{(n-1) 2^{n}+2^{n-2}}{2^{n-2}-1} \leq \frac{(n-1) 2^{n}+2^{n}}{2^{n-3}}=8 n
$$
So $2^{n} \leq 8 n \Longrightarrow n \leq 5$. Testing $n=3,4,5$ :
- For $n=3$ we get $x=17$ which is greater than $2^{4}$.
- For $n=4$ we get $x=\frac{49}{3}$ which works.
- For $n=5$ we get $x=\frac{129}{7}$ which is less than $2^{5}$.
We see that only $n=4$ and $x=\frac{49}{3}$ works.
|
{
"resource_path": "HarvardMIT/segmented/en-231-2019-nov-thm-solutions.jsonl",
"problem_match": "\n8. ",
"solution_match": "\n## Proposed by: Krit Boonsiriseth and Milan Haiman\n\n"
}
|
d38cb03c-8a02-5004-941b-484d895f9836
| 610,109
|
For dinner, Priya is eating grilled pineapple spears. Each spear is in the shape of the quadrilateral PINE, with $P I=6 \mathrm{~cm}, I N=15 \mathrm{~cm}, N E=6 \mathrm{~cm}, E P=25 \mathrm{~cm}$, and $\angle N E P+\angle E P I=60^{\circ}$. What is the area of each spear, in $\mathrm{cm}^{2}$ ?
|
Answer: $\frac{100 \sqrt{3}}{3}$
We consider a configuration composed of 2 more quadrilaterals congruent to PINE. Let them be $P^{\prime} I^{\prime} N^{\prime} E^{\prime}$, with $E^{\prime}=P$ and $N^{\prime}=I$, and $P^{\prime \prime} I^{\prime \prime} N^{\prime \prime} E^{\prime \prime}$ with $P^{\prime \prime}=E, E^{\prime \prime}=P^{\prime}, N^{\prime \prime}=I^{\prime}$, and $I^{\prime \prime}=N$. Notice that this forms an equilateral triangle of side length 25 since $\angle P P^{\prime} P^{\prime \prime}=\angle P P^{\prime \prime} P^{\prime}=\angle P^{\prime} P P^{\prime \prime}=$ $60^{\circ}$. Also, we see that the inner triangle $N N^{\prime} N^{\prime \prime}$ forms an equilateral triangle of side length 15 since all the side lengths are equal. So the area inside the big equilateral triangle and outside the small one is $\frac{625 \sqrt{3}}{4}-\frac{225 \sqrt{3}}{4}=100 \sqrt{3}$. Since there are two other congruent quadrilaterals to PINE, we have that the area of one of them is $\frac{100 \sqrt{3}}{3}$.
|
\frac{100 \sqrt{3}}{3}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
For dinner, Priya is eating grilled pineapple spears. Each spear is in the shape of the quadrilateral PINE, with $P I=6 \mathrm{~cm}, I N=15 \mathrm{~cm}, N E=6 \mathrm{~cm}, E P=25 \mathrm{~cm}$, and $\angle N E P+\angle E P I=60^{\circ}$. What is the area of each spear, in $\mathrm{cm}^{2}$ ?
|
Answer: $\frac{100 \sqrt{3}}{3}$
We consider a configuration composed of 2 more quadrilaterals congruent to PINE. Let them be $P^{\prime} I^{\prime} N^{\prime} E^{\prime}$, with $E^{\prime}=P$ and $N^{\prime}=I$, and $P^{\prime \prime} I^{\prime \prime} N^{\prime \prime} E^{\prime \prime}$ with $P^{\prime \prime}=E, E^{\prime \prime}=P^{\prime}, N^{\prime \prime}=I^{\prime}$, and $I^{\prime \prime}=N$. Notice that this forms an equilateral triangle of side length 25 since $\angle P P^{\prime} P^{\prime \prime}=\angle P P^{\prime \prime} P^{\prime}=\angle P^{\prime} P P^{\prime \prime}=$ $60^{\circ}$. Also, we see that the inner triangle $N N^{\prime} N^{\prime \prime}$ forms an equilateral triangle of side length 15 since all the side lengths are equal. So the area inside the big equilateral triangle and outside the small one is $\frac{625 \sqrt{3}}{4}-\frac{225 \sqrt{3}}{4}=100 \sqrt{3}$. Since there are two other congruent quadrilaterals to PINE, we have that the area of one of them is $\frac{100 \sqrt{3}}{3}$.
|
{
"resource_path": "HarvardMIT/segmented/en-231-2019-nov-thm-solutions.jsonl",
"problem_match": "\n9. ",
"solution_match": "\nProposed by: Milan Haiman\n"
}
|
d587d6b5-52e7-5d16-aa19-401c05204d7f
| 610,110
|
For dessert, Melinda eats a spherical scoop of ice cream with diameter 2 inches. She prefers to eat her ice cream in cube-like shapes, however. She has a special machine which, given a sphere placed in space, cuts it through the planes $x=n, y=n$, and $z=n$ for every integer $n$ (not necessarily positive). Melinda centers the scoop of ice cream uniformly at random inside the cube $0 \leq x, y, z \leq 1$, and then cuts it into pieces using her machine. What is the expected number of pieces she cuts the ice cream into?
|
Answer: $7+\frac{13 \pi}{3}$
Note that if we consider the division of $\mathbb{R}^{3}$ into unit cubes by the given planes, we only need to compute the sum of the probabilities that the ice cream scoop intersects each cube. There are three types of cubes that can be intersected:
- The cube $0 \leq x, y, z \leq 1$ in which the center lies, as well as the 6 face-adjacent cubes are always intersected, for a total of 7 .
- The cubes edge-adjacent to the center cube are intersected if the center of the ice cream lies within 1 unit of the connecting edge, which happens with probability $\frac{\pi}{4}$. There are 12 such cubes, for a total of $3 \pi$.
- The cubes corner-adjacent to the center cube are intersected if the center of the ice cream lies within 1 unit of the connecting corner, which happens with probability $\frac{\pi}{6}$. There are 8 such cubes, for a total of $\frac{4 \pi}{3}$.
Adding these all up gives our answer of $7+\frac{13 \pi}{3}$.
An alternate solution is possible:
We compute the number of regions into which a convex region $S$ in $\mathbb{R}^{3}$ is divided by planes: Let $a$ be the number of planes intersecting $S$. Let $b$ be the number of lines (intersections of two planes) passing through $S$. Let $c$ be the number of points (intersections of three planes) lying inside $S$. Then $S$ is divided into $a+b+c+1$ regions. Then the computation for the problem is fairly straight forward. Note that the only planes, lines, and points that can intersect the ice cream scoop $I$ are the faces, edges, and vertices of the cube $0 \leq x, y, z \leq 1$. The computation is essentially the same as in the first solution. The scoop intersects each of the 6 faces with probability 1 , each of the 12 edges with probability $\frac{\pi}{4}$, and each of the 8 vertices with probability $\frac{\pi}{6}$, for a total expected number of regions $1+6+3 \pi+\frac{4 \pi}{3}=7+\frac{13 \pi}{3}$.
|
7+\frac{13 \pi}{3}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
For dessert, Melinda eats a spherical scoop of ice cream with diameter 2 inches. She prefers to eat her ice cream in cube-like shapes, however. She has a special machine which, given a sphere placed in space, cuts it through the planes $x=n, y=n$, and $z=n$ for every integer $n$ (not necessarily positive). Melinda centers the scoop of ice cream uniformly at random inside the cube $0 \leq x, y, z \leq 1$, and then cuts it into pieces using her machine. What is the expected number of pieces she cuts the ice cream into?
|
Answer: $7+\frac{13 \pi}{3}$
Note that if we consider the division of $\mathbb{R}^{3}$ into unit cubes by the given planes, we only need to compute the sum of the probabilities that the ice cream scoop intersects each cube. There are three types of cubes that can be intersected:
- The cube $0 \leq x, y, z \leq 1$ in which the center lies, as well as the 6 face-adjacent cubes are always intersected, for a total of 7 .
- The cubes edge-adjacent to the center cube are intersected if the center of the ice cream lies within 1 unit of the connecting edge, which happens with probability $\frac{\pi}{4}$. There are 12 such cubes, for a total of $3 \pi$.
- The cubes corner-adjacent to the center cube are intersected if the center of the ice cream lies within 1 unit of the connecting corner, which happens with probability $\frac{\pi}{6}$. There are 8 such cubes, for a total of $\frac{4 \pi}{3}$.
Adding these all up gives our answer of $7+\frac{13 \pi}{3}$.
An alternate solution is possible:
We compute the number of regions into which a convex region $S$ in $\mathbb{R}^{3}$ is divided by planes: Let $a$ be the number of planes intersecting $S$. Let $b$ be the number of lines (intersections of two planes) passing through $S$. Let $c$ be the number of points (intersections of three planes) lying inside $S$. Then $S$ is divided into $a+b+c+1$ regions. Then the computation for the problem is fairly straight forward. Note that the only planes, lines, and points that can intersect the ice cream scoop $I$ are the faces, edges, and vertices of the cube $0 \leq x, y, z \leq 1$. The computation is essentially the same as in the first solution. The scoop intersects each of the 6 faces with probability 1 , each of the 12 edges with probability $\frac{\pi}{4}$, and each of the 8 vertices with probability $\frac{\pi}{6}$, for a total expected number of regions $1+6+3 \pi+\frac{4 \pi}{3}=7+\frac{13 \pi}{3}$.
|
{
"resource_path": "HarvardMIT/segmented/en-231-2019-nov-thm-solutions.jsonl",
"problem_match": "\n10. ",
"solution_match": "\nProposed by: Carl Schildkraut\n"
}
|
28aa24c7-fd8a-5bc5-a10d-0d30f7e3c17f
| 610,111
|
Let $P(x)=x^{3}+x^{2}-r^{2} x-2020$ be a polynomial with roots $r, s, t$. What is $P(1)$ ?
|
Plugging in $x=r$ gives $r^{2}=2020$. This means $P(1)=2-r^{2}-2020=-4038$.
|
-4038
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Let $P(x)=x^{3}+x^{2}-r^{2} x-2020$ be a polynomial with roots $r, s, t$. What is $P(1)$ ?
|
Plugging in $x=r$ gives $r^{2}=2020$. This means $P(1)=2-r^{2}-2020=-4038$.
|
{
"resource_path": "HarvardMIT/segmented/en-232-2020-feb-algnt-solutions.jsonl",
"problem_match": "\n1. ",
"solution_match": "\nSolution 1: "
}
|
826806e2-b178-5ce2-9d60-69e8ddf4f56f
| 610,112
|
Let $a=256$. Find the unique real number $x>a^{2}$ such that
$$
\log _{a} \log _{a} \log _{a} x=\log _{a^{2}} \log _{a^{2}} \log _{a^{2}} x
$$
|
Answer: $2^{32}$
|
2^{32}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Let $a=256$. Find the unique real number $x>a^{2}$ such that
$$
\log _{a} \log _{a} \log _{a} x=\log _{a^{2}} \log _{a^{2}} \log _{a^{2}} x
$$
|
Answer: $2^{32}$
|
{
"resource_path": "HarvardMIT/segmented/en-232-2020-feb-algnt-solutions.jsonl",
"problem_match": "\n3. ",
"solution_match": "\nProposed by: James Lin\n"
}
|
764b81eb-1466-55f2-929a-4f6debbbe36e
| 610,114
|
For positive integers $n$ and $k$, let $\mho(n, k)$ be the number of distinct prime divisors of $n$ that are at least $k$. For example, $\mho(90,3)=2$, since the only prime factors of 90 that are at least 3 are 3 and 5 . Find the closest integer to
$$
\sum_{n=1}^{\infty} \sum_{k=1}^{\infty} \frac{\mho(n, k)}{3^{n+k-7}}
$$
|
## Answer: 167
|
167
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
For positive integers $n$ and $k$, let $\mho(n, k)$ be the number of distinct prime divisors of $n$ that are at least $k$. For example, $\mho(90,3)=2$, since the only prime factors of 90 that are at least 3 are 3 and 5 . Find the closest integer to
$$
\sum_{n=1}^{\infty} \sum_{k=1}^{\infty} \frac{\mho(n, k)}{3^{n+k-7}}
$$
|
## Answer: 167
|
{
"resource_path": "HarvardMIT/segmented/en-232-2020-feb-algnt-solutions.jsonl",
"problem_match": "\n4. ",
"solution_match": "\nProposed by: Daniel Zhu\n\n"
}
|
67cf1bfb-2355-58c5-8363-bf082cf763c4
| 610,115
|
A positive integer $N$ is piquant if there exists a positive integer $m$ such that if $n_{i}$ denotes the number of digits in $m^{i}$ (in base 10), then $n_{1}+n_{2}+\cdots+n_{10}=N$. Let $p_{M}$ denote the fraction of the first $M$ positive integers that are piquant. Find $\lim _{M \rightarrow \infty} p_{M}$.
|
Answer: $\frac{32}{55}$
|
\frac{32}{55}
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
A positive integer $N$ is piquant if there exists a positive integer $m$ such that if $n_{i}$ denotes the number of digits in $m^{i}$ (in base 10), then $n_{1}+n_{2}+\cdots+n_{10}=N$. Let $p_{M}$ denote the fraction of the first $M$ positive integers that are piquant. Find $\lim _{M \rightarrow \infty} p_{M}$.
|
Answer: $\frac{32}{55}$
|
{
"resource_path": "HarvardMIT/segmented/en-232-2020-feb-algnt-solutions.jsonl",
"problem_match": "\n5. ",
"solution_match": "\nProposed by: James Lin\n"
}
|
7dd1952f-45fd-576d-9c39-646a5b9214c2
| 610,116
|
A polynomial $P(x)$ is a base-n polynomial if it is of the form $a_{d} x^{d}+a_{d-1} x^{d-1}+\cdots+a_{1} x+a_{0}$, where each $a_{i}$ is an integer between 0 and $n-1$ inclusive and $a_{d}>0$. Find the largest positive integer $n$ such that for any real number $c$, there exists at most one base- $n$ polynomial $P(x)$ for which $P(\sqrt{2}+\sqrt{3})=c$.
|
It is equivalent to determine the largest $n$ such that we cannot find two distinct base$n$ polynomials $P_{1}$ and $P_{2}$ such that $P_{1}(\sqrt{2}+\sqrt{3})=P_{2}(\sqrt{2}+\sqrt{3})$. The difference of two base- $n$ polynomials is a polynomial with integer coefficients whose absolute values are less than $n$, and all such polynomials are the difference of two base- $n$ polynomials. We compute the minimal polynomial of $x=\sqrt{2}+\sqrt{3}$ first: since $x^{2}=5+2 \sqrt{6}$, we have $\left(x^{2}-5\right)^{2}=24$ so $x^{4}-10 x^{2}+1=0$. Therefore $\sqrt{2}+\sqrt{3}$ is a root of $\left(x^{2}+1\right)\left(x^{4}-10 x^{2}+1\right)=x^{6}-9 x^{4}-9 x^{2}+1$. The coefficients of this polynomial have magnitude at most 9 , so $n<10$.
In the other direction, observe that $(\sqrt{2}+\sqrt{3})^{k}$ is of the form $a+b \sqrt{6}$ for integers $a$ and $b$ if $k$ is even, and $a \sqrt{2}+b \sqrt{3}$ if $k$ is odd. As no integer linear combination of the first expression can equal the second, we can treat these cases separately. Suppose $Q(x)=c_{d} x^{2 d}+c_{d-1} x^{2 d-2}+\cdots+c_{0}$ is an even polynomial with $\left|c_{i}\right|<9$ for all $i$ and $c_{d} \neq 0$. Let $y=(\sqrt{2}+\sqrt{3})^{2}=5+2 \sqrt{6}$ and observe that $y>9$. Then
$$
\begin{aligned}
\left|c_{d} y^{d}\right| & \geq y^{d} \\
& >\frac{8}{y-1}\left(y^{d}-1\right) \\
& =8 y^{d-1}+8 y^{d-2}+\cdots+8 y+8 \\
& \geq\left|c_{d-1} y^{d-1}+c_{d-2} y^{d-2}+\cdots+c_{0}\right|
\end{aligned}
$$
Therefore $Q(\sqrt{2}+\sqrt{3})=c_{d} y^{d}+c_{d-1} y^{d-1}+\cdots+c_{0} \neq 0$, so no two distinct base-9 polynomials coincide at $x=\sqrt{2}+\sqrt{3}$.
The same logic applies for the odd polynomial case after dividing out a factor of $\sqrt{2}+\sqrt{3}$, so $n=9$ works.
|
9
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
A polynomial $P(x)$ is a base-n polynomial if it is of the form $a_{d} x^{d}+a_{d-1} x^{d-1}+\cdots+a_{1} x+a_{0}$, where each $a_{i}$ is an integer between 0 and $n-1$ inclusive and $a_{d}>0$. Find the largest positive integer $n$ such that for any real number $c$, there exists at most one base- $n$ polynomial $P(x)$ for which $P(\sqrt{2}+\sqrt{3})=c$.
|
It is equivalent to determine the largest $n$ such that we cannot find two distinct base$n$ polynomials $P_{1}$ and $P_{2}$ such that $P_{1}(\sqrt{2}+\sqrt{3})=P_{2}(\sqrt{2}+\sqrt{3})$. The difference of two base- $n$ polynomials is a polynomial with integer coefficients whose absolute values are less than $n$, and all such polynomials are the difference of two base- $n$ polynomials. We compute the minimal polynomial of $x=\sqrt{2}+\sqrt{3}$ first: since $x^{2}=5+2 \sqrt{6}$, we have $\left(x^{2}-5\right)^{2}=24$ so $x^{4}-10 x^{2}+1=0$. Therefore $\sqrt{2}+\sqrt{3}$ is a root of $\left(x^{2}+1\right)\left(x^{4}-10 x^{2}+1\right)=x^{6}-9 x^{4}-9 x^{2}+1$. The coefficients of this polynomial have magnitude at most 9 , so $n<10$.
In the other direction, observe that $(\sqrt{2}+\sqrt{3})^{k}$ is of the form $a+b \sqrt{6}$ for integers $a$ and $b$ if $k$ is even, and $a \sqrt{2}+b \sqrt{3}$ if $k$ is odd. As no integer linear combination of the first expression can equal the second, we can treat these cases separately. Suppose $Q(x)=c_{d} x^{2 d}+c_{d-1} x^{2 d-2}+\cdots+c_{0}$ is an even polynomial with $\left|c_{i}\right|<9$ for all $i$ and $c_{d} \neq 0$. Let $y=(\sqrt{2}+\sqrt{3})^{2}=5+2 \sqrt{6}$ and observe that $y>9$. Then
$$
\begin{aligned}
\left|c_{d} y^{d}\right| & \geq y^{d} \\
& >\frac{8}{y-1}\left(y^{d}-1\right) \\
& =8 y^{d-1}+8 y^{d-2}+\cdots+8 y+8 \\
& \geq\left|c_{d-1} y^{d-1}+c_{d-2} y^{d-2}+\cdots+c_{0}\right|
\end{aligned}
$$
Therefore $Q(\sqrt{2}+\sqrt{3})=c_{d} y^{d}+c_{d-1} y^{d-1}+\cdots+c_{0} \neq 0$, so no two distinct base-9 polynomials coincide at $x=\sqrt{2}+\sqrt{3}$.
The same logic applies for the odd polynomial case after dividing out a factor of $\sqrt{2}+\sqrt{3}$, so $n=9$ works.
|
{
"resource_path": "HarvardMIT/segmented/en-232-2020-feb-algnt-solutions.jsonl",
"problem_match": "\n6. ",
"solution_match": "\nSolution: "
}
|
44702dce-63b1-5509-845a-39e65884e2d2
| 610,117
|
Find the sum of all positive integers $n$ for which
$$
\frac{15 \cdot n!^{2}+1}{2 n-3}
$$
is an integer.
|
It is clear that $n=1$ and $n=2$ work so assume that $n>2$. If $2 n-3$ is composite then its smallest prime factor is at most $\frac{2 n-3}{2}<n$ so will be coprime to $15 \cdot n!^{2}+1$. Therefore assume that $2 n-3=p$ is prime. We can rewrite the numerator as
$$
(-1)^{n} \cdot 15 \cdot\left(1 \cdot 2 \cdots \frac{p+3}{2}\right) \cdot\left(\frac{p-3}{2} \cdot \frac{p-1}{2} \cdots(p-1)\right)+1 \quad(\bmod p)
$$
By Wilson's Theorem, $(p-1)!\equiv-1(\bmod p)$, so the expression simplifies to
$$
(-1)^{n+1} \cdot 15 \cdot \frac{p-3}{2} \cdot \frac{p-1}{2} \cdot \frac{p+1}{2} \cdot \frac{p+3}{2}+1 \equiv(-1)^{n+1} \cdot \frac{135}{16}+1 \quad(\bmod p)
$$
If $p \equiv 3(\bmod 4)$, then we have
$$
\frac{135+16}{16} \equiv \frac{151}{16} \equiv 0 \quad(\bmod p)
$$
If $p \equiv 1(\bmod 4)$, then we have
$$
\frac{135-16}{16} \equiv \frac{119}{16} \equiv 0 \quad(\bmod p)
$$
So $p$ must be a prime divisor of 151 or 119 , which means that $p \in\{7,17,151\}$. All of these numbers work aside from $7($ because $7 \equiv 3(\bmod 4))$ and the corresponding values of $n$ are 10 and 77 . The sum of the solutions is then $1+2+10+77=90$.
|
90
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Find the sum of all positive integers $n$ for which
$$
\frac{15 \cdot n!^{2}+1}{2 n-3}
$$
is an integer.
|
It is clear that $n=1$ and $n=2$ work so assume that $n>2$. If $2 n-3$ is composite then its smallest prime factor is at most $\frac{2 n-3}{2}<n$ so will be coprime to $15 \cdot n!^{2}+1$. Therefore assume that $2 n-3=p$ is prime. We can rewrite the numerator as
$$
(-1)^{n} \cdot 15 \cdot\left(1 \cdot 2 \cdots \frac{p+3}{2}\right) \cdot\left(\frac{p-3}{2} \cdot \frac{p-1}{2} \cdots(p-1)\right)+1 \quad(\bmod p)
$$
By Wilson's Theorem, $(p-1)!\equiv-1(\bmod p)$, so the expression simplifies to
$$
(-1)^{n+1} \cdot 15 \cdot \frac{p-3}{2} \cdot \frac{p-1}{2} \cdot \frac{p+1}{2} \cdot \frac{p+3}{2}+1 \equiv(-1)^{n+1} \cdot \frac{135}{16}+1 \quad(\bmod p)
$$
If $p \equiv 3(\bmod 4)$, then we have
$$
\frac{135+16}{16} \equiv \frac{151}{16} \equiv 0 \quad(\bmod p)
$$
If $p \equiv 1(\bmod 4)$, then we have
$$
\frac{135-16}{16} \equiv \frac{119}{16} \equiv 0 \quad(\bmod p)
$$
So $p$ must be a prime divisor of 151 or 119 , which means that $p \in\{7,17,151\}$. All of these numbers work aside from $7($ because $7 \equiv 3(\bmod 4))$ and the corresponding values of $n$ are 10 and 77 . The sum of the solutions is then $1+2+10+77=90$.
|
{
"resource_path": "HarvardMIT/segmented/en-232-2020-feb-algnt-solutions.jsonl",
"problem_match": "\n7. ",
"solution_match": "\nSolution: "
}
|
d6076cf5-09fc-5d91-832d-c58df9215a0d
| 610,118
|
Let $P(x)=x^{2020}+x+2$, which has 2020 distinct roots. Let $Q(x)$ be the monic polynomial of degree $\binom{2020}{2}$ whose roots are the pairwise products of the roots of $P(x)$. Let $\alpha$ satisfy $P(\alpha)=4$. Compute the sum of all possible values of $Q\left(\alpha^{2}\right)^{2}$.
|
Answer: $2020 \cdot 2^{2019}$
|
2020 \cdot 2^{2019}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Let $P(x)=x^{2020}+x+2$, which has 2020 distinct roots. Let $Q(x)$ be the monic polynomial of degree $\binom{2020}{2}$ whose roots are the pairwise products of the roots of $P(x)$. Let $\alpha$ satisfy $P(\alpha)=4$. Compute the sum of all possible values of $Q\left(\alpha^{2}\right)^{2}$.
|
Answer: $2020 \cdot 2^{2019}$
|
{
"resource_path": "HarvardMIT/segmented/en-232-2020-feb-algnt-solutions.jsonl",
"problem_match": "\n9. ",
"solution_match": "\n## Proposed by: Milan Haiman\n\n"
}
|
604296f1-e4ae-54c9-a836-08482813efcd
| 610,120
|
How many ways can the vertices of a cube be colored red or blue so that the color of each vertex is the color of the majority of the three vertices adjacent to it?
|
If all vertices of the cube are of the same color, then there are 2 ways. Otherwise, look at a red vertex. Since it must have at least 2 red neighbors, there is a face of the cube containing 3 red vertices. The last vertex on this face must also be red. Similarly, all vertices on the opposite face must be blue. Thus, all vertices on one face of the cube are red while the others are blue. Since a cube has 6 faces, the answer is $2+6=8$.
|
8
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
How many ways can the vertices of a cube be colored red or blue so that the color of each vertex is the color of the majority of the three vertices adjacent to it?
|
If all vertices of the cube are of the same color, then there are 2 ways. Otherwise, look at a red vertex. Since it must have at least 2 red neighbors, there is a face of the cube containing 3 red vertices. The last vertex on this face must also be red. Similarly, all vertices on the opposite face must be blue. Thus, all vertices on one face of the cube are red while the others are blue. Since a cube has 6 faces, the answer is $2+6=8$.
|
{
"resource_path": "HarvardMIT/segmented/en-232-2020-feb-comb-solutions.jsonl",
"problem_match": "\n1. ",
"solution_match": "\nSolution: "
}
|
cef88f24-3563-5110-95c0-42879b528d29
| 610,122
|
How many positive integers at most 420 leave different remainders when divided by each of 5,6 , and 7 ?
|
Note that $210=5 \cdot 6 \cdot 7$ and $5,6,7$ are pairwise relatively prime. So, by the Chinese Remainder Theorem, we can just consider the remainders $n$ leaves when divided by each of $5,6,7$. To construct an $n$ that leaves distinct remainders, first choose its remainder modulo 5 , then modulo 6 , then modulo 7 . We have $5=6-1=7-2$ choices for each remainder. Finally, we multiply by 2 because $420=2 \cdot 210$. The answer is $2 \cdot 5^{3}=250$.
|
250
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
How many positive integers at most 420 leave different remainders when divided by each of 5,6 , and 7 ?
|
Note that $210=5 \cdot 6 \cdot 7$ and $5,6,7$ are pairwise relatively prime. So, by the Chinese Remainder Theorem, we can just consider the remainders $n$ leaves when divided by each of $5,6,7$. To construct an $n$ that leaves distinct remainders, first choose its remainder modulo 5 , then modulo 6 , then modulo 7 . We have $5=6-1=7-2$ choices for each remainder. Finally, we multiply by 2 because $420=2 \cdot 210$. The answer is $2 \cdot 5^{3}=250$.
|
{
"resource_path": "HarvardMIT/segmented/en-232-2020-feb-comb-solutions.jsonl",
"problem_match": "\n2. ",
"solution_match": "\nSolution: "
}
|
c8bf5d11-7dcb-50e5-86a0-19b649327824
| 610,123
|
Given an $8 \times 8$ checkerboard with alternating white and black squares, how many ways are there to choose four black squares and four white squares so that no two of the eight chosen squares are in the same row or column?
|
Number both the rows and the columns from 1 to 8, and say that black squares are the ones where the rows and columns have the same parity. We will use, e.g. "even rows" to refer to rows 2,4 , 6,8 . Choosing 8 squares all in different rows and columns is equivalent to matching rows to columns.
For each of the 8 rows, we first decide whether they will be matched with a column of the same parity as itself (resulting in a black square) or with one of a different parity (resulting in a white square). Since we want to choose 4 squares of each color, the 4 rows matched to same-parity columns must contain 2 even rows and 2 odd rows. There are $\binom{4}{2}^{2}=6^{2}$ ways to choose 2 odd rows and 2 even rows to match with same-parity columns.
After choosing the above, we have fixed which 4 rows should be matched with odd columns (while the other 4 should be matched with even columns). Then there are $(4!)^{2}=24^{2}$ ways to assign the columns to the rows, so the answer is $(6 \cdot 24)^{2}=144^{2}=20736$.
|
20736
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Given an $8 \times 8$ checkerboard with alternating white and black squares, how many ways are there to choose four black squares and four white squares so that no two of the eight chosen squares are in the same row or column?
|
Number both the rows and the columns from 1 to 8, and say that black squares are the ones where the rows and columns have the same parity. We will use, e.g. "even rows" to refer to rows 2,4 , 6,8 . Choosing 8 squares all in different rows and columns is equivalent to matching rows to columns.
For each of the 8 rows, we first decide whether they will be matched with a column of the same parity as itself (resulting in a black square) or with one of a different parity (resulting in a white square). Since we want to choose 4 squares of each color, the 4 rows matched to same-parity columns must contain 2 even rows and 2 odd rows. There are $\binom{4}{2}^{2}=6^{2}$ ways to choose 2 odd rows and 2 even rows to match with same-parity columns.
After choosing the above, we have fixed which 4 rows should be matched with odd columns (while the other 4 should be matched with even columns). Then there are $(4!)^{2}=24^{2}$ ways to assign the columns to the rows, so the answer is $(6 \cdot 24)^{2}=144^{2}=20736$.
|
{
"resource_path": "HarvardMIT/segmented/en-232-2020-feb-comb-solutions.jsonl",
"problem_match": "\n4. ",
"solution_match": "\nSolution: "
}
|
bf0788ef-e6bd-5265-b9af-4bb361e8c368
| 610,125
|
Let $S$ be a set of intervals defined recursively as follows:
- Initially, $[1,1000]$ is the only interval in $S$.
- If $l \neq r$ and $[l, r] \in S$, then both $\left[l,\left\lfloor\frac{l+r}{2}\right\rfloor\right],\left[\left\lfloor\frac{l+r}{2}\right\rfloor+1, r\right] \in S$.
(Note that $S$ can contain intervals such as [1, 1], which contain a single integer.) An integer $i$ is chosen uniformly at random from the range [1,1000]. What is the expected number of intervals in $S$ which contain $i$ ?
|
The answer is given by computing the sum of the lengths of all intervals in $S$ and dividing this value by 1000 , where the length of an interval $[i, j]$ is given by $j-i+1$. An interval may be categorized based on how many times $[1,1000]$ must be split to attain it. An interval that is derived from splitting $[1,1000] k$ times will be called a $k$-split.
The only 0 -split is $[1,1000]$, with a total length of 1000 . The 1 -splits are $[1,500]$ and $[501,1000]$, with a total length of 1000 . As long as none of the $k$-splits have length 1 , the $(k+1)$-splits will have the same total length. Since the length of the intervals is reduced by half each time (rounded down), we find that the sum of the lengths of the $k$-splits is 1000 for $0 \leq k \leq 9$.
Note that the 9 -splits consist of $2^{10}-1000$ intervals of length 1 and $1000-2^{9}$ intervals of length 2. Then the 10 -splits consist of $2\left(1000-2^{9}\right)$ intervals of length 1 , with total length $2\left(1000-2^{9}\right)$. The total interval length across all splits is equal to $12(1000)-2^{10}$, so our answer is
$$
12-\frac{2^{10}}{1000}=10.976
$$
|
10.976
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Let $S$ be a set of intervals defined recursively as follows:
- Initially, $[1,1000]$ is the only interval in $S$.
- If $l \neq r$ and $[l, r] \in S$, then both $\left[l,\left\lfloor\frac{l+r}{2}\right\rfloor\right],\left[\left\lfloor\frac{l+r}{2}\right\rfloor+1, r\right] \in S$.
(Note that $S$ can contain intervals such as [1, 1], which contain a single integer.) An integer $i$ is chosen uniformly at random from the range [1,1000]. What is the expected number of intervals in $S$ which contain $i$ ?
|
The answer is given by computing the sum of the lengths of all intervals in $S$ and dividing this value by 1000 , where the length of an interval $[i, j]$ is given by $j-i+1$. An interval may be categorized based on how many times $[1,1000]$ must be split to attain it. An interval that is derived from splitting $[1,1000] k$ times will be called a $k$-split.
The only 0 -split is $[1,1000]$, with a total length of 1000 . The 1 -splits are $[1,500]$ and $[501,1000]$, with a total length of 1000 . As long as none of the $k$-splits have length 1 , the $(k+1)$-splits will have the same total length. Since the length of the intervals is reduced by half each time (rounded down), we find that the sum of the lengths of the $k$-splits is 1000 for $0 \leq k \leq 9$.
Note that the 9 -splits consist of $2^{10}-1000$ intervals of length 1 and $1000-2^{9}$ intervals of length 2. Then the 10 -splits consist of $2\left(1000-2^{9}\right)$ intervals of length 1 , with total length $2\left(1000-2^{9}\right)$. The total interval length across all splits is equal to $12(1000)-2^{10}$, so our answer is
$$
12-\frac{2^{10}}{1000}=10.976
$$
|
{
"resource_path": "HarvardMIT/segmented/en-232-2020-feb-comb-solutions.jsonl",
"problem_match": "\n5. ",
"solution_match": "\nSolution: "
}
|
d0a690a4-ef1f-5601-a26a-10c6700acb29
| 610,126
|
Anne-Marie has a deck of 16 cards, each with a distinct positive factor of 2002 written on it. She shuffles the deck and begins to draw cards from the deck without replacement. She stops when there exists a nonempty subset of the cards in her hand whose numbers multiply to a perfect square. What is the expected number of cards in her hand when she stops?
|
Answer: $\frac{837}{208}$
|
\frac{837}{208}
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Anne-Marie has a deck of 16 cards, each with a distinct positive factor of 2002 written on it. She shuffles the deck and begins to draw cards from the deck without replacement. She stops when there exists a nonempty subset of the cards in her hand whose numbers multiply to a perfect square. What is the expected number of cards in her hand when she stops?
|
Answer: $\frac{837}{208}$
|
{
"resource_path": "HarvardMIT/segmented/en-232-2020-feb-comb-solutions.jsonl",
"problem_match": "\n7. ",
"solution_match": "\nProposed by: Michael Ren\n"
}
|
adc98376-025d-56dc-9cc5-849e3ce2e1f5
| 610,128
|
Let $\Gamma_{1}$ and $\Gamma_{2}$ be concentric circles with radii 1 and 2 , respectively. Four points are chosen on the circumference of $\Gamma_{2}$ independently and uniformly at random, and are then connected to form a convex quadrilateral. What is the probability that the perimeter of this quadrilateral intersects $\Gamma_{1}$ ?
|
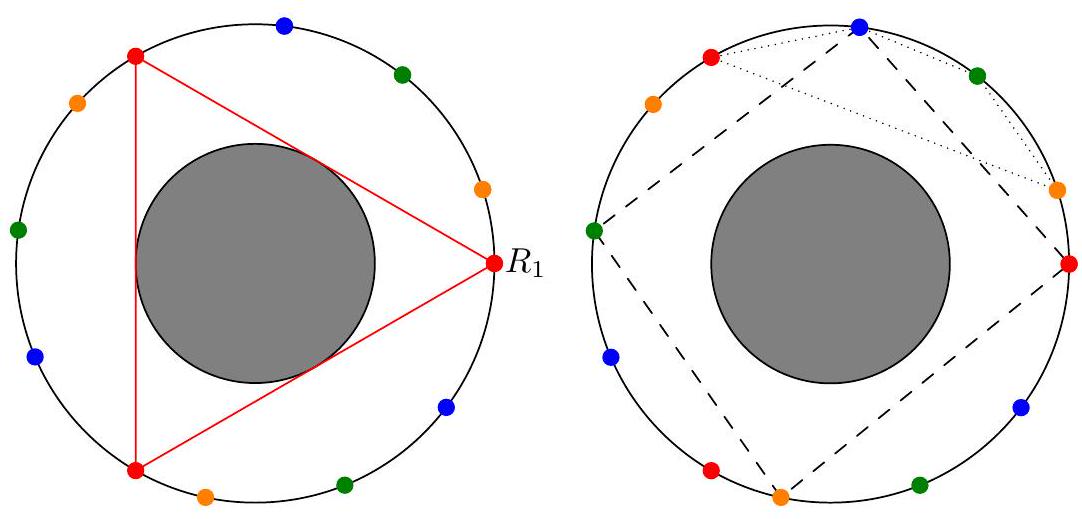
Define a triplet as three points on $\Gamma_{2}$ that form the vertices of an equilateral triangle. Note that due to the radii being 1 and 2, the sides of a triplet are all tangent to $\Gamma_{1}$. Rather than choosing four points on $\Gamma_{2}$ uniformly at random, we will choose four triplets of $\Gamma_{2}$ uniformly at random and then choose a random point from each triplet. (This results in the same distribution.) Assume without loss of generality that the first step creates 12 distinct points, as this occurs with probability 1.
In the set of twelve points, a segment between two of those points does not intersect $\Gamma_{1}$ if and only if they are at most three vertices apart. (In the diagram shown above, the segments connecting $R_{1}$ to the other red vertices are tangent to $\Gamma_{1}$, so the segments connecting $R_{1}$ to the six closer vertices do not intersect $\Gamma_{1}$.) There are two possibilities for the perimeter of the convex quadrilateral to not intersect $\Gamma_{1}$ : either the convex quadrilateral contains $\Gamma_{1}$ or is disjoint from it.
## Case 1: The quadrilateral contains $\Gamma_{1}$.
Each of the four segments of the quadrilateral passes at most three vertices, so the only possibility is that every third vertex is chosen. This is shown by the dashed quadrilateral in the diagram, and there are 3 such quadrilaterals.
## Case 2: The quadrilateral does not contain $\Gamma_{1}$.
In this case, all of the chosen vertices are at most three apart. This is only possible if we choose four consecutive vertices, which is shown by the dotted quadrilateral in the diagram. There are 12 such quadrilaterals.
Regardless of how the triplets are chosen, there are 81 ways to pick four points and $12+3=15$ of these choices result in a quadrilateral whose perimeter does not intersect $\Gamma_{1}$. The desired probability is $1-\frac{5}{27}=\frac{22}{27}$.
Remark. The problem can easily be generalized for a larger number of vertices, where $\Gamma_{1}$ and $\Gamma_{2}$ are the inscribed and circumscribed circles of a regular $n$-gon and $n+1$ points are chosen uniformly at random on $\Gamma_{2}$. The probability that the perimeter of the convex $(n+1)$-gon formed by those vertices intersects $\Gamma_{1}$ is $1-\frac{n+2}{n^{n}}$.
|
\frac{22}{27}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $\Gamma_{1}$ and $\Gamma_{2}$ be concentric circles with radii 1 and 2 , respectively. Four points are chosen on the circumference of $\Gamma_{2}$ independently and uniformly at random, and are then connected to form a convex quadrilateral. What is the probability that the perimeter of this quadrilateral intersects $\Gamma_{1}$ ?
|

Define a triplet as three points on $\Gamma_{2}$ that form the vertices of an equilateral triangle. Note that due to the radii being 1 and 2, the sides of a triplet are all tangent to $\Gamma_{1}$. Rather than choosing four points on $\Gamma_{2}$ uniformly at random, we will choose four triplets of $\Gamma_{2}$ uniformly at random and then choose a random point from each triplet. (This results in the same distribution.) Assume without loss of generality that the first step creates 12 distinct points, as this occurs with probability 1.
In the set of twelve points, a segment between two of those points does not intersect $\Gamma_{1}$ if and only if they are at most three vertices apart. (In the diagram shown above, the segments connecting $R_{1}$ to the other red vertices are tangent to $\Gamma_{1}$, so the segments connecting $R_{1}$ to the six closer vertices do not intersect $\Gamma_{1}$.) There are two possibilities for the perimeter of the convex quadrilateral to not intersect $\Gamma_{1}$ : either the convex quadrilateral contains $\Gamma_{1}$ or is disjoint from it.
## Case 1: The quadrilateral contains $\Gamma_{1}$.
Each of the four segments of the quadrilateral passes at most three vertices, so the only possibility is that every third vertex is chosen. This is shown by the dashed quadrilateral in the diagram, and there are 3 such quadrilaterals.
## Case 2: The quadrilateral does not contain $\Gamma_{1}$.
In this case, all of the chosen vertices are at most three apart. This is only possible if we choose four consecutive vertices, which is shown by the dotted quadrilateral in the diagram. There are 12 such quadrilaterals.
Regardless of how the triplets are chosen, there are 81 ways to pick four points and $12+3=15$ of these choices result in a quadrilateral whose perimeter does not intersect $\Gamma_{1}$. The desired probability is $1-\frac{5}{27}=\frac{22}{27}$.
Remark. The problem can easily be generalized for a larger number of vertices, where $\Gamma_{1}$ and $\Gamma_{2}$ are the inscribed and circumscribed circles of a regular $n$-gon and $n+1$ points are chosen uniformly at random on $\Gamma_{2}$. The probability that the perimeter of the convex $(n+1)$-gon formed by those vertices intersects $\Gamma_{1}$ is $1-\frac{n+2}{n^{n}}$.
|
{
"resource_path": "HarvardMIT/segmented/en-232-2020-feb-comb-solutions.jsonl",
"problem_match": "\n8. ",
"solution_match": "\n## Solution:\n\n"
}
|
cd8643bb-eaa5-585a-86f4-9f539419e72b
| 610,129
|
Farmer James wishes to cover a circle with circumference $10 \pi$ with six different types of colored arcs. Each type of arc has radius 5 , has length either $\pi$ or $2 \pi$, and is colored either red, green, or blue. He has an unlimited number of each of the six arc types. He wishes to completely cover his circle without overlap, subject to the following conditions:
- Any two adjacent arcs are of different colors.
- Any three adjacent arcs where the middle arc has length $\pi$ are of three different colors.
Find the number of distinct ways Farmer James can cover his circle. Here, two coverings are equivalent if and only if they are rotations of one another. In particular, two colorings are considered distinct if they are reflections of one another, but not rotations of one another.
|
Fix an orientation of the circle, and observe that the the problem is equivalent to finding the number of ways to color ten equal arcs of the circle such that each arc is one of three different colors, and any two arcs which are separated by exactly one arc are of different colors. We can consider every other arc, so we are trying to color just five arcs so that no two adjacent arcs are of the same color. This is independent from the coloring of the other five arcs.
Let $a_{i}$ be the number of ways to color $i$ arcs in three colors so that no two adjacent arcs are the same color. Note that $a_{1}=3$ and $a_{2}=6$. We claim that $a_{i}+a_{i+1}=3 \cdot 2^{i}$ for $i \geq 2$. To prove this, observe that $a_{i}$ counts the number of ways to color $i+1$ points in a line so that no two adjacent points are the same color, and the first and $(i+1)$ th points are the same color. Meanwhile, $a_{i+1}$ counts the number of ways to color $i+1$ points in a line so that no two adjacent points are the same color, and the first and $(i+1)$ th points are different colors. Then $a_{i}+a_{i+1}$ is the number of ways to color $i+1$ points in a line so that no two adjacent points are the same color. There are clearly $3 \cdot 2^{i}$ ways to do this, as we pick the colors from left to right, with 3 choices for the first color and 2 for the rest. We then compute $a_{3}=6, a_{4}=18, a_{5}=30$. Then we can color the whole original circle by picking one of the 30 possible colorings for each of the two sets of 5 alternating arcs, for $30^{2}=900$ total.
Now, we must consider the rotational symmetry. If a configuration has no rotational symmetry, then we have counted it 10 times. If a configuration has $180^{\circ}$ rotational symmetry, then we have counted it 5 times. This occurs exactly when we have picked the same coloring from our 30 for both choices, and in exactly one particular orientation, so there are 30 such cases. Having $72^{\circ}$ or $36^{\circ}$ rotational
symmetry is impossible, as arcs with exactly one arc between them must be different colors. Then after we correct for overcounting our answer is
$$
\frac{900-30}{10}+\frac{30}{5}=93
$$
|
93
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Farmer James wishes to cover a circle with circumference $10 \pi$ with six different types of colored arcs. Each type of arc has radius 5 , has length either $\pi$ or $2 \pi$, and is colored either red, green, or blue. He has an unlimited number of each of the six arc types. He wishes to completely cover his circle without overlap, subject to the following conditions:
- Any two adjacent arcs are of different colors.
- Any three adjacent arcs where the middle arc has length $\pi$ are of three different colors.
Find the number of distinct ways Farmer James can cover his circle. Here, two coverings are equivalent if and only if they are rotations of one another. In particular, two colorings are considered distinct if they are reflections of one another, but not rotations of one another.
|
Fix an orientation of the circle, and observe that the the problem is equivalent to finding the number of ways to color ten equal arcs of the circle such that each arc is one of three different colors, and any two arcs which are separated by exactly one arc are of different colors. We can consider every other arc, so we are trying to color just five arcs so that no two adjacent arcs are of the same color. This is independent from the coloring of the other five arcs.
Let $a_{i}$ be the number of ways to color $i$ arcs in three colors so that no two adjacent arcs are the same color. Note that $a_{1}=3$ and $a_{2}=6$. We claim that $a_{i}+a_{i+1}=3 \cdot 2^{i}$ for $i \geq 2$. To prove this, observe that $a_{i}$ counts the number of ways to color $i+1$ points in a line so that no two adjacent points are the same color, and the first and $(i+1)$ th points are the same color. Meanwhile, $a_{i+1}$ counts the number of ways to color $i+1$ points in a line so that no two adjacent points are the same color, and the first and $(i+1)$ th points are different colors. Then $a_{i}+a_{i+1}$ is the number of ways to color $i+1$ points in a line so that no two adjacent points are the same color. There are clearly $3 \cdot 2^{i}$ ways to do this, as we pick the colors from left to right, with 3 choices for the first color and 2 for the rest. We then compute $a_{3}=6, a_{4}=18, a_{5}=30$. Then we can color the whole original circle by picking one of the 30 possible colorings for each of the two sets of 5 alternating arcs, for $30^{2}=900$ total.
Now, we must consider the rotational symmetry. If a configuration has no rotational symmetry, then we have counted it 10 times. If a configuration has $180^{\circ}$ rotational symmetry, then we have counted it 5 times. This occurs exactly when we have picked the same coloring from our 30 for both choices, and in exactly one particular orientation, so there are 30 such cases. Having $72^{\circ}$ or $36^{\circ}$ rotational
symmetry is impossible, as arcs with exactly one arc between them must be different colors. Then after we correct for overcounting our answer is
$$
\frac{900-30}{10}+\frac{30}{5}=93
$$
|
{
"resource_path": "HarvardMIT/segmented/en-232-2020-feb-comb-solutions.jsonl",
"problem_match": "\n9. ",
"solution_match": "\nSolution: "
}
|
f14bd2fe-0416-50b6-9fff-5977eef8efad
| 610,130
|
Max repeatedly throws a fair coin in a hurricane. For each throw, there is a $4 \%$ chance that the coin gets blown away. He records the number of heads $H$ and the number of tails $T$ before the coin is lost. (If the coin is blown away on a toss, no result is recorded for that toss.) What is the expected value of $|H-T|$ ?
|
Answer: $\frac{24}{7}$
|
\frac{24}{7}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Max repeatedly throws a fair coin in a hurricane. For each throw, there is a $4 \%$ chance that the coin gets blown away. He records the number of heads $H$ and the number of tails $T$ before the coin is lost. (If the coin is blown away on a toss, no result is recorded for that toss.) What is the expected value of $|H-T|$ ?
|
Answer: $\frac{24}{7}$
|
{
"resource_path": "HarvardMIT/segmented/en-232-2020-feb-comb-solutions.jsonl",
"problem_match": "\n10. ",
"solution_match": "\nProposed by: Krit Boonsiriseth\n"
}
|
0848b58b-bee8-5119-b2fa-e1690130682b
| 610,131
|
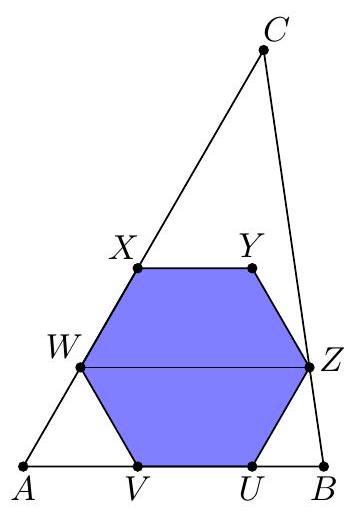
Let $A B C$ be a triangle with $A B=5, A C=8$, and $\angle B A C=60^{\circ}$. Let $U V W X Y Z$ be a regular hexagon that is inscribed inside $A B C$ such that $U$ and $V$ lie on side $B A, W$ and $X$ lie on side $A C$, and $Z$ lies on side $C B$. What is the side length of hexagon $U V W X Y Z$ ?
|
Let the side length of $U V W X Y Z$ be $s$. We have $W Z=2 s$ and $W Z \| A B$ by properties of regular hexagons. Thus, triangles $W C Z$ and $A C B$ are similar. $A W V$ is an equilateral triangle, so we have $A W=s$. Thus, using similar triangles, we have
$$
\frac{W C}{W Z}=\frac{A C}{A B} \Longrightarrow \frac{8-s}{2 s}=\frac{8}{5},
$$
so $5(8-s)=8(2 s) \Longrightarrow s=\frac{40}{21}$.
|
\frac{40}{21}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $A B C$ be a triangle with $A B=5, A C=8$, and $\angle B A C=60^{\circ}$. Let $U V W X Y Z$ be a regular hexagon that is inscribed inside $A B C$ such that $U$ and $V$ lie on side $B A, W$ and $X$ lie on side $A C$, and $Z$ lies on side $C B$. What is the side length of hexagon $U V W X Y Z$ ?
|
Let the side length of $U V W X Y Z$ be $s$. We have $W Z=2 s$ and $W Z \| A B$ by properties of regular hexagons. Thus, triangles $W C Z$ and $A C B$ are similar. $A W V$ is an equilateral triangle, so we have $A W=s$. Thus, using similar triangles, we have
$$
\frac{W C}{W Z}=\frac{A C}{A B} \Longrightarrow \frac{8-s}{2 s}=\frac{8}{5},
$$
so $5(8-s)=8(2 s) \Longrightarrow s=\frac{40}{21}$.

|
{
"resource_path": "HarvardMIT/segmented/en-232-2020-feb-geo-solutions.jsonl",
"problem_match": "\n2. ",
"solution_match": "\nSolution: "
}
|
cddd5f14-e6f2-5c0f-9bd4-8c216bf75244
| 610,133
|
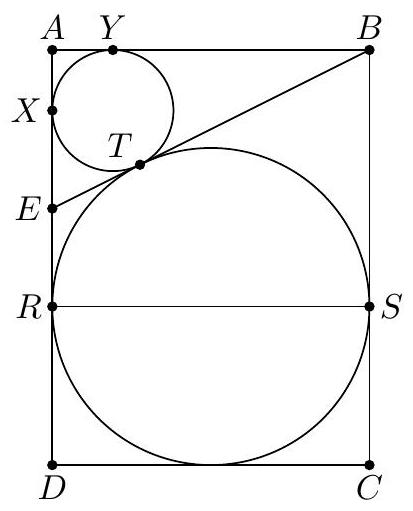
Let $A B C D$ be a rectangle and $E$ be a point on segment $A D$. We are given that quadrilateral $B C D E$ has an inscribed circle $\omega_{1}$ that is tangent to $B E$ at $T$. If the incircle $\omega_{2}$ of $A B E$ is also tangent to $B E$ at $T$, then find the ratio of the radius of $\omega_{1}$ to the radius of $\omega_{2}$.
|
Let $\omega_{1}$ be tangent to $A D, B C$ at $R, S$ and $\omega_{2}$ be tangent to $A D, A B$ at $X, Y$. Let $A X=A Y=r, E X=E T=E R=a, B Y=B T=B S=b$. Then noting that $R S \| C D$, we see that $A B S R$ is a rectangle, so $r+2 a=b$. Therefore $A E=a+r, A B=b+r=2(a+r)$, and so $B E=(a+r) \sqrt{5}$. On the other hand, $B E=b+a=r+3 a$. This implies that $a=\frac{1+\sqrt{5}}{2} r$. The desired ratio is then $\frac{R S}{2 A Y}=\frac{A B}{2 r}=\frac{a+r}{r}=\frac{3+\sqrt{5}}{2}$.
|
\frac{3+\sqrt{5}}{2}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $A B C D$ be a rectangle and $E$ be a point on segment $A D$. We are given that quadrilateral $B C D E$ has an inscribed circle $\omega_{1}$ that is tangent to $B E$ at $T$. If the incircle $\omega_{2}$ of $A B E$ is also tangent to $B E$ at $T$, then find the ratio of the radius of $\omega_{1}$ to the radius of $\omega_{2}$.
|
Let $\omega_{1}$ be tangent to $A D, B C$ at $R, S$ and $\omega_{2}$ be tangent to $A D, A B$ at $X, Y$. Let $A X=A Y=r, E X=E T=E R=a, B Y=B T=B S=b$. Then noting that $R S \| C D$, we see that $A B S R$ is a rectangle, so $r+2 a=b$. Therefore $A E=a+r, A B=b+r=2(a+r)$, and so $B E=(a+r) \sqrt{5}$. On the other hand, $B E=b+a=r+3 a$. This implies that $a=\frac{1+\sqrt{5}}{2} r$. The desired ratio is then $\frac{R S}{2 A Y}=\frac{A B}{2 r}=\frac{a+r}{r}=\frac{3+\sqrt{5}}{2}$.

|
{
"resource_path": "HarvardMIT/segmented/en-232-2020-feb-geo-solutions.jsonl",
"problem_match": "\n4. ",
"solution_match": "\nSolution: "
}
|
60f68d9f-df44-5719-814f-740de2be6d0e
| 610,135
|
Let $A B C D E F$ be a regular hexagon with side length 2. A circle with radius 3 and center at $A$ is drawn. Find the area inside quadrilateral $B C D E$ but outside the circle.
|
Answer: $4 \sqrt{3}-\frac{3}{2} \pi$
|
4 \sqrt{3}-\frac{3}{2} \pi
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $A B C D E F$ be a regular hexagon with side length 2. A circle with radius 3 and center at $A$ is drawn. Find the area inside quadrilateral $B C D E$ but outside the circle.
|
Answer: $4 \sqrt{3}-\frac{3}{2} \pi$
|
{
"resource_path": "HarvardMIT/segmented/en-232-2020-feb-geo-solutions.jsonl",
"problem_match": "\n5. ",
"solution_match": "\nProposed by: Carl Joshua Quines\n"
}
|
5b40886a-91b6-533d-a204-1ce06715a18d
| 610,136
|
Let $\Gamma$ be a circle, and $\omega_{1}$ and $\omega_{2}$ be two non-intersecting circles inside $\Gamma$ that are internally tangent to $\Gamma$ at $X_{1}$ and $X_{2}$, respectively. Let one of the common internal tangents of $\omega_{1}$ and $\omega_{2}$ touch $\omega_{1}$ and $\omega_{2}$ at $T_{1}$ and $T_{2}$, respectively, while intersecting $\Gamma$ at two points $A$ and $B$. Given that $2 X_{1} T_{1}=X_{2} T_{2}$ and that $\omega_{1}, \omega_{2}$, and $\Gamma$ have radii 2, 3, and 12 , respectively, compute the length of $A B$.
|
Let $\omega_{1}, \omega_{2}, \Gamma$ have centers $O_{1}, O_{2}, O$ and radii $r_{1}, r_{2}, R$ respectively. Let $d$ be the distance from $O$ to $A B$ (signed so that it is positive if $O$ and $O_{1}$ are on the same side of $A B$ ).
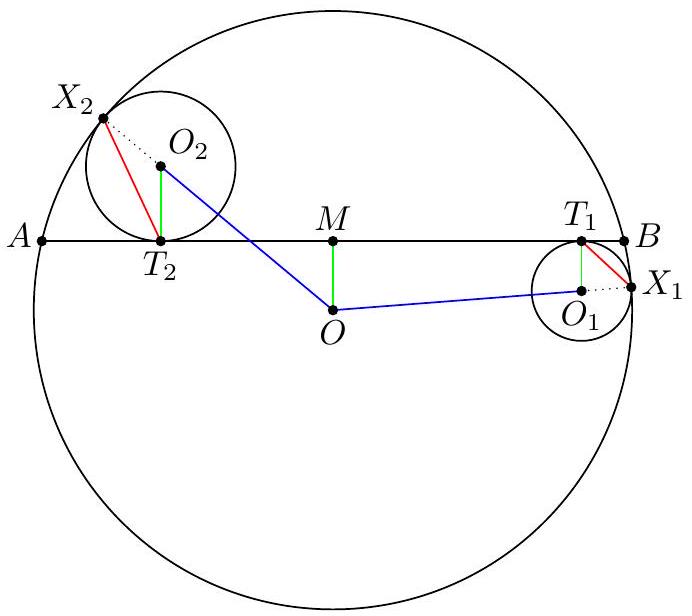
Note that
$$
\begin{array}{r}
O O_{i}=R-r_{i} \\
\cos \angle T_{1} O_{1} O=\frac{O_{1} T_{1}-O M}{O O_{1}}=\frac{r_{1}-d}{R-r_{1}} \\
\cos \angle T_{2} O_{2} O=\frac{O_{2} T_{2}+O M}{O O_{1}}=\frac{r_{2}+d}{R-r_{2}}
\end{array}
$$
Then
$$
\begin{aligned}
X_{1} T_{1} & =r_{1} \sqrt{2-2 \cos \angle X_{1} O_{1} T_{1}} \\
& =r_{i} \sqrt{2+2 \cos \angle T_{1} O_{1} O} \\
& =r_{1} \sqrt{2+2 \frac{r_{1}-d}{R-r_{1}}} \\
& =r_{1} \sqrt{2 \frac{R-d}{R-r_{1}}} .
\end{aligned}
$$
Likewise,
$$
X_{2} T_{2}=r_{2} \sqrt{2 \frac{R+d}{R-r_{2}}}
$$
From $2 X_{1} T_{1}=X_{2} T_{2}$ we have
$$
8 r_{1}^{2}\left(\frac{R-d}{R-r_{1}}\right)=4 X_{1} T_{1}^{2}=X_{2} T_{2}^{2}=2 r_{2}^{2}\left(\frac{R+d}{R-r_{2}}\right) .
$$
Plugging in $r_{1}=2, r_{2}=3, R=12$ and solving yields $d=\frac{36}{13}$. Hence $A B=2 \sqrt{R^{2}-d^{2}}=\frac{96 \sqrt{10}}{13}$.
|
\frac{96 \sqrt{10}}{13}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $\Gamma$ be a circle, and $\omega_{1}$ and $\omega_{2}$ be two non-intersecting circles inside $\Gamma$ that are internally tangent to $\Gamma$ at $X_{1}$ and $X_{2}$, respectively. Let one of the common internal tangents of $\omega_{1}$ and $\omega_{2}$ touch $\omega_{1}$ and $\omega_{2}$ at $T_{1}$ and $T_{2}$, respectively, while intersecting $\Gamma$ at two points $A$ and $B$. Given that $2 X_{1} T_{1}=X_{2} T_{2}$ and that $\omega_{1}, \omega_{2}$, and $\Gamma$ have radii 2, 3, and 12 , respectively, compute the length of $A B$.
|
Let $\omega_{1}, \omega_{2}, \Gamma$ have centers $O_{1}, O_{2}, O$ and radii $r_{1}, r_{2}, R$ respectively. Let $d$ be the distance from $O$ to $A B$ (signed so that it is positive if $O$ and $O_{1}$ are on the same side of $A B$ ).

Note that
$$
\begin{array}{r}
O O_{i}=R-r_{i} \\
\cos \angle T_{1} O_{1} O=\frac{O_{1} T_{1}-O M}{O O_{1}}=\frac{r_{1}-d}{R-r_{1}} \\
\cos \angle T_{2} O_{2} O=\frac{O_{2} T_{2}+O M}{O O_{1}}=\frac{r_{2}+d}{R-r_{2}}
\end{array}
$$
Then
$$
\begin{aligned}
X_{1} T_{1} & =r_{1} \sqrt{2-2 \cos \angle X_{1} O_{1} T_{1}} \\
& =r_{i} \sqrt{2+2 \cos \angle T_{1} O_{1} O} \\
& =r_{1} \sqrt{2+2 \frac{r_{1}-d}{R-r_{1}}} \\
& =r_{1} \sqrt{2 \frac{R-d}{R-r_{1}}} .
\end{aligned}
$$
Likewise,
$$
X_{2} T_{2}=r_{2} \sqrt{2 \frac{R+d}{R-r_{2}}}
$$
From $2 X_{1} T_{1}=X_{2} T_{2}$ we have
$$
8 r_{1}^{2}\left(\frac{R-d}{R-r_{1}}\right)=4 X_{1} T_{1}^{2}=X_{2} T_{2}^{2}=2 r_{2}^{2}\left(\frac{R+d}{R-r_{2}}\right) .
$$
Plugging in $r_{1}=2, r_{2}=3, R=12$ and solving yields $d=\frac{36}{13}$. Hence $A B=2 \sqrt{R^{2}-d^{2}}=\frac{96 \sqrt{10}}{13}$.
|
{
"resource_path": "HarvardMIT/segmented/en-232-2020-feb-geo-solutions.jsonl",
"problem_match": "\n7. ",
"solution_match": "\nSolution 1: "
}
|
ef306b0e-bd0b-5de3-8c17-40a94af5a616
| 610,138
|
Circles $\omega_{a}, \omega_{b}, \omega_{c}$ have centers $A, B, C$, respectively and are pairwise externally tangent at points $D, E, F$ (with $D \in B C, E \in C A, F \in A B$ ). Lines $B E$ and $C F$ meet at $T$. Given that $\omega_{a}$ has radius 341 , there exists a line $\ell$ tangent to all three circles, and there exists a circle of radius 49 tangent to all three circles, compute the distance from $T$ to $\ell$.
|
We will use the following notation: let $\omega$ be the circle of radius 49 tangent to each of $\omega_{a}, \omega_{b}, \omega_{c}$. Let $\omega_{a}, \omega_{b}, \omega_{c}$ have radii $r_{a}, r_{b}, r_{c}$ respectively. Let $\gamma$ be the incircle of $A B C$, with center $I$ and radius $r$. Note that $D E F$ is the intouch triangle of $A B C$ and $\gamma$ is orthogonal to $\omega_{a}, \omega_{b}, \omega_{c}$ (i.e. $I D, I E, I F$ are the common internal tangents). Since $A D, B E, C F$ are concurrent at $T$, we have $K=A B \cap D E$ satisfies $(A, B ; F, K)=-1$, so $K$ is the external center of homothety of $\omega_{a}$ and $\omega_{b}$. In particular, $K$ lies on $\ell$. Similarly, $B C \cap E F$ also lies on $\ell$, so $\ell$ is the polar of $T$ to $\gamma$. Hence $I T \perp \ell$ so if $L$ is the foot from $I$ to $\ell$, we have $I T \cdot I L=r^{2}$.
An inversion about $\gamma$ preserves $\omega_{a}, \omega_{b}, \omega_{c}$ and sends $\ell$ to the circle with diameter $I T$. Since inversion preserves tangency, the circle with diameter $I T$ must be $\omega$. Therefore $I T=98$ by the condition of the problem statement. Letting $a, b, c$ be the radii of $\omega_{a}, \omega_{b}, \omega_{c}$ respectively and invoking Heron's formula as well as $A=r s$ for triangle $A B C$, we see that $\gamma$ has radius
$$
r=\sqrt{\frac{r_{a} r_{b} r_{c}}{r_{a}+r_{b}+r_{c}}} .
$$
We will compute this quantity using Descartes' theorem. Note that there are two circles tangent to $\omega_{a}$, $\omega_{b}, \omega_{c}$, one with radius $I T / 2$ and one with radius $\infty$. By Descartes' circle theorem, we have (where $k_{a}:=1 / a$ is the curvature)
$$
k_{a}+k_{b}+k_{c}+2 \sqrt{k_{a} k_{b}+k_{b} k_{c}+k_{a} k_{c}}=\frac{1}{I T / 2}
$$
and
$$
k_{a}+k_{b}+k_{c}-2 \sqrt{k_{a} k_{b}+k_{b} k_{c}+k_{c} k_{a}}=0
$$
which implies
$$
\sqrt{\frac{r_{a}+r_{b}+r_{c}}{r_{a} r_{b} r_{c}}}=\sqrt{k_{a} k_{b}+k_{b} k_{c}+k_{c} k_{a}}=\frac{1}{2 I T} .
$$
Therefore $r=2 I T$, which means $I L=\frac{r^{2}}{I T}=4 I T$ and $T L=3 I T=294$.
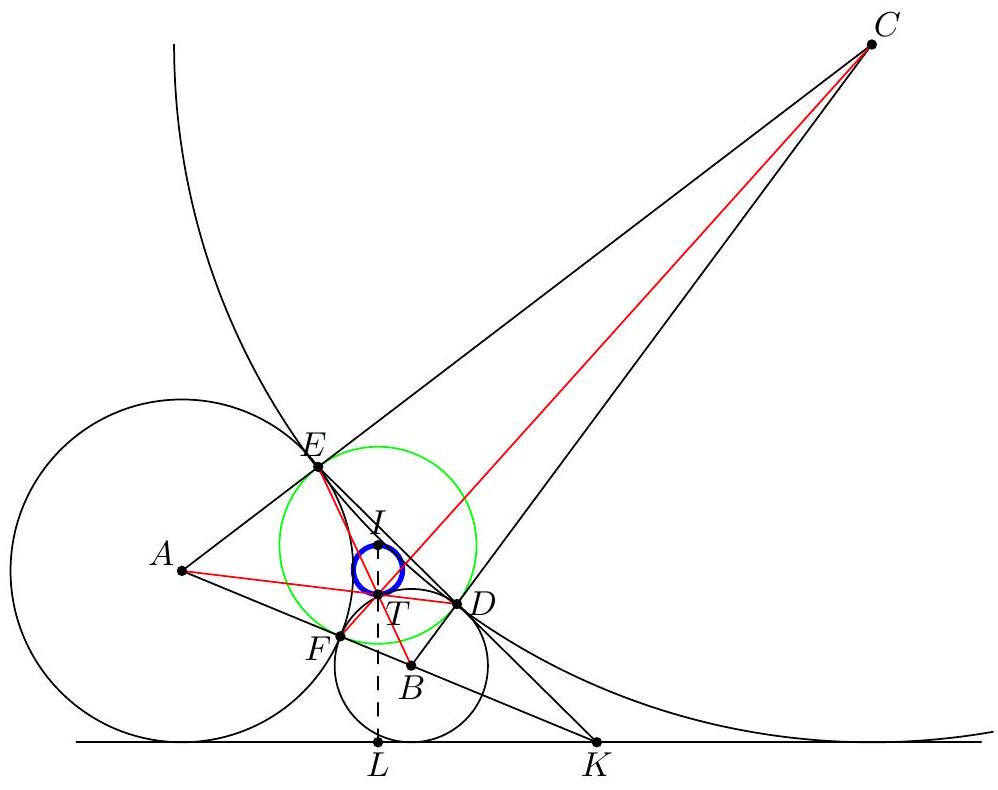
|
294
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Circles $\omega_{a}, \omega_{b}, \omega_{c}$ have centers $A, B, C$, respectively and are pairwise externally tangent at points $D, E, F$ (with $D \in B C, E \in C A, F \in A B$ ). Lines $B E$ and $C F$ meet at $T$. Given that $\omega_{a}$ has radius 341 , there exists a line $\ell$ tangent to all three circles, and there exists a circle of radius 49 tangent to all three circles, compute the distance from $T$ to $\ell$.
|
We will use the following notation: let $\omega$ be the circle of radius 49 tangent to each of $\omega_{a}, \omega_{b}, \omega_{c}$. Let $\omega_{a}, \omega_{b}, \omega_{c}$ have radii $r_{a}, r_{b}, r_{c}$ respectively. Let $\gamma$ be the incircle of $A B C$, with center $I$ and radius $r$. Note that $D E F$ is the intouch triangle of $A B C$ and $\gamma$ is orthogonal to $\omega_{a}, \omega_{b}, \omega_{c}$ (i.e. $I D, I E, I F$ are the common internal tangents). Since $A D, B E, C F$ are concurrent at $T$, we have $K=A B \cap D E$ satisfies $(A, B ; F, K)=-1$, so $K$ is the external center of homothety of $\omega_{a}$ and $\omega_{b}$. In particular, $K$ lies on $\ell$. Similarly, $B C \cap E F$ also lies on $\ell$, so $\ell$ is the polar of $T$ to $\gamma$. Hence $I T \perp \ell$ so if $L$ is the foot from $I$ to $\ell$, we have $I T \cdot I L=r^{2}$.
An inversion about $\gamma$ preserves $\omega_{a}, \omega_{b}, \omega_{c}$ and sends $\ell$ to the circle with diameter $I T$. Since inversion preserves tangency, the circle with diameter $I T$ must be $\omega$. Therefore $I T=98$ by the condition of the problem statement. Letting $a, b, c$ be the radii of $\omega_{a}, \omega_{b}, \omega_{c}$ respectively and invoking Heron's formula as well as $A=r s$ for triangle $A B C$, we see that $\gamma$ has radius
$$
r=\sqrt{\frac{r_{a} r_{b} r_{c}}{r_{a}+r_{b}+r_{c}}} .
$$
We will compute this quantity using Descartes' theorem. Note that there are two circles tangent to $\omega_{a}$, $\omega_{b}, \omega_{c}$, one with radius $I T / 2$ and one with radius $\infty$. By Descartes' circle theorem, we have (where $k_{a}:=1 / a$ is the curvature)
$$
k_{a}+k_{b}+k_{c}+2 \sqrt{k_{a} k_{b}+k_{b} k_{c}+k_{a} k_{c}}=\frac{1}{I T / 2}
$$
and
$$
k_{a}+k_{b}+k_{c}-2 \sqrt{k_{a} k_{b}+k_{b} k_{c}+k_{c} k_{a}}=0
$$
which implies
$$
\sqrt{\frac{r_{a}+r_{b}+r_{c}}{r_{a} r_{b} r_{c}}}=\sqrt{k_{a} k_{b}+k_{b} k_{c}+k_{c} k_{a}}=\frac{1}{2 I T} .
$$
Therefore $r=2 I T$, which means $I L=\frac{r^{2}}{I T}=4 I T$ and $T L=3 I T=294$.

|
{
"resource_path": "HarvardMIT/segmented/en-232-2020-feb-geo-solutions.jsonl",
"problem_match": "\n9. ",
"solution_match": "\nSolution 1: "
}
|
5bb93a78-0bd0-5e49-9c18-d2ee18337386
| 610,140
|
Let $\Gamma$ be a circle of radius 1 centered at $O$. A circle $\Omega$ is said to be friendly if there exist distinct circles $\omega_{1}, \omega_{2}, \ldots, \omega_{2020}$, such that for all $1 \leq i \leq 2020, \omega_{i}$ is tangent to $\Gamma, \Omega$, and $\omega_{i+1}$. (Here, $\omega_{2021}=\omega_{1}$.) For each point $P$ in the plane, let $f(P)$ denote the sum of the areas of all friendly circles centered at $P$. If $A$ and $B$ are points such that $O A=\frac{1}{2}$ and $O B=\frac{1}{3}$, determine $f(A)-f(B)$.
|
Let $P$ satisfy $O P=x$. (For now, we focus on $f(P)$ and ignore the $A$ and $B$ from the problem statement.) The key idea is that if we invert at some point along $O P$ such that the images of $\Gamma$ and $\Omega$ are concentric, then $\omega_{i}$ still exist. Suppose that this inversion fixes $\Gamma$ and takes $\Omega$ to $\Omega^{\prime}$ of radius $r$ (and $X$ to $X^{\prime}$ in general). If the inversion is centered at a point $Q$ along ray $O P$ such that $O Q=d$, then the radius of inversion is $\sqrt{d^{2}-1}$. Let the diameter of $\Omega$ meet $O Q$ at $A$ and $B$ with $A$ closer to $Q$ than $B$. Then, $\left(A B ; P P_{\infty}\right)=-1$ inverts to $\left(A^{\prime} B^{\prime} ; P^{\prime} Q\right)=-1$, where $P_{\infty}$ is the point at infinity along line $O P$, so $P^{\prime}$ is the inverse of $Q$ in $\Omega^{\prime}$. We can compute $O P^{\prime}=\frac{r^{2}}{d}$ so $P^{\prime} Q=d-\frac{r^{2}}{d}$ and $P Q=\frac{d^{2}-1}{d-\frac{r^{2}}{d}}$. Thus, we get the equation $\frac{d^{2}-1}{d-\frac{r^{2}}{d}}+x=d$, which rearranges to $\frac{1-r^{2}}{d^{2}-r^{2}} d=x$, or $d^{2}-x^{-1}\left(1-r^{2}\right) d-r^{2}=0$. Now, we note that the radius of $\Omega$ is
$$
\frac{1}{2} A B=\frac{1}{2}\left(\frac{d^{2}-1}{d-r}-\frac{d^{2}-1}{d+r}\right)=\frac{r\left(d^{2}-1\right)}{d^{2}-r^{2}}=r\left(1+\frac{r^{2}-1}{d^{2}-r^{2}}\right)=r\left(1-\frac{x}{d}\right)
$$
The quadratic formula gives us that $d=\frac{\left(1-r^{2}\right) \pm \sqrt{r^{4}-\left(2-4 x^{2}\right) r^{2}+1}}{2 x}$, so $\frac{x}{d}=-\frac{1-r^{2} \pm \sqrt{r^{4}-\left(2-4 x^{2}\right) r^{2}+1}}{2 r^{2}}$, which means that the radius of $\Omega$ is
$$
\frac{r^{2}+1 \pm \sqrt{r^{4}-\left(2-4 x^{2}\right) r^{2}+1}}{2 r}=\frac{r+\frac{1}{r} \pm \sqrt{r^{2}+\frac{1}{r^{2}}-2+4 x^{2}}}{2}
$$
Note that if $r$ gives a valid chain of 2020 circles, so will $\frac{1}{r}$ by homothety/inversion. Thus, we can think of each pair of $r, \frac{1}{r}$ as giving rise to two possible values of the radius of $\Omega$, which are $\frac{r+\frac{1}{r} \pm \sqrt{r^{2}+\frac{1}{r^{2}}-1}}{2}$. This means that the pairs have the same sum of radii as the circles centered at $O$, and the product of the radii is $1-x^{2}$. (A simpler way to see this is to note that inversion at $P$ with radius $\sqrt{1-x^{2}}$ swaps the two circles.) From this, it follows that the difference between the sum of the areas for each pair is $2 \pi\left(\frac{1}{2^{2}}-\frac{1}{3^{2}}\right)=\frac{5}{18} \pi$. There are $\frac{\varphi(2020)}{2}=400$ such pairs, which can be explicitly computed as $\frac{1-\sin \frac{\pi k}{2020}}{1+\sin \frac{\pi k}{2020}}, \frac{1+\sin \frac{\pi k}{2020}}{1-\sin \frac{\pi k}{2020}}$ for positive integers $k<1010$ relatively prime to 2020 . Thus, the answer is $\frac{1000}{9} \pi$.
|
\frac{1000}{9} \pi
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $\Gamma$ be a circle of radius 1 centered at $O$. A circle $\Omega$ is said to be friendly if there exist distinct circles $\omega_{1}, \omega_{2}, \ldots, \omega_{2020}$, such that for all $1 \leq i \leq 2020, \omega_{i}$ is tangent to $\Gamma, \Omega$, and $\omega_{i+1}$. (Here, $\omega_{2021}=\omega_{1}$.) For each point $P$ in the plane, let $f(P)$ denote the sum of the areas of all friendly circles centered at $P$. If $A$ and $B$ are points such that $O A=\frac{1}{2}$ and $O B=\frac{1}{3}$, determine $f(A)-f(B)$.
|
Let $P$ satisfy $O P=x$. (For now, we focus on $f(P)$ and ignore the $A$ and $B$ from the problem statement.) The key idea is that if we invert at some point along $O P$ such that the images of $\Gamma$ and $\Omega$ are concentric, then $\omega_{i}$ still exist. Suppose that this inversion fixes $\Gamma$ and takes $\Omega$ to $\Omega^{\prime}$ of radius $r$ (and $X$ to $X^{\prime}$ in general). If the inversion is centered at a point $Q$ along ray $O P$ such that $O Q=d$, then the radius of inversion is $\sqrt{d^{2}-1}$. Let the diameter of $\Omega$ meet $O Q$ at $A$ and $B$ with $A$ closer to $Q$ than $B$. Then, $\left(A B ; P P_{\infty}\right)=-1$ inverts to $\left(A^{\prime} B^{\prime} ; P^{\prime} Q\right)=-1$, where $P_{\infty}$ is the point at infinity along line $O P$, so $P^{\prime}$ is the inverse of $Q$ in $\Omega^{\prime}$. We can compute $O P^{\prime}=\frac{r^{2}}{d}$ so $P^{\prime} Q=d-\frac{r^{2}}{d}$ and $P Q=\frac{d^{2}-1}{d-\frac{r^{2}}{d}}$. Thus, we get the equation $\frac{d^{2}-1}{d-\frac{r^{2}}{d}}+x=d$, which rearranges to $\frac{1-r^{2}}{d^{2}-r^{2}} d=x$, or $d^{2}-x^{-1}\left(1-r^{2}\right) d-r^{2}=0$. Now, we note that the radius of $\Omega$ is
$$
\frac{1}{2} A B=\frac{1}{2}\left(\frac{d^{2}-1}{d-r}-\frac{d^{2}-1}{d+r}\right)=\frac{r\left(d^{2}-1\right)}{d^{2}-r^{2}}=r\left(1+\frac{r^{2}-1}{d^{2}-r^{2}}\right)=r\left(1-\frac{x}{d}\right)
$$
The quadratic formula gives us that $d=\frac{\left(1-r^{2}\right) \pm \sqrt{r^{4}-\left(2-4 x^{2}\right) r^{2}+1}}{2 x}$, so $\frac{x}{d}=-\frac{1-r^{2} \pm \sqrt{r^{4}-\left(2-4 x^{2}\right) r^{2}+1}}{2 r^{2}}$, which means that the radius of $\Omega$ is
$$
\frac{r^{2}+1 \pm \sqrt{r^{4}-\left(2-4 x^{2}\right) r^{2}+1}}{2 r}=\frac{r+\frac{1}{r} \pm \sqrt{r^{2}+\frac{1}{r^{2}}-2+4 x^{2}}}{2}
$$
Note that if $r$ gives a valid chain of 2020 circles, so will $\frac{1}{r}$ by homothety/inversion. Thus, we can think of each pair of $r, \frac{1}{r}$ as giving rise to two possible values of the radius of $\Omega$, which are $\frac{r+\frac{1}{r} \pm \sqrt{r^{2}+\frac{1}{r^{2}}-1}}{2}$. This means that the pairs have the same sum of radii as the circles centered at $O$, and the product of the radii is $1-x^{2}$. (A simpler way to see this is to note that inversion at $P$ with radius $\sqrt{1-x^{2}}$ swaps the two circles.) From this, it follows that the difference between the sum of the areas for each pair is $2 \pi\left(\frac{1}{2^{2}}-\frac{1}{3^{2}}\right)=\frac{5}{18} \pi$. There are $\frac{\varphi(2020)}{2}=400$ such pairs, which can be explicitly computed as $\frac{1-\sin \frac{\pi k}{2020}}{1+\sin \frac{\pi k}{2020}}, \frac{1+\sin \frac{\pi k}{2020}}{1-\sin \frac{\pi k}{2020}}$ for positive integers $k<1010$ relatively prime to 2020 . Thus, the answer is $\frac{1000}{9} \pi$.
|
{
"resource_path": "HarvardMIT/segmented/en-232-2020-feb-geo-solutions.jsonl",
"problem_match": "\n10. ",
"solution_match": "\nSolution: "
}
|
083067bb-d032-5dd0-9516-a34f03c72d55
| 610,141
|
Let $A B C$ be a triangle and $D, E$, and $F$ be the midpoints of sides $B C, C A$, and $A B$ respectively. What is the maximum number of circles which pass through at least 3 of these 6 points?
|
All $\binom{6}{3}=20$ triples of points can produce distinct circles aside from the case where the three points are collinear $(B D C, C E A, A F B)$.
|
20
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $A B C$ be a triangle and $D, E$, and $F$ be the midpoints of sides $B C, C A$, and $A B$ respectively. What is the maximum number of circles which pass through at least 3 of these 6 points?
|
All $\binom{6}{3}=20$ triples of points can produce distinct circles aside from the case where the three points are collinear $(B D C, C E A, A F B)$.
|
{
"resource_path": "HarvardMIT/segmented/en-232-2020-feb-guts-solutions.jsonl",
"problem_match": "\n3. [4]",
"solution_match": "\nSolution: "
}
|
1267c4f7-0082-596e-937e-74cb6d4adb9f
| 610,144
|
Compute the value of $\sqrt{105^{3}-104^{3}}$, given that it is a positive integer.
|
First compute $105^{3}-104^{3}=105^{2}+105 \cdot 104+104^{2}=3 \cdot 105 \cdot 104+1=32761$. Note that $180^{2}=32400$, so $181^{2}=180^{2}+2 \cdot 180+1=32761$ as desired.
|
181
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Compute the value of $\sqrt{105^{3}-104^{3}}$, given that it is a positive integer.
|
First compute $105^{3}-104^{3}=105^{2}+105 \cdot 104+104^{2}=3 \cdot 105 \cdot 104+1=32761$. Note that $180^{2}=32400$, so $181^{2}=180^{2}+2 \cdot 180+1=32761$ as desired.
|
{
"resource_path": "HarvardMIT/segmented/en-232-2020-feb-guts-solutions.jsonl",
"problem_match": "\n4. [4]",
"solution_match": "\nSolution 1: "
}
|
05d8cdc7-ca5b-5c17-aaf0-4f62596465e7
| 610,145
|
Alice, Bob, and Charlie roll a 4,5 , and 6 -sided die, respectively. What is the probability that a number comes up exactly twice out of the three rolls?
|
There are $4 \cdot 5 \cdot 6=120$ different ways that the dice can come up. The common number can be any of $1,2,3,4$, or 5 : there are $3+4+5=12$ ways for it to be each of $1,2,3$, or 4 , because we pick one of the three people's rolls to disagree, and there are 3,4 , and 5 ways that roll can come up (for Alice, Bob, and Charlie respectively). Finally, there are 4 ways for Bob and Charlie to both roll a 5 and Alice to roll any number. Thus there are 52 different ways to satisfy the problem condition, and our answer is $\frac{52}{120}=\frac{13}{30}$.
|
\frac{13}{30}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Alice, Bob, and Charlie roll a 4,5 , and 6 -sided die, respectively. What is the probability that a number comes up exactly twice out of the three rolls?
|
There are $4 \cdot 5 \cdot 6=120$ different ways that the dice can come up. The common number can be any of $1,2,3,4$, or 5 : there are $3+4+5=12$ ways for it to be each of $1,2,3$, or 4 , because we pick one of the three people's rolls to disagree, and there are 3,4 , and 5 ways that roll can come up (for Alice, Bob, and Charlie respectively). Finally, there are 4 ways for Bob and Charlie to both roll a 5 and Alice to roll any number. Thus there are 52 different ways to satisfy the problem condition, and our answer is $\frac{52}{120}=\frac{13}{30}$.
|
{
"resource_path": "HarvardMIT/segmented/en-232-2020-feb-guts-solutions.jsonl",
"problem_match": "\n5. [5]",
"solution_match": "\nSolution 1: "
}
|
2cbd2664-645d-5a94-962b-2dacc7baa5f3
| 610,146
|
Two sides of a regular $n$-gon are extended to meet at a $28^{\circ}$ angle. What is the smallest possible value for $n$ ?
|
We note that if we inscribe the $n$-gon in a circle, then according to the inscribed angle theorem, the angle between two sides is $\frac{1}{2}$ times some $x-y$, where $x$ and $y$ are integer multiples of the arc measure of one side of the $n$-gon. Thus, the angle is equal to $\frac{1}{2}$ times an integer multiple of $\frac{360}{n}$, so $\frac{1}{2} \cdot k \cdot \frac{360}{n}=28$ for some integer $k$. Simplifying gives $7 n=45 k$, and since all $k$ are clearly attainable, the smallest possible value of $n$ is 45 .
|
45
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Two sides of a regular $n$-gon are extended to meet at a $28^{\circ}$ angle. What is the smallest possible value for $n$ ?
|
We note that if we inscribe the $n$-gon in a circle, then according to the inscribed angle theorem, the angle between two sides is $\frac{1}{2}$ times some $x-y$, where $x$ and $y$ are integer multiples of the arc measure of one side of the $n$-gon. Thus, the angle is equal to $\frac{1}{2}$ times an integer multiple of $\frac{360}{n}$, so $\frac{1}{2} \cdot k \cdot \frac{360}{n}=28$ for some integer $k$. Simplifying gives $7 n=45 k$, and since all $k$ are clearly attainable, the smallest possible value of $n$ is 45 .
|
{
"resource_path": "HarvardMIT/segmented/en-232-2020-feb-guts-solutions.jsonl",
"problem_match": "\n6. [5]",
"solution_match": "\nSolution: "
}
|
a471cbc7-c763-531e-9dc2-c99d2a10a240
| 610,147
|
Ana and Banana are rolling a standard six-sided die. Ana rolls the die twice, obtaining $a_{1}$ and $a_{2}$, then Banana rolls the die twice, obtaining $b_{1}$ and $b_{2}$. After Ana's two rolls but before Banana's two rolls, they compute the probability $p$ that $a_{1} b_{1}+a_{2} b_{2}$ will be a multiple of 6 . What is the probability that $p=\frac{1}{6}$ ?
|
If either $a_{1}$ or $a_{2}$ is relatively prime to 6 , then $p=\frac{1}{6}$. If one of them is a multiple of 2 but not 6 , while the other is a multiple of 3 but not 6 , we also have $p=\frac{1}{6}$. In other words, $p=\frac{1}{6}$ if $\operatorname{gcd}\left(a_{1}, a_{2}\right)$ is coprime to 6 , and otherwise $p \neq \frac{1}{6}$. The probability that $p=\frac{1}{6}$ is $\frac{\left(3^{2}-1\right)\left(2^{2}-1\right)}{6^{2}}=\frac{2}{3}$ where $\frac{q^{2}-1}{q^{2}}$ corresponds to the probability that at least one of $a_{1}$ and $a_{2}$ is not divisible by $q$ for $q=2,3$.
|
\frac{2}{3}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Ana and Banana are rolling a standard six-sided die. Ana rolls the die twice, obtaining $a_{1}$ and $a_{2}$, then Banana rolls the die twice, obtaining $b_{1}$ and $b_{2}$. After Ana's two rolls but before Banana's two rolls, they compute the probability $p$ that $a_{1} b_{1}+a_{2} b_{2}$ will be a multiple of 6 . What is the probability that $p=\frac{1}{6}$ ?
|
If either $a_{1}$ or $a_{2}$ is relatively prime to 6 , then $p=\frac{1}{6}$. If one of them is a multiple of 2 but not 6 , while the other is a multiple of 3 but not 6 , we also have $p=\frac{1}{6}$. In other words, $p=\frac{1}{6}$ if $\operatorname{gcd}\left(a_{1}, a_{2}\right)$ is coprime to 6 , and otherwise $p \neq \frac{1}{6}$. The probability that $p=\frac{1}{6}$ is $\frac{\left(3^{2}-1\right)\left(2^{2}-1\right)}{6^{2}}=\frac{2}{3}$ where $\frac{q^{2}-1}{q^{2}}$ corresponds to the probability that at least one of $a_{1}$ and $a_{2}$ is not divisible by $q$ for $q=2,3$.
|
{
"resource_path": "HarvardMIT/segmented/en-232-2020-feb-guts-solutions.jsonl",
"problem_match": "\n7. [5]",
"solution_match": "\nSolution: "
}
|
4f76e3cb-06e0-5db3-b016-1377c9926db5
| 610,148
|
Tessa picks three real numbers $x, y, z$ and computes the values of the eight expressions of the form $\pm x \pm y \pm z$. She notices that the eight values are all distinct, so she writes the expressions down in increasing order. For example, if $x=2, y=3, z=4$, then the order she writes them down is
$$
-x-y-z,+x-y-z,-x+y-z,-x-y+z,+x+y-z,+x-y+z,-x+y+z,+x+y+z
$$
How many possible orders are there?
|
Answer: 96
|
96
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Tessa picks three real numbers $x, y, z$ and computes the values of the eight expressions of the form $\pm x \pm y \pm z$. She notices that the eight values are all distinct, so she writes the expressions down in increasing order. For example, if $x=2, y=3, z=4$, then the order she writes them down is
$$
-x-y-z,+x-y-z,-x+y-z,-x-y+z,+x+y-z,+x-y+z,-x+y+z,+x+y+z
$$
How many possible orders are there?
|
Answer: 96
|
{
"resource_path": "HarvardMIT/segmented/en-232-2020-feb-guts-solutions.jsonl",
"problem_match": "\n8. [5]",
"solution_match": "\nProposed by: Yuan Yao\n"
}
|
b24affa6-1a99-529f-a2a1-3d515b45c7ca
| 610,149
|
Jarris is a weighted tetrahedral die with faces $F_{1}, F_{2}, F_{3}, F_{4}$. He tosses himself onto a table, so that the probability he lands on a given face is proportional to the area of that face (i.e. the probability he lands on face $F_{i}$ is $\frac{\left[F_{i}\right]}{\left[F_{1}\right]+\left[F_{2}\right]+\left[F_{3}\right]+\left[F_{4}\right]}$ where $[K]$ is the area of $\left.K\right)$. Let $k$ be the maximum distance any part of Jarris is from the table after he rolls himself. Given that Jarris has an inscribed sphere of radius 3 and circumscribed sphere of radius 10, find the minimum possible value of the expected value of $k$.
|
Since the maximum distance to the table is just the height, the expected value is equal to $\frac{\sum_{i=1}^{4} h_{i}\left[F_{i}\right]}{\sum_{i=1}^{4}\left[F_{i}\right]}$. Let $V$ be the volume of Jarris. Recall that $V=\frac{1}{3} h_{i}\left[F_{i}\right]$ for any $i$, but also $V=\frac{r}{3}\left(\sum_{i=1}^{4}\left[F_{i}\right]\right)$
where $r$ is the inradius (by decomposing into four tetrahedra with a vertex at the incenter). Therefore
$$
\frac{\sum_{i=1}^{4} h_{i}\left[F_{i}\right]}{\sum_{i=1}^{4}\left[F_{i}\right]}=\frac{12 V}{3 V / r}=4 r=12 .
$$
|
12
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Jarris is a weighted tetrahedral die with faces $F_{1}, F_{2}, F_{3}, F_{4}$. He tosses himself onto a table, so that the probability he lands on a given face is proportional to the area of that face (i.e. the probability he lands on face $F_{i}$ is $\frac{\left[F_{i}\right]}{\left[F_{1}\right]+\left[F_{2}\right]+\left[F_{3}\right]+\left[F_{4}\right]}$ where $[K]$ is the area of $\left.K\right)$. Let $k$ be the maximum distance any part of Jarris is from the table after he rolls himself. Given that Jarris has an inscribed sphere of radius 3 and circumscribed sphere of radius 10, find the minimum possible value of the expected value of $k$.
|
Since the maximum distance to the table is just the height, the expected value is equal to $\frac{\sum_{i=1}^{4} h_{i}\left[F_{i}\right]}{\sum_{i=1}^{4}\left[F_{i}\right]}$. Let $V$ be the volume of Jarris. Recall that $V=\frac{1}{3} h_{i}\left[F_{i}\right]$ for any $i$, but also $V=\frac{r}{3}\left(\sum_{i=1}^{4}\left[F_{i}\right]\right)$
where $r$ is the inradius (by decomposing into four tetrahedra with a vertex at the incenter). Therefore
$$
\frac{\sum_{i=1}^{4} h_{i}\left[F_{i}\right]}{\sum_{i=1}^{4}\left[F_{i}\right]}=\frac{12 V}{3 V / r}=4 r=12 .
$$
|
{
"resource_path": "HarvardMIT/segmented/en-232-2020-feb-guts-solutions.jsonl",
"problem_match": "\n10. [6]",
"solution_match": "\nSolution: "
}
|
a049d0d3-60ad-597d-8a32-2d1f4807058a
| 610,151
|
Find the number of ordered pairs of positive integers $(x, y)$ with $x, y \leq 2020$ such that $3 x^{2}+10 x y+$ $3 y^{2}$ is the power of some prime.
|
We can factor as $(3 x+y)(x+3 y)$. If $x \geq y$, we need $\frac{3 x+y}{x+3 y} \in\{1,2\}$ to be an integer. So we get the case where $x=y$, in which we need both to be a power of 2 , or the case $x=5 y$, in which case we need $y$ to be a power of 2 . This gives us $11+9+9=29$ solutions, where we account for $y=5 x$ as well.
|
29
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Find the number of ordered pairs of positive integers $(x, y)$ with $x, y \leq 2020$ such that $3 x^{2}+10 x y+$ $3 y^{2}$ is the power of some prime.
|
We can factor as $(3 x+y)(x+3 y)$. If $x \geq y$, we need $\frac{3 x+y}{x+3 y} \in\{1,2\}$ to be an integer. So we get the case where $x=y$, in which we need both to be a power of 2 , or the case $x=5 y$, in which case we need $y$ to be a power of 2 . This gives us $11+9+9=29$ solutions, where we account for $y=5 x$ as well.
|
{
"resource_path": "HarvardMIT/segmented/en-232-2020-feb-guts-solutions.jsonl",
"problem_match": "\n11. [6]",
"solution_match": "\nSolution: "
}
|
f7c65493-4e9a-5430-9022-d1246fcf14d1
| 610,152
|
An $11 \times 11$ grid is labeled with consecutive rows $0,1,2, \ldots, 10$ and columns $0,1,2, \ldots, 10$ so that it is filled with integers from 1 to $2^{10}$, inclusive, and the sum of all of the numbers in row $n$ and in column $n$ are both divisible by $2^{n}$. Find the number of possible distinct grids.
|
We begin by filling the 10 by 10 grid formed by rows and columns 1 through 10 with any values, which we can do in $\left(2^{10}\right)^{100}=2^{1000}$ ways. Then in column 0 , there is at most 1 way to fill in the square in row 10,2 ways for the square in row 9 , down to $2^{10}$ ways in row 0 . Similarly, there is 1 way to fill in the square in row 0 and column 10, 2 ways to fill in the square in row 0 and column 9 , etc. Overall, the number of ways to fill out the squares in row or column 0 is $2^{1} \cdot 2^{2} \cdot 2^{3} \cdots 2^{9} \cdot 2^{10} \cdot 2^{9} \cdot 2^{8} \cdots 2^{1}=2^{100}$, so the number of possible distinct grids $2^{1000} \cdot 2^{100}=2^{1100}$.
|
2^{1100}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
An $11 \times 11$ grid is labeled with consecutive rows $0,1,2, \ldots, 10$ and columns $0,1,2, \ldots, 10$ so that it is filled with integers from 1 to $2^{10}$, inclusive, and the sum of all of the numbers in row $n$ and in column $n$ are both divisible by $2^{n}$. Find the number of possible distinct grids.
|
We begin by filling the 10 by 10 grid formed by rows and columns 1 through 10 with any values, which we can do in $\left(2^{10}\right)^{100}=2^{1000}$ ways. Then in column 0 , there is at most 1 way to fill in the square in row 10,2 ways for the square in row 9 , down to $2^{10}$ ways in row 0 . Similarly, there is 1 way to fill in the square in row 0 and column 10, 2 ways to fill in the square in row 0 and column 9 , etc. Overall, the number of ways to fill out the squares in row or column 0 is $2^{1} \cdot 2^{2} \cdot 2^{3} \cdots 2^{9} \cdot 2^{10} \cdot 2^{9} \cdot 2^{8} \cdots 2^{1}=2^{100}$, so the number of possible distinct grids $2^{1000} \cdot 2^{100}=2^{1100}$.
|
{
"resource_path": "HarvardMIT/segmented/en-232-2020-feb-guts-solutions.jsonl",
"problem_match": "\n12. [6]",
"solution_match": "\nSolution: "
}
|
6d0173f0-4f54-5a63-aef3-ac64d8580bf8
| 610,153
|
Let $\triangle A B C$ be a triangle with $A B=7, B C=1$, and $C A=4 \sqrt{3}$. The angle trisectors of $C$ intersect $\overline{A B}$ at $D$ and $E$, and lines $\overline{A C}$ and $\overline{B C}$ intersect the circumcircle of $\triangle C D E$ again at $X$ and $Y$, respectively. Find the length of $X Y$.
|
Let $O$ be the cirumcenter of $\triangle C D E$. Observe that $\triangle A B C \sim \triangle X Y C$. Moreover, $\triangle A B C$ is a right triangle because $1^{2}+(4 \sqrt{3})^{2}=7^{2}$, so the length $X Y$ is just equal to $2 r$, where $r$ is the radius of the circumcircle of $\triangle C D E$. Since $D$ and $E$ are on the angle trisectors of angle $C$, we see that $\triangle O D E, \triangle X D O$, and $\triangle Y E O$ are equilateral. The length of the altitude from $C$ to $A B$ is $\frac{4 \sqrt{3}}{7}$. The distance from $C$ to $X Y$ is $\frac{X Y}{A B} \cdot \frac{4 \sqrt{3}}{7}=\frac{2 r}{7} \cdot \frac{4 \sqrt{3}}{7}$, while the distance between lines $X Y$ and $A B$ is $\frac{r \sqrt{3}}{2}$. Hence we have
$$
\frac{4 \sqrt{3}}{7}=\frac{2 r}{7} \cdot \frac{4 \sqrt{3}}{7}+\frac{r \sqrt{3}}{2}
$$
Solving for $r$ gives that $r=\frac{56}{65}$, so $X Y=\frac{112}{65}$.

|
\frac{112}{65}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $\triangle A B C$ be a triangle with $A B=7, B C=1$, and $C A=4 \sqrt{3}$. The angle trisectors of $C$ intersect $\overline{A B}$ at $D$ and $E$, and lines $\overline{A C}$ and $\overline{B C}$ intersect the circumcircle of $\triangle C D E$ again at $X$ and $Y$, respectively. Find the length of $X Y$.
|
Let $O$ be the cirumcenter of $\triangle C D E$. Observe that $\triangle A B C \sim \triangle X Y C$. Moreover, $\triangle A B C$ is a right triangle because $1^{2}+(4 \sqrt{3})^{2}=7^{2}$, so the length $X Y$ is just equal to $2 r$, where $r$ is the radius of the circumcircle of $\triangle C D E$. Since $D$ and $E$ are on the angle trisectors of angle $C$, we see that $\triangle O D E, \triangle X D O$, and $\triangle Y E O$ are equilateral. The length of the altitude from $C$ to $A B$ is $\frac{4 \sqrt{3}}{7}$. The distance from $C$ to $X Y$ is $\frac{X Y}{A B} \cdot \frac{4 \sqrt{3}}{7}=\frac{2 r}{7} \cdot \frac{4 \sqrt{3}}{7}$, while the distance between lines $X Y$ and $A B$ is $\frac{r \sqrt{3}}{2}$. Hence we have
$$
\frac{4 \sqrt{3}}{7}=\frac{2 r}{7} \cdot \frac{4 \sqrt{3}}{7}+\frac{r \sqrt{3}}{2}
$$
Solving for $r$ gives that $r=\frac{56}{65}$, so $X Y=\frac{112}{65}$.

|
{
"resource_path": "HarvardMIT/segmented/en-232-2020-feb-guts-solutions.jsonl",
"problem_match": "\n13. [8]",
"solution_match": "\nSolution: "
}
|
6d00766e-fe37-5920-b66d-1a4f8346f3e1
| 610,154
|
Let $\varphi(n)$ denote the number of positive integers less than or equal to $n$ which are relatively prime to $n$. Let $S$ be the set of positive integers $n$ such that $\frac{2 n}{\varphi(n)}$ is an integer. Compute the sum
$$
\sum_{n \in S} \frac{1}{n}
$$
|
Answer: $\frac{10}{3}$
|
\frac{10}{3}
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Let $\varphi(n)$ denote the number of positive integers less than or equal to $n$ which are relatively prime to $n$. Let $S$ be the set of positive integers $n$ such that $\frac{2 n}{\varphi(n)}$ is an integer. Compute the sum
$$
\sum_{n \in S} \frac{1}{n}
$$
|
Answer: $\frac{10}{3}$
|
{
"resource_path": "HarvardMIT/segmented/en-232-2020-feb-guts-solutions.jsonl",
"problem_match": "\n14. [8]",
"solution_match": "\nProposed by: Joseph Heerens, James Lin\n"
}
|
103db72f-73b7-530c-8eb1-eae1c72b0b2a
| 610,155
|
You have six blocks in a row, labeled 1 through 6 , each with weight 1 . Call two blocks $x \leq y$ connected when, for all $x \leq z \leq y$, block $z$ has not been removed. While there is still at least one block remaining, you choose a remaining block uniformly at random and remove it. The cost of this operation is the sum of the weights of the blocks that are connected to the block being removed, including itself. Compute the expected total cost of removing all the blocks.
|
Note that the total cost is the total number of ordered pairs $(x, y)$ with $1 \leq x, y \leq 6$ such that $x$ and $y$ are connected right before $x$ gets removed.
The probability that blocks $x$ and $y$ are connected just before block $x$ is removed is simply $\frac{1}{|x-y|+1}$, since all of the $|x-y|+1$ relevant blocks are equally likely to be removed first. Summing over $1 \leq x, y \leq 6$, combining terms with the same value of $|x-y|$, we get
$$
\frac{2}{6}+\frac{4}{5}+\frac{6}{4}+\frac{8}{3}+\frac{10}{2}+6=\frac{163}{10}
$$
|
\frac{163}{10}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
You have six blocks in a row, labeled 1 through 6 , each with weight 1 . Call two blocks $x \leq y$ connected when, for all $x \leq z \leq y$, block $z$ has not been removed. While there is still at least one block remaining, you choose a remaining block uniformly at random and remove it. The cost of this operation is the sum of the weights of the blocks that are connected to the block being removed, including itself. Compute the expected total cost of removing all the blocks.
|
Note that the total cost is the total number of ordered pairs $(x, y)$ with $1 \leq x, y \leq 6$ such that $x$ and $y$ are connected right before $x$ gets removed.
The probability that blocks $x$ and $y$ are connected just before block $x$ is removed is simply $\frac{1}{|x-y|+1}$, since all of the $|x-y|+1$ relevant blocks are equally likely to be removed first. Summing over $1 \leq x, y \leq 6$, combining terms with the same value of $|x-y|$, we get
$$
\frac{2}{6}+\frac{4}{5}+\frac{6}{4}+\frac{8}{3}+\frac{10}{2}+6=\frac{163}{10}
$$
|
{
"resource_path": "HarvardMIT/segmented/en-232-2020-feb-guts-solutions.jsonl",
"problem_match": "\n15. [8]",
"solution_match": "\nSolution: "
}
|
8cef55f0-5fd8-5a69-ab65-e39312854cb2
| 610,156
|
Let $A B C$ be a triangle with incircle tangent to the perpendicular bisector of $B C$. If $B C=A E=$ 20, where $E$ is the point where the $A$-excircle touches $B C$, then compute the area of $\triangle A B C$.
|
Let the incircle and $B C$ touch at $D$, the incircle and perpendicular bisector touch at $X, Y$ be the point opposite $D$ on the incircle, and $M$ be the midpoint of $B C$. Recall that $A, Y$, and $E$ are collinear by homothety at $A$. Additionally, we have $M D=M X=M E$ so $\angle D X Y=\angle D X E=90^{\circ}$. Therefore $E, X$, and $Y$ are collinear. Since $M X \perp B C$, we have $\angle A E B=45^{\circ}$. The area of $A B C$ is
$$
\frac{1}{2} B C \cdot A E \cdot \sin \angle A E B=100 \sqrt{2}
$$
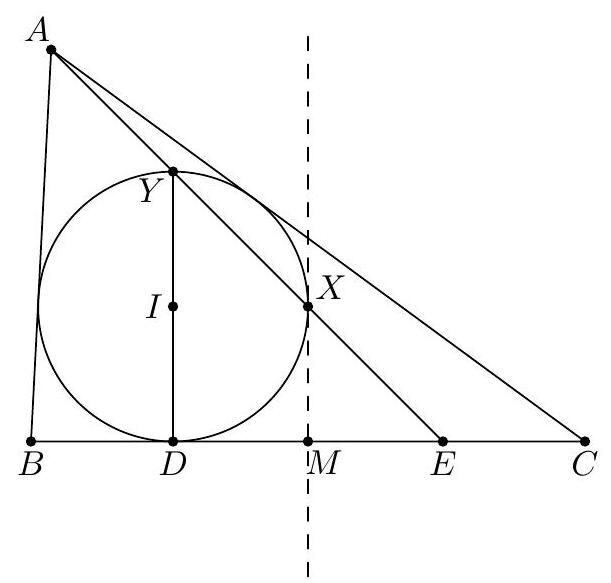
|
100 \sqrt{2}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $A B C$ be a triangle with incircle tangent to the perpendicular bisector of $B C$. If $B C=A E=$ 20, where $E$ is the point where the $A$-excircle touches $B C$, then compute the area of $\triangle A B C$.
|
Let the incircle and $B C$ touch at $D$, the incircle and perpendicular bisector touch at $X, Y$ be the point opposite $D$ on the incircle, and $M$ be the midpoint of $B C$. Recall that $A, Y$, and $E$ are collinear by homothety at $A$. Additionally, we have $M D=M X=M E$ so $\angle D X Y=\angle D X E=90^{\circ}$. Therefore $E, X$, and $Y$ are collinear. Since $M X \perp B C$, we have $\angle A E B=45^{\circ}$. The area of $A B C$ is
$$
\frac{1}{2} B C \cdot A E \cdot \sin \angle A E B=100 \sqrt{2}
$$

|
{
"resource_path": "HarvardMIT/segmented/en-232-2020-feb-guts-solutions.jsonl",
"problem_match": "\n17. [10]",
"solution_match": "\nSolution: "
}
|
21c8036c-96ec-54b6-97b3-76a381be15b4
| 610,158
|
A vertex-induced subgraph is a subset of the vertices of a graph together with any edges whose endpoints are both in this subset.
An undirected graph contains 10 nodes and $m$ edges, with no loops or multiple edges. What is the minimum possible value of $m$ such that this graph must contain a nonempty vertex-induced subgraph where all vertices have degree at least 5 ?
|
Suppose that we want to find the vertex-induced subgraph of maximum size where each vertex has degree at least 5 . To do so, we start with the entire graph and repeatedly remove any vertex with degree less than 5 .
If there are vertices left after this process terminates, then the subgraph induced by these vertices must have all degrees at least 5 . Conversely, if there is a vertex-induced subgraph where all degrees are at least 5 , then none of these vertices can be removed during the removing process. Thus, there are vertices remaining after this process if and only if such a vertex-induced subgraph exists.
If the process ends with an empty graph, the largest possible number of edges are removed when the first 5 removed vertices all have 4 edges at the time of removal, and the last 5 vertices are all connected to each other, resulting in $5 \times 4+4+3+2+1+0=30$ removed edges. The answer is $30+1=31$.
|
31
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
A vertex-induced subgraph is a subset of the vertices of a graph together with any edges whose endpoints are both in this subset.
An undirected graph contains 10 nodes and $m$ edges, with no loops or multiple edges. What is the minimum possible value of $m$ such that this graph must contain a nonempty vertex-induced subgraph where all vertices have degree at least 5 ?
|
Suppose that we want to find the vertex-induced subgraph of maximum size where each vertex has degree at least 5 . To do so, we start with the entire graph and repeatedly remove any vertex with degree less than 5 .
If there are vertices left after this process terminates, then the subgraph induced by these vertices must have all degrees at least 5 . Conversely, if there is a vertex-induced subgraph where all degrees are at least 5 , then none of these vertices can be removed during the removing process. Thus, there are vertices remaining after this process if and only if such a vertex-induced subgraph exists.
If the process ends with an empty graph, the largest possible number of edges are removed when the first 5 removed vertices all have 4 edges at the time of removal, and the last 5 vertices are all connected to each other, resulting in $5 \times 4+4+3+2+1+0=30$ removed edges. The answer is $30+1=31$.
|
{
"resource_path": "HarvardMIT/segmented/en-232-2020-feb-guts-solutions.jsonl",
"problem_match": "\n18. [10]",
"solution_match": "\nSolution: "
}
|
1a0323d2-d64f-54cb-b73b-f7b831e68224
| 610,159
|
The Fibonacci numbers are defined by $F_{0}=0, F_{1}=1$, and $F_{n}=F_{n-1}+F_{n-2}$ for $n \geq 2$. There exist unique positive integers $n_{1}, n_{2}, n_{3}, n_{4}, n_{5}, n_{6}$ such that
$$
\sum_{i_{1}=0}^{100} \sum_{i_{2}=0}^{100} \sum_{i_{3}=0}^{100} \sum_{i_{4}=0}^{100} \sum_{i_{5}=0}^{100} F_{i_{1}+i_{2}+i_{3}+i_{4}+i_{5}}=F_{n_{1}}-5 F_{n_{2}}+10 F_{n_{3}}-10 F_{n_{4}}+5 F_{n_{5}}-F_{n_{6}}
$$
Find $n_{1}+n_{2}+n_{3}+n_{4}+n_{5}+n_{6}$.
|
We make use of the identity
$$
\sum_{i=0}^{\ell} F_{i}=F_{\ell+2}-1
$$
(easily proven by induction) which implies
$$
\sum_{i=k}^{\ell} F_{i}=F_{\ell+2}-F_{k+1}
$$
Applying this several times yields
$$
\begin{aligned}
& \sum_{i_{1}=0}^{100} \sum_{i_{2}=0}^{100} \sum_{i_{3}=0}^{100} \sum_{i_{4}=0}^{100} \sum_{i_{5}=0}^{100} F_{i_{1}+i_{2}+i_{3}+i_{4}+i_{5}} \\
= & \sum_{i_{1}=0}^{100} \sum_{i_{2}=0}^{100} \sum_{i_{3}=0}^{100} \sum_{i_{4}=0}^{100}\left(F_{i_{1}+i_{2}+i_{3}+i_{4}+102}-F_{i_{1}+i_{2}+i_{3}+i_{4}+1}\right) \\
= & \sum_{i_{1}=0}^{100} \sum_{i_{2}=0}^{100} \sum_{i_{3}=0}^{100}\left(F_{i_{1}+i_{2}+i_{3}+204}-2 F_{i_{1}+i_{2}+i_{3}+103}+F_{i_{1}+i_{2}+i_{3}+2}\right) \\
= & \sum_{i_{1}=0}^{100} \sum_{i_{2}=0}^{100}\left(F_{i_{1}+i_{2}+306}-3 F_{i_{1}+i_{2}+205}+3 F_{i_{1}+i_{2}+104}-F_{i_{1}+i_{2}+3}\right) \\
= & \sum_{i_{1}=0}^{100}\left(F_{i_{1}+408}-4 F_{i_{1}+307}+6 F_{i_{1}+206}-4 F_{i_{1}+105}+F_{i_{1}+4}\right) \\
= & F_{510}-5 F_{409}+10 F_{308}-10 F_{207}+5 F_{106}-F_{5} .
\end{aligned}
$$
This representation is unique because the Fibonacci terms grow exponentially quickly, so e.g. the $F_{510}$ term dominates, forcing $n_{1}=510$ and similarly for the other terms. The final answer is
$$
510+409+308+207+106+5=1545
$$
|
1545
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
The Fibonacci numbers are defined by $F_{0}=0, F_{1}=1$, and $F_{n}=F_{n-1}+F_{n-2}$ for $n \geq 2$. There exist unique positive integers $n_{1}, n_{2}, n_{3}, n_{4}, n_{5}, n_{6}$ such that
$$
\sum_{i_{1}=0}^{100} \sum_{i_{2}=0}^{100} \sum_{i_{3}=0}^{100} \sum_{i_{4}=0}^{100} \sum_{i_{5}=0}^{100} F_{i_{1}+i_{2}+i_{3}+i_{4}+i_{5}}=F_{n_{1}}-5 F_{n_{2}}+10 F_{n_{3}}-10 F_{n_{4}}+5 F_{n_{5}}-F_{n_{6}}
$$
Find $n_{1}+n_{2}+n_{3}+n_{4}+n_{5}+n_{6}$.
|
We make use of the identity
$$
\sum_{i=0}^{\ell} F_{i}=F_{\ell+2}-1
$$
(easily proven by induction) which implies
$$
\sum_{i=k}^{\ell} F_{i}=F_{\ell+2}-F_{k+1}
$$
Applying this several times yields
$$
\begin{aligned}
& \sum_{i_{1}=0}^{100} \sum_{i_{2}=0}^{100} \sum_{i_{3}=0}^{100} \sum_{i_{4}=0}^{100} \sum_{i_{5}=0}^{100} F_{i_{1}+i_{2}+i_{3}+i_{4}+i_{5}} \\
= & \sum_{i_{1}=0}^{100} \sum_{i_{2}=0}^{100} \sum_{i_{3}=0}^{100} \sum_{i_{4}=0}^{100}\left(F_{i_{1}+i_{2}+i_{3}+i_{4}+102}-F_{i_{1}+i_{2}+i_{3}+i_{4}+1}\right) \\
= & \sum_{i_{1}=0}^{100} \sum_{i_{2}=0}^{100} \sum_{i_{3}=0}^{100}\left(F_{i_{1}+i_{2}+i_{3}+204}-2 F_{i_{1}+i_{2}+i_{3}+103}+F_{i_{1}+i_{2}+i_{3}+2}\right) \\
= & \sum_{i_{1}=0}^{100} \sum_{i_{2}=0}^{100}\left(F_{i_{1}+i_{2}+306}-3 F_{i_{1}+i_{2}+205}+3 F_{i_{1}+i_{2}+104}-F_{i_{1}+i_{2}+3}\right) \\
= & \sum_{i_{1}=0}^{100}\left(F_{i_{1}+408}-4 F_{i_{1}+307}+6 F_{i_{1}+206}-4 F_{i_{1}+105}+F_{i_{1}+4}\right) \\
= & F_{510}-5 F_{409}+10 F_{308}-10 F_{207}+5 F_{106}-F_{5} .
\end{aligned}
$$
This representation is unique because the Fibonacci terms grow exponentially quickly, so e.g. the $F_{510}$ term dominates, forcing $n_{1}=510$ and similarly for the other terms. The final answer is
$$
510+409+308+207+106+5=1545
$$
|
{
"resource_path": "HarvardMIT/segmented/en-232-2020-feb-guts-solutions.jsonl",
"problem_match": "\n19. [10]",
"solution_match": "\nSolution: "
}
|
586a5bcf-a0ca-5f3b-b71f-1e3cf9c3b404
| 610,160
|
We call a positive integer $t$ good if there is a sequence $a_{0}, a_{1}, \ldots$ of positive integers satisfying $a_{0}=15, a_{1}=t$, and
$$
a_{n-1} a_{n+1}=\left(a_{n}-1\right)\left(a_{n}+1\right)
$$
for all positive integers $n$. Find the sum of all good numbers.
|
Answer: 296
|
296
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
We call a positive integer $t$ good if there is a sequence $a_{0}, a_{1}, \ldots$ of positive integers satisfying $a_{0}=15, a_{1}=t$, and
$$
a_{n-1} a_{n+1}=\left(a_{n}-1\right)\left(a_{n}+1\right)
$$
for all positive integers $n$. Find the sum of all good numbers.
|
Answer: 296
|
{
"resource_path": "HarvardMIT/segmented/en-232-2020-feb-guts-solutions.jsonl",
"problem_match": "\n21. [12]",
"solution_match": "\nProposed by: Krit Boonsiriseth\n"
}
|
b40f9b9e-69b8-5895-bb0d-3e66c41c09a7
| 610,162
|
Let $A$ be a set of integers such that for each integer $m$, there exists an integer $a \in A$ and positive integer $n$ such that $a^{n} \equiv m(\bmod 100)$. What is the smallest possible value of $|A|$ ?
|
Work in $R=\mathbb{Z} / 100 \mathbb{Z} \cong \mathbb{Z} / 4 \mathbb{Z} \times \mathbb{Z} / 25 \mathbb{Z}$.
Call an element $r \in R$ type $(s, t)$ if $s=\nu_{2}(r) \leq 2$ and $t=\nu_{5}(r) \leq 2$. Also, define an element $r \in R$ to be coprime if it is of type $(0,0)$, powerful if it is of types $(0,2),(2,0)$, or $(2,2)$, and marginal otherwise.
Then, note that if if $r \in R$ is marginal, then any power of $r$ is powerful. Therefore all marginal elements must be in $A$.
We claim that all powerful elements are the cube of some marginal element. To show this take a powerful element $r$. In modulo 4 or 25 , if $r$ is a unit, then since 3 is coprime to both the sizes of $(\mathbb{Z} / 4 \mathbb{Z})^{\times}$and $(\mathbb{Z} / 25 \mathbb{Z})^{\times}$, it is the cube of some element. Otherwise, if $r$ is zero then it is the cube of 2 or 5 , respectively (since this case happens at least once this means that the constructed cube root is marginal).
We now claim that 4 additional elements are needed to generate the coprime elements. To see this, note that $R^{\times} \cong \mathbb{Z} / 2 \mathbb{Z} \times \mathbb{Z} / 20 \mathbb{Z}$ since there are primitive roots $\bmod 4$ and 25 . Under this isomorphism, one can show that $(1,1),(1,2),(1,4)$, and $(0,1)$ generate anything, and that no element in $R^{\times}$has more than one of these as a multiple.
To wrap up, note that there are $100-(20+1)(2+1)=37$ marginal elements, so 41 elements are needed in total.
|
41
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Let $A$ be a set of integers such that for each integer $m$, there exists an integer $a \in A$ and positive integer $n$ such that $a^{n} \equiv m(\bmod 100)$. What is the smallest possible value of $|A|$ ?
|
Work in $R=\mathbb{Z} / 100 \mathbb{Z} \cong \mathbb{Z} / 4 \mathbb{Z} \times \mathbb{Z} / 25 \mathbb{Z}$.
Call an element $r \in R$ type $(s, t)$ if $s=\nu_{2}(r) \leq 2$ and $t=\nu_{5}(r) \leq 2$. Also, define an element $r \in R$ to be coprime if it is of type $(0,0)$, powerful if it is of types $(0,2),(2,0)$, or $(2,2)$, and marginal otherwise.
Then, note that if if $r \in R$ is marginal, then any power of $r$ is powerful. Therefore all marginal elements must be in $A$.
We claim that all powerful elements are the cube of some marginal element. To show this take a powerful element $r$. In modulo 4 or 25 , if $r$ is a unit, then since 3 is coprime to both the sizes of $(\mathbb{Z} / 4 \mathbb{Z})^{\times}$and $(\mathbb{Z} / 25 \mathbb{Z})^{\times}$, it is the cube of some element. Otherwise, if $r$ is zero then it is the cube of 2 or 5 , respectively (since this case happens at least once this means that the constructed cube root is marginal).
We now claim that 4 additional elements are needed to generate the coprime elements. To see this, note that $R^{\times} \cong \mathbb{Z} / 2 \mathbb{Z} \times \mathbb{Z} / 20 \mathbb{Z}$ since there are primitive roots $\bmod 4$ and 25 . Under this isomorphism, one can show that $(1,1),(1,2),(1,4)$, and $(0,1)$ generate anything, and that no element in $R^{\times}$has more than one of these as a multiple.
To wrap up, note that there are $100-(20+1)(2+1)=37$ marginal elements, so 41 elements are needed in total.
|
{
"resource_path": "HarvardMIT/segmented/en-232-2020-feb-guts-solutions.jsonl",
"problem_match": "\n22. [12]",
"solution_match": "\nSolution: "
}
|
1875c259-0edb-57bd-9889-e0580724ad5a
| 610,163
|
A function $f: A \rightarrow A$ is called idempotent if $f(f(x))=f(x)$ for all $x \in A$. Let $I_{n}$ be the number of idempotent functions from $\{1,2, \ldots, n\}$ to itself. Compute
$$
\sum_{n=1}^{\infty} \frac{I_{n}}{n!}
$$
|
Answer: $e^{e}-1$
|
e^{e}-1
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
A function $f: A \rightarrow A$ is called idempotent if $f(f(x))=f(x)$ for all $x \in A$. Let $I_{n}$ be the number of idempotent functions from $\{1,2, \ldots, n\}$ to itself. Compute
$$
\sum_{n=1}^{\infty} \frac{I_{n}}{n!}
$$
|
Answer: $e^{e}-1$
|
{
"resource_path": "HarvardMIT/segmented/en-232-2020-feb-guts-solutions.jsonl",
"problem_match": "\n23. [12]",
"solution_match": "\nProposed by: Carl Schildkraut\n"
}
|
3a183831-0fcf-5198-9794-078a5c59f2f3
| 610,164
|
In $\triangle A B C, \omega$ is the circumcircle, $I$ is the incenter and $I_{A}$ is the $A$-excenter. Let $M$ be the midpoint of arc $\widehat{B A C}$ on $\omega$, and suppose that $X, Y$ are the projections of $I$ onto $M I_{A}$ and $I_{A}$ onto $M I$, respectively. If $\triangle X Y I_{A}$ is an equilateral triangle with side length 1 , compute the area of $\triangle A B C$.
|
Using Fact 5, we know that $I I_{A}$ intersects the circle $(A B C)$ at $M_{A}$, which is the center of $\left(I I_{A} B C X Y\right)$. Let $R$ be the radius of the latter circle. We have $R=\frac{1}{\sqrt{3}}$.
We have $\angle A I M=\angle Y I I_{A}=\angle Y I X=\frac{\pi}{3}$. Also, $\angle I I_{A} M=\angle I M I_{A}$ by calculating the angles from the equilateral triangle. Using 90-60-30 triangles, we have:
$$
\begin{gathered}
A I=\frac{1}{2} M I=\frac{1}{2} I I_{A}=R \\
A M=\frac{\sqrt{3}}{2} M I=\sqrt{3} R \\
M M_{A}^{2}=A M^{2}+A M_{A}^{2}=7 R^{2}
\end{gathered}
$$
Now, let $J$ and $N$ be the feet of the altitudes from $A$ and $B$ respectively on $M M_{A}$. Note that as $M$ is an arc midpoint of $B C, N$ is actually the midpoint of $B C$.
$$
\begin{aligned}
& M_{A} J=\frac{A M_{A}^{2}}{M M_{A}}=\frac{4}{\sqrt{7}} R \\
& M_{A} N=\frac{B M_{A}^{2}}{M M_{A}}=\frac{1}{\sqrt{7}} R
\end{aligned}
$$
Thus $J N=\frac{3}{\sqrt{7}} R$. Also, we have,
$$
B N^{2}=M_{A} N \cdot M N=\frac{6}{7} R^{2}
$$
Now, $[A B C]=\frac{1}{2} J N \cdot B C=J N \cdot B N=\frac{3 \sqrt{6}}{7} R^{2}=\frac{\sqrt{6}}{7}$.
|
\frac{\sqrt{6}}{7}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
In $\triangle A B C, \omega$ is the circumcircle, $I$ is the incenter and $I_{A}$ is the $A$-excenter. Let $M$ be the midpoint of arc $\widehat{B A C}$ on $\omega$, and suppose that $X, Y$ are the projections of $I$ onto $M I_{A}$ and $I_{A}$ onto $M I$, respectively. If $\triangle X Y I_{A}$ is an equilateral triangle with side length 1 , compute the area of $\triangle A B C$.
|
Using Fact 5, we know that $I I_{A}$ intersects the circle $(A B C)$ at $M_{A}$, which is the center of $\left(I I_{A} B C X Y\right)$. Let $R$ be the radius of the latter circle. We have $R=\frac{1}{\sqrt{3}}$.
We have $\angle A I M=\angle Y I I_{A}=\angle Y I X=\frac{\pi}{3}$. Also, $\angle I I_{A} M=\angle I M I_{A}$ by calculating the angles from the equilateral triangle. Using 90-60-30 triangles, we have:
$$
\begin{gathered}
A I=\frac{1}{2} M I=\frac{1}{2} I I_{A}=R \\
A M=\frac{\sqrt{3}}{2} M I=\sqrt{3} R \\
M M_{A}^{2}=A M^{2}+A M_{A}^{2}=7 R^{2}
\end{gathered}
$$
Now, let $J$ and $N$ be the feet of the altitudes from $A$ and $B$ respectively on $M M_{A}$. Note that as $M$ is an arc midpoint of $B C, N$ is actually the midpoint of $B C$.
$$
\begin{aligned}
& M_{A} J=\frac{A M_{A}^{2}}{M M_{A}}=\frac{4}{\sqrt{7}} R \\
& M_{A} N=\frac{B M_{A}^{2}}{M M_{A}}=\frac{1}{\sqrt{7}} R
\end{aligned}
$$
Thus $J N=\frac{3}{\sqrt{7}} R$. Also, we have,
$$
B N^{2}=M_{A} N \cdot M N=\frac{6}{7} R^{2}
$$
Now, $[A B C]=\frac{1}{2} J N \cdot B C=J N \cdot B N=\frac{3 \sqrt{6}}{7} R^{2}=\frac{\sqrt{6}}{7}$.
|
{
"resource_path": "HarvardMIT/segmented/en-232-2020-feb-guts-solutions.jsonl",
"problem_match": "\n24. [12]",
"solution_match": "\nSolution 1: "
}
|
3f0f1113-97dd-594c-a821-e2b185b8acd5
| 610,165
|
Let $S$ be the set of $3^{4}$ points in four-dimensional space where each coordinate is in $\{-1,0,1\}$. Let $N$ be the number of sequences of points $P_{1}, P_{2}, \ldots, P_{2020}$ in $S$ such that $P_{i} P_{i+1}=2$ for all $1 \leq i \leq 2020$ and $P_{1}=(0,0,0,0)$. (Here $P_{2021}=P_{1}$.) Find the largest integer $n$ such that $2^{n}$ divides $N$.
|
From $(0,0,0,0)$ we have to go to $( \pm 1, \pm 1, \pm 1, \pm 1)$, and from $(1,1,1,1)$ (or any of the other similar points), we have to go to $(0,0,0,0)$ or $(-1,1,1,1)$ and its cyclic shifts. If $a_{i}$ is the number of ways to go from $(1,1,1,1)$ to point of the form $( \pm 1, \pm 1, \pm 1, \pm 1)$ in $i$ steps, then we need to find $\nu_{2}\left(16 a_{2018}\right)$. To find a recurrence relation for $a_{i}$, note that to get to some point in $( \pm 1, \pm 1, \pm 1, \pm 1)$, we must either come from a previous point of the form $( \pm 1, \pm 1, \pm 1, \pm 1)$ or the point $(0,0,0,0)$. In order to go to one point of the form $( \pm 1, \pm 1, \pm 1, \pm 1)$ through $(0,0,0,0)$ from the point $( \pm 1, \pm 1, \pm 1, \pm 1)$, we have one way of going to the origin and 16 ways to pick which point we go to after the origin.
Additionally, if the previous point we visit is another point of the form $( \pm 1, \pm 1, \pm 1, \pm 1)$ then we have 4 possible directions to go in. Therefore the recurrence relation for $a_{i}$ is $a_{i}=4 a_{i-1}+16 a_{i-2}$. Solving the linear recurrence yields
$$
a_{i}=\frac{1}{\sqrt{5}}(2+2 \sqrt{5})^{i}-\frac{1}{\sqrt{5}}(2-2 \sqrt{5})^{i}=4^{i} F_{i+1},
$$
so it suffices to find $\nu_{2}\left(F_{2019}\right)$. We have $F_{n} \equiv 0,1,1,2,3,1(\bmod 4)$ for $n \equiv 0,1,2,3,4,5(\bmod 6)$, so $\nu_{2}\left(F_{2019}\right)=1$, and the answer is $4+2 \cdot 2018+1=4041$.
|
4041
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Let $S$ be the set of $3^{4}$ points in four-dimensional space where each coordinate is in $\{-1,0,1\}$. Let $N$ be the number of sequences of points $P_{1}, P_{2}, \ldots, P_{2020}$ in $S$ such that $P_{i} P_{i+1}=2$ for all $1 \leq i \leq 2020$ and $P_{1}=(0,0,0,0)$. (Here $P_{2021}=P_{1}$.) Find the largest integer $n$ such that $2^{n}$ divides $N$.
|
From $(0,0,0,0)$ we have to go to $( \pm 1, \pm 1, \pm 1, \pm 1)$, and from $(1,1,1,1)$ (or any of the other similar points), we have to go to $(0,0,0,0)$ or $(-1,1,1,1)$ and its cyclic shifts. If $a_{i}$ is the number of ways to go from $(1,1,1,1)$ to point of the form $( \pm 1, \pm 1, \pm 1, \pm 1)$ in $i$ steps, then we need to find $\nu_{2}\left(16 a_{2018}\right)$. To find a recurrence relation for $a_{i}$, note that to get to some point in $( \pm 1, \pm 1, \pm 1, \pm 1)$, we must either come from a previous point of the form $( \pm 1, \pm 1, \pm 1, \pm 1)$ or the point $(0,0,0,0)$. In order to go to one point of the form $( \pm 1, \pm 1, \pm 1, \pm 1)$ through $(0,0,0,0)$ from the point $( \pm 1, \pm 1, \pm 1, \pm 1)$, we have one way of going to the origin and 16 ways to pick which point we go to after the origin.
Additionally, if the previous point we visit is another point of the form $( \pm 1, \pm 1, \pm 1, \pm 1)$ then we have 4 possible directions to go in. Therefore the recurrence relation for $a_{i}$ is $a_{i}=4 a_{i-1}+16 a_{i-2}$. Solving the linear recurrence yields
$$
a_{i}=\frac{1}{\sqrt{5}}(2+2 \sqrt{5})^{i}-\frac{1}{\sqrt{5}}(2-2 \sqrt{5})^{i}=4^{i} F_{i+1},
$$
so it suffices to find $\nu_{2}\left(F_{2019}\right)$. We have $F_{n} \equiv 0,1,1,2,3,1(\bmod 4)$ for $n \equiv 0,1,2,3,4,5(\bmod 6)$, so $\nu_{2}\left(F_{2019}\right)=1$, and the answer is $4+2 \cdot 2018+1=4041$.
|
{
"resource_path": "HarvardMIT/segmented/en-232-2020-feb-guts-solutions.jsonl",
"problem_match": "\n25. [15]",
"solution_match": "\nSolution: "
}
|
d2548bc6-15c2-5228-8328-b91ea852a329
| 610,166
|
Let $A B C D$ be a cyclic quadrilateral, and let segments $A C$ and $B D$ intersect at $E$. Let $W$ and $Y$ be the feet of the altitudes from $E$ to sides $D A$ and $B C$, respectively, and let $X$ and $Z$ be the midpoints of sides $A B$ and $C D$, respectively. Given that the area of $A E D$ is 9 , the area of $B E C$ is 25 , and $\angle E B C-\angle E C B=30^{\circ}$, then compute the area of $W X Y Z$.
|
Answer: $17+\frac{15}{2} \sqrt{3}$
|
17+\frac{15}{2} \sqrt{3}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $A B C D$ be a cyclic quadrilateral, and let segments $A C$ and $B D$ intersect at $E$. Let $W$ and $Y$ be the feet of the altitudes from $E$ to sides $D A$ and $B C$, respectively, and let $X$ and $Z$ be the midpoints of sides $A B$ and $C D$, respectively. Given that the area of $A E D$ is 9 , the area of $B E C$ is 25 , and $\angle E B C-\angle E C B=30^{\circ}$, then compute the area of $W X Y Z$.
|
Answer: $17+\frac{15}{2} \sqrt{3}$
|
{
"resource_path": "HarvardMIT/segmented/en-232-2020-feb-guts-solutions.jsonl",
"problem_match": "\n26. [15]",
"solution_match": "\nProposed by: James Lin\n"
}
|
ff0935aa-6841-5a04-abd6-905efd39337d
| 610,167
|
Let $\left\{a_{i}\right\}_{i \geq 0}$ be a sequence of real numbers defined by
$$
a_{n+1}=a_{n}^{2}-\frac{1}{2^{2020 \cdot 2^{n}-1}}
$$
for $n \geq 0$. Determine the largest value for $a_{0}$ such that $\left\{a_{i}\right\}_{i \geq 0}$ is bounded.
|
Let $a_{0}=\frac{1}{\sqrt{2}^{2020}}\left(t+\frac{1}{t}\right)$, with $t \geq 1$. (If $a_{0}<\frac{1}{\sqrt{2}^{2018}}$ then no real $t$ exists, but we ignore these values because $a_{0}$ is smaller.) Then, we can prove by induction that
$$
a_{n}=\frac{1}{\sqrt{2}^{2020 \cdot 2^{n}}}\left(t^{2^{n}}+\frac{1}{t^{2^{n}}}\right) .
$$
For this to be bounded, it is easy to see that we just need
$$
\frac{t^{2^{n}}}{\sqrt{2}^{2020 \cdot 2^{n}}}=\left(\frac{t}{\sqrt{2}^{2020}}\right)^{2^{n}}
$$
to be bounded, since the second term approaches 0 . We see that this is is equivalent to $t \leq 2^{2020 / 2}$, which means
$$
a_{0} \leq \frac{1}{\sqrt{2}^{2020}}\left(\sqrt{2}^{2020}+\left(\frac{1}{\sqrt{2}}\right)^{2020}\right)=1+\frac{1}{2^{2020}}
$$
|
1+\frac{1}{2^{2020}}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Let $\left\{a_{i}\right\}_{i \geq 0}$ be a sequence of real numbers defined by
$$
a_{n+1}=a_{n}^{2}-\frac{1}{2^{2020 \cdot 2^{n}-1}}
$$
for $n \geq 0$. Determine the largest value for $a_{0}$ such that $\left\{a_{i}\right\}_{i \geq 0}$ is bounded.
|
Let $a_{0}=\frac{1}{\sqrt{2}^{2020}}\left(t+\frac{1}{t}\right)$, with $t \geq 1$. (If $a_{0}<\frac{1}{\sqrt{2}^{2018}}$ then no real $t$ exists, but we ignore these values because $a_{0}$ is smaller.) Then, we can prove by induction that
$$
a_{n}=\frac{1}{\sqrt{2}^{2020 \cdot 2^{n}}}\left(t^{2^{n}}+\frac{1}{t^{2^{n}}}\right) .
$$
For this to be bounded, it is easy to see that we just need
$$
\frac{t^{2^{n}}}{\sqrt{2}^{2020 \cdot 2^{n}}}=\left(\frac{t}{\sqrt{2}^{2020}}\right)^{2^{n}}
$$
to be bounded, since the second term approaches 0 . We see that this is is equivalent to $t \leq 2^{2020 / 2}$, which means
$$
a_{0} \leq \frac{1}{\sqrt{2}^{2020}}\left(\sqrt{2}^{2020}+\left(\frac{1}{\sqrt{2}}\right)^{2020}\right)=1+\frac{1}{2^{2020}}
$$
|
{
"resource_path": "HarvardMIT/segmented/en-232-2020-feb-guts-solutions.jsonl",
"problem_match": "\n27. [15]",
"solution_match": "\nSolution: "
}
|
5aa51c94-141a-5ad2-9ec5-46ccb77d52cc
| 610,168
|
Let $\triangle A B C$ be a triangle inscribed in a unit circle with center $O$. Let $I$ be the incenter of $\triangle A B C$, and let $D$ be the intersection of $B C$ and the angle bisector of $\angle B A C$. Suppose that the circumcircle of $\triangle A D O$ intersects $B C$ again at a point $E$ such that $E$ lies on $I O$. If $\cos A=\frac{12}{13}$, find the area of $\triangle A B C$.
|
Consider the following lemma:
Lemma. $A D \perp E O$.
Proof. By the Shooting Lemma, the reflection of the midpoint $M$ of arc $B C$ not containing $A$ over $B C$ lies on $(A D O)$. Hence
$$
\measuredangle A D E+\measuredangle D E O=\measuredangle M D C+\measuredangle D M^{\prime} O=\measuredangle M D C+\measuredangle M^{\prime} M D=90^{\circ}
$$
This is enough to imply $A D \perp E O$.
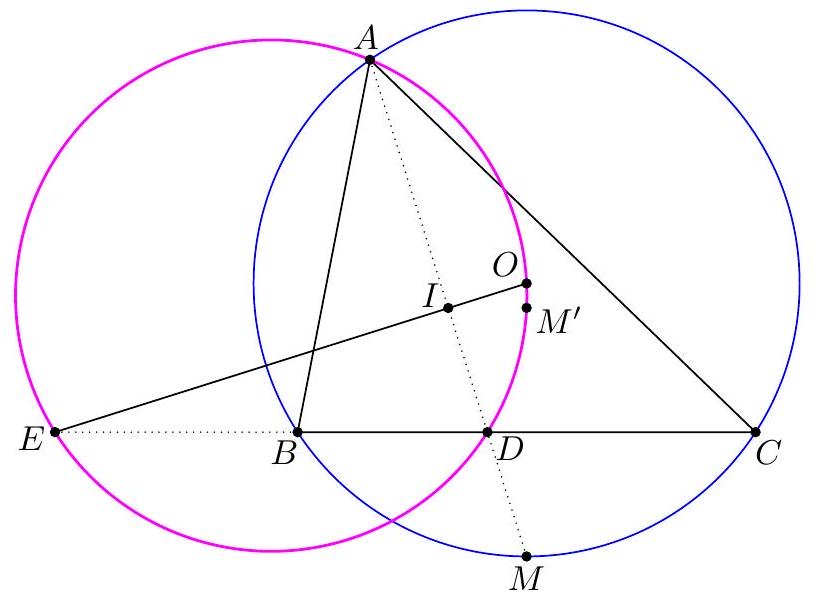
Thus $I$ is the foot from $O$ onto $A D$. Now
$$
A I^{2}+I O^{2}=A O^{2}
$$
By Euler's formula,
$$
\left(\frac{r}{\sin \frac{A}{2}}\right)^{2}+R^{2}-2 R r=R^{2}
$$
Hence
$$
r=2 R \sin ^{2} \frac{A}{2}
$$
Then
$$
s=a+\frac{r}{\tan \frac{A}{2}}=a+R \sin A=3 R \sin A
$$
and
$$
[A B C]=r s=\left(2 R \sin ^{2} \frac{A}{2}\right)(3 R \sin A)
$$
Since $R=1$, we get
$$
[A B C]=3(1-\cos A) \sin A
$$
Plugging in $\sin A=\frac{5}{13}$ and $\cos A=\frac{12}{13}$, we get
$$
[A B C]=3 \cdot \frac{1}{13} \cdot \frac{5}{13}=\frac{15}{169}
$$
Remark. On the contest, this problem stated that $\triangle A B C$ is an acute triangle and that $\sin A=\frac{5}{13}$, rather than $\cos A=\frac{12}{13}$. This is erroneous because there is no acute triangle satisfying the conditions of the problem statement (the given diagram is not accurate). We apologize for the mistake.
|
\frac{15}{169}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $\triangle A B C$ be a triangle inscribed in a unit circle with center $O$. Let $I$ be the incenter of $\triangle A B C$, and let $D$ be the intersection of $B C$ and the angle bisector of $\angle B A C$. Suppose that the circumcircle of $\triangle A D O$ intersects $B C$ again at a point $E$ such that $E$ lies on $I O$. If $\cos A=\frac{12}{13}$, find the area of $\triangle A B C$.
|
Consider the following lemma:
Lemma. $A D \perp E O$.
Proof. By the Shooting Lemma, the reflection of the midpoint $M$ of arc $B C$ not containing $A$ over $B C$ lies on $(A D O)$. Hence
$$
\measuredangle A D E+\measuredangle D E O=\measuredangle M D C+\measuredangle D M^{\prime} O=\measuredangle M D C+\measuredangle M^{\prime} M D=90^{\circ}
$$
This is enough to imply $A D \perp E O$.

Thus $I$ is the foot from $O$ onto $A D$. Now
$$
A I^{2}+I O^{2}=A O^{2}
$$
By Euler's formula,
$$
\left(\frac{r}{\sin \frac{A}{2}}\right)^{2}+R^{2}-2 R r=R^{2}
$$
Hence
$$
r=2 R \sin ^{2} \frac{A}{2}
$$
Then
$$
s=a+\frac{r}{\tan \frac{A}{2}}=a+R \sin A=3 R \sin A
$$
and
$$
[A B C]=r s=\left(2 R \sin ^{2} \frac{A}{2}\right)(3 R \sin A)
$$
Since $R=1$, we get
$$
[A B C]=3(1-\cos A) \sin A
$$
Plugging in $\sin A=\frac{5}{13}$ and $\cos A=\frac{12}{13}$, we get
$$
[A B C]=3 \cdot \frac{1}{13} \cdot \frac{5}{13}=\frac{15}{169}
$$
Remark. On the contest, this problem stated that $\triangle A B C$ is an acute triangle and that $\sin A=\frac{5}{13}$, rather than $\cos A=\frac{12}{13}$. This is erroneous because there is no acute triangle satisfying the conditions of the problem statement (the given diagram is not accurate). We apologize for the mistake.
|
{
"resource_path": "HarvardMIT/segmented/en-232-2020-feb-guts-solutions.jsonl",
"problem_match": "\n28. [15]",
"solution_match": "\nSolution: "
}
|
ae5922ad-a997-5c53-b187-dc6aec46bd2e
| 610,169
|
Let $S=\{(x, y) \mid x>0, y>0, x+y<200$, and $x, y \in \mathbb{Z}\}$. Find the number of parabolas $\mathcal{P}$ with vertex $V$ that satisfy the following conditions:
- $\mathcal{P}$ goes through both $(100,100)$ and at least one point in $S$,
- $V$ has integer coordinates, and
- $\mathcal{P}$ is tangent to the line $x+y=0$ at $V$.
|
We perform the linear transformation $(x, y) \rightarrow(x-y, x+y)$, which has the reverse transformation $(a, b) \rightarrow\left(\frac{a+b}{2}, \frac{b-a}{2}\right)$. Then the equivalent problem has a parabola has a vertical axis of symmetry, goes through $A=(0,200)$, a point $B=(u, v)$ in
$$
S^{\prime}=\{(x, y) \mid x+y>0, x>y, y<200, x, y \in \mathbb{Z}, \text { and } x \equiv y \bmod 2\}
$$
and a new vertex $W=(w, 0)$ on $y=0$ with $w$ even. Then $\left(1-\frac{u}{w}\right)^{2}=\frac{v}{200}$. The only way the RHS can be the square of a rational number is if $\frac{u}{w}=\frac{v^{\prime}}{10}$ where $v=2\left(10-v^{\prime}\right)^{2}$. Since $v$ is even, we can find conditions so that $u, w$ are both even:
$$
\begin{aligned}
v^{\prime} \in\{1,3,7,9\} & \Longrightarrow\left(2 v^{\prime}\right)|u, 20| w \\
v^{\prime} \in\{2,4,6,8\} & \Longrightarrow v^{\prime}|u, 10| w \\
v^{\prime}=5 & \Longrightarrow 2|u, 4| w
\end{aligned}
$$
It follows that any parabola that goes through $v^{\prime} \in\{3,7,9\}$ has a point with $v^{\prime}=1$, and any parabola that goes through $v^{\prime} \in\{4,6,8\}$ has a point with $v^{\prime}=2$. We then count the following parabolas:
- The number of parabolas going through $(2 k, 162)$, where $k$ is a nonzero integer with $|2 k|<162$.
- The number of parabolas going through $(2 k, 128)$ not already counted, where $k$ is a nonzero integer with $|2 k|<128$. (Note that this passes through $(k, 162)$.)
- The number of parabolas going through $(2 k, 50)$ not already counted, where $k$ is a nonzero integer with $|2 k|<50$. (Note that this passes through $\left(\frac{2 k}{5}, 162\right)$, and any overlap must have been counted in the first case.)
The number of solutions is then
$$
2\left(80+\frac{1}{2} \cdot 64+\frac{4}{5} \cdot 25\right)=264
$$
|
264
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Let $S=\{(x, y) \mid x>0, y>0, x+y<200$, and $x, y \in \mathbb{Z}\}$. Find the number of parabolas $\mathcal{P}$ with vertex $V$ that satisfy the following conditions:
- $\mathcal{P}$ goes through both $(100,100)$ and at least one point in $S$,
- $V$ has integer coordinates, and
- $\mathcal{P}$ is tangent to the line $x+y=0$ at $V$.
|
We perform the linear transformation $(x, y) \rightarrow(x-y, x+y)$, which has the reverse transformation $(a, b) \rightarrow\left(\frac{a+b}{2}, \frac{b-a}{2}\right)$. Then the equivalent problem has a parabola has a vertical axis of symmetry, goes through $A=(0,200)$, a point $B=(u, v)$ in
$$
S^{\prime}=\{(x, y) \mid x+y>0, x>y, y<200, x, y \in \mathbb{Z}, \text { and } x \equiv y \bmod 2\}
$$
and a new vertex $W=(w, 0)$ on $y=0$ with $w$ even. Then $\left(1-\frac{u}{w}\right)^{2}=\frac{v}{200}$. The only way the RHS can be the square of a rational number is if $\frac{u}{w}=\frac{v^{\prime}}{10}$ where $v=2\left(10-v^{\prime}\right)^{2}$. Since $v$ is even, we can find conditions so that $u, w$ are both even:
$$
\begin{aligned}
v^{\prime} \in\{1,3,7,9\} & \Longrightarrow\left(2 v^{\prime}\right)|u, 20| w \\
v^{\prime} \in\{2,4,6,8\} & \Longrightarrow v^{\prime}|u, 10| w \\
v^{\prime}=5 & \Longrightarrow 2|u, 4| w
\end{aligned}
$$
It follows that any parabola that goes through $v^{\prime} \in\{3,7,9\}$ has a point with $v^{\prime}=1$, and any parabola that goes through $v^{\prime} \in\{4,6,8\}$ has a point with $v^{\prime}=2$. We then count the following parabolas:
- The number of parabolas going through $(2 k, 162)$, where $k$ is a nonzero integer with $|2 k|<162$.
- The number of parabolas going through $(2 k, 128)$ not already counted, where $k$ is a nonzero integer with $|2 k|<128$. (Note that this passes through $(k, 162)$.)
- The number of parabolas going through $(2 k, 50)$ not already counted, where $k$ is a nonzero integer with $|2 k|<50$. (Note that this passes through $\left(\frac{2 k}{5}, 162\right)$, and any overlap must have been counted in the first case.)
The number of solutions is then
$$
2\left(80+\frac{1}{2} \cdot 64+\frac{4}{5} \cdot 25\right)=264
$$
|
{
"resource_path": "HarvardMIT/segmented/en-232-2020-feb-guts-solutions.jsonl",
"problem_match": "\n30. [18]",
"solution_match": "\nSolution: "
}
|
3c9d6ba8-eeb8-5871-aac9-614fb9a69774
| 610,171
|
Anastasia is taking a walk in the plane, starting from $(1,0)$. Each second, if she is at $(x, y)$, she moves to one of the points $(x-1, y),(x+1, y),(x, y-1)$, and $(x, y+1)$, each with $\frac{1}{4}$ probability. She stops as soon as she hits a point of the form $(k, k)$. What is the probability that $k$ is divisible by 3 when she stops?
|
Answer: $\frac{3-\sqrt{3}}{3}$ or $1-\frac{1}{\sqrt{3}}$
|
\frac{3-\sqrt{3}}{3}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Anastasia is taking a walk in the plane, starting from $(1,0)$. Each second, if she is at $(x, y)$, she moves to one of the points $(x-1, y),(x+1, y),(x, y-1)$, and $(x, y+1)$, each with $\frac{1}{4}$ probability. She stops as soon as she hits a point of the form $(k, k)$. What is the probability that $k$ is divisible by 3 when she stops?
|
Answer: $\frac{3-\sqrt{3}}{3}$ or $1-\frac{1}{\sqrt{3}}$
|
{
"resource_path": "HarvardMIT/segmented/en-232-2020-feb-guts-solutions.jsonl",
"problem_match": "\n31. [18]",
"solution_match": "\nProposed by: Michael Ren\n"
}
|
0e4f7e41-af8f-5624-9cfc-d0b7c5016168
| 610,172
|
Find the smallest real constant $\alpha$ such that for all positive integers $n$ and real numbers $0=y_{0}<$ $y_{1}<\cdots<y_{n}$, the following inequality holds:
$$
\alpha \sum_{k=1}^{n} \frac{(k+1)^{3 / 2}}{\sqrt{y_{k}^{2}-y_{k-1}^{2}}} \geq \sum_{k=1}^{n} \frac{k^{2}+3 k+3}{y_{k}} \text {. }
$$
|
Answer: $\frac{16 \sqrt{2}}{9}$
|
\frac{16 \sqrt{2}}{9}
|
Yes
|
Yes
|
math-word-problem
|
Inequalities
|
Find the smallest real constant $\alpha$ such that for all positive integers $n$ and real numbers $0=y_{0}<$ $y_{1}<\cdots<y_{n}$, the following inequality holds:
$$
\alpha \sum_{k=1}^{n} \frac{(k+1)^{3 / 2}}{\sqrt{y_{k}^{2}-y_{k-1}^{2}}} \geq \sum_{k=1}^{n} \frac{k^{2}+3 k+3}{y_{k}} \text {. }
$$
|
Answer: $\frac{16 \sqrt{2}}{9}$
|
{
"resource_path": "HarvardMIT/segmented/en-232-2020-feb-guts-solutions.jsonl",
"problem_match": "\n32. [18]",
"solution_match": "\nProposed by: Andrew Gu\n"
}
|
b7ddf51c-30af-5229-97db-a7635929d642
| 610,173
|
Estimate
$$
N=\prod_{n=1}^{\infty} n^{n^{-1.25}}
$$
An estimate of $E>0$ will receive $\lfloor 22 \min (N / E, E / N)\rfloor$ points.
|
We approximate
$$
\ln N=\sum_{n=1}^{\infty} \frac{\ln n}{n^{5 / 4}}
$$
with an integral as
$$
\begin{aligned}
\int_{1}^{\infty} \frac{\ln x}{x^{5 / 4}} d x & =\left.\left(-4 x^{-1 / 4} \ln x-16 x^{-1 / 4}\right)\right|_{1} ^{\infty} \\
& =16
\end{aligned}
$$
Therefore $e^{16}$ is a good approximation. We can estimate $e^{16}$ by repeated squaring:
$$
\begin{aligned}
e & \approx 2.72 \\
e^{2} & \approx 7.4 \\
e^{4} & \approx 55 \\
e^{8} & \approx 3000 \\
e^{16} & \approx 9000000
\end{aligned}
$$
The true value of $e^{16}$ is around 8886111, which is reasonably close to the value of $N$. Both $e^{16}$ and 9000000 would be worth 20 points.
|
9000000
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Estimate
$$
N=\prod_{n=1}^{\infty} n^{n^{-1.25}}
$$
An estimate of $E>0$ will receive $\lfloor 22 \min (N / E, E / N)\rfloor$ points.
|
We approximate
$$
\ln N=\sum_{n=1}^{\infty} \frac{\ln n}{n^{5 / 4}}
$$
with an integral as
$$
\begin{aligned}
\int_{1}^{\infty} \frac{\ln x}{x^{5 / 4}} d x & =\left.\left(-4 x^{-1 / 4} \ln x-16 x^{-1 / 4}\right)\right|_{1} ^{\infty} \\
& =16
\end{aligned}
$$
Therefore $e^{16}$ is a good approximation. We can estimate $e^{16}$ by repeated squaring:
$$
\begin{aligned}
e & \approx 2.72 \\
e^{2} & \approx 7.4 \\
e^{4} & \approx 55 \\
e^{8} & \approx 3000 \\
e^{16} & \approx 9000000
\end{aligned}
$$
The true value of $e^{16}$ is around 8886111, which is reasonably close to the value of $N$. Both $e^{16}$ and 9000000 would be worth 20 points.
|
{
"resource_path": "HarvardMIT/segmented/en-232-2020-feb-guts-solutions.jsonl",
"problem_match": "\n33. [22]",
"solution_match": "\nSolution: "
}
|
d09d118f-e1d4-518d-8ad4-2a048d680f5c
| 610,174
|
For odd primes $p$, let $f(p)$ denote the smallest positive integer $a$ for which there does not exist an integer $n$ satisfying $p \mid n^{2}-a$. Estimate $N$, the sum of $f(p)^{2}$ over the first $10^{5}$ odd primes $p$.
An estimate of $E>0$ will receive $\left\lfloor 22 \min (N / E, E / N)^{3}\right\rfloor$ points.
|
Note that the smallest quadratic nonresidue $a$ is always a prime, because if $a=b c$ with $b, c>1$ then one of $b$ and $c$ is also a quadratic nonresidue. We apply the following heuristic: if $p_{1}$, $p_{2}, \ldots$ are the primes in increasing order, then given a "uniform random prime" $q$, the values of $\left(\frac{p_{1}}{q}\right),\left(\frac{p_{2}}{q}\right), \ldots$ are independent and are 1 with probability $\frac{1}{2}$ and -1 with probability $\frac{1}{2}$.
Of course, there is no such thing as a uniform random prime. More rigorously, for any $n$, the joint distributions of $\left(\frac{p_{1}}{q}\right), \ldots,\left(\frac{p_{n}}{q}\right)$ where $q$ is a uniform random prime less than $N$ converges in distribution
to $n$ independent coin flips between 1 and -1 as $N \rightarrow \infty$. For ease of explanation, we won't adopt this more formal view, but it is possible to make the following argument rigorous by looking at primes $q<N$ and sending $N \rightarrow \infty$. Given any $n$, the residue of $q \bmod n$ is uniform over the $\varphi(n)$ residues $\bmod n$ that are relatively prime to $n$. By quadratic reciprocity, conditioned on either $q \equiv 1(\bmod 4)$ or $q \equiv 3(\bmod 4)$, exactly half of the nonzero residues $\bmod p_{n}$ satisfy $\left(\frac{p_{n}}{q}\right)=1$ and exactly half satisfy $\left(\frac{p_{n}}{q}\right)=-1$ for odd $p_{n}$ (the case of $p_{n}=2$ is slightly different and one must look mod 8 , but the result is the same). The residue of $q \bmod 8, p_{2}, p_{3}, \ldots, p_{n}$ are independent as these are pairwise relatively prime, yielding our heuristic.
Thus, we may model our problem of finding the smallest quadratic nonresidue with the following process: independent fair coins are flipped for each prime, and we take the smallest prime that flipped heads. We can estimate the expected value of $f(p)^{2}$ as $\sum_{n=1}^{\infty} \frac{p_{n}^{2}}{2^{n}}$. Looking at the first few terms gives us
$$
\frac{2^{2}}{2}+\frac{3^{2}}{4}+\frac{5^{2}}{8}+\frac{7^{2}}{16}+\frac{11^{2}}{32}+\frac{13^{2}}{64}+\frac{17^{2}}{128}+\frac{19^{2}}{256}+\frac{23^{2}}{512}+\frac{29^{2}}{1024} \approx 22
$$
The terms after this decay rapidly, so a good approximation is $E=22 \cdot 10^{5}$, good enough for 20 points. The more inaccurate $E=20 \cdot 10^{5}$ earns 15 points.
This Python code computes the exact answer:
```
def smallest_nqr(p):
for a in range(1,p):
if pow(a,(p-1)//2,p)==p-1:
return a
```
import sympy
print (sum([smallest_nqr(p) $* * 2$ for p in sympy.ntheory.primerange(3,sympy.prime(10**5+2))]))
Remark. In 1961, Erdős showed that as $N \rightarrow \infty$, the average value of $f(p)$ over odd primes $p<N$ will converge to $\sum_{n=1}^{\infty} \frac{p_{n}}{2^{n}} \approx 3.675$.
|
22 \cdot 10^{5}
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
For odd primes $p$, let $f(p)$ denote the smallest positive integer $a$ for which there does not exist an integer $n$ satisfying $p \mid n^{2}-a$. Estimate $N$, the sum of $f(p)^{2}$ over the first $10^{5}$ odd primes $p$.
An estimate of $E>0$ will receive $\left\lfloor 22 \min (N / E, E / N)^{3}\right\rfloor$ points.
|
Note that the smallest quadratic nonresidue $a$ is always a prime, because if $a=b c$ with $b, c>1$ then one of $b$ and $c$ is also a quadratic nonresidue. We apply the following heuristic: if $p_{1}$, $p_{2}, \ldots$ are the primes in increasing order, then given a "uniform random prime" $q$, the values of $\left(\frac{p_{1}}{q}\right),\left(\frac{p_{2}}{q}\right), \ldots$ are independent and are 1 with probability $\frac{1}{2}$ and -1 with probability $\frac{1}{2}$.
Of course, there is no such thing as a uniform random prime. More rigorously, for any $n$, the joint distributions of $\left(\frac{p_{1}}{q}\right), \ldots,\left(\frac{p_{n}}{q}\right)$ where $q$ is a uniform random prime less than $N$ converges in distribution
to $n$ independent coin flips between 1 and -1 as $N \rightarrow \infty$. For ease of explanation, we won't adopt this more formal view, but it is possible to make the following argument rigorous by looking at primes $q<N$ and sending $N \rightarrow \infty$. Given any $n$, the residue of $q \bmod n$ is uniform over the $\varphi(n)$ residues $\bmod n$ that are relatively prime to $n$. By quadratic reciprocity, conditioned on either $q \equiv 1(\bmod 4)$ or $q \equiv 3(\bmod 4)$, exactly half of the nonzero residues $\bmod p_{n}$ satisfy $\left(\frac{p_{n}}{q}\right)=1$ and exactly half satisfy $\left(\frac{p_{n}}{q}\right)=-1$ for odd $p_{n}$ (the case of $p_{n}=2$ is slightly different and one must look mod 8 , but the result is the same). The residue of $q \bmod 8, p_{2}, p_{3}, \ldots, p_{n}$ are independent as these are pairwise relatively prime, yielding our heuristic.
Thus, we may model our problem of finding the smallest quadratic nonresidue with the following process: independent fair coins are flipped for each prime, and we take the smallest prime that flipped heads. We can estimate the expected value of $f(p)^{2}$ as $\sum_{n=1}^{\infty} \frac{p_{n}^{2}}{2^{n}}$. Looking at the first few terms gives us
$$
\frac{2^{2}}{2}+\frac{3^{2}}{4}+\frac{5^{2}}{8}+\frac{7^{2}}{16}+\frac{11^{2}}{32}+\frac{13^{2}}{64}+\frac{17^{2}}{128}+\frac{19^{2}}{256}+\frac{23^{2}}{512}+\frac{29^{2}}{1024} \approx 22
$$
The terms after this decay rapidly, so a good approximation is $E=22 \cdot 10^{5}$, good enough for 20 points. The more inaccurate $E=20 \cdot 10^{5}$ earns 15 points.
This Python code computes the exact answer:
```
def smallest_nqr(p):
for a in range(1,p):
if pow(a,(p-1)//2,p)==p-1:
return a
```
import sympy
print (sum([smallest_nqr(p) $* * 2$ for p in sympy.ntheory.primerange(3,sympy.prime(10**5+2))]))
Remark. In 1961, Erdős showed that as $N \rightarrow \infty$, the average value of $f(p)$ over odd primes $p<N$ will converge to $\sum_{n=1}^{\infty} \frac{p_{n}}{2^{n}} \approx 3.675$.
|
{
"resource_path": "HarvardMIT/segmented/en-232-2020-feb-guts-solutions.jsonl",
"problem_match": "\n34. [22]",
"solution_match": "\nSolution: "
}
|
380bd376-68b0-5908-8ce7-4396d1e765c2
| 610,175
|
Let $n$ be a fixed positive integer, and choose $n$ positive integers $a_{1}, \ldots, a_{n}$. Given a permutation $\pi$ on the first $n$ positive integers, let $S_{\pi}=\left\{i \left\lvert\, \frac{a_{i}}{\pi(i)}\right.\right.$ is an integer $\}$. Let $N$ denote the number of distinct sets $S_{\pi}$ as $\pi$ ranges over all such permutations. Determine, in terms of $n$, the maximum value of $N$ over all possible values of $a_{1}, \ldots, a_{n}$.
|
The answer is $2^{n}-n$.
Let $D=\left(d_{i j}\right)$ be the matrix where $d_{i j}$ is 1 if $i$ is a divisor of $a_{j}$ and 0 otherwise. For a subset $S$ of $[n]$, let $D_{S}$ be the matrix obtained from $D$ by flipping $(0 \leftrightarrow 1)$ every entry $d_{i j}$ where $j \notin S$. Observe that $S=S_{\pi}$ if and only if $\left(D_{S}\right)_{\pi(i) i}=1$ for all $i$.
To show that $N \leq 2^{n}-n$ we consider two cases. If all the rows of $D$ are distinct, then there exist $n$ different possibilities for $S$ that set a row equal to zero. In this case, there is clearly no $\pi$ so that $S_{\pi}=S$. Thus there are at most $2^{n}-n$ possible $S_{\pi}$. Otherwise, if two rows in $D$ are the same, then choose an $S_{0}$ such that $D_{S_{0}}$ has two zero rows. Then, the $n+1$ sets $S$ that are at most "one element away" from $S_{0}$ are such that $D_{S}$ only has one column with nonzero entries in those two rows. This makes it impossible for $S_{\pi}=S$ as well, so $N \leq 2^{n}-n-1$.
Now we construct $N=2^{n}-n$ by setting $a_{j}=j$. By Hall's marriage theorem, it suffices to prove the following:
Assuming that $D_{S}$ has no completely-zero rows, given a set $I=\left\{i_{1}, i_{2}, \ldots, i_{k}\right\}$ there exist at least $k$ values of $j$ so that there exists an $i \in I$ so that $\left(D_{S}\right)_{i j}=1$. Call such $j$ admissible.
Without loss of generality assume $i_{1}<i_{2}<\cdots<i_{k}$.
Note that if $\left\{d_{i j} \mid i \in I\right\}=\{0,1\}$, then $j$ is admissible. Therefore the $k-1$ numbers $i_{1}, i_{2}, \ldots, i_{k-1}$ are admissible, since for $\alpha<k, i_{\alpha}$ divides $i_{\alpha}$ but $i_{k}$ does not. So we only need to find one more admissible $j$. Assume that $i_{k}$ is not admissible; now it must be the case that all the $i_{\alpha}$ are divisors of $i_{k}$.
At this point we note that the $k=1$ case is easy, since no row of $D_{S}$ is zero. Moreover, if $k=2$, $\left\{\left(D_{S}\right)_{i_{1} i_{1}},\left(D_{S}\right)_{i_{2} i_{1}}\right\}=\{0,1\}$, so in the row with the zero there must be 1 somewhere, yielding a second admissible column.
In the case where $k \geq 3$, note that $i_{1} \leq i_{k} / 3$. Therefore $i_{k}-i_{1} \notin I$, but $i_{1}$ divides $i_{k}-i_{1}$ and $i_{k}$ does not. Thus we have found the last admissible column. Having exhausted all cases, we are done.
|
2^{n}-n
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Let $n$ be a fixed positive integer, and choose $n$ positive integers $a_{1}, \ldots, a_{n}$. Given a permutation $\pi$ on the first $n$ positive integers, let $S_{\pi}=\left\{i \left\lvert\, \frac{a_{i}}{\pi(i)}\right.\right.$ is an integer $\}$. Let $N$ denote the number of distinct sets $S_{\pi}$ as $\pi$ ranges over all such permutations. Determine, in terms of $n$, the maximum value of $N$ over all possible values of $a_{1}, \ldots, a_{n}$.
|
The answer is $2^{n}-n$.
Let $D=\left(d_{i j}\right)$ be the matrix where $d_{i j}$ is 1 if $i$ is a divisor of $a_{j}$ and 0 otherwise. For a subset $S$ of $[n]$, let $D_{S}$ be the matrix obtained from $D$ by flipping $(0 \leftrightarrow 1)$ every entry $d_{i j}$ where $j \notin S$. Observe that $S=S_{\pi}$ if and only if $\left(D_{S}\right)_{\pi(i) i}=1$ for all $i$.
To show that $N \leq 2^{n}-n$ we consider two cases. If all the rows of $D$ are distinct, then there exist $n$ different possibilities for $S$ that set a row equal to zero. In this case, there is clearly no $\pi$ so that $S_{\pi}=S$. Thus there are at most $2^{n}-n$ possible $S_{\pi}$. Otherwise, if two rows in $D$ are the same, then choose an $S_{0}$ such that $D_{S_{0}}$ has two zero rows. Then, the $n+1$ sets $S$ that are at most "one element away" from $S_{0}$ are such that $D_{S}$ only has one column with nonzero entries in those two rows. This makes it impossible for $S_{\pi}=S$ as well, so $N \leq 2^{n}-n-1$.
Now we construct $N=2^{n}-n$ by setting $a_{j}=j$. By Hall's marriage theorem, it suffices to prove the following:
Assuming that $D_{S}$ has no completely-zero rows, given a set $I=\left\{i_{1}, i_{2}, \ldots, i_{k}\right\}$ there exist at least $k$ values of $j$ so that there exists an $i \in I$ so that $\left(D_{S}\right)_{i j}=1$. Call such $j$ admissible.
Without loss of generality assume $i_{1}<i_{2}<\cdots<i_{k}$.
Note that if $\left\{d_{i j} \mid i \in I\right\}=\{0,1\}$, then $j$ is admissible. Therefore the $k-1$ numbers $i_{1}, i_{2}, \ldots, i_{k-1}$ are admissible, since for $\alpha<k, i_{\alpha}$ divides $i_{\alpha}$ but $i_{k}$ does not. So we only need to find one more admissible $j$. Assume that $i_{k}$ is not admissible; now it must be the case that all the $i_{\alpha}$ are divisors of $i_{k}$.
At this point we note that the $k=1$ case is easy, since no row of $D_{S}$ is zero. Moreover, if $k=2$, $\left\{\left(D_{S}\right)_{i_{1} i_{1}},\left(D_{S}\right)_{i_{2} i_{1}}\right\}=\{0,1\}$, so in the row with the zero there must be 1 somewhere, yielding a second admissible column.
In the case where $k \geq 3$, note that $i_{1} \leq i_{k} / 3$. Therefore $i_{k}-i_{1} \notin I$, but $i_{1}$ divides $i_{k}-i_{1}$ and $i_{k}$ does not. Thus we have found the last admissible column. Having exhausted all cases, we are done.
|
{
"resource_path": "HarvardMIT/segmented/en-232-2020-feb-team-solutions.jsonl",
"problem_match": "\n10. [60]",
"solution_match": "\nSolution: "
}
|
ef005cb8-1f93-5575-8e0d-b6346e9d3b35
| 610,187
|
Sir Alex is coaching a soccer team of $n$ players of distinct heights. He wants to line them up so that for each player $P$, the total number of players that are either to the left of $P$ and taller than $P$ or to the right of $P$ and shorter than $P$ is even. In terms of $n$, how many possible orders are there?
|
We want to determine the number of permutations $\pi$ of $1, \ldots, n$ such that every number is involved in an even number of inversions. The key observation is that the number of inversions $k$ is involved in has the same parity as $\pi(k)-k$. This is since $\pi(k)-k$ can be interpreted as the number of $i$ with $\pi(i)<\pi(k)$ minus the number of $i$ with $i<k$, meaning that $i$ is counted with a weight of $\pm 1 \equiv 1(\bmod 2)$ if and only if $i$ is in an inversion with $k$.
From this, it follows that such permutations are the ones that permute the even and odd numbers, so the answer is $\left\lfloor\frac{n}{2}\right\rfloor!\left\lceil\frac{n}{2}\right\rceil$ !.
|
\left\lfloor\frac{n}{2}\right\rfloor!\left\lceil\frac{n}{2}\right\rceil
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Sir Alex is coaching a soccer team of $n$ players of distinct heights. He wants to line them up so that for each player $P$, the total number of players that are either to the left of $P$ and taller than $P$ or to the right of $P$ and shorter than $P$ is even. In terms of $n$, how many possible orders are there?
|
We want to determine the number of permutations $\pi$ of $1, \ldots, n$ such that every number is involved in an even number of inversions. The key observation is that the number of inversions $k$ is involved in has the same parity as $\pi(k)-k$. This is since $\pi(k)-k$ can be interpreted as the number of $i$ with $\pi(i)<\pi(k)$ minus the number of $i$ with $i<k$, meaning that $i$ is counted with a weight of $\pm 1 \equiv 1(\bmod 2)$ if and only if $i$ is in an inversion with $k$.
From this, it follows that such permutations are the ones that permute the even and odd numbers, so the answer is $\left\lfloor\frac{n}{2}\right\rfloor!\left\lceil\frac{n}{2}\right\rceil$ !.
|
{
"resource_path": "HarvardMIT/segmented/en-234-tournaments-2020-hmic-solutions.jsonl",
"problem_match": "\n1. [6]",
"solution_match": "\nSolution: "
}
|
79b98971-1923-595e-9439-ed1a25c40021
| 610,188
|
In the Cartesian plane, a line segment with midpoint $(2020,11)$ has one endpoint at $(a, 0)$ and the other endpoint on the line $y=x$. Compute $a$.
|
Let the other endpoint be $(t, t)$. The midpoint of $(a, 0)$ and $(t, t)$ is $\left(\frac{a+t}{2}, \frac{t}{2}\right)$. So, we know that $\frac{a+t}{2}=2020$ and $\frac{t}{2}=11$. The second equation yields $t=22$. Substituting this into the first yields $a=2 \cdot 2020-22=4018$.
|
4018
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
In the Cartesian plane, a line segment with midpoint $(2020,11)$ has one endpoint at $(a, 0)$ and the other endpoint on the line $y=x$. Compute $a$.
|
Let the other endpoint be $(t, t)$. The midpoint of $(a, 0)$ and $(t, t)$ is $\left(\frac{a+t}{2}, \frac{t}{2}\right)$. So, we know that $\frac{a+t}{2}=2020$ and $\frac{t}{2}=11$. The second equation yields $t=22$. Substituting this into the first yields $a=2 \cdot 2020-22=4018$.
|
{
"resource_path": "HarvardMIT/segmented/en-241-2020-nov-gen-solutions.jsonl",
"problem_match": "\n1. ",
"solution_match": "\nSolution: "
}
|
4332619b-7bdb-566d-931d-cfb521160a46
| 610,193
|
Let $T$ be a trapezoid with two right angles and side lengths $4,4,5$, and $\sqrt{17}$. Two line segments are drawn, connecting the midpoints of opposite sides of $T$ and dividing $T$ into 4 regions. If the difference between the areas of the largest and smallest of these regions is $d$, compute $240 d$.
|
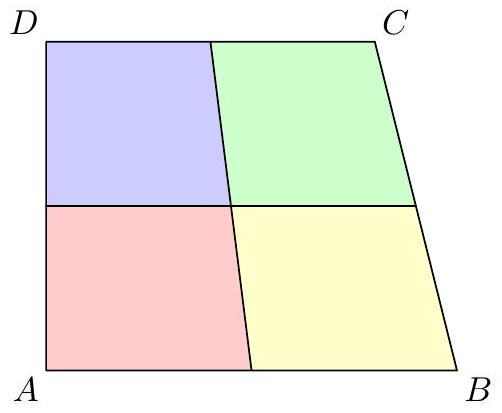
By checking all the possibilities, one can show that $T$ has height 4 and base lengths 4 and 5 . Orient $T$ so that the shorter base is on the top.
Then, the length of the cut parallel to the bases is $\frac{4+5}{2}=\frac{9}{2}$. Thus, the top two pieces are trapezoids with height 2 and base lengths 2 and $\frac{9}{4}$, while the bottom two pieces are trapezoids with height 2 and base lengths $\frac{9}{4}$ and $\frac{5}{2}$. Thus, using the area formula for a trapezoid, the difference between the largest and smallest areas is
$$
d=\frac{\left(\frac{5}{2}+\frac{9}{4}-\frac{9}{4}-2\right) \cdot 2}{2}=\frac{1}{2}
$$
|
120
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $T$ be a trapezoid with two right angles and side lengths $4,4,5$, and $\sqrt{17}$. Two line segments are drawn, connecting the midpoints of opposite sides of $T$ and dividing $T$ into 4 regions. If the difference between the areas of the largest and smallest of these regions is $d$, compute $240 d$.
|

By checking all the possibilities, one can show that $T$ has height 4 and base lengths 4 and 5 . Orient $T$ so that the shorter base is on the top.
Then, the length of the cut parallel to the bases is $\frac{4+5}{2}=\frac{9}{2}$. Thus, the top two pieces are trapezoids with height 2 and base lengths 2 and $\frac{9}{4}$, while the bottom two pieces are trapezoids with height 2 and base lengths $\frac{9}{4}$ and $\frac{5}{2}$. Thus, using the area formula for a trapezoid, the difference between the largest and smallest areas is
$$
d=\frac{\left(\frac{5}{2}+\frac{9}{4}-\frac{9}{4}-2\right) \cdot 2}{2}=\frac{1}{2}
$$
|
{
"resource_path": "HarvardMIT/segmented/en-241-2020-nov-gen-solutions.jsonl",
"problem_match": "\n2. ",
"solution_match": "\n## Solution:\n\n"
}
|
fe97a449-88ed-5b30-86e0-f6381e800243
| 610,194
|
Jody has 6 distinguishable balls and 6 distinguishable sticks, all of the same length. How many ways are there to use the sticks to connect the balls so that two disjoint non-interlocking triangles are formed? Consider rotations and reflections of the same arrangement to be indistinguishable.
|
For two disjoint triangles to be formed, three of the balls must be connected into a triangle by three of the sticks, and the three remaining balls must be connected by the three remaining sticks.
There are $\binom{6}{3}$ ways to pick the 3 balls for the first triangle. Note that once we choose the 3 balls for the first triangle, the remaining 3 balls must form the vertices of the second triangle.
Now that we have determined the vertices of each triangle, we can assign the 6 sticks to the 6 total edges in the two triangles. Because any ordering of the 6 sticks works, there are $6!=720$ total ways to assign the sticks as edges.
Finally, because the order of the two triangles doesn't matter (i.e. our initial choice of 3 balls could have been used for the second triangle), we must divide by 2 to correct for overcounting. Hence the final answer is $\binom{6}{3} \cdot 6!/ 2=7200$.
|
7200
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Jody has 6 distinguishable balls and 6 distinguishable sticks, all of the same length. How many ways are there to use the sticks to connect the balls so that two disjoint non-interlocking triangles are formed? Consider rotations and reflections of the same arrangement to be indistinguishable.
|
For two disjoint triangles to be formed, three of the balls must be connected into a triangle by three of the sticks, and the three remaining balls must be connected by the three remaining sticks.
There are $\binom{6}{3}$ ways to pick the 3 balls for the first triangle. Note that once we choose the 3 balls for the first triangle, the remaining 3 balls must form the vertices of the second triangle.
Now that we have determined the vertices of each triangle, we can assign the 6 sticks to the 6 total edges in the two triangles. Because any ordering of the 6 sticks works, there are $6!=720$ total ways to assign the sticks as edges.
Finally, because the order of the two triangles doesn't matter (i.e. our initial choice of 3 balls could have been used for the second triangle), we must divide by 2 to correct for overcounting. Hence the final answer is $\binom{6}{3} \cdot 6!/ 2=7200$.
|
{
"resource_path": "HarvardMIT/segmented/en-241-2020-nov-gen-solutions.jsonl",
"problem_match": "\n3. ",
"solution_match": "\nSolution 1: "
}
|
8d2d3f68-ee38-5824-9311-ee4f20986320
| 610,195
|
Compute the sum of all positive integers $a \leq 26$ for which there exist integers $b$ and $c$ such that $a+23 b+15 c-2$ and $2 a+5 b+14 c-8$ are both multiples of 26 .
|
Assume $b$ and $c$ exist. Considering the two values modulo 13, we find
$$
\begin{cases}a+10 b+2 c \equiv 2 & (\bmod 13) \\ 2 a+5 b+c \equiv 8 & (\bmod 13)\end{cases}
$$
Subtracting twice the second equation from the first, we get $-3 a \equiv-14(\bmod 13)$. So, we have $a \equiv 9$ $(\bmod 13)$. Therefore we must either have $a=9$ or $a=22$.
Moreover, both $a=9$ and $a=22$ yield solutions with $b=0$ and $c=3,16$, depending on the value of $a$. Thus the answer is $9+22=31$.
|
31
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Compute the sum of all positive integers $a \leq 26$ for which there exist integers $b$ and $c$ such that $a+23 b+15 c-2$ and $2 a+5 b+14 c-8$ are both multiples of 26 .
|
Assume $b$ and $c$ exist. Considering the two values modulo 13, we find
$$
\begin{cases}a+10 b+2 c \equiv 2 & (\bmod 13) \\ 2 a+5 b+c \equiv 8 & (\bmod 13)\end{cases}
$$
Subtracting twice the second equation from the first, we get $-3 a \equiv-14(\bmod 13)$. So, we have $a \equiv 9$ $(\bmod 13)$. Therefore we must either have $a=9$ or $a=22$.
Moreover, both $a=9$ and $a=22$ yield solutions with $b=0$ and $c=3,16$, depending on the value of $a$. Thus the answer is $9+22=31$.
|
{
"resource_path": "HarvardMIT/segmented/en-241-2020-nov-gen-solutions.jsonl",
"problem_match": "\n5. ",
"solution_match": "\nSolution: "
}
|
54128a35-b48d-5534-985d-18d261f28a69
| 610,197
|
A sphere is centered at a point with integer coordinates and passes through the three points $(2,0,0)$, $(0,4,0),(0,0,6)$, but not the origin $(0,0,0)$. If $r$ is the smallest possible radius of the sphere, compute $r^{2}$.
|
Let $(x, y, z)$ be the center of the sphere. By the given condition, we have
$$
(x-2)^{2}+y^{2}+z^{2}=x^{2}+(y-4)^{2}+z^{2}=x^{2}+y^{2}+(z-6)^{2} .
$$
Subtracting $x^{2}+y^{2}+z^{2}$ yields
$$
x^{2}-(x-2)^{2}=y^{2}-(y-4)^{2}=z^{2}-(z-6)^{2},
$$
or
$$
4(x-1)=8(y-2)=12(z-3)
$$
Therefore $(x-1, y-2, z-3)$ must be $(6 t, 3 t, 2 t)$ for some integer $t$. Checking small values of $t$ yields that the possibilities for $(x, y, z)$ closest to $(2,0,0)$ are $(-5,-1,1),(1,2,3)$, and $(7,5,5)$. The second yields a sphere that passes through the origin and is thus forbidden. The other two yield $r^{2}=51$ and $r^{2}=75$, so 51 is the answer.
|
51
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
A sphere is centered at a point with integer coordinates and passes through the three points $(2,0,0)$, $(0,4,0),(0,0,6)$, but not the origin $(0,0,0)$. If $r$ is the smallest possible radius of the sphere, compute $r^{2}$.
|
Let $(x, y, z)$ be the center of the sphere. By the given condition, we have
$$
(x-2)^{2}+y^{2}+z^{2}=x^{2}+(y-4)^{2}+z^{2}=x^{2}+y^{2}+(z-6)^{2} .
$$
Subtracting $x^{2}+y^{2}+z^{2}$ yields
$$
x^{2}-(x-2)^{2}=y^{2}-(y-4)^{2}=z^{2}-(z-6)^{2},
$$
or
$$
4(x-1)=8(y-2)=12(z-3)
$$
Therefore $(x-1, y-2, z-3)$ must be $(6 t, 3 t, 2 t)$ for some integer $t$. Checking small values of $t$ yields that the possibilities for $(x, y, z)$ closest to $(2,0,0)$ are $(-5,-1,1),(1,2,3)$, and $(7,5,5)$. The second yields a sphere that passes through the origin and is thus forbidden. The other two yield $r^{2}=51$ and $r^{2}=75$, so 51 is the answer.
|
{
"resource_path": "HarvardMIT/segmented/en-241-2020-nov-gen-solutions.jsonl",
"problem_match": "\n6. ",
"solution_match": "\nSolution: "
}
|
50fba742-2c5d-5090-a257-e62764e057f1
| 610,198
|
In the Cartesian plane, a perfectly reflective semicircular room is bounded by the upper half of the unit circle centered at $(0,0)$ and the line segment from $(-1,0)$ to $(1,0)$. David stands at the point $(-1,0)$ and shines a flashlight into the room at an angle of $46^{\circ}$ above the horizontal. How many times does the light beam reflect off the walls before coming back to David at $(-1,0)$ for the first time?
|
Note that when the beam reflects off the $x$-axis, we can reflect the entire room across the $x$-axis instead. Therefore, the number of times the beam reflects off a circular wall in our semicircular room is equal to the number of times the beam reflects off a circular wall in a room bounded by the unit circle centered at $(0,0)$. Furthermore, the number of times the beam reflects off the $x$-axis wall in our semicircular room is equal to the number of times the beam crosses the $x$-axis in the room bounded by the unit circle. We will count each of these separately.
We first find the number of times the beam reflects off a circular wall. Note that the path of the beam is made up of a series of chords of equal length within the unit circle, each chord connecting the points from two consecutive reflections. Through simple angle chasing, we find that the angle subtended by each chord is $180-2 \cdot 46=88^{\circ}$. Therefore, the $n$th point of reflection in the unit circle is $(-\cos (88 n), \sin (88 n))$. The beam returns to $(-1,0)$ when
$$
88 n \equiv 0 \quad(\bmod 360) \Longleftrightarrow 11 n \equiv 0 \quad(\bmod 45) \rightarrow n=45
$$
but since we're looking for the number of time the beam is reflected before it comes back to David, we only count $45-1=44$ of these reflections.
Next, we consider the number of times the beam is reflected off the $x$-axis. This is simply the number of times the beam crosses the $x$-axis in the unit circle room before returning to David, which happens every $180^{\circ}$ around the circle. Thus, we have $\frac{88 \cdot 45}{180}-1=21$ reflections off the $x$-axis, where we subtract 1 to remove the instance when the beam returns to $(-1,0)$. Thus, the total number of reflections is $44+21=65$.
|
65
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
In the Cartesian plane, a perfectly reflective semicircular room is bounded by the upper half of the unit circle centered at $(0,0)$ and the line segment from $(-1,0)$ to $(1,0)$. David stands at the point $(-1,0)$ and shines a flashlight into the room at an angle of $46^{\circ}$ above the horizontal. How many times does the light beam reflect off the walls before coming back to David at $(-1,0)$ for the first time?
|
Note that when the beam reflects off the $x$-axis, we can reflect the entire room across the $x$-axis instead. Therefore, the number of times the beam reflects off a circular wall in our semicircular room is equal to the number of times the beam reflects off a circular wall in a room bounded by the unit circle centered at $(0,0)$. Furthermore, the number of times the beam reflects off the $x$-axis wall in our semicircular room is equal to the number of times the beam crosses the $x$-axis in the room bounded by the unit circle. We will count each of these separately.
We first find the number of times the beam reflects off a circular wall. Note that the path of the beam is made up of a series of chords of equal length within the unit circle, each chord connecting the points from two consecutive reflections. Through simple angle chasing, we find that the angle subtended by each chord is $180-2 \cdot 46=88^{\circ}$. Therefore, the $n$th point of reflection in the unit circle is $(-\cos (88 n), \sin (88 n))$. The beam returns to $(-1,0)$ when
$$
88 n \equiv 0 \quad(\bmod 360) \Longleftrightarrow 11 n \equiv 0 \quad(\bmod 45) \rightarrow n=45
$$
but since we're looking for the number of time the beam is reflected before it comes back to David, we only count $45-1=44$ of these reflections.
Next, we consider the number of times the beam is reflected off the $x$-axis. This is simply the number of times the beam crosses the $x$-axis in the unit circle room before returning to David, which happens every $180^{\circ}$ around the circle. Thus, we have $\frac{88 \cdot 45}{180}-1=21$ reflections off the $x$-axis, where we subtract 1 to remove the instance when the beam returns to $(-1,0)$. Thus, the total number of reflections is $44+21=65$.
|
{
"resource_path": "HarvardMIT/segmented/en-241-2020-nov-gen-solutions.jsonl",
"problem_match": "\n9. ",
"solution_match": "\nSolution: "
}
|
1ffff1e4-cb93-5553-8347-497129adfe4f
| 610,201
|
A sequence of positive integers $a_{1}, a_{2}, a_{3}, \ldots$ satisfies
$$
a_{n+1}=n\left\lfloor\frac{a_{n}}{n}\right\rfloor+1
$$
for all positive integers $n$. If $a_{30}=30$, how many possible values can $a_{1}$ take? (For a real number $x$, $\lfloor x\rfloor$ denotes the largest integer that is not greater than $x$.)
|
Answer: 274
|
274
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
A sequence of positive integers $a_{1}, a_{2}, a_{3}, \ldots$ satisfies
$$
a_{n+1}=n\left\lfloor\frac{a_{n}}{n}\right\rfloor+1
$$
for all positive integers $n$. If $a_{30}=30$, how many possible values can $a_{1}$ take? (For a real number $x$, $\lfloor x\rfloor$ denotes the largest integer that is not greater than $x$.)
|
Answer: 274
|
{
"resource_path": "HarvardMIT/segmented/en-241-2020-nov-gen-solutions.jsonl",
"problem_match": "\n10. ",
"solution_match": "\nProposed by: Carl Joshua Quines\n"
}
|
f6452027-fe1a-51a3-84bb-51e721c17be6
| 610,202
|
Let $a$ be a positive integer such that $2 a$ has units digit 4. What is the sum of the possible units digits of $3 a$ ?
|
If $2 a$ has last digit 4 , then the last digit of $a$ is either 2 or 7 . In the former case, $3 a$ has last digit 6 , and in the latter case, $3 a$ has last digit 1 . This gives a final answer of $6+1=7$.
|
7
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Let $a$ be a positive integer such that $2 a$ has units digit 4. What is the sum of the possible units digits of $3 a$ ?
|
If $2 a$ has last digit 4 , then the last digit of $a$ is either 2 or 7 . In the former case, $3 a$ has last digit 6 , and in the latter case, $3 a$ has last digit 1 . This gives a final answer of $6+1=7$.
|
{
"resource_path": "HarvardMIT/segmented/en-241-2020-nov-guts-solutions.jsonl",
"problem_match": "\n2. [5]",
"solution_match": "\nSolution: "
}
|
73f7942c-1845-5fbc-a9a3-eec72bab9378
| 610,204
|
How many six-digit multiples of 27 have only 3,6 , or 9 as their digits?
|
Divide by 3 . We now want to count the number of six-digit multiples of 9 that only have 1 , 2 , or 3 as their digits. Due to the divisibility rule for 9 , we only need to consider when the digit sum is a multiple of 9 . Note that $3 \cdot 6=18$ is the maximum digit sum.
If the sum is 18 , the only case is 333333 .
Otherwise, the digit sum is 9 . The possibilities here, up to ordering of the digits, are 111222 and 111123. The first has $\binom{6}{3}=20$ cases, while the second has $6 \cdot 5=30$. Thus the final answer is $1+20+30=51$.
|
51
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
How many six-digit multiples of 27 have only 3,6 , or 9 as their digits?
|
Divide by 3 . We now want to count the number of six-digit multiples of 9 that only have 1 , 2 , or 3 as their digits. Due to the divisibility rule for 9 , we only need to consider when the digit sum is a multiple of 9 . Note that $3 \cdot 6=18$ is the maximum digit sum.
If the sum is 18 , the only case is 333333 .
Otherwise, the digit sum is 9 . The possibilities here, up to ordering of the digits, are 111222 and 111123. The first has $\binom{6}{3}=20$ cases, while the second has $6 \cdot 5=30$. Thus the final answer is $1+20+30=51$.
|
{
"resource_path": "HarvardMIT/segmented/en-241-2020-nov-guts-solutions.jsonl",
"problem_match": "\n3. [5]",
"solution_match": "\nSolution: "
}
|
9b5a51b7-4f38-5ef7-9805-9de9fecfe3bf
| 610,205
|
The points $(0,0),(1,2),(2,1),(2,2)$ in the plane are colored red while the points $(1,0),(2,0),(0,1),(0,2)$ are colored blue. Four segments are drawn such that each one connects a red point to a blue point and each colored point is the endpoint of some segment. The smallest possible sum of the lengths of the segments can be expressed as $a+\sqrt{b}$, where $a, b$ are positive integers. Compute $100 a+b$.
|
If $(2,2)$ is connected to $(0,1)$ or $(1,0)$, then the other 6 points can be connected with segments of total length 3 , which is minimal. This leads to a total length of $3+\sqrt{5}$.
On the other hand, if $(2,2)$ is connected to $(0,2)$ or $(0,2)$, then connecting the other points with segments of total length 2 is impossible, so the minimal length is at least $2+2+\sqrt{2}=4+\sqrt{2}>3+\sqrt{5}$.
|
305
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
The points $(0,0),(1,2),(2,1),(2,2)$ in the plane are colored red while the points $(1,0),(2,0),(0,1),(0,2)$ are colored blue. Four segments are drawn such that each one connects a red point to a blue point and each colored point is the endpoint of some segment. The smallest possible sum of the lengths of the segments can be expressed as $a+\sqrt{b}$, where $a, b$ are positive integers. Compute $100 a+b$.
|

If $(2,2)$ is connected to $(0,1)$ or $(1,0)$, then the other 6 points can be connected with segments of total length 3 , which is minimal. This leads to a total length of $3+\sqrt{5}$.
On the other hand, if $(2,2)$ is connected to $(0,2)$ or $(0,2)$, then connecting the other points with segments of total length 2 is impossible, so the minimal length is at least $2+2+\sqrt{2}=4+\sqrt{2}>3+\sqrt{5}$.
|
{
"resource_path": "HarvardMIT/segmented/en-241-2020-nov-guts-solutions.jsonl",
"problem_match": "\n5. [6]",
"solution_match": "\n## Solution:\n\n"
}
|
f953f03b-4285-5af6-ad2c-90911db4524a
| 610,207
|
If $x, y, z$ are real numbers such that $x y=6, x-z=2$, and $x+y+z=9$, compute $\frac{x}{y}-\frac{z}{x}-\frac{z^{2}}{x y}$. Proposed by: Ragulan Sivakumar
|
Let $k=\frac{x}{y}-\frac{z}{x}-\frac{z^{2}}{x y}=\frac{x^{2}-y z-z^{2}}{x y}$. We have
$$
k+1=\frac{x^{2}+x y-y z-z^{2}}{x y}=\frac{x^{2}-x z+x y-y z+z x-z^{2}}{x y}=\frac{(x+y+z)(x-z)}{x y}=\frac{9 \cdot 2}{6}=3,
$$
so $k=2$.
|
2
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
If $x, y, z$ are real numbers such that $x y=6, x-z=2$, and $x+y+z=9$, compute $\frac{x}{y}-\frac{z}{x}-\frac{z^{2}}{x y}$. Proposed by: Ragulan Sivakumar
|
Let $k=\frac{x}{y}-\frac{z}{x}-\frac{z^{2}}{x y}=\frac{x^{2}-y z-z^{2}}{x y}$. We have
$$
k+1=\frac{x^{2}+x y-y z-z^{2}}{x y}=\frac{x^{2}-x z+x y-y z+z x-z^{2}}{x y}=\frac{(x+y+z)(x-z)}{x y}=\frac{9 \cdot 2}{6}=3,
$$
so $k=2$.
|
{
"resource_path": "HarvardMIT/segmented/en-241-2020-nov-guts-solutions.jsonl",
"problem_match": "\n6. [6]",
"solution_match": "\nSolution: "
}
|
08062338-78d6-5ee7-8564-21769a4188eb
| 610,208
|
Compute the maximum number of sides of a polygon that is the cross-section of a regular hexagonal prism.
|
Note that since there are 8 faces to a regular hexagonal prism and a cross-section may only intersect a face once, the upper bound for our answer is 8 .
Indeed, we can construct a cross-section of the prism with 8 sides. Let $A B C D E F$ and $A^{\prime} B^{\prime} C^{\prime} D^{\prime} E^{\prime} F^{\prime}$ be the two bases of the prism, with $A$ being directly over $A^{\prime}$. Choose points $P$ and $Q$ on line segments $A B$ and $B C$, respectively, and choose points $P^{\prime}$ and $Q^{\prime}$ on segments $D^{\prime} E^{\prime}$ and $E^{\prime} F^{\prime}$, respectively, such that $P Q \| P^{\prime} Q^{\prime}$. Then, the cross-section of the prism from the plane that goes through $P, Q, P^{\prime}$, and $Q^{\prime}$ forms a polygon with 8 sides.
|
8
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Compute the maximum number of sides of a polygon that is the cross-section of a regular hexagonal prism.
|
Note that since there are 8 faces to a regular hexagonal prism and a cross-section may only intersect a face once, the upper bound for our answer is 8 .
Indeed, we can construct a cross-section of the prism with 8 sides. Let $A B C D E F$ and $A^{\prime} B^{\prime} C^{\prime} D^{\prime} E^{\prime} F^{\prime}$ be the two bases of the prism, with $A$ being directly over $A^{\prime}$. Choose points $P$ and $Q$ on line segments $A B$ and $B C$, respectively, and choose points $P^{\prime}$ and $Q^{\prime}$ on segments $D^{\prime} E^{\prime}$ and $E^{\prime} F^{\prime}$, respectively, such that $P Q \| P^{\prime} Q^{\prime}$. Then, the cross-section of the prism from the plane that goes through $P, Q, P^{\prime}$, and $Q^{\prime}$ forms a polygon with 8 sides.

|
{
"resource_path": "HarvardMIT/segmented/en-241-2020-nov-guts-solutions.jsonl",
"problem_match": "\n7. [7]",
"solution_match": "\nSolution: "
}
|
216d8218-3905-5021-8e66-2050a8be7869
| 610,209
|
A small village has $n$ people. During their yearly elections, groups of three people come up to a stage and vote for someone in the village to be the new leader. After every possible group of three people has voted for someone, the person with the most votes wins.
This year, it turned out that everyone in the village had the exact same number of votes! If $10 \leq n \leq$ 100 , what is the number of possible values of $n$ ?
|
Answer: 61
|
61
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
A small village has $n$ people. During their yearly elections, groups of three people come up to a stage and vote for someone in the village to be the new leader. After every possible group of three people has voted for someone, the person with the most votes wins.
This year, it turned out that everyone in the village had the exact same number of votes! If $10 \leq n \leq$ 100 , what is the number of possible values of $n$ ?
|
Answer: 61
|
{
"resource_path": "HarvardMIT/segmented/en-241-2020-nov-guts-solutions.jsonl",
"problem_match": "\n8. [7]",
"solution_match": "\nProposed by: Vincent Bian\n"
}
|
47b53b89-e081-5b12-b80f-82b17e7b40d1
| 610,210
|
A fair coin is flipped eight times in a row. Let $p$ be the probability that there is exactly one pair of consecutive flips that are both heads and exactly one pair of consecutive flips that are both tails. If $p=\frac{a}{b}$, where $a, b$ are relatively prime positive integers, compute $100 a+b$.
|
Separate the sequence of coin flips into alternating blocks of heads and tails. Of the blocks of heads, exactly one block has length 2 , and all other blocks have length 1 . The same statement applies to blocks of tails. Thus, if there are $k$ blocks in total, there are $k-2$ blocks of length 1 and 2 blocks of length 2 , leading to $k+2$ coins in total. We conclude that $k=6$, meaning that there are 3 blocks of heads and 3 blocks of tails.
The blocks of heads must have lengths $1,1,2$ in some order, and likewise for tails. There are $3^{2}=9$ ways to choose these two orders, and 2 ways to assemble these blocks into a sequence, depending on whether the first coin flipped is heads or tails. Thus the final probability is $18 / 2^{8}=9 / 128$.
|
90128
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
A fair coin is flipped eight times in a row. Let $p$ be the probability that there is exactly one pair of consecutive flips that are both heads and exactly one pair of consecutive flips that are both tails. If $p=\frac{a}{b}$, where $a, b$ are relatively prime positive integers, compute $100 a+b$.
|
Separate the sequence of coin flips into alternating blocks of heads and tails. Of the blocks of heads, exactly one block has length 2 , and all other blocks have length 1 . The same statement applies to blocks of tails. Thus, if there are $k$ blocks in total, there are $k-2$ blocks of length 1 and 2 blocks of length 2 , leading to $k+2$ coins in total. We conclude that $k=6$, meaning that there are 3 blocks of heads and 3 blocks of tails.
The blocks of heads must have lengths $1,1,2$ in some order, and likewise for tails. There are $3^{2}=9$ ways to choose these two orders, and 2 ways to assemble these blocks into a sequence, depending on whether the first coin flipped is heads or tails. Thus the final probability is $18 / 2^{8}=9 / 128$.
|
{
"resource_path": "HarvardMIT/segmented/en-241-2020-nov-guts-solutions.jsonl",
"problem_match": "\n9. [7]",
"solution_match": "\nSolution: "
}
|
585affc2-5b6a-57c1-97a4-7d5bd95b3147
| 610,211
|
The number 3003 is the only number known to appear eight times in Pascal's triangle, at positions
$$
\binom{3003}{1},\binom{3003}{3002},\binom{a}{2},\binom{a}{a-2},\binom{15}{b},\binom{15}{15-b},\binom{14}{6},\binom{14}{8}
$$
Compute $a+b(15-b)$.
|
Answer: 128
|
128
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
The number 3003 is the only number known to appear eight times in Pascal's triangle, at positions
$$
\binom{3003}{1},\binom{3003}{3002},\binom{a}{2},\binom{a}{a-2},\binom{15}{b},\binom{15}{15-b},\binom{14}{6},\binom{14}{8}
$$
Compute $a+b(15-b)$.
|
Answer: 128
|
{
"resource_path": "HarvardMIT/segmented/en-241-2020-nov-guts-solutions.jsonl",
"problem_match": "\n10. [8]",
"solution_match": "\nProposed by: Carl Joshua Quines\n"
}
|
f4864579-e4a4-56b7-b2ea-192d4375b44d
| 610,212
|
In a single-elimination tournament consisting of $2^{9}=512$ teams, there is a strict ordering on the skill levels of the teams, but Joy does not know that ordering. The teams are randomly put into a bracket and they play out the tournament, with the better team always beating the worse team. Joy is then given the results of all 511 matches and must create a list of teams such that she can guarantee that the third-best team is on the list. What is the minimum possible length of Joy's list?
|
The best team must win the tournament. The second-best team has to be one of the 9 teams that the first best team beat; call these teams marginal. The third best team must have lost to either the best or the second-best team, so it must either be marginal or have lost to a marginal team. Since there is exactly one marginal team that won $k$ games for each integer $0 \leq k \leq 8$, we can then conclude that there are $1+2+\cdots+9=45$ teams that are either marginal or lost to a marginal team. Moreover, it is not hard to construct a scenario in which the third-best team is any of these 45 teams, so we cannot do better.
|
45
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
In a single-elimination tournament consisting of $2^{9}=512$ teams, there is a strict ordering on the skill levels of the teams, but Joy does not know that ordering. The teams are randomly put into a bracket and they play out the tournament, with the better team always beating the worse team. Joy is then given the results of all 511 matches and must create a list of teams such that she can guarantee that the third-best team is on the list. What is the minimum possible length of Joy's list?
|
The best team must win the tournament. The second-best team has to be one of the 9 teams that the first best team beat; call these teams marginal. The third best team must have lost to either the best or the second-best team, so it must either be marginal or have lost to a marginal team. Since there is exactly one marginal team that won $k$ games for each integer $0 \leq k \leq 8$, we can then conclude that there are $1+2+\cdots+9=45$ teams that are either marginal or lost to a marginal team. Moreover, it is not hard to construct a scenario in which the third-best team is any of these 45 teams, so we cannot do better.
|
{
"resource_path": "HarvardMIT/segmented/en-241-2020-nov-guts-solutions.jsonl",
"problem_match": "\n12. [8]",
"solution_match": "\nSolution: "
}
|
3e3bb7e8-3cfc-54d1-9cc9-137a15d78d67
| 610,214
|
Wendy is playing darts with a circular dartboard of radius 20 . Whenever she throws a dart, it lands uniformly at random on the dartboard. At the start of her game, there are 2020 darts placed randomly on the board. Every turn, she takes the dart farthest from the center, and throws it at the board again. What is the expected number of darts she has to throw before all the darts are within 10 units of the center?
|
Consider an individual dart. There is a $\frac{1}{4}$ probability it is already within 10 units of the center. If not, for every throw there is a $\frac{1}{4}$ probability it is not thrown again. Thus, if $E$ is the expected value of times it is thrown, we find $E=1+\frac{3}{4} E \Longrightarrow E=4$.
As a result, the expected number of times each dart is thrown is $\frac{3}{4} \cdot 4=3$. By linearity of expectation, the answer is $2020 \cdot 3=6060$.
|
6060
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Wendy is playing darts with a circular dartboard of radius 20 . Whenever she throws a dart, it lands uniformly at random on the dartboard. At the start of her game, there are 2020 darts placed randomly on the board. Every turn, she takes the dart farthest from the center, and throws it at the board again. What is the expected number of darts she has to throw before all the darts are within 10 units of the center?
|
Consider an individual dart. There is a $\frac{1}{4}$ probability it is already within 10 units of the center. If not, for every throw there is a $\frac{1}{4}$ probability it is not thrown again. Thus, if $E$ is the expected value of times it is thrown, we find $E=1+\frac{3}{4} E \Longrightarrow E=4$.
As a result, the expected number of times each dart is thrown is $\frac{3}{4} \cdot 4=3$. By linearity of expectation, the answer is $2020 \cdot 3=6060$.
|
{
"resource_path": "HarvardMIT/segmented/en-241-2020-nov-guts-solutions.jsonl",
"problem_match": "\n13. [9]",
"solution_match": "\nSolution: "
}
|
f01ba7fc-75ea-549a-8b49-db0cc343d445
| 610,215
|
A point $(x, y)$ is selected uniformly at random from the unit square $S=\{(x, y) \mid 0 \leq x \leq 1,0 \leq$ $y \leq 1\}$. If the probability that $(3 x+2 y, x+4 y)$ is in $S$ is $\frac{a}{b}$, where $a, b$ are relatively prime positive integers, compute $100 a+b$.
|
Under the transformation $(x, y) \mapsto(3 x+2 y, x+4 y), S$ is mapped to a parallelogram with vertices $(0,0),(3,1),(5,5)$, and $(2,4)$. Using the shoelace formula, the area of this parallelogram is 10 .
The intersection of the image parallelogram and $S$ is the quadrilateral with vertices $(0,0),\left(1, \frac{1}{3}\right),(1,1)$, and $\left(\frac{1}{2}, 1\right)$. To get this quadrilateral, we take away a right triangle with legs 1 and $\frac{1}{2}$ and a right triangle with legs 1 and $\frac{1}{3}$ from the unit square. So the quadrilateral has area $1-\frac{1}{2} \cdot \frac{1}{2}-\frac{1}{2} \cdot \frac{1}{3}=\frac{7}{12}$. Then the fraction of the image parallelogram that lies within $S$ is $\frac{7}{12}=\frac{7}{120}$, which is the probability that a point stays in $S$ after the mapping.
|
701
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
A point $(x, y)$ is selected uniformly at random from the unit square $S=\{(x, y) \mid 0 \leq x \leq 1,0 \leq$ $y \leq 1\}$. If the probability that $(3 x+2 y, x+4 y)$ is in $S$ is $\frac{a}{b}$, where $a, b$ are relatively prime positive integers, compute $100 a+b$.
|

Under the transformation $(x, y) \mapsto(3 x+2 y, x+4 y), S$ is mapped to a parallelogram with vertices $(0,0),(3,1),(5,5)$, and $(2,4)$. Using the shoelace formula, the area of this parallelogram is 10 .
The intersection of the image parallelogram and $S$ is the quadrilateral with vertices $(0,0),\left(1, \frac{1}{3}\right),(1,1)$, and $\left(\frac{1}{2}, 1\right)$. To get this quadrilateral, we take away a right triangle with legs 1 and $\frac{1}{2}$ and a right triangle with legs 1 and $\frac{1}{3}$ from the unit square. So the quadrilateral has area $1-\frac{1}{2} \cdot \frac{1}{2}-\frac{1}{2} \cdot \frac{1}{3}=\frac{7}{12}$. Then the fraction of the image parallelogram that lies within $S$ is $\frac{7}{12}=\frac{7}{120}$, which is the probability that a point stays in $S$ after the mapping.
|
{
"resource_path": "HarvardMIT/segmented/en-241-2020-nov-guts-solutions.jsonl",
"problem_match": "\n14. [9]",
"solution_match": "\nSolution:\n"
}
|
1278375d-794a-5e35-a21b-ae60db69e4c7
| 610,216
|
For a real number $r$, the quadratics $x^{2}+(r-1) x+6$ and $x^{2}+(2 r+1) x+22$ have a common real root. The sum of the possible values of $r$ can be expressed as $\frac{a}{b}$, where $a, b$ are relatively prime positive integers. Compute $100 a+b$.
|
Let the common root be $s$. Then,
$$
s^{2}+(r-1) s+6=s^{2}+(2 r+1) s+22
$$
and $s=-\frac{16}{r+2}$. Substituting this into $s^{2}+(r-1) s+6=0$ yields
$$
\frac{256}{(r+2)^{2}}-\frac{16(r-1)}{r+2}+6=0
$$
After multiplying both sides by $(r+2)^{2}$, the equation becomes
$$
256-16(r-1)(r+2)+6(r+2)^{2}=0
$$
which simplifies into
$$
5 r^{2}-4 r-156=0
$$
Thus, by Vieta's Formulas, the sum of the possible values of $r$ is $\frac{4}{5}$.
|
100 \cdot 4 + 5
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
For a real number $r$, the quadratics $x^{2}+(r-1) x+6$ and $x^{2}+(2 r+1) x+22$ have a common real root. The sum of the possible values of $r$ can be expressed as $\frac{a}{b}$, where $a, b$ are relatively prime positive integers. Compute $100 a+b$.
|
Let the common root be $s$. Then,
$$
s^{2}+(r-1) s+6=s^{2}+(2 r+1) s+22
$$
and $s=-\frac{16}{r+2}$. Substituting this into $s^{2}+(r-1) s+6=0$ yields
$$
\frac{256}{(r+2)^{2}}-\frac{16(r-1)}{r+2}+6=0
$$
After multiplying both sides by $(r+2)^{2}$, the equation becomes
$$
256-16(r-1)(r+2)+6(r+2)^{2}=0
$$
which simplifies into
$$
5 r^{2}-4 r-156=0
$$
Thus, by Vieta's Formulas, the sum of the possible values of $r$ is $\frac{4}{5}$.
|
{
"resource_path": "HarvardMIT/segmented/en-241-2020-nov-guts-solutions.jsonl",
"problem_match": "\n15. [9]",
"solution_match": "\nSolution: "
}
|
63577ea4-d63f-5af2-b154-357c28443c78
| 610,217
|
Three players play tic-tac-toe together. In other words, the three players take turns placing an "A", "B", and "C", respectively, in one of the free spots of a $3 \times 3$ grid, and the first player to have three of their label in a row, column, or diagonal wins. How many possible final boards are there where the player who goes third wins the game? (Rotations and reflections are considered different boards, but the order of placement does not matter.)
|
In all winning cases for the third player, every spot in the grid must be filled. There are two ways that player C wins along a diagonal, and six ways that player C wins along a row or column. In the former case, any arrangement of the As and Bs is a valid board, since every other row, column, and diagonal is blocked. So there are $\binom{6}{3}=20$ different finishing boards each for this case. However, in the latter case, we must make sure players A and B do not complete a row or column of their own, so only $20-2=18$ of the finishing boards are valid. The final answer is $2 \cdot 20+6 \cdot 18=148$.
|
148
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Three players play tic-tac-toe together. In other words, the three players take turns placing an "A", "B", and "C", respectively, in one of the free spots of a $3 \times 3$ grid, and the first player to have three of their label in a row, column, or diagonal wins. How many possible final boards are there where the player who goes third wins the game? (Rotations and reflections are considered different boards, but the order of placement does not matter.)
|
In all winning cases for the third player, every spot in the grid must be filled. There are two ways that player C wins along a diagonal, and six ways that player C wins along a row or column. In the former case, any arrangement of the As and Bs is a valid board, since every other row, column, and diagonal is blocked. So there are $\binom{6}{3}=20$ different finishing boards each for this case. However, in the latter case, we must make sure players A and B do not complete a row or column of their own, so only $20-2=18$ of the finishing boards are valid. The final answer is $2 \cdot 20+6 \cdot 18=148$.
|
{
"resource_path": "HarvardMIT/segmented/en-241-2020-nov-guts-solutions.jsonl",
"problem_match": "\n16. [10]",
"solution_match": "\nSolution: "
}
|
35af6e09-e873-5158-bfd1-d4c9c49d0277
| 610,218
|
Let $\mathbb{N}_{>1}$ denote the set of positive integers greater than 1 . Let $f: \mathbb{N}_{>1} \rightarrow \mathbb{N}_{>1}$ be a function such that $f(m n)=f(m) f(n)$ for all $m, n \in \mathbb{N}_{>1}$. If $f(101!)=101$ !, compute the number of possible values of $f(2020 \cdot 2021)$.
|
For a prime $p$ and positive integer $n$, we let $v_{p}(n)$ denote the largest nonnegative integer $k$ such that $p^{k} \mid n$. Note that $f$ is determined by its action on primes. Since $f(101!)=101!$, by counting prime factors, $f$ must permute the set of prime factors of 101!; moreover, if $p$ and $q$ are prime factors of 101 ! and $f(p)=q$, we must have $v_{p}(101!)=v_{q}(101!)$. This clearly gives $f(2)=2, f(5)=5$, so it suffices to find the number of possible values for $f\left(43 \cdot 47 \cdot 101\right.$ ). (We can factor $2021=45^{2}-2^{2}=43 \cdot 47$.)
There are 4 primes with $v_{p}(101!)=2$ (namely, $37,41,43,47$ ), so there are 6 possible values for $f(43 \cdot 47)$. Moreover, there are 11 primes with $v_{p}(101!)=1$ (namely, 53, 59, 61, 67, 71, 73, 79, 83, 89, $97,101)$. Hence there are 66 possible values altogether.
|
66
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Let $\mathbb{N}_{>1}$ denote the set of positive integers greater than 1 . Let $f: \mathbb{N}_{>1} \rightarrow \mathbb{N}_{>1}$ be a function such that $f(m n)=f(m) f(n)$ for all $m, n \in \mathbb{N}_{>1}$. If $f(101!)=101$ !, compute the number of possible values of $f(2020 \cdot 2021)$.
|
For a prime $p$ and positive integer $n$, we let $v_{p}(n)$ denote the largest nonnegative integer $k$ such that $p^{k} \mid n$. Note that $f$ is determined by its action on primes. Since $f(101!)=101!$, by counting prime factors, $f$ must permute the set of prime factors of 101!; moreover, if $p$ and $q$ are prime factors of 101 ! and $f(p)=q$, we must have $v_{p}(101!)=v_{q}(101!)$. This clearly gives $f(2)=2, f(5)=5$, so it suffices to find the number of possible values for $f\left(43 \cdot 47 \cdot 101\right.$ ). (We can factor $2021=45^{2}-2^{2}=43 \cdot 47$.)
There are 4 primes with $v_{p}(101!)=2$ (namely, $37,41,43,47$ ), so there are 6 possible values for $f(43 \cdot 47)$. Moreover, there are 11 primes with $v_{p}(101!)=1$ (namely, 53, 59, 61, 67, 71, 73, 79, 83, 89, $97,101)$. Hence there are 66 possible values altogether.
|
{
"resource_path": "HarvardMIT/segmented/en-241-2020-nov-guts-solutions.jsonl",
"problem_match": "\n17. [10]",
"solution_match": "\nSolution: "
}
|
a5bd2616-90d3-5a71-8433-0d18eb0b1716
| 610,219
|
Suppose Harvard Yard is a $17 \times 17$ square. There are 14 dorms located on the perimeter of the Yard. If $s$ is the minimum distance between two dorms, the maximum possible value of $s$ can be expressed as $a-\sqrt{b}$ where $a, b$ are positive integers. Compute $100 a+b$.
|
If two neighboring dorms are separated by a distance of more than $s$, we can move them slightly closer together and adjust the other dorms, increasing $s$. Therefore, in an optimal arrangement, the dorms form an equilateral 14 -gon with side length $s$.
By scaling, the problem is now equivalent to finding the smallest $a$ such that there exist 14 vertices on the boundary of an $a \times a$ square that form an equilateral 14 -gon with side length 1 . Such a 14 -gon must be centrally symmetric, yielding the following picture:
We know that $x_{1}^{2}+y_{1}^{2}=x_{2}^{2}+y_{2}^{2}=1$ and $x_{1}+x_{2}+3=y_{1}+y_{2}+2=a$. Moreover, if these equations are satisfied, then such a 14 -gon exists. We now consider the vectors $\vec{v}_{1}=\left(x_{1}, y_{1}\right)$ and $\vec{v}_{2}=\left(x_{2}, y_{2}\right)$. These unit vectors are in the first quadrant and add to $(a-3, a-2)$, which lies on the line $y=x+1$.
Since $\vec{v}_{1}$ and $\vec{v}_{2}$ must lie on the first quadrant, from the above diagram we deduce that the minimum value of $a$ occurs when one of $\vec{v}_{1}, \vec{v}_{2}$ is $(0,1)$, meaning that $(a-3, a-2)=\left(\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2}+1\right)$. This means that $a=\frac{\sqrt{2}}{2}+3$, so the maximum possible value of $s$ is
$$
\frac{17}{\frac{\sqrt{2}}{2}+3}=17 \cdot \frac{3-\frac{\sqrt{2}}{2}}{17 / 2}=6-\sqrt{2}
$$
|
602
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Suppose Harvard Yard is a $17 \times 17$ square. There are 14 dorms located on the perimeter of the Yard. If $s$ is the minimum distance between two dorms, the maximum possible value of $s$ can be expressed as $a-\sqrt{b}$ where $a, b$ are positive integers. Compute $100 a+b$.
|
If two neighboring dorms are separated by a distance of more than $s$, we can move them slightly closer together and adjust the other dorms, increasing $s$. Therefore, in an optimal arrangement, the dorms form an equilateral 14 -gon with side length $s$.
By scaling, the problem is now equivalent to finding the smallest $a$ such that there exist 14 vertices on the boundary of an $a \times a$ square that form an equilateral 14 -gon with side length 1 . Such a 14 -gon must be centrally symmetric, yielding the following picture:

We know that $x_{1}^{2}+y_{1}^{2}=x_{2}^{2}+y_{2}^{2}=1$ and $x_{1}+x_{2}+3=y_{1}+y_{2}+2=a$. Moreover, if these equations are satisfied, then such a 14 -gon exists. We now consider the vectors $\vec{v}_{1}=\left(x_{1}, y_{1}\right)$ and $\vec{v}_{2}=\left(x_{2}, y_{2}\right)$. These unit vectors are in the first quadrant and add to $(a-3, a-2)$, which lies on the line $y=x+1$.

Since $\vec{v}_{1}$ and $\vec{v}_{2}$ must lie on the first quadrant, from the above diagram we deduce that the minimum value of $a$ occurs when one of $\vec{v}_{1}, \vec{v}_{2}$ is $(0,1)$, meaning that $(a-3, a-2)=\left(\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2}+1\right)$. This means that $a=\frac{\sqrt{2}}{2}+3$, so the maximum possible value of $s$ is
$$
\frac{17}{\frac{\sqrt{2}}{2}+3}=17 \cdot \frac{3-\frac{\sqrt{2}}{2}}{17 / 2}=6-\sqrt{2}
$$
|
{
"resource_path": "HarvardMIT/segmented/en-241-2020-nov-guts-solutions.jsonl",
"problem_match": "\n18. [10]",
"solution_match": "\nSolution: "
}
|
16064c70-4c9d-5a1d-b416-383131afad96
| 610,220
|
Let $\omega_{1}$ be a circle of radius 5 , and let $\omega_{2}$ be a circle of radius 2 whose center lies on $\omega_{1}$. Let the two circles intersect at $A$ and $B$, and let the tangents to $\omega_{2}$ at $A$ and $B$ intersect at $P$. If the area of $\triangle A B P$ can be expressed as $\frac{a \sqrt{b}}{c}$, where $b$ is square-free and $a, c$ are relatively prime positive integers, compute $100 a+10 b+c$.
|
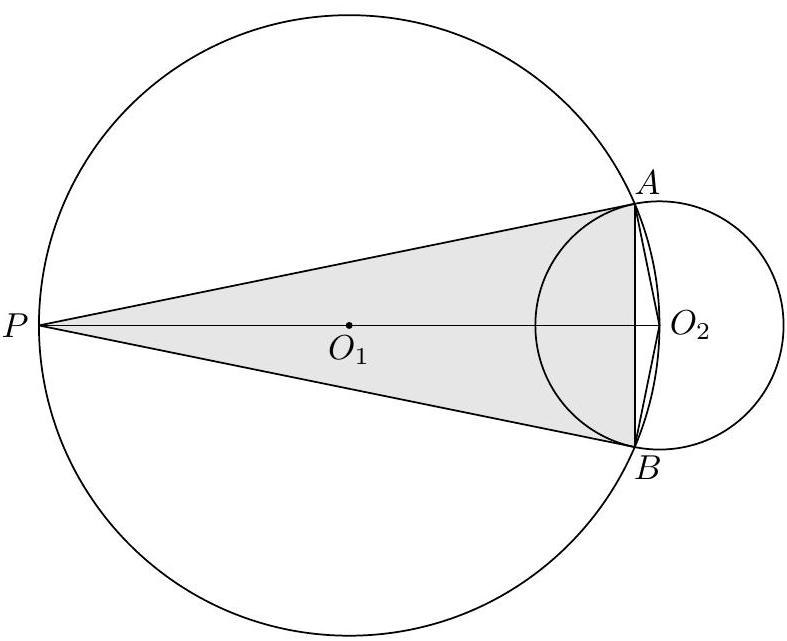
Let $O_{1}$ and $O_{2}$ be the centers of $\omega_{1}$ and $\omega_{2}$, respectively. Because
$$
\angle O_{2} A P+\angle O_{2} B P=90^{\circ}+90^{\circ}=180^{\circ},
$$
quadrilateral $O_{2} A P B$ is cyclic. But $O_{2}, A$, and $B$ lie on $\omega_{1}$, so $P$ lies on $\omega_{1}$ and $O_{2} P$ is a diameter of $\omega_{1}$.
From the Pythagorean theorem on triangle $P A O_{2}$, we can calculate $A P=4 \sqrt{6}$, so $\sin \angle A O_{2} P=\frac{2 \sqrt{6}}{5}$ and $\cos \angle A O_{2} P=\frac{1}{5}$. Because $\triangle A O_{2} P$ and $\triangle B O_{2} P$ are congruent, we have
$$
\sin \angle A P B=\sin 2 \angle A O_{2} P=2 \sin \angle A O_{2} P \cos \angle A O_{2} P=\frac{4 \sqrt{6}}{25}
$$
implying that
$$
[A P B]=\frac{P A \cdot P B}{2} \sin \angle A P B=\frac{192 \sqrt{6}}{25} .
$$
|
192 \sqrt{6}/25
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $\omega_{1}$ be a circle of radius 5 , and let $\omega_{2}$ be a circle of radius 2 whose center lies on $\omega_{1}$. Let the two circles intersect at $A$ and $B$, and let the tangents to $\omega_{2}$ at $A$ and $B$ intersect at $P$. If the area of $\triangle A B P$ can be expressed as $\frac{a \sqrt{b}}{c}$, where $b$ is square-free and $a, c$ are relatively prime positive integers, compute $100 a+10 b+c$.
|

Let $O_{1}$ and $O_{2}$ be the centers of $\omega_{1}$ and $\omega_{2}$, respectively. Because
$$
\angle O_{2} A P+\angle O_{2} B P=90^{\circ}+90^{\circ}=180^{\circ},
$$
quadrilateral $O_{2} A P B$ is cyclic. But $O_{2}, A$, and $B$ lie on $\omega_{1}$, so $P$ lies on $\omega_{1}$ and $O_{2} P$ is a diameter of $\omega_{1}$.
From the Pythagorean theorem on triangle $P A O_{2}$, we can calculate $A P=4 \sqrt{6}$, so $\sin \angle A O_{2} P=\frac{2 \sqrt{6}}{5}$ and $\cos \angle A O_{2} P=\frac{1}{5}$. Because $\triangle A O_{2} P$ and $\triangle B O_{2} P$ are congruent, we have
$$
\sin \angle A P B=\sin 2 \angle A O_{2} P=2 \sin \angle A O_{2} P \cos \angle A O_{2} P=\frac{4 \sqrt{6}}{25}
$$
implying that
$$
[A P B]=\frac{P A \cdot P B}{2} \sin \angle A P B=\frac{192 \sqrt{6}}{25} .
$$
|
{
"resource_path": "HarvardMIT/segmented/en-241-2020-nov-guts-solutions.jsonl",
"problem_match": "\n20. [11]",
"solution_match": "\n## Solution:\n\n"
}
|
02b17475-fdb7-5ed7-a51c-8260be808bce
| 610,222
|
Let $f(n)$ be the number of distinct prime divisors of $n$ less than 6 . Compute
$$
\sum_{n=1}^{2020} f(n)^{2}
$$
|
Define
$$
\mathbf{1}_{a \mid n}= \begin{cases}1 & a \mid n \\ 0 & \text { otherwise }\end{cases}
$$
Then
$$
\begin{aligned}
f(n)^{2} & =\left(\mathbf{1}_{2 \mid n}+\mathbf{1}_{3 \mid n}+\mathbf{1}_{5 \mid n}\right)^{2} \\
& =\mathbf{1}_{2 \mid n}+\mathbf{1}_{3 \mid n}+\mathbf{1}_{5 \mid n}+2\left(\mathbf{1}_{2 \mid n} \mathbf{1}_{3 \mid n}+\mathbf{1}_{2 \mid n} \mathbf{1}_{5 \mid n}+\mathbf{1}_{3 \mid n} \mathbf{1}_{5 \mid n}\right) \\
& =\mathbf{1}_{2 \mid n}+\mathbf{1}_{3 \mid n}+\mathbf{1}_{5 \mid n}+2\left(\mathbf{1}_{6 \mid n}+\mathbf{1}_{10 \mid n}+\mathbf{1}_{15 \mid n}\right)
\end{aligned}
$$
So summing $f(n)^{2}$ over integers $1 \leq n \leq 2020$ is the same as summing 1 for each time $n$ is divisible by 2,3 , or 5 , and additionally summing 2 for each time $n$ is divisible by 6,10 , or 15 .
$$
\begin{aligned}
\sum_{n=1}^{2020} f(n)^{2} & =\left\lfloor\frac{2020}{2}\right\rfloor+\left\lfloor\frac{2020}{3}\right\rfloor+\left\lfloor\frac{2020}{5}\right\rfloor+2\left(\left\lfloor\frac{2020}{6}\right\rfloor+\left\lfloor\frac{2020}{10}\right\rfloor+\left\lfloor\frac{2020}{15}\right\rfloor\right) \\
& =1010+673+404+2(336+202+134)=3431
\end{aligned}
$$
|
3431
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Let $f(n)$ be the number of distinct prime divisors of $n$ less than 6 . Compute
$$
\sum_{n=1}^{2020} f(n)^{2}
$$
|
Define
$$
\mathbf{1}_{a \mid n}= \begin{cases}1 & a \mid n \\ 0 & \text { otherwise }\end{cases}
$$
Then
$$
\begin{aligned}
f(n)^{2} & =\left(\mathbf{1}_{2 \mid n}+\mathbf{1}_{3 \mid n}+\mathbf{1}_{5 \mid n}\right)^{2} \\
& =\mathbf{1}_{2 \mid n}+\mathbf{1}_{3 \mid n}+\mathbf{1}_{5 \mid n}+2\left(\mathbf{1}_{2 \mid n} \mathbf{1}_{3 \mid n}+\mathbf{1}_{2 \mid n} \mathbf{1}_{5 \mid n}+\mathbf{1}_{3 \mid n} \mathbf{1}_{5 \mid n}\right) \\
& =\mathbf{1}_{2 \mid n}+\mathbf{1}_{3 \mid n}+\mathbf{1}_{5 \mid n}+2\left(\mathbf{1}_{6 \mid n}+\mathbf{1}_{10 \mid n}+\mathbf{1}_{15 \mid n}\right)
\end{aligned}
$$
So summing $f(n)^{2}$ over integers $1 \leq n \leq 2020$ is the same as summing 1 for each time $n$ is divisible by 2,3 , or 5 , and additionally summing 2 for each time $n$ is divisible by 6,10 , or 15 .
$$
\begin{aligned}
\sum_{n=1}^{2020} f(n)^{2} & =\left\lfloor\frac{2020}{2}\right\rfloor+\left\lfloor\frac{2020}{3}\right\rfloor+\left\lfloor\frac{2020}{5}\right\rfloor+2\left(\left\lfloor\frac{2020}{6}\right\rfloor+\left\lfloor\frac{2020}{10}\right\rfloor+\left\lfloor\frac{2020}{15}\right\rfloor\right) \\
& =1010+673+404+2(336+202+134)=3431
\end{aligned}
$$
|
{
"resource_path": "HarvardMIT/segmented/en-241-2020-nov-guts-solutions.jsonl",
"problem_match": "\n21. [11]",
"solution_match": "\nSolution: "
}
|
b4ecc3ae-4463-5509-8e20-0f0c8160fa14
| 610,223
|
In triangle $A B C, A B=32, A C=35$, and $B C=x$. What is the smallest positive integer $x$ such that $1+\cos ^{2} A, \cos ^{2} B$, and $\cos ^{2} C$ form the sides of a non-degenerate triangle?
|
By the triangle inequality, we wish $\cos ^{2} B+\cos ^{2} C>1+\cos ^{2} A$. The other two inequalities are always satisfied, since $1+\cos ^{2} A \geq 1 \geq \cos ^{2} B, \cos ^{2} C$. Rewrite the above as
$$
2-\sin ^{2} B-\sin ^{2} C>2-\sin ^{2} A
$$
so it is equivalent to $\sin ^{2} B+\sin ^{2} C<\sin ^{2} A$. By the law of $\operatorname{sines}, \sin A: \sin B: \sin C=B C: A C: A B$. Therefore,
$$
\sin ^{2} B+\sin ^{2} C<\sin ^{2} A \Longleftrightarrow C A^{2}+A B^{2}<x^{2}
$$
Since $C A^{2}+A B^{2}=2249$, the smallest possible value of $x$ such that $x^{2}>2249$ is 48 .
|
48
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
In triangle $A B C, A B=32, A C=35$, and $B C=x$. What is the smallest positive integer $x$ such that $1+\cos ^{2} A, \cos ^{2} B$, and $\cos ^{2} C$ form the sides of a non-degenerate triangle?
|
By the triangle inequality, we wish $\cos ^{2} B+\cos ^{2} C>1+\cos ^{2} A$. The other two inequalities are always satisfied, since $1+\cos ^{2} A \geq 1 \geq \cos ^{2} B, \cos ^{2} C$. Rewrite the above as
$$
2-\sin ^{2} B-\sin ^{2} C>2-\sin ^{2} A
$$
so it is equivalent to $\sin ^{2} B+\sin ^{2} C<\sin ^{2} A$. By the law of $\operatorname{sines}, \sin A: \sin B: \sin C=B C: A C: A B$. Therefore,
$$
\sin ^{2} B+\sin ^{2} C<\sin ^{2} A \Longleftrightarrow C A^{2}+A B^{2}<x^{2}
$$
Since $C A^{2}+A B^{2}=2249$, the smallest possible value of $x$ such that $x^{2}>2249$ is 48 .
|
{
"resource_path": "HarvardMIT/segmented/en-241-2020-nov-guts-solutions.jsonl",
"problem_match": "\n22. [12]",
"solution_match": "\nSolution: "
}
|
71edb769-ff6f-59fc-9aa4-7cc9052c30ef
| 610,224
|
Two points are chosen inside the square $\{(x, y) \mid 0 \leq x, y \leq 1\}$ uniformly at random, and a unit square is drawn centered at each point with edges parallel to the coordinate axes. The expected area of the union of the two squares can be expressed as $\frac{a}{b}$, where $a, b$ are relatively prime positive integers. Compute $100 a+b$.
|

Let $\Delta x$ and $\Delta y$ be the positive differences between the $x$ coordinates and $y$ coordinates of the centers of the squares, respectively. Then, the length of the intersection of the squares along the $x$ dimension is $1-\Delta x$, and likewise the length along the $y$ dimension is $1-\Delta y$. In order to find the expectation of $\Delta x$ and $\Delta y$, we can find the volume of the set of points $(a, b, c)$ such that $0 \leq a, b \leq 1$ and $c \leq|a-b|$. This set is composed of the two pyramids of volume $\frac{1}{6}$ shown below:
Since the expected distance between two points on a unit interval is therefore $\frac{1}{3}$, we have that $\mathbb{E}[1-\Delta x]=\mathbb{E}[1-\Delta y]=\frac{2}{3}$. The expectation of the product of independent variables equals the product of their expectations, so the expected area of intersection is $\frac{4}{9}$ and the expected area of union is $2-\frac{4}{9}=\frac{14}{9}$.
|
1409
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Two points are chosen inside the square $\{(x, y) \mid 0 \leq x, y \leq 1\}$ uniformly at random, and a unit square is drawn centered at each point with edges parallel to the coordinate axes. The expected area of the union of the two squares can be expressed as $\frac{a}{b}$, where $a, b$ are relatively prime positive integers. Compute $100 a+b$.
|

Let $\Delta x$ and $\Delta y$ be the positive differences between the $x$ coordinates and $y$ coordinates of the centers of the squares, respectively. Then, the length of the intersection of the squares along the $x$ dimension is $1-\Delta x$, and likewise the length along the $y$ dimension is $1-\Delta y$. In order to find the expectation of $\Delta x$ and $\Delta y$, we can find the volume of the set of points $(a, b, c)$ such that $0 \leq a, b \leq 1$ and $c \leq|a-b|$. This set is composed of the two pyramids of volume $\frac{1}{6}$ shown below:

Since the expected distance between two points on a unit interval is therefore $\frac{1}{3}$, we have that $\mathbb{E}[1-\Delta x]=\mathbb{E}[1-\Delta y]=\frac{2}{3}$. The expectation of the product of independent variables equals the product of their expectations, so the expected area of intersection is $\frac{4}{9}$ and the expected area of union is $2-\frac{4}{9}=\frac{14}{9}$.
|
{
"resource_path": "HarvardMIT/segmented/en-241-2020-nov-guts-solutions.jsonl",
"problem_match": "\n23. [12]",
"solution_match": "\nSolution:\n"
}
|
fb65efb5-2c9c-54d2-9cd2-f052286dc0c2
| 610,225
|
Compute the number of positive integers less than 10 ! which can be expressed as the sum of at most 4 (not necessarily distinct) factorials.
|
Answer: 648
|
648
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Compute the number of positive integers less than 10 ! which can be expressed as the sum of at most 4 (not necessarily distinct) factorials.
|
Answer: 648
|
{
"resource_path": "HarvardMIT/segmented/en-241-2020-nov-guts-solutions.jsonl",
"problem_match": "\n24. [12]",
"solution_match": "\nProposed by: Sheldon Kieren Tan\n"
}
|
c1fb1fbc-9ce5-59d9-a0a6-eb19c1c43555
| 610,226
|
Let $a_{1}, a_{2}, a_{3}, \ldots$ be a sequence of positive integers where $a_{1}=\sum_{i=0}^{100} i$ ! and $a_{i}+a_{i+1}$ is an odd perfect square for all $i \geq 1$. Compute the smallest possible value of $a_{1000}$.
|
Note that $a_{1} \equiv 1+1+2+6 \equiv 2(\bmod 8)$. Since $a_{1}+a_{2}$ must be an odd perfect square, we must have $a_{1}+a_{2} \equiv 1(\bmod 8) \Longrightarrow a_{2} \equiv 7(\bmod 8)$. Similarly, since $a_{2}+a_{3}$ is an odd perfect
square, we must have $a_{3} \equiv 2(\bmod 8)$. We can continue this to get $a_{2 k-1} \equiv 2(\bmod 8)$ and $a_{2 k} \equiv 7$ $(\bmod 8)$, so in particular, we have $a_{1000} \equiv 7(\bmod 8)$, so $a_{1000} \geq 7$.
Now, note that we can find some large enough odd perfect square $t^{2}$ such that $t^{2}-a_{1} \geq 23$. Let $a_{2}=t^{2}-a_{1}$. Since $a_{2} \equiv 7(\bmod 8)$, we can let $a_{2}-7=8 k$ for some integer $k \geq 2$. Now, since we have $(2 k+1)^{2}-(2 k-1)^{2}=8 k$, if we let $a_{3}=(2 k-1)^{2}-7$, then
$$
a_{2}+a_{3}=a_{2}+\left((2 k-1)^{2}-7\right)=(2 k-1)^{2}+\left(a_{2}-7\right)=(2 k-1)^{2}+8 k=(2 k+1)^{2}
$$
which is an odd perfect square. Now, we can let $a_{4}=7$ and we will get $a_{3}+a_{4}=(2 k-1)^{2}$. From here, we can let $2=a_{5}=a_{7}=a_{9}=\cdots$ and $7=a_{4}=a_{6}=a_{8}=\cdots$, which tells us that the least possible value for $a_{1000}$ is 7 .
|
7
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Let $a_{1}, a_{2}, a_{3}, \ldots$ be a sequence of positive integers where $a_{1}=\sum_{i=0}^{100} i$ ! and $a_{i}+a_{i+1}$ is an odd perfect square for all $i \geq 1$. Compute the smallest possible value of $a_{1000}$.
|
Note that $a_{1} \equiv 1+1+2+6 \equiv 2(\bmod 8)$. Since $a_{1}+a_{2}$ must be an odd perfect square, we must have $a_{1}+a_{2} \equiv 1(\bmod 8) \Longrightarrow a_{2} \equiv 7(\bmod 8)$. Similarly, since $a_{2}+a_{3}$ is an odd perfect
square, we must have $a_{3} \equiv 2(\bmod 8)$. We can continue this to get $a_{2 k-1} \equiv 2(\bmod 8)$ and $a_{2 k} \equiv 7$ $(\bmod 8)$, so in particular, we have $a_{1000} \equiv 7(\bmod 8)$, so $a_{1000} \geq 7$.
Now, note that we can find some large enough odd perfect square $t^{2}$ such that $t^{2}-a_{1} \geq 23$. Let $a_{2}=t^{2}-a_{1}$. Since $a_{2} \equiv 7(\bmod 8)$, we can let $a_{2}-7=8 k$ for some integer $k \geq 2$. Now, since we have $(2 k+1)^{2}-(2 k-1)^{2}=8 k$, if we let $a_{3}=(2 k-1)^{2}-7$, then
$$
a_{2}+a_{3}=a_{2}+\left((2 k-1)^{2}-7\right)=(2 k-1)^{2}+\left(a_{2}-7\right)=(2 k-1)^{2}+8 k=(2 k+1)^{2}
$$
which is an odd perfect square. Now, we can let $a_{4}=7$ and we will get $a_{3}+a_{4}=(2 k-1)^{2}$. From here, we can let $2=a_{5}=a_{7}=a_{9}=\cdots$ and $7=a_{4}=a_{6}=a_{8}=\cdots$, which tells us that the least possible value for $a_{1000}$ is 7 .
|
{
"resource_path": "HarvardMIT/segmented/en-241-2020-nov-guts-solutions.jsonl",
"problem_match": "\n25. [13]",
"solution_match": "\nSolution: "
}
|
b5e72094-eb49-56f8-86be-937e9be51000
| 610,227
|
Two players play a game where they are each given 10 indistinguishable units that must be distributed across three locations. (Units cannot be split.) At each location, a player wins at that location if the number of units they placed there is at least 2 more than the units of the other player. If both players distribute their units randomly (i.e. there is an equal probability of them distributing their units for any attainable distribution across the 3 locations), the probability that at least one location is won by one of the players can be expressed as $\frac{a}{b}$, where $a, b$ are relatively prime positive integers. Compute $100 a+b$.
|
By stars and bars, the total number of distributions is $\binom{12}{2}^{2}=66^{2}$. If no locations are won, either both distributions are identical or the difference between the two is $(1,0,-1)$, in some order. The first case has 66 possibilities. If the difference is $(1,0,-1)$, we can construct all such possiblities by choosing nonnegative integers $a, b, c$ that sum to 9 , and having the two players choose $(a+1, b, c)$ and $(a, b, c+1)$. This can be done in $\binom{11}{2}=55$ ways. In total, the second case has $6 \cdot 55=5 \cdot 66$ possibilities.
Thus the probability that no locations are won is $\frac{6 \cdot 66}{66^{2}}=\frac{1}{11}$, meaning that the answer is $\frac{10}{11}$.
|
1001
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Two players play a game where they are each given 10 indistinguishable units that must be distributed across three locations. (Units cannot be split.) At each location, a player wins at that location if the number of units they placed there is at least 2 more than the units of the other player. If both players distribute their units randomly (i.e. there is an equal probability of them distributing their units for any attainable distribution across the 3 locations), the probability that at least one location is won by one of the players can be expressed as $\frac{a}{b}$, where $a, b$ are relatively prime positive integers. Compute $100 a+b$.
|
By stars and bars, the total number of distributions is $\binom{12}{2}^{2}=66^{2}$. If no locations are won, either both distributions are identical or the difference between the two is $(1,0,-1)$, in some order. The first case has 66 possibilities. If the difference is $(1,0,-1)$, we can construct all such possiblities by choosing nonnegative integers $a, b, c$ that sum to 9 , and having the two players choose $(a+1, b, c)$ and $(a, b, c+1)$. This can be done in $\binom{11}{2}=55$ ways. In total, the second case has $6 \cdot 55=5 \cdot 66$ possibilities.
Thus the probability that no locations are won is $\frac{6 \cdot 66}{66^{2}}=\frac{1}{11}$, meaning that the answer is $\frac{10}{11}$.
|
{
"resource_path": "HarvardMIT/segmented/en-241-2020-nov-guts-solutions.jsonl",
"problem_match": "\n26. [13]",
"solution_match": "\nSolution: "
}
|
b559a3cb-cfa7-5540-a1fc-839d50bcedf7
| 610,228
|
In $\triangle A B C, D$ and $E$ are the midpoints of $B C$ and $C A$, respectively. $A D$ and $B E$ intersect at $G$. Given that $G E C D$ is cyclic, $A B=41$, and $A C=31$, compute $B C$.
|
By Power of a Point,
$$
\frac{2}{3} A D^{2}=A D \cdot A G=A E \cdot A C=\frac{1}{2} \cdot 31^{2}
$$
so $A D^{2}=\frac{3}{4} \cdot 31^{2}$. The median length formula yields
$$
A D^{2}=\frac{1}{4}\left(2 A B^{2}+2 A C^{2}-B C^{2}\right)
$$
whence
$$
B C=\sqrt{2 A B^{2}+2 A C^{2}-4 A D^{2}}=\sqrt{2 \cdot 41^{2}+2 \cdot 31^{2}-3 \cdot 31^{2}}=49
$$
|
49
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
In $\triangle A B C, D$ and $E$ are the midpoints of $B C$ and $C A$, respectively. $A D$ and $B E$ intersect at $G$. Given that $G E C D$ is cyclic, $A B=41$, and $A C=31$, compute $B C$.
|

By Power of a Point,
$$
\frac{2}{3} A D^{2}=A D \cdot A G=A E \cdot A C=\frac{1}{2} \cdot 31^{2}
$$
so $A D^{2}=\frac{3}{4} \cdot 31^{2}$. The median length formula yields
$$
A D^{2}=\frac{1}{4}\left(2 A B^{2}+2 A C^{2}-B C^{2}\right)
$$
whence
$$
B C=\sqrt{2 A B^{2}+2 A C^{2}-4 A D^{2}}=\sqrt{2 \cdot 41^{2}+2 \cdot 31^{2}-3 \cdot 31^{2}}=49
$$
|
{
"resource_path": "HarvardMIT/segmented/en-241-2020-nov-guts-solutions.jsonl",
"problem_match": "\n27. [13]",
"solution_match": "\nSolution:\n"
}
|
2f9576fa-abb0-579e-b0d2-c05cccd53c40
| 610,229
|
Bernie has 2020 marbles and 2020 bags labeled $B_{1}, \ldots, B_{2020}$ in which he randomly distributes the marbles (each marble is placed in a random bag independently). If $E$ the expected number of integers $1 \leq i \leq 2020$ such that $B_{i}$ has at least $i$ marbles, compute the closest integer to $1000 E$.
|
Let $p_{i}$ be the probability that a bag has $i$ marbles. Then, by linearity of expectation, we find
$$
E=\left(p_{1}+p_{2}+\cdots\right)+\left(p_{2}+p_{3}+\cdots\right)+\cdots=p_{1}+2 p_{2}+3 p_{3}+\cdots
$$
This is precisely the expected value of the number of marbles in a bag. By symmetry, this is 1 .
|
1000
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Bernie has 2020 marbles and 2020 bags labeled $B_{1}, \ldots, B_{2020}$ in which he randomly distributes the marbles (each marble is placed in a random bag independently). If $E$ the expected number of integers $1 \leq i \leq 2020$ such that $B_{i}$ has at least $i$ marbles, compute the closest integer to $1000 E$.
|
Let $p_{i}$ be the probability that a bag has $i$ marbles. Then, by linearity of expectation, we find
$$
E=\left(p_{1}+p_{2}+\cdots\right)+\left(p_{2}+p_{3}+\cdots\right)+\cdots=p_{1}+2 p_{2}+3 p_{3}+\cdots
$$
This is precisely the expected value of the number of marbles in a bag. By symmetry, this is 1 .
|
{
"resource_path": "HarvardMIT/segmented/en-241-2020-nov-guts-solutions.jsonl",
"problem_match": "\n28. [15]",
"solution_match": "\nSolution: "
}
|
b27cfa7e-7ee2-5560-be84-59f6228e5148
| 610,230
|
In acute triangle $A B C$, let $H$ be the orthocenter and $D$ the foot of the altitude from $A$. The circumcircle of triangle $B H C$ intersects $A C$ at $E \neq C$, and $A B$ at $F \neq B$. If $B D=3, C D=7$, and $\frac{A H}{H D}=\frac{5}{7}$, the area of triangle $A E F$ can be expressed as $\frac{a}{b}$, where $a, b$ are relatively prime positive integers. Compute $100 a+b$.
|
Let $A H$ intersect the circumcircle of $\triangle A B C$ again at $P$, and the circumcircle of $\triangle B H C$ again at $Q$. Because $\angle B H C=180-\angle A=\angle B P C, P$ is the reflection of $H$ over $D$. Thus, we know that $P D=H D$. From power of a point and $A D=\frac{12 H D}{7}$,
$$
B D \cdot C D=A D \cdot P D=\frac{12 H D^{2}}{7}
$$
From this, $H D=\frac{7}{2}$ and $A H=\frac{5}{2}$. Furthermore, because $\triangle B H C$ is the reflection of $\triangle B P C$ over $B C$, the circumcircle of $\triangle B H C$ is the reflection of the circumcircle of $\triangle A B C$ over $B C$. Then, $A Q=$ $2 A D=12$. Applying Power of a Point,
$$
A C \cdot A E=A B \cdot A F=A H \cdot A Q=30
$$
We can compute $A C=\sqrt{85}$ and $A B=3 \sqrt{5}$, which means that $A E=\frac{6 \sqrt{85}}{17}$ and $A F=2 \sqrt{5}$. Also, $[A B C]=\frac{B C \cdot A D}{2}=30$. Therefore,
$$
[A E F]=\frac{A E \cdot A F}{A C \cdot A B} \cdot[A B C]=\frac{4}{17} \cdot 30=\frac{120}{17}
$$
|
12017
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
In acute triangle $A B C$, let $H$ be the orthocenter and $D$ the foot of the altitude from $A$. The circumcircle of triangle $B H C$ intersects $A C$ at $E \neq C$, and $A B$ at $F \neq B$. If $B D=3, C D=7$, and $\frac{A H}{H D}=\frac{5}{7}$, the area of triangle $A E F$ can be expressed as $\frac{a}{b}$, where $a, b$ are relatively prime positive integers. Compute $100 a+b$.
|

Let $A H$ intersect the circumcircle of $\triangle A B C$ again at $P$, and the circumcircle of $\triangle B H C$ again at $Q$. Because $\angle B H C=180-\angle A=\angle B P C, P$ is the reflection of $H$ over $D$. Thus, we know that $P D=H D$. From power of a point and $A D=\frac{12 H D}{7}$,
$$
B D \cdot C D=A D \cdot P D=\frac{12 H D^{2}}{7}
$$
From this, $H D=\frac{7}{2}$ and $A H=\frac{5}{2}$. Furthermore, because $\triangle B H C$ is the reflection of $\triangle B P C$ over $B C$, the circumcircle of $\triangle B H C$ is the reflection of the circumcircle of $\triangle A B C$ over $B C$. Then, $A Q=$ $2 A D=12$. Applying Power of a Point,
$$
A C \cdot A E=A B \cdot A F=A H \cdot A Q=30
$$
We can compute $A C=\sqrt{85}$ and $A B=3 \sqrt{5}$, which means that $A E=\frac{6 \sqrt{85}}{17}$ and $A F=2 \sqrt{5}$. Also, $[A B C]=\frac{B C \cdot A D}{2}=30$. Therefore,
$$
[A E F]=\frac{A E \cdot A F}{A C \cdot A B} \cdot[A B C]=\frac{4}{17} \cdot 30=\frac{120}{17}
$$
|
{
"resource_path": "HarvardMIT/segmented/en-241-2020-nov-guts-solutions.jsonl",
"problem_match": "\n29. [15]",
"solution_match": "\n## Solution:\n\n"
}
|
aa86673b-e315-5e8f-a731-2a81bd2e8f26
| 610,231
|
Let $a_{1}, a_{2}, a_{3}, \ldots$ be a sequence of positive real numbers that satisfies
$$
\sum_{n=k}^{\infty}\binom{n}{k} a_{n}=\frac{1}{5^{k}}
$$
for all positive integers $k$. The value of $a_{1}-a_{2}+a_{3}-a_{4}+\cdots$ can be expressed as $\frac{a}{b}$, where $a, b$ are relatively prime positive integers. Compute $100 a+b$.
|
Answer: 542
|
542
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Let $a_{1}, a_{2}, a_{3}, \ldots$ be a sequence of positive real numbers that satisfies
$$
\sum_{n=k}^{\infty}\binom{n}{k} a_{n}=\frac{1}{5^{k}}
$$
for all positive integers $k$. The value of $a_{1}-a_{2}+a_{3}-a_{4}+\cdots$ can be expressed as $\frac{a}{b}$, where $a, b$ are relatively prime positive integers. Compute $100 a+b$.
|
Answer: 542
|
{
"resource_path": "HarvardMIT/segmented/en-241-2020-nov-guts-solutions.jsonl",
"problem_match": "\n30. [15]",
"solution_match": "\nProposed by: Akash Das\n"
}
|
d5dbcc45-7508-50bc-b31b-2c1116a350b3
| 610,232
|
For some positive real $\alpha$, the set $S$ of positive real numbers $x$ with $\{x\}>\alpha x$ consists of the union of several intervals, with total length 20.2. The value of $\alpha$ can be expressed as $\frac{a}{b}$, where $a, b$ are relatively prime positive integers. Compute $100 a+b$. (Here, $\{x\}=x-\lfloor x\rfloor$ is the fractional part of $x$.) Proposed by: Daniel Zhu
|
If we note that $x=\{x\}+\lfloor x\rfloor$, then we can rewrite our given inequality as $\{x\}>\frac{\alpha}{1-\alpha}\lfloor x\rfloor$. However, since $\{x\}<1$, we know that we must have $\frac{\alpha}{1-\alpha}\lfloor x\rfloor<\{x\}<1$, so each interval is of the form $\left(n+\frac{\alpha}{1-\alpha} n, n+1\right)$ for some integer $n$, which has length $\frac{1-(n+1) \alpha}{1-\alpha}$. If we let $k$ be the smallest integer such that $\frac{1-(k+1) \alpha}{1-\alpha}<0$, then the total length of all our intervals is the sum
$$
\sum_{n=0}^{k-1} \frac{1-(n+1) \alpha}{1-\alpha}=\frac{k-\frac{k(k+1)}{2} \alpha}{1-\alpha}
$$
If we set this to 20.2 , we can solve for $\alpha$ to get
$$
\alpha=\frac{k-20.2}{\frac{k(k+1)}{2}-20.2} .
$$
Since we defined $k$ to be the smallest integer such that $1-(k+1) \alpha<0$, we know that $k$ is the largest integer such that $k \alpha<1$. If we plug in our value for $\alpha$, we get that this is equivalent to
$$
\frac{k^{2}-20.2 k}{\frac{k(k+1)}{2}-20.2}<1 \Longrightarrow k<40.4
$$
Thus, we have $k=40$, and plugging this in for our formula for $\alpha$ gives us
$$
\alpha=\frac{40-20.2}{\frac{40 \cdot 41}{2}-20.2}=\frac{33}{1333} .
$$
|
331333
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
For some positive real $\alpha$, the set $S$ of positive real numbers $x$ with $\{x\}>\alpha x$ consists of the union of several intervals, with total length 20.2. The value of $\alpha$ can be expressed as $\frac{a}{b}$, where $a, b$ are relatively prime positive integers. Compute $100 a+b$. (Here, $\{x\}=x-\lfloor x\rfloor$ is the fractional part of $x$.) Proposed by: Daniel Zhu
|
If we note that $x=\{x\}+\lfloor x\rfloor$, then we can rewrite our given inequality as $\{x\}>\frac{\alpha}{1-\alpha}\lfloor x\rfloor$. However, since $\{x\}<1$, we know that we must have $\frac{\alpha}{1-\alpha}\lfloor x\rfloor<\{x\}<1$, so each interval is of the form $\left(n+\frac{\alpha}{1-\alpha} n, n+1\right)$ for some integer $n$, which has length $\frac{1-(n+1) \alpha}{1-\alpha}$. If we let $k$ be the smallest integer such that $\frac{1-(k+1) \alpha}{1-\alpha}<0$, then the total length of all our intervals is the sum
$$
\sum_{n=0}^{k-1} \frac{1-(n+1) \alpha}{1-\alpha}=\frac{k-\frac{k(k+1)}{2} \alpha}{1-\alpha}
$$
If we set this to 20.2 , we can solve for $\alpha$ to get
$$
\alpha=\frac{k-20.2}{\frac{k(k+1)}{2}-20.2} .
$$
Since we defined $k$ to be the smallest integer such that $1-(k+1) \alpha<0$, we know that $k$ is the largest integer such that $k \alpha<1$. If we plug in our value for $\alpha$, we get that this is equivalent to
$$
\frac{k^{2}-20.2 k}{\frac{k(k+1)}{2}-20.2}<1 \Longrightarrow k<40.4
$$
Thus, we have $k=40$, and plugging this in for our formula for $\alpha$ gives us
$$
\alpha=\frac{40-20.2}{\frac{40 \cdot 41}{2}-20.2}=\frac{33}{1333} .
$$
|
{
"resource_path": "HarvardMIT/segmented/en-241-2020-nov-guts-solutions.jsonl",
"problem_match": "\n31. [17]",
"solution_match": "\nSolution: "
}
|
2cc5c78a-78d5-5680-8f6d-f3252a2cb797
| 610,233
|
The numbers $1,2, \ldots, 10$ are written in a circle. There are four people, and each person randomly selects five consecutive integers (e.g. $1,2,3,4,5$, or $8,9,10,1,2$ ). If the probability that there exists some number that was not selected by any of the four people is $p$, compute $10000 p$.
|
Answer: 3690
|
3690
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
The numbers $1,2, \ldots, 10$ are written in a circle. There are four people, and each person randomly selects five consecutive integers (e.g. $1,2,3,4,5$, or $8,9,10,1,2$ ). If the probability that there exists some number that was not selected by any of the four people is $p$, compute $10000 p$.
|
Answer: 3690
|
{
"resource_path": "HarvardMIT/segmented/en-241-2020-nov-guts-solutions.jsonl",
"problem_match": "\n32. [17]",
"solution_match": "\nProposed by: Hahn Lheem\n"
}
|
19ee5660-033f-597b-a98b-8e985fbb1209
| 610,234
|
In quadrilateral $A B C D$, there exists a point $E$ on segment $A D$ such that $\frac{A E}{E D}=\frac{1}{9}$ and $\angle B E C$ is a right angle. Additionally, the area of triangle $C E D$ is 27 times more than the area of triangle $A E B$. If $\angle E B C=\angle E A B, \angle E C B=\angle E D C$, and $B C=6$, compute the value of $A D^{2}$.
|
Extend sides $A B$ and $C D$ to intersect at point $F$. The angle conditions yield $\triangle B E C \sim \triangle A F D$, so $\angle A F D=90^{\circ}$. Therefore, since $\angle B F C$ and $\angle B E C$ are both right angles, quadrilateral $E B F C$ is cyclic and
$$
\angle E F C=\angle E B C=90^{\circ}-\angle E C B=90^{\circ}-\angle E D F
$$
implying that $E F \perp A D$.
Since $A F D$ is a right triangle, we have $\left(\frac{F A}{F D}\right)^{2}=\frac{A E}{E D}=\frac{1}{9}$, so $\frac{F A}{F D}=\frac{1}{3}$. Therefore $\frac{E B}{E C}=\frac{1}{3}$. Since the area of $C E D$ is 27 times more than the area of $A E B, E D=9 \cdot E A$, and $E C=3 \cdot E B$, we get that $\angle D E C=\angle A E B=45^{\circ}$. Since $B E C F$ is cyclic, we obtain $\angle F B C=\angle F C B=45^{\circ}$, so $F B=F C$.
Since $B C=6$, we get $F B=F C=3 \sqrt{2}$. From $\triangle E A B \sim \triangle E F C$ we find $A B=\frac{1}{3} F C=\sqrt{2}$, so $F A=4 \sqrt{2}$. Similarly, $F D=12 \sqrt{2}$. It follows that $A D^{2}=F A^{2}+F D^{2}=320$.
|
320
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
In quadrilateral $A B C D$, there exists a point $E$ on segment $A D$ such that $\frac{A E}{E D}=\frac{1}{9}$ and $\angle B E C$ is a right angle. Additionally, the area of triangle $C E D$ is 27 times more than the area of triangle $A E B$. If $\angle E B C=\angle E A B, \angle E C B=\angle E D C$, and $B C=6$, compute the value of $A D^{2}$.
|

Extend sides $A B$ and $C D$ to intersect at point $F$. The angle conditions yield $\triangle B E C \sim \triangle A F D$, so $\angle A F D=90^{\circ}$. Therefore, since $\angle B F C$ and $\angle B E C$ are both right angles, quadrilateral $E B F C$ is cyclic and
$$
\angle E F C=\angle E B C=90^{\circ}-\angle E C B=90^{\circ}-\angle E D F
$$
implying that $E F \perp A D$.
Since $A F D$ is a right triangle, we have $\left(\frac{F A}{F D}\right)^{2}=\frac{A E}{E D}=\frac{1}{9}$, so $\frac{F A}{F D}=\frac{1}{3}$. Therefore $\frac{E B}{E C}=\frac{1}{3}$. Since the area of $C E D$ is 27 times more than the area of $A E B, E D=9 \cdot E A$, and $E C=3 \cdot E B$, we get that $\angle D E C=\angle A E B=45^{\circ}$. Since $B E C F$ is cyclic, we obtain $\angle F B C=\angle F C B=45^{\circ}$, so $F B=F C$.
Since $B C=6$, we get $F B=F C=3 \sqrt{2}$. From $\triangle E A B \sim \triangle E F C$ we find $A B=\frac{1}{3} F C=\sqrt{2}$, so $F A=4 \sqrt{2}$. Similarly, $F D=12 \sqrt{2}$. It follows that $A D^{2}=F A^{2}+F D^{2}=320$.
|
{
"resource_path": "HarvardMIT/segmented/en-241-2020-nov-guts-solutions.jsonl",
"problem_match": "\n33. [17]",
"solution_match": "\n## Solution:\n\n"
}
|
47086cf4-6ff8-5619-981a-e5b010f59370
| 610,235
|
Estimate $A$, the number of times an 8-digit number appears in Pascal's triangle. An estimate of $E$ earns $\max (0,\lfloor 20-|A-E| / 200\rfloor)$ points.
|
We can obtain a good estimate by only counting terms of the form $\binom{a}{1},\binom{a}{2},\binom{a}{a-1}$, and $\binom{a}{a-2}$. The last two cases are symmetric to the first two, so we will only consider the first two and multiply by 2 at the end.
Since $\binom{a}{1}=a$, there are 90000000 values of $a$ for which $\binom{a}{1}$ has eight digits. Moreover, since $\binom{a}{2} \approx a^{2} / 2$, the values of $a$ for which $\binom{a}{2}$ has eight digits vary from about $\sqrt{2 \cdot 10^{7}}$ to $\sqrt{2 \cdot 10^{8}}$, leading to about $10^{4} \sqrt{2}\left(1-10^{-1 / 2}\right) \approx 14000 \cdot 0.69=9660$ values for $a$.
Therefore, these terms yield an estimate of 180019320, good enough for 13 points. Of course, one would expect this to be an underestimate, and even rounding up to 180020000 would give 16 points.
|
180020000
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Estimate $A$, the number of times an 8-digit number appears in Pascal's triangle. An estimate of $E$ earns $\max (0,\lfloor 20-|A-E| / 200\rfloor)$ points.
|
We can obtain a good estimate by only counting terms of the form $\binom{a}{1},\binom{a}{2},\binom{a}{a-1}$, and $\binom{a}{a-2}$. The last two cases are symmetric to the first two, so we will only consider the first two and multiply by 2 at the end.
Since $\binom{a}{1}=a$, there are 90000000 values of $a$ for which $\binom{a}{1}$ has eight digits. Moreover, since $\binom{a}{2} \approx a^{2} / 2$, the values of $a$ for which $\binom{a}{2}$ has eight digits vary from about $\sqrt{2 \cdot 10^{7}}$ to $\sqrt{2 \cdot 10^{8}}$, leading to about $10^{4} \sqrt{2}\left(1-10^{-1 / 2}\right) \approx 14000 \cdot 0.69=9660$ values for $a$.
Therefore, these terms yield an estimate of 180019320, good enough for 13 points. Of course, one would expect this to be an underestimate, and even rounding up to 180020000 would give 16 points.
|
{
"resource_path": "HarvardMIT/segmented/en-241-2020-nov-guts-solutions.jsonl",
"problem_match": "\n35. [20]",
"solution_match": "\nSolution: "
}
|
55395588-b607-5a27-93a4-ff6d39334342
| 610,237
|
Let $p_{i}$ be the $i$ th prime. Let
$$
f(x)=\sum_{i=1}^{50} p_{i} x^{i-1}=2+3 x+\cdots+229 x^{49}
$$
If $a$ is the unique positive real number with $f(a)=100$, estimate $A=\lfloor 100000 a\rfloor$. An estimate of $E$ will earn $\max (0,\lfloor 20-|A-E| / 250\rfloor)$ points.
|
Note $f(x)$ is increasing. Since $f(0)=2$ and $f(1) \approx 50000$, we have $0<a<1$.
Since we know that $p_{50}=229$, we can crudely bound
$$
f(x) \lesssim \sum_{i=1}^{\infty} 5 i x^{i-1}=\frac{5}{(1-x)^{2}}
$$
Setting this equal to 100 yields $x=1-20^{-1 / 2} \approx 0.78$, so this is a good lower bound for $a$, though just outside the window to receive points.
A better estimate can be obtained by noting that since $p_{25}=100$, it is more accurate to write
$$
f(x) \lesssim \sum_{i=1}^{\infty} 4 i x^{i-1}=\frac{4}{(1-x)^{2}}
$$
which yields $a=0.8$, good enough for 5 points.
However, we can do better. If we know that $a \approx 0.8$, the "most significant terms" will occur at the $i$ where $p_{i} / p_{i+1} \approx 0.8$. The first few primes are $2,3,5,7,11,13,17,19,23,29,31$, so this transition occurs roughly at $p_{8}=19$. Thus, it is more accurate to approximate $f(x)=\sum_{i=1}^{\infty} \frac{19}{8} i x^{i-1}$, so $a=1-\sqrt{19 / 800} \approx 1-40^{-1 / 2} \approx 0.85$, good enough for 14 points.
Repeating this process again with the new estimate for $a$ reveals that $p_{9}=23$ may have been a better choice, which yield $a=1-\sqrt{23 / 900} \approx 1-\sqrt{0.0256}=0.84$. This is good enough for 18 points.
|
0.84
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Let $p_{i}$ be the $i$ th prime. Let
$$
f(x)=\sum_{i=1}^{50} p_{i} x^{i-1}=2+3 x+\cdots+229 x^{49}
$$
If $a$ is the unique positive real number with $f(a)=100$, estimate $A=\lfloor 100000 a\rfloor$. An estimate of $E$ will earn $\max (0,\lfloor 20-|A-E| / 250\rfloor)$ points.
|
Note $f(x)$ is increasing. Since $f(0)=2$ and $f(1) \approx 50000$, we have $0<a<1$.
Since we know that $p_{50}=229$, we can crudely bound
$$
f(x) \lesssim \sum_{i=1}^{\infty} 5 i x^{i-1}=\frac{5}{(1-x)^{2}}
$$
Setting this equal to 100 yields $x=1-20^{-1 / 2} \approx 0.78$, so this is a good lower bound for $a$, though just outside the window to receive points.
A better estimate can be obtained by noting that since $p_{25}=100$, it is more accurate to write
$$
f(x) \lesssim \sum_{i=1}^{\infty} 4 i x^{i-1}=\frac{4}{(1-x)^{2}}
$$
which yields $a=0.8$, good enough for 5 points.
However, we can do better. If we know that $a \approx 0.8$, the "most significant terms" will occur at the $i$ where $p_{i} / p_{i+1} \approx 0.8$. The first few primes are $2,3,5,7,11,13,17,19,23,29,31$, so this transition occurs roughly at $p_{8}=19$. Thus, it is more accurate to approximate $f(x)=\sum_{i=1}^{\infty} \frac{19}{8} i x^{i-1}$, so $a=1-\sqrt{19 / 800} \approx 1-40^{-1 / 2} \approx 0.85$, good enough for 14 points.
Repeating this process again with the new estimate for $a$ reveals that $p_{9}=23$ may have been a better choice, which yield $a=1-\sqrt{23 / 900} \approx 1-\sqrt{0.0256}=0.84$. This is good enough for 18 points.
|
{
"resource_path": "HarvardMIT/segmented/en-241-2020-nov-guts-solutions.jsonl",
"problem_match": "\n36. [20]",
"solution_match": "\nSolution: "
}
|
761a785f-9e18-5d47-97bf-db8f9ef47c44
| 610,238
|
For how many positive integers $n \leq 1000$ does the equation in real numbers
$$
x^{\lfloor x\rfloor}=n
$$
have a positive solution for $x$ ? (For a real number $x,\lfloor x\rfloor$ denotes the largest integer that is not greater than $x$.)
|
Answer: 412
|
412
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
For how many positive integers $n \leq 1000$ does the equation in real numbers
$$
x^{\lfloor x\rfloor}=n
$$
have a positive solution for $x$ ? (For a real number $x,\lfloor x\rfloor$ denotes the largest integer that is not greater than $x$.)
|
Answer: 412
|
{
"resource_path": "HarvardMIT/segmented/en-241-2020-nov-team-solutions.jsonl",
"problem_match": "\n1. [20]",
"solution_match": "\nProposed by: John Michael Wu\n"
}
|
29f5cb8b-3425-5e8c-8eaa-0c4be11c7a20
| 610,239
|
How many ways are there to arrange the numbers $\{1,2,3,4,5,6,7,8\}$ in a circle so that every two adjacent elements are relatively prime? Consider rotations and reflections of the same arrangement to be indistinguishable.
|
Note that 6 can only be adjacent to 1,5 , and 7 , so there are $\binom{3}{2}=3$ ways to pick its neighbors. Since each of 1,5 , and 7 is relatively prime to every number in $\{1,2,3,4,5,6,7,8\}$ but itself (and hence can have arbitrary neighbors), without loss of generality suppose we have picked 1 and 5 as neighbors of 6 . Observe that fixing the positions of 1,5 , and 6 eliminates the indistinguishability of rotations and reflections.
Now, we have to consecutively arrange $\{2,3,4,7,8\}$ so that no two of 2,4 , and 8 are adjacent. There are $3!\cdot 2!=12$ ways of doing so, so the final answer is $3 \cdot 12=36$.
|
36
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
How many ways are there to arrange the numbers $\{1,2,3,4,5,6,7,8\}$ in a circle so that every two adjacent elements are relatively prime? Consider rotations and reflections of the same arrangement to be indistinguishable.
|
Note that 6 can only be adjacent to 1,5 , and 7 , so there are $\binom{3}{2}=3$ ways to pick its neighbors. Since each of 1,5 , and 7 is relatively prime to every number in $\{1,2,3,4,5,6,7,8\}$ but itself (and hence can have arbitrary neighbors), without loss of generality suppose we have picked 1 and 5 as neighbors of 6 . Observe that fixing the positions of 1,5 , and 6 eliminates the indistinguishability of rotations and reflections.
Now, we have to consecutively arrange $\{2,3,4,7,8\}$ so that no two of 2,4 , and 8 are adjacent. There are $3!\cdot 2!=12$ ways of doing so, so the final answer is $3 \cdot 12=36$.
|
{
"resource_path": "HarvardMIT/segmented/en-241-2020-nov-team-solutions.jsonl",
"problem_match": "\n2. [25]",
"solution_match": "\nSolution: "
}
|
88a246a7-cdc5-5c54-8f32-33ae2c033610
| 610,240
|
Marisa has two identical cubical dice labeled with the numbers $\{1,2,3,4,5,6\}$. However, the two dice are not fair, meaning that they can land on each face with different probability. Marisa rolls the two dice and calculates their sum. Given that the sum is 2 with probability 0.04 , and 12 with probability 0.01 , the maximum possible probability of the sum being 7 is $p$. Compute $\lfloor 100 p\rfloor$.
|
Let $p_{i}$ be the probability that the dice lands on the number $i$. The problem gives that $p_{1}^{2}=0.04, p_{6}^{2}=0.01$, so we have
$$
p_{1}=0.2, \quad p_{6}=0.1, \quad p_{2}+p_{3}+p_{4}+p_{5}=0.7
$$
We are asked to maximize
$$
2\left(p_{1} p_{6}+p_{2} p_{5}+p_{3} p_{4}\right)=2\left(0.02+p_{2} p_{5}+p_{3} p_{4}\right)
$$
Let $x=p_{2}+p_{5}$ and $y=p_{3}+p_{4}$. Then by AM-GM, $p_{2} p_{5} \leq \frac{x^{2}}{4}, p_{3} p_{4} \leq \frac{y^{2}}{4}$. Also,
$$
\frac{x^{2}+y^{2}}{4} \leq \frac{x^{2}+2 x y+y^{2}}{4}=\frac{(x+y)^{2}}{4}=\frac{0.7^{2}}{4}=0.1225
$$
Hence,
$$
2\left(p_{1} p_{6}+p_{2} p_{5}+p_{3} p_{4}\right) \leq 2(0.02+0.1225)=0.285
$$
where equality holds if $p_{2}=p_{5}=0.35, p_{3}=p_{4}=0$.
Thus, we conclude that $p=0.285$ and $\lfloor 100 p\rfloor=28$.
|
28
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Marisa has two identical cubical dice labeled with the numbers $\{1,2,3,4,5,6\}$. However, the two dice are not fair, meaning that they can land on each face with different probability. Marisa rolls the two dice and calculates their sum. Given that the sum is 2 with probability 0.04 , and 12 with probability 0.01 , the maximum possible probability of the sum being 7 is $p$. Compute $\lfloor 100 p\rfloor$.
|
Let $p_{i}$ be the probability that the dice lands on the number $i$. The problem gives that $p_{1}^{2}=0.04, p_{6}^{2}=0.01$, so we have
$$
p_{1}=0.2, \quad p_{6}=0.1, \quad p_{2}+p_{3}+p_{4}+p_{5}=0.7
$$
We are asked to maximize
$$
2\left(p_{1} p_{6}+p_{2} p_{5}+p_{3} p_{4}\right)=2\left(0.02+p_{2} p_{5}+p_{3} p_{4}\right)
$$
Let $x=p_{2}+p_{5}$ and $y=p_{3}+p_{4}$. Then by AM-GM, $p_{2} p_{5} \leq \frac{x^{2}}{4}, p_{3} p_{4} \leq \frac{y^{2}}{4}$. Also,
$$
\frac{x^{2}+y^{2}}{4} \leq \frac{x^{2}+2 x y+y^{2}}{4}=\frac{(x+y)^{2}}{4}=\frac{0.7^{2}}{4}=0.1225
$$
Hence,
$$
2\left(p_{1} p_{6}+p_{2} p_{5}+p_{3} p_{4}\right) \leq 2(0.02+0.1225)=0.285
$$
where equality holds if $p_{2}=p_{5}=0.35, p_{3}=p_{4}=0$.
Thus, we conclude that $p=0.285$ and $\lfloor 100 p\rfloor=28$.
|
{
"resource_path": "HarvardMIT/segmented/en-241-2020-nov-team-solutions.jsonl",
"problem_match": "\n4. [35]",
"solution_match": "\nSolution: "
}
|
4217e35d-f25a-5f61-ad88-a903bcf3169d
| 610,242
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.