problem
stringlengths 14
7.96k
| solution
stringlengths 3
10k
| answer
stringlengths 1
91
| problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | question_type
stringclasses 1
value | problem_type
stringclasses 8
values | problem_raw
stringlengths 14
7.96k
| solution_raw
stringlengths 3
10k
| metadata
dict | uuid
stringlengths 36
36
| id
int64 22.6k
612k
|
|---|---|---|---|---|---|---|---|---|---|---|---|
On a chessboard, a queen attacks every square it can reach by moving from its current square along a row, column, or diagonal without passing through a different square that is occupied by a chess piece. Find the number of ways in which three indistinguishable queens can be placed on an $8 \times 8$ chess board so that each queen attacks both others.
|
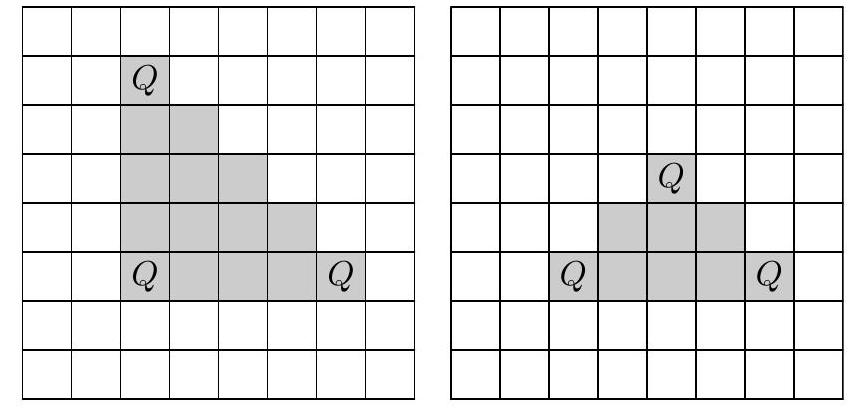
The configuration of three cells must come in a 45-45-90 triangle. There are two cases, both shown above: the triangle has legs parallel to the axes, or it has its hypotenuse parallel to an axis. The first case can be solved by noticing that each selection of four cells in the shape of a square corresponds to four such possibilities. There are $7^{2}$ possible squares of size $2 \times 2,6^{2}$ possible squares of size $3 \times 3$, and so on. The total for this first case is thus $4\left(7^{2}+6^{2}+\cdots+1^{2}\right)=560$. The second case can also be done by casework: each triangle in this case can be completed into an $n+1$ by $2 n+1$ rectangle, of which there are $7 \cdot 6+6 \cdot 4+5 \cdot 2$ (for $n=1,2,3$ respectively). Multiply this by 4 to get all orientations of the triangle. The final answer is $560+4(7 \cdot 6+6 \cdot 4+5 \cdot 2)=864$.
|
864
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
On a chessboard, a queen attacks every square it can reach by moving from its current square along a row, column, or diagonal without passing through a different square that is occupied by a chess piece. Find the number of ways in which three indistinguishable queens can be placed on an $8 \times 8$ chess board so that each queen attacks both others.
|

The configuration of three cells must come in a 45-45-90 triangle. There are two cases, both shown above: the triangle has legs parallel to the axes, or it has its hypotenuse parallel to an axis. The first case can be solved by noticing that each selection of four cells in the shape of a square corresponds to four such possibilities. There are $7^{2}$ possible squares of size $2 \times 2,6^{2}$ possible squares of size $3 \times 3$, and so on. The total for this first case is thus $4\left(7^{2}+6^{2}+\cdots+1^{2}\right)=560$. The second case can also be done by casework: each triangle in this case can be completed into an $n+1$ by $2 n+1$ rectangle, of which there are $7 \cdot 6+6 \cdot 4+5 \cdot 2$ (for $n=1,2,3$ respectively). Multiply this by 4 to get all orientations of the triangle. The final answer is $560+4(7 \cdot 6+6 \cdot 4+5 \cdot 2)=864$.
|
{
"resource_path": "HarvardMIT/segmented/en-251-2021-nov-guts-solutions.jsonl",
"problem_match": "\n20. [11]",
"solution_match": "\n## Solution:\n\n"
}
|
50648b6b-7dcb-5d85-a87f-190e377e0fe2
| 610,365
|
Circle $\omega$ is inscribed in rhombus $H M_{1} M_{2} T$ so that $\omega$ is tangent to $\overline{H M_{1}}$ at $A, \overline{M_{1} M_{2}}$ at $I, \overline{M_{2} T}$ at $M$, and $\overline{T H}$ at $E$. Given that the area of $H M_{1} M_{2} T$ is 1440 and the area of $E M T$ is 405 , find the area of $A I M E$.
|
Answer: 540
|
540
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Circle $\omega$ is inscribed in rhombus $H M_{1} M_{2} T$ so that $\omega$ is tangent to $\overline{H M_{1}}$ at $A, \overline{M_{1} M_{2}}$ at $I, \overline{M_{2} T}$ at $M$, and $\overline{T H}$ at $E$. Given that the area of $H M_{1} M_{2} T$ is 1440 and the area of $E M T$ is 405 , find the area of $A I M E$.
|
Answer: 540
|
{
"resource_path": "HarvardMIT/segmented/en-251-2021-nov-guts-solutions.jsonl",
"problem_match": "\n21. [11]",
"solution_match": "\nProposed by: Joseph Heerens\n"
}
|
690d454a-f40a-5545-bf51-118ea4732e53
| 610,366
|
Two distinct squares on a $4 \times 4$ chessboard are chosen, with each pair of squares equally likely to be chosen. A knight is placed on one of the squares. The expected value of the minimum number of moves it takes for the knight to reach the other squarecan be written as $\frac{m}{n}$, where $m, n$ are positive integers and $\operatorname{gcd}(m, n)=1$. Find $100 m+n$.
|
We can do casework based on the position of the knight: corner, edge, or center. In each case, we can quickly compute all 15 distances by writing a 1 down in all squares reachable from the original square, then writing a 2 down in all blank squares reachable from a square with a 1 , writing a 3 down in all blank squares reachable from a square with a 2 , and so on. The resulting tables are below:
| 0 | 3 | 2 | 5 |
| :--- | :--- | :--- | :--- |
| 3 | 4 | 1 | 2 |
| 2 | 1 | 4 | 3 |
| 5 | 2 | 3 | 2 |
| 3 | 0 | 3 | 2 |
| :--- | :--- | :--- | :--- |
| 2 | 3 | 2 | 1 |
| 1 | 2 | 1 | 4 |
| 2 | 3 | 2 | 3 |
| 4 | 3 | 2 | 1 |
| :--- | :--- | :--- | :--- |
| 3 | 0 | 3 | 2 |
| 2 | 3 | 2 | 1 |
| 1 | 2 | 1 | 4 |
The expectation can be computed by weighing the sum of the distances in each of these tables by the number of squares of that type:
$$
\begin{aligned}
\frac{1}{16 \cdot 15} & (4(2 \cdot 1+5 \cdot 2+4 \cdot 3+2 \cdot 4+2 \cdot 5)+8(3 \cdot 1+6 \cdot 2+5 \cdot 3+1 \cdot 4)+4(4 \cdot 1+5 \cdot 2+4 \cdot 3+2 \cdot 4)) \\
& =\frac{1}{240}(168+272+136) \\
& =\frac{12}{5}
\end{aligned}
$$
|
100 \cdot 12 + 5
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Two distinct squares on a $4 \times 4$ chessboard are chosen, with each pair of squares equally likely to be chosen. A knight is placed on one of the squares. The expected value of the minimum number of moves it takes for the knight to reach the other squarecan be written as $\frac{m}{n}$, where $m, n$ are positive integers and $\operatorname{gcd}(m, n)=1$. Find $100 m+n$.
|
We can do casework based on the position of the knight: corner, edge, or center. In each case, we can quickly compute all 15 distances by writing a 1 down in all squares reachable from the original square, then writing a 2 down in all blank squares reachable from a square with a 1 , writing a 3 down in all blank squares reachable from a square with a 2 , and so on. The resulting tables are below:
| 0 | 3 | 2 | 5 |
| :--- | :--- | :--- | :--- |
| 3 | 4 | 1 | 2 |
| 2 | 1 | 4 | 3 |
| 5 | 2 | 3 | 2 |
| 3 | 0 | 3 | 2 |
| :--- | :--- | :--- | :--- |
| 2 | 3 | 2 | 1 |
| 1 | 2 | 1 | 4 |
| 2 | 3 | 2 | 3 |
| 4 | 3 | 2 | 1 |
| :--- | :--- | :--- | :--- |
| 3 | 0 | 3 | 2 |
| 2 | 3 | 2 | 1 |
| 1 | 2 | 1 | 4 |
The expectation can be computed by weighing the sum of the distances in each of these tables by the number of squares of that type:
$$
\begin{aligned}
\frac{1}{16 \cdot 15} & (4(2 \cdot 1+5 \cdot 2+4 \cdot 3+2 \cdot 4+2 \cdot 5)+8(3 \cdot 1+6 \cdot 2+5 \cdot 3+1 \cdot 4)+4(4 \cdot 1+5 \cdot 2+4 \cdot 3+2 \cdot 4)) \\
& =\frac{1}{240}(168+272+136) \\
& =\frac{12}{5}
\end{aligned}
$$
|
{
"resource_path": "HarvardMIT/segmented/en-251-2021-nov-guts-solutions.jsonl",
"problem_match": "\n22. [12]",
"solution_match": "\n## Solution:\n\n"
}
|
332d9ee1-17bd-5c36-b16e-a4add5b5b2d0
| 610,367
|
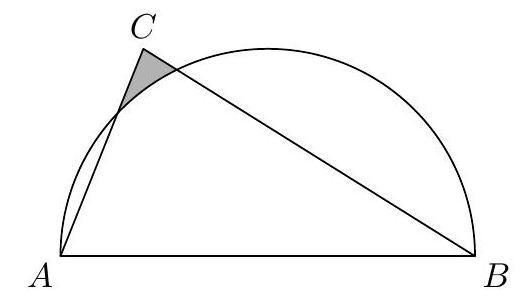
Side $\overline{A B}$ of $\triangle A B C$ is the diameter of a semicircle, as shown below. If $A B=3+\sqrt{3}, B C=3 \sqrt{2}$, and $A C=2 \sqrt{3}$, then the area of the shaded region can be written as $\frac{a+(b+c \sqrt{d}) \pi}{e}$, where $a, b, c, d, e$ are integers, $e$ is positive, $d$ is square-free, and $\operatorname{gcd}(a, b, c, e)=1$. Find $10000 a+1000 b+100 c+10 d+e$.
|
Drop an altitude to point $D$ on $\overline{A B}$ from $C$ and let $x=A D$. Solving for $x$, we find
$$
\begin{aligned}
12-x^{2}=18-(3+\sqrt{3}-x)^{2} & \Rightarrow 12=18-9-6 \sqrt{3}-3+2(3+\sqrt{3}) x-x^{2} \\
& \Rightarrow 6+6 \sqrt{3}=(6+2 \sqrt{3}) x \\
& \Rightarrow x=\sqrt{3}
\end{aligned}
$$
So $A C=2 A D$, from which we have $\angle C A D=60^{\circ}$. Also, $C D=A D \sqrt{3}=3$ and $B D=A B-A D=$ $3+\sqrt{3}-\sqrt{3}=3$, so $\angle D B C=45^{\circ}$. Then, if $E$ is the intersection of the circle with $\overline{A C}, F$ is the intersection of the circle with $\overline{B C}$, and $O$ is the midpoint of $\overline{A B}, \angle A O E=60^{\circ}$ and $\angle B O F=90^{\circ}$. Then, letting $r=\frac{A B}{2}$, we get that the area of the part of $\triangle A B C$ that lies inside the semicircle is
$$
\begin{aligned}
\frac{1}{2} \pi r^{2}-\left(\frac{1}{4}+\frac{1}{6}\right) \pi r^{2}+\frac{1}{2} r^{2} \sin 60^{\circ}+\frac{1}{2} r^{2} \sin 90^{\circ} & =\frac{1}{12} \pi r^{2}+\frac{\sqrt{3}}{4} r^{2}+\frac{1}{2} r^{2} \\
& =\frac{1}{12}(\pi+3 \sqrt{3}+6) r^{2}
\end{aligned}
$$
So the desired area is
$$
\begin{aligned}
3 r-\frac{1}{12}(\pi+3 \sqrt{3}+6) r^{2} & =\frac{9+3 \sqrt{3}}{2}-\frac{1}{8}(\pi+3 \sqrt{3}+6)(2+\sqrt{3}) \\
& =\frac{1}{2}(9+3 \sqrt{3})-\frac{1}{8}(2+\sqrt{3}) \pi-\frac{1}{8}(21+12 \sqrt{3}) \\
& =\frac{15-(2+\sqrt{3}) \pi}{8} .
\end{aligned}
$$
|
\frac{15-(2+\sqrt{3}) \pi}{8}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Side $\overline{A B}$ of $\triangle A B C$ is the diameter of a semicircle, as shown below. If $A B=3+\sqrt{3}, B C=3 \sqrt{2}$, and $A C=2 \sqrt{3}$, then the area of the shaded region can be written as $\frac{a+(b+c \sqrt{d}) \pi}{e}$, where $a, b, c, d, e$ are integers, $e$ is positive, $d$ is square-free, and $\operatorname{gcd}(a, b, c, e)=1$. Find $10000 a+1000 b+100 c+10 d+e$.

|
Drop an altitude to point $D$ on $\overline{A B}$ from $C$ and let $x=A D$. Solving for $x$, we find
$$
\begin{aligned}
12-x^{2}=18-(3+\sqrt{3}-x)^{2} & \Rightarrow 12=18-9-6 \sqrt{3}-3+2(3+\sqrt{3}) x-x^{2} \\
& \Rightarrow 6+6 \sqrt{3}=(6+2 \sqrt{3}) x \\
& \Rightarrow x=\sqrt{3}
\end{aligned}
$$
So $A C=2 A D$, from which we have $\angle C A D=60^{\circ}$. Also, $C D=A D \sqrt{3}=3$ and $B D=A B-A D=$ $3+\sqrt{3}-\sqrt{3}=3$, so $\angle D B C=45^{\circ}$. Then, if $E$ is the intersection of the circle with $\overline{A C}, F$ is the intersection of the circle with $\overline{B C}$, and $O$ is the midpoint of $\overline{A B}, \angle A O E=60^{\circ}$ and $\angle B O F=90^{\circ}$. Then, letting $r=\frac{A B}{2}$, we get that the area of the part of $\triangle A B C$ that lies inside the semicircle is
$$
\begin{aligned}
\frac{1}{2} \pi r^{2}-\left(\frac{1}{4}+\frac{1}{6}\right) \pi r^{2}+\frac{1}{2} r^{2} \sin 60^{\circ}+\frac{1}{2} r^{2} \sin 90^{\circ} & =\frac{1}{12} \pi r^{2}+\frac{\sqrt{3}}{4} r^{2}+\frac{1}{2} r^{2} \\
& =\frac{1}{12}(\pi+3 \sqrt{3}+6) r^{2}
\end{aligned}
$$
So the desired area is
$$
\begin{aligned}
3 r-\frac{1}{12}(\pi+3 \sqrt{3}+6) r^{2} & =\frac{9+3 \sqrt{3}}{2}-\frac{1}{8}(\pi+3 \sqrt{3}+6)(2+\sqrt{3}) \\
& =\frac{1}{2}(9+3 \sqrt{3})-\frac{1}{8}(2+\sqrt{3}) \pi-\frac{1}{8}(21+12 \sqrt{3}) \\
& =\frac{15-(2+\sqrt{3}) \pi}{8} .
\end{aligned}
$$
|
{
"resource_path": "HarvardMIT/segmented/en-251-2021-nov-guts-solutions.jsonl",
"problem_match": "\n23. [12]",
"solution_match": "\nSolution: "
}
|
06ffe758-ebea-5d1b-8656-046bf2f8bf7d
| 610,368
|
Find the number of subsets $S$ of $\{1,2, \ldots, 48\}$ satisfying both of the following properties:
- For each integer $1 \leq k \leq 24$, exactly one of $2 k-1$ and $2 k$ is in $S$.
- There are exactly nine integers $1 \leq m \leq 47$ so that both $m$ and $m+1$ are in $S$.
|
This problem can be thought of as laying down a series of $1 \times 2$ dominoes, with each one having either the left or right square marked. The second condition states that exactly 9 pairs of consecutive dominoes will have the leftmost one with the right square marked and the rightmost one with the left square marked. Therefore, this problem can be thought of as laying down a series of dominoes with the left square marked, followed by a series with the right square marked, followed by left square and so on and so forth, with the pattern LRLRLRL...LR. However, the left end is not guaranteed to be left marked dominoes and the right end is not guaranteed to be right marked dominoes. However, we can add a left marked domino to the left end and a right marked domino to the right end without changing the number of right-left combinations in the sequence. Further, there will be 10 of each left and right blocks, and a total of 26 dominoes, such that each block has at least 1 domino. If there are $a_{1}, a_{2}, \ldots, a_{20}$ dominoes in each block, then $a_{1}+a_{2}+\ldots+a_{20}=26$ and $a_{i}>0$ for all $1 \leq i \leq 20$. Therefore, from stars and bars, we find that there are $\binom{25}{6}$ ways to select the dominoes and thus the subset $S$. Surprisingly, $\binom{25}{6}$ is not too hard to compute and is just 177100.
|
177100
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Find the number of subsets $S$ of $\{1,2, \ldots, 48\}$ satisfying both of the following properties:
- For each integer $1 \leq k \leq 24$, exactly one of $2 k-1$ and $2 k$ is in $S$.
- There are exactly nine integers $1 \leq m \leq 47$ so that both $m$ and $m+1$ are in $S$.
|
This problem can be thought of as laying down a series of $1 \times 2$ dominoes, with each one having either the left or right square marked. The second condition states that exactly 9 pairs of consecutive dominoes will have the leftmost one with the right square marked and the rightmost one with the left square marked. Therefore, this problem can be thought of as laying down a series of dominoes with the left square marked, followed by a series with the right square marked, followed by left square and so on and so forth, with the pattern LRLRLRL...LR. However, the left end is not guaranteed to be left marked dominoes and the right end is not guaranteed to be right marked dominoes. However, we can add a left marked domino to the left end and a right marked domino to the right end without changing the number of right-left combinations in the sequence. Further, there will be 10 of each left and right blocks, and a total of 26 dominoes, such that each block has at least 1 domino. If there are $a_{1}, a_{2}, \ldots, a_{20}$ dominoes in each block, then $a_{1}+a_{2}+\ldots+a_{20}=26$ and $a_{i}>0$ for all $1 \leq i \leq 20$. Therefore, from stars and bars, we find that there are $\binom{25}{6}$ ways to select the dominoes and thus the subset $S$. Surprisingly, $\binom{25}{6}$ is not too hard to compute and is just 177100.
|
{
"resource_path": "HarvardMIT/segmented/en-251-2021-nov-guts-solutions.jsonl",
"problem_match": "\n24. [12]",
"solution_match": "\nSolution: "
}
|
56ffed92-0df8-5fd3-bc88-2851d818c3db
| 610,369
|
Let $x, y, z$ be real numbers satisfying
$$
\begin{aligned}
2 x+y+4 x y+6 x z & =-6 \\
y+2 z+2 x y+6 y z & =4 \\
x-z+2 x z-4 y z & =-3
\end{aligned}
$$
Find $x^{2}+y^{2}+z^{2}$.
|
We multiply the first, second, and third equations by $\frac{1}{2},-\frac{1}{2}$, and -1 , respectively, then add the three resulting equations. This gives $x y+x z+y z=-2$. Doing the same with the coefficients $-1,2$, and 3 gives $x+y+z=5$, from which $(x+y+z)^{2}=25$. So $x^{2}+y^{2}+z^{2}=25-2 \cdot-2=29$.
|
29
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Let $x, y, z$ be real numbers satisfying
$$
\begin{aligned}
2 x+y+4 x y+6 x z & =-6 \\
y+2 z+2 x y+6 y z & =4 \\
x-z+2 x z-4 y z & =-3
\end{aligned}
$$
Find $x^{2}+y^{2}+z^{2}$.
|
We multiply the first, second, and third equations by $\frac{1}{2},-\frac{1}{2}$, and -1 , respectively, then add the three resulting equations. This gives $x y+x z+y z=-2$. Doing the same with the coefficients $-1,2$, and 3 gives $x+y+z=5$, from which $(x+y+z)^{2}=25$. So $x^{2}+y^{2}+z^{2}=25-2 \cdot-2=29$.
|
{
"resource_path": "HarvardMIT/segmented/en-251-2021-nov-guts-solutions.jsonl",
"problem_match": "\n25. [13]",
"solution_match": "\nSolution: "
}
|
6dd47cca-2525-5332-984d-1474491c67dd
| 610,370
|
$O$ is the center of square $A B C D$, and $M$ and $N$ are the midpoints of $\overline{B C}$ and $\overline{A D}$, respectively. Points $A^{\prime}, B^{\prime}, C^{\prime}, D^{\prime}$ are chosen on $\overline{A O}, \overline{B O}, \overline{C O}, \overline{D O}$, respectively, so that $A^{\prime} B^{\prime} M C^{\prime} D^{\prime} N$ is an equiangular hexagon. The ratio $\frac{\left[A^{\prime} B^{\prime} M C^{\prime} D^{\prime} N\right]}{[A B C D]}$ can be written as $\frac{a+b \sqrt{c}}{d}$, where $a, b, c, d$ are integers, $d$ is positive, $c$ is square-free, and $\operatorname{gcd}(a, b, d)=1$. Find $1000 a+100 b+10 c+d$.
|
Assume without loss of generality that the side length of $A B C D$ is 1 so that the area of the square is also 1 . This also means that $O M=O N=\frac{1}{2}$. As $A^{\prime} B^{\prime} M C^{\prime} D^{\prime} N$ is equiangular, it can be seen that $\angle A^{\prime} N O=60^{\circ}$, and also by symmetry, that $A^{\prime} B^{\prime} \| A B$, so $\angle O A^{\prime} B^{\prime}=45^{\circ}$ and $\angle O A^{\prime} N=75^{\circ}$. Therefore, $A^{\prime} N O$ is a $45-60-75$ triangle, which has sides in ratio $2: 1+\sqrt{3}: \sqrt{6}$, so we may compute that $A^{\prime} O=\frac{\sqrt{6}}{1+\sqrt{3}} \cdot \frac{1}{2}=\frac{3 \sqrt{2}-\sqrt{6}}{4}$. Further, the area of $A^{\prime} N O$ can be found by taking the altitude to $N O$, which has length of $\frac{1}{2} \cdot \frac{\sqrt{3}}{1+\sqrt{3}}=\frac{3-\sqrt{3}}{4}$, so the area is $\frac{1}{2} \cdot \frac{1}{2} \cdot \frac{3-\sqrt{3}}{4}=\frac{3-\sqrt{3}}{16}$. The area of $O A^{\prime} B^{\prime}$ is $\frac{1}{2}\left(\frac{3 \sqrt{2}-\sqrt{6}}{4}\right)^{2}=\frac{6-3 \sqrt{3}}{8}$.
Combining everything together, we can find that $\left[A^{\prime} B^{\prime} M C^{\prime} D^{\prime} N\right]=4\left[A^{\prime} N O\right]+2\left[O A^{\prime} B^{\prime}\right]=\frac{3-\sqrt{3}}{4}+$ $\frac{6-3 \sqrt{3}}{4}=\frac{9-4 \sqrt{3}}{4}$. Therefore, our answer is $9000-400+30+4=8634$.
|
8634
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
$O$ is the center of square $A B C D$, and $M$ and $N$ are the midpoints of $\overline{B C}$ and $\overline{A D}$, respectively. Points $A^{\prime}, B^{\prime}, C^{\prime}, D^{\prime}$ are chosen on $\overline{A O}, \overline{B O}, \overline{C O}, \overline{D O}$, respectively, so that $A^{\prime} B^{\prime} M C^{\prime} D^{\prime} N$ is an equiangular hexagon. The ratio $\frac{\left[A^{\prime} B^{\prime} M C^{\prime} D^{\prime} N\right]}{[A B C D]}$ can be written as $\frac{a+b \sqrt{c}}{d}$, where $a, b, c, d$ are integers, $d$ is positive, $c$ is square-free, and $\operatorname{gcd}(a, b, d)=1$. Find $1000 a+100 b+10 c+d$.
|
Assume without loss of generality that the side length of $A B C D$ is 1 so that the area of the square is also 1 . This also means that $O M=O N=\frac{1}{2}$. As $A^{\prime} B^{\prime} M C^{\prime} D^{\prime} N$ is equiangular, it can be seen that $\angle A^{\prime} N O=60^{\circ}$, and also by symmetry, that $A^{\prime} B^{\prime} \| A B$, so $\angle O A^{\prime} B^{\prime}=45^{\circ}$ and $\angle O A^{\prime} N=75^{\circ}$. Therefore, $A^{\prime} N O$ is a $45-60-75$ triangle, which has sides in ratio $2: 1+\sqrt{3}: \sqrt{6}$, so we may compute that $A^{\prime} O=\frac{\sqrt{6}}{1+\sqrt{3}} \cdot \frac{1}{2}=\frac{3 \sqrt{2}-\sqrt{6}}{4}$. Further, the area of $A^{\prime} N O$ can be found by taking the altitude to $N O$, which has length of $\frac{1}{2} \cdot \frac{\sqrt{3}}{1+\sqrt{3}}=\frac{3-\sqrt{3}}{4}$, so the area is $\frac{1}{2} \cdot \frac{1}{2} \cdot \frac{3-\sqrt{3}}{4}=\frac{3-\sqrt{3}}{16}$. The area of $O A^{\prime} B^{\prime}$ is $\frac{1}{2}\left(\frac{3 \sqrt{2}-\sqrt{6}}{4}\right)^{2}=\frac{6-3 \sqrt{3}}{8}$.
Combining everything together, we can find that $\left[A^{\prime} B^{\prime} M C^{\prime} D^{\prime} N\right]=4\left[A^{\prime} N O\right]+2\left[O A^{\prime} B^{\prime}\right]=\frac{3-\sqrt{3}}{4}+$ $\frac{6-3 \sqrt{3}}{4}=\frac{9-4 \sqrt{3}}{4}$. Therefore, our answer is $9000-400+30+4=8634$.
|
{
"resource_path": "HarvardMIT/segmented/en-251-2021-nov-guts-solutions.jsonl",
"problem_match": "\n27. [13]",
"solution_match": "\nSolution: "
}
|
8d008e86-ceb1-54bb-aefd-ee396d904f4b
| 610,372
|
Find the smallest positive integer $n$ such that the divisors of $n$ can be partitioned into three sets with equal sums.
|
I claim the answer is 120 . First, note that $120=2^{3} \cdot 3 \cdot 5$, so the sum of divisors is $(1+2+4+8)(1+3)(1+5)=15 \cdot 4 \cdot 6=360$. Thus, we need to split the divisors into groups summing to 120 . But then we can just take $\{120\},\{20,40,60\},\{1,2,3,4,5,6,8,10,12,15,24,30\}$. Thus, 120 works.
Now we need to show 120 is the lowest. Let $s(n)$ be the sum of divisors. Since $n$ will be in one of the piles, we need $s(n) \geq 3 n$. First, we claim that $n$ must have at least 3 distinct prime divisors. Surely, if it had 2 distinct prime divisors, say $p$ and $q$, so that $n=p^{a} q^{b}$, then the sum of divisors is
$$
\left(1+p+p^{2}+\ldots+p^{a}\right)\left(1+q+q^{2}+\ldots+q^{b}\right)=p^{a} q^{b}\left(1+\frac{1}{p}+\ldots+\frac{1}{p^{a}}\right)\left(1+\frac{1}{q}+\ldots+\frac{1}{q^{b}}\right)
$$
However, the expression $1+\frac{1}{p}+\ldots+\frac{1}{p^{a}}$ is maximized when $p$ is minimized, and further, as $a$ is finite must be at most $\frac{1}{1-\frac{1}{p}}=\frac{p}{p-1}$. Thus, the sum of divisors is less than
$$
p^{a} q^{b} \frac{p}{p-1} \frac{q}{q-1} \leq n \cdot 2 \cdot \frac{3}{2}=3 n
$$
Thus, $n$ can't have 2 distinct prime divisors and must have at least 3 distinct prime divisors.
As we already discovered 120 works, we need not worry about 4 distinct prime divisors, as the value of $n$ would be at least $2 \cdot 3 \cdot 5 \cdot 7=210$. We now work through the numbers with 3 distinct divisors. If 2 is not one of them, then the only number that works is $105=3 \cdot 5 \cdot 7$, which has a sum of divisors that is not large enough. Therefore, 2 must be a prime divisor of $n$. Additionally, if 3 is not a divisor, then our options are $2 \cdot 5 \cdot 7$ and $2 \cdot 5 \cdot 11$, which also do not work. Therefore, 3 must also be a prime divisor. Then, if 5 is not a prime divisor, then if $n$ is $2 \cdot 3 \cdot p$, it has a sum of divisors of $(1+2)(1+3)(1+p)=n \cdot \frac{3}{2} \cdot \frac{4}{3} \cdot \frac{p+1}{p}$, which is only at least $3 n$ if $p$ is exactly 2 , which is not feasible. Additionally, if we use $2^{2}$, then the sum of divisors is $(1+2+4)(1+3)(1+p)=n \cdot \frac{7}{4} \cdot \frac{4}{3} \cdot \frac{p}{p+1}$, so $\frac{p+1}{p}>\frac{9}{7} \Longrightarrow p<4.5$, which also can't happen. Further, we can't have $3^{2}$ be a divisor of $n$ as $2 \cdot 3^{2} \cdot 5$ is the only value less than 120 with this, and that also does not work. Lastly, we just need to check $2^{3} \cdot 3 \cdot p$, which has a sum of divisors of $(1+2+4+8)(1+3)(1+p)=n \cdot \frac{15}{8} \cdot \frac{4}{3} \cdot \frac{p+1}{p}=n \cdot \frac{5}{2} \cdot \frac{p}{p+1}$, so $p=5$ and that works. This means that $n=120$ is the smallest value for which $s(n) \geq 3 n$, and thus is our answer.
|
120
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Find the smallest positive integer $n$ such that the divisors of $n$ can be partitioned into three sets with equal sums.
|
I claim the answer is 120 . First, note that $120=2^{3} \cdot 3 \cdot 5$, so the sum of divisors is $(1+2+4+8)(1+3)(1+5)=15 \cdot 4 \cdot 6=360$. Thus, we need to split the divisors into groups summing to 120 . But then we can just take $\{120\},\{20,40,60\},\{1,2,3,4,5,6,8,10,12,15,24,30\}$. Thus, 120 works.
Now we need to show 120 is the lowest. Let $s(n)$ be the sum of divisors. Since $n$ will be in one of the piles, we need $s(n) \geq 3 n$. First, we claim that $n$ must have at least 3 distinct prime divisors. Surely, if it had 2 distinct prime divisors, say $p$ and $q$, so that $n=p^{a} q^{b}$, then the sum of divisors is
$$
\left(1+p+p^{2}+\ldots+p^{a}\right)\left(1+q+q^{2}+\ldots+q^{b}\right)=p^{a} q^{b}\left(1+\frac{1}{p}+\ldots+\frac{1}{p^{a}}\right)\left(1+\frac{1}{q}+\ldots+\frac{1}{q^{b}}\right)
$$
However, the expression $1+\frac{1}{p}+\ldots+\frac{1}{p^{a}}$ is maximized when $p$ is minimized, and further, as $a$ is finite must be at most $\frac{1}{1-\frac{1}{p}}=\frac{p}{p-1}$. Thus, the sum of divisors is less than
$$
p^{a} q^{b} \frac{p}{p-1} \frac{q}{q-1} \leq n \cdot 2 \cdot \frac{3}{2}=3 n
$$
Thus, $n$ can't have 2 distinct prime divisors and must have at least 3 distinct prime divisors.
As we already discovered 120 works, we need not worry about 4 distinct prime divisors, as the value of $n$ would be at least $2 \cdot 3 \cdot 5 \cdot 7=210$. We now work through the numbers with 3 distinct divisors. If 2 is not one of them, then the only number that works is $105=3 \cdot 5 \cdot 7$, which has a sum of divisors that is not large enough. Therefore, 2 must be a prime divisor of $n$. Additionally, if 3 is not a divisor, then our options are $2 \cdot 5 \cdot 7$ and $2 \cdot 5 \cdot 11$, which also do not work. Therefore, 3 must also be a prime divisor. Then, if 5 is not a prime divisor, then if $n$ is $2 \cdot 3 \cdot p$, it has a sum of divisors of $(1+2)(1+3)(1+p)=n \cdot \frac{3}{2} \cdot \frac{4}{3} \cdot \frac{p+1}{p}$, which is only at least $3 n$ if $p$ is exactly 2 , which is not feasible. Additionally, if we use $2^{2}$, then the sum of divisors is $(1+2+4)(1+3)(1+p)=n \cdot \frac{7}{4} \cdot \frac{4}{3} \cdot \frac{p}{p+1}$, so $\frac{p+1}{p}>\frac{9}{7} \Longrightarrow p<4.5$, which also can't happen. Further, we can't have $3^{2}$ be a divisor of $n$ as $2 \cdot 3^{2} \cdot 5$ is the only value less than 120 with this, and that also does not work. Lastly, we just need to check $2^{3} \cdot 3 \cdot p$, which has a sum of divisors of $(1+2+4+8)(1+3)(1+p)=n \cdot \frac{15}{8} \cdot \frac{4}{3} \cdot \frac{p+1}{p}=n \cdot \frac{5}{2} \cdot \frac{p}{p+1}$, so $p=5$ and that works. This means that $n=120$ is the smallest value for which $s(n) \geq 3 n$, and thus is our answer.
|
{
"resource_path": "HarvardMIT/segmented/en-251-2021-nov-guts-solutions.jsonl",
"problem_match": "\n28. [15]",
"solution_match": "\nSolution: "
}
|
2d3be9dd-00c9-58d7-9c4f-c933f664d07e
| 610,373
|
Kevin writes down the positive integers $1,2, \ldots, 15$ on a blackboard. Then, he repeatedly picks two random integers $a, b$ on the blackboard, erases them, and writes down $\operatorname{gcd}(a, b)$ and $\operatorname{lcm}(a, b)$. He does this until he is no longer able to change the set of numbers written on the board. Find the maximum sum of the numbers on the board after this process.
|
Since $v_{p}(\operatorname{gcd}(a, b))=\min \left(v_{p}(a), v_{p}(b)\right)$ and $v_{p}(\operatorname{lcm}(a, b))=\max \left(v_{p}(a), v_{p}(b)\right)$, we may show the following:
Claim. For any prime $p$ and non-negative integer $k$, the number of numbers $n$ on the board such that $v_{p}(n)=k$ doesn't change throughout this process.
Let the 15 final numbers on the board be $a_{1} \leq a_{2} \leq a_{3} \cdots \leq a_{15}$. Note that $a_{i} \mid a_{j}$ for all $i<j$. For each prime $p$, let $X_{p, i}=v_{p}\left(a_{i}\right)$. Note that by the lemma, we have
$$
\begin{aligned}
\left(X_{2,1}, X_{2,2}, \ldots, X_{2,15}\right) & =(0,0,0,0,0,0,0,0,1,1,1,1,2,2,3) \\
\left(X_{3,1}, X_{3,2}, \ldots, X_{3,15}\right) & =(0,0,0,0,0,0,0,0,0,0,1,1,1,1,2) \\
\left(X_{5,1}, X_{5,2}, \ldots, X_{5,15}\right) & =(0,0,0,0,0,0,0,0,0,0,0,0,1,1,1) \\
\left(X_{7,1}, X_{7,2}, \ldots, X_{7,15}\right) & =(0,0,0,0,0,0,0,0,0,0,0,0,0,1,1) \\
\left(X_{11,1}, X_{11,2}, \ldots, X_{11,15}\right) & =(0,0,0,0,0,0,0,0,0,0,0,0,0,0,1) \\
\left(X_{13,1}, X_{13,2}, \ldots, X_{13,15}\right) & =(0,0,0,0,0,0,0,0,0,0,0,0,0,0,1)
\end{aligned}
$$
Thus, since $a_{i}=\prod_{p} p^{X_{p, i}}$ for each $i$, so we get the 15 final numbers on the board are
$$
1,1,1,1,1,1,1,1,2,2,6,6,60,420, \text { and } 360360
$$
Adding these up gives 360854 .
|
360854
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Kevin writes down the positive integers $1,2, \ldots, 15$ on a blackboard. Then, he repeatedly picks two random integers $a, b$ on the blackboard, erases them, and writes down $\operatorname{gcd}(a, b)$ and $\operatorname{lcm}(a, b)$. He does this until he is no longer able to change the set of numbers written on the board. Find the maximum sum of the numbers on the board after this process.
|
Since $v_{p}(\operatorname{gcd}(a, b))=\min \left(v_{p}(a), v_{p}(b)\right)$ and $v_{p}(\operatorname{lcm}(a, b))=\max \left(v_{p}(a), v_{p}(b)\right)$, we may show the following:
Claim. For any prime $p$ and non-negative integer $k$, the number of numbers $n$ on the board such that $v_{p}(n)=k$ doesn't change throughout this process.
Let the 15 final numbers on the board be $a_{1} \leq a_{2} \leq a_{3} \cdots \leq a_{15}$. Note that $a_{i} \mid a_{j}$ for all $i<j$. For each prime $p$, let $X_{p, i}=v_{p}\left(a_{i}\right)$. Note that by the lemma, we have
$$
\begin{aligned}
\left(X_{2,1}, X_{2,2}, \ldots, X_{2,15}\right) & =(0,0,0,0,0,0,0,0,1,1,1,1,2,2,3) \\
\left(X_{3,1}, X_{3,2}, \ldots, X_{3,15}\right) & =(0,0,0,0,0,0,0,0,0,0,1,1,1,1,2) \\
\left(X_{5,1}, X_{5,2}, \ldots, X_{5,15}\right) & =(0,0,0,0,0,0,0,0,0,0,0,0,1,1,1) \\
\left(X_{7,1}, X_{7,2}, \ldots, X_{7,15}\right) & =(0,0,0,0,0,0,0,0,0,0,0,0,0,1,1) \\
\left(X_{11,1}, X_{11,2}, \ldots, X_{11,15}\right) & =(0,0,0,0,0,0,0,0,0,0,0,0,0,0,1) \\
\left(X_{13,1}, X_{13,2}, \ldots, X_{13,15}\right) & =(0,0,0,0,0,0,0,0,0,0,0,0,0,0,1)
\end{aligned}
$$
Thus, since $a_{i}=\prod_{p} p^{X_{p, i}}$ for each $i$, so we get the 15 final numbers on the board are
$$
1,1,1,1,1,1,1,1,2,2,6,6,60,420, \text { and } 360360
$$
Adding these up gives 360854 .
|
{
"resource_path": "HarvardMIT/segmented/en-251-2021-nov-guts-solutions.jsonl",
"problem_match": "\n29. [15]",
"solution_match": "\nSolution: "
}
|
f543ca06-3b7e-5608-a0c7-06555c392621
| 610,374
|
The function $f: \mathbb{Z}^{2} \rightarrow \mathbb{Z}$ satisfies
- $f(x, 0)=f(0, y)=0$, and
- $f(x, y)=f(x-1, y)+f(x, y-1)+x+y$
for all nonnegative integers $x$ and $y$. Find $f(6,12)$.
|
We claim $f(x, y)=\binom{x+y+2}{x+1}-(x+y+2)$. Indeed, the hypothesis holds true for our base cases $f(x, 0)$ and $f(0, y)$, and moreover,
$f(x-1, y)+f(x, y-1)+x+y=\binom{x+y+1}{x}+\binom{x+y+1}{x+1}-2(x+y+1)+x+y=\binom{x+y+2}{x+1}-(x+y+2)$.
Thus, the final answer is $\binom{20}{7}-20=77500$.
Here is a way to derive this formula from scratch. The idea is that the second condition harks back to the Pascal's triangle rule, sans some modifications. Write $f(x, y)=g(x, y)-x-y$, so then $g(0, t)=g(t, 0)=t$ and $g(x, y)=g(x-1, y)+g(x, y-1)+2$. Then, letting $g(x, y)=h(x, y)-2$ gives $h(x, y)=h(x-1, y)+h(x, y-1)$, which is exactly Pascal's rule. We are given the base cases $h(0, t)=h(t, 0)=t+2$, which is starting "inside" of Pascal's triangle, so $h(x, y)=\binom{x+y+2}{x+1}$.
|
77500
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
The function $f: \mathbb{Z}^{2} \rightarrow \mathbb{Z}$ satisfies
- $f(x, 0)=f(0, y)=0$, and
- $f(x, y)=f(x-1, y)+f(x, y-1)+x+y$
for all nonnegative integers $x$ and $y$. Find $f(6,12)$.
|
We claim $f(x, y)=\binom{x+y+2}{x+1}-(x+y+2)$. Indeed, the hypothesis holds true for our base cases $f(x, 0)$ and $f(0, y)$, and moreover,
$f(x-1, y)+f(x, y-1)+x+y=\binom{x+y+1}{x}+\binom{x+y+1}{x+1}-2(x+y+1)+x+y=\binom{x+y+2}{x+1}-(x+y+2)$.
Thus, the final answer is $\binom{20}{7}-20=77500$.
Here is a way to derive this formula from scratch. The idea is that the second condition harks back to the Pascal's triangle rule, sans some modifications. Write $f(x, y)=g(x, y)-x-y$, so then $g(0, t)=g(t, 0)=t$ and $g(x, y)=g(x-1, y)+g(x, y-1)+2$. Then, letting $g(x, y)=h(x, y)-2$ gives $h(x, y)=h(x-1, y)+h(x, y-1)$, which is exactly Pascal's rule. We are given the base cases $h(0, t)=h(t, 0)=t+2$, which is starting "inside" of Pascal's triangle, so $h(x, y)=\binom{x+y+2}{x+1}$.
|
{
"resource_path": "HarvardMIT/segmented/en-251-2021-nov-guts-solutions.jsonl",
"problem_match": "\n30. [15]",
"solution_match": "\nSolution: "
}
|
310bd87d-8aad-5ecc-837b-30a30ad23419
| 610,375
|
For positive integers $n$, let $f(n)$ be the product of the digits of $n$. Find the largest positive integer $m$ such that
$$
\sum_{n=1}^{\infty} \frac{f(n)}{m^{\left\lfloor\log _{10} n\right\rfloor}}
$$
is an integer.
|
We know that if $S_{\ell}$ is the set of all positive integers with $\ell$ digits, then
$$
\begin{aligned}
& \sum_{n \in S_{\ell}} \frac{f(n)}{k^{\left\lfloor\log _{10}(n)\right\rfloor}=} \sum_{n \in S_{\ell}} \frac{f(n)}{k^{\ell-1}}=\frac{(0+1+2+\ldots+9)^{\ell}}{k^{\ell-1}}= \\
& 45 \cdot\left(\frac{45}{k}\right)^{\ell-1} .
\end{aligned}
$$
Thus, we can see that
$$
\sum_{n=1}^{\infty} \frac{f(n)}{k\left\lfloor\log _{10}(n)\right\rfloor}=\sum_{\ell=1}^{\infty} \sum_{n \in S_{\ell}} \frac{f(n)}{k\left\lfloor\log _{10}(n)\right\rfloor}=\sum_{\ell=1}^{\infty} 45 \cdot\left(\frac{45}{k}\right)^{\ell-1}=\frac{45}{1-\frac{45}{k}}=\frac{45 k}{k-45}=45+\frac{2025}{k-45}
$$
It is clear that the largest integer $k$ that will work is when $k-45=2025 \Longrightarrow k=2070$.
|
2070
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
For positive integers $n$, let $f(n)$ be the product of the digits of $n$. Find the largest positive integer $m$ such that
$$
\sum_{n=1}^{\infty} \frac{f(n)}{m^{\left\lfloor\log _{10} n\right\rfloor}}
$$
is an integer.
|
We know that if $S_{\ell}$ is the set of all positive integers with $\ell$ digits, then
$$
\begin{aligned}
& \sum_{n \in S_{\ell}} \frac{f(n)}{k^{\left\lfloor\log _{10}(n)\right\rfloor}=} \sum_{n \in S_{\ell}} \frac{f(n)}{k^{\ell-1}}=\frac{(0+1+2+\ldots+9)^{\ell}}{k^{\ell-1}}= \\
& 45 \cdot\left(\frac{45}{k}\right)^{\ell-1} .
\end{aligned}
$$
Thus, we can see that
$$
\sum_{n=1}^{\infty} \frac{f(n)}{k\left\lfloor\log _{10}(n)\right\rfloor}=\sum_{\ell=1}^{\infty} \sum_{n \in S_{\ell}} \frac{f(n)}{k\left\lfloor\log _{10}(n)\right\rfloor}=\sum_{\ell=1}^{\infty} 45 \cdot\left(\frac{45}{k}\right)^{\ell-1}=\frac{45}{1-\frac{45}{k}}=\frac{45 k}{k-45}=45+\frac{2025}{k-45}
$$
It is clear that the largest integer $k$ that will work is when $k-45=2025 \Longrightarrow k=2070$.
|
{
"resource_path": "HarvardMIT/segmented/en-251-2021-nov-guts-solutions.jsonl",
"problem_match": "\n31. [17]",
"solution_match": "\nSolution: "
}
|
d5afa36d-79f9-54f4-8ad6-75951e36f0ac
| 610,376
|
There are $N$ lockers, labeled from 1 to $N$, placed in clockwise order around a circular hallway. Initially, all lockers are open. Ansoon starts at the first locker and always moves clockwise. When she is at locker $n$ and there are more than $n$ open lockers, she keeps locker $n$ open and closes the next $n$ open lockers, then repeats the process with the next open locker. If she is at locker $n$ and there are at most $n$ lockers still open, she keeps locker $n$ open and closes all other lockers. She continues this process until only one locker is left open. What is the smallest integer $N>2021$ such that the last open locker is locker 1?
|
Note that in the first run-through, we will leave all lockers $2^{n}-1$ open. This is because after having locker $2^{n}-1$ open, we will close the next $2^{n}-1$ lockers and then start at locker $2^{n}-1+2^{n}-1+1=2^{n+1}-1$. Now we want 1 to be the last locker that is open. We know that if $N<2046$, then closing 1023 lockers after 1023 will lead us to close locker 1 . However, if $N=2046$, then locker 1 will stay open, 3 will close, 7 will stay open, closing the next 10 and then 1 stays open and we close locker 7 , therefore $N=2046$ does work.
|
2046
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
There are $N$ lockers, labeled from 1 to $N$, placed in clockwise order around a circular hallway. Initially, all lockers are open. Ansoon starts at the first locker and always moves clockwise. When she is at locker $n$ and there are more than $n$ open lockers, she keeps locker $n$ open and closes the next $n$ open lockers, then repeats the process with the next open locker. If she is at locker $n$ and there are at most $n$ lockers still open, she keeps locker $n$ open and closes all other lockers. She continues this process until only one locker is left open. What is the smallest integer $N>2021$ such that the last open locker is locker 1?
|
Note that in the first run-through, we will leave all lockers $2^{n}-1$ open. This is because after having locker $2^{n}-1$ open, we will close the next $2^{n}-1$ lockers and then start at locker $2^{n}-1+2^{n}-1+1=2^{n+1}-1$. Now we want 1 to be the last locker that is open. We know that if $N<2046$, then closing 1023 lockers after 1023 will lead us to close locker 1 . However, if $N=2046$, then locker 1 will stay open, 3 will close, 7 will stay open, closing the next 10 and then 1 stays open and we close locker 7 , therefore $N=2046$ does work.
|
{
"resource_path": "HarvardMIT/segmented/en-251-2021-nov-guts-solutions.jsonl",
"problem_match": "\n32. [17]",
"solution_match": "\nSolution: "
}
|
fafefa5a-d90b-5b37-b3c4-5d4d00d7a42c
| 610,377
|
Point $P$ lies inside equilateral triangle $A B C$ so that $\angle B P C=120^{\circ}$ and $A P \sqrt{2}=B P+C P$. $\frac{A P}{A B}$ can be written as $\frac{a \sqrt{b}}{c}$, where $a, b, c$ are integers, $c$ is positive, $b$ is square-free, and $\operatorname{gcd}(a, c)=1$. Find $100 a+10 b+c$.
|
Let $O$ be the center of $A B C$. First, we draw in the circumcircle of $A B C$ and the circumcircle of $B O C$, labeled $\omega_{1}$ and $\omega_{2}$, respectively. Note that $\omega_{1}$ is the reflection of $\omega_{2}$ over $B C$ and that $P$ lies on $\omega_{2}$. Now, let $P_{C}$ be the second intersection of ray $C P$ with $\omega_{1}$. Additionally, label the second intersections of ray $A P$ with $\omega_{1}$ and $\omega_{2}$ be $M$ and $X$, respectively. Lastly, let $A^{\prime}$ be the diametrically opposite point from $A$ on $\omega_{1}$.
We first note that $A^{\prime}$ is the center of $\omega_{2}$. Thus, $A^{\prime}$ lies on the perpendicular bisector of segment $P X$. But since $A A^{\prime}$ is a diameter of $\omega_{1}$, this also means that the midpoint of $P X$ lies on $\omega_{1}$. This implies that $M$ is the midpoint of $P X$.
From a simple angle chase, we have $\angle P_{C} P B=180-\angle B P C=60^{\circ}$. Also, $\angle B P_{C} C=\angle B A C=60^{\circ}$. Therefore, we find that triangle $B P P_{C}$ is equilateral with side length $B P$.
Now we begin computations. By Law of Cosines in triangle $B P C$, we see that $B P^{2}+C P^{2}+B P \cdot C P=$ $B C^{2}=A B^{2}$. However, we can rewrite this as
$$
A B^{2}=B P^{2}+C P^{2}+B P \cdot C P=(B P+C P)^{2}-B P \cdot C P=2 \cdot A P^{2}-B P \cdot C P
$$
To find an equation for $\frac{A P}{A B}$, it suffices to simplify the expression $B P \cdot C P$. Since $B P P_{C}$ is equilateral, we can proceed through Power of a Point. By looking at $\omega_{1}$, we see that
$$
B P \cdot C P=P P_{C} \cdot C P=A P \cdot P M=\frac{1}{2} \cdot A P \cdot A X
$$
Then, from Power of a Point on $\omega_{2}$, we see that
$$
\frac{1}{2} \cdot A P \cdot A X=\frac{1}{2} \cdot A P \cdot(A X-A P)=\frac{1}{2} \cdot A P \cdot A X-\frac{1}{2} \cdot A P^{2}=\frac{1}{2}\left(A B^{2}-A P^{2}\right)
$$
Combining everything, we find that $B P \cdot C P=\frac{1}{2}\left(A B^{2}-A P^{2}\right)$ which means that
$$
A B^{2}=2 \cdot A P^{2}-\frac{1}{2}\left(A B^{2}-A P^{2}\right) \Longrightarrow \frac{5}{2} A B^{2}=\frac{3}{2} A P^{2} \Longrightarrow \frac{A P}{A B}=\frac{\sqrt{15}}{5} .
$$
|
155
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Point $P$ lies inside equilateral triangle $A B C$ so that $\angle B P C=120^{\circ}$ and $A P \sqrt{2}=B P+C P$. $\frac{A P}{A B}$ can be written as $\frac{a \sqrt{b}}{c}$, where $a, b, c$ are integers, $c$ is positive, $b$ is square-free, and $\operatorname{gcd}(a, c)=1$. Find $100 a+10 b+c$.
|
Let $O$ be the center of $A B C$. First, we draw in the circumcircle of $A B C$ and the circumcircle of $B O C$, labeled $\omega_{1}$ and $\omega_{2}$, respectively. Note that $\omega_{1}$ is the reflection of $\omega_{2}$ over $B C$ and that $P$ lies on $\omega_{2}$. Now, let $P_{C}$ be the second intersection of ray $C P$ with $\omega_{1}$. Additionally, label the second intersections of ray $A P$ with $\omega_{1}$ and $\omega_{2}$ be $M$ and $X$, respectively. Lastly, let $A^{\prime}$ be the diametrically opposite point from $A$ on $\omega_{1}$.
We first note that $A^{\prime}$ is the center of $\omega_{2}$. Thus, $A^{\prime}$ lies on the perpendicular bisector of segment $P X$. But since $A A^{\prime}$ is a diameter of $\omega_{1}$, this also means that the midpoint of $P X$ lies on $\omega_{1}$. This implies that $M$ is the midpoint of $P X$.
From a simple angle chase, we have $\angle P_{C} P B=180-\angle B P C=60^{\circ}$. Also, $\angle B P_{C} C=\angle B A C=60^{\circ}$. Therefore, we find that triangle $B P P_{C}$ is equilateral with side length $B P$.
Now we begin computations. By Law of Cosines in triangle $B P C$, we see that $B P^{2}+C P^{2}+B P \cdot C P=$ $B C^{2}=A B^{2}$. However, we can rewrite this as
$$
A B^{2}=B P^{2}+C P^{2}+B P \cdot C P=(B P+C P)^{2}-B P \cdot C P=2 \cdot A P^{2}-B P \cdot C P
$$
To find an equation for $\frac{A P}{A B}$, it suffices to simplify the expression $B P \cdot C P$. Since $B P P_{C}$ is equilateral, we can proceed through Power of a Point. By looking at $\omega_{1}$, we see that
$$
B P \cdot C P=P P_{C} \cdot C P=A P \cdot P M=\frac{1}{2} \cdot A P \cdot A X
$$
Then, from Power of a Point on $\omega_{2}$, we see that
$$
\frac{1}{2} \cdot A P \cdot A X=\frac{1}{2} \cdot A P \cdot(A X-A P)=\frac{1}{2} \cdot A P \cdot A X-\frac{1}{2} \cdot A P^{2}=\frac{1}{2}\left(A B^{2}-A P^{2}\right)
$$
Combining everything, we find that $B P \cdot C P=\frac{1}{2}\left(A B^{2}-A P^{2}\right)$ which means that
$$
A B^{2}=2 \cdot A P^{2}-\frac{1}{2}\left(A B^{2}-A P^{2}\right) \Longrightarrow \frac{5}{2} A B^{2}=\frac{3}{2} A P^{2} \Longrightarrow \frac{A P}{A B}=\frac{\sqrt{15}}{5} .
$$
|
{
"resource_path": "HarvardMIT/segmented/en-251-2021-nov-guts-solutions.jsonl",
"problem_match": "\n33. [17]",
"solution_match": "\nSolution: "
}
|
03aac20e-7ad9-57c4-a8f3-b44ba6019ded
| 610,378
|
Suppose two distinct competitors of the HMMT 2021 November contest are chosen uniformly at random. Let $p$ be the probability that they can be labelled $A$ and $B$ so that $A$ 's score on the General round is strictly greater than $B$ 's, and $B$ 's score on the theme round is strictly greater than $A$ 's. Estimate $P=\lfloor 10000 p\rfloor$.
An estimate of $E$ will earn $\left\lfloor 20 \min \left(\frac{A}{E}, \frac{E}{A}\right)^{6}\right\rfloor$ points.
|
If competitors' scores on the General and Theme rounds were completely uncorrelated, we would expect the answer to be approximately $\frac{1}{2}$. If they were maximally correlated, we would expect the answer to be exactly 0 . It turns out that guessing $\frac{1}{4} \rightarrow 2500$ achieves almost full points $-17 / 20$.
One could try to come up with a more concrete model of what is happening. For example, we could start by looking only at the number of questions answered on each test, rather than the score, and assuming that two competitors could satisfy the desired property only if they have similar skill levels. In the case that they are similarly skilled, we assume it's $50 / 50$ who wins on each test.
How do we determine the probability that two random competitors are similarly skilled? We could make some reasonable guess about the distribution of number of questions solved on the general round and assume that two competitors are similarly skilled if the number of questions they answered differs by exactly 1 . Most of the action on the general round happens in the first five problems, so let's assume that $\frac{1}{6}$ of competitors answer 1 problem, $\frac{1}{3}$ answer $2, \frac{1}{3}$ answer 3 , and $\frac{1}{6}$ answer 4 . Then two competitors are similarly skilled with probability $\frac{4}{9}$, which gives a final estimate of $\frac{2}{9} \rightarrow 2222$.
This is farther from the true answer and only achieves 11 points, but one can imagine slight changes to this model that lead to a better estimate. For example, one could guess a different distribution of general round scores. Also, one could assume that slight differences in the subject distribution across
the tests can in fact cause Theme round scores of competitors who score similarly on the General round to in fact be weakly inversely correlated (since many students are stronger in one subject area than others), so that the probability that the higher General scorer scores lower on the Theme round is a little greater than $50 \%$.
|
2222
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Suppose two distinct competitors of the HMMT 2021 November contest are chosen uniformly at random. Let $p$ be the probability that they can be labelled $A$ and $B$ so that $A$ 's score on the General round is strictly greater than $B$ 's, and $B$ 's score on the theme round is strictly greater than $A$ 's. Estimate $P=\lfloor 10000 p\rfloor$.
An estimate of $E$ will earn $\left\lfloor 20 \min \left(\frac{A}{E}, \frac{E}{A}\right)^{6}\right\rfloor$ points.
|
If competitors' scores on the General and Theme rounds were completely uncorrelated, we would expect the answer to be approximately $\frac{1}{2}$. If they were maximally correlated, we would expect the answer to be exactly 0 . It turns out that guessing $\frac{1}{4} \rightarrow 2500$ achieves almost full points $-17 / 20$.
One could try to come up with a more concrete model of what is happening. For example, we could start by looking only at the number of questions answered on each test, rather than the score, and assuming that two competitors could satisfy the desired property only if they have similar skill levels. In the case that they are similarly skilled, we assume it's $50 / 50$ who wins on each test.
How do we determine the probability that two random competitors are similarly skilled? We could make some reasonable guess about the distribution of number of questions solved on the general round and assume that two competitors are similarly skilled if the number of questions they answered differs by exactly 1 . Most of the action on the general round happens in the first five problems, so let's assume that $\frac{1}{6}$ of competitors answer 1 problem, $\frac{1}{3}$ answer $2, \frac{1}{3}$ answer 3 , and $\frac{1}{6}$ answer 4 . Then two competitors are similarly skilled with probability $\frac{4}{9}$, which gives a final estimate of $\frac{2}{9} \rightarrow 2222$.
This is farther from the true answer and only achieves 11 points, but one can imagine slight changes to this model that lead to a better estimate. For example, one could guess a different distribution of general round scores. Also, one could assume that slight differences in the subject distribution across
the tests can in fact cause Theme round scores of competitors who score similarly on the General round to in fact be weakly inversely correlated (since many students are stronger in one subject area than others), so that the probability that the higher General scorer scores lower on the Theme round is a little greater than $50 \%$.
|
{
"resource_path": "HarvardMIT/segmented/en-251-2021-nov-guts-solutions.jsonl",
"problem_match": "\n34. [20]",
"solution_match": "\nSolution: "
}
|
ac2c9f0e-0403-5b69-9c64-1b5cbaccbdf4
| 610,379
|
Let $N$ be the number of ways in which the letters in "HMMTHMMTHMMTHMMTHMMTHMMT" ("HMMT" repeated six times) can be rearranged so that each letter is adjacent to another copy of the same letter. For example, "MMMMMMTTTTTTHHHHHHHHHHHH" satisfies this property, but "HMMMMMTTTTTTHННННННННННМ" does not. Estimate $N$.
An estimate of $E$ will earn $\left\lfloor 20 \min \left(\frac{N}{E}, \frac{E}{N}\right)^{4}\right\rfloor$ points.
|
We first count the number of arrangements for which each block of consecutive identical letters has even size. Pair up the letters into 3 pairs of $H, 6$ pairs of $M$, and 3 pairs of $T$, then rearrange the pairs. There are $\frac{12!}{6!3!3!}=18480$ ways to do this.
In the original problem, we may estimate the number of arrangements by computing the fraction of arrangements with all even blocks. We estimate this by counting the number of ways to split the 6 Hs , 12 Ms , and 6 Ts into blocks, and collating the proportions of splittings which use all even blocks:
- We can split 6 as $6,4+2,3+3$, and $2+4$. Exactly $3 / 4$ of the splittings have all even blocks.
- We can split 12 into $12,10+2, \ldots, 2+10,8+2+2,7+3+2,6+4+2,5+5+2,6+3+3$, $5+4+3,6+2+2+2,5+3+2+2,4+4+2+2,4+3+3+2,3+3+3+3,4+2+2+2+2$, $3+3+2+2+2,2+2+2+2+2+2$.
Stars and bars to expand from the pairs variant gives 79000
The following $\mathrm{C}++$ code outputs the exact answer:
```
#include <bits/stdc++.h>
using namespace std;
#define IJK iii[0]][iii[1]][iii[2]
#define ijk i][j][k
#define MAX_N 100
#define S 3
#define N 6
long long dp[2][3] [MAX_N] [MAX_N] [MAX_N];
int main()
{
dp[1][0][0][0][0] = 1;
for (int i = 0; i <= N; i++)
for (int j = 0; j <= 2*N; j++)
for (int k = 0; k <= N; k++)
for (int c = 0; c < S; c++)
for (int l = 0; l < S; l++)
{
int iii[] = { i, j, k }; iii[l]++;
dp[0][l][IJK] += (c != l || !(i + j + k)) * dp[1][c][ijk];
dp[1][l][IJK] += (c == l && i + j + k) * (dp[1][c][ijk] + dp[0][c][ijk]);
}
long long a = 0;
for (int i = 0; i < S; i++) a += dp[1][i][N][2 * N][N];
cout << a << endl;
return 0;
}
```
|
79000
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Let $N$ be the number of ways in which the letters in "HMMTHMMTHMMTHMMTHMMTHMMT" ("HMMT" repeated six times) can be rearranged so that each letter is adjacent to another copy of the same letter. For example, "MMMMMMTTTTTTHHHHHHHHHHHH" satisfies this property, but "HMMMMMTTTTTTHННННННННННМ" does not. Estimate $N$.
An estimate of $E$ will earn $\left\lfloor 20 \min \left(\frac{N}{E}, \frac{E}{N}\right)^{4}\right\rfloor$ points.
|
We first count the number of arrangements for which each block of consecutive identical letters has even size. Pair up the letters into 3 pairs of $H, 6$ pairs of $M$, and 3 pairs of $T$, then rearrange the pairs. There are $\frac{12!}{6!3!3!}=18480$ ways to do this.
In the original problem, we may estimate the number of arrangements by computing the fraction of arrangements with all even blocks. We estimate this by counting the number of ways to split the 6 Hs , 12 Ms , and 6 Ts into blocks, and collating the proportions of splittings which use all even blocks:
- We can split 6 as $6,4+2,3+3$, and $2+4$. Exactly $3 / 4$ of the splittings have all even blocks.
- We can split 12 into $12,10+2, \ldots, 2+10,8+2+2,7+3+2,6+4+2,5+5+2,6+3+3$, $5+4+3,6+2+2+2,5+3+2+2,4+4+2+2,4+3+3+2,3+3+3+3,4+2+2+2+2$, $3+3+2+2+2,2+2+2+2+2+2$.
Stars and bars to expand from the pairs variant gives 79000
The following $\mathrm{C}++$ code outputs the exact answer:
```
#include <bits/stdc++.h>
using namespace std;
#define IJK iii[0]][iii[1]][iii[2]
#define ijk i][j][k
#define MAX_N 100
#define S 3
#define N 6
long long dp[2][3] [MAX_N] [MAX_N] [MAX_N];
int main()
{
dp[1][0][0][0][0] = 1;
for (int i = 0; i <= N; i++)
for (int j = 0; j <= 2*N; j++)
for (int k = 0; k <= N; k++)
for (int c = 0; c < S; c++)
for (int l = 0; l < S; l++)
{
int iii[] = { i, j, k }; iii[l]++;
dp[0][l][IJK] += (c != l || !(i + j + k)) * dp[1][c][ijk];
dp[1][l][IJK] += (c == l && i + j + k) * (dp[1][c][ijk] + dp[0][c][ijk]);
}
long long a = 0;
for (int i = 0; i < S; i++) a += dp[1][i][N][2 * N][N];
cout << a << endl;
return 0;
}
```
|
{
"resource_path": "HarvardMIT/segmented/en-251-2021-nov-guts-solutions.jsonl",
"problem_match": "\n36. [20]",
"solution_match": "\nSolution: "
}
|
bff50dde-975c-5e2e-9c2e-923e34984606
| 610,381
|
Let $A B C D$ be a parallelogram. Let $E$ be the midpoint of $A B$ and $F$ be the midpoint of $C D$. Points $P$ and $Q$ are on segments $E F$ and $C F$, respectively, such that $A, P$, and $Q$ are collinear. Given that $E P=5, P F=3$, and $Q F=12$, find $C Q$.
|
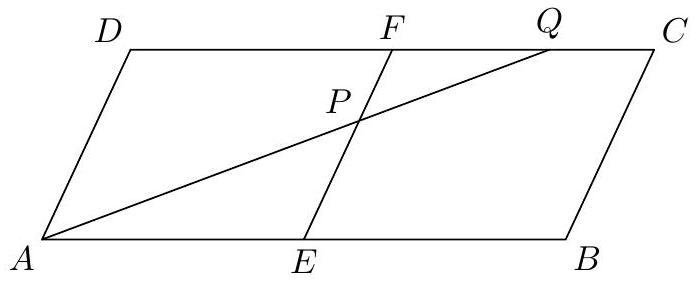
Triangles $P F Q$ and $P E A$ are similar, so $A E=F Q \cdot \frac{P E}{P F}=12 \cdot \frac{5}{3}=20$. Now, $C Q=C F-Q F=$ $20-12=8$.
|
8
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $A B C D$ be a parallelogram. Let $E$ be the midpoint of $A B$ and $F$ be the midpoint of $C D$. Points $P$ and $Q$ are on segments $E F$ and $C F$, respectively, such that $A, P$, and $Q$ are collinear. Given that $E P=5, P F=3$, and $Q F=12$, find $C Q$.
|

Triangles $P F Q$ and $P E A$ are similar, so $A E=F Q \cdot \frac{P E}{P F}=12 \cdot \frac{5}{3}=20$. Now, $C Q=C F-Q F=$ $20-12=8$.
|
{
"resource_path": "HarvardMIT/segmented/en-251-2021-nov-team-solutions.jsonl",
"problem_match": "\n1. [20]",
"solution_match": "\n## Solution:\n\n"
}
|
94768d55-94f4-5a72-b4b6-b7d59e60a5cf
| 610,382
|
Joey wrote a system of equations on a blackboard, where each of the equations was of the form $a+b=c$ or $a \cdot b=c$ for some variables or integers $a, b, c$. Then Sean came to the board and erased all of the plus signs and multiplication signs, so that the board reads:
$$
\begin{array}{ll}
x & z=15 \\
x & y=12 \\
x & x=36
\end{array}
$$
If $x, y, z$ are integer solutions to the original system, find the sum of all possible values of $100 x+10 y+z$. Proposed by: David Vulakh
|
The bottom line gives $x=-6, x=6$ or $x=18$. If $x=-6, y$ can be -2 or 18 and $z$ must be 21 , so the possible values for $100 x+10 y+z$ are -599 and -399 . If $x=6, y$ can be 2 or 6 and $z$ must be 9 , so the possible values are 629 and 669 . If $x=18, y$ must be -6 and $z$ must be -3 , so the only possible value is 1737 . The total sum is 2037 .
|
2037
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Joey wrote a system of equations on a blackboard, where each of the equations was of the form $a+b=c$ or $a \cdot b=c$ for some variables or integers $a, b, c$. Then Sean came to the board and erased all of the plus signs and multiplication signs, so that the board reads:
$$
\begin{array}{ll}
x & z=15 \\
x & y=12 \\
x & x=36
\end{array}
$$
If $x, y, z$ are integer solutions to the original system, find the sum of all possible values of $100 x+10 y+z$. Proposed by: David Vulakh
|
The bottom line gives $x=-6, x=6$ or $x=18$. If $x=-6, y$ can be -2 or 18 and $z$ must be 21 , so the possible values for $100 x+10 y+z$ are -599 and -399 . If $x=6, y$ can be 2 or 6 and $z$ must be 9 , so the possible values are 629 and 669 . If $x=18, y$ must be -6 and $z$ must be -3 , so the only possible value is 1737 . The total sum is 2037 .
|
{
"resource_path": "HarvardMIT/segmented/en-251-2021-nov-team-solutions.jsonl",
"problem_match": "\n2. [25]",
"solution_match": "\nSolution: "
}
|
757ca9b2-e9b1-520f-b2af-3d24f54cdb63
| 610,383
|
Suppose $m$ and $n$ are positive integers for which
- the sum of the first $m$ multiples of $n$ is 120 , and
- the sum of the first $m^{3}$ multiples of $n^{3}$ is 4032000 .
Determine the sum of the first $m^{2}$ multiples of $n^{2}$.
|
Answer: 20800
|
20800
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Suppose $m$ and $n$ are positive integers for which
- the sum of the first $m$ multiples of $n$ is 120 , and
- the sum of the first $m^{3}$ multiples of $n^{3}$ is 4032000 .
Determine the sum of the first $m^{2}$ multiples of $n^{2}$.
|
Answer: 20800
|
{
"resource_path": "HarvardMIT/segmented/en-251-2021-nov-team-solutions.jsonl",
"problem_match": "\n3. [30]",
"solution_match": "\nProposed by: Sean Li\n"
}
|
383b8b74-512f-546b-85ce-b0362acf1927
| 610,384
|
Find the number of 10-digit numbers $\overline{a_{1} a_{2} \cdots a_{10}}$ which are multiples of 11 such that the digits are non-increasing from left to right, i.e. $a_{i} \geq a_{i+1}$ for each $1 \leq i \leq 9$.
|
It is well known that $\overline{a_{1} a_{2} \cdots a_{10}}$ is divisible by 11 if and only if $S=a_{1}-a_{2}+a_{3}-\cdots-a_{10}$ is. By the non-increasing condition, we deduce that
$$
S=\left(a_{1}-a_{2}\right)+\left(a_{3}-a_{4}\right)+\cdots+\left(a_{9}-a_{10}\right) \geq 0
$$
Also,
$$
S=a_{1}-\left(a_{2}-a_{3}\right)-\cdots-\left(a_{8}-a_{9}\right)-a_{10} \leq a_{1} \leq 9
$$
Therefore, $S=0$, our number must be of the form $\overline{a a b b c c d d e e}$. Since all numbers of this form work $(\overline{a a b b c c d d e e}=11 \cdot \overline{a 0 b 0 c 0 d 0 e})$, it suffices to find the number of tuples ( $a, b, c, d, e$ ) so that $9 \geq a \geq b \geq c \geq d \geq e \geq 0$ and $a>0$. The number of tuples satisfying the first condition is $\binom{14}{5}=14 \cdot 13 \cdot 11=2002$. To account for the second condition, we subtract one tuple (all zeroes), yielding a final answer of 2001.
|
2001
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Find the number of 10-digit numbers $\overline{a_{1} a_{2} \cdots a_{10}}$ which are multiples of 11 such that the digits are non-increasing from left to right, i.e. $a_{i} \geq a_{i+1}$ for each $1 \leq i \leq 9$.
|
It is well known that $\overline{a_{1} a_{2} \cdots a_{10}}$ is divisible by 11 if and only if $S=a_{1}-a_{2}+a_{3}-\cdots-a_{10}$ is. By the non-increasing condition, we deduce that
$$
S=\left(a_{1}-a_{2}\right)+\left(a_{3}-a_{4}\right)+\cdots+\left(a_{9}-a_{10}\right) \geq 0
$$
Also,
$$
S=a_{1}-\left(a_{2}-a_{3}\right)-\cdots-\left(a_{8}-a_{9}\right)-a_{10} \leq a_{1} \leq 9
$$
Therefore, $S=0$, our number must be of the form $\overline{a a b b c c d d e e}$. Since all numbers of this form work $(\overline{a a b b c c d d e e}=11 \cdot \overline{a 0 b 0 c 0 d 0 e})$, it suffices to find the number of tuples ( $a, b, c, d, e$ ) so that $9 \geq a \geq b \geq c \geq d \geq e \geq 0$ and $a>0$. The number of tuples satisfying the first condition is $\binom{14}{5}=14 \cdot 13 \cdot 11=2002$. To account for the second condition, we subtract one tuple (all zeroes), yielding a final answer of 2001.
|
{
"resource_path": "HarvardMIT/segmented/en-251-2021-nov-team-solutions.jsonl",
"problem_match": "\n4. [35]",
"solution_match": "\nSolution: "
}
|
3da47a32-636f-50b2-a558-5c54cbfef4f3
| 610,385
|
How many ways are there to place 31 knights in the cells of an $8 \times 8$ unit grid so that no two attack one another?
(A knight attacks another knight if the distance between the centers of their cells is exactly $\sqrt{5}$.)
|
Consider coloring the squares of the chessboard so that 32 are black and 32 are white, and no two squares of the same color share a side. Then a knight in a square of one color only attacks squares of the opposite color. Any arrangement of knights in which all 31 are placed on the same color therefore works: there are 64 such arrangements (one for each square, in which that square is empty and the others of the same color are occupied). Also, if a knight is placed in a corner, it only attacks two squares. Therefore, for each corner, it is possible to place a knight in one corner and in all squares of theopposite color except the two attacked by the corner night. This gives 68 total arrangements. one can prove that no others are possible.
|
68
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
How many ways are there to place 31 knights in the cells of an $8 \times 8$ unit grid so that no two attack one another?
(A knight attacks another knight if the distance between the centers of their cells is exactly $\sqrt{5}$.)
|
Consider coloring the squares of the chessboard so that 32 are black and 32 are white, and no two squares of the same color share a side. Then a knight in a square of one color only attacks squares of the opposite color. Any arrangement of knights in which all 31 are placed on the same color therefore works: there are 64 such arrangements (one for each square, in which that square is empty and the others of the same color are occupied). Also, if a knight is placed in a corner, it only attacks two squares. Therefore, for each corner, it is possible to place a knight in one corner and in all squares of theopposite color except the two attacked by the corner night. This gives 68 total arrangements. one can prove that no others are possible.
|
{
"resource_path": "HarvardMIT/segmented/en-251-2021-nov-team-solutions.jsonl",
"problem_match": "\n5. [40]",
"solution_match": "\nSolution: "
}
|
2d028ddb-2053-5d37-9f4e-bbb5a4bb8982
| 610,386
|
The taxicab distance between points $\left(x_{1}, y_{1}\right)$ and $\left(x_{2}, y_{2}\right)$ is $\left|x_{2}-x_{1}\right|+\left|y_{2}-y_{1}\right|$. A regular octagon is positioned in the $x y$ plane so that one of its sides has endpoints $(0,0)$ and $(1,0)$. Let $S$ be the set of all points inside the octagon whose taxicab distance from some octagon vertex is at most $\frac{2}{3}$. The area of $S$ can be written as $\frac{m}{n}$, where $m, n$ are positive integers and $\operatorname{gcd}(m, n)=1$. Find $100 m+n$.
|
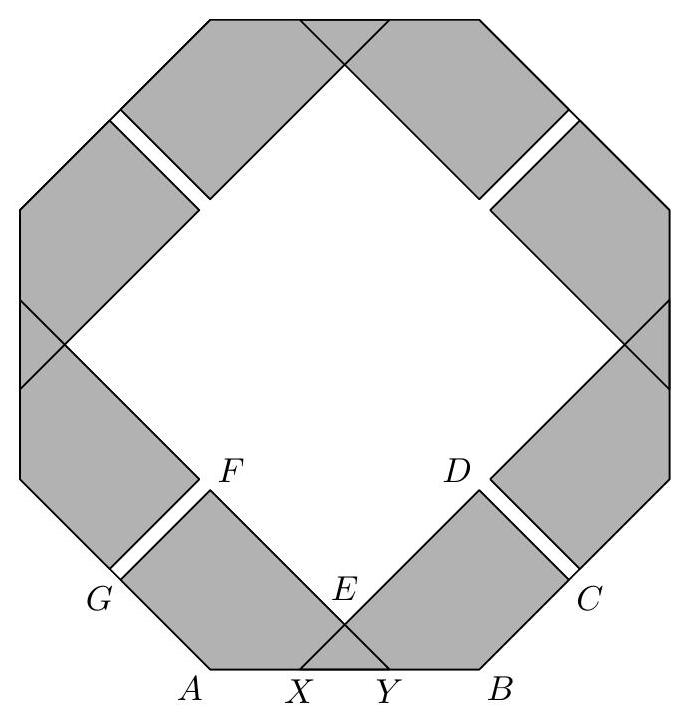
In the taxicab metric, the set of points that lie at most $d$ units away from some fixed point $P$ form a square centered at $P$ with vertices at a distance of $d$ from $P$ in directions parallel to the axes. The diagram above depicts the intersection of an octagon with eight such squares for $d=\frac{2}{3}$ centered at its vertices. (Note that since $\sqrt{2}>\frac{2}{3} \cdot 2$, the squares centered at adjacent vertices that are diagonal from each other do not intersect.) The area of the entire shaded region is $4[A B C D E F G]=4(2([A F G]+$ $[A Y F])-[E X Y])$, which is easy to evaluate since $A F G, A Y F$, and $E X Y$ are all 45-45-90-degree triangles. Since $A F=\frac{2}{3}, G F=\frac{\sqrt{2}}{3}$, and $E X=\frac{1}{3 \sqrt{2}}$, the desired area is $4\left(\frac{2}{9}+\frac{4}{9}-\frac{1}{36}\right)=\frac{23}{9}$.
|
\frac{23}{9}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
The taxicab distance between points $\left(x_{1}, y_{1}\right)$ and $\left(x_{2}, y_{2}\right)$ is $\left|x_{2}-x_{1}\right|+\left|y_{2}-y_{1}\right|$. A regular octagon is positioned in the $x y$ plane so that one of its sides has endpoints $(0,0)$ and $(1,0)$. Let $S$ be the set of all points inside the octagon whose taxicab distance from some octagon vertex is at most $\frac{2}{3}$. The area of $S$ can be written as $\frac{m}{n}$, where $m, n$ are positive integers and $\operatorname{gcd}(m, n)=1$. Find $100 m+n$.
|

In the taxicab metric, the set of points that lie at most $d$ units away from some fixed point $P$ form a square centered at $P$ with vertices at a distance of $d$ from $P$ in directions parallel to the axes. The diagram above depicts the intersection of an octagon with eight such squares for $d=\frac{2}{3}$ centered at its vertices. (Note that since $\sqrt{2}>\frac{2}{3} \cdot 2$, the squares centered at adjacent vertices that are diagonal from each other do not intersect.) The area of the entire shaded region is $4[A B C D E F G]=4(2([A F G]+$ $[A Y F])-[E X Y])$, which is easy to evaluate since $A F G, A Y F$, and $E X Y$ are all 45-45-90-degree triangles. Since $A F=\frac{2}{3}, G F=\frac{\sqrt{2}}{3}$, and $E X=\frac{1}{3 \sqrt{2}}$, the desired area is $4\left(\frac{2}{9}+\frac{4}{9}-\frac{1}{36}\right)=\frac{23}{9}$.
|
{
"resource_path": "HarvardMIT/segmented/en-251-2021-nov-team-solutions.jsonl",
"problem_match": "\n6. [40]",
"solution_match": "\nSolution:\n"
}
|
0d0eb121-5c1d-5752-8948-19783f217454
| 610,387
|
Let $f(x)=x^{3}+3 x-1$ have roots $a, b, c$. Given that
$$
\frac{1}{a^{3}+b^{3}}+\frac{1}{b^{3}+c^{3}}+\frac{1}{c^{3}+a^{3}}
$$
can be written as $\frac{m}{n}$, where $m, n$ are positive integers and $\operatorname{gcd}(m, n)=1$, find $100 m+n$.
|
We know that $a^{3}=-3 a+1$ and similarly for $b, c$, so
$$
\frac{1}{a^{3}+b^{3}}=\frac{1}{2-3 a-3 b}=\frac{1}{2+3 c}=\frac{1}{3(2 / 3+c)} .
$$
Now,
$$
f(x-2 / 3)=x^{3}-2 x^{2}+\frac{13}{3} x-\frac{89}{27}
$$
has roots $a+2 / 3, b+2 / 3$, and $c+2 / 3$. Thus the answer is, by Vieta's formulas,
$$
\frac{1}{3} \frac{(a+2 / 3)(b+2 / 3)+(a+2 / 3)(c+2 / 3)+(b+2 / 3)(c+2 / 3)}{(a+2 / 3)(b+2 / 3)(c+2 / 3)}=\frac{13 / 3}{3 \cdot 89 / 27}=\frac{39}{89}
$$
|
39/89
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Let $f(x)=x^{3}+3 x-1$ have roots $a, b, c$. Given that
$$
\frac{1}{a^{3}+b^{3}}+\frac{1}{b^{3}+c^{3}}+\frac{1}{c^{3}+a^{3}}
$$
can be written as $\frac{m}{n}$, where $m, n$ are positive integers and $\operatorname{gcd}(m, n)=1$, find $100 m+n$.
|
We know that $a^{3}=-3 a+1$ and similarly for $b, c$, so
$$
\frac{1}{a^{3}+b^{3}}=\frac{1}{2-3 a-3 b}=\frac{1}{2+3 c}=\frac{1}{3(2 / 3+c)} .
$$
Now,
$$
f(x-2 / 3)=x^{3}-2 x^{2}+\frac{13}{3} x-\frac{89}{27}
$$
has roots $a+2 / 3, b+2 / 3$, and $c+2 / 3$. Thus the answer is, by Vieta's formulas,
$$
\frac{1}{3} \frac{(a+2 / 3)(b+2 / 3)+(a+2 / 3)(c+2 / 3)+(b+2 / 3)(c+2 / 3)}{(a+2 / 3)(b+2 / 3)(c+2 / 3)}=\frac{13 / 3}{3 \cdot 89 / 27}=\frac{39}{89}
$$
|
{
"resource_path": "HarvardMIT/segmented/en-251-2021-nov-team-solutions.jsonl",
"problem_match": "\n7. [45]",
"solution_match": "\nSolution: "
}
|
b8fe8bfe-4f88-5486-8007-2bd1ad6f650f
| 610,388
|
Paul and Sara are playing a game with integers on a whiteboard, with Paul going first. When it is Paul's turn, he can pick any two integers on the board and replace them with their product; when
it is Sara's turn, she can pick any two integers on the board and replace them with their sum. Play continues until exactly one integer remains on the board. Paul wins if that integer is odd, and Sara wins if it is even.
Initially, there are 2021 integers on the board, each one sampled uniformly at random from the set $\{0,1,2,3, \ldots, 2021\}$. Assuming both players play optimally, the probability that Paul wins is $\frac{m}{n}$, where $m, n$ are positive integers and $\operatorname{gcd}(m, n)=1$. Find the remainder when $m+n$ is divided by 1000 .
|
Answer: 383
|
383
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Paul and Sara are playing a game with integers on a whiteboard, with Paul going first. When it is Paul's turn, he can pick any two integers on the board and replace them with their product; when
it is Sara's turn, she can pick any two integers on the board and replace them with their sum. Play continues until exactly one integer remains on the board. Paul wins if that integer is odd, and Sara wins if it is even.
Initially, there are 2021 integers on the board, each one sampled uniformly at random from the set $\{0,1,2,3, \ldots, 2021\}$. Assuming both players play optimally, the probability that Paul wins is $\frac{m}{n}$, where $m, n$ are positive integers and $\operatorname{gcd}(m, n)=1$. Find the remainder when $m+n$ is divided by 1000 .
|
Answer: 383
|
{
"resource_path": "HarvardMIT/segmented/en-251-2021-nov-team-solutions.jsonl",
"problem_match": "\n8. [50]",
"solution_match": "\n## Proposed by: David Vulakh\n\n"
}
|
b8a5b8bd-9209-51cc-baf8-d7aa462a6b2e
| 610,389
|
Let $N$ be the smallest positive integer for which
$$
x^{2}+x+1 \quad \text { divides } \quad 166-\sum_{d \mid N, d>0} x^{d}
$$
Find the remainder when $N$ is divided by 1000.
|
Answer: 672
|
672
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Let $N$ be the smallest positive integer for which
$$
x^{2}+x+1 \quad \text { divides } \quad 166-\sum_{d \mid N, d>0} x^{d}
$$
Find the remainder when $N$ is divided by 1000.
|
Answer: 672
|
{
"resource_path": "HarvardMIT/segmented/en-251-2021-nov-team-solutions.jsonl",
"problem_match": "\n9. [55]",
"solution_match": "\nProposed by: Joseph Heerens\n"
}
|
a1a4117e-1e64-5d01-a0fb-bb3c78b9fede
| 610,390
|
Three faces $\mathcal{X}, \mathcal{Y}, \mathcal{Z}$ of a unit cube share a common vertex. Suppose the projections of $\mathcal{X}, \mathcal{Y}, \mathcal{Z}$ onto a fixed plane $\mathcal{P}$ have areas $x, y, z$, respectively. If $x: y: z=6: 10: 15$, then $x+y+z$ can be written as $\frac{m}{n}$, where $m, n$ are positive integers and $\operatorname{gcd}(m, n)=1$. Find $100 m+n$.
|
Answer: 3119
|
3119
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Three faces $\mathcal{X}, \mathcal{Y}, \mathcal{Z}$ of a unit cube share a common vertex. Suppose the projections of $\mathcal{X}, \mathcal{Y}, \mathcal{Z}$ onto a fixed plane $\mathcal{P}$ have areas $x, y, z$, respectively. If $x: y: z=6: 10: 15$, then $x+y+z$ can be written as $\frac{m}{n}$, where $m, n$ are positive integers and $\operatorname{gcd}(m, n)=1$. Find $100 m+n$.
|
Answer: 3119
|
{
"resource_path": "HarvardMIT/segmented/en-251-2021-nov-team-solutions.jsonl",
"problem_match": "\n10. [60]",
"solution_match": "\nProposed by: Sean Li\n"
}
|
3b6f2663-0016-565d-82d2-f696e1c6e2c4
| 610,391
|
Let $n$ be the answer to this problem. In acute triangle $A B C$, point $D$ is located on side $B C$ so that $\angle B A D=\angle D A C$ and point $E$ is located on $A C$ so that $B E \perp A C$. Segments $B E$ and $A D$ intersect at $X$ such that $\angle B X D=n^{\circ}$. Given that $\angle X B A=16^{\circ}$, find the measure of $\angle B C A$.
|
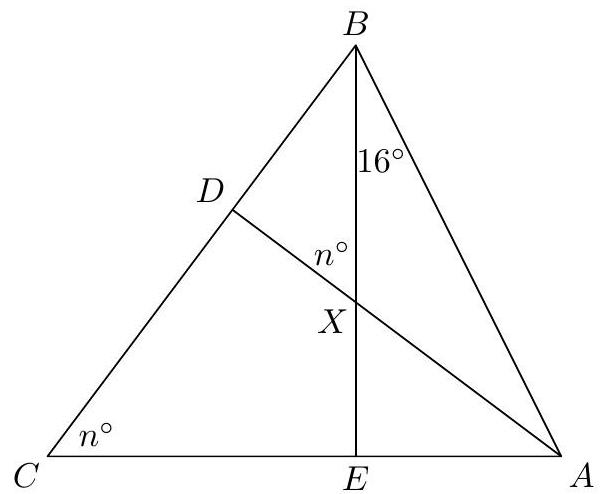
Since $B E \perp A C, \angle B A E=90^{\circ}-\angle A B E=74^{\circ}$. Now, $n^{\circ}=180-\angle B X A=\angle E B A+\angle B A D=$ $16^{\circ}+\frac{74^{\circ}}{2}=53^{\circ}$.
|
53
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $n$ be the answer to this problem. In acute triangle $A B C$, point $D$ is located on side $B C$ so that $\angle B A D=\angle D A C$ and point $E$ is located on $A C$ so that $B E \perp A C$. Segments $B E$ and $A D$ intersect at $X$ such that $\angle B X D=n^{\circ}$. Given that $\angle X B A=16^{\circ}$, find the measure of $\angle B C A$.
|

Since $B E \perp A C, \angle B A E=90^{\circ}-\angle A B E=74^{\circ}$. Now, $n^{\circ}=180-\angle B X A=\angle E B A+\angle B A D=$ $16^{\circ}+\frac{74^{\circ}}{2}=53^{\circ}$.
|
{
"resource_path": "HarvardMIT/segmented/en-251-2021-nov-thm-solutions.jsonl",
"problem_match": "\n1. ",
"solution_match": "\n## Solution:\n\n"
}
|
5a3e4036-c8ec-5054-9c21-0857928013ff
| 610,392
|
Let $n$ be the answer to this problem. An urn contains white and black balls. There are $n$ white balls and at least two balls of each color in the urn. Two balls are randomly drawn from the urn without replacement. Find the probability, in percent, that the first ball drawn is white and the second is black.
|
Let the number of black balls in the urn be $k \geq 2$. Then the probability of drawing a white ball first is $\frac{n}{n+k}$, and the probability of drawing a black ball second is $\frac{k}{n+k-1}$. This gives us the equation
$$
\frac{n k}{(n+k)(n+k-1)}=\frac{n}{100}
$$
from which we get
$$
(n+k)(n+k-1)=100 k
$$
Let $m=n+k$. Since $100 \mid m(m-1)$, we must have that either 100 divides one of $m, m-1$ or 25 divides one of $m, m-1$ and 4 divides the other. Since $m, m-1>k$, if either of $m$ or $m-1$ is greater than or equal to 100 , the product $m(m-1)>100 k$. Therefore, the only possible values for $m$ are 25 and 76 .
If $m=25$, we have
$$
m(m-1)=600 \Longrightarrow k=6 \Longrightarrow n=19
$$
If $m=76$, we have
$$
m(m-1)=5700 \Longrightarrow k=57 \Longrightarrow n=19
$$
So $n=19$ is the unique solution.
|
19
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Let $n$ be the answer to this problem. An urn contains white and black balls. There are $n$ white balls and at least two balls of each color in the urn. Two balls are randomly drawn from the urn without replacement. Find the probability, in percent, that the first ball drawn is white and the second is black.
|
Let the number of black balls in the urn be $k \geq 2$. Then the probability of drawing a white ball first is $\frac{n}{n+k}$, and the probability of drawing a black ball second is $\frac{k}{n+k-1}$. This gives us the equation
$$
\frac{n k}{(n+k)(n+k-1)}=\frac{n}{100}
$$
from which we get
$$
(n+k)(n+k-1)=100 k
$$
Let $m=n+k$. Since $100 \mid m(m-1)$, we must have that either 100 divides one of $m, m-1$ or 25 divides one of $m, m-1$ and 4 divides the other. Since $m, m-1>k$, if either of $m$ or $m-1$ is greater than or equal to 100 , the product $m(m-1)>100 k$. Therefore, the only possible values for $m$ are 25 and 76 .
If $m=25$, we have
$$
m(m-1)=600 \Longrightarrow k=6 \Longrightarrow n=19
$$
If $m=76$, we have
$$
m(m-1)=5700 \Longrightarrow k=57 \Longrightarrow n=19
$$
So $n=19$ is the unique solution.
|
{
"resource_path": "HarvardMIT/segmented/en-251-2021-nov-thm-solutions.jsonl",
"problem_match": "\n2. ",
"solution_match": "\nSolution: "
}
|
befa8d12-0869-5b60-905f-a3562174a913
| 610,393
|
Let $n$ be the answer to this problem. Hexagon $A B C D E F$ is inscribed in a circle of radius 90 . The area of $A B C D E F$ is $8 n, A B=B C=D E=E F$, and $C D=F A$. Find the area of triangle $A B C$.
|
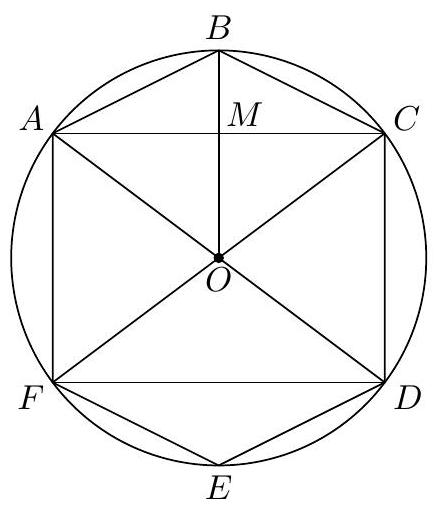
Let $O$ be the center of the circle, and let $O B$ intersect $A C$ at point $M$; note $O B$ is the perpendicular bisector of $A C$. Since triangles $A B C$ and $D E F$ are congruent, $A C D F$ has area $6 n$, meaning that $A O C$ has area $3 n / 2$. It follows that $\frac{B M}{O M}=\frac{2}{3}$. Therefore $O M=54$ and $M B=36$, so by the Pythagorean theorem, $M A=\sqrt{90^{2}-54^{2}}=72$. Thus, $A B C$ has area $72 \cdot 36=2592$.
|
2592
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $n$ be the answer to this problem. Hexagon $A B C D E F$ is inscribed in a circle of radius 90 . The area of $A B C D E F$ is $8 n, A B=B C=D E=E F$, and $C D=F A$. Find the area of triangle $A B C$.
|

Let $O$ be the center of the circle, and let $O B$ intersect $A C$ at point $M$; note $O B$ is the perpendicular bisector of $A C$. Since triangles $A B C$ and $D E F$ are congruent, $A C D F$ has area $6 n$, meaning that $A O C$ has area $3 n / 2$. It follows that $\frac{B M}{O M}=\frac{2}{3}$. Therefore $O M=54$ and $M B=36$, so by the Pythagorean theorem, $M A=\sqrt{90^{2}-54^{2}}=72$. Thus, $A B C$ has area $72 \cdot 36=2592$.
|
{
"resource_path": "HarvardMIT/segmented/en-251-2021-nov-thm-solutions.jsonl",
"problem_match": "\n3. ",
"solution_match": "\n## Solution:\n\n"
}
|
0ea5ac23-fcd8-5a12-bf89-c980351fa620
| 610,394
|
Let $n$ be the answer to this problem. We define the digit sum of a date as the sum of its 4 digits when expressed in mmdd format (e.g. the digit sum of 13 May is $0+5+1+3=9$ ). Find the number of dates in the year 2021 with digit sum equal to the positive integer $n$.
|
This problem is an exercise in how to do ugly computations efficiently.
Let $f(n)$ be the number of days with digit sum $n$. Also, let $g(n)$ be the number of days with digit sum $n$, under the assumption that every month has 30 days. Let $h(n)$ be the number of positive integers from 1 to 30 with integer sum $n$. We now do computation:
$$
\begin{array}{c|ccccccccccc}
n & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 \\
\hline h(n) & 2 & 3 & 4 & 3 & 3 & 3 & 3 & 3 & 3 & 2 & 1
\end{array}
$$
Observe that $g(n)=\sum_{k=1}^{3} 2 h(n-k)+\sum_{k=4}^{9} h(n-k)$. Also, to move from $g(n)$ to $f(n)$ we need to add in "01-31", "03-31", "05-31", "07-31", "08-31", "10-31", "12-31" and subtract "02-29", "02-30". Therefore we find
| $n$ | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| $\sum_{k=1}^{3} h(n-k)$ | 2 | 5 | 9 | 10 | 10 | 9 | 9 | 9 | 9 | 8 | 6 | 3 | 1 | | | | | | |
| $\sum_{k=4}^{9} h(n-k)$ | | | 2 | 5 | 9 | 12 | 15 | 18 | 19 | 19 | 18 | 17 | 15 | 12 | 9 | 6 | 3 | 1 | |
| $g(n)$ | 4 | 10 | 18 | 22 | 25 | 27 | 30 | 33 | 36 | 35 | 31 | 24 | 19 | 15 | 12 | 9 | 6 | 3 | 1 |
| $f(n)$ | 4 | 10 | 18 | 23 | 25 | 29 | 30 | 34 | 36 | 36 | 32 | 23 | 19 | 15 | 12 | 9 | 6 | 3 | 1 |
Evidently the answer is 15 .
While the above computation is a bit tedious in practice, the work one has to do can be dramatically cut down if one notices that if $n \leq 10$ or so, $f(n)$ is significantly larger than $n$. Thus one only really
needs to compute the latter half of the table.
|
15
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Let $n$ be the answer to this problem. We define the digit sum of a date as the sum of its 4 digits when expressed in mmdd format (e.g. the digit sum of 13 May is $0+5+1+3=9$ ). Find the number of dates in the year 2021 with digit sum equal to the positive integer $n$.
|
This problem is an exercise in how to do ugly computations efficiently.
Let $f(n)$ be the number of days with digit sum $n$. Also, let $g(n)$ be the number of days with digit sum $n$, under the assumption that every month has 30 days. Let $h(n)$ be the number of positive integers from 1 to 30 with integer sum $n$. We now do computation:
$$
\begin{array}{c|ccccccccccc}
n & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 \\
\hline h(n) & 2 & 3 & 4 & 3 & 3 & 3 & 3 & 3 & 3 & 2 & 1
\end{array}
$$
Observe that $g(n)=\sum_{k=1}^{3} 2 h(n-k)+\sum_{k=4}^{9} h(n-k)$. Also, to move from $g(n)$ to $f(n)$ we need to add in "01-31", "03-31", "05-31", "07-31", "08-31", "10-31", "12-31" and subtract "02-29", "02-30". Therefore we find
| $n$ | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| $\sum_{k=1}^{3} h(n-k)$ | 2 | 5 | 9 | 10 | 10 | 9 | 9 | 9 | 9 | 8 | 6 | 3 | 1 | | | | | | |
| $\sum_{k=4}^{9} h(n-k)$ | | | 2 | 5 | 9 | 12 | 15 | 18 | 19 | 19 | 18 | 17 | 15 | 12 | 9 | 6 | 3 | 1 | |
| $g(n)$ | 4 | 10 | 18 | 22 | 25 | 27 | 30 | 33 | 36 | 35 | 31 | 24 | 19 | 15 | 12 | 9 | 6 | 3 | 1 |
| $f(n)$ | 4 | 10 | 18 | 23 | 25 | 29 | 30 | 34 | 36 | 36 | 32 | 23 | 19 | 15 | 12 | 9 | 6 | 3 | 1 |
Evidently the answer is 15 .
While the above computation is a bit tedious in practice, the work one has to do can be dramatically cut down if one notices that if $n \leq 10$ or so, $f(n)$ is significantly larger than $n$. Thus one only really
needs to compute the latter half of the table.
|
{
"resource_path": "HarvardMIT/segmented/en-251-2021-nov-thm-solutions.jsonl",
"problem_match": "\n4. ",
"solution_match": "\nSolution: "
}
|
4bac941d-6f5d-514d-aed7-1a46594809a3
| 610,395
|
Let $n$ be the answer to this problem. The polynomial $x^{n}+a x^{2}+b x+c$ has real coefficients and exactly $k$ real roots. Find the sum of the possible values of $k$.
|
Note that the roots to the above polynomial must satisfy $x^{n}=-a x^{2}-b x-c$. Therefore, it suffices to consider how many times a parabola can intersect the graph $x^{n}$. For $n \leq 2$, a parabola can intersect $x^{n} 0,1$, or 2 times, so the sum of the possible values of $k$ is 3 . Therefore, we know we must have $n>2$. If $n$ is odd, then a parabola can intersect $x^{n} 0,1,2$, or 3 times, so the sum of the possible values of $k$ is 6 , which isn't odd. Thus, we must have $n$ is even and $n>2$. In this case a parabola can intersect $x^{n} 0,1,2,3$, or 4 times, so the sum of the possible values of $k$ in this case is 10 . Thus, we must have $n=10$.
Here is a more rigorous justification of the above reasoning for $n>2$ : consider $f(x)=x^{n}+a x^{2}+b x+c$. Note that $f^{\prime \prime \prime}(x)=n(n-1)(n-2) x^{n-3}$, which has at most one real root. However, it is known that if a differentiable function $f(x)$ has $k$ real roots, $f^{\prime}(x)$ must have at least $k-1$ real roots, with at least one in between any pair of real roots of $f(x)$ (Proof sketch: apply Rolle's theorem many times.). Therefore, if $f(x)$ has at least five real roots, applying the above result three times yields that $f^{\prime \prime \prime}(x)$ has at least two real roots, a contradiction. Moreover, if $f(x)$ has four real roots and $n$ is odd, then since nonreal roots come in pairs we know that at least one of these real roots $c$ has multiplicity at least 2. Therefore, $f^{\prime}(x)$ has three real roots in between the roots of $f(x)$, plus one real root at $c$. Thus $f^{\prime}(x)$ has at least four real roots, implying that $f^{\prime \prime \prime}(x)$ has at least two real roots, again a contradiction.
|
10
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Let $n$ be the answer to this problem. The polynomial $x^{n}+a x^{2}+b x+c$ has real coefficients and exactly $k$ real roots. Find the sum of the possible values of $k$.
|
Note that the roots to the above polynomial must satisfy $x^{n}=-a x^{2}-b x-c$. Therefore, it suffices to consider how many times a parabola can intersect the graph $x^{n}$. For $n \leq 2$, a parabola can intersect $x^{n} 0,1$, or 2 times, so the sum of the possible values of $k$ is 3 . Therefore, we know we must have $n>2$. If $n$ is odd, then a parabola can intersect $x^{n} 0,1,2$, or 3 times, so the sum of the possible values of $k$ is 6 , which isn't odd. Thus, we must have $n$ is even and $n>2$. In this case a parabola can intersect $x^{n} 0,1,2,3$, or 4 times, so the sum of the possible values of $k$ in this case is 10 . Thus, we must have $n=10$.
Here is a more rigorous justification of the above reasoning for $n>2$ : consider $f(x)=x^{n}+a x^{2}+b x+c$. Note that $f^{\prime \prime \prime}(x)=n(n-1)(n-2) x^{n-3}$, which has at most one real root. However, it is known that if a differentiable function $f(x)$ has $k$ real roots, $f^{\prime}(x)$ must have at least $k-1$ real roots, with at least one in between any pair of real roots of $f(x)$ (Proof sketch: apply Rolle's theorem many times.). Therefore, if $f(x)$ has at least five real roots, applying the above result three times yields that $f^{\prime \prime \prime}(x)$ has at least two real roots, a contradiction. Moreover, if $f(x)$ has four real roots and $n$ is odd, then since nonreal roots come in pairs we know that at least one of these real roots $c$ has multiplicity at least 2. Therefore, $f^{\prime}(x)$ has three real roots in between the roots of $f(x)$, plus one real root at $c$. Thus $f^{\prime}(x)$ has at least four real roots, implying that $f^{\prime \prime \prime}(x)$ has at least two real roots, again a contradiction.
|
{
"resource_path": "HarvardMIT/segmented/en-251-2021-nov-thm-solutions.jsonl",
"problem_match": "\n5. ",
"solution_match": "\nSolution: "
}
|
a08dba44-465b-591f-b79e-58546eb8ba8e
| 610,396
|
Let $n$ be the answer to this problem. $a$ and $b$ are positive integers satisfying
$$
\begin{aligned}
& 3 a+5 b \equiv 19 \quad(\bmod n+1) \\
& 4 a+2 b \equiv 25 \quad(\bmod n+1)
\end{aligned}
$$
Find $2 a+6 b$.
|
Answer: 96
|
96
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Let $n$ be the answer to this problem. $a$ and $b$ are positive integers satisfying
$$
\begin{aligned}
& 3 a+5 b \equiv 19 \quad(\bmod n+1) \\
& 4 a+2 b \equiv 25 \quad(\bmod n+1)
\end{aligned}
$$
Find $2 a+6 b$.
|
Answer: 96
|
{
"resource_path": "HarvardMIT/segmented/en-251-2021-nov-thm-solutions.jsonl",
"problem_match": "\n6. ",
"solution_match": "\nProposed by: David Vulakh\n"
}
|
fefcd9ad-acac-5270-b08e-63155686bede
| 610,397
|
Let $n$ be the answer to this problem. Box $B$ initially contains $n$ balls, and Box $A$ contains half as many balls as Box $B$. After 80 balls are moved from Box $A$ to Box $B$, the ratio of balls in Box $A$ to Box $B$ is now $\frac{p}{q}$, where $p, q$ are positive integers with $\operatorname{gcd}(p, q)=1$. Find $100 p+q$.
|
Originally, box $A$ has $n / 2$ balls and $B$ has $n$ balls. After moving, box $A$ has $n / 2-80$ balls and $B$ has $n+80$ balls. The answer to the problem is thus
$$
\frac{100(n / 2-80)+(n+80)}{\operatorname{gcd}(n / 2-80, n+80)}=\frac{51 n-80 \cdot 99}{\operatorname{gcd}(n / 2-80, n+80)} \stackrel{?}{=} n
$$
Write $d=\operatorname{gcd}(n / 2-80, n+80)=\operatorname{gcd}(n / 2-80,240)$. Then the problem is equivalent $n d=51 n-80 \cdot 99$ or $(51-d) n=80 \cdot 99$, with $d \mid 240$.
Let's try to solve this. Either $51-d$ or $n$ must be divisible by 5 . In the latter case, where $n$ is divisible by 5 , we see that $d$ must be as well. Therefore $d$ is either 0 or $1 \bmod 5$.
If $n$ is divisible by 4 , then we know that $d$ is even and thus $51-d$ is odd. Therefore, since $16 \mid 80 \cdot 99$, $n$ must be divisible by 16 , meaning that $d$ is divisible by 8 . Alternatively, if $n$ is not divisible by 4 , then since $16 \mid 80 \cdot 99,51-d$ must be divisible by 8 , meaning that $d$ is $3 \bmod 8$. Therefore $d$ is either 0 or $3 \bmod 8$.
Putting these results together, we find that $d$ must either be $0,11,16$, or $35 \bmod 40$. Since $d$ is a divisor of 240 and less than 51 , we conclude that $d$ is either 16 or 40 . If $d=16$, then $51-d=35$, which does not divide $80 \cdot 99$. If $d=40$, then we get $n=720$, which ends up working.
|
720
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Let $n$ be the answer to this problem. Box $B$ initially contains $n$ balls, and Box $A$ contains half as many balls as Box $B$. After 80 balls are moved from Box $A$ to Box $B$, the ratio of balls in Box $A$ to Box $B$ is now $\frac{p}{q}$, where $p, q$ are positive integers with $\operatorname{gcd}(p, q)=1$. Find $100 p+q$.
|
Originally, box $A$ has $n / 2$ balls and $B$ has $n$ balls. After moving, box $A$ has $n / 2-80$ balls and $B$ has $n+80$ balls. The answer to the problem is thus
$$
\frac{100(n / 2-80)+(n+80)}{\operatorname{gcd}(n / 2-80, n+80)}=\frac{51 n-80 \cdot 99}{\operatorname{gcd}(n / 2-80, n+80)} \stackrel{?}{=} n
$$
Write $d=\operatorname{gcd}(n / 2-80, n+80)=\operatorname{gcd}(n / 2-80,240)$. Then the problem is equivalent $n d=51 n-80 \cdot 99$ or $(51-d) n=80 \cdot 99$, with $d \mid 240$.
Let's try to solve this. Either $51-d$ or $n$ must be divisible by 5 . In the latter case, where $n$ is divisible by 5 , we see that $d$ must be as well. Therefore $d$ is either 0 or $1 \bmod 5$.
If $n$ is divisible by 4 , then we know that $d$ is even and thus $51-d$ is odd. Therefore, since $16 \mid 80 \cdot 99$, $n$ must be divisible by 16 , meaning that $d$ is divisible by 8 . Alternatively, if $n$ is not divisible by 4 , then since $16 \mid 80 \cdot 99,51-d$ must be divisible by 8 , meaning that $d$ is $3 \bmod 8$. Therefore $d$ is either 0 or $3 \bmod 8$.
Putting these results together, we find that $d$ must either be $0,11,16$, or $35 \bmod 40$. Since $d$ is a divisor of 240 and less than 51 , we conclude that $d$ is either 16 or 40 . If $d=16$, then $51-d=35$, which does not divide $80 \cdot 99$. If $d=40$, then we get $n=720$, which ends up working.
|
{
"resource_path": "HarvardMIT/segmented/en-251-2021-nov-thm-solutions.jsonl",
"problem_match": "\n7. ",
"solution_match": "\nSolution: "
}
|
5a9bd61d-dd70-5d6e-ba18-b9bfbdeffad2
| 610,398
|
Let $n$ be the answer to this problem. Given $n>0$, find the number of distinct (i.e. non-congruent), non-degenerate triangles with integer side lengths and perimeter $n$.
|
We explicitly compute the number of triangles satisfying the problem conditions for any $n$. There are three kinds of triangles: isosceles and scalene. (Equilateral triangles are isosceles.)
- Case 1: Isosceles. A triangle with side lengths $a, a, b$ must satisfy $2 a>b$ and $2 a+b=n$. So $2 a$ can be any even integer in the interval $(n / 2, n)$. There are thus $\lfloor(n-1) / 2\rfloor-\lfloor n / 4\rfloor$ triangles here.
- Case 2: Scalene. A triangle with side lengths $a, b, c$ must satisfy $a, b, c<n / 2$ and $a+b+c=n$. There are $\binom{n-1}{2}$ triples satisfying the second condition, $3\binom{\lfloor n / 2\rfloor}{ 2}$ of which violate condition 1 (since at most one side is at least $n / 2$, we can do casework on which side). We then remove the isosceles triangles and divide by 6 to account for ordering the sides. If there are no equilateral triangles (i.e. if $3 \nmid n$ ), our answer here is
$$
\frac{1}{6}\left(\binom{n-1}{2}-3\binom{\lfloor n / 2\rfloor}{ 2}-3(\lfloor(n-1) / 2\rfloor-\lfloor n / 4\rfloor)\right) .
$$
Otherwise, the answer is
$$
\frac{1}{6}\left(\binom{n-1}{2}-3\binom{\lfloor n / 2\rfloor}{ 2}-3(\lfloor(n-1) / 2\rfloor-\lfloor n / 4\rfloor-1)-1\right)
$$
The key observation is that almost all triangles are scalene, and there are are roughly $\frac{1}{6}\left(n^{2} / 2-3 n^{2} / 8\right)=$ $n^{2} / 48$ scalene triangles. Hence, $n \approx 48$. Checking $n=48$ yields
$$
(23-12)+\frac{1}{6}\left(\binom{47}{2}-3\binom{24}{2}-3 \cdot(23-12-1)-1\right)=48
$$
Hence, the answer is 48.
Remark 1. In fact, the number of distinct triangles with perimeter $n$ and integer sides is $\left[n^{2} / 48\right]$ when $n$ is even and $\left[(n+3)^{2} / 48\right]$ when $n$ is odd, where [•] is the nearest integer function. This follows by analyzing $n$ modulo 12 .
Remark 2. The problem statement originally omitted the condition $n>0$, so an answer of 0 was also counted as correct.
|
48
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $n$ be the answer to this problem. Given $n>0$, find the number of distinct (i.e. non-congruent), non-degenerate triangles with integer side lengths and perimeter $n$.
|
We explicitly compute the number of triangles satisfying the problem conditions for any $n$. There are three kinds of triangles: isosceles and scalene. (Equilateral triangles are isosceles.)
- Case 1: Isosceles. A triangle with side lengths $a, a, b$ must satisfy $2 a>b$ and $2 a+b=n$. So $2 a$ can be any even integer in the interval $(n / 2, n)$. There are thus $\lfloor(n-1) / 2\rfloor-\lfloor n / 4\rfloor$ triangles here.
- Case 2: Scalene. A triangle with side lengths $a, b, c$ must satisfy $a, b, c<n / 2$ and $a+b+c=n$. There are $\binom{n-1}{2}$ triples satisfying the second condition, $3\binom{\lfloor n / 2\rfloor}{ 2}$ of which violate condition 1 (since at most one side is at least $n / 2$, we can do casework on which side). We then remove the isosceles triangles and divide by 6 to account for ordering the sides. If there are no equilateral triangles (i.e. if $3 \nmid n$ ), our answer here is
$$
\frac{1}{6}\left(\binom{n-1}{2}-3\binom{\lfloor n / 2\rfloor}{ 2}-3(\lfloor(n-1) / 2\rfloor-\lfloor n / 4\rfloor)\right) .
$$
Otherwise, the answer is
$$
\frac{1}{6}\left(\binom{n-1}{2}-3\binom{\lfloor n / 2\rfloor}{ 2}-3(\lfloor(n-1) / 2\rfloor-\lfloor n / 4\rfloor-1)-1\right)
$$
The key observation is that almost all triangles are scalene, and there are are roughly $\frac{1}{6}\left(n^{2} / 2-3 n^{2} / 8\right)=$ $n^{2} / 48$ scalene triangles. Hence, $n \approx 48$. Checking $n=48$ yields
$$
(23-12)+\frac{1}{6}\left(\binom{47}{2}-3\binom{24}{2}-3 \cdot(23-12-1)-1\right)=48
$$
Hence, the answer is 48.
Remark 1. In fact, the number of distinct triangles with perimeter $n$ and integer sides is $\left[n^{2} / 48\right]$ when $n$ is even and $\left[(n+3)^{2} / 48\right]$ when $n$ is odd, where [•] is the nearest integer function. This follows by analyzing $n$ modulo 12 .
Remark 2. The problem statement originally omitted the condition $n>0$, so an answer of 0 was also counted as correct.
|
{
"resource_path": "HarvardMIT/segmented/en-251-2021-nov-thm-solutions.jsonl",
"problem_match": "\n8. ",
"solution_match": "\nSolution: "
}
|
e619e3cf-bd11-56bd-99db-45339192c89b
| 610,399
|
Let $n$ be the answer to this problem. Suppose square $A B C D$ has side-length 3 . Then, congruent non-overlapping squares $E H G F$ and $I H J K$ of side-length $\frac{n}{6}$ are drawn such that $A, C$, and $H$ are collinear, $E$ lies on $B C$ and $I$ lies on $C D$. Given that $A J G$ is an equilateral triangle, then the area of $A J G$ is $a+b \sqrt{c}$, where $a, b, c$ are positive integers and $c$ is not divisible by the square of any prime. Find $a+b+c$.
|
The fact that $E H G F$ and $I H J K$ have side length $n / 6$ ends up being irrelevant.
Since $A$ and $H$ are both equidistant from $G$ and $J$, we conclude that the line $A C H M$ is the perpendicular bisector of $G J$.
Now, define the point $C^{\prime}$ so that the spiral similarity centered at $J$ sends $M$ and $H$ to $C^{\prime}$ and $I$, respectively. Since $\triangle J M C^{\prime} \sim \triangle J H I, J M \perp M C^{\prime}$, so $C^{\prime}$ is on line $A M$. Moreover, since the spiral similarity rotates by $\angle H J I=45^{\circ}$, we conclude that $I C^{\prime}$ is at a $45^{\circ}$ angle to $H M$, implying that $C^{\prime}$ is on line $C D$. Therefore $C^{\prime}=C$, implying that $\angle M J C=\angle H J I=45^{\circ}$. As a result, $J$ lies on line $B C$. To finish, simply note that $\angle B A J=75^{\circ}$, so by $A J=A B / \cos 75^{\circ}$. So
$$
[A J G]=\frac{\sqrt{3}}{4} A J^{2}=\frac{9 \sqrt{3}}{4} \frac{1}{\cos ^{2} 75^{\circ}}=\frac{9 \sqrt{3}}{4} \frac{2}{1+\cos 150^{\circ}}=\frac{9 \sqrt{3}}{2-\sqrt{3}}=18 \sqrt{3}+27 .
$$
|
18 \sqrt{3} + 27
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $n$ be the answer to this problem. Suppose square $A B C D$ has side-length 3 . Then, congruent non-overlapping squares $E H G F$ and $I H J K$ of side-length $\frac{n}{6}$ are drawn such that $A, C$, and $H$ are collinear, $E$ lies on $B C$ and $I$ lies on $C D$. Given that $A J G$ is an equilateral triangle, then the area of $A J G$ is $a+b \sqrt{c}$, where $a, b, c$ are positive integers and $c$ is not divisible by the square of any prime. Find $a+b+c$.
|

The fact that $E H G F$ and $I H J K$ have side length $n / 6$ ends up being irrelevant.
Since $A$ and $H$ are both equidistant from $G$ and $J$, we conclude that the line $A C H M$ is the perpendicular bisector of $G J$.
Now, define the point $C^{\prime}$ so that the spiral similarity centered at $J$ sends $M$ and $H$ to $C^{\prime}$ and $I$, respectively. Since $\triangle J M C^{\prime} \sim \triangle J H I, J M \perp M C^{\prime}$, so $C^{\prime}$ is on line $A M$. Moreover, since the spiral similarity rotates by $\angle H J I=45^{\circ}$, we conclude that $I C^{\prime}$ is at a $45^{\circ}$ angle to $H M$, implying that $C^{\prime}$ is on line $C D$. Therefore $C^{\prime}=C$, implying that $\angle M J C=\angle H J I=45^{\circ}$. As a result, $J$ lies on line $B C$. To finish, simply note that $\angle B A J=75^{\circ}$, so by $A J=A B / \cos 75^{\circ}$. So
$$
[A J G]=\frac{\sqrt{3}}{4} A J^{2}=\frac{9 \sqrt{3}}{4} \frac{1}{\cos ^{2} 75^{\circ}}=\frac{9 \sqrt{3}}{4} \frac{2}{1+\cos 150^{\circ}}=\frac{9 \sqrt{3}}{2-\sqrt{3}}=18 \sqrt{3}+27 .
$$
|
{
"resource_path": "HarvardMIT/segmented/en-251-2021-nov-thm-solutions.jsonl",
"problem_match": "\n10. ",
"solution_match": "\n## Solution:\n\n"
}
|
595c114d-cdce-50e4-b175-230a502344ac
| 610,401
|
Positive integers $a, b$, and $c$ are all powers of $k$ for some positive integer $k$. It is known that the equation $a x^{2}-b x+c=0$ has exactly one real solution $r$, and this value $r$ is less than 100 . Compute the maximum possible value of $r$.
|
Note that for there to be exactly one solution, the discriminant must be 0 , so $b^{2}-4 a c=0$. Thus, $b$ is even, so $k=2$. Since $r=\frac{b}{2 a}$, then $r$ is also a power of 2 , and the largest power of 2 less than 100 is 64 . This is achieved by $(x-64)^{2}=x^{2}-128 x+4096$.
|
64
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Positive integers $a, b$, and $c$ are all powers of $k$ for some positive integer $k$. It is known that the equation $a x^{2}-b x+c=0$ has exactly one real solution $r$, and this value $r$ is less than 100 . Compute the maximum possible value of $r$.
|
Note that for there to be exactly one solution, the discriminant must be 0 , so $b^{2}-4 a c=0$. Thus, $b$ is even, so $k=2$. Since $r=\frac{b}{2 a}$, then $r$ is also a power of 2 , and the largest power of 2 less than 100 is 64 . This is achieved by $(x-64)^{2}=x^{2}-128 x+4096$.
|
{
"resource_path": "HarvardMIT/segmented/en-252-2022-feb-algnt-solutions.jsonl",
"problem_match": "\n1. ",
"solution_match": "\nSolution: "
}
|
922ce131-459e-5e0d-a6e1-7dc15ab1c8b5
| 610,402
|
Compute the number of positive integers that divide at least two of the integers in the set $\left\{1^{1}, 2^{2}, 3^{3}, 4^{4}, 5^{5}, 6^{6}, 7^{7}, 8^{8}, 9^{9}, 10^{10}\right\}$.
|
For a positive integer $n$, let rad $n$ be the product of the distinct prime factors of $n$. Observe that if $n \mid m^{m}$, all prime factors of $n$ must divide $m$, so $\operatorname{rad} n \mid m$.
Therefore, if $n$ is such an integer, $\operatorname{rad} n$ must divide at least two of the numbers in $\{1,2,3,4,5,6,7,8,9,10\}$, implying that rad $n$ is either $1,2,3$, or 5 . These have $1,10,6$, and 5 cases, respectively, for a total of 22 .
|
22
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Compute the number of positive integers that divide at least two of the integers in the set $\left\{1^{1}, 2^{2}, 3^{3}, 4^{4}, 5^{5}, 6^{6}, 7^{7}, 8^{8}, 9^{9}, 10^{10}\right\}$.
|
For a positive integer $n$, let rad $n$ be the product of the distinct prime factors of $n$. Observe that if $n \mid m^{m}$, all prime factors of $n$ must divide $m$, so $\operatorname{rad} n \mid m$.
Therefore, if $n$ is such an integer, $\operatorname{rad} n$ must divide at least two of the numbers in $\{1,2,3,4,5,6,7,8,9,10\}$, implying that rad $n$ is either $1,2,3$, or 5 . These have $1,10,6$, and 5 cases, respectively, for a total of 22 .
|
{
"resource_path": "HarvardMIT/segmented/en-252-2022-feb-algnt-solutions.jsonl",
"problem_match": "\n2. ",
"solution_match": "\nSolution: "
}
|
33d39bf8-e8d7-5cb9-9e50-a637d43a66b3
| 610,403
|
Let $x_{1}, x_{2}, \ldots, x_{2022}$ be nonzero real numbers. Suppose that $x_{k}+\frac{1}{x_{k+1}}<0$ for each $1 \leq k \leq 2022$, where $x_{2023}=x_{1}$. Compute the maximum possible number of integers $1 \leq n \leq 2022$ such that $x_{n}>0$.
|
Let the answer be $M$. If $M>1011$, there would exist two consecutive positive terms $x_{k}, x_{k+1}$ which contradicts the assumption that $x_{k}+\frac{1}{x_{k+1}}<0$. Thus, $M \leq 1011$. If $M=1011$, then the $2022 x_{i}$ s must alternate between positive and negative. WLOG, assume $x_{2 k-1}>0$ and $x_{2 k}<0$ for each $k$. Then, we have
$$
\begin{aligned}
& x_{2 k-1}+\frac{1}{x_{2 k}}<0 \Longrightarrow\left|x_{2 k-1} x_{2 k}\right|<1, \\
& x_{2 k}+\frac{1}{x_{2 k+1}}<0 \Longrightarrow\left|x_{2 k} x_{2 k+1}\right|>1 .
\end{aligned}
$$
Multiplying the first equation over all $k$ gives us $\prod_{i=1}^{2022}\left|x_{i}\right|<1$, while multiplying the second equation over all $k$ gives us $\prod_{i=1}^{2022}\left|x_{i}\right|>1$. Thus, we must have $M<1011$.
$M=1010$ is possible by the following construction:
$$
1,-\frac{1}{2}, 3,-\frac{1}{4}, \ldots, 2019,-\frac{1}{2020},-10000,-10000
$$
|
1010
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Let $x_{1}, x_{2}, \ldots, x_{2022}$ be nonzero real numbers. Suppose that $x_{k}+\frac{1}{x_{k+1}}<0$ for each $1 \leq k \leq 2022$, where $x_{2023}=x_{1}$. Compute the maximum possible number of integers $1 \leq n \leq 2022$ such that $x_{n}>0$.
|
Let the answer be $M$. If $M>1011$, there would exist two consecutive positive terms $x_{k}, x_{k+1}$ which contradicts the assumption that $x_{k}+\frac{1}{x_{k+1}}<0$. Thus, $M \leq 1011$. If $M=1011$, then the $2022 x_{i}$ s must alternate between positive and negative. WLOG, assume $x_{2 k-1}>0$ and $x_{2 k}<0$ for each $k$. Then, we have
$$
\begin{aligned}
& x_{2 k-1}+\frac{1}{x_{2 k}}<0 \Longrightarrow\left|x_{2 k-1} x_{2 k}\right|<1, \\
& x_{2 k}+\frac{1}{x_{2 k+1}}<0 \Longrightarrow\left|x_{2 k} x_{2 k+1}\right|>1 .
\end{aligned}
$$
Multiplying the first equation over all $k$ gives us $\prod_{i=1}^{2022}\left|x_{i}\right|<1$, while multiplying the second equation over all $k$ gives us $\prod_{i=1}^{2022}\left|x_{i}\right|>1$. Thus, we must have $M<1011$.
$M=1010$ is possible by the following construction:
$$
1,-\frac{1}{2}, 3,-\frac{1}{4}, \ldots, 2019,-\frac{1}{2020},-10000,-10000
$$
|
{
"resource_path": "HarvardMIT/segmented/en-252-2022-feb-algnt-solutions.jsonl",
"problem_match": "\n3. ",
"solution_match": "\nSolution: "
}
|
4caffed5-7217-5c7f-8572-03dc089a24cf
| 610,404
|
Compute the sum of all 2-digit prime numbers $p$ such that there exists a prime number $q$ for which $100 q+p$ is a perfect square.
|
All squares must end with $0,1,4,5,6$, or 9 , meaning that $p$ must end with 1 and 9 . Moreover, since all odd squares are $1 \bmod 4$, we know that $p$ must be $1 \bmod 4$. This rules all primes except for $41,61,29,89$. Since $17^{2}=289,19^{2}=361,23^{2}=529,89,61$, and 29 all work. To finish, we claim that 41 does not work. If $100 q+41$ were a square, then since all odd squares are 1 mod 8 we find that $4 q+1 \equiv 1(\bmod 8)$, implying that $q$ is even. But 241 is not a square, contradiction.
The final answer is $29+61+89=179$.
|
179
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Compute the sum of all 2-digit prime numbers $p$ such that there exists a prime number $q$ for which $100 q+p$ is a perfect square.
|
All squares must end with $0,1,4,5,6$, or 9 , meaning that $p$ must end with 1 and 9 . Moreover, since all odd squares are $1 \bmod 4$, we know that $p$ must be $1 \bmod 4$. This rules all primes except for $41,61,29,89$. Since $17^{2}=289,19^{2}=361,23^{2}=529,89,61$, and 29 all work. To finish, we claim that 41 does not work. If $100 q+41$ were a square, then since all odd squares are 1 mod 8 we find that $4 q+1 \equiv 1(\bmod 8)$, implying that $q$ is even. But 241 is not a square, contradiction.
The final answer is $29+61+89=179$.
|
{
"resource_path": "HarvardMIT/segmented/en-252-2022-feb-algnt-solutions.jsonl",
"problem_match": "\n4. ",
"solution_match": "\nSolution: "
}
|
25e5aefe-e322-5204-9df0-1258d6eb5321
| 610,405
|
Given a positive integer $k$, let $\|k\|$ denote the absolute difference between $k$ and the nearest perfect square. For example, $\|13\|=3$ since the nearest perfect square to 13 is 16 . Compute the smallest positive integer $n$ such that
$$
\frac{\|1\|+\|2\|+\cdots+\|n\|}{n}=100 .
$$
|
Note that from $n=m^{2}$ to $n=(m+1)^{2},\|n\|$ increases from 0 to a peak of $m$ (which is repeated twice), and then goes back down to 0 . Therefore
$$
\sum_{n=1}^{m^{2}}\|n\|=\sum_{k=1}^{m-1} 2(1+2+\cdots+k)=\sum_{k=1}^{m-1} 2\binom{k+1}{2}=2\binom{m+1}{3}=\frac{m}{3}\left(m^{2}-1\right)
$$
In particular, if $n=m^{2}-1$,
$$
\frac{\|1\|+\|2\|+\cdots+\|n\|}{n}=\frac{m}{3},
$$
so $n=300^{2}-1$ satisfies the condition. However, this does not prove that there are not smaller solutions for $n$.
Let $N=300^{2}-1$ and suppose that $N-k$ satisfies the condition. Then, we know that
$$
\frac{\|N\|+\|N-1\|+\cdots\|N-(k-1)\|}{k}=100 .
$$
Since $\|N-k\|=k+1$ for $k \leq 298$, one can show that $k=199$ works. By looking at further terms, one can convince oneself that no larger value of $k$ works. Thus, the answer is $300^{2}-1-199=90000-200=$ 89800.
|
89800
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Given a positive integer $k$, let $\|k\|$ denote the absolute difference between $k$ and the nearest perfect square. For example, $\|13\|=3$ since the nearest perfect square to 13 is 16 . Compute the smallest positive integer $n$ such that
$$
\frac{\|1\|+\|2\|+\cdots+\|n\|}{n}=100 .
$$
|
Note that from $n=m^{2}$ to $n=(m+1)^{2},\|n\|$ increases from 0 to a peak of $m$ (which is repeated twice), and then goes back down to 0 . Therefore
$$
\sum_{n=1}^{m^{2}}\|n\|=\sum_{k=1}^{m-1} 2(1+2+\cdots+k)=\sum_{k=1}^{m-1} 2\binom{k+1}{2}=2\binom{m+1}{3}=\frac{m}{3}\left(m^{2}-1\right)
$$
In particular, if $n=m^{2}-1$,
$$
\frac{\|1\|+\|2\|+\cdots+\|n\|}{n}=\frac{m}{3},
$$
so $n=300^{2}-1$ satisfies the condition. However, this does not prove that there are not smaller solutions for $n$.
Let $N=300^{2}-1$ and suppose that $N-k$ satisfies the condition. Then, we know that
$$
\frac{\|N\|+\|N-1\|+\cdots\|N-(k-1)\|}{k}=100 .
$$
Since $\|N-k\|=k+1$ for $k \leq 298$, one can show that $k=199$ works. By looking at further terms, one can convince oneself that no larger value of $k$ works. Thus, the answer is $300^{2}-1-199=90000-200=$ 89800.
|
{
"resource_path": "HarvardMIT/segmented/en-252-2022-feb-algnt-solutions.jsonl",
"problem_match": "\n5. ",
"solution_match": "\nSolution: "
}
|
2d4a9959-baef-599d-9306-7dc34f4dacbe
| 610,406
|
Let $f$ be a function from $\{1,2, \ldots, 22\}$ to the positive integers such that $m n \mid f(m)+f(n)$ for all $m, n \in\{1,2, \ldots, 22\}$. If $d$ is the number of positive divisors of $f(20)$, compute the minimum possible value of $d$.
|
Let $L=\operatorname{lcm}(1,2, \ldots, 22)$. We claim that the possible values of $f(20)$ are the multiples of $20 L$. If we can prove this, we will be done, since the minimum value of $d$ will be the number of divisors of $20 L=2^{6} \cdot 3^{2} \cdot 5^{2} \cdot 7 \cdot 11 \cdot 13 \cdot 17 \cdot 19$, which has $7 \cdot 3^{2} \cdot 2^{5}=2016$ factors.
First let's construct such an $f$. For any positive integer $a$, I claim that $f(n)=a L n$ works. Indeed, for any $m, n$, we find that $f(m)=a L m$ is divisible by $m n$, since $n \mid L$. Thus the condition is satisfied.
Now let's prove that $f(20)$ must be a multiple of $20 L$. Take any prime $p$, and let $q$ be the largest power of $p$ at most 22. If $p \neq 2$, we know that $q^{2} \mid 2 f(q)$, meaning that $q^{2} \mid f(q)$. Then, using the fact that $20 q \mid f(q)+f(20)$, we find that $\operatorname{gcd}\left(20 q, q^{2}\right) \mid f(q), f(q)+f(20)$, implying that
$$
\nu_{p}(f(20)) \geq \nu_{p}\left(\operatorname{gcd}\left(20 q, q^{2}\right)\right)=\nu_{p}(20 q)=\nu_{p}(20 L)
$$
Now suppose $p=2$. Then $2^{8}=16^{2} \mid 2 f(16)$, so $2^{7} \mid f(16)$. Then, since $5 \cdot 2^{6}=20 \cdot 16 \mid f(16)+f(20)$, we find that $2^{7} \mid f(20)$. Since $7=\nu_{2}(20 L)$, we are done.
|
2016
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Let $f$ be a function from $\{1,2, \ldots, 22\}$ to the positive integers such that $m n \mid f(m)+f(n)$ for all $m, n \in\{1,2, \ldots, 22\}$. If $d$ is the number of positive divisors of $f(20)$, compute the minimum possible value of $d$.
|
Let $L=\operatorname{lcm}(1,2, \ldots, 22)$. We claim that the possible values of $f(20)$ are the multiples of $20 L$. If we can prove this, we will be done, since the minimum value of $d$ will be the number of divisors of $20 L=2^{6} \cdot 3^{2} \cdot 5^{2} \cdot 7 \cdot 11 \cdot 13 \cdot 17 \cdot 19$, which has $7 \cdot 3^{2} \cdot 2^{5}=2016$ factors.
First let's construct such an $f$. For any positive integer $a$, I claim that $f(n)=a L n$ works. Indeed, for any $m, n$, we find that $f(m)=a L m$ is divisible by $m n$, since $n \mid L$. Thus the condition is satisfied.
Now let's prove that $f(20)$ must be a multiple of $20 L$. Take any prime $p$, and let $q$ be the largest power of $p$ at most 22. If $p \neq 2$, we know that $q^{2} \mid 2 f(q)$, meaning that $q^{2} \mid f(q)$. Then, using the fact that $20 q \mid f(q)+f(20)$, we find that $\operatorname{gcd}\left(20 q, q^{2}\right) \mid f(q), f(q)+f(20)$, implying that
$$
\nu_{p}(f(20)) \geq \nu_{p}\left(\operatorname{gcd}\left(20 q, q^{2}\right)\right)=\nu_{p}(20 q)=\nu_{p}(20 L)
$$
Now suppose $p=2$. Then $2^{8}=16^{2} \mid 2 f(16)$, so $2^{7} \mid f(16)$. Then, since $5 \cdot 2^{6}=20 \cdot 16 \mid f(16)+f(20)$, we find that $2^{7} \mid f(20)$. Since $7=\nu_{2}(20 L)$, we are done.
|
{
"resource_path": "HarvardMIT/segmented/en-252-2022-feb-algnt-solutions.jsonl",
"problem_match": "\n6. ",
"solution_match": "\nSolution: "
}
|
b41aefe7-863f-571d-aad4-d89ca0888228
| 610,407
|
Let $\left(x_{1}, y_{1}\right),\left(x_{2}, y_{2}\right),\left(x_{3}, y_{3}\right),\left(x_{4}, y_{4}\right)$, and $\left(x_{5}, y_{5}\right)$ be the vertices of a regular pentagon centered at $(0,0)$. Compute the product of all positive integers $k$ such that the equality
$$
x_{1}^{k}+x_{2}^{k}+x_{3}^{k}+x_{4}^{k}+x_{5}^{k}=y_{1}^{k}+y_{2}^{k}+y_{3}^{k}+y_{4}^{k}+y_{5}^{k}
$$
must hold for all possible choices of the pentagon.
|
Without loss of generality let the vertices of the pentagon lie on the unit circle. Then, if $f(\theta)=\cos (\theta)^{k}$ and $g(\theta)=\sum_{j=0}^{4} f(\theta+2 j \pi / 5)$, the condition becomes $g(\theta)=g(\pi / 2-\theta)$, or $g(\theta)=$ $g(\theta+\pi / 2)$, since $g$ is an odd function.
Write $f \asymp g$ if $f=c g$ for some nonzero constant $c$ that we don't care about. Since $\cos \theta \asymp e^{i \theta}+e^{-i \theta}$, we find that
$$
f(\theta) \asymp \sum_{\ell \in \mathbb{Z}}\binom{k}{\frac{k+\ell}{2}} e^{i \ell \theta}
$$
where $\binom{a}{b}$ is defined to be zero if $b$ is not an integer in the interval $[0, a]$. It is also true that
$$
\sum_{j=0}^{4} e^{i \ell(\theta+2 j \pi / 5)}= \begin{cases}5 e^{i \theta} & 5 \mid \ell \\ 0 & \text { else }\end{cases}
$$
so
$$
g(\theta) \asymp \sum_{\ell \in 5 \mathbb{Z}}\binom{k}{\frac{k+\ell}{2}} e^{i \ell \theta}
$$
This is periodic with period $\pi / 2$ if and only if all terms with $\ell$ not a multiple of 4 are equal to 0 . However, we know that the nonzero terms are exactly the $\ell$ that (1) are multiples of $5,(2)$ are of the same parity as $k$, and (3) satisfy $|\ell| \leq k$. Hence, if $k$ is even, the condition is satisfied if and only if $k<10$ (else the $\ell=10$ term is nonzero), and if $k$ is odd, the condition is satisfied if and only if $k<5$ (else the $\ell=5$ term is nonzero). Our final answer is $1 \cdot 2 \cdot 3 \cdot 4 \cdot 6 \cdot 8=1152$.
|
1152
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Let $\left(x_{1}, y_{1}\right),\left(x_{2}, y_{2}\right),\left(x_{3}, y_{3}\right),\left(x_{4}, y_{4}\right)$, and $\left(x_{5}, y_{5}\right)$ be the vertices of a regular pentagon centered at $(0,0)$. Compute the product of all positive integers $k$ such that the equality
$$
x_{1}^{k}+x_{2}^{k}+x_{3}^{k}+x_{4}^{k}+x_{5}^{k}=y_{1}^{k}+y_{2}^{k}+y_{3}^{k}+y_{4}^{k}+y_{5}^{k}
$$
must hold for all possible choices of the pentagon.
|
Without loss of generality let the vertices of the pentagon lie on the unit circle. Then, if $f(\theta)=\cos (\theta)^{k}$ and $g(\theta)=\sum_{j=0}^{4} f(\theta+2 j \pi / 5)$, the condition becomes $g(\theta)=g(\pi / 2-\theta)$, or $g(\theta)=$ $g(\theta+\pi / 2)$, since $g$ is an odd function.
Write $f \asymp g$ if $f=c g$ for some nonzero constant $c$ that we don't care about. Since $\cos \theta \asymp e^{i \theta}+e^{-i \theta}$, we find that
$$
f(\theta) \asymp \sum_{\ell \in \mathbb{Z}}\binom{k}{\frac{k+\ell}{2}} e^{i \ell \theta}
$$
where $\binom{a}{b}$ is defined to be zero if $b$ is not an integer in the interval $[0, a]$. It is also true that
$$
\sum_{j=0}^{4} e^{i \ell(\theta+2 j \pi / 5)}= \begin{cases}5 e^{i \theta} & 5 \mid \ell \\ 0 & \text { else }\end{cases}
$$
so
$$
g(\theta) \asymp \sum_{\ell \in 5 \mathbb{Z}}\binom{k}{\frac{k+\ell}{2}} e^{i \ell \theta}
$$
This is periodic with period $\pi / 2$ if and only if all terms with $\ell$ not a multiple of 4 are equal to 0 . However, we know that the nonzero terms are exactly the $\ell$ that (1) are multiples of $5,(2)$ are of the same parity as $k$, and (3) satisfy $|\ell| \leq k$. Hence, if $k$ is even, the condition is satisfied if and only if $k<10$ (else the $\ell=10$ term is nonzero), and if $k$ is odd, the condition is satisfied if and only if $k<5$ (else the $\ell=5$ term is nonzero). Our final answer is $1 \cdot 2 \cdot 3 \cdot 4 \cdot 6 \cdot 8=1152$.
|
{
"resource_path": "HarvardMIT/segmented/en-252-2022-feb-algnt-solutions.jsonl",
"problem_match": "\n7. ",
"solution_match": "\nSolution: "
}
|
d62152f8-e866-5081-8977-16356ca1b038
| 610,408
|
Positive integers $a_{1}, a_{2}, \ldots, a_{7}, b_{1}, b_{2}, \ldots, b_{7}$ satisfy $2 \leq a_{i} \leq 166$ and $a_{i}^{b_{i}} \equiv a_{i+1}^{2}(\bmod 167)$ for each $1 \leq i \leq 7$ (where $a_{8}=a_{1}$ ). Compute the minimum possible value of $b_{1} b_{2} \cdots b_{7}\left(b_{1}+b_{2}+\cdots+b_{7}\right)$.
|
Let $B=b_{1} b_{2} \cdots b_{7}-128$. Since
$$
a_{1}^{b_{1} b_{2} \cdots b_{7}} \equiv a_{2}^{2 b_{2} b_{3} \cdots b_{7}} \equiv a_{3}^{4 b_{3} b_{4} \cdots b_{7}} \equiv \cdots \equiv a_{1}^{128} \quad(\bmod 167)
$$
we find that $a_{1}^{B} \equiv 1(\bmod 167)$. Similarly, $a_{i}^{B} \equiv 1(\bmod 167)$ for all $i$. Since 167 is a prime and $167-1=2 \cdot 83$, we know that the order of each individual $a_{i}$ (since $a_{i} \neq 1$ ) must be either 2 of a multiple of 83 . If $B$ is not a multiple of 83 , then it follows that all the $a_{i}$ must be -1 , which implies that all the $b_{i}$ must be even, meaning that the minimum possible value of $b_{1} b_{2} \cdots b_{7}\left(b_{1}+b_{2}+\cdots b_{7}\right)$ is $2^{7} \cdot 14>1000$.
Oh the other hand, if $B$ is a multiple of 83 , then the smallest possible values for $b_{1} b_{2} \cdots b_{7}$ are 45 and 128. If $b_{1} b_{2} \cdots b_{7}=45$, then the smallest possible value for $b_{1}+b_{2}+\cdots+b_{7}$ is $5+3+3+1+1+1+1=15$, so the minimum possible value for $b_{1} b_{2} \cdots b_{7}\left(b_{1}+b_{2}+\cdots b_{7}\right)$ is $45 \cdot 15=675$. This can be achieved by letting $g$ be an element of order 83 and setting $a_{1}=g, a_{2}=g^{1 / 2}, a_{3}=g^{1 / 4}, a_{4}=g^{1 / 8}, a_{5}=g^{1 / 16}, a_{6}=$ $g^{3 / 32}, a_{7}=g^{9 / 64}($ all exponents are taken mod 83).
If $b_{1} b_{2} \cdots b_{7} \geq 128$, then by the AM-GM inequality we have
$$
b_{1} b_{2} \cdots b_{7}\left(b_{1}+b_{2}+\cdots b_{7}\right) \geq 7\left(b_{1} b_{2} \cdots b_{7}\right)^{8 / 7} \geq 7 \cdot 2^{8}>1000
$$
Therefore 675 is optimal.
|
675
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Positive integers $a_{1}, a_{2}, \ldots, a_{7}, b_{1}, b_{2}, \ldots, b_{7}$ satisfy $2 \leq a_{i} \leq 166$ and $a_{i}^{b_{i}} \equiv a_{i+1}^{2}(\bmod 167)$ for each $1 \leq i \leq 7$ (where $a_{8}=a_{1}$ ). Compute the minimum possible value of $b_{1} b_{2} \cdots b_{7}\left(b_{1}+b_{2}+\cdots+b_{7}\right)$.
|
Let $B=b_{1} b_{2} \cdots b_{7}-128$. Since
$$
a_{1}^{b_{1} b_{2} \cdots b_{7}} \equiv a_{2}^{2 b_{2} b_{3} \cdots b_{7}} \equiv a_{3}^{4 b_{3} b_{4} \cdots b_{7}} \equiv \cdots \equiv a_{1}^{128} \quad(\bmod 167)
$$
we find that $a_{1}^{B} \equiv 1(\bmod 167)$. Similarly, $a_{i}^{B} \equiv 1(\bmod 167)$ for all $i$. Since 167 is a prime and $167-1=2 \cdot 83$, we know that the order of each individual $a_{i}$ (since $a_{i} \neq 1$ ) must be either 2 of a multiple of 83 . If $B$ is not a multiple of 83 , then it follows that all the $a_{i}$ must be -1 , which implies that all the $b_{i}$ must be even, meaning that the minimum possible value of $b_{1} b_{2} \cdots b_{7}\left(b_{1}+b_{2}+\cdots b_{7}\right)$ is $2^{7} \cdot 14>1000$.
Oh the other hand, if $B$ is a multiple of 83 , then the smallest possible values for $b_{1} b_{2} \cdots b_{7}$ are 45 and 128. If $b_{1} b_{2} \cdots b_{7}=45$, then the smallest possible value for $b_{1}+b_{2}+\cdots+b_{7}$ is $5+3+3+1+1+1+1=15$, so the minimum possible value for $b_{1} b_{2} \cdots b_{7}\left(b_{1}+b_{2}+\cdots b_{7}\right)$ is $45 \cdot 15=675$. This can be achieved by letting $g$ be an element of order 83 and setting $a_{1}=g, a_{2}=g^{1 / 2}, a_{3}=g^{1 / 4}, a_{4}=g^{1 / 8}, a_{5}=g^{1 / 16}, a_{6}=$ $g^{3 / 32}, a_{7}=g^{9 / 64}($ all exponents are taken mod 83).
If $b_{1} b_{2} \cdots b_{7} \geq 128$, then by the AM-GM inequality we have
$$
b_{1} b_{2} \cdots b_{7}\left(b_{1}+b_{2}+\cdots b_{7}\right) \geq 7\left(b_{1} b_{2} \cdots b_{7}\right)^{8 / 7} \geq 7 \cdot 2^{8}>1000
$$
Therefore 675 is optimal.
|
{
"resource_path": "HarvardMIT/segmented/en-252-2022-feb-algnt-solutions.jsonl",
"problem_match": "\n8. ",
"solution_match": "\nSolution: "
}
|
1aa14755-9998-5ec1-8510-7b1cf4098c4f
| 610,409
|
Suppose $P(x)$ is a monic polynomial of degree 2023 such that
$$
P(k)=k^{2023} P\left(1-\frac{1}{k}\right)
$$
for every positive integer $1 \leq k \leq 2023$. Then $P(-1)=\frac{a}{b}$, where $a$ and $b$ relatively prime integers. Compute the unique integer $0 \leq n<2027$ such that $b n-a$ is divisible by the prime 2027 .
|
Answer: 406
|
406
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Suppose $P(x)$ is a monic polynomial of degree 2023 such that
$$
P(k)=k^{2023} P\left(1-\frac{1}{k}\right)
$$
for every positive integer $1 \leq k \leq 2023$. Then $P(-1)=\frac{a}{b}$, where $a$ and $b$ relatively prime integers. Compute the unique integer $0 \leq n<2027$ such that $b n-a$ is divisible by the prime 2027 .
|
Answer: 406
|
{
"resource_path": "HarvardMIT/segmented/en-252-2022-feb-algnt-solutions.jsonl",
"problem_match": "\n9. ",
"solution_match": "\nProposed by: Akash Das\n"
}
|
08849943-d57d-533c-9205-92848657ebde
| 610,410
|
Compute the smallest positive integer $n$ for which there are at least two odd primes $p$ such that
$$
\sum_{k=1}^{n}(-1)^{\nu_{p}(k!)}<0
$$
Note: for a prime $p$ and a positive integer $m, \nu_{p}(m)$ is the exponent of the largest power of $p$ that divides $m$; for example, $\nu_{3}(18)=2$.
|
Answer: 229
|
229
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Compute the smallest positive integer $n$ for which there are at least two odd primes $p$ such that
$$
\sum_{k=1}^{n}(-1)^{\nu_{p}(k!)}<0
$$
Note: for a prime $p$ and a positive integer $m, \nu_{p}(m)$ is the exponent of the largest power of $p$ that divides $m$; for example, $\nu_{3}(18)=2$.
|
Answer: 229
|
{
"resource_path": "HarvardMIT/segmented/en-252-2022-feb-algnt-solutions.jsonl",
"problem_match": "\n10. ",
"solution_match": "\nProposed by: Krit Boonsiriseth\n"
}
|
c8c50221-fb3f-50bb-9c6a-11efe3096f77
| 610,411
|
Sets $A, B$, and $C$ satisfy $|A|=92,|B|=35,|C|=63,|A \cap B|=16,|A \cap C|=51,|B \cap C|=19$. Compute the number of possible values of $|A \cap B \cap C|$.
|
Suppose $|A \cap B \cap C|=n$. Then there are $16-n$ elements in $A$ and $B$ but not $C, 51-n$ in $A$ and $C$ but not $B$, and $19-n$ in $B$ and $C$ but not $A$. Furthermore, there are $25+n$ elements that are only in $A, n$ only in $B$, and $n-7$ that are only in $C$. Therefore, $7 \leq n \leq 16$, so there are 10 possible values.
|
10
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Sets $A, B$, and $C$ satisfy $|A|=92,|B|=35,|C|=63,|A \cap B|=16,|A \cap C|=51,|B \cap C|=19$. Compute the number of possible values of $|A \cap B \cap C|$.
|
Suppose $|A \cap B \cap C|=n$. Then there are $16-n$ elements in $A$ and $B$ but not $C, 51-n$ in $A$ and $C$ but not $B$, and $19-n$ in $B$ and $C$ but not $A$. Furthermore, there are $25+n$ elements that are only in $A, n$ only in $B$, and $n-7$ that are only in $C$. Therefore, $7 \leq n \leq 16$, so there are 10 possible values.
|
{
"resource_path": "HarvardMIT/segmented/en-252-2022-feb-comb-solutions.jsonl",
"problem_match": "\n1. ",
"solution_match": "\nSolution: "
}
|
32b1b6bb-d884-59b4-8fa2-f640418d71e1
| 610,412
|
Compute the number of ways to color 3 cells in a $3 \times 3$ grid so that no two colored cells share an edge.
|
If the middle square is colored, then two of the four corner squares must be colored, and there are $\binom{4}{2}=6$ ways to do this. If the middle square is not colored, then after coloring one of the 8 other squares, there are always 6 ways to place the other two squares. However, the number of possibilities is overcounted by a factor of 3 , so there are 16 ways where the middle square is not colored. This leads to a total of 22 .
|
22
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Compute the number of ways to color 3 cells in a $3 \times 3$ grid so that no two colored cells share an edge.
|
If the middle square is colored, then two of the four corner squares must be colored, and there are $\binom{4}{2}=6$ ways to do this. If the middle square is not colored, then after coloring one of the 8 other squares, there are always 6 ways to place the other two squares. However, the number of possibilities is overcounted by a factor of 3 , so there are 16 ways where the middle square is not colored. This leads to a total of 22 .
|
{
"resource_path": "HarvardMIT/segmented/en-252-2022-feb-comb-solutions.jsonl",
"problem_match": "\n2. ",
"solution_match": "\nSolution: "
}
|
8d1ad4b4-8e72-5874-8a64-a18c00f27ae6
| 610,413
|
Michel starts with the string $H M M T$. An operation consists of either replacing an occurrence of $H$ with $H M$, replacing an occurrence of $M M$ with $M O M$, or replacing an occurrence of $T$ with $M T$. For example, the two strings that can be reached after one operation are $H M M M T$ and $H M O M T$. Compute the number of distinct strings Michel can obtain after exactly 10 operations.
|
Each final string is of the form $H M x M T$, where $x$ is a string of length 10 consisting of $M \mathrm{~s}$ and $O$ s. Further, no two $O$ s can be adjacent. It is not hard to prove that this is a necessary and sufficient condition for being a final string.
Let $f(n)$ be the number of strings of length $n$ consisting of $M$ s and $O$ where no two $O$ s are adjacent. Any such string of length $n+2$ must either end in $M$, in which case removing the $M$ results in a valid string of length $n+1$, or $M O$, in which case removing the $M O$ results in a valid string of length $n$. Therefore, $f(n+2)=f(n)+f(n+1)$. Since $f(1)=2$ and $f(2)=3$, applying the recursion leads to $f(10)=144$.
|
144
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Michel starts with the string $H M M T$. An operation consists of either replacing an occurrence of $H$ with $H M$, replacing an occurrence of $M M$ with $M O M$, or replacing an occurrence of $T$ with $M T$. For example, the two strings that can be reached after one operation are $H M M M T$ and $H M O M T$. Compute the number of distinct strings Michel can obtain after exactly 10 operations.
|
Each final string is of the form $H M x M T$, where $x$ is a string of length 10 consisting of $M \mathrm{~s}$ and $O$ s. Further, no two $O$ s can be adjacent. It is not hard to prove that this is a necessary and sufficient condition for being a final string.
Let $f(n)$ be the number of strings of length $n$ consisting of $M$ s and $O$ where no two $O$ s are adjacent. Any such string of length $n+2$ must either end in $M$, in which case removing the $M$ results in a valid string of length $n+1$, or $M O$, in which case removing the $M O$ results in a valid string of length $n$. Therefore, $f(n+2)=f(n)+f(n+1)$. Since $f(1)=2$ and $f(2)=3$, applying the recursion leads to $f(10)=144$.
|
{
"resource_path": "HarvardMIT/segmented/en-252-2022-feb-comb-solutions.jsonl",
"problem_match": "\n3. ",
"solution_match": "\nSolution: "
}
|
375370b7-549e-5acc-98ff-724e202fa161
| 610,414
|
Five cards labeled $1,3,5,7,9$ are laid in a row in that order, forming the five-digit number 13579 when read from left to right. A swap consists of picking two distinct cards, and then swapping them. After three swaps, the cards form a new five-digit number $n$ when read from left to right. Compute the expected value of $n$.
|
For a given card, let $p(n)$ denote the probability that it is in its original position after $n$ swaps. Then $p(n+1)=p(n) \cdot \frac{3}{5}+(1-p(n)) \cdot \frac{1}{10}$, by casework on whether the card is in the correct position or not after $n$ swaps. In particular, $p(0)=1, p(1)=3 / 5, p(2)=2 / 5$, and $p(3)=3 / 10$.
For a certain digit originally occupied with the card labeled $d$, we see that, at the end of the process, the card at the digit is $d$ with probability $3 / 10$ and equally likely to be one of the four non- $d$ cards with probability $7 / 10$. Thus the expected value of the card at this digit is
$$
\frac{3 d}{10}+\frac{7}{10} \frac{25-d}{4}=\frac{12 d+175-7 d}{40}=\frac{d+35}{8}
$$
By linearity of expectation, our final answer is therefore
$$
\frac{13579+35 \cdot 11111}{8}=\frac{402464}{8}=50308
$$
|
50308
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Five cards labeled $1,3,5,7,9$ are laid in a row in that order, forming the five-digit number 13579 when read from left to right. A swap consists of picking two distinct cards, and then swapping them. After three swaps, the cards form a new five-digit number $n$ when read from left to right. Compute the expected value of $n$.
|
For a given card, let $p(n)$ denote the probability that it is in its original position after $n$ swaps. Then $p(n+1)=p(n) \cdot \frac{3}{5}+(1-p(n)) \cdot \frac{1}{10}$, by casework on whether the card is in the correct position or not after $n$ swaps. In particular, $p(0)=1, p(1)=3 / 5, p(2)=2 / 5$, and $p(3)=3 / 10$.
For a certain digit originally occupied with the card labeled $d$, we see that, at the end of the process, the card at the digit is $d$ with probability $3 / 10$ and equally likely to be one of the four non- $d$ cards with probability $7 / 10$. Thus the expected value of the card at this digit is
$$
\frac{3 d}{10}+\frac{7}{10} \frac{25-d}{4}=\frac{12 d+175-7 d}{40}=\frac{d+35}{8}
$$
By linearity of expectation, our final answer is therefore
$$
\frac{13579+35 \cdot 11111}{8}=\frac{402464}{8}=50308
$$
|
{
"resource_path": "HarvardMIT/segmented/en-252-2022-feb-comb-solutions.jsonl",
"problem_match": "\n5. ",
"solution_match": "\nSolution: "
}
|
3321e6f7-8b3a-52f9-a9be-1439b0547100
| 610,416
|
Let $S=\left\{(x, y) \in \mathbb{Z}^{2} \mid 0 \leq x \leq 11,0 \leq y \leq 9\right\}$. Compute the number of sequences $\left(s_{0}, s_{1}, \ldots, s_{n}\right)$ of elements in $S$ (for any positive integer $n \geq 2$ ) that satisfy the following conditions:
- $s_{0}=(0,0)$ and $s_{1}=(1,0)$,
- $s_{0}, s_{1}, \ldots, s_{n}$ are distinct,
- for all integers $2 \leq i \leq n, s_{i}$ is obtained by rotating $s_{i-2}$ about $s_{i-1}$ by either $90^{\circ}$ or $180^{\circ}$ in the clockwise direction.
|
Let $a_{n}$ be the number of such possibilities where there $n 90^{\circ}$ turns. Note that $a_{0}=10$ and $a_{1}=11 \cdot 9$.
Now suppose $n=2 k$ with $k \geq 1$. The path traced out by the $s_{i}$ is uniquely determined by a choice of $k+1$ nonnegative $x$-coordinates and $k$ positive $y$-coordinates indicating where to turn and when to stop. If $n=2 k+1$, the path is uniquely determined by a choice of $k+1$ nonnegative $x$-coordinates and $k+1$ positive $y$-coordinates.
As a result, our final answer is
$$
10+11 \cdot 9+\binom{12}{2}\binom{9}{1}+\binom{12}{2}\binom{9}{2}+\cdots=-12+\binom{12}{0}\binom{9}{0}+\binom{12}{1}\binom{9}{0}+\binom{12}{1}\binom{9}{1}+\cdots
$$
One can check that
$$
\sum_{k=0}^{9}\binom{12}{k}\binom{9}{k}=\sum_{k=0}^{9}\binom{12}{k}\binom{9}{9-k}=\binom{21}{9}
$$
by Vandermonde's identity. Similarly,
$$
\sum_{k=0}^{9}\binom{12}{k+1}\binom{9}{k}=\sum_{k=0}^{9}\binom{12}{k+1}\binom{9}{9-k}=\binom{21}{10}
$$
Thus our final answer is
$$
\begin{aligned}
\binom{22}{10}-12 & =-12+\frac{22 \cdot 21 \cdot 2 \cdot 19 \cdot 2 \cdot 17 \cdot 2 \cdot 15 \cdot 2 \cdot 13}{6!} \\
& =-12+7 \cdot 11 \cdot 13 \cdot \frac{2^{5} \cdot 3^{2} \cdot 5 \cdot 19 \cdot 17}{2^{4} \cdot 3^{2} \cdot 5} \\
& =-12+1001 \cdot 2 \cdot 17 \cdot 19 \\
& =646646-12=646634 .
\end{aligned}
$$
|
646634
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Let $S=\left\{(x, y) \in \mathbb{Z}^{2} \mid 0 \leq x \leq 11,0 \leq y \leq 9\right\}$. Compute the number of sequences $\left(s_{0}, s_{1}, \ldots, s_{n}\right)$ of elements in $S$ (for any positive integer $n \geq 2$ ) that satisfy the following conditions:
- $s_{0}=(0,0)$ and $s_{1}=(1,0)$,
- $s_{0}, s_{1}, \ldots, s_{n}$ are distinct,
- for all integers $2 \leq i \leq n, s_{i}$ is obtained by rotating $s_{i-2}$ about $s_{i-1}$ by either $90^{\circ}$ or $180^{\circ}$ in the clockwise direction.
|
Let $a_{n}$ be the number of such possibilities where there $n 90^{\circ}$ turns. Note that $a_{0}=10$ and $a_{1}=11 \cdot 9$.
Now suppose $n=2 k$ with $k \geq 1$. The path traced out by the $s_{i}$ is uniquely determined by a choice of $k+1$ nonnegative $x$-coordinates and $k$ positive $y$-coordinates indicating where to turn and when to stop. If $n=2 k+1$, the path is uniquely determined by a choice of $k+1$ nonnegative $x$-coordinates and $k+1$ positive $y$-coordinates.
As a result, our final answer is
$$
10+11 \cdot 9+\binom{12}{2}\binom{9}{1}+\binom{12}{2}\binom{9}{2}+\cdots=-12+\binom{12}{0}\binom{9}{0}+\binom{12}{1}\binom{9}{0}+\binom{12}{1}\binom{9}{1}+\cdots
$$
One can check that
$$
\sum_{k=0}^{9}\binom{12}{k}\binom{9}{k}=\sum_{k=0}^{9}\binom{12}{k}\binom{9}{9-k}=\binom{21}{9}
$$
by Vandermonde's identity. Similarly,
$$
\sum_{k=0}^{9}\binom{12}{k+1}\binom{9}{k}=\sum_{k=0}^{9}\binom{12}{k+1}\binom{9}{9-k}=\binom{21}{10}
$$
Thus our final answer is
$$
\begin{aligned}
\binom{22}{10}-12 & =-12+\frac{22 \cdot 21 \cdot 2 \cdot 19 \cdot 2 \cdot 17 \cdot 2 \cdot 15 \cdot 2 \cdot 13}{6!} \\
& =-12+7 \cdot 11 \cdot 13 \cdot \frac{2^{5} \cdot 3^{2} \cdot 5 \cdot 19 \cdot 17}{2^{4} \cdot 3^{2} \cdot 5} \\
& =-12+1001 \cdot 2 \cdot 17 \cdot 19 \\
& =646646-12=646634 .
\end{aligned}
$$
|
{
"resource_path": "HarvardMIT/segmented/en-252-2022-feb-comb-solutions.jsonl",
"problem_match": "\n7. ",
"solution_match": "\nSolution: "
}
|
414f91ed-b4ae-54d4-85eb-6f3ba3d64818
| 610,418
|
Random sequences $a_{1}, a_{2}, \ldots$ and $b_{1}, b_{2}, \ldots$ are chosen so that every element in each sequence is chosen independently and uniformly from the set $\{0,1,2,3, \ldots, 100\}$. Compute the expected value of the smallest nonnegative integer $s$ such that there exist positive integers $m$ and $n$ with
$$
s=\sum_{i=1}^{m} a_{i}=\sum_{j=1}^{n} b_{j} .
$$
|
Let's first solve the problem, ignoring the possibility that the $a_{i}$ and $b_{i}$ can be zero. Call a positive integer $s$ an $A$-sum if $s=\sum_{i=1}^{m} a_{i}$ for some nonnegative integer $m$ (in particular, 0 is always an $A$-sum). Define the term $B$-sum similarly. Let $E$ be the expected value of the smallest positive integer that is both an $A$-sum and a $B$-sum.
The first key observation to make is that if $s$ is both an $A$-sum and a $B$-sum, then the distance to the next number that is both an $A$-sum and a $B$-sum is $E$. To see this, note that if
$$
s=\sum_{i=1}^{m} a_{i}=\sum_{j=1}^{n} b_{i}
$$
the distance to the next number that is both an $A$-sum and a $B$-sum is the minimal positive integer $t$ so that there exist $m^{\prime}$ and $n^{\prime}$ so that
$$
t=\sum_{i=1}^{m^{\prime}} a_{m+i}=\sum_{j=1}^{n^{\prime}} b_{n+i}
$$
This is the same question of which we defined $E$ to be the answer, but with renamed variables, so the expected value of $t$ is $E$. As a result, we conclude that the expected density of numbers that are both $A$-sums and $B$-sums is $\frac{1}{E}$.
We now compute this density. Note that since the expected value of $a_{i}$ is $\frac{101}{2}$, the density of $A$-sums is $\frac{2}{101}$. Also, the density of $B$-sums if $\frac{2}{101}$. Moreover, as $n$ goes to infinity, the probability that $n$ is an $A$-sum approaches $\frac{2}{101}$ and the probability that $n$ is a $B$-sum approaches $\frac{2}{101}$. Thus, the density of numbers that are simultaneously $A$-sums and $B$-sums is $\frac{4}{101^{2}}$, so $E=\frac{101^{2}}{4}$.
We now add back the possibility that some of the $a_{i}$ and $b_{i}$ can be 0 . The only way this changes our answer is that the $s$ we seek can be 0 , which happens if and only if $a_{1}=b_{1}=0$. Thus our final answer is
$$
\frac{1}{101^{2}} \cdot 0+\frac{101^{2}-1}{101^{2}} \cdot \frac{101^{2}}{4}=\frac{101^{2}-1}{4}=2550
$$
|
2550
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Random sequences $a_{1}, a_{2}, \ldots$ and $b_{1}, b_{2}, \ldots$ are chosen so that every element in each sequence is chosen independently and uniformly from the set $\{0,1,2,3, \ldots, 100\}$. Compute the expected value of the smallest nonnegative integer $s$ such that there exist positive integers $m$ and $n$ with
$$
s=\sum_{i=1}^{m} a_{i}=\sum_{j=1}^{n} b_{j} .
$$
|
Let's first solve the problem, ignoring the possibility that the $a_{i}$ and $b_{i}$ can be zero. Call a positive integer $s$ an $A$-sum if $s=\sum_{i=1}^{m} a_{i}$ for some nonnegative integer $m$ (in particular, 0 is always an $A$-sum). Define the term $B$-sum similarly. Let $E$ be the expected value of the smallest positive integer that is both an $A$-sum and a $B$-sum.
The first key observation to make is that if $s$ is both an $A$-sum and a $B$-sum, then the distance to the next number that is both an $A$-sum and a $B$-sum is $E$. To see this, note that if
$$
s=\sum_{i=1}^{m} a_{i}=\sum_{j=1}^{n} b_{i}
$$
the distance to the next number that is both an $A$-sum and a $B$-sum is the minimal positive integer $t$ so that there exist $m^{\prime}$ and $n^{\prime}$ so that
$$
t=\sum_{i=1}^{m^{\prime}} a_{m+i}=\sum_{j=1}^{n^{\prime}} b_{n+i}
$$
This is the same question of which we defined $E$ to be the answer, but with renamed variables, so the expected value of $t$ is $E$. As a result, we conclude that the expected density of numbers that are both $A$-sums and $B$-sums is $\frac{1}{E}$.
We now compute this density. Note that since the expected value of $a_{i}$ is $\frac{101}{2}$, the density of $A$-sums is $\frac{2}{101}$. Also, the density of $B$-sums if $\frac{2}{101}$. Moreover, as $n$ goes to infinity, the probability that $n$ is an $A$-sum approaches $\frac{2}{101}$ and the probability that $n$ is a $B$-sum approaches $\frac{2}{101}$. Thus, the density of numbers that are simultaneously $A$-sums and $B$-sums is $\frac{4}{101^{2}}$, so $E=\frac{101^{2}}{4}$.
We now add back the possibility that some of the $a_{i}$ and $b_{i}$ can be 0 . The only way this changes our answer is that the $s$ we seek can be 0 , which happens if and only if $a_{1}=b_{1}=0$. Thus our final answer is
$$
\frac{1}{101^{2}} \cdot 0+\frac{101^{2}-1}{101^{2}} \cdot \frac{101^{2}}{4}=\frac{101^{2}-1}{4}=2550
$$
|
{
"resource_path": "HarvardMIT/segmented/en-252-2022-feb-comb-solutions.jsonl",
"problem_match": "\n8. ",
"solution_match": "\nSolution: "
}
|
b7809ee9-866e-5cad-b9f7-60d86ae245dc
| 610,419
|
Consider permutations $\left(a_{0}, a_{1}, \ldots, a_{2022}\right)$ of $(0,1, \ldots, 2022)$ such that
- $a_{2022}=625$,
- for each $0 \leq i \leq 2022, a_{i} \geq \frac{625 i}{2022}$,
- for each $0 \leq i \leq 2022,\left\{a_{i}, \ldots, a_{2022}\right\}$ is a set of consecutive integers (in some order).
The number of such permutations can be written as $\frac{a!}{b!c!}$ for positive integers $a, b, c$, where $b>c$ and $a$ is minimal. Compute $100 a+10 b+c$.
|
Ignore the second condition for now. The permutations we seek are in bijection with the $\binom{2022}{625}$ ways to choose 625 indices $i \leq 2021$ so that $a_{i}<625$. These are in bijection with up-right lattice paths from $(0,0)$ to $(625,1397)$ in the following way: a step $(i, j) \rightarrow(i+1, j)$ indicates that $a_{i+j}=i$, while a step $(i, j) \rightarrow(i, j+1)$ indicates that $a_{i+j}=2022-j$.
Under this bijection, the second condition now becomes: for every right step $(i, j) \rightarrow(i+1, j)$, we have $i \geq \frac{625}{2022}(i+j)$, which is equivalent to $j \leq \frac{1397}{625} i$. In other words, we want to count the number of paths from $(0,0)$ to $(625,1397)$ that stay under the line $y=\frac{1397}{625} x$.
This can be counted via a standard shifting argument. Given a path from $(0,0)$ to $(625,1397)$, one can shift it by moving the first step to the end. We claim that exactly one of these cyclic shifts has the property of lying under the lines $y=\frac{1397}{625} x$. If we can show this, it follows that the answer is $\frac{2021!}{1397!625!}$, since, as $\operatorname{gcd}(2022,625)=1$, all the cyclic shifts are distinct. (It is true that the 2021 is minimal and that, given the numerator, the form of the denominator is unique. However, proving this is a bit annoying so we omit it here.)
To see that exactly one cyclic shift lies under the line, imagine extending a path infinitely in both directions in a periodic manner. A cyclic shift corresponds to taking a subset of this path between two points $P$ and $Q$ at distance 2022 along the path. Note that the condition of the path lying below the line corresponds to the infinite path lying below line $P Q$, so the unique $P, Q$ that satisfy this condition are those that lie on the highest line of slope $\frac{1397}{625}$ that touches the path. Since $\operatorname{gcd}(2022,625)=1$, these points are unique.
|
2021001397625
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Consider permutations $\left(a_{0}, a_{1}, \ldots, a_{2022}\right)$ of $(0,1, \ldots, 2022)$ such that
- $a_{2022}=625$,
- for each $0 \leq i \leq 2022, a_{i} \geq \frac{625 i}{2022}$,
- for each $0 \leq i \leq 2022,\left\{a_{i}, \ldots, a_{2022}\right\}$ is a set of consecutive integers (in some order).
The number of such permutations can be written as $\frac{a!}{b!c!}$ for positive integers $a, b, c$, where $b>c$ and $a$ is minimal. Compute $100 a+10 b+c$.
|
Ignore the second condition for now. The permutations we seek are in bijection with the $\binom{2022}{625}$ ways to choose 625 indices $i \leq 2021$ so that $a_{i}<625$. These are in bijection with up-right lattice paths from $(0,0)$ to $(625,1397)$ in the following way: a step $(i, j) \rightarrow(i+1, j)$ indicates that $a_{i+j}=i$, while a step $(i, j) \rightarrow(i, j+1)$ indicates that $a_{i+j}=2022-j$.
Under this bijection, the second condition now becomes: for every right step $(i, j) \rightarrow(i+1, j)$, we have $i \geq \frac{625}{2022}(i+j)$, which is equivalent to $j \leq \frac{1397}{625} i$. In other words, we want to count the number of paths from $(0,0)$ to $(625,1397)$ that stay under the line $y=\frac{1397}{625} x$.
This can be counted via a standard shifting argument. Given a path from $(0,0)$ to $(625,1397)$, one can shift it by moving the first step to the end. We claim that exactly one of these cyclic shifts has the property of lying under the lines $y=\frac{1397}{625} x$. If we can show this, it follows that the answer is $\frac{2021!}{1397!625!}$, since, as $\operatorname{gcd}(2022,625)=1$, all the cyclic shifts are distinct. (It is true that the 2021 is minimal and that, given the numerator, the form of the denominator is unique. However, proving this is a bit annoying so we omit it here.)
To see that exactly one cyclic shift lies under the line, imagine extending a path infinitely in both directions in a periodic manner. A cyclic shift corresponds to taking a subset of this path between two points $P$ and $Q$ at distance 2022 along the path. Note that the condition of the path lying below the line corresponds to the infinite path lying below line $P Q$, so the unique $P, Q$ that satisfy this condition are those that lie on the highest line of slope $\frac{1397}{625}$ that touches the path. Since $\operatorname{gcd}(2022,625)=1$, these points are unique.
|
{
"resource_path": "HarvardMIT/segmented/en-252-2022-feb-comb-solutions.jsonl",
"problem_match": "\n9. ",
"solution_match": "\nSolution: "
}
|
2977b678-6028-50e2-aae8-ae5ecd8807e3
| 610,420
|
Let $S$ be a set of size 11. A random 12 -tuple $\left(s_{1}, s_{2}, \ldots, s_{12}\right)$ of elements of $S$ is chosen uniformly at random. Moreover, let $\pi: S \rightarrow S$ be a permutation of $S$ chosen uniformly at random. The probability that $s_{i+1} \neq \pi\left(s_{i}\right)$ for all $1 \leq i \leq 12$ (where $s_{13}=s_{1}$ ) can be written as $\frac{a}{b}$ where $a$ and $b$ are relatively prime positive integers. Compute $a$.
|
Given a permutation $\pi$, let $\nu(\pi)$ be the number of fixed points of $\pi$. We claim that if we fix $\pi$, then the probability that the condition holds, over the randomness of $s_{i}$, is $\frac{10^{12}+\nu\left(\pi^{12}\right)-1}{11^{12}}$. Note that a point in $S$ is a fixed point of $\pi^{12}$ if and only if the length of its cycle in $\pi$ is $1,2,3,4$, or 6 , which happens with probability $\frac{5}{11}$, as each cycle length from 1 to 11 is equally likely. Therefore, the answer is
$$
\mathbb{E}_{\pi}\left[\frac{10^{12}+\nu\left(\pi^{12}\right)-1}{11^{12}}\right]=\frac{10^{12}+4}{11^{12}}
$$
Since 11 does not divide $10^{12}+4$ this fraction is simplified.
We now prove the claim. Instead of counting $\left(s_{1}, s_{2}, \ldots, s_{12}\right)$, we count tuples $\left(t_{1}, t_{2}, \ldots, t_{12}\right)$ so that $t_{i} \neq t_{i+1}$ for $1 \leq i \leq 11$ and $t_{1} \neq \pi^{12}\left(t_{12}\right)$. A bijection between the two is to let $t_{i}=\pi^{-i}\left(s_{i}\right)$. To do this, fix a $t_{1}$. If $t_{1}$ is a fixed point of $\pi^{12}$, we need to count the possibilities for $t_{2}, \ldots, t_{12}$ so that $t_{1} \neq t_{2}, t_{2} \neq t_{3}, \ldots, t_{12} \neq t_{1}$. This can be done via recursion: if $a_{k}$ is the number of $t_{2}, \ldots, t_{k+1}$ so that $t_{1} \neq t_{2}, t_{2} \neq t_{3}, \ldots, t_{k+1} \neq t_{1}$, then $a_{0}=0$, while for $n \geq 0$ we have $a_{n+1}=9 a_{n}+10\left(10^{n}-a_{n}\right)=$ $10^{n+1}-a_{n}$; thus $a_{11}=10^{11}-10^{10}+\cdots+10^{1}=\frac{1}{11}\left(10^{12}+10\right)$. Similarly, if $t_{1}$ is not a fixed point of $\pi^{12}$, there are $\frac{1}{11}\left(10^{12}-1\right)$ ways. Therefore, number of possible $\left(t_{1}, \ldots, t_{n}\right)$ is
$$
\frac{10^{12}}{11}\left(\nu\left(\pi^{12}\right)+\left(11-\nu\left(\pi^{12}\right)\right)\right)+\frac{1}{11}\left(10 \nu\left(\pi^{12}\right)-\left(11-\nu\left(\pi^{12}\right)\right)\right)=10^{12}+\nu\left(\pi^{12}\right)-1
$$
as desired.
|
10^{12}+4
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Let $S$ be a set of size 11. A random 12 -tuple $\left(s_{1}, s_{2}, \ldots, s_{12}\right)$ of elements of $S$ is chosen uniformly at random. Moreover, let $\pi: S \rightarrow S$ be a permutation of $S$ chosen uniformly at random. The probability that $s_{i+1} \neq \pi\left(s_{i}\right)$ for all $1 \leq i \leq 12$ (where $s_{13}=s_{1}$ ) can be written as $\frac{a}{b}$ where $a$ and $b$ are relatively prime positive integers. Compute $a$.
|
Given a permutation $\pi$, let $\nu(\pi)$ be the number of fixed points of $\pi$. We claim that if we fix $\pi$, then the probability that the condition holds, over the randomness of $s_{i}$, is $\frac{10^{12}+\nu\left(\pi^{12}\right)-1}{11^{12}}$. Note that a point in $S$ is a fixed point of $\pi^{12}$ if and only if the length of its cycle in $\pi$ is $1,2,3,4$, or 6 , which happens with probability $\frac{5}{11}$, as each cycle length from 1 to 11 is equally likely. Therefore, the answer is
$$
\mathbb{E}_{\pi}\left[\frac{10^{12}+\nu\left(\pi^{12}\right)-1}{11^{12}}\right]=\frac{10^{12}+4}{11^{12}}
$$
Since 11 does not divide $10^{12}+4$ this fraction is simplified.
We now prove the claim. Instead of counting $\left(s_{1}, s_{2}, \ldots, s_{12}\right)$, we count tuples $\left(t_{1}, t_{2}, \ldots, t_{12}\right)$ so that $t_{i} \neq t_{i+1}$ for $1 \leq i \leq 11$ and $t_{1} \neq \pi^{12}\left(t_{12}\right)$. A bijection between the two is to let $t_{i}=\pi^{-i}\left(s_{i}\right)$. To do this, fix a $t_{1}$. If $t_{1}$ is a fixed point of $\pi^{12}$, we need to count the possibilities for $t_{2}, \ldots, t_{12}$ so that $t_{1} \neq t_{2}, t_{2} \neq t_{3}, \ldots, t_{12} \neq t_{1}$. This can be done via recursion: if $a_{k}$ is the number of $t_{2}, \ldots, t_{k+1}$ so that $t_{1} \neq t_{2}, t_{2} \neq t_{3}, \ldots, t_{k+1} \neq t_{1}$, then $a_{0}=0$, while for $n \geq 0$ we have $a_{n+1}=9 a_{n}+10\left(10^{n}-a_{n}\right)=$ $10^{n+1}-a_{n}$; thus $a_{11}=10^{11}-10^{10}+\cdots+10^{1}=\frac{1}{11}\left(10^{12}+10\right)$. Similarly, if $t_{1}$ is not a fixed point of $\pi^{12}$, there are $\frac{1}{11}\left(10^{12}-1\right)$ ways. Therefore, number of possible $\left(t_{1}, \ldots, t_{n}\right)$ is
$$
\frac{10^{12}}{11}\left(\nu\left(\pi^{12}\right)+\left(11-\nu\left(\pi^{12}\right)\right)\right)+\frac{1}{11}\left(10 \nu\left(\pi^{12}\right)-\left(11-\nu\left(\pi^{12}\right)\right)\right)=10^{12}+\nu\left(\pi^{12}\right)-1
$$
as desired.
|
{
"resource_path": "HarvardMIT/segmented/en-252-2022-feb-comb-solutions.jsonl",
"problem_match": "\n10. ",
"solution_match": "\nSolution: "
}
|
96411776-972d-52a6-a389-9f2aac245445
| 610,421
|
Let $A B C$ be a triangle with $\angle A=60^{\circ}$. Line $\ell$ intersects segments $A B$ and $A C$ and splits triangle $A B C$ into an equilateral triangle and a quadrilateral. Let $X$ and $Y$ be on $\ell$ such that lines $B X$ and $C Y$ are perpendicular to $\ell$. Given that $A B=20$ and $A C=22$, compute $X Y$.
|
Let the intersection points of $\ell$ with $A B$ and $A C$ be $B^{\prime}$ and $C^{\prime}$. Note that $A B^{\prime}+A C^{\prime}=$ $2 B^{\prime} C^{\prime}, B B^{\prime}=2 X B^{\prime}$, and $C C^{\prime}=2 Y C^{\prime}$. Adding gives us
$$
A B+A C=A B^{\prime}+A C^{\prime}+B B^{\prime}+C C^{\prime}=2\left(B^{\prime} C^{\prime}+X B^{\prime}+Y C^{\prime}\right)=2 X Y
$$
Thus, $X Y=\frac{20+22}{2}=21$.
|
21
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $A B C$ be a triangle with $\angle A=60^{\circ}$. Line $\ell$ intersects segments $A B$ and $A C$ and splits triangle $A B C$ into an equilateral triangle and a quadrilateral. Let $X$ and $Y$ be on $\ell$ such that lines $B X$ and $C Y$ are perpendicular to $\ell$. Given that $A B=20$ and $A C=22$, compute $X Y$.
|
Let the intersection points of $\ell$ with $A B$ and $A C$ be $B^{\prime}$ and $C^{\prime}$. Note that $A B^{\prime}+A C^{\prime}=$ $2 B^{\prime} C^{\prime}, B B^{\prime}=2 X B^{\prime}$, and $C C^{\prime}=2 Y C^{\prime}$. Adding gives us
$$
A B+A C=A B^{\prime}+A C^{\prime}+B B^{\prime}+C C^{\prime}=2\left(B^{\prime} C^{\prime}+X B^{\prime}+Y C^{\prime}\right)=2 X Y
$$
Thus, $X Y=\frac{20+22}{2}=21$.
|
{
"resource_path": "HarvardMIT/segmented/en-252-2022-feb-geo-solutions.jsonl",
"problem_match": "\n1. ",
"solution_match": "\nSolution: "
}
|
0b32c6cc-d375-5ac6-881d-ad2af7baa21e
| 610,422
|
Rectangle $R_{0}$ has sides of lengths 3 and 4. Rectangles $R_{1}, R_{2}$, and $R_{3}$ are formed such that:
- all four rectangles share a common vertex $P$,
- for each $n=1,2,3$, one side of $R_{n}$ is a diagonal of $R_{n-1}$,
- for each $n=1,2,3$, the opposite side of $R_{n}$ passes through a vertex of $R_{n-1}$ such that the center of $R_{n}$ is located counterclockwise of the center of $R_{n-1}$ with respect to $P$.
Compute the total area covered by the union of the four rectangles.
|
Let $A B C D$ be $R_{0}$ such that $\overline{A B}=3$ and $\overline{B C}=4$. Then, let $\overline{A C}$ be a side length of $R_{1}$ and let the other two vertices be $E$ and $F$ such that $B$ lies on segment $E F$. Notice that the area of $\triangle A B C$ is both half of the area of $R_{0}$ and half of the area of $R_{1}$. This means forming $R_{1}$ adds half of the area of $R_{0}$ to the union of rectangles. Similarly, forming $R_{2}$ adds half of the area of $R_{1}$ to the union of all rectangles, and the same for $R_{3}$. This means the total area of the union of rectangles is given by
$$
\left[R_{0}\right]+\frac{1}{2}\left[R_{1}\right]+\frac{1}{2}\left[R_{2}\right]+\frac{1}{2}\left[R_{3}\right]=\left[R_{0}\right]+\frac{1}{2}\left[R_{0}\right]+\frac{1}{2}\left[R_{0}\right]+\frac{1}{2}\left[R_{0}\right]=\frac{5}{2}\left[R_{0}\right]=\frac{5}{2}(3 \cdot 4)=30
$$
Note that in the above equation, $[X]$ denotes the area of shape $X$.
|
30
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Rectangle $R_{0}$ has sides of lengths 3 and 4. Rectangles $R_{1}, R_{2}$, and $R_{3}$ are formed such that:
- all four rectangles share a common vertex $P$,
- for each $n=1,2,3$, one side of $R_{n}$ is a diagonal of $R_{n-1}$,
- for each $n=1,2,3$, the opposite side of $R_{n}$ passes through a vertex of $R_{n-1}$ such that the center of $R_{n}$ is located counterclockwise of the center of $R_{n-1}$ with respect to $P$.

Compute the total area covered by the union of the four rectangles.
|
Let $A B C D$ be $R_{0}$ such that $\overline{A B}=3$ and $\overline{B C}=4$. Then, let $\overline{A C}$ be a side length of $R_{1}$ and let the other two vertices be $E$ and $F$ such that $B$ lies on segment $E F$. Notice that the area of $\triangle A B C$ is both half of the area of $R_{0}$ and half of the area of $R_{1}$. This means forming $R_{1}$ adds half of the area of $R_{0}$ to the union of rectangles. Similarly, forming $R_{2}$ adds half of the area of $R_{1}$ to the union of all rectangles, and the same for $R_{3}$. This means the total area of the union of rectangles is given by
$$
\left[R_{0}\right]+\frac{1}{2}\left[R_{1}\right]+\frac{1}{2}\left[R_{2}\right]+\frac{1}{2}\left[R_{3}\right]=\left[R_{0}\right]+\frac{1}{2}\left[R_{0}\right]+\frac{1}{2}\left[R_{0}\right]+\frac{1}{2}\left[R_{0}\right]=\frac{5}{2}\left[R_{0}\right]=\frac{5}{2}(3 \cdot 4)=30
$$
Note that in the above equation, $[X]$ denotes the area of shape $X$.
|
{
"resource_path": "HarvardMIT/segmented/en-252-2022-feb-geo-solutions.jsonl",
"problem_match": "\n2. ",
"solution_match": "\nSolution: "
}
|
d59e9e26-0b81-5fc5-a621-f0e6844d9783
| 610,423
|
Let $A B C D$ and $A E F G$ be unit squares such that the area of their intersection is $\frac{20}{21}$. Given that $\angle B A E<45^{\circ}, \tan \angle B A E$ can be expressed as $\frac{a}{b}$ for relatively prime positive integers $a$ and $b$. Compute $100 a+b$.
|
Suppose the two squares intersect at a point $X \neq A$. If $\mathcal{S}$ is the region formed by the intersection of the squares, note that line $A X$ splits $\mathcal{S}$ into two congruent pieces of area $\frac{10}{21}$. Each of these pieces is a right triangle with one leg of length 1 , so the other leg must have length $\frac{20}{21}$. Thus, if the two squares are displaced by an angle of $\theta$, then $90-\theta=2 \arctan \frac{20}{21}$. Though there is some ambiguity in how the points are labeled, the fact that $\angle B A F<45^{\circ}$ tells us that $\angle B A F=\theta$. Therefore
$$
\tan \angle B A F=\frac{1}{\tan \left(2 \arctan \frac{20}{21}\right)}=\frac{1-\frac{20^{2}}{21^{2}}}{2 \cdot \frac{20}{21}}=\frac{41}{840} .
$$
|
4101
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $A B C D$ and $A E F G$ be unit squares such that the area of their intersection is $\frac{20}{21}$. Given that $\angle B A E<45^{\circ}, \tan \angle B A E$ can be expressed as $\frac{a}{b}$ for relatively prime positive integers $a$ and $b$. Compute $100 a+b$.
|
Suppose the two squares intersect at a point $X \neq A$. If $\mathcal{S}$ is the region formed by the intersection of the squares, note that line $A X$ splits $\mathcal{S}$ into two congruent pieces of area $\frac{10}{21}$. Each of these pieces is a right triangle with one leg of length 1 , so the other leg must have length $\frac{20}{21}$. Thus, if the two squares are displaced by an angle of $\theta$, then $90-\theta=2 \arctan \frac{20}{21}$. Though there is some ambiguity in how the points are labeled, the fact that $\angle B A F<45^{\circ}$ tells us that $\angle B A F=\theta$. Therefore
$$
\tan \angle B A F=\frac{1}{\tan \left(2 \arctan \frac{20}{21}\right)}=\frac{1-\frac{20^{2}}{21^{2}}}{2 \cdot \frac{20}{21}}=\frac{41}{840} .
$$
|
{
"resource_path": "HarvardMIT/segmented/en-252-2022-feb-geo-solutions.jsonl",
"problem_match": "\n3. ",
"solution_match": "\nSolution: "
}
|
7489ff70-160e-590a-9e2d-14f2ca88dbb1
| 610,424
|
Parallel lines $\ell_{1}, \ell_{2}, \ell_{3}, \ell_{4}$ are evenly spaced in the plane, in that order. Square $A B C D$ has the property that $A$ lies on $\ell_{1}$ and $C$ lies on $\ell_{4}$. Let $P$ be a uniformly random point in the interior of $A B C D$ and let $Q$ be a uniformly random point on the perimeter of $A B C D$. Given that the probability that $P$ lies between $\ell_{2}$ and $\ell_{3}$ is $\frac{53}{100}$, the probability that $Q$ lies between $\ell_{2}$ and $\ell_{3}$ can be expressed as $\frac{a}{b}$, where $a$ and $b$ are relatively prime positive integers. Compute $100 a+b$.
|
The first thing to note is that the area of $A B C D$ does not matter in this problem, so for the sake of convenience, introduce coordinates so that $A=(0,0), B=(1,0)$, and $C=(0,1)$.
Suppose $A$ and $B$ lie on the same side of $\ell_{2}$. Then, by symmetry, $C$ and $D$ lie on the same side of $\ell_{3}$. Now suppose $B C$ intersects $\ell_{2}$ and $\ell_{3}$ at $X$ and $Y$, respectively, and that $D A$ intersects $\ell_{2}$ and $\ell_{3}$ at $U$ and $V$, respectively. Note that $X Y V U$ is a parallelogram. Since $B C=B X+X Y+Y C=B X+2 X Y>2 X Y$, we have that $X Y$ is less than half the side length of the square, so the area of $X Y V U$ is at most half of the area of square $A B C D$. However, since $0.53>\frac{1}{2}$, this can't happen. Similar reasoning applies if $B$ and $C$ lie on the same side of $\ell_{3}$. Therefore, points $B$ and $D$ lie between $\ell_{2}$ and $\ell_{3}$.
Let $A B$ and $A D$ intersect $\ell_{2}$ at points $M$ and $N$, respectively. Let $r=A M$ and $s=A N$. By symmetry, $[A M N]=0.235$, so $r s=0.47$. Additionally, in coordinates line $\ell_{2}$ is just $\frac{x}{r}+\frac{y}{s}=1$. Therefore line $\ell_{4}$ is given by $\frac{x}{r}+\frac{y}{s}=3$. Since $C=(1,1)$ lies on this line, $\frac{1}{r}+\frac{1}{s}=3$.
The answer that we want is
$$
1-\frac{2 r+2 s}{4}=1-\frac{r+s}{2}
$$
On the other hand, the condition $\frac{1}{r}+\frac{1}{s}=3$ rearranges to $3 r s=r+s$, so $r+s=1.41$. Thus the answer is $1-\frac{1.41}{2}=0.295=\frac{59}{200}$.
|
\frac{59}{200}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Parallel lines $\ell_{1}, \ell_{2}, \ell_{3}, \ell_{4}$ are evenly spaced in the plane, in that order. Square $A B C D$ has the property that $A$ lies on $\ell_{1}$ and $C$ lies on $\ell_{4}$. Let $P$ be a uniformly random point in the interior of $A B C D$ and let $Q$ be a uniformly random point on the perimeter of $A B C D$. Given that the probability that $P$ lies between $\ell_{2}$ and $\ell_{3}$ is $\frac{53}{100}$, the probability that $Q$ lies between $\ell_{2}$ and $\ell_{3}$ can be expressed as $\frac{a}{b}$, where $a$ and $b$ are relatively prime positive integers. Compute $100 a+b$.
|
The first thing to note is that the area of $A B C D$ does not matter in this problem, so for the sake of convenience, introduce coordinates so that $A=(0,0), B=(1,0)$, and $C=(0,1)$.
Suppose $A$ and $B$ lie on the same side of $\ell_{2}$. Then, by symmetry, $C$ and $D$ lie on the same side of $\ell_{3}$. Now suppose $B C$ intersects $\ell_{2}$ and $\ell_{3}$ at $X$ and $Y$, respectively, and that $D A$ intersects $\ell_{2}$ and $\ell_{3}$ at $U$ and $V$, respectively. Note that $X Y V U$ is a parallelogram. Since $B C=B X+X Y+Y C=B X+2 X Y>2 X Y$, we have that $X Y$ is less than half the side length of the square, so the area of $X Y V U$ is at most half of the area of square $A B C D$. However, since $0.53>\frac{1}{2}$, this can't happen. Similar reasoning applies if $B$ and $C$ lie on the same side of $\ell_{3}$. Therefore, points $B$ and $D$ lie between $\ell_{2}$ and $\ell_{3}$.
Let $A B$ and $A D$ intersect $\ell_{2}$ at points $M$ and $N$, respectively. Let $r=A M$ and $s=A N$. By symmetry, $[A M N]=0.235$, so $r s=0.47$. Additionally, in coordinates line $\ell_{2}$ is just $\frac{x}{r}+\frac{y}{s}=1$. Therefore line $\ell_{4}$ is given by $\frac{x}{r}+\frac{y}{s}=3$. Since $C=(1,1)$ lies on this line, $\frac{1}{r}+\frac{1}{s}=3$.
The answer that we want is
$$
1-\frac{2 r+2 s}{4}=1-\frac{r+s}{2}
$$
On the other hand, the condition $\frac{1}{r}+\frac{1}{s}=3$ rearranges to $3 r s=r+s$, so $r+s=1.41$. Thus the answer is $1-\frac{1.41}{2}=0.295=\frac{59}{200}$.
|
{
"resource_path": "HarvardMIT/segmented/en-252-2022-feb-geo-solutions.jsonl",
"problem_match": "\n4. ",
"solution_match": "\nSolution: "
}
|
89d0f50d-f43d-5f83-9d10-ed9f9d14e611
| 610,425
|
Let triangle $A B C$ be such that $A B=A C=22$ and $B C=11$. Point $D$ is chosen in the interior of the triangle such that $A D=19$ and $\angle A B D+\angle A C D=90^{\circ}$. The value of $B D^{2}+C D^{2}$ can be expressed as $\frac{a}{b}$, where $a$ and $b$ are relatively prime positive integers. Compute $100 a+b$.
|
Rotate triangle $A B D$ about $A$ so that $B$ coincides with $C$. Let $D$ map to $D^{\prime}$ under this. Note that $C D D^{\prime}$ is a right triangle with right angle at $C$. Also, note that $A D D^{\prime}$ is similar to $A B C$. Thus, we have $D D^{\prime}=\frac{A D}{2}=\frac{19}{2}$. Finally, note that
$$
B D^{2}+C D^{2}=C D^{\prime 2}+C D^{2}=D D^{\prime 2}=\frac{361}{4}
$$
|
9025
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let triangle $A B C$ be such that $A B=A C=22$ and $B C=11$. Point $D$ is chosen in the interior of the triangle such that $A D=19$ and $\angle A B D+\angle A C D=90^{\circ}$. The value of $B D^{2}+C D^{2}$ can be expressed as $\frac{a}{b}$, where $a$ and $b$ are relatively prime positive integers. Compute $100 a+b$.
|
Rotate triangle $A B D$ about $A$ so that $B$ coincides with $C$. Let $D$ map to $D^{\prime}$ under this. Note that $C D D^{\prime}$ is a right triangle with right angle at $C$. Also, note that $A D D^{\prime}$ is similar to $A B C$. Thus, we have $D D^{\prime}=\frac{A D}{2}=\frac{19}{2}$. Finally, note that
$$
B D^{2}+C D^{2}=C D^{\prime 2}+C D^{2}=D D^{\prime 2}=\frac{361}{4}
$$
|
{
"resource_path": "HarvardMIT/segmented/en-252-2022-feb-geo-solutions.jsonl",
"problem_match": "\n5. ",
"solution_match": "\nSolution: "
}
|
ddcd6546-e23c-592b-8967-b91b41c52bae
| 610,426
|
Let $A B C D$ be a rectangle inscribed in circle $\Gamma$, and let $P$ be a point on minor arc $A B$ of $\Gamma$. Suppose that $P A \cdot P B=2, P C \cdot P D=18$, and $P B \cdot P C=9$. The area of rectangle $A B C D$ can be expressed as $\frac{a \sqrt{b}}{c}$, where $a$ and $c$ are relatively prime positive integers and $b$ is a squarefree positive integer. Compute $100 a+10 b+c$.
|
We have
$$
P D \cdot P A=\frac{(P A \cdot P B)(P D \cdot P C)}{(P B \cdot P C)}=\frac{2 \cdot 18}{9}=4
$$
Let $\alpha=\angle D P C=180^{\circ}-\angle A P B$ and $\beta=\angle A P D=\angle B P C$. Note that $\alpha+\beta=90^{\circ}$. We have, letting $x=A B=C D$ and $y=A D=B C$,
$$
2[P A D]+2[P B C]=y(d(P, A D)+d(P, B C))=y \cdot x=[A B C D]
$$
Here $d(X, \ell)$ is used to denote the distance from $X$ to line $\ell$. By the trig area formula, the left-hand side is
$$
P A \cdot P D \cdot \sin \beta+P B \cdot P C \cdot \sin \beta=13 \sin \beta
$$
Similarly, we have $[A B C D]=16 \sin \alpha$. Thus, letting $K=[A B C D]$,
$$
1=\sin ^{2} \alpha+\sin ^{2} \beta=\frac{K^{2}}{13^{2}}+\frac{K^{2}}{16^{2}}=\frac{425}{13^{2} \cdot 16^{2}} K^{2}
$$
giving $K=\frac{208}{\sqrt{425}}=\frac{208 \sqrt{17}}{85}$.
|
20801785
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $A B C D$ be a rectangle inscribed in circle $\Gamma$, and let $P$ be a point on minor arc $A B$ of $\Gamma$. Suppose that $P A \cdot P B=2, P C \cdot P D=18$, and $P B \cdot P C=9$. The area of rectangle $A B C D$ can be expressed as $\frac{a \sqrt{b}}{c}$, where $a$ and $c$ are relatively prime positive integers and $b$ is a squarefree positive integer. Compute $100 a+10 b+c$.
|
We have
$$
P D \cdot P A=\frac{(P A \cdot P B)(P D \cdot P C)}{(P B \cdot P C)}=\frac{2 \cdot 18}{9}=4
$$
Let $\alpha=\angle D P C=180^{\circ}-\angle A P B$ and $\beta=\angle A P D=\angle B P C$. Note that $\alpha+\beta=90^{\circ}$. We have, letting $x=A B=C D$ and $y=A D=B C$,
$$
2[P A D]+2[P B C]=y(d(P, A D)+d(P, B C))=y \cdot x=[A B C D]
$$
Here $d(X, \ell)$ is used to denote the distance from $X$ to line $\ell$. By the trig area formula, the left-hand side is
$$
P A \cdot P D \cdot \sin \beta+P B \cdot P C \cdot \sin \beta=13 \sin \beta
$$
Similarly, we have $[A B C D]=16 \sin \alpha$. Thus, letting $K=[A B C D]$,
$$
1=\sin ^{2} \alpha+\sin ^{2} \beta=\frac{K^{2}}{13^{2}}+\frac{K^{2}}{16^{2}}=\frac{425}{13^{2} \cdot 16^{2}} K^{2}
$$
giving $K=\frac{208}{\sqrt{425}}=\frac{208 \sqrt{17}}{85}$.
|
{
"resource_path": "HarvardMIT/segmented/en-252-2022-feb-geo-solutions.jsonl",
"problem_match": "\n6. ",
"solution_match": "\nSolution: "
}
|
10ff8d80-c286-5df1-87e2-b894ea6fdea1
| 610,427
|
Point $P$ is located inside a square $A B C D$ of side length 10. Let $O_{1}, O_{2}, O_{3}, O_{4}$ be the circumcenters of $P A B, P B C, P C D$, and $P D A$, respectively. Given that $P A+P B+P C+P D=23 \sqrt{2}$ and the area of $O_{1} O_{2} O_{3} O_{4}$ is 50 , the second largest of the lengths $O_{1} O_{2}, O_{2} O_{3}, O_{3} O_{4}, O_{4} O_{1}$ can be written as $\sqrt{\frac{a}{b}}$, where $a$ and $b$ are relatively prime positive integers. Compute $100 a+b$.
|
Note that $O_{1} O_{3}$ and $O_{2} O_{4}$ are perpendicular and intersect at $O$, the center of square $A B C D$. Also note that $O_{1} O_{2}, O_{2} O_{3}, O_{3} O_{4}, O_{4} O_{1}$ are the perpendiculars of $P B, P C, P D, P A$, respectively. Let $d_{1}=O O_{1}, d_{2}=O O_{2}, d_{3}=O O_{3}$, and $d_{4}=O O_{4}$. Note that that since the area of $O_{1} O_{2} O_{3} O_{4}=50$, we have that $\left(d_{1}+d_{3}\right)\left(d_{2}+d_{4}\right)=100$. Also note that the area of octagon $A O_{1} B O_{2} C O_{3} D O_{4}$ is twice the area of $O_{1} O_{2} O_{3} O_{4}$, which is the same as the area of $A B C D$. Note that the difference between the area of this octagon and $A B C D$ is $\frac{1}{2} \cdot 10\left[\left(d_{1}-5\right)+\left(d_{2}-5\right)+\left(d_{3}-5\right)+\left(d_{4}-5\right)\right]$. Since this must equal 0 , we have $d_{1}+d_{2}+d_{3}+d_{4}=20$. Combining this with the fact that $\left(d_{1}+d_{3}\right)\left(d_{2}+d_{4}\right)=100$ gives us $d_{1}+d_{3}=d_{2}+d_{4}=10$, so $O_{1} O_{3}=O_{2} O_{4}=10$. Note that if we translate $A B$ by 10 to coincide with $D C$, then $O_{1}$ would coincide with $O_{3}$, and thus if $P$ translates to $P^{\prime}$, then $P C P^{\prime} D$ is cyclic. In other words, we have $\angle A P B$ and $\angle C P D$ are supplementary.
Fix any $\alpha \in\left(0^{\circ}, 180^{\circ}\right)$. There are at most two points $P$ in $A B C D$ such that $\angle A P B=\alpha$ and $\angle C P D=180^{\circ}-\alpha$ (two circular arcs intersect at most twice). Let $P^{\prime}$ denote the unique point on $A C$ such that $\angle A P^{\prime} B=\alpha$, and let $P^{*}$ denote the unique point on $B D$ such that $\angle A P^{*} B=\alpha$. Note that it is not hard to see that in we have $\angle C P^{\prime} D=\angle C P^{*} D=180^{\circ}-\alpha$. Thus, we have $P=P^{\prime}$ or $P=P^{*}$, so $P$ must lie on one of the diagonals. Without loss of generality, assume $P=P^{\prime}(P$ is on $A C)$. Note that $O_{1} O_{2} O_{3} O_{4}$ is an isosceles trapezoid with bases $O_{1} O_{4}$ and $O_{2} O_{3}$. Additionally, the height of the trapezoid is $\frac{A C}{2}=5 \sqrt{2}$. Since the area of trapezoid is $O_{1} O_{2} O_{3} O_{4}$, we have the midlength of the
trapezoid is $\frac{50}{5 \sqrt{2}}=5 \sqrt{2}$. Additionally, note that $\angle P O_{1} B=2 \angle P A B=90^{\circ}$. Similarly $\angle P O_{2} B=90^{\circ}$. Combining this with the fact that $O_{1} O_{2}$ perpendicular bisects $P B$, we get that $P O_{1} B O_{2}$ is a square, so $O_{1} O_{2}=P B=\frac{23 \sqrt{2}-10 \sqrt{2}}{2}=\frac{13 \sqrt{2}}{2}=\sqrt{\frac{169}{2}}$. Since this is the second largest side of $O_{1} O_{2} O_{3} O_{4}$, we are done.
|
16902
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Point $P$ is located inside a square $A B C D$ of side length 10. Let $O_{1}, O_{2}, O_{3}, O_{4}$ be the circumcenters of $P A B, P B C, P C D$, and $P D A$, respectively. Given that $P A+P B+P C+P D=23 \sqrt{2}$ and the area of $O_{1} O_{2} O_{3} O_{4}$ is 50 , the second largest of the lengths $O_{1} O_{2}, O_{2} O_{3}, O_{3} O_{4}, O_{4} O_{1}$ can be written as $\sqrt{\frac{a}{b}}$, where $a$ and $b$ are relatively prime positive integers. Compute $100 a+b$.
|
Note that $O_{1} O_{3}$ and $O_{2} O_{4}$ are perpendicular and intersect at $O$, the center of square $A B C D$. Also note that $O_{1} O_{2}, O_{2} O_{3}, O_{3} O_{4}, O_{4} O_{1}$ are the perpendiculars of $P B, P C, P D, P A$, respectively. Let $d_{1}=O O_{1}, d_{2}=O O_{2}, d_{3}=O O_{3}$, and $d_{4}=O O_{4}$. Note that that since the area of $O_{1} O_{2} O_{3} O_{4}=50$, we have that $\left(d_{1}+d_{3}\right)\left(d_{2}+d_{4}\right)=100$. Also note that the area of octagon $A O_{1} B O_{2} C O_{3} D O_{4}$ is twice the area of $O_{1} O_{2} O_{3} O_{4}$, which is the same as the area of $A B C D$. Note that the difference between the area of this octagon and $A B C D$ is $\frac{1}{2} \cdot 10\left[\left(d_{1}-5\right)+\left(d_{2}-5\right)+\left(d_{3}-5\right)+\left(d_{4}-5\right)\right]$. Since this must equal 0 , we have $d_{1}+d_{2}+d_{3}+d_{4}=20$. Combining this with the fact that $\left(d_{1}+d_{3}\right)\left(d_{2}+d_{4}\right)=100$ gives us $d_{1}+d_{3}=d_{2}+d_{4}=10$, so $O_{1} O_{3}=O_{2} O_{4}=10$. Note that if we translate $A B$ by 10 to coincide with $D C$, then $O_{1}$ would coincide with $O_{3}$, and thus if $P$ translates to $P^{\prime}$, then $P C P^{\prime} D$ is cyclic. In other words, we have $\angle A P B$ and $\angle C P D$ are supplementary.
Fix any $\alpha \in\left(0^{\circ}, 180^{\circ}\right)$. There are at most two points $P$ in $A B C D$ such that $\angle A P B=\alpha$ and $\angle C P D=180^{\circ}-\alpha$ (two circular arcs intersect at most twice). Let $P^{\prime}$ denote the unique point on $A C$ such that $\angle A P^{\prime} B=\alpha$, and let $P^{*}$ denote the unique point on $B D$ such that $\angle A P^{*} B=\alpha$. Note that it is not hard to see that in we have $\angle C P^{\prime} D=\angle C P^{*} D=180^{\circ}-\alpha$. Thus, we have $P=P^{\prime}$ or $P=P^{*}$, so $P$ must lie on one of the diagonals. Without loss of generality, assume $P=P^{\prime}(P$ is on $A C)$. Note that $O_{1} O_{2} O_{3} O_{4}$ is an isosceles trapezoid with bases $O_{1} O_{4}$ and $O_{2} O_{3}$. Additionally, the height of the trapezoid is $\frac{A C}{2}=5 \sqrt{2}$. Since the area of trapezoid is $O_{1} O_{2} O_{3} O_{4}$, we have the midlength of the
trapezoid is $\frac{50}{5 \sqrt{2}}=5 \sqrt{2}$. Additionally, note that $\angle P O_{1} B=2 \angle P A B=90^{\circ}$. Similarly $\angle P O_{2} B=90^{\circ}$. Combining this with the fact that $O_{1} O_{2}$ perpendicular bisects $P B$, we get that $P O_{1} B O_{2}$ is a square, so $O_{1} O_{2}=P B=\frac{23 \sqrt{2}-10 \sqrt{2}}{2}=\frac{13 \sqrt{2}}{2}=\sqrt{\frac{169}{2}}$. Since this is the second largest side of $O_{1} O_{2} O_{3} O_{4}$, we are done.
|
{
"resource_path": "HarvardMIT/segmented/en-252-2022-feb-geo-solutions.jsonl",
"problem_match": "\n7. ",
"solution_match": "\nSolution: "
}
|
d7833adb-8929-5b96-9da0-a57f4de9cf38
| 610,428
|
Let $\mathcal{E}$ be an ellipse with foci $A$ and $B$. Suppose there exists a parabola $\mathcal{P}$ such that
- $\mathcal{P}$ passes through $A$ and $B$,
- the focus $F$ of $\mathcal{P}$ lies on $\mathcal{E}$,
- the orthocenter $H$ of $\triangle F A B$ lies on the directrix of $\mathcal{P}$.
If the major and minor axes of $\mathcal{E}$ have lengths 50 and 14 , respectively, compute $A H^{2}+B H^{2}$.
|
Let $D$ and $E$ be the projections of $A$ and $B$ onto the directrix of $\mathcal{P}$, respectively. Also, let $\omega_{A}$ be the circle centered at $A$ with radius $A D=A F$, and define $\omega_{B}$ similarly.
If $M$ is the midpoint of $\overline{D E}$, then $M$ lies on the radical axis of $\omega_{A}$ and $\omega_{B}$ since $M D^{2}=M E^{2}$. Since $F$ lies on both $\omega_{A}$ and $\omega_{B}$, it follows that $M F$ is the radical axis of the two circles. Moreover, $M F \perp A B$, so we must have $M=H$.
Let $N$ be the midpoint of $\overline{A B}$. We compute that $A D+B E=A F+F B=50$, so $H N=\frac{1}{2}(A D+B E)=$ 25. Since $A B=2 \sqrt{25^{2}-7^{2}}=48$, we have
$$
\begin{aligned}
25^{2}=H N^{2} & =\frac{1}{2}\left(A H^{2}+B H^{2}\right)-\frac{1}{4} A B^{2} \\
& =\frac{1}{2}\left(A H^{2}+B H^{2}\right)-24^{2} .
\end{aligned}
$$
by the median lengtb formula. Thus $A H^{2}+B H^{2}=2\left(25^{2}+24^{2}\right)=2402$.
|
2402
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $\mathcal{E}$ be an ellipse with foci $A$ and $B$. Suppose there exists a parabola $\mathcal{P}$ such that
- $\mathcal{P}$ passes through $A$ and $B$,
- the focus $F$ of $\mathcal{P}$ lies on $\mathcal{E}$,
- the orthocenter $H$ of $\triangle F A B$ lies on the directrix of $\mathcal{P}$.
If the major and minor axes of $\mathcal{E}$ have lengths 50 and 14 , respectively, compute $A H^{2}+B H^{2}$.
|
Let $D$ and $E$ be the projections of $A$ and $B$ onto the directrix of $\mathcal{P}$, respectively. Also, let $\omega_{A}$ be the circle centered at $A$ with radius $A D=A F$, and define $\omega_{B}$ similarly.
If $M$ is the midpoint of $\overline{D E}$, then $M$ lies on the radical axis of $\omega_{A}$ and $\omega_{B}$ since $M D^{2}=M E^{2}$. Since $F$ lies on both $\omega_{A}$ and $\omega_{B}$, it follows that $M F$ is the radical axis of the two circles. Moreover, $M F \perp A B$, so we must have $M=H$.
Let $N$ be the midpoint of $\overline{A B}$. We compute that $A D+B E=A F+F B=50$, so $H N=\frac{1}{2}(A D+B E)=$ 25. Since $A B=2 \sqrt{25^{2}-7^{2}}=48$, we have
$$
\begin{aligned}
25^{2}=H N^{2} & =\frac{1}{2}\left(A H^{2}+B H^{2}\right)-\frac{1}{4} A B^{2} \\
& =\frac{1}{2}\left(A H^{2}+B H^{2}\right)-24^{2} .
\end{aligned}
$$
by the median lengtb formula. Thus $A H^{2}+B H^{2}=2\left(25^{2}+24^{2}\right)=2402$.
|
{
"resource_path": "HarvardMIT/segmented/en-252-2022-feb-geo-solutions.jsonl",
"problem_match": "\n8. ",
"solution_match": "\nSolution: "
}
|
a107af18-771d-52a4-a377-a8a7bb5a606c
| 610,429
|
Let $A_{1} B_{1} C_{1}, A_{2} B_{2} C_{2}$, and $A_{3} B_{3} C_{3}$ be three triangles in the plane. For $1 \leq i \leq 3$, let $D_{i}, E_{i}$, and $F_{i}$ be the midpoints of $B_{i} C_{i}, A_{i} C_{i}$, and $A_{i} B_{i}$, respectively. Furthermore, for $1 \leq i \leq 3$ let $G_{i}$ be the centroid of $A_{i} B_{i} C_{i}$.
Suppose that the areas of the triangles $A_{1} A_{2} A_{3}, B_{1} B_{2} B_{3}, C_{1} C_{2} C_{3}, D_{1} D_{2} D_{3}, E_{1} E_{2} E_{3}$, and $F_{1} F_{2} F_{3}$ are $2,3,4,20,21$, and 2020, respectively. Compute the largest possible area of $G_{1} G_{2} G_{3}$.
|
Let $P_{i}(x, y, z)$ be the point with barycentric coordinates $(x, y, z)$ in triangle $A_{i} B_{i} C_{i}$. Note that since this is linear in $x, y$, and $z$, the signed area of triangle $P_{1}(x, y, z) P_{2}(x, y, z) P_{3}(x, y, z)$ is a homogenous quadratic polynomial in $x, y$, and $z$; call it $f(x, y, z)$.
We now claim that
$$
f\left(\frac{1}{3}, \frac{1}{3}, \frac{1}{3}\right)=\frac{4 f\left(\frac{1}{2}, \frac{1}{2}, 0\right)+4 f\left(\frac{1}{2}, 0, \frac{1}{2}\right)+4 f\left(0, \frac{1}{2}, \frac{1}{2}\right)-f(1,0,0)-f(0,1,0)-f(0,0,1)}{9}
$$
This is easy to verify for $f \in\left\{x^{2}, y^{2}, z^{2}, x y, x z, y z\right\}$, after which the statement follows for general $f$ by linearity. Then, assuming that we can arbitrarily choose the signs of the areas, the area is maximized at
$$
\frac{4 \cdot 2061+9}{9}=229 \cdot 4+1=917
$$
Now it remains to show that this best-case scenario is actually possible. The first step is to first show that these values from an actual $f$, i.e. that one can fit a homogenous quadratic polynomial through
every six possible values for $f$ at the six given points. One way to see this is to note that by choosing the coefficients for $x^{2}, y^{2}$, and $z^{2}$, the values at the vertices of the triangle can be matched, while adding any of the $x y, x z$, and $y z$ terms influences only one of the midpoints, so they can be matched as well.
Now we show that this particular $f$ can be realized by a choice of triangles. To do this, note that by continuity there must exist $x_{0}, y_{0}$, and $z_{0}$ with $f\left(x_{0}, y_{0}, z_{0}\right)=0$, since $f(1,0,0)$ and $f\left(\frac{1}{2}, \frac{1}{2}, 0\right)$ are different signs, and introduce the new coordinates $u=x-x_{0}$ and $v=y-y_{0}$; then $f$ can be written as $a u^{2}+b u v+c v^{2}+d u+e v$. Now, one can let $P_{1}(u, v)=(0,0), P_{2}(u, v)=(u, v)$, and $P_{3}(u, v)=(-c v-e, a u+b v+d)$. This can be shown to reproduce the desired $f$.
Finally, to address the condition that the original triangles must be nondegenerate, we can perturb each of the $P_{i}$ by a constant, which doesn't affect $f$ as areas are translation-invariant. This concludes the proof.
|
917
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $A_{1} B_{1} C_{1}, A_{2} B_{2} C_{2}$, and $A_{3} B_{3} C_{3}$ be three triangles in the plane. For $1 \leq i \leq 3$, let $D_{i}, E_{i}$, and $F_{i}$ be the midpoints of $B_{i} C_{i}, A_{i} C_{i}$, and $A_{i} B_{i}$, respectively. Furthermore, for $1 \leq i \leq 3$ let $G_{i}$ be the centroid of $A_{i} B_{i} C_{i}$.
Suppose that the areas of the triangles $A_{1} A_{2} A_{3}, B_{1} B_{2} B_{3}, C_{1} C_{2} C_{3}, D_{1} D_{2} D_{3}, E_{1} E_{2} E_{3}$, and $F_{1} F_{2} F_{3}$ are $2,3,4,20,21$, and 2020, respectively. Compute the largest possible area of $G_{1} G_{2} G_{3}$.
|
Let $P_{i}(x, y, z)$ be the point with barycentric coordinates $(x, y, z)$ in triangle $A_{i} B_{i} C_{i}$. Note that since this is linear in $x, y$, and $z$, the signed area of triangle $P_{1}(x, y, z) P_{2}(x, y, z) P_{3}(x, y, z)$ is a homogenous quadratic polynomial in $x, y$, and $z$; call it $f(x, y, z)$.
We now claim that
$$
f\left(\frac{1}{3}, \frac{1}{3}, \frac{1}{3}\right)=\frac{4 f\left(\frac{1}{2}, \frac{1}{2}, 0\right)+4 f\left(\frac{1}{2}, 0, \frac{1}{2}\right)+4 f\left(0, \frac{1}{2}, \frac{1}{2}\right)-f(1,0,0)-f(0,1,0)-f(0,0,1)}{9}
$$
This is easy to verify for $f \in\left\{x^{2}, y^{2}, z^{2}, x y, x z, y z\right\}$, after which the statement follows for general $f$ by linearity. Then, assuming that we can arbitrarily choose the signs of the areas, the area is maximized at
$$
\frac{4 \cdot 2061+9}{9}=229 \cdot 4+1=917
$$
Now it remains to show that this best-case scenario is actually possible. The first step is to first show that these values from an actual $f$, i.e. that one can fit a homogenous quadratic polynomial through
every six possible values for $f$ at the six given points. One way to see this is to note that by choosing the coefficients for $x^{2}, y^{2}$, and $z^{2}$, the values at the vertices of the triangle can be matched, while adding any of the $x y, x z$, and $y z$ terms influences only one of the midpoints, so they can be matched as well.
Now we show that this particular $f$ can be realized by a choice of triangles. To do this, note that by continuity there must exist $x_{0}, y_{0}$, and $z_{0}$ with $f\left(x_{0}, y_{0}, z_{0}\right)=0$, since $f(1,0,0)$ and $f\left(\frac{1}{2}, \frac{1}{2}, 0\right)$ are different signs, and introduce the new coordinates $u=x-x_{0}$ and $v=y-y_{0}$; then $f$ can be written as $a u^{2}+b u v+c v^{2}+d u+e v$. Now, one can let $P_{1}(u, v)=(0,0), P_{2}(u, v)=(u, v)$, and $P_{3}(u, v)=(-c v-e, a u+b v+d)$. This can be shown to reproduce the desired $f$.
Finally, to address the condition that the original triangles must be nondegenerate, we can perturb each of the $P_{i}$ by a constant, which doesn't affect $f$ as areas are translation-invariant. This concludes the proof.
|
{
"resource_path": "HarvardMIT/segmented/en-252-2022-feb-geo-solutions.jsonl",
"problem_match": "\n9. ",
"solution_match": "\nSolution: "
}
|
b1908ffc-96f7-5989-835d-2809c95f459b
| 610,430
|
Suppose $\omega$ is a circle centered at $O$ with radius 8 . Let $A C$ and $B D$ be perpendicular chords of $\omega$. Let $P$ be a point inside quadrilateral $A B C D$ such that the circumcircles of triangles $A B P$ and $C D P$ are tangent, and the circumcircles of triangles $A D P$ and $B C P$ are tangent. If $A C=2 \sqrt{61}$ and $B D=6 \sqrt{7}$, then $O P$ can be expressed as $\sqrt{a}-\sqrt{b}$ for positive integers $a$ and $b$. Compute $100 a+b$.
|
Let $X=A C \cap B D, Q=A B \cap C D$ and $R=B C \cap A D$. Since $Q A \cdot Q B=Q C \cdot Q D, Q$ is on the radical axis of $(A B P)$ and $(C D P)$, so $Q$ lies on the common tangent at $P$. Thus, $Q P^{2}=Q A \cdot Q B$. Similarly, $R A \cdot R C=R P^{2}$. Let $M$ be the Miquel point of quadrilateral $A B C D$ : in particular, $M=O X \cap Q R$ is the foot from $O$ to $Q R$. By properties of the Miquel point, $A B M R$ and $A C M Q$ are cyclic. Thus,
$$
\begin{aligned}
Q P^{2} & =Q A \cdot Q B \\
R P^{2} & =R A \cdot R C \\
Q P^{2}+R P^{2} & =Q M \cdot Q R+R M \cdot R Q=(Q R+R M) Q R=Q R^{2}
\end{aligned}
$$
As a result, $\angle Q P R=90^{\circ}$.
Now, let $P^{\prime}$ the inverse of $P$ with respect to $\omega$. Note that by properties of inversion, $\left(A B P^{\prime}\right)$ and $\left(C D P^{\prime}\right)$ are tangent, and $\left(A C P^{\prime}\right)$ and $\left(B D P^{\prime}\right)$ are also tangent.
But now,
$$
\begin{aligned}
Q P^{2}=Q P^{\prime 2} & =Q A \cdot Q B \\
R P^{2}=R P^{\prime 2} & =R A \cdot R C \\
Q P^{2}+R P^{2}=Q P^{\prime 2}+R P^{\prime 2} & =Q R^{2} .
\end{aligned}
$$
Thus, $P Q P^{\prime} R$ is a cyclic kite, so $P$ and $P^{\prime}$ are reflections of each other across $Q R$. In particular, since $O, P, P^{\prime}$ are collinear, then $M$ lies on line $O P P^{\prime}$.
We can now compute $O P$ by using the fact that $O P+\frac{r^{2}}{O P}=2 O M=\frac{2 r^{2}}{O X}$, where $r=8$. Since $O X$ can be computed to equal 2 quite easily, then $O P+\frac{64}{O P}=64$, or $O P^{2}-64 O P+64=0$. Solving this yields $O P=32 \pm 8 \sqrt{15}$, and because $P$ is inside the circle, $O P=32-8 \sqrt{15}=\sqrt{1024}-\sqrt{960}$.
|
102400+960
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Suppose $\omega$ is a circle centered at $O$ with radius 8 . Let $A C$ and $B D$ be perpendicular chords of $\omega$. Let $P$ be a point inside quadrilateral $A B C D$ such that the circumcircles of triangles $A B P$ and $C D P$ are tangent, and the circumcircles of triangles $A D P$ and $B C P$ are tangent. If $A C=2 \sqrt{61}$ and $B D=6 \sqrt{7}$, then $O P$ can be expressed as $\sqrt{a}-\sqrt{b}$ for positive integers $a$ and $b$. Compute $100 a+b$.
|
Let $X=A C \cap B D, Q=A B \cap C D$ and $R=B C \cap A D$. Since $Q A \cdot Q B=Q C \cdot Q D, Q$ is on the radical axis of $(A B P)$ and $(C D P)$, so $Q$ lies on the common tangent at $P$. Thus, $Q P^{2}=Q A \cdot Q B$. Similarly, $R A \cdot R C=R P^{2}$. Let $M$ be the Miquel point of quadrilateral $A B C D$ : in particular, $M=O X \cap Q R$ is the foot from $O$ to $Q R$. By properties of the Miquel point, $A B M R$ and $A C M Q$ are cyclic. Thus,
$$
\begin{aligned}
Q P^{2} & =Q A \cdot Q B \\
R P^{2} & =R A \cdot R C \\
Q P^{2}+R P^{2} & =Q M \cdot Q R+R M \cdot R Q=(Q R+R M) Q R=Q R^{2}
\end{aligned}
$$
As a result, $\angle Q P R=90^{\circ}$.
Now, let $P^{\prime}$ the inverse of $P$ with respect to $\omega$. Note that by properties of inversion, $\left(A B P^{\prime}\right)$ and $\left(C D P^{\prime}\right)$ are tangent, and $\left(A C P^{\prime}\right)$ and $\left(B D P^{\prime}\right)$ are also tangent.
But now,
$$
\begin{aligned}
Q P^{2}=Q P^{\prime 2} & =Q A \cdot Q B \\
R P^{2}=R P^{\prime 2} & =R A \cdot R C \\
Q P^{2}+R P^{2}=Q P^{\prime 2}+R P^{\prime 2} & =Q R^{2} .
\end{aligned}
$$
Thus, $P Q P^{\prime} R$ is a cyclic kite, so $P$ and $P^{\prime}$ are reflections of each other across $Q R$. In particular, since $O, P, P^{\prime}$ are collinear, then $M$ lies on line $O P P^{\prime}$.
We can now compute $O P$ by using the fact that $O P+\frac{r^{2}}{O P}=2 O M=\frac{2 r^{2}}{O X}$, where $r=8$. Since $O X$ can be computed to equal 2 quite easily, then $O P+\frac{64}{O P}=64$, or $O P^{2}-64 O P+64=0$. Solving this yields $O P=32 \pm 8 \sqrt{15}$, and because $P$ is inside the circle, $O P=32-8 \sqrt{15}=\sqrt{1024}-\sqrt{960}$.
|
{
"resource_path": "HarvardMIT/segmented/en-252-2022-feb-geo-solutions.jsonl",
"problem_match": "\n10. ",
"solution_match": "\nSolution: "
}
|
f1991bbc-3c34-5d32-9ac7-4741debca0ae
| 610,431
|
A regular 2022-gon has perimeter 6.28. To the nearest positive integer, compute the area of the 2022-gon.
|
Note that the area of a regular 2022-gon is approximately equal to the area of its circumcircle, and the perimeter of a regular 2022-gon approximately equals the perimeter of its circumcircle. Since the perimeter is $6.28 \approx 2 \pi$, the circumradius $R \approx 1$, so the area of the 2022 -gon is approximately $R^{2} \pi \approx \pi \approx 3$.
|
3
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
A regular 2022-gon has perimeter 6.28. To the nearest positive integer, compute the area of the 2022-gon.
|
Note that the area of a regular 2022-gon is approximately equal to the area of its circumcircle, and the perimeter of a regular 2022-gon approximately equals the perimeter of its circumcircle. Since the perimeter is $6.28 \approx 2 \pi$, the circumradius $R \approx 1$, so the area of the 2022 -gon is approximately $R^{2} \pi \approx \pi \approx 3$.
|
{
"resource_path": "HarvardMIT/segmented/en-252-2022-feb-guts-solutions.jsonl",
"problem_match": "\n1. [5]",
"solution_match": "\nSolution: "
}
|
2677b77f-8e74-5dda-a3e8-e8c3784aef5a
| 610,432
|
Three distinct vertices are randomly selected among the five vertices of a regular pentagon. Let $p$ be the probability that the triangle formed by the chosen vertices is acute. Compute $10 p$.
|
The only way for the three vertices to form an acute triangle is if they consist of two adjacent vertices and the vertex opposite their side. Since there are 5 ways to choose this and $\binom{5}{3}=10$ ways to choose the three vertices, we have $p=\frac{5}{10}=\frac{1}{2}$.
|
5
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Three distinct vertices are randomly selected among the five vertices of a regular pentagon. Let $p$ be the probability that the triangle formed by the chosen vertices is acute. Compute $10 p$.
|
The only way for the three vertices to form an acute triangle is if they consist of two adjacent vertices and the vertex opposite their side. Since there are 5 ways to choose this and $\binom{5}{3}=10$ ways to choose the three vertices, we have $p=\frac{5}{10}=\frac{1}{2}$.
|
{
"resource_path": "HarvardMIT/segmented/en-252-2022-feb-guts-solutions.jsonl",
"problem_match": "\n2. [5]",
"solution_match": "\nSolution: "
}
|
f2d7e848-79a1-5903-88b8-7480245fe7e2
| 610,433
|
Herbert rolls 6 fair standard dice and computes the product of all of his rolls. If the probability that the product is prime can be expressed as $\frac{a}{b}$ for relatively prime positive integers $a$ and $b$, compute $100 a+b$.
|
The only way this can happen is if 5 of the dice roll 1 and the last die rolls a prime number $(2,3$, or 5$)$. There are 6 ways to choose the die that rolls the prime, and 3 ways to choose the prime. Thus, the probability is $\frac{3 \cdot 6}{6^{6}}=\frac{1}{2592}$.
|
103
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Herbert rolls 6 fair standard dice and computes the product of all of his rolls. If the probability that the product is prime can be expressed as $\frac{a}{b}$ for relatively prime positive integers $a$ and $b$, compute $100 a+b$.
|
The only way this can happen is if 5 of the dice roll 1 and the last die rolls a prime number $(2,3$, or 5$)$. There are 6 ways to choose the die that rolls the prime, and 3 ways to choose the prime. Thus, the probability is $\frac{3 \cdot 6}{6^{6}}=\frac{1}{2592}$.
|
{
"resource_path": "HarvardMIT/segmented/en-252-2022-feb-guts-solutions.jsonl",
"problem_match": "\n3. [5]",
"solution_match": "\nSolution: "
}
|
dab817ff-cd88-5dbb-a324-ab28be309005
| 610,434
|
For a real number $x$, let $[x]$ be $x$ rounded to the nearest integer and $\langle x\rangle$ be $x$ rounded to the nearest tenth. Real numbers $a$ and $b$ satisfy $\langle a\rangle+[b]=98.6$ and $[a]+\langle b\rangle=99.3$. Compute the minimum possible value of $[10(a+b)]$.
(Here, any number equally between two integers or tenths of integers, respectively, is rounded up. For example, $[-4.5]=-4$ and $\langle 4.35\rangle=4.4$.)
|
Without loss of generality, let $a$ and $b$ have the same integer part or integer parts that differ by at most 1 , as we can always repeatedly subtract 1 from the larger number and add 1 to the smaller to get another solution.
Next, we note that the decimal part of $a$ must round to .6 and the decimal part of $b$ must round to .3 . We note that $(a, b)=(49.55,49.25)$ is a solution and is clearly minimal in fractional parts, giving us $[10(a+b)]=988$.
|
988
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
For a real number $x$, let $[x]$ be $x$ rounded to the nearest integer and $\langle x\rangle$ be $x$ rounded to the nearest tenth. Real numbers $a$ and $b$ satisfy $\langle a\rangle+[b]=98.6$ and $[a]+\langle b\rangle=99.3$. Compute the minimum possible value of $[10(a+b)]$.
(Here, any number equally between two integers or tenths of integers, respectively, is rounded up. For example, $[-4.5]=-4$ and $\langle 4.35\rangle=4.4$.)
|
Without loss of generality, let $a$ and $b$ have the same integer part or integer parts that differ by at most 1 , as we can always repeatedly subtract 1 from the larger number and add 1 to the smaller to get another solution.
Next, we note that the decimal part of $a$ must round to .6 and the decimal part of $b$ must round to .3 . We note that $(a, b)=(49.55,49.25)$ is a solution and is clearly minimal in fractional parts, giving us $[10(a+b)]=988$.
|
{
"resource_path": "HarvardMIT/segmented/en-252-2022-feb-guts-solutions.jsonl",
"problem_match": "\n4. [5]",
"solution_match": "\nSolution: "
}
|
620f0c92-1257-5f58-815c-75d91322d0b8
| 610,435
|
A jar contains 8 red balls and 2 blue balls. Every minute, a ball is randomly removed. The probability that there exists a time during this process where there are more blue balls than red balls in the jar can be expressed as $\frac{a}{b}$ for relatively prime integers $a$ and $b$. Compute $100 a+b$.
|
One can show that the condition in the problem is satisfied if and only the last ball drown is blue (which happens with probability $\frac{1}{5}$ ), or the blue balls are drawn second-to-last and third-to-last (which happens with probability $\frac{1}{\binom{10}{2}}=\frac{1}{45}$ ). Thus the total probability is $\frac{10}{45}=\frac{2}{9}$.
|
209
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
A jar contains 8 red balls and 2 blue balls. Every minute, a ball is randomly removed. The probability that there exists a time during this process where there are more blue balls than red balls in the jar can be expressed as $\frac{a}{b}$ for relatively prime integers $a$ and $b$. Compute $100 a+b$.
|
One can show that the condition in the problem is satisfied if and only the last ball drown is blue (which happens with probability $\frac{1}{5}$ ), or the blue balls are drawn second-to-last and third-to-last (which happens with probability $\frac{1}{\binom{10}{2}}=\frac{1}{45}$ ). Thus the total probability is $\frac{10}{45}=\frac{2}{9}$.
|
{
"resource_path": "HarvardMIT/segmented/en-252-2022-feb-guts-solutions.jsonl",
"problem_match": "\n7. [6]",
"solution_match": "\nSolution: "
}
|
0a7eb837-f071-5f99-9cd7-0be4979d37a6
| 610,438
|
For any positive integer $n$, let $\tau(n)$ denote the number of positive divisors of $n$. If $n$ is a positive integer such that $\frac{\tau\left(n^{2}\right)}{\tau(n)}=3$, compute $\frac{\tau\left(n^{7}\right)}{\tau(n)}$.
|
Answer: 29
|
29
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
For any positive integer $n$, let $\tau(n)$ denote the number of positive divisors of $n$. If $n$ is a positive integer such that $\frac{\tau\left(n^{2}\right)}{\tau(n)}=3$, compute $\frac{\tau\left(n^{7}\right)}{\tau(n)}$.
|
Answer: 29
|
{
"resource_path": "HarvardMIT/segmented/en-252-2022-feb-guts-solutions.jsonl",
"problem_match": "\n8. [6]",
"solution_match": "\nProposed by: Sean Li\n"
}
|
38817b77-9ec2-5992-b9f1-029b54b296c3
| 610,439
|
An $E$-shape is a geometric figure in the two-dimensional plane consisting of three rays pointing in the same direction, along with a line segment such that
- the endpoints of the rays all lie on the segment,
- the segment is perpendicular to all three rays,
- both endpoints of the segment are endpoints of rays.
Suppose two $E$-shapes intersect each other $N$ times in the plane for some positive integer $N$. Compute the maximum possible value of $N$.
|
Define a $C$-shape to be an $E$-shape without the middle ray. Then, an $E$-shape consists of a ray and a $C$-shape. Two $C$-shapes can intersect at most 6 times, a $C$-shape and a ray can intersect at most 2 times, and two rays can intersect at most 1 time. Thus, the number of intersections of two $E$-shapes is at most $6+2+2+1=11$.
|
11
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
An $E$-shape is a geometric figure in the two-dimensional plane consisting of three rays pointing in the same direction, along with a line segment such that
- the endpoints of the rays all lie on the segment,
- the segment is perpendicular to all three rays,
- both endpoints of the segment are endpoints of rays.
Suppose two $E$-shapes intersect each other $N$ times in the plane for some positive integer $N$. Compute the maximum possible value of $N$.
|
Define a $C$-shape to be an $E$-shape without the middle ray. Then, an $E$-shape consists of a ray and a $C$-shape. Two $C$-shapes can intersect at most 6 times, a $C$-shape and a ray can intersect at most 2 times, and two rays can intersect at most 1 time. Thus, the number of intersections of two $E$-shapes is at most $6+2+2+1=11$.
|
{
"resource_path": "HarvardMIT/segmented/en-252-2022-feb-guts-solutions.jsonl",
"problem_match": "\n9. [7]",
"solution_match": "\nSolution: "
}
|
bcf3e5df-609d-513e-bc60-4ea57988bc4b
| 610,440
|
A positive integer $n$ is loose it has six positive divisors and satisfies the property that any two positive divisors $a<b$ of $n$ satisfy $b \geq 2 a$. Compute the sum of all loose positive integers less than 100 .
|
Note that the condition in the problem implies that for any divisor $d$ of $n$, if $d$ is odd then all other divisors of $n$ cannot lie in the interval $\left[\left\lceil\frac{d}{2}\right\rceil, 2 d-1\right]$. If $d$ is even, then all other divisors cannot lie in the interval $\left[\frac{d}{2}+1,2 d-1\right]$.
We first find that $n$ must be of the form $p^{5}$ or $p^{2} q$ for primes $p$ and $q$. If $n=p^{5}$, the only solution is when $p=2$ and $n=32$.
Otherwise, $n=p^{2} q$. Since $100>n>p^{2}$, so $p \leq 7$. Now we can do casework on $p$. When $p=2$, we find that $q$ cannot lie in $[2,3]$ or $[3,7]$, so we must have $q \geq 11$. All such values for $q$ work, giving solutions $n=44,52,68,76,92$. When $p=3$, we find that $q$ cannot lie in $[2,5]$ or $[5,17]$, so we must have that $q \geq 19$, so there are no solutions in this case. When $p=5$ or $p=7$, the only solution occurs when $q=2$ (since otherwise $n>100$ ). This gives us the solutions $n=50$ and $n=98$. Adding these values of $n$ gives 512 .
|
512
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
A positive integer $n$ is loose it has six positive divisors and satisfies the property that any two positive divisors $a<b$ of $n$ satisfy $b \geq 2 a$. Compute the sum of all loose positive integers less than 100 .
|
Note that the condition in the problem implies that for any divisor $d$ of $n$, if $d$ is odd then all other divisors of $n$ cannot lie in the interval $\left[\left\lceil\frac{d}{2}\right\rceil, 2 d-1\right]$. If $d$ is even, then all other divisors cannot lie in the interval $\left[\frac{d}{2}+1,2 d-1\right]$.
We first find that $n$ must be of the form $p^{5}$ or $p^{2} q$ for primes $p$ and $q$. If $n=p^{5}$, the only solution is when $p=2$ and $n=32$.
Otherwise, $n=p^{2} q$. Since $100>n>p^{2}$, so $p \leq 7$. Now we can do casework on $p$. When $p=2$, we find that $q$ cannot lie in $[2,3]$ or $[3,7]$, so we must have $q \geq 11$. All such values for $q$ work, giving solutions $n=44,52,68,76,92$. When $p=3$, we find that $q$ cannot lie in $[2,5]$ or $[5,17]$, so we must have that $q \geq 19$, so there are no solutions in this case. When $p=5$ or $p=7$, the only solution occurs when $q=2$ (since otherwise $n>100$ ). This gives us the solutions $n=50$ and $n=98$. Adding these values of $n$ gives 512 .
|
{
"resource_path": "HarvardMIT/segmented/en-252-2022-feb-guts-solutions.jsonl",
"problem_match": "\n10. [7]",
"solution_match": "\nSolution: "
}
|
0cd87030-9a68-5baf-ba32-ffc0dd8339c3
| 610,441
|
A regular dodecagon $P_{1} P_{2} \cdots P_{12}$ is inscribed in a unit circle with center $O$. Let $X$ be the intersection of $P_{1} P_{5}$ and $O P_{2}$, and let $Y$ be the intersection of $P_{1} P_{5}$ and $O P_{4}$. Let $A$ be the area of the region bounded by $X Y, X P_{2}, Y P_{4}$, and minor arc $\widehat{P_{2} P_{4}}$. Compute $\lfloor 120 A\rfloor$.
|
The area of sector $O P_{2} P_{4}$ is one sixth the area of the circle because its angle is $60^{\circ}$. The desired area is just that of the sector subtracted by the area of equilateral triangle $O X Y$.
Note that the altitude of this triangle is the distance from $O$ to $P_{1} P_{5}$, which is $\frac{1}{2}$. Thus, the side length of the triangle is $\frac{\sqrt{3}}{3}$, implying that the area is $\frac{\sqrt{3}}{12}$. Thus, we find that $A=\frac{\pi}{6}-\frac{\sqrt{3}}{12}$. Thus, $120 A=20 \pi-10 \sqrt{3} \approx 62.8-17.3$, which has floor 45 .
|
45
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
A regular dodecagon $P_{1} P_{2} \cdots P_{12}$ is inscribed in a unit circle with center $O$. Let $X$ be the intersection of $P_{1} P_{5}$ and $O P_{2}$, and let $Y$ be the intersection of $P_{1} P_{5}$ and $O P_{4}$. Let $A$ be the area of the region bounded by $X Y, X P_{2}, Y P_{4}$, and minor arc $\widehat{P_{2} P_{4}}$. Compute $\lfloor 120 A\rfloor$.
|
The area of sector $O P_{2} P_{4}$ is one sixth the area of the circle because its angle is $60^{\circ}$. The desired area is just that of the sector subtracted by the area of equilateral triangle $O X Y$.
Note that the altitude of this triangle is the distance from $O$ to $P_{1} P_{5}$, which is $\frac{1}{2}$. Thus, the side length of the triangle is $\frac{\sqrt{3}}{3}$, implying that the area is $\frac{\sqrt{3}}{12}$. Thus, we find that $A=\frac{\pi}{6}-\frac{\sqrt{3}}{12}$. Thus, $120 A=20 \pi-10 \sqrt{3} \approx 62.8-17.3$, which has floor 45 .
|
{
"resource_path": "HarvardMIT/segmented/en-252-2022-feb-guts-solutions.jsonl",
"problem_match": "\n11. [7]",
"solution_match": "\nSolution: "
}
|
d24ad190-9acb-5c92-881e-ccaa7b475729
| 610,442
|
A unit square $A B C D$ and a circle $\Gamma$ have the following property: if $P$ is a point in the plane not contained in the interior of $\Gamma$, then $\min (\angle A P B, \angle B P C, \angle C P D, \angle D P A) \leq 60^{\circ}$. The minimum possible area of $\Gamma$ can be expressed as $\frac{a \pi}{b}$ for relatively prime positive integers $a$ and $b$. Compute $100 a+b$.
|
Note that the condition for $\Gamma$ in the problem is equivalent to the following condition: if $\min (\angle A P B, \angle B P C, \angle C P D, \angle D P A)>60^{\circ}$, then $P$ is contained in the interior of $\Gamma$. Let $X_{1}, X_{2}, X_{3}$, and $X_{4}$ be the four points in $A B C D$ such that $A B X_{1}, B C X_{2}, C D X_{3}$, and $D A X_{4}$ are all equilateral triangles. Now, let $\Omega_{1}, \Omega_{2}, \Omega_{3}$, and $\Omega_{4}$ be the respective circumcircles of these triangles, and let the centers of these circles be $O_{1}, O_{2}, O_{3}$, and $O_{4}$. Note that the set of points $P$ such that $\angle A P B, \angle B P C, \angle C P D, \angle D P A>60^{\circ}$ is the intersection of $\Omega_{1}, \Omega_{2}, \Omega_{3}$, and $\Omega_{4}$. We want to find the area of the minimum circle containing this intersection.
Let $\Gamma_{1}$ and $\Gamma_{2}$ intersect at $B$ and $B^{\prime}$. Define $C^{\prime}, D^{\prime}$ and $A^{\prime}$ similarly. It is not hard to see that the circumcircle of square $A^{\prime} B^{\prime} C^{\prime} D^{\prime}$ is the desired circle. Now observe that $\angle A B^{\prime} D^{\prime}=\angle A B^{\prime} D=60^{\circ}$. Similarly, $\angle A D^{\prime} B^{\prime}=60^{\circ}$, so $A B^{\prime} D^{\prime}$ is equilateral. Its height is the distance from $A$ to $B^{\prime} D^{\prime}$, which is $\frac{1}{\sqrt{2}}$, so its side length is $\frac{\sqrt{6}}{3}$. This is also the diameter of the desired circle, so its area is $\frac{\pi}{4} \cdot \frac{6}{9}=\frac{\pi}{6}$.
|
101
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
A unit square $A B C D$ and a circle $\Gamma$ have the following property: if $P$ is a point in the plane not contained in the interior of $\Gamma$, then $\min (\angle A P B, \angle B P C, \angle C P D, \angle D P A) \leq 60^{\circ}$. The minimum possible area of $\Gamma$ can be expressed as $\frac{a \pi}{b}$ for relatively prime positive integers $a$ and $b$. Compute $100 a+b$.
|
Note that the condition for $\Gamma$ in the problem is equivalent to the following condition: if $\min (\angle A P B, \angle B P C, \angle C P D, \angle D P A)>60^{\circ}$, then $P$ is contained in the interior of $\Gamma$. Let $X_{1}, X_{2}, X_{3}$, and $X_{4}$ be the four points in $A B C D$ such that $A B X_{1}, B C X_{2}, C D X_{3}$, and $D A X_{4}$ are all equilateral triangles. Now, let $\Omega_{1}, \Omega_{2}, \Omega_{3}$, and $\Omega_{4}$ be the respective circumcircles of these triangles, and let the centers of these circles be $O_{1}, O_{2}, O_{3}$, and $O_{4}$. Note that the set of points $P$ such that $\angle A P B, \angle B P C, \angle C P D, \angle D P A>60^{\circ}$ is the intersection of $\Omega_{1}, \Omega_{2}, \Omega_{3}$, and $\Omega_{4}$. We want to find the area of the minimum circle containing this intersection.
Let $\Gamma_{1}$ and $\Gamma_{2}$ intersect at $B$ and $B^{\prime}$. Define $C^{\prime}, D^{\prime}$ and $A^{\prime}$ similarly. It is not hard to see that the circumcircle of square $A^{\prime} B^{\prime} C^{\prime} D^{\prime}$ is the desired circle. Now observe that $\angle A B^{\prime} D^{\prime}=\angle A B^{\prime} D=60^{\circ}$. Similarly, $\angle A D^{\prime} B^{\prime}=60^{\circ}$, so $A B^{\prime} D^{\prime}$ is equilateral. Its height is the distance from $A$ to $B^{\prime} D^{\prime}$, which is $\frac{1}{\sqrt{2}}$, so its side length is $\frac{\sqrt{6}}{3}$. This is also the diameter of the desired circle, so its area is $\frac{\pi}{4} \cdot \frac{6}{9}=\frac{\pi}{6}$.
|
{
"resource_path": "HarvardMIT/segmented/en-252-2022-feb-guts-solutions.jsonl",
"problem_match": "\n12. [7]",
"solution_match": "\nSolution: "
}
|
044edacf-bbd3-5388-ac60-0da6d1db1b44
| 610,443
|
Let $z_{1}, z_{2}, z_{3}, z_{4}$ be the solutions to the equation $x^{4}+3 x^{3}+3 x^{2}+3 x+1=0$. Then $\left|z_{1}\right|+\left|z_{2}\right|+\left|z_{3}\right|+\left|z_{4}\right|$ can be written as $\frac{a+b \sqrt{c}}{d}$, where $c$ is a square-free positive integer, and $a, b, d$ are positive integers with $\operatorname{gcd}(a, b, d)=1$. Compute $1000 a+100 b+10 c+d$.
|
Note that $x=0$ is clearly not a solution, so we can divide the equation by $x^{2}$ to get $\left(x^{2}+2+\frac{1}{x^{2}}\right)+3\left(x+\frac{1}{x}\right)+1=0$. Letting $y=x+\frac{1}{x}$, we get that $y^{2}+3 y+1=0$, so $y=x+\frac{1}{x}=\frac{-3 \pm \sqrt{5}}{2}$. Since $\frac{-3+\sqrt{5}}{2}$ has absolute value less than 2 , the associated $x$ are on the unit circle, and thus the two solutions for $x$ in this case each have magnitude 1. For $\frac{-3-\sqrt{5}}{2}$, the roots are negative reals that are reciprocals of each other. Thus, the sum of their absolute values is the absolute value of their sum, which is $\frac{3+\sqrt{5}}{2}$. Thus, the sum of the magnitudes of the four solutions are $1+1+\frac{3+\sqrt{5}}{2}=\frac{7+\sqrt{5}}{2}$.
|
7152
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Let $z_{1}, z_{2}, z_{3}, z_{4}$ be the solutions to the equation $x^{4}+3 x^{3}+3 x^{2}+3 x+1=0$. Then $\left|z_{1}\right|+\left|z_{2}\right|+\left|z_{3}\right|+\left|z_{4}\right|$ can be written as $\frac{a+b \sqrt{c}}{d}$, where $c$ is a square-free positive integer, and $a, b, d$ are positive integers with $\operatorname{gcd}(a, b, d)=1$. Compute $1000 a+100 b+10 c+d$.
|
Note that $x=0$ is clearly not a solution, so we can divide the equation by $x^{2}$ to get $\left(x^{2}+2+\frac{1}{x^{2}}\right)+3\left(x+\frac{1}{x}\right)+1=0$. Letting $y=x+\frac{1}{x}$, we get that $y^{2}+3 y+1=0$, so $y=x+\frac{1}{x}=\frac{-3 \pm \sqrt{5}}{2}$. Since $\frac{-3+\sqrt{5}}{2}$ has absolute value less than 2 , the associated $x$ are on the unit circle, and thus the two solutions for $x$ in this case each have magnitude 1. For $\frac{-3-\sqrt{5}}{2}$, the roots are negative reals that are reciprocals of each other. Thus, the sum of their absolute values is the absolute value of their sum, which is $\frac{3+\sqrt{5}}{2}$. Thus, the sum of the magnitudes of the four solutions are $1+1+\frac{3+\sqrt{5}}{2}=\frac{7+\sqrt{5}}{2}$.
|
{
"resource_path": "HarvardMIT/segmented/en-252-2022-feb-guts-solutions.jsonl",
"problem_match": "\n13. [9]",
"solution_match": "\nSolution: "
}
|
44000423-d151-5af6-90bb-3d41389a904e
| 610,444
|
The area of the largest regular hexagon that can fit inside of a rectangle with side lengths 20 and 22 can be expressed as $a \sqrt{b}-c$, for positive integers $a, b$, and $c$, where $b$ is squarefree. Compute $100 a+10 b+c$.
|
Let $s$ be the sidelength of the hexagon. We can view this problem as finding the maximal rectangle of with sides $s$ and $s \sqrt{3}$ that can fit inside this rectangle. Let $A B C D$ be a rectangle with $A B=20$ and $B C=22$ and let $X Y Z W$ be an inscribed rectangle with $X$ on $A B$ and $Y$ on $B C$ with $X Y=s$ and $Y Z=s \sqrt{3}$. Let $B X=a$ and $B Y=b$. Then, by similar triangles, we have $A X=b \sqrt{3}$ and $C Y=a \sqrt{3}$. Thus, we have $a+b \sqrt{3}=20$ and $a \sqrt{3}+b=22$. Solving gives us $a=11 \sqrt{3}-10$ and $b=10 \sqrt{3}-11$, so $s^{2}=a^{2}+b^{2}=884-440 \sqrt{3}$. Thus, the area of the hexagon is $\frac{s^{2} \cdot 3 \sqrt{3}}{2}=1326 \sqrt{3}-1980$.
|
1326 \sqrt{3}-1980
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
The area of the largest regular hexagon that can fit inside of a rectangle with side lengths 20 and 22 can be expressed as $a \sqrt{b}-c$, for positive integers $a, b$, and $c$, where $b$ is squarefree. Compute $100 a+10 b+c$.
|
Let $s$ be the sidelength of the hexagon. We can view this problem as finding the maximal rectangle of with sides $s$ and $s \sqrt{3}$ that can fit inside this rectangle. Let $A B C D$ be a rectangle with $A B=20$ and $B C=22$ and let $X Y Z W$ be an inscribed rectangle with $X$ on $A B$ and $Y$ on $B C$ with $X Y=s$ and $Y Z=s \sqrt{3}$. Let $B X=a$ and $B Y=b$. Then, by similar triangles, we have $A X=b \sqrt{3}$ and $C Y=a \sqrt{3}$. Thus, we have $a+b \sqrt{3}=20$ and $a \sqrt{3}+b=22$. Solving gives us $a=11 \sqrt{3}-10$ and $b=10 \sqrt{3}-11$, so $s^{2}=a^{2}+b^{2}=884-440 \sqrt{3}$. Thus, the area of the hexagon is $\frac{s^{2} \cdot 3 \sqrt{3}}{2}=1326 \sqrt{3}-1980$.
|
{
"resource_path": "HarvardMIT/segmented/en-252-2022-feb-guts-solutions.jsonl",
"problem_match": "\n14. [9]",
"solution_match": "\nSolution: "
}
|
1c07e8b6-aa6e-5795-9ed0-38648f94a5f9
| 610,445
|
Let $N$ be the number of triples of positive integers $(a, b, c)$ satisfying
$$
a \leq b \leq c, \quad \operatorname{gcd}(a, b, c)=1, \quad a b c=6^{2020}
$$
Compute the remainder when $N$ is divided by 1000.
|
Answer: 602
|
602
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Let $N$ be the number of triples of positive integers $(a, b, c)$ satisfying
$$
a \leq b \leq c, \quad \operatorname{gcd}(a, b, c)=1, \quad a b c=6^{2020}
$$
Compute the remainder when $N$ is divided by 1000.
|
Answer: 602
|
{
"resource_path": "HarvardMIT/segmented/en-252-2022-feb-guts-solutions.jsonl",
"problem_match": "\n15. [9]",
"solution_match": "\nProposed by: Benjamin Wu\n"
}
|
70ba6f20-90d4-5442-8c30-1dd92c3618be
| 610,446
|
Let $A B C$ be an acute triangle with $A$-excircle $\Gamma$. Let the line through $A$ perpendicular to $B C$ intersect $B C$ at $D$ and intersect $\Gamma$ at $E$ and $F$. Suppose that $A D=D E=E F$. If the maximum value of $\sin B$ can be expressed as $\frac{\sqrt{a}+\sqrt{b}}{c}$ for positive integers $a, b$, and $c$, compute the minimum possible value of $a+b+c$.
|
First note that we can assume $A B<A C$. Suppose $\Gamma$ is tangent to $B C$ at $T$. Let $A D=$ $D E=E F=x$. Then, by Power of a Point, we have $D T^{2}=D E \cdot D F=x \cdot 2 x=2 x^{2} \Longrightarrow D T=x \sqrt{2}$. Note that $C T=s-b$, and since the length of the tangent from $A$ to $\Gamma$ is $s$, we have $s^{2}=A E \cdot A F=6 x^{2}$, so $C T=x \sqrt{6}-b$. Since $B C=B D+D T+T C$, we have $B D=B C-x \sqrt{2}-(x \sqrt{6}-b)=a+b-x(\sqrt{2}+\sqrt{6})$. Since $a+b=2 s-c=2 x \sqrt{6}-c$, we have $B D=x(\sqrt{6}-\sqrt{2})-c$. Now, by Pythagorean Theorem, we have $c^{2}=A B^{2}=A D^{2}+B D^{2}=x^{2}+[x(\sqrt{6}-\sqrt{2})-c]^{2}$. Simplifying gives $x^{2}(9-4 \sqrt{3})=x c(2 \sqrt{6}-2 \sqrt{2})$. This yields
$$
\frac{x}{c}=\frac{2 \sqrt{6}-2 \sqrt{2}}{9-4 \sqrt{3}}=\frac{6 \sqrt{2}+10 \sqrt{6}}{33}=\frac{\sqrt{72}+\sqrt{600}}{33}
$$
|
\frac{\sqrt{72}+\sqrt{600}}{33}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $A B C$ be an acute triangle with $A$-excircle $\Gamma$. Let the line through $A$ perpendicular to $B C$ intersect $B C$ at $D$ and intersect $\Gamma$ at $E$ and $F$. Suppose that $A D=D E=E F$. If the maximum value of $\sin B$ can be expressed as $\frac{\sqrt{a}+\sqrt{b}}{c}$ for positive integers $a, b$, and $c$, compute the minimum possible value of $a+b+c$.
|
First note that we can assume $A B<A C$. Suppose $\Gamma$ is tangent to $B C$ at $T$. Let $A D=$ $D E=E F=x$. Then, by Power of a Point, we have $D T^{2}=D E \cdot D F=x \cdot 2 x=2 x^{2} \Longrightarrow D T=x \sqrt{2}$. Note that $C T=s-b$, and since the length of the tangent from $A$ to $\Gamma$ is $s$, we have $s^{2}=A E \cdot A F=6 x^{2}$, so $C T=x \sqrt{6}-b$. Since $B C=B D+D T+T C$, we have $B D=B C-x \sqrt{2}-(x \sqrt{6}-b)=a+b-x(\sqrt{2}+\sqrt{6})$. Since $a+b=2 s-c=2 x \sqrt{6}-c$, we have $B D=x(\sqrt{6}-\sqrt{2})-c$. Now, by Pythagorean Theorem, we have $c^{2}=A B^{2}=A D^{2}+B D^{2}=x^{2}+[x(\sqrt{6}-\sqrt{2})-c]^{2}$. Simplifying gives $x^{2}(9-4 \sqrt{3})=x c(2 \sqrt{6}-2 \sqrt{2})$. This yields
$$
\frac{x}{c}=\frac{2 \sqrt{6}-2 \sqrt{2}}{9-4 \sqrt{3}}=\frac{6 \sqrt{2}+10 \sqrt{6}}{33}=\frac{\sqrt{72}+\sqrt{600}}{33}
$$
|
{
"resource_path": "HarvardMIT/segmented/en-252-2022-feb-guts-solutions.jsonl",
"problem_match": "\n16. [9]",
"solution_match": "\nSolution: "
}
|
64ea0fb1-4f22-5f41-b541-a526d0bcced6
| 610,447
|
Compute the number of positive real numbers $x$ that satisfy
$$
\left(3 \cdot 2^{\left\lfloor\log _{2} x\right\rfloor}-x\right)^{16}=2022 x^{13}
$$
|
Let $f(x)=3 \cdot 2^{\left\lfloor\log _{2} x\right\rfloor}-x$. Note that for each integer $i$, if $x \in\left[2^{i}, 2^{i+1}\right)$, then $f(x)=3 \cdot 2^{i}-x$. This is a line segment from $\left(2^{i}, 2^{i+1}\right)$ to $\left(2^{i+1}, 2^{i}\right)$, including the first endpoint but not the second.
Now consider the function $f(x)^{16} / x^{13}$. This consists of segments of decreasing functions connecting $\left(2^{i}, 2^{3 i+16}\right)$ and $\left(2^{i+1}, 2^{3 i-13}\right)$. Note that for each $-1 \leq i \leq 7$, we have that $2^{3 i-13} \leq 2^{10}<2022<$ $2^{11} \leq 2^{3 i+16}$. This gives us 9 solutions in total.
|
9
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Compute the number of positive real numbers $x$ that satisfy
$$
\left(3 \cdot 2^{\left\lfloor\log _{2} x\right\rfloor}-x\right)^{16}=2022 x^{13}
$$
|
Let $f(x)=3 \cdot 2^{\left\lfloor\log _{2} x\right\rfloor}-x$. Note that for each integer $i$, if $x \in\left[2^{i}, 2^{i+1}\right)$, then $f(x)=3 \cdot 2^{i}-x$. This is a line segment from $\left(2^{i}, 2^{i+1}\right)$ to $\left(2^{i+1}, 2^{i}\right)$, including the first endpoint but not the second.
Now consider the function $f(x)^{16} / x^{13}$. This consists of segments of decreasing functions connecting $\left(2^{i}, 2^{3 i+16}\right)$ and $\left(2^{i+1}, 2^{3 i-13}\right)$. Note that for each $-1 \leq i \leq 7$, we have that $2^{3 i-13} \leq 2^{10}<2022<$ $2^{11} \leq 2^{3 i+16}$. This gives us 9 solutions in total.
|
{
"resource_path": "HarvardMIT/segmented/en-252-2022-feb-guts-solutions.jsonl",
"problem_match": "\n17. [11]",
"solution_match": "\nSolution: "
}
|
fea88371-f258-5ae0-b3e0-7645259fc368
| 610,448
|
Compute the number of permutations $\pi$ of the set $\{1,2, \ldots, 10\}$ so that for all (not necessarily distinct) $m, n \in\{1,2, \ldots, 10\}$ where $m+n$ is prime, $\pi(m)+\pi(n)$ is prime.
|
Since $\pi$ sends pairs $(m, n)$ with $m+n$ prime to pairs ( $m^{\prime}, n^{\prime}$ ) with $m^{\prime}+n^{\prime}$ prime, and there are only finitely many such pairs, we conclude that if $m+n$ is composite, then so is $\pi(m)+\pi(n)$. Also note that $2 \pi(1)=\pi(1)+\pi(1)$ is prime because $2=1+1$ is prime. Thus, $\pi(1)=1$. Now, since $1+2,1+4,1+6$, and $1+10$ are all prime, we know that $\pi(2), \pi(4), \pi(6)$, and $\pi(10)$ are all even. Additionally, since $8+2,8+6,8+6$, and $8+10$ are all composite, it is not hard to see that $\pi(8)$ must also be even. Therefore $\pi$ preserves parity.
Now, draw a bipartite graph between the odd and even numbers where we have an edge between $a$ and $b$ if and only if $a+b$ composite. We now only need to compute automorphisms of this graph that fix 1 . Note that the edges are precisely $1-8-7-2,3-6-9$, and $4-5-10$. Since 1 is a fixed point of $\pi$, we know that $\pi$ fixes $1,8,7$, and 2 . Additionally, $\pi(6)=6$ and $\pi(5)=5$. We can swap 3 and 9 , as well as 4 and 10 . Thus, there are $2 \cdot 2=4$ possible permutations.
|
4
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Compute the number of permutations $\pi$ of the set $\{1,2, \ldots, 10\}$ so that for all (not necessarily distinct) $m, n \in\{1,2, \ldots, 10\}$ where $m+n$ is prime, $\pi(m)+\pi(n)$ is prime.
|
Since $\pi$ sends pairs $(m, n)$ with $m+n$ prime to pairs ( $m^{\prime}, n^{\prime}$ ) with $m^{\prime}+n^{\prime}$ prime, and there are only finitely many such pairs, we conclude that if $m+n$ is composite, then so is $\pi(m)+\pi(n)$. Also note that $2 \pi(1)=\pi(1)+\pi(1)$ is prime because $2=1+1$ is prime. Thus, $\pi(1)=1$. Now, since $1+2,1+4,1+6$, and $1+10$ are all prime, we know that $\pi(2), \pi(4), \pi(6)$, and $\pi(10)$ are all even. Additionally, since $8+2,8+6,8+6$, and $8+10$ are all composite, it is not hard to see that $\pi(8)$ must also be even. Therefore $\pi$ preserves parity.
Now, draw a bipartite graph between the odd and even numbers where we have an edge between $a$ and $b$ if and only if $a+b$ composite. We now only need to compute automorphisms of this graph that fix 1 . Note that the edges are precisely $1-8-7-2,3-6-9$, and $4-5-10$. Since 1 is a fixed point of $\pi$, we know that $\pi$ fixes $1,8,7$, and 2 . Additionally, $\pi(6)=6$ and $\pi(5)=5$. We can swap 3 and 9 , as well as 4 and 10 . Thus, there are $2 \cdot 2=4$ possible permutations.
|
{
"resource_path": "HarvardMIT/segmented/en-252-2022-feb-guts-solutions.jsonl",
"problem_match": "\n18. [11]",
"solution_match": "\nSolution: "
}
|
0764abc0-7e82-5c0d-bc09-787555bad221
| 610,449
|
In right triangle $A B C$, a point $D$ is on hypotenuse $A C$ such that $B D \perp A C$. Let $\omega$ be a circle with center $O$, passing through $C$ and $D$ and tangent to line $A B$ at a point other than $B$. Point $X$ is chosen on $B C$ such that $A X \perp B O$. If $A B=2$ and $B C=5$, then $B X$ can be expressed as $\frac{a}{b}$ for relatively prime positive integers $a$ and $b$. Compute $100 a+b$.
|
Note that since $A D \cdot A C=A B^{2}$, we have the tangency point of $\omega$ and $A B$ is $B^{\prime}$, the reflection of $B$ across $A$. Let $Y$ be the second intersection of $\omega$ and $B C$. Note that by power of point, we have $B Y \cdot B C=B B^{\prime 2}=4 A B^{2} \Longrightarrow B Y=\frac{4 A B^{2}}{B C}$. Note that $A X$ is the radical axis of $\omega$ and the degenerate circle at $B$, so we have $X B^{2}=X Y \cdot X C$, so
$$
B X^{2}=(B C-B X)(B Y-B X)=B X^{2}-B X(B C+B Y)+B C \cdot B Y
$$
This gives us
$$
B X=\frac{B C \cdot B Y}{B C+B Y}=\frac{4 A B^{2} \cdot B C}{4 A B^{2}+B C^{2}}=\frac{80}{41}
$$
|
8041
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
In right triangle $A B C$, a point $D$ is on hypotenuse $A C$ such that $B D \perp A C$. Let $\omega$ be a circle with center $O$, passing through $C$ and $D$ and tangent to line $A B$ at a point other than $B$. Point $X$ is chosen on $B C$ such that $A X \perp B O$. If $A B=2$ and $B C=5$, then $B X$ can be expressed as $\frac{a}{b}$ for relatively prime positive integers $a$ and $b$. Compute $100 a+b$.
|
Note that since $A D \cdot A C=A B^{2}$, we have the tangency point of $\omega$ and $A B$ is $B^{\prime}$, the reflection of $B$ across $A$. Let $Y$ be the second intersection of $\omega$ and $B C$. Note that by power of point, we have $B Y \cdot B C=B B^{\prime 2}=4 A B^{2} \Longrightarrow B Y=\frac{4 A B^{2}}{B C}$. Note that $A X$ is the radical axis of $\omega$ and the degenerate circle at $B$, so we have $X B^{2}=X Y \cdot X C$, so
$$
B X^{2}=(B C-B X)(B Y-B X)=B X^{2}-B X(B C+B Y)+B C \cdot B Y
$$
This gives us
$$
B X=\frac{B C \cdot B Y}{B C+B Y}=\frac{4 A B^{2} \cdot B C}{4 A B^{2}+B C^{2}}=\frac{80}{41}
$$
|
{
"resource_path": "HarvardMIT/segmented/en-252-2022-feb-guts-solutions.jsonl",
"problem_match": "\n19. [11]",
"solution_match": "\nSolution: "
}
|
c9d8affe-31df-50f7-aa8b-4070f115a302
| 610,450
|
Let $\pi$ be a uniformly random permutation of the set $\{1,2, \ldots, 100\}$. The probability that $\pi^{20}(20)=$ 20 and $\pi^{21}(21)=21$ can be expressed as $\frac{a}{b}$, where $a$ and $b$ are relatively prime positive integers. Compute $100 a+b$. (Here, $\pi^{k}$ means $\pi$ iterated $k$ times.)
|
We look at the cycles formed by $\pi$. Let $\operatorname{ord}_{\pi}(n)$ denote the smallest $m$ such that $\pi^{m}(n)=n$. In particular, the condition implies that $\operatorname{ord}_{\pi}(20) \mid 20$ and $\operatorname{ord}_{\pi}(21) \mid 21$.
Claim 1. 20 and 21 cannot be in the same cycle.
Proof. If 20 and 21 were in the same cycle, then $x=\operatorname{ord}_{\pi}(20)=\operatorname{ord}_{\pi}(21)$ for some $x$. Then $x>1$ since the cycle contains both 20 and 21 , but $x|20, x| 21$ implies $x=1$, a contradiction.
Claim 2. The probability that $a=\operatorname{ord}_{\pi}(20), b=\operatorname{ord}_{\pi}(21)$ for some fixed $a, b$ such that $a+b \leq 100$ is $\frac{1}{99 \cdot 100}$.
Proof. We can just count these permutations. We first choose $a-1$ elements of $[100] \backslash\{20,21\}$ to be in the cycle of 20 , then we similarly choose $b-1$ to be in the cycle of 21 . We then have $(a-1)$ ! ways to reorder within the cycle of $20,(b-1)$ ! ways to reorder within the cycle of 21 , and $(100-a-b)$ ! ways to permute the remaining elements. The total number of ways is just
$$
\frac{98!}{(a-1)!(b-1)!(100-a-b)!} \cdot(a-1)!(b-1)!(100-a-b)!=98!,
$$
so the probability this happens is just $\frac{98!}{100!}=\frac{1}{9900}$.
Now, since $\operatorname{ord}_{\pi}(20) \mid 20$ and $\operatorname{ord}_{\pi}(21) \mid 21$, we have 6 possible values for $\operatorname{ord}_{\pi}(20)$ and 4 for $\operatorname{ord}_{\pi}(21)$, so in total we have a $\frac{6 \cdot 4}{9900}=\frac{2}{825}$ probability that the condition is satisfied.
|
203
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Let $\pi$ be a uniformly random permutation of the set $\{1,2, \ldots, 100\}$. The probability that $\pi^{20}(20)=$ 20 and $\pi^{21}(21)=21$ can be expressed as $\frac{a}{b}$, where $a$ and $b$ are relatively prime positive integers. Compute $100 a+b$. (Here, $\pi^{k}$ means $\pi$ iterated $k$ times.)
|
We look at the cycles formed by $\pi$. Let $\operatorname{ord}_{\pi}(n)$ denote the smallest $m$ such that $\pi^{m}(n)=n$. In particular, the condition implies that $\operatorname{ord}_{\pi}(20) \mid 20$ and $\operatorname{ord}_{\pi}(21) \mid 21$.
Claim 1. 20 and 21 cannot be in the same cycle.
Proof. If 20 and 21 were in the same cycle, then $x=\operatorname{ord}_{\pi}(20)=\operatorname{ord}_{\pi}(21)$ for some $x$. Then $x>1$ since the cycle contains both 20 and 21 , but $x|20, x| 21$ implies $x=1$, a contradiction.
Claim 2. The probability that $a=\operatorname{ord}_{\pi}(20), b=\operatorname{ord}_{\pi}(21)$ for some fixed $a, b$ such that $a+b \leq 100$ is $\frac{1}{99 \cdot 100}$.
Proof. We can just count these permutations. We first choose $a-1$ elements of $[100] \backslash\{20,21\}$ to be in the cycle of 20 , then we similarly choose $b-1$ to be in the cycle of 21 . We then have $(a-1)$ ! ways to reorder within the cycle of $20,(b-1)$ ! ways to reorder within the cycle of 21 , and $(100-a-b)$ ! ways to permute the remaining elements. The total number of ways is just
$$
\frac{98!}{(a-1)!(b-1)!(100-a-b)!} \cdot(a-1)!(b-1)!(100-a-b)!=98!,
$$
so the probability this happens is just $\frac{98!}{100!}=\frac{1}{9900}$.
Now, since $\operatorname{ord}_{\pi}(20) \mid 20$ and $\operatorname{ord}_{\pi}(21) \mid 21$, we have 6 possible values for $\operatorname{ord}_{\pi}(20)$ and 4 for $\operatorname{ord}_{\pi}(21)$, so in total we have a $\frac{6 \cdot 4}{9900}=\frac{2}{825}$ probability that the condition is satisfied.
|
{
"resource_path": "HarvardMIT/segmented/en-252-2022-feb-guts-solutions.jsonl",
"problem_match": "\n20. [11]",
"solution_match": "\nSolution: "
}
|
d2589c79-aacd-55e7-ab2f-a07f27b50408
| 610,451
|
In the Cartesian plane, let $A=(0,0), B=(200,100)$, and $C=(30,330)$. Compute the number of ordered pairs $(x, y)$ of integers so that $\left(x+\frac{1}{2}, y+\frac{1}{2}\right)$ is in the interior of triangle $A B C$.
|
Answer: 31480
|
31480
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
In the Cartesian plane, let $A=(0,0), B=(200,100)$, and $C=(30,330)$. Compute the number of ordered pairs $(x, y)$ of integers so that $\left(x+\frac{1}{2}, y+\frac{1}{2}\right)$ is in the interior of triangle $A B C$.
|
Answer: 31480
|
{
"resource_path": "HarvardMIT/segmented/en-252-2022-feb-guts-solutions.jsonl",
"problem_match": "\n21. [12]",
"solution_match": "\nProposed by: Ankit Bisain\n"
}
|
3f39f68f-dbf9-5fab-a611-e985a95c750d
| 610,452
|
The function $f(x)$ is of the form $a x^{2}+b x+c$ for some integers $a, b$, and $c$. Given that
$$
\begin{aligned}
\{f(177883), f(348710), & f(796921), f(858522)\} \\
= & \{1324754875645,1782225466694,1984194627862,4388794883485\}
\end{aligned}
$$
compute $a$.
|
We first match the outputs to the inputs. To start, we observe that since $a \geq 0$ (since the answer to the problem is nonnegative), we must either have $f(858522) \approx 4.39 \cdot 10^{12}$ or $f(177883) \approx$ $4.39 \cdot 10^{12}$. However, since 858522 is relatively close to 796921 , the first case is unrealistic, meaning that the second case must be true.
Now, looking mod 2 , we find that $f(796921) \approx 1.32 \cdot 10^{12}$. Additionally, we find that mod $5, f(1) \equiv$ $f(3) \equiv 0(\bmod 5)$, so $f(x) \equiv a(x-1)(x-3)(\bmod 5)$. Modulo 5 , we now have $\{3 a, 4 a\}=\{f(0), f(2)\}=$ $\{2,4\}$, so it follows that $a \equiv 3(\bmod 5), f(349710) \approx 1.78 \cdot 10^{12}$ and $f(858522) \approx 1.98 \cdot 10^{12}$.
There are several ways to finish from here. One (somewhat tedious) method is to use mod 9, which tells us that $f(7)=7, f(5)=8, f(3)=4$, which tells you that $a \equiv 5(\bmod 9)$ (take a finite difference). This tells you that $a \equiv 23(\bmod 45)$, and $a \geq 68$ can be ruled out for being too large.
Another method is to work with the numbers themselves. One way to do this is to note that for quadratic polynomials,
$$
f^{\prime}\left(\frac{x+y}{2}\right)=\frac{f(y)-f(x)}{y-x}
$$
Using this for $\{177883,348710\}$ and $\{796921,858522\}$, we find that $f^{\prime}(260000) \approx-1500000$ and $f^{\prime}(830000) \approx 1000000$. Thus $f^{\prime}$ (which we know must be linear with slope $2 a$ ) has slope just less than 50.
Either way, we find that $a=23$. The actual polynomial is $8529708870514-27370172 x+23 x^{2}$.
|
23
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
The function $f(x)$ is of the form $a x^{2}+b x+c$ for some integers $a, b$, and $c$. Given that
$$
\begin{aligned}
\{f(177883), f(348710), & f(796921), f(858522)\} \\
= & \{1324754875645,1782225466694,1984194627862,4388794883485\}
\end{aligned}
$$
compute $a$.
|
We first match the outputs to the inputs. To start, we observe that since $a \geq 0$ (since the answer to the problem is nonnegative), we must either have $f(858522) \approx 4.39 \cdot 10^{12}$ or $f(177883) \approx$ $4.39 \cdot 10^{12}$. However, since 858522 is relatively close to 796921 , the first case is unrealistic, meaning that the second case must be true.
Now, looking mod 2 , we find that $f(796921) \approx 1.32 \cdot 10^{12}$. Additionally, we find that mod $5, f(1) \equiv$ $f(3) \equiv 0(\bmod 5)$, so $f(x) \equiv a(x-1)(x-3)(\bmod 5)$. Modulo 5 , we now have $\{3 a, 4 a\}=\{f(0), f(2)\}=$ $\{2,4\}$, so it follows that $a \equiv 3(\bmod 5), f(349710) \approx 1.78 \cdot 10^{12}$ and $f(858522) \approx 1.98 \cdot 10^{12}$.
There are several ways to finish from here. One (somewhat tedious) method is to use mod 9, which tells us that $f(7)=7, f(5)=8, f(3)=4$, which tells you that $a \equiv 5(\bmod 9)$ (take a finite difference). This tells you that $a \equiv 23(\bmod 45)$, and $a \geq 68$ can be ruled out for being too large.
Another method is to work with the numbers themselves. One way to do this is to note that for quadratic polynomials,
$$
f^{\prime}\left(\frac{x+y}{2}\right)=\frac{f(y)-f(x)}{y-x}
$$
Using this for $\{177883,348710\}$ and $\{796921,858522\}$, we find that $f^{\prime}(260000) \approx-1500000$ and $f^{\prime}(830000) \approx 1000000$. Thus $f^{\prime}$ (which we know must be linear with slope $2 a$ ) has slope just less than 50.
Either way, we find that $a=23$. The actual polynomial is $8529708870514-27370172 x+23 x^{2}$.
|
{
"resource_path": "HarvardMIT/segmented/en-252-2022-feb-guts-solutions.jsonl",
"problem_match": "\n22. [12]",
"solution_match": "\nSolution: "
}
|
3a0cfd4a-5961-5097-93f9-17ec491edefd
| 610,453
|
Let $A B C D$ be an isosceles trapezoid such that $A B=17, B C=D A=25$, and $C D=31$. Points $P$ and $Q$ are selected on sides $A D$ and $B C$, respectively, such that $A P=C Q$ and $P Q=25$. Suppose that the circle with diameter $P Q$ intersects the sides $A B$ and $C D$ at four points which are vertices of a convex quadrilateral. Compute the area of this quadrilateral.
|
Let the midpoint of $P Q$ be $M$; note that $M$ lies on the midline of $A B C D$. Let $B^{\prime} C^{\prime}$ be a translate of $B C$ (parallel to $A B$ and $C D$ ) so that $M$ is the midpoint of $B^{\prime}$ and $C^{\prime}$. Since $M B^{\prime}=M C^{\prime}=25 / 2=$ $M P=M Q, B^{\prime}$ and $C^{\prime}$ are one of the four intersections of the circle with diameter $P Q$ and the sides $A B$ and $C D$. We may also define $A^{\prime}$ and $D^{\prime}$ similarly and get that they are also among the four points.
It follows that the desired quadrilateral is $B^{\prime} D^{\prime} C^{\prime} A^{\prime}$, which is a rectangle with height equal to the height of $A B C D$ (which is 24 ), and width equal to $\frac{1}{2}(31-17)=7$. Thus the area is $24 \cdot 7=168$.
|
168
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $A B C D$ be an isosceles trapezoid such that $A B=17, B C=D A=25$, and $C D=31$. Points $P$ and $Q$ are selected on sides $A D$ and $B C$, respectively, such that $A P=C Q$ and $P Q=25$. Suppose that the circle with diameter $P Q$ intersects the sides $A B$ and $C D$ at four points which are vertices of a convex quadrilateral. Compute the area of this quadrilateral.
|
Let the midpoint of $P Q$ be $M$; note that $M$ lies on the midline of $A B C D$. Let $B^{\prime} C^{\prime}$ be a translate of $B C$ (parallel to $A B$ and $C D$ ) so that $M$ is the midpoint of $B^{\prime}$ and $C^{\prime}$. Since $M B^{\prime}=M C^{\prime}=25 / 2=$ $M P=M Q, B^{\prime}$ and $C^{\prime}$ are one of the four intersections of the circle with diameter $P Q$ and the sides $A B$ and $C D$. We may also define $A^{\prime}$ and $D^{\prime}$ similarly and get that they are also among the four points.
It follows that the desired quadrilateral is $B^{\prime} D^{\prime} C^{\prime} A^{\prime}$, which is a rectangle with height equal to the height of $A B C D$ (which is 24 ), and width equal to $\frac{1}{2}(31-17)=7$. Thus the area is $24 \cdot 7=168$.
|
{
"resource_path": "HarvardMIT/segmented/en-252-2022-feb-guts-solutions.jsonl",
"problem_match": "\n23. [12]",
"solution_match": "\n## Solution:\n\n"
}
|
7c375a96-d2ad-50a6-bd0b-d149708e8058
| 610,454
|
Let $S_{0}$ be a unit square in the Cartesian plane with horizontal and vertical sides. For any $n>0$, the shape $S_{n}$ is formed by adjoining 9 copies of $S_{n-1}$ in a $3 \times 3$ grid, and then removing the center copy. For example, $S_{3}$ is shown below:

Let $a_{n}$ be the expected value of $\left|x-x^{\prime}\right|+\left|y-y^{\prime}\right|$, where $(x, y)$ and $\left(x^{\prime}, y^{\prime}\right)$ are two points chosen randomly within $S_{n}$. There exist relatively prime positive integers $a$ and $b$ such that
$$
\lim _{n \rightarrow \infty} \frac{a_{n}}{3^{n}}=\frac{a}{b} .
$$
Compute $100 a+b$.
|
By symmetry, we only need to consider the $x$-distance, then we can multiply our answer by 2. Let this quantity be $g(n)=a_{n} / 2$.
Divide the $n$th iteration fractal into three meta-columns of equal width. Then the probability that a random point is in the first, second, and third meta-columns is $\frac{3}{8}, \frac{2}{8}$, and $\frac{3}{8}$, respectively. If the two points end up in neighboring meta columns, the expected value of their $x$-distance is simply the width of a meta-column, which is $3^{n-1}$. If they end up in opposite meta-columns (the left and right ones), it is twice this amount, which is $2 \cdot 3^{n-1}$. Finally, if the two points lie in the same meta-column, which happens with probability $\left(\frac{3}{8}\right)^{2}+\left(\frac{2}{8}\right)^{2}+\left(\frac{3}{8}\right)^{2}=\frac{11}{32}$, the expected $x$-distance is just $g(n-1)$. Thus, we have
$$
g(n)=3^{n-1}\left(2 \cdot \frac{3}{8} \cdot \frac{2}{8}+2 \cdot \frac{2}{8} \cdot \frac{3}{8}\right)+\left(2 \cdot 3^{n-1}\right)\left(2 \cdot \frac{3}{8} \cdot \frac{3}{8}\right)+\frac{11}{32} g(n-1)=\frac{15}{16} \cdot 3^{n-1}+\frac{11}{32} g(n-1)
$$
As $n$ grows, say this is asymptotic to $g(n)=3^{n} C$. For some constant $C$. Then we can write $3^{n} C=\frac{15}{16} \cdot 3^{n-1}+\frac{11}{32} \cdot 3^{n-1} C \Longrightarrow C=\frac{6}{17}$. Our final answer is twice this, which is $\frac{12}{17}$.
|
12017
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Let $S_{0}$ be a unit square in the Cartesian plane with horizontal and vertical sides. For any $n>0$, the shape $S_{n}$ is formed by adjoining 9 copies of $S_{n-1}$ in a $3 \times 3$ grid, and then removing the center copy. For example, $S_{3}$ is shown below:

Let $a_{n}$ be the expected value of $\left|x-x^{\prime}\right|+\left|y-y^{\prime}\right|$, where $(x, y)$ and $\left(x^{\prime}, y^{\prime}\right)$ are two points chosen randomly within $S_{n}$. There exist relatively prime positive integers $a$ and $b$ such that
$$
\lim _{n \rightarrow \infty} \frac{a_{n}}{3^{n}}=\frac{a}{b} .
$$
Compute $100 a+b$.
|
By symmetry, we only need to consider the $x$-distance, then we can multiply our answer by 2. Let this quantity be $g(n)=a_{n} / 2$.
Divide the $n$th iteration fractal into three meta-columns of equal width. Then the probability that a random point is in the first, second, and third meta-columns is $\frac{3}{8}, \frac{2}{8}$, and $\frac{3}{8}$, respectively. If the two points end up in neighboring meta columns, the expected value of their $x$-distance is simply the width of a meta-column, which is $3^{n-1}$. If they end up in opposite meta-columns (the left and right ones), it is twice this amount, which is $2 \cdot 3^{n-1}$. Finally, if the two points lie in the same meta-column, which happens with probability $\left(\frac{3}{8}\right)^{2}+\left(\frac{2}{8}\right)^{2}+\left(\frac{3}{8}\right)^{2}=\frac{11}{32}$, the expected $x$-distance is just $g(n-1)$. Thus, we have
$$
g(n)=3^{n-1}\left(2 \cdot \frac{3}{8} \cdot \frac{2}{8}+2 \cdot \frac{2}{8} \cdot \frac{3}{8}\right)+\left(2 \cdot 3^{n-1}\right)\left(2 \cdot \frac{3}{8} \cdot \frac{3}{8}\right)+\frac{11}{32} g(n-1)=\frac{15}{16} \cdot 3^{n-1}+\frac{11}{32} g(n-1)
$$
As $n$ grows, say this is asymptotic to $g(n)=3^{n} C$. For some constant $C$. Then we can write $3^{n} C=\frac{15}{16} \cdot 3^{n-1}+\frac{11}{32} \cdot 3^{n-1} C \Longrightarrow C=\frac{6}{17}$. Our final answer is twice this, which is $\frac{12}{17}$.
|
{
"resource_path": "HarvardMIT/segmented/en-252-2022-feb-guts-solutions.jsonl",
"problem_match": "\n24. [12]",
"solution_match": "\nSolution: "
}
|
214dc20f-0331-56c7-8b7c-3376d672bd51
| 610,455
|
Let $A B C$ be an acute scalene triangle with circumcenter $O$ and centroid $G$. Given that $A G O$ is a right triangle, $A O=9$, and $B C=15$, let $S$ be the sum of all possible values for the area of triangle $A G O$. Compute $S^{2}$.
|
Answer: 288
|
288
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $A B C$ be an acute scalene triangle with circumcenter $O$ and centroid $G$. Given that $A G O$ is a right triangle, $A O=9$, and $B C=15$, let $S$ be the sum of all possible values for the area of triangle $A G O$. Compute $S^{2}$.
|
Answer: 288
|
{
"resource_path": "HarvardMIT/segmented/en-252-2022-feb-guts-solutions.jsonl",
"problem_match": "\n25. [14]",
"solution_match": "\nProposed by: Akash Das\n"
}
|
616ffd24-8564-51de-a71b-fee62ce14ee6
| 610,456
|
Diana is playing a card game against a computer. She starts with a deck consisting of a single card labeled 0.9. Each turn, Diana draws a random card from her deck, while the computer generates a card with a random real number drawn uniformly from the interval [ 0,1$]$. If the number on Diana's card is larger, she keeps her current card and also adds the computer's card to her deck. Otherwise, the computer takes Diana's card. After $k$ turns, Diana's deck is empty. Compute the expected value of $k$.
|
By linearity of expectation, we can treat the number of turns each card contributes to the total independently. Let $f(x)$ be the expected number of turns a card of value $x$ contributes (we want $f(0.9)$ ). If we have a card of value $x$, we lose it after 1 turn with probability $1-x$. If we don't lose it after the first turn, which happens with probability $x$, then given this, the expected number of turns this card contributes is $f(x)+\frac{1}{x} \int_{0}^{x} f(t) d t$. Thus, we can write the equation
$$
f(x)=1+x f(x)+\int_{0}^{x} f(t) d t
$$
Differentiating both sides gives us
$$
f^{\prime}(x)=x f^{\prime}(x)+f(x)+f(x) \Longrightarrow \frac{f^{\prime}(x)}{f(x)}=\frac{2}{1-x}
$$
Integrating gives us $\ln f(x)=-2 \ln (1-x)+C \Longrightarrow f(x)=\frac{e^{C}}{(1-x)^{2}}$. Since $f(0)=1$, we know that $C=0$, so $f(x)=(1-x)^{-2}$. Thus, we have $f(0.9)=(1-0.9)^{-2}=100$.
|
100
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Diana is playing a card game against a computer. She starts with a deck consisting of a single card labeled 0.9. Each turn, Diana draws a random card from her deck, while the computer generates a card with a random real number drawn uniformly from the interval [ 0,1$]$. If the number on Diana's card is larger, she keeps her current card and also adds the computer's card to her deck. Otherwise, the computer takes Diana's card. After $k$ turns, Diana's deck is empty. Compute the expected value of $k$.
|
By linearity of expectation, we can treat the number of turns each card contributes to the total independently. Let $f(x)$ be the expected number of turns a card of value $x$ contributes (we want $f(0.9)$ ). If we have a card of value $x$, we lose it after 1 turn with probability $1-x$. If we don't lose it after the first turn, which happens with probability $x$, then given this, the expected number of turns this card contributes is $f(x)+\frac{1}{x} \int_{0}^{x} f(t) d t$. Thus, we can write the equation
$$
f(x)=1+x f(x)+\int_{0}^{x} f(t) d t
$$
Differentiating both sides gives us
$$
f^{\prime}(x)=x f^{\prime}(x)+f(x)+f(x) \Longrightarrow \frac{f^{\prime}(x)}{f(x)}=\frac{2}{1-x}
$$
Integrating gives us $\ln f(x)=-2 \ln (1-x)+C \Longrightarrow f(x)=\frac{e^{C}}{(1-x)^{2}}$. Since $f(0)=1$, we know that $C=0$, so $f(x)=(1-x)^{-2}$. Thus, we have $f(0.9)=(1-0.9)^{-2}=100$.
|
{
"resource_path": "HarvardMIT/segmented/en-252-2022-feb-guts-solutions.jsonl",
"problem_match": "\n26. [14]",
"solution_match": "\nSolution: "
}
|
d9172f77-27a8-5cf3-b357-ee295c399c8c
| 610,457
|
In three-dimensional space, let $S$ be the region of points $(x, y, z)$ satisfying $-1 \leq z \leq 1$. Let $S_{1}, S_{2}, \ldots, S_{2022}$ be 2022 independent random rotations of $S$ about the origin ( $0,0,0$ ). The expected volume of the region $S_{1} \cap S_{2} \cap \cdots \cap S_{2022}$ can be expressed as $\frac{a \pi}{b}$, for relatively prime positive integers $a$ and $b$. Compute $100 a+b$.
|
Consider a point $P$ of distance $r$ from the origin. The distance from the origin of a random projection of $P$ onto a line is uniform from 0 to $r$. Therefore, if $r<1$ then the probability of $P$ being in all the sets is 1 , while for $r \geq 1$ it is $r^{-2022}$. Therefore the volume is
$$
\frac{4 \pi}{3}+4 \pi \int_{1}^{\infty} r^{2} r^{-2022} d r=4 \pi\left(\frac{1}{3}+\frac{1}{2019}\right)=\frac{2696 \pi}{2019}
$$
|
271619
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
In three-dimensional space, let $S$ be the region of points $(x, y, z)$ satisfying $-1 \leq z \leq 1$. Let $S_{1}, S_{2}, \ldots, S_{2022}$ be 2022 independent random rotations of $S$ about the origin ( $0,0,0$ ). The expected volume of the region $S_{1} \cap S_{2} \cap \cdots \cap S_{2022}$ can be expressed as $\frac{a \pi}{b}$, for relatively prime positive integers $a$ and $b$. Compute $100 a+b$.
|
Consider a point $P$ of distance $r$ from the origin. The distance from the origin of a random projection of $P$ onto a line is uniform from 0 to $r$. Therefore, if $r<1$ then the probability of $P$ being in all the sets is 1 , while for $r \geq 1$ it is $r^{-2022}$. Therefore the volume is
$$
\frac{4 \pi}{3}+4 \pi \int_{1}^{\infty} r^{2} r^{-2022} d r=4 \pi\left(\frac{1}{3}+\frac{1}{2019}\right)=\frac{2696 \pi}{2019}
$$
|
{
"resource_path": "HarvardMIT/segmented/en-252-2022-feb-guts-solutions.jsonl",
"problem_match": "\n27. [14]",
"solution_match": "\nSolution: "
}
|
f19864df-37e0-540f-8566-c4bd399e43e0
| 610,458
|
Compute the nearest integer to
$$
100 \sum_{n=1}^{\infty} 3^{n} \sin ^{3}\left(\frac{\pi}{3^{n}}\right)
$$
|
Answer: 236
|
236
|
Yes
|
Yes
|
math-word-problem
|
Calculus
|
Compute the nearest integer to
$$
100 \sum_{n=1}^{\infty} 3^{n} \sin ^{3}\left(\frac{\pi}{3^{n}}\right)
$$
|
Answer: 236
|
{
"resource_path": "HarvardMIT/segmented/en-252-2022-feb-guts-solutions.jsonl",
"problem_match": "\n28. [14]",
"solution_match": "\nProposed by: Akash Das\n"
}
|
939fd74a-ae90-52d3-9653-875b16c3786b
| 610,459
|
Let $\left(x_{1}, y_{1}\right), \ldots,\left(x_{k}, y_{k}\right)$ be the distinct real solutions to the equation
$$
\left(x^{2}+y^{2}\right)^{6}=\left(x^{2}-y^{2}\right)^{4}=\left(2 x^{3}-6 x y^{2}\right)^{3}
$$
Then $\sum_{i=1}^{k}\left(x_{i}+y_{i}\right)$ can be expressed as $\frac{a}{b}$, where $a$ and $b$ are relatively prime positive integers. Compute $100 a+b$.
|
Using polar coordinates, we can transform the problem to finding the intersections between $r=\cos 2 \theta$ and $r=2 \cos 3 \theta$. Drawing this out gives us a four-leaf clover and a large 3-leaf clover, which intersect at 7 points (one point being the origin). Note that since this graph is symmetric about the $x$ axis, we are only interested in finding the $x$-coordinates, which is $r \cos \theta=\cos 2 \theta \cos \theta=2 \cos ^{3} \theta-\cos \theta$.
Now note that all points of intersection satisfy
$$
\cos 2 \theta=2 \cos 3 \theta \Longleftrightarrow 8 \cos ^{3} \theta-2 \cos ^{2} \theta-6 \cos \theta+1=0 .
$$
Now, we want to compute the sum of $2 \cos ^{3} \theta-\cos \theta$ over all values of $\cos \theta$ that satisfy the above cubic. In other words, if the solutions for $\cos \theta$ to the above cubic are $a, b$, and $c$, we want $2 \sum_{\text {cyc }} 2 a^{3}-a$, since each value for $\cos \theta$ generates two solutions (symmetric about the $x$-axis).
This is
$$
\sum_{\mathrm{cyc}} 4 a^{3}-2 a=\sum_{\mathrm{cyc}} a^{2}+a-\frac{1}{2}
$$
where we have used the fact that $a^{3}=a^{2}+3 a-\frac{1}{2}$. By Vieta's formulas, $a+b+c=\frac{1}{4}$, while
$$
a^{2}+b^{2}+c^{2}=\left(\frac{1}{4}\right)^{2}+2 \cdot \frac{3}{4}=\frac{25}{16}
$$
Thus the final answer is $\frac{5}{16}$.
|
\frac{5}{16}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Let $\left(x_{1}, y_{1}\right), \ldots,\left(x_{k}, y_{k}\right)$ be the distinct real solutions to the equation
$$
\left(x^{2}+y^{2}\right)^{6}=\left(x^{2}-y^{2}\right)^{4}=\left(2 x^{3}-6 x y^{2}\right)^{3}
$$
Then $\sum_{i=1}^{k}\left(x_{i}+y_{i}\right)$ can be expressed as $\frac{a}{b}$, where $a$ and $b$ are relatively prime positive integers. Compute $100 a+b$.
|
Using polar coordinates, we can transform the problem to finding the intersections between $r=\cos 2 \theta$ and $r=2 \cos 3 \theta$. Drawing this out gives us a four-leaf clover and a large 3-leaf clover, which intersect at 7 points (one point being the origin). Note that since this graph is symmetric about the $x$ axis, we are only interested in finding the $x$-coordinates, which is $r \cos \theta=\cos 2 \theta \cos \theta=2 \cos ^{3} \theta-\cos \theta$.
Now note that all points of intersection satisfy
$$
\cos 2 \theta=2 \cos 3 \theta \Longleftrightarrow 8 \cos ^{3} \theta-2 \cos ^{2} \theta-6 \cos \theta+1=0 .
$$
Now, we want to compute the sum of $2 \cos ^{3} \theta-\cos \theta$ over all values of $\cos \theta$ that satisfy the above cubic. In other words, if the solutions for $\cos \theta$ to the above cubic are $a, b$, and $c$, we want $2 \sum_{\text {cyc }} 2 a^{3}-a$, since each value for $\cos \theta$ generates two solutions (symmetric about the $x$-axis).
This is
$$
\sum_{\mathrm{cyc}} 4 a^{3}-2 a=\sum_{\mathrm{cyc}} a^{2}+a-\frac{1}{2}
$$
where we have used the fact that $a^{3}=a^{2}+3 a-\frac{1}{2}$. By Vieta's formulas, $a+b+c=\frac{1}{4}$, while
$$
a^{2}+b^{2}+c^{2}=\left(\frac{1}{4}\right)^{2}+2 \cdot \frac{3}{4}=\frac{25}{16}
$$
Thus the final answer is $\frac{5}{16}$.
|
{
"resource_path": "HarvardMIT/segmented/en-252-2022-feb-guts-solutions.jsonl",
"problem_match": "\n30. [16]",
"solution_match": "\nSolution: "
}
|
a9a3d9c8-0cdb-5ffd-8be6-be24035216ea
| 610,461
|
For a point $P=(x, y)$ in the Cartesian plane, let $f(P)=\left(x^{2}-y^{2}, 2 x y-y^{2}\right)$. If $S$ is the set of all $P$ so that the sequence $P, f(P), f(f(P)), f(f(f(P))), \ldots$ approaches $(0,0)$, then the area of $S$ can be expressed as $\pi \sqrt{r}$ for some positive real number $r$. Compute $\lfloor 100 r\rfloor$.
|
For a point $P=(x, y)$, let $z(P)=x+y \omega$, where $\omega$ is a nontrivial third root of unity. Then
$$
\begin{aligned}
z(f(P))=\left(x^{2}-y^{2}\right)+\left(2 x y-y^{2}\right) \omega=x^{2}+2 x y \omega+y^{2}( & -1-\omega) \\
& =x^{2}+2 x y \omega+y^{2} \omega^{2}=(x+y \omega)^{2}=z(P)^{2}
\end{aligned}
$$
Applying this recursively gives us $z\left(f^{n}(P)\right)=z\left(f^{n-1}(P)\right)^{2}=z\left(f^{n-2}(P)\right)^{4}=\cdots=z(P)^{2^{n}}$. Thus the condition $f^{n}(P) \rightarrow(0,0)$ is equivalent to $|z(P)|<1$. The region of such points is the preimage of the unit disk (area $\pi$ ) upon the "shear" sending $(0,1)$ to $\left(-\frac{1}{2}, \frac{\sqrt{3}}{2}\right)$. This shear multiplies areas by a factor of $\frac{\sqrt{3}}{2}$, so the original area was $\frac{2 \pi}{\sqrt{3}}=\pi \sqrt{\frac{4}{3}}$.
|
133
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
For a point $P=(x, y)$ in the Cartesian plane, let $f(P)=\left(x^{2}-y^{2}, 2 x y-y^{2}\right)$. If $S$ is the set of all $P$ so that the sequence $P, f(P), f(f(P)), f(f(f(P))), \ldots$ approaches $(0,0)$, then the area of $S$ can be expressed as $\pi \sqrt{r}$ for some positive real number $r$. Compute $\lfloor 100 r\rfloor$.
|
For a point $P=(x, y)$, let $z(P)=x+y \omega$, where $\omega$ is a nontrivial third root of unity. Then
$$
\begin{aligned}
z(f(P))=\left(x^{2}-y^{2}\right)+\left(2 x y-y^{2}\right) \omega=x^{2}+2 x y \omega+y^{2}( & -1-\omega) \\
& =x^{2}+2 x y \omega+y^{2} \omega^{2}=(x+y \omega)^{2}=z(P)^{2}
\end{aligned}
$$
Applying this recursively gives us $z\left(f^{n}(P)\right)=z\left(f^{n-1}(P)\right)^{2}=z\left(f^{n-2}(P)\right)^{4}=\cdots=z(P)^{2^{n}}$. Thus the condition $f^{n}(P) \rightarrow(0,0)$ is equivalent to $|z(P)|<1$. The region of such points is the preimage of the unit disk (area $\pi$ ) upon the "shear" sending $(0,1)$ to $\left(-\frac{1}{2}, \frac{\sqrt{3}}{2}\right)$. This shear multiplies areas by a factor of $\frac{\sqrt{3}}{2}$, so the original area was $\frac{2 \pi}{\sqrt{3}}=\pi \sqrt{\frac{4}{3}}$.
|
{
"resource_path": "HarvardMIT/segmented/en-252-2022-feb-guts-solutions.jsonl",
"problem_match": "\n31. [16]",
"solution_match": "\nSolution: "
}
|
5dd57ec4-0b68-5cc7-9612-26637746c1e3
| 610,462
|
An ant starts at the point $(0,0)$ in the Cartesian plane. In the first minute, the ant faces towards $(1,0)$ and walks one unit. Each subsequent minute, the ant chooses an angle $\theta$ uniformly at random in the interval $\left[-90^{\circ}, 90^{\circ}\right]$, and then turns an angle of $\theta$ clockwise (negative values of $\theta$ correspond to counterclockwise rotations). Then, the ant walks one unit. After $n$ minutes, the ant's distance from $(0,0)$ is $d_{n}$. Let the expected value of $d_{n}^{2}$ be $a_{n}$. Compute the closest integer to
$$
10 \lim _{n \rightarrow \infty} \frac{a_{n}}{n} .
$$
|
Answer: 45
|
45
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
An ant starts at the point $(0,0)$ in the Cartesian plane. In the first minute, the ant faces towards $(1,0)$ and walks one unit. Each subsequent minute, the ant chooses an angle $\theta$ uniformly at random in the interval $\left[-90^{\circ}, 90^{\circ}\right]$, and then turns an angle of $\theta$ clockwise (negative values of $\theta$ correspond to counterclockwise rotations). Then, the ant walks one unit. After $n$ minutes, the ant's distance from $(0,0)$ is $d_{n}$. Let the expected value of $d_{n}^{2}$ be $a_{n}$. Compute the closest integer to
$$
10 \lim _{n \rightarrow \infty} \frac{a_{n}}{n} .
$$
|
Answer: 45
|
{
"resource_path": "HarvardMIT/segmented/en-252-2022-feb-guts-solutions.jsonl",
"problem_match": "\n32. [16]",
"solution_match": "\nProposed by: Carl Schildkraut\n"
}
|
1dd7586e-950b-545b-83da-d969146dadd9
| 610,463
|
Estimate $A$, the number of unordered triples of integers $(a, b, c)$ so that there exists a nondegenerate triangle with side lengths $a, b$, and $c$ fitting inside a $100 \times 100$ square. An estimate of $E$ earns $\max (0,\lfloor 20-|A-E| / 1000\rfloor)$ points.
|
Let's first count the number of such triangles with perimeter equal to $p$. By Stars and Bars, there are $\binom{p}{2} \approx \frac{p^{2}}{2}$ ordered triples of positive integers that sum to $p$. Additionally, note that only about a quarter of them satisfy the triangle inequality, we have only $\frac{p^{2}}{8}$ possible triples. Dividing by 3 ! gives us approximately $\frac{p^{2}}{48}$ nondegenerate triangles with perimeter $p$. Summing this from $p=1$ to $n$ gives us approximately $\frac{n^{3}}{144}$ triangles with perimeter at most $n$.
Now, note that there are two "extremes" for our triangles. One extreme is a triangle that is very close to a line. In that case, we have that the maximum perimeter is $200 \sqrt{2} \approx 283$. In the other extreme, we have a triangle that is very close to an equilateral triangle, in which case we have the maximum perimeter is $3 \cdot \frac{100}{\cos 15^{\circ}} \approx 311$. Thus, as a compromise between these extremes, we can plug in $n=300$ to get a value of $\frac{300^{3}}{144}=187500$, which would have earned 13 points.
|
187500
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Estimate $A$, the number of unordered triples of integers $(a, b, c)$ so that there exists a nondegenerate triangle with side lengths $a, b$, and $c$ fitting inside a $100 \times 100$ square. An estimate of $E$ earns $\max (0,\lfloor 20-|A-E| / 1000\rfloor)$ points.
|
Let's first count the number of such triangles with perimeter equal to $p$. By Stars and Bars, there are $\binom{p}{2} \approx \frac{p^{2}}{2}$ ordered triples of positive integers that sum to $p$. Additionally, note that only about a quarter of them satisfy the triangle inequality, we have only $\frac{p^{2}}{8}$ possible triples. Dividing by 3 ! gives us approximately $\frac{p^{2}}{48}$ nondegenerate triangles with perimeter $p$. Summing this from $p=1$ to $n$ gives us approximately $\frac{n^{3}}{144}$ triangles with perimeter at most $n$.
Now, note that there are two "extremes" for our triangles. One extreme is a triangle that is very close to a line. In that case, we have that the maximum perimeter is $200 \sqrt{2} \approx 283$. In the other extreme, we have a triangle that is very close to an equilateral triangle, in which case we have the maximum perimeter is $3 \cdot \frac{100}{\cos 15^{\circ}} \approx 311$. Thus, as a compromise between these extremes, we can plug in $n=300$ to get a value of $\frac{300^{3}}{144}=187500$, which would have earned 13 points.
|
{
"resource_path": "HarvardMIT/segmented/en-252-2022-feb-guts-solutions.jsonl",
"problem_match": "\n34. [20]",
"solution_match": "\nSolution: "
}
|
3e8a81d8-6e27-5613-8bd5-bcb2efc0f559
| 610,465
|
A random permutation of $\{1,2, \ldots, 100\}$ is given. It is then sorted to obtain the sequence $(1,2, \ldots, 100)$ as follows: at each step, two of the numbers which are not in their correct positions are selected at random, and the two numbers are swapped. If $s$ is the expected number of steps (i.e. swaps) required to obtain the sequence $(1,2, \cdots, 100)$, then estimate $A=\lfloor s\rfloor$. An estimate of $E$ earns $\max \left(0,\left\lfloor 20-\frac{1}{2}|A-E|\right\rfloor\right)$ points.
|
Let $f(n)$ be the expected number of steps if there are $n$ elements out of order. Let's consider one of these permutations and suppose that $a$ and $b$ are random elements that are out of order. The probability that swapping $a$ and $b$ sends $a$ to the proper place is $\frac{1}{n-1}$, and the probability that it sends $b$ to the proper place is $\frac{1}{n-1}$. Thus we can approximate
$$
f(n) \approx 1+\frac{2}{n-1} f(n-1)+\frac{n-3}{n-1} f(n)
$$
(The chance that both get sent to the right place decreases the overall probability that the number of fixed points increases, but also decreases the expected number of moves after the swap. These effects largely cancel out.)
As a result, we conclude that
$$
f(n) \approx f(n-1)+\frac{n-1}{2}
$$
and since $f(0)=0$ we have $f(n) \approx \frac{n(n-1)}{4}$. At the beginning, the expected number of elements that are in the right place is 1 , so the answer is approximately $f(99) \approx \frac{99 \cdot 98}{4} \approx 2425$. This is good enough for 19 points.
|
2425
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
A random permutation of $\{1,2, \ldots, 100\}$ is given. It is then sorted to obtain the sequence $(1,2, \ldots, 100)$ as follows: at each step, two of the numbers which are not in their correct positions are selected at random, and the two numbers are swapped. If $s$ is the expected number of steps (i.e. swaps) required to obtain the sequence $(1,2, \cdots, 100)$, then estimate $A=\lfloor s\rfloor$. An estimate of $E$ earns $\max \left(0,\left\lfloor 20-\frac{1}{2}|A-E|\right\rfloor\right)$ points.
|
Let $f(n)$ be the expected number of steps if there are $n$ elements out of order. Let's consider one of these permutations and suppose that $a$ and $b$ are random elements that are out of order. The probability that swapping $a$ and $b$ sends $a$ to the proper place is $\frac{1}{n-1}$, and the probability that it sends $b$ to the proper place is $\frac{1}{n-1}$. Thus we can approximate
$$
f(n) \approx 1+\frac{2}{n-1} f(n-1)+\frac{n-3}{n-1} f(n)
$$
(The chance that both get sent to the right place decreases the overall probability that the number of fixed points increases, but also decreases the expected number of moves after the swap. These effects largely cancel out.)
As a result, we conclude that
$$
f(n) \approx f(n-1)+\frac{n-1}{2}
$$
and since $f(0)=0$ we have $f(n) \approx \frac{n(n-1)}{4}$. At the beginning, the expected number of elements that are in the right place is 1 , so the answer is approximately $f(99) \approx \frac{99 \cdot 98}{4} \approx 2425$. This is good enough for 19 points.
|
{
"resource_path": "HarvardMIT/segmented/en-252-2022-feb-guts-solutions.jsonl",
"problem_match": "\n35. [20]",
"solution_match": "\nSolution: "
}
|
03d49f63-43ab-52eb-975b-cdb9c015e454
| 610,466
|
For a cubic polynomial $P(x)$ with complex roots $z_{1}, z_{2}, z_{3}$, let
$$
M(P)=\frac{\max \left(\left|z_{1}-z_{2}\right|,\left|z_{1}-z_{3}\right|,\left|z_{2}-z_{3}\right|\right)}{\min \left(\left|z_{1}-z_{2}\right|,\left|z_{1}-z_{3}\right|,\left|z_{2}-z_{3}\right|\right)}
$$
Over all polynomials $P(x)=x^{3}+a x^{2}+b x+c$, where $a, b, c$ are nonnegative integers at most 100 and $P(x)$ has no repeated roots, the twentieth largest possible value of $M(P)$ is $m$. Estimate $A=\lfloor m\rfloor$. An estimate of $E$ earns $\max \left(0,\left\lfloor 20-20|3 \ln (A / E)|^{1 / 2}\right\rfloor\right)$ points.
|
Consider fixing $a$ and $b$. Then, we know that $P^{\prime}(x)=3 x^{2}+2 a x+b$, which has a root at approximately $r \approx-b / 2 a$, which is rather small compared to 100 . Then $P(r) \approx-b^{2} / 4 a$. Assuming that this is greater than about -100 , then the value of $c$ that produces the roots that are closest together is the closest integer to $-P(r)$ (the chance when this creates a double root is pretty rare. Let $-P(r)=c+s$, so that we can now assume that $s$ is uniformly distributed in $(-1 / 2,1 / 2)$. One can
show that the difference between these roots is about $2 \sqrt{|s| / a}$. Since these roots are rather small, by Vieta's formulas the other root is near $-a$, so $M(P)$ is about $\frac{1}{2} \sqrt{a^{3} /|s|}$.
It's clear from this discussion that $a$ needs to be reasonably large for $M(P)$ to be large. Thus the condition $P(r)>-100$ is satisfied close to all the time - we will henceforth ignore it.
Set some $L$ and let's consider the expected number of $P$ so that $M(P)>L$. Then, for a given $a, b$, we need $|s|<a^{3} /(2 L)^{2}$. Summing over all $a$ and $b$, we find the probability is $2 \cdot 100 \cdot 100^{4} / 4 \cdot 1 /(2 L)^{2}$. Setting this equal to 20 gives us
$$
L^{2}=\frac{10^{10}}{160} \Longrightarrow L \approx 7900
$$
This is good enough for 14 points.
|
7900
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
For a cubic polynomial $P(x)$ with complex roots $z_{1}, z_{2}, z_{3}$, let
$$
M(P)=\frac{\max \left(\left|z_{1}-z_{2}\right|,\left|z_{1}-z_{3}\right|,\left|z_{2}-z_{3}\right|\right)}{\min \left(\left|z_{1}-z_{2}\right|,\left|z_{1}-z_{3}\right|,\left|z_{2}-z_{3}\right|\right)}
$$
Over all polynomials $P(x)=x^{3}+a x^{2}+b x+c$, where $a, b, c$ are nonnegative integers at most 100 and $P(x)$ has no repeated roots, the twentieth largest possible value of $M(P)$ is $m$. Estimate $A=\lfloor m\rfloor$. An estimate of $E$ earns $\max \left(0,\left\lfloor 20-20|3 \ln (A / E)|^{1 / 2}\right\rfloor\right)$ points.
|
Consider fixing $a$ and $b$. Then, we know that $P^{\prime}(x)=3 x^{2}+2 a x+b$, which has a root at approximately $r \approx-b / 2 a$, which is rather small compared to 100 . Then $P(r) \approx-b^{2} / 4 a$. Assuming that this is greater than about -100 , then the value of $c$ that produces the roots that are closest together is the closest integer to $-P(r)$ (the chance when this creates a double root is pretty rare. Let $-P(r)=c+s$, so that we can now assume that $s$ is uniformly distributed in $(-1 / 2,1 / 2)$. One can
show that the difference between these roots is about $2 \sqrt{|s| / a}$. Since these roots are rather small, by Vieta's formulas the other root is near $-a$, so $M(P)$ is about $\frac{1}{2} \sqrt{a^{3} /|s|}$.
It's clear from this discussion that $a$ needs to be reasonably large for $M(P)$ to be large. Thus the condition $P(r)>-100$ is satisfied close to all the time - we will henceforth ignore it.
Set some $L$ and let's consider the expected number of $P$ so that $M(P)>L$. Then, for a given $a, b$, we need $|s|<a^{3} /(2 L)^{2}$. Summing over all $a$ and $b$, we find the probability is $2 \cdot 100 \cdot 100^{4} / 4 \cdot 1 /(2 L)^{2}$. Setting this equal to 20 gives us
$$
L^{2}=\frac{10^{10}}{160} \Longrightarrow L \approx 7900
$$
This is good enough for 14 points.
|
{
"resource_path": "HarvardMIT/segmented/en-252-2022-feb-guts-solutions.jsonl",
"problem_match": "\n36. [20]",
"solution_match": "\nSolution: "
}
|
3215587e-1f4f-5399-813c-120f18984ec7
| 610,467
|
Call a simple graph $G$ quasi-colorable if we can color each edge blue, red, green, and white such that
- for each vertex $v$ of degree 3 in $G$, the three edges containing $v$ as an endpoint are either colored blue, red, and green, or all three edges are white,
- not all edges are white.
A connected graph $G$ has $a$ vertices of degree $4, b$ vertices of degree 3, and no other vertices, where $a$ and $b$ are positive integers. Find the smallest real number $c$ so that the following statement is true: "If $a / b>c$, then $G$ is quasi-colorable."
|
Consider a graph $G$ such that $\frac{a}{b}>\frac{1}{4}$. Note that the number of edges is $\frac{4 a+3 b}{2}$. Additionally, if any two vertices of degree 4 are adjacent, we can simply color that edge red and every other edge in $G$ white to get a valid quasi-coloring. Thus, suppose no two vertices of degree 4 are adjacent. Then, consider the subgraph $G^{\prime}$ resulting from removing all vertices of degree 4. Note that $G^{\prime}$ has $\frac{4 a+3 b}{2}-4 a=\frac{3 b-4 a}{2}<\frac{3 b-b}{2}=b$ edges. Thus, $G^{\prime}$ has fewer edges than vertices, which means that one of it's connected components must be a tree $T$. In this tree $T$, we can just select some arbitrary vertex $v$, and perform a breadth-first search on $T$, greedily coloring the edges as we go along. What this means is that we partition the vertices of $T$ into disjoint subsets $S_{0}=\{v\}, S_{1}, S_{2}, \ldots$, where $S_{j}$ contains all vertices of $T$ whose distance to $v$ is exactly $j$, and then we color edges between $S_{0}$ and $S_{1}$, and then greedily color the edges between $S_{1}$ and $S_{2}$, and so on. Once we color all the edges in $T$, we can color the edges between vertices in $T$ and the vertices of degree 4 appropriately, and color the remaining edges white to get a valid quasi-coloring.
To show that $c=\frac{1}{4}$ is indeed the smallest possible solution, consider the graph shown below. This graph is not quasi-colorable (one can see that coloring the tails of this graph is impossible).

If there are $N$ degree vertices of degree 4 , there are $4 N+10$ vertices of degree 3 . Since $\frac{N}{4 N+10} \rightarrow \frac{1}{4}$ as $N \rightarrow \infty$, we have that for each value $c<\frac{1}{4}$, one can find a graph with $a=N_{0}$ vertices of degree 4 and $b=4 N_{0}+10$ vertices of degree 3 such that $\frac{a}{b}=\frac{N_{0}}{4 N_{0}+10}>c$.
|
\frac{1}{4}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Call a simple graph $G$ quasi-colorable if we can color each edge blue, red, green, and white such that
- for each vertex $v$ of degree 3 in $G$, the three edges containing $v$ as an endpoint are either colored blue, red, and green, or all three edges are white,
- not all edges are white.
A connected graph $G$ has $a$ vertices of degree $4, b$ vertices of degree 3, and no other vertices, where $a$ and $b$ are positive integers. Find the smallest real number $c$ so that the following statement is true: "If $a / b>c$, then $G$ is quasi-colorable."
|
Consider a graph $G$ such that $\frac{a}{b}>\frac{1}{4}$. Note that the number of edges is $\frac{4 a+3 b}{2}$. Additionally, if any two vertices of degree 4 are adjacent, we can simply color that edge red and every other edge in $G$ white to get a valid quasi-coloring. Thus, suppose no two vertices of degree 4 are adjacent. Then, consider the subgraph $G^{\prime}$ resulting from removing all vertices of degree 4. Note that $G^{\prime}$ has $\frac{4 a+3 b}{2}-4 a=\frac{3 b-4 a}{2}<\frac{3 b-b}{2}=b$ edges. Thus, $G^{\prime}$ has fewer edges than vertices, which means that one of it's connected components must be a tree $T$. In this tree $T$, we can just select some arbitrary vertex $v$, and perform a breadth-first search on $T$, greedily coloring the edges as we go along. What this means is that we partition the vertices of $T$ into disjoint subsets $S_{0}=\{v\}, S_{1}, S_{2}, \ldots$, where $S_{j}$ contains all vertices of $T$ whose distance to $v$ is exactly $j$, and then we color edges between $S_{0}$ and $S_{1}$, and then greedily color the edges between $S_{1}$ and $S_{2}$, and so on. Once we color all the edges in $T$, we can color the edges between vertices in $T$ and the vertices of degree 4 appropriately, and color the remaining edges white to get a valid quasi-coloring.
To show that $c=\frac{1}{4}$ is indeed the smallest possible solution, consider the graph shown below. This graph is not quasi-colorable (one can see that coloring the tails of this graph is impossible).

If there are $N$ degree vertices of degree 4 , there are $4 N+10$ vertices of degree 3 . Since $\frac{N}{4 N+10} \rightarrow \frac{1}{4}$ as $N \rightarrow \infty$, we have that for each value $c<\frac{1}{4}$, one can find a graph with $a=N_{0}$ vertices of degree 4 and $b=4 N_{0}+10$ vertices of degree 3 such that $\frac{a}{b}=\frac{N_{0}}{4 N_{0}+10}>c$.
|
{
"resource_path": "HarvardMIT/segmented/en-254-tournaments-2022-hmic-solutions.jsonl",
"problem_match": "\n4. [10]",
"solution_match": "\nSolution 1: "
}
|
c388f6dc-dc82-54d4-8cfc-f68028221ec6
| 610,481
|
Emily's broken clock runs backwards at five times the speed of a regular clock. Right now, it is displaying the wrong time. How many times will it display the correct time in the next 24 hours? It is an analog clock (i.e. a clock with hands), so it only displays the numerical time, not AM or PM. Emily's clock also does not tick, but rather updates continuously.
|
When comparing Emily's clock with a normal clock, the difference between the two times decreases by 6 seconds for every 1 second that passes. Since this difference is treated as 0 whenever it is a multiple of 12 hours, the two clocks must agree once every $\frac{12}{6}=2$ hours. Thus, in a 24 hour period it will agree 12 times.
|
12
|
Yes
|
Yes
|
math-word-problem
|
Logic and Puzzles
|
Emily's broken clock runs backwards at five times the speed of a regular clock. Right now, it is displaying the wrong time. How many times will it display the correct time in the next 24 hours? It is an analog clock (i.e. a clock with hands), so it only displays the numerical time, not AM or PM. Emily's clock also does not tick, but rather updates continuously.
|
When comparing Emily's clock with a normal clock, the difference between the two times decreases by 6 seconds for every 1 second that passes. Since this difference is treated as 0 whenever it is a multiple of 12 hours, the two clocks must agree once every $\frac{12}{6}=2$ hours. Thus, in a 24 hour period it will agree 12 times.
|
{
"resource_path": "HarvardMIT/segmented/en-261-2022-nov-gen-solutions.jsonl",
"problem_match": "\n1. ",
"solution_match": "\nSolution: "
}
|
84772ebf-173c-59b0-a3dd-cd7df0b0661a
| 610,483
|
How many ways are there to arrange the numbers $1,2,3,4,5,6$ on the vertices of a regular hexagon such that exactly 3 of the numbers are larger than both of their neighbors? Rotations and reflections are considered the same.
|
Label the vertices of the hexagon $a b c d e f$.
The numbers that are larger than both of their neighbors can't be adjacent, so assume (by rotation) that these numbers take up slots ace. We also have that 6 and 5 cannot be smaller than both of their neighbors, so assume (by rotation and reflection) that $a=6$ and $c=5$.
Now, we need to insert $1,2,3,4$ into $b, d, e, f$ such that $e$ is the largest among $d, e, f$. There are 4 ways to choose $b$, which uniquely determines $e$, and 2 ways to choose the ordering of $d$, $f$, giving $4 \cdot 2=8$ total ways.
|
8
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
How many ways are there to arrange the numbers $1,2,3,4,5,6$ on the vertices of a regular hexagon such that exactly 3 of the numbers are larger than both of their neighbors? Rotations and reflections are considered the same.
|
Label the vertices of the hexagon $a b c d e f$.
The numbers that are larger than both of their neighbors can't be adjacent, so assume (by rotation) that these numbers take up slots ace. We also have that 6 and 5 cannot be smaller than both of their neighbors, so assume (by rotation and reflection) that $a=6$ and $c=5$.
Now, we need to insert $1,2,3,4$ into $b, d, e, f$ such that $e$ is the largest among $d, e, f$. There are 4 ways to choose $b$, which uniquely determines $e$, and 2 ways to choose the ordering of $d$, $f$, giving $4 \cdot 2=8$ total ways.
|
{
"resource_path": "HarvardMIT/segmented/en-261-2022-nov-gen-solutions.jsonl",
"problem_match": "\n2. ",
"solution_match": "\nSolution: "
}
|
a654566c-a541-58c9-9c38-2fdf5b9d5f12
| 610,484
|
An apartment building consists of 20 rooms numbered $1,2, \ldots, 20$ arranged clockwise in a circle. To move from one room to another, one can either walk to the next room clockwise (i.e. from room $i$ to room $(i+1)(\bmod 20))$ or walk across the center to the opposite room (i.e. from room $i$ to room $(i+10)(\bmod 20))$. Find the number of ways to move from room 10 to room 20 without visiting the same room twice.
|
One way is to walk directly from room 10 to 20 . Else, divide the rooms into 10 pairs $A_{0}=(10,20), A_{1}=(1,11), A_{2}=(2,12), \ldots, A_{9}=(9,19)$. Notice that
- each move is either between rooms in $A_{i}$ and $A_{(i+1)(\bmod 10)}$ for some $i \in\{0,1, \ldots, 9\}$, or between rooms in the same pair, meaning that our path must pass through $A_{0}, A_{1}, \ldots, A_{9}$ in that order before coming back to room 20 in $A_{0}$,
- in each of the pairs $A_{1}, A_{2}, \ldots, A_{8}$, we can choose to walk between rooms in that pair 0 or 1 times, and
- we have to walk between rooms 9 and 19 if and only if we first reach $A_{9}$ at room 9 (so the choice of walking between $A_{9}$ is completely determined by previous choices).
Thus, the number of ways to walk from room 10 to 20 is $1+2^{8}=257$.
|
257
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
An apartment building consists of 20 rooms numbered $1,2, \ldots, 20$ arranged clockwise in a circle. To move from one room to another, one can either walk to the next room clockwise (i.e. from room $i$ to room $(i+1)(\bmod 20))$ or walk across the center to the opposite room (i.e. from room $i$ to room $(i+10)(\bmod 20))$. Find the number of ways to move from room 10 to room 20 without visiting the same room twice.
|
One way is to walk directly from room 10 to 20 . Else, divide the rooms into 10 pairs $A_{0}=(10,20), A_{1}=(1,11), A_{2}=(2,12), \ldots, A_{9}=(9,19)$. Notice that
- each move is either between rooms in $A_{i}$ and $A_{(i+1)(\bmod 10)}$ for some $i \in\{0,1, \ldots, 9\}$, or between rooms in the same pair, meaning that our path must pass through $A_{0}, A_{1}, \ldots, A_{9}$ in that order before coming back to room 20 in $A_{0}$,
- in each of the pairs $A_{1}, A_{2}, \ldots, A_{8}$, we can choose to walk between rooms in that pair 0 or 1 times, and
- we have to walk between rooms 9 and 19 if and only if we first reach $A_{9}$ at room 9 (so the choice of walking between $A_{9}$ is completely determined by previous choices).
Thus, the number of ways to walk from room 10 to 20 is $1+2^{8}=257$.
|
{
"resource_path": "HarvardMIT/segmented/en-261-2022-nov-gen-solutions.jsonl",
"problem_match": "\n5. ",
"solution_match": "\nSolution: "
}
|
eca0c5a0-dd96-5f29-9035-e139d89b483f
| 610,487
|
In a plane, equilateral triangle $A B C$, square $B C D E$, and regular dodecagon $D E F G H I J K L M N O$ each have side length 1 and do not overlap. Find the area of the circumcircle of $\triangle A F N$.
|
Answer: $(2+\sqrt{3}) \pi$
|
(2+\sqrt{3}) \pi
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
In a plane, equilateral triangle $A B C$, square $B C D E$, and regular dodecagon $D E F G H I J K L M N O$ each have side length 1 and do not overlap. Find the area of the circumcircle of $\triangle A F N$.
|
Answer: $(2+\sqrt{3}) \pi$
|
{
"resource_path": "HarvardMIT/segmented/en-261-2022-nov-gen-solutions.jsonl",
"problem_match": "\n6. ",
"solution_match": "\nProposed by: Kevin Zhao\n"
}
|
ed2aabd7-726e-5bd8-bb45-4ea7b9952c95
| 610,488
|
In circle $\omega$, two perpendicular chords intersect at a point $P$. The two chords have midpoints $M_{1}$ and $M_{2}$ respectively, such that $P M_{1}=15$ and $P M_{2}=20$. Line $M_{1} M_{2}$ intersects $\omega$ at points $A$ and $B$, with $M_{1}$ between $A$ and $M_{2}$. Compute the largest possible value of $B M_{2}-A M_{1}$.
|
Let $O$ be the center of $\omega$ and let $M$ be the midpoint of $A B$ (so $M$ is the foot of $O$ to $M_{1} M_{2}$ ). Since $O M_{1} P M_{2}$ is a rectangle, we easily get that $M M_{1}=16$ and $M M_{2}=9$. Thus, $B M_{2}-A M_{1}=$ $M M_{1}-M M_{2}=7$.
|
7
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
In circle $\omega$, two perpendicular chords intersect at a point $P$. The two chords have midpoints $M_{1}$ and $M_{2}$ respectively, such that $P M_{1}=15$ and $P M_{2}=20$. Line $M_{1} M_{2}$ intersects $\omega$ at points $A$ and $B$, with $M_{1}$ between $A$ and $M_{2}$. Compute the largest possible value of $B M_{2}-A M_{1}$.
|
Let $O$ be the center of $\omega$ and let $M$ be the midpoint of $A B$ (so $M$ is the foot of $O$ to $M_{1} M_{2}$ ). Since $O M_{1} P M_{2}$ is a rectangle, we easily get that $M M_{1}=16$ and $M M_{2}=9$. Thus, $B M_{2}-A M_{1}=$ $M M_{1}-M M_{2}=7$.
|
{
"resource_path": "HarvardMIT/segmented/en-261-2022-nov-gen-solutions.jsonl",
"problem_match": "\n7. ",
"solution_match": "\n## Solution:\n\n"
}
|
6f790191-0fed-5d87-a5c0-bd0b18ead571
| 610,489
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.