problem
stringlengths 14
7.96k
| solution
stringlengths 3
10k
| answer
stringlengths 1
91
| problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | question_type
stringclasses 1
value | problem_type
stringclasses 8
values | problem_raw
stringlengths 14
7.96k
| solution_raw
stringlengths 3
10k
| metadata
dict | uuid
stringlengths 36
36
| id
int64 22.6k
612k
|
|---|---|---|---|---|---|---|---|---|---|---|---|
Let $\ell$ be the line through $(0,0)$ and tangent to the curve $y=x^{3}+x+16$. Find the slope of $\ell$.
|
13 Let the point of tangency be $\left(t, t^{3}+t+16\right)$, then the slope of $\ell$ is $\left(t^{3}+t+16\right) / t$. On the other hand, since $d y / d x=3 x^{2}+1$, the slope of $\ell$ is $3 t^{2}+1$. Therefore,
$$
\frac{t^{3}+t+16}{t}=3 t^{2}+1
$$
Simplifying, we get $t^{3}=8$, so $t=2$. It follows that the slope is $3(2)^{2}+1=13$.
|
13
|
Yes
|
Yes
|
math-word-problem
|
Calculus
|
Let $\ell$ be the line through $(0,0)$ and tangent to the curve $y=x^{3}+x+16$. Find the slope of $\ell$.
|
13 Let the point of tangency be $\left(t, t^{3}+t+16\right)$, then the slope of $\ell$ is $\left(t^{3}+t+16\right) / t$. On the other hand, since $d y / d x=3 x^{2}+1$, the slope of $\ell$ is $3 t^{2}+1$. Therefore,
$$
\frac{t^{3}+t+16}{t}=3 t^{2}+1
$$
Simplifying, we get $t^{3}=8$, so $t=2$. It follows that the slope is $3(2)^{2}+1=13$.
|
{
"resource_path": "HarvardMIT/segmented/en-112-2008-feb-calc-solutions.jsonl",
"problem_match": "\n2. [3]",
"solution_match": "\nAnswer: "
}
|
30ff8a2f-8fa5-5f1d-90b2-7b817f808675
| 608,263
|
Find all $y>1$ satisfying $\int_{1}^{y} x \ln x d x=\frac{1}{4}$.
|
$\sqrt{\sqrt{e}}$ Applying integration by parts with $u=\ln x$ and $v=\frac{1}{2} x^{2}$, we get
$$
\int_{1}^{y} x \ln x d x=\left.\frac{1}{2} x^{2} \ln x\right|_{1} ^{y}-\frac{1}{2} \int_{1}^{y} x d x=\frac{1}{2} y^{2} \ln y-\frac{1}{4} y^{2}+\frac{1}{4}
$$
So $y^{2} \ln y=\frac{1}{2} y^{2}$. Since $y>1$, we obtain $\ln y=\frac{1}{2}$, and thus $y=\sqrt{e}$.
|
\sqrt{e}
|
Yes
|
Yes
|
math-word-problem
|
Calculus
|
Find all $y>1$ satisfying $\int_{1}^{y} x \ln x d x=\frac{1}{4}$.
|
$\sqrt{\sqrt{e}}$ Applying integration by parts with $u=\ln x$ and $v=\frac{1}{2} x^{2}$, we get
$$
\int_{1}^{y} x \ln x d x=\left.\frac{1}{2} x^{2} \ln x\right|_{1} ^{y}-\frac{1}{2} \int_{1}^{y} x d x=\frac{1}{2} y^{2} \ln y-\frac{1}{4} y^{2}+\frac{1}{4}
$$
So $y^{2} \ln y=\frac{1}{2} y^{2}$. Since $y>1$, we obtain $\ln y=\frac{1}{2}$, and thus $y=\sqrt{e}$.
|
{
"resource_path": "HarvardMIT/segmented/en-112-2008-feb-calc-solutions.jsonl",
"problem_match": "\n3. [4]",
"solution_match": "\nAnswer: "
}
|
d960c4e3-f769-5504-a828-82b12050f550
| 608,264
|
Let $f(x)=\sin ^{6}\left(\frac{x}{4}\right)+\cos ^{6}\left(\frac{x}{4}\right)$ for all real numbers $x$. Determine $f^{(2008)}(0)$ (i.e., $f$ differentiated 2008 times and then evaluated at $x=0$ ).
|
| $\frac{3}{8}$ |
| :---: |
| We have |
$$
\begin{aligned}
\sin ^{6} x+\cos ^{6} x & =\left(\sin ^{2} x+\cos ^{2} x\right)^{3}-3 \sin ^{2} x \cos ^{2} x\left(\sin ^{2} x+\cos ^{2} x\right) \\
& =1-3 \sin ^{2} x \cos ^{2} x=1-\frac{3}{4} \sin ^{2} 2 x=1-\frac{3}{4}\left(\frac{1-\cos 4 x}{2}\right) \\
& =\frac{5}{8}+\frac{3}{8} \cos 4 x
\end{aligned}
$$
It follows that $f(x)=\frac{5}{8}+\frac{3}{8} \cos x$. Thus $f^{(2008)}(x)=\frac{3}{8} \cos x$. Evaluating at $x=0$ gives $\frac{3}{8}$.
|
\frac{3}{8}
|
Yes
|
Yes
|
math-word-problem
|
Calculus
|
Let $f(x)=\sin ^{6}\left(\frac{x}{4}\right)+\cos ^{6}\left(\frac{x}{4}\right)$ for all real numbers $x$. Determine $f^{(2008)}(0)$ (i.e., $f$ differentiated 2008 times and then evaluated at $x=0$ ).
|
| $\frac{3}{8}$ |
| :---: |
| We have |
$$
\begin{aligned}
\sin ^{6} x+\cos ^{6} x & =\left(\sin ^{2} x+\cos ^{2} x\right)^{3}-3 \sin ^{2} x \cos ^{2} x\left(\sin ^{2} x+\cos ^{2} x\right) \\
& =1-3 \sin ^{2} x \cos ^{2} x=1-\frac{3}{4} \sin ^{2} 2 x=1-\frac{3}{4}\left(\frac{1-\cos 4 x}{2}\right) \\
& =\frac{5}{8}+\frac{3}{8} \cos 4 x
\end{aligned}
$$
It follows that $f(x)=\frac{5}{8}+\frac{3}{8} \cos x$. Thus $f^{(2008)}(x)=\frac{3}{8} \cos x$. Evaluating at $x=0$ gives $\frac{3}{8}$.
|
{
"resource_path": "HarvardMIT/segmented/en-112-2008-feb-calc-solutions.jsonl",
"problem_match": "\n5. [4]",
"solution_match": "\nAnswer: "
}
|
dada6427-e099-5e4b-b174-c233e6e13356
| 608,266
|
Determine the value of $\lim _{n \rightarrow \infty} \sum_{k=0}^{n}\binom{n}{k}^{-1}$.
|
2 Let $S_{n}$ denote the sum in the limit. For $n \geq 1$, we have $S_{n} \geq\binom{ n}{0}^{-1}+\binom{n}{n}^{-1}=2$. On the other hand, for $n \geq 3$, we have
$$
S_{n}=\binom{n}{0}^{-1}+\binom{n}{1}^{-1}+\binom{n}{n-1}^{-1}+\binom{n}{n}^{-1}+\sum_{k=2}^{n-2}\binom{n}{k}^{-1} \leq 2+\frac{2}{n}+(n-3)\binom{n}{2}^{-1}
$$
which goes to 2 as $n \rightarrow \infty$. Therefore, $S_{n} \rightarrow 2$.
|
2
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Determine the value of $\lim _{n \rightarrow \infty} \sum_{k=0}^{n}\binom{n}{k}^{-1}$.
|
2 Let $S_{n}$ denote the sum in the limit. For $n \geq 1$, we have $S_{n} \geq\binom{ n}{0}^{-1}+\binom{n}{n}^{-1}=2$. On the other hand, for $n \geq 3$, we have
$$
S_{n}=\binom{n}{0}^{-1}+\binom{n}{1}^{-1}+\binom{n}{n-1}^{-1}+\binom{n}{n}^{-1}+\sum_{k=2}^{n-2}\binom{n}{k}^{-1} \leq 2+\frac{2}{n}+(n-3)\binom{n}{2}^{-1}
$$
which goes to 2 as $n \rightarrow \infty$. Therefore, $S_{n} \rightarrow 2$.
|
{
"resource_path": "HarvardMIT/segmented/en-112-2008-feb-calc-solutions.jsonl",
"problem_match": "\n6. [5]",
"solution_match": "\nAnswer: "
}
|
84bba2f2-139a-5d3c-a011-2b7715d2ec8c
| 608,267
|
Find $p$ so that $\lim _{x \rightarrow \infty} x^{p}(\sqrt[3]{x+1}+\sqrt[3]{x-1}-2 \sqrt[3]{x})$ is some non-zero real number.
|
$\sqrt{\frac{5}{3}}$ Make the substitution $t=\frac{1}{x}$. Then the limit equals to
$$
\lim _{t \rightarrow 0} t^{-p}\left(\sqrt[3]{\frac{1}{t}+1}+\sqrt[3]{\frac{1}{t}-1}-2 \sqrt[3]{\frac{1}{t}}\right)=\lim _{t \rightarrow 0} t^{-p-\frac{1}{3}}(\sqrt[3]{1+t}+\sqrt[3]{1-t}-2)
$$
We need the degree of the first nonzero term in the MacLaurin expansion of $\sqrt[3]{1+t}+\sqrt[3]{1-t}-2$. We have
$$
\sqrt[3]{1+t}=1+\frac{1}{3} t-\frac{1}{9} t^{2}+o\left(t^{2}\right), \quad \sqrt[3]{1-t}=1-\frac{1}{3} t-\frac{1}{9} t^{2}+o\left(t^{2}\right)
$$
It follows that $\sqrt[3]{1+t}+\sqrt[3]{1-t}-2=-\frac{2}{9} t^{2}+o\left(t^{2}\right)$. By consider the degree of the leading term, it follows that $-p-\frac{1}{3}=-2$. So $p=\frac{5}{3}$.
|
\frac{5}{3}
|
Yes
|
Yes
|
math-word-problem
|
Calculus
|
Find $p$ so that $\lim _{x \rightarrow \infty} x^{p}(\sqrt[3]{x+1}+\sqrt[3]{x-1}-2 \sqrt[3]{x})$ is some non-zero real number.
|
$\sqrt{\frac{5}{3}}$ Make the substitution $t=\frac{1}{x}$. Then the limit equals to
$$
\lim _{t \rightarrow 0} t^{-p}\left(\sqrt[3]{\frac{1}{t}+1}+\sqrt[3]{\frac{1}{t}-1}-2 \sqrt[3]{\frac{1}{t}}\right)=\lim _{t \rightarrow 0} t^{-p-\frac{1}{3}}(\sqrt[3]{1+t}+\sqrt[3]{1-t}-2)
$$
We need the degree of the first nonzero term in the MacLaurin expansion of $\sqrt[3]{1+t}+\sqrt[3]{1-t}-2$. We have
$$
\sqrt[3]{1+t}=1+\frac{1}{3} t-\frac{1}{9} t^{2}+o\left(t^{2}\right), \quad \sqrt[3]{1-t}=1-\frac{1}{3} t-\frac{1}{9} t^{2}+o\left(t^{2}\right)
$$
It follows that $\sqrt[3]{1+t}+\sqrt[3]{1-t}-2=-\frac{2}{9} t^{2}+o\left(t^{2}\right)$. By consider the degree of the leading term, it follows that $-p-\frac{1}{3}=-2$. So $p=\frac{5}{3}$.
|
{
"resource_path": "HarvardMIT/segmented/en-112-2008-feb-calc-solutions.jsonl",
"problem_match": "\n7. [5]",
"solution_match": "\nAnswer: "
}
|
eff6674b-e27b-59f3-b73a-b22d2dec19f4
| 608,268
|
Let $T=\int_{0}^{\ln 2} \frac{2 e^{3 x}+e^{2 x}-1}{e^{3 x}+e^{2 x}-e^{x}+1} d x$. Evaluate $e^{T}$.
|
$\frac{11}{4}$ Divide the top and bottom by $e^{x}$ to obtain that
$$
T=\int_{0}^{\ln 2} \frac{2 e^{2 x}+e^{x}-e^{-x}}{e^{2 x}+e^{x}-1+e^{-x}} d x
$$
Notice that $2 e^{2 x}+e^{x}-e^{-x}$ is the derivative of $e^{2 x}+e^{x}-1+e^{-x}$, and so
$$
T=\left[\ln \left|e^{2 x}+e^{x}-1+e^{-x}\right|\right]_{0}^{\ln 2}=\ln \left(4+2-1+\frac{1}{2}\right)-\ln 2=\ln \left(\frac{11}{4}\right)
$$
Therefore, $e^{T}=\frac{11}{4}$.
|
\frac{11}{4}
|
Yes
|
Yes
|
math-word-problem
|
Calculus
|
Let $T=\int_{0}^{\ln 2} \frac{2 e^{3 x}+e^{2 x}-1}{e^{3 x}+e^{2 x}-e^{x}+1} d x$. Evaluate $e^{T}$.
|
$\frac{11}{4}$ Divide the top and bottom by $e^{x}$ to obtain that
$$
T=\int_{0}^{\ln 2} \frac{2 e^{2 x}+e^{x}-e^{-x}}{e^{2 x}+e^{x}-1+e^{-x}} d x
$$
Notice that $2 e^{2 x}+e^{x}-e^{-x}$ is the derivative of $e^{2 x}+e^{x}-1+e^{-x}$, and so
$$
T=\left[\ln \left|e^{2 x}+e^{x}-1+e^{-x}\right|\right]_{0}^{\ln 2}=\ln \left(4+2-1+\frac{1}{2}\right)-\ln 2=\ln \left(\frac{11}{4}\right)
$$
Therefore, $e^{T}=\frac{11}{4}$.
|
{
"resource_path": "HarvardMIT/segmented/en-112-2008-feb-calc-solutions.jsonl",
"problem_match": "\n8. $[7]$",
"solution_match": "\nAnswer: "
}
|
6ec7118f-a6c4-524f-8b5b-b9ca25e17545
| 608,269
|
Evaluate the limit $\lim _{n \rightarrow \infty} n^{-\frac{1}{2}\left(1+\frac{1}{n}\right)}\left(1^{1} \cdot 2^{2} \cdots \cdots n^{n}\right)^{\frac{1}{n^{2}}}$.
|
$e^{-1 / 4}$ Taking the logarithm of the expression inside the limit, we find that it is
$$
-\frac{1}{2}\left(1+\frac{1}{n}\right) \ln n+\frac{1}{n^{2}} \sum_{k=1}^{n} k \ln k=\frac{1}{n} \sum_{k=1}^{n} \frac{k}{n} \ln \left(\frac{k}{n}\right)
$$
We can recognize this as the as Riemann sum expansion for the integral $\int_{0}^{1} x \ln x d x$, and thus the limit of the above sum as $n \rightarrow \infty$ equals to the value of this integral. Evaluating this integral using integration by parts, we find that
$$
\int_{0}^{1} x \ln x d x=\left.\frac{1}{2} x^{2} \ln x\right|_{0} ^{1}-\int_{0}^{1} \frac{x}{2} d x=-\frac{1}{4}
$$
Therefore, the original limit is $e^{-1 / 4}$.
|
e^{-1 / 4}
|
Yes
|
Yes
|
math-word-problem
|
Calculus
|
Evaluate the limit $\lim _{n \rightarrow \infty} n^{-\frac{1}{2}\left(1+\frac{1}{n}\right)}\left(1^{1} \cdot 2^{2} \cdots \cdots n^{n}\right)^{\frac{1}{n^{2}}}$.
|
$e^{-1 / 4}$ Taking the logarithm of the expression inside the limit, we find that it is
$$
-\frac{1}{2}\left(1+\frac{1}{n}\right) \ln n+\frac{1}{n^{2}} \sum_{k=1}^{n} k \ln k=\frac{1}{n} \sum_{k=1}^{n} \frac{k}{n} \ln \left(\frac{k}{n}\right)
$$
We can recognize this as the as Riemann sum expansion for the integral $\int_{0}^{1} x \ln x d x$, and thus the limit of the above sum as $n \rightarrow \infty$ equals to the value of this integral. Evaluating this integral using integration by parts, we find that
$$
\int_{0}^{1} x \ln x d x=\left.\frac{1}{2} x^{2} \ln x\right|_{0} ^{1}-\int_{0}^{1} \frac{x}{2} d x=-\frac{1}{4}
$$
Therefore, the original limit is $e^{-1 / 4}$.
|
{
"resource_path": "HarvardMIT/segmented/en-112-2008-feb-calc-solutions.jsonl",
"problem_match": "\n9. [7]",
"solution_match": "\nAnswer: "
}
|
58b9703f-62f5-58b9-bdfe-36b3e045b901
| 608,270
|
Evaluate the integral $\int_{0}^{1} \ln x \ln (1-x) d x$.
|
$2-\frac{\pi^{2}}{6}$ We have the MacLaurin expansion $\ln (1-x)=-x-\frac{x^{2}}{2}-\frac{x^{3}}{3}-\cdots$. So
$$
\int_{0}^{1} \ln x \ln (1-x) d x=-\int_{0}^{1} \ln x \sum_{n=1}^{\infty} \frac{x^{n}}{n} d x=-\sum_{n=1}^{\infty} \frac{1}{n} \int_{0}^{1} x^{n} \ln x d x
$$
Using integration by parts, we get
$$
\int_{0}^{1} x^{n} \ln x d x=\left.\frac{x^{n+1} \ln x}{n+1}\right|_{0} ^{1}-\int_{0}^{1} \frac{x^{n}}{n+1} d x=-\frac{1}{(n+1)^{2}}
$$
(We used the fact that $\lim _{x \rightarrow 0} x^{n} \ln x=0$ for $n>0$, which can be proven using l'Hôpital's rule.) Therefore, the original integral equals to
$$
\sum_{n=1}^{\infty} \frac{1}{n(n+1)^{2}}=\sum_{n=1}^{\infty}\left(\frac{1}{n}-\frac{1}{n+1}-\frac{1}{(n+1)^{2}}\right)
$$
Telescoping the sum and using the well-known identity $\sum_{n=0}^{\infty} \frac{1}{n^{2}}=\frac{\pi^{2}}{6}$, we see that the above sum is equal to $2-\frac{\pi^{2}}{6}$.
|
2-\frac{\pi^{2}}{6}
|
Yes
|
Yes
|
math-word-problem
|
Calculus
|
Evaluate the integral $\int_{0}^{1} \ln x \ln (1-x) d x$.
|
$2-\frac{\pi^{2}}{6}$ We have the MacLaurin expansion $\ln (1-x)=-x-\frac{x^{2}}{2}-\frac{x^{3}}{3}-\cdots$. So
$$
\int_{0}^{1} \ln x \ln (1-x) d x=-\int_{0}^{1} \ln x \sum_{n=1}^{\infty} \frac{x^{n}}{n} d x=-\sum_{n=1}^{\infty} \frac{1}{n} \int_{0}^{1} x^{n} \ln x d x
$$
Using integration by parts, we get
$$
\int_{0}^{1} x^{n} \ln x d x=\left.\frac{x^{n+1} \ln x}{n+1}\right|_{0} ^{1}-\int_{0}^{1} \frac{x^{n}}{n+1} d x=-\frac{1}{(n+1)^{2}}
$$
(We used the fact that $\lim _{x \rightarrow 0} x^{n} \ln x=0$ for $n>0$, which can be proven using l'Hôpital's rule.) Therefore, the original integral equals to
$$
\sum_{n=1}^{\infty} \frac{1}{n(n+1)^{2}}=\sum_{n=1}^{\infty}\left(\frac{1}{n}-\frac{1}{n+1}-\frac{1}{(n+1)^{2}}\right)
$$
Telescoping the sum and using the well-known identity $\sum_{n=0}^{\infty} \frac{1}{n^{2}}=\frac{\pi^{2}}{6}$, we see that the above sum is equal to $2-\frac{\pi^{2}}{6}$.
|
{
"resource_path": "HarvardMIT/segmented/en-112-2008-feb-calc-solutions.jsonl",
"problem_match": "\n10. [8]",
"solution_match": "\nAnswer: "
}
|
34d32836-1097-5713-bf14-b430b951bbf0
| 608,271
|
A $3 \times 3 \times 3$ cube composed of 27 unit cubes rests on a horizontal plane. Determine the number of ways of selecting two distinct unit cubes from a $3 \times 3 \times 1$ block (the order is irrelevant) with the property that the line joining the centers of the two cubes makes a $45^{\circ}$ angle with the horizontal plane.
|
60 There are 6 such slices, and each slice gives 10 valid pairs (with no overcounting). Therefore, there are 60 such pairs.
|
60
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
A $3 \times 3 \times 3$ cube composed of 27 unit cubes rests on a horizontal plane. Determine the number of ways of selecting two distinct unit cubes from a $3 \times 3 \times 1$ block (the order is irrelevant) with the property that the line joining the centers of the two cubes makes a $45^{\circ}$ angle with the horizontal plane.
|
60 There are 6 such slices, and each slice gives 10 valid pairs (with no overcounting). Therefore, there are 60 such pairs.
|
{
"resource_path": "HarvardMIT/segmented/en-112-2008-feb-comb-solutions.jsonl",
"problem_match": "\n1. [3]",
"solution_match": "\nAnswer: "
}
|
e259d1be-5f8a-54ba-b52d-170bdfa3e06a
| 608,272
|
Farmer John has 5 cows, 4 pigs, and 7 horses. How many ways can he pair up the animals so that every pair consists of animals of different species? Assume that all animals are distinguishable from each other. (Please write your answer as an integer, without any incomplete computations.)
|
100800 Since there are 9 cow and pigs combined and 7 horses, there must be a pair with 1 cow and 1 pig, and all the other pairs must contain a horse. There are $4 \times 5$ ways of selecting the cow-pig pair, and 7! ways to select the partners for the horses. It follows that the answer is $4 \times 5 \times 7!=100800$.
|
100800
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Farmer John has 5 cows, 4 pigs, and 7 horses. How many ways can he pair up the animals so that every pair consists of animals of different species? Assume that all animals are distinguishable from each other. (Please write your answer as an integer, without any incomplete computations.)
|
100800 Since there are 9 cow and pigs combined and 7 horses, there must be a pair with 1 cow and 1 pig, and all the other pairs must contain a horse. There are $4 \times 5$ ways of selecting the cow-pig pair, and 7! ways to select the partners for the horses. It follows that the answer is $4 \times 5 \times 7!=100800$.
|
{
"resource_path": "HarvardMIT/segmented/en-112-2008-feb-comb-solutions.jsonl",
"problem_match": "\n3. [4]",
"solution_match": "\nAnswer: "
}
|
b2b439c5-0916-59bb-b142-c42a838a91ca
| 608,274
|
Kermit the frog enjoys hopping around the infinite square grid in his backyard. It takes him 1 Joule of energy to hop one step north or one step south, and 1 Joule of energy to hop one step east or one step west. He wakes up one morning on the grid with 100 Joules of energy, and hops till he falls asleep with 0 energy. How many different places could he have gone to sleep?
|
10201
It is easy to see that the coordinates of the frog's final position must have the same parity. Suppose that the frog went to sleep at $(x, y)$. Then, we have that $-100 \leq y \leq 100$ and $|x| \leq 100-|y|$, so $x$ can take on the values $-100+|y|,-98+|y|, \ldots, 100-|y|$. There are $101-|y|$ such values, so the total number of such locations is
$$
\sum_{y=-100}^{100} 101-|y|=201 \cdot 101-2 \cdot \frac{100(100+1)}{2}=101^{2}=10201
$$
|
10201
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Kermit the frog enjoys hopping around the infinite square grid in his backyard. It takes him 1 Joule of energy to hop one step north or one step south, and 1 Joule of energy to hop one step east or one step west. He wakes up one morning on the grid with 100 Joules of energy, and hops till he falls asleep with 0 energy. How many different places could he have gone to sleep?
|
10201
It is easy to see that the coordinates of the frog's final position must have the same parity. Suppose that the frog went to sleep at $(x, y)$. Then, we have that $-100 \leq y \leq 100$ and $|x| \leq 100-|y|$, so $x$ can take on the values $-100+|y|,-98+|y|, \ldots, 100-|y|$. There are $101-|y|$ such values, so the total number of such locations is
$$
\sum_{y=-100}^{100} 101-|y|=201 \cdot 101-2 \cdot \frac{100(100+1)}{2}=101^{2}=10201
$$
|
{
"resource_path": "HarvardMIT/segmented/en-112-2008-feb-comb-solutions.jsonl",
"problem_match": "\n4. [4]",
"solution_match": "\nAnswer: "
}
|
2b1badfb-3776-51ae-b31c-c0d9e29ebd00
| 608,275
|
Let $S$ be the smallest subset of the integers with the property that $0 \in S$ and for any $x \in S$, we have $3 x \in S$ and $3 x+1 \in S$. Determine the number of non-negative integers in $S$ less than 2008.
|
128 Write the elements of $S$ in their ternary expansion (i.e. base 3). Then the second condition translates into, if $\overline{d_{1} d_{2} \cdots d_{k}} \in S$, then $\overline{d_{1} d_{2} \cdots d_{k} 0}$ and $\overline{d_{1} d_{2} \cdots d_{k} 1}$ are also in $S$. It follows that $S$ is the set of nonnegative integers whose tertiary representation contains only the digits 0 and 1. Since $2 \cdot 3^{6}<2008<3^{7}$, there are $2^{7}=128$ such elements less than 2008 . Therefore, there are 128 such non-negative elements.
|
128
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Let $S$ be the smallest subset of the integers with the property that $0 \in S$ and for any $x \in S$, we have $3 x \in S$ and $3 x+1 \in S$. Determine the number of non-negative integers in $S$ less than 2008.
|
128 Write the elements of $S$ in their ternary expansion (i.e. base 3). Then the second condition translates into, if $\overline{d_{1} d_{2} \cdots d_{k}} \in S$, then $\overline{d_{1} d_{2} \cdots d_{k} 0}$ and $\overline{d_{1} d_{2} \cdots d_{k} 1}$ are also in $S$. It follows that $S$ is the set of nonnegative integers whose tertiary representation contains only the digits 0 and 1. Since $2 \cdot 3^{6}<2008<3^{7}$, there are $2^{7}=128$ such elements less than 2008 . Therefore, there are 128 such non-negative elements.
|
{
"resource_path": "HarvardMIT/segmented/en-112-2008-feb-comb-solutions.jsonl",
"problem_match": "\n5. [5]",
"solution_match": "\nAnswer: "
}
|
f72b258a-2f34-58f7-9ae3-b797c341c4eb
| 608,276
|
Let $P_{1}, P_{2}, \ldots, P_{8}$ be 8 distinct points on a circle. Determine the number of possible configurations made by drawing a set of line segments connecting pairs of these 8 points, such that: (1) each $P_{i}$ is the endpoint of at most one segment and (2) two no segments intersect. (The configuration with no edges drawn is allowed. An example of a valid configuration is shown below.)
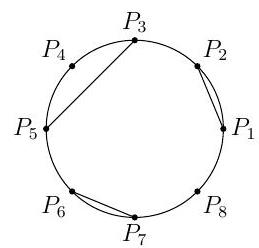
|
323 Let $f(n)$ denote the number of valid configurations when there are $n$ points on the circle. Let $P$ be one of the points. If $P$ is not the end point of an edge, then there are $f(n-1)$ ways to connect the remaining $n-1$ points. If $P$ belongs to an edge that separates the circle so that there are $k$ points on one side and $n-k-2$ points on the other side, then there are $f(k) f(n-k-2)$ ways of finishing the configuration. Thus, $f(n)$ satisfies the recurrence relation
$$
f(n)=f(n-1)+f(0) f(n-2)+f(1) f(n-3)+f(2) f(n-4)+\cdots+f(n-2) f(0), n \geq 2
$$
The initial conditions are $f(0)=f(1)=1$. Using the recursion, we find that $f(2)=2, f(3)=4, f(4)=$ $9, f(5)=21, f(6)=51, f(7)=127, f(8)=323$.
Remark: These numbers are known as the Motzkin numbers. This is sequence A001006 in the On-Line Encyclopedia of Integer Sequences (http://www.research.att.com/~njas/sequences/A001006). In
Richard Stanley's Enumerative Combinatorics Volume 2, one can find 13 different interpretations of Motzkin numbers in exercise 6.38.
|
323
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Let $P_{1}, P_{2}, \ldots, P_{8}$ be 8 distinct points on a circle. Determine the number of possible configurations made by drawing a set of line segments connecting pairs of these 8 points, such that: (1) each $P_{i}$ is the endpoint of at most one segment and (2) two no segments intersect. (The configuration with no edges drawn is allowed. An example of a valid configuration is shown below.)

|
323 Let $f(n)$ denote the number of valid configurations when there are $n$ points on the circle. Let $P$ be one of the points. If $P$ is not the end point of an edge, then there are $f(n-1)$ ways to connect the remaining $n-1$ points. If $P$ belongs to an edge that separates the circle so that there are $k$ points on one side and $n-k-2$ points on the other side, then there are $f(k) f(n-k-2)$ ways of finishing the configuration. Thus, $f(n)$ satisfies the recurrence relation
$$
f(n)=f(n-1)+f(0) f(n-2)+f(1) f(n-3)+f(2) f(n-4)+\cdots+f(n-2) f(0), n \geq 2
$$
The initial conditions are $f(0)=f(1)=1$. Using the recursion, we find that $f(2)=2, f(3)=4, f(4)=$ $9, f(5)=21, f(6)=51, f(7)=127, f(8)=323$.
Remark: These numbers are known as the Motzkin numbers. This is sequence A001006 in the On-Line Encyclopedia of Integer Sequences (http://www.research.att.com/~njas/sequences/A001006). In
Richard Stanley's Enumerative Combinatorics Volume 2, one can find 13 different interpretations of Motzkin numbers in exercise 6.38.
|
{
"resource_path": "HarvardMIT/segmented/en-112-2008-feb-comb-solutions.jsonl",
"problem_match": "\n7. [6]",
"solution_match": "\nAnswer: "
}
|
afdb7d6f-771f-569c-b58f-6c00cf68ba0e
| 608,278
|
Determine the number of ways to select a sequence of 8 sets $A_{1}, A_{2}, \ldots, A_{8}$, such that each is a subset (possibly empty) of $\{1,2\}$, and $A_{m}$ contains $A_{n}$ if $m$ divides $n$.
|
2025 Consider an arbitrary $x \in\{1,2\}$, and let us consider the number of ways for $x$ to be in some of the sets so that the constraints are satisfied. We divide into a few cases:
- Case: $x \notin A_{1}$. Then $x$ cannot be in any of the sets. So there is one possibility.
- Case: $x \in A_{1}$ but $x \notin A_{2}$. Then the only other sets that $x$ could be in are $A_{3}, A_{5}, A_{7}$, and $x$ could be in some collection of them. There are 8 possibilities in this case.
- Case: $x \in A_{2}$. Then $x \in A_{1}$ automatically. There are 4 independent choices to be make here: (1) whether $x \in A_{5} ;(2)$ whether $x \in A_{7}$; (3) whether $x \in A_{3}$, and if yes, whether $x \in A_{6}$; (4) whether $x \in A_{4}$, and if yes, whether $x \in A_{8}$. There are $2 \times 2 \times 3 \times 3=36$ choices here.
Therefore, there are $1+8+36=45$ ways to place $x$ into some of the sets. Since the choices for $x=1$ and $x=2$ are made independently, we see that the total number of possibilities is $45^{2}=2025$.
Remark: The solution could be guided by the following diagram. Set $A$ is above $B$ and connected to $B$ if and only if $A \subset B$. Such diagrams are known as Hasse diagrams, which are used to depict partially ordered sets.
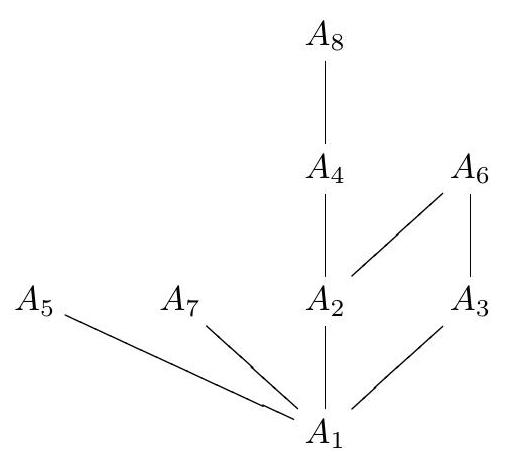
|
2025
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Determine the number of ways to select a sequence of 8 sets $A_{1}, A_{2}, \ldots, A_{8}$, such that each is a subset (possibly empty) of $\{1,2\}$, and $A_{m}$ contains $A_{n}$ if $m$ divides $n$.
|
2025 Consider an arbitrary $x \in\{1,2\}$, and let us consider the number of ways for $x$ to be in some of the sets so that the constraints are satisfied. We divide into a few cases:
- Case: $x \notin A_{1}$. Then $x$ cannot be in any of the sets. So there is one possibility.
- Case: $x \in A_{1}$ but $x \notin A_{2}$. Then the only other sets that $x$ could be in are $A_{3}, A_{5}, A_{7}$, and $x$ could be in some collection of them. There are 8 possibilities in this case.
- Case: $x \in A_{2}$. Then $x \in A_{1}$ automatically. There are 4 independent choices to be make here: (1) whether $x \in A_{5} ;(2)$ whether $x \in A_{7}$; (3) whether $x \in A_{3}$, and if yes, whether $x \in A_{6}$; (4) whether $x \in A_{4}$, and if yes, whether $x \in A_{8}$. There are $2 \times 2 \times 3 \times 3=36$ choices here.
Therefore, there are $1+8+36=45$ ways to place $x$ into some of the sets. Since the choices for $x=1$ and $x=2$ are made independently, we see that the total number of possibilities is $45^{2}=2025$.
Remark: The solution could be guided by the following diagram. Set $A$ is above $B$ and connected to $B$ if and only if $A \subset B$. Such diagrams are known as Hasse diagrams, which are used to depict partially ordered sets.

|
{
"resource_path": "HarvardMIT/segmented/en-112-2008-feb-comb-solutions.jsonl",
"problem_match": "\n8. [6]",
"solution_match": "\nAnswer: "
}
|
f98fc16d-9e65-5c31-ae3b-396e1ce39beb
| 608,279
|
On an infinite chessboard (whose squares are labeled by $(x, y)$, where $x$ and $y$ range over all integers), a king is placed at $(0,0)$. On each turn, it has probability of 0.1 of moving to each of the four edgeneighboring squares, and a probability of 0.05 of moving to each of the four diagonally-neighboring squares, and a probability of 0.4 of not moving. After 2008 turns, determine the probability that the king is on a square with both coordinates even. An exact answer is required.
|
| $\frac{1}{4}+\frac{3}{4 \cdot 5^{2008}}$ |
| :---: |
| Since only the parity of the coordinates are relevant, it is equivalent to | consider a situation where the king moves $(1,0)$ with probability 0.2 , moves $(0,1)$ with probability 0.2 , moves $(1,1)$ with probability 0.2 , and stays put with probability 0.4 . This can be analyzed using the generating function
$$
f(x, y)=(0.4+2 \times 0.1 x+2 \times 0.1 y+4 \times 0.05 x y)^{2008}=\frac{(2+x+y+x y)^{2008}}{5^{2008}} .
$$
We wish to find the sum of the coefficients of the terms $x^{a} y^{b}$, where both $a$ and $b$ are even. This is simply equal to $\frac{1}{4}(f(1,1)+f(1,-1)+f(-1,1)+f(-1,-1))$. We have $f(1,1)=1$ and $f(1,-1)=$ $f(-1,1)=f(-1,-1)=1 / 5^{2008}$. Therefore, the answer is
$$
\frac{1}{4}(f(1,1)+f(1,-1)+f(-1,1)+f(-1,-1))=\frac{1}{4}\left(1+\frac{3}{5^{2008}}\right)=\frac{1}{4}+\frac{3}{4 \cdot 5^{2008}}
$$
|
\frac{1}{4}+\frac{3}{4 \cdot 5^{2008}}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
On an infinite chessboard (whose squares are labeled by $(x, y)$, where $x$ and $y$ range over all integers), a king is placed at $(0,0)$. On each turn, it has probability of 0.1 of moving to each of the four edgeneighboring squares, and a probability of 0.05 of moving to each of the four diagonally-neighboring squares, and a probability of 0.4 of not moving. After 2008 turns, determine the probability that the king is on a square with both coordinates even. An exact answer is required.
|
| $\frac{1}{4}+\frac{3}{4 \cdot 5^{2008}}$ |
| :---: |
| Since only the parity of the coordinates are relevant, it is equivalent to | consider a situation where the king moves $(1,0)$ with probability 0.2 , moves $(0,1)$ with probability 0.2 , moves $(1,1)$ with probability 0.2 , and stays put with probability 0.4 . This can be analyzed using the generating function
$$
f(x, y)=(0.4+2 \times 0.1 x+2 \times 0.1 y+4 \times 0.05 x y)^{2008}=\frac{(2+x+y+x y)^{2008}}{5^{2008}} .
$$
We wish to find the sum of the coefficients of the terms $x^{a} y^{b}$, where both $a$ and $b$ are even. This is simply equal to $\frac{1}{4}(f(1,1)+f(1,-1)+f(-1,1)+f(-1,-1))$. We have $f(1,1)=1$ and $f(1,-1)=$ $f(-1,1)=f(-1,-1)=1 / 5^{2008}$. Therefore, the answer is
$$
\frac{1}{4}(f(1,1)+f(1,-1)+f(-1,1)+f(-1,-1))=\frac{1}{4}\left(1+\frac{3}{5^{2008}}\right)=\frac{1}{4}+\frac{3}{4 \cdot 5^{2008}}
$$
|
{
"resource_path": "HarvardMIT/segmented/en-112-2008-feb-comb-solutions.jsonl",
"problem_match": "\n9. [7]",
"solution_match": "\nAnswer: "
}
|
7ac55031-d8df-5979-90ac-3abb2f571f68
| 608,280
|
Determine the number of 8-tuples of nonnegative integers $\left(a_{1}, a_{2}, a_{3}, a_{4}, b_{1}, b_{2}, b_{3}, b_{4}\right)$ satisfying $0 \leq$ $a_{k} \leq k$, for each $k=1,2,3,4$, and $a_{1}+a_{2}+a_{3}+a_{4}+2 b_{1}+3 b_{2}+4 b_{3}+5 b_{4}=19$.
|
1540 For each $k=1,2,3,4$, note that set of pairs $\left(a_{k}, b_{k}\right)$ with $0 \leq a_{k} \leq k$ maps bijectively to the set of nonnegative integers through the map $\left(a_{k}, b_{k}\right) \mapsto a_{k}+(k+1) b_{k}$, as $a_{k}$ is simply the remainder of $a_{k}+(k+1) b_{k}$ upon division by $k+1$. By letting $x_{k}=a_{k}+(k+1) b_{k}$, we see that the problem is equivalent to finding the number of quadruples of nonnegative integers $\left(x_{1}, x_{2}, x_{3}, x_{4}\right)$ such that $x_{1}+x_{2}+x_{3}+x_{4}=19$. This is the same as finding the number of quadruples of positive integers $\left(x_{1}+1, x_{2}+1, x_{3}+1, x_{4}+1\right)$ such that $x_{1}+x_{2}+x_{3}+x_{4}=23$. By a standard "dots and bars" argument, we see that the answer is $\binom{22}{3}=1540$.
A generating functions solution is also available. It's not hard to see that the answer is the coefficient of $x^{19}$ in
$$
\begin{aligned}
& (1+x)\left(1+x+x^{2}\right)\left(1+x+x^{2}+x^{3}\right)\left(1+x+x^{2}+x^{3}+x^{4}\right) \\
& \quad\left(1+x^{2}+x^{4}+\cdots\right)\left(1+x^{3}+x^{6}+\cdots\right)\left(1+x^{4}+x^{8}+\cdots\right)\left(1+x^{5}+x^{10}+\cdots\right) \\
= & \left(\frac{1-x^{2}}{1-x}\right)\left(\frac{1-x^{3}}{1-x}\right)\left(\frac{1-x^{4}}{1-x}\right)\left(\frac{1-x^{5}}{1-x}\right)\left(\frac{1}{1-x^{2}}\right)\left(\frac{1}{1-x^{3}}\right)\left(\frac{1}{1-x^{4}}\right)\left(\frac{1}{1-x^{5}}\right) \\
= & \frac{1}{(1-x)^{4}}=(1-x)^{-4} .
\end{aligned}
$$
Using binomial theorem, we find that the coefficient of $x^{19}$ in $(1-x)^{-4}$ is $(-1)^{19}\binom{-4}{19}=\binom{22}{19}=1540$.
|
1540
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Determine the number of 8-tuples of nonnegative integers $\left(a_{1}, a_{2}, a_{3}, a_{4}, b_{1}, b_{2}, b_{3}, b_{4}\right)$ satisfying $0 \leq$ $a_{k} \leq k$, for each $k=1,2,3,4$, and $a_{1}+a_{2}+a_{3}+a_{4}+2 b_{1}+3 b_{2}+4 b_{3}+5 b_{4}=19$.
|
1540 For each $k=1,2,3,4$, note that set of pairs $\left(a_{k}, b_{k}\right)$ with $0 \leq a_{k} \leq k$ maps bijectively to the set of nonnegative integers through the map $\left(a_{k}, b_{k}\right) \mapsto a_{k}+(k+1) b_{k}$, as $a_{k}$ is simply the remainder of $a_{k}+(k+1) b_{k}$ upon division by $k+1$. By letting $x_{k}=a_{k}+(k+1) b_{k}$, we see that the problem is equivalent to finding the number of quadruples of nonnegative integers $\left(x_{1}, x_{2}, x_{3}, x_{4}\right)$ such that $x_{1}+x_{2}+x_{3}+x_{4}=19$. This is the same as finding the number of quadruples of positive integers $\left(x_{1}+1, x_{2}+1, x_{3}+1, x_{4}+1\right)$ such that $x_{1}+x_{2}+x_{3}+x_{4}=23$. By a standard "dots and bars" argument, we see that the answer is $\binom{22}{3}=1540$.
A generating functions solution is also available. It's not hard to see that the answer is the coefficient of $x^{19}$ in
$$
\begin{aligned}
& (1+x)\left(1+x+x^{2}\right)\left(1+x+x^{2}+x^{3}\right)\left(1+x+x^{2}+x^{3}+x^{4}\right) \\
& \quad\left(1+x^{2}+x^{4}+\cdots\right)\left(1+x^{3}+x^{6}+\cdots\right)\left(1+x^{4}+x^{8}+\cdots\right)\left(1+x^{5}+x^{10}+\cdots\right) \\
= & \left(\frac{1-x^{2}}{1-x}\right)\left(\frac{1-x^{3}}{1-x}\right)\left(\frac{1-x^{4}}{1-x}\right)\left(\frac{1-x^{5}}{1-x}\right)\left(\frac{1}{1-x^{2}}\right)\left(\frac{1}{1-x^{3}}\right)\left(\frac{1}{1-x^{4}}\right)\left(\frac{1}{1-x^{5}}\right) \\
= & \frac{1}{(1-x)^{4}}=(1-x)^{-4} .
\end{aligned}
$$
Using binomial theorem, we find that the coefficient of $x^{19}$ in $(1-x)^{-4}$ is $(-1)^{19}\binom{-4}{19}=\binom{22}{19}=1540$.
|
{
"resource_path": "HarvardMIT/segmented/en-112-2008-feb-comb-solutions.jsonl",
"problem_match": "\n10. [7]",
"solution_match": "\nAnswer: "
}
|
d2b5ff83-f6cd-52d4-aaf1-1b435ed66926
| 608,281
|
Let $A B C D$ be a unit square (that is, the labels $A, B, C, D$ appear in that order around the square). Let $X$ be a point outside of the square such that the distance from $X$ to $A C$ is equal to the distance from $X$ to $B D$, and also that $A X=\frac{\sqrt{2}}{2}$. Determine the value of $C X^{2}$.
|
$\quad \frac{5}{2}$
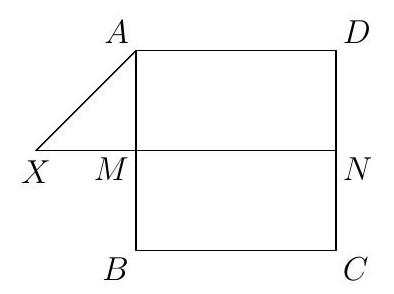
Since $X$ is equidistant from $A C$ and $B D$, it must lie on either the perpendicular bisector of $A B$ or the perpendicular bisector of $A D$. It turns that the two cases yield the same answer, so we will just assume the first case. Let $M$ be the midpoint of $A B$ and $N$ the midpoint of $C D$. Then, $X M$ is perpendicular to $A B$, so $X M=\frac{1}{2}$ and thus $X N=\frac{3}{2}, N C=\frac{1}{2}$. By the Pythagorean Theorem we find $X C=\frac{\sqrt{10}}{2}$ and the answer follows.
|
\frac{5}{2}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $A B C D$ be a unit square (that is, the labels $A, B, C, D$ appear in that order around the square). Let $X$ be a point outside of the square such that the distance from $X$ to $A C$ is equal to the distance from $X$ to $B D$, and also that $A X=\frac{\sqrt{2}}{2}$. Determine the value of $C X^{2}$.
|
$\quad \frac{5}{2}$

Since $X$ is equidistant from $A C$ and $B D$, it must lie on either the perpendicular bisector of $A B$ or the perpendicular bisector of $A D$. It turns that the two cases yield the same answer, so we will just assume the first case. Let $M$ be the midpoint of $A B$ and $N$ the midpoint of $C D$. Then, $X M$ is perpendicular to $A B$, so $X M=\frac{1}{2}$ and thus $X N=\frac{3}{2}, N C=\frac{1}{2}$. By the Pythagorean Theorem we find $X C=\frac{\sqrt{10}}{2}$ and the answer follows.
|
{
"resource_path": "HarvardMIT/segmented/en-112-2008-feb-gen1-solutions.jsonl",
"problem_match": "\n1. [2]",
"solution_match": "\nAnswer: "
}
|
0506ac02-f6ce-517d-af24-67cdfecc3535
| 608,282
|
Find the smallest positive integer $n$ such that $107 n$ has the same last two digits as $n$.
|
50 The two numbers have the same last two digits if and only if 100 divides their difference $106 n$, which happens if and only if 50 divides $n$.
|
50
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Find the smallest positive integer $n$ such that $107 n$ has the same last two digits as $n$.
|
50 The two numbers have the same last two digits if and only if 100 divides their difference $106 n$, which happens if and only if 50 divides $n$.
|
{
"resource_path": "HarvardMIT/segmented/en-112-2008-feb-gen1-solutions.jsonl",
"problem_match": "\n2. [3]",
"solution_match": "\nAnswer: "
}
|
c8cf6c63-1433-59b8-aba5-1d0a7130526a
| 608,283
|
There are 5 dogs, 4 cats, and 7 bowls of milk at an animal gathering. Dogs and cats are distinguishable, but all bowls of milk are the same. In how many ways can every dog and cat be paired with either a member of the other species or a bowl of milk such that all the bowls of milk are taken?
|
20 Since there are 9 dogs and cats combined and 7 bowls of milk, there can only be one dog-cat pair, and all the other pairs must contain a bowl of milk. There are $4 \times 5$ ways of selecting the dog-cat pair, and only one way of picking the other pairs, since the bowls of milk are indistinguishable, so the answer is $4 \times 5=20$.
|
20
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
There are 5 dogs, 4 cats, and 7 bowls of milk at an animal gathering. Dogs and cats are distinguishable, but all bowls of milk are the same. In how many ways can every dog and cat be paired with either a member of the other species or a bowl of milk such that all the bowls of milk are taken?
|
20 Since there are 9 dogs and cats combined and 7 bowls of milk, there can only be one dog-cat pair, and all the other pairs must contain a bowl of milk. There are $4 \times 5$ ways of selecting the dog-cat pair, and only one way of picking the other pairs, since the bowls of milk are indistinguishable, so the answer is $4 \times 5=20$.
|
{
"resource_path": "HarvardMIT/segmented/en-112-2008-feb-gen1-solutions.jsonl",
"problem_match": "\n3. [3]",
"solution_match": "\nAnswer: "
}
|
e6212586-a2aa-5220-ad19-3420d95b5450
| 608,284
|
The equation $x^{3}-9 x^{2}+8 x+2=0$ has three real roots $p, q, r$. Find $\frac{1}{p^{2}}+\frac{1}{q^{2}}+\frac{1}{r^{2}}$.
|
25 From Vieta's relations, we have $p+q+r=9, p q+q r+p r=8$ and $p q r=-2$. So
$$
\frac{1}{p^{2}}+\frac{1}{q^{2}}+\frac{1}{r^{2}}=\frac{(p q+q r+r p)^{2}-2(p+q+r)(p q r)}{(p q r)^{2}}=\frac{8^{2}-2 \cdot 9 \cdot(-2)}{(-2)^{2}}=25
$$
|
25
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
The equation $x^{3}-9 x^{2}+8 x+2=0$ has three real roots $p, q, r$. Find $\frac{1}{p^{2}}+\frac{1}{q^{2}}+\frac{1}{r^{2}}$.
|
25 From Vieta's relations, we have $p+q+r=9, p q+q r+p r=8$ and $p q r=-2$. So
$$
\frac{1}{p^{2}}+\frac{1}{q^{2}}+\frac{1}{r^{2}}=\frac{(p q+q r+r p)^{2}-2(p+q+r)(p q r)}{(p q r)^{2}}=\frac{8^{2}-2 \cdot 9 \cdot(-2)}{(-2)^{2}}=25
$$
|
{
"resource_path": "HarvardMIT/segmented/en-112-2008-feb-gen1-solutions.jsonl",
"problem_match": "\n7. [5]",
"solution_match": "\nAnswer: "
}
|
8f1a3edd-c5c5-5822-aa86-46485d65b962
| 608,286
|
Four students from Harvard, one of them named Jack, and five students from MIT, one of them named Jill, are going to see a Boston Celtics game. However, they found out that only 5 tickets remain, so 4 of them must go back. Suppose that at least one student from each school must go see the game, and at least one of Jack and Jill must go see the game, how many ways are there of choosing which 5 people can see the game?
|
104 Let us count the number of way of distributing the tickets so that one of the conditions is violated. There is 1 way to give all the tickets to MIT students, and $\binom{7}{5}$ ways to give all the tickets to the 7 students other than Jack and Jill. Therefore, the total number of valid ways is $\binom{9}{5}-1-\binom{7}{5}=104$.
|
104
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Four students from Harvard, one of them named Jack, and five students from MIT, one of them named Jill, are going to see a Boston Celtics game. However, they found out that only 5 tickets remain, so 4 of them must go back. Suppose that at least one student from each school must go see the game, and at least one of Jack and Jill must go see the game, how many ways are there of choosing which 5 people can see the game?
|
104 Let us count the number of way of distributing the tickets so that one of the conditions is violated. There is 1 way to give all the tickets to MIT students, and $\binom{7}{5}$ ways to give all the tickets to the 7 students other than Jack and Jill. Therefore, the total number of valid ways is $\binom{9}{5}-1-\binom{7}{5}=104$.
|
{
"resource_path": "HarvardMIT/segmented/en-112-2008-feb-gen2-solutions.jsonl",
"problem_match": "\n1. [2]",
"solution_match": "\nAnswer: "
}
|
0d30f8a4-0a7d-5ea0-9b14-1f4591ddd257
| 608,290
|
Suppose that $a, b, c, d$ are real numbers satisfying $a \geq b \geq c \geq d \geq 0, a^{2}+d^{2}=1, b^{2}+c^{2}=1$, and $a c+b d=1 / 3$. Find the value of $a b-c d$.
|
$\frac{2 \sqrt{2}}{3}$ We have
$$
(a b-c d)^{2}=\left(a^{2}+d^{2}\right)\left(b^{2}+c^{2}\right)-(a c+b d)^{2}=(1)(1)-\left(\frac{1}{3}\right)^{2}=\frac{8}{9}
$$
Since $a \geq b \geq c \geq d \geq 0, a b-c d \geq 0$, so $a b-c d=\frac{2 \sqrt{2}}{3}$.
Comment: Another way to solve this problem is to use the trigonometric substitutions $a=\sin \theta$, $b=\sin \phi, c=\cos \phi, d=\cos \theta$.
|
\frac{2 \sqrt{2}}{3}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Suppose that $a, b, c, d$ are real numbers satisfying $a \geq b \geq c \geq d \geq 0, a^{2}+d^{2}=1, b^{2}+c^{2}=1$, and $a c+b d=1 / 3$. Find the value of $a b-c d$.
|
$\frac{2 \sqrt{2}}{3}$ We have
$$
(a b-c d)^{2}=\left(a^{2}+d^{2}\right)\left(b^{2}+c^{2}\right)-(a c+b d)^{2}=(1)(1)-\left(\frac{1}{3}\right)^{2}=\frac{8}{9}
$$
Since $a \geq b \geq c \geq d \geq 0, a b-c d \geq 0$, so $a b-c d=\frac{2 \sqrt{2}}{3}$.
Comment: Another way to solve this problem is to use the trigonometric substitutions $a=\sin \theta$, $b=\sin \phi, c=\cos \phi, d=\cos \theta$.
|
{
"resource_path": "HarvardMIT/segmented/en-112-2008-feb-gen2-solutions.jsonl",
"problem_match": "\n4. [3]",
"solution_match": "\nAnswer: "
}
|
d8c0113b-3d7d-56d1-bcae-03b115c5e278
| 608,293
|
How many different values can $\angle A B C$ take, where $A, B, C$ are distinct vertices of a cube?
|
5 . In a unit cube, there are 3 types of triangles, with side lengths $(1,1, \sqrt{2}),(1, \sqrt{2}, \sqrt{3})$ and $(\sqrt{2}, \sqrt{2}, \sqrt{2})$. Together they generate 5 different angle values.
|
5
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
How many different values can $\angle A B C$ take, where $A, B, C$ are distinct vertices of a cube?
|
5 . In a unit cube, there are 3 types of triangles, with side lengths $(1,1, \sqrt{2}),(1, \sqrt{2}, \sqrt{3})$ and $(\sqrt{2}, \sqrt{2}, \sqrt{2})$. Together they generate 5 different angle values.
|
{
"resource_path": "HarvardMIT/segmented/en-112-2008-feb-geo-solutions.jsonl",
"problem_match": "\n1. [3]",
"solution_match": "\nAnswer: "
}
|
e59d683a-1a7d-5629-82b3-466c744969b5
| 608,297
|
Let $A B C$ be an equilateral triangle. Let $\Omega$ be its incircle (circle inscribed in the triangle) and let $\omega$ be a circle tangent externally to $\Omega$ as well as to sides $A B$ and $A C$. Determine the ratio of the radius of $\Omega$ to the radius of $\omega$.
|
$\quad 3$ Label the diagram as shown below, where $\Omega$ and $\omega$ also denote the center of the corresponding circles. Note that $A M$ is a median and $\Omega$ is the centroid of the equilateral triangle. So $A M=3 M \Omega$. Since $M \Omega=N \Omega$, it follows that $A M / A N=3$, and triangle $A B C$ is the image of triangle $A B^{\prime} C^{\prime}$ after a scaling by a factor of 3 , and so the two incircles must also be related by a scale factor of 3 .
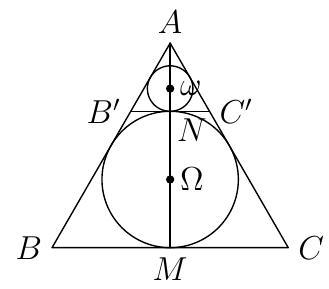
|
3
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $A B C$ be an equilateral triangle. Let $\Omega$ be its incircle (circle inscribed in the triangle) and let $\omega$ be a circle tangent externally to $\Omega$ as well as to sides $A B$ and $A C$. Determine the ratio of the radius of $\Omega$ to the radius of $\omega$.
|
$\quad 3$ Label the diagram as shown below, where $\Omega$ and $\omega$ also denote the center of the corresponding circles. Note that $A M$ is a median and $\Omega$ is the centroid of the equilateral triangle. So $A M=3 M \Omega$. Since $M \Omega=N \Omega$, it follows that $A M / A N=3$, and triangle $A B C$ is the image of triangle $A B^{\prime} C^{\prime}$ after a scaling by a factor of 3 , and so the two incircles must also be related by a scale factor of 3 .

|
{
"resource_path": "HarvardMIT/segmented/en-112-2008-feb-geo-solutions.jsonl",
"problem_match": "\n2. [3]",
"solution_match": "\nAnswer: "
}
|
9dd4b7f8-0eb7-5579-b963-ec4525f47241
| 608,298
|
Let $A B C$ be a triangle with $\angle B A C=90^{\circ}$. A circle is tangent to the sides $A B$ and $A C$ at $X$ and $Y$ respectively, such that the points on the circle diametrically opposite $X$ and $Y$ both lie on the side $B C$. Given that $A B=6$, find the area of the portion of the circle that lies outside the triangle.
|
$\pi-2$ Let $O$ be the center of the circle, and $r$ its radius, and let $X^{\prime}$ and $Y^{\prime}$ be the points diametrically opposite $X$ and $Y$, respectively. We have $O X^{\prime}=O Y^{\prime}=r$, and $\angle X^{\prime} O Y^{\prime}=90^{\circ}$. Since triangles $X^{\prime} O Y^{\prime}$ and $B A C$ are similar, we see that $A B=A C$. Let $X^{\prime \prime}$ be the projection of $Y^{\prime}$ onto $A B$. Since $X^{\prime \prime} B Y^{\prime}$ is similar to $A B C$, and $X^{\prime \prime} Y^{\prime}=r$, we have $X^{\prime \prime} B=r$. It follows that $A B=3 r$, so $r=2$.
Then, the desired area is the area of the quarter circle minus that of the triangle $X^{\prime} O Y^{\prime}$. And the answer is $\frac{1}{4} \pi r^{2}-\frac{1}{2} r^{2}=\pi-2$.
|
\pi-2
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
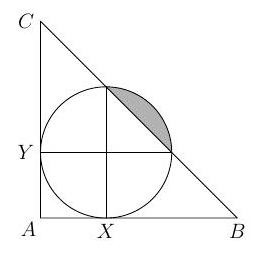
Let $A B C$ be a triangle with $\angle B A C=90^{\circ}$. A circle is tangent to the sides $A B$ and $A C$ at $X$ and $Y$ respectively, such that the points on the circle diametrically opposite $X$ and $Y$ both lie on the side $B C$. Given that $A B=6$, find the area of the portion of the circle that lies outside the triangle.

|
$\pi-2$ Let $O$ be the center of the circle, and $r$ its radius, and let $X^{\prime}$ and $Y^{\prime}$ be the points diametrically opposite $X$ and $Y$, respectively. We have $O X^{\prime}=O Y^{\prime}=r$, and $\angle X^{\prime} O Y^{\prime}=90^{\circ}$. Since triangles $X^{\prime} O Y^{\prime}$ and $B A C$ are similar, we see that $A B=A C$. Let $X^{\prime \prime}$ be the projection of $Y^{\prime}$ onto $A B$. Since $X^{\prime \prime} B Y^{\prime}$ is similar to $A B C$, and $X^{\prime \prime} Y^{\prime}=r$, we have $X^{\prime \prime} B=r$. It follows that $A B=3 r$, so $r=2$.

Then, the desired area is the area of the quarter circle minus that of the triangle $X^{\prime} O Y^{\prime}$. And the answer is $\frac{1}{4} \pi r^{2}-\frac{1}{2} r^{2}=\pi-2$.
|
{
"resource_path": "HarvardMIT/segmented/en-112-2008-feb-geo-solutions.jsonl",
"problem_match": "\n3. [4]",
"solution_match": "\nAnswer: "
}
|
71bfca02-16cd-5ea0-978a-0c90a9b0b968
| 608,299
|
In a triangle $A B C$, take point $D$ on $B C$ such that $D B=14, D A=13, D C=4$, and the circumcircle of $A D B$ is congruent to the circumcircle of $A D C$. What is the area of triangle $A B C$ ?
|
108
The fact that the two circumcircles are congruent means that the chord $A D$ must subtend the same angle in both circles. That is, $\angle A B C=\angle A C B$, so $A B C$ is isosceles. Drop the perpendicular $M$ from $A$ to $B C$; we know $M C=9$ and so $M D=5$ and by Pythagoras on $A M D, A M=12$. Therefore, the area of $A B C$ is $\frac{1}{2}(A M)(B C)=\frac{1}{2}(12)(18)=108$.
|
108
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
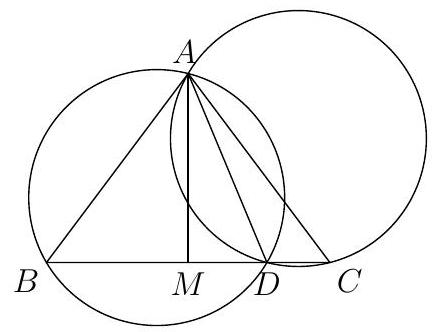
In a triangle $A B C$, take point $D$ on $B C$ such that $D B=14, D A=13, D C=4$, and the circumcircle of $A D B$ is congruent to the circumcircle of $A D C$. What is the area of triangle $A B C$ ?
|
108

The fact that the two circumcircles are congruent means that the chord $A D$ must subtend the same angle in both circles. That is, $\angle A B C=\angle A C B$, so $A B C$ is isosceles. Drop the perpendicular $M$ from $A$ to $B C$; we know $M C=9$ and so $M D=5$ and by Pythagoras on $A M D, A M=12$. Therefore, the area of $A B C$ is $\frac{1}{2}(A M)(B C)=\frac{1}{2}(12)(18)=108$.
|
{
"resource_path": "HarvardMIT/segmented/en-112-2008-feb-geo-solutions.jsonl",
"problem_match": "\n4. [4]",
"solution_match": "\nAnswer: "
}
|
ed9893ee-ca84-5274-a1f9-3d33da7e252f
| 608,285
|
Let $A B C$ be a triangle with $\angle A=45^{\circ}$. Let $P$ be a point on side $B C$ with $P B=3$ and $P C=5$. Let $O$ be the circumcenter of $A B C$. Determine the length $O P$.
|
$\sqrt{\sqrt{17}}$ Using extended Sine law, we find the circumradius of $A B C$ to be $R=\frac{B C}{2 \sin A}=4 \sqrt{2}$. By considering the power of point $P$, we find that $R^{2}-O P^{2}=P B \cdot P C=15$. So $O P=\sqrt{R^{2}-15}=$ $\sqrt{16 \cdot 2-15}=\sqrt{17}$.
|
\sqrt{17}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $A B C$ be a triangle with $\angle A=45^{\circ}$. Let $P$ be a point on side $B C$ with $P B=3$ and $P C=5$. Let $O$ be the circumcenter of $A B C$. Determine the length $O P$.
|
$\sqrt{\sqrt{17}}$ Using extended Sine law, we find the circumradius of $A B C$ to be $R=\frac{B C}{2 \sin A}=4 \sqrt{2}$. By considering the power of point $P$, we find that $R^{2}-O P^{2}=P B \cdot P C=15$. So $O P=\sqrt{R^{2}-15}=$ $\sqrt{16 \cdot 2-15}=\sqrt{17}$.
|
{
"resource_path": "HarvardMIT/segmented/en-112-2008-feb-geo-solutions.jsonl",
"problem_match": "\n6. [5]",
"solution_match": "\nAnswer: "
}
|
3b90564b-dda4-5fbe-a623-49f971ddf9e3
| 608,301
|
Let $C_{1}$ and $C_{2}$ be externally tangent circles with radius 2 and 3 , respectively. Let $C_{3}$ be a circle internally tangent to both $C_{1}$ and $C_{2}$ at points $A$ and $B$, respectively. The tangents to $C_{3}$ at $A$ and $B$ meet at $T$, and $T A=4$. Determine the radius of $C_{3}$.
|
8 Let $D$ be the point of tangency between $C_{1}$ and $C_{2}$. We see that $T$ is the radical center of the three circles, and so it must lie on the radical axis of $C_{1}$ and $C_{2}$, which happens to be their common tangent $T D$. So $T D=4$.
We have
$$
\tan \frac{\angle A T D}{2}=\frac{2}{T D}=\frac{1}{2}, \quad \text { and } \quad \tan \frac{\angle B T D}{2}=\frac{3}{T D}=\frac{3}{4} .
$$
Thus, the radius of $C_{3}$ equals to
$$
\begin{aligned}
T A \tan \frac{\angle A T B}{2} & =4 \tan \left(\frac{\angle A T D+\angle B T D}{2}\right) \\
& =4 \cdot \frac{\tan \frac{\angle A T D}{2}+\tan \frac{\angle B T D}{2}}{1-\tan \frac{\angle A T D}{2} \tan \frac{\angle B T D}{2}} \\
& =4 \cdot \frac{\frac{1}{2}+\frac{3}{4}}{1-\frac{1}{2} \cdot \frac{3}{4}} \\
& =8 .
\end{aligned}
$$
|
8
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
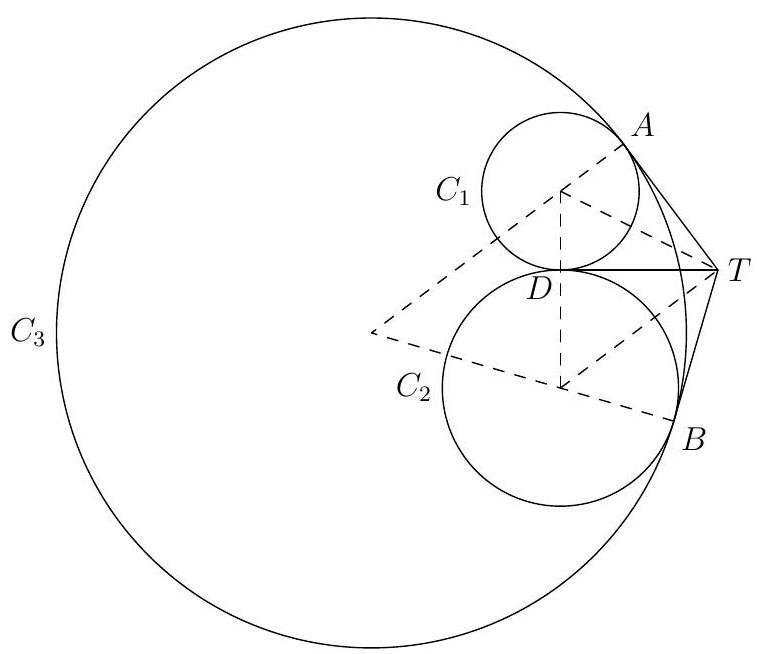
Let $C_{1}$ and $C_{2}$ be externally tangent circles with radius 2 and 3 , respectively. Let $C_{3}$ be a circle internally tangent to both $C_{1}$ and $C_{2}$ at points $A$ and $B$, respectively. The tangents to $C_{3}$ at $A$ and $B$ meet at $T$, and $T A=4$. Determine the radius of $C_{3}$.
|
8 Let $D$ be the point of tangency between $C_{1}$ and $C_{2}$. We see that $T$ is the radical center of the three circles, and so it must lie on the radical axis of $C_{1}$ and $C_{2}$, which happens to be their common tangent $T D$. So $T D=4$.

We have
$$
\tan \frac{\angle A T D}{2}=\frac{2}{T D}=\frac{1}{2}, \quad \text { and } \quad \tan \frac{\angle B T D}{2}=\frac{3}{T D}=\frac{3}{4} .
$$
Thus, the radius of $C_{3}$ equals to
$$
\begin{aligned}
T A \tan \frac{\angle A T B}{2} & =4 \tan \left(\frac{\angle A T D+\angle B T D}{2}\right) \\
& =4 \cdot \frac{\tan \frac{\angle A T D}{2}+\tan \frac{\angle B T D}{2}}{1-\tan \frac{\angle A T D}{2} \tan \frac{\angle B T D}{2}} \\
& =4 \cdot \frac{\frac{1}{2}+\frac{3}{4}}{1-\frac{1}{2} \cdot \frac{3}{4}} \\
& =8 .
\end{aligned}
$$
|
{
"resource_path": "HarvardMIT/segmented/en-112-2008-feb-geo-solutions.jsonl",
"problem_match": "\n7. [6]",
"solution_match": "\nAnswer: "
}
|
0b7e4e3b-ccca-5fa7-bd25-e942612cb81b
| 608,302
|
Let $A B C$ be an equilateral triangle with side length 2 , and let $\Gamma$ be a circle with radius $\frac{1}{2}$ centered at the center of the equilateral triangle. Determine the length of the shortest path that starts somewhere on $\Gamma$, visits all three sides of $A B C$, and ends somewhere on $\Gamma$ (not necessarily at the starting point). Express your answer in the form of $\sqrt{p}-q$, where $p$ and $q$ are rational numbers written as reduced fractions.
|
$\sqrt{\frac{28}{3}}-1$ Suppose that the path visits sides $A B, B C, C A$ in this order. Construct points $A^{\prime}, B^{\prime}, C^{\prime}$ so that $C^{\prime}$ is the reflection of $C$ across $A B, A^{\prime}$ is the reflection of $A$ across $B C^{\prime}$, and $B^{\prime}$ is the reflection of $B$ across $A^{\prime} C^{\prime}$. Finally, let $\Gamma^{\prime}$ be the circle with radius $\frac{1}{2}$ centered at the center of $A^{\prime} B^{\prime} C^{\prime}$. Note that $\Gamma^{\prime}$ is the image of $\Gamma$ after the three reflections: $A B, B C^{\prime}, C^{\prime} A^{\prime}$.
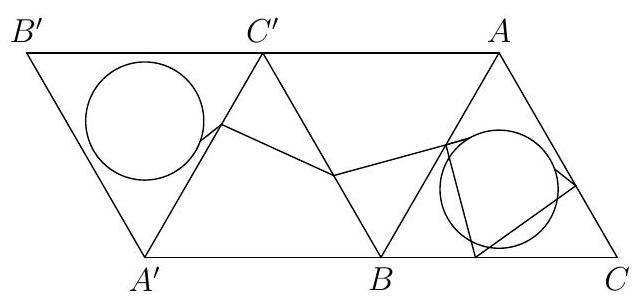
When the path hits $A B$, let us reflect the rest of the path across $A B$ and follow this reflected path. When we hit $B C^{\prime}$, let us reflect the rest of the path across $B C^{\prime}$, and follow the new path. And when we hit $A^{\prime} C^{\prime}$, reflect the rest of the path across $A^{\prime} C^{\prime}$ and follow the new path. We must eventually end up at $\Gamma^{\prime}$.
It is easy to see that the shortest path connecting some point on $\Gamma$ to some point on $\Gamma^{\prime}$ lies on the line connecting the centers of the two circles. We can easily find the distance between the two centers to be $\sqrt{3^{2}+\left(\frac{1}{\sqrt{3}}\right)^{2}}=\sqrt{\frac{28}{3}}$. Therefore, the length of the shortest path connecting $\Gamma$ to $\Gamma^{\prime}$ has length $\sqrt{\frac{28}{3}}-1$. By reflecting this path three times back into $A B C$, we get a path that satisfies our conditions.
|
\sqrt{\frac{28}{3}}-1
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $A B C$ be an equilateral triangle with side length 2 , and let $\Gamma$ be a circle with radius $\frac{1}{2}$ centered at the center of the equilateral triangle. Determine the length of the shortest path that starts somewhere on $\Gamma$, visits all three sides of $A B C$, and ends somewhere on $\Gamma$ (not necessarily at the starting point). Express your answer in the form of $\sqrt{p}-q$, where $p$ and $q$ are rational numbers written as reduced fractions.
|
$\sqrt{\frac{28}{3}}-1$ Suppose that the path visits sides $A B, B C, C A$ in this order. Construct points $A^{\prime}, B^{\prime}, C^{\prime}$ so that $C^{\prime}$ is the reflection of $C$ across $A B, A^{\prime}$ is the reflection of $A$ across $B C^{\prime}$, and $B^{\prime}$ is the reflection of $B$ across $A^{\prime} C^{\prime}$. Finally, let $\Gamma^{\prime}$ be the circle with radius $\frac{1}{2}$ centered at the center of $A^{\prime} B^{\prime} C^{\prime}$. Note that $\Gamma^{\prime}$ is the image of $\Gamma$ after the three reflections: $A B, B C^{\prime}, C^{\prime} A^{\prime}$.

When the path hits $A B$, let us reflect the rest of the path across $A B$ and follow this reflected path. When we hit $B C^{\prime}$, let us reflect the rest of the path across $B C^{\prime}$, and follow the new path. And when we hit $A^{\prime} C^{\prime}$, reflect the rest of the path across $A^{\prime} C^{\prime}$ and follow the new path. We must eventually end up at $\Gamma^{\prime}$.
It is easy to see that the shortest path connecting some point on $\Gamma$ to some point on $\Gamma^{\prime}$ lies on the line connecting the centers of the two circles. We can easily find the distance between the two centers to be $\sqrt{3^{2}+\left(\frac{1}{\sqrt{3}}\right)^{2}}=\sqrt{\frac{28}{3}}$. Therefore, the length of the shortest path connecting $\Gamma$ to $\Gamma^{\prime}$ has length $\sqrt{\frac{28}{3}}-1$. By reflecting this path three times back into $A B C$, we get a path that satisfies our conditions.
|
{
"resource_path": "HarvardMIT/segmented/en-112-2008-feb-geo-solutions.jsonl",
"problem_match": "\n8. [6]",
"solution_match": "\nAnswer: "
}
|
13efb027-cb83-52b2-aa80-e6cc0d192b8e
| 608,289
|
Let $A B C$ be a triangle with $B C=2007, C A=2008, A B=2009$. Let $\omega$ be an excircle of $A B C$ that touches the line segment $B C$ at $D$, and touches extensions of lines $A C$ and $A B$ at $E$ and $F$, respectively (so that $C$ lies on segment $A E$ and $B$ lies on segment $A F$ ). Let $O$ be the center of $\omega$. Let $\ell$ be the line through $O$ perpendicular to $A D$. Let $\ell$ meet line $E F$ at $G$. Compute the length $D G$.
|
2014024 Let line $A D$ meet $\omega$ again at $H$. Since $A F$ and $A E$ are tangents to $\omega$ and $A D H$ is a secant, we see that $D E H F$ is a harmonic quadrilateral. This implies that the pole of $A D$ with respect to $\omega$ lies on $E F$. Since $\ell \perp A D$, the pole of $A D$ lies on $\ell$. It follows that the pole of $A D$ is $G$.
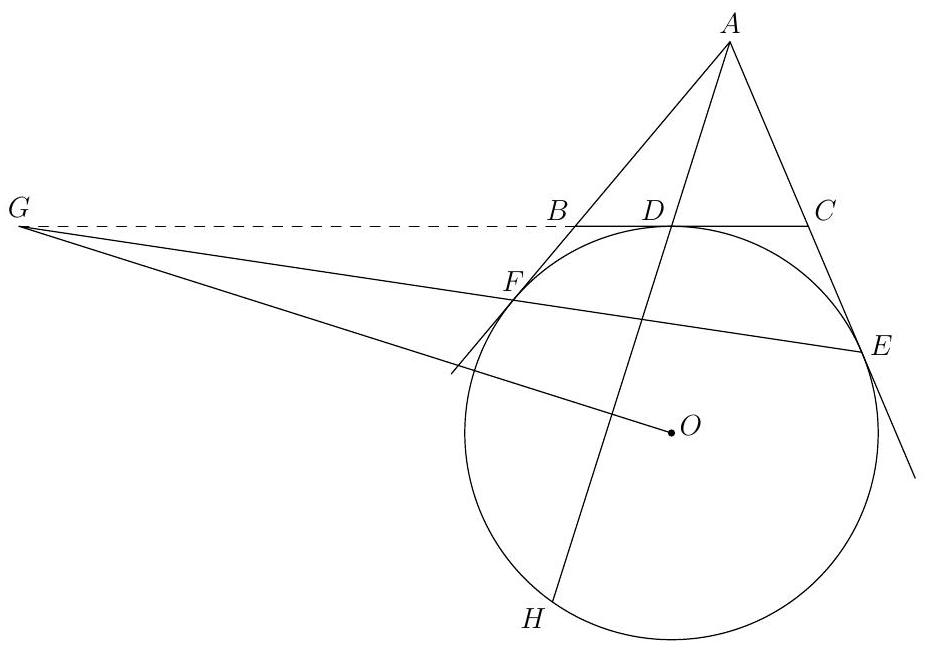
Thus, $G$ must lie on the tangent to $\omega$ at $D$, so $C, D, B, G$ are collinear. Furthermore, since the pencil of lines $(A E, A F ; A D, A G)$ is harmonic, by intersecting it with the line $B C$, we see that $(C, B ; D, G)$ is harmonic as well. This means that
$$
\frac{B D}{D C} \cdot \frac{C G}{G B}=-1
$$
(where the lengths are directed.) The semiperimeter of $A B C$ is $s=\frac{1}{2}(2007+2008+2009)=3012$. So $B D=s-2009=1003$ and $C D=s-2008=1004$. Let $x=D G$, then the above equations gives
$$
\frac{1003}{1004} \cdot \frac{x+1004}{x-1003}=1
$$
Solving gives $x=2014024$.
Remark: If you are interested to learn about projective geometry, check out the last chapter of Geometry Revisited by Coxeter and Greitzer or Geometric Transformations III by Yaglom.
|
2014024
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $A B C$ be a triangle with $B C=2007, C A=2008, A B=2009$. Let $\omega$ be an excircle of $A B C$ that touches the line segment $B C$ at $D$, and touches extensions of lines $A C$ and $A B$ at $E$ and $F$, respectively (so that $C$ lies on segment $A E$ and $B$ lies on segment $A F$ ). Let $O$ be the center of $\omega$. Let $\ell$ be the line through $O$ perpendicular to $A D$. Let $\ell$ meet line $E F$ at $G$. Compute the length $D G$.
|
2014024 Let line $A D$ meet $\omega$ again at $H$. Since $A F$ and $A E$ are tangents to $\omega$ and $A D H$ is a secant, we see that $D E H F$ is a harmonic quadrilateral. This implies that the pole of $A D$ with respect to $\omega$ lies on $E F$. Since $\ell \perp A D$, the pole of $A D$ lies on $\ell$. It follows that the pole of $A D$ is $G$.

Thus, $G$ must lie on the tangent to $\omega$ at $D$, so $C, D, B, G$ are collinear. Furthermore, since the pencil of lines $(A E, A F ; A D, A G)$ is harmonic, by intersecting it with the line $B C$, we see that $(C, B ; D, G)$ is harmonic as well. This means that
$$
\frac{B D}{D C} \cdot \frac{C G}{G B}=-1
$$
(where the lengths are directed.) The semiperimeter of $A B C$ is $s=\frac{1}{2}(2007+2008+2009)=3012$. So $B D=s-2009=1003$ and $C D=s-2008=1004$. Let $x=D G$, then the above equations gives
$$
\frac{1003}{1004} \cdot \frac{x+1004}{x-1003}=1
$$
Solving gives $x=2014024$.
Remark: If you are interested to learn about projective geometry, check out the last chapter of Geometry Revisited by Coxeter and Greitzer or Geometric Transformations III by Yaglom.
|
{
"resource_path": "HarvardMIT/segmented/en-112-2008-feb-geo-solutions.jsonl",
"problem_match": "\n10. [7]",
"solution_match": "\nAnswer: "
}
|
6e82ecf4-1173-5f2d-856f-6ebd51e73231
| 608,303
|
Given right triangle $A B C$, with $A B=4, B C=3$, and $C A=5$. Circle $\omega$ passes through $A$ and is tangent to $B C$ at $C$. What is the radius of $\omega$ ?
|
$\quad \frac{25}{8}$ Let $O$ be the center of $\omega$, and let $M$ be the midpoint of $A C$. Since $O A=O C$, $O M \perp A C$. Also, $\angle O C M=\angle B A C$, and so triangles $A B C$ and $C M O$ are similar. Then, $C O / C M=$ $A C / A B$, from which we obtain that the radius of $\omega$ is $C O=\frac{25}{8}$.
|
\frac{25}{8}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Given right triangle $A B C$, with $A B=4, B C=3$, and $C A=5$. Circle $\omega$ passes through $A$ and is tangent to $B C$ at $C$. What is the radius of $\omega$ ?
|
$\quad \frac{25}{8}$ Let $O$ be the center of $\omega$, and let $M$ be the midpoint of $A C$. Since $O A=O C$, $O M \perp A C$. Also, $\angle O C M=\angle B A C$, and so triangles $A B C$ and $C M O$ are similar. Then, $C O / C M=$ $A C / A B$, from which we obtain that the radius of $\omega$ is $C O=\frac{25}{8}$.
|
{
"resource_path": "HarvardMIT/segmented/en-112-2008-feb-guts-solutions.jsonl",
"problem_match": "\n2. [5]",
"solution_match": "\nAnswer: "
}
|
88d1cdb7-64ae-5d41-a52a-3ded80569ec7
| 608,305
|
How many ways can you color the squares of a $2 \times 2008$ grid in 3 colors such that no two squares of the same color share an edge?
|
$2 \cdot 3^{2008}$ Denote the colors $A, B, C$. The left-most column can be colored in 6 ways. For each subsequent column, if the $k$ th column is colored with $A B$, then the $(k+1)$ th column can only be colored with one of $B A, B C, C A$. That is, if we have colored the first $k$ columns, then there are 3 ways to color the $(k+1)$ th column. It follows that the number of ways of coloring the board is $6 \times 3^{2007}$.
## $11^{\text {th }}$ HARVARD-MIT MATHEMATICS TOURNAMENT, 23 FEBRUARY 2008 - GUTS ROUND
|
6 \times 3^{2007}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
How many ways can you color the squares of a $2 \times 2008$ grid in 3 colors such that no two squares of the same color share an edge?
|
$2 \cdot 3^{2008}$ Denote the colors $A, B, C$. The left-most column can be colored in 6 ways. For each subsequent column, if the $k$ th column is colored with $A B$, then the $(k+1)$ th column can only be colored with one of $B A, B C, C A$. That is, if we have colored the first $k$ columns, then there are 3 ways to color the $(k+1)$ th column. It follows that the number of ways of coloring the board is $6 \times 3^{2007}$.
## $11^{\text {th }}$ HARVARD-MIT MATHEMATICS TOURNAMENT, 23 FEBRUARY 2008 - GUTS ROUND
|
{
"resource_path": "HarvardMIT/segmented/en-112-2008-feb-guts-solutions.jsonl",
"problem_match": "\n3. [5]",
"solution_match": "\nAnswer: "
}
|
c4888bb8-91c7-5e93-aa38-db93ccd17622
| 608,306
|
A Vandal and a Moderator are editing a Wikipedia article. The article originally is error-free. Each day, the Vandal introduces one new error into the Wikipedia article. At the end of the day, the moderator checks the article and has a $2 / 3$ chance of catching each individual error still in the article. After 3 days, what is the probability that the article is error-free?
|
$\frac{416}{729}$ Consider the error that was introduced on day 1. The probability that the Moderator misses this error on all three checks is $1 / 3^{3}$, so the probability that this error gets removed is $1-\frac{1}{3^{3}}$. Similarly, the probability that the moderator misses the other two errors are $1-\frac{1}{3^{2}}$ and $1-\frac{1}{3}$. So the probability that the article is error-free is
$$
\left(1-\frac{1}{3^{3}}\right)\left(1-\frac{1}{3^{2}}\right)\left(1-\frac{1}{3}\right)=\frac{416}{729}
$$
|
\frac{416}{729}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
A Vandal and a Moderator are editing a Wikipedia article. The article originally is error-free. Each day, the Vandal introduces one new error into the Wikipedia article. At the end of the day, the moderator checks the article and has a $2 / 3$ chance of catching each individual error still in the article. After 3 days, what is the probability that the article is error-free?
|
$\frac{416}{729}$ Consider the error that was introduced on day 1. The probability that the Moderator misses this error on all three checks is $1 / 3^{3}$, so the probability that this error gets removed is $1-\frac{1}{3^{3}}$. Similarly, the probability that the moderator misses the other two errors are $1-\frac{1}{3^{2}}$ and $1-\frac{1}{3}$. So the probability that the article is error-free is
$$
\left(1-\frac{1}{3^{3}}\right)\left(1-\frac{1}{3^{2}}\right)\left(1-\frac{1}{3}\right)=\frac{416}{729}
$$
|
{
"resource_path": "HarvardMIT/segmented/en-112-2008-feb-guts-solutions.jsonl",
"problem_match": "\n5. [6]",
"solution_match": "\nAnswer: "
}
|
594def3c-9440-5d3a-b2d7-e86ef1ce8267
| 608,308
|
Given that $x+\sin y=2008$ and $x+2008 \cos y=2007$, where $0 \leq y \leq \pi / 2$, find the value of $x+y$.
|
$2007+\frac{\pi}{2}$ Subtracting the two equations gives $\sin y-2008 \cos y=1$. But since $0 \leq y \leq \pi / 2$, the maximum of $\sin y$ is 1 and the minimum of $\cos y$ is 0 , so we must have $\sin y=1$, so $y=\pi / 2$ and $x+y=2007+\frac{\pi}{2}$.
|
2007+\frac{\pi}{2}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Given that $x+\sin y=2008$ and $x+2008 \cos y=2007$, where $0 \leq y \leq \pi / 2$, find the value of $x+y$.
|
$2007+\frac{\pi}{2}$ Subtracting the two equations gives $\sin y-2008 \cos y=1$. But since $0 \leq y \leq \pi / 2$, the maximum of $\sin y$ is 1 and the minimum of $\cos y$ is 0 , so we must have $\sin y=1$, so $y=\pi / 2$ and $x+y=2007+\frac{\pi}{2}$.
|
{
"resource_path": "HarvardMIT/segmented/en-112-2008-feb-guts-solutions.jsonl",
"problem_match": "\n7. [6]",
"solution_match": "\nAnswer: "
}
|
91fe7774-092c-5962-bac1-1c3d54e7fb69
| 608,310
|
Trodgor the dragon is burning down a village consisting of 90 cottages. At time $t=0$ an angry peasant arises from each cottage, and every 8 minutes ( 480 seconds) thereafter another angry peasant spontaneously generates from each non-burned cottage. It takes Trodgor 5 seconds to either burn a peasant or to burn a cottage, but Trodgor cannot begin burning cottages until all the peasants around him have been burned. How many seconds does it take Trodgor to burn down the entire village?
|
1920 We look at the number of cottages after each wave of peasants. Let $A_{n}$ be the number of cottages remaining after $8 n$ minutes. During each 8 minute interval, Trodgor burns a total of $480 / 5=96$ peasants and cottages. Trodgor first burns $A_{n}$ peasants and spends the remaining time burning $96-A_{n}$ cottages. Therefore, as long as we do not reach negative cottages, we have the recurrence relation $A_{n+1}=A_{n}-\left(96-A_{n}\right)$, which is equivalent to $A_{n+1}=2 A_{n}-96$. Computing the first few terms of the series, we get that $A_{1}=84, A_{2}=72, A_{3}=48$, and $A_{4}=0$. Therefore, it takes Trodgor 32 minutes, which is 1920 seconds.
|
1920
|
Yes
|
Yes
|
math-word-problem
|
Logic and Puzzles
|
Trodgor the dragon is burning down a village consisting of 90 cottages. At time $t=0$ an angry peasant arises from each cottage, and every 8 minutes ( 480 seconds) thereafter another angry peasant spontaneously generates from each non-burned cottage. It takes Trodgor 5 seconds to either burn a peasant or to burn a cottage, but Trodgor cannot begin burning cottages until all the peasants around him have been burned. How many seconds does it take Trodgor to burn down the entire village?
|
1920 We look at the number of cottages after each wave of peasants. Let $A_{n}$ be the number of cottages remaining after $8 n$ minutes. During each 8 minute interval, Trodgor burns a total of $480 / 5=96$ peasants and cottages. Trodgor first burns $A_{n}$ peasants and spends the remaining time burning $96-A_{n}$ cottages. Therefore, as long as we do not reach negative cottages, we have the recurrence relation $A_{n+1}=A_{n}-\left(96-A_{n}\right)$, which is equivalent to $A_{n+1}=2 A_{n}-96$. Computing the first few terms of the series, we get that $A_{1}=84, A_{2}=72, A_{3}=48$, and $A_{4}=0$. Therefore, it takes Trodgor 32 minutes, which is 1920 seconds.
|
{
"resource_path": "HarvardMIT/segmented/en-112-2008-feb-guts-solutions.jsonl",
"problem_match": "\n8. [6]",
"solution_match": "\nAnswer: "
}
|
eed6d64a-6084-56b9-9c92-640c57da0b33
| 608,311
|
Consider a circular cone with vertex $V$, and let $A B C$ be a triangle inscribed in the base of the cone, such that $A B$ is a diameter and $A C=B C$. Let $L$ be a point on $B V$ such that the volume of the cone is 4 times the volume of the tetrahedron $A B C L$. Find the value of $B L / L V$.
|
$\sqrt{\frac{\pi}{4-\pi}}$ Let $R$ be the radius of the base, $H$ the height of the cone, $h$ the height of the pyramid and let $B L / L V=x / y$. Let [•] denote volume. Then [cone] $=\frac{1}{3} \pi R^{2} H$ and $[A B C L]=\frac{1}{3} \pi R^{2} h$ and $h=\frac{x}{x+y} H$. We are given that $[$ cone $]=4[A B C L]$, so $x / y=\frac{\pi}{4-\pi}$.
## $11^{\text {th }}$ HARVARD-MIT MATHEMATICS TOURNAMENT, 23 FEBRUARY 2008 - GUTS ROUND
|
\sqrt{\frac{\pi}{4-\pi}}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Consider a circular cone with vertex $V$, and let $A B C$ be a triangle inscribed in the base of the cone, such that $A B$ is a diameter and $A C=B C$. Let $L$ be a point on $B V$ such that the volume of the cone is 4 times the volume of the tetrahedron $A B C L$. Find the value of $B L / L V$.
|
$\sqrt{\frac{\pi}{4-\pi}}$ Let $R$ be the radius of the base, $H$ the height of the cone, $h$ the height of the pyramid and let $B L / L V=x / y$. Let [•] denote volume. Then [cone] $=\frac{1}{3} \pi R^{2} H$ and $[A B C L]=\frac{1}{3} \pi R^{2} h$ and $h=\frac{x}{x+y} H$. We are given that $[$ cone $]=4[A B C L]$, so $x / y=\frac{\pi}{4-\pi}$.
## $11^{\text {th }}$ HARVARD-MIT MATHEMATICS TOURNAMENT, 23 FEBRUARY 2008 - GUTS ROUND
|
{
"resource_path": "HarvardMIT/segmented/en-112-2008-feb-guts-solutions.jsonl",
"problem_match": "\n9. [6]",
"solution_match": "\nAnswer: "
}
|
5675d6ff-fcc0-58ba-b1ca-e5989da83829
| 608,312
|
Find the number of subsets $S$ of $\{1,2, \ldots 63\}$ the sum of whose elements is 2008 .
|
6 Note that $1+2+\cdots+63=2016$. So the problem is equivalent to finding the number of subsets of $\{1,2, \cdots 63\}$ whose sum of elements is 8 . We can count this by hand: $\{8\},\{1,7\},\{2,6\}$, $\{3,5\},\{1,2,5\},\{1,3,4\}$.
|
6
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Find the number of subsets $S$ of $\{1,2, \ldots 63\}$ the sum of whose elements is 2008 .
|
6 Note that $1+2+\cdots+63=2016$. So the problem is equivalent to finding the number of subsets of $\{1,2, \cdots 63\}$ whose sum of elements is 8 . We can count this by hand: $\{8\},\{1,7\},\{2,6\}$, $\{3,5\},\{1,2,5\},\{1,3,4\}$.
|
{
"resource_path": "HarvardMIT/segmented/en-112-2008-feb-guts-solutions.jsonl",
"problem_match": "\n10. [7]",
"solution_match": "\nAnswer: "
}
|
46102784-3f72-54f1-bc6b-d135a7dfddcd
| 608,313
|
Let $f(r)=\sum_{j=2}^{2008} \frac{1}{j^{r}}=\frac{1}{2^{r}}+\frac{1}{3^{r}}+\cdots+\frac{1}{2008^{r}}$. Find $\sum_{k=2}^{\infty} f(k)$.
|
$\frac{2007}{2008}$ We change the order of summation:
$$
\sum_{k=2}^{\infty} \sum_{j=2}^{2008} \frac{1}{j^{k}}=\sum_{j=2}^{2008} \sum_{k=2}^{\infty} \frac{1}{j^{k}}=\sum_{j=2}^{2008} \frac{1}{j^{2}\left(1-\frac{1}{j}\right)}=\sum_{j=2}^{2008} \frac{1}{j(j-1)}=\sum_{j=2}^{2008}\left(\frac{1}{j-1}-\frac{1}{j}\right)=1-\frac{1}{2008}=\frac{2007}{2008}
$$
|
\frac{2007}{2008}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Let $f(r)=\sum_{j=2}^{2008} \frac{1}{j^{r}}=\frac{1}{2^{r}}+\frac{1}{3^{r}}+\cdots+\frac{1}{2008^{r}}$. Find $\sum_{k=2}^{\infty} f(k)$.
|
$\frac{2007}{2008}$ We change the order of summation:
$$
\sum_{k=2}^{\infty} \sum_{j=2}^{2008} \frac{1}{j^{k}}=\sum_{j=2}^{2008} \sum_{k=2}^{\infty} \frac{1}{j^{k}}=\sum_{j=2}^{2008} \frac{1}{j^{2}\left(1-\frac{1}{j}\right)}=\sum_{j=2}^{2008} \frac{1}{j(j-1)}=\sum_{j=2}^{2008}\left(\frac{1}{j-1}-\frac{1}{j}\right)=1-\frac{1}{2008}=\frac{2007}{2008}
$$
|
{
"resource_path": "HarvardMIT/segmented/en-112-2008-feb-guts-solutions.jsonl",
"problem_match": "\n11. [7]",
"solution_match": "\nAnswer: "
}
|
1bcb122d-b3ce-571f-810d-012aed5ab297
| 608,314
|
Suppose we have an (infinite) cone $\mathcal{C}$ with apex $A$ and a plane $\pi$. The intersection of $\pi$ and $\mathcal{C}$ is an ellipse $\mathcal{E}$ with major axis $B C$, such that $B$ is closer to $A$ than $C$, and $B C=4, A C=5, A B=3$. Suppose we inscribe a sphere in each part of $\mathcal{C}$ cut up by $\mathcal{E}$ with both spheres tangent to $\mathcal{E}$. What is the ratio of the radii of the spheres (smaller to larger)?
|
$\sqrt{\frac{1}{3}}$ It can be seen that the points of tangency of the spheres with $E$ must lie on its major axis due to symmetry. Hence, we consider the two-dimensional cross-section with plane $A B C$. Then the two spheres become the incentre and the excentre of the triangle $A B C$, and we are looking for the ratio of the inradius to the exradius. Let $s, r, r_{a}$ denote the semiperimeter, inradius, and exradius (opposite to $A$ ) of the triangle $A B C$. We know that the area of $A B C$ can be expressed as both $r s$ and $r_{a}(s-|B C|)$, and so $\frac{r}{r_{a}}=\frac{s-|B C|}{s}$. For the given triangle, $s=6$ and $a=4$, so the required ratio is $\frac{1}{3}$.
$11^{\text {th }}$ HARVARD-MIT MATHEMATICS TOURNAMENT, 23 FEBRUARY 2008 - GUTS ROUND
|
\frac{1}{3}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Suppose we have an (infinite) cone $\mathcal{C}$ with apex $A$ and a plane $\pi$. The intersection of $\pi$ and $\mathcal{C}$ is an ellipse $\mathcal{E}$ with major axis $B C$, such that $B$ is closer to $A$ than $C$, and $B C=4, A C=5, A B=3$. Suppose we inscribe a sphere in each part of $\mathcal{C}$ cut up by $\mathcal{E}$ with both spheres tangent to $\mathcal{E}$. What is the ratio of the radii of the spheres (smaller to larger)?
|
$\sqrt{\frac{1}{3}}$ It can be seen that the points of tangency of the spheres with $E$ must lie on its major axis due to symmetry. Hence, we consider the two-dimensional cross-section with plane $A B C$. Then the two spheres become the incentre and the excentre of the triangle $A B C$, and we are looking for the ratio of the inradius to the exradius. Let $s, r, r_{a}$ denote the semiperimeter, inradius, and exradius (opposite to $A$ ) of the triangle $A B C$. We know that the area of $A B C$ can be expressed as both $r s$ and $r_{a}(s-|B C|)$, and so $\frac{r}{r_{a}}=\frac{s-|B C|}{s}$. For the given triangle, $s=6$ and $a=4$, so the required ratio is $\frac{1}{3}$.
$11^{\text {th }}$ HARVARD-MIT MATHEMATICS TOURNAMENT, 23 FEBRUARY 2008 - GUTS ROUND
|
{
"resource_path": "HarvardMIT/segmented/en-112-2008-feb-guts-solutions.jsonl",
"problem_match": "\n12. [7]",
"solution_match": "\nAnswer: "
}
|
0e9eee9c-d796-5aa0-97d7-d6fd57b00a06
| 608,315
|
Let $P(x)$ be a polynomial with degree 2008 and leading coefficient 1 such that
$$
P(0)=2007, P(1)=2006, P(2)=2005, \ldots, P(2007)=0 .
$$
Determine the value of $P(2008)$. You may use factorials in your answer.
|
$2008!-1$ Consider the polynomial $Q(x)=P(x)+x-2007$. The given conditions
 we know that $Q(x)$ is also a polynomial with degree 2008 and leading coefficient 1 . It follows that $Q(x)=x(x-1)(x-2)(x-3) \cdots(x-2007)$. Thus
$$
P(x)=x(x-1)(x-2)(x-3) \cdots(x-2007)-x+2007 .
$$
Setting $x=2008$ gives the answer.
|
2008!-1
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Let $P(x)$ be a polynomial with degree 2008 and leading coefficient 1 such that
$$
P(0)=2007, P(1)=2006, P(2)=2005, \ldots, P(2007)=0 .
$$
Determine the value of $P(2008)$. You may use factorials in your answer.
|
$2008!-1$ Consider the polynomial $Q(x)=P(x)+x-2007$. The given conditions
 we know that $Q(x)$ is also a polynomial with degree 2008 and leading coefficient 1 . It follows that $Q(x)=x(x-1)(x-2)(x-3) \cdots(x-2007)$. Thus
$$
P(x)=x(x-1)(x-2)(x-3) \cdots(x-2007)-x+2007 .
$$
Setting $x=2008$ gives the answer.
|
{
"resource_path": "HarvardMIT/segmented/en-112-2008-feb-guts-solutions.jsonl",
"problem_match": "\n13. [8]",
"solution_match": "\nAnswer: "
}
|
8e41b057-b942-5583-8581-7c66af553008
| 608,316
|
Evaluate the infinite sum $\sum_{n=1}^{\infty} \frac{n}{n^{4}+4}$.
|
| $\frac{3}{8}$ |
| :---: |
| We have |
$$
\begin{aligned}
\sum_{n=1}^{\infty} \frac{n}{n^{4}+4} & =\sum_{n=1}^{\infty} \frac{n}{\left(n^{2}+2 n+2\right)\left(n^{2}-2 n+2\right)} \\
& =\frac{1}{4} \sum_{n=1}^{\infty}\left(\frac{1}{n^{2}-2 n+2}-\frac{1}{n^{2}+2 n+2}\right) \\
& =\frac{1}{4} \sum_{n=1}^{\infty}\left(\frac{1}{(n-1)^{2}+1}-\frac{1}{(n+1)^{2}+1}\right)
\end{aligned}
$$
Observe that the sum telescopes. From this we find that the answer is $\frac{1}{4}\left(\frac{1}{0^{2}+1}+\frac{1}{1^{2}+1}\right)=\frac{3}{8}$.
|
\frac{3}{8}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Evaluate the infinite sum $\sum_{n=1}^{\infty} \frac{n}{n^{4}+4}$.
|
| $\frac{3}{8}$ |
| :---: |
| We have |
$$
\begin{aligned}
\sum_{n=1}^{\infty} \frac{n}{n^{4}+4} & =\sum_{n=1}^{\infty} \frac{n}{\left(n^{2}+2 n+2\right)\left(n^{2}-2 n+2\right)} \\
& =\frac{1}{4} \sum_{n=1}^{\infty}\left(\frac{1}{n^{2}-2 n+2}-\frac{1}{n^{2}+2 n+2}\right) \\
& =\frac{1}{4} \sum_{n=1}^{\infty}\left(\frac{1}{(n-1)^{2}+1}-\frac{1}{(n+1)^{2}+1}\right)
\end{aligned}
$$
Observe that the sum telescopes. From this we find that the answer is $\frac{1}{4}\left(\frac{1}{0^{2}+1}+\frac{1}{1^{2}+1}\right)=\frac{3}{8}$.
|
{
"resource_path": "HarvardMIT/segmented/en-112-2008-feb-guts-solutions.jsonl",
"problem_match": "\n14. [8]",
"solution_match": "\nAnswer: "
}
|
b7614a4e-fda8-50ba-bc04-e494b8441880
| 608,317
|
In a game show, Bob is faced with 7 doors, 2 of which hide prizes. After he chooses a door, the host opens three other doors, of which one is hiding a prize. Bob chooses to switch to another door. What is the probability that his new door is hiding a prize?
|
| $\frac{5}{21}$ | If Bob initially chooses a door with a prize, then he will not find a prize by switching. |
| :---: | :---: | :---: | With probability $5 / 7$ his original door does not hide the prize. After the host opens the three doors, the remaining three doors have equal probability of hiding the prize. Therefore, the probability that Bob finds the prize is $\frac{5}{7} \times \frac{1}{3}=\frac{5}{21}$.
Remark: This problem can be easily recognized as a variation of the classic Monty Hall problem.
$11^{\text {th }}$ HARVARD-MIT MATHEMATICS TOURNAMENT, 23 FEBRUARY 2008 - GUTS ROUND
|
\frac{5}{21}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
In a game show, Bob is faced with 7 doors, 2 of which hide prizes. After he chooses a door, the host opens three other doors, of which one is hiding a prize. Bob chooses to switch to another door. What is the probability that his new door is hiding a prize?
|
| $\frac{5}{21}$ | If Bob initially chooses a door with a prize, then he will not find a prize by switching. |
| :---: | :---: | :---: | With probability $5 / 7$ his original door does not hide the prize. After the host opens the three doors, the remaining three doors have equal probability of hiding the prize. Therefore, the probability that Bob finds the prize is $\frac{5}{7} \times \frac{1}{3}=\frac{5}{21}$.
Remark: This problem can be easily recognized as a variation of the classic Monty Hall problem.
$11^{\text {th }}$ HARVARD-MIT MATHEMATICS TOURNAMENT, 23 FEBRUARY 2008 - GUTS ROUND
|
{
"resource_path": "HarvardMIT/segmented/en-112-2008-feb-guts-solutions.jsonl",
"problem_match": "\n15. [8]",
"solution_match": "\nAnswer: "
}
|
88b0cb43-d587-52d1-a9d6-0d9470d56336
| 608,318
|
Point $A$ lies at $(0,4)$ and point $B$ lies at $(3,8)$. Find the $x$-coordinate of the point $X$ on the $x$-axis maximizing $\angle A X B$.
|
$\quad 5 \sqrt{2}-3$ Let $X$ be a point on the $x$-axis and let $\theta=\angle A X B$. We can easily see that the circle with diameter $A B$ does not meet the $x$-axis, so $\theta \leq \pi$. Thus, maximizing $\theta$ is equivalent to maximizing $\sin \theta$. By the Law of Sines, this in turn is equivalent to minimizing the circumradius of triangle $A B X$. This will occur when the circumcircle of $A B X$ is the smaller of the two circles through $A$ and $B$ tangent to the $x$-axis. So let $X$ now be this point of tangency. Extend line $A B$ to meet the $x$-axis at $C=(-3,0)$; by Power of a Point $C X^{2}=C A \cdot C B=50$ so $C X=5 \sqrt{2}$. Clearly $X$ has larger $x$-coordinate than $C$, so the $x$-coordinate of $X$ is $5 \sqrt{2}-3$.
|
5 \sqrt{2}-3
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Point $A$ lies at $(0,4)$ and point $B$ lies at $(3,8)$. Find the $x$-coordinate of the point $X$ on the $x$-axis maximizing $\angle A X B$.
|
$\quad 5 \sqrt{2}-3$ Let $X$ be a point on the $x$-axis and let $\theta=\angle A X B$. We can easily see that the circle with diameter $A B$ does not meet the $x$-axis, so $\theta \leq \pi$. Thus, maximizing $\theta$ is equivalent to maximizing $\sin \theta$. By the Law of Sines, this in turn is equivalent to minimizing the circumradius of triangle $A B X$. This will occur when the circumcircle of $A B X$ is the smaller of the two circles through $A$ and $B$ tangent to the $x$-axis. So let $X$ now be this point of tangency. Extend line $A B$ to meet the $x$-axis at $C=(-3,0)$; by Power of a Point $C X^{2}=C A \cdot C B=50$ so $C X=5 \sqrt{2}$. Clearly $X$ has larger $x$-coordinate than $C$, so the $x$-coordinate of $X$ is $5 \sqrt{2}-3$.
|
{
"resource_path": "HarvardMIT/segmented/en-112-2008-feb-guts-solutions.jsonl",
"problem_match": "\n16. [9]",
"solution_match": "\nAnswer: "
}
|
8375425b-e9d6-5424-b179-d7357808f87b
| 608,319
|
Solve the equation
$$
\sqrt{x+\sqrt{4 x+\sqrt{16 x+\sqrt{\ldots+\sqrt{4^{2008} x+3}}}}}-\sqrt{x}=1
$$
Express your answer as a reduced fraction with the numerator and denominator written in their prime factorization.
|
$\frac{1}{2^{4016}}$ Rewrite the equation to get
$$
\sqrt{x+\sqrt{4 x+\sqrt{16 x+\sqrt{\ldots+\sqrt{4^{2008} x+3}}}}}=\sqrt{x}+1
$$
Squaring both sides yields
$$
\sqrt{4 x+\sqrt{\ldots+\sqrt{4^{2008} x+3}}}=2 \sqrt{x}+1
$$
Squaring again yields
$$
\sqrt{16 x+\sqrt{\ldots+\sqrt{4^{2008} x+3}}}=4 \sqrt{x}+1
$$
One can see that by continuing this process one gets
$$
\sqrt{4^{2008} x+3}=2^{2008} \sqrt{x}+1
$$
so that $2 \cdot 2^{2008} \sqrt{x}=2$. Hence $x=4^{-2008}$. It is also easy to check that this is indeed a solution to the original equation.
|
\frac{1}{2^{4016}}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Solve the equation
$$
\sqrt{x+\sqrt{4 x+\sqrt{16 x+\sqrt{\ldots+\sqrt{4^{2008} x+3}}}}}-\sqrt{x}=1
$$
Express your answer as a reduced fraction with the numerator and denominator written in their prime factorization.
|
$\frac{1}{2^{4016}}$ Rewrite the equation to get
$$
\sqrt{x+\sqrt{4 x+\sqrt{16 x+\sqrt{\ldots+\sqrt{4^{2008} x+3}}}}}=\sqrt{x}+1
$$
Squaring both sides yields
$$
\sqrt{4 x+\sqrt{\ldots+\sqrt{4^{2008} x+3}}}=2 \sqrt{x}+1
$$
Squaring again yields
$$
\sqrt{16 x+\sqrt{\ldots+\sqrt{4^{2008} x+3}}}=4 \sqrt{x}+1
$$
One can see that by continuing this process one gets
$$
\sqrt{4^{2008} x+3}=2^{2008} \sqrt{x}+1
$$
so that $2 \cdot 2^{2008} \sqrt{x}=2$. Hence $x=4^{-2008}$. It is also easy to check that this is indeed a solution to the original equation.
|
{
"resource_path": "HarvardMIT/segmented/en-112-2008-feb-guts-solutions.jsonl",
"problem_match": "\n17. [9]",
"solution_match": "\nAnswer: "
}
|
8296e9f6-01dc-55fc-9ae1-ea14ed3df9a1
| 608,320
|
Let $A B C$ be a right triangle with $\angle A=90^{\circ}$. Let $D$ be the midpoint of $A B$ and let $E$ be a point on segment $A C$ such that $A D=A E$. Let $B E$ meet $C D$ at $F$. If $\angle B F C=135^{\circ}$, determine $B C / A B$.
|
$\frac{\sqrt{13}}{2}$ Let $\alpha=\angle A D C$ and $\beta=\angle A B E$. By exterior angle theorem, $\alpha=\angle B F D+\beta=$ $45^{\circ}+\beta$. Also, note that $\tan \beta=A E / A B=A D / A B=1 / 2$. Thus,
$$
1=\tan 45^{\circ}=\tan (\alpha-\beta)=\frac{\tan \alpha-\tan \beta}{1+\tan \alpha \tan \beta}=\frac{\tan \alpha-\frac{1}{2}}{1+\frac{1}{2} \tan \alpha}
$$
Solving for $\tan \alpha$ gives $\tan \alpha=3$. Therefore, $A C=3 A D=\frac{3}{2} A B$. Using Pythagorean Theorem, we find that $B C=\frac{\sqrt{13}}{2} A B$. So the answer is $\frac{\sqrt{13}}{2}$.
## $11^{\text {th }}$ HARVARD-MIT MATHEMATICS TOURNAMENT, 23 FEBRUARY 2008 - GUTS ROUND
|
\frac{\sqrt{13}}{2}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $A B C$ be a right triangle with $\angle A=90^{\circ}$. Let $D$ be the midpoint of $A B$ and let $E$ be a point on segment $A C$ such that $A D=A E$. Let $B E$ meet $C D$ at $F$. If $\angle B F C=135^{\circ}$, determine $B C / A B$.
|
$\frac{\sqrt{13}}{2}$ Let $\alpha=\angle A D C$ and $\beta=\angle A B E$. By exterior angle theorem, $\alpha=\angle B F D+\beta=$ $45^{\circ}+\beta$. Also, note that $\tan \beta=A E / A B=A D / A B=1 / 2$. Thus,
$$
1=\tan 45^{\circ}=\tan (\alpha-\beta)=\frac{\tan \alpha-\tan \beta}{1+\tan \alpha \tan \beta}=\frac{\tan \alpha-\frac{1}{2}}{1+\frac{1}{2} \tan \alpha}
$$
Solving for $\tan \alpha$ gives $\tan \alpha=3$. Therefore, $A C=3 A D=\frac{3}{2} A B$. Using Pythagorean Theorem, we find that $B C=\frac{\sqrt{13}}{2} A B$. So the answer is $\frac{\sqrt{13}}{2}$.
## $11^{\text {th }}$ HARVARD-MIT MATHEMATICS TOURNAMENT, 23 FEBRUARY 2008 - GUTS ROUND
|
{
"resource_path": "HarvardMIT/segmented/en-112-2008-feb-guts-solutions.jsonl",
"problem_match": "\n18. [9]",
"solution_match": "\nAnswer: "
}
|
b4714ff2-f502-5603-99fe-c7684d1c715c
| 608,321
|
Let $A B C D$ be a regular tetrahedron, and let $O$ be the centroid of triangle $B C D$. Consider the point $P$ on $A O$ such that $P$ minimizes $P A+2(P B+P C+P D)$. Find $\sin \angle P B O$.
|
| $\frac{1}{6}$ |
| :---: |
| We translate the problem into one about 2-D geometry. Consider the right triangle | $A B O$, and $P$ is some point on $A O$. Then, the choice of $P$ minimizes $P A+6 P B$. Construct the line $\ell$ through $A$ but outside the triangle $A B O$ so that $\sin \angle(A O, \ell)=\frac{1}{6}$. For whichever $P$ chosen, let $Q$ be the projection of $P$ onto $\ell$, then $P Q=\frac{1}{6} A P$. Then, since $P A+6 P B=6(P Q+P B)$, it is equivalent to minimize $P Q+P B$. Observe that this sum is minimized when $B, P, Q$ are collinear and the line through them is perpendicular to $\ell$ (so that $P Q+P B$ is simply the distance from $B$ to $\ell$ ). Then, $\angle A Q B=90^{\circ}$, and since $\angle A O B=90^{\circ}$ as well, we see that $A, Q, P, B$ are concyclic. Therefore, $\angle P B O=\angle O P A=\angle(A O, \ell)$, and the sine of this angle is therefore $\frac{1}{6}$.
|
\frac{1}{6}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $A B C D$ be a regular tetrahedron, and let $O$ be the centroid of triangle $B C D$. Consider the point $P$ on $A O$ such that $P$ minimizes $P A+2(P B+P C+P D)$. Find $\sin \angle P B O$.
|
| $\frac{1}{6}$ |
| :---: |
| We translate the problem into one about 2-D geometry. Consider the right triangle | $A B O$, and $P$ is some point on $A O$. Then, the choice of $P$ minimizes $P A+6 P B$. Construct the line $\ell$ through $A$ but outside the triangle $A B O$ so that $\sin \angle(A O, \ell)=\frac{1}{6}$. For whichever $P$ chosen, let $Q$ be the projection of $P$ onto $\ell$, then $P Q=\frac{1}{6} A P$. Then, since $P A+6 P B=6(P Q+P B)$, it is equivalent to minimize $P Q+P B$. Observe that this sum is minimized when $B, P, Q$ are collinear and the line through them is perpendicular to $\ell$ (so that $P Q+P B$ is simply the distance from $B$ to $\ell$ ). Then, $\angle A Q B=90^{\circ}$, and since $\angle A O B=90^{\circ}$ as well, we see that $A, Q, P, B$ are concyclic. Therefore, $\angle P B O=\angle O P A=\angle(A O, \ell)$, and the sine of this angle is therefore $\frac{1}{6}$.
|
{
"resource_path": "HarvardMIT/segmented/en-112-2008-feb-guts-solutions.jsonl",
"problem_match": "\n19. [10]",
"solution_match": "\nAnswer: "
}
|
c6e54850-e9e0-53a7-80a9-6e0cf8e8e3f5
| 608,322
|
For how many ordered triples $(a, b, c)$ of positive integers are the equations $a b c+9=a b+b c+c a$ and $a+b+c=10$ satisfied?
|
21 Subtracting the first equation from the second, we obtain $1-a-b-c+a b+b c+c a-a b c=$ $(1-a)(1-b)(1-c)=0$. Since $a, b$, and $c$ are positive integers, at least one must equal 1 . Note that $a=b=c=1$ is not a valid triple, so it suffices to consider the cases where exactly two or one of $a, b, c$ are equal to 1 . If $a=b=1$, we obtain $c=8$ and similarly for the other two cases, so this gives 3 ordered triples. If $a=1$, then we need $b+c=9$, which has 6 solutions for $b, c \neq 1$; a similar argument for $b$ and $c$ gives a total of 18 such solutions. It is easy to check that all the solutions we found are actually solutions to the original equations. Adding, we find $18+3=21$ total triples.
|
21
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
For how many ordered triples $(a, b, c)$ of positive integers are the equations $a b c+9=a b+b c+c a$ and $a+b+c=10$ satisfied?
|
21 Subtracting the first equation from the second, we obtain $1-a-b-c+a b+b c+c a-a b c=$ $(1-a)(1-b)(1-c)=0$. Since $a, b$, and $c$ are positive integers, at least one must equal 1 . Note that $a=b=c=1$ is not a valid triple, so it suffices to consider the cases where exactly two or one of $a, b, c$ are equal to 1 . If $a=b=1$, we obtain $c=8$ and similarly for the other two cases, so this gives 3 ordered triples. If $a=1$, then we need $b+c=9$, which has 6 solutions for $b, c \neq 1$; a similar argument for $b$ and $c$ gives a total of 18 such solutions. It is easy to check that all the solutions we found are actually solutions to the original equations. Adding, we find $18+3=21$ total triples.
|
{
"resource_path": "HarvardMIT/segmented/en-112-2008-feb-guts-solutions.jsonl",
"problem_match": "\n20. [10]",
"solution_match": "\nAnswer: "
}
|
46e4eafd-f901-557f-95c9-87d6ba05878e
| 608,323
|
Let $A B C$ be a triangle with $A B=5, B C=4$ and $A C=3$. Let $\mathcal{P}$ and $\mathcal{Q}$ be squares inside $A B C$ with disjoint interiors such that they both have one side lying on $A B$. Also, the two squares each have an edge lying on a common line perpendicular to $A B$, and $\mathcal{P}$ has one vertex on $A C$ and $\mathcal{Q}$ has one vertex on $B C$. Determine the minimum value of the sum of the areas of the two squares.
|
$\frac{144}{49}$ Let the side lengths of $\mathcal{P}$ and $\mathcal{Q}$ be $a$ and $b$, respectively. Label two of the vertices of $\mathcal{P}$ as $D$ and $E$ so that $D$ lies on $A B$ and $E$ lies on $A C$, and so that $D E$ is perpendicular to $A B$. The triangle $A D E$ is similar to $A C B$. So $A D=\frac{3}{4} a$. Using similar arguments, we find that
$$
\frac{3 a}{4}+a+b+\frac{4 b}{3}=A B=5
$$
so
$$
\frac{a}{4}+\frac{b}{3}=\frac{5}{7}
$$
Using Cauchy-Schwarz inequality, we get
$$
\left(a^{2}+b^{2}\right)\left(\frac{1}{4^{2}}+\frac{1}{3^{2}}\right) \geq\left(\frac{a}{4}+\frac{b}{3}\right)^{2}=\frac{25}{49}
$$
It follows that
$$
a^{2}+b^{2} \geq \frac{144}{49}
$$
Equality occurs at $a=\frac{36}{35}$ and $b=\frac{48}{35}$.
$$
11^{\text {th }} \text { HARVARD-MIT MATHEMATICS TOURNAMENT, } 23 \text { FEBRUARY } 2008 \text { - GUTS ROUND }
$$
|
\frac{144}{49}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $A B C$ be a triangle with $A B=5, B C=4$ and $A C=3$. Let $\mathcal{P}$ and $\mathcal{Q}$ be squares inside $A B C$ with disjoint interiors such that they both have one side lying on $A B$. Also, the two squares each have an edge lying on a common line perpendicular to $A B$, and $\mathcal{P}$ has one vertex on $A C$ and $\mathcal{Q}$ has one vertex on $B C$. Determine the minimum value of the sum of the areas of the two squares.

|
$\frac{144}{49}$ Let the side lengths of $\mathcal{P}$ and $\mathcal{Q}$ be $a$ and $b$, respectively. Label two of the vertices of $\mathcal{P}$ as $D$ and $E$ so that $D$ lies on $A B$ and $E$ lies on $A C$, and so that $D E$ is perpendicular to $A B$. The triangle $A D E$ is similar to $A C B$. So $A D=\frac{3}{4} a$. Using similar arguments, we find that
$$
\frac{3 a}{4}+a+b+\frac{4 b}{3}=A B=5
$$
so
$$
\frac{a}{4}+\frac{b}{3}=\frac{5}{7}
$$
Using Cauchy-Schwarz inequality, we get
$$
\left(a^{2}+b^{2}\right)\left(\frac{1}{4^{2}}+\frac{1}{3^{2}}\right) \geq\left(\frac{a}{4}+\frac{b}{3}\right)^{2}=\frac{25}{49}
$$
It follows that
$$
a^{2}+b^{2} \geq \frac{144}{49}
$$
Equality occurs at $a=\frac{36}{35}$ and $b=\frac{48}{35}$.
$$
11^{\text {th }} \text { HARVARD-MIT MATHEMATICS TOURNAMENT, } 23 \text { FEBRUARY } 2008 \text { - GUTS ROUND }
$$
|
{
"resource_path": "HarvardMIT/segmented/en-112-2008-feb-guts-solutions.jsonl",
"problem_match": "\n21. [10]",
"solution_match": "\nAnswer: "
}
|
ed60c6fb-7875-5d16-8312-7f6ca4c63bf0
| 608,324
|
For a positive integer $n$, let $\theta(n)$ denote the number of integers $0 \leq x<2010$ such that $x^{2}-n$ is divisible by 2010. Determine the remainder when $\sum_{n=0}^{2009} n \cdot \theta(n)$ is divided by 2010.
|
335 Let us consider the sum $\sum_{n=0}^{2009} n \cdot \theta(n)(\bmod 2010)$ in a another way. Consider the sum $0^{2}+1^{2}+2^{2}+\cdots+2007^{2}(\bmod 2010)$. For each $0 \leq n<2010$, in the latter sum, the term $n$ appears $\theta(n)$ times, so the sum is congruent to $\sum_{n=0}^{2009} n \cdot \theta(n)$. In other words,
$$
\sum_{n=0}^{2009} n \cdot \theta(n)=\sum_{n=0}^{2009} n^{2}=\frac{(2009)(2009+1)(2 \cdot 2009+1)}{6} \equiv(-1) \cdot \frac{2010}{6} \cdot(-1)=335 \quad(\bmod 2010)
$$
|
335
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
For a positive integer $n$, let $\theta(n)$ denote the number of integers $0 \leq x<2010$ such that $x^{2}-n$ is divisible by 2010. Determine the remainder when $\sum_{n=0}^{2009} n \cdot \theta(n)$ is divided by 2010.
|
335 Let us consider the sum $\sum_{n=0}^{2009} n \cdot \theta(n)(\bmod 2010)$ in a another way. Consider the sum $0^{2}+1^{2}+2^{2}+\cdots+2007^{2}(\bmod 2010)$. For each $0 \leq n<2010$, in the latter sum, the term $n$ appears $\theta(n)$ times, so the sum is congruent to $\sum_{n=0}^{2009} n \cdot \theta(n)$. In other words,
$$
\sum_{n=0}^{2009} n \cdot \theta(n)=\sum_{n=0}^{2009} n^{2}=\frac{(2009)(2009+1)(2 \cdot 2009+1)}{6} \equiv(-1) \cdot \frac{2010}{6} \cdot(-1)=335 \quad(\bmod 2010)
$$
|
{
"resource_path": "HarvardMIT/segmented/en-112-2008-feb-guts-solutions.jsonl",
"problem_match": "\n22. [10]",
"solution_match": "\nAnswer: "
}
|
cceb7844-007b-5b52-8859-d9b02bd0f975
| 608,325
|
Two mathematicians, Kelly and Jason, play a cooperative game. The computer selects some secret positive integer $n<60$ (both Kelly and Jason know that $n<60$, but that they don't know what the value of $n$ is). The computer tells Kelly the unit digit of $n$, and it tells Jason the number of divisors of $n$. Then, Kelly and Jason have the following dialogue:
Kelly: I don't know what $n$ is, and I'm sure that you don't know either. However, I know that $n$ is divisible by at least two different primes.
Jason: Oh, then I know what the value of $n$ is.
Kelly: Now I also know what $n$ is.
Assuming that both Kelly and Jason speak truthfully and to the best of their knowledge, what are all the possible values of $n$ ?
|
10 The only way in which Kelly can know that $n$ is divisible by at least two different primes is if she is given 0 as the unit digit of $n$, since if she received anything else, then there is some number with that unit digit and not divisible by two primes (i.e., $1,2,3,4,5,16,7,8,9$ ). Then, after Kelly says the first line, Jason too knows that $n$ is divisible by 10 .
The number of divisors of $10,20,30,40,50$ are $4,6,8,8,6$, respectively. So unless Jason received 4 , he cannot otherwise be certain of what $n$ is. It follows that Jason received 4 , and thus $n=10$.
|
10
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Two mathematicians, Kelly and Jason, play a cooperative game. The computer selects some secret positive integer $n<60$ (both Kelly and Jason know that $n<60$, but that they don't know what the value of $n$ is). The computer tells Kelly the unit digit of $n$, and it tells Jason the number of divisors of $n$. Then, Kelly and Jason have the following dialogue:
Kelly: I don't know what $n$ is, and I'm sure that you don't know either. However, I know that $n$ is divisible by at least two different primes.
Jason: Oh, then I know what the value of $n$ is.
Kelly: Now I also know what $n$ is.
Assuming that both Kelly and Jason speak truthfully and to the best of their knowledge, what are all the possible values of $n$ ?
|
10 The only way in which Kelly can know that $n$ is divisible by at least two different primes is if she is given 0 as the unit digit of $n$, since if she received anything else, then there is some number with that unit digit and not divisible by two primes (i.e., $1,2,3,4,5,16,7,8,9$ ). Then, after Kelly says the first line, Jason too knows that $n$ is divisible by 10 .
The number of divisors of $10,20,30,40,50$ are $4,6,8,8,6$, respectively. So unless Jason received 4 , he cannot otherwise be certain of what $n$ is. It follows that Jason received 4 , and thus $n=10$.
|
{
"resource_path": "HarvardMIT/segmented/en-112-2008-feb-guts-solutions.jsonl",
"problem_match": "\n23. [10]",
"solution_match": "\nAnswer: "
}
|
633a89d1-e2fd-522e-a005-1f5eb376fe55
| 608,326
|
Suppose that $A B C$ is an isosceles triangle with $A B=A C$. Let $P$ be the point on side $A C$ so that $A P=2 C P$. Given that $B P=1$, determine the maximum possible area of $A B C$.
|
$\sqrt{\frac{9}{10}}$ Let $Q$ be the point on $A B$ so that $A Q=2 B Q$, and let $X$ be the intersection of $B P$ and $C Q$. The key observation that, as we will show, $B X$ and $C X$ are fixed lengths, and the ratio of areas $[A B C] /[B C X]$ is constant. So, to maximize $[A B C]$, it is equivalent to maximize $[B C X]$.
Using Menelaus' theorem on $A B P$, we have
$$
\frac{B X \cdot P C \cdot A Q}{X P \cdot C A \cdot Q B}=1
$$
Since $P C / C A=1 / 3$ and $A Q / Q B=2$, we get $B X / X P=3 / 2$. It follows that $B X=3 / 5$. By symmetry, $C X=3 / 5$.
Also, we have
$$
[A B C]=3[B P C]=3 \cdot \frac{5}{3}[B X C]=5[B X C]
$$
Note that $[B X C]$ is maximized when $\angle B X C=90^{\circ}$ (one can check that this configuration is indeed possible). Thus, the maximum value of $[B X C]$ is $\frac{1}{2} B X \cdot C X=\frac{1}{2}\left(\frac{3}{5}\right)^{2}=\frac{9}{50}$. It follows that the maximum value of $[A B C]$ is $\frac{9}{10}$.
## $11^{\text {th }}$ HARVARD-MIT MATHEMATICS TOURNAMENT, 23 FEBRUARY 2008 - GUTS ROUND
|
\frac{9}{10}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Suppose that $A B C$ is an isosceles triangle with $A B=A C$. Let $P$ be the point on side $A C$ so that $A P=2 C P$. Given that $B P=1$, determine the maximum possible area of $A B C$.
|
$\sqrt{\frac{9}{10}}$ Let $Q$ be the point on $A B$ so that $A Q=2 B Q$, and let $X$ be the intersection of $B P$ and $C Q$. The key observation that, as we will show, $B X$ and $C X$ are fixed lengths, and the ratio of areas $[A B C] /[B C X]$ is constant. So, to maximize $[A B C]$, it is equivalent to maximize $[B C X]$.
Using Menelaus' theorem on $A B P$, we have
$$
\frac{B X \cdot P C \cdot A Q}{X P \cdot C A \cdot Q B}=1
$$
Since $P C / C A=1 / 3$ and $A Q / Q B=2$, we get $B X / X P=3 / 2$. It follows that $B X=3 / 5$. By symmetry, $C X=3 / 5$.
Also, we have
$$
[A B C]=3[B P C]=3 \cdot \frac{5}{3}[B X C]=5[B X C]
$$
Note that $[B X C]$ is maximized when $\angle B X C=90^{\circ}$ (one can check that this configuration is indeed possible). Thus, the maximum value of $[B X C]$ is $\frac{1}{2} B X \cdot C X=\frac{1}{2}\left(\frac{3}{5}\right)^{2}=\frac{9}{50}$. It follows that the maximum value of $[A B C]$ is $\frac{9}{10}$.
## $11^{\text {th }}$ HARVARD-MIT MATHEMATICS TOURNAMENT, 23 FEBRUARY 2008 - GUTS ROUND
|
{
"resource_path": "HarvardMIT/segmented/en-112-2008-feb-guts-solutions.jsonl",
"problem_match": "\n24. [10]",
"solution_match": "\nAnswer: "
}
|
680e6b71-b3eb-5880-9082-a495afb6c1e3
| 608,327
|
Alice and the Cheshire Cat play a game. At each step, Alice either (1) gives the cat a penny, which causes the cat to change the number of (magic) beans that Alice has from $n$ to $5 n$ or (2) gives the cat a nickel, which causes the cat to give Alice another bean. Alice wins (and the cat disappears) as soon as the number of beans Alice has is greater than 2008 and has last two digits 42 . What is the minimum number of cents Alice can spend to win the game, assuming she starts with 0 beans?
|
35 Consider the number of beans Alice has in base 5 . Note that $2008=31013_{5}, 42=132_{5}$, and $100=400_{5}$. Now, suppose Alice has $d_{k} \cdots d_{2} d_{1}$ beans when she wins; the conditions for winning mean that these digits must satisfy $d_{2} d_{1}=32, d_{k} \cdots d_{3} \geq 310$, and $d_{k} \cdots d_{3}=4 i+1$ for some $i$. To gain these $d_{k} \cdots d_{2} d_{1}$ beans, Alice must spend at least $5\left(d_{1}+d_{2}+\cdots+d_{k}\right)+k-1$ cents (5 cents to get each bean in the "units digit" and $k-1$ cents to promote all the beans). We now must have $k \geq 5$ because $d_{k} \cdots d_{2} d_{1}>2008$. If $k=5$, then $d_{k} \geq 3$ since $d_{k} \cdots d_{3} \geq 3100$; otherwise, we have $d_{k} \geq 1$. Therefore, if $k=5$, we have $5\left(d_{1}+d_{2}+\cdots+d_{k}\right)+k-1 \geq 44>36$; if $k>5$, we have $5\left(d_{1}+d_{2}+\cdots+d_{k}\right)+k-1 \geq 30+k-1 \geq 35$. But we can attain 36 cents by taking $d_{k} \cdots d_{3}=1000$, so this is indeed the minimum.
|
35
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Alice and the Cheshire Cat play a game. At each step, Alice either (1) gives the cat a penny, which causes the cat to change the number of (magic) beans that Alice has from $n$ to $5 n$ or (2) gives the cat a nickel, which causes the cat to give Alice another bean. Alice wins (and the cat disappears) as soon as the number of beans Alice has is greater than 2008 and has last two digits 42 . What is the minimum number of cents Alice can spend to win the game, assuming she starts with 0 beans?
|
35 Consider the number of beans Alice has in base 5 . Note that $2008=31013_{5}, 42=132_{5}$, and $100=400_{5}$. Now, suppose Alice has $d_{k} \cdots d_{2} d_{1}$ beans when she wins; the conditions for winning mean that these digits must satisfy $d_{2} d_{1}=32, d_{k} \cdots d_{3} \geq 310$, and $d_{k} \cdots d_{3}=4 i+1$ for some $i$. To gain these $d_{k} \cdots d_{2} d_{1}$ beans, Alice must spend at least $5\left(d_{1}+d_{2}+\cdots+d_{k}\right)+k-1$ cents (5 cents to get each bean in the "units digit" and $k-1$ cents to promote all the beans). We now must have $k \geq 5$ because $d_{k} \cdots d_{2} d_{1}>2008$. If $k=5$, then $d_{k} \geq 3$ since $d_{k} \cdots d_{3} \geq 3100$; otherwise, we have $d_{k} \geq 1$. Therefore, if $k=5$, we have $5\left(d_{1}+d_{2}+\cdots+d_{k}\right)+k-1 \geq 44>36$; if $k>5$, we have $5\left(d_{1}+d_{2}+\cdots+d_{k}\right)+k-1 \geq 30+k-1 \geq 35$. But we can attain 36 cents by taking $d_{k} \cdots d_{3}=1000$, so this is indeed the minimum.
|
{
"resource_path": "HarvardMIT/segmented/en-112-2008-feb-guts-solutions.jsonl",
"problem_match": "\n25. [12]",
"solution_match": "\nAnswer: "
}
|
647a1724-a403-5fe8-a97f-028c3f30e1b1
| 608,328
|
Let $\mathcal{P}$ be a parabola, and let $V_{1}$ and $F_{1}$ be its vertex and focus, respectively. Let $A$ and $B$ be points on $\mathcal{P}$ so that $\angle A V_{1} B=90^{\circ}$. Let $\mathcal{Q}$ be the locus of the midpoint of $A B$. It turns out that $\mathcal{Q}$ is also a parabola, and let $V_{2}$ and $F_{2}$ denote its vertex and focus, respectively. Determine the ratio $F_{1} F_{2} / V_{1} V_{2}$.
|
$\frac{7}{8}$ Since all parabolas are similar, we may assume that $\mathcal{P}$ is the curve $y=x^{2}$. Then, if $A=\left(a, a^{2}\right)$ and $B=\left(b, b^{2}\right)$, the condition that $\angle A V_{1} B=90^{\circ}$ gives $a b+a^{2} b^{2}=0$, or $a b=-1$. Then, the midpoint of $A B$ is
$$
\frac{A+B}{2}=\left(\frac{a+b}{2}, \frac{a^{2}+b^{2}}{2}\right)=\left(\frac{a+b}{2}, \frac{(a+b)^{2}-2 a b}{2}\right)=\left(\frac{a+b}{2}, \frac{(a+b)^{2}}{2}+1\right) .
$$
(Note that $a+b$ can range over all real numbers under the constraint $a b=-1$.) It follows that the locus of the midpoint of $A B$ is the curve $y=2 x^{2}+1$.
Recall that the focus of $y=a x^{2}$ is $\left(0, \frac{1}{4 a}\right)$. We find that $V_{1}=(0,0), V_{2}=(0,1), F_{1}=\left(0, \frac{1}{4}\right)$, $F_{2}=\left(0,1+\frac{1}{8}\right)$. Therefore, $F_{1} F_{2} / V_{1} V_{2}=\frac{7}{8}$.
|
\frac{7}{8}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $\mathcal{P}$ be a parabola, and let $V_{1}$ and $F_{1}$ be its vertex and focus, respectively. Let $A$ and $B$ be points on $\mathcal{P}$ so that $\angle A V_{1} B=90^{\circ}$. Let $\mathcal{Q}$ be the locus of the midpoint of $A B$. It turns out that $\mathcal{Q}$ is also a parabola, and let $V_{2}$ and $F_{2}$ denote its vertex and focus, respectively. Determine the ratio $F_{1} F_{2} / V_{1} V_{2}$.
|
$\frac{7}{8}$ Since all parabolas are similar, we may assume that $\mathcal{P}$ is the curve $y=x^{2}$. Then, if $A=\left(a, a^{2}\right)$ and $B=\left(b, b^{2}\right)$, the condition that $\angle A V_{1} B=90^{\circ}$ gives $a b+a^{2} b^{2}=0$, or $a b=-1$. Then, the midpoint of $A B$ is
$$
\frac{A+B}{2}=\left(\frac{a+b}{2}, \frac{a^{2}+b^{2}}{2}\right)=\left(\frac{a+b}{2}, \frac{(a+b)^{2}-2 a b}{2}\right)=\left(\frac{a+b}{2}, \frac{(a+b)^{2}}{2}+1\right) .
$$
(Note that $a+b$ can range over all real numbers under the constraint $a b=-1$.) It follows that the locus of the midpoint of $A B$ is the curve $y=2 x^{2}+1$.
Recall that the focus of $y=a x^{2}$ is $\left(0, \frac{1}{4 a}\right)$. We find that $V_{1}=(0,0), V_{2}=(0,1), F_{1}=\left(0, \frac{1}{4}\right)$, $F_{2}=\left(0,1+\frac{1}{8}\right)$. Therefore, $F_{1} F_{2} / V_{1} V_{2}=\frac{7}{8}$.
|
{
"resource_path": "HarvardMIT/segmented/en-112-2008-feb-guts-solutions.jsonl",
"problem_match": "\n26. [12]",
"solution_match": "\nAnswer: "
}
|
c14fcf56-f710-50fb-826f-c39b4afb9a48
| 608,329
|
Cyclic pentagon $A B C D E$ has a right angle $\angle A B C=90^{\circ}$ and side lengths $A B=15$ and $B C=20$. Supposing that $A B=D E=E A$, find $C D$.
|
7 By Pythagoras, $A C=25$. Since $\overline{A C}$ is a diameter, angles $\angle A D C$ and $\angle A E C$ are also right, so that $C E=20$ and $A D^{2}+C D^{2}=A C^{2}$ as well. Beginning with Ptolemy's theorem,
$$
\begin{aligned}
& (A E \cdot C D+A C \cdot D E)^{2}=A D^{2} \cdot E C^{2}=\left(A C^{2}-C D^{2}\right) E C^{2} \\
& \quad \Longrightarrow C D^{2}\left(A E^{2}+E C^{2}\right)+2 \cdot C D \cdot A E^{2} \cdot A C+A C^{2}\left(D E^{2}-E C^{2}\right)=0 \\
& \quad \Longrightarrow C D^{2}+2 C D\left(\frac{A E^{2}}{A C}\right)+D E^{2}-E C^{2}=0
\end{aligned}
$$
It follows that $C D^{2}+18 C D-175=0$, from which $C D=7$.
Remark: A simple trigonometric solution is possible. One writes $\alpha=\angle A C E=\angle E C D \Longrightarrow \angle D A C=$ $90^{\circ}-2 \alpha$ and applies double angle formula.
## $11^{\text {th }}$ HARVARD-MIT MATHEMATICS TOURNAMENT, 23 FEBRUARY 2008 - GUTS ROUND
|
7
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Cyclic pentagon $A B C D E$ has a right angle $\angle A B C=90^{\circ}$ and side lengths $A B=15$ and $B C=20$. Supposing that $A B=D E=E A$, find $C D$.
|
7 By Pythagoras, $A C=25$. Since $\overline{A C}$ is a diameter, angles $\angle A D C$ and $\angle A E C$ are also right, so that $C E=20$ and $A D^{2}+C D^{2}=A C^{2}$ as well. Beginning with Ptolemy's theorem,
$$
\begin{aligned}
& (A E \cdot C D+A C \cdot D E)^{2}=A D^{2} \cdot E C^{2}=\left(A C^{2}-C D^{2}\right) E C^{2} \\
& \quad \Longrightarrow C D^{2}\left(A E^{2}+E C^{2}\right)+2 \cdot C D \cdot A E^{2} \cdot A C+A C^{2}\left(D E^{2}-E C^{2}\right)=0 \\
& \quad \Longrightarrow C D^{2}+2 C D\left(\frac{A E^{2}}{A C}\right)+D E^{2}-E C^{2}=0
\end{aligned}
$$
It follows that $C D^{2}+18 C D-175=0$, from which $C D=7$.
Remark: A simple trigonometric solution is possible. One writes $\alpha=\angle A C E=\angle E C D \Longrightarrow \angle D A C=$ $90^{\circ}-2 \alpha$ and applies double angle formula.
## $11^{\text {th }}$ HARVARD-MIT MATHEMATICS TOURNAMENT, 23 FEBRUARY 2008 - GUTS ROUND
|
{
"resource_path": "HarvardMIT/segmented/en-112-2008-feb-guts-solutions.jsonl",
"problem_match": "\n27. [12]",
"solution_match": "\nAnswer: "
}
|
6b6f3edd-666b-5d54-afd6-8cac12e5a487
| 608,330
|
Let $P$ be a polyhedron where every face is a regular polygon, and every edge has length 1. Each vertex of $P$ is incident to two regular hexagons and one square. Choose a vertex $V$ of the polyhedron. Find the volume of the set of all points contained in $P$ that are closer to $V$ than to any other vertex.
|
$\quad \frac{\sqrt{2}}{3}$ Observe that $P$ is a truncated octahedron, formed by cutting off the corners from a regular octahedron with edge length 3 . So, to compute the value of $P$, we can find the volume of the octahedron, and then subtract off the volume of truncated corners. Given a square pyramid where each triangular face an equilateral triangle, and whose side length is $s$, the height of the pyramid is $\frac{\sqrt{2}}{2} s$, and thus the volume is $\frac{1}{3} \cdot s^{2} \cdot \frac{\sqrt{2}}{2} s=\frac{\sqrt{2}}{6} s^{3}$. The side length of the octahedron is 3 , and noting that the octahedron is made up of two square pyramids, its volume must be is $2 \cdot \frac{\sqrt{2}(3)^{3}}{6}=9 \sqrt{2}$. The six "corners" that we remove are all square pyramids, each with volume $\frac{\sqrt{2}}{6}$, and so the resulting polyhedron $P$ has volume $9 \sqrt{2}-6 \cdot \frac{\sqrt{2}}{6}=8 \sqrt{2}$.
Finally, to find the volume of all points closer to one particular vertex than any other vertex, note that due to symmetry, every point in $P$ (except for a set with zero volume), is closest to one of the 24 vertices. Due to symmetry, it doesn't matter which $V$ is picked, so we can just divide the volume of $P$ by 24 to obtain the answer $\frac{\sqrt{2}}{3}$.
|
\frac{\sqrt{2}}{3}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $P$ be a polyhedron where every face is a regular polygon, and every edge has length 1. Each vertex of $P$ is incident to two regular hexagons and one square. Choose a vertex $V$ of the polyhedron. Find the volume of the set of all points contained in $P$ that are closer to $V$ than to any other vertex.
|
$\quad \frac{\sqrt{2}}{3}$ Observe that $P$ is a truncated octahedron, formed by cutting off the corners from a regular octahedron with edge length 3 . So, to compute the value of $P$, we can find the volume of the octahedron, and then subtract off the volume of truncated corners. Given a square pyramid where each triangular face an equilateral triangle, and whose side length is $s$, the height of the pyramid is $\frac{\sqrt{2}}{2} s$, and thus the volume is $\frac{1}{3} \cdot s^{2} \cdot \frac{\sqrt{2}}{2} s=\frac{\sqrt{2}}{6} s^{3}$. The side length of the octahedron is 3 , and noting that the octahedron is made up of two square pyramids, its volume must be is $2 \cdot \frac{\sqrt{2}(3)^{3}}{6}=9 \sqrt{2}$. The six "corners" that we remove are all square pyramids, each with volume $\frac{\sqrt{2}}{6}$, and so the resulting polyhedron $P$ has volume $9 \sqrt{2}-6 \cdot \frac{\sqrt{2}}{6}=8 \sqrt{2}$.
Finally, to find the volume of all points closer to one particular vertex than any other vertex, note that due to symmetry, every point in $P$ (except for a set with zero volume), is closest to one of the 24 vertices. Due to symmetry, it doesn't matter which $V$ is picked, so we can just divide the volume of $P$ by 24 to obtain the answer $\frac{\sqrt{2}}{3}$.
|
{
"resource_path": "HarvardMIT/segmented/en-112-2008-feb-guts-solutions.jsonl",
"problem_match": "\n28. [15]",
"solution_match": "\nAnswer: "
}
|
054f1d7b-5fb0-53ce-a203-4ad88cf0cdea
| 608,331
|
Let $(x, y)$ be a pair of real numbers satisfying
$$
56 x+33 y=\frac{-y}{x^{2}+y^{2}}, \quad \text { and } \quad 33 x-56 y=\frac{x}{x^{2}+y^{2}}
$$
Determine the value of $|x|+|y|$.
|
$\frac{11}{65}$ Observe that
$$
\frac{1}{x+y i}=\frac{x-y i}{x^{2}+y^{2}}=33 x-56 y+(56 x+33 y) i=(33+56 i)(x+y i)
$$
So
$$
(x+y i)^{2}=\frac{1}{33+56 i}=\frac{1}{(7+4 i)^{2}}=\left(\frac{7-4 i}{65}\right)^{2}
$$
It follows that $(x, y)= \pm\left(\frac{7}{65},-\frac{4}{65}\right)$.
|
\frac{11}{65}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Let $(x, y)$ be a pair of real numbers satisfying
$$
56 x+33 y=\frac{-y}{x^{2}+y^{2}}, \quad \text { and } \quad 33 x-56 y=\frac{x}{x^{2}+y^{2}}
$$
Determine the value of $|x|+|y|$.
|
$\frac{11}{65}$ Observe that
$$
\frac{1}{x+y i}=\frac{x-y i}{x^{2}+y^{2}}=33 x-56 y+(56 x+33 y) i=(33+56 i)(x+y i)
$$
So
$$
(x+y i)^{2}=\frac{1}{33+56 i}=\frac{1}{(7+4 i)^{2}}=\left(\frac{7-4 i}{65}\right)^{2}
$$
It follows that $(x, y)= \pm\left(\frac{7}{65},-\frac{4}{65}\right)$.
|
{
"resource_path": "HarvardMIT/segmented/en-112-2008-feb-guts-solutions.jsonl",
"problem_match": "\n29. [15]",
"solution_match": "\nAnswer: "
}
|
2ed36278-c798-59c3-8339-236a4aaca455
| 608,332
|
Let $\mathcal{C}$ be the hyperbola $y^{2}-x^{2}=1$. Given a point $P_{0}$ on the $x$-axis, we construct a sequence of points $\left(P_{n}\right)$ on the $x$-axis in the following manner: let $\ell_{n}$ be the line with slope 1 passing passing
through $P_{n}$, then $P_{n+1}$ is the orthogonal projection of the point of intersection of $\ell_{n}$ and $\mathcal{C}$ onto the $x$-axis. (If $P_{n}=0$, then the sequence simply terminates.)
Let $N$ be the number of starting positions $P_{0}$ on the $x$-axis such that $P_{0}=P_{2008}$. Determine the remainder of $N$ when divided by 2008.
|
254 Let $P_{n}=\left(x_{n}, 0\right)$. Then the $\ell_{n}$ meet $\mathcal{C}$ at $\left(x_{n+1}, x_{n+1}-x_{n}\right)$. Since this point lies on the hyperbola, we have $\left(x_{n+1}-x_{n}\right)^{2}-x_{n+1}^{2}=1$. Rearranging this equation gives
$$
x_{n+1}=\frac{x_{n}^{2}-1}{2 x_{n}}
$$
Choose a $\theta_{0} \in(0, \pi)$ with $\cot \theta_{0}=x_{0}$, and define $\theta_{n}=2^{n} \theta_{0}$. Using the double-angle formula, we have
$$
\cot \theta_{n+1}=\cot \left(2 \theta_{n}\right)=\frac{\cot ^{2} \theta_{n}-1}{2 \cot \theta_{n}}
$$
It follows by induction that $x_{n}=\cot \theta_{n}$. Then, $P_{0}=P_{2008}$ corresponds to $\cot \theta_{0}=\cot \left(2^{2008} \theta_{0}\right)$ (assuming that $P_{0}$ is never at the origin, or equivalently, $2^{n} \theta$ is never an integer multiple of $\pi$ ). So, we need to find the number of $\theta_{0} \in(0, \pi)$ with the property that $2^{2008} \theta_{0}-\theta_{0}=k \pi$ for some integer $k$. We have $\theta_{0}=\frac{k \pi}{2^{2008}-1}$, so $k$ can be any integer between 1 and $2^{2008}-2$ inclusive (and note that since the denominator is odd, the sequence never terminates). It follows that the number of starting positions is $N=2^{2008}-2$.
Finally, we need to compute the remainder when $N$ is divided by 2008 . We have $2008=2^{3} \times 251$. Using Fermat's Little Theorem with 251 , we get $2^{2008} \equiv\left(2^{250}\right)^{4} \cdot 256 \equiv 1^{4} \cdot 5=5(\bmod 251)$. So we have $N \equiv 3(\bmod 251)$ and $N \equiv-2(\bmod 8)$. Using Chinese Remainder Theorem, we get $N \equiv 254$ $(\bmod 2008)$.
|
254
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Let $\mathcal{C}$ be the hyperbola $y^{2}-x^{2}=1$. Given a point $P_{0}$ on the $x$-axis, we construct a sequence of points $\left(P_{n}\right)$ on the $x$-axis in the following manner: let $\ell_{n}$ be the line with slope 1 passing passing
through $P_{n}$, then $P_{n+1}$ is the orthogonal projection of the point of intersection of $\ell_{n}$ and $\mathcal{C}$ onto the $x$-axis. (If $P_{n}=0$, then the sequence simply terminates.)
Let $N$ be the number of starting positions $P_{0}$ on the $x$-axis such that $P_{0}=P_{2008}$. Determine the remainder of $N$ when divided by 2008.
|
254 Let $P_{n}=\left(x_{n}, 0\right)$. Then the $\ell_{n}$ meet $\mathcal{C}$ at $\left(x_{n+1}, x_{n+1}-x_{n}\right)$. Since this point lies on the hyperbola, we have $\left(x_{n+1}-x_{n}\right)^{2}-x_{n+1}^{2}=1$. Rearranging this equation gives
$$
x_{n+1}=\frac{x_{n}^{2}-1}{2 x_{n}}
$$
Choose a $\theta_{0} \in(0, \pi)$ with $\cot \theta_{0}=x_{0}$, and define $\theta_{n}=2^{n} \theta_{0}$. Using the double-angle formula, we have
$$
\cot \theta_{n+1}=\cot \left(2 \theta_{n}\right)=\frac{\cot ^{2} \theta_{n}-1}{2 \cot \theta_{n}}
$$
It follows by induction that $x_{n}=\cot \theta_{n}$. Then, $P_{0}=P_{2008}$ corresponds to $\cot \theta_{0}=\cot \left(2^{2008} \theta_{0}\right)$ (assuming that $P_{0}$ is never at the origin, or equivalently, $2^{n} \theta$ is never an integer multiple of $\pi$ ). So, we need to find the number of $\theta_{0} \in(0, \pi)$ with the property that $2^{2008} \theta_{0}-\theta_{0}=k \pi$ for some integer $k$. We have $\theta_{0}=\frac{k \pi}{2^{2008}-1}$, so $k$ can be any integer between 1 and $2^{2008}-2$ inclusive (and note that since the denominator is odd, the sequence never terminates). It follows that the number of starting positions is $N=2^{2008}-2$.
Finally, we need to compute the remainder when $N$ is divided by 2008 . We have $2008=2^{3} \times 251$. Using Fermat's Little Theorem with 251 , we get $2^{2008} \equiv\left(2^{250}\right)^{4} \cdot 256 \equiv 1^{4} \cdot 5=5(\bmod 251)$. So we have $N \equiv 3(\bmod 251)$ and $N \equiv-2(\bmod 8)$. Using Chinese Remainder Theorem, we get $N \equiv 254$ $(\bmod 2008)$.
|
{
"resource_path": "HarvardMIT/segmented/en-112-2008-feb-guts-solutions.jsonl",
"problem_match": "\n31. [18]",
"solution_match": "\nAnswer: "
}
|
c5ec6bc8-6daf-50d2-9bff-293f405908a4
| 608,334
|
Cyclic pentagon $A B C D E$ has side lengths $A B=B C=5, C D=D E=12$, and $A E=14$. Determine the radius of its circumcircle.
|
$\frac{225 \sqrt{11}}{88}$ Let $C^{\prime}$ be the point on minor arc $B C D$ such that $B C^{\prime}=12$ and $C^{\prime} D=5$, and write $A C^{\prime}=B D=C^{\prime} E=x, A D=y$, and $B D=z$. Ptolemy applied to quadrilaterals $A B C^{\prime} D, B C^{\prime} D E$, and $A B D E$ gives
$$
\begin{aligned}
& x^{2}=12 y+5^{2} \\
& x^{2}=5 z+12^{2} \\
& y z=14 x+5 \cdot 12
\end{aligned}
$$
Then
$$
\left(x^{2}-5^{2}\right)\left(x^{2}-12^{2}\right)=5 \cdot 12 y z=5 \cdot 12 \cdot 14 x+5^{2} \cdot 12^{2}
$$
from which $x^{3}-169 x-5 \cdot 12 \cdot 14=0$. Noting that $x>13$, the rational root theorem leads quickly to the root $x=15$. Then triangle $B C D$ has area $\sqrt{16 \cdot 1 \cdot 4 \cdot 11}=8 \sqrt{11}$ and circumradius $R=\frac{5 \cdot 12 \cdot 15}{4 \cdot 8 \sqrt{11}}=$ $\frac{225 \sqrt{11}}{88}$.
|
\frac{225 \sqrt{11}}{88}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Cyclic pentagon $A B C D E$ has side lengths $A B=B C=5, C D=D E=12$, and $A E=14$. Determine the radius of its circumcircle.
|
$\frac{225 \sqrt{11}}{88}$ Let $C^{\prime}$ be the point on minor arc $B C D$ such that $B C^{\prime}=12$ and $C^{\prime} D=5$, and write $A C^{\prime}=B D=C^{\prime} E=x, A D=y$, and $B D=z$. Ptolemy applied to quadrilaterals $A B C^{\prime} D, B C^{\prime} D E$, and $A B D E$ gives
$$
\begin{aligned}
& x^{2}=12 y+5^{2} \\
& x^{2}=5 z+12^{2} \\
& y z=14 x+5 \cdot 12
\end{aligned}
$$
Then
$$
\left(x^{2}-5^{2}\right)\left(x^{2}-12^{2}\right)=5 \cdot 12 y z=5 \cdot 12 \cdot 14 x+5^{2} \cdot 12^{2}
$$
from which $x^{3}-169 x-5 \cdot 12 \cdot 14=0$. Noting that $x>13$, the rational root theorem leads quickly to the root $x=15$. Then triangle $B C D$ has area $\sqrt{16 \cdot 1 \cdot 4 \cdot 11}=8 \sqrt{11}$ and circumradius $R=\frac{5 \cdot 12 \cdot 15}{4 \cdot 8 \sqrt{11}}=$ $\frac{225 \sqrt{11}}{88}$.
|
{
"resource_path": "HarvardMIT/segmented/en-112-2008-feb-guts-solutions.jsonl",
"problem_match": "\n32. [18]",
"solution_match": "\nAnswer: "
}
|
f6fdbfad-2f42-5247-8e18-1c5c559e08bb
| 608,335
|
Let $a, b, c$ be nonzero real numbers such that $a+b+c=0$ and $a^{3}+b^{3}+c^{3}=a^{5}+b^{5}+c^{5}$. Find the value of $a^{2}+b^{2}+c^{2}$.
|
$\quad \frac{6}{5}$ Let $\sigma_{1}=a+b+c, \sigma_{2}=a b+b c+c a$ and $\sigma_{3}=a b c$ be the three elementary symmetric polynomials. Since $a^{3}+b^{3}+c^{3}$ is a symmetric polynomial, it can be written as a polynomial in $\sigma_{1}, \sigma_{2}$ and $\sigma_{3}$. Now, observe that $\sigma_{1}=0$, and so we only need to worry about the terms not containing $\sigma_{1}$. By considering the degrees of the terms, we see that the only possibility is $\sigma_{3}$. That is, $a^{3}+b^{3}+c^{3}=k \sigma_{3}$ for some constant $k$. By setting $a=b=1, c=-2$, we see that $k=3$.
By similar reasoning, we find that $a^{5}+b^{5}+c^{5}=h \sigma_{2} \sigma_{3}$ for some constant $h$. By setting $a=b=1$ and $c=-2$, we get $h=-5$.
So, we now know that $a+b+c=0$ implies
$$
a^{3}+b^{3}+c^{3}=3 a b c \quad \text { and } \quad a^{5}+b^{5}+c^{5}=-5 a b c(a b+b c+c a)
$$
Then $a^{3}+b^{3}+c^{3}=a^{5}+b^{5}+c^{5}$ implies that $3 a b c=-5 a b c(a b+b c+c a)$. Given that $a, b, c$ are nonzero, we get $a b+b c+c a=-\frac{3}{5}$. Then, $a^{2}+b^{2}+c^{2}=(a+b+c)^{2}-2(a b+b c+c a)=\frac{6}{5}$.
## $11^{\text {th }}$ HARVARD-MIT MATHEMATICS TOURNAMENT, 23 FEBRUARY 2008 - GUTS ROUND
|
\frac{6}{5}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Let $a, b, c$ be nonzero real numbers such that $a+b+c=0$ and $a^{3}+b^{3}+c^{3}=a^{5}+b^{5}+c^{5}$. Find the value of $a^{2}+b^{2}+c^{2}$.
|
$\quad \frac{6}{5}$ Let $\sigma_{1}=a+b+c, \sigma_{2}=a b+b c+c a$ and $\sigma_{3}=a b c$ be the three elementary symmetric polynomials. Since $a^{3}+b^{3}+c^{3}$ is a symmetric polynomial, it can be written as a polynomial in $\sigma_{1}, \sigma_{2}$ and $\sigma_{3}$. Now, observe that $\sigma_{1}=0$, and so we only need to worry about the terms not containing $\sigma_{1}$. By considering the degrees of the terms, we see that the only possibility is $\sigma_{3}$. That is, $a^{3}+b^{3}+c^{3}=k \sigma_{3}$ for some constant $k$. By setting $a=b=1, c=-2$, we see that $k=3$.
By similar reasoning, we find that $a^{5}+b^{5}+c^{5}=h \sigma_{2} \sigma_{3}$ for some constant $h$. By setting $a=b=1$ and $c=-2$, we get $h=-5$.
So, we now know that $a+b+c=0$ implies
$$
a^{3}+b^{3}+c^{3}=3 a b c \quad \text { and } \quad a^{5}+b^{5}+c^{5}=-5 a b c(a b+b c+c a)
$$
Then $a^{3}+b^{3}+c^{3}=a^{5}+b^{5}+c^{5}$ implies that $3 a b c=-5 a b c(a b+b c+c a)$. Given that $a, b, c$ are nonzero, we get $a b+b c+c a=-\frac{3}{5}$. Then, $a^{2}+b^{2}+c^{2}=(a+b+c)^{2}-2(a b+b c+c a)=\frac{6}{5}$.
## $11^{\text {th }}$ HARVARD-MIT MATHEMATICS TOURNAMENT, 23 FEBRUARY 2008 - GUTS ROUND
|
{
"resource_path": "HarvardMIT/segmented/en-112-2008-feb-guts-solutions.jsonl",
"problem_match": "\n33. [18]",
"solution_match": "\nAnswer: "
}
|
1278f55e-8ef3-5297-bdd8-3fc21bad9a66
| 608,336
|
NUMB3RS. The RSA Factoring Challenge, which ended in 2007, challenged computational mathematicians to factor extremely large numbers that were the product of two prime numbers. The largest number successfully factored in this challenge was RSA-640, which has 193 decimal digits and carried a prize of $\$ 20,000$. The next challenge number carried prize of $\$ 30,000$, and contains $N$ decimal digits. Your task is to submit a guess for $N$. Only the team(s) that have the closest guess(es) receives points. If $k$ teams all have the closest guesses, then each of them receives $\left\lceil\frac{20}{k}\right\rceil$ points.
|
212 For more information, see the Wikipedia entry at http://en.wikipedia.org/wiki/ RSA_Factoring_Challenge.
RSA-640 was factored in November 2005, and the effort took approximately 302.2 GHz -Opteron-CPU years over five months of calendar time.
|
212
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
NUMB3RS. The RSA Factoring Challenge, which ended in 2007, challenged computational mathematicians to factor extremely large numbers that were the product of two prime numbers. The largest number successfully factored in this challenge was RSA-640, which has 193 decimal digits and carried a prize of $\$ 20,000$. The next challenge number carried prize of $\$ 30,000$, and contains $N$ decimal digits. Your task is to submit a guess for $N$. Only the team(s) that have the closest guess(es) receives points. If $k$ teams all have the closest guesses, then each of them receives $\left\lceil\frac{20}{k}\right\rceil$ points.
|
212 For more information, see the Wikipedia entry at http://en.wikipedia.org/wiki/ RSA_Factoring_Challenge.
RSA-640 was factored in November 2005, and the effort took approximately 302.2 GHz -Opteron-CPU years over five months of calendar time.
|
{
"resource_path": "HarvardMIT/segmented/en-112-2008-feb-guts-solutions.jsonl",
"problem_match": "\n35. ",
"solution_match": "\nAnswer: "
}
|
b8816897-286f-5c44-be03-4d590b1a0cf4
| 608,338
|
Determine the number of ways of walking from $(0,0)$ to $(5,5)$ using only up and right unit steps such that the path does not pass through any of the following points: $(1,1),(1,4),(4,1),(4,4)$.

|
In the following figure, each lattice point (with the bottom-left-most point $(0,0)$ ) is labeled with the number of ways of reaching there from $(0,0)$. With the exception of the forbidden points, the labels satisfy the recursion formula $f(x, y)=f(x-1, y)+f(x, y-1)$. We see from the diagram that there are 34 ways to reach $(5,5)$.
| 1 | 1 | 5 | 17 | 17 | 34 |
| :--- | :--- | :--- | :--- | :--- | :--- | :--- |
| 1 | 0 | 4 | 12 | 0 | 17 |
| 1 | 2 | 4 | 8 | 12 | 17 |
| 1 | 1 | 2 | 4 | 4 | 5 |
| 1 | 0 | 1 | 2 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 |
|
34
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Determine the number of ways of walking from $(0,0)$ to $(5,5)$ using only up and right unit steps such that the path does not pass through any of the following points: $(1,1),(1,4),(4,1),(4,4)$.

|
In the following figure, each lattice point (with the bottom-left-most point $(0,0)$ ) is labeled with the number of ways of reaching there from $(0,0)$. With the exception of the forbidden points, the labels satisfy the recursion formula $f(x, y)=f(x-1, y)+f(x, y-1)$. We see from the diagram that there are 34 ways to reach $(5,5)$.
| 1 | 1 | 5 | 17 | 17 | 34 |
| :--- | :--- | :--- | :--- | :--- | :--- | :--- |
| 1 | 0 | 4 | 12 | 0 | 17 |
| 1 | 2 | 4 | 8 | 12 | 17 |
| 1 | 1 | 2 | 4 | 4 | 5 |
| 1 | 0 | 1 | 2 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 |
|
{
"resource_path": "HarvardMIT/segmented/en-112-2008-feb-team1-solutions.jsonl",
"problem_match": "\n1. [20]",
"solution_match": "\nSolution: "
}
|
aea69a9d-e5d7-5955-8332-6023395a9fa6
| 608,340
|
Let $n>4$ be a positive integer. Determine the number of ways to walk from $(0,0)$ to $(n, 2)$ using only up and right unit steps such that the path does not meet the lines $y=x$ or $y=x-n+2$ except at the start and at the end.
|
It is easy to see the the first two steps and the last two steps must all be right steps. So we need to compute the number of walks from $(2,0)$ to $(n-2,0)$ that does not pass through $(2,2)$ and $(n-2,0)$. There are $\binom{n-2}{2}$ paths from $(2,0)$ to $(n-2,0)$, and exactly two of them are invalid. So the answer is $\binom{n-2}{2}-2=\frac{1}{2}(n-2)(n-3)-2=\frac{1}{2}\left(n^{2}-5 n+2\right)$.
|
\frac{1}{2}\left(n^{2}-5 n+2\right)
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Let $n>4$ be a positive integer. Determine the number of ways to walk from $(0,0)$ to $(n, 2)$ using only up and right unit steps such that the path does not meet the lines $y=x$ or $y=x-n+2$ except at the start and at the end.
|
It is easy to see the the first two steps and the last two steps must all be right steps. So we need to compute the number of walks from $(2,0)$ to $(n-2,0)$ that does not pass through $(2,2)$ and $(n-2,0)$. There are $\binom{n-2}{2}$ paths from $(2,0)$ to $(n-2,0)$, and exactly two of them are invalid. So the answer is $\binom{n-2}{2}-2=\frac{1}{2}(n-2)(n-3)-2=\frac{1}{2}\left(n^{2}-5 n+2\right)$.
|
{
"resource_path": "HarvardMIT/segmented/en-112-2008-feb-team1-solutions.jsonl",
"problem_match": "\n3. [20]",
"solution_match": "\nSolution: "
}
|
8a78fe4d-b1fd-5726-94c4-32f77b6655e0
| 608,342
|
Let $n>6$ be a positive integer. Determine the number of ways to walk from $(0,0)$ to $(n, 3)$ using only up and right unit steps such that the path does not meet the lines $y=x$ or $y=x-n+3$ except at the start and at the end.
|
$\quad \frac{1}{6}(n-6)(n-1)(n+1)$ Consider the first point of the path that lies on $x=3$. There are two possibilities for this point: $(3,0)$ and $(3,1)$, and there is exactly one valid way of getting to each point from the origin. Similarly, consider the last point of the path that lies on $x=n-3$. There are two possibilities: $(n-3,2)$ and $(n-3,3)$, and there is exactly one valid way of getting to the destination from each of the two points. Now we count the number of valid paths from each of $(3,0)$ and $(3,1)$, to each of $(n-3,2)$ and $(n-3,3)$, and the answer will be the sum.
- From $(3,1)$ to $(n-3,2)$ : there are no forbidden points along the way, so there are $n-5$ ways.
- From $(3,0)$ to $(n-3,2)$ : the path must not pass through $(n-3,0)$, and there is exactly one invalid path. So there are $\binom{n-4}{2}-1$ ways.
- From $(3,1)$ to $(n-3,3)$ : the path must not pass through $(3,3)$, and there is exactly one invalid path. So there are $\binom{n-4}{2}-1$ ways.
- From $(3,0)$ to $(n-3,3)$ : the path must not pass through $(n-3,0)$ and $(3,3)$, and there are exactly two invalid paths. So there are $\binom{n-3}{3}-2$ ways.
Summing, we obtain the answer:
$n-5+\binom{n-4}{2}-1+\binom{n-4}{2}-1+\binom{n-3}{3}-2=\frac{n^{3}-6 n^{2}-n+6}{6}=\frac{(n-6)(n-1)(n+1)}{6}$.
## Lattice and Centroids [130]
A d-dimensional lattice point is a point of the form $\left(x_{1}, x_{2}, \ldots, x_{d}\right)$ where $x_{1}, x_{2}, \ldots, x_{d}$ are all integers. For a set of $d$-dimensional points, their centroid is the point found by taking the coordinatewise average of the given set of points.
Let $f(n, d)$ denote the minimal number $f$ such that any set of $f$ lattice points in the $d$-dimensional Euclidean space contains a subset of size $n$ whose centroid is also a lattice point.
|
\frac{1}{6}(n-6)(n-1)(n+1)
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Let $n>6$ be a positive integer. Determine the number of ways to walk from $(0,0)$ to $(n, 3)$ using only up and right unit steps such that the path does not meet the lines $y=x$ or $y=x-n+3$ except at the start and at the end.
|
$\quad \frac{1}{6}(n-6)(n-1)(n+1)$ Consider the first point of the path that lies on $x=3$. There are two possibilities for this point: $(3,0)$ and $(3,1)$, and there is exactly one valid way of getting to each point from the origin. Similarly, consider the last point of the path that lies on $x=n-3$. There are two possibilities: $(n-3,2)$ and $(n-3,3)$, and there is exactly one valid way of getting to the destination from each of the two points. Now we count the number of valid paths from each of $(3,0)$ and $(3,1)$, to each of $(n-3,2)$ and $(n-3,3)$, and the answer will be the sum.
- From $(3,1)$ to $(n-3,2)$ : there are no forbidden points along the way, so there are $n-5$ ways.
- From $(3,0)$ to $(n-3,2)$ : the path must not pass through $(n-3,0)$, and there is exactly one invalid path. So there are $\binom{n-4}{2}-1$ ways.
- From $(3,1)$ to $(n-3,3)$ : the path must not pass through $(3,3)$, and there is exactly one invalid path. So there are $\binom{n-4}{2}-1$ ways.
- From $(3,0)$ to $(n-3,3)$ : the path must not pass through $(n-3,0)$ and $(3,3)$, and there are exactly two invalid paths. So there are $\binom{n-3}{3}-2$ ways.
Summing, we obtain the answer:
$n-5+\binom{n-4}{2}-1+\binom{n-4}{2}-1+\binom{n-3}{3}-2=\frac{n^{3}-6 n^{2}-n+6}{6}=\frac{(n-6)(n-1)(n+1)}{6}$.
## Lattice and Centroids [130]
A d-dimensional lattice point is a point of the form $\left(x_{1}, x_{2}, \ldots, x_{d}\right)$ where $x_{1}, x_{2}, \ldots, x_{d}$ are all integers. For a set of $d$-dimensional points, their centroid is the point found by taking the coordinatewise average of the given set of points.
Let $f(n, d)$ denote the minimal number $f$ such that any set of $f$ lattice points in the $d$-dimensional Euclidean space contains a subset of size $n$ whose centroid is also a lattice point.
|
{
"resource_path": "HarvardMIT/segmented/en-112-2008-feb-team1-solutions.jsonl",
"problem_match": "\n4. [30]",
"solution_match": "\nAnswer: "
}
|
7c6a09f2-ec33-5123-a804-06495731eeab
| 608,343
|
Determine the number of juggling sequences of length $n$ with exactly 1 ball.
|
$2^{n}-1$. Solution: With 1 ball, we simply need to decide at times should the ball land in our hand. That is, we need to choose a non-empty subset of $\{0,1,2, \ldots, n-1\}$ where the ball lands. It follows that the answer is $2^{n}-1$.
|
2^{n}-1
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Determine the number of juggling sequences of length $n$ with exactly 1 ball.
|
$2^{n}-1$. Solution: With 1 ball, we simply need to decide at times should the ball land in our hand. That is, we need to choose a non-empty subset of $\{0,1,2, \ldots, n-1\}$ where the ball lands. It follows that the answer is $2^{n}-1$.
|
{
"resource_path": "HarvardMIT/segmented/en-112-2008-feb-team2-solutions.jsonl",
"problem_match": "\n7. [30]",
"solution_match": "\nAnswer: "
}
|
9be8c8a3-382d-525b-96e8-09c6bfcc8582
| 608,360
|
Evaluate
$$
\sin \left(1998^{\circ}+237^{\circ}\right) \sin \left(1998^{\circ}-1653^{\circ}\right)
$$
|
$-\frac{1}{4}$. We have $\sin \left(1998^{\circ}+237^{\circ}\right) \sin \left(1998^{\circ}-1653^{\circ}\right)=\sin \left(2235^{\circ}\right) \sin \left(345^{\circ}\right)=\sin \left(75^{\circ}\right) \sin \left(-15^{\circ}\right)=$ $-\sin \left(75^{\circ}\right) \sin \left(15^{\circ}\right)=-\sin \left(15^{\circ}\right) \cos \left(15^{\circ}\right)=-\frac{\sin \left(30^{\circ}\right)}{2}=-\frac{1}{4}$.
|
-\frac{1}{4}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Evaluate
$$
\sin \left(1998^{\circ}+237^{\circ}\right) \sin \left(1998^{\circ}-1653^{\circ}\right)
$$
|
$-\frac{1}{4}$. We have $\sin \left(1998^{\circ}+237^{\circ}\right) \sin \left(1998^{\circ}-1653^{\circ}\right)=\sin \left(2235^{\circ}\right) \sin \left(345^{\circ}\right)=\sin \left(75^{\circ}\right) \sin \left(-15^{\circ}\right)=$ $-\sin \left(75^{\circ}\right) \sin \left(15^{\circ}\right)=-\sin \left(15^{\circ}\right) \cos \left(15^{\circ}\right)=-\frac{\sin \left(30^{\circ}\right)}{2}=-\frac{1}{4}$.
|
{
"resource_path": "HarvardMIT/segmented/en-12-1998-feb-adv-solutions.jsonl",
"problem_match": "\n1. ",
"solution_match": "\nAnswer: "
}
|
ff2567c1-bf54-5c5a-97ef-d12bf23df132
| 608,369
|
Find the sum of the infinite series
$$
1+2\left(\frac{1}{1998}\right)+3\left(\frac{1}{1998}\right)^{2}+4\left(\frac{1}{1998}\right)^{3}+\ldots
$$
|
$\left(\frac{1998}{1997}\right)^{2}$ or $\frac{3992004}{3988009}$. We can rewrite the sum as
$\left(1+\frac{1}{1998}+\left(\frac{1}{1998}\right)^{2}+\ldots\right)+\left(\frac{1}{1998}+\left(\frac{1}{1998}\right)^{2}+\left(\frac{1}{1998}\right)^{3}+\ldots\right)+\left(\left(\frac{1}{1998}\right)^{2}+\left(\frac{1}{1998}\right)^{3}+\ldots\right)+\ldots$.
Evaluating each of the infinite sums gives
$\frac{1}{1-\frac{1}{1998}}+\frac{\frac{1}{1998}}{1-\frac{1}{1998}}+\frac{\left(\frac{1}{1998}\right)^{2}}{1-\frac{1}{1998}}+\ldots=\frac{1998}{1997} \cdot\left(1+\frac{1}{1998}+\left(\frac{1}{1998}\right)^{2}+\ldots\right)=\frac{1998}{1997} \cdot\left(1+\frac{1}{1998}+\left(\frac{1}{1998}\right)^{2}+\ldots\right)$,
which is equal to $\left(\frac{1998}{1997}\right)^{2}$, or $\frac{3992004}{3988009}$, as desired.
|
\left(\frac{1998}{1997}\right)^{2}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Find the sum of the infinite series
$$
1+2\left(\frac{1}{1998}\right)+3\left(\frac{1}{1998}\right)^{2}+4\left(\frac{1}{1998}\right)^{3}+\ldots
$$
|
$\left(\frac{1998}{1997}\right)^{2}$ or $\frac{3992004}{3988009}$. We can rewrite the sum as
$\left(1+\frac{1}{1998}+\left(\frac{1}{1998}\right)^{2}+\ldots\right)+\left(\frac{1}{1998}+\left(\frac{1}{1998}\right)^{2}+\left(\frac{1}{1998}\right)^{3}+\ldots\right)+\left(\left(\frac{1}{1998}\right)^{2}+\left(\frac{1}{1998}\right)^{3}+\ldots\right)+\ldots$.
Evaluating each of the infinite sums gives
$\frac{1}{1-\frac{1}{1998}}+\frac{\frac{1}{1998}}{1-\frac{1}{1998}}+\frac{\left(\frac{1}{1998}\right)^{2}}{1-\frac{1}{1998}}+\ldots=\frac{1998}{1997} \cdot\left(1+\frac{1}{1998}+\left(\frac{1}{1998}\right)^{2}+\ldots\right)=\frac{1998}{1997} \cdot\left(1+\frac{1}{1998}+\left(\frac{1}{1998}\right)^{2}+\ldots\right)$,
which is equal to $\left(\frac{1998}{1997}\right)^{2}$, or $\frac{3992004}{3988009}$, as desired.
|
{
"resource_path": "HarvardMIT/segmented/en-12-1998-feb-adv-solutions.jsonl",
"problem_match": "\n3. ",
"solution_match": "\nAnswer: "
}
|
e6d16972-f40d-55df-8df5-2201025a04bd
| 608,371
|
How many positive integers less than 1998 are relatively prime to 1547 ? (Two integers are relatively prime if they have no common factors besides 1.)
|
1487. The factorization of 1547 is $7 \cdot 13 \cdot 17$, so we wish to find the number of positive integers less than 1998 that are not divisible by 7,13 , or 17 . By the Principle of Inclusion-Exclusion, we first subtract the numbers that are divisible by one of 7,13 , and 17 , add back those that are divisible by two of 7,13 , and 17 , then subtract those divisible by three of them. That is,
$$
1997-\left\lfloor\frac{1997}{7}\right\rfloor-\left\lfloor\frac{1997}{13}\right\rfloor-\left\lfloor\frac{1997}{17}\right\rfloor+\left\lfloor\frac{1997}{7 \cdot 13}\right\rfloor+\left\lfloor\frac{1997}{7 \cdot 17}\right\rfloor+\left\lfloor\frac{1997}{13 \cdot 17}\right\rfloor-\left\lfloor\frac{1997}{7 \cdot 13 \cdot 17}\right\rfloor,
$$
or 1487.
|
1487
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
How many positive integers less than 1998 are relatively prime to 1547 ? (Two integers are relatively prime if they have no common factors besides 1.)
|
1487. The factorization of 1547 is $7 \cdot 13 \cdot 17$, so we wish to find the number of positive integers less than 1998 that are not divisible by 7,13 , or 17 . By the Principle of Inclusion-Exclusion, we first subtract the numbers that are divisible by one of 7,13 , and 17 , add back those that are divisible by two of 7,13 , and 17 , then subtract those divisible by three of them. That is,
$$
1997-\left\lfloor\frac{1997}{7}\right\rfloor-\left\lfloor\frac{1997}{13}\right\rfloor-\left\lfloor\frac{1997}{17}\right\rfloor+\left\lfloor\frac{1997}{7 \cdot 13}\right\rfloor+\left\lfloor\frac{1997}{7 \cdot 17}\right\rfloor+\left\lfloor\frac{1997}{13 \cdot 17}\right\rfloor-\left\lfloor\frac{1997}{7 \cdot 13 \cdot 17}\right\rfloor,
$$
or 1487.
|
{
"resource_path": "HarvardMIT/segmented/en-12-1998-feb-adv-solutions.jsonl",
"problem_match": "\n5. ",
"solution_match": "\nAnswer: "
}
|
edc9b46d-4760-5b45-b9f5-db506ba129e4
| 608,373
|
In the diagram below, how many distinct paths are there from January 1 to December 31, moving from one adjacent dot to the next either to the right, down, or diagonally down to the right?
| Jan. $1->$ | * | * | * | * | * | * | * | * | * | * | |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| | * | * | | * | * | | * | * | | * | |
| | * | * | * | * | * | * | * | * | * | * | |
| | * | | | * | | | * | * | | * | |
| | * | * | * | * | * | * | * | * | * | * | <-Dec. 31 |
|
372. For each dot in the diagram, we can count the number of paths from January 1 to it by adding the number of ways to get to the dots to the left of it, above it, and above and to the left of it, starting from the topmost leftmost dot. This yields the following numbers of paths:
| Jan. $1->$ | $* 1$ | $* 1$ | $* 1$ | $* 1$ | $* 1$ | $* 1$ | $* 1$ | $* 1$ | $* 1$ |
| ---: | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- |$* 1$
So the number of paths from January 1 to December 31 is 372 .
|
372
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
In the diagram below, how many distinct paths are there from January 1 to December 31, moving from one adjacent dot to the next either to the right, down, or diagonally down to the right?
| Jan. $1->$ | * | * | * | * | * | * | * | * | * | * | |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| | * | * | | * | * | | * | * | | * | |
| | * | * | * | * | * | * | * | * | * | * | |
| | * | | | * | | | * | * | | * | |
| | * | * | * | * | * | * | * | * | * | * | <-Dec. 31 |
|
372. For each dot in the diagram, we can count the number of paths from January 1 to it by adding the number of ways to get to the dots to the left of it, above it, and above and to the left of it, starting from the topmost leftmost dot. This yields the following numbers of paths:
| Jan. $1->$ | $* 1$ | $* 1$ | $* 1$ | $* 1$ | $* 1$ | $* 1$ | $* 1$ | $* 1$ | $* 1$ |
| ---: | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- |$* 1$
So the number of paths from January 1 to December 31 is 372 .
|
{
"resource_path": "HarvardMIT/segmented/en-12-1998-feb-adv-solutions.jsonl",
"problem_match": "\n6. ",
"solution_match": "\nAnswer: "
}
|
53a30336-e104-5a36-ab68-7fea5cd5577c
| 608,374
|
The Houson Association of Mathematics Educators decides to hold a grand forum on mathematics education and invites a number of politicians from the United States to participate. Around lunch time the politicians decide to play a game. In this game, players can score 19 points for pegging the coordinator of the gathering with a spit ball, 9 points for downing an entire cup of the forum's interpretation of coffee, or 8 points for quoting more than three consecutive words from the speech Senator Bobbo delivered before lunch. What is the product of the two greatest scores that a player cannot score in this game?
|
1209. Attainable scores are positive integers that can be written in the form $8 a+9 b+19 c$, where $a, b$, and $c$ are nonnegative integers. Consider attainable number of points modulo 8 .
Scores that are $0(\bmod 8)$ can be obtained with $8 a$ for positive $a$.
Scores that are $1(\bmod 8)$ greater than or equal to 9 can be obtained with $9+8 a$ for nonnegative $a$.
Scores that are $2(\bmod 8)$ greater than or equal to 18 can be obtained with $9 \cdot 2+8 a$.
Scores that are $3(\bmod 8)$ greater than or equal to 19 can be obtained with $19+8 a$.
Scores that are $4(\bmod 8)$ greater than or equal to $19+9=28$ can be obtained with $19+9+8 a$.
Scores that are $5(\bmod 8)$ greater than or equal to $19+9 \cdot 2=37$ can be obtained with $19+9 \cdot 2+8 a$.
Scores that are $6(\bmod 8)$ greater than or equal to $19 \cdot 2=38$ can be obtained with $19 \cdot 2+8 a$.
Scores that are $7(\bmod 8)$ greater than or equal to $19 \cdot 2+9=47$ can be obtained with $19 \cdot 2+9+8 a$.
So the largest two unachievable values are 39 and 31. Multiplying them gives 1209.
|
1209
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
The Houson Association of Mathematics Educators decides to hold a grand forum on mathematics education and invites a number of politicians from the United States to participate. Around lunch time the politicians decide to play a game. In this game, players can score 19 points for pegging the coordinator of the gathering with a spit ball, 9 points for downing an entire cup of the forum's interpretation of coffee, or 8 points for quoting more than three consecutive words from the speech Senator Bobbo delivered before lunch. What is the product of the two greatest scores that a player cannot score in this game?
|
1209. Attainable scores are positive integers that can be written in the form $8 a+9 b+19 c$, where $a, b$, and $c$ are nonnegative integers. Consider attainable number of points modulo 8 .
Scores that are $0(\bmod 8)$ can be obtained with $8 a$ for positive $a$.
Scores that are $1(\bmod 8)$ greater than or equal to 9 can be obtained with $9+8 a$ for nonnegative $a$.
Scores that are $2(\bmod 8)$ greater than or equal to 18 can be obtained with $9 \cdot 2+8 a$.
Scores that are $3(\bmod 8)$ greater than or equal to 19 can be obtained with $19+8 a$.
Scores that are $4(\bmod 8)$ greater than or equal to $19+9=28$ can be obtained with $19+9+8 a$.
Scores that are $5(\bmod 8)$ greater than or equal to $19+9 \cdot 2=37$ can be obtained with $19+9 \cdot 2+8 a$.
Scores that are $6(\bmod 8)$ greater than or equal to $19 \cdot 2=38$ can be obtained with $19 \cdot 2+8 a$.
Scores that are $7(\bmod 8)$ greater than or equal to $19 \cdot 2+9=47$ can be obtained with $19 \cdot 2+9+8 a$.
So the largest two unachievable values are 39 and 31. Multiplying them gives 1209.
|
{
"resource_path": "HarvardMIT/segmented/en-12-1998-feb-adv-solutions.jsonl",
"problem_match": "\n7. ",
"solution_match": "\nAnswer: "
}
|
c89e2949-8475-535b-b0bd-2b30524e1e64
| 608,375
|
Given any two positive real numbers $x$ and $y$, then $x \diamond y$ is a positive real number defined in terms of $x$ and $y$ by some fixed rule. Suppose the operation $x \diamond y$ satisfies the equations $(x \cdot y) \diamond y=x(y \diamond y)$ and $(x \diamond 1) \diamond x=x \diamond 1$ for all $x, y>0$. Given that $1 \diamond 1=1$, find $19 \diamond 98$.
|
19. Note first that $x \diamond 1=(x \cdot 1) \diamond 1=x \cdot(1 \diamond 1)=x \cdot 1=x$. Also, $x \diamond x=(x \diamond 1) \diamond x=x \diamond 1=x$. Now, we have $(x \cdot y) \diamond y=x \cdot(y \diamond y)=x \cdot y$. So $19 \diamond 98=\left(\frac{19}{98} \cdot 98\right) \diamond 98=\frac{19}{98} \cdot(98 \diamond 98)=\frac{19}{98} \cdot 98=19$.
|
19
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Given any two positive real numbers $x$ and $y$, then $x \diamond y$ is a positive real number defined in terms of $x$ and $y$ by some fixed rule. Suppose the operation $x \diamond y$ satisfies the equations $(x \cdot y) \diamond y=x(y \diamond y)$ and $(x \diamond 1) \diamond x=x \diamond 1$ for all $x, y>0$. Given that $1 \diamond 1=1$, find $19 \diamond 98$.
|
19. Note first that $x \diamond 1=(x \cdot 1) \diamond 1=x \cdot(1 \diamond 1)=x \cdot 1=x$. Also, $x \diamond x=(x \diamond 1) \diamond x=x \diamond 1=x$. Now, we have $(x \cdot y) \diamond y=x \cdot(y \diamond y)=x \cdot y$. So $19 \diamond 98=\left(\frac{19}{98} \cdot 98\right) \diamond 98=\frac{19}{98} \cdot(98 \diamond 98)=\frac{19}{98} \cdot 98=19$.
|
{
"resource_path": "HarvardMIT/segmented/en-12-1998-feb-adv-solutions.jsonl",
"problem_match": "\n8. ",
"solution_match": "\nAnswer: "
}
|
99fdbb07-aca5-5a93-b23b-337013c17c2c
| 608,376
|
Bob's Rice ID number has six digits, each a number from 1 to 9 , and any digit can be used any number of times. The ID number satisfies the following property: the first two digits is a number divisible by 2 , the first three digits is a number divisible by 3 , etc. so that the ID number itself is divisible by 6 . One ID number that satisfies this condition is 123252 . How many different possibilities are there for Bob's ID number?
|
324 . We will count the number of possibilities for each digit in Bob's ID number, then multiply them to find the total number of possibilities for Bob's ID number. There are 3 possibilities for the first digit given any last 5 digits, because the entire number must be divisible by 3 , so the sum of the digits must be divisible by 3 . Because the first two digits are a number divisible by 2 , the second digit must be $2,4,6$, or 8 , which is 4 possibilities. Because the first five digits are a number divisible by 5 , the fifth digit must be a 5 . Now, if the fourth digit is a 2 , then the last digit has two choices, 2,8 , and the third digit has 5 choices, $1,3,5,7,9$. If the fourth digit is a 4 , then the last digit must be a 6 , and the third digit has 4 choices, $2,4,6,8$. If the fourth digit is a 6 , then the last digit must be a 4 , and the third digit has 5 choices, $1,3,5,7,9$. If the fourth digit is an 8 , then the last digit has two choices, 2,8 , and the third digit has 4 choices, $2,4,6,8$. So there are a total of $3 \cdot 4(2 \cdot 5+4+5+2 \cdot 4)=3 \cdot 4 \cdot 27=324$ possibilities for Bob's ID number.
|
324
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Bob's Rice ID number has six digits, each a number from 1 to 9 , and any digit can be used any number of times. The ID number satisfies the following property: the first two digits is a number divisible by 2 , the first three digits is a number divisible by 3 , etc. so that the ID number itself is divisible by 6 . One ID number that satisfies this condition is 123252 . How many different possibilities are there for Bob's ID number?
|
324 . We will count the number of possibilities for each digit in Bob's ID number, then multiply them to find the total number of possibilities for Bob's ID number. There are 3 possibilities for the first digit given any last 5 digits, because the entire number must be divisible by 3 , so the sum of the digits must be divisible by 3 . Because the first two digits are a number divisible by 2 , the second digit must be $2,4,6$, or 8 , which is 4 possibilities. Because the first five digits are a number divisible by 5 , the fifth digit must be a 5 . Now, if the fourth digit is a 2 , then the last digit has two choices, 2,8 , and the third digit has 5 choices, $1,3,5,7,9$. If the fourth digit is a 4 , then the last digit must be a 6 , and the third digit has 4 choices, $2,4,6,8$. If the fourth digit is a 6 , then the last digit must be a 4 , and the third digit has 5 choices, $1,3,5,7,9$. If the fourth digit is an 8 , then the last digit has two choices, 2,8 , and the third digit has 4 choices, $2,4,6,8$. So there are a total of $3 \cdot 4(2 \cdot 5+4+5+2 \cdot 4)=3 \cdot 4 \cdot 27=324$ possibilities for Bob's ID number.
|
{
"resource_path": "HarvardMIT/segmented/en-12-1998-feb-adv-solutions.jsonl",
"problem_match": "\n9. ",
"solution_match": "\nAnswer: "
}
|
eb183f22-245d-5392-aa81-36d2af38a8cd
| 608,377
|
In the fourth annual Swirled Series, the Oakland Alphas are playing the San Francisco Gammas. The first game is played in San Francisco and succeeding games alternate in location. San Francisco has a $50 \%$ chance of winning their home games, while Oakland has a probability of $60 \%$ of winning at home. Normally, the serios will stretch on forever until one team gets a three-game lead, in which case they are declared the winners. However, after each game in San Francisco there is a $50 \%$ chance of an earthquake, which will cause the series to end with the team that has won more games declared the winner. What is the probability that the Gammas will win?
|
| $\frac{34}{73} \cdot$ | Let $F(x)$ be the probability that the Gammas will win the series if they are ahead by |
| :--- | :--- | $x$ games and are about to play in San Francisco, and let $A(x)$ be the probability that the Gammas will win the series if they are ahead by $x$ games and are about to play in Oakland. Then we have
$$
\begin{gathered}
F(2)=\frac{3}{4}+\frac{A(1)}{4} \\
A(1)=\frac{6 F(0)}{10}+\frac{4 F(2)}{10} \\
F(0)=\frac{1}{4}+\frac{A(1)}{4}+\frac{A(-1)}{4} \\
A(-1)=\frac{6 F(-2)}{10}+\frac{4 F(0)}{10} \\
F(-2)=\frac{A(-1)}{4}
\end{gathered}
$$
Plugging $A(1)=\frac{6 F(0)}{10}+\frac{4 F(2)}{10}$ into $F(2)=\frac{3}{4}+\frac{A(1)}{4}$, we get
$$
\begin{gathered}
F(2)=\frac{3}{4}+\frac{1}{4}\left(\frac{6 F(0)}{10}+\frac{4 F(2)}{10}\right) \\
\frac{9 F(2)}{10}=\frac{3}{4}+\frac{6 F(0)}{40} \Leftrightarrow F(2)=\frac{5}{6}+\frac{F(0)}{6}
\end{gathered}
$$
Plugging $A(-1)=\frac{6 F(-2)}{10}+\frac{4 F(0)}{10}$ into $F(-2)=\frac{A(-1)}{4}$, we get
$$
\frac{34 A(-1)}{40}=\frac{4 F(0)}{10} \Leftrightarrow F(-2)=\frac{2 F(0)}{17}
$$
Now,
$$
F(0)=\frac{1}{4}+\frac{1}{4}\left(\frac{6 F(0)}{10}+\frac{4 F(2)}{10}\right)+\frac{1}{4}\left(\frac{6 F(-2)}{10}+\frac{4 F(0)}{10}\right)
$$
This simplifies to $F(0)=\frac{1}{4}+\frac{F(0)}{4}+\frac{F(2)}{10}+\frac{6 F(-2)}{40}$. Then, plugging our formulas in, we get
$$
\begin{gathered}
F(0)=\frac{1}{4}+\frac{F(0)}{4}+\frac{1}{10}\left(\frac{5}{6}+\frac{F(0)}{6}\right)+\frac{3 F(0)}{170} \\
\frac{73 F(0)}{102}=\frac{1}{3} \Leftrightarrow F(0)=\frac{34}{73}
\end{gathered}
$$
Since $F(0)$ is the situation before the Series has started, the probability that the Gammas will win is $\frac{34}{73}$.
|
\frac{34}{73}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
In the fourth annual Swirled Series, the Oakland Alphas are playing the San Francisco Gammas. The first game is played in San Francisco and succeeding games alternate in location. San Francisco has a $50 \%$ chance of winning their home games, while Oakland has a probability of $60 \%$ of winning at home. Normally, the serios will stretch on forever until one team gets a three-game lead, in which case they are declared the winners. However, after each game in San Francisco there is a $50 \%$ chance of an earthquake, which will cause the series to end with the team that has won more games declared the winner. What is the probability that the Gammas will win?
|
| $\frac{34}{73} \cdot$ | Let $F(x)$ be the probability that the Gammas will win the series if they are ahead by |
| :--- | :--- | $x$ games and are about to play in San Francisco, and let $A(x)$ be the probability that the Gammas will win the series if they are ahead by $x$ games and are about to play in Oakland. Then we have
$$
\begin{gathered}
F(2)=\frac{3}{4}+\frac{A(1)}{4} \\
A(1)=\frac{6 F(0)}{10}+\frac{4 F(2)}{10} \\
F(0)=\frac{1}{4}+\frac{A(1)}{4}+\frac{A(-1)}{4} \\
A(-1)=\frac{6 F(-2)}{10}+\frac{4 F(0)}{10} \\
F(-2)=\frac{A(-1)}{4}
\end{gathered}
$$
Plugging $A(1)=\frac{6 F(0)}{10}+\frac{4 F(2)}{10}$ into $F(2)=\frac{3}{4}+\frac{A(1)}{4}$, we get
$$
\begin{gathered}
F(2)=\frac{3}{4}+\frac{1}{4}\left(\frac{6 F(0)}{10}+\frac{4 F(2)}{10}\right) \\
\frac{9 F(2)}{10}=\frac{3}{4}+\frac{6 F(0)}{40} \Leftrightarrow F(2)=\frac{5}{6}+\frac{F(0)}{6}
\end{gathered}
$$
Plugging $A(-1)=\frac{6 F(-2)}{10}+\frac{4 F(0)}{10}$ into $F(-2)=\frac{A(-1)}{4}$, we get
$$
\frac{34 A(-1)}{40}=\frac{4 F(0)}{10} \Leftrightarrow F(-2)=\frac{2 F(0)}{17}
$$
Now,
$$
F(0)=\frac{1}{4}+\frac{1}{4}\left(\frac{6 F(0)}{10}+\frac{4 F(2)}{10}\right)+\frac{1}{4}\left(\frac{6 F(-2)}{10}+\frac{4 F(0)}{10}\right)
$$
This simplifies to $F(0)=\frac{1}{4}+\frac{F(0)}{4}+\frac{F(2)}{10}+\frac{6 F(-2)}{40}$. Then, plugging our formulas in, we get
$$
\begin{gathered}
F(0)=\frac{1}{4}+\frac{F(0)}{4}+\frac{1}{10}\left(\frac{5}{6}+\frac{F(0)}{6}\right)+\frac{3 F(0)}{170} \\
\frac{73 F(0)}{102}=\frac{1}{3} \Leftrightarrow F(0)=\frac{34}{73}
\end{gathered}
$$
Since $F(0)$ is the situation before the Series has started, the probability that the Gammas will win is $\frac{34}{73}$.
|
{
"resource_path": "HarvardMIT/segmented/en-12-1998-feb-adv-solutions.jsonl",
"problem_match": "\n10. ",
"solution_match": "\nAnswer: "
}
|
7a4b3095-18dd-55ba-a3ab-9f09c86f52bb
| 608,378
|
The cost of 3 hamburgers, 5 milk shakes, and 1 order of fries at a certain fast food restaurant is $\$ 23.50$. At the same restaurant, the cost of 5 hamburgers, 9 milk shakes, and 1 order of fries is $\$ 39.50$. What is the cost of 2 hamburgers, 2 milk shakes ,and 2 orders of fries at this restaurant?
|
Let $H=$ hamburger, $M=$ milk shake, and $F=$ order of fries. Then $3 H+5 M+F=\$ 23.50$. Multiplying the equation by 2 yields $6 H+10 M+2 F=\$ 47$. Also, it is given that $5 H+9 M+F=\$ 39.50$. Then subtracting the following equations
$$
\begin{aligned}
& 6 H+10 M+2 F=\$ 47.00 \\
& 5 H+9 M+F=\$ 39.50
\end{aligned}
$$
yields $H+M+F=\$ 7.50$. Multiplying the equation by 2 yields $2 H+2 M+2 F=\$ 15$.
|
15
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
The cost of 3 hamburgers, 5 milk shakes, and 1 order of fries at a certain fast food restaurant is $\$ 23.50$. At the same restaurant, the cost of 5 hamburgers, 9 milk shakes, and 1 order of fries is $\$ 39.50$. What is the cost of 2 hamburgers, 2 milk shakes ,and 2 orders of fries at this restaurant?
|
Let $H=$ hamburger, $M=$ milk shake, and $F=$ order of fries. Then $3 H+5 M+F=\$ 23.50$. Multiplying the equation by 2 yields $6 H+10 M+2 F=\$ 47$. Also, it is given that $5 H+9 M+F=\$ 39.50$. Then subtracting the following equations
$$
\begin{aligned}
& 6 H+10 M+2 F=\$ 47.00 \\
& 5 H+9 M+F=\$ 39.50
\end{aligned}
$$
yields $H+M+F=\$ 7.50$. Multiplying the equation by 2 yields $2 H+2 M+2 F=\$ 15$.
|
{
"resource_path": "HarvardMIT/segmented/en-12-1998-feb-alg-solutions.jsonl",
"problem_match": "\n1. Problem: ",
"solution_match": "\nSolution: "
}
|
fe3e5ba4-24a3-5ec9-b9ba-ec46958ab9f4
| 608,379
|
Bobbo starts swimming at 2 feet/s across a 100 foot wide river with a current of 5 feet/s. Bobbo doesn't know that there is a waterfall 175 feet from where he entered the river. He realizes his predicament midway across the river. What is the minimum speed that Bobbo must increase to make it to the other side of the river safely?
|
When Bobbo is midway across the river, he has travelled 50 feet. Going at a speed of 2 feet $/ \mathrm{s}$, this means that Bobbo has already been in the river for $\frac{50 \text { feet }}{20 \text { feet } / \mathrm{s}}=25 \mathrm{~s}$. Then he has traveled 5 feet $/ \mathrm{s} \cdot 25 \mathrm{~s}=125$ feet down the river. Then he has 175 feet- 125 feet $=50$ feet left to travel downstream before he hits the waterfall.
Bobbo travels at a rate of 5 feet/s downstream. Thus there are $\frac{50 \mathrm{feet}}{5 \text { feet } / \mathrm{s}}=10 \mathrm{~s}$ before he hits the waterfall. He still has to travel 50 feet horizontally across the river. Thus he must travel at a speed of $\frac{50 \text { feet }}{10 \mathrm{~s}}=5$ feet $/ \mathrm{s}$. This is a 3 feet/s difference from Bobbo's original speed of 2 feet $/ \mathrm{s}$.
|
3
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Bobbo starts swimming at 2 feet/s across a 100 foot wide river with a current of 5 feet/s. Bobbo doesn't know that there is a waterfall 175 feet from where he entered the river. He realizes his predicament midway across the river. What is the minimum speed that Bobbo must increase to make it to the other side of the river safely?
|
When Bobbo is midway across the river, he has travelled 50 feet. Going at a speed of 2 feet $/ \mathrm{s}$, this means that Bobbo has already been in the river for $\frac{50 \text { feet }}{20 \text { feet } / \mathrm{s}}=25 \mathrm{~s}$. Then he has traveled 5 feet $/ \mathrm{s} \cdot 25 \mathrm{~s}=125$ feet down the river. Then he has 175 feet- 125 feet $=50$ feet left to travel downstream before he hits the waterfall.
Bobbo travels at a rate of 5 feet/s downstream. Thus there are $\frac{50 \mathrm{feet}}{5 \text { feet } / \mathrm{s}}=10 \mathrm{~s}$ before he hits the waterfall. He still has to travel 50 feet horizontally across the river. Thus he must travel at a speed of $\frac{50 \text { feet }}{10 \mathrm{~s}}=5$ feet $/ \mathrm{s}$. This is a 3 feet/s difference from Bobbo's original speed of 2 feet $/ \mathrm{s}$.
|
{
"resource_path": "HarvardMIT/segmented/en-12-1998-feb-alg-solutions.jsonl",
"problem_match": "\n2. Problem: ",
"solution_match": "\nSolution: "
}
|
994a5f19-98d1-58f9-a1ea-f1734cc53d10
| 608,380
|
Find the sum of every even positive integer less than 233 not divisible by 10 .
|
We find the sum of all positive even integers less than 233 and then subtract all the positive integers less than 233 that are divisible by 10 .
$2+4+\ldots+232=2(1+2+\ldots+116)=116 \cdot 117=13572$. The sum of all positive integers less than 233 that are divisible by 10 is $10+20+\ldots+230=10(1+2+\ldots+23)=2760$. Then our answer is $13572-2760=10812$.
|
10812
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Find the sum of every even positive integer less than 233 not divisible by 10 .
|
We find the sum of all positive even integers less than 233 and then subtract all the positive integers less than 233 that are divisible by 10 .
$2+4+\ldots+232=2(1+2+\ldots+116)=116 \cdot 117=13572$. The sum of all positive integers less than 233 that are divisible by 10 is $10+20+\ldots+230=10(1+2+\ldots+23)=2760$. Then our answer is $13572-2760=10812$.
|
{
"resource_path": "HarvardMIT/segmented/en-12-1998-feb-alg-solutions.jsonl",
"problem_match": "\n3. Problem: ",
"solution_match": "\nSolution: "
}
|
e8dbaab5-8343-5da4-bd10-0fb637f1f3cb
| 608,381
|
A man named Juan has three rectangular solids, each having volume 128. Two of the faces of one solid have areas 4 and 32 . Two faces of another solid have areas 64 and 16 . Finally, two faces of the last solid have areas 8 and 32 . What is the minimum possible exposed surface area of the tallest tower Juan can construct by stacking his solids one on top of the other, face to face? (Assume that the base of the tower is not exposed).
|
Suppose that $x, y, z$ are the sides of the following solids. Then Volume $=x y z=128$. For the first solid, without loss of generality (with respect to assigning lengths to $x, y, z$ ), $x y=4$ and $y z=32$. Then $x y^{2} z=128$. Then $y=1$. Solving the remaining equations yields $x=4$ and $z=32$. Then the first solid has dimensions $4 \times 1 \times 32$.
For the second solid, without loss of generality, $x y=64$ and $y z=16$. Then $x y^{2} z=1024$. Then $y=8$. Solving the remaining equations yields $x=8$ and $z=2$. Then the second solid has dimensions $8 \times 8 \times 2$.
For the third solid, without loss of generality, $x y=8$ and $y z=32$. Then $y=2$. Solving the remaining equations yields $x=4$ and $z=16$. Then the third solid has dimensions $4 \times 2 \times 16$.
To obtain the tallest structure, Juan must stack the boxes such that the longest side of each solid is oriented vertically. Then for the first solid, the base must be $1 \times 4$, so that the side of length 32 can
contribute to the height of the structure. Similarly, for the second solid, the base must be $8 \times 2$, so that the side of length 8 can contribute to the height. Finally, for the third solid, the base must be $4 \times 2$. Thus the structure is stacked, from bottom to top: second solid, third solid, first solid. This order is necessary, so that the base of each solid will fit entirely on the top of the solid directly beneath it.
All the side faces of the solids contribute to the surface area of the final solid. The side faces of the bottom solid have area $8 \cdot(8+2+8+2)=160$. The side faces of the middle solid have area $16 \cdot(4+2+4+2)=192$. The sides faces of the top solid have area $32 \cdot(4+1+4+1)=320$.
Furthermore, the top faces of each of the solids are exposed. The top face of the bottom solid is partially obscured by the middle solid. Thus the total exposed area of the top face of the bottom solid is $8 \cdot 2-4 \cdot 2=8$. The top face of the middle solid is partially obscured by the top solid. Thus the total exposed area of the top face of the middle solid is $4 \cdot 2-4 \cdot 1=4$. The top face of the top solid is fully exposed. Thus the total exposed area of the top face of the top solid is $4 \cdot 1=4$.
Then the total surface area of the entire structure is $160+192+320+8+4+4=688$.
|
688
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
A man named Juan has three rectangular solids, each having volume 128. Two of the faces of one solid have areas 4 and 32 . Two faces of another solid have areas 64 and 16 . Finally, two faces of the last solid have areas 8 and 32 . What is the minimum possible exposed surface area of the tallest tower Juan can construct by stacking his solids one on top of the other, face to face? (Assume that the base of the tower is not exposed).
|
Suppose that $x, y, z$ are the sides of the following solids. Then Volume $=x y z=128$. For the first solid, without loss of generality (with respect to assigning lengths to $x, y, z$ ), $x y=4$ and $y z=32$. Then $x y^{2} z=128$. Then $y=1$. Solving the remaining equations yields $x=4$ and $z=32$. Then the first solid has dimensions $4 \times 1 \times 32$.
For the second solid, without loss of generality, $x y=64$ and $y z=16$. Then $x y^{2} z=1024$. Then $y=8$. Solving the remaining equations yields $x=8$ and $z=2$. Then the second solid has dimensions $8 \times 8 \times 2$.
For the third solid, without loss of generality, $x y=8$ and $y z=32$. Then $y=2$. Solving the remaining equations yields $x=4$ and $z=16$. Then the third solid has dimensions $4 \times 2 \times 16$.
To obtain the tallest structure, Juan must stack the boxes such that the longest side of each solid is oriented vertically. Then for the first solid, the base must be $1 \times 4$, so that the side of length 32 can
contribute to the height of the structure. Similarly, for the second solid, the base must be $8 \times 2$, so that the side of length 8 can contribute to the height. Finally, for the third solid, the base must be $4 \times 2$. Thus the structure is stacked, from bottom to top: second solid, third solid, first solid. This order is necessary, so that the base of each solid will fit entirely on the top of the solid directly beneath it.
All the side faces of the solids contribute to the surface area of the final solid. The side faces of the bottom solid have area $8 \cdot(8+2+8+2)=160$. The side faces of the middle solid have area $16 \cdot(4+2+4+2)=192$. The sides faces of the top solid have area $32 \cdot(4+1+4+1)=320$.
Furthermore, the top faces of each of the solids are exposed. The top face of the bottom solid is partially obscured by the middle solid. Thus the total exposed area of the top face of the bottom solid is $8 \cdot 2-4 \cdot 2=8$. The top face of the middle solid is partially obscured by the top solid. Thus the total exposed area of the top face of the middle solid is $4 \cdot 2-4 \cdot 1=4$. The top face of the top solid is fully exposed. Thus the total exposed area of the top face of the top solid is $4 \cdot 1=4$.
Then the total surface area of the entire structure is $160+192+320+8+4+4=688$.
|
{
"resource_path": "HarvardMIT/segmented/en-12-1998-feb-alg-solutions.jsonl",
"problem_match": "\n5. Problem: ",
"solution_match": "\nSolution: "
}
|
6db27429-cd58-5dd1-9cb7-176cc0848f86
| 608,383
|
How many pairs of positive integers $(a, b)$ with $\leq b$ satisfy $\frac{1}{a}+\frac{1}{b}=\frac{1}{6}$ ?
|
$\frac{1}{a}+\frac{1}{b}=\frac{1}{6} \Rightarrow \frac{a+b}{a b}=\frac{1}{6} \Rightarrow a b=6 a+6 b \Rightarrow a b-6 a-6 b=0$. Factoring yields $(a-b)(b-6)-36=0$. Then $(a-6)(b-6)=36$. Because $a$ and $b$ are positive integers, only the factor pairs of 36 are possible values of $a-6$ and $b-6$. The possible pairs are:
$$
\begin{aligned}
& a-6=1, b-6=36 \\
& a-6=2, b-6=18 \\
& a-6=3, b-6=12 \\
& a-6=4, b-6=9 \\
& a-6=6, b-6=6
\end{aligned}
$$
Because $a \leq b$, the symmetric cases, such as $a-6=12, b-6=3$ are not applicable. Then there are 5 possible pairs.
|
5
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
How many pairs of positive integers $(a, b)$ with $\leq b$ satisfy $\frac{1}{a}+\frac{1}{b}=\frac{1}{6}$ ?
|
$\frac{1}{a}+\frac{1}{b}=\frac{1}{6} \Rightarrow \frac{a+b}{a b}=\frac{1}{6} \Rightarrow a b=6 a+6 b \Rightarrow a b-6 a-6 b=0$. Factoring yields $(a-b)(b-6)-36=0$. Then $(a-6)(b-6)=36$. Because $a$ and $b$ are positive integers, only the factor pairs of 36 are possible values of $a-6$ and $b-6$. The possible pairs are:
$$
\begin{aligned}
& a-6=1, b-6=36 \\
& a-6=2, b-6=18 \\
& a-6=3, b-6=12 \\
& a-6=4, b-6=9 \\
& a-6=6, b-6=6
\end{aligned}
$$
Because $a \leq b$, the symmetric cases, such as $a-6=12, b-6=3$ are not applicable. Then there are 5 possible pairs.
|
{
"resource_path": "HarvardMIT/segmented/en-12-1998-feb-alg-solutions.jsonl",
"problem_match": "\n6. Problem: ",
"solution_match": "\nSolution: "
}
|
721c6820-b7c9-5745-8a46-e00377d1cc69
| 608,384
|
Given that three roots of $f(x)=x^{4}+a x^{2}+b x+c$ are $2,-3$, and 5 , what is the value of $a+b+c$ ?
|
By definition, the coefficient of $x^{3}$ is negative the sum of the roots. In $f(x)$, the coefficient of $x^{3}$ is 0 . Thus the sum of the roots of $f(x)$ is 0 . Then the fourth root is -4 . Then $f(x)=(x-2)(x+3)(x-5)(x+4)$. Notice that $f(1)$ is $1+a+b+c$. Thus our answer is $f(1)-1=(1-2)(1+3)(1-5)(1+4)-1=79$.
|
79
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Given that three roots of $f(x)=x^{4}+a x^{2}+b x+c$ are $2,-3$, and 5 , what is the value of $a+b+c$ ?
|
By definition, the coefficient of $x^{3}$ is negative the sum of the roots. In $f(x)$, the coefficient of $x^{3}$ is 0 . Thus the sum of the roots of $f(x)$ is 0 . Then the fourth root is -4 . Then $f(x)=(x-2)(x+3)(x-5)(x+4)$. Notice that $f(1)$ is $1+a+b+c$. Thus our answer is $f(1)-1=(1-2)(1+3)(1-5)(1+4)-1=79$.
|
{
"resource_path": "HarvardMIT/segmented/en-12-1998-feb-alg-solutions.jsonl",
"problem_match": "\n7. Problem: ",
"solution_match": "\nSolution: "
}
|
0d449504-5e21-5364-81f7-34e3378f9b8f
| 608,385
|
Suppose $f(x)$ is a rational function such that $3 f\left(\frac{1}{x}\right)+\frac{2 f(x)}{x}=x^{2}$ for $x \neq 0$. Find $f(-2)$.
|
Let $x=\frac{-1}{2}$. Then
$$
\begin{aligned}
& 3 f(-2)+\frac{2 f\left(\frac{-1}{2}\right)}{\frac{-1}{2}}=\frac{1}{4} \\
& \Rightarrow 3 f(-2)-4 f\left(\frac{-1}{2}\right)= \frac{1}{4}
\end{aligned}
$$
Let $x=-2$. Then
$$
\begin{aligned}
& 3 f\left(\frac{-1}{2}\right)+\frac{2 f(-2)}{-2}=4 \\
\Rightarrow 3 f\left(\frac{-1}{2}\right)-f(-2) & =4
\end{aligned}
$$
Solving this system of equations $\{(1),(2)\}$ for $f(-2)$ yields $f(-2)=\frac{67}{20}$.
|
\frac{67}{20}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Suppose $f(x)$ is a rational function such that $3 f\left(\frac{1}{x}\right)+\frac{2 f(x)}{x}=x^{2}$ for $x \neq 0$. Find $f(-2)$.
|
Let $x=\frac{-1}{2}$. Then
$$
\begin{aligned}
& 3 f(-2)+\frac{2 f\left(\frac{-1}{2}\right)}{\frac{-1}{2}}=\frac{1}{4} \\
& \Rightarrow 3 f(-2)-4 f\left(\frac{-1}{2}\right)= \frac{1}{4}
\end{aligned}
$$
Let $x=-2$. Then
$$
\begin{aligned}
& 3 f\left(\frac{-1}{2}\right)+\frac{2 f(-2)}{-2}=4 \\
\Rightarrow 3 f\left(\frac{-1}{2}\right)-f(-2) & =4
\end{aligned}
$$
Solving this system of equations $\{(1),(2)\}$ for $f(-2)$ yields $f(-2)=\frac{67}{20}$.
|
{
"resource_path": "HarvardMIT/segmented/en-12-1998-feb-alg-solutions.jsonl",
"problem_match": "\n9. Problem: ",
"solution_match": "\nSolution: "
}
|
aaed8f40-1d38-50b5-a165-603aae3a6747
| 608,387
|
G.H. Hardy once went to visit Srinivasa Ramanujan in the hospital, and he started the conversation with: "I came here in taxi-cab number 1729. That number seems dull to me, which I hope isn't a bad omen." "Nonsense," said Ramanujan. "The number isn't dull at all. It's quite interesting. It's the smallest number that can be expressed as the sum of two cubes in two different ways." Ramanujan had immediately seen that $1729=12^{3}+1^{3}=10^{3}+9^{3}$. What is the smallest positive integer representable as the sum of the cubes of three positive integers in two different ways?
|
Let this smallest positive integer be represented as $a^{3}+b^{3}+c^{3}=d^{3}+e^{3}+f^{3}$. By inspection, a solution is not possible with the first 4 cubes. We prove that it is impossible to write the same number as two different sums of the first 5 cubes. Because we necessarily need to use the 5 th cube (otherwise, this proof would be for the first 4 cubes), we have $5^{3}+b^{3}+c^{3}=d^{3}+e^{3}+f^{3}$. Without loss of generality, suppose $d=5$. By inspection, there is no solution to $b^{3}+c^{3}=e^{3}+f^{3}$, such that $b, c, e, f \leq 5$ and $b, c$ and $e, f$ are unique.
Then none of $d, e, f$ are 5 . Then at least two must be 4 , otherwise the RHS would be too small. Without loss of generality, suppose $d=e=4$. Then $b^{3}+c^{3}=3+f^{3}$. By inspection, there are no possible solutions if $b, c, f \leq 4$.
Thus if $a=5$, there are no solutions.
Suppose that there is a solution within the first 6 cubes. Then $a=6$. By the same analysis as above, $d=e=5$, otherwise the RHS would be too small. Then $b^{3}+c^{3}=34+f^{3}$. By inspection, we see that a possible solution is $b=3, c=2, f=1$. Then the desired integer is $6^{3}+3^{3}+2^{3}=251$.
|
251
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
G.H. Hardy once went to visit Srinivasa Ramanujan in the hospital, and he started the conversation with: "I came here in taxi-cab number 1729. That number seems dull to me, which I hope isn't a bad omen." "Nonsense," said Ramanujan. "The number isn't dull at all. It's quite interesting. It's the smallest number that can be expressed as the sum of two cubes in two different ways." Ramanujan had immediately seen that $1729=12^{3}+1^{3}=10^{3}+9^{3}$. What is the smallest positive integer representable as the sum of the cubes of three positive integers in two different ways?
|
Let this smallest positive integer be represented as $a^{3}+b^{3}+c^{3}=d^{3}+e^{3}+f^{3}$. By inspection, a solution is not possible with the first 4 cubes. We prove that it is impossible to write the same number as two different sums of the first 5 cubes. Because we necessarily need to use the 5 th cube (otherwise, this proof would be for the first 4 cubes), we have $5^{3}+b^{3}+c^{3}=d^{3}+e^{3}+f^{3}$. Without loss of generality, suppose $d=5$. By inspection, there is no solution to $b^{3}+c^{3}=e^{3}+f^{3}$, such that $b, c, e, f \leq 5$ and $b, c$ and $e, f$ are unique.
Then none of $d, e, f$ are 5 . Then at least two must be 4 , otherwise the RHS would be too small. Without loss of generality, suppose $d=e=4$. Then $b^{3}+c^{3}=3+f^{3}$. By inspection, there are no possible solutions if $b, c, f \leq 4$.
Thus if $a=5$, there are no solutions.
Suppose that there is a solution within the first 6 cubes. Then $a=6$. By the same analysis as above, $d=e=5$, otherwise the RHS would be too small. Then $b^{3}+c^{3}=34+f^{3}$. By inspection, we see that a possible solution is $b=3, c=2, f=1$. Then the desired integer is $6^{3}+3^{3}+2^{3}=251$.
|
{
"resource_path": "HarvardMIT/segmented/en-12-1998-feb-alg-solutions.jsonl",
"problem_match": "\n10. Problem: ",
"solution_match": "\nSolution: "
}
|
0cb7a024-7ddc-5cba-bd77-dcdee4636d11
| 608,388
|
Farmer Tim is lost in the densely-forested Cartesian plane. Starting from the origin he walks a sinusoidal path in search of home; that is, after $t$ minutes he is at position $(t, \sin t)$.
Five minutes after he sets out, Alex enters the forest at the origin and sets out in search of Tim. He walks in such a way that after he has been in the forest for $m$ minutes, his position is $(m, \cos t)$.
What is the greatest distance between Alex and Farmer Tim while they are walking in these paths?
|
At arbitrary time $t$, Farmer Tim is at position $(t, \sin t)$ and Alex is at position $(t-5, \cos t)$. Hence at time $t$, the distance, $d$, between Tim and Alex is $d=\sqrt{(\sin t-\cos t)^{2}+25}$. To find the maximum value of $d$, we solve for $t$ such that $\frac{d d}{d t}=0$.
$\frac{d d}{d t}=\frac{(\sin t-\cos t)(\cos t+\sin t)}{\sqrt{(\sin t-\cos t)^{2}+25}}$. Then $\frac{d d}{d t}=0 \Rightarrow \sin ^{2} t-\cos ^{2} t=0 \Rightarrow \sin ^{2} t=\cos ^{2} t$. Equality happens if $t$ is any constant multiple of $\frac{\pi}{4}$.
Notice that to maximize $d$, we need to maximize $(\sin t-\cos t)^{2}$. This is achieved when $\cos t=-\sin t$. Because we determined earlier that $t$ is a constant multiple of $\frac{\pi}{4}$, then with this new condition, we see that $t$ must be a constant multiple of $\frac{3 \pi}{4}$.
Then $(\sin t-\cos t)^{2}=2 \Rightarrow d=\sqrt{29}$.
|
\sqrt{29}
|
Yes
|
Yes
|
math-word-problem
|
Calculus
|
Farmer Tim is lost in the densely-forested Cartesian plane. Starting from the origin he walks a sinusoidal path in search of home; that is, after $t$ minutes he is at position $(t, \sin t)$.
Five minutes after he sets out, Alex enters the forest at the origin and sets out in search of Tim. He walks in such a way that after he has been in the forest for $m$ minutes, his position is $(m, \cos t)$.
What is the greatest distance between Alex and Farmer Tim while they are walking in these paths?
|
At arbitrary time $t$, Farmer Tim is at position $(t, \sin t)$ and Alex is at position $(t-5, \cos t)$. Hence at time $t$, the distance, $d$, between Tim and Alex is $d=\sqrt{(\sin t-\cos t)^{2}+25}$. To find the maximum value of $d$, we solve for $t$ such that $\frac{d d}{d t}=0$.
$\frac{d d}{d t}=\frac{(\sin t-\cos t)(\cos t+\sin t)}{\sqrt{(\sin t-\cos t)^{2}+25}}$. Then $\frac{d d}{d t}=0 \Rightarrow \sin ^{2} t-\cos ^{2} t=0 \Rightarrow \sin ^{2} t=\cos ^{2} t$. Equality happens if $t$ is any constant multiple of $\frac{\pi}{4}$.
Notice that to maximize $d$, we need to maximize $(\sin t-\cos t)^{2}$. This is achieved when $\cos t=-\sin t$. Because we determined earlier that $t$ is a constant multiple of $\frac{\pi}{4}$, then with this new condition, we see that $t$ must be a constant multiple of $\frac{3 \pi}{4}$.
Then $(\sin t-\cos t)^{2}=2 \Rightarrow d=\sqrt{29}$.
|
{
"resource_path": "HarvardMIT/segmented/en-12-1998-feb-calc-solutions.jsonl",
"problem_match": "\n1. Problem: ",
"solution_match": "\nSolution: "
}
|
764c35b9-3cb0-55c8-b5a2-03d386afbe10
| 608,389
|
Find the area of the region bounded by the graphs of $y=x^{2}, y=x$, and $x=2$.
|
There are two regions to consider. First, there is the region bounded by $y=x^{2}$ and $y=x$, in the interval $[0,1]$. In this interval, the values of $y=x$ are greater than the values of $y=x^{2}$, thus the area is calculated by $\int_{0}^{1}\left(x-x^{2}\right) d x$.
Second, there is the region bounded by $y=x^{2}$ and $y=x$ and $x=2$, in the interval [1,2]. In this interval, the values of $y=x^{2}$ are greater than the values of $y=x$, thus the area is calculated by $\int_{1}^{2}\left(x^{2}-x\right) d x$. Then the total area of the region bounded by the three graphs is $\int_{0}^{1}\left(x-x^{2}\right) d x+\int_{1}^{2}\left(x^{2}-x\right) d x=1$.
|
1
|
Yes
|
Yes
|
math-word-problem
|
Calculus
|
Find the area of the region bounded by the graphs of $y=x^{2}, y=x$, and $x=2$.
|
There are two regions to consider. First, there is the region bounded by $y=x^{2}$ and $y=x$, in the interval $[0,1]$. In this interval, the values of $y=x$ are greater than the values of $y=x^{2}$, thus the area is calculated by $\int_{0}^{1}\left(x-x^{2}\right) d x$.
Second, there is the region bounded by $y=x^{2}$ and $y=x$ and $x=2$, in the interval [1,2]. In this interval, the values of $y=x^{2}$ are greater than the values of $y=x$, thus the area is calculated by $\int_{1}^{2}\left(x^{2}-x\right) d x$. Then the total area of the region bounded by the three graphs is $\int_{0}^{1}\left(x-x^{2}\right) d x+\int_{1}^{2}\left(x^{2}-x\right) d x=1$.
|
{
"resource_path": "HarvardMIT/segmented/en-12-1998-feb-calc-solutions.jsonl",
"problem_match": "\n3. Problem: ",
"solution_match": "\nSolution: "
}
|
beb63b7f-6978-5701-88e1-5f2adb928d9b
| 608,391
|
Let $f(x)=1+\frac{x}{2}+\frac{x^{2}}{4}+\frac{x^{3}}{8}+\ldots$, for $-1 \leq x \leq 1$. Find $\sqrt{e^{\int_{0}^{1} f(x) d x}}$.
|
Observe that $f(x)$ is merely an infinite geometric series. Thus $f(x)=\frac{1}{1-\frac{x}{2}}=\frac{2}{2-x}$. Then $\int_{0}^{1} \frac{2}{2-x}=2 \ln 2$. Then $\sqrt{e^{2 \ln 2}}=\sqrt{2^{2}}=2$.
|
2
|
Yes
|
Yes
|
math-word-problem
|
Calculus
|
Let $f(x)=1+\frac{x}{2}+\frac{x^{2}}{4}+\frac{x^{3}}{8}+\ldots$, for $-1 \leq x \leq 1$. Find $\sqrt{e^{\int_{0}^{1} f(x) d x}}$.
|
Observe that $f(x)$ is merely an infinite geometric series. Thus $f(x)=\frac{1}{1-\frac{x}{2}}=\frac{2}{2-x}$. Then $\int_{0}^{1} \frac{2}{2-x}=2 \ln 2$. Then $\sqrt{e^{2 \ln 2}}=\sqrt{2^{2}}=2$.
|
{
"resource_path": "HarvardMIT/segmented/en-12-1998-feb-calc-solutions.jsonl",
"problem_match": "\n4. Problem: ",
"solution_match": "\nSolution: "
}
|
ac8757d5-3ce3-54ae-b208-c85345a6972d
| 608,392
|
Edward, the author of this test, had to escape from prison to work in the grading room today. He stopped to rest at a place 1,875 feet from the prison and was spotted by a guard with a crossbow. The guard fired an arrow with an initial velocity of $100 \mathrm{ft} / \mathrm{s}$. At the same time, Edward started running away with an acceleration of $1 \mathrm{ft} / \mathrm{s}^{2}$. Assuming that air resistance causes the arrow to decelerate at $1 \mathrm{ft} / \mathrm{s}^{2}$ and that it does hit Edward, how fast was the arrow moving at the moment of impact (in $\mathrm{ft} / \mathrm{s}$ )?
|
We use the formula for distance, $d=\frac{1}{2} a t^{2}+v t+d_{0}$. Then after $t$ seconds, Edward is at location $1875+\frac{1}{2}(1)\left(t^{2}\right)$ from the prison. After $t$ seconds, the arrow is at location $\frac{1}{2}(-1)\left(t^{2}\right)+100 t$ from the prison. When the arrow hits Edward, both objects are at the same distance away from the tower. Hence $1875+\frac{1}{2}(1)\left(t^{2}\right)=\frac{1}{2}(-1)\left(t^{2}\right)+100 t$. Solving for $t$ yields $t^{2}-100 t+1875=0 \Rightarrow t=25$ or $t=75$. Then it must be $t=25$, because after the arrow hits Edward, he will stop running.
After 25 seconds, the arrow is moving at a velocity of $100-25(1)=75 \mathrm{ft} / \mathrm{s}$.
|
75
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Edward, the author of this test, had to escape from prison to work in the grading room today. He stopped to rest at a place 1,875 feet from the prison and was spotted by a guard with a crossbow. The guard fired an arrow with an initial velocity of $100 \mathrm{ft} / \mathrm{s}$. At the same time, Edward started running away with an acceleration of $1 \mathrm{ft} / \mathrm{s}^{2}$. Assuming that air resistance causes the arrow to decelerate at $1 \mathrm{ft} / \mathrm{s}^{2}$ and that it does hit Edward, how fast was the arrow moving at the moment of impact (in $\mathrm{ft} / \mathrm{s}$ )?
|
We use the formula for distance, $d=\frac{1}{2} a t^{2}+v t+d_{0}$. Then after $t$ seconds, Edward is at location $1875+\frac{1}{2}(1)\left(t^{2}\right)$ from the prison. After $t$ seconds, the arrow is at location $\frac{1}{2}(-1)\left(t^{2}\right)+100 t$ from the prison. When the arrow hits Edward, both objects are at the same distance away from the tower. Hence $1875+\frac{1}{2}(1)\left(t^{2}\right)=\frac{1}{2}(-1)\left(t^{2}\right)+100 t$. Solving for $t$ yields $t^{2}-100 t+1875=0 \Rightarrow t=25$ or $t=75$. Then it must be $t=25$, because after the arrow hits Edward, he will stop running.
After 25 seconds, the arrow is moving at a velocity of $100-25(1)=75 \mathrm{ft} / \mathrm{s}$.
|
{
"resource_path": "HarvardMIT/segmented/en-12-1998-feb-calc-solutions.jsonl",
"problem_match": "\n6. Problem: ",
"solution_match": "\nSolution: "
}
|
8a69db34-7d87-51e5-96d8-2f01074b65c5
| 608,393
|
A parabola is inscribed in equilateral triangle $A B C$ of side length 1 in the sense that $A C$ and $B C$ are tangent to the parabola at $A$ and $B$, respectively. Find the area between $A B$ and the parabola.
|
Suppose $A=(0,0), B=(1,0)$, and $C=\left(\frac{1}{2}, \frac{\sqrt{3}}{2}\right)$. Then the parabola in question goes through $(0,0)$ and $(1,0)$ and has tangents with slopes of $\sqrt{3}$ and $-\sqrt{3}$, respectively, at these points. Suppose the parabola has equation $y=a x^{2}+b x+c$. Then $\frac{d y}{d x}=2 a x+b$.
At point $(0,0), \frac{d y}{d x}=b$. Also the slope at $(0,0)$, as we determined earlier, is $\sqrt{3}$. Hence $b=\sqrt{3}$. Similarly, at point $(1,0), \frac{d y}{d x}=2 a+b$. The slope at $(1,0)$, as we determined earlier, is $-\sqrt{3}$. Then $a=-\sqrt{3}$.
Since the parabola goes through $(0,0), c=0$. Hence the equation of the parabola is $y=-\sqrt{3} x^{2}+\sqrt{3} x$. The desired area is simply the area under the parabolic curve in the interval $[0,1]$.
Hence $\int_{0}^{1}\left(-\sqrt{3} x^{2}+\sqrt{3} x\right) d x=\frac{\sqrt{3}}{6}$.
|
\frac{\sqrt{3}}{6}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
A parabola is inscribed in equilateral triangle $A B C$ of side length 1 in the sense that $A C$ and $B C$ are tangent to the parabola at $A$ and $B$, respectively. Find the area between $A B$ and the parabola.
|
Suppose $A=(0,0), B=(1,0)$, and $C=\left(\frac{1}{2}, \frac{\sqrt{3}}{2}\right)$. Then the parabola in question goes through $(0,0)$ and $(1,0)$ and has tangents with slopes of $\sqrt{3}$ and $-\sqrt{3}$, respectively, at these points. Suppose the parabola has equation $y=a x^{2}+b x+c$. Then $\frac{d y}{d x}=2 a x+b$.
At point $(0,0), \frac{d y}{d x}=b$. Also the slope at $(0,0)$, as we determined earlier, is $\sqrt{3}$. Hence $b=\sqrt{3}$. Similarly, at point $(1,0), \frac{d y}{d x}=2 a+b$. The slope at $(1,0)$, as we determined earlier, is $-\sqrt{3}$. Then $a=-\sqrt{3}$.
Since the parabola goes through $(0,0), c=0$. Hence the equation of the parabola is $y=-\sqrt{3} x^{2}+\sqrt{3} x$. The desired area is simply the area under the parabolic curve in the interval $[0,1]$.
Hence $\int_{0}^{1}\left(-\sqrt{3} x^{2}+\sqrt{3} x\right) d x=\frac{\sqrt{3}}{6}$.
|
{
"resource_path": "HarvardMIT/segmented/en-12-1998-feb-calc-solutions.jsonl",
"problem_match": "\n7. Problem: ",
"solution_match": "\nSolution: "
}
|
31a9c2d4-552c-595f-9b78-711c3ef79141
| 608,394
|
Evaluate $\sum_{n=1}^{\infty} \frac{1}{n \cdot 2^{n-1}}$.
|
Note that if we take the integral of $f(x)$ in problem 4, we get the function $F(x)=x+\frac{x^{2}}{2 \cdot 2}+$ $\frac{x^{3}}{3 \cdot 2^{2}}+\ldots$. Evaluating this integral in the interval $[0,1]$, we get $1+\frac{1}{2 \cdot 2}+\frac{1}{3 \cdot 2^{2}}+\ldots$, which is the desired sum.
Hence $\int_{0}^{1} \frac{2}{2-x} d x=2 \ln 2$.
|
2 \ln 2
|
Yes
|
Yes
|
math-word-problem
|
Calculus
|
Evaluate $\sum_{n=1}^{\infty} \frac{1}{n \cdot 2^{n-1}}$.
|
Note that if we take the integral of $f(x)$ in problem 4, we get the function $F(x)=x+\frac{x^{2}}{2 \cdot 2}+$ $\frac{x^{3}}{3 \cdot 2^{2}}+\ldots$. Evaluating this integral in the interval $[0,1]$, we get $1+\frac{1}{2 \cdot 2}+\frac{1}{3 \cdot 2^{2}}+\ldots$, which is the desired sum.
Hence $\int_{0}^{1} \frac{2}{2-x} d x=2 \ln 2$.
|
{
"resource_path": "HarvardMIT/segmented/en-12-1998-feb-calc-solutions.jsonl",
"problem_match": "\n9. Problem: ",
"solution_match": "\nSolution: "
}
|
bf499065-f54a-5239-a47e-a8594bc205da
| 608,396
|
Let $S$ be the locus of all points $(x, y)$ in the first quadrant such that $\frac{x}{t}+\frac{y}{1-t}=1$ for some $t$ with $0<t<1$. Find the area of $S$.
|
Solving for $t$ in the given equation, we get $t^{2}+(y-x-1) t+x=0$. Using the quadratic equation, we get $t=\frac{(x+1-y) \pm \sqrt{(y-x-1)^{2}-4 x}}{2}$. For all valid combinations of $(x, y), t$ is positive and less than 1 (this is easy to see by inspection). All valid combinations of $(x, y)$ are those that make $(y-x-1)^{2}-4 x \geq 0$.
Solving for $y$ in the equation $(y-x-1)^{2}-4 x=0$ yields $y^{2}-(2 x+2) y+(x-1)^{2} \geq 0 \Rightarrow y=(x+1) \pm 2 \sqrt{x}$. In the original equation, it is given that $\frac{x}{t}+\frac{y}{1-t}=1$, and $0<t<1$. This implies that $x, y<1$. Then the only possible $y<1$ that satisfies $(y-x-1)^{2}-4 x=0$ is $y=x+1-2 \sqrt{x}$.
Then to satisfy the inequality $(y-x-1)^{2}-4 x \geq 0$, we must have $y \leq x+1-2 \sqrt{x}$. Recall that this is when $0<y<1$. Hence we integrate in the interval $[0,1]: \in_{0}^{1} x+1-2 \sqrt{x}=\frac{1}{6}$.
|
\frac{1}{6}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Let $S$ be the locus of all points $(x, y)$ in the first quadrant such that $\frac{x}{t}+\frac{y}{1-t}=1$ for some $t$ with $0<t<1$. Find the area of $S$.
|
Solving for $t$ in the given equation, we get $t^{2}+(y-x-1) t+x=0$. Using the quadratic equation, we get $t=\frac{(x+1-y) \pm \sqrt{(y-x-1)^{2}-4 x}}{2}$. For all valid combinations of $(x, y), t$ is positive and less than 1 (this is easy to see by inspection). All valid combinations of $(x, y)$ are those that make $(y-x-1)^{2}-4 x \geq 0$.
Solving for $y$ in the equation $(y-x-1)^{2}-4 x=0$ yields $y^{2}-(2 x+2) y+(x-1)^{2} \geq 0 \Rightarrow y=(x+1) \pm 2 \sqrt{x}$. In the original equation, it is given that $\frac{x}{t}+\frac{y}{1-t}=1$, and $0<t<1$. This implies that $x, y<1$. Then the only possible $y<1$ that satisfies $(y-x-1)^{2}-4 x=0$ is $y=x+1-2 \sqrt{x}$.
Then to satisfy the inequality $(y-x-1)^{2}-4 x \geq 0$, we must have $y \leq x+1-2 \sqrt{x}$. Recall that this is when $0<y<1$. Hence we integrate in the interval $[0,1]: \in_{0}^{1} x+1-2 \sqrt{x}=\frac{1}{6}$.
|
{
"resource_path": "HarvardMIT/segmented/en-12-1998-feb-calc-solutions.jsonl",
"problem_match": "\n10. Problem: ",
"solution_match": "\nSolution: "
}
|
9a94e1bf-1000-5196-bfaf-31ad6abf70f9
| 608,397
|
Find the minimum of $x^{2}-2 x$ over all real numbers $x$.
|
-1 Write $x^{2}-2 x=x^{2}-2 x+1-1=(x-1)^{2}-1$. Since $(x-1)^{2} \geq 0$, it is clear that the minimum is -1 .
Alternate method: The graph of $y=x^{2}-2 x$ is a parabola that opens up. Therefore, the minimum occurs at its vertex, which is at $\frac{-b}{2 a}=\frac{-(-2)}{2}=1$. But $1^{2}-2 \cdot 1=-1$, so the minimum is -1 .
|
-1
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Find the minimum of $x^{2}-2 x$ over all real numbers $x$.
|
-1 Write $x^{2}-2 x=x^{2}-2 x+1-1=(x-1)^{2}-1$. Since $(x-1)^{2} \geq 0$, it is clear that the minimum is -1 .
Alternate method: The graph of $y=x^{2}-2 x$ is a parabola that opens up. Therefore, the minimum occurs at its vertex, which is at $\frac{-b}{2 a}=\frac{-(-2)}{2}=1$. But $1^{2}-2 \cdot 1=-1$, so the minimum is -1 .
|
{
"resource_path": "HarvardMIT/segmented/en-121-2008-nov-gen1-solutions.jsonl",
"problem_match": "\n1. [2]",
"solution_match": "\nAnswer: "
}
|
d0db9821-de4f-54f9-b4c1-ea820fdaa0bc
| 608,398
|
What is the units digit of $7^{2009}$ ?
|
7 Note that the units digits of $7^{1}, 7^{2}, 7^{3}, 7^{4}, 7^{5}, 7^{6}, \ldots$ follows the pattern $7,9,3,1,7,9,3,1, \ldots$. The 2009th term in this sequence should be 7 .
Alternate method: Note that the units digit of $7^{4}$ is equal to 1 , so the units digit of $\left(7^{4}\right)^{502}$ is also 1. But $\left(7^{4}\right)^{502}=7^{2008}$, so the units digit of $7^{2008}$ is 1 , and therefore the units digit of $7^{2009}$ is 7 .
|
7
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
What is the units digit of $7^{2009}$ ?
|
7 Note that the units digits of $7^{1}, 7^{2}, 7^{3}, 7^{4}, 7^{5}, 7^{6}, \ldots$ follows the pattern $7,9,3,1,7,9,3,1, \ldots$. The 2009th term in this sequence should be 7 .
Alternate method: Note that the units digit of $7^{4}$ is equal to 1 , so the units digit of $\left(7^{4}\right)^{502}$ is also 1. But $\left(7^{4}\right)^{502}=7^{2008}$, so the units digit of $7^{2008}$ is 1 , and therefore the units digit of $7^{2009}$ is 7 .
|
{
"resource_path": "HarvardMIT/segmented/en-121-2008-nov-gen1-solutions.jsonl",
"problem_match": "\n2. [3]",
"solution_match": "\nAnswer: "
}
|
cd0b97bc-5ec7-5f76-9717-75365c5e0908
| 608,399
|
How many diagonals does a regular undecagon (11-sided polygon) have?
|
44 There are 8 diagonals coming from the first vertex, 8 more from the next, 7 from the next, 6 from the next, 5 from the next, etc., and 1 from the last, for $8+8+7+6+5+4+3+2+1=44$ total.
Third method: Each vertex has 8 diagonals touching it. There are 11 vertices. Since each diagonal touches two vertices, this counts every diagonal twice, so there are $\frac{8 \cdot 11}{2}=44$ diagonals.
|
44
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
How many diagonals does a regular undecagon (11-sided polygon) have?
|
44 There are 8 diagonals coming from the first vertex, 8 more from the next, 7 from the next, 6 from the next, 5 from the next, etc., and 1 from the last, for $8+8+7+6+5+4+3+2+1=44$ total.
Third method: Each vertex has 8 diagonals touching it. There are 11 vertices. Since each diagonal touches two vertices, this counts every diagonal twice, so there are $\frac{8 \cdot 11}{2}=44$ diagonals.
|
{
"resource_path": "HarvardMIT/segmented/en-121-2008-nov-gen1-solutions.jsonl",
"problem_match": "\n3. [3]",
"solution_match": "\nAnswer: "
}
|
b032c9e6-1a68-53d5-b7eb-d1f263d767a0
| 608,400
|
Joe has a triangle with area $\sqrt{3}$. What's the smallest perimeter it could have?
|
6 The minimum occurs for an equilateral triangle. The area of an equilateral triangle with side-length $s$ is $\frac{\sqrt{3}}{4} s^{2}$, so if the area is $\sqrt{3}$ then $s=\sqrt{\sqrt{3} \frac{4}{\sqrt{3}}}=2$. Multiplying by 3 to get the perimeter yields the answer.
|
6
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Joe has a triangle with area $\sqrt{3}$. What's the smallest perimeter it could have?
|
6 The minimum occurs for an equilateral triangle. The area of an equilateral triangle with side-length $s$ is $\frac{\sqrt{3}}{4} s^{2}$, so if the area is $\sqrt{3}$ then $s=\sqrt{\sqrt{3} \frac{4}{\sqrt{3}}}=2$. Multiplying by 3 to get the perimeter yields the answer.
|
{
"resource_path": "HarvardMIT/segmented/en-121-2008-nov-gen1-solutions.jsonl",
"problem_match": "\n5. [5]",
"solution_match": "\nAnswer: "
}
|
43a698a2-d5e7-59cf-9fd5-43a62f8ac206
| 608,402
|
How many integers between 2 and 100 inclusive cannot be written as $m \cdot n$, where $m$ and $n$ have no common factors and neither $m$ nor $n$ is equal to 1 ? Note that there are 25 primes less than 100 .
|
35 A number cannot be written in the given form if and only if it is a power of a prime. We can see this by considering the prime factorization. Suppose that $k=p_{1}^{e_{1}} p_{2}^{e_{2}} \cdots p_{n}^{e_{n}}$, with $p_{1}, \ldots, p_{n}$ primes. Then we can write $m=p_{1}^{e_{1}}$ and $n=p_{2}^{e_{2}} \cdots p_{n}^{e_{n}}$. So, we want to find the powers of primes that are less than or equal to 100 . There are 25 primes, as given in the problem statement. The squares of primes are $2^{2}, 3^{2}, 5^{2}, 7^{2}$. The cubes of primes are $2^{3}, 3^{3}$. The fourth powers of primes are $2^{4}, 3^{4}$. The fifth powers of primes are $2^{5}$, The sixth powers of primes are $2^{6}$. There are no seventh or higher powers of primes between 2 and 100 . This adds 10 non-primes to the list, so that in total there are $10+25=35$ such integers.
|
35
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
How many integers between 2 and 100 inclusive cannot be written as $m \cdot n$, where $m$ and $n$ have no common factors and neither $m$ nor $n$ is equal to 1 ? Note that there are 25 primes less than 100 .
|
35 A number cannot be written in the given form if and only if it is a power of a prime. We can see this by considering the prime factorization. Suppose that $k=p_{1}^{e_{1}} p_{2}^{e_{2}} \cdots p_{n}^{e_{n}}$, with $p_{1}, \ldots, p_{n}$ primes. Then we can write $m=p_{1}^{e_{1}}$ and $n=p_{2}^{e_{2}} \cdots p_{n}^{e_{n}}$. So, we want to find the powers of primes that are less than or equal to 100 . There are 25 primes, as given in the problem statement. The squares of primes are $2^{2}, 3^{2}, 5^{2}, 7^{2}$. The cubes of primes are $2^{3}, 3^{3}$. The fourth powers of primes are $2^{4}, 3^{4}$. The fifth powers of primes are $2^{5}$, The sixth powers of primes are $2^{6}$. There are no seventh or higher powers of primes between 2 and 100 . This adds 10 non-primes to the list, so that in total there are $10+25=35$ such integers.
|
{
"resource_path": "HarvardMIT/segmented/en-121-2008-nov-gen1-solutions.jsonl",
"problem_match": "\n8. [7]",
"solution_match": "\nAnswer: "
}
|
bf005865-3560-5a38-9328-51b261be32f5
| 608,405
|
Find the product of all real $x$ for which
$$
2^{3 x+1}-17 \cdot 2^{2 x}+2^{x+3}=0
$$
|
-3 We can re-write the equation as $2^{x}\left(2 \cdot\left(2^{x}\right)^{2}-17 \cdot\left(2^{x}\right)+8\right)=0$, or $2 \cdot\left(2^{x}\right)^{2}-17 \cdot\left(2^{x}\right)+8=0$. Make the substitution $y=2^{x}$. Then we have $2 y^{2}-17 y+8=0$, which has solutions (by the quadratic formula) $y=\frac{17 \pm \sqrt{289-64}}{4}=\frac{17 \pm 15}{4}=8, \frac{1}{2}$, so $2^{x}=8, \frac{1}{2}$ and $x=3,-1$. The product of these numbers is -3 .
|
-3
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Find the product of all real $x$ for which
$$
2^{3 x+1}-17 \cdot 2^{2 x}+2^{x+3}=0
$$
|
-3 We can re-write the equation as $2^{x}\left(2 \cdot\left(2^{x}\right)^{2}-17 \cdot\left(2^{x}\right)+8\right)=0$, or $2 \cdot\left(2^{x}\right)^{2}-17 \cdot\left(2^{x}\right)+8=0$. Make the substitution $y=2^{x}$. Then we have $2 y^{2}-17 y+8=0$, which has solutions (by the quadratic formula) $y=\frac{17 \pm \sqrt{289-64}}{4}=\frac{17 \pm 15}{4}=8, \frac{1}{2}$, so $2^{x}=8, \frac{1}{2}$ and $x=3,-1$. The product of these numbers is -3 .
|
{
"resource_path": "HarvardMIT/segmented/en-121-2008-nov-gen1-solutions.jsonl",
"problem_match": "\n9. [7]",
"solution_match": "\nAnswer: "
}
|
450266b0-530d-5044-9dd4-8c9d98982e78
| 608,406
|
Find the largest positive integer $n$ such that $n^{3}+4 n^{2}-15 n-18$ is the cube of an integer.
|
19 Note that the next cube after $n^{3}$ is $(n+1)^{3}=n^{3}+3 n^{2}+3 n+1$. After that, it is $(n+2)^{3}=n^{3}+6 n^{2}+12 n+8 . n^{3}+6 n^{3}+12 n+8$ is definitely bigger than $n^{3}+4 n^{2}-15 n-18$, so the largest cube that $n^{3}+4 n^{2}-15 n-18$ could be is $(n+1)^{3}$. On the other hand, for $n \geq 4, n^{3}+4 n^{2}-15 n-18$ is larger than $(n-2)^{3}=n^{3}-6 n^{2}+12 n-8$ (as $4 n^{2}-15 n-18>-6 n^{2}+12 n-8 \Longleftrightarrow 10 n^{2}-27 n-10>0$, which is true for $n \geq 4$ ).
So, we will check for all solutions to $n^{3}+4 n^{2}-15 n-18=(n-1)^{3}, n^{3},(n+1)^{3}$. The first case yields
$$
n^{3}+4 n^{2}-15 n-18=n^{3}-3 n^{2}+3 n-1 \Longleftrightarrow 7 n^{2}-18 n-17=0
$$
which has no integer solutions. The second case yields
$$
n^{3}+4 n^{2}-15 n-18=n^{3} \Longleftrightarrow 4 n^{2}-15 n-18=0
$$
which also has no integer solutions. The final case yields
$$
n^{3}+4 n^{2}-15 n-18=n^{3}+3 n^{2}+3 n+1 \Longleftrightarrow n^{2}-18 n-19=0
$$
which has integer solutions $n=-1,19$. So, the largest possible $n$ is 19 .
Remark: The easiest way to see that the first two polynomials have no integer solutions is using the Rational Root Theorem, which states that the rational solutions of a polynomial $a x^{n}+\ldots+b$ are all of the form $\pm \frac{b^{\prime}}{a^{\prime}}$, where $b^{\prime}$ divides $b$ and $a^{\prime}$ divides $a$.
|
19
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Find the largest positive integer $n$ such that $n^{3}+4 n^{2}-15 n-18$ is the cube of an integer.
|
19 Note that the next cube after $n^{3}$ is $(n+1)^{3}=n^{3}+3 n^{2}+3 n+1$. After that, it is $(n+2)^{3}=n^{3}+6 n^{2}+12 n+8 . n^{3}+6 n^{3}+12 n+8$ is definitely bigger than $n^{3}+4 n^{2}-15 n-18$, so the largest cube that $n^{3}+4 n^{2}-15 n-18$ could be is $(n+1)^{3}$. On the other hand, for $n \geq 4, n^{3}+4 n^{2}-15 n-18$ is larger than $(n-2)^{3}=n^{3}-6 n^{2}+12 n-8$ (as $4 n^{2}-15 n-18>-6 n^{2}+12 n-8 \Longleftrightarrow 10 n^{2}-27 n-10>0$, which is true for $n \geq 4$ ).
So, we will check for all solutions to $n^{3}+4 n^{2}-15 n-18=(n-1)^{3}, n^{3},(n+1)^{3}$. The first case yields
$$
n^{3}+4 n^{2}-15 n-18=n^{3}-3 n^{2}+3 n-1 \Longleftrightarrow 7 n^{2}-18 n-17=0
$$
which has no integer solutions. The second case yields
$$
n^{3}+4 n^{2}-15 n-18=n^{3} \Longleftrightarrow 4 n^{2}-15 n-18=0
$$
which also has no integer solutions. The final case yields
$$
n^{3}+4 n^{2}-15 n-18=n^{3}+3 n^{2}+3 n+1 \Longleftrightarrow n^{2}-18 n-19=0
$$
which has integer solutions $n=-1,19$. So, the largest possible $n$ is 19 .
Remark: The easiest way to see that the first two polynomials have no integer solutions is using the Rational Root Theorem, which states that the rational solutions of a polynomial $a x^{n}+\ldots+b$ are all of the form $\pm \frac{b^{\prime}}{a^{\prime}}$, where $b^{\prime}$ divides $b$ and $a^{\prime}$ divides $a$.
|
{
"resource_path": "HarvardMIT/segmented/en-121-2008-nov-gen1-solutions.jsonl",
"problem_match": "\n10. [8]",
"solution_match": "\nAnswer: "
}
|
d73e9d02-061c-508a-ac10-3dee8cce7b1d
| 608,407
|
A triangle has sides of length 9,40 , and 41 . What is its area?
|
180 Observe that $9^{2}+40^{2}=41^{2}$, so this triangle is right and therefore has area $\frac{1}{2} \cdot 9 \cdot 40=$ 180.
|
180
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
A triangle has sides of length 9,40 , and 41 . What is its area?
|
180 Observe that $9^{2}+40^{2}=41^{2}$, so this triangle is right and therefore has area $\frac{1}{2} \cdot 9 \cdot 40=$ 180.
|
{
"resource_path": "HarvardMIT/segmented/en-121-2008-nov-gen2-solutions.jsonl",
"problem_match": "\n1. [3]",
"solution_match": "\nAnswer: "
}
|
87b70c0e-e91b-5e81-b118-adb6bbc0dd38
| 608,408
|
Let $A B C$ be a triangle, and let $M$ be the midpoint of side $A B$. If $A B$ is 17 units long and $C M$ is 8 units long, find the maximum possible value of the area of $A B C$.
|
68 Let $h$ be the length of the altitude from $C$ to $A B$. Observe that $K=\frac{1}{2} \cdot h \cdot A B \leq$ $\frac{1}{2} \cdot C M \cdot A B=68$ and that equality is achieved when $C M \perp A B$.
|
68
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $A B C$ be a triangle, and let $M$ be the midpoint of side $A B$. If $A B$ is 17 units long and $C M$ is 8 units long, find the maximum possible value of the area of $A B C$.
|
68 Let $h$ be the length of the altitude from $C$ to $A B$. Observe that $K=\frac{1}{2} \cdot h \cdot A B \leq$ $\frac{1}{2} \cdot C M \cdot A B=68$ and that equality is achieved when $C M \perp A B$.
|
{
"resource_path": "HarvardMIT/segmented/en-121-2008-nov-gen2-solutions.jsonl",
"problem_match": "\n2. [4]",
"solution_match": "\nAnswer: "
}
|
2d3078d0-8aa1-5814-b199-ea55abb955a1
| 608,409
|
Let $D E F$ be a triangle and $H$ the foot of the altitude from $D$ to $E F$. If $D E=60, D F=35$, and $D H=21$, what is the difference between the minimum and the maximum possible values for the area of $D E F$ ?
|
588 Observe that the two possible configurations come from $D E F$ obtuse and $D E F$ acute. In either case, we have that $H F=\sqrt{35^{2}-21^{2}}=28$ and $E H=\sqrt{60^{2}-21^{2}}=9 \sqrt{39}$. This means that $H F-E H$, so in the two cases the values of $E F$ are $F H+E H$ and $E H-F H$. The difference in area is hence $\frac{1}{2} \cdot 2 \cdot F H \cdot D H=28 \cdot 21=588$.
|
588
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $D E F$ be a triangle and $H$ the foot of the altitude from $D$ to $E F$. If $D E=60, D F=35$, and $D H=21$, what is the difference between the minimum and the maximum possible values for the area of $D E F$ ?
|
588 Observe that the two possible configurations come from $D E F$ obtuse and $D E F$ acute. In either case, we have that $H F=\sqrt{35^{2}-21^{2}}=28$ and $E H=\sqrt{60^{2}-21^{2}}=9 \sqrt{39}$. This means that $H F-E H$, so in the two cases the values of $E F$ are $F H+E H$ and $E H-F H$. The difference in area is hence $\frac{1}{2} \cdot 2 \cdot F H \cdot D H=28 \cdot 21=588$.
|
{
"resource_path": "HarvardMIT/segmented/en-121-2008-nov-gen2-solutions.jsonl",
"problem_match": "\n3. [5]",
"solution_match": "\nAnswer: "
}
|
fb3a50fc-2e79-55b1-a308-d3a9b06284ff
| 608,410
|
Right triangle $X Y Z$, with hypotenuse $Y Z$, has an incircle of radius $\frac{3}{8}$ and one leg of length 3. Find the area of the triangle.
|
$\quad \frac{21}{16}$ Let the other leg have length $x$. Then the tangents from $Y$ and $Z$ to the incircle have length $x-\frac{3}{8}$ and $3-\frac{3}{8}$. So the hypotenuse has length $x+\frac{9}{4}$, the semiperimeter of the triangle is $x+\frac{21}{8}$, and the area of the triangle is $\frac{3}{8}\left(x+\frac{21}{8}\right)$. But the area can also be calculated as $\frac{3 x}{2}$. Setting these expressions equal, we find $x=\frac{7}{8}$ and the area is $\frac{21}{16}$.
|
\frac{21}{16}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Right triangle $X Y Z$, with hypotenuse $Y Z$, has an incircle of radius $\frac{3}{8}$ and one leg of length 3. Find the area of the triangle.
|
$\quad \frac{21}{16}$ Let the other leg have length $x$. Then the tangents from $Y$ and $Z$ to the incircle have length $x-\frac{3}{8}$ and $3-\frac{3}{8}$. So the hypotenuse has length $x+\frac{9}{4}$, the semiperimeter of the triangle is $x+\frac{21}{8}$, and the area of the triangle is $\frac{3}{8}\left(x+\frac{21}{8}\right)$. But the area can also be calculated as $\frac{3 x}{2}$. Setting these expressions equal, we find $x=\frac{7}{8}$ and the area is $\frac{21}{16}$.
|
{
"resource_path": "HarvardMIT/segmented/en-121-2008-nov-gen2-solutions.jsonl",
"problem_match": "\n4. [6]",
"solution_match": "\nAnswer: "
}
|
332a6562-0c33-585b-8a37-1e4126730f0c
| 608,411
|
A triangle has altitudes of length 15,21 , and 35 . Find its area.
|
$\quad 245 \sqrt{3}$ If $A$ is the area of the triangle, the sides are $\frac{2 A}{15}, \frac{2 A}{21}$, and $\frac{2 A}{35}$. So the triangle is similar to a $\frac{1}{15}, \frac{1}{21}, \frac{1}{35}$ triangle, which is similar to a $3,5,7$ triangle. Let the sides be $3 k, 5 k$, and $7 k$. Then the angle between the sides of length $3 k$ and $7 k$ is $120^{\circ}$, so the area is $\frac{15 \sqrt{3}}{4} k^{2}$. But the area can also be calculated as $\frac{(3 k)(35)}{2}=\frac{105 k}{2}$. Setting these values equal, $k=\frac{14 \sqrt{3}}{3}$ and the area is $245 \sqrt{3}$.
Chessboards [25]
Joe B. is playing with some chess pieces on a $6 \times 6$ chessboard. Help him find out some things.
|
245 \sqrt{3}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
A triangle has altitudes of length 15,21 , and 35 . Find its area.
|
$\quad 245 \sqrt{3}$ If $A$ is the area of the triangle, the sides are $\frac{2 A}{15}, \frac{2 A}{21}$, and $\frac{2 A}{35}$. So the triangle is similar to a $\frac{1}{15}, \frac{1}{21}, \frac{1}{35}$ triangle, which is similar to a $3,5,7$ triangle. Let the sides be $3 k, 5 k$, and $7 k$. Then the angle between the sides of length $3 k$ and $7 k$ is $120^{\circ}$, so the area is $\frac{15 \sqrt{3}}{4} k^{2}$. But the area can also be calculated as $\frac{(3 k)(35)}{2}=\frac{105 k}{2}$. Setting these values equal, $k=\frac{14 \sqrt{3}}{3}$ and the area is $245 \sqrt{3}$.
Chessboards [25]
Joe B. is playing with some chess pieces on a $6 \times 6$ chessboard. Help him find out some things.
|
{
"resource_path": "HarvardMIT/segmented/en-121-2008-nov-gen2-solutions.jsonl",
"problem_match": "\n5. [7]",
"solution_match": "\nAnswer: "
}
|
a6dc5e1c-0cf5-5080-afdd-151b932334e6
| 608,412
|
Joe B. first places the black king in one corner of the board. In how many of the 35 remaining squares can he place a white bishop so that it does not check the black king?
|
30 Any square not on the diagonal containing the corner is a possible location, and there are $36-6=30$ such squares.
|
30
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Joe B. first places the black king in one corner of the board. In how many of the 35 remaining squares can he place a white bishop so that it does not check the black king?
|
30 Any square not on the diagonal containing the corner is a possible location, and there are $36-6=30$ such squares.
|
{
"resource_path": "HarvardMIT/segmented/en-121-2008-nov-gen2-solutions.jsonl",
"problem_match": "\n1. [3]",
"solution_match": "\nAnswer: "
}
|
f91be076-3f2c-50c7-9ee7-fbffa4b3bcb9
| 608,413
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.