problem
stringlengths 14
7.96k
| solution
stringlengths 3
10k
| answer
stringlengths 1
91
| problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | question_type
stringclasses 1
value | problem_type
stringclasses 8
values | problem_raw
stringlengths 14
7.96k
| solution_raw
stringlengths 3
10k
| metadata
dict | uuid
stringlengths 36
36
| id
int64 22.6k
612k
|
|---|---|---|---|---|---|---|---|---|---|---|---|
In triangle $A B C, \angle A B C=50^{\circ}$ and $\angle A C B=70^{\circ}$. Let $D$ be the midpoint of side $B C$. A circle is tangent to $B C$ at $B$ and is also tangent to segment $A D$; this circle instersects $A B$ again at $P$. Another circle is tangent to $B C$ at $C$ and is also tangent to segment $A D$; this circle intersects $A C$ again at $Q$. Find $\angle A P Q$ (in degrees).
|
70
Suppose the circles are tangent to $A D$ at $E, F$, respectively; then, by equal tangents, $D E=D B=D C=D F \Rightarrow E=F$ (as shown). So, by the Power of a Point Theorem, $A P \cdot A B=A E^{2}=A F^{2}=A Q \cdot A C \Rightarrow A P / A Q=A C / A B \Rightarrow \triangle A P Q \sim \triangle A C B$, giving $\angle A P Q=\angle A C B=70^{\circ}$.
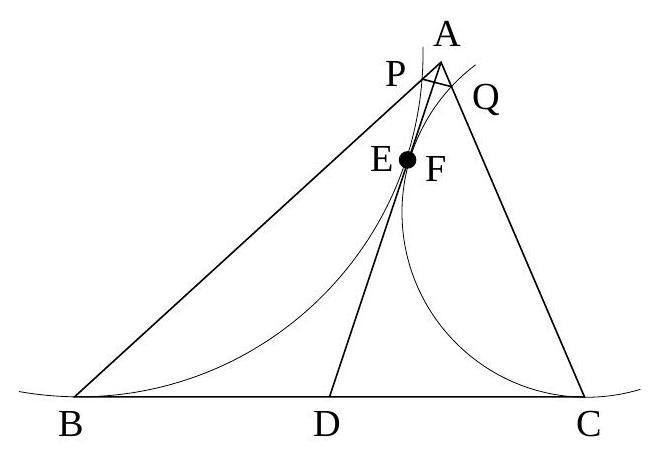
|
70
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
In triangle $A B C, \angle A B C=50^{\circ}$ and $\angle A C B=70^{\circ}$. Let $D$ be the midpoint of side $B C$. A circle is tangent to $B C$ at $B$ and is also tangent to segment $A D$; this circle instersects $A B$ again at $P$. Another circle is tangent to $B C$ at $C$ and is also tangent to segment $A D$; this circle intersects $A C$ again at $Q$. Find $\angle A P Q$ (in degrees).
|
70
Suppose the circles are tangent to $A D$ at $E, F$, respectively; then, by equal tangents, $D E=D B=D C=D F \Rightarrow E=F$ (as shown). So, by the Power of a Point Theorem, $A P \cdot A B=A E^{2}=A F^{2}=A Q \cdot A C \Rightarrow A P / A Q=A C / A B \Rightarrow \triangle A P Q \sim \triangle A C B$, giving $\angle A P Q=\angle A C B=70^{\circ}$.

|
{
"resource_path": "HarvardMIT/segmented/en-62-2003-feb-geo-solutions.jsonl",
"problem_match": "\n9. ",
"solution_match": "\nSolution: "
}
|
fa13c03a-56b1-50ae-b4ce-a7bba01dc032
| 611,137
|
Convex quadrilateral $M A T H$ is given with $H M / M T=3 / 4$, and $\angle A T M=\angle M A T=$ $\angle A H M=60^{\circ} . N$ is the midpoint of $M A$, and $O$ is a point on $T H$ such that lines $M T, A H, N O$ are concurrent. Find the ratio $H O / O T$.
|
$9 / 16$
Triangle $M A T$ is equilateral, so $H M / A T=H M / M T=3 / 4$. Also, $\angle A H M=\angle A T M$, so the quadrilateral is cyclic. Now, let $P$ be the intersection of $M T, A H, N O$. Extend $M H$ and $N O$ to intersect at point $Q$. Then by Menelaus's theorem, applied to triangle
$A H M$ and line $Q N P$, we have
$$
\frac{H Q}{Q M} \cdot \frac{M N}{N A} \cdot \frac{A P}{P H}=1
$$
while applying the same theorem to triangle THM and line $Q P O$ gives
$$
\frac{H Q}{Q M} \cdot \frac{M P}{P T} \cdot \frac{T O}{O H}=1
$$
Combining gives $H O / O T=(M P / P T) \cdot(A N / N M) \cdot(H P / P A)=(M P / P A) \cdot(H P / P T)$ (because $A N / N M=1$ ). But since $M A T H$ is cyclic, $\triangle A P T \sim \triangle M P H$, so $M P / P A=$ $H P / P T=H M / A T=3 / 4$, and the answer is $(3 / 4)^{2}=9 / 16$. (See figure.)
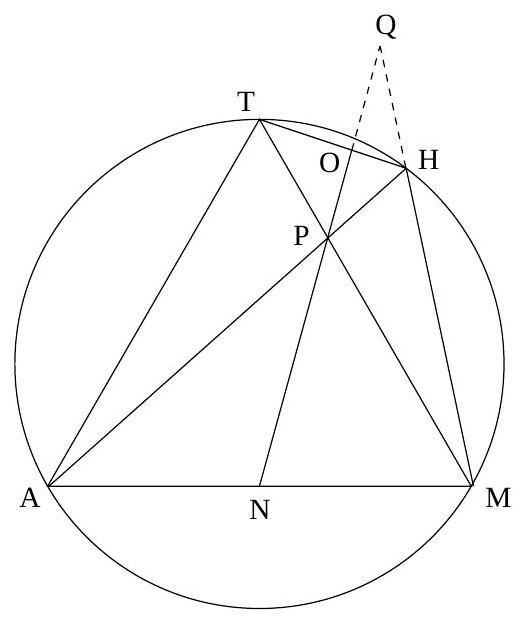
|
\frac{9}{16}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Convex quadrilateral $M A T H$ is given with $H M / M T=3 / 4$, and $\angle A T M=\angle M A T=$ $\angle A H M=60^{\circ} . N$ is the midpoint of $M A$, and $O$ is a point on $T H$ such that lines $M T, A H, N O$ are concurrent. Find the ratio $H O / O T$.
|
$9 / 16$
Triangle $M A T$ is equilateral, so $H M / A T=H M / M T=3 / 4$. Also, $\angle A H M=\angle A T M$, so the quadrilateral is cyclic. Now, let $P$ be the intersection of $M T, A H, N O$. Extend $M H$ and $N O$ to intersect at point $Q$. Then by Menelaus's theorem, applied to triangle
$A H M$ and line $Q N P$, we have
$$
\frac{H Q}{Q M} \cdot \frac{M N}{N A} \cdot \frac{A P}{P H}=1
$$
while applying the same theorem to triangle THM and line $Q P O$ gives
$$
\frac{H Q}{Q M} \cdot \frac{M P}{P T} \cdot \frac{T O}{O H}=1
$$
Combining gives $H O / O T=(M P / P T) \cdot(A N / N M) \cdot(H P / P A)=(M P / P A) \cdot(H P / P T)$ (because $A N / N M=1$ ). But since $M A T H$ is cyclic, $\triangle A P T \sim \triangle M P H$, so $M P / P A=$ $H P / P T=H M / A T=3 / 4$, and the answer is $(3 / 4)^{2}=9 / 16$. (See figure.)

|
{
"resource_path": "HarvardMIT/segmented/en-62-2003-feb-geo-solutions.jsonl",
"problem_match": "\n10. ",
"solution_match": "\nSolution: "
}
|
3076fb2b-859b-5aad-b154-fd1607f673d6
| 611,138
|
Simplify $\sqrt[2003]{2 \sqrt{11}-3 \sqrt{5}} \cdot \sqrt[4006]{89+12 \sqrt{55}}$.
|
-1
Note that $(2 \sqrt{11}+3 \sqrt{5})^{2}=89+12 \sqrt{55}$. So, we have
$$
\begin{aligned}
\sqrt[2003]{2 \sqrt{11}-3 \sqrt{5}} \cdot \sqrt[4006]{89+12 \sqrt{55}} & =\sqrt[2003]{2 \sqrt{11}-3 \sqrt{5}} \cdot \sqrt[2003]{2 \sqrt{11}+3 \sqrt{5}} \\
& =\sqrt[2003]{(2 \sqrt{11})^{2}-(3 \sqrt{5})^{2}}=\sqrt[2003]{-1}=-1
\end{aligned}
$$
|
-1
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Simplify $\sqrt[2003]{2 \sqrt{11}-3 \sqrt{5}} \cdot \sqrt[4006]{89+12 \sqrt{55}}$.
|
-1
Note that $(2 \sqrt{11}+3 \sqrt{5})^{2}=89+12 \sqrt{55}$. So, we have
$$
\begin{aligned}
\sqrt[2003]{2 \sqrt{11}-3 \sqrt{5}} \cdot \sqrt[4006]{89+12 \sqrt{55}} & =\sqrt[2003]{2 \sqrt{11}-3 \sqrt{5}} \cdot \sqrt[2003]{2 \sqrt{11}+3 \sqrt{5}} \\
& =\sqrt[2003]{(2 \sqrt{11})^{2}-(3 \sqrt{5})^{2}}=\sqrt[2003]{-1}=-1
\end{aligned}
$$
|
{
"resource_path": "HarvardMIT/segmented/en-62-2003-feb-guts-solutions.jsonl",
"problem_match": "\n1. ",
"solution_match": "\nSolution: "
}
|
855669d3-45bb-52a3-96c2-df444162f562
| 611,139
|
The graph of $x^{4}=x^{2} y^{2}$ is a union of $n$ different lines. What is the value of $n$ ?
|
3
The equation $x^{4}-x^{2} y^{2}=0$ factors as $x^{2}(x+y)(x-y)=0$, so its graph is the union of the three lines $x=0, x+y=0$, and $x-y=0$.
|
3
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
The graph of $x^{4}=x^{2} y^{2}$ is a union of $n$ different lines. What is the value of $n$ ?
|
3
The equation $x^{4}-x^{2} y^{2}=0$ factors as $x^{2}(x+y)(x-y)=0$, so its graph is the union of the three lines $x=0, x+y=0$, and $x-y=0$.
|
{
"resource_path": "HarvardMIT/segmented/en-62-2003-feb-guts-solutions.jsonl",
"problem_match": "\n2. ",
"solution_match": "\n## Solution: "
}
|
ba350347-0450-5447-9d38-fc393291dcfb
| 611,140
|
If $a$ and $b$ are positive integers that can each be written as a sum of two squares, then $a b$ is also a sum of two squares. Find the smallest positive integer $c$ such that $c=a b$, where $a=x^{3}+y^{3}$ and $b=x^{3}+y^{3}$ each have solutions in integers $(x, y)$, but $c=x^{3}+y^{3}$ does not.
|
4
We can't have $c=1=1^{3}+0^{3}$ or $c=2=1^{3}+1^{3}$, and if $c=3$, then $a$ or $b= \pm 3$ which is not a sum of two cubes (otherwise, flipping signs of $x$ and $y$ if necessary, we would get either a sum of two nonnegative cubes to equal 3, which clearly does not happen, or a difference of two nonnegative cubes to equal 3 , but the smallest difference between two successive cubes $\geq 1$ is $2^{3}-1^{3}=7$ ). However, $c=4$ does meet the conditions, with $a=b=2=1^{3}+1^{3}$ (an argument similar to the above shows that there are no $x, y$ with $4=x^{3}+y^{3}$ ), so 4 is the answer.
|
4
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
If $a$ and $b$ are positive integers that can each be written as a sum of two squares, then $a b$ is also a sum of two squares. Find the smallest positive integer $c$ such that $c=a b$, where $a=x^{3}+y^{3}$ and $b=x^{3}+y^{3}$ each have solutions in integers $(x, y)$, but $c=x^{3}+y^{3}$ does not.
|
4
We can't have $c=1=1^{3}+0^{3}$ or $c=2=1^{3}+1^{3}$, and if $c=3$, then $a$ or $b= \pm 3$ which is not a sum of two cubes (otherwise, flipping signs of $x$ and $y$ if necessary, we would get either a sum of two nonnegative cubes to equal 3, which clearly does not happen, or a difference of two nonnegative cubes to equal 3 , but the smallest difference between two successive cubes $\geq 1$ is $2^{3}-1^{3}=7$ ). However, $c=4$ does meet the conditions, with $a=b=2=1^{3}+1^{3}$ (an argument similar to the above shows that there are no $x, y$ with $4=x^{3}+y^{3}$ ), so 4 is the answer.
|
{
"resource_path": "HarvardMIT/segmented/en-62-2003-feb-guts-solutions.jsonl",
"problem_match": "\n3. ",
"solution_match": "\nSolution: "
}
|
4939de0f-ec2c-502b-b4f4-756db540795e
| 611,141
|
Let $z=1-2 i$. Find $\frac{1}{z}+\frac{2}{z^{2}}+\frac{3}{z^{3}}+\cdots$.
|
$(2 i-1) / 4$
Let $x=\frac{1}{z}+\frac{2}{z^{2}}+\frac{3}{z^{3}}+\cdots$, so $z \cdot x=\left(1+\frac{2}{z}+\frac{3}{z^{2}}+\frac{4}{z^{3}}+\cdots\right)$. Then $z \cdot x-x=$ $1+\frac{1}{z}+\frac{1}{z^{2}}+\frac{1}{z^{3}}+\cdots=\frac{1}{1-1 / z}=\frac{z}{z-1}$. Solving for $x$ in terms of $z$, we obtain $x=\frac{z}{(z-1)^{2}}$. Plugging in the original value of $z$ produces $x=(2 i-1) / 4$.
|
\frac{2i-1}{4}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Let $z=1-2 i$. Find $\frac{1}{z}+\frac{2}{z^{2}}+\frac{3}{z^{3}}+\cdots$.
|
$(2 i-1) / 4$
Let $x=\frac{1}{z}+\frac{2}{z^{2}}+\frac{3}{z^{3}}+\cdots$, so $z \cdot x=\left(1+\frac{2}{z}+\frac{3}{z^{2}}+\frac{4}{z^{3}}+\cdots\right)$. Then $z \cdot x-x=$ $1+\frac{1}{z}+\frac{1}{z^{2}}+\frac{1}{z^{3}}+\cdots=\frac{1}{1-1 / z}=\frac{z}{z-1}$. Solving for $x$ in terms of $z$, we obtain $x=\frac{z}{(z-1)^{2}}$. Plugging in the original value of $z$ produces $x=(2 i-1) / 4$.
|
{
"resource_path": "HarvardMIT/segmented/en-62-2003-feb-guts-solutions.jsonl",
"problem_match": "\n4. ",
"solution_match": "\nSolution: "
}
|
b668fddf-455b-5d31-a2a6-b352afd907f4
| 611,142
|
Compute the surface area of a cube inscribed in a sphere of surface area $\pi$.
|
2
The sphere's radius $r$ satisfies $4 \pi r^{2}=\pi \Rightarrow r=1 / 2$, so the cube has body diagonal 1 , hence side length $1 / \sqrt{3}$. So, its surface area is $6(1 / \sqrt{3})^{2}=2$.
|
2
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Compute the surface area of a cube inscribed in a sphere of surface area $\pi$.
|
2
The sphere's radius $r$ satisfies $4 \pi r^{2}=\pi \Rightarrow r=1 / 2$, so the cube has body diagonal 1 , hence side length $1 / \sqrt{3}$. So, its surface area is $6(1 / \sqrt{3})^{2}=2$.
|
{
"resource_path": "HarvardMIT/segmented/en-62-2003-feb-guts-solutions.jsonl",
"problem_match": "\n5. ",
"solution_match": "\nSolution: "
}
|
e84c325d-7996-5d9a-bab4-7eb9787b0022
| 611,143
|
Define the Fibonacci numbers by $F_{0}=0, F_{1}=1, F_{n}=F_{n-1}+F_{n-2}$ for $n \geq 2$. For how many $n, 0 \leq n \leq 100$, is $F_{n}$ a multiple of 13 ?
|
15
The sequence of remainders modulo 13 begins $0,1,1,2,3,5,8,0$, and then we have $F_{n+7} \equiv 8 F_{n}$ modulo 13 by a straightforward induction. In particular, $F_{n}$ is a multiple of 13 if and only if $7 \mid n$, so there are 15 such $n$.
|
15
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Define the Fibonacci numbers by $F_{0}=0, F_{1}=1, F_{n}=F_{n-1}+F_{n-2}$ for $n \geq 2$. For how many $n, 0 \leq n \leq 100$, is $F_{n}$ a multiple of 13 ?
|
15
The sequence of remainders modulo 13 begins $0,1,1,2,3,5,8,0$, and then we have $F_{n+7} \equiv 8 F_{n}$ modulo 13 by a straightforward induction. In particular, $F_{n}$ is a multiple of 13 if and only if $7 \mid n$, so there are 15 such $n$.
|
{
"resource_path": "HarvardMIT/segmented/en-62-2003-feb-guts-solutions.jsonl",
"problem_match": "\n6. ",
"solution_match": "\n## Solution: "
}
|
d04a1c84-aa37-5307-99ee-cfc8004a7259
| 611,144
|
$a$ and $b$ are integers such that $a+\sqrt{b}=\sqrt{15+\sqrt{216}}$. Compute $a / b$.
|
$1 / 2$
Squaring both sides gives $a^{2}+b+2 a \sqrt{b}=15+\sqrt{216}$; separating rational from irrational parts, we get $a^{2}+b=15,4 a^{2} b=216$, so $a^{2}$ and $b$ equal 6 and 9. $a$ is an integer, so $a^{2}=9, b=6 \Rightarrow a / b=3 / 6=1 / 2$. (We cannot have $a=-3$, since $a+\sqrt{b}$ is positive.)
|
\frac{1}{2}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
$a$ and $b$ are integers such that $a+\sqrt{b}=\sqrt{15+\sqrt{216}}$. Compute $a / b$.
|
$1 / 2$
Squaring both sides gives $a^{2}+b+2 a \sqrt{b}=15+\sqrt{216}$; separating rational from irrational parts, we get $a^{2}+b=15,4 a^{2} b=216$, so $a^{2}$ and $b$ equal 6 and 9. $a$ is an integer, so $a^{2}=9, b=6 \Rightarrow a / b=3 / 6=1 / 2$. (We cannot have $a=-3$, since $a+\sqrt{b}$ is positive.)
|
{
"resource_path": "HarvardMIT/segmented/en-62-2003-feb-guts-solutions.jsonl",
"problem_match": "\n7. ",
"solution_match": "\nSolution: "
}
|
dd11a449-5ece-5d41-b033-b9f4b23504a7
| 611,145
|
How many solutions in nonnegative integers $(a, b, c)$ are there to the equation
$$
2^{a}+2^{b}=c!\quad ?
$$
|
5
We can check that $2^{a}+2^{b}$ is never divisible by 7 , so we must have $c<7$. The binary representation of $2^{a}+2^{b}$ has at most two 1 's. Writing 0 !, 1 !, 2 !, $\ldots, 6$ ! in binary, we can check that the only possibilities are $c=2,3,4$, giving solutions $(0,0,2),(1,2,3),(2,1,3)$, $(3,4,4),(4,3,4)$.
|
5
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
How many solutions in nonnegative integers $(a, b, c)$ are there to the equation
$$
2^{a}+2^{b}=c!\quad ?
$$
|
5
We can check that $2^{a}+2^{b}$ is never divisible by 7 , so we must have $c<7$. The binary representation of $2^{a}+2^{b}$ has at most two 1 's. Writing 0 !, 1 !, 2 !, $\ldots, 6$ ! in binary, we can check that the only possibilities are $c=2,3,4$, giving solutions $(0,0,2),(1,2,3),(2,1,3)$, $(3,4,4),(4,3,4)$.
|
{
"resource_path": "HarvardMIT/segmented/en-62-2003-feb-guts-solutions.jsonl",
"problem_match": "\n8. ",
"solution_match": "\n## Solution: "
}
|
4d91bebd-8594-5881-b15c-b162dca64b5e
| 611,146
|
For $x$ a real number, let $f(x)=0$ if $x<1$ and $f(x)=2 x-2$ if $x \geq 1$. How many solutions are there to the equation
$$
f(f(f(f(x))))=x ?
$$
|
2
Certainly 0,2 are fixed points of $f$ and therefore solutions. On the other hand, there can be no solutions for $x<0$, since $f$ is nonnegative-valued; for $0<x<2$, we have $0 \leq f(x)<x<2$ (and $f(0)=0$ ), so iteration only produces values below $x$, and for $x>2, f(x)>x$, and iteration produces higher values. So there are no other solutions.
|
2
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
For $x$ a real number, let $f(x)=0$ if $x<1$ and $f(x)=2 x-2$ if $x \geq 1$. How many solutions are there to the equation
$$
f(f(f(f(x))))=x ?
$$
|
2
Certainly 0,2 are fixed points of $f$ and therefore solutions. On the other hand, there can be no solutions for $x<0$, since $f$ is nonnegative-valued; for $0<x<2$, we have $0 \leq f(x)<x<2$ (and $f(0)=0$ ), so iteration only produces values below $x$, and for $x>2, f(x)>x$, and iteration produces higher values. So there are no other solutions.
|
{
"resource_path": "HarvardMIT/segmented/en-62-2003-feb-guts-solutions.jsonl",
"problem_match": "\n9. ",
"solution_match": "\n## Solution: "
}
|
ee63b6cc-bcd6-5dde-aa89-764fe014ea99
| 611,147
|
Suppose that $A, B, C, D$ are four points in the plane, and let $Q, R, S, T, U, V$ be the respective midpoints of $A B, A C, A D, B C, B D, C D$. If $Q R=2001, S U=2002, T V=$ 2003, find the distance between the midpoints of $Q U$ and $R V$.
|
2001
This problem has far more information than necessary: $Q R$ and $U V$ are both parallel to $B C$, and $Q U$ and $R V$ are both parallel to $A D$. Hence, $Q U V R$ is a parallelogram, and the desired distance is simply the same as the side length $Q R$, namely 2001. (See figure, next page.)
|
2001
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Suppose that $A, B, C, D$ are four points in the plane, and let $Q, R, S, T, U, V$ be the respective midpoints of $A B, A C, A D, B C, B D, C D$. If $Q R=2001, S U=2002, T V=$ 2003, find the distance between the midpoints of $Q U$ and $R V$.
|
2001
This problem has far more information than necessary: $Q R$ and $U V$ are both parallel to $B C$, and $Q U$ and $R V$ are both parallel to $A D$. Hence, $Q U V R$ is a parallelogram, and the desired distance is simply the same as the side length $Q R$, namely 2001. (See figure, next page.)
|
{
"resource_path": "HarvardMIT/segmented/en-62-2003-feb-guts-solutions.jsonl",
"problem_match": "\n10. ",
"solution_match": "\n## Solution: "
}
|
8406caff-877a-5c92-a6fe-418ca73ecf3f
| 611,148
|
Find the smallest positive integer $n$ such that $1^{2}+2^{2}+3^{2}+4^{2}+\cdots+n^{2}$ is divisible by 100 .
|
24
The sum of the first $n$ squares equals $n(n+1)(2 n+1) / 6$, so we require $n(n+1)(2 n+1)$ to be divisible by $600=24 \cdot 25$. The three factors are pairwise relatively prime, so
one of them must be divisible by 25 . The smallest $n$ for which this happens is $n=12$ $(2 n+1=25)$, but then we do not have enough factors of 2 . The next smallest is $n=24(n+1=25)$, and this works, so 24 is the answer.
|
24
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Find the smallest positive integer $n$ such that $1^{2}+2^{2}+3^{2}+4^{2}+\cdots+n^{2}$ is divisible by 100 .
|
24
The sum of the first $n$ squares equals $n(n+1)(2 n+1) / 6$, so we require $n(n+1)(2 n+1)$ to be divisible by $600=24 \cdot 25$. The three factors are pairwise relatively prime, so

one of them must be divisible by 25 . The smallest $n$ for which this happens is $n=12$ $(2 n+1=25)$, but then we do not have enough factors of 2 . The next smallest is $n=24(n+1=25)$, and this works, so 24 is the answer.
|
{
"resource_path": "HarvardMIT/segmented/en-62-2003-feb-guts-solutions.jsonl",
"problem_match": "\n11. ",
"solution_match": "\n## Solution: "
}
|
db92218f-2a88-5dd6-8072-28f60fcba193
| 611,149
|
If $x y=5$ and $x^{2}+y^{2}=21$, compute $x^{4}+y^{4}$.
|
391
We have $441=\left(x^{2}+y^{2}\right)^{2}=x^{4}+y^{4}+2(x y)^{2}=x^{4}+y^{4}+50$, yielding $x^{4}+y^{4}=391$.
|
391
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
If $x y=5$ and $x^{2}+y^{2}=21$, compute $x^{4}+y^{4}$.
|
391
We have $441=\left(x^{2}+y^{2}\right)^{2}=x^{4}+y^{4}+2(x y)^{2}=x^{4}+y^{4}+50$, yielding $x^{4}+y^{4}=391$.
|
{
"resource_path": "HarvardMIT/segmented/en-62-2003-feb-guts-solutions.jsonl",
"problem_match": "\n13. ",
"solution_match": "\nSolution: "
}
|
f776eee7-21c2-5d7f-b232-2033039e5c6c
| 611,151
|
A positive integer will be called "sparkly" if its smallest (positive) divisor, other than 1, equals the total number of divisors (including 1). How many of the numbers $2,3, \ldots, 2003$ are sparkly?
|
3
Suppose $n$ is sparkly; then its smallest divisor other than 1 is some prime $p$. Hence, $n$ has $p$ divisors. However, if the full prime factorization of $n$ is $p_{1}^{e_{1}} p_{2}^{e_{2}} \cdots p_{r}^{e_{r}}$, the number of divisors is $\left(e_{1}+1\right)\left(e_{2}+1\right) \cdots\left(e_{r}+1\right)$. For this to equal $p$, only one factor can be greater than 1 , so $n$ has only one prime divisor - namely $p$ - and we get $e_{1}=p-1 \Rightarrow n=p^{p-1}$. Conversely, any number of the form $p^{p-1}$ is sparkly. There are just three such numbers in the desired range $\left(2^{1}, 3^{2}, 5^{4}\right)$, so the answer is 3 .
|
3
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
A positive integer will be called "sparkly" if its smallest (positive) divisor, other than 1, equals the total number of divisors (including 1). How many of the numbers $2,3, \ldots, 2003$ are sparkly?
|
3
Suppose $n$ is sparkly; then its smallest divisor other than 1 is some prime $p$. Hence, $n$ has $p$ divisors. However, if the full prime factorization of $n$ is $p_{1}^{e_{1}} p_{2}^{e_{2}} \cdots p_{r}^{e_{r}}$, the number of divisors is $\left(e_{1}+1\right)\left(e_{2}+1\right) \cdots\left(e_{r}+1\right)$. For this to equal $p$, only one factor can be greater than 1 , so $n$ has only one prime divisor - namely $p$ - and we get $e_{1}=p-1 \Rightarrow n=p^{p-1}$. Conversely, any number of the form $p^{p-1}$ is sparkly. There are just three such numbers in the desired range $\left(2^{1}, 3^{2}, 5^{4}\right)$, so the answer is 3 .
|
{
"resource_path": "HarvardMIT/segmented/en-62-2003-feb-guts-solutions.jsonl",
"problem_match": "\n14. ",
"solution_match": "\nSolution: "
}
|
5ae425a8-1f1f-5ce4-aa57-672130057063
| 611,152
|
The product of the digits of a 5 -digit number is 180 . How many such numbers exist?
|
360
Let the digits be $a, b, c, d, e$. Then $a b c d e=180=2^{2} \cdot 3^{2} \cdot 5$. We observe that there are 6 ways to factor 180 into digits $a, b, c, d, e$ (ignoring differences in ordering): $180=$ $1 \cdot 1 \cdot 4 \cdot 5 \cdot 9=1 \cdot 1 \cdot 5 \cdot 6 \cdot 6=1 \cdot 2 \cdot 2 \cdot 5 \cdot 9=1 \cdot 2 \cdot 3 \cdot 5 \cdot 6=1 \cdot 3 \cdot 3 \cdot 4 \cdot 5=2 \cdot 2 \cdot 3 \cdot 3 \cdot 5$. There are (respectively) $60,30,60,120,60$, and 30 permutations of these breakdowns, for a total of 360 numbers.
|
360
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
The product of the digits of a 5 -digit number is 180 . How many such numbers exist?
|
360
Let the digits be $a, b, c, d, e$. Then $a b c d e=180=2^{2} \cdot 3^{2} \cdot 5$. We observe that there are 6 ways to factor 180 into digits $a, b, c, d, e$ (ignoring differences in ordering): $180=$ $1 \cdot 1 \cdot 4 \cdot 5 \cdot 9=1 \cdot 1 \cdot 5 \cdot 6 \cdot 6=1 \cdot 2 \cdot 2 \cdot 5 \cdot 9=1 \cdot 2 \cdot 3 \cdot 5 \cdot 6=1 \cdot 3 \cdot 3 \cdot 4 \cdot 5=2 \cdot 2 \cdot 3 \cdot 3 \cdot 5$. There are (respectively) $60,30,60,120,60$, and 30 permutations of these breakdowns, for a total of 360 numbers.
|
{
"resource_path": "HarvardMIT/segmented/en-62-2003-feb-guts-solutions.jsonl",
"problem_match": "\n15. ",
"solution_match": "\nSolution: "
}
|
8ddccd47-bfc4-5ac7-9b0e-bbc7ee7b4d4c
| 611,153
|
What fraction of the area of a regular hexagon of side length 1 is within distance $\frac{1}{2}$ of at least one of the vertices?
|
$\pi \sqrt{3} / 9$
The hexagon has area $6(\sqrt{3} / 4)(1)^{2}=3 \sqrt{3} / 2$. The region we want consists of six $120^{\circ}$ arcs of circles of radius $1 / 2$, whichcan be reassembled into two circles of radius $1 / 2$. So its area is $\pi / 2$, and the ratio of areas is $\pi \sqrt{3} / 9$.
|
\pi \sqrt{3} / 9
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
What fraction of the area of a regular hexagon of side length 1 is within distance $\frac{1}{2}$ of at least one of the vertices?
|
$\pi \sqrt{3} / 9$
The hexagon has area $6(\sqrt{3} / 4)(1)^{2}=3 \sqrt{3} / 2$. The region we want consists of six $120^{\circ}$ arcs of circles of radius $1 / 2$, whichcan be reassembled into two circles of radius $1 / 2$. So its area is $\pi / 2$, and the ratio of areas is $\pi \sqrt{3} / 9$.
|
{
"resource_path": "HarvardMIT/segmented/en-62-2003-feb-guts-solutions.jsonl",
"problem_match": "\n16. ",
"solution_match": "\nSolution: "
}
|
dafded58-5f62-5683-b381-5f5de873f4ac
| 611,154
|
There are 10 cities in a state, and some pairs of cities are connected by roads. There are 40 roads altogether. A city is called a "hub" if it is directly connected to every other city. What is the largest possible number of hubs?
|
6
If there are $h$ hubs, then $\binom{h}{2}$ roads connect the hubs to each other, and each hub is connected to the other $10-h$ cities; we thus get $\binom{h}{2}+h(10-h)$ distinct roads. So, $40 \geq\binom{ h}{2}+h(10-h)=-h^{2} / 2+19 h / 2$, or $80 \geq h(19-h)$. The largest $h \leq 10$ satisfying this condition is $h=6$, and conversely, if we connect each of 6 cities to every other city and place the remaining $40-\left[\binom{6}{2}+6(10-6)\right]=1$ road wherever we wish, we can achieve 6 hubs. So 6 is the answer.
|
6
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
There are 10 cities in a state, and some pairs of cities are connected by roads. There are 40 roads altogether. A city is called a "hub" if it is directly connected to every other city. What is the largest possible number of hubs?
|
6
If there are $h$ hubs, then $\binom{h}{2}$ roads connect the hubs to each other, and each hub is connected to the other $10-h$ cities; we thus get $\binom{h}{2}+h(10-h)$ distinct roads. So, $40 \geq\binom{ h}{2}+h(10-h)=-h^{2} / 2+19 h / 2$, or $80 \geq h(19-h)$. The largest $h \leq 10$ satisfying this condition is $h=6$, and conversely, if we connect each of 6 cities to every other city and place the remaining $40-\left[\binom{6}{2}+6(10-6)\right]=1$ road wherever we wish, we can achieve 6 hubs. So 6 is the answer.
|
{
"resource_path": "HarvardMIT/segmented/en-62-2003-feb-guts-solutions.jsonl",
"problem_match": "\n17. ",
"solution_match": "\nSolution: "
}
|
f7fc3b88-73b8-5077-acc0-b736f7a0f85f
| 611,155
|
Find the sum of the reciprocals of all the (positive) divisors of 144.
|
403/144
As $d$ ranges over the divisors of 144 , so does $144 / d$, so the sum of $1 / d$ is $1 / 144$ times the sum of the divisors of 144 . Using the formula for the sum of the divisors of a number (or just counting them out by hand), we get that this sum is 403, so the answer is 403/144.
|
\frac{403}{144}
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Find the sum of the reciprocals of all the (positive) divisors of 144.
|
403/144
As $d$ ranges over the divisors of 144 , so does $144 / d$, so the sum of $1 / d$ is $1 / 144$ times the sum of the divisors of 144 . Using the formula for the sum of the divisors of a number (or just counting them out by hand), we get that this sum is 403, so the answer is 403/144.
|
{
"resource_path": "HarvardMIT/segmented/en-62-2003-feb-guts-solutions.jsonl",
"problem_match": "\n18. ",
"solution_match": "\n## Solution: "
}
|
6c494065-1e2e-5397-b640-dbd0b6b2d432
| 611,156
|
Let $r, s, t$ be the solutions to the equation $x^{3}+a x^{2}+b x+c=0$. What is the value of $(r s)^{2}+(s t)^{2}+(r t)^{2}$ in terms of $a, b$, and $c$ ?
|
$b^{2}-2 a c$
We have $(x-r)(x-s)(x-t)=x^{3}+a x^{2}+b x+c$, so
$$
a=-(r+s+t), \quad b=r s+s t+r t, \quad c=-r s t .
$$
So we have
$$
(r s)^{2}+(s t)^{2}+(r t)^{2}=(r s+s t+r t)^{2}-2 r s t(r+s+t)=b^{2}-2 a c .
$$
|
b^{2}-2 a c
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Let $r, s, t$ be the solutions to the equation $x^{3}+a x^{2}+b x+c=0$. What is the value of $(r s)^{2}+(s t)^{2}+(r t)^{2}$ in terms of $a, b$, and $c$ ?
|
$b^{2}-2 a c$
We have $(x-r)(x-s)(x-t)=x^{3}+a x^{2}+b x+c$, so
$$
a=-(r+s+t), \quad b=r s+s t+r t, \quad c=-r s t .
$$
So we have
$$
(r s)^{2}+(s t)^{2}+(r t)^{2}=(r s+s t+r t)^{2}-2 r s t(r+s+t)=b^{2}-2 a c .
$$
|
{
"resource_path": "HarvardMIT/segmented/en-62-2003-feb-guts-solutions.jsonl",
"problem_match": "\n19. ",
"solution_match": "\nSolution: "
}
|
1b852de0-74a0-56a4-b012-ed3212bbcdde
| 611,157
|
What is the smallest number of regular hexagons of side length 1 needed to completely cover a disc of radius 1 ?
|
3
First, we show that two hexagons do not suffice. Specifically, we claim that a hexagon covers less than half of the disc's boundary. First, a hexagon of side length 1 may be inscribed in a circle, and this covers just 6 points. Translating the hexagon vertically upward (regardless of its orientation) will cause it to no longer touch any point on the lower half of the circle, so that it now covers less than half of the boundary. By rotational symmetry, the same argument applies to translation in any other direction, proving the claim. Then, two hexagons cannot possibly cover the disc.
The disc can be covered by three hexagons as follows. Let $P$ be the center of the circle. Put three non-overlapping hexagons together at point $P$. This will cover the circle, since each hexagon will cover a $120^{\circ}$ sector of the circle.
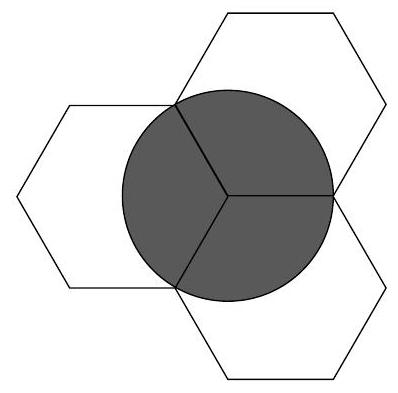
|
3
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
What is the smallest number of regular hexagons of side length 1 needed to completely cover a disc of radius 1 ?
|
3
First, we show that two hexagons do not suffice. Specifically, we claim that a hexagon covers less than half of the disc's boundary. First, a hexagon of side length 1 may be inscribed in a circle, and this covers just 6 points. Translating the hexagon vertically upward (regardless of its orientation) will cause it to no longer touch any point on the lower half of the circle, so that it now covers less than half of the boundary. By rotational symmetry, the same argument applies to translation in any other direction, proving the claim. Then, two hexagons cannot possibly cover the disc.
The disc can be covered by three hexagons as follows. Let $P$ be the center of the circle. Put three non-overlapping hexagons together at point $P$. This will cover the circle, since each hexagon will cover a $120^{\circ}$ sector of the circle.

|
{
"resource_path": "HarvardMIT/segmented/en-62-2003-feb-guts-solutions.jsonl",
"problem_match": "\n20. ",
"solution_match": "\nSolution: "
}
|
42794722-aaec-57f4-b860-5eeeb6b83db6
| 611,158
|
$r$ and $s$ are integers such that
$$
3 r \geq 2 s-3 \text { and } 4 s \geq r+12 .
$$
What is the smallest possible value of $r / s$ ?
|
$1 / 2$
We simply plot the two inequalities in the $s r$-plane and find the lattice point satisfying both inequalities such that the slope from it to the origin is as low as possible. We find that this point is $(2,4)$ (or $(3,6))$, as circled in the figure, so the answer is $2 / 4=1 / 2$.
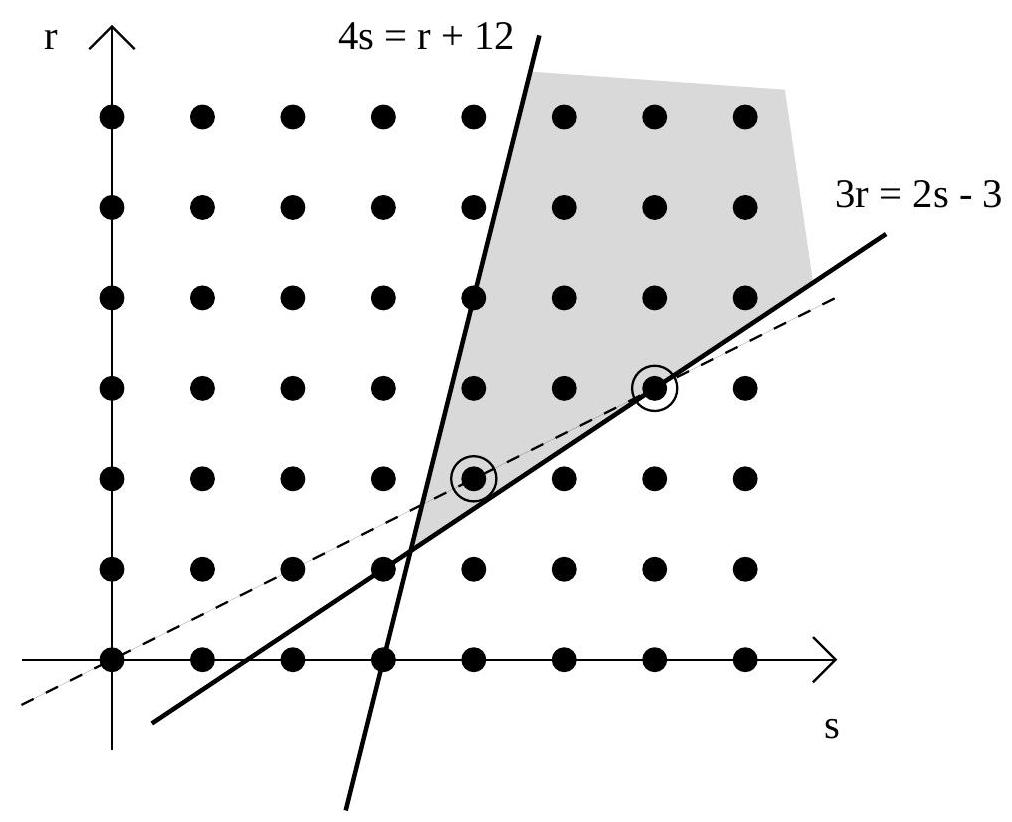
|
\frac{1}{2}
|
Yes
|
Yes
|
math-word-problem
|
Inequalities
|
$r$ and $s$ are integers such that
$$
3 r \geq 2 s-3 \text { and } 4 s \geq r+12 .
$$
What is the smallest possible value of $r / s$ ?
|
$1 / 2$
We simply plot the two inequalities in the $s r$-plane and find the lattice point satisfying both inequalities such that the slope from it to the origin is as low as possible. We find that this point is $(2,4)$ (or $(3,6))$, as circled in the figure, so the answer is $2 / 4=1 / 2$.

|
{
"resource_path": "HarvardMIT/segmented/en-62-2003-feb-guts-solutions.jsonl",
"problem_match": "\n21. ",
"solution_match": "\nSolution: "
}
|
671bc24a-3111-5bb0-aac7-e94d09431d81
| 611,159
|
There are 100 houses in a row on a street. A painter comes and paints every house red. Then, another painter comes and paints every third house (starting with house number 3) blue. Another painter comes and paints every fifth house red (even if it is already red), then another painter paints every seventh house blue, and so forth, alternating between red and blue, until 50 painters have been by. After this is finished, how many houses will be red?
|
52
House $n$ ends up red if and only if the largest odd divisor of $n$ is of the form $4 k+1$. We have 25 values of $n=4 k+1 ; 13$ values of $n=2(4 k+1)$ (given by $k=0,1,2, \ldots, 12$ ); 7 values of $n=4(4 k+1)(k=0,1, \ldots, 6) ; 3$ values of $n=8(4 k+1)(k=0,1,2) ; 2$ of the form $n=16(4 k+1)$ (for $k=0,1)$; 1 of the form $n=32(4 k+1)$; and 1 of the form $n=64(4 k+1)$. Thus we have a total of $25+13+7+3+2+1+1=52$ red houses.
|
52
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
There are 100 houses in a row on a street. A painter comes and paints every house red. Then, another painter comes and paints every third house (starting with house number 3) blue. Another painter comes and paints every fifth house red (even if it is already red), then another painter paints every seventh house blue, and so forth, alternating between red and blue, until 50 painters have been by. After this is finished, how many houses will be red?
|
52
House $n$ ends up red if and only if the largest odd divisor of $n$ is of the form $4 k+1$. We have 25 values of $n=4 k+1 ; 13$ values of $n=2(4 k+1)$ (given by $k=0,1,2, \ldots, 12$ ); 7 values of $n=4(4 k+1)(k=0,1, \ldots, 6) ; 3$ values of $n=8(4 k+1)(k=0,1,2) ; 2$ of the form $n=16(4 k+1)$ (for $k=0,1)$; 1 of the form $n=32(4 k+1)$; and 1 of the form $n=64(4 k+1)$. Thus we have a total of $25+13+7+3+2+1+1=52$ red houses.
|
{
"resource_path": "HarvardMIT/segmented/en-62-2003-feb-guts-solutions.jsonl",
"problem_match": "\n22. ",
"solution_match": "\n## Solution: "
}
|
4527c562-9705-5a59-af96-cdefaa6e38c0
| 611,160
|
How many lattice points are enclosed by the triangle with vertices $(0,99),(5,100)$, and (2003, 500)? Don't count boundary points.
|
0
Using the determinant formula, we get that the area of the triangle is
$$
\left|\begin{array}{cc}
5 & 1 \\
2003 & 401
\end{array}\right| / 2=1
$$
There are 4 lattice points on the boundary of the triangle (the three vertices and $(1004,300))$, so it follows from Pick's Theorem that there are 0 in the interior.
|
0
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
How many lattice points are enclosed by the triangle with vertices $(0,99),(5,100)$, and (2003, 500)? Don't count boundary points.
|
0
Using the determinant formula, we get that the area of the triangle is
$$
\left|\begin{array}{cc}
5 & 1 \\
2003 & 401
\end{array}\right| / 2=1
$$
There are 4 lattice points on the boundary of the triangle (the three vertices and $(1004,300))$, so it follows from Pick's Theorem that there are 0 in the interior.
|
{
"resource_path": "HarvardMIT/segmented/en-62-2003-feb-guts-solutions.jsonl",
"problem_match": "\n23. ",
"solution_match": "\nSolution: "
}
|
aefd8e4a-90aa-59f2-b573-8549e202ea68
| 611,161
|
Compute the radius of the inscribed circle of a triangle with sides 15,16 , and 17 .
|
$\sqrt{21}$
Hero's formula gives that the area is $\sqrt{24 \cdot 9 \cdot 8 \cdot 7}=24 \sqrt{21}$. Then, using the result that the area of a triangle equals the inradius times half the perimeter, we see that the radius is $\sqrt{21}$.
|
\sqrt{21}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Compute the radius of the inscribed circle of a triangle with sides 15,16 , and 17 .
|
$\sqrt{21}$
Hero's formula gives that the area is $\sqrt{24 \cdot 9 \cdot 8 \cdot 7}=24 \sqrt{21}$. Then, using the result that the area of a triangle equals the inradius times half the perimeter, we see that the radius is $\sqrt{21}$.
|
{
"resource_path": "HarvardMIT/segmented/en-62-2003-feb-guts-solutions.jsonl",
"problem_match": "\n24. ",
"solution_match": "\nSolution: "
}
|
df41a6e2-813b-5a48-9b31-fa7abfc5c26f
| 611,162
|
Let $A B C$ be an isosceles triangle with apex $A$. Let $I$ be the incenter. If $A I=3$ and the distance from $I$ to $B C$ is 2 , then what is the length of $B C$ ?
|
$4 \sqrt{5}$
Let $X$ and $Y$ be the points where the incircle touches $A B$ and $B C$, respectively. Then $A X I$ and $A Y B$ are similar right triangles. Since $I$ is the incenter, we have $I X=I Y=2$. Using the Pythagorean theorem on triangle $A X I$, we find $A X=\sqrt{5}$. By similarity, $A Y / A X=B Y / I X$. Plugging in the numbers given, $5 / \sqrt{5}=B Y / 2$, so $B Y=2 \sqrt{5} . Y$ is the midpoint of $B C$, so $B C=4 \sqrt{5}$.
|
4 \sqrt{5}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $A B C$ be an isosceles triangle with apex $A$. Let $I$ be the incenter. If $A I=3$ and the distance from $I$ to $B C$ is 2 , then what is the length of $B C$ ?
|
$4 \sqrt{5}$
Let $X$ and $Y$ be the points where the incircle touches $A B$ and $B C$, respectively. Then $A X I$ and $A Y B$ are similar right triangles. Since $I$ is the incenter, we have $I X=I Y=2$. Using the Pythagorean theorem on triangle $A X I$, we find $A X=\sqrt{5}$. By similarity, $A Y / A X=B Y / I X$. Plugging in the numbers given, $5 / \sqrt{5}=B Y / 2$, so $B Y=2 \sqrt{5} . Y$ is the midpoint of $B C$, so $B C=4 \sqrt{5}$.
|
{
"resource_path": "HarvardMIT/segmented/en-62-2003-feb-guts-solutions.jsonl",
"problem_match": "\n25. ",
"solution_match": "\n## Solution: "
}
|
70144984-6d80-5461-9c79-b4ab609393c6
| 611,163
|
The rational numbers $x$ and $y$, when written in lowest terms, have denominators 60 and 70 , respectively. What is the smallest possible denominator of $x+y$ ?
|
84
Write $x+y=a / 60+b / 70=(7 a+6 b) / 420$. Since $a$ is relatively prime to 60 and $b$ is relatively prime to 70 , it follows that none of the primes $2,3,7$ can divide $7 a+6 b$, so we won't be able to cancel any of these factors in the denominator. Thus, after reducing to lowest terms, the denominator will still be at least $2^{2} \cdot 3 \cdot 7=84$ (the product of the powers of 2,3 , and 7 dividing 420). On the other hand, 84 is achievable, by taking (e.g.) $1 / 60+3 / 70=25 / 420=5 / 84$. So 84 is the answer.
|
84
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
The rational numbers $x$ and $y$, when written in lowest terms, have denominators 60 and 70 , respectively. What is the smallest possible denominator of $x+y$ ?
|
84
Write $x+y=a / 60+b / 70=(7 a+6 b) / 420$. Since $a$ is relatively prime to 60 and $b$ is relatively prime to 70 , it follows that none of the primes $2,3,7$ can divide $7 a+6 b$, so we won't be able to cancel any of these factors in the denominator. Thus, after reducing to lowest terms, the denominator will still be at least $2^{2} \cdot 3 \cdot 7=84$ (the product of the powers of 2,3 , and 7 dividing 420). On the other hand, 84 is achievable, by taking (e.g.) $1 / 60+3 / 70=25 / 420=5 / 84$. So 84 is the answer.
|
{
"resource_path": "HarvardMIT/segmented/en-62-2003-feb-guts-solutions.jsonl",
"problem_match": "\n27. ",
"solution_match": "\n## Solution: "
}
|
3d1d4324-cf70-5b4f-a1b6-6429b9c68dde
| 611,165
|
A point in three-space has distances $2,6,7,8,9$ from five of the vertices of a regular octahedron. What is its distance from the sixth vertex?
|
$\sqrt{21}$
By a simple variant of the British Flag Theorem, if $A B C D$ is a square and $P$ any point in space, $A P^{2}+C P^{2}=B P^{2}+D P^{2}$. Four of the five given vertices must form a square $A B C D$, and by experimentation we find their distances to the given point $P$ must be $A P=2, B P=6, C P=9, D P=7$. Then $A, C$, and the other two vertices $E, F$ also form a square $A E C F$, so $85=A P^{2}+C P^{2}=E P^{2}+F P^{2}=8^{2}+F P^{2} \Rightarrow F P=\sqrt{21}$.
|
\sqrt{21}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
A point in three-space has distances $2,6,7,8,9$ from five of the vertices of a regular octahedron. What is its distance from the sixth vertex?
|
$\sqrt{21}$
By a simple variant of the British Flag Theorem, if $A B C D$ is a square and $P$ any point in space, $A P^{2}+C P^{2}=B P^{2}+D P^{2}$. Four of the five given vertices must form a square $A B C D$, and by experimentation we find their distances to the given point $P$ must be $A P=2, B P=6, C P=9, D P=7$. Then $A, C$, and the other two vertices $E, F$ also form a square $A E C F$, so $85=A P^{2}+C P^{2}=E P^{2}+F P^{2}=8^{2}+F P^{2} \Rightarrow F P=\sqrt{21}$.
|
{
"resource_path": "HarvardMIT/segmented/en-62-2003-feb-guts-solutions.jsonl",
"problem_match": "\n28. ",
"solution_match": "\nSolution: "
}
|
16f6157c-2782-57c9-9813-e5ef0e193295
| 611,166
|
A palindrome is a positive integer that reads the same backwards as forwards, such as 82328. What is the smallest 5 -digit palindrome that is a multiple of 99 ?
|
54945
Write the number as $X Y Z Y X$. This is the same as $10000 X+1000 Y+100 Z+10 Y+X=$ $99(101 X+10 Y+Z)+20 Y+2 X+Z$. We thus want $20 Y+2 X+Z$ to be a multiple of 99 , with $X$ as small as possible. This expression cannot be larger than $20 \cdot 9+2 \cdot 9+9=207$, and it is greater than 0 (since $X \neq 0$ ), so for this to be a multiple of 99 , it must equal 99 or 198. Consider these two cases.
To get 198, we must have $Y=9$, which then leaves $2 X+Z=18$. The smallest possible $X$ is 5 , and then $Z$ becomes 8 and we have the number 59895 .
To get 99 , we must have $Y=4$. Then, $2 X+Z=19$, and, as above, we find the minimal $X$ is 5 and then $Z=9$. This gives us the number 54945 . This is smaller than the other number, so it is the smallest number satisfying the conditions of the problem.
|
54945
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
A palindrome is a positive integer that reads the same backwards as forwards, such as 82328. What is the smallest 5 -digit palindrome that is a multiple of 99 ?
|
54945
Write the number as $X Y Z Y X$. This is the same as $10000 X+1000 Y+100 Z+10 Y+X=$ $99(101 X+10 Y+Z)+20 Y+2 X+Z$. We thus want $20 Y+2 X+Z$ to be a multiple of 99 , with $X$ as small as possible. This expression cannot be larger than $20 \cdot 9+2 \cdot 9+9=207$, and it is greater than 0 (since $X \neq 0$ ), so for this to be a multiple of 99 , it must equal 99 or 198. Consider these two cases.
To get 198, we must have $Y=9$, which then leaves $2 X+Z=18$. The smallest possible $X$ is 5 , and then $Z$ becomes 8 and we have the number 59895 .
To get 99 , we must have $Y=4$. Then, $2 X+Z=19$, and, as above, we find the minimal $X$ is 5 and then $Z=9$. This gives us the number 54945 . This is smaller than the other number, so it is the smallest number satisfying the conditions of the problem.
|
{
"resource_path": "HarvardMIT/segmented/en-62-2003-feb-guts-solutions.jsonl",
"problem_match": "\n29. ",
"solution_match": "\nSolution: "
}
|
180050f6-8bd2-50a0-a9d6-0213b3fe7e49
| 611,167
|
The sequence $a_{1}, a_{2}, a_{3}, \ldots$ of real numbers satisfies the recurrence
$$
a_{n+1}=\frac{a_{n}^{2}-a_{n-1}+2 a_{n}}{a_{n-1}+1} .
$$
Given that $a_{1}=1$ and $a_{9}=7$, find $a_{5}$.
|
3
Let $b_{n}=a_{n}+1$. Then the recurrence becomes $b_{n+1}-1=\left(b_{n}^{2}-b_{n-1}\right) / b_{n-1}=b_{n}^{2} / b_{n-1}-1$, so $b_{n+1}=b_{n}^{2} / b_{n-1}$. It follows that the sequence $\left(b_{n}\right)$ is a geometric progression, from which $b_{5}^{2}=b_{1} b_{9}=2 \cdot 8=16 \Rightarrow b_{5}= \pm 4$. However, since all $b_{n}$ are real, they either alternate in sign or all have the same sign (depending on the sign of the progression's common ratio); either way, $b_{5}$ has the same sign as $b_{1}$, so $b_{5}=4 \Rightarrow a_{5}=3$.
|
3
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
The sequence $a_{1}, a_{2}, a_{3}, \ldots$ of real numbers satisfies the recurrence
$$
a_{n+1}=\frac{a_{n}^{2}-a_{n-1}+2 a_{n}}{a_{n-1}+1} .
$$
Given that $a_{1}=1$ and $a_{9}=7$, find $a_{5}$.
|
3
Let $b_{n}=a_{n}+1$. Then the recurrence becomes $b_{n+1}-1=\left(b_{n}^{2}-b_{n-1}\right) / b_{n-1}=b_{n}^{2} / b_{n-1}-1$, so $b_{n+1}=b_{n}^{2} / b_{n-1}$. It follows that the sequence $\left(b_{n}\right)$ is a geometric progression, from which $b_{5}^{2}=b_{1} b_{9}=2 \cdot 8=16 \Rightarrow b_{5}= \pm 4$. However, since all $b_{n}$ are real, they either alternate in sign or all have the same sign (depending on the sign of the progression's common ratio); either way, $b_{5}$ has the same sign as $b_{1}$, so $b_{5}=4 \Rightarrow a_{5}=3$.
|
{
"resource_path": "HarvardMIT/segmented/en-62-2003-feb-guts-solutions.jsonl",
"problem_match": "\n30. ",
"solution_match": "\nSolution: "
}
|
3dd34db6-0f61-55a2-87b8-fde29cfdfdb7
| 611,168
|
A cylinder of base radius 1 is cut into two equal parts along a plane passing through the center of the cylinder and tangent to the two base circles. Suppose that each piece's surface area is $m$ times its volume. Find the greatest lower bound for all possible values of $m$ as the height of the cylinder varies.
|
3
Let $h$ be the height of the cylinder. Then the volume of each piece is half the volume of the cylinder, so it is $\frac{1}{2} \pi h$. The base of the piece has area $\pi$, and the ellipse formed by the cut has area $\pi \cdot 1 \cdot \sqrt{1+\frac{h^{2}}{4}}$ because its area is the product of the semiaxes times $\pi$. The rest of the area of the piece is half the lateral area of the cylinder, so it is $\pi h$. Thus, the value of $m$ is
$$
\begin{aligned}
\frac{\pi+\pi \sqrt{1+h^{2} / 4}+\pi h}{\pi h / 2} & =\frac{2+2 h+\sqrt{4+h^{2}}}{h} \\
& =\frac{2}{h}+2+\sqrt{\frac{4}{h^{2}}+1}
\end{aligned}
$$
a decreasing function of $h$ whose limit as $h \rightarrow \infty$ is 3 . Therefore the greatest lower bound of $m$ is 3 .
|
3
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
A cylinder of base radius 1 is cut into two equal parts along a plane passing through the center of the cylinder and tangent to the two base circles. Suppose that each piece's surface area is $m$ times its volume. Find the greatest lower bound for all possible values of $m$ as the height of the cylinder varies.
|
3
Let $h$ be the height of the cylinder. Then the volume of each piece is half the volume of the cylinder, so it is $\frac{1}{2} \pi h$. The base of the piece has area $\pi$, and the ellipse formed by the cut has area $\pi \cdot 1 \cdot \sqrt{1+\frac{h^{2}}{4}}$ because its area is the product of the semiaxes times $\pi$. The rest of the area of the piece is half the lateral area of the cylinder, so it is $\pi h$. Thus, the value of $m$ is
$$
\begin{aligned}
\frac{\pi+\pi \sqrt{1+h^{2} / 4}+\pi h}{\pi h / 2} & =\frac{2+2 h+\sqrt{4+h^{2}}}{h} \\
& =\frac{2}{h}+2+\sqrt{\frac{4}{h^{2}}+1}
\end{aligned}
$$
a decreasing function of $h$ whose limit as $h \rightarrow \infty$ is 3 . Therefore the greatest lower bound of $m$ is 3 .
|
{
"resource_path": "HarvardMIT/segmented/en-62-2003-feb-guts-solutions.jsonl",
"problem_match": "\n31. ",
"solution_match": "\n## Solution: "
}
|
2e4a3eca-cf0a-5bf4-b52c-3c323e436ac7
| 611,169
|
If $x, y$, and $z$ are real numbers such that $2 x^{2}+y^{2}+z^{2}=2 x-4 y+2 x z-5$, find the maximum possible value of $x-y+z$.
|
4
The equation rearranges as $(x-1)^{2}+(y+2)^{2}+(x-z)^{2}=0$, so we must have $x=1$, $y=-2, z=1$, giving us 4 .
|
4
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
If $x, y$, and $z$ are real numbers such that $2 x^{2}+y^{2}+z^{2}=2 x-4 y+2 x z-5$, find the maximum possible value of $x-y+z$.
|
4
The equation rearranges as $(x-1)^{2}+(y+2)^{2}+(x-z)^{2}=0$, so we must have $x=1$, $y=-2, z=1$, giving us 4 .
|
{
"resource_path": "HarvardMIT/segmented/en-62-2003-feb-guts-solutions.jsonl",
"problem_match": "\n32. ",
"solution_match": "\nSolution: "
}
|
32d44a7f-27d3-5e78-9e32-3100a27777bb
| 611,170
|
We are given triangle $A B C$, with $A B=9, A C=10$, and $B C=12$, and a point $D$ on $B C$. $B$ and $C$ are reflected in $A D$ to $B^{\prime}$ and $C^{\prime}$, respectively. Suppose that lines $B C^{\prime}$ and $B^{\prime} C$ never meet (i.e., are parallel and distinct). Find $B D$.
|
6
The lengths of $A B$ and $A C$ are irrelevant. Because the figure is symmetric about $A D$, lines $B C^{\prime}$ and $B^{\prime} C$ meet if and only if they meet at a point on line $A D$. So, if they never meet, they must be parallel to $A D$. Because $A D$ and $B C^{\prime}$ are parallel, triangles $A B D$ and $A D C^{\prime}$ have the same area. Then $A B D$ and $A D C$ also have the same area. Hence, $B D$ and $C D$ must have the same length, so $B D=\frac{1}{2} B C=6$.
|
6
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
We are given triangle $A B C$, with $A B=9, A C=10$, and $B C=12$, and a point $D$ on $B C$. $B$ and $C$ are reflected in $A D$ to $B^{\prime}$ and $C^{\prime}$, respectively. Suppose that lines $B C^{\prime}$ and $B^{\prime} C$ never meet (i.e., are parallel and distinct). Find $B D$.
|
6
The lengths of $A B$ and $A C$ are irrelevant. Because the figure is symmetric about $A D$, lines $B C^{\prime}$ and $B^{\prime} C$ meet if and only if they meet at a point on line $A D$. So, if they never meet, they must be parallel to $A D$. Because $A D$ and $B C^{\prime}$ are parallel, triangles $A B D$ and $A D C^{\prime}$ have the same area. Then $A B D$ and $A D C$ also have the same area. Hence, $B D$ and $C D$ must have the same length, so $B D=\frac{1}{2} B C=6$.
|
{
"resource_path": "HarvardMIT/segmented/en-62-2003-feb-guts-solutions.jsonl",
"problem_match": "\n33. ",
"solution_match": "\nSolution: "
}
|
57598210-7de3-54c6-a15d-cd47de9ba763
| 611,171
|
$O K R A$ is a trapezoid with $O K$ parallel to $R A$. If $O K=12$ and $R A$ is a positive integer, how many integer values can be taken on by the length of the segment in the trapezoid, parallel to $O K$, through the intersection of the diagonals?
|
10
Let $R A=x$. If the diagonals intersect at $X$, and the segment is $P Q$ with $P$ on $K R$, then $\triangle P K X \sim \triangle R K A$ and $\triangle O K X \sim \triangle R A X$ (by equal angles), giving $R A / P X=$ $A K / X K=1+A X / X K=1+A R / O K=(x+12) / 12$, so $P X=12 x /(12+x)$. Similarly $X Q=12 x /(12+x)$ also, so $P Q=24 x /(12+x)=24-\frac{288}{12+x}$. This has to be an integer. $288=2^{5} 3^{2}$, so it has $(5+1)(3+1)=18$ divisors. $12+x$ must be one of these. We also exclude the 8 divisors that don't exceed 12 , so our final answer is 10 .
|
10
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
$O K R A$ is a trapezoid with $O K$ parallel to $R A$. If $O K=12$ and $R A$ is a positive integer, how many integer values can be taken on by the length of the segment in the trapezoid, parallel to $O K$, through the intersection of the diagonals?
|
10
Let $R A=x$. If the diagonals intersect at $X$, and the segment is $P Q$ with $P$ on $K R$, then $\triangle P K X \sim \triangle R K A$ and $\triangle O K X \sim \triangle R A X$ (by equal angles), giving $R A / P X=$ $A K / X K=1+A X / X K=1+A R / O K=(x+12) / 12$, so $P X=12 x /(12+x)$. Similarly $X Q=12 x /(12+x)$ also, so $P Q=24 x /(12+x)=24-\frac{288}{12+x}$. This has to be an integer. $288=2^{5} 3^{2}$, so it has $(5+1)(3+1)=18$ divisors. $12+x$ must be one of these. We also exclude the 8 divisors that don't exceed 12 , so our final answer is 10 .
|
{
"resource_path": "HarvardMIT/segmented/en-62-2003-feb-guts-solutions.jsonl",
"problem_match": "\n34. ",
"solution_match": "\nSolution: "
}
|
906c0f8f-ec0d-59c3-a09a-2b51b8830222
| 611,172
|
A certain lottery has tickets labeled with the numbers $1,2,3, \ldots, 1000$. The lottery is run as follows: First, a ticket is drawn at random. If the number on the ticket is odd, the drawing ends; if it is even, another ticket is randomly drawn (without replacement). If this new ticket has an odd number, the drawing ends; if it is even, another ticket is randomly drawn (again without replacement), and so forth, until an odd number is drawn. Then, every person whose ticket number was drawn (at any point in the process) wins a prize.
You have ticket number 1000. What is the probability that you get a prize?
|
$1 / 501$
Notice that the outcome is the same as if the lottery instead draws all the tickets, in random order, and awards a prize to the holder of the odd ticket drawn earliest and each even ticket drawn before it. Thus, the probability of your winning is the probability that, in a random ordering of the tickets, your ticket precedes all the odd tickets. This, in turn, equals the probability that your ticket is the first in the setconsisting of your own and all odd-numbered tickets, irrespective of the other even-numbered tickets. Since all 501! orderings of these tickets are equally likely, the desired probability is $1 / 501$.
|
\frac{1}{501}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
A certain lottery has tickets labeled with the numbers $1,2,3, \ldots, 1000$. The lottery is run as follows: First, a ticket is drawn at random. If the number on the ticket is odd, the drawing ends; if it is even, another ticket is randomly drawn (without replacement). If this new ticket has an odd number, the drawing ends; if it is even, another ticket is randomly drawn (again without replacement), and so forth, until an odd number is drawn. Then, every person whose ticket number was drawn (at any point in the process) wins a prize.
You have ticket number 1000. What is the probability that you get a prize?
|
$1 / 501$
Notice that the outcome is the same as if the lottery instead draws all the tickets, in random order, and awards a prize to the holder of the odd ticket drawn earliest and each even ticket drawn before it. Thus, the probability of your winning is the probability that, in a random ordering of the tickets, your ticket precedes all the odd tickets. This, in turn, equals the probability that your ticket is the first in the setconsisting of your own and all odd-numbered tickets, irrespective of the other even-numbered tickets. Since all 501! orderings of these tickets are equally likely, the desired probability is $1 / 501$.
|
{
"resource_path": "HarvardMIT/segmented/en-62-2003-feb-guts-solutions.jsonl",
"problem_match": "\n35. ",
"solution_match": "\nSolution: "
}
|
4f6fabec-dffa-5ea1-b317-93cdf7ce8e9c
| 611,173
|
A teacher must divide 221 apples evenly among 403 students. What is the minimal number of pieces into which she must cut the apples? (A whole uncut apple counts as one piece.)
|
611
Consider a bipartite graph, with 221 vertices representing the apples and 403 vertices representing the students; each student is connected to each apple that she gets a
piece of. The number of pieces then equals the number of edges in the graph. Each student gets a total of $221 / 403=17 / 31$ apple, but each component of the graph represents a complete distribution of an integer number of apples to an integer number of students and therefore uses at least 17 apple vertices and 31 student vertices. Then we have at most $221 / 17=403 / 31=13$ components in the graph, so there are at least $221+403-13=611$ edges. On the other hand, if we simply distribute in the straightforward manner - proceeding through the students, cutting up a new apple whenever necessary but never returning to a previous apple or student - we can create a graph without cycles, and each component does involve 17 apples and 31 students. Thus, we get 13 trees, and 611 edges is attainable.
|
611
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
A teacher must divide 221 apples evenly among 403 students. What is the minimal number of pieces into which she must cut the apples? (A whole uncut apple counts as one piece.)
|
611
Consider a bipartite graph, with 221 vertices representing the apples and 403 vertices representing the students; each student is connected to each apple that she gets a
piece of. The number of pieces then equals the number of edges in the graph. Each student gets a total of $221 / 403=17 / 31$ apple, but each component of the graph represents a complete distribution of an integer number of apples to an integer number of students and therefore uses at least 17 apple vertices and 31 student vertices. Then we have at most $221 / 17=403 / 31=13$ components in the graph, so there are at least $221+403-13=611$ edges. On the other hand, if we simply distribute in the straightforward manner - proceeding through the students, cutting up a new apple whenever necessary but never returning to a previous apple or student - we can create a graph without cycles, and each component does involve 17 apples and 31 students. Thus, we get 13 trees, and 611 edges is attainable.
|
{
"resource_path": "HarvardMIT/segmented/en-62-2003-feb-guts-solutions.jsonl",
"problem_match": "\n36. ",
"solution_match": "\n## Solution: "
}
|
8ab4097b-1169-5a5a-8621-4a195db39b0f
| 611,174
|
A quagga is an extinct chess piece whose move is like a knight's, but much longer: it can move 6 squares in any direction (up, down, left, or right) and then 5 squares in a perpendicular direction. Find the number of ways to place 51 quaggas on an $8 \times 8$ chessboard in such a way that no quagga attacks another. (Since quaggas are naturally belligerent creatures, a quagga is considered to attack quaggas on any squares it can move to, as well as any other quaggas on the same square.)
|
68
Represent the 64 squares of the board as vertices of a graph, and connect two vertices by an edge if a quagga can move from one to the other. The resulting graph consists of 4 paths of length 5 and 4 paths of length 3 (given by the four rotations of the two paths shown, next page), and 32 isolated vertices. Each path of length 5 can accommodate at most 3 nonattacking quaggas in a unique way (the first, middle, and last vertices), and each path of length 3 can accommodate at most 2 nonattacking quaggas in a unique way; thus, the maximum total number of nonattacking quaggas we can have is $4 \cdot 3+4 \cdot 2+32=52$. For 51 quaggas to fit, then, just one component of the graph must contain one less quagga than its maximum.
If this component is a path of length 5 , there are $\binom{5}{2}-4=6$ ways to place the two quaggas on nonadjacent vertices, and then all the other locations are forced; the 4 such paths then give us $4 \cdot 6=24$ possibilities this way. If it is a path of length 3 , there are 3 ways to place one quagga, and the rest of the board is forced, so we have $4 \cdot 3=12$ possibilities here. Finally, if it is one of the 32 isolated vertices, we simply leave this square empty, and the rest of the board is forced, so we have 32 possibilities here. So the total is $24+12+32=68$ different arrangements.
|
68
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
A quagga is an extinct chess piece whose move is like a knight's, but much longer: it can move 6 squares in any direction (up, down, left, or right) and then 5 squares in a perpendicular direction. Find the number of ways to place 51 quaggas on an $8 \times 8$ chessboard in such a way that no quagga attacks another. (Since quaggas are naturally belligerent creatures, a quagga is considered to attack quaggas on any squares it can move to, as well as any other quaggas on the same square.)
|
68
Represent the 64 squares of the board as vertices of a graph, and connect two vertices by an edge if a quagga can move from one to the other. The resulting graph consists of 4 paths of length 5 and 4 paths of length 3 (given by the four rotations of the two paths shown, next page), and 32 isolated vertices. Each path of length 5 can accommodate at most 3 nonattacking quaggas in a unique way (the first, middle, and last vertices), and each path of length 3 can accommodate at most 2 nonattacking quaggas in a unique way; thus, the maximum total number of nonattacking quaggas we can have is $4 \cdot 3+4 \cdot 2+32=52$. For 51 quaggas to fit, then, just one component of the graph must contain one less quagga than its maximum.
If this component is a path of length 5 , there are $\binom{5}{2}-4=6$ ways to place the two quaggas on nonadjacent vertices, and then all the other locations are forced; the 4 such paths then give us $4 \cdot 6=24$ possibilities this way. If it is a path of length 3 , there are 3 ways to place one quagga, and the rest of the board is forced, so we have $4 \cdot 3=12$ possibilities here. Finally, if it is one of the 32 isolated vertices, we simply leave this square empty, and the rest of the board is forced, so we have 32 possibilities here. So the total is $24+12+32=68$ different arrangements.
|
{
"resource_path": "HarvardMIT/segmented/en-62-2003-feb-guts-solutions.jsonl",
"problem_match": "\n37. ",
"solution_match": "\n## Solution: "
}
|
865ab415-cd82-55cb-9f7e-60f6758fabfd
| 611,175
|
In the figure, if $A E=3, C E=1, B D=C D=2$, and $A B=5$, find $A G$.
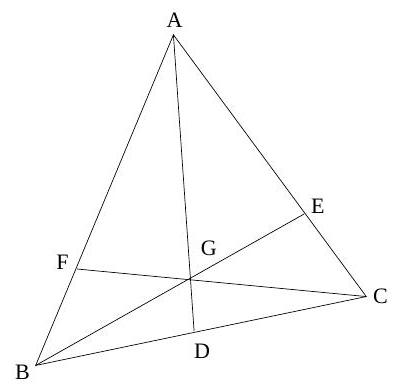
|
$3 \sqrt{66} / 7$
By Stewart's Theorem, $A D^{2} \cdot B C+C D \cdot B D \cdot B C=A B^{2} \cdot C D+A C^{2} \cdot B D$, so $A D^{2}=\left(5^{2} \cdot 2+4^{2} \cdot 2-2 \cdot 2 \cdot 4\right) / 4=(50+32-16) / 4=33 / 2$. By Menelaus's Theorem applied to line $B G E$ and triangle $A C D, D G / G A \cdot A E / E C \cdot C B / B D=1$, so $D G / G A=1 / 6 \Rightarrow A D / A G=7 / 6$. Thus $A G=6 \cdot A D / 7=3 \sqrt{66} / 7$.
|
\frac{3 \sqrt{66}}{7}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
In the figure, if $A E=3, C E=1, B D=C D=2$, and $A B=5$, find $A G$.

|
$3 \sqrt{66} / 7$
By Stewart's Theorem, $A D^{2} \cdot B C+C D \cdot B D \cdot B C=A B^{2} \cdot C D+A C^{2} \cdot B D$, so $A D^{2}=\left(5^{2} \cdot 2+4^{2} \cdot 2-2 \cdot 2 \cdot 4\right) / 4=(50+32-16) / 4=33 / 2$. By Menelaus's Theorem applied to line $B G E$ and triangle $A C D, D G / G A \cdot A E / E C \cdot C B / B D=1$, so $D G / G A=1 / 6 \Rightarrow A D / A G=7 / 6$. Thus $A G=6 \cdot A D / 7=3 \sqrt{66} / 7$.
|
{
"resource_path": "HarvardMIT/segmented/en-62-2003-feb-guts-solutions.jsonl",
"problem_match": "\n39. ",
"solution_match": "\nSolution: "
}
|
e8d4c0ab-2dd0-5cea-b6b8-65bf4ad0ba8c
| 611,177
|
All the sequences consisting of five letters from the set $\{T, U, R, N, I, P\}$ (with repetitions allowed) are arranged in alphabetical order in a dictionary. Two sequences are called "anagrams" of each other if one can be obtained by rearranging the letters of the
other. How many pairs of anagrams are there that have exactly 100 other sequences between them in the dictionary?
|
0
Convert each letter to a digit in base $6: I \mapsto 0, N \mapsto 1, P \mapsto 2, R \mapsto 3, T \mapsto 4, U \mapsto 5$. Then the dictionary simply consists of all base-6 integers from $00000_{6}$ to $55555_{6}$ in numerical order. If one number can be obtained from another by a rearrangement of digits, then the numbers are congruent modulo 5 (this holds because a number $a^{a b c d e_{6}}$ $=6^{4} \cdot a+6^{3} \cdot b+6^{2} \cdot c+6 \cdot d+e$ is congruent modulo 5 to $a+b+c+d+e$ ), but if there are 100 other numbers between them, then their difference is 101 , which is not divisible by 5 . So there are no such pairs.
|
0
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
All the sequences consisting of five letters from the set $\{T, U, R, N, I, P\}$ (with repetitions allowed) are arranged in alphabetical order in a dictionary. Two sequences are called "anagrams" of each other if one can be obtained by rearranging the letters of the
other. How many pairs of anagrams are there that have exactly 100 other sequences between them in the dictionary?
|
0
Convert each letter to a digit in base $6: I \mapsto 0, N \mapsto 1, P \mapsto 2, R \mapsto 3, T \mapsto 4, U \mapsto 5$. Then the dictionary simply consists of all base-6 integers from $00000_{6}$ to $55555_{6}$ in numerical order. If one number can be obtained from another by a rearrangement of digits, then the numbers are congruent modulo 5 (this holds because a number $a^{a b c d e_{6}}$ $=6^{4} \cdot a+6^{3} \cdot b+6^{2} \cdot c+6 \cdot d+e$ is congruent modulo 5 to $a+b+c+d+e$ ), but if there are 100 other numbers between them, then their difference is 101 , which is not divisible by 5 . So there are no such pairs.
|
{
"resource_path": "HarvardMIT/segmented/en-62-2003-feb-guts-solutions.jsonl",
"problem_match": "\n40. ",
"solution_match": "\nSolution: "
}
|
8216538f-d27e-5828-98b2-c55e2054c123
| 611,178
|
A hotel consists of a $2 \times 8$ square grid of rooms, each occupied by one guest. All the guests are uncomfortable, so each guest would like to move to one of the adjoining rooms (horizontally or vertically). Of course, they should do this simultaneously, in such a way that each room will again have one guest. In how many different ways can they collectively move?
|
1156
Imagine that the rooms are colored black and white, checkerboard-style. Each guest in a black room moves to an adjacent white room (and vice versa). If, for each such guest, we place a domino over the original room and the new room, we obtain a covering of the $2 \times n$ grid by $n$ dominoes, since each black square is used once and each white square is used once. Applying a similar procedure to each guest who begins in a white room and moves to a black room, we obtain a second domino tiling. Conversely, it is readily verified that any pair of such tilings uniquely determines a movement pattern. Also, it is easy to prove by induction that the number of domino tilings of a $2 \times n$ grid is the $(n+1)$ th Fibonacci number (this holds for the base cases $n=1,2$, and for a $2 \times n$ rectangle, the two rightmost squares either belong to one vertical domino, leaving a $2 \times(n-1)$ rectangle to be covered arbitrarily, or to two horizontal dominoes which also occupy the adjoining squares, leaving a $2 \times(n-2)$ rectangle to be covered freely; hence, the numbers of tilings satisfy the Fibonacci recurrence). So the number of domino tilings of a $2 \times 8$ grid is 34 , and the number of pairs of such tilings is $34^{2}=1156$, the answer.
|
1156
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
A hotel consists of a $2 \times 8$ square grid of rooms, each occupied by one guest. All the guests are uncomfortable, so each guest would like to move to one of the adjoining rooms (horizontally or vertically). Of course, they should do this simultaneously, in such a way that each room will again have one guest. In how many different ways can they collectively move?
|
1156
Imagine that the rooms are colored black and white, checkerboard-style. Each guest in a black room moves to an adjacent white room (and vice versa). If, for each such guest, we place a domino over the original room and the new room, we obtain a covering of the $2 \times n$ grid by $n$ dominoes, since each black square is used once and each white square is used once. Applying a similar procedure to each guest who begins in a white room and moves to a black room, we obtain a second domino tiling. Conversely, it is readily verified that any pair of such tilings uniquely determines a movement pattern. Also, it is easy to prove by induction that the number of domino tilings of a $2 \times n$ grid is the $(n+1)$ th Fibonacci number (this holds for the base cases $n=1,2$, and for a $2 \times n$ rectangle, the two rightmost squares either belong to one vertical domino, leaving a $2 \times(n-1)$ rectangle to be covered arbitrarily, or to two horizontal dominoes which also occupy the adjoining squares, leaving a $2 \times(n-2)$ rectangle to be covered freely; hence, the numbers of tilings satisfy the Fibonacci recurrence). So the number of domino tilings of a $2 \times 8$ grid is 34 , and the number of pairs of such tilings is $34^{2}=1156$, the answer.
|
{
"resource_path": "HarvardMIT/segmented/en-62-2003-feb-guts-solutions.jsonl",
"problem_match": "\n41. ",
"solution_match": "\nSolution: "
}
|
a7e8de25-62a9-50d5-a952-10d36931b5fb
| 611,179
|
A tightrope walker stands in the center of a rope of length 32 meters. Every minute she walks forward one meter with probability $3 / 4$ and backward one meter with probability $1 / 4$. What is the probability that she reaches the end in front of her before the end behind her?
|
$3^{16} /\left(3^{16}+1\right)$
After one minute, she is three times as likely to be one meter forward as one meter back. After two minutes she is either in the same place, two meters forward, or two meters back. The chance of being two meters forward is clearly $(3 / 4)^{2}$ and thus $3^{2}=9$ times greater than the chance of being two back $\left((1 / 4)^{2}\right)$. We can group the minutes into two-minute periods and ignore the periods of no net movement, so we can consider her to be moving 2 meters forward or backward each period, where forward movement is $3^{2}$ times as likely as backward movement. Repeating the argument inductively, we eventually find that she is $3^{16}$ times more likely to move 16 meters forward than 16
meters backward, and thus the probability is $3^{16} /\left(3^{16}+1\right)$ that she will meet the front end of the rope first.
|
\frac{3^{16}}{3^{16}+1}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
A tightrope walker stands in the center of a rope of length 32 meters. Every minute she walks forward one meter with probability $3 / 4$ and backward one meter with probability $1 / 4$. What is the probability that she reaches the end in front of her before the end behind her?
|
$3^{16} /\left(3^{16}+1\right)$
After one minute, she is three times as likely to be one meter forward as one meter back. After two minutes she is either in the same place, two meters forward, or two meters back. The chance of being two meters forward is clearly $(3 / 4)^{2}$ and thus $3^{2}=9$ times greater than the chance of being two back $\left((1 / 4)^{2}\right)$. We can group the minutes into two-minute periods and ignore the periods of no net movement, so we can consider her to be moving 2 meters forward or backward each period, where forward movement is $3^{2}$ times as likely as backward movement. Repeating the argument inductively, we eventually find that she is $3^{16}$ times more likely to move 16 meters forward than 16
meters backward, and thus the probability is $3^{16} /\left(3^{16}+1\right)$ that she will meet the front end of the rope first.
|
{
"resource_path": "HarvardMIT/segmented/en-62-2003-feb-guts-solutions.jsonl",
"problem_match": "\n42. ",
"solution_match": "\nSolution: "
}
|
0f647085-0966-5227-8af1-fdaf8a48e4c1
| 611,180
|
Suppose $A$ is a set with $n$ elements, and $k$ is a divisor of $n$. Find the number of consistent $k$-configurations of $A$ of order 1 .
|
Given such a $k$-configuration, we can write out all the elements of one of the $k$-element subsets, then all the elements of another subset, and so forth, eventually obtaining an ordering of all $n$ elements of $A$. Conversely, given any ordering of the elements of $A$, we can construct a consistent $k$-configuration of order 1 from it by grouping together the first $k$ elements, then the next $k$ elements, and so forth. In fact, each consistent $k$-configuration of order 1 corresponds to $(n / k)!(k!)^{n / k}$ different such orderings, since the elements of $A$ within each of the $n / k k$-element subsets can be ordered in $k$ ! ways, and the various subsets can also be ordered with respect to each other in $(n / k)$ ! different ways. Thus, since there are $n$ ! orderings of the elements of $A$, we get $\frac{n!}{(n / k)!(k!)^{n / k}}$ different consistent $k$-configurations of order 1 .
|
\frac{n!}{(n / k)!(k!)^{n / k}}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Suppose $A$ is a set with $n$ elements, and $k$ is a divisor of $n$. Find the number of consistent $k$-configurations of $A$ of order 1 .
|
Given such a $k$-configuration, we can write out all the elements of one of the $k$-element subsets, then all the elements of another subset, and so forth, eventually obtaining an ordering of all $n$ elements of $A$. Conversely, given any ordering of the elements of $A$, we can construct a consistent $k$-configuration of order 1 from it by grouping together the first $k$ elements, then the next $k$ elements, and so forth. In fact, each consistent $k$-configuration of order 1 corresponds to $(n / k)!(k!)^{n / k}$ different such orderings, since the elements of $A$ within each of the $n / k k$-element subsets can be ordered in $k$ ! ways, and the various subsets can also be ordered with respect to each other in $(n / k)$ ! different ways. Thus, since there are $n$ ! orderings of the elements of $A$, we get $\frac{n!}{(n / k)!(k!)^{n / k}}$ different consistent $k$-configurations of order 1 .
|
{
"resource_path": "HarvardMIT/segmented/en-62-2003-feb-team-solutions.jsonl",
"problem_match": "\n2. ",
"solution_match": "\nSolution: "
}
|
686bbf28-34f9-535d-bc31-97ced333bc48
| 611,182
|
(a) Let $A_{n}=\left\{a_{1}, a_{2}, a_{3}, \ldots, a_{n}, b\right\}$, for $n \geq 3$, and let $C_{n}$ be the 2-configuration consisting of $\left\{a_{i}, a_{i+1}\right\}$ for all $1 \leq i \leq n-1,\left\{a_{1}, a_{n}\right\}$, and $\left\{a_{i}, b\right\}$ for $1 \leq i \leq n$. Let $S_{e}(n)$ be the number of subsets of $C_{n}$ that are consistent of order $e$. Find $S_{e}(101)$ for $e=1,2$, and 3 .
|
For convenience, we assume the $a_{i}$ are indexed modulo 101, so that $a_{i+1}=a_{1}$ when $a_{i}=a_{101}$.
In any consistent subset of $C_{101}$ of order $1, b$ must be paired with exactly one $a_{i}$, say $a_{1}$. Then, $a_{2}$ cannot be paired with $a_{1}$, so it must be paired with $a_{3}$, and likewise we find we use the pairs $\left\{a_{4}, a_{5}\right\},\left\{a_{6}, a_{7}\right\}, \ldots,\left\{a_{100}, a_{101}\right\}$ - and this does give us a consistent subset of order 1. Similarly, pairing $b$ with any other $a_{i}$ would give us a unique extension to a consistent configuration of order 1 . Thus, we have one such 2-configuration for each $i$, giving $S_{1}(101)=101$ altogether.
In a consistent subset of order $2, b$ must be paired with two other elements. Suppose one of them is $a_{i}$. Then $a_{i}$ is also paired with either $a_{i-1}$ or $a_{i+1}$, say $a_{i+1}$. But then $a_{i-1}$ needs to be paired up with two other elements, and $a_{i}$ is not available, so it must be paired with $a_{i-2}$ and $b$. Now $b$ has its two pairs determined, so nothing else can be paired with $b$. Thus, for $j \neq i-1, i$, we have that $a_{j}$ must be paired with $a_{j-1}$ and $a_{j+1}$. So our subset must be of the form
$$
\left\{\left\{b, a_{i}\right\},\left\{a_{i}, a_{i+1}\right\},\left\{a_{i+1}, a_{i+2}\right\}, \ldots,\left\{a_{101}, a_{1}\right\}, \ldots,\left\{a_{i-2}, a_{i-1}\right\},\left\{a_{i-1}, b\right\}\right\}
$$
for some $i$. On the other hand, for any $i=1, \ldots, 101$, this gives a subset meeting our requirements. So, we have 101 possibilities, and $S_{2}(101)=101$.
Finally, in a consistent subset of order 3 , each $a_{i}$ must be paired with $a_{i-1}, a_{i+1}$, and $b$. But then $b$ occurs in 101 pairs, not just 3 , so we have a contradiction. Thus, no such subset exists, so $S_{3}(101)=0$.
(b) Let $A=\{V, W, X, Y, Z, v, w, x, y, z\}$. Find the number of subsets of the 2 configuration
$$
\begin{gathered}
\{\{V, W\},\{W, X\},\{X, Y\},\{Y, Z\},\{Z, V\},\{v, x\},\{v, y\},\{w, y\},\{w, z\},\{x, z\}, \\
\{V, v\},\{W, w\},\{X, x\},\{Y, y\},\{Z, z\}\}
\end{gathered}
$$
that are consistent of order 1.
|
101
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
(a) Let $A_{n}=\left\{a_{1}, a_{2}, a_{3}, \ldots, a_{n}, b\right\}$, for $n \geq 3$, and let $C_{n}$ be the 2-configuration consisting of $\left\{a_{i}, a_{i+1}\right\}$ for all $1 \leq i \leq n-1,\left\{a_{1}, a_{n}\right\}$, and $\left\{a_{i}, b\right\}$ for $1 \leq i \leq n$. Let $S_{e}(n)$ be the number of subsets of $C_{n}$ that are consistent of order $e$. Find $S_{e}(101)$ for $e=1,2$, and 3 .
|
For convenience, we assume the $a_{i}$ are indexed modulo 101, so that $a_{i+1}=a_{1}$ when $a_{i}=a_{101}$.
In any consistent subset of $C_{101}$ of order $1, b$ must be paired with exactly one $a_{i}$, say $a_{1}$. Then, $a_{2}$ cannot be paired with $a_{1}$, so it must be paired with $a_{3}$, and likewise we find we use the pairs $\left\{a_{4}, a_{5}\right\},\left\{a_{6}, a_{7}\right\}, \ldots,\left\{a_{100}, a_{101}\right\}$ - and this does give us a consistent subset of order 1. Similarly, pairing $b$ with any other $a_{i}$ would give us a unique extension to a consistent configuration of order 1 . Thus, we have one such 2-configuration for each $i$, giving $S_{1}(101)=101$ altogether.
In a consistent subset of order $2, b$ must be paired with two other elements. Suppose one of them is $a_{i}$. Then $a_{i}$ is also paired with either $a_{i-1}$ or $a_{i+1}$, say $a_{i+1}$. But then $a_{i-1}$ needs to be paired up with two other elements, and $a_{i}$ is not available, so it must be paired with $a_{i-2}$ and $b$. Now $b$ has its two pairs determined, so nothing else can be paired with $b$. Thus, for $j \neq i-1, i$, we have that $a_{j}$ must be paired with $a_{j-1}$ and $a_{j+1}$. So our subset must be of the form
$$
\left\{\left\{b, a_{i}\right\},\left\{a_{i}, a_{i+1}\right\},\left\{a_{i+1}, a_{i+2}\right\}, \ldots,\left\{a_{101}, a_{1}\right\}, \ldots,\left\{a_{i-2}, a_{i-1}\right\},\left\{a_{i-1}, b\right\}\right\}
$$
for some $i$. On the other hand, for any $i=1, \ldots, 101$, this gives a subset meeting our requirements. So, we have 101 possibilities, and $S_{2}(101)=101$.
Finally, in a consistent subset of order 3 , each $a_{i}$ must be paired with $a_{i-1}, a_{i+1}$, and $b$. But then $b$ occurs in 101 pairs, not just 3 , so we have a contradiction. Thus, no such subset exists, so $S_{3}(101)=0$.
(b) Let $A=\{V, W, X, Y, Z, v, w, x, y, z\}$. Find the number of subsets of the 2 configuration
$$
\begin{gathered}
\{\{V, W\},\{W, X\},\{X, Y\},\{Y, Z\},\{Z, V\},\{v, x\},\{v, y\},\{w, y\},\{w, z\},\{x, z\}, \\
\{V, v\},\{W, w\},\{X, x\},\{Y, y\},\{Z, z\}\}
\end{gathered}
$$
that are consistent of order 1.
|
{
"resource_path": "HarvardMIT/segmented/en-62-2003-feb-team-solutions.jsonl",
"problem_match": "\n3. ",
"solution_match": "\nSolution: "
}
|
e293149f-4a7d-51b7-96dd-d2127af69747
| 611,183
|
How many ordered pairs of integers (a,b) satisfy all of the following inequalities?
$$
\begin{aligned}
a^{2}+b^{2} & <16 \\
a^{2}+b^{2} & <8 a \\
a^{2}+b^{2} & <8 b
\end{aligned}
$$
|
6
This is easiest to see by simply graphing the inequalities. They correspond to the (strict) interiors of circles of radius 4 and centers at $(0,0),(4,0),(0,4)$, respectively. So we can see that there are 6 lattice points in their intersection (circled in the figure).
|
6
|
Yes
|
Yes
|
math-word-problem
|
Inequalities
|
How many ordered pairs of integers (a,b) satisfy all of the following inequalities?
$$
\begin{aligned}
a^{2}+b^{2} & <16 \\
a^{2}+b^{2} & <8 a \\
a^{2}+b^{2} & <8 b
\end{aligned}
$$
|
6
This is easiest to see by simply graphing the inequalities. They correspond to the (strict) interiors of circles of radius 4 and centers at $(0,0),(4,0),(0,4)$, respectively. So we can see that there are 6 lattice points in their intersection (circled in the figure).

|
{
"resource_path": "HarvardMIT/segmented/en-72-2004-feb-alg-solutions.jsonl",
"problem_match": "\n1. ",
"solution_match": "\nSolution: "
}
|
3c2cbf8a-d8d5-5153-bc96-b3c251e82b2f
| 611,191
|
Find the largest number $n$ such that (2004!)! is divisible by (( $n!)!$ )!.
|
For positive integers $a, b$, we have
$$
a!\mid b!\quad \Leftrightarrow \quad a!\leq b!\quad \Leftrightarrow \quad a \leq b .
$$
Thus,
$$
((n!)!)!\mid(2004!)!\Leftrightarrow(n!)!\leq 2004!\Leftrightarrow n!\leq 2004 \quad \Leftrightarrow \quad n \leq 6 .
$$
|
6
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Find the largest number $n$ such that (2004!)! is divisible by (( $n!)!$ )!.
|
For positive integers $a, b$, we have
$$
a!\mid b!\quad \Leftrightarrow \quad a!\leq b!\quad \Leftrightarrow \quad a \leq b .
$$
Thus,
$$
((n!)!)!\mid(2004!)!\Leftrightarrow(n!)!\leq 2004!\Leftrightarrow n!\leq 2004 \quad \Leftrightarrow \quad n \leq 6 .
$$
|
{
"resource_path": "HarvardMIT/segmented/en-72-2004-feb-alg-solutions.jsonl",
"problem_match": "\n2. ",
"solution_match": "\nSolution:\n"
}
|
c64c3b81-c1e4-55cc-948d-c3345dfa13f3
| 611,192
|
Compute:
$$
\left\lfloor\frac{2005^{3}}{2003 \cdot 2004}-\frac{2003^{3}}{2004 \cdot 2005}\right\rfloor .
$$
|
8
Let $x=2004$. Then the expression inside the floor brackets is
$$
\frac{(x+1)^{3}}{(x-1) x}-\frac{(x-1)^{3}}{x(x+1)}=\frac{(x+1)^{4}-(x-1)^{4}}{(x-1) x(x+1)}=\frac{8 x^{3}+8 x}{x^{3}-x}=8+\frac{16 x}{x^{3}-x} .
$$
Since $x$ is certainly large enough that $0<16 x /\left(x^{3}-x\right)<1$, the answer is 8 .
|
8
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Compute:
$$
\left\lfloor\frac{2005^{3}}{2003 \cdot 2004}-\frac{2003^{3}}{2004 \cdot 2005}\right\rfloor .
$$
|
8
Let $x=2004$. Then the expression inside the floor brackets is
$$
\frac{(x+1)^{3}}{(x-1) x}-\frac{(x-1)^{3}}{x(x+1)}=\frac{(x+1)^{4}-(x-1)^{4}}{(x-1) x(x+1)}=\frac{8 x^{3}+8 x}{x^{3}-x}=8+\frac{16 x}{x^{3}-x} .
$$
Since $x$ is certainly large enough that $0<16 x /\left(x^{3}-x\right)<1$, the answer is 8 .
|
{
"resource_path": "HarvardMIT/segmented/en-72-2004-feb-alg-solutions.jsonl",
"problem_match": "\n3. ",
"solution_match": "\nSolution: "
}
|
a51fa557-84dc-5fb9-8e4d-d01dc0d12314
| 611,193
|
Evaluate the sum
$$
\frac{1}{2\lfloor\sqrt{1}\rfloor+1}+\frac{1}{2\lfloor\sqrt{2}\rfloor+1}+\frac{1}{2\lfloor\sqrt{3}\rfloor+1}+\cdots+\frac{1}{2\lfloor\sqrt{100}\rfloor+1} .
$$
|
190/21
The first three terms all equal $1 / 3$, then the next five all equal $1 / 5$; more generally, for each $a=1,2, \ldots, 9$, the terms $1 /\left(2\left\lfloor\sqrt{a^{2}}\right\rfloor+1\right)$ to $1 /\left(2\left\lfloor\sqrt{a^{2}+2 a}\right\rfloor+1\right)$ all equal $1 /(2 a+1)$, and there are $2 a+1$ such terms. Thus our terms can be arranged into 9 groups, each with sum 1 , and only the last term $1 /(2\lfloor\sqrt{100}\rfloor+1)$ remains, so the answer is $9+1 / 21=190 / 21$.
|
\frac{190}{21}
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Evaluate the sum
$$
\frac{1}{2\lfloor\sqrt{1}\rfloor+1}+\frac{1}{2\lfloor\sqrt{2}\rfloor+1}+\frac{1}{2\lfloor\sqrt{3}\rfloor+1}+\cdots+\frac{1}{2\lfloor\sqrt{100}\rfloor+1} .
$$
|
190/21
The first three terms all equal $1 / 3$, then the next five all equal $1 / 5$; more generally, for each $a=1,2, \ldots, 9$, the terms $1 /\left(2\left\lfloor\sqrt{a^{2}}\right\rfloor+1\right)$ to $1 /\left(2\left\lfloor\sqrt{a^{2}+2 a}\right\rfloor+1\right)$ all equal $1 /(2 a+1)$, and there are $2 a+1$ such terms. Thus our terms can be arranged into 9 groups, each with sum 1 , and only the last term $1 /(2\lfloor\sqrt{100}\rfloor+1)$ remains, so the answer is $9+1 / 21=190 / 21$.
|
{
"resource_path": "HarvardMIT/segmented/en-72-2004-feb-alg-solutions.jsonl",
"problem_match": "\n4. ",
"solution_match": "\n## Solution: "
}
|
e5eac5f1-ca86-57eb-962c-75066b697f97
| 611,194
|
There exists a positive real number $x$ such that $\cos \left(\tan ^{-1}(x)\right)=x$. Find the value of $x^{2}$.
|
$(-1+\sqrt{5}) / 2$
Draw a right triangle with legs $1, x$; then the angle $\theta$ opposite $x$ is $\tan ^{-1} x$, and we can compute $\cos (\theta)=1 / \sqrt{x^{2}+1}$. Thus, we only need to solve $x=1 / \sqrt{x^{2}+1}$. This is equivalent to $x \sqrt{x^{2}+1}=1$. Square both sides to get $x^{4}+x^{2}=1 \Rightarrow x^{4}+x^{2}-1=0$. Use the quadratic formula to get the solution $x^{2}=(-1+\sqrt{5}) / 2$ (unique since $x^{2}$ must be positive).
|
\frac{-1+\sqrt{5}}{2}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
There exists a positive real number $x$ such that $\cos \left(\tan ^{-1}(x)\right)=x$. Find the value of $x^{2}$.
|
$(-1+\sqrt{5}) / 2$
Draw a right triangle with legs $1, x$; then the angle $\theta$ opposite $x$ is $\tan ^{-1} x$, and we can compute $\cos (\theta)=1 / \sqrt{x^{2}+1}$. Thus, we only need to solve $x=1 / \sqrt{x^{2}+1}$. This is equivalent to $x \sqrt{x^{2}+1}=1$. Square both sides to get $x^{4}+x^{2}=1 \Rightarrow x^{4}+x^{2}-1=0$. Use the quadratic formula to get the solution $x^{2}=(-1+\sqrt{5}) / 2$ (unique since $x^{2}$ must be positive).
|
{
"resource_path": "HarvardMIT/segmented/en-72-2004-feb-alg-solutions.jsonl",
"problem_match": "\n5. ",
"solution_match": "\nSolution: "
}
|
b06aa000-482e-54a7-9a63-bfbcdd4bbad3
| 611,195
|
If $x, y, k$ are positive reals such that
$$
3=k^{2}\left(\frac{x^{2}}{y^{2}}+\frac{y^{2}}{x^{2}}\right)+k\left(\frac{x}{y}+\frac{y}{x}\right),
$$
find the maximum possible value of $k$.
|
$$
(-1+\sqrt{7}) / 2
$$
We have $3=k^{2}\left(x^{2} / y^{2}+y^{2} / x^{2}\right)+k(x / y+y / x) \geq 2 k^{2}+2 k$, hence $7 \geq 4 k^{2}+4 k+1=$ $(2 k+1)^{2}$, hence $k \leq(\sqrt{7}-1) / 2$. Obviously $k$ can assume this value, if we let $x=y=1$.
|
\frac{-1 + \sqrt{7}}{2}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
If $x, y, k$ are positive reals such that
$$
3=k^{2}\left(\frac{x^{2}}{y^{2}}+\frac{y^{2}}{x^{2}}\right)+k\left(\frac{x}{y}+\frac{y}{x}\right),
$$
find the maximum possible value of $k$.
|
$$
(-1+\sqrt{7}) / 2
$$
We have $3=k^{2}\left(x^{2} / y^{2}+y^{2} / x^{2}\right)+k(x / y+y / x) \geq 2 k^{2}+2 k$, hence $7 \geq 4 k^{2}+4 k+1=$ $(2 k+1)^{2}$, hence $k \leq(\sqrt{7}-1) / 2$. Obviously $k$ can assume this value, if we let $x=y=1$.
|
{
"resource_path": "HarvardMIT/segmented/en-72-2004-feb-alg-solutions.jsonl",
"problem_match": "\n7. ",
"solution_match": "\nSolution:\n\n"
}
|
e04a9da9-4674-5625-8083-b7649c46bbc4
| 611,197
|
Let $x$ be a real number such that $x^{3}+4 x=8$. Determine the value of $x^{7}+64 x^{2}$.
|
128
For any integer $n \geq 0$, the given implies $x^{n+3}=-4 x^{n+1}+8 x^{n}$, so we can rewrite any such power of $x$ in terms of lower powers. Carrying out this process iteratively gives
$$
\begin{aligned}
x^{7} & =-4 x^{5}+8 x^{4} \\
& =8 x^{4}+16 x^{3}-32 x^{2} \\
& =16 x^{3}-64 x^{2}+64 x \\
& =-64 x^{2}+128 .
\end{aligned}
$$
Thus, our answer is 128 .
|
128
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Let $x$ be a real number such that $x^{3}+4 x=8$. Determine the value of $x^{7}+64 x^{2}$.
|
128
For any integer $n \geq 0$, the given implies $x^{n+3}=-4 x^{n+1}+8 x^{n}$, so we can rewrite any such power of $x$ in terms of lower powers. Carrying out this process iteratively gives
$$
\begin{aligned}
x^{7} & =-4 x^{5}+8 x^{4} \\
& =8 x^{4}+16 x^{3}-32 x^{2} \\
& =16 x^{3}-64 x^{2}+64 x \\
& =-64 x^{2}+128 .
\end{aligned}
$$
Thus, our answer is 128 .
|
{
"resource_path": "HarvardMIT/segmented/en-72-2004-feb-alg-solutions.jsonl",
"problem_match": "\n8. ",
"solution_match": "\nSolution: "
}
|
a0828d66-ec76-5205-a142-8712ec849017
| 611,198
|
A sequence of positive integers is defined by $a_{0}=1$ and $a_{n+1}=a_{n}^{2}+1$ for each $n \geq 0$. Find $\operatorname{gcd}\left(a_{999}, a_{2004}\right)$.
|
677
If $d$ is the relevant greatest common divisor, then $a_{1000}=a_{999}^{2}+1 \equiv 1=a_{0}(\bmod d)$, which implies (by induction) that the sequence is periodic modulo $d$, with period 1000 . In particular, $a_{4} \equiv a_{2004} \equiv 0$. So $d$ must divide $a_{4}$. Conversely, we can see that $a_{5}=a_{4}^{2}+1 \equiv 1=a_{0}$ modulo $a_{4}$, so (again by induction) the sequence is periodic modulo $a_{4}$ with period 5 , and hence $a_{999}, a_{2004}$ are indeed both divisible by $a_{4}$. So the answer is $a_{4}$, which we can compute directly; it is 677 .
|
677
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
A sequence of positive integers is defined by $a_{0}=1$ and $a_{n+1}=a_{n}^{2}+1$ for each $n \geq 0$. Find $\operatorname{gcd}\left(a_{999}, a_{2004}\right)$.
|
677
If $d$ is the relevant greatest common divisor, then $a_{1000}=a_{999}^{2}+1 \equiv 1=a_{0}(\bmod d)$, which implies (by induction) that the sequence is periodic modulo $d$, with period 1000 . In particular, $a_{4} \equiv a_{2004} \equiv 0$. So $d$ must divide $a_{4}$. Conversely, we can see that $a_{5}=a_{4}^{2}+1 \equiv 1=a_{0}$ modulo $a_{4}$, so (again by induction) the sequence is periodic modulo $a_{4}$ with period 5 , and hence $a_{999}, a_{2004}$ are indeed both divisible by $a_{4}$. So the answer is $a_{4}$, which we can compute directly; it is 677 .
|
{
"resource_path": "HarvardMIT/segmented/en-72-2004-feb-alg-solutions.jsonl",
"problem_match": "\n9. ",
"solution_match": "\nSolution: "
}
|
d2e75d26-7aee-5328-a2e0-675f00d17484
| 611,199
|
There exists a polynomial $P$ of degree 5 with the following property: if $z$ is a complex number such that $z^{5}+2004 z=1$, then $P\left(z^{2}\right)=0$. Calculate the quotient $P(1) / P(-1)$.
|
-2010012/2010013
Let $z_{1}, \ldots, z_{5}$ be the roots of $Q(z)=z^{5}+2004 z-1$. We can check these are distinct (by using the fact that there's one in a small neighborhood of each root of $z^{5}+2004 z$, or by noting that $Q(z)$ is relatively prime to its derivative). And certainly none of the roots of $Q$ is the negative of another, since $z^{5}+2004 z=1$ implies $(-z)^{5}+2004(-z)=-1$, so their squares are distinct as well. Then, $z_{1}^{2}, \ldots, z_{5}^{2}$ are the roots of $P$, so if we write $C$ for the leading coefficient of $P$, we have
$$
\begin{aligned}
\frac{P(1)}{P(-1)} & =\frac{C\left(1-z_{1}^{2}\right) \cdots\left(1-z_{5}^{2}\right)}{C\left(-1-z_{1}^{2}\right) \cdots\left(-1-z_{5}^{2}\right)} \\
& =\frac{\left[\left(1-z_{1}\right) \cdots\left(1-z_{5}\right)\right] \cdot\left[\left(1+z_{1}\right) \cdots\left(1+z_{5}\right)\right]}{\left[\left(i-z_{1}\right) \cdots\left(i-z_{5}\right)\right] \cdot\left[\left(i+z_{1}\right) \cdots\left(i+z_{5}\right)\right]} \\
& =\frac{\left[\left(1-z_{1}\right) \cdots\left(1-z_{5}\right)\right] \cdot\left[\left(-1-z_{1}\right) \cdots\left(-1-z_{5}\right)\right]}{\left[\left(i-z_{1}\right) \cdots\left(i-z_{5}\right)\right] \cdot\left[\left(-i-z_{1}\right) \cdots\left(-i-z_{5}\right)\right]} \\
& =\frac{\left(1^{5}+2004 \cdot 1-1\right)\left(-1^{5}+2004 \cdot(-1)-1\right)}{\left(i^{5}+2004 \cdot i-1\right)\left(-i^{5}+2004 \cdot(-i)-1\right)} \\
& =\frac{(2004)(-2006)}{(-1+2005 i)(-1-2005 i)} \\
& =-\frac{2005^{2}-1}{2005^{2}+1} \\
& =-4020024 / 4020026=-2010012 / 2010013 .
\end{aligned}
$$
Alternative Solution: In fact, we can construct the polynomial $P$ explicitly (up to multiplication by a constant). We write $P\left(z^{2}\right)$ as a polynomial in $z$; it must use only
even powers of $z$ and be divisible by $z^{5}+2004 z-1$, so we are inspired to try a difference of squares,
$$
P\left(z^{2}\right)=\left(z^{5}+2004 z-1\right)\left(z^{5}+2004 z+1\right)=\left(z^{5}+2004 z\right)^{2}-1^{2}=z^{2}\left(z^{4}+2004\right)^{2}-1,
$$
giving
$$
P(z)=z\left(z^{2}+2004\right)^{2}-1 .
$$
Now plugging in $z=1$ and $z=-1$ rapidly gives $\left(2005^{2}-1\right) /\left(-2005^{2}-1\right)$ as before.
|
-\frac{2010012}{2010013}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
There exists a polynomial $P$ of degree 5 with the following property: if $z$ is a complex number such that $z^{5}+2004 z=1$, then $P\left(z^{2}\right)=0$. Calculate the quotient $P(1) / P(-1)$.
|
-2010012/2010013
Let $z_{1}, \ldots, z_{5}$ be the roots of $Q(z)=z^{5}+2004 z-1$. We can check these are distinct (by using the fact that there's one in a small neighborhood of each root of $z^{5}+2004 z$, or by noting that $Q(z)$ is relatively prime to its derivative). And certainly none of the roots of $Q$ is the negative of another, since $z^{5}+2004 z=1$ implies $(-z)^{5}+2004(-z)=-1$, so their squares are distinct as well. Then, $z_{1}^{2}, \ldots, z_{5}^{2}$ are the roots of $P$, so if we write $C$ for the leading coefficient of $P$, we have
$$
\begin{aligned}
\frac{P(1)}{P(-1)} & =\frac{C\left(1-z_{1}^{2}\right) \cdots\left(1-z_{5}^{2}\right)}{C\left(-1-z_{1}^{2}\right) \cdots\left(-1-z_{5}^{2}\right)} \\
& =\frac{\left[\left(1-z_{1}\right) \cdots\left(1-z_{5}\right)\right] \cdot\left[\left(1+z_{1}\right) \cdots\left(1+z_{5}\right)\right]}{\left[\left(i-z_{1}\right) \cdots\left(i-z_{5}\right)\right] \cdot\left[\left(i+z_{1}\right) \cdots\left(i+z_{5}\right)\right]} \\
& =\frac{\left[\left(1-z_{1}\right) \cdots\left(1-z_{5}\right)\right] \cdot\left[\left(-1-z_{1}\right) \cdots\left(-1-z_{5}\right)\right]}{\left[\left(i-z_{1}\right) \cdots\left(i-z_{5}\right)\right] \cdot\left[\left(-i-z_{1}\right) \cdots\left(-i-z_{5}\right)\right]} \\
& =\frac{\left(1^{5}+2004 \cdot 1-1\right)\left(-1^{5}+2004 \cdot(-1)-1\right)}{\left(i^{5}+2004 \cdot i-1\right)\left(-i^{5}+2004 \cdot(-i)-1\right)} \\
& =\frac{(2004)(-2006)}{(-1+2005 i)(-1-2005 i)} \\
& =-\frac{2005^{2}-1}{2005^{2}+1} \\
& =-4020024 / 4020026=-2010012 / 2010013 .
\end{aligned}
$$
Alternative Solution: In fact, we can construct the polynomial $P$ explicitly (up to multiplication by a constant). We write $P\left(z^{2}\right)$ as a polynomial in $z$; it must use only
even powers of $z$ and be divisible by $z^{5}+2004 z-1$, so we are inspired to try a difference of squares,
$$
P\left(z^{2}\right)=\left(z^{5}+2004 z-1\right)\left(z^{5}+2004 z+1\right)=\left(z^{5}+2004 z\right)^{2}-1^{2}=z^{2}\left(z^{4}+2004\right)^{2}-1,
$$
giving
$$
P(z)=z\left(z^{2}+2004\right)^{2}-1 .
$$
Now plugging in $z=1$ and $z=-1$ rapidly gives $\left(2005^{2}-1\right) /\left(-2005^{2}-1\right)$ as before.
|
{
"resource_path": "HarvardMIT/segmented/en-72-2004-feb-alg-solutions.jsonl",
"problem_match": "\n10. ",
"solution_match": "\nSolution: "
}
|
f8a34cbf-ebad-5206-aefa-fe8f5828d5e2
| 611,200
|
Suppose the function $f(x)-f(2 x)$ has derivative 5 at $x=1$ and derivative 7 at $x=2$. Find the derivative of $f(x)-f(4 x)$ at $x=1$.
|
Let $g(x)=f(x)-f(2 x)$. Then we want the derivative of
$$
f(x)-f(4 x)=(f(x)-f(2 x))+(f(2 x)-f(4 x))=g(x)+g(2 x)
$$
at $x=1$. This is $g^{\prime}(x)+2 g^{\prime}(2 x)$ at $x=1$, or $5+2 \cdot 7=19$.
|
19
|
Yes
|
Yes
|
math-word-problem
|
Calculus
|
Suppose the function $f(x)-f(2 x)$ has derivative 5 at $x=1$ and derivative 7 at $x=2$. Find the derivative of $f(x)-f(4 x)$ at $x=1$.
|
Let $g(x)=f(x)-f(2 x)$. Then we want the derivative of
$$
f(x)-f(4 x)=(f(x)-f(2 x))+(f(2 x)-f(4 x))=g(x)+g(2 x)
$$
at $x=1$. This is $g^{\prime}(x)+2 g^{\prime}(2 x)$ at $x=1$, or $5+2 \cdot 7=19$.
|
{
"resource_path": "HarvardMIT/segmented/en-72-2004-feb-calc-solutions.jsonl",
"problem_match": "\n2. ",
"solution_match": "\nSolution:\n"
}
|
4662d1d5-5090-52af-bf73-2b20c8c3166d
| 611,202
|
Find $\lim _{x \rightarrow \infty}\left(\sqrt[3]{x^{3}+x^{2}}-\sqrt[3]{x^{3}-x^{2}}\right)$.
|
$2 / 3$
Observe that
$\lim _{x \rightarrow \infty}\left[(x+1 / 3)-\sqrt[3]{x^{3}+x^{2}}\right]=\lim _{x \rightarrow \infty} \frac{x / 3+1 / 27}{\left(\sqrt[3]{x^{3}+x^{2}}\right)^{2}+\left(\sqrt[3]{x^{3}+x^{2}}\right)(x+1 / 3)+(x+1 / 3)^{2}}$,
by factoring the numerator as a difference of cubes. The numerator is linear in $x$, while the denominator is at least $3 x^{2}$, so the limit as $x \rightarrow \infty$ is 0 . By similar arguments, $\lim _{x \rightarrow \infty}\left[(x-1 / 3)-\sqrt[3]{x^{3}-x^{2}}\right]=0$. So, the desired limit equals
$$
2 / 3+\lim _{x \rightarrow \infty}\left[(x-1 / 3)-\sqrt[3]{x^{3}-x^{2}}\right]-\lim _{x \rightarrow \infty}\left[(x+1 / 3)-\sqrt[3]{x^{3}+x^{2}}\right]=2 / 3
$$
|
\frac{2}{3}
|
Yes
|
Yes
|
math-word-problem
|
Calculus
|
Find $\lim _{x \rightarrow \infty}\left(\sqrt[3]{x^{3}+x^{2}}-\sqrt[3]{x^{3}-x^{2}}\right)$.
|
$2 / 3$
Observe that
$\lim _{x \rightarrow \infty}\left[(x+1 / 3)-\sqrt[3]{x^{3}+x^{2}}\right]=\lim _{x \rightarrow \infty} \frac{x / 3+1 / 27}{\left(\sqrt[3]{x^{3}+x^{2}}\right)^{2}+\left(\sqrt[3]{x^{3}+x^{2}}\right)(x+1 / 3)+(x+1 / 3)^{2}}$,
by factoring the numerator as a difference of cubes. The numerator is linear in $x$, while the denominator is at least $3 x^{2}$, so the limit as $x \rightarrow \infty$ is 0 . By similar arguments, $\lim _{x \rightarrow \infty}\left[(x-1 / 3)-\sqrt[3]{x^{3}-x^{2}}\right]=0$. So, the desired limit equals
$$
2 / 3+\lim _{x \rightarrow \infty}\left[(x-1 / 3)-\sqrt[3]{x^{3}-x^{2}}\right]-\lim _{x \rightarrow \infty}\left[(x+1 / 3)-\sqrt[3]{x^{3}+x^{2}}\right]=2 / 3
$$
|
{
"resource_path": "HarvardMIT/segmented/en-72-2004-feb-calc-solutions.jsonl",
"problem_match": "\n3. ",
"solution_match": "\nSolution: "
}
|
817a739e-9842-5049-943f-c491dfe39581
| 611,203
|
Let $f(x)=\cos (\cos (\cos (\cos (\cos (\cos (\cos (\cos x)))))))$, and suppose that the number $a$ satisfies the equation $a=\cos a$. Express $f^{\prime}(a)$ as a polynomial in $a$.
|
$a^{8}-4 a^{6}+6 a^{4}-4 a^{2}+1$
This is an exercise using the chain rule. Define $f_{0}(x)=x$ and $f_{n}(x)=\cos f_{n-1}(x)$ for $n \geq 0$. We will show by induction that $f_{n}(a)=a$ and $f_{n}^{\prime}(a)=(-\sin a)^{n}$ for all $n$. The case $n=0$ is clear. Then $f_{n}(a)=\cos f_{n-1}(a)=\cos a=a$, and
$$
f_{n}^{\prime}(a)=f_{n-1}^{\prime}(a) \cdot\left(-\sin f_{n-1}(a)\right)=(-\sin a)^{n-1} \cdot(-\sin a)=(-\sin a)^{n}
$$
by induction. Now, $f(x)=f_{8}(x)$, so $f^{\prime}(a)=(-\sin a)^{8}=\sin ^{8} a$. But $\sin ^{2} a=1-$ $\cos ^{2} a=1-a^{2}$, so $f^{\prime}(a)=\left(1-a^{2}\right)^{4}=a^{8}-4 a^{6}+6 a^{4}-4 a^{2}+1$.
|
a^{8}-4 a^{6}+6 a^{4}-4 a^{2}+1
|
Yes
|
Yes
|
math-word-problem
|
Calculus
|
Let $f(x)=\cos (\cos (\cos (\cos (\cos (\cos (\cos (\cos x)))))))$, and suppose that the number $a$ satisfies the equation $a=\cos a$. Express $f^{\prime}(a)$ as a polynomial in $a$.
|
$a^{8}-4 a^{6}+6 a^{4}-4 a^{2}+1$
This is an exercise using the chain rule. Define $f_{0}(x)=x$ and $f_{n}(x)=\cos f_{n-1}(x)$ for $n \geq 0$. We will show by induction that $f_{n}(a)=a$ and $f_{n}^{\prime}(a)=(-\sin a)^{n}$ for all $n$. The case $n=0$ is clear. Then $f_{n}(a)=\cos f_{n-1}(a)=\cos a=a$, and
$$
f_{n}^{\prime}(a)=f_{n-1}^{\prime}(a) \cdot\left(-\sin f_{n-1}(a)\right)=(-\sin a)^{n-1} \cdot(-\sin a)=(-\sin a)^{n}
$$
by induction. Now, $f(x)=f_{8}(x)$, so $f^{\prime}(a)=(-\sin a)^{8}=\sin ^{8} a$. But $\sin ^{2} a=1-$ $\cos ^{2} a=1-a^{2}$, so $f^{\prime}(a)=\left(1-a^{2}\right)^{4}=a^{8}-4 a^{6}+6 a^{4}-4 a^{2}+1$.
|
{
"resource_path": "HarvardMIT/segmented/en-72-2004-feb-calc-solutions.jsonl",
"problem_match": "\n4. ",
"solution_match": "\nSolution: "
}
|
b5934a72-7e67-56f5-be56-14eb1cded5e1
| 611,204
|
A mouse is sitting in a toy car on a negligibly small turntable. The car cannot turn on its own, but the mouse can control when the car is launched and when the car stops (the car has brakes). When the mouse chooses to launch, the car will immediately leave the turntable on a straight trajectory at 1 meter per second.
Suddenly someone turns on the turntable; it spins at 30 rpm . Consider the set $S$ of points the mouse can reach in his car within 1 second after the turntable is set in motion. (For example, the arrows in the figure below represent two possible paths the mouse can take.) What is the area of $S$, in square meters?
|
$\pi / 6$
The mouse can wait while the table rotates through some angle $\theta$ and then spend the remainder of the time moving along that ray at $1 \mathrm{~m} / \mathrm{s}$. He can reach any point between the starting point and the furthest reachable point along the ray, $(1-\theta / \pi)$ meters out. So the area is given by the polar integral
$$
\int_{0}^{\pi} \frac{(1-\theta / \pi)^{2}}{2} d \theta=\frac{1}{2} \cdot \frac{1}{\pi^{2}} \int_{0}^{\pi} \phi^{2} d \phi=\pi / 6
$$
(where we have used the change of variables $\phi=\pi-\theta$ ).
|
\pi / 6
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
A mouse is sitting in a toy car on a negligibly small turntable. The car cannot turn on its own, but the mouse can control when the car is launched and when the car stops (the car has brakes). When the mouse chooses to launch, the car will immediately leave the turntable on a straight trajectory at 1 meter per second.
Suddenly someone turns on the turntable; it spins at 30 rpm . Consider the set $S$ of points the mouse can reach in his car within 1 second after the turntable is set in motion. (For example, the arrows in the figure below represent two possible paths the mouse can take.) What is the area of $S$, in square meters?

|
$\pi / 6$
The mouse can wait while the table rotates through some angle $\theta$ and then spend the remainder of the time moving along that ray at $1 \mathrm{~m} / \mathrm{s}$. He can reach any point between the starting point and the furthest reachable point along the ray, $(1-\theta / \pi)$ meters out. So the area is given by the polar integral
$$
\int_{0}^{\pi} \frac{(1-\theta / \pi)^{2}}{2} d \theta=\frac{1}{2} \cdot \frac{1}{\pi^{2}} \int_{0}^{\pi} \phi^{2} d \phi=\pi / 6
$$
(where we have used the change of variables $\phi=\pi-\theta$ ).
|
{
"resource_path": "HarvardMIT/segmented/en-72-2004-feb-calc-solutions.jsonl",
"problem_match": "\n5. ",
"solution_match": "\n## Solution: "
}
|
b12412ef-f625-50f3-872e-bb95b8d22b48
| 611,205
|
For $x>0$, let $f(x)=x^{x}$. Find all values of $x$ for which $f(x)=f^{\prime}(x)$.
|
1
Let $g(x)=\log f(x)=x \log x$. Then $f^{\prime}(x) / f(x)=g^{\prime}(x)=1+\log x$. Therefore $f(x)=f^{\prime}(x)$ when $1+\log x=1$, that is, when $x=1$.
|
1
|
Yes
|
Yes
|
math-word-problem
|
Calculus
|
For $x>0$, let $f(x)=x^{x}$. Find all values of $x$ for which $f(x)=f^{\prime}(x)$.
|
1
Let $g(x)=\log f(x)=x \log x$. Then $f^{\prime}(x) / f(x)=g^{\prime}(x)=1+\log x$. Therefore $f(x)=f^{\prime}(x)$ when $1+\log x=1$, that is, when $x=1$.
|
{
"resource_path": "HarvardMIT/segmented/en-72-2004-feb-calc-solutions.jsonl",
"problem_match": "\n6. ",
"solution_match": "\nSolution: "
}
|
047f9aa7-ab91-5766-b9f3-85462b24a4ea
| 611,206
|
Find the area of the region in the $x y$-plane satisfying $x^{6}-x^{2}+y^{2} \leq 0$.
|
$\pi / 2$
Rewrite the condition as $|y| \leq \sqrt{x^{2}-x^{6}}$. The right side is zero when $x$ is $-1,0$, or 1 , and it bounds an area symmetric about the $x$ - and $y$-axes. Therefore, we can calculate the area by the integral
$$
2 \int_{-1}^{1} \sqrt{x^{2}-x^{6}} d x=4 \int_{0}^{1} x \sqrt{1-x^{4}} d x=2 \int_{0}^{1} \sqrt{1-u^{2}} d u=\pi / 2
$$
|
\pi / 2
|
Yes
|
Yes
|
math-word-problem
|
Inequalities
|
Find the area of the region in the $x y$-plane satisfying $x^{6}-x^{2}+y^{2} \leq 0$.
|
$\pi / 2$
Rewrite the condition as $|y| \leq \sqrt{x^{2}-x^{6}}$. The right side is zero when $x$ is $-1,0$, or 1 , and it bounds an area symmetric about the $x$ - and $y$-axes. Therefore, we can calculate the area by the integral
$$
2 \int_{-1}^{1} \sqrt{x^{2}-x^{6}} d x=4 \int_{0}^{1} x \sqrt{1-x^{4}} d x=2 \int_{0}^{1} \sqrt{1-u^{2}} d u=\pi / 2
$$
|
{
"resource_path": "HarvardMIT/segmented/en-72-2004-feb-calc-solutions.jsonl",
"problem_match": "\n7. ",
"solution_match": "\nSolution: "
}
|
bdf3a5e8-7fba-5128-8f97-31982fbe94db
| 611,207
|
If $x$ and $y$ are real numbers with $(x+y)^{4}=x-y$, what is the maximum possible value of $y$ ?
|
$$
3 \sqrt[3]{2} / 16
$$
By drawing the graph of the curve (as shown), which is just a $135^{\circ}$ clockwise rotation and scaling of $y=x^{4}$, we see that the maximum is achieved at the unique point where $d y / d x=0$. Implicit differentiation gives $4(d y / d x+1)(x+y)^{3}=1-d y / d x$, so setting $d y / d x=0$ gives $4(x+y)^{3}=1$. So $x+y=1 / \sqrt[3]{4}=\sqrt[3]{2} / 2$, and $x-y=(x+y)^{4}=\sqrt[3]{2} / 8$. Subtracting and dividing by 2 gives $y=(\sqrt[3]{2} / 2-\sqrt[3]{2} / 8) / 2=3 \sqrt[3]{2} / 16$.
|
\frac{3 \sqrt[3]{2}}{16}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
If $x$ and $y$ are real numbers with $(x+y)^{4}=x-y$, what is the maximum possible value of $y$ ?
|
$$
3 \sqrt[3]{2} / 16
$$
By drawing the graph of the curve (as shown), which is just a $135^{\circ}$ clockwise rotation and scaling of $y=x^{4}$, we see that the maximum is achieved at the unique point where $d y / d x=0$. Implicit differentiation gives $4(d y / d x+1)(x+y)^{3}=1-d y / d x$, so setting $d y / d x=0$ gives $4(x+y)^{3}=1$. So $x+y=1 / \sqrt[3]{4}=\sqrt[3]{2} / 2$, and $x-y=(x+y)^{4}=\sqrt[3]{2} / 8$. Subtracting and dividing by 2 gives $y=(\sqrt[3]{2} / 2-\sqrt[3]{2} / 8) / 2=3 \sqrt[3]{2} / 16$.

|
{
"resource_path": "HarvardMIT/segmented/en-72-2004-feb-calc-solutions.jsonl",
"problem_match": "\n8. ",
"solution_match": "\nSolution:\n\n"
}
|
2666de8b-071f-57a2-9600-5361ee04e7f2
| 611,208
|
Find the positive constant $c_{0}$ such that the series
$$
\sum_{n=0}^{\infty} \frac{n!}{(c n)^{n}}
$$
converges for $c>c_{0}$ and diverges for $0<c<c_{0}$.
|
$1 / e$
The ratio test tells us that the series converges if
$$
\lim _{n \rightarrow \infty} \frac{(n+1)!/(c(n+1))^{n+1}}{n!/(c n)^{n}}=\frac{1}{c} \cdot \lim _{n \rightarrow \infty}\left(\frac{n}{n+1}\right)^{n}
$$
is less than one and diverges if it is greater than one. But
$$
\lim _{n \rightarrow \infty}\left(\frac{n}{n+1}\right)^{n}=\lim _{n \rightarrow \infty}\left(1+\frac{1}{n}\right)^{-n}=\frac{1}{e} .
$$
Then the limit above is just $1 / c e$, so the series converges for $c>1 / e$ and diverges for $0<c<1 / e$.
|
\frac{1}{e}
|
Yes
|
Yes
|
math-word-problem
|
Calculus
|
Find the positive constant $c_{0}$ such that the series
$$
\sum_{n=0}^{\infty} \frac{n!}{(c n)^{n}}
$$
converges for $c>c_{0}$ and diverges for $0<c<c_{0}$.
|
$1 / e$
The ratio test tells us that the series converges if
$$
\lim _{n \rightarrow \infty} \frac{(n+1)!/(c(n+1))^{n+1}}{n!/(c n)^{n}}=\frac{1}{c} \cdot \lim _{n \rightarrow \infty}\left(\frac{n}{n+1}\right)^{n}
$$
is less than one and diverges if it is greater than one. But
$$
\lim _{n \rightarrow \infty}\left(\frac{n}{n+1}\right)^{n}=\lim _{n \rightarrow \infty}\left(1+\frac{1}{n}\right)^{-n}=\frac{1}{e} .
$$
Then the limit above is just $1 / c e$, so the series converges for $c>1 / e$ and diverges for $0<c<1 / e$.
|
{
"resource_path": "HarvardMIT/segmented/en-72-2004-feb-calc-solutions.jsonl",
"problem_match": "\n9. ",
"solution_match": "\nSolution: "
}
|
0de7eec2-12dc-5fda-a7d9-e18d7c133a68
| 611,209
|
Let $P(x)=x^{3}-\frac{3}{2} x^{2}+x+\frac{1}{4}$. Let $P^{[1]}(x)=P(x)$, and for $n \geq 1$, let $P^{[n+1]}(x)=$ $P^{[n]}(P(x))$. Evaluate $\int_{0}^{1} P^{[2004]}(x) d x$.
|
$1 / 2$
By Note that $P(1-x)=1-P(x)$. It follows easily by induction that $P^{[k]}(1-x)=$ $1-P^{[k]}(x)$ for all positive integers $k$. Hence
$$
\begin{aligned}
\int_{0}^{1} P^{[2004]}(x) d x & =\int_{0}^{1} 1-P^{[2004]}(1-x) d x \\
& =1-\int_{0}^{1} P^{[2004]}(1-x) d x \\
& =1-\int_{0}^{1} P^{[2004]}(u) d u \quad(u=1-x)
\end{aligned}
$$
Hence $\int_{0}^{1} P^{[2004]}(x) d x=1 / 2$.
|
\frac{1}{2}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Let $P(x)=x^{3}-\frac{3}{2} x^{2}+x+\frac{1}{4}$. Let $P^{[1]}(x)=P(x)$, and for $n \geq 1$, let $P^{[n+1]}(x)=$ $P^{[n]}(P(x))$. Evaluate $\int_{0}^{1} P^{[2004]}(x) d x$.
|
$1 / 2$
By Note that $P(1-x)=1-P(x)$. It follows easily by induction that $P^{[k]}(1-x)=$ $1-P^{[k]}(x)$ for all positive integers $k$. Hence
$$
\begin{aligned}
\int_{0}^{1} P^{[2004]}(x) d x & =\int_{0}^{1} 1-P^{[2004]}(1-x) d x \\
& =1-\int_{0}^{1} P^{[2004]}(1-x) d x \\
& =1-\int_{0}^{1} P^{[2004]}(u) d u \quad(u=1-x)
\end{aligned}
$$
Hence $\int_{0}^{1} P^{[2004]}(x) d x=1 / 2$.
|
{
"resource_path": "HarvardMIT/segmented/en-72-2004-feb-calc-solutions.jsonl",
"problem_match": "\n10. ",
"solution_match": "\nSolution: "
}
|
5a14e4ba-1fe0-5a6a-8e56-1565fa597a80
| 611,210
|
There are 1000 rooms in a row along a long corridor. Initially the first room contains 1000 people and the remaining rooms are empty. Each minute, the following happens: for each room containing more than one person, someone in that room decides it is too crowded and moves to the next room. All these movements are simultaneous (so nobody moves more than once within a minute). After one hour, how many different rooms will have people in them?
|
31
We can prove by induction on $n$ that the following pattern holds for $0 \leq n \leq 499$ : after $2 n$ minutes, the first room contains $1000-2 n$ people and the next $n$ rooms each contain 2 people, and after $2 n+1$ minutes, the first room contains $1000-(2 n+1)$ people, the next $n$ rooms each contain 2 people, and the next room after that contains 1 person. So, after 60 minutes, we have one room with 940 people and 30 rooms with 2 people each.
|
31
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
There are 1000 rooms in a row along a long corridor. Initially the first room contains 1000 people and the remaining rooms are empty. Each minute, the following happens: for each room containing more than one person, someone in that room decides it is too crowded and moves to the next room. All these movements are simultaneous (so nobody moves more than once within a minute). After one hour, how many different rooms will have people in them?
|
31
We can prove by induction on $n$ that the following pattern holds for $0 \leq n \leq 499$ : after $2 n$ minutes, the first room contains $1000-2 n$ people and the next $n$ rooms each contain 2 people, and after $2 n+1$ minutes, the first room contains $1000-(2 n+1)$ people, the next $n$ rooms each contain 2 people, and the next room after that contains 1 person. So, after 60 minutes, we have one room with 940 people and 30 rooms with 2 people each.
|
{
"resource_path": "HarvardMIT/segmented/en-72-2004-feb-comb-solutions.jsonl",
"problem_match": "\n1. ",
"solution_match": "\n## Solution: "
}
|
ca47c62c-6b55-5fae-a904-09d13a842988
| 611,211
|
How many ways can you mark 8 squares of an $8 \times 8$ chessboard so that no two marked squares are in the same row or column, and none of the four corner squares is marked? (Rotations and reflections are considered different.)
|
21600
In the top row, you can mark any of the 6 squares that is not a corner. In the bottom row, you can then mark any of the 5 squares that is not a corner and not in the same column as the square just marked. Then, in the second row, you have 6 choices for a square not in the same column as either of the two squares already marked; then there are 5 choices remaining for the third row, and so on down to 1 for the seventh row, in which you make the last mark. Thus, altogether, there are $6 \cdot 5 \cdot(6 \cdot 5 \cdots 1)=30 \cdot 6!=30 \cdot 720=21600$ possible sets of squares.
|
21600
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
How many ways can you mark 8 squares of an $8 \times 8$ chessboard so that no two marked squares are in the same row or column, and none of the four corner squares is marked? (Rotations and reflections are considered different.)
|
21600
In the top row, you can mark any of the 6 squares that is not a corner. In the bottom row, you can then mark any of the 5 squares that is not a corner and not in the same column as the square just marked. Then, in the second row, you have 6 choices for a square not in the same column as either of the two squares already marked; then there are 5 choices remaining for the third row, and so on down to 1 for the seventh row, in which you make the last mark. Thus, altogether, there are $6 \cdot 5 \cdot(6 \cdot 5 \cdots 1)=30 \cdot 6!=30 \cdot 720=21600$ possible sets of squares.
|
{
"resource_path": "HarvardMIT/segmented/en-72-2004-feb-comb-solutions.jsonl",
"problem_match": "\n2. ",
"solution_match": "\n## Solution: "
}
|
905d52d4-6054-55ae-ad07-8663ab2d9797
| 611,212
|
A class of 10 students took a math test. Each problem was solved by exactly 7 of the students. If the first nine students each solved 4 problems, how many problems did the tenth student solve?
|
6
Suppose the last student solved $n$ problems, and the total number of problems on the test was $p$. Then the total number of correct solutions written was $7 p$ (seven per problem), and also equal to $36+n$ (the sum of the students' scores), so $p=(36+n) / 7$. The smallest $n \geq 0$ for which this is an integer is $n=6$. But we also must have $n \leq p$, so $7 n \leq 36+n$, and solving gives $n \leq 6$. Thus $n=6$ is the answer.
|
6
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
A class of 10 students took a math test. Each problem was solved by exactly 7 of the students. If the first nine students each solved 4 problems, how many problems did the tenth student solve?
|
6
Suppose the last student solved $n$ problems, and the total number of problems on the test was $p$. Then the total number of correct solutions written was $7 p$ (seven per problem), and also equal to $36+n$ (the sum of the students' scores), so $p=(36+n) / 7$. The smallest $n \geq 0$ for which this is an integer is $n=6$. But we also must have $n \leq p$, so $7 n \leq 36+n$, and solving gives $n \leq 6$. Thus $n=6$ is the answer.
|
{
"resource_path": "HarvardMIT/segmented/en-72-2004-feb-comb-solutions.jsonl",
"problem_match": "\n3. ",
"solution_match": "\n## Solution: "
}
|
e1af011e-cf73-525b-befb-12f195e38fee
| 611,213
|
Andrea flips a fair coin repeatedly, continuing until she either flips two heads in a row (the sequence $H H$ ) or flips tails followed by heads (the sequence $T H$ ). What is the probability that she will stop after flipping $H H$ ?
|
$1 / 4$
The only way that Andrea can ever flip $H H$ is if she never flips $T$, in which case she must flip two heads immediately at the beginning. This happens with probability $\frac{1}{4}$.
|
\frac{1}{4}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Andrea flips a fair coin repeatedly, continuing until she either flips two heads in a row (the sequence $H H$ ) or flips tails followed by heads (the sequence $T H$ ). What is the probability that she will stop after flipping $H H$ ?
|
$1 / 4$
The only way that Andrea can ever flip $H H$ is if she never flips $T$, in which case she must flip two heads immediately at the beginning. This happens with probability $\frac{1}{4}$.
|
{
"resource_path": "HarvardMIT/segmented/en-72-2004-feb-comb-solutions.jsonl",
"problem_match": "\n4. ",
"solution_match": "\nSolution: "
}
|
490655e6-7bdb-5245-822b-5355a7d5dddf
| 611,214
|
A best-of-9 series is to be played between two teams; that is, the first team to win 5 games is the winner. The Mathletes have a chance of $2 / 3$ of winning any given game. What is the probability that exactly 7 games will need to be played to determine a winner?
|
$20 / 81$
If the Mathletes are to win, they must win exactly 5 out of the 7 games. One of the 5 games they win must be the 7th game, because otherwise they would win the tournament before 7 games are completed. Thus, in the first 6 games, the Mathletes must win 4 games and lose 2. The probability of this happening and the Mathletes winning the last game is
$$
\left[\binom{6}{2} \cdot\left(\frac{2}{3}\right)^{4} \cdot\left(\frac{1}{3}\right)^{2}\right] \cdot\left(\frac{2}{3}\right) .
$$
Likewise, the probability of the other team winning on the 7th game is
$$
\left[\binom{6}{2} \cdot\left(\frac{1}{3}\right)^{4} \cdot\left(\frac{2}{3}\right)^{2}\right] \cdot\left(\frac{1}{3}\right)
$$
Summing these values, we obtain 160/729 $+20 / 729=20 / 81$.
|
\frac{20}{81}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
A best-of-9 series is to be played between two teams; that is, the first team to win 5 games is the winner. The Mathletes have a chance of $2 / 3$ of winning any given game. What is the probability that exactly 7 games will need to be played to determine a winner?
|
$20 / 81$
If the Mathletes are to win, they must win exactly 5 out of the 7 games. One of the 5 games they win must be the 7th game, because otherwise they would win the tournament before 7 games are completed. Thus, in the first 6 games, the Mathletes must win 4 games and lose 2. The probability of this happening and the Mathletes winning the last game is
$$
\left[\binom{6}{2} \cdot\left(\frac{2}{3}\right)^{4} \cdot\left(\frac{1}{3}\right)^{2}\right] \cdot\left(\frac{2}{3}\right) .
$$
Likewise, the probability of the other team winning on the 7th game is
$$
\left[\binom{6}{2} \cdot\left(\frac{1}{3}\right)^{4} \cdot\left(\frac{2}{3}\right)^{2}\right] \cdot\left(\frac{1}{3}\right)
$$
Summing these values, we obtain 160/729 $+20 / 729=20 / 81$.
|
{
"resource_path": "HarvardMIT/segmented/en-72-2004-feb-comb-solutions.jsonl",
"problem_match": "\n5. ",
"solution_match": "\nSolution: "
}
|
e472d406-248b-50f1-91d2-ab444629ac4f
| 611,215
|
A committee of 5 is to be chosen from a group of 9 people. How many ways can it be chosen, if Bill and Karl must serve together or not at all, and Alice and Jane refuse to serve with each other?
|
41
If Bill and Karl are on the committee, there are $\binom{7}{3}=35$ ways for the other group members to be chosen. However, if Alice and Jane are on the committee with Bill and Karl, there are $\binom{5}{1}=5$ ways for the last member to be chosen, yielding 5 unacceptable committees. If Bill and Karl are not on the committee, there are $\binom{7}{5}=21$ ways for the 5 members to be chosen, but again if Alice and Jane were to be on the committee, there would be $\binom{5}{3}=10$ ways to choose the other three members, yielding 10 more unacceptable committees. So, we obtain $(35-5)+(21-10)=41$ ways the committee can be chosen.
|
41
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
A committee of 5 is to be chosen from a group of 9 people. How many ways can it be chosen, if Bill and Karl must serve together or not at all, and Alice and Jane refuse to serve with each other?
|
41
If Bill and Karl are on the committee, there are $\binom{7}{3}=35$ ways for the other group members to be chosen. However, if Alice and Jane are on the committee with Bill and Karl, there are $\binom{5}{1}=5$ ways for the last member to be chosen, yielding 5 unacceptable committees. If Bill and Karl are not on the committee, there are $\binom{7}{5}=21$ ways for the 5 members to be chosen, but again if Alice and Jane were to be on the committee, there would be $\binom{5}{3}=10$ ways to choose the other three members, yielding 10 more unacceptable committees. So, we obtain $(35-5)+(21-10)=41$ ways the committee can be chosen.
|
{
"resource_path": "HarvardMIT/segmented/en-72-2004-feb-comb-solutions.jsonl",
"problem_match": "\n6. ",
"solution_match": "\n## Solution: "
}
|
bb802840-9541-520a-95df-02586e8b7a03
| 69,533
|
We have a polyhedron such that an ant can walk from one vertex to another, traveling only along edges, and traversing every edge exactly once. What is the smallest possible total number of vertices, edges, and faces of this polyhedron?
|
20
This is obtainable by construction. Consider two tetrahedrons glued along a face; this gives us 5 vertices, 9 edges, and 6 faces, for a total of 20 , and one readily checks that the required Eulerian path exists. Now, to see that we cannot do better, first notice that the number $v$ of vertices is at least 5 , since otherwise we must have a tetrahedron, which does not have an Eulerian path. Each vertex is incident to at least 3 edges, and
in fact, since there is an Eulerian path, all except possibly two vertices are incident to an even number of edges. So the number of edges is at least $(3+3+4+4+4) / 2$ (since each edge meets two vertices) $=9$. Finally, if $f=4$ then each face must be a triangle, because there are only 3 other faces for it to share edges with, and we are again in the case of a tetrahedron, which is impossible; therefore $f \geq 5$. So $f+v+e \geq 5+5+9=19$. But since $f+v-e=2-2 g$ (where $g$ is the number of holes in the polyhedron), $f+v+e$ must be even. This strengthens our bound to 20 as needed.
|
20
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
We have a polyhedron such that an ant can walk from one vertex to another, traveling only along edges, and traversing every edge exactly once. What is the smallest possible total number of vertices, edges, and faces of this polyhedron?
|
20
This is obtainable by construction. Consider two tetrahedrons glued along a face; this gives us 5 vertices, 9 edges, and 6 faces, for a total of 20 , and one readily checks that the required Eulerian path exists. Now, to see that we cannot do better, first notice that the number $v$ of vertices is at least 5 , since otherwise we must have a tetrahedron, which does not have an Eulerian path. Each vertex is incident to at least 3 edges, and
in fact, since there is an Eulerian path, all except possibly two vertices are incident to an even number of edges. So the number of edges is at least $(3+3+4+4+4) / 2$ (since each edge meets two vertices) $=9$. Finally, if $f=4$ then each face must be a triangle, because there are only 3 other faces for it to share edges with, and we are again in the case of a tetrahedron, which is impossible; therefore $f \geq 5$. So $f+v+e \geq 5+5+9=19$. But since $f+v-e=2-2 g$ (where $g$ is the number of holes in the polyhedron), $f+v+e$ must be even. This strengthens our bound to 20 as needed.
|
{
"resource_path": "HarvardMIT/segmented/en-72-2004-feb-comb-solutions.jsonl",
"problem_match": "\n7. ",
"solution_match": "\n## Solution: "
}
|
5e40cd73-7805-584d-aff7-653e7efe1efc
| 69,544
|
Urn A contains 4 white balls and 2 red balls. Urn B contains 3 red balls and 3 black balls. An urn is randomly selected, and then a ball inside of that urn is removed. We then repeat the process of selecting an urn and drawing out a ball, without returning the first ball. What is the probability that the first ball drawn was red, given that the second ball drawn was black?
|
$7 / 15$
This is a case of conditional probability; the answer is the probability that the first ball is red and the second ball is black, divided by the probability that the second ball is black.
First, we compute the numerator. If the first ball is drawn from Urn A, we have a probability of $2 / 6$ of getting a red ball, then a probability of $1 / 2$ of drawing the second ball from Urn B, and a further probability of $3 / 6$ of drawing a black ball. If the first ball is drawn from Urn B, we have probability $3 / 6$ of getting a red ball, then $1 / 2$ of drawing the second ball from Urn B, and $3 / 5$ of getting a black ball. So our numerator is
$$
\frac{1}{2}\left(\frac{2}{6} \cdot \frac{1}{2} \cdot \frac{3}{6}+\frac{3}{6} \cdot \frac{1}{2} \cdot \frac{3}{5}\right)=\frac{7}{60} .
$$
We similarly compute the denominator: if the first ball is drawn from Urn A, we have a probability of $1 / 2$ of drawing the second ball from Urn B, and $3 / 6$ of drawing a black ball. If the first ball is drawn from Urn B, then we have probability $3 / 6$ that it is red, in which case the second ball will be black with probability $(1 / 2) \cdot(3 / 5)$, and probability $3 / 6$ that the first ball is black, in which case the second is black with probability $(1 / 2) \cdot(2 / 5)$. So overall, our denominator is
$$
\frac{1}{2}\left(\frac{1}{2} \cdot \frac{3}{6}+\frac{3}{6}\left[\frac{1}{2} \cdot \frac{3}{5}+\frac{1}{2} \cdot \frac{2}{5}\right]\right)=\frac{1}{4}
$$
Thus, the desired conditional probability is $(7 / 60) /(1 / 4)=7 / 15$.
|
\frac{7}{15}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Urn A contains 4 white balls and 2 red balls. Urn B contains 3 red balls and 3 black balls. An urn is randomly selected, and then a ball inside of that urn is removed. We then repeat the process of selecting an urn and drawing out a ball, without returning the first ball. What is the probability that the first ball drawn was red, given that the second ball drawn was black?
|
$7 / 15$
This is a case of conditional probability; the answer is the probability that the first ball is red and the second ball is black, divided by the probability that the second ball is black.
First, we compute the numerator. If the first ball is drawn from Urn A, we have a probability of $2 / 6$ of getting a red ball, then a probability of $1 / 2$ of drawing the second ball from Urn B, and a further probability of $3 / 6$ of drawing a black ball. If the first ball is drawn from Urn B, we have probability $3 / 6$ of getting a red ball, then $1 / 2$ of drawing the second ball from Urn B, and $3 / 5$ of getting a black ball. So our numerator is
$$
\frac{1}{2}\left(\frac{2}{6} \cdot \frac{1}{2} \cdot \frac{3}{6}+\frac{3}{6} \cdot \frac{1}{2} \cdot \frac{3}{5}\right)=\frac{7}{60} .
$$
We similarly compute the denominator: if the first ball is drawn from Urn A, we have a probability of $1 / 2$ of drawing the second ball from Urn B, and $3 / 6$ of drawing a black ball. If the first ball is drawn from Urn B, then we have probability $3 / 6$ that it is red, in which case the second ball will be black with probability $(1 / 2) \cdot(3 / 5)$, and probability $3 / 6$ that the first ball is black, in which case the second is black with probability $(1 / 2) \cdot(2 / 5)$. So overall, our denominator is
$$
\frac{1}{2}\left(\frac{1}{2} \cdot \frac{3}{6}+\frac{3}{6}\left[\frac{1}{2} \cdot \frac{3}{5}+\frac{1}{2} \cdot \frac{2}{5}\right]\right)=\frac{1}{4}
$$
Thus, the desired conditional probability is $(7 / 60) /(1 / 4)=7 / 15$.
|
{
"resource_path": "HarvardMIT/segmented/en-72-2004-feb-comb-solutions.jsonl",
"problem_match": "\n8. ",
"solution_match": "\n## Solution: "
}
|
50a5cec5-17cf-5239-8e84-fd4879d5dd3a
| 69,556
|
A classroom consists of a $5 \times 5$ array of desks, to be filled by anywhere from 0 to 25 students, inclusive. No student will sit at a desk unless either all other desks in its row or all others in its column are filled (or both). Considering only the set of desks that are occupied (and not which student sits at each desk), how many possible arrangements are there?
|
962
The set of empty desks must be of the form (non-full rows) $\times$ (non-full columns): each empty desk is in a non-full column and a non-full row, and the given condition implies that each desk in such a position is empty. So if there are fewer than 25 students, then
both of these sets are nonempty; we have $2^{5}-1=31$ possible sets of non-full rows, and 31 sets of non-full columns, for 961 possible arrangements. Alternatively, there may be 25 students, and then only 1 arrangement is possible. Thus there are 962 possibilities altogether.
|
962
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
A classroom consists of a $5 \times 5$ array of desks, to be filled by anywhere from 0 to 25 students, inclusive. No student will sit at a desk unless either all other desks in its row or all others in its column are filled (or both). Considering only the set of desks that are occupied (and not which student sits at each desk), how many possible arrangements are there?
|
962
The set of empty desks must be of the form (non-full rows) $\times$ (non-full columns): each empty desk is in a non-full column and a non-full row, and the given condition implies that each desk in such a position is empty. So if there are fewer than 25 students, then
both of these sets are nonempty; we have $2^{5}-1=31$ possible sets of non-full rows, and 31 sets of non-full columns, for 961 possible arrangements. Alternatively, there may be 25 students, and then only 1 arrangement is possible. Thus there are 962 possibilities altogether.
|
{
"resource_path": "HarvardMIT/segmented/en-72-2004-feb-comb-solutions.jsonl",
"problem_match": "\n9. ",
"solution_match": "\nSolution: "
}
|
a3b8446c-47c4-5135-9e8f-3d5acfa7a015
| 611,216
|
In a game similar to three card monte, the dealer places three cards on the table: the queen of spades and two red cards. The cards are placed in a row, and the queen starts in the center; the card configuration is thus RQR. The dealer proceeds to move. With each move, the dealer randomly switches the center card with one of the two edge cards (so the configuration after the first move is either RRQ or QRR). What is the probability that, after 2004 moves, the center card is the queen?
|
$1 / 3+1 /\left(3 \cdot 2^{2003}\right)$
If the probability that the queen is the center card after move n is $p_{n}$, then the probability that the queen is an edge card is $1-p_{n}$, and the probability that the queen is the center card after move $n+1$ is $p_{n+1}=\left(1-p_{n}\right) / 2$. This recursion allows us to calculate the first few values of $p_{n}$. We might then notice in $1,0, \frac{1}{2}, \frac{1}{4}, \frac{3}{8}, \frac{5}{16}, \frac{11}{32}, \cdots$, that the value of each fraction is close to $1 / 3$, and getting closer for larger $n$. In fact subtracting $1 / 3$ from each fraction yields $\frac{2}{3},-\frac{1}{3}, \frac{1}{6},-\frac{1}{12}, \frac{1}{24},-\frac{1}{48}, \cdots$. This suggests the formula $p_{n}=\frac{1}{3}+\frac{2}{3}\left(-\frac{1}{2}\right)^{n}$, and one can then prove that this formula is in fact correct by induction. Thus, $p(2004)=\frac{1}{3}+\frac{2}{3}\left(-\frac{1}{2}\right)^{2004}=\frac{1}{3}+\frac{1}{3 \cdot 2^{2003}}$.
The recurrence can also be solved without guessing - by generating functions, for example, or by using the fundamental theorem of linear recurrences, which ensures that the solution is of the form $p_{n}=a+b(-1 / 2)^{n}$ for some constants $a, b$.
|
\frac{1}{3}+\frac{1}{3 \cdot 2^{2003}}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
In a game similar to three card monte, the dealer places three cards on the table: the queen of spades and two red cards. The cards are placed in a row, and the queen starts in the center; the card configuration is thus RQR. The dealer proceeds to move. With each move, the dealer randomly switches the center card with one of the two edge cards (so the configuration after the first move is either RRQ or QRR). What is the probability that, after 2004 moves, the center card is the queen?
|
$1 / 3+1 /\left(3 \cdot 2^{2003}\right)$
If the probability that the queen is the center card after move n is $p_{n}$, then the probability that the queen is an edge card is $1-p_{n}$, and the probability that the queen is the center card after move $n+1$ is $p_{n+1}=\left(1-p_{n}\right) / 2$. This recursion allows us to calculate the first few values of $p_{n}$. We might then notice in $1,0, \frac{1}{2}, \frac{1}{4}, \frac{3}{8}, \frac{5}{16}, \frac{11}{32}, \cdots$, that the value of each fraction is close to $1 / 3$, and getting closer for larger $n$. In fact subtracting $1 / 3$ from each fraction yields $\frac{2}{3},-\frac{1}{3}, \frac{1}{6},-\frac{1}{12}, \frac{1}{24},-\frac{1}{48}, \cdots$. This suggests the formula $p_{n}=\frac{1}{3}+\frac{2}{3}\left(-\frac{1}{2}\right)^{n}$, and one can then prove that this formula is in fact correct by induction. Thus, $p(2004)=\frac{1}{3}+\frac{2}{3}\left(-\frac{1}{2}\right)^{2004}=\frac{1}{3}+\frac{1}{3 \cdot 2^{2003}}$.
The recurrence can also be solved without guessing - by generating functions, for example, or by using the fundamental theorem of linear recurrences, which ensures that the solution is of the form $p_{n}=a+b(-1 / 2)^{n}$ for some constants $a, b$.
|
{
"resource_path": "HarvardMIT/segmented/en-72-2004-feb-comb-solutions.jsonl",
"problem_match": "\n10. ",
"solution_match": "\nSolution: "
}
|
3730124a-5928-59ee-9646-924cdf9f7dbd
| 69,580
|
What is the largest whole number that is equal to the product of its digits?
|
9
Suppose the number $n$ has $k+1$ digits, the first of which is $d$. Then the number is at least $d \cdot 10^{k}$. On the other hand, each of the digits after the first is at most 9 , so the product of the digits is at most $d \cdot 9^{k}$. Thus, if $n$ equals the product of its digits, then
$$
d \cdot 10^{k} \leq n \leq d \cdot 9^{k}
$$
which forces $k=0$, i.e., the number has only one digit. So $n=9$ is clearly the largest possible value.
|
9
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
What is the largest whole number that is equal to the product of its digits?
|
9
Suppose the number $n$ has $k+1$ digits, the first of which is $d$. Then the number is at least $d \cdot 10^{k}$. On the other hand, each of the digits after the first is at most 9 , so the product of the digits is at most $d \cdot 9^{k}$. Thus, if $n$ equals the product of its digits, then
$$
d \cdot 10^{k} \leq n \leq d \cdot 9^{k}
$$
which forces $k=0$, i.e., the number has only one digit. So $n=9$ is clearly the largest possible value.
|
{
"resource_path": "HarvardMIT/segmented/en-72-2004-feb-gen1-solutions.jsonl",
"problem_match": "\n2. ",
"solution_match": "\nSolution: "
}
|
70005019-b683-53a9-afef-c8dfb99d0461
| 611,217
|
Suppose $f$ is a function that assigns to each real number $x$ a value $f(x)$, and suppose the equation
$$
f\left(x_{1}+x_{2}+x_{3}+x_{4}+x_{5}\right)=f\left(x_{1}\right)+f\left(x_{2}\right)+f\left(x_{3}\right)+f\left(x_{4}\right)+f\left(x_{5}\right)-8
$$
holds for all real numbers $x_{1}, x_{2}, x_{3}, x_{4}, x_{5}$. What is $f(0)$ ?
|
2
Plug in $x_{1}=x_{2}=x_{3}=x_{4}=x_{5}=0$. Then the equation reads $f(0)=5 f(0)-8$, so $4 f(0)=8$, so $f(0)=2$.
|
2
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Suppose $f$ is a function that assigns to each real number $x$ a value $f(x)$, and suppose the equation
$$
f\left(x_{1}+x_{2}+x_{3}+x_{4}+x_{5}\right)=f\left(x_{1}\right)+f\left(x_{2}\right)+f\left(x_{3}\right)+f\left(x_{4}\right)+f\left(x_{5}\right)-8
$$
holds for all real numbers $x_{1}, x_{2}, x_{3}, x_{4}, x_{5}$. What is $f(0)$ ?
|
2
Plug in $x_{1}=x_{2}=x_{3}=x_{4}=x_{5}=0$. Then the equation reads $f(0)=5 f(0)-8$, so $4 f(0)=8$, so $f(0)=2$.
|
{
"resource_path": "HarvardMIT/segmented/en-72-2004-feb-gen1-solutions.jsonl",
"problem_match": "\n3. ",
"solution_match": "\nSolution: "
}
|
4ba204e6-601d-5a60-9ed7-d91a1cef6063
| 611,218
|
A rectangle has perimeter 10 and diagonal $\sqrt{15}$. What is its area?
|
5
If the sides are $x$ and $y$, we have $2 x+2 y=10$, so $x+y=5$, and $\sqrt{x^{2}+y^{2}}=\sqrt{15}$, so $x^{2}+y^{2}=15$. Squaring the first equation gives $x^{2}+2 x y+y^{2}=25$, and subtracting the second equation gives $2 x y=10$, so the area is $x y=5$.
|
5
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
A rectangle has perimeter 10 and diagonal $\sqrt{15}$. What is its area?
|
5
If the sides are $x$ and $y$, we have $2 x+2 y=10$, so $x+y=5$, and $\sqrt{x^{2}+y^{2}}=\sqrt{15}$, so $x^{2}+y^{2}=15$. Squaring the first equation gives $x^{2}+2 x y+y^{2}=25$, and subtracting the second equation gives $2 x y=10$, so the area is $x y=5$.
|
{
"resource_path": "HarvardMIT/segmented/en-72-2004-feb-gen1-solutions.jsonl",
"problem_match": "\n5. ",
"solution_match": "\nSolution: "
}
|
36fef509-8684-5776-bfb6-443d5f917190
| 611,219
|
Let $A C E$ be a triangle with a point $B$ on segment $A C$ and a point $D$ on segment $C E$ such that $B D$ is parallel to $A E$. A point $Y$ is chosen on segment $A E$, and segment $C Y$ is drawn. Let $X$ be the intersection of $C Y$ and $B D$. If $C X=5, X Y=3$, what is the ratio of the area of trapezoid $A B D E$ to the area of triangle $B C D$ ?
|
$39 / 25$
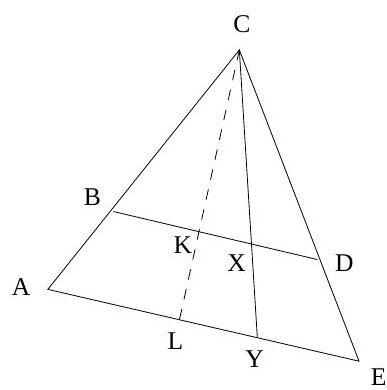
Draw the altitude from $C$ to $A E$, intersecting line $B D$ at $K$ and line $A E$ at $L$. Then $C K$ is the altitude of triangle $B C D$, so triangles $C K X$ and $C L Y$ are similar. Since $C Y / C X=8 / 5, C L / C K=8 / 5$. Also triangles $C K B$ and $C L A$ are similar, so that $C A / C B=8 / 5$, and triangles $B C D$ and $A C E$ are similar, so that $A E / B D=8 / 5$. The area of $A C E$ is $(1 / 2)(A E)(C L)$, and the area of $B C D$ is $(1 / 2)(B D)(C K)$, so the
ratio of the area of $A C E$ to the area of $B C D$ is $64 / 25$. Therefore, the ratio of the area of $A B D E$ to the area of $B C D$ is $39 / 25$.
|
\frac{39}{25}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $A C E$ be a triangle with a point $B$ on segment $A C$ and a point $D$ on segment $C E$ such that $B D$ is parallel to $A E$. A point $Y$ is chosen on segment $A E$, and segment $C Y$ is drawn. Let $X$ be the intersection of $C Y$ and $B D$. If $C X=5, X Y=3$, what is the ratio of the area of trapezoid $A B D E$ to the area of triangle $B C D$ ?
|
$39 / 25$

Draw the altitude from $C$ to $A E$, intersecting line $B D$ at $K$ and line $A E$ at $L$. Then $C K$ is the altitude of triangle $B C D$, so triangles $C K X$ and $C L Y$ are similar. Since $C Y / C X=8 / 5, C L / C K=8 / 5$. Also triangles $C K B$ and $C L A$ are similar, so that $C A / C B=8 / 5$, and triangles $B C D$ and $A C E$ are similar, so that $A E / B D=8 / 5$. The area of $A C E$ is $(1 / 2)(A E)(C L)$, and the area of $B C D$ is $(1 / 2)(B D)(C K)$, so the
ratio of the area of $A C E$ to the area of $B C D$ is $64 / 25$. Therefore, the ratio of the area of $A B D E$ to the area of $B C D$ is $39 / 25$.
|
{
"resource_path": "HarvardMIT/segmented/en-72-2004-feb-gen1-solutions.jsonl",
"problem_match": "\n7. ",
"solution_match": "\nSolution: "
}
|
089f4e0c-35b5-5621-9d46-a66438384290
| 611,221
|
You have a $10 \times 10$ grid of squares. You write a number in each square as follows: you write $1,2,3, \ldots, 10$ from left to right across the top row, then $11,12, \ldots, 20$ across the second row, and so on, ending with a 100 in the bottom right square. You then write a second number in each square, writing $1,2, \ldots, 10$ in the first column (from top to bottom), then $11,12, \ldots, 20$ in the second column, and so forth.
When this process is finished, how many squares will have the property that their two numbers sum to 101 ?
|
10
The number in the $i$ th row, $j$ th column will receive the numbers $10(i-1)+j$ and $10(j-1)+i$, so the question is how many pairs $(i, j)(1 \leq i, j \leq 10)$ will have
$$
101=[10(i-1)+j]+[10(j-1)+i] \quad \Leftrightarrow \quad 121=11 i+11 j=11(i+j) .
$$
Now it is clear that this is achieved by the ten pairs $(1,10),(2,9),(3,8), \ldots,(10,1)$ and no others.
|
10
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
You have a $10 \times 10$ grid of squares. You write a number in each square as follows: you write $1,2,3, \ldots, 10$ from left to right across the top row, then $11,12, \ldots, 20$ across the second row, and so on, ending with a 100 in the bottom right square. You then write a second number in each square, writing $1,2, \ldots, 10$ in the first column (from top to bottom), then $11,12, \ldots, 20$ in the second column, and so forth.
When this process is finished, how many squares will have the property that their two numbers sum to 101 ?
|
10
The number in the $i$ th row, $j$ th column will receive the numbers $10(i-1)+j$ and $10(j-1)+i$, so the question is how many pairs $(i, j)(1 \leq i, j \leq 10)$ will have
$$
101=[10(i-1)+j]+[10(j-1)+i] \quad \Leftrightarrow \quad 121=11 i+11 j=11(i+j) .
$$
Now it is clear that this is achieved by the ten pairs $(1,10),(2,9),(3,8), \ldots,(10,1)$ and no others.
|
{
"resource_path": "HarvardMIT/segmented/en-72-2004-feb-gen1-solutions.jsonl",
"problem_match": "\n8. ",
"solution_match": "\nSolution: "
}
|
2bca8b37-87df-55f7-8b02-74dc41c390af
| 611,222
|
A floor is tiled with equilateral triangles of side length 1 , as shown. If you drop a needle of length 2 somewhere on the floor, what is the largest number of triangles it could end up intersecting? (Only count the triangles whose interiors are met by the needle - touching along edges or at corners doesn't qualify.)

|
8
Let $L$ be the union of all the lines of the tiling. Imagine walking from one end of the needle to the other. We enter a new triangle precisely when we cross one of the lines of the tiling. Therefore, the problem is equivalent to maximizing the number of times the needle crosses $L$. Now, the lines of the tiling each run in one of three directions. It is clear that the needle cannot cross more than three lines in any given direction, since the lines are a distance $\sqrt{3} / 2$ apart and the needle would therefore have to be of length greater than $3 \sqrt{3} / 2>2$. Moreover, it cannot cross three lines in each of two different directions. To see this, notice that its endpoints would have to lie in either the two light-shaded regions or the two dark-shaded regions shown, but the closest two points of such opposite regions are at a distance of 2 (twice the length of a side of a triangle), so the needle cannot penetrate both regions.

Therefore, the needle can cross at most three lines in one direction and two lines in each of the other two directions, making for a maximum of $3+2+2=7$ crossings and $7+1=8$ triangles intersected. The example shows that 8 is achievable, as long as the needle has length greater than $\sqrt{3}<2$.
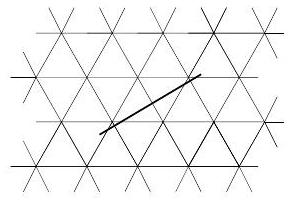
|
8
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
A floor is tiled with equilateral triangles of side length 1 , as shown. If you drop a needle of length 2 somewhere on the floor, what is the largest number of triangles it could end up intersecting? (Only count the triangles whose interiors are met by the needle - touching along edges or at corners doesn't qualify.)

|
8
Let $L$ be the union of all the lines of the tiling. Imagine walking from one end of the needle to the other. We enter a new triangle precisely when we cross one of the lines of the tiling. Therefore, the problem is equivalent to maximizing the number of times the needle crosses $L$. Now, the lines of the tiling each run in one of three directions. It is clear that the needle cannot cross more than three lines in any given direction, since the lines are a distance $\sqrt{3} / 2$ apart and the needle would therefore have to be of length greater than $3 \sqrt{3} / 2>2$. Moreover, it cannot cross three lines in each of two different directions. To see this, notice that its endpoints would have to lie in either the two light-shaded regions or the two dark-shaded regions shown, but the closest two points of such opposite regions are at a distance of 2 (twice the length of a side of a triangle), so the needle cannot penetrate both regions.

Therefore, the needle can cross at most three lines in one direction and two lines in each of the other two directions, making for a maximum of $3+2+2=7$ crossings and $7+1=8$ triangles intersected. The example shows that 8 is achievable, as long as the needle has length greater than $\sqrt{3}<2$.

|
{
"resource_path": "HarvardMIT/segmented/en-72-2004-feb-gen1-solutions.jsonl",
"problem_match": "\n10. ",
"solution_match": "\nSolution: "
}
|
59f72bb0-b1f5-5094-8a1d-8e1048643096
| 611,223
|
Find the largest number $n$ such that (2004!)! is divisible by (( $n!)!)!$.
|
6
For positive integers $a, b$, we have
$$
a!\mid b!\quad \Leftrightarrow \quad a!\leq b!\quad \Leftrightarrow \quad a \leq b
$$
Thus,
$$
((n!)!)!\mid(2004!)!\Leftrightarrow(n!)!\leq 2004!\Leftrightarrow n!\leq 2004 \Leftrightarrow n \leq 6 .
$$
|
6
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Find the largest number $n$ such that (2004!)! is divisible by (( $n!)!)!$.
|
6
For positive integers $a, b$, we have
$$
a!\mid b!\quad \Leftrightarrow \quad a!\leq b!\quad \Leftrightarrow \quad a \leq b
$$
Thus,
$$
((n!)!)!\mid(2004!)!\Leftrightarrow(n!)!\leq 2004!\Leftrightarrow n!\leq 2004 \Leftrightarrow n \leq 6 .
$$
|
{
"resource_path": "HarvardMIT/segmented/en-72-2004-feb-gen2-solutions.jsonl",
"problem_match": "\n1. ",
"solution_match": "\nSolution: "
}
|
ebf325e8-d6b0-5ebc-bab7-db7f2760decf
| 611,224
|
How many ordered pairs of integers $(a, b)$ satisfy all of the following inequalities?
$$
\begin{aligned}
a^{2}+b^{2} & <16 \\
a^{2}+b^{2} & <8 a \\
a^{2}+b^{2} & <8 b
\end{aligned}
$$
|
This is easiest to see by simply graphing the inequalities. They correspond to the (strict) interiors of circles of radius 4 and centers at $(0,0),(4,0),(0,4)$, respectively. So we can see that there are 6 lattice points in their intersection (circled in the figure).
|
6
|
Yes
|
Yes
|
math-word-problem
|
Inequalities
|
How many ordered pairs of integers $(a, b)$ satisfy all of the following inequalities?
$$
\begin{aligned}
a^{2}+b^{2} & <16 \\
a^{2}+b^{2} & <8 a \\
a^{2}+b^{2} & <8 b
\end{aligned}
$$
|
This is easiest to see by simply graphing the inequalities. They correspond to the (strict) interiors of circles of radius 4 and centers at $(0,0),(4,0),(0,4)$, respectively. So we can see that there are 6 lattice points in their intersection (circled in the figure).

|
{
"resource_path": "HarvardMIT/segmented/en-72-2004-feb-gen2-solutions.jsonl",
"problem_match": "\n3. ",
"solution_match": "\n## Solution:\n\n"
}
|
0c9fdc68-f128-54ac-987c-d331beac2578
| 611,225
|
A horse stands at the corner of a chessboard, a white square. With each jump, the horse can move either two squares horizontally and one vertically or two vertically and one horizontally (like a knight moves). The horse earns two carrots every time it lands on a black square, but it must pay a carrot in rent to rabbit who owns the chessboard for every move it makes. When the horse reaches the square on which it began, it can leave. What is the maximum number of carrots the horse can earn without touching any square more than twice?

|
0
The horse must alternate white and black squares, and it ends on the same square where it started. Thus it lands on the same number of black squares ( $b$ ) as white squares $(w)$. Thus, its net earnings will be $2 b-(b+w)=b-w=0$ carrots, regardless of its path.
|
0
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
A horse stands at the corner of a chessboard, a white square. With each jump, the horse can move either two squares horizontally and one vertically or two vertically and one horizontally (like a knight moves). The horse earns two carrots every time it lands on a black square, but it must pay a carrot in rent to rabbit who owns the chessboard for every move it makes. When the horse reaches the square on which it began, it can leave. What is the maximum number of carrots the horse can earn without touching any square more than twice?

|
0
The horse must alternate white and black squares, and it ends on the same square where it started. Thus it lands on the same number of black squares ( $b$ ) as white squares $(w)$. Thus, its net earnings will be $2 b-(b+w)=b-w=0$ carrots, regardless of its path.
|
{
"resource_path": "HarvardMIT/segmented/en-72-2004-feb-gen2-solutions.jsonl",
"problem_match": "\n4. ",
"solution_match": "\n## Solution: "
}
|
4507c131-a285-53c9-8291-62605286aca5
| 611,226
|
Eight strangers are preparing to play bridge. How many ways can they be grouped into two bridge games - that is, into unordered pairs of unordered pairs of people?
|
315
Putting 8 people into 4 pairs and putting those 4 pairs into 2 pairs of pairs are independent. If the people are numbered from 1 to 8 , there are 7 ways to choose the person to pair with person 1. Then there are 5 ways to choose the person to pair with the person who has the lowest remaining number, 3 ways to choose the next, and 1 way to choose the last (because there are only 2 people remaining). Thus, there are $7 \cdot 5 \cdot 3 \cdot 1$ ways to assign 8 people to pairs and similarly there are $3 \cdot 1$ ways to assign 4 pairs to 2 pairs of pairs, so there are $7 \cdot 5 \cdot 3 \cdot 3=315$ ways.
|
315
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Eight strangers are preparing to play bridge. How many ways can they be grouped into two bridge games - that is, into unordered pairs of unordered pairs of people?
|
315
Putting 8 people into 4 pairs and putting those 4 pairs into 2 pairs of pairs are independent. If the people are numbered from 1 to 8 , there are 7 ways to choose the person to pair with person 1. Then there are 5 ways to choose the person to pair with the person who has the lowest remaining number, 3 ways to choose the next, and 1 way to choose the last (because there are only 2 people remaining). Thus, there are $7 \cdot 5 \cdot 3 \cdot 1$ ways to assign 8 people to pairs and similarly there are $3 \cdot 1$ ways to assign 4 pairs to 2 pairs of pairs, so there are $7 \cdot 5 \cdot 3 \cdot 3=315$ ways.
|
{
"resource_path": "HarvardMIT/segmented/en-72-2004-feb-gen2-solutions.jsonl",
"problem_match": "\n5. ",
"solution_match": "\nSolution:\n"
}
|
87a1eff3-1c85-589f-acd6-496dcef1ff14
| 611,227
|
$a$ and $b$ are positive integers. When written in binary, $a$ has 2004 1's, and $b$ has 2005 1's (not necessarily consecutive). What is the smallest number of 1 's $a+b$ could possibly have?
|
1
Consider the following addition:
$$
=\begin{array}{r}
111 \cdots 100 \cdots 01 \\
+
\end{array} \frac{11 \cdots 11}{1000 \cdots \cdots \cdots 00}
$$
By making the blocks of 1 's and 0 's appropriately long, we can ensure that the addends respectively contain 2004 and 2005 1's. (To be precise, we get $a=2^{4008}-2^{2005}+1$ and $b=2^{2005}-1$.) Then the sum has only one 1 . And clearly it is not possible to get any less than one 1.
|
1
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
$a$ and $b$ are positive integers. When written in binary, $a$ has 2004 1's, and $b$ has 2005 1's (not necessarily consecutive). What is the smallest number of 1 's $a+b$ could possibly have?
|
1
Consider the following addition:
$$
=\begin{array}{r}
111 \cdots 100 \cdots 01 \\
+
\end{array} \frac{11 \cdots 11}{1000 \cdots \cdots \cdots 00}
$$
By making the blocks of 1 's and 0 's appropriately long, we can ensure that the addends respectively contain 2004 and 2005 1's. (To be precise, we get $a=2^{4008}-2^{2005}+1$ and $b=2^{2005}-1$.) Then the sum has only one 1 . And clearly it is not possible to get any less than one 1.
|
{
"resource_path": "HarvardMIT/segmented/en-72-2004-feb-gen2-solutions.jsonl",
"problem_match": "\n6. ",
"solution_match": "\nSolution: "
}
|
a0f12dd5-d9a2-5868-8aea-1aa3da4ef42e
| 611,228
|
Farmer John is grazing his cows at the origin. There is a river that runs east to west 50 feet north of the origin. The barn is 100 feet to the south and 80 feet to the east of the origin. Farmer John leads his cows to the river to take a swim, then the cows leave the river from the same place they entered and Farmer John leads them to the barn. He does this using the shortest path possible, and the total distance he travels is $d$ feet. Find the value of $d$.
|
$\square$
Suppose we move the barn to its reflection across the river's edge. Then paths from the origin to the river and then to the old barn location correspond to paths from the origin to the river and then to the new barn location, by reflecting the second part of the path across the river, and corresponding paths have the same length. Now the shortest path from the origin to the river and then to the new barn location is a straight line. The new barn location is 200 feet north and 80 feet east of the origin, so the value of $d$ is $\sqrt{200^{2}+80^{2}}=40 \sqrt{29}$.
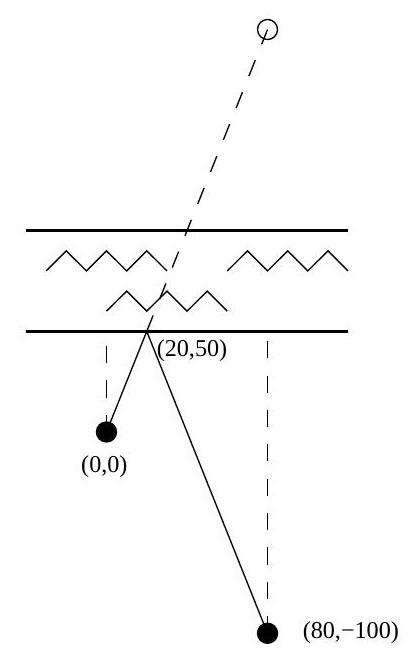
|
40 \sqrt{29}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Farmer John is grazing his cows at the origin. There is a river that runs east to west 50 feet north of the origin. The barn is 100 feet to the south and 80 feet to the east of the origin. Farmer John leads his cows to the river to take a swim, then the cows leave the river from the same place they entered and Farmer John leads them to the barn. He does this using the shortest path possible, and the total distance he travels is $d$ feet. Find the value of $d$.
|
$\square$
Suppose we move the barn to its reflection across the river's edge. Then paths from the origin to the river and then to the old barn location correspond to paths from the origin to the river and then to the new barn location, by reflecting the second part of the path across the river, and corresponding paths have the same length. Now the shortest path from the origin to the river and then to the new barn location is a straight line. The new barn location is 200 feet north and 80 feet east of the origin, so the value of $d$ is $\sqrt{200^{2}+80^{2}}=40 \sqrt{29}$.

|
{
"resource_path": "HarvardMIT/segmented/en-72-2004-feb-gen2-solutions.jsonl",
"problem_match": "\n7. ",
"solution_match": "\nSolution: "
}
|
326032f9-3d06-5bb8-9085-b879f7c22b5b
| 611,229
|
A freight train leaves the town of Jenkinsville at 1:00 PM traveling due east at constant speed. Jim, a hobo, sneaks onto the train and falls asleep. At the same time, Julie leaves Jenkinsville on her bicycle, traveling along a straight road in a northeasterly direction (but not due northeast) at 10 miles per hour. At 1:12 PM, Jim rolls over in his sleep and falls from the train onto the side of the tracks. He wakes up and immediately begins walking at 3.5 miles per hour directly towards the road on which Julie is riding. Jim reaches the road at 2:12 PM, just as Julie is riding by. What is the speed of the train in miles per hour?
|
62.5
Julie's distance is $(10 \mathrm{mph}) \cdot(6 / 5 \mathrm{hrs})=12$ miles. Jim's walking distance, after falling off the train, is $(3.5 \mathrm{mph}) \cdot(1 \mathrm{hr})=3.5$ miles at a right angle to the road. Therefore, Jim rode the train for $\sqrt{12^{2}+3.5^{2}}=\frac{1}{2} \sqrt{24^{2}+7^{2}}=25 / 2$ miles, and its speed is $(25 / 2 \mathrm{mi}) /(1 / 5 \mathrm{hr})=62.5 \mathrm{mph}$.
|
62.5
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
A freight train leaves the town of Jenkinsville at 1:00 PM traveling due east at constant speed. Jim, a hobo, sneaks onto the train and falls asleep. At the same time, Julie leaves Jenkinsville on her bicycle, traveling along a straight road in a northeasterly direction (but not due northeast) at 10 miles per hour. At 1:12 PM, Jim rolls over in his sleep and falls from the train onto the side of the tracks. He wakes up and immediately begins walking at 3.5 miles per hour directly towards the road on which Julie is riding. Jim reaches the road at 2:12 PM, just as Julie is riding by. What is the speed of the train in miles per hour?
|
62.5
Julie's distance is $(10 \mathrm{mph}) \cdot(6 / 5 \mathrm{hrs})=12$ miles. Jim's walking distance, after falling off the train, is $(3.5 \mathrm{mph}) \cdot(1 \mathrm{hr})=3.5$ miles at a right angle to the road. Therefore, Jim rode the train for $\sqrt{12^{2}+3.5^{2}}=\frac{1}{2} \sqrt{24^{2}+7^{2}}=25 / 2$ miles, and its speed is $(25 / 2 \mathrm{mi}) /(1 / 5 \mathrm{hr})=62.5 \mathrm{mph}$.
|
{
"resource_path": "HarvardMIT/segmented/en-72-2004-feb-gen2-solutions.jsonl",
"problem_match": "\n8. ",
"solution_match": "\nSolution: "
}
|
39f693fd-c0e7-58ab-8d90-31df242af4b1
| 611,230
|
Given is a regular tetrahedron of volume 1 . We obtain a second regular tetrahedron by reflecting the given one through its center. What is the volume of their intersection?
|
$1 / 2$
Imagine placing the tetrahedron $A B C D$ flat on a table with vertex $A$ at the top. By vectors or otherwise, we see that the center is $3 / 4$ of the way from $A$ to the bottom face, so the reflection of this face lies in a horizontal plane halfway between $A$ and $B C D$. In particular, it cuts off the smaller tetrahedron obtained by scaling the original tetrahedron by a factor of $1 / 2$ about $A$. Similarly, the reflections of the other three faces cut off tetrahedra obtained by scaling $A B C D$ by $1 / 2$ about $B, C$, and $D$. On the other hand, the octahedral piece remaining remaining after we remove these four smaller tetrahedra is in the intersection of $A B C D$ with its reflection, since the reflection sends this piece to itself. So the answer we seek is just the volume of this piece, which is
(volume of $A B C D)-4 \cdot($ volume of $A B C D$ scaled by a factor of $1 / 2$ )
$$
=1-4(1 / 2)^{3}=1 / 2 .
$$
|
\frac{1}{2}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Given is a regular tetrahedron of volume 1 . We obtain a second regular tetrahedron by reflecting the given one through its center. What is the volume of their intersection?
|
$1 / 2$
Imagine placing the tetrahedron $A B C D$ flat on a table with vertex $A$ at the top. By vectors or otherwise, we see that the center is $3 / 4$ of the way from $A$ to the bottom face, so the reflection of this face lies in a horizontal plane halfway between $A$ and $B C D$. In particular, it cuts off the smaller tetrahedron obtained by scaling the original tetrahedron by a factor of $1 / 2$ about $A$. Similarly, the reflections of the other three faces cut off tetrahedra obtained by scaling $A B C D$ by $1 / 2$ about $B, C$, and $D$. On the other hand, the octahedral piece remaining remaining after we remove these four smaller tetrahedra is in the intersection of $A B C D$ with its reflection, since the reflection sends this piece to itself. So the answer we seek is just the volume of this piece, which is
(volume of $A B C D)-4 \cdot($ volume of $A B C D$ scaled by a factor of $1 / 2$ )
$$
=1-4(1 / 2)^{3}=1 / 2 .
$$
|
{
"resource_path": "HarvardMIT/segmented/en-72-2004-feb-gen2-solutions.jsonl",
"problem_match": "\n9. ",
"solution_match": "\nSolution: "
}
|
a6c4c4e0-5b83-5aba-bab4-15ecc2b28795
| 611,231
|
A lattice point is a point whose coordinates are both integers. Suppose Johann walks in a line from the point $(0,2004)$ to a random lattice point in the interior (not on the boundary) of the square with vertices $(0,0),(0,99),(99,99),(99,0)$. What is the probability that his path, including the endpoints, contains an even number of lattice points?
|
$3 / 4$
If Johann picks the point $(a, b)$, the path will contain $\operatorname{gcd}(a, 2004-b)+1$ points. There will be an odd number of points in the path if $\operatorname{gcd}(a, 2004-b)$ is even, which is true if and only if $a$ and $b$ are both even. Since there are $49^{2}$ points with $a, b$ both even and $98^{2}$ total points, the probability that the path contains an even number of points is
$$
\frac{98^{2}-49^{2}}{98^{2}}=\frac{49^{2}\left(2^{2}-1^{2}\right)}{49^{2}\left(2^{2}\right)}=\frac{3}{4} .
$$
|
\frac{3}{4}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
A lattice point is a point whose coordinates are both integers. Suppose Johann walks in a line from the point $(0,2004)$ to a random lattice point in the interior (not on the boundary) of the square with vertices $(0,0),(0,99),(99,99),(99,0)$. What is the probability that his path, including the endpoints, contains an even number of lattice points?
|
$3 / 4$
If Johann picks the point $(a, b)$, the path will contain $\operatorname{gcd}(a, 2004-b)+1$ points. There will be an odd number of points in the path if $\operatorname{gcd}(a, 2004-b)$ is even, which is true if and only if $a$ and $b$ are both even. Since there are $49^{2}$ points with $a, b$ both even and $98^{2}$ total points, the probability that the path contains an even number of points is
$$
\frac{98^{2}-49^{2}}{98^{2}}=\frac{49^{2}\left(2^{2}-1^{2}\right)}{49^{2}\left(2^{2}\right)}=\frac{3}{4} .
$$
|
{
"resource_path": "HarvardMIT/segmented/en-72-2004-feb-gen2-solutions.jsonl",
"problem_match": "\n10. ",
"solution_match": "\nSolution: "
}
|
0f55c310-4e96-55be-989b-cc3b86488b1f
| 611,232
|
In trapezoid $A B C D, A D$ is parallel to $B C . \angle A=\angle D=45^{\circ}$, while $\angle B=\angle C=135^{\circ}$. If $A B=6$ and the area of $A B C D$ is 30 , find $B C$.
|
$\square$
Draw altitudes from $B$ and $C$ to $A D$ and label the points of intersection $X$ and $Y$, respectively. Then $A B X$ and $C D Y$ are $45^{\circ}-45^{\circ}-90^{\circ}$ triangles with $B X=C Y=3 \sqrt{2}$. So, the area of $A B X$ and the area of $C D Y$ are each 9 , meaning that the area of rectangle $B C Y X$ is 12. Since $B X=3 \sqrt{2}, B C=12 /(3 \sqrt{2})=2 \sqrt{2}$.
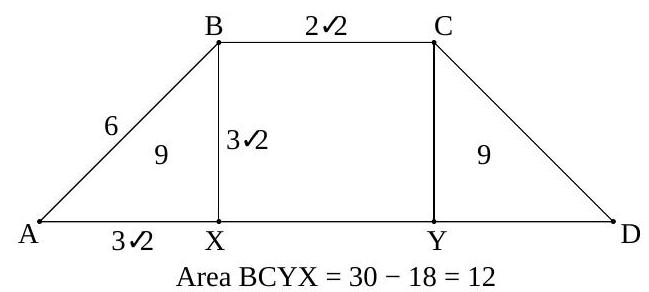
|
2\sqrt{2}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
In trapezoid $A B C D, A D$ is parallel to $B C . \angle A=\angle D=45^{\circ}$, while $\angle B=\angle C=135^{\circ}$. If $A B=6$ and the area of $A B C D$ is 30 , find $B C$.
|
$\square$
Draw altitudes from $B$ and $C$ to $A D$ and label the points of intersection $X$ and $Y$, respectively. Then $A B X$ and $C D Y$ are $45^{\circ}-45^{\circ}-90^{\circ}$ triangles with $B X=C Y=3 \sqrt{2}$. So, the area of $A B X$ and the area of $C D Y$ are each 9 , meaning that the area of rectangle $B C Y X$ is 12. Since $B X=3 \sqrt{2}, B C=12 /(3 \sqrt{2})=2 \sqrt{2}$.

|
{
"resource_path": "HarvardMIT/segmented/en-72-2004-feb-geo-solutions.jsonl",
"problem_match": "\n1. ",
"solution_match": "\nSolution: "
}
|
eb23a18f-ed74-50fd-9b5a-2d57da25feff
| 611,233
|
A parallelogram has 3 of its vertices at $(1,2),(3,8)$, and $(4,1)$. Compute the sum of the possible $x$-coordinates for the 4th vertex.
|
8
There are 3 possible locations for the 4th vertex. Let $(a, b)$ be its coordinates. If it is opposite to vertex $(1,2)$, then since the midpoints of the diagonals of a parallelogram coincide, we get $\left(\frac{a+1}{2}, \frac{b+2}{2}\right)=\left(\frac{3+4}{2}, \frac{8+1}{2}\right)$. Thus $(a, b)=(6,7)$. By similar reasoning for the other possible choices of opposite vertex, the other possible positions for the fourth vertex are $(0,9)$ and $(2,-5)$, and all of these choices do give parallelograms. So the answer is $6+0+2=8$.
|
8
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
A parallelogram has 3 of its vertices at $(1,2),(3,8)$, and $(4,1)$. Compute the sum of the possible $x$-coordinates for the 4th vertex.
|
8
There are 3 possible locations for the 4th vertex. Let $(a, b)$ be its coordinates. If it is opposite to vertex $(1,2)$, then since the midpoints of the diagonals of a parallelogram coincide, we get $\left(\frac{a+1}{2}, \frac{b+2}{2}\right)=\left(\frac{3+4}{2}, \frac{8+1}{2}\right)$. Thus $(a, b)=(6,7)$. By similar reasoning for the other possible choices of opposite vertex, the other possible positions for the fourth vertex are $(0,9)$ and $(2,-5)$, and all of these choices do give parallelograms. So the answer is $6+0+2=8$.
|
{
"resource_path": "HarvardMIT/segmented/en-72-2004-feb-geo-solutions.jsonl",
"problem_match": "\n2. ",
"solution_match": "\nSolution: "
}
|
58c787ed-aad9-563f-8f1d-58a966871f77
| 611,234
|
A swimming pool is in the shape of a circle with diameter 60 ft . The depth varies linearly along the east-west direction from 3 ft at the shallow end in the east to 15 ft at the diving end in the west (this is so that divers look impressive against the sunset) but does not vary at all along the north-south direction. What is the volume of the pool, in $\mathrm{ft}^{3}$ ?
|
$8100 \pi$
Take another copy of the pool, turn it upside-down, and put the two together to form a cylinder. It has height 18 ft and radius 30 ft , so the volume is $\pi(30 \mathrm{ft})^{2} \cdot 18 \mathrm{ft}=$ $16200 \pi \mathrm{ft}^{3}$; since our pool is only half of that, the answer is $8100 \pi \mathrm{ft}^{3}$.
|
8100 \pi
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
A swimming pool is in the shape of a circle with diameter 60 ft . The depth varies linearly along the east-west direction from 3 ft at the shallow end in the east to 15 ft at the diving end in the west (this is so that divers look impressive against the sunset) but does not vary at all along the north-south direction. What is the volume of the pool, in $\mathrm{ft}^{3}$ ?
|
$8100 \pi$
Take another copy of the pool, turn it upside-down, and put the two together to form a cylinder. It has height 18 ft and radius 30 ft , so the volume is $\pi(30 \mathrm{ft})^{2} \cdot 18 \mathrm{ft}=$ $16200 \pi \mathrm{ft}^{3}$; since our pool is only half of that, the answer is $8100 \pi \mathrm{ft}^{3}$.
|
{
"resource_path": "HarvardMIT/segmented/en-72-2004-feb-geo-solutions.jsonl",
"problem_match": "\n3. ",
"solution_match": "\nSolution: "
}
|
68919fe9-37ee-53b1-921b-3305a6714e2b
| 611,235
|
$P$ is inside rectangle $A B C D . P A=2, P B=3$, and $P C=10$. Find $P D$.
|
$\sqrt{95}$
Draw perpendiculars from $P$ to $E$ on $A B, F$ on $B C, G$ on $C D$, and $H$ on $D A$, and let $A H=B F=w, H D=F C=x, A E=D G=y$, and $E B=G C=z$. Then $P A^{2}=w^{2}+y^{2}, P B^{2}=w^{2}+z^{2}, P C^{2}=x^{2}+z^{2}$, and $P D^{2}=x^{2}+y^{2}$. Adding and subtracting, we see that $P D^{2}=P A^{2}-P B^{2}+P C^{2}=95$, so $P D=\sqrt{95}$.
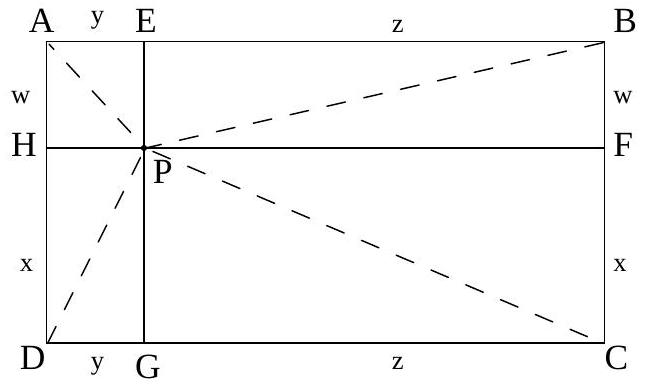
|
\sqrt{95}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
$P$ is inside rectangle $A B C D . P A=2, P B=3$, and $P C=10$. Find $P D$.
|
$\sqrt{95}$
Draw perpendiculars from $P$ to $E$ on $A B, F$ on $B C, G$ on $C D$, and $H$ on $D A$, and let $A H=B F=w, H D=F C=x, A E=D G=y$, and $E B=G C=z$. Then $P A^{2}=w^{2}+y^{2}, P B^{2}=w^{2}+z^{2}, P C^{2}=x^{2}+z^{2}$, and $P D^{2}=x^{2}+y^{2}$. Adding and subtracting, we see that $P D^{2}=P A^{2}-P B^{2}+P C^{2}=95$, so $P D=\sqrt{95}$.

|
{
"resource_path": "HarvardMIT/segmented/en-72-2004-feb-geo-solutions.jsonl",
"problem_match": "\n4. ",
"solution_match": "\n## Solution: "
}
|
e7d87fbf-b097-51a1-a2f0-a9cf5b179479
| 611,236
|
Find the area of the region of the $x y$-plane defined by the inequality $|x|+|y|+|x+y| \leq 1$.
|
$3 / 4$
To graph this region we divide the $x y$-plane into six sectors depending on which of $x, y, x+y$ are $\geq 0$, or $\leq 0$. The inequality simplifies in each case:
| Sector | Inequality | Simplified inequality |
| :---: | :---: | :---: |
| $x \geq 0, y \geq 0, x+y \geq 0$ | $x+y+(x+y) \leq 1$ | $x+y \leq 1 / 2$ |
| $x \geq 0, y \leq 0, x+y \geq 0$ | $x-y+(x+y) \leq 1$ | $x \leq 1 / 2$ |
| $x \geq 0, y \leq 0, x+y \leq 0$ | $x-y-(x+y) \leq 1$ | $y \geq-1 / 2$ |
| $x \leq 0, y \geq 0, x+y \geq 0$ | $-x+y+(x+y) \leq 1$ | $y \leq 1 / 2$ |
| $x \leq 0, y \geq 0, x+y \leq 0$ | $-x+y-(x+y) \leq 1$ | $x \geq-1 / 2$ |
| $x \leq 0, y \leq 0, x+y \leq 0$ | $-x-y-(x+y) \leq 1$ | $x+y \geq-1 / 2$ |
We then draw the region; we get a hexagon as shown. The hexagon intersects each region in an isosceles right triangle of area $1 / 8$, so the total area is $6 \cdot 1 / 8=3 / 4$.
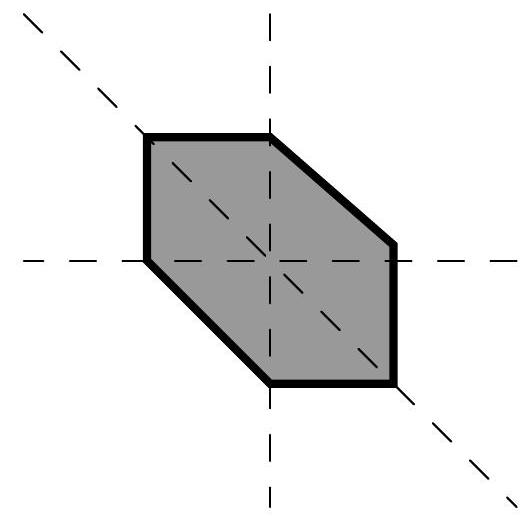
|
\frac{3}{4}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Find the area of the region of the $x y$-plane defined by the inequality $|x|+|y|+|x+y| \leq 1$.
|
$3 / 4$
To graph this region we divide the $x y$-plane into six sectors depending on which of $x, y, x+y$ are $\geq 0$, or $\leq 0$. The inequality simplifies in each case:
| Sector | Inequality | Simplified inequality |
| :---: | :---: | :---: |
| $x \geq 0, y \geq 0, x+y \geq 0$ | $x+y+(x+y) \leq 1$ | $x+y \leq 1 / 2$ |
| $x \geq 0, y \leq 0, x+y \geq 0$ | $x-y+(x+y) \leq 1$ | $x \leq 1 / 2$ |
| $x \geq 0, y \leq 0, x+y \leq 0$ | $x-y-(x+y) \leq 1$ | $y \geq-1 / 2$ |
| $x \leq 0, y \geq 0, x+y \geq 0$ | $-x+y+(x+y) \leq 1$ | $y \leq 1 / 2$ |
| $x \leq 0, y \geq 0, x+y \leq 0$ | $-x+y-(x+y) \leq 1$ | $x \geq-1 / 2$ |
| $x \leq 0, y \leq 0, x+y \leq 0$ | $-x-y-(x+y) \leq 1$ | $x+y \geq-1 / 2$ |
We then draw the region; we get a hexagon as shown. The hexagon intersects each region in an isosceles right triangle of area $1 / 8$, so the total area is $6 \cdot 1 / 8=3 / 4$.

|
{
"resource_path": "HarvardMIT/segmented/en-72-2004-feb-geo-solutions.jsonl",
"problem_match": "\n5. ",
"solution_match": "\nSolution: "
}
|
48ffb435-3341-553e-9040-c785b1d8dca6
| 611,237
|
In trapezoid $A B C D$ shown, $A D$ is parallel to $B C$, and $A B=6, B C=7, C D=$ $8, A D=17$. If sides $A B$ and $C D$ are extended to meet at $E$, find the resulting angle at $E$ (in degrees).
|
90
Choose point $F$ on $A D$ so that $B C D F$ is a parallelogram. Then $B F=C D=8$, and $A F=A D-D F=A D-B C=10$, so $\triangle A B F$ is a 6-8-10 right triangle. The required angle is equal to $\angle A B F=90^{\circ}$.
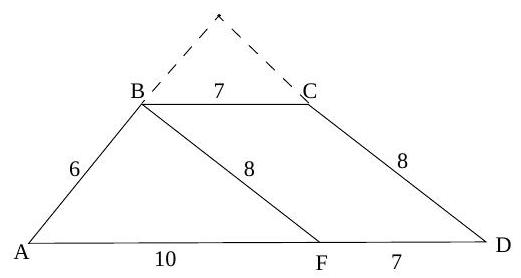
|
90
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
In trapezoid $A B C D$ shown, $A D$ is parallel to $B C$, and $A B=6, B C=7, C D=$ $8, A D=17$. If sides $A B$ and $C D$ are extended to meet at $E$, find the resulting angle at $E$ (in degrees).
|
90
Choose point $F$ on $A D$ so that $B C D F$ is a parallelogram. Then $B F=C D=8$, and $A F=A D-D F=A D-B C=10$, so $\triangle A B F$ is a 6-8-10 right triangle. The required angle is equal to $\angle A B F=90^{\circ}$.

|
{
"resource_path": "HarvardMIT/segmented/en-72-2004-feb-geo-solutions.jsonl",
"problem_match": "\n6. ",
"solution_match": "\nSolution: "
}
|
cf7f2b3e-d5ff-5947-8023-55d3585835aa
| 611,238
|
Yet another trapezoid $A B C D$ has $A D$ parallel to $B C . A C$ and $B D$ intersect at $P$. If $[A D P] /[B C P]=1 / 2$, find $[A D P] /[A B C D]$. (Here the notation $\left[P_{1} \cdots P_{n}\right]$ denotes the area of the polygon $P_{1} \cdots P_{n}$.)
|
$3-2 \sqrt{2}$
A homothety (scaling) about $P$ takes triangle $A D P$ into $B C P$, since $A D, B C$ are parallel and $A, P, C ; B, P, D$ are collinear. The ratio of homothety is thus $\sqrt{2}$. It follows that, if we rescale to put $[A D P]=1$, then $[A B P]=[C D P]=\sqrt{2}$, just by the ratios of lengths of bases. So $[A B C D]=3+2 \sqrt{2}$, so $[A D P] /[A B C D]=1 /(3+2 \sqrt{2})$. Simplifying this, we get $3-2 \sqrt{2}$.
|
3-2 \sqrt{2}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Yet another trapezoid $A B C D$ has $A D$ parallel to $B C . A C$ and $B D$ intersect at $P$. If $[A D P] /[B C P]=1 / 2$, find $[A D P] /[A B C D]$. (Here the notation $\left[P_{1} \cdots P_{n}\right]$ denotes the area of the polygon $P_{1} \cdots P_{n}$.)
|
$3-2 \sqrt{2}$
A homothety (scaling) about $P$ takes triangle $A D P$ into $B C P$, since $A D, B C$ are parallel and $A, P, C ; B, P, D$ are collinear. The ratio of homothety is thus $\sqrt{2}$. It follows that, if we rescale to put $[A D P]=1$, then $[A B P]=[C D P]=\sqrt{2}$, just by the ratios of lengths of bases. So $[A B C D]=3+2 \sqrt{2}$, so $[A D P] /[A B C D]=1 /(3+2 \sqrt{2})$. Simplifying this, we get $3-2 \sqrt{2}$.
|
{
"resource_path": "HarvardMIT/segmented/en-72-2004-feb-geo-solutions.jsonl",
"problem_match": "\n7. ",
"solution_match": "\nSolution: "
}
|
ca8dbbb5-4936-5a0a-b535-318f319ad568
| 611,239
|
A triangle has side lengths 18,24 , and 30 . Find the area of the triangle whose vertices are the incenter, circumcenter, and centroid of the original triangle.
|
3
There are many solutions to this problem, which is straightforward. The given triangle is a right 3-4-5 triangle, so the circumcenter is the midpoint of the hypotenuse. Coordinatizing for convenience, put the vertex at $(0,0)$ and the other vertices at $(0,18)$ and $(24,0)$. Then the circumcenter is $(12,9)$. The centroid is at one-third the sum of the three vertices, which is $(8,6)$. Finally, since the area equals the inradius times half the perimeter, we can see that the inradius is $(18 \cdot 24 / 2) /([18+24+30] / 2)=6$. So the incenter of the triangle is $(6,6)$. So the small triangle has a base of length 2 and a height of 3 , hence its area is 3 .
|
3
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
A triangle has side lengths 18,24 , and 30 . Find the area of the triangle whose vertices are the incenter, circumcenter, and centroid of the original triangle.
|
3
There are many solutions to this problem, which is straightforward. The given triangle is a right 3-4-5 triangle, so the circumcenter is the midpoint of the hypotenuse. Coordinatizing for convenience, put the vertex at $(0,0)$ and the other vertices at $(0,18)$ and $(24,0)$. Then the circumcenter is $(12,9)$. The centroid is at one-third the sum of the three vertices, which is $(8,6)$. Finally, since the area equals the inradius times half the perimeter, we can see that the inradius is $(18 \cdot 24 / 2) /([18+24+30] / 2)=6$. So the incenter of the triangle is $(6,6)$. So the small triangle has a base of length 2 and a height of 3 , hence its area is 3 .
|
{
"resource_path": "HarvardMIT/segmented/en-72-2004-feb-geo-solutions.jsonl",
"problem_match": "\n8. ",
"solution_match": "\n## Solution: "
}
|
e21c8904-5770-5840-a2b2-873cff806793
| 611,240
|
Given is a regular tetrahedron of volume 1. We obtain a second regular tetrahedron by reflecting the given one through its center. What is the volume of their intersection?
|
$1 / 2$
Imagine placing the tetrahedron $A B C D$ flat on a table with vertex $A$ at the top. By vectors or otherwise, we see that the center is $3 / 4$ of the way from $A$ to the bottom face, so the reflection of this face lies in a horizontal plane halfway between $A$ and $B C D$. In particular, it cuts off the smaller tetrahedron obtained by scaling the original tetrahedron by a factor of $1 / 2$ about $A$. Similarly, the reflections of the other three faces cut off tetrahedra obtained by scaling $A B C D$ by $1 / 2$ about $B, C$, and $D$. On the other hand, the octahedral piece remaining remaining after we remove these four smaller tetrahedra is in the intersection of $A B C D$ with its reflection, since the reflection sends this piece to itself. So the answer we seek is just the volume of this piece, which is
(volume of $A B C D)-4 \cdot($ volume of $A B C D$ scaled by a factor of $1 / 2$ )
$$
=1-4(1 / 2)^{3}=1 / 2 .
$$
|
\frac{1}{2}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Given is a regular tetrahedron of volume 1. We obtain a second regular tetrahedron by reflecting the given one through its center. What is the volume of their intersection?
|
$1 / 2$
Imagine placing the tetrahedron $A B C D$ flat on a table with vertex $A$ at the top. By vectors or otherwise, we see that the center is $3 / 4$ of the way from $A$ to the bottom face, so the reflection of this face lies in a horizontal plane halfway between $A$ and $B C D$. In particular, it cuts off the smaller tetrahedron obtained by scaling the original tetrahedron by a factor of $1 / 2$ about $A$. Similarly, the reflections of the other three faces cut off tetrahedra obtained by scaling $A B C D$ by $1 / 2$ about $B, C$, and $D$. On the other hand, the octahedral piece remaining remaining after we remove these four smaller tetrahedra is in the intersection of $A B C D$ with its reflection, since the reflection sends this piece to itself. So the answer we seek is just the volume of this piece, which is
(volume of $A B C D)-4 \cdot($ volume of $A B C D$ scaled by a factor of $1 / 2$ )
$$
=1-4(1 / 2)^{3}=1 / 2 .
$$
|
{
"resource_path": "HarvardMIT/segmented/en-72-2004-feb-geo-solutions.jsonl",
"problem_match": "\n9. ",
"solution_match": "\n## Solution: "
}
|
00a02788-a69d-59df-9b43-70b264f371dc
| 611,241
|
Right triangle $X Y Z$ has right angle at $Y$ and $X Y=228, Y Z=2004$. Angle $Y$ is trisected, and the angle trisectors intersect $X Z$ at $P$ and $Q$ so that $X, P, Q, Z$ lie on $X Z$ in that order. Find the value of $(P Y+Y Z)(Q Y+X Y)$.
|
1370736
The triangle's area is $(228 \cdot 2004) / 2=228456$. All the angles at $Y$ are 30 degrees, so by the sine area formula, the areas of the three small triangles in the diagram are $Q Y \cdot Y Z / 4, P Y \cdot Q Y / 4$, and $X Y \cdot P Y / 4$, which sum to the area of the triangle. So expanding $(P Y+Y Z)(Q Y+X Y)$, we see that it equals
$$
4 \cdot 228456+X Y \cdot Y Z=6 \cdot 228456=1370736
$$
|
1370736
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Right triangle $X Y Z$ has right angle at $Y$ and $X Y=228, Y Z=2004$. Angle $Y$ is trisected, and the angle trisectors intersect $X Z$ at $P$ and $Q$ so that $X, P, Q, Z$ lie on $X Z$ in that order. Find the value of $(P Y+Y Z)(Q Y+X Y)$.
|
1370736
The triangle's area is $(228 \cdot 2004) / 2=228456$. All the angles at $Y$ are 30 degrees, so by the sine area formula, the areas of the three small triangles in the diagram are $Q Y \cdot Y Z / 4, P Y \cdot Q Y / 4$, and $X Y \cdot P Y / 4$, which sum to the area of the triangle. So expanding $(P Y+Y Z)(Q Y+X Y)$, we see that it equals
$$
4 \cdot 228456+X Y \cdot Y Z=6 \cdot 228456=1370736
$$

|
{
"resource_path": "HarvardMIT/segmented/en-72-2004-feb-geo-solutions.jsonl",
"problem_match": "\n10. ",
"solution_match": "\nSolution: "
}
|
d2a1cc54-5cdf-5ae3-97ee-78d3b2acf8ce
| 611,242
|
Find the value of
$$
\binom{6}{1} 2^{1}+\binom{6}{2} 2^{2}+\binom{6}{3} 2^{3}+\binom{6}{4} 2^{4}+\binom{6}{5} 2^{5}+\binom{6}{6} 2^{6} .
$$
|
This sum is the binomial expansion of $(1+2)^{6}$, except that it is missing the first term, $\binom{6}{0} 2^{0}=1$. So we get $3^{6}-1=728$.
|
728
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Find the value of
$$
\binom{6}{1} 2^{1}+\binom{6}{2} 2^{2}+\binom{6}{3} 2^{3}+\binom{6}{4} 2^{4}+\binom{6}{5} 2^{5}+\binom{6}{6} 2^{6} .
$$
|
This sum is the binomial expansion of $(1+2)^{6}$, except that it is missing the first term, $\binom{6}{0} 2^{0}=1$. So we get $3^{6}-1=728$.
|
{
"resource_path": "HarvardMIT/segmented/en-72-2004-feb-guts-solutions.jsonl",
"problem_match": "\n1. ",
"solution_match": "\nSolution:\n"
}
|
f9afadd9-1193-5857-bc7a-2c58ebb18c02
| 611,243
|
If the three points
$$
\begin{aligned}
& (1, a, b) \\
& (a, 2, b) \\
& (a, b, 3)
\end{aligned}
$$
are collinear (in 3 -space), what is the value of $a+b$ ?
|
4
The first two points are distinct (otherwise we would have $a=1$ and $a=2$ simultaneously), and they both lie on the plane $z=b$, so the whole line is in this plane and $b=3$. Reasoning similarly with the last two points gives $a=1$, so $a+b=4$.
|
4
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
If the three points
$$
\begin{aligned}
& (1, a, b) \\
& (a, 2, b) \\
& (a, b, 3)
\end{aligned}
$$
are collinear (in 3 -space), what is the value of $a+b$ ?
|
4
The first two points are distinct (otherwise we would have $a=1$ and $a=2$ simultaneously), and they both lie on the plane $z=b$, so the whole line is in this plane and $b=3$. Reasoning similarly with the last two points gives $a=1$, so $a+b=4$.
|
{
"resource_path": "HarvardMIT/segmented/en-72-2004-feb-guts-solutions.jsonl",
"problem_match": "\n2. ",
"solution_match": "\nSolution: "
}
|
198cdbb6-4f25-5765-8bad-7c4b053e64c2
| 611,244
|
If the system of equations
$$
\begin{aligned}
& |x+y|=99 \\
& |x-y|=c
\end{aligned}
$$
has exactly two real solutions $(x, y)$, find the value of $c$.
|
0
If $c<0$, there are no solutions. If $c>0$ then we have four possible systems of linear equations given by $x+y= \pm 99, x-y= \pm c$, giving four solutions $(x, y)$. So we must have $c=0$, and then we do get two solutions ( $x=y$, so they must both equal $\pm 99 / 2$ ).
|
0
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
If the system of equations
$$
\begin{aligned}
& |x+y|=99 \\
& |x-y|=c
\end{aligned}
$$
has exactly two real solutions $(x, y)$, find the value of $c$.
|
0
If $c<0$, there are no solutions. If $c>0$ then we have four possible systems of linear equations given by $x+y= \pm 99, x-y= \pm c$, giving four solutions $(x, y)$. So we must have $c=0$, and then we do get two solutions ( $x=y$, so they must both equal $\pm 99 / 2$ ).
|
{
"resource_path": "HarvardMIT/segmented/en-72-2004-feb-guts-solutions.jsonl",
"problem_match": "\n3. ",
"solution_match": "\n## Solution: "
}
|
9d6c640f-ce03-5e6e-a782-e59c53a85e8d
| 611,245
|
A tree grows in a rather peculiar manner. Lateral cross-sections of the trunk, leaves, branches, twigs, and so forth are circles. The trunk is 1 meter in diameter to a height of 1 meter, at which point it splits into two sections, each with diameter .5 meter. These sections are each one meter long, at which point they each split into two sections, each with diameter .25 meter. This continues indefinitely: every section of tree is 1 meter long and splits into two smaller sections, each with half the diameter of the previous.
What is the total volume of the tree?
|
$\pi / 2$
If we count the trunk as level 0 , the two sections emerging from it as level 1 , and so forth, then the $n$th level consists of $2^{n}$ sections each with diameter $1 / 2^{n}$, for a volume of $2^{n}\left(\pi / 4 \cdot 2^{-2 n}\right)=(\pi / 4) \cdot 2^{-n}$. So the total volume is given by a simple infinite sum,
$$
.25 \pi \cdot(1+1 / 2+1 / 4+\ldots)=.25 \pi \cdot 2=\pi / 2 .
$$
|
\pi / 2
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
A tree grows in a rather peculiar manner. Lateral cross-sections of the trunk, leaves, branches, twigs, and so forth are circles. The trunk is 1 meter in diameter to a height of 1 meter, at which point it splits into two sections, each with diameter .5 meter. These sections are each one meter long, at which point they each split into two sections, each with diameter .25 meter. This continues indefinitely: every section of tree is 1 meter long and splits into two smaller sections, each with half the diameter of the previous.
What is the total volume of the tree?
|
$\pi / 2$
If we count the trunk as level 0 , the two sections emerging from it as level 1 , and so forth, then the $n$th level consists of $2^{n}$ sections each with diameter $1 / 2^{n}$, for a volume of $2^{n}\left(\pi / 4 \cdot 2^{-2 n}\right)=(\pi / 4) \cdot 2^{-n}$. So the total volume is given by a simple infinite sum,
$$
.25 \pi \cdot(1+1 / 2+1 / 4+\ldots)=.25 \pi \cdot 2=\pi / 2 .
$$
|
{
"resource_path": "HarvardMIT/segmented/en-72-2004-feb-guts-solutions.jsonl",
"problem_match": "\n4. ",
"solution_match": "\nSolution: "
}
|
38d1f33c-b4f7-51d3-8bc6-784fd993a431
| 611,246
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.