problem
stringlengths 14
7.96k
| solution
stringlengths 3
10k
| answer
stringlengths 1
91
| problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | question_type
stringclasses 1
value | problem_type
stringclasses 8
values | problem_raw
stringlengths 14
7.96k
| solution_raw
stringlengths 3
10k
| metadata
dict | uuid
stringlengths 36
36
| id
int64 22.6k
612k
|
|---|---|---|---|---|---|---|---|---|---|---|---|
Augustin has six $1 \times 2 \times \pi$ bricks. He stacks them, one on top of another, to form a tower six bricks high. Each brick can be in any orientation so long as it rests flat on top of the next brick below it (or on the floor). How many distinct heights of towers can he make?
|
28
If there are $k$ bricks which are placed so that they contribute either 1 or 2 height, then the height of these $k$ bricks can be any integer from $k$ to $2 k$. Furthermore, towers with different values of $k$ cannot have the same height. Thus, for each $k$ there are $k+1$ possible tower heights, and since $k$ is any integer from 0 to 6 , there are $1+2+3+4+5+6+7=28$ possible heights.
|
28
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Augustin has six $1 \times 2 \times \pi$ bricks. He stacks them, one on top of another, to form a tower six bricks high. Each brick can be in any orientation so long as it rests flat on top of the next brick below it (or on the floor). How many distinct heights of towers can he make?
|
28
If there are $k$ bricks which are placed so that they contribute either 1 or 2 height, then the height of these $k$ bricks can be any integer from $k$ to $2 k$. Furthermore, towers with different values of $k$ cannot have the same height. Thus, for each $k$ there are $k+1$ possible tower heights, and since $k$ is any integer from 0 to 6 , there are $1+2+3+4+5+6+7=28$ possible heights.
|
{
"resource_path": "HarvardMIT/segmented/en-72-2004-feb-guts-solutions.jsonl",
"problem_match": "\n5. ",
"solution_match": "\nSolution: "
}
|
7e8324e8-385e-56f2-bf9e-7f41ee8bbbd3
| 611,247
|
Find the smallest integer $n$ such that $\sqrt{n+99}-\sqrt{n}<1$.
|
2402
This is equivalent to
$$
\begin{aligned}
\sqrt{n+99} & <\sqrt{n}+1 \\
n+99 & <n+1+2 \sqrt{n} \\
49 & <\sqrt{n}
\end{aligned}
$$
So the smallest integer $n$ with this property is $49^{2}+1=2402$.
|
2402
|
Yes
|
Yes
|
math-word-problem
|
Inequalities
|
Find the smallest integer $n$ such that $\sqrt{n+99}-\sqrt{n}<1$.
|
2402
This is equivalent to
$$
\begin{aligned}
\sqrt{n+99} & <\sqrt{n}+1 \\
n+99 & <n+1+2 \sqrt{n} \\
49 & <\sqrt{n}
\end{aligned}
$$
So the smallest integer $n$ with this property is $49^{2}+1=2402$.
|
{
"resource_path": "HarvardMIT/segmented/en-72-2004-feb-guts-solutions.jsonl",
"problem_match": "\n6. ",
"solution_match": "\nSolution: "
}
|
9d27788d-fd99-5a8d-b126-293d217a55b9
| 611,248
|
Find the shortest distance from the line $3 x+4 y=25$ to the circle $x^{2}+y^{2}=6 x-8 y$.
|
$7 / 5$
The circle is $(x-3)^{2}+(y+4)^{2}=5^{2}$. The center $(3,-4)$ is a distance of
$$
\frac{|3 \cdot 3+4 \cdot-4-25|}{\sqrt{3^{2}+4^{2}}}=\frac{32}{5}
$$
from the line, so we subtract 5 for the radius of the circle and get $7 / 5$.
|
\frac{7}{5}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Find the shortest distance from the line $3 x+4 y=25$ to the circle $x^{2}+y^{2}=6 x-8 y$.
|
$7 / 5$
The circle is $(x-3)^{2}+(y+4)^{2}=5^{2}$. The center $(3,-4)$ is a distance of
$$
\frac{|3 \cdot 3+4 \cdot-4-25|}{\sqrt{3^{2}+4^{2}}}=\frac{32}{5}
$$
from the line, so we subtract 5 for the radius of the circle and get $7 / 5$.
|
{
"resource_path": "HarvardMIT/segmented/en-72-2004-feb-guts-solutions.jsonl",
"problem_match": "\n7. ",
"solution_match": "\nSolution: "
}
|
8f654c5b-6f68-56e7-b354-adb75e837564
| 611,249
|
I have chosen five of the numbers $\{1,2,3,4,5,6,7\}$. If I told you what their product was, that would not be enough information for you to figure out whether their sum was even or odd. What is their product?
|
420
Giving you the product of the five numbers is equivalent to telling you the product of the two numbers I didn't choose. The only possible products that are achieved by more than one pair of numbers are $12(\{3,4\}$ and $\{2,6\})$ and $6(\{1,6\}$ and $\{2,3\})$. But in the second case, you at least know that the two unchosen numbers have odd sum (and so the five chosen numbers have odd sum also). Therefore, the first case must hold, and the product of the five chosen numbers is
$$
1 \cdot 2 \cdot 5 \cdot 6 \cdot 7=1 \cdot 3 \cdot 4 \cdot 5 \cdot 7=420
$$
|
420
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
I have chosen five of the numbers $\{1,2,3,4,5,6,7\}$. If I told you what their product was, that would not be enough information for you to figure out whether their sum was even or odd. What is their product?
|
420
Giving you the product of the five numbers is equivalent to telling you the product of the two numbers I didn't choose. The only possible products that are achieved by more than one pair of numbers are $12(\{3,4\}$ and $\{2,6\})$ and $6(\{1,6\}$ and $\{2,3\})$. But in the second case, you at least know that the two unchosen numbers have odd sum (and so the five chosen numbers have odd sum also). Therefore, the first case must hold, and the product of the five chosen numbers is
$$
1 \cdot 2 \cdot 5 \cdot 6 \cdot 7=1 \cdot 3 \cdot 4 \cdot 5 \cdot 7=420
$$
|
{
"resource_path": "HarvardMIT/segmented/en-72-2004-feb-guts-solutions.jsonl",
"problem_match": "\n8. ",
"solution_match": "\nSolution: "
}
|
1c0da341-2889-542c-adb8-044490a45ea7
| 611,250
|
A positive integer $n$ is picante if $n$ ! ends in the same number of zeroes whether written in base 7 or in base 8 . How many of the numbers $1,2, \ldots, 2004$ are picante?
|
4
The number of zeroes in base 7 is the total number of factors of 7 in $1 \cdot 2 \cdots n$, which is
$$
\lfloor n / 7\rfloor+\left\lfloor n / 7^{2}\right\rfloor+\left\lfloor n / 7^{3}\right\rfloor+\cdots .
$$
The number of zeroes in base 8 is $\lfloor a\rfloor$, where
$$
a=\left(\lfloor n / 2\rfloor+\left\lfloor n / 2^{2}\right\rfloor+\left\lfloor n / 2^{3}\right\rfloor+\cdots\right) / 3
$$
is one-third the number of factors of 2 in the product $n$ !. Now $\left\lfloor n / 2^{k}\right\rfloor / 3 \geq\left\lfloor n / 7^{k}\right\rfloor$ for all $k$, since $\left(n / 2^{k}\right) / 3 \geq n / 7^{k}$. But $n$ can only be picante if the two sums differ by at most $2 / 3$, so in particular this requires $\left(\left\lfloor n / 2^{2}\right\rfloor\right) / 3 \leq\left\lfloor n / 7^{2}\right\rfloor+2 / 3 \Leftrightarrow\lfloor n / 4\rfloor \leq 3\lfloor n / 49\rfloor+2$. This cannot happen for $n \geq 12$; checking the remaining few cases by hand, we find $n=1,2,3,7$ are picante, for a total of 4 values.
|
4
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
A positive integer $n$ is picante if $n$ ! ends in the same number of zeroes whether written in base 7 or in base 8 . How many of the numbers $1,2, \ldots, 2004$ are picante?
|
4
The number of zeroes in base 7 is the total number of factors of 7 in $1 \cdot 2 \cdots n$, which is
$$
\lfloor n / 7\rfloor+\left\lfloor n / 7^{2}\right\rfloor+\left\lfloor n / 7^{3}\right\rfloor+\cdots .
$$
The number of zeroes in base 8 is $\lfloor a\rfloor$, where
$$
a=\left(\lfloor n / 2\rfloor+\left\lfloor n / 2^{2}\right\rfloor+\left\lfloor n / 2^{3}\right\rfloor+\cdots\right) / 3
$$
is one-third the number of factors of 2 in the product $n$ !. Now $\left\lfloor n / 2^{k}\right\rfloor / 3 \geq\left\lfloor n / 7^{k}\right\rfloor$ for all $k$, since $\left(n / 2^{k}\right) / 3 \geq n / 7^{k}$. But $n$ can only be picante if the two sums differ by at most $2 / 3$, so in particular this requires $\left(\left\lfloor n / 2^{2}\right\rfloor\right) / 3 \leq\left\lfloor n / 7^{2}\right\rfloor+2 / 3 \Leftrightarrow\lfloor n / 4\rfloor \leq 3\lfloor n / 49\rfloor+2$. This cannot happen for $n \geq 12$; checking the remaining few cases by hand, we find $n=1,2,3,7$ are picante, for a total of 4 values.
|
{
"resource_path": "HarvardMIT/segmented/en-72-2004-feb-guts-solutions.jsonl",
"problem_match": "\n9. ",
"solution_match": "\nSolution: "
}
|
02ff864a-46f7-52f3-aeb0-c24102a2fc74
| 611,251
|
Let $f(x)=x^{2}+x^{4}+x^{6}+x^{8}+\cdots$, for all real $x$ such that the sum converges. For how many real numbers $x$ does $f(x)=x$ ?
|
2
Clearly $x=0$ works. Otherwise, we want $x=x^{2} /\left(1-x^{2}\right)$, or $x^{2}+x-1=0$. Discard the negative root (since the sum doesn't converge there), but $(-1+\sqrt{5}) / 2$ works, for a total of 2 values.
|
2
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Let $f(x)=x^{2}+x^{4}+x^{6}+x^{8}+\cdots$, for all real $x$ such that the sum converges. For how many real numbers $x$ does $f(x)=x$ ?
|
2
Clearly $x=0$ works. Otherwise, we want $x=x^{2} /\left(1-x^{2}\right)$, or $x^{2}+x-1=0$. Discard the negative root (since the sum doesn't converge there), but $(-1+\sqrt{5}) / 2$ works, for a total of 2 values.
|
{
"resource_path": "HarvardMIT/segmented/en-72-2004-feb-guts-solutions.jsonl",
"problem_match": "\n10. ",
"solution_match": "\nSolution: "
}
|
c2f717a2-ba68-5335-81bd-fd80c9c7c74f
| 611,252
|
A convex quadrilateral is drawn in the coordinate plane such that each of its vertices $(x, y)$ satisfies the equations $x^{2}+y^{2}=73$ and $x y=24$. What is the area of this quadrilateral?
|
110
The vertices all satisfy $(x+y)^{2}=x^{2}+y^{2}+2 x y=73+2 \cdot 24=121$, so $x+y= \pm 11$. Similarly, $(x-y)^{2}=x^{2}+y^{2}-2 x y=73-2 \cdot 24=25$, so $x-y= \pm 5$. Thus, there are four solutions: $(x, y)=(8,3),(3,8),(-3,-8),(-8,-3)$. All four of these solutions satisfy the original equations. The quadrilateral is therefore a rectangle with side lengths of $5 \sqrt{2}$ and $11 \sqrt{2}$, so its area is 110 .
|
110
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
A convex quadrilateral is drawn in the coordinate plane such that each of its vertices $(x, y)$ satisfies the equations $x^{2}+y^{2}=73$ and $x y=24$. What is the area of this quadrilateral?
|
110
The vertices all satisfy $(x+y)^{2}=x^{2}+y^{2}+2 x y=73+2 \cdot 24=121$, so $x+y= \pm 11$. Similarly, $(x-y)^{2}=x^{2}+y^{2}-2 x y=73-2 \cdot 24=25$, so $x-y= \pm 5$. Thus, there are four solutions: $(x, y)=(8,3),(3,8),(-3,-8),(-8,-3)$. All four of these solutions satisfy the original equations. The quadrilateral is therefore a rectangle with side lengths of $5 \sqrt{2}$ and $11 \sqrt{2}$, so its area is 110 .
|
{
"resource_path": "HarvardMIT/segmented/en-72-2004-feb-guts-solutions.jsonl",
"problem_match": "\n12. ",
"solution_match": "\nSolution: "
}
|
7f8d42e1-10fe-5e10-be87-ec8728e03236
| 611,254
|
If $a_{1}=1, a_{2}=0$, and $a_{n+1}=a_{n}+\frac{a_{n+2}}{2}$ for all $n \geq 1$, compute $a_{2004}$.
|
$\quad-2^{1002}$
By writing out the first few terms, we find that $a_{n+4}=-4 a_{n}$. Indeed,
$$
a_{n+4}=2\left(a_{n+3}-a_{n+2}\right)=2\left(a_{n+2}-2 a_{n+1}\right)=2\left(-2 a_{n}\right)=-4 a_{n} .
$$
Then, by induction, we get $a_{4 k}=(-4)^{k}$ for all positive integers $k$, and setting $k=501$ gives the answer.
|
-2^{1002}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
If $a_{1}=1, a_{2}=0$, and $a_{n+1}=a_{n}+\frac{a_{n+2}}{2}$ for all $n \geq 1$, compute $a_{2004}$.
|
$\quad-2^{1002}$
By writing out the first few terms, we find that $a_{n+4}=-4 a_{n}$. Indeed,
$$
a_{n+4}=2\left(a_{n+3}-a_{n+2}\right)=2\left(a_{n+2}-2 a_{n+1}\right)=2\left(-2 a_{n}\right)=-4 a_{n} .
$$
Then, by induction, we get $a_{4 k}=(-4)^{k}$ for all positive integers $k$, and setting $k=501$ gives the answer.
|
{
"resource_path": "HarvardMIT/segmented/en-72-2004-feb-guts-solutions.jsonl",
"problem_match": "\n14. ",
"solution_match": "\n## Solution: "
}
|
0bb338af-74e2-5d08-9434-ec4dab3cc3a5
| 611,256
|
An $n$-string is a string of digits formed by writing the numbers $1,2, \ldots, n$ in some order (in base ten). For example, one possible 10-string is
35728910461
What is the smallest $n>1$ such that there exists a palindromic $n$-string?
|
The following is such a string for $n=19$ :
$$
9|18| 7|16| 5|14| 3|12| 1|10| 11|2| 13|4| 15|6| 17|8| 19
$$
where the vertical bars indicate breaks between the numbers. On the other hand, to see that $n=19$ is the minimum, notice that only one digit can occur an odd number of times in a palindromic $n$-string (namely the center digit). If $n \leq 9$, then (say) the digits 1,2 each appear once in any $n$-string, so we cannot have a palindrome. If $10 \leq n \leq 18$, then 0,9 each appear once, and we again cannot have a palindrome. So 19 is the smallest possible $n$.
|
19
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
An $n$-string is a string of digits formed by writing the numbers $1,2, \ldots, n$ in some order (in base ten). For example, one possible 10-string is
35728910461
What is the smallest $n>1$ such that there exists a palindromic $n$-string?
|
The following is such a string for $n=19$ :
$$
9|18| 7|16| 5|14| 3|12| 1|10| 11|2| 13|4| 15|6| 17|8| 19
$$
where the vertical bars indicate breaks between the numbers. On the other hand, to see that $n=19$ is the minimum, notice that only one digit can occur an odd number of times in a palindromic $n$-string (namely the center digit). If $n \leq 9$, then (say) the digits 1,2 each appear once in any $n$-string, so we cannot have a palindrome. If $10 \leq n \leq 18$, then 0,9 each appear once, and we again cannot have a palindrome. So 19 is the smallest possible $n$.
|
{
"resource_path": "HarvardMIT/segmented/en-72-2004-feb-guts-solutions.jsonl",
"problem_match": "\n16. ",
"solution_match": "\nSolution:\n"
}
|
da8aeffd-a84e-5397-b499-668bec89f79d
| 611,258
|
Kate has four red socks and four blue socks. If she randomly divides these eight socks into four pairs, what is the probability that none of the pairs will be mismatched? That is, what is the probability that each pair will consist either of two red socks or of two blue socks?
|
$3 / 35$
The number of ways Kate can divide the four red socks into two pairs is $\binom{4}{2} / 2=3$. The number of ways she can divide the four blue socks into two pairs is also 3 . Therefore, the number of ways she can form two pairs of red socks and two pairs of blue socks is
$3 \cdot 3=9$. The total number of ways she can divide the eight socks into four pairs is $[8!/(2!\cdot 2!\cdot 2!\cdot 2!)] / 4!=105$, so the probability that the socks come out paired correctly is $9 / 105=3 / 35$.
To see why 105 is the correct denominator, we can look at each 2 ! term as representing the double counting of pair $(a b)$ and pair ( $b a$ ), while the 4 ! term represents the number of different orders in which we can select the same four pairs. Alternatively, we know that there are three ways to select two pairs from four socks. To select three pairs from six socks, there are five different choices for the first sock's partner and then three ways to pair up the remaining four socks, for a total of $5 \cdot 3=15$ pairings. To select four pairs from eight socks, there are seven different choices for the first sock's partner and then fifteen ways to pair up the remaining six socks, for a total of $7 \cdot 15=105$ pairings.
|
\frac{3}{35}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Kate has four red socks and four blue socks. If she randomly divides these eight socks into four pairs, what is the probability that none of the pairs will be mismatched? That is, what is the probability that each pair will consist either of two red socks or of two blue socks?
|
$3 / 35$
The number of ways Kate can divide the four red socks into two pairs is $\binom{4}{2} / 2=3$. The number of ways she can divide the four blue socks into two pairs is also 3 . Therefore, the number of ways she can form two pairs of red socks and two pairs of blue socks is
$3 \cdot 3=9$. The total number of ways she can divide the eight socks into four pairs is $[8!/(2!\cdot 2!\cdot 2!\cdot 2!)] / 4!=105$, so the probability that the socks come out paired correctly is $9 / 105=3 / 35$.
To see why 105 is the correct denominator, we can look at each 2 ! term as representing the double counting of pair $(a b)$ and pair ( $b a$ ), while the 4 ! term represents the number of different orders in which we can select the same four pairs. Alternatively, we know that there are three ways to select two pairs from four socks. To select three pairs from six socks, there are five different choices for the first sock's partner and then three ways to pair up the remaining four socks, for a total of $5 \cdot 3=15$ pairings. To select four pairs from eight socks, there are seven different choices for the first sock's partner and then fifteen ways to pair up the remaining six socks, for a total of $7 \cdot 15=105$ pairings.
|
{
"resource_path": "HarvardMIT/segmented/en-72-2004-feb-guts-solutions.jsonl",
"problem_match": "\n17. ",
"solution_match": "\nSolution: "
}
|
f3925d60-8199-5a27-843c-518d7cedf9d4
| 611,259
|
The Fibonacci numbers are defined by $F_{1}=F_{2}=1$, and $F_{n}=F_{n-1}+F_{n-2}$ for $n \geq 3$. If the number
$$
\frac{F_{2003}}{F_{2002}}-\frac{F_{2004}}{F_{2003}}
$$
is written as a fraction in lowest terms, what is the numerator?
|
1
Before reducing, the numerator is $F_{2003}^{2}-F_{2002} F_{2004}$. We claim $F_{n}^{2}-F_{n-1} F_{n+1}=$ $(-1)^{n+1}$, which will immediately imply that the answer is 1 (no reducing required). This claim is straightforward to prove by induction on $n$ : it holds for $n=2$, and if it holds for some $n$, then
$F_{n+1}^{2}-F_{n} F_{n+2}=F_{n+1}\left(F_{n-1}+F_{n}\right)-F_{n}\left(F_{n}+F_{n+1}\right)=F_{n+1} F_{n-1}-F_{n}^{2}=-(-1)^{n+1}=(-1)^{n+2}$.
|
1
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
The Fibonacci numbers are defined by $F_{1}=F_{2}=1$, and $F_{n}=F_{n-1}+F_{n-2}$ for $n \geq 3$. If the number
$$
\frac{F_{2003}}{F_{2002}}-\frac{F_{2004}}{F_{2003}}
$$
is written as a fraction in lowest terms, what is the numerator?
|
1
Before reducing, the numerator is $F_{2003}^{2}-F_{2002} F_{2004}$. We claim $F_{n}^{2}-F_{n-1} F_{n+1}=$ $(-1)^{n+1}$, which will immediately imply that the answer is 1 (no reducing required). This claim is straightforward to prove by induction on $n$ : it holds for $n=2$, and if it holds for some $n$, then
$F_{n+1}^{2}-F_{n} F_{n+2}=F_{n+1}\left(F_{n-1}+F_{n}\right)-F_{n}\left(F_{n}+F_{n+1}\right)=F_{n+1} F_{n-1}-F_{n}^{2}=-(-1)^{n+1}=(-1)^{n+2}$.
|
{
"resource_path": "HarvardMIT/segmented/en-72-2004-feb-guts-solutions.jsonl",
"problem_match": "\n19. ",
"solution_match": "\nSolution: "
}
|
dc904e62-4f77-5f70-b24c-98c793d5aca1
| 611,261
|
Two positive rational numbers $x$ and $y$, when written in lowest terms, have the property that the sum of their numerators is 9 and the sum of their denominators is 10 . What is the largest possible value of $x+y$ ?
|
$73 / 9$
For fixed denominators $a<b$ (with sum 10), we maximize the sum of the fractions by giving the smaller denominator as large a numerator as possible: $8 / a+1 / b$. Then, if $a \geq 2$, this quantity is at most $8 / 2+1 / 1=5$, which is clearly smaller than the sum we get by setting $a=1$, namely $8 / 1+1 / 9=73 / 9$. So this is the answer.
|
\frac{73}{9}
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Two positive rational numbers $x$ and $y$, when written in lowest terms, have the property that the sum of their numerators is 9 and the sum of their denominators is 10 . What is the largest possible value of $x+y$ ?
|
$73 / 9$
For fixed denominators $a<b$ (with sum 10), we maximize the sum of the fractions by giving the smaller denominator as large a numerator as possible: $8 / a+1 / b$. Then, if $a \geq 2$, this quantity is at most $8 / 2+1 / 1=5$, which is clearly smaller than the sum we get by setting $a=1$, namely $8 / 1+1 / 9=73 / 9$. So this is the answer.
|
{
"resource_path": "HarvardMIT/segmented/en-72-2004-feb-guts-solutions.jsonl",
"problem_match": "\n20. ",
"solution_match": "\nSolution: "
}
|
566b543d-1172-5d72-a7d9-049790da2c68
| 611,262
|
I have written a strictly increasing sequence of six positive integers, such that each number (besides the first) is a multiple of the one before it, and the sum of all six numbers is 79 . What is the largest number in my sequence?
|
48
If the fourth number is $\geq 12$, then the last three numbers must sum to at least $12+$ $2 \cdot 12+2^{2} \cdot 12=84>79$. This is impossible, so the fourth number must be less than 12. Then the only way we can have the required divisibilities among the first four numbers is if they are $1,2,4,8$. So the last two numbers now sum to $79-15=64$. If we call these numbers $8 a, 8 a b(a, b>1)$ then we get $a(1+b)=a+a b=8$, which forces $a=2, b=3$. So the last two numbers are 16,48 .
|
48
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
I have written a strictly increasing sequence of six positive integers, such that each number (besides the first) is a multiple of the one before it, and the sum of all six numbers is 79 . What is the largest number in my sequence?
|
48
If the fourth number is $\geq 12$, then the last three numbers must sum to at least $12+$ $2 \cdot 12+2^{2} \cdot 12=84>79$. This is impossible, so the fourth number must be less than 12. Then the only way we can have the required divisibilities among the first four numbers is if they are $1,2,4,8$. So the last two numbers now sum to $79-15=64$. If we call these numbers $8 a, 8 a b(a, b>1)$ then we get $a(1+b)=a+a b=8$, which forces $a=2, b=3$. So the last two numbers are 16,48 .
|
{
"resource_path": "HarvardMIT/segmented/en-72-2004-feb-guts-solutions.jsonl",
"problem_match": "\n22. ",
"solution_match": "\nSolution: "
}
|
0ea623e4-8f94-5d02-822f-de40c8f6309f
| 611,264
|
Find the largest integer $n$ such that $3^{512}-1$ is divisible by $2^{n}$.
|
11
Write
$$
\begin{aligned}
3^{512}-1 & =\left(3^{256}+1\right)\left(3^{256}-1\right)=\left(3^{256}+1\right)\left(3^{128}+1\right)\left(3^{128}-1\right) \\
& =\cdots=\left(3^{256}+1\right)\left(3^{128}+1\right) \cdots(3+1)(3-1)
\end{aligned}
$$
Now each factor $3^{2^{k}}+1, k \geq 1$, is divisible by just one factor of 2 , since $3^{2^{k}}+1=$ $\left(3^{2}\right)^{2^{k-1}}+1 \equiv 1^{2^{k-1}}+1=2(\bmod 4)$. Thus we get 8 factors of 2 here, and the remaining terms $(3+1)(3-1)=8$ give us 3 more factors of 2 , for a total of 11 .
|
11
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Find the largest integer $n$ such that $3^{512}-1$ is divisible by $2^{n}$.
|
11
Write
$$
\begin{aligned}
3^{512}-1 & =\left(3^{256}+1\right)\left(3^{256}-1\right)=\left(3^{256}+1\right)\left(3^{128}+1\right)\left(3^{128}-1\right) \\
& =\cdots=\left(3^{256}+1\right)\left(3^{128}+1\right) \cdots(3+1)(3-1)
\end{aligned}
$$
Now each factor $3^{2^{k}}+1, k \geq 1$, is divisible by just one factor of 2 , since $3^{2^{k}}+1=$ $\left(3^{2}\right)^{2^{k-1}}+1 \equiv 1^{2^{k-1}}+1=2(\bmod 4)$. Thus we get 8 factors of 2 here, and the remaining terms $(3+1)(3-1)=8$ give us 3 more factors of 2 , for a total of 11 .
|
{
"resource_path": "HarvardMIT/segmented/en-72-2004-feb-guts-solutions.jsonl",
"problem_match": "\n23. ",
"solution_match": "\nSolution: "
}
|
e83bc1b1-3083-5a17-b96e-b69d0f5523cf
| 611,265
|
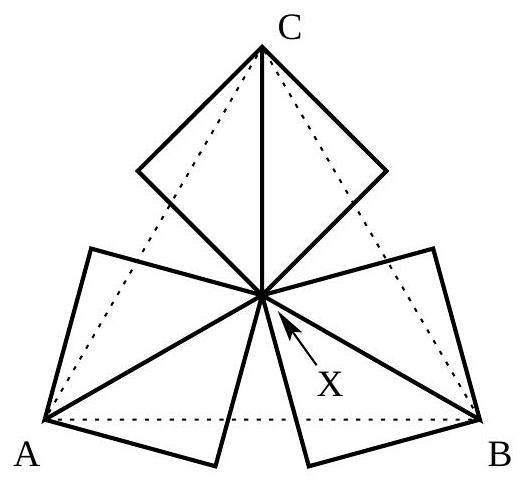
We say a point is contained in a square if it is in its interior or on its boundary. Three unit squares are given in the plane such that there is a point contained in all three. Furthermore, three points $A, B, C$, are given, each contained in at least one of the squares. Find the maximum area of triangle $A B C$.
|
$3 \sqrt{3} / 2$
Let $X$ be a point contained in all three squares. The distance from $X$ to any point in any of the three squares is at most $\sqrt{2}$, the length of the diagonal of the squares. Therefore, triangle $A B C$ is contained in a circle of radius $\sqrt{2}$, so its circumradius is at most $\sqrt{2}$. The triangle with greatest area that satisfies this property is the equilateral triangle in a circle of radius $\sqrt{2}$. (This can be proved, for example, by considering that the maximum altitude to any given side is obtained by putting the opposite vertex at the midpoint of its arc, and it follows that all the vertices are equidistant.) The equilateral triangle is also attainable, since making $X$ the circumcenter and positioning the squares such that $A X, B X$, and $C X$ are diagonals (of the three squares) and $A B C$ is equilateral, leads to such a triangle. This triangle has area $3 \sqrt{3} / 2$, which may be calculated, for example, using the sine formula for area applied to $A B X, A C X$, and $B C X$, to get $3 / 2(\sqrt{2})^{2} \sin 120^{\circ}$. (See diagram, next page.)
|
\frac{3 \sqrt{3}}{2}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
We say a point is contained in a square if it is in its interior or on its boundary. Three unit squares are given in the plane such that there is a point contained in all three. Furthermore, three points $A, B, C$, are given, each contained in at least one of the squares. Find the maximum area of triangle $A B C$.
|
$3 \sqrt{3} / 2$
Let $X$ be a point contained in all three squares. The distance from $X$ to any point in any of the three squares is at most $\sqrt{2}$, the length of the diagonal of the squares. Therefore, triangle $A B C$ is contained in a circle of radius $\sqrt{2}$, so its circumradius is at most $\sqrt{2}$. The triangle with greatest area that satisfies this property is the equilateral triangle in a circle of radius $\sqrt{2}$. (This can be proved, for example, by considering that the maximum altitude to any given side is obtained by putting the opposite vertex at the midpoint of its arc, and it follows that all the vertices are equidistant.) The equilateral triangle is also attainable, since making $X$ the circumcenter and positioning the squares such that $A X, B X$, and $C X$ are diagonals (of the three squares) and $A B C$ is equilateral, leads to such a triangle. This triangle has area $3 \sqrt{3} / 2$, which may be calculated, for example, using the sine formula for area applied to $A B X, A C X$, and $B C X$, to get $3 / 2(\sqrt{2})^{2} \sin 120^{\circ}$. (See diagram, next page.)
|
{
"resource_path": "HarvardMIT/segmented/en-72-2004-feb-guts-solutions.jsonl",
"problem_match": "\n24. ",
"solution_match": "\nSolution: "
}
|
c097dfd9-2a98-54bb-8941-d332563717c7
| 611,266
|
Suppose $x^{3}-a x^{2}+b x-48$ is a polynomial with three positive roots $p, q$, and $r$ such that $p<q<r$. What is the minimum possible value of $1 / p+2 / q+3 / r$ ?
|
$3 / 2$
We know $p q r=48$ since the product of the roots of a cubic is the constant term. Now,
$$
\frac{1}{p}+\frac{2}{q}+\frac{3}{r} \geq 3 \sqrt[3]{\frac{6}{p q r}}=\frac{3}{2}
$$
by AM-GM, with equality when $1 / p=2 / q=3 / r$. This occurs when $p=2, q=4$, $r=6$, so $3 / 2$ is in fact the minimum possible value.
|
\frac{3}{2}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Suppose $x^{3}-a x^{2}+b x-48$ is a polynomial with three positive roots $p, q$, and $r$ such that $p<q<r$. What is the minimum possible value of $1 / p+2 / q+3 / r$ ?

|
$3 / 2$
We know $p q r=48$ since the product of the roots of a cubic is the constant term. Now,
$$
\frac{1}{p}+\frac{2}{q}+\frac{3}{r} \geq 3 \sqrt[3]{\frac{6}{p q r}}=\frac{3}{2}
$$
by AM-GM, with equality when $1 / p=2 / q=3 / r$. This occurs when $p=2, q=4$, $r=6$, so $3 / 2$ is in fact the minimum possible value.
|
{
"resource_path": "HarvardMIT/segmented/en-72-2004-feb-guts-solutions.jsonl",
"problem_match": "\n25. ",
"solution_match": "\nSolution: "
}
|
7bfb79d1-a9a6-545c-b4c1-5c13061ea859
| 611,267
|
How many of the integers $1,2, \ldots, 2004$ can be represented as $(m n+1) /(m+n)$ for positive integers $m$ and $n$ ?
|
2004
For any positive integer $a$, we can let $m=a^{2}+a-1, n=a+1$ to see that every positive integer has this property, so the answer is 2004.
|
2004
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
How many of the integers $1,2, \ldots, 2004$ can be represented as $(m n+1) /(m+n)$ for positive integers $m$ and $n$ ?
|
2004
For any positive integer $a$, we can let $m=a^{2}+a-1, n=a+1$ to see that every positive integer has this property, so the answer is 2004.
|
{
"resource_path": "HarvardMIT/segmented/en-72-2004-feb-guts-solutions.jsonl",
"problem_match": "\n26. ",
"solution_match": "\nSolution: "
}
|
a243cec8-ac2d-554d-9d15-3e0f0fc879ec
| 611,268
|
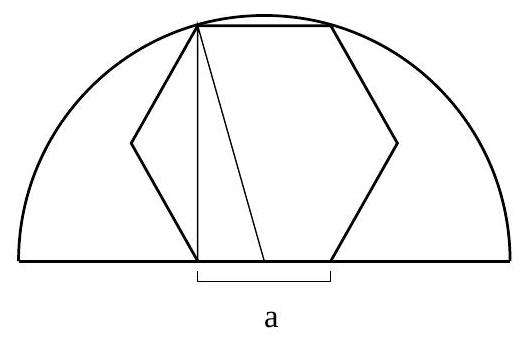
A regular hexagon has one side along the diameter of a semicircle, and the two opposite vertices on the semicircle. Find the area of the hexagon if the diameter of the semicircle is 1 .
|
$3 \sqrt{3} / 26$
The midpoint of the side of the hexagon on the diameter is the center of the circle. Draw the segment from this center to a vertex of the hexagon on the circle. This segment, whose length is $1 / 2$, is the hypotenuse of a right triangle whose legs have lengths $a / 2$ and $a \sqrt{3}$, where $a$ is a side of the hexagon. So $1 / 4=a^{2}(1 / 4+3)$, so $a^{2}=1 / 13$. The hexagon consists of 6 equilateral triangles of side length $a$, so the area of the hexagon is $3 a^{2} \sqrt{3} / 2=3 \sqrt{3} / 26$.
|
\frac{3 \sqrt{3}}{26}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
A regular hexagon has one side along the diameter of a semicircle, and the two opposite vertices on the semicircle. Find the area of the hexagon if the diameter of the semicircle is 1 .
|
$3 \sqrt{3} / 26$
The midpoint of the side of the hexagon on the diameter is the center of the circle. Draw the segment from this center to a vertex of the hexagon on the circle. This segment, whose length is $1 / 2$, is the hypotenuse of a right triangle whose legs have lengths $a / 2$ and $a \sqrt{3}$, where $a$ is a side of the hexagon. So $1 / 4=a^{2}(1 / 4+3)$, so $a^{2}=1 / 13$. The hexagon consists of 6 equilateral triangles of side length $a$, so the area of the hexagon is $3 a^{2} \sqrt{3} / 2=3 \sqrt{3} / 26$.

|
{
"resource_path": "HarvardMIT/segmented/en-72-2004-feb-guts-solutions.jsonl",
"problem_match": "\n27. ",
"solution_match": "\nSolution: "
}
|
aa32c862-9f59-59ce-b919-eacafdaee27c
| 611,269
|
Find the value of
$$
\binom{2003}{1}+\binom{2003}{4}+\binom{2003}{7}+\cdots+\binom{2003}{2002}
$$
|
$\left(2^{2003}-2\right) / 3$
Let $\omega=-1 / 2+i \sqrt{3} / 2$ be a complex cube root of unity. Then, by the binomial theorem, we have
$$
\begin{aligned}
\omega^{2}(\omega+1)^{2003} & =\binom{2003}{0} \omega^{2}+\binom{2003}{1} \omega^{3}+\binom{2003}{2} \omega^{4}+\cdots+\binom{2003}{2003} \omega^{2005} \\
2^{2003} & =\binom{2003}{0}+\binom{2003}{1}+\binom{2003}{2}+\cdots+\binom{2003}{2003} \\
\omega^{-2}\left(\omega^{-1}+1\right)^{2003} & =\binom{2003}{0} \omega^{-2}+\binom{2003}{1} \omega^{-3}+\binom{2003}{2} \omega^{-4}+\cdots+\binom{2003}{2003} \omega^{-2005}
\end{aligned}
$$
If we add these together, then the terms $\binom{2003}{n}$ for $n \equiv 1(\bmod 3)$ appear with coefficient 3 , while the remaining terms appear with coefficient $1+\omega+\omega^{2}=0$. Thus the desired sum is just $\left(\omega^{2}(\omega+1)^{2003}+2^{2003}+\omega^{-2}\left(\omega^{-1}+1\right)^{2003}\right) / 3$. Simplifying using $\omega+1=-\omega^{2}$ and $\omega^{-1}+1=-\omega$ gives $\left(-1+2^{2003}+-1\right) / 3=\left(2^{2003}-2\right) / 3$.
|
\frac{2^{2003}-2}{3}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Find the value of
$$
\binom{2003}{1}+\binom{2003}{4}+\binom{2003}{7}+\cdots+\binom{2003}{2002}
$$
|
$\left(2^{2003}-2\right) / 3$
Let $\omega=-1 / 2+i \sqrt{3} / 2$ be a complex cube root of unity. Then, by the binomial theorem, we have
$$
\begin{aligned}
\omega^{2}(\omega+1)^{2003} & =\binom{2003}{0} \omega^{2}+\binom{2003}{1} \omega^{3}+\binom{2003}{2} \omega^{4}+\cdots+\binom{2003}{2003} \omega^{2005} \\
2^{2003} & =\binom{2003}{0}+\binom{2003}{1}+\binom{2003}{2}+\cdots+\binom{2003}{2003} \\
\omega^{-2}\left(\omega^{-1}+1\right)^{2003} & =\binom{2003}{0} \omega^{-2}+\binom{2003}{1} \omega^{-3}+\binom{2003}{2} \omega^{-4}+\cdots+\binom{2003}{2003} \omega^{-2005}
\end{aligned}
$$
If we add these together, then the terms $\binom{2003}{n}$ for $n \equiv 1(\bmod 3)$ appear with coefficient 3 , while the remaining terms appear with coefficient $1+\omega+\omega^{2}=0$. Thus the desired sum is just $\left(\omega^{2}(\omega+1)^{2003}+2^{2003}+\omega^{-2}\left(\omega^{-1}+1\right)^{2003}\right) / 3$. Simplifying using $\omega+1=-\omega^{2}$ and $\omega^{-1}+1=-\omega$ gives $\left(-1+2^{2003}+-1\right) / 3=\left(2^{2003}-2\right) / 3$.
|
{
"resource_path": "HarvardMIT/segmented/en-72-2004-feb-guts-solutions.jsonl",
"problem_match": "\n28. ",
"solution_match": "\nSolution: "
}
|
d2207408-ea77-5a9d-9c8d-2446cb7f4c13
| 611,270
|
A regular dodecahedron is projected orthogonally onto a plane, and its image is an $n$-sided polygon. What is the smallest possible value of $n$ ?
|
6
We can achieve 6 by projecting onto a plane perpendicular to an edge of the dodecaheron. Indeed, if we imagine viewing the dodecahedron in such a direction, then 4 of the faces are projected to line segments (namely, the two faces adjacent to the edge and the two opposite faces), and of the remaining 8 faces, 4 appear on the front of the dodecahedron and the other 4 are on the back. Thus, the dodecahedron appears as shown.
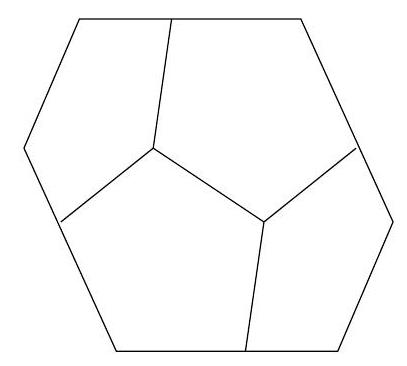
To see that we cannot do better, note that, by central symmetry, the number of edges of the projection must be even. So we just need to show that the answer cannot be 4 . But if the projection had 4 sides, one of the vertices would give a projection forming an acute angle, which is not possible. So 6 is the answer.
|
6
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
A regular dodecahedron is projected orthogonally onto a plane, and its image is an $n$-sided polygon. What is the smallest possible value of $n$ ?
|
6
We can achieve 6 by projecting onto a plane perpendicular to an edge of the dodecaheron. Indeed, if we imagine viewing the dodecahedron in such a direction, then 4 of the faces are projected to line segments (namely, the two faces adjacent to the edge and the two opposite faces), and of the remaining 8 faces, 4 appear on the front of the dodecahedron and the other 4 are on the back. Thus, the dodecahedron appears as shown.

To see that we cannot do better, note that, by central symmetry, the number of edges of the projection must be even. So we just need to show that the answer cannot be 4 . But if the projection had 4 sides, one of the vertices would give a projection forming an acute angle, which is not possible. So 6 is the answer.
|
{
"resource_path": "HarvardMIT/segmented/en-72-2004-feb-guts-solutions.jsonl",
"problem_match": "\n29. ",
"solution_match": "\nSolution: "
}
|
a0fc03a1-8ba2-56ee-aab1-885bc153062d
| 611,271
|
We have an $n$-gon, and each of its vertices is labeled with a number from the set $\{1, \ldots, 10\}$. We know that for any pair of distinct numbers from this set there is
at least one side of the polygon whose endpoints have these two numbers. Find the smallest possible value of $n$.
|
Each number be paired with each of the 9 other numbers, but each vertex can be used in at most 2 different pairs, so each number must occur on at least $\lceil 9 / 2\rceil=5$ different vertices. Thus, we need at least $10 \cdot 5=50$ vertices, so $n \geq 50$.
To see that $n=50$ is feasible, let the numbers $1, \ldots, 10$ be the vertices of a complete graph. Then each vertex has degree 9 , and there are $\binom{10}{2}=45$ edges. If we attach extra copies of the edges $1-2,3-4,5-6,7-8$, and $9-10$, then every vertex will have degree 10 . In particular, the graph has an Eulerian tour, so we can follow this tour, successively numbering vertices of the 50 -gon according to the vertices of the graph we visit. Then, for each edge of the graph, there will be a corresponding edge of the polygon with the same two vertex labels on its endpoints. It follows that every pair of distinct numbers occurs at the endpoints of some edge of the polygon, and so $n=50$ is the answer.
|
50
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
We have an $n$-gon, and each of its vertices is labeled with a number from the set $\{1, \ldots, 10\}$. We know that for any pair of distinct numbers from this set there is
at least one side of the polygon whose endpoints have these two numbers. Find the smallest possible value of $n$.
|
Each number be paired with each of the 9 other numbers, but each vertex can be used in at most 2 different pairs, so each number must occur on at least $\lceil 9 / 2\rceil=5$ different vertices. Thus, we need at least $10 \cdot 5=50$ vertices, so $n \geq 50$.
To see that $n=50$ is feasible, let the numbers $1, \ldots, 10$ be the vertices of a complete graph. Then each vertex has degree 9 , and there are $\binom{10}{2}=45$ edges. If we attach extra copies of the edges $1-2,3-4,5-6,7-8$, and $9-10$, then every vertex will have degree 10 . In particular, the graph has an Eulerian tour, so we can follow this tour, successively numbering vertices of the 50 -gon according to the vertices of the graph we visit. Then, for each edge of the graph, there will be a corresponding edge of the polygon with the same two vertex labels on its endpoints. It follows that every pair of distinct numbers occurs at the endpoints of some edge of the polygon, and so $n=50$ is the answer.
|
{
"resource_path": "HarvardMIT/segmented/en-72-2004-feb-guts-solutions.jsonl",
"problem_match": "\n30. ",
"solution_match": "\nSolution:\n"
}
|
61428846-4fda-5fa9-9efa-99dd50bd1469
| 611,272
|
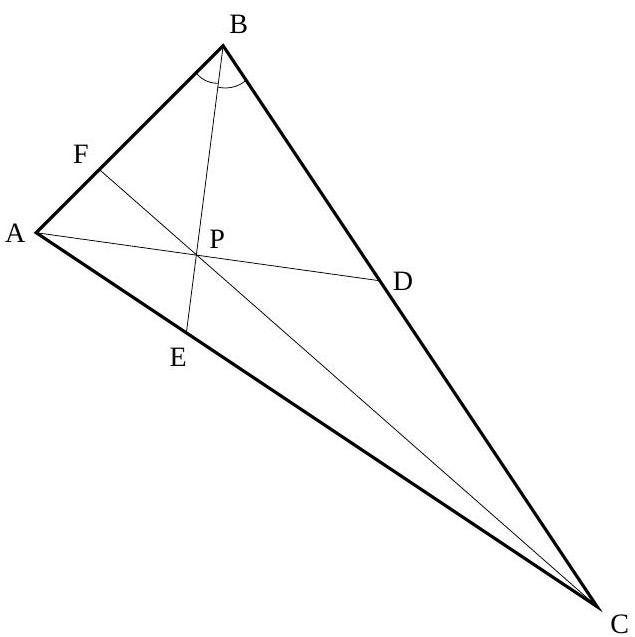
$P$ is a point inside triangle $A B C$, and lines $A P, B P, C P$ intersect the opposite sides $B C, C A, A B$ in points $D, E, F$, respectively. It is given that $\angle A P B=90^{\circ}$, and that $A C=B C$ and $A B=B D$. We also know that $B F=1$, and that $B C=999$. Find $A F$.
|
499/500
Let $A C=B C=s, A B=B D=t$. Since $B P$ is the altitude in isosceles triangle $A B D$, it bisects angle $B$. So, the Angle Bisector Theorem in triangle $A B C$ given $A E / E C=A B / B C=t / s$. Meanwhile, $C D / D B=(s-t) / t$. Now Ceva's theorem gives us
$$
\begin{gathered}
\frac{A F}{F B}=\left(\frac{A E}{E C}\right) \cdot\left(\frac{C D}{D B}\right)=\frac{s-t}{s} \\
\Rightarrow \frac{A B}{F B}=1+\frac{s-t}{s}=\frac{2 s-t}{s} \Rightarrow F B=\frac{s t}{2 s-t} .
\end{gathered}
$$
Now we know $s=999$, but we need to find $t$ given that $s t /(2 s-t)=F B=1$. So $s t=2 s-t \Rightarrow t=2 s /(s+1)$, and then
$$
A F=F B \cdot \frac{A F}{F B}=1 \cdot \frac{s-t}{s}=\frac{\left(s^{2}-s\right) /(s+1)}{s}=\frac{s-1}{s+1}=\frac{499}{500} .
$$
|
\frac{499}{500}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
$P$ is a point inside triangle $A B C$, and lines $A P, B P, C P$ intersect the opposite sides $B C, C A, A B$ in points $D, E, F$, respectively. It is given that $\angle A P B=90^{\circ}$, and that $A C=B C$ and $A B=B D$. We also know that $B F=1$, and that $B C=999$. Find $A F$.
|
499/500

Let $A C=B C=s, A B=B D=t$. Since $B P$ is the altitude in isosceles triangle $A B D$, it bisects angle $B$. So, the Angle Bisector Theorem in triangle $A B C$ given $A E / E C=A B / B C=t / s$. Meanwhile, $C D / D B=(s-t) / t$. Now Ceva's theorem gives us
$$
\begin{gathered}
\frac{A F}{F B}=\left(\frac{A E}{E C}\right) \cdot\left(\frac{C D}{D B}\right)=\frac{s-t}{s} \\
\Rightarrow \frac{A B}{F B}=1+\frac{s-t}{s}=\frac{2 s-t}{s} \Rightarrow F B=\frac{s t}{2 s-t} .
\end{gathered}
$$
Now we know $s=999$, but we need to find $t$ given that $s t /(2 s-t)=F B=1$. So $s t=2 s-t \Rightarrow t=2 s /(s+1)$, and then
$$
A F=F B \cdot \frac{A F}{F B}=1 \cdot \frac{s-t}{s}=\frac{\left(s^{2}-s\right) /(s+1)}{s}=\frac{s-1}{s+1}=\frac{499}{500} .
$$
|
{
"resource_path": "HarvardMIT/segmented/en-72-2004-feb-guts-solutions.jsonl",
"problem_match": "\n31. ",
"solution_match": "\nSolution: "
}
|
327cb972-d44f-515a-9fe8-3bcb0552677b
| 611,273
|
A plane $P$ slices through a cube of volume 1 with a cross-section in the shape of a regular hexagon. This cube also has an inscribed sphere, whose intersection with $P$ is a circle. What is the area of the region inside the regular hexagon but outside the circle?
|
$\quad(3 \sqrt{3}-\pi) / 4$
One can show that the hexagon must have as its vertices the midpoints of six edges of the cube, as illustrated; for example, this readily follows from the fact that opposite sides of the hexagons and the medians between them are parallel. We then conclude that the side of the hexagon is $\sqrt{2} / 2$ (since it cuts off an isosceles triangle of leg $1 / 2$ from each face), so the area is $(3 / 2)(\sqrt{2} / 2)^{2}(\sqrt{3})=3 \sqrt{3} / 4$. Also, the plane passes through the center of the sphere by symmetry, so it cuts out a cross section of radius $1 / 2$, whose area (which is contained entirely inside the hexagon) is then $\pi / 4$. The sought area is thus $(3 \sqrt{3}-\pi) / 4$.
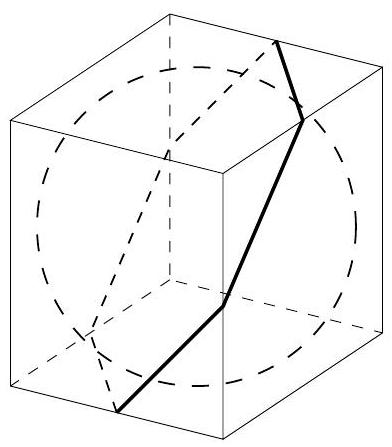
|
(3 \sqrt{3}-\pi) / 4
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
A plane $P$ slices through a cube of volume 1 with a cross-section in the shape of a regular hexagon. This cube also has an inscribed sphere, whose intersection with $P$ is a circle. What is the area of the region inside the regular hexagon but outside the circle?
|
$\quad(3 \sqrt{3}-\pi) / 4$
One can show that the hexagon must have as its vertices the midpoints of six edges of the cube, as illustrated; for example, this readily follows from the fact that opposite sides of the hexagons and the medians between them are parallel. We then conclude that the side of the hexagon is $\sqrt{2} / 2$ (since it cuts off an isosceles triangle of leg $1 / 2$ from each face), so the area is $(3 / 2)(\sqrt{2} / 2)^{2}(\sqrt{3})=3 \sqrt{3} / 4$. Also, the plane passes through the center of the sphere by symmetry, so it cuts out a cross section of radius $1 / 2$, whose area (which is contained entirely inside the hexagon) is then $\pi / 4$. The sought area is thus $(3 \sqrt{3}-\pi) / 4$.

|
{
"resource_path": "HarvardMIT/segmented/en-72-2004-feb-guts-solutions.jsonl",
"problem_match": "\n33. ",
"solution_match": "\n## Solution: "
}
|
a4a70167-8ebb-5c1a-aa94-9d649e1e2a9f
| 611,275
|
There are eleven positive integers $n$ such that there exists a convex polygon with $n$ sides whose angles, in degrees, are unequal integers that are in arithmetic progression. Find the sum of these values of $n$.
|
106
The sum of the angles of an $n$-gon is $(n-2) 180$, so the average angle measure is $(n-2) 180 / n$. The common difference in this arithmetic progression is at least 1 , so the difference between the largest and smallest angles is at least $n-1$. So the largest angle is at least $(n-1) / 2+(n-2) 180 / n$. Since the polygon is convex, this quantity is no larger than 179: $(n-1) / 2-360 / n \leq-1$, so that $360 / n-n / 2 \geq 1 / 2$. Multiplying by $2 n$ gives $720-n^{2} \geq n$. So $n(n+1) \leq 720$, which forces $n \leq 26$. Of course, since the common difference is an integer, and the angle measures are integers, $(n-2) 180 / n$ must be an integer or a half integer, so $(n-2) 360 / n=360-720 / n$ is an integer, and then $720 / n$ must be an integer. This leaves only $n=3,4,5,6,8,9,10,12,15,16,18,20,24$ as possibilities. When $n$ is even, $(n-2) 180 / n$ is not an angle of the polygon, but the mean of the two middle angles. So the common difference is at least 2 when $(n-2) 180 / n$ is an integer. For $n=20$, the middle angle is 162 , so the largest angle is at least $162+38 / 2=181$, since 38 is no larger than the difference between the smallest and largest angles. For $n=24$, the middle angle is 165 , again leading to a contradiction. So no solution exists for $n=20,24$. All of the others possess solutions:
| $n$ | angles |
| :---: | :--- |
| 3 | $59,60,61$ |
| 4 | $87,89,91,93$ |
| 5 | $106,107,108,109,110$ |
| 6 | $115,117,119,121,123,125$ |
| 8 | $128,130,132,134,136,138,140,142$ |
| 9 | $136, \ldots, 144$ |
| 10 | $135,137,139, \ldots, 153$ |
| 12 | $139,141,143, \ldots, 161$ |
| 15 | $149,150, \ldots, 163$ |
| 16 | $150,151, \ldots, 165$ |
| 18 | $143,145, \ldots, 177$ |
(These solutions are quite easy to construct.) The desired value is then $3+4+5+6+$ $8+9+10+12+15+16+18=106$.
|
106
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
There are eleven positive integers $n$ such that there exists a convex polygon with $n$ sides whose angles, in degrees, are unequal integers that are in arithmetic progression. Find the sum of these values of $n$.
|
106
The sum of the angles of an $n$-gon is $(n-2) 180$, so the average angle measure is $(n-2) 180 / n$. The common difference in this arithmetic progression is at least 1 , so the difference between the largest and smallest angles is at least $n-1$. So the largest angle is at least $(n-1) / 2+(n-2) 180 / n$. Since the polygon is convex, this quantity is no larger than 179: $(n-1) / 2-360 / n \leq-1$, so that $360 / n-n / 2 \geq 1 / 2$. Multiplying by $2 n$ gives $720-n^{2} \geq n$. So $n(n+1) \leq 720$, which forces $n \leq 26$. Of course, since the common difference is an integer, and the angle measures are integers, $(n-2) 180 / n$ must be an integer or a half integer, so $(n-2) 360 / n=360-720 / n$ is an integer, and then $720 / n$ must be an integer. This leaves only $n=3,4,5,6,8,9,10,12,15,16,18,20,24$ as possibilities. When $n$ is even, $(n-2) 180 / n$ is not an angle of the polygon, but the mean of the two middle angles. So the common difference is at least 2 when $(n-2) 180 / n$ is an integer. For $n=20$, the middle angle is 162 , so the largest angle is at least $162+38 / 2=181$, since 38 is no larger than the difference between the smallest and largest angles. For $n=24$, the middle angle is 165 , again leading to a contradiction. So no solution exists for $n=20,24$. All of the others possess solutions:
| $n$ | angles |
| :---: | :--- |
| 3 | $59,60,61$ |
| 4 | $87,89,91,93$ |
| 5 | $106,107,108,109,110$ |
| 6 | $115,117,119,121,123,125$ |
| 8 | $128,130,132,134,136,138,140,142$ |
| 9 | $136, \ldots, 144$ |
| 10 | $135,137,139, \ldots, 153$ |
| 12 | $139,141,143, \ldots, 161$ |
| 15 | $149,150, \ldots, 163$ |
| 16 | $150,151, \ldots, 165$ |
| 18 | $143,145, \ldots, 177$ |
(These solutions are quite easy to construct.) The desired value is then $3+4+5+6+$ $8+9+10+12+15+16+18=106$.
|
{
"resource_path": "HarvardMIT/segmented/en-72-2004-feb-guts-solutions.jsonl",
"problem_match": "\n35. ",
"solution_match": "\n## Solution: "
}
|
0bb45d7b-afbd-5380-a50f-f3a2b93da2d6
| 611,277
|
For a string of $P$ 's and $Q$ 's, the value is defined to be the product of the positions of the $P$ 's. For example, the string $P P Q P Q Q$ has value $1 \cdot 2 \cdot 4=8$.
Also, a string is called antipalindromic if writing it backwards, then turning all the $P$ 's into $Q$ 's and vice versa, produces the original string. For example, $P P Q P Q Q$ is antipalindromic.
There are $2^{1002}$ antipalindromic strings of length 2004. Find the sum of the reciprocals of their values.
|
$2005^{1002} / 2004$ !
Consider the product
$$
\left(\frac{1}{1}+\frac{1}{2004}\right)\left(\frac{1}{2}+\frac{1}{2003}\right)\left(\frac{1}{3}+\frac{1}{2002}\right) \cdots\left(\frac{1}{1002}+\frac{1}{1003}\right) .
$$
This product expands to $2^{1002}$ terms, and each term gives the reciprocal of the value of a corresponding antipalindromic string of $P$ 's and $Q$ 's as follows: if we choose the term $1 / n$ for the $n$th factor, then our string has a $P$ in position $n$ and $Q$ in position $2005-n$; if we choose the term $1 /(2005-n)$, then we get a $Q$ in position $n$ and $P$ in position $2005-n$. Conversely, each antipalindromic string has its value represented by exactly one of our $2^{1002}$ terms. So the value of the product is the number we are looking for. But when we simplify this product, the $n$th factor becomes $1 / n+1 /(2005-n)=2005 / n(2005-n)$. Multiplying these together, we get 1002 factors of 2005 in the numerator and each integer from 1 to 2004 exactly once in the denominator, for a total of $2005^{1002}$ /2004!.
|
\frac{2005^{1002}}{2004!}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
For a string of $P$ 's and $Q$ 's, the value is defined to be the product of the positions of the $P$ 's. For example, the string $P P Q P Q Q$ has value $1 \cdot 2 \cdot 4=8$.
Also, a string is called antipalindromic if writing it backwards, then turning all the $P$ 's into $Q$ 's and vice versa, produces the original string. For example, $P P Q P Q Q$ is antipalindromic.
There are $2^{1002}$ antipalindromic strings of length 2004. Find the sum of the reciprocals of their values.
|
$2005^{1002} / 2004$ !
Consider the product
$$
\left(\frac{1}{1}+\frac{1}{2004}\right)\left(\frac{1}{2}+\frac{1}{2003}\right)\left(\frac{1}{3}+\frac{1}{2002}\right) \cdots\left(\frac{1}{1002}+\frac{1}{1003}\right) .
$$
This product expands to $2^{1002}$ terms, and each term gives the reciprocal of the value of a corresponding antipalindromic string of $P$ 's and $Q$ 's as follows: if we choose the term $1 / n$ for the $n$th factor, then our string has a $P$ in position $n$ and $Q$ in position $2005-n$; if we choose the term $1 /(2005-n)$, then we get a $Q$ in position $n$ and $P$ in position $2005-n$. Conversely, each antipalindromic string has its value represented by exactly one of our $2^{1002}$ terms. So the value of the product is the number we are looking for. But when we simplify this product, the $n$th factor becomes $1 / n+1 /(2005-n)=2005 / n(2005-n)$. Multiplying these together, we get 1002 factors of 2005 in the numerator and each integer from 1 to 2004 exactly once in the denominator, for a total of $2005^{1002}$ /2004!.
|
{
"resource_path": "HarvardMIT/segmented/en-72-2004-feb-guts-solutions.jsonl",
"problem_match": "\n36. ",
"solution_match": "\nSolution: "
}
|
77fe7ad9-9307-5f92-bc74-0f882f4060b0
| 611,278
|
Simplify $\prod_{k=1}^{2004} \sin (2 \pi k / 4009)$.
|
## $\frac{\sqrt{4009}}{2^{2004}}$
Let $\zeta=e^{2 \pi i / 4009}$ so that $\sin (2 \pi k / 4009)=\frac{\zeta^{k}-\zeta^{-k}}{2 i}$ and $x^{4009}-1=\prod_{k=0}^{4008}\left(x-\zeta^{k}\right)$. Hence $1+x+\cdots+x^{4008}=\prod_{k=1}^{4008}\left(x-\zeta^{k}\right)$. Comparing constant coefficients gives $\prod_{k=1}^{4008} \zeta^{k}=1$, setting $x=1$ gives $\prod_{k=1}^{40 \overline{0} \overline{8}}\left(1-\zeta^{k}\right)=4009$, and setting $x=-1$ gives $\prod_{k=1}^{4008}\left(1+\zeta^{k}\right)=1$. Now, note that $\sin (2 \pi(4009-k) / 4009)=-\sin (2 \pi k / 4009)$, so
$$
\begin{aligned}
\left(\prod_{k=1}^{2004} \sin (2 \pi k / 4009)\right)^{2} & =(-1)^{2004} \prod_{k=1}^{4008} \sin (2 \pi k / 4009) \\
& =\prod_{k=1}^{4008} \frac{\zeta^{k}-\zeta^{-k}}{2 i} \\
& =\frac{1}{(2 i)^{4008}} \prod_{k=1}^{4008} \frac{\zeta^{2 k}-1}{\zeta^{k}} \\
& =\frac{1}{2^{4008}} \prod_{k=1}^{4008}\left(\zeta^{2 k}-1\right) \\
& =\frac{1}{2^{4008}} \prod_{k=1}^{4008}\left(\zeta^{k}-1\right)\left(\zeta^{k}+1\right) \\
& =\frac{4009 \cdot 1}{2^{4008}} .
\end{aligned}
$$
However, $\sin (x)$ is nonnegative on the interval $[0, \pi]$, so our product is positive. Hence it is $\frac{\sqrt{4009}}{2^{2004}}$.
|
\frac{\sqrt{4009}}{2^{2004}}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Simplify $\prod_{k=1}^{2004} \sin (2 \pi k / 4009)$.
|
## $\frac{\sqrt{4009}}{2^{2004}}$
Let $\zeta=e^{2 \pi i / 4009}$ so that $\sin (2 \pi k / 4009)=\frac{\zeta^{k}-\zeta^{-k}}{2 i}$ and $x^{4009}-1=\prod_{k=0}^{4008}\left(x-\zeta^{k}\right)$. Hence $1+x+\cdots+x^{4008}=\prod_{k=1}^{4008}\left(x-\zeta^{k}\right)$. Comparing constant coefficients gives $\prod_{k=1}^{4008} \zeta^{k}=1$, setting $x=1$ gives $\prod_{k=1}^{40 \overline{0} \overline{8}}\left(1-\zeta^{k}\right)=4009$, and setting $x=-1$ gives $\prod_{k=1}^{4008}\left(1+\zeta^{k}\right)=1$. Now, note that $\sin (2 \pi(4009-k) / 4009)=-\sin (2 \pi k / 4009)$, so
$$
\begin{aligned}
\left(\prod_{k=1}^{2004} \sin (2 \pi k / 4009)\right)^{2} & =(-1)^{2004} \prod_{k=1}^{4008} \sin (2 \pi k / 4009) \\
& =\prod_{k=1}^{4008} \frac{\zeta^{k}-\zeta^{-k}}{2 i} \\
& =\frac{1}{(2 i)^{4008}} \prod_{k=1}^{4008} \frac{\zeta^{2 k}-1}{\zeta^{k}} \\
& =\frac{1}{2^{4008}} \prod_{k=1}^{4008}\left(\zeta^{2 k}-1\right) \\
& =\frac{1}{2^{4008}} \prod_{k=1}^{4008}\left(\zeta^{k}-1\right)\left(\zeta^{k}+1\right) \\
& =\frac{4009 \cdot 1}{2^{4008}} .
\end{aligned}
$$
However, $\sin (x)$ is nonnegative on the interval $[0, \pi]$, so our product is positive. Hence it is $\frac{\sqrt{4009}}{2^{2004}}$.
|
{
"resource_path": "HarvardMIT/segmented/en-72-2004-feb-guts-solutions.jsonl",
"problem_match": "\n37. ",
"solution_match": "\n## Solution:\n\n"
}
|
c881a637-6dc9-5989-b1f0-b76a00fb9842
| 611,279
|
Let $S=\left\{p_{1} p_{2} \cdots p_{n} \mid p_{1}, p_{2}, \ldots, p_{n}\right.$ are distinct primes and $\left.p_{1}, \ldots, p_{n}<30\right\}$. Assume 1 is in $S$. Let $a_{1}$ be an element of $S$. We define, for all positive integers $n$ :
$$
\begin{gathered}
a_{n+1}=a_{n} /(n+1) \quad \text { if } a_{n} \text { is divisible by } n+1 \\
a_{n+1}=(n+2) a_{n} \\
\text { if } a_{n} \text { is not divisible by } n+1
\end{gathered}
$$
How many distinct possible values of $a_{1}$ are there such that $a_{j}=a_{1}$ for infinitely many $j$ 's?
|
512
If $a_{1}$ is odd, then we can see by induction that $a_{j}=(j+1) a_{1}$ when $j$ is even and $a_{j}=a_{1}$ when $j$ is odd (using the fact that no even $j$ can divide $a_{1}$ ). So we have infinitely many $j$ 's for which $a_{j}=a_{1}$.
If $a_{1}>2$ is even, then $a_{2}$ is odd, since $a_{2}=a_{1} / 2$, and $a_{1}$ may have only one factor of 2. Now, in general, let $p=\min \left(\left\{p_{1}, \ldots, p_{n}\right\} \backslash\{2\}\right)$. Suppose $1<j<p$. By induction, we have $a_{j}=(j+1) a_{1} / 2$ when $j$ is odd, and $a_{j}=a_{1} / 2$ when $j$ is even. So $a_{i} \neq a_{1}$ for all $1<j<p$. It follows that $a_{p}=a_{1} / 2 p$. Then, again using induction, we get for all nonnegative integers $k$ that $a_{p+k}=a_{p}$ if $k$ is even, and $a_{p+k}=(p+k+1) a_{p}$ if $k$ is odd. Clearly, $a_{p} \neq a_{1}$ and $p+k+1 \neq 2 p$ when $k$ is odd (the left side is odd, and the right side even). It follows that $a_{j}=a_{1}$ for no $j>1$. Finally, when $a_{1}=2$, we can check inductively that $a_{j}=j+1$ for $j$ odd and $a_{j}=1$ for $j$ even.
So our answer is just the number of odd elements in $S$. There are 9 odd prime numbers smaller than 30 , so the answer is $2^{9}=512$.
|
512
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Let $S=\left\{p_{1} p_{2} \cdots p_{n} \mid p_{1}, p_{2}, \ldots, p_{n}\right.$ are distinct primes and $\left.p_{1}, \ldots, p_{n}<30\right\}$. Assume 1 is in $S$. Let $a_{1}$ be an element of $S$. We define, for all positive integers $n$ :
$$
\begin{gathered}
a_{n+1}=a_{n} /(n+1) \quad \text { if } a_{n} \text { is divisible by } n+1 \\
a_{n+1}=(n+2) a_{n} \\
\text { if } a_{n} \text { is not divisible by } n+1
\end{gathered}
$$
How many distinct possible values of $a_{1}$ are there such that $a_{j}=a_{1}$ for infinitely many $j$ 's?
|
512
If $a_{1}$ is odd, then we can see by induction that $a_{j}=(j+1) a_{1}$ when $j$ is even and $a_{j}=a_{1}$ when $j$ is odd (using the fact that no even $j$ can divide $a_{1}$ ). So we have infinitely many $j$ 's for which $a_{j}=a_{1}$.
If $a_{1}>2$ is even, then $a_{2}$ is odd, since $a_{2}=a_{1} / 2$, and $a_{1}$ may have only one factor of 2. Now, in general, let $p=\min \left(\left\{p_{1}, \ldots, p_{n}\right\} \backslash\{2\}\right)$. Suppose $1<j<p$. By induction, we have $a_{j}=(j+1) a_{1} / 2$ when $j$ is odd, and $a_{j}=a_{1} / 2$ when $j$ is even. So $a_{i} \neq a_{1}$ for all $1<j<p$. It follows that $a_{p}=a_{1} / 2 p$. Then, again using induction, we get for all nonnegative integers $k$ that $a_{p+k}=a_{p}$ if $k$ is even, and $a_{p+k}=(p+k+1) a_{p}$ if $k$ is odd. Clearly, $a_{p} \neq a_{1}$ and $p+k+1 \neq 2 p$ when $k$ is odd (the left side is odd, and the right side even). It follows that $a_{j}=a_{1}$ for no $j>1$. Finally, when $a_{1}=2$, we can check inductively that $a_{j}=j+1$ for $j$ odd and $a_{j}=1$ for $j$ even.
So our answer is just the number of odd elements in $S$. There are 9 odd prime numbers smaller than 30 , so the answer is $2^{9}=512$.
|
{
"resource_path": "HarvardMIT/segmented/en-72-2004-feb-guts-solutions.jsonl",
"problem_match": "\n38. ",
"solution_match": "\n## Solution: "
}
|
551c71ab-3e70-5913-91ed-2d1ff98cb782
| 611,280
|
You want to arrange the numbers $1,2,3, \ldots, 25$ in a sequence with the following property: if $n$ is divisible by $m$, then the $n$th number is divisible by the $m$ th number. How many such sequences are there?
|
24
Let the rearranged numbers be $a_{1}, \ldots, a_{25}$. The number of pairs $(n, m)$ with $n \mid m$ must equal the number of pairs with $a_{n} \mid a_{m}$, but since each pair of the former type is also of the latter type, the converse must be true as well. Thus, $n \mid m$ if and only if $a_{n} \mid a_{m}$. Now for each $n=1,2, \ldots, 6$, the number of values divisible by $n$ uniquely determines $n$, so $n=a_{n}$. Similarly, 7, 8 must either be kept fixed by the rearrangement or interchanged, because they are the only values that divide exactly 2 other numbers in the sequence; since 7 is prime and 8 is not, we conclude they are kept fixed. Then we can easily check by induction that $n=a_{n}$ for all larger composite numbers $n \leq 25$ (by using $m=a_{m}$ for all proper factors $m$ of $n$ ) and $n=11$ (because it is the only prime that divides exactly 1 other number). So we have only the primes $n=13,17,19,23$ left to rearrange, and it is easily seen that these can be permuted arbitrarily, leaving 4 ! possible orderings altogether.
|
24
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
You want to arrange the numbers $1,2,3, \ldots, 25$ in a sequence with the following property: if $n$ is divisible by $m$, then the $n$th number is divisible by the $m$ th number. How many such sequences are there?
|
24
Let the rearranged numbers be $a_{1}, \ldots, a_{25}$. The number of pairs $(n, m)$ with $n \mid m$ must equal the number of pairs with $a_{n} \mid a_{m}$, but since each pair of the former type is also of the latter type, the converse must be true as well. Thus, $n \mid m$ if and only if $a_{n} \mid a_{m}$. Now for each $n=1,2, \ldots, 6$, the number of values divisible by $n$ uniquely determines $n$, so $n=a_{n}$. Similarly, 7, 8 must either be kept fixed by the rearrangement or interchanged, because they are the only values that divide exactly 2 other numbers in the sequence; since 7 is prime and 8 is not, we conclude they are kept fixed. Then we can easily check by induction that $n=a_{n}$ for all larger composite numbers $n \leq 25$ (by using $m=a_{m}$ for all proper factors $m$ of $n$ ) and $n=11$ (because it is the only prime that divides exactly 1 other number). So we have only the primes $n=13,17,19,23$ left to rearrange, and it is easily seen that these can be permuted arbitrarily, leaving 4 ! possible orderings altogether.
|
{
"resource_path": "HarvardMIT/segmented/en-72-2004-feb-guts-solutions.jsonl",
"problem_match": "\n39. ",
"solution_match": "\nSolution: "
}
|
885fcc5b-4661-5bfe-a2c7-3222ed016228
| 611,281
|
You would like to provide airline service to the 10 cities in the nation of Schizophrenia, by instituting a certain number of two-way routes between cities. Unfortunately, the government is about to divide Schizophrenia into two warring countries of five cities
each, and you don't know which cities will be in each new country. All airplane service between the two new countries will be discontinued. However, you want to make sure that you set up your routes so that, for any two cities in the same new country, it will be possible to get from one city to the other (without leaving the country).
What is the minimum number of routes you must set up to be assured of doing this, no matter how the government divides up the country?
|
30
Each city $C$ must be directly connected to at least 6 other cities, since otherwise the government could put $C$ in one country and all its connecting cities in the other country, and there would be no way out of $C$. This means that we have 6 routes for each of 10 cities, counted twice (since each route has two endpoints) $\Rightarrow 6 \cdot 10 / 2=30$ routes. On the other hand, this is enough: picture the cities arranged around a circle, and each city connected to its 3 closest neighbors in either direction. Then if $C$ and $D$ are in the same country but mutually inaccessible, this means that on each arc of the circle between $C$ and $D$, there must be (at least) three consecutive cities in the other country. Then this second country would have 6 cities, which is impossible. So our arrangement achieves the goal with 30 routes.
|
30
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
You would like to provide airline service to the 10 cities in the nation of Schizophrenia, by instituting a certain number of two-way routes between cities. Unfortunately, the government is about to divide Schizophrenia into two warring countries of five cities
each, and you don't know which cities will be in each new country. All airplane service between the two new countries will be discontinued. However, you want to make sure that you set up your routes so that, for any two cities in the same new country, it will be possible to get from one city to the other (without leaving the country).
What is the minimum number of routes you must set up to be assured of doing this, no matter how the government divides up the country?
|
30
Each city $C$ must be directly connected to at least 6 other cities, since otherwise the government could put $C$ in one country and all its connecting cities in the other country, and there would be no way out of $C$. This means that we have 6 routes for each of 10 cities, counted twice (since each route has two endpoints) $\Rightarrow 6 \cdot 10 / 2=30$ routes. On the other hand, this is enough: picture the cities arranged around a circle, and each city connected to its 3 closest neighbors in either direction. Then if $C$ and $D$ are in the same country but mutually inaccessible, this means that on each arc of the circle between $C$ and $D$, there must be (at least) three consecutive cities in the other country. Then this second country would have 6 cities, which is impossible. So our arrangement achieves the goal with 30 routes.
|
{
"resource_path": "HarvardMIT/segmented/en-72-2004-feb-guts-solutions.jsonl",
"problem_match": "\n40. ",
"solution_match": "\nSolution: "
}
|
f0092245-8188-505b-ad8e-e211d5b07978
| 611,282
|
A tetrahedron has all its faces triangles with sides $13,14,15$. What is its volume?
|
$42 \sqrt{55}$
Let $A B C$ be a triangle with $A B=13, B C=14, C A=15$. Let $A D, B E$ be altitudes. Then $B D=5, C D=9$. (If you don't already know this, it can be deduced from the Pythagorean Theorem: $C D^{2}-B D^{2}=\left(C D^{2}+A D^{2}\right)-\left(B D^{2}+A D^{2}\right)=A C^{2}-A B^{2}=56$, while $C D+B D=B C=14$, giving $C D-B D=56 / 14=4$, and now solve the linear system.) Also, $A D=\sqrt{A B^{2}-B D^{2}}=12$. Similar reasoning gives $A E=33 / 5$, $E C=42 / 5$.
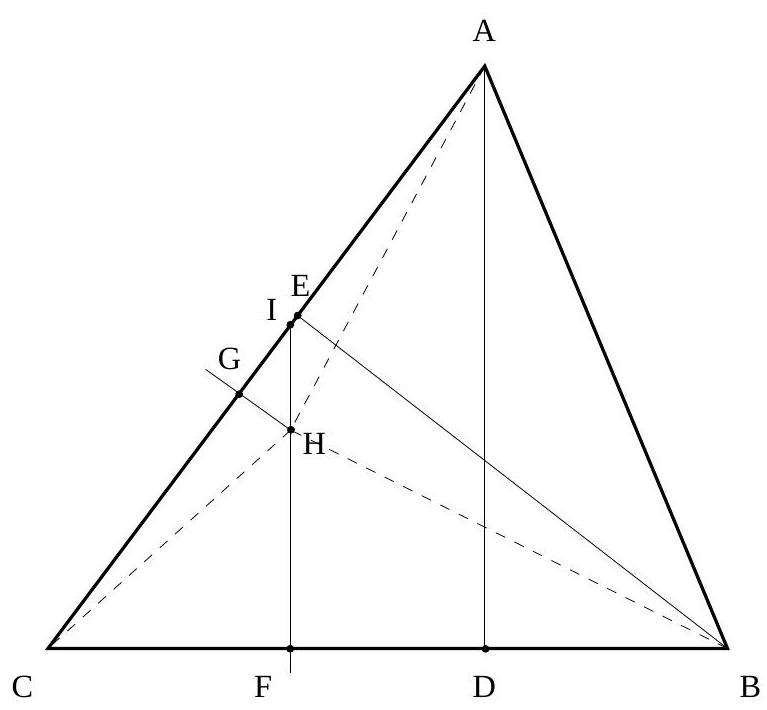
Now let $F$ be the point on $B C$ such that $C F=B D=5$, and let $G$ be on $A C$ such that $C G=A E=33 / 5$. Imagine placing face $A B C$ flat on the table, and letting $X$ be a point in space with $C X=13, B X=14$. By mentally rotating triangle $B C X$
about line $B C$, we can see that $X$ lies on the plane perpendicular to $B C$ through $F$. In particular, this holds if $X$ is the fourth vertex of our tetrahedron $A B C X$. Similarly, $X$ lies on the plane perpendicular to $A C$ through $G$. Let the mutual intersection of these two planes and plane $A B C$ be $H$. Then $X H$ is the altitude of the tetrahedron.
To find $X H$, extend $F H$ to meet $A C$ at $I$. Then $\triangle C F I \sim \triangle C D A$, a 3-4-5 triangle, so $F I=C F \cdot 4 / 3=20 / 3$, and $C I=C F \cdot 5 / 3=25 / 3$. Then $I G=C I-C G=26 / 15$, and $H I=I G \cdot 5 / 4=13 / 6$. This leads to $H F=F I-H I=9 / 2$, and finally $X H=\sqrt{X F^{2}-H F^{2}}=\sqrt{A D^{2}-H F^{2}}=3 \sqrt{55} / 2$.
Now $X A B C$ is a tetrahedron whose base $\triangle A B C$ has area $A D \cdot B C / 2=12 \cdot 14 / 2=84$, and whose height $X H$ is $3 \sqrt{55} / 2$, so its volume is $(84)(3 \sqrt{55} / 2) / 3=42 \sqrt{55}$.
|
42 \sqrt{55}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
A tetrahedron has all its faces triangles with sides $13,14,15$. What is its volume?
|
$42 \sqrt{55}$
Let $A B C$ be a triangle with $A B=13, B C=14, C A=15$. Let $A D, B E$ be altitudes. Then $B D=5, C D=9$. (If you don't already know this, it can be deduced from the Pythagorean Theorem: $C D^{2}-B D^{2}=\left(C D^{2}+A D^{2}\right)-\left(B D^{2}+A D^{2}\right)=A C^{2}-A B^{2}=56$, while $C D+B D=B C=14$, giving $C D-B D=56 / 14=4$, and now solve the linear system.) Also, $A D=\sqrt{A B^{2}-B D^{2}}=12$. Similar reasoning gives $A E=33 / 5$, $E C=42 / 5$.

Now let $F$ be the point on $B C$ such that $C F=B D=5$, and let $G$ be on $A C$ such that $C G=A E=33 / 5$. Imagine placing face $A B C$ flat on the table, and letting $X$ be a point in space with $C X=13, B X=14$. By mentally rotating triangle $B C X$
about line $B C$, we can see that $X$ lies on the plane perpendicular to $B C$ through $F$. In particular, this holds if $X$ is the fourth vertex of our tetrahedron $A B C X$. Similarly, $X$ lies on the plane perpendicular to $A C$ through $G$. Let the mutual intersection of these two planes and plane $A B C$ be $H$. Then $X H$ is the altitude of the tetrahedron.
To find $X H$, extend $F H$ to meet $A C$ at $I$. Then $\triangle C F I \sim \triangle C D A$, a 3-4-5 triangle, so $F I=C F \cdot 4 / 3=20 / 3$, and $C I=C F \cdot 5 / 3=25 / 3$. Then $I G=C I-C G=26 / 15$, and $H I=I G \cdot 5 / 4=13 / 6$. This leads to $H F=F I-H I=9 / 2$, and finally $X H=\sqrt{X F^{2}-H F^{2}}=\sqrt{A D^{2}-H F^{2}}=3 \sqrt{55} / 2$.
Now $X A B C$ is a tetrahedron whose base $\triangle A B C$ has area $A D \cdot B C / 2=12 \cdot 14 / 2=84$, and whose height $X H$ is $3 \sqrt{55} / 2$, so its volume is $(84)(3 \sqrt{55} / 2) / 3=42 \sqrt{55}$.
|
{
"resource_path": "HarvardMIT/segmented/en-72-2004-feb-guts-solutions.jsonl",
"problem_match": "\n41. ",
"solution_match": "\nSolution: "
}
|
639c9937-7056-5e09-9660-1251f59a4cf3
| 611,283
|
$S$ is a set of complex numbers such that if $u, v \in S$, then $u v \in S$ and $u^{2}+v^{2} \in S$. Suppose that the number $N$ of elements of $S$ with absolute value at most 1 is finite. What is the largest possible value of $N$ ?
|
13
First, if $S$ contained some $u \neq 0$ with absolute value $<1$, then (by the first condition) every power of $u$ would be in $S$, and $S$ would contain infinitely many different numbers of absolute value $<1$. This is a contradiction. Now suppose $S$ contains some number $u$ of absolute value 1 and argument $\theta$. If $\theta$ is not an integer multiple of $\pi / 6$, then $u$ has some power $v$ whose argument lies strictly between $\theta+\pi / 3$ and $\theta+\pi / 2$. Then $u^{2}+v^{2}=u^{2}\left(1+(v / u)^{2}\right)$ has absolute value between 0 and 1 , since $(v / u)^{2}$ lies on the unit circle with angle strictly between $2 \pi / 3$ and $\pi$. But $u^{2}+v^{2} \in S$, so this is a contradiction.
This shows that the only possible elements of $S$ with absolute value $\leq 1$ are 0 and the points on the unit circle whose arguments are multiples of $\pi / 6$, giving $N \leq 1+12=13$. To show that $N=13$ is attainable, we need to show that there exists a possible set $S$ containing all these points. Let $T$ be the set of all numbers of the form $a+b \omega$, where $a, b$ are integers are $\omega$ is a complex cube root of 1 . Since $\omega^{2}=-1-\omega, T$ is closed under multiplication and addition. Then, if we let $S$ be the set of numbers $u$ such that $u^{2} \in T, S$ has the required properties, and it contains the 13 complex numbers specified, so we're in business.
|
13
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
$S$ is a set of complex numbers such that if $u, v \in S$, then $u v \in S$ and $u^{2}+v^{2} \in S$. Suppose that the number $N$ of elements of $S$ with absolute value at most 1 is finite. What is the largest possible value of $N$ ?
|
13
First, if $S$ contained some $u \neq 0$ with absolute value $<1$, then (by the first condition) every power of $u$ would be in $S$, and $S$ would contain infinitely many different numbers of absolute value $<1$. This is a contradiction. Now suppose $S$ contains some number $u$ of absolute value 1 and argument $\theta$. If $\theta$ is not an integer multiple of $\pi / 6$, then $u$ has some power $v$ whose argument lies strictly between $\theta+\pi / 3$ and $\theta+\pi / 2$. Then $u^{2}+v^{2}=u^{2}\left(1+(v / u)^{2}\right)$ has absolute value between 0 and 1 , since $(v / u)^{2}$ lies on the unit circle with angle strictly between $2 \pi / 3$ and $\pi$. But $u^{2}+v^{2} \in S$, so this is a contradiction.
This shows that the only possible elements of $S$ with absolute value $\leq 1$ are 0 and the points on the unit circle whose arguments are multiples of $\pi / 6$, giving $N \leq 1+12=13$. To show that $N=13$ is attainable, we need to show that there exists a possible set $S$ containing all these points. Let $T$ be the set of all numbers of the form $a+b \omega$, where $a, b$ are integers are $\omega$ is a complex cube root of 1 . Since $\omega^{2}=-1-\omega, T$ is closed under multiplication and addition. Then, if we let $S$ be the set of numbers $u$ such that $u^{2} \in T, S$ has the required properties, and it contains the 13 complex numbers specified, so we're in business.
|
{
"resource_path": "HarvardMIT/segmented/en-72-2004-feb-guts-solutions.jsonl",
"problem_match": "\n42. ",
"solution_match": "\n## Solution: "
}
|
eaae2be6-3f12-51a2-80b4-13ef3f55466e
| 611,284
|
Shown on your answer sheet is a $20 \times 20$ grid. Place as many queens as you can so that each of them attacks at most one other queen. (A queen is a chess piece that can
move any number of squares horizontally, vertically, or diagonally.) It's not very hard to get 20 queens, so you get no points for that, but you get 5 points for each further queen beyond 20 . You can mark the grid by placing a dot in each square that contains a queen.
|
An elementary argument shows there cannot be more than 26 queens: we cannot have more than 2 in a row or column (or else the middle queen would attack the other two), so if we had 27 queens, there would be at least 7 columns with more than one queen and thus at most 13 queens that are alone in their respective columns. Similarly, there would be at most 13 queens that are alone in their respective rows. This leaves $27-13-13=1$ queen who is not alone in her row or column, and she therefore attacks two other queens, contradiction.
Of course, this is not a very strong argument since it makes no use of the diagonals. The best possible number of queens is not known to us; the following construction gives 23:
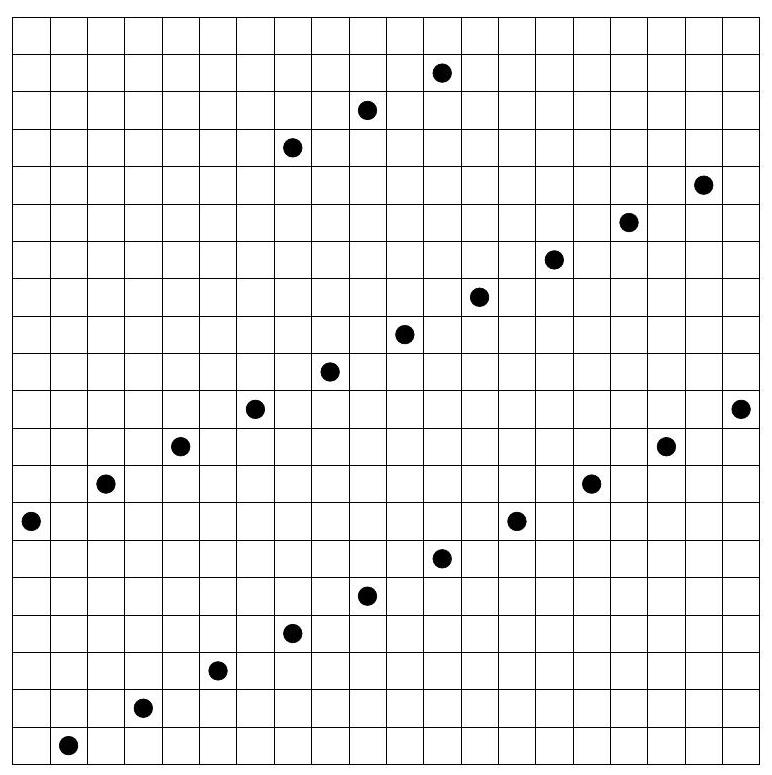
|
23
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Shown on your answer sheet is a $20 \times 20$ grid. Place as many queens as you can so that each of them attacks at most one other queen. (A queen is a chess piece that can
move any number of squares horizontally, vertically, or diagonally.) It's not very hard to get 20 queens, so you get no points for that, but you get 5 points for each further queen beyond 20 . You can mark the grid by placing a dot in each square that contains a queen.
|
An elementary argument shows there cannot be more than 26 queens: we cannot have more than 2 in a row or column (or else the middle queen would attack the other two), so if we had 27 queens, there would be at least 7 columns with more than one queen and thus at most 13 queens that are alone in their respective columns. Similarly, there would be at most 13 queens that are alone in their respective rows. This leaves $27-13-13=1$ queen who is not alone in her row or column, and she therefore attacks two other queens, contradiction.
Of course, this is not a very strong argument since it makes no use of the diagonals. The best possible number of queens is not known to us; the following construction gives 23:

|
{
"resource_path": "HarvardMIT/segmented/en-72-2004-feb-guts-solutions.jsonl",
"problem_match": "\n44. ",
"solution_match": "\nSolution: "
}
|
79309886-ef5a-5ab4-8952-53a5aadcb69e
| 611,286
|
A binary string of length $n$ is a sequence of $n$ digits, each of which is 0 or 1 . The distance between two binary strings of the same length is the number of positions in which they disagree; for example, the distance between the strings 01101011 and 00101110 is 3 since they differ in the second, sixth, and eighth positions.
Find as many binary strings of length 8 as you can, such that the distance between any two of them is at least 3 . You get one point per string.
|
The maximum possible number of such strings is 20 . An example of a set
attaining this bound is
| 00000000 | 00110101 |
| :--- | :--- |
| 11001010 | 10011110 |
| 11100001 | 01101011 |
| 11010100 | 01100110 |
| 10111001 | 10010011 |
| 01111100 | 11001101 |
| 00111010 | 10101100 |
| 01010111 | 11110010 |
| 00001111 | 01011001 |
| 10100111 | 11111111 |
This example is taken from page 57 of F. J. MacWilliams and N. J. A. Sloane, The Theory of Error Correcting Codes (New York: Elsevier Publishing, 1977). The proof that 20 is the best possible is elementary but too long to reproduce here; see pages 537-541 of MacWilliams and Sloane for details.
In general, a set of $M$ strings of length $n$ such that any two have a distance of at least $d$ is called an $(n, M, d)$-code. These objects are of basic importance in coding theory, which studies how to transmit information through a channel with a known error rate. For example, since the code given above has minimum distance 3, I can transmit to you a message consisting of strings in this code, and even if there is a possible error rate of one digit in each string, you will still be able to determine the intended message uniquely.
|
20
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
A binary string of length $n$ is a sequence of $n$ digits, each of which is 0 or 1 . The distance between two binary strings of the same length is the number of positions in which they disagree; for example, the distance between the strings 01101011 and 00101110 is 3 since they differ in the second, sixth, and eighth positions.
Find as many binary strings of length 8 as you can, such that the distance between any two of them is at least 3 . You get one point per string.
|
The maximum possible number of such strings is 20 . An example of a set
attaining this bound is
| 00000000 | 00110101 |
| :--- | :--- |
| 11001010 | 10011110 |
| 11100001 | 01101011 |
| 11010100 | 01100110 |
| 10111001 | 10010011 |
| 01111100 | 11001101 |
| 00111010 | 10101100 |
| 01010111 | 11110010 |
| 00001111 | 01011001 |
| 10100111 | 11111111 |
This example is taken from page 57 of F. J. MacWilliams and N. J. A. Sloane, The Theory of Error Correcting Codes (New York: Elsevier Publishing, 1977). The proof that 20 is the best possible is elementary but too long to reproduce here; see pages 537-541 of MacWilliams and Sloane for details.
In general, a set of $M$ strings of length $n$ such that any two have a distance of at least $d$ is called an $(n, M, d)$-code. These objects are of basic importance in coding theory, which studies how to transmit information through a channel with a known error rate. For example, since the code given above has minimum distance 3, I can transmit to you a message consisting of strings in this code, and even if there is a possible error rate of one digit in each string, you will still be able to determine the intended message uniquely.
|
{
"resource_path": "HarvardMIT/segmented/en-72-2004-feb-guts-solutions.jsonl",
"problem_match": "\n45. ",
"solution_match": "\nSolution: "
}
|
11bdc1f3-9f31-54f0-a327-83cec7a3e597
| 611,287
|
How many real numbers $x$ are solutions to the following equation?
$$
|x-1|=|x-2|+|x-3|
$$
|
2
If $x<1$, the equation becomes $(1-x)=(2-x)+(3-x)$ which simplifies to $x=4$, contradicting the assumption $x<1$. If $1 \leq x \leq 2$, we get $(x-1)=(2-x)+(3-x)$, which gives $x=2$. If $2 \leq x \leq 3$, we get $(x-1)=(x-2)+(3-x)$, which again gives $x=2$. If $x \geq 3$, we get $(x-1)=(x-2)+(x-3)$, or $x=4$. So 2 and 4 are the only solutions, and the answer is 2 .
|
2
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
How many real numbers $x$ are solutions to the following equation?
$$
|x-1|=|x-2|+|x-3|
$$
|
2
If $x<1$, the equation becomes $(1-x)=(2-x)+(3-x)$ which simplifies to $x=4$, contradicting the assumption $x<1$. If $1 \leq x \leq 2$, we get $(x-1)=(2-x)+(3-x)$, which gives $x=2$. If $2 \leq x \leq 3$, we get $(x-1)=(x-2)+(3-x)$, which again gives $x=2$. If $x \geq 3$, we get $(x-1)=(x-2)+(x-3)$, or $x=4$. So 2 and 4 are the only solutions, and the answer is 2 .
|
{
"resource_path": "HarvardMIT/segmented/en-82-2005-feb-alg-solutions.jsonl",
"problem_match": "\n1. ",
"solution_match": "\n## Solution: "
}
|
225b1935-2487-5da3-a85a-111d6aef8e03
| 611,304
|
How many real numbers $x$ are solutions to the following equation?
$$
2003^{x}+2004^{x}=2005^{x}
$$
|
1
Rewrite the equation as $(2003 / 2005)^{x}+(2004 / 2005)^{x}=1$. The left side is strictly decreasing in $x$, so there cannot be more than one solution. On the other hand, the left side equals $2>1$ when $x=0$ and goes to 0 when $x$ is very large, so it must equal 1 somewhere in between. Therefore there is one solution.
|
1
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
How many real numbers $x$ are solutions to the following equation?
$$
2003^{x}+2004^{x}=2005^{x}
$$
|
1
Rewrite the equation as $(2003 / 2005)^{x}+(2004 / 2005)^{x}=1$. The left side is strictly decreasing in $x$, so there cannot be more than one solution. On the other hand, the left side equals $2>1$ when $x=0$ and goes to 0 when $x$ is very large, so it must equal 1 somewhere in between. Therefore there is one solution.
|
{
"resource_path": "HarvardMIT/segmented/en-82-2005-feb-alg-solutions.jsonl",
"problem_match": "\n2. ",
"solution_match": "\n## Solution: "
}
|
285d891d-b596-56eb-90d9-ff0602a5349c
| 611,305
|
Let $x, y$, and $z$ be distinct real numbers that sum to 0 . Find the maximum possible value of
$$
\frac{x y+y z+z x}{x^{2}+y^{2}+z^{2}} .
$$
|
$-1 / 2$
Note that $0=(x+y+z)^{2}=x^{2}+y^{2}+z^{2}+2 x y+2 y z+2 z x$. Rearranging, we get that $x y+y z+z x=-\frac{1}{2}\left(x^{2}+y^{2}+z^{2}\right)$, so that in fact the quantity is always equal to $-1 / 2$.
|
-\frac{1}{2}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Let $x, y$, and $z$ be distinct real numbers that sum to 0 . Find the maximum possible value of
$$
\frac{x y+y z+z x}{x^{2}+y^{2}+z^{2}} .
$$
|
$-1 / 2$
Note that $0=(x+y+z)^{2}=x^{2}+y^{2}+z^{2}+2 x y+2 y z+2 z x$. Rearranging, we get that $x y+y z+z x=-\frac{1}{2}\left(x^{2}+y^{2}+z^{2}\right)$, so that in fact the quantity is always equal to $-1 / 2$.
|
{
"resource_path": "HarvardMIT/segmented/en-82-2005-feb-alg-solutions.jsonl",
"problem_match": "\n3. ",
"solution_match": "\nSolution: "
}
|
7d788c6c-e102-5575-aaf3-2332caeb43e6
| 611,306
|
If $a, b, c>0$, what is the smallest possible value of $\left\lfloor\frac{a+b}{c}\right\rfloor+\left\lfloor\frac{b+c}{a}\right\rfloor+\left\lfloor\frac{c+a}{b}\right\rfloor$ ? (Note that $\lfloor x\rfloor$ denotes the greatest integer less than or equal to $x$.)
|
4
Since $\lfloor x\rfloor>x-1$ for all $x$, we have that
$$
\begin{aligned}
\left\lfloor\frac{a+b}{c}\right\rfloor+\left\lfloor\frac{b+c}{a}\right\rfloor+\left\lfloor\frac{c+a}{b}\right\rfloor & >\frac{a+b}{c}+\frac{b+c}{a}+\frac{c+a}{b}-3 \\
& =\left(\frac{a}{b}+\frac{b}{a}\right)+\left(\frac{b}{c}+\frac{c}{b}\right)+\left(\frac{c}{a}+\frac{a}{c}\right)-3
\end{aligned}
$$
But by the AM-GM inequality, each of the first three terms in the last line is at least 2. Therefore, the lefthand side is greater than $2+2+2-3=3$. Since it is an integer, the smallest value it can be is 4 . This is in fact attainable by letting $(a, b, c)=(6,8,9)$.
|
4
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
If $a, b, c>0$, what is the smallest possible value of $\left\lfloor\frac{a+b}{c}\right\rfloor+\left\lfloor\frac{b+c}{a}\right\rfloor+\left\lfloor\frac{c+a}{b}\right\rfloor$ ? (Note that $\lfloor x\rfloor$ denotes the greatest integer less than or equal to $x$.)
|
4
Since $\lfloor x\rfloor>x-1$ for all $x$, we have that
$$
\begin{aligned}
\left\lfloor\frac{a+b}{c}\right\rfloor+\left\lfloor\frac{b+c}{a}\right\rfloor+\left\lfloor\frac{c+a}{b}\right\rfloor & >\frac{a+b}{c}+\frac{b+c}{a}+\frac{c+a}{b}-3 \\
& =\left(\frac{a}{b}+\frac{b}{a}\right)+\left(\frac{b}{c}+\frac{c}{b}\right)+\left(\frac{c}{a}+\frac{a}{c}\right)-3
\end{aligned}
$$
But by the AM-GM inequality, each of the first three terms in the last line is at least 2. Therefore, the lefthand side is greater than $2+2+2-3=3$. Since it is an integer, the smallest value it can be is 4 . This is in fact attainable by letting $(a, b, c)=(6,8,9)$.
|
{
"resource_path": "HarvardMIT/segmented/en-82-2005-feb-alg-solutions.jsonl",
"problem_match": "\n4. ",
"solution_match": "\nSolution: "
}
|
2351c5bf-c093-5c15-8965-7c91561fa3db
| 611,307
|
Ten positive integers are arranged around a circle. Each number is one more than the greatest common divisor of its two neighbors. What is the sum of the ten numbers?
|
28
First note that all the integers must be at least 2, because the greatest common divisor of any two positive integers is at least 1 . Let $n$ be the largest integer in the circle. The greatest common divisor of its two neighbors is $n-1$. Therefore, each of the two neighbors is at least $n-1$ but at most $n$, so since $n-1 \nmid n$ for $n-1 \geq 2$, they must both be equal to $n-1$. Let $m$ be one of the numbers on the other side of $n-1$ from $n$. Then $\operatorname{gcd}(n, m)=n-2$. Since $n-2 \geq 0, n-2 \mid n$ only for $n=3$ or 4 . If $n=3$, each number must be 2 or 3 , and it is easy to check that there is no solution. If $n=4$, then it is again not hard to find that there is a unique solution up to rotation, namely 4322343223. The only possible sum is therefore 28 .
|
28
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Ten positive integers are arranged around a circle. Each number is one more than the greatest common divisor of its two neighbors. What is the sum of the ten numbers?
|
28
First note that all the integers must be at least 2, because the greatest common divisor of any two positive integers is at least 1 . Let $n$ be the largest integer in the circle. The greatest common divisor of its two neighbors is $n-1$. Therefore, each of the two neighbors is at least $n-1$ but at most $n$, so since $n-1 \nmid n$ for $n-1 \geq 2$, they must both be equal to $n-1$. Let $m$ be one of the numbers on the other side of $n-1$ from $n$. Then $\operatorname{gcd}(n, m)=n-2$. Since $n-2 \geq 0, n-2 \mid n$ only for $n=3$ or 4 . If $n=3$, each number must be 2 or 3 , and it is easy to check that there is no solution. If $n=4$, then it is again not hard to find that there is a unique solution up to rotation, namely 4322343223. The only possible sum is therefore 28 .
|
{
"resource_path": "HarvardMIT/segmented/en-82-2005-feb-alg-solutions.jsonl",
"problem_match": "\n5. ",
"solution_match": "\n## Solution: "
}
|
fc7f220a-1767-5d6b-84b3-d9efd562c595
| 69,649
|
Find the sum of the $x$-coordinates of the distinct points of intersection of the plane curves given by $x^{2}=x+y+4$ and $y^{2}=y-15 x+36$.
|
0
Substituting $y=x^{2}-x-4$ into the second equation yields
$$
\begin{aligned}
0 & =\left(x^{2}-x-4\right)^{2}-\left(x^{2}-x-4\right)+15 x-36 \\
& =x^{4}-2 x^{3}-7 x^{2}+8 x+16-x^{2}+x+4+15 x-36 \\
& =x^{4}-2 x^{3}-8 x^{2}+24 x-16 \\
& =(x-2)\left(x^{3}-8 x+8\right)=(x-2)^{2}\left(x^{2}+2 x-4\right) .
\end{aligned}
$$
This quartic has three distinct real roots at $x=2,-1 \pm \sqrt{5}$. Each of these yields a distinct point of intersection, so the answer is their sum, 0 .
|
0
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Find the sum of the $x$-coordinates of the distinct points of intersection of the plane curves given by $x^{2}=x+y+4$ and $y^{2}=y-15 x+36$.
|
0
Substituting $y=x^{2}-x-4$ into the second equation yields
$$
\begin{aligned}
0 & =\left(x^{2}-x-4\right)^{2}-\left(x^{2}-x-4\right)+15 x-36 \\
& =x^{4}-2 x^{3}-7 x^{2}+8 x+16-x^{2}+x+4+15 x-36 \\
& =x^{4}-2 x^{3}-8 x^{2}+24 x-16 \\
& =(x-2)\left(x^{3}-8 x+8\right)=(x-2)^{2}\left(x^{2}+2 x-4\right) .
\end{aligned}
$$
This quartic has three distinct real roots at $x=2,-1 \pm \sqrt{5}$. Each of these yields a distinct point of intersection, so the answer is their sum, 0 .

|
{
"resource_path": "HarvardMIT/segmented/en-82-2005-feb-alg-solutions.jsonl",
"problem_match": "\n6. ",
"solution_match": "\nSolution: "
}
|
68e92791-6d59-520e-9602-538e9b877fe1
| 611,308
|
Let $x$ be a positive real number. Find the maximum possible value of
$$
\frac{x^{2}+2-\sqrt{x^{4}+4}}{x} .
$$
|
$2 \sqrt{2}-2$
Rationalizing the numerator, we get
$$
\begin{aligned}
\frac{x^{2}+2-\sqrt{x^{4}+4}}{x} \cdot \frac{x^{2}+2+\sqrt{x^{4}+4}}{x^{2}+2+\sqrt{x^{4}+4}} & =\frac{\left(x^{2}+2\right)^{2}-\left(x^{4}+4\right)}{x\left(x^{2}+2+\sqrt{x^{4}+4}\right)} \\
& =\frac{4 x^{2}}{x\left(x^{2}+2+\sqrt{x^{4}+4}\right)} \\
& =\frac{4}{\frac{1}{x}\left(x^{2}+2+\sqrt{x^{4}+4}\right)} \\
& =\frac{4}{x+\frac{2}{x}+\sqrt{x^{2}+\frac{4}{x^{2}}}}
\end{aligned}
$$
Since we wish to maximize this quantity, we wish to minimize the denominator. By AM-GM, $x+\frac{2}{x} \geq 2 \sqrt{2}$ and $x^{2}+\frac{4}{x^{2}} \geq 4$, so that the denominator is at least $2 \sqrt{2}+2$. Therefore,
$$
\frac{x^{2}+2-\sqrt{x^{4}+4}}{x} \leq \frac{4}{2 \sqrt{2}+2}=2 \sqrt{2}-2,
$$
with equality when $x=\sqrt{2}$.
|
2 \sqrt{2}-2
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Let $x$ be a positive real number. Find the maximum possible value of
$$
\frac{x^{2}+2-\sqrt{x^{4}+4}}{x} .
$$
|
$2 \sqrt{2}-2$
Rationalizing the numerator, we get
$$
\begin{aligned}
\frac{x^{2}+2-\sqrt{x^{4}+4}}{x} \cdot \frac{x^{2}+2+\sqrt{x^{4}+4}}{x^{2}+2+\sqrt{x^{4}+4}} & =\frac{\left(x^{2}+2\right)^{2}-\left(x^{4}+4\right)}{x\left(x^{2}+2+\sqrt{x^{4}+4}\right)} \\
& =\frac{4 x^{2}}{x\left(x^{2}+2+\sqrt{x^{4}+4}\right)} \\
& =\frac{4}{\frac{1}{x}\left(x^{2}+2+\sqrt{x^{4}+4}\right)} \\
& =\frac{4}{x+\frac{2}{x}+\sqrt{x^{2}+\frac{4}{x^{2}}}}
\end{aligned}
$$
Since we wish to maximize this quantity, we wish to minimize the denominator. By AM-GM, $x+\frac{2}{x} \geq 2 \sqrt{2}$ and $x^{2}+\frac{4}{x^{2}} \geq 4$, so that the denominator is at least $2 \sqrt{2}+2$. Therefore,
$$
\frac{x^{2}+2-\sqrt{x^{4}+4}}{x} \leq \frac{4}{2 \sqrt{2}+2}=2 \sqrt{2}-2,
$$
with equality when $x=\sqrt{2}$.
|
{
"resource_path": "HarvardMIT/segmented/en-82-2005-feb-alg-solutions.jsonl",
"problem_match": "\n7. ",
"solution_match": "\nSolution: "
}
|
aad72a11-afc6-5fc3-8d34-96afe59b728b
| 611,309
|
Compute
$$
\sum_{n=0}^{\infty} \frac{n}{n^{4}+n^{2}+1}
$$
|
$1 / 2$
Note that
$$
n^{4}+n^{2}+1=\left(n^{4}+2 n^{2}+1\right)-n^{2}=\left(n^{2}+1\right)^{2}-n^{2}=\left(n^{2}+n+1\right)\left(n^{2}-n+1\right)
$$
Decomposing into partial fractions, we find that
$$
\frac{n}{n^{4}+n^{2}+1}=\frac{1}{2}\left(\frac{1}{n^{2}-n+1}-\frac{1}{n^{2}+n+1}\right) .
$$
Now, note that if $f(n)=\frac{1}{n^{2}-n+1}$, then $f(n+1)=\frac{1}{(n+1)^{2}-(n+1)+1}=\frac{1}{n^{2}+n+1}$. It follows that
$$
\sum_{n=0}^{\infty} \frac{n}{n^{4}+n^{2}+1}=\frac{1}{2}((f(0)-f(1))+(f(1)-f(2))+(f(2)-f(3))+\cdots) .
$$
Since $f(n)$ tends towards 0 as $n$ gets large, this sum telescopes to $f(0) / 2=1 / 2$.
|
\frac{1}{2}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Compute
$$
\sum_{n=0}^{\infty} \frac{n}{n^{4}+n^{2}+1}
$$
|
$1 / 2$
Note that
$$
n^{4}+n^{2}+1=\left(n^{4}+2 n^{2}+1\right)-n^{2}=\left(n^{2}+1\right)^{2}-n^{2}=\left(n^{2}+n+1\right)\left(n^{2}-n+1\right)
$$
Decomposing into partial fractions, we find that
$$
\frac{n}{n^{4}+n^{2}+1}=\frac{1}{2}\left(\frac{1}{n^{2}-n+1}-\frac{1}{n^{2}+n+1}\right) .
$$
Now, note that if $f(n)=\frac{1}{n^{2}-n+1}$, then $f(n+1)=\frac{1}{(n+1)^{2}-(n+1)+1}=\frac{1}{n^{2}+n+1}$. It follows that
$$
\sum_{n=0}^{\infty} \frac{n}{n^{4}+n^{2}+1}=\frac{1}{2}((f(0)-f(1))+(f(1)-f(2))+(f(2)-f(3))+\cdots) .
$$
Since $f(n)$ tends towards 0 as $n$ gets large, this sum telescopes to $f(0) / 2=1 / 2$.
|
{
"resource_path": "HarvardMIT/segmented/en-82-2005-feb-alg-solutions.jsonl",
"problem_match": "\n8. ",
"solution_match": "\n## Solution: "
}
|
70039676-e82f-582d-81d2-fcf962137b57
| 611,310
|
The number $27,000,001$ has exactly four prime factors. Find their sum.
|
652
First, we factor
$$
\begin{aligned}
27 x^{6}+1 & =\left(3 x^{2}\right)^{3}+1 \\
& =\left(3 x^{2}+1\right)\left(9 x^{4}-3 x^{2}+1\right) \\
& =\left(3 x^{2}+1\right)\left(\left(9 x^{4}+6 x^{2}+1\right)-9 x^{2}\right) \\
& =\left(3 x^{2}+1\right)\left(\left(3 x^{2}+1\right)^{2}-(3 x)^{2}\right) \\
& =\left(3 x^{2}+1\right)\left(3 x^{2}+3 x+1\right)\left(3 x^{2}-3 x+1\right)
\end{aligned}
$$
Letting $x=10$, we get that $27000001=301 \cdot 331 \cdot 271$. A quick check shows that $301=7 \cdot 43$, so that $27000001=7 \cdot 43 \cdot 271 \cdot 331$. Each factor here is prime, and their sum is 652 .
|
652
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
The number $27,000,001$ has exactly four prime factors. Find their sum.
|
652
First, we factor
$$
\begin{aligned}
27 x^{6}+1 & =\left(3 x^{2}\right)^{3}+1 \\
& =\left(3 x^{2}+1\right)\left(9 x^{4}-3 x^{2}+1\right) \\
& =\left(3 x^{2}+1\right)\left(\left(9 x^{4}+6 x^{2}+1\right)-9 x^{2}\right) \\
& =\left(3 x^{2}+1\right)\left(\left(3 x^{2}+1\right)^{2}-(3 x)^{2}\right) \\
& =\left(3 x^{2}+1\right)\left(3 x^{2}+3 x+1\right)\left(3 x^{2}-3 x+1\right)
\end{aligned}
$$
Letting $x=10$, we get that $27000001=301 \cdot 331 \cdot 271$. A quick check shows that $301=7 \cdot 43$, so that $27000001=7 \cdot 43 \cdot 271 \cdot 331$. Each factor here is prime, and their sum is 652 .
|
{
"resource_path": "HarvardMIT/segmented/en-82-2005-feb-alg-solutions.jsonl",
"problem_match": "\n9. ",
"solution_match": "\nSolution: "
}
|
ac526486-e161-5418-96d5-5562fb976223
| 611,311
|
Find the sum of the absolute values of the roots of $x^{4}-4 x^{3}-4 x^{2}+16 x-8=0$.
|
$2+2 \sqrt{2}+2 \sqrt{3}$
$$
\begin{aligned}
x^{4}-4 x^{3}-4 x^{2}+16 x-8 & =\left(x^{4}-4 x^{3}+4 x^{2}\right)-\left(8 x^{2}-16 x+8\right) \\
& =x^{2}(x-2)^{2}-8(x-1)^{2} \\
& =\left(x^{2}-2 x\right)^{2}-(2 \sqrt{2} x-2 \sqrt{2})^{2} \\
& =\left(x^{2}-(2+2 \sqrt{2}) x+2 \sqrt{2}\right)\left(x^{2}-(2-2 \sqrt{2}) x-2 \sqrt{2}\right)
\end{aligned}
$$
But noting that $(1+\sqrt{2})^{2}=3+2 \sqrt{2}$ and completing the square,
$$
\begin{aligned}
x^{2}-(2+2 \sqrt{2}) x+2 \sqrt{2} & =x^{2}-(2+2 \sqrt{2}) x+3+2 \sqrt{2}-3 \\
& =(x-(1+\sqrt{2}))^{2}-(\sqrt{3})^{2} \\
& =(x-1-\sqrt{2}+\sqrt{3})(x-1-\sqrt{2}-\sqrt{3}) .
\end{aligned}
$$
Likewise,
$$
x^{2}-(2-2 \sqrt{2}) x-2 \sqrt{2}=(x-1+\sqrt{2}+\sqrt{3})(x-1+\sqrt{2}-\sqrt{3})
$$
so the roots of the quartic are $1 \pm \sqrt{2} \pm \sqrt{3}$. Only one of these is negative, namely $1-\sqrt{2}-\sqrt{3}$, so the sum of the absolute values of the roots is
$(1+\sqrt{2}+\sqrt{3})+(1+\sqrt{2}-\sqrt{3})+(1-\sqrt{2}+\sqrt{3})-(1-\sqrt{2}-\sqrt{3})=2+2 \sqrt{2}+2 \sqrt{3}$.
|
2+2 \sqrt{2}+2 \sqrt{3}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Find the sum of the absolute values of the roots of $x^{4}-4 x^{3}-4 x^{2}+16 x-8=0$.
|
$2+2 \sqrt{2}+2 \sqrt{3}$
$$
\begin{aligned}
x^{4}-4 x^{3}-4 x^{2}+16 x-8 & =\left(x^{4}-4 x^{3}+4 x^{2}\right)-\left(8 x^{2}-16 x+8\right) \\
& =x^{2}(x-2)^{2}-8(x-1)^{2} \\
& =\left(x^{2}-2 x\right)^{2}-(2 \sqrt{2} x-2 \sqrt{2})^{2} \\
& =\left(x^{2}-(2+2 \sqrt{2}) x+2 \sqrt{2}\right)\left(x^{2}-(2-2 \sqrt{2}) x-2 \sqrt{2}\right)
\end{aligned}
$$
But noting that $(1+\sqrt{2})^{2}=3+2 \sqrt{2}$ and completing the square,
$$
\begin{aligned}
x^{2}-(2+2 \sqrt{2}) x+2 \sqrt{2} & =x^{2}-(2+2 \sqrt{2}) x+3+2 \sqrt{2}-3 \\
& =(x-(1+\sqrt{2}))^{2}-(\sqrt{3})^{2} \\
& =(x-1-\sqrt{2}+\sqrt{3})(x-1-\sqrt{2}-\sqrt{3}) .
\end{aligned}
$$
Likewise,
$$
x^{2}-(2-2 \sqrt{2}) x-2 \sqrt{2}=(x-1+\sqrt{2}+\sqrt{3})(x-1+\sqrt{2}-\sqrt{3})
$$
so the roots of the quartic are $1 \pm \sqrt{2} \pm \sqrt{3}$. Only one of these is negative, namely $1-\sqrt{2}-\sqrt{3}$, so the sum of the absolute values of the roots is
$(1+\sqrt{2}+\sqrt{3})+(1+\sqrt{2}-\sqrt{3})+(1-\sqrt{2}+\sqrt{3})-(1-\sqrt{2}-\sqrt{3})=2+2 \sqrt{2}+2 \sqrt{3}$.
|
{
"resource_path": "HarvardMIT/segmented/en-82-2005-feb-alg-solutions.jsonl",
"problem_match": "\n10. ",
"solution_match": "\nSolution: "
}
|
0a1a972c-1a23-5a34-9ed2-a7a1c1725e93
| 611,312
|
Let $f(x)=x^{3}+a x+b$, with $a \neq b$, and suppose the tangent lines to the graph of $f$ at $x=a$ and $x=b$ are parallel. Find $f(1)$.
|
1
Since $f^{\prime}(x)=3 x^{2}+a$, we must have $3 a^{2}+a=3 b^{2}+a$. Then $a^{2}=b^{2}$, and since $a \neq b$, $a=-b$. Thus $f(1)=1+a+b=1$.
|
1
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Let $f(x)=x^{3}+a x+b$, with $a \neq b$, and suppose the tangent lines to the graph of $f$ at $x=a$ and $x=b$ are parallel. Find $f(1)$.
|
1
Since $f^{\prime}(x)=3 x^{2}+a$, we must have $3 a^{2}+a=3 b^{2}+a$. Then $a^{2}=b^{2}$, and since $a \neq b$, $a=-b$. Thus $f(1)=1+a+b=1$.
|
{
"resource_path": "HarvardMIT/segmented/en-82-2005-feb-calc-solutions.jsonl",
"problem_match": "\n1. ",
"solution_match": "\n## Solution: "
}
|
5803bad4-cb34-5af3-80d2-7dfe5d458d17
| 611,313
|
A plane curve is parameterized by $x(t)=\int_{t}^{\infty} \frac{\cos u}{u} d u$ and $y(t)=\int_{t}^{\infty} \frac{\sin u}{u} d u$ for $1 \leq t \leq$ 2. What is the length of the curve?
|
$\ln 2$
By the Second Fundamental Theorem of Calculus, $\frac{d x}{d t}=-\frac{\cos t}{t}$ and $\frac{d y}{d t}=-\frac{\sin t}{t}$. Therefore, the length of the curve is
$$
\int_{1}^{2} \sqrt{\left(\frac{d x}{d t}\right)^{2}+\left(\frac{d y}{d t}\right)^{2}} d t=\int_{1}^{2} \sqrt{\frac{\cos ^{2} t}{t^{2}}+\frac{\sin ^{2} t}{t^{2}}} d t=\int_{1}^{2} \frac{1}{t} d t=[\ln t]_{1}^{2}=\ln 2
$$
|
\ln 2
|
Yes
|
Yes
|
math-word-problem
|
Calculus
|
A plane curve is parameterized by $x(t)=\int_{t}^{\infty} \frac{\cos u}{u} d u$ and $y(t)=\int_{t}^{\infty} \frac{\sin u}{u} d u$ for $1 \leq t \leq$ 2. What is the length of the curve?
|
$\ln 2$
By the Second Fundamental Theorem of Calculus, $\frac{d x}{d t}=-\frac{\cos t}{t}$ and $\frac{d y}{d t}=-\frac{\sin t}{t}$. Therefore, the length of the curve is
$$
\int_{1}^{2} \sqrt{\left(\frac{d x}{d t}\right)^{2}+\left(\frac{d y}{d t}\right)^{2}} d t=\int_{1}^{2} \sqrt{\frac{\cos ^{2} t}{t^{2}}+\frac{\sin ^{2} t}{t^{2}}} d t=\int_{1}^{2} \frac{1}{t} d t=[\ln t]_{1}^{2}=\ln 2
$$
|
{
"resource_path": "HarvardMIT/segmented/en-82-2005-feb-calc-solutions.jsonl",
"problem_match": "\n2. ",
"solution_match": "\nSolution: "
}
|
62a5aa87-aafc-5a40-9a7d-ab364bd8d889
| 611,314
|
Let $f: \mathbf{R} \rightarrow \mathbf{R}$ be a continuous function with $\int_{0}^{1} f(x) f^{\prime}(x) d x=0$ and $\int_{0}^{1} f(x)^{2} f^{\prime}(x) d x=$ 18. What is $\int_{0}^{1} f(x)^{4} f^{\prime}(x) d x$ ?
|
486/5
$$
\begin{gathered}
0=\int_{0}^{1} f(x) f^{\prime}(x) d x=\int_{f(0)}^{f(1)} u d u=\frac{1}{2}\left(f(1)^{2}-f(0)^{2}\right), \text { and } \\
18=\int_{0}^{1} f(x)^{2} f^{\prime}(x) d x=\int_{f(0)}^{f(1)} u^{2} d u=\frac{1}{3}\left(f(1)^{3}-f(0)^{3}\right) .
\end{gathered}
$$
The first equation implies $f(0)= \pm f(1)$. The second equation shows that $f(0) \neq f(1)$, and in fact $54=f(1)^{3}-f(0)^{3}=2 f(1)^{3}$, so $f(1)=3$ and $f(0)=-3$. Then
$$
\int_{0}^{1} f(x)^{4} f^{\prime}(x) d x=\int_{f(0)}^{f(1)} u^{4} d u=\frac{1}{5}\left(f(1)^{5}-f(0)^{5}\right)=\frac{1}{5}(243+243)=\frac{486}{5} .
$$
|
\frac{486}{5}
|
Yes
|
Yes
|
math-word-problem
|
Calculus
|
Let $f: \mathbf{R} \rightarrow \mathbf{R}$ be a continuous function with $\int_{0}^{1} f(x) f^{\prime}(x) d x=0$ and $\int_{0}^{1} f(x)^{2} f^{\prime}(x) d x=$ 18. What is $\int_{0}^{1} f(x)^{4} f^{\prime}(x) d x$ ?
|
486/5
$$
\begin{gathered}
0=\int_{0}^{1} f(x) f^{\prime}(x) d x=\int_{f(0)}^{f(1)} u d u=\frac{1}{2}\left(f(1)^{2}-f(0)^{2}\right), \text { and } \\
18=\int_{0}^{1} f(x)^{2} f^{\prime}(x) d x=\int_{f(0)}^{f(1)} u^{2} d u=\frac{1}{3}\left(f(1)^{3}-f(0)^{3}\right) .
\end{gathered}
$$
The first equation implies $f(0)= \pm f(1)$. The second equation shows that $f(0) \neq f(1)$, and in fact $54=f(1)^{3}-f(0)^{3}=2 f(1)^{3}$, so $f(1)=3$ and $f(0)=-3$. Then
$$
\int_{0}^{1} f(x)^{4} f^{\prime}(x) d x=\int_{f(0)}^{f(1)} u^{4} d u=\frac{1}{5}\left(f(1)^{5}-f(0)^{5}\right)=\frac{1}{5}(243+243)=\frac{486}{5} .
$$
|
{
"resource_path": "HarvardMIT/segmented/en-82-2005-feb-calc-solutions.jsonl",
"problem_match": "\n3. ",
"solution_match": "\nSolution: "
}
|
edc8be38-3ae8-5de6-8816-2fc0d553c030
| 611,315
|
Calculate
$$
\lim _{x \rightarrow 0^{+}}\left(x^{x^{x}}-x^{x}\right) .
$$
|
-1
We first calculate $\lim _{x \rightarrow 0^{+}} x^{x}$ : it is just $\exp \left(\lim _{x \rightarrow 0^{+}} x \ln x\right)$. But
$$
\lim _{x \rightarrow 0^{+}} x \ln x=\lim _{x \rightarrow 0^{+}} \frac{\ln x}{1 / x}=\lim _{x \rightarrow 0^{+}} \frac{1 / x}{-1 / x^{2}}=\lim _{x \rightarrow 0^{+}}-x=0
$$
by L'Hôpital's Rule. Therefore $\lim _{x \rightarrow 0^{+}} x^{x}=1$. Then $\lim _{x \rightarrow 0^{+}} x^{x^{x}}=0^{1}=0$, so $\lim _{x \rightarrow 0^{+}}\left(x^{x^{x}}-x^{x}\right)=-1$.
|
-1
|
Yes
|
Yes
|
math-word-problem
|
Calculus
|
Calculate
$$
\lim _{x \rightarrow 0^{+}}\left(x^{x^{x}}-x^{x}\right) .
$$
|
-1
We first calculate $\lim _{x \rightarrow 0^{+}} x^{x}$ : it is just $\exp \left(\lim _{x \rightarrow 0^{+}} x \ln x\right)$. But
$$
\lim _{x \rightarrow 0^{+}} x \ln x=\lim _{x \rightarrow 0^{+}} \frac{\ln x}{1 / x}=\lim _{x \rightarrow 0^{+}} \frac{1 / x}{-1 / x^{2}}=\lim _{x \rightarrow 0^{+}}-x=0
$$
by L'Hôpital's Rule. Therefore $\lim _{x \rightarrow 0^{+}} x^{x}=1$. Then $\lim _{x \rightarrow 0^{+}} x^{x^{x}}=0^{1}=0$, so $\lim _{x \rightarrow 0^{+}}\left(x^{x^{x}}-x^{x}\right)=-1$.
|
{
"resource_path": "HarvardMIT/segmented/en-82-2005-feb-calc-solutions.jsonl",
"problem_match": "\n5. ",
"solution_match": "\nSolution: "
}
|
fa384e77-4c9b-5a54-beaa-8d2df112438d
| 611,317
|
The graph of $r=2+\cos 2 \theta$ and its reflection over the line $y=x$ bound five regions in the plane. Find the area of the region containing the origin.
|
$9 \pi / 2-8$
The original graph is closer to the origin than its reflection for $\theta \in\left(\frac{\pi}{4}, \frac{3 \pi}{4}\right) \cup\left(\frac{5 \pi}{4}, \frac{7 \pi}{4}\right)$, and the region is symmetric about the origin. Therefore the area we wish to find is the polar integral
$$
\begin{aligned}
4 \int_{\frac{\pi}{4}}^{\frac{3 \pi}{4}} \frac{1}{2}(2+\cos 2 \theta)^{2} d \theta & =2 \int_{\frac{\pi}{4}}^{\frac{3 \pi}{4}}\left(4+4 \cos 2 \theta+\cos ^{2} 2 \theta\right) d \theta \\
& =2 \int_{\frac{\pi}{4}}^{\frac{3 \pi}{4}}\left(4+4 \cos 2 \theta+\frac{1}{2}(1+\cos 4 \theta)\right) d \theta \\
& =\left[9 \theta+4 \sin 2 \theta+\frac{1}{4} \sin 4 \theta\right]_{\frac{\pi}{4}}^{\frac{3 \pi}{4}} \\
& =\left(\frac{27 \pi}{4}-4\right)-\left(\frac{9 \pi}{4}+4\right)=\frac{9 \pi}{2}-8
\end{aligned}
$$
|
\frac{9 \pi}{2}-8
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
The graph of $r=2+\cos 2 \theta$ and its reflection over the line $y=x$ bound five regions in the plane. Find the area of the region containing the origin.
|
$9 \pi / 2-8$

The original graph is closer to the origin than its reflection for $\theta \in\left(\frac{\pi}{4}, \frac{3 \pi}{4}\right) \cup\left(\frac{5 \pi}{4}, \frac{7 \pi}{4}\right)$, and the region is symmetric about the origin. Therefore the area we wish to find is the polar integral
$$
\begin{aligned}
4 \int_{\frac{\pi}{4}}^{\frac{3 \pi}{4}} \frac{1}{2}(2+\cos 2 \theta)^{2} d \theta & =2 \int_{\frac{\pi}{4}}^{\frac{3 \pi}{4}}\left(4+4 \cos 2 \theta+\cos ^{2} 2 \theta\right) d \theta \\
& =2 \int_{\frac{\pi}{4}}^{\frac{3 \pi}{4}}\left(4+4 \cos 2 \theta+\frac{1}{2}(1+\cos 4 \theta)\right) d \theta \\
& =\left[9 \theta+4 \sin 2 \theta+\frac{1}{4} \sin 4 \theta\right]_{\frac{\pi}{4}}^{\frac{3 \pi}{4}} \\
& =\left(\frac{27 \pi}{4}-4\right)-\left(\frac{9 \pi}{4}+4\right)=\frac{9 \pi}{2}-8
\end{aligned}
$$
|
{
"resource_path": "HarvardMIT/segmented/en-82-2005-feb-calc-solutions.jsonl",
"problem_match": "\n6. ",
"solution_match": "\nSolution: "
}
|
1b049353-50c6-556d-93e0-f4bfceccbd7f
| 611,318
|
Two ants, one starting at $(-1,1)$, the other at $(1,1)$, walk to the right along the parabola $y=x^{2}$ such that their midpoint moves along the line $y=1$ with constant speed 1. When the left ant first hits the line $y=\frac{1}{2}$, what is its speed?
|
$3 \sqrt{3}-3$
When the left ant first hits the line $y=\frac{1}{2}$, the right ant hits the line $y=\frac{3}{2}$. The left ant is then at $\left(-\frac{\sqrt{2}}{2}, \frac{1}{2}\right)$, and the right ant is at $\left(\frac{\sqrt{6}}{2}, \frac{3}{2}\right)$. Let the left ant have velocity with components $v_{x}$ and $v_{y}$, the right ant velocity with components $w_{x}$ and $w_{y}$. Since $\frac{d y}{d x}=2 x, \frac{v_{y}}{v_{x}}=-\sqrt{2}$ and $\frac{w_{y}}{w_{x}}=\sqrt{6}$. Since the midpoint of the ants moves at speed 1 along the line $y=1, \frac{1}{2}\left(v_{x}+w_{x}\right)=1$ and $\frac{1}{2}\left(v_{y}+w_{y}\right)=0$. Therefore, $\sqrt{2} v_{x}=-v_{y}=w_{y}=\sqrt{6} w_{x}=\sqrt{6}\left(2-v_{x}\right)$. Solving for $v_{x}$ gives $\frac{2 \sqrt{6}}{\sqrt{6}+\sqrt{2}}=3-\sqrt{3}$. Then the speed of the left ant is
$$
\sqrt{v_{x}^{2}+v_{y}^{2}}=\sqrt{v_{x}^{2}+\left(-\sqrt{2} v_{x}\right)^{2}}=\sqrt{3}\left|v_{x}\right|=3 \sqrt{3}-3
$$
|
3 \sqrt{3}-3
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Two ants, one starting at $(-1,1)$, the other at $(1,1)$, walk to the right along the parabola $y=x^{2}$ such that their midpoint moves along the line $y=1$ with constant speed 1. When the left ant first hits the line $y=\frac{1}{2}$, what is its speed?
|
$3 \sqrt{3}-3$
When the left ant first hits the line $y=\frac{1}{2}$, the right ant hits the line $y=\frac{3}{2}$. The left ant is then at $\left(-\frac{\sqrt{2}}{2}, \frac{1}{2}\right)$, and the right ant is at $\left(\frac{\sqrt{6}}{2}, \frac{3}{2}\right)$. Let the left ant have velocity with components $v_{x}$ and $v_{y}$, the right ant velocity with components $w_{x}$ and $w_{y}$. Since $\frac{d y}{d x}=2 x, \frac{v_{y}}{v_{x}}=-\sqrt{2}$ and $\frac{w_{y}}{w_{x}}=\sqrt{6}$. Since the midpoint of the ants moves at speed 1 along the line $y=1, \frac{1}{2}\left(v_{x}+w_{x}\right)=1$ and $\frac{1}{2}\left(v_{y}+w_{y}\right)=0$. Therefore, $\sqrt{2} v_{x}=-v_{y}=w_{y}=\sqrt{6} w_{x}=\sqrt{6}\left(2-v_{x}\right)$. Solving for $v_{x}$ gives $\frac{2 \sqrt{6}}{\sqrt{6}+\sqrt{2}}=3-\sqrt{3}$. Then the speed of the left ant is
$$
\sqrt{v_{x}^{2}+v_{y}^{2}}=\sqrt{v_{x}^{2}+\left(-\sqrt{2} v_{x}\right)^{2}}=\sqrt{3}\left|v_{x}\right|=3 \sqrt{3}-3
$$
|
{
"resource_path": "HarvardMIT/segmented/en-82-2005-feb-calc-solutions.jsonl",
"problem_match": "\n7. ",
"solution_match": "\nSolution: "
}
|
ebe91856-ef22-54a8-a5e2-eaa78c37648d
| 611,319
|
If $f$ is a continuous real function such that $f(x-1)+f(x+1) \geq x+f(x)$ for all $x$, what is the minimum possible value of $\int_{1}^{2005} f(x) d x$ ?
|
2010012
Let $g(x)=f(x)-x$. Then
$$
g(x-1)+x-1+g(x+1)+x+1 \geq x+g(x)+x
$$
or $g(x-1)+g(x+1) \geq g(x)$. But now,
$$
g(x+3) \geq g(x+2)-g(x+1) \geq-g(x)
$$
Therefore
$$
\begin{aligned}
\int_{a}^{a+6} g(x) d x & =\int_{a}^{a+3} g(x) d x+\int_{a+3}^{a+6} g(x) d x \\
& =\int_{a}^{a+3}(g(x)+g(x+3)) d x \geq 0
\end{aligned}
$$
It follows that
$$
\int_{1}^{2005} g(x)=\sum_{n=0}^{333} \int_{6 n+1}^{6 n+7} g(x) d x \geq 0
$$
so that
$$
\int_{1}^{2005} f(x) d x=\int_{1}^{2005}(g(x)+x) d x \geq \int_{1}^{2005} x d x=\left[\frac{x^{2}}{2}\right]_{1}^{2005}=\frac{2005^{2}-1}{2}=2010012
$$
Equality holds for $f(x)=x$.
|
2010012
|
Yes
|
Yes
|
math-word-problem
|
Calculus
|
If $f$ is a continuous real function such that $f(x-1)+f(x+1) \geq x+f(x)$ for all $x$, what is the minimum possible value of $\int_{1}^{2005} f(x) d x$ ?
|
2010012
Let $g(x)=f(x)-x$. Then
$$
g(x-1)+x-1+g(x+1)+x+1 \geq x+g(x)+x
$$
or $g(x-1)+g(x+1) \geq g(x)$. But now,
$$
g(x+3) \geq g(x+2)-g(x+1) \geq-g(x)
$$
Therefore
$$
\begin{aligned}
\int_{a}^{a+6} g(x) d x & =\int_{a}^{a+3} g(x) d x+\int_{a+3}^{a+6} g(x) d x \\
& =\int_{a}^{a+3}(g(x)+g(x+3)) d x \geq 0
\end{aligned}
$$
It follows that
$$
\int_{1}^{2005} g(x)=\sum_{n=0}^{333} \int_{6 n+1}^{6 n+7} g(x) d x \geq 0
$$
so that
$$
\int_{1}^{2005} f(x) d x=\int_{1}^{2005}(g(x)+x) d x \geq \int_{1}^{2005} x d x=\left[\frac{x^{2}}{2}\right]_{1}^{2005}=\frac{2005^{2}-1}{2}=2010012
$$
Equality holds for $f(x)=x$.
|
{
"resource_path": "HarvardMIT/segmented/en-82-2005-feb-calc-solutions.jsonl",
"problem_match": "\n8. ",
"solution_match": "\nSolution: "
}
|
e51998ad-2f72-5aef-bf45-6c0855619373
| 611,320
|
Compute
$$
\sum_{k=0}^{\infty} \frac{4}{(4 k)!}
$$
|
$e+1 / e+2 \cos 1$
This is the power series
$$
4+\frac{4 x^{4}}{4!}+\frac{4 x^{8}}{8!}+\cdots
$$
evaluated at $x=1$. But this power series can be written as the sum
$$
\begin{aligned}
& \left(1+\frac{x}{1!}+\frac{x^{2}}{2!}+\frac{x^{3}}{3!}+\frac{x^{4}}{4!}+\frac{x^{5}}{5!}+\frac{x^{6}}{6!}+\frac{x^{7}}{7!}+\cdots\right) \\
+ & \left(1-\frac{x}{1!}+\frac{x^{2}}{2!}-\frac{x^{3}}{3!}+\frac{x^{4}}{4!}-\frac{x^{5}}{5!}+\frac{x^{6}}{6!}-\frac{x^{7}}{7!}+\cdots\right) \\
+ & 2\left(1-\frac{x^{2}}{2!}+\frac{x^{4}}{4!}-\frac{x^{6}}{6!}+\cdots\right) \\
= & e^{x}+e^{-x}+2 \cos x .
\end{aligned}
$$
It follows that the quantity is $e+1 / e+2 \cos 1$.
|
e + \frac{1}{e} + 2 \cos 1
|
Yes
|
Yes
|
math-word-problem
|
Calculus
|
Compute
$$
\sum_{k=0}^{\infty} \frac{4}{(4 k)!}
$$
|
$e+1 / e+2 \cos 1$
This is the power series
$$
4+\frac{4 x^{4}}{4!}+\frac{4 x^{8}}{8!}+\cdots
$$
evaluated at $x=1$. But this power series can be written as the sum
$$
\begin{aligned}
& \left(1+\frac{x}{1!}+\frac{x^{2}}{2!}+\frac{x^{3}}{3!}+\frac{x^{4}}{4!}+\frac{x^{5}}{5!}+\frac{x^{6}}{6!}+\frac{x^{7}}{7!}+\cdots\right) \\
+ & \left(1-\frac{x}{1!}+\frac{x^{2}}{2!}-\frac{x^{3}}{3!}+\frac{x^{4}}{4!}-\frac{x^{5}}{5!}+\frac{x^{6}}{6!}-\frac{x^{7}}{7!}+\cdots\right) \\
+ & 2\left(1-\frac{x^{2}}{2!}+\frac{x^{4}}{4!}-\frac{x^{6}}{6!}+\cdots\right) \\
= & e^{x}+e^{-x}+2 \cos x .
\end{aligned}
$$
It follows that the quantity is $e+1 / e+2 \cos 1$.
|
{
"resource_path": "HarvardMIT/segmented/en-82-2005-feb-calc-solutions.jsonl",
"problem_match": "\n9. ",
"solution_match": "\nSolution: "
}
|
ebe78b52-6dec-5912-abcf-f16304d794a9
| 611,321
|
Let $f: \mathbf{R} \rightarrow \mathbf{R}$ be a smooth function such that $f^{\prime}(x)=f(1-x)$ for all $x$ and $f(0)=1$. Find $f(1)$.
|
$\quad \sec 1+\tan 1$
Differentiating the given equation gives $f^{\prime \prime}(x)=-f(x)$. This has solutions of the form $A \cos (x)+B \sin (x)$. Since $f(0)=1, A=1$. Then $f^{\prime}(x)=B \cos (x)-\sin (x)$ and
$$
\begin{aligned}
f(1-x) & =\cos (1-x)+B \sin (1-x) \\
& =\cos 1 \cos x+\sin 1 \sin x+B \sin 1 \cos x-B \cos 1 \sin x \\
& =(\cos 1+B \sin 1) \cos x+(\sin 1-B \cos 1) \sin x
\end{aligned}
$$
Therefore, $B=\cos 1+B \sin 1$ and $-1=\sin 1-B \cos 1$, both of which yield as solutions
$$
B=\frac{\cos 1}{1-\sin 1}=\frac{1+\sin 1}{\cos 1}=\sec 1+\tan 1
$$
|
\sec 1+\tan 1
|
Yes
|
Yes
|
math-word-problem
|
Calculus
|
Let $f: \mathbf{R} \rightarrow \mathbf{R}$ be a smooth function such that $f^{\prime}(x)=f(1-x)$ for all $x$ and $f(0)=1$. Find $f(1)$.
|
$\quad \sec 1+\tan 1$
Differentiating the given equation gives $f^{\prime \prime}(x)=-f(x)$. This has solutions of the form $A \cos (x)+B \sin (x)$. Since $f(0)=1, A=1$. Then $f^{\prime}(x)=B \cos (x)-\sin (x)$ and
$$
\begin{aligned}
f(1-x) & =\cos (1-x)+B \sin (1-x) \\
& =\cos 1 \cos x+\sin 1 \sin x+B \sin 1 \cos x-B \cos 1 \sin x \\
& =(\cos 1+B \sin 1) \cos x+(\sin 1-B \cos 1) \sin x
\end{aligned}
$$
Therefore, $B=\cos 1+B \sin 1$ and $-1=\sin 1-B \cos 1$, both of which yield as solutions
$$
B=\frac{\cos 1}{1-\sin 1}=\frac{1+\sin 1}{\cos 1}=\sec 1+\tan 1
$$
|
{
"resource_path": "HarvardMIT/segmented/en-82-2005-feb-calc-solutions.jsonl",
"problem_match": "\n10. ",
"solution_match": "\n## Solution: "
}
|
dd65734a-3bb5-5ea6-8642-2dc5ee3c18df
| 611,322
|
A true-false test has ten questions. If you answer five questions "true" and five "false," your score is guaranteed to be at least four. How many answer keys are there for which this is true?
|
22
Suppose that either nine or ten of the questions have the same answer. Then no matter which five questions we pick to have this answer, we will be right at least four times. Conversely, suppose that there are at least two questions with each answer; we will show that we can get a score less than four. By symmetry, assume there are at least five questions whose answer is true. Then if we label five of these false, not only will we get these five wrong, but we will also have answered all the false questions with true, for a total of at least seven incorrect. There are 2 ways for all the questions to have the same answer, and $2 \cdot 10=20$ ways for one question to have a different answer from the others, for a total of 22 ways.
|
22
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
A true-false test has ten questions. If you answer five questions "true" and five "false," your score is guaranteed to be at least four. How many answer keys are there for which this is true?
|
22
Suppose that either nine or ten of the questions have the same answer. Then no matter which five questions we pick to have this answer, we will be right at least four times. Conversely, suppose that there are at least two questions with each answer; we will show that we can get a score less than four. By symmetry, assume there are at least five questions whose answer is true. Then if we label five of these false, not only will we get these five wrong, but we will also have answered all the false questions with true, for a total of at least seven incorrect. There are 2 ways for all the questions to have the same answer, and $2 \cdot 10=20$ ways for one question to have a different answer from the others, for a total of 22 ways.
|
{
"resource_path": "HarvardMIT/segmented/en-82-2005-feb-comb-solutions.jsonl",
"problem_match": "\n1. ",
"solution_match": "\nSolution: "
}
|
0e1450ed-cfd6-51c4-b71c-ff023ae9f7de
| 611,323
|
How many nonempty subsets of $\{1,2,3, \ldots, 12\}$ have the property that the sum of the largest element and the smallest element is 13 ?
|
1365
If $a$ is the smallest element of such a set, then $13-a$ is the largest element, and for the remaining elements we may choose any (or none) of the $12-2 a$ elements $a+1, a+2, \ldots,(13-a)-1$. Thus there are $2^{12-2 a}$ such sets whose smallest element is $a$. Also, $13-a \geq a$ clearly implies $a<7$. Summing over all $a=1,2, \ldots, 6$, we get a total of
$$
2^{10}+2^{8}+2^{6}+\cdots+2^{0}=4^{5}+4^{4}+\cdots+4^{0}=\left(4^{6}-1\right) /(4-1)=4095 / 3=1365
$$
possible sets.
|
1365
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
How many nonempty subsets of $\{1,2,3, \ldots, 12\}$ have the property that the sum of the largest element and the smallest element is 13 ?
|
1365
If $a$ is the smallest element of such a set, then $13-a$ is the largest element, and for the remaining elements we may choose any (or none) of the $12-2 a$ elements $a+1, a+2, \ldots,(13-a)-1$. Thus there are $2^{12-2 a}$ such sets whose smallest element is $a$. Also, $13-a \geq a$ clearly implies $a<7$. Summing over all $a=1,2, \ldots, 6$, we get a total of
$$
2^{10}+2^{8}+2^{6}+\cdots+2^{0}=4^{5}+4^{4}+\cdots+4^{0}=\left(4^{6}-1\right) /(4-1)=4095 / 3=1365
$$
possible sets.
|
{
"resource_path": "HarvardMIT/segmented/en-82-2005-feb-comb-solutions.jsonl",
"problem_match": "\n2. ",
"solution_match": "\nSolution: "
}
|
ddc4ea48-2dfc-58ae-892c-69ae6833de8c
| 611,324
|
The Red Sox play the Yankees in a best-of-seven series that ends as soon as one team wins four games. Suppose that the probability that the Red Sox win Game $n$ is $\frac{n-1}{6}$. What is the probability that the Red Sox will win the series?
|
$1 / 2$
Note that if we imagine that the series always continues to seven games even after one team has won four, this will never change the winner of the series. Notice also that the probability that the Red Sox will win Game $n$ is precisely the probability that the Yankees will win Game $8-n$. Therefore, the probability that the Yankees win at least four games is the same as the probability that the Red Sox win at least four games, namely $1 / 2$.
|
\frac{1}{2}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
The Red Sox play the Yankees in a best-of-seven series that ends as soon as one team wins four games. Suppose that the probability that the Red Sox win Game $n$ is $\frac{n-1}{6}$. What is the probability that the Red Sox will win the series?
|
$1 / 2$
Note that if we imagine that the series always continues to seven games even after one team has won four, this will never change the winner of the series. Notice also that the probability that the Red Sox will win Game $n$ is precisely the probability that the Yankees will win Game $8-n$. Therefore, the probability that the Yankees win at least four games is the same as the probability that the Red Sox win at least four games, namely $1 / 2$.
|
{
"resource_path": "HarvardMIT/segmented/en-82-2005-feb-comb-solutions.jsonl",
"problem_match": "\n3. ",
"solution_match": "\n## Solution: "
}
|
6fdb8dcf-fec6-5ac0-9bd8-4261a0462e95
| 611,325
|
In how many ways can 4 purple balls and 4 green balls be placed into a $4 \times 4$ grid such that every row and column contains one purple ball and one green ball? Only one ball may be placed in each box, and rotations and reflections of a single configuration are considered different.
|
216
There are $4!=24$ ways to place the four purple balls into the grid. Choose any purple ball, and place two green balls, one in its row and the other in its column. There are four boxes that do not yet lie in the same row or column as a green ball, and at least one of these contains a purple ball (otherwise the two rows containing green balls would contain the original purple ball as well as the two in the columns not containing green balls). It is then easy to see that there is a unique way to place the remaining green balls. Therefore, there are a total of $24 \cdot 9=216$ ways.
|
216
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
In how many ways can 4 purple balls and 4 green balls be placed into a $4 \times 4$ grid such that every row and column contains one purple ball and one green ball? Only one ball may be placed in each box, and rotations and reflections of a single configuration are considered different.
|
216
There are $4!=24$ ways to place the four purple balls into the grid. Choose any purple ball, and place two green balls, one in its row and the other in its column. There are four boxes that do not yet lie in the same row or column as a green ball, and at least one of these contains a purple ball (otherwise the two rows containing green balls would contain the original purple ball as well as the two in the columns not containing green balls). It is then easy to see that there is a unique way to place the remaining green balls. Therefore, there are a total of $24 \cdot 9=216$ ways.
|
{
"resource_path": "HarvardMIT/segmented/en-82-2005-feb-comb-solutions.jsonl",
"problem_match": "\n4. ",
"solution_match": "\n## Solution: "
}
|
27059042-5eee-5abe-9d6e-ebc290a14004
| 611,326
|
Doug and Ryan are competing in the 2005 Wiffle Ball Home Run Derby. In each round, each player takes a series of swings. Each swing results in either a home run or an out, and an out ends the series. When Doug swings, the probability that he will hit a home run is $1 / 3$. When Ryan swings, the probability that he will hit a home run is $1 / 2$. In one round, what is the probability that Doug will hit more home runs than Ryan hits?
|
$1 / 5$
Denote this probability by $p$. Doug hits more home runs if he hits a home run on his first try when Ryan does not, or if they both hit home runs on their first try and Doug hits more home runs thereafter. The probability of the first case occurring is $\frac{1}{3} \cdot \frac{1}{2}=\frac{1}{6}$, and the probability of the second case occurring is $\frac{1}{3} \cdot \frac{1}{2} \cdot p=\frac{p}{6}$. Therefore $p=\frac{1}{6}+\frac{p}{6}$, which we solve to find $p=\frac{1}{5}$.
|
\frac{1}{5}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Doug and Ryan are competing in the 2005 Wiffle Ball Home Run Derby. In each round, each player takes a series of swings. Each swing results in either a home run or an out, and an out ends the series. When Doug swings, the probability that he will hit a home run is $1 / 3$. When Ryan swings, the probability that he will hit a home run is $1 / 2$. In one round, what is the probability that Doug will hit more home runs than Ryan hits?
|
$1 / 5$
Denote this probability by $p$. Doug hits more home runs if he hits a home run on his first try when Ryan does not, or if they both hit home runs on their first try and Doug hits more home runs thereafter. The probability of the first case occurring is $\frac{1}{3} \cdot \frac{1}{2}=\frac{1}{6}$, and the probability of the second case occurring is $\frac{1}{3} \cdot \frac{1}{2} \cdot p=\frac{p}{6}$. Therefore $p=\frac{1}{6}+\frac{p}{6}$, which we solve to find $p=\frac{1}{5}$.
|
{
"resource_path": "HarvardMIT/segmented/en-82-2005-feb-comb-solutions.jsonl",
"problem_match": "\n5. ",
"solution_match": "\n## Solution: "
}
|
f0bcb861-48ae-551f-a388-4b8e8d56c5f0
| 611,327
|
Three fair six-sided dice, each numbered 1 through 6 , are rolled. What is the probability that the three numbers that come up can form the sides of a triangle?
|
$37 / 72$
Denote this probability by $p$, and let the three numbers that come up be $x, y$, and $z$. We will calculate $1-p$ instead: $1-p$ is the probability that $x \geq y+z, y \geq z+x$, or $z \geq x+y$. Since these three events are mutually exclusive, $1-p$ is just 3 times the probability that $x \geq y+z$. This happens with probability $(0+1+3+6+10+15) / 216=35 / 216$, so the answer is $1-3 \cdot(35 / 216)=1-35 / 72=37 / 72$.
|
\frac{37}{72}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Three fair six-sided dice, each numbered 1 through 6 , are rolled. What is the probability that the three numbers that come up can form the sides of a triangle?
|
$37 / 72$
Denote this probability by $p$, and let the three numbers that come up be $x, y$, and $z$. We will calculate $1-p$ instead: $1-p$ is the probability that $x \geq y+z, y \geq z+x$, or $z \geq x+y$. Since these three events are mutually exclusive, $1-p$ is just 3 times the probability that $x \geq y+z$. This happens with probability $(0+1+3+6+10+15) / 216=35 / 216$, so the answer is $1-3 \cdot(35 / 216)=1-35 / 72=37 / 72$.
|
{
"resource_path": "HarvardMIT/segmented/en-82-2005-feb-comb-solutions.jsonl",
"problem_match": "\n6. ",
"solution_match": "\nSolution: "
}
|
93ff27cc-47b0-5647-ad7d-531de16caeea
| 611,328
|
What is the maximum number of bishops that can be placed on an $8 \times 8$ chessboard such that at most three bishops lie on any diagonal?
|
38
If the chessboard is colored black and white as usual, then any diagonal is a solid color, so we may consider bishops on black and white squares separately. In one direction, the lengths of the black diagonals are $2,4,6,8,6,4$, and 2 . Each of these can have at most three bishops, except the first and last which can have at most two, giving a total of at most $2+3+3+3+3+3+2=19$ bishops on black squares. Likewise there can be at most 19 bishops on white squares for a total of at most 38 bishops. This is indeed attainable as in the diagram below.

|
38
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
What is the maximum number of bishops that can be placed on an $8 \times 8$ chessboard such that at most three bishops lie on any diagonal?
|
38
If the chessboard is colored black and white as usual, then any diagonal is a solid color, so we may consider bishops on black and white squares separately. In one direction, the lengths of the black diagonals are $2,4,6,8,6,4$, and 2 . Each of these can have at most three bishops, except the first and last which can have at most two, giving a total of at most $2+3+3+3+3+3+2=19$ bishops on black squares. Likewise there can be at most 19 bishops on white squares for a total of at most 38 bishops. This is indeed attainable as in the diagram below.

|
{
"resource_path": "HarvardMIT/segmented/en-82-2005-feb-comb-solutions.jsonl",
"problem_match": "\n7. ",
"solution_match": "\n## Solution: "
}
|
d907389a-1119-562a-8714-dfc2cae4b37c
| 611,329
|
Every second, Andrea writes down a random digit uniformly chosen from the set $\{1,2,3,4\}$. She stops when the last two numbers she has written sum to a prime number. What is the probability that the last number she writes down is 1 ?
|
15/44
Let $p_{n}$ be the probability that the last number she writes down is 1 when the first number she writes down is $n$. Suppose she starts by writing 2 or 4 . Then she can continue writing either 2 or 4 , but the first time she writes 1 or 3 , she stops. Therefore $p_{2}=p_{4}=\frac{1}{2}$. Suppose she starts by writing 1 . Then she stops if she writes 1 , 2 , or 4 , but continues if she writes 3 . Therefore $p_{1}=\frac{1}{4}\left(1+p_{3}\right)$. If she starts by writing 3 , then she stops if she writes 2 or 4 and otherwise continues. Therefore $p_{3}=\frac{1}{4}\left(p_{1}+p_{3}\right)=\frac{1}{16}\left(1+5 p_{3}\right)$. Solving gives $p_{3}=\frac{1}{11}$ and $p_{1}=\frac{3}{11}$. The probability we want to find is therefore $\frac{1}{4}\left(p_{1}+p_{2}+p_{3}+p_{4}\right)=\frac{15}{44}$.
|
\frac{15}{44}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Every second, Andrea writes down a random digit uniformly chosen from the set $\{1,2,3,4\}$. She stops when the last two numbers she has written sum to a prime number. What is the probability that the last number she writes down is 1 ?
|
15/44
Let $p_{n}$ be the probability that the last number she writes down is 1 when the first number she writes down is $n$. Suppose she starts by writing 2 or 4 . Then she can continue writing either 2 or 4 , but the first time she writes 1 or 3 , she stops. Therefore $p_{2}=p_{4}=\frac{1}{2}$. Suppose she starts by writing 1 . Then she stops if she writes 1 , 2 , or 4 , but continues if she writes 3 . Therefore $p_{1}=\frac{1}{4}\left(1+p_{3}\right)$. If she starts by writing 3 , then she stops if she writes 2 or 4 and otherwise continues. Therefore $p_{3}=\frac{1}{4}\left(p_{1}+p_{3}\right)=\frac{1}{16}\left(1+5 p_{3}\right)$. Solving gives $p_{3}=\frac{1}{11}$ and $p_{1}=\frac{3}{11}$. The probability we want to find is therefore $\frac{1}{4}\left(p_{1}+p_{2}+p_{3}+p_{4}\right)=\frac{15}{44}$.
|
{
"resource_path": "HarvardMIT/segmented/en-82-2005-feb-comb-solutions.jsonl",
"problem_match": "\n8. ",
"solution_match": "\nSolution: "
}
|
ab754c7c-dc0c-56b7-b930-bb5c3361ccc2
| 611,330
|
Eight coins are arranged in a circle heads up. A move consists of flipping over two adjacent coins. How many different sequences of six moves leave the coins alternating heads up and tails up?
|
7680
Imagine we flip over two adjacent coins by pushing a button halfway between them. Then the outcome depends only on the parities of the number of times that each button is pushed. To flip any coin, we must push the two buttons adjacent to that coin a total of an odd number of times. To flip every other coin, the parities must then progress around the circle as even, even, odd, odd, even, even, odd, odd. There are 4 ways to assign these parities. If we assume each button is pressed either once or not at all, this accounts for only four presses, so some button is also pressed twice more. Suppose this button was already pushed once. There are 4 of these, and the number of possible sequences of presses is then $6!/ 3!=120$. Suppose it has not already been pressed. There are 4 of these as well, and the number of possible sequences is $6!/ 2!=360$. The total number of sequences is then $4(4 \cdot 120+4 \cdot 360)=7680$.
|
7680
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Eight coins are arranged in a circle heads up. A move consists of flipping over two adjacent coins. How many different sequences of six moves leave the coins alternating heads up and tails up?
|
7680
Imagine we flip over two adjacent coins by pushing a button halfway between them. Then the outcome depends only on the parities of the number of times that each button is pushed. To flip any coin, we must push the two buttons adjacent to that coin a total of an odd number of times. To flip every other coin, the parities must then progress around the circle as even, even, odd, odd, even, even, odd, odd. There are 4 ways to assign these parities. If we assume each button is pressed either once or not at all, this accounts for only four presses, so some button is also pressed twice more. Suppose this button was already pushed once. There are 4 of these, and the number of possible sequences of presses is then $6!/ 3!=120$. Suppose it has not already been pressed. There are 4 of these as well, and the number of possible sequences is $6!/ 2!=360$. The total number of sequences is then $4(4 \cdot 120+4 \cdot 360)=7680$.
|
{
"resource_path": "HarvardMIT/segmented/en-82-2005-feb-comb-solutions.jsonl",
"problem_match": "\n9. ",
"solution_match": "\n## Solution: "
}
|
15ac0e99-cf98-580f-a279-0dc375ec15a8
| 611,331
|
You start out with a big pile of $3^{2004}$ cards, with the numbers $1,2,3, \ldots, 3^{2004}$ written on them. You arrange the cards into groups of three any way you like; from each group, you keep the card with the largest number and discard the other two. You now again arrange these $3^{2003}$ remaining cards into groups of three any way you like, and in each group, keep the card with the smallest number and discard the other two. You now have $3^{2002}$ cards, and you again arrange these into groups of three and keep the largest number in each group. You proceed in this manner, alternating between keeping the largest number and keeping the smallest number in each group, until you have just one card left.
How many different values are possible for the number on this final card?
|
$\quad 3^{2004}-2 \cdot 3^{1002}+2$
We claim that if you have cards numbered $1,2, \ldots, 3^{2 n}$ and perform $2 n$ successive grouping operations, then $c$ is a possible value for your last remaining card if and only if
$$
3^{n} \leq c \leq 3^{2 n}-3^{n}+1
$$
This gives $3^{2 n}-2 \cdot 3^{n}+2$ possible values of $c$, for a final answer of $3^{2004}-2 \cdot 3^{1002}+2$. Indeed, notice that the last remaining card $c$ must have been the largest of some set of three at the $(2 n-1)$ th step; each of these was in turn the largest of some set of three (and so $c$ was the largest of some set of 9 cards) remaining at the $(2 n-3)$ th step; each of these was in turn the largest of some set of three (and so $c$ was the largest of some set of 27 ) remaining at the $(2 n-5)$ th step; continuing in this manner, we get that $c$ was the largest of some $3^{n}$ cards at the first step, so $c \geq 3^{n}$. A similar analysis of all of the steps in which we save the smallest card gives that $c$ is the smallest of some set of $3^{n}$ initial cards, so $c \leq 3^{2 n}-3^{n}+1$.
To see that any $c$ in this interval is indeed possible, we will carry out the groupings inductively so that, after $2 i$ steps, the following condition is satisfied: if the numbers remaining are $a_{1}<a_{2}<\cdots<a_{3^{2(n-i)}}$, then $c$ is one of these, and there are at least $3^{n-i}-1$ numbers smaller than $c$ and at least $3^{n-i}-1$ numbers larger than $c$. This is certainly true when $i=0$, so it suffices to show that if it holds for some $i<n$, we can perform the grouping so that the condition will still hold for $i+1$. Well, we first group the smallest numbers as $\left\{a_{1}, a_{2}, a_{3}\right\},\left\{a_{4}, a_{5}, a_{6}\right\}, \ldots,\left\{a_{3^{n-i}-5}, a_{3^{n-i}-4}, a_{3^{n-i}-3}\right\}$. We then group the remaining numbers in such a way that $c$ and the largest $3^{n-i}-1$ numbers are each the largest in its respective group; it is easy to see that we can do this. After retaining the largest number in each group, we will then have at least $3^{n-i-1}-1$ numbers smaller than $c$ remaining and at least $3^{n-i}-1$ numbers larger than $c$ remaining. And for the next grouping, we similarly group the largest $3^{n-i}-3$ numbers into $3^{n-i-1}-1$ groups, and arrange the remaining numbers so that the smallest $3^{n-i-1}-1$ numbers and $c$ are all the smallest in their groups. After this round of discarding, then $c$ will be retained, and we will still have at least $3^{n-i-1}-1$ numbers larger than $c$ and $3^{n-i-1}$ numbers smaller than $c$. This proves the induction step, and now the solution is complete.
|
3^{2004}-2 \cdot 3^{1002}+2
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
You start out with a big pile of $3^{2004}$ cards, with the numbers $1,2,3, \ldots, 3^{2004}$ written on them. You arrange the cards into groups of three any way you like; from each group, you keep the card with the largest number and discard the other two. You now again arrange these $3^{2003}$ remaining cards into groups of three any way you like, and in each group, keep the card with the smallest number and discard the other two. You now have $3^{2002}$ cards, and you again arrange these into groups of three and keep the largest number in each group. You proceed in this manner, alternating between keeping the largest number and keeping the smallest number in each group, until you have just one card left.
How many different values are possible for the number on this final card?
|
$\quad 3^{2004}-2 \cdot 3^{1002}+2$
We claim that if you have cards numbered $1,2, \ldots, 3^{2 n}$ and perform $2 n$ successive grouping operations, then $c$ is a possible value for your last remaining card if and only if
$$
3^{n} \leq c \leq 3^{2 n}-3^{n}+1
$$
This gives $3^{2 n}-2 \cdot 3^{n}+2$ possible values of $c$, for a final answer of $3^{2004}-2 \cdot 3^{1002}+2$. Indeed, notice that the last remaining card $c$ must have been the largest of some set of three at the $(2 n-1)$ th step; each of these was in turn the largest of some set of three (and so $c$ was the largest of some set of 9 cards) remaining at the $(2 n-3)$ th step; each of these was in turn the largest of some set of three (and so $c$ was the largest of some set of 27 ) remaining at the $(2 n-5)$ th step; continuing in this manner, we get that $c$ was the largest of some $3^{n}$ cards at the first step, so $c \geq 3^{n}$. A similar analysis of all of the steps in which we save the smallest card gives that $c$ is the smallest of some set of $3^{n}$ initial cards, so $c \leq 3^{2 n}-3^{n}+1$.
To see that any $c$ in this interval is indeed possible, we will carry out the groupings inductively so that, after $2 i$ steps, the following condition is satisfied: if the numbers remaining are $a_{1}<a_{2}<\cdots<a_{3^{2(n-i)}}$, then $c$ is one of these, and there are at least $3^{n-i}-1$ numbers smaller than $c$ and at least $3^{n-i}-1$ numbers larger than $c$. This is certainly true when $i=0$, so it suffices to show that if it holds for some $i<n$, we can perform the grouping so that the condition will still hold for $i+1$. Well, we first group the smallest numbers as $\left\{a_{1}, a_{2}, a_{3}\right\},\left\{a_{4}, a_{5}, a_{6}\right\}, \ldots,\left\{a_{3^{n-i}-5}, a_{3^{n-i}-4}, a_{3^{n-i}-3}\right\}$. We then group the remaining numbers in such a way that $c$ and the largest $3^{n-i}-1$ numbers are each the largest in its respective group; it is easy to see that we can do this. After retaining the largest number in each group, we will then have at least $3^{n-i-1}-1$ numbers smaller than $c$ remaining and at least $3^{n-i}-1$ numbers larger than $c$ remaining. And for the next grouping, we similarly group the largest $3^{n-i}-3$ numbers into $3^{n-i-1}-1$ groups, and arrange the remaining numbers so that the smallest $3^{n-i-1}-1$ numbers and $c$ are all the smallest in their groups. After this round of discarding, then $c$ will be retained, and we will still have at least $3^{n-i-1}-1$ numbers larger than $c$ and $3^{n-i-1}$ numbers smaller than $c$. This proves the induction step, and now the solution is complete.
|
{
"resource_path": "HarvardMIT/segmented/en-82-2005-feb-comb-solutions.jsonl",
"problem_match": "\n10. ",
"solution_match": "\nSolution: "
}
|
c1ddfe2d-e246-5573-91a7-ab5e1d7bb081
| 611,332
|
Let $A B C D$ be a regular tetrahedron with side length 2 . The plane parallel to edges $A B$ and $C D$ and lying halfway between them cuts $A B C D$ into two pieces. Find the surface area of one of these pieces.
|
$1+2 \sqrt{3}$
The plane intersects each face of the tetrahedron in a midline of the face; by symmetry it follows that the intersection of the plane with the tetrahedron is a square of side length 1. The surface area of each piece is half the total surface area of the tetrahedron plus the area of the square, that is, $\frac{1}{2} \cdot 4 \cdot \frac{2^{2} \sqrt{3}}{4}+1=1+2 \sqrt{3}$.
|
1+2 \sqrt{3}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $A B C D$ be a regular tetrahedron with side length 2 . The plane parallel to edges $A B$ and $C D$ and lying halfway between them cuts $A B C D$ into two pieces. Find the surface area of one of these pieces.
|
$1+2 \sqrt{3}$
The plane intersects each face of the tetrahedron in a midline of the face; by symmetry it follows that the intersection of the plane with the tetrahedron is a square of side length 1. The surface area of each piece is half the total surface area of the tetrahedron plus the area of the square, that is, $\frac{1}{2} \cdot 4 \cdot \frac{2^{2} \sqrt{3}}{4}+1=1+2 \sqrt{3}$.
|
{
"resource_path": "HarvardMIT/segmented/en-82-2005-feb-gen1-solutions.jsonl",
"problem_match": "\n3. ",
"solution_match": "\nSolution: "
}
|
77afc5f5-671c-55cb-871c-824bbb83d036
| 611,333
|
Find all real solutions to $x^{3}+(x+1)^{3}+(x+2)^{3}=(x+3)^{3}$.
|
3
The equation simplifies to $3 x^{3}+9 x^{2}+15 x+9=x^{3}+9 x^{2}+27 x+27$, or equivalently, $2 x^{3}-12 x-18=2(x-3)\left(x^{2}+3 x+3\right)=0$. The discriminant of $x^{2}+3 x+3$ is $-3<0$, so the only real solution is $x=3$.
|
3
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Find all real solutions to $x^{3}+(x+1)^{3}+(x+2)^{3}=(x+3)^{3}$.
|
3
The equation simplifies to $3 x^{3}+9 x^{2}+15 x+9=x^{3}+9 x^{2}+27 x+27$, or equivalently, $2 x^{3}-12 x-18=2(x-3)\left(x^{2}+3 x+3\right)=0$. The discriminant of $x^{2}+3 x+3$ is $-3<0$, so the only real solution is $x=3$.
|
{
"resource_path": "HarvardMIT/segmented/en-82-2005-feb-gen1-solutions.jsonl",
"problem_match": "\n4. ",
"solution_match": "\nSolution: "
}
|
2266dc5f-518f-5bf1-b875-7093eba46f40
| 611,334
|
In an election, there are two candidates, $A$ and $B$, who each have 5 supporters. Each supporter, independent of other supporters, has a $\frac{1}{2}$ probability of voting for his or her candidate and a $\frac{1}{2}$ probability of being lazy and not voting. What is the probability of a tie (which includes the case in which no one votes)?
|
63/256
The probability that exactly $k$ supporters of $A$ vote and exactly $k$ supporters of $B$ vote is $\binom{5}{k}^{2} \cdot \frac{1}{2^{10}}$. Summing over $k$ from 0 to 5 gives
$$
\left(\frac{1}{2^{10}}\right)(1+25+100+100+25+1)=\frac{252}{1024}=\frac{63}{256} .
$$
|
\frac{63}{256}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
In an election, there are two candidates, $A$ and $B$, who each have 5 supporters. Each supporter, independent of other supporters, has a $\frac{1}{2}$ probability of voting for his or her candidate and a $\frac{1}{2}$ probability of being lazy and not voting. What is the probability of a tie (which includes the case in which no one votes)?
|
63/256
The probability that exactly $k$ supporters of $A$ vote and exactly $k$ supporters of $B$ vote is $\binom{5}{k}^{2} \cdot \frac{1}{2^{10}}$. Summing over $k$ from 0 to 5 gives
$$
\left(\frac{1}{2^{10}}\right)(1+25+100+100+25+1)=\frac{252}{1024}=\frac{63}{256} .
$$
|
{
"resource_path": "HarvardMIT/segmented/en-82-2005-feb-gen1-solutions.jsonl",
"problem_match": "\n6. ",
"solution_match": "\n## Solution: "
}
|
797c3081-9dab-52cd-bdf8-8b492bc2f55b
| 611,335
|
A triangular piece of paper of area 1 is folded along a line parallel to one of the sides and pressed flat. What is the minimum possible area of the resulting figure?
|
$2 / 3$
Let the triangle be denoted $A B C$, and suppose we fold parallel to $B C$. Let the distance from $A$ to $B C$ be $h$, and suppose we fold along a line at a distance of $c h$ from $A$. We will assume that neither angle $B$ nor $C$ is obtuse, for the area of overlap will only be smaller if either is obtuse. If $c \leq \frac{1}{2}$, then $A$ does not fold past the edge $B C$, so the overlap is a triangle similar to the original with height ch; the area of the figure is then $1-c^{2} \geq \frac{3}{4}$. Suppose $c>\frac{1}{2}$, so that $A$ does fold past $B C$. Then the overlap is a trapezoid formed by taking a triangle of height $c h$ similar to the original and removing a triangle of height $(2 c-1) h$ similar to the original. The area of the resulting figure is thus $1-c^{2}+(2 c-1)^{2}=3 c^{2}-4 c+2$. This is minimized when $c=\frac{2}{3}$, when the area is $\frac{2}{3}<\frac{3}{4}$; the minimum possible area is therefore $\frac{2}{3}$.
|
\frac{2}{3}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
A triangular piece of paper of area 1 is folded along a line parallel to one of the sides and pressed flat. What is the minimum possible area of the resulting figure?
|
$2 / 3$
Let the triangle be denoted $A B C$, and suppose we fold parallel to $B C$. Let the distance from $A$ to $B C$ be $h$, and suppose we fold along a line at a distance of $c h$ from $A$. We will assume that neither angle $B$ nor $C$ is obtuse, for the area of overlap will only be smaller if either is obtuse. If $c \leq \frac{1}{2}$, then $A$ does not fold past the edge $B C$, so the overlap is a triangle similar to the original with height ch; the area of the figure is then $1-c^{2} \geq \frac{3}{4}$. Suppose $c>\frac{1}{2}$, so that $A$ does fold past $B C$. Then the overlap is a trapezoid formed by taking a triangle of height $c h$ similar to the original and removing a triangle of height $(2 c-1) h$ similar to the original. The area of the resulting figure is thus $1-c^{2}+(2 c-1)^{2}=3 c^{2}-4 c+2$. This is minimized when $c=\frac{2}{3}$, when the area is $\frac{2}{3}<\frac{3}{4}$; the minimum possible area is therefore $\frac{2}{3}$.
|
{
"resource_path": "HarvardMIT/segmented/en-82-2005-feb-gen1-solutions.jsonl",
"problem_match": "\n9. ",
"solution_match": "\nSolution: "
}
|
61e697f0-7c72-5d21-9144-595f6c2f96e4
| 611,336
|
What is the smallest integer $x$ larger than 1 such that $x^{2}$ ends in the same three digits as $x$ does?
|
376
The condition is that $1000 \mid x^{2}-x=x(x-1)$. Since $1000=2^{3} \cdot 5^{3}$, and 2 cannot divide both $x$ and $x-1,2^{3}=8$ must divide one of them. Similarly, $5^{3}=125$ must divide either $x$ or $x-1$. We try successive values of $x$ that are congruent to 0 or 1 modulo 125 and see which ones have the property that $x$ or $x-1$ is divisible by 8 . It is easy to check that $125,126,250,251$, and 375 do not work, but the next value, 376 , does, so this is the answer.
|
376
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
What is the smallest integer $x$ larger than 1 such that $x^{2}$ ends in the same three digits as $x$ does?
|
376
The condition is that $1000 \mid x^{2}-x=x(x-1)$. Since $1000=2^{3} \cdot 5^{3}$, and 2 cannot divide both $x$ and $x-1,2^{3}=8$ must divide one of them. Similarly, $5^{3}=125$ must divide either $x$ or $x-1$. We try successive values of $x$ that are congruent to 0 or 1 modulo 125 and see which ones have the property that $x$ or $x-1$ is divisible by 8 . It is easy to check that $125,126,250,251$, and 375 do not work, but the next value, 376 , does, so this is the answer.
|
{
"resource_path": "HarvardMIT/segmented/en-82-2005-feb-gen1-solutions.jsonl",
"problem_match": "\n10. ",
"solution_match": "\nSolution: "
}
|
6c46a906-572e-5053-988b-9dbee49a954c
| 611,337
|
The volume of a cube (in cubic inches) plus three times the total length of its edges (in inches) is equal to twice its surface area (in square inches). How many inches long is its long diagonal?
|
$6 \sqrt{3}$
If the side length of the cube is $s$ inches, then the condition implies $s^{3}+3 \cdot 12 s=2 \cdot 6 s^{2}$, or $s\left(s^{2}-12 s+36\right)=s(s-6)^{2}=0$. Therefore $s=6$, and the long diagonal has length $s \sqrt{3}=6 \sqrt{3}$.
|
6 \sqrt{3}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
The volume of a cube (in cubic inches) plus three times the total length of its edges (in inches) is equal to twice its surface area (in square inches). How many inches long is its long diagonal?
|
$6 \sqrt{3}$
If the side length of the cube is $s$ inches, then the condition implies $s^{3}+3 \cdot 12 s=2 \cdot 6 s^{2}$, or $s\left(s^{2}-12 s+36\right)=s(s-6)^{2}=0$. Therefore $s=6$, and the long diagonal has length $s \sqrt{3}=6 \sqrt{3}$.
|
{
"resource_path": "HarvardMIT/segmented/en-82-2005-feb-gen2-solutions.jsonl",
"problem_match": "\n1. ",
"solution_match": "\n## Solution: "
}
|
0b0ca467-8fa0-5a48-a461-354937ae4026
| 83,635
|
Working together, Jack and Jill can paint a house in 3 days; Jill and Joe can paint the same house in 4 days; or Joe and Jack can paint the house in 6 days. If Jill, Joe, and Jack all work together, how many days will it take them?
|
$8 / 3$
Suppose that Jack paints $x$ houses per day, Jill paints $y$ houses per day, and Joe paints $z$ houses per day. Together, Jack and Jill paint $1 / 3$ of a house in a day - that is,
$$
x+y=1 / 3 .
$$
Similarly,
$$
y+z=1 / 4
$$
and
$$
z+x=1 / 6
$$
Adding all three equations and dividing by 2 gives
$$
x+y+z=3 / 8
$$
So, working together, the three folks can paint $3 / 8$ houses in a day, or $8 / 3$ days per house.
|
\frac{8}{3}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Working together, Jack and Jill can paint a house in 3 days; Jill and Joe can paint the same house in 4 days; or Joe and Jack can paint the house in 6 days. If Jill, Joe, and Jack all work together, how many days will it take them?
|
$8 / 3$
Suppose that Jack paints $x$ houses per day, Jill paints $y$ houses per day, and Joe paints $z$ houses per day. Together, Jack and Jill paint $1 / 3$ of a house in a day - that is,
$$
x+y=1 / 3 .
$$
Similarly,
$$
y+z=1 / 4
$$
and
$$
z+x=1 / 6
$$
Adding all three equations and dividing by 2 gives
$$
x+y+z=3 / 8
$$
So, working together, the three folks can paint $3 / 8$ houses in a day, or $8 / 3$ days per house.
|
{
"resource_path": "HarvardMIT/segmented/en-82-2005-feb-gen2-solutions.jsonl",
"problem_match": "\n3. ",
"solution_match": "\nSolution: "
}
|
07611987-f4f0-5b30-a454-726078218b41
| 611,339
|
In how many ways can 8 people be arranged in a line if Alice and Bob must be next to each other, and Carol must be somewhere behind Dan?
|
5040
Let us place Alice and Bob as a single person; there are then $7!=5040$ different arrangements. Alice can be in front of Bob or vice versa, multiplying the number of possibilities by 2, but Carol is behind Dan in exactly half of those, so that the answer is just 5040 .
|
5040
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
In how many ways can 8 people be arranged in a line if Alice and Bob must be next to each other, and Carol must be somewhere behind Dan?
|
5040
Let us place Alice and Bob as a single person; there are then $7!=5040$ different arrangements. Alice can be in front of Bob or vice versa, multiplying the number of possibilities by 2, but Carol is behind Dan in exactly half of those, so that the answer is just 5040 .
|
{
"resource_path": "HarvardMIT/segmented/en-82-2005-feb-gen2-solutions.jsonl",
"problem_match": "\n4. ",
"solution_match": "\nSolution: "
}
|
afaed0d4-43c9-57ba-bf72-1e4d9b061725
| 611,340
|
You and I play the following game on an $8 \times 8$ square grid of boxes: Initially, every box is empty. On your turn, you choose an empty box and draw an $X$ in it; if any of the four adjacent boxes are empty, you mark them with an $X$ as well. (Two boxes are adjacent if they share an edge.) We alternate turns, with you moving first, and whoever draws the last $X$ wins. How many choices do you have for a first move that will enable you to guarantee a win no matter how I play?
|
0
I can follow a symmetry strategy: whenever you play in the box $S$, I play in the image of $S$ under the $180^{\circ}$ rotation about the center of the board. This ensures that the board will always be centrally symmetric at the beginning of your turn. Thus, if you play in an empty box $S$, its symmetric image $S^{\prime}$ is also empty at the beginning of your turn, and it remains so after your turn, since the even size of the board ensures that $S$ can be neither equal to nor adjacent to $S^{\prime}$. In particular, I always have a move available. Since the first person without an available move loses, you are guaranteed to lose. So the answer is that you have 0 choices for a first move that will guarantee your win.
|
0
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
You and I play the following game on an $8 \times 8$ square grid of boxes: Initially, every box is empty. On your turn, you choose an empty box and draw an $X$ in it; if any of the four adjacent boxes are empty, you mark them with an $X$ as well. (Two boxes are adjacent if they share an edge.) We alternate turns, with you moving first, and whoever draws the last $X$ wins. How many choices do you have for a first move that will enable you to guarantee a win no matter how I play?
|
0
I can follow a symmetry strategy: whenever you play in the box $S$, I play in the image of $S$ under the $180^{\circ}$ rotation about the center of the board. This ensures that the board will always be centrally symmetric at the beginning of your turn. Thus, if you play in an empty box $S$, its symmetric image $S^{\prime}$ is also empty at the beginning of your turn, and it remains so after your turn, since the even size of the board ensures that $S$ can be neither equal to nor adjacent to $S^{\prime}$. In particular, I always have a move available. Since the first person without an available move loses, you are guaranteed to lose. So the answer is that you have 0 choices for a first move that will guarantee your win.
|
{
"resource_path": "HarvardMIT/segmented/en-82-2005-feb-gen2-solutions.jsonl",
"problem_match": "\n5. ",
"solution_match": "\nSolution: "
}
|
408add56-8bcd-5142-8dcc-7e47d8c140fe
| 611,341
|
A cube with side length 2 is inscribed in a sphere. A second cube, with faces parallel to the first, is inscribed between the sphere and one face of the first cube. What is the length of a side of the smaller cube?
|
$2 / 3$
First note that the long diagonal of the cube has length $2 \sqrt{3}$, so the radius of the sphere is $\sqrt{3}$. Let $x$ be the side length of the smaller cube. Then the distance from the center of the sphere to the far face of the smaller cube is $1+x$, while the distance from the center of the far face to a vertex lying on the sphere is $\frac{x \sqrt{2}}{2}$. Therefore, the square of the radius is $3=(1+x)^{2}+\frac{x^{2}}{2}$, or $3 x^{2}+4 x-4=(3 x-2)(x+2)=0$, so $x=\frac{2}{3}$.
|
\frac{2}{3}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
A cube with side length 2 is inscribed in a sphere. A second cube, with faces parallel to the first, is inscribed between the sphere and one face of the first cube. What is the length of a side of the smaller cube?
|
$2 / 3$
First note that the long diagonal of the cube has length $2 \sqrt{3}$, so the radius of the sphere is $\sqrt{3}$. Let $x$ be the side length of the smaller cube. Then the distance from the center of the sphere to the far face of the smaller cube is $1+x$, while the distance from the center of the far face to a vertex lying on the sphere is $\frac{x \sqrt{2}}{2}$. Therefore, the square of the radius is $3=(1+x)^{2}+\frac{x^{2}}{2}$, or $3 x^{2}+4 x-4=(3 x-2)(x+2)=0$, so $x=\frac{2}{3}$.
|
{
"resource_path": "HarvardMIT/segmented/en-82-2005-feb-gen2-solutions.jsonl",
"problem_match": "\n6. ",
"solution_match": "\n## Solution: "
}
|
c481cdf1-c343-5766-92f0-824d5b8ef6ad
| 611,342
|
In how many ways can the cells of a $4 \times 4$ table be filled in with the digits $1,2, \ldots, 9$ so that each of the 4 -digit numbers formed by the columns is divisible by each of the 4-digit numbers formed by the rows?
|
9
If $a$ and $b$ are 4-digit numbers with the same first digit, and $a$ divides $b$, then since $b<a+1000 \leq 2 a, b$ must equal $a$. In particular, since the number formed by the first row of the table divides the number in the first column (and both have the same first digit), these numbers must be equal; call their common value $n$. Then, for $k=2,3$, or 4 , we find that the number in the $k$ th column and the number in the $k$ th row have the same first digit (namely the $k$ th digit of $n$ ), so by the same reasoning, they are equal. Also, the smallest number $b$ formed by any column is divisible by the largest number $a$ formed by any row, but by the symmetry just proven, $a$ is also the largest number formed by any column, so $a \geq b$. Since $b$ is divisible by $a$, we must have equality. Then all columns contain the same number - and hence all rows also contain the same
number - which is only possible if all 16 cells contain the same digit. Conversely, for each $d=1, \ldots, 9$, filling in all 16 cells with the digit $d$ clearly gives a table meeting the required condition, so we have exactly 9 such tables, one for each digit.
|
9
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
In how many ways can the cells of a $4 \times 4$ table be filled in with the digits $1,2, \ldots, 9$ so that each of the 4 -digit numbers formed by the columns is divisible by each of the 4-digit numbers formed by the rows?
|
9
If $a$ and $b$ are 4-digit numbers with the same first digit, and $a$ divides $b$, then since $b<a+1000 \leq 2 a, b$ must equal $a$. In particular, since the number formed by the first row of the table divides the number in the first column (and both have the same first digit), these numbers must be equal; call their common value $n$. Then, for $k=2,3$, or 4 , we find that the number in the $k$ th column and the number in the $k$ th row have the same first digit (namely the $k$ th digit of $n$ ), so by the same reasoning, they are equal. Also, the smallest number $b$ formed by any column is divisible by the largest number $a$ formed by any row, but by the symmetry just proven, $a$ is also the largest number formed by any column, so $a \geq b$. Since $b$ is divisible by $a$, we must have equality. Then all columns contain the same number - and hence all rows also contain the same
number - which is only possible if all 16 cells contain the same digit. Conversely, for each $d=1, \ldots, 9$, filling in all 16 cells with the digit $d$ clearly gives a table meeting the required condition, so we have exactly 9 such tables, one for each digit.
|
{
"resource_path": "HarvardMIT/segmented/en-82-2005-feb-gen2-solutions.jsonl",
"problem_match": "\n9. ",
"solution_match": "\nSolution: "
}
|
e4733147-6679-5201-99d5-e1d0262fefc8
| 611,344
|
Let $\lfloor x\rfloor$ denote the greatest integer less than or equal to $x$. How many positive integers less than 2005 can be expressed in the form $\lfloor x\lfloor x\rfloor\rfloor$ for some positive real $x$ ?
|
990
Let $\{x\}=x-\lfloor x\rfloor$ be the fractional part of $x$. Note that
$$
\lfloor x\lfloor x\rfloor\rfloor=\lfloor(\lfloor x\rfloor+\{x\})\lfloor x\rfloor\rfloor=\lfloor x\rfloor^{2}+\lfloor\{x\}\lfloor x\rfloor\rfloor .
$$
Because $\{x\}$ may take on any value in the half-open interval $[0,1)$, the quantity $\lfloor\{x\}\lfloor x\rfloor\rfloor$ can take on any integer value between 0 and $\lfloor x\rfloor-1$, inclusive.
If $\lfloor x\rfloor=n$, then $\lfloor x\lfloor x\rfloor\rfloor$ can be any of the numbers $n^{2}, n^{2}+1, \ldots, n^{2}+n-1$. In other words, there are precisely $n$ possible values that $\lfloor x\lfloor x\rfloor\rfloor$ can take, and moreover, all of them are less than $(n+1)^{2}$. Because $44^{2}+43=1979<2005$ and $45^{2}=2025>2005$, $n$ can range between 1 and 44, inclusive. Therefore, the answer is
$$
\sum_{n=1}^{44} n=\frac{44 \cdot 45}{2}=990
$$
|
990
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Let $\lfloor x\rfloor$ denote the greatest integer less than or equal to $x$. How many positive integers less than 2005 can be expressed in the form $\lfloor x\lfloor x\rfloor\rfloor$ for some positive real $x$ ?
|
990
Let $\{x\}=x-\lfloor x\rfloor$ be the fractional part of $x$. Note that
$$
\lfloor x\lfloor x\rfloor\rfloor=\lfloor(\lfloor x\rfloor+\{x\})\lfloor x\rfloor\rfloor=\lfloor x\rfloor^{2}+\lfloor\{x\}\lfloor x\rfloor\rfloor .
$$
Because $\{x\}$ may take on any value in the half-open interval $[0,1)$, the quantity $\lfloor\{x\}\lfloor x\rfloor\rfloor$ can take on any integer value between 0 and $\lfloor x\rfloor-1$, inclusive.
If $\lfloor x\rfloor=n$, then $\lfloor x\lfloor x\rfloor\rfloor$ can be any of the numbers $n^{2}, n^{2}+1, \ldots, n^{2}+n-1$. In other words, there are precisely $n$ possible values that $\lfloor x\lfloor x\rfloor\rfloor$ can take, and moreover, all of them are less than $(n+1)^{2}$. Because $44^{2}+43=1979<2005$ and $45^{2}=2025>2005$, $n$ can range between 1 and 44, inclusive. Therefore, the answer is
$$
\sum_{n=1}^{44} n=\frac{44 \cdot 45}{2}=990
$$
|
{
"resource_path": "HarvardMIT/segmented/en-82-2005-feb-gen2-solutions.jsonl",
"problem_match": "\n10. ",
"solution_match": "\nSolution: "
}
|
892b4160-f262-5796-acd1-f5e802fb8743
| 611,345
|
Let $A B C D$ be a rectangle with area 1 , and let $E$ lie on side $C D$. What is the area of the triangle formed by the centroids of triangles $A B E, B C E$, and $A D E$ ?
|
$1 / 9$
Let the centroids of $A B E, B C E$, and $A D E$ be denoted by $X, Y$, and $Z$, respectively. Let $d(P, Q R)$ denote the distance from $P$ to line $Q R$. Since the centroid lies two-thirds of the distance from each vertex to the midpoint of the opposite edge, $d(X, A B)=$ $d(Y, C D)=d(Z, C D)=\frac{1}{3} B C$, so $Y Z$ is parallel to $C D$ and $d(X, Y Z)=B C-$ $\frac{2}{3} B C=\frac{1}{3} B C$. Likewise, $d(Z, A D)=\frac{1}{3} D E$ and $d(Y, B C)=\frac{1}{3} C E$, so that since $Y Z$ is perpendicular to $A D$ and $B C$, we have that $Y Z=C D-\frac{1}{3}(D E+C E)=\frac{2}{3} C D$. Therefore, the area of $X Y Z$ is $\frac{1}{2}\left(\frac{1}{3} B C\right)\left(\frac{2}{3} C D\right)=\frac{1}{9} B C \cdot C D=\frac{1}{9}$.
|
\frac{1}{9}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $A B C D$ be a rectangle with area 1 , and let $E$ lie on side $C D$. What is the area of the triangle formed by the centroids of triangles $A B E, B C E$, and $A D E$ ?
|
$1 / 9$
Let the centroids of $A B E, B C E$, and $A D E$ be denoted by $X, Y$, and $Z$, respectively. Let $d(P, Q R)$ denote the distance from $P$ to line $Q R$. Since the centroid lies two-thirds of the distance from each vertex to the midpoint of the opposite edge, $d(X, A B)=$ $d(Y, C D)=d(Z, C D)=\frac{1}{3} B C$, so $Y Z$ is parallel to $C D$ and $d(X, Y Z)=B C-$ $\frac{2}{3} B C=\frac{1}{3} B C$. Likewise, $d(Z, A D)=\frac{1}{3} D E$ and $d(Y, B C)=\frac{1}{3} C E$, so that since $Y Z$ is perpendicular to $A D$ and $B C$, we have that $Y Z=C D-\frac{1}{3}(D E+C E)=\frac{2}{3} C D$. Therefore, the area of $X Y Z$ is $\frac{1}{2}\left(\frac{1}{3} B C\right)\left(\frac{2}{3} C D\right)=\frac{1}{9} B C \cdot C D=\frac{1}{9}$.

|
{
"resource_path": "HarvardMIT/segmented/en-82-2005-feb-geo-solutions.jsonl",
"problem_match": "\n3. ",
"solution_match": "\nSolution: "
}
|
97a1a81c-c4cd-57d2-a5d4-1306deaa9415
| 611,346
|
Let $A B C D$ be a tetrahedron such that edges $A B, A C$, and $A D$ are mutually perpendicular. Let the areas of triangles $A B C, A C D$, and $A D B$ be denoted by $x, y$, and $z$, respectively. In terms of $x, y$, and $z$, find the area of triangle $B C D$.
|
$\sqrt{x^{2}+y^{2}+z^{2}}$
Place $A, B, C$, and $D$ at $(0,0,0),(b, 0,0),(0, c, 0)$, and $(0,0, d)$ in Cartesian coordinate space, with $b, c$, and $d$ positive. Then the plane through $B, C$, and $D$ is given by the equation $\frac{x}{b}+\frac{y}{c}+\frac{z}{d}=1$. The distance from the origin to this plane is then
$$
\frac{1}{\sqrt{\frac{1}{b^{2}}+\frac{1}{c^{2}}+\frac{1}{d^{2}}}}=\frac{b c d}{\sqrt{b^{2} c^{2}+c^{2} d^{2}+d^{2} b^{2}}}=\frac{b c d}{2 \sqrt{x^{2}+y^{2}+z^{2}}}
$$
Then if the area of $B C D$ is $K$, the volume of the tetrahedron is
$$
\frac{b c d}{6}=\frac{b c d K}{6 \sqrt{x^{2}+y^{2}+z^{2}}}
$$
implying $K=\sqrt{x^{2}+y^{2}+z^{2}}$.
Alternative Solution: The area of $B C D$ is also half the length of the cross product of the vectors $\overrightarrow{B C}=(0,-c, d)$ and $\overrightarrow{B D}=(-b, 0, d)$. This cross product is $(-c d,-d b,-b c)=-2(y, z, x)$, which has length $2 \sqrt{x^{2}+y^{2}+z^{2}}$. Thus the area of $B C D$ is $\sqrt{x^{2}+y^{2}+z^{2}}$.
|
\sqrt{x^{2}+y^{2}+z^{2}}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $A B C D$ be a tetrahedron such that edges $A B, A C$, and $A D$ are mutually perpendicular. Let the areas of triangles $A B C, A C D$, and $A D B$ be denoted by $x, y$, and $z$, respectively. In terms of $x, y$, and $z$, find the area of triangle $B C D$.
|
$\sqrt{x^{2}+y^{2}+z^{2}}$
Place $A, B, C$, and $D$ at $(0,0,0),(b, 0,0),(0, c, 0)$, and $(0,0, d)$ in Cartesian coordinate space, with $b, c$, and $d$ positive. Then the plane through $B, C$, and $D$ is given by the equation $\frac{x}{b}+\frac{y}{c}+\frac{z}{d}=1$. The distance from the origin to this plane is then
$$
\frac{1}{\sqrt{\frac{1}{b^{2}}+\frac{1}{c^{2}}+\frac{1}{d^{2}}}}=\frac{b c d}{\sqrt{b^{2} c^{2}+c^{2} d^{2}+d^{2} b^{2}}}=\frac{b c d}{2 \sqrt{x^{2}+y^{2}+z^{2}}}
$$
Then if the area of $B C D$ is $K$, the volume of the tetrahedron is
$$
\frac{b c d}{6}=\frac{b c d K}{6 \sqrt{x^{2}+y^{2}+z^{2}}}
$$
implying $K=\sqrt{x^{2}+y^{2}+z^{2}}$.
Alternative Solution: The area of $B C D$ is also half the length of the cross product of the vectors $\overrightarrow{B C}=(0,-c, d)$ and $\overrightarrow{B D}=(-b, 0, d)$. This cross product is $(-c d,-d b,-b c)=-2(y, z, x)$, which has length $2 \sqrt{x^{2}+y^{2}+z^{2}}$. Thus the area of $B C D$ is $\sqrt{x^{2}+y^{2}+z^{2}}$.
|
{
"resource_path": "HarvardMIT/segmented/en-82-2005-feb-geo-solutions.jsonl",
"problem_match": "\n7. ",
"solution_match": "\nSolution: "
}
|
310176c9-c07f-5c19-b532-46986d7f00bb
| 611,348
|
Let $T$ be a triangle with side lengths 26,51 , and 73 . Let $S$ be the set of points inside $T$ which do not lie within a distance of 5 of any side of $T$. Find the area of $S$.
|
$135 / 28$
Note that the sides of $S$ are parallel to the sides of $T$, so $S$ is a triangle similar to $T$. The semiperimeter of $T$ is $s=\frac{1}{2}(26+51+73)=75$. By Heron's formula, the area of $T$ is $\sqrt{75 \cdot 49 \cdot 24 \cdot 2}=420$. If $r$ is the inradius of $T$, then the area of $T$ is $r s$, so $r=420 / 75=28 / 5$. It follows that the inradius of $S$ is $r-5=3 / 5$, and the ratio of similitude between $S$ and $T$ is $3 / 28$. Therefore, the area of $S$ is $420 \cdot(3 / 28)^{2}=135 / 28$.
|
\frac{135}{28}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $T$ be a triangle with side lengths 26,51 , and 73 . Let $S$ be the set of points inside $T$ which do not lie within a distance of 5 of any side of $T$. Find the area of $S$.
|
$135 / 28$
Note that the sides of $S$ are parallel to the sides of $T$, so $S$ is a triangle similar to $T$. The semiperimeter of $T$ is $s=\frac{1}{2}(26+51+73)=75$. By Heron's formula, the area of $T$ is $\sqrt{75 \cdot 49 \cdot 24 \cdot 2}=420$. If $r$ is the inradius of $T$, then the area of $T$ is $r s$, so $r=420 / 75=28 / 5$. It follows that the inradius of $S$ is $r-5=3 / 5$, and the ratio of similitude between $S$ and $T$ is $3 / 28$. Therefore, the area of $S$ is $420 \cdot(3 / 28)^{2}=135 / 28$.
|
{
"resource_path": "HarvardMIT/segmented/en-82-2005-feb-geo-solutions.jsonl",
"problem_match": "\n8. ",
"solution_match": "\nSolution: "
}
|
0f46b92c-0094-5906-9110-9be8d7aefb8e
| 611,349
|
Let $A C$ be a diameter of a circle $\omega$ of radius 1 , and let $D$ be the point on $A C$ such that $C D=1 / 5$. Let $B$ be the point on $\omega$ such that $D B$ is perpendicular to $A C$, and let $E$ be the midpoint of $D B$. The line tangent to $\omega$ at $B$ intersects line $C E$ at the point $X$. Compute $A X$.
|
3
We first show that $A X$ is perpendicular to $A C$. Let the tangent to $\omega$ at $A$ intersect $C B$ at $Z$ and $C E$ at $X^{\prime}$. Since $Z A$ is parallel to $B D$ and $B E=E D, Z X^{\prime}=X^{\prime} A$. Therefore, $X^{\prime}$ is the midpoint of the hypotenuse of the right triangle $A B Z$, so it is also its circumcenter. Thus $X^{\prime} A=X^{\prime} B$, and since $X^{\prime} A$ is tangent to $\omega$ and $B$ lies on $\omega$, we must have that $X^{\prime} B$ is tangent to $\omega$, so $X=X^{\prime}$.
Let $O$ be the center of $\omega$. Then $O D=\frac{4}{5}$, so $B D=\frac{3}{5}$ and $D E=\frac{3}{10}$. Then $A X=$ $D E \cdot \frac{A C}{D C}=\frac{3}{10} \cdot \frac{2}{1 / 5}=3$.
|
3
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $A C$ be a diameter of a circle $\omega$ of radius 1 , and let $D$ be the point on $A C$ such that $C D=1 / 5$. Let $B$ be the point on $\omega$ such that $D B$ is perpendicular to $A C$, and let $E$ be the midpoint of $D B$. The line tangent to $\omega$ at $B$ intersects line $C E$ at the point $X$. Compute $A X$.
|
3
We first show that $A X$ is perpendicular to $A C$. Let the tangent to $\omega$ at $A$ intersect $C B$ at $Z$ and $C E$ at $X^{\prime}$. Since $Z A$ is parallel to $B D$ and $B E=E D, Z X^{\prime}=X^{\prime} A$. Therefore, $X^{\prime}$ is the midpoint of the hypotenuse of the right triangle $A B Z$, so it is also its circumcenter. Thus $X^{\prime} A=X^{\prime} B$, and since $X^{\prime} A$ is tangent to $\omega$ and $B$ lies on $\omega$, we must have that $X^{\prime} B$ is tangent to $\omega$, so $X=X^{\prime}$.
Let $O$ be the center of $\omega$. Then $O D=\frac{4}{5}$, so $B D=\frac{3}{5}$ and $D E=\frac{3}{10}$. Then $A X=$ $D E \cdot \frac{A C}{D C}=\frac{3}{10} \cdot \frac{2}{1 / 5}=3$.

|
{
"resource_path": "HarvardMIT/segmented/en-82-2005-feb-geo-solutions.jsonl",
"problem_match": "\n9. ",
"solution_match": "\nSolution: "
}
|
e6b66683-d8d3-556b-937a-5e62d739aac7
| 611,350
|
Let $A B$ be the diameter of a semicircle $\Gamma$. Two circles, $\omega_{1}$ and $\omega_{2}$, externally tangent to each other and internally tangent to $\Gamma$, are tangent to the line $A B$ at $P$ and $Q$, respectively, and to semicircular arc $A B$ at $C$ and $D$, respectively, with $A P<A Q$. Suppose $F$ lies on $\Gamma$ such that $\angle F Q B=\angle C Q A$ and that $\angle A B F=80^{\circ}$. Find $\angle P D Q$ in degrees.
|
35
Extend the semicircle centered at $O$ to an entire circle $\omega$, and let the reflection of $F$ over $A B$ be $F^{\prime}$. Then $C Q F^{\prime}$ is a straight line. Also, the homothety centered at $C$ taking $\omega_{1}$ into $\omega$ takes $P$ to a point $X$ on $\omega$ and $A B$ to the parallel line tangent to $\omega$ at $X$. Therefore, $X$ is the midpoint of semicircle $A X B$, and $C, P$, and $X$ lie on a line. Similarly, $D, Q$, and $X$ lie on a line. So,
$$
45^{\circ}=\angle X C B=\angle P C B=\angle P C Q+\angle Q C B=\angle P C Q+10^{\circ},
$$
since $\angle Q C B=\angle F^{\prime} C B=\angle F^{\prime} A B=\angle F A B=90^{\circ}-\angle A B F=10^{\circ}$. Thus $\angle P C Q=35^{\circ}$. We will show that $\angle P C Q=\angle P D Q$ to get that $\angle P D Q=35^{\circ}$.
Note that $\angle X P Q$ subtends the sum of arcs $A C$ and $B X$, which is equal to arc $X C$. Therefore $\angle X P Q=\angle C D X$, so $C D Q P$ is cyclic and $\angle P C Q=\angle P D Q$. The conclusion follows.
|
35
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $A B$ be the diameter of a semicircle $\Gamma$. Two circles, $\omega_{1}$ and $\omega_{2}$, externally tangent to each other and internally tangent to $\Gamma$, are tangent to the line $A B$ at $P$ and $Q$, respectively, and to semicircular arc $A B$ at $C$ and $D$, respectively, with $A P<A Q$. Suppose $F$ lies on $\Gamma$ such that $\angle F Q B=\angle C Q A$ and that $\angle A B F=80^{\circ}$. Find $\angle P D Q$ in degrees.
|
35
Extend the semicircle centered at $O$ to an entire circle $\omega$, and let the reflection of $F$ over $A B$ be $F^{\prime}$. Then $C Q F^{\prime}$ is a straight line. Also, the homothety centered at $C$ taking $\omega_{1}$ into $\omega$ takes $P$ to a point $X$ on $\omega$ and $A B$ to the parallel line tangent to $\omega$ at $X$. Therefore, $X$ is the midpoint of semicircle $A X B$, and $C, P$, and $X$ lie on a line. Similarly, $D, Q$, and $X$ lie on a line. So,
$$
45^{\circ}=\angle X C B=\angle P C B=\angle P C Q+\angle Q C B=\angle P C Q+10^{\circ},
$$
since $\angle Q C B=\angle F^{\prime} C B=\angle F^{\prime} A B=\angle F A B=90^{\circ}-\angle A B F=10^{\circ}$. Thus $\angle P C Q=35^{\circ}$. We will show that $\angle P C Q=\angle P D Q$ to get that $\angle P D Q=35^{\circ}$.
Note that $\angle X P Q$ subtends the sum of arcs $A C$ and $B X$, which is equal to arc $X C$. Therefore $\angle X P Q=\angle C D X$, so $C D Q P$ is cyclic and $\angle P C Q=\angle P D Q$. The conclusion follows.

|
{
"resource_path": "HarvardMIT/segmented/en-82-2005-feb-geo-solutions.jsonl",
"problem_match": "\n10. ",
"solution_match": "\n## Solution: "
}
|
00877ad9-a4c3-51d7-84e0-b3f3e2a2b40a
| 611,351
|
Find the largest positive integer $n$ such that $1+2+3+\cdots+n^{2}$ is divisible by $1+2+$ $3+\cdots+n$.
|
1
The statement is
$$
\frac{n(n+1)}{2}\left|\frac{n^{2}\left(n^{2}+1\right)}{2} \Leftrightarrow n+1\right| n\left(n^{2}+1\right)=n^{3}+n .
$$
But $n+1$ also divides $(n+1)\left(n^{2}-n+2\right)=n^{3}+n+2$, so $n+1$ must divide 2. Hence, $n$ cannot be greater than 1 . And $n=1$ clearly works, so that is the answer.
|
1
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Find the largest positive integer $n$ such that $1+2+3+\cdots+n^{2}$ is divisible by $1+2+$ $3+\cdots+n$.
|
1
The statement is
$$
\frac{n(n+1)}{2}\left|\frac{n^{2}\left(n^{2}+1\right)}{2} \Leftrightarrow n+1\right| n\left(n^{2}+1\right)=n^{3}+n .
$$
But $n+1$ also divides $(n+1)\left(n^{2}-n+2\right)=n^{3}+n+2$, so $n+1$ must divide 2. Hence, $n$ cannot be greater than 1 . And $n=1$ clearly works, so that is the answer.
|
{
"resource_path": "HarvardMIT/segmented/en-82-2005-feb-guts-solutions.jsonl",
"problem_match": "\n1. ",
"solution_match": "\nSolution: "
}
|
07ac8a07-e0e7-5ce6-9068-582abd38a01a
| 611,352
|
Let $x, y$, and $z$ be positive real numbers such that $(x \cdot y)+z=(x+z) \cdot(y+z)$. What is the maximum possible value of $x y z$ ?
|
$1 / 27$
The condition is equivalent to $z^{2}+(x+y-1) z=0$. Since $z$ is positive, $z=1-x-y$, so $x+y+z=1$. By the AM-GM inequality,
$$
x y z \leq\left(\frac{x+y+z}{3}\right)^{3}=\frac{1}{27}
$$
with equality when $x=y=z=\frac{1}{3}$.
|
\frac{1}{27}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Let $x, y$, and $z$ be positive real numbers such that $(x \cdot y)+z=(x+z) \cdot(y+z)$. What is the maximum possible value of $x y z$ ?
|
$1 / 27$
The condition is equivalent to $z^{2}+(x+y-1) z=0$. Since $z$ is positive, $z=1-x-y$, so $x+y+z=1$. By the AM-GM inequality,
$$
x y z \leq\left(\frac{x+y+z}{3}\right)^{3}=\frac{1}{27}
$$
with equality when $x=y=z=\frac{1}{3}$.
|
{
"resource_path": "HarvardMIT/segmented/en-82-2005-feb-guts-solutions.jsonl",
"problem_match": "\n2. ",
"solution_match": "\n## Solution: "
}
|
8adde65e-278b-5a77-b54e-3ff4f3c17b9b
| 611,353
|
Find the sum
$$
\frac{2^{1}}{4^{1}-1}+\frac{2^{2}}{4^{2}-1}+\frac{2^{4}}{4^{4}-1}+\frac{2^{8}}{4^{8}-1}+\cdots .
$$
|
1
Notice that
$$
\frac{2^{2^{k}}}{4^{2^{k}}-1}=\frac{2^{2^{k}}+1}{4^{2^{k}}-1}-\frac{1}{4^{2^{k}}-1}=\frac{1}{2^{2^{k}}-1}-\frac{1}{4^{2^{k}}-1}=\frac{1}{4^{2^{k-1}}-1}-\frac{1}{4^{2^{k}}-1} .
$$
Therefore, the sum telescopes as
$$
\left(\frac{1}{4^{2^{-1}}-1}-\frac{1}{4^{2^{0}}-1}\right)+\left(\frac{1}{4^{2^{0}}-1}-\frac{1}{4^{2^{1}}-1}\right)+\left(\frac{1}{4^{2^{1}}-1}-\frac{1}{4^{2^{2}}-1}\right)+\cdots
$$
and evaluates to $1 /\left(4^{2^{-1}}-1\right)=1$.
|
1
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Find the sum
$$
\frac{2^{1}}{4^{1}-1}+\frac{2^{2}}{4^{2}-1}+\frac{2^{4}}{4^{4}-1}+\frac{2^{8}}{4^{8}-1}+\cdots .
$$
|
1
Notice that
$$
\frac{2^{2^{k}}}{4^{2^{k}}-1}=\frac{2^{2^{k}}+1}{4^{2^{k}}-1}-\frac{1}{4^{2^{k}}-1}=\frac{1}{2^{2^{k}}-1}-\frac{1}{4^{2^{k}}-1}=\frac{1}{4^{2^{k-1}}-1}-\frac{1}{4^{2^{k}}-1} .
$$
Therefore, the sum telescopes as
$$
\left(\frac{1}{4^{2^{-1}}-1}-\frac{1}{4^{2^{0}}-1}\right)+\left(\frac{1}{4^{2^{0}}-1}-\frac{1}{4^{2^{1}}-1}\right)+\left(\frac{1}{4^{2^{1}}-1}-\frac{1}{4^{2^{2}}-1}\right)+\cdots
$$
and evaluates to $1 /\left(4^{2^{-1}}-1\right)=1$.
|
{
"resource_path": "HarvardMIT/segmented/en-82-2005-feb-guts-solutions.jsonl",
"problem_match": "\n3. ",
"solution_match": "\nSolution: "
}
|
0e1f0554-5390-57a3-aab1-ab9007645820
| 611,354
|
What is the probability that in a randomly chosen arrangement of the numbers and letters in "HMMT2005," one can read either "HMMT" or " 2005 " from left to right? (For example, in "5HM0M20T," one can read "HMMT.")
|
$23 / 144$
To read "HMMT," there are $\binom{8}{4}$ ways to place the letters, and $\frac{4!}{2}$ ways to place the numbers. Similarly, there are $\binom{8}{4} \frac{4!}{2}$ arrangements where one can read " 2005 ." The number of arrangements in which one can read both is just $\binom{8}{4}$. The total number of arrangements is $\frac{8!}{4}$, thus the answer is
$$
\frac{\binom{8}{4} \frac{4!}{2}+\binom{8}{4} \frac{4!}{2}-\binom{8}{4}}{\frac{8!}{4}}=\binom{8}{4} \frac{4}{8!} \cdot 23=\frac{23}{144} .
$$
|
\frac{23}{144}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
What is the probability that in a randomly chosen arrangement of the numbers and letters in "HMMT2005," one can read either "HMMT" or " 2005 " from left to right? (For example, in "5HM0M20T," one can read "HMMT.")
|
$23 / 144$
To read "HMMT," there are $\binom{8}{4}$ ways to place the letters, and $\frac{4!}{2}$ ways to place the numbers. Similarly, there are $\binom{8}{4} \frac{4!}{2}$ arrangements where one can read " 2005 ." The number of arrangements in which one can read both is just $\binom{8}{4}$. The total number of arrangements is $\frac{8!}{4}$, thus the answer is
$$
\frac{\binom{8}{4} \frac{4!}{2}+\binom{8}{4} \frac{4!}{2}-\binom{8}{4}}{\frac{8!}{4}}=\binom{8}{4} \frac{4}{8!} \cdot 23=\frac{23}{144} .
$$
|
{
"resource_path": "HarvardMIT/segmented/en-82-2005-feb-guts-solutions.jsonl",
"problem_match": "\n4. ",
"solution_match": "\nSolution: "
}
|
6f9788ed-6b68-57c7-9c04-9e6894b6c624
| 611,355
|
For how many integers $n$ between 1 and 2005 , inclusive, is $2 \cdot 6 \cdot 10 \cdots(4 n-2)$ divisible by $n!$ ?
|
2005
Note that
$$
\begin{aligned}
2 \cdot 6 \cdot 10 \cdots(4 n-2) & =2^{n} \cdot 1 \cdot 3 \cdot 5 \cdots(2 n-1) \\
& =2^{n} \cdot \frac{1 \cdot 2 \cdot 3 \cdots 2 n}{2 \cdot 4 \cdot 6 \cdots 2 n} \\
& =\frac{1 \cdot 2 \cdot 3 \cdots 2 n}{1 \cdot 2 \cdot 3 \cdots n}
\end{aligned}
$$
that is, it is just $(2 n)!/ n!$. Therefore, since $(2 n)!/(n!)^{2}=\binom{2 n}{n}$ is always an integer, the answer is 2005.
|
2005
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
For how many integers $n$ between 1 and 2005 , inclusive, is $2 \cdot 6 \cdot 10 \cdots(4 n-2)$ divisible by $n!$ ?
|
2005
Note that
$$
\begin{aligned}
2 \cdot 6 \cdot 10 \cdots(4 n-2) & =2^{n} \cdot 1 \cdot 3 \cdot 5 \cdots(2 n-1) \\
& =2^{n} \cdot \frac{1 \cdot 2 \cdot 3 \cdots 2 n}{2 \cdot 4 \cdot 6 \cdots 2 n} \\
& =\frac{1 \cdot 2 \cdot 3 \cdots 2 n}{1 \cdot 2 \cdot 3 \cdots n}
\end{aligned}
$$
that is, it is just $(2 n)!/ n!$. Therefore, since $(2 n)!/(n!)^{2}=\binom{2 n}{n}$ is always an integer, the answer is 2005.
|
{
"resource_path": "HarvardMIT/segmented/en-82-2005-feb-guts-solutions.jsonl",
"problem_match": "\n5. ",
"solution_match": "\n## Solution: "
}
|
3be40421-1699-52d3-a49c-841fa791d267
| 611,356
|
Let $m \circ n=(m+n) /(m n+4)$. Compute $((\cdots((2005 \circ 2004) \circ 2003) \circ \cdots \circ 1) \circ 0)$.
|
$1 / 12$
Note that $m \circ 2=(m+2) /(2 m+4)=\frac{1}{2}$, so the quantity we wish to find is just $\left(\frac{1}{2} \circ 1\right) \circ 0=\frac{1}{3} \circ 0=1 / 12$.
|
\frac{1}{12}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Let $m \circ n=(m+n) /(m n+4)$. Compute $((\cdots((2005 \circ 2004) \circ 2003) \circ \cdots \circ 1) \circ 0)$.
|
$1 / 12$
Note that $m \circ 2=(m+2) /(2 m+4)=\frac{1}{2}$, so the quantity we wish to find is just $\left(\frac{1}{2} \circ 1\right) \circ 0=\frac{1}{3} \circ 0=1 / 12$.
|
{
"resource_path": "HarvardMIT/segmented/en-82-2005-feb-guts-solutions.jsonl",
"problem_match": "\n6. ",
"solution_match": "\n## Solution: "
}
|
b58edacc-da14-5dd3-b4ea-0d852cc891cd
| 611,357
|
Five people of different heights are standing in line from shortest to tallest. As it happens, the tops of their heads are all collinear; also, for any two successive people, the horizontal distance between them equals the height of the shorter person. If the shortest person is 3 feet tall and the tallest person is 7 feet tall, how tall is the middle person, in feet?
|
$\sqrt{21}$
If $A, B$, and $C$ are the tops of the heads of three successive people and $D, E$, and $F$ are their respective feet, let $P$ be the foot of the perpendicular from $A$ to $B E$ and let $Q$ be the foot of the perpendicular from $B$ to $C F$. Then, by equal angles, $\triangle A B P \sim \triangle B C Q$, so
$$
\frac{C F}{B E}=\frac{C F}{B Q}=\frac{C Q}{B Q}+1=\frac{B P}{A P}+1=\frac{B E}{A P}=\frac{B E}{A D}
$$
Therefore the heights of successive people are in geometric progression. Hence, the heights of all five people are in geometric progression, so the middle height is $\sqrt{3 \cdot 7}=$ $\sqrt{21}$ feet.
|
\sqrt{21}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Five people of different heights are standing in line from shortest to tallest. As it happens, the tops of their heads are all collinear; also, for any two successive people, the horizontal distance between them equals the height of the shorter person. If the shortest person is 3 feet tall and the tallest person is 7 feet tall, how tall is the middle person, in feet?
|
$\sqrt{21}$
If $A, B$, and $C$ are the tops of the heads of three successive people and $D, E$, and $F$ are their respective feet, let $P$ be the foot of the perpendicular from $A$ to $B E$ and let $Q$ be the foot of the perpendicular from $B$ to $C F$. Then, by equal angles, $\triangle A B P \sim \triangle B C Q$, so
$$
\frac{C F}{B E}=\frac{C F}{B Q}=\frac{C Q}{B Q}+1=\frac{B P}{A P}+1=\frac{B E}{A P}=\frac{B E}{A D}
$$
Therefore the heights of successive people are in geometric progression. Hence, the heights of all five people are in geometric progression, so the middle height is $\sqrt{3 \cdot 7}=$ $\sqrt{21}$ feet.

|
{
"resource_path": "HarvardMIT/segmented/en-82-2005-feb-guts-solutions.jsonl",
"problem_match": "\n7. ",
"solution_match": "\nSolution: "
}
|
fdabf2f1-7998-5420-945c-03fee25d6889
| 611,358
|
Let $A B C D$ be a convex quadrilateral inscribed in a circle with shortest side $A B$. The ratio $[B C D] /[A B D]$ is an integer (where $[X Y Z]$ denotes the area of triangle $X Y Z$.) If the lengths of $A B, B C, C D$, and $D A$ are distinct integers no greater than 10 , find the largest possible value of $A B$.
|
5
Note that
$$
\frac{[B C D]}{[A B D]}=\frac{\frac{1}{2} B C \cdot C D \cdot \sin C}{\frac{1}{2} D A \cdot A B \cdot \sin A}=\frac{B C \cdot C D}{D A \cdot A B}
$$
since $\angle A$ and $\angle C$ are supplementary. If $A B \geq 6$, it is easy to check that no assignment of lengths to the four sides yields an integer ratio, but if $A B=5$, we can let $B C=10$, $C D=9$, and $D A=6$ for a ratio of 3 . The maximum value for $A B$ is therefore 5 .
|
5
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $A B C D$ be a convex quadrilateral inscribed in a circle with shortest side $A B$. The ratio $[B C D] /[A B D]$ is an integer (where $[X Y Z]$ denotes the area of triangle $X Y Z$.) If the lengths of $A B, B C, C D$, and $D A$ are distinct integers no greater than 10 , find the largest possible value of $A B$.
|
5
Note that
$$
\frac{[B C D]}{[A B D]}=\frac{\frac{1}{2} B C \cdot C D \cdot \sin C}{\frac{1}{2} D A \cdot A B \cdot \sin A}=\frac{B C \cdot C D}{D A \cdot A B}
$$
since $\angle A$ and $\angle C$ are supplementary. If $A B \geq 6$, it is easy to check that no assignment of lengths to the four sides yields an integer ratio, but if $A B=5$, we can let $B C=10$, $C D=9$, and $D A=6$ for a ratio of 3 . The maximum value for $A B$ is therefore 5 .
|
{
"resource_path": "HarvardMIT/segmented/en-82-2005-feb-guts-solutions.jsonl",
"problem_match": "\n8. ",
"solution_match": "\nSolution: "
}
|
2219bd69-809e-5cdf-8f99-e1c359f357c0
| 611,359
|
Farmer Bill's 1000 animals - ducks, cows, and rabbits - are standing in a circle. In order to feel safe, every duck must either be standing next to at least one cow or between two rabbits. If there are 600 ducks, what is the least number of cows there can be for this to be possible?
|
201
Suppose Bill has $r$ rabbits and $c$ cows. At most $r-1$ ducks can be between two rabbits: each rabbit can serve up to two such ducks, so at most $2 r / 2=r$ ducks will each be served by two rabbits, but we cannot have equality, since this would require alternating between rabbits and ducks all the way around the circle, contradicting the fact that more than half the animals are ducks. Also, at most $2 c$ ducks can each be adjacent to a cow. So we need $600 \leq r-1+2 c=(400-c)-1+2 c$, giving $c \geq 201$. Conversely, an arrangement with 201 cows is possible:
$$
\underbrace{R D R D R \cdots D R}_{199_{R}, 198 D} \underbrace{D C D D C D D C D \cdots D C D}_{201 C, 402 D} .
$$
So 201 is the answer.
|
201
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Farmer Bill's 1000 animals - ducks, cows, and rabbits - are standing in a circle. In order to feel safe, every duck must either be standing next to at least one cow or between two rabbits. If there are 600 ducks, what is the least number of cows there can be for this to be possible?
|
201
Suppose Bill has $r$ rabbits and $c$ cows. At most $r-1$ ducks can be between two rabbits: each rabbit can serve up to two such ducks, so at most $2 r / 2=r$ ducks will each be served by two rabbits, but we cannot have equality, since this would require alternating between rabbits and ducks all the way around the circle, contradicting the fact that more than half the animals are ducks. Also, at most $2 c$ ducks can each be adjacent to a cow. So we need $600 \leq r-1+2 c=(400-c)-1+2 c$, giving $c \geq 201$. Conversely, an arrangement with 201 cows is possible:
$$
\underbrace{R D R D R \cdots D R}_{199_{R}, 198 D} \underbrace{D C D D C D D C D \cdots D C D}_{201 C, 402 D} .
$$
So 201 is the answer.
|
{
"resource_path": "HarvardMIT/segmented/en-82-2005-feb-guts-solutions.jsonl",
"problem_match": "\n9. ",
"solution_match": "\nSolution: "
}
|
4a1356ac-249b-52e9-855b-2f1dcb580c3b
| 611,360
|
You are given a set of cards labeled from 1 to 100 . You wish to make piles of three cards such that in any pile, the number on one of the cards is the product of the numbers on the other two cards. However, no card can be in more than one pile. What is the maximum number of piles you can form at once?
|
8
Certainly, the two factors in any pile cannot both be at least 10 , since then the product would be at least $10 \times 11>100$. Also, the number 1 can not appear in any pile, since then the other two cards in the pile would have to be the same. So each pile must use
one of the numbers $2,3, \ldots, 9$ as one of the factors, meaning we have at most 8 piles. Conversely, it is easy to construct a set of 8 such piles, for example:
$$
\begin{array}{llll}
\{9,11,99\} & \{8,12,96\} & \{7,13,91\} & \{6,14,84\} \\
\{5,15,75\} & \{4,16,64\} & \{3,17,51\} & \{2,18,36\}
\end{array}
$$
|
8
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
You are given a set of cards labeled from 1 to 100 . You wish to make piles of three cards such that in any pile, the number on one of the cards is the product of the numbers on the other two cards. However, no card can be in more than one pile. What is the maximum number of piles you can form at once?
|
8
Certainly, the two factors in any pile cannot both be at least 10 , since then the product would be at least $10 \times 11>100$. Also, the number 1 can not appear in any pile, since then the other two cards in the pile would have to be the same. So each pile must use
one of the numbers $2,3, \ldots, 9$ as one of the factors, meaning we have at most 8 piles. Conversely, it is easy to construct a set of 8 such piles, for example:
$$
\begin{array}{llll}
\{9,11,99\} & \{8,12,96\} & \{7,13,91\} & \{6,14,84\} \\
\{5,15,75\} & \{4,16,64\} & \{3,17,51\} & \{2,18,36\}
\end{array}
$$
|
{
"resource_path": "HarvardMIT/segmented/en-82-2005-feb-guts-solutions.jsonl",
"problem_match": "\n10. ",
"solution_match": "\nSolution: "
}
|
90b35f57-12f3-587f-a61a-486fc0698a77
| 611,361
|
The Dingoberry Farm is a 10 mile by 10 mile square, broken up into 1 mile by 1 mile patches. Each patch is farmed either by Farmer Keith or by Farmer Ann. Whenever Ann farms a patch, she also farms all the patches due west of it and all the patches due south of it. Ann puts up a scarecrow on each of her patches that is adjacent to exactly two of Keith's patches (and nowhere else). If Ann farms a total of 30 patches, what is the largest number of scarecrows she could put up?
|
7
Whenever Ann farms a patch $P$, she also farms all the patches due west of $P$ and due south of $P$. So, the only way she can put a scarecrow on $P$ is if Keith farms the patch immediately north of $P$ and the patch immediately east of $P$, in which case Ann cannot farm any of the patches due north of $P$ or due east of $P$. That is, Ann can only put a scarecrow on $P$ if it is the easternmost patch she farms in its east-west row, and the northernmost in its north-south column. In particular, all of her scarecrow patches are in different rows and columns. Suppose that she puts up $n$ scarecrows. The farthest south of these must be in the 10th row or above, so she farms at least 1 patch in that column; the second-farthest south must be in the 9 th row above, so she farms at least 2 patches in that column; the third-farthest south must be in the 8th row or above, so she farms at least 3 patches in that column, and so forth, for a total of at least
$$
1+2+\cdots+n=n(n+1) / 2
$$
patches. If Ann farms a total of $30<8 \cdot 9 / 2$ patches, then we have $n<8$. On the other hand, $n=7$ scarecrows are possible, as shown:
|
7
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
The Dingoberry Farm is a 10 mile by 10 mile square, broken up into 1 mile by 1 mile patches. Each patch is farmed either by Farmer Keith or by Farmer Ann. Whenever Ann farms a patch, she also farms all the patches due west of it and all the patches due south of it. Ann puts up a scarecrow on each of her patches that is adjacent to exactly two of Keith's patches (and nowhere else). If Ann farms a total of 30 patches, what is the largest number of scarecrows she could put up?
|
7
Whenever Ann farms a patch $P$, she also farms all the patches due west of $P$ and due south of $P$. So, the only way she can put a scarecrow on $P$ is if Keith farms the patch immediately north of $P$ and the patch immediately east of $P$, in which case Ann cannot farm any of the patches due north of $P$ or due east of $P$. That is, Ann can only put a scarecrow on $P$ if it is the easternmost patch she farms in its east-west row, and the northernmost in its north-south column. In particular, all of her scarecrow patches are in different rows and columns. Suppose that she puts up $n$ scarecrows. The farthest south of these must be in the 10th row or above, so she farms at least 1 patch in that column; the second-farthest south must be in the 9 th row above, so she farms at least 2 patches in that column; the third-farthest south must be in the 8th row or above, so she farms at least 3 patches in that column, and so forth, for a total of at least
$$
1+2+\cdots+n=n(n+1) / 2
$$
patches. If Ann farms a total of $30<8 \cdot 9 / 2$ patches, then we have $n<8$. On the other hand, $n=7$ scarecrows are possible, as shown:

|
{
"resource_path": "HarvardMIT/segmented/en-82-2005-feb-guts-solutions.jsonl",
"problem_match": "\n11. ",
"solution_match": "\nSolution: "
}
|
e6598d34-894e-5347-9ebe-be8bdccfaaa3
| 611,362
|
Two vertices of a cube are given in space. The locus of points that could be a third vertex of the cube is the union of $n$ circles. Find $n$.
|
10
Let the distance between the two given vertices be 1. If the two given vertices are adjacent, then the other vertices lie on four circles, two of radius 1 and two of radius $\sqrt{2}$. If the two vertices are separated by a diagonal of a face of the cube, then the locus of possible vertices adjacent to both of them is a circle of radius $\frac{1}{2}$, the locus of
possible vertices adjacent to exactly one of them is two circles of radius $\frac{\sqrt{2}}{2}$, and the locus of possible vertices adjacent to neither of them is a circle of radius $\frac{\sqrt{3}}{2}$. If the two given vertices are separated by a long diagonal, then each of the other vertices lie on one of two circles of radius $\frac{\sqrt{2}}{3}$, for a total of 10 circles.
|
10
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Two vertices of a cube are given in space. The locus of points that could be a third vertex of the cube is the union of $n$ circles. Find $n$.
|
10
Let the distance between the two given vertices be 1. If the two given vertices are adjacent, then the other vertices lie on four circles, two of radius 1 and two of radius $\sqrt{2}$. If the two vertices are separated by a diagonal of a face of the cube, then the locus of possible vertices adjacent to both of them is a circle of radius $\frac{1}{2}$, the locus of
possible vertices adjacent to exactly one of them is two circles of radius $\frac{\sqrt{2}}{2}$, and the locus of possible vertices adjacent to neither of them is a circle of radius $\frac{\sqrt{3}}{2}$. If the two given vertices are separated by a long diagonal, then each of the other vertices lie on one of two circles of radius $\frac{\sqrt{2}}{3}$, for a total of 10 circles.
|
{
"resource_path": "HarvardMIT/segmented/en-82-2005-feb-guts-solutions.jsonl",
"problem_match": "\n12. ",
"solution_match": "\nSolution: "
}
|
fdf6f426-b3e3-5fb4-ac3a-48b50c9bbd53
| 611,363
|
Triangle $A B C$ has $A B=1, B C=\sqrt{7}$, and $C A=\sqrt{3}$. Let $\ell_{1}$ be the line through $A$ perpendicular to $A B, \ell_{2}$ the line through $B$ perpendicular to $A C$, and $P$ the point of intersection of $\ell_{1}$ and $\ell_{2}$. Find $P C$.
|
3
By the Law of Cosines, $\angle B A C=\cos ^{-1} \frac{3+1-7}{2 \sqrt{3}}=\cos ^{-1}\left(-\frac{\sqrt{3}}{2}\right)=150^{\circ}$. If we let $Q$ be the intersection of $\ell_{2}$ and $A C$, we notice that $\angle Q B A=90^{\circ}-\angle Q A B=90^{\circ}-30^{\circ}=60^{\circ}$. It follows that triangle $A B P$ is a 30-60-90 triangle and thus $P B=2$ and $P A=\sqrt{3}$. Finally, we have $\angle P A C=360^{\circ}-\left(90^{\circ}+150^{\circ}\right)=120^{\circ}$, and
$$
P C=\left(P A^{2}+A C^{2}-2 P A \cdot A C \cos 120^{\circ}\right)^{1 / 2}=(3+3+3)^{1 / 2}=3 .
$$
|
3
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Triangle $A B C$ has $A B=1, B C=\sqrt{7}$, and $C A=\sqrt{3}$. Let $\ell_{1}$ be the line through $A$ perpendicular to $A B, \ell_{2}$ the line through $B$ perpendicular to $A C$, and $P$ the point of intersection of $\ell_{1}$ and $\ell_{2}$. Find $P C$.
|
3
By the Law of Cosines, $\angle B A C=\cos ^{-1} \frac{3+1-7}{2 \sqrt{3}}=\cos ^{-1}\left(-\frac{\sqrt{3}}{2}\right)=150^{\circ}$. If we let $Q$ be the intersection of $\ell_{2}$ and $A C$, we notice that $\angle Q B A=90^{\circ}-\angle Q A B=90^{\circ}-30^{\circ}=60^{\circ}$. It follows that triangle $A B P$ is a 30-60-90 triangle and thus $P B=2$ and $P A=\sqrt{3}$. Finally, we have $\angle P A C=360^{\circ}-\left(90^{\circ}+150^{\circ}\right)=120^{\circ}$, and
$$
P C=\left(P A^{2}+A C^{2}-2 P A \cdot A C \cos 120^{\circ}\right)^{1 / 2}=(3+3+3)^{1 / 2}=3 .
$$

|
{
"resource_path": "HarvardMIT/segmented/en-82-2005-feb-guts-solutions.jsonl",
"problem_match": "\n13. ",
"solution_match": "\nSolution: "
}
|
317bed84-fe8f-56b2-b8c1-eea7ca3352c7
| 611,364
|
Three noncollinear points and a line $\ell$ are given in the plane. Suppose no two of the points lie on a line parallel to $\ell$ (or $\ell$ itself). There are exactly $n$ lines perpendicular to $\ell$ with the following property: the three circles with centers at the given points and tangent to the line all concur at some point. Find all possible values of $n$.
|
1
The condition for the line is that each of the three points lies at an equal distance from the line as from some fixed point; in other words, the line is the directrix of a parabola containing the three points. Three noncollinear points in the coordinate plane determine a quadratic polynomial in $x$ unless two of the points have the same $x$-coordinate. Therefore, given the direction of the directrix, three noncollinear points determine a parabola, unless two of the points lie on a line perpendicular to the directrix. This case is ruled out by the given condition, so the answer is 1 .
|
1
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Three noncollinear points and a line $\ell$ are given in the plane. Suppose no two of the points lie on a line parallel to $\ell$ (or $\ell$ itself). There are exactly $n$ lines perpendicular to $\ell$ with the following property: the three circles with centers at the given points and tangent to the line all concur at some point. Find all possible values of $n$.
|
1
The condition for the line is that each of the three points lies at an equal distance from the line as from some fixed point; in other words, the line is the directrix of a parabola containing the three points. Three noncollinear points in the coordinate plane determine a quadratic polynomial in $x$ unless two of the points have the same $x$-coordinate. Therefore, given the direction of the directrix, three noncollinear points determine a parabola, unless two of the points lie on a line perpendicular to the directrix. This case is ruled out by the given condition, so the answer is 1 .
|
{
"resource_path": "HarvardMIT/segmented/en-82-2005-feb-guts-solutions.jsonl",
"problem_match": "\n14. ",
"solution_match": "\nSolution: "
}
|
5e916bb8-4958-5053-ab51-9d2b73fcdc0f
| 611,365
|
Let $S$ be the set of lattice points inside the circle $x^{2}+y^{2}=11$. Let $M$ be the greatest area of any triangle with vertices in $S$. How many triangles with vertices in $S$ have area $M$ ?
|
16
The boundary of the convex hull of $S$ consists of points with $(x, y)$ or $(y, x)=(0, \pm 3)$, $( \pm 1, \pm 3)$, and $( \pm 2, \pm 2)$. For any triangle $T$ with vertices in $S$, we can increase its area by moving a vertex not on the boundary to some point on the boundary. Thus,
if $T$ has area $M$, its vertices are all on the boundary of $S$. The next step is to see (either by inspection or by noting that T has area no larger than that of an equilateral triangle inscribed in a circle of radius $\sqrt{10}$, which has area less than 13) that $M=12$. There are 16 triangles with area 12 , all congruent to one of the following three: vertices $(2,2),(1,-3)$, and $(-3,1)$; vertices $(3,-1),(-3,-1)$, and $(1,3)$; or vertices $(3,-1)$, $(-3,-1)$, and $(0,3)$.
|
16
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $S$ be the set of lattice points inside the circle $x^{2}+y^{2}=11$. Let $M$ be the greatest area of any triangle with vertices in $S$. How many triangles with vertices in $S$ have area $M$ ?
|
16
The boundary of the convex hull of $S$ consists of points with $(x, y)$ or $(y, x)=(0, \pm 3)$, $( \pm 1, \pm 3)$, and $( \pm 2, \pm 2)$. For any triangle $T$ with vertices in $S$, we can increase its area by moving a vertex not on the boundary to some point on the boundary. Thus,
if $T$ has area $M$, its vertices are all on the boundary of $S$. The next step is to see (either by inspection or by noting that T has area no larger than that of an equilateral triangle inscribed in a circle of radius $\sqrt{10}$, which has area less than 13) that $M=12$. There are 16 triangles with area 12 , all congruent to one of the following three: vertices $(2,2),(1,-3)$, and $(-3,1)$; vertices $(3,-1),(-3,-1)$, and $(1,3)$; or vertices $(3,-1)$, $(-3,-1)$, and $(0,3)$.
|
{
"resource_path": "HarvardMIT/segmented/en-82-2005-feb-guts-solutions.jsonl",
"problem_match": "\n15. ",
"solution_match": "\nSolution: "
}
|
95f799a1-19bd-52f0-878f-f0042b766a2b
| 611,366
|
A regular octahedron has a side length of 1 . What is the distance between two opposite faces?
|
$\sqrt{6} / 3$
Imagine orienting the octahedron so that the two opposite faces are horizontal. Project onto a horizontal plane; these two faces are congruent equilateral triangles which (when projected) have the same center and opposite orientations. Hence, the vertices of the octahedron project to the vertices of a regular hexagon $A B C D E F$.
Let $O$ be the center of the hexagon and $M$ the midpoint of $A C$. Now $A B M$ is a 30-60-90 triangle, so $A B=A M /(\sqrt{3} / 2)=(1 / 2) /(\sqrt{3} / 2)=\sqrt{3} / 3$. If we let $d$ denote the desired vertical distance between the opposite faces (which project to $A C E$ and $B D F$ ), then by the Pythagorean Theorem, $A B^{2}+d^{2}=1^{2}$, so $d=\sqrt{1-A B^{2}}=\sqrt{6} / 3$.
|
\sqrt{6} / 3
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
A regular octahedron has a side length of 1 . What is the distance between two opposite faces?
|
$\sqrt{6} / 3$
Imagine orienting the octahedron so that the two opposite faces are horizontal. Project onto a horizontal plane; these two faces are congruent equilateral triangles which (when projected) have the same center and opposite orientations. Hence, the vertices of the octahedron project to the vertices of a regular hexagon $A B C D E F$.

Let $O$ be the center of the hexagon and $M$ the midpoint of $A C$. Now $A B M$ is a 30-60-90 triangle, so $A B=A M /(\sqrt{3} / 2)=(1 / 2) /(\sqrt{3} / 2)=\sqrt{3} / 3$. If we let $d$ denote the desired vertical distance between the opposite faces (which project to $A C E$ and $B D F$ ), then by the Pythagorean Theorem, $A B^{2}+d^{2}=1^{2}$, so $d=\sqrt{1-A B^{2}}=\sqrt{6} / 3$.
|
{
"resource_path": "HarvardMIT/segmented/en-82-2005-feb-guts-solutions.jsonl",
"problem_match": "\n16. ",
"solution_match": "\nSolution: "
}
|
0b62e1fe-698f-5486-9d02-55b6ebcbb62a
| 611,367
|
If $a, b$, and $c$ are random real numbers from 0 to 1 , independently and uniformly chosen, what is the average (expected) value of the smallest of $a, b$, and $c$ ?
|
$1 / 4$
Let $d$ be a fourth random variable, also chosen uniformly from $[0,1]$. For fixed $a, b$, and $c$, the probability that $d<\min \{a, b, c\}$ is evidently equal to $\min \{a, b, c\}$. Hence,
if we average over all choices of $a, b, c$, the average value of $\min \{a, b, c\}$ is equal to the probability that, when $a, b, c$, and $d$ are independently randomly chosen, $d<$ $\min \{a, b, c\}$, i.e., that $d$ is the smallest of the four variables. On the other hand, by symmetry, the probability that $d$ is the smallest of the four is simply equal to $1 / 4$, so that is our answer.
|
\frac{1}{4}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
If $a, b$, and $c$ are random real numbers from 0 to 1 , independently and uniformly chosen, what is the average (expected) value of the smallest of $a, b$, and $c$ ?
|
$1 / 4$
Let $d$ be a fourth random variable, also chosen uniformly from $[0,1]$. For fixed $a, b$, and $c$, the probability that $d<\min \{a, b, c\}$ is evidently equal to $\min \{a, b, c\}$. Hence,
if we average over all choices of $a, b, c$, the average value of $\min \{a, b, c\}$ is equal to the probability that, when $a, b, c$, and $d$ are independently randomly chosen, $d<$ $\min \{a, b, c\}$, i.e., that $d$ is the smallest of the four variables. On the other hand, by symmetry, the probability that $d$ is the smallest of the four is simply equal to $1 / 4$, so that is our answer.
|
{
"resource_path": "HarvardMIT/segmented/en-82-2005-feb-guts-solutions.jsonl",
"problem_match": "\n18. ",
"solution_match": "\nSolution: "
}
|
e9d7905c-cdbd-5a49-bbe8-6f6b84110686
| 611,369
|
Regular tetrahedron $A B C D$ is projected onto a plane sending $A, B, C$, and $D$ to $A^{\prime}, B^{\prime}, C^{\prime}$, and $D^{\prime}$ respectively. Suppose $A^{\prime} B^{\prime} C^{\prime} D^{\prime}$ is a convex quadrilateral with $A^{\prime} B^{\prime}=A^{\prime} D^{\prime}$ and $C^{\prime} B^{\prime}=C^{\prime} D^{\prime}$, and suppose that the area of $A^{\prime} B^{\prime} C^{\prime} D^{\prime}=4$. Given these conditions, the set of possible lengths of $A B$ consists of all real numbers in the interval $[a, b)$. Compute $b$.
|
$2 \sqrt[4]{6}$
The value of $b$ occurs when the quadrilateral $A^{\prime} B^{\prime} C^{\prime} D^{\prime}$ degenerates to an isosceles triangle. This occurs when the altitude from $A$ to $B C D$ is parallel to the plane. Let $s=A B$. Then the altitude from $A$ intersects the center $E$ of face $B C D$. Since $E B=\frac{s}{\sqrt{3}}$, it follows that $A^{\prime} C^{\prime}=A E=\sqrt{s^{2}-\frac{s^{2}}{3}}=\frac{s \sqrt{6}}{3}$. Then since $B D$ is parallel to the plane, $B^{\prime} D^{\prime}=s$. Then the area of $A^{\prime} B^{\prime} C^{\prime} D^{\prime}$ is $4=\frac{1}{2} \cdot \frac{s^{2} \sqrt{6}}{3}$, implying $s^{2}=4 \sqrt{6}$, or $s=2 \sqrt[4]{6}$.
|
2 \sqrt[4]{6}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Regular tetrahedron $A B C D$ is projected onto a plane sending $A, B, C$, and $D$ to $A^{\prime}, B^{\prime}, C^{\prime}$, and $D^{\prime}$ respectively. Suppose $A^{\prime} B^{\prime} C^{\prime} D^{\prime}$ is a convex quadrilateral with $A^{\prime} B^{\prime}=A^{\prime} D^{\prime}$ and $C^{\prime} B^{\prime}=C^{\prime} D^{\prime}$, and suppose that the area of $A^{\prime} B^{\prime} C^{\prime} D^{\prime}=4$. Given these conditions, the set of possible lengths of $A B$ consists of all real numbers in the interval $[a, b)$. Compute $b$.
|
$2 \sqrt[4]{6}$
The value of $b$ occurs when the quadrilateral $A^{\prime} B^{\prime} C^{\prime} D^{\prime}$ degenerates to an isosceles triangle. This occurs when the altitude from $A$ to $B C D$ is parallel to the plane. Let $s=A B$. Then the altitude from $A$ intersects the center $E$ of face $B C D$. Since $E B=\frac{s}{\sqrt{3}}$, it follows that $A^{\prime} C^{\prime}=A E=\sqrt{s^{2}-\frac{s^{2}}{3}}=\frac{s \sqrt{6}}{3}$. Then since $B D$ is parallel to the plane, $B^{\prime} D^{\prime}=s$. Then the area of $A^{\prime} B^{\prime} C^{\prime} D^{\prime}$ is $4=\frac{1}{2} \cdot \frac{s^{2} \sqrt{6}}{3}$, implying $s^{2}=4 \sqrt{6}$, or $s=2 \sqrt[4]{6}$.
|
{
"resource_path": "HarvardMIT/segmented/en-82-2005-feb-guts-solutions.jsonl",
"problem_match": "\n19. ",
"solution_match": "\nSolution: "
}
|
df19044e-50ca-5b5d-81cc-817958a57b2f
| 611,370
|
If $n$ is a positive integer, let $s(n)$ denote the sum of the digits of $n$. We say that $n$ is zesty if there exist positive integers $x$ and $y$ greater than 1 such that $x y=n$ and $s(x) s(y)=s(n)$. How many zesty two-digit numbers are there?
|
34
Let $n$ be a zesty two-digit number, and let $x$ and $y$ be as in the problem statement. Clearly if both $x$ and $y$ are one-digit numbers, then $s(x) s(y)=n \neq s(n)$. Thus either $x$ is a two-digit number or $y$ is. Assume without loss of generality that it is $x$. If $x=10 a+b, 1 \leq a \leq 9$ and $0 \leq b \leq 9$, then $n=10 a y+b y$. If both $a y$ and by are less than 10 , then $s(n)=a y+b y$, but if either is at least 10 , then $s(n)<a y+b y$. It follows that the two digits of $n$ share a common factor greater than 1 , namely $y$. It is now easy to count the zesty two-digit numbers by first digit starting with 2 ; there are a total of $5+4+5+2+7+2+5+4=34$.
|
34
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
If $n$ is a positive integer, let $s(n)$ denote the sum of the digits of $n$. We say that $n$ is zesty if there exist positive integers $x$ and $y$ greater than 1 such that $x y=n$ and $s(x) s(y)=s(n)$. How many zesty two-digit numbers are there?
|
34
Let $n$ be a zesty two-digit number, and let $x$ and $y$ be as in the problem statement. Clearly if both $x$ and $y$ are one-digit numbers, then $s(x) s(y)=n \neq s(n)$. Thus either $x$ is a two-digit number or $y$ is. Assume without loss of generality that it is $x$. If $x=10 a+b, 1 \leq a \leq 9$ and $0 \leq b \leq 9$, then $n=10 a y+b y$. If both $a y$ and by are less than 10 , then $s(n)=a y+b y$, but if either is at least 10 , then $s(n)<a y+b y$. It follows that the two digits of $n$ share a common factor greater than 1 , namely $y$. It is now easy to count the zesty two-digit numbers by first digit starting with 2 ; there are a total of $5+4+5+2+7+2+5+4=34$.
|
{
"resource_path": "HarvardMIT/segmented/en-82-2005-feb-guts-solutions.jsonl",
"problem_match": "\n20. ",
"solution_match": "\nSolution: "
}
|
d2904787-7073-5ed0-a7cd-7fedb6e9794c
| 611,371
|
In triangle $A B C$ with altitude $A D, \angle B A C=45^{\circ}, D B=3$, and $C D=2$. Find the area of triangle $A B C$.
|
15
Suppose first that $D$ lies between $B$ and $C$. Let $A B C$ be inscribed in circle $\omega$, and extend $A D$ to intersect $\omega$ again at $E$. Note that $A$ subtends a quarter of the circle, so in particular, the chord through $C$ perpendicular to $B C$ and parallel to $A D$ has length $B C=5$. Therefore, $A D=5+D E$. By power of a point, $6=B D \cdot D C=A D \cdot D E=$ $A D^{2}-5 A D$, implying $A D=6$, so the area of $A B C$ is $\frac{1}{2} B C \cdot A D=15$.
If $D$ does not lie between $B$ and $C$, then $B C=1$, so $A$ lies on a circle of radius $\sqrt{2} / 2$ through $B$ and $C$. But then it is easy to check that the perpendicular to $B C$ through $D$ cannot intersect the circle, a contradiction.
|
15
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
In triangle $A B C$ with altitude $A D, \angle B A C=45^{\circ}, D B=3$, and $C D=2$. Find the area of triangle $A B C$.
|
15
Suppose first that $D$ lies between $B$ and $C$. Let $A B C$ be inscribed in circle $\omega$, and extend $A D$ to intersect $\omega$ again at $E$. Note that $A$ subtends a quarter of the circle, so in particular, the chord through $C$ perpendicular to $B C$ and parallel to $A D$ has length $B C=5$. Therefore, $A D=5+D E$. By power of a point, $6=B D \cdot D C=A D \cdot D E=$ $A D^{2}-5 A D$, implying $A D=6$, so the area of $A B C$ is $\frac{1}{2} B C \cdot A D=15$.
If $D$ does not lie between $B$ and $C$, then $B C=1$, so $A$ lies on a circle of radius $\sqrt{2} / 2$ through $B$ and $C$. But then it is easy to check that the perpendicular to $B C$ through $D$ cannot intersect the circle, a contradiction.

|
{
"resource_path": "HarvardMIT/segmented/en-82-2005-feb-guts-solutions.jsonl",
"problem_match": "\n21. ",
"solution_match": "\nSolution: "
}
|
5b0fb172-4adf-5b37-8741-7a70b146d226
| 611,372
|
Find
$$
\{\ln (1+e)\}+\left\{\ln \left(1+e^{2}\right)\right\}+\left\{\ln \left(1+e^{4}\right)\right\}+\left\{\ln \left(1+e^{8}\right)\right\}+\cdots,
$$
where $\{x\}=x-\lfloor x\rfloor$ denotes the fractional part of $x$.
|
$1-\ln (e-1)$
Since $\ln \left(1+e^{2^{k}}\right)$ is just larger than $2^{k}$, its fractional part is $\ln \left(1+e^{2^{k}}\right)-\ln e^{2^{k}}=$ $\ln \left(1+e^{-2^{k}}\right)$. But now notice that
$$
\prod_{k=0}^{n}\left(1+x^{2^{k}}\right)=1+x+x^{2}+\cdots+x^{2^{n+1}-1}
$$
(This is easily proven by induction or by noting that every nonnegative integer less than $2^{n+1}$ has a unique ( $n+1$ )-bit binary expansion.) If $|x|<1$, this product converges to $\frac{1}{1-x}$ as $n$ goes to infinity. Therefore,
$$
\sum_{k=0}^{\infty} \ln \left(1+e^{-2^{k}}\right)=\ln \prod_{k=0}^{\infty}\left(1+\left(e^{-1}\right)^{2^{k}}\right)=\ln \frac{1}{1-e^{-1}}=\ln \frac{e}{e-1}=1-\ln (e-1)
$$
|
1-\ln (e-1)
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Find
$$
\{\ln (1+e)\}+\left\{\ln \left(1+e^{2}\right)\right\}+\left\{\ln \left(1+e^{4}\right)\right\}+\left\{\ln \left(1+e^{8}\right)\right\}+\cdots,
$$
where $\{x\}=x-\lfloor x\rfloor$ denotes the fractional part of $x$.
|
$1-\ln (e-1)$
Since $\ln \left(1+e^{2^{k}}\right)$ is just larger than $2^{k}$, its fractional part is $\ln \left(1+e^{2^{k}}\right)-\ln e^{2^{k}}=$ $\ln \left(1+e^{-2^{k}}\right)$. But now notice that
$$
\prod_{k=0}^{n}\left(1+x^{2^{k}}\right)=1+x+x^{2}+\cdots+x^{2^{n+1}-1}
$$
(This is easily proven by induction or by noting that every nonnegative integer less than $2^{n+1}$ has a unique ( $n+1$ )-bit binary expansion.) If $|x|<1$, this product converges to $\frac{1}{1-x}$ as $n$ goes to infinity. Therefore,
$$
\sum_{k=0}^{\infty} \ln \left(1+e^{-2^{k}}\right)=\ln \prod_{k=0}^{\infty}\left(1+\left(e^{-1}\right)^{2^{k}}\right)=\ln \frac{1}{1-e^{-1}}=\ln \frac{e}{e-1}=1-\ln (e-1)
$$
|
{
"resource_path": "HarvardMIT/segmented/en-82-2005-feb-guts-solutions.jsonl",
"problem_match": "\n22. ",
"solution_match": "\nSolution: "
}
|
1ac57152-bb33-5b5b-a671-1a923d9583d0
| 611,373
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.